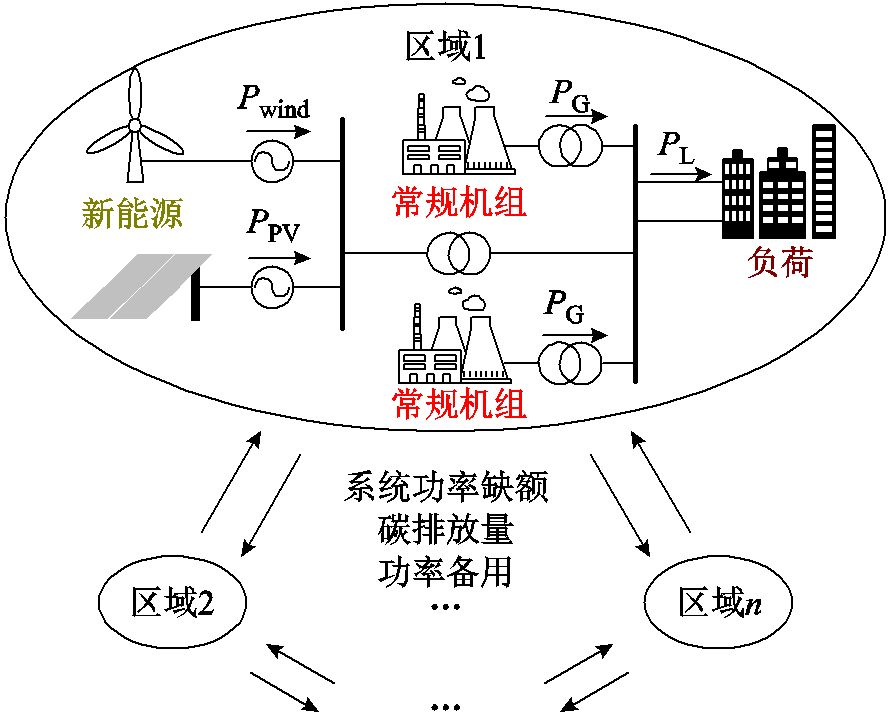
图1 互联区域间信息交互
Fig.1 Inter-regional information interaction
摘要 针对多区域互联系统考虑全局不等式约束的低碳经济调度分布式求解问题,提出一种分布式低碳经济调度优化方法。首先,为实现多区域互联系统低碳化运行,利用互联系统碳排放量约束调控各区域中发电单元出力,构建低碳经济调度模型;随后,基于对偶理论和变量分解方法对多区域互联系统低碳经济调度模型进行分解,将低碳经济调度问题分解为与各区域相关的子问题,再利用交替方向乘子法(ADMM)搭建各区域协同优化求解框架;迭代求解过程中,通过迭代互联区域之间相邻单元或节点拉格朗日乘子信息的交换实现分布式低碳经济调度模型求解,该经济调度优化模型,在有效降低各区域间信息传递量、充分保障各区域单元信息隐私性要求的同时,满足优化区域“即插即用”的需求;最后,通过IEEE 6节点测试系统和72节点测试系统进行算例分析,验证了所提方法的有效性。
关键词:多耦合约束 碳排放量约束 分布式经济调度 对偶理论 变量分解 交替方向乘子法(ADMM)
为加快减排步伐,我国明确提出2030年“碳达峰”与2060年“碳中和”目标,积极推动能源行业低碳化和清洁化[1]。电力行业作为碳排放水平较高的国民经济基础性产业,是推动“双碳”目标完成的关键角色[2-3]。在此背景下,电力系统经济调度向低碳化转变已成为必然趋势。制定兼顾运行安全与低碳的经济调度方案,成为当代电力行业面临的重要挑战。
在多区域互联电力系统中,一方面,各区域通过负荷的错峰效益及备用共享可提高系统运行的经济性与可靠性。另一方面,随着新型电力系统构建的加快,各区域内可调控出力设备逐渐增多,在为多区域互联电力系统稳定运行提出更高要求的同时,也为其经济调度带来更多的优化方案。在“双碳”背景下,可以通过区域间信息交互,实现各区域内部出力单元碳排放互补,在合理的减排目标基础上制定相应的低碳经济调度策略。
为满足政策减排需求,在经济调度模型中引入系统碳排放量约束,调控各区域中碳排放参数不同的发电单元出力,可实现系统低碳经济调度。该方案在集中式优化调度中最为普遍,但随着电力系统的不断发展,多区域互联电力系统中可调用的单元逐渐增多,集中式经济调度所需的极大通信带宽难以得到满足,且计算和信息储存需求随之急剧增长,存在扩展性差、易受单点故障影响问题[4-5]。分布式经济调度策略可将经济调度问题分解为各区域单元求解问题,通过子区域内部独立优化及相邻区域协调优化实现整个系统的优化调度[6]。
分布式经济调度在保证各区域信息隐私性的同时,能够降低系统对通信带宽及信息储存的需求,已成为研究的热点。关于分布式经济调度的研究,文献[7]根据辅助问题原理对电网区域进行划分,随后制定了互联区域协调调度策略,实现了多目标分区并行优化,但在模型中所需构建的目标函数非常复杂。文献[8]中在一致性算法的基础上引入了innovation项,通过此项可将每个单元的功率缺额反映到本地乘子中,并基于一致性算法扩散开,但其需要两个参数随着一致性迭代过程不断趋于零,其收敛效果与两个参数的衰减策略密切相关,参数衰减策略的合理性决定了算法能否收敛到最优值。文献[9]应用一致性算法实现计及柔性负荷的电力系统分布式经济调度,但仍然需要一个与发电机组或柔性负荷相关联的控制器用于获取系统总的功率缺额。对此,文献[10]提出一种基于一致性算法和梯度下降法的算法,其仅需节点间进行局部信息的交换即可实现各节点获取功率缺额,平衡电力系统中的供应与需求,解决了信息交互隐私性问题。
此外,交替方向乘子法(Alternating Direction Multiplier Method, ADMM)处理速度快,算法收敛性好,目前被广泛应用于电力系统分布式经济调度中。其本质是将原始问题分解为多个更小的子问题,在每次迭代更新中分别求解每一个子问题的优化算法,这种方法弥补了优化问题中存在二次惩罚项的缺点[11-13]。文献[14]构建了以系统的运行成本与碳排放量惩罚项最小为目标函数的综合能源经济调度模型,利用ADMM求解,实现低碳经济调度,但不同惩罚因子对应不同最优解,出力决策易受主观因素影响。文献[15-16]利用ADMM提出一种完全分布式电力系统动态经济调度方法,该算法并不依赖负责乘子更新的数据中心,无需全局协调和同步迭代,同时采用多时段优化方法实现了完全分布式的调度策略。文献[17]采用二分法解决经济调度问题,但各单元每次更新拉格朗日乘子之前需要基于一致性算法获取全局的功率缺额和拉格朗日乘子信息。分布式经济调度问题的研究已取得了一定的成效,但涉及的方法只能处理含有一项全局等式约束和若干局部约束的经济调度问题,对于含有全局不等式约束(例如备用约束、系统碳排放量约束)的经济调度问题,这些方法存在一定的局限性。
对此,本文主要工作和创新点如下:
1)在包含多类型可调度资源的多区域互联系统中引入全局不等式约束-系统碳排放量约束, 根据减排需求调控各出力单元的出力决策,实现分布式低碳经济调度。
2)针对同时包含全局等式约束(功率平衡约束)和全局不等式约束(备用约束、系统碳排放量约束)的经济调度问题,基于对偶理论和变量分解方法构建完全分布式的调度模型,与已有分布式经济调度相比更具有普适性。
3)基于ADMM设计模型求解方法,搭建各区域协同优化的迭代求解框架。迭代求解过程中,各互联区域仅需与相邻区域进行拉格朗日乘子信息交换即可实现整体的优化,有效降低各区域间信息传递量,充分保障各区域单元信息隐私性。
最后通过IEEE 6节点系统及72节点测试系统算例分析验证了所提方法的有效性。
本文以含有多种类型机组及新能源的n个区域互联电力系统为研究对象,其中区域内部单元包含负荷、燃煤机组、燃气机组或新能源。燃气机组较燃煤机组碳排放系数小,但其出力成本较高,在以系统低运行成本为目标调度的情况下,系统必然选择燃煤机组优先出力[18]。为降低系统碳排放量,满足减排需求,以系统运行成本最小为目标函数,考虑系统碳排放量约束调整机组出力可以实现低碳经济调度。但含全局不等式的经济调度问题较难实现分布式求解。
关于多区域互联系统经济调度的信息交互如图1所示。相邻区域直接通过传递系统功率缺额、碳排放量、系统功率备用等信息交互调整自身可调控设备出力,实现系统调度优化。在包含全局不等式碳排放约束的经济调度模型中,当各区域单元内部负荷预测值和发电机组、风电等的运行状态信息对外不可知时,如何通过相邻区域之间有限信息的交换和迭代优化实现分布式低碳经济调度,保证系统满足碳排放约束兼顾经济性运行是本文研究的主要问题。

图1 互联区域间信息交互
Fig.1 Inter-regional information interaction
针对含有全局不等式约束的经济调度模型,本文基于对偶理论和变量分解方法对其进行分解,构造与单个区域优化问题相关的拉格朗日函数,互联区域之间需要交换的信息由图1中功率缺额、碳排放量等代替为拉格朗日乘子信息,充分保证了各区域的信息隐私性。随后根据ADMM设计了模型的分布式迭代求解框架,实现含全局不等式约束的分布式低碳经济调度。整体研究架构如图2所示。
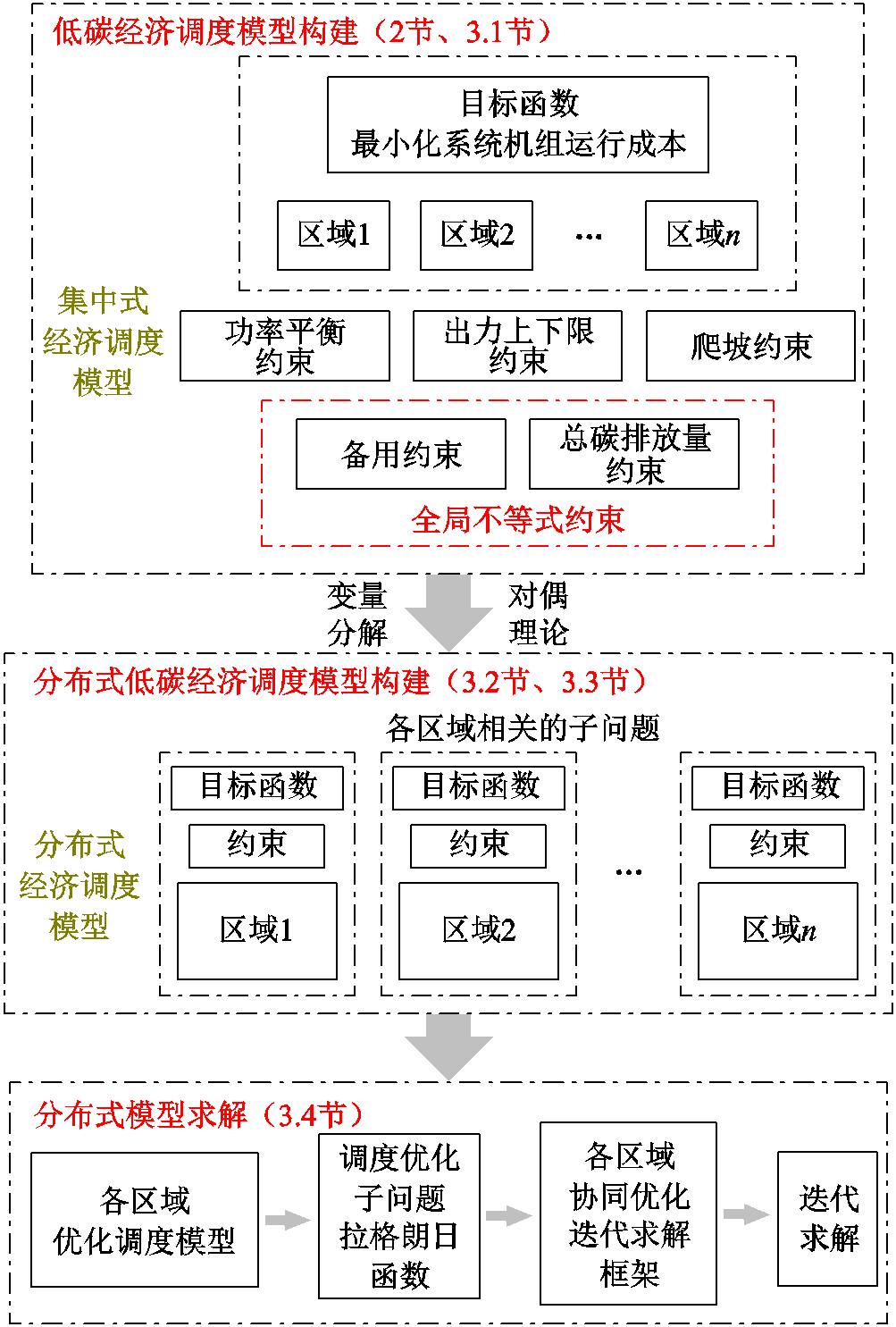
图2 研究框架
Fig.2 Research framework
本文为实现多区域互联电力系统在满足减排要求的基础上经济运行,目标函数设定为系统出力单元运行成本最小,即
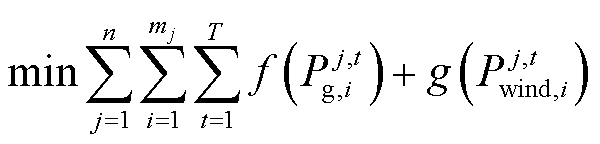 (1)
(1)
式中,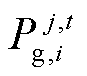 、
、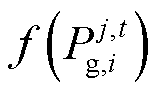 分别为区域j中机组i在t时刻出力及出力成本;
分别为区域j中机组i在t时刻出力及出力成本;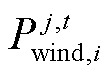 、
、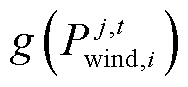 分别为区域j中风机i在t时刻出力及出力成本,若j区域i单元为纯负荷节点,则
分别为区域j中风机i在t时刻出力及出力成本,若j区域i单元为纯负荷节点,则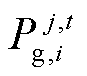 、
、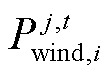 视为零;mj为j区域内单元数目。此外定义时段构成的集合为ζ={1,…,T},每个时段时长为Δt(min);区域j中单元构成的集合为vj={1,…,mj},区域构成的集合为v={v1,…,vn}。
视为零;mj为j区域内单元数目。此外定义时段构成的集合为ζ={1,…,T},每个时段时长为Δt(min);区域j中单元构成的集合为vj={1,…,mj},区域构成的集合为v={v1,…,vn}。
本文所选机组的成本为出力决策的二次函数,式(1)中出力成本函数表达式为
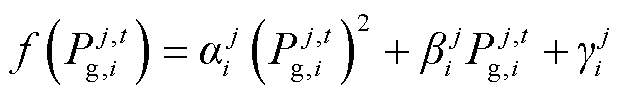 (2)
(2)
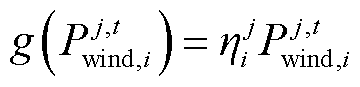 (3)
(3)
式中,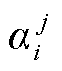 、
、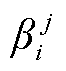 、
、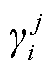 为区域j中机组i出力成本系数;
为区域j中机组i出力成本系数;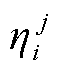 为通过区域j中风机i运维成本及装机投资成本换算的度电成本。
为通过区域j中风机i运维成本及装机投资成本换算的度电成本。
随后,为保证构建的分布式低碳经济调度问题“凸性”,对各区域单元成本曲线进行分段线性化,为搭建ADMM分布式迭代求解框架作铺垫,边际成本函数曲线如图3所示。图3中,第j个区域出力单元i的边际发电成本分为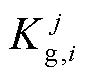 段;
段;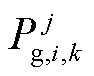 、
、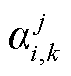 分别为区域j中第i个出力单元中机组第k段的发电、发电边际运行成本;
分别为区域j中第i个出力单元中机组第k段的发电、发电边际运行成本;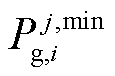 为区域j中第i个出力单元的出力下限;为便于模型矩阵的构建,针对风机发电成本作相同处理,亦可认为风机
为区域j中第i个出力单元的出力下限;为便于模型矩阵的构建,针对风机发电成本作相同处理,亦可认为风机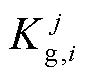 =1。
=1。
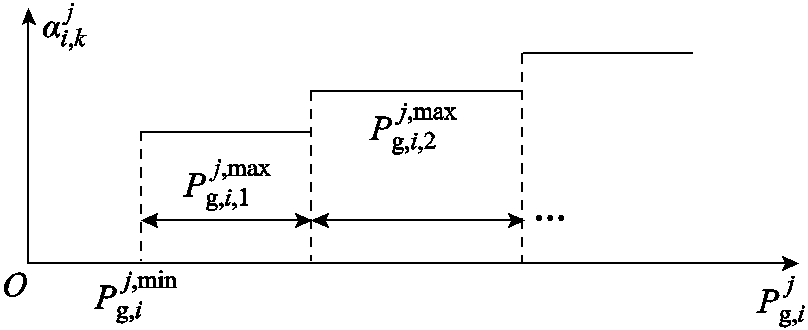
图3 发电边际成本函数线性化
Fig.3 Linearization of marginal cost function of power generation
首先确定系统基准情况下的总碳排放量[19],在此基础上考虑一定减排系数,有
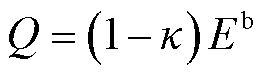 (4)
(4)
式中,Q为系统碳排放约束总量;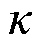 为减排系数,在本文中取15%;Eb为基准情况下碳排放总量。
为减排系数,在本文中取15%;Eb为基准情况下碳排放总量。
多区域互联系统低碳经济调度考虑的约束条件如下:
1)系统功率平衡约束
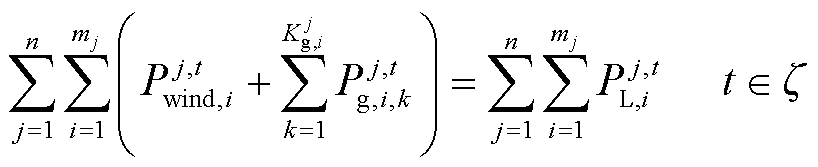 (5)
(5)
式中,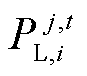 为区域j中第i个单元对自身负荷的预测值,若无负荷即为零。
为区域j中第i个单元对自身负荷的预测值,若无负荷即为零。
2)旋转备用约束
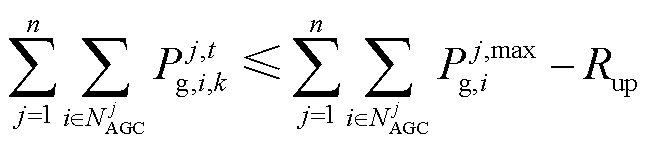 (6)
(6)
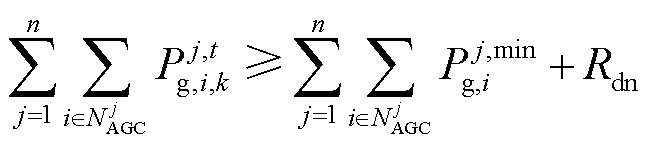 (7)
(7)
式中,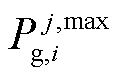 为区域j中单元i的出力上限;
为区域j中单元i的出力上限;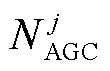 为区域j中参与自动发电控制(Automatic Generation Control, AGC)调整的单元构成的集合;Rup、Rdn分别为系统所需的向上备用、向下备用容量。
为区域j中参与自动发电控制(Automatic Generation Control, AGC)调整的单元构成的集合;Rup、Rdn分别为系统所需的向上备用、向下备用容量。
3)系统碳排放量约束
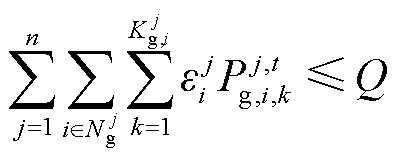 (8)
(8)
式中,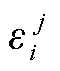 为区域j中第i个出力单元的碳排放系数,若单元i不包含常规机组,
为区域j中第i个出力单元的碳排放系数,若单元i不包含常规机组,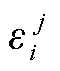 =0;
=0;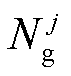 为区域j中含可调度设备的单元构成的集合。
为区域j中含可调度设备的单元构成的集合。
4)机组出力上、下限约束
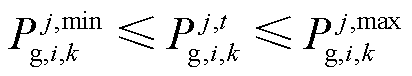 (9)
(9)
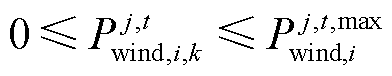 (10)
(10)
式中,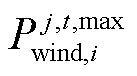 为区域j中风机i在t时刻出力预测值。
为区域j中风机i在t时刻出力预测值。
5)机组爬坡约束
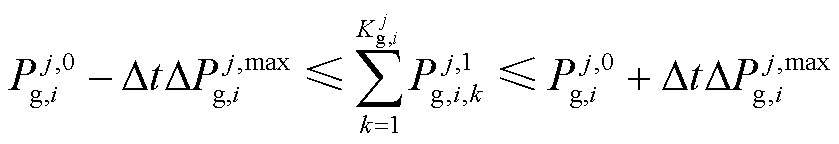 (11)
(11)
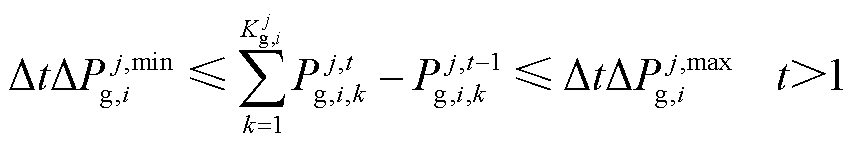 (12)
(12)
式中,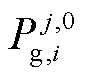 为机组的初始出力;
为机组的初始出力;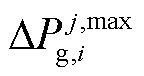 为第i个区域单元出力的最大爬坡速率。
为第i个区域单元出力的最大爬坡速率。
在第2节中构建的含有全局不等式约束的经济调度模型通常采用集中式计算,但随着电力系统中可调控设备的不断接入,集中式经济调度面临的问题也越发严重。在本节中,基于ADMM处理分布式优化调度问题具有较好的收敛性、鲁棒性及高效性,构建了含有全局不等式约束的分布式低碳经济调度模型,并设计了相应的求解方法。
第2节中构建的低碳经济调度模型可表示为如式(13)和式(14)所示的线性规划问题,定义为模型A。
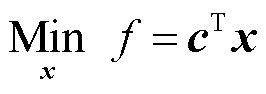 (13)
(13)
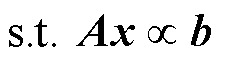 (14)
(14)
式中,c为各区域中出力单元的边际发电成本系数组成的n维列向量;x为各出力单元的发电输出功率决策组成的n维的列向量;A、b分别为通过约束条件构成的常数矩阵和列向量;“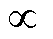 ”表示矩阵之间的大小关系,其中与功率平衡约束相关的“
”表示矩阵之间的大小关系,其中与功率平衡约束相关的“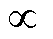 ”为“=”,与其余约束相关的“
”为“=”,与其余约束相关的“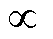 ”为“≤”。c、A、b形式为
”为“≤”。c、A、b形式为
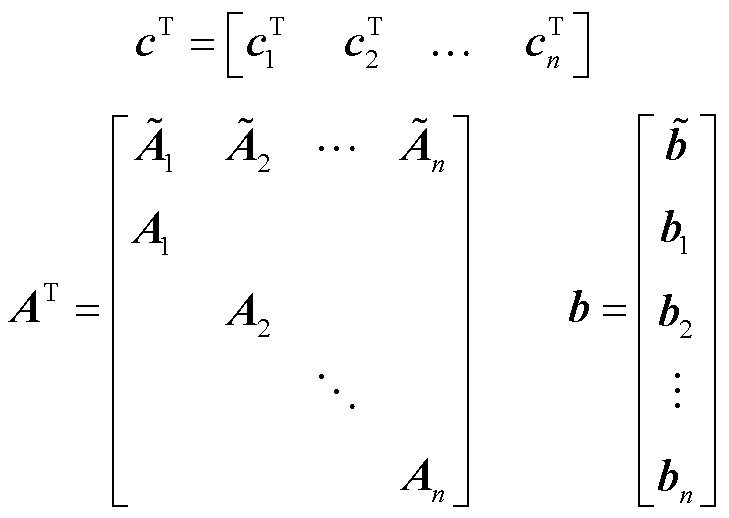
式中,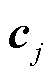 为第j个区域给出的边际发电成本系数矩阵;
为第j个区域给出的边际发电成本系数矩阵;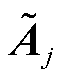 、
、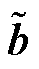 为与全局约束相关的系数矩阵;Aj、bj为与局部约束相关的系数矩阵。
为与全局约束相关的系数矩阵;Aj、bj为与局部约束相关的系数矩阵。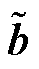 、cj、
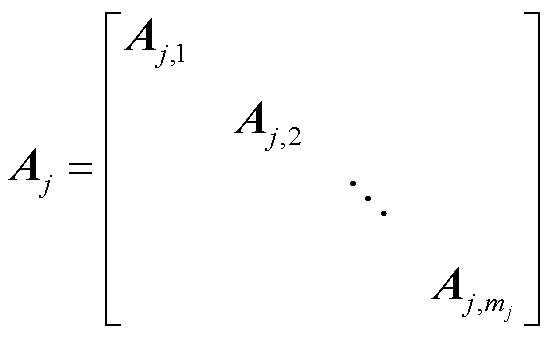
、cj、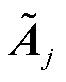 、Aj、bj的具体形式为
、Aj、bj的具体形式为
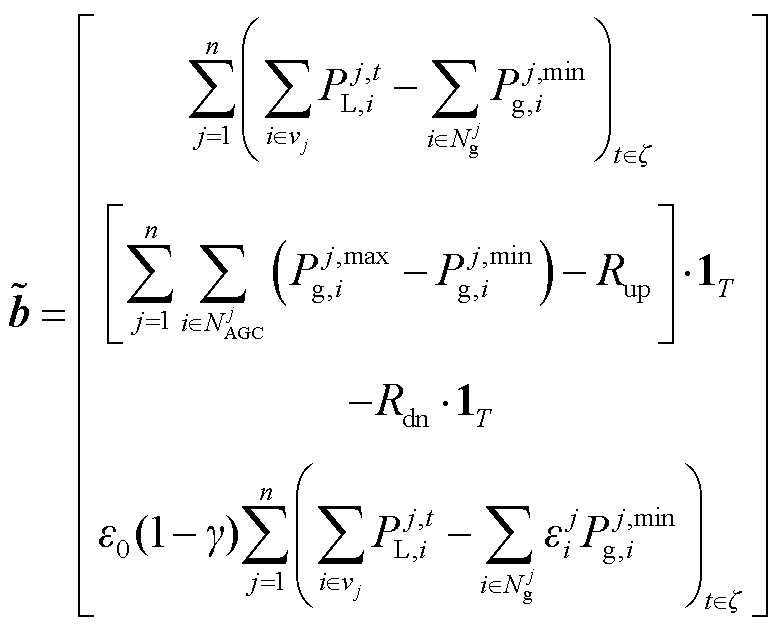
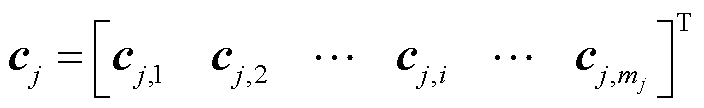
式中,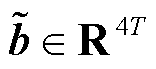 ;
;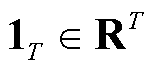 为元素都为1的列向量;
为元素都为1的列向量;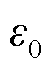 为基准碳排放量以及系统负荷计算的碳排放系数,有
为基准碳排放量以及系统负荷计算的碳排放系数,有
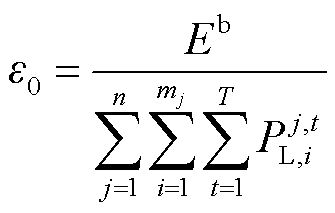 (15)
(15)
1)若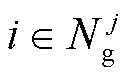 ,则
,则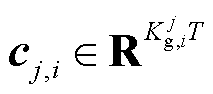 ,有
,有
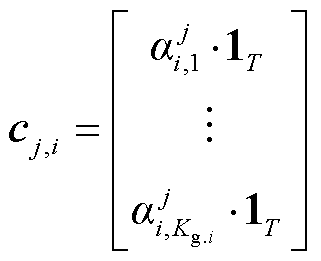
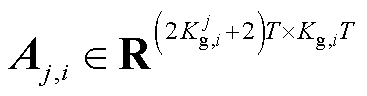
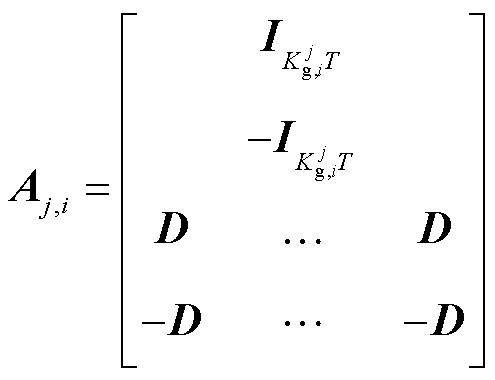
式中,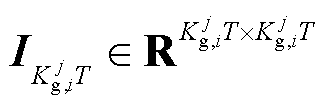 为单位矩阵;
为单位矩阵;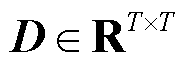 ,表示为
,表示为
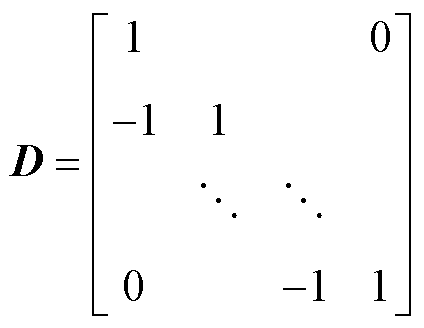
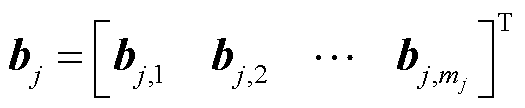
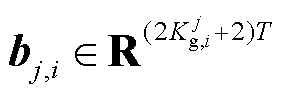
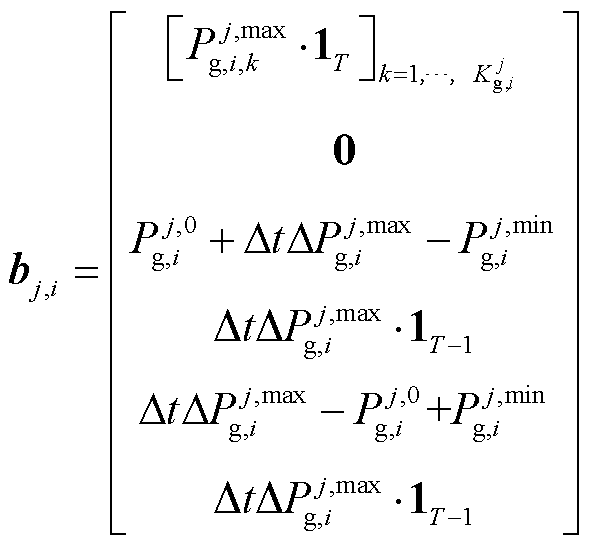
式中,0为元素都为0的列向量,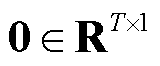 。
。
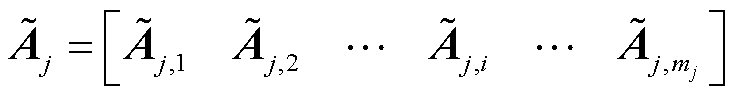
(1)若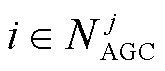 ,则
,则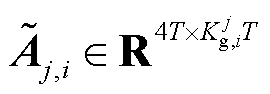 ,有
,有
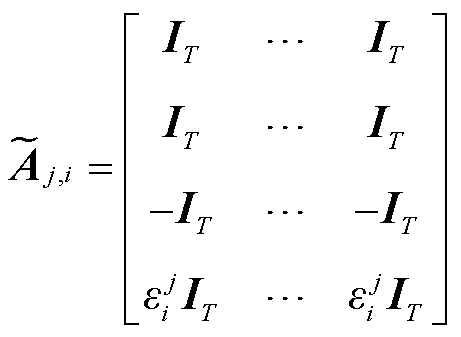
(2)若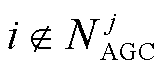 ,
,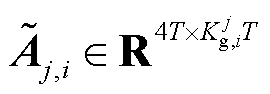 ,有
,有
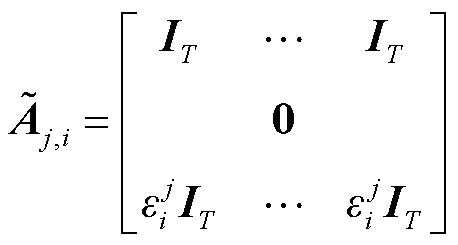
式中,IT为单位矩阵,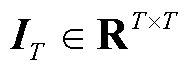 ;0为元素全为0的矩阵,
;0为元素全为0的矩阵,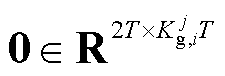 。
。
(3)若i为风电,则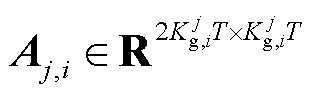 ,
,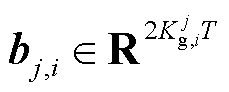 。
。
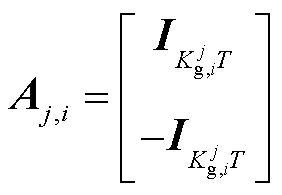
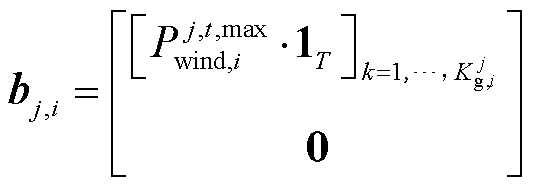
2)若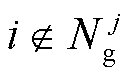 ,则
,则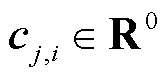 、
、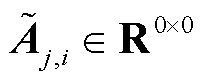 、
、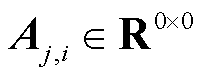 、
、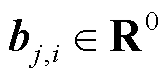 。
。
在解决分布式动态经济调度问题过程中,关键在于对所构建模型的分布式求解。对于包含全局不等式的模型A很难直接对其进行分布式求解,本文首先基于对偶原理构建模型A的对偶模型,随后采用变量分解方法对原问题的对偶模型进行分解,最后设计相应的分布式求解算法。
对模型A分解的目的是将经济调度问题分解为一系列子问题,使优化求解过程中对拉格朗日乘子的协调过程、对出力的决策过程都在各区域上分布式进行。分解步骤分以下两步。
1)求模型A的对偶问题
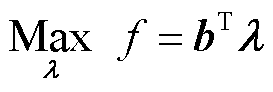 (16)
(16)
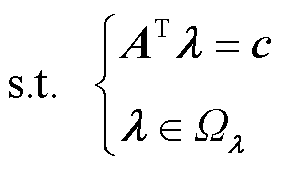 (17)
(17)
式中,λ为与约束式(14)相关的乘子,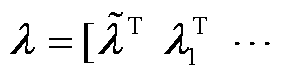
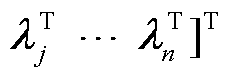 ,
,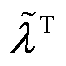 为与全局约束相关的乘子,λj为与第j个区域局部约束相关的乘子;Ωλ为λ取值范围,与等式约束相关的乘子取值范围为(-∞, +∞),与其他约束相关的乘子取值范围为(-∞, 0]。
为与全局约束相关的乘子,λj为与第j个区域局部约束相关的乘子;Ωλ为λ取值范围,与等式约束相关的乘子取值范围为(-∞, +∞),与其他约束相关的乘子取值范围为(-∞, 0]。
2)对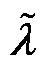 、
、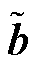 的分解
的分解
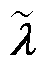 表示与全局约束相关的乘子,将其分解为与各区域相关的局部变量,对与各区域相关的局部约束λj不作处理;
表示与全局约束相关的乘子,将其分解为与各区域相关的局部变量,对与各区域相关的局部约束λj不作处理;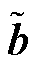 表示与全局约束相关的约束值,将
表示与全局约束相关的约束值,将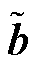 分解为与各区域相关的系数矩阵,对与各区域相关的局部约束值bj不作处理。
分解为与各区域相关的系数矩阵,对与各区域相关的局部约束值bj不作处理。
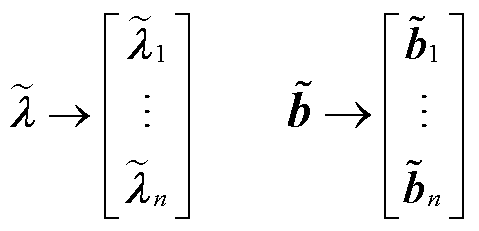
式中,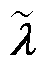 分解后的元素满足
分解后的元素满足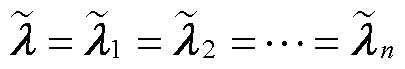 ;
;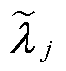 (j=1,…,n)为将
(j=1,…,n)为将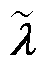 分解后与第j个区域相关的局部变量;
分解后与第j个区域相关的局部变量;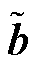 分解后的元素满足
分解后的元素满足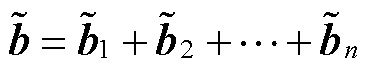 ,
,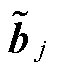 (j=1,…,n)为与区域j相关的全局不等式约束值,
(j=1,…,n)为与区域j相关的全局不等式约束值,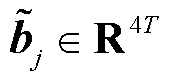 。设区域j中第iR个单元可知系统整体的备用,具体形式如下。
。设区域j中第iR个单元可知系统整体的备用,具体形式如下。
1)若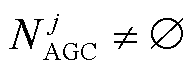 ,即j区域中存在单元
,即j区域中存在单元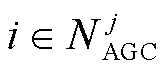
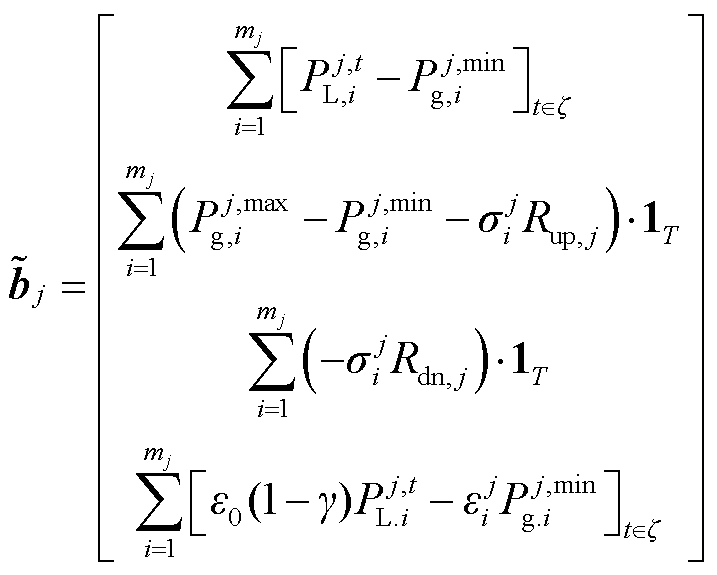
2)若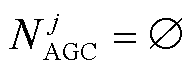 ,但j区域中存在单元
,但j区域中存在单元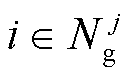
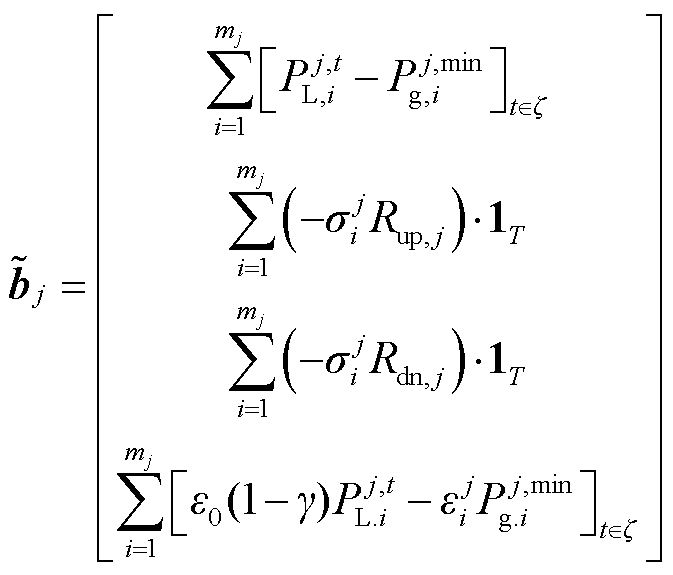
3)若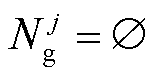
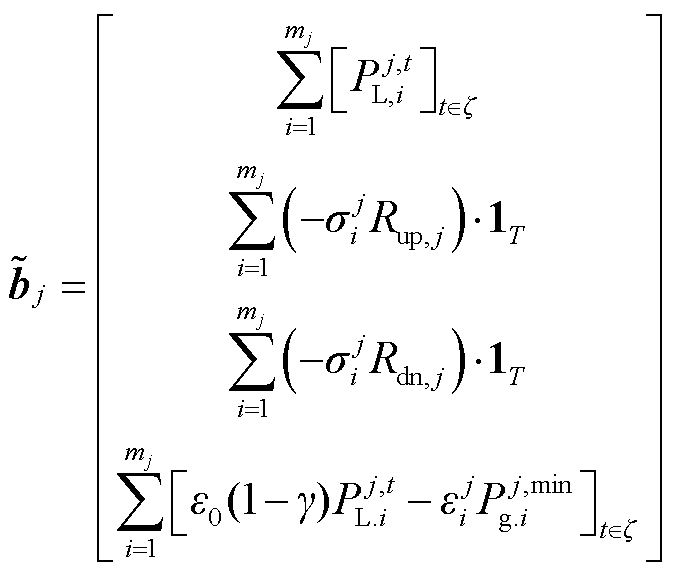
式中,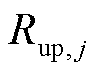 、
、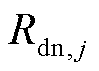 分别为由区域j的负荷计算出的向上、向下备用容量;
分别为由区域j的负荷计算出的向上、向下备用容量;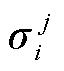 由第j个区域单元i是否可知系统整体的备用需求决定,若可知,则
由第j个区域单元i是否可知系统整体的备用需求决定,若可知,则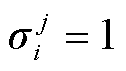 ,反之,则
,反之,则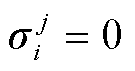 。
。
通过以上两步工作,可得到能够分布式求解的模型B,表示为
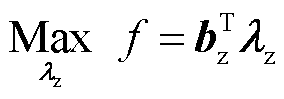 (18)
(18)
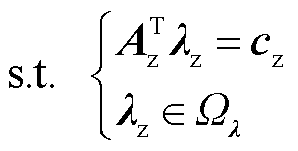 (19)
(19)
其中,λz、bz、Az、cz的形式为
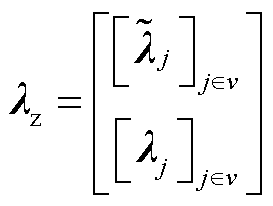
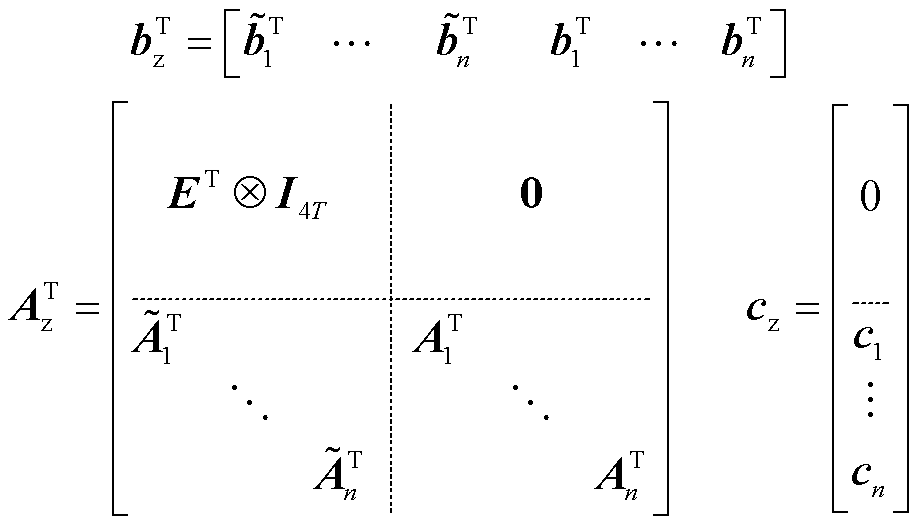
式中,E为点-边关联矩阵; 表示Kronecker乘积。
表示Kronecker乘积。
此时每个区域都对应一子问题,即
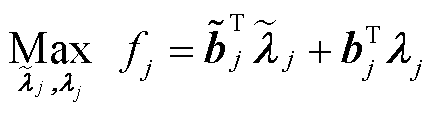 (20)
(20)
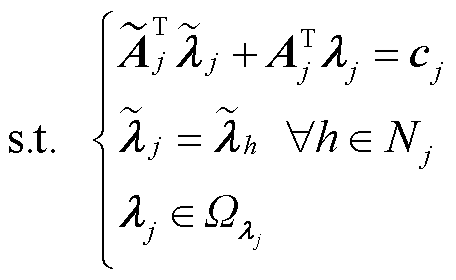 (21)
(21)
式中,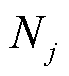 为与点j相邻的点的集合。
为与点j相邻的点的集合。
至此,通过将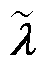 、
、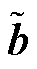 分解为与各区域相关的局部变量,将经济调度问题分解为与各区域相关的子问题,并根据各区域之间的信息拓扑关联构造了各子问题中相应局部变量的关联约束,实现了对模型A的分解。
分解为与各区域相关的局部变量,将经济调度问题分解为与各区域相关的子问题,并根据各区域之间的信息拓扑关联构造了各子问题中相应局部变量的关联约束,实现了对模型A的分解。
各区域之间能够实现信息交互的前提为存在电气联系,即各区域之间的信息网络拓扑决定了它们之间能否实现信息交互。信息网络拓扑可表示为各节点之间的有向图:G=(v, ε),其中,v为点的集合,表示各区域,v ={1, 2,…,n};ε=v×v为边的集合,表示各区域之间的信息拓扑结构关系;与点j相邻的点的集合用Nj表示,Nj={ Nj+,Nj- },其中Nj+为与点j相连并由点j指出的点集;Nj-为与点j相连并指向点j的点集;G=(v, ε)的点-边关联矩阵为E。
本节基于ADMM设计对模型A的分布式解法,首先构造与单个区域优化子问题对应的拉格朗日函数,可通过与模型B对应的增广拉格朗日函数推导得出。模型B对应的增广拉格朗日函数为
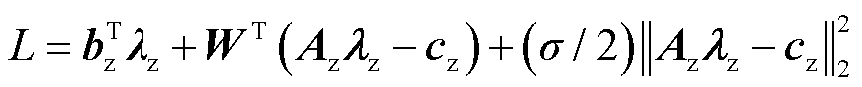 (22)
(22)
式中,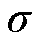 为常数惩罚因子,即迭代步长,为提高算法收敛性,采用文献[20]提出的一种动态乘子更新策略;
为常数惩罚因子,即迭代步长,为提高算法收敛性,采用文献[20]提出的一种动态乘子更新策略;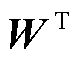 为与约束
为与约束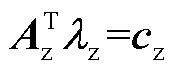 相关的乘子向量,其形式为
相关的乘子向量,其形式为
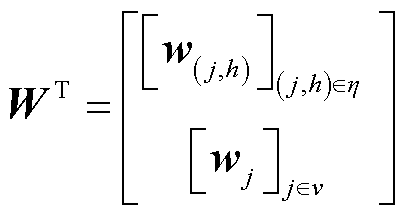
式中,h为相邻区域构成的集合;w(j,h)为互联区域优化子问题之间关联约束相关的乘子;wj为与单个区域优化子问题局部约束相关的乘子,等价于各区域单元的出力矩阵。
对Az、W、cz进行分解,可得到
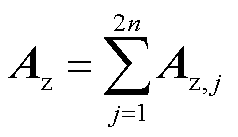 (23)
(23)
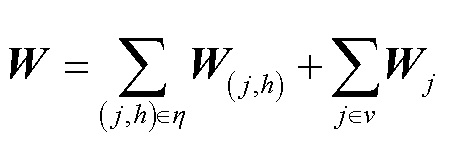 (24)
(24)
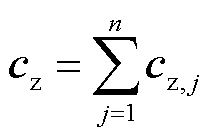 (25)
(25)
式中,Az,j为Az的第j列;W(j,h)、Wj、cz,j分别为
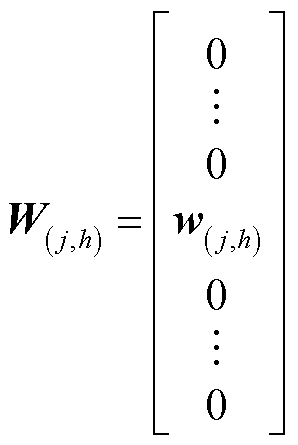
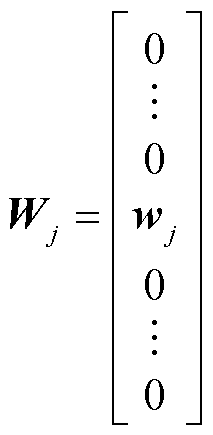
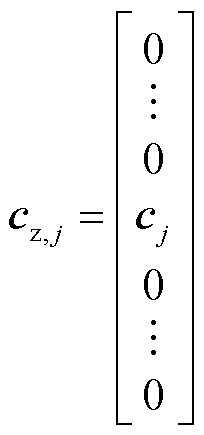
将式(23)~式(25)代入式(22),化简可得与各区域优化子问题对应的增广拉格朗日函数为
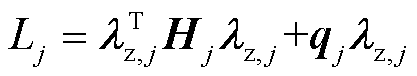 (26)
(26)
式中,Hj、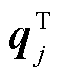 可根据区域j的局部信息和相邻区域的关联信息计算得出。
可根据区域j的局部信息和相邻区域的关联信息计算得出。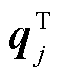 、Hj与
、Hj与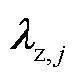 分别为
分别为
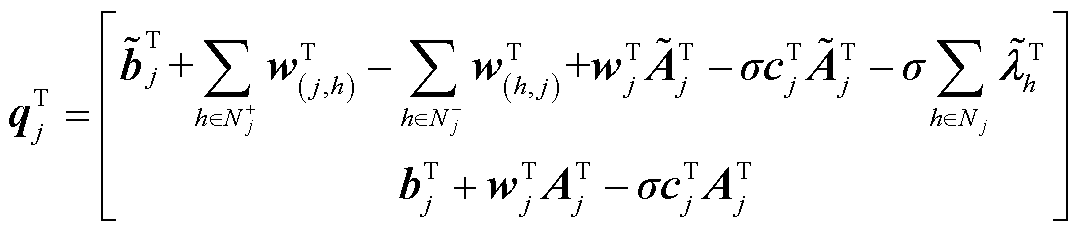
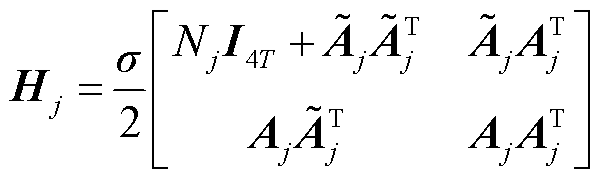
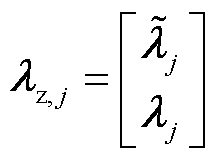
至此得到了与单个区域优化子问题对应的拉格朗日函数。
根据文献[21]提出的颜色法,将所有的区域分为两类,第一类区域构成的集合为P1,第二类区域构成的集合为P2,有N={P1∪P2}且P1∩P2= ,要求相邻区域分类不同,可通过合理规划信息网络拓扑来满足这一要求。对模型B的求解步骤如下:
,要求相邻区域分类不同,可通过合理规划信息网络拓扑来满足这一要求。对模型B的求解步骤如下:
1)对各区域数据初始化, 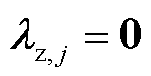 、
、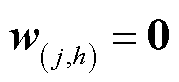 ,
,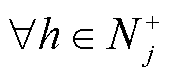 、
、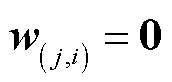 ,
,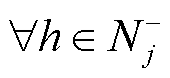 、
、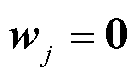 。
。
2)针对各区域优化模型进行求解,得到第k次迭代与各区域相关的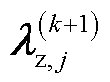 。
。
3)相邻区域间进行信息传递,更新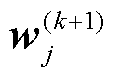 、
、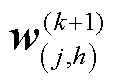 、
、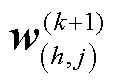 ,更新过程如图4所示。
,更新过程如图4所示。
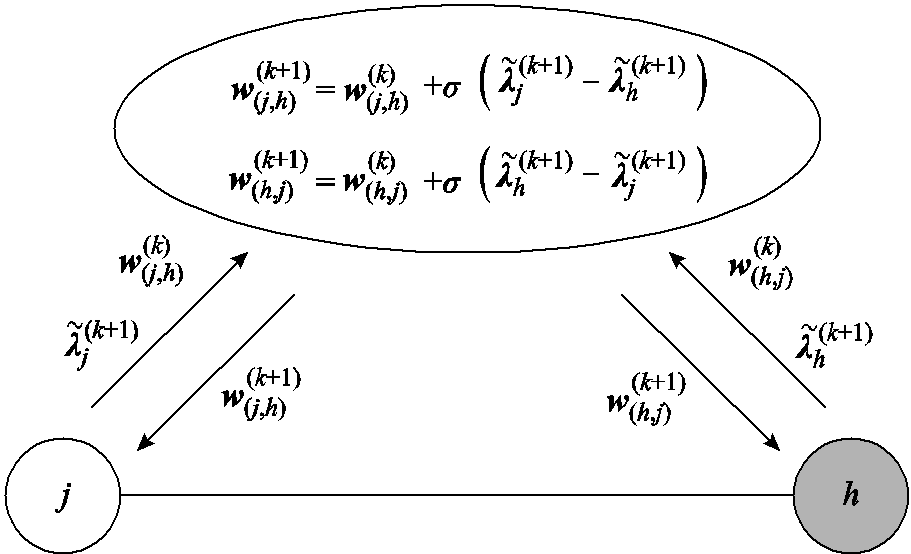
图4 互联区域乘子信息交互示意图
Fig.4 Interconnected area multiplier information interaction diagram
4)判断迭代次数是否满足初始设定,不满足则返回步骤2),满足则迭代结束。
关于模型B分布式求解流程如图5所示。在优化过程中,同类区域的优化在时序上是并行的,而不同类区域的优化在时序上是串行的,通过两类区域的交替迭代计算实现分布式优化。当各区域优化完成后,单个区域不断与相邻区域之间通过互联的单元或节点交换与各约束相关的乘子,并根据交换信息协调、更新自身下次迭代相应的乘子。
信息交互过程也可以理解为相邻区域不断交换各自关于发电边际成本、备用边际成本的报价,并根据交换结果评估与各自运行约束相关的机会成本和发电、备用的边际成本,根据评估结果调整各自对发电的决策。通过区域之间的多次协商和决策调整,最终得到各自的最优调度安排,保证系统在完成减排目标下经济性运行。在优化过程中,各区域对外可知的信息仅仅是关于边际成本的报价,而内部负荷预测值、发电单元的运行状态信息对外部并不可知,仅通过互联区域之间有限信息的交换即可实现低碳经济调度。
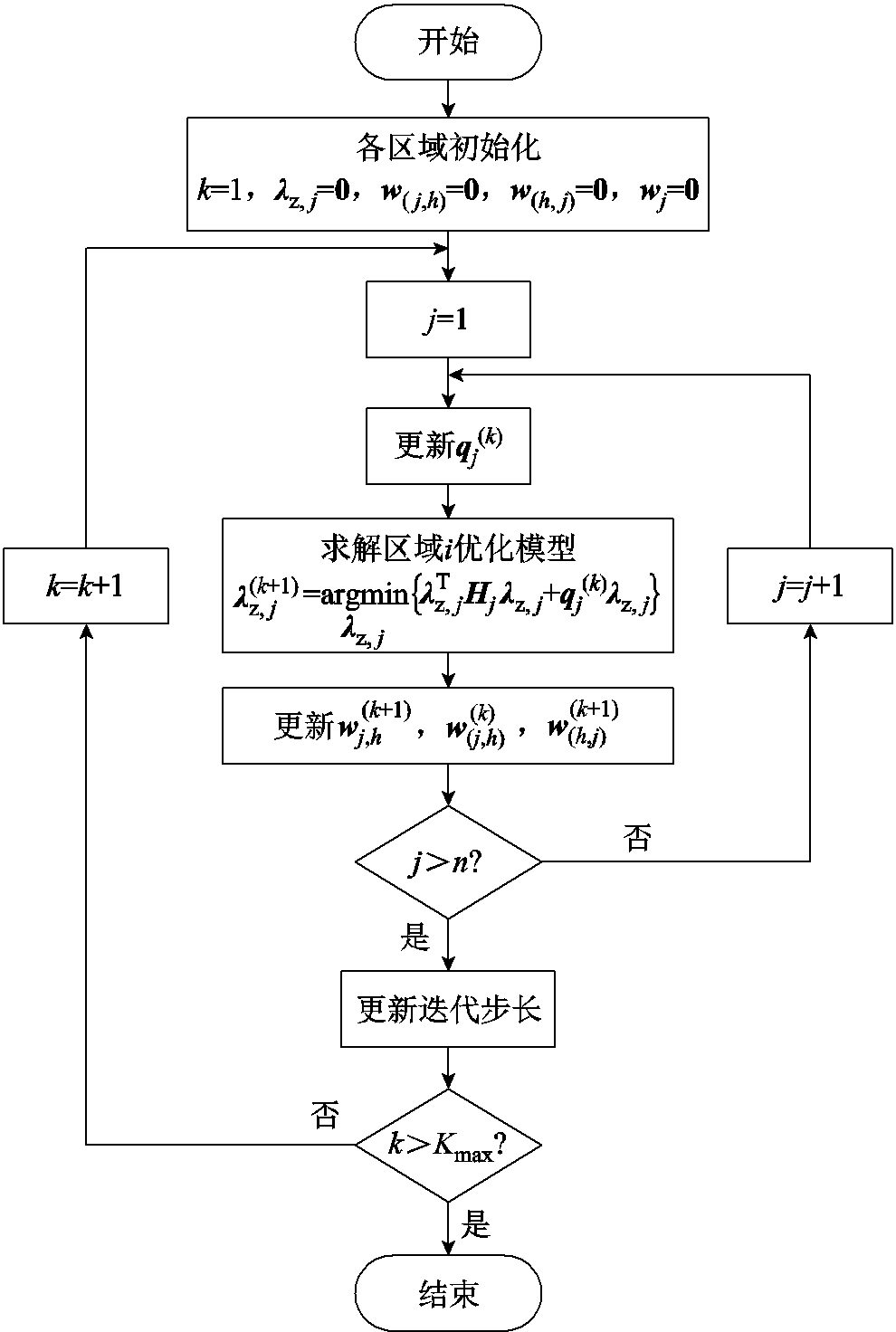
图5 模型B分布式求解流程
Fig.5 Distributed solving flowchart of Model B
根据3.4节设计的模型解法,每个区域优化时只用到相邻区域的信息,而相邻区域分类不同,可知每个区域在优化过程中并不会用到同类区域的信息,因此每次迭代过程中同类区域之间的计算次序并不影响优化的结果,两类单元的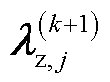 更新过程可表示为
更新过程可表示为
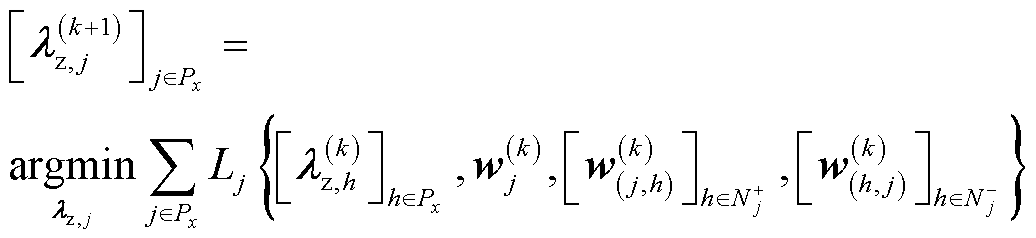 (27)
(27)
式中,x为区域的类别,在本文中为1或2。
此时,区域单元被分成两类的多区域互联系统分布式优化就等价于对两个互联区域分布式优化,关于这一算法的收敛性证明见文献[21]。
根据文献[21],定义原始残差r(k)和对偶残差s(k)分别为
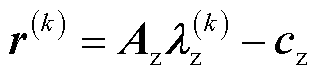 (28)
(28)
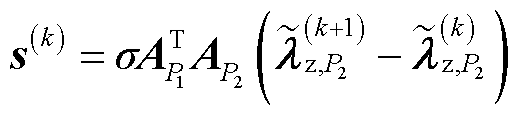 (29)
(29)
式中,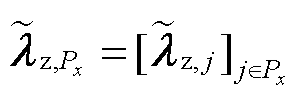 ;
;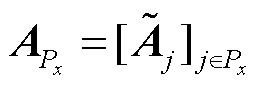 。
。
根据文献[22],收敛准则为
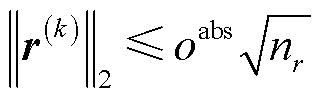 (30)
(30)
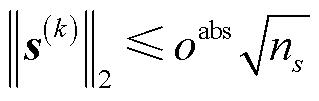 (31)
(31)
式中,nr、ns分别为向量r、s所含元素的个数;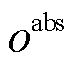 为收敛允许的绝对误差,本文选择
为收敛允许的绝对误差,本文选择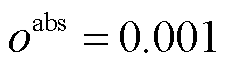 。
。
在迭代过程中,原始残差r、对偶残差s对各区域来讲并不可知,可设定最大收敛次数Kmax,当迭代次数k>Kmax,则迭代结束。可根据仿真实验中算法的收敛效果来选取Kmax。
基于所提的分布式经济调度方法,所有区域被分为两类且相邻区域分类不同,因此各区域只需知道各自的分类即可安排自身的计算时序。若有新的区域要并入分布式调度网络,仅需根据相邻区域的种类即可对自身进行分类,并设计相应的信息拓扑结构,以满足相邻区域不同种类这一要求。新的区域接入分布式调度网络后,其自身和相邻区域都能根据新的信息网络拓扑结构调整各自的优化决策。若原有区域要退出分布式调度网络,仅需停止其与相邻区域的通信,不会对其他各区域之间的分布式计算过程造成不良影响,剩余部分的分布式调度网络仍以其运行成本最小化为目标进行分布式优化。由此可见,该调度方法可有效满足“即插即用”的需求。
基于所提出的方法对IEEE 6节点测试系统和72节点测试系统的低碳经济调度问题展开分析,以验证该方法的有效性。编程开发平台为64-bit Matlab R2018b,计算机配置为Intel Core i5-8300H,2.30 GHz,8 GB RAM。
将IEEE 6节点系统划分为4个区域,各区域之间的信息网络拓扑结构如图6所示。在单元3中包含50 MW风电机组,发电机的运行参数见附表1。选取典型日作为研究对象,各节点的负荷及风电出力预测曲线如附图1所示,单个时段长度为15 min。
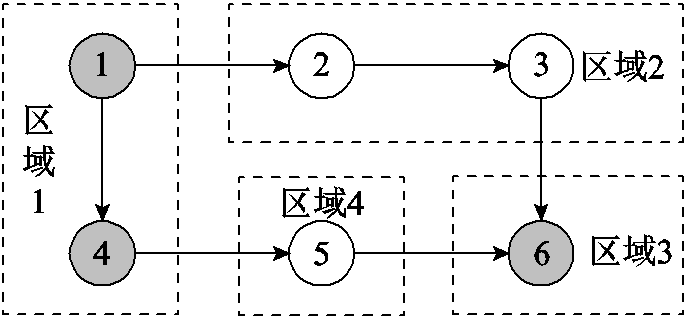
图6 IEEE 6节点系统信息网络拓扑
Fig.6 IEEE 6 system information network topology
在IEEE 6节点系统算例分析中,迭代步长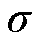 初值取0.15。图7为机组日出力决策曲线。在碳排放约束作用下,由于机组
初值取0.15。图7为机组日出力决策曲线。在碳排放约束作用下,由于机组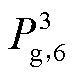 的发电成本以及碳排放系数较高,该机组以最小出力运行。
的发电成本以及碳排放系数较高,该机组以最小出力运行。
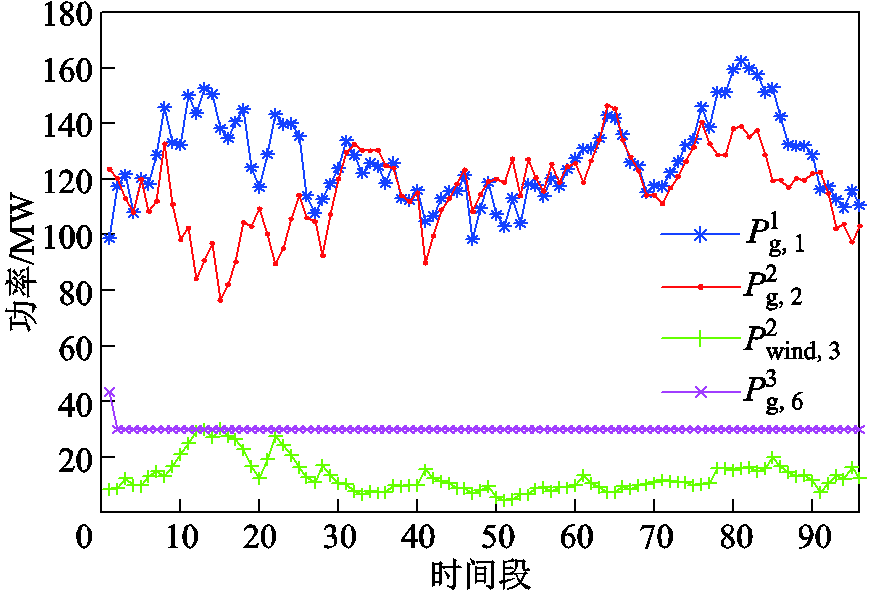
图7 日经济调度各机组出力曲线
Fig.7 Output curves of units in daily economic dispatch
选取典型日调度前四个时段算例结果进行收敛性分析。对偶残差及原始残差随迭代次数增加的变化曲线如图8所示,当迭代次数为247时分布式计算达到收敛要求。
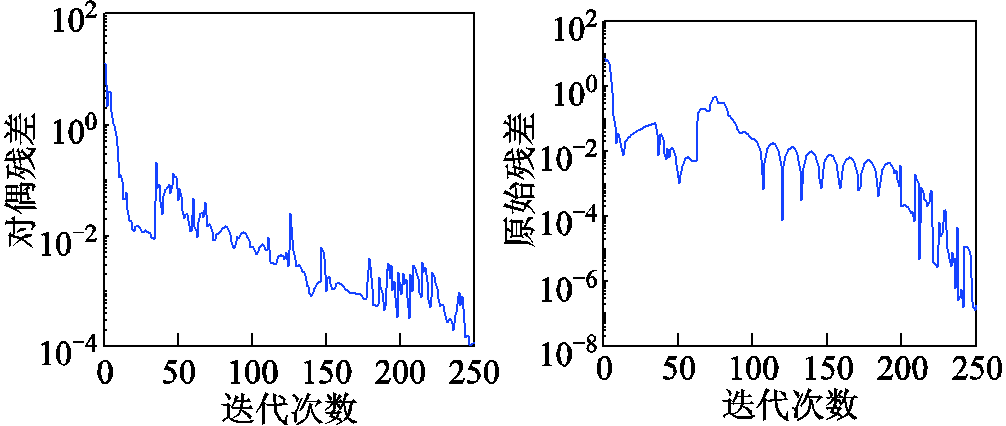
图8 收敛曲线
Fig.8 Convergence curves
当迭代次数为247时,分布式经济调度成本为82 868.04元,与集中式经济调度成本82144.40元的相对误差为0.88%,两者结果十分相近。
图9为前四个时段的机组出力决策随迭代次数增加变化曲线。在迭代次数达到150左右时,系统机组出力已满足功率平衡约束,随后,机组出力因互联区域间不断交换乘子逐渐趋于收敛。
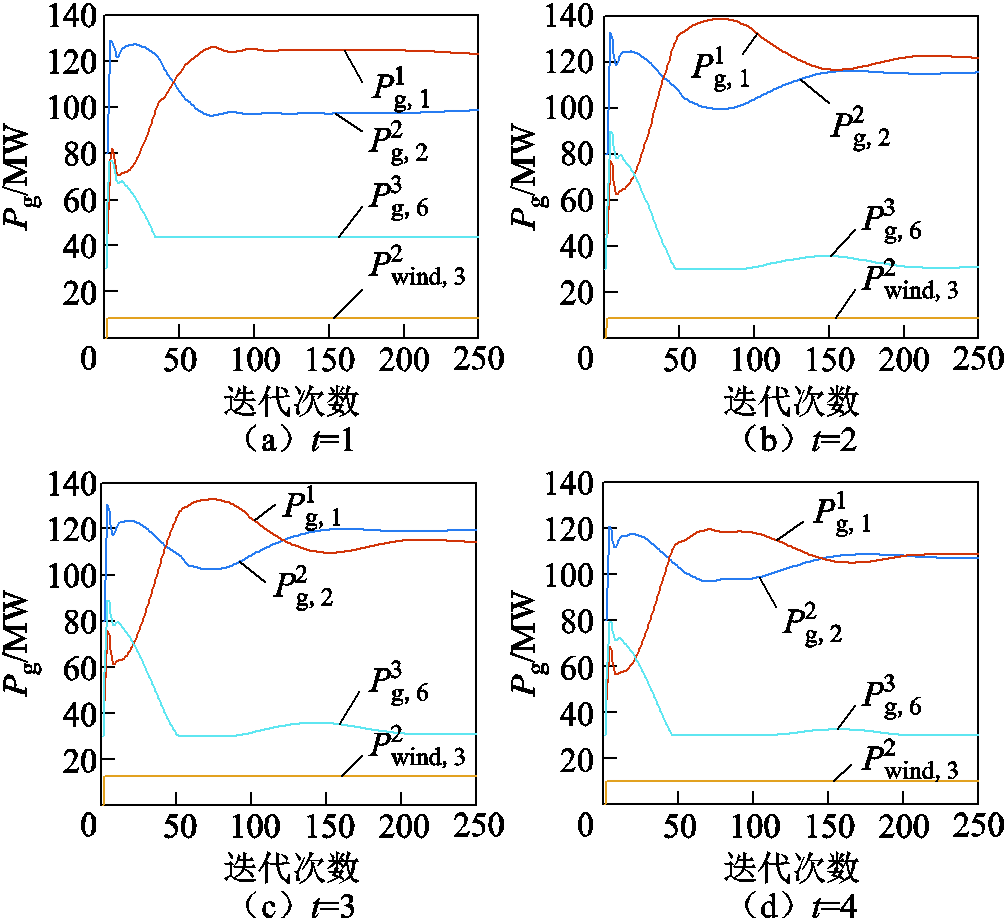
图9 机组发电决策值迭代变化曲线
Fig.9 Curves of unit power generation decision value changing with iteration
图10为考虑碳排放约束后分布式与集中式经济调度各机组决策值求解结果差值。各时间段差值范围在-1.30~1.28 MW之间,相对误差较小。
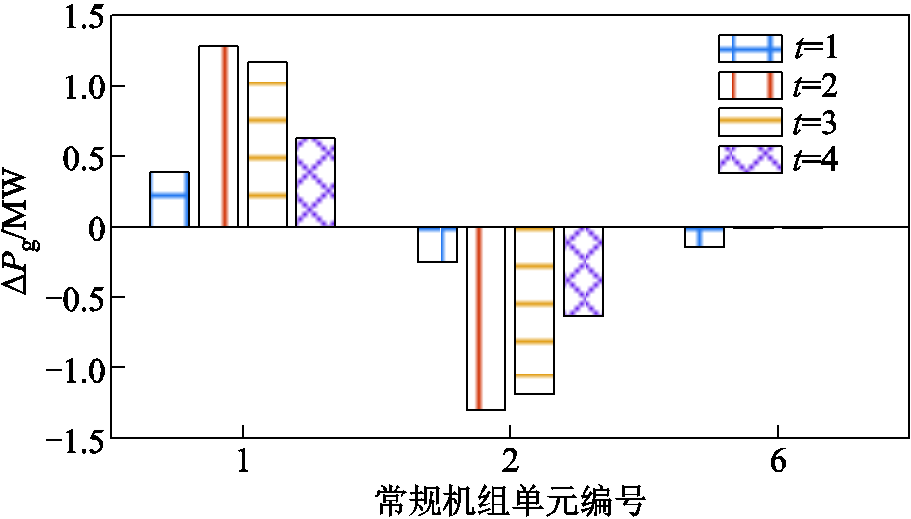
图10 分布式与集中式调度发电决策差值
Fig.10 Decision difference between distributed and centralized dispatching power generation
碳排放约束加入前后各机组在前四个时间段的碳排放量对比如图11所示。火电机组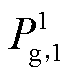 、
、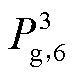 碳排放量大幅减少,
碳排放量大幅减少,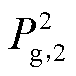 碳排放量增加。系统碳排放量由224 t降低至190.06 t,降低15.15%,满足碳排放约束。
碳排放量增加。系统碳排放量由224 t降低至190.06 t,降低15.15%,满足碳排放约束。
本节以72节点测试系统为例,进一步验证本文所提方法在大规模系统中应用的有效性与实用性。首先对72节点18机测试系统划分为6区域互联电力系统,并构建了三种网络拓扑结构,对其进行算例结果对比;随后对区域数量进行变换,对比相同规模系统不同区域数量分布式求解结果;最后,通过互联区域通信故障验证了本文方法满足优化区域“即插即用”的需求。
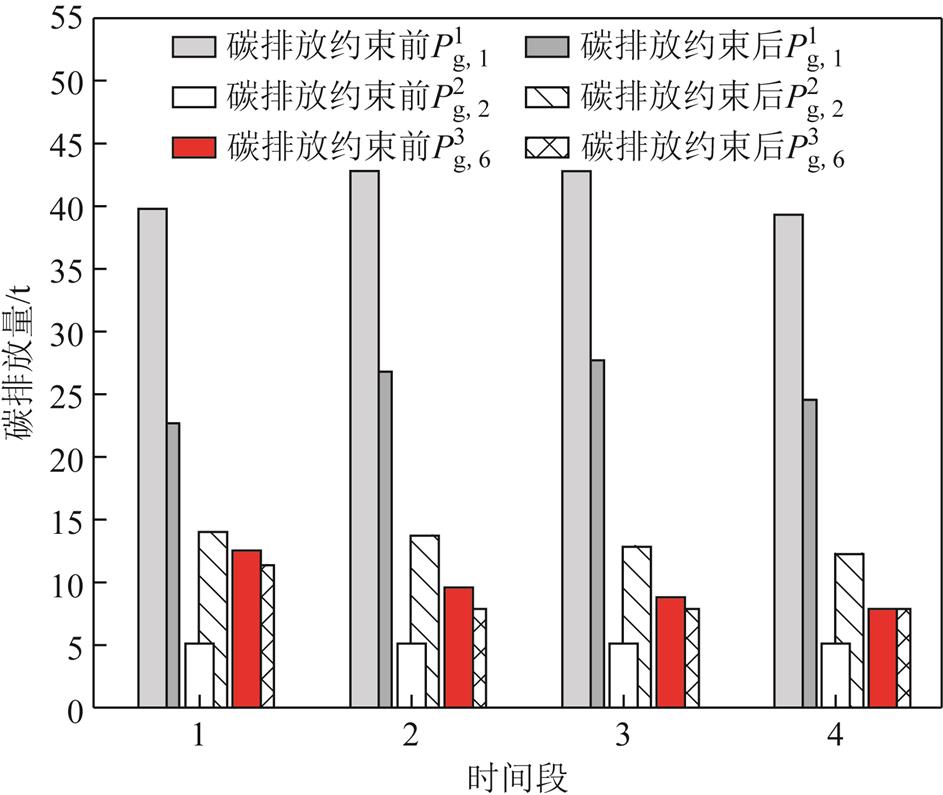
图11 碳排放约束前后机组碳排放量对比
Fig.11 Comparison of unit carbon emissions before and after carbon emission constraints
5.2.1 72节点6区域测试系统三种拓扑结构对比
在本节中,对72节点6区域测试系统三种网络拓扑结构进行分布式低碳经济调度优化,并对其分布式求解结果进行对比。72节点6区域测试系统三种网络拓扑结构如图12所示。关于各区域节点分配情况见附表2。
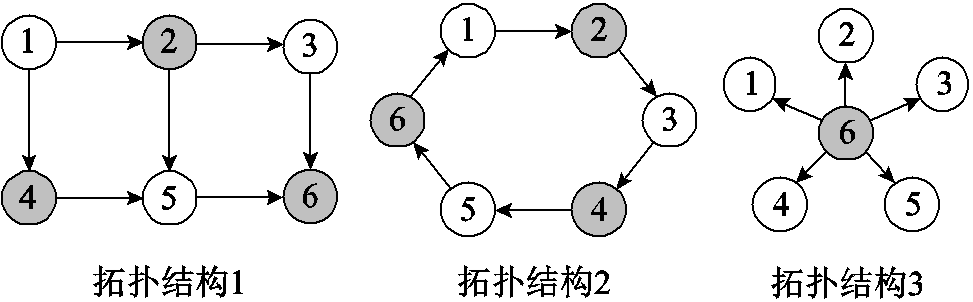
图12 72节点六区域测试系统三种拓扑结构
Fig.12 Three topology structures of 72-node 6-area test system
72节点6区域测试系统三种网络拓扑结构分布式低碳经济调度模型计算结果见表1。通过表1可以看出,三种网络拓扑收敛所需迭代次数及迭代时间并没有很大差别,且关于分布式求解结果与集中式经济调度结果相对误差很小,求解结果可视为一致。即关于同一系统,不同互联区域拓扑在该方法下都能取得与集中式经济调度相近的优化结果,验证了该方法对不同网络拓扑的通用性。
表1 72节点6区域测试系统三种网络拓扑求解结果
Tab.1 Results of three network topologies for 72-node 6-area test system

网络拓扑类别迭代次数迭代时间/s与集中式经济调度成本相对误差(%) 13712930.10 23672070.08 33422420.13
5.2.2 72节点测试系统三种分区方式对比
在本节中,对72节点测试系统三种分区方式进行算例分析。为保证算例结果对比合理性,三种分区方式的网络拓扑全部采用辐射型。72节点测试系统三种分区网络拓扑结构如图13所示。
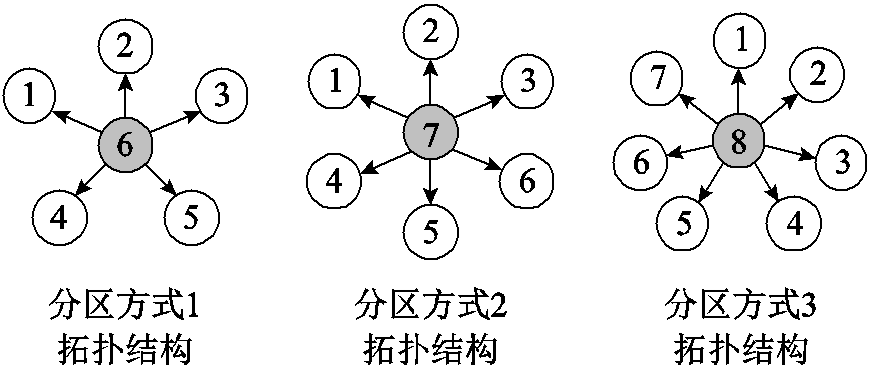
图13 72节点测试系统三种分区拓扑结构
Fig.13 Three partition topology structures of 72-node test system
对比三种分区方式的分布式求解结果见表2。由表2可知,在同一规模的电力系统中,随着互联区域数量的增加,达到收敛所需迭代次数略微增大。此外,关于模型分布式求解结果较集中式误差很小,所得目标函数值基本一致。即关于同一算例系统,在互联区域数量不同情况下都能取得与集中式经济调度相近的优化结果,验证了该方法在同一测试系统不同分区条件下的适用性。
表2 72节点测试系统三种分区方式求解结果
Tab.2 Solution results of three partition methods for 72-node test system

分区方式类别迭代次数迭代时间/s与集中式经济调度成本相对误差(%) 13422420.13 23582550.15 33742130.14
5.2.3 “即插即用”算例分析
以72节点6区域拓扑结构1为研究对象,设定区域1在迭代次数150~170时发生通信故障无法与其互联区域进行信息交互,退出多区域互联系统;迭代次数为170时,通信故障修复。
发生故障与未发生故障两种情况求解所得到的对偶残差及原始残差迭代变化曲线如图14所示。从图14可看出,当区域1退出及加入互联系统时,对偶残差及原始残差曲线出现剧烈波动,但通过区域间的信息交互,又逐渐趋于稳定,最终达到收敛,证明了该方法满足优化区域“即插即用”的需求。
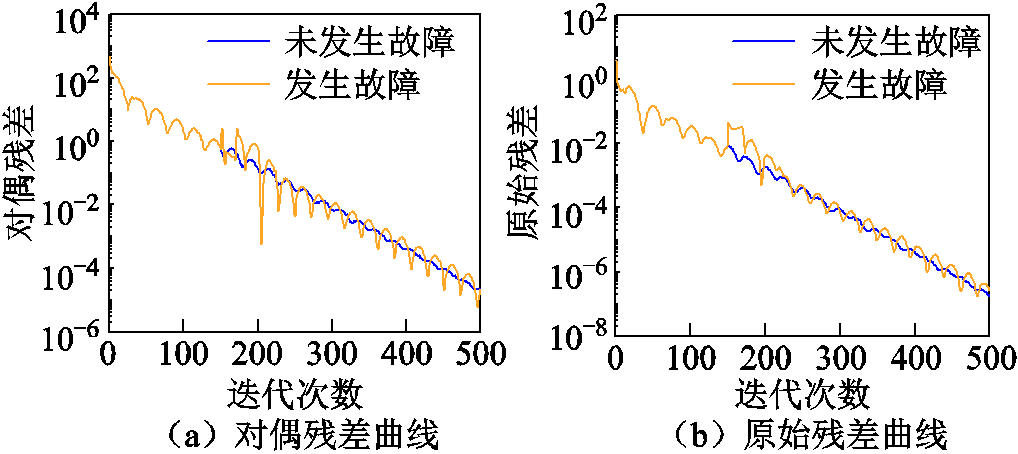
图14 收敛曲线对比
Fig.14 Convergence curve comparison
在“双碳”目标的推动下,为实现含有多类型机组电力系统在满足政策减排目标的同时最小化系统运行成本,构建了分布式低碳经济调度模型,基于ADMM设计了模型的分布式求解方法,并通过算例进行验证,得到如下结论:
1)针对多区域互联电力系统构建了分布式低碳经济调度模型,可对系统中多种可调控资源进行低碳经济调度优化,通过系统碳排放约束调整系统中各碳排放系数不同的设备出力,在满足减排目标的基础上,确定经济性最优的运行策略。
2)针对含有全局不等式约束的经济调度模型,提出一种分布式低碳经济调度方法,采用完全分布式调度结构。所提方法可以解决同时含全局等式约束和全局不等式约束的经济调度问题,与已有分布式经济调度方法相比更具有普适性。
3)各区域仅需通过内部单元的运行状态和相邻区域的拉格朗日乘子信息即可实现整体的优化,不需要相邻区域之间功率缺额信息的交换,充分满足各区域信息独立且私密性的要求,同时也满足优化区域单元“即插即用”的需求。
下一步工作将对算法进行改进以加快其收敛速度,并进一步丰富完善各区域内部可控单元的模型。
附 录
附表1 IEEE 6节点系统发电参数
App.Tab. 1 Generation parameters of the IEEE 6 bus system

序号AGCα/(元/MW2)β/(元/MW)γ/元/MW 1是0.004 6899.604 920200 2否0.312 6183.365 586162 6否0.042 72133.562 220100
(续)

序号/MW/(MW/min)Kg/MWε/[t/(MW·h)] 1805.24950.920 2454.38900.455 6301.14601.050
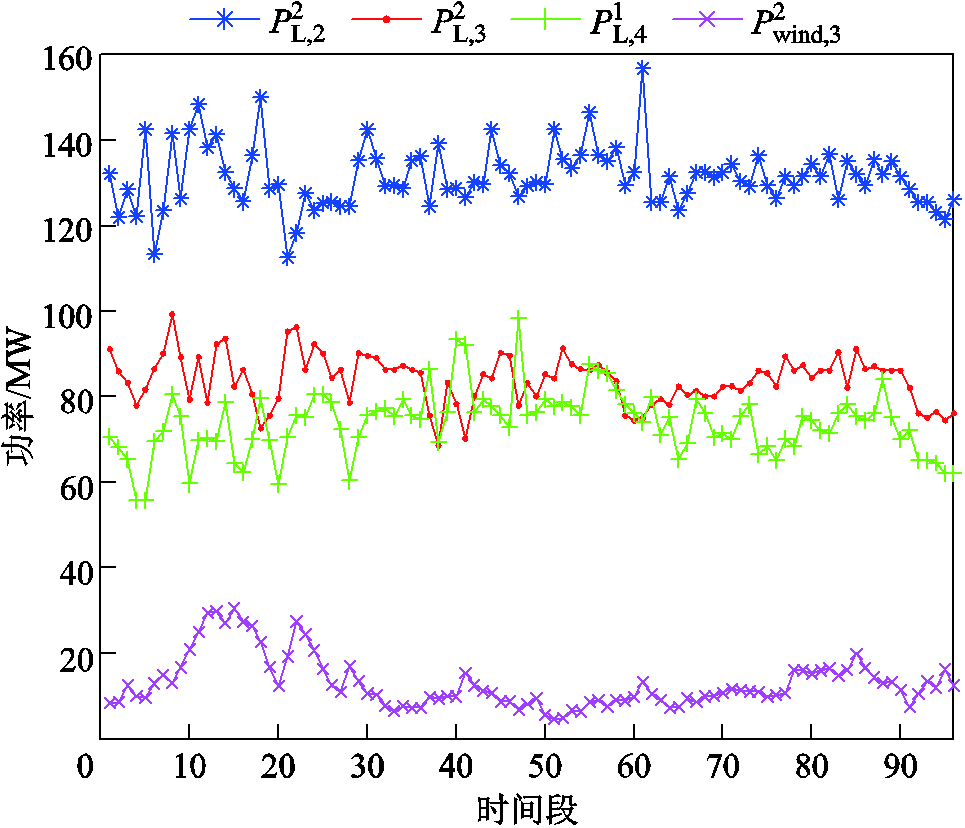
附图1 节点负荷及风电出力的预测曲线
App.Fig.1 Prediction curves of node load and wind power output
附表2 72节点测试系统分区信息
App.Tab.2 72 node test system partition information

区域编号6区域系统7区域系统8区域系统 1666 2121212 3303018 46612 5666 61266 7—66 8——6
参考文献
[1] 刘哲远, 邢海军, 程浩忠, 等. 考虑碳排放流及需求响应的综合能源系统双层优化调度[J]. 高电压技术, 2023, 49(1): 169-178.
Liu Zheyuan, Xing Haijun, Cheng Haozhong, et al. Bi-level optimal scheduling of integrated energy system considering carbon emission flow and demand response[J]. High Voltage Engineering, 2023, 49(1): 169-178.
[2] 盛戈皞, 钱勇, 罗林根, 等. 面向新型电力系统的电力设备运行维护关键技术及其应用展望[J]. 高电压技术, 2021, 47(9): 3072-3084.
Sheng Gehao, Qian Yong, Luo Lingen, et al. Key technologies and application prospects for operation and maintenance of power equipment in new type power system[J]. High Voltage Engineering, 2021, 47(9): 3072-3084.
[3] 彭元, 娄素华, 吴耀武, 等. 考虑储液式碳捕集电厂的含风电系统低碳经济调度[J]. 电工技术学报, 2021, 36(21): 4508-4516.
Peng Yuan, Lou Suhua, Wu Yaowu, et al. Low-carbon economic dispatch of power system with wind power considering solvent-storaged carbon capture power plant[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4508-4516.
[4] 李忠文, 程志平, 张书源, 等. 考虑经济调度及电压恢复的直流微电网分布式二次控制[J]. 电工技术学报, 2021, 36(21): 4482-4492.
Li Zhongwen, Cheng Zhiping, Zhang Shuyuan, et al. Distributed secondary control for economic dispatch and voltage restoration of DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4482-4492.
[5] 夏世威, 邹唯薇, 张茜, 等. 基于交替方向乘子法的电力系统分散式经济调度[J]. 电力系统自动化, 2019, 43(6): 100-106.
Xia Shiwei, Zou Weiwei, Zhang Qian, et al. Decentralized economic dispatch for power system based on alternating direction method of multipliers[J]. Automation of Electric Power Systems, 2019, 43(6): 100-106.
[6] 陈厚合, 王子璇, 张儒峰, 等. 含虚拟电厂的风电并网系统分布式优化调度建模[J]. 中国电机工程学报, 2019, 39(9): 2615-2625.
Chen Houhe, Wang Zixuan, Zhang Rufeng, et al. Decentralized optimal dispatching modeling for wind power integrated power system with virtual power plant[J]. Proceedings of the CSEE, 2019, 39(9): 2615-2625.
[7] 喻洁, 李扬, 夏安邦. 兼顾环境保护与经济效益的发电调度分布式优化策略[J]. 中国电机工程学报, 2009, 29(16): 63-68.
Yu Jie, Li Yang, Xia Anbang. Distributed optimization of generation dispatch schedule considering environmental protection and economic profits[J]. Proceedings of the CSEE, 2009, 29(16): 63-68.
[8] Kar S, Hug G. Distributed robust economic dispatch in power systems: a consensus innovations approach[C]//2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 2012: 1-8.
[9] 谢俊, 陈凯旋, 岳东, 等. 基于多智能体系统一致性算法的电力系统分布式经济调度策略[J]. 电力自动化设备, 2016, 36(2): 112-117.
Xie Jun, Chen Kaixuan, Yue Dong, et al. Distributed economic dispatch based on consensus algorithm of multi agent system for power system[J]. Electric Power Automation Equipment, 2016, 36(2): 112-117.
[10] 马锴, 于洋庆, 朱善迎, 等. 基于梯度下降和一致性的电网分布式经济调度算法[J]. 中国科学: 信息科学, 2018, 48(10): 1364-1380.
Ma Kai, Yu Yangqing, Zhu Shanying, et al. Distributed algorithm for economic dispatch based on gradient descent and consensus in power grid[J]. Scientia Sinica (Informationis), 2018, 48(10): 1364-1380.
[11] 陈伟俊, 罗洪林, 彭建文. 随机ADMM算法及其在电力系统凸经济调度问题中的应用[J]. 应用数学和力学, 2021, 42(9): 979-988.
Chen Weijun, Luo Honglin, Peng Jianwen. The random ADMM and its application to convex economic dispatch problems of power systems[J]. Applied Mathematics and Mechanics, 2021, 42(9): 979-988.
[12] Wang Yamin, Wu Lei, Wang Shouxiang. A fully-decentralized consensus-based ADMM approach for DC-OPF with demand response[J]. IEEE Transactions on Smart Grid, 2017, 8(6): 2637-2647.
[13] 杨珺, 侯俊浩, 刘亚威, 等. 分布式协同控制方法及在电力系统中的应用综述[J]. 电工技术学报, 2021, 36(19): 4035-4049.
Yang Jun, Hou Junhao, Liu Yawei, et al. Distributed cooperative control method and application in power system[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4035-4049.
[14] 史佳琪, 胡浩, 张建华. 计及多个独立运营商的综合能源系统分布式低碳经济调度[J]. 电网技术, 2019, 43(1): 127-136.
Shi Jiaqi, Hu Hao, Zhang Jianhua. Distributed low-carbon economy scheduling for integrated energy system with multiple individual energy-hubs[J]. Power System Technology, 2019, 43(1): 127-136.
[15] 杨青润, 李澄, 丁涛, 等. 基于交替方向乘子法的电力系统完全分布式动态经济调度方法[J]. 控制理论与应用, 2018, 35(5): 709-716.
Yang Qingrun, Li Cheng, Ding Tao, et al. Fully distributed dynamic economical dispatching method for power system based on alternating direction multiplier method[J]. Control Theory & Applications, 2018, 35(5): 709-716.
[16] 李佩杰, 陆镛, 白晓清, 等. 基于交替方向乘子法的动态经济调度分散式优化[J]. 中国电机工程学报, 2015, 35(10): 2428-2435.
Li Peijie, Lu Yong, Bai Xiaoqing, et al. Decentralized optimization for dynamic economic dispatch based on alternating direction method of multipliers[J]. Proceedings of the CSEE, 2015, 35(10): 2428-2435.
[17] Xing Hao, Mou Yuting, Fu Minyue, et al. Distributed bisection method for economic power dispatch in smart grid[J]. IEEE Transactions on Power Systems, 2015, 30(6): 3024-3035.
[18] 李国庆, 王冲, 雷顺波, 等. 考虑碳捕集技术的电力系统双层优化配置[J]. 电力自动化设备, 2023, 43(1): 25-31.
Li Guoqing, Wang Chong, Lei Shunbo, et al. Bi-level optimal allocation of power system considering carbon capture technology[J]. Electric Power Automation Equipment, 2023, 43(1): 25-31.
[19] 王澹, 蒋传文, 李磊, 等. 考虑碳排放权分配及需求侧资源的安全约束机组组合问题研究[J]. 电网技术, 2016, 40(11): 3355-3362.
Wang Tan, Jiang Chuanwen, Li Lei, et al. Security constrained unit commitment problem considering carbon emission allocation and demand side resources[J]. Power System Technology, 2016, 40(11): 3355-3362.
[20] 陈哲, 王橹裕, 郭创新, 等. 基于风险的多区互联电力系统分布式鲁棒动态经济调度[J]. 电力系统自动化, 2021, 45(23): 113-122.
Chen Zhe, Wang Luyu, Guo Chuangxin, et al. Risk-based distributed robust dynamic economic dispatch for interconnected multi-regional power systems[J]. Automation of Electric Power Systems, 2021, 45(23): 113-122.
[21] Stephen B, Neal P, Eric C, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Distributed Optimization and Statistical Learning Via the Alternating Direction Method of Multipliers, 2011, 3(1): 1-122.
[22] Matt K, Eric C, Javad L, et al. Dynamic network energy management via proximal message passing[J]. Dynamic Network Energy Management Via Proximal Message Passing, 2014, 1(2): 73-126.
Abstract In a multi-area interconnected power system, to meet the needs of emission reduction policies, carbon emission constraints can be added to the economic dispatch model to regulate the output of the unit and achieve low-carbon economic dispatch of the system. This method is the most common in centralized economic dispatch. Because centralized optimal dispatch requires great communication bandwidth and large computing and information storage requirements, distributed economic dispatch has become a research hotspot. In recent years, scholars have made some achievements in the research of distributed economic dispatch, but the methods involved can only solve the economic dispatch problem with a global equality constraint and several local constraints. For the economic dispatch problem with global inequality constraints, these methods are not applicable. Therefore, this paper proposes a new distributed low-carbon economic scheduling method. The proposed method can solve the economic scheduling problem with global equality constraints and global inequality constraints, which is more universal than the existing distributed economic scheduling methods.
First, a low-carbon economic dispatch model is constructed to determine the objective function and the corresponding equality constraints and inequality constraints. Then, based on the duality principle, the original problem is transformed into a corresponding dual problem. Then, the dual problem model is decomposed by the variable decomposition method, so that the objective function and constraints are transformed into optimization sub-problems related to a single region. Finally, based on ADMM, an iterative solution framework for the collaborative optimization of each region is designed.
To improve the convergence of the algorithm and avoid the problem of penalty factor parameter selection, a dynamic multiplier update strategy is adopted. The emission reduction factor is set at 15%. According to the method proposed in this paper, the IEEE 6 node test system and the 72-node test system are optimized for distributed low-carbon economy scheduling. In the example of the IEEE 6 node system, the convergence condition is reached when iterating 247 times. The relative error of distributed economic dispatch is 0.88% compared with centralized operation cost, and the calculation result can be regarded as consistent. The carbon emission of the system is reduced from 224 t to 190.06 t, which is reduced by 15.15% and meets the carbon emission constraint. Then, the 72-node test system is analyzed, and the distributed solution effects of different network topology types and partition methods are compared. The universality of the method to different network topologies and the applicability under different partition conditions of the same test system is verified. Finally, the communication fault in the interconnected area verifies that the method meets the needs of “plug and play” in the optimized area.
Through the example analysis, it is verified that the method can effectively reduce the amount of information transmission between regions, fully guarantee the requirements of information privacy of each regional unit, meet the demand of “plug and play” in the optimization region, and realize the distributed low-carbon economic dispatch of the multi-area interconnected system. The next work will improve the algorithm to accelerate its convergence speed, and further enrich and improve the model of controllable units within each region.
keywords:Multiple coupling constraints, carbon emission constraint, distributed economic dispatch, duality theory, variance decomposition, alternating direction multiplier method (ADMM)
中图分类号:TM73
DOI:10.19595/j.cnki.1000-6753.tces.221745
内蒙古自治区科学技术厅揭榜挂帅项目(2022JBGS0044)和东北电力大学博士科研启动基金(BSJXM-2021102)资助。
收稿日期 2022-09-14
改稿日期 2022-11-30
李军徽 男,1976年生,教授,硕士生导师,博士,研究方向为新能源发电运行与控制,储能技术在电力系统中的应用。E-mail:lijunhui@neepu.edu.cn
朱星旭 男,1989年生,讲师,硕士生导师,研究方向为电力系统运行与控制。E-mail:neduzxx@163.com(通信作者)
(编辑 赫蕾)