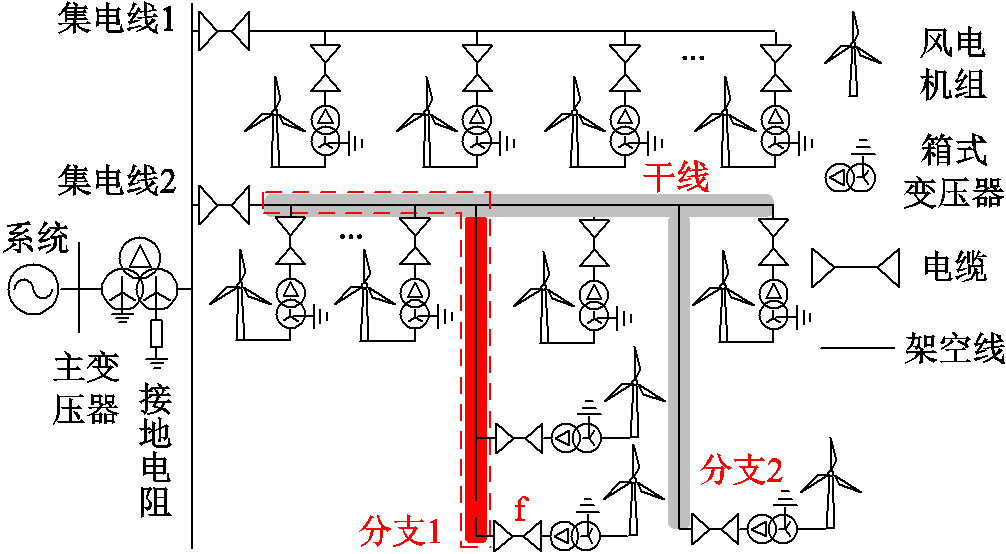
图1 风电场拓扑结构
Fig.1 Topology of wind farms
摘要 由于风电场集电线线路短、连接风机多且风机间距小,传统行波测距等故障定位方法难以适用。为此该文提出一种图学习与零序分量相结合的新型层次化单相接地故障定位方案。首先,计及集电线拓扑信息构建图数据,应用图卷积神经网络进行图分类建模判断集电线故障区域;然后,为克服样本不平衡的影响,结合迁移学习进行模型串联,并引入代价敏感机制后处理分类结果;最后,利用风电场接地方式与箱变接线特点,基于双端零序分量推导与风机无关的故障区域测距公式。所提方案可跨越风机实现定位,并能克服数据不同步的影响,所需测点少,适用于含分支集电线。仿真表明,图卷积神经网络相对传统深度网络判断正确率更高,模型串联结合代价敏感机制可有效克服样本不平衡影响;故障区域判断与测距效果不受故障位置、过渡电阻和风速的影响。
关键词:风电场 集电线 单相接地故障 故障定位 图卷积神经网络 零序分量 样本不平衡 数据不同步
当前,我国风电的装机容量与发电量已多年位列全球第一[1],在实现“双碳”目标,构建新型电力系统背景下,风电势必会迎来进一步的发展。但是,我国风电场大多位于戈壁、海岸等环境较为恶劣的地区,集电线短路故障易发[2],而集电线线路短、连接风机多、风机间距小又使得自动化定位难度很大,易造成弃风窝电,使风电企业备受困扰。
目前故障定位技术的研究多集中在输配电线路,主流定位方法包括故障分析法[3-7]、行波法[8-11]、人工智能法[12-15]。文献[5]基于FTU(feeder terminal unit)告警信息,利用整数线性规划有效地实现了主动配电网的故障区段定位;但是一条集电线会连接十几台风机,因此所含区段众多,且单条集电线一般在10 km左右,实施类似方案需在有限长线路上安装大量FTU,风电企业一般较难接受。文献[11]通过计算故障行波零模与线模分量到达时间之差确定配电网故障区段,然后利用传统行波法进行故障测距;但是由于电源密集接入,风机间距小,应用行波法跨风机测距会导致行波折反射频繁,在风机间测距又面临所需装置多、测距相对误差过大等问题。文献[12-15]分别采用模糊C均值聚类算法、卷积神经网络、AdaBoost-Elman集成神经网络实现了输配电网故障线路识别与多端直流、特高压直流输电线的故障定位。人工智能技术有着优秀的自主学习、复杂特征提取及非线性表达能力,虽然面临小样本学习及模型泛化能力的挑战,但其能依靠大数据自主形成输入输出映射关系,实现“端到端”模型构建,这一优势使其非常适用于解决复杂机理问题,因此其在故障定位领域有广泛应用空间,研究意义重大。
风电场集电线结构特殊,故障定位困难,目前相关研究成果较少。文献[16-17]在风机之间分布式安装测点,以避免风机对故障测距的影响,成功实施了风机间的单端阻抗法测距与单端行波法测距。然而,上述方案需在线路上安装大量测点,同时也面临前文所述风机间行波测距的难点。文献[2]注意到集电线零序电流远大于风机电流的事实,近似认为各风机提供的故障电流相等,基于对风机电流的估计改进了传统单端阻抗法,通过逐段搜索实现了跨越风机的故障测距。文献[18]采用极限梯度提升算法建立回归模型,同样能够跨越风机完成集电线故障测距;作者依靠人工智能算法的学习、表达能力拟合风机特性,较好地解决了风机影响难以表征的问题,为在集电线故障测距中消除风机影响提供了新的思路。同时,文献[2,18]只需在集电线首端安装测点;但是,当它们应用于含分支集电线时会出现伪根。从整体上看,风机影响、集电线分支及测点数目是集电线故障定位面临的几大难点,还需进一步研究以实现以上各点的有效统筹。
针对以上难点,本文将图学习理论与零序分量相结合实施故障定位。首先分析了风电场的特点。然后基于图学习理论构建图卷积神经网络基模型,在基模型的基础上结合多级分类模型串联与代价敏感学习形成完整故障区域判断模型。进一步,利用风电场零序特征较明显、零序网络不含风机的事实,从零序分量出发实现故障区域的故障测距。另外,为避免故障区域误判造成定位失败,文章还设计了故障区域误判处理机制。最后,搭建仿真模型验证该方案性能,并与其他方案进行了比较。
风电场典型拓扑结构如图1所示。风机在多点密集接入集电线,且集电线长度有限[17],一般在10 km左右,因此相邻风机间距很小[2,18]。集电线往往由架空线、电缆混合构成,但电缆很短,长则几百米,短则十几米。同时,与风机相连的箱式变压器(简称箱变)高压侧采用三角形联结以限制谐波与零序电流的流入[2,19],满足风电场安全性及风机性能指标,目前风电场广泛采用中性点经电阻接地的接地方式[2],通过主变压器(简称主变)或接地变压器(简称接地变)实现接地。另外,某些集电线可能含有分支,但是分支数目要远少于配电网,分支拓扑也更为简单,典型含分支的集电线如图1集电线2。

图1 风电场拓扑结构
Fig.1 Topology of wind farms
电力系统中单相接地故障占绝大多数[20],本文只针对单相接地进行定位。由于电缆短路故障往往为三相故障,且风电场中电缆很短,因此单相接地故障定位仅针对架空线即可。为实现集电线尤其是含分支集电线的故障定位,本文在故障集电线跳闸后首先判断出故障区域,图1含分支集电线可分为干线(蓝色部分)、分支1(橙色部分)、分支2(绿色部分)共三个区域;之后再针对故障区域进行故障测距。对于不含分支的集电线,直接测距即可。
现有可跨越风机测距的方案[2,18]应用于含分支集电线时会出现伪故障点,原因在于其只利用了干线首端测点的电压电流信息,而不同区域的故障可能在干线首端产生相同电压电流。因此本文在测距前先行判断故障区域以排除伪故障点。然而,由上述分析也可知,仅依靠干线首端电压电流测点不能实现故障区域的判断。
实际上,当干线首端故障信息相同时,其他位置会存在差异化信息,因此本文适当增加测点,通过多点信息融合进行信息互补来识别不同区域的故障。考虑到在集电线末端风机箱变处安装测点相较集电线中间段在工程实现上更方便,且新增测点少,同时契合后续故障测距量测需求,本文在干线首端测点的基础上只在干线与各分支末端增加测点。随着测量技术的发展,即使是在线路上安装的同步相量测量装置目前也已被研制[21],所以上述测点配置的硬件需求能得到满足,且实现成本不高。
风机不同于传统电源,其故障特性特殊[22-23],且集电线为密集风电源接入结构,所接电源数目远多于配电网;同时,新增测点位于线路末端,相比于线路中部的测点可获取的故障信息有限,所以直接建立各测点所测电气量与故障区域的解析关系十分不易。因此,本文借助深度学习强大的数据挖掘、特征提取与“端到端”模型构建能力,增强多点信息融合深度,充分挖掘可获取量所含故障信息,无需建立解析关系即能实现故障区域判断。
图神经网络是一种新兴深度网络,以其优秀的图数据处理能力备受青睐,目前已被应用在机械、电气设备故障诊断等领域[24-25]。该网络的处理对象是图,图由节点及连接节点的边构成,其中边表征节点间的连接关系,节点与边都可以拥有自己的属性。相较一般图像,图不仅能表征属性信息,还能表征各节点之间的连接关系即结构信息。
对于风电场故障区域判断来讲,一方面风电场中含分支集电线属于树状辐射型网,是一个天然的图结构;另一方面,采用图的表征方式在使电气量属性信息得以利用的同时,可以借助图的结构信息,通过节点间的消息传递充分挖掘各处电气量信息之间的依赖关系,这一特点与本文所采用的多点信息融合思想非常契合,能够有效加深多点信息之间的融合度,反映更丰富的故障特征。所以,本文将故障区域判断建模成图分类问题,应用作为图神经网络之一的图卷积神经网络(Graph Convolutional Network, GCN)实现故障区域判断。目前关于GCN在风电场集电线故障定位方面的研究尚未见报道。
2.1.1 图卷积神经网络
GCN的核心是图卷积层,图卷积层可使图节点对自身特征与邻居节点特征进行聚合生成新的节点。一般图卷积层表示为
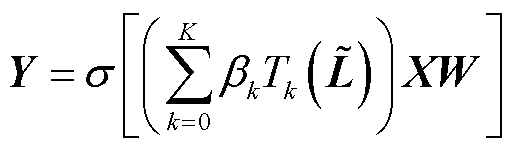 (1)
(1)
式中,X、Y分别为输入、输出节点特征矩阵;W为对X进行仿射变换的一个参数化权重矩阵,可以加强网络拟合能力;σ[·]为激活函数;Tk(·)为k阶Chebyshev多项式;βk为对应Chebyshev系数;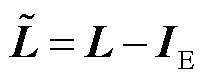 ,L为拉普拉斯矩阵,IE为单位矩阵;K为所选Chebyshev多项式的最大阶数,一般取1~3即可满足拟合精度,本文取K=2。
,L为拉普拉斯矩阵,IE为单位矩阵;K为所选Chebyshev多项式的最大阶数,一般取1~3即可满足拟合精度,本文取K=2。
2.1.2 图池化
本文的故障区域判断为图分类问题,因此需要采用图池化机制对图卷积层学习到的节点特征进行全局融合,生成图表示特征。本文应用文献[26]提出的自注意力池化层参与实现全局信息提取。
自注意力池化层能充分利用图结构信息,同时有着合理的时间、空间复杂度,其首先通过图卷积按照式(2)自适应学习节点重要度(式(2)实际上是令式(1)的K为1,β1、β0分别为-1、1所得);然后按照TopK机制只保留前kN个节点(k为池化率(0≤k≤1),N为节点总数),更新图的结构。
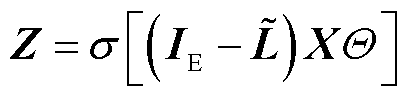 (2)
(2)
式中,Z为节点重要度矩阵;Θ为自注意力池化层的权重系数。
2.2.1 图的构建
节点与边是图的两大要素,为了应用图数据处理方法解决故障区域判断问题,需要对节点、边的物理意义进行规定,构建图数据。
本文中干线首端测点需测量三相电压电流相量,其余测点测量三相电压相量。规定每个测点为一个节点,并取干线首端节点的属性信息为三相电压电流及正、负零序电压电流的有效值,其他节点为三相电压及正、负零序电压的有效值,这样可有效地消除相量不同步的影响。节点属性即为故障特征量。
由于本文并没有在分支与干线的连接点处配置测点,因此节点之间的边不能直接根据集电线的路径定义。为此,本文引入“投影”的概念,也就是将分支末端的测点等效地沿分支向干线移动直至到达干线。投影时最终所到达的位置即为该测点在干线上的投影点。投影后,按照干线的路径容易得到分支末端测点的投影点与干线首末端测点之间的连接关系,以此作为实际测点间的连接关系来确定节点间的边,得到表征边的邻接矩阵。图1所示含分支集电线的投影过程及结果如图2所示。
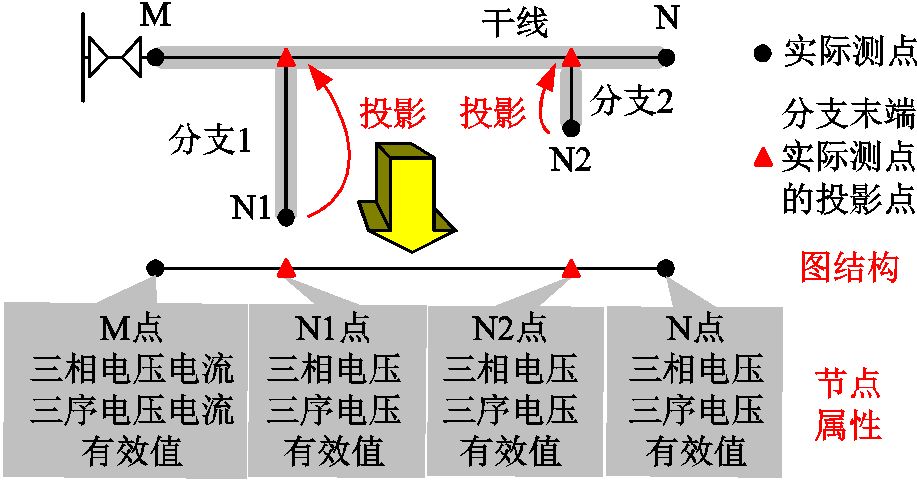
图2 图的构建
Fig.2 Construction of the graph
2.2.2 基模型的构建
在图卷积层、自注意力池化层的基础上,采用图3所示网络结构作为故障区域判断的基模型,模型输入为2.2.1节所得图数据,输出为故障区域类别。
自注意力池化层可以对节点特征进行融合,但还未彻底生成图表示特征,因此添加读出层,采用最大值池化与均值池化对图池化层得到的新图进行一次性聚合,输出表征整图属性的图表示特征。然后输入全连接层构成的多层感知机完成图分类。
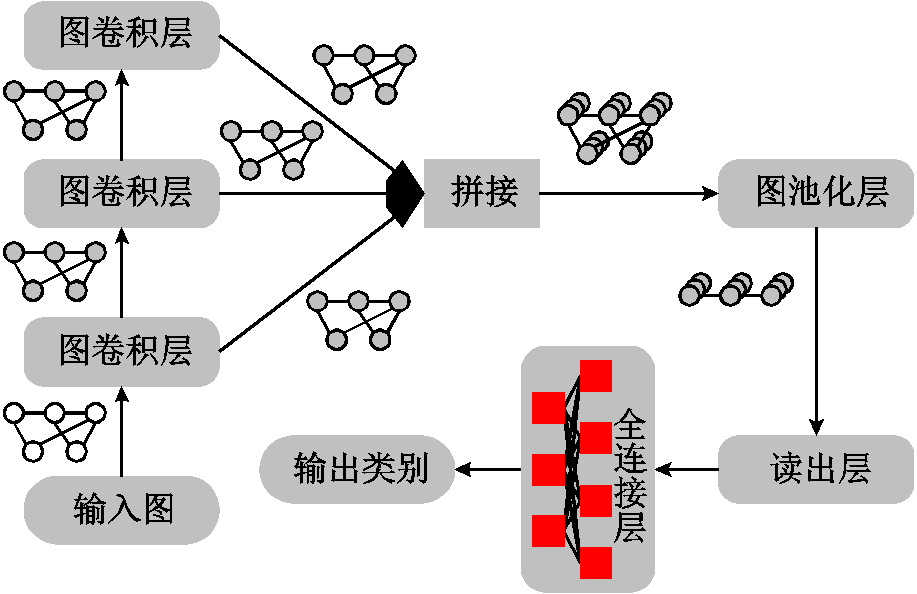
图3 基模型结构
Fig.3 Structure of the base model
由工程实际可知,有时风电场会存在集电线干线远长于分支的情况,这就会导致在样本分布相近的情况下干线故障样本远多于各类分支故障样本,从而出现样本不平衡问题。若直接使用原始样本集(即样本集中每个故障区域单独作为一个类别),并单纯采用基模型构建故障区域判断模型,会导致模型存在很大的偏向性,分类结果会偏向于样本数目更多的类别。为解决该问题,本文一方面重构原始样本集,进行模型串联,另一方面引入代价敏感学习,使用代价矩阵对分类结果进行调整。
2.3.1 串联分类模型的构建
尽管一条分支的故障样本相对于干线来讲数量差距较大,但若将所有分支的故障样本整合为分支故障这一类,就可以在一定程度上减轻样本不平衡。并且,不同分支都属于集电线的分支部分,存在共同特征,如,对于各分支末端节点的投影点,干线首末端节点总是分别位于其上游、下游;不同于干线故障,各分支故障时,干线末端节点总不是零序电压最大的节点。因此,将各分支的故障样本归为一类是合理的。基于上述思想构成分支故障样本集,使其与干线故障样本集一起进行分支故障、干线故障二分类,得到初级分类器。
之后,仅使用分支故障样本集,将分支1故障~分支n故障(n为一条集电线上分支的总数)各作为一类,形成次级分类器。次级分类器的构建是基于分支之间的差异性,如不同分支末端的节点到其他节点的路径不同、不同分支故障时各节点之间负序、零序电压的大小关系不同。上述两级分类器均采用基模型网络结构,二者构成串联分类模型,共同完成故障区域的最终判断。
相对于其他深度网络,GCN的样本需求量相对较少,更能适应样本规模较少的情况[25],但是在建立次级分类器时,由于分支较短,故障样本数目过于有限,GCN仍然容易出现过拟合、模型性能不佳等问题。因此,本文进一步引入迁移学习。迁移学习是指将在源域上学习到的知识应用到另一相似领域即目标域中的机器学习方法[27],其可以解决目标域中样本不足所导致的无法有效建模问题。
本文借助迁移学习使用训练完成的初级分类器辅助后续次级分类器的构建。因为两个分类器任务性质相近,所以采用迁移学习能够使次级分类器在小样本下取得很好的效果。本文此处应用的是模型微调形式的迁移学习,即首先建立次级分类器的结构,除输出层外其余部分均与初级分类器结构相同;然后,以初级分类器训练所得参数初始化次级分类器(不含输出层),并采用分支故障样本进行训练,调整次级分类器的全局参数。
2.3.2 代价敏感学习
经过上述处理,样本不平衡可以得到一定程度的解决,但是当所有分支的长度之和与干线相比还是相差较大或各分支之间长度相差较大时,初级或次级分类器还会存在一定偏向性。因此进一步引入代价敏感学习,利用代价矩阵纠正模型的偏向性。
代价敏感学习是指在机器学习中,为不同类别赋予不同误分类代价,主要用于不同类别误分后果严重性不同的分类问题[28-29]。当认为少数类的误分后果比多数类更严重时,就可使用代价敏感学习解决C样本不平衡问题。代价敏感学习的核心是代价矩阵,以二分类为例的代价矩阵C见表1。表中,1与0分别表示正、负类,C(i, j)为类别i的实例被误分为类别j的代价(i, j=0, 1),一般可令对角线元素为0,只设置非对角线元素以简化矩阵。
表1 二分类问题的代价矩阵
Tab.1 Cost matrix of binary classification

预测类别为正类预测类别为负类 真实类别为正类C(1,1)C(1,0) 真实类别为负类C(0,1)C(0,0)
本文采用后处理形式的代价敏感学习,其基于贝叶斯风险理论对训练完成后的分类模型进行分类结果的后处理[29]。首先应用前文建立的图神经网络得到输入样本对应的类别概率,然后结合代价矩阵通过式(3)确定最终分类类别。
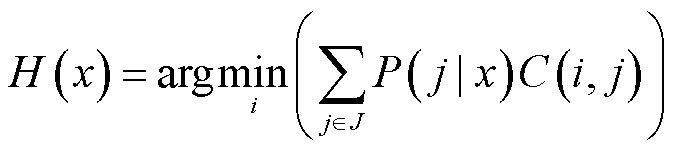 (3)
(3)
式中,x为输入样本;H(x)为x的输出类别;J为所有类别构成的集合;P(j|x)为x属于类别j的后验概率;argmin表示取最小值对应的类别。式(3)的含义在于计及各类别误分类代价后选择总误分类代价最小的分类结果作为最终类别。
2.3.3 故障区域判断模型的建立
模型串联与代价敏感学习实质上是分别从样本集角度、分类结果后处理角度应对样本不平衡问题。前者相对来讲更为本质,后者容易损失多数类的正确率。因此当干线、分支故障样本数量相差较大时,应先进行模型串联,若串联后模型仍有较大偏向性,再考虑在某一级或两级模型中引入代价敏感学习。当干线、各分支故障样本数量相近时,直接使用基模型即可。为了保持方案的完整性,后文所述方案均进行模型串联,并在两级模型中均引入代价敏感学习。综上所述,可得故障区域判断模型的训练、测试与应用流程如图4所示。
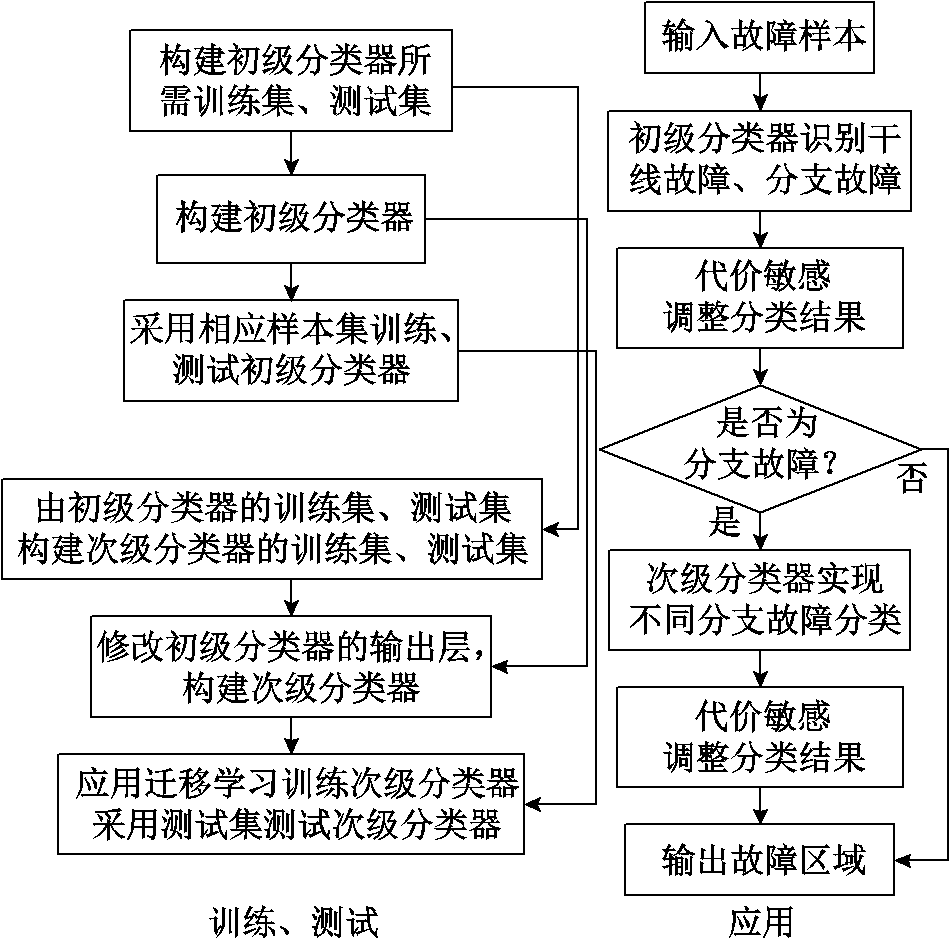
图4 模型训练、测试与应用流程
Fig.4 Flow chart of training, testing and application of the model
1)获取测点量测信息,形成节点属性;对实际集电线拓扑进行投影操作,形成邻接矩阵。
2)构建初级分类器所需样本集,并对该样本集进行训练集、测试集划分。在划分时,首先按照干线故障、分支1~分支n故障共n+1类进行分层划分;然后,分别将所得训练集、测试集中各类分支故障样本整合为分支故障一个类别。
3)由步骤2)所得训练集、测试集中的分支故障样本分别构成次级分类器所需的训练集、测试集。由于步骤2)进行了n+1层的分层划分,本步骤所得样本集相当于进行了n层的划分。
4)搭建初级分类器,首先设置隐含层神经元数目、迭代次数、求解器、初始学习率、学习率衰减系数、代价矩阵等超参数;然后进行训练、测试。
5)搭建次级分类器,首先设置输出层神经元数目、迭代次数、求解器、初始学习率、学习率衰减系数、代价矩阵等超参数;然后以初级分类器训练所得参数初始化次级分类器,并进行训练、测试。
6)实际应用时,用初级分类器(含代价敏感后处理)进行干线故障、分支故障识别;若判断为分支故障,则将故障样本进一步输入次级分类器(含代价敏感后处理),得到具体故障区域。
如前所述,风机故障特性复杂,但风机箱变高压侧采用三角形联结使风机并不参与构建风电场零序网络。因此利用零序分量测距无需考虑风机影响,有独特优势。另外,当前风电场广泛采用中性点经电阻接地,在出现单相接地时此类系统零序电流较大[30],远大于中性点不接地系统[2],因此零序特征较为明显,可安装零序电流保护切除故障[30-31],并且目前在风电场中已有研究成功地实现了基于零序电流的故障检测[32]。由此可见,利用零序分量进行风电场故障测距既有独特优势,又切实可行。
由于线路对地电容会给零序分量带来一定影响,因此为提高故障测距的准确性,也将对地电容考虑在内。具体考虑方式为,将故障集电线的总对地电容各取二分之一等效在干线首端、故障区域末端。假设图1所示风电场的f点出现单相接地故障,可得相应零序网络如图5。图1虚线框内为f点故障时参与零序网络构成的故障集电线范围,即故障区域末端至干线首端的集电线。
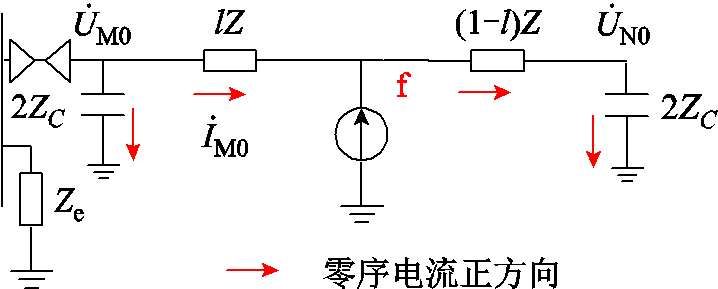
图5 集电线单相接地时风电场零序网络
Fig.5 Zero-sequence network of the wind farm with single-phase-to-ground faults on collecting lines
图5中,f为故障点;Ze为故障集电线以外部分的等效零序阻抗:ZC为故障集电线的总对地电容对应阻抗;Z为故障集电线上故障区域末端到干线首端的线路阻抗;l为故障距离比,即故障点至干线首端的距离(故障距离)与故障区域末端至干线首端的距离之比,有0≤l≤1;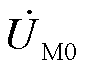 、
、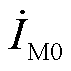 分别为干线首端零序电压、零序电流;
分别为干线首端零序电压、零序电流;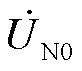 为故障区域末端零序电压。
为故障区域末端零序电压。
根据图5,采用干线首端或故障区域末端电气量均可计算出故障点零序电压,并且两者所得故障点零序电压相等,由此可得
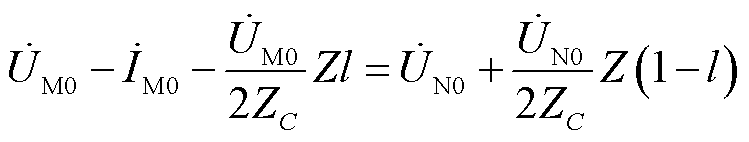 (4)
(4)
为避免测距准确性受到数据不同步的影响,对式(4)等号两边同时取模值二次方,可得
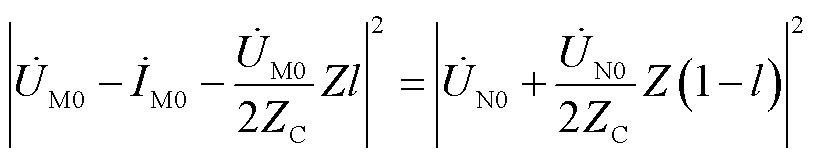 (5)
(5)
对式(5)进行整理可得
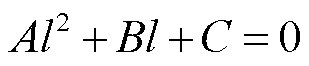 (6)
(6)
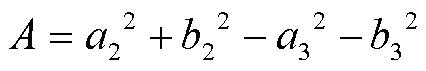 (7)
(7)
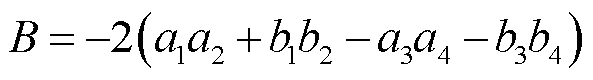 (8)
(8)
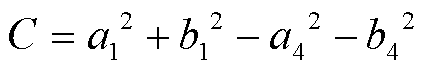 (9)
(9)
 (10)
(10)
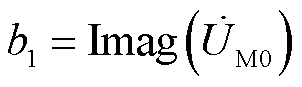 (11)
(11)
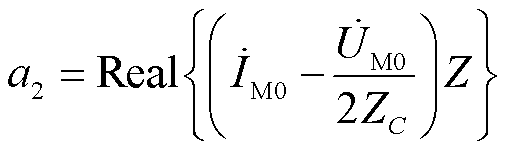 (12)
(12)
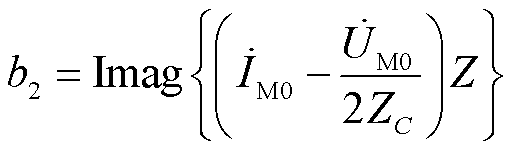 (13)
(13)
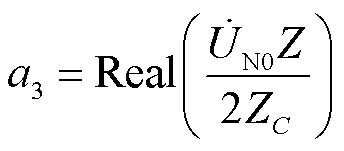 (14)
(14)
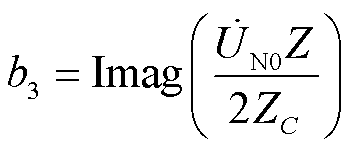 (15)
(15)
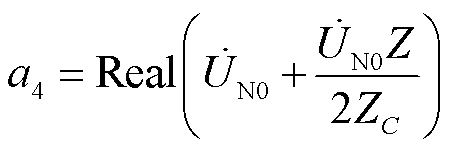 (16)
(16)
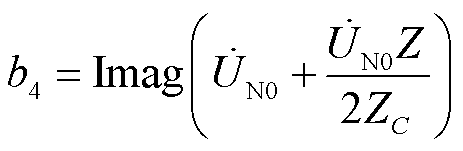 (17)
(17)
式中,Real、Imag分别表示取相量的实部、虚部。式(6)为实系数一元二次方程,采用解析法可解得两个实数解,结合l的大小限制,就能获得符合实际的l值,完成故障区域的故障测距。
由于测距误差的存在,对于靠近故障区域首末端的一些故障,所得测距结果可能会超出故障区域的实际范围。本文定义故障区域首端到干线首端的线路长度至故障区域末端到干线首端的线路长度为故障区域的准确测距范围;并将准确测距范围的下限减m、上限加m,得到故障区域的有效测距范围。当测距结果位于上述两测距范围的下限(上限)之间时,表明实际故障点位于故障区域首端(末端)附近。根据后文仿真结果,再计及实际存在的线路参数误差、测量误差等,可取m=150 m。
为尽可能减小线路参数与相量计算误差,可通过现场实测获取线路参数实际值;同时可采用罗氏线圈电流互感器测量电流,误差能控制在1%左右。
前文故障区域判断模型在绝大多数情况下能够保证判断的准确性,但是对于区域分界点即干线-分支连接点附近的故障来讲,由于它们所产生的故障信息差异较小,可能出现故障区域误判。为此,本文进一步设计了故障区域误判处理机制。
若故障区域判断结果为干线故障,且故障测距后现场人员并未在计算所得故障位置(称作原始故障位置)及其附近查找到故障,则表明实际故障区域为某一分支。此时对所有分支按照其与原始故障位置的距离(该距离是指分支与干线的连接点到原始故障位置的距离)进行升序排序;依序假设故障点位于某分支上进行测距,并检查测距结果的有效性,即检查测距结果是否位于相应分支的有效测距范围内;若测距结果有效且现场人员由测距结果能够查找到故障点,则定位结束,反之重新假设故障位于下一分支,重复以上步骤,直到获得有效测距结果且能够查找到故障点。
若故障区域判断结果为某分支故障,且故障测距后测距结果无效,或测距结果有效但是现场人员未能在判断所得分支(称作原始分支)上查找到故障,则表明实际故障区域为干线或其他某分支。首先假设干线故障进行测距,若在干线上能查找到故障点,则定位结束;否则,对原始分支以外的分支按照其与原始分支的距离(该距离是指其余分支与干线的连接点到原始分支与干线的连接点的距离)进行升序排序。依序假设故障点位于某分支进行测距,并检查测距结果的有效性。若测距结果有效且现场人员按照测距结果能够查找到故障点,则定位结束;反之重新假设下一分支故障。重复以上步骤,直到获得有效测距结果且可以查找到故障点。
使用PSCAD/EMTDC参照某实际风电场结构搭建如图6所示的仿真模型。
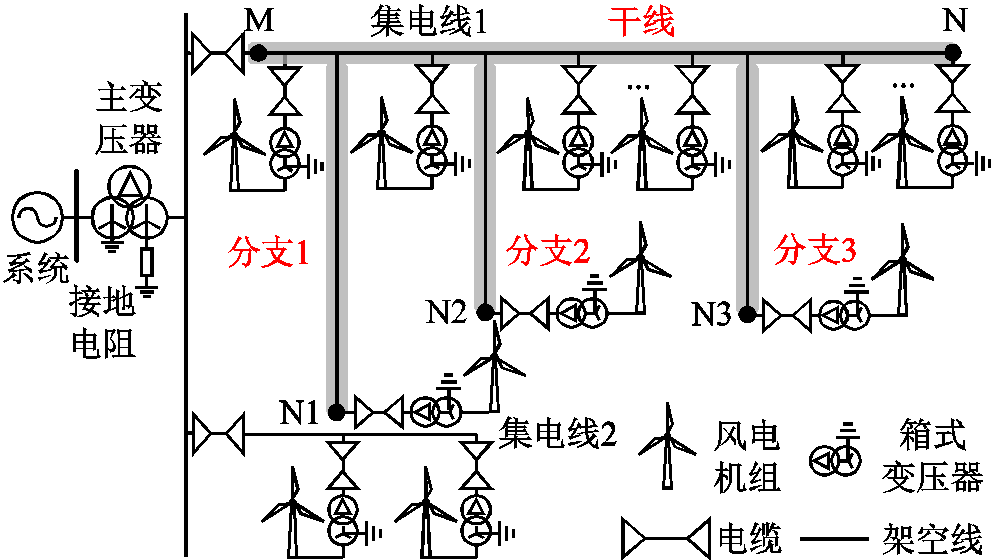
图6 风电场仿真模型
Fig.6 Simulation model of wind farm
本文以图6所示集电线1为研究对象,构建其对应图数据时所得投影结果如图7所示。图6中,主变压器额定电压为220 kV/35 kV/10.5 kV,在中压侧经67.3 Ω电阻接地。集电线1前端通过400 m电缆接入升压站,其上连接有11台双馈风机,均经箱变、100 m电缆与架空线相连接。每台风机额定功率为2 MW,额定风速为11 m/s,端电压为0.69 kV。集电线1采用LGJ 120/25型号架空线,其含有三条分支,线路参数及干线、各分支的长度分别见表2、表3。
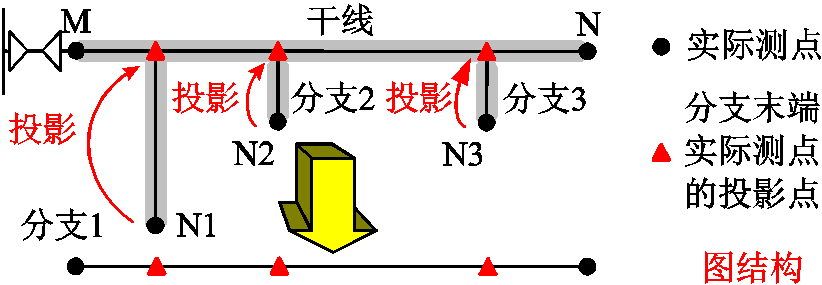
图7 仿真模型对应投影结果
Fig.7 Projection results of the simulation model
表2 架空线参数
Tab.2 Parameter of the over-head line

参数数值 正/负序零序 电阻/(Ω/km)0.2630.447 1 电感/(H/km)0.001 250.003 74 电容/(F/km)1×10-112.14×10-11
表3 架空线长度
Tab.3 Length of the over-head line

区域长度/m 干线9533.37 分支1800 分支2300.23 分支3214.15
5.1.1 样本集的形成与模型超参数设置
图6所示集电线1包含干线、分支1~3共四个区域。建立故障区域判断样本集时,各故障样本的图结构相同,所含节点的属性取值不同。本文在集电线上每隔100 m左右设置一个故障点,并且每个故障点设置0、50、100、150、200 Ω的过渡电阻,同时为尽可能地反映风电场实际运行状况,又设置了额定风速、低风速运行场景,对应风速分别为11、7.5 m/s,最终得到包含1 040组样本的样本集。上述样本集只包含A相接地故障,对于B或C相接地,可通过转相等效为A相接地。对所得样本集按照4:1的比例划分得到训练集、测试集。
在上述样本集中,干线故障与分支故障样本数之比为7:1,分支故障中分支1~3的故障样本数之比为8:3:2。由此可知,各类故障之间存在明显样本不平衡,且干线、分支故障之间的不平衡也较严重,各分支之间的不平衡较弱,同时考虑到各分支并不直接相连,可分性强,因此在模型串联的基础上进一步只针对初级分类器使用代价敏感学习即可,后文准确的分类结果可验证该处理方式的合理性。
5.1.2 判断效果与分析
GCN模型不宜过深[25],考虑到模型层数较少时更易训练、样本需求更少,本文构建初级与次级分类器时均设置2层图卷积层、1层图池化层,且图池化层池化比例为0.5。模型训练时,采用Adam优化器,并应用分段学习率衰减,学习率衰减比例为0.5,同时为防止模型过拟合,引入dropout机制与Adam的权重衰减进行正则化处理,dropout比例为一般取值0.5。初级分类器其他超参数取值如下:各图卷积层神经元数目为64,优化器初始学习率为0.005,权重衰减系数为0.000 1,代价矩阵为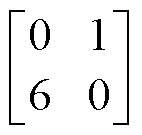 。
。
次级分类器其他超参数取值如下:优化器初始学习率为0.005,权重衰减系数为0.000 1。
采用五折交叉验证分析初级分类器与次级分类器的分类性能,所得各级分类器五条训练集损失曲线的平均值曲线如图8所示,初级分类器各折测试集的分类结果如图9所示。另外得到次级分类器各折测试集中各类别的分类正确率均为100%。
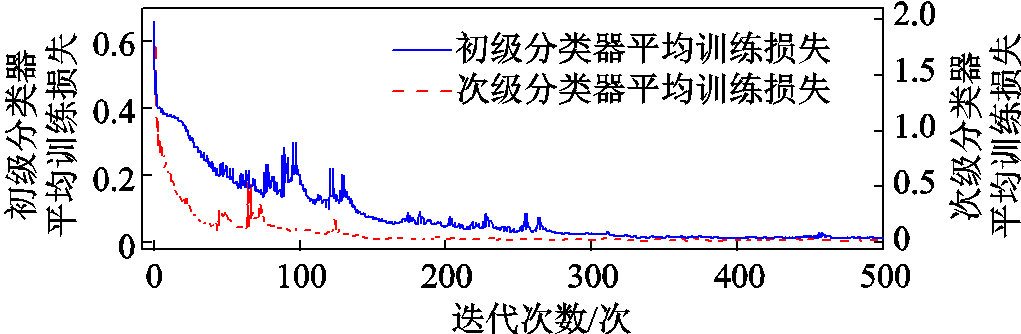
图8 分类器训练集损失曲线
Fig.8 Classifier loss curve of the train set
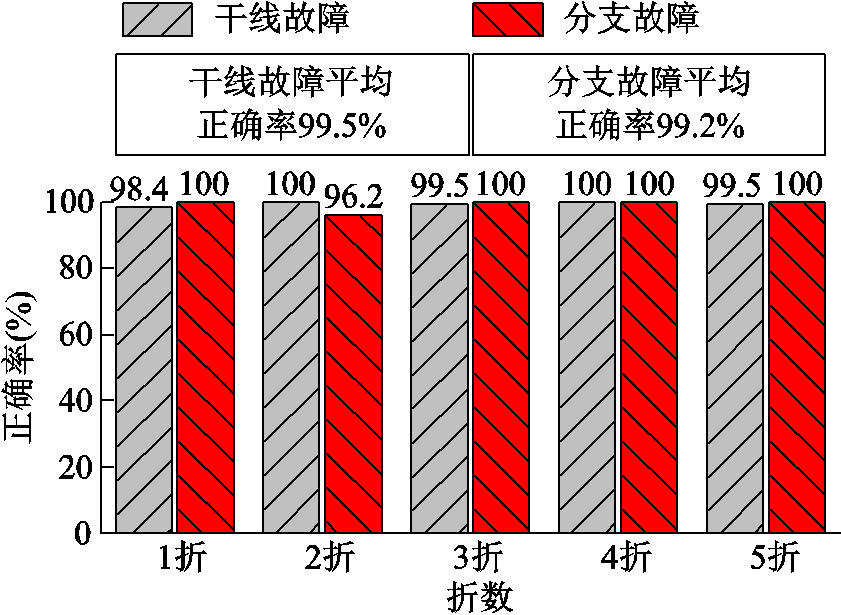
图9 初级分类器的测试集分类结果
Fig.9 Test-set classification result of the primary classifier
由图8可以看到,各级分类器在训练时都能较好地收敛,模型性能不断提升。由图9以及次级分类器的分类正确率可知,所得故障区域判断模型较为准确,干线故障、分支故障的平均正确率都接近100%,判断效果不受样本不平衡的影响。这表明所提方法能够作为一种有效的故障区域判断方法。进一步,分析初级分类器各折测试集误分的故障样本可知,所有出现误判的故障均是干线、分支上最靠近干线-分支连接点的故障。这些故障位于干线、分支的分界点周围,故障特征十分相近,因此出现误判。但是,这些误判在第4节所提误判处理机制的辅助下都会得到纠正,最终仍能准确定位故障。另外,针对不平衡样本下的分类器,灵敏度(Sensitive)、特效度(Specificity)、AUC(area under curve)值能够较好地对其性能做出评价,上述灵敏度与特效度即本文各类故障的正确率。进一步计算各折所得模型的AUC值,其中最大值为1,最小为0.99,可见所提模型拥有较好的分类性能。
前文形成的训练集、测试集含有不同故障位置、过渡电阻、风速下的故障样本,因此本文所构建的故障区域判断模型针对不同故障位置、过渡电阻、风速下的故障都是有效的,上述测试集准确的分类结果验证了此有效性。另外,由于模型所需输入量仅为电压电流有效值,因此故障区域判断效果不被数据不同步影响。
5.1.3 与单一分类模型的对比
为了验证模型串联对解决样本不平衡问题的有效性,在不引入代价敏感学习的情况下,对比单一分类模型与串联分类模型的分类正确率。单一分类模型直接采用基模型,一次性实现干线与各分支的分类。使用相同的训练集、测试集对其进行参数选择、训练与测试,所得分类结果如图10所示。计算两模型的干线故障总平均正确率(等于干线故障平均正确率)、分支故障总平均正确率(即所有分支平均正确率的平均值),所得结果见表4。
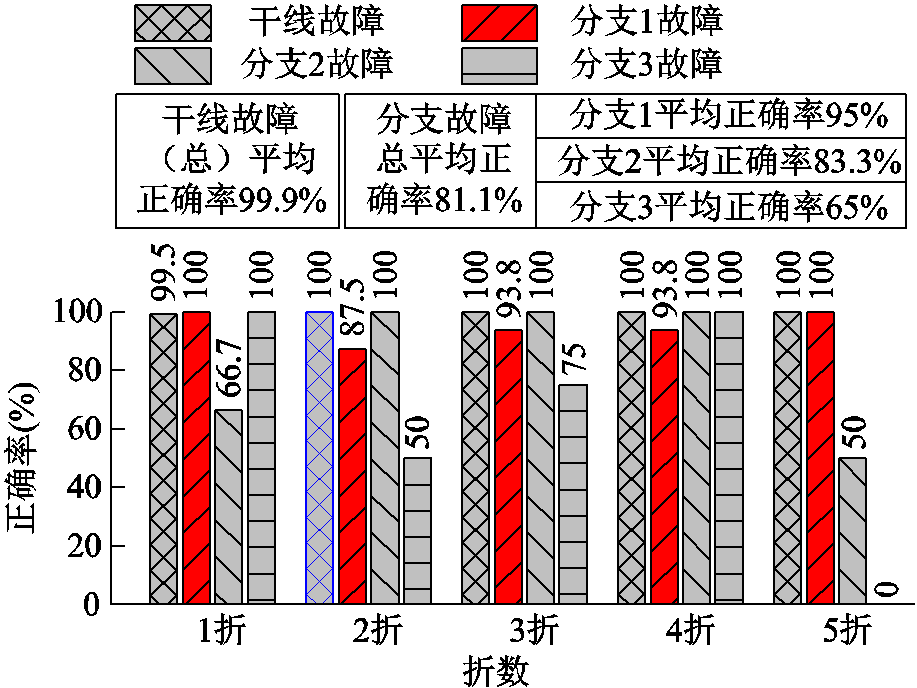
图10 单一分类模型的测试集分类结果
Fig.10 Test-set classification result of the single classification model
表4 总平均正确率对比
Tab.4 Comparison of the total average accuracy

模型干线故障总平均正确率(%)分支故障总平均正确率(%) 单一分类模型99.981.1 串联分类模型10093.1
由图10可知,由于各类样本数量不平衡,仅使用单一分类模型时,多数类的正确率高,少数类的正确率低,分支1~3的平均正确率分别只有95%、83.3%、65%,最终干线故障总平均正确率为99.9%,而分支故障总平均正确率仅为81.1%。由表4对比可知,通过样本整合、模型串联,分支故障总平均正确率提升了12%。因此可以看出,存在样本不平衡时,仅建立单一分类模型并不能获得满意的分类效果,而模型串联能够有效提升分支故障分类正确率,起到了缓解样本不平衡的作用。
5.1.4 与不含代价敏感学习的对比
模型串联能够在一定程度上缓解样本不平衡,但是由于分支总长与干线长度仍存在较大差距,不加处理时,由表4可知,干线、分支故障总平均正确率分别为100%、93.1%,依然存在一定偏向性。
当引入代价敏感学习对分类结果进行调整时,由图9可知,初级分类器的干线故障、分支故障平均正确率分别为99.5%、99.2%,计及100%的次级分类器分类正确率,可知分支故障总平均正确率为99.2%。比较可得,在代价敏感学习的干预下,干线故障总平均正确率下降0.5%,但是分支故障总平均正确率提升了6.1%。由此可见,在模型串联的基础上进一步应用代价敏感学习,能够很好地克服样本不平衡的影响。
5.1.5 与传统深度神经网络的对比
为对比GCN与传统深度神经网络的性能,搭建全连接层构成的传统深度神经网络(Deep Neural Network, DNN)。构建DNN的样本集时,将各测点所获电压电流有效值整合为一个特征向量。DNN所用训练集、测试集包含的故障场景都与GCN一致。另外,同样使用DNN搭建串联分类模型,并引入代价敏感学习。五折交叉验证时DNN初级分类器的各折测试集分类正确率如图11所示;另外,DNN次级分类器的各折测试集分类正确率都为100%。
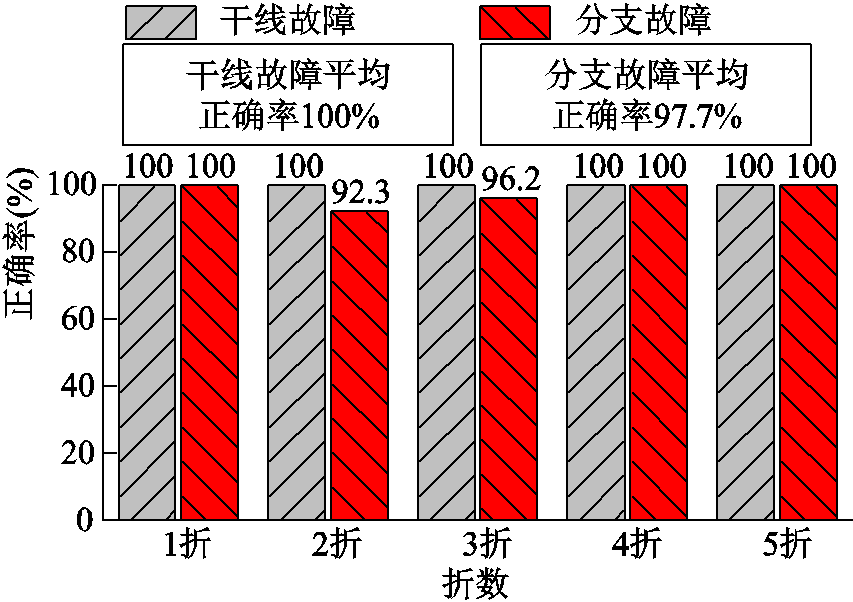
图11 DNN初级分类器的测试集分类结果
Fig.11 Test-set classification result of the DNN-based primary classifier
与5.1.2节GCN的分类结果比较可得,虽然两种网络的次级分类器分类正确率都为100%,但是对于图9与图11所示的初级分类器分类结果,在两种网络干线故障平均正确率相当的情况下,GCN的分支故障平均正确率更高,接近100%,DNN在第二折的分支故障正确率仅为92.3%。另外,各折所得DNN模型的AUC值中,最大值为1,最小为0.97,而前文所述本文模型的最小AUC值为0.99。因此从整体来看,GCN效果更佳。这主要得益于GCN计及风电场拓扑结构,利用了更丰富的故障信息,使得干线、分支故障的可分性更好。
5.2.1 不同故障位置下的故障测距
在图6所示集电线1的不同位置设置A相接地故障,过渡电阻均为0 Ω,风机均运行在额定工况下。所提测距方法的测距结果见表5。
由表5可知,以上故障位置的测距误差均小于70 m,这表明针对不同位置的单相接地,本文都能准确实现故障测距。还可以看到,相对于干线故障,分支故障的测距误差稍大,其主要与第3节所采用的电容等效方式有关。当分支故障时,故障区域末端即为故障分支末端,干线-故障分支连接点至干线末端之间的线路为主要的旁支线路(即不位于干线首端与故障区域末端之间的线路)。由于故障分支较短,因此相比于干线首端,主要旁支线路更靠近故障区域末端,且该部分线路较长,对地电容较大,所以两端均分电容的等效误差稍大,增大了测距误差。相比之下,干线故障时,故障区域末端为干线末端,旁支线路为各分支,而各分支都较短,此时电容等效误差较小,因此测距误差更小。
表5 不同故障位置下的测距结果
Tab.5 Localization result under different fault locations

故障区域实际故障距离/m所得故障距离/m测距误差/m 干线9091.841.84 4418.344418.830.49 7290.037289.55-0.48 分支12833.872873.0839.21 分支22853.752918.8365.08 分支37054.187113.9359.75
5.2.2 不同过渡电阻下的故障测距
额定风速下,分别在干线、分支2上各选一个故障位置设置A相接地,各故障点处均设置0、50、150、200 Ω的过渡电阻,所得结果见表6。
表6 不同过渡电阻下的测距结果
Tab.6 Localization result under different values of fault resistance
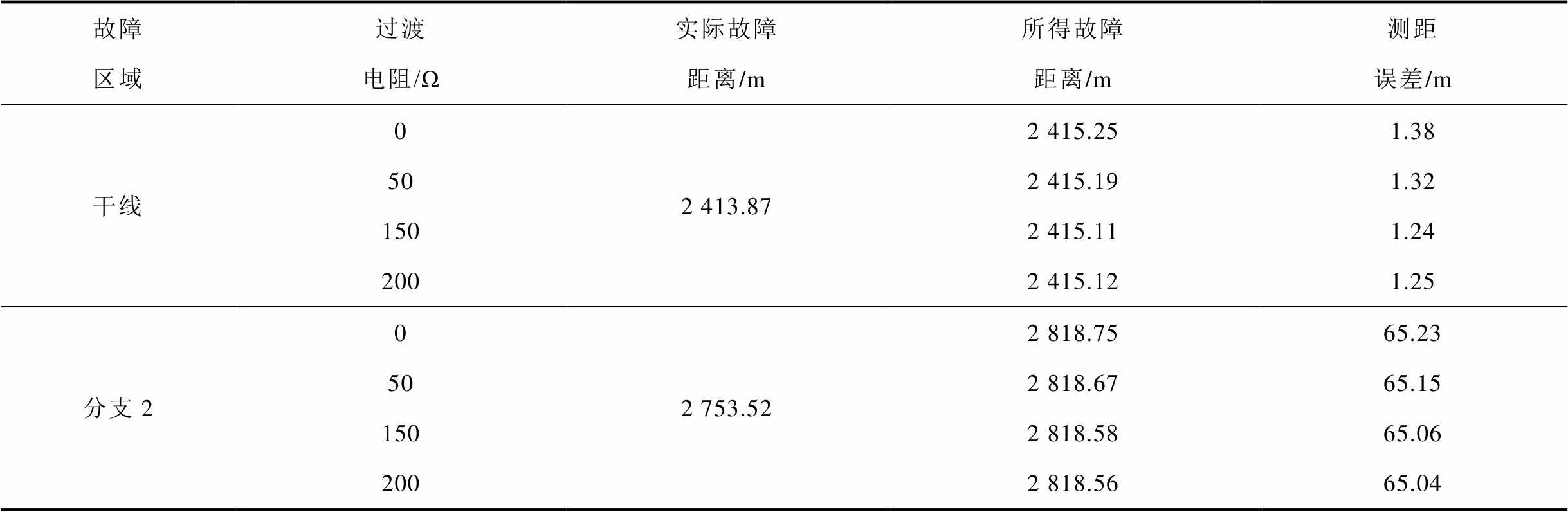
故障区域过渡电阻/Ω实际故障距离/m所得故障距离/m测距误差/m 干线02413.872415.251.38 502415.191.32 1502415.111.24 2002415.121.25 分支202753.522818.7565.23 502818.6765.15 1502818.5865.06 2002818.5665.04
由表6可知,测距误差随着过渡电阻的变化并没有出现较大波动,都维持在较低数值,这表明本文所提测距方法的性能不被过渡电阻影响。这主要是因为本文测距方法基于双端量构建,在测距公式中消除了过渡电阻。
5.2.3 不同风速下的故障测距
风速不同、风机的输出功率不同,有可能会对测距性能造成影响。因此分别设置7.5 m/s与11 m/s的风速,在干线、分支2上模拟过渡电阻为0 Ω的A相接地。所得测距结果见表7。
表7 不同风速下的测距结果
Tab.7 Localization results under different values of wind speed

故障区域风速/ (m/s)实际故障距离/m所得故障距离/m测距误差/m 干线7.52413.872416.082.21 112415.251.38 分支27.52753.522819.6666.14 112818.7565.23
由表7可知,两故障点在额定风速及低风速下测距误差都较为接近且数值较小。这表明风速并不会对所提测距方法的性能造成影响。其原因在于本文测距公式采用零序分量推导,零序电压电流的大小取决于故障时的零序网络,而风机并不参与零序网络的构成,因此测距效果与风机运行状况无关。
5.2.4 数据不同步状况下的故障测距
在干线、分支2上模拟额定风速下过渡电阻为0 Ω的A相接地,并以干线首端测点为参考,在干线末端、分支2末端测点所得数据中加入2°、10°、50°、90°的不同步角。所得测距结果见表8。
表8 数据不同步下的测距结果
Tab.8 Localization result with asynchronous data

故障区域不同步角/(°)实际故障距离/m所得故障距离/m测距误差/m 干线22413.872415.251.38 102413.872415.251.38 502413.872415.251.38 902413.872415.251.38 分支222753.522818.7565.23 102753.522818.7565.23 502753.522818.7565.23 902753.522818.7565.23
由表8可知,对于不同大小的不同步角,干线、分支故障的测距误差都一直保持恒定,测距结果均没有被影响。因此可知,数据不同步不会对本文测距方法造成不利影响。这得益于本文测距公式由相量模值相等原则建立,能较好地消除不同步角的影响。
5.2.5 测距方法对比
本文测距方法属于阻抗法测距,因此与文献[2]所提方法进行对比。在干线上共设置两处A相接地,故障距离分别为9 074.37 m、9 434.37 m,风速均为额定风速,过渡电阻为0 Ω。所得测距误差如图12所示。
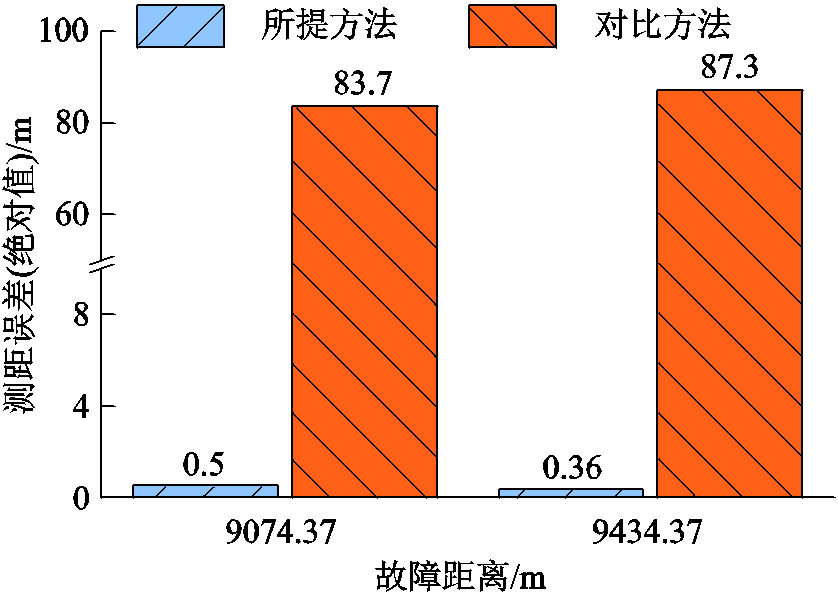
图12 测距误差对比
Fig.12 Comparison of the localization error
由图12可知,对于上述故障,虽然两种方法的测距误差都在100 m以内,但是相比较而言,本文所提测距方法的准确性高于文献[2]。因为本文方法基于风电场零序分量构建,能够天然地将风机影响排除在外,所以测距准确性较高;文献[2]虽然引入假设,较好地估计了风机电流,但是与实际仍存在一定误差,降低了测距准确性。
为验证本文误判处理机制的有效性,分别假设某分支2故障误判为干线故障、某干线故障误判为分支2故障、某分支1故障误判为分支2故障,应用所提处理机制进行处理,所得结果见表9。以上各故障场景下故障类型均为A相接地,过渡电阻均为0 Ω,风速均为额定值。由于图6中集电线1共有四个区域,因此最多只需重新测距3次。
表9 故障区域误判处理结果
Tab.9 Result of the misidentification processing mechanism of faulty area

实际故障区域实际故障距离/m所得故障区域所得故障距离/m重新测距1所得故障距离/m重新测距2所得故障距离/m重新测距3所得故障距离/m最终测距误差/m 分支22753.52干线2554.84\2818.75(分支2)√——65.23 干线4418.34分支22619.12\4418.83(干线)√——0.49 分支12533.87分支22100.03\\2035.36(干线)\2573.28(分支1)√—39.41
注:表中括号内为重新测距时的假设故障区域;\\表示所得故障距离不在对应故障区域的有效测距范围内;\表示所得故障距离在对应故障区域的有效测距范围内,但在对应故障区域上查找不到故障点;√表示所得故障距离在对应故障区域的有效测距范围内,且对应故障区域上可查找到故障点;—表示不再执行相应测距。
由表9可知,无论是干线误判还是分支误判,按照所提误判处理机制最终都能成功地确定正确的故障区域,并得到准确测距结果,同时本文设定的故障假设顺序也使得并非所有误判都需对其余所有区域进行重新测距,因此纠错效率较高。以上表明,所提误判处理机制可以有效地纠正前期故障区域误判结果,确保了故障定位整体方案的有效性。
为验证测量误差对所提方案的影响,在测试集中对各特征量随机增加-5%~5%的测量误差后进行测试,所得干线故障(总)平均正确率为97.6%,分支故障总平均正确率为97.0%。同时,对干线上故障距离2 413.87 m处、分支2上故障距离2 753.52 m处的A相接地进行测距时,均分别在干线首端测点与故障区域末端测点添加-5%、5%的测量误差,所得测距误差分别为92.63 m、125.08 m。由上述结果可知,测量误差确实会降低所提方案的定位精度,但是最终定位误差仍在可接受范围内。随着测量技术的进步,测量误差的影响可进一步减小。
本文将图学习与零序分量相结合实现了风电场集电线单相接地故障定位,主要结论如下:
1)采用图数据表征集电线故障信息,应用GCN构建故障区域判断模型,可综合利用电气量信息与结构信息,使多点信息融合更充分,验证表明,模型正确率高于传统深度学习方法;同时,模型串联结合代价敏感学习能有效应对样本不平衡问题。
2)充分利用集电线零序特征较明显、零序网络不含风机的事实,推导出基于零序分量的风机无关测距公式,从而实现了较少测点下跨越多风机的故障测距,并且正确率较高。
3)所提定位方案能够有效地实现含分支集电线的故障定位;并且整体方案只需在干线两端及各分支末端安装测点,所需测点少。
4)所提定位方案在测点数据不同步的条件下仍能够准确地实现故障定位,并且定位效果不受故障位置、过渡电阻和风速等因素的影响。
另外注意到,GCN存在过平滑问题,使其难以通过深度堆叠进一步提升特征提取能力;同时,本文在处理故障区域误判时仍需少量人工介入。以上问题有待于后续研究。
参考文献
[1] 王恰. 中国风电产业40年发展成就与展望[J]. 中国能源, 2020, 42(9): 28-32, 9.
Wang Qia. Achievements and prospects of China’s wind power industry development for 40 years[J]. Energy of China, 2020, 42(9): 28-32, 9.
[2] 王宾, 任萱. 中性点经小电阻接地风电场集电线路单相接地故障测距研究[J]. 中国电机工程学报, 2021, 41(6): 2136-2144.
Wang Bin, Ren Xuan. Single-line-to-ground fault location in wind farm collection line with neutral point grounding with resistor[J]. Proceedings of the CSEE, 2021, 41(6): 2136-2144.
[3] 刘鑫, 滕欢, 梁梦可, 等. 基于电流偏差2-范数的有源配电网故障距离定位[J]. 电工技术学报, 2019, 34(增刊2): 720-728.
Liu Xin, Teng Huan, Liang Mengke, et al. Fault location of active distribution network based on current deviation 2-norm[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 720-728.
[4] 王守鹏, 赵冬梅, 商立群, 等. 基于线路分段参数的非全程同塔双回线故障定位算法[J]. 电工技术学报, 2017, 32(20): 261-270.
Wang Shoupeng, Zhao Dongmei, Shang Liqun, et al. Fault location algorithm for non-complete double-circuit lines on the same tower based on line segmentation parameters[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 261-270.
[5] 李振钊, 王增平, 张玉玺, 等. 基于升维线性规划的主动配电网故障区段定位方法[J]. 电力系统自动化, 2021, 45(24): 122-132.
Li Zhenzhao, Wang Zengping, Zhang Yuxi, et al. Fault location method of active distribution network based on ascending dimension linear programming[J]. Automation of Electric Power Systems, 2021, 45(24): 122-132.
[6] 王小君, 任欣玉, 和敬涵, 等. 基于μPMU相量信息的配电网络故障测距方法[J]. 电网技术, 2019, 43(3): 810-817.
Wang Xiaojun, Ren Xinyu, He Jinghan, et al. Distribution network fault location based on μPMU information[J]. Power System Technology, 2019, 43(3): 810-817.
[7] 张健磊, 高湛军, 陈明, 等. 考虑复故障的有源配电网故障定位方法[J]. 电工技术学报, 2021, 36(11): 2265-2276.
Zhang Jianlei, Gao Zhanjun, Chen Ming, et al. Fault location method for active distribution networks considering combination faults[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2265-2276.
[8] 邓丰, 徐帆, 曾哲, 等. 基于多源暂态信息融合的单端故障定位方法[J]. 电工技术学报, 2022, 37(13): 3201-3212.
Deng Feng, Xu Fan, Zeng Zhe, et al. Single-ended fault location method based on multi-source transient information fusion[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3201-3212.
[9] 于华楠, 马聪聪, 王鹤. 基于压缩感知估计行波自然频率的输电线路故障定位方法研究[J]. 电工技术学报, 2017, 32(23): 140-148.
Yu Huanan, Ma Congcong, Wang He. Transmission line fault location method based on compressed sensing estimation of traveling wave natural frequencies[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 140-148.
[10] 邓丰, 梅龙军, 唐欣, 等. 基于时频域行波全景波形的配电网故障选线方法[J]. 电工技术学报, 2021, 36(13): 2861-2870.
Deng Feng, Mei Longjun, Tang Xin, et al. Faulty line selection method of distribution network based on time-frequency traveling wave panoramic waveform[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2861-2870.
[11] 胡明峰, 刘洋, 华斌. 量测装置优化配置下的分布式配电网故障定位方法[J]. 电网技术, 2021, 45(7): 2616-2622.
Hu Mingfeng, Liu Yang, Hua Bin. Distributed fault location for distribution networks under optimal configuration of measuring devices[J]. Power System Technology, 2021, 45(7): 2616-2622.
[12] 张大海, 张晓炜, 孙浩, 等. 基于卷积神经网络的交直流输电系统故障诊断[J]. 电力系统自动化, 2022, 46(5): 132-145.
Zhang Dahai, Zhang Xiaowei, Sun Hao, et al. Fault diagnosis for AC/DC transmission system based on convolutional neural network[J]. Automation of Electric Power Systems, 2022, 46(5): 132-145.
[13] 喻锟, 胥鹏博, 曾祥君, 等. 基于模糊测度融合诊断的配电网接地故障选线[J]. 电工技术学报, 2022, 37(3): 623-633.
Yu Kun, Xu Pengbo, Zeng Xiangjun, et al. Grounding fault line selection of distribution networks based on fuzzy measures integrated diagnosis[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 623-633.
[14] 王浩, 杨东升, 周博文, 等. 基于并联卷积神经网络的多端直流输电线路故障诊断[J]. 电力系统自动化, 2020, 44(12): 84-92.
Wang Hao, Yang Dongsheng, Zhou Bowen, et al. Fault diagnosis of multi-terminal HVDC transmission line based on parallel convolutional neural network[J]. Automation of Electric Power Systems, 2020, 44(12): 84-92.
[15] 邢超, 高敬业, 毕贵红, 等. 基于集成神经网络的特高压直流输电线路初始电压行波小波变换模极大值比单端测距方法[J]. 电力自动化设备, 2022, 42(11): 128-134.
Xing Chao, Gao Jingye, Bi Guihong, et al. Single-ended location method based on integrated neural network for modulus maximum ratio of traveling wave wavelet transform of initial voltage of UHVDC transmission lines[J]. Electric Power Automation Equipment, 2022, 42(11): 128-134.
[16] 彭华, 朱永利, 袁胜辉. 风电场集电线路单相接地故障组合测距[J]. 仪器仪表学报, 2020, 41(9): 88-97.
Peng Hua, Zhu Yongli, Yuan Shenghui. Combined fault location for single-phase grounding of wind farm collection line[J]. Chinese Journal of Scientific Instrument, 2020, 41(9): 88-97.
[17] 张科, 朱永利, 郑艳艳, 等. 风电场输电线路单相接地故障定位研究[J]. 太阳能学报, 2020, 41(5): 114-120.
Zhang Ke, Zhu Yongli, Zheng Yanyan, et al. Fault location of single-phase earth in transmission lines of wind farm[J]. Acta Energiae Solaris Sinica, 2020, 41(5): 114-120.
[18] 彭华, 朱永利. 基于apFFT频谱校正和XGBoost的风电场集电线路单相接地故障测距[J]. 电工技术学报, 2020, 35(23): 4931-4939.
Peng Hua, Zhu Yongli. Single phase grounding fault location for power lines of wind farm based on apFFT spectrum correction and XGBoost algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4931-4939.
[19] Hoerauf R. Considerations in wind farm grounding designs[J]. IEEE Transactions on Industry Applications, 2014, 50(2): 1348-1355.
[20] 马伟, 裘愉涛, 丁冬, 等. 基于阻尼最小二乘法的单相接地故障定位方案[J]. 电网技术, 2018, 42(9): 3049-3054.
Ma Wei, Qiu Yutao, Ding Dong, et al. Single-phase grounding fault location scheme based on levenberg-marquarat algorithm[J]. Power System Technology, 2018, 42(9): 3049-3054.
[21] 谢潇磊, 刘亚东, 孙鹏, 等. 新型配电网线路P MU装置的研制[J]. 电力系统自动化, 2016, 40(12): 15-20, 52.
Xie Xiaolei, Liu Yadong, Sun Peng, et al. Development of novel PMU device for distribution network lines[J]. Automation of Electric Power Systems, 2016, 40(12): 15-20, 52.
[22] 袁冰, 王宾, 陆元园, 等. 风电场并网线路单相接地故障单端测距误差特性分析[J]. 电力系统保护与控制, 2016, 44(19): 63-69.
Yuan Bing, Wang Bin, Lu Yuanyuan, et al. Error analysis of single-end fault location for single-line-to-ground fault in transmission line with wind farm connection[J]. Power System Protection and Control, 2016, 44(19): 63-69.
[23] 王晨清, 宋国兵, 迟永宁, 等. 风电系统故障特征分析[J]. 电力系统自动化, 2015, 39(21): 52-58.
Wang Chenqing, Song Guobing, Chi Yongning, et al. Fault characteristics analysis of wind power system[J]. Automation of Electric Power Systems, 2015, 39(21): 52-58.
[24] Zhang Dingcheng, Stewart E, Entezami M, et al. Intelligent acoustic-based fault diagnosis of roller bearings using a deep graph convolutional network[J]. Measurement, 2020, 156: 107585.
[25] 张翼, 朱永利. 图信号与图卷积网络相结合的局部放电模式识别方法[J]. 中国电机工程学报, 2021, 41(18): 6472-6481.
Zhang Yi, Zhu Yongli. A partial discharge pattern recognition method combining graph signal and graph convolutional network[J]. Proceedings of the CSEE, 2021, 41(18): 6472-6481.
[26] Lee J, Lee I, Kang J. Self-attention graph pooling[C]//Proceedings of the 36th International Conference on Machine Learning, Long Beach, USA, 2019: 1-10.
[27] 陈剑, 杜文娟, 王海风. 基于对抗式迁移学习的含柔性高压直流输电的风电系统次同步振荡源定位[J]. 电工技术学报, 2021, 36(22): 4703-4715.
Chen Jian, Du Wenjuan, Wang Haifeng. Location method of subsynchronous oscillation source in wind power system with VSC-HVDC based on adversarial transfer learning[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4703-4715.
[28] Correa Bahnsen A, Aouada D, Ottersten B. Example-dependent cost-sensitive decision trees[J]. Expert Systems with Applications, 2015, 42(19): 6609-6619.
[29] Bahnsen A C, Stojanovic A, Aouada D, et al. Cost sensitive credit card fraud detection using Bayes minimum risk[C]//2013 12th International Conference on Machine Learning and Applications, Miami, FL, USA, 2014: 333-338.
[30] 曾德辉, 王钢, 李海锋, 等. 小电阻接地配电网多回线故障分析与自适应零序电流保护[J]. 电力自动化设备, 2019, 39(5): 45-52.
Zeng Dehui, Wang Gang, Li Haifeng, et al. Fault analysis of multi-feeder grounding fault and self-adaptive zero-sequence current protection scheme for low-resistance grounding distribution network[J]. Electric Power Automation Equipment, 2019, 39(5): 45-52.
[31] 陈福锋, 赵谦, 兰金波, 等. 风电场汇流线路同步采样及差动保护[J]. 电力系统自动化, 2013, 37(14): 19-24.
Chen Fufeng, Zhao Qian, Lan Jinbo, et al. Synchronous sampling and differential protections of collector lines in wind farms[J]. Automation of Electric Power Systems, 2013, 37(14): 19-24.
[32] Wang Bin, Ni Jiang, Geng Jianzhao, et al. Arc flash fault detection in wind farm collection feeders based on current waveform analysis[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(2): 211-219.
Abstract In wind farms, collecting lines are short with a large number of wind turbines connected to it, and fault characteristics of wind turbines are different from those of traditional power sources, so dense connection of special power sources is the typical characteristic of collecting lines. The elimination of influence of wind turbines, applicability of collecting lines with line branches and reduction of measurement points are key challenges faced by the fault localization for collecting lines. Given these above challenges, it is difficult for the fault localization method in transmission and distribution networks to apply in wind farms, and the existing fault localization method of collecting lines cannot effectively address all these challenges. Therefore, a new hierarchical fault localization scheme for single-phase-to-ground faults on collecting lines combining graph learning and zero-sequence components is proposed, which can achieve precise fault localization across wind turbines with the applicability of collecting lines containing line branches considered and a few measurement points used.
Firstly, the graph data is constructed according to electrical information at measurement points and collecting line topology, and GCN (graph convolution neural network) is used as base-models for graph classification modeling to obtain the identification model of faulty areas which consists of a primary classifier and a secondary classifier; in the process of identification model construction, in order to overcome the impact of sample imbalance, multiple classifier models are connected in series with transfer learning combined, and cost sensitive learning based on Bayes minimum risk is also introduced to post-process classification results. Then, considering the neutral-point grounding type of wind farms and the winding connection characteristic of box-type transformers, a wind-turbine-independent fault distance calculation formula is derived based on zero-sequence components, and thus the fault point in faulty areas can be obtained by zero-sequence components. Besides, a misidentification processing mechanism for faulty areas is also proposed to correct the misidentification which occurs rarely. This above proposed fault localization scheme does not require strict data synchronization, can take into account both of structural and attribute information of collecting lines to identify the faulty area with limited fault data provided by a few measurement points, and can overcome influence of wind turbines to achieve the fault distance calculation.
Verification results show that with the graph data constructed, faulty areas can be effectively identified by GCN, and the identification accuracy of all faulty areas reaches over 99%, which is higher than traditional DNN (deep neural network); besides, in the process of dealing with sample imbalance, model series connection increases the total average accuracy of branch faults by 12%, and further this above accuracy achieves another 6.1% improvement with cost sensitive learning introduced, which verifies the feasibility of the sample imbalance treatment strategy in this paper. The fault distance calculation method proposed for faulty areas can overcome the influence of fault locations, fault resistance, wind speed and data asynchronization, and errors of fault distance is no more than 150 m. In addition, the proposed misidentification processing mechanism is also proved to be effective and efficient in correcting misidentification of faulty areas.
keywords:Wind farm, collecting line, single-phase-to-ground fault, fault localization, graph convolutional neural network, zero-sequence component, sample imbalance, asynchronous data
中图分类号:TM76
DOI:10.19595/j.cnki.1000-6753.tces.221031
国家自然科学基金(51677072)和中国国电集团公司科技项目(GDDL-KJ-2017-02)资助。
收稿日期 2022-06-06
改稿日期 2023-04-30
丁 嘉 男,1997年生,博士研究生,研究方向为电力线故障定位。E-mail:jia_ding_0132@163.com(通信作者)
朱永利 男,1963年生,教授,博士生导师,研究方向为电力设备故障诊断、电力设备大数据分析与智能电网等。E-mail:yonglipw@163.com
(编辑 赫蕾)