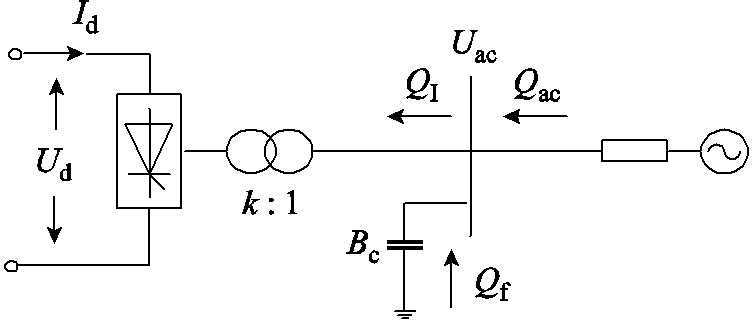
图1 换流站无功功率交换示意图
Fig.1 Schematic diagram of reactive power exchange of converter station
摘要 该文分析了逆变站无功功率随直流电流与关断角变化的趋势，对准稳态下关断角、直流电流及无功功率的可运行范围进行解析，并提出一种基于逆变站动态无功控制的后续换相失败抑制方法。该方法通过对整流侧低压限流单元参数进行整定，并且在逆变侧根据测得的交流母线电压及直流电流实时计算关断角指令，对故障期间逆变站的无功功率进行控制。最后，在电磁暂态仿真软件PSCAD/EMTDC中以CIGRE高压直流标准测试模型及贵广Ⅱ回直流输电工程模型为算例进行仿真验证，结果表明所提方法能够有效地提升系统的故障支撑能力，降低系统发生后续换相失败的概率。
关键词：高压直流 无功功率 换相失败 故障恢复
基于电网换相换流器的高压直流输电（Line Commutated Converter based High Voltage Direct Current, LCC-HVDC）技术在远距离、大容量输电中具有重要地位[1-2]。在“强直弱交”背景下，高压直流输电系统发生换相失败将对交直流混联电网安全产生不利影响[3-4]。交流侧故障是高压直流系统发生换相失败的主要原因[5]，在交流故障发生或切除、甚至是系统恢复过程中，受换流母线电压变化、直流控制等影响，换流站对交流系统造成的无功功率冲击很可能引发后续换相失败[6-9]，甚至引发多馈入直流系统中的相继换相失败[10]，对系统的安全稳定运行造成威胁。
近年来，交流故障下换流站无功功率特性成为了研究热点。无功补偿设备由于响应时间较长，通常难以及时响应以抑制后续换相失败，因此常被作为辅助手段[11-14]。从无功功率与直流控制方式的角度出发，文献[15]指出，换相失败初始恢复阶段的定熄弧角控制给出的熄弧角指令具有较大的超调量，进而引起无功功率的超调量。文献[16]分析了在交流母线电压波动下，逆变站低压限流功能（Voltage Dependent Current Order Limitation, VDCOL）启动点、直流控制方式等对逆变站无功动态特性的影响。文献[17-18]优化了低压限流器启动电压，但实际上未改变系统的稳态运行点。文献[19]通过控制直流电流减少逆变器无功消耗，使逆变站产生盈余的容性无功。文献[20]分析了VDCOL参数设置与换流站消耗的无功功率的关系，以换流站向交流系统注入无功功率为目标给出了VDCOL参数的设置范围。文献[21]在交流故障期间根据无功功率交换量期望值及实测换流母线电压实时计算出直流电流指令，取代VDCOL功能，实现无功功率交换量的实时定量控制。文献[22]在定无功控制的基础上，确定了不同故障类型下直流电流受换流母线电压约束的可运行范围，结果表明定无功控制策略能够有效改善系统的恢复性能。文献[23]采用瞬时无功功率理论计算交流滤波器补偿后的无功功率，以确定逆变器的期望无功消耗。文献[24]同时考虑了无功平衡与定关断角的约束，提出替代VDCOL的直流电流实时计算方法。
上述研究大多采用控制直流电流的方式改善交流故障期间换流站的无功平衡，而在准稳态过程中，整流侧处于定电流控制，逆变侧处于定关断角控制，即逆变侧计算得到的电流指令需要从逆变侧传输至整流侧实现。但在实际工程中，整流侧与逆变侧之间需要考虑15～20 ms延时，可能造成控制效果变差。为了避免两侧换流站之间的电流指令传输导致控制作用滞后，本文以逆变站关断角为控制量，提出一种基于逆变站动态无功控制的双端协调的控制策略。首先分析了逆变站无功功率动态特性，对准稳态下关断角、直流电流及无功功率的可运行范围进行了解析。在此基础上，对整流侧低压限流单元参数进行整定，并在逆变侧根据测得的交流母线电压及直流电流实时计算关断角指令，对故障期间逆变站的无功功率进行控制。最后电磁暂态仿真表明所提方法能够有效提升系统的故障支撑能力，并且降低了系统发生后续换相失败的概率。
高压直流输电系统换流站与交流系统间的（以逆变站为例）无功功率交换示意图如图1所示。
图1 换流站无功功率交换示意图
Fig.1 Schematic diagram of reactive power exchange of converter station
图1中，Uac为交流母线线电压有效值，Id为直流电流，Ud为直流电压，k为换流变压器匝比，Qf为交流滤波器所补偿的无功功率，QI为换流器消耗的无功功率，Qac为换流站与交流系统间的无功功率交换量。由图1可知，逆变站交流母线处的无功平衡公式为
（1）
式中，Qac为负，表示交流系统从逆变站吸收无功功率；Qac为正，表示交流系统向逆变站提供无功功率。
逆变站消耗的无功功率QI为
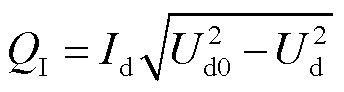（2）
式中，Ud0为换流变压器阀侧的理想空载直流电压。
对于12脉动换流器，Qac与Uac、Id和关断角γ的关系为[17]
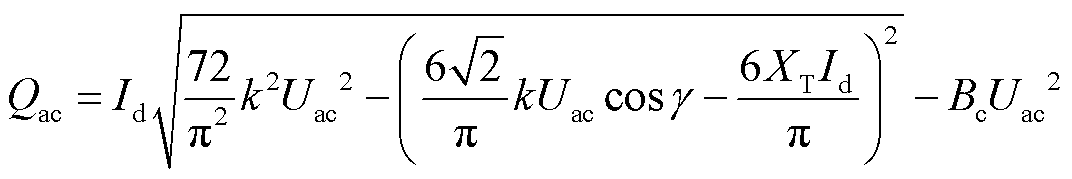（3）
式中，Bc为无功补偿装置等值容纳；XT为换流变压器二次侧的等值换相电抗。
在逆变侧交流系统出现短路故障时，换流母线电压跌落，使得滤波器组供给无功功率Qf不足，逆变站自身消耗的无功功率QI随直流电流及换流母线电压波动而波动，则交直流系统间将出现大幅无功波动，其变化量由受端交流系统承担。由于无功功率与换流母线电压幅值紧密耦合，则无功功率冲击将进一步影响换流母线的电压稳定，很可能引发后续换相失败。因此，若换流站能够通过直流控制实现无功功率平衡，则可以在故障期间对换流母线电压起到一定的支撑作用。
本文以CIGRE高压直流标准测试模型及贵广Ⅱ回直流输电工程模型为算例，其基本参数见表1。
表1 直流输电模型基本参数
Tab.1 Basic parameters of HVDC model
参数CIGRE高压直流标准测试模型贵广Ⅱ回直流输电工程模型 额定直流电压UdN/kV500500 额定直流电流IdN/kA23 换流母线额定电压Uac/kV230525 换流变压器匝比k209:230196.5:525 换相电抗XT/Ω13.315 27.042 31 等值容纳Bc/S0.011 840.003 10
式（3）中将Qac对Id求偏导可得
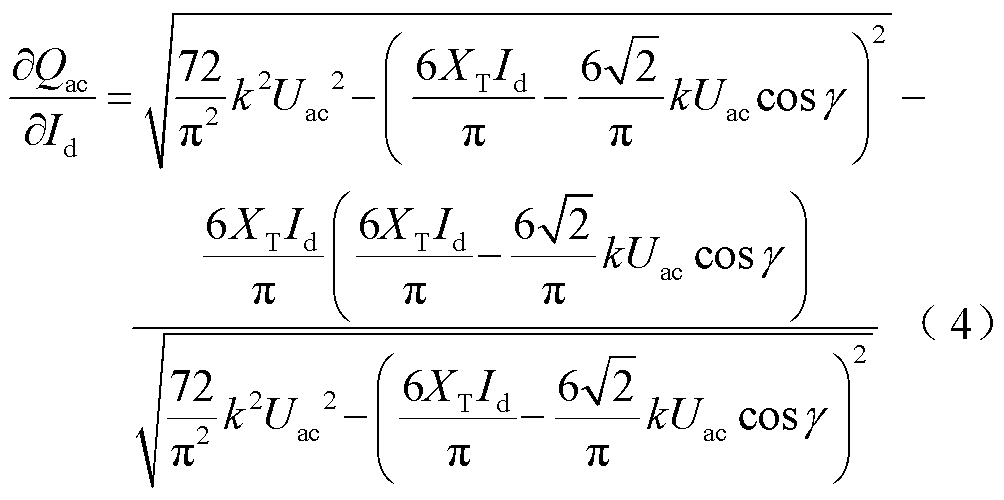
同理，将Qac对关断角γ求偏导可得
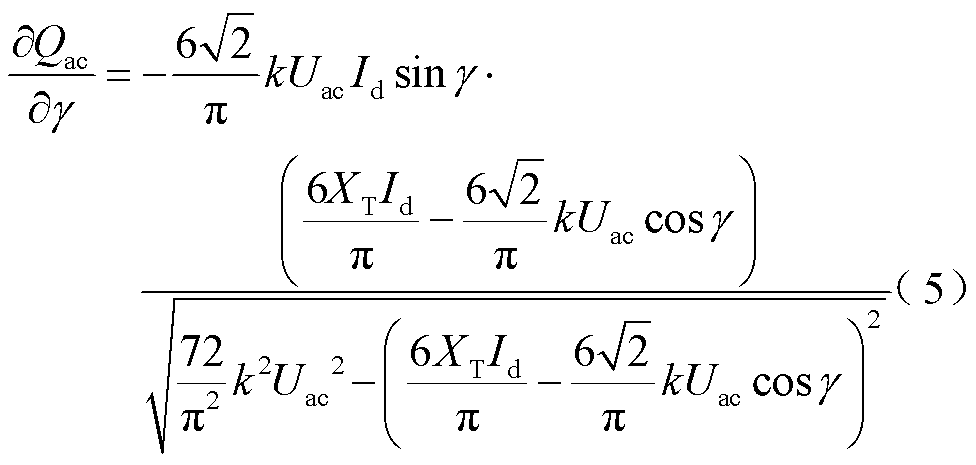
代入表1参数，可得到不同的交流电压下的偏导数，如图2所示。
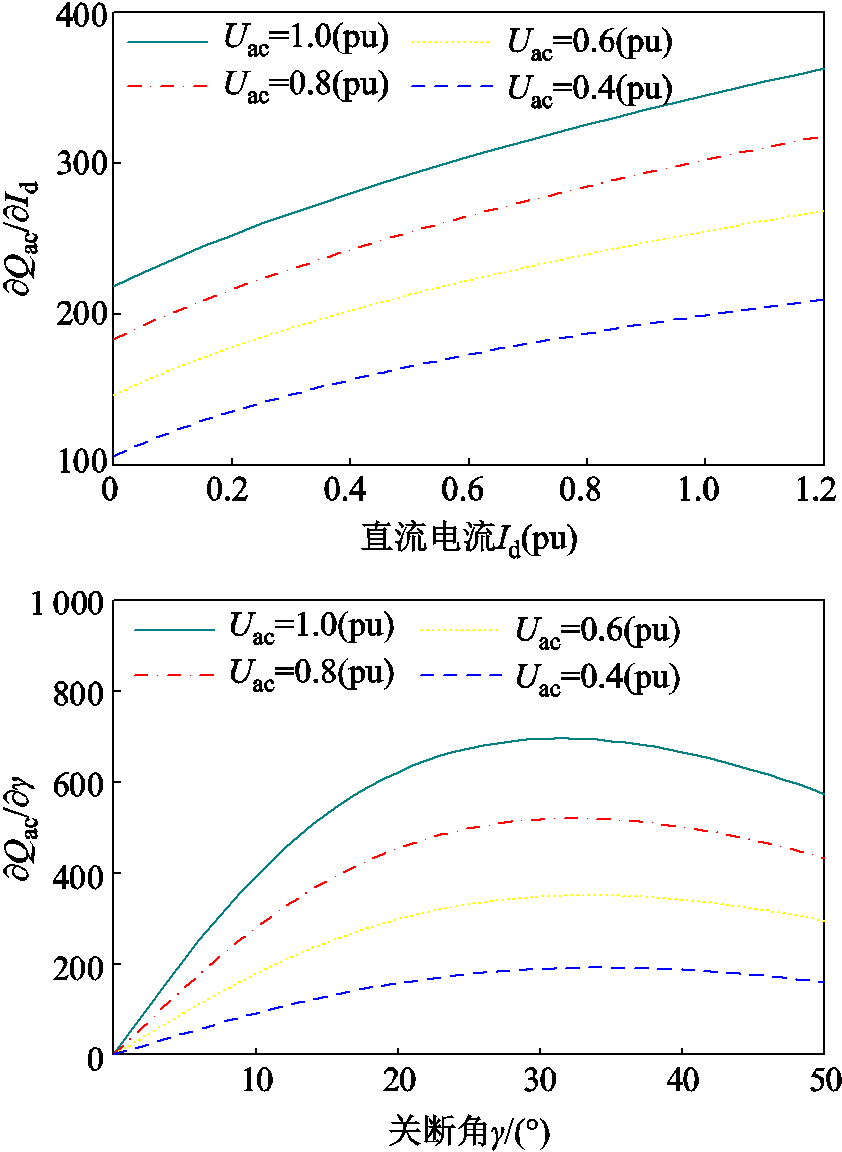
图2 不同交流电压下无功交换量关于直流电流、关断角的偏导数
Fig.2 Partial derivatives of Qac with respect to Id andγ under different AC voltages
由图2可以看到，在不同交流电压下偏导数均为正数，说明关断角、直流电流的增大均伴随着换流站吸收的无功功率的增加。而在实际电网中，换流站与交流系统间的无功功率与直流电流、关断角及交流电压相互耦合，任一电气量的调整都将引起其他量的变化。通过在极控制级调节触发延迟角大小，可以控制直流电流或关断角等电气量。以逆变侧为例，减小触发延迟角可以增大关断角，增大换相面积，但此时换流器消耗的无功功率也增大，从交流侧吸收更多的无功功率，对故障中的交流系统造成更大的无功负担，很可能反而引发换相失败。因此，触发延迟角的调节应该同时考虑换流站吸收无功功率的影响，避免对交流系统造成无功冲击。
稳态下无功交换量对直流电流的偏导数与对关断角的偏导数关系为
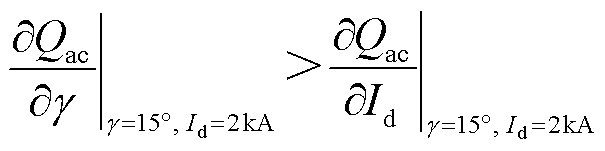（6）
即关断角变化对无功功率的影响要大于电流变化带来的影响，无功功率关于关断角的灵敏度更高。因此，通过改变关断角参考值来调节无功功率比通过改变电流更为快速。
为了在交流故障期间充分挖掘换流器的无功调节能力，可以通过控制关断角对交直流系统中的无功交换量进行控制，对换流母线电压起到支撑作用，从而避免发生后续换相失败。
对于12脉动换流器，由准稳态公式可得
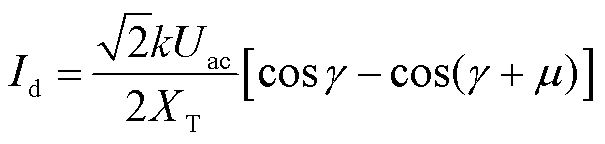（7）
式中，μ为换相重叠角。正常工况下μ不超过30°，则可运行范围边界处，关断角满足
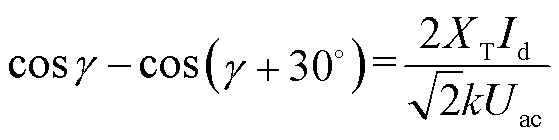（8）
代入CIGRE高压直流标准测试模型具体参数，可解得
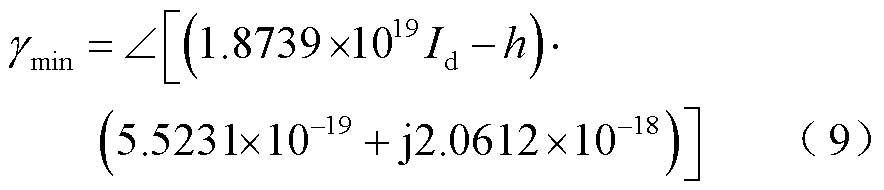
其中
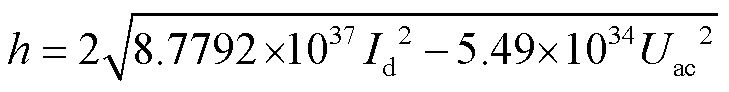（11）
由式（9）～式（11）可以得到CIGRE高压直流标准测试模型及贵广Ⅱ回直流输电工程模型的关断角可运行范围分别为（γmin, γmax）。代入贵广Ⅱ回直流输电工程模型具体参数，同样可以解得相应范围。
在CIGRE高压直流标准测试模型中，准稳态下γ=15°。由于其VDCOL输入为直流线路中点电压Uvdcol，中点距离换流站的阻抗为2.5 Ω，代入式（8）后可得到令换相角μ≤30°时，直流电流与线路中点电压的电流限定曲线表达式（标么值）：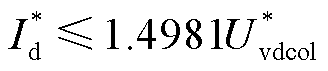
。
因此，CIGRE高压直流标准测试模型的直流电流可运行范围与VDCOL曲线[18]的关系如图3所示。
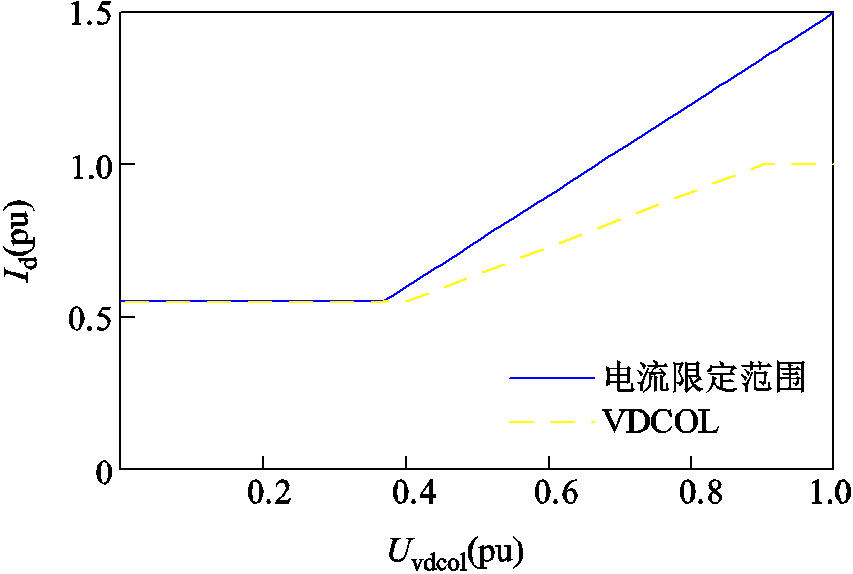
图3 VDCOL与电流可运行范围（CIGRE）
Fig.3 The VDCOL and the operating range of current (CIGRE)
从图3可以看出，当VDCOL曲线位于蓝色实线左半侧区域时，其直流电流指令Id不满足μ≤30°的条件，这意味着当系统运行在该区域对应的工况时，满足μ≤30°条件的直流电流要小于VDCOL输出的指令，故在此区域VDCOL控制下的逆变器发生换相失败的风险相应增加。
同理，代入贵广Ⅱ回直流输电工程模型的运行参数，其中逆变侧运行在定关断角控制，关断角γ=17°。可以得到当换相角μ≤30°时直流电流与逆变侧电压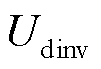
的关系：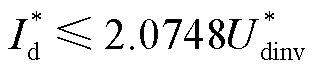
。考虑直流线路阻抗12.2 Ω，得到当换相角μ≤30°时直流电流与整流侧电压
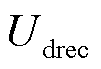的电流限定曲线：
。
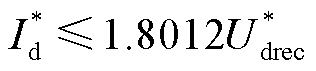因此，贵广Ⅱ回直流输电工程模型整流侧、逆变侧VDCOL与对应的电流可运行范围关系如图4所示。
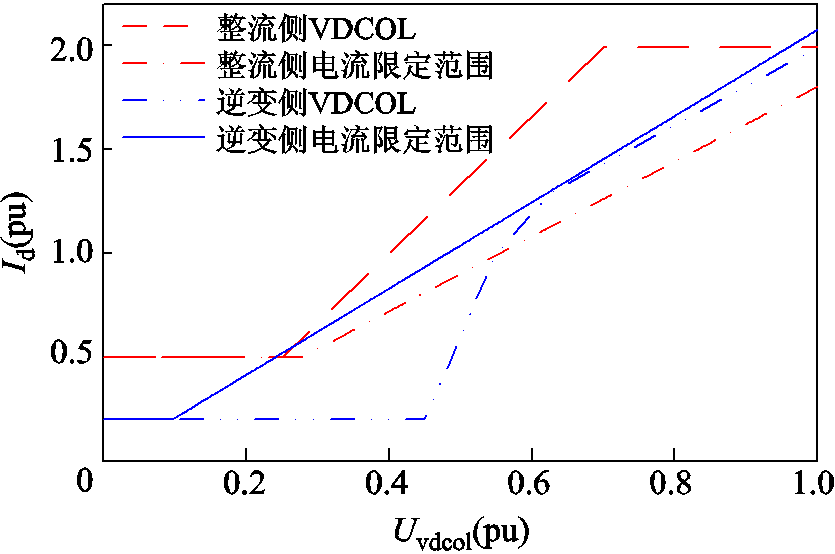
图4 整流侧、逆变侧VDCOL与电流可运行范围（贵广Ⅱ）
Fig.4 The VDCOL and the operating range of current on the rectifier and inverter (Guiguang Ⅱ)
由图4可知，贵广Ⅱ回直流输电工程模型逆变侧VDCOL位于电流可运行范围内，整流侧VDCOL不满足准稳态下具有可运行点的要求，需要重新整定。
由式（3）可知，无功功率是由直流电流、交流电压及关断角共同决定的。设故障时交流电压的变化范围为0.3(pu)～1.0(pu)，直流电流变化范围为0.2(pu)～1.1(pu)。由于在实际12脉动直流工程的准稳态过程中，触发角最小值约110°，换相角最大值为30°，则关断角变化范围为0～40°。将交流电压、直流电流、关断角变化范围以及μ≤30°代入式（8），可得如图5所示的无功功率可调节范围。
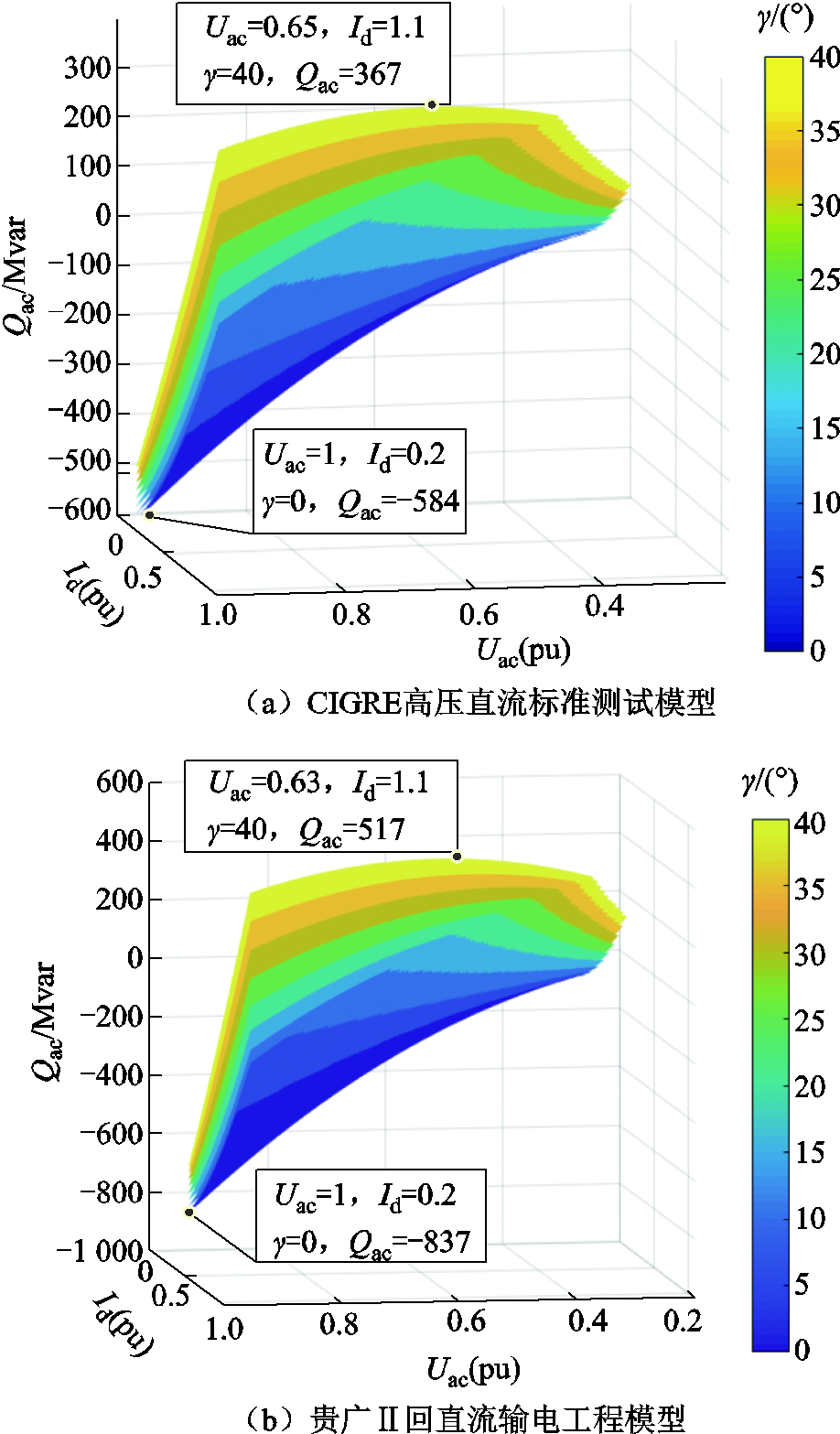
图5 不同关断角、直流电流、交流电压下对应的无功功率可调节范围
Fig.5 Adjustable range of reactive power under different extinction angle, DC current and AC voltage
图5中不同颜色表示关断角0°～40°的不同大小。随着关断角的变大，交流系统需要向换流站提供更多无功功率，其变化范围为-584～367 Mvar（CIGRE），-873～518 Mvar（贵广Ⅱ）。
图6为γ取额定值时的无功变化情况，其变化范围为-554～157 Mvar（CIGRE），-783～294 Mvar（贵广Ⅱ）。在故障发展过程中，电压变化程度一般没有直流电流严重，即故障过程中无功功率明显受直流电流变化的影响，很可能使换流站从交流系统吸收大量无功功率。
图6 γ取额定值时的无功功率可调节范围
Fig.6 Adjustable range of the reactive power when γ takes the rated value
为了在交流故障期间控制换流站与交流系统之间的无功交换量，本文提出了基于逆变站动态无功控制的后续换相失败抑制方法：在逆变侧通过控制关断角对无功功率进行控制，在整流侧根据准稳态方程整定出满足逆变侧无功定量需求的直流电流指令。
CIGRE高压直流标准测试模型在稳态下Qac=-60Mvar。又由于对称故障下交直流系统无功交换量为负值时，更有利于系统的恢复[19]，则令设定的逆变侧交直流系统的无功交换量为Qac_ord= -60Mvar。由式（3）可以得到
（12）
由式（9）～式（11）及式（12）可以得到CIGRE高压直流标准测试模型关断角限定范围及无功指令的关系如图7所示。
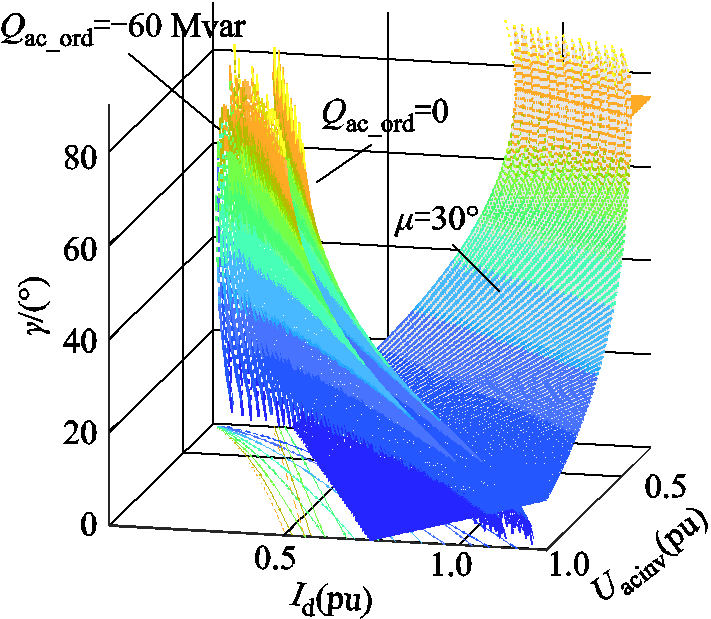
图7 定无功关断角指令及满足换相角的关断角范围（CIGRE）
Fig.7 Extinction angle order under constant reactive power control and the operating range of extinction angle satisfying commutation angle(CIGRE)
对应贵广Ⅱ回直流输电工程模型，令Qac_ord=-100Mvar，由式（12）可以得到无功定量控制关断角随交流电压与直流电流的关系。再根据式（8）得到关断角的可运行范围，与定无功关断角指令值进行对比，得到图8。
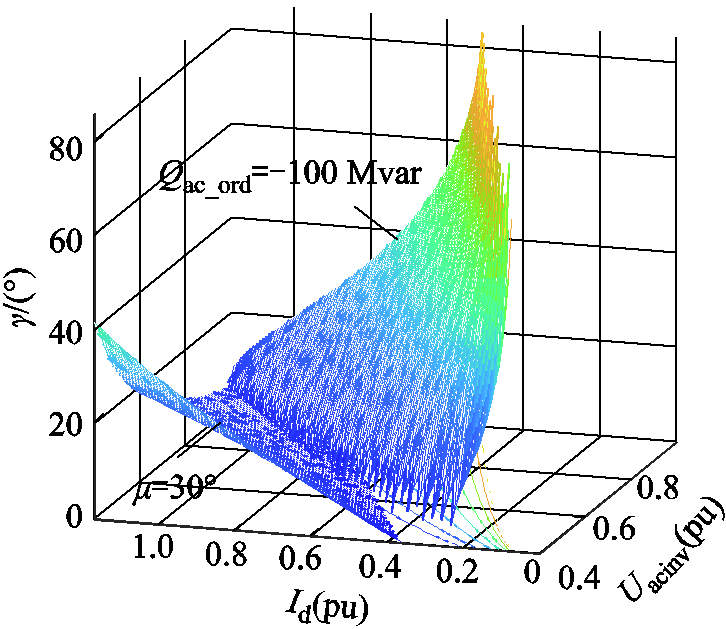
图8 定无功关断角指令及满足换相角的关断角范围（贵广Ⅱ）
Fig.8 Extinction angle order under constant reactive power control and operating range of extinction angle satisfying commutation angle (Guiguang Ⅱ)
图7与图8中，“μ=30°”标识的曲面上各点表示不同交流电压、直流电流下，正好使得μ=30°条件的关断角取值。曲面内侧上方所包裹的范围内，满足μ≤30°的条件，即12脉动换流器可以正常换相。可以看到，关断角的可运行范围受到直流电流、交流电压的共同影响。升高交流电压可以使得关断角可调节范围增大；而增大直流电流后，关断角可调节范围逐渐变小。
动态无功控制指令基本上处于满足μ≤30°的空间范围内。在同一直流电流和交流电压下，降低关断角，可以降低换流站消耗的无功功率；对于同一交流电压与关断角指令，降低直流电流可以使得换流站从交流系统吸收较少无功功率，对换流母线电压恢复起到支撑作用。
CIGRE高压直流标准测试模型中VDCOL参数是在经验值的基础上通过仿真统计来整定的，无理论依据。本文从无功控制的角度，推导VDCOL电流指令值。为防止电流断续，直流电流最小值与原系统中一致，为0.55(pu)。
当逆变侧交直流系统无功交换量的期望值设为Qac_ord=-60Mvar时，令γ=15°，由式（12）可得
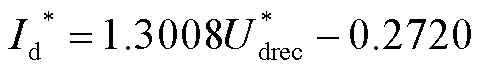（13）
该曲线可以使CIGRE高压直流标准测试模型在故障准稳态下，无功交换量Qac =-60Mvar。
代入贵广Ⅱ回直流输电工程模型参数，令γ=17°，Qac_ord=-100Mvar，由式（12）可以得到满足逆变站原系统无功需求的电流指令值。又由于在实际运行过程中，直流电流由整流侧控制，可以得到直流电流指令值与整流侧电压的关系为
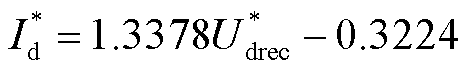（14）
对比贵广Ⅱ回直流输电工程模型整流侧原VDCOL、2.2节中的电流限定范围及式（14）计算得到的电流指令值，如图9所示。
图9 整流侧电流指令值对比（贵广Ⅱ）
Fig.9 Comparison of current instruction values on the rectifier side (Guiguang Ⅱ)
由图9可知式（14）对应的电流指令值满足μ≤30°的条件。电流指令值的最小值保持与原系统一致。
另外，整流侧和逆变侧具有不同的VDCOL曲线。在相同电压水平下，逆变侧的电流参考值设置的比整流侧小，以加快故障的恢复速度，缩短逆变侧电流控制的时间。按照式（14），取直流电流降低0.1(pu)的电流裕度，可以得到逆变侧的VDCOL曲线为
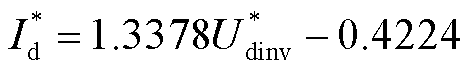（15）
动态无功控制下逆变侧的关断角指令及整流侧的直流电流指令值生成环节如图10所示。
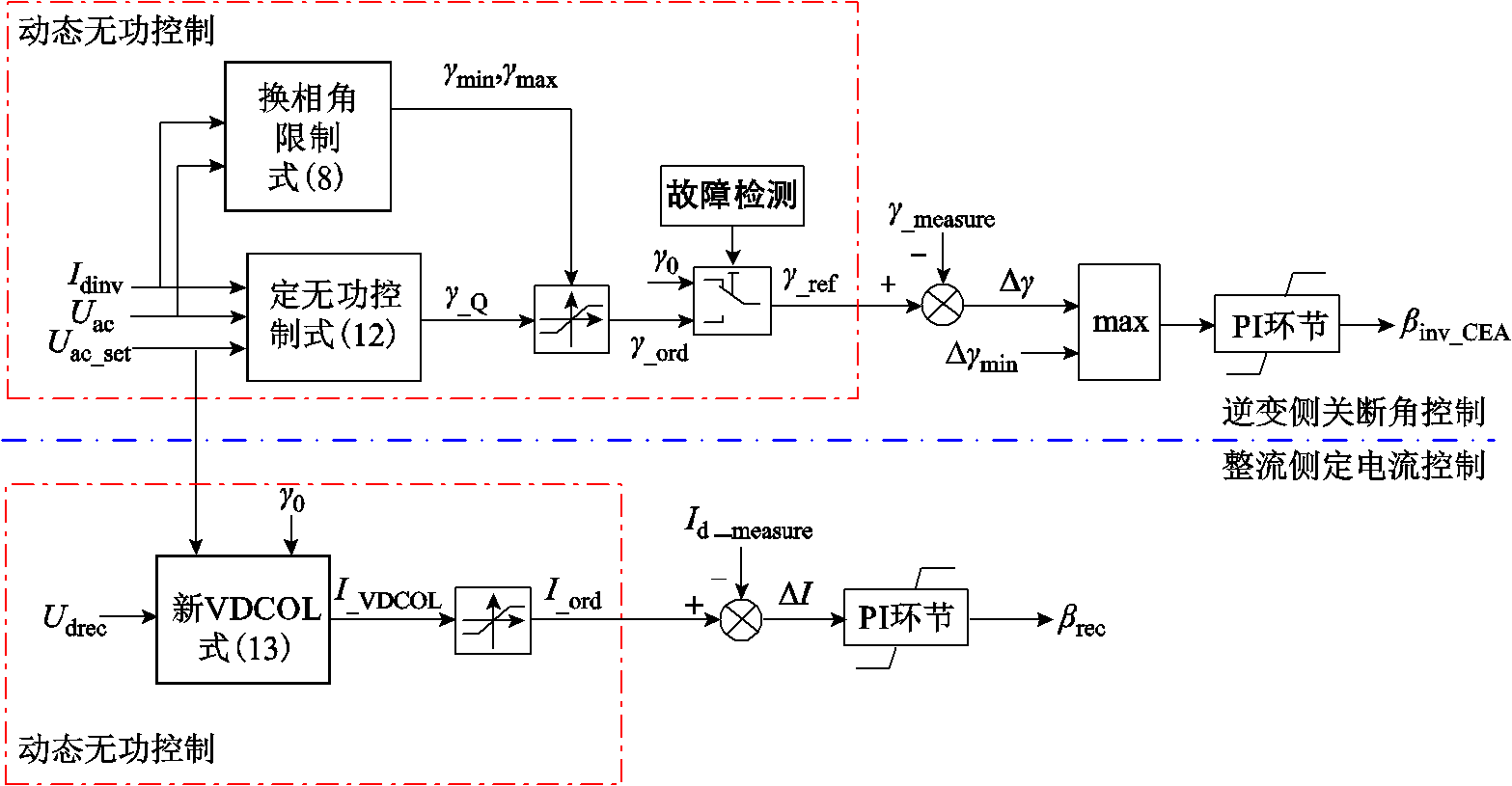
图10 动态无功控制下的关断角及直流电流指令值生成环节
Fig.10 Extinction angle and DC current order under constant reactive power control
图10中，γ_measure为关断角测量值，Id_measure为直流电流测量值，Dγmin为CIGRE系统的最小关断角误差量。在逆变侧通过实时测量换流母线交流电压Uac与直流电流Idinv来求解式（8）与式（12），得到可运行范围约束下的无功定量关断角指令γ_Q。由于在故障发生时刻后一段时间内，直流电流激增，此时式（12）无解，则保持
输出，在故障发生40 ms后，再接入定无功关断角控制，直到故障结束。在整流侧，根据Qac_ord及额定关断角
对整流侧低压限流单元参数进行整定，如式（13）所示。最终根据上述关断角和电流指令给出系统的触发角指令。
基于逆变站动态无功控制的后续换相失败抑制方法流程如图11所示。
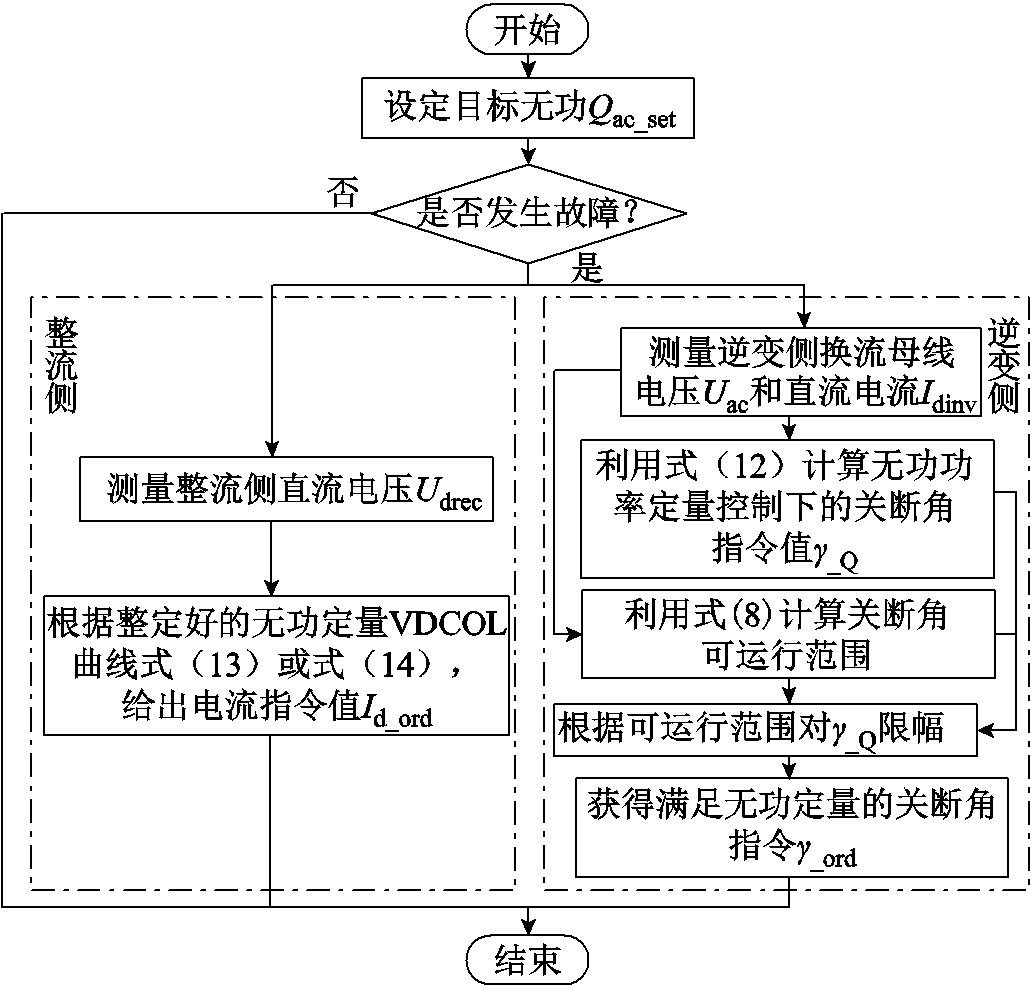
图11 基于逆变站动态无功控制的后续换相失败抑制方法流程
Fig.11 A method based on constant reactive power control of inverter to suppress the subsequent commutation failure in HVDC System
如图11所示，一方面，在逆变侧通过控制关断角对逆变站无功功率进行控制，当逆变侧检测到的交流母线电压或直流电流值发生变化，可以直接通过改变逆变侧的关断角来实时控制无功交换量；关断角、直流电压、逆变侧交流电压互相耦合，并满足准稳态方程约束。
另一方面，在整流侧根据准稳态方程求出直流电流可运行范围，并根据给出的新电流指令，使其满足额定关断角时逆变侧的无功定量需求。由整流侧测得直流电压，实时给出直流电流指令，不再由逆变侧传输，避免传输延迟对系统性能的恶化。
以CIGRE高压直流输电标准测试系统为基本算例，其采用12脉动换流器，额定直流电压为500 kV，额定直流电流为2 kA。设置3 s时发生三相故障，持续时间500 ms，故障电感0.15 H。对比未延时的CIGRE系统、考虑两侧传输延时20 ms的CIGRE系统及采用动态无功控制的CIGRE系统的故障响应。改进前后的电气量响应如图12所示。
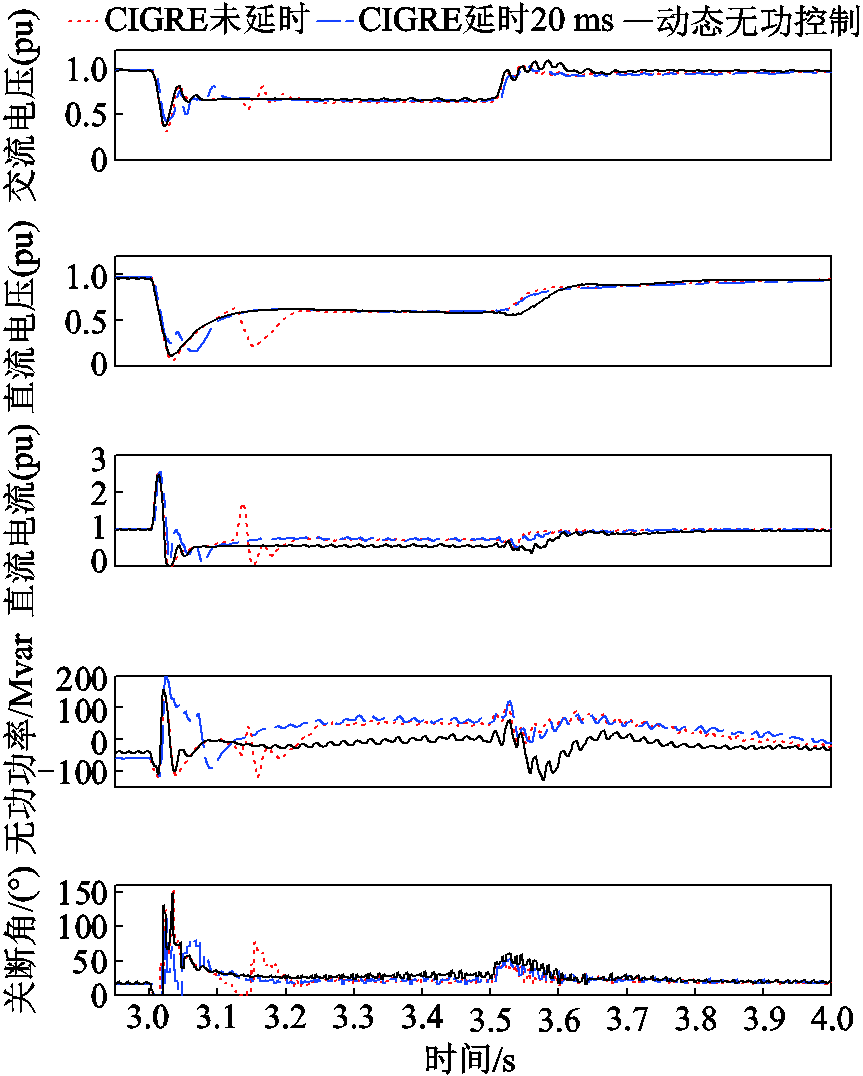
图12 改进前后的电气量响应（CIGRE）
Fig.12 Electrical response before and after improvement(CIGRE)
故障后，没有采用动态无功控制的系统关断角均两次跌落至0°，发生后续换相失败。如红点线所示，首次换相失败后，由于控制目标冲突[25]，引发了后续换相失败；如蓝色虚线所示，在具有20 ms传输延时的情况下，直流电流不能及时根据故障后电压进行控制，导致故障后吸收大量无功功率，并且更快地引发了后续换相失败。在动态无功控制策略下，换流站从交流系统吸收了更少的无功功率，各电气量振幅更小，故障期间无功交换量保持稳定，且未发生后续换相失败。
进一步地，将整流侧逆变侧具有20 ms传输延时的系统称为原系统，采用动态无功控制的系统称为改进系统。采用后续换相失败免疫因子指标（Subsequent Commutation Failure Immunity Index, SCFII）和换相失败概率指标（Subsequent Commutation Failure Probability Index, SCFPI）对改进前后系统的换相失败免疫性能进行测试[26]。
设置逆变侧交流母线发生三相短路故障，持续时间500 ms。改进后SCFII由102%提升至158%，说明动态无功控制策略能显著提升系统抑制后续换相失败的能力。
改进前后的SCFPI如图13所示。从图13可以看出，原系统在交流电压跌落0.35(pu)时开始发生后续换相失败，改进系统则可以承受交流电压跌落0.4(pu)。即改进系统发生后续换相失败对应的故障水平比原系统高。说明动态无功控制策略有效地提高了系统的换相失败免疫性能以及故障穿越能力。
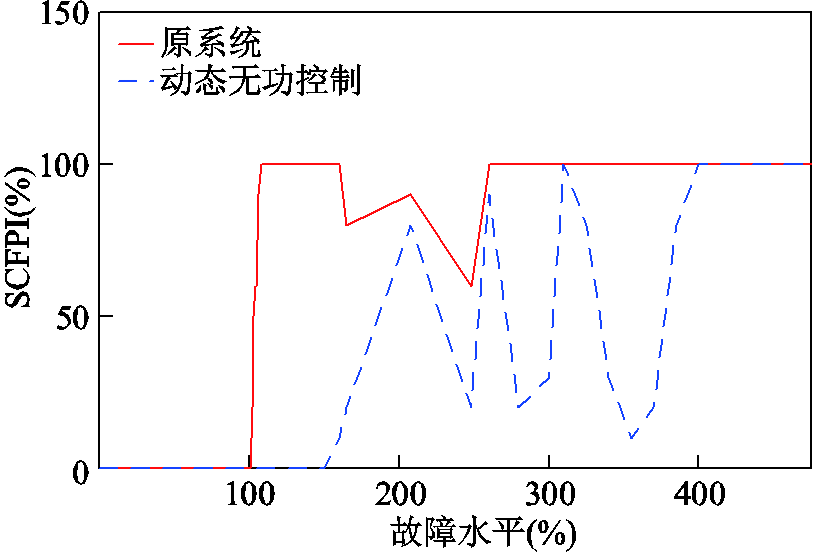
图13 后续换相失败概率指标比较（CIGRE）
Fig.13 Comparison of subsequent commutation failure probability indicators（CIGRE）
在贵广Ⅱ回直流输电工程模型中验证所提动态无功控制策略。对比原贵广Ⅱ系统与采用动态无功控制策略的系统，分别设置逆变侧交流母线处发生三相短路故障，持续时间500 ms。其中改进后SCFII由6 887%提升至14 327%，说明动态无功控制能显著提升贵广Ⅱ系统抑制后续换相失败的能力。
改进前后的电气量响应如图14所示。可以看到，故障后，原系统运行在经验设置下的VDCOL参数不合理，导致电流不断发生大幅波动，无法进入稳定运行点。在故障恢复阶段，发生了后续换相失败。而在动态无功控制策略下，直流电压可以更快恢复到额定值，直流电流波动幅度比原系统更小，故障期间无功交换量保持稳定，且未发生后续换相失败。
图14 改进前后的电气量响应（贵广Ⅱ）
Fig.14 Electrical response before and after improvement(Guiguang Ⅱ)
后续换相失败概率指标比较如图15所示，原系统在交流电压跌落量达到0.65(pu)左右开始发生后续换相失败，改进后系统则约为0.8(pu)。改进后系统在交流电压跌落更多时，才发生后续换相失败，说明改进的电流指令值对提升系统的换相失败抵御能力具有积极作用。
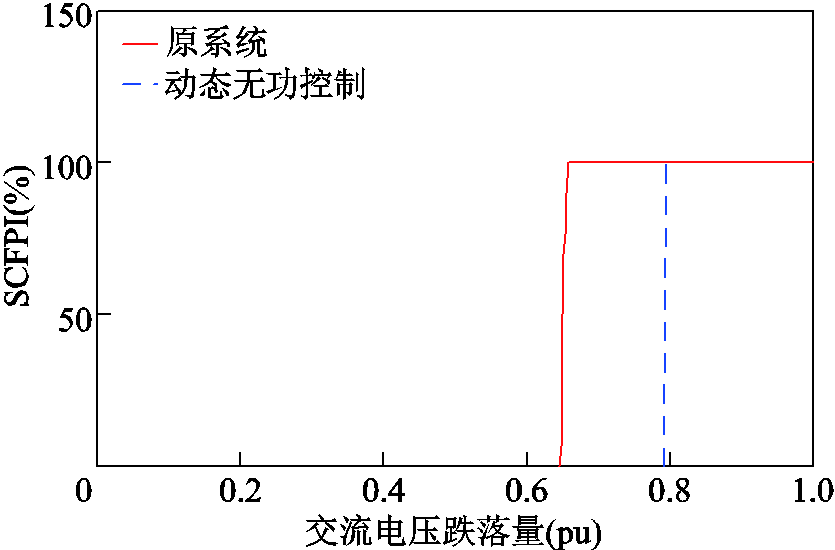
图15 后续换相失败概率指标比较（贵广Ⅱ）
Fig.15 Comparison of subsequent Commutation failure probability indices (Guiguang Ⅱ)
本文根据12脉动换流器正常工况下的运行要求，对准稳态下关断角、直流电流及无功功率的可运行范围进行了解析，为低压限流单元参数的设置提供了理论依据；提出了一种基于逆变站动态无功控制的后续换相失败抑制方法，通过对整流侧低压限流单元参数进行整定，并且在逆变侧根据换流母线电压及直流电流实时计算关断角参考值，对故障期间逆变站无功功率进行控制。在电磁暂态仿真程序PSCAD/EMTDC中以CIGRE高压直流标准测试模型及贵广Ⅱ回直流输电工程模型为算例，仿真验证了所提方法能够有效降低系统发生后续换相失败的概率，有效提高了系统的故障穿越能力。
本文主要研究了三相对称故障下的逆变站动态无功控制策略，针对单相接地故障的动态无功控制方法有待进一步展开。
参考文献
[1] 刘振亚, 张启平. 国家电网发展模式研究[J]. 中国电机工程学报, 2013, 33(7): 1-10, 25.
Liu Zhenya, Zhang Qiping. Study on the development mode of national power grid of China[J]. Proceedings of the CSEE, 2013, 33(7): 1-10, 25.
[2] 郑超, 汤涌, 马世英, 等. 直流参与稳定控制的典型场景及技术需求[J]. 中国电机工程学报, 2014, 34(22): 3750-3759.
Zheng Chao, Tang Yong, Ma Shiying, et al. A survey on typical scenarios and technology needs for HVDC participated into stability control[J]. Proceedings of the CSEE, 2014, 34(22): 3750-3759.
[3] 金璇, 杨万开, 徐永海. UHVDC分层接入方式谐波对换相失败影响的研究[J]. 电网技术, 2021, 45(9): 3763-3771.
Jin Xuan, Yang Wankai, Xu Yonghai. Commutation failure impacted by harmonics in UHVDC split connection grid system[J]. Power System Technology, 2021, 45(9): 3763-3771.
[4] 张艳霞, 卢静怡, 张富贺, 等. 基于临界故障时刻的换相失败预测方法[J]. 电网技术, 2021, 45(10): 4066-4075.
Zhang Yanxia, Lu Jingyi, Zhang Fuhe, et al. Commutation failure prediction considering critical fault moment[J]. Power System Technology, 2021, 45(10): 4066-4075.
[5] 邓瑜佳. 交直流混联系统换相失败下的保护与故障定位方法[D]. 成都: 西南交通大学, 2019.
[6] 屠竞哲, 张健, 曾兵, 等. 直流换相失败及恢复过程暂态无功特性及控制参数影响[J]. 高电压技术, 2017, 43(7): 2131-2139.
Tu Jingzhe, Zhang Jian, Zeng Bing, et al. HVDC transient reactive power characteristics and impact of control system parameters during commutation failure and recovery[J]. High Voltage Engineering, 2017, 43(7): 2131-2139.
[7] Shao Yao, Tang Yong. Fast evaluation of commutation failure risk in multi-infeed HVDC systems[J]. IEEE Transactions on Power Systems, 2018, 33(1): 646-653.
[8] 李培平, 姚伟, 高东学, 等. 基于电化学储能的多馈入直流系统暂态控制及影响因素分析[J]. 电工技术学报, 2021, 36(增刊1): 154-167.
Li Peiping, Yao Wei, Gao Dongxue, et al. Transient control and influencing factors analysis of multi-infeed HVDC system based on electrochemical energy storage[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 154-167.
[9] 王增平, 刘席洋, 郑博文, 等. 基于电压波形拟合的换相失败快速预测与抑制措施[J]. 电工技术学报, 2020, 35(7): 1454-1463.
Wang Zengping, Liu Xiyang, Zheng Bowen, et al. The research on fast prediction and suppression measures of commutation failure based on voltage waveform fitting[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1454-1463.
[10] 许汉平, 杨炜晨, 张东寅, 等. 考虑换相失败相互影响的多馈入高压直流系统换相失败判断方法[J]. 电工技术学报, 2020, 35(8): 1776-1786.
Xu Hanping, Yang Weichen, Zhang Dongyin, et al. Commutation failure judgment method for multi-infeed HVDC systems considering the interaction of commutation failures[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1776-1786.
[11] Sadek K, Pereira M, Brandt D P, et al. Capacitor commutated converter circuit configurations for DC transmission[J]. IEEE Transactions on Power Delivery, 1998, 13(4): 1257-1264.
[12] 张志文, 雷诗婕, 翟承达, 等. 高压直流输电系统吸收与并联电容换相换流器特性分析[J]. 电工技术学报, 2019, 34(增刊2): 684-691.
Zhang Zhiwen, Lei Shijie, Zhai Chengda, et al. The characteristic analysis of HVDC system with absorption and shunt capacitance commutated converter[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 684-691.
[13] Xue Ying, Zhang Xiaoping. Reactive power and AC voltage control of LCC HVDC system with controllable capacitors[J]. IEEE Transactions on Power Systems, 2016, 32(1): 753-764.
[14] 李辉, 王震, 周挺, 等. 含同步调相机的直流受端换流站全工况下多模式协调控制策略[J]. 电工技术学报, 2020, 35(17): 3678-3690.
Li Hui, Wang Zhen, Zhou Ting, et al. Multi-mode coordinated control strategy for DC receiving converter station with synchronous condenser under full operating conditions[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3678-3690.
[15] 杨欢欢, 朱林, 蔡泽祥, 等. 直流控制对直流系统无功动态特性的影响分析[J]. 电网技术, 2014, 38(10): 2631-2637.
Yang Huanhuan, Zhu Lin, Cai Zexiang, et al. Influence of HVDC control on HVDC reactive power dynamic characteristic[J]. Power System Technology, 2014, 38(10): 2631-2637.
[16] 王贺楠, 郑超, 任杰, 等. 直流逆变站动态无功轨迹及优化措施[J]. 电网技术, 2015, 39(5): 1254-1260.
Wang Henan, Zheng Chao, Ren Jie, et al. Dynamic reactive power trajectory of HVDC inverter station and its optimization measures[J]. Power System Technology, 2015, 39(5): 1254-1260.
[17] 郭春义, 李春华, 刘羽超, 等. 一种抑制传统直流输电连续换相失败的虚拟电阻电流限制控制方法[J]. 中国电机工程学报, 2016, 36(18): 4930-4937, 5117.
Guo Chunyi, Li Chunhua, Liu Yuchao, et al. A DC current limitation control method based on virtual-resistance to mitigate the continuous commutation failure for conventional HVDC[J]. Proceedings of the CSEE, 2016, 36(18): 4930-4937, 5117.
[18] 李瑞鹏, 李永丽, 陈晓龙. 一种抑制直流输电连续换相失败的控制方法[J]. 中国电机工程学报, 2018, 38(17): 5029-5042, 5300.
Li Ruipeng, Li Yongli, Chen Xiaolong. A control method for suppressing the continuous commutation failure of HVDC transmission[J]. Proceedings of the CSEE, 2018, 38(17): 5029-5042, 5300.
[19] 郑超, 马世英, 盛灿辉, 等. 以直流逆变站为动态无功源的暂态电压稳定控制[J]. 中国电机工程学报, 2014, 34(34): 6141-6149.
Zheng Chao, Ma Shiying, Sheng Canhui, et al. Transient voltage stability control based on the HVDC inverter station acting as dynamic reactive source[J]. Proceedings of the CSEE, 2014, 34(34): 6141-6149.
[20] 李瑶佳, 汪娟娟, 李子林, 等. 考虑高压直流输电系统无功特性的低压限流参数设置[J]. 电力系统保护与控制, 2017, 45(16): 16-23.
Li Yaojia, Wang Juanjuan, Li Zilin, et al. VDCOL parameters setting influenced by reactive power characteristics of HVDC system[J]. Power System Protection and Control, 2017, 45(16): 16-23.
[21] 黄梦华, 汪娟娟, 李瑶佳, 等. 高压直流定无功功率交流故障恢复方法[J]. 电力系统自动化, 2018, 42(3): 143-148.
Huang Menghua, Wang Juanjuan, Li Yaojia, et al. Constant reactive power control during AC fault recovery for HVDC[J]. Automation of Electric Power Systems, 2018, 42(3): 143-148.
[22] 汪娟娟, 黄梦华, 傅闯. 交流故障下高压直流运行特性及恢复策略研究[J]. 中国电机工程学报, 2019, 39(2): 514-523, 648.
Wang Juanjuan, Huang Menghua, Fu Chuang. Research on operational characteristics and recovery strategy of HVDC under AC fault[J]. Proceedings of the CSEE, 2019, 39(2): 514-523, 648.
[23] Wang Juanjuan, Huang Menghua, Fu Chuang, et al. A new recovery strategy of HVDC system during AC faults[J]. IEEE Transactions on Power Delivery, 2019, 34(2): 486-495.
[24] 汪家铭, 徐谦, 戴攀, 等. 基于无功反馈控制的后续换相失败抑制方法[J]. 电力系统自动化, 2021, 45(12): 101-108.
Wang Jiaming, Xu Qian, Dai Pan, et al. Suppression method of subsequent commutation failure based on reactive power feedback control[J]. Automation of Electric Power Systems, 2021, 45(12): 101-108.
[25] 刘磊, 林圣, 刘健, 等. 控制器交互不当引发后续换相失败的机理分析[J]. 电网技术, 2019, 43(10): 3562-3568.
Liu Lei, Lin Sheng, Liu Jian, et al. Mechanism analysis of subsequent commutation failures caused by improper interaction of controllers[J]. Power System Technology, 2019, 43(10): 3562-3568.
[26] 郑睿娜, 汪娟娟, 文兆新, 等. 基于交流故障快速检测的高压直流换相失败抑制方法[J]. 电网技术, 2022, 46(3): 851-859.
Zheng Ruina, Wang Juanjuan, Wen Zhaoxin, et al. A method based on fast fault detection of inverter-side AC system to suppress the commutation failure in HVDC system[J]. Power System Technology, 2022, 46(3): 851-859.
Abstract AC side fault is the main reason for commutation failure of HVDC system. In the process of AC fault occurrence or removal, or even system recovery, the reactive power impact caused by converter station to AC system is likely to cause subsequent commutation failure due to the influence of commutation bus voltage change and DC control. However, due to the long response time, reactive power compensation equipment is usually difficult to respond in time to suppress subsequent commutation failure, so it is often used as an auxiliary means. In recent years, many methods have been proposed to control the reactive power by optimizing the DC control mode, but most of them do not take into account the transmission delay between the rectifier side and the inverter side. In order to solve these problems, this paper proposes a two-terminal coordination control strategy based on dynamic reactive power control of the inverter station, taking the extinction Angle of the inverter station as the control quantity.
Firstly, the variation trend of reactive power of inverter with DC current and extinction angle is analyzed. The operating range of extinction angle, DC current and reactive power in quasi-steady state is analyzed.
Then, a method based on constant reactive power control of inverter to suppress the subsequent commutation failure is proposed.
By setting the new VDCOL(voltage dependent current order limitation) parameters on the rectifier, and calculating the reference value of the extinction angle in real time according to the AC bus voltage and DC current on the inverter, the reactive power of the inverter is controlled during AC fault.
On the one hand, the inverter side controls the reactive power of the inverter station by controlling the extinction Angle. When the AC bus voltage or DC current value detected by the inverter side changes, the reactive power switching capacity can be controlled in real time by directly changing the extinction Angle of the inverter side. The extinction Angle, DC voltage and inverter side AC voltage are coupled to each other and meet the constraints of quasi-steady state equation.
On the other hand, the operation range of DC current can be calculated according to the quasi-steady-state equation on the rectifier side, and according to the new current instruction given, it can meet the reactive power quantitative demand of the inverter side at the rated extinction Angle. The DC voltage measured by the rectifier side gives the DC current instruction in real time, which is no longer transmitted by the inverter side, so as to avoid the deterioration of the system performance caused by the transmission delay.
Finally, the CIGRE HVDC model and GuiGuang Ⅱ HVDC model in PSCAD/EMTDC are taken as examples. After the improvement, subsequent commutation failure occurs when AC fault is more serious, and the system recovers more smoothly. The results verify that the proposed method can effectively improve the system's support capability during AC fault and reduce the probability of subsequent commutation failure.
This paper mainly studies the dynamic reactive power control strategy of inverter station under three-phase symmetric fault, and the dynamic reactive power control method for single-phase ground fault needs to be further developed.
keywords：High voltage direct current(HVDC), reactive power, commutation failure, fault recovery
中图分类号：TM712
DOI:10.19595/j.cnki.1000-6753.tces.221109
国家自然科学基金资助项目（52277102）。
收稿日期 2022-06-14
改稿日期 2022-07-14
汪娟娟 女，1974年生，教授，博士生导师，研究方向为电力系统稳定与控制、高压直流输电等。E-mail：epjjwang@scut.edu.cn
郑睿娜 女，1997年生，硕士，研究方向为高压直流输电。E-mail：121803325@qq.com（通信作者）
（编辑 赫蕾）