基于不确定与扰动估计器的直流配电网电压鲁棒控制
林 莉1 范 米1 林雨露1 罗 皓1,2 王静芝1 谭惠丹1
(1. 雪峰山能源装备安全国家野外科学观测研究站(重庆大学) 重庆 400044 2.国网四川省电力公司经济技术研究院 成都 610041)
摘要 为保证在直流配电网母线电压鲁棒控制的同时,实现各源换流器之间电流的合理分配,基于不确定与扰动估计器(UDE)控制方法提出一种电压鲁棒控制策略,分别应用于直流配电网换流站级和换流阀级的控制。换流站级控制器设计重点在于解决负载电流参考值的给定和UDE控制的实现:将容量比引入下垂控制,提出考虑电流精确分配的负载电流参考值设定方法,该方法既充分考虑了各源换流器容量又避免了电流分配受线路参数影响的因素;以各源换流器输出电流能够渐进跟踪该参考值为控制目标,设计UDE控制律,这是实现电压鲁棒控制的关键。换流阀级控制方法应用UDE控制理论对电压源型换流器内环电流控制受到的不确定与扰动因素进行估计并补偿,设计了其UDE鲁棒控制律,证明UDE内环电流鲁棒控制器具有二自由度特性,且控制器参数解耦,简化了参数整定方法。改进后的控制器在提高电流控制抗扰性和鲁棒性的同时,解决了传统PI控制参数整定繁琐的问题。以三端直流配电网为例,对比仿真验证了所提策略的有效性。
关键词:直流配电网 电压鲁棒控制 不确定与扰动估计器 下垂控制 二自由度特性
0 引言
系统内功率平衡是直流配电网稳定运行的最基本要求,这一要求体现在直流电压的稳定。作为小惯性系统,直流系统参数的不确定性、系统外部扰动甚至是换流站投切、电源出力不稳定等都会导致直流母线电压失稳和负荷功率分配不均[1-4]。因此,有效地控制直流系统电压稳定、合理分配各个功率单元的电流是直流配电网稳定控制的关键。
直流系统以换流站为核心,按控制信息传输方向分为:直流系统调度级控制、换流站级控制、换流阀级控制。
直流配电网换流站级电压控制方法主要有三种:主从控制、电压下垂控制和电压裕度控制[5]。其中直流电压下垂控制是有差调节,通过负斜率特性调整直流电压与功率或电流之间的关系,从而实现对系统功率平衡的实时控制。对于多端换流站,直流电压下垂控制因其调节能力强、不需要站间通信系统,在直流配电网中得到了广泛应用[6-9]。但下垂系数受线路阻抗的影响,从而影响各换流站端口电压,进而影响系统负荷电流在各换流站之间的合理分配。这个不足是直流系统协调控制研究需解决的核心问题之一。文献[10]采用自适应比例积分(Proportional Integral, PI)控制器调节下垂电阻,以消除微电网中各单元的共流误差。文献[11]提出一种适用于直流微电网的二级控制技术,以分散方式控制直流母线电压,通过分布式策略实现精确的功率分配。文献[12]提出变下垂和移压两种方法来实现电压稳定和负载合理分配的控制目标。上述文献从不同角度对直流配电网的电压源型换流器(Voltage Source Converter,VSC)下垂控制作出了改进,都取得了一定的控制效果。但功率精确分配与直流母线电压之间的协调控制仍是一个值得探索研究的重要方向。
目前,换流阀级控制普遍采用电压、电流双闭环PI控制:外部电压环通常是一个PI控制器,调节直流母线电压并为内环提供参考电流;内环则用来调节交流电流以跟踪参考电流。该控制器结构简单,但控制参数具有耦合特性,整定较为繁琐,同时抗扰性较差,对系统参数不确定性与外部动态干扰较为敏感,难以满足系统在较大扰动情况下的稳定性要求[13-14]。针对VSC传统双环PI控制的不足,文献多对双环控制中的电流内环控制进行研究,以方便准确地调节直流母线电压。为了获得更好的输出性能和更强的鲁棒性,文献[15]分析了PI调节器参数对系统性能的影响,提出参数整定的具体方法,但整定方法较为繁琐。文献[16]提出最大d轴电压控制方法,提高了电流控制的响应速度。但上述改进方法仍然存在算法复杂、不易实现的问题。因此,对于VSC同步坐标系PI电流控制器的控制方法和参数整定方法仍待进一步研究。
不确定与扰动估计器(Uncertainty and Disturbance Estimator, UDE)控制方法能够快速估计系统不确定性动态和外部干扰,具有优良的鲁棒控制性能,可以应用于多种不同类型的系统,如不确定系统、非线性系统、时变系统和时滞系统[17-19]。文献[20]应用UDE控制方法对并联逆变器的下垂控制进行了改进,将系统干扰、模型的非线性和不确定性应用控制理论进行估计和补偿后,实现了并联逆变器功率分配不受逆变器输出阻抗的影响。文献[21]提出一种基于UDE的单相整流器鲁棒控制策略,以实现直流电压的精确调节。直流配电系统作为小惯性系统,存在直流系统建模及参数误差、系统故障等各种不确定与扰动,因此应用UDE理论解决不确定与扰动因素对直流母线电压稳定和换流站功率分配的影响,具有较好的研究前景和优势。
为提高直流配电网在各种工况下的电压跟踪性和抗扰性,同时实现负载电流的合理分配,本文首先针对换流站级传统下垂控制的不足,基于UDE控制理论提出了直流配电网VSC鲁棒下垂控制方法,核心是解决负载电流参考值的给定和UDE控制的实现。为提高换流阀级电流内环PI控制的抗扰性,设计了UDE内环电流鲁棒控制器,对于包括直流换流站投切、负荷变化、系统参数漂移、建模误差等在内的不确定性与扰动,该控制器可实现预测和补偿,具有较强的抗扰性和鲁棒性。同时,通过模型推导发现该控制器具有二自由度特性,两个核心参数解耦,进而提出了简便有效的参数整定流程。最后,通过仿真模拟直流配电网的运行工况,验证了所提控制策略的有效性。
1 换流站级UDE鲁棒下垂控制设计
UDE控制律的特点有[19]:①能够对控制系统包括与系统状态、控制输入相关的参数化误差及建模误差,以及系统未知扰动在内的、多种类别的不确定与扰动进行估计并补偿;②系统状态变量对参考状态变量具有较好的跟踪性。
为保证直流母线电压稳定在设定值下依然可以实现各源换流器负载电流的精确分配,且下垂控制器对直流配电网的各项扰动具备一定的鲁棒性,本节将基于UDE理论对下垂控制进行改进设计,控制器结构如图1所示。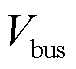 为公共直流母线实际电压值;
为公共直流母线实际电压值;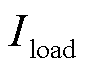 为公共直流母线上总负载电流,通过站间信息交换获取;
为公共直流母线上总负载电流,通过站间信息交换获取;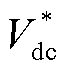 为直流配电网公共母线的电压设定值;
为直流配电网公共母线的电压设定值;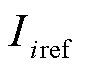 为第i个源换流器负载电流参考值;
为第i个源换流器负载电流参考值;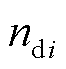 为第i个源换流器的下垂系数;
为第i个源换流器的下垂系数;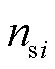 为第i个源换流器的容量比例系数;
为第i个源换流器的容量比例系数;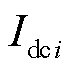 为各源换流器支路负载电流;
为各源换流器支路负载电流;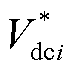 为第i个换流器输出电压参考值;
为第i个换流器输出电压参考值;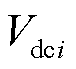 为第i个换流器输出电压;
为第i个换流器输出电压;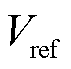 为双环控制的输入电压参考值。根据控制目标该控制器结构分为两部分:①负载电流参考值给定部分,其主要功能是根据下垂原理设定合理的负载电流参考值;②UDE控制部分,通过设计UDE控制律使得各源换流器的实际输出负载电流能够渐进跟踪负载电流参考值,同时能提供VSC电压外环控制所需的参考量。
为双环控制的输入电压参考值。根据控制目标该控制器结构分为两部分:①负载电流参考值给定部分,其主要功能是根据下垂原理设定合理的负载电流参考值;②UDE控制部分,通过设计UDE控制律使得各源换流器的实际输出负载电流能够渐进跟踪负载电流参考值,同时能提供VSC电压外环控制所需的参考量。
1.1 负载电流参考值的设定
在直流配电系统中,不同源换流器的等效下垂系数中通常含线路电阻,从而使得各源换流器之间负载电流的分配与线路电阻相关,这不仅影响了负载电流的分配精度,同时也将影响直流系统电压稳定控制能力。本文为减弱线路电阻的影响,提高系统功率分配精度,改善系统电压运行水平,将源换流器容量引入分配单元,由此设计出图1中负载电流参考值的控制律为
式中,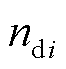 按各源换流器容量比例设定;
按各源换流器容量比例设定;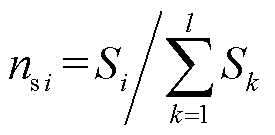 ,
,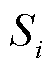 为第i个源换流器容量,
为第i个源换流器容量,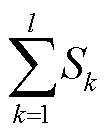 为参与运行的所有源换流器容量之和。
为参与运行的所有源换流器容量之和。
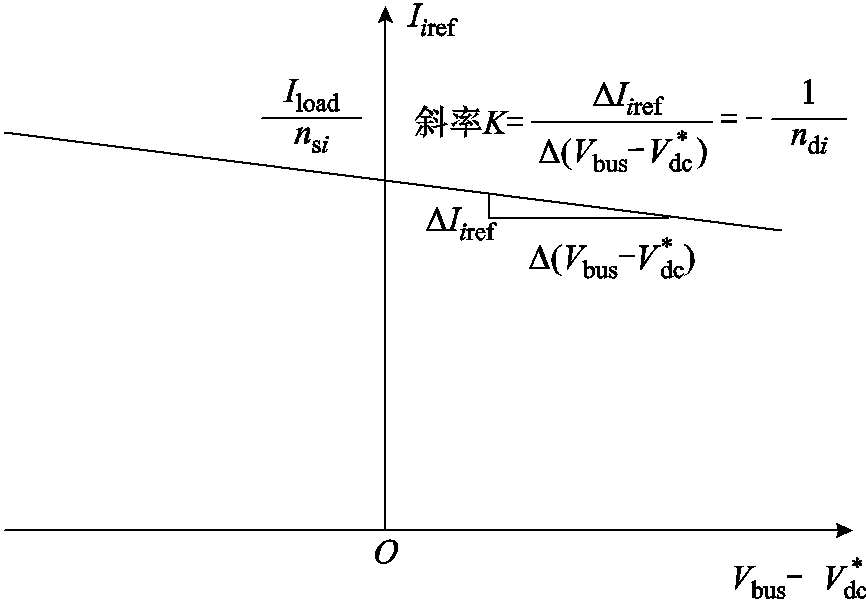
式(1)表达的源换流器参考负载电流的下垂控制特性如图2所示。当直流配电系统处于理想的稳态情况下运行时,公共直流母线电压实际值等于其设定值,此时各支路的负载电流参考值为
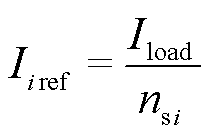 (2)
(2)
即负载电流参考值按容量比分配实际总负载电流。当系统出现小扰动,母线电压实际值出现偏差,根据下垂控制原理,若直流母线电压升高,则通过式(1)中的比例调节使得支路负载电流参考值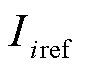 减小,直到直流母线电压
减小,直到直流母线电压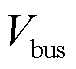 下降至设定值
下降至设定值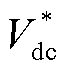 ,恢复到前述的系统理想稳态情况。
,恢复到前述的系统理想稳态情况。
1.2 UDE控制部分控制律的设计
UDE控制器设计的核心是:通过使用适当的滤波器,估计系统中存在的不确定与未知扰动信号,并将其用于合成实用的鲁棒控制器[19]。本节将设计基于UDE的鲁棒下垂控制律。
根据电路的基尔霍夫定律,各源换流器支路负载电流满足
式中,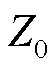 为支路总阻抗,是换流器输出阻抗
为支路总阻抗,是换流器输出阻抗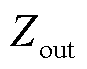 与线路阻抗
与线路阻抗 之和,即
之和,即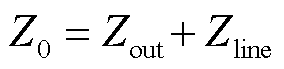 。
。
由于系统参数、模型测量参数等存在不确定以及干扰因素,故系统状态变量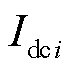 在进入UDE控制部分时需通过低通滤波器滤除高频不确定以及干扰量,即
在进入UDE控制部分时需通过低通滤波器滤除高频不确定以及干扰量,即
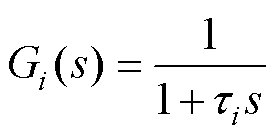 (4)
(4)
式中,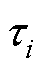 为时间常数。
为时间常数。
在控制过程中的不确定与扰动函数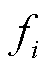 表达式可写为
表达式可写为
式中,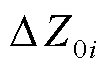 为第i个换流器支路总阻抗的不确定性与动态变化;
为第i个换流器支路总阻抗的不确定性与动态变化;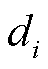 为系统参数不准确和系统未知扰动。
为系统参数不准确和系统未知扰动。
考虑低通滤波器以及不确定和干扰信号后,式(3)可改写为
式中, 为卷积符号;
为卷积符号;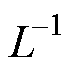 为拉普拉斯逆变换符号。
为拉普拉斯逆变换符号。
对式(6)两端同时求导可得支路负载电流的不确定动态模型为
式中,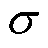 为系统的集总不确定与扰动,
为系统的集总不确定与扰动,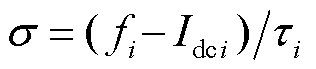 。
。
进一步地将式(7)移项改写为
根据UDE控制方法,选择合适带宽的滤波器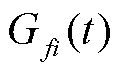 使不确定和扰动信号对应的频率成分通过,则
使不确定和扰动信号对应的频率成分通过,则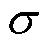 预测值为
预测值为
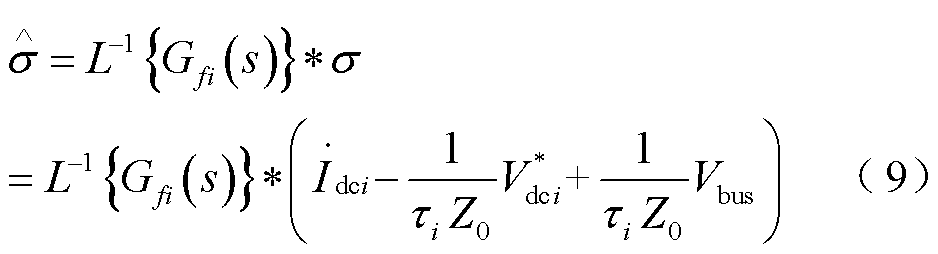
鲁棒下垂控制器的设计目标是:确保源换流器支路负载电流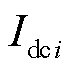 能渐进跟踪负载电流参考值
能渐进跟踪负载电流参考值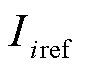 。设各源换流器支路负载电流的跟踪误差为
。设各源换流器支路负载电流的跟踪误差为
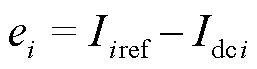 (10)
(10)
则满足UDE理论所需的动态方程[22]为
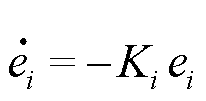 (11)
(11)
式中,Ki为误差反馈增益系数,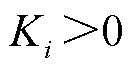 。
。
结合式(7)、式(10)和式(11)可得
将式(9)预测值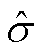 代替式(12)中的
代替式(12)中的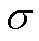 可得
可得
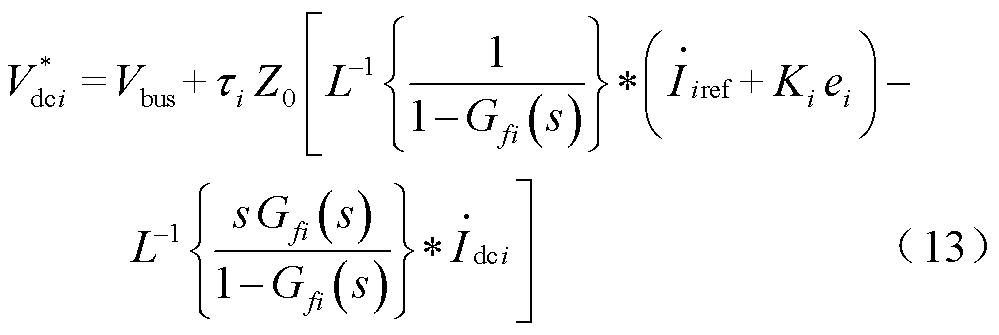
式(13)即为基于UDE的鲁棒下垂控制律,结合图1可知,提供系统参考指令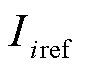 是该控制律能正常工作的必要条件之一,此参考指令由UDE鲁棒下垂控制器的负载电流参考值给定部分提供。同时,该控制律正常工作的另一必要条件是获得各源换流器支路负载电流
是该控制律能正常工作的必要条件之一,此参考指令由UDE鲁棒下垂控制器的负载电流参考值给定部分提供。同时,该控制律正常工作的另一必要条件是获得各源换流器支路负载电流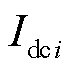 。
。
2 换流阀级UDE鲁棒控制策略
在换流阀级控制层,VSC一般采用电压外环和电流内环构成的双环控制。在内环电流控制环节运用传统PI控制,理论上能够实现零稳态误差的跟踪效果。然而,在直流配电网运行环境下产生的各种参数不确定性与系统扰动下,电流内环PI控制常表现出抗扰性能不佳,且通过试凑方法整定PI增益参数的过程繁琐。
为此,本节将应用不确定与扰动估计控制理论设计VSC内环鲁棒电流控制器,通过滤波器将参数误差、建模误差、外部未知干扰等不确定与扰动进行估计和补偿,使得控制器能够快速实现优越的鲁棒控制效果,即电流内环输出电流具有较好的跟踪性和抗扰性,进而提高对直流母线电压控制的稳定性。同时,该控制器具有二自由度特性,仅有两个不耦合的控制参数需整定,从而极大地简化了控制器参数整定过程。
2.1 VSC内环电流控制器的UDE动态模型
VSC内环电流控制部分在dq坐标系下的数学模型[23]为
式中,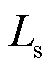 为交流侧等效电感与漏感;
为交流侧等效电感与漏感;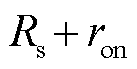 为交流侧等效电阻;
为交流侧等效电阻;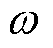 为交流系统角频率;
为交流系统角频率;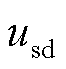 和
和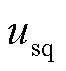 分别为dq坐标系下的交流源电压;
分别为dq坐标系下的交流源电压;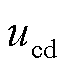 和
和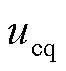 分别为VSC在dq坐标系下的控制信号;
分别为VSC在dq坐标系下的控制信号;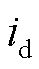 和
和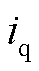 为交流侧电流分量。
为交流侧电流分量。
由式(14)建立VSC内环电流动态模型为[24]
式中,下标“0”表示该参数额定值;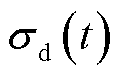 和
和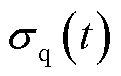 分别为d轴和q轴的集总不确定与扰动,可表示为
分别为d轴和q轴的集总不确定与扰动,可表示为
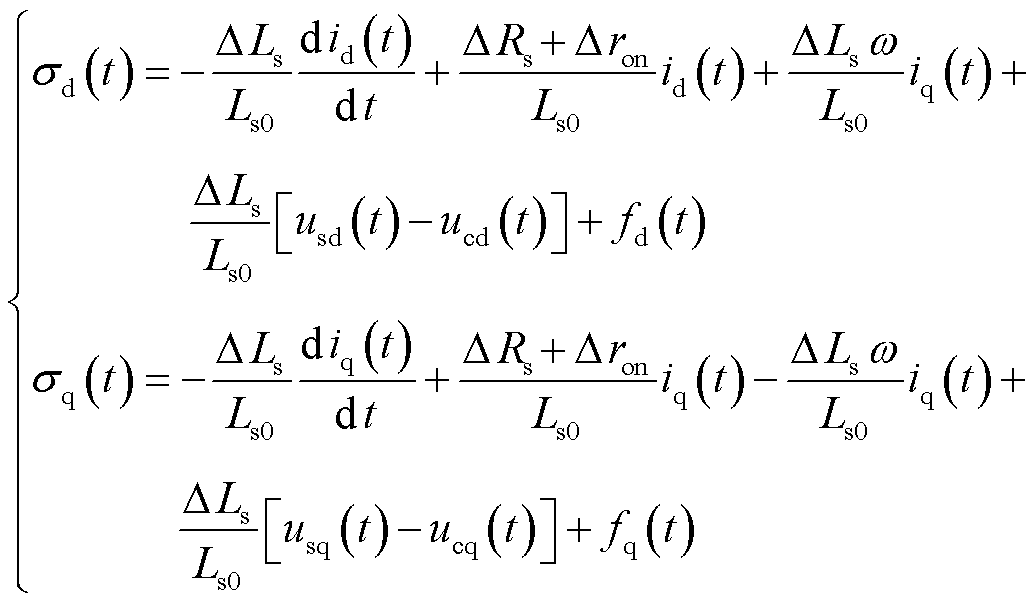 (16)
(16)
式中,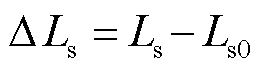 ;
;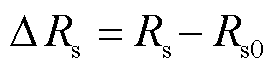 ;
;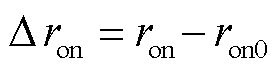 ;
;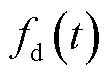 和
和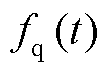 分别为d轴和q轴的未知扰动,统一表达为
分别为d轴和q轴的未知扰动,统一表达为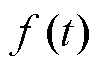 。
。
式(15)和式(16)一起构成VSC内环电流控制部分的状态空间表达式,即VSC内环电流控制部分的UDE动态模型,该模型考虑的不确定与干扰包括:与系统状态、控制输入相关的参数化误差及建模误差,如系统结构参数、系统状态id和iq、控制输入ucd和ucq等不确定性,以及系统的未知扰动,如电源/负荷变化、系统故障等对公共直流母线电压造成的难以预测的扰动。
2.2 控制参考模型设计及不确定与扰动估计
复杂的具有不确定和干扰的多变量线性时变系统状态空间模型[25]为
式中,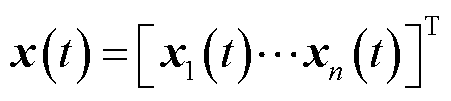 为系统状态向量;
为系统状态向量;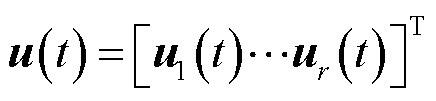 为控制输入向量;
为控制输入向量;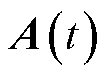 和
和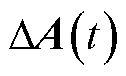 分别为已知和未知的状态矩阵,维数为n×n;
分别为已知和未知的状态矩阵,维数为n×n;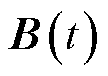 和
和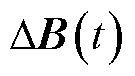 分别为已知和未知的控制矩阵,维数为n×r;
分别为已知和未知的控制矩阵,维数为n×r;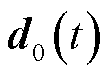 为已知扰动向量;
为已知扰动向量;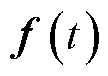 为未知扰动向量。
为未知扰动向量。
函数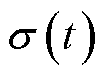 为集总不确定与扰动,包含不确定动态、非线性动态与未知扰动项[25],即
为集总不确定与扰动,包含不确定动态、非线性动态与未知扰动项[25],即
因此,式(17)可写为
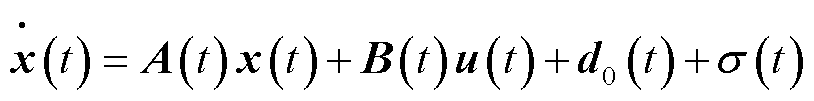 (19)
(19)
令状态矢量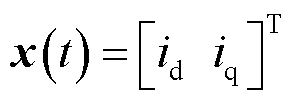 ,控制输入矢量
,控制输入矢量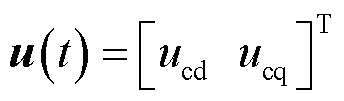 ,已知的外部干扰矢量
,已知的外部干扰矢量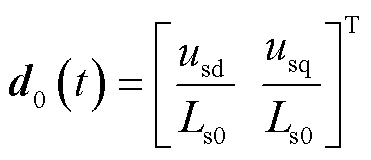 。对比式(15)与式(19)的系统状态空间模型,可得
。对比式(15)与式(19)的系统状态空间模型,可得
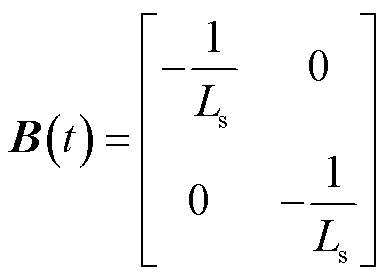 (21)
(21)
式中,A(t)、B(t)为常数矩阵,分别另记为A、B。
根据UDE控制理论,选择参考模型[26]为
式中,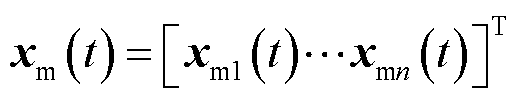 为参考状态向量;
为参考状态向量;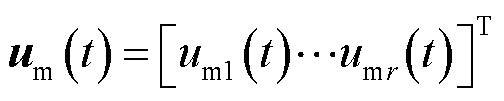 为系统参考指令;
为系统参考指令;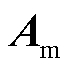 和
和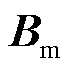 皆为常数矩阵,且
皆为常数矩阵,且
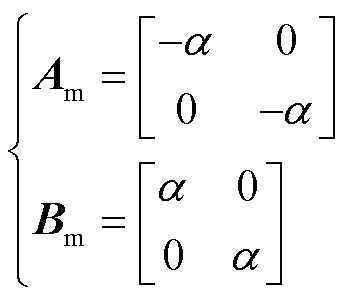 (23)
(23)
式中,α为滤波器带宽常数。
定义参考模型和系统模型间的误差为
UDE控制的设计目标是寻找一个控制律来获得期望的稳定的误差动态[19,26],有
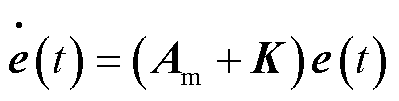 (25)
(25)
式中,K为误差反馈增益的常值矩阵。
因此,需确定一个控制输入矢量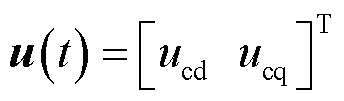 ,使得状态矢量
,使得状态矢量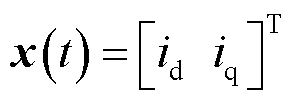 趋近于参考状态矢量
趋近于参考状态矢量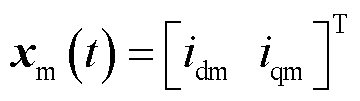 ,即跟踪误差渐进收敛为0。
,即跟踪误差渐进收敛为0。
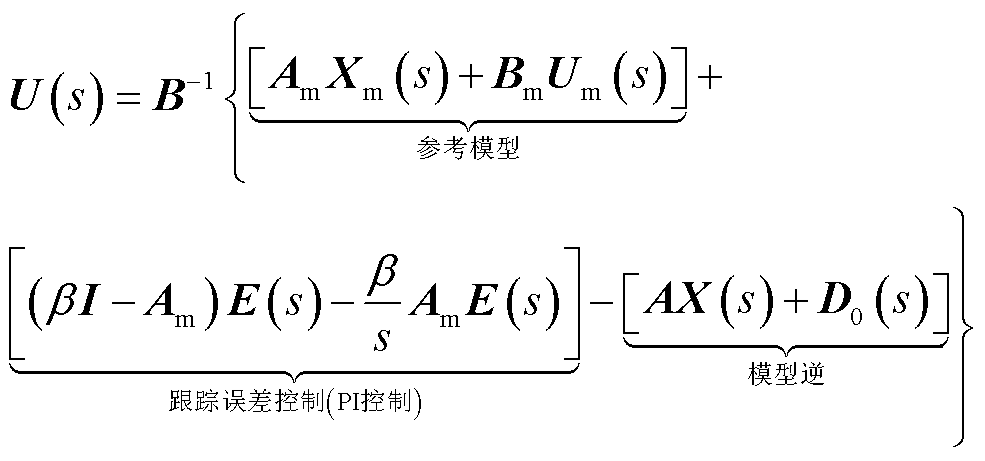
联立式(19)、式(22)、式(24)、式(25)可得控制输入矢量为
已知系统参考指令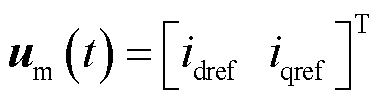 ,将VSC电流内环控制参考模型写作
,将VSC电流内环控制参考模型写作
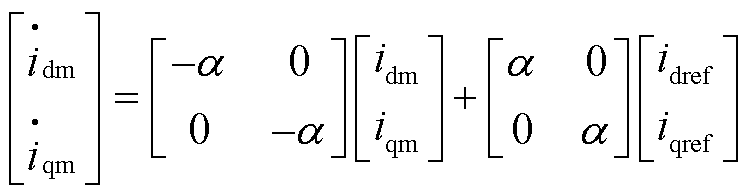 (27)
(27)
通常选择低通滤波器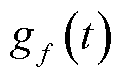 使不确定和扰动信号对应的频率成分通过,则
使不确定和扰动信号对应的频率成分通过,则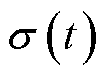 可被预测为
可被预测为
代入式(26)替代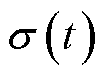 ,且设置矩阵K为零矩阵,则有
,且设置矩阵K为零矩阵,则有
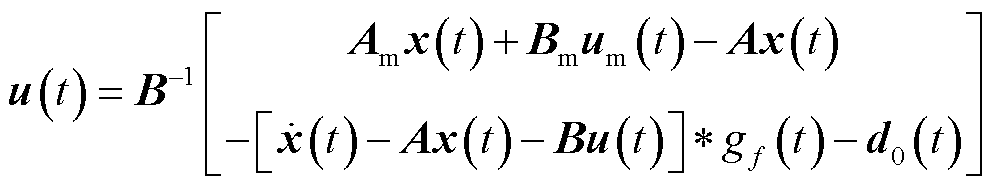 (29)
(29)
对式(29)求解可得到UDE时域控制律为
式中,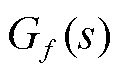 为带宽为β的低通滤波器。
为带宽为β的低通滤波器。
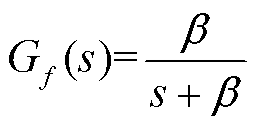 (31)
(31)
将式(30)的控制率进行拉普拉斯变换得到
其中
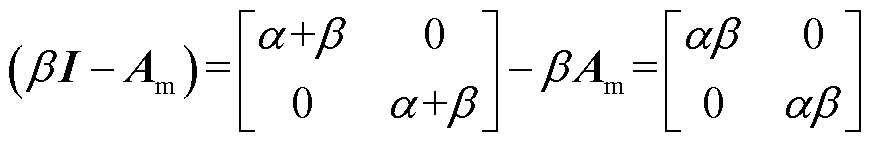 (33)
(33)
式中,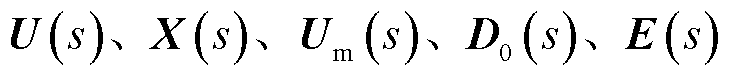 分别为
分别为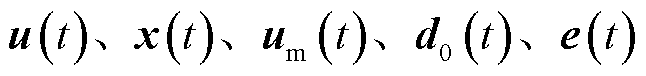 的拉普拉斯变换。
的拉普拉斯变换。
若令PI控制中比例系数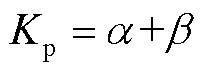 ,积分系数
,积分系数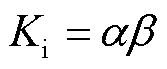 ,则跟踪误差
,则跟踪误差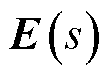 的控制律在形式上可以近似等效为PI控制。因此,由式(32)可知,基于UDE的VSC电流内环鲁棒控制律包括三个部分:①参考模型部分,为前馈微分形式,用于产生期望系统变量
的控制律在形式上可以近似等效为PI控制。因此,由式(32)可知,基于UDE的VSC电流内环鲁棒控制律包括三个部分:①参考模型部分,为前馈微分形式,用于产生期望系统变量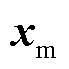 及其导数,同时加速暂态过程;②类PI控制器形式的跟踪误差控制部分,用来驱动系统的状态变量跟踪参考模型;③模型逆部分,用以补偿和对消模型中的已知动态部分。
及其导数,同时加速暂态过程;②类PI控制器形式的跟踪误差控制部分,用来驱动系统的状态变量跟踪参考模型;③模型逆部分,用以补偿和对消模型中的已知动态部分。
将式(33)代入式(32),整理后可得
2.3 控制器二自由度参数整定
2.3.1 控制器的二自由度特性
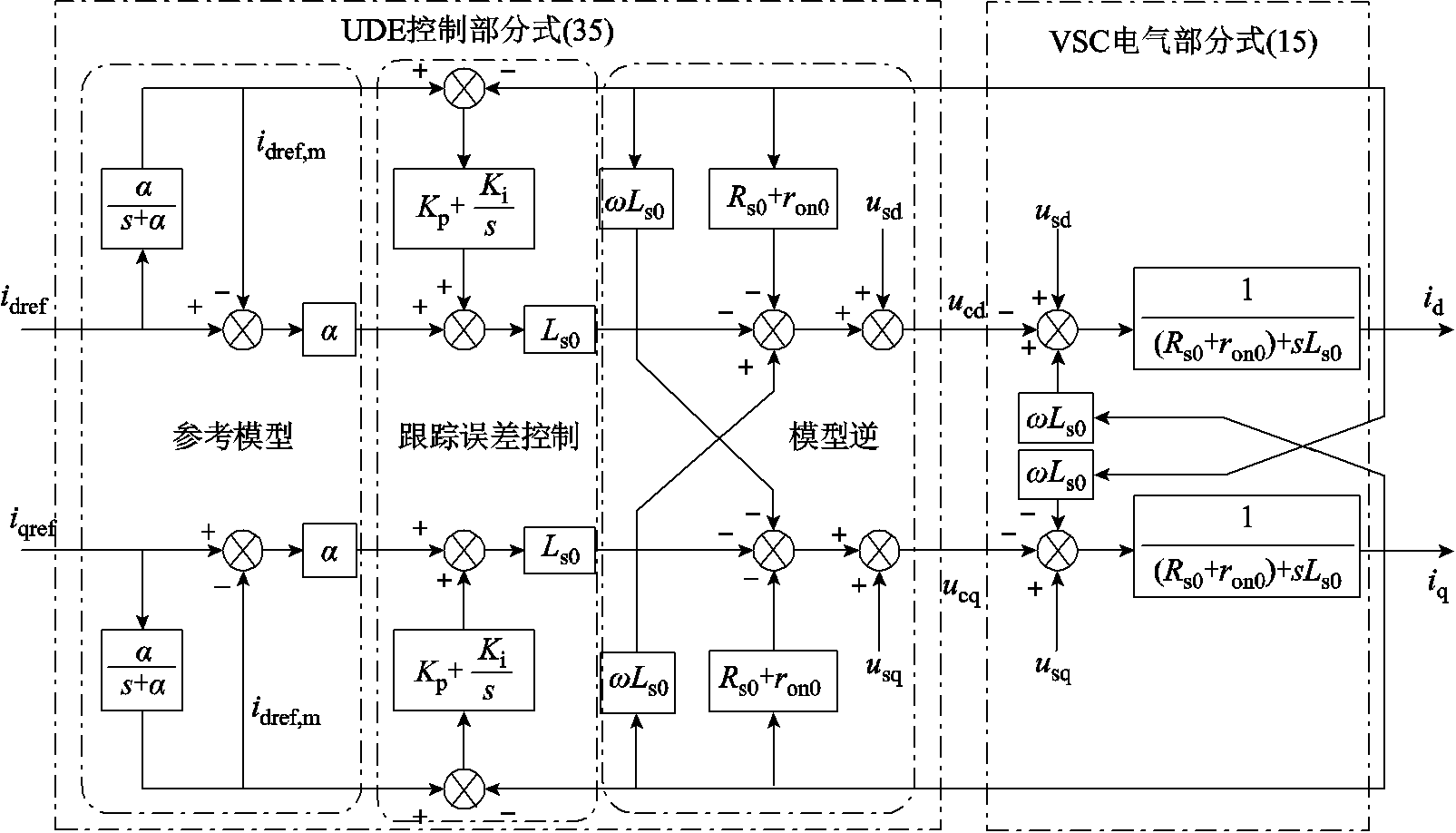
根据式(34)和图3可以看出,基于UDE理论设计VSC电流内环鲁棒控制器时,控制器参数整定仅涉及两个参数,即两个滤波器带宽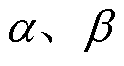 的选取。
的选取。
将式(26)、式(28)代入式(19)可得
两端进行拉普拉斯变换得到
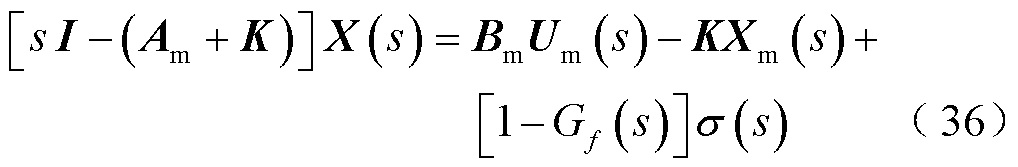
对式(22)进行拉普拉斯变换得
将式(37)代入式(36)可得
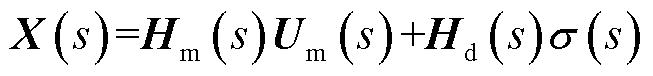 (38)
(38)
其中
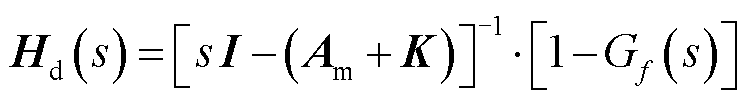 (40)
(40)
依据2.2节设计UDE电流内环鲁棒控制律时通常设矩阵K为零矩阵,代入式(39)和式(40)可得
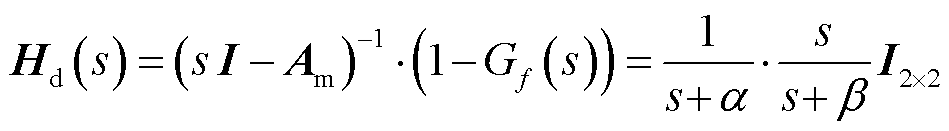 (42)
(42)
由此可给出式(38)对应的等效控制框图,如图4所示,图中,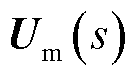 为系统参考指令,
为系统参考指令,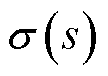 为集总不确定与扰动。
为集总不确定与扰动。
由图4可知,UDE控制在参考跟踪和干扰抑制之间可实现解耦控制,即体现了UDE控制律的二自由度特性。系统的期望点响应由参考模型决定,在选定了合适的参考模型后,模型参数α不变。系统干扰响应由滤波器Gf (s)决定,干扰信号先后经过一个带宽为α的低通滤波器和带宽为β的频率选择器得到两次抑制。
同时可知,二自由度的控制可通过选取两个带宽参数α和β来实现,两个参数在频域的控制效果互相解耦,不相互影响。这极大地简化了基于UDE的VSC鲁棒电流控制器的参数整定。
2.3.2 控制器二自由度参数整定流程
为实现VSC理想的内环电流控制效果,要求状态变量即内环电流输出量id、iq能较好地跟踪各自参考值的同时,还应减弱直流配电网系统中存在的集总不确定与扰动σ对控制输入ucd、ucq的影响。
由式(16)可知,VSC电流内环控制中存在的集总不确定与扰动共包括三项:直流配电网系统中存在的未知外部干扰、系统状态id和iq的未知不确定项、控制输入ucd和ucq的未知不确定项。因此集总不确定与扰动σ的频谱包括了这三项频谱。由此,UDE控制器的设计关键在于滤波器的带宽应覆盖集总不确定与扰动σ的频谱,否则可能因对σ估计不足而造成控制器的鲁棒性能有所降低。
α作为设计期望模型而提出的参数,由式(27)可知其本质为期望系统输出与其输入之间实现渐进的低通滤波器时间常数。又由式(32)得知,α的取值应尽量大,以保证系统的带宽和收敛速度,但α过大又可能使系统发散。β与设计的低通滤波器 Gf (s)有关。由式(42)和式(32)可知,提高β的取值有利于提高UDE的抗扰能力和等效PI调节的跟踪性能。
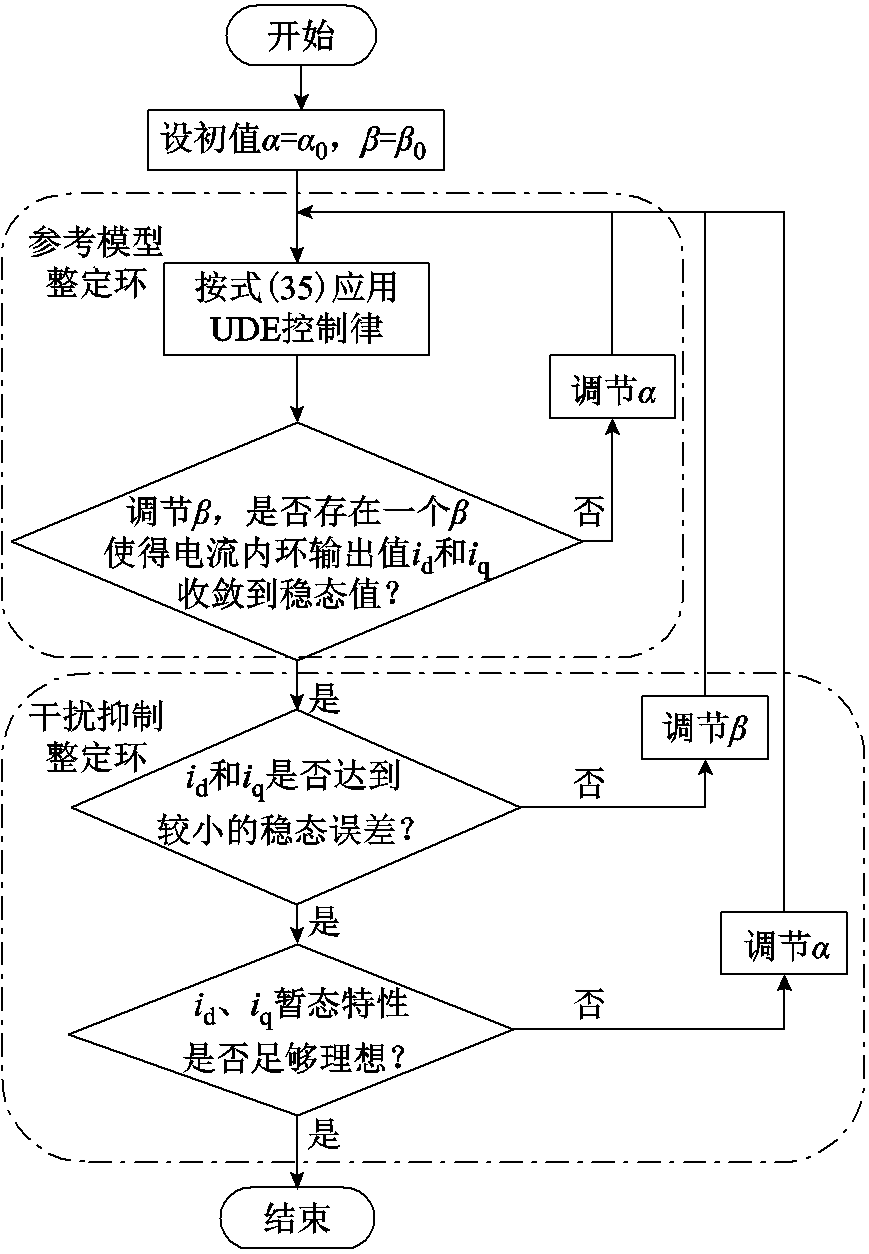
据此提出基于UDE的VSC电流内环鲁棒控制器参数二自由度整定流程如图5所示。参数整定时分为参考模型和干扰抑制两个整定环,且参数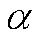 和β在频域的解耦特性,使得调参过程基本呈线性,各自整定最佳值时不会互相影响。
和β在频域的解耦特性,使得调参过程基本呈线性,各自整定最佳值时不会互相影响。
3 仿真验证
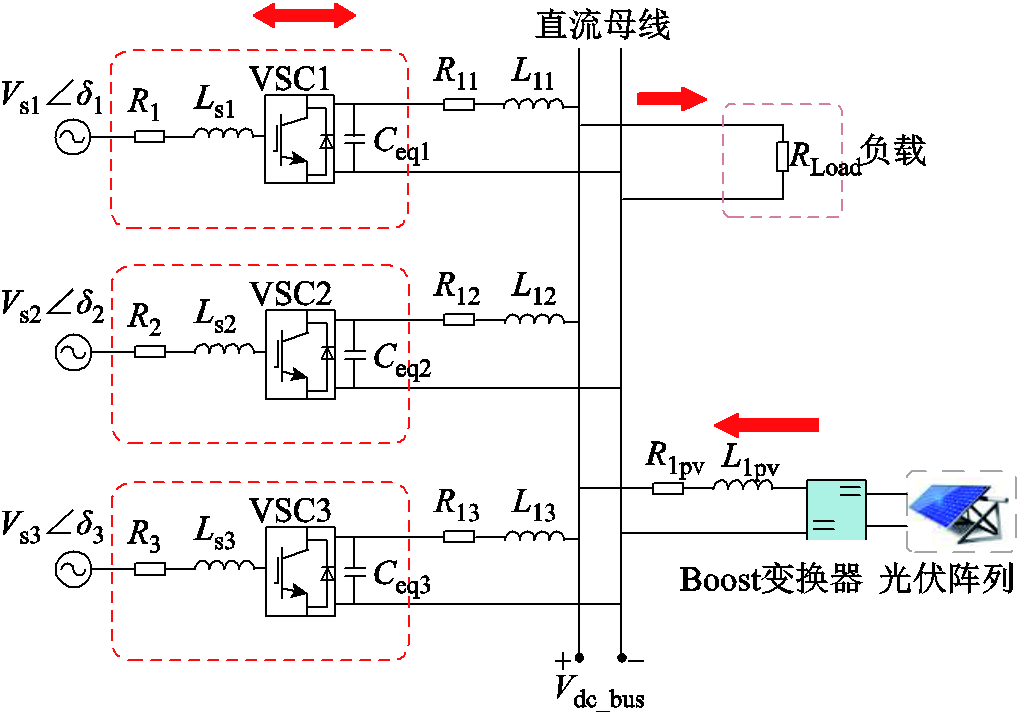
采用图6所示的典型三端直流系统[27]在PSCAD/EMTDC软件对比仿真验证本文设计的控制器效果。该系统主要分为三个区域:①VSC1、VSC2、VSC3分别与380 V、50 Hz的交流电网连接构成第一区域,通过传统下垂控制/UDE鲁棒下垂控制对换流器直流侧出口电流进行管理,以维持直流母线电压稳定;②第二区域为通过Boost升压直流变压器与直流母线相连的光伏模块,Boost换流器采用传统PI控制;③第三区域为无源负载。系统参数及控制器参数见表1~表3。
表1 仿真系统参数
Tab.1 System parameters
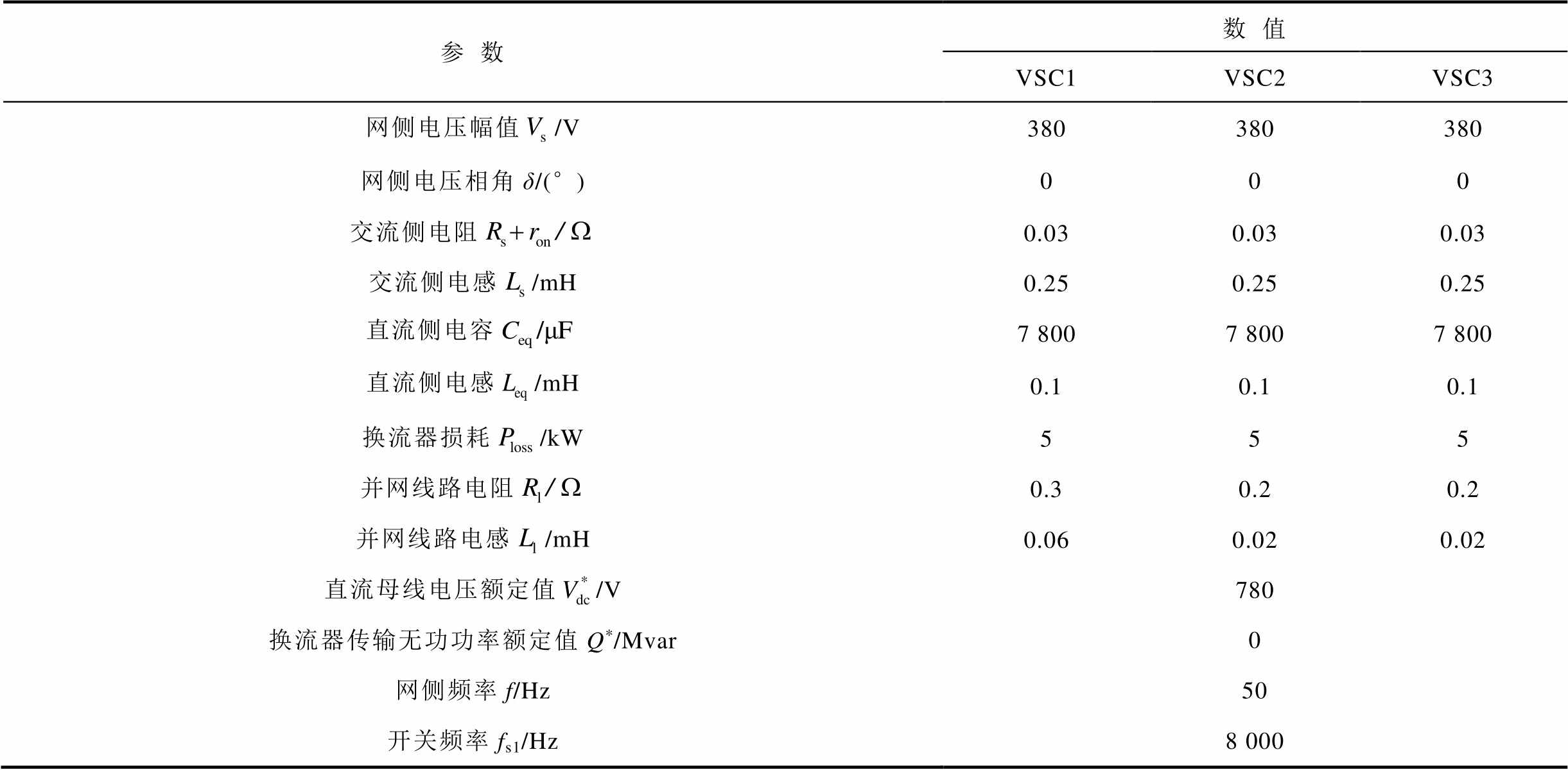
参数数值 VSC1VSC2VSC3 网侧电压幅值/V380380380 网侧电压相角δ/(°)000 交流侧电阻0.030.030.03 交流侧电感/mH0.250.250.25 直流侧电容7 8007 8007 800 直流侧电感/mH0.10.10.1 换流器损耗/kW555 并网线路电阻0.30.20.2 并网线路电感/mH0.060.020.02 直流母线电压额定值/V780 换流器传输无功功率额定值Q*/Mvar0 网侧频率f/Hz50 开关频率fs1/Hz8 000
表2 光伏系统仿真参数
Tab.2 Parameters of PV system

参数数值 温度T/℃20 辐射强度G/(W/m2)600 最大传输有功功率Ppvmax/MW0.5 滤波电感/mH0.1 滤波电容3 000 并网线路电阻0.2 并网线路电感/mH0.01 开关频率fs2/Hz3 600
表3 控制器仿真参数
Tab.3 Parameters of the controller

控制器环节参数数值 VSC内环(d轴)0.5 1/0.08 VSC外环(d轴)3.5 1/0.003 5 VSC内环(q轴)0.5 1/0.08 VSC外环(q轴)0.3 1/0.02 下垂控制环节d/(kV/kA)0.05 Boost变压器环节1 0.5
3.1 换流站级UDE鲁棒控制策略性能仿真
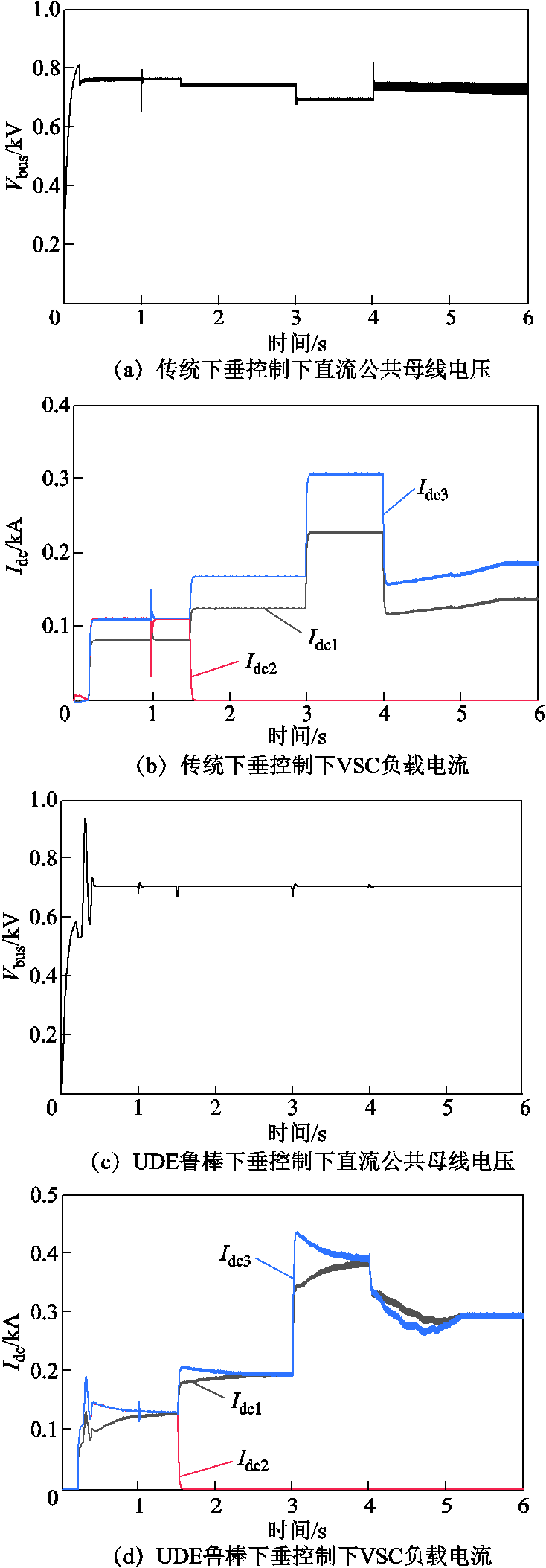
将传统下垂控制和UDE鲁棒下垂控制分别应用于各源换流器控制,对比仿真以验证本文提出的UDE鲁棒下垂控制对系统各源换流器的控制性能。仿真设置:系统总仿真时间为6 s,0.2 s时接入直流系统所有控制信号;1 s时VSC2的直流侧电容参数Ceq发生变化,变为15.6 mF;1.5 s时VSC2因故障退出系统运行;3 s时0.28 MW的阻性负荷接入直流公共母线;4 s时光伏单元接入直流公共母线。两种控制策略下的仿真结果如图7所示,图7a和图7b分别为传统下垂控制下直流公共母线电压和VSC负载电流,图7c和图7d分别为UDE鲁棒下垂控制下直流公共母线电压和VSC负载电流。
由图7a和图7c可看出,当直流系统启动后连续发生参数变化、VSC2退出、负荷增加、光伏单元接入扰动时,传统下垂控制下对应五个特征时段的直流母线电压稳态值分别为760.1、775.6、740.6、708.8、746.7 V,相比于额定电压780 V均出现较大变化。而UDE鲁棒下垂控制下五个特征时段的直流母线电压分别为780.07、780.03、780.06、778.50、780.07 V,略有振荡,但均能在较短时间内恢复到780 V附近。在所提的UDE鲁棒下垂控制方法作用下,扰动后的直流母线电压能快速恢复稳定,且稳态电压偏移小,显然,系统具有较好的抗扰性和稳定性,即系统电压控制具有较好的鲁棒性。
同时,对比图7b和图7d可分析两种控制策略对各VSC负载电流分配的控制能力。仿真时,各VSC负载电流的控制目标为按各自容量等比例分配。以1.5 s时刻VSC2退出运行为例,图7b中,对于相同容量的VSC1和VSC3,各自的负载电流分别稳定在0.124 6、0.169 3 kA直至第3 s即下一个扰动时刻,并未做到均流。表明传统下垂控制受线路阻抗不同等因素影响,无法实现负载电流按换流器容量比例精确分配。而在本文所提的UDE鲁棒下垂控制作用下,如图7d所示,当VSC2退出时,VSC1和VSC3的负载电流由1.5 s时刻的0.181 3、0.211 0 kA,于2.3 s调整到同一个电流值0.194 kA。表明所提鲁棒下垂控制器能使负载电流跟踪按容量等比例计算出的各支路负载电流参考值,从而达到电流精确分配的目的。而负载电流精确分配的实现有利于改善直流母线电压控制的鲁棒性。
3.2 换流阀级UDE鲁棒控制策略性能仿真
3.2.1 UDE内环鲁棒电流控制性能对比仿真
对于VSC电流内环控制器而言,控制效果直接体现在电流内环输出量id和iq的跟踪性和抗扰性。与此同时,对VSC控制器进行改进的根本目的是提高直流母线电压控制的鲁棒性,这是衡量电流内环控制器控制效果的另一指标。
图6所示的三端直流系统中,以任意一个VSC为研究对象,仿真验证本文所提UDE电流内环鲁棒控制方法与传统PI控制方法的控制效果。
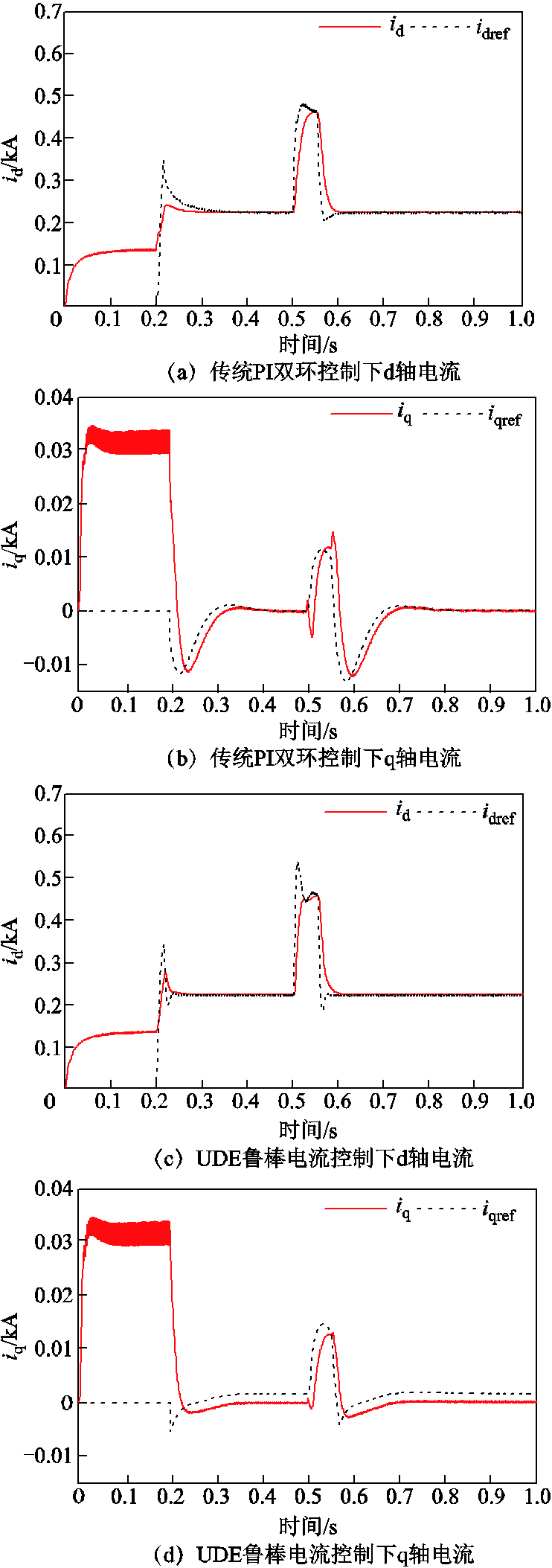
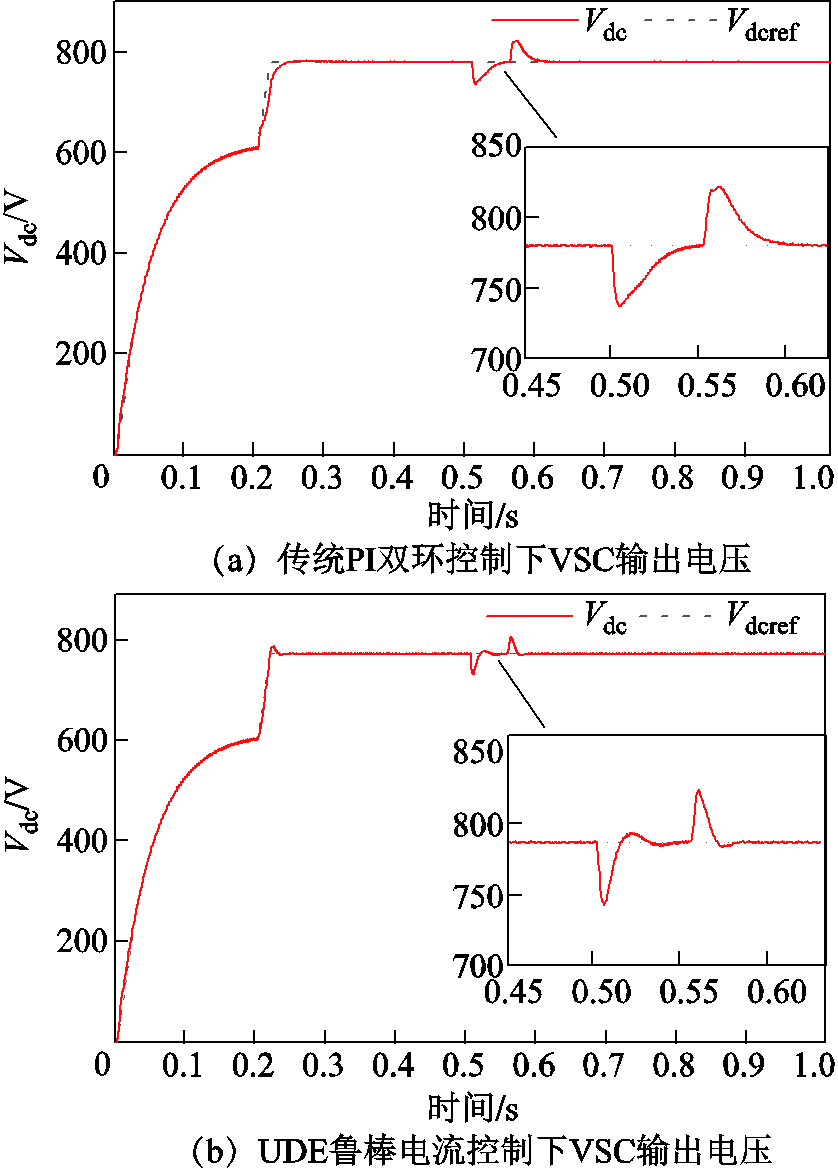
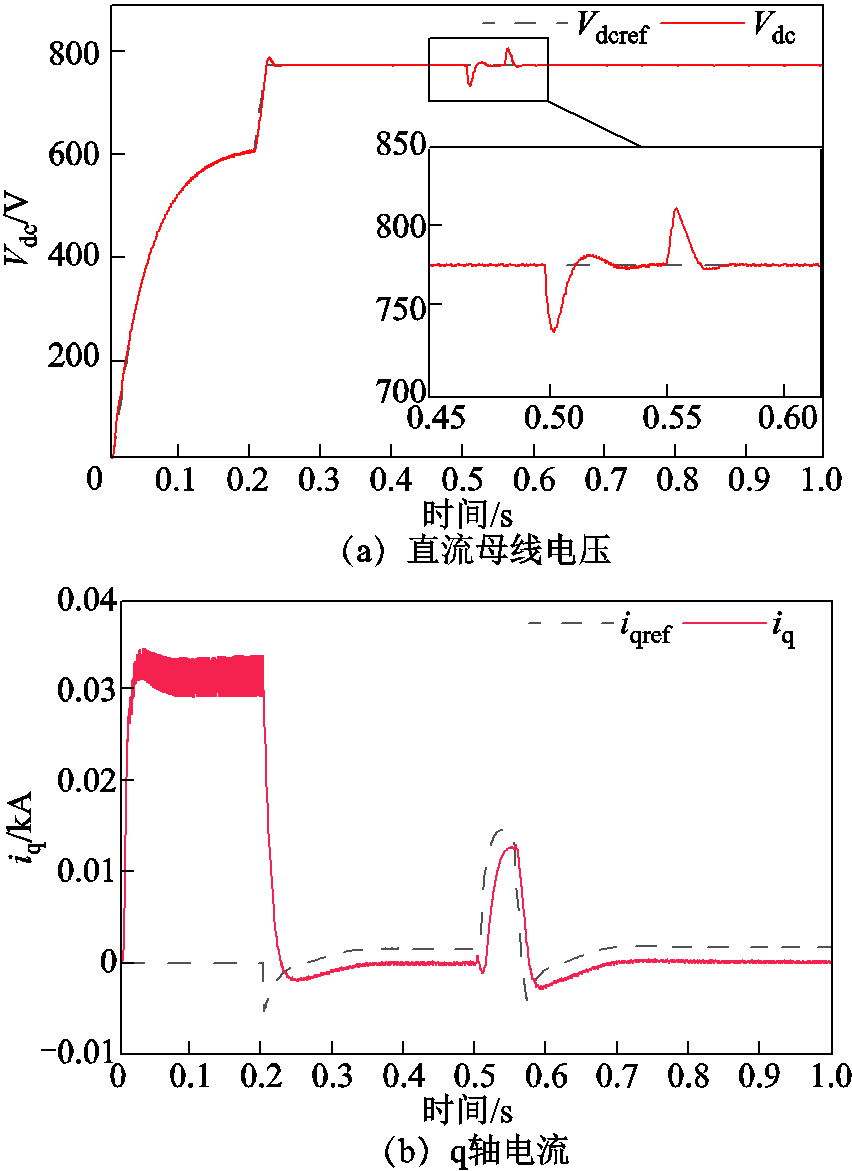
仿真设置:仿真总时长为1 s,0.2 s时接入直流系统的所有控制,0.2~0.5 s为系统正常运行区间,0.5~0.55 s为交流电网发生单相接地故障区间,0.55~1 s为故障恢复后的运行区间。PI控制器外环参数见表3,VSC电流内环UDE控制参数α=3 000 rad/s、β=3 000 rad/s。仿真结果如图8、图9所示。图8a和图8b分别为传统PI双环控制下d轴和q轴电流,图8c和图8d分别为UDE鲁棒电流控制下d轴和q轴电流。图9a和图9b分别为传统PI双环控制和UDE鲁棒电流控制下VSC输出电压。
从图8b和图8d可知,稳态情况下两种控制方法的q轴电流分量的跟踪性均在理想范围内,其原因是在VSC双环控制中q轴电流参考值设置为0 A。对于鲁棒性,在交流系统故障发生和消失的0.5 s、0.55 s时刻,传统PI控制的q轴电流峰值分别为0.014 8 kA和-0.013 kA,基于UDE的内环电流鲁棒控制分别为0.013 kA和-0.002 kA,实际q轴电流的波动范围明显小于前者,表明所设计的内环电流鲁棒控制的参考电流值和实际值的鲁棒性均明显优于传统PI控制。
从图8a和图8c可知,对于d轴电流,稳态情况下均有较好的跟踪性;在0.2 s控制接入时,相比于传统PI控制,UDE鲁棒控制短暂地出现了较高的峰值;但二者调整到稳态值的时刻分别为0.29 s和0.25 s,表明所提控制方法响应速度快。
由图9可以看出,电流内环在应用传统PI控制和UDE鲁棒控制时,直流母线电压虽有较小的稳态误差,但还是都能较好地跟踪期望的直流母线参考电压780 V。对于暂态特性,在交流电源端单相接地故障发生的0.5 s时刻和故障消除的0.55 s时刻,两种控制方法下直流母线电压回到电压稳态值的恢复时间分别为0.050 s和0.041 s,说明UDE内环鲁棒电流控制下表现出了更快的响应速度;故障发生后,对应0.5 s和0.55 s两个时刻的直流电压峰值,传统PI控制下为736.7 V和821.6 V,UDE内环鲁棒电流控制下为739.3 V和814.5 V,在故障后电压超调量方面二者区别不大。
由图8和图9三组波形对比说明,应用基于UDE的内环电流鲁棒控制后,故障出现和消除时刻对VSC电流内环输出量id和iq带来的影响被极大地削弱,所接入的直流母线电压的鲁棒性也明显提高。
3.2.2 二自由度带宽参数整定方法验证仿真
本节将仿真分析两个调节参数α和β对UDE电流内环鲁棒控制器的稳定性、跟踪性及暂态特性产生的影响,仿真设置同3.2.1节。
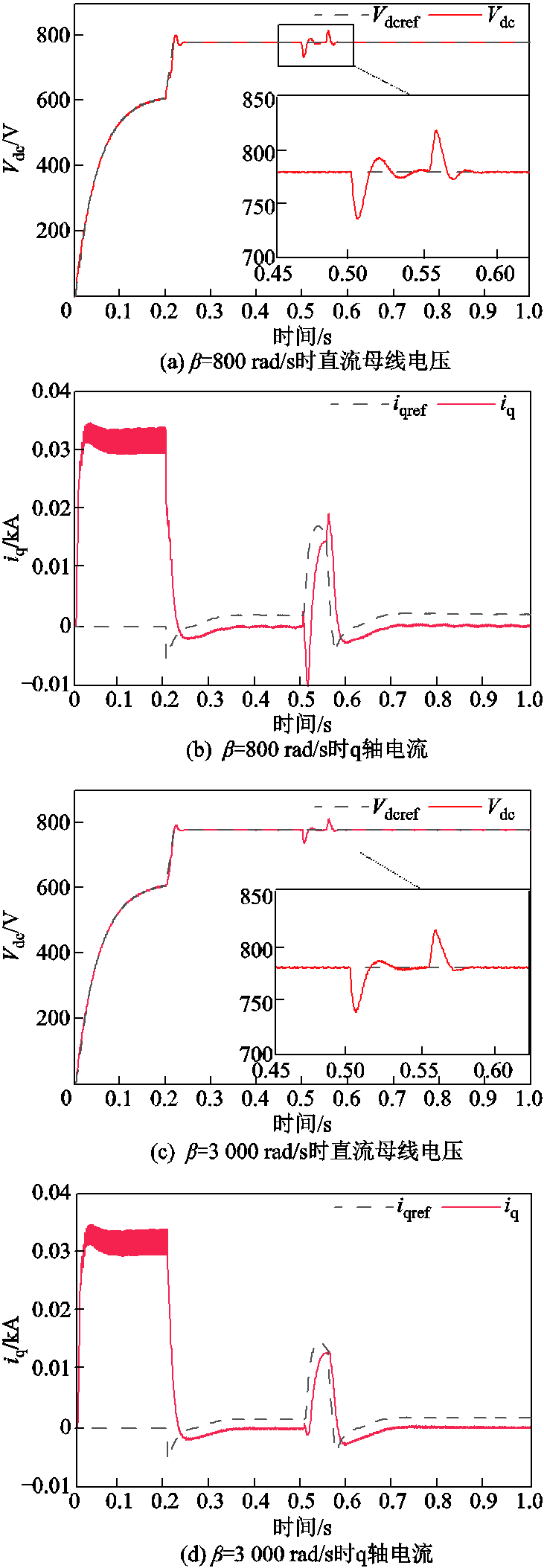
根据图5所示的二自由度带宽参数整定方法,第一步需针对参考模型整定环选定一个合适的α以保证控制系统的稳定。图10为α=800 rad/s调节β时的直流母线电压和q轴电流,图10a和图10b对应β=800 rad/s,图10c和图10d对应β=3 000 rad/s。
在α=800 rad/s的情况下,比较图10a和图10c,当交流系统在0.5 s发生故障时,β=800 rad/s下的直流母线电压在0.55 s故障消失前未达到稳态设定值,而增大β至3 000 rad/s时直流母线电压在0.55 s前可达到稳态设定值,表明在α一定的情况下,增大β有利于增强扰动过程中控制器调节的稳定性,改善暂态性能。当故障消失系统恢复稳态运行时,β=800 rad/s和β=3 000 rad/s下直流母线电压分别稳定在781.29 V和780.13 V,表明在α一定的情况下,增大β值可以使VSC获得更满意的电压跟踪控制效果。对比q轴电流波形,图10b和图10d所示第一个电流波峰值分别为-0.01 kA和0.013 2 kA,随着β值的增大,波形更加平稳,且电流的跟踪性能也在增强。显然,增大β有利于改善VSC的控制性能。
根据图5,当二自由度带宽参数整定进入到干扰抑制整定环后,其过程是取到合适的β值后,再调节α值以获得更加满意的控制效果。根据图10的仿真结果,为保障较好的控制效果,仿真选定β=3 000 rad/s,此时逐步增加α直至3 000 rad/s,仿真结果如图11所示。
在相同β下,对比图10c,图11a对应的直流母线电压稳态值为780.10 V,在跟踪性上优于前者;图11b所示的q轴电流在0.5 s受到交流系统短路扰动后,第一个电流波峰值为0.013 0 kA,小于图10d的0.013 2 kA,在选定β后增加α值可以获得更满意的跟踪性和暂态性。
同时,在对图10和图11的仿真过程中发现,α和β两个参数整定过程解耦,不会因一个参数的变化而影响另一个的最优值,避免了耦合参数整定时需要不断试凑的繁琐。
由此验证了前序理论分析得到的结论:UDE电流内环两个控制参数对系统性能均有调节作用,且调节效果解耦,所提的参数整定方法可行,调参便捷性优于传统PI控制的试凑法。
3.3 UDE综合鲁棒控制策略性能验证
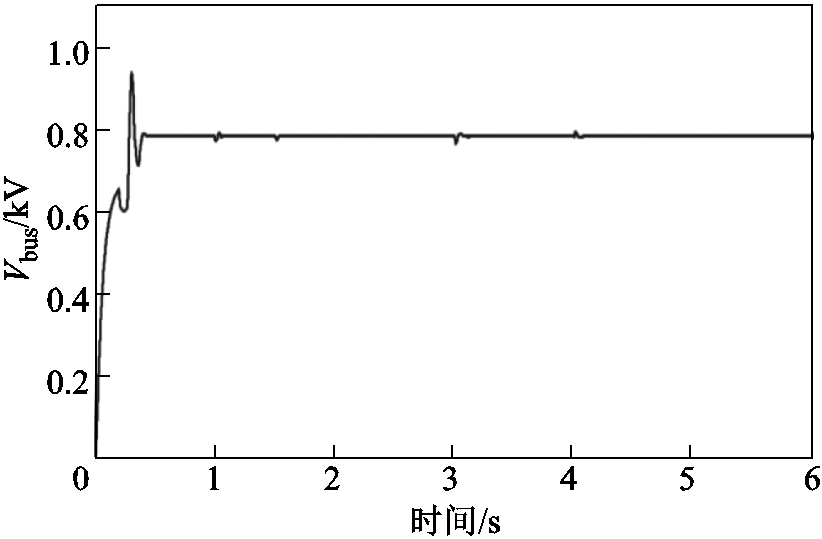
将本文所提的换流站级改进下垂控制和换流阀内环电流鲁棒控制同时应用于图6所示的三源直流配电网中,其仿真设置同3.1节,UDE综合鲁棒控制下的直流母线电压仿真曲线如图12所示。
对比图7c中应用传统PI内环电流控制、UDE鲁棒下垂控制的仿真结果,发现综合改进后的系统依然可保持直流母线电压的稳定性,电压维持在设定值780 V左右。尤其在0.2 s时刻各源换流器投入时直流母线电压振荡峰值有所降低,由图7c所示的传统PI内环电流控制的1.032 2 kV下降至图12中的0.931 5 kV,说明在应用UDE内环电流鲁棒控制器后,直流母线电压的抗干扰能力有所提高。再次验证了本文所提直流配电网综合鲁棒控制器在实现负荷电流精确分配的同时,对直流母线电压的控制也具有较好的鲁棒性。
4 结论
为提高不同工况下直流配电网电压稳定性,同时实现负载电流在各源换流器间的合理分配,借鉴UDE控制理论,本文分别从换流站级和换流阀级研究了直流配电网电压鲁棒控制方法,通过理论分析与仿真验证得到了以下结论:
1)在换流站级控制层,提出了基于UDE的鲁棒下垂控制方法,仿真结果表明,在VSC投切、系统参数变化等扰动工况下,所提控制方法可以实现各源换流器支路按容量等比例分配负载电流,相比于传统下垂控制具有更优越的负载电流分配性能,同时,对直流母线电压具有更好的鲁棒控制效果。
2)在换流阀级控制层,设计了基于UDE的VSC内环鲁棒电流控制器,并提出了控制参数的整定方法。对比受扰后直流母线电压、VSC内环输出电流仿真结果表明,所提控制器在扰动过程中不仅拥有优良的电流跟踪性能,同时在电压控制方面具有更强的抗干扰性和更好的动态性能。
本文围绕直流配电网的直流母线电压稳定性和负荷电流合理分配问题展开了研究,但仍存在一些未涉及或仍待后续研究解决的问题,如:在控制器设计时考虑控制信号的延时,设计系统时可考虑不同类型负载和分布式电源接入等。
参考文献
[1] 刘子文, 苗世洪, 范志华, 等. 基于自适应下垂特性的孤立直流微电网功率精确分配与电压无偏差控制策略[J]. 电工技术学报, 2019, 34(4): 795-806.
Liu Ziwen, Miao Shihong, Fan Zhihua, et al. Accurate power allocation and zero steady-state error voltage control of the islanding DC microgird based on adaptive droop characteristics[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 795-806.
[2] 周敏, 吕振宇, 王琦, 等. 直流配电网换流站分布式有功–电压二级优化控制策略[J]. 中国电机工程学报, 2020, 40(24): 8002-8011, 8237.
Zhou Min, Lü Zhenyu, Wang Qi, et al. Distributed secondary power and voltage optimal control strategy for converter station in DC distribution network[J]. Proceedings of the CSEE, 2020, 40(24): 8002-8011, 8237.
[3] 唐欣, 蔡明君, 唐惟楚, 等. 辐射型直流配电网母线电压跌落峰值的定量计算方法[J]. 电工技术学报, 2022, 37(12): 3108-3116.
Tang Xin, Cai Mingjun, Tang Weichu, et al. Quantitative calculation method of bus voltage sag peak value in radial DC distribution network[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3108-3116.
[4] 金国彬, 潘狄, 陈庆, 等. 考虑源荷不确定性的直流配电网模糊随机日前优化调度[J]. 电工技术学报, 2021, 36(21): 4517-4528.
Jin Guobin, Pan Di, Chen Qing, et al. Fuzzy random day-ahead optimal dispatch of DC distribution network considering the uncertainty of source-load[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4517-4528.
[5] 朱珊珊, 汪飞, 郭慧, 等. 直流微电网下垂控制技术研究综述[J]. 中国电机工程学报, 2018, 38(1): 72-84, 344.
Zhu Shanshan, Wang Fei, Guo Hui, et al. Overview of droop control in DC microgrid[J]. Proceedings of the CSEE, 2018, 38(1): 72-84, 344.
[6] 李忠文, 程志平, 张书源, 等. 考虑经济调度及电压恢复的直流微电网分布式二次控制[J]. 电工技术学报, 2021, 36(21): 4482-4492.
Li Zhongwen, Cheng Zhiping, Zhang Shuyuan, et al. Distributed secondary control for economic dispatch and voltage restoration of DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4482-4492.
[7] 支娜, 丁可, 黄庆辉, 等. 基于P-U下垂特性的虚拟直流电机控制策略[J]. 电工技术学报, 2021, 36(6): 1238-1248.
Zhi Na, Ding Ke, Huang Qinghui, et al. A virtual DC motor control strategy based on P-U drooping characteristics[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1238-1248.
[8] 李霞林, 郭力, 王成山, 等. 直流微电网关键技术研究综述[J]. 中国电机工程学报, 2016, 36(1): 2-17.
Li Xialin, Guo Li, Wang Chengshan, et al. Key technologies of DC microgrids: an overview[J]. Proceedings of the CSEE, 2016, 36(1): 2-17.
[9] 王宇彬, 杨晓东, 谢路耀, 等. 基于滑模控制的直流微电网一致性控制策略[J]. 电工技术学报, 2021, 36(增刊2): 530-540, 553.
Wang Yubin, Yang Xiaodong, Xie Luyao, et al. Consensus algorithm strategy of DC microgrid based on sliding mode control[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 530-540, 553.
[10] Mokhtar M, Marei M I, El-Sattar A A. An adaptive droop control scheme for DC microgrids integrating sliding mode voltage and current controlled boost converters[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 1685-1693.
[11] da Silva W W A G, Oliveira T R, Donoso-Garcia P F. Hybrid distributed and decentralized secondary control strategy to attain accurate power sharing and improved voltage restoration in DC microgrids[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 6458-6469.
[12] Wang Panbao, Lu Xiaonan, Yang Xu, et al. An improved distributed secondary control method for DC microgrids with enhanced dynamic current sharing performance[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6658-6673.
[13] 余希瑞, 周林, 郭珂, 等. 含新能源发电接入的电力系统低频振荡阻尼控制研究综述[J]. 中国电机工程学报, 2017, 37(21): 6278-6290.
Yu Xirui, Zhou Lin, Guo Ke, et al. A survey on low frequency oscillation damping control in power system integrated with new energy power generation[J]. Proceedings of the CSEE, 2017, 37(21): 6278-6290.
[14] 朱进权, 葛琼璇, 王晓新, 等. 基于自抗扰和负载功率前馈的高速磁悬浮系统PWM整流器控制策略[J]. 电工技术学报, 2021, 36(2): 320-329.
Zhu Jinquan, Ge Qiongxuan, Wang Xiaoxin, et al. Control strategy for PWM rectifier of high-speed maglev based on active disturbance rejection control and load power feed-forward[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 320-329.
[15] 汪万伟, 尹华杰, 管霖. 双闭环矢量控制的电压型PWM整流器参数整定[J]. 电工技术学报, 2010, 25(2): 67-72, 79.
Wang Wanwei, Yin Huajie, Guan Lin. Parameter setting for double closed-loop vector control of voltage source PWM rectifier[J]. Transactions of China Electrotechnical Society, 2010, 25(2): 67-72, 79.
[16] 钟炎平, 张勋, 陈耀军. PWM整流器电流快速动态响应控制研究[J]. 控制工程, 2016, 23(2): 269-272.
Zhong Yanping, Zhang Xun, Chen Yaojun. Research on fast transient response control of PWM rectifier[J]. Control Engineering of China, 2016, 23(2): 269-272.
[17] Zhong Qingchang, Rees D. Control of uncertain LTI systems based on an uncertainty and disturbance estimator[J]. Journal of Dynamic Systems, Measurement, and Control, 2004, 126(4): 905-910.
[18] Kuperman A, Zhong Qingchang. Control of uncertain linear systems with a state delay based on an uncertainty and disturbance estimator[J]. IFAC Proceedings Volumes, 2009, 42(6): 279-283.
[19] Tian Zhen, Zhong Qingchang, Ren Beibei, et al. Stabilisability analysis and design of UDE-based robust control[J]. IET Control Theory & Applications, 2019, 13(10): 1445-1453.
[20] Zhong Qingchang, Wang Yeqin, Ren Beibei. UDE-based robust droop control of inverters in parallel operation[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 7552-7562.
[21] Wang Yeqin, Dong Yiting, Ren Beibei, et al. UDE-based robust control for AC/DC converters[C]// IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 2018: 1550-1555.
[22] Ren Beibei, Zhong Qingchang, Chen Jinhao. Robust control for a class of nonaffine nonlinear systems based on the uncertainty and disturbance estimator[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5881-5888.
[23] 瞿博, 吕征宇. 三相电压型PWM整流器小信号建模及其控制器设计[J]. 电工技术学报, 2010, 25(5): 103-108.
Qu Bo, Lü Zhengyu. Small-signal modeling and controller design of three-phase voltage source PWM rectifier[J]. Transactions of China Electrotechnical Society, 2010, 25(5): 103-108.
[24] 张学, 裴玮, 邓卫, 等. 含恒功率负载的交直流混联配电系统稳定性分析[J]. 中国电机工程学报, 2017, 37(19): 5572-5582, 5834.
Zhang Xue, Pei Wei, Deng Wei, et al. Stability analysis of AC/DC hybrid distribution system with constant power loads[J]. Proceedings of the CSEE, 2017, 37(19): 5572-5582, 5834.
[25] Zhong Qingchang, Kuperman A, Stobart R K. Design of UDE-based controllers from their two-degree-of-freedom nature[J]. International Journal of Robust and Nonlinear Control, 2011, 21(17): 1994-2008.
[26] Stobart R K, Kuperman A, Zhong Qingchang. Uncertainty and disturbance estimator–based control for uncertain LTI-SISO systems with state delays[J]. Journal of Dynamic Systems, Measurement, and Control, 2011, 133(2): 493-502.
[27] 林莉, 马明辉, 金鑫, 等. 考虑VSC交直流侧瞬时功率的直流配网母线电压鲁棒控制策略[J]. 中国电机工程学报, 2021, 41(17): 5827-5842.
Lin Li, Ma Minghui, Jin Xin, et al. DC-bus voltage robust control of VSC considering the instantaneous power of AC-and DC-side in DC distribution network[J]. Proceedings of the CSEE, 2021, 41(17): 5827-5842.
Uncertainty and Disturbance Estimator-Based Control for Voltage Robust Controller in DC Distribution Network
Lin Li1 Fan Mi1 Lin Yulu1 Luo Hao1,2 Wang Jingzhi1 Tan Huidan1
(1. Xuefeng Mountain Energy Equipment Safety National Observation and Research Station Chongqing University Chongqing 400044 China 2. State Grid Sichuan Economic Research Institute Chengdu 610041 China)
Abstract The power system's power supply capacity, quality, and reliability can all be improved with the help of a DC distribution network, which also offers a practical and effective access interface for distributed energy. Therefore, the DC distribution network has become a development direction of power supply in the future. However, the DC distribution network is susceptible to system uncertainties and interference since it is a small inertial system, which leads to large fluctuations and even instability of the DC bus voltage. To address these issues, this paper proposes a voltage robust control strategy based on the uncertainty and disturbance estimator (UDE) control method, which is applied to the converter station level and converter valve level control of the DC distribution network, respectively.
At the converter station level, firstly, the capacity ratio of each converter station is introduced into the droop control, and the setting method of load current reference value is proposed to solve the influence of line impedance on load current distribution in the traditional droop control. Then, according to the UDE control theory, the uncertain dynamic model of the load current of each source converter branch is constructed. Finally, taking the load current output from each source converter can gradually track the reference value of the load current as the control objective, and the converter station level UDE robust droop control method is designed. At the converter valve level, firstly, the system state space model is constructed with the dq-axis current in the voltage source converter (VSC) inner loop as the state variable. Secondly, the dq-axis current reference vector is established according to the UDE standard model. Finally, to make the state vector of the dq-axis current tend to the reference vector, the control input vector is determined.
The simulation results of the three source DC distribution network system in PSCAD/EMTDC software show that, firstly, for the converter station level, under various disturbances, the minimum steady-state voltage of the disturbed DC bus is 740.6 V under the traditional droop control, which is a large deviation compared with the rated voltage of 780 V. When VSC2 suddenly exits, for VSC1 and VSC3 with the same capacity, their respective load currents are stable at 0.124 6 kA and 0.169 3 kA respectively, and current sharing is not achieved according to capacity. The lowest DC bus voltage under UDE robust droop control is 778.50 V, which is sTab.at the rated voltage of 780V. When VSC2 suddenly exits, the load current of VSC1 and VSC3 is finally adjusted to 0.194 kA, realizing current sharing. Then, at the converter valve level, when the AC system fails, compared with the traditional PI dual loop control and UDE robust current control, the corresponding DC bus voltage is 821.6 V and 814.5 V respectively. When the fault disappears, and the time for the system to recover to stability is 0.050 s and 0.041 s respectively. At the time of fault occurrence and disappearance, the peak value of q-axis current of traditional PI dual loop control is 0.0148 kA and -0.013 kA respectively, while that of UDE robust current control is 0.013 kA and -0.002 kA respectively, and the fluctuation range of q-axis current is smaller than the former.
The following findings can be drawn by the simulation analysis: (1) At the converter station level, the UDE robust droop control approach outperforms the conventional droop control method in terms of load current distribution and has a greater robust control impact on the DC bus voltage. (2) At the converter valve level, UDE robust current control has stronger anti-interference and better dynamic performance in voltage control in addition to good current tracking performance in the process of disturbance.
Keywords:DC distribution network, voltage robust control, uncertainty and disturbance estimator (UDE), droop control, two-degree-of-freedom characteristic
中图分类号:TM721
DOI:10.19595/j.cnki.1000-6753.tces.221012
收稿日期 2022-06-01
改稿日期 2022-08-08
作者简介
林 莉 女,1974年生,副教授,硕士生导师,研究方向为电力系统运行与控制。E-mail:linli@cqu.edu.cn(通信作者)
范 米 男,1996年生,硕士研究生,研究方向为直流配电网运行控制。E-mail:eamiyfan@163.com
(编辑 赫蕾)
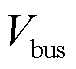 为公共直流母线实际电压值;
为公共直流母线实际电压值;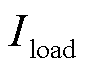 为公共直流母线上总负载电流,通过站间信息交换获取;
为公共直流母线上总负载电流,通过站间信息交换获取;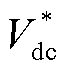 为直流配电网公共母线的电压设定值;
为直流配电网公共母线的电压设定值;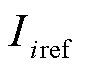 为第i个源换流器负载电流参考值;
为第i个源换流器负载电流参考值;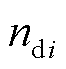 为第i个源换流器的下垂系数;
为第i个源换流器的下垂系数;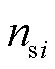 为第i个源换流器的容量比例系数;
为第i个源换流器的容量比例系数;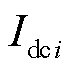 为各源换流器支路负载电流;
为各源换流器支路负载电流;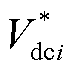 为第i个换流器输出电压参考值;
为第i个换流器输出电压参考值;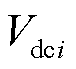 为第i个换流器输出电压;
为第i个换流器输出电压;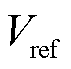 为双环控制的输入电压参考值。根据控制目标该控制器结构分为两部分:①负载电流参考值给定部分,其主要功能是根据下垂原理设定合理的负载电流参考值;②UDE控制部分,通过设计UDE控制律使得各源换流器的实际输出负载电流能够渐进跟踪负载电流参考值,同时能提供VSC电压外环控制所需的参考量。
为双环控制的输入电压参考值。根据控制目标该控制器结构分为两部分:①负载电流参考值给定部分,其主要功能是根据下垂原理设定合理的负载电流参考值;②UDE控制部分,通过设计UDE控制律使得各源换流器的实际输出负载电流能够渐进跟踪负载电流参考值,同时能提供VSC电压外环控制所需的参考量。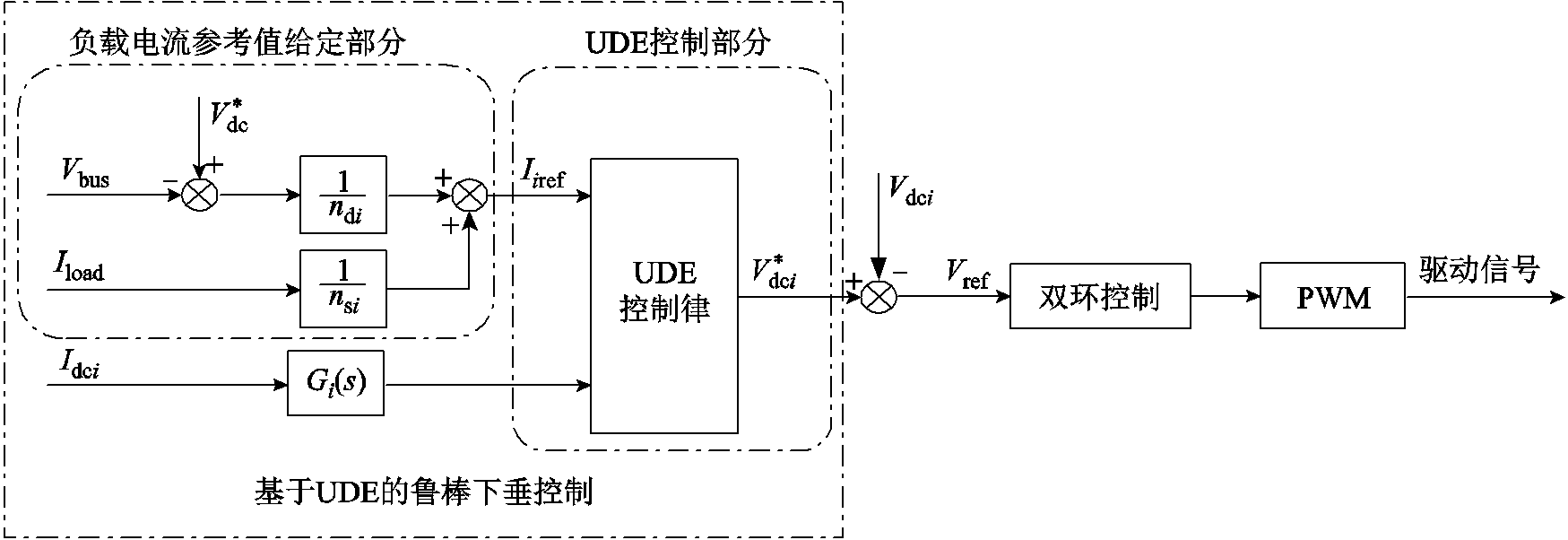
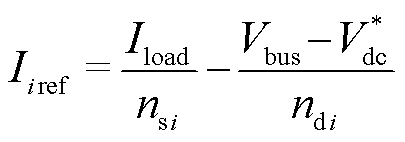 (1)
(1)
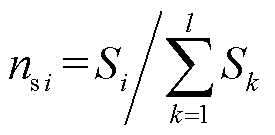 ,
,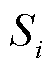 为第i个源换流器容量,
为第i个源换流器容量,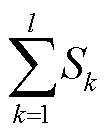 为参与运行的所有源换流器容量之和。
为参与运行的所有源换流器容量之和。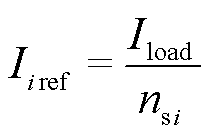 (2)
(2)
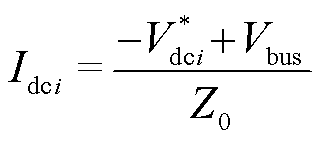 (3)
(3)
 为支路总阻抗,是换流器输出阻抗
为支路总阻抗,是换流器输出阻抗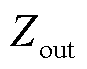 与线路阻抗
与线路阻抗 之和,即
之和,即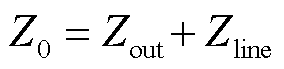 。
。 (4)
(4)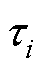 为时间常数。
为时间常数。 表达式可写为
表达式可写为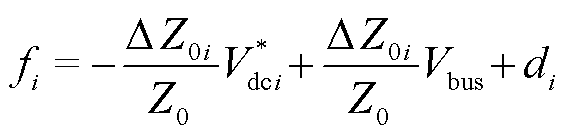 (5)
(5)
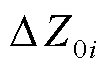 为第i个换流器支路总阻抗的不确定性与动态变化;
为第i个换流器支路总阻抗的不确定性与动态变化;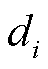 为系统参数不准确和系统未知扰动。
为系统参数不准确和系统未知扰动。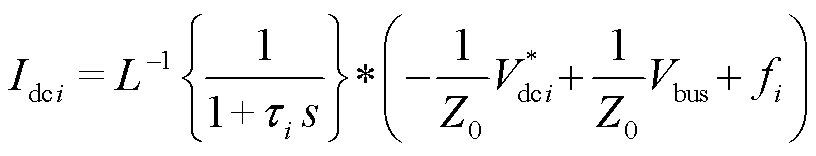 (6)
(6)
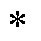 为卷积符号;
为卷积符号;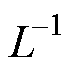 为拉普拉斯逆变换符号。
为拉普拉斯逆变换符号。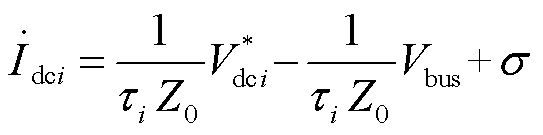 (7)
(7)
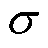 为系统的集总不确定与扰动,
为系统的集总不确定与扰动,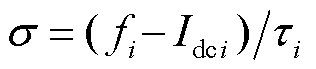 。
。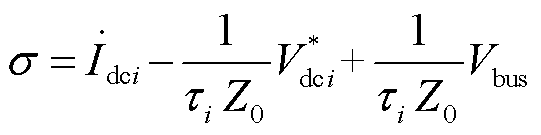 (8)
(8)
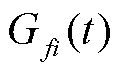 使不确定和扰动信号对应的频率成分通过,则
使不确定和扰动信号对应的频率成分通过,则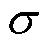 预测值为
预测值为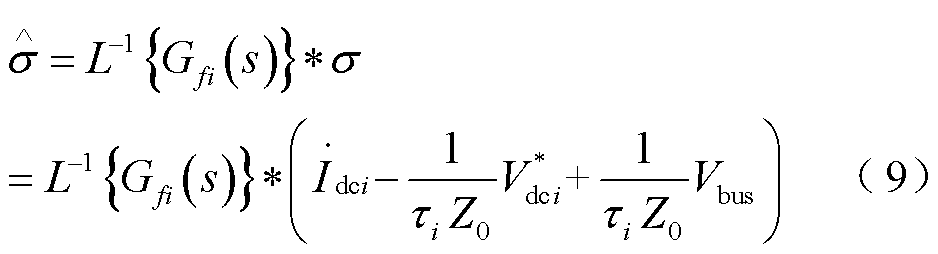
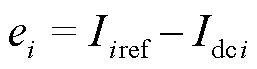 (10)
(10)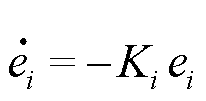 (11)
(11)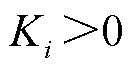 。
。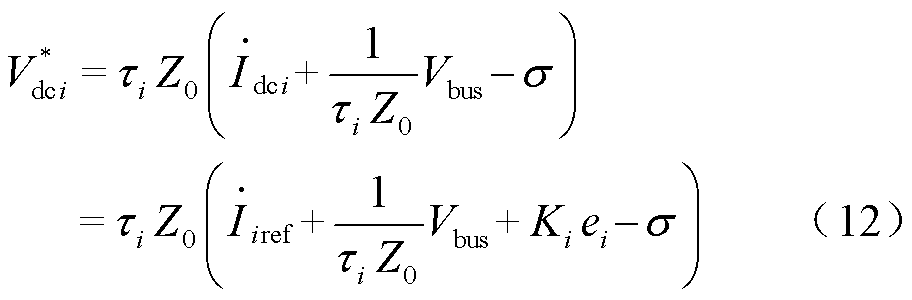
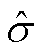 代替式(12)中的
代替式(12)中的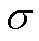 可得
可得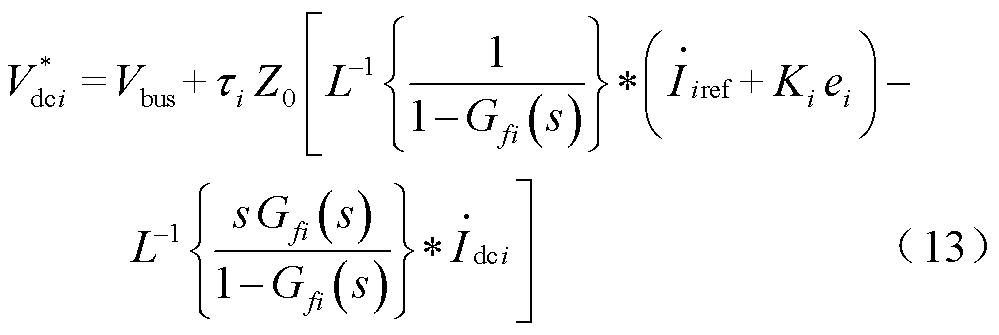
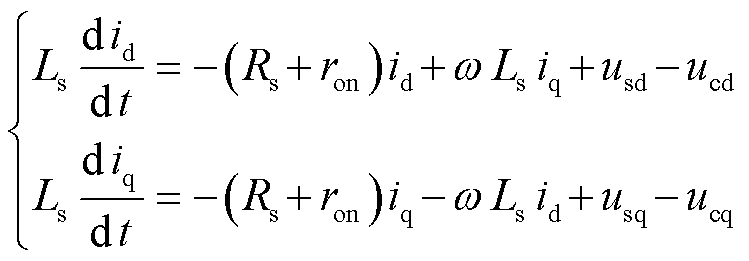 (14)
(14)
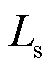 为交流侧等效电感与漏感;
为交流侧等效电感与漏感;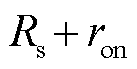 为交流侧等效电阻;
为交流侧等效电阻;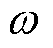 为交流系统角频率;
为交流系统角频率;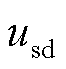 和
和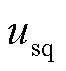 分别为dq坐标系下的交流源电压;
分别为dq坐标系下的交流源电压;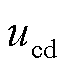 和
和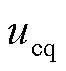 分别为VSC在dq坐标系下的控制信号;
分别为VSC在dq坐标系下的控制信号;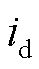 和
和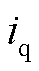 为交流侧电流分量。
为交流侧电流分量。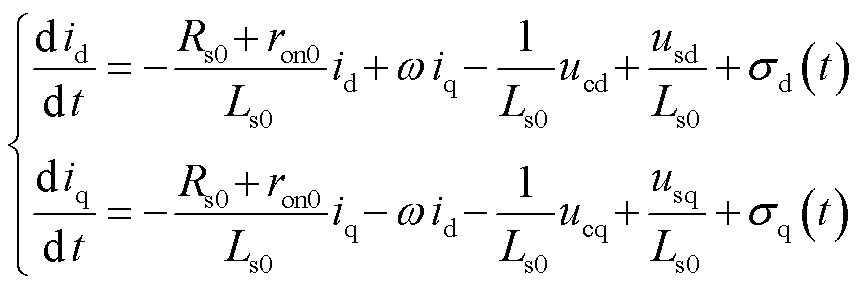 (15)
(15)
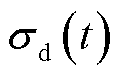 和
和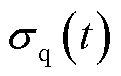 分别为d轴和q轴的集总不确定与扰动,可表示为
分别为d轴和q轴的集总不确定与扰动,可表示为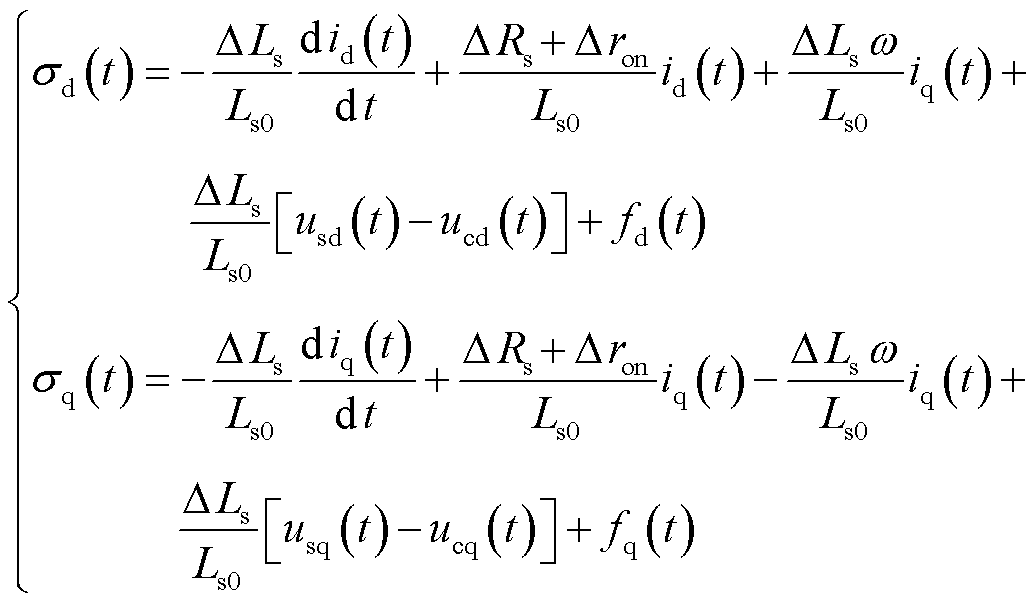 (16)
(16)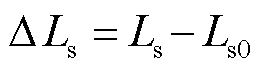 ;
;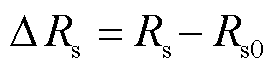 ;
;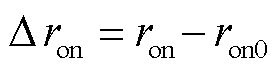 ;
;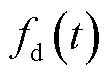 和
和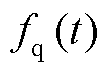 分别为d轴和q轴的未知扰动,统一表达为
分别为d轴和q轴的未知扰动,统一表达为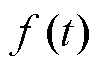 。
。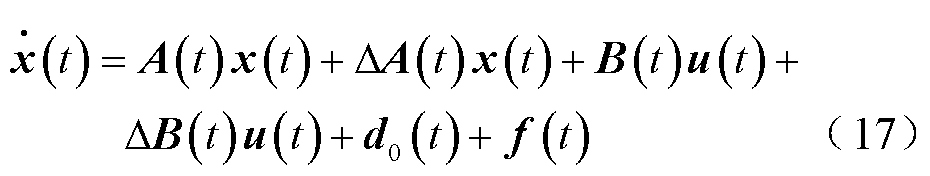
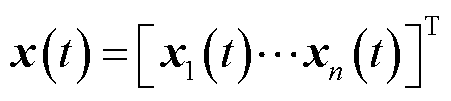 为系统状态向量;
为系统状态向量;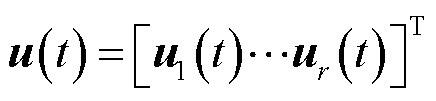 为控制输入向量;
为控制输入向量;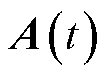 和
和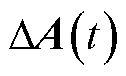 分别为已知和未知的状态矩阵,维数为n×n;
分别为已知和未知的状态矩阵,维数为n×n;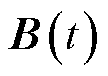 和
和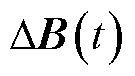 分别为已知和未知的控制矩阵,维数为n×r;
分别为已知和未知的控制矩阵,维数为n×r;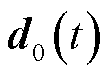 为已知扰动向量;
为已知扰动向量;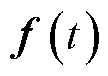 为未知扰动向量。
为未知扰动向量。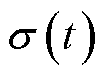 为集总不确定与扰动,包含不确定动态、非线性动态与未知扰动项
为集总不确定与扰动,包含不确定动态、非线性动态与未知扰动项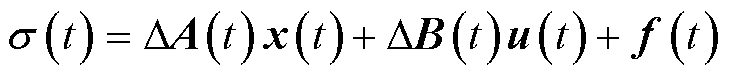 (18)
(18)
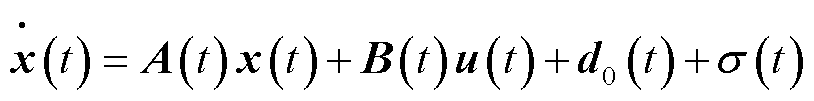 (19)
(19)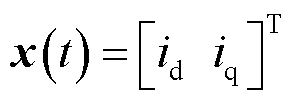 ,控制输入矢量
,控制输入矢量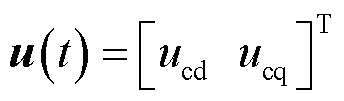 ,已知的外部干扰矢量
,已知的外部干扰矢量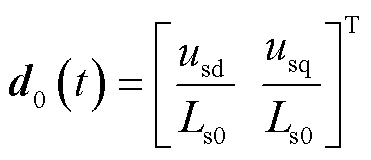 。对比式(15)与式(19)的系统状态空间模型,可得
。对比式(15)与式(19)的系统状态空间模型,可得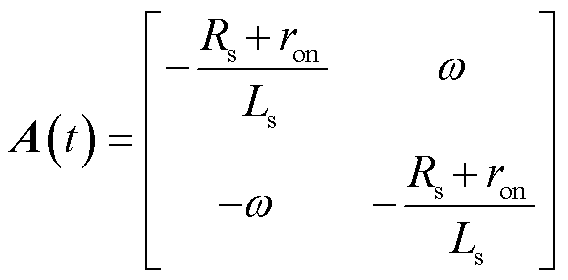 (20)
(20)
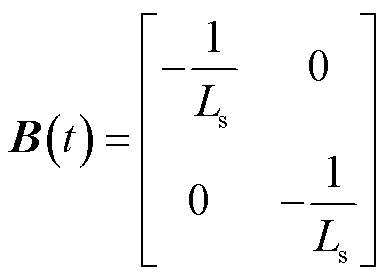 (21)
(21)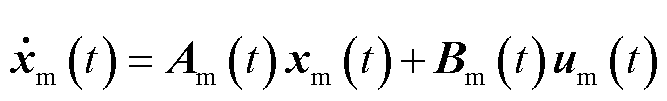 (22)
(22)
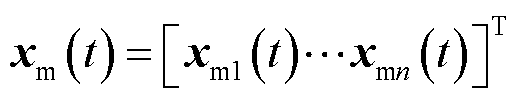 为参考状态向量;
为参考状态向量;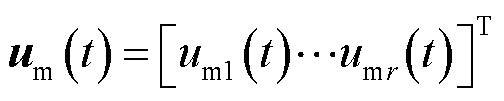 为系统参考指令;
为系统参考指令;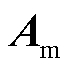 和
和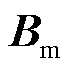 皆为常数矩阵,且
皆为常数矩阵,且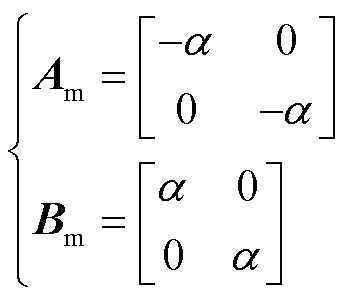 (23)
(23)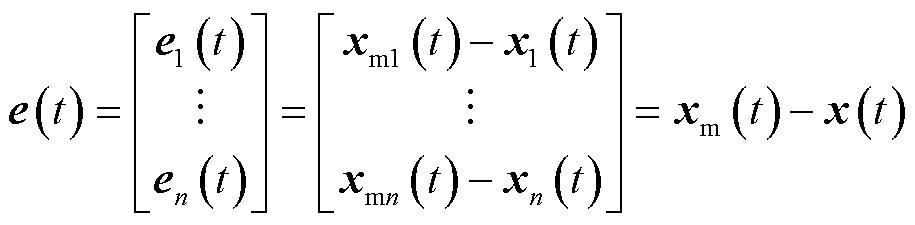 (24)
(24)
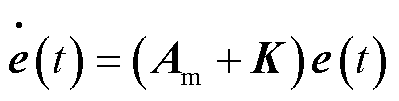 (25)
(25)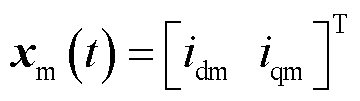 ,即跟踪误差渐进收敛为0。
,即跟踪误差渐进收敛为0。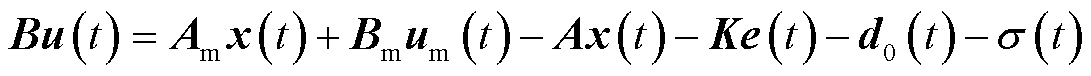 (26)
(26)
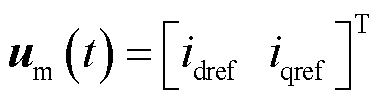 ,将VSC电流内环控制参考模型写作
,将VSC电流内环控制参考模型写作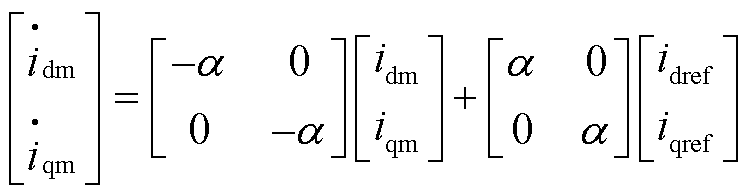 (27)
(27)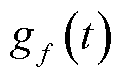 使不确定和扰动信号对应的频率成分通过,则
使不确定和扰动信号对应的频率成分通过,则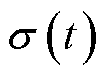 可被预测为
可被预测为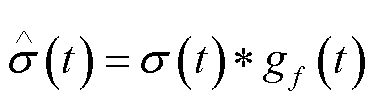 (28)
(28)
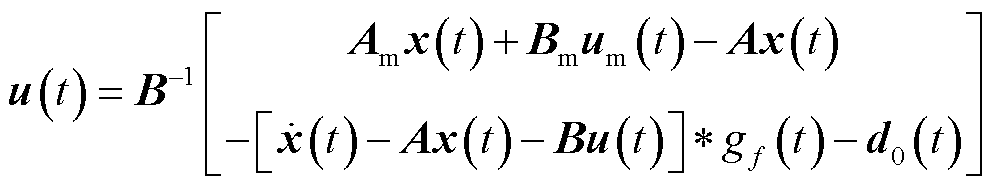 (29)
(29)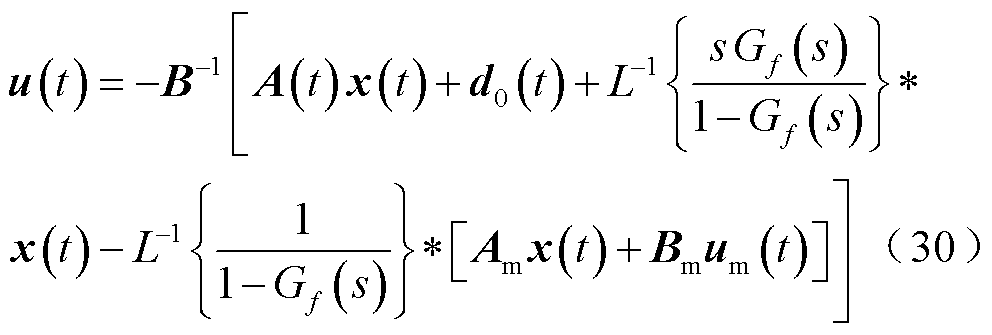
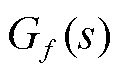 为带宽为β的低通滤波器。
为带宽为β的低通滤波器。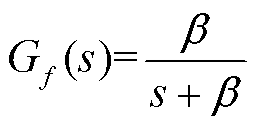 (31)
(31) (32)
(32)
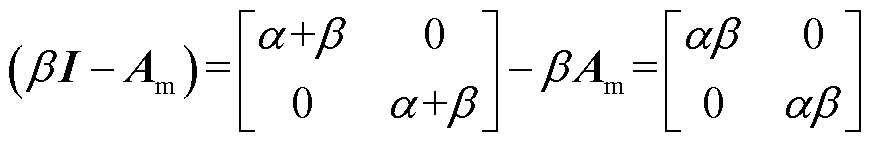 (33)
(33) 分别为
分别为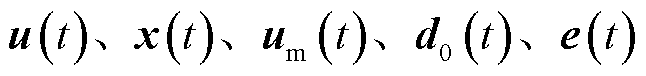 的拉普拉斯变换。
的拉普拉斯变换。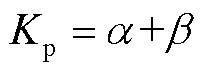 ,积分系数
,积分系数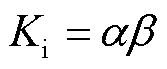 ,则跟踪误差
,则跟踪误差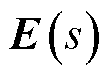 的控制律在形式上可以近似等效为PI控制。因此,由式(32)可知,基于UDE的VSC电流内环鲁棒控制律包括三个部分:①参考模型部分,为前馈微分形式,用于产生期望系统变量
的控制律在形式上可以近似等效为PI控制。因此,由式(32)可知,基于UDE的VSC电流内环鲁棒控制律包括三个部分:①参考模型部分,为前馈微分形式,用于产生期望系统变量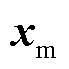 及其导数,同时加速暂态过程;②类PI控制器形式的跟踪误差控制部分,用来驱动系统的状态变量跟踪参考模型;③模型逆部分,用以补偿和对消模型中的已知动态部分。
及其导数,同时加速暂态过程;②类PI控制器形式的跟踪误差控制部分,用来驱动系统的状态变量跟踪参考模型;③模型逆部分,用以补偿和对消模型中的已知动态部分。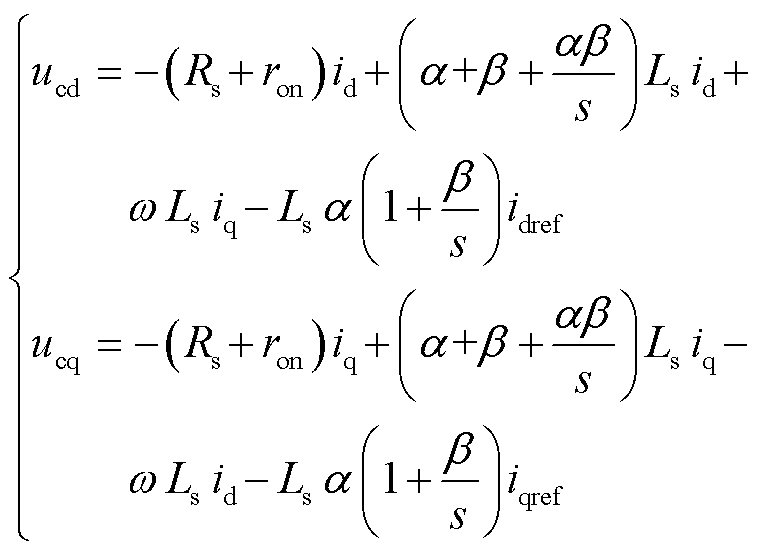 (34)
(34)
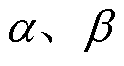 的选取。
的选取。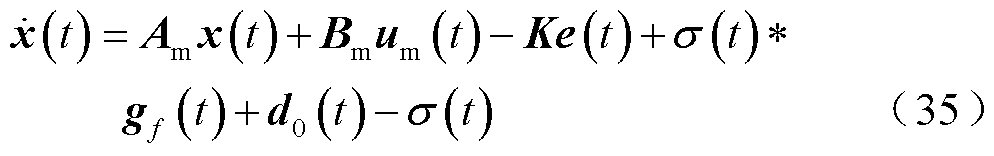
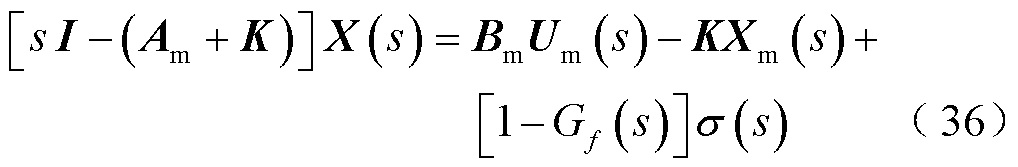
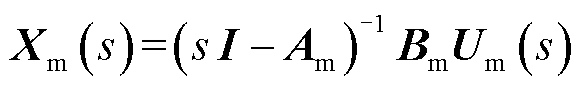 (37)
(37)
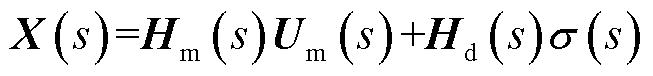 (38)
(38)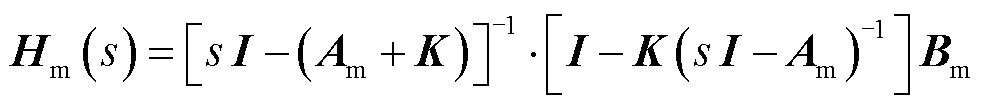 (39)
(39)
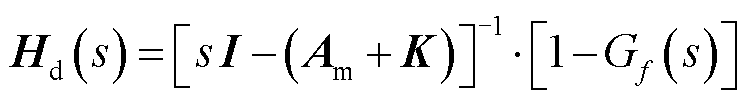 (40)
(40)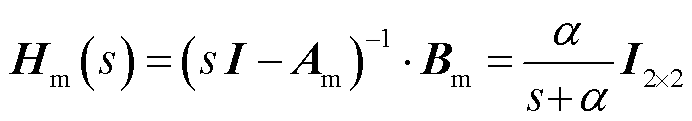 (41)
(41)
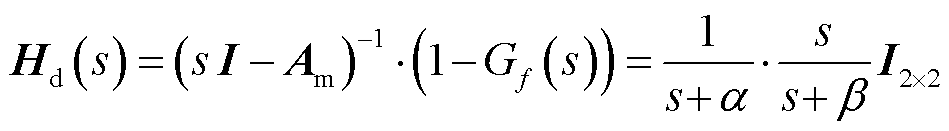 (42)
(42)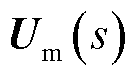 为系统参考指令,
为系统参考指令,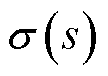 为集总不确定与扰动。
为集总不确定与扰动。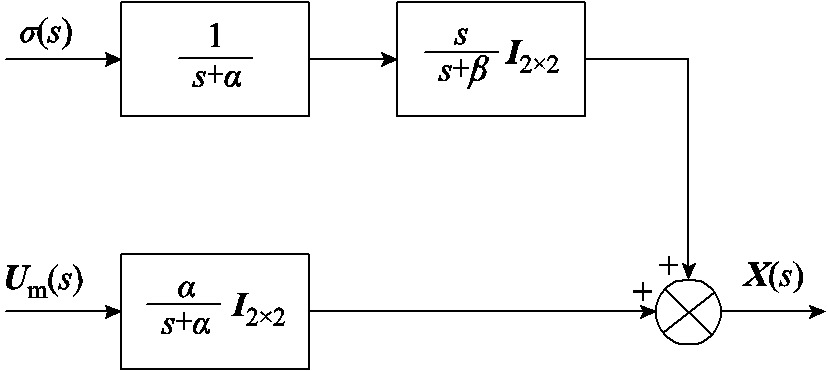
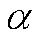 和β在频域的解耦特性,使得调参过程基本呈线性,各自整定最佳值时不会互相影响。
和β在频域的解耦特性,使得调参过程基本呈线性,各自整定最佳值时不会互相影响。