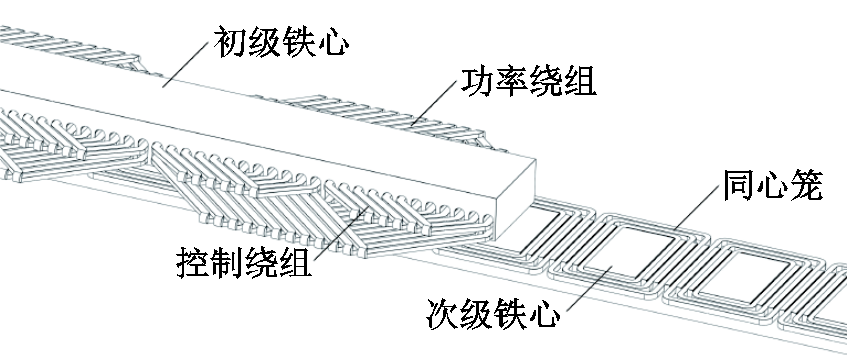
图1 NLS-LDFM结构示意图
Fig.1 Structure diagram of NLS-LDFM
摘要 同心笼次级直线双馈电机是由无刷双馈感应电机演变而来的一种新型直线电机，在城市轨道交通中具有良好的应用前景。然而，因初级铁心开断导致的静态端部效应，电机绕组中含有较大的负序电流和直接耦合电流。针对该问题，该文提出了一种基于脉振电压矢量前馈和静态端部效应电流抑制的补偿策略。首先，分析了静态端部效应在初级绕组中产生的谐波电流成分，推导了产生静态端部效应电流的脉振电动势，并采用脉振电压矢量前馈对其进行抑制；然后，基于混合二阶-三阶广义积分器及瞬时对称分量法，将各频率电流正负序分量变换到同步旋转坐标系中进行控制，以进一步抑制负序电流和直接耦合电流，从而对静态端部效应进行有效补偿；最后，通过仿真和实验验证了静态端部效应补偿策略的有效性。
关键词：直线双馈电机 静态端部效应 脉振电压前馈 特定频率电流提取
城市轨道交通列车牵引方式主要分为旋转电机牵引和直线电机牵引两种。直线电机牵引系统无需机械传动装置，可直接产生沿运动方向的电磁推力，具有转弯半径小、爬坡能力强、隧道盾构面小、噪声小、维护成本低等优势，在国内外城市地铁、轻轨和磁悬浮中得到了广泛的应用[1-3]。
目前城市轨道交通直线牵引系统主要采用直线感应电机（Linear Induction Machine, LIM）和直线同步电机（Linear Synchronous Machine, LSM）[4]。其中LIM多采用短初级单边平板型结构，具有结构简单、维护量小、造价低等优点，在中低速磁浮和直线地铁牵引系统中得到广泛应用。然而受动态端部效应影响，LIM的推力等关键性能指标会随着速度的升高而下降[5]。LSM多采用长初级单边平板型结构，具有效率和功率因数较高等优点，多用于高速磁浮列车。但因其需要在长距离轨道上铺设电枢绕组并分段变频供电，建设及运行维护成本相对较高[6]。
相比上述两种直线电机驱动系统，直线双馈电机（Linear Doubly-Fed Machine, LDFM）驱动系统因其功率因数可调、运行方式灵活等优势逐渐引起国内外学者关注。根据两套馈电绕组所处位置不同，LDFM可分为双边励磁型和单边励磁型两种。双边励磁型LDFM初、次级均嵌放绕组，可独立调整次级电流，国内外学者对其展开了广泛的研究[7-9]。单边励磁型LDFM工作原理与无刷双馈感应电机类似，初级嵌有两套极对数不同的三相绕组，次级可分为笼型、磁阻型、绕线型等多种结构，其中笼型次级结构简单且轨道建设成本较低。
本文所研究的同心笼次级直线双馈电机（Nest-Loop Secondary Linear Doubly-Fed Machine, NLS-LDFM）最早由俄勒冈州立大学提出[10-11]，A. K. Wallace教授团队首次指出了NLS-LDFM在轨道交通应用中的潜在优势，但研究过程并未考虑端部效应对电机性能的影响。近年来，华中科技大学对NLS-LDFM端部效应作用规律开展了部分研究工作[12]。研究表明，NLS-LDFM的静态端部效应除了使每套绕组三相不对称，还会导致两套绕组间发生直接耦合，即静态端部效应会在初级两套绕组中同时产生负序电流和直接耦合电流。负序电流分量会使电机产生反向推力，削弱电机平均推力。直接耦合的能量传递发生在初级两套绕组之间，并不产生有效的推力和有功功率，因此会导致电机功率因数和效率下降，对电机运行产生不利影响。
针对电机绕组三相不对称问题，一般可通过增加绕组极对数予以改善[13]。然而，NLS-LDFM通常采用“和调制”方案，在运行速度范围一定且尺寸有限的情况下，其极对数较少，难以通过增加极对数的方式降低三相不对称度，更无法削弱直接耦合。负序电流和直接耦合电流对于基波正序电流而言为谐波电流，电机谐波电流抑制策略主要有多旋转PI控制[14]、比例积分-准谐振控制[15]、前馈谐波电压注入控制[16]、复矢量PI控制[17]和重复控制[18]等。上述方法考虑的低频谐波通常以5、7次谐波为主，其频率均远高于NLS-LDFM绕组基波电流频率。在功率绕组中，直接耦合电流的频率为控制绕组的工作频率。两套初级绕组的基波频率相近，难以实现对直接耦合电流的精确提取和抑制。因此亟须研究静态端部效应补偿策略，以抑制初级绕组中的负序电流和直接耦合电流，从而提升NLS-LDFM的推力、功率因数和效率等。
据此，本文首先分析NLS-LDFM的静态端部效应及其产生的谐波电流成分。然后，基于静态端部效应脉振电感与直接耦合互感矩阵分析，推导脉振反电动势表达式，并将其作为前馈电压补偿到初级绕组中。同时，为提高补偿精度，采用混合二阶-三阶广义积分器（Mixed Second- and Third-Order Generalized Integrator, MSTOGI）提取基波电流和直接耦合电流，并应用瞬时对称分量法获取相应电流的正、负序分量，进而采用多同步旋转坐标变换（Multiple Synchronous Rotating Frame Transformation, MSRFT）将其分别变换到各自频率对应的旋转坐标系进行闭环控制。最后，在功率绕组级联异步运行模式下，通过仿真和实验验证NLS-LDFM静态端部效应补偿策略的有效性。
NLS-LDFM结构示意图如图1所示，电机采用短初级单边平板型结构，初级嵌有两套极对数分别为pp和pc的单层绕组，分别称为功率绕组（Power Winding, PW）和控制绕组（Control Winding, CW）。次级沿每一段初级纵向长度L均匀嵌放pp+pc巢同心笼，每巢同心笼包含3个笼环，每个笼环独立，各自构成一个闭合回路。
图1 NLS-LDFM结构示意图
Fig.1 Structure diagram of NLS-LDFM
NLS-LDFM初级两套绕组产生的气隙行波磁通密度分别为
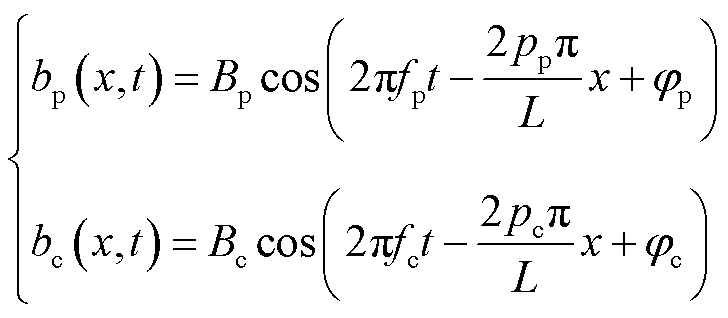（1）
式中，下角标p、c分别表示功率绕组和控制绕组；B为气隙行波磁通密度幅值；f为绕组通电频率；p为极对数；x为空间位置；φ为初始相位。
为产生稳定的电磁推力，同心笼产生的两组气隙行波磁通密度须与对应的初级行波磁通密度保持相对静止。因此，两组气隙行波磁通密度应在次级同心笼环中产生单一频率的感应电动势，继而产生单一频率的感应电流。两组磁场在次级同心笼中产生的感应电流频率分别为
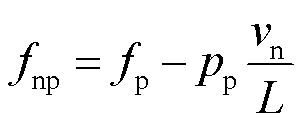（2）
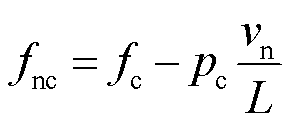（3）
式中，vn为电机的机械运行速度。
采用“和调制”方案时，次级产生的两组气隙行波磁通密度相对次级沿相反方向运动，因此有
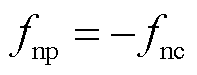（4）
由式（2）～式（4）可得电机的运行速度与初级两套绕组通电频率的关系为
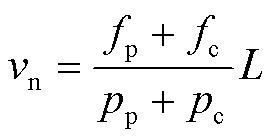（5）
式（5）表明，在电机极对数p和初级纵向长度L一定时，电机稳定运行的速度由两套绕组通电频率唯一确定。另外，当电机运行速度一定时，在功率绕组（控制绕组）施加频率为fp（fc）的激励，则在控制绕组（功率绕组）中能够感应出频率为fc（fp）的电动势，fp和fc的关系满足式（5）。
与一般短初级直线电机静态端部效应类似，在三相对称电压激励下，NLS-LDFM的三相不对称电流将产生除正常工作的正向行波磁场，还会产生反向行波磁场和沿气隙均匀分布的脉振磁场。其中，脉振磁场会使极对数不同的两套初级绕组发生直接耦合，即在pp（pc）对极绕组中通电时，pc（pp）对极绕组中可以感应出频率为fp（fc）的电动势。当该套绕组构成通路时，便会产生频率为fp（fc）的感应电流。
与旋转无刷双馈感应电机不同，由于NLS-LDFM中存在直接耦合现象，功率绕组和控制绕组间的互感矩阵并不为0。根据文献[19]的分析，当C相绕组位于初级的中部，A、B相绕组分别靠近初级两侧端部时，可推导得到初级两套绕组的直接耦合互感矩阵为
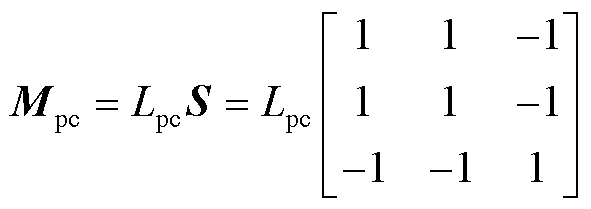（6）
式中，Lpc为直接耦合互感的幅值，其表达式为
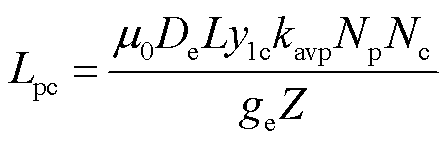（7）
式中，μ0为真空磁导率；De为等效初级横向长度；y1为绕组节距；kav为绕组脉振系数；N为绕组每相串联匝数；ge为等效气隙长度；Z为初级槽数。
同时，脉振磁场也是使得三相单层绕组不对称的根本原因。定义绕组脉振磁通路径所对应的电感为脉振电感，可得功率绕组和控制绕组的脉振电感矩阵分别为
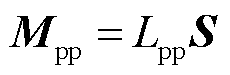（8）
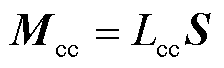（9）
式中，Lpp和Lcc分别为功率绕组和控制绕组脉振电感的幅值，其表达式分别为
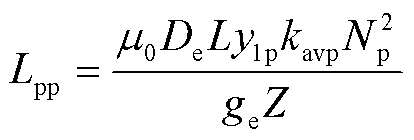（10）
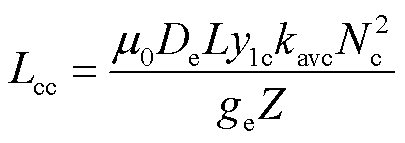（11）
忽略电机及逆变器等非线性因素产生的谐波电流，绘制NLS-LDFM静态端部效应耦合关系示意图如图2所示。
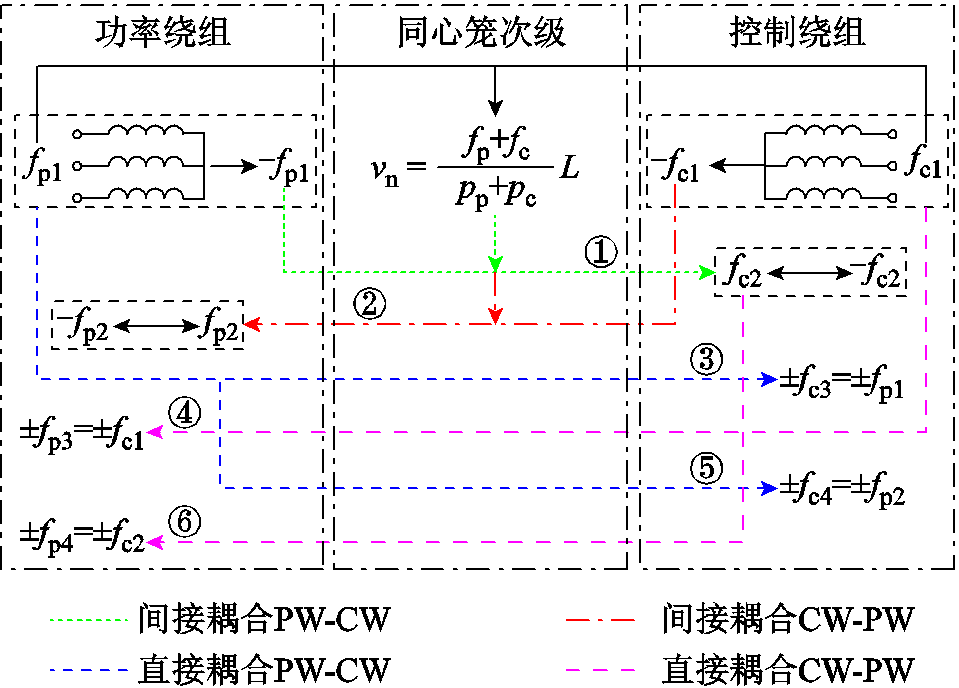
图2 NLS-LDFM静态端部效应耦合关系
Fig.2 Coupling relationship of static end effect in NLS-LDFM
受静态端部效应影响，电机中除基波正序电流经次级作用的间接耦合过程外，还存在负序电流的间接耦合（箭头①②所示），以及不经过次级作用的直接耦合过程（箭头③～⑥所示）。间接耦合可产生正序或负序电流，而直接耦合产生的电流正负序均存在。因其他频率电流的负序含量相对较小，间接耦合作用相对较弱，可忽略除基波以外其他频率负序电流的间接耦合过程。
由于三相绕组不对称，当功率绕组和控制绕组工作电流的频率分别为fp1和fc1时，会分别产生频率为-fp1和-fc1的负序电流。负序电流经次级的磁场调制作用，又会产生另一频率的电流，在电机运行速度一定时，其频率可根据式（5）计算得到
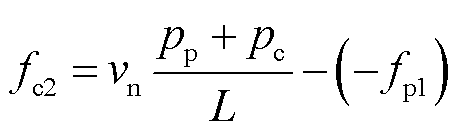（12）
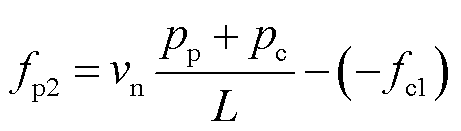（13）
即功率绕组（控制绕组）频率为-fp1（-fc1）的负序电流所产生的反向行波磁场将通过次级磁场调制作用在控制绕组（功率绕组）中产生频率为fc2（fp2）的感应电动势及电流。
经过负序电流的间接耦合作用后，初级绕组中均含有两种频率为fp1和fp2（fc1和fc2）的电流。受直接耦合影响，一套绕组中能够感应出另一套绕组中所有频率的电流。如图2中箭头③（④）所示，功率绕组（控制绕组）中基波频率为fp1（fc1）的电流能够通过直接耦合作用在控制绕组（功率绕组）中产生频率为fc3（fp3）的正、负序电流，且满足
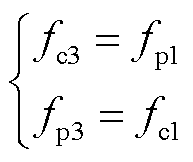（14）
类似地，图2中箭头⑤（⑥）所示的过程为功率绕组（控制绕组）中经间接耦合产生的频率为fp2（fc2）的电流，再次通过直接耦合在控制绕组（功率绕组）中产生频率为fc4（fp4）的正、负序电流，称为“间接-直接二次耦合”。二次耦合产生的电流频率为
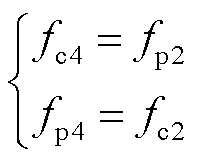（15）
当仅考虑基波负序电流的间接耦合作用、基波电流的直接耦合作用和二次耦合作用时，功率绕组（控制绕组）中主要含有四种频率的电流，每种频率的电流均三相不对称。对每套绕组而言，其中有两种频率的电流是绕组自身的工作电流或二次耦合电流，另外两种频率的电流则是来源于另一套绕组的直接耦合或间接耦合作用。
基于静态端部效应分析结果，可以将初级功率绕组磁链表示为
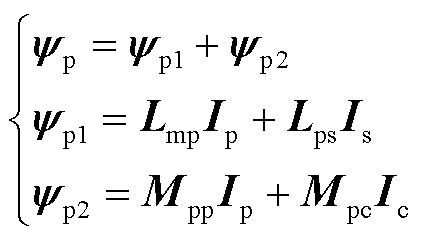（16）
式中，Lmp、Lps、Mpp和Mpc分别为功率绕组励磁电感、功率绕组与次级的互感、功率绕组脉振电感和直接耦合互感；下角标s表示次级同心笼；ψp1为三相对称电感对应的磁链；ψp2为功率绕组表征静态端部效应的磁链。
进一步得到功率绕组电压表达式为
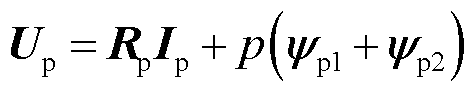（17）
式中，p表示微分算子d/dt。将式（16）中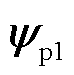
和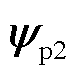
的表达式代入式（17）可得
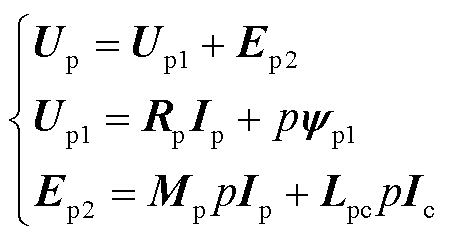（18）
式中，Ep2为反映三相绕组不对称的反电动势和直接耦合反电动势，合成后定义为脉振反电动势。
将式（6）直接耦合互感和式（8）脉振电感的表达式代入式（18）中。因三相绕组为星形联结，由基尔霍夫电流定律可得三相反电动势表达式为
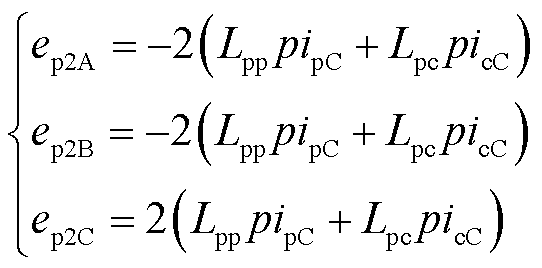（19）
式中，ep2为一相脉振反电动势的瞬时值，下标A、B、C分别表示三相绕组；ipC和icC分别为功率绕组和控制绕组C相电流。
由式（19）可知，对于由端部效应产生的脉振反电动势，A、B相相位相同且与C相相位相反，脉振反电动势的瞬时值随两套绕组C相电流对时间的导数变化而变化。
由上述分析可知，可采用脉振反电动势作为激励等效三相绕组的不对称与直接耦合现象。若将脉振反电动势作为前馈电压补偿到初级三相绕组中，则可抵消其产生的不对称电流与直接耦合电流。三相不平衡的脉振反电动势合成的空间电压矢量为
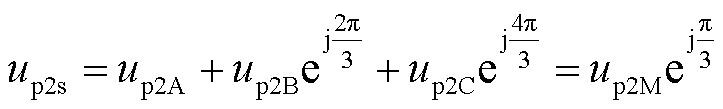（20）
式中，up2M为参考脉振电压矢量的幅值，其表达式为
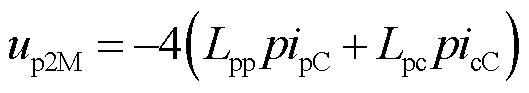（21）
由式（20）和式（21）可知，三相脉振电动势合成后得到的幅值随时间正弦变化，但空间位置恒定的脉振电压矢量，其幅值是单相脉振电动势的2倍，相位与中间相（C相）电动势相反。将三相合成脉振电压矢量分解到两相静止ab坐标轴上可得
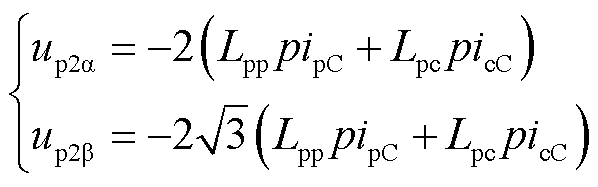（22）
式（22）即可作为两相静止ab坐标系下静态端部效应前馈电压补偿量。在空间平面坐标系中绘制出脉振电压矢量的示意图如图3所示。
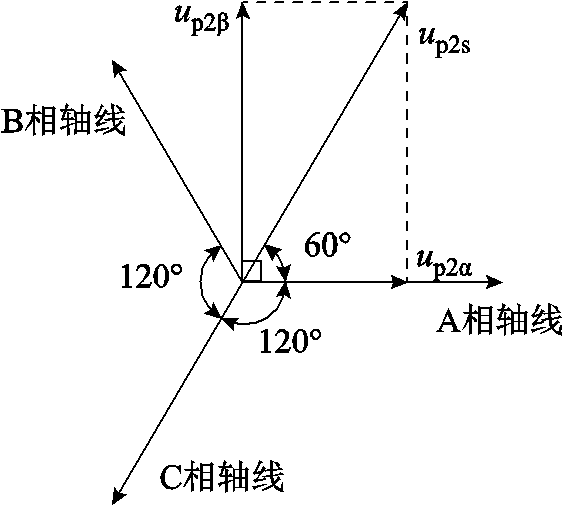
图3 脉振电压矢量示意图
Fig.3 Schematic diagram of pulsating voltage vector
由于脉振电压的表达式中含有功率绕组和控制绕组电流对于时间的导数项，在数字控制系统中直接对电流求导可能会将噪声放大，引起系统的不稳定。因此本文采用二阶线性跟踪微分器（Trace Differentiator, TD）作为数字微分器来求取电流的导数[20]。
作为一种开环的前馈补偿方法，脉振电压矢量补偿具有实时补偿、动态响应快等优点，但较依赖脉振电感与直接耦合互感参数，当参数误差较大时，补偿精度将显著降低。为提高补偿精度，本文进一步对特定频率的负序电流和直接耦合电流进行抑制，一般可采用二阶广义积分器（Second Order Generalized Integrator, SOGI）提取特定频率的电流，SOGI闭环传递函数表达式为[21]
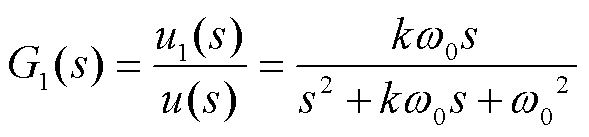（23）
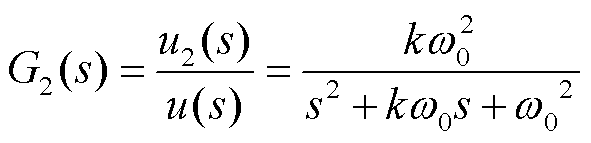（24）
式中，u、u1、u2分别为输入信号、同相输出信号和正交输出信号；k和ω0分别为增益系数和谐振角频率。G1(s)相当于带通滤波器，仅在谐振频率附近具有正增益，对于低频和高频信号均有一定的滤波作用；G2(s)相当于低通滤波器，正交输出信号则不能滤除低频信号的干扰。
NLS-LDFM的基波电流和直接耦合电流频率较为接近，且直接耦合电流频率低于基波电流频率。采用瞬时对称分量法获取电流正、负序分量时需使用正交信号作为输入，因此需降低正交输出信号对低频谐波分量的敏感度。本文采用MSTOGI提取不同频率的电流，其结构框图如图4所示。
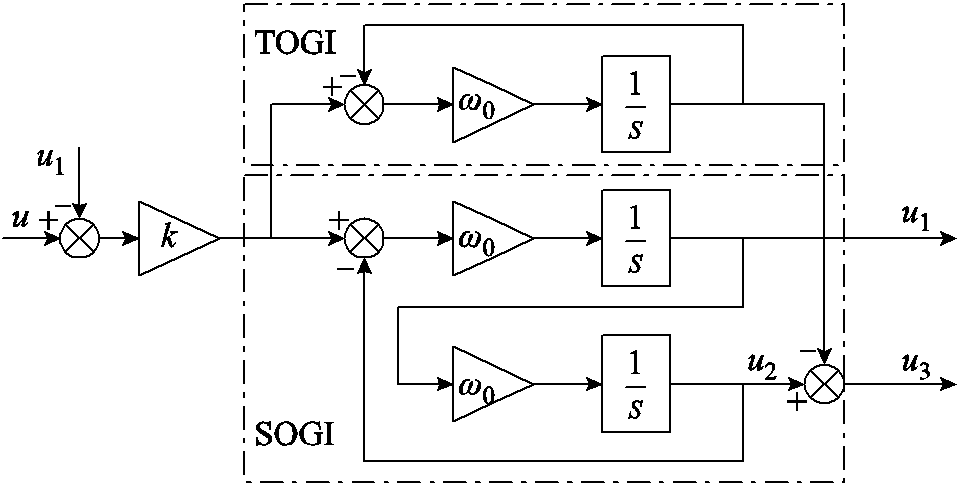
图4 MSTOGI结构框图
Fig.4 Structure diagram of MSTOGI
MSTOGI通过在SOGI基础上增加一条估计低频分量的通路，在同相输出信号仍为二阶的情况下，将正交输出信号转化为三阶，可有效降低积分器输出信号对于低频谐波分量的敏感度，同时保持和SOGI相同的动态响应速度和参数特性。其中u3为带低频补偿的正交输出信号，其闭环传递函数表达式为[22]
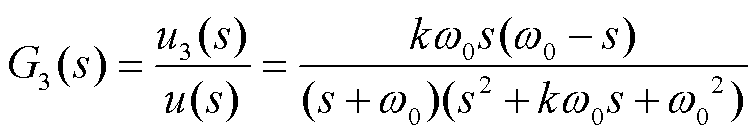（25）
令k=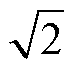
，w0=100p，绘制G2(s)和G3(s)的伯德图如图5所示，由幅频特性曲线可知，G2(s)对于频率低于ω0的信号具有正增益，而G3(s)对于频率低于ω0的信号增益为负，可以抑制输入信号中的直流分量和低频分量。由相频特性曲线可知，G2(s)和G3(s)在ω0处的相位均滞后输入信号90°。因此采用u3代替u2作为正交输出信号更为合适。
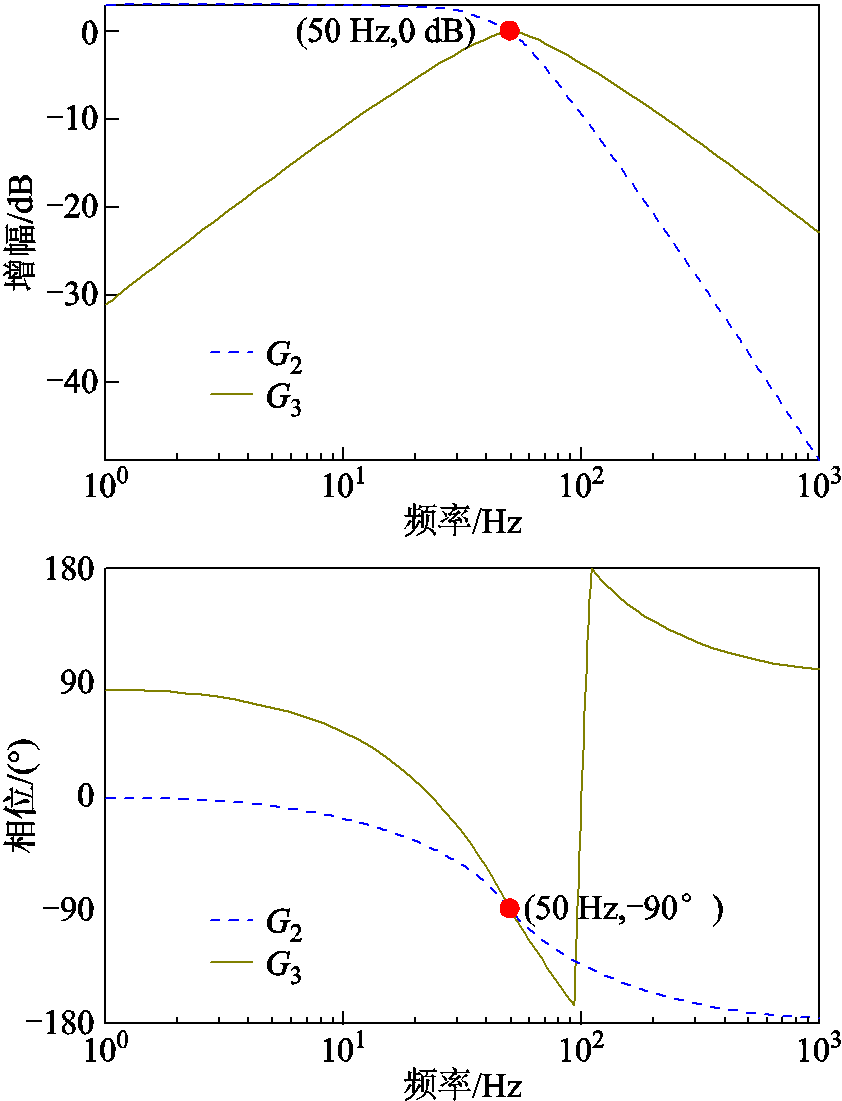
图5 MSTOGI正交信号伯德图对比
Fig.5 Bode diagram for orthogonal signal of MSTOGI
图4中的增益系数k会对MSTOGI的动态响应和滤波性能产生影响。k越大时，系统输出的响应速度越快，但谐振频率处通带变大使得滤波性能变差。反之，当k越小时，滤波性能越好但动态响应速度变慢[23]。
除提取电流中特定频率的信号，还需要对相应频率的电流信号进行正、负序分解。根据瞬时对称分量法可得三相静止ABC坐标系中的正序分量表达式为
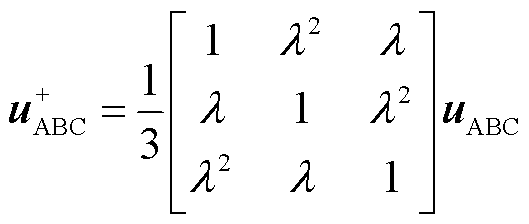（26）
式中，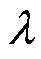
为时域相位滞后120°的偏移算子，
。
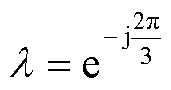将三相静止ABC坐标系中的瞬时正序分量变换到两相静止ab坐标系下可得
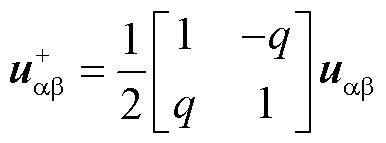（27）
同样地，可以得到两相静止ab坐标系下瞬时负序分量表达式为
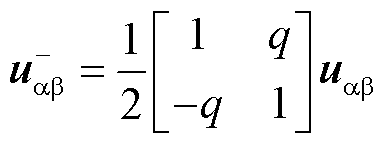（28）
式中，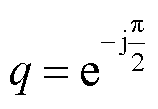
为时域内相位滞后90°的偏移算子；上标“+”和“-”分别表示正序和负序分量。
利用MSTOGI正交输出信号的相位滞后输入信号90°的特性，可将电机功率绕组或控制绕组的三相电流变换到ab坐标系下，那么在ab坐标系下初级电流的正、负序分量可以分别表示为
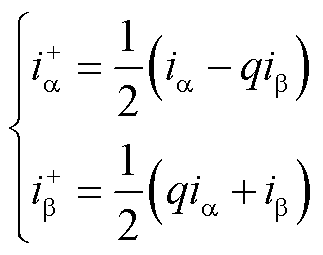（29）
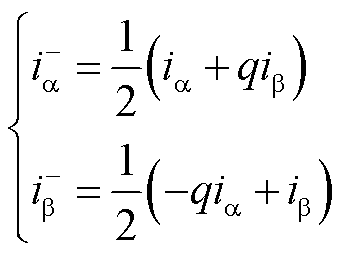（30）
本文将经过谐波解耦后的电流作为MSTOGI的输入信号[24]，以减小其他频率电流干扰，提高信号的提取精度。采用多个MSTOGI和正负序分量计算器（Positive- and Negative-Sequence Caculator, PNSC）可以实现特定频率电流信号的提取与正、负序分解。信号提取及分解过程如图6所示，包含两相静止坐标变换模块、双MSTOGI模块（Dual MSTOGI, DMSTOGI）和PNSC。
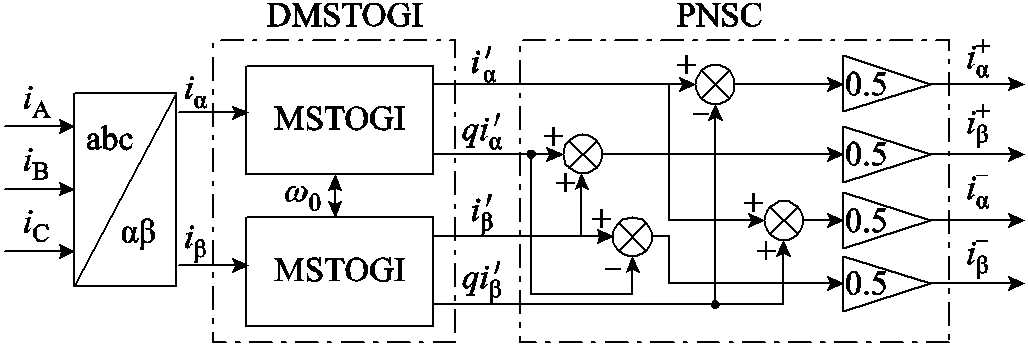
图6 特定频率电流正负序提取模块结构框图
Fig.6 Block diagram of positive- and negative-sequence current extraction module at specific frequency
由第2节分析可知，静态端部效应会使NLS-LDFM两套初级绕组分别产生脉振反电动势，进而在绕组中产生负序电流和另一绕组基波频率的直接耦合电流。
本文提出的功率绕组静态端部效应补偿方法如图7所示，控制绕组的补偿方法与之相同。补偿方法主要包含两部分：①采集功率绕组和控制绕组的C相电流，并利用跟踪微分器分别获取C相电流对时间的导数，由式（22）得到脉振电压矢量在两相静止ab坐标系下的前馈补偿量；②采集功率绕组电流并对其进行谐波解耦，在静止ab坐标系下应用DMSTOGI和PNSC提取基波和直接耦合电流的正、负序分量，再将其变换到相应的同步旋转坐标系下进行闭环控制。
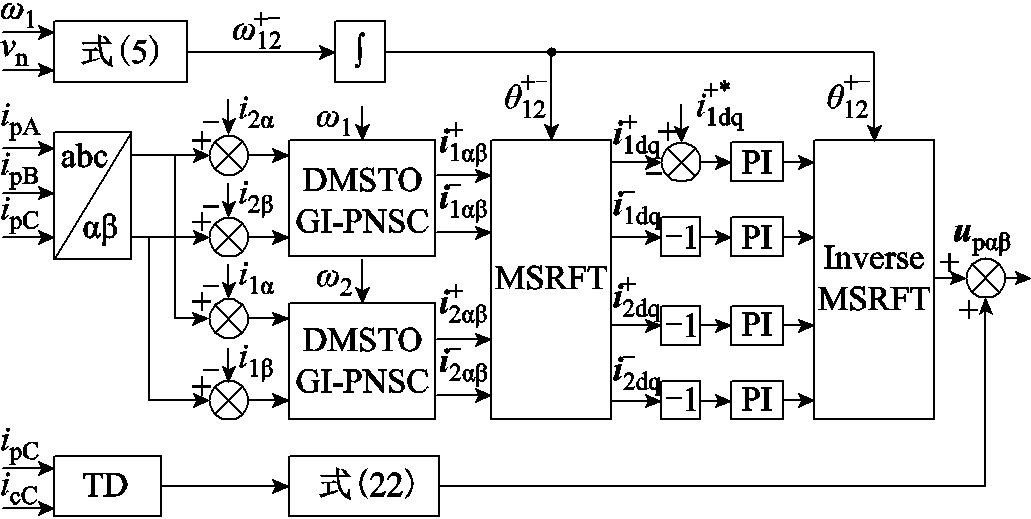
图7 NLS-LDFM静态端部效应补偿框图
Fig.7 Block diagram of compensating static end effect for NLS-LDFM
在两相静止ab坐标系下得到功率绕组静态端部效应补偿量upαβ后，将其实时补偿到功率绕组中。该方法动态响应较快，但作为一种开环补偿方式，其补偿精度较依赖电机参数的准确性，易出现欠补偿或过补偿现象。因此加入基于MSTOGI的电流控制环节对含量较大的基波负序电流和直接耦合电流进行抑制，以提升补偿精度。本文中功率绕组的基波电流和直接耦合电流频率接近，因此需要取较小的增益系数k以增强MSTOGI的滤波性能。
当电流提取模块精度较高时，电流的控制精度也会得到提升。理想情况下，当基波负序分量被抑制到0后，控制绕组中将不会产生频率为fc2的电流，功率绕组中也就不会产生频率为fp4的电流。当直接耦合电流被抑制到0以后，功率绕组频率为fp3的电流分量亦为0。因此，当功率绕组基波负序电流和直接耦合电流得到完全抑制时，功率绕组除基波正序电流外仅含由静态端部效应引起的频率为fp2的谐波电流，可通过抑制控制绕组中的基波负序电流消除该频率的电流。
为验证静态端部效应补偿方法的有效性，通过Matlab/Simulink对一台2/4对极的3 kW NLS-LDFM进行仿真分析，仿真中所用的直接耦合互感Lpc为0.55 mH，功率绕组脉振电感Lpp为0.57 mH。仿真中仅考虑由静态端部效应产生的谐波电流成分。
以功率绕组静态端部效应补偿为例，仿真在功率绕组级联异步运行模式下进行。为便于对比分析，仅给定电流参考值，以保持基波正序电流幅值不变。在补偿静态端部效应前，功率绕组的d、q轴电流分别给定20 A和0 A，频率为50 Hz。当采用控制策略补偿静态端部效应时，在给定d轴基波正序电流20 A的基础上，将基波负序电流及直接耦合电流给定值设为0 A。电机运行速度保持为4.5 m/s，由式（5）可得直接耦合电流的频率为-20 Hz。仿真结果如图8～图12所示。
图8 功率绕组三相电流波形
Fig.8 The three phase current waveform of power winding
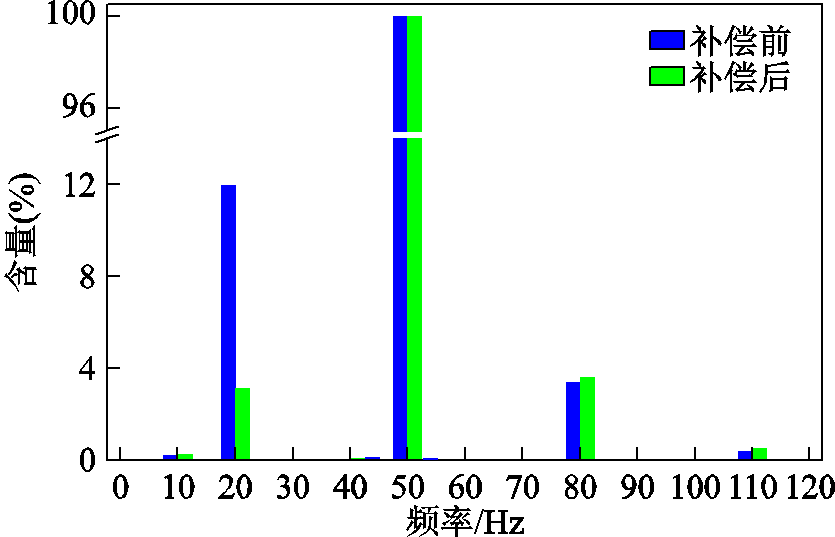
图9 功率绕组C相电流FFT波形
Fig.9 The FFT waveform of phase-C current in power winding
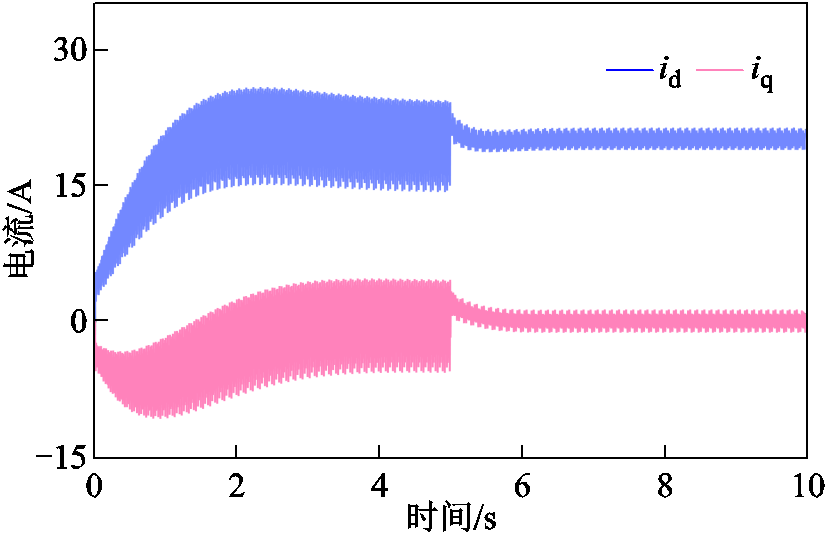
图10 功率绕组dq轴电流波形
Fig.10 The dq-axis current waveform of power winding
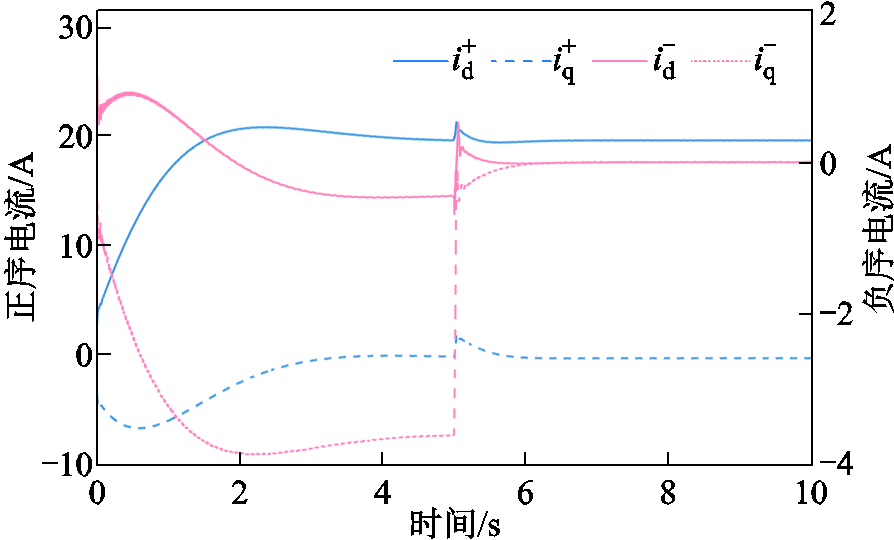
图11 功率绕组基波正负序dq轴电流波形
Fig.11 The fundamental positive and negative sequence current waveforms of power winding in dq-axis
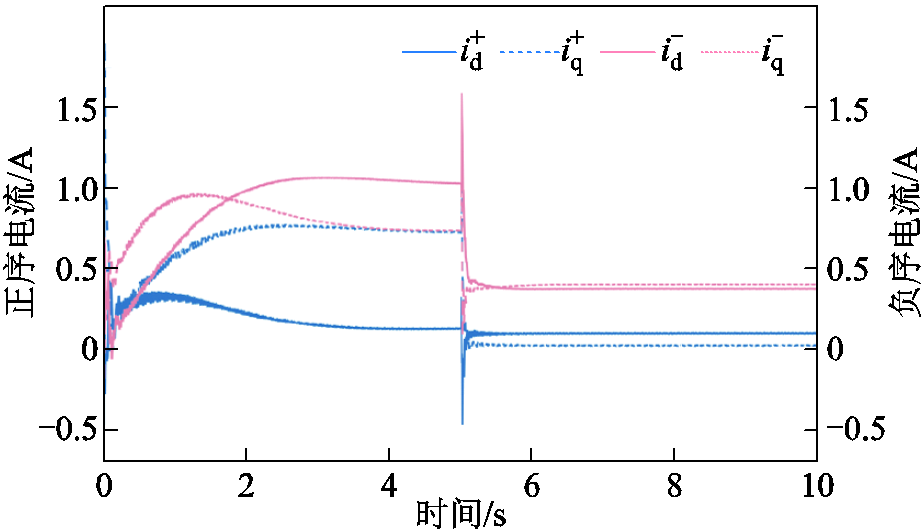
图12 功率绕组直接耦合正负序dq轴电流波形
Fig.12 The direct-coupling positive- and negative- sequence current waveforms of power winding in dq-axis
图8为功率绕组的三相电流波形。t=0～5 s时未采用静态端部效应补偿策略，发现三相电流不对称度较大，表明功率绕组中产生了负序电流。在t=5 s时施加静态端部效应补偿策略，稳态时三相电流不对称度明显降低，三相电流幅值基本相同。表明负序电流得到了有效抑制。
对补偿前后的功率绕组C相电流做快速傅里叶变换（Fast Fourier Transform, FFT），得到其对比波形如图9所示。其中频率为20 Hz的电流含量（谐波幅值/基波幅值×100%）由补偿前的12.0%降低到了补偿后的3.1%。表明直接耦合电流得到了有效抑制。
图10为功率绕组dq轴电流波形。静态端部效应补偿前dq轴电流波动较大，因为在基波正序旋转坐标系下，静态端部效应引起的负序电流和直接耦合电流均为交流量。补偿后的负序电流和直接耦合电流含量降低，因此dq轴电流波动显著减小。
利用基于MSTOGI和PNSC的谐波及正负序分解模块可提取特定基波电流和直接耦合的正负序分量。
图11为基波正负序dq轴电流波形。补偿前负序电流的dq轴分量分别为-0.45 A和-3.6 A，可得负序电流的幅值为3.63 A。施加静态端部效应补偿后，经历了短暂的过渡过程，基波正序电流dq轴分量保持不变，而基波负序电流dq轴分量稳定在0附近，其幅值也基本为0。
图12为直接耦合的正负序dq轴电流波形。施加补偿后电流正、负序分量均减小，直接耦合电流正、负序分量幅值分别由0.76 A和1.3 A减小到了0.1 A和0.56 A。结果表明，基波负序dq轴电流和直接耦合正负序dq轴电流均能够被抑制。
为进一步验证静态端部效应补偿方法的有效性，本文采用如图13所示的3 kW弧形NLS-LDFM实验平台进行验证。该平台包含两套弧形初级和一个圆形次级，实验过程中给任意一套初级通电即可。负载电机为一台永磁同步发电机，发电机三相绕组经交流调压器与负载电阻箱相连，通过调节调压器的输出电压来调节NLS-LDFM的负载。由于弧形电机初级铁心开断，其端部效应作用规律及电磁特性和直线电机相同，因此采用弧形电机进行实验验证是合理的。
图13 NLS-LDFM实验平台
Fig.13 The experimental platform of NLS-LDFM
实验样机由于气隙不均、加工装配偏差等原因，电机电磁参数与设计值存在一定偏差。实验中所采用的直接耦合互感Lpc为2.0 mH，功率绕组脉振电感Lpp为1.9 mH。
实验所用的变频器为背靠背双三相逆变器，每个三相逆变器分别与功率绕组和控制绕组连接。通过控制逆变器IGBT的开关状态可灵活控制NLS-LDFM的运行方式。本文主要在功率绕组侧进行静态端部效应补偿，因此在功率绕组级联异步运行模式下实验。通过将控制绕组侧逆变器下桥臂IGBT全部开通、上桥臂IGBT全部关断实现控制绕组三相短接。实验中功率绕组的激励方式与4.1节相同。通过调节负载使电机稳定运行在4.5 m/s，此时直接耦合电流频率为-20 Hz。实验结果如图14～图17所示。
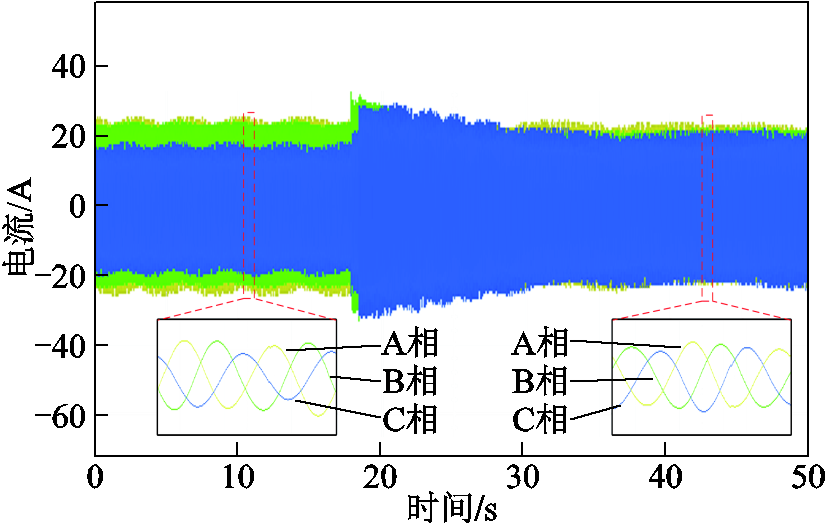
图14 功率绕组三相电流实验波形
Fig.14 The three phase current waveforms of power winding in experiment
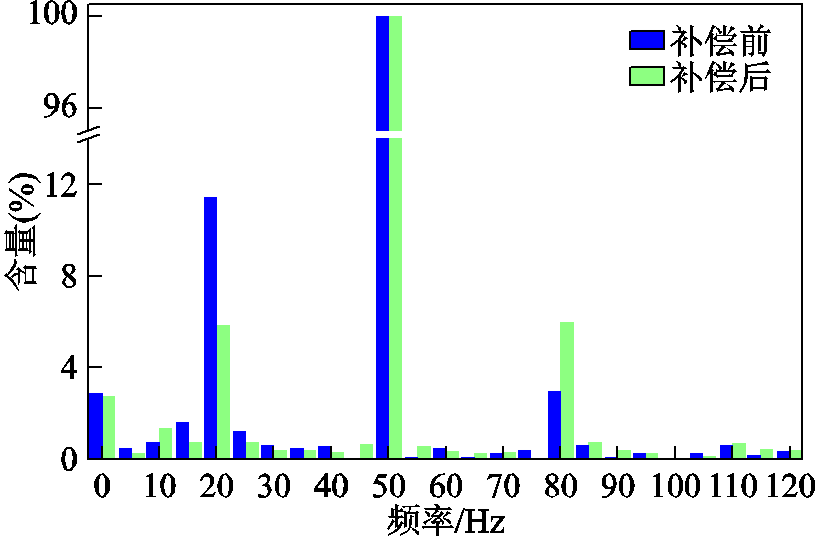
图15 功率绕组C相电流FFT波形
Fig.15 The FFT waveform of phase-C current in power winding
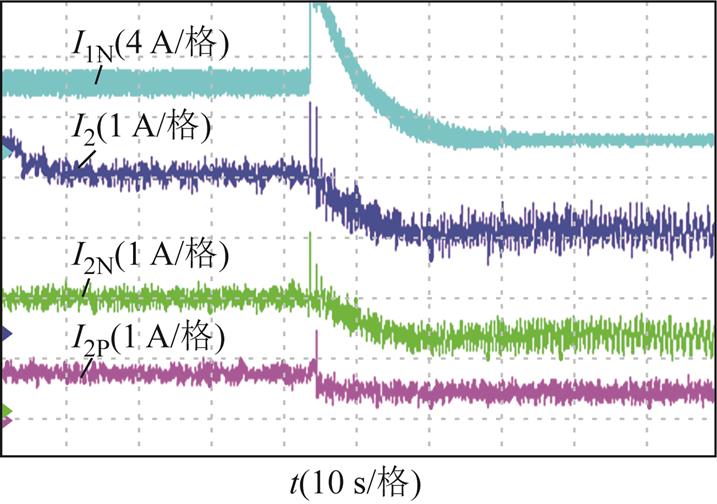
图16 基波负序电流和直接耦合电流幅值波形
Fig.16 The amplitude of negative-sequence and direct-coupling current
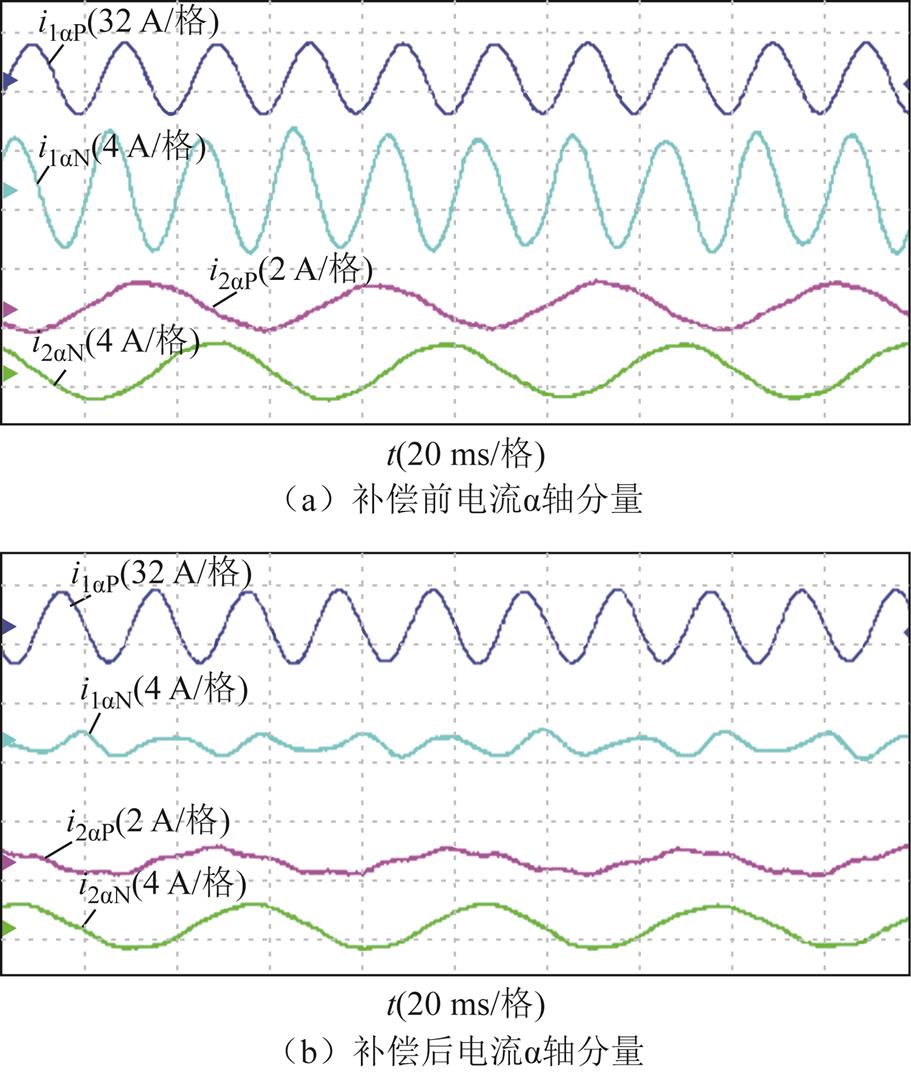
图17 功率绕组基波和直接耦合电流正负序的a轴分量
Fig.17 The positive- and negative-sequence of the power winding fundamental and the direct-coupling current in a-axis
图14为功率绕组三相电流波形。在静态端部效应补偿前，三相电流明显不对称，其中A、B相电流幅值相近，C相电流幅值较小，三相电流有效值分别为16.6 A、17.1 A和12.8 A。在t=18 s时实施静态端部效应补偿策略，补偿后的三相电流幅值基本相同，三相电流有效值分别为15.9 A、15.6 A和15.3 A，三相不对称度（最大相电流之差/三相平均电流×100%）由27.7%降低到了3.9%，表明负序电流得到了有效抑制。
施加静态端部效应补偿后功率绕组三相电流的过渡时间较长，除电机本身参数影响外，是由于该策略通过注入电压来补偿相应的电流，但在任意dq同步旋转坐标系下电压与电流之间存在交叉耦合项，且同步旋转坐标系变换角度由角频率积分得到，未考虑积分初值，难以准确解耦。本文通过忽略交叉耦合项，可近似认为功率绕组dq轴电压与对应的电流呈线性关系。但积分初值引起变换角度的误差，只会影响直流量id和iq的相对大小。不论积分初值如何选取，只要保证积分频率准确，id和iq在各自同步旋转坐标系下均为直流量，积分初值的选取对于电流的控制精度没有影响。
对补偿前后功率绕组C相电流作FFT分析，得到如图15所示的FFT波形。其中，频率为20 Hz的电流含量由11.4%降低到了5.8%，表明补偿后直接耦合电流得到了较好的抑制。但功率绕组频率为 80 Hz的电流含量却升高。其原因为：施加补偿后，三相电流不对称度减小，C相基波电流幅值增大（仿真中C相电流幅值由17.5 A增大至20 A，实验中C相电流幅值由17.3 A增大至21.8 A）。因此在控制绕组中产生的50 Hz直接耦合反电动势幅值和负序电流含量增大。由式（5）可知，控制绕组中频率为50 Hz的负序电流会经过次级耦合作用在功率绕组中产生频率为80 Hz的电流，所以在补偿后功率绕组中频率为80 Hz的电流含量增大。
图16为静态端部效应补偿前后电流幅值的波形，由上至下的曲线分别为功率绕组基波负序电流幅值I1N、直接耦合电流幅值I2、直接耦合负序电流幅值I2N和直接耦合正序电流幅值I2P，其中I2=I2P+I2N。施加补偿后，I1N由4.8 A减小至0.8 A，I2由2.6 A减小到了1.6 A。负序电流和直接耦合电流均得到了一定程度的抑制。
图17为静态端部效应补偿前后功率绕组基波电流和直接耦合电流正负序的a轴分量。由上至下的曲线分别为基波正、负序电流和直接耦合正、负序电流的a轴分量。补偿后基波正序电流保持不变，基波负序电流和直接耦合电流均减小。图中基波正序电流波形正弦度较好，而负序电流和直接耦合正负序电流中还有其他谐波分量，进行控制时会受到不同程度的影响。
针对同心笼次级直线双馈电机静态端部效应，本文提出了一种基于脉振电压矢量前馈和静态端部效应电流抑制的补偿策略。仿真及实验结果均表明：该补偿策略可有效降低绕组的负序电流和直接耦合电流。在样机实验中：三相电流不对称度由27.7%减小至3.9%，直接耦合电流含量由11.4%减小至5.8%。下一步工作，将继续研究双馈同步运行模式下基于矢量控制的初级两套绕组同时补偿策略，进一步提升直线双馈电机驱动性能。
参考文献
[1] 范瑜, 李文球, 杨中平. 国外直线电机轮轨交通[M]. 北京: 中国科学技术出版社, 2010.
[2] 曹瑞武, 苏恩超, 张学. 轨道交通用次级分段型直线磁通切换永磁电机研究[J]. 电工技术学报, 2020, 35(5): 1001-1012.
Cao Ruiwu, Su Enchao, Zhang Xue. Investigation of linear flux-switching permanent magnet motor with segmented secondary for rail transit[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1001-1012.
[3] Xu Wei, Sun Guangyong, Wen Guilin, et al. Equivalent circuit derivation and performance analysis of a single-sided linear induction motor based on the winding function theory[J]. IEEE Transactions on Vehicular Technology, 2012, 61(4): 1515-1525.
[4] 吕刚. 直线电机在轨道交通中的应用与关键技术综述[J]. 中国电机工程学报, 2020, 40(17): 5665-5674.
Lü Gang. Review of the application and key technology in the linear motor for the rail transit[J]. Proceedings of the CSEE, 2020, 40(17): 5665-5674.
[5] 徐伟, 肖新宇, 董定昊, 等. 直线感应电机效率优化控制技术综述[J]. 电工技术学报, 2021, 36(5): 902-915, 934.
Xu Wei, Xiao Xinyu, Dong Dinghao, et al. Review on efficiency optimization control strategies of linear induction machines[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 902-915, 934.
[6] Lü Gang, Zhang Zhixuan, Li Xiaodong. Three-dimensional electromagnetic characteristics analysis of novel linear synchronous motor under lateral and yaw conditions of MAGLEV[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(1): 29-36.
[7] Kang Jinsong, Mu Siyuan, Ding Hao. Long stator linear doubly-fed motor for high-speed maglev integrated suspension, propulsion and contactless power supply[C]//2021 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 2021: 1-5.
[8] 曾志凌. 城轨列车双馈直线驱动电机电磁计算与设计[D]. 成都: 西南交通大学, 2015.
[9] Yang Bo, Henke M, Grotstollen H. Pitch analysis and control design for the linear motor of a railway carriage[C]//Conference Record of the 2001 IEEE Industry Applications Conference. 36th IAS Annual Meeting (Cat. No.01CH37248), Chicago, IL, USA, 2002: 2360-2365.
[10] Seifkhani F. Investigation, analysis and design of the linear brushless doubly-fed machine[D]. Corvallis: Oregon State University, 1991.
[11] Saifkhani F, Wallace A K. A linear brushless doubly-fed machine drive for traction applications[C]//1993 Fifth European Conference on Power Electronics and Applications, Brighton, UK, 2002: 344-348.
[12] 葛健. 同心笼次级直线双馈电机端部效应及运行特性分析[D]. 武汉: 华中科技大学, 2019.
[13] 刘慧娟, 马杰芳, 张千, 李雨蔓. 双边型长初级直线感应电机电磁推力特性研究[J]. 中国电机工程学报, 2019, 39(增刊1): 268-277.
Liu Huijuan, Ma Jiefang, Zhang Qian, Li Yuman. Research on electromagnetic thrust characteristic of double sided long primary linear induction motor[J]. Proceedings of the CSEE, 2019, 39(S1): 268-277.
[14] Liu Gang, Chen Baodong, Wang Kun, et al. Selective Current harmonic suppression for high-speed PMSM based on high-precision harmonic detection method[J]. IEEE Transactions on Industrial Informatics, 2019, 15(6): 3457-3468.
[15] 张海洋, 许海平, 方程, 等. 基于比例积分-准谐振控制器的直驱式永磁同步电机转矩脉动抑制方法[J]. 电工技术学报, 2017, 32(19): 41-51.
Zhang Haiyang, Xu Haiping, Fang Cheng, et al. Torque ripple suppression method of direct-drive permanent magnet synchronous motor based on proportional-integral and quasi resonant controller[J]. Transactions of China Electrotechnical Society, 2017, 32(19): 41-51.
[16] 钟再敏, 江尚, 康劲松, 等. 永磁同步电机谐波电压与电流的耦合模型及前馈控制[J]. 电工技术学报, 2017, 32(18): 131-142.
Zhong Zaimin, Jiang Shang, Kang Jinsong, et al. A harmonic voltage and current coupling permanent magnet synchronous motor model and feedforward control[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 131-142.
[17] 郭小强. 光伏并网逆变器通用比例复数积分控制策略[J]. 中国电机工程学报, 2015, 35(13): 3393-3399.
Guo Xiaoqiang. Generalized proportional complex integral control scheme for PV grid-connected inverters[J]. Proceedings of the CSEE, 2015, 35(13): 3393-3399.
[18] 武永燎, 李红, 宋欣达, 等. 基于改进型重复控制器的永磁同步电机电流谐波抑制方法研究[J]. 电工技术学报, 2019, 34(11): 2277-2286.
Wu Yongliao, Li Hong, Song Xinda, et al. Suppression of harmonic current in permanent magnet synchronous motors using improved repetitive controller[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2277-2286.
[19] Ge Jian, Xu Wei, Liu Yi, et al. Investigation on winding theory for short primary linear machines[J]. IEEE Transactions on Vehicular Technology, 2021, 70(8): 7400-7412.
[20] 闫光亚, 艾武, 陈冰, 等. 永磁直线同步电机ADRC控制系统[J]. 电工技术学报, 2011, 26(9): 60-66.
Yan Guangya, Ai Wu, Chen Bing, et al. PMLSM active disturbance rejection control[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 60-66.
[21] Zhao Rende, Xin Zhen, Loh P C, et al. A novel flux estimator based on multiple second-order generalized integrators and frequency-locked loop for induction motor drives[J]. IEEE Transactions on Power Electronics, 2017, 32(8): 6286-6296.
[22] Zhang Chunjiang, Zhao Xiaojun, Wang Xiaohuan, et al. A grid synchronization PLL method based on mixed second- and third-order generalized integrator for DC offset elimination and frequency adaptability[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(3): 1517-1526.
[23] Rodríguez P, Luna A, Muñoz-Aguilar R S, et al. A stationary reference frame grid synchronization system for three-phase grid-connected power converters under adverse grid conditions[J]. IEEE Transactions on Power Electronics, 2012, 27(1): 99-112.
[24] Xu Wei, Yu Kailiang, Liu Yi, et al. Improved coordinated control of standalone brushless doubly fed induction generator supplying nonlinear loads[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8382-8393.
Abstract At present, linear induction machines (LIMs) and linear synchronous machines (LSMs) are mainly used for linear traction system adopted to urban rail transit. As a new type of linear machine, the nest-loop secondary linear doubly-fed machine (NLS-LDFM) and its drive system have gradually attracted the attention of scholars for its advantages of adjustable power factor and flexible operation mode. However, the static end effect exists in NLS-LDFM due to the cut-open primary iron core. It generates the pulsating magnetic field which is evenly distributed along the direction of motion. The phenomenon not only leads to two sets of asymmetrical three-phase windings but also direct-coupling between them. Therefore, the static end effect can produce both negative-sequence current and direct-coupling current in the primary windings. Therein, the negative-sequence current can produce negative thrust, which can weaken the average thrust. And the direct-coupling current does not produce effective thrust or active power. Thus, the static end effect will lead to the reduction of power factor and efficiency in the NLS-LDFM.
Firstly, based on the law of static end effect and the working principle of NLS-LDFM, the main components of harmonic current generated by static end effect are analyzed. Most of the harmonic currents generated by the static end effect can be compensated by suppressing the fundamental negative-sequence current and direct-coupling current. Secondly, based on the analysis of static end effect pulsating inductance matrix and direct-coupling mutual inductance matrix, the expression of pulsating electromotive force is derived. It can be compensated to the primary windings as feedforward voltage to suppress the negative-sequence current and direct-coupling current. Thirdly, a mixed second- and third-order generalized integrator (MSTOGI) is used to extract fundamental current and direct-coupling current to improve the compensation accuracy. The corresponding positive- and negative-sequence components are obtained by using instantaneous symmetric component method. Finally, the effectiveness of proposed compensation strategy is verified by simulation and experiment.
The simulation results show that when the static end effect compensation strategy is not adopted, the three-phase current is very asymmetrical, indicating that the negative-sequence current is of high content. After applying the static end effect compensation strategy, the negative sequence current is effectively suppressed and the three-phase current becomes more symmetrical. By fast Fourier transform analysis of C-phase current of power winding, the current content of direct-coupling decreases from 12.0% to 3.1% after compensation. In experiments, the asymmetry of three-phase current in the power winding decreases from 27.7% to 3.9%, and the content of direct-coupling current decreases from 11.4% to 5.8%.
The following conclusions can be drawn from the simulation and experiment analysis: (1) The static end effect of NLS-LDFM will generate harmonic current and negative-sequence current of various frequencies, of which the fundamental negative-sequence current and direct-coupling current are the main components. (2) The proposed current control process based MSTOGI and pulsating voltage feedforward can suppress the fundamental negative-sequence current and direct-coupling current, which can effectively compensate the static end effect in NLS-LDFM.
keywords：Linear doubly-fed machine (LDFM), static end effect, pulsating voltage feedforward, selective frequency current extraction
中图分类号：TM359.4
DOI:10.19595/j.cnki.1000-6753.tces.221058
国家自然科学基金面上项目（51877093）、四川省重点研发项目（2021YFG0081）、深圳市基础研究专项（自然科学基金）基础研究面上项目（JCYJ20190809101205546）、华中科技大学“双一流”建设国际合作专项（5001131076）资助。
收稿日期 2022-06-06
改稿日期 2022-07-01
包 振 男，1998年生，博士研究生，研究方向为直线电机控制。E-mail：zhenbao@hust.edu.cn
葛 健 男，1994年生，博士后，研究方向为直线电机特性分析。E-mail：gejian1994@hust.edu.cn（通信作者）
（编辑 郭丽军）