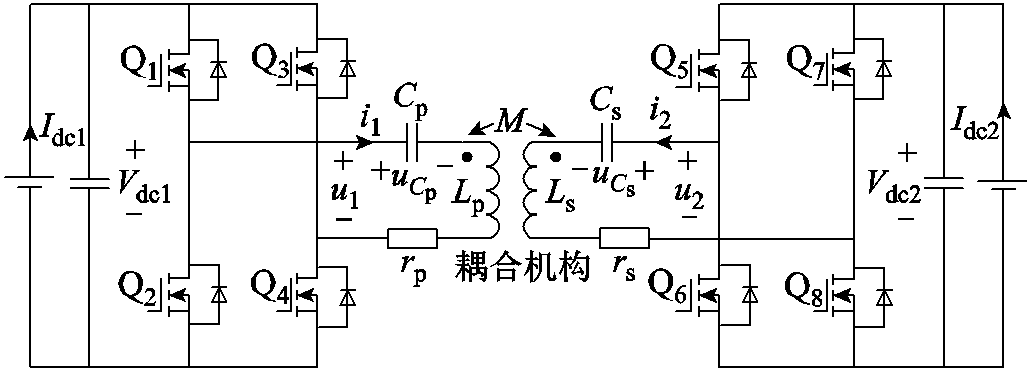
图1 SS补偿的感应式无线电能传输系统主电路
Fig.1 Main circuit of the SS compensated bidirectional inductive power transfer system
摘要 在宽功率范围内实现高效功率传输是无线电能传输系统的基本要求。为提升全功率范围下无线电能传输系统的效率，该文提出了一种双侧多周期不对称电压激励方法。该方法在一、二次侧采用一种具有多个周期的不对称激励电压波形，当系统需要降功率运行时，根据功率大小对构成多周期激励电压波形的各个半周期脉宽依次进行缩减。同时，通过调节二次侧激励电压波形相对于电流波形之间的位置关系，实现宽功率范围内的开关器件零电压开通。通过各个半周期脉宽随功率降低依次缩减的变化模式，使激励电压相位差随功率的逐渐降低而出现多次回归至峰值的非单调变化特性，平抑了宽功率范围内激励电压相位差的波动幅度而将其维持于较高值，进而实现宽功率范围内的效率提升。实验结果表明，所提方法在宽功率范围内的效率不低于传统方法的效率，在大部分功率点的效率高于传统方法的效率。所提多周期不对称电压激励方法无需任何额外硬件电路，可在宽功率范围内实现效率提升。
关键词：感应式无线电能传输（IPT） 双侧多周期不对称电压激励控制 效率优化 零电压开通
感应式无线电能传输技术（Inductive Power Transfer, IPT）可使电能在互相之间存在电气隔离的两个系统中进行传输。由于其无需任何电气连接，具有安全方便的特点，因此在一些场合，例如电子产品的无线充电、电动汽车无线充电、轨道交通等得到了广泛的应用[1-5]。
感应式无线电能传输系统包括高频逆变环节、谐振环节、高频整流环节。高频逆变环节将直流逆变为高频交流，施加在谐振环节的输入端。谐振环节包括一次侧补偿网络、耦合机构（线圈）和二次侧补偿网络，负责电能的无线传输。高频整流环节将谐振环节输出端的交流电整流为直流电。传统感应式无线电能传输系统的二次侧的高频整流环节往往采用二极管不控整流桥，而传输功率、充电过程的调控采用后级级联的DC-DC变换器实现。由于这种变换方式需要两级变换，因此其损耗较大、系统结构复杂。为了降低变换器的级数以降低系统损耗和复杂程度，可以将二次侧的二极管不控整流桥用可控有源整流桥代替[6-14]，与中间谐振环节和一次侧的高频逆变环节共同构成一种中间环节为谐振网络的双有源全桥结构的变换器拓扑。通过对二次侧可控整流桥的控制，可实现传输功率的调节，从而省去为实现功率调节所需的额外级联的DC-DC变换环节，使整个系统的结构较为简单。此外，二次侧采用有源可控整流桥，还使电能的双向流动成为可能；通过对双侧的逆变桥和整流桥的控制，还可实现传输效率的优化[6-14]。
鉴于该双有源全桥结构的无线电能传输变换器拓扑存在的种种优势，诸多文献对该变换器拓扑展开了研究。文献[9,11]针对该变换器拓扑提出了一种双侧双移相（Dual Phase Shift, DPS）控制方法，通过调整两侧全桥产生的激励电压的脉冲宽度角，使得两侧谐振网络的电流应力均衡，从而降低谐振网络的损耗，实现效率优化。然而，该双侧双移相控制方法无法实现所有开关器件的零电压开通，开关器件的开关损耗较大，导致系统在中载和轻载下的传输效率低下。为了实现所有开关器件的零电压开通，降低开关损耗，文献[8,13-14]提出了一种双侧三移相（Triple Phase Shift, TPS）控制方法。该方法引入两侧全桥变换器的激励电压的基波分量之间的相位差作为额外控制量，同时配合两侧激励电压的脉冲宽度角的调节，使得所有开关器件均能实现零电压开通，并且实现两侧谐振网络电流应力的均衡，从而优化系统的整体效率。然而，在该三移相控制方法中，所有开关管的零电压开通是通过降低激励电压基波相位差来实现的，而较低的激励电压基波相位差将会使得一次侧、二次侧的功率因数较低，相比于双移相控制，在传输同等的功率下需要较高的谐振电流幅值，使得导通损耗增加。文献[15]在一次侧、二次侧全桥的直流侧分别加入软开关辅助电路，使整个系统在双移相控制下即可实现所有开关器件的零电压开通，而不需要以牺牲功率因数为代价。然而，该方法中的额外软开关辅助电路增加了系统的成本，设计较为复杂。且软开关辅助电路同样存在着一定的损耗，相比于传统的硬开关双移相方法，系统的效率提升不高。
鉴于以上问题，为了使感应式无线电能传输系统在宽功率范围下取得较高的效率，文献[16]提出了一种单周期双侧不对称电压激励控制（One Period Asymmetrical Voltage Control, 1P-AVC）方法，通过采用不对称的激励电压波形，削弱了实现零电压开通与实现较高的一次侧、二次侧功率因数两者之间的矛盾，从而在宽功率范围下实现了效率的提升。然而，文献[16]所提出的基于单个周期的双侧不对称电压激励控制方法在低功率段的效率较低，仍具有一定的改进空间。为此，本文在文献[16]方法的基础上，将基于单个周期的双侧不对称电压激励控制方法拓展到多个周期，提出一种多周期不对称电压激励控制（Multiple Period Asymmetrical Voltage Control, MP-AVC）方法。相比于单个周期的不对称激励电压控制，所提多周期不对称电压激励控制方法是一种更一般、更广义的形式，前者可归为后者的一种特殊情况。该方法在多个谐振频率所对应的周期内采用不对称的激励电压波形，当需要降功率运行时，以特定的次序对激励电压波形的各个半周期脉冲宽度角先后进行缩减，在实现激励电压幅值降低的同时，使基波功率因数值多次重复出现“减小-增大”的变化趋势，进一步平抑全功率范围内基波功率因数值的波动幅度，使其在较高的区间内波动，同时尽可能地保障各开关器件的零电压开通，进而在宽传输功率范围内获得更高的传输效率。首先，对串联-串联（Series-Series, SS）补偿的双有源全桥结构的感应式无线电能传输系统的基本特性进行介绍，给出影响中间谐振环节的传输效率的因素；其次，对所提多周期不对称电压激励方法进行阐述，并与传统方法进行对比；最后，通过实验对所提方法进行验证并给出结论。
SS补偿的双有源全桥结构的感应式无线电能传输系统的主电路拓扑如图1所示。其中，Vdc1为一次侧全桥变换器的直流侧电压；Vdc2为二次侧全桥变换器的直流侧电压；u1、u2分别为一次侧、二次侧全桥变换器输出的激励电压；i1、i2分别为一次侧、二次侧线圈中的电流；Q1～Q4为一次侧全桥变换器的开关管；Q5～Q8为二次侧全桥变换器的开关管；Cp、Cs分别为一次侧、二次侧的补偿电容；Lp、Ls分别为耦合机构（线圈）一次绕组、二次绕组的自感；M为耦合机构的一次、二次绕组之间的互感系数；rp、rs分别为表征一次侧、二次侧损耗的等效电阻。
图1 SS补偿的感应式无线电能传输系统主电路
Fig.1 Main circuit of the SS compensated bidirectional inductive power transfer system
本文所采用的SS补偿网络的参数选取方式为全补偿，即一次侧补偿电容Cp在工作频率处的容抗完全抵消耦合机构一次线圈Lp的感抗，二次侧补偿电容Cs在工作频率处的容抗完全抵消耦合机构二次线圈Ls的感抗，即
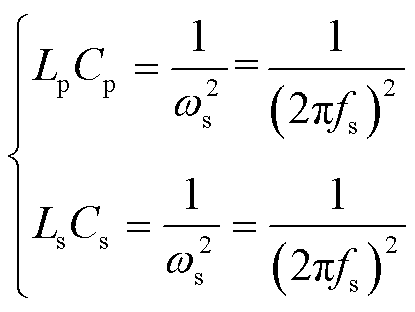（1）
式中，ωs、fs分别为工作角频率和工作频率。由于中间谐振环节具有较强的带通滤波特性，高于谐振频率fs的谐波成分在很大程度上被滤除。为方便分析，可采用基波分析法，仅考虑频率为fs的基波成分，则图1所示的中间谐振环节的等效电路如图2所示。
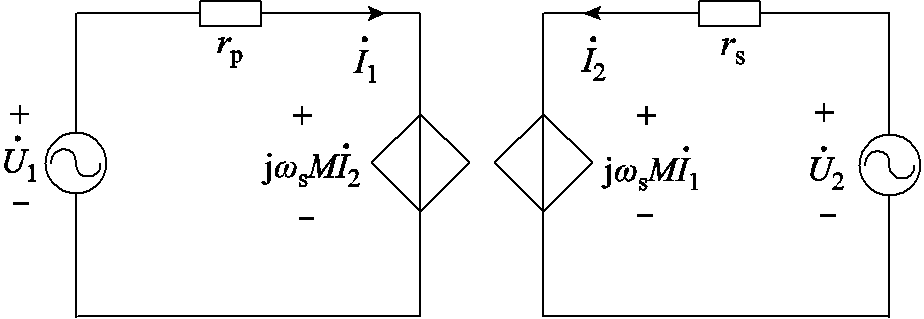
图2 SS补偿的IPT系统中间环节等效电路
Fig.2 The equivalent circuit of the intermediate circuit of the SS compensated IPT system
根据如图2所示的等效电路，可解得一次侧、二次侧谐振电流分别为
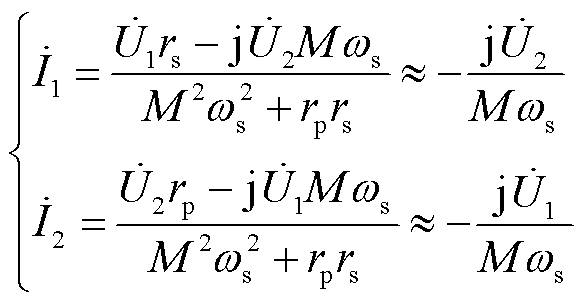（2）
式中，
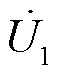和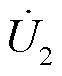
分别为一次侧和二次侧激励电压的基波分量。
可见，当忽略一次侧、二次侧的等效损耗电阻rp、rs后，二次侧谐振电流的基波分量滞后于一次侧激励电压的基波分量90°，一次侧谐振电流的基波分量滞后于二次侧激励电压的基波分量90°。
定义一次侧、二次侧激励电压的基波分量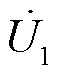、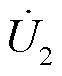之间的相位差为δ，以二次侧激励电压基波分量超前于一次侧激励电压基波分量为正，即
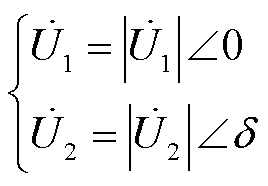（3）
则可得到理想情况下的传输功率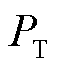
为
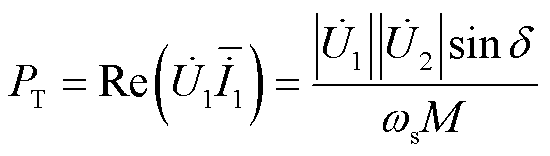（4）
式中，“-”代表电流相量的共轭。由式（4）可见，传输功率的大小与一次侧、二次侧激励电压的基波幅值的乘积成正比，此外，还与一次侧、二次侧激励电压的相位差δ的正弦值成正比。因此，通过控制一次侧、二次侧激励电压幅值的大小，可以调节传输功率的大小；而通过改变一次侧、二次侧激励电压的相位差δ，可改变传输功率值的大小和功率传输方向。
IPT系统的中间环节，包括一次侧补偿网络、耦合机构和二次侧补偿网络。以功率从一次侧流向二次侧为例，中间环节的传输效率为
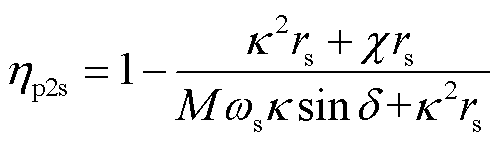（5）
式中，κ为激励电压比；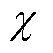
为等效损耗电阻之比。二者分别定义为
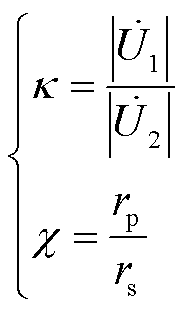（6）
当中间环节的传输效率取得最大值时，激励电压比κ为
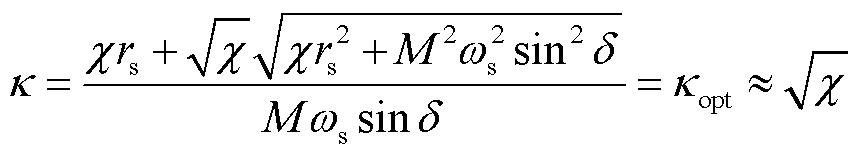（7）
式中，κopt为最优激励电压比。式（7）表示当实际的激励电压比κ等于最优激励电压比κopt时，中间环节的传输效率达到最大值。由式（7）可知，最优激励电压比与传输功率的大小无关，其所描述的条件又被称为负载匹配条件。
由式（5）还可得，无论功率传输方向如何，一次侧、二次侧激励电压基波之间的相位差δ对中间环节的传输效率亦存在影响。以κopt=1、rp=rs=0.32 Ω、M=35 μH、频率为85 kHz为例，激励电压比κ和一次侧、二次侧激励电压相位差δ对中间谐振环节的传输效率的影响如图3所示。当|δ|接近90°时，中间环节的传输效率最高；而当|δ|偏离90°时，传输效率将会降低。虽然图3所示的结果是基于以上的特定参数值得到的，对于其他参数值，图3所示的规律仍然成立，具有普适性。
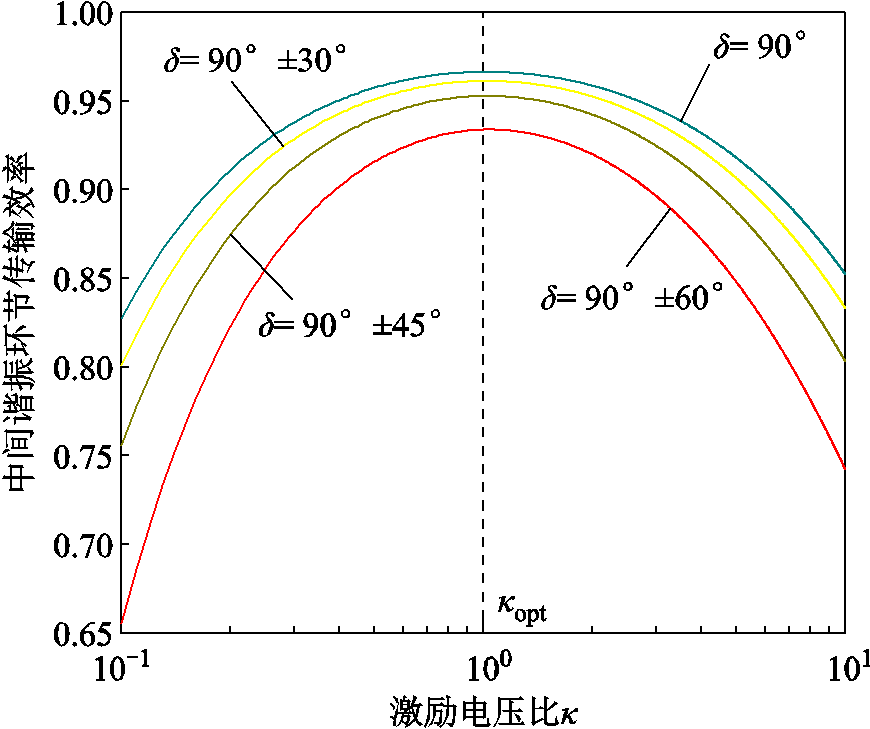
图3 激励电压比κ和相位差δ对中间谐振环节传输效率的影响
Fig.3 The influence of the excitation voltage ratio κ and phase difference δ to the transfer efficiency of the intermediate resonance circuit
对于传统的双侧双移相（DPS）控制方法和双侧三移相（TPS）控制方法，全桥变换器产生的激励电压波形的正负半周对称。在实现负载匹配的条件下，DPS控制以牺牲开关损耗为代价，得到较高的功率因数和较高的|δ|值，从而实现较高的中间谐振环节的传输效率。而TPS控制则以牺牲功率因数、|δ|值为代价，在相对较高的中间谐振环节损耗及开关管的导通损耗的条件下实现所有开关器件的零电压开通，进而降低开关损耗，以优化系统整体效率。对于TPS控制，传输功率越低，则为实现所有开关器件的零电压开通，对功率因数的牺牲程度越高，使得传输同等功率时所需的电流幅值越大，在某些特定的情况下，谐振腔与开关管的导通损耗的增量可能超过所有开关管实现零电压开通所减小的开关损耗，使得系统采用TPS控制相比于DPS控制并不能带来效率的提升，因此采用DPS和TPS两种控制方法的系统在中载和轻载下效率较低。
为削弱传统对称三移相控制中一次侧和二次侧在实现较低的中间谐振环节损耗与实现较低的开关损耗两个目标之间的矛盾，从而在更低的中间谐振环节损耗的情况下实现所有开关器件的零电压开通，基于单周期的双侧不对称电压激励方法被提出[16]。为了削弱两个目标之间的矛盾，进一步提高系统在宽功率范围下的整体效率，本节提出一种多周期不对称电压激励方法。
对于N个周期的不对称激励电压，其波形如图4所示。该波形由全桥变换器产生，重复周期为NTs，其中Ts=1/fs。该重复周期内的激励电压波形由N个周期为Ts的激励电压波形构成，每个周期内的激励电压电平存在三种状态，分别为正电平P、负电平N和零电平O，激励电压在各电平之间变化的边沿分别为上升沿①、下降沿②、下降沿③、上升沿④。定义第m（m=1,2,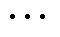
, N）个周期内的激励电压波形的正脉冲宽度角和负脉冲宽度角分别为
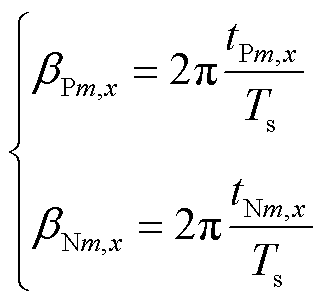（8）
式中，tPm,x和tNm,x分别为第m个周期内激励电压正电平和负电平所持续的时间，x=1代表一次侧，x=2代表二次侧。
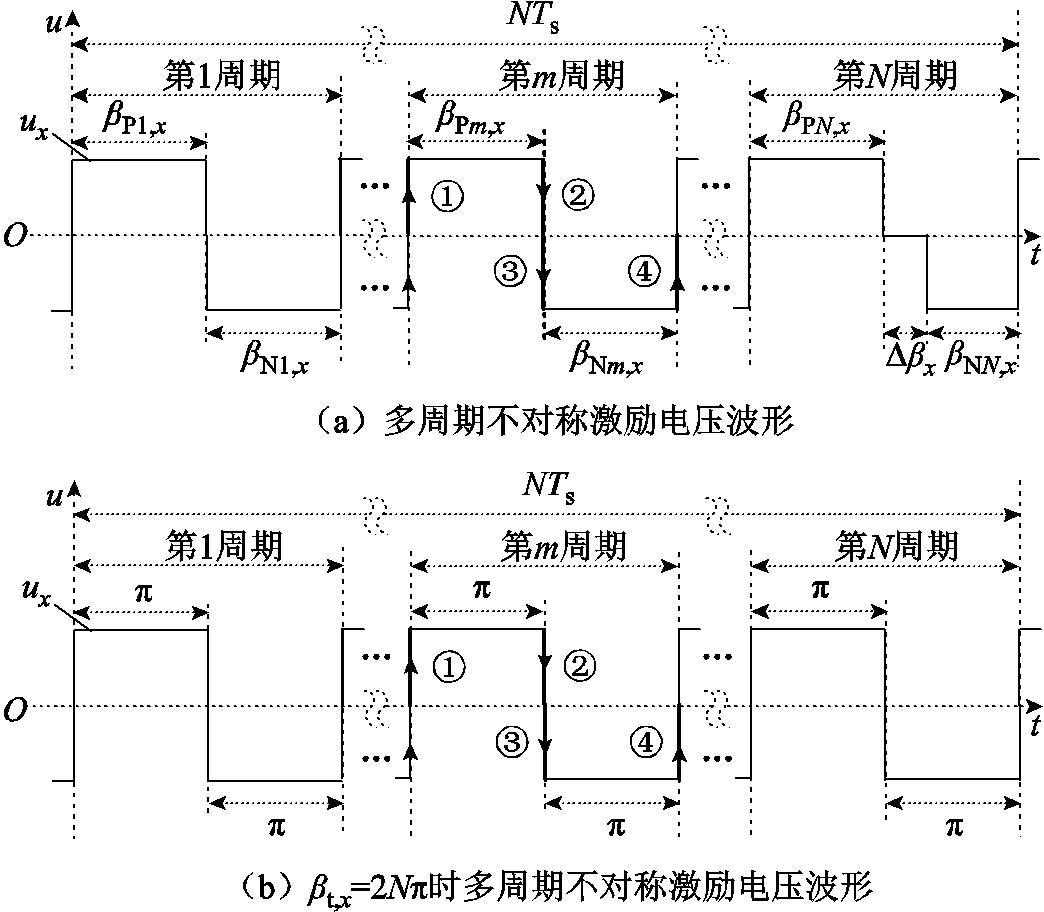
图4 多周期不对称激励电压波形
Fig.4 The waveforms of multi-period asymmetrical excitation voltage
定义整个激励电压波形ux(t)在重复周期NTs内的总正脉冲宽度角βPt,x、总负脉冲宽度角βNt,x及总脉冲宽度角βt,x分别为
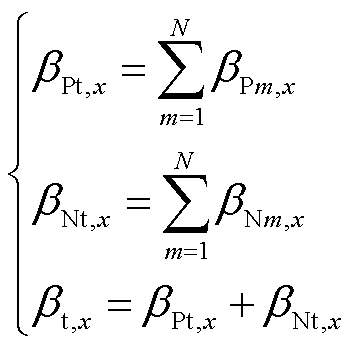（9）
在实际系统中，总脉冲宽度角βt,x由控制环路调节器事先给定，根据βt,x值以特定的规则确定重复周期NTs内的各个周期Ts内的激励电压波形。该波形的确定规则如下。
首先，规定βt,x取值为2Nπ时的激励电压波形。当βt,x=2Nπ时，激励电压波形如图4b所示，其各个周期Ts内的正脉冲宽度角和负脉冲宽度角均为π。从第1周期至第N周期的N个周期中，总共有2N个半周期。当βt,x取其他值时，计算出βt,x相对于2Nπ的减小量Δβt,x为
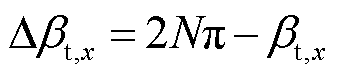（10）
随后，根据Δβt,x计算出需要将正电平或负电平脉冲宽度角缩减至零的半周期的个数p为
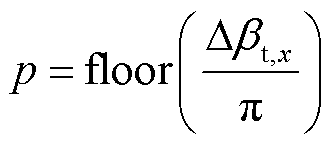（11）
式中，floor(·)代表向下取整运算。将激励电压波形在图4b的基础上，选取p+1个半周期，分别记为λ1, λ2,…, λp, λp+1，并将λ1～λp半周期内的正电平或负电平脉冲宽度角置为零，对应时间段内的电平变为零电平。同时，将第λp+1个半周期内的正或负电平的脉冲宽度角缩减，缩减量为
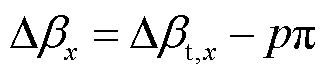（12）
其中，对正电平或负电平脉冲宽度进行置零或缩减的半周期序号λ1, λ2,…, λp, λp+1可以按一定的规则进行选取，从而达到降低低于开关工作频率fs的次谐波（sub-harmonic）的目的，也可采用较为简单的方式进行选取，例如将多周期激励电压波形序列中的后p个Ts/2半周期的正或负脉冲宽度角置为零，将倒数第p+1个Ts/2半周期的正或负脉冲宽度角削减Δβx。
第λp+1个半周期的正脉冲或负脉冲宽度角的缩减是通过将该半周期内的边沿向中间位置移动得到的，根据全桥变换器的工作模式对半周期内位置固定的边沿与所移动的边沿进行选择。如果所需缩减脉宽的半周期为正半周期，则若全桥变换器处于整流模式，令边沿②的位置保持不变，而将边沿①向右移动Δβx；若该全桥变换器处于逆变模式，则令边沿①的位置保持不变，而将边沿②向左移动Δβx。边沿移动所经过的区间Δβx内的激励电压电平由正电平变为零电平。如果所需缩减脉宽的半周期为负半周期，当全桥变换器处于整流模式时，则令边沿④的位置保持不变，而将边沿③向右移动Δβx；当该全桥变换器处于逆变模式时，则令边沿③的位置保持不变，而将边沿④向左移动Δβx。边沿移动所经过的区间Δβx内的激励电压电平由负电平变为零电平。
由于中间谐振环节具有带通特性，偏离fs的频率分量在很大程度上被衰减，因此可认为起到功率传输作用的成分主要是频率为谐振频率fs的分量。根据以上的规则确定了多周期激励电压的波形后，为求出激励电压波形的频率为fs的分量的幅值与相位，以第1周期的起始时刻为参考点，对多周期激励电压波形进行傅里叶分析，可得到激励电压的fs分量的幅值为
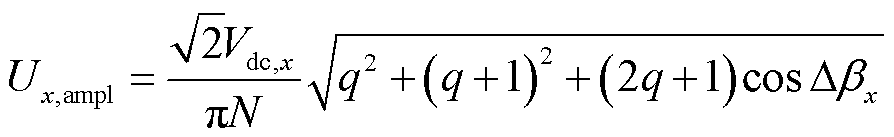（13）
其中
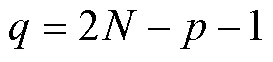（14）
激励电压的fs分量相对于参考点之间的相位差为
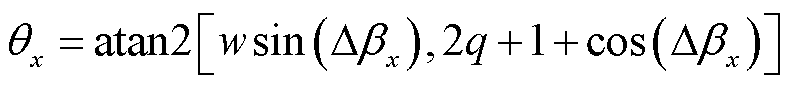（15）
式中，atan2(·)为四象限反正切函数；w为与激励电压波形相关的参数，当激励电压波形为逆变模式时，w取值为1，当激励电压波形为整流模式时，w取值为-1；θx为激励电压ux的频率为fs的分量波形由负到正的过零点与参考点之间的相位差，以正值代表过零点超前于参考点，负值代表过零点滞后于参考点。激励电压的fs分量的幅值和相位与前文所述的半周期序号λ1, λ2,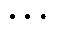
, λp, λp+1的选取方式无关。
对于一次侧的变换器，仅需根据一次侧总脉冲宽度角βt,1及其运行状态（逆变或整流）生成其多周期激励电压波形。而对于二次侧的变换器，不仅需要根据二次侧总脉冲宽度角βt,2及其运行状态生成相应的多周期激励电压波形，还需对激励电压波形与二次侧谐振电流i2波形之间的相对位置进行调整，从而使双侧变换器的开关器件可在大部分情况下实现零电压开通。该相对位置的调整可通过锁相环实现。在后文中，将以能量由一次侧传输至二次侧为例进行分析和说明。此时，二次侧变换器处于整流模式，需将二次侧多周期激励电压波形的参考点（第1周期起始时刻）控制在滞后于二次侧谐振电流波形i2由正到负的过零点相位α的位置。则可得到频率为fs的二次侧激励电压分量与二次电流基波分量之间的相角（二次侧功率因数角）为
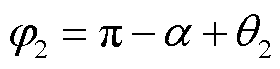（16）
由于二次电流的fs分量与一次侧激励电压的fs分量之间存在90°的滞后角，可得一次侧、二次侧激励电压的fs分量之间的相位差δ为
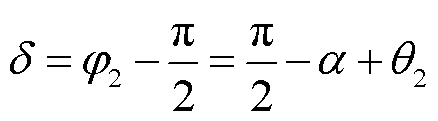（17）
由于一次电流的fs分量与二次侧激励电压的fs分量之间存在90°的滞后角，可得到频率为fs的一次侧激励电压分量与一次电流分量之间的相角（一次侧功率因数角）为
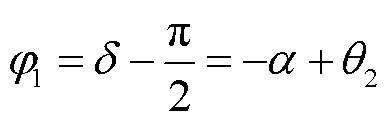（18）
由式（16）～式（18）可见，相位差δ与一次侧、二次侧功率因数角φ1、φ2之间存在明确的对应关系，当δ越接近90°，则一次侧、二次侧端口的功率因数的绝对值越高，反之亦然。因此，“提高激励电压相位差δ”与“提高功率因数”两种表达方式是等价的。
以两个周期的不对称激励电压波形为例对波形的产生进行说明，当采用二周期不对称激励电压控制（Two Period Asymmetrical Voltage Control, 2P-AVC）时，一次侧变换器处于逆变模式，二次侧变换器处于整流模式。一次侧、二次侧变换器激励电压总脉冲宽度角在不同范围内取值时，一次侧、二次侧激励电压波形分别如图5、图6所示。
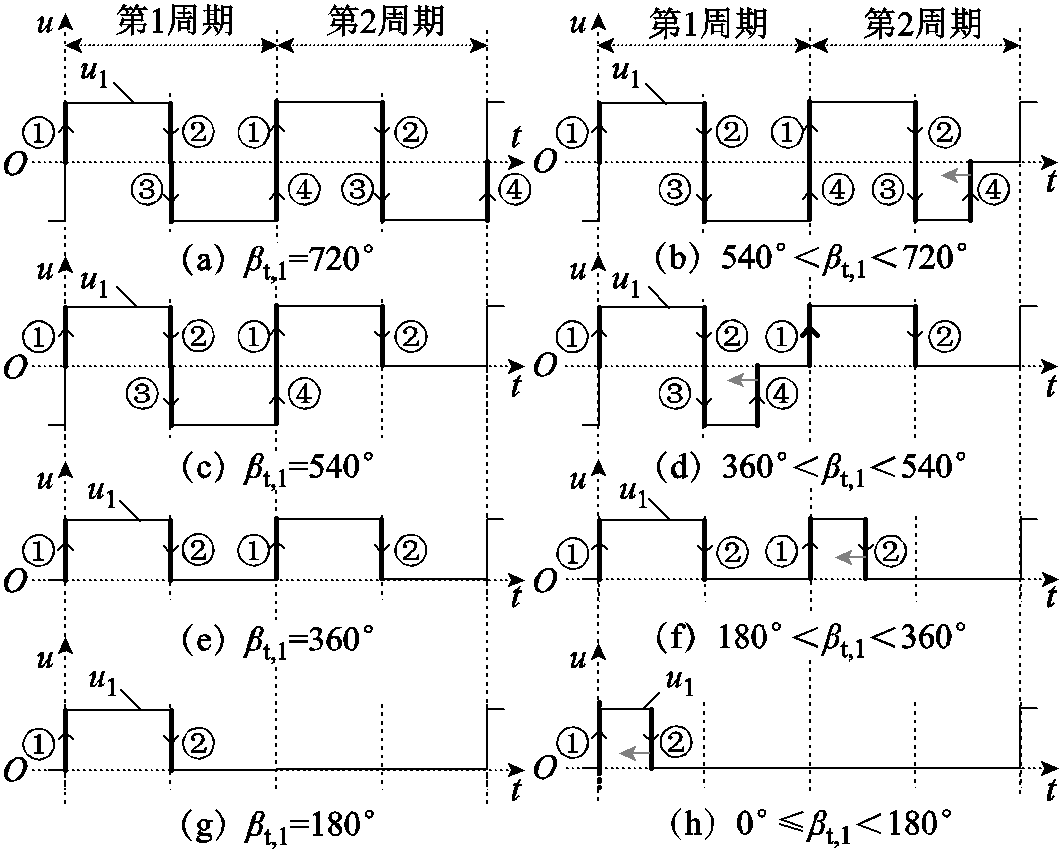
图5 一次侧二周期不对称激励电压波形
Fig.5 The waveforms of two-period asymmetrical excitation voltage of primary side
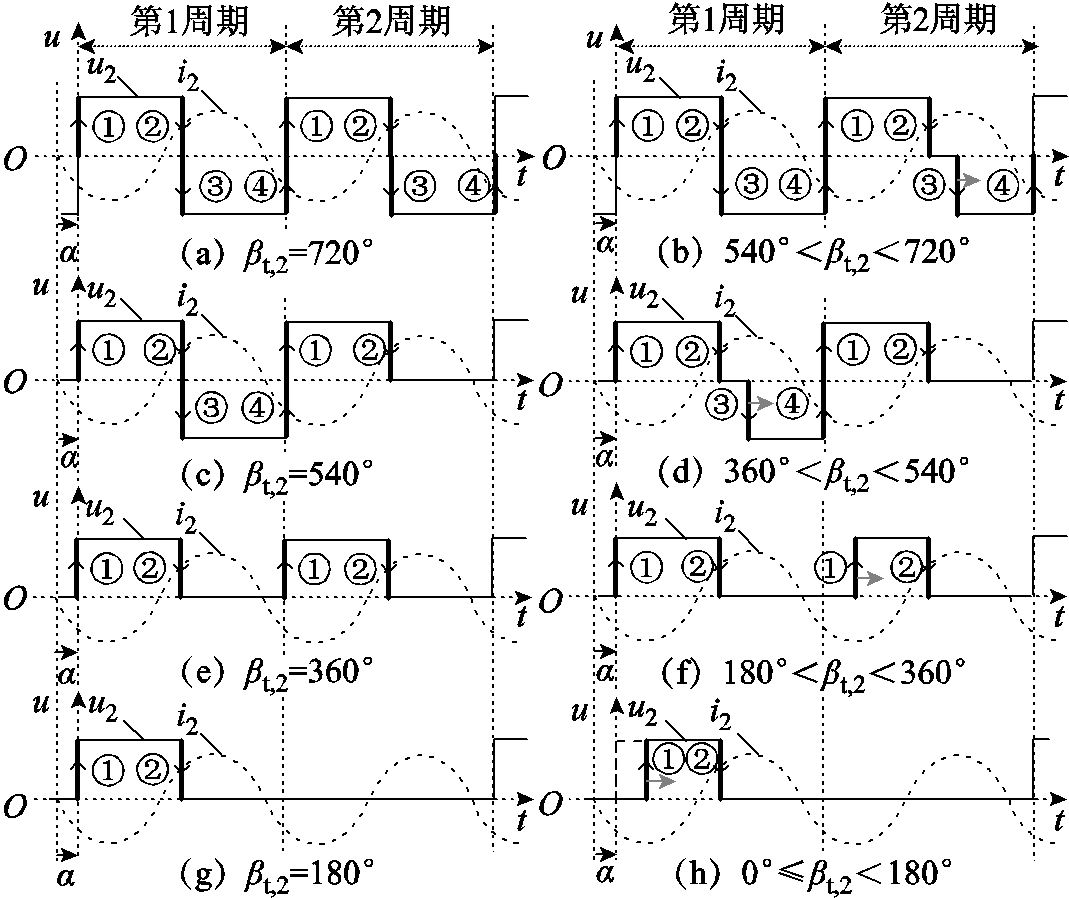
图6 二次侧二周期不对称激励电压波形
Fig.6 The waveforms of two-period asymmetrical excitation voltage of secondary side
如图5所示，对于处于逆变模式的一次侧变换器的二周期激励电压，当βt,1为720°时，激励电压波形为正、负电平脉冲宽度均为180°的两电平波形。两周期内的正负脉宽角总和为720°。当βt,2在区间(540°, 720°]内减小时，令第二周期的边沿④向左移动(720°-βt,1)，直至第二周期的负脉宽减小至零；当βt,1在区间(360°, 540°]内减小时，令第一周期边沿④向左移动(540°-βt,1)，直至第一周期的负脉宽减小至零；当βt,1在区间(180°, 360°]内减小时，令第二周期边沿②向左移动(360°-βt,1)，直至第二周期的正脉宽减小至零；当βt,1在区间[0°, 180°]内减小时，令第一周期边沿②向左移动(180°- βt,1)，直至第一周期的正脉宽减小至零。
对于处于整流模式的二次侧变换器的二周期激励电压，其波形如图6所示。第一周期的起始时刻与电流i2基波分量由正到负的过零点之间存在滞后角α。当βt,2分别在区间(540°, 720°]、(360°, 540°]、(180°, 360°]和[0°, 180°]内减小时，分别令第二周期边沿③、第一周期边沿③、第二周期边沿①和第一周期边沿①分别向右移动(720°- βt,2)、(540°-βt,2)、(360°-βt,2)和(180°-βt,2)，直至对应周期内的正或负脉宽角减小至零。
则以上所述的二周期不对称激励电压波形的频率为fs的电压分量幅值为
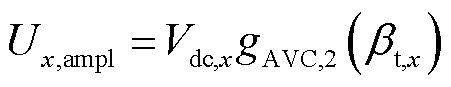（19）
其中
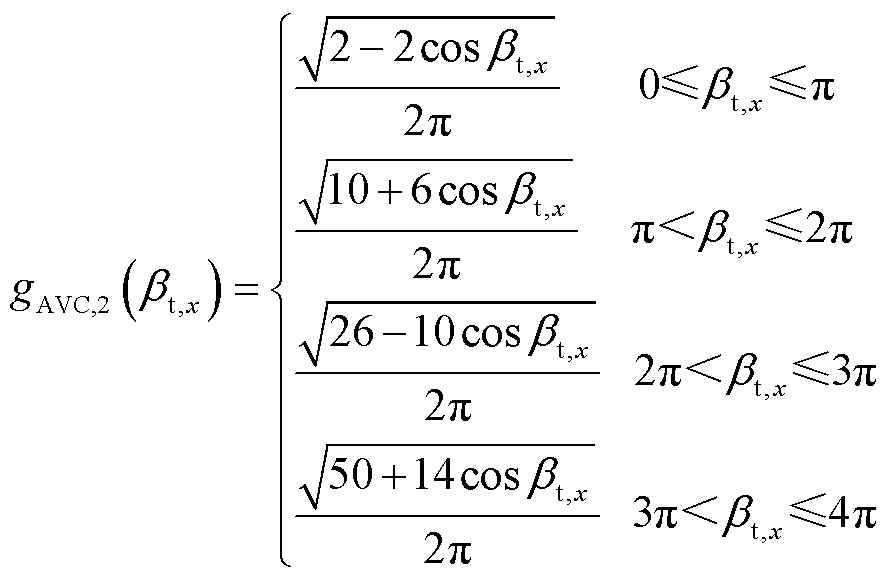（20）
由式（20）可知，函数gAVC,2(βt,x)在区间[0, 4π]内连续且单调递增，值域为[0, 4/π]。
激励电压的fs分量相对于参考点之间的相位差为
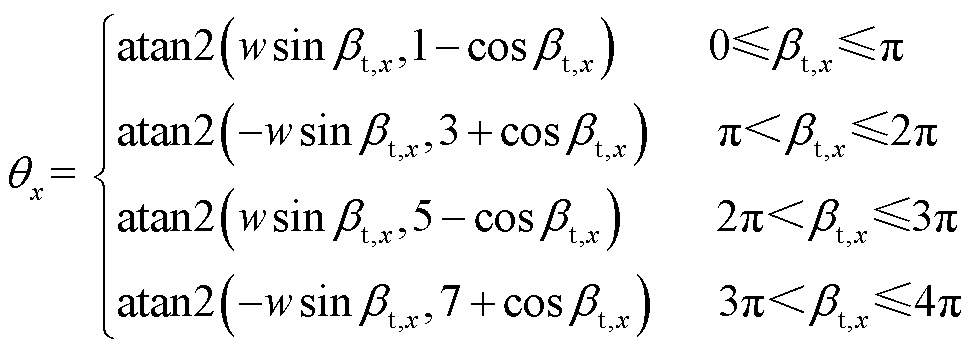（21）
对于电路中的各个开关管，为实现其零电压开通，需保证在该开关管的驱动信号由低电平变为高电平之前，其端电压被导通的反向并联二极管钳位至零。当一次侧、二次侧谐振电流i1、i2的参考方向取图1所示的方向时，为使全桥变换器开关管实现零电压开通，在各个周期的边沿①、②、③、④的时刻，该侧谐振电路的瞬时值需分别为负值、正值、正值、负值。为尽量满足该条件，需对二次侧的滞后角α进行调节。在大部分工作点内，存在一个使所有开关器件均可实现零电压开通的α值的取值范围。而由式（5）、式（16）～式（18）可见，较大的α值将会导致δ值和功率因数偏低，从而降低中间谐振环节的传输效率。因此，α值应取可使所有开关器件实现零电压开通的最小值。计算得到二次侧的滞后角α与一次侧和二次侧激励电压的脉冲宽度角β1t与β2t之间的关系为
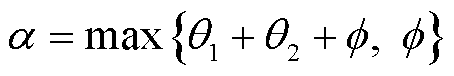（22）
式中，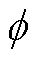
为额外的裕度角，可取值为10°，用于确保死区电流足够高以抽走开关管结电容的电荷，从而使开关器件实现零电压开通。
为提高中间谐振环节的传输效率，由1.2节的结论可知，还需满足负载匹配条件，即使激励电压比值接近最优激励电压比。在所提双侧多周期不对称电压激励方法中，需对双侧的激励电压脉冲宽度角进行调节，以使实际的激励电压比κ等于或尽可能接近最优激励电压比κopt，即
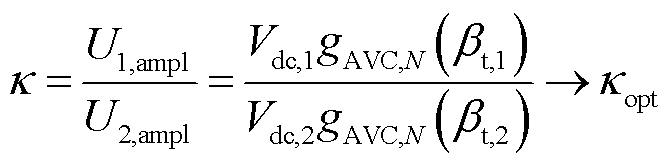（23）
式中，gAVC,N(βt,x)为关于N周期的不对称激励电压的总脉冲宽度角的函数，其函数值为N周期激励电压的fs的分量的幅值与直流侧电压值之比，在0≤βt,x≤2Nπ范围内连续，且随βt,x的增加单调递增。
根据式（13）、式（15）、式（17）、式（22），可得到所提多周期不对称电压激励方法在不同周期数N的情况下，一次侧、二次侧激励电压的频率为fs的分量之间的相位差δ与激励电压fs分量幅值U1,ampl、U2,ampl之间的关系。对于对称三移相（TPS）控制，当其正负脉冲宽度角为π时，其激励电压波形与总脉冲宽度角为2Nπ的N个周期的不对称激励电压波形完全一致，取此时的激励电压fs分量幅值为基值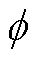，取值为10°，得到在TPS控制、单周期、二周期和三周期不对称激励电压控制（Three Period Asymmetrical Voltage Control, 3P-AVC）下的相位差δ与一次侧、二次侧激励电压标幺值U1*、U2*之间的关系分别如图7a～图7d所示。
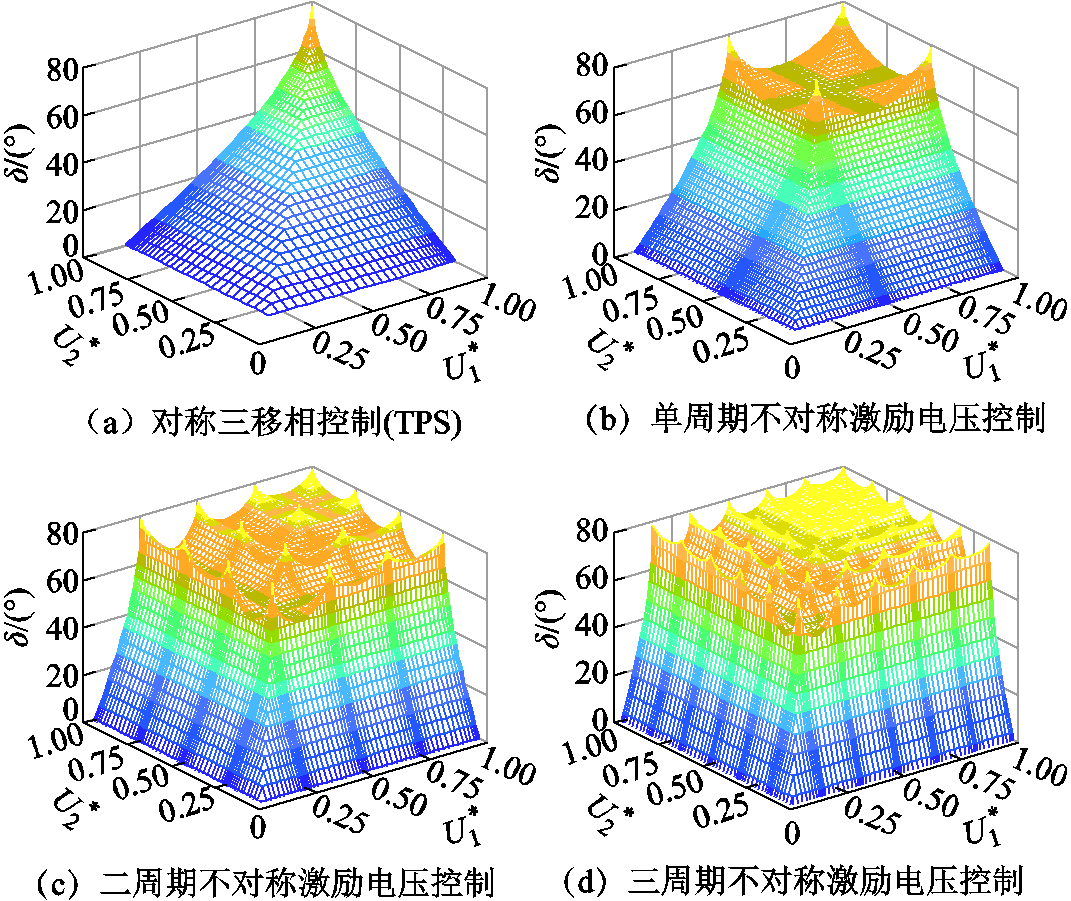
图7 相位差δ与激励电压标幺值U1*、U2*之间的关系
Fig.7 The relationship between the normalized excitaiton voltage U1*, U2* and phase difference δ
由图7可见，对于传统的对称三移相控制TPS，处于实现开关管零电压开通条件下的δ值在(U1*, U2*)=(1,1)处达到最大值，随着U1*或U2*的降低，δ值逐渐下降，对应一次侧、二次侧的功率因数逐渐降低。对于单个或多个周期的不对称激励电压控制，随着U1*或U2*的取值从1逐渐降低，δ值呈现出多次“下降-上升”的变化趋势，当U1*和U2*取值为1/(2N)的正整数倍时，δ值回归到峰值。例如，对于N=1的单周期不对称激励电压控制，当两侧的激励电压标幺值取值为1/2和1时，对应的δ值达到最大；对于N=2的二周期不对称激励电压控制，当两侧的激励电压标幺值取值为1/4、1/2、3/4和1时，对应的δ值达到最大；对于N=3的三周期不对称激励电压控制，当两侧的激励电压标幺值取值为1/6、1/3、1/2、2/3、5/6和1时，对应的δ值达到最大。这是由于，当U1*=m1/(2N)且U2*=m2/(2N)（其中m1, m2为正整数，且m1, m2≤2N）时，βt,1、βt,2的值分别为m1π和m2π，而根据第2节所述的波形生成规则，此时一次侧和二次侧的激励电压波形恰好分别有m1个和m2个完整的半周期。此时，与βt,1、βt,2取值为2Nπ（即U1*=U2*=1）的情况类似，由式（15）可得到θ1=θ2=0°，再根据式（22），二次侧的滞后角α只需取最小值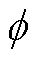即可实现开关器件零电压开通，因此由式（17）可得，此时δ=π/2-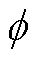，取得最大值。
由图7还可得，在相同的(U1*, U2*)条件下，所提的多周期不对称激励电压控制方法的δ值不小于对称三移相控制TPS的δ值，在绝大多数情况大于对称三移相控制TPS的δ值。随着周期数的增加，将会出现更大范围的δ较大的区域。这实际上是与由式（15）所描述的θx随βt,x的变化而变化的规律有关，θx所描述的实际上是激励电压的fs分量相对于第1周期的起始时刻参考点之间的相位偏移，当βt,x为π的正整数倍时，θx为零。对于N周期的不对称激励电压波形，当由于βt,x降低，而使其中的个别半周期的脉冲边沿发生移动、脉冲宽度角发生变化或缺失时，会使θx相对于零出现偏移，而此时其余的半周期波形还是保持完整的（即正或负脉冲宽度角为180°），由傅里叶级数分析可得，这些完整的半周期对整体激励电压波形的fs分量的相位差的偏移θx，起到了一定的抑制、平抑的作用，且当完整的半周期数越多（即βt,x越大、对应功率值越高、周期数N越大），这种抑制整体相位差偏移θx的作用就越强，|θx|的值就越小，因此，在对应变化区间内的δ的值就相对更大。
考虑不同方法在同等功率、同等激励电压之比的情况下的相位差δ的大小关系，首先以U1*=U2*=1、δ=π/2-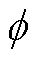时的传输功率为基值，定义功率标幺值P*为
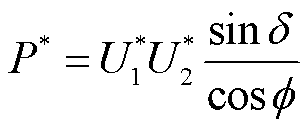（24）
功率P*随着U1*或U2*的增加而增大。定义激励电压标幺值U1*、U2*之比为
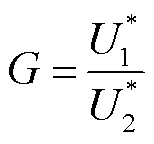（25）
当给定了P*值和G值，则至多可确定1个工作点(U1*, U2*)。由此，给出了不同控制方法下，不同P*和G值情况下的相位差δ，如图8中的曲面所示，图8中的各个峰值点即对应图7中的各个峰值点。对比图8b与图8a可见，在相同的P*和G的情况下，单周期不对称激励电压控制的相位差δ值高于对称三移相控制的δ值；而对比图8c与图8b，以及对比图8d与图8b可见，多个周期不对称激励电压控制的相位差δ值大于单周期不对称激励电压控制的δ值。在功率标幺值P*和激励电压标幺值之比G一定的情况下，相位差δ值越大，则所需U1*、U2*值越小，因此一次侧、二次侧的谐振电流值更小，在中间谐振环节产生的功率损耗也更小。对于以上三种都能实现开关器件零电压开通的方法，整体效率主要由中间谐振环节的损耗决定，中间谐振环节的损耗越小，则整体效率越高。因此，不对称激励电压控制方法的效率优于对称方法，而多个周期的不对称激励电压控制方法的效率优于单个周期的方法。
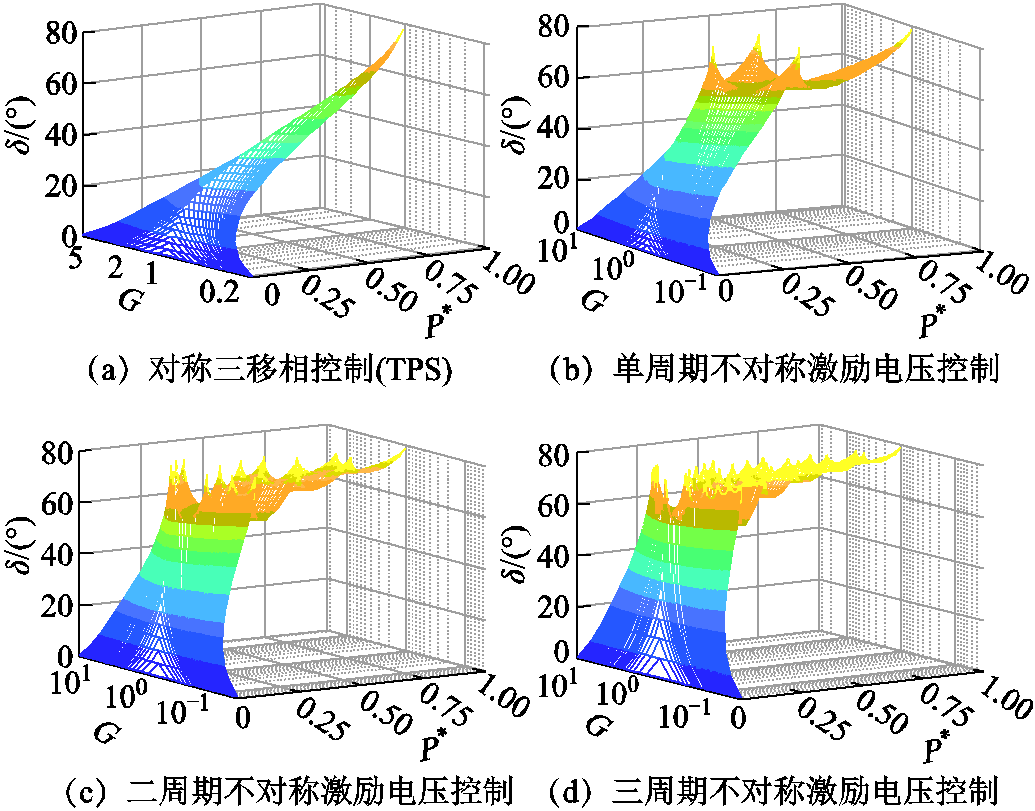
图8 不同方法的相位差δ与P*、G的关系
Fig.8 The relationship between P*, G and phase difference δ
以二周期和三周期不对称电压激励控制方法为例，对所提多周期不对称电压激励控制方法的有效性进行实验验证，所搭建的实验平台如图9所示，实验平台的参数见表1。系统额定传输功率为3.7 kW，一次侧、二次侧直流侧电压为300 V，功率传输方向为由一次侧传输至二次侧。
图9 实验平台
Fig.9 The experiment platform
表1 实验平台参数
Tab.1 Parameters of the experiment platform
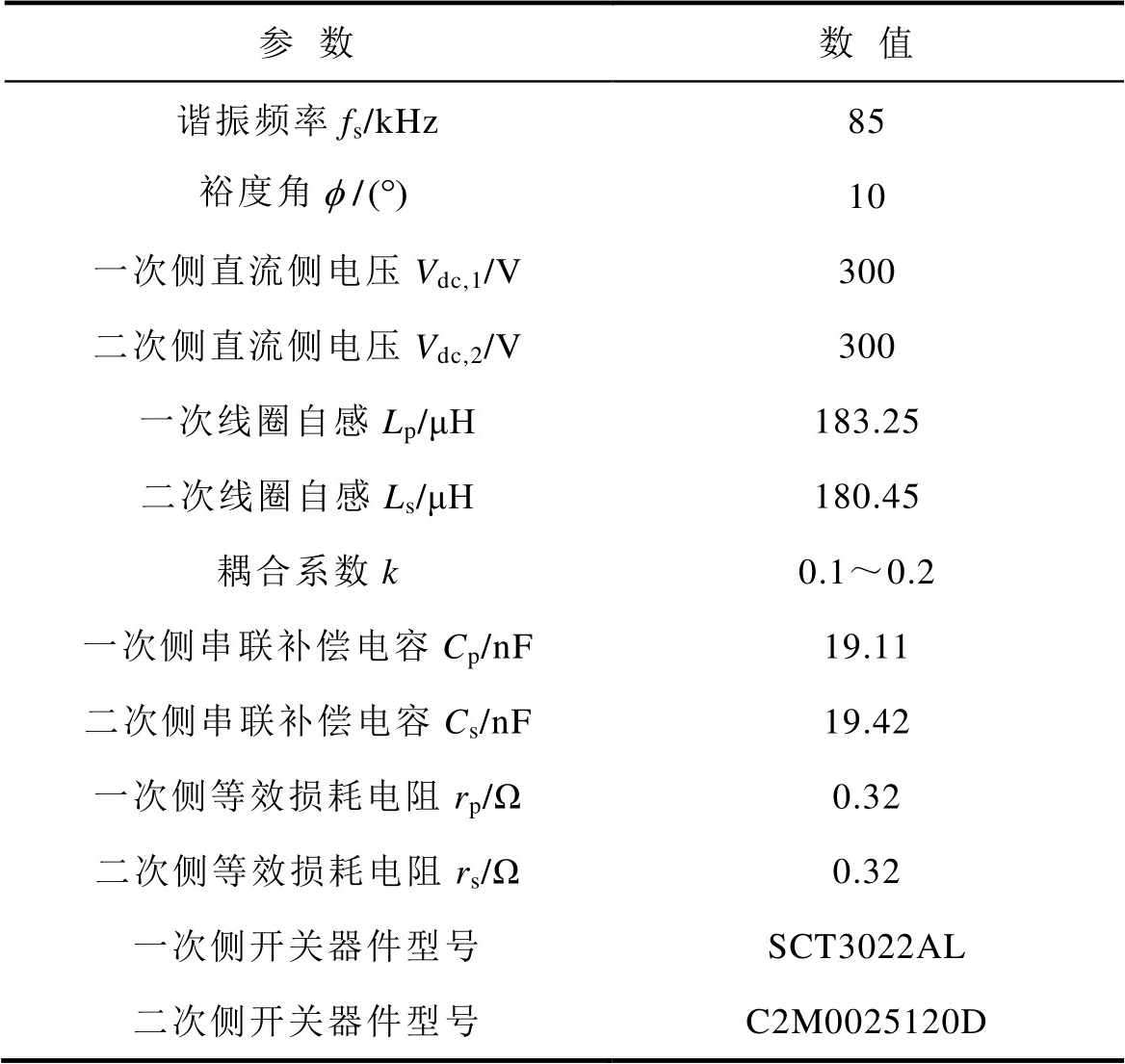
参数数值 谐振频率fs/kHz85 裕度角10 一次侧直流侧电压Vdc,1/V300 二次侧直流侧电压Vdc,2/V300 一次线圈自感Lp/μH183.25 二次线圈自感Ls/μH180.45 耦合系数k0.1～0.2 一次侧串联补偿电容Cp/nF19.11 二次侧串联补偿电容Cs/nF19.42 一次侧等效损耗电阻rp/Ω0.32 二次侧等效损耗电阻rs/Ω0.32 一次侧开关器件型号SCT3022AL 二次侧开关器件型号C2M0025120D
当耦合系数k=0.2时，实验测得采用二周期不对称电压激励时，不同脉冲宽度角取值区间的一次侧、二次侧激励电压与谐振电流波形如图10所示。为实现所有开关器件的零电压开通，以图1为参考方向，在激励电压由零电平变为正电平、由正电平变为零电平、由零电平变为负电平、由负电平变为零电平所对应的时刻的谐振电流分别应该为负值、正值、正值、负值，显然，图10所示的激励电压波形满足该条件，所有开关器件实现了零电压开通。
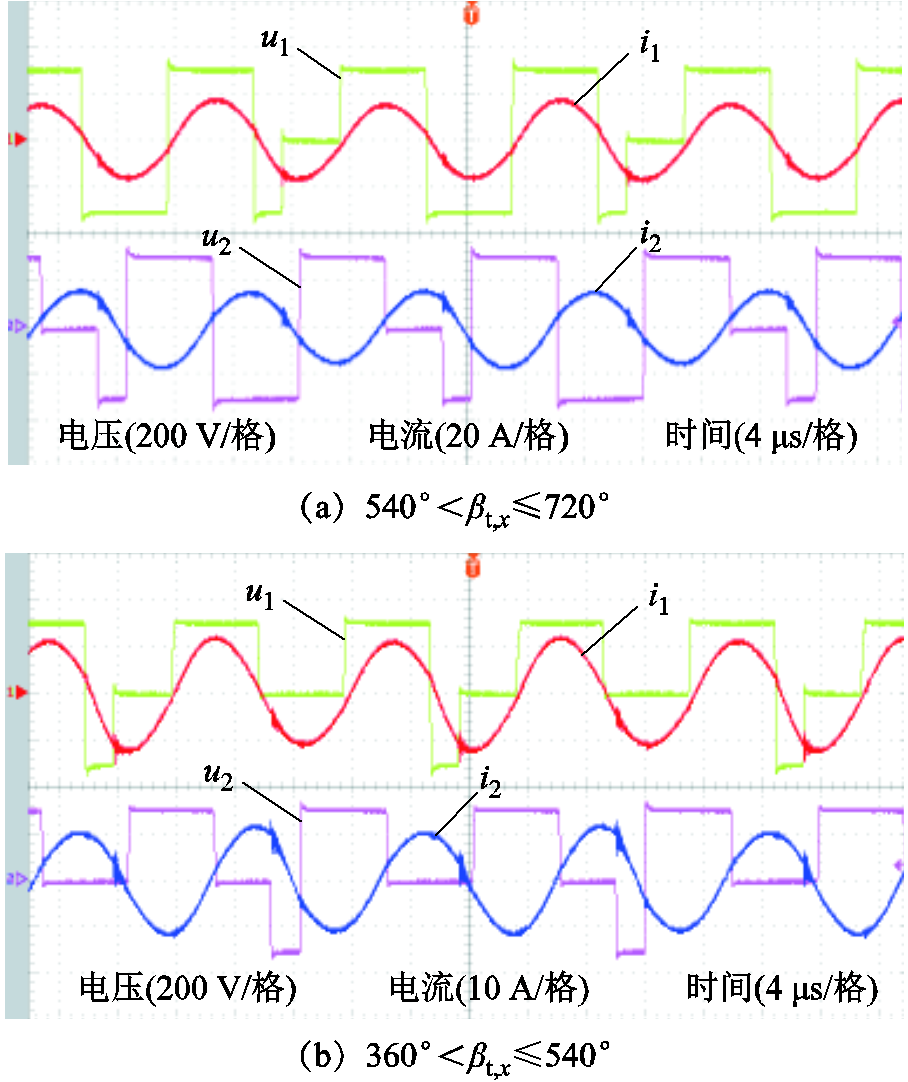
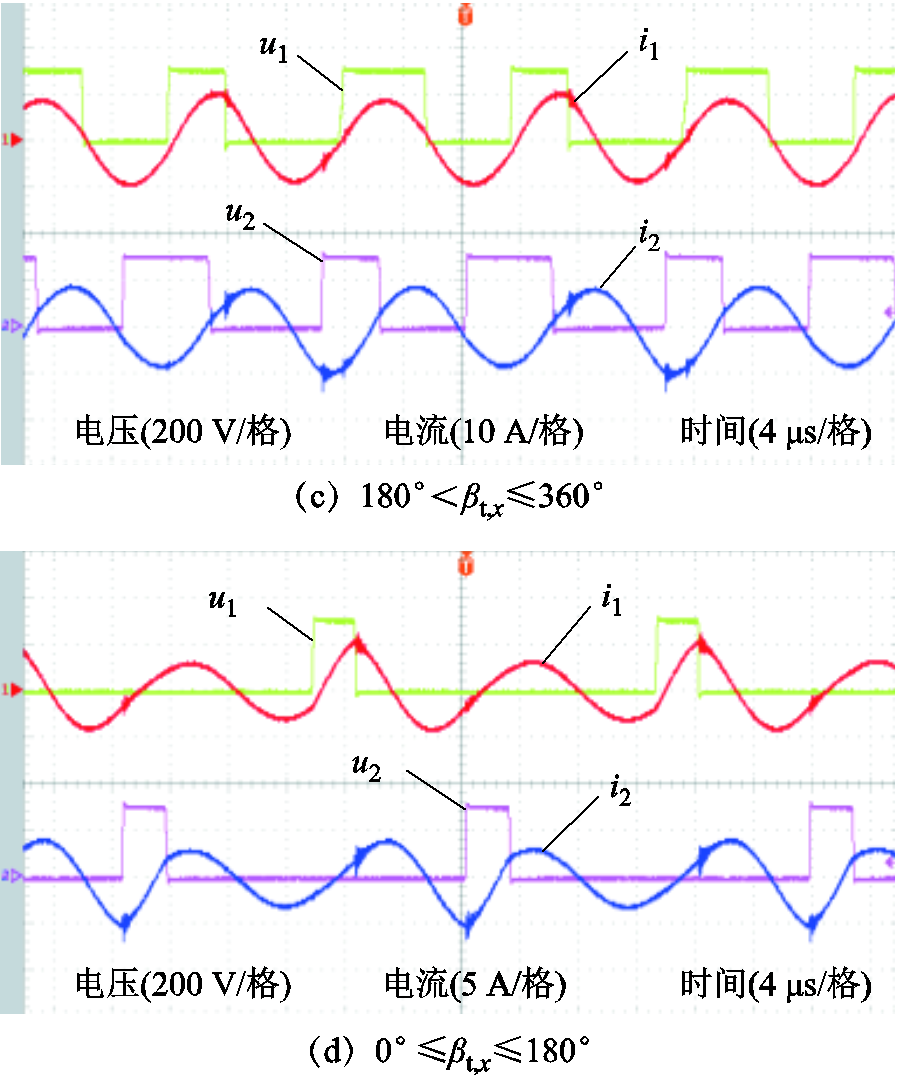
图10 二周期不对称电压激励实验波形
Fig.10 The experiment waveforms of 2P-AVC
耦合系数k=0.2时，DC-DC效率如图11所示。由图11可见，随着负载功率值的降低，传统的DPS和TPS方法的效率在全功率范围内呈现出单调下降的趋势。而对于单周期的不对称电压激励控制（1P-AVC）方法，3.7 kW满功率时的效率为97%；随着负载功率由满功率逐渐下降，其效率值先下降，当效率值下降至最低点95.8%时，负载功率值约为2.1 kW；随着负载功率的继续下降，效率逐渐回升，当功率下降至约0.9 kW时，效率达到第二个峰值点，为96.4%；此后效率再逐渐下降，表现出“先下降、后上升、再下降”的三段单调区间。而对于二周期的不对称电压激励控制（2P-AVC）方法，随着负载功率值的降低，其效率特性呈现出了三段“下降-上升”式的区间和极轻载下的单调递减的区间，总共呈现出七段单调区间。效率曲线的峰值所对应的功率及效率分别约为（3.7 kW, 97%）、（2.1 kW, 97%）、（0.9 kW, 96.9%）、（0.3 kW, 95%）。其中，当功率值约为2.1 kW时，2P-AVC方法的效率（97%）高出1P-AVC方法的效率（95.8%）约1.2%；当功率值在0.3 kW左右时，2P-AVC方法的效率（95%）高出1P-AVC方法的效率（93.5%）约1.5%。在2P-AVC效率曲线的谷值处，其效率仍高于1P-AVC方法的效率。在更轻的负载功率下，效率的提升更为明显，例如当功率值在130 W附近时，2P-AVC方法的效率为92.6%，高出1P-AVC方法的效率（89.6%）约3%。这种多峰值的效率曲线是由δ值多次回归至峰值而导致的。通过该多峰值、非单调的效率特性，平抑了在整个功率范围内的效率值的波动，进而获得宽功率范围内的高效率。在各个负载功率下，所提2P-AVC方法的DC-DC效率均优于1P-AVC方法、传统的TPS控制和DPS控制的效率。相比于传统的TPS控制和DPS控制，负载功率越低，所提2P-AVC方法对效率的改善就越明显。
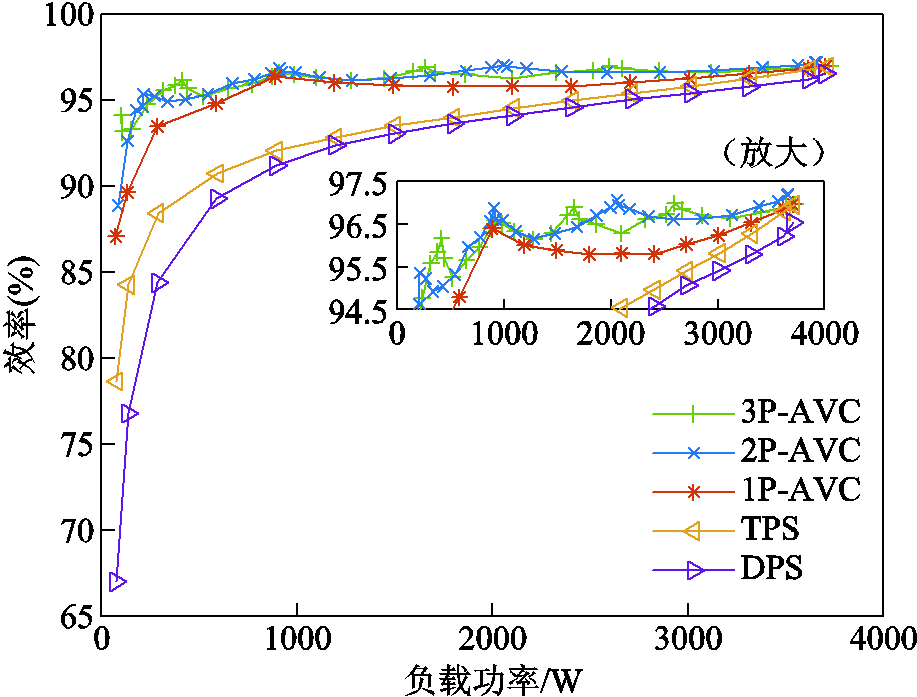
图11 k=0.2情况下的DC-DC效率
Fig.11 DC-DC efficiency with k=0.2
对于三周期的不对称电压激励控制（3P-AVC）方法，与2P-AVC类似，其效率曲线仍以峰值为分界点，呈现出多段“下降-上升”的特性，效率曲线的峰值所对应的功率及效率分别约为(3.7 kW, 97%)、(2.6 kW, 97%)、(1.7 kW, 96.9%)、(0.9 kW, 96.6%)、(0.4 kW, 96.2%)。与2P-AVC相比，在全功率范围内，对于不同的功率点，3P-AVC的效率可能高于、低于2P-AVC的效率，或与2P-AVC的效率基本持平。这是由于对于2P-AVC和3P-AVC两种方法，δ值的峰值个数不同，以及达到峰值所对应的功率不完全相同所导致的。在实验条件下，对于2P-AVC，当P*为1/16、1/4、9/16和1等特殊值时，δ值达到最大，对应的效率回归到峰值。而对于3P-AVC，当P*为1/36、1/9、1/4、4/9、25/36和1等特殊值时，δ值达到最大，对应的效率回归到峰值。因此，在P*=1/4时，对应功率约为0.9 kW，两种方法的δ值相同，都处于峰值，两者效率基本持平。而当P*取值为某一种方法的其他特殊值时，对于另一种方法，该值并不是可令δ值达到峰值的特殊值，因此，后者在该点的效率小于前者。虽然对于2P-AVC与3P-AVC两种方法，其中任意一种方法的效率在整体功率段并不完全高于另一种，但相比于1P-AVC，通过采用多个周期的不对称电压激励控制，两种方法的效率还是得到了明显的提升。
当耦合系数k降至0.1时，DC-DC效率如图12所示。由图12可见，所提2P-AVC方法的效率曲线仍出现了多段“下降-上升”式的区间，在相同负载功率情况下的效率明显高于传统的TPS和DPS方法的效率。在中功率、高功率段，所提方法的效率不低于1P-AVC方法的效率，且在低功率段，所提方法的效率明显高于1P-AVC方法的效率，例如，当功率值在0.6 kW左右时，2P-AVC方法的效率92.6%高出1P-AVC方法的效率88.9%约3.7%；在最轻负载功率值约为85 W情况下，2P-AVC方法的效率85%比1P-AVC方法的效率77%高约8%。对于3P-AVC方法，与2P-AVC类似，其效率不低于1P-AVC的效率，在整个功率段的效率表现效果基本与2P-AVC持平。由此，所提方法的正确性和有效性得到验证。在实际应用中，综合考虑方法实现的复杂度与效率提升效果，采用2P-AVC方法就可以在整个功率段范围内达到较高的效率。由实验测得的效率关系还可发现，3P-AVC和2P-AVC的效率峰值呈现出了明显的互补的特点，若能将两种方法混合，形成一种混合周期的方法，则可以获得相比于3P-AVC和2P-AVC更优的整体效率特性，这是后续工作中值得研究的方向。
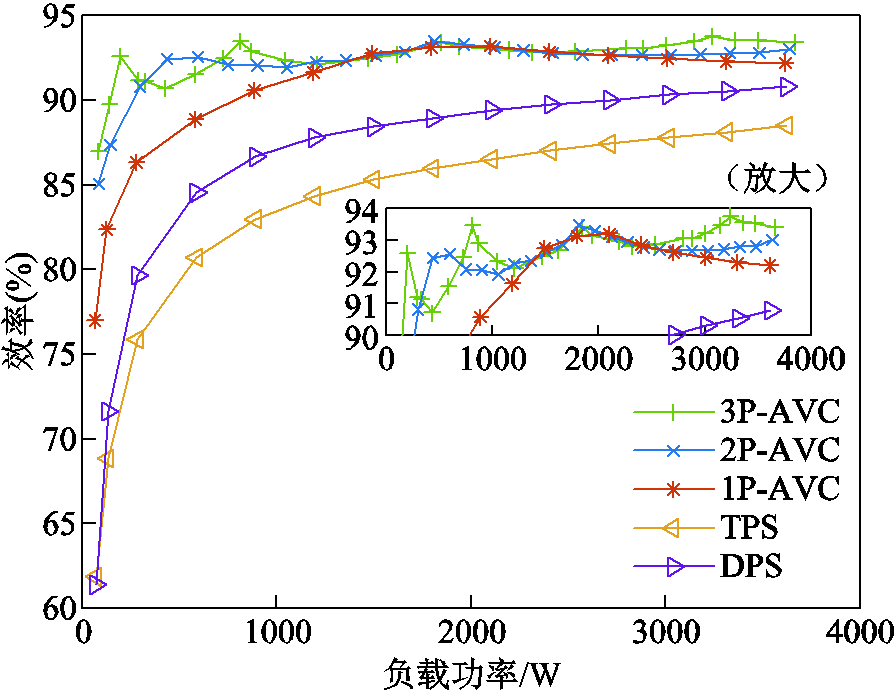
图12 k=0.1情况下的DC-DC效率
Fig.12 DC-DC efficiency with k=0.1
本文介绍了全补偿的串联-串联无线电能传输系统的基本特性及影响中间谐振环节的传输效率的因素，提出了一种无线电能传输系统的多周期不对称电压激励方法，可实现开关器件的零电压开通以及中间谐振环节的效率提升。实验结果表明，相比于传统的TPS和DPS控制，所提方法可显著地提高效率；相比于1P-AVC方法，通过将基于单周期的不对称电压激励控制方法拓展到多个周期，所提MP-AVC方法可进一步提升效率，且无需任何额外的硬件电路，成本低、实用性强，具有较好的应用前景。
参考文献
[1] 薛明, 杨庆新, 章鹏程, 等. 无线电能传输技术应用研究现状与关键问题[J]. 电工技术学报, 2021, 36(8): 1547-1568.
Xue Ming, Yang Qingxin, Zhang Pengcheng, et al. Application status and key issues of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.
[2] 李阳, 石少博, 刘雪莉, 等. 磁场耦合式无线电能传输耦合机构综述[J]. 电工技术学报, 2021, 36(增刊2): 389-403.
Li Yang, Shi Shaobo, Liu Xueli, et al. Overview of magnetic coupling mechanism for wireless power transfer[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 389-403.
[3] 陈凯楠, 蒋烨, 檀添, 等. 轨道交通350kW大功率无线电能传输系统研究[J]. 电工技术学报, 2022, 37(10): 2411-2421, 2445.
Chen Kainan, Jiang Ye, Tan Tian, et al. Research on 350kW high power wireless power transfer system for rail transit[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2411-2421, 2445.
[4] 贾金亮, 闫晓强. 磁耦合谐振式无线电能传输特性研究动态[J]. 电工技术学报, 2020, 35(20): 4217-4231.
Jia Jinliang, Yan Xiaoqiang. Research tends of magnetic coupling resonant wireless power transfer characteristics[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4217-4231.
[5] 沈栋, 杜贵平, 丘东元, 等. 无线电能传输系统电磁兼容研究现况及发展趋势[J]. 电工技术学报, 2020, 35(13): 2855-2869.
Shen Dong, Du Guiping, Qiu Dongyuan, et al. Research status and development trend of electromagnetic compatibility of wireless power transmission system[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2855-2869.
[6] 陈凯楠, 赵争鸣, 刘方, 等. 电动汽车双向无线充电系统谐振拓扑分析[J]. 电力系统自动化, 2017, 41(2): 66-72.
Chen Kainan, Zhao Zhengming, Liu Fang, et al. Analysis of resonant topology for Bi-directional wireless charging of electric vehicle[J]. Automation of Electric Power Systems, 2017, 41(2): 66-72.
[7] 李砚玲, 孙跃, 戴欣, 等. LCL型双向感应电能传输系统建模及控制[J]. 重庆大学学报, 2012, 35(10): 117-123.
Li Yanling, Sun Yue, Dai Xin, et al. Modeling and control of an LCL bi-directional inductive power transfer system[J]. Journal of Chongqing University, 2012, 35(10): 117-123.
[8] 刘方, 陈凯楠, 蒋烨, 等. 双向无线电能传输系统效率优化控制策略研究[J]. 电工技术学报, 2019, 34(5): 891-901.
Liu Fang, Chen Kainan, Jiang Ye, et al. Research on the overall efficiency optimization of the bidirectional wireless power transfer system[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 891-901.
[9] Nguyen B X, Vilathgamuwa D M, Foo G H B, et al. An efficiency optimization scheme for bidirectional inductive power transfer systems[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6310-6319.
[10] Liu Xin, Wang Tianfeng, Yang Xijun, et al. Analysis and design of a wireless power transfer system with dual active bridges[J]. Energies, 2017, 10(10): 1588.
[11] Li Yong, Hu Jiefeng, Chen Feibin, et al. Dual-phase-shift control scheme with current-stress and efficiency optimization for wireless power transfer systems[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2018, 65(9): 3110-3121.
[12] Zhang Xiaoming, Cai Tao, Duan Shanxu, et al. A control strategy for efficiency optimization and wide ZVS operation range in bidirectional inductive power transfer system[J]. IEEE Transactions on Industrial Electronics, 2019, 66(8): 5958-5969.
[13] Jiang Yongbin, Wang Laili, Fang Jingyang, et al. A high-efficiency ZVS wireless power transfer system for electric vehicle charging with variable angle phase shift control[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(2): 2356-2372.
[14] Jiang Yongbin, Wang Laili, Fang Jingyang, et al. A joint control with variable ZVS angles for dynamic efficiency optimization in wireless power transfer system[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 11064-11081.
[15] Wang Chu, Chen Min, Cui Hongzhi, et al. A novel soft-switching dual-side phase shift circuit for wireless power transfer[C]//2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 2019: 5344-5351.
[16] Jia Shuran, Chen Changsong, Duan Shanxu, et al. Dual-side asymmetrical voltage-cancelation control for bidirectional inductive power transfer systems[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 8061-8071.
Abstract Achieving high power transmission efficiency over a wide power range is the basic requirement of a wireless power transfer system. For inductive power transfer (IPT) systems with dual active full bridge structure, the conventional one-period (1P) asymmetrical voltage excitation control (AVC) method has achieved higher efficiency in comparison to the symmetrical dual-phase-shift (DPS) and triple-phase-shift (TPS) control method. To further improve the efficiency under a wide power range, this paper extends the conventional 1P-AVC method to multi-period AVC (MP-AVC) method for series-series compensated inductive power transfer (SS-IPT) system.
By analyzing the SS-IPT system, it has been found that the power transfer efficiency of the intermediate resonant network depends on the ratio of the fundamental excitation voltages and the phase difference between them. The efficiency decreases when the fundamental excitation voltage ratio deviates from its optimal value or the phase difference deviates from 90°. To improve the power transfer efficiency of the intermediate resonant network while maintaining zero-voltage turning-on of the switches at the majority of the operating points, the asymmetrical excitation voltage waveform consisting of multiple periods has been proposed and used for both the primary side and the secondary side. When the system is needed to operate at a reduced power, the pulse width of every half period that composes the multi-period excitation voltage waveform is decreased sequentially according to the power amount. And the relative position of the excitation voltage waveform to the current waveform is also adjusted to achieve wide-power-range zero-voltage turning-on for the power switches. The primary-side and secondary-side excitation voltage waveforms are also controlled to keep the voltage ratio close to the optimal voltage ratio for higher efficiency. By utilizing the sequentially-decreasing variation pattern of the half-period pulse width with the reduction of power amount, the non-monotonic variation characteristic of the excitation voltage phase difference periodically returning to its peak value for multiple times can be achieved, which smooths out the fluctuation magnitude of the excitation voltage phase difference and maintains the excitation voltage phase difference at a high value, increasing the maximum achievable phase difference under the constraint of zero-voltage turning-on of all switching devices, and can lead to efficiency improvement in a wide power range.
The experiment results has shown that the efficiency curves of the proposed 2P-AVC and 3P-AVC method have a multi-peak characteristic, and the number of peaks increases with the increasing of the number of periods. The efficiency achieved with the proposed two-period and three-period AVC (2P-AVC and 3P-AVC) method is equal to or higher than the efficiency achieved with conventional DPS, TPS or 1P-AVC method over the full power range, especially at light-loading conditions. The rated power of the experiment platform is 3.7 kW. At the coupling coefficient of 0.2, the efficiency with 2P-AVC is 92.6% at a light loading condition about 130 W, which is 3 percentage points higher than that with 1P-AVC. At the coupling coefficient of 0.1, the efficiency with 2P-AVC is 85% at about 85W, which is 8 percentage points higher than that with 1P-AVC. Besides, the zero-voltage turning-on is achieved with the proposed control method.
The multi-peak efficiency curve characteristic obtained from the experiment has verified the periodical-returning characteristic of the phase difference with the varying of power, which smooths out the power transfer efficiency in a wide power range. The proposed MP-AVC method does not require any additional hardware circuits and can significantly improve the overall efficiency especially at light-loading conditions.
keywords：Inductive power transfer (IPT), dual-side multi-period asymmetrical voltage excitation control, efficiency optimization, zero-voltage turning-on
中图分类号：TM46
DOI:10.19595/j.cnki.1000-6753.tces.221078
国家自然科学基金资助项目（51977086）。
收稿日期 2022-06-09
改稿日期 2022-08-26
贾舒然 男，1995年生，博士研究生，研究方向为无线电能传输。E-mail：jia_shuran@qq.com
段善旭 男，1970年生，教授，博士生导师，研究方向为分布式可再生能源发电系统控制。E-mail：duanshanxu@hust.edu.cn（通信作者）
（编辑 李冰）