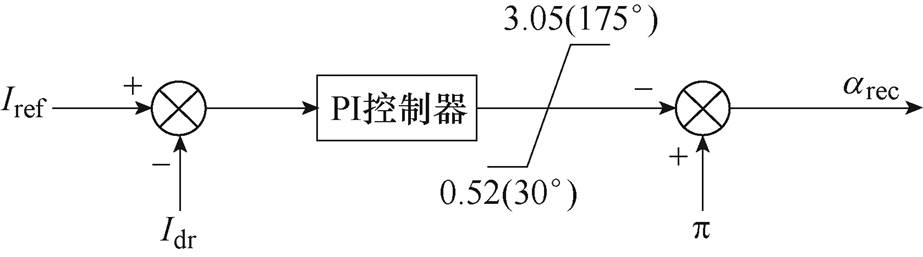
图1 整流侧控制框图
Fig.1 Rectifier side control block diagram
摘要 通常认为高压直流输电（HVDC）的换相失败是由受端交流系统或换流阀故障引起，但工程实践中发现，送端交流故障同样可能引发逆变器的换相失败。目前，针对此类换相失败的研究较少，且大多局限于传统的母线电压幅值特征，对其机理研究不够深入。鉴于此，首先通过分析故障后的交直流系统响应，指出与一般受端故障不同，送端交流故障引发的换相失败发生在故障切除后的恢复阶段，且受端母线电压幅值大小不是其关键因素。在此基础上，对故障切除后的受端母线电压相位特性进行剖析，得出有功功率的恢复会导致受端母线电压相位前移，进而压缩关断裕度并造成触发延迟。进一步地，在不同故障程度下分析了系统换相失败过程对应的触发指令与直流电流的变化。结果表明，当送端故障相对轻微，受端保持定关断角（CEA）控制时，相位前移及突增的直流电流是导致逆变器换相失败的主要原因；而在送端故障程度加深，受端切换至定电流（CC）控制后，相位前移是换相失败的主要原因。最后，基于CIGRE标准模型，仿真验证了分析的正确性。
关键词：换相失败 送端交流故障 相位偏移 关断角 触发指令
高压直流（High Voltoge Direct Current, HVDC）输电凭借其输送容量大、传输距离远等优势，已经成为解决我国能源资源与负荷中心逆向分布问题的重要手段[1]。然而，由于晶闸管不具备自关断能力，一旦受端换相电压受扰，逆变侧就有可能发生换相失败，造成直流功率迅速下降，严重时甚至导致直流闭锁，电能供应彻底中断[2]。
目前，对于换相失败的研究主要集中在换相失败机理[3-5]、判定指标[6-9]及抑制策略[8-13]这三个方面，且绝大部分研究重点关注由受端交流故障引发的换相失败情形，很少提及送端故障对逆变器换相的影响。实际上，由于送受端存在电气耦合，送端交流系统故障也可能引发逆变器的换相失败，目前国内外学者对这方面的研究尚处于初步阶段。文献[14]首次研究了送端交流侧故障引发换相失败的问题，指出恢复过程中电流偏差环节的不良激活引发了换相失败。文献[15]通过分析受端控制响应的全过程，得出逆变器无功消耗过多是导致换相失败的主要原因。文献[14-15]虽然分析的过程不同，但是最终将换相失败都归结于换流母线电压幅值的降低上。文献[16]针对送端不同故障程度进行划分，得出轻微故障下过大的电流以及严重故障下控制器的交互不当造成了换相失败的发生。
总的来说，上述文献虽然对于送端交流故障引发的换相失败问题进行了分析并得到了一些结论，但仍有许多内容亟待进一步的研究。一方面，由于送端故障后的交直流系统响应与受端故障有很大的不同，而现有研究仍局限在受端交流故障的分析思路中，对于送端故障引发换相失败的机理揭示还不够深入；另一方面，由于换相失败影响因素较多，若仅考虑单一变量来判断是否发生换相失败，其结果有可能出现偏差。
鉴于此，本文首先，分析了送端交流系统故障后的交直流系统响应，重点关注关断角和受端换流母线电压两个关键电气量的变化趋势，明确了送端交流系统故障与常规受端故障导致逆变器换相失败的特征差异。在此基础上，进一步剖析了送端故障后功率变化引起受端换流母线电压相位偏移的机理，并研究了在故障恢复阶段相位偏移给换流阀带来的换相失败风险。此外，在不同程度的送端交流故障下，分析了逆变器换相失败时的直流电流以及触发指令特征，对换相失败影响因素进行了更为全面的研究。最后，基于CIGRE HVDC标准测试模型，仿真验证了理论分析的正确性。
以典型的HVDC系统为例，其两端控制结构如图1和图2所示。图中，Iref、Idr分别为整流侧的直流电流参考值、测量值，Udi、Idi分别为逆变侧直流电压、直流电流，Iord为系统主控制极输出的直流电流参考值，bCC、bCEA分别为逆变侧定电流（Constant Current, CC）控制和定关断角（Constant Extinction Angle, CEA）控制输出的超前触发角，binv为逆变侧输出的超前触发角，ainv为逆变侧输出的触发角指令，gm为关断角实测值，gref为关断角参考值。
图1 整流侧控制框图
Fig.1 Rectifier side control block diagram
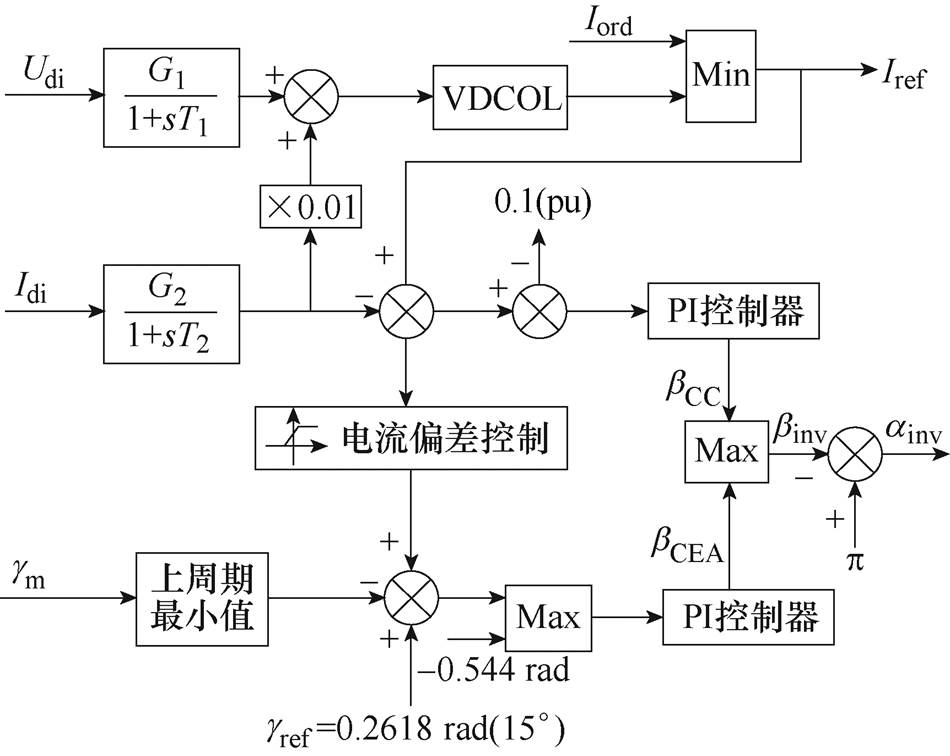
图2 逆变侧控制框图
Fig.2 Inverter side control block diagram
整流侧通常采用CC控制模式。其输入为直流电流测量值与参考值之差，经过PI控制，计算得整流侧触发角arec。
逆变侧通常有CEA控制以及CC控制，两者中间配以电流偏差控制（Current Error Controller, CEC）以平稳过渡。系统运行过程中，CEA控制、CC控制同时投入，最终取两者输出较大者，与p 相减得到触发指令ainv。稳态工况下，逆变侧处于CEA控制，只有当直流电流减小时，才有可能切换至CC控制。为了避免两端定电流控制同时工作造成系统不稳，逆变侧的电流整定值比整流侧小0.1(pu)。
送端交流侧不同故障程度下，两侧换流器的控制响应存在较大的差异；为了表述方便，现针对本文研究的问题，根据受端控制器是否发生切换将不同的系统响应划分为两类，送端不同故障程度下两类控制响应发展框图如图3所示。结合图3，对这两类故障响应作简要分析。
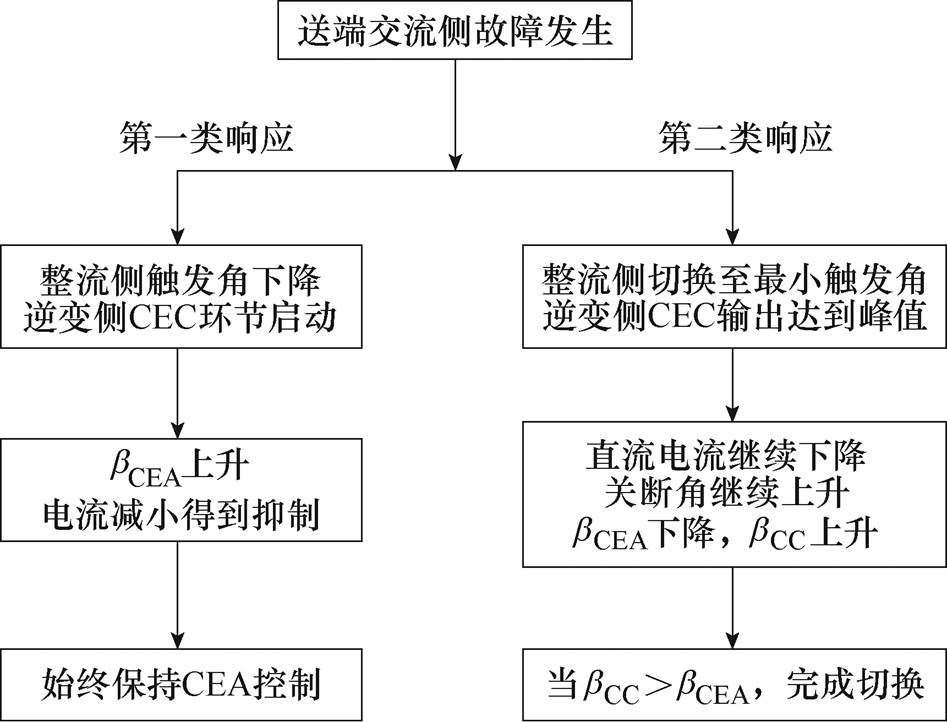
图3 送端不同故障程度下两类控制响应发展框图
Fig.3 Development block diagram of two types of control responses under different fault degrees at the sending end
送端交流侧故障程度相对轻微时，系统会表现为第一类响应：随着交流电压的下降，整流侧控制最先动作，通过降低触发角以提升送端直流电压；对于逆变侧，当直流电流小于整流侧电流参考值后，CEC环节启动，增加CEA控制输出，降低受端直流电压，功率传输得以维持。切除故障后，若不发生换相失败，受端继续保持CEA控制，系统逐渐恢复到稳态。
随着送端故障程度的加深，故障后整流侧会迅速切换到最小触发角控制，逆变侧控制响应前半段与第一类响应的控制逻辑相同。但是，随着CEC环节输出达到峰值，依然无法抑制直流电流的减小。此时，受端CC控制便开始动作，bCC逐渐增大，直至超过bCEA，接管逆变侧控制，即呈现为图3中的第二类响应。故障切除后，随着电流的恢复，bCC逐渐减小，与不断增大的bCEA再次相交，逆变侧重新由CEA控制接管。
以CIGRE HVDC标准测试系统为例，在送端设置三相接地短路故障，送端交流电压跌落至0.62(pu)，故障发生在1 s，持续0.1 s，其响应如图4所示。图中，Uacr、Uaci分别为送端、受端换流母线电压有效值。
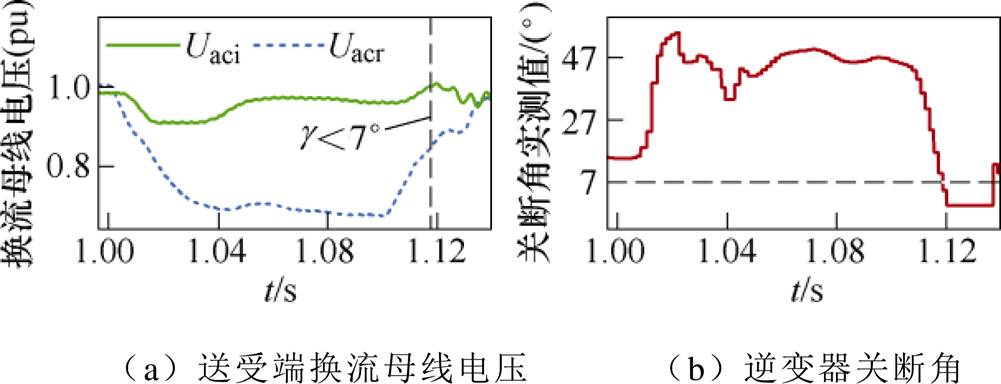
图4 送端故障发生后系统响应
Fig.4 System response after sending end failure
可以看到，短路故障发生后，送端交流母线电压迅速下降，受端交流母线电压也有一定程度的下降；在此期间，逆变器的关断角呈现增大的趋势；1.1 s故障切除后，伴随着系统的恢复，关断角反而迅速跌落，发生了换相失败。
本节以该波形为基础，对送端交流故障后的关键特征进行分析。
HVDC系统中直流电压、电流的关系可表示为
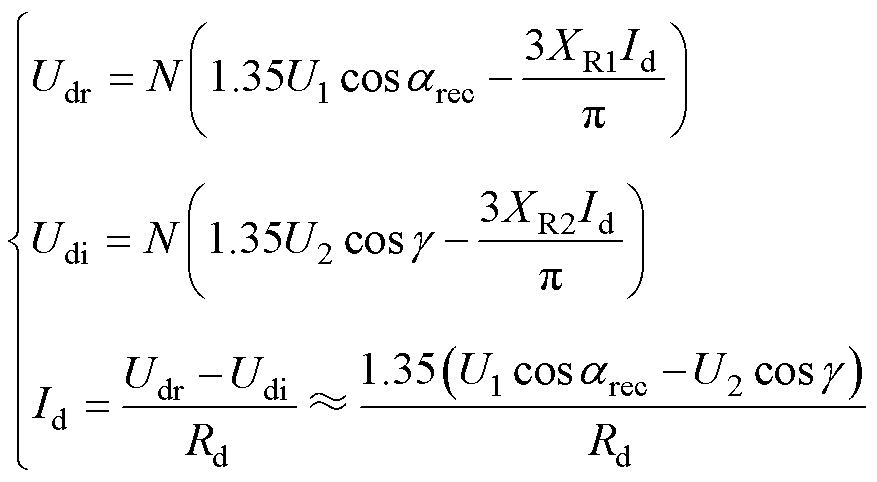（1）
式中，Udr为整流侧直流电压；XR1、XR2分别为整流侧、逆变侧的等效换相阻抗；Rd为直流线路等值电阻；N为单极6脉波桥的个数；U1、U2分别为整流侧、逆变侧换流变压器阀侧空载线电压有效值；g为逆变侧的关断角；Id为直流线路电流。
根据上文分析可知，送端故障发生后，交流电压迅速下降，整流侧的直流电压也随之降低。在此期间，逆变侧虽然可能切换至不同的控制模式，但是不论逆变侧处于何种控制，送端直流电压Udr降低后，根据式（1），为了维持直流电流，逆变侧直流电压Udi也要降低，即此时必须增大关断角，而且送端故障程度越严重，关断角增大幅度越高。关断角的增大也就决定了送端故障期间不会引起逆变器的换相失败。
另一方面，受端换流母线电压的跌落也是导致逆变器换相失败的常见原因之一。因此，为了彻底厘清送端故障引发换相失败的本质原因，有必要对故障后的受端换流母线电压进行初步分析。
由于故障发生在送端交流母线，受端母线电压的大小主要与直流侧逆变器的无功消耗有关。一般逆变器的无功特性[17]可以表示为
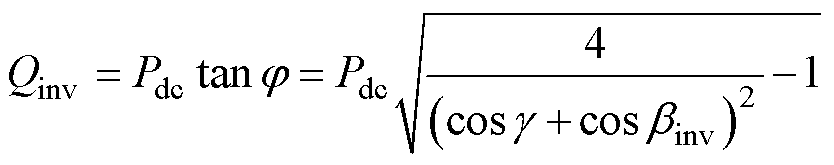（2）
式中，Qinv为逆变器消耗的无功功率；Pdc为直流功率；j 为逆变侧的功率因数角。
由式（2）可知，逆变器消耗的无功功率不仅与逆变侧的功率因数角有关，还会受到直流功率的影响，因此送端故障发生后，直到故障切除前，受端换流母线电压可能呈现两种不同的变化趋势。第一种情况下，送端故障后，若关断角增加导致的功率因素增长幅度超过直流功率的下降幅度，则逆变器消耗无功增大，需要向受端交流电网吸收无功缺额，受端换流母线电压也会因此降低，正如图4a中所示。第二种情况下，一般发生在送端故障极其严重时，此时直流功率的下降幅度超过功率因数的上升幅度，这就使得故障期间逆变器消耗的无功功率相比稳态更少，不需要向交流电网吸收无功功率，甚至向受端交流电网输送无功功率，受端换流母线电压在故障期间相较稳态反而更大。但是不论是上述何种情形，当送端交流故障切除后，受端母线电压的恢复与关断角的减小总是同步进行，其值不会处于一个较低的水平，也就不存在母线电压突然跌落导致逆变器换相失败的条件。
综上所述，送端交流故障引发逆变器换相失败的特征与受端故障有很大差异。从触发事件看，只有在送端交流系统故障切除后才有可能发生换相失败；从系统响应看，送端故障切除后，伴随着关断角下降直至换相失败，受端换流母线电压一直处于恢复状态，因而其幅值大小并不是引发逆变器换相失败的主导因素。所以对于送端故障引发换相失败的研究，不能局限于常规的受端故障分析的思路，要从问题的源头着手对机理进行重新分析。
高压直流输电的受端系统通常由逆变器、换流变压器、无功补偿设备以及受端交流电网等组成，其中受端交流电网一般等值为理想电压源和等值阻抗的串联组合[15]，其等值模型如图5所示。图中，Up为换流母线电压，Us为理想电压源电压，Zs为等值阻抗，P、Q分别为受端电网的有功、无功功率。
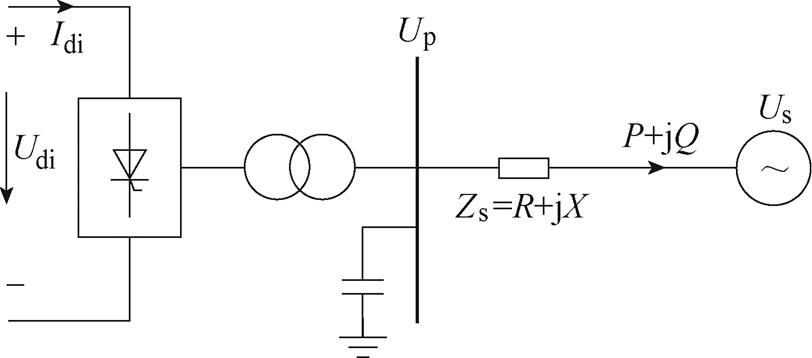
图5 高压直流输电受端系统等值模型
Fig.5 Equivalent model of HVDC receiver system
由于等值阻抗Zs的存在，换流母线电压Up和理想电压源电压Us之间存在电压降落。以Us为参考，则电压降落的横分量dU和纵分量DU分别表示为
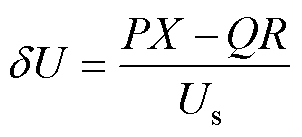（3）
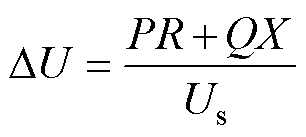（4）
结合式（3）、式（4）可进一步求得母线电压Up与电压源Us的相位差d 为
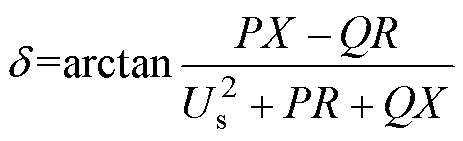（5）
在确定的受端交流系统下，式（5）中的电压源电压Us和阻抗参数R、X基本不变，相位差d 只受传输到受端电网的功率P、Q的影响。在高压电网中，又有X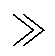
R，即电压降落的横分量主要取决于有功功率；而相位差又主要由电压降落的横分量决定[15]，所以可进一步得到d 主要与传输到受端电网的有功功率P有关。同时，Us作为理想电压源，其电压波形始终保持正弦规律，那么相位差d 的变化实际上就直接表征了换流母线电压Up的相位偏移。换言之，传输到受端电网有功功率P的变化直接决定着Up的相位偏移，以此为依据，可以忽略式（5）中的次要因素，将其进行简化得到Up的相位偏移量
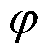为
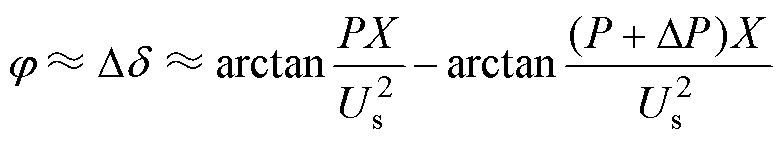（6）
式中，Dd 为换流母线电压相位差的变化量；DP为交流系统有功变化量；X为受端系统等值电抗。
另一方面，由于不同的有功功率变化速率对母线电压的偏移影响程度也有所差异，并且考虑到换相失败只发生在故障切除后，所以有必要对系统恢复期间的有功恢复速率进行分析。若忽略换流器及线路损耗，传输到受端系统的有功功率可以表示为
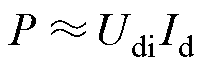（7）
基于式（7），可以根据直流电压、电流的恢复特性大体将故障恢复分为三个阶段，具体如图6所示。
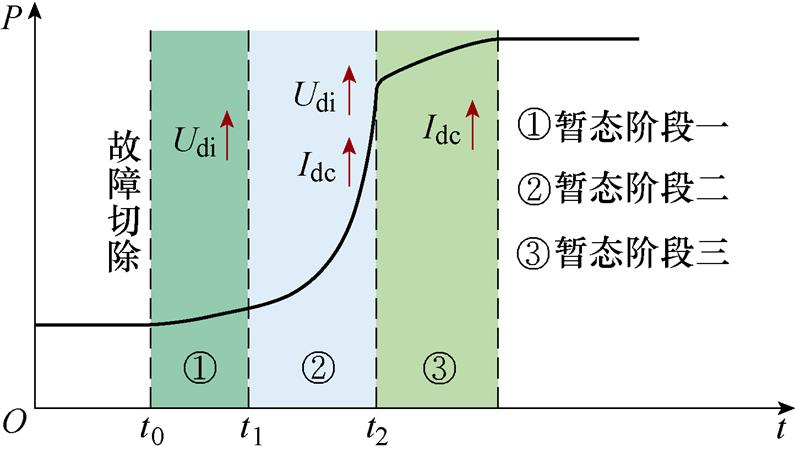
图6 送端故障切除后功率恢复的三个阶段
Fig.6 Three stages of DC power recovery after sending-end fault removal
暂态阶段一，也就是t0～t1之间，故障切除后，虽然受端直流电压Udi由于关断角的减小开始恢复，但由于系统对于直流电压的测量时间常数相对较大，低压限流控制器难以及时动作，仍然保持着输出较低的直流电流指令值，导致直流电流恢复延后，故这一阶段的直流功率恢复得很慢。该阶段通常持续数毫秒。
暂态阶段二，低压限流控制器开始动作，直流电流开始迅速回升，再结合直流电压的增长，使得t1～t2之间的功率恢复非常快。该阶段的持续时间取决于送端交流电压的恢复时间，一般在十几毫秒内完成，也正是在该阶段，受端换流母线电压相位前移最严重。
暂态阶段三，Udi随着送端交流电压的恢复，已基本回到稳态水平，此阶段有功功率的恢复主要取决于直流电流，由两端控制系统发挥主导作用，整体的恢复速率偏慢。若不发生换相失败，将一直持续到恢复稳态。
为验证上述理论分析的正确性，同样以1.3节中的仿真设置为例，利用式（5）计算所得的相位差以及对应的实际受端交流电压波形如图7所示。
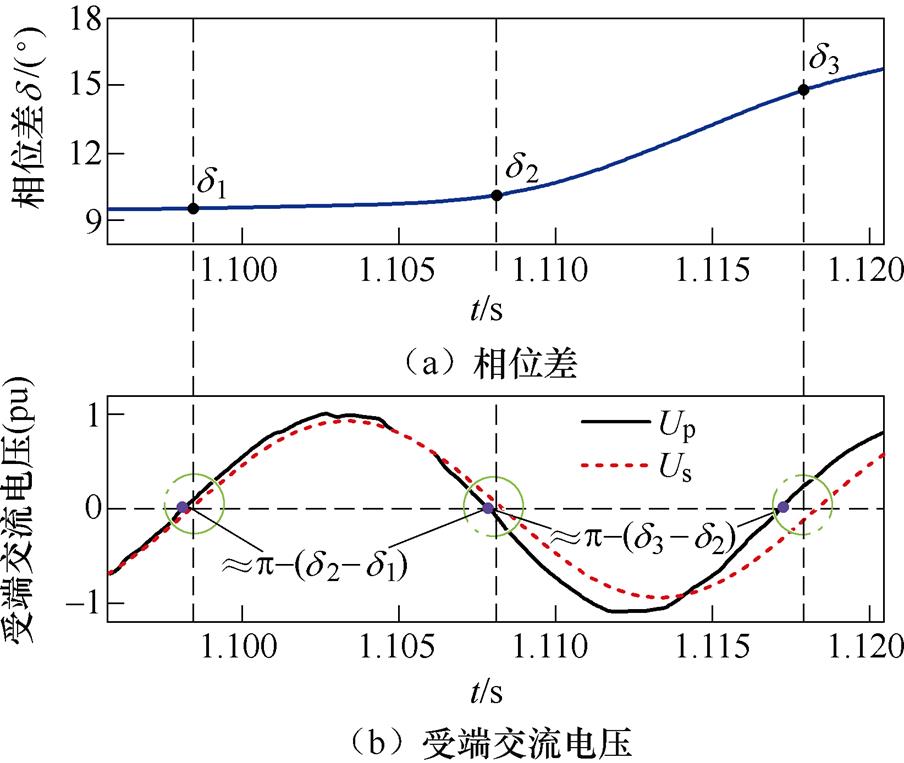
图7 故障恢复期间的受端交流电压与相位差的关系
Fig.7 The relationship between the AC voltage at receiving end and the phase angle difference during fault recovery
可以看到，故障切除前，系统达到稳态，受端交流母线电压Up与理想电压源电压Us之间保持着恒定的相位差d1；随着1.1 s故障的切除，有功功率开始恢复，相位差也逐渐增大。在故障恢复初期，相位差变化速率很慢，接近10 ms才增长了1.5 °左右；而在后续的半个周期内，恢复速率大幅增长，与上述分析基本一致。同时，相位差d1、d2和d3的不断递增体现在波形上就对应着受端换流母线电压Up相位的不断前移，从图7也能看出，相位差d 的变化量在一定程度上直接反映了受端换流母线电压的相位前移程度。
2.2.1 母线电压相位前移对关断裕度的影响
第2.1节最后提到，送端故障切除后，有功功率的恢复会导致受端换流母线电压相位前移，这一特征势必会传递到变压器的阀侧，影响到换相电压。为更清楚直观地展现相位前移对换相过程的影响，本节基于换相电压面积理论[16]，结合图8对相位前移下的关断裕度进行分析。图8中，下标1为故障工况变量，下标0为稳态工况变量，m 为换相位，a为触发角，g 为关断角。
稳态时，逆变侧换相电压三相对称，根据换相工作原理[3]，逆变器的换相过程、关断裕度可以分别表示为
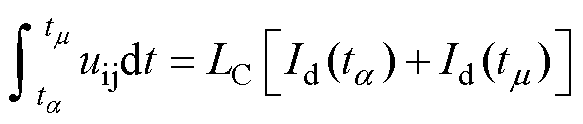（8）
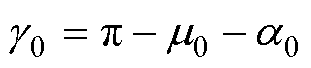（9）
其中
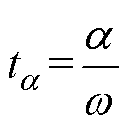
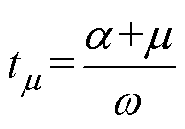
式中，uij为逆变侧的换相电压；Id(ta)、Id(tm)分别为换相开始及换相结束时刻的直流电流；w 为系统角频率；LC为换相等效电感。
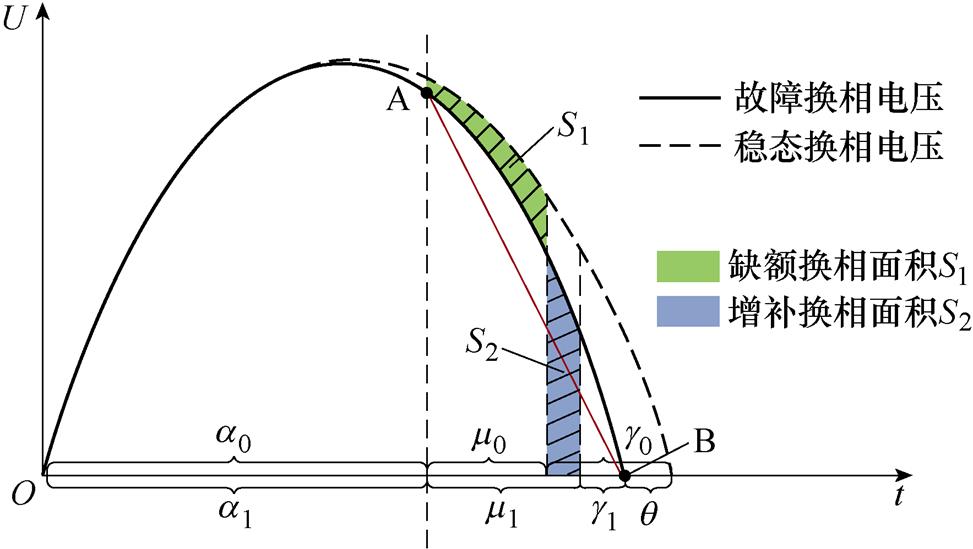
图8 换相电压相位前移时的关断裕度分析
Fig.8 Analysis of turn-off margin when commutation voltage phase moves forward
由式（8）、式（9）可以发现，直流电流增大、换相电压减小以及触发时刻推迟都会迫使换相时间延长，进而影响关断裕度。所以为了突出体现相位前移对关断裕度的影响，这里假设换相期间的直流电流、换相时刻的触发角与稳态保持一致，后续再分别对这两个假设作单独讨论。
根据直流电流的假设，由式（8）可得，故障工况和稳态工况下的换相电压时间面积必须相等，而由图8可见，换相电压相位前移后，波形被压缩，触发后的换相电压较稳态时要小，所以换流阀只能通过延长换相时间，即增大m 来弥补这部分换相面积缺额。此外，由于相位前移后的换相电压波形已经不是标准正弦，无法直接代入正弦电压表达式，在此，利用A、B两点构成的直线去等效前移后的换相电压[16]，有
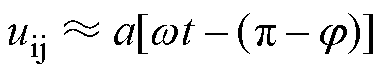（10）
其中
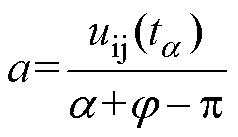
式中，uij(ta)为触发时刻的换相电压。
将式（10）代入式（8）并令需求换相面积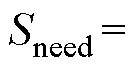
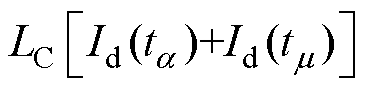，可以解得相位前移后的换相角为
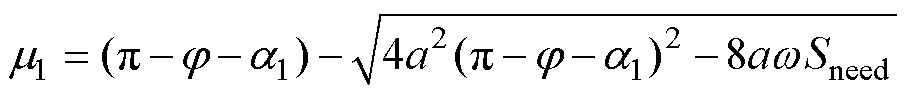（11）
最终，可以得到相位前移后的关断裕度为
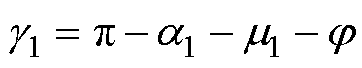（12）
综上所述，换相电压的相位前移会对换相过程产生十分不利的影响，不仅直接压缩了关断裕度，还会造成换相电压减小、换相结束时刻延迟。而且相位前移越严重，关断裕度越小，换相失败的风险也越高。
2.2.2 母线电压相位前移对触发偏差的影响
为了避免发生谐波不稳定，现阶段高压直流输电工程普遍采用等相位间隔触发控制[18-21]，具体工作原理如图9所示。图中，qs为锁相环的输出相位，aord为触发脉冲指令。
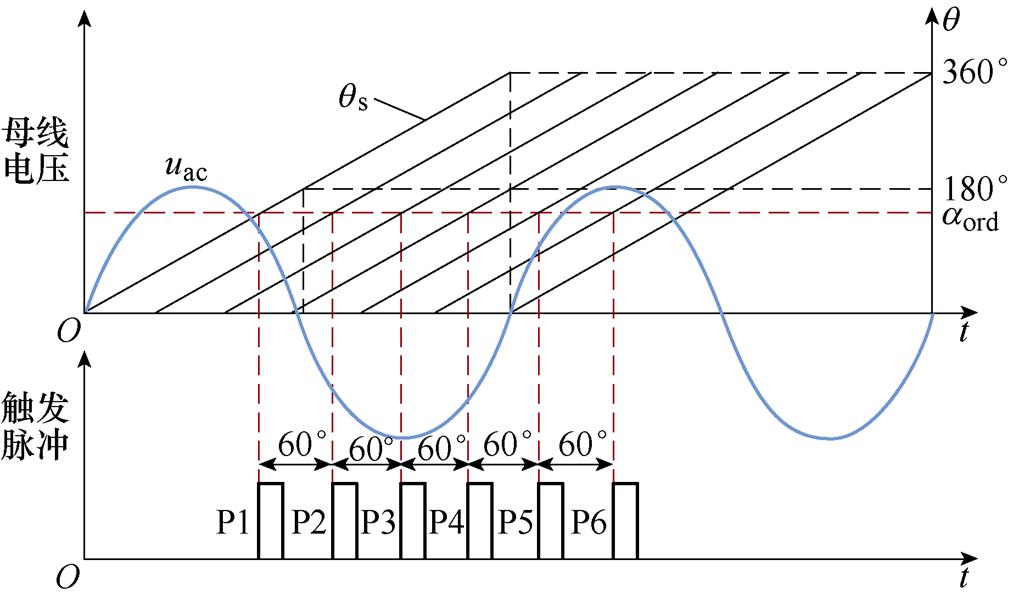
图9 等相位间隔触发控制工作原理
Fig.9 Working principle of equal-phase interval trigger control
以Yy型换流变所连换流器为例，锁相环根据输入的换流母线电压得到A相电压相位，将其延迟30 °得到阀1对应换相电压Uac的相位qs，并以此为基准，依次延后60 °得到其他阀的相位信息；触发脉冲发生器再将这六个斜坡信号与极控系统输出的触发指令aord相比较，当两者相等时，便输出一个脉冲信号，用于对应换流阀的触发。由上述工作原理可知，锁相环对母线电压相位获取的准确性是后续能否准确触发的关键。
现有直流工程通常采用的是同步参考坐标系锁相环（Synchronous Reference Frame Phase-Locked Loop, SRF-PLL），其结构简单、易于实现，具体原理如图10所示。图中，Vd、Vq为变化后的电压信号，kp、ki分别为锁相环比例、积分常数，w0为稳态角频率，q 为锁相环输出。锁相环首先对输入的交流三相电压进行Clarke和Park变换得到相位误差信号Vq，再对其归一化，通过PI控制对Vq进行调节使其趋于零，从而锁住相位[21-22]。
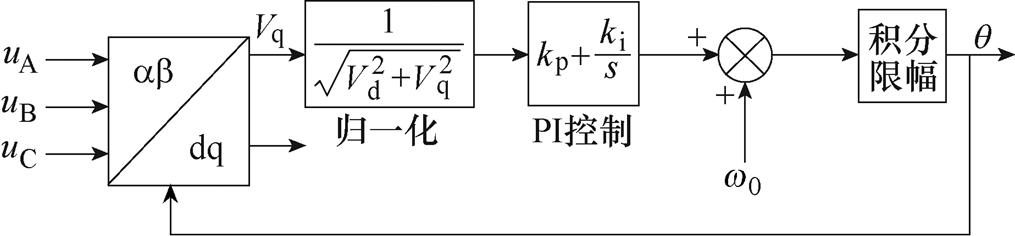
图10 锁相环的结构框图
Fig.10 Block diagram of phase locked loop
一方面，SRF-PLL的动态响应速度与kp成正比，kp越大，锁相环的动态性能越好；另一方面，由于SRF-PLL本身锁相原理的限制，SRF-PLL很容易受到谐波的影响[17]，此时若将kp设计过大，又会放大谐波等噪声的干扰，造成系统持续振荡，进入稳态时间变长。所以，在设计参数时，需要综合考虑两方面的因素。在实际工程中，为了避免谐波对同步锁相的影响，通常会牺牲锁相环的一部分动态性能，将其带宽设置得很小[18]。以送端换流母线处发生三相短路故障为例，其逆变侧A相交流电压以及对应的锁相环输出信号如图11所示。
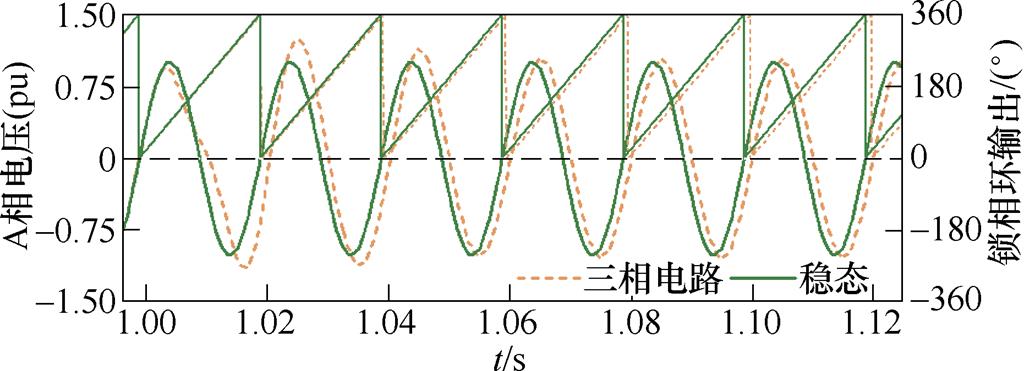
图11 送端三相短路后的A相电压以及锁相环输出
Fig.11 A-phase voltage and phase-locked loop output
可以看到，送端交流侧三相短路故障发生后，逆变侧A相电压的相位在一个电周期内迅速前移，而锁相环输出在故障前期基本不变，维持在故障前稳态水平，在后续一百多毫秒内经过不断修正，才与故障后实际电压相位基本吻合。所以稳态时，由于SRF-PLL获取的同步相位能够与逆变侧换流母线电压相位保持一致，实际触发角便能够与触发指令一致。在故障发生或者故障切除后的暂态过程中，当逆变侧换流母线电压相位发生偏移，锁相环较差的动态性能决定了其不能够在极短时间内快速地锁住实际相位，这就会导致逆变器的实际触发角与触发指令之间产生偏差。
同样以故障恢复阶段为例，分析受端换流母线电压相位前移对逆变器触发偏差的的具体影响，如图12所示。图12中，qact为逆变侧换流母线电压实际相位，qs为锁相环输出相位，aact为实际触发角。
由图12可见，当故障切除后，逆变侧换流母线电压迅速前移，锁相环由于其动态响应速度缓慢，输出不能及时更新，且需要较长的时间才能够重新锁定实际电压，其输出qs在故障切除后始终滞后实际相位qact，而触发脉冲发生器仍以qs作为后续触发控制的相位基准，这就导致了换流阀的实际触发角超出触发指令值，相当于对换相阀延迟触发，关断角也因此在短时间内快速减小，严重时就有可能导致换相失败。
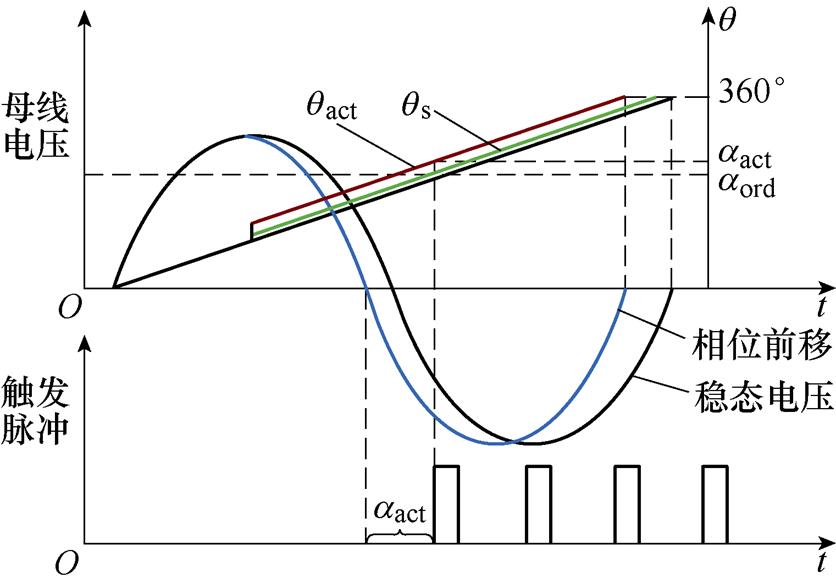
图12 相位前移对触发偏差的影响
Fig.12 Effect of phase advance on trigger deviation
在第2节分析相位前移特征对换相的影响时，为了突出重点，均假设换相期间的直流电流以及换相时刻的触发角没有变化。实际上，在故障恢复期间，当逆变侧处于不同控制方式时，直流电流和触发角的变化会有较大的差异，进而对换相过程有着不同的影响。所以本节在明确了相位前移对换相影响的基础上，再结合逆变侧的控制响应，着重讨论不同故障水平下的直流电流以及触发角特征。
第2.2.2节已经研究过实际触发角与触发指令的偏差问题，所以这部分对触发角差异的分析主要是针对极控系统输出的触发指令。
对于送端发生较轻微故障时，系统处于第一类响应，逆变侧不存在控制切换，始终保持CEA控制。故障切除后，逆变侧的关断角随着直流电流的恢复开始减小。由于CEA模式直接对关断角进行控制，对恢复过程中关断角的减小能够及时地响应，一旦关断角小于稳态指令值，逆变器将会输出更大的控制指令值binv，即更小的触发指令aord。所以，一般送端故障较轻微，受端依旧保持CEA控制时，此时逆变器若发生换相失败，其对应的触发角指令往往比稳态情形小。
当送端交流侧故障加深，逆变侧发生控制切换。故障切除后，需要从CC控制切换回CEA控制；受端系统响应表现为电流回升，关断角减小，继而CC输出逐渐减小，CEA输出逐渐增大，最终在触发角稳态值附近完成控制切换；实际上，换相失败也通常发生在控制器切换附近[13]。所以，一般当送端故障较严重、受端发生控制切换时，逆变器若发生换相失败，其对应的触发角指令与稳态情形基本一致。
送端故障较轻微时，系统处于第一类控制响应，受端不发生控制切换。故障切除后，送端交流电压、直流电压回升，直流电流开始增大，而直流电流的后续变化只取决于两端的直流电压差[23]。逆变侧不同控制对直流电流的影响示意图如图13所示，整流侧由于处于CC控制模式，对于电流实际值Im与指令值Iord的差异总能快速地反应，并通过PI输出相应的触发角来改变直流电压；而逆变侧的CEA控制对于电流的偏差响应，是通过电流影响关断角，进而接收到关断角的变化，再通过PI输出去改变直流电压，从对电流的控制响应速度上要明显滞后于整流侧，这也就使得故障恢复期间，逆变侧直流电压并不能及时地跟踪整流侧电压，两端电压差变大，电流往往超过参考值。所以，一般送端故障较轻微，受端依旧保持CEA控制时，逆变器若发生换相失败，其对应的直流电流往往比稳态情形大。
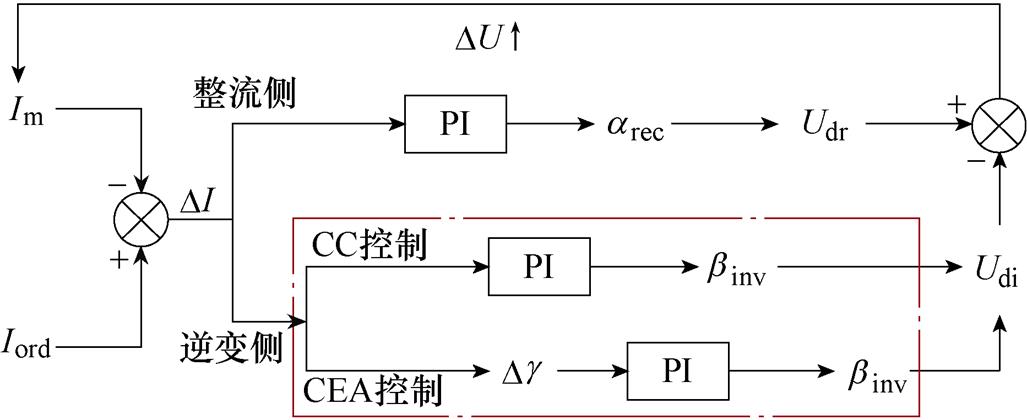
图13 逆变侧不同控制对直流电流的影响示意图
Fig.13 Schematic diagram of the influence of different controls on the inverter side on the DC current
送端交流侧故障程度加深，系统处于第二类响应，恢复阶段逆变侧与整流侧一致，也处于CC控制模式，对电流直接控制，不存在上述响应速度慢的问题，保证了电流在恢复期间能够较快地跟踪电流参考值。所以，一般当送端故障较严重，受端发生控制切换时，逆变器若发生换相失败，其对应的直流电流与稳态情形基本一致。
总结来说，当送端故障程度相对轻微，受端依旧保持CEA控制时，系统能够对恢复期间关断角的减小快速响应，进而输出较小的触发指令，但是由于受到换相电压相位前移以及电流过大的双重影响，依然有可能发生换相失败；而当送端故障加深，受端控制器切换至CC控制后，相位前移往往是换相失败的主要原因。
为验证上述机理的正确性，在PSCAD/EMTDC中采用CIGRE HVDC标准系统进行仿真测试。逆变器关断角稳态值为15 °，触发角稳态值为142 °，此系统整流侧逆变侧交流系统短路比（Short Circuit Ratio, SCR）为2.5，均为弱交流系统。
由于高压电网中，线路阻抗主要以感性为主，所以当交流系统发生远端线路接地短路故障时，可以将换流母线处的接地阻抗设置为感性，并通过调整接地电感的大小来模拟故障点与换流母线之间的电气距离。设置三种仿真案例如下。
（1）案例1，取接地电感Lf=0.8 H，故障后稳态送端交流母线电压有效值下降至0.86(pu)，故障在1 s发生，持续0.1 s后清除。其逆变侧各电气量、控制量如图14所示，图15、图16分别为受端交流侧线电压波形及换相电压波形。图15中，Us为受端理想电压源线电压，Up为受端换流母线线电压，经变压后即得各换流阀换相电压。
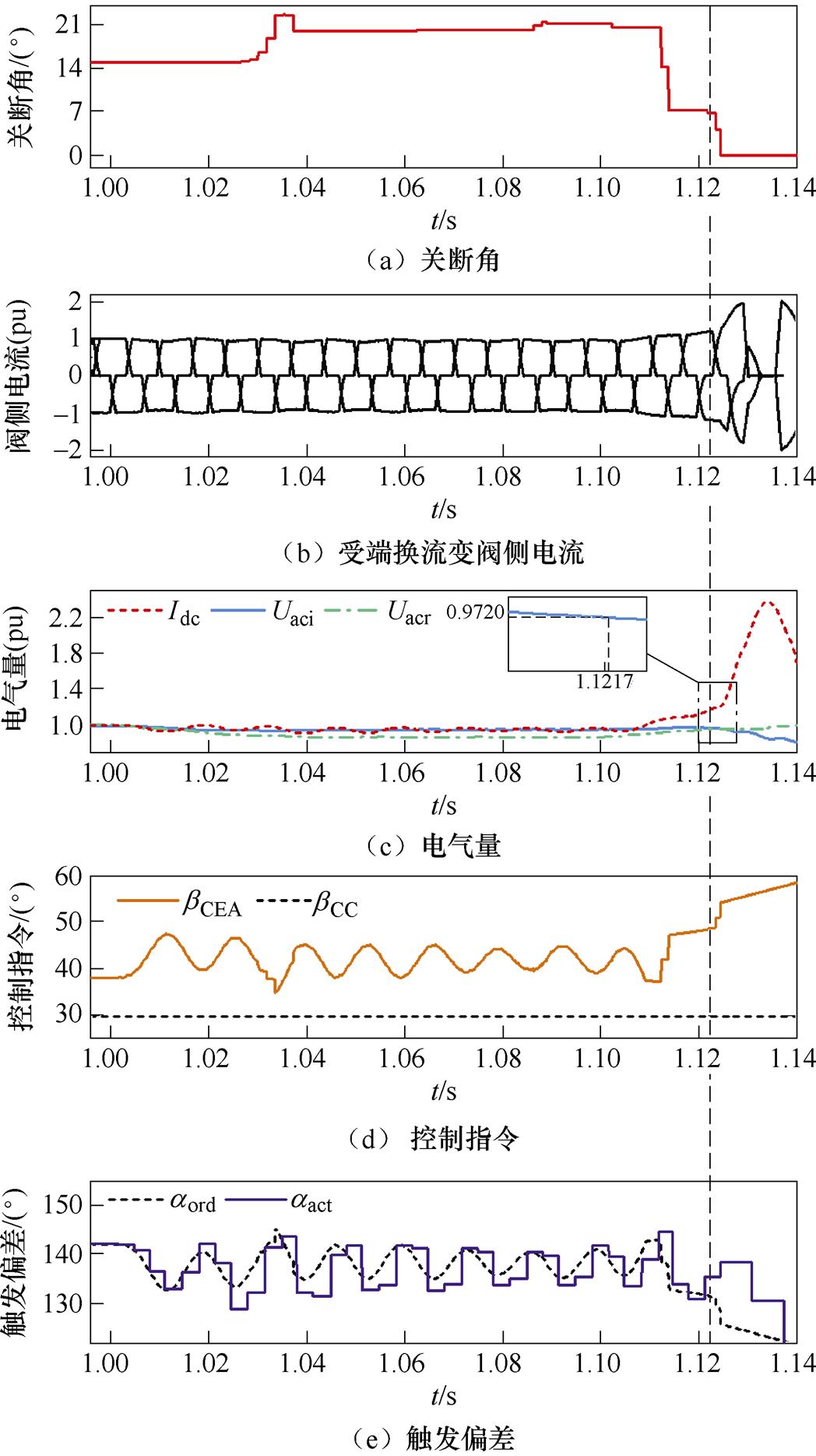
图14 案例1的交直流系统响应过程
Fig.14 AC-DC system response process in case 1
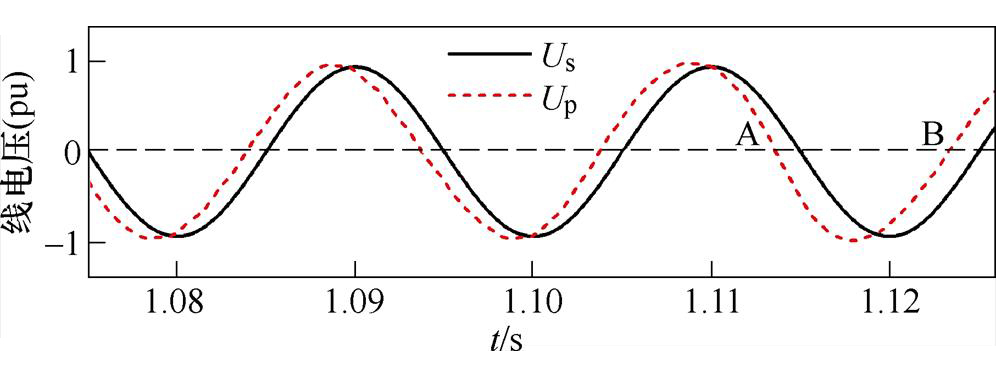
图15 案例1的受端交流线电压
Fig.15 AC line voltage at the receiving end in case 1
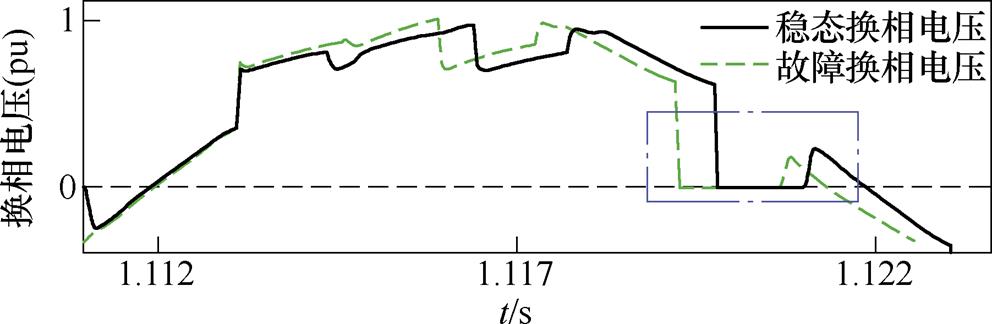
图16 案例1的换流阀换相电压
Fig.16 Commutation valve commutation voltage in case 1
首先，由图14a、图14c可以看出，送端交流侧故障发生后，Uacr、Idc迅速降低，关断角从稳态时的15 °增加到20 °左右，受端换流母线电压Uaci也因此略微降低。在图14d、图14e中，bCEA与bCC并无交点，逆变侧始终保持CEA控制，属于第一类响应；触发指令与实际触发基本保持一致。
1.1 s时故障切除，关断角迅速跌落，在1.121 7 s直接跌破临界值，发生换相失败，这一点也能从图14b中换流变阀侧电流的变化验证。整体来看，以该换相失败时刻为基准，Uaci在1.121 7 s处于0.972 (pu)，已经恢复到稳态值附近，说明受端母线电压幅值大小并不是此次换相失败的主导因素。此外，从故障切除到换相失败期间，逆变器输出的控制指令不断上升，在1.121 7 s时已经超过稳态值10 °左右；同时，也由于CEA控制的局限性，恢复过程系统也未能及时抑制直流电流的突增，这些都与上述的理论分析相吻合。结合图16、图17的电压波形对换相失败的原因进一步分析。由图15可知，Up在故障切除后并没有立刻大幅度变化，而是在直流电流上升后，才呈现较为明显的相位前移趋势。以Up过零点A、B为例，B点相比A点的相位前移程度进一步加深，也就使得这一段的交流电压波形受到压缩，对换相产生不利的影响。这一点由图16的换相电压波形体现得更加直观。点画线框中对应着关断角跌破临界值时的阀换相过程。可以看到，尽管极控系统输出了更大的控制指令，使得换流阀较稳态提前触发，但受到直流电流增长和换相电压前移的双重影响后，触发后的换相时间相比稳态不减反增，再加上过零点前移，导致关断角相比稳态大幅度降低，引发了换相失败。
（2）案例2，取接地电感Lf =0.4 H，故障后稳态送端交流母线电压有效值下降至0.78(pu)，故障在1 s发生，持续0.1 s后清除。其逆变侧各电气量、控制量如图17所示，图18、图19分别为受端交流侧线电压波形及换相电压波形。
图17 案例2的交直流系统响应过程
Fig.17 AC-DC system response process in case 2
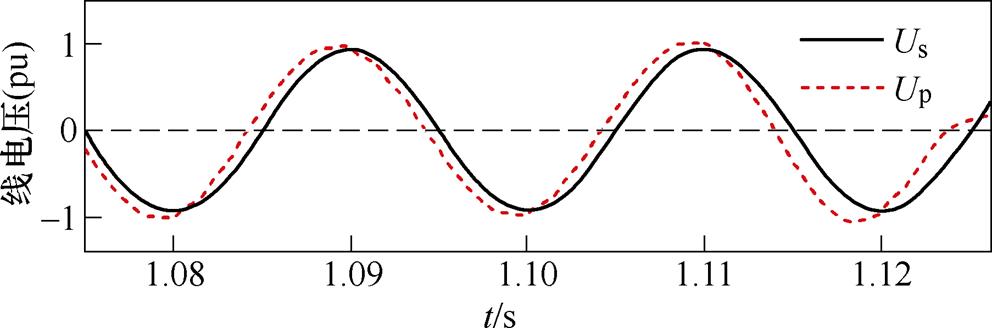
图18 案例2的受端交流线电压
Fig.18 AC line voltage at the receiving end in case 2
从图17可以看出，案例2的系统响应属于第二类。另外，故障期间关断角、直流电流、换流母线电压的变化趋势与案例1类似，只是程度有所差异。1.1 s故障切除后，关断角迅速跌落，在1.118 s跌破临界值。同样地，对应换相失败时刻，Uaci已经恢复到0.99(pu)，也再次印证了Uaci的幅值大小不是此类换相失败的关键因素。另外，算例2故障期间发生控制切换，按照定义属于严重故障。故障切除后，Idc在CC控制下稳步增长，不会出现骤升现象；其对应的控制指令也基本与稳态一致，与上述分析吻合。
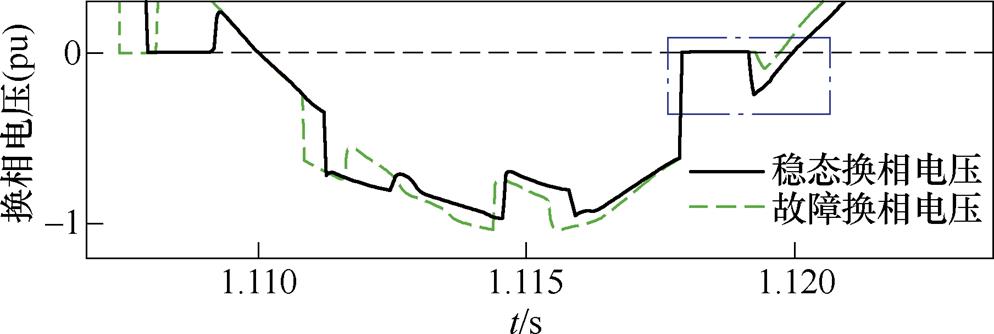
图19 案例2的换流阀换相电压
Fig.19 Commutation valve commutation voltage in case 2
但是若仅通过该控制指令去分析对应的阀换相过程，有可能出现误差。因为从图17e看到，故障期间实际触发角aact未能完全跟踪触发指令aord，两者之间存在偏差，说明此时锁相环已不能及时更新母线电压Up的相位。按照2.2.2节分析，在故障切除后，Up发生相位前移，理论上应该造成aact＞aord，但从图中看到，由于0.1 s的故障持续时间尚不足以让锁相环成功锁相，在故障切除时aact仍然小于aord；故随着Up重新前移，相当于锁相环“锁住”了相位，使得触发偏差再次缩小。所以，针对本次的换相失败过程分析，仅依据逆变器的控制指令，也基本能满足需要。
结合图18、图19能够发现，该案例换相失败的主要原因仍然是恢复期间Up的相位前移。图18中的换流母线电压前移规律与算例1一致，这里不做赘述。重点关注图19中关断角跌破临界值的换相过程：故障情形下，换流阀与稳态相比基本同时触发；触发后，由于直流电流与稳态水平一致，换相时间仅受换相电压相位前移的影响，超出稳态水平，再加上正向过零点提前，压缩了关断裕度，最终引发换相失败。
（3）案例3，取接地电感Lf =0.15 H，故障后稳态送端交流母线电压有效值下降至0.55(pu)，故障在1 s发生，持续0.1 s后清除。其逆变侧各电气量、控制量如图20所示，图21、图22分别为受端交流侧线电压波形及换相电压波形。
按照定义，案例3下的系统响应仍然属于第二类，但从仿真结果看，该案例与算例2的故障特征存在差异。首先，该算例下换相失败的发生是在故障切除时刻的两个电周期以后，依据功率恢复速率分段定义，属于暂态第三阶段，该阶段功率恢复慢，相位前移程度较轻微，对关断裕度的直接影响不大。其次，结合图21、图22可知，在暂态第二阶段，也就是1.105 s到1.12 s附近，虽然逆变器同样会面临换流母线电压相位前移严重的问题，但由于故障程度深，此时的电流尚未完全恢复，控制指令也维持在较大的水平，系统是能够度过这个换相失败高发区段的。到了暂态第三阶段，触发偏差的问题开始体现，如图20e所示，换相失败过程对应的实际触发角已经大于触发指令8 °左右，对换相产生不利的影响。实际上，从图22的阀换相失败过程也可以看出，正是由于该触发偏差，系统对换流阀延迟触发，换相时间延长，才最终导致了换相失败的发生。
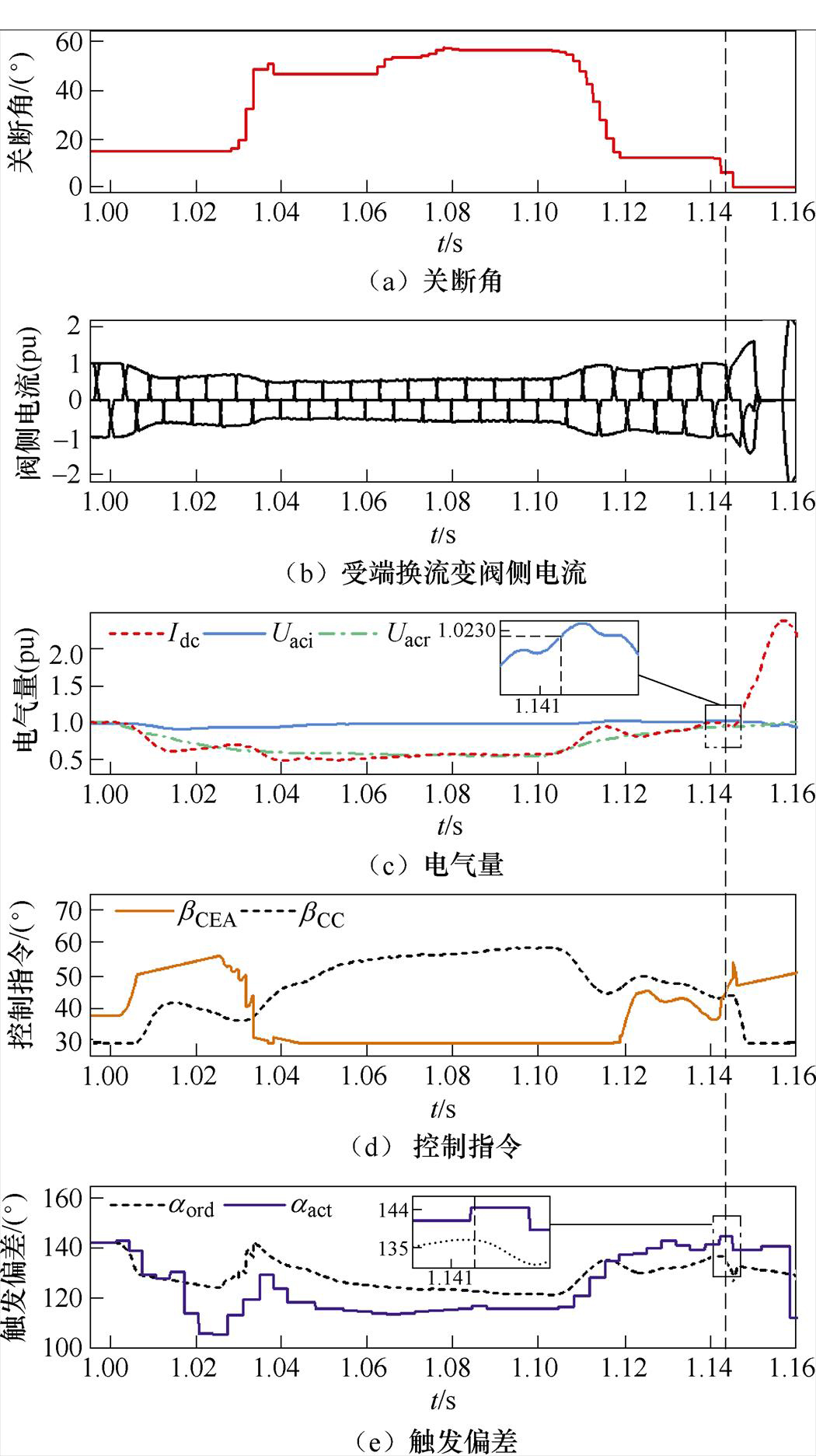
图20 案例3的交直流系统响应过程
Fig.20 AC-DC system response process in case 3
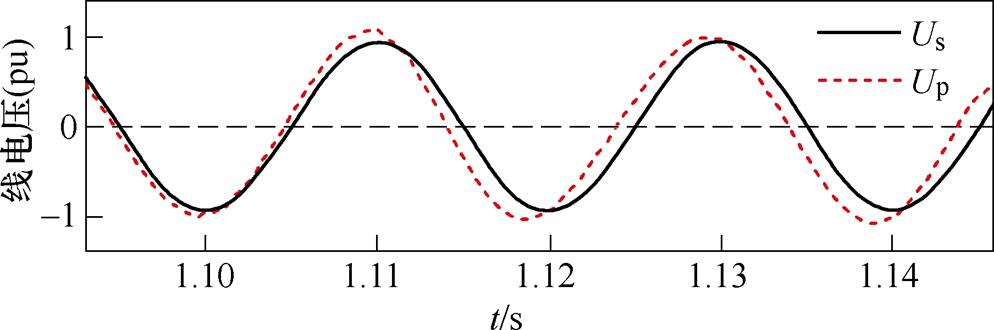
图21 案例3的受端交流线电压
Fig.21 AC line voltage at the receiving end in case
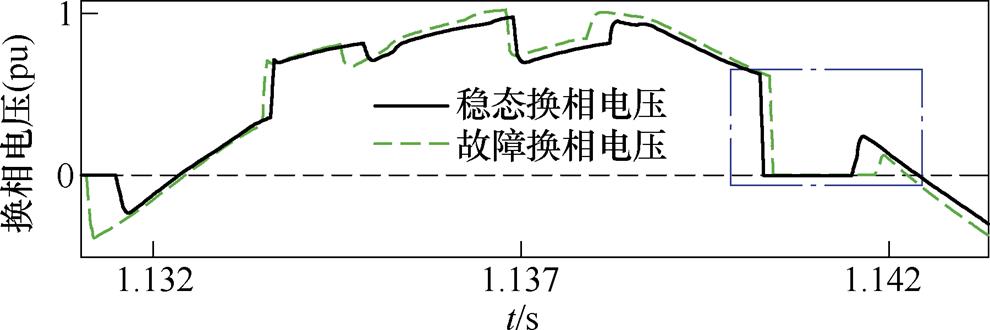
图22 算例3的换流阀换相电压
Fig.22 Commutation valve commutation voltage in case 3
由于CIGRE HVDC标准测试系统中逆变侧为弱交流系统，而交流系统强度与暂态过程中换流母线电压的稳定具有强相关性，所以有必要进一步探讨不同交流系统强度下送端故障对受端换相失败的影响。不同SCR下送端故障与逆变器的换相失败关系如图23所示。本文以短路容量与额定传输功率的比值SCR表征系统强度[12]，分别在送端不同故障类型下调整逆变侧交流系统短路比为2.5、3.5、4.5，设置故障时刻为1 s，故障持续时间为0.1 s，故障电感为0.6～0.1 H。仿真结果如下。
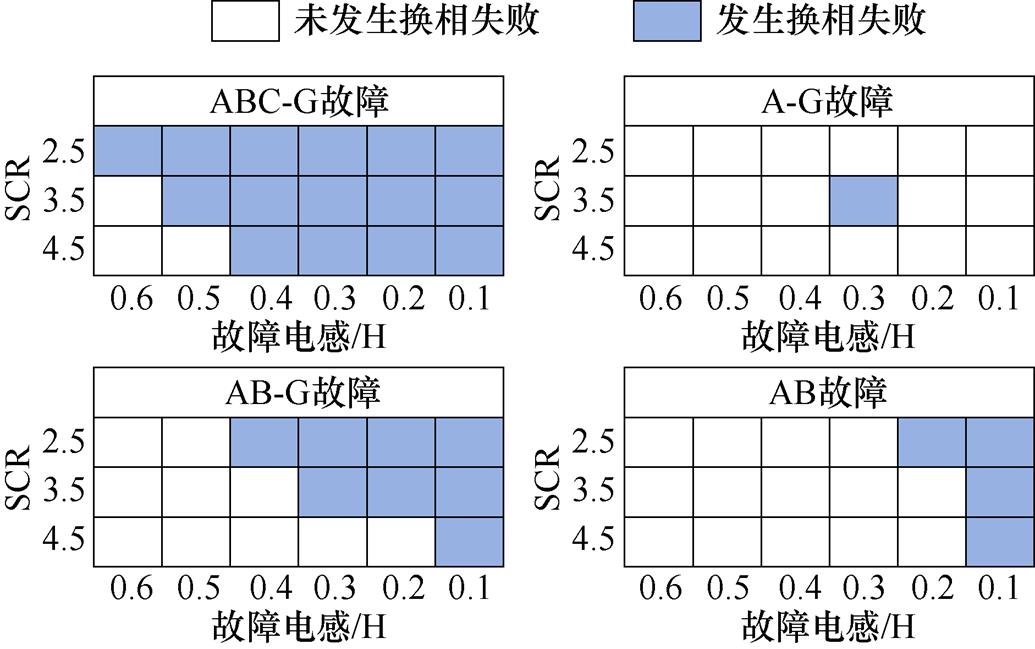
图23 不同SCR下送端故障与逆变器的换相失败关系
Fig.23 Relationship between different SCR downlink faults and inverter commutation failure
首先，由仿真结果发现，当送端三相短路接地故障时，随着受端交流系统强度的增大，较轻微故障程度下的换相失败现象消失了，同样地，在其他故障类型中也存在类似结论。这是由于在提高了受端交流系统强度后，交流系统的等效阻抗减小，暂态过程中换流母线电压的偏移程度受有功功率的影响减轻，逆变器的换相失败风险也因此随之减小。这也说明了可以通过适当增加受端交流系统强度来抑制送端故障引发的换相失败。此外，整体来看，除了单相接地故障基本不发生换相失败外，其他的三种故障类型，随着故障程度的加深，送端故障引发换相失败的可能性都在不断增大；而相同短路比、故障电感下，各种故障类型引发受端换相失败概率顺序为三相故障＞两相短路接地＞两相短路＞单相接地，这都是由不同故障对传输功率的影响程度不同带来的必然结果，所以在后续故障穿越的研究中，也应该以此为依据，以穿越最严重的三相故障为目标进行。
本文通过分析送端交流故障后的交直流系统响应，剖析了送端交流故障引发逆变器换相失败的机理，主要结论如下：
1）送端交流故障与受端交流故障引发逆变器换相失败有很大差异，送端交流故障引发的换相失败只发生在故障切除后的恢复阶段，且换流母线电压幅值大小并不是影响此类换相失败的关键因素。
2）送端故障切除后，有功功率的恢复会导致受端换流母线电压相位前移。这不仅直接压缩了换相面积，造成关断裕度减小，还给触发控制带来困难，导致实际触发角超过触发指令，增大了换相失败的风险。
3）不同故障程度下的换相失败原因存在差异。当送端故障程度较严重，受端切换至CC控制时，相位前移往往是导致逆变器换相失败的主要原因；当故障相对轻微，受端不发生控制切换时，除了相位前移，恢复过程中突增的直流电流也会对换相造成不利的影响。
后续将依据恢复阶段的相位偏移特性以及不同故障程度下的其他影响因素特征，从两侧系统的触发控制着手，开展送端交流故障引发逆变器的换相失败抑制策略研究。
参考文献
[1] 李培平, 周泓宇, 姚伟, 等. 多馈入结构背景下的高压直流输电系统换相失败研究综述[J]. 电网技术, 2022, 46(3): 834-850.
Li Peiping, Zhou Hongyu, Yao Wei, et al. Review of commutation failure on HVDC transmission system under background of multi-infeed structure[J]. Power System Technology, 2022, 46(3): 834-850.
[2] 王增平, 刘席洋, 李林泽, 等. 多馈入直流输电系统换相失败边界条件[J]. 电工技术学报, 2017, 32(10): 12-19.
Wang Zengping, Liu Xiyang, Li Linze, et al. Boun- dary conditions of commutation failure in multi- infeed HVDC systems[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 12-19.
[3] 王玲, 文俊, 李亚男, 等. 谐波对多馈入直流输电系统换相失败的影响[J]. 电工技术学报, 2017, 32(3): 27-34.
Wang Ling, Wen Jun, Li Yanan, et al. The harmonic effects on commutation faliure of multi-infeed direct current transmission systems[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 27-34.
[4] 程道卫, 刘天琪, 张金, 等. 多落点直流输电系统换相失败影响因素的仿真分析[J]. 电网技术, 2010, 34(11): 59-64.
Cheng Daowei, Liu Tianqi, Zhang Jin, et al. Simu- lative analysis on factors impacting commutation failure in multi-terminal HVDC transmission system[J]. Power System Technology, 2010, 34(11): 59-64.
[5] 吴萍, 林伟芳, 孙华东, 等. 多馈入直流输电系统换相失败机制及特性[J]. 电网技术, 2012, 36(5): 269-274.
Wu Ping, Lin Weifang, Sun Huadong, et al. Research and electromechanical transient simulation on mechanism of commutation failure in multi-infeed HVDC power transmission system[J]. Power System Technology, 2012, 36(5): 269-274.
[6] 高本锋, 王刚, 刘毅, 等. LCC-HVDC送端电网等值方案研究[J]. 电工技术学报, 2021, 36(15): 3250- 3263, 3271.
Gao Benfeng, Wang Gang, Liu Yi, et al. Study on equivalence method of AC system in sending-end of LCC-HVDC[J]. Transactions of China Electro- technical Society, 2021, 36(15): 3250-3263, 3271.
[7] 解润生, 张国荣, 高凯, 等. 适用于频变输电线的动态相量谐波分析建模与仿真[J]. 电工技术学报, 2021, 36(15): 3200-3210.
Xie Runsheng, Zhang Guorong, Gao Kai, et al. Modeling and simulation of dynamic phasor harmonic analysis for frequency-dependent transmission line[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3200-3210.
[8] 许汉平, 杨炜晨, 张东寅, 等. 考虑换相失败相互影响的多馈入高压直流系统换相失败判断方法[J]. 电工技术学报, 2020, 35(8): 1776-1786.
Xu Hanping, Yang Weichen, Zhang Dongyin, et al. Commutation failure judgment method for multi- infeed HVDC systems considering the interaction of commutation failures[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1776-1786.
[9] 夏成军, 王真, 杜兆斌. 考虑直流系统控制方式的多馈入交互作用因子实用计算方法[J]. 电网技术, 2017, 41(11): 3532-3540.
Xia Chengjun, Wang Zhen, Du Zhaobin. Practical calculation method for multi-infeed interaction factor considering HVDC system control modes[J]. Power System Technology, 2017, 41(11): 3532-3540.
[10] Andersen B R, Xu Lie. Hybrid HVDC system for power transmission to island networks[J]. IEEE Transactions on Power Delivery, 2004, 19(4): 1884- 1890.
[11] Son H I, Kim H M. An algorithm for effective mitigation of commutation failure in high-voltage direct-current systems[J]. IEEE Transactions on Power Delivery, 2016, 31(4): 1437-1446.
[12] 王增平, 刘席洋, 郑博文, 等. 基于电压波形拟合的换相失败快速预测与抑制措施[J]. 电工技术学报, 2020, 35(7): 1454-1463.
Wang Zengping, Liu Xiyang, Zheng Bowen, et al. The research on fast prediction and suppression measures of commutation failure based on voltage waveform fitting[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1454-1463.
[13] 束洪春, 代月, 安娜, 等. 基于线性回归的柔性直流电网纵联保护方法[J]. 电工技术学报, 2022, 37(13): 3213-3226, 3288.
Shu Hongchun, Dai Yue, An Na, et al. Pilot protection method of flexible DC grid based on linear regression[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3213-3226, 3288.
[14] Xiao Hao, Li Yinhong, Lan Tongkun. Sending end AC faults can cause commutation failure in LCC- HVDC inverters[J]. IEEE Transactions on Power Delivery, 2020, 35(5): 2554-2557.
[15] 林圣, 雷雨晴, 刘健, 等. HVDC送端系统故障引发受端换相失败分析[J]. 中国电机工程学报, 2022, 42(5): 1669-1680.
Lin Sheng, Lei Yuqing, Liu Jian, et al. Analysis of receiving-side commutation failure mechanism caused by HVDC sending-side system fault[J]. Proceedings of the CSEE, 2022, 42(5): 1669-1680.
[16] Hong Lerong, Zhou Xiaoping, Xia Haitao, et al. Mechanism and prevention of commutation failure in LCC-HVDC caused by sending end AC faults[J]. IEEE Transactions on Power Delivery, 2021, 36(1): 473-476.
[17] 汤奕, 郑晨一, 楼伯良, 等. 抑制连续换相失败的直流功率控制策略[J]. 电网技术, 2019, 43(10): 3514-3522.
Tang Yi, Zheng Chenyi, Lou Boliang, et al. Research on DC power control strategy for mitigating continuous commutation failure[J]. Power System Technology, 2019, 43(10): 3514-3522.
[18] 汪娟娟, 文兆新, 傅闯, 等. 基于换相电压相位检测的高压直流故障恢复策略[J]. 电网技术, 2019, 43(10): 3504-3514.
Wang Juanjuan, Wen Zhaoxin, Fu Chuang, et al. HVDC fault recovery strategy based on phase change detection of commutation voltage[J]. Power System Technology, 2019, 43(10): 3504-3514.
[19] 王子民, 傅闯, 汪娟娟, 等. 锁相环对HVDC系统后续换相失败的影响研究[J]. 中国电机工程学报, 2019, 39(23): 6836-6843, 7097.
Wang Zimin, Fu Chuang, Wang Juanjuan, et al. Study on the influence of phase-locked loop on follow-up commutation failure of HVDC system[J]. Proceedings of the CSEE, 2019, 39(23): 6836-6843, 7097.
[20] 曾君, 岑德海, 陈润, 等. 针对直流偏移和谐波干扰的单相锁相环[J]. 电工技术学报, 2021, 36(16): 3504-3515.
Zeng Jun, Cen Dehai, Chen Run, et al. Single-phase phase-locked loop for DC offset and harmonic inter- ference[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3504-3515.
[21] 何宇, 漆汉宏, 邓小龙. 基于全复数型滤波器的三相锁相环技术[J]. 电工技术学报, 2021, 36(10): 2115-2126.
He Yu, Qi Hanhong, Deng Xiaolong. A three-phase phase-locked loop technique based on all complex coefficient filter[J]. Transactions of China Electro- technical Society, 2021, 36(10): 2115-2126.
[22] 龚英明, 汪娟娟, 王子民, 等. 一种应用于高压直流输电的新型锁相环[J]. 电网技术, 2019, 43(11): 4097-4104.
Gong Yingming, Wang Juanjuan, Wang Zimin, et al. A novel phase-locked loop for HVDC[J]. Power System Technology, 2019, 43(11): 4097-4104.
[23] 朱仁龙, 周小平, 罗安, 等. 基于电压时间换相面积预测的换相失败抑制方法[J]. 电力系统自动化, 2022, 46(3): 156-163.
Zhu Renlong, Zhou Xiaoping, Luo An, et al. Commutation failure mitigation method based on voltage-time commutation area prediction[J]. Auto- mation of Electric Power Systems, 2022, 46(3): 156-163.
Abstract It is generally believed that the commutation failure of high-voltage direct current transmission (HVDC) is caused by the failure of the receiving-end AC system or the converter valve. However, in engineering practice, it is found that the sending-end AC system failure may also cause the commutation failure of the inverter. At present, most research is limited to the amplitude characteristics of the traditional bus voltage, and its electrical coupling and control coordination needs to be studied.
Firstly, by analyzing the response of the AC/DC system after the sending-side fault occurs, it is pointed out that, different from the general receiving-side AC fault, the commutation failure caused by the sending-side AC fault generally occurs in the recovery stage after the fault is removed. Moreover, the magnitude of the bus voltage is not a key factor in such commutation failures. On this basis, the phase characteristics of the bus voltage at the receiving end after the fault is removed are analyzed using the relationship between the active transmission power and the phase angle of the bus voltage. Based on the phase characteristics, the possible commutation failure risk is obtained. The analysis shows that after the fault is removed, restoring the active power transmitted from the sending system to the receiving end will lead to the phase advance of the commutation bus voltage at the receiving end. The phase advance of the bus voltage will not only make the commutation voltage zero-crossing point earlier, but also it will directly compress the commutation area, reduce the turn-off margin from two aspects, and increase the risk of commutation failure. On the other hand, the phase advance will also cause the actual trigger angle of the inverter to exceed the trigger command value, which delays the triggering of the commutator valve on the inverter side during the recovery process and induces commutation failure. In addition, in order to more comprehensively consider other influencing factors of commutation failure, according to the controller response at both ends, this paper further analyzes the changing characteristics of the trigger command and DC current corresponding to the inverter commutation failure process under different fault degrees of the sending-end AC system. The results show that when the AC fault at the sending end is slight and the inverter maintains constant turn-off angle control before and after the fault is removed, the phase shift of the bus voltage at the receiving end and the sudden increase of DC current cause the commutation failure of the inverter. When the fault degree of the sending end deepens and the receiving end inverter switches to constant current control, the phase advance of the bus voltage is often the main reason for the commutation failure. Finally, based on the CIGRE-HVDC simulation model, the correctness of the analysis is verified from the turn-off angle, the voltage of the converter valve, and the voltage and current of the AC and DC systems.
keywords：Commutation failure, sending AC failure, phase offset, turn-off angle, trigger command
DOI: 10.19595/j.cnki.1000-6753.tces.220989
中图分类号：TM711
国家自然科学基金委员会-国家电网公司智能电网联合基金资助项目（U2066210）。
收稿日期 2022-06-01
改稿日期 2022-06-15
朱 海 男，1998年生，硕士研究生，主要研究方向为直流输电控制与保护。E-mail: 20121546@bjtu.edu.cn
郝亮亮 男，1985年生，副教授，博士生导师，主要研究方向为电力系统主设备故障分析及保护、直流输电控制与保护、励磁控制。E-mail: llhao@bjtu.edu.cn（通信作者）
（编辑 崔文静）