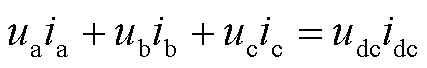 (1)
(1)
摘要 由于以光伏、风电为代表的可再生能源的间歇性、随机性特征,当分布式电源高渗透率并入电网时往往导致供电线路有功、无功功率的波动,造成有源配电网潮流分布与控制复杂化,网损增加,频率和电压品质下降。为了改善这一状况,该文参考静止无功补偿器(STATCOM)的电压源型换流器(VSC)结构提出一种基于旋转移相变压器(RPST)的电压源型无功补偿器(VSVC)的新拓扑,分析VSVC在容性和感性两种典型工况下的工作原理;研究VSVC并联稳态数学模型,应用瞬时无功理论,提出一种包含功率外环控制和电流内环控制的双闭环控制策略,具有良好的鲁棒性和控制精度。最后,通过仿真和实验验证了该文所提拓扑结构以及控制策略的有效性,满足有源配电网无功补偿器的灵活配置,可实现无功功率的连续、双向调节,并具有易实现高电压、大容量化,以及成本低、易运维、抗冲击性强和耐受性好等优势。
关键词:电压源型无功补偿器 旋转移相变压器 无功补偿 新型配电网
2020年9月,习近平主席在第75届联合国大会上提出了“碳达峰,碳中和”的战略目标[1-2]。国家电网和南方电网公司为响应“双碳”目标,提出建设新型电力系统。接入大量分布式新能源和分布式储能的新型配电网是新型电力系统实现“双碳”的重要环节[3-6]。随着分布式新能源的快速发展及其渗透率逐渐升高,新能源并网点电压跌落使得并网变换器功率传输能力受限以及功率反送引起的电压越限成为了制约分布式新能源发展的瓶颈问题[7-8]。随着电能替代加速推进,电动汽车、空调等非线性负荷逐年增加,系统对无功的需求也日益增大。及时补偿系统所需无功功率,不仅可以减小线路损耗,提高配电网的传输能力,而且可以稳定电网电压,提高用电设备的工作效率,有利于电网的经济稳定运行[9]。另外,新型配电网中电力电子设备大规模应用导致的配电系统谐波问题也不容忽视。
静止无功补偿器(Static Var Compensator, SVC)具有装置简单、造价低廉、调节效率较高[10-13]的优点。晶闸管投切电容器(Thyristor Switching Capacitor, TSC)和晶闸管控制电抗器(Thyratron Control Reactor, TCR)都属于SVC。其中TSC由于电容投切,只能实现无功分级调节 [14];TCR通过改变晶闸管的触发延迟角可以连续调节注入的无功功率,但调节过程中存在谐波问题[15]。基于电压源型换流器(Voltage Source Converter, VSC)的静止同步补偿器(Static Synchronous Compensator, STATCOM)和静止同步串联补偿器(Static Synchronous Series Compensator, SSSC)由于响应迅速的特点,在近几年中快速发展。STATCOM可以提供连续动态的无功支撑,谐波问题也有了很大改善[16-18]。SSSC通过调节输出电压既可以控制线路传输有功,也可以向系统补偿无功。但由于电力电子器件的耐压问题和成本较高,难以实现大容量、高电压和大范围推广使用[19]。因此,现有的无功补偿装置难以同时满足精准性和经济性两个方面。
考虑到SVC和STATCOM具有优势互补的特点,一些学者提出将两种装置进行串并联组成混合补偿装置,可以同时兼顾补偿效果和设备成本。文献[20]提出一种TSC与STATCOM串联复合系统, TSC承受主要压降,补偿大部分无功功率,但TSC分级调节会给STATCOM带来一定冲击。文献[21]采用多组TSC与STATCOM并联,大容量TSC实现无功“粗补”,小容量STATCOM实现无功“精补”,有效减小了STATCOM的容量,降低了整个设备的成本。但并联点电压跌落会直接影响TSC的无功出力,使得整个装置的无功补偿容量快速下降。文献[22]提出一种基于模型预测控制的SVC与STATCOM协调控制策略,考虑到SVC与STATCOM之间的交互影响问题,协调控制策略较为复杂。文献[23]提出了一种可控串联补偿装置(Thyristor Controlled Series Compensator, TCSC)和STATCOM联合控制的方法,提供充足的无功功率来改善风电并网系统在受到大扰动时的电压稳定性问题。除了采用上述混合装置,为了有效减小器件电压应力,有学者提出了将级联型多电平变流器(Cascaded H-Bridge, CHB)或模块化多电平变流器(Modular Multilevel Converter, MMC)与STATCOM相结合[24],分别设计出级联H桥型STATCOM和MMC-STATCOM。文献[25]提出将级联型STATCOM接入配电变压器高压侧三角形绕组,能够有效降低注入点电压,减少级联数,提升补偿容量,但由于没有公共直流侧,二倍频分量会对直流电压产生影响。文献[26]提出了对MMC-STATCOM电容电压的控制策略,由于子模块电容能量控制是MMC-STATCOM提供稳定无功支持的关键,因此针对电容电压的控制策略较为复杂,需考虑相与相之间、同一相内上下桥臂之间、同一桥臂内不同模块之间的能量平衡。另外,有些学者也提出了新思路,文献[27]提出一种串联型电力电子调压设备,用电力弹簧(Electric Spring, ES)拓扑结构有效解决低电压台区因光伏发电倒送引起的用户端电压波动问题。
针对上述问题,本文借鉴VSC的工作原理[28]以及旋转潮流控制器(Rotary Power Flow Controller, RPFC)的电压合成机理[29-30],提出一种基于旋转移相变压器(Rotary Phase Shifting Transformer, RPST)的电压源型无功补偿器(Voltage Source Var Compensator, VSVC)新拓扑,其具有连续、双向无功调节能力,且易实现高电压、大容量化,同时运维方便、经济性好,抗冲击性和耐受性好。因此,本文对该VSVC的拓扑结构及工作原理展开分析,进一步提出一种适用于该设备的无功补偿控制策略,给出相关参数的设计方法,最后通过仿真和样机验证本文所提拓扑结构及控制策略的可行性和有效性。
电压源型换流器(VSC)的拓扑结构如图1所示,e表示电源电动势;L表示VSC与电网间的连接电感;ia、ib、ic表示VSC交流侧电流;ua、ub、uc表示VSC交流侧电压;udc表示VSC直流侧电压;idc表示VSC直流侧电流。若不计功率开关管桥路损耗,由功率平衡关系可得
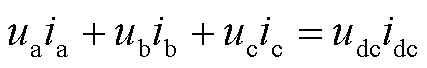 (1)
(1)
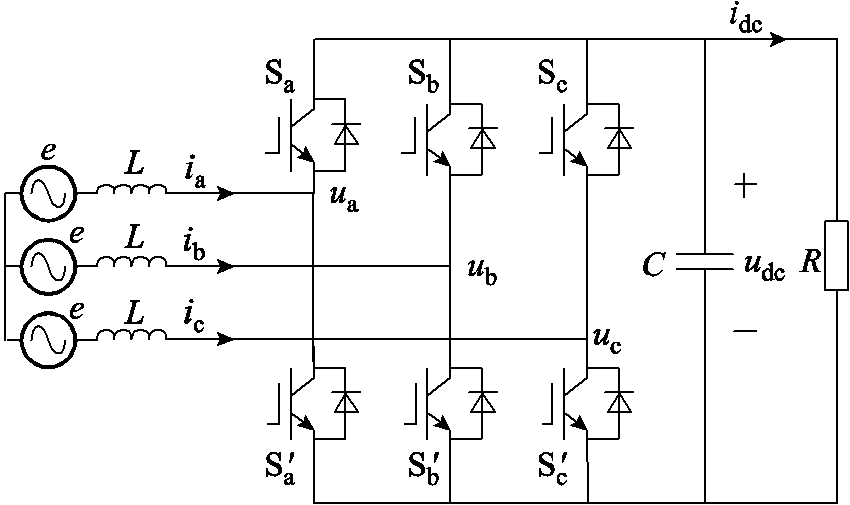
图1 电压源型换流器拓扑结构
Fig.1 Topology of voltage source converter
由式(1)可知,控制电路的任意一侧即可实现对另一侧的直接控制。
以电源电动势E为参考相量,通过控制功率开关管桥路改变VSC交流侧电压的大小和相位,进而改变VSC的网侧特性,实现VSC的四象限运行,其交流侧稳态相量关系如图2所示。当VSC交流侧电压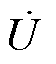 位于A点,VSC交流侧电流
位于A点,VSC交流侧电流 滞后
滞后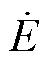 相位90°,此时VSC运行在纯感性区域,只从电网吸收无功功率,如图2a所示。当
相位90°,此时VSC运行在纯感性区域,只从电网吸收无功功率,如图2a所示。当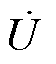 位于B点,
位于B点, 与
与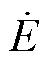 同相位,此时VSC运行在正阻性区域,如图2b所示。当
同相位,此时VSC运行在正阻性区域,如图2b所示。当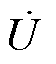 位于C点,
位于C点, 超前E相位90°,此时VSC运行在纯容性区域,只向电网发出无功功率,如图2c所示。当
超前E相位90°,此时VSC运行在纯容性区域,只向电网发出无功功率,如图2c所示。当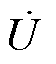 位于D点,
位于D点, 与
与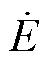 反相位,此时VSC运行在负阻性区域,如图2d所示。
反相位,此时VSC运行在负阻性区域,如图2d所示。
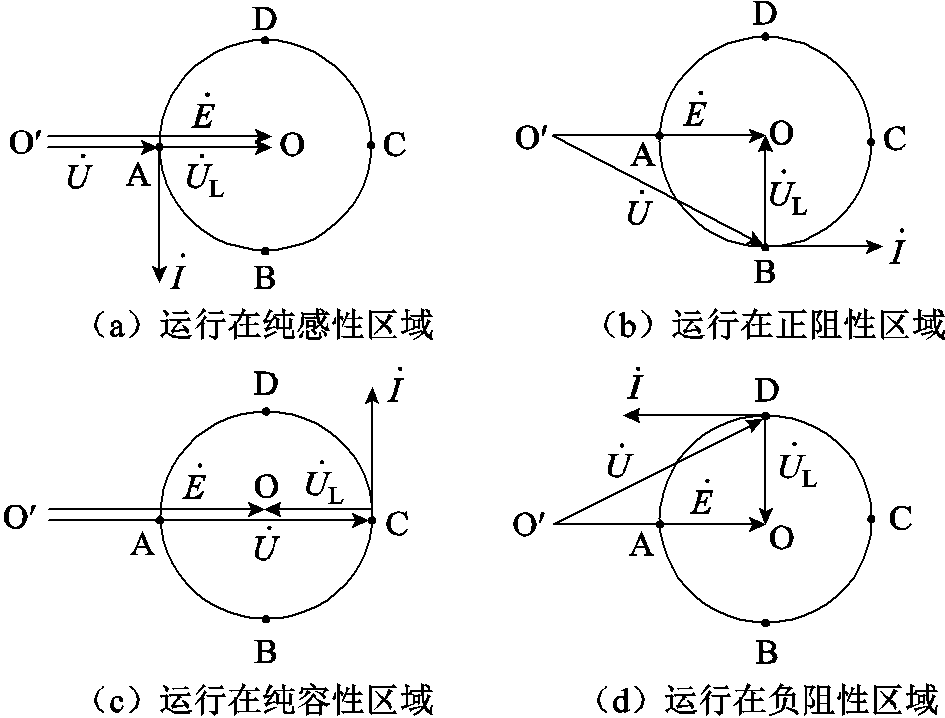
图2 VSC交流侧稳态相量关系
Fig.2 VSC AC side steady-state phasor relationship
旋转移相变压器(RPST)采用绕线式转子异步电机的结构,RPST的接线结构如图3所示。转子绕组作为一次绕组接电源,定子绕组作为二次绕组接负载。一次绕组由包括伺服电动机、齿轮和转子轴在内的转子驱动装置控制,根据需要旋转一定的角度,以达到调整输出电压相对于输入电压的相位差的目的。由于RPST一般采用多对级,因此在实际调节中只需要转动很小的角度就可以实现所需相位调节,调节范围可达到180°电角度。
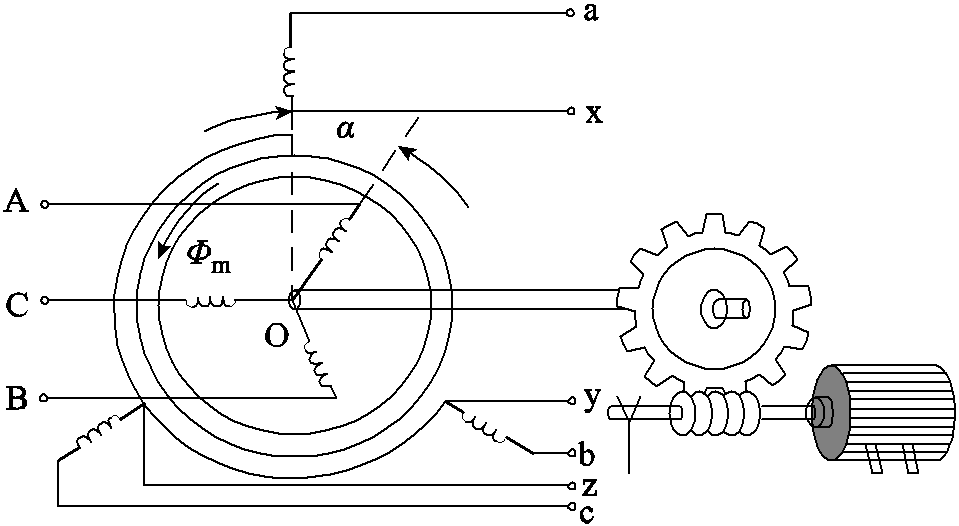
图3 RPST的接线结构
Fig.3 Wiring diagram of RPST
假设RPST为一对极,当一次绕组接电源后,电源向RPST供给励磁电流,该电流在一、二次铁心及其之间的气隙中产生旋转磁场,磁通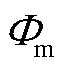 为逆时针方向,旋转磁场切割一、二次绕组后产生感应电动势
为逆时针方向,旋转磁场切割一、二次绕组后产生感应电动势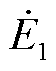 、
、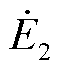 ,其幅值与一、二次绕组的匝数成正比,而相位取决于一、二次绕组的相对位置。当一次绕组逆着旋转磁场方向旋转a角度,如图4a所示,此时二次绕组超前一次绕组a角度,存在以下关系
,其幅值与一、二次绕组的匝数成正比,而相位取决于一、二次绕组的相对位置。当一次绕组逆着旋转磁场方向旋转a角度,如图4a所示,此时二次绕组超前一次绕组a角度,存在以下关系
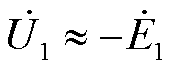 (2)
(2)
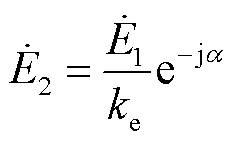 (3)
(3)
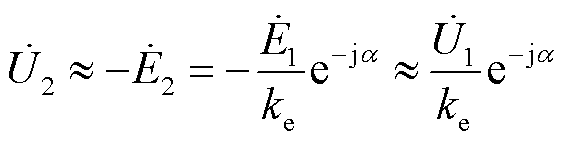 (4)
(4)
式中,ke为一、二次绕组有效匝数比。输入、输出电压及一、二次绕组感应电动势相量如图4b所示。
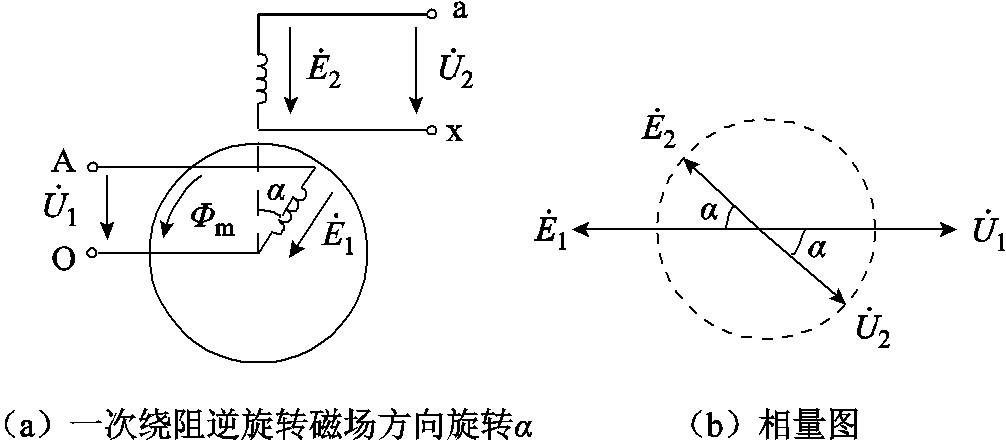
图4 RPST单相原理
Fig.4 RPST single-phase schematic
本文借鉴已有VSC的拓扑及工作原理,用两台并联的RPST代替功率开关管桥路,提出一种基于RPST的VSVC,其拓扑结构如图5所示。
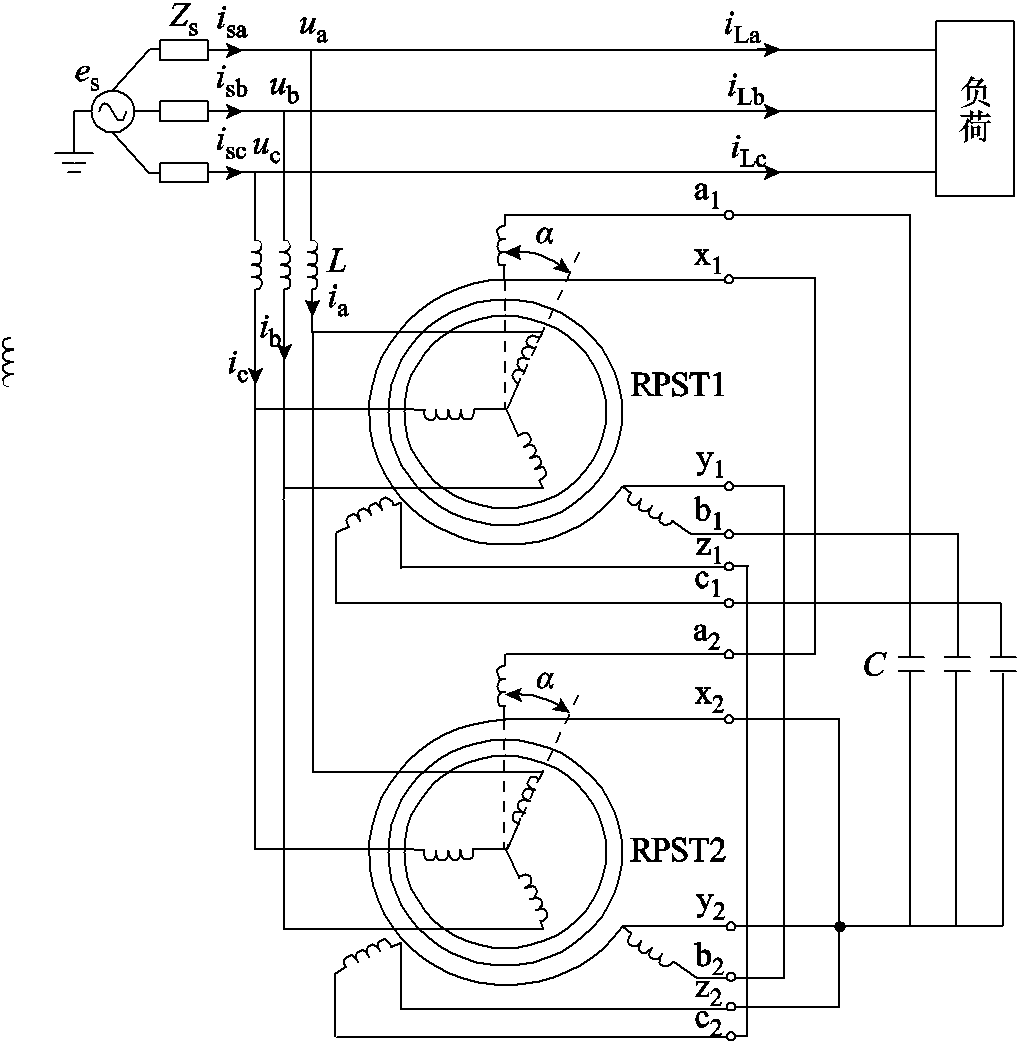
图5 基于RPST的VSVC拓扑结构
Fig.5 Topology of VSVC based on RPST
VSVC主要由两台RPST、连接电感L以及补偿电容C构成。es表示系统电源电动势;Zs表示电源的等效阻抗;isa、isb、isc分别为电源侧三相电流;ua、ub、uc分别为并联点三相电压;ia、ib、ic分别为VSVC三相补偿电流;iLa、iLb、iLc分别为负荷侧三相电流;两台RPST的一次绕组并联,经过连接电感接入电网,二次绕组串联后连接成三相星形联结在补偿电容两侧。RPST可以等效为一台移相变压器,一、二次侧存在一定电压比关系,而相位差取决于一、二次绕组的相对位置角。因此,只要调节2台RPST的转子位置角,就可以连续调节电容两侧电压的幅值和相位,从而改变电容发出的无功功率。一方面,使用两台RPST代替原有的功率开关管桥路,可以大大地降低整个设备的投资成本,满足经济性要求,实现高电压、大容量化、方便运维且抗冲击性能好、耐受性高;另一方面,电容两侧电压连续可调,VSVC可实现对负荷无功功率的全补偿。
为阐述VSVC的工作原理,根据图5所示拓扑结构,建立VSVC稳态运行时的单相等效电路,如图6所示,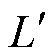 表示计及RPST自电感的等效连接电感;C表示补偿电容;
表示计及RPST自电感的等效连接电感;C表示补偿电容;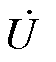 表示VSVC并联点电压,
表示VSVC并联点电压,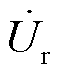 表示一次电压;
表示一次电压;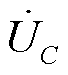 表示电容两侧电压;
表示电容两侧电压; 表示补偿电流;
表示补偿电流;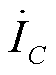 表示流过电容的电流。电压、电流参考方向如图6中所示。
表示流过电容的电流。电压、电流参考方向如图6中所示。
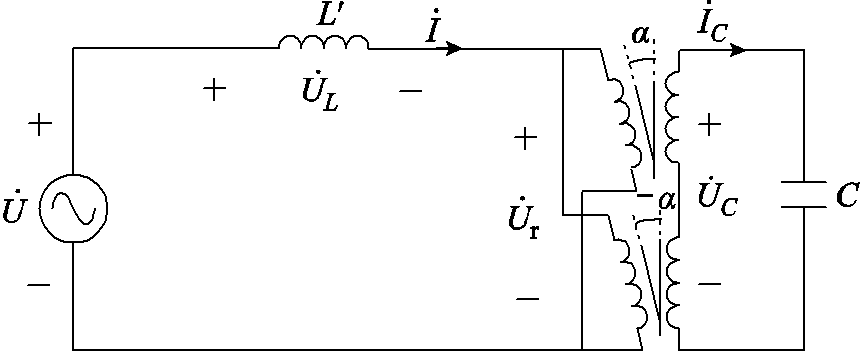
图6 单相等效电路
Fig.6 Single-phase equivalent circuit diagram
设RPST一次侧和二次侧的绕组匝数相同,对一次回路列写KVL方程得
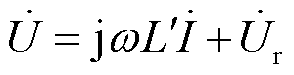 (5)
(5)
单相VSVC输出的视在功率S可表示为
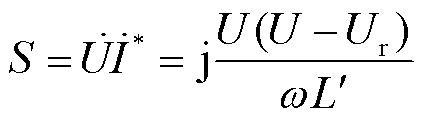 (6)
(6)
因此,单相补偿无功功率为
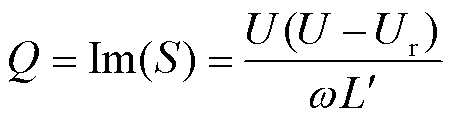 (7)
(7)
由式(7)可知,当U>Ur时,Q>0,VSVC吸收无功功率;当U<Ur时,Q<0,VSVC发出无功功率。因此,VSVC既可以吸收无功功率,也可以发出无功功率,能够灵活补偿系统所需无功功率。
VSVC的两种理想运行方式相量图如图7所示。以电网侧并联点电压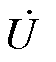 为参考相量,
为参考相量,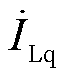 为负荷电流的无功分量,要使电源侧功率因数维持在1,需要VSVC的补偿电流满足
为负荷电流的无功分量,要使电源侧功率因数维持在1,需要VSVC的补偿电流满足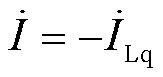 ;
;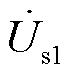 和
和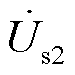 表示两台RPST二次电压。由于两台RPST一次侧并联,二次侧串联,故
表示两台RPST二次电压。由于两台RPST一次侧并联,二次侧串联,故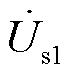 和
和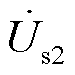 幅值相近,相位不同,共同合成电容两侧电压
幅值相近,相位不同,共同合成电容两侧电压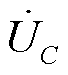 。
。
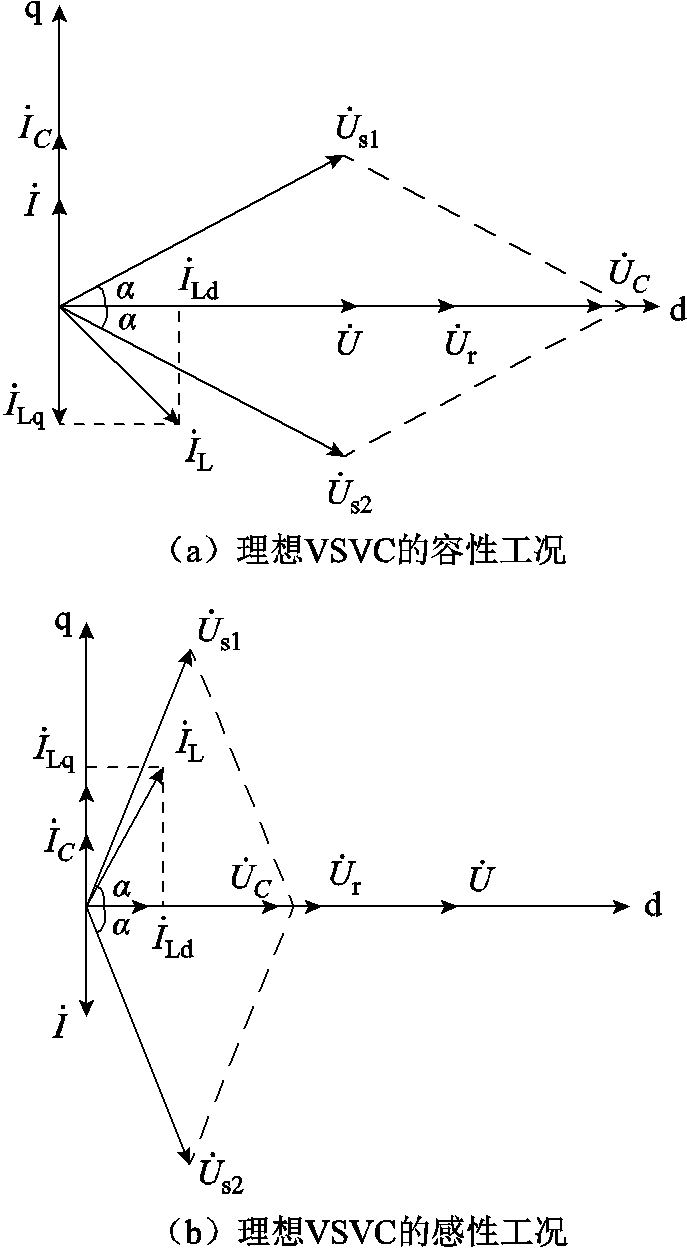
图7 两种理想运行方式相量图
Fig.7 Phasor diagram of two ideal operating modes
图7a为理想VSVC的容性工况,此时负荷呈感性,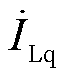 位于
位于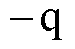 轴方向,α较小,电容两侧电压
轴方向,α较小,电容两侧电压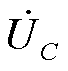 幅值较大,RPST一次电压
幅值较大,RPST一次电压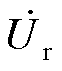 大于并联点电压
大于并联点电压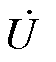 ,补偿电流
,补偿电流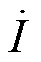 超前并联点电压
超前并联点电压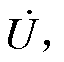 VSVC在网侧呈现纯电容特性,向电网发出无功功率。图7b为理想VSVC的感性工况。此时负荷呈容性,
VSVC在网侧呈现纯电容特性,向电网发出无功功率。图7b为理想VSVC的感性工况。此时负荷呈容性,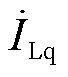 位于
位于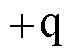 轴方向,α较大,电容两侧电压
轴方向,α较大,电容两侧电压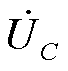 幅值较小,RPST一次电压
幅值较小,RPST一次电压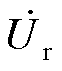 小于并联点电压
小于并联点电压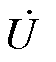 ,补偿电流
,补偿电流 滞后并联点电压
滞后并联点电压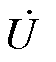 ,VSVC在网侧呈现纯电感特性,从电网吸收无功功率。
,VSVC在网侧呈现纯电感特性,从电网吸收无功功率。
本节根据VSVC的拓扑结构推导其并联稳态数学模型,为了提高控制策略的精准性,应用瞬时无功理论,建立包括功率外环控制以及电流内环控制的双闭环控制策略。
VSVC接入电网的单相等效电路如图8所示。ZL表示负载阻抗;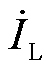 表示负载电流;
表示负载电流;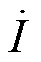 表示VSVC的补偿电流;L′表示计及RPST自电感的等效连接电感;
表示VSVC的补偿电流;L′表示计及RPST自电感的等效连接电感;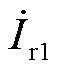 、
、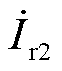 表示两台RPST的一次电流;kRPST为RPST的电压比;a1和a2分别为两台RPST的移相角,不考虑系统电阻损耗。
表示两台RPST的一次电流;kRPST为RPST的电压比;a1和a2分别为两台RPST的移相角,不考虑系统电阻损耗。
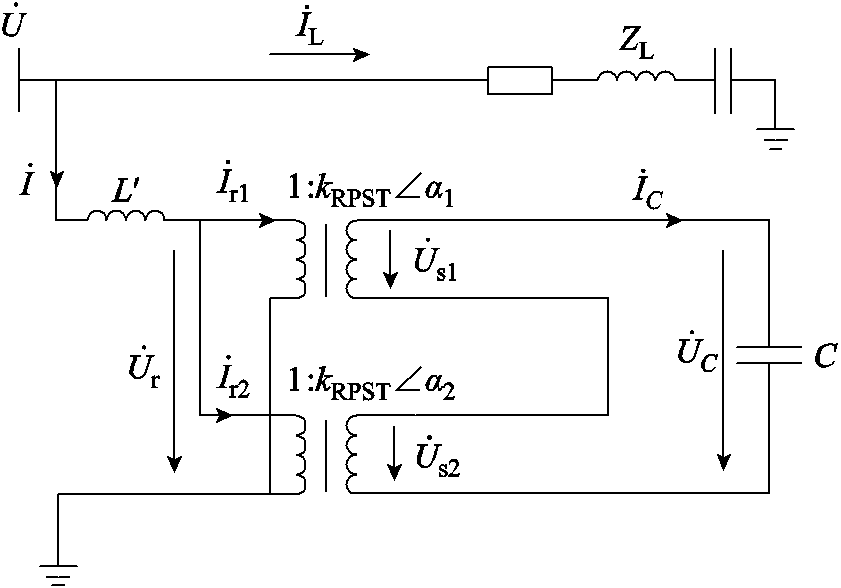
图8 系统单相等效电路
Fig.8 System single-phase equivalent circuit
根据变压器原理,两台RPST的一次、二次电压的关系可表示为
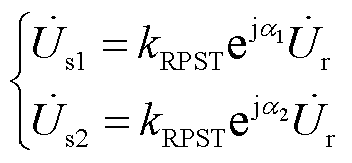 (8)
(8)
根据矢量合成原理,二次绕组串联后得到电容电压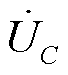 为
为
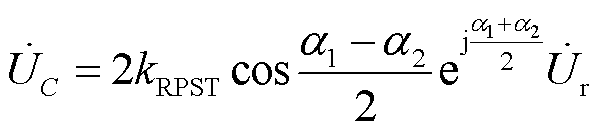 (9)
(9)
同理,根据电流关系可得
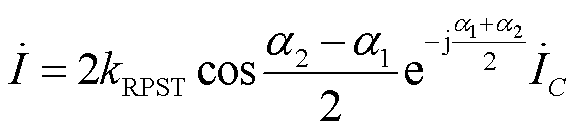 (10)
(10)
当取a1=-a2=a,TRPST=1时,则式(9)、式(10)可简化为
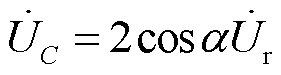 (11)
(11)
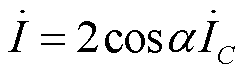 (12)
(12)
由式(5)可知VSVC的补偿电流可表示为
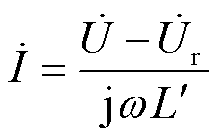 (13)
(13)
已知电容两侧电压,可得电容发出的无功功率为
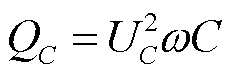 (14)
(14)
根据VSVC的补偿电流,电感吸收的无功功率为
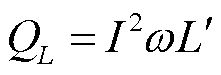 (15)
(15)
因此,VSVC向电网补偿无功可表示为
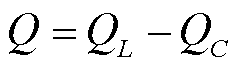 (16)
(16)
将式(14)、式(15)代入式(16),近似化简后可得VSVC补偿无功与并网点电压、一次电压及RPST移相角的关系为
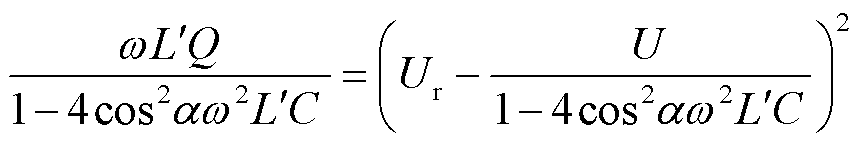 (17)
(17)
当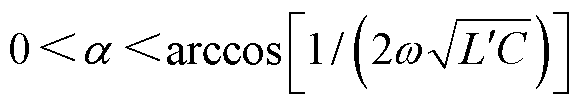 时,Q<0,说明此时电容发出的无功功率大于电感吸收的无功功率,因此VSVC对外发出无功功率,可补偿感性负荷,由于无功功率流动的方向即电压降落的方向,此时RPST一次电压
时,Q<0,说明此时电容发出的无功功率大于电感吸收的无功功率,因此VSVC对外发出无功功率,可补偿感性负荷,由于无功功率流动的方向即电压降落的方向,此时RPST一次电压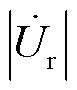 大于并联点电压
大于并联点电压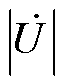 ,符合图7a。
,符合图7a。
当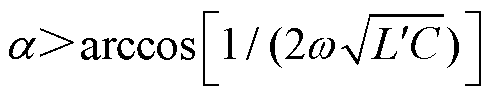 时,Q>0,说明此时电感吸收的无功功率大于电容发出的无功功率,因此VSVC从电网吸收无功,可补偿容性负荷,此时RPST一次电压
时,Q>0,说明此时电感吸收的无功功率大于电容发出的无功功率,因此VSVC从电网吸收无功,可补偿容性负荷,此时RPST一次电压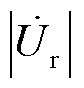 小于电网并联点电压
小于电网并联点电压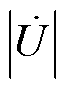 ,符合图7b。
,符合图7b。
设伺服电动机转速为rs,RPST一次绕组的机械转速为rm,电角度转速为re,单位均为rad/s,齿轮传动比为c,RPST极对数为p。一般rs为固定值,根据齿轮传动比可得RPST一次绕组的机械转速为
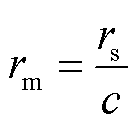 (18)
(18)
RPST的电角度转速为
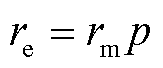 (19)
(19)
当RPST的始末移相角分别为a0和a时,所需调节时间可表示为
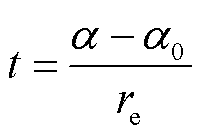 (20)
(20)
由于VSVC的正弦交流电路中同时存在电感和电容元件,当调节电路元件参数和RPST移相角时,可能会出现谐振现象。因此,特别针对VSVC的谐振点展开研究。
已知电容两侧电压和电流关系为
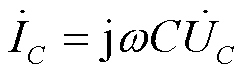 (21)
(21)
依次将式(21)、式(11)和式(5)代入式(12)可得
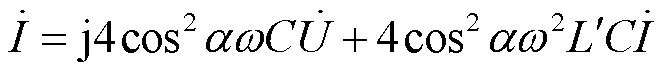 (22)
(22)
化简可得
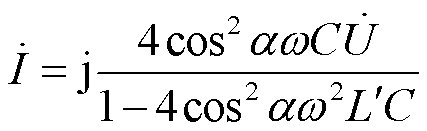 (23)
(23)
VSVC的等效阻抗可表示为
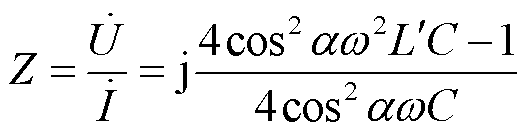 (24)
(24)
因此,谐振频率为
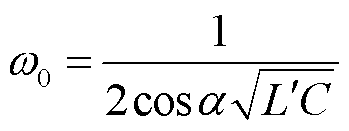 (25)
(25)
谐振移相角为
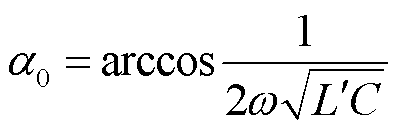 (26)
(26)
构建基于RPST的VSVC控制方案,控制系统框图如图9所示。
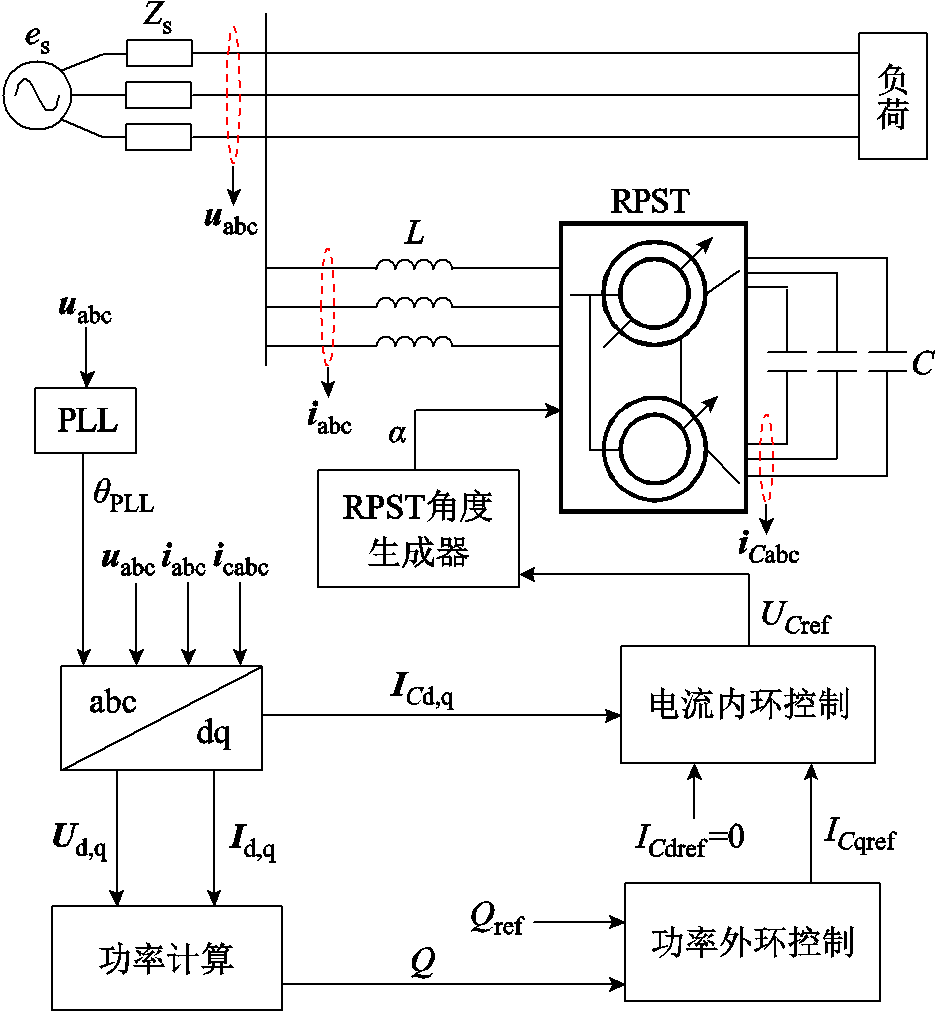
图9 控制系统框图
Fig.9 Control system block diagram
VSVC的控制策略在dq旋转坐标系下实现,通过锁相环(Phase Locked Loop, PLL)将并网点电压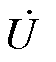 固定在d轴上,dq坐标系以电网基波角速度w旋转,图中qPLL为锁相环输出角度。根据图9给出的VSVC无功功率控制环路可知:控制系统通过无功功率外环以及无功电流内环分别实现VSVC补偿无功Q对无功指令值Qref、二次侧输出无功电流ICq对无功电流指令值ICqref的跟踪。本文暂不考虑对VSVC有功部分的控制,因此后文分析中认为ICd=ICdref=0。
固定在d轴上,dq坐标系以电网基波角速度w旋转,图中qPLL为锁相环输出角度。根据图9给出的VSVC无功功率控制环路可知:控制系统通过无功功率外环以及无功电流内环分别实现VSVC补偿无功Q对无功指令值Qref、二次侧输出无功电流ICq对无功电流指令值ICqref的跟踪。本文暂不考虑对VSVC有功部分的控制,因此后文分析中认为ICd=ICdref=0。
VSVC内外环控制框图如图10所示。要维持电源侧功率因数为1,需要VSVC提供负荷所需全部无功功率。因此,选择负荷侧所需无功功率作为无功功率指令Qref,由功率控制环实现Q对Qref的跟踪并生成二次侧所发无功功率指令QC,经过计算得到二次侧无功电流指令ICqref,再经过无功电流控制环实现二次侧无功电流ICq对ICqref的跟踪,并限制该值在1.1倍额定电流之内。另外,经过有功电流控制环实现二次侧有功电流ICd对ICdref的跟踪。由于a1=-a2,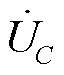 固定在+d轴上,而RPST二次侧为电容,IC位于+q轴上,因此二次电流以无功电流分量为主。将ICd和ICq的理想值输入幅角转化模块,得到二次电流的幅值|IC|和相位θi,进而得到电容两侧电压的幅值|UC|,电压角度θu滞后电流角度90°。根据电压的幅值和相位计算得到电容电压的d轴分量,将该值输入RPST角度生成器,由式(11)可得RPST移相角a,即a1=a,a2=-a。为避免发生谐振现象,在谐振移相角a0附近设置移相角死区,死区范围为[-e, e ]。当a0-e<a<a0时,令a=a0-e;当a0<a<a0+e时,令a=a0+e,其中e 的取值可根据实际应用场景需要来确定。将移相信号a 输入RPST模块,实现无功补偿的目的。
固定在+d轴上,而RPST二次侧为电容,IC位于+q轴上,因此二次电流以无功电流分量为主。将ICd和ICq的理想值输入幅角转化模块,得到二次电流的幅值|IC|和相位θi,进而得到电容两侧电压的幅值|UC|,电压角度θu滞后电流角度90°。根据电压的幅值和相位计算得到电容电压的d轴分量,将该值输入RPST角度生成器,由式(11)可得RPST移相角a,即a1=a,a2=-a。为避免发生谐振现象,在谐振移相角a0附近设置移相角死区,死区范围为[-e, e ]。当a0-e<a<a0时,令a=a0-e;当a0<a<a0+e时,令a=a0+e,其中e 的取值可根据实际应用场景需要来确定。将移相信号a 输入RPST模块,实现无功补偿的目的。
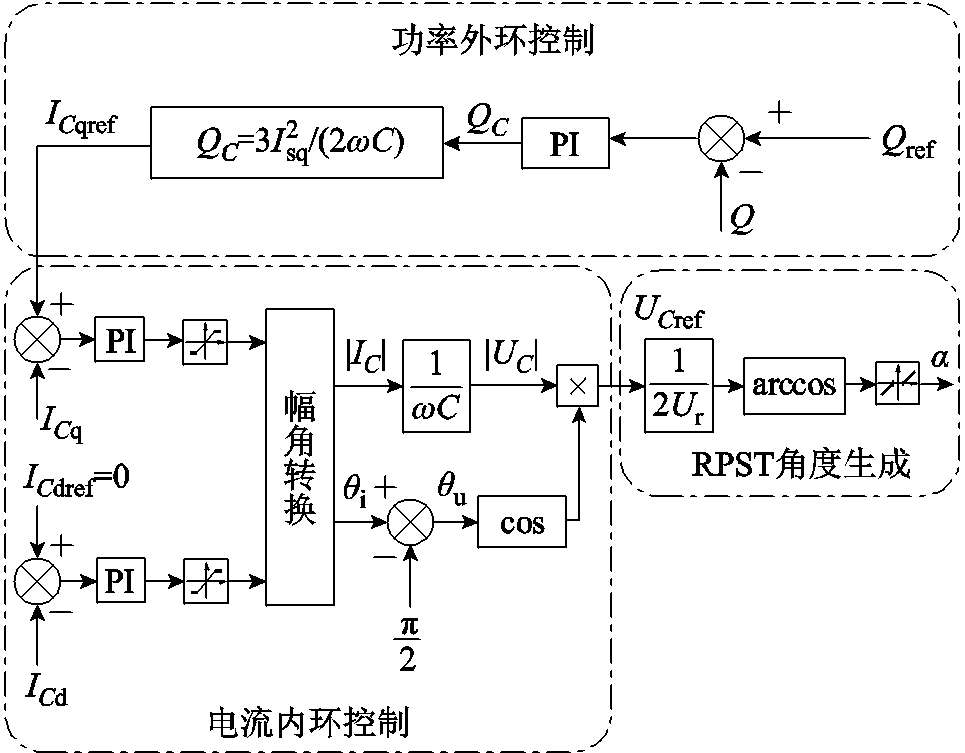
图10 VSVC内外环控制框图
Fig.10 Control block diagram of the inner and outer loops of VSVC
本文拟对电网电压为690 V,以吸收无功功率为正,双向补偿容量均为1 Mvar的VSVC进行容量选取、一次侧电感、二次侧电容选择和谐振移相角分析。
RPST要从电网吸收无功功率来励磁和供给一、二次绕组的漏抗,其中大部分无功功率用来励磁。由于RPST运行在额定电压时,励磁电流可以达到额定电流的20%~25%,因此吸收的无功功率可以达到RPST容量的20%~25%。本文按照25%确定RPST的容量。
VSVC吸收的最大无功功率为1 Mvar,单台RPST吸收无功为0.5 Mvar,因此每台RPST的容量应为
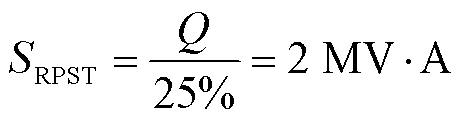 (27)
(27)
当电网电压为690 V时,补偿容量共计2 Mvar,VSVC的相电流有效值为
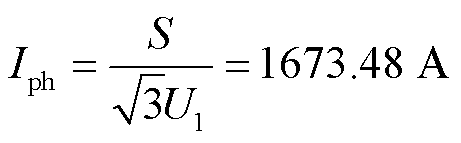 (28)
(28)
式中,U1为电网线电压的有效值。
连接电抗标幺值X*按0.15进行选取[31],则连接电感值为
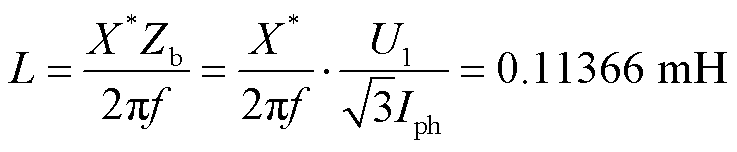 (29)
(29)
式中,Zb为系统阻抗的基准值。
二次侧电容按照最大发出无功功率1 Mvar计算,考虑到RPST自身存在阻抗,且为阻感性,为了满足无功补偿需求,在设计电容值时,应该考虑RPST吸收的无功功率,设计裕度取1.1。
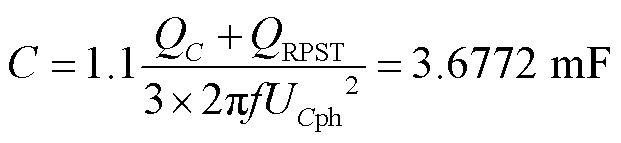 (30)
(30)
式中,QRPST为RPST吸收无功功率;UCph为电容两侧最大相电压的有效值,这里取额定相电压有效值的2倍。
VSVC吸收的最大无功为1 Mvar,此时相电流可表示为
 (31)
(31)
计及RPST内电抗的等效电抗L′可表示为
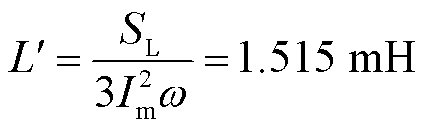 (32)
(32)
由式(26)可得谐振移相角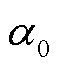 为
为
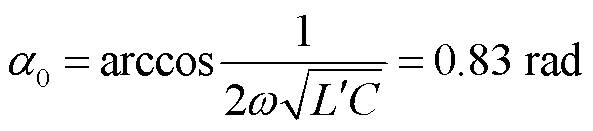 (33)
(33)
e取0.03 rad,因此死区范围设为0.80~0.86 rad。
采用Matlab/Simulink仿真平台搭建额定电压为690 V,双向补偿容量为1 Mvar的三相VSVC系统模型,对VSVC的工作原理及控制策略进行仿真验证。仿真系统如图5所示,仿真系统参数见表1。
表1 仿真系统参数
Tab.1 Simulation system parameters

参数数值 电网电压es/V690 电源等效阻抗Zs/Ω0.01+j1×10-5 电感L/mH0.113 66 RPST额定容量/(MV∙A)2 RPST额定电压/V690 RPST定子侧阻抗Zs(pu)0.010 8+j0.102 RPST转子侧阻抗Zr(pu)0.010 21+j0.11 RPST励磁电感Lm(pu)3.362 电容C/mF3.677 2
考虑到VSVC具有感性工况和容性工况,首先对其设计的补偿范围进行仿真验证,测试参数设计方案的有效性,然后分别对这两种典型工况下VSVC的补偿效果进行研究分析。为验证该设备及控制策略在额定补偿范围可实现全范围补偿,分别在容性和感性工况下,针对无功功率大、中、小情况进行仿真分析。
VSVC设计的调节范围为-1~1 Mvar,即当设备运行在最大容性工况时,RPST的移相角为0°,电容两端的电压最高,设备发出1 Mvar无功功率。当设备运行在最大感性工况时,RPST的移相角为90°,电容两端的电压接近于0,此时设备吸收 1 Mvar无功功率。VSVC的调节范围如图11所示,VSVC初始运行在最大容性工况,5 s时切换到最大感性工况。考虑到极限状态时设备运行的稳定性,其调节范围略大于理想设计范围。
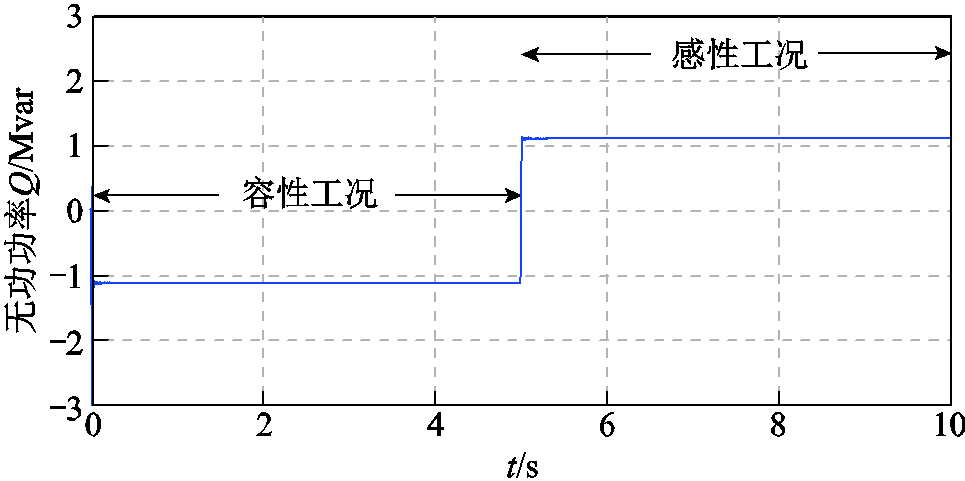
图11 调节范围
Fig.11 Adjustment range
5.2.1 容性工况
为验证VSVC在容性工况下的调节效果,在线路末端设置感性负荷PLoad+jQLoad=(1+j1) MV∙A。初始时刻VSVC暂未投入,两台RPST的移相角a1和a2为±90°,电容两侧合成电压UC为0,线路上实际潮流为Pline+jQline=(0.947+j0.947) MV∙A,电源侧功率因数为0.605,放大后三相电压和电流如图12a所示,电源输出的电压和电流相位有偏差且电流滞后于电压。在0.05 s时投入VSVC,a1和a2在0.08 s左右调节至稳态,UC高于VSVC并联点电压U,此时负荷线路上功功率Pline+jQline=(0.957+j0.957) MV∙A,VSVC发出0.957 Mvar无功功率,电源侧无功功率几乎为0,功率因数提高到1,此时电源侧三相电压和电流相位相同,补偿后三相电压和电流波形如图12b所示。RPST移相角和电压波形如图12c所示。
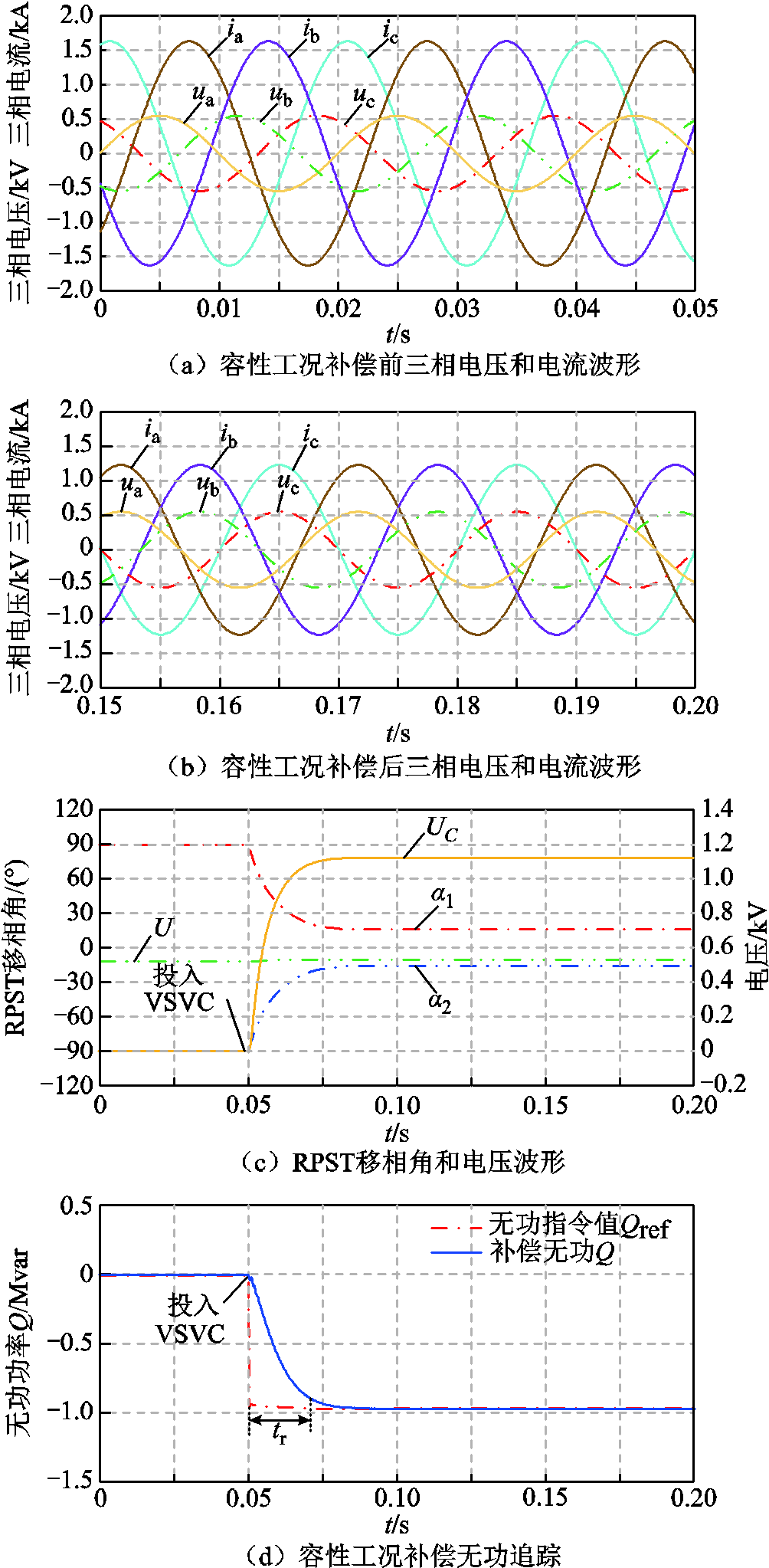
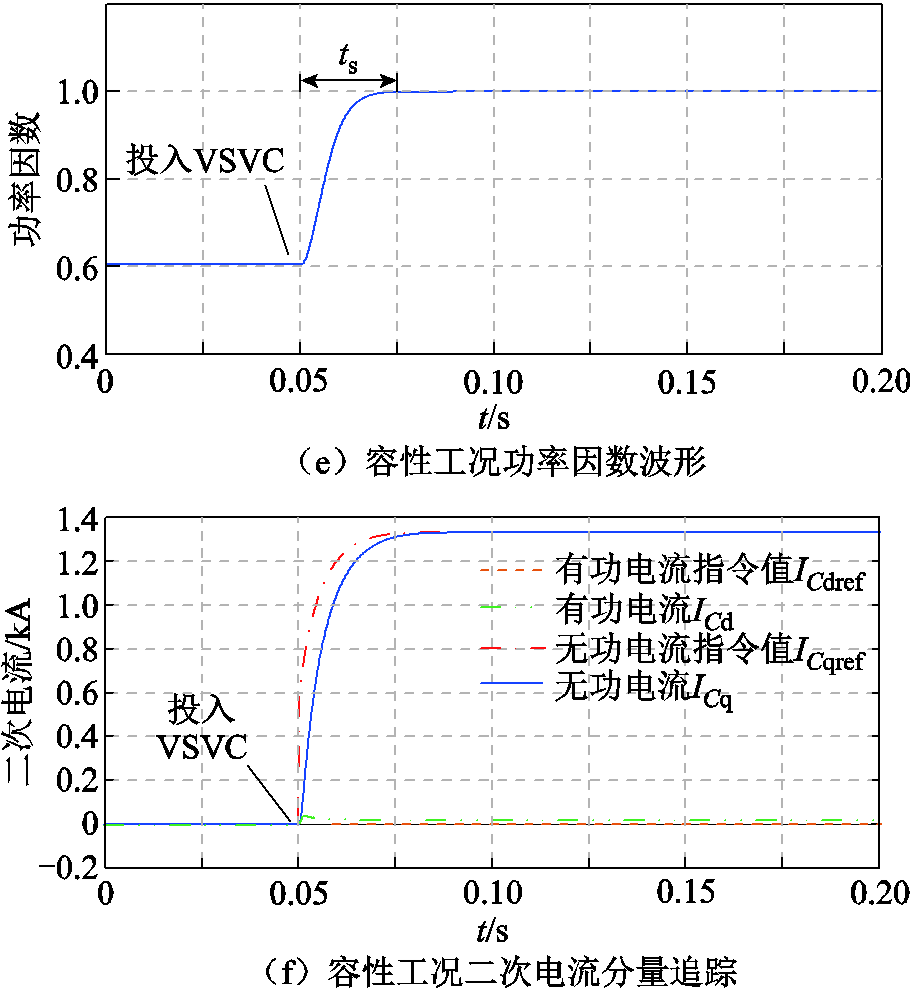
图12 VSVC容性工况调节效果仿真结果
Fig.12 Simulation results of regulation effect in VSVC capacitive condition
采用动态性能指标对VSVC容性工况下调节效果进行分析,主要包括动态响应时间tr、调节时间ts、超调量σ和稳态误差。补偿无功功率Q对无功指令值Qref的追踪如图12d所示,0~0.05 s时,VSVC未参与调节,无功功率指令值为0,此时,补偿无功功率Q=0。0.05 s时投入VSVC,经过响应时间tr=0.021 s,Q的变化量达到无功功率指令值Qref和初始值之差的90%,经过调节时间ts=0.025 s,Q保持在无功指令值Qref的95%~105%范围内,超调量σ为0,实际发出无功为0.957 Mvar,与无功功率指令值的稳态误差为0。功率因数波形如图12e所示,VSVC投入运行后,功率因数由0.605提高到1。二次电流分量追踪如图12f所示,未超过电流限值。
5.2.2 感性工况
为验证VSVC在感性工况下的调节效果,在线路末端设置容性负荷PLoad+jQLoad=(1-j1) MV∙A,初始时刻VSVC暂未投入,两台RPST的移相角a1和a2为±90°,电容两侧合成电压UC为0,线路上实际潮流为Pline+jQline=(0.971-j0.971) MV∙A,电源侧功率因数为0.793,放大后三相电压和电流如图13a所示,电源侧电压和电流相位有偏差且电流超前电压。在0.05 s时投入VSVC,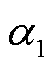 和
和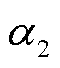 在0.03 s左右调节至稳态,UC未超过VSVC并联点电压U,此时负荷线路上功率Pline+jQline=(0.958-j0.958) MV∙A,VSVC吸收0.958 Mvar无功功率,电源侧无功功率几乎为0,功率因数提高到1,此时电源侧三相电压和电流相位相同,补偿后三相电压和电流波形如图13b所示。RPST移相角和电压波形如图13c所示。
在0.03 s左右调节至稳态,UC未超过VSVC并联点电压U,此时负荷线路上功率Pline+jQline=(0.958-j0.958) MV∙A,VSVC吸收0.958 Mvar无功功率,电源侧无功功率几乎为0,功率因数提高到1,此时电源侧三相电压和电流相位相同,补偿后三相电压和电流波形如图13b所示。RPST移相角和电压波形如图13c所示。
补偿无功功率Q对无功功率指令值Qref的追踪如图13d所示,0~0.05 s时,VSVC未参与调节,Qref=0,此时,吸收无功功率为0。0.05 s时投入VSVC,经过响应时间tr=0.013 s,Q的变化量达到无功功率指令值Qref和其初始值之差的90%,经过调节时间ts=0.023 s,Q保持在无功指令值Qref的95%~105%范围内,超调量σ为15.6%,实际吸收无功功率为0.958 Mvar,与无功功率指令值的稳态误差为0。功率因数波形如图13e所示,VSVC投入运行后,功率因数由0.793提高到1.0。二次电流分量追踪如图13f所示,未超过电流限值。
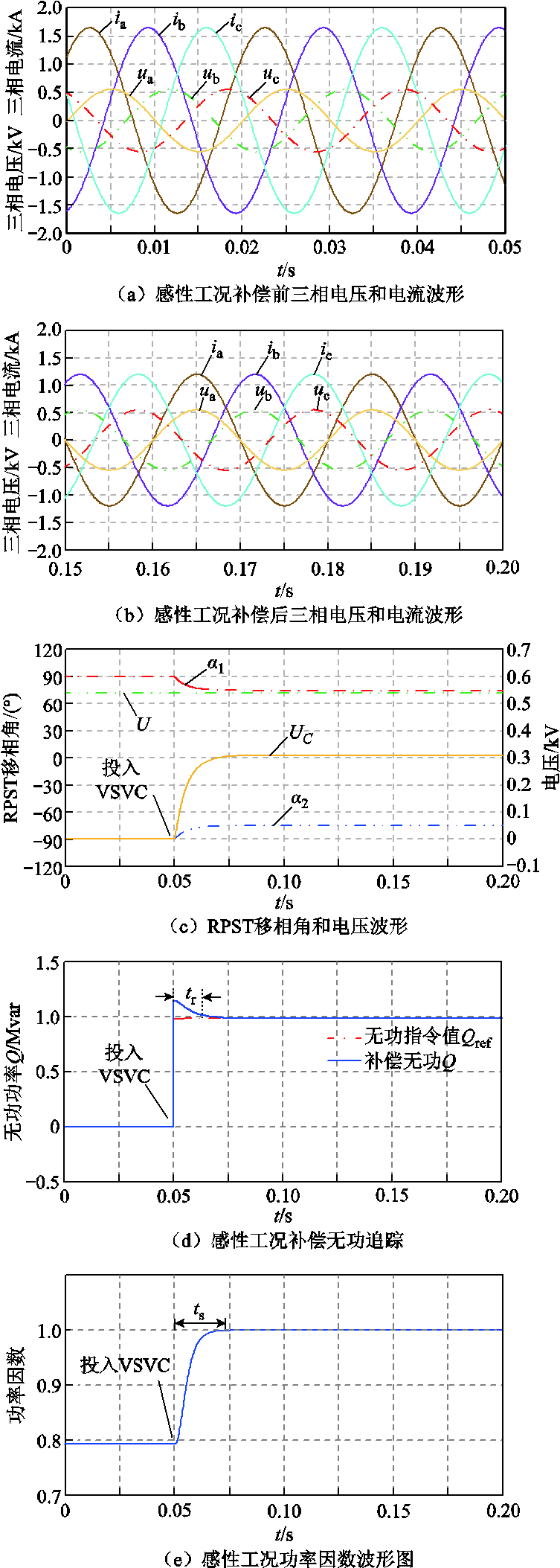
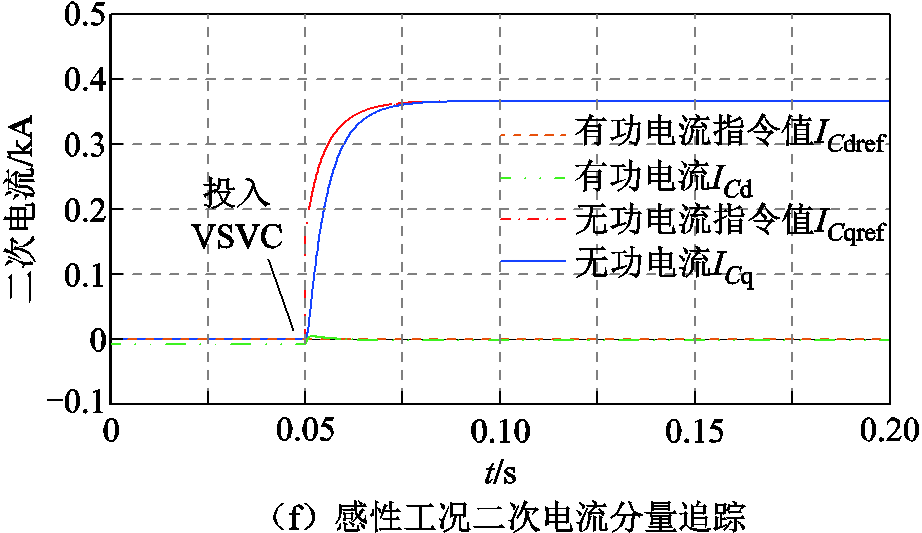
图13 VSVC感性工况调节效果仿真结果
Fig.13 Simulation results of regulation effect in VSVC inductive condition
为了体现VSVC在额定补偿范围内的连续、双向补偿能力,本文分别在容性工况和感性工况下设置无功负荷变动,验证VSVC在全范围都具有良好的无功补偿能力。
5.3.1 容性工况
VSVC发出无功的最大值为1 Mvar。因此,有功负荷为1 MW时,设置初始感性无功负荷0.3 Mvar,0.5 s时增加到0.6 Mvar,1 s时再增加到1 Mvar,分析VSVC在容性工况下的全范围补偿能力。
容性工况下无功功率追踪、功率因数波形以及二次电流追踪如图14所示。初始感性无功负荷为0.3 Mvar,VSVC零时刻投入,电源侧功率因数达到1.0,无超调且无误差,VSVC实现对感性无功负荷的全补偿;0.5 s时增加0.3 Mvar感性无功负荷,功率因数降至0.960,降落幅度约为4%,经过0.029 s响应时间和0.031 s调节时间,实现补偿无功Q对无功功率指令值Qref的追踪,无超调且无误差,功率因数重新提高至1.0。1 s时增加0.4 Mvar感性无功负荷,功率因数降至0.933,降落幅度约为6.7%,响应时间为0.030 s,调节时间为0.033 s,无超调且无误差,功率因数重新提高至1.0。无功电流ICq对无功电流指令值ICqref有良好的追踪性,可实现容性工况下全范围无功补偿。
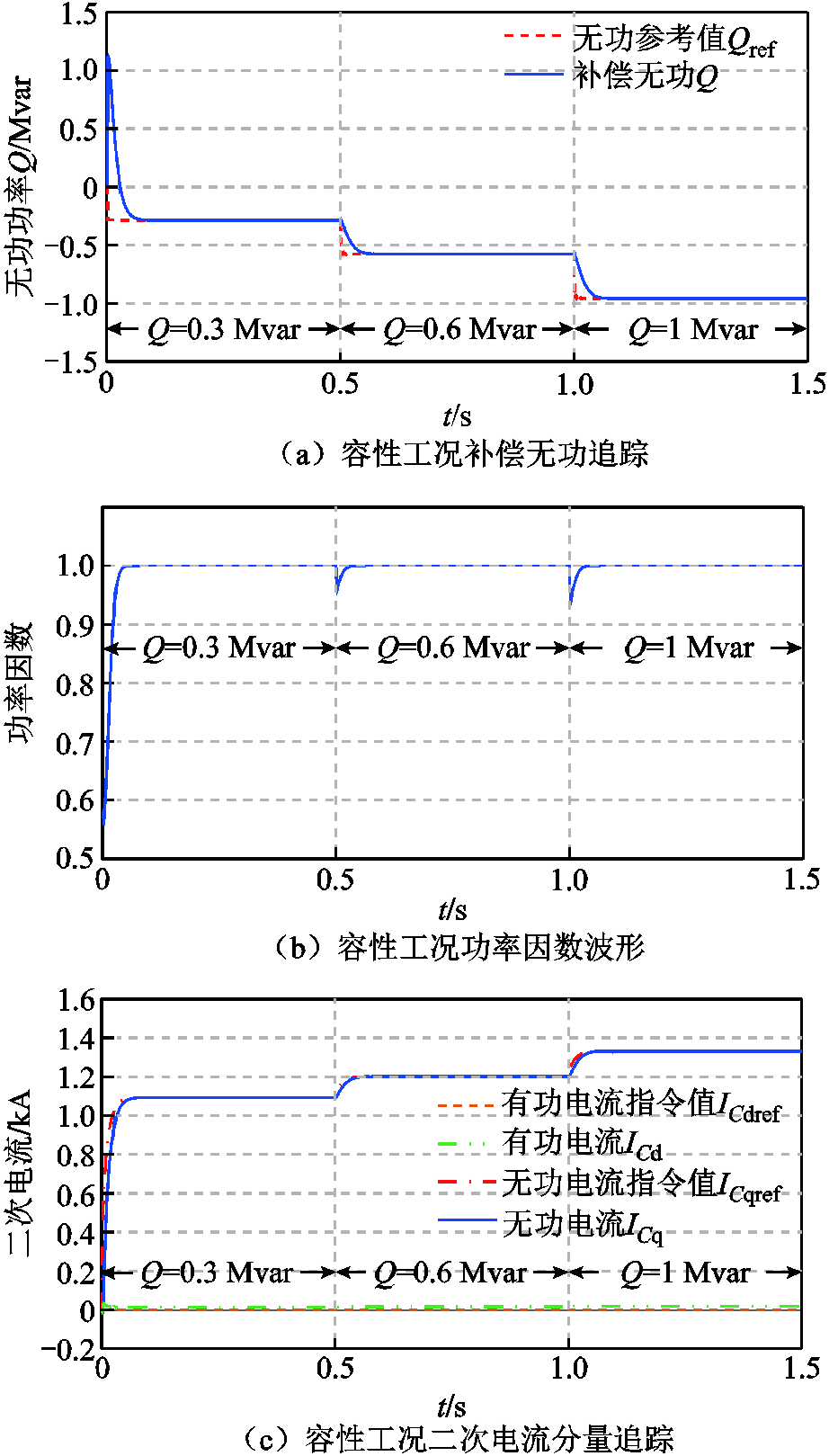
图14 VSVC容性工况全范围补偿能力仿真结果
Fig.14 Simulation results of full-range compensation capability in VSVC capacitive conditions
5.3.2 感性工况
VSVC吸收无功的最大值为1 Mvar。因此,有功负荷为1 MW时,设置初始容性无功负荷0.3 Mvar,0.5 s时增加到0.6 Mvar,1 s时再增加到1 Mvar,分析VSVC在感性工况下的全范围补偿能力。
感性工况下无功功率追踪、功率因数波形以及二次电流分量追踪如图15所示。初始容性无功负荷0.3Mvar,VSVC零时刻投入,电源侧功率因数达到1.0,无超调且无误差,VSVC实现对容性无功负荷的全补偿;0.5 s时增加0.3 Mvar容性无功负荷,功率因数降至0.958,降落幅度约为4.2%,经过0.028 s响应时间和0.033 s调节时间,实现补偿无功Q对无功功率指令值Qref的追踪,无超调且无误差,功率因数重新提高至1.0。1 s时增加0.4 Mvar容性无功负荷,功率因数降至0.929,降落幅度约为7.1%,响应时间为0.029 s,调节时间为0.035 s,无超调且无误差,功率因数重新提高至1.0。无功电流ICq对无功电流指令值ICqref有良好的追踪性,可实现感性工况下全范围无功补偿。
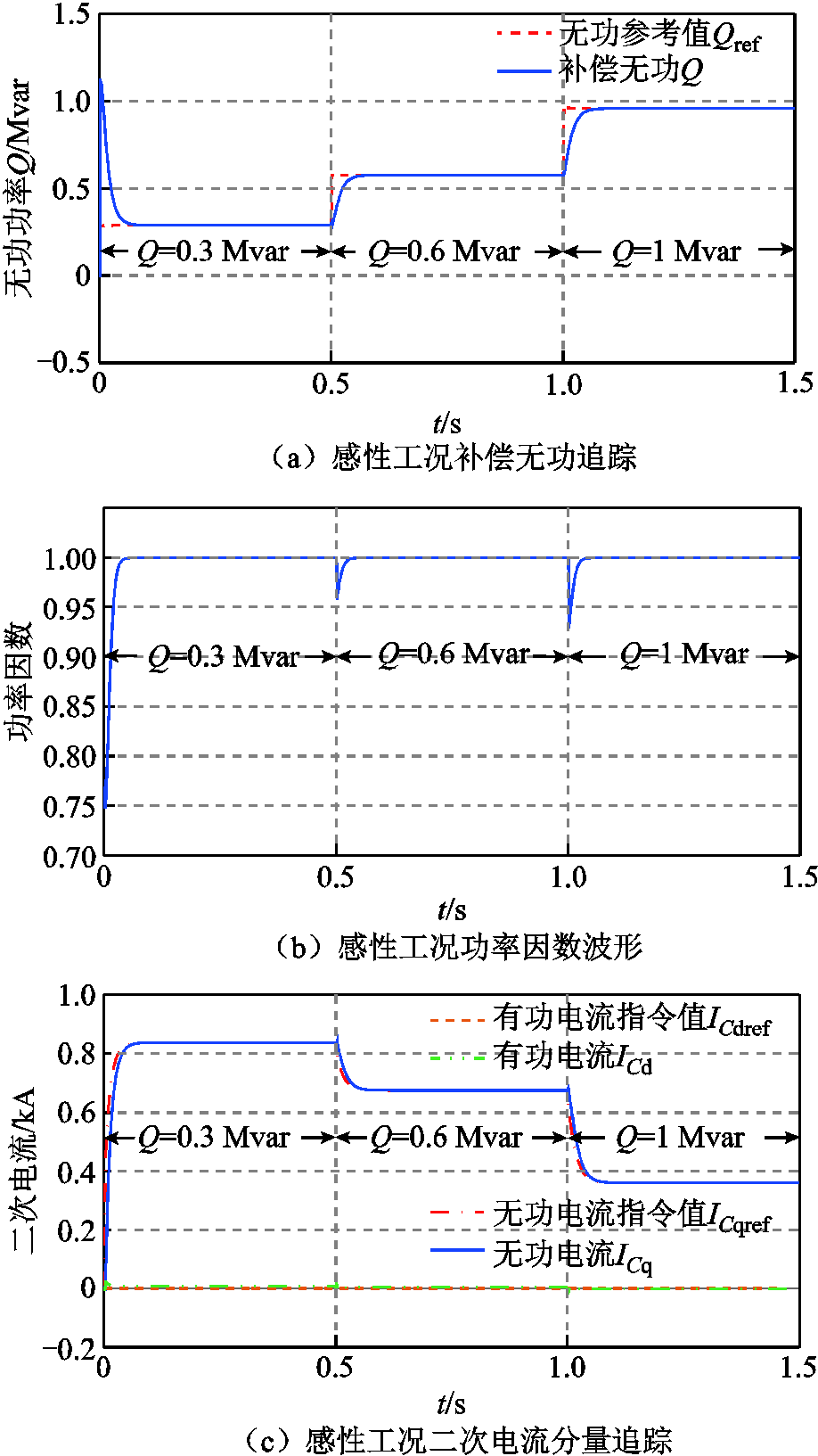
图15 VSVC感性工况全范围补偿能力仿真结果
Fig.15 Simulation results of full-range compensation capability in VSVC inductive conditions
为了说明VSVC具有良好的发展应用前景,特别将VSVC与发展已较为成熟的SVC、STATCOM、SSSC在技术和经济方面进行综合性对比。
SVC目前在电力系统中应用较广泛,主要通过控制晶闸管的通断来改变补偿无功,SVC输出的最大无功与系统电压的二次方成正比,当系统电压降落时,SVC的补偿无功也会迅速减小,响应时间约为十毫秒级,运行损耗比相同容量的STATCOM低2%左右,采用晶闸管,成本低于STATCOM、SSSC采用的可关断晶闸管和绝缘栅双极型晶体管[32]。STATCOM和SSSC的突出优点是调节精度高,响应迅速(以ms为单位),其中STATCOM具有很强的无功补偿能力,而SSSC主要用于串联补偿,进行潮流调控,具有一定无功补偿能力,但二者都因使用电力电子器件导致成本高于相同容量的传统变压器成本,运行损耗通常在6%~8%,控制策略复杂,运维难度大[33]。VSVC的优势在于无功补偿能力与STATCOM相近,运行可靠性较高,响应时间在百毫秒级别,抗冲击性能好,控制策略简单,只需控制两台RPST的旋转移相角,而且RPST的结构与绕线转子异步电动机相似,成本较低,运行损耗一般在2%~4%。为更加直观地反映其技术、经济特性,表2对其进行了详细对比,其中“√√√”表示特性最好,“√√”表示特性一般,“√”表示特性较差。
表2 VSVC与SVC、STATCOM、SSSC的对比
Tab.2 Comparison of VSVC with SVC, STATCOM and SSSC
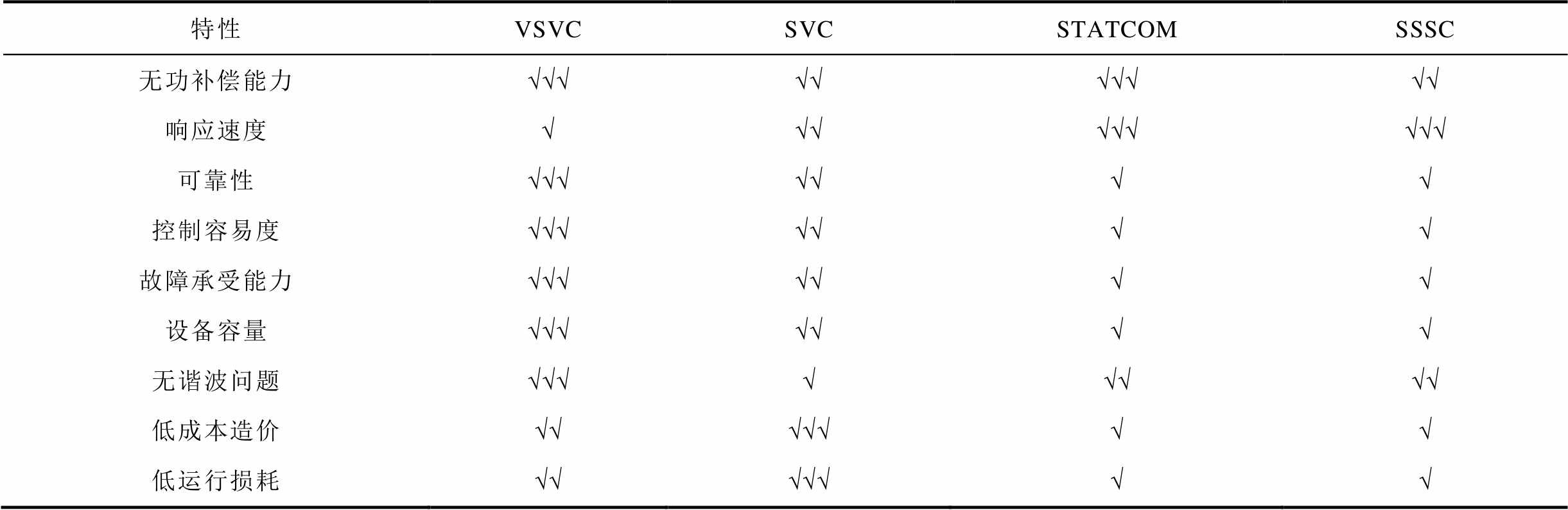
特性VSVCSVCSTATCOMSSSC 无功补偿能力√√√√√√√√√√ 响应速度√√√√√√√√√ 可靠性√√√√√√√ 控制容易度√√√√√√√ 故障承受能力√√√√√√√ 设备容量√√√√√√√ 无谐波问题√√√√√√√√ 低成本造价√√√√√√√ 低运行损耗√√√√√√√
通过对比发现,VSVC在很多方面具有明显的优势,只有响应速度略逊色于其他三种无功补偿装置。由于各装置不同的技术经济特点,可以适用于不同的电力系统场景。STATCOM、SSSC动态调节能力强,响应速度快,但成本造价和运行损耗都较高,适用于多目标控制和动态响应要求较高的场景。SVC由TSC、TCR配合可实现精准补偿,补偿容量与系统电压的正相关特性使得SVC在电压降落时出力受限,适用于对动态响应时间有一定要求的非关键系统节点。VSVC的主要优势在于:既可以实现精准补偿,同时又具有耐受性好、可靠性高、经济性好、控制简单、易高电压和大容量化等特点,可适用于对装置可靠性和经济性要求高于响应时间的应用场景,尤其在高电压、大容量场景下,具有很高的性价比,还可对电力系统进行多点无功补偿,优化潮流分布。
为进一步验证本文所提VSVC拓扑结构及其控制策略的有效性,搭建380 V的VSVC样机实验平台,如图16所示。其中,补偿电容为380 V/6.6 kvar,RPST的一次、二次绕组电压比为380 V/100 V,连接电感值可根据工作模式选取,设二次侧合成电压为0时为设备初始状态。为充分体现VSVC的连续、双向调节能力以及对实际应用场景的广泛适用性,实验分为两种工作模式。工作模式1中VSVC以发出无功功率为主,主要补偿感性负荷;工作模式2中VSVC以吸收无功功率为主,主要补偿容性负荷。

图16 实验样机
1,2—RPST 3—DSP处理器 4,5—补偿电容 6—示波器 7,8—两台RPST的伺服电动机 9,10—传动齿轮
Fig.16 Test prototype
图17为工作模式1初始状态下一次、二次侧A相电压和电流,图中已将一次电压归算至二次侧。PRST二次侧合成电压uA2幅值约为0,一次电流iA1约为2 A,二次电流iA2约为0。初始状态测得两台RPST和连接电感吸收无功功率约0.26 kvar,流过连接电感的电流有效值约为1.4 A,得到计及RPST内电抗的等效连接电感为140 mH。二次侧电容电压最大值约为200 V,将380 V/6.6 kvar电容归算到200 V,最大补偿容量为1.83 kvar。此时VSVC的理想补偿范围为-1.57~0.26 kvar。
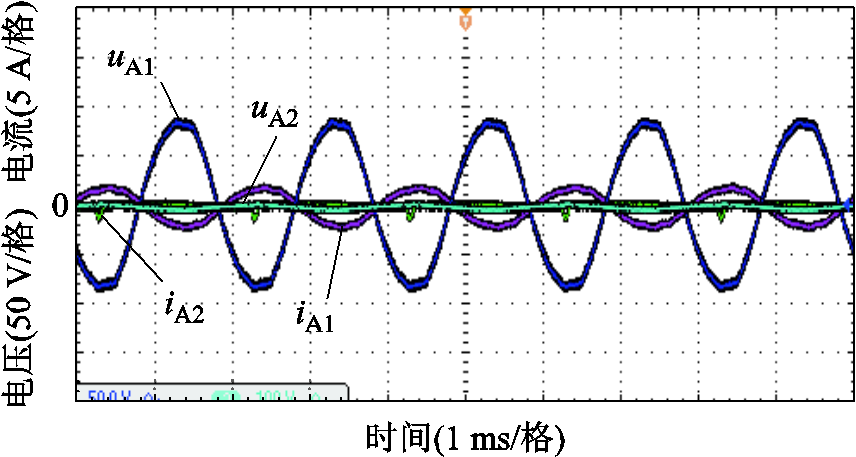
图17 工作模式1初始状态下一次、二次侧A相电压和电流
Fig.17 In the initial state of operation mode 1, the first and secondary side A phase voltage and current
图18为工作模式1下VSVC补偿范围测试。RPST初始移相角为±90°,电容两侧合成电压为0,电容发出的无功功率为0,VSVC吸收无功功率达到最大值0.25 kvar左右;将两台RPST移相角均调节至0°,电容两侧合成电压达到最大值,VSVC发出无功功率达到最大值约为1.6 kvar。图18a为RPST移相角,图18b为VSVC实际无功补偿范围,与理想补偿范围相近。
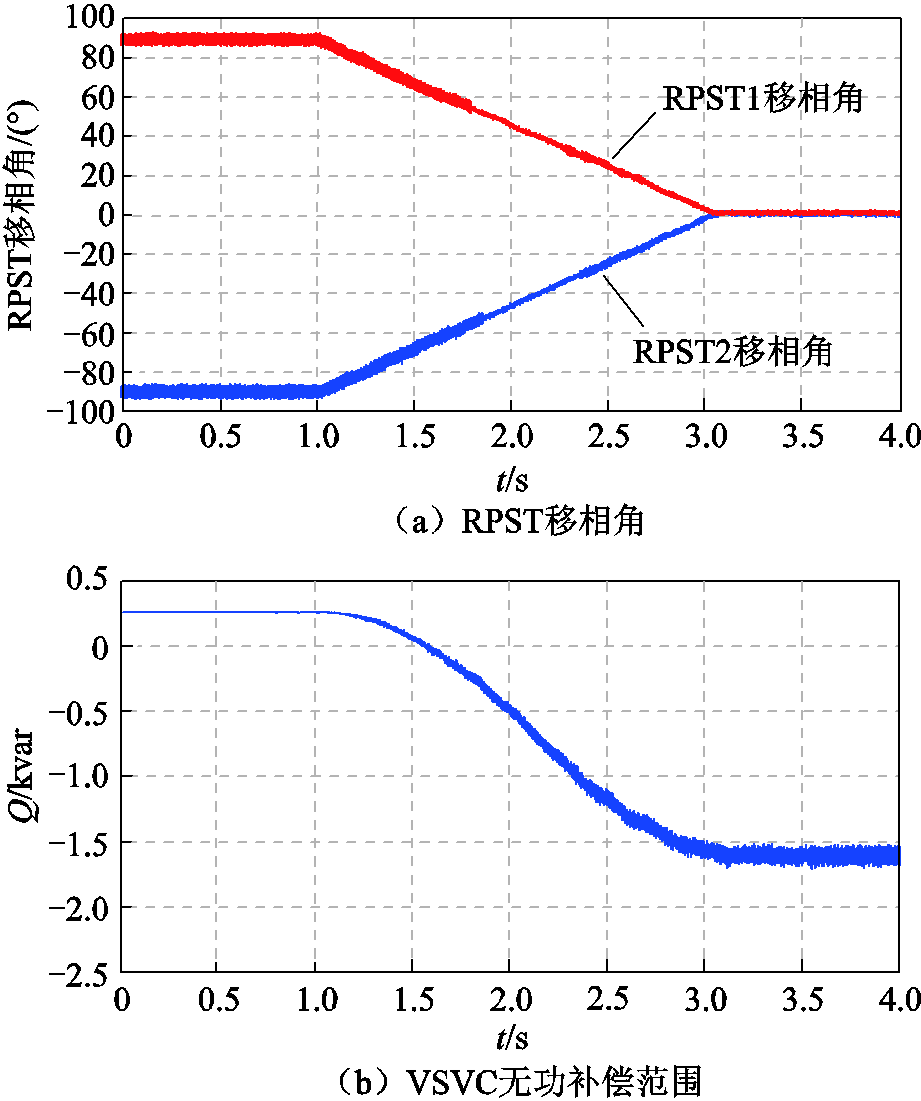
图18 工作模式1下VSVC补偿范围测试
Fig.18 VSVC compensation range test in working mode 1
图19为工作模式1下定无功功率闭环补偿实验结果。VSVC零时刻起运行在初始状态,此时VSVC吸收无功功率达到最大值0.25 kvar左右;随后给定补偿无功指令值Qref =-0.5 kvar,测量VSVC实际补偿无功Q,Qref和Q经过比较器后生成信号控制伺服电动机调节RPST移相角,使VSVC发出无功达到给定值-0.5 kvar;随后将Qref先后变动至 -1.5 kvar、-0.8 kvar。两台RPST移相角如图19a所示,补偿无功功率如图19b所示。
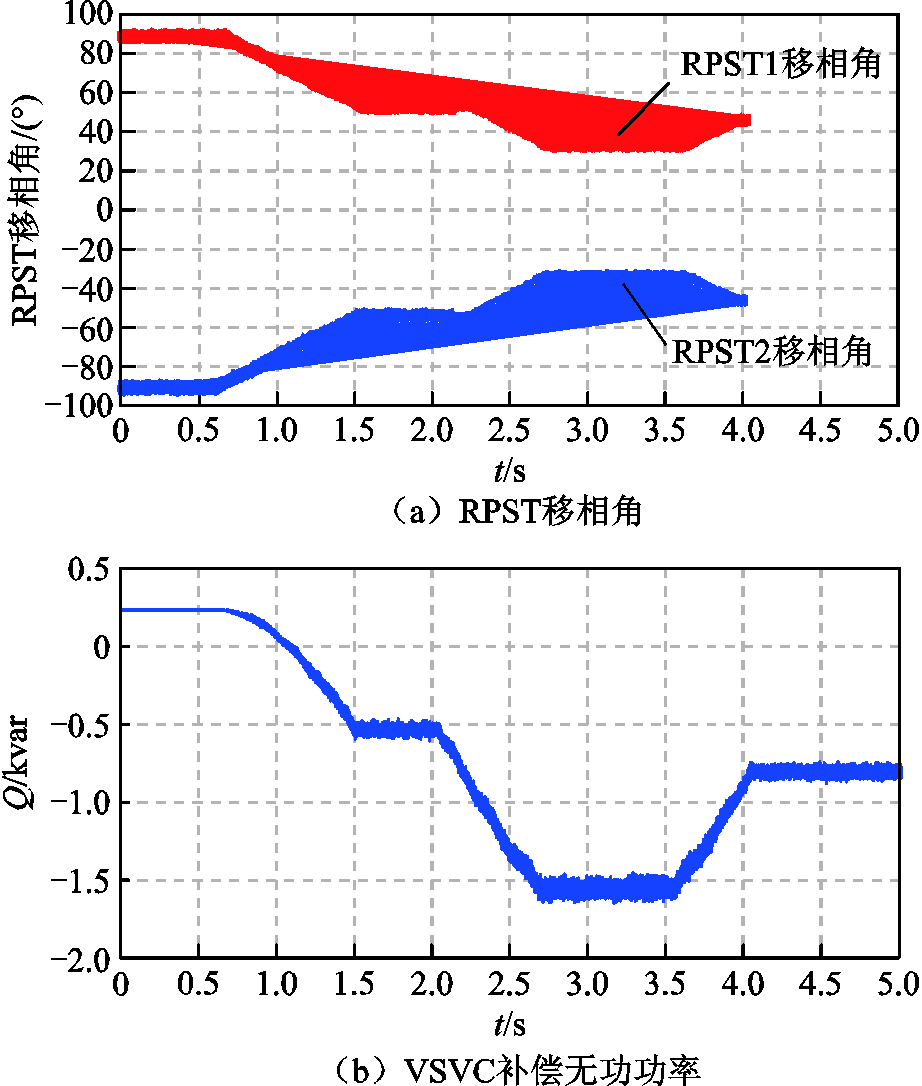
图19 工作模式1下VSVC定无功功率补偿波形
Fig.19 VSVC constant reactive power compensation waveform in working mode 1
图20为工作模式2初始状态下一、二次侧A相电压和电流,同样将一次电压归算至二次侧。RPST二次侧合成电压uA2幅值约为0,一次电流iA1约为4A,二次电流iA2约为0。初始状态测得两台RPST和连接电感吸收无功功率约1.32 kvar,初始状态流过连接电感的电流有效值为2.8 A,得到计及RPST内电抗的等效连接电感为179 mH。由二次侧电容最大补偿容量为1.83 kvar可知,此时VSVC的理想补偿范围为-0.51~1.32 kvar。

图20 工作模式2初始状态下一、二次侧A相电压和电流
Fig.20 In the initial state of operation mode 2, the first and secondary side A phase voltage and current
图21为工作模式2下VSVC补偿范围测试,测试方法与工作方式1相同。VSVC吸收的无功功率最大值为1.3 kvar左右,发出无功功率的最大值约为-0.5 kvar。图21a为RPST移相角度,图21b为VSVC实际无功补偿范围,与理想补偿范围相近。
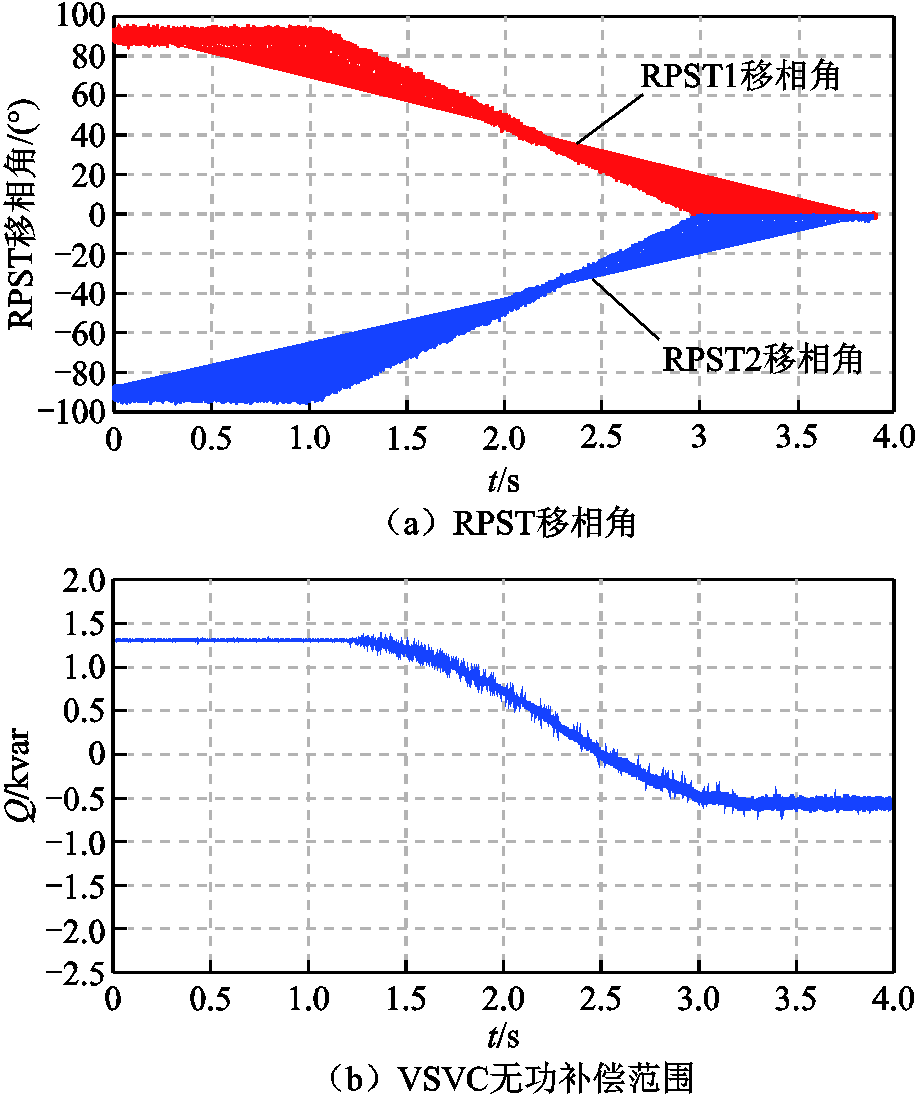
图21 工作模式2下VSVC补偿范围测试
Fig.21 VSVC compensation range test in working mode 2
图22为工作模式2下定无功功率闭环补偿实验结果。VSVC零时刻起运行在初始状态,此时VSVC吸收无功功率达到最大值1.3 kvar左右;随后给定补偿无功指令值Qref=0.5 kvar,测量VSVC实际补偿无功Q,Qref和Q经过比较器后生成信号控制伺服电动机调节RPST移相角,使VSVC发出无功达到给定值;随后将Qref调节至-0.5 kvar、0.5 kvar。两台RPST移相角如图22a所示,补偿无功功率如图22b所示。
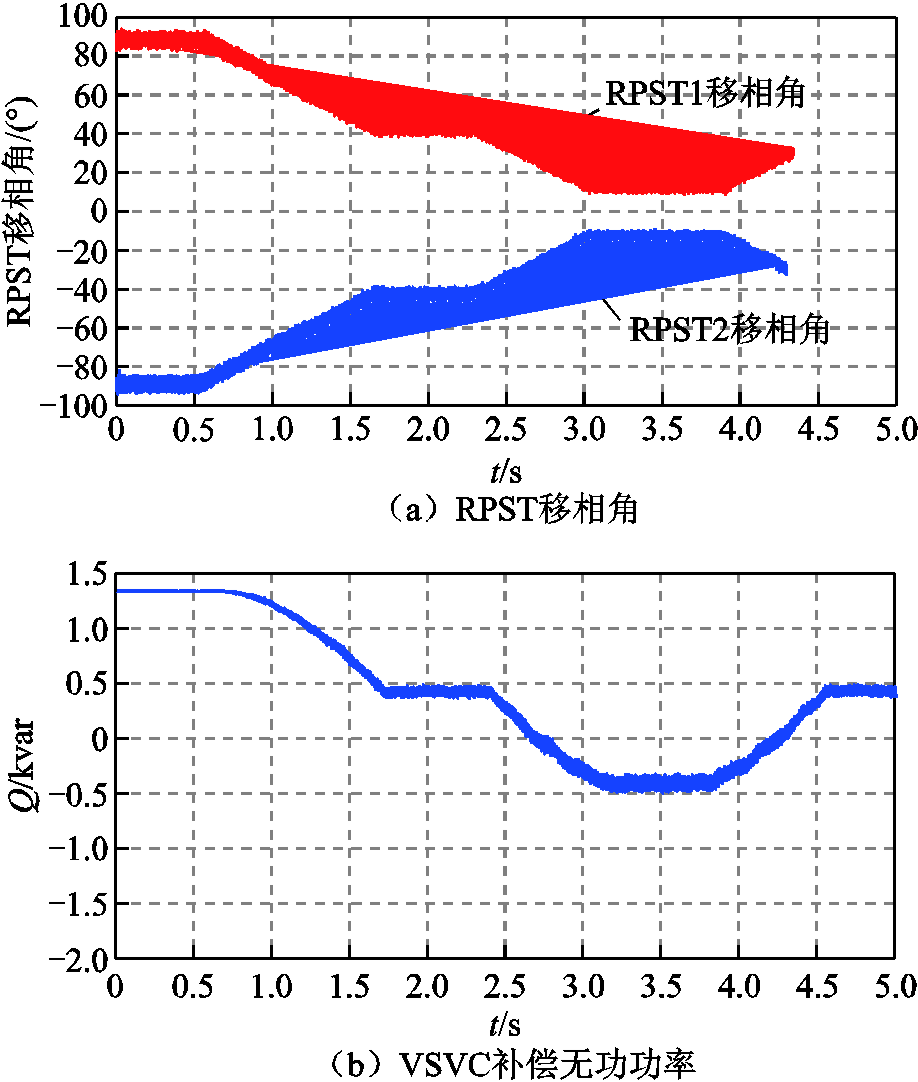
图22 工作模式2下VSVC定无功功率补偿波形
Fig.22 VSVC constant reactive power compensation waveform in working mode 2
通过图18和图21可以证明,VSVC可实现连续、双向无功补偿,并根据实际应用场景选择偏向于补偿感性或容性负荷,验证了VSVC拓扑结构和工作原理的理论分析。通过图19和图22可以证明,VSVC可实现实际电力系统要求的闭环补偿,通过给定补偿无功模拟实际电力系统中测量得到的无功指令值Qref,与实际补偿无功Q经比较器后来控制伺服电动机调节RPST移相角,改变电容两侧合成电压,进而调节VSVC补偿无功功率,验证了本文所提控制策略的可行性。由于VSVC调节速度与伺服电动机转速、RPST极对数和转子轴齿轮比有关,因此后续有待进一步改进。
本文提出了一种基于RPST的电压源型无功补偿器(VSVC)拓扑结构;分析其在不同工况下的工作原理;研究VSVC的并联稳态数学模型,构建控制方案;根据参数设计结果进行仿真分析,并利用样机进行实验验证,得出如下结论:
1)VSVC参考了VSC的拓扑结构以及RPST的移相调压功能,用RPST代替VSC的功率开关管桥路,提出一种新型并联无功补偿设备的拓扑结构,其具有结构简单,建设成本低,无需单独提供电源及隔离变压器,易实现高电压、大容量,且成本经济、易运维、抗冲击性强和耐受性好等优势。
2)本文应用瞬时无功理论,提出一种适用于VSVC,包括功率外环控制及电流内环控制的双闭环控制策略,可实现连续、双向无功补偿,具有鲁棒性强、控制精度高、调节性能好的特点。
3)通过仿真及实验验证了本文所提VSVC拓扑结构及其控制策略应用于新型配电网的有效性,为无功补偿装置及其控制策略提供了新思路。
本文仅对VSVC的无功补偿能力进行了初步研究,验证了其拓扑结构和控制策略的有效性。后续关于优化试验样机设计和提高动态补偿能力还需要进一步开展研究。
参考文献
[1] 舒印彪, 张丽英, 张运洲, 等. 我国电力碳达峰、碳中和路径研究[J]. 中国工程科学, 2021, 23(6): 1-14. Shu Yinbiao, Zhang Liying, Zhang Yunzhou, et al. Carbon peak and carbon neutrality path for China’s power industry[J]. Strategic Study of CAE, 2021, 23(6): 1-14.
[2] 魏泓屹, 卓振宇, 张宁, 等. 中国电力系统碳达峰·碳中和转型路径优化与影响因素分析[J]. 电力系统自动化, 2022, 46(19): 1-12. Wei Hongyi, Zhuo Zhenyu, Zhang Ning, et al. Transition path optimization and influencing factor analysis of carbon emission peak and carbon neutrality for power system of China[J]. Automation of Electric Power Systems, 2022, 46(19): 1-12.
[3] 刘东奇, 曾祥君, 王耀南. 边缘计算架构下配电台区虚拟电站控制策略[J]. 电工技术学报, 2021, 36(13): 2852-2860, 2870. Liu Dongqi, Zeng Xiangjun, Wang Yaonan. Control strategy of virtual power station in distribution transformer area under edge computing architecture[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2852-2860, 2870.
[4] 黄大为, 王孝泉, 于娜, 等. 计及光伏出力不确定性的配电网混合时间尺度无功/电压控制策略[J]. 电工技术学报, 2022, 37(17): 4377-4389. Huang Dawei, Wang Xiaoquan, Yu Na, et al. Hybrid timescale voltage/var control in distribution network considering PV power uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4377-4389.
[5] 唐爱红, 翟晓辉, 卢智键, 等. 一种适用于配电网的新分布式潮流控制器拓扑[J]. 电工技术学报, 2021, 36(16): 3400-3409. Tang Aihong, Zhai Xiaohui, Lu Zhijian, et al. A novel topology of distributed power flow controller for distribution network[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3400-3409.
[6] Liao Huilian. Review on distribution network optimization under uncertainty[J]. Energies, 2019, 12(17): 3369.
[7] 刘健, 同向前, 潘忠美, 等. 考虑过电压因素时分布式光伏电源的准入容量[J]. 电力系统保护与控制, 2014, 42(6): 45-51. Liu Jian, Tong Xiangqian, Pan Zhongmei, et al. The maximum power of distributed PV generation according to over-voltage in distribution network[J]. Power System Protection and Control, 2014, 42(6): 45-51.
[8] Morozovska K, Heleno M, Meza A V, et al. Including dynamic line rating into the optimal planning of distributed energy resources[J]. IEEE Transactions on Smart Grid, 2021, 12(6): 5052-5059.
[9] 雷二涛, 尹项根, 赖锦木, 等. 配电变压器-静止同步补偿器的补偿机理及无源控制技术[J]. 电工技术学报, 2017, 32(16): 284-293. Lei Ertao, Yin Xianggen, Lai Jinmu, et al. Compensation mechanism and passivity-based control technology for distribution transformer-static synchronous compensator[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 284-293.
[10] 付伟, 刘天琪, 李兴源, 等. 静止无功补偿器运行特性分析和控制方法综述[J]. 电力系统保护与控制, 2014, 42(22): 147-154. Fu Wei, Liu Tianqi, Li Xingyuan, et al. Analysis of operating characteristic and survey of control methods used in static var compensator[J]. Power System Protection and Control, 2014, 42(22): 147-154.
[11] 张前进, 周林, 李海啸, 等. 考虑SVG补偿装置的大型光伏并网系统振荡分析与抑制[J]. 中国电机工程学报, 2019, 39(9): 2636-2643. Zhang Qianjin, Zhou Lin, Li Haixiao, et al. Oscillation analysis and suppression of large-scale grid-connected photovoltaic system considering SVG equipment[J]. Proceedings of the CSEE, 2019, 39(9): 2636-2643.
[12] 颜湘武, 常文斐, 崔森, 等. 基于线性自抗扰控制的静止无功补偿器抑制弱交流风电系统次同步振荡策略[J]. 电工技术学报, 2022, 37(11): 2825-2836. Yan Xiangwu, Chang Wenfei, Cui Sen, et al. Sub-synchronous oscillation suppression strategy of weak AC wind power system with static var compensator based on linear active disturbance rejection control[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2825-2836.
[13] De S, Debnath S. Optimal switching strategy of an SVC to improve the power quality in a distribution network[J]. IET Science, Measurement & Technology, 2019, 13(5): 640-649.
[14] Chen Hao, Prasai A, Divan D. A modular isolated topology for instantaneous reactive power compensation[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 975-986.
[15] Dionise T J. Assessing the performance of a static var compensator for an electric arc furnace[J]. IEEE Transactions on Industry Applications, 2014, 50(3): 1619-1629.
[16] 周兴达, 陆帅. 一种基于消弧线圈和静止同步补偿器协同作用的配电网消弧结构与方法[J]. 电工技术学报, 2019, 34(6): 1251-1262. Zhou Xingda, Lu Shuai. An arc-suppression method based on the coordinated operation of the petersen coil and the static synchronous compensator in distribution networks[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1251-1262
[17] 陆道荣, 魏缪宇, 于宇, 等. 一种基于方波注入的星形级联静止同步补偿器的负序电流补偿策略[J]. 电工技术学报, 2022, 37(6): 1482-1494. Lu Daorong, Wei Miaoyu, Yu Yu, et al. Zero-sequence-voltage injection based on square-wave to balance cluster voltages for star-connected cascaded STATCOM[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1482-1494.
[18] Miremad A, Khalaj Monfared K, Iman-Eini H, et al. Design and control of a STATCOM based on hybrid cascaded H-bridge and full-bridge neutral point clamped multilevel inverter[J]. IET Power Electronics, 2020, 13(17): 4019-4030.
[19] Wei Tianliu, Mao Chengxiong, Lu Jiming, et al. Low cost hybrid reactive power compensator using coordination control strategies[J]. IET Generation, Transmission & Distribution, 2016, 10(8): 1805-1814.
[20] 彭星, 姜飞, 涂春鸣, 等. TSC与STATCOM串联复合系统及其控制方法[J]. 电网技术, 2021, 45(10): 4114-4124. Peng Xing, Jiang Fei, Tu Chunming, et al. TSC and STATCOM series composite system and its control method[J]. Power System Technology, 2021, 45(10): 4114-4124.
[21] 赵伟, 罗安, 唐杰, 等. 静止无功发生器与晶闸管投切电容器协同运行混合无功补偿系统[J]. 中国电机工程学报, 2009, 29(19): 92-98. Zhao Wei, Luo An, Tang Jie, et al. Hybrid var compensator based on the coordinated operation of STATCOM and TSC[J]. Proceedings of the CSEE, 2009, 29(19): 92-98.
[22] 李帅虎, 向振宇, 彭寒梅, 等. 基于模型预测控制的SVC与STATCOM协调控制器[J]. 电网技术, 2019, 43(11): 4218-4224. Li Shuaihu, Xiang Zhenyu, Peng Hanmei, et al. SVC and STATCOM coordination controller based on model predictive control[J]. Power System Technology, 2019, 43(11): 4218-4224.
[23] 郑丽平, 匡洪海, 张曙云, 等. TCSC-STATCOM控制对风电并网系统电压稳定性的改善[J]. 电力系统保护与控制, 2017, 45(22): 90-95. Zheng Liping, Kuang Honghai, Zhang Shuyun, et al. Voltage stability improvement of wind power integrated system using TCSC-STATCOM control[J]. Power System Protection and Control, 2017, 45(22): 90-95.
[24] 秦海鸿, 赵海伟, 马策宇, 等. 基于模块化多电平变换器的静止同步补偿器桥臂不对称及其控制策略[J]. 电工技术学报, 2016, 31(14): 183-192. Qin Haihong, Zhao Haiwei, Ma Ceyu, et al. Asymmetric bridge arm of static synchronous compensator based on modular multilevel converter and its control strategy[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 183-192.
[25] 陈玉, 文明浩, 尹项根, 等. 配电变压器集成式级联STATCOM原理与设计[J]. 电工技术学报, 2018, 33(12): 2861-2872. Chen Yu, Wen Minghao, Yin Xianggen, et al. Principle and design of the cascaded STATCOM integrated with distribution transformer[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2861-2872.
[26] 刘星, 汤自安, 张凯. 基于能量分析的MMC-STATCOM电容电压三级平衡控制[J]. 高电压技术, 2018, 44(7): 2222-2230. Liu Xing, Tang Zian, Zhang Kai. Three-level capacitor voltage balance control of MMC-STATCOM based on energy analysis[J]. High Voltage Engineering, 2018, 44(7): 2222-2230.
[27] 颜湘武, 贾焦心, 王德胜, 等. 基于电力弹簧的低压台区用户侧电压调节方法[J]. 电工技术学报, 2020, 35(12): 2623-2631. Yan Xiangwu, Jia Jiaoxin, Wang Desheng, et al. User-side voltage regulation method for transformer areas based on electric spring[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2623-2631.
[28] 张兴, 张崇巍. PWM整流器及其控制[M]. 北京: 机械工业出版社, 2012.
[29] 谭振龙, 张春朋, 姜齐荣, 等. 旋转潮流控制器稳态特性研究[J]. 电网技术, 2015, 39(7): 1921-1926. Tan Zhenlong, Zhang Chunpeng, Jiang Qirong, et al. Study on steady state characteristics of rotary power flow controller[J]. Power System Technology, 2015, 39(7): 1921-1926.
[30] Haddadi A M, Kazemi A. Optimal power flow control by rotary power flow controller[J]. Advances in Electrical and Computer Engineering, 2011, 11(2): 79-86.
[31] 姜志鹏, 周辉, 宋俊燕, 等. 干式空心电抗器温度场计算与试验分析[J]. 电工技术学报, 2017, 32(3): 218-224.Jiang Zhipeng, Zhou Hui, Song Junyan, et al. Temperature field calculation and experimental analysis of dry-type air-core reactor[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 218-224.
[32] 周建丰, 顾亚琴, 韦寿祺. SVC与STATCOM的综合比较分析[J]. 电力自动化设备, 2007, 27(12): 57-60. Zhou Jianfeng, Gu Yaqin, Wei Shouqi. Comprehensive comparative analysis of SVC and STATCOM[J]. Electric Power Automation Equipment, 2007, 27(12): 57-60.
[33] 谭振龙, 张春朋, 姜齐荣, 等. 旋转潮流控制器与统一潮流控制器和Sen Transformer的对比[J]. 电网技术, 2016, 40(3): 868-874. Tan Zhenlong, Zhang Chunpeng, Jiang Qirong, et al. Comparative research on rotary power flow controller, unified power flow controller and Sen transformer[J]. Power System Technology, 2016, 40(3): 868-874.
Abstract The proportion of renewable energy represented by photovoltaic and wind power connected to the grid is increasing annually. Due to their intermittent and stochastic characteristics, it often leads to complicate power distribution, increase network losses, and degrade frequency and voltage quality. However, the existing reactive power compensation equipment cannot satisfy both accurate compensation and low cost. In recent years, scholars have also proposed some hybrid compensation devices, but most of the topologies still suffer from the dynamic response problems caused by capacitor switching. To solve the above problems, this paper proposes a topology of voltage source var compensator (VSVC) based on rotating phase shift transformer (RPST) with reference to the voltage source converter (VSC) structure of static synchronous compensator (STATCOM), which can realize continuous and bidirectional reactive power compensation by adjusting the phase shift angle of RPST.
First, two primary windings of the RPSTs are connected in parallel to the grid through the connecting inductor, while the secondary windings are wired in a star pattern on both sides of the compensation capacitor. By adjusting the phase shift angle of the two RPSTs, a variable voltage phase can be synthesized on both sides of the compensation capacitor, regulating the compensated reactive power of the VSVC. When the phase shift angle is small, the amplitude of the synthesized capacitor voltage is large. The VSVC operates in a capacitive condition, emitting reactive power to the grid. When the phase shift angle is large, the capacitor voltage amplitude is small and the VSVC works in an inductive condition, absorbing reactive power from the grid. A dual closed-loop control strategy including power external loop control and current internal loop control is constructed based on VSVC to obtain the phase shift angle of the two RPSTs and then realize the closed-loop control of reactive power.
Simulation results for VSVC indicate that when an inductive load of (1+j1)MV×A is set at the end of the line, VSVC is not put in at the initial moment. The power factor on the power side is 0.605, with the current phase on the power side lagging behind the voltage. The VSVC is put in at 0.05 s, which operates under capacitive condition and raises the power factor to 1 at about 0.03 s. When a capacitive load of (1-j1)MV×A is set at the end of the line, the power factor of the power side is 0.793 before VSVC is put in, and the phase of the current ahead of the voltage phase. The VSVC is put into working in inductive condition and raises the power factor to 1 around 0.03 s. The response time is less than 0.02 s under both operating conditions, the regulation time is no more than 0.03 s, the overshoot is lower than 20%, and the steady-state error is 0. The inductive and capacitive reactive load changes are set at the end of the line respectively. The initial reactive load is 0.3 MVar when the active load is 1 MW, increasing to 0.6 Mvar at 0.5 s, and then increasing to 1 Mvar at 1 s, with response time around 0.030 s and regulation time around 0.035 s, without overshoot and error. It proves that VSVC can achieve full range of reactive power compensation in both capacitive and inductive operating conditions. The experimental results show that VSVC can achieve the closed-loop compensation required by real power systems, and the adjustment speed is related to the servo motor speed, RPST pole pair number and rotor shaft gear ratio.
The following conclusions can be drawn from the simulation and experimental analysis: (1) VSVC utilizes the phase shifting function of RPST to synthesize a voltage phase with fixed phase and continuously variable amplitude on both sides of the capacitor, which has continuous and bidirectional reactive power compensation capability. (2) Applying the instantaneous reactive power theory, a double closed-loop control strategy applicable to VSVC is proposed, which has the characteristics of strong robustness and excellent control accuracy. (3) Simulations and experiments verify the effectiveness of the proposed topology and control strategy.
keywords:Voltage source var compensator (VSVC), rotary phase shifting transformer (RPST), reactive power compensation, new distribution network
DOI: 10.19595/j.cnki.1000-6753.tces.220189
中图分类号:TM761
北京市自然科学基金项目(3212037)、国网河北省科技项目“雄安城市配电网电压和潮流数字化精准调控技术研究与应用(SGHEDK00DYJS2000286)”资助。
收稿日期 2022-01-30
改稿日期 2022-04-20
颜湘武 男,1965年生,教授,博士生导师,研究方向为新能源电力系统分析与控制、现代电力变换、新型储能与节能技术等。E-mail:xiangwuy@ncepu.edu.cn
郭 燕 女,1996年生,硕士研究生,研究方向为电力系统潮流调控技术。E-mail:guo_y77@163.com(通信作者)
(编辑 郭丽军)