控制锅炉高温蒸汽，调节蝶阀
控制高压缸蒸汽进入量，通过抽汽调节蝶阀
控制抽汽蒸汽供给的热源输出热功率及蒸汽进入低压缸做功输出的电功率。热源与供热首站交换热量供应工业企业内部热负荷。考虑企业区域面积较小，供热管道空间上分布较为有限，热量传输过程影响可以忽略[22]。同时，CHP机组承担园区企业自用电及辐射区域生产生活的部分用电，供电不足部分由大电网调度风电、常规火电机组来满足。摘要 园区企业对自备热电联产（CHP）机组进行技术改造可以显著提升其快速调节能力，但是调度过程对CHP机组动态过程精细化建模不足，导致调度方案难以匹配CHP机组的运行状态。该文提出一种考虑园区自备CHP机组状态运行约束的电热耦合系统（CEHS）动态优化调度方法。首先，考虑CHP机组快速调节下的电能、流量、压力等状态量特性建立机组的动态约束，进而构建CEHS动态优化调度模型；然后，针对含微分方程约束的CEHS动态优化难以求解的问题，提出一种动态自适应粒子群-径向基拟序贯双层优化求解策略；最后，基于改进的IEEE 30节点系统验证该文所提方法的正确性和有效性。
关键词：电热耦合系统 状态运行约束 径向基函数 拟序贯法 双层动态优化
园区大型工业企业因生产工艺需要，常配备热电联产（Combined Heat and Power, CHP）机组来供应全部热力需求[1-2]，但是，自备CHP机组电热耦合特性限制了电出力的调节速率，成为制约新能源消纳的一个重要因素。通过对CHP机组进行控制改造赋予其快速调节能力[3]，再将自备电厂纳入电热综合能源体系中进行一体化调度[4]，可以有效地缓解当前电网调节备用不足带来的新能源消纳困境。
现有CHP机组主要通过低压缸切除、加装储热和电锅炉、高中压缸旁路供热等灵活性改造方案拓展CHP机组可行运行域[5]，然后以代数方程运行约束参与到电热耦合系统（Combined Electrical and Heating System, CEHS）调度中。文献[6]构建了两阶段CHP机组爬坡速率和备用容量代数方程约束，证明变特性调节对扩大风电上网空间有一定作用；文献[7-9]通过对增加电锅炉、热泵、储热等装置改造CHP机组，采用备用容量、爬坡速率的代数约束，研究其对电网优化调度问题的经济性影响；针对CHP机组电热特性，研究其改造后的调度灵活性[10-11]，并考虑集中供热系统中CHP机组电出力灵活性约束，实现电力系统多时间尺度灵活性的最优分配[12]。但是，对工业企业而言，上述CHP机组改造方案一方面面临改造成本过高，增加企业成本负担；另一方面上述可行域的拓展并未实质改变机组的调节速率，限制了企业自备CHP机组参与系统备用的能力。近年来，在CHP机组运行过程中采用优化控制策略[13]进行快速调节能力提升，是一种适用于企业自备CHP机组改造的成本低、综合优势大的方案[14]。这类具有快速调节能力的CHP机组模型已在电网调频[15]、新能源消纳[16]等场景中得到了应用。但是，在调度场景中，控制技术改造后的CHP机组的代数方程建模方式无法计及优化控制策略对CHP机组压力安全、供热稳定等状态动态过程的影响，调度结果会导致CHP机组运行状态的安全越线，严重影响这类CEHS调度方案的可行性。
考虑优化控制改造CHP机组运行约束的CEHS优化调度，是一个含微分代数方程（Differential Algebraic Equation, DAE）约束的动态优化问题。现有文献中考虑机组代数方程约束的优化调度求解方法，难以同时满足系统经济调度与机组状态运行约束的计算要求。大多数含DAE约束问题的优化求解均是将模型离散转化为非线性规划（Nonlinear Programming, NLP）问题，再用各种NLP求解器或智能优化算法进行求解[17]。其中，采用联立法[18]将连续控制变量作为优化量来处理动态优化问题较容易，但其离散后产生的大规模问题，需要特殊的分解技术和复杂的数学处理。文献[19]将调度系统中光伏、负荷等状态量，以及机组出力等动作量进行离散，形成了维数灾难问题；采用离散方法[17]处理调度系统动作空间中的连续量[20-21]，会导致决策动作域中信息被删除、调度方案可行性降低等问题。因此，在兼顾求解效率与精度时，现有方法均面临求解策略与离散适用性的挑战。
综上分析，本文提出考虑园区自备CHP机组状态运行约束的CEHS动态优化调度方法。首先，基于含优化控制策略的CHP机组机理模型分析，构建CHP机组运行动态约束；然后，在此基础上建立CEHS优化调度模型，提出一种动态自适应粒子群算法（Dynamic Adaptive Particle Swarm Optimization, DAPSO）-径向基拟序贯法的双层优化求解策略，基于径向基函数的拟序贯法求解内层CHP机组控制过程动态优化问题，利用DAPSO生成外层CEHS调度方案；最后，算例分析验证考虑CHP机组状态运行约束对CEHS优化调度的必要性和优势。
本文含园区自备CHP机组的电热耦合系统结构如图1所示。园区企业自备CHP机组服从电网统一调度，控制器通过调节控制锅炉高温蒸汽，调节蝶阀控制高压缸蒸汽进入量，通过抽汽调节蝶阀控制抽汽蒸汽供给的热源输出热功率及蒸汽进入低压缸做功输出的电功率。热源与供热首站交换热量供应工业企业内部热负荷。考虑企业区域面积较小，供热管道空间上分布较为有限，热量传输过程影响可以忽略[22]。同时，CHP机组承担园区企业自用电及辐射区域生产生活的部分用电，供电不足部分由大电网调度风电、常规火电机组来满足。
CHP机组运行区域的任意电出力、热出力水平都可用凸区域顶点的线性组合[6,8]表示（本文机组的顶点见附表1），其与CHP机组电出力爬坡约束[10]、CHP机组备用容量约束[8]共同构成CEHS优化调度中CHP机组的运行约束，如式（1）所示，本文称之为CHP机组的静态运行约束。
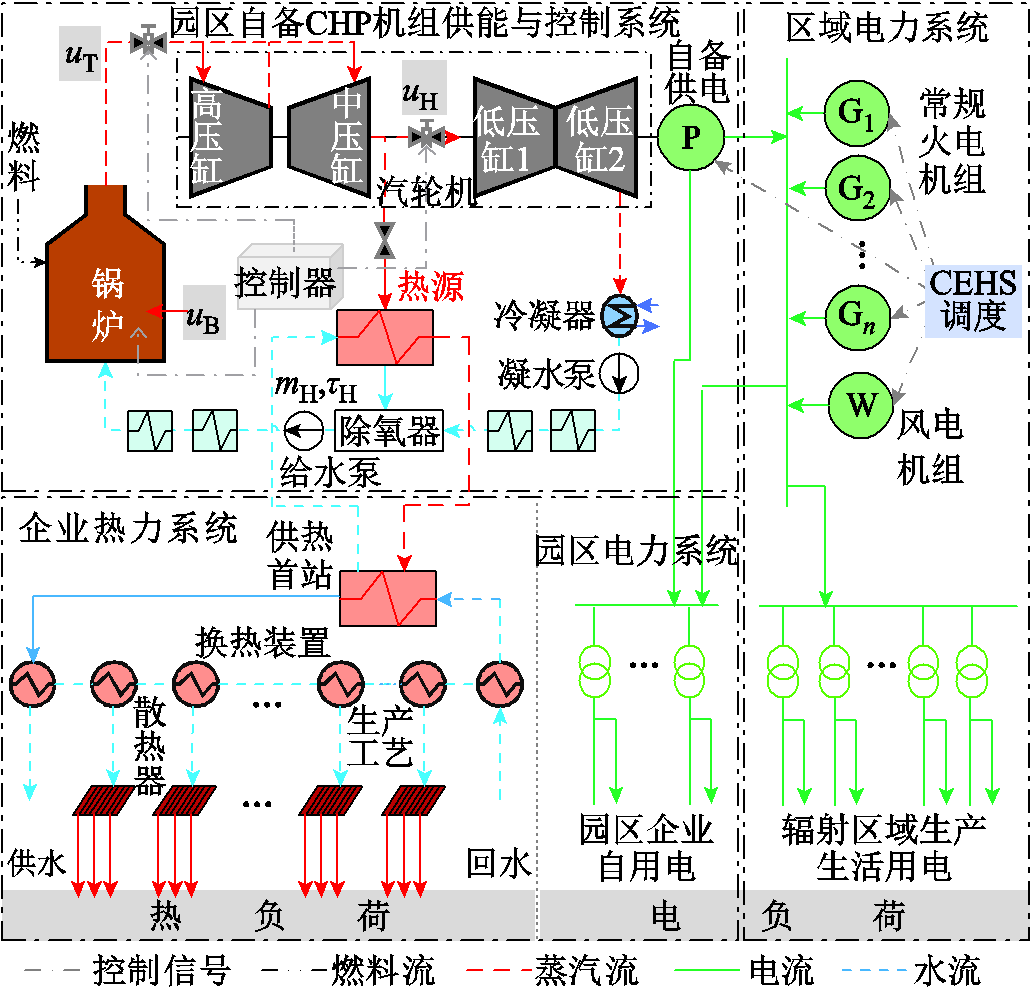
图1 园区型CEHS结构
Fig.1 Structure diagram of park CEHS
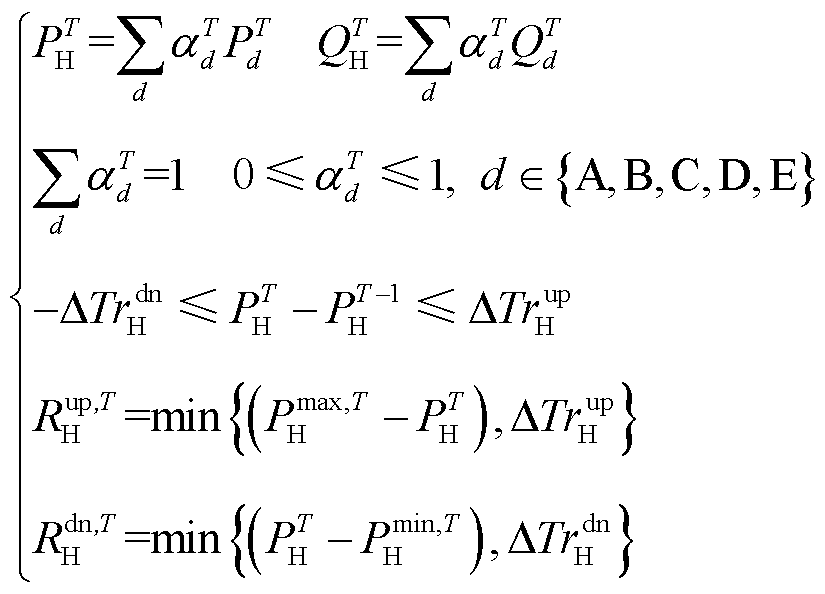（1）
式中，
、
分别为T时段机组的电出力、热出力；d为可行域顶点编号；
为T时段各顶点系数；∆T为爬坡时间；
、
分别为上备用、下备用容量；
、
分别为T时段允许的最大、最小电出力；
、
分别为向上、向下爬坡速率。
300 MW CHP机组[16]电出力响应曲线如图2所示，初始时刻运行点A1为
=(262.63,150)。经优化控制改造的CHP机组爬坡速率可提高到4%～5%
/min[14]（为机组额定功率），采用静态运行约束（本文、均取4.5 %/min）时，机组出力可达目标运行点B1为
=(262.63,217.5)。但运行中受到机组主蒸汽压力安全限制（压力限值），实际只能到运行点C1为=(262.63,210)。同时，静态运行约束计算的机组出力变化过程，会出现机组压力的波动峰值超越安全上限、蒸汽流量波动增大影响机组稳定供热等情况。
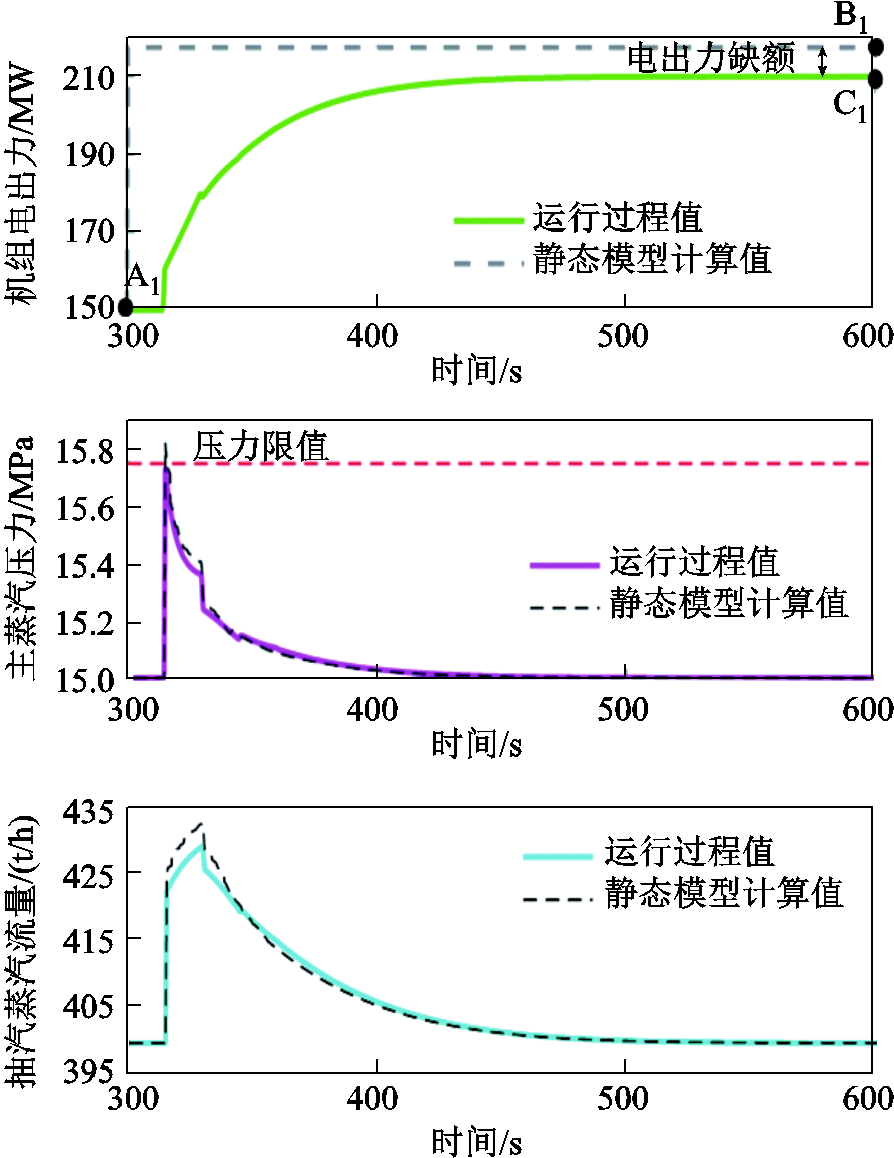
图2 CHP机组运行特性
Fig.2 Operation characteristics of CHP unit
上述现象表明，CHP机组静态运行约束无法展现机组压力、流量等状态量变化引起的安全性、稳定性问题，可能会导致机组运行时调节难以实施或引发安全事故。因此，为确保CEHS精细化调度，需要量化分析CHP机组优化控制改造后的特性，建立精确的CHP机组状态运行约束模型。
本文考虑CHP机组优化控制过程的动态约束模型结构如图3所示。
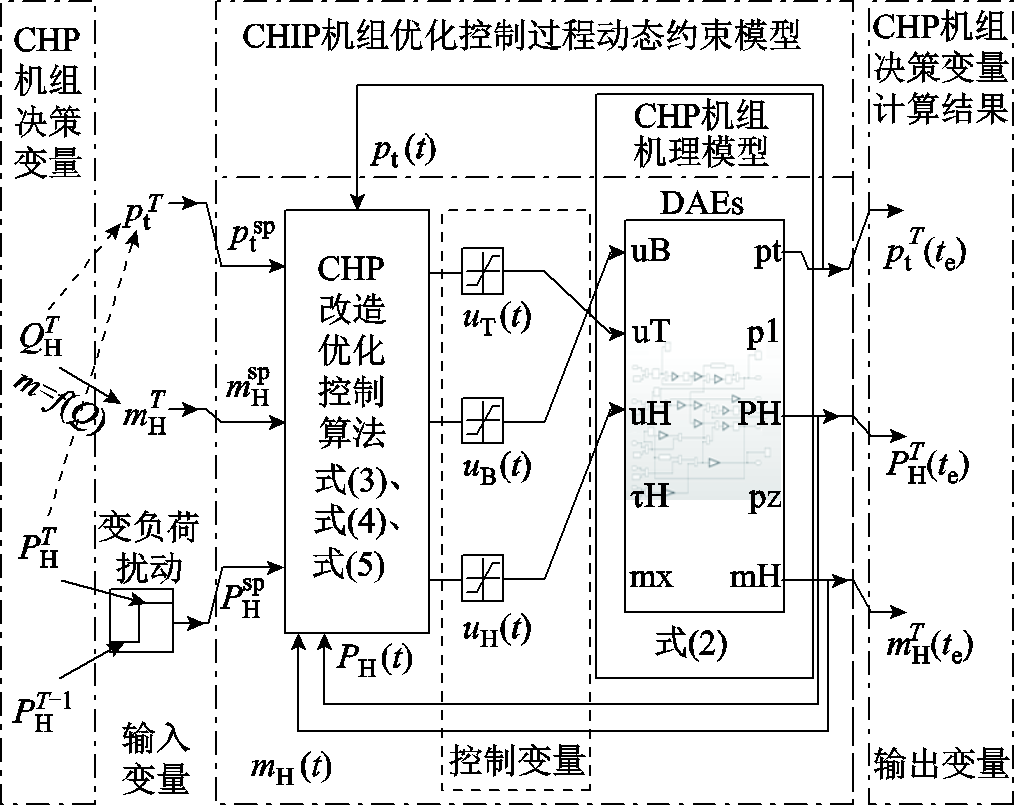
图3 CHP机组动态约束模型结构
Fig.3 Structure of dynamic constraints of CHP unit
将纯凝机组负荷-压力简化非线性动态模型[23]与单元机组非线性动态模型[24]结合，建立抽汽式CHP机组运行机理模型，有
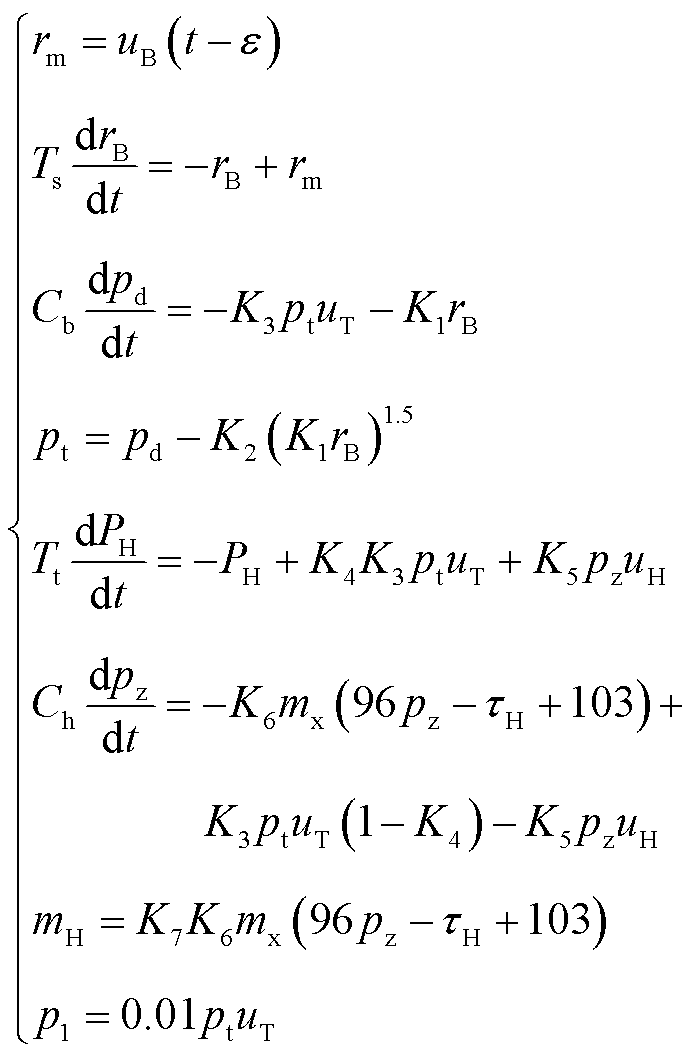（2）
式中，
为进入磨煤机的煤量；
为进入锅炉的煤粉量；
为汽包压力；
为汽轮机供热抽汽压力；
为机组循环水流量；
为机组循环水回水温度；
为汽轮机一级压力；
为机组主蒸汽压力；
为供热抽汽流量；
为机组发电功率；为机组燃料量；为高压缸进汽调节阀开度；为供热抽汽调节蝶阀开度；
、
、
、
、
、
、
为静态参数；
为制粉过程迟延时间；
为制粉惯性时间；
为锅炉蓄热系数；
为汽轮机惯性时间；
为机组加热器蓄热系数。
本文优化控制改造是针对上述模型采用电热协调控制方法提升机组快速响应能力，增强机组的短期电出力灵活性。CHP机组的、、作为输入变量，、、为控制变量。为实现电功率准确跟踪、热功率快速恢复和机组运行安全稳定的控制目标，
、
和
的优化控制算法[13]如式（3）所示。
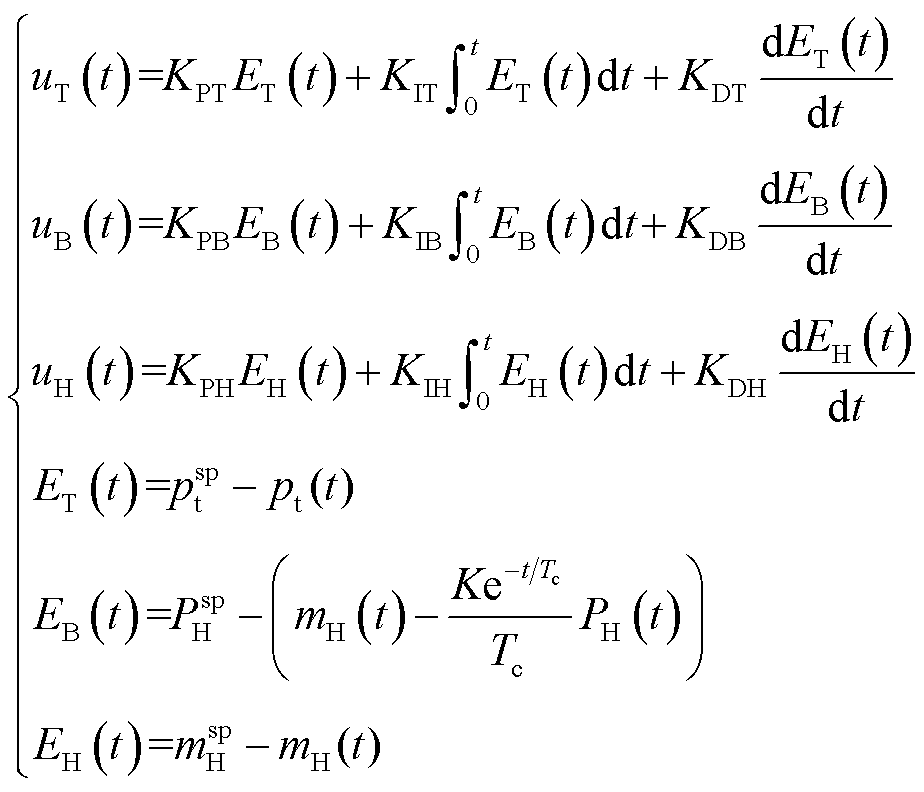（3）
式中，
、
、
，
、
、
，
、
、
、
、
为、、优化控制参数；
、
、
分别为CHP机组主蒸汽压力、发电功率、供热抽汽流量设定值。
考虑到机组安全稳定，调节过程应满足式（4）所示路径约束；同时，各输出变量稳态值不能超出允许的误差范围，还应满足式（5）所示终值约束。
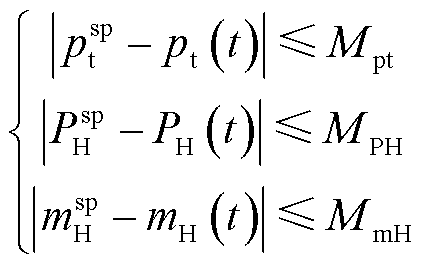（4）
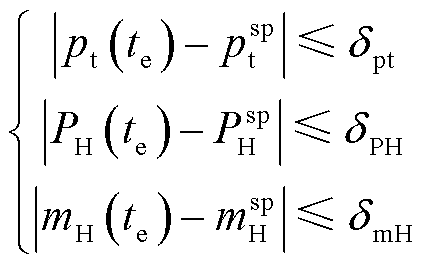（5）
式中，
为主蒸汽压力波动范围（取设定值
[25]）；
为电功率的波动范围（取±1 MW）；
为抽汽蒸汽流量的波动范围（取±50 t/h）；
为主蒸汽压力的误差范围（取设定值
）；
为电功率的误差范围（取±0.1 MW）；
为抽汽蒸汽流量的误差范围（取±5 t/h）。
综上所述，式（2）～式（5）构成优化控制改造的CHP机组状态运行动态约束。
本文优化调度以CEHS运行成本最小为目标，即
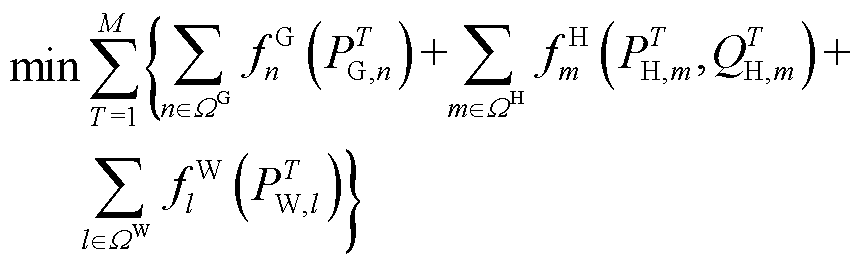(6)
其中
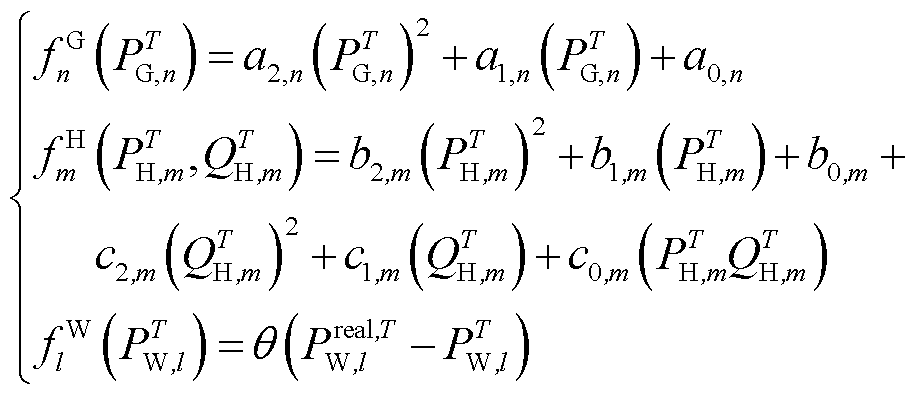（7）
式中，
为火电机组运行成本；
、
、
为成本系数；
为火电机组出力；
为CHP机组运行成本，成本系数为
、
、
、
、
、
；、
分别为CHP机组电、热出力；
为风电惩罚成本，
为成本系数；
为风电机组出力；
为预测风电出力；
、
、
分别为火电、CHP、风电机组集合；
、
、
分别为火电、CHP、风电机组数量；T为调度时段数；M为调度总时段数。决策变量有
、
、
、
，其中、为CHP机组运行过程动态约束模型的输出设定值。
1）火电机组出力约束、爬坡约束。
（8）
（9）
（10）
（11）
式中，
为火电机组爬坡速率；
、
分别为火电机组出力最小值、最大值；
、
分别为火电机组上备用、下备用。
2）风电机组运行约束。
（12）
3）CEHS电功率平衡与热功率平衡约束。
（13）
（14）
式中，
为电负荷需求；
为热负荷需求。
4）电力系统网络安全约束。
（15）
式中，
为支路
时段
的传输功率；
、
分别为支路最大传输功率下界、上界；
为电力系统中的所有传输线路。
5）CHP机组状态运行动态约束，如式（2）～式（5）所示，将其写成DAEs模型的标准形式为
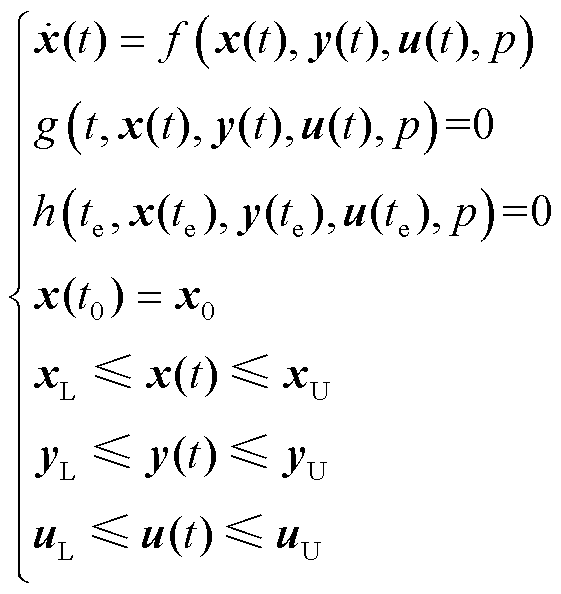（16）
其中
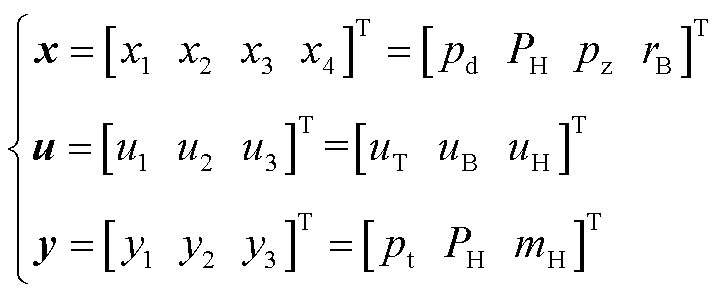（17）
式中，
为控制变量；
和
分别为控制变量的上限、下限；
为代数状态变量；
和
分别为代数状态变量的上限、下限；
为微分状态变量；
和
分别为微分状态变量的上限、下限；
为与
无关的待优化参数；f为CHP机组DAEs模型，对应式（2）；
为模型路径约束，对应式（3）、式（4）；
为模型在时刻te的终值约束，对应式（5）。
6）热力系统通过式（18）～式（20）计算CHP机组热量波动及供热区域温度变化。
（18）
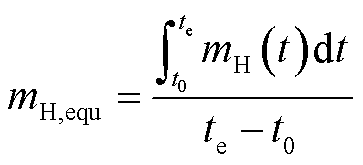（19）
（20）
式中，
为CHP机组热功率；
为供热抽汽焓降；
为流量调节过程值；
为平均等效流量；
和
为机组优化控制的起始和终止时间点；
为供热区域热容；
为供热区域温度；
为温度变化速率。
根据生产工艺需求，5 min内温度变化要小于0.5℃，2 h内温度变化小于1～2℃[26]，可由式（20）换算成热量变化约束，有
（21）
（22）
式中，
、
分别为5 min、2 h内允许的热量变化值。
本文建立的考虑CHP机组状态运行约束的CEHS动态优化调度模型，需要同时求解外层系统经济调度优化问题和内层机组运行过程动态优化问题。外层以最小化
为目标，优化调度CEHS决策变量，采用智能算法迭代寻优调度方案，获得各机组出力，其中，CHP机组电、热出力值作为内层动态优化的设定值；内层以最小化
为目标，引导输出变量逼近期望的设定值，使机组控制过程收敛、控制变量尽量平滑，采用拟序贯法进行求解。
1）外层优化模型
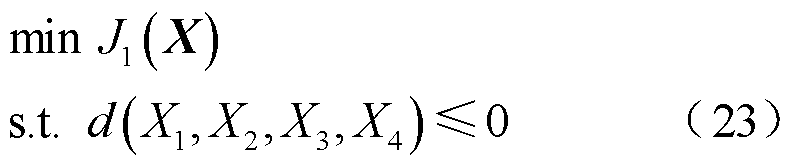
式中，目标函数对应式（6）、式（7）；X为优化调度变量组成的决策向量，
，分别为火电、风电机组出力以及CHP机组电、热出力；
为优化调度决策变量的约束，对应式（8）～式（22）。
2）内层优化模型
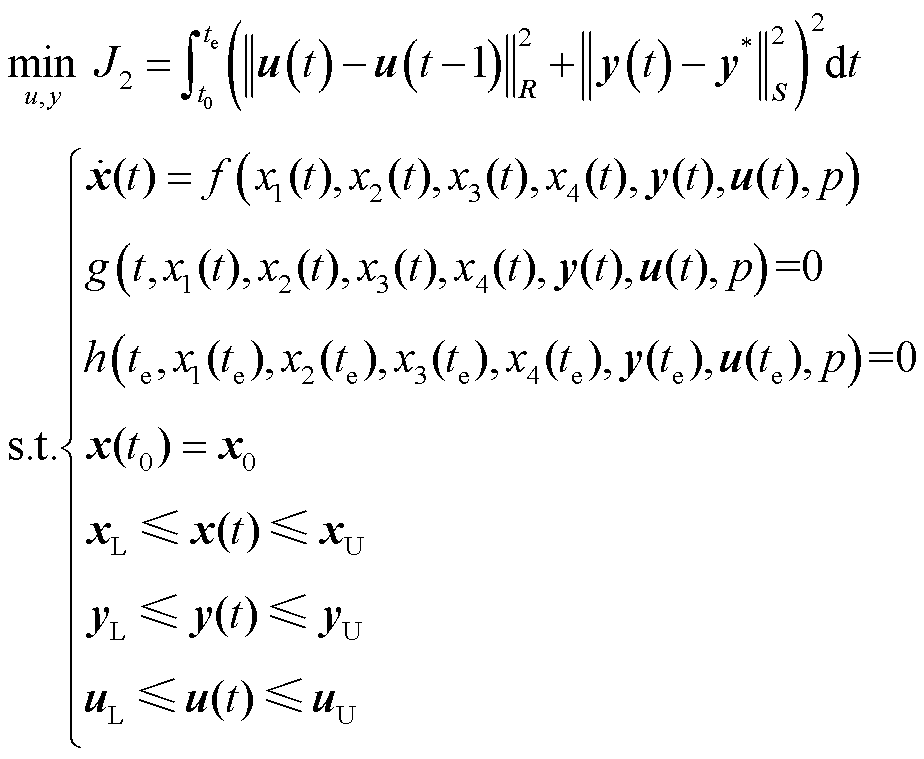（24）
其中
（25）
（26）
式中，
为输出变量的设定值；u(t)为第个时刻的控制变量，
最小使得控制变量平稳变化；
为第
个时刻控制对象的测量输出，作为第个时刻闭环系统的反馈；
和
为正定权矩阵，通过归一化来确定初始值。
考虑到上述CEHS优化调度是一个复杂的非线性动态优化问题，可采用高效处理多种约束寻优的粒子群算法进行求解。与其他算法相比，DAPSO在用于本文的CEHS优化调度时，表现出了相对出色的收敛能力和求解精度[27]，其数学描述为
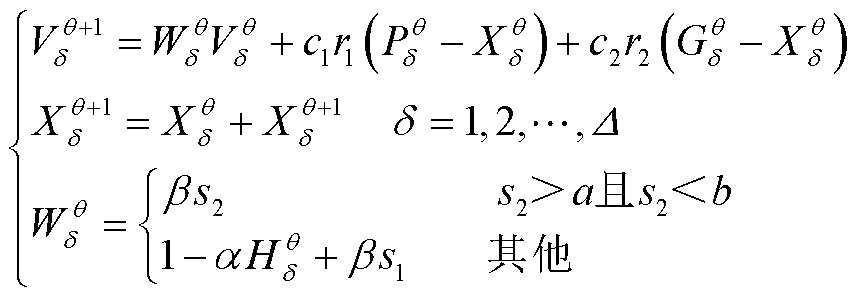（27）
式中，
为第
个粒子在
次迭代时的速度；
、
、
分别为第个粒子在次迭代时的速度、位置、惯性权重；和为加速系数（
）；
和
为
内变化的随机数；
为第个粒子在次迭代中的最好位置；
为整个群体在次迭代中的最好位置；
；
、
为控制聚集度因子的阈值，
，
；
为进化速度因子；
、
分别为适应值、空间聚集度因子；
为迭代中的粒子总数。
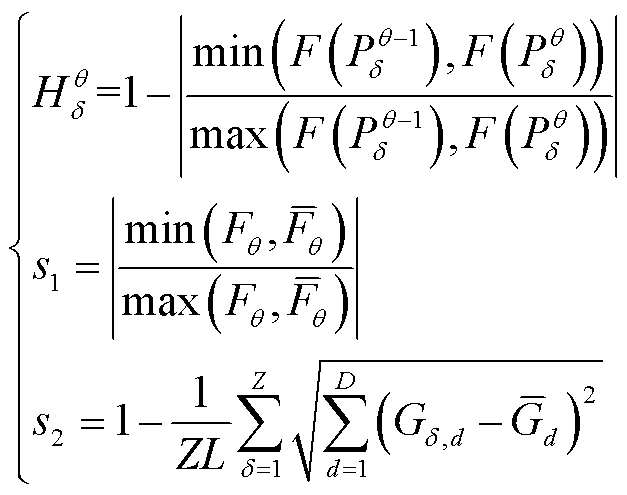（28）
式中，
为的适应值；
为第次迭代中的最佳适应值；
为第次迭代中的平均适应值；Z为种群规模；L为搜索空间的最长半径；D为解空间的维数；
为第个粒子的第
维坐标；
为所有粒子第维坐标的平均值。
CEHS双层动态优化调度求解流程如图4所示。基于DAPSO的外层调度优化算法步骤如下：
1）根据CEHS优化调度问题设置DAPSO参数，生成调度方案的决策变量。
2）加载CEHS调度模型的数据，决策变量
、
代入非CHP机组的约束进行检验。
3）决策变量
、、
、输入CHP机组DAEs模型进行动态优化计算，检验决策变量是否满足优化控制特性约束。
4）若调度方案的决策变量不满足步骤2）、步骤3）的任一约束条件时，决策变量乘以较大惩罚系数后计算调度模型目标函数值输出。
5）若调度方案的决策变量满足全部约束条件，则计算目标函数值输出，比较函数最小值保留。
6）迭代次数
，利用式（27）、式（28）更新下一次调度方案种群，直到满足设置的迭代次数终止条件。
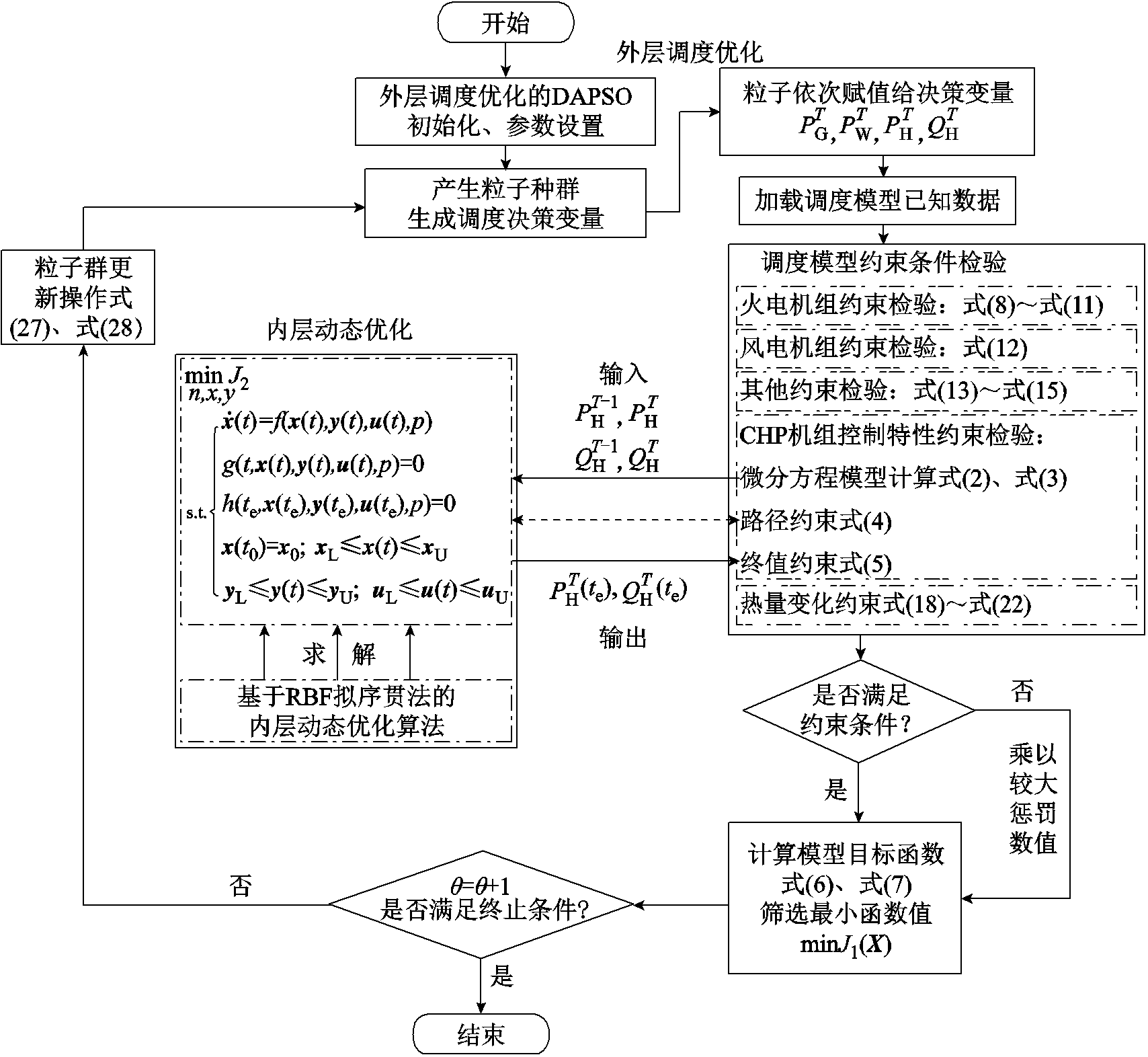
图4 CEHS优化调度模型求解流程
Fig.4 Solution flow of CEHS optimal scheduling model
拟序贯法[17]结合序贯算法和联立算法的优点，适合求解带路径约束的大规模强非线性动态优化问题，其结构如图5所示。在模拟计算层中，控制变量被表示为每一时间单元内的常量函数或线性函数，状态变量采用以径向基函数（Radical Basis Function, RBF）为基的正交配置法离散。将DAEs离散为非线性代数方程组，通过牛顿迭代法求解，得到离散点上状态变量值。由离散点上状态变量关于控制变量的导数公式，计算出灵敏度矩阵，优化计算层从中获取目标函数对控制变量的梯度信息。控制变量分段函数值成为优化问题的决策变量，状态变量仅以路径约束形式出现，原问题简化为NLP问题，可采用序列二次规划算法求解。
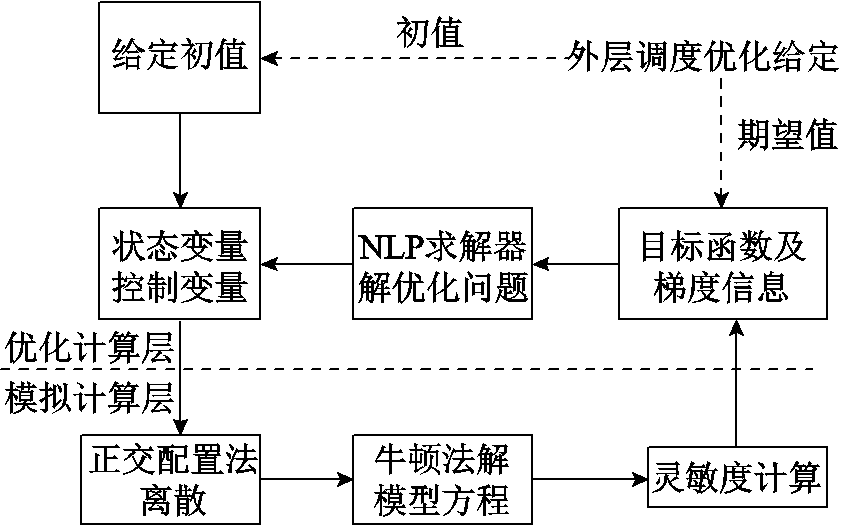
图5 拟序贯算法结构
Fig.5 Structure of quasi sequential algorithm
基于RBF拟序贯法的内层动态优化方法步骤如下：
1）给定初值。给定控制变量初值
、状态变量初值
、优化时间
和
及所有变量的边界约束。
2）变量离散。离散式（16）的DAEs模型是利用一元数值逼近方法将各连续变量沿时间轴进行离散。采用RBF实施离散后的NLP模型具有更简洁的公式描述，更易实现编程求解。先对导函数
进行逼近，然后通过积分得到原函数x(t)的逼近。
对于给定CHP机组DAEs初值问题，有
（29）
已知
，对于任意给定
，可用式（30）进行插值，且满足式（31）条件。
（30）
（31）
式中，
为实系数；
为一元函数(基函数)；
为RBF插值的中心。
将CHP机组优化控制时间离散为时间序列
，可用式（32）对式（30）进行逼近。
（32）
对
进行不定积分，可得
（33）
令
，则
（34）
易得初值问题的离散格式为
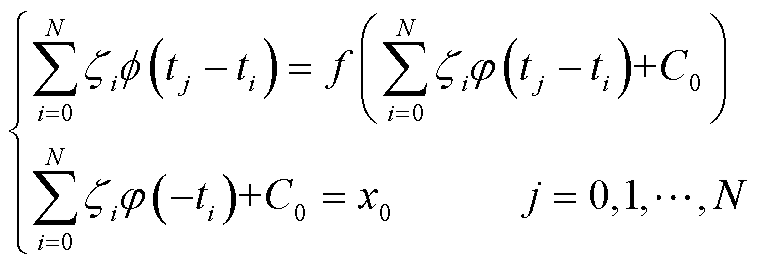（35）
联立求解式（35）得和
的值，代入式（34）可得离散点处变量值
，可通过求差方式消去。将记为，则简化式（35）为
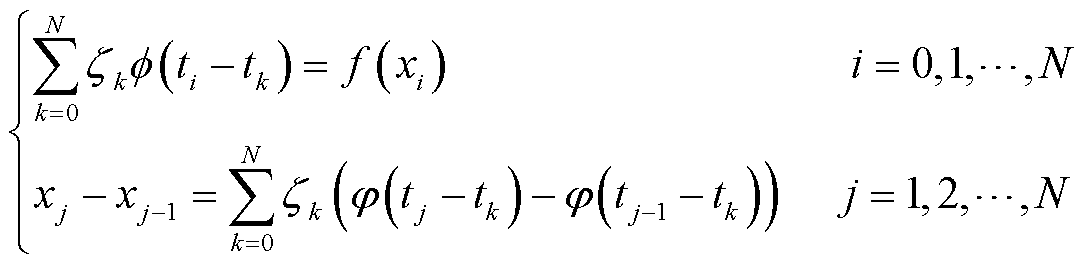（36）
基函数常采用RBF形式[28]，其中逆Multi-Quadric函数最适合求解DAEs[29]，
为给定正数（
）。对于大多数DAEs优化模型，当
可使求解过程易于收敛[30]，即
（37）
对进行不定积分可得
（38）
式（24）所示的动态优化问题，所有变量都是时间
的函数。仅考虑式（24）的离散化，对优化控制时段
进行等距划分，可得时间序列
，且有
，
。将各时间点
所对应各变量分别记为、
和
，按式（36）对式（24）进行离散，可得如下NLP模型
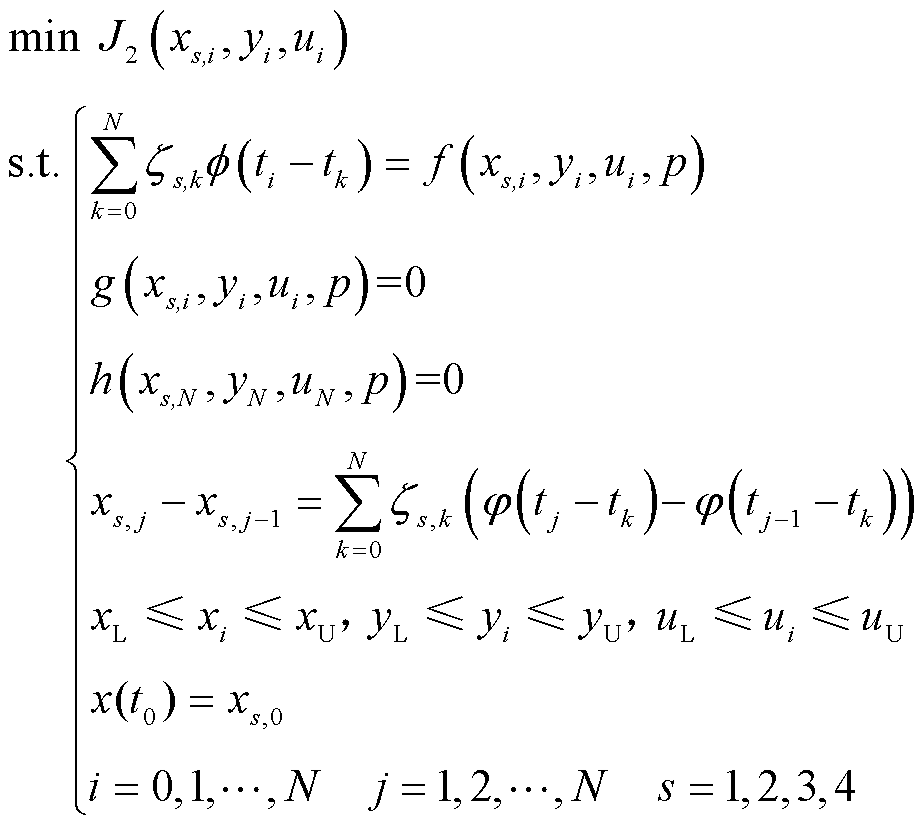（39）
3）模型计算。在每个优化迭代中都要进行一次DAEs模型的模拟，在模拟层对离散后的非线性方程组采用牛顿迭代法进行计算，得到状态变量的值。
4）灵敏度计算。在模型计算的同时，得到状态变量对控制变量和时间变量的灵敏度信息矩阵。
5）优化层计算。每次优化迭代过程，重复步骤4），利用NLP求解器求解经模拟层处理后的NLP问题，直至达到优化的收敛精度，寻得最优解。
本文采用改进的IEEE 30节点系统构建CEHS模型，其结构如图6所示，其中节点1、2、8、13为火电机组、5为CHP机组，节点11处接入150 MW风电场。弃风惩罚成本850元/(MW·h)，CHP机组运行相关参数见附表1～附表5，火电机组参数见附表6。调度时长为2 h，5 min为一个时段，共24个时段。电、热负荷、风电预测功率，如附图1所示。
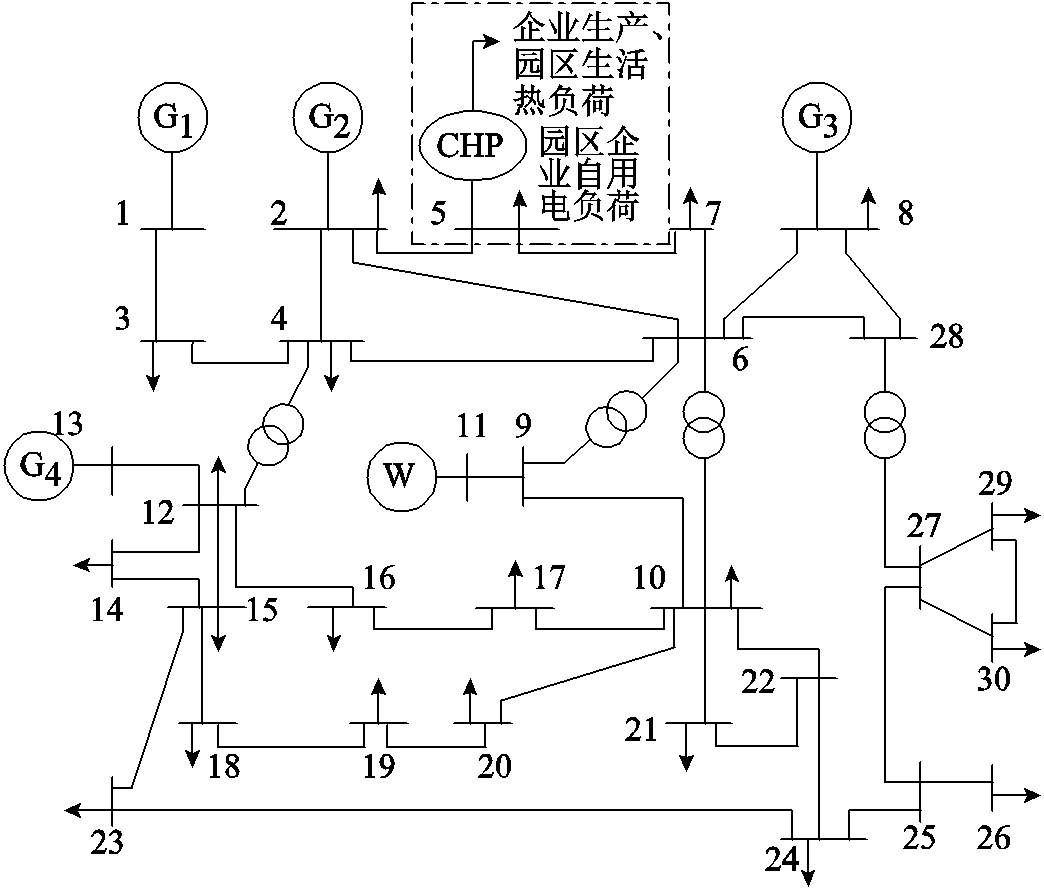
图6 改进的IEEE 30节点CEHS结构
Fig.6 Structure of improved IEEE 30 node CEHS
本文设置如下三种算例来分析采用本文调度模型后在系统调度经济性与机组运行安全性的优势。
算例1：未充分考虑控制改造的CHP机组静态运行约束（如式（1））的CEHS调度模型，其爬坡率一般为2%
/min[31]（约束过于严格），采用CPLEX求解器求解。
算例2：考虑优化控制改造的CHP机组状态运行动态约束（如式（16））的CEHS调度模型（模拟实际运行状态的约束），采用双层求解策略求解。
算例3：过度充分考虑控制改造CHP机组静态约束（如式（1））的CEHS调度模型，如1.1节所述本文爬坡率取4.5%/min（约束过于宽松），采用CPLEX求解器求解。
算例1、算例2、算例3调度方案的各机组出力结果如图7所示。与算例2调度结果相比，算例3差别较小，而算例1在风电、CHP电出力上差别较大。在1、3、5、6、9、12、15、18、20、22、24时段，算例2的风电机组出力比算例1分别增加了24.72、30、18.27、4.93、21.47、8.08、23.33、16.7、11.87、30、30 MW，系统风电消纳量提升10.22%；与算例1相比，算例2的CHP机组、火电机组电出力总体上分别降低了4.3%、0.09%。可见，充分考虑CHP机组改造后CEHS的风电利用率显著提高，耗煤机组出力明显降低。
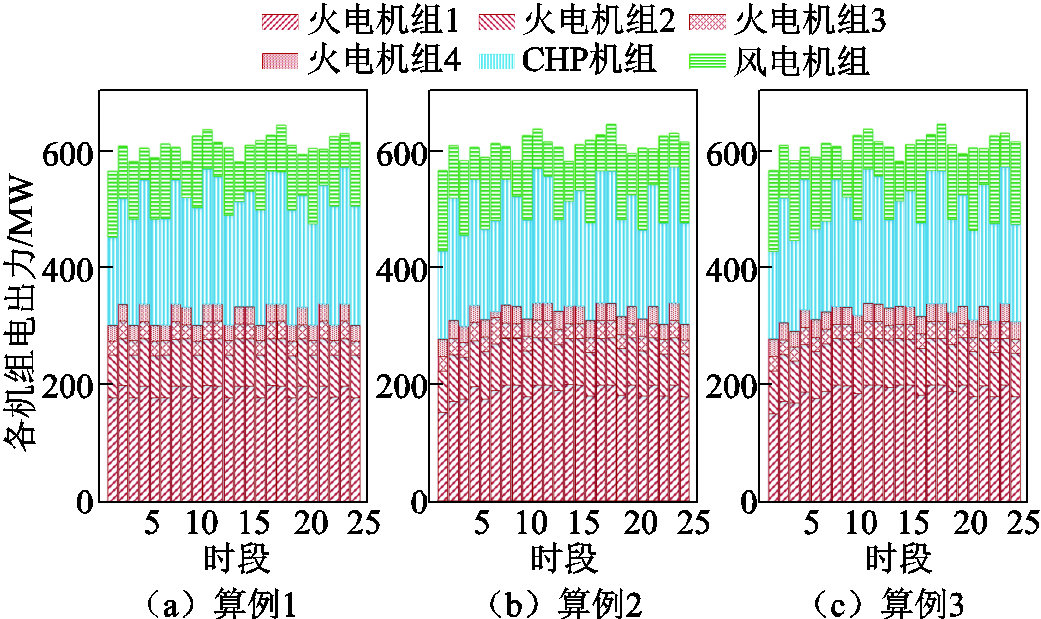
图7 不同算例下调度结果
Fig.7 Scheduling results under different cases
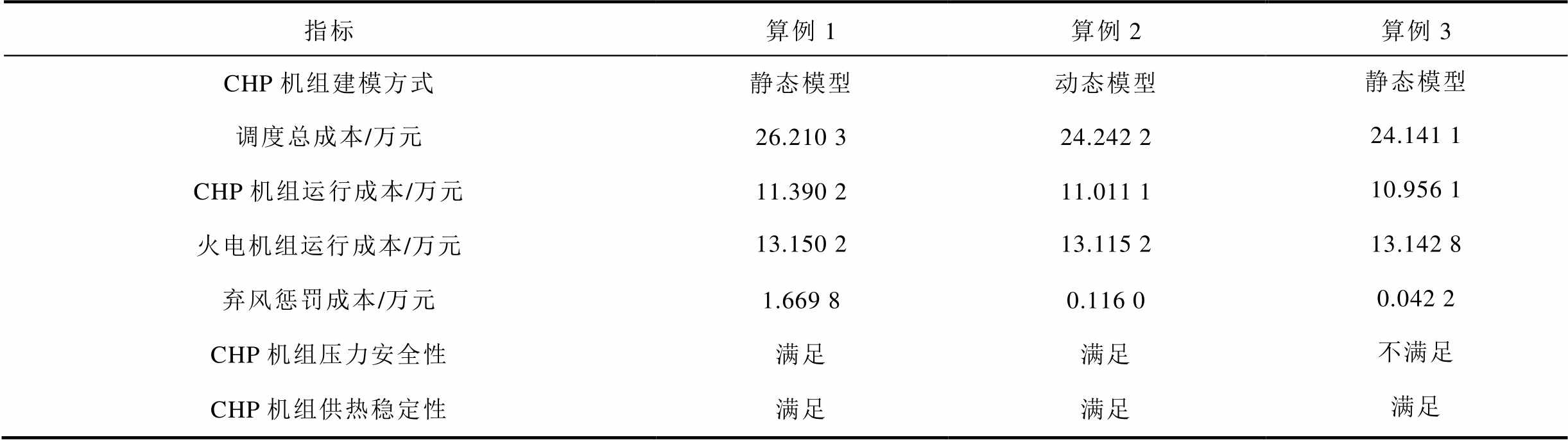
经调度计算可知，算例3与算例2在调度成本、各机组出力总量方面差别较小。表1给出了不同算例的调度成本，总体上算例2比算例1减少了19 681元，主要是弃风成本大幅降低，此外，CHP机组、火电机组出力降低使运行成本小幅减少。可以看出，充分考虑CHP机组改造特性的系统在调度成本上具有明显优势。同时，考虑CHP机组静态模型的调度优化在系统经济性、机组安全性方面，与CHP机组动态建模相比也存在明显不足。
表1 不同算例下调度方案计算指标对比
Tab.1 Comparison of calculation indexes of scheduling scheme under different cases
指标算例1算例2算例3 CHP机组建模方式静态模型动态模型静态模型 调度总成本/万元26.210 324.242 224.141 1 CHP机组运行成本/万元11.390 211.011 110.956 1 火电机组运行成本/万元13.150 213.115 213.142 8 弃风惩罚成本/万元1.669 80.116 00.042 2 CHP机组压力安全性满足满足不满足 CHP机组供热稳定性满足满足满足
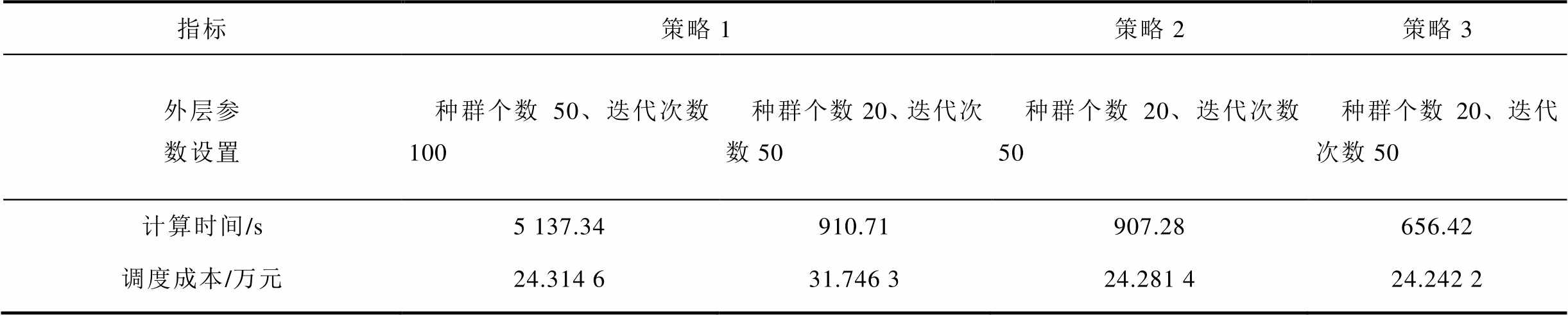
为了验证本文所提求解策略的优越性与有效性，针对算例2中本文所构建的调度模型分别采用如下三种双层求解策略进行仿真计算，其求解结果见表2。
表2 不同求解策略下算例2的求解结果对比
Tab.2 Comparison of solution results of case 2 under different solution strategies
指标策略1策略2策略3 外层参数设置种群个数50、迭代次数100种群个数20、迭代次数50种群个数20、迭代次数50种群个数20、迭代次数50 计算时间/s5 137.34910.71907.28656.42 调度成本/万元24.314 631.746 324.281 424.242 2
策略1：采用传统的外层PSO优化调度+内层联立法（Lagrange离散格式）[18]动态优化。
策略2：采用改进外层DAPSO优化调度+内层联立法（Lagrange离散格式）动态优化。
策略3：采用本文所提外层DAPSO优化调度+内层拟序贯法（RBF离散格式）动态优化。
设置外层优化算法参数为种群个数20、迭代次数50时，与求解策略2相比，策略1的调度成本陷入局部最优无法准确寻优到最小调度成本，通过增大策略1的参数设置虽然可以寻优到更小的调度成本，但在计算时间上大大增加，无法满足计算的实时性需求。在设置种群个数20、迭代次数50时，通过对比策略2与策略3的计算结果，在保证调度成本最优的情况下，策略3计算时间更短。这是由于采用基于RBF离散格式的拟序贯法在求解动态优化问题时的优势作用，如图8所示，所提拟序贯法求解CHP机组时，每一次迭代中20个种群的平均计算时间均小于联立法，提升了内层优化的求解效率。数据表明，本文所提外层DAPSO优化调度+内层拟序贯法（RBF离散格式）动态优化的双层求解策略较好地兼顾了计算效率与求解精度。
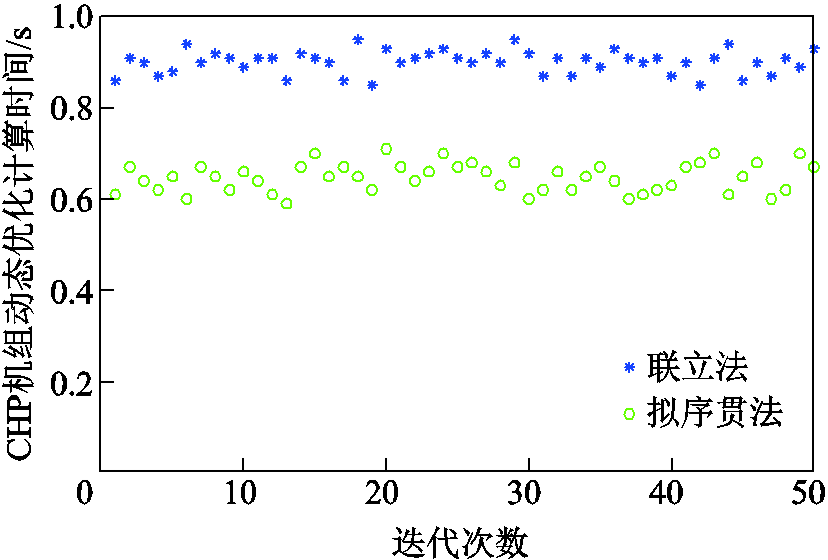
图8 算例2中CHP机组动态优化计算时间
Fig.8 Dynamic optimization calculation time of CHP unit in case 2
在算例1、算例2、算例3调度方案下，24个时段CHP机组运行点分布情况如图9所示。算例1运行点分布较为集中，离可行域上下边界较远；而算例2、3有更多的运行点靠近下边界，且分布范围也更大。例如，算例1在24时段运行点为（257.10, 203.28），而算例2为（257.10, 173.28）、算例3为（257.10, 165.78）。相比算例1，算例2有10个运行点更接近下边界、有5个点离上边界更近，而采用更加宽松约束的算例3又有更多运行点接近下边界。这是因为优化控制改造后CHP机组爬坡能力更强，充分考虑其运行约束的调度方案使CHP电功率优化区间更大。因此，企业自备CHP机组改造对改善系统运行灵活性有积极作用，充分考虑机组改造后所具有的更深调节范围为风电消纳提供了条件。
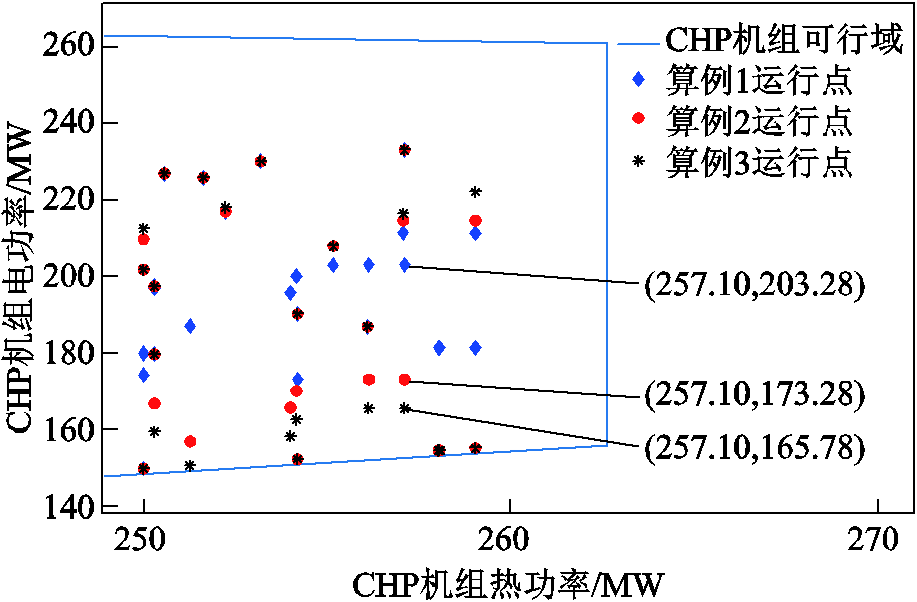
图9 不同算例下CHP机组运行点分布情况
Fig.9 Distribution of operation points of CHP unit under different cases
算例1、算例2、算例3下CHP机组电出力与风电消纳情况如图10所示。与算例1相比，在时段1、3、5、6、9、12、15、18、20、22、24，算例2、算例3的CHP机组电出力均向下爬坡到更小值，相应时段的风电消纳均有所增加。以5时段为例，算例1的CHP机组电出力由211.58 MW减少到181.58 MW，算例2由214.84 MW减少到155.42 MW，同时风电消纳增加52.29 MW。因而，在调度中合理地构建优化控制改造的CHP机组运行特性模型来匹配风电变化，能够有效缓解弃风现象。
图10 不同算例下CHP机组出力与风电消纳
Fig.10 CHP unit output and wind power consumption under different cases
运行备用是对系统可能出现的预想事故或负荷波动而预留的灵活性备用容量，机组出力序列确定时其预留容量通常是固定的。不同算例下CHP机组备用容量对比如图11所示，算例1的CHP机组备用容量可调范围较为有限，应对系统电功率波动能力有限；而算例2、3中机组备用可调节上下限较大，其对电负荷、风电预测不确定性的应对潜力也较大。因此，充分考虑CHP机组优化控制改造的运行特性，为企业自备电厂实现对电网企业的辅助服务提供了可能。
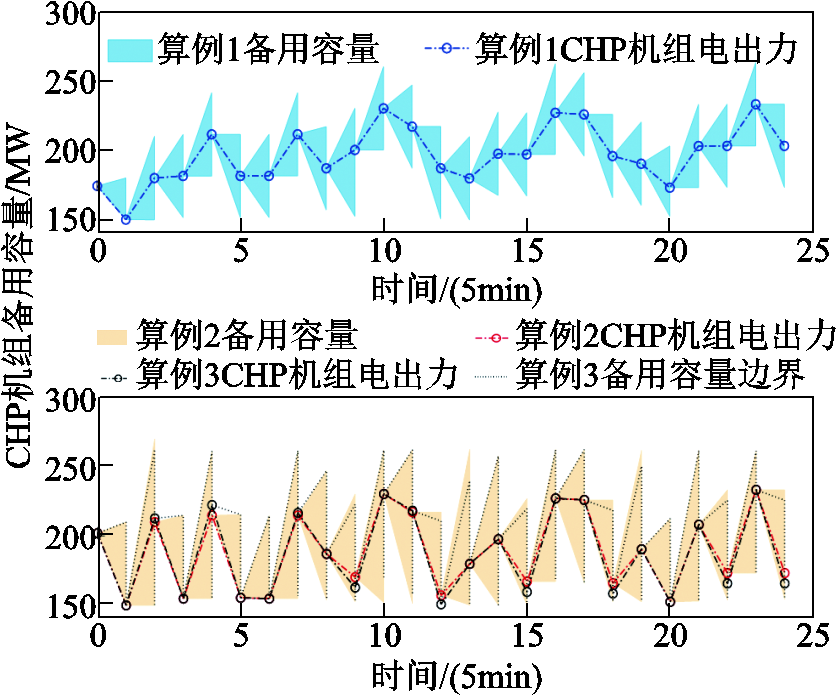
图11 不同算例下CHP机组备用容量对比
Fig.11 Comparison of reserve capacity of CHP unit under different cases
CHP机组动态约束（算例2）与静态约束（算例3）的不同算例在调度成本、其他机组出力方面差别较小，但对CHP机组运行的电出力跟踪准确性、压力安全性、供热稳定性等方面需进一步分析。
不同算例下CHP机组电出力如图12所示，CHP机组的实际运行过程值在2、4、7、9、12、15、18、24时段出现了对算例3中机组调度值跟踪失配的情况，机组存在电出力缺额，将会导致算例3的调度方案难以实施、方案可行性降低。而采用CHP机组动态约束的算例2的调度值与实际运行过程值匹配度较高，能够实现机组过程值对调度值的准确跟踪，其CEHS调度方案可行。
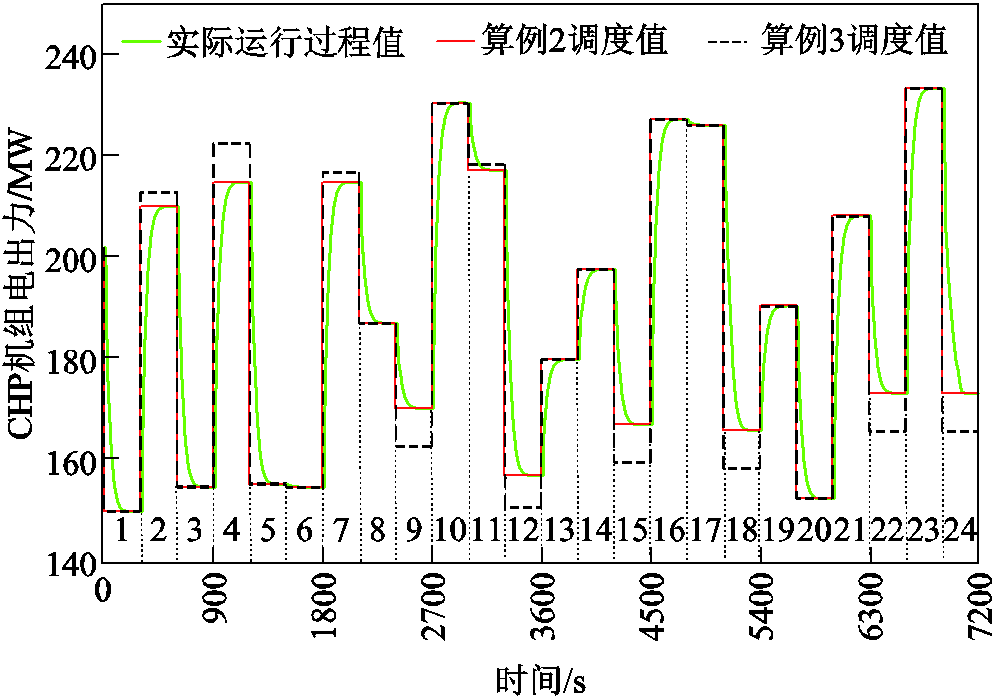
图12 不同算例下CHP机组电出力
Fig.12 Power output of CHP unit under different cases
调度方案执行过程中，CHP机组主蒸汽压力变化关系到机组运行的安全稳定。不同算例下CHP机组主蒸汽压力如图13所示，算例2中主蒸汽压力设定值为15.00 MPa时，向上、向下最大峰值分别为15.74 MPa、14.39 MPa，未超设定值±5%的波动范围，且稳态均达到设定值；11、17、18、24时段压力设定为15.50 MPa，稳态均达到设定值，且峰值在限值范围内。数据表明，机组运行过程动态约束的压力波动对机组安全并无影响。这是因为CHP机组动态建模方式（如式（2）～式（5））可刻画出CHP机组主蒸汽压力
在变负荷过程中的变化规律，并通过调节过程路径约束限制超压安全越线情况。而算例3的建模方式无法考虑主蒸汽压力的动态调节过程约束，变负荷调节过大将导致机组调节过程压力超过安全约束的上限值（如图13中2、4、10、16、23、24时段），将给CHP机组稳定运行造成安全隐患。
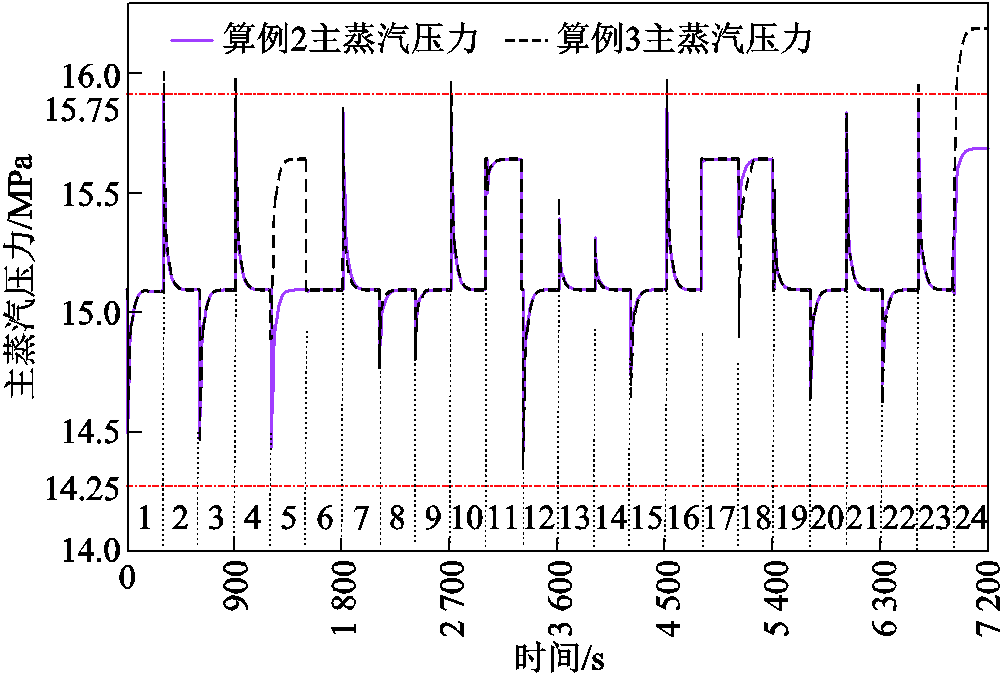
图13 不同算例下CHP机组主蒸汽压力
Fig.13 Main steam pressure of CHP unit under different cases
CHP机组优化控制过程中，抽汽蒸汽流量的设定值随热需求值变化，按式（19）计算。如图14所示，算例2各时段稳态均达到设定值，调节过程的峰值波动未超出设定值±50 t/h的偏差范围。与算例2相比，算例3在多个时段调节过程的峰值波动更大，平均流量等效值偏离需求稳态值更远，将会给供热要求较高的工业生产工艺带来不利影响。
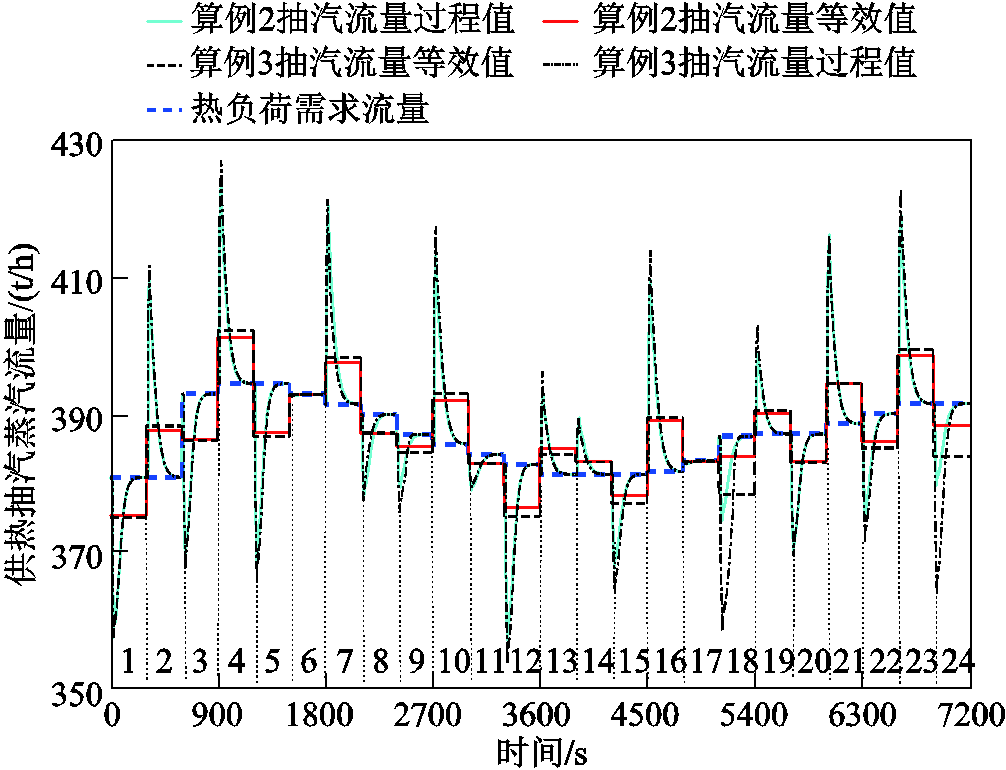
图14 不同算例下CHP机组抽汽蒸汽流量
Fig.14 Extraction steam flow of CHP unit under different cases
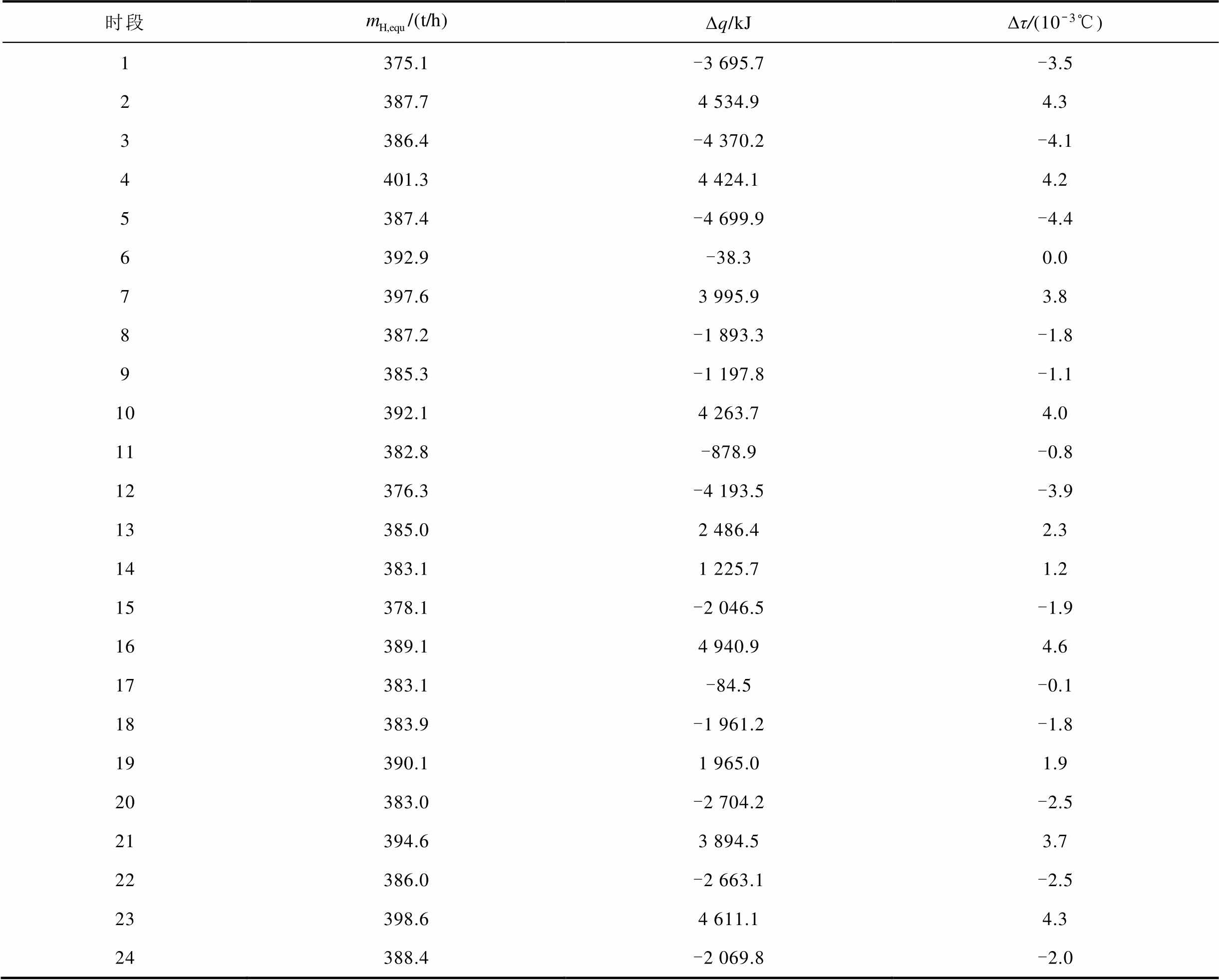
算例2的CHP机组热出力波动引起的热量、温度变化，见表3，其中mH,equ为平均等效抽汽蒸汽流量，∆q为热量变化值，∆τ为300 s温度变化值。算例2在各时段热量增减引起的温度变化均较小，总体来看，2 h内CHP机组平均多产生热量3 845.2 kJ，该热量导致供热区域温度升高3.62×10-3℃。同理计算算例3的相应指标，最终引起供热区域温度降低0.11×10-3℃。数据表明，两种算例中CHP机组动态调节过程产生的热量波动对生活供热温度需求并无影响。
表3 算例2抽汽蒸汽流量波动对热出力与温度的影响
Tab.3 Influence of extraction steam flow fluctuation on thermal output and temperature in case 2
时段∆q/kJ∆τ/(10-3℃) 1375.1-3 695.7-3.5 2387.74 534.94.3 3386.4-4 370.2-4.1 4401.34 424.14.2 5387.4-4 699.9-4.4 6392.9-38.30.0 7397.63 995.93.8 8387.2-1 893.3-1.8 9385.3-1 197.8-1.1 10392.14 263.74.0 11382.8-878.9-0.8 12376.3-4 193.5-3.9 13385.02 486.42.3 14383.11 225.71.2 15378.1-2 046.5-1.9 16389.14 940.94.6 17383.1-84.5-0.1 18383.9-1 961.2-1.8 19390.11 965.01.9 20383.0-2 704.2-2.5 21394.63 894.53.7 22386.0-2 663.1-2.5 23398.64 611.14.3 24388.4-2 069.8-2.0
本文深入分析了CHP机组优化控制改造的运行特性，并提出了一种考虑CHP机组运行过程约束的CEHS动态优化调度模型，得到以下结论：
1）园区自备CHP机组改造对改善CEHS运行域的灵活性具有积极作用，改造后机组运行的快速调节特性，使其能合理匹配风电变化、及时响应系统不确定性波动。将优化控制改造后CHP机组状态运行约束充分考虑到CEHS调度优化中，其具备的更深电出力调节能力可减少调度成本、促进风电消纳。
2）CHP机组状态运行约束动态模型在机组运行的出力调节准确性、压力安全性、供热稳定性方面比静态约束表现得更加合理，可更好地保证CHP机组安全稳定运行，提高调度方案的可行性。
CHP机组动态建模的微分代数方程在优化求解时形成大规模数值计算问题，随着机组数量的增加，计算成本也会成倍增加。因此，下一步需要研究在保证一定求解精度下的动态优化问题的快速求解方法。
附 录
附表1 CHP机组典型工作点参数
App.Tab.1 Typical operating point parameters
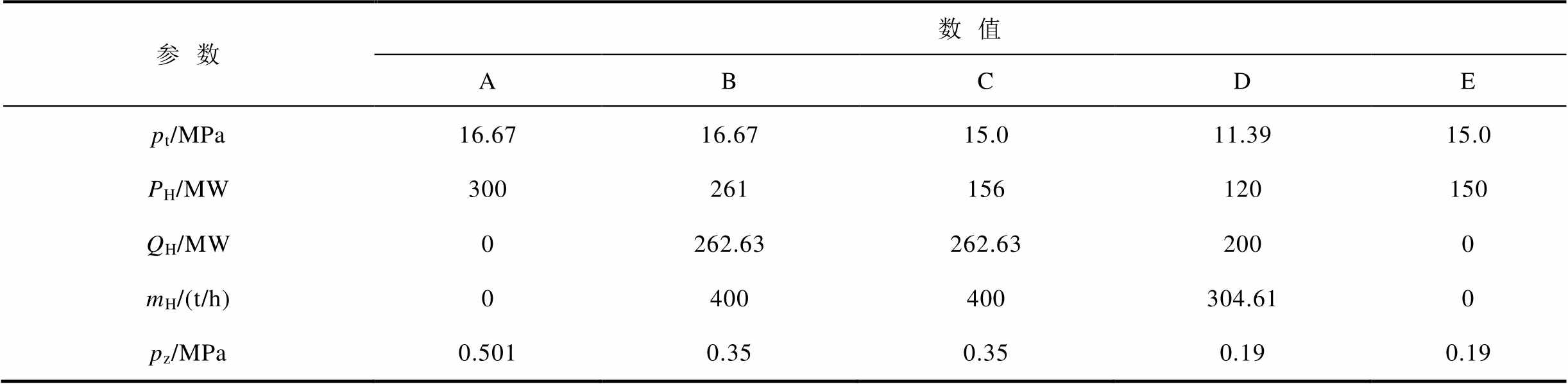
参数数值 ABCDE pt/MPa16.6716.6715.011.3915.0 PH/MW300261156120150 QH/MW0262.63262.632000 mH/(t/h)0400400304.610 pz/MPa0.5010.350.350.190.19
附表2 CHP机组供热工况运行参数
App.Tab.2 Working point parameters of CHP unit
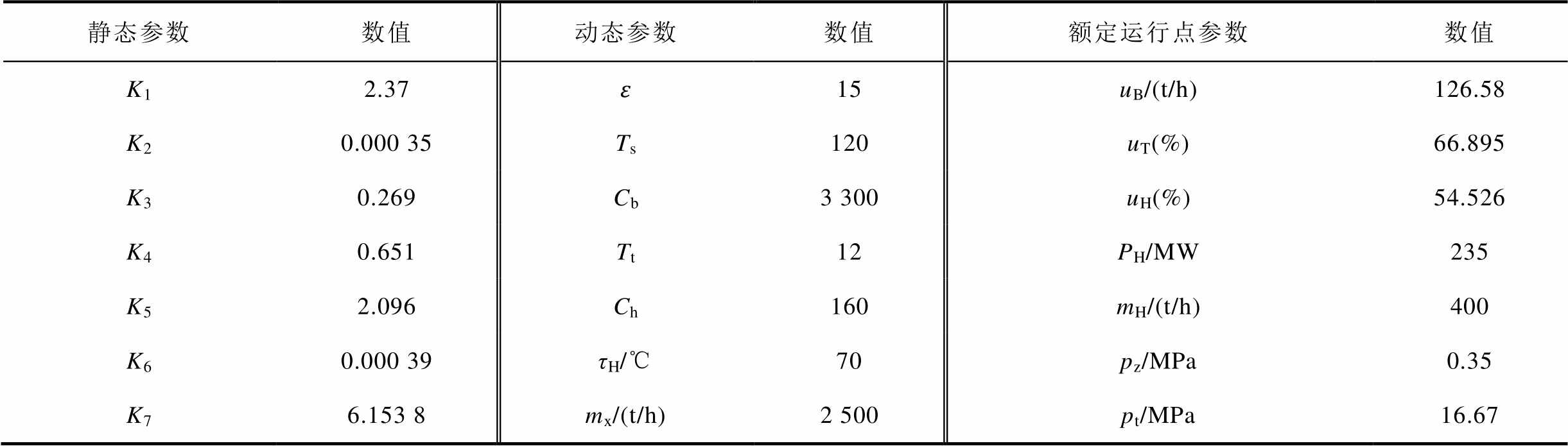
静态参数数值动态参数数值额定运行点参数数值 K12.37ɛ15uB/(t/h)126.58 K20.000 35Ts120uT(%)66.895 K30.269Cb3 300uH(%)54.526 K40.651Tt12PH/MW235 K52.096Ch160mH/(t/h)400 K60.000 39τH/℃70pz/MPa0.35 K76.153 8mx/(t/h)2 500pt/MPa16.67
附表3 CHP机组控制系统参数
App.Tab.3 CHP unit control system parameters
参数数值 KPT-0.9 KIT-1 KDT0 KPB0.1 KIB0.01 KDB0 KPH0.01 KIH10 KDH0 K0.5 Tc15
附表4 热力系统参数
App.Tab.4 Thermal system parameters
参数数值 供热区域热容Csys/(kJ/℃)3.189 6×108 机组供热抽汽焓降∆h/(kJ/kg)2.363 7×103
附表5 CHP机组成本系数
App.Tab.5 Cost coefficient of CHP unit
参数数值参数数值 b0/(元/h)2 740c0/[元/(MW2·h)]0.002 54 b2/[元/(MW2·h)]0.006 98c2/[元/(MW2·h)]0.000 233 b1/[元/(MW·h)]212c1/[元/(MW·h)]38.4
附表6 火电机组成本运行参数
App.Tab.6 Operation parameters of thermal power unit
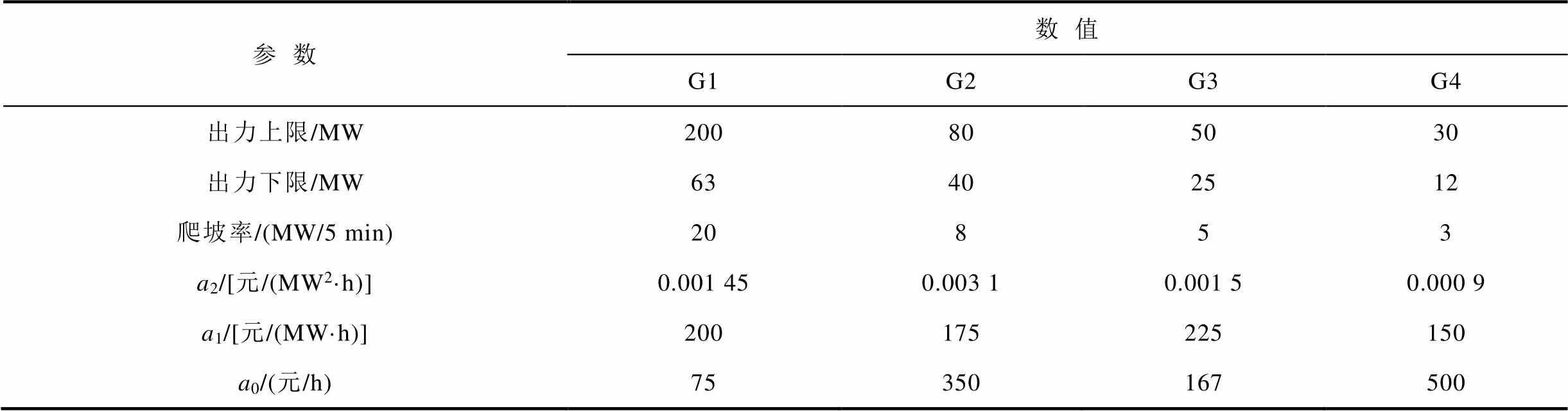
参数数值 G1G2G3G4 出力上限/MW200805030 出力下限/MW63402512 爬坡率/(MW/5 min)20853 a2/[元/(MW2·h)]0.001 450.003 10.001 50.000 9 a1/[元/(MW·h)]200175225150 a0/(元/h)75350167500
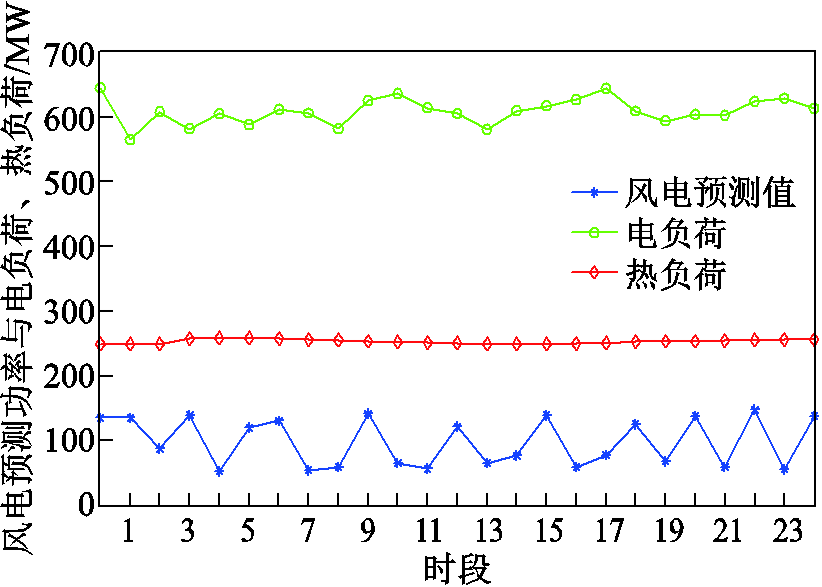
附图1 电、热负荷及风电预测数据
App.Fig.1 Forecast data of power, heat load and wind power
参考文献
[1] 陈岑, 武传涛, 林湘宁, 等. 计及上下游市场的园区综合能源商购售能策略[J]. 电工技术学报, 2022, 37(1): 220-231. Chen Cen, Wu Chuantao, Lin Xiangning, et al. Purchase and sale strategies of park integrated energy suppliers in wholesale and retail markets[J]. Transactionsof China Electrotechnical Society, 2022, 37(1): 220-231.
[2] 熊宇峰, 司杨, 郑天文, 等. 基于主从博弈的工业园区综合能源系统氢储能优化配置[J]. 电工技术学报, 2021, 36(3): 507-516. Xiong Yufeng, Si Yang, Zheng Tianwen, et al. Optimal configuration of hydrogen storage in industrial park integrated energy system based on stackelberg game[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 507-516.
[3] 刘鑫屏, 田亮, 王琪. 补偿风电扰动的供热机组快速变负荷控制方法[J]. 电力系统自动化, 2014, 38(6): 26-32. Liu Xinping, Tian Liang, Wang Qi. A control method of rapid load change for heat supply units compensating wind power disturbance[J]. Automation of Electric Power Systems, 2014, 38(6): 26-32.
[4] 潘超, 范宫博, 王锦鹏, 等. 灵活性资源参与的电热综合能源系统低碳优化[J].电工技术学报,2023, 38(6): 1633-1647.Pan Chao, Fan Gongbo, Wang Jinpeng, et al. Low-carbon optimization of electric and heating integrated energy system with flexible resource participation[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1633-1647.
[5] Wang Jiawei, You Shi, Zong Yi, et al. Flexibility of combined heat and power plants: a review of technologies and operation strategies[J]. Applied Energy, 2019, 252: 113445.
[6] Zhang Menglin, Wu Qiuwei, Wen Jinyu, et al. Two-stage stochastic optimal operation of integrated electricity and heat system considering reserve of flexible devices and spatial-temporal correlation of wind power[J]. Applied Energy, 2020, 275: 115357.
[7] Liu Ming, Wang Shan, Zhao Yongliang, et al. Heat-power decoupling technologies for coal-fired CHP plants: operation flexibility and thermodynamic performance[J]. Energy, 2019, 188: 116074.
[8] Chen Hongkun, Yu Yanjuan, Jiang Xin. Optimal scheduling of combined heat and power units with heat storage for the improvement of wind power integration[C]//2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi'an, China, 2016: 1508-1512.
[9] Chen Heng, Yao Xianhuai, Li Juan, et al. Thermodynamic analysis of a novel combined heat and power system incorporating a CO2 heat pump cycle for enhancing flexibility[J]. Applied Thermal Engineering, 2019, 161: 114160.
[10] Tan Jin, Wu Qiuwei, Hu Qinran, et al. Adaptive robust energy and reserve co-optimization of integrated electricity and heating system considering wind uncertainty[J]. Applied Energy, 2020, 260: 114230.
[11] 王昀, 谢海鹏, 孙啸天, 等. 计及激励型综合需求响应的电-热综合能源系统日前经济调度[J]. 电工技术学报, 2021, 36(9): 1926-1934. Wang Yun, Xie Haipeng, Sun Xiaotian, et al. Day-ahead economic dispatch for electricity-heating integrated energy system considering incentive integrated demand response[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1926-1934.
[12] 张磊, 罗毅, 罗恒恒, 等. 基于集中供热系统储热特性的热电联产机组多时间尺度灵活性协调调度[J]. 中国电机工程学报, 2018, 38(4): 985-998, 1275. Zhang Lei, Luo Yi, Luo Hengheng, et al. Scheduling of integrated heat and power system considering multiple time-scale flexibility of CHP unit based on heat characteristic of DHS[J]. Proceedings of the CSEE, 2018, 38(4): 985-998, 1275.
[13] Wang Wei, Liu Jizhen, Zeng Deliang, et al. Modeling and flexible load control of combined heat and power units[J]. Applied Thermal Engineering, 2020, 166: 114624.
[14] Wang Wei, Jing Sitong, Sun Yang, et al. Combined heat and power control considering thermal inertia of district heating network for flexible electric power regulation[J]. Energy, 2019, 169: 988-999.
[15] 王玮, 孙阳, 刘吉臻, 等. 适应电网快速调频的热电联产机组新型变负荷控制策略[J]. 电力系统自动化, 2018, 42(21): 63-69. Wang Wei, Sun Yang, Liu Jizhen, et al. Load-change control strategy for combined heat and power units adapted to rapid frequency regulation of power grid[J]. Automation of Electric Power Systems, 2018, 42(21): 63-69.
[16] 王琪. 风电规模化并网条件下供热机组优化控制研究[D]. 北京: 华北电力大学, 2013.
[17] 洪伟荣. 大规模动态过程优化的拟序贯算法研究[D]. 杭州: 浙江大学, 2005.
[18] 陈荣华, 王可心, 邵之江. 自主泊车的全联立动态优化方法[J]. 控制理论与应用, 2016, 33(5): 561-568. Chen Ronghua, Wang Kexin, Shao Zhijiang. Simultaneous dynamic optimization for autonomous parking[J]. Control Theory & Applications, 2016, 33(5): 561-568.
[19] 刘洪, 李吉峰, 葛少云, 等. 基于多主体博弈与强化学习的并网型综合能源微网协调调度[J]. 电力系统自动化, 2019, 43(1): 40-48. Liu Hong, Li Jifeng, Ge Shaoyun, et al. Coordinated scheduling of grid-connected integrated energy microgrid based on multi-agent game and reinforcement learning[J]. Automation of Electric Power Systems, 2019, 43(1): 40-48.
[20] Foruzan E, Soh L K, Asgarpoor S. Reinforcement learning approach for optimal distributed energy management in a microgrid[J]. IEEE Transactions on Power Systems, 2018, 33(5): 5749-5758.
[21] Ji Ying, Wang Jianhui, Xu Jiacan, et al. Real-time energy management of a microgrid using deep reinforcement learning[J]. Energies, 2019, 12(12): 2291.
[22] 孙博昭. 350MW超临界机组可调式蒸汽喷射器工业供热应用研究[D]. 北京: 华北电力大学, 2021.
[23] 刘鑫屏, 田亮, 王琪, 等. 供热机组发电负荷-机前压力-抽汽压力简化非线性动态模型[J]. 动力工程学报, 2014, 34(2): 115-121. Liu Xinping, Tian Liang, Wang Qi, et al. Simplified nonlinear dynamic model of generating load-throttle pressure-extraction pressure for heating units[J]. Journal of Chinese Society of Power Engineering, 2014, 34(2): 115-121.
[24] 田亮. 单元机组非线性动态模型的研究[D]. 保定: 华北电力大学, 2005.
[25] 田亮, 练海晴, 刘鑫屏, 等. 直流锅炉蒸汽压力与中间点温度耦合特性分析[J]. 中国电机工程学报, 2017, 37(4): 1142-1151. Tian Liang, Lian Haiqing, Liu Xinping, et al. Coupling characteristics of steam pressure and intermediate point temperature for once-through boiler[J]. Proceedings of the CSEE, 2017, 37(4): 1142-1151.
[26] Cheung T, Schiavon S, Parkinson T, et al. Analysis of the accuracy on PMV-PPD model using the ASHRAE global thermal comfort database II[J]. Building and Environment, 2019, 153: 205-217.
[27] Fu Wenfeng, Yang Xueming, Wang Lanjing, et al. Feedwater heating allocation optimization for large capacity steam turbine unit based on particle swarm optimization[J]. Journal of Energy Resources Technology, 2015, 137(4): 042005.
[28] 王柏育. 散乱数据拟合的一种无网格方法及其应用[D]. 长沙: 湖南大学, 2014.
[29] Mai-Duy N. Solving high order ordinary differential equations with radial basis function networks[J]. International Journal for Numerical Methods in Engineering, 2005, 62(6): 824-852.
[30] 王志强. 微分代数方程动态优化问题的快速求解策略研究[D]. 杭州: 浙江大学, 2012.
[31] 邓拓宇. 供热机组储能特性分析与快速变负荷控制[D]. 北京: 华北电力大学, 2016.
Abstract The technical reformation of self-provided combined heat and power (CHP) units by park enterprises can significantly improve their fast regulation capability. However, the dynamic process of the CHP unit is not finely modeled in the scheduling process, which makes it difficult for the scheduling scheme to match the operation state of CHP units. This paper proposed a combined electrical and heating system (CEHS) dynamic optimal scheduling method considering the state operation constraints of the park's self-provided CHP units.
In the park-type CEHS, the enterprise's self-provided CHP units are subject to the unified dispatching of the power grid, which supplies the enterprise's own power and part of the power for production and living in the radiation area. The shortage of power supply is met by the grid dispatching wind power and conventional thermal power units. The heat source of CHP unit exchanges heat with the first heating station to supply the internal heat load of industrial enterprises. Firstly, considering the characteristics of electric energy, flow, pressure and other state variables under the rapid regulation of CHP unit, the dynamic constraints of the unit in the form of differential algebraic equations (DAEs) are established.
Secondly, a CEHS dynamic optimization scheduling model considering the state operation constraints of the self-provided CHP units in the park is constructed. Aiming at the problem that CEHS dynamic optimization with DAEs constraints is difficult to solve, a dynamic adaptive particle swarm optimization (DAPSO)-radial basis quasi sequential bi-level optimization strategy is proposed. The outer layer optimizes the CEHS decision variables with the objective of minimizing the CEHS operation cost. The DAPSO algorithm is used to iteratively optimize the scheduling scheme to obtain the output of each unit. The electric and thermal output values of CHP units are taken as the setting values for dynamic optimization in the inner layer. The inner layer aims at minimizing the performance index of the control process of the CHP units. By guiding the output variables to approach the desired set value, the unit control process converges and the control variables are smoothed as much as possible. For the dynamic optimization problem of the optimal control of the inner unit, the radial basis function (RBF) format is used to discretize the variables, and the discretized nonlinear programming problem is solved by the quasi sequential method.
Finally, the correctness and effectiveness of the proposed method were verified based on the improved IEEE30 node system. The simulation results show that the wind power consumption capacity of the system can be improved after fully considering the control characteristics of CHP units. The flexibility of CHP unit modification provides the possibility for enterprise self-provided power plants to realize auxiliary services to the grid. The data show that the bi-level solution strategy of outer DAPSO optimal scheduling + inner quasi sequential method (RBF discrete format) dynamic optimization is a good balance of computational efficiency and solution accuracy. The optimal scheduling of CHP unit dynamic modeling has obvious advantages in system economy and unit safety.
keywords：Combined electrical and heating system, state operation constraints, radial basis function, quasi-sequential method, bi-level dynamic optimization
DOI:10.19595/j.cnki.1000-6753.tces.220910
中图分类号：TM732
国家自然科学基金项目（52007103）、湖北省科技重大专项项目（2020AEA012）和三峡大学学位论文培优基金项目（2021BSPY013）资助。
收稿日期 2022-05-26
改稿日期 2022-12-22
黄悦华 男，1972年生，教授，博士生导师，研究方向为智能电网，新能源微电网、综合能源系统。E-mail：hyh@ctgu.edu.cn
张 磊 男，1986年生，博士，副教授，研究方向为大规模新能源接入电力系统的优化调度。E-mail：leizhang3188@163.com（通信作者）
（编辑 赫 蕾）