
图1 城市轨道交通供电系统
Fig.1 Urban rail transit power supply system
摘要 直流牵引供电系统杂散电流产生的直流干扰问题日趋严重。为研究杂散电流的干扰程度,将直流牵引供电回流系统与杂散电流扩散模型进行联合仿真。考虑段场与正线之间的互相影响,建立段场集中点电流源泄漏与正线沿线钢轨分布式泄漏共同作用下的动态杂散电流在分层介质中的扩散模型。提出分层模型的精细积分主元加权迭代方法,从而避免一般方法求解失败的问题,实现高精度、高效率求解分层格林函数。以中国实际地铁工程为例,采用该文模型对段场的杂散电流和附近土壤地表电位梯度的现场测试进行过程还原,实测与仿真结果误差在8.46%以内。直流牵引供电系统正线与段场之间采用阻断式连接方案,可使得附近土壤的地表电位梯度降低46.53%。
关键词:直流牵引供电系统 钢轨电位 杂散电流 扩散模型 联合仿真
直流牵引供电系统杂散电流问题由来已久,且日益凸显。在地铁列车实际运行过程中,多列车移动负荷随时间动态变化,引起全线杂散电流动态变化,造成地铁沿线附近地电位不断波动。对埋地金属结构、油气管道的直流干扰问题逐渐突出。
众多学者对轨道交通杂散电流的沿线分布特性进行了研究。如基于电阻网络的方法,建立将各金属结构、道床及大地等效成电阻和过渡电阻的电路模型,并推导出各金属结构电压、电流的解析表达式[1-2]。在直流牵引轨道电位和杂散电流分析中应考虑回流系统采用固定电流和直流电阻性参数进行计算分析[3]。实际运行过程中,多牵引变电所并列运行,多列车移动负荷随时间动态变化,引起全线钢轨电位、杂散电流动态变化,造成地铁沿线附近地电位不断波动,埋地金属结构受到的腐蚀也随之变化[4]。
文献[5-6]认为采用走行轨回流的直流牵引供电系统存在轨道电位与杂散电流问题,给城市轨道交通安全运行带来隐患。提出一种基于可变电阻模块的电力电子动模实验平台,采用双向可变电阻模块模拟列车运行工况,结合牵引变电站接地方式,模拟杂散电流和钢轨电位分布的研究逐渐受到关注。
文献[7-8]对电力系统传统潮流算法进行了改进,提出基于诺顿等值的多平衡节点处理方法。该方法既能解算具有多个平衡节点的同一电网潮流问题,又能够同时解算相互解列的、各自内部具有多个平衡节点的不同子网潮流问题。Y. S. Tzeng和C. H. Lee搭建了台北地铁的Simulink线路仿真[9],Simulink平台的搭建主要通过电子元件的组合,实现一个可变或者动态的杂散电流评估。
文献[10]对多区间多列车并列运行情况下电流跨区间传输现象进行分析,理论研究了电流跨区间传输对钢轨电位的影响。文献[11]建立了钢轨电位限制装置和段场等效电路的通用模型,并提出计及回流设备行为过程的直流牵引供电计算方法。为了治理埋地金属结构的电化学腐蚀问题,需要确定杂散电流干扰范围和影响程度,并采取相应的防治措施。
为了准确高效地计算城市轨道交通长线路杂散电流,基于CDEGS软件提出一种长线路杂散电流仿真建模方法[12]。在杂散电流电阻网络模型和电流场分布公式的基础上,提出基于地表电位梯度的地铁杂散电流动态干扰范围评估模型[13]。
I. Cotton等系统地介绍了杂散电流对埋地管道、扣件系统、第三方建筑的腐蚀机理。多数学者通过CDEGS软件工具对电气工程进行建模,解决电力系统接地、电磁场、电磁干扰等问题。I. Cotton、C. Charalambous等利用MALZ模块对杂散电流进行建模,分析了不同影响因素[14]。
对于病态代数方程的求解,H. J. Kim等通过改善病态方程的条件给出一种无需迭代运算的求解方法[15]。富明慧等利用精细积分法的思想,通过改良病态矩阵,提出了病态代数矩阵求逆的精细积分方法[16]。S. M. Rump通过引入摄动矩阵提出一种求解病态矩阵逆的迭代法[17]。潘卓洪等提出多精度多分辨率法计算格林函数,从而求解地表电位分布[18]。
综合国内外研究文献来看,目前的研究主要集中在回流系统建模和杂散电流防护等方面,影响钢轨电位与杂散电流的因素众多,但未考虑段场与正线叠加对杂散电流分布和扩散的影响。本文研究综合考虑段场和正线的多列车复杂运行工况下的杂散电流分布特性和在大地的扩散问题,将回流系统与杂散电流扩散模型进行联合仿真。回流系统通过分布参数与集中参数进行等效替换,采用节点电压法进行供电计算,得到线路跨区间钢轨电位和杂散电流泄漏分布;考虑介质分层情况,提出分层模型的精细积分迭代方法,建立杂散电流在地中电位分布的模型,获得地表电位梯度随时间动态变化过程。结合国内实际线路的工程案例,对比实测与仿真的钢轨电位和地表电位梯度分布过程,讨论了正线与段场之间的不同连接方式对直流干扰传播过程的影响。
传统的杂散电流模型计算中只考虑某一时刻的分布结果。杂散电流计算不仅需要耗费大量的计算内存,而且列车取流与位置均在动态变化,无法实现动态评估。本文所提的将回流系统与杂散电流扩散模型进行联合仿真,不仅可以动态评估某一时间段的动态杂散电流,并且可以减小计算代价,得到高精度高效率的计算结果。
城市轨道交通回流系统主要包括牵引变电所、列车、钢轨、排流网和段场等,如图1所示。当段场内的列检库钢轨采用直接接地或者维修中接触网和钢轨之间悬挂临时地线时,段场钢轨将接地。

图1 城市轨道交通供电系统
Fig.1 Urban rail transit power supply system
正线与段场之间的钢轨设置钢轨绝缘节,其两端并联连接装置(Connecting Device, CD)。现有CD主要包括:单向导通装置和响应式触发装置(该装置在正常运行时,阻断正线和段场钢轨电气连接;列车到来时,短暂闭合导通)。
在对回流系统进行建模时,采用“钢轨、排流网、地”的三层网络模型。钢轨与大地存在过渡电阻,为模拟钢轨电位与杂散电流情况,通过π型单元电路纵向连接,回流系统分布式电路等效模型,对应切面的位置为x1~xN,如图2所示。图中,rr为单位长度钢轨纵向电阻,rs为单位长度排流网纵向电阻,rrs为单位长度钢轨对排流网电阻,rse为单位长度排流网对地电阻。
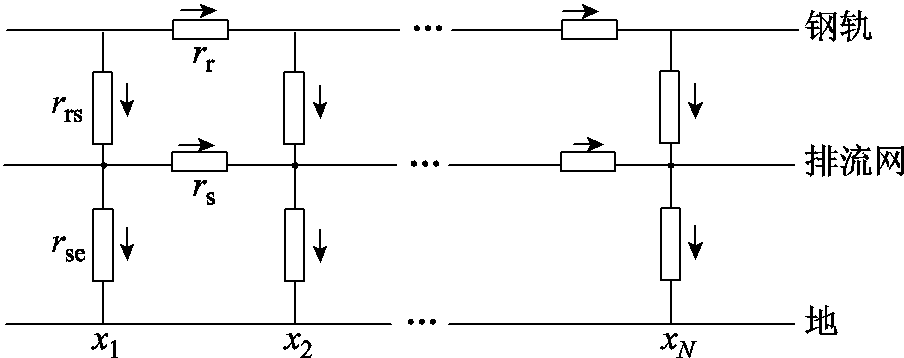
图2 正线钢轨、排流网、地回路分布式电路模型
Fig.2 Distributed circuit model for mainline rail, stray current collection network and ground loop
采用文献[3]的钢轨、地回路集中参数等值方法,可将切面的位置x1~xN等效为xj-1和xj之间钢轨、地回路集中参数电路,如图3所示。
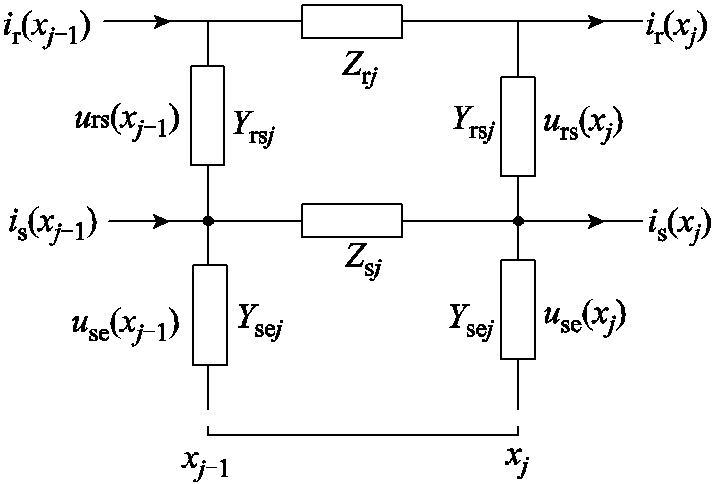
图3 集中参数等效电路
Fig.3 Equivalent circuit of centralized parameters
图3中,ir(xj-1)、ir(xj)是在xj-1、xj处的钢轨电流。is(xj-1)、is(xj)是在xj-1、xj处的排流网电流。urs(xj-1)、urs(xj)是在xj-1、xj处的钢轨对排流网电压。use(xj-1)、use(xj)是在xj-1、xj处的排流网对地电压。Zrj是xj和xj-1之间钢轨的等效纵向电阻。Zsj是xj和xj-1之间排流网的等效纵向电阻。Yrsj是xj和xj-1之间钢轨对排流网的等效电导。Ysej是xj和xj-1之间排流网对地的等效电导。其表达式分别为
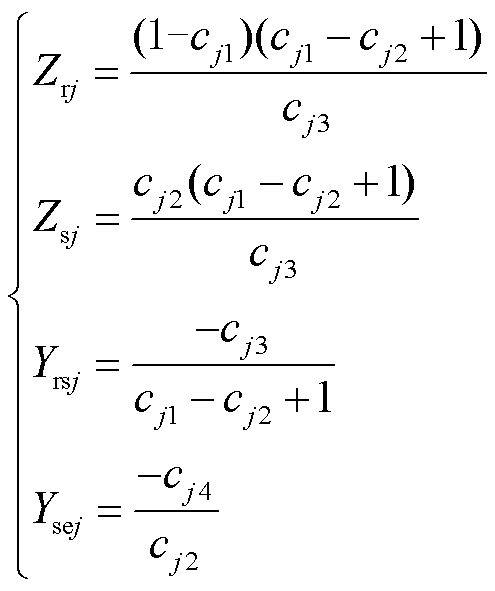 (1)
(1)
式中,cj1~cj4只与单位长度钢轨、地回路分布式参数及距离有关。
段场与正线之间通过CD连接,也将影响全线的钢轨电位和杂散电流分布。段场在直流牵引供电系统的建模如图4所示。图中,R1为出入线与正线间连接钢轨的纵向电阻;Rz1、Rz2分别为咽喉区和库前CD的等效电阻;R2为咽喉区CD与库前CD间的钢轨电阻;R3为库前CD与段场末端间的钢轨电阻;Rd1、Rd2、Rd3为相应区段的钢轨对地过渡电阻;R0为段场末端采用不同钢轨接地方式下的钢轨对地电阻。
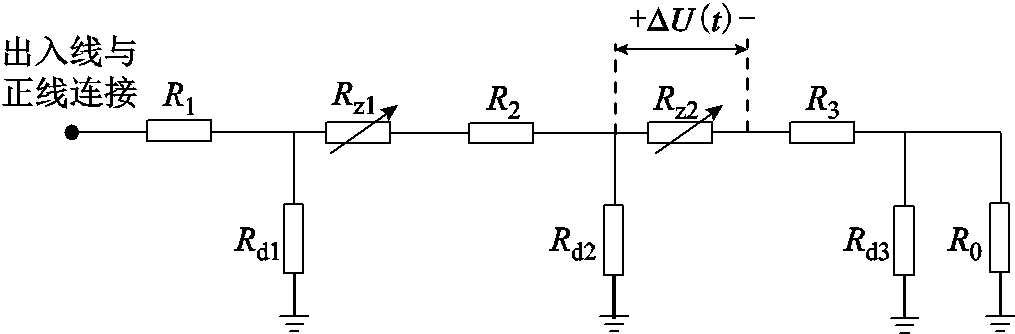
图4 段场等效电路模型
Fig.4 Equivalent circuit model of depot
将回流系统分布式参数模型转换为集中参数模型,建立回流系统集中参数等值网络,由链式电路可得,对应切面的编号为切面0~m+n+2,如图5所示。在线路起点和线路终点间,某一特定时间有n个牵引变电所整流机组, m个列车。线路起点为切面0,终点为切面m+n+2,以列车或牵引所为节点分界面,切面n为第n个节点位置,相邻两个节点为一个区间,共有m+n+3个区间,不同切面的位置用xj表示。列车等效为功率源,牵引变电所用诺顿定理等效。
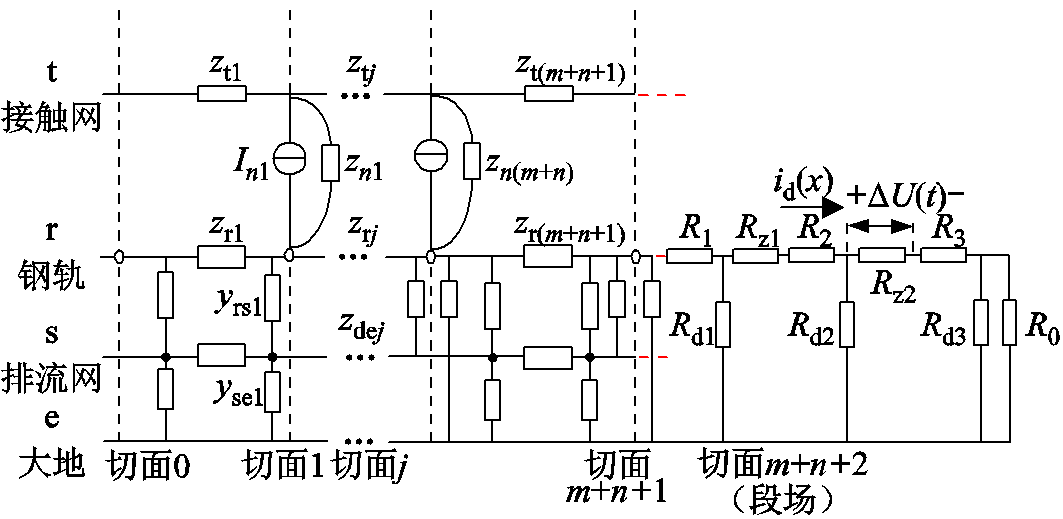
图5 牵引供电系统回流链式电路模型
Fig.5 Reflux chain circuit model of traction power supply system
图5中,t代表接触网,r代表钢轨,s代表排流网,e代表大地。Ztj是xj和xj-1之间接触网的等效纵向电阻。In(m+n)、Zn(m+n)分别为第m+n切面下列车的等效电流源和等效阻抗。系统等效为集中参数后,基于各接口之间的变化关系得链式电路构成的节点电压方程为
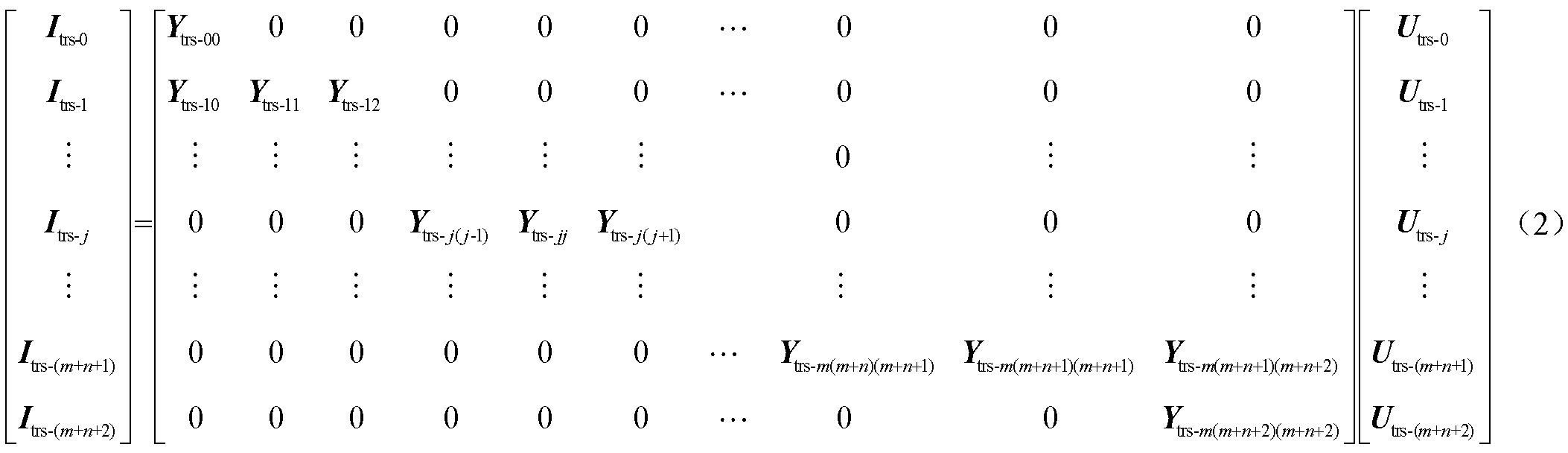
式中,Itrs-j为节点注入电流元素,Itrs-j= [Itj Irj Isj]T;Utrs-j为节点电压元素,Utrs-j= [Utj Urj Usj]T;Ytrs-jj为自导纳矩阵;其他元素为互导纳矩阵。
为了研究正线和段场动态杂散电流在土壤的电位分布,建立杂散电流在分层介质中的扩散模型。地铁杂散电流在双层介质中的扩散模型如图6所示。第一层介质为混凝土层,钢轨置于混凝土层表面,排流网在混凝土层;第二层介质为土壤层。

图6 杂散电流在分层介质中的扩散模型
Fig.6 Diffusion model of stray current in layered media
轨道交通回流系统杂散电流源包括沿线正线排流网向地中泄漏的电流和段场作为点电流源向地中泄漏的电流。基于点电流源在分层介质中的地电位分布,采用叠加原理,可以得到正线和段场泄漏的杂散电流在任意土壤层位置的电位分布。
当电路表示为如图3所示的集中电路时,在xj线路位置处,如式(3)所示,ir(xj)与ir(xj+(n-1)dx)的关系可以用ir(xj), is(xj), urs(xj), use(xj)表示。将式(3)进行还原全线钢轨电位分布。
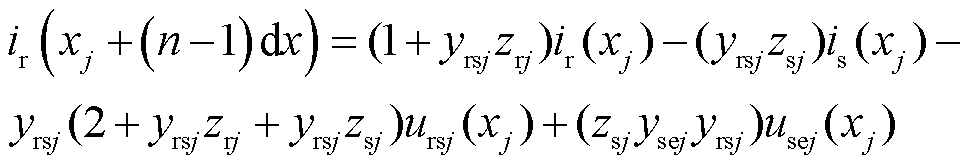 (3)
(3)
假设段场的坐标为(xdp, ydp, 0)。段场泄漏的电流造成的地电位 分布的计算公式[19]为
分布的计算公式[19]为
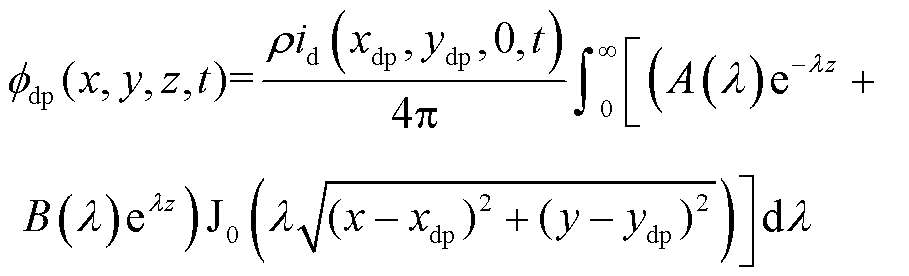 (4)
(4)
式中,ρ为第二层土壤电阻率(土壤层)(Ω·m);id(xdp, ydp,0, t)为t时刻、段场坐标为(xdp, ydp, 0)向地中泄漏的电流(A);J0(·)为第一类零阶贝塞尔函数;(x, y, z)为所求电位点坐标; l为控制精度常数;z为计算距离(m);A、B为待定系数。
沿线排流网泄漏电流产生的地电位分布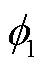 ,源点在混凝土层,场点在土壤层时的格林函数为
,源点在混凝土层,场点在土壤层时的格林函数为
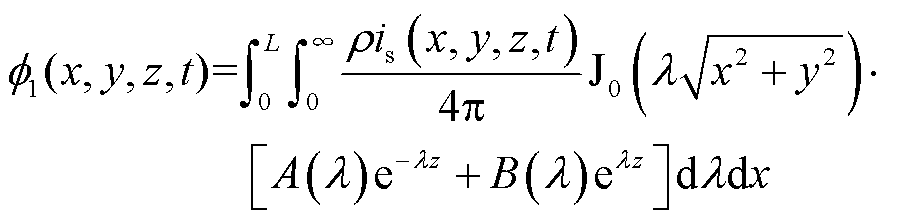 (5)
(5)
式中,is(x, y, z, t)为在t时刻、任意x位置、dx长度上排流网向地中泄漏的电流(A);
根据叠加定理,正线泄漏的杂散电流与段场杂散电流在土壤层中地电位分布叠加后为
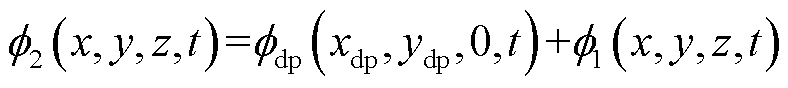 (6)
(6)
将式(5)进行李普希兹积分,可得杂散电流在土壤层中任意位置地电位分布。
在分层模型中,利用Prony法求解格林函数中A(λ)、B(λ)的过程中面临严重的病态矩阵求逆问题,将病态问题转换为易解的良性问题显得格外重要。主元加权的权重由加权因子q和加权矩阵P决定,对各个主元叠加不同的权值,从而更好地降低条件数。
设求解B(λ)时的病态矩阵为B,B为n阶正定矩阵,利用主元加权对其进行改善[20]。
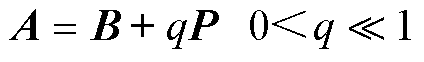 (7)
(7)
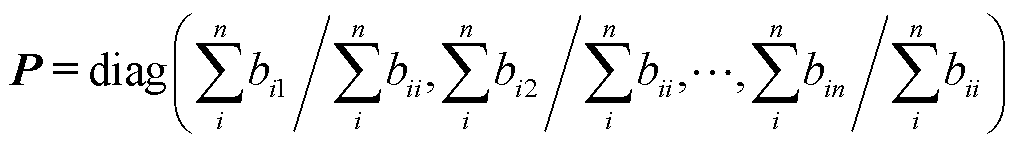 (8)
(8)
可以得出
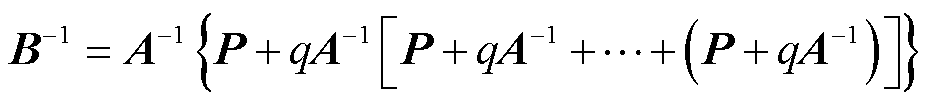 (9)
(9)
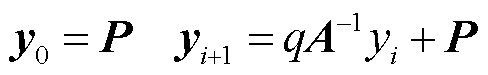 (10)
(10)
可得
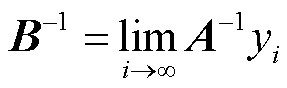 (11)
(11)
对于A求逆,I为n阶单位矩阵,有
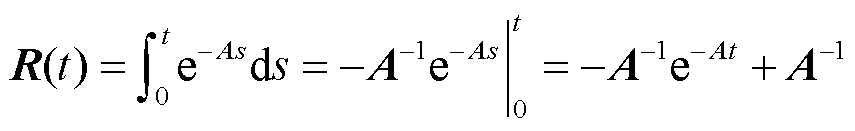 (12)
(12)
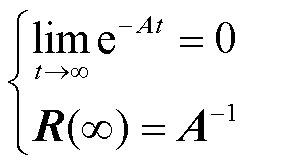 (13)
(13)
 (14)
(14)
取时间常数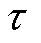 ,即
,即
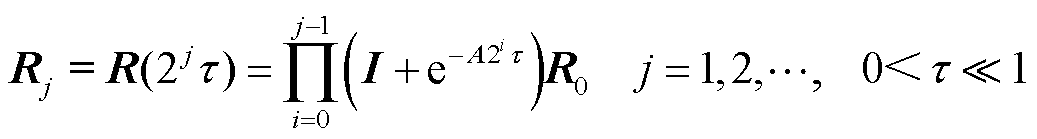 (15)
(15)
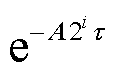 可由精细积分法计算,将其泰勒展开,有
可由精细积分法计算,将其泰勒展开,有
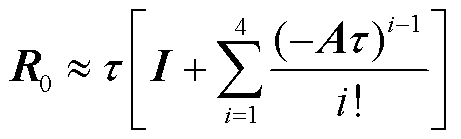 (16)
(16)
 (17)
(17)
可得迭代式(18)。
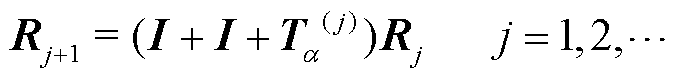 (18)
(18)
根据式(18),当j足够大,可得A-1,代回式(11)得到B-1。
回流系统杂散电流的分布与扩散的联合仿真计算步骤见表1。
表1 联合仿真计算过程
Tab.1 Co-simulated calculation process

序号联合仿真主要步骤 1t时刻,扫描列车运行图,得到列车位置和功率的分布。输入第一层混凝土层电阻率、第二层土壤层电阻率、控制精度常量l、计算点坐标(x0, y0, z0)等,设迭代次数it=1。 2初始化供电系统计算参数,设置潮流计算收敛精度x。 3扫描全线元件,根据整流机组、段场、CD等t时刻状态,形成式(2)的节点导纳矩阵。 4根据求解得到的各节点电压、支路信息等,判断各误差是否满足收敛精度x,计算误差大于x,根据当前列车网压,按照功率源模型更新列车电流,回到步骤3,it=it+1。 5判断列车节点电压是否达到车载制动电阻启动电压Uon。若达到,启动车载制动电阻,返回步骤3,it=it+1;否则退出循环,系统求解已收敛。 6将t时刻潮流计算结果代入多区间联合的分布模型计算钢轨电压和杂散电流分布计算t时刻沿线钢轨电位和杂散电流分布。确立不同位置的边界条件。 7根据式(2)链式电路构成的节点电压方程结算各点钢轨电位和支路电流分布,采用式(5)计算杂散电流的扩散模型;输入q、、P控制精度,求得土壤层中任意位置电位分布,计算t时刻下(x0,y0,z0)地表电位梯度叠加后的模。 8判断是否达到仿真结束时刻,若是,直流牵引供电回流系统与杂散电流扩散联合仿真计算模型仿真结束;否则t=t+1,返回步骤6。 9联合仿真计算完成。
为研究计算方法的有效性,在户外场地埋设裸露铜制导线,实测裸露导线沿线地表电位分布,并与计算结果进行对比。测试原理如图7所示,导线铺设长度为30 m,中间间隔1 m,左右两部分均存在5°偏折,裸露导线埋地总长度为29.11 m,埋地深度为0.1 m。裸露导线直径为0.05 m,相对电阻率为0.018 25,相对磁导率为1。土壤的分层参数为第一层土壤电阻率为60 Ω·m,深度为3 m;第二层土壤电阻率为35 Ω·m,深度为无限。
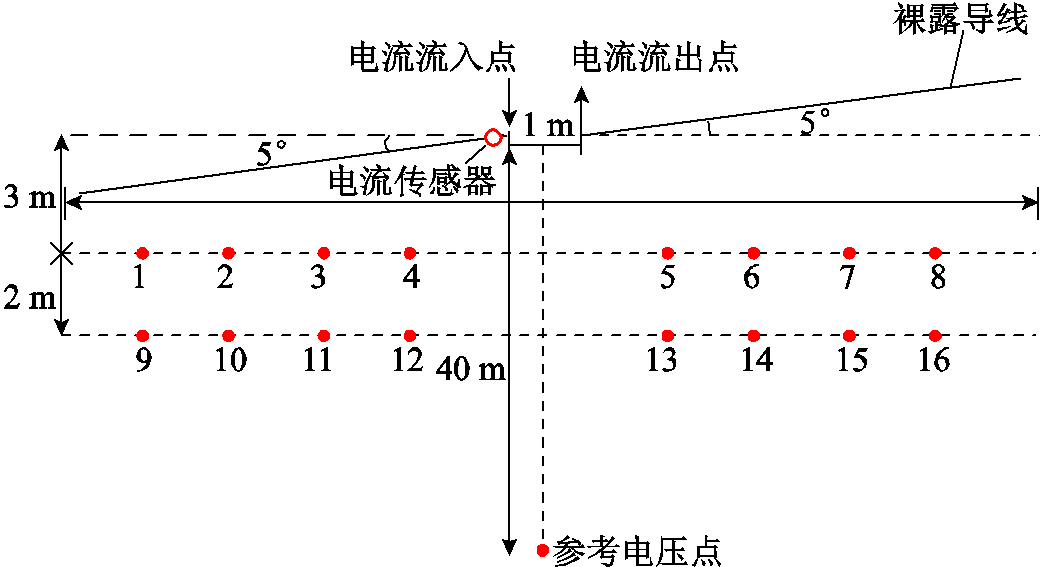
图7 测试原理
Fig.7 Test schematic diagram
电压测试点如图7所示,利用硫酸铜电极作为参比电极,对各个点的地表电位进行测量。计算范围取30 m×30 m。
实测结果和仿真计算结果如图8和图9所示,裸露导线分别通以3 A和4 A稳定电流,曲线为杂散电流扩散模型中计算出的仿真电位分布。平均误差为6.98%,可以看出,计算与实测的结果有很好的一致性,杂散电流扩散模型有很高的准确性。

图8 通入3 A电流地表电位分布
Fig.8 Surface potential distribution of the current injecting 3 A
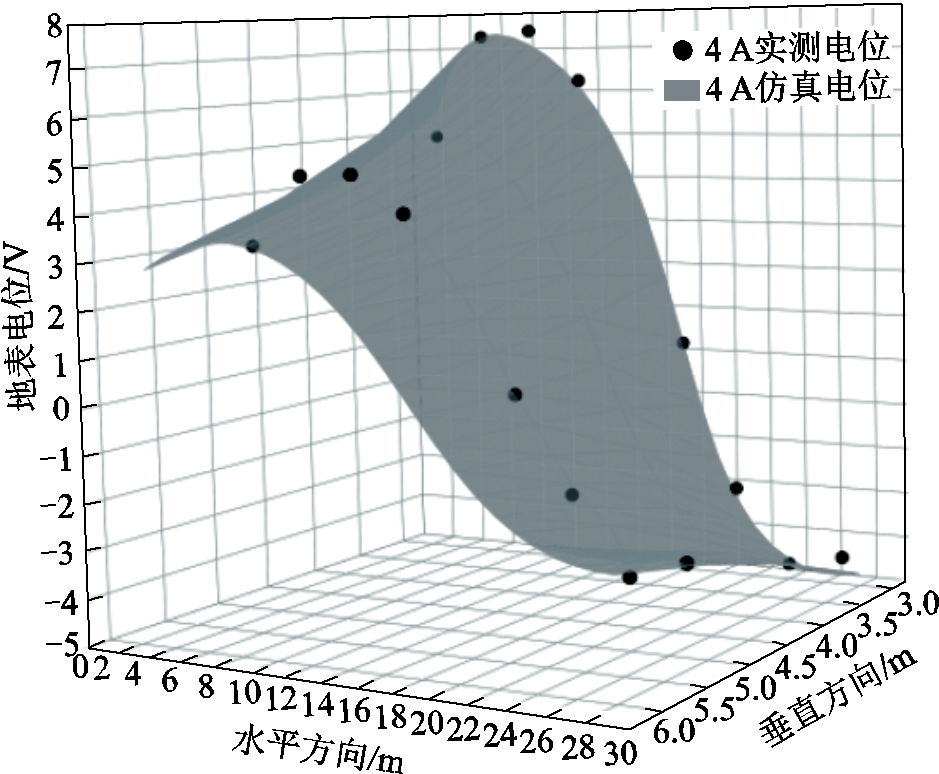
图9 通入4 A电流地表电位分布
Fig.9 Surface potential distribution of the current injecting 4 A
本文精细积分主元加权迭代法取q=10-9,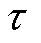 =10-12。与其他算法进行对比,结果见表2。
=10-12。与其他算法进行对比,结果见表2。
表2 本文结果与其他算法对比
Tab.2 Comparison of the results of this paper with the results of other algorithms

算法绝对误差迭代次数 本文方法1.6×10-103 文献[16]的精细积分法7.4×10-732 文献[18]的多精度多分辨率法2×10-85
由表2的实验结果可以看出,本文算法精度与迭代次数均优于精细积分法和多精度多分辨率法。
以国内某实际地铁线路为例,通过实测和模型分析地铁沿线杂散电流的分布和扩散过程。该线路全长24.124 km,采用DC 1 500 V接触轨授流,钢轨回流。全线共设置13个车站,1段1场,车站线路图与车辆段A位置如图10所示。其中,车辆段A位于车站13附近,与正线交界处为21.44 km处。在车辆段的东南方向6.52 km处,B点处设立地表电位梯度监测点。该地轨道交通线路少,附近也无其他高压直流输电线路,可忽略其他直流电流泄漏对测试点B的直流干扰影响。
段场咽喉区单向导通装置测试原理及电流参考方向如图11所示。在图10中的A点,监测车辆段A咽喉区单导正线一侧对地电压、车辆段一侧对地电压和单导电流如图11所示。监测过程中,A、B点监测采用GPS对时,各信号同步监测。
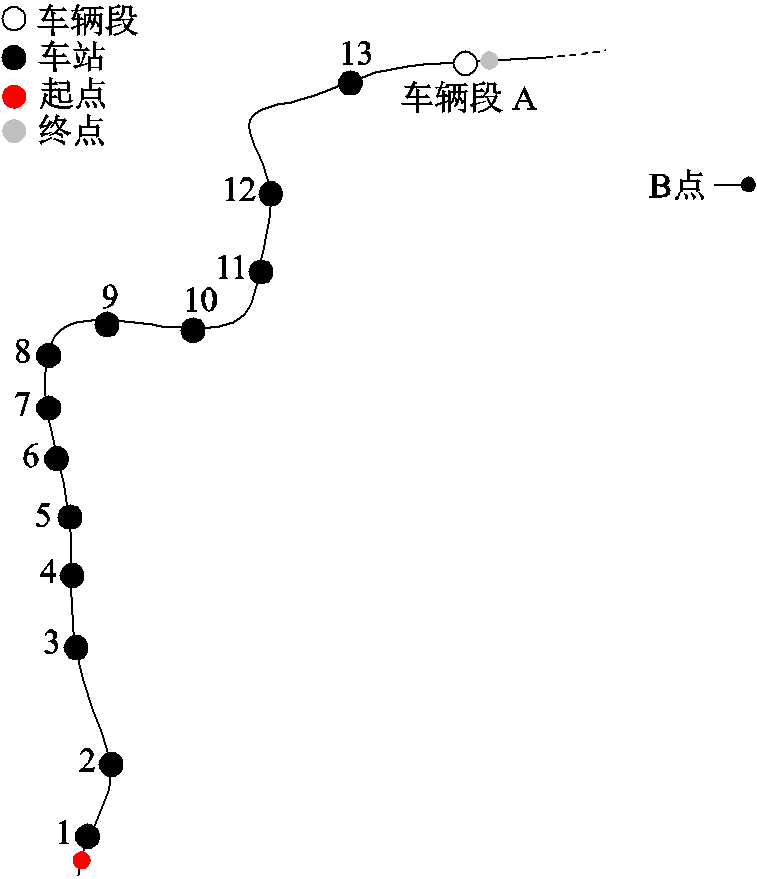
图10 车站线路图与车辆段A位置
Fig.10 Station route map and location of depot A
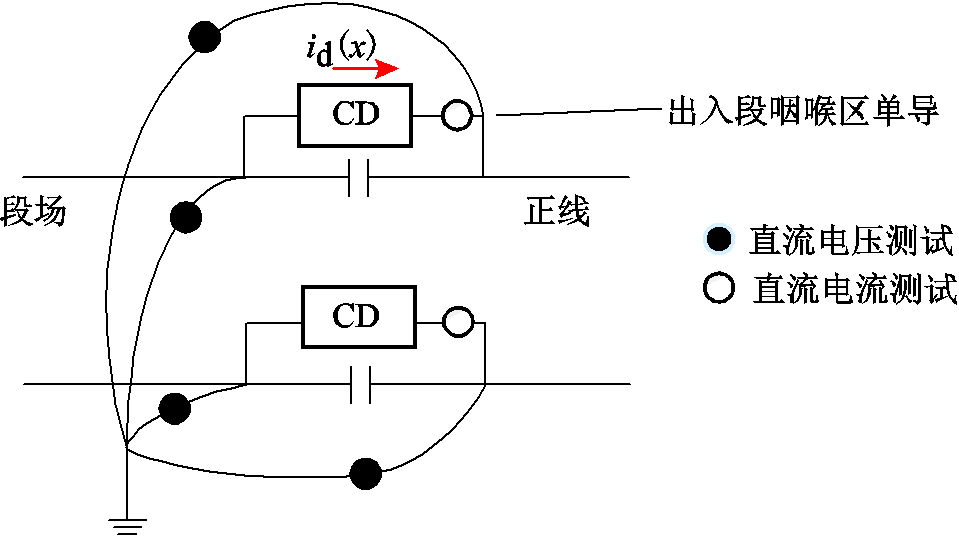
图11 段场咽喉区单向导通装置测试原理及电流参考方向(咽喉区流入正线为正)
Fig.11 Test principle and current reference direction of the unidirectional connection device in the throat area of the depot (positive direction of inflow to the mainline in the throat area)
实验中设计了两种工况:Case1,单向导通装置投入,监测时间为17:00—18:00;Case2,移除单向导通装置的二极管支路和晶闸管支路熔断器,实现车辆段与正线之间钢轨的电气阻断,监测时间为次日的17:00—18:00。
监测17:00—18:00时CD处的电流(咽喉区流入正线为正方向)、B点的地表电位梯度,结果如图12~图14所示。Case1情况下,咽喉区流入正线电流与B点地表电位梯度模波动明显,具有相同趋势。Case1中实测咽喉区流入正线电流绝对值最大达351.58 A,B点地表电位波动在4.12~7.26 mV/m范围内;Case2实测B点地表电位梯度模波动较小,在3.62~3.88 mV/m范围内。
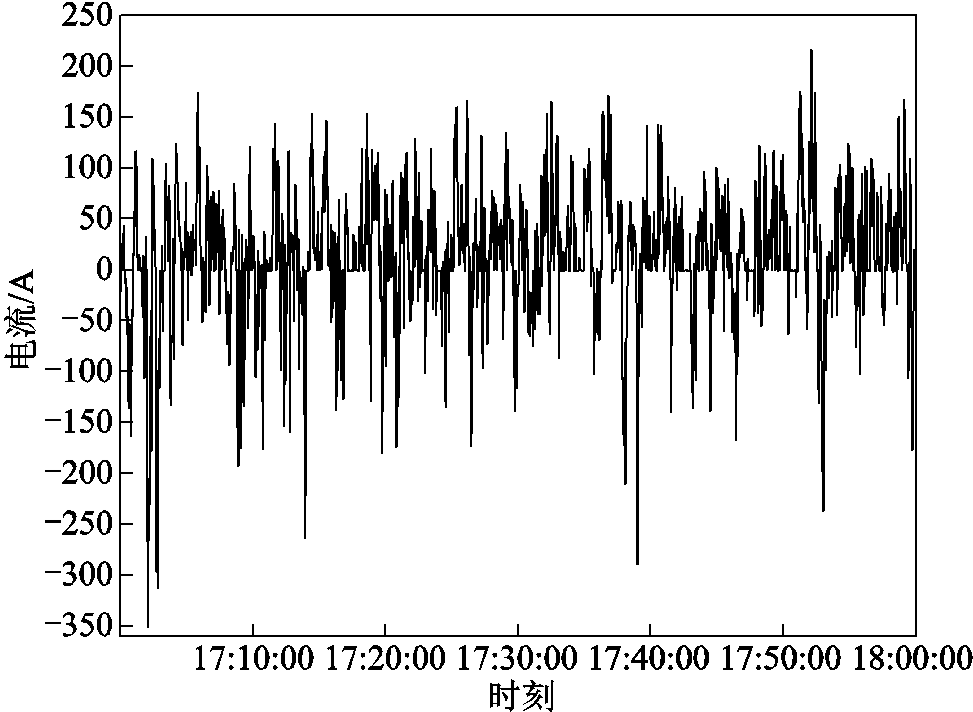
图12 Case1实测咽喉区流入正线电流
Fig.12 Case1 measured inflow positive current in throat area
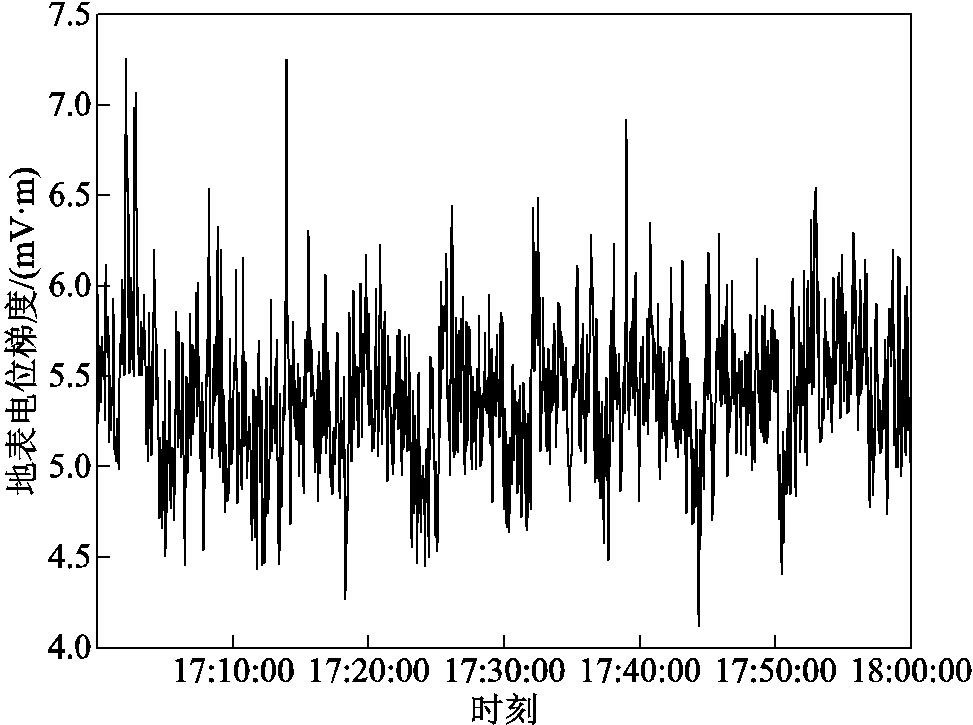
图13 Case1实测B点地表电位梯度模
Fig.13 Case1 measured surface potential gradient mode at point B
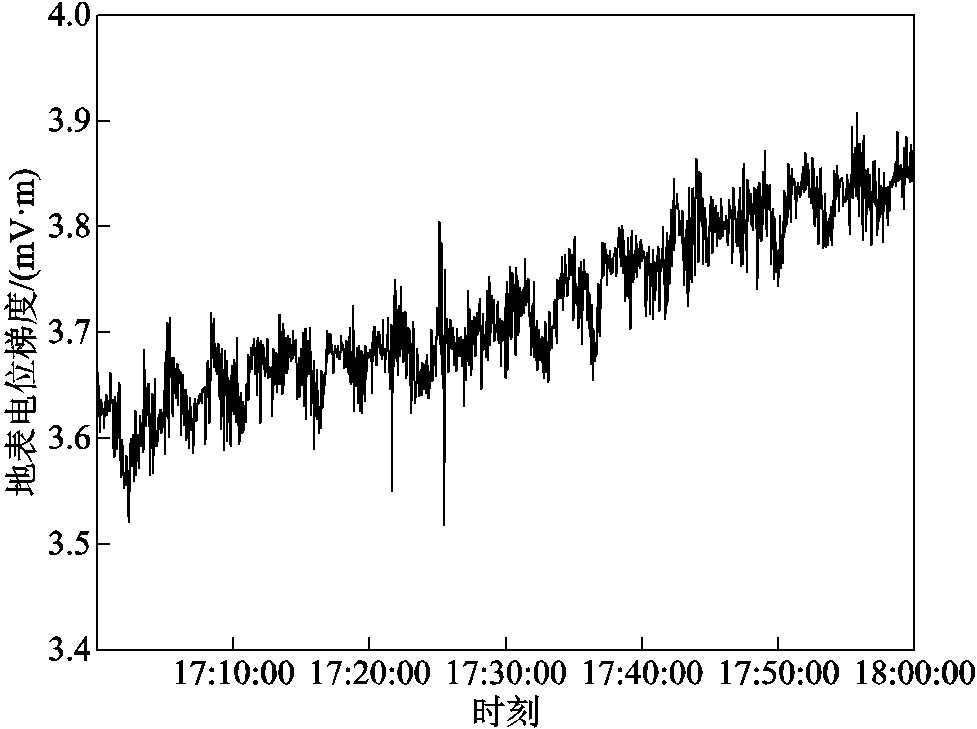
图14 Case2实测B点地表电位梯度模
Fig.14 Case2 measured surface potential gradient mode at point B
5.3.1 计算条件的确定
列车运行过程采用实际运行图还原实际情景。抽测了该段线路正线的部分区间和段场的钢轨对地过渡电阻,该段线路轨道区间经过了钢轨扣件污染清理、排除道床积水等措施,钢轨对地过渡电阻提高到了16.556 Ω·km[21]。段场附近的土壤电阻率经过测试为58.4 Ω·m。
采用本文提出的直流牵引供电回流系统与杂散电流扩散的联合仿真计算方法还原实验现场情况。列车采用6辆编组B型车,4动2拖,最高速度100 km/h,发车间隔360 s,上下行列车运行曲线如图15所示。假设测试这两日,相同时间段列车的运行情况相同。
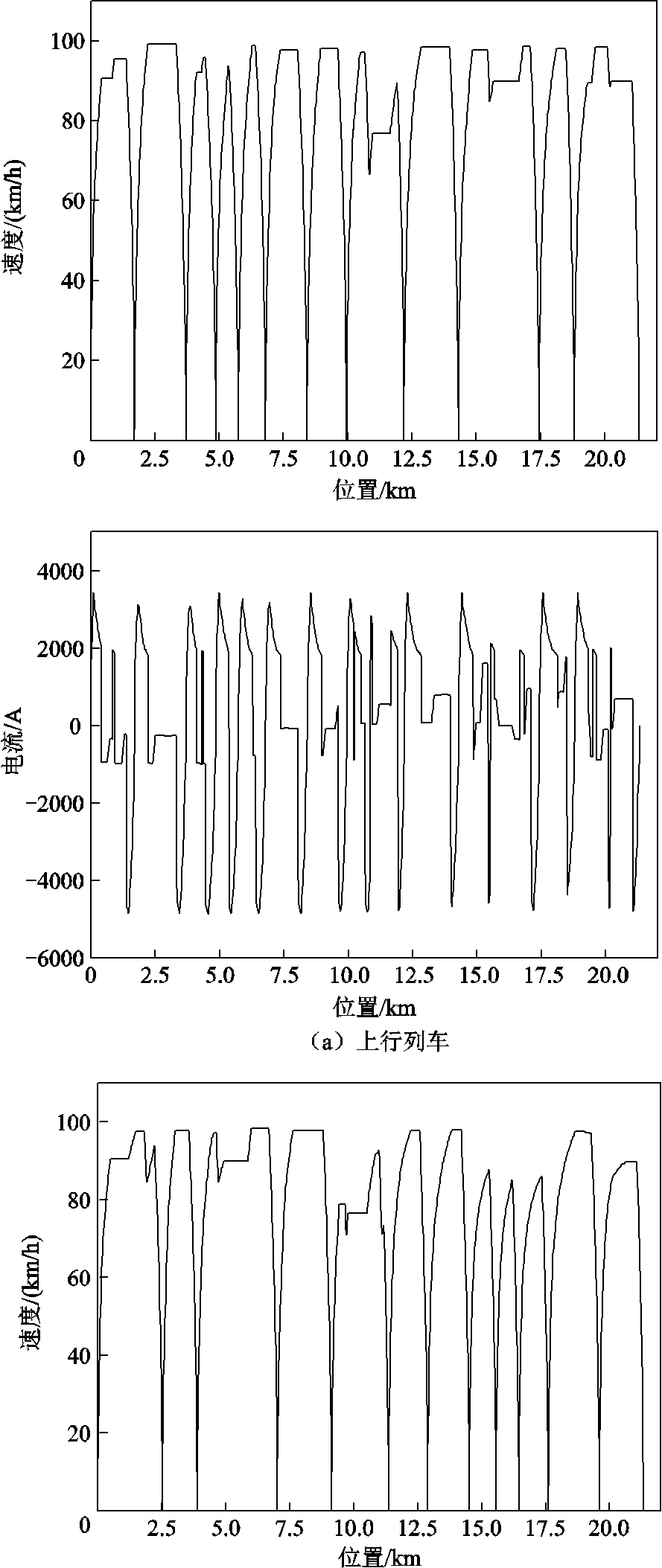
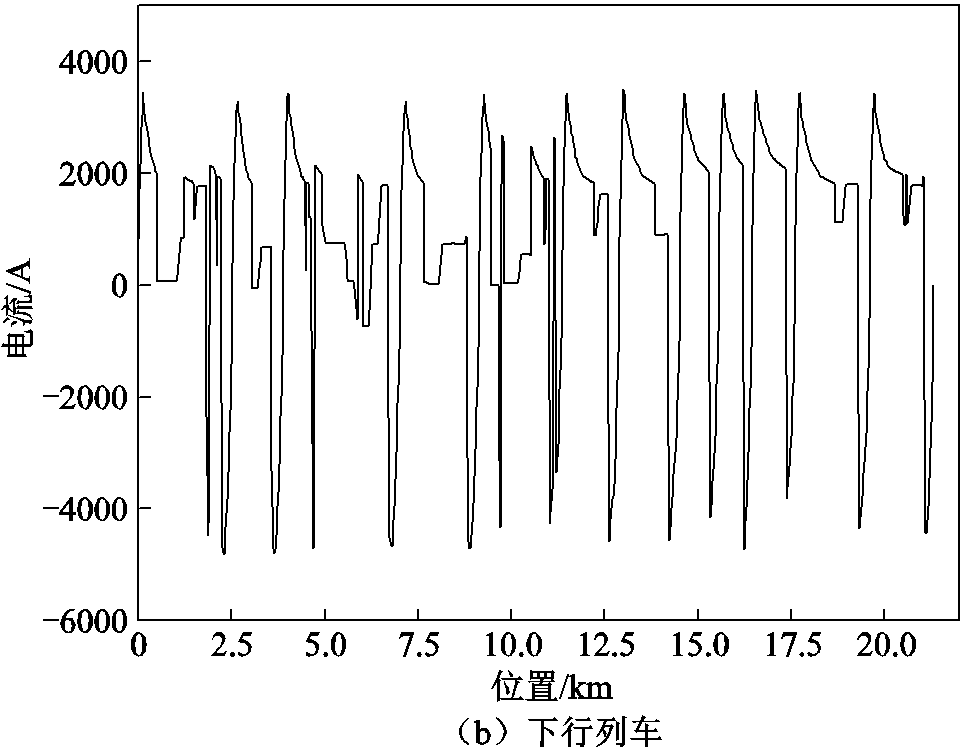
图15 上下行列车运行曲线
Fig.15 Running curves of up-and-down trains
本文选取每个切面以1~200 m作为剖分单位间隔范围,讨论本文方法与现有方法剖分单位间隔的变化对地电位梯度计算中精度和效率的影响。选取1、50、100、150和200 m作为系统剖分间隔。抽取17:10:00—17:11:00的地电位梯度实测结果进行对比,最大误差为仿真结果与实测的最大偏差,结果如图16所示。
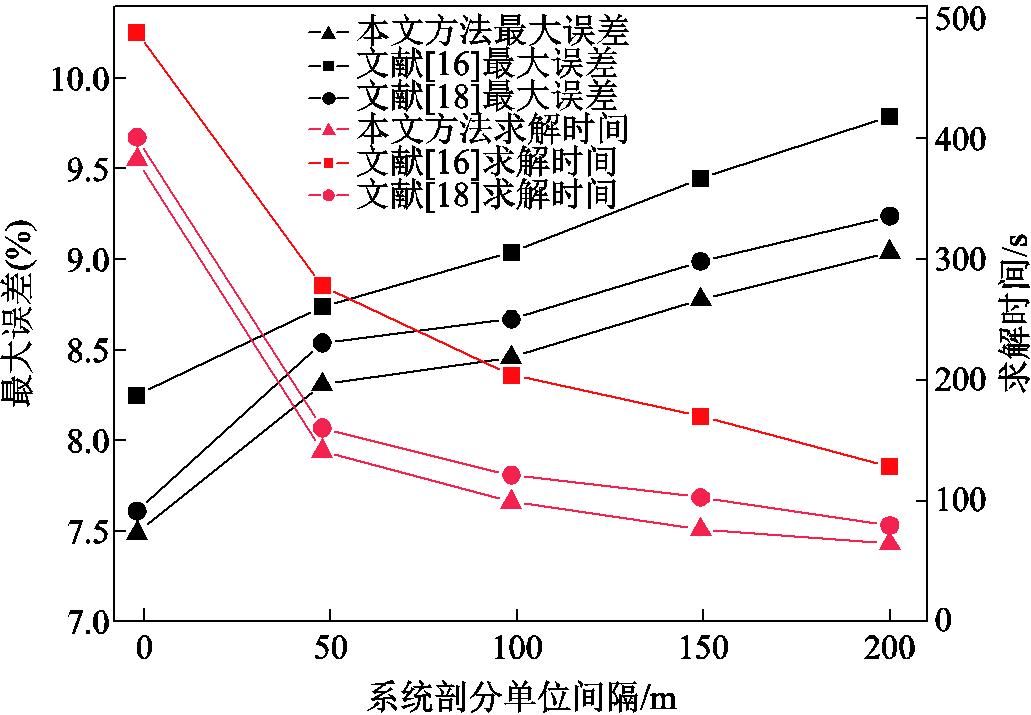
图16 剖分单位间隔对最大误差与求解时间
Fig.16 Maximum error and operation time of interval pair of subdivision elements
随着剖分单位间隔的增大,三种方法的计算结果与实测之间的最大偏差都呈增大趋势,当最大剖分单位间隔小于200 m时,最大偏差均小于10%。当系统剖分间隔为100 m时,求解时间是系统剖分间隔1 m的3.91倍。考虑到列车(注入电流源)车长影响、计算效率等因素,本文后续分析的剖分单位间隔设为100 m。本文方法通过主元加权再进行精细积分迭代,有效降低迭代次数,在格林函数的求解精度和效率上均高于文献[16]的精细积分法与文献[18]的多精度多分辨率法。
5.3.2 Case1情况下
采用该线路实际运行图模拟多列车运行情况,使用本文提出的回流系统与杂散电流扩散的联合仿真模型,还原测试过程。以其中一段地表电位梯度最严重的结果(17:01:01—17:07:00)为例,咽喉区单导电流实测结果与仿真数据对比如图17所示。由图17可知,咽喉区最大流入正线电流达106.62 A,最小流入正线电流达-330.28 A。当单向导通装置导通时,正线和段场连通导致钢轨电位保持一致,大量电流经由单向导通装置及维修接地支路流入车辆段地网形成杂散电流。
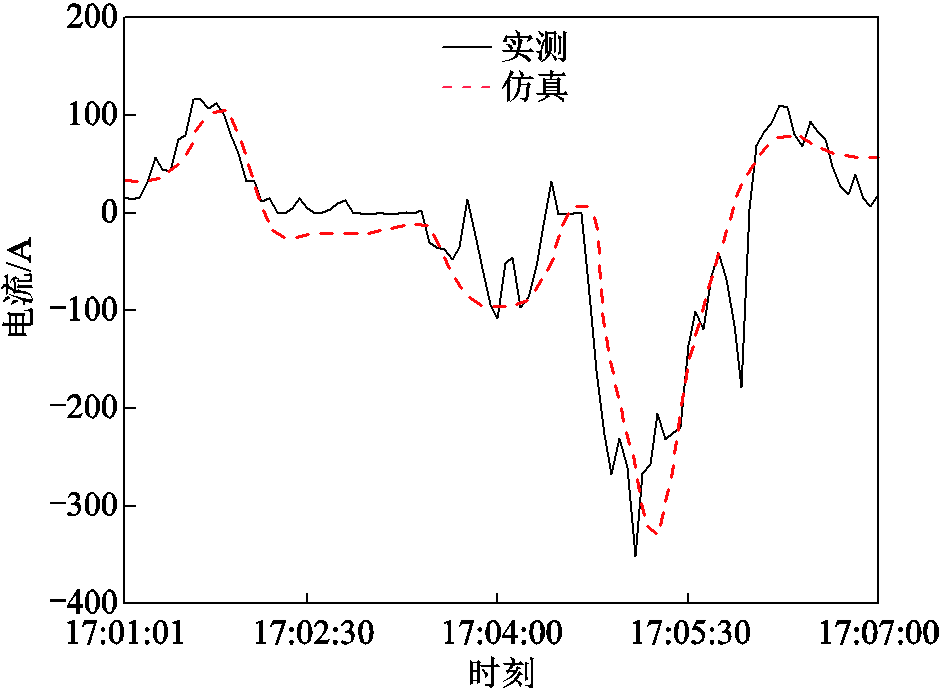
图17 Case1咽喉区单导电流对比(360 s)
Fig.17 Comparison of unidirectional connection device current in the throat area of Case1 (360 s)
B位置处的地表电位梯度实测结果与仿真结果对比如图18所示,最大地表电位梯度模为6.77 mV/m,最小地表电位梯度模为4.87 mV/m。当地表电位梯度大于5 mV/m时,杂散电流的程度强。
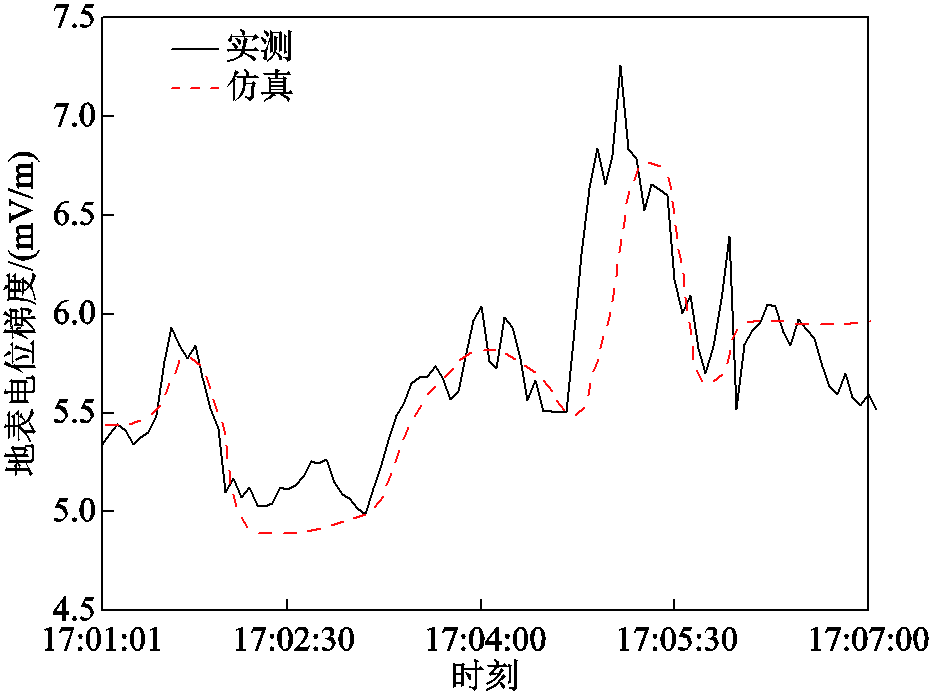
图18 Case1 B点地表电位梯度模对比(360 s)
Fig.18 Comparison of surface potential gradient mode at point B of Case1 (360 s)
对段场流入正线电流和地表电位梯度与实际情况进行误差分析,误差在8.46%以内。
5.3.3 Case2情况下
咽喉区单导装置内二极管支路被取消,并且晶闸管的触发信号已经更改为光电信号,即当有列车经过时才会触发晶闸管导通。在正常运营的时间段由于无列车出入车辆段,单导装置中的晶闸管不导通,使得正线上的钢轨电位无法侵入至该车辆段A。
B点地表电位梯度模实测结果与仿真数据如图19所示,最大地表电位梯度模为3.62 mV/m,最小地表电位梯度模为3.54 mV/m;当地表电位梯度在0.5~5 mV/m之间时,杂散电流的强度适中。
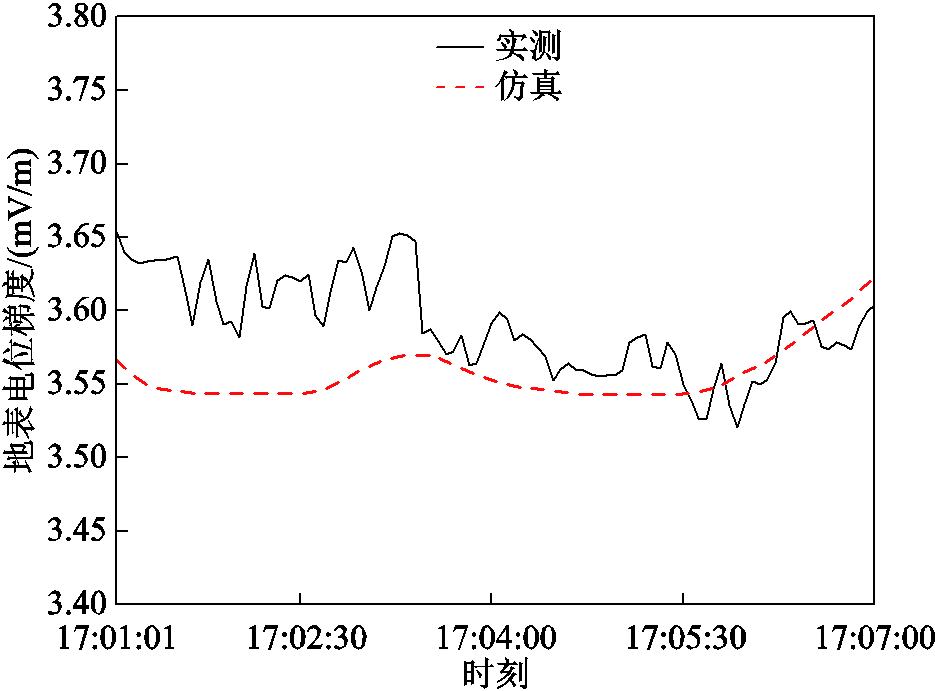
图19 Case2 B点地表电位梯度模对比(360 s)
Fig.19 Comparison of surface potential gradient mode at point B of Case2 (360 s)
对段场流入的正线电流和地表电位梯度与实际情况进行误差分析,误差在8.23%以内。Case2相比Case1,B位置处最大地表电位梯度模减小46.53%。采用直流牵引供电回流系统与分层介质杂散电流扩散的联合仿真计算模型来计算段场流入正线电流与地表电位梯度是有效的。
1)本文建立了考虑咽喉区与正线连接装置(CD)行为过程的直流牵引供电回流系统与杂散电流扩散的联合仿真计算模型。回流系统通过分布参数与集中参数进行等效替换,通过供电计算得到线路多区间钢轨电位分布;考虑介质分层情况,建立段场点电源叠加正线沿线杂散电流在地中电位分布的模型,基于点电流源在分层介质中的地中电位分布模型,获得地表电位梯度随时间动态变化的模型。
2)针对求解格林函数遇到病态矩阵的问题,本文提出了分层模型的精细积分主元加权迭代方法,可以高精度、高效率地求解分层格林函数。通过物理实验验证杂散电流在地中电位分布的模型的有效性,实测与仿真平均误差在6.98%以内。
3)通过国内某地铁线路实测验证了联合仿真模型在钢轨电位、杂散电流、地表电位梯度的有效性。实测与仿真相对比误差范围在8.46%以内,说明模型是有效的。
4)段场钢轨采用直接接地的方式,单向导通装置成为段场与正线连接的桥梁,段场在单向导通装置投入工况下咽喉区最大流入正线电流达106.62 A,最小流入正线电流达-330.28 A,距段场6.52 km处最大地表电位梯度模为6.77 mV/m,杂散电流的程度强。在移除单向导通装置的二极管支路和晶闸管支路熔断器工况下上行单导电流流入正线明显减少,最大地表电位梯度模为3.62 mV/m,相比在单向导通装置投入工况下减小46.53%。
参考文献
[1] 朱峰, 李嘉成, 曾海波, 等. 城市轨道交通轨地过渡电阻对杂散电流分布特性的影响[J]. 高电压技术, 2018, 44(8): 2738-2745. Zhu Feng, Li Jiacheng, Zeng Haibo, et al. Influence of rail-to-ground resistance of urban transit systems on distribution characteristics of stray current[J]. High Voltage Engineering, 2018, 44(8): 2738-2745.
[2] 顾靖达, 杨晓峰, 郑琼林, 等. 基于不同接地方式与列车工况的负阻变换器牵引供电系统轨道电位与杂散电流[J]. 电工技术学报, 2021, 36(8): 1703-1717. Gu Jingda, Yang Xiaofeng, Zheng T Q, et al. Rail potential and stray current on negative resistance converter traction power system under different grounding schemes and train conditions[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1703-1717.
[3] Liu Wei, Li Tian, Zheng Jie, et al. Evaluation of the effect of stray current collection system in DC-electrified railway system[J]. IEEE Transactions on Vehicular Technology, 2021, 70(7): 6542-6553.
[4] Du Guifu, Wang Jun, Jiang Xingxing, et al. Evaluation of rail potential and stray current with dynamic traction networks in multitrain subway systems[J]. IEEE Transactions on Transportation Electrification, 2020, 6(2): 784-796.
[5] 杨晓峰, 薛皓, 郑琼林. 基于双向可变电阻模块的杂散电流与轨道电位动态模拟系统[J]. 电工技术学报, 2019, 34(13): 2793-2805. Yang Xiaofeng, Xue Hao, Zheng T Q. Stray current and rail potential dynamic simulation system based on bidirectional variable resistance module[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2793-2805.
[6] 王慧康, 杨晓峰, 倪梦涵, 等. 轨道电位与杂散电流动模实验平台[J]. 电工技术学报, 2020, 35(17): 3609-3618. Wang Huikang, Yang Xiaofeng, Ni Menghan, et al. Rail potential and stray current dynamic emulator[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3609-3618.
[7] 于继来, 王江, 柳焯. 电力系统潮流算法的几点改进[J]. 中国电机工程学报, 2001, 21(9): 88-93. Yu Jilai, Wang Jiang, Liu Zhuo. Improvements on usual load flow algorithms of power system[J]. Proceedings of the CSEE, 2001, 21(9): 88-93.
[8] 吴命利. 电气化铁道牵引网的统一链式电路模型[J]. 中国电机工程学报, 2010, 30(28): 52-58. Wu Mingli. Uniform chain circuit model for traction networks of electric railways[J]. Proceedings of the CSEE, 2010, 30(28): 52-58.
[9] Tzeng Y S, Lee C H. Analysis of rail potential and stray currents in a direct-current transit system[J]. IEEE Transactions on Power Delivery, 2010, 25(3): 1516-1525.
[10] 杜贵府, 张栋梁, 王崇林, 等. 直流牵引供电系统电流跨区间传输对钢轨电位影响[J]. 电工技术学报, 2016, 31(11): 129-139. Du Guifu, Zhang Dongliang, Wang Chonglin, et al. Effect of traction current transmission among power sections on rail potential in DC mass transit system[J]. Transactions of China Electrotechnical Society, 2016, 31(11): 129-139.
[11] 刘炜, 杨龙, 李国玉, 等. 计及回流系统设备行为过程的钢轨电位动态仿真[J]. 电工技术学报, 2022, 37(4): 1000-1009. Liu Wei, Yang Long, Li Guoyu, et al. Dynamic simulation of rail potential considering the equipment behavior process of recirculation system[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 1000-1009.
[12] 王爱民, 林圣, 李俊逸, 等. 城市轨道交通长线路杂散电流仿真模型[J]. 高电压技术, 2020, 46(4): 1379-1386. Wang Aimin, Lin Sheng, Li Junyi, et al. Stray current simulation model of the long line of DC metro systems[J]. High Voltage Engineering, 2020, 46(4): 1379-1386.
[13] 刘炜, 郑杰, 李田, 等. 排流装置对直流牵引供电系统杂散电流分布的影响[J]. 电工技术学报, 2022, 37(18): 4565-4574. Liu Wei, Zheng Jie, Li Tian, et al. The influence of drainage device on stray current distribution in DC traction power supply system[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4565-4574.
[14] Cotton I, Charalambous C, Aylott P, et al. Stray current control in DC mass transit systems[J]. IEEE Transactions on Vehicular Technology, 2005, 54(2): 722-730.
[15] Kim H J, Choi K, Lee H B, et al. A new algorithm for solving ill conditioned linear systems[J]. IEEE Transactions on Magnetics, 1996, 32(3): 1373-1376.
[16] 富明慧, 张文志. 病态代数方程的精细积分解法[J]. 计算力学学报, 2011, 28(4): 530-534. Fu Minghui, Zhang Wenzhi. Precise integration method for solving ill-conditioned algebraic equations[J]. Chinese Journal of Computational Mechanics, 2011, 28(4): 530-534.
[17] Rump S M. Approximate inverses of almost singular matrices still contain useful information[R]. Technical Report 90.1, Faculty for Information and Communication Sciences, Hamburg University of Technology, 1990.
[18] 潘卓洪, 李嘉思, 刘曳君, 等. 分层土壤接地格林函数的多精度多分辨率计算[J]. 中国电机工程学报, 2019, 39(15): 4451-4459. Pan Zhuohong, Li Jiasi, Liu Yejun, et al. Multi-precision-resolution computation of the green’s function for the grounding problems of layered soils[J]. Proceedings of the CSEE, 2019, 39(15): 4451-4459.
[19] 刘炜, 尹乙臣, 潘卫国, 等. 直流动态杂散电流在分层介质中的扩散模型[J]. 电工技术学报, 2021, 36(23): 4864-4873. Liu Wei, Yin Yichen, Pan Weiguo, et al. Diffusion model of DC dynamic stray current in layered soil[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4864-4873.
[20] 薛正林. 基于主元加权的病态线性方程组算法研究[D]. 成都: 四川师范大学, 2016.
[21] 刘炜, 李富强, 唐靖坤, 等. 城市轨道走行轨过渡电阻测量方法与计算误差[J]. 高电压技术, 2020, 46(8): 2856-2863. Liu Wei, Li Fuqiang, Tang Jingkun, et al. Measurement method and calculation error of rail-to-earth resistance in urban rail[J]. High Voltage Engineering, 2020, 46(8): 2856-2863.
Abstract Currently, there are many factors affecting the rail potential and stray current, but the influence of the superposition of the depot and the mainline on the distribution and diffusion of stray current is not considered. Considering the complex operation conditions of multiple trains in the depot and main line, the distribution characteristics of stray current and its diffusion in the ground were studied. The return system and the stray current diffusion model were jointly simulated. The layered model based on the precise integration principal component weighted iteration method can dynamically evaluate the dynamic stray current in a certain period, reduce the calculation cost, and obtain high-precision and efficient calculation results. The return system was equivalently replaced by distributed parameters and concentrated parameters, and the node voltage method is used for power supply calculation. The distribution of the rail potential and stray current leakage across the line is obtained. Considering the layered soil medium, the model of the stray current potential distribution in the ground along the mainline superimposed by the power supply at the section points was established. Based on the ground potential distribution model of the point current source in layered medium, the dynamic change model of the ground potential gradient with time was obtained.
It is important to transform the ill-conditioned problem into a benign problem that is easy to solve for the problem of solving the ill-conditioned matrix of Green's function. The weight of the principal component weighting was determined by the weighting factor q and the weighting matrix P. Different weights were superimposed on each principal component to better reduce the number of conditions. A precise integration principal component weighted iteration method for the layered model was proposed, which can solve Green's function of the layered model with high accuracy and efficiency. The validity of the layered model of stray current potential distribution in the ground was verified by physical experiments and the average error between the field results and calculated results is within 6.98%.
Combined with the engineering case of the actual line in China, comparing the field measured and calculated rail potential and ground potential gradient distribution process, the relative error range between the field measured and calculated results is within 8.46%, which shows that the model is effective. The influence of different connection modes between the mainline and the depot on the DC interference propagation process was discussed. The rail in the depot is directly grounded, and the one-way conduction device becomes the bridge connecting the depot and the mainline. The maximum current flowing into the mainline in the throat area reaches 106.62 A and the minimum current flowing into the main line reaches -330.28 A when the unidirectional connection device was put into operation. The maximum surface potential gradient mode at 6.52 km away from the depot is 6.77 mV/m, and the degree of stray current is serious. Under the condition of removing the diode branch and thyristor branch fuses of the unidirectional connection device, the upstream unidirectional connection device current flowing into the mainline was significantly reduced, and the maximum ground potential gradient modulus is 3.62 mV/m, which is 46.53% less than that under the operating condition of the unidirectional connection device.
keywords:DC traction power supply system, rail potential, stray current, diffusion model, co-simulation
DOI:10.19595/j.cnki.1000-6753.tces.220937
中图分类号:TM922
四川省自然科学基金资助项目(2022NSFSC0463)。
收稿日期 2022-05-26
改稿日期 2023-02-25
刘 炜 男,1982年生,副教授,博士生导师,研究方向为杂散电流,牵引供电系统设计仿真,再生制动能量利用。E-mail:liuwei_8208@swjtu.cn(通信作者)
周林杰 男,1997年生,硕士研究生,研究方向为城市轨道牵引供电系统理论及其仿真,杂散电流和钢轨电位理论及其控制。E-mail:linjiezhou@my.swjtu.edu.cn
(编辑 赫 蕾)