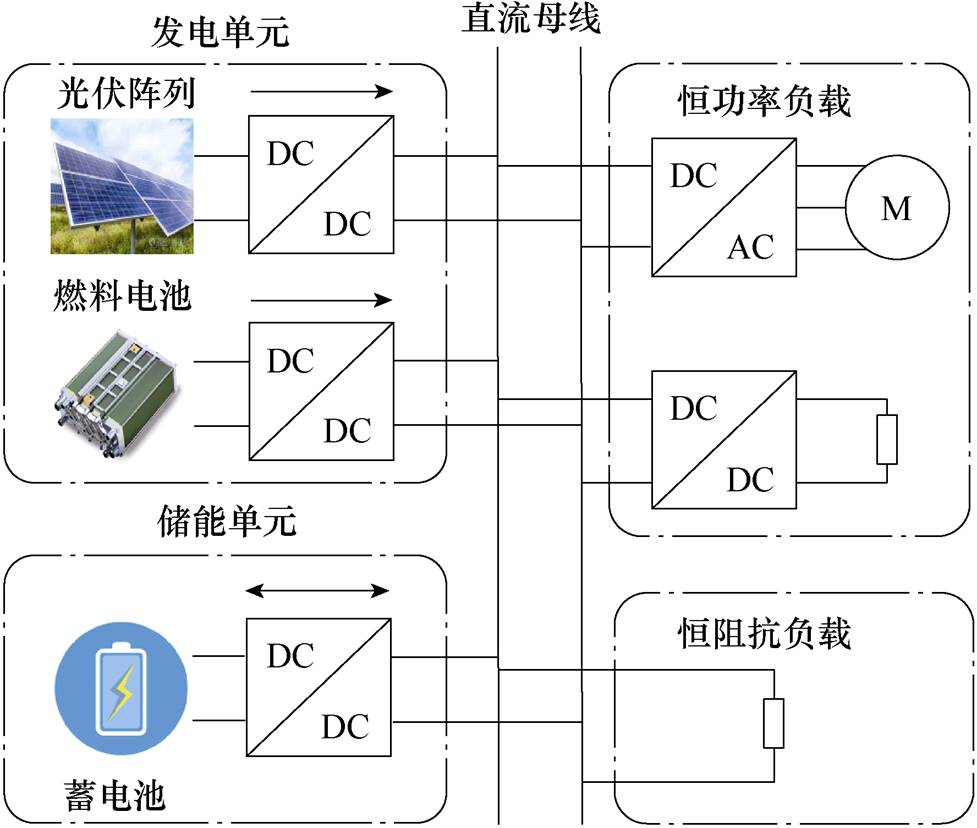
图1 典型直流微电网示意图
Fig.1 Schematic diagram of a typical DC microgrid
摘要 为解决直流微电网中Boost变换器带恒功率负载引起的不稳定问题，提出一种自适应反步控制。首先，采用坐标变换将系统模型转换为标准形式，避免寄生电阻对主控制器的影响。其次，为了改善系统的鲁棒性，利用扩展非线性干扰观测器和基于变换器动态模型设计的输入电压观测器在线估计和补偿外部扰动、寄生电阻与集总不确定项干扰。经过优化后的自适应反步控制可以在系统初始参数有限且不精准的前提下运行。之后运用李雅普诺夫与混合势函数理论验证控制器的大信号稳定性，并给出控制器参数设计原则，保证了输出电压的全局轨迹跟踪和快速动态响应。最后，通过仿真与实验验证了所提控制在恒功率负载高度渗透直流微电网下的有效性与优越性。
关键词：直流微电网 Boost变换器 恒功率负载 反步控制器 扩展非线性干扰观测器 大信号稳定
微电网作为未来智能电力系统的重要组成部分，代表了分布式能源聚合向电网供能的发展趋 势[1-3]。近年来，光伏阵列、燃料电池、储能单元与直流负载的渗透率逐渐提高，直流微电网提供了能源与负载的有效集成，并且相比于交流微电网，直流微电网无须考虑无功补偿、频率调节、趋肤效应，在提高系统供电可靠性和电能质量上，直流微电网具有天然优势[4-6]。
典型直流微电网示意图如图1所示，分布式能源与储能装置通过电力电子变换器与直流母线相连，进而将能量供给至负载侧。微电网负载主要分为恒阻抗负载（Constant Impedance Load, CIL）与恒功率负载（Constant Power Load, CPL）两类。对于CPL，在微电网中的形式为闭环调节的电力电子变换器，其输入端表现为负阻抗特性，降低整体系统阻尼，并倾向于破坏馈线系统和上游变换器的稳定性，造成系统的崩溃[7-8]。
图1 典型直流微电网示意图
Fig.1 Schematic diagram of a typical DC microgrid
为解决恒功率负载造成的不稳定现象，国内外学者进行大量的研究。文献[9-11]提出的阻尼法，通过添加无源器件或修改控制回路从而改善系统阻尼，但仅可在平衡点小邻域内保证渐近稳定性。文献[12-14]采用李雅普诺夫、T-S（Takagi-Sugeno）模糊模型与混合势函数理论推导线性控制下微电网的稳定判据与渐近稳定域。但上述方法均未对满足大信号稳定性的变换器控制器进行设计与研究。直流微电网是一个高度非线性系统，线性控制技术需在稳定裕度与动态性能之间做出取舍。
为了克服上述缺陷，许多非线性控制算法被提出。文献[15-16]分别提出基于PI的无源控制和反步控制，通过反馈调节补偿扰动造成的输出误差，在面对扰动时以相对缓慢方式的做出反应，存在动态性能差、超调大等问题。文献[17]提出一种复合离散滑模控制应用于微电网变换器中，具有良好的鲁棒性，但滑模面造成的系统抖振不可避免。文献[18-19]提出的自适应能量整形控制和有限时间控制能够确保带恒功率负载的功率变换器大信号稳定，然而控制算法依赖传感器获取输入电压，导致了系统成本增加与可靠性降低。非线性干扰观测器（Nonlinear Disturbance Observer, NDO）作为在线估计系统干扰的有效技术，为补偿不精准的系统模型、参数和外部扰动提供有效的解决方案[20]。文献[21-22]分别提出基于NDO的无源控制和反步控制，通过添加NDO环节将估计的外部扰动以前馈通道方式补偿至主控制器，以提高直流微电网带恒功率负载功率变换器的稳定性与鲁棒性。然而，控制器需大量参数进行设计和一般的动态性能。
本文考虑系统寄生电阻带来的未知干扰[23]，提出基于扩展非线性干扰观测器（Extended Nonlinear Disturbance Observer, ENDO）[24]的自适应反步控制（Adaptive Back-Stepping Control, ABSC），以解决直流微电网带混合负载升压转换器的不稳定问题。首先采用坐标变换，避免寄生电阻对主控制器的影响并将其转化为最小相位问题。在反步控制中设计电压观测器和ENDO进行优化，在线估计和补偿外部扰动（电源侧与负载侧）、寄生电阻与集总不确定项干扰，并使其在无输入电压和初始负载信息的情况下运行。通过李雅普诺夫与混合势函数理论进行稳定性分析，得到控制器参数选取准则和大信号稳定判据，使系统在已知参数少、模型不精准与外部扰动下也能确保快速、准确地跟踪输出电压标称值，且混合负载下大信号稳定。最后，通过仿真与实验验证了所提控制策略的有效性与优越性。
对图1所示的直流微电网系统模型进行简化，分布式电源仅考虑其输出特性，将其等效为电压源；将闭环调节的负载变换器等效为恒功率负载（CPLs）；将工作模式下需恒定阻抗运行的负载等效为恒阻抗负载（CILs）；功率变换器连接分布式电源与直流母线进而将能量供给至负载侧。
图2是将图1简化的级联系统，由分布式电源、Boost变换器与恒功率负载构成。对于一般数学建模，通常将其视为理想电路，而忽略寄生电阻对系统的影响[25]。但实际上，如电感、电容、二极管与开关管中存在的寄生电阻对电路性能存在着不可忽略的影响，因此直流微电网系统简化结构如图2所示。
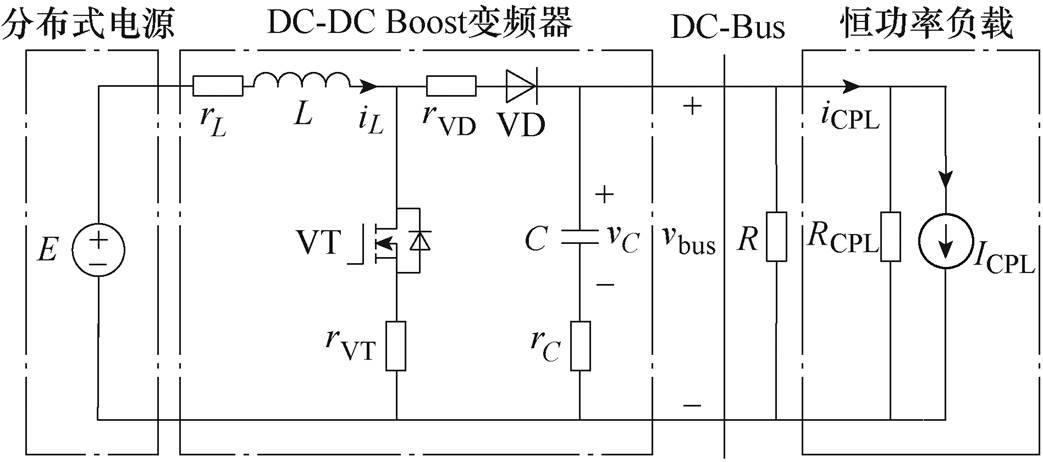
图2 含寄生电阻的直流微电网简化结构
Fig.2 Simplified structure diagram of DC microgrid with parasitic resistance
图2中，E为Boost变换器供电的分布式电源，L、C分别为电感和电容，VT、VD分别为开关管与二极管，rL、rC、rVT和rVD分别为电感、电容、开关管与续流二极管的寄生电阻，R为恒阻抗负载，恒功率负载采用负电阻RCPL与电流源ICPL并联的等效模型表示[26]，iCPL为恒功率负载输入电流，其中RCPL=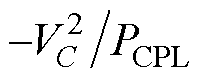
，ICPL=2PCPL/VC。系统工作在连续导通模式（Continuous Conduction Mode, CCM），其状态空间平均模型为
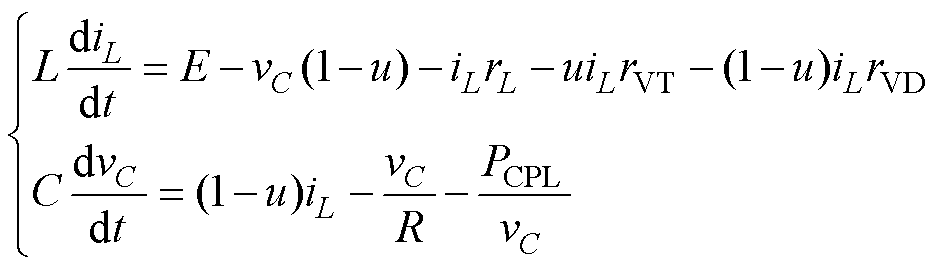（1）
式中，iL为电感电流；E、vC分别为系统输入、输出电压；u为开关管占空比（0＜u＜1
；PCPL为恒功率负载消耗功率。当系统稳态时，电容相当于开路，因此，iC≈0、iCrC可忽略不计，将余下的寄生电阻扰动统一定义为dis=iLrL+uiLrVT+(1-u)iLrVD，式（1）简化为
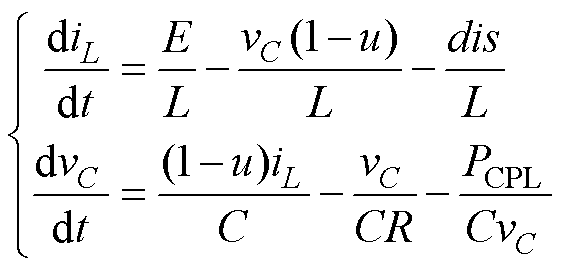（2）
对式（2）进行拉氏变换，可得混合负载下含寄生电阻的直流微电网系统传递函数为
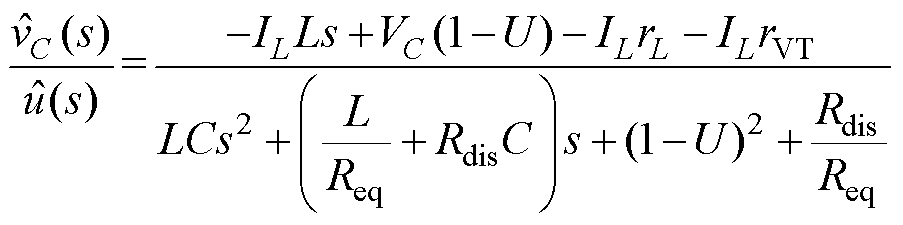（3）
式中，
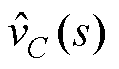和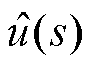
分别为输出电压和占空比的扰动量；U、IL和VC分别为占空比、电感电流和输出电压的稳态值；Req=R//RCPL，Rdis=rL+UrVT+(1-U)rVD。
根据恒阻抗负载与寄生电阻表现为正阻抗，恒功率负载表现为负阻抗，因此，直流微电网中发生级联时，会降低系统整体阻尼。由式（3）可得出变换器根轨迹与动态响应如图3所示。图3a表示恒阻抗负载与寄生电阻占主导地位时，其整体呈现为正阻尼，系统根轨迹极点位于平面左半轴，系统处于稳定状态。随着恒功率负载逐渐增大趋于主导地位时，其整体呈现为负阻尼，系统根轨迹极点位于平面右半轴，造成系统不稳定。图3b描绘了开环控制时混合负载下Boost变换器的动态响应。在0.4 s之前，恒功率负载占主导地位，系统的动态响应为极限循环振荡。0.4 s之后，通过向系统中额外注入恒阻抗负载使其占主导地位，系统的动态响应逐渐趋于稳定。然而，加入额外的恒阻抗负载虽可使系统保持稳定，但会加重不必要的能量损耗，对直流微电网的经济稳定运行造成不利影响。
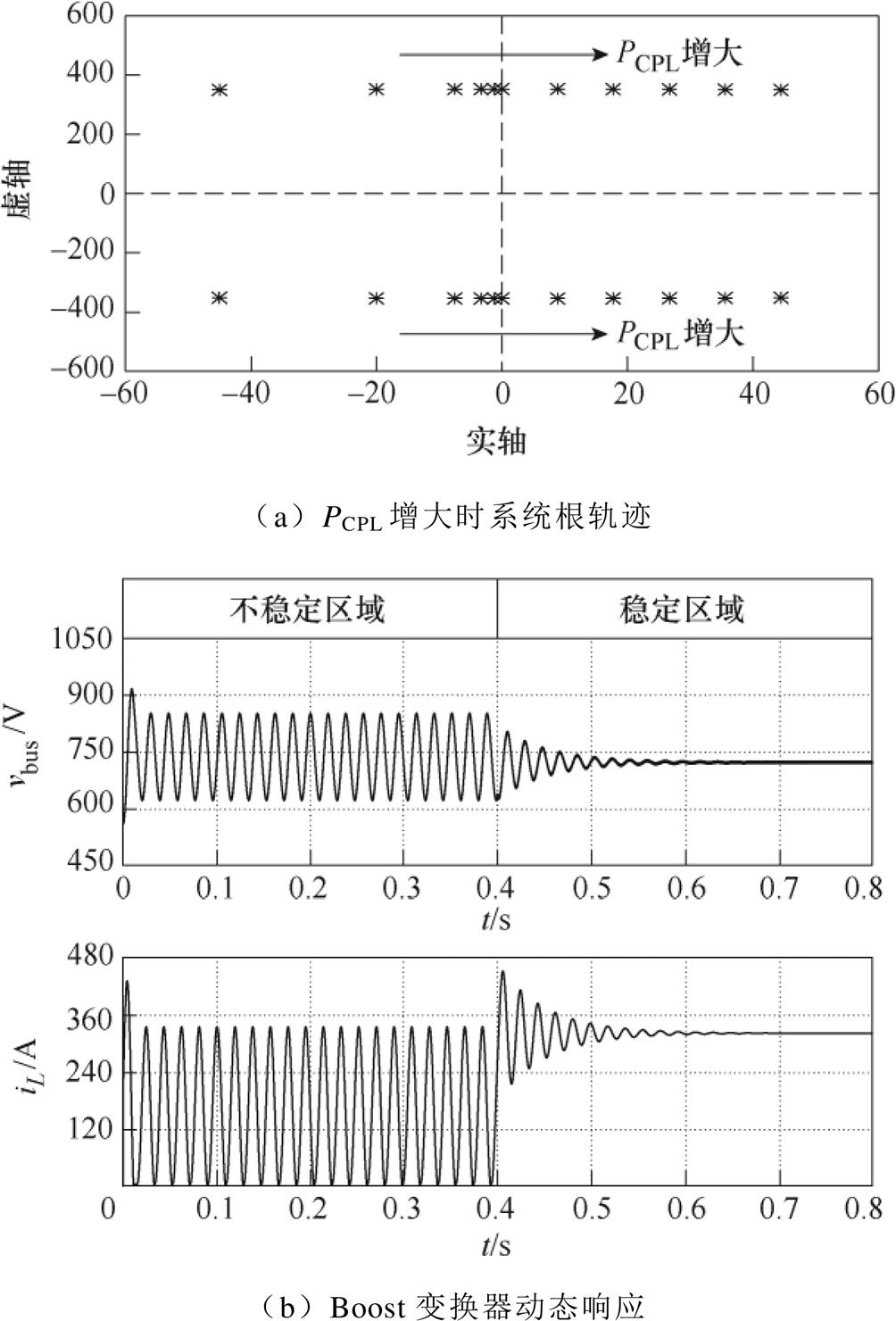
图3 变换器根轨迹与动态响应
Fig.3 Root locus and dynamic response of converter
直流微电网内部为高度非线性系统，由式（3）可知，Boost变换器含有非最小相位特性，如果直接控制输出电压，会导致动态响应缓慢和超调增大。因此，利用精确反馈线性化进行坐标转换为布鲁诺夫斯基标准形式，将状态变量重新定义为系统储能与总输入功率进行间接控制，从而解决非最小相位问题，且避免了系统寄生电阻对主控制器的影响。
系统中存储总能量表达式为
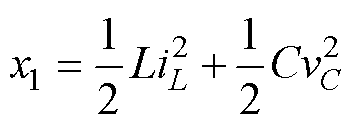（4）
式中，x1对时间的导数为
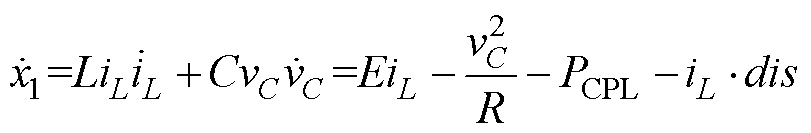（5）
根据式（5），可将新状态变量（总输入功率）和扰动分别定义为
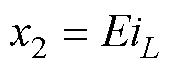（6）
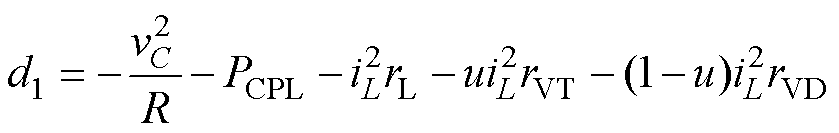（7）
结合式（2）、式（7），直流微电网总功率可表示为
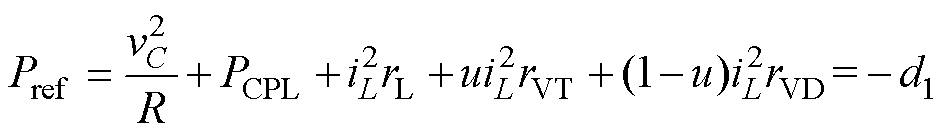（8）
式（6）中，x2对时间的导数为
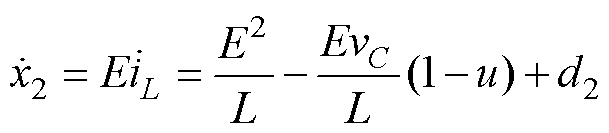（9）
式中，d2为不确定项引起的扰动，如系统噪声、寄生电阻干扰与参数不确定性；系统的平均状态方程式（2）可以重新转换为标准形式，即
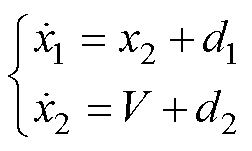（10）
式中，V为间接控制率；d1为外部扰动项与寄生电阻项（dis）；d2为集总不确定项。至此，通过坐标变换将d1和d2单独剥离出来，从而使主控制器（反步控制）正常设计而无须考虑dis，最终利用ENDO的在线估计和前馈补偿消除d1和d2对主控制器的影响。根据式（9）与式（10），初始系统方程式（2）的最终控制率转化为
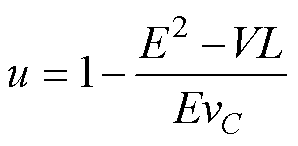（11）
为了稳定混合负载下含寄生电阻的Boost变换器，使其具有强大的稳定性与鲁棒性。设计了一种自适应反步控制（Back Stepping Controller, BSC），自适应反步控制框图如图4所示，控制器主要分为三部分：分布式电源电压观测器、扩展非线性干扰观测器（ENDO）和改进反步控制的设计。电压观测器用来估计输入电压，扩展非线性干扰观测器估计各种外部扰动、寄生电阻与集总不确定项干扰，前馈补偿至反步控制器中，使其生成PWM脉冲信号，用于驱动Boost变换器的开关管。最后，利用李雅普诺夫函数与混合势函数稳定性条件验证了所提控制器的全局稳定性。
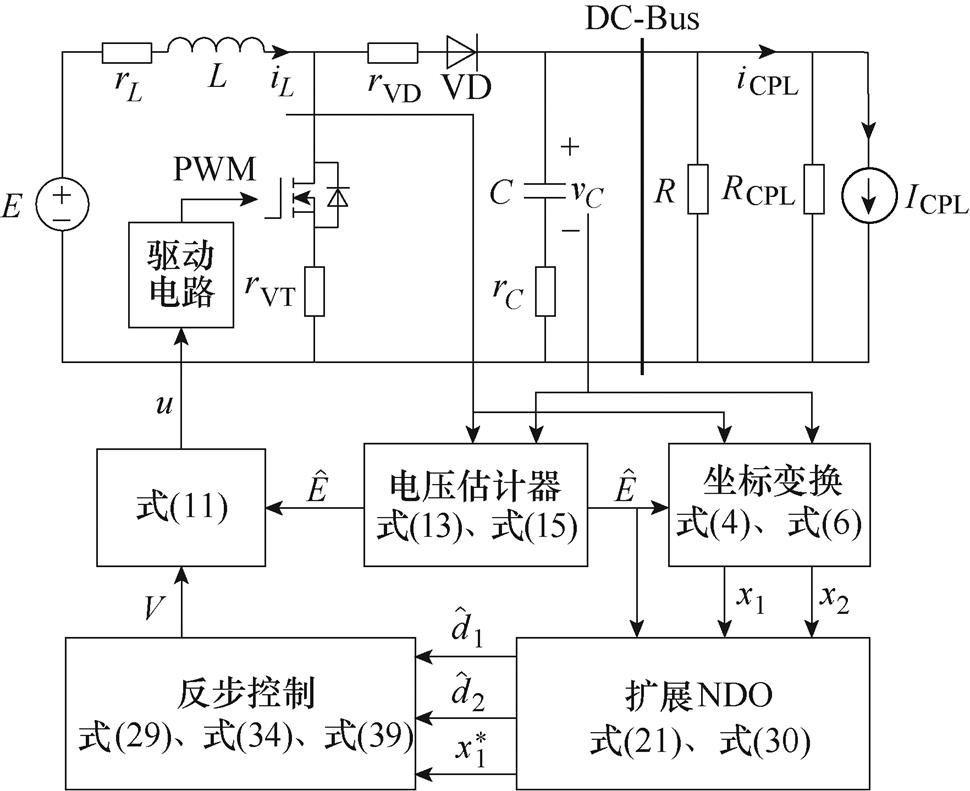
图4 自适应反步控制框图
Fig.4 Adaptive back-stepping control block diagram
本文在考虑电源侧输入-输出特性下，将分布式电源等效为电压源。由于直流微电网中的分布式能源的强间歇性与随机性，其电压通常是未知且时变的。为了保证控制器的稳定性，减少传感器数量，设计了一个观测器来估计电源电压。定义误差为
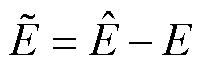（12）
式中，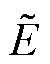
为输入电压估计误差；
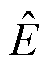为输入电压估计值。电压观测器被设计为
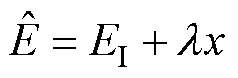（13）
式中，EI为辅助变量；l 为估计器增益；x为式（2）中的电感电流iL。式（12）中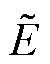，对时间的导数为
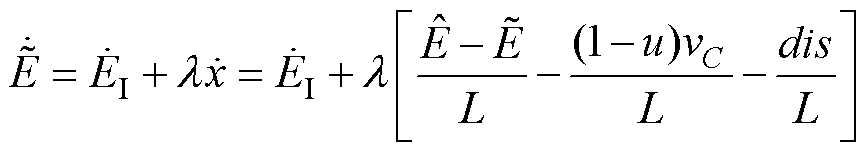（14）
为了确保所设计估计器的全局稳定性，必须确保其满足李雅普诺夫稳定性条件，因此辅助变量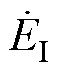
被设计为
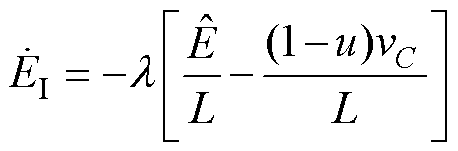（15）
将式（15）代入式（14）中简化可得
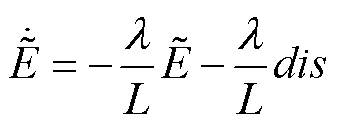（16）
根据式（16）可知，由于寄生电阻引起的干扰项dis，无法使设计的电压观测器满足李雅普诺夫间接稳定性条件。因此定义李雅普诺夫函数H为
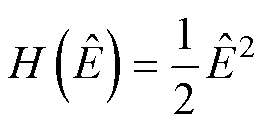（17）
李雅普诺夫函数H对时间的导数为
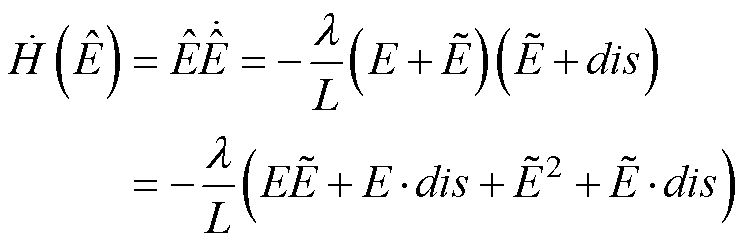（18）
将不等式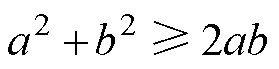
代入式（18）中，可简化为
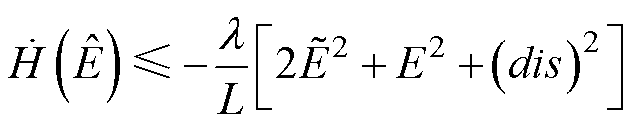（19）
由式（19）可得，通过选取电压观测器增益 l＞0，使设计的李雅普诺夫函数满足直接稳定性条件，且H中自变量趋近于无穷时，李雅普诺夫函数H→∞，可确保所设计的电源电压观测器大信号 稳定。
所设计的扰动di（i=1, 2）是由总负载随机性波动、系统内部不确定参数和不确定项干扰所引起的，从实际角度出发，其扰动值的变化频率远低于系统开关频率，因此存在如下条件
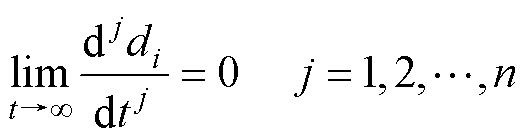（20）
本文使用的扩展非线性干扰观测器主要用来估计各种外部扰动、寄生电阻与集总不确定项干扰，前馈补偿至反步控制器中，输出电压追踪额定电压值。使用的ENDO进一步估计扰动的时间导数，对比传统的NDO具有更好的动态响应。
首先对干扰项d1和集总不确定项d2进行估计
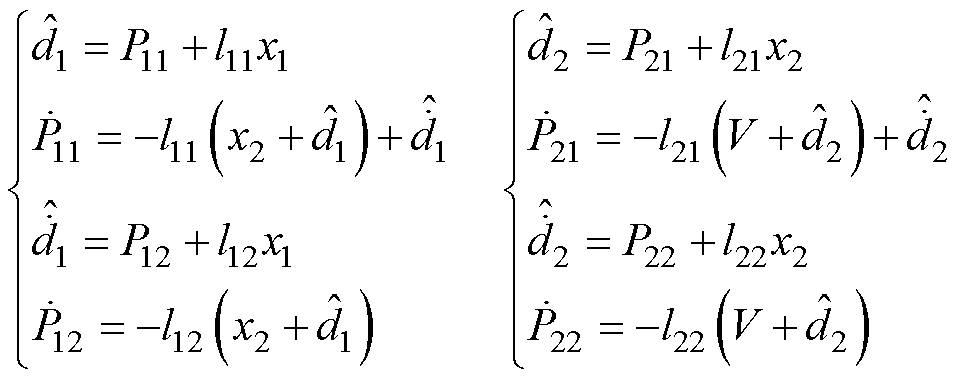（21）
式中，Pi1、Pi2（i=1, 2）为ENDO的辅助变量；li1、li2（i=1, 2）为ENDO的增益；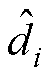
（i=1, 2）为干扰项估计值；
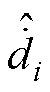（i=1, 2）为干扰项导数估计值。
根据式（21），估计误差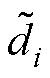
（i=1, 2）可被定义为
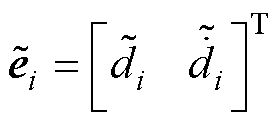（22）
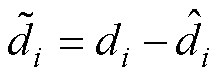（23）
结合式（10）、式（21）、式（23），化简可得
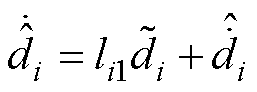（24）
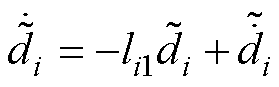（25）
同理结合式（10）、式（21），化简可得
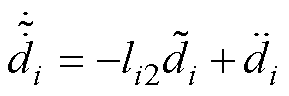（26）
观测器的动态误差表达式表示为
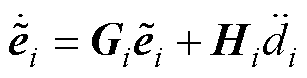（27）
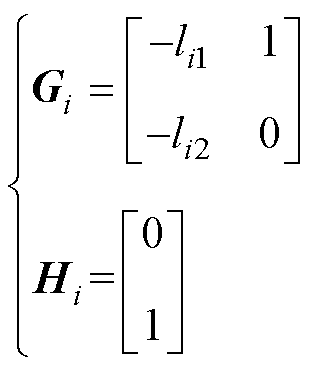（28）
根据式（20）对扰动导数的条件，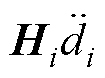
可被忽略不计，式（27）可通过选取合适的增益系数来确保ENDO满足李雅普诺夫间接稳定条件，以保证设计的ENDO全局稳定性。
为了稳定直流微电网内混合负载下Boost变换器设计了一种基于ENDO与输入电压观测的自适应反步控制，分为两部分：
1）寻找标称值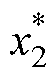
BSC的目标是使坐标转换后新状态变量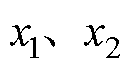
跟踪标称值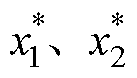
，因此定义状态变量误差为
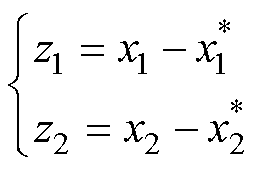（29）
将式（8）代入式（4）中简化可得标称值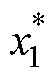
为
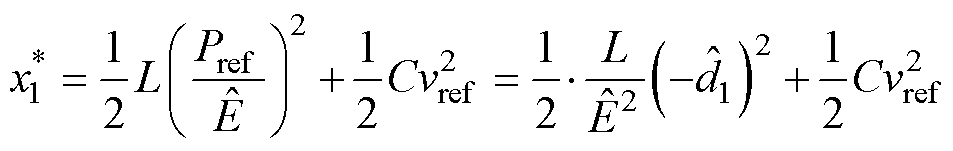（30）
式（29）中，z1对时间的导数为
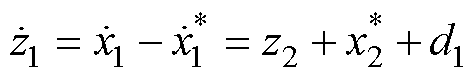（31）
定义李雅普诺夫函数V1为
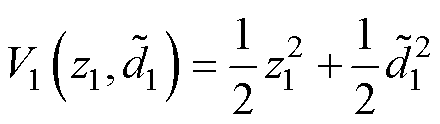（32）
式中，李雅普诺夫函数V1对时间的导数为
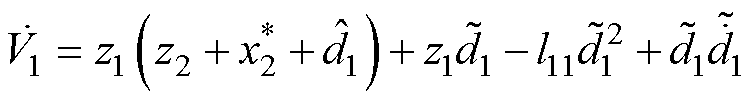（33）
为了使设计的V1满足李雅普诺夫稳定条件，标称值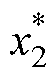被设计为
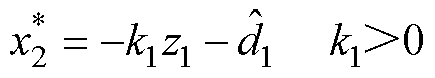（34）
将式（23）、式（24）、式（34）代入式（33）中，简化可得
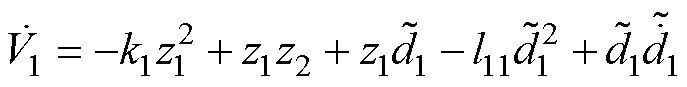（35）
由式（35）可知，不能保证所设计的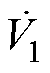
满足李雅普诺夫负定条件，因此应当进行下一步骤。
2）寻找虚拟控制律V
式（29）中，z2对时间的导数为
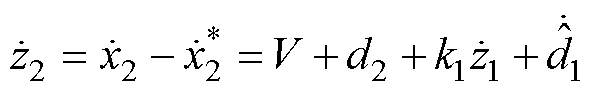（36）
定义李雅普诺夫函数V2为
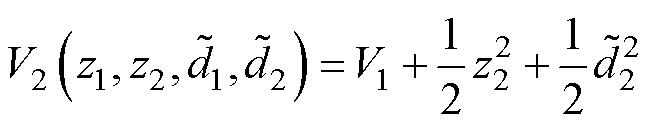（37）
选取V2对时间的导数，并将式（24）、式（34）、式（36）代入可简化为
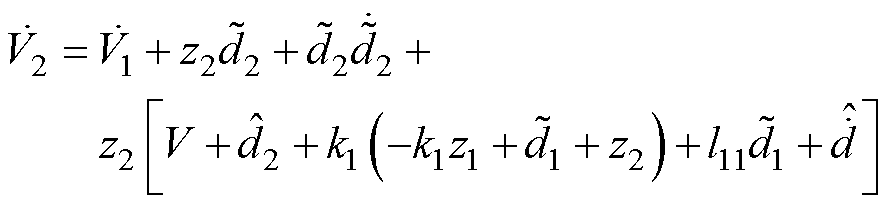（38）
为了使设计的V2满足李雅普诺夫稳定条件，虚拟控制律V被设计为
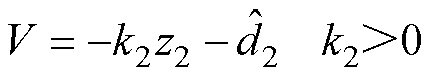（39）
通过将式（24）、式（25）、式（33）、式（39）代入式（38）中可得
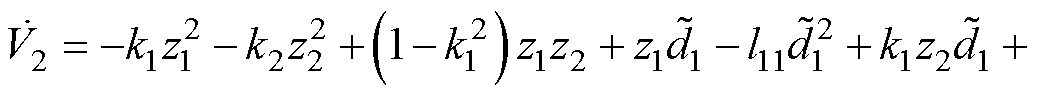
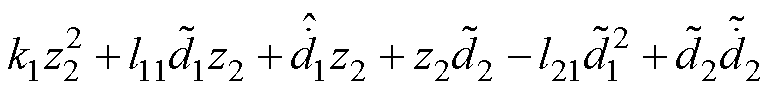（40）
将不等式2ab≤a2+b2代入式（40）中简化可得
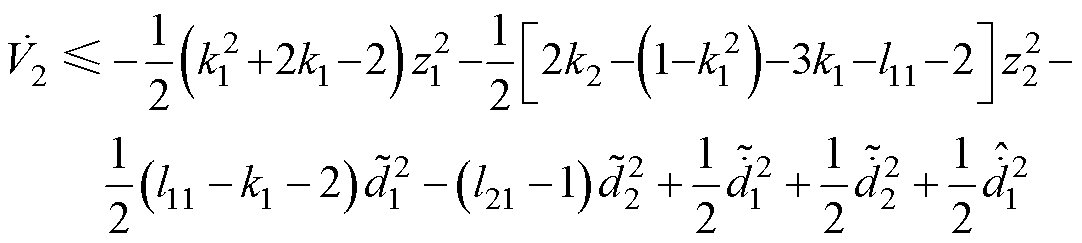（41）
为了使构造的函数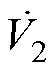
满足李雅普诺夫负定条件，式（41）中的参数选取应遵循
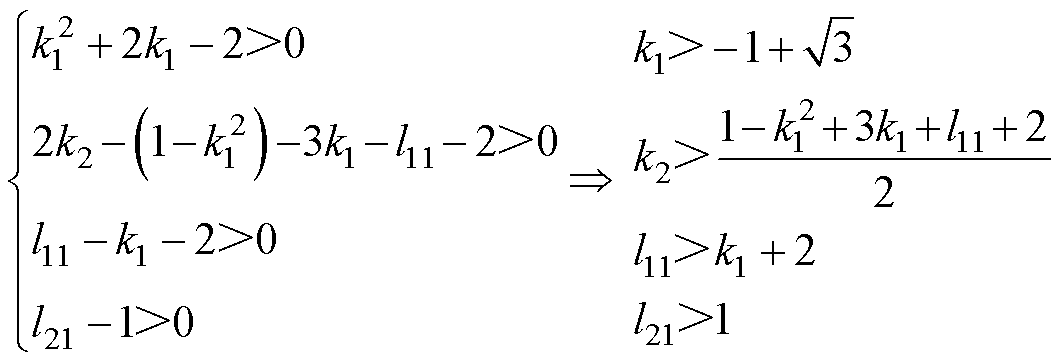（42）
当控制器参数选取满足式（42）时，构建的V2符合李雅普诺夫函数直接稳定条件，因此闭环系统为渐近稳定，这意味着经过坐标转换的新状态变量能够追踪标称值，因此直流母线电压可达到参考值，并且在观测器ENDO与电压观测器协助下，系统输出稳定无误差，具有良好的鲁棒性。
该控制器的设计过程也适用直流微电网内其他DC-DC变换器，如Buck、Buck-Boost变换器。采用坐标变换将系统模型转化为布鲁诺夫斯基标准形式，利用类似步骤设计控制律，此种建模方法使控制器无须考虑模型差异而统一应用。此外，控制器可搭配下垂控制实现多变换器之间的协调运行。
混合势函数理论在1964年被提出，是一种李雅普诺夫函数的特殊形式，为非线性电路提供了统一的研究方法，且提出了非线性系统的大信号稳定判据[27]。混合势函数标准形式表述为
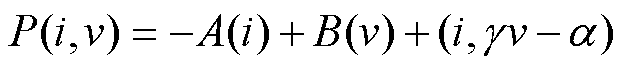（43）
式中，A(i)为电路中非储能元件电流势函数；B(v)为电路中非储能元件电压势函数；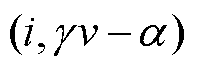
为电容与其他非储能元件能量。
本节基于混合势函数第三定理，对自适应反步控制的大信号稳定性进行分析。首先对系统模型进行重构，直流微电网大信号等效电路如图5所示。变换器等效输出电流为(1-u)iL，电容中寄生电阻稳态时iC≈0，因此忽略不计。恒功率负载采用大信号模型表示，等效为受直流母线电压控制的电流源，其混合势函数表述为
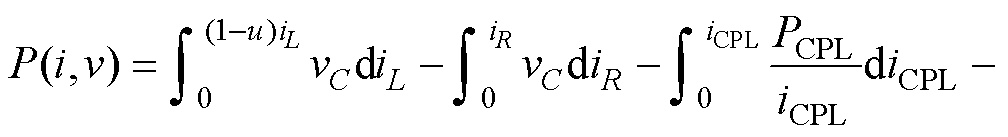
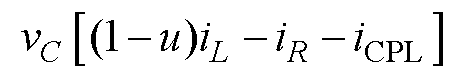（44）
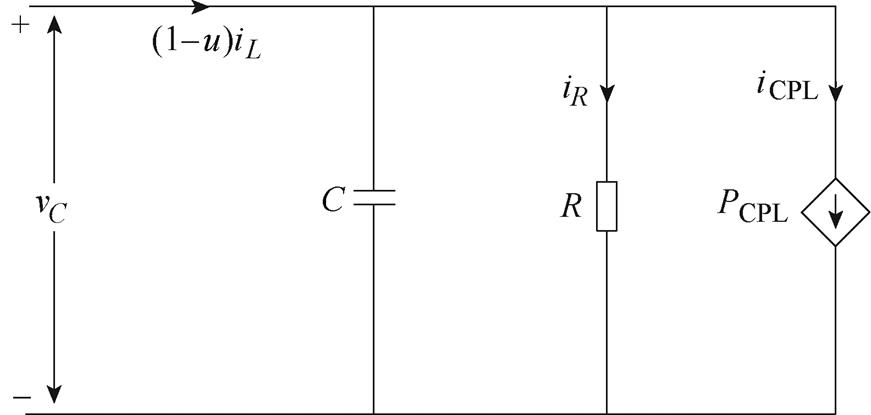
图5 直流微电网大信号等效电路
Fig.5 DC microgrid large signal equivalent circuit
将式（44）转化为一般形式为
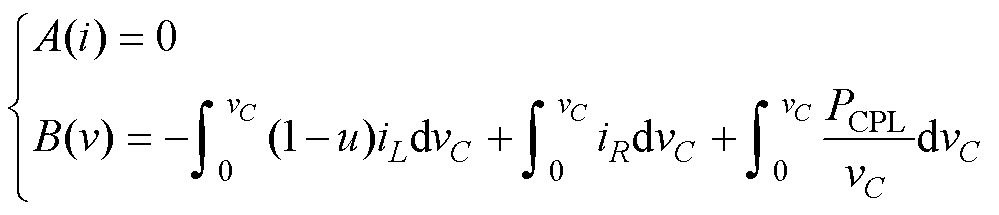（45）
将式（45）中电流势函数与电压势函数分别对电流变量iL、电压变量vC进行二次求导可得
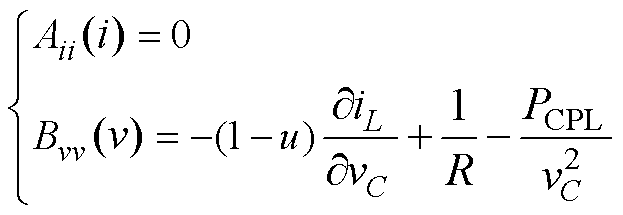（46）
结合由反步控制所得式（6）、式（29）、式（34），可得L-1/2Aii(i)L-1/2和C-1/2Bvv(v)C-1/2的最小特征值为
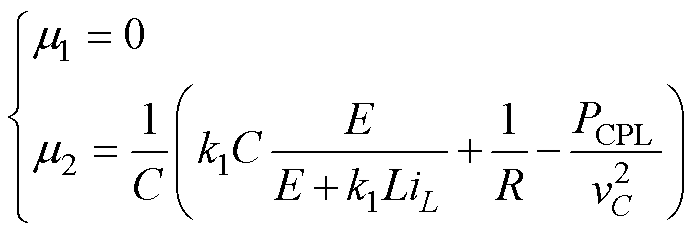（47）
根据混合势函数第三定理可知，直流微电网系统大信号稳定判据为
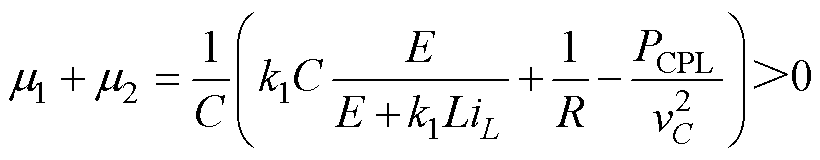（48）
式（48）所示判据给定了恒功率负载功率PCPL、恒阻抗负载R、电容C和反步增益k1的系统大信号稳定关系，且该判据结构简单，为系统参数设计提供了重要依据，能够确保直流微电网在大扰动条件下系统稳定。系统的大信号稳定边界如图6所示，当恒功率负载增大时，系统趋于不稳定，此时需要较大的增益系数k1平衡系统，与李雅普诺夫理论获得的渐近稳定取值相对比，更具体和直观地展现出系统与控制器之间的稳定关系。
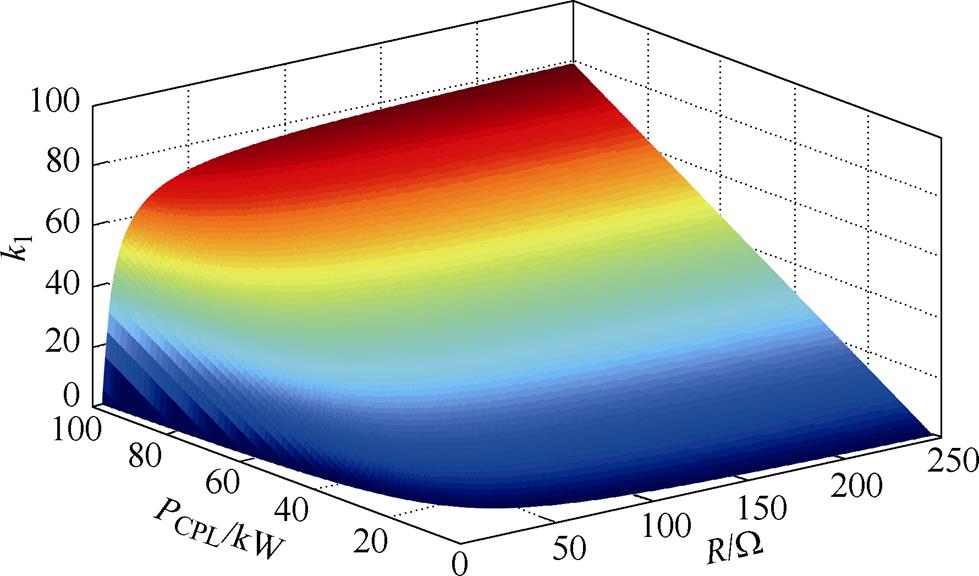
图6 系统大信号稳定边界
Fig.6 System large signal stability boundary diagram
为验证本文所提控制策略的有效性，在Matlab/ Simulink环境中进行仿真研究，并且基于RT-Lab搭建了硬件在环（Hardware-in-Loop, HIL）实验平台，HIL平台包括上位机（PC端）、下位机（OP5600实时模拟器）与TMS320F28379D数字信号处理器（DSP）。硬件在环实验流程如图7所示，该平台允许将Simulink中搭建的表1含寄生电阻直流微电网简化模型参数放入OP5600实时模拟器中实现硬件在环，DSP的ADC模块接收由下位机OP5600输出的模拟信号（iL, vC），并执行由上位机PC端向DSP提供的自适应反步控制算法，由DSP输出的ePWM信号通过OP5600数字信号输入端口送回直流微电网模型实现闭环控制。
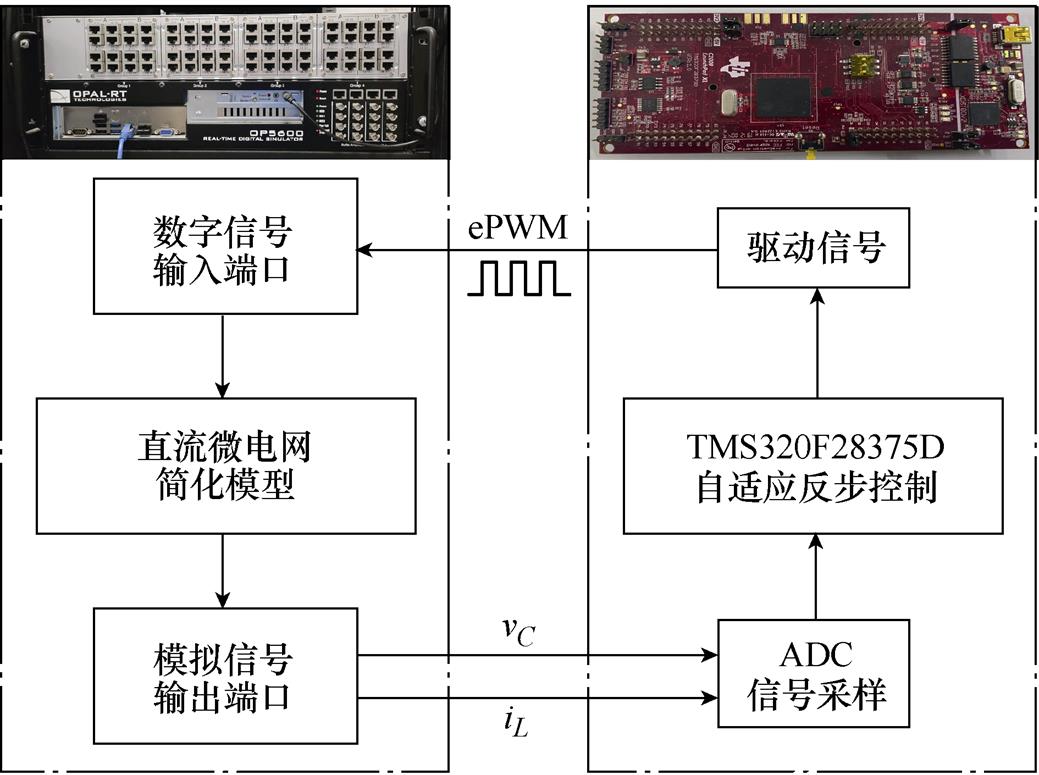
图7 硬件在环实验流程
Fig.7 Hardware-in-loop experiment flowchart
表1 含寄生电阻直流微电网模型参数
Tab.1 Model parameters of DC microgrid with parasitic resistance
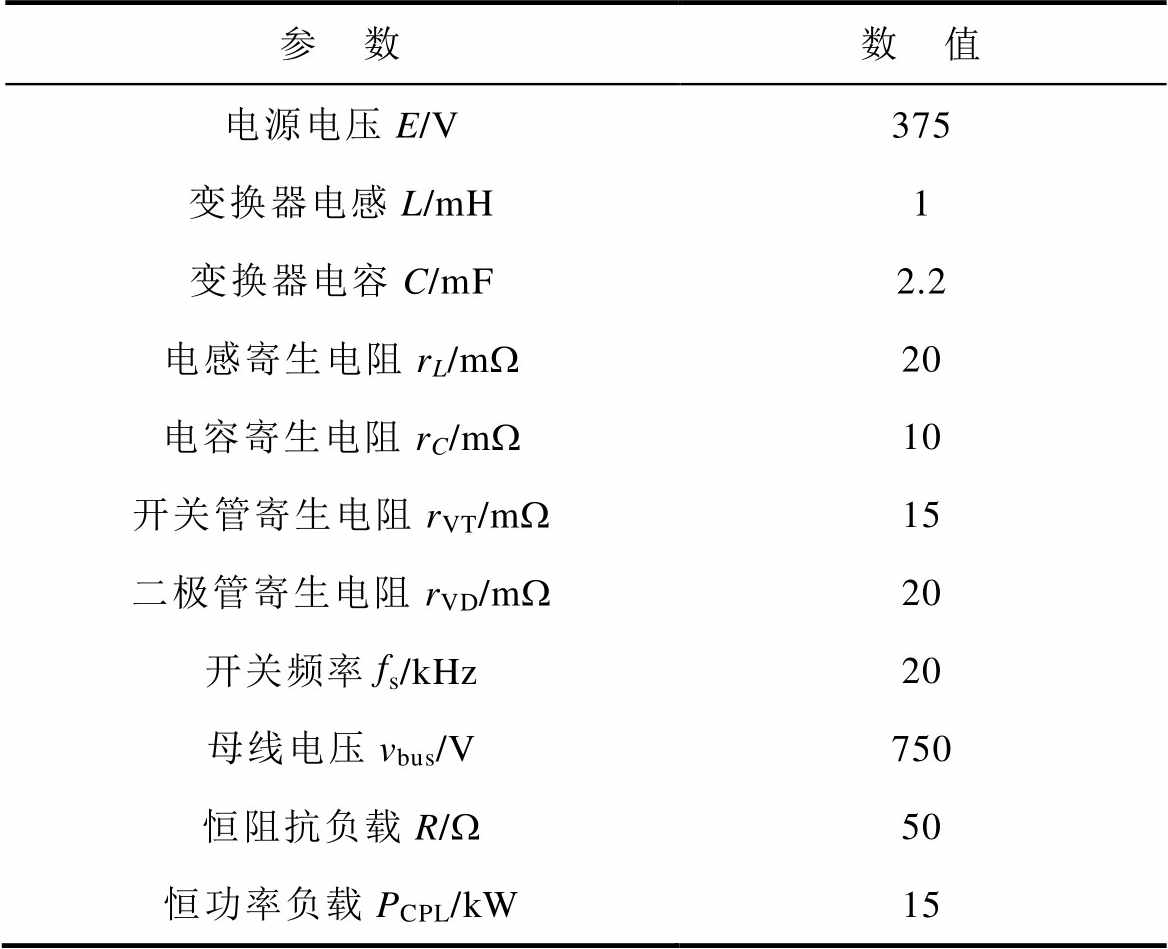
参 数数 值 电源电压E/V375 变换器电感L/mH1 变换器电容C/mF2.2 电感寄生电阻rL/mW20 电容寄生电阻rC/mW10 开关管寄生电阻rVT/mW15 二极管寄生电阻rVD/mW20 开关频率fs/kHz20 母线电压vbus/V750 恒阻抗负载R/W50 恒功率负载PCPL/kW15
为了验证所提控制策略的鲁棒性，将所提控制与BSC+NDO进行性能比较。所提控制器参数见表2，BSC参数k1、k2与ENDO参数li1、li2在满足渐近稳定与大信号稳定判据的基础上，各参数增加有利于系统动态性能和功率估计值收敛速度，但过大会造成对测量噪声更加敏感；对于电压观测器增益l，选值偏小会导致输入电压估计值收敛速度较差；反之，则会造成估计值纹波较大。因此，应根据控制要求合理选择控制器增益系数。采用文献[22]中控制器进行对比，并在表3中总结控制器性能比较结果。本文为更接近实际工程，在多种复杂工况下进行仿真实验，验证了所提的自适应反步控制在各种环境下均能稳定运行。
表2 控制器参数
Tab.2 Controller parameters
参 数数 值 li11 540 li21 000 k1800 k24 000 l25
本节测试了输入电压变化时的鲁棒性。系统初始输入电压为375 V，在0.08 s时输入电压突增至425 V，0.04 s后输入电压跌至345 V。图8为输入电压变化时直流微电网系统动态响应。
由图8a可知，BSC+NDO在输入电压突增（375 V→425 V）时会产生4.8 V瞬时电压偏差，突减（425 V→345 V）时会产生8 V瞬时电压偏差，可以在25 ms内消除直流母线电压偏差。但本文所提的自适应反步控制所设计的电压观测器提供的估计值在短时间内精确收敛至实际电压值，因此产生的瞬时电压偏差仅为0.9 V（输入电压突增）和1.5 V（输入电压突减），仅需3 ms使直流母线电压稳态无误差，相比于BSC+NDO，其超调量与恢复时间分别减少81.25%和88%，并且电感电流无反向超调。图8b为输入电压扰动下硬件在环实验波形。
表3 控制器性能对比
Tab.3 Controller performance comparison
控制器稳定性参数信息输入电压突变恒功率负载突变恒阻抗负载突变 恢复时间/ms超调量/V恢复时间/ms超调量/V恢复时间/ms超调量/V PI小信号稳定2—————— BSC+NDO[22]全局渐近稳定6254.88207.4207.7 ABSC大信号稳定430.91.554.354.5
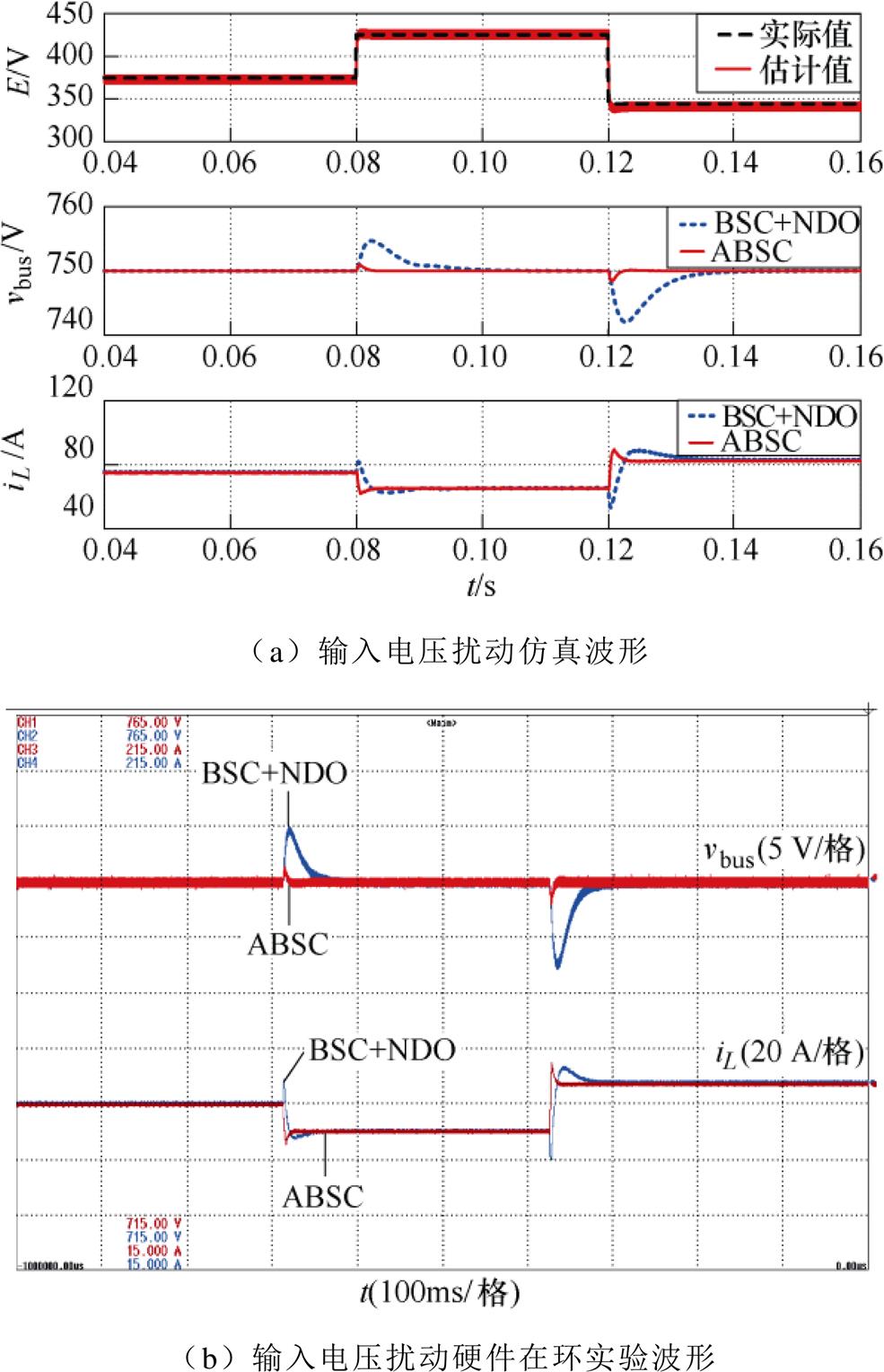
图8 输入电压扰动下的动态响应
Fig.8 Dynamic response under input voltage disturbance
通过在混合负载（CIL和CPL）下阶跃变化CPL以获得负载扰动测试。系统初始CPL为15 kW，在0.08 s时由15 kW突增至25 kW，经过0.04 s后由25 kW跌至15 kW。图9为CPL变化期间直流微电网系统动态响应。
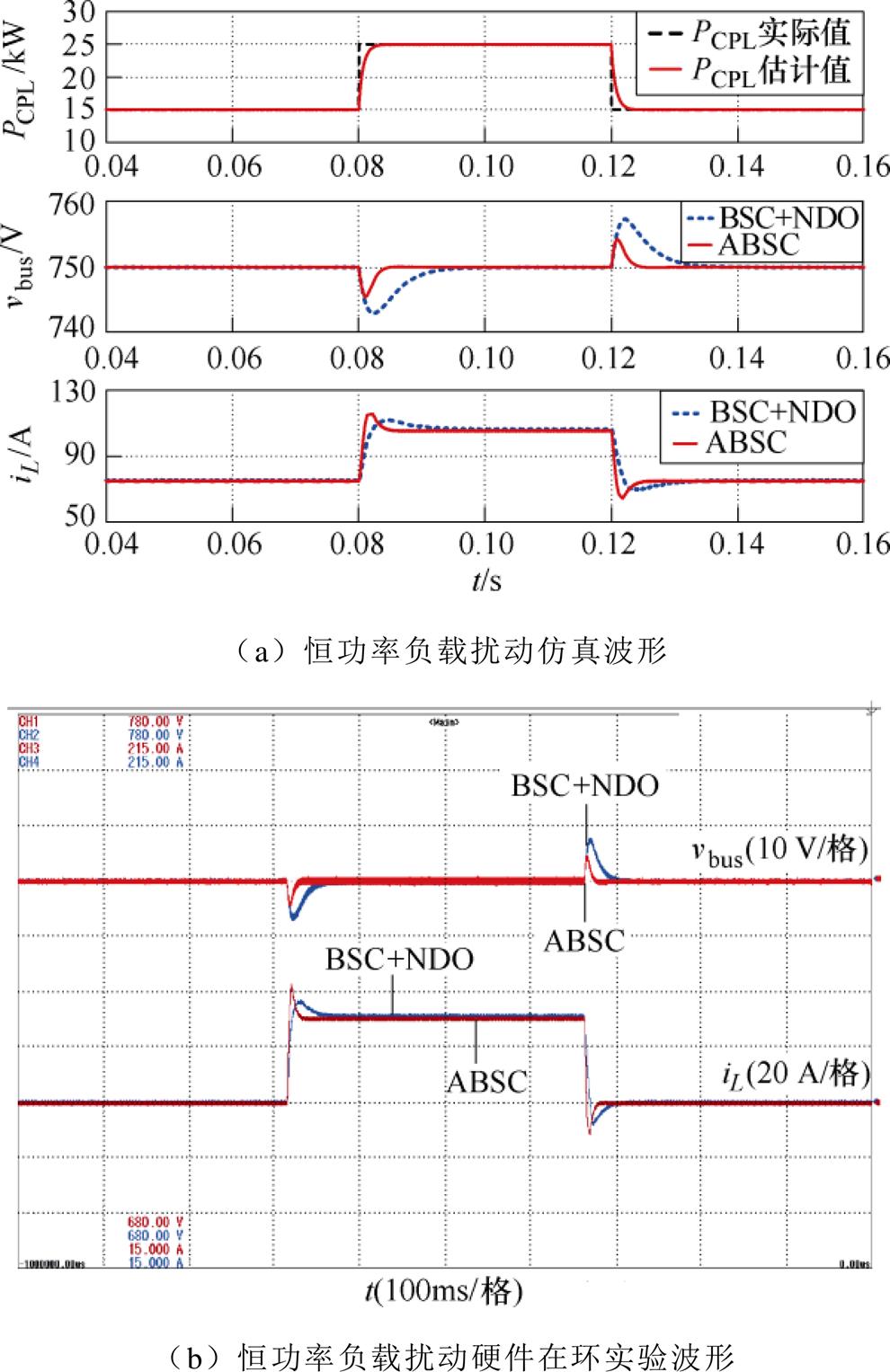
图9 恒功率负载扰动下的动态响应
Fig.9 Dynamic response under CPL disturbance
由图9a可知，BSC+NDO在CPL阶跃扰动下会产生7.4 V瞬时电压偏差，虽可以通过NDO协助在20 ms后消除电压误差，但出现了超调量大、恢复时间长的性能问题。为了克服上述问题，通过采用ENDO来代替NDO，ENDO提供的功率估计值在短时间内精确收敛至功率实际值，本文的自适应反步控制在CPL阶跃扰动下仅产生4.3 V瞬时电压偏差、5 ms的恢复时间，相比于BSC+NDO其超调量与恢复时间分别减少41.89%和75%，直流母线电压始终保持稳定，并且具有强大的动态性能。图9b为CPL扰动下硬件在环实验波形。
为了模拟直流微电网最坏情况下的系统状态，通过移除全部CIL，使系统整体处于负阻尼状态。系统初始CIL为50 W，在0.08 s时CIL全部移除，经过0.04 s后重新加载CIL。图10为CIL变化期间直流微电网系统动态响应。
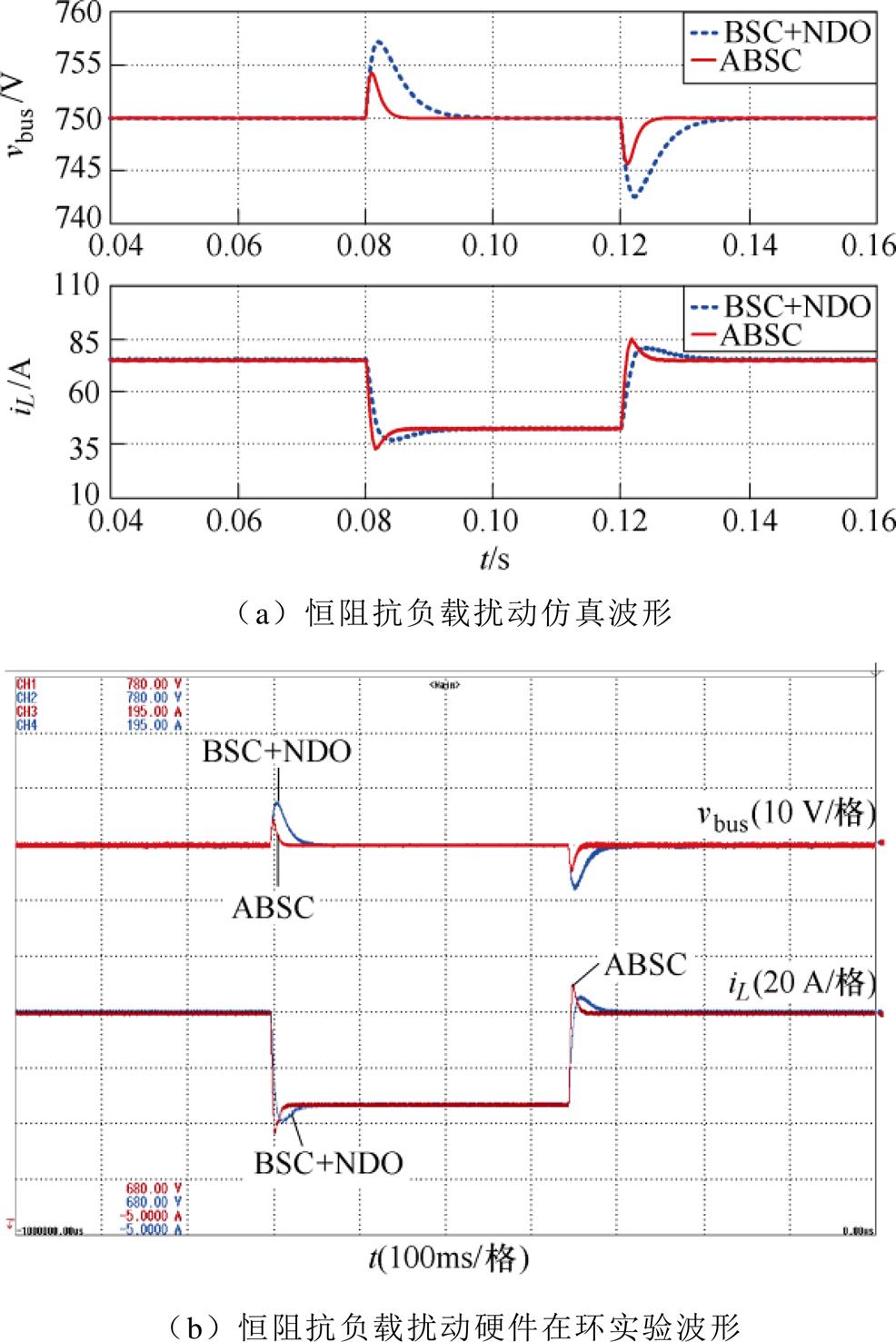
图10 恒阻抗负载扰动下的动态响应
Fig.10 Dynamic response under CIL disturbance
由图10a可知，BSC+NDO在CIL阶跃扰动而造成的系统处于纯恒功率负载环境下，会产生7.7 V瞬时电压偏差，通过NDO协助下在20 ms后消除误差，出现了超调量大、恢复时间长的性能问题。本文的自适应反步控制在CIL阶跃扰动下仅产生4.5 V电压偏差、5 ms恢复时间，相比于BSC+NDO，其超调量与恢复时间分别减少41.56%和75%，直流母线电压始终保持稳定，并且具有强大的动态性能。图10b为CIL扰动下硬件在环实验波形。
为了验证自适应反步控制对模型参数不确定的鲁棒性，在不同电感与电容偏差值的基础下，进行CPL扰动的仿真研究与硬件在环实验。系统初始CPL为15 kW，在0.12 s时由15 kW突增至25 kW，经0.02 s后由25 kW跌至15 kW。图11为电感和电容与标称值相差-30%、0和30%的系统动态响应。
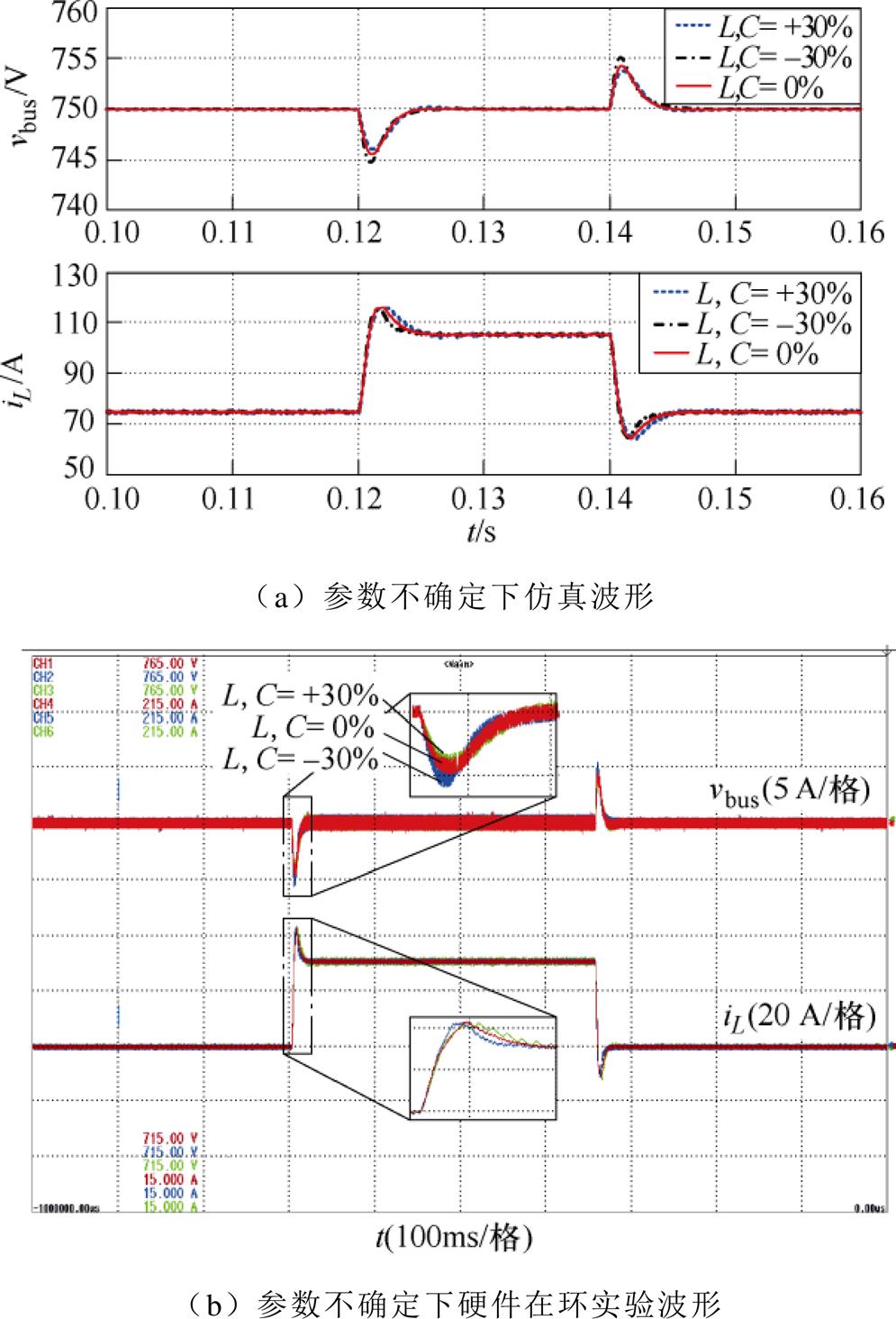
图11 参数不确定性下的动态响应
Fig.11 Dynamic response under uncertainty of parameters
由图11a可知，对于上述情况下，在负载变化周期内，直流母线电压均可在5 ms内准确追踪750 V直流母线电压参考值。因此，自适应反步控制实现了对模型参数不确定和考虑寄生电阻下对系统具有鲁棒性，能更好地适用于各种恶劣条件下的工业应用。图11b为模型参数不确定下硬件在环实验波形。
为了验证控制器对极限循环振荡系统是否具有稳定化的能力，系统应以最坏情况下运行，以确保各种恶劣环境下均可运行。根据式（48）分析可知，恒阻抗负载有利于系统稳定性，因此当负载侧仅存在恒功率负载时，系统受纯粹的负阻抗特性支配处于最坏的稳定状况。本工况以此为基础进行测试，系统在纯恒功率负载60 kW的重载情况下开环（固定占空比u=0.5）启动，平衡点不稳定，此时系统处于极限循环振荡状态。在0.3 s时，切换至自适应反步控制，极限循环振荡状态被抑制，电感电流趋于稳定，直流母线电压控制在额定值750 V。图12为控制器切换测试下系统的动态响应。
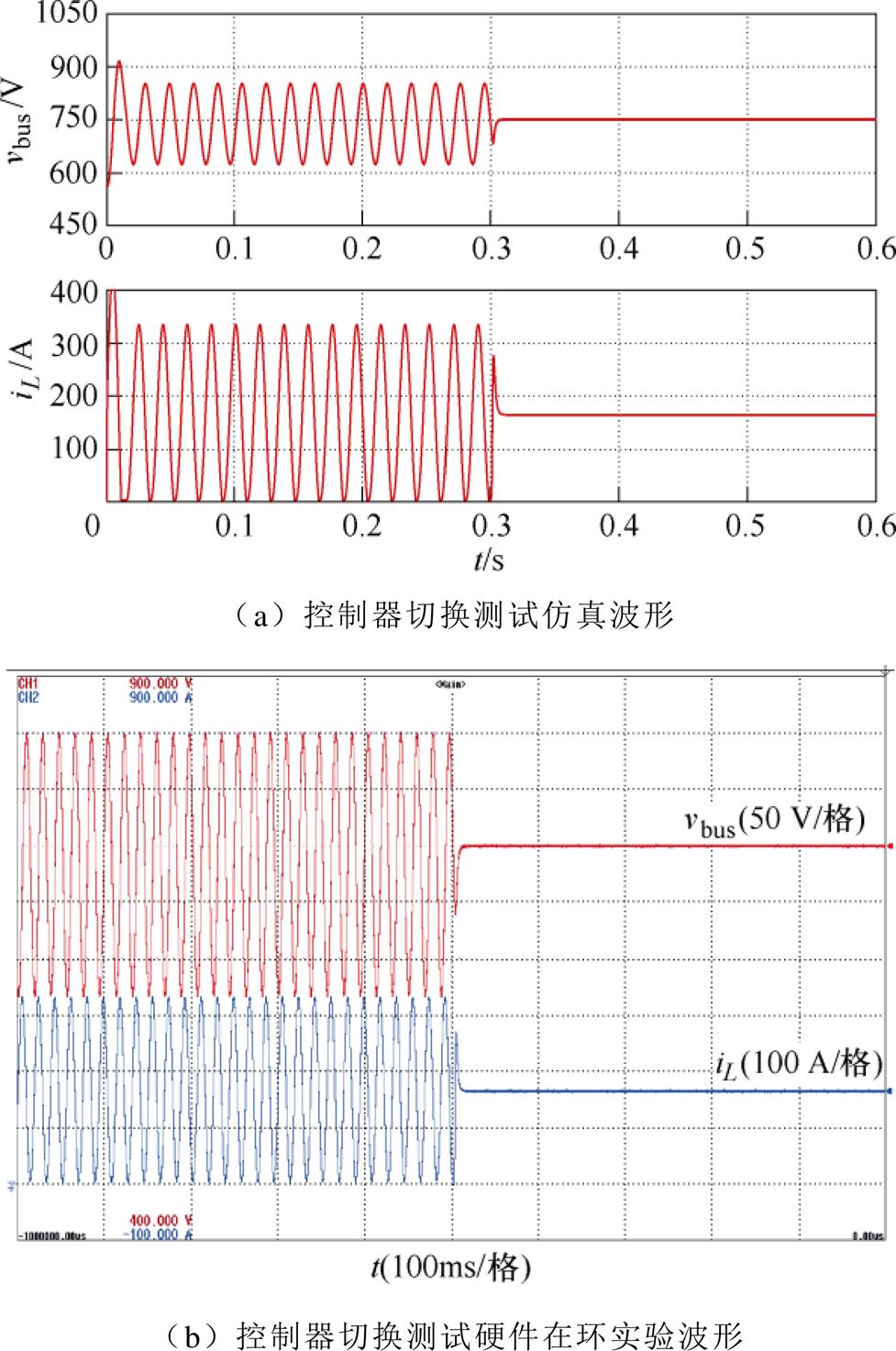
图12 控制器切换测试下的动态响应
Fig.12 Dynamic response under controller switching test
为了验证自适应反步控制在大信号稳定性上的优势，将其与经典双闭环PI控制器进行比较。图13为大信号稳定性测试时系统动态响应。在0.2 s时，CPL由15 kW突增至30 kW，与PI控制相比，自适应反步控制的超调量与恢复时间分别减少57.14%和92.5%。在0.4 s时，CPL由30 kW突增至60 kW时，自适应反步控制仍可保证系统稳定运行，而PI控制器出现明显振荡，导致系统崩溃。基于上述比较，自适应反步控制展现了在大信号稳定性方面的优越性，从而为直流微电网系统提供了更宽的稳定裕度。
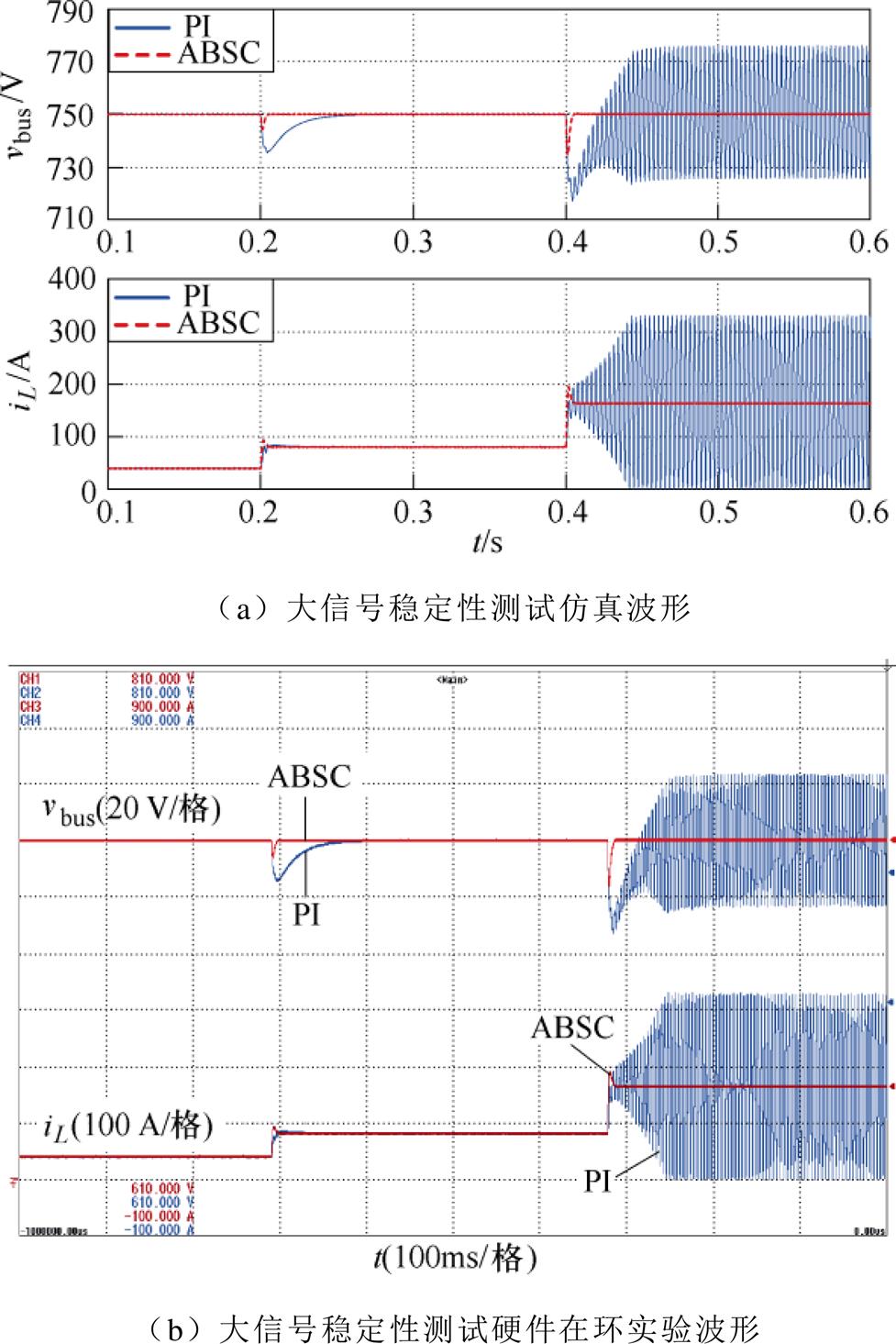
图13 大信号稳定性测试下的动态响应
Fig.13 Dynamic response under large signal stability test
受限于实验室条件，搭建了基于DSP控制器的低压（48 V）直流微电网实验平台，以验证仿真与硬件在环实验结果。图14为直流微电网系统实验平台，该平台包括直流电源、升压变换器、驱动电路、采样电路、混合负载和DSP。图4所示控制算法在DSP控制器中实现，生成PWM脉冲信号，经驱动电路功率放大后送至升压变换器，其实验装置参数见表4，输出信号经过电压、电流采样调理电路后发送至DSP控制器以实现闭环运行。负载侧主要分为两类：电阻性负载用于模拟CIL，电子负载设置在恒定功率模式下运行用于模拟CPL。
图14 直流微电网系统实验平台
Fig.14 DC microgrid system experiment platform
表4 直流微电网实验平台参数
Tab.4 Parameters of DC microgrid experimental platform
参 数数 值 电源电压E/V24 变换器电感L/mH1 变换器电容C/mF1 恒阻抗负载R/W50 开关频率fs/kHz20 直流母线电压vbus/V48 恒功率负载PCPL/W50
针对工况1的实验验证，输入电压扰动下的实验波形如图15所示。系统稳定一段时间后，输入电压突减至15 V，经过一段时间后输入电压增至26 V。可以观察到在输入电压变化期间，系统输出电压仍被精准的控制在48 V，并且具有快速恢复时间与良好鲁棒性能。
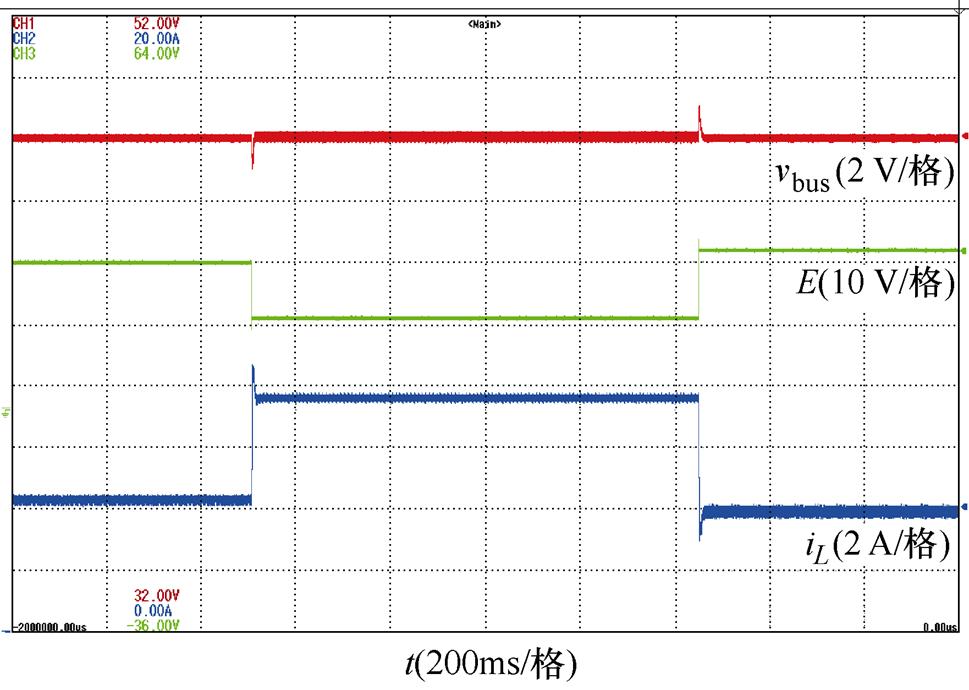
图15 输入电压扰动下的实验波形
Fig.15 Experimental waveforms under input voltage disturbance
针对工况2的实验验证，恒功率负载扰动下系统实验波形如图16所示。系统稳定一段时间后，将CPL由50 W突增至100 W，经过一段时间后CPL恢复至50 W。可以观察到在CPL变化期间，直流母线电压具有快速恢复时间与良好鲁棒性能。
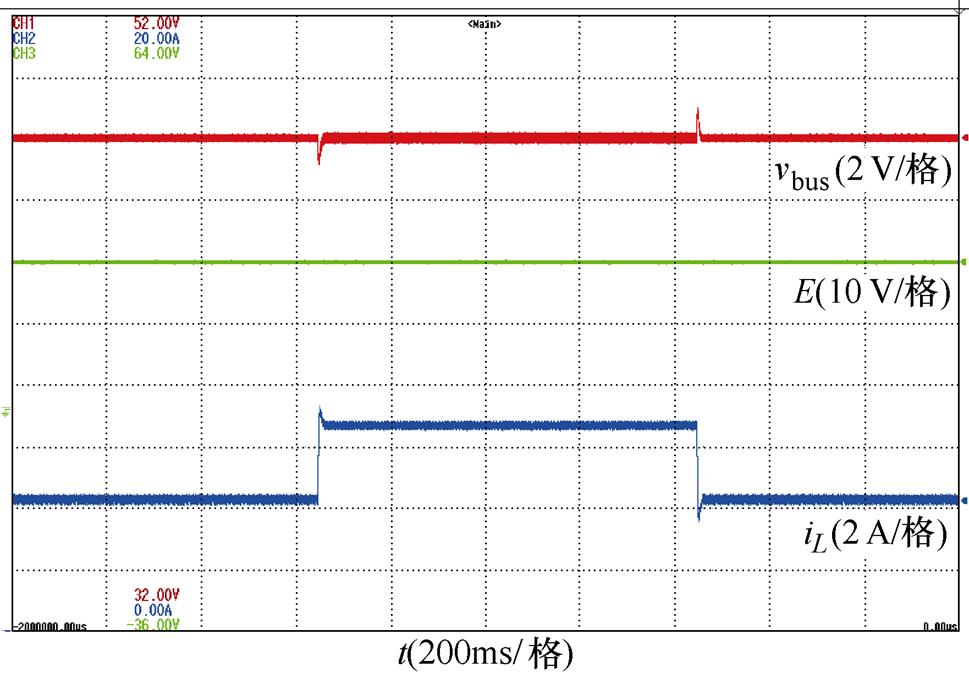
图16 恒功率负载扰动下系统实验波形
Fig.16 Experimental waveforms under CPL disturbance
针对工况3的实验验证，通过移除全部CIL以达到系统稳定性最差的条件，负载侧仅剩下CPL。恒阻抗负载扰动下系统实验波形如图17所示。系统稳定一段时间后，将CIL切除，经过一段时间后重新加载CIL。可以得到，即使系统向仅有CPL供给能量时，仍可保证直流母线电压稳定输出且具有良好的鲁棒性能。
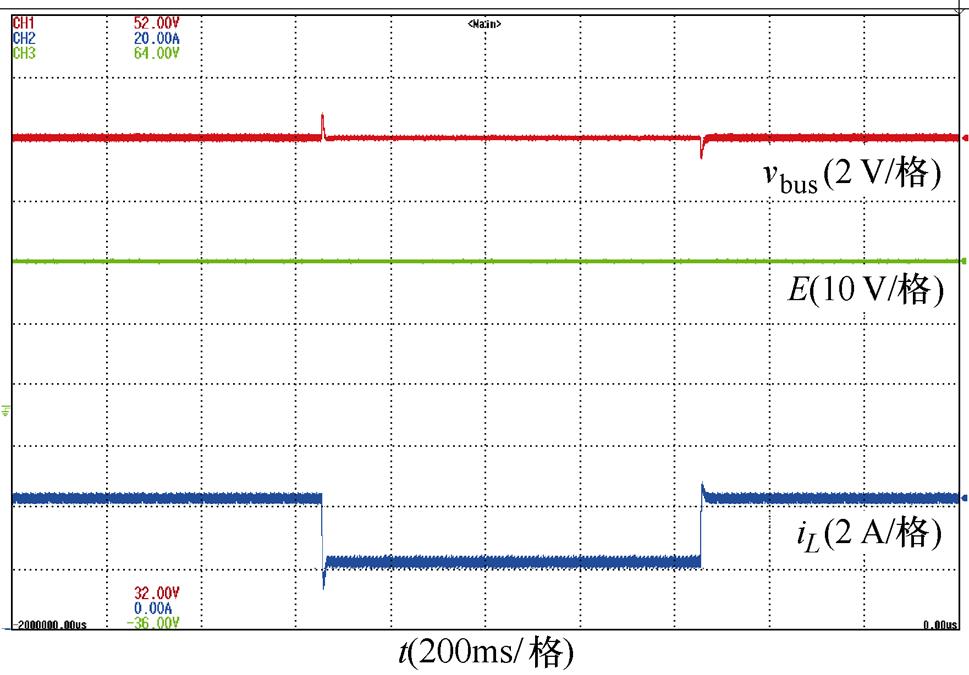
图17 恒阻抗负载扰动下系统实验波形
Fig.17 Experimental waveforms under CIL disturbance
针对工况4的实验验证，由于更换电路器件过于繁琐，因此通过将控制器中参数与实际硬件系统参数产生偏差来完成实验。图18为在控制器参数中电感与电容标称值相差-30%和30%时系统动态响应。对于上述两种情况，在负载阶跃变化下，直流母线电压总能恢复至期望输出电压，所提出的控制对系统参数不确定性具有良好的鲁棒性能。
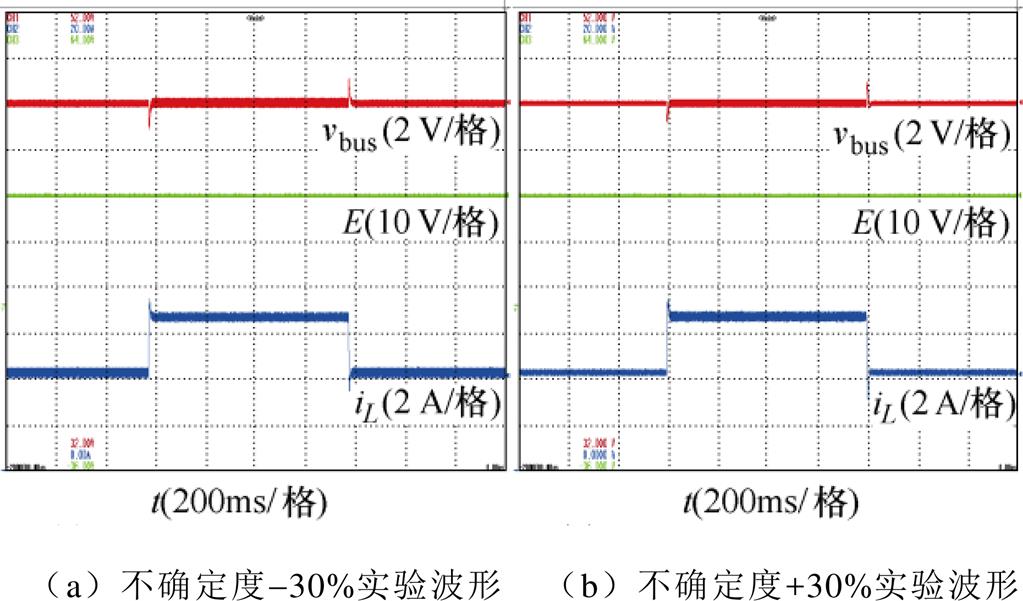
图18 模型不确定度下的实验波形
Fig.18 Experimental waveforms under model uncertainty
针对工况5，首先进行了控制器切换实验验证，控制器切换实验波形如图19所示。系统在带有CPL 150 W情况下开环启动，发生极限循环振荡，经过一段时间后，切换至提议控制，系统趋于稳定，母线电压维持在48 V。
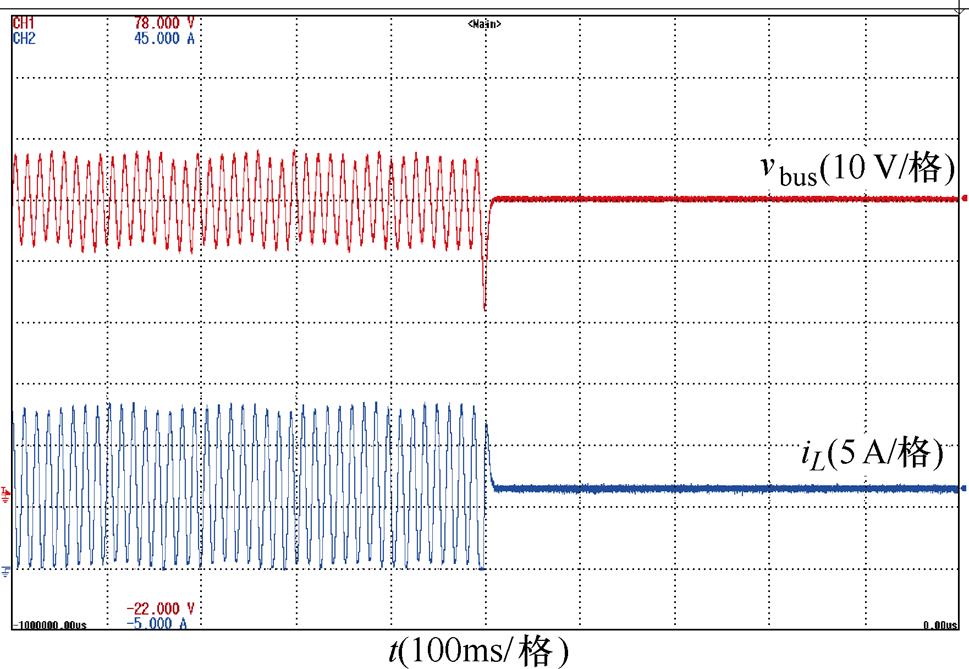
图19 控制器切换实验波形
Fig.19 Controller switching experimental waveforms
为了进一步验证大信号稳定性，将自适应反步控制与双闭环PI控制进行对比实验，大信号稳定性测试实验波形如图20所示。系统初始负载CPL为50 W，当CPL阶跃至100 W时，自适应反步控制的恢复时间与超调量均优于PI控制。继续增加CPL至200 W，此时PI控制出现明显振荡导致系统崩溃，而自适应反步控制仍可确保系统稳定运行。
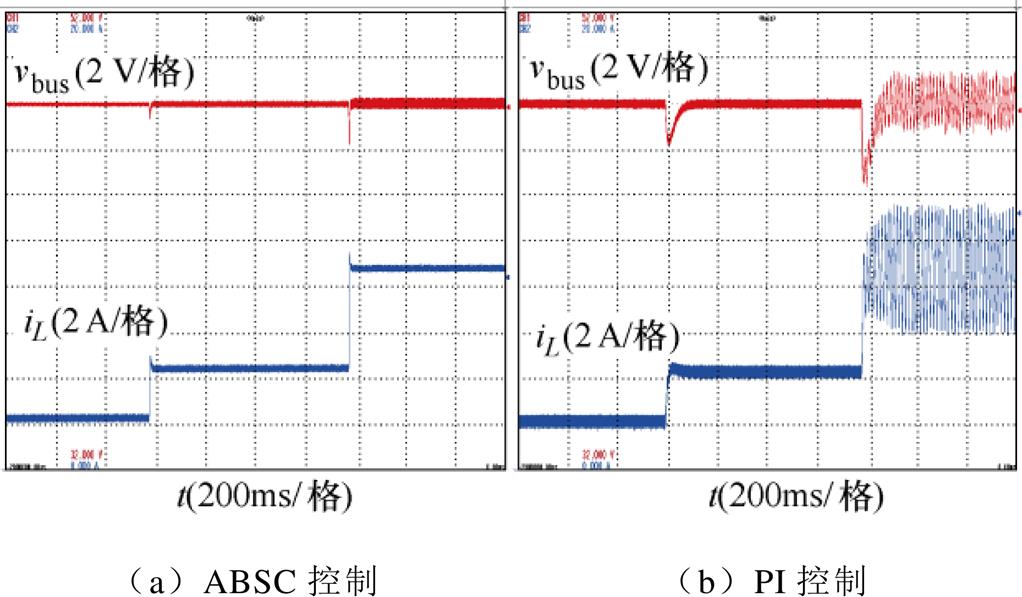
图20 大信号稳定性测试实验波形
Fig.20 Large signal stability test experimental waveforms
本文以直流微电网内部Boost变换器为研究对象，提出一种自适应反步控制策略，以解决恒功率负载引起的系统不稳定问题。首先，采用坐标变换将系统模型转换为标准形式，避免了寄生电阻对主控制器的影响。然后，通过扩展非线性干扰观测器与基于变换器动态模型设计的输入电压观测器对外部扰动（电源侧与负载侧）、寄生电阻和集总不确定项干扰进行估计并补偿，减轻控制器对传感器的依赖并消除直流母线电压稳态误差，显著提高了系统稳定性和鲁棒性。之后，运用李雅普诺夫与混合势函数理论，得到稳定性判据和控制器参数选取准则，保证了系统的大信号稳定性。最后，通过硬件在环与实验同时验证了自适应反步控制的有效性与优越性。本文控制器的设计步骤也适用于微电网内其他变换器拓扑。
参考文献
[1] Xu Luona, Guerrero J M, Lashab A, et al. A review of DC shipboard microgrids part I: power architectures, energy storage and power converters[J]. IEEE Transactions on Power Electronics, 2022, 37(5): 5155-5172.
[2] 朱晓荣, 李铮, 孟凡奇. 基于不同网架结构的直流微电网稳定性分析[J]. 电工技术学报, 2021, 36(1): 166-178.
Zhu Xiaorong, Li Zheng, Meng Fanqi. Stability analysis of DC microgrid based on different grid structures[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 166-178.
[3] 程林, 万宇翔, 齐宁, 等. 含多种分布式资源的配用电系统运行可靠性研究评述及展望[J]. 电力系统自动化, 2021, 45(22): 191-207.
Cheng Lin, Wan Yuxiang, Qi Ning, et al. Review and prospect of research on operation reliability of power distribution and consumption system considering various distributed energy resources[J]. Automation of Electric Power Systems, 2021, 45(22): 191-207.
[4] Alshareef M, Lin Zhengyu, Li Fulong, et al. A grid interface current control strategy for DC micro- grids[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(3): 249-256.
[5] 郭慧, 汪飞, 顾永文, 等. 基于电压分层控制的直流微电网及其储能扩容单元功率协调控制策略[J]. 电工技术学报, 2022, 37(12): 3117-3131.
Guo Hui, Wang Fei, Gu Yongwen, et al. Coordinated power control strategy for DC microgrid and storage expansion unit based on voltage hierarchical control[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3117-3131.
[6] Peyghami S, Palensky P, Blaabjerg F. An overview on the reliability of modern power electronic based power systems[J]. IEEE Open Journal of Power Electronics, 2020, 1: 34-50.
[7] 黄远胜, 刘和平, 苗轶如, 等. 基于并联虚拟电阻的级联DC-DC变换器稳定控制方法[J]. 电工技术学报, 2020, 35(18): 3927-3937.
Huang Yuansheng, Liu Heping, Miao Yiru, et al. Cascaded DC-DC converter stability control method based on paralleling virtual resistor[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3927-3937.
[8] Singh S, Gautam A R, Fulwani D. Constant power loads and their effects in DC distributed power systems: a review[J]. Renewable and Sustainable Energy Reviews, 2017, 72: 407-421.
[9] Cespedes M, Xing Lei, Sun Jian. Constant-power load system stabilization by passive damping[J]. IEEE Transactions on Power Electronics, 2011, 26(7): 1832-1836.
[10] 季宇, 王东旭, 吴红斌, 等. 提高直流微电网稳定性的有源阻尼方法[J]. 电工技术学报, 2018, 33(2): 370-379.
Ji Yu, Wang Dongxu, Wu Hongbin, et al. The active damping method for improving the stability of DC microgrid[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 370-379.
[11] Zhang Xin, Zhong Qingchang, Kadirkamanathan V, et al. Source-side series-virtual-impedance control to improve the cascaded system stability and the dynamic performance of its source converter[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5854-5866.
[12] 滕昌鹏, 王玉斌, 周博恺, 等. 含恒功率负载的直流微网大信号稳定性分析[J]. 电工技术学报, 2019, 34(5): 973-982.
Teng Changpeng, Wang Yubin, Zhou Bokai, et al. Large-signal stability analysis of DC microgrid with constant power loads[J]. Transactions of China Elec- trotechnical Society, 2019, 34(5): 973-982.
[13] Jiang Jianbo, Liu Fei, Pan Shangzhi, et al. A conservatism-free large signal stability analysis method for DC microgrid based on mixed potential theory[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 11342-11351.
[14] 刘宿城, 李响, 秦强栋, 等. 直流微电网集群的大信号稳定性分析[J]. 电工技术学报, 2022, 37(12): 3132-3147.
Liu Sucheng, Li Xiang, Qin Qiangdong, et al. Large signal stability analysis for DC microgrid clusters[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3132-3147.
[15] Zeng Jianwu, Zhang Zhe, Qiao Wei. An inter- connection and damping assignment passivity-based controller for a DC-DC Boost converter with a constant power load[J]. IEEE Transactions on Industry Applications, 2014, 50(4): 2314-2322.
[16] Khan M S, Ahmad I, Abideen F Z U. Output voltage regulation of FC-UC based hybrid electric vehicle using integral backstepping control[J]. IEEE Access, 2019, 7: 65693-65702.
[17] Zheng Changming, Dragičević T, Zhang Jiasheng, et al. Composite robust quasi-sliding mode control of DC-DC Buck converter with constant power loads[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(2): 1455-1464.
[18] He Wei, Ortega R. Design and implementation of adaptive energy shaping control for DC-DC converters with constant power loads[J]. IEEE Transactions on Industrial Informatics, 2020, 16(8): 5053-5064.
[19] Yuan Cong, Bai Hao, Ma Rui, et al. Large-signal stability analysis and design of finite-time controller for the electric vehicle DC power system[J]. IEEE Transactions on Industry Applications, 2022, 58(1): 868-878.
[20] Chen Wenhua, Yang Jun, Guo Lei, et al. Disturbance- observer-based control and related methods-an overview[J]. IEEE Transactions on Industrial Elec- tronics, 2016, 63(2): 1083-1095.
[21] Hassan M A, Su Chunlian, Chen Fuzen, et al. Adaptive passivity-based control of DC-DC Boost power converter supplying constant power and constant voltage loads[J]. IEEE Transactions on Industrial Electronics, 2022, 69(6): 6204-6214.
[22] Xu Qianwen, Zhang Chuanlin, Wen Changyun, et al. A novel composite nonlinear controller for stabi- lization of constant power load in DC microgrid[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 752-761.
[23] 崔健, 王久和, 李建国, 等. 基于扩张状态观测器估计补偿的Buck变换器带恒功率负载无源控制[J]. 电工技术学报, 2019, 34(增刊1): 171-180.
Cui Jian, Wang Jiuhe, Li Jianguo, et al. Research on passivity-based control of Buck converter with constant power load based on extend state observer estimating and compensating[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 171- 180.
[24] Ginoya D, Shendge P D, Phadke S B. Sliding mode control for mismatched uncertain systems using an extended disturbance observer[J]. IEEE Transactions on Industrial Electronics, 2014, 61(4): 1983-1992.
[25] Li Po, Li Ruiyu, Shao Tianying, et al. Composite adaptive model predictive control for DC-DC Boost converters[J]. IET Power Electronics, 2018, 11(10): 1706-1717.
[26] Gui Yonghao, Han Renke, Guerrero J M, et al. Large- signal stability improvement of DC-DC converters in DC microgrid[J]. IEEE Transactions on Energy Conversion, 2021, 36(3): 2534-2544.
[27] 游逍遥, 刘和平, 苗轶如, 等. 带恒功率负载的双极性直流系统稳定性分析及其有源阻尼方法[J]. 电工技术学报, 2022, 37(4): 918-930.
You Xiaoyao, Liu Heping, Miao Yiru, et al. Stability analysis and active damping method of the bipolar DC system with constant power loads[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 918-930.
Abstract The DC microgrid has many loads: constant impedance load (CIL) and constant power load (CPL). The negative impedance characteristic of CPL will reduce the system damping and cause the system to collapse. However, the traditional linear control only guarantees stability in the small neighborhood of the equilibrium point and needs to make a trade-off between the stability margin and the dynamic performance. In recent years, many nonlinear control methods have been proposed, but most require parameter design and general dynamic performance. In order to solve these problems, this paper proposes an adaptive backstepping control, which guarantees the global large signal stability and fast dynamic response of the system.
Firstly, the model is transformed into Brunovsky’s canonical form using the exact feedback linearization technique to solve the non-minimum phase problem and avoid the influence of parasitic resistance on the primary controller. Secondly, to improve the robustness of the system, an extended nonlinear disturbance observer and an input voltage observer based on the dynamic model of the converter are used to estimate and compensate for external disturbances, parasitic resistance, and lumped uncertainty disturbances online. The optimized adaptive backstepping control can operate with limited and imprecise initial parameters of the system. The large-signal stability of the controller is verified based on Lyapunov and mixed potential function theory. The design principle of controller parameters and the stability boundary diagram of the system are given to ensure global trajectory tracking and fast dynamic response of the output voltage.
The simulation and hardware in the loop experiment of DC microgrid under various working conditions, compared with the literature in Ref.[22], show that when the input voltage step changes, the overshoot and recovery time are reduced by 81.25% and 88%, respectively, and the inductance current does not reverse overshoot. When the CPL step changes, its overshoot and recovery time are reduced by 41.89% and 75%, respectively. When the CIL step changes, the overshoot and recovery time are reduced by 41.56% and 75%, respectively. At the same time, the proposed control is robust to model parameter uncertainties and parasitic parameters, which can be better applied to industrial applications under various harsh conditions. In addition, the proposed control is tested for controller switching and large signal stability. Compared with the classical PI control, the overshoot and recovery time of the proposed control are reduced by 57.14% and 92.5%, respectively. Finally, the effectiveness and superiority of the proposed control are further verified through the DC microgrid experimental platform.
The following conclusions are drawn from the simulation and experimental results: (1) Compared with BSC+NDO, it reduces the parameters required for controller design and the dependence on sensors, considers the system parasitic parameter interference, and has good stability and robustness. (2) Compared with classical PI control, the proposed control can stabilize the limit cycle oscillation system and has a better dynamic response. (3) A mixed potential function large signal stability criterion for nonlinear control is proposed, and the controller parameter design criteria and large signal stability boundary diagram are provided.
keywords：DC microgrid, Boost converter, constant power load, back stepping controller, extended non- linear disturbance observer, large signal stability
DOI: 10.19595/j.cnki.1000-6753.tces.220609
中图分类号：TM46
国家自然科学基金青年项目（52007049）和河北省自然科学基金项目（E2020202177）资助。
收稿日期 2022-04-18
改稿日期 2022-05-05
张泽华 男，1997年生，硕士研究生，研究方向为直流微电网系统的稳定性分析与先进控制策略。E-mail: zzh_hebut@126.com
宋桂英 女，1971年生，副教授，硕士生导师，研究方向为永磁同步电机控制与微电网技术。E-mail: sgyxl@hebut.edu.cn（通信作者）
（编辑 陈 诚）