图1 主从式控制结构
Fig.1 Master-slave control structure
摘要 分布式控制在级联H桥（CHB）变换器并联的电源中可提升输出容量及可靠性。然而，常规分布式控制器可能由于硬件或控制参数的不匹配而导致输出功率不平衡，从而在CHB支路之间形成不稳定的环流，这将导致：①支路电流的稳定性与跟踪性能变差；②均流电抗器易饱和。对此该文提出一种基于Luenberger观测器状态重构的主从模型预测控制，所提策略可以实现参考电流跟踪和环流抑制的控制优化。此外，通过载波可以轻松实现级联H桥交错和并联控制器同步，从而固定开关频率。基于推导出的电流预测模型，当多个并联CHB支路具有不同的输出功率时，可以实现优化的电流跟踪响应并消除环流。仿真和实验结果验证了所提方法的有效性。
关键词：预测控制 级联H桥变换器 并联 主从控制结构 电流跟踪 环流 观测器
采用级联H桥（Cascaded H-Bridge, CHB）变换器模块化并联是大功率应用的有效拓扑，对于具有输出高电压和输出大电流要求的高功率设备，并联CHB变换器的做法已出现在托卡马克磁体控制电源中[1]。线圈两端更高的电压产生更快的电流变化率，输出端更多的电平则可有效降低滤波成本。为了在负载线圈两端输出更高的电压与更多的电平，CHB变换器的级联H桥可以交错级联。H桥交错级联可以提高等效开关频率，同时减少纹波、响应延迟和开关噪声等问题。通常载波移相脉宽调制（Carrier Phase Shifted Pulse Width Modulation, CPSPWM）用于管理交错H桥的开关动作，根据文献[2-4]的研究，CPSPWM具有响应速度快、输出功率均衡和滤波成本低的优点，因此，CPSPWM可以显著提高级联系统输出性能。
为了输出更高的电流，CHB变换器也可以通过均流电抗器并联[5]。这样，每个CHB支路的输出电流在公共负载处汇流为总电流，因此可以在功率器件允许的范围内获得更高的输出并降低成本。并联的主要问题是因支路之间输出特性差异而注入的环流，过大的环流幅值导致均流电抗器易饱和、电流跟踪性能下降并危害系统稳定性。环流可能由硬件参数或控制参数不匹配引起，如均流电抗器、直流母线电压不等或器件差异如开关延时、死区时间等原因。通常增加均流电感可以获得满意的环流抑制，但成本和体积会大幅增加，并且随着均流电抗器电压的升高，负载电感的电流导数会降低，不利于总电流的快速跟踪，因此通过增加均流电抗器抑制环流会带来一些实际问题。
为了减小均流电抗器，并联变换器可以采用同步载波并输出相同的参考电流[6]。假设每个支路具有相同幅度的参考电流与直流母线电压，并且在完全理想状态下运行，并联支路间将不存在环流，那么可以说在理想条件下实现功率平均分配的脉冲宽度调制（Pulse Width Modulation, PWM）方案可以最小化均流电抗器电感值。但是对于非平均功率的并联系统，在输出功率不等时，即使增大均流电抗器也难以抑制严重的功率失衡引入的环流。可行的做法之一是在控制回路中增加环流抑制环节，一些简单的环流消除控制器通常由线性PID控制器实 现[7-8]，这种控制策略无需支路之间进行通信，因此控制结构属于完全分散式控制。
在最近的研究中，模型预测控制（Model Predictive Control, MPC）已被用作并联系统的控制策略，具有响应速度快、约束灵活、控制性能良好等优点[9-11]。固定开关频率MPC目前是应用场景较多的一种有吸引力的控制策略[12]，然而对并联CHB变换器的MPC研究并不多。并联系统通常是多输入状态的，即输出与多个输入存在耦合，当预测模型能够准确描述并联系统行为时，MPC将具有良好的控制性能。因此，MPC需要在并行控制器之间建立通信接口以共享耦合信息[13]。
在完全分散式结构中，由于控制器之间无通信通道，因此无法主动平衡功率来抑制环流，只能在环流出现后通过线性控制器被动减弱。随着技术的进步，有很多方法可以实现分布式控制器之间快速稳定的通信和协同控制。文献[14]设计了一种协调控制结构的环流抑制。文献[15]在并联三电平逆变器中提出了无差拍的环流抑制策略。文献[16]采用主从控制结构来抑制T型三电平逆变器的环流。在传统主从控制方案中，每个控制器必须与所有其他控制器共享数据形成信息冗余以提高可靠性，从而避免主机故障时系统无法正常工作。但需要相当多的通信数量，因此传统主从控制方案的系统开关频率受到并联数量与通信次数的较大限制。为了提高开关频率以获得更好的输出质量，可以采用改进的主从控制方案[13, 17-18]。文献[13]在模块化多电平变换器（Modular Multilevel Converter, MMC）的并联应用中，在主控制器内执行抑制低频零序环流的MPC，并在从控制器中执行固定开关频率的交错PWM实施控制量，可以有效抑制低频零序环流，但是零序环流的预测模型不具有闭环观测能力。文献[17]在级联H桥型静止同步补偿器（Static Synchronous Compensator, STATCOM）的并联应用中，提出在主控制器内执行简化的分枝定界算法，从而将有限控制集（Finite Control Set, FCS）遍历以选取最优控制矢量，并在9个从控制器中执行开关动作，该策略可以将FCS-MPC最优矢量选择的耗时降低至线性时间，但是开关频率不固定且最优控制矢量计算量大。文献[18]在中性点钳位（Neutral Point Clamped, NPC）逆变器的并联应用中，提出在主控制器内执行比例谐振与超前补偿的控制策略，并在从控制器内执行正弦PWM的电流注入方法，从而改善谐波与控制带宽。结果表明，该方法的开关频率高达50 kHz，但是该方法控制参数多且整定困难。在这些文献中从控制器仅与主控制器通信，无需与其他从控制器通信，则通信数量可以减少到从控制器的数量，主从式控制结构如图1所示。因此改进的主从控制方案可以有效缓解系统的通信时间成本，从而在交错H桥或并联CHB支路数量较多时获得更高的输出质量，其可靠性也已在工业应用中得到证明[9]。
图1 主从式控制结构
Fig.1 Master-slave control structure
本文创新之处在于提出一种基于载波的主从MPC方案，适用于M个H桥交错级联、N个CHB支路同步并联的电源。与现有的完全分散式控制相比，主从控制结构组成的通信协同能有效抑制并联支路输出功率不等导致的环流。在提出的方法中，MPC与CPSPWM相结合以实现级联H桥的交错与固定开关频率。通过采用移相交错技术，将单个CHB支路的控制频率提高到级联H桥数量的倍数。因此，MPC（快速响应、优化性能）和CPSPWM（高等效开关频率和低成本滤波）的优点可以结合起来，进一步提高跟踪性能。在主控制器中，通过Luenberger观测器将支路电流重构为流过公共负载电感的电流与支路环流，完成包括参考跟踪误差最小化和环流抑制在内的最优电流控制。并且在并联支路输出功率不等时，可以保证环流抑制能力的同时尽量减小均流电抗器。所提策略的有效性已在多达6个并联七电平CHB支路的仿真与两个并联五电平CHB支路的实验中得到验证。
并联CHB电源拓扑结构如图2所示。单个CHB支路级联M个H桥以提高输出电压，共有N个CHB支路通过均流电抗器连接至负载电感；Lb为均流电抗器；LH为负载电感；Rb和RH分别为均流电抗器、负载电感的等效电阻；uHjk为第j个CHB支路的第k个H桥输出电压；udc为H桥模块的直流侧输入电压；ij为第j个CHB支路的输出电流；iH为负载电感的总输出电流。本文的工程背景是磁体电源，因此电源具有电流源性质。忽略负载电感及线路中微弱电阻，由基尔霍夫电压定律可得并联CHB电源的数学模型描述为
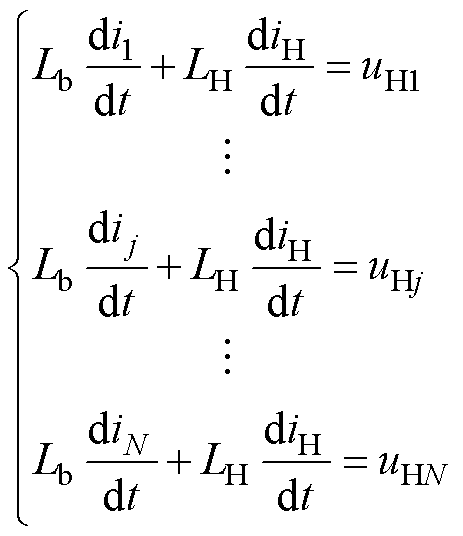（1）
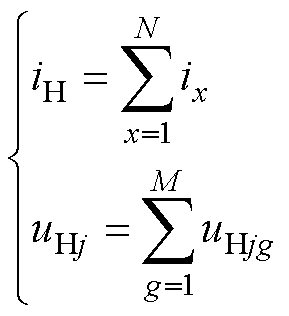（2）
式中，uHj为第j个CHB支路的输出电压，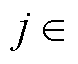
。
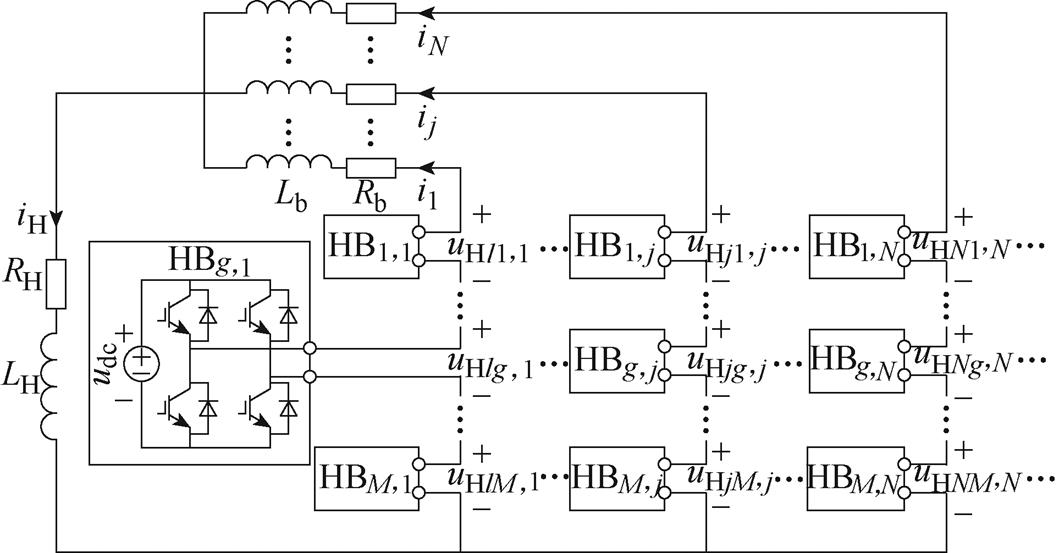
图2 模块化并联CHB电源
Fig.2 Modular parallel CHB power supply
任意CHB支路中流动有两种路径的电流，分别为公共负载电流以及不平衡功率而导致的环流，第j个CHB支路电流分解为公共负载电流与环流，如图3所示。因此第j个CHB支路电流ij可分解为公共负载电感电流iHj及N-1个环流iccjx（x=1,…, N, x≠j），即
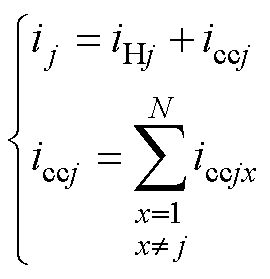（3）
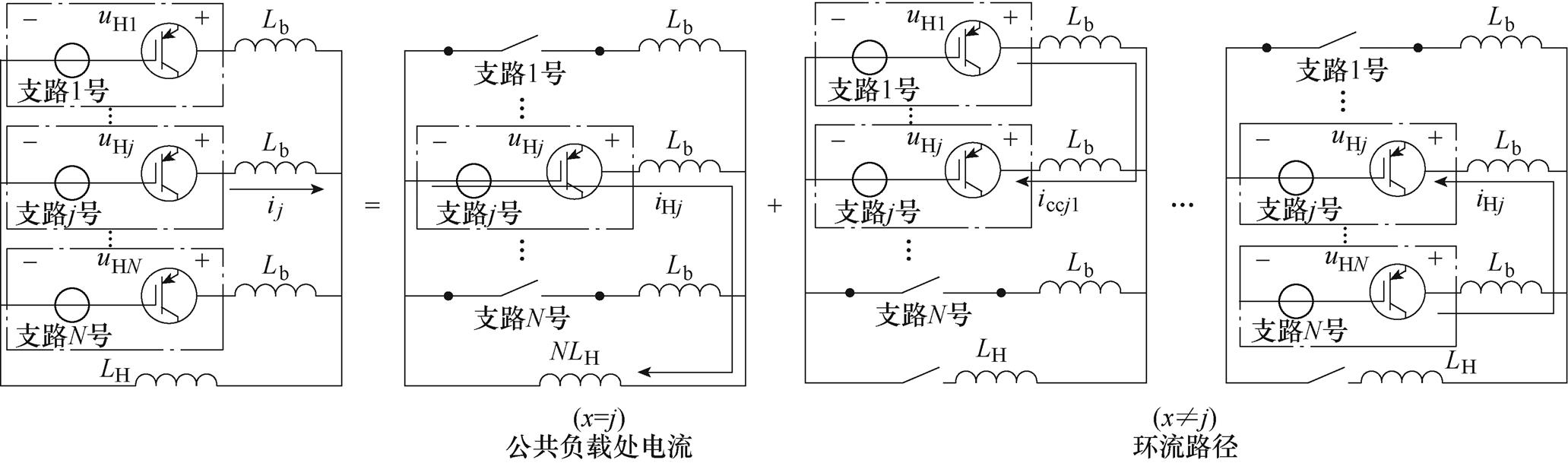
图3 第j个CHB支路电流分解为公共负载电流与环流
Fig.3 Current of the jth CHB branch is decomposed into the common load current and the circulating current
式中，iccjx为第j个支路与第x个支路之间的环流；iccj为第j个支路中的总环流。在实际CHB支路中设置的电流传感器仅可测量支路电流ij，而无法有效测量上述两种路径的电流，即第j个支路电流中含有的公共负载电感电流以及环流属于不可测状态。采用Luenberger状态观测器实现对上述两种不可测电流状态的监测。以第j个CHB支路为例，首先将支路电流ij写为多变量状态方程为
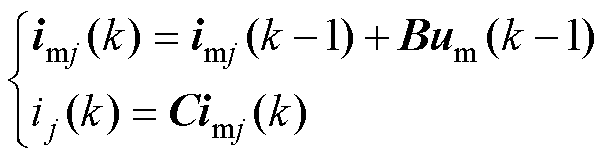（4）
其中
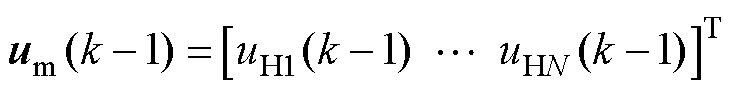
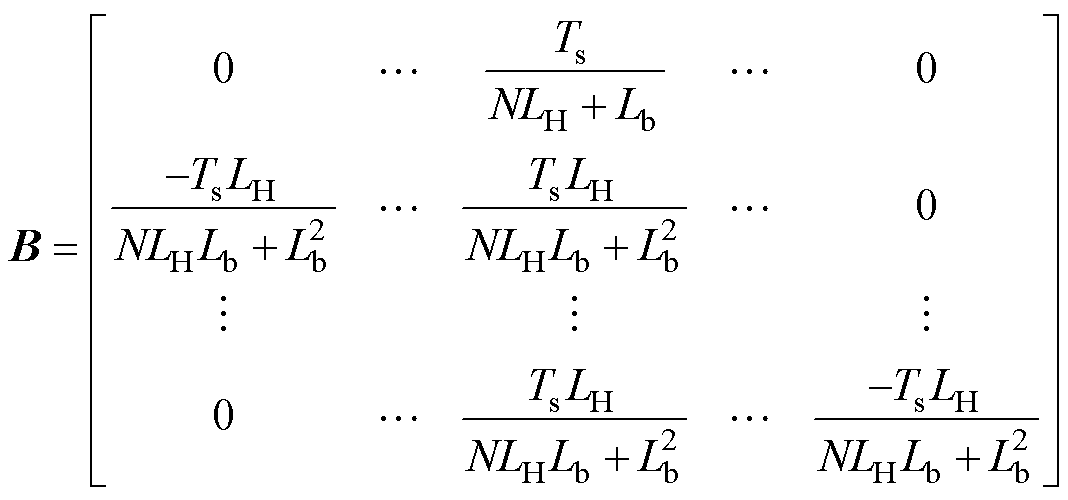
式中，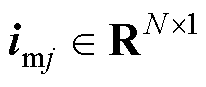
为电流状态向量；
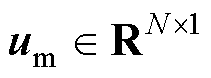为输入向量；
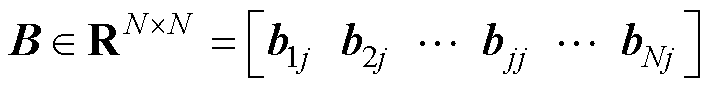为输入增益矩阵；
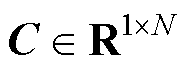为输出增益向量；Ts为采样频率；ij(k)为第j个CHB支路在第k时刻的输出电流。采用Luenberger状态观测器对支路电流状态进行重构得
（5）
式中，
为观测电流状态向量；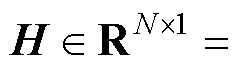
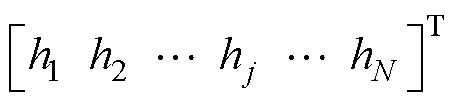为误差反馈增益向量；
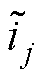为观测支路电流。为了使观测误差渐近稳定，令式（5）减去式（4），可得误差状态方程为
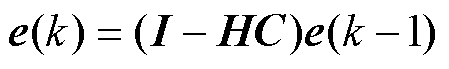（6）
式中，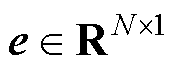
为误差状态向量；I为单位阵；A= I-HC为误差增益矩阵。误差方程的特征根通过求解
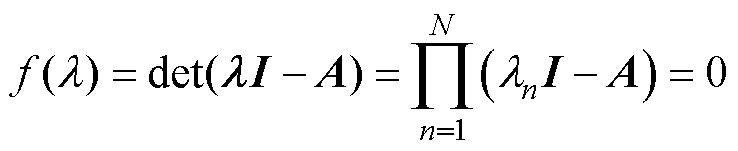获得。其中det(∙)为行列式计算函数；l 为增益矩阵的特征根。因此，离散观测误差的稳定性条件为特征根分布在单元圆内，即
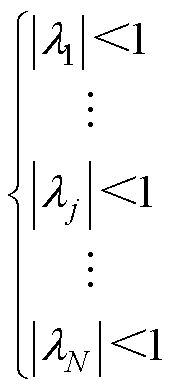（7）
选取满足式（7）的误差状态反馈增益向量H，可得到渐近稳定的Luenberger观测器，即可重构第j个支路电流中含有的公共负载电感电流iHj以及总环流iccj，为多目标优化建立基础。以第j个CHB支路为例，所提出的Luenberger观测器如图4所示，图中，bij为输入增益矩阵B的列向量，hi为误差反馈增益向量H的行元素。由图4可知，第j个支路电流被分解为公共负载电感电流与第j个支路的总环流，其中第j个支路的公共负载电感电流仅与自身输出电压相关，而与其他所有并联支路输出无关，因此可通过Luenberger观测支路电流状态。而第j个CHB支路的总环流在并联耦合系统中与其他所有支路输出相关，即环流由所有并联输出电压差激励，因此可通过Luenberger观测器将总环流进一步分解为N-1个环流iccjx（x=1,…, N, x≠j）。
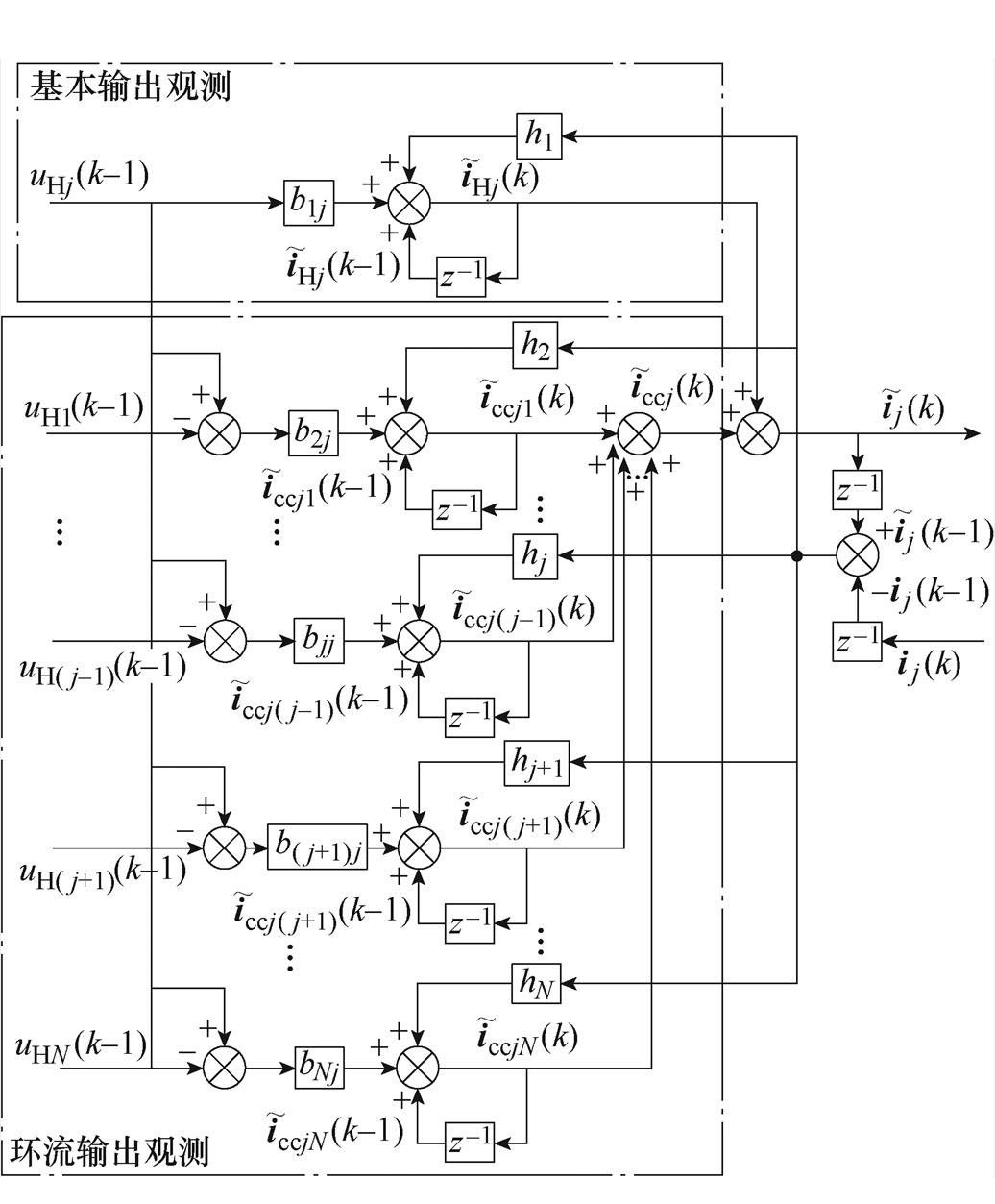
图4 Luenberger观测器重构CHB支路电流
Fig.4 Reconstructing the CHB branch current by the Luenberger observer
本节提出一种基于载波的主从MPC结构，以实现并联CHB支路的电流参考跟踪及环流抑制，基于载波的交错级联与同步并联如图5所示。N个同步并联的控制器采用主从控制结构，主控制器输出载波相位信号强制同步从控制器之间的相位，使并行控制器具有相同的优化时序。待主控制器完成最优控制量的计算后下发至从控制器，并由CPSPWM进一步独立管理，基于载波实现的M个交错级联H桥产生更高的等效开关频率。所提方法适用于N个CHB支路并联，并且从控制器之间无需通信。
主从模型预测控制框图如图6所示，其中
为各CHB支路最优控制量，
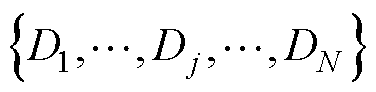为支路更新的占空比。首先，采样值上传到主控制器后通过Luenberger观测器将每个支路电流重构为公共负载电感电流与环流，再将重构电流状态的一步超前预测作为单步优化初始值以补偿数字控制固有的占空比装载、更新延迟；其次，令每个支路中流过公共负载电感的电流跟踪指令值，令环流跟踪0，从而建立跟踪误差二次方最小准则的多目标评价函数；然后，将每个支路的评价函数联立以得到全局优化的最优控制量；最后，将计算出的各支路最优控制量由通信模块下发给从控制器，再由CPSPWM在关联H桥更新时刻独立管理每个CHB支路的占空比，载波移相调制时序如图7所示，图中，
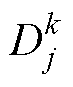为第k时刻第j支路更新的占空比。CPSPWM在每个载波峰谷点时刻触发采样，特别注意的是，级联H桥的交错技术提高了等效开关频率，因此需要在等效开关周期Ts而不是开关周期MTs内完成控制过程以保持所更新控制量的最优性。
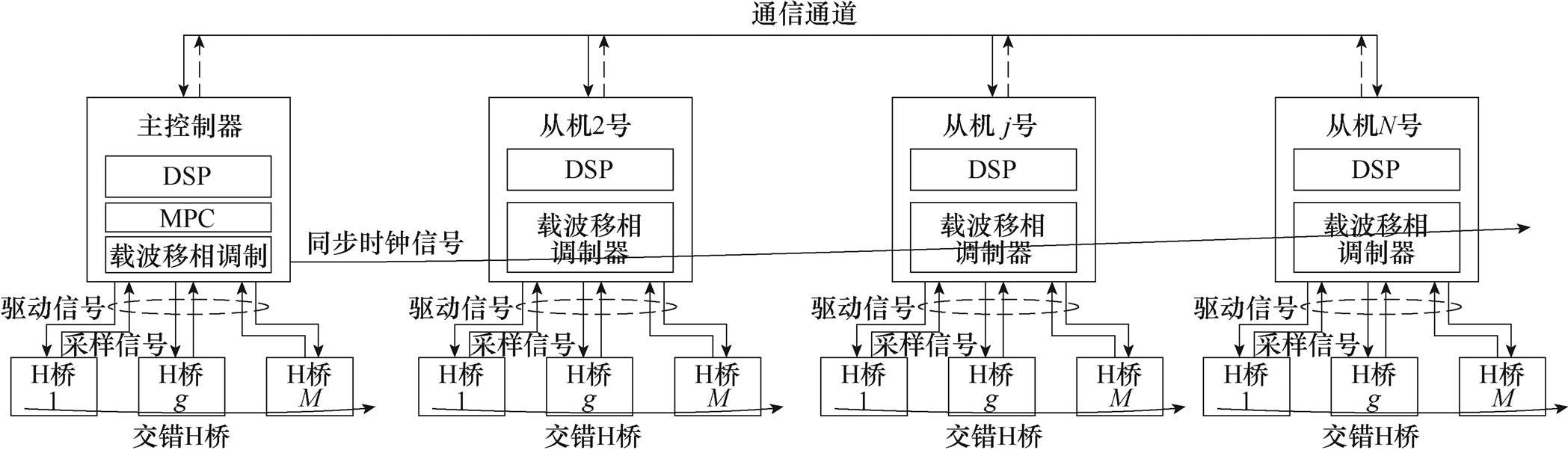
图5 基于载波的交错级联与同步并联
Fig.5 Carrier-based interleaved cascade and synchronous parallel
图6 主从模型预测控制框图
Fig.6 Master-slave model predictive control block diagram
MPC通过数学模型对系统未来行为做出合理预测并计算出使得评价函数最小的最优控制量。由第1节的分析可知，任意CHB支路输出的电流不仅有其自身的输出功率，还包括因支路间可能存在的不平衡功率而导致的环流。通过Luenberger观测器对支路电流进行状态重构可以得到各支路的公共负载电感电流与环流的单步预测如式（8）、式（9）所示。在提出的MPC方法中，CHB变换器输出电压可以被等效为一个整体，CHB变换器输出电压状态见表1。
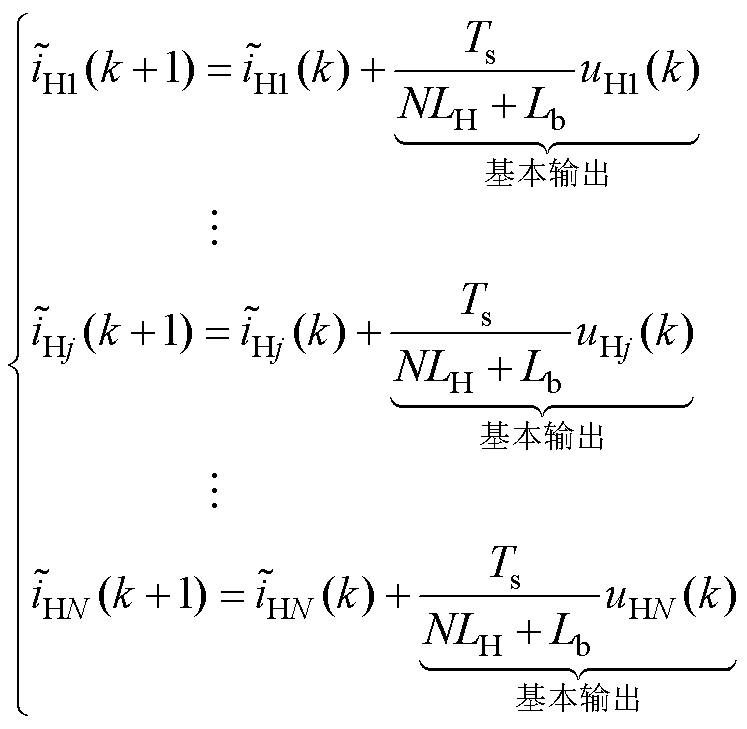（8）
图7 载波移相调制时序
Fig.7 Timing of the carrier phase-shifted modulator
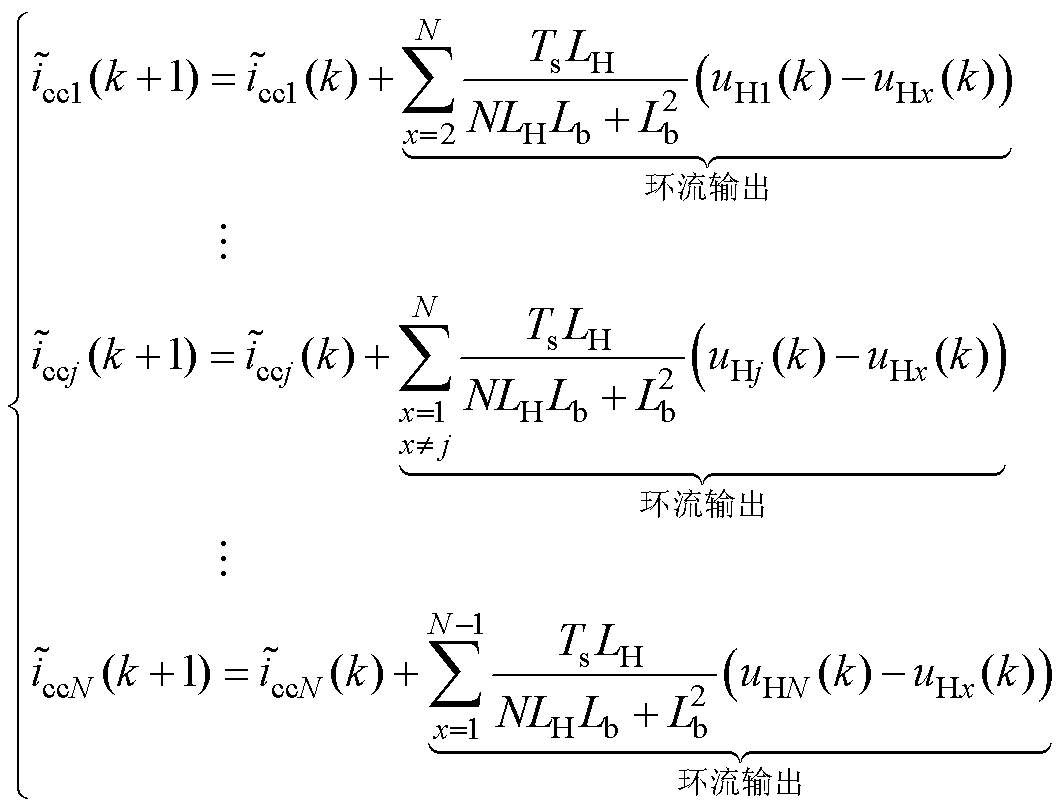（9）
表1 CHB变换器输出电压状态
Tab.1 CHB converter output voltage status
状态输出电压uo符号 1uHv1 20v2 3-uHv3
（1）状态“1”表示所有的级联H桥均投入并输出正电压，CHB变换器输出电压用uH表示，将状态“1”记为v1。
（2）状态“2”表示所有的级联H桥均不投入并输出零电压，CHB变换器输出电压用0表示，将状态“2”记为v2。
（3）状态“3”表示所有的级联H桥均投入并输出负电压，CHB变换器输出电压用-uH表示，将状态“3”记为v3。
特别指出，上述虚拟的电平状态仅用于建立预测模型并计算最优控制量，并不直接用于实际CHB支路控制。
在将CHB支路输出电压视为一个整体后，各支路公共负载电流与环流的单步预测模型可以写为控制量的函数，即
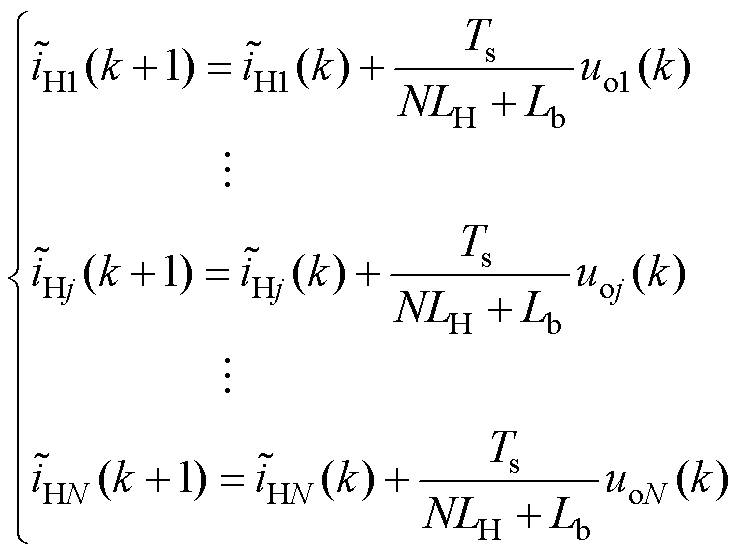（10）
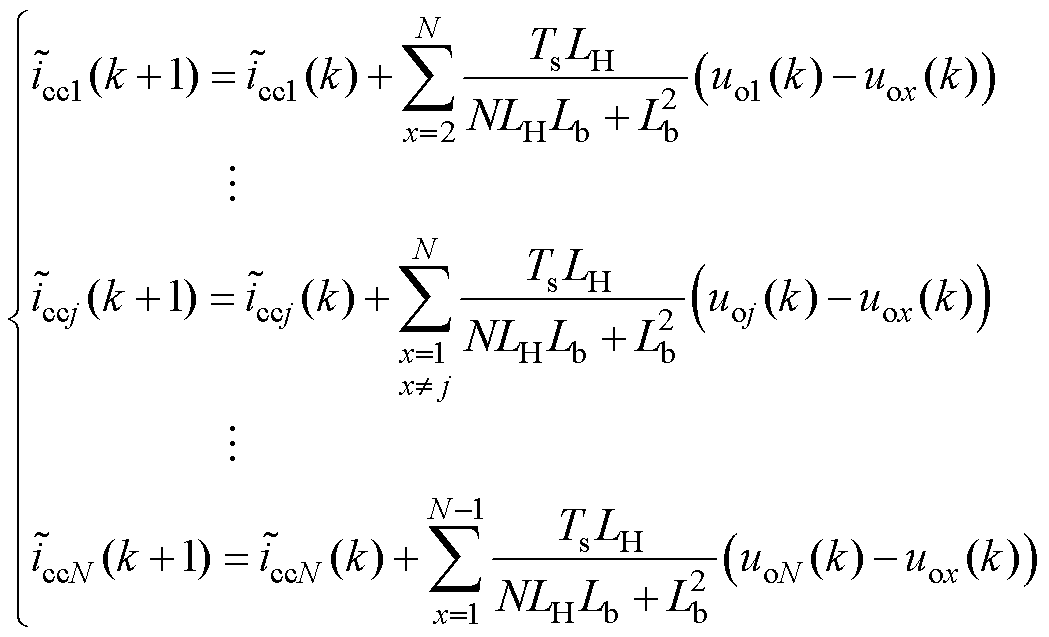（11）
式中，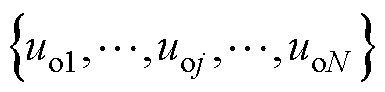
为由非零电平和零电平组成的平均电压。v1的电流导数为正，v3的电流导数为负，v2的电流导数为零表示直流侧与负载电感没有功率交换。因此，在每个采样周期内仅有一种状态组合v1/v2或v3/v2被选中以计算最优控制量。
所提出MPC控制器有两个主要的控制目标：①支路电流参考跟踪；②抑制环流。对于并联CHB支路应独立跟踪每个支路的电流参考，这是通过控制公共负载电流中每个支路的基本输出完成的。此外由于硬件参数失配或输出功率不平衡引起的环流需要系统全局优化，因此第j个支路的评价函数
应当评估当前支路基本输出跟踪电流参考的性能，以及全局控制量对当前支路环流的影响。所提出的MPC采用与传统MPC相同的评价函数最小化思想，但是并联耦合系统的全局优化需要考虑所有N个并联支路输出。在采样周期内逐一评估所有支路评价函数并反复迭代得到全局优化的方案会耗费大量计算时间，并且系统可能陷入局部最优而不是全局最优，因此提出MPC控制器在无约束条件时直接建立全局优化的评价函数为
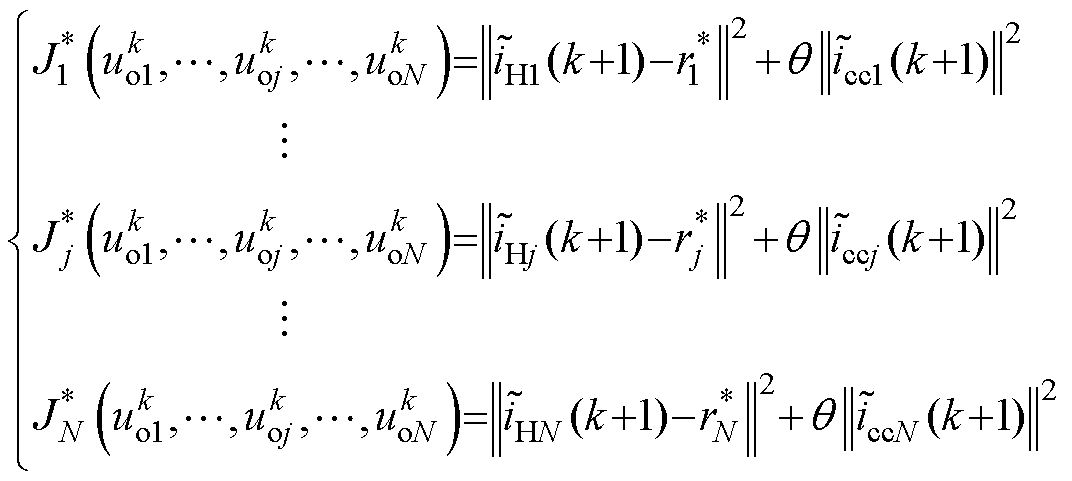（12）
式中，
为第j个支路的参考电流；q 为环流抑制的权重。虽然公共负载电流中第j个CHB支路的基本输出独立于其他所有支路，但第j个支路的环流取决于所有支路的输出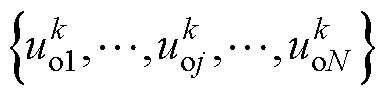
，因此为了获得全局最优控制量，对式（12）求导可得
（13）
将公共负载电流单步预测模型式（10）与环流的单步预测模型式（11）代入式（13），可知最优控制量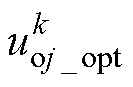
可以在式（13）中求解N个支路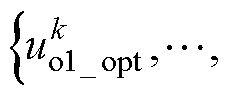
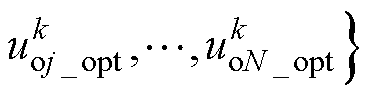。考虑到数字控制器的占空比装载、更新机制存在一个控制拍的延时，因此通常MPC单步优化实际需要预测两步，即将第一步预测作为优化的初始值以计算实际作用在k+2时刻的最优控制量。但由于仍然是向后优化一个控制拍，因此属于单步优化范畴，本节不再单独给出考虑数字延时的最优解。
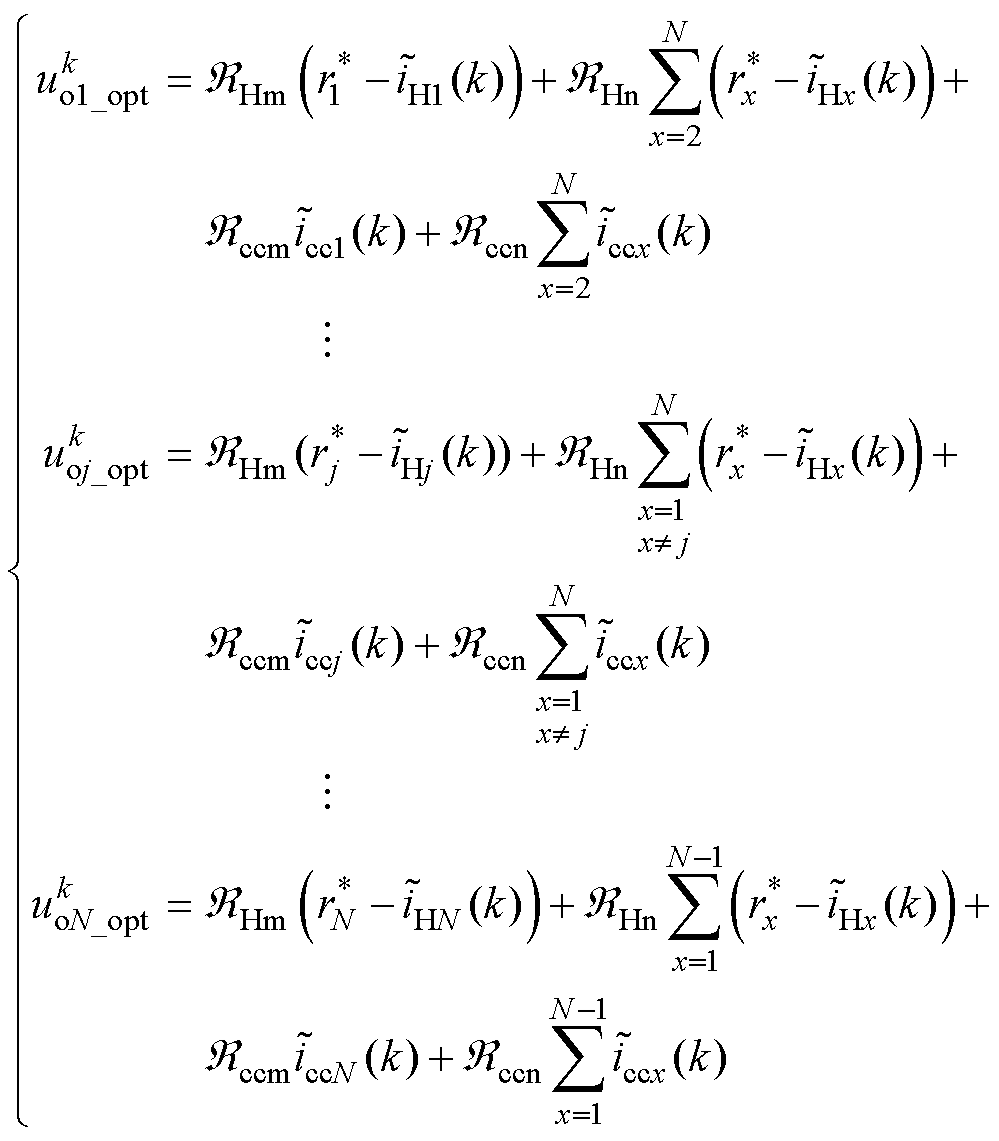（14）
其中
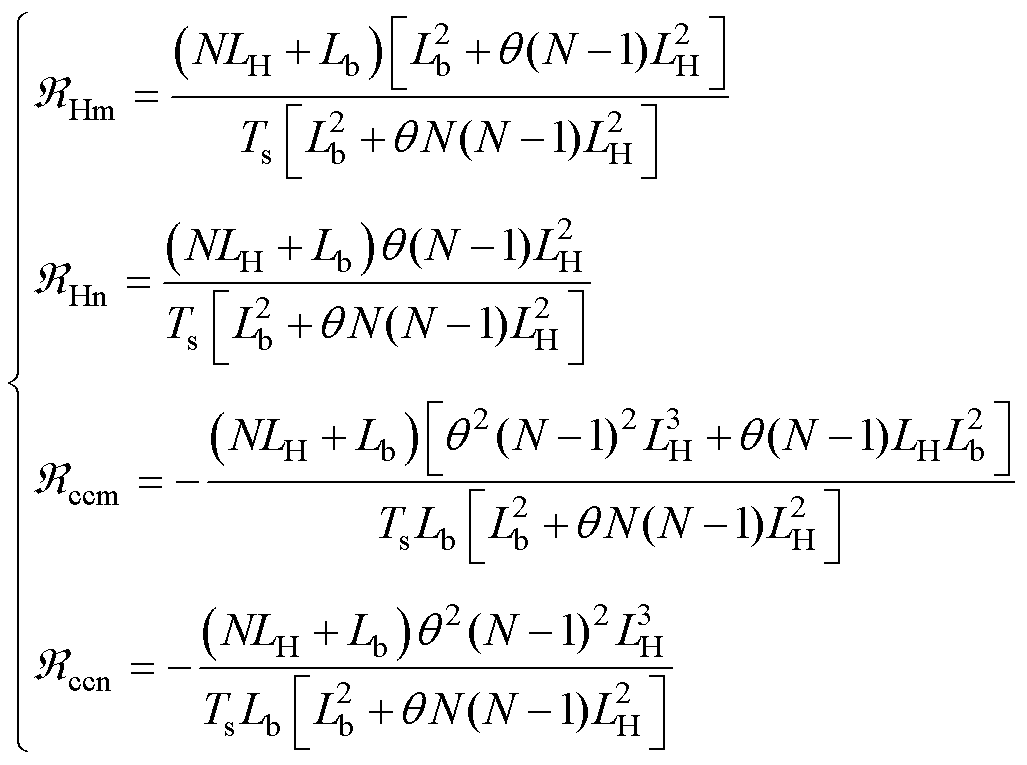
由上述推导，可以得到所有并联支路的最优控制量，其最终下发至从机由各自的CPSPWM在关联H桥的采样时刻实现。通过所提出的MPC策略可以在并联N个支路的CHB电源中实现各支路电流参考跟踪及环流抑制，也可以实现H桥的交错与并联同步以获得更好的输出质量，并且提出的主从策略也仅需少量的通信资源即可实现全局协同 控制。
为了验证有效性，在Matlab/Simulink中搭建了并联6个7L-CHB支路的电源（N=6, M=3）。通过仿真证明所提出方法的参考跟踪与环流抑制，并与常规线性控制器进行对比。所提出的方法也对不同的N和M值进行了验证，本节不再详述。
在验证所提方法的控制性能之前，首先仿真测试Luenberger观测器重构支路负载电流与环流，并在此基础上通过式（10）与式（11）对支路电流状态进行单步预测。即由式（10）得到各支路公共负载电流的一步预测，由式（11）得到各支路环流的一步预测，最终由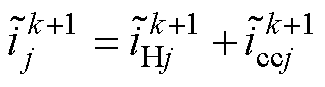
得到支路电流。为了在6个并联支路中产生一定幅值的环流，设置各支路输出电流参考互异，即r1=5 A, r2=10 A, r3= 7.5 A, r4=10 A, r5=6.5 A, r6=10 A。电流预测模型仿真波形如图8所示，图中，实线波形为采样值，虚线波形为提出的预测模型，由图8可知，状态重构后各支路电流预测值几乎与实际电流曲线重合，在支路5中出现预测模型的最大绝对误差为0.83 A，因此可以验证提出的Luenberger观测器与预测模型对此类并联系统行为描述的准确性。
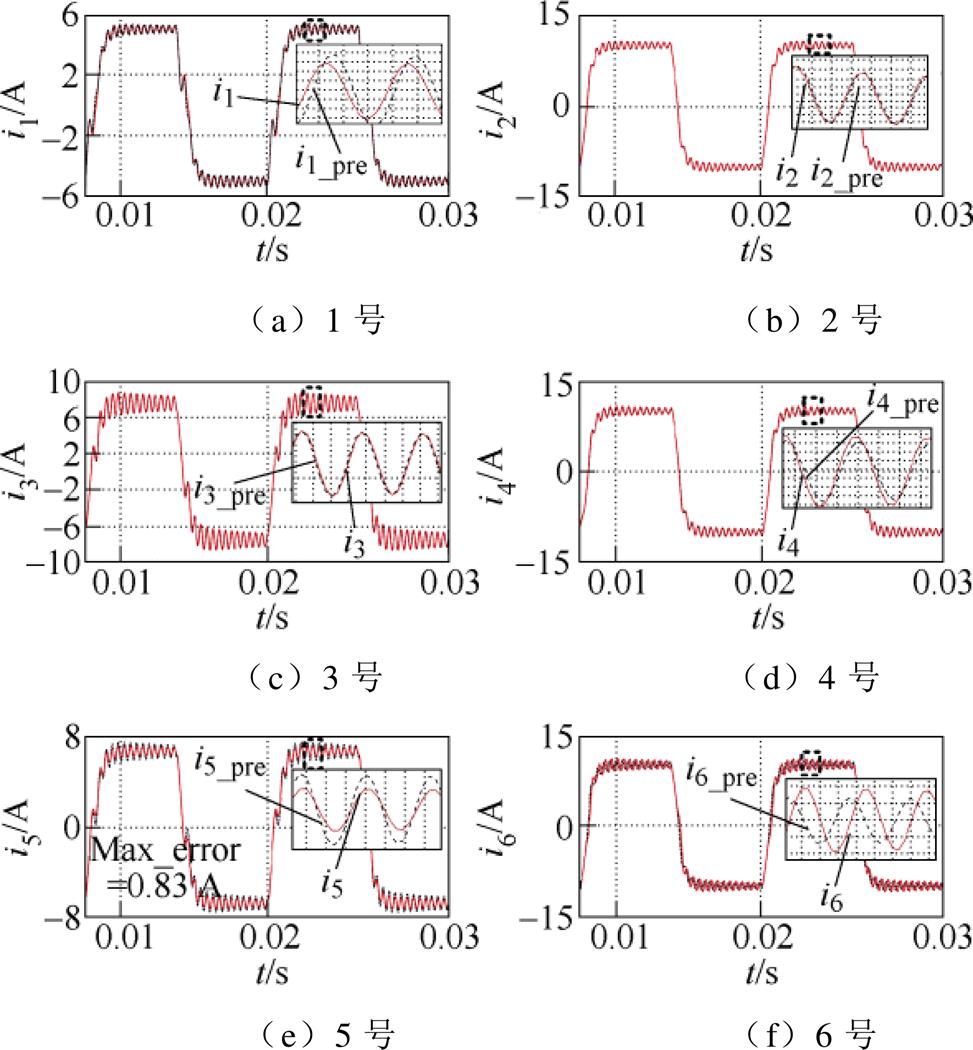
图8 电流预测模型仿真波形
Fig.8 Simulation waveforms of current prediction model
当CHB支路因硬件参数失配而具有不同的输出功率时，通过仿真评估了所提出MPC策略的电流跟踪与环流抑制。运行工况设定如下：6个并联支路的电流参考均为10 A，各支路均流电抗器标称值为2 mH且偏离标称值±5 %。线性控制器的支路电流跟踪波形如图9所示，图中，虚线为支路电流参考波形，实线为支路电流波形。由图9可知，因并联均流电抗器参数失配而各支路输出功率不平衡将导致支路间产生环流，跟踪电流在平顶阶段出现较大的振荡幅度，明显降低稳态跟踪精度。提出策略在均流电感2 mH时各支路电流跟踪如图10所示，任意CHB支路都实现了电流参考跟踪，并且支路间几乎没有出现环流，支路电流快速跟踪参考且一致性较好。
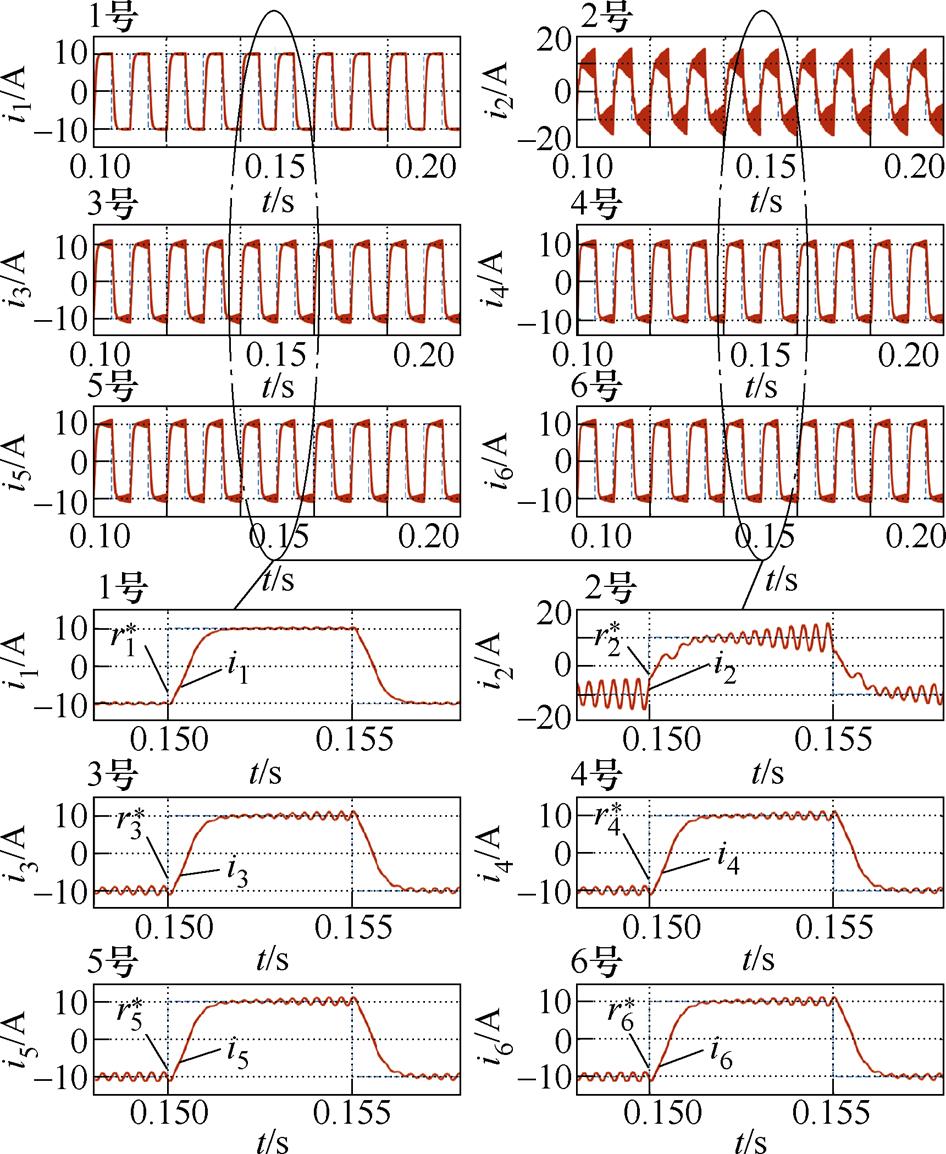
图9 常规控制器在均流电感2 mH时支路电流跟踪波形
Fig.9 Branch current tracking waveforms of the conventional controller when current-sharing reactor is 2 mH
均流电抗器的成本与体积通常需要设计者综合考虑，随着均流电感的增加可以获得满意的环流抑制，但是成本和体积会大幅提高。因此，有必要测试所提策略在减小均流电抗器后的跟踪性能，以提供潜在的缩减成本和体积的方案。进一步地，减小均流电感至0.5 mH并设定各并联均流电抗器偏离标称值5 %，由于均流电感减小后，环流抑制性能下降，因此常规策略的控制参数需重新整定，仿真结果如图11所示。由图11可知，常规控制策略此时通过整定控制参数也无法实现稳定电流跟踪，支路电流波形出现幅值较大的环流并失去稳定性。提出策略在均流电感0.5 mH时各支路电流跟踪如图12所示，在调整预测模型中有关参数后各支路电流可以快速、稳定地跟踪参考，并且环流抑制效果佳，仅在平顶阶段出现微弱的振荡纹波。
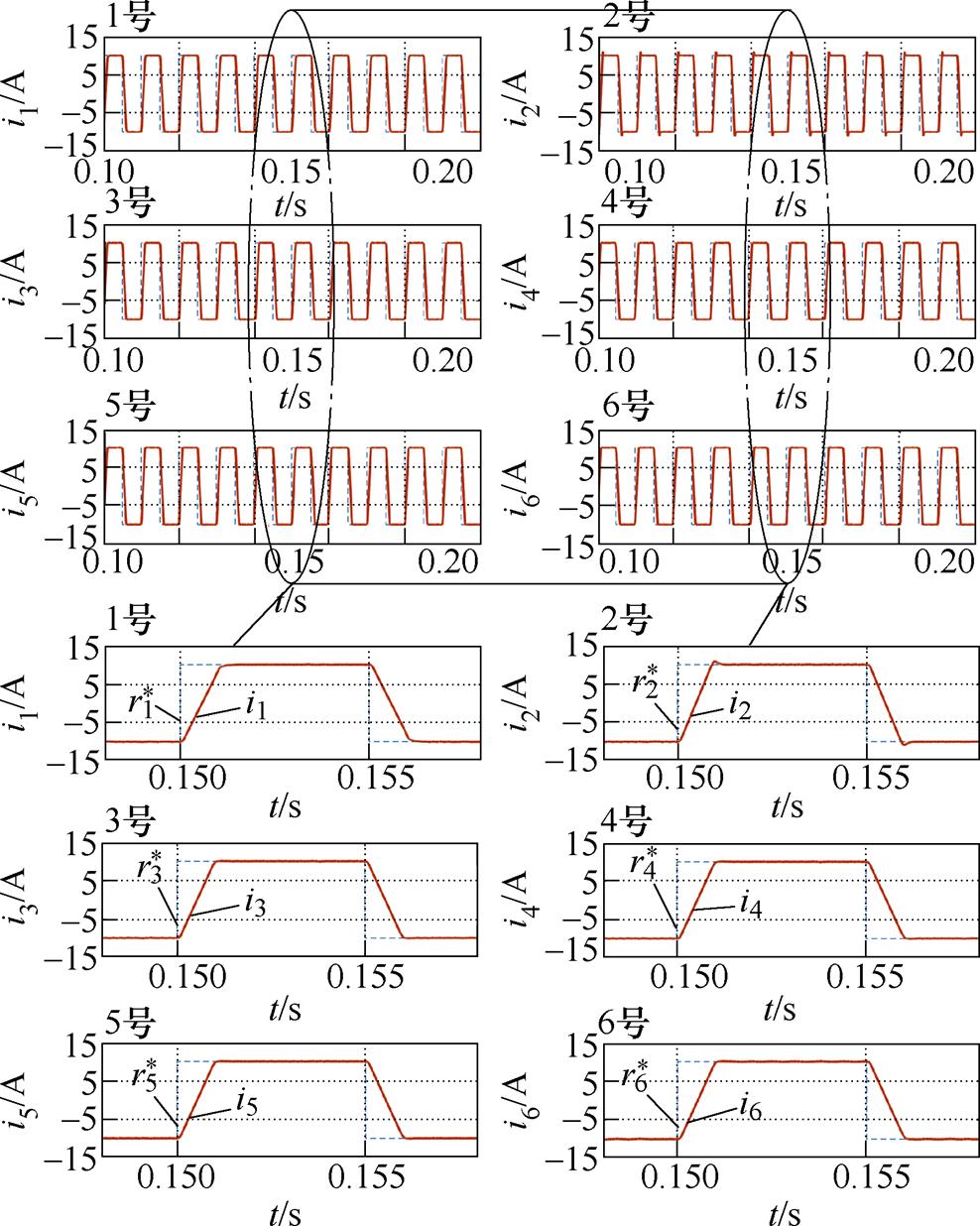
图10 提出策略在均流电感2 mH时各支路电流跟踪
Fig.10 Each branch current tracking of the proposed strategy when current-sharing reactor is 2 mH
图11 常规控制器在均流电感0.5 mH时支路电流跟踪
Fig.11 Branch current tracking of the conventional controller when current-sharing reactor is 0.5 mH
图12 提出策略在均流电感0.5 mH时各支路电流跟踪
Fig.12 Each branch current tracking of the proposed strategy when current-sharing reactor is 0.5 mH
两并联5L-CHB电源实验样机如图13所示，详细参数见表2。图中标号含义如下：①三相调压器；②隔离变压器；③不控整流桥；④直流侧电容；⑤级联H桥变换器；⑥示波器；⑦两条支路的均流电抗器；⑧公共负载电感；⑨主控制器；⑩从控制器；,参考信号发生器。系统采用DSP28335作为主控制器和从控制器实现数字控制，主控制器在载波的零点产生相位同步信号，并对所有并联变换器进行同步。共有两个CHB支路并联为公共负载电感输出功率，每个CHB支路级联两个H桥模块，交错的H桥占空比由各自的CPSPWM管理。H桥单侧桥臂的载波频率设置为5 kHz，采用双倍采样模式即开关频率为10 kHz，等效开关频率为20 kHz，如图14中的载波H1和载波H2所示。
支路1号用作主控制器，支路2号用作从控制器，两者之间进行实时通信交换数据以完成所提出的控制策略。为保障数据的稳定传输，所使用的串行外设接口通信波特率设置为4.69 Mbit/s，即单向传输整型数据耗时约3.5 ms，因此主控制器与从控制器在一个采样周期内的接收与发送理论耗时7 ms，实际测试为8 ms，如图14所示。所提出Luenberger观测与MPC算法的计算时间测试为15 ms，因此所提策略的程序执行时间共计23 ms，在等效开关周期50 ms内还有较大的裕度。所提策略的程序执行时间主要受到级联H桥数量M与并联CHB支路数量N的限制。级联H桥数量越多，等效开关频率越高，则程序执行的限制时间越短。而并联CHB支路数量越多，则主控制器与从控制器的通信耗时越多。因此在应对较多的M与N时，考虑到算法程序，有必要选择更先进的数字处理器或者进一步优化通信。
图13 两并联5L-CHB电源实验样机
Fig.13 Prototype of the parallel 5L-CHB power supply
表2 实验型样机参数
Tab.2 Parameters of the experiment
参 数数 值 级联H桥数量N2 并联CHB数量M2 直流侧电压Vdc/V200 直流侧电容C/mF10 负载线圈电感LH/mH2 均流电抗器感值Lb/mH2 载波频率fc/kHz5
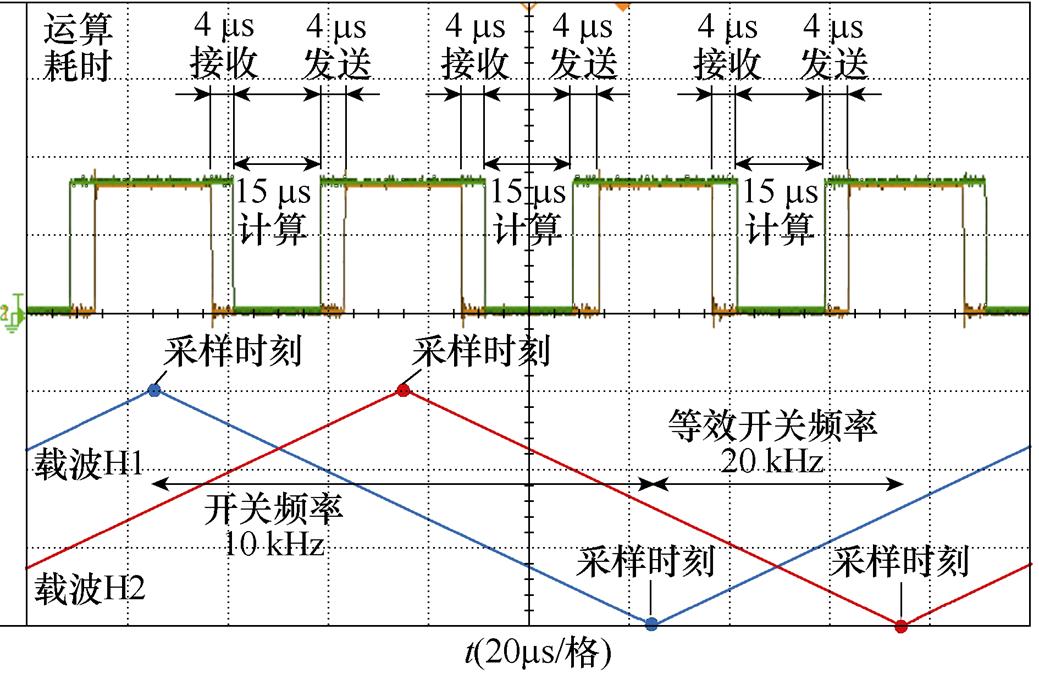
图14 数字控制器执行时间
Fig.14 Digital controller operating time
为了验证本文提出的策略在环流抑制及优化电流跟踪的效果，本节实验设定在输出功率不平衡为50 %的工况下进行。
第一组稳态实验的均流电抗器标称参数为2 mH，由于电感参数无法任意变化，因此设置CHB变换器具有不同的电流参考（r1=8 A, r2=4 A），此时并联支路因输出参考不同而产生幅值明显的环流。图15给出了常规线性控制策略下电流跟踪和输出电压的波形，图15a中，第一路波形为电流参考，第二路波形为支路1号电流i1，第三路波形为支路2号电流i2，第四路波形为公共负载电流iH。由图15a可知，并联CHB支路输出功率相差50 %时在支路间产生幅值明显的环流，支路1号与支路2号电流跟踪平顶阶段出现大幅振荡，使得支路电流跟踪的稳态精度下降。而公共负载电流iH中没有出现环流，因此环流仅在并联支路间流动。图15b中，第二路波形为支路1号输出电压U1，第三路波形为支路2号输出电压U2。通过CPSPWM管理交错的H桥，由图15b可知，CHB支路可以输出5个不同的电压电平并且等效开关频率提高到20 kHz，这将有利于缩短电流响应的延迟、减小滤波成本并提高电流跟踪精度。所提出MPC策略的实验结果如图16所示，支路1号与支路2号在上升阶段快速跟踪各自参考，经过短暂超调后进入平顶阶段而最终稳定在参考值，没有出现环流引起的振荡纹波。支路1号与支路2号的电流超调原因是预测模型与实际物理模型不可避免的参数失配，这可以通过进一步微调模型参数缓解。因此并联CHB支路输出功率相差50 %时在支路间产生的环流分量得到有效抑制，所提策略有利于提高支路电流的稳态跟踪精度与调节速度。
图15 均流电抗器2 mH时常规策略的稳态性能
Fig.15 Steady-state performance of the conventional method when the current-sharing reactor is 2 mH
第二组稳态实验的均流电抗器受制于实验条件而降低至标称参数1 mH，同样设置并联CHB支路具有不同的电流跟踪参考r1=8 A, r2=4 A，由于此时均流电抗器的环流抑制能力下降，因此需适当降低线性控制器参数，主要是减小比例增益系数。图17给出了常规线性控制策略下电流跟踪波形，由图17可知，减小均流电抗器后即使随之降低线性控制器参数，并联支路间环流幅值仍进一步增大，电流跟踪稳态性能进一步降低，并且过大的环流幅值可能造成均流电抗器的饱和而危害系统稳定性。图18给出了所提出MPC策略的电流跟踪波形，支路1号与支路2号同样在上升阶段快速跟踪各自参考，在平顶阶段稳定在指令值，可以在降低均流电抗器后有效抑制环流分量并且实现参考跟踪。
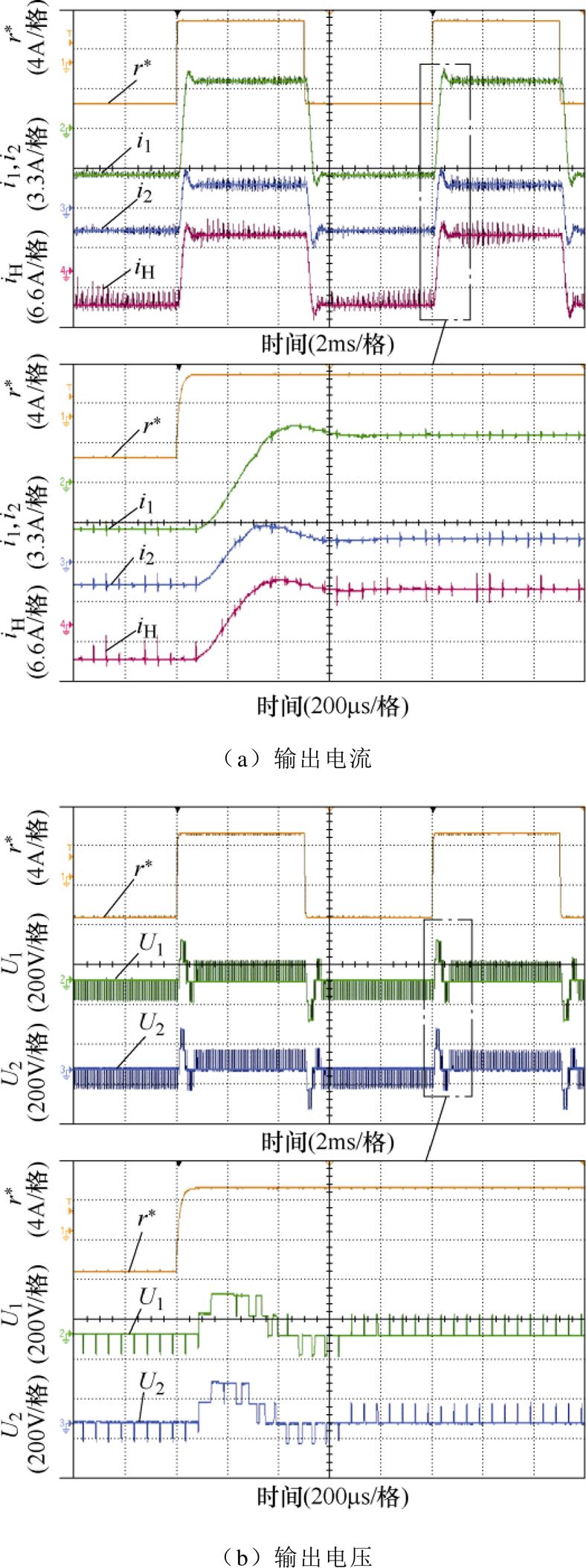
图16 均流电抗器2 mH时提出策略的稳态性能
Fig.16 Steady-state performance of the proposed method when the current-sharing reactor is 2 mH
图17 均流电抗器1 mH时常规策略的稳态性能
Fig.17 Steady-state performance of the conventional method when the current-sharing reactor is 1 mH
图18 均流电抗器1 mH时提出策略的稳态性能
Fig.18 Steady-state performance of the proposed method when the current-sharing reactor is 1 mH
在动态实验中对比评估所提策略的瞬态响应，动态实验的均流电抗器采用标称参数2 mH，设置并联CHB支路具有不同的电流跟踪参考并且参考信号在某一时刻其幅值阶跃突变，在突变时刻前电流参考幅值为r1=4 A, r2=2 A，而在突变时刻后参考幅值为r1=8 A, r2=4 A，此时并联支路在突变前后均因输出参考不同而产生幅值明显的环流。图19给出了常规线性控制策略下电流跟踪波形。由图19可知，常规线性控制策略虽然实现了突变指令的跟踪，但是在突变前后各支路电流波形具有明显的环流，并且随着参考信号的突变，支路间环流幅值进一步增加而加剧了跟踪性能的下降。所提出MPC策略的瞬态性能如图20所示，支路1号与支路2号的电流瞬态响应实现了突变指令的跟踪，并且响应过程的跟踪性能优良，在参考信号突变前后支路均没有出现明显的环流分量，仅存在短暂的超调过程。
本文设计了一种基于Luenberger观测器的主从MPC控制以优化电流跟踪和抑制环流，适用于N个CHB支路并联的磁体电源，仿真和实验结果验证了所提策略的有效性。与常规分布式线性控制器相比，该策略具有更好的动态性能与环流抑制效果，结果表明：
图19 常规策略的瞬态性能
Fig.19 Transient performance of the conventional method
图20 提出MPC策略的瞬态性能
Fig.20 Transient performance of the proposed MPC method
1）支路电流跟踪性能得到提高，具体为稳态跟踪精度高、动态调整时间短。
2）环流得到有效抑制。在控制周期足够容纳算法运行时间的条件下，本文工作可以扩展到任意数量（N, M）的并联CHB电源中。
参考文献
[1] Huang Haihong, Yan Teng, Wang Haixin. Application of a current and voltage mixed control mode for the new fast control power supply at EAST[J]. Plasma Science and Technology, 2014, 16(4): 420-423.
[2] 蔡信健, 吴振兴, 孙乐, 等. 直流电压不均衡的级联H桥多电平变频器载波移相PWM调制策略的设计[J]. 电工技术学报, 2016, 31(1): 119-127.
Cai Xinjian, Wu Zhenxing, Sun Le, et al. Design for phase-shifted carrier pulse width modulation of cascaded H-bridge multi-level inverters with non- equal DC voltages[J]. Transactions of China Elec- trotechnical Society, 2016, 31(1): 119-127.
[3] 陈轶涵, 郭鸿浩, 陈家伟. 基于载波移相控制的模块化串并联逆变器非理想条件谐波特性分析[J]. 电工技术学报, 2020, 35(8): 1690-1704.
Chen Yihan, Guo Honghao, Chen Jiawei. Analysis of harmonic characteristics in non-ideal conditions of modular series/parallel inverter based on carrier phase shifted control[J]. Transactions of China Electro- technical Society, 2020, 35(8): 1690-1704.
[4] 谢江华, 张方华, 张帅, 等. 基于载波移相控制的高功率密度双降压式全桥逆变器[J]. 电工技术学报, 2016, 31(13): 1-9.
Xie Jianghua, Zhang Fanghua, Zhang Shuai, et al. A high power density dual-buck full-bridge inverter based on carrier phase-shift control[J]. Transactions of China Electrotechnical Society, 2016, 31(13): 1-9.
[5] Wu Xiajie, Xiong Chenglin, Yang Shunfeng, et al. A simplified space vector pulse width modulation scheme for three-phase cascaded H-bridge inverters[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4192-4204.
[6] Huang Haihong, Bi Nanxia, Wang Haixin. The analysis and experimental research of the second- generation EAST active feedback power supply[J]. Fusion Engineering and Design, 2018, 126: 174-179.
[7] Wang Fei, Wang Yong, Gao Qiang, et al. A control strategy for suppressing circulating currents in parallel-connected PMSM drives with individual DC links[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1680-1691.
[8] Wei Baoze, Guerrero J M, Vásquez J C, et al. A circulating-current suppression method for parallel- connected voltage-source inverters with common DC and AC buses[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3758-3769.
[9] 贾成禹, 王旭东, 周凯. 基于线性变参数模型预测控制的内置式永磁同步电机转速控制器设计[J]. 电工技术学报, 2020, 35(22): 4666-4677.
Jia Chengyu, Wang Xudong, Zhou Kai. Design of interior permanent magnet synchronous motor speed controller based on linear parameter-varying model predictive control[J]. Transactions of China Electro- technical Society, 2020, 35(22): 4666-4677.
[10] 年珩, 叶余桦. 三端口隔离双向DC-DC变换器模型预测控制技术[J]. 电工技术学报, 2020, 35(16): 3478-3488.
Nian Heng, Ye Yuhua. Model predictive control of three-port isolated bidirectional DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3478-3488.
[11] 杨海涛, 江晶晶, 赵敏, 等. 基于模型预测控制的区域综合能源系统运行优化方法[J]. 电气技术, 2022, 23(4): 7-13.
Yang Haitao, Jiang Jingjing, Zhao Min, et al. Operational optimization method of regional inter- grated energy system based on model predictive control[J]. Electrical Engineering, 2022, 23(4): 7-13.
[12] Llor A M, Solano E. Direct model-predictive control with variable commutation instant: application to a parallel multicell converter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(8): 5293-5300.
[13] Jiang Changpeng, Quan Zhongyi, Zhou Dehong, et al. A centralized CB-MPC to suppress low-frequency ZSCC in modular parallel converters[J]. IEEE Transa- ctions on Industrial Electronics, 2021, 68(4): 2760- 2771.
[14] Zhang Xueguang, Wang Tianyi, Wang Xiongfei, et al. A coordinate control strategy for circulating current suppression in multiparalleled three-phase inverters[J]. IEEE Transactions on Industrial Electronics, 2017, 64(1): 838-847.
[15] Zhang Xueguang, Zhang Wenjie, Chen Jiaming, et al. Deadbeat control strategy of circulating currents in parallel connection system of three-phase PWM converter[J]. IEEE Transactions on Energy Conver- sion, 2014, 29(2): 406-417.
[16] Sun Kai, Lin Xiang, Li Yunwei, et al. Improved modulation mechanism of parallel-operated T-type three-level PWM rectifiers for neutral-point potential balancing and circulating current suppression[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 7466-7479.
[17] Zhang Yonglei, Wu Xiaojie, Yuan Xibo. A simplified branch and bound approach for model predictive control of multilevel cascaded H-bridge STATCOM[J]. IEEE Transactions on Industrial Electronics, 2017, 64(10): 7634-7644.
[18] Brüske S, Pugliese S, Flacke S, et al. High-frequency grid current control of parallel inverters[C]//2018 44th Annual Conference of the IEEE Industrial Elec- tronics Society, Washington, DC, US, 2018: 1835-1841.
Abstract When the cascaded H-bridge (CHB) converter with an isolated DC-link is used as a power supply in parallel through the current-sharing reactor, the distributed controller will form an unstable circulating current between the parallel branches due to the parameter difference. However, when the output power is unbalanced, the conventional linear controller cannot actively suppress the circulating current, resulting in degraded reference tracking performances. Recent studies have proposed parallel methods based on improved master-slave predictive control. However, the problems of more stable circulating current observation and a large amount of computation still exist. Therefore, this paper proposes a parallel method of carrier-based model predictive control (MPC) and improved master-slave control. When the output power is unbalanced, the reference tracking and a circulating current suppression are realized by optimizing the global control value through the proposed prediction model.
Firstly, the master controller reconstructs the branch current into the common load inductor current and the branch circulating current through the Luenberger observer. Secondly, a global cost function is established to optimize the reference tracking and the circulating current suppression. Finally, the globally optimized control values are sent to the slave controllers, and the interleaved H-bridges are managed by the respective carrier phase shifted pulse width modulation (CPSPWM) modulator. The master and slave controllers have similar optimized timing based on the carrier, and slave controllers only communicate with the master controller. In the proposed method, the Luenberger outputs stable state observations, the MPC solves the global optimal control values, the CPSPWM modulator fixes the switching frequency of the interleaved H-bridge, and the improved master-slave control reduces the communication resource. Therefore, the proposed method can realize stable reference tracking and the circulating current suppression in the parallel CHB power supply.
The results show that when the current-sharing reactor is 2 mH or 1mH and the current reference difference reaches 50 %, the proposed method quickly tracks the steady-state reference after a small overshoot. The steady-state deviation is much smaller than the conventional linear controller. It is shown that the proposed method has a more stable dynamic tracking performance, with the reference suddenly changing when the amplitude step mutation of the reference signal is added. A 5 % mismatching of the current-sharing reactor is operated in the simulated test. The results show that the proposed method can effectively suppress the circulating current caused by the difference in hardware parameters. Observation errors of the proposed Luenberger observer are measured in simulation. The maximum deviation of the branch current is 0.83 A, almost following the sampling current. The program time of the proposed method is about 23 ms in DSP28335, which is less than the sampling period of 20 kHz.
The analysis of the results leads to the conclusion that: (1) Compared with the parallel scheme of the conventional linear controller, the branch’s current reference tracking performance is improved. Specifically in terms of high steady-state tracking accuracy and short dynamic adjustment time. (2) The circulating current caused by the unbalanced output power is effectively suppressed. (3) The proposed algorithm can be extended to any number of the multi-parallel CHB branches if the sampling period is sufficient to operate the program.
keywords：Predictive control, cascaded H-bridge converter, parallel, master-slave control structure, current tracking, circulating current, observer
DOI: 10.19595/j.cnki.1000-6753.tces.221041
中图分类号：TL62; TM46
区域创新发展联合基金资助项目（重点支持项目）（U22A20225）。
收稿日期 2022-06-06
改稿日期 2022-11-09
黄海宏 男，1973年生，教授，博士生导师，研究方向为电力电子技术和自动控制。E-mail: hhaihong741@126.com
颜碧琛 男，1995年生，博士研究生，研究方向为电力电子技术和预测控制。E-mail: yanbichen@mail.hfut.edu.cn（通信作者）
（编辑 陈 诚）