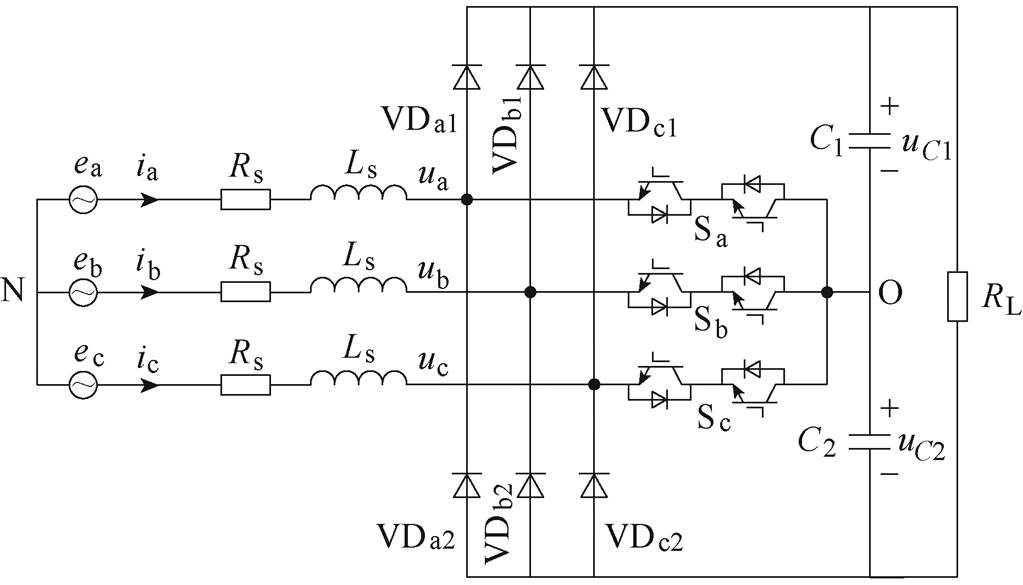
图1 Vienna整流器拓扑
Fig.1 Topology of Vienna rectifier
摘要 Vienna整流器是一种控制简单、可靠性高的升压型整流器,被广泛应用到风能发电系统、航空电源以及新能源电动汽车等领域。由于Vienna整流器结构的特性,传统的调制方法会导致电流过零点畸变。因此,该文从调制波分解的角度分析电流过零点畸变产生的原因,针对现有的调制策略存在的不足,在其基础上进行改进,提出一种在维持直流侧中点电压平衡的情况下,可以最大程度地降低电流畸变的调制方法。该文将Vienna整流器的传统空间矢量调制、具有过零钳位的空间矢量调制与所提调制方法进行了比较,通过实验验证了所提调制方法的可行性和优 越性。
关键词:Vienna整流器 调制方法 中点电压平衡 电流过零点畸变
近年来,Vienna整流器因其可靠性高、控制简单的特点在工业领域有着广泛应用[1-3],如风力发电系统[4-5]、航空电源[6]、通信电源[7]、电动汽车充电系统[8-9]等。
本文研究的Vienna整流器结构外管由两个二极管构成,内管由两个带反并联二极管的IGBT反向串联构成,两个内管的通断信号保持一致。Vienna整流器与传统三电平整流器的区别在于Vienna整流器的能量不能双向流动,开关器件数量较其他三电平整流器少,结构更简单、成本更低。
Vienna整流器的调制策略一直是研究的热点,调制策略的优劣可以通过性能指标衡量,主要的性能指标有:①直流母线电压波动较小;②网侧电流谐波含量小于规定值,系统可实现单位功率因数运行;③中点电压平衡,直流侧上下电容电压大小近似相等。目前常用的调制方法有基于载波的脉宽调制(Carrier-Based Pulse Width Modulation, CBPWM)[10]和空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)[11-12]。文献[13-14]表明,CBPWM和SVPWM在一定条件下是等效的。
输入电流的总谐波畸变率(Total Harmonic Distortion, THD)是衡量整流装置性能的重要指标。文献[15]分析了Vienna电流过零点畸变产生的原因,为了解决过零点畸变,国内外学者已经提出了多种基于CBPWM和SVPWM的调制策略。文献[16]提出了一种优化输入电流过零点附近扇区内冗余矢量分配的方法,通过重新计算冗余矢量的作用时间来缓解过零点畸变,但此方法无法应用到Vienna整流器的全部运行状态,在调制度较高时将会失效。文献[17]提出了通过零序电压将输入电流控制到与桥臂电压同相位,这种方法在一定程度上优化了Vienna的电流波形,但从本质上降低了Vienna整流器网侧的功率因数。文献[18]提出了一种基于CBPWM的调制方法,根据功率因数来补偿参考电压,这种方法可以保证Vienna整流器的输入电流正弦,但是在调制度较高时,补偿后的参考电压将会导致其他相过调制,改变了线电压关系,同样会产生电流畸变。文献[19-20]均提出了混合调制策略;文献[19]提出了一种注入最小无功电流以避免过调制的方法;文献[20]提出了一种基于SVPWM在过零点钳位(Zero-Crossing Clamped SVPWM, ZCC- SVM)的方法来降低谐波失真。文献[21-22]都是三电平变流器下的调制波分解方法;文献[21]是通过计算三相不同电平的占空比来得到双调制波;文献[22]将中间相的调制波分解,重新排列冗余矢量的位置,可以优化输出线电压的谐波分布。本文参考以上两种方法,结合Vienna整流器输出电平受其输入电流约束的特性,提出了一种基于Vienna整流器的双调制波分解的方法,在处理中点电压平衡和过零点畸变时分析更为简单。
中点电压平衡是Vienna整流器稳定运行的重要指标,文献[23-24]分析了三电平变流器中点电压自平衡特性,由于并网变流器的中点电压自平衡时间过长,中点电压会导致较大的偏移,中点电压偏移将会导致功率器件过电压,严重的话甚至引发危险。文献[25]提出了一种具有分段式直流分量注入的新型CBPWM方法,不仅可以使输入电流保持低谐波失真,而且可以在不平衡条件下使直流侧电压振荡降至最低。文献[26]提出了一种通用的三相Vienna整流器设计框架来处理中点电压平衡问题,主要通过基于零序电压注入的CBPWM来实现。文献[27]提出了一种注入零序电压分量实现中点振荡和偏移控制的方法,通过计算补偿系数,动态补偿注入的零序电压分量,实现中点电压平衡控制与振荡抑制。
为了最大程度降低Vienna整流器输入电流过零点畸变并保持中点电压平衡,本文提出了一种在单位功率因数运行条件下的调制方法。首先介绍了Vienna整流器的拓扑结构,探讨了双调制波分离的方法,并通过注入零序电压实现中点电压平衡。简要分析了电流过零点畸变的原因,提出了处理电流过零点畸变的调制方法,通过实验与其他调制方法进行对比,验证了所提调制方法的可行性和优越性。
Vienna整流器拓扑结构如图1所示,三相三电平Vienna整流器每一相的内管由两个带反并联二极管的IGBT反向串联组成,外管由两个二极管组成。C1和C2分别为其直流侧的上、下电容,当整流器的上下电容平衡时,uC1=uC2=udc/2,Ls和Rs分别为三相交流侧的输入滤波电感及其等效电阻;ex(x= a, b, c)为三相电网电压。
定义输入电流从电网流向整流器为正方向,以图1中直流侧上、下电容的中点O作为电压参考点,Sx(x=a, b, c)表示内管的导通状态,当Sx=1时,内管导通;当Sx=0时,内管关断。Sx=1时,由于内管导通,所以无论输入电流为正还是负,桥臂电压均为0,该状态为电平1。Sx=0时,若输入电流为正,其从二极管VDx1流入正母线,桥臂电压为udc/2,该状态为电平2;若输入电流为负,桥臂与负母线相连,桥臂电压为-udc/2,该状态为电平0。Vienna整流器输出电平见表1。

图1 Vienna整流器拓扑
Fig.1 Topology of Vienna rectifier
表1 Vienna整流器输出电平
Tab.1 Vienna rectifier output level
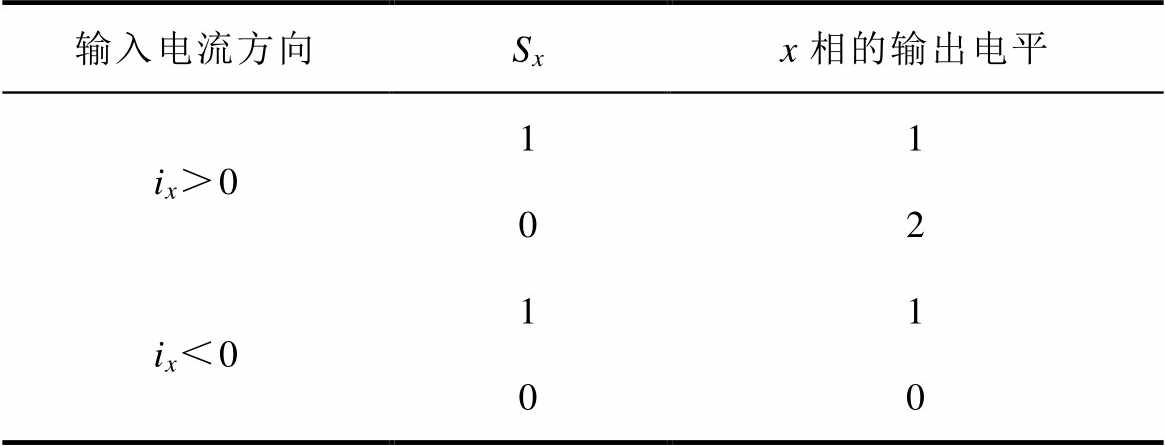
输入电流方向Sxx相的输出电平 ix>011 02 ix<011 00
不同于T型三电平变流器中外管的双向导通特性,Vienna整流器的输出电平不仅与内管的开关状态有关,还与输入电流ix的方向有关。ix>0时无法输出电平0;ix<0时无法输出电平2。这种输出状态与电流的约束关系是Vienna整流器和T型三电平变流器的最大区别点之一。这将给Vienna整流器带来诸如电流畸变等问题。
图2给出了Vienna整流器的控制框图,电压外环通过PI调节器得到d轴电流给定值,电流内环采用无差拍控制(Deadbeat Control, DBC)方法,经过反Clarke变换得到三相调制电压。调制策略是本文研究的重点。本文提出了基于调制波分解的可最大程度降低Vienna整流器输入电流过零点畸变并保持中点电压平衡的调制方法。
Vienna整流器的调制策略一般为SVPWM或CBPWM。CBPWM较SVPWM省略了分区判别、矢量作用时间计算和重新组合的过程,计算负担大大降低,使其更适合在高频场合应用,如以SiC等宽禁带器件组成的Vienna整流器中,因此本文主要讨论低计算负担的CBPWM算法。
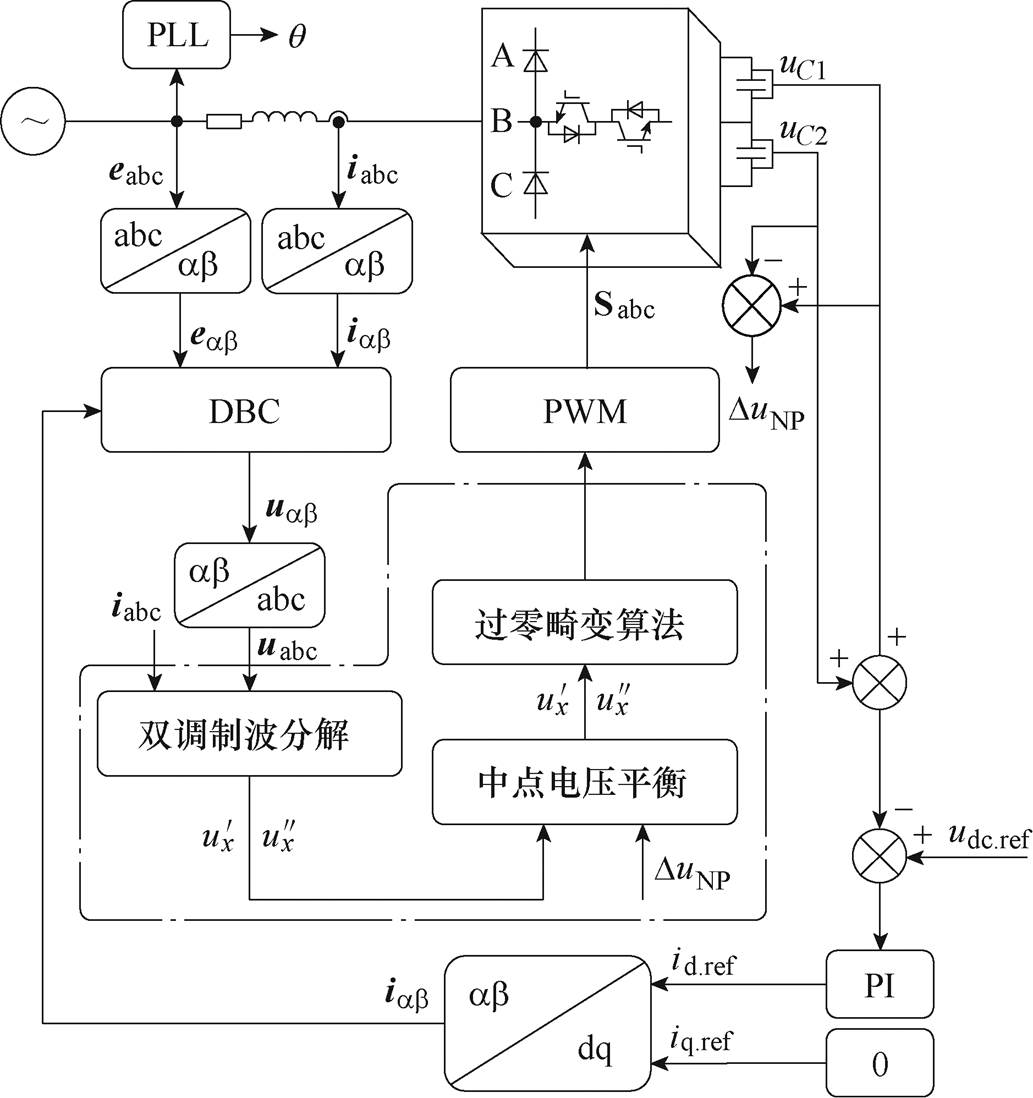
图2 Vienna整流器基于所提调制方法的控制框图
Fig.2 Control block diagram of Vienna rectifier based on the proposed modulation method
CBPWM的核心在于调制波,将调制波与载波相比较产生所需要的PWM序列。在本文中,调制波ux被分解为双调制波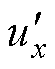 和
和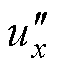 ,
,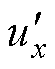 ,
,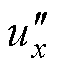 ∈[0, udc/2],当超出这个范围即发生过调制。定义
∈[0, udc/2],当超出这个范围即发生过调制。定义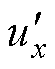 为固定调制波,
为固定调制波,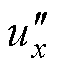 为自由调制波,则有
为自由调制波,则有
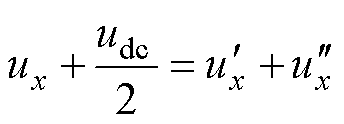 (1)
(1)
由表1可知,ix>0时,调制只能发生在电平1、2之间,电平0无法参与调制;ix<0时,调制只能发生在电平0、1之间,电平2无法参与调制;基于上述特点,限定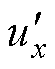 为
为
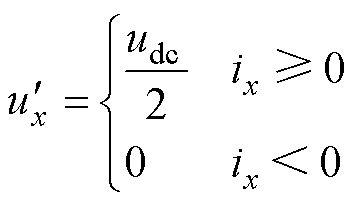 (2)
(2)
值得注意的是,对调制波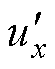 的限制是强制的,它是由Vienna整流器的换流特点决定的。还需确定调制波
的限制是强制的,它是由Vienna整流器的换流特点决定的。还需确定调制波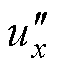 ,其基本形式可以写为
,其基本形式可以写为
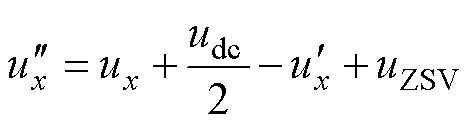 (3)
(3)
式中,uZSV为注入的零序电压。
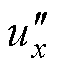 为可变的调制波,通过改变调制波
为可变的调制波,通过改变调制波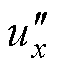 可实现Vienna整流器的中点电压平衡、抑制电流过零点畸变等目标。为了便于描述,将三相电压按大小排序为umax、umid、umin,并且将其对应的电流记为imax、imid、imin。在三相三线制系统中,电压电流满足
可实现Vienna整流器的中点电压平衡、抑制电流过零点畸变等目标。为了便于描述,将三相电压按大小排序为umax、umid、umin,并且将其对应的电流记为imax、imid、imin。在三相三线制系统中,电压电流满足
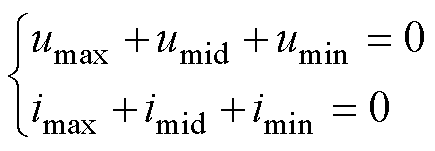 (4)
(4)
Vienna整流器一般运行在单位功率因数或接近单位功率因数,则三相调制波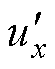 可以写为
可以写为
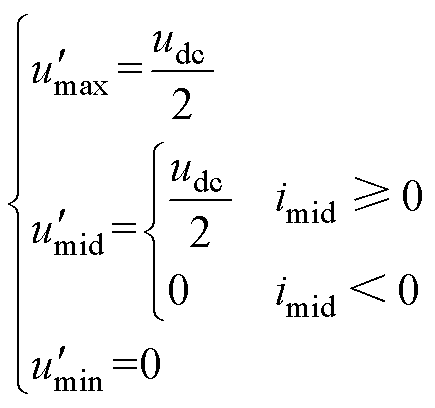 (5)
(5)
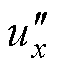 可以写为
可以写为
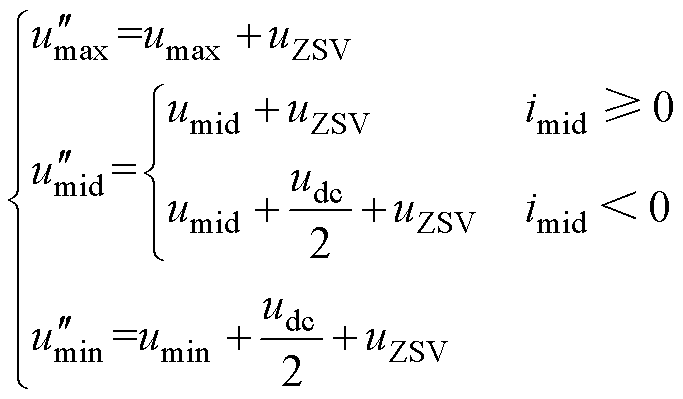 (6)
(6)
图3给出了双调制波合成PWM序列的过程。将分解后的双调制波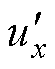 和
和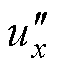 与同一载波比较,得到两个独立的开关序列
与同一载波比较,得到两个独立的开关序列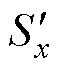 和
和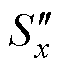 ,通过将
,通过将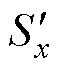 和
和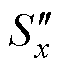 相加得到最终输出的开关序列Sout,x。
相加得到最终输出的开关序列Sout,x。
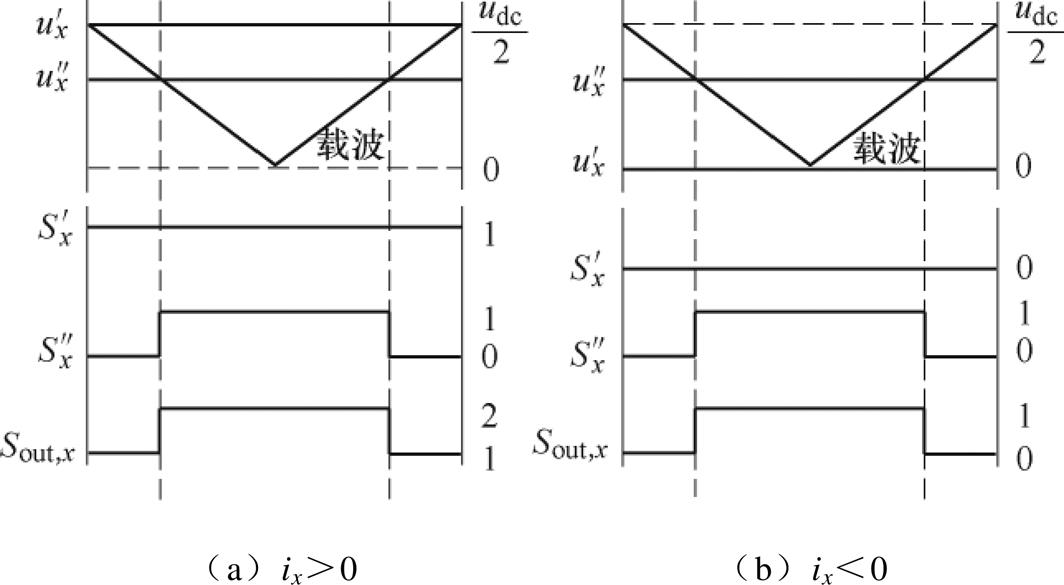
图3 双调制波合成PWM序列
Fig.3 PWM sequence generation of modulation wave decomposition
采用双调制波分解,调制自由度增加,算法实现更为灵活,但复杂度相对增加。当这一方式应用于Vienna整流器时,由于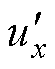 受电流方向限定,因而复杂度降低,且其在分析中点电压控制和过零点畸变问题方面具有一定优势,因而本文采用双调制波分解的方法。
受电流方向限定,因而复杂度降低,且其在分析中点电压控制和过零点畸变问题方面具有一定优势,因而本文采用双调制波分解的方法。
从中点抽取或者注入电流可以改变中点电压。一方面,因为调制引入的电流会导致中点电压偏移;另一方面,由中点电压控制算法引入中点电流可以使中点电压恢复至平衡状态。本文在输入电流和输入电压同相位的情况下,分析中点电压平衡。假定上下电容的差值DuNP=uC1-uC2,为了使中点电压恢复至平衡状态,则一个载波周期需要向中点注入的平均电流为
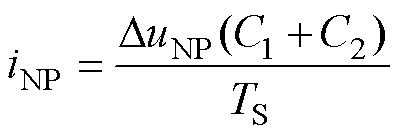 (7)
(7)
式中,TS为开关周期。
只有当某一相输出电平1时,才会向中点注入或抽取电流,在一个开关周期内注入中点电流iNP为
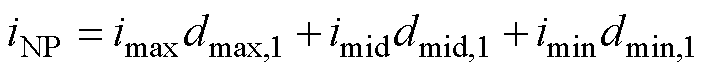 (8)
(8)
式中,dmax,1、dmid,1、dmin,1分别为各相电平1的占空比,在不同电流方向下的表达式为
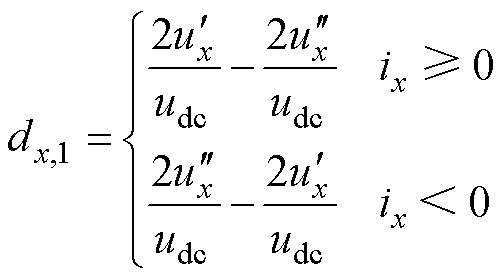 (9)
(9)
由式(8)和式(9)可得iNP为
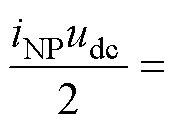
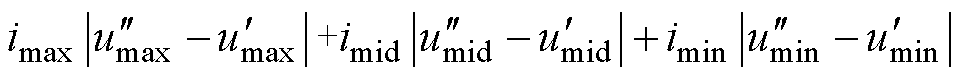 (10)
(10)
以imid≥0为例,则自由调制波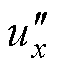 为
为
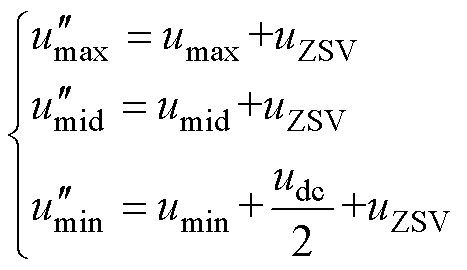 (11)
(11)
为了在一个载波周期内平衡中点电压,注入的零序电压应使中点电流满足式(7)要求。结合式(7)、式(10)和式(11)可以得到
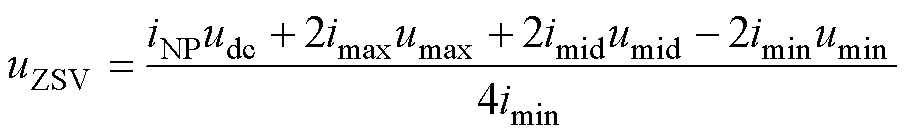 (12)
(12)
对于双调制波必须满足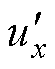 和
和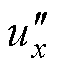 ∈[0, udc/2]这一约束条件,超出这个条件将会发生过调制,约束不等式为
∈[0, udc/2]这一约束条件,超出这个条件将会发生过调制,约束不等式为
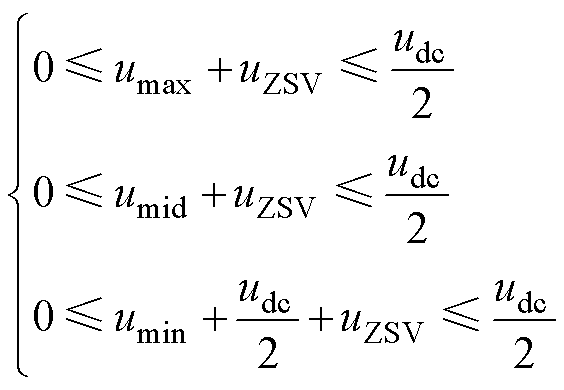 (13)
(13)
即所注入的零序电压uZSV的范围为
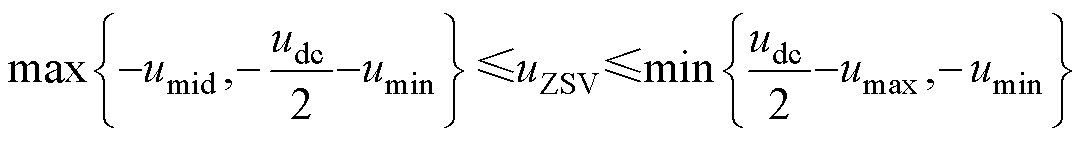 (14)
(14)
同理,当imid<0时,可以得到其注入的电压uZSV为
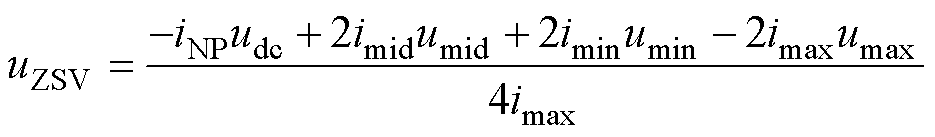 (15)
(15)
注入的电压uZSV必须满足范围
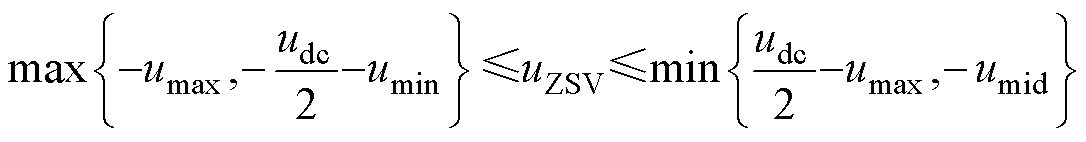 (16)
(16)
一般情况下,Vienna整流器都工作在网侧单位功率因数,即e和i同相位。在稳态情况下,Vienna整流器的输入电压相量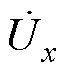 、电网电压相量
、电网电压相量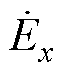 和电流相量
和电流相量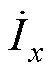 满足
满足
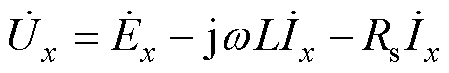 (17)
(17)
式中,Rs为寄生电阻,其值较小可以忽略,式(17)可简写为
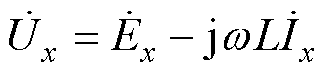 (18)
(18)
Vienna整流器电压电流的相量关系如图4a所示。通常假设系统在单位功率因数下运行,电网电压和输入电流保持同相位。由其相量可知,由于电感的存在,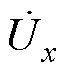 会滞后电流
会滞后电流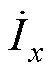 一个角度θ,这将导致
一个角度θ,这将导致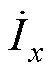 和
和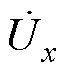 出现异号的情况,如图4b所示。
出现异号的情况,如图4b所示。
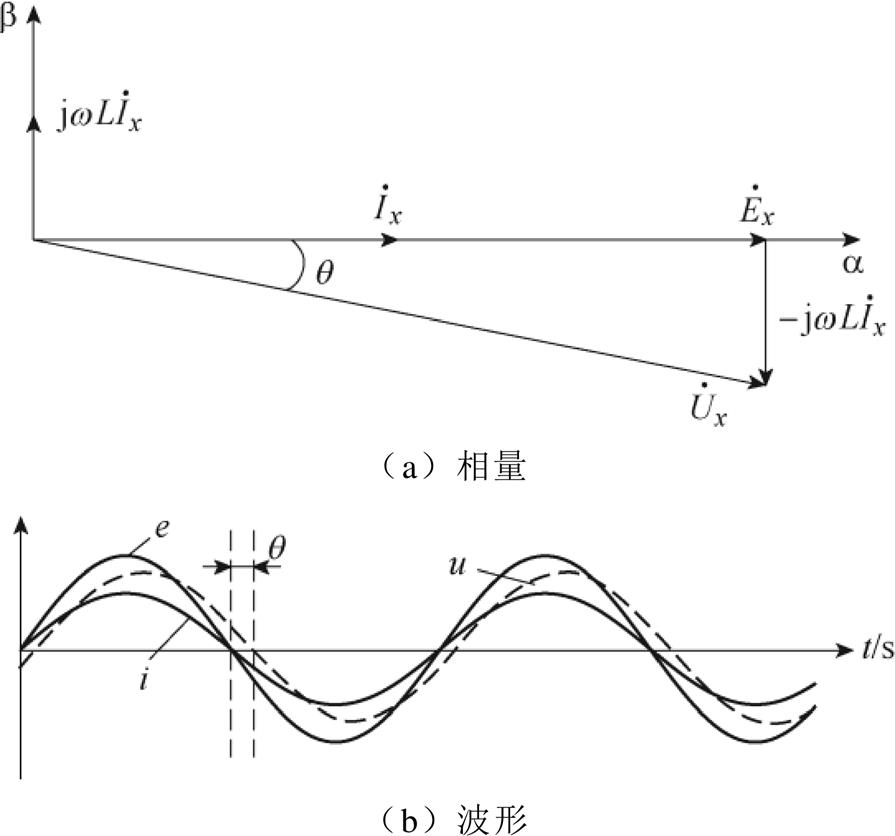
图4 电流电压相量及波形
Fig.4 Phasor and waveforms diagram of voltage and current
从调制波的角度分析,假设输入电流由负到正过零时,umid<0, imid>0,中间相双调制波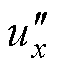 可以表示为
可以表示为
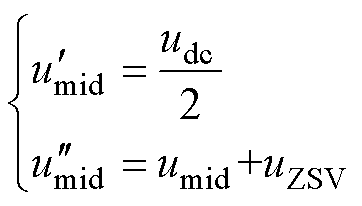 (19)
(19)
当不进行任何处理,即uZSV=0的情况下,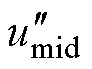 不满足
不满足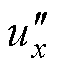 ∈[0, udc/2]这一约束条件,即会发生过调制,导致电流发生畸变。
∈[0, udc/2]这一约束条件,即会发生过调制,导致电流发生畸变。
4.2.1 电流过零点畸变的抑制
为了处理电流过零点畸变,需要将过零相钳位至电平1,即通过改变uZSV的大小来处理这种情况。在输入电流由负到正过零时,自由调制波可写为
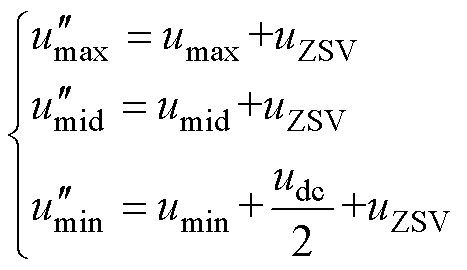 (20)
(20)
为将中间相钳位到电平1,需要满足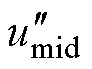 =0,即使uZSV=-umid成立,将其代入式(20)可得
=0,即使uZSV=-umid成立,将其代入式(20)可得
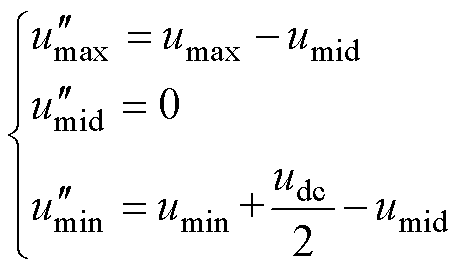 (21)
(21)
结合约束条件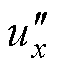 ∈[0, udc/2]可得
∈[0, udc/2]可得
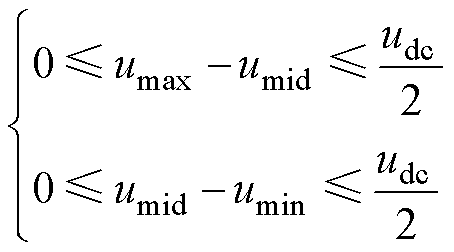 (22)
(22)
电流由正到负时的情形可参考上述过程,这里不再赘述。
式(22)表示可以通过注入零序电压的方法来抑制电流过零点畸变的约束条件。当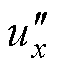 不满足式(22)时,注入零序电压将导致某一相过调制,如果再将过调制相钳位,三相间的线电压关系将全被改变,仍存在电流畸变。为了应对这一问题,采用两相钳位、一相调制的方法,但需要尽量保证线电压关系不变。此时电流过零点畸变不能被完全抑制,只能被适当缓解。
不满足式(22)时,注入零序电压将导致某一相过调制,如果再将过调制相钳位,三相间的线电压关系将全被改变,仍存在电流畸变。为了应对这一问题,采用两相钳位、一相调制的方法,但需要尽量保证线电压关系不变。此时电流过零点畸变不能被完全抑制,只能被适当缓解。
4.2.2 电流过零点畸变的缓解
当输入电流由负到正过零时,中间相电压本应在电平0、1之间调制,为抑制过零点畸变使中间相钳位,需注入正的零序电压,若不能满足umax-umid≤ udc/2,将导致umax过调制。此时最大相和中间相均出现钳位,仅能调制最小相,调制波的变化如图5所示。
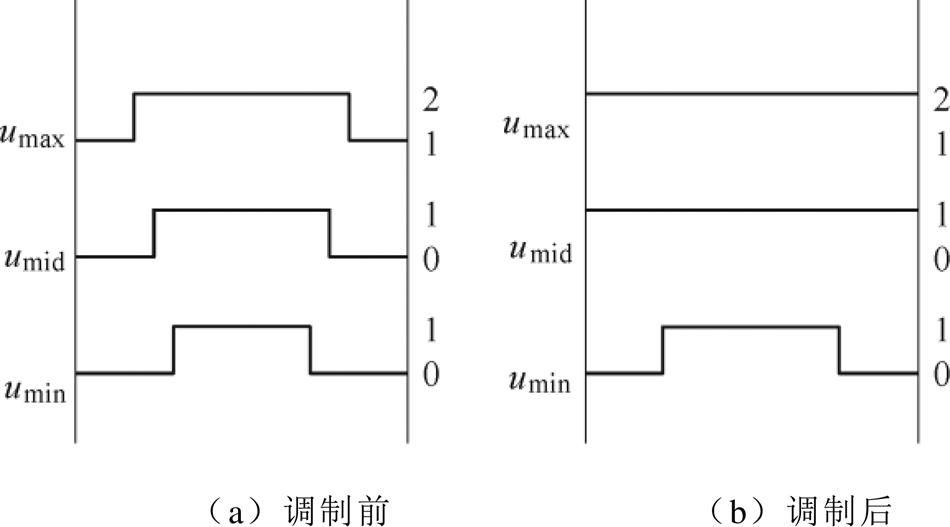
图5 中间相电流由负到正过零时的调制波变化情况
Fig.5 Variation of the modulating waveforms when the current changes from negative to positive
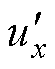 的值由电流方向决定,此时原始的自由调制波
的值由电流方向决定,此时原始的自由调制波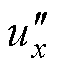 可表示为
可表示为
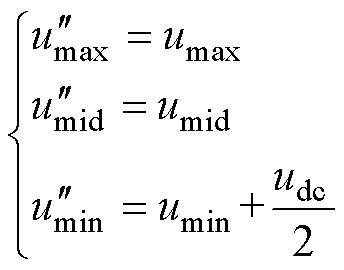 (23)
(23)
将最大相和中间相分别钳位至电平2和电平1,通过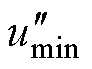 调制,即有
调制,即有
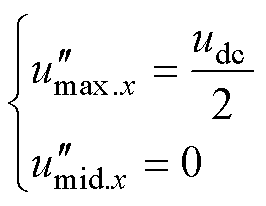 (24)
(24)
令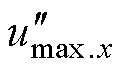 、
、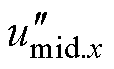 和
和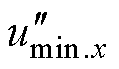 (x=1, 2, 3)表示调制电压在下述方法中的值,对于
(x=1, 2, 3)表示调制电压在下述方法中的值,对于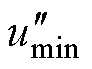 的计算有如下几种处理方法:
的计算有如下几种处理方法:
方法一:保证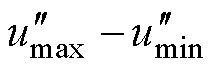 线电压关系不变,即满足
线电压关系不变,即满足
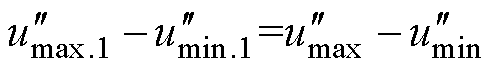 (25)
(25)
化简得到
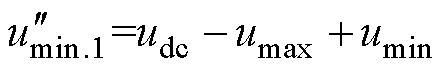 (26)
(26)
方法二:保证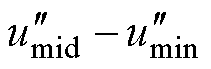 线电压关系不变,有
线电压关系不变,有
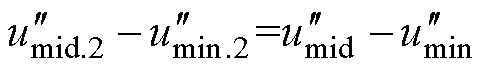 (27)
(27)
化简得到
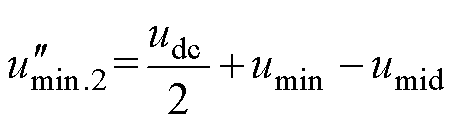 (28)
(28)
上述方法中,方法一和方法二都保证其中一相的线电压关系不变。本文结合上述两种方法,提出一种最小合成误差方法即方法三,以最大程度缓解过零点畸变,其证明过程见附录。
方法三:采用对方法一和方法二取平均的方法,即
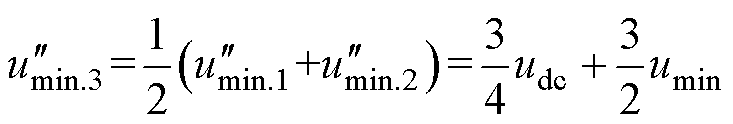 (29)
(29)
综上可得,自由调制波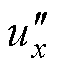 为
为
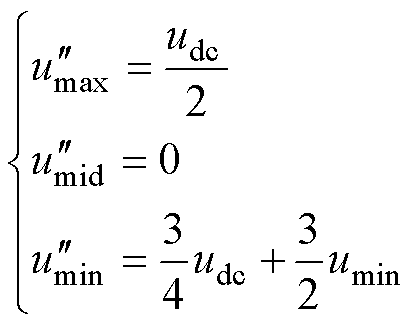 (30)
(30)
类似地,当输入电流由正到负过零时,中间相电压本应在电平1、2之间调制,为抑制过零点畸变使中间相钳位,需注入负的零序电压,若不能满足umid-umin≤udc/2,将导致umin过调制。此时中间相和最小相均出现钳位,仅能调制最大相,调制波的变化如图6所示。
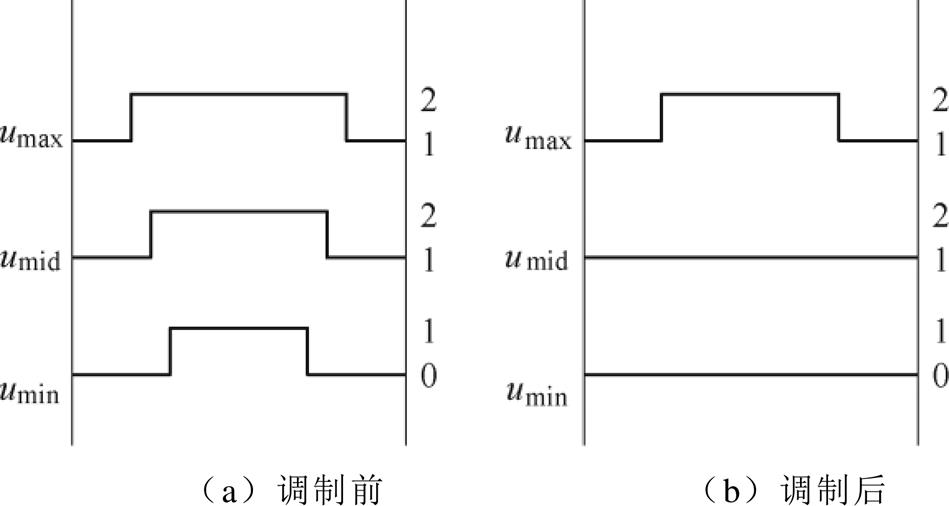
图6 中间相电流由正到负过零时的调制波变化情况
Fig.6 Variation of the modulated waveforms when the current changes from positive to negative
此时,原始的自由调制波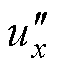 为
为
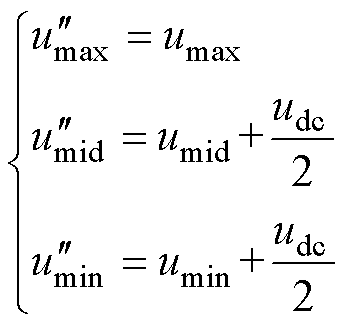 (31)
(31)
将中间相和最小相分别钳位至电平1和0,通过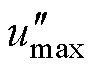 调制,即有
调制,即有
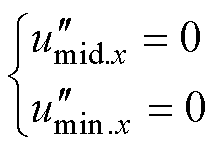 (32)
(32)
同样有如下三种处理方法:
方法一:保证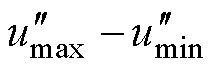 线电压关系不变有
线电压关系不变有
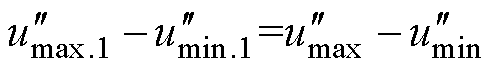 (33)
(33)
化简得到
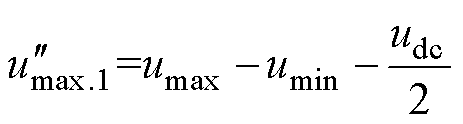 (34)
(34)
方法二:保证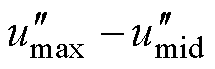 线电压关系不变,有
线电压关系不变,有
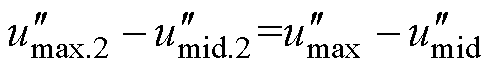 (35)
(35)
化简得到
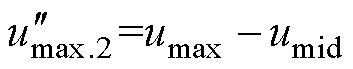 (36)
(36)
方法三:折中上述两种方法,有
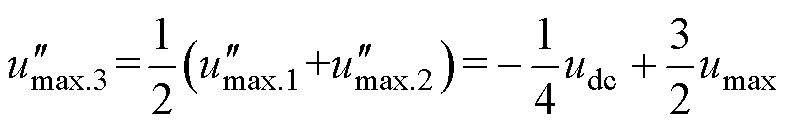 (37)
(37)
综上可得,自由调制波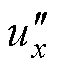 为
为
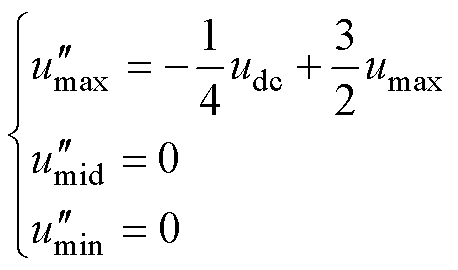 (38)
(38)
本文所采用的调制算法流程如图7所示,在输入电流非过零区域,通过零序电压注入平衡中点电位,而在输入电流过零点的一小段区域内,通过零序电压注入实现过零相钳位。若过零相钳位导致最大相或最小相过调制时,采用所提的方法三,以最大程度缓解过零点畸变。
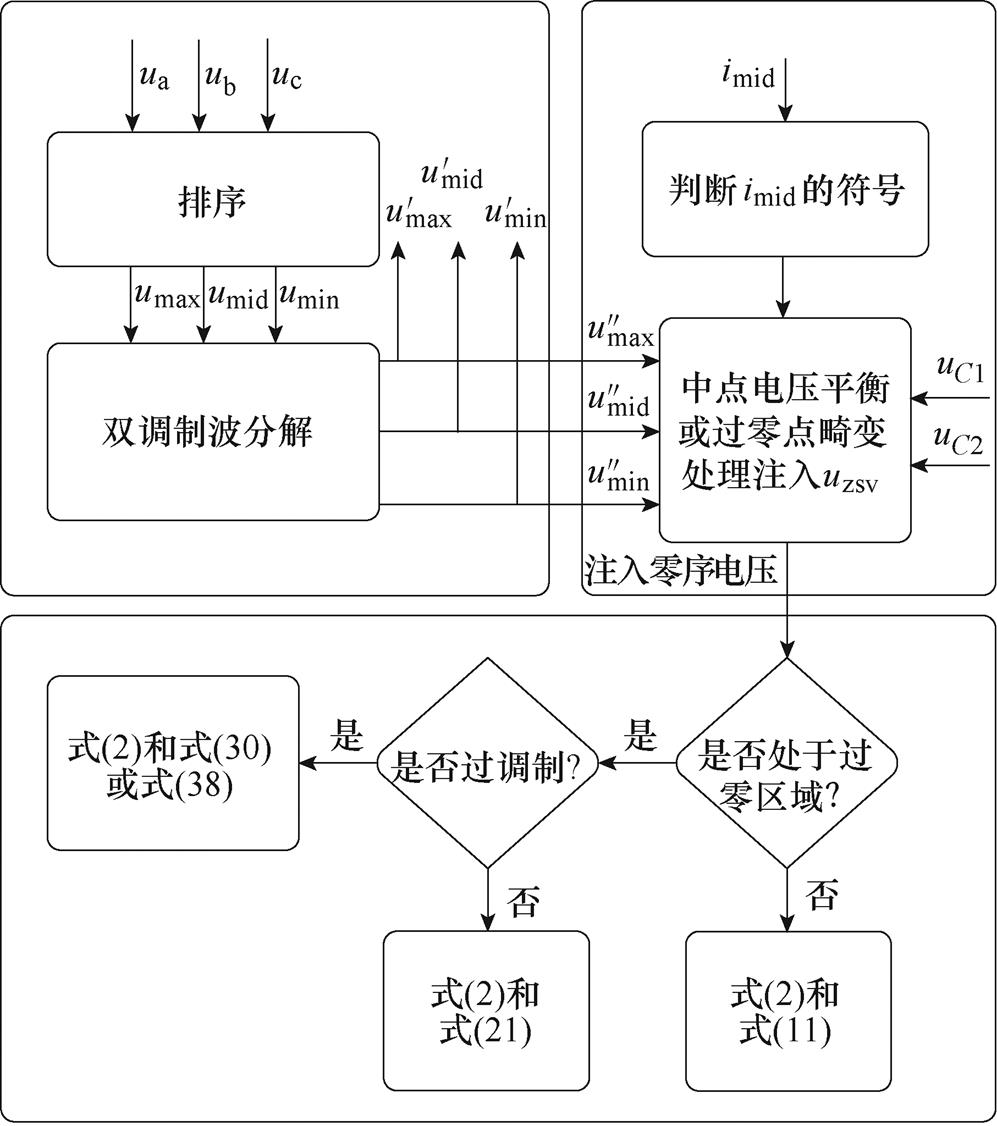
图7 所提调制算法的流程
Fig.7 The flow chart of the proposed modulation method
为了验证理论分析,搭建了Vienna整流器的实验平台如图8所示,系统参数见表2。实验部分包括稳态实验和动态实验两个部分。稳态实验将本文所提方法与SVPWM、文献[20]提出的ZCC-SVM相比较,通过稳态实验波形和THD数据分析不同调制方法下抑制电流畸变的效果。动态实验主要是在负载和直流侧电压突变时验证所提调制方法的可行性和稳定性。

图8 Vienna整流器的实验平台
Fig.8 Experimental platform of Vienna rectifier
图9给出了调制度为0.5时,SVPWM、ZCC- SVM和本文所提调制策略的稳态实验结果,此时对应电网电压情形1和负载情形1。图9a~图9c分别给出了直流侧上下电容电压、三相输入电流、A相电压、AB两相间的线电压,以及A相调制波分解的双调制波。由图9c可见,固定调制波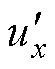 与电流的极性相关,如式(2)所示,当电流为正时,
与电流的极性相关,如式(2)所示,当电流为正时,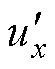 =udc/2,电流为负时,
=udc/2,电流为负时,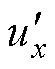 =0。由图9a~图9c可以看出,采用SVPWM时,电流在过零点区域畸变比较明显,而采用ZCC-SVM和所提调制方法时,输入电流无明显过零点畸变现象。为定量分析,图9d~图9f分别给出三种调制方法对应的A相输入电流频谱,相比于SVPWM,从THD可以看出,ZCC-SVM和所提调制方法有了明显降低,这是由于电流过零点畸变得到了很好的抑制。在低调制度下,ZCC-SVM和所提调制方法的电流过零点畸变抑制效果几乎一致,这是因为在电流过零点区域,零序电压的注入不会引起过调制。
=0。由图9a~图9c可以看出,采用SVPWM时,电流在过零点区域畸变比较明显,而采用ZCC-SVM和所提调制方法时,输入电流无明显过零点畸变现象。为定量分析,图9d~图9f分别给出三种调制方法对应的A相输入电流频谱,相比于SVPWM,从THD可以看出,ZCC-SVM和所提调制方法有了明显降低,这是由于电流过零点畸变得到了很好的抑制。在低调制度下,ZCC-SVM和所提调制方法的电流过零点畸变抑制效果几乎一致,这是因为在电流过零点区域,零序电压的注入不会引起过调制。
表2 系统参数
Tab.2 Parameters of the system

参 数数 值 直流侧电压/V600 直流侧上下电容/mF1 000 电网电压情形1/V122 电网电压情形2/V220 网侧输入电感/mH3 负载情形1/W150 负载情形2/W50 开关频率/kHz10 基波频率/Hz50
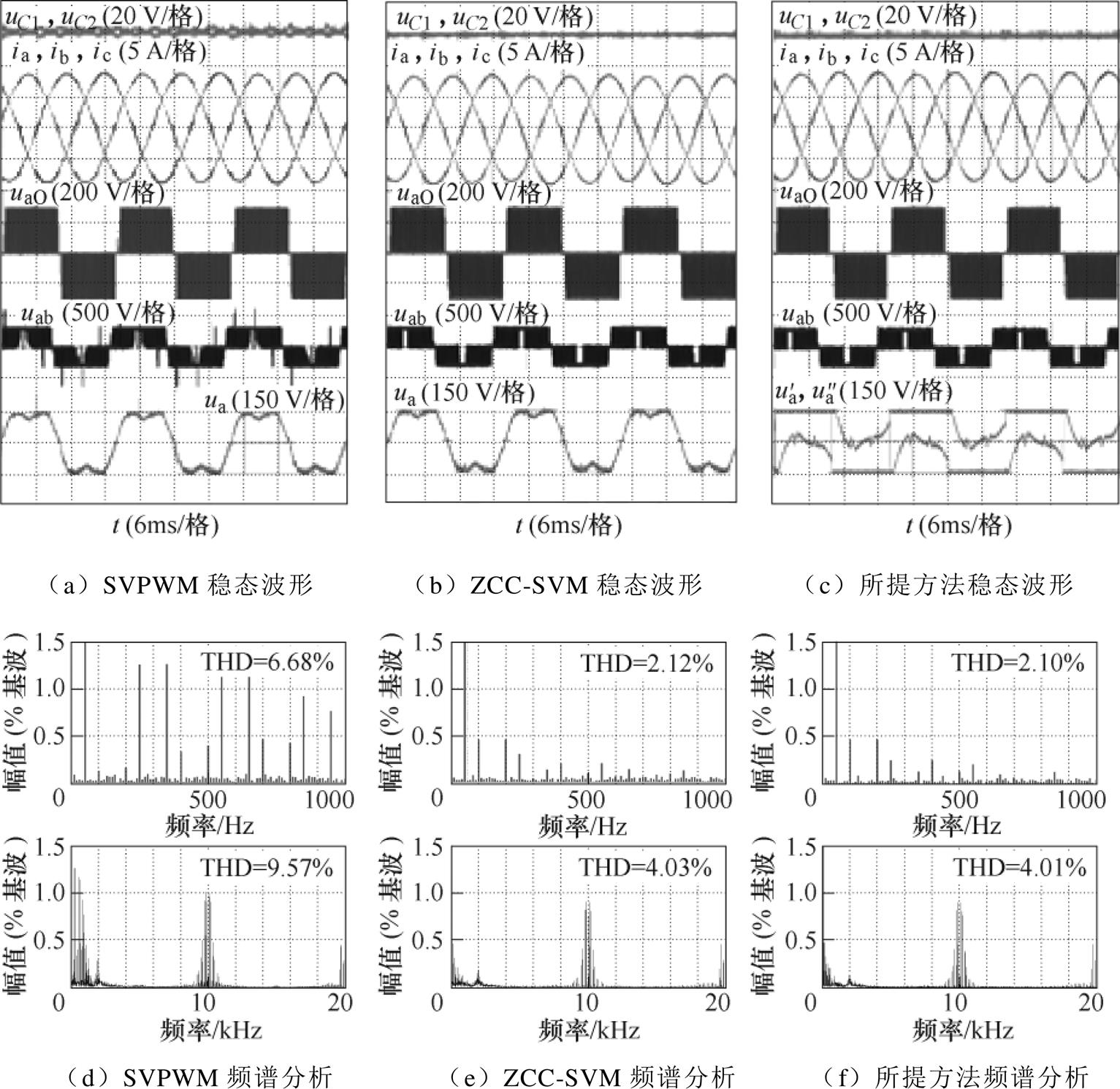
图9 调制度为0.5时,三种调制方式的稳态实验结果
Fig.9 When the modulation degree is 0.5, the steady state experimental results of the three modulation methods
图10给出了在调制度为0.9时三种调制方式的稳态实验结果对比,此时对应电网电压情形2和负载情形2。由图10可以看出,在采用所提调制算法时,输入电流波形质量最好。在高调制度时,为抑制过零点畸变注入的零序电压将使后两种算法均出现过调制,由于所提调制算法采用了最小合成误差原则,因而过零畸变抑制效果优于ZCC-SVM。对比图10e和图10f可以看出,相比于ZCC-SVM,采用所提方法时低频THD由3.64%降至3.04%,高频THD由5.34%降至4.56%,由低频频谱可见电流5、7次谐波有了明显降低。

图10 调制度为0.9,三种调制方式的稳态实验结果
Fig.10 When the modulation degree is 0.9, the steady state experimental results of the three modulation methods
表3给了文献[12]中提出的混合空间矢量调制(Hybrid, HSVPWM)、文献[28]中提出的基于载波振荡消除的空间矢量调制(Carrier Based-Oscillation Cancel SVM, CB-OCSVM)、SVM、过零畸变消除的空间矢量调制(Zero Crossing Cancel SVW, ZCC-SVM)和所提方法在m=0.9时额定负载下的输入电流THD、中点电压平衡能力和开关损耗方面的定量对比。所提方法在输入电流THD的处理和中点电压平衡方面均为最佳,几种方法的开关损耗没有明显的差别。
表3 不同调制方法对比结果
Tab.3 Comparison results of different modulation methods
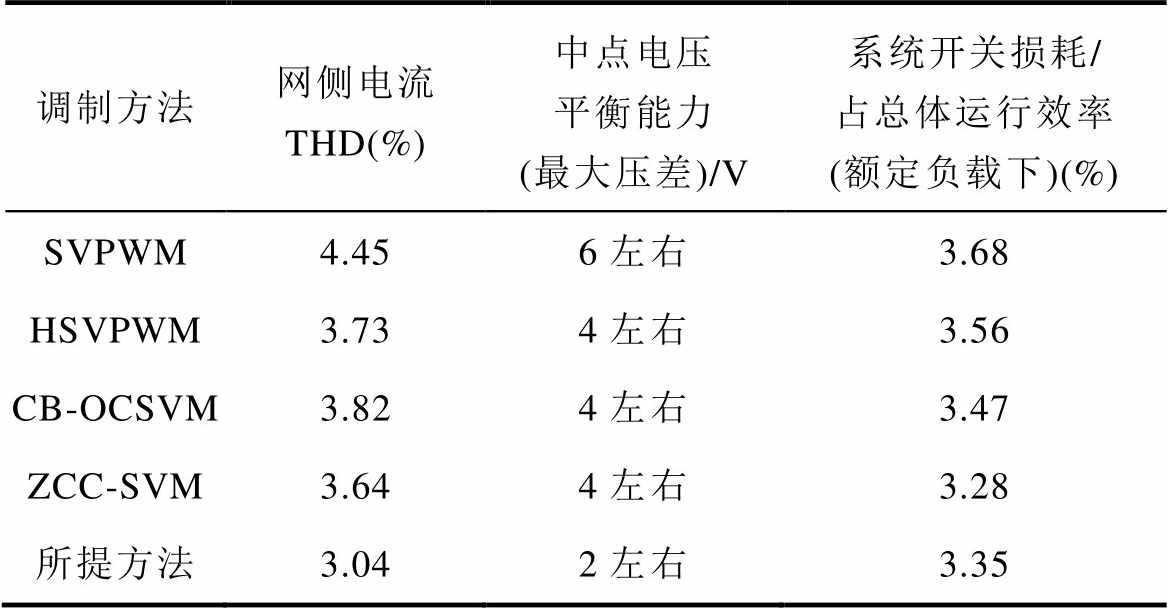
调制方法网侧电流 THD(%)中点电压平衡能力 (最大压差)/V系统开关损耗/占总体运行效率 (额定负载下)(%) SVPWM4.456左右3.68 HSVPWM3.734左右3.56 CB-OCSVM3.824左右3.47 ZCC-SVM3.644左右3.28 所提方法3.042左右3.35
图11给出了电流过零点畸变的缓解方法中提到的方法一和方法二在m=0.9时的实验结果和频谱分析。从实验结果来看,这两种处理方法下的输入电流质量均不如图10c中所提方法的输入电流,在过零点处有明显的畸变,频谱分析可见其THD均高于方法三即所提方法的THD。
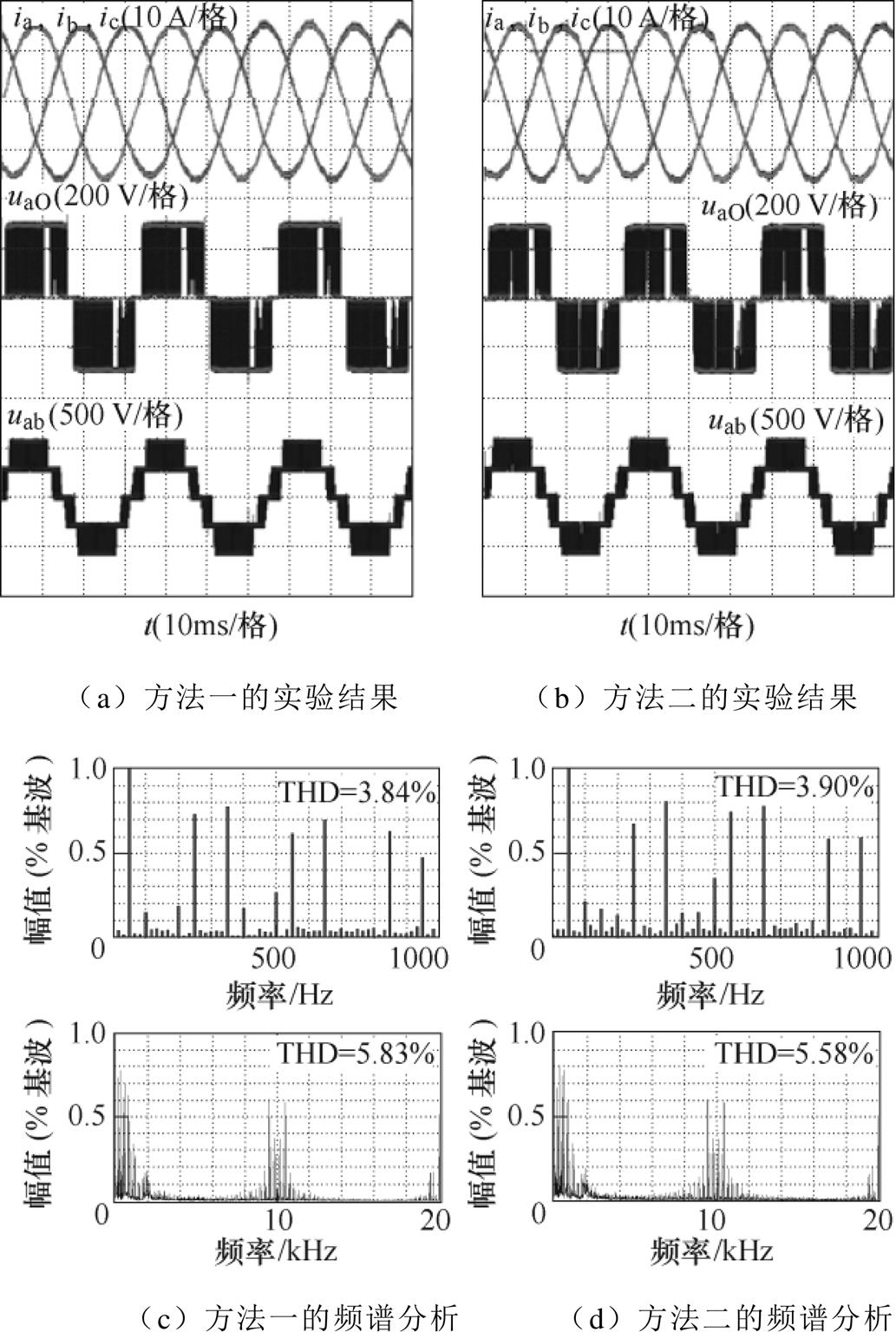
图11 m=0.9时方法一和方法二的实验波形
Fig.11 When the modulation degree is 0.9, the experimental waveforms of method 1 and method 2
图12给出了本调制算法在不同调制度下中点电压的恢复能力,上下电容电压初值分别为320 V和280 V。由图12可知,本文所提调制策略具有较好的中点电压恢复能力。
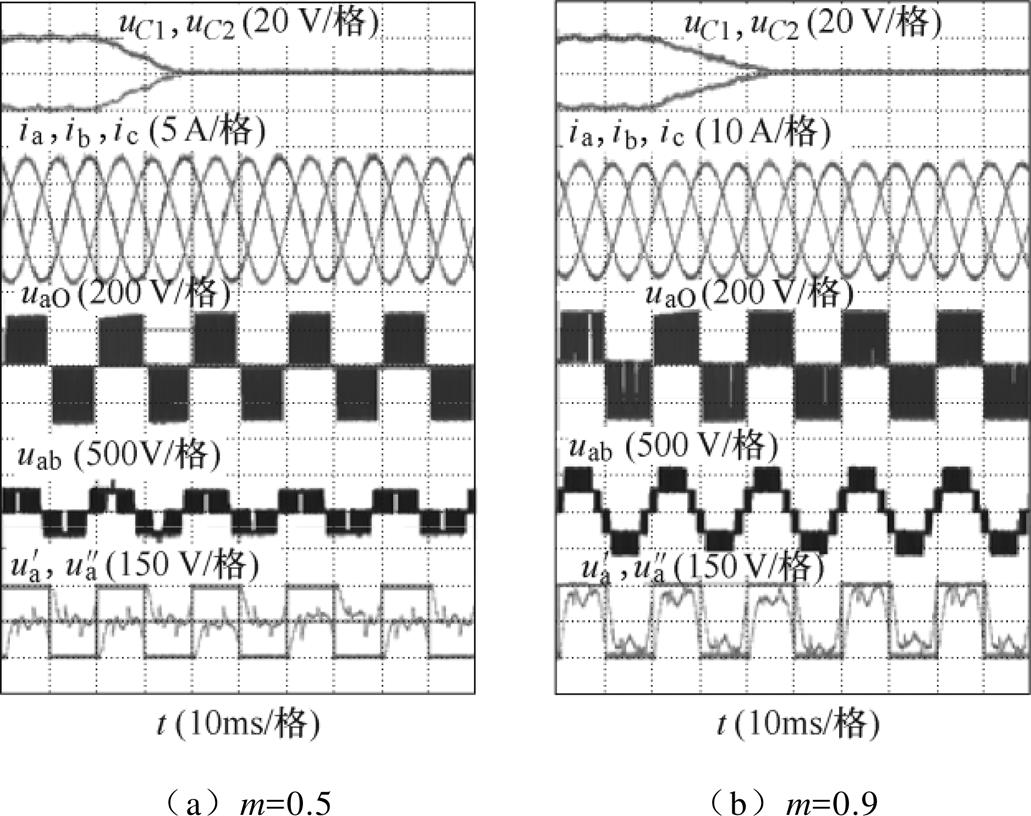
图12 中点电压恢复实验
Fig.12 Neutral point voltage recovery experiments
图13~图16给出了本调制算法在不同调制度下的负载突变和直流侧突变实验。由动态实验结果同样可以看出,本文所提调制算法具有很好地控制直流侧电压波动和输入电流畸变的能力。
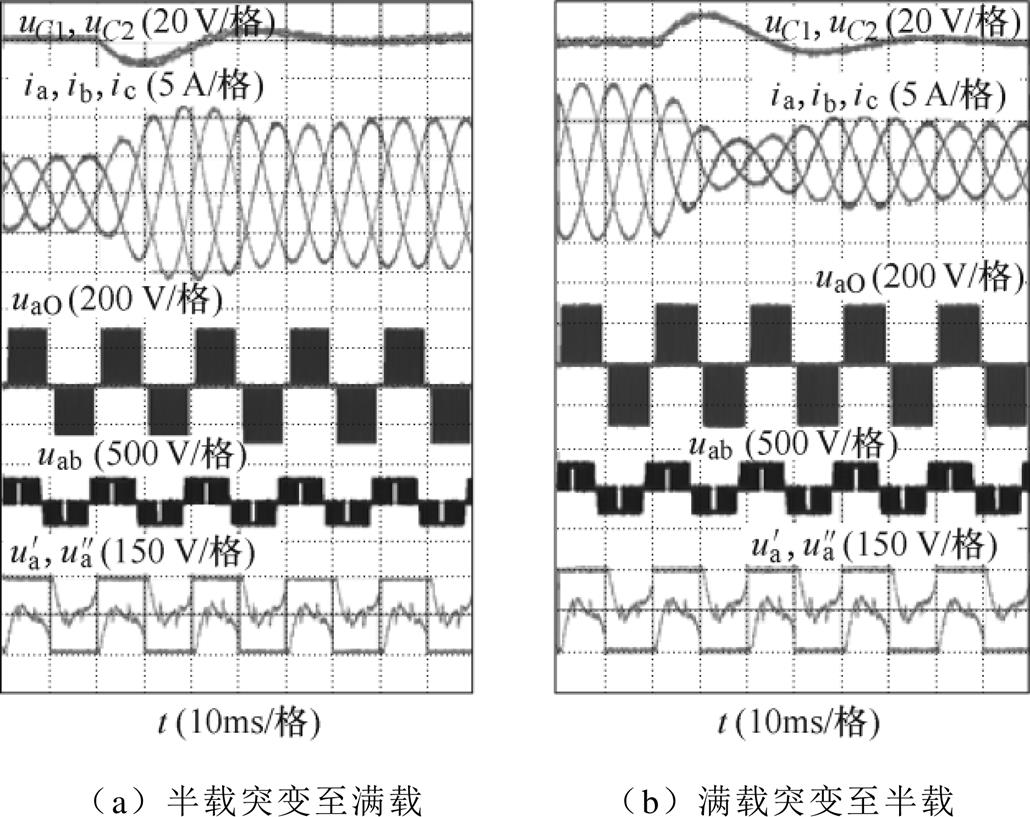
图13 m=0.5时负载突变实验
Fig.13 Load step change when m=0.5
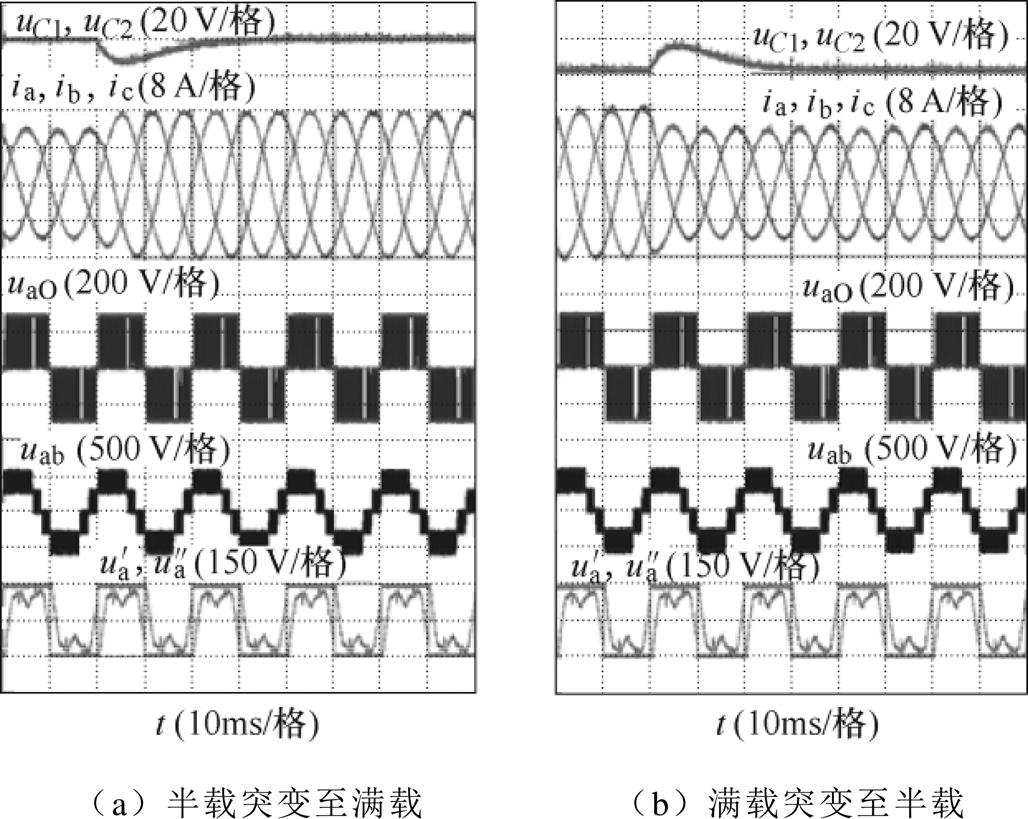
图14 m=0.9时负载突变实验
Fig.14 Load step change when m=0.9
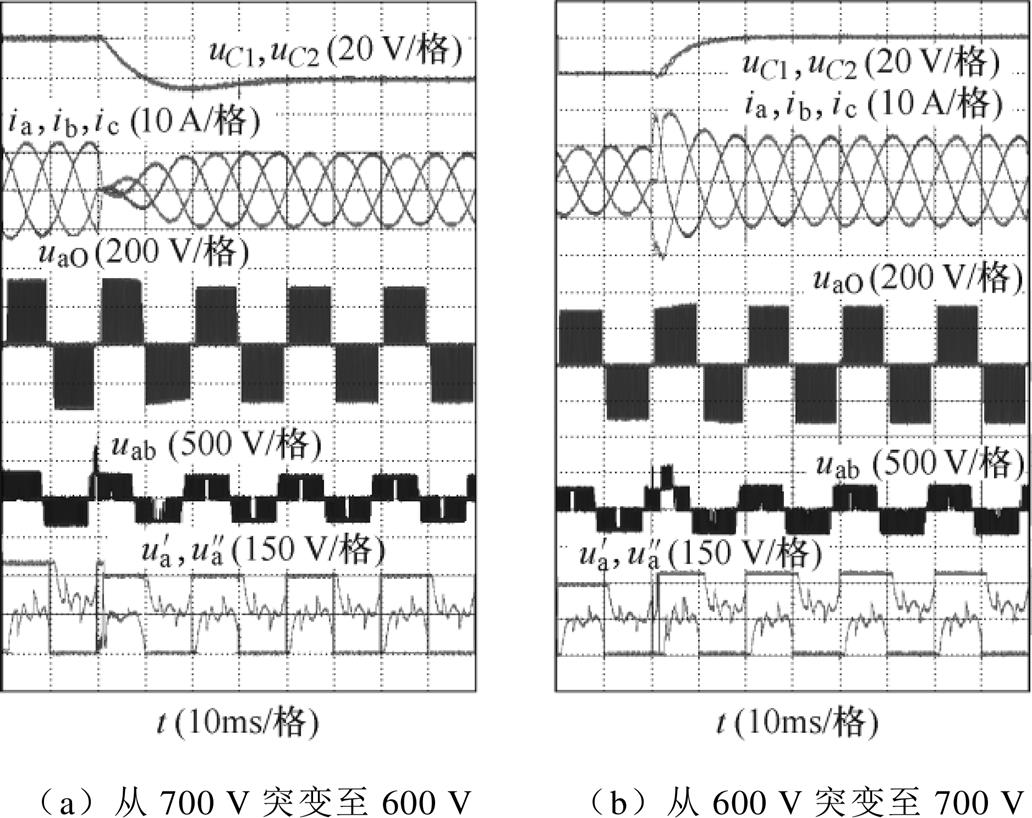
图15 m=0.5时直流侧突变实验
Fig.15 DC side voltage step change when m=0.5
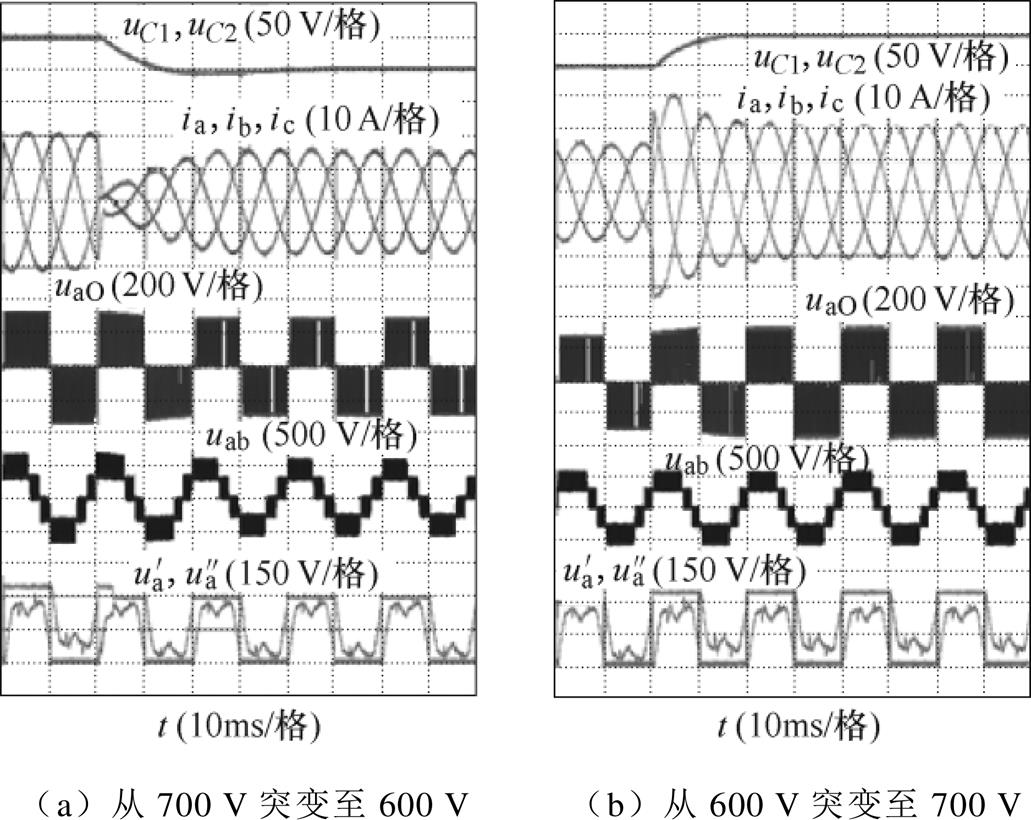
图16 m=0.9时直流侧突变实验
Fig.16 DC side voltage step change when m=0.9
为了维持中点电压平衡并抑制电流过零点畸变,本文在基于双调制波分解的CBPWM下,提出了一种合成误差最小的调制方法来改善高调制度下常规钳位方法无法处理的过零区域。在低调制度时,传统的钳位方法能够很好地抑制过零点畸变,高调制度时通过利用两相钳位,一相调制的方法可以最大程度地缓解过零点畸变问题。在全调制度范围内,通过计算中点电流注入相应的零序电压能够很好地实现中点电压平衡。实验结果验证了所提调制算法的优越性。
附 录
对于文中方法三的证明,需要在αβ轴坐标系下分析,参考电压矢量uref可以表示为uα,ref+juβ,ref, αβ轴和abc轴的等效公式为
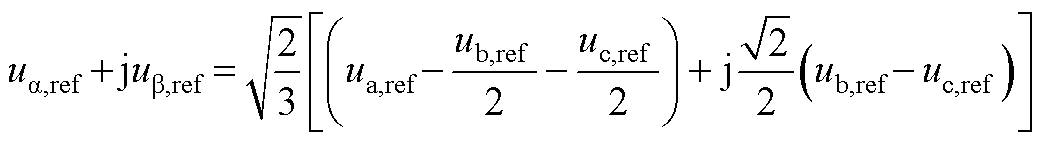 (A1)
(A1)
定义矢量[2, 1, 1]表示umax输出电平2,umid和umin输出电平1。分别对由负到正和由正到负两种情形进行 讨论。
情形一:电流由负到正过零,umax-umid>udc/2,将umax钳为电平2,umid钳为电平1,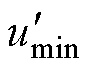 已经固定,
已经固定,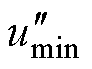 在[0, udc/2]之间实现调制。定义[2, 1, 1]作用时间的占空比为d(d∈[0, 1]),即可得到矢量[2, 1, 0]作用时间的占空比为1-d。在αβ轴下引入误差函数F(d),为了量化整流器的实际输出电压矢量
在[0, udc/2]之间实现调制。定义[2, 1, 1]作用时间的占空比为d(d∈[0, 1]),即可得到矢量[2, 1, 0]作用时间的占空比为1-d。在αβ轴下引入误差函数F(d),为了量化整流器的实际输出电压矢量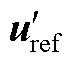 与参考电压矢量uref之间的误差,F(d)表示为
与参考电压矢量uref之间的误差,F(d)表示为
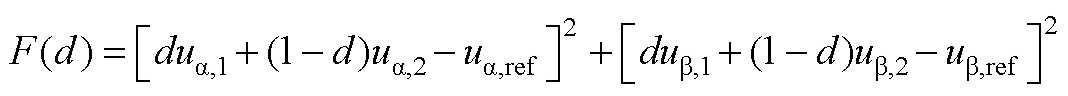 (A2)
(A2)
其中矢量[2, 1, 1]和[2, 1, 0]在ab 轴下的具体表达式分别为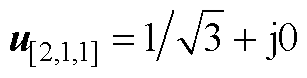 和
和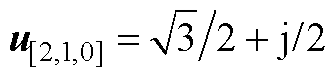 。为了使其合成误差最小,式(A2)中的F(d)应取最小值。通过计算化简式(A2)可得,F(d)为关于d的二次项系数大于零的二次函数,定义dmin为函数F(d)取最小值时对应的d值为
。为了使其合成误差最小,式(A2)中的F(d)应取最小值。通过计算化简式(A2)可得,F(d)为关于d的二次项系数大于零的二次函数,定义dmin为函数F(d)取最小值时对应的d值为
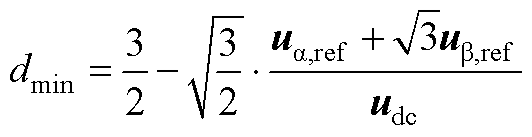 (A3)
(A3)
解出式(A3)即可得到在最小合成误差的调制方法下矢量[2, 1, 1]的占空比。在abc轴下实际输出电压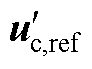 与占空比的表达式为
与占空比的表达式为
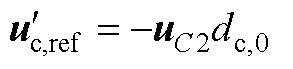 (A4)
(A4)
式中,dc,0为C相电平0的占空比,通过计算可以得到其自由调制波为
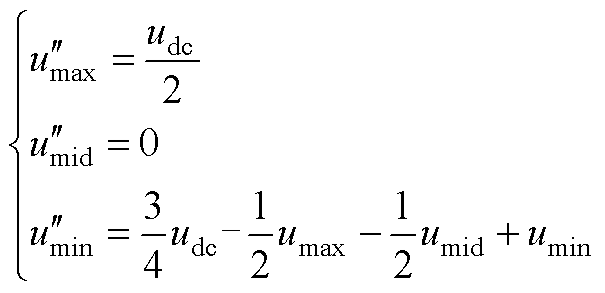 (A5)
(A5)
结合式(2)化简得到的双调制波为
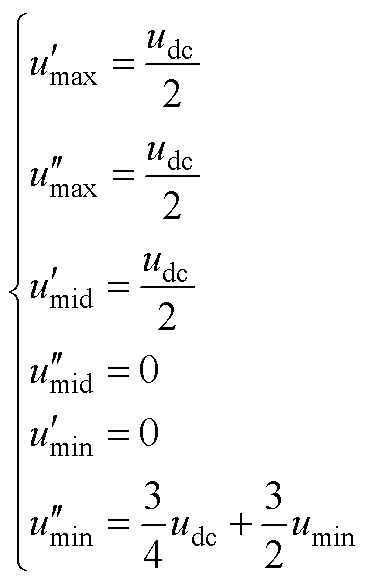 (A6)
(A6)
情形二:电流由正到负过零时umid-umin>udc/2,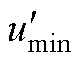 已经固定,
已经固定,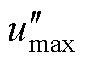 实现调制,umid钳位电平1,umin钳位电平0。类似地,在矢量[2, 1, 0]和[1, 1, 0]之间调制,得到的分离的调制波为
实现调制,umid钳位电平1,umin钳位电平0。类似地,在矢量[2, 1, 0]和[1, 1, 0]之间调制,得到的分离的调制波为
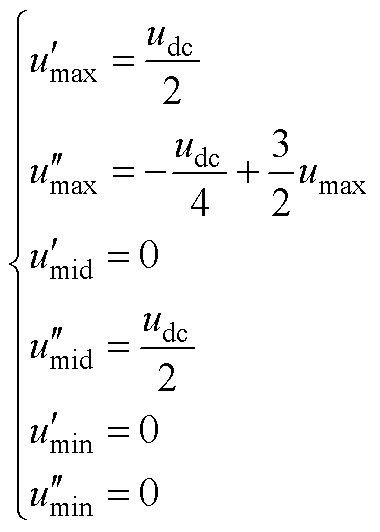 (A7)
(A7)
上述分析得到的结果与正文结果一致,即可证明此方法合成误差最小。
参考文献
[1] 周运红, 张爱民, 黄晶晶, 等. 基于动态事件触发的Vienna整流器模型预测控制[J]. 电工技术学报, 2022, 37(8): 2040-2050.
Zhou Yunhong, Zhang Aimin, Huang Jingjing, et al. Dynamic event-triggered model predictive control for Vienna rectifier[J]. Transactions of China Electro- technical Society, 2022, 37(8): 2040-2050.
[2] 肖蕙蕙, 苏新柱, 郭强, 等. 三相Vienna整流器无网压传感器预测电流控制策略[J]. 电工技术学报, 2021, 36(6): 1304-1312.
Xiao Huihui, Su Xinzhu, Guo Qiang, et al. Predi- ctive current control of three-phase Vienna rectifier without grid voltage sensors[J]. Transactions ofChina Electrotechnical Society, 2021, 36(6): 1304-1312.
[3] 党超亮, 王飞, 刘丁, 等. 基于优选矢量合成的Vienna整流器滑模预测控制[J]. 中国电机工程学报, 2022, 42(23): 8699-8708.
Dang Chaoliang, Wang Fei, Liu Ding, et al. Sliding mode predictive control of Vienna rectifier based on optimal vector synthesis[J]. Proceedings of the CSEE, 2022, 42(23): 8699-8708.
[4] Satpathy A S, Kastha D, Kishore N K. Vienna rectifier-fed squirrel cage induction generator based stand-alone wind energy conversion system[J]. IEEE Transactions on Power Electronics, 2021, 36(9): 10186-10198.
[5] Monteiro A P, Jacobina C B, Bahia F A C, et al. Dual Vienna rectifiers with a single DC-link for wind energy conversion system applications[C]//IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, 2020: 2189-2195.
[6] 郝振洋, 徐子梁, 陈宇, 等. 航空Vienna整流器故障诊断与容错控制[J]. 电工技术学报, 2020, 35(24): 5152-5163.
Hao Zhenyang, Xu Ziliang, Chen Yu, et al. Fault diagnosis and fault tolerant control for aviation Vienna rectifier[J]. Transactions of China Electro- technical Society, 2020, 35(24): 5152-5163.
[7] Adhikari J, Iv P, Panda S K. Reduction of input current harmonic distortions and balancing of output voltages of the Vienna rectifier under supply voltage disturbances[J]. IEEE Transactions on Power Elec- tronic, 2017, 32(7): 5802-5812.
[8] Rajendran G, Vaithilingam C A, Misron N, et al. Voltage oriented controller based Vienna rectifier for electric vehicle charging stations[J]. IEEE Access, 2021, 9: 50798-50809.
[9] Pandey R, Singh B. An electric vehicle charger based on Vienna rectifier and resonant LLC converter[C]// IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 2021: 1-6.
[10] 朱文杰, 陈昌松, 段善旭. 一种改善Vienna整流器输入电流品质的载波钳位调制方法[J]. 电工技术学报, 2019, 34(8): 1677-1688.
Zhu Wenjie, Chen Changsong, Duan Shanxu. A carrier-based modulation method with clamped area for input current performance of Vienna rectifier[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1677-1688.
[11] 杨青松, 石健将. 带中点电位波动的Vienna整流器改进SVPWM策略[J]. 电力电子技术, 2021, 55(7): 130-133.
Yang Qingsong, Shi Jianjiang. Improved SVPWM strategy for Vienna rectifier with midpoint potential fluctuation[J]. Power Electronics, 2021, 55(7): 130- 133.
[12] 陈杰, 沈禹廷, 沈佳茜, 等. 三相VIENNA整流器的混合空间矢量脉宽调制策略[J]. 电工技术学报, 2021, 36(增刊2): 665-675.
Chen Jie, Shen Yuting, Shen Jiaqian, et al. Hybrid space vector pulse width modulation strategy for three-phase VIENNA rectifier[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 665-675.
[13] Hang Lijun, Li Bin, Zhang Ming, et al. Equivalence of SVM and carrier-based PWM in three-phase/ wire/level Vienna rectifier and capability of unbalanced- load control[J]. IEEE Transactions on Industrial Elec- tronics, 2014, 61(1): 20-28.
[14] 李洪亮, 姜建国, 乔树通. 三电平SVPWM与SPWM本质联系及对输出电压谐波的分析[J]. 电力系统自动化, 2015, 39(12): 130-137.
Li Hongliang, Jiang Jianguo, Qiao Shutong. Essential relationship between three-level SVPWM and SPWM and analysis on output voltage harmonic[J]. Auto- mation of Electric Power Systems, 2015, 39(12): 130-137.
[15] Xu Houjian, Yao Wenxin, Shao Shuai. Improved SVPWM schemes for Vienna rectifiers without current distortion[C]//IEEE Energy Conversion Con- gress and Exposition (ECCE), Cincinnati, OH, 2017: 3410-3414.
[16] 王涛, 陈昌松, 段善旭, 等. 用于改善电流过零点畸变的Vienna整流器空间矢量调制策略[J]. 电工技术学报, 2019, 34(18): 3854-3864.
Wang Tao, Chen Changsong, Duan Shanxu, et al. An improved space-vector modulation for Vienna recti- fier to eliminating current distortion around zero crossing point[J]. Transactions of China Electro- technical Society, 2019, 34(18): 3854-3864.
[17] Ding Wenlong, Zhang Chenghui, Gao Feng, et al. A zero-sequence component injection modulation method with compensation for current harmonic mitigation of a Vienna rectifier[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 801-814.
[18] Lee J S, Lee K B. A novel carrier-based PWM method for Vienna rectifier with a variable power factor[J]. IEEE Transactions on Industrial Electronics, 2016, 63(1): 3-12.
[19] Molligoda D, Ceballos S, Pou J, et al. Hybrid modulation strategy for the Vienna rectifier[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 1283-1295.
[20] Wang Tao, Chen Changsong, Liu Peng, et al. A hybrid space-vector modulation method for harmonics and current ripple reduction of interleaved Vienna rectifier[J]. IEEE Transactions on Industrial Elec- tronics, 2020, 67(10): 8088-8099.
[21] Jiang Weidong, Wang Lei, Wang Jinping, et al. A carrier-based virtual space vector modulation with active neutral-point voltage control for a neutral- point-clamped three-level inverter[J]. IEEE Transa- ctions Industrial Electronics, 2018, 65(11): 8687- 8696.
[22] 谢路耀, 金新民, 吴学智, 等. 基于零序电压注入与调制波分解的三电平脉宽调制策略[J]. 电工技术学报, 2014, 29(10): 27-37.
Xie Luyao, Jin Xinmin, Wu Xuezhi, et al. Three-level pulse width modulation strategy based on zero- sequence voltage injection and modulation-waves decomposition[J]. Transactions of China Electro- technical Society, 2014, 29(10): 27-37.
[23] 陈鹏飞, 唐芬, 吴学智, 等. 三电平并网变流器中点电位自平衡特性分析及拓扑改进[J]. 电力系统自动化, 2019, 43(24): 171-180.
Chen Pengfei, Tang Fen, Wu Xuezhi, et al. Self- balancing characteristic analysis of neutral point potential and improved topology of three-level grid- connected converter[J]. Automation of Electric Power Systems, 2019, 43(24): 171-180.
[24] 石祥花, 许津铭, 谢少军. 三电平中点钳位变换器电容电压自平衡机理与均压控制策略[J]. 电力系统自动化, 2014, 38(7): 95-100, 111.
Shi Xianghua, Xu Jinming, Xie Shaojun. Natural- capacitor voltage balancing mechanism and voltage balance trategies for 3L-NPC inverters[J]. Auto- mation of Electric Power Systems, 2014, 38(7): 95- 100, 111.
[25] Ding Wenlong, Qiu Han, Duan Bin, et al. A novel segmented component injection scheme to minimize the oscillation of DC-link voltage under balanced and unbalanced conditions for Vienna rectifier[J]. IEEE Transactions on Power Electronics, 2019, 34(10): 9536-9551.
[26] Li Xing, Han Jian, Sun Yao, et al. A generalized design framework for neutral point voltage balance of three-phase Vienna rectifiers[J]. IEEE Transactions on Power Electronics, 2019, 34(10): 10221-10232.
[27] 丁文龙, 刘家君, 段彬, 等. VIENNA整流器中点电位振荡抑制与平衡控制研究[J]. 中国电机工程学报, 2017, 37(24): 7284-7293, 7443.
Ding Wenlong, Liu Jiajun, Duan Bin, et al. Investi- gation of neutral-point voltage oscillation suppression and balancing control in VIENNA rectifiers[J]. Pro- ceedings of the CSEE, 2017, 37(24): 7284-7293, 7443.
[28] 赵志宏, 吴佳衡, 冯义龙, 等. Vienna整流器输入电流畸变与中点电位振荡综合优化调制策略研究[J]. 中国电机工程学报, 2022, 42(15): 5685-5697.
Zhao Zhihong, Wu Jiaheng, Feng Yilong, et al. Com- prehensive study on modulation strategy for Vienna rectifier input current distortion and midpoint potential oscillation[J]. Proceedings of the CSEE, 2022, 42(15): 5685-5697.
Abstract As a three-phase power factor corrector, the Vienna rectifier has the advantages of high reliability and simple control. It is widely used and plays an important role in power unidirectional flow fields, such as communication power supply, electric vehicle, wind power, and aeronautical power supply. Carrier-based pulse width modulation (CB-PWM) and space vector modulation (SVM) are usually used to achieve unity power factor and neutral point voltage balance. However, these modulation methods have the problem of current zero-crossing point distortion, which is also one of the characteristics of Vienna rectifier topology. Different symbols of modulation voltage and current cause current distortion. Many modulation strategies have been proposed to solve the zero-crossing distortion. However, only some can perfectly applied to the full modulation range or the modulation strategy to overmodulate the modulation voltage. This paper presents a modulation method that can minimize the current zero-crossing distortion while maintaining the neutral point voltage balance on the DC side. Because the Vienna output level is limited by the current symbol, this paper uses the dual modulation wave decomposition method to deal with neutral point voltage balance and zero-crossing distortion.
Neutral point voltage balance is an important indicator of the stable operation of the Vienna rectifier. An unbalanced neutral point voltage can cause serious DC side offset, leading to over-voltage of power devices and causing danger. In order to balance the neutral point voltage, this paper calculates the average current to be extracted or injected during a carrier cycle by detecting the difference in capacitance voltage between the upper and lower DC sides obtained from the feedback. Combined with the expression of the duty cycle of each level, the zero-sequence voltage to be injected is calculated to balance the neutral point voltage.
In order to deal with the current zero crossing distortion, the modulation wave is divided into fixed modulation and free modulation waves. The fixed modulation wave is affected by the current symbol. In the current zero crossing area, a zero-sequence voltage is injected to clamp its zero-crossing phase voltage to 0. Injecting zero sequence voltage in high regulation will over-modulate, changing the relationship between line voltage and causing current distortion. The current zero crossing distortion cannot be wholly suppressed in high modulation. This paper uses a minimum synthetic error method in high modulation to minimize the change of line voltage. When the current zero crossing, the modulation voltage is obtained by calculation, instead of injecting zero-sequence voltage. Thus, the current zero crossing distortion can be alleviated to the greatest extent when injecting zero sequence voltage over modulation.
The steady-state experimental results of SVPWM, ZCC-SVM (Zero-Crossing Clamped SVPWM), and the proposed method are compared. When the modulation index is 0.5, the distortion of the SVPWM modulation strategy in the current zero crossing region is obvious, while the input current of ZCC-SVM and the proposed modulation method has no obvious zero crossing distortion. When the modulation index is low, the suppression effect of current zero crossing distortion of ZCC-SVM and the proposed modulation method is almost the same, because in the region of current zero crossing, the injection of zero sequence voltage will not cause over-modulation. When the modulation index is 0.9, the zero-sequence voltage injected by the ZCC-SVM method to suppress zero crossing distortion will be over-modulated. Compared with ZCC-SVM, since the proposed modulation algorithm adopts the minimum synthesis error method, the low-frequency THD (Total Harmonic Distortion) is reduced from 3.64% to 3.04%, the high-frequency THD is reduced from 5.34% to 4.56%, and the 5th and 7th harmonics of the input current are significantly reduced.
keywords:Vienna rectifier, modulation method, neutral point voltage balance, current zero crossing distortion
DOI: 10.19595/j.cnki.1000-6753.tces.221055
中图分类号:TM461
国家自然科学基金面上资助项目(52077050)。
收稿日期 2022-06-06
改稿日期 2022-08-01
姜卫东 男,1976年出生,博士,教授,研究方向为电能质量控制技术、并网变流器控制技术、电机控制技术。E-mail: ahjwd@163.com(通信作者)
胡业波 男,1998年出生,硕士研究生,研究方向为电力电子与电力传动。E-mail: 958141021@qq.com
(编辑 陈 诚)