一种基于ghg 坐标系的三电平四桥臂逆变器简化空间矢量脉宽调制方法
张 志1,2 陈浩辉1,2 陈思哲2 张兆云1 李义云1
(1. 东莞理工学院电子工程与智能化学院 东莞 523808 2. 广东工业大学自动化学院 广州 510006)
摘要 针对中点钳位型三电平四桥臂逆变器拓扑,该文提出一种基于ghg 坐标系的简化三维空间矢量脉宽调制方法。该方法以各冗余小矢量为中心点,将原矢量空间降阶分解为若干个两电平四桥臂矢量空间,仅需要简单的坐标变换和计算就能得到开关器件的占空比,还能自动获取冗余矢量和相邻电压矢量并优化组成开关序列,克服了传统三电平空间矢量调制方法存在过多的四面体选择、占空比计算过程存在较多的三角函数运算和需人工查找冗余矢量并存储大量开关序列的缺点。同时,针对中点电位平衡的问题,提出一种通过调节冗余矢量占空比以精确补偿电容电荷量的计算方法。所提简化调制方法能拓展应用于多电平四桥臂逆变器中。最后,通过仿真和实验结果验证了该文所提方法的正确性和有效性。
关键词:三维空间矢量脉宽调制 冗余矢量 空间矢量降阶分解 中点电位平衡
0 引言
在中低压三相四线制供电系统中,多种电力电子变流器拓扑被用于提供恒定电压或解决电流谐波等电能质量问题[1]。相较于带D/YN型变压器的三相三线制逆变器和带分裂电容三相四线制逆变器,四桥臂逆变器体积更小且不存在直流侧电容分压不均等问题[2-3],通过增加一个桥臂,提供了更多的控制自由度,具有更强的带负载能力和抑制网侧功率倍频波动的能力[4]。因此,该拓扑在有源电力滤波 器[5]、静止无功功率补偿器[6]和可再生能源与电网的接口装置[7]等设备中得到了广泛的应用。
由于多电平四桥臂逆变器相较于传统两电平四桥臂逆变器拓扑具有开关器件电压变化率更低、输出电压波形正弦度更高和可工作于更高的电压等级以及功率等级等优点,对其控制策略和调制方式的研究也越来越多[8-11]。然而,调制过程随开关器件数量的增加变得相当复杂。由于三维空间矢量脉宽调制(Three-Dimensional Space Vector Pulse Width Modulation, 3DSVPWM)方法相比于正弦脉宽调制方法具有更高的直流电压利用率和易于数字化实现的特点,因而得到广泛研究[12-15],以下从坐标系选取和矢量空间简化方法这两个角度对现有的中点钳位型三电平四桥臂逆变器(以下简称为三电平四桥臂逆变器)3DSVPWM方法进行概述。
从坐标系选取的角度进行分析,传统调制过程一般在abg 坐标系或abc坐标系下进行。在abg 坐标系下,坐标变换与相邻电压矢量占空比的计算过程中存在大量三角函数运算,增加了处理器的计算负担[16-20]。在abc坐标系下,占空比计算得到了简化,但三电平矢量空间失去坐标平面对称性,不能直观分析参考电压矢量的运动过程,且中点电位平衡控制相对复杂[21]。同时,在该坐标系下不利于三相四线制变流器对零序分量的直接控制。
从矢量空间简化的角度进行分析,传统调制方法通常会在矢量空间中指定某一特定空间作为子空间以简化调制过程。文献[17-18]中提出一种在abg 坐标系下,以矢量空间投影平面上小扇区延展出的五面体作为子空间的简化调制方法。该方案虽对矢量空间进行了一定程度的简化,但子空间中存在大量的四面体切分斜面方程需要计算,且各四面体对应的开关序列和占空比系数矩阵也各不相同,占用较多存储空间。文献[19]是前一种调制方法的简化形式,将参考电压矢量转移到第1与第2大扇区中,相应地简化了计算过程并减少了存储量,但其过程仍非常繁琐。对于中点电位的调节,文献[19]中提出了电容能量变化率小于零即两电容电压趋于一致的中点电位调节原理。文献[20]提出一种在abc坐标系下,以矢量空间中小正方体作为子空间的简化调制方法。该方案运用向下取整的计算方式对占空比计算过程进行了简化,然而,取整坐标对应的空间矢量不一定是冗余矢量,形成的开关序列并非全是最优序列,不能有效调节直流侧中点电位,会造成功率器件开关损耗较大和电压应力较高。文献[21]将文献[20]的子空间平面化以实现空间降维。然而,该方案将子空间从abc坐标系转移到abg 坐标系下,使得占空比计算过程中包含了三角函数。同时,该方案未简化开关序列的判断过程,且每个调制周期中会发生两次两个桥臂开关同时跳变的情况。对于中点电位的调节,提出了一种带PI调节器的冗余矢量占空比调节的方法。
由上述分析可见,现有的三电平四桥臂3DSVPWM方法主要存在以下不足:①子空间内部结构复杂且含有较多四面体;②空间矢量的开关状态需先行推导并存储;③需人工寻找各四面体中的冗余矢量并存储相应的开关序列。此外,现有方法实施过程相对复杂,且缺乏直接拓展应用至多电平的能力。
本文针对上述问题,提出一种基于ghg 坐标系的三电平四桥臂逆变器简化3DSVPWM方法。该方法具有以下特点:
(1)以各冗余矢量为中心点建立两电平矢量空间,并选取第1小扇区中的五面体作为子空间,将子空间中包含的四面体数量减少为4个。
(2)主动计算出空间矢量的开关状态,不需先行推导及存储。
(3)开关序列以小矢量为首发矢量,优化了矢量作用顺序,有效了减少开关损耗。该调制方法可以推广应用至任意多电平四桥臂逆变器。
1 三电平矢量空间的可分解性分析
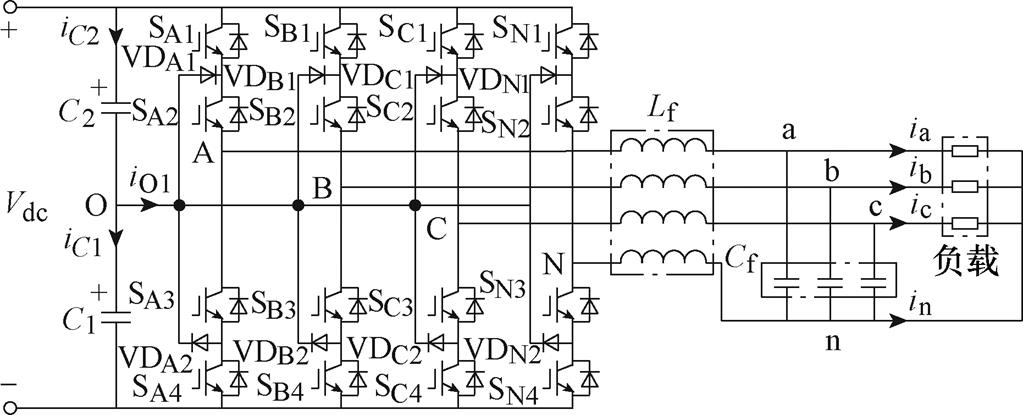
三电平四桥臂逆变器如图1所示,各桥臂上有4个开关器件,各器件的开关状态可表示为
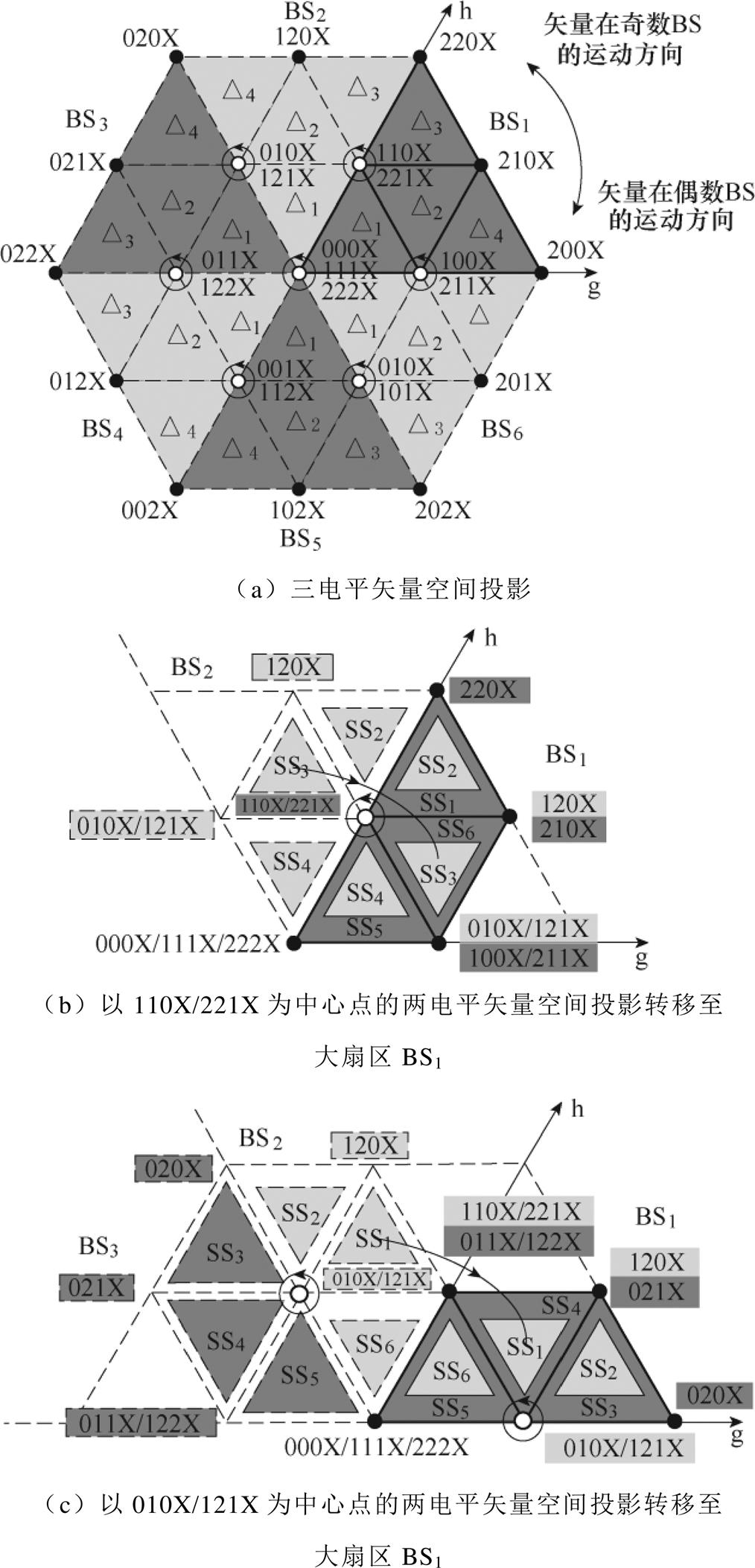
为使81种开关状态组成的矢量空间具有平面对称性,以及避免占空比计算过程中出现复杂的三角函数运算,运用式(2)将空间矢量转换到ghg 坐标系中,形成如图2所示的三维空间矢量。图2a为两电平矢量空间,图2b和图2c为三电平矢量空间。
式中,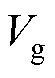 、
、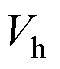 、
、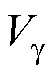 为参考电压矢量在ghg 坐标系上的投影值;
为参考电压矢量在ghg 坐标系上的投影值;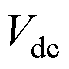 为直流电压;M为电平数量。
为直流电压;M为电平数量。
相较于两电平矢量空间,三电平矢量空间结构随着空间矢量个数的指数级增长而变得愈加复杂,四面体也从两电平的24个增加至192个,因此,有必要对矢量空间进行简化分析。
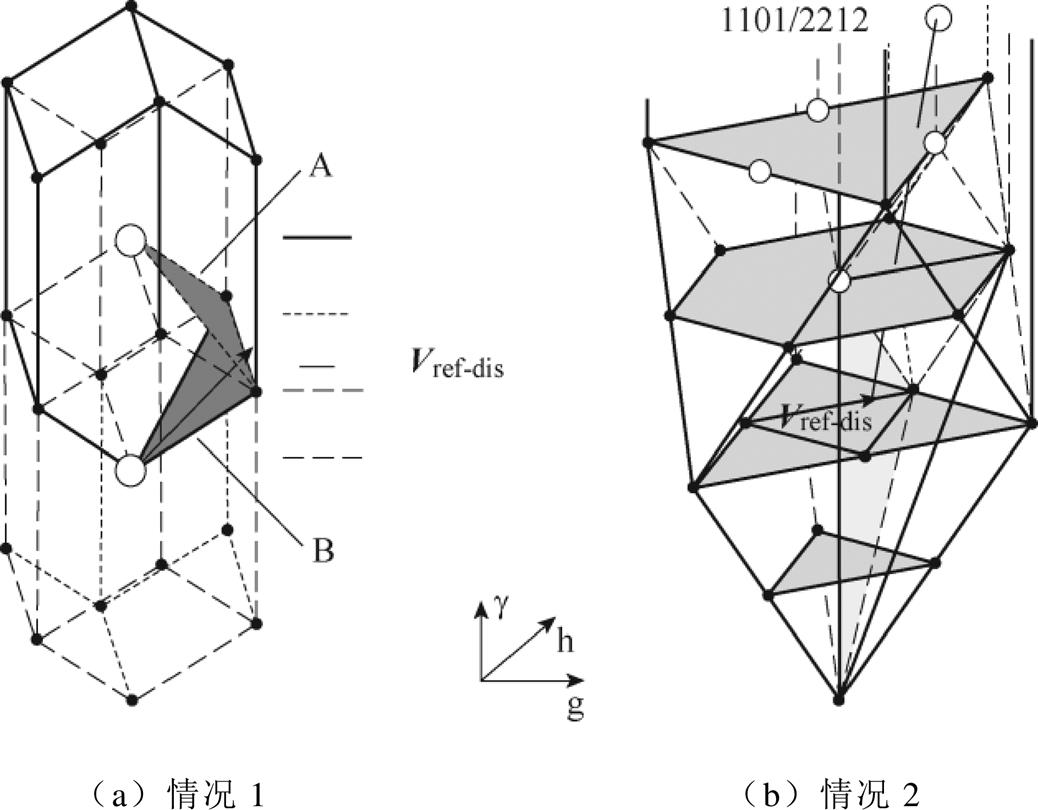
在ghg 坐标系下,两电平矢量空间及三电平矢量空间遵循如下规律:①两者在gh平面上均投影成M-1层六边形,且在g 轴上分布的层数均为6M-5层;②三电平矢量空间内部包含14个以冗余矢量为中心点的两电平矢量空间,表1给出了各冗余矢量包含的正负小矢量及其坐标,并在图2b与图2c中以白心点进行标注,同时上述两图中分别给出了以1100/2211、1101/2212,以及1110/2221、0001/1112为中心点的两电平矢量空间构建示意图。由中心点所构建的14个两电平矢量空间可完全填充原三电平矢量空间。
表1 冗余矢量及其坐标
Tab.1 Redundant vectors with coordinates

冗余矢量空间坐标正小矢量负小矢量 (1, 0, 1)21111000 (0, 1, 2)22111100 (-1, 1, 1)12110100 (-1, 0, 2)12210110 (-1, -1, 1)11210010 (1, -1, 2)21211010 (0, 0, 3)22211110 (1, 0, -2)21121001 (0, 1, -1)22121101 (-1, 1, -2)12120101 (-1, 0, -1)12220111 (-1, -1, -2)11220011 (1, -1, -1)21221011 (0, 0, -3)11120001
在实际应用中,由于参考电压矢量在矢量空间中的运动轨迹具有不确定性,需运用合适的方法判断参考电压矢量所在的四面体,并计算占空比及开关序列。基于三电平矢量空间可被分解的特性,只需判断参考电压矢量所在的两电平矢量空间,并移至其中,三电平调制过程可简化成两电平调制过程,减小了分析难度和计算量。
简化的3DSVPWM方法包含以下3个主要步骤:
(1)建立三电平矢量空间划分规则,并将参考电压矢量移至两电平矢量空间中。
(2)在两电平矢量空间第1小扇区中计算占空比和最优开关序列。
(3)调整冗余矢量占空比使直流侧中点电位平衡。
2 改进的两电平3DSVPWM方法
传统两电平四桥臂3DSVPWM过程中的主要工作是在矢量空间中确定相邻电压矢量并计算各矢量的占空比。三电平矢量空间分解出的各两电平矢量空间与传统两电平矢量空间在结构上具有一致性,可将两电平中的占空比计算方式运用于三电平中,但空间矢量需与三电平矢量空间中的相对应。为使参考电压矢量在各分解出的两电平矢量空间中的调制过程具有统一性,对传统两电平调制方法进行一般化处理,使其具备主动构建空间矢量和开关序列的能力。
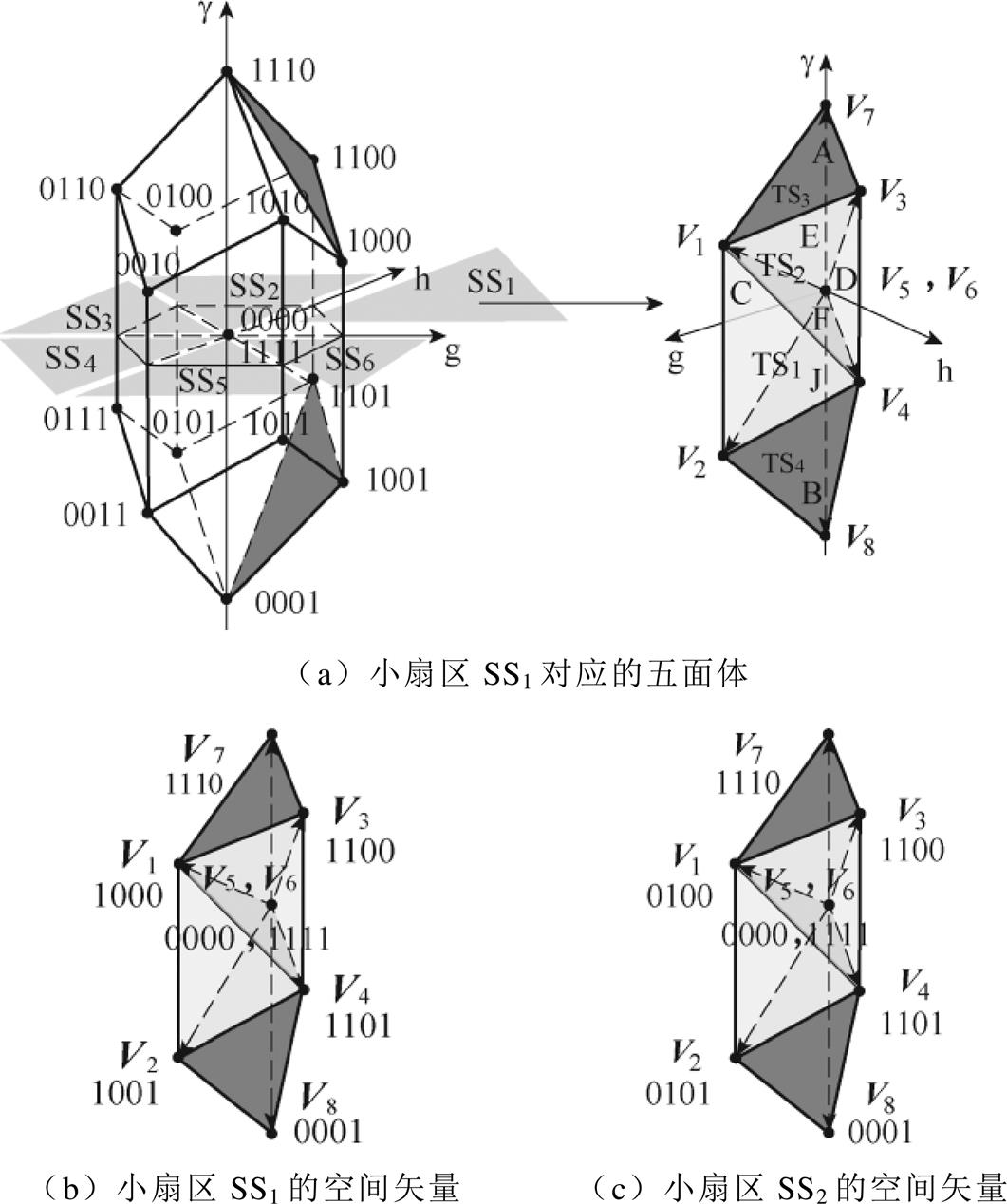
在两电平矢量空间中,将参考电压矢量从各小扇区(SS2~SS6)转移至第1小扇区(SS1),见表2。转移后各小扇区的空间矢量与小扇区SS1中原有空间矢量的位置相互重合,使得原矢量空间的十二面体简化为小扇区SS1的五面体,如图3a所示。该五面体中存在4个四面体(TS1, TS2, TS3, TS4)及8个基准矢量(V1, V2, V3, V4, V5, V6, V7, V8)。图3b与图3c中展示了小扇区SS1及小扇区SS2中基准矢量V1~V8对应的空间矢量分布情况。可见,简化后产生的五面体具备表达原两电平空间结构和空间矢量的能力。
区别于直接旋转至小扇区SS1,表2所示的转换方式可使得各小扇区中的四面体转移至小扇区SS1后与原小扇区SS1的四面体重合,且参考电压矢量在四面体中所处的相对位置不变,保证了转换后占空比计算的有效性及统一性。该坐标转换方式同样适用于三电平矢量空间,可保持空间的原有特征。
表2 转移至第1小扇区中的参考电压矢量投影值
Tab.2 Transfer to the projection value of the reference voltage vector in SS1
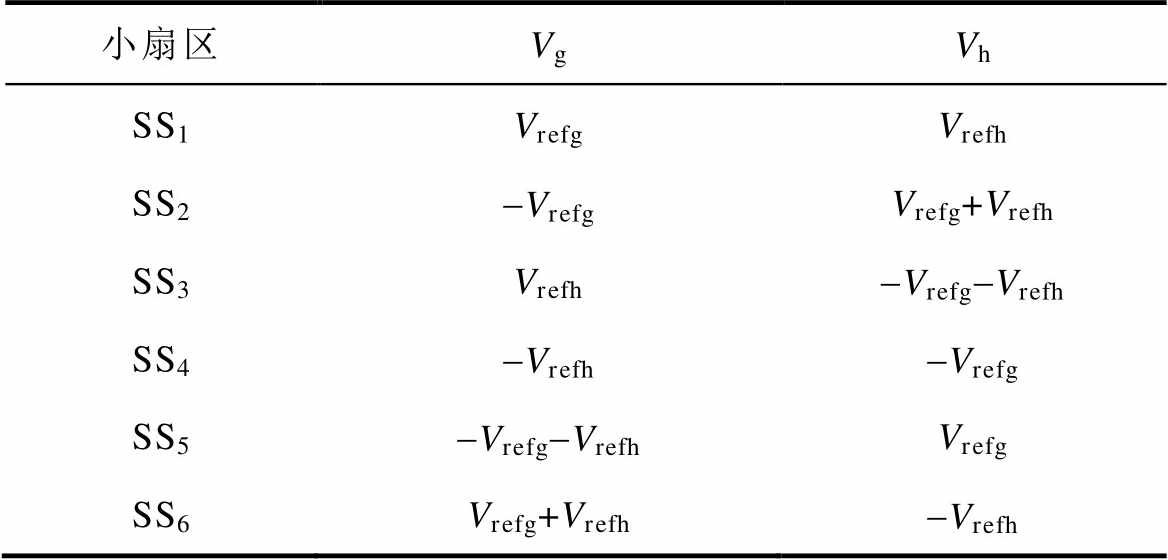
小扇区VgVh SS1VrefgVrefh SS2-VrefgVrefg+Vrefh SS3Vrefh-Vrefg-Vrefh SS4-Vrefh-Vrefg SS5-Vrefg-VrefhVrefg SS6Vrefg+Vrefh-Vrefh
注:Vrefg、Vrefh为参考电压矢量在gh平面上的投影值;Vg、Vh为矢量转移至SS1上的投影值。
由于参考电压矢量转移至小扇区SS1中,参与调制计算的四面体总数减少为4个,基准矢量作用顺序及占空比计算结果见表3和如式(3)所示。表3中,系数a=3/Tpwm,Tpwm为调制周期。以一个调制周期内开关损耗最小为目标,各相邻电压矢量仅有一个开关状态发生单位跳变,并采用9段式开关序列。表3中给出了第2~4个基准矢量的作用顺序,第1个与第5个矢量均为中心点矢量V5与V6。例如,当参考电压矢量在四面体TS1中时,基准矢量作用顺序为V5, V1, V2, V4, V6, V4, V2, V1, V5。与文献[22]中的传统调制方法相比,占空比系数矩阵及开关序列的判断过程经扇区转换得到了简化,且实现了无三角函数运算。
表3 第1小扇区的调制信息
Tab.3 Modulation information for SS1

四面体判断条件基准矢量占空比/a TS1F>0且J>0V1, V2, V4J, F, C TS2E>0且F<0V1, V3, V4D, -F, E TS3E<0V1, V3, V7D, C,-E TS4J<0V8, V2, V4-J, D, C
三电平矢量空间在ghg 坐标系下可分解出14个两电平矢量空间,分别由不同的空间矢量构成,现有的调制方法需进行重复的空间分解操作及复杂的开关状态查找工作以组成开关序列。由于各分解出的两电平空间矢量遵循传统两电平空间矢量的构建规则,可根据此规律计算相邻电压矢量并组成开关序列,避免了传统算法中繁杂的步骤。两电平空间矢量可根据中心点矢量V5(0000)、V6(1111)进行构建,空间矢量的构建见表4。若符合小扇区和基准矢量的要求,选取V6中对应相的开关状态;若不符,则对V5对应相的开关状态进行选取。
表4 空间矢量的构建
Tab.4 Construction of space vector
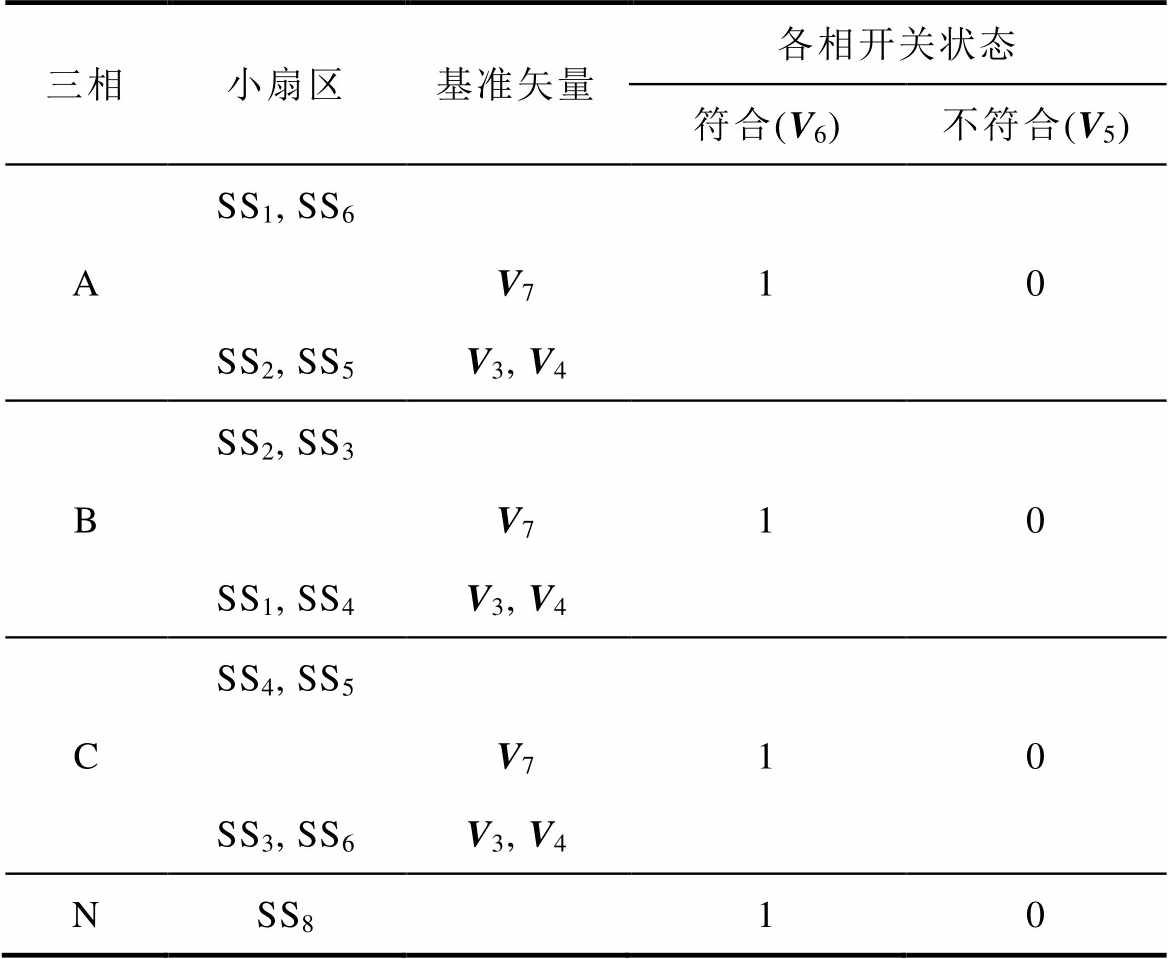
三相小扇区基准矢量各相开关状态 符合(V6)不符合(V5) ASS1, SS610 V7 SS2, SS5V3, V4 BSS2, SS310 V7 SS1, SS4V3, V4 CSS4, SS510 V7 SS3, SS6V3, V4 NSS810
以参考矢量在图3c小扇区SS2与四面体TS1中为例,需运用基准矢量V5, V1, V2, V4, V6进行合成。基准矢量V1可在V6的B相开关状态符合小扇区为SS2的条件时,将其B相开关状态选取为V6的B相开关状态“1”,A、C、D相开关状态均不符合小扇区和基准矢量的要求,选取V5对应相开关状态“0”,则构建的空间矢量(0100)与原空间矢量相符。该序列中V2和V4的开关状态(0100)和(1101)计算过程同理。
在三电平各分解出的两电平矢量空间中,中心点矢量为冗余矢量,两电平中的V5(0000) 被替换成负小矢量,V6(1111) 被替换成正小矢量。以图2b中两电平矢量空间中心点1101/2212为例,有V5(1101)和V6(2212),而开关序列中各空间矢量的构建方式则与上述两电平的相同。相较于传统固定的开关序列选取方式,该方法具有灵活的空间矢量构建能力,以及主动计算最优开关序列的能力,可应用至任意电平的四桥臂逆变器降维调制过程中。
3 基于空间分解三电平3DSVPWM方法
在三电平矢量空间中,参考电压矢量可分为水平与垂直两个维度进行分析。首先,分析参考电压矢量在gh平面上的投影规律,以及在g 轴上与冗余矢量之间的层数关系,选取空间位移中心点,并将参考电压矢量移至该中心点所表示的两电平矢量空间中。然后,计算中心点所包含的冗余矢量,并对位移参考电压矢量进行调制。最后,输出以负小矢量为首发矢量的最优开关序列,减少开关损耗和平衡直流侧中点电位。
3.1 矢量空间的分解及空间位移中心点的选取
首先,对三电平矢量空间在gh平面上的投影进行分析,投影平面如图4a所示。为简化调制过程,将参考电压矢量从第2~6大扇区(BS2~BS6)转移到第1大扇区(BS1)中,各大扇区转换关系与表2各小扇区转换关系相同。图4b与图4c以投影的方式展示了转换后各转移两电平小扇区与转移中心点之间的对应关系。由于小扇区是四面体的投影,从图中可知,转移后的小扇区与中心点的相接关系不变,即矢量空间中各中心点与四面体的相接关系不变,保持了矢量空间的原有特征。基于此对应关系,对大扇区BS1~BS6中的小扇区用三角形(△)进行标识,则参考电压矢量转移至大扇区BS1后的运动轨迹如图4a所示。
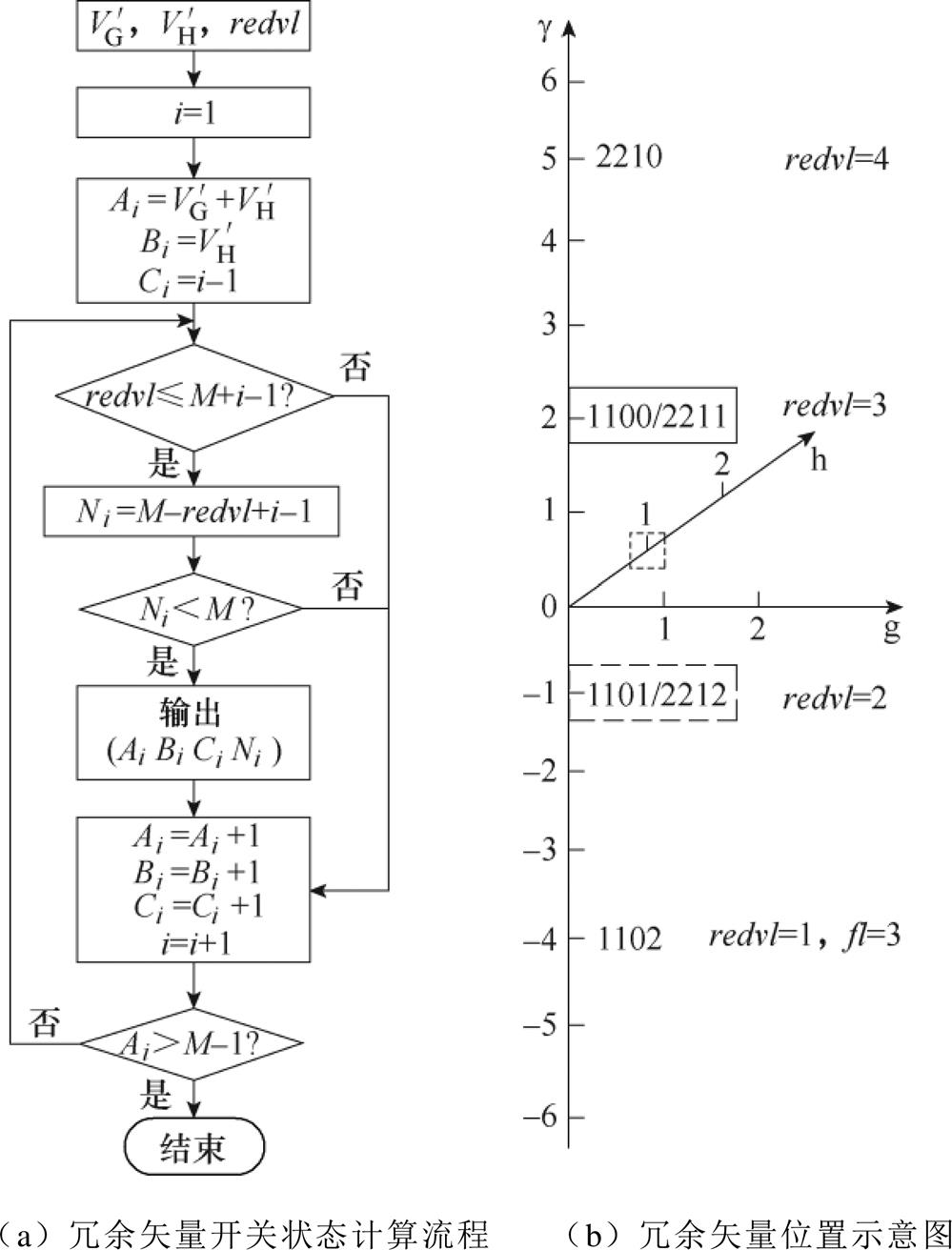
在大扇区BS1中,采用向下取整函数floor( )选取平面位移中心点,并将参考电压矢量投影移至该中心点。
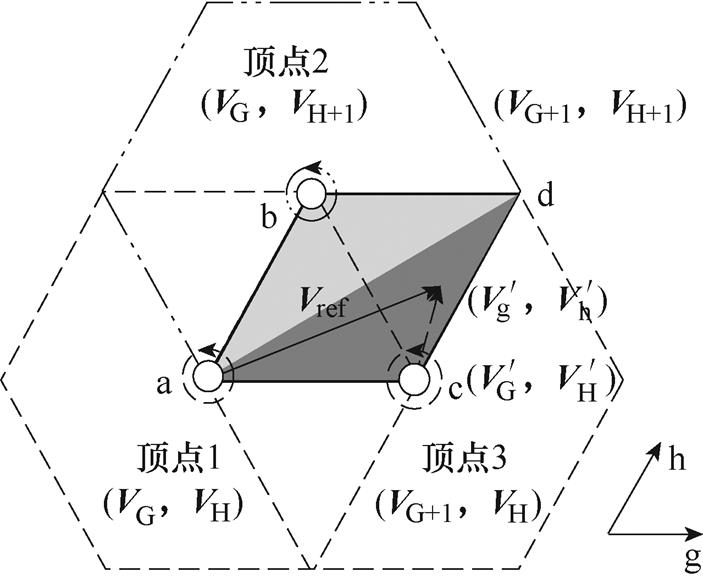
式中,VG、VH分别为g、h平面上矢量的投影坐标取整后的结果。当调制度较低时,经过取整后,中心点可能落在原点(000X/111X/222X)处,从而失去对中点电位的调节作用。为避免该情况,当参考电压矢量投影取整后位于矢量平面原点时,根据参考电压矢量位于三角形abd或三角形acd,平面位移中心点的选取如图5所示,将取整坐标相应往外移动一个单位作为平面位移中心点(顶点2/顶点3)。当取整后不是位于原点处,则直接以取整坐标作为平面位移中心点(顶点1)。将选定的平面位移中心点记为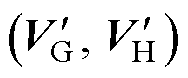 ,位移参考电压矢量记为
,位移参考电压矢量记为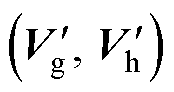 。
。
对电压矢量在g 轴上的分布规律进行分析。为对垂直分布的两电平矢量空间建立划分规则,以矢量空间中电压矢量所在层作为判断的基准,将与参考电压矢量距离最小的冗余矢量作为空间位移中心点,并将该中心点所表示的两电平矢量空间作为参考电压矢量选定的简化矢量空间。
参考电压矢量在矢量空间中的层数(reference vector’s layer, refvl)计算方式为
将冗余矢量相对于其所在纵向空间中首层(first layer, fl)矢量的层数定义为冗余矢量层(redundant vector’s layer, redvl),以图2b中心点1101/2212为例,相对于首层矢量1102,有redvl=2。则与参考电压矢量相近的冗余矢量层的计算方式为
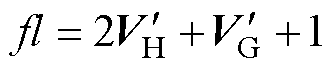 (6)
(6)
式中,abs( )为绝对值函数,当2≤redvl≤3时,参考电压矢量位于两组冗余矢量之间,通过式(8)与式(9)选取与之距离较小的冗余矢量作为空间位移中心点,并将该距离值作为参考电压矢量移至两电平矢量空间中的Vg 值,记为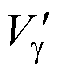 。当redvl<2或redvl>3时,上述选择方式可能会使空间位移中心点落在原矢量空间的表面,而冗余矢量全部位于矢量空间的内部。为使空间位移中心点包含冗余矢量,若redvl<2,取redvl=2,若redvl>3,取redvl=3,两者距离计算方式为
。当redvl<2或redvl>3时,上述选择方式可能会使空间位移中心点落在原矢量空间的表面,而冗余矢量全部位于矢量空间的内部。为使空间位移中心点包含冗余矢量,若redvl<2,取redvl=2,若redvl>3,取redvl=3,两者距离计算方式为
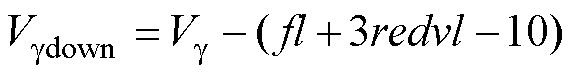 (9)
(9)
式中,Vgup为参考电压矢量与位于其之上的冗余矢量之间的距离;Vgdown为参考电压矢量与位于其之下的冗余矢量之间的距离。
以Vg 值不同的两个参考电压矢量为例,给出空间位移中心点及位移参考电压矢量的计算过程。当矢量Vref1=(0.1, 1.1, 0.2)时,通过向下取整的计算方法选取平面位移中心点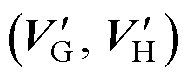 =(0, 1),矢量所在层refvl=7,对应的冗余矢量层redvl=2,即参考电压矢量位于两个两电平矢量空间之间,由Vγup=-1.8,Vγdown=1.2可知,参考电压矢量与位于其之下的冗余矢量组1100/2211更为接近,故有
=(0, 1),矢量所在层refvl=7,对应的冗余矢量层redvl=2,即参考电压矢量位于两个两电平矢量空间之间,由Vγup=-1.8,Vγdown=1.2可知,参考电压矢量与位于其之下的冗余矢量组1100/2211更为接近,故有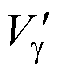 =1.2。因此,Vref1的位移参考电压矢量为
=1.2。因此,Vref1的位移参考电压矢量为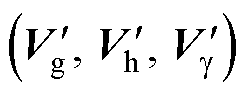 =(0.1, 0.1, 1.2),空间位移中心点为
=(0.1, 0.1, 1.2),空间位移中心点为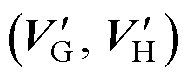 =(0, 1),redvl=2。当参考电压矢量为Vref2=(0.1, 1.1, -2.9) 时,平面位移中心点
=(0, 1),redvl=2。当参考电压矢量为Vref2=(0.1, 1.1, -2.9) 时,平面位移中心点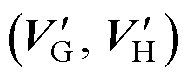 =(0, 1),矢量所在层refvl=4,对应的冗余矢量层redvl=1,由于选择的冗余矢量可能落于矢量空间的表面,取redvl=2,则
=(0, 1),矢量所在层refvl=4,对应的冗余矢量层redvl=1,由于选择的冗余矢量可能落于矢量空间的表面,取redvl=2,则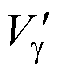 =Vγdown=-1.9。因此,Vref2的位移参考电压矢量
=Vγdown=-1.9。因此,Vref2的位移参考电压矢量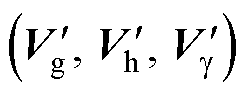 = (0.1, 0.1, -1.9),空间位移中心点
= (0.1, 0.1, -1.9),空间位移中心点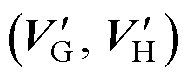 =(0, 1),redvl=2,与Vref1相同。
=(0, 1),redvl=2,与Vref1相同。
3.2 空间位移中心点的修正
由于两电平矢量空间为非规则六棱柱,会存在位移参考电压矢量(Vref-dis)过调制的问题。具体以两种方式呈现:其一,是当位移参考电压矢量位于上下两个两电平矢量空间之间时,会在中间夹层的微小空间处出现矢量超出上斜面或下斜面的情况,如图6a所示;其二,是当选取的两电平矢量空间为最靠下的一个时,会出现位移参考电压矢量超出下斜面的情况,如图6b所示。同理,当选取的两电平矢量空间为最靠上时,会出现位移参考电压矢量超出上斜面的情况。
两类过调制问题可归结为位移参考电压矢量超出了两电平矢量空间的上斜面或下斜面。为简化问题,将位移参考电压矢量转移至小扇区SS1,只需判断是否超出如图3a所示的A、B斜面即可。当出现过调制情况1时,做出上移或下移一个空间位移中心点的修正;当出现过调制情况2时,使用图5投影小扇区中所关联的其他中心点进行调制。根据分解出的两电平矢量空间的相互覆盖规律,若在最下方两电平矢量空间中出现下斜面超调的情况,按照顶点2-顶点3-顶点1的顺序进行修正,并取redvl=2,若在最上方两电平矢量空间中出现上斜面超调的情况,则按照顶点3-顶点2-顶点1的顺序进行修正,并取redvl=4-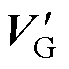 。
。
3.3 相邻电压矢量占空比及开关序列的计算方式
根据伏秒平衡原理以及矢量的可叠加性原理,位移参考电压矢量在两电平矢量空间中计算出的占空比就是参考电压矢量在原矢量空间中各相邻电压矢量的占空比。由于在解决过调制问题的过程中,已将位移参考电压矢量转移至小扇区SS1,故可直接运用第2节中所提的简化两电平3DSVPWM方法对位移参考电压矢量进行占空比计算。而开关序列中的相邻电压矢量是由中心点处冗余矢量的四桥臂开关状态组成的,其中前三桥臂和第四桥臂的开关状态分别与平面位移中心及其所在层相关联,计算流程如图7a所示。
以图2b矢量空间中的中心点1101/2212为例,其平面位移中心点坐标为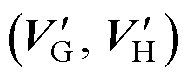 =(0, 1),冗余矢量层为redvl=2,在g 轴方向上的位置如图7b所示。通过图7a所示的方法可得,空间位移中心点包含的冗余矢量为1101/2212,与原空间矢量相符。以该冗余矢量为空间位移中心点,假设位移参考电压矢量在两电平矢量空间小扇区SS1与四面体TS1中,可对占空比计算原理进行具体描述为
=(0, 1),冗余矢量层为redvl=2,在g 轴方向上的位置如图7b所示。通过图7a所示的方法可得,空间位移中心点包含的冗余矢量为1101/2212,与原空间矢量相符。以该冗余矢量为空间位移中心点,假设位移参考电压矢量在两电平矢量空间小扇区SS1与四面体TS1中,可对占空比计算原理进行具体描述为
式中,Vref为参考电压矢量;Vdref为位移参考电压矢量;Voref为空间位移中心点矢量,V5(1101) 和V6(2212) 为Voref包含的一组冗余矢量。
3.4 中点电位平衡调节策略
根据基尔霍夫电流定律,各电容上的电流随着直流侧中点电流的变化而变化,因而导致了电容电荷量发生波动,致使中点电位不平衡。以各电容电荷量误差之和最小为调节目标,对冗余矢量占空比进行调整,使中点电位保持相对稳定。
直流侧电容电荷量主要由三部分组成:①上一调制周期留下的固有电荷量差值Qerr;②这一调制周期新开关序列对电容电荷量的初始补充值Qs; ③调节新开关序列中小矢量的占空比对电容所产生的电荷调节量Qterr。电容电荷量实时误差值DQC为Qerr与Qs之和,调整目标为
中点支路电流iox计算公式如式(12)所示。文献[19]已给出各大扇区中4个桥臂对中点电流贡献的对应关系,即
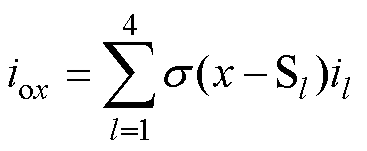 (12)
(12)
式中,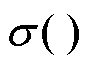 函数为冲击函数;x为中点支路序号,x=1, 2,…, M-2;l为桥臂数,l=1, 2, 3, 4;Sl为各桥臂的工作状态,Sl=0, 1,…, M-1。三电平逆变器对应M=3,下述同理。
函数为冲击函数;x为中点支路序号,x=1, 2,…, M-2;l为桥臂数,l=1, 2, 3, 4;Sl为各桥臂的工作状态,Sl=0, 1,…, M-1。三电平逆变器对应M=3,下述同理。
在一个调制周期内,新开关序列在各电容上电荷量的初始补充值的计算方法为
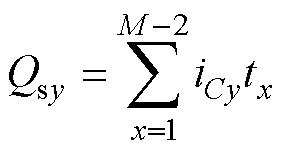 (14)
(14)
式中,y为直流侧电容序号,y=1, 2,…, M-1;iCy为第y个电容电流;Qsy为第y个电容的初始新增电荷量;tx为电流iCy流经电容Cy的时长,可通过开关序列的占空比得出。
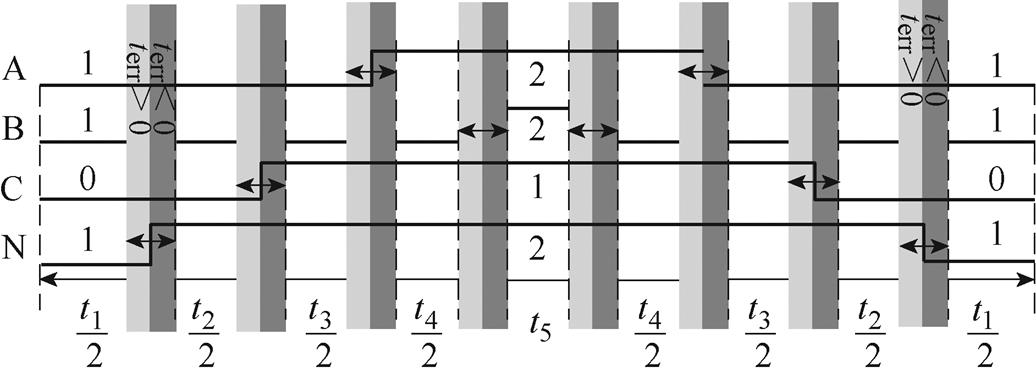
根据调整目标,有如式(15)所示的冗余矢量占空比调节方式。当中心点为1101/2212时,占空比调节量为terr,调整示意图如图8所示。
4 拓展
本文所提的三电平3DSVPWM方法可拓展为M(M≥3)电平3DSVPWM方法。由于M电平矢量空间内部两电平矢量空间的分布特征与三电平的完全一致,故可运用前述方法对M电平矢量空间进行分解,并结合改进的两电平3DSVPWM方法对参考电压矢量进行调制。
(1)计算平面位移中心点及平面位移矢量。运用表1将参考电压矢量转移至大扇区BS1中。为保持参考电压矢量在多电平矢量空间中的平面位移中心点与三电平的选取方式相同,结合式(4)与式(16)判断矢量投影所在的平面六边形层数。
当slayer≠M-1时,根据参考电压矢量位于图5中的三角形abd或三角形acd区域,将取整坐标相应往外移动一个单位;当slayer=M-1时,参考电压矢量投影位于最外两层六边形之间,取整后的gh坐标即为平面位移中心点。将平面位移矢量记为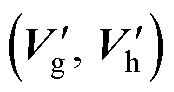 ,平面位移中心点记为
,平面位移中心点记为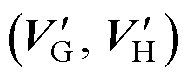 。
。
(2)计算空间位移中心点及g 轴方向上的位移量。中心点与参考电压矢量所在层及与之相近的冗余矢量层有关,式(17)对式(6)参考电压矢量所在层的计算做了一般化处理,冗余矢量层的计算方式为
当redvl≥2且redvl≤2M-2-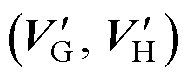 时,参考电压矢量位于两组冗余矢量之间,选取与之距离较小的冗余矢量作为空间位移中心点,如式(18)、式(19)所示,并将较小值记为
时,参考电压矢量位于两组冗余矢量之间,选取与之距离较小的冗余矢量作为空间位移中心点,如式(18)、式(19)所示,并将较小值记为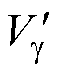 。为使空间中心点包含冗余矢量,若redvl<2,取redvl=2,若redvl>2M-2-
。为使空间中心点包含冗余矢量,若redvl<2,取redvl=2,若redvl>2M-2-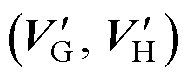 ,取redvl=2M-2-
,取redvl=2M-2-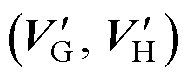 ,两者距离计算方式均如式(19)所示。将空间位移矢量记为
,两者距离计算方式均如式(19)所示。将空间位移矢量记为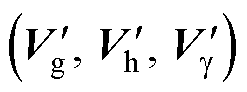 ,空间位移中心点记为
,空间位移中心点记为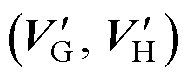 。
。
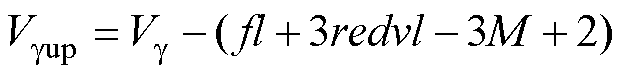 (18)
(18)
(3)修正空间位移中心点。当位移参考电压矢量出现过调制情况1时,做出上移或下移一个中心点的修正。当出现过调制情况2时,中心点修正顺序与三电平的相同,若在最下方两电平空间出现下斜面超调的状况时,取redvl=2;若在最上方两电平空间出现上斜面超调的状况时,则取redvl= 2M-2-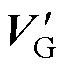 。
。
(4)计算占空比及选取最佳开关序列。对于M电平矢量空间,运用图7a可计算出多组冗余矢量。为使各中点电位平衡效果达到最优,先运用一般化的两电平3DSVPWM对各序列进行占空比计算,然后通过式(12)~式(14)计算当各序列作用时,各电容上电荷量实时误差值,并结合式(20)选取最佳开关序列。
式中,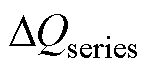 为一个开关序列所造成的电容电荷量实时误差值之和。通过求取电容电荷量误差之和最小项,即min(
为一个开关序列所造成的电容电荷量实时误差值之和。通过求取电容电荷量误差之和最小项,即min(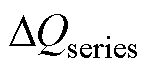 ),可选取最佳开关序列。
),可选取最佳开关序列。
(5)平衡中点电位。采用三电平中点电位平衡方式对冗余矢量的占空比进行调整,使得各电容上的电荷量保持在同一水平上。
将上述调制方式运用到四电平四桥臂逆变器中。传统调制算法需对矢量空间中612个四面体涉及的占空比系数矩阵及开关序列进行具体分析,而运用本文所提计算方式只需改变M即可,避免了空间分解并减小了调制过程的计算量。将逆变器参数设置如下,电平数M=4,直流侧电压Vdc=700 V,给定三相对称电压,设置调制比m=0.9,四电平四桥臂逆变器输出线电压如图9所示。
5 仿真与实验
为验证本文提出的三电平四桥臂逆变器3DSVPWM策略的正确性和有效性,搭建了基于Matlab/Simulink软件的仿真模型进行仿真验证,并通过dSPACE-SCALEXIO进行半实物仿真实验。仿真和实验参数见表5。
表5 仿真和实验参数
Tab.5 Parameters for simulation and experiment
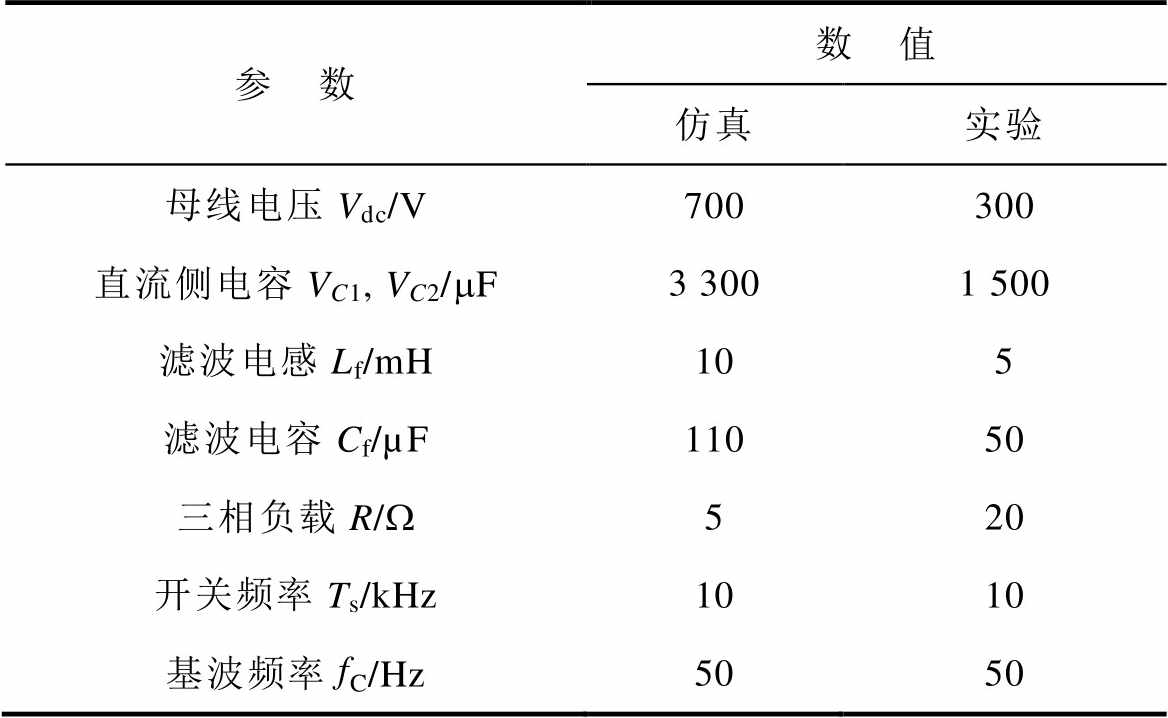
参 数数 值 仿真实验 母线电压Vdc/V700300 直流侧电容VC1, VC2/mF3 3001 500 滤波电感Lf/mH105 滤波电容Cf/µF11050 三相负载R/W520 开关频率Ts/kHz1010 基波频率fC/Hz5050
5.1 仿真证明
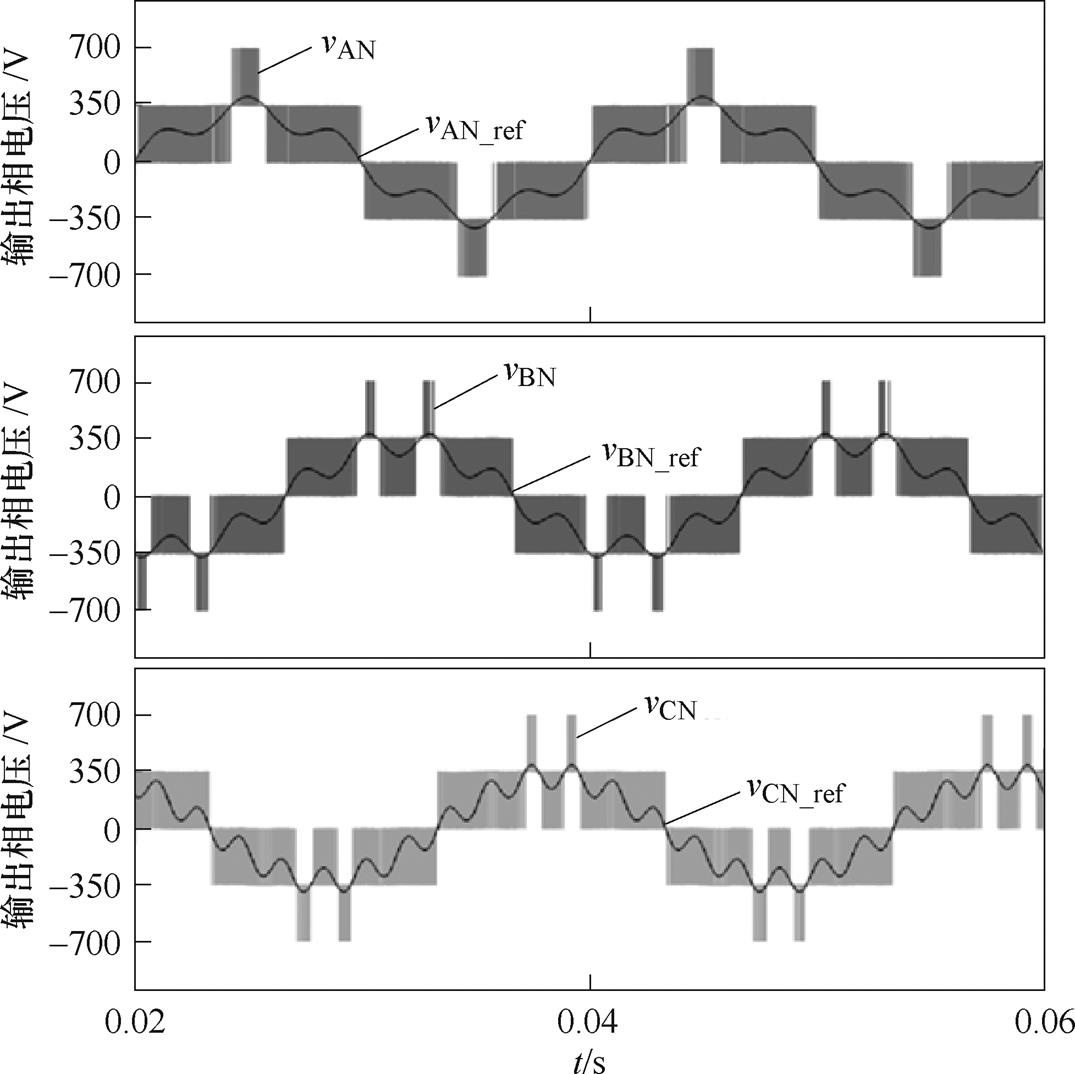
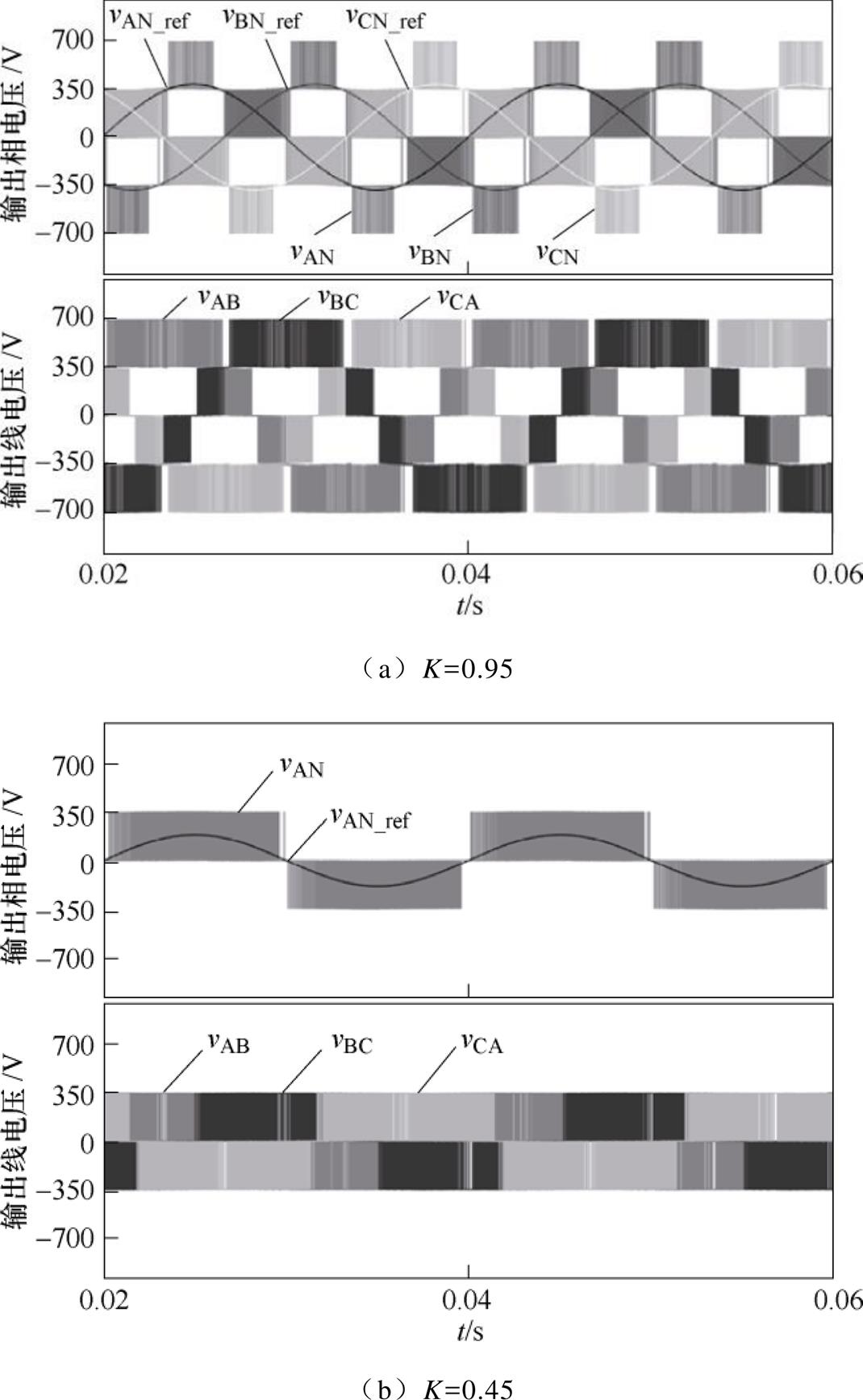
验证本文所提调制方法在逆变器给定三相电压平衡的状况下输出电压的正确性,分别在调制比较大及较小的情况下给定三相对称电压,参考电压表达式如式(21)所示,取K=0.95, 0.45。图10a与图10b分别为K=0.95与K=0.45时,三电平四桥臂逆变器输出的相电压与线电压。其中,图10b中的输出相电压为A相参考电压与输出电压的对应关系。
由图10可知,当相电压与线电压幅值大于Vdc/2时,输出电平的数量为5个,而电平数量的增加使得输出波形更接近正弦波,可减小滤波器的大小。
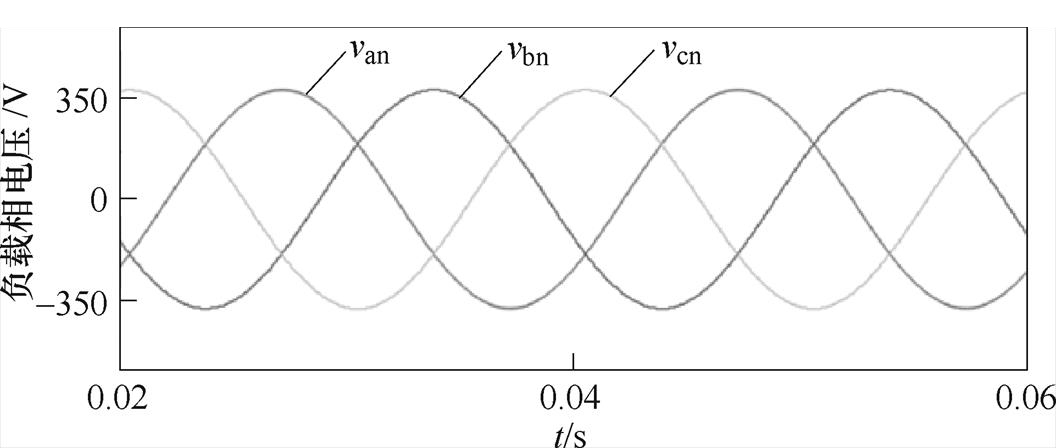
当K=0.95时,逆变器给三相对称电阻性负载供电,负载的相电压仿真波形如图11所示。
由图11可知,负载各相电压的正弦度较高,其中A相电压畸变率为0.25%,各相周期均为20 ms,相位差为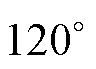 。
。
验证给定三相参考电压不平衡的状况下逆变器输出电压的正确性。改变式(21)中的三相正弦电压幅值并注入高次谐波,三相参考电压如式(22)所示,输出相电压仿真波形如图12所示。
当参考电压不平衡时,所提调制方法通过计算占空比及开关序列,进而得到各桥臂开关器件的触发信号,由图12可知,逆变器能较好地跟踪参考电压。
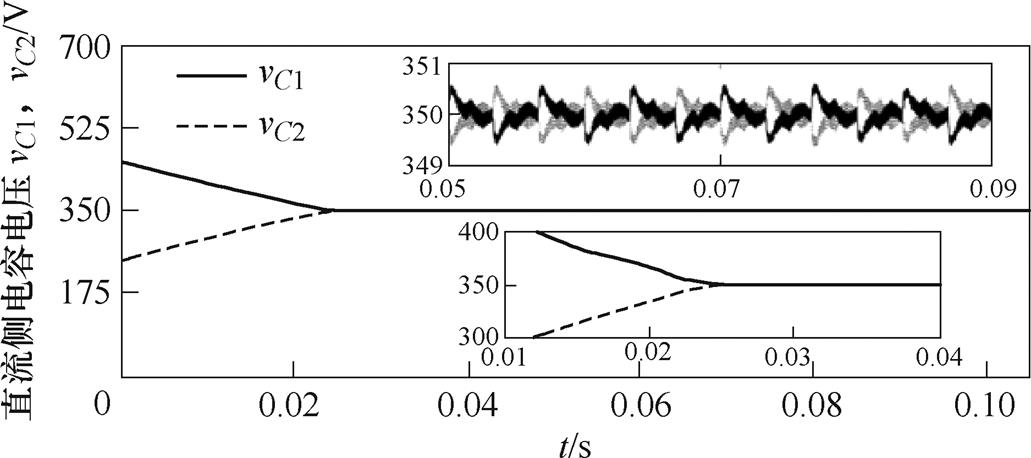
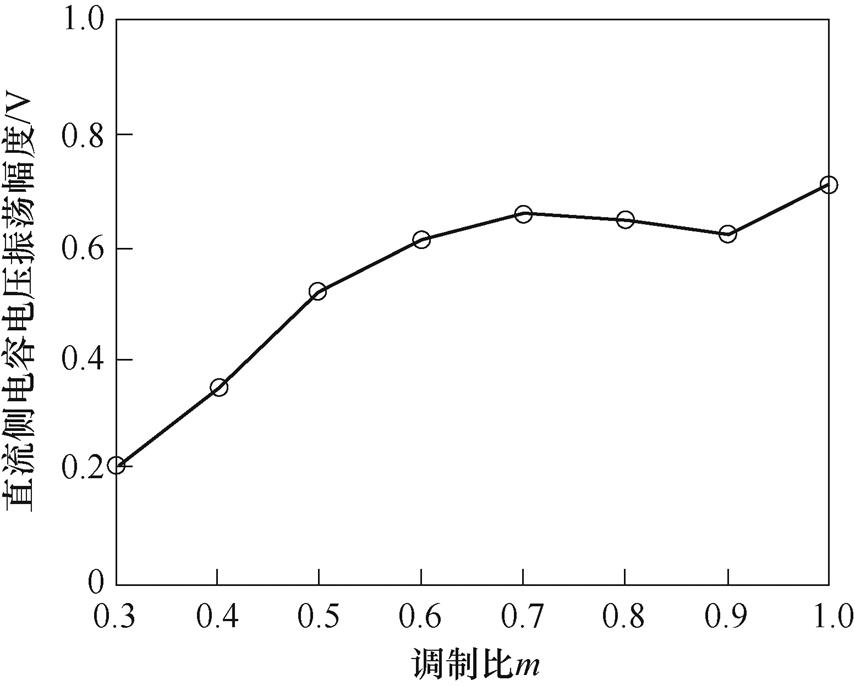
验证中点电位平衡算法的有效性。在调制比为m=0.9的情况下,给定直流侧电容C1的初始电压250 V,C2的初始电压为450 V,两电容电压仿真波形如图13所示。经过0.025 s,中点电位达到相对平衡的状态,并且伴有3倍于基频的振荡,振荡幅度为0.63 V。图14给出各调制比下中点电位振荡幅度,当调制比小于等于1时,所提调制方法可较好地抑制中点电位振荡,振荡幅度小于1 V。
5.2 实验验证
为进一步验证所提调制方法的正确性,本文基于dSPACE平台对三电平四桥臂逆变器进行了半实物仿真实验,通过采集直流侧电容电压以及四桥臂输出电感电流实时分析出各调制周期内冗余矢量占空比的调整量,对直流侧中点电位进行控制。实验参数见表5。实验平台如图15所示。
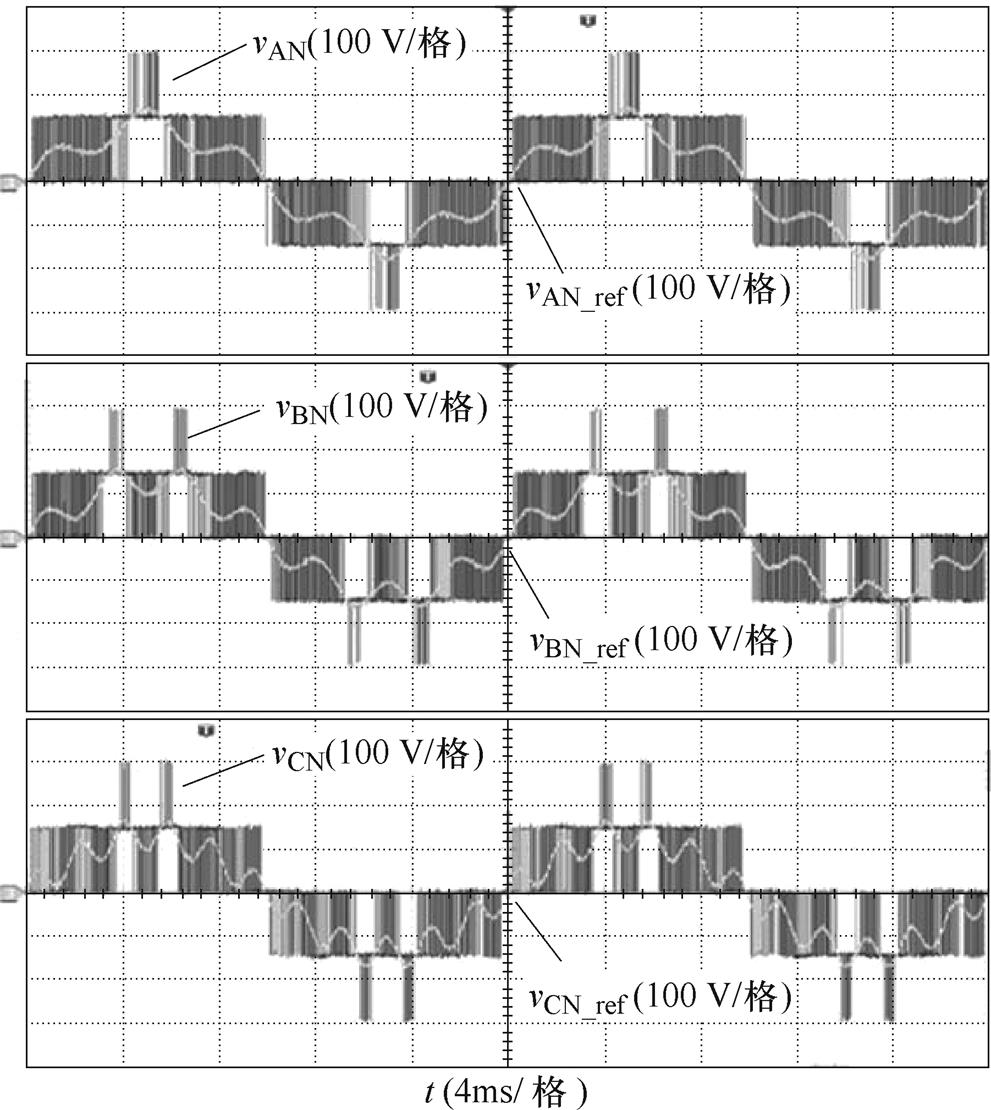
图16a和图16b分别为给定三相参考电压平衡的状态下,三电平四桥臂逆变器在K=0.95, 0.45时输出相电压和线电压的实验波形。负载相电压的波形如图16c所示,各相电压正弦度较高。在参数取值一致的条件下,实验与仿真对应的调制比是相同的,实验和仿真波形基本一致。
图17为参考电压不平衡时,四桥臂逆变器输出的相电压波形。由图可知,所提调制算法能快速跟踪参考电压,满足电压波形可能大幅畸变的实际工况。在相同调制比的前提下,实验和仿真波形基本一致。
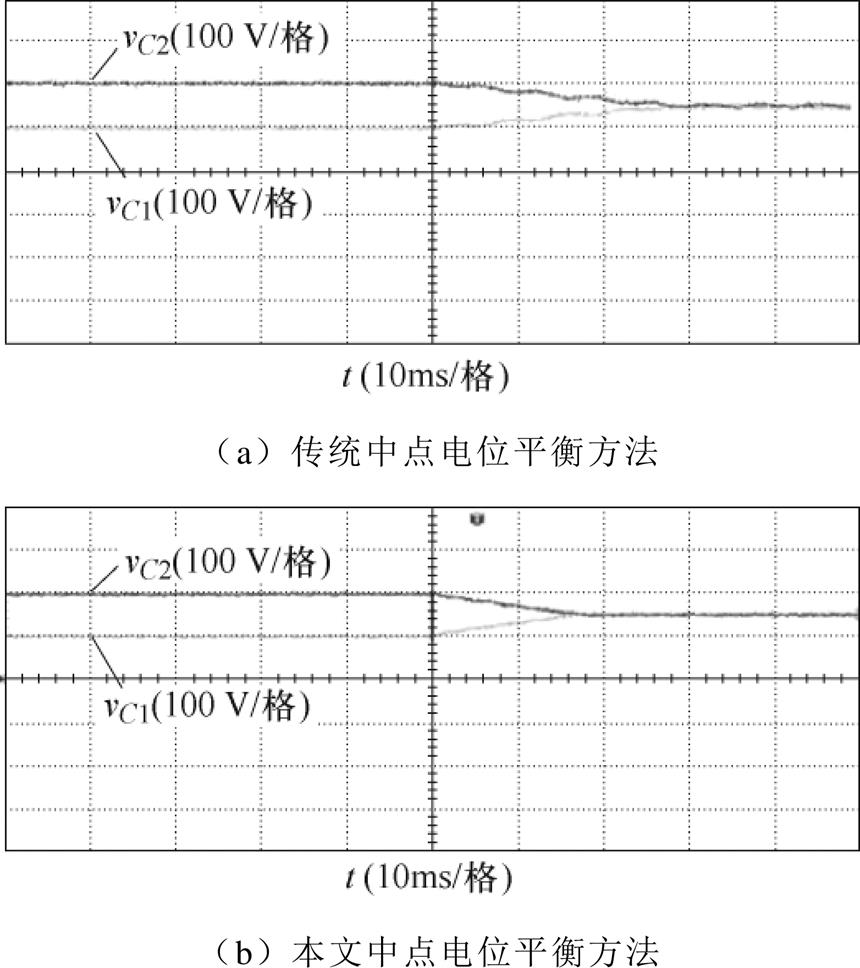
为了验证本文所提简化3DSVPWM方法对直流侧电容电压的平衡能力,当调制比m=0.9时,将直流侧电容C1的初始电压设为100 V,电容C2的初始电压设为200 V,基于传统方法[21]下的直流侧电容电压波形如图18a所示,采用本文所提方法下的直流侧电容电压波形如图18b所示。由图可知,采用本文所提的控制方法能使得直流侧电容电压较快的实现平衡,优于传统控制方法。另外,采用传统控制方法直流侧电容电压存在波动较大的问题,如图18b所示,电容电压呈现3倍于基频的振荡且幅度较大,而本文所提方法通过对电容电荷量进行精确计算,有效抑制电容电压波动,两电容的电压相较于传统方法一致性更强。
表6将各种三电平四桥臂逆变器调制方案进行了比较和归纳,本文所提调制算法具有占空比计算简单、自动识别冗余矢量及计算开关序列的优点,简化了三电平3DSVPWM方法的实现过程。同时,本文对电容电荷量的组成部分进行了详细分析,具备精确补偿的特点,有效抑制了电容电压波动和保持电容电压水平相对一致。需要指出,由于本文所提调制方法具有可拓展性,随着电平数的增加,矢量空间简化过程计算量保持不变,并可运用一般化的两电平3DSVPWM计算出占空比。由于支持自动计算开关序列,有效避免了由于四面体指数级增长带来占空比系数矩阵及开关序列存储量飞跃式增长的不足,同时大幅减少了多电平调制过程中的计 算量。
表6 各种三电平四桥臂逆变器调制方案对比
Tab.6 Comparison of different modulation schemes of three-level four-leg inverter
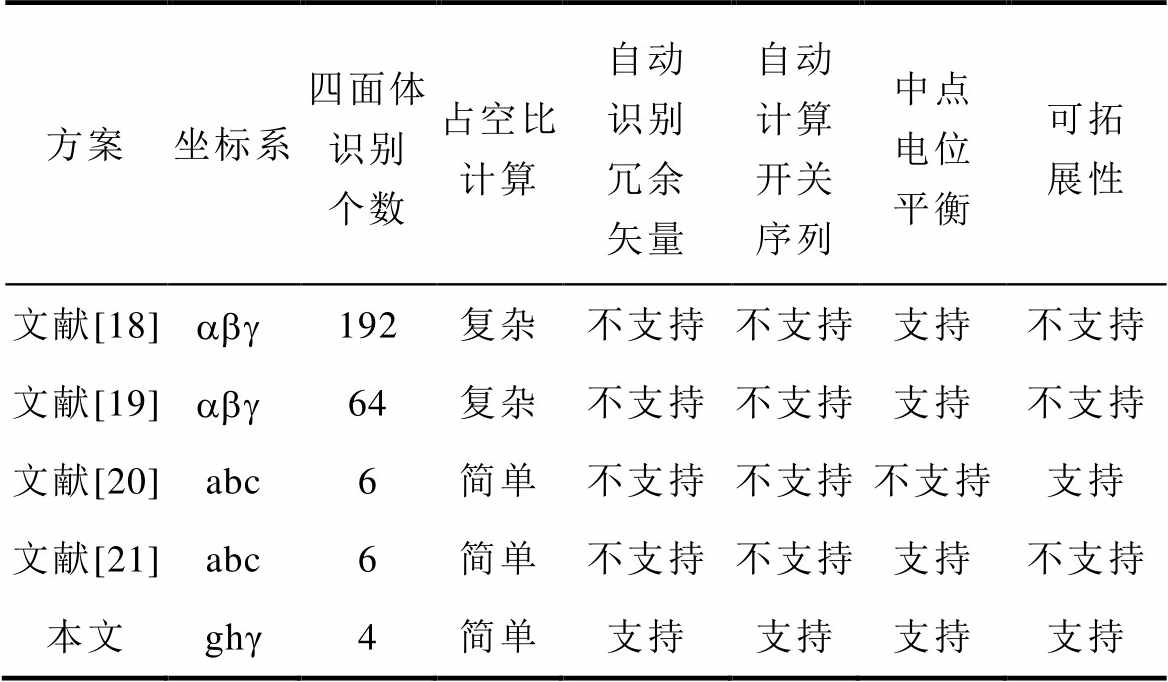
方案坐标系四面体识别个数占空比计算自动识别冗余矢量自动计算开关序列中点电位平衡可拓展性 文献[18]abg 192复杂不支持不支持支持不支持 文献[19]abg 64复杂不支持不支持支持不支持 文献[20]abc6简单不支持不支持不支持支持 文献[21]abc6简单不支持不支持支持不支持 本文ghγ4简单支持支持支持支持
6 结论
本文针对传统三电平四桥臂空间矢量调制方法存在空间结构复杂、占空比计算过程中包含较多三角函数和开关序列运算过程中需要较多存储空间等不足,提出了一种基于ghγ坐标系的简化空间矢量脉宽调制方法。该方法充分发挥坐标系优势,将三电平矢量空间分解为若干两电平矢量空间,并通过矢量位移的方式简化了调制过程,可自动产生包含冗余矢量的最优开关序列,保证直流侧两电容的中点电位平衡。仿真及实验验证了所提调制方式的正确性。此外,由于对两电平3DSVPWM方法进行了一般化处理的改进,该调制方式可拓展至更高电平,且计算量不会大幅增加。
参考文献
[1] 游建章, 郭谋发. 含四桥臂H桥变流器的不对称配电网综合补偿方法[J]. 电工技术学报, 2022, 37(11): 2849-2858.
You Jianzhang, Guo Moufa. Comprehensive com- pensation method for asymmetric distribution network with four-arm H-bridge converter[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2849- 2858.
[2] 陈轶涵, 郭鸿浩, 陈杰, 等. 中频三相四桥臂逆变器控制策略不平衡负载状态相量模型分析[J]. 电工技术学报, 2019, 34(9): 1912-1923.
Chen Yihan, Guo Honghao, Chen Jie, et al. Analysis on control strategies for unsymmetrical state of medium frequency three phase four leg inverter based on vector model[J]. Transactions of China Electro- technical Society, 2019, 34(9): 1912-1923.
[3] 付永升, 李静, 胡文婷, 等. 不平衡负载下车载三相四线双向充电器中线桥臂控制与软启动设计[J]. 电工技术学报, 2019, 34(24): 5176-5188.
Fu Yongsheng, Li Jing, Hu Wenting, et al. Neutral leg control and soft-start design of 3-phase 4-wire on-board bidirectional charger under imbalance load condition[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5176-5188.
[4] 徐永海, 张蒙蒙, 杨依睿, 等. 不平衡负载下四桥臂逆变器双重准比例复数积分控制策略[J]. 电力系统保护与控制, 2020, 48(7): 141-150.
Xu Yonghai, Zhang Mengmeng, Yang Yirui, et al. Dual quasi-proportional complex integral control strategy of the four-leg inverter with unbalanced load[J]. Power System Protection and Control, 2020, 48(7): 141-150.
[5] 周娟, 秦静, 王子绩, 等. 内置重复控制器无差拍控制在有源滤波器中的应用[J]. 电工技术学报, 2013, 28(2): 233-238.
Zhou Juan, Qin Jing, Wang Ziji, et al. Application of deadbeat control with plug-in repetitive controller in active power filter[J]. Transactions of China Electro- technical Society, 2013, 28(2): 233-238.
[6] 李勇, 刘宏, 刘乾易, 等. 四桥臂SVG改进电流检测方法及控制策略[J]. 电力系统及其自动化学报, 2019, 31(4): 123-131.
Li Yong, Liu Hong, Liu Qianyi, et al. Improved current detection method and control strategy for four-leg SVG[J]. Proceedings of the CSU-EPSA, 2019, 31(4): 123-131.
[7] 谭翠兰, 邢彦一, 陈启宏, 等. 三相四桥臂并网逆变器重复控制积分抗饱和策略[J]. 电工技术学报, 2019, 34(17): 3631-3639.
Tan Cuilan, Xing Yanyi, Chen Qihong, et al. Anti- windup strategy of repetitive controller for three- phase four-leg grid-tied inverter[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3631- 3639.
[8] 倪梦涵, 杨晓峰, 王淼, 等. 多电平均压型直流变换器输入电流纹波抑制策略[J]. 电工技术学报, 2021, 36(16): 3354-3364.
Ni Menghan, Yang Xiaofeng, Wang Miao, et al. Input current ripple suppression strategy of multilevel voltage-balancing DC-DC converter[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3354-3364.
[9] 王要强, 张亨泰, 赖锦木, 等. 低应力高电平开关电容逆变器及其调制策略[J]. 电工技术学报, 2021, 36(20): 4237-4248.
Wang Yaoqiang, Zhang Hengtai, Lai Jinmu, et al. Topology and modulation strategy for switched capacitor inverter with low voltage stress and high level[J]. Transactions of China Electrotechnical Society, 2021, 36(20): 4237-4248.
[10] 茆美琴, 程德健, 袁敏, 等. 基于暂态能量流的模块化多电平高压直流电网接地优化配置[J]. 电工技术学报, 2022, 37(3): 739-749.
Mao Meiqin, Cheng Dejian, Yuan Min, et al. Optimal allocation of grounding system in high voltage direct current grid with modular multi-level converters based on transient energy flow[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 739- 749.
[11] Chee S J, Kim H S, Sul S K, et al. Common-mode voltage reduction of three-level four-leg PWM con- verter[J]. IEEE Transactions on Industry Applications, 2015, 51(5): 4006-4016.
[12] 王宝诚, 郭小强, 杨勇, 等. 三电平四桥臂光伏逆变器漏电流抑制研究[J]. 中国电机工程学报, 2018, 38(14): 4194-4201, 4325.
Wang Baocheng, Guo Xiaoqiang, Yang Yong, et al. Research on leakage current suppression for three- level four-leg PV inverter[J]. Proceedings of the CSEE, 2018, 38(14): 4194-4201, 4325.
[13] 江畅, 程启明, 马信乔, 等. 不平衡电网电压下基于模块化多电平变流器的统一电能质量调节器的微分平坦控制[J]. 电工技术学报, 2021, 36(16): 3410-3421.
Jiang Chang, Cheng Qiming, Ma Xinqiao, et al. Differential flat control for unified power quality controller based on modular multilevel converter under unbalanced grid voltage[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3410- 3421.
[14] Tabart Q, Vechiu I, Etxeberria A, et al. Hybrid energy storage system microgrids integration for power quality improvement using four-leg three-level NPC inverter and second-order sliding mode control[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 424-435.
[15] Tsai M J, Chen H C, Cheng Potai. Eliminating the neutral-point oscillation of the four-wire NPC active power filter[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(7): 6233-6240.
[16] Golwala H, Chudamani R. New three-dimensional space vector-based switching signal generation technique without null vectors and with reduced switching losses for a grid-connected four-leg inverter[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1026-1035.
[17] Roh C, Kwak S, Choi S. Three-phase three-level four-leg NPC converters with advanced model predictive control[J]. Journal of Power Electronics, 2021, 21(10): 1574-1584.
[18] Rojas F, Kennel R, Cardenas R, et al. A new space-vector-modulation algorithm for a three-level four-leg NPC inverter[J]. IEEE Transactions on Energy Conversion, 2017, 32(1): 23-35.
[19] Bouzidi M, Benaissa A, Barkat S. Hybrid direct power/current control using feedback linearization of three-level four-leg voltage source shunt active power filter[J]. International Journal of Electrical Power & Energy Systems, 2014, 61: 629-646.
[20] Franquelo L G, Prats M A M, Portillo R C, et al. Three-dimensional space-vector modulation algorithm for four-leg multilevel converters using abc coor- dinates[J]. IEEE Transactions on Industrial Elec- tronics, 2006, 53(2): 458-466.
[21] Rojas F, Cárdenas R, Kennel R, et al. A simplified space-vector modulation algorithm for four-leg NPC converters[J]. IEEE Transactions on Power Elec- tronics, 2017, 32(11): 8371-8380.
[22] 杨智彭, 何晋伟, 王成山. 面向独立供电系统的四桥臂电流源变流器3D-SVPWM方法[J]. 电力系统自动化, 2020, 44(16): 145-153.
Yang Zhipeng, He Jinwei, Wang Chengshan. Three- dimensional space vector pulse width modulation method of four-leg current-source converter for independent power supply system[J]. Automation of Electric Power Systems, 2020, 44(16): 145-153.
A Simplified Space Vector Pulse Width Modulation Method Based on ghg Coordinates System for the Three-Level Four-Leg Inverter
Zhang Zhi1,2 Chen Haohui1,2 Chen Sizhe2 Zhang Zhaoyun1 Li Yiyun1
(1. School of Electrical Engineering and Intelligence Dongguan University of Technology Dongguan 523808 China 2. School of Automation Guangdong University of Technology Guangzhou 510006 China)
Abstract The topology of the three-level, four-leg neutral-point-clamped (3L4L-NPC) inverter is more complex than the traditional two-level and three-leg ones, which complicates the vector space (VS) and space vector pulse width modulation (SVPMW) algorithm. Traditional methods designate a subspace under the abg and abc coordinates system to simplify the VS. However, the disadvantages of excess tetrahedrons in the subspace, manually finding for redundant vectors, lots of storage space for switching sequences and poor scalability remain unsolved. This paper proposes a simplified SVPWM method based on the ghg coordinates system. By decomposing the three-level VS into several two-level ones and designating the first small sectors as subspaces, combining the exact charge adjusting method for capacitance voltage on DC-side, duty cycles and switching sequences of the 3L4L-NPC inverter can be automatically calculated.
Firstly, the decomposability of the three-level VS is discussed. Since it has the same characteristics in both horizontal and vertical dimensions as the two-level one, the three-level VS can be replaced by the two-level ones with redundant vectors as center points. Secondly, the two-level SVPWM method is simplified. Duty cycles and switching sequences can be calculated automatically through integer computation and space vector construction in the first small sector, which can be extended to the decomposed two-level VSs. Thirdly, rules for dividing the three-level VS are established. The selected two-level VS and its redundant vectors are calculated using the hexagonal layer where the reference voltage vector locates on gh plane and g axis. Combining the improved two-level SVPWM method, tetrahedrons containing modulation information can be found without global searching. Finally, the charge that causes fluctuations in the capacitance voltage on the DC side is classified into three types: the charge difference left over from the previous modulation cycle, the initial supplementary charge in this cycle, and the adjustment charge provided by small vectors in this cycle. Charge error is caused by the first two types. The stability of capacitor voltages can be maintained by a linear calculation that makes the sum of the third type and the charge error zero. In addition, the above three-level modulation process is extended to make it applicable to multi-level inverters.
Simulation of the algorithm was first performed on Matlab/Simulink platform. When the three-phase balanced reference voltage was set at different modulation ratios, the output voltage was three and five levels at smaller and larger modulation ratios, respectively, and the latter was closer to a sinusoidal waveform. Then, harmonics were injected into the reference voltage, which generated non-saddle modulation waves. The output voltages transformed their levels when the reference values crossed half of the DC source. Next, the voltages of two capacitors on the DC side were set at 250 V and 450 V with the modulation ratio of m=0.9 and DC source voltage at Vdc=700 V. After 0.025 s, the neutral-point potential reached relative equilibrium and was accompanied by three times oscillation of fundamental frequency with an amplitude of 0.63 V. Meanwhile, the neutral-point potential oscillations were less than 1 V when modulation ratios were less than or equal to 1. Furthermore, semi-physical simulations were carried out with dSPACE-SCALEXIO. The results showed that the three-level four-leg inverter could accurately output voltages with different modulation ratios and asymmetric voltages. A compared test was carried out when DC-side capacitor voltages were set at 100 V and 300 V. The conventional control method used about 30 ms to stabilize the voltage, and three times fluctuations occurred. In contrast, capacitor voltages could be balanced without 20 ms and maintained smoothly through the proposed method. In addition, a multi-level simulation with a large modulation ratio was implemented on a four-level four-leg inverter, which outputs three-phase line voltage with seven levels.
The following conclusions can be drawn from the simulation and experimental analyses. (1) Compared with the traditional SVPMW method, the proposed one does not require manual decomposition of three-level VS and large storage space, and can automatically calculate duty cycles and switching sequences under different operating conditions. (2) The proposed neutral-point potential balancing method can make two capacitor voltages on the DC-side consistent more quickly by accurately calculating the capacitor charge. (3) The proposed modulation method can be extended to multi-level inverters by changing the level.
keywords:Three-dimensional space vector pulse width modulation, redundant vector, vector space reduced-order decomposition, neutral-point potential balance
DOI: 10.19595/j.cnki.1000-6753.tces.221040
中图分类号:TM464
广东省基础与应用基础研究基金项目(2022A1515140009)和东莞市科技特派员项目(20221800500072)资助。
收稿日期 2022-06-06
改稿日期 2022-08-18
作者简介
张 志 男,1981年生,博士,副教授,硕士生导师,研究方向为并网逆变器装置拓扑及波形控制技术、谐振软开关技术。E-mail: zhangz@dgut.edu.cn(通信作者)
陈浩辉 男,1997年生,硕士研究生,研究方向为三电平四桥臂逆变器调制技术。E-mail: haohui_nexus@163.com
(编辑 陈 诚)
 (1)
(1)
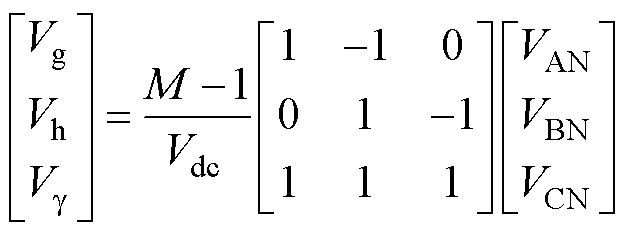 (2)
(2)
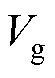 、
、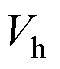 、
、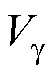 为参考电压矢量在gh
为参考电压矢量在gh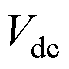 为直流电压;M为电平数量。
为直流电压;M为电平数量。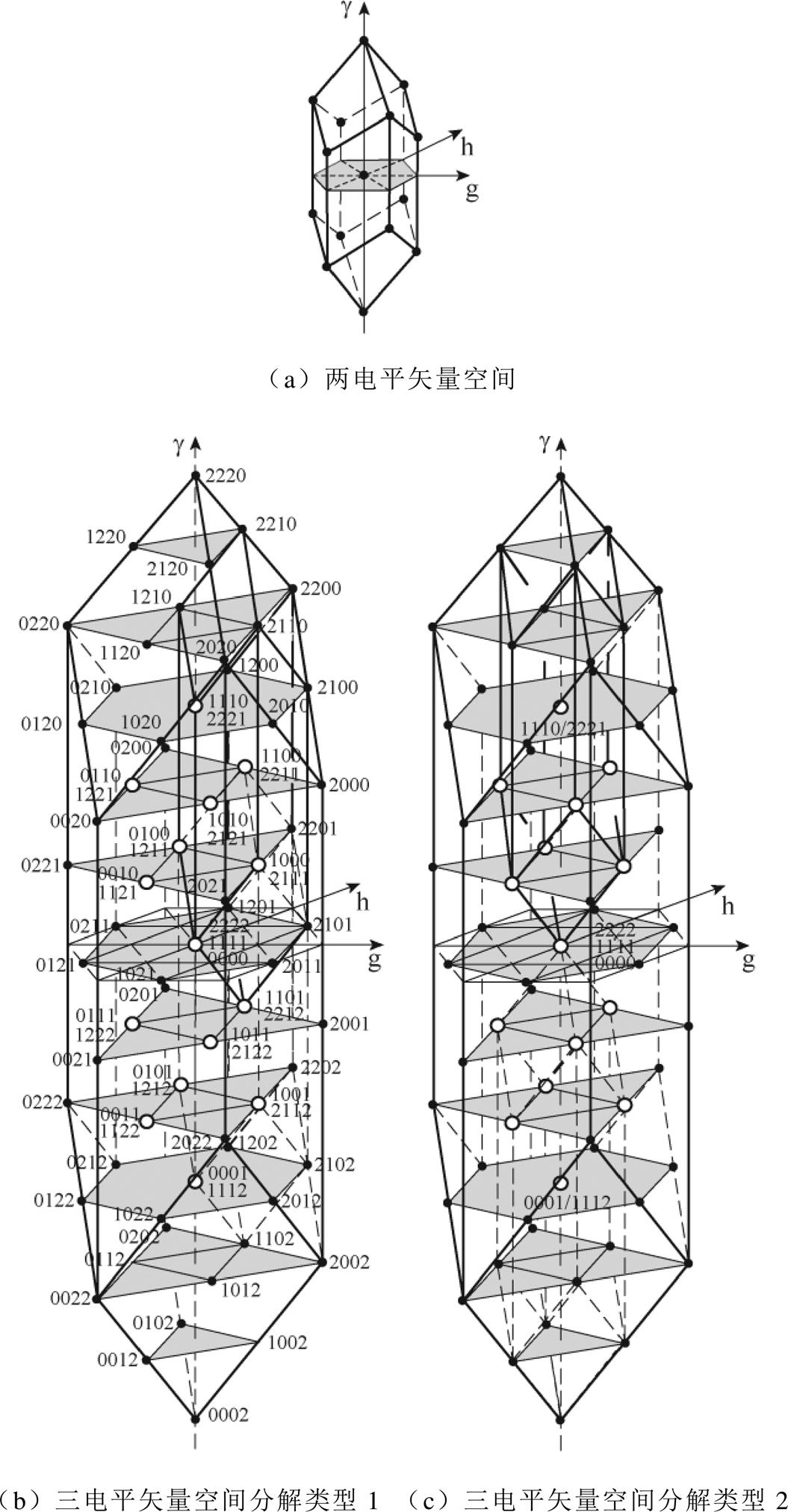


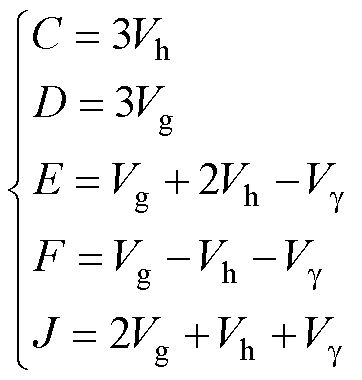 (3)
(3)


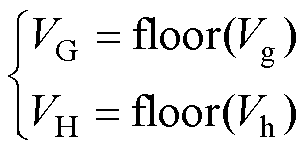 (4)
(4)
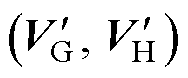 ,位移参考电压矢量记为
,位移参考电压矢量记为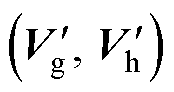 。
。
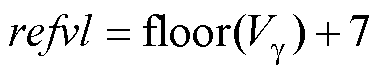 (5)
(5)
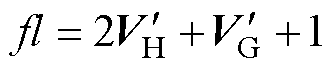 (6)
(6)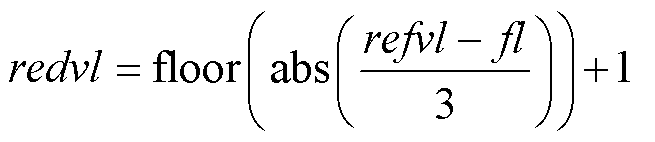 (7)
(7)
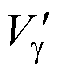 。当redvl<2或redvl>3时,上述选择方式可能会使空间位移中心点落在原矢量空间的表面,而冗余矢量全部位于矢量空间的内部。为使空间位移中心点包含冗余矢量,若redvl<2,取redvl=2,若redvl>3,取redvl=3,两者距离计算方式为
。当redvl<2或redvl>3时,上述选择方式可能会使空间位移中心点落在原矢量空间的表面,而冗余矢量全部位于矢量空间的内部。为使空间位移中心点包含冗余矢量,若redvl<2,取redvl=2,若redvl>3,取redvl=3,两者距离计算方式为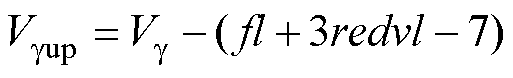 (8)
(8)
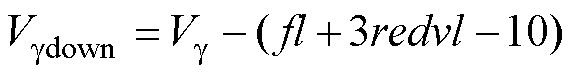 (9)
(9)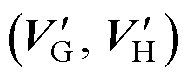 =(0, 1),矢量所在层refvl=7,对应的冗余矢量层redvl=2,即参考电压矢量位于两个两电平矢量空间之间,由V
=(0, 1),矢量所在层refvl=7,对应的冗余矢量层redvl=2,即参考电压矢量位于两个两电平矢量空间之间,由V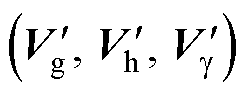 =(0.1, 0.1, 1.2),空间位移中心点为
=(0.1, 0.1, 1.2),空间位移中心点为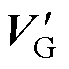 。
。
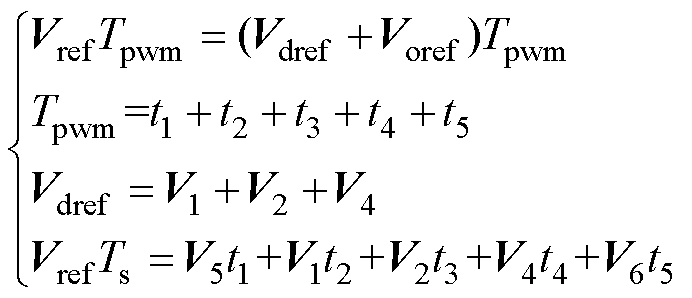 (10)
(10)
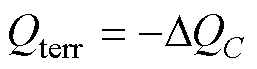 (11)
(11)
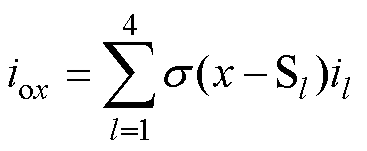 (12)
(12)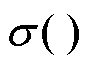 函数为冲击函数;x为中点支路序号,x=1, 2,…, M
函数为冲击函数;x为中点支路序号,x=1, 2,…, M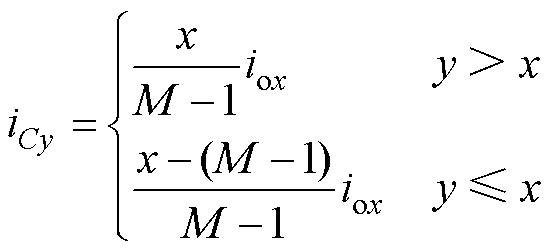 (13)
(13)
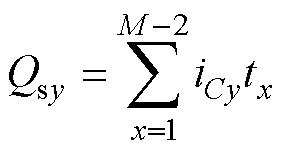 (14)
(14)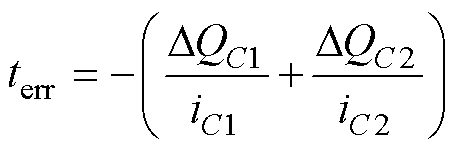 (15)
(15)
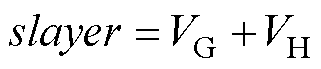 (16)
(16)
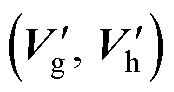 ,平面位移中心点记为
,平面位移中心点记为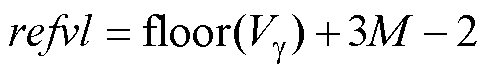 (17)
(17)
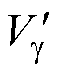 。为使空间中心点包含冗余矢量,若redvl<2,取redvl=2,若redvl>2M
。为使空间中心点包含冗余矢量,若redvl<2,取redvl=2,若redvl>2M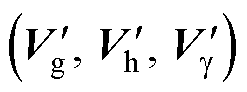 ,空间位移中心点记为
,空间位移中心点记为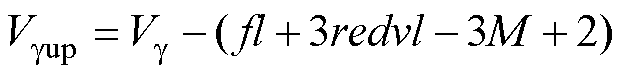 (18)
(18)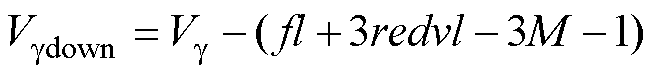 (19)
(19)
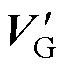
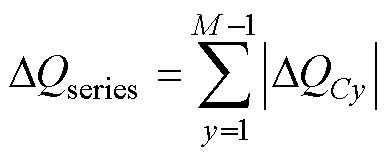 (20)
(20)
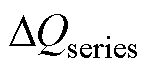 为一个开关序列所造成的电容电荷量实时误差值之和。通过求取电容电荷量误差之和最小项,即min(
为一个开关序列所造成的电容电荷量实时误差值之和。通过求取电容电荷量误差之和最小项,即min(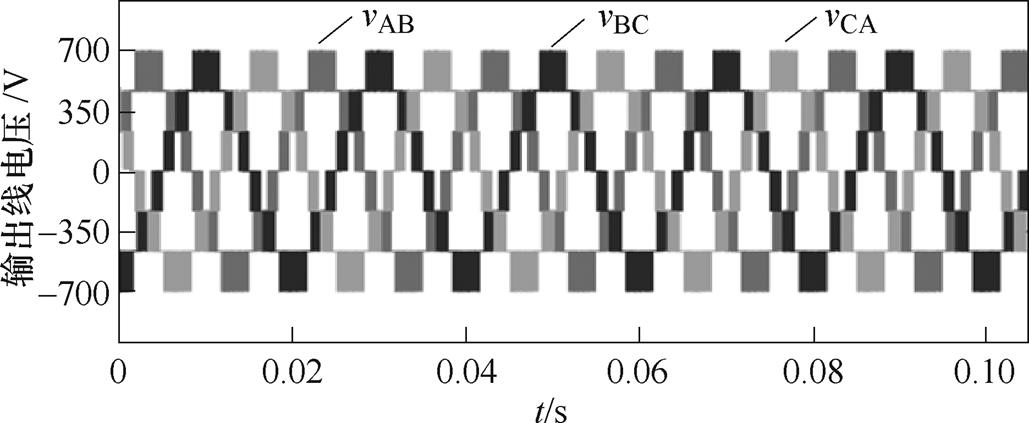

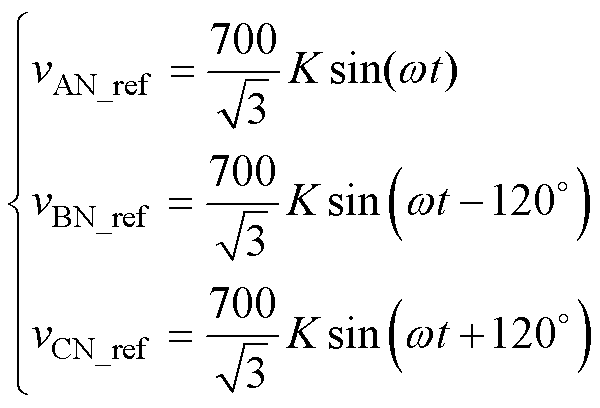 (21)
(21)
 。
。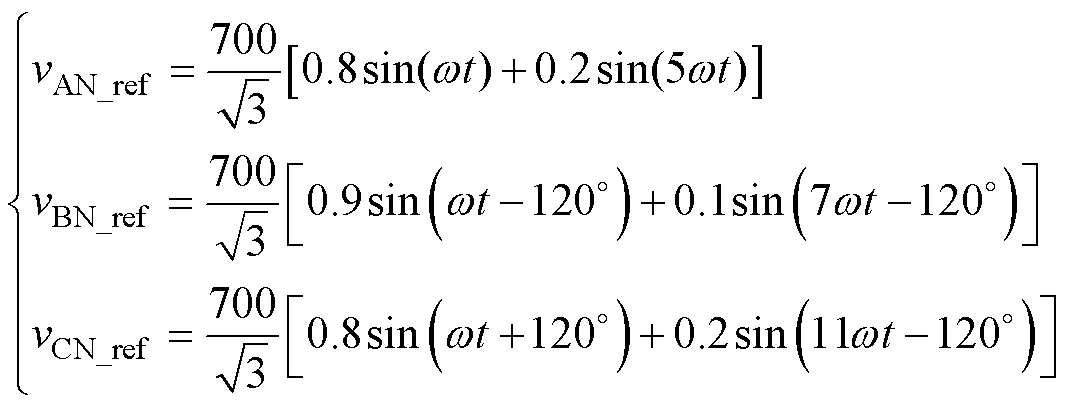 (22)
(22)