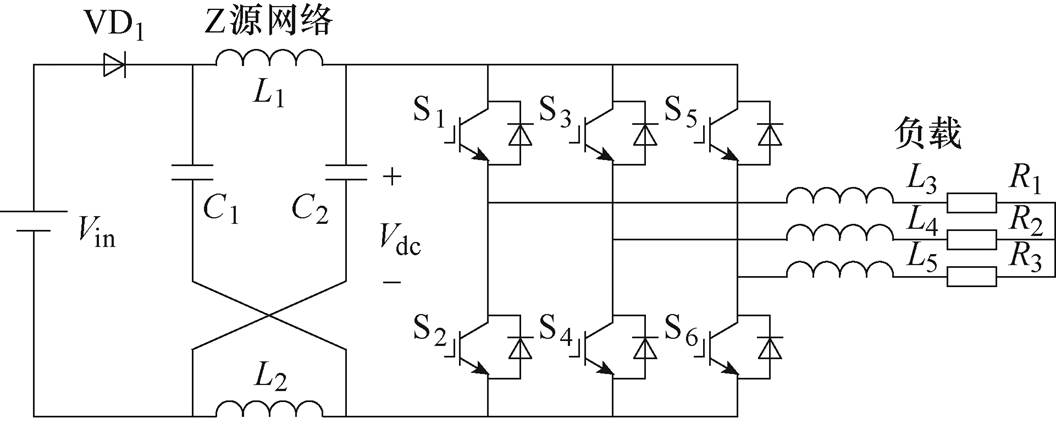
图1 Z源逆变器拓扑结构
Fig.1 Z-source inverter topology
摘要 现有的Z源逆变器调制策略较少考虑功率因数的变化。当功率因数变化时,由于通过开关器件的电流发生相位变化,原有调制策略所产生的开关器件损耗便不是最优的。该文提出一种广义Z源逆变器空间矢量调制(ZSVM2)策略,可以实现功率因数小于1时开关损耗最优。该文通过分析Z源逆变器独有的直通电流分布情况,得到开关损耗的计算方法。通过移动开关器件所通过的直通电流与交流电流相对位置,找到最低开关损耗发生位置。最后,通过Matlab/Simulink并联合PLECS仿真证明了所提出调制方法的有效性,同时搭建了小功率平台进行实验验证。该策略不与其他控制策略冲突,可以在此基础上叠加其他策略。
关键词:Z源逆变器 开关损耗优化 Z源逆变器空间矢量调制(ZSVM2) 空间矢量调制
随着清洁能源的快速发展,风电、光伏等新能源发电占电力系统发电比重越来越大。电力电子变换器在新能源并网发电、电机驱动等方面的应用也越来越广泛。发展更高效率、更高可靠性、更高功率密度和更经济的电力电子变换器的需求已经迫在眉睫。
在燃料电池或光伏发电领域,由于其电压不稳定,一般需要应用两级式逆变器,即先将直流电压升压变换,再使用传统逆变器将直流转换为交流。Z源逆变器(Z-Source Inverter, ZSI)的研制可以替代两级式的结构,通过增加Z源网络和特殊的直通调制方式可以实现直流链路的升压。不仅如此,Z源逆变器特殊的结构使得其可实现上下桥臂直通。因此Z源逆变器可以不需要考虑死区,增加了系统的可靠性。
Z源逆变器于2003年被彭方正教授首先提出[1],经过多年发展已经有了丰富的变化。2008年四种准Z源逆变器(quasi-Z-Source Inverter, qZSI)[2]:输入电流连续的电压源型准Z源逆变器、输入电流断续的电压源型准Z源逆变器、输入电流连续的电流源型准Z源逆变器及输入电流不连续的电流源型准Z源逆变器。通过改变电源与阻抗网络之间的连接方式,使得电压源型准Z源逆变器降低了阻抗网络中电容电压的应力,抑制了启动冲击电流,但输出电压增益并未得到提高和改善,仍与传统Z源逆变器相同。
此后又发展出适应负载大范围变动的高性能Z源逆变器[3],通过利用开关电感单元来替换基本Z阻抗网络中的单个电感的开关电感型Z源逆变器,使用元器件数更少的变压器型Z源逆变器(Trans- Z-Source Inverter, Trans-qZSI)[4],Γ型Z源逆变器(Γ-Z-Source Inverter, Γ-ZSI)[5],开关电感准Z源逆变器(Switch-Inductance quasi-Z-Source Inverter, SI-qZSI)[6],开关耦合电感准Z源逆变器(Switch- Couple-Inductance quasi-Z-Source Inverter, SCI- qZSI)[7],减轻了占空比D和调制度M的约束效应的耦合电感倍压器型准Z源逆变器(Coupled- inductor Multiplier Voltage Rectifier cell embedded qZSIs, CMVR-qZSI)[8]。新型Z源逆变器在减少器件数量、提高升压比等方面有明显进步。
Z源逆变器调制发展也跟随拓扑发展。Z源逆变器早期调制方法一般采用基于载波的调制方法。在此基础发展出了简单升压调制、最大升压调制[9]、最大恒定升压调制[10]以及移位三角调制[11]等。早期调制方式主要以探索拓扑升压能力及器件电压电流应力为讨论点。此后又发展出了空间矢量调制,其中包括了Z源逆变器空间矢量调制(Z-source inverter Space Vector Modulations, ZSVMs)策略如ZSVM6[12]、ZSVM4[13]、ZSVM3[14]、ZSVM2[15]及ZSVM1[16]等一系列调制方法。近些年,Z源逆变器调制方法在降低开关损耗、优化电感纹波等方面也有了许多进展。文献[17]提出了一种新型的双开关频率调制方法,用于解耦调制度M与占空比D,可以减小开关损耗。文献[18]提出一种不连续空间矢量调制方法,用于减少开关损耗。电感纹波减小可以减小电感值,进而减小电感体积,提高功率密度。通过将直通时间由均分变为不均分,可以最大化的减小电感纹波[19-21]。三电平Z源逆变器可以进一步提高逆变器功率,改善输出电能质量。文献[22]分析了单Z源三电平逆变器并提出了控制方法。文献[23]提出了一种新的Z源三电平T型逆变器的调制方法。新的调制方法还在发展中,但结合功率因数变化的调制方法还较少。因此,在变功率因数下讨论开关损耗等问题是有意义的。
本文首先分析Z源逆变器在ZSVM2下开关器件电流情况;然后分析变功率因数下Z源逆变器开关损耗,通过对计算结果的分析,得到了在功率因数变化时,通过移动直通矢量发生的位置,保持最优的开关损耗的计算结果;最后通过Matlab/Simulink联合PLECS仿真验证所提出的控制策略的有效性。此外,搭建小功率Z源逆变器实验平台进行了实验测试,以验证所提调制策略的正确性。
Z源逆变器拓扑结构如图1所示,三相Z源逆变器在直流输入源和两电平之间插入了一个Z源网络,该网络包括L1、L2两个电感值相等的电感器,C1、C2两个电容值相等电容器和二极管VD1。Vin为直流侧供电电压,Vdc为直流链路电压,R1、R2、R3和L3、L4、L5分别为负载侧电阻和电感。

图1 Z源逆变器拓扑结构
Fig.1 Z-source inverter topology
对于Z源逆变器空间矢量调制,交流侧电压幅值为
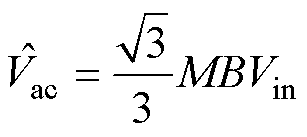 (1)
(1)
式中,M=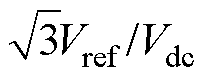 为调制度;B为升压比。以第Ⅰ扇区为例,每个矢量所需时间为
为调制度;B为升压比。以第Ⅰ扇区为例,每个矢量所需时间为
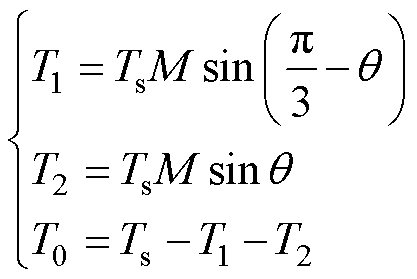 (2)
(2)
式中,Ts为开关周期。
通常,直通矢量作用时间被包含在零矢量作用时间当中。直通矢量占空比D为
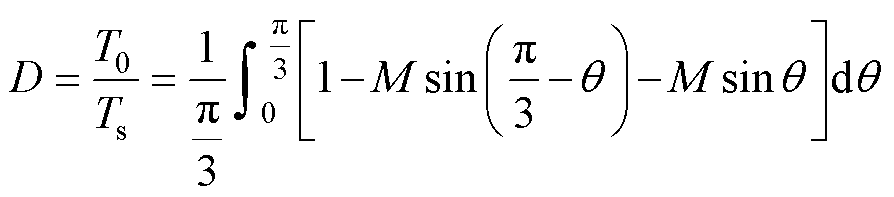 (3)
(3)
对于空间矢量调制而言,零矢量作用时间T0不一定要全部使用直通矢量,下面定义直通时间Tsh与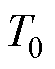 比值D0为
比值D0为
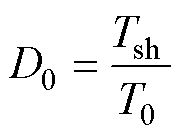 (4)
(4)
直通电流定义为当上桥臂与下桥臂同时导通时,同时通过上桥臂和下桥臂的电流。根据功率输入输出关系,不考虑电感的波动部分,直通电流的平均值可计算[24]为
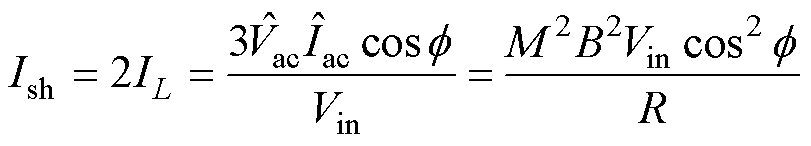 (5)
(5)
式中,IL为Z源网络电感电流;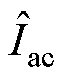 为交流侧电流幅值;R为负载侧电阻;f 为功率因数角。对于ZSVM2,通常认为在一个开关周期内,插入4次直通矢量。在单个开关周期中只有两相桥臂存在直通时间。所以,对于每个单相桥臂而言,直通时间只存在6个扇区当中的4个,下面以A相桥臂为例进行分析。ZSVM2开关时间序列如图2所示。
为交流侧电流幅值;R为负载侧电阻;f 为功率因数角。对于ZSVM2,通常认为在一个开关周期内,插入4次直通矢量。在单个开关周期中只有两相桥臂存在直通时间。所以,对于每个单相桥臂而言,直通时间只存在6个扇区当中的4个,下面以A相桥臂为例进行分析。ZSVM2开关时间序列如图2所示。
开关状态由100变为sh00电流流向如图3所示。图3中,定义A相电流由左向右流动为正。当负载为功率因数接近1的阻感负载,A相电流为正时,A相电流与通过A相上桥臂开关管的电流相等,而下桥臂流过的电流由续流二极管实现;当A相电流为负时,对于A相下桥臂所通过的电流等于负载A相的相电流,上桥臂电流由续流二极管实现。
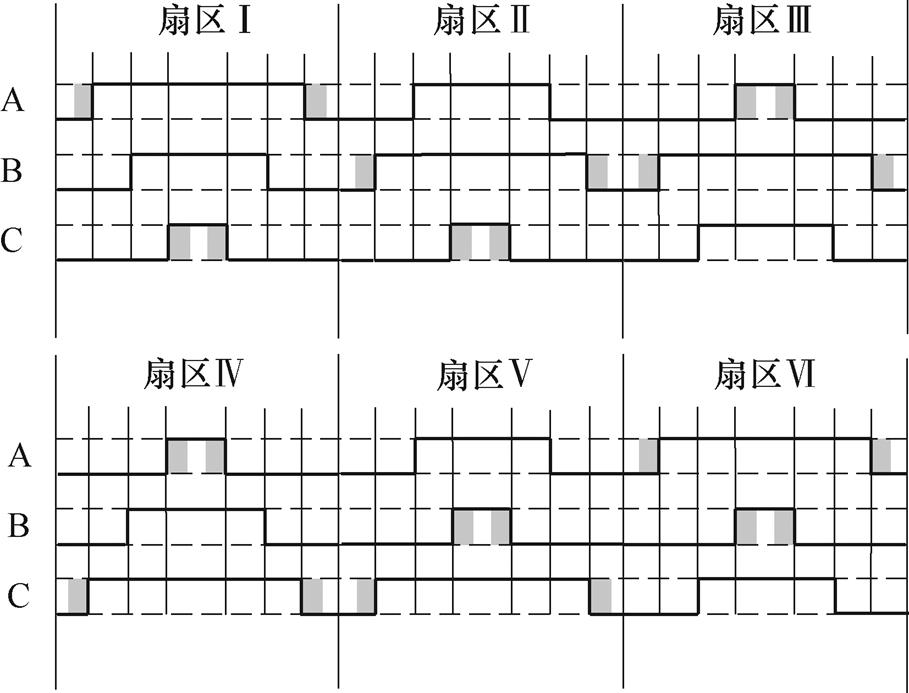
图2 ZSVM2开关时间序列
Fig.2 ZSVM2 switch time series
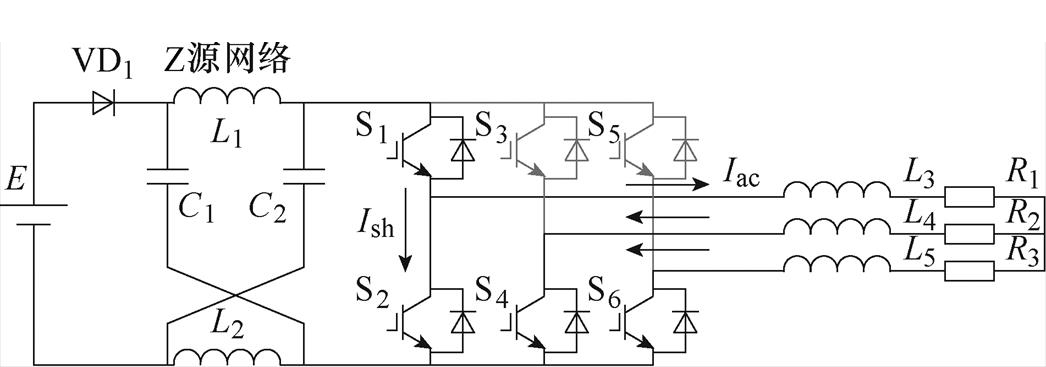
图3 开关状态由100变为sh00电流流向
Fig.3 Switch state changes from 100 to sh00 current direction
当考虑直通矢量时,A相桥臂电流通过情况会变得复杂。直通电流会受到上一个状态Iac的影响。当状态由100→sh00时,在阻感负载下,上桥臂通过的电流为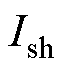 ,下桥臂通过的电流为Ish-Iac。上桥臂所通过的直通电流为
,下桥臂通过的电流为Ish-Iac。上桥臂所通过的直通电流为
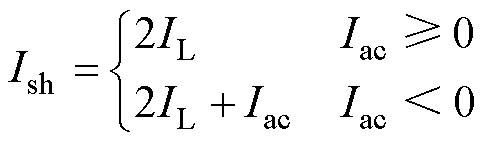 (6)
(6)
对于功率因数接近1的阻感负载而言,相电流Iac为正弦波形状。在功率因数接近1时,A相开关器件通过的电流的平均值为
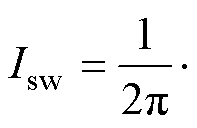
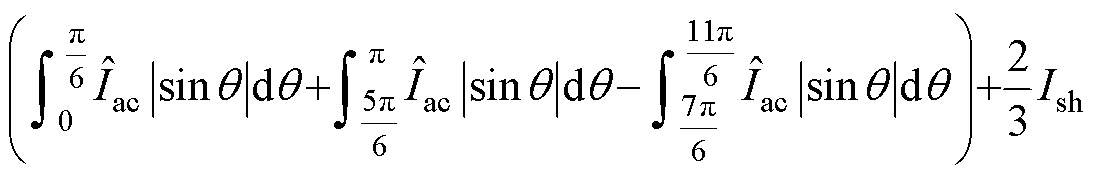 (7)
(7)
以上分析可知,从通过开关器件电流角度来看,Z源三相逆变器与常规三相逆变器通过电流的差异就在于直通电流的分布。当Z源三相逆变器增加了直通矢量后,在部分区域叠加直通电流。一般地,直通电流大于Iac。此时则需要满足
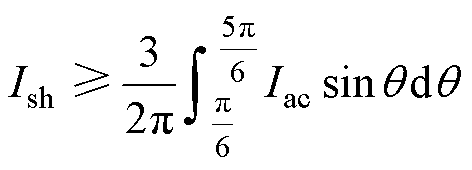 (8)
(8)
由式(8)可得
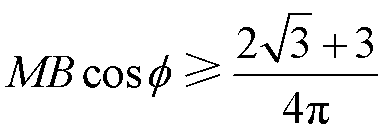 (9)
(9)
对于逆变器开关器件的开关损耗[18, 25]表示为
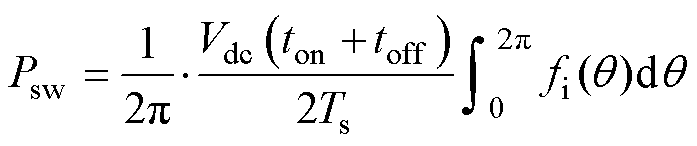 (10)
(10)
式中,Vdc为直流链路电压;ton、toff分别为器件开、关时间。根据式(10),逆变器开关损耗受到了直流链路电压大小、开关损耗及开通和关断时间的影响。在Z源逆变器运行当中,直流链路电压虽有少量波动但其波动不大,可认为保持恒定。稳定运行中,逆变器开关频率通常不变化。开通、关断时间ton和toff会受到器件型号、电流大小等方面的影响。但当开关电流增加时,ton和toff通常是少量增加的。由于增加量较少同时又不影响通过平均电流分析计算开关损耗大小趋势,为了简便计算,这里认为此参数不变。因此,评估开关损耗差异主要在开关器件在开关时刻所通过的电流。
下面来分析开关器件在功率因数不为1的情况。当功率因数不为1时,Iac电流会跟随功率因数变化而滞后。但是直通电流产生的位置是合成电压参考矢量的,可以认为不变,这产生了Ish与Iac之间的位置变化。
对于开关器件,开关电流的平均值为
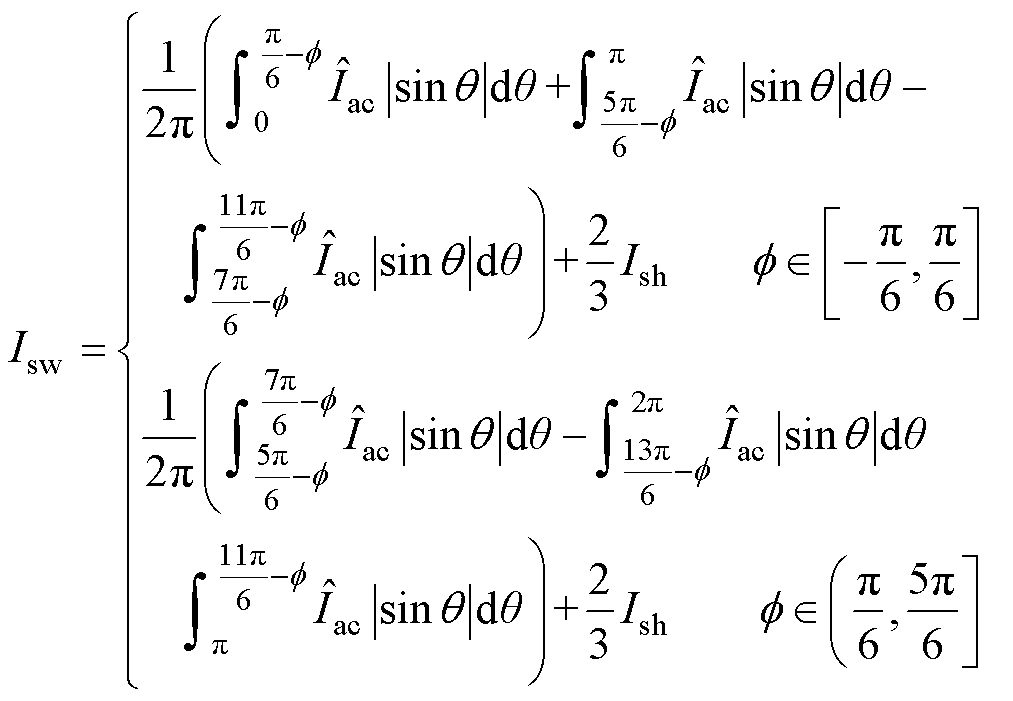 (11)
(11)
由式(11)化简得到
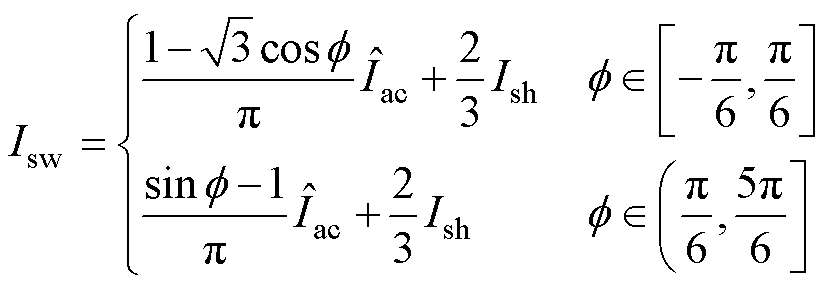 (12)
(12)
由式(12)可知,为了方便计算变功率因数下开关电流的变化情况,考虑稳定工作状态时逆变器其他参数不变的前提下,Iac和Ish不变,则平均开关电流与功率因数角j 有关,设系数
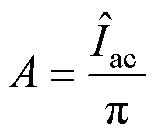 (13)
(13)
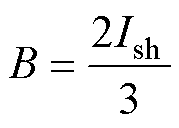 (14)
(14)
则有
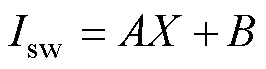 (15)
(15)
其中
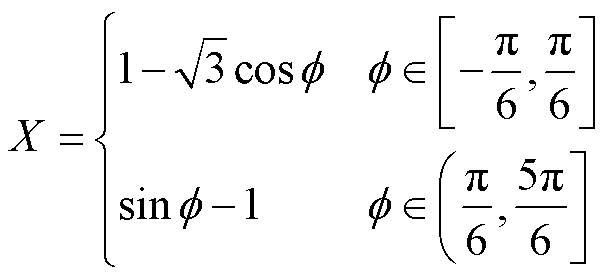 (16)
(16)
由式(16)可知,开关电流变化值与X有关。经过分析可知,当j =0°时,X值最小。这意味着此时开关器件平均电流最小,此时最小值为
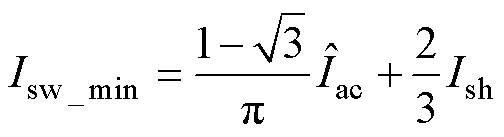 (17)
(17)
系数X与功率因数角关系如图4所示。以上分析可知,X为平均开关电流的变化值。实际上,Iac和Ish的幅值也会随着j 的变化而变化。因此在图4中,可以认为是当Iac和Ish为定值时,Ish与Iac之间的相位关系引起的平均开关电流变化情况。当Iac和Ish相对位置关系与j =0°相同时,开关器件电流在Iac影响下平均电流最小。
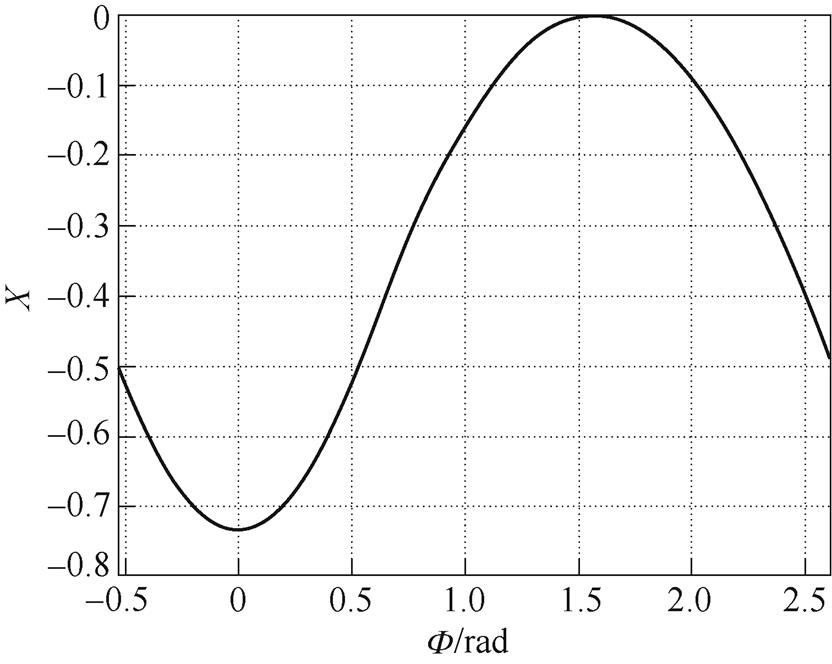
图4 X与功率因数角关系
Fig.4 Relationship between X and power factor angle
推荐的开关损耗调制方法是在ZSVM2的基础上进行的。ZSVM2在一个开关周期当中使用两相桥臂产生直通矢量,因此有了可以调节直通电流Ish和Iac相对位置的条件。第3节的讨论说明不采用其他方法时,两者相对位置在功率因数角j =0°时平均开关电流最低,也就是开关损耗最低。下面介绍如何实现直通电流跟随Iac移动的调制方法。
当负载出现功率因数角j 时,不改变原有扇区开关顺序,将产生直通矢量的顺序向后延迟j 角度。此时恰好可以让负半周开关电流始终保持最小,也就能够产生最小的开关损耗。对于矢量调制而言,可分别产生直通矢量和向量开关时间。
以第Ⅰ扇区为例,当功率因数角在0~p/3之间时,将0~j 之间的直通矢量产生桥臂由原始A、C相变为图2扇区Ⅵ中的A、B相。此时j ~p/3之间的直通矢量产生桥臂不变。当功率因数进一步变大至p/3~2p/3之间时,此时p/3~j 之间直通产生桥臂为B、C相,而j ~2p/3之间直通产生桥臂为A、B相。同理可推广至其他功率因数角进行修正。对于0~p/3之间的调制情况如图5所示。
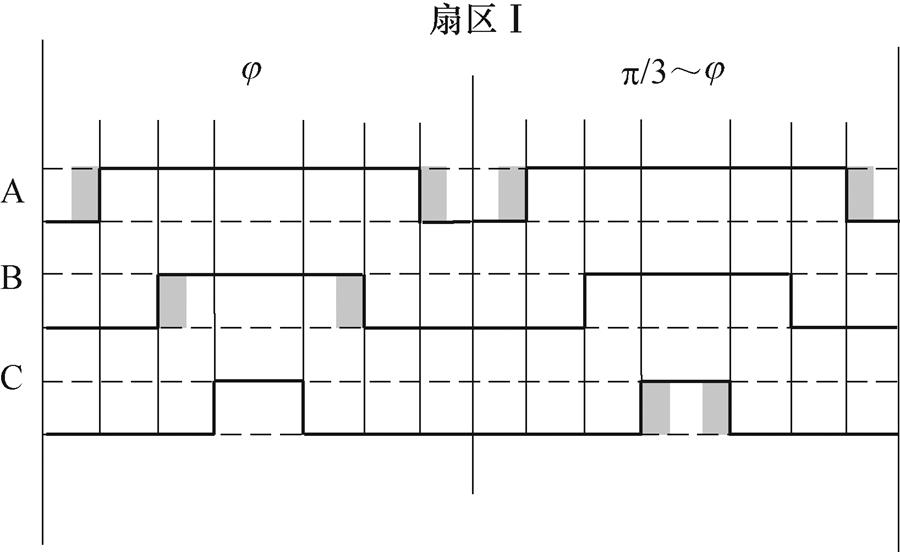
图5 移位j 角度后,第Ⅰ扇区调制序列
Fig.5 After shifting by j angle, the first sector modulation sequence
换种角度来看,原ZSVM2方式是根据交流侧电压Vac来产生直通矢量区域的,而推荐的改进型ZSVM2策略是根据交流侧电流Iac来确定直通矢量区域。这使得当开关器件通过直通电流时,可以有更大的Iac来抵消开关器件所通过的直通电流,进而到达减少损耗的目的。ZSVM2策略与推荐的改进ZSVM2策略直通矢量发生区域对比如图6所示。
根据式(12),可得到采用推荐的调制算法开关电流平均值Isw_r和不采用推荐调制算法开关电流平均值Isw的平均电流比(Average Current Ratio, ACR),即
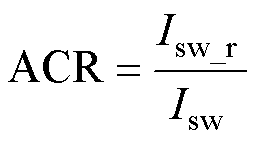 (18)
(18)
ACR系数表示的是当负载功率因数变动时,其他参数不变的情况下,由使用推荐调制和原ZSVM2调制方法开关电流的比值。
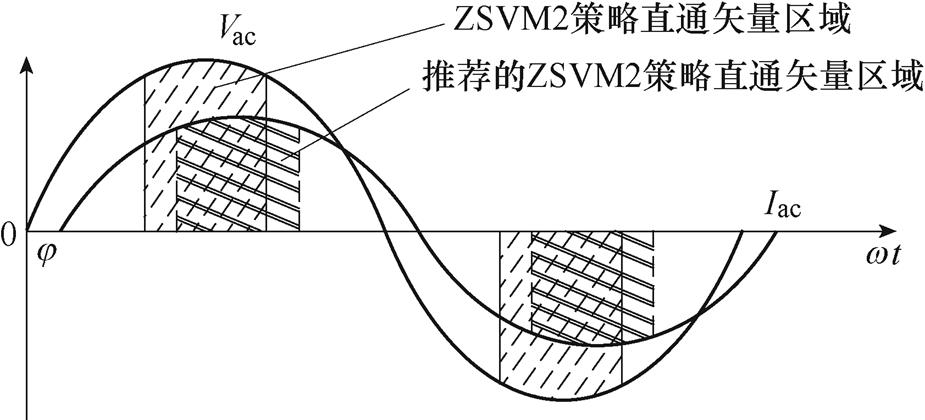
图6 ZSVM2策略与推荐的改进ZSVM2策略直通矢量发生区域对比
Fig.6 Comparison of ZSVM2 strategy and the proposed improved ZSVM2 strategy in the shoot-through vector region
由式(18)可得
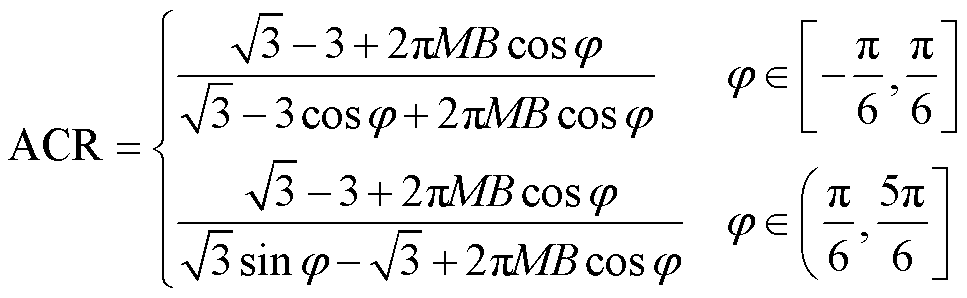 (19)
(19)
更换Ish与Iac相对位置关系不影响逆变器的工作参数,所以除平均开关电流差异并无其他参数变化。事实上,ZSVM2、ZSVM1等在一个开关周期内不使用所有桥臂直通的调制方法都可以使用这种相位移动的方法降低平均开关电流。ZSVM6由于在一个开关周期内所有的桥臂都参与直通矢量的产生,所以在相应扇区内无法移动直通矢量产生位置。由式(18)关系可得到ACR与调制度和功率因数的关系,如图7所示。
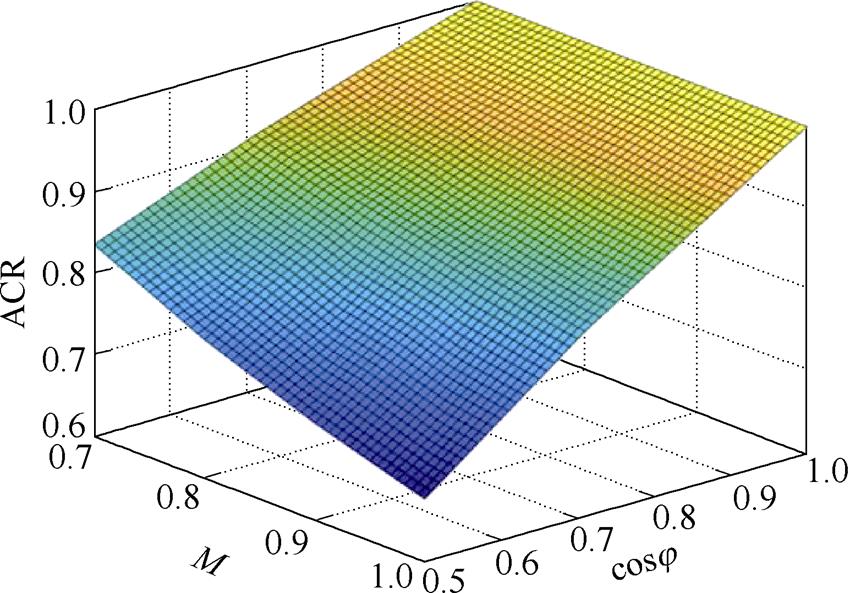
图7 ACR与调制度和功率因数的关系(D0=1)
Fig.7 Relationship between average current ratio and power factor (D0=1)
图7所示为D0=1时,改变调制度M和功率因数角之后其平均电流比(ACR)的值。它表示输出相同交流侧电压情况下,当功率因数越低,调制度越高时,其降低幅度越大,即损耗优化的效果越好。如图7所示的开关损耗比较关系,是考虑了原ZSVM2与推荐ZSVM2在平均电流比之间的差异。当调制度变化时,保持D0不变,其直流链路电压会改变,整体开关损耗因此变化,损耗的优化效果随之变化。但将ZSVM2变为推荐调制并不影响直流链路电压,只是影响通过器件的电流,通过优化电流实现损耗的优化。当调制度降低时(保持D0不变),直通电流增加,交流侧电流可抵消部分并减弱,而开关损耗优化效果降低。
本文使用的是空间矢量调制。根据式(3)计算完成矢量发生时间,直通矢量计算叠加在零矢量发生时间。同时设定直通矢量占零矢量时间比D0,通过调节D0可调节直通矢量时间。
Z源逆变器开关器件的导通损耗通常可分为两部分:一部分为非直通状态的导通损耗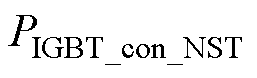 ;另一部分为直通状态下的导通损耗
;另一部分为直通状态下的导通损耗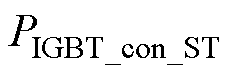 。对于非直通状态,其电流与传统逆变器计算方法并无差异。对于直通状态,导通损耗要考虑直通电流的影响。
。对于非直通状态,其电流与传统逆变器计算方法并无差异。对于直通状态,导通损耗要考虑直通电流的影响。
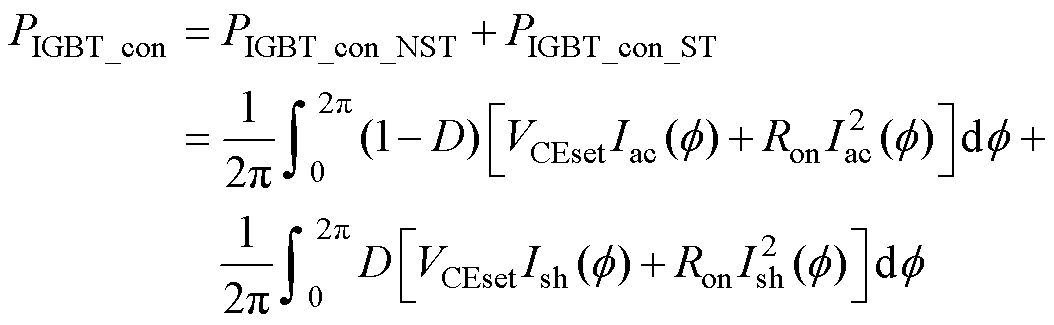 (20)
(20)
式中,VCEset为开关器件导通电压;Ron为开关器件的导通电阻。
推荐的调制方式并不影响直通占空比,而VCEsat和Ron为器件固有参数,且变化主要体现在电流上。Z源逆变器直通状态下其等效电路为LC电路,短时间内认为直通电流不变,此时导通电流计算方法与开关电流类似。当使用推荐调制时,结合式(19)可知,功率因数不为1时,推荐调制策略可降低器件所通过直通电流的平均值。因此推荐的调制策略可降低导通电流,从而降低导通损耗。
续流二极管损耗主要包括导通损耗和反向恢复损耗两部分。续流二极管导通损耗主要产生在所在桥臂Iac<0部分,其表达式为
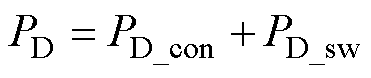 (21)
(21)
式中,PD_con为续流二极管导通损耗;PD_sw为续流二极管开关损耗。续流二极管导通损耗可定义为
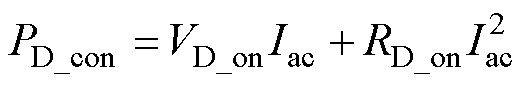 (22)
(22)
式中,VD_on为续流二极管导通压降;RD_on为续流二极管导通电阻。
所推荐的调制策略将直通电流产生区域更多的与Iac<0部分进行抵消。这不仅降低了直通电流,也少量降低了续流二极管导通时通过的电流值Iac的平均值。类似地,续流二极管导通电流也有所降低。
反向恢复损耗非常小,通常可忽略不计,其大小也与导通电流有关,即
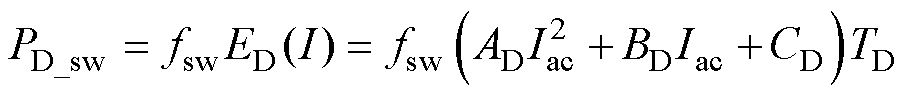 (23)
(23)
式中,AD、BD、CD为测试条件下开关能力损耗随电流变化的二次拟合曲线;TD为温度修正系数;fsw为开关频率。根据式(23)可得,当通过的续流二极管电流降低时,其反向恢复损耗也有所降低。
4.3.1 推荐调制策略对电压应力和电流应力影响
由于改进的ZSVM2策略不改变升压比,因此不改变直流链路电压,开关器件电压应力也无改变。
Z源逆变器电流应力通常由其通过的直通电流及其波动值决定。电流应力可表示为
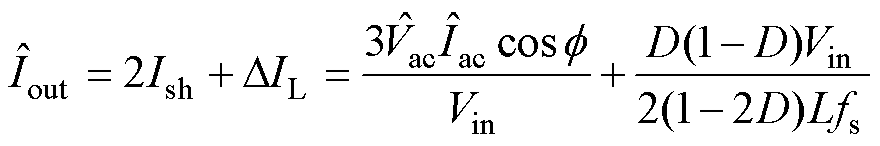 (24)
(24)
式中,L为Z源网络电感值。当使用推荐调制策略时,以上参数均不改变,但推荐的调制策略改变交流电流Iac和Ish之间相对位置,因此在功率因数变化时,可以降低Iac<0部分的电流应力。Z源逆变器单相直通电流应力通常由直通电流决定。
推荐的调制方式并不建议使用三相直通。三相直通虽然可将每相直通电流降低至原来的1/3,但三相直通使得推荐的调制策略在相位变化时电流优化失效。当使用三相直通时,无法实现变功率因数下的电流优化效果。
4.3.2 推荐调制策略对共模电压影响
在不同矢量下对Z源逆变器的共模电压情况也有所不同,由于推荐的ZSVM2策略合成电压参考矢量时,与原ZSVM2策略并无差异。因此推荐的调制方式不改变原有的共模电压情况。
4.3.3 推荐调制策略对电感纹波影响
Z源逆变器电感纹波优化对于电感选值有较大益处。下面以第Ⅰ扇区,功率因数角位于0~p/3之间为例,分析改进型ZSVM2策略与原ZSVM2策略在电感纹波之间的差异。
当功率因数角位于0~p/3之间时,对于第Ⅰ扇区,0~j 之间的直通矢量产生桥臂发生更换;而在j ~p/3之间时,直通矢量则不需要更换。因此改进后的ZSVM2策略需要考虑两部分的电感纹波情况。对于ZSVM2策略,其纹波为
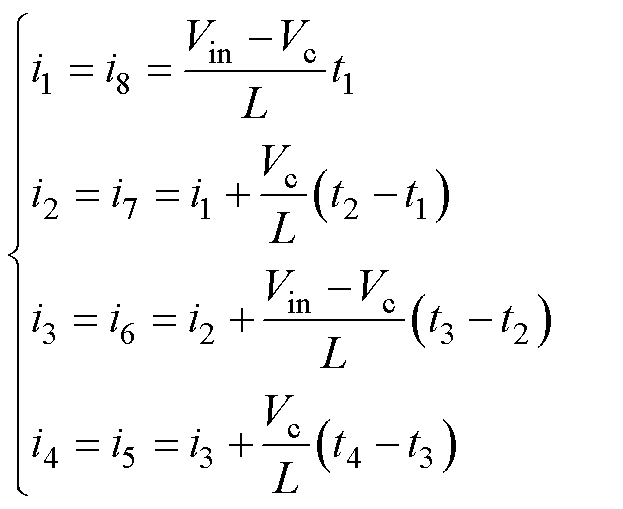 (25)
(25)
其中
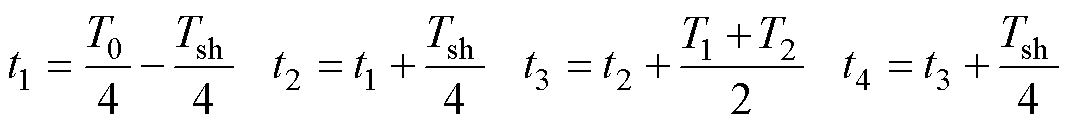
此时最大纹波为
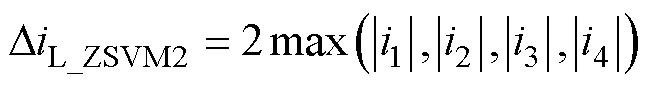 (26)
(26)
对于改进的ZSVM2策略,0~j 部分纹波为
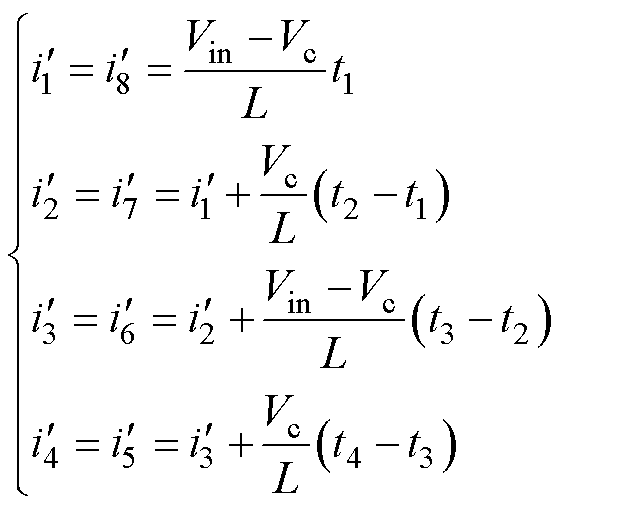 (27)
(27)
其中
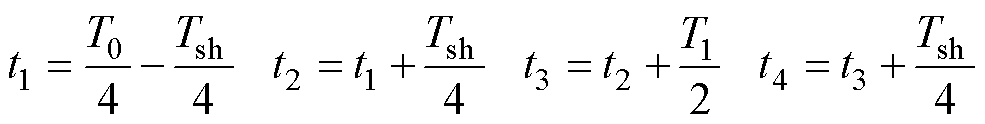
推荐调制最大纹波为
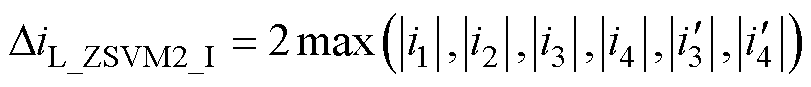 (28)
(28)
对于ZSVM2,最大电感纹波产生在j =p/6时,其最大纹波电流为
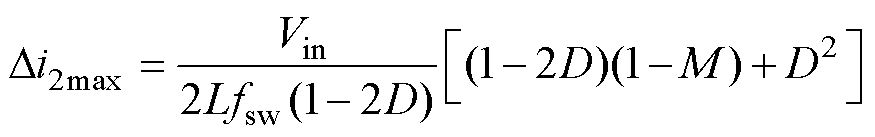 (29)
(29)
对于改进的ZSVM2,最大电感纹波产生在j = p/3时,其最大纹波电流为
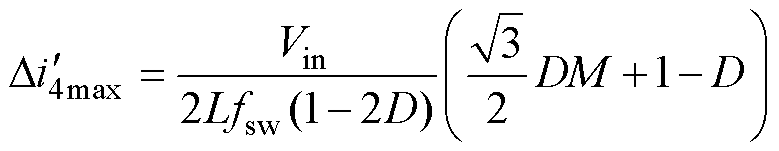 (30)
(30)
根据式(29)与式(30),改进的ZSVM2电感纹波增加情况还需根据M和D以及功率因数角进行判断。改进的ZSVM2最大电感纹波出现在j =p/3时,与ZSVM2最大电感纹波出现功率因数角条件不同。改进的ZSVM2策略并不影响纹波优化策略的使用,可采用不等分或移动直通时间进行电感纹波优化。ZSVM2与推荐的改进ZSVM2方法电感纹波情况如图8所示。
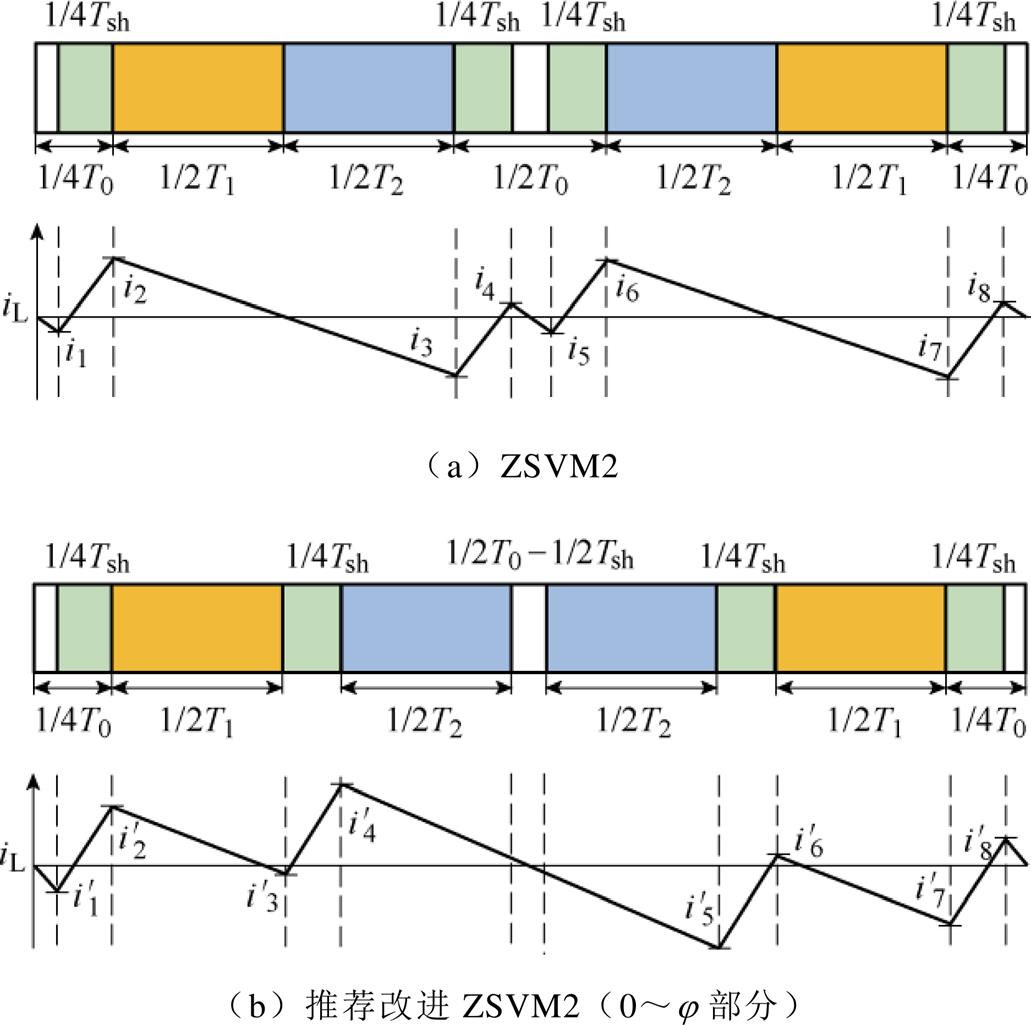
图8 ZSVM2与推荐的改进ZSVM2方法电感纹波情况
Fig.8 ZSVM2 and proposed improved ZSVM2 method inductance ripple
搭建了仿真及实验平台验证所提出的调制策略的有效性。Z源网络电感和电容分别为1 300 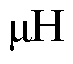 和1 000
和1 000 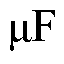 。三相负载分别为(R=12.5 W, L=1 mH)、(R= 12.5 W, L=10.67 mH)、(R=12.5 W, L=23 mH);功率因数分别为0.999 8、0.966、0.866,交流输出频率为50 Hz,开关频率为10 kHz。
。三相负载分别为(R=12.5 W, L=1 mH)、(R= 12.5 W, L=10.67 mH)、(R=12.5 W, L=23 mH);功率因数分别为0.999 8、0.966、0.866,交流输出频率为50 Hz,开关频率为10 kHz。
首先比较不同功率因数下Ish和Iac的相对位置关系。图9所示为仿真参数Vin=70 V,D0=0.9,M=0.8,功率因数分别为0.999 8、0.966、0.866时,A相桥臂器件两端开关电流。可以清晰地看到,对于ZSVM2,直通电流与Iac相对位置随着功率因数变化而变化。
当功率因数变小时,Iac电流相应相右移动,而Ish不变。图9d为推荐的调制A相上桥臂电流。可以看到,相比于原ZSVM2策略直通电流产生位置,改进的ZSVM2策略直通矢量产生位置向右移动了p/6,直通电流产生区域也移动了p/6,直通电流与Iac相对位置恰好发生在与图9a中功率因数接近1时相同的位置。
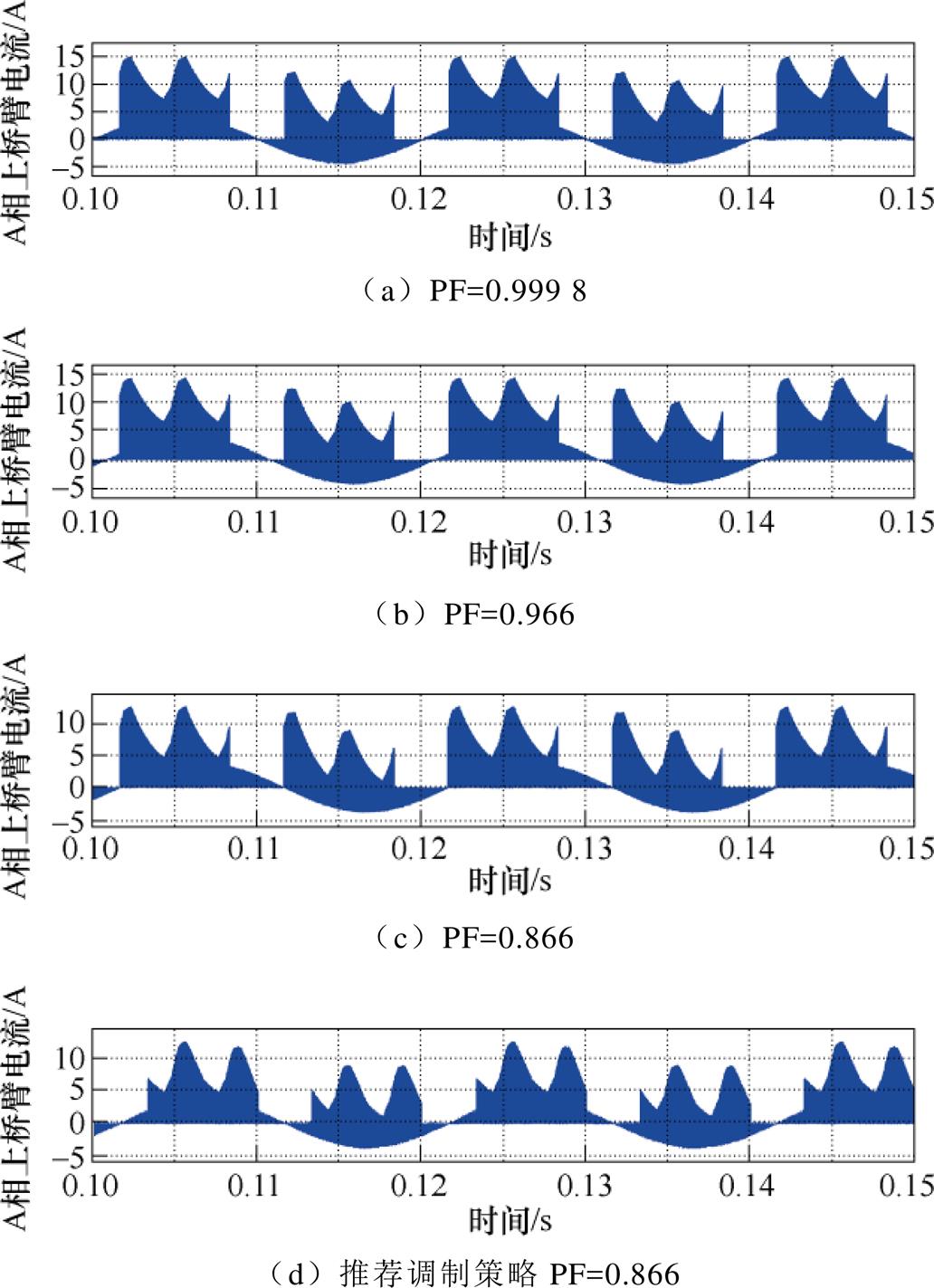
图9 A相上桥臂电流仿真
Fig.9 A-phase upper leg current simulation
通过使用Matlab/Simulink联合PLECS进行仿真。开关管损耗和续流二极管损耗分别见表1和表2。仿真参数与图9一致。PLECS模型采用的器件型号为英飞凌IHW30N65R5。由表1和表2可看出,推荐调制的损耗优化效果。
表1 ZSVM2开关器件损耗
Tab.1 ZSVM2 switching device losses (单位: W)
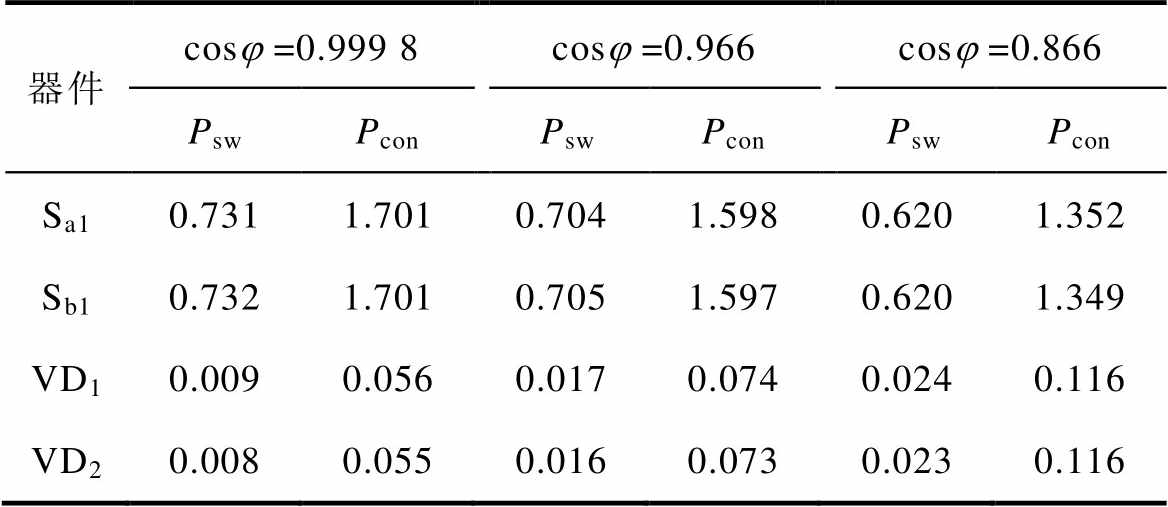
器件cosj=0.999 8cosj=0.966cosj=0.866 PswPconPswPconPswPcon Sa10.7311.7010.7041.5980.6201.352 Sb10.7321.7010.7051.5970.6201.349 VD10.0090.0560.0170.0740.0240.116 VD20.0080.0550.0160.0730.0230.116
实验表明,当使用了推荐的调制策略时,无论平均开关电流还是导通电流都有所降低。因此,无论是开关管还是续流二极管,开关损耗和导通损耗都有所降低。采用PLECS器件模型开通损耗与关断损耗大小不同,而且开关损耗与电流关系也非完全呈线性,因此仿真与此前模型分析有少量差异,但损耗减少趋势和优化损耗效果不变。当功率因数越大时,使用推荐调制损耗减少的效果越好。
表2 推荐调制开关器件损耗
Tab.2 Recommended modulation switching device losses (单位: W)
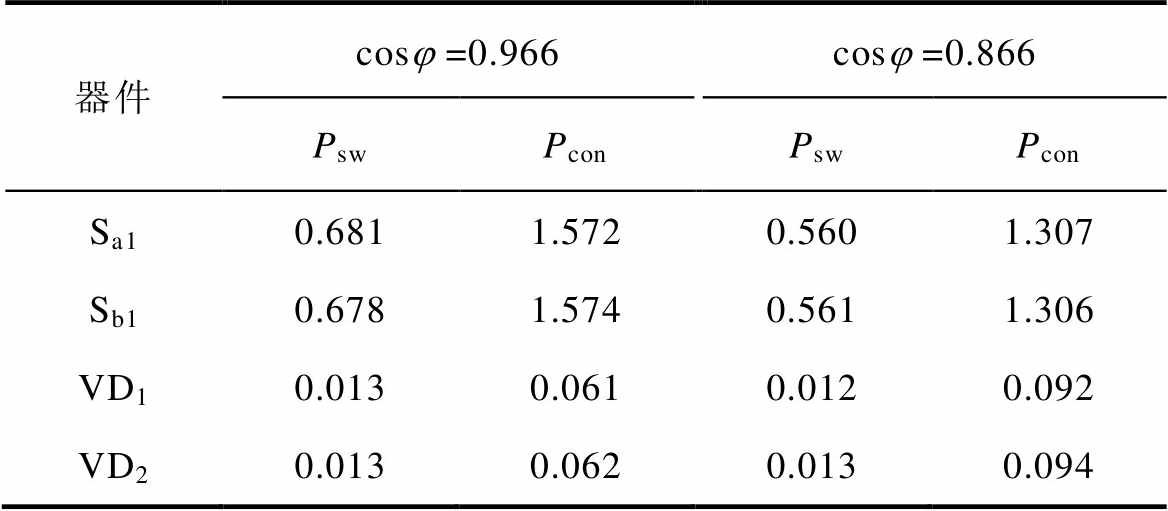
器件cosj=0.966cosj=0.866 PswPconPswPcon Sa10.6811.5720.5601.307 Sb10.6781.5740.5611.306 VD10.0130.0610.0120.092 VD20.0130.0620.0130.094
图10为不同输出功率下ZSVM2策略与推荐调制策略效率对比。仿真负载功率因数PF=0.866,D0= 0.85,调制度M分别为1, 0.9, 0.8, 0.7, 0.65, 0.6,对应输出功率分别为141.32 W,165.81 W,205.57 W,283.5 W,352.83 W,470.34 W。PF=0.966时,R=12.5 W, L=10.67 mH,对应输出功率分别为153.72 W,180.96 W,225.37 W,380.78 W,383.02 W,500 W。如图10所示,调制策略可提高逆变器效率,功率因数越小时效率优化越明显。
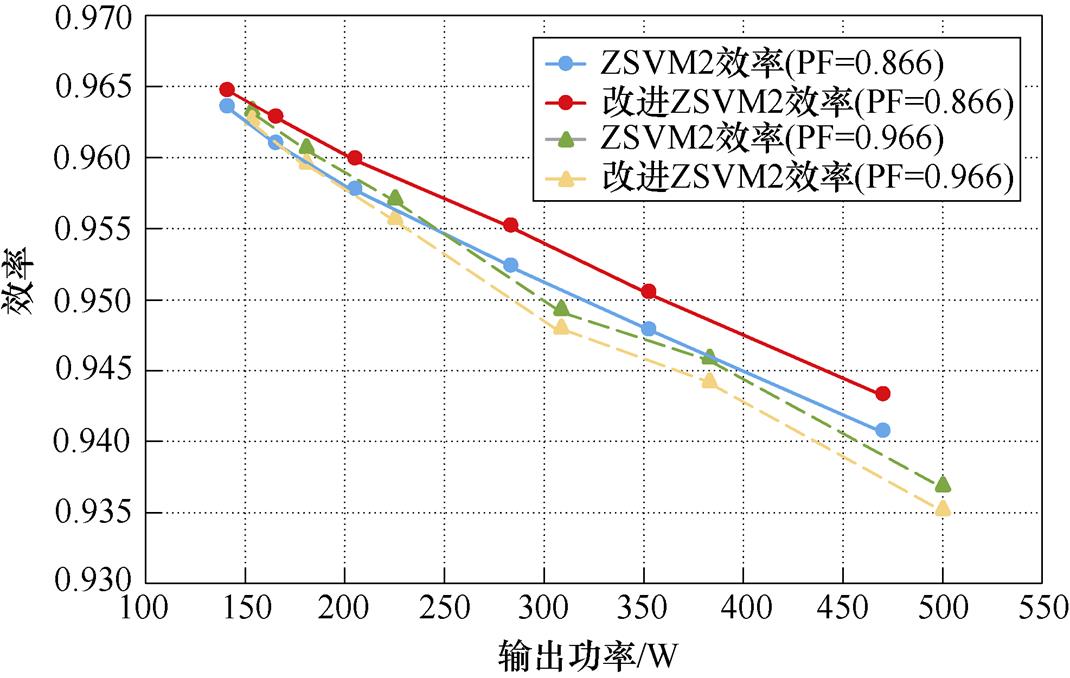
图10 不同输出功率下ZSVM2策略与改进ZSVM2策略的效率对比
Fig.10 Efficiency comparison of ZSVM2 strategy and improved ZSVM2 strategy under different output power
图11为不同调制度下ZSVM2策略与推荐调制策略输出电流总谐波畸变率(Total Harmonic Dis- tortion, THD)对比。仿真参数与图10一致。可以看到推荐的改进ZSVM2策略THD略有上升。
为验证前述分析的有效性,搭建了小功率实验平台。其中包括直流稳压电源、Z源网络板、三相阻感负载、三相逆变器、示波器、差分探头等。三相逆变器控制器型号为德州仪器公司的TMS320F28335,开关管采用英飞凌IHW30N65R5。实验平台及其组成如图12所示。
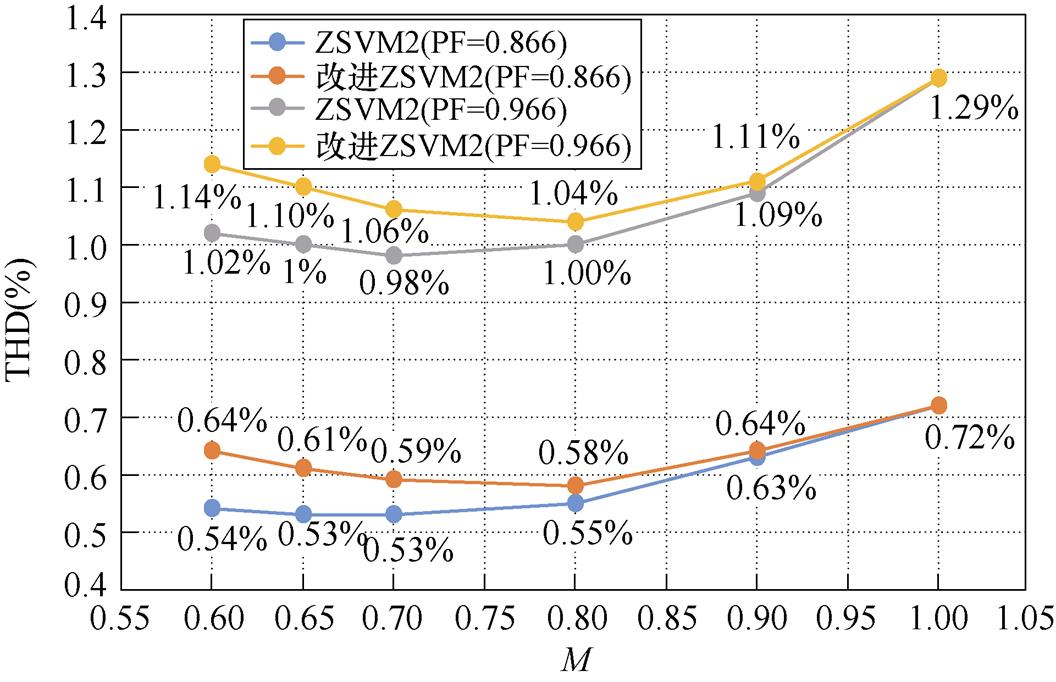
图11 不同调制度下,ZSVM2策略与改进ZSVM2策略的输出电流总谐波畸变率对比
Fig.11 Total harmonic distortion rate of output current of ZSVM2 strategy and improved ZSVM2 strategy under different modulation ratios

图12 实验平台及其组成
Fig.12 Experimental platform and composition
实验平台使用与图9及表1、表2仿真相同的参数,分别采集A相上桥臂电流以及直流链路电压验证所推荐的调制方法有效性。图13为PF=0.866时,直流链路电压和A相上桥臂电流。实验波形可以看出,推荐的调制方法不改变直流链路电压。A相上桥臂开关器件通过的电流波形与图9c仿真波形基本一致。图14为PF=0.866时,使用推荐调制直流链路电压和A相上桥臂电流。从图9中可以看到与仿真类似的波形效果。当使用推荐的改进调制时,开关器件通过的直通电流与交流侧电流相对位置关系发生变化,直通矢量发生区域位于平均电流降低位置,实现开关器件损耗的最优化。
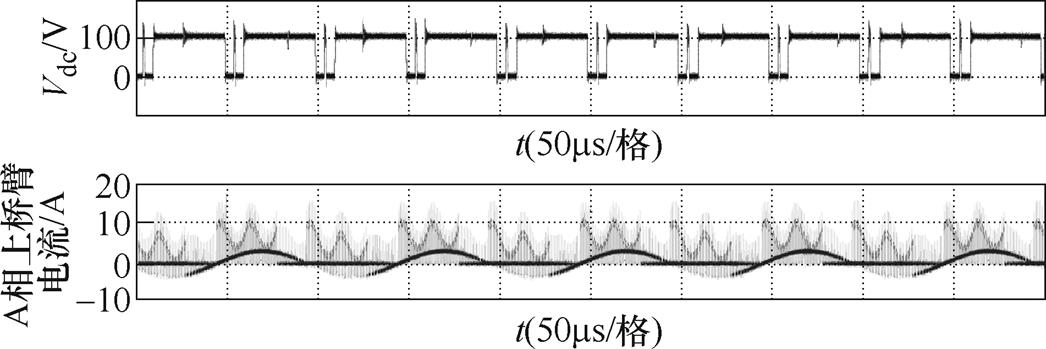
图13 PF=0.866时,直流链路电压和A相上桥臂电流实验波形
Fig.13 When PF=0.866,DC-link voltage and A-phase upper leg current experimental waveforms
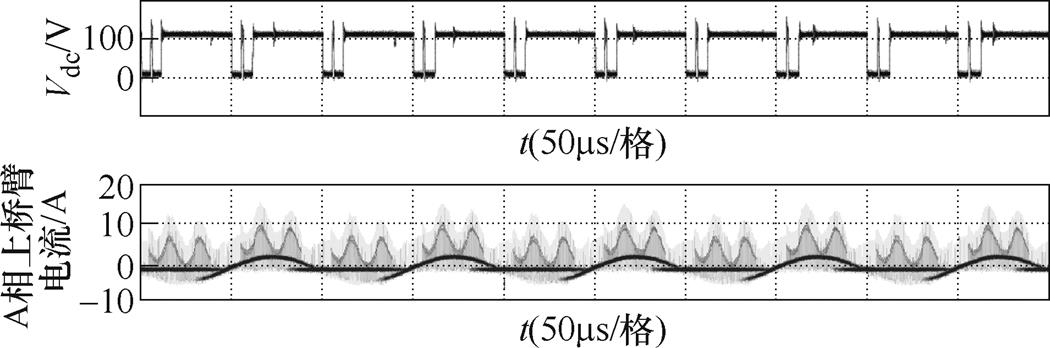
图14 PF=0.866时,使用推荐调制直流链路电压和A相上桥臂电流实验波形
Fig.14 When PF=0.866, use the proposed modulation strategy DC-link voltage and A-phase upper leg current experimental waveforms
图15通过热成像仪验证所采用调制方法的有效性。可见,当使用推荐调制时,IGBT器件的温度有所降低,导致了器件损耗的降低。
本文提出了一种广义ZSVM2策略可减少开关器件开关损耗。详细推导了传统ZSVM2策略和所提出的改进调制方法在平均电流上的差异。经过分析可知,当直通电流Ish与Iac相对位置关系与负载功率因数为1两者位置关系相同时,可以实现最小开关损耗。推荐调制策略开关损耗优化效果与负载功率因数角有关。本文分析了推荐的调制策略对导通损耗、电感纹波等方面的影响。仿真和实验结果均表明,所提出的策略可有效减少开关损耗和器件总损耗。同时,该策略不与其他控制策略相冲突,可以在此基础上叠加其他策略。该策略给稳定工作在负载功率因数不为1的Z源逆变器提供了减少开关损耗的实用方法。

图15 实验平台IGBT器件红外热像
Fig.15 IGBT temperature of experimental platform under the proposed modulation strategy
参考文献
[1] 彭方正, 房绪鹏, 顾斌, 等. Z源变换器[J]. 电工技术学报, 2004, 19(2): 47-51.
Peng Fangzheng, Fang Xupeng, Gu Bin, et al. Z- source converter[J]. Transactions of China Electro- technical Society, 2004, 19(2): 47-51.
[2] Anderson J, Peng Fangzheng. A class of quasi- Z-source inverters[C]//2008 IEEE Industry Appli- cations Society Annual Meeting, Edmonton, AB, Canada, 2008: 1-7.
[3] 丁新平, 钱照明, 崔彬, 等. 适应负载大范围变动的高性能Z源逆变器[J]. 电工技术学报, 2008, 23(2): 61-67.
Ding Xinping, Qian Zhaoming, Cui Bin, et al. A high-performance Z-source inverter operating at wide-range load[J]. Transactions of China Electro- technical Society, 2008, 23(2): 61-67.
[4] Qian Wei, Peng Fangzheng, Cha H. Trans-Z-source inverters[C]//2010 International Power Electronics Conference, Sapporo, Japan, 2010: 1874-1881.
[5] Loh P C, Li Ding, Blaabjerg F. Γ-Z-source inverters[J]. IEEE Transactions on Power Electronics, 2013, 28(11): 4880-4884.
[6] Li Linlin, Tang Yu. A high set-up quasi-Z-source inverter based on voltage-lifting unit[C]//2014 IEEE Energy Conversion Congress and Exposition, Pittsburgh, PA, USA, 2014: 1880-1886.
[7] Ahmed H F, Cha H, Kim S H, et al. Switched- coupled-inductor quasi-Z-source inverter[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1241-1254.
[8] Ding Xinping, Li Kai, Hao Yangyang, et al. Family of the coupled-inductor multiplier voltage rectifier quasi- Z-source inverters[J]. IEEE Transactions on Industrial Electronics, 2021, 68(6): 4903-4915.
[9] Peng Fangzheng, Shen Miaosen, Qian Zhaoming. Maximum Boost control of the Z-source inverter[J]. IEEE Transactions on Power Electronics, 2005, 20(4): 833-838.
[10] Shen Miaosen, Wang Jin, Joseph A, et al. Constant Boost control of the Z-source inverter to minimize current ripple and voltage stress[J]. IEEE Transa- ctions on Industry Applications, 2006, 42(3): 770- 778.
[11] Ding Xinping, Qian Zhaoming, Xie Yeyuan, et al. A novel ZVS Z-source rectifier[C]//2006 Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition, Dallas, USA, 2006: 1-5.
[12] Loh P C, Vilathgamuwa D M, Lai Y S, et al. Pulse- width modulation of Z-source inverters[J]. IEEE Transactions on Power Electronics, 2005, 20(6): 1346-1355.
[13] Jung J W, Keyhani A. Control of a fuel cell based Z-source converter[J]. IEEE Transactions on Energy Conversion, 2007, 22(2): 467-476.
[14] Zhang Qianfan, Na Tuopu, Song Liwei, et al. A novel modulation for soft-switching three-phase quasi-Z- source rectifier without auxiliary circuit[J]. IEEE Transactions on Industrial Electronics, 2018, 65(6): 5157-5166.
[15] Ali U S, Kamaraj V. A novel space vector PWM for Z-source inverter[C]//2011 1st International Conference on Electrical Energy Systems, Chennai, India, 2011: 82-85.
[16] Liu Yushan, Ge Baoming, Abu-Rub H, et al. Overview of space vector modulations for three- phase Z-source/quasi-Z-source inverters[J]. IEEE Transactions on Power Electronics, 2014, 29(4): 2098-2108.
[17] Mohammadi M, Moghani J S, Milimonfared J. A novel dual switching frequency modulation for Z- source and quasi-Z-source inverters[J]. IEEE Transa- ctions on Industrial Electronics, 2018, 65(6): 5167- 5176.
[18] Abdelhakim A, Davari P, Blaabjerg F, et al. Switching loss reduction in the three-phase quasi-Z-source inverters utilizing modified space vector modulation strategies[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 4045-4060.
[19] 董帅, 张千帆, 王睿, 等. SVPWM控制时双向Z源逆变器电容电压纹波分析[J]. 电工技术学报, 2017, 32(24): 107-114.
Dong Shuai, Zhang Qianfan, Wang Rui, et al. Analysis of capacitor voltage ripple for bi-directional Z-source inverters based on SVPWM[J]. Transactions of China Electrotechnical Society, 2017, 32(24): 107-114.
[20] He Yuyao, Xu Yuhao, Chen Jinping. New space vector modulation strategies to reduce inductor current ripple of Z-source inverter[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(3): 2643- 2654.
[21] Liu Wenjie, Yang Yongheng, Kerekes T, et al. Inductor current ripple analysis and reduction for quasi-Z-source inverters with an improved ZSVM6 strategy[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 7693-7704.
[22] Loh P C, Lim S W, Gao Feng, et al. Three level Z-source inverters using a single LC impedance network[J]. IEEE Transactions on Power Electronics, 2007, 22(2): 706-711.
[23] Xing Xiangyang, Zhang Chenghui, Chen Alian, et al. Space-vector-modulated method for boosting and neutral voltage balancing in Z-source three-level T-type inverter[J]. IEEE Transactions on Industry Applications, 2016, 52(2): 1621-1631.
[24] Dong Shuai, Zhang Qianfan, Cheng Shukang. Analysis of critical inductance and capacitor voltage ripple for a bi-directional Z-source inverter[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 4009-4015.
[25] Hava A M, Kerkman R J, Lipo T A. A high- performance generalized discontinuous PWM algri- thm[J]. IEEE Transactions on Industry Applications, 1998, 34(5): 1059-1071.
Abstract A Z-source inverter is a topology that can replace a two-stage inverter. It can increase the voltage of the DC link by adding a Z-source network and shoot-through vector. The shoot-through current generated by the shoot-through vector is usually large, which increases the switching device losses of the Z-source inverter. In recent studies, some modulation strategies to reduce switching losses, such as DPWM, have been proposed. However, these modulation strategies seldom consider the variation of load power factor. When the load power factor changes, the current phase through the switching device changes, and the switching device losses caused by the original modulation strategy are not optimal. This paper proposes a generalized ZSVM2 modulation strategy. By moving the relative position between the shoot-through current and the AC output current of the switching device, the switching losses are optimized when the load power factor changes.
First, the current passing through the switching device using the ZSVM2 modulation strategy is analyzed. According to the phase relationship between the AC output current and the shoot-through current, the relationship between the average current of the device and the power factor is obtained. Through formula derivation, when the power factor is 1, the phase relationship between the AC output current and the shoot-through current can achieve the lowest average switching current. Secondly, an improved modulation strategy is proposed. During a switching period, the ZSVM2 strategy has a bridge arm that does not use the shoot-through vector. The proposed strategy exploits this to move the shoot-through current relative to the AC output current. When the power factor is less than 1, the AC output current lags the voltage angle φ, and at this time, the shoot-through vector follows the AC output current and also lags the angle j. In this way, the position of the shoot-through vector can be determined according to the output current of the AC side, and the optimal effect of switching losses can be achieved. The proposed improved modulation strategy does not change parameters such as the boost factor of the original modulation strategy, so the switching losses can be compared by the average current of the device. Through the derivation of the formula, it can be known that when the power factor is lower, the switching loss optimization of the proposed modulation strategy is better. The proposed modulation strategy optimizes the average current through the device and thus reduces conduction losses. Finally, due to the redistribution of the bridge arm with the shoot-through vector, the maximum value of the inductance ripple of the proposed modulation is no longer generated at j =p/6. However, it must be re-determined according to the actual operating power factor and modulation parameters. The improved modulation does not affect the use of the inductor ripple optimized modulation algorithm. The proposed modulation strategy can also be applied to the ZSVM1 modulation strategy.
The loss optimization effect is verified by Matlab/Simulink combined with PLECS simulation. The results show that when the power factor is 0.966 and 0.866, the proposed modulation strategy can reduce the switching losses by 3.3% and 9.7%, and the conduction losses by 1.6% and 3.2%, respectively. Simulations show that the proposed modulation strategy slightly increases the total harmonic content THD of the AC output current. A low-power test platform is built to verify the loss optimization effect. The thermal imager shows that when the power factor is 0.866, compared with the ZSVM2 modulation strategy, the proposed ZSVM2 modulation reduces the temperature of the switching device by 1-2 degrees Celsius.
keywords:Z-source inverter, switching losses optimization, Z-source inverter space vector modulations 2 (ZSVM2), space vector modulation
DOI: 10.19595/j.cnki.1000-6753.tces.221183
中图分类号:TM464
江苏省研究生科研与实践创新计划(KYCX22_2533)和中国矿业大学未来科学家计划(2022WLKXJ126)资助项目。
收稿日期 2022-06-21
改稿日期 2022-09-05
姜翼展 男,1988年生,博士研究生,研究方向为Z源逆变器调制和控制策略。E-mail: 290998441@qq.com(通信作者)
张经纬 男,1991年生,博士研究生,研究方向为大功率模块智能驱动技术。E-mail: tb19130011b4@cumt.edu.cn
(编辑 陈 诚)