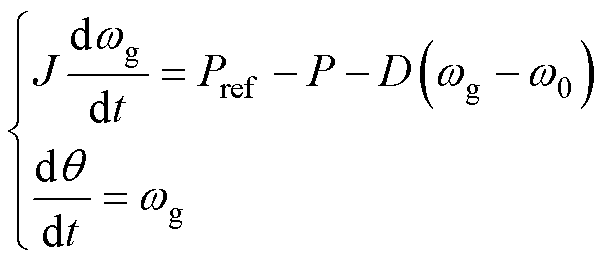 (1)
(1)
摘要 新能源并网换流器采用虚拟同步机(VSG)控制有利于提升电网惯量和阻尼水平,但在电网电压不平衡时存在输出电流畸变和瞬时功率脉动的问题。为灵活调控不平衡电网下VSG输出电流质量与功率纹波,该文提出一种VSG多模式协调策略。首先,研究不平衡电网下的VSG瞬时功率脉动抑制机理,在功率恒定模式分析并网电流谐波特征的基础上,利用VSG虚拟功率计算电流参考指令并引入协调系数对其修正;其次,在多谐振电流内环控制下实现VSG电流平衡-功率恒定多模式协调,并研究协调系数影响及其取值区间选取方法;最后,通过仿真与实验结果验证了该文理论分析与所提控制策略的有效性。
关键词:虚拟同步机 不平衡电网 电流质量 功率纹波 协调控制
在我国“碳达峰、碳中和”目标下电力系统呈现出高比例新能源并网的发展趋势,预计到2060年我国风光能源装机容量和发电量将突破70.1亿kW和11.9亿万kW·h,占电力装机总容量和总发电量比重分别超过85%和69.2%[1-3]。与传统同步电机相比,新能源通过电力电子换流器并网存在低惯量、弱阻尼特点,难以主动为电网提供频率与电压支撑,不利于电网的安全稳定运行[4]。针对以上问题,虚拟同步机(Virtual Synchronous Generator, VSG)技术应运而生[5-6]。VSG通过模拟同步电机的机械与电磁特性以实现电网等效惯量和阻尼提升,在新能源发电并网领域备受关注[7-8]。
构建以新能源为主体的新型电力系统,其核心指标之一为确保新能源并网换流器向电网输送高质量电流与稳定功率。正常电网工况下,通过合理设计VSG控制系统及参数[9-10]不难实现新能源高质量并网。然而我国新能源集中并网地区往往呈现出电网结构薄弱、缺乏无功支撑等特点,易受新能源功率间歇性、强波动性影响,出现电压不平衡现象[11]。与矢量控制类似,当网压不平衡时,VSG控制存在输出电流畸变和瞬时功率二倍频脉动现象[12-13],这无疑会给新能源并网电能质量带来显著的负面影响。因此,研究不平衡电网下的VSG控制策略以抑制电流畸变和功率脉动具有重要意义。
针对上述问题,文献[14-15]开展了不平衡电网VSG正序电流内环设计,然而所提策略仅能实现电流平衡目标。文献[16]在双dq坐标系下提出VSG正、负序电流控制方法,虽可实现电流平衡、有功功率恒定或无功功率恒定三种控制目标,但显著增加了控制复杂度。文献[17]在两相静止坐标系下利用谐振控制器补偿VSG负序电压以实现多种目标,然而难以实现精确的电流跟踪。以上研究均采用基波负序控制思路,不仅难以兼顾有功和无功功率脉动抑制,正负序分离环节还增大了计算负担[18]。对此,文献[19]提出基于拓展功率的VSG策略,无需正负序分离且可实现有功和无功功率同时恒定,然而未考虑不同目标间的协调。已有方法均缺乏对优化目标间影响关系的研究,实现单一目标优化时可能导致其他目标恶化,因此,需提出简单有效、灵活可调的不平衡电网VSG协调控制策略。
本文在分析不平衡电网下VSG并网瞬时功率脉动机理后,深入研究了功率恒定模式下VSG并网电流的谐波分布及其影响规律。以此为基础,首先在两相静止坐标系下利用VSG虚拟功率计算并网电流参考指令并引入协调系数进行修正,通过多谐振电流内环控制基频电流同时补偿谐波电流,实现不平衡电网下VSG多模式协调控制。接着量化分析了协调系数对VSG电流质量、功率纹波的影响并给出其取值区间计算方法。最后通过仿真和实验对本文理论分析与控制策略有效性进行验证。
VSG的本质是从控制层面模拟同步电机动态特性,使得并网换流器外特性等效为同步电机以获得相应的惯量/阻尼特征。传统VSG往往采用二阶同步电机模型,分为有功-频率环和无功-电压环两部分。其中,换流器输出电压相位由有功-频率环产生,其数学模型满足
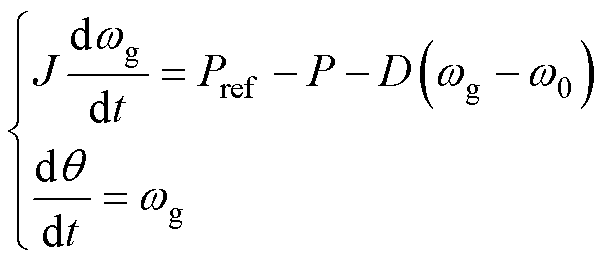 (1)
(1)
式中,J为虚拟转动惯量; 和q 分别为VSG内电动势角频率和相位;D为阻尼系数;
和q 分别为VSG内电动势角频率和相位;D为阻尼系数;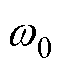 为额定角频率;Pref和P分别为有功功率参考值和实际值。
为额定角频率;Pref和P分别为有功功率参考值和实际值。
换流器输出电压幅值由VSG无功-电压环产生,反映了同步电机的励磁调节特性,即
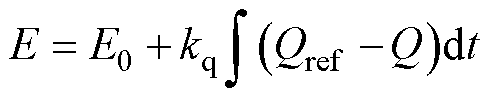 (2)
(2)
式中,E0为额定电压幅值;kq为积分系数;Qref和Q分别为无功功率的参考值和实际值。
有功-频率环生成的相位q 与无功-电压环的幅值E通过式(3)得到VSG参考电压uvj(j=a, b, c),由此可得如图1所示虚拟同步机控制的并网换流器模型。图1中,Rm、Lm为换流器等效并网电阻和电感,usj、isj为采样电网电压与电流,Ls为网侧电感,ugj为网侧电压,Udc为直流电压。当发生网压不平衡时,图1中的VSG并网换流器不具备控制负序和谐波电流以及抑制功率脉动的能力,不仅并网电能质量严重恶化,甚至可能威胁自身安全运行。
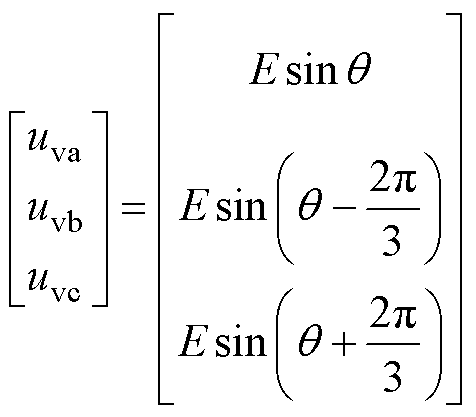 (3)
(3)
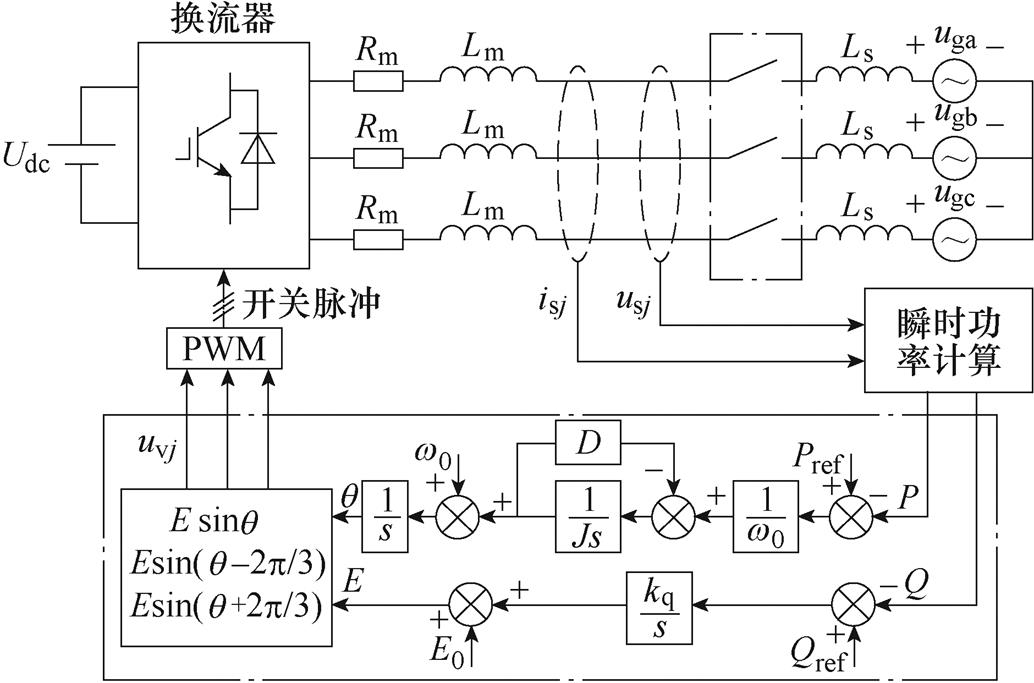
图1 虚拟同步机控制的并网换流器模型
Fig.1 Model of grid-connected converter under VSG
对于图1所示的三相三线制系统,系统内部无零序电流回路,此时不平衡电网电压usj与电流isj可由对应正序、负序分量分别表示为
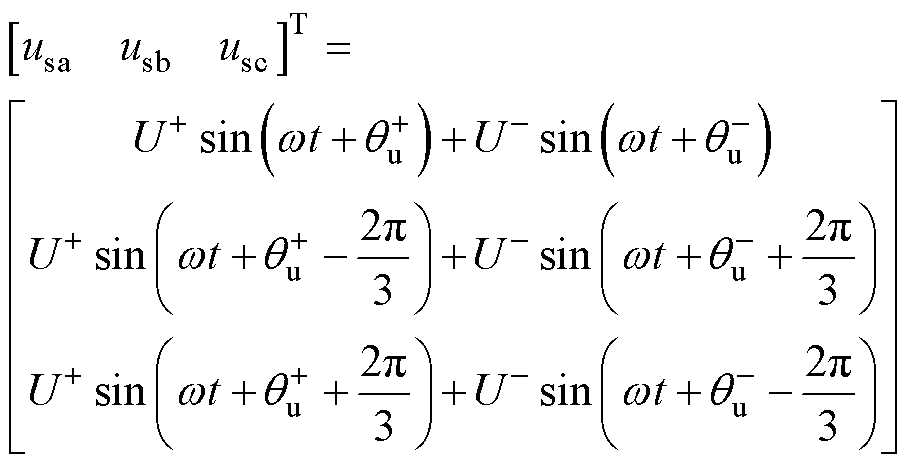 (4)
(4)
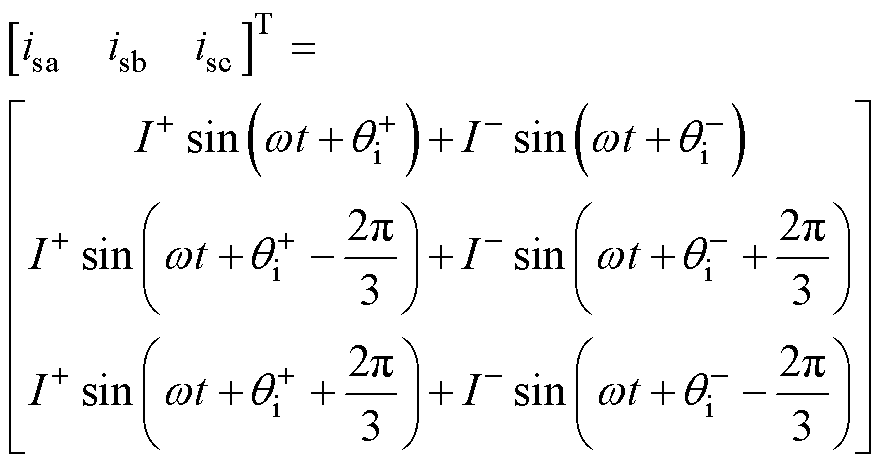 (5)
(5)
式中, 、
、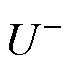 和
和 、
、 分别为电网电压和电流的正、负序分量幅值;
分别为电网电压和电流的正、负序分量幅值;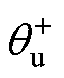 、
、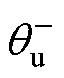 和
和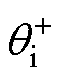 、
、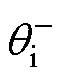 分别为电网电压和电流的正、负序分量初相位;
分别为电网电压和电流的正、负序分量初相位;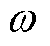 为电网额定角频率。
为电网额定角频率。
式(4)和式(5)经过Clarke变换可得电网电压、电流在两相静止坐标系下的表达式为
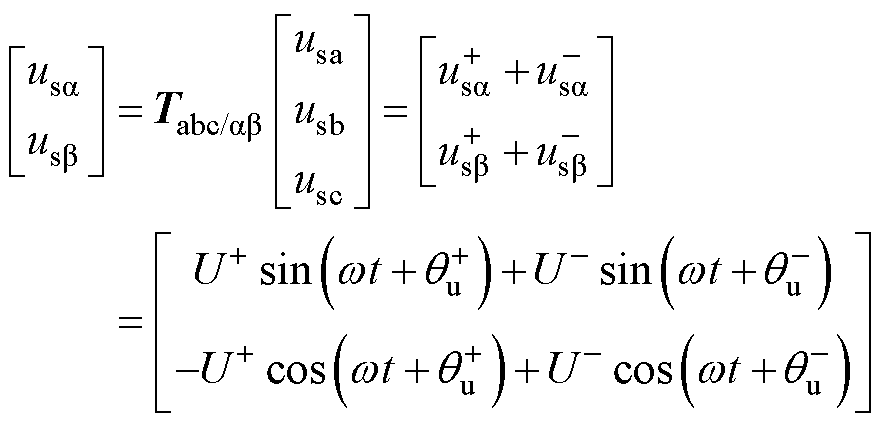 (6)
(6)
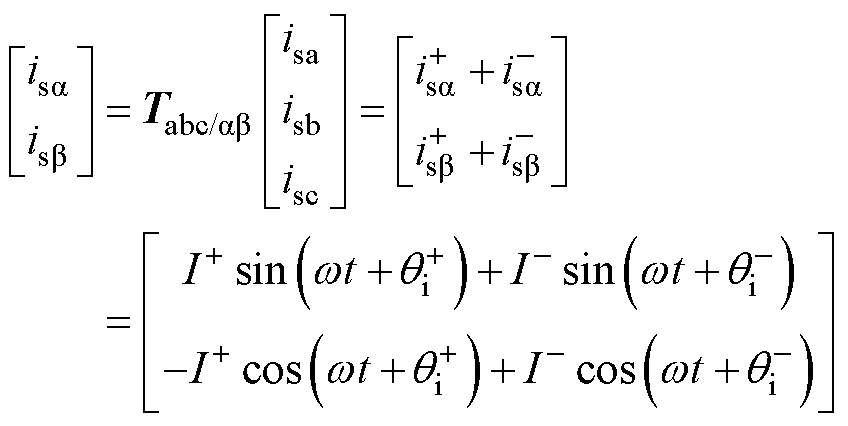 (7)
(7)
式中,下标“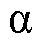 、
、 ”分别表示电网电压usj和电网电流isj在
”分别表示电网电压usj和电网电流isj在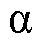 轴和
轴和 轴上的分量;
轴上的分量;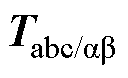 为恒幅值Clarke变换矩阵。
为恒幅值Clarke变换矩阵。
由于负序分量的存在,根据瞬时功率理论可得VSG输出瞬时有功功率P包括直流分量与脉动分量两部分,瞬时无功功率同理。
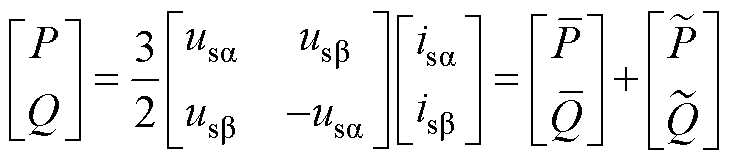 (8)
(8)
其中,瞬时有功、无功功率直流分量分别表示为
 (9)
(9)
而瞬时有功、无功功率脉动分量可分别表示为
 (10)
(10)
在不平衡电网工况下,若控制电网电流负序分量 =0,此时电网电流仅存在正序分量;但由式(10)可知,由于电网电压负序分量
=0,此时电网电流仅存在正序分量;但由式(10)可知,由于电网电压负序分量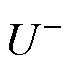 不为0,VSG瞬时有功、无功功率必然存在二倍频脉动分量,且功率脉动幅值与负序电压幅值、正序电流幅值成正比。当电网电流负序分量
不为0,VSG瞬时有功、无功功率必然存在二倍频脉动分量,且功率脉动幅值与负序电压幅值、正序电流幅值成正比。当电网电流负序分量 不为0时,此时有功/无功功率脉动幅值
不为0时,此时有功/无功功率脉动幅值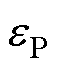 、
、 分别为
分别为
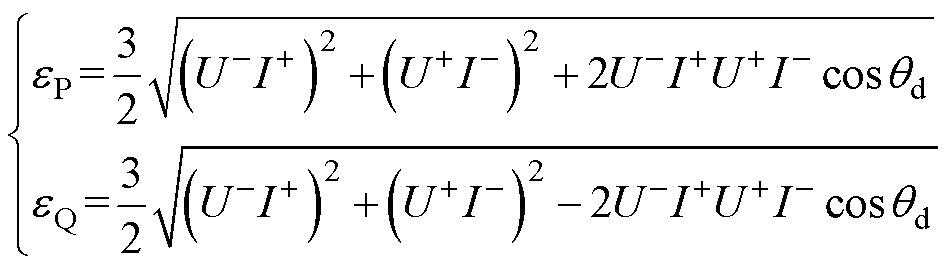 (11)
(11)
其中
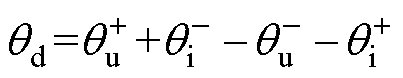
对式(11)量化分析,不失一般性,设定电网电压正序分量幅值为0.8(pu),负序分量幅值为0.2(pu),电网电流正序分量幅值为1.0(pu),此时有功、无功功率脉动幅值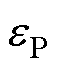 、
、 与电网电流负序分量
与电网电流负序分量 及qd间的三维关系如图2所示。
及qd间的三维关系如图2所示。

图2 有功、无功功率脉动幅值与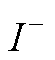 、qd间的关系
、qd间的关系
Fig.2 The relation ship between  ,
, 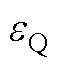 and
and 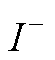 , qd
, qd
图2表明,VSG有功恒定和无功恒定模式下其输出负序电流幅值相等而相位相反,有功和无功功率脉动抑制难以同时兼顾。若将有功恒定作为控制目标将导致无功功率脉动增大;反之,亦然。
为同时抑制VSG有功、无功功率脉动(称之为“功率恒定模式”),需使得有功脉动分量与无功脉动分量幅值均为0,此时并网电流中将出现一系列低次谐波[20]。针对功率恒定模式下VSG并网电流畸变机理与谐波特征展开分析。
功率恒定模式下VSG输出功率仅包含直流分量,可得并网电流满足
 (12)
(12)
考虑电网电压负序分量,式(12)可表示为
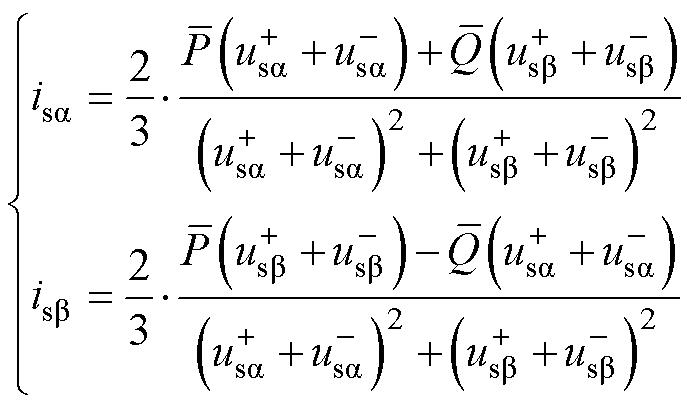 (13)
(13)
式(13)通过Clarke逆变换可得到三相静止坐标系下的电网电流isj表达式。以a相为例,假设电网电压的正、负序分量初始相位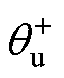 、
、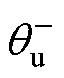 均为零,isa满足
均为零,isa满足
 (14)
(14)
不难发现,isa为周期函数且满足狄利克雷条件,因此根据傅里叶定理可以将其展开为直流分量、基波分量与各次谐波分量之和,即
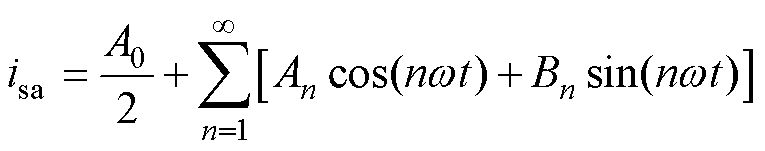 (15)
(15)
式中,A0为直流分量幅值,VSG正常运行时输出电流不含直流分量,即A0=0;An与Bn分别为余弦与正弦各次波动成分的幅值,选取积分区间[-p, p],An、Bn具体表达式分别为
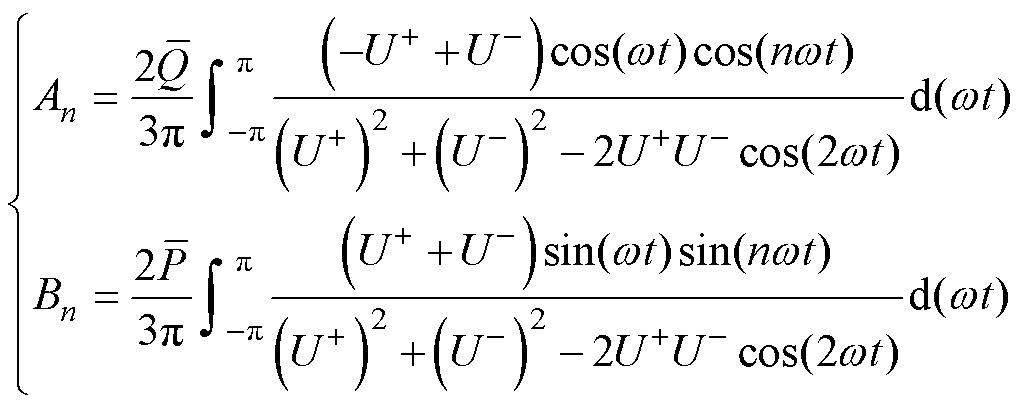 (16)
(16)
由式(16)可知,An、Bn分别与无功、有功功率大小成正比,同时两者与电网电压正、负序分量幅值相关。
由于换流器功率因数仅影响输出电流相位而不影响其幅值,不失一般性,假设VSG工作于额定功率因数,输出有功功率为1.0(pu),无功功率为0(pu),进一步量化分析VSG在功率恒定模式下并网电流成分及其影响规律。考虑到式(15)求解时涉及到多个变量且函数形式较为复杂,为简化分析计算步骤,本文采用函数遍历求解方式,给出电流基波、各次谐波幅值 与电网电压正、负序分量
与电网电压正、负序分量 、
、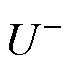 间直观的三维关系,如图3所示。
间直观的三维关系,如图3所示。

图3 各次波动成分幅值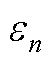 与
与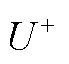 、
、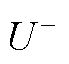 间的关系
间的关系
Fig.3 The relationship between 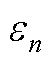 ,
, 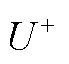 and
and 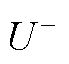
根据图3不难发现,功率恒定模式下VSG并网电流中除基波外还包含3、5、7等低次奇次谐波成分。其中基波分量幅值仅与电网电压正序分量相关。而各次谐波电流幅值随着谐波次数n的升高而减小,与电网电压正、负序分量均相关,其变化趋势为随着电网不平衡度升高而增大。
综上所述,不平衡电网下VSG的瞬时功率直流分量即VSG与电网交换的平均功率,取决于其并网电流中的基波成分;而VSG瞬时功率中的二倍频脉动分量则由各奇次谐波电流共同控制。
因此合理设计VSG控制系统使其在基频与3、5、7次等主要谐波频率处增益足够大,即可实现VSG功率参考值跟踪的同时调控二倍频功率脉动。若控制VSG并网电流跟踪式(12)中电流参考指令,虽三相电流存在畸变,但其有功、无功功率脉动均可完全抑制,处于功率恒定模式。在此基础上逐步抑制并网电流中奇次谐波,VSG功率平均值维持不变,仅二倍频脉动抑制效果削弱;若将对应奇次谐波抑制为零,此时VSG三相电流平衡且不存在谐波,即为电流平衡模式,然而难以避免瞬时有功、无功功率存在二倍频脉动。基于上述思路可完成不平衡电网下VSG多模式协调切换,实现对其输出电流质量与功率纹波灵活统一的调控。
与传统功率控制中并网功率跟踪给定参考值不同,VSG实际并网功率反映了同步电机的惯量/阻尼特征。为不改变VSG上述特性,引入虚拟功率作为式(12)并网电流参考指令计算的功率参考值。
将传统VSG环节中式(3)生成的参考电压uvj变换到ab 坐标系得到uva、uvb,由此计算虚拟电流iva、ivb 表达式为
 (17)
(17)
式中,Dua=usa-uva;Duβ=usb-uvb;Rv、Lv分别为虚拟电阻和电感。由于VSG有功-频率环、无功-电压环中均有积分环节存在,因此虚拟阻抗取值不依赖实际电路参数,本文中设定Rv=Rm,Lv=Lm。
为便于算法实现,引入a、b 轴交叉项对式(17)进行降阶化简,得到稳态虚拟电流表达式为
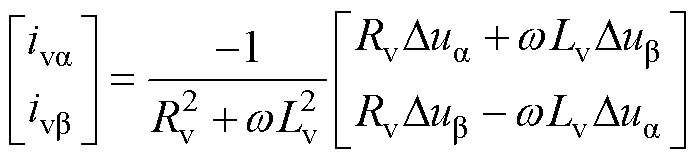 (18)
(18)
进一步结合电网电压计算出VSG虚拟功率参考值Pv、Qv表达式为
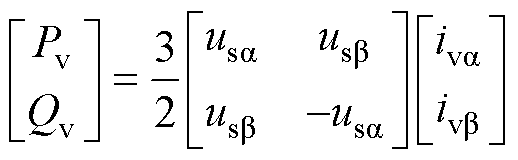 (19)
(19)
由于负序网压会导致虚拟功率参考值中存在二倍频脉动,经过二倍频陷波器可避免功率脉动影响后续控制环节性能。陷波器参数设置合理时仅在陷波频率处增益较小而不妨碍其他频率成分通过,因此对系统动态性能影响较小。陷波器传递函数为
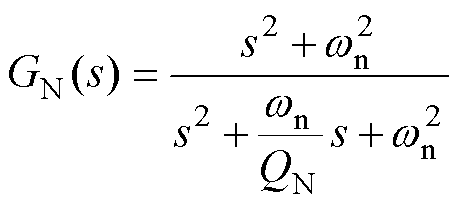 (20)
(20)
式中,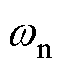 为陷波角频率;QN为品质因数。
为陷波角频率;QN为品质因数。
多谐振电流内环主要由基波控制器与谐波补偿器两部分组成。将陷波后的 、
、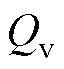 作为式(12)功率参考指令,可得VSG并网电流参考指令为
作为式(12)功率参考指令,可得VSG并网电流参考指令为
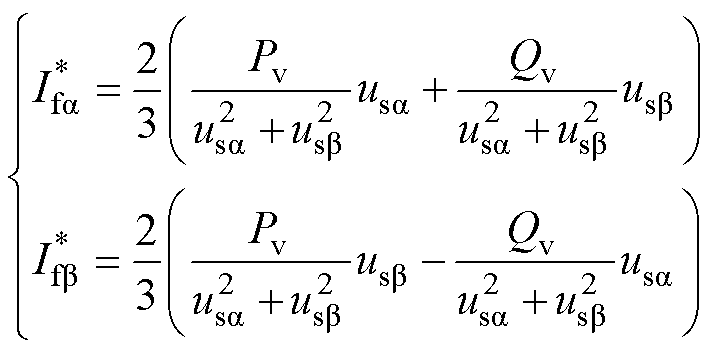 (21)
(21)
采用准比例谐振的基波控制器对VSG并网基频电流进行控制,其传递函数为

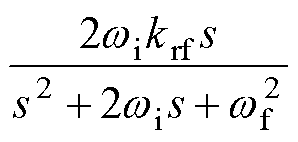 (22)
(22)
式中,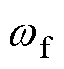 为基频电流角频率;
为基频电流角频率;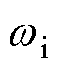 为截止角频率;kpf和krf分别为VSG基波控制器的比例和谐振系数。
为截止角频率;kpf和krf分别为VSG基波控制器的比例和谐振系数。
引入协调系数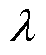 对式(21)并网电流参考指令进行修正,
对式(21)并网电流参考指令进行修正,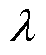 取值范围为[0, 1]。
取值范围为[0, 1]。
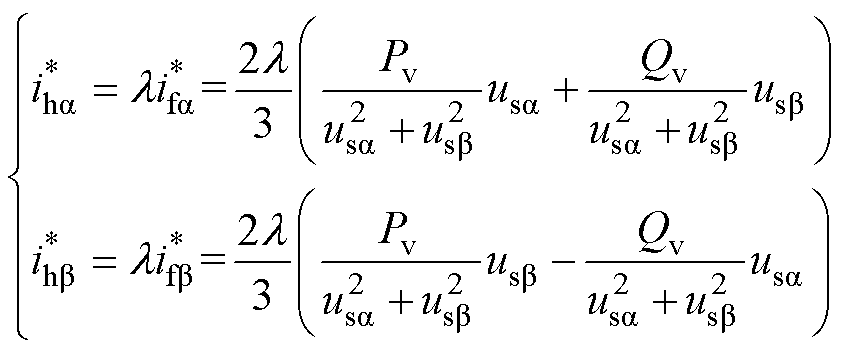 (23)
(23)
通过谐波补偿器跟踪修正后的电流参考指令,对3、5、7次主要谐波进行控制,其传递函数为
 (24)
(24)
式中,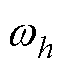 为对应次谐波电流角频率;
为对应次谐波电流角频率;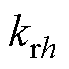 为谐振系数。
为谐振系数。
若三相电网电压平衡,VSG并网电流参考指令中仅存在基频成分,此时谐波补偿器不起作用;当电网电压出现不平衡时,谐波补偿器迅速控制VSG并网电流中的3、5、7次谐波跟踪式(23)中对应谐波参考值,无需故障检测即可快速响应。
将基波控制器和谐波补偿器输出调节量与前馈网压叠加,经过Clarke逆变换得到换流器三相参考调制波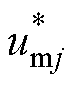 ,不平衡电网下VSG电流平衡-功率恒定多模式协调策略整体框图如图4所示。
,不平衡电网下VSG电流平衡-功率恒定多模式协调策略整体框图如图4所示。

图4 不平衡电网下VSG电流平衡-功率恒定多模式协调策略整体框图
Fig.4 Overall block diagram of VSG balanced-current and constant-power multi-mode coordination strategy
协调系数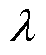 是实现VSG多模式协调的关键参数,灵活、合理地设置其数值可实现调控不平衡电网下VSG输出电流、功率质量的目的。根据2.2节分析,协调系数
是实现VSG多模式协调的关键参数,灵活、合理地设置其数值可实现调控不平衡电网下VSG输出电流、功率质量的目的。根据2.2节分析,协调系数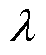 的对VSG电流、功率质量调控具体可体现为电流总谐波畸变率(Total Harmonic Distortion, THD)与功率纹波两个方面。
的对VSG电流、功率质量调控具体可体现为电流总谐波畸变率(Total Harmonic Distortion, THD)与功率纹波两个方面。
VSG多模式协调策略下输出电流THD与协调系数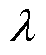 的关系满足
的关系满足
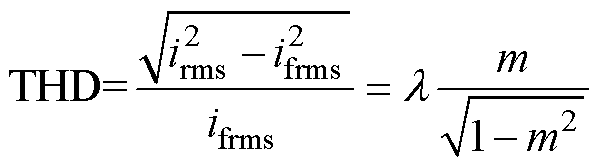 (25)
(25)
式中,m为电网不平衡度,m=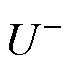 /
/ ;irms为电流有效值;ifrms为电流基频成分有效值。
;irms为电流有效值;ifrms为电流基频成分有效值。
由于VSG有功、无功功率脉动幅值在电流平衡-功率恒定多模式协调过程中均相等,因此对两者不作区分。以有功功率为例,功率纹波表达式为
 (26)
(26)
根据式(25)和式(26)可以得到如图5所示VSG输出电流THD、功率纹波 与协调系数、电网不平衡度的三维关系。
与协调系数、电网不平衡度的三维关系。
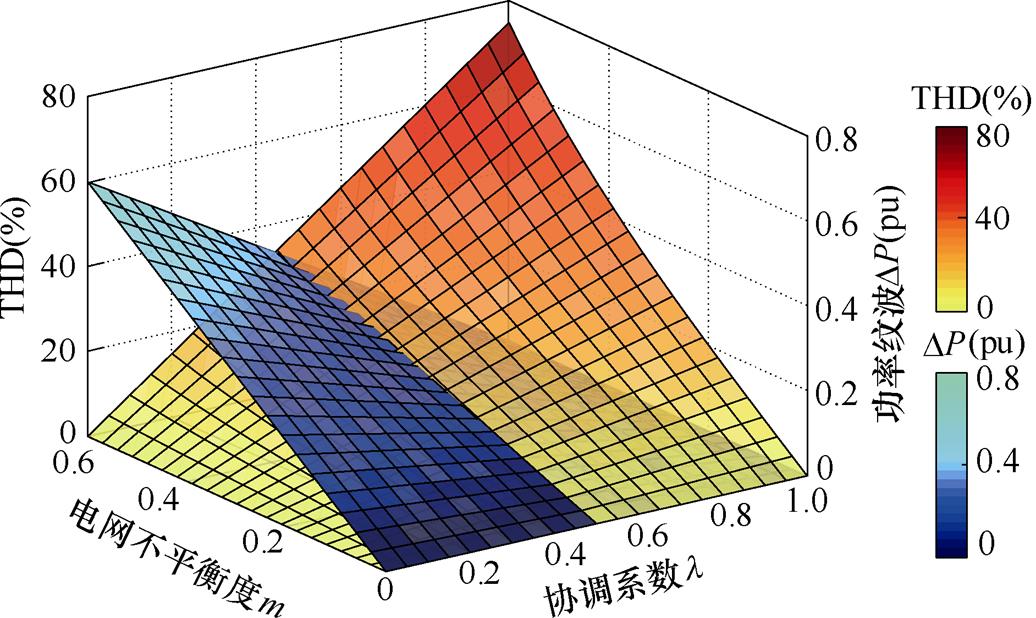
图5 协调系数 影响分析
影响分析
Fig.5 The influences of coordination coefficient 
当 =0时VSG处于电流平衡模式,输出电流质量最佳,但功率纹波达到峰值;随着
=0时VSG处于电流平衡模式,输出电流质量最佳,但功率纹波达到峰值;随着 取值增大,VSG并网电流THD逐渐增大,而功率纹波逐渐减小;当
取值增大,VSG并网电流THD逐渐增大,而功率纹波逐渐减小;当 =1时,VSG处于功率恒定模式,并网电流畸变严重,但有功、无功功率趋于恒定。因此,应根据实际应用场景对VSG并网电流THD与功率纹波稳态指标选取合理的协调系数取值区间。
=1时,VSG处于功率恒定模式,并网电流畸变严重,但有功、无功功率趋于恒定。因此,应根据实际应用场景对VSG并网电流THD与功率纹波稳态指标选取合理的协调系数取值区间。
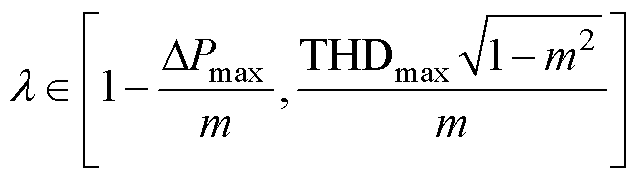 (27)
(27)
式中, 为稳态功率纹波上限;THDmax为并网电流THD上限。
为稳态功率纹波上限;THDmax为并网电流THD上限。
以光伏虚拟同步机的单相电压跌落场景为例,根据相电压UT跌落幅度划分为浅度跌落(0.9(pu)≤ UT<1.0(pu) 、中度跌落(0.2(pu)≤UT<0.9(pu)
、中度跌落(0.2(pu)≤UT<0.9(pu) 与深度跌落(0(pu)≤UT<0.2(pu)),其中深度跌落发生时光伏VSG 0.15 s即可切出[21],因此不对其展开讨论。表1列出了光伏VSG相应指标及协调系数参考取值区间。
与深度跌落(0(pu)≤UT<0.2(pu)),其中深度跌落发生时光伏VSG 0.15 s即可切出[21],因此不对其展开讨论。表1列出了光伏VSG相应指标及协调系数参考取值区间。
表1 光伏VSG指标与参考协调取值区间
Tab.1 Photovoltaic VSG index and the range of 

场景0.9(pu)≤UT<1.0(pu)0.2(pu)≤UT<0.9(pu) 运行需求应持续正常运行应符合相应低电压穿越要求,一定时间内不允许脱网 稳态电流THD(%)≤5≤5 稳态功率误差(%)≤1建议≤10 协调系数参考取值区间
本文中仿真及实验验证均采用模块化多电平换流器(Modular Multilevel Converter, MMC)拓扑。MMC作为典型的中高压、大功率DC-AC换流器拓扑,具有模块化程度高、电压等级易拓展、输出电压谐波含量低等诸多优势,在新能源并网、柔性直流输电等领域有着广泛的应用[22-23]。
MMC采用图4中给出的VSG电流平衡-功率恒定多模式协调策略,结合载波层叠调制与子模块排序均压算法,环流抑制策略则采用通用环流抑制策略,相关MMC底层控制可参考文献[24]。
为了验证所提策略及协调系数影响规律的有效性,在Matlab/Simulink环境下搭建了三相五电平MMC模型进行仿真证明,其参数见表2。
表2 MMC模型仿真参数
Tab.2 Parameters of MMC simulation model

参 数数 值 额定容量/(MV·A)20 直流电压/kV20 交流线电压有效值/kV10 单桥臂子模块数4 交流侧电阻/W0.1 子模块电容/mF5.6 桥臂电感/mH4
4.1.1 控制模式切换与功率指令阶跃响应
为验证本文所提VSG策略控制模式切换以及不同模式下功率指令阶跃响应性能,设置b相电网电压跌落至额定值0.6(pu),此时电网电压不平衡度约为15.4%,在此工况下进行仿真:0.2 s前VSG运行于额定工况且功率因数为1,设置协调系数 为0,VSG处于电流平衡模式,有功功率参考指令20 MW,无功功率参考指令0 Mvar;0.4 s时有功功率指令阶跃至15 MW,VSG运行于3/4额定容量避免过电流;0.8 s时恢复有功功率指令至初始值;1.0 s后设置协调系数
为0,VSG处于电流平衡模式,有功功率参考指令20 MW,无功功率参考指令0 Mvar;0.4 s时有功功率指令阶跃至15 MW,VSG运行于3/4额定容量避免过电流;0.8 s时恢复有功功率指令至初始值;1.0 s后设置协调系数 =1,VSG切换为功率恒定模式;接着1.2 s时设置有功功率参考指令阶跃至16 MW,无功功率参考指令阶跃至12 Mvar,功率因数0.8,部分容量用于输出无功功率支撑电网电压;1.6 s时恢复至额定值。上述仿真过程波形如图6所示。
=1,VSG切换为功率恒定模式;接着1.2 s时设置有功功率参考指令阶跃至16 MW,无功功率参考指令阶跃至12 Mvar,功率因数0.8,部分容量用于输出无功功率支撑电网电压;1.6 s时恢复至额定值。上述仿真过程波形如图6所示。

图6 模式切换与功率指令阶跃仿真波形
Fig.6 Simulation waveforms of mode switching and power reference steps
不难发现,1.0 s时协调系数 由0切换至1,VSG输出模式由电流平衡平滑、迅速地转化为功率恒定模式,切换时间小于0.05 s,验证了电流平衡-功率恒定模式切换的有效性与快速性。在0.4 s和1.2 s功率指令发生阶跃时,VSG虚拟功率参考值Pv、Qv与输出有功、无功功率P、Q均能有效跟踪功率参考指令,同时其暂态变化过程呈现类似同步发电机的惯量/阻尼特性。整个功率阶跃过程大约在0.1 s内完成,说明无论VSG处于电流平衡还是功率恒定模式,其功率指令阶跃响应均具有良好的动态性能。
由0切换至1,VSG输出模式由电流平衡平滑、迅速地转化为功率恒定模式,切换时间小于0.05 s,验证了电流平衡-功率恒定模式切换的有效性与快速性。在0.4 s和1.2 s功率指令发生阶跃时,VSG虚拟功率参考值Pv、Qv与输出有功、无功功率P、Q均能有效跟踪功率参考指令,同时其暂态变化过程呈现类似同步发电机的惯量/阻尼特性。整个功率阶跃过程大约在0.1 s内完成,说明无论VSG处于电流平衡还是功率恒定模式,其功率指令阶跃响应均具有良好的动态性能。
4.1.2 VSG多模式协调控制及协调系数取值验证
VSG给定有功功率参考指令20 MW,无功功率参考指令0 Mvar,设置b相电压跌落至额定值0.7(pu),电压不平衡度约为11.1%,验证了本文所提策略实现多模式协调控制的有效值以及协调系数取值区间计算方法的正确性。0.3 s前设置协调系数 为0,此时VSG处于电流平衡模式;0.3~0.5 s期间使协调系数
为0,此时VSG处于电流平衡模式;0.3~0.5 s期间使协调系数 线性增大至1,实现由电流平衡向功率恒定的多模式协调切换过程;0.5 s后协调系数
线性增大至1,实现由电流平衡向功率恒定的多模式协调切换过程;0.5 s后协调系数 维持为1,VSG运行于功率恒定模式,仿真波形如图7所示。
维持为1,VSG运行于功率恒定模式,仿真波形如图7所示。
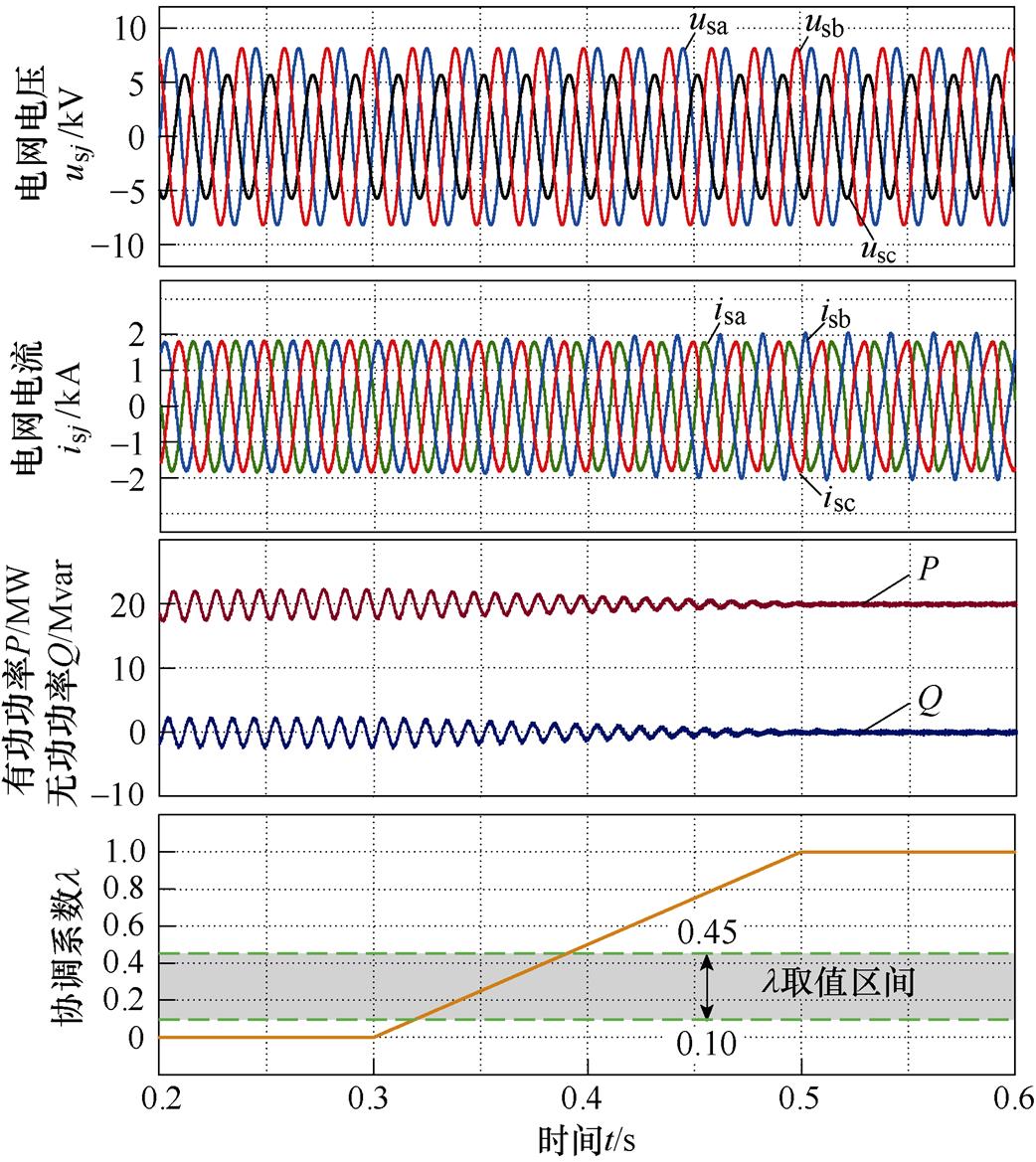
图7 多模式协调控制仿真波形
Fig.7 Simulation waveforms of multi-mode coordination
由图7可知,0.3 s前VSG输出电流三相几乎完全平衡,选取0.2~0.3 s电流波形进行快速傅里叶变换得到其电流THD约为0.97%,但此时VSG输出有功、无功功率存在幅值约为0.11(pu)的二倍频脉动成分。在0.3~0.5 s间,随着协调系数 增大,VSG实现由电流平衡模式过渡到功率恒定模式的多模式协调,该过程中VSG输出电流畸变程度有所增大,但有功、无功功率二倍频脉动逐渐减小。0.5 s后,VSG切换至功率恒定模式,此时输出有功、无功功率二倍频脉动幅值抑制至约0.002(pu),输出电流THD为11.22%,与理论计算吻合。接着根据表1给出的协调系数取值区间表达式,计算得到
增大,VSG实现由电流平衡模式过渡到功率恒定模式的多模式协调,该过程中VSG输出电流畸变程度有所增大,但有功、无功功率二倍频脉动逐渐减小。0.5 s后,VSG切换至功率恒定模式,此时输出有功、无功功率二倍频脉动幅值抑制至约0.002(pu),输出电流THD为11.22%,与理论计算吻合。接着根据表1给出的协调系数取值区间表达式,计算得到 参考取值范围为[0.10, 0.45],选取上述区间内外若干数值点计算VSG稳态电流THD与二倍频功率纹波,其结果见表3。仿真波形与表3结果充分验证了本文所提VSG多模式协调控制有效性与协调系数影响分析及其取值区间计算方法的正确性。
参考取值范围为[0.10, 0.45],选取上述区间内外若干数值点计算VSG稳态电流THD与二倍频功率纹波,其结果见表3。仿真波形与表3结果充分验证了本文所提VSG多模式协调控制有效性与协调系数影响分析及其取值区间计算方法的正确性。
表3 不同协调系数下VSG电流THD与功率纹波
Tab.3 VSG output parameters under different values of 

协调系数l稳态电流THD(%)二倍频功率纹波(pu)是否处于取值区间是否满足指标 0.051.20.107>0.10否否 0.152.00.091是是 0.253.00.085是是 0.404.60.068是是 0.505.7>50.057否否
为进一步验证本文理论分析以及所提VSG多模式协调策略的有效性,搭建如图8所示的三相五电平MMC实验平台,系统参数见表4。

图8 三相五电平MMC实验平台
Fig.8 Three-phase 5-level MMC experimental prototype
表4 MMC实验平台参数
Tab.4 Parameters of MMC experimental prototype
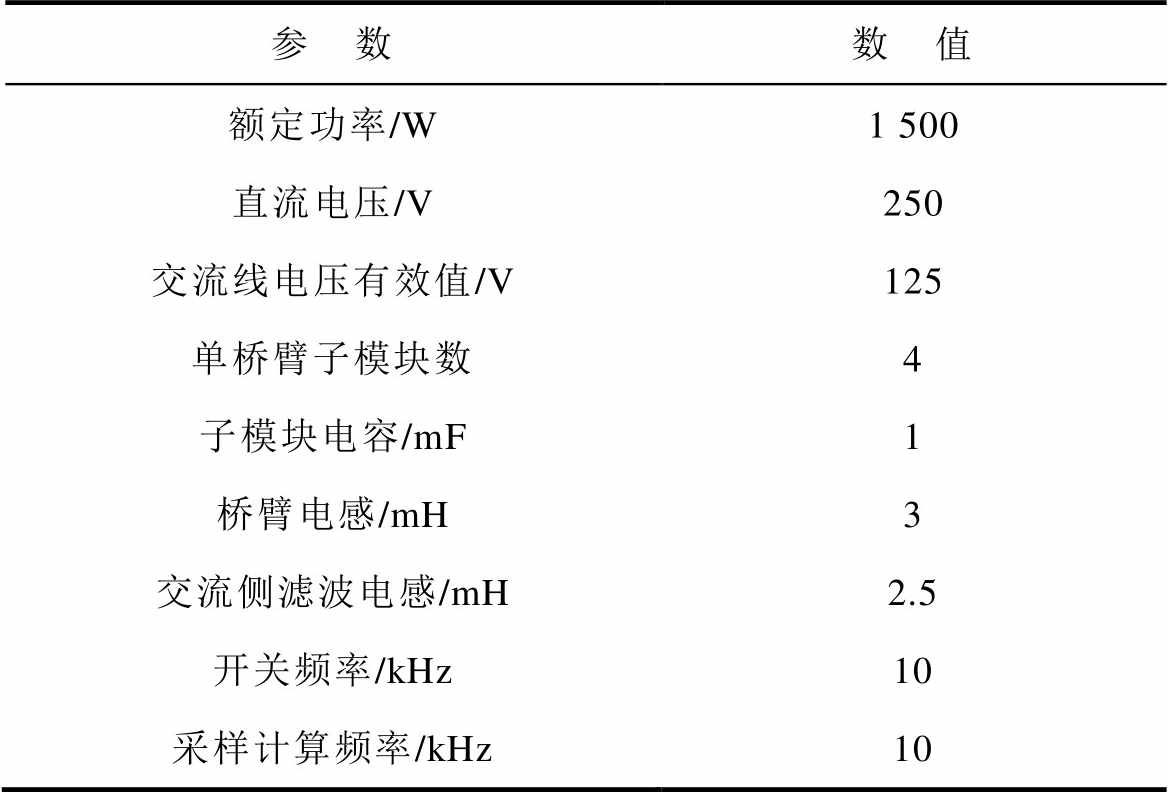
参 数数 值 额定功率/W1 500 直流电压/V250 交流线电压有效值/V125 单桥臂子模块数4 子模块电容/mF1 桥臂电感/mH3 交流侧滤波电感/mH2.5 开关频率/kHz10 采样计算频率/kHz10
在网侧b相电压降低至0.6(pu)的不平衡工况下分别针对VSG电流平衡、功率恒定模式以及多模式协调控制工况进行实验验证。图9和图10分别为电流平衡和功率恒定模式下的VSG输出波形。可以观察到,在电流平衡模式下VSG输出电流三相正弦度较好,但此时有功、无功功率存在二倍频脉动,脉动峰-峰值约为0.33(pu);图10实验结果显示,功率恒定模式下VSG瞬时有功、无功功率二倍频脉动得到较好抑制,但输出电流存在一定畸变。
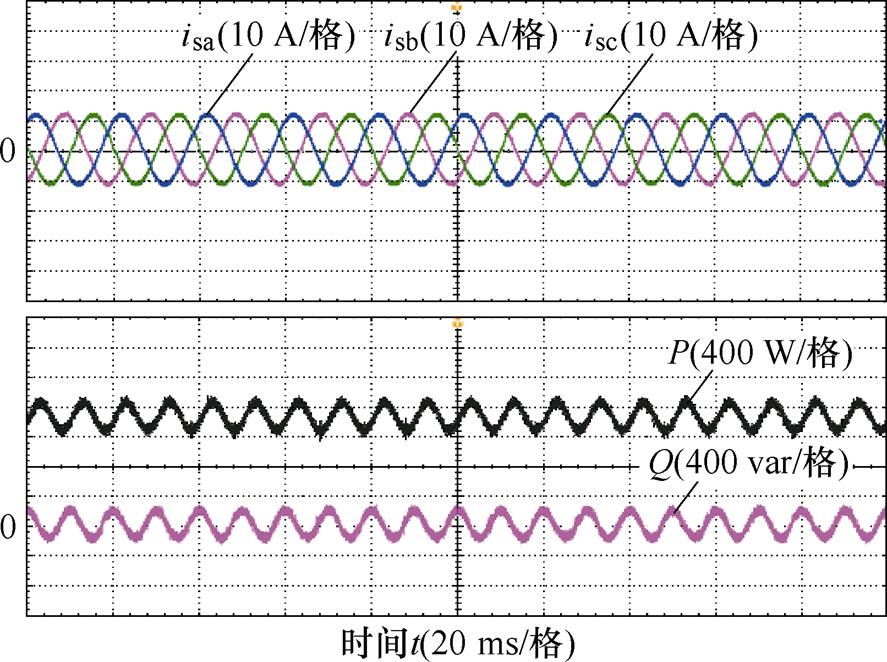
图9 电流平衡模式下VSG输出波形
Fig.9 VSG output waveforms of balanced-current mode
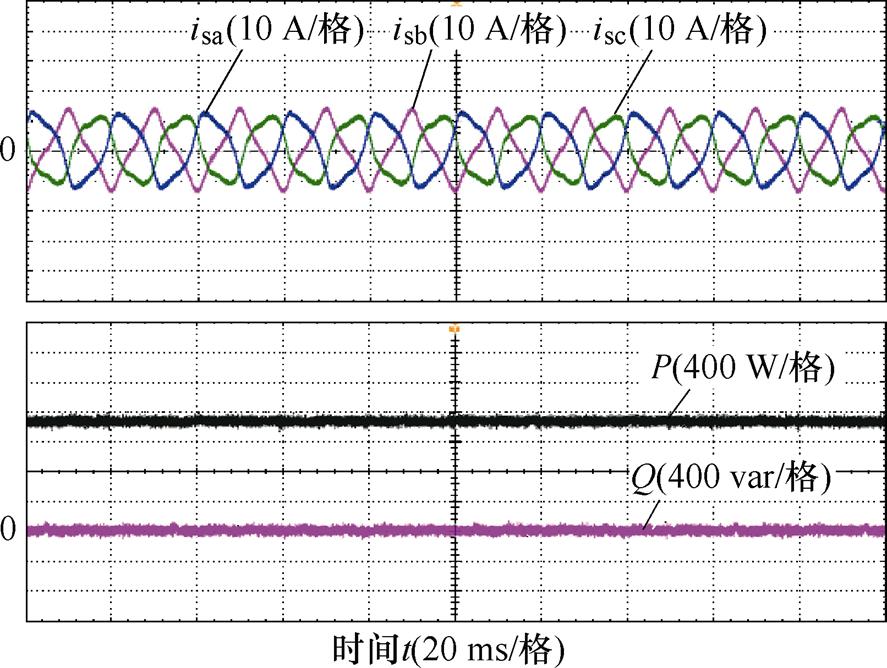
图10 功率恒定模式下VSG输出波形
Fig.10 VSG output waveforms of constant-power mode
为进一步验证准确性,取三个电流周期进行快速傅里叶变换分析两种模式下VSG三相电流谐波成分,结果如图11所示。不难发现,在功率恒定模式下VSG三相电流均存在3、5、7次谐波,且幅值随谐波次序升高而减小。而切换为电流平衡模式后,3、5、7次谐波均得到了较好的抑制,此时VSG输出电流中几乎仅包含三相平衡的基频分量。上述实验分析结果验证了本文理论分析与所提VSG电流平衡-功率恒定多模式协调策略的有效性。
图12为协调系数 由0线性增大至1过程中的VSG输出电流与功率波形。可见随着协调系数
由0线性增大至1过程中的VSG输出电流与功率波形。可见随着协调系数 的增大,VSG输出电流畸变程度增大,功率脉动幅值降低,实现了电流平衡-功率恒定多模式协调切换。为进一步验证本文协调系数影响分析的正确性,对VSG多模式协调切换过程中的电流THD、功率纹波参数进行量化分析,并与理论计算值对照,其结果如图13所示。图13对比结果显示,VSG多模式协调切换过程中,随着协调系数
的增大,VSG输出电流畸变程度增大,功率脉动幅值降低,实现了电流平衡-功率恒定多模式协调切换。为进一步验证本文协调系数影响分析的正确性,对VSG多模式协调切换过程中的电流THD、功率纹波参数进行量化分析,并与理论计算值对照,其结果如图13所示。图13对比结果显示,VSG多模式协调切换过程中,随着协调系数 取值增大,电流THD线性增大同时功率纹波线性减小,其变化趋势与理论计算较为贴近。实际应用中可参考式(27)中协调系数取值区间选取方式,综合VSG输出电流THD、功率纹波指标需求以最终选定适宜的协调系数。
取值增大,电流THD线性增大同时功率纹波线性减小,其变化趋势与理论计算较为贴近。实际应用中可参考式(27)中协调系数取值区间选取方式,综合VSG输出电流THD、功率纹波指标需求以最终选定适宜的协调系数。

图11 两种模式下VSG电流谐波成分分析
Fig.11 Analysis of VSG harmonic current components in two modes
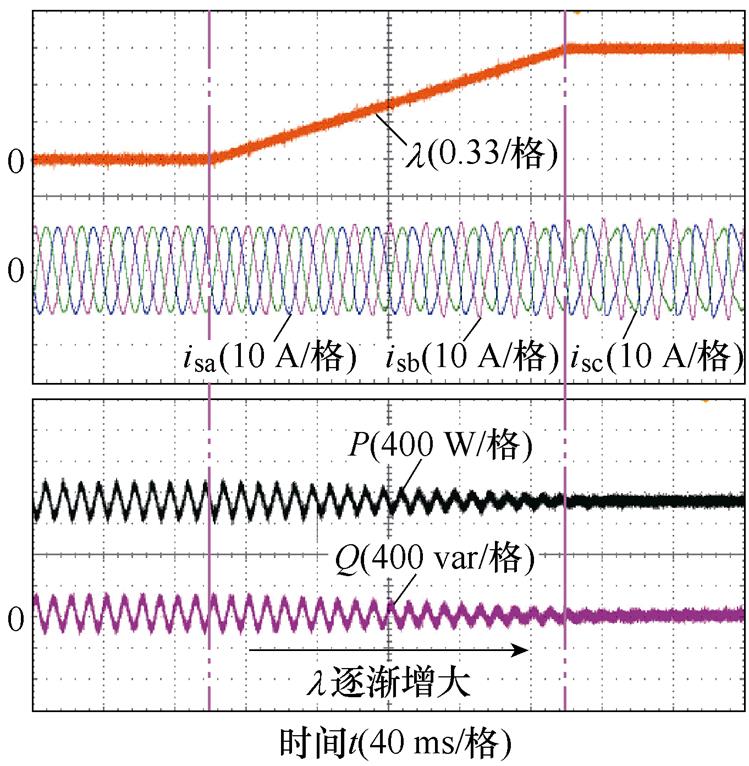
图12 多模式协调过程波形
Fig.12 Waveforms of multi-mode coordination process
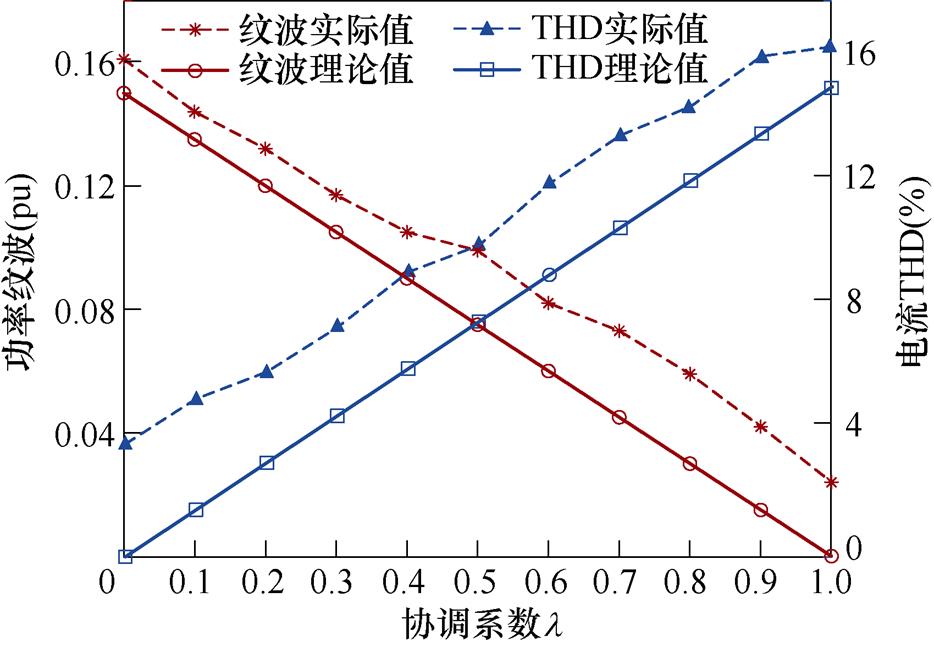
图13 实验值与理论值对照
Fig.13 Comparison of experimental and theoretical results
本文分析了不平衡电网下VSG瞬时功率脉动与输出电流畸变机理,提出一种VSG电流平衡-功率恒定多模式协调策略,并对协调系数影响及其取值区间选取方法展开讨论,研究结果表明:
1)基波负序控制难以实现功率恒定模式,在该模式下VSG输出电流将不可避免地存在低次奇次谐波,谐波幅值与电网不平衡度呈正相关。
2)本文所提策略可实现不平衡电压下VSG电流平衡-功率恒定多模式协调控制,灵活调控VSG输出电流质量和功率纹波,且动态响应性能较优。
3)该方法无需正负序分离与双dq坐标变换,简化控制结构并减轻了计算负担,具有一定工程应用价值。
参考文献
[1] 周孝信, 陈树勇, 鲁宗相, 等. 能源转型中我国新一代电力系统的技术特征[J]. 中国电机工程学报, 2018, 38(7): 1893-1904, 2205.
Zhou Xiaoxin, Chen Shuyong, Lu Zongxiang, et al. Technology features of the new generation power system in China[J]. Proceedings of the CSEE, 2018, 38(7): 1893-1904, 2205.
[2] 刘钊汛, 秦亮, 杨诗琦, 等. 面向新型电力系统的电力电子变流器虚拟同步控制方法评述[J]. 电网技术, 2023, 47(1): 1-16.
Liu Zhaoxun, Qin Liang, Yang Shiqi, et al. Review on virtual synchronous generator control technology of power electronic converter in power system based on new energy[J]. Power System Technology, 2023, 47(1): 1-16.
[3] 张子扬, 张宁, 杜尔顺, 等. 双高电力系统频率安全问题评述及其应对措施[J]. 中国电机工程学报, 2022, 42(1): 1-25.
Zhang Ziyang, Zhang Ning, Du Ershun, et al. Review and countermeasures on frequency security issues of power systems with high shares of renewables and power electronics[J]. Proceedings of the CSEE, 2022, 42(1): 1-25.
[4] 郑军铭, 冯丽, 蔡志远, 等. 提高短时中断故障期间新能源微电网稳定性的惯性储能永磁发电机组[J]. 电工技术学报, 2022, 37(23): 6000-6010.
Zheng Junming, Feng Li, Cai Zhiyuan, et al. The inertia motivity permanent magnet machine set for improving the stability of new energy microgrid during short-term interruption[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6000- 6010.
[5] Zhong Qingchang, Weiss G. Synchronverters: inver- ters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.
[6] 于彦雪, 关万琳, 陈晓光, 等. 基于序阻抗的虚拟同步机同步频率谐振现象[J]. 电工技术学报, 2022, 37(10): 2584-2595.
Yu Yanxue, Guan Wanlin, Chen Xiaoguang, et al. Synchronous frequency resonance in virtual syn- chronous generator based on sequence-impedance[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2584-2595.
[7] 胡石阳, 刘国荣. 基于虚拟同步机的新能源并网智能控制研究[J]. 电气技术, 2022, 23(10): 10-17.
Hu Shiyang, Liu Guorong. Research on intelligent control of grid connected new energy based on virtual synchronous machine[J]. Electrical Engineering, 2022, 23(10): 10-17.
[8] 章艳, 高晗, 张萌. 不同虚拟同步机控制下双馈风机系统频率响应差异研究[J]. 电工技术学报, 2020, 35(13): 2889-2900.
Zhang Yan, Gao Han, Zhang Meng. Research on frequency response difference of doubly-fed indu- ction generator system controlled by different virtual synchronous generator controls[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2889- 2900.
[9] 孟建辉, 王毅, 石新春, 等. 基于虚拟同步发电机的分布式逆变电源控制策略及参数分析[J]. 电工技术学报, 2014, 29(12): 1-10.
Meng Jianhui, Wang Yi, Shi Xinchun, et al. Control strategy and parameter analysis of distributed inverters based on VSG[J]. Transactions of China Electrotechnical Society, 2014, 29(12): 1-10.
[10] 颜湘武, 张伟超, 崔森, 等. 基于虚拟同步机的电压源逆变器频率响应时域特性和自适应参数设计[J]. 电工技术学报, 2021, 36(增刊1): 241-254.
Yan Xiangwu, Zhang Weichao, Cui Sen, et al. Frequency response characteristics and adaptive parameter tuning of voltage-sourced converters under VSG control[J]. Transactions of China Electro- technical Society, 2021, 36(S1): 241-254.
[11] 刘其辉, 逄思敏, 吴林林, 等. 大规模风电汇集系统电压不平衡机理、因素及影响规律[J]. 电工技术学报, 2022, 37(21): 5435-5450.
Liu Qihui, Pang Simin, Wu Linlin, et al. The mechanism, factors and influence rules of voltage imbalance in wind power integration areas[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(21): 5435-5450.
[12] 缪惠宇, 梅飞, 张宸宇, 等. 基于虚拟阻抗的虚拟同步整流器三相不平衡控制策略[J]. 电工技术学报, 2019, 34(17): 3622-3630.
Miao Huiyu, Mei Fei, Zhang Chenyu, et al. Three phase unbalanced control strategy for virtual syn- chronous rectifier based on virtual impedance[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3622-3630.
[13] 韦徵, 姬秋华, 王伟, 等. 适用于电网不对称下的自同步电压源逆变器控制策略[J]. 电力系统自动化, 2021, 45(10): 124-131.
Wei Zheng, Ji Qiuhua, Wang Wei, et al. Control strategy of self-synchronous voltage source inverter for asymmetric power grid[J]. Automation of Electric Power Systems, 2021, 45(10): 124-131.
[14] 陈天一, 陈来军, 汪雨辰, 等. 考虑不平衡电网电压的虚拟同步发电机平衡电流控制方法[J]. 电网技术, 2016, 40(3): 904-909.
Chen Tianyi, Chen Laijun, Wang Yuchen, et al. Balanced current control of virtual synchronous generator considering unbalanced grid voltage[J]. Power System Technology, 2016, 40(3): 904-909.
[15] Zheng Xuemei, Wang Chao, Pang Songnan. Injecting positive-sequence current virtual synchronous gen- erator control under unbalanced grid[J]. IET Rene- wable Power Generation, 2019, 13(1): 165-170.
[16] 万晓凤, 胡海林, 聂晓艺, 等. 电网电压不平衡时的改进虚拟同步机控制策略[J]. 电网技术, 2017, 41(11): 3573-3581.
Wan Xiaofeng, Hu Hailin, Nie Xiaoyi, et al. An improved control strategy for virtual synchronous generator under unbalanced grid voltage[J]. Power System Technology, 2017, 41(11): 3573-3581.
[17] 肖湘宁, 陈萌. 不平衡电压下虚拟同步发电机功率控制策略[J]. 电力自动化设备, 2017, 37(8): 193-200.
Xiao Xiangning, Chen Meng. Power control of virtual synchronous generator under unbalanced grid voltage[J]. Electric Power Automation Equipment, 2017, 37(8): 193-200.
[18] Wang Yichao, Li Xiangqi, Li Yan. Power-current coordinated control without sequence extraction under unbalanced voltage conditions[J]. IET Power Electronics, 2020, 13(11): 2274-2280.
[19] 王仰铭, 孙丹, 年珩, 等. 不平衡电网下自同步虚拟同步机拓展功率控制策略研究[J]. 电网技术, 2020, 44(9): 3368-3375.
Wang Yangming, Sun Dan, Nian Heng, et al. Extended power control strategy of self-synchronized virtual synchronous generator under unbalanced power grid[J]. Power System Technology, 2020, 44(9): 3368-3375.
[20] 郭小强, 张学, 卢志刚, 等. 不平衡电网电压下光伏并网逆变器功率/电流质量协调控制策略[J]. 中国电机工程学报, 2014, 34(3): 346-353.
Guo Xiaoqiang, Zhang Xue, Lu Zhigang, et al. Coordinate control of power and current quality for grid-connected PV inverters under unbalanced grid voltage[J]. Proceedings of the CSEE, 2014, 34(3): 346-353.
[21] 国家市场监督管理总局, 国家标准化管理委员会. 光伏发电并网逆变器技术要求: GB/T 37408-2019[S]. 北京: 中国标准出版社, 2019.
[22] 杨晓峰, 林智钦, 郑琼林, 等. 模块组合多电平变换器的研究综述[J]. 中国电机工程学报, 2013, 33(6): 1-15.
Yang Xiaofeng, Lin Zhiqin, Zheng Trillion Q, et al. A review of modular multilevel converters[J]. Pro- ceedings of the CSEE, 2013, 33(6): 1-15.
[23] 孟沛彧, 向往, 潘尔生, 等. 分址建设直流输电系统拓扑方案与运行特性研究[J]. 电工技术学报, 2022, 37(19): 4808-4822.
Meng Peiyu, Xiang Wang, Pan Ersheng, et al. Research on topology and operation characteristics of HVDC transmission system based on site-division construction[J]. Transactions of China Electro- technical Society, 2022, 37(19): 4808-4822.
[24] Pan Zixun, Yang Xiaofeng, Li Zejie, et al. Coor- dinated power control strategy of modified electrical energy router[C]//IEEE Energy Conversion Congress and Exposition(ECCE), Detroit, MI, USA, 2020: 4849-4856.
Abstract Virtual synchronous generator control has been widely studied in renewable energy generation to provide equivalent inertia support for the power grid. However, current distortion and power oscillation occur severely when the grid voltage becomes unbalanced, significantly aggravating the power supply quality of renewable energy generation. The existing methods generally take the fundamental-frequency negative-sequence component as the VSG control object to solve the above issues. It is obvious that positive-negative sequence separation increases the calculation burden, and active and reactive power oscillations cannot be suppressed simultaneously. In addition, the mutual influence between optimization targets is rarely considered, so the realization of one optimization target may lead to the deterioration of the others. Therefore, this paper proposes a multi-mode coordination control of VSG and quantitatively analyzes the restrictive relation of VSG current distortion and power fluctuation under an unbalanced power grid.
This paper first analyzes the VSG power oscillation mechanism under an unbalanced power grid and then further studies the harmonic components of VSG grid-connected current in constant-power mode. The results indicate that VSG grid-connected current contains low-order odd harmonic components, and the proportion determines double-line frequency active and reactive power oscillation. On this basis, the initial current reference is obtained from VSG virtual power calculation to maintain the operating characteristics of the synchronous machine. Then a multi-resonance current inner loop controls the fundamental frequency current and the harmonic components. It should be noted that the coordination coefficient is introduced to modify the current reference of the harmonic controller, thereby realizing the VSG multi-mode coordination control. Finally, the influence of the coordination coefficient on VSG current quality and power ripple is quantified, and the calculation method of selection range is given.
In order to validate the effectiveness of the proposed method, a modular multilevel converter (MMC) is selected as the grid-connected AC-DC topology, and the simulation and experiment are respectively performed on Matlab/Simulink platform and a three-phase five-level MMC prototype. In the simulation, the power step performance of the proposed method is well verified under balanced-current and constant-power modes. After that, VSG multi-mode coordination control and the corresponding coordination coefficient selection method are simulated, which verifies the proposed method. As for the experiment, the verification is carried out when the b-phase voltage drops to 0.6(pu). The experiment waveforms and the components of VSG current under the two typical modes further verified the validity of the aforementioned theoretical analysis and the control strategy. In the process of VSG multi-mode coordination, the experimental results show that the trends of current total harmonic distortion and the power ripple are consistent with the theoretical calculation.
The following conclusions can be drawn from this paper: (1) Under an unbalanced power grid, the VSG grid-connected current appears as low-order odd harmonic components in constant-power mode, and the amplitude is positively related to the voltage imbalance degree. (2) The proposed method can realize the multi-mode coordinated control between balanced-current and constant-power modes to flexibly regulate the VSG output current quality and power ripple. (3) This method simplifies the control and reduces the calculation burden without positive-negative sequence separation and double dq transformation.
keywords:Virtual synchronous generator, unbalanced power grid, current quality, power ripple, coor- dinated control
DOI: 10.19595/j.cnki.1000-6753.tces.L10082
中图分类号:TM46
新能源与储能运行控制国家重点实验室(中国电力科学研究院有限公司)开放基金资助项目(DGB51202101307)。
收稿日期 2023-01-13
改稿日期 2023-02-16
潘子迅 男,1998年生,硕士研究生,研究方向为模块化多电平换流器控制技术与应用。E-mail: 20121478@bjtu.edu.cn
杨晓峰 男,1980年生,副教授,博士生导师,研究方向为多电平变换器、柔性直流输电、宽禁带半导体及电力电子技术在轨道交通中的应用等。E-mail: xfyang@bjtu.edu.cn(通信作者)
(编辑 陈 诚)