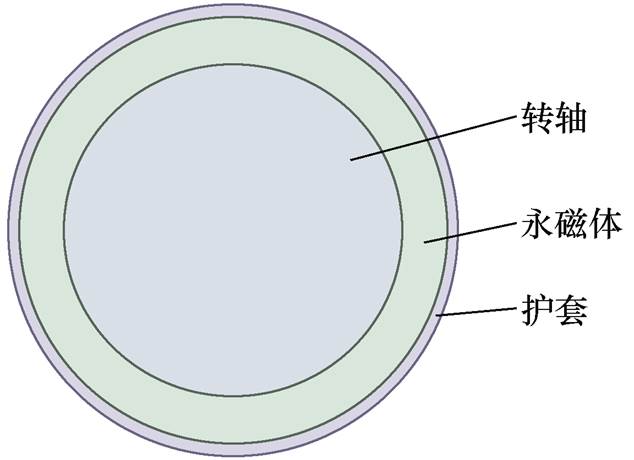
图1 表贴式高速永磁电机转子示意图
Fig.1 Cross section of surface mounted HSPMM rotor
摘要 该文对高速永磁电机(HSPMM)转子过盈方式对转子应力的影响进行研究。首先,在二维极坐标下建立了转子各部位统一几何模型的应力场数学模型,可求解不同边界条件下转轴、永磁体和护套的径向应力和周向应力。然后,基于建立的应力场数学模型得到不同过盈方式下转子应力的解析计算方法,分析了不同过盈方式对转子应力的影响。在此基础上,提出“虚拟过盈”概念及虚拟过盈下的应力计算表达式,分析了其准确度并解释了其物理意义。最后,通过有限元(FEM)分析方法对一台额定功率为50 kW、额定转速为40 000 r/min的高速永磁电机进行分析,说明了不同的过盈方式导致转子应力的差异,验证了理论分析的合理性。
关键词:高速永磁电机 应力 过盈 数学模型
高速电机体积小、结构紧凑、功率密度高,与高速原动机或负载相连时可省去齿轮箱等机械设备,提高系统的可靠性。高速电机在涡轮机、油泵、飞轮储能等场合有着广泛应用[1-5]。在众多高速电机拓扑中,永磁电机凭借其效率高、结构简单等优势,在高速电机领域得到了较多关注[6-8]。
高速永磁电机(High Speed Permanent Magnet Machine, HSPMM)转子多采用实心转子和表贴式永磁体结构[9-10]。永磁体的抗拉强度通常较低,若不对永磁体加以保护,在高速旋转时永磁体会破碎以至整体断裂,导致电机损坏[11-12]。因此,高速永磁电机需要用高强度材料(如钛合金[13]、碳纤维[14])制成的护套来保护永磁体。通过永磁体和护套之间的过盈配合来给永磁体施加一定的压力,以抵消高速旋转时的离心力[15]。
在进行高速电机设计时,其应力的计算和校验至关重要。因此,众多学者围绕高速永磁电机转子强度开展了相关研究。文献[5, 12, 16]研究了护套厚度对转子应力的影响,文献[17]提出了一种护套厚度最小的设计方法,文献[10, 18-19]对不同材料的护套以及护套表面开槽对转子应力的影响进行了分析。除了研究温度[10, 20]、永磁体间填充物[12, 16]、轴间填充物[21]对转子强度的影响外,过盈量[5, 12, 16, 22]对转子应力的影响也是众多学者关注的问题。
现有研究主要关注过盈量对转子应力的影响,往往忽略了过盈方式这一影响因素。事实上,护套和永磁体之间的过盈配合对转子整体应力的影响很大[22]。受限于电磁功率,或为了提高材料利用率,留给永磁体或护套的应力裕量有限。若设计时未考虑不同过盈方式下电机转子应力分布差异,当电机运行点位于材料应力极限值附近时,转子强度的安全度将大大降低,甚至可能导致高速永磁电机设计失败。因此,过盈方式对高速永磁电机转子的应力影响不可忽视,在核算转子应力时必须加以重视。
本文首先建立了表贴式高速永磁电机转子应力求解的数学模型。在此基础上,研究了不同过盈方式对转子应力的影响,并提出了“虚拟过盈”的概念。进一步地,通过有限元分析方法对一台额定功率为50 kW,额定转速为40 000 r/min的高速永磁电机进行了分析,说明在护套厚度较小时,虽然过盈量相同,但不同的过盈方式将导致明显的应力差异,尤其是永磁体上的应力。最后,在额定转速和超转两种工况下,对比了不同过盈方式下转子核心部件(永磁体和护套)的应力,以更高的安全度为准则,确定了更优的过盈方式。
本文以表贴式高速永磁电机转子结构进行分析,如图1所示。电机转子由转轴、永磁体和护套组成,它们都可归结为圆筒结构,如图2所示。圆筒内半径为R1,外半径为R2,转轴可视为R1=0的圆筒。做应力分析时做如下假设:①忽略万有引力;②认为转子位于真空之中;③不考虑轴向应力与应变;④不考虑磁致伸缩效应及磁力。

图1 表贴式高速永磁电机转子示意图
Fig.1 Cross section of surface mounted HSPMM rotor
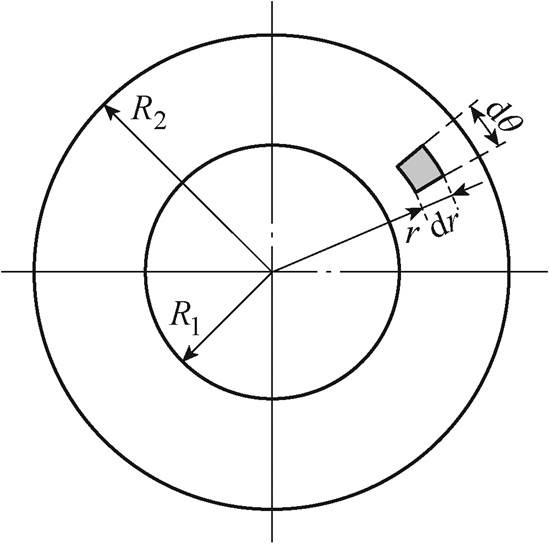
图2 一般圆筒尺寸
Fig.2 Cylinder dimension
取图2中一微元体drdq 于圆筒上并对其进行受力分析。微元体ABCD所受应力的参考方向如图3所示,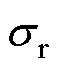 为径向正应力,
为径向正应力,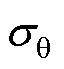 为周向正应力,应力为正时表示拉应力,为负时表示压应力。
为周向正应力,应力为正时表示拉应力,为负时表示压应力。
径向应力和周向应力的关系[23]为
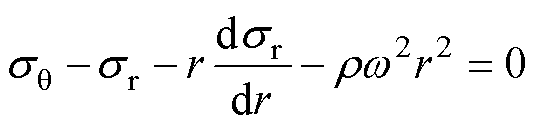 (1)
(1)
式中,r 为材料密度;w 为旋转机械角速度。
将式(1)结合弹性本构方程和柔度矩阵[24]得
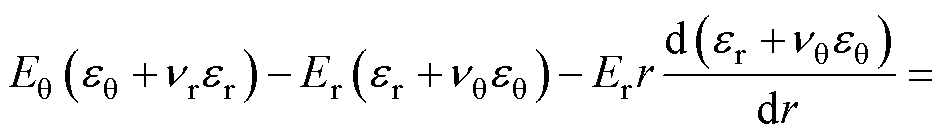
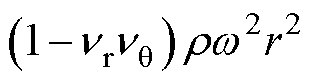 (2)
(2)
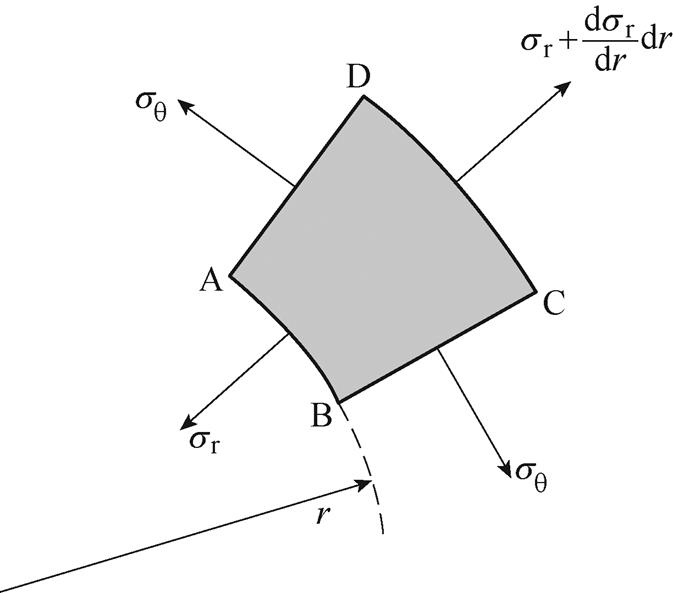
图3 微元体应力
Fig.3 Stress of miro unit
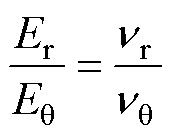 (3)
(3)
式中,er为径向正应变;eq 为周向正应变;Er、Eq分别为材料的径向和周向杨氏模量;nq、nr分别为材料的周向和径向泊松比。
当材料各相同性时,有
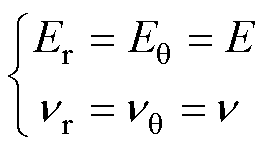 (4)
(4)
式中,E和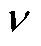 分别为材料杨氏模量和泊松比。
分别为材料杨氏模量和泊松比。
式(2)中有er、eq 两个未知量,需加上形变的“几何条件”进行求解。在物体形变过程中,微元体的空间位置(径向位置)会发生变化,可用位移u来表示,u是r的函数。图4展示了微元体的位移(实线为初始位置,虚线为终末位置)。根据应变定义,可表达为
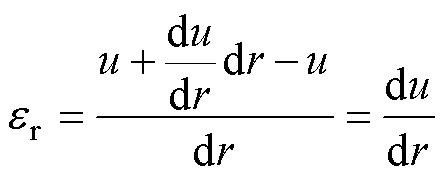 (5)
(5)
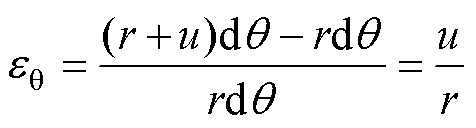 (6)
(6)
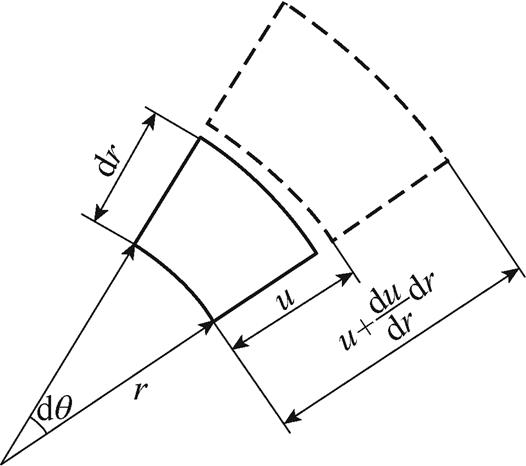
图4 微元体的位移
Fig.4 Displacement of miro unit
将式(5)、式(6)代入式(2),并结合式(3)得
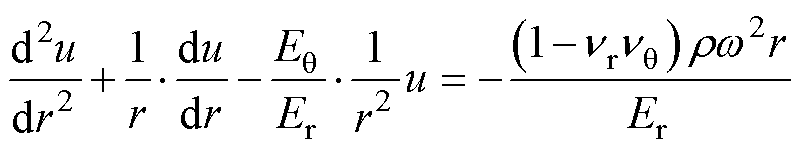 (7)
(7)
由式(7)可得
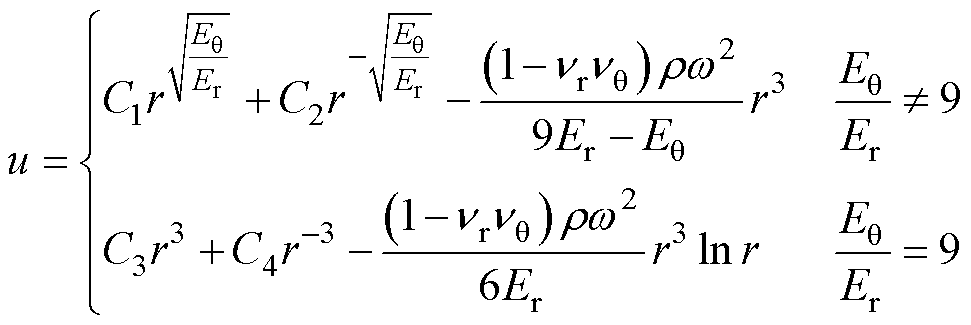 (8)
(8)
式中,C1~C4为由边界条件确定的积分常数。目前,对转子应力分析中,主要考虑周向/径向杨氏模量之比不等于9的各向异性材料[17, 25],因此本文对于周向/径向杨氏模量之比等于9的材料不展开分析。当材料各向同性时,式(8)可表示为
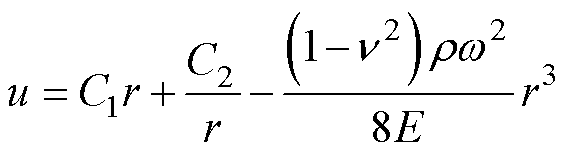 (9)
(9)
令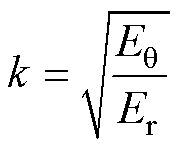 ,把式(9)代入式(5)和式(6),结合弹性本构方程得到应力表达式,分别为
,把式(9)代入式(5)和式(6),结合弹性本构方程得到应力表达式,分别为
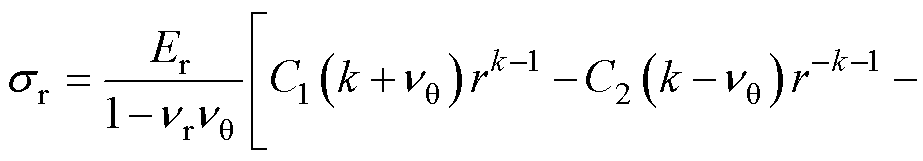
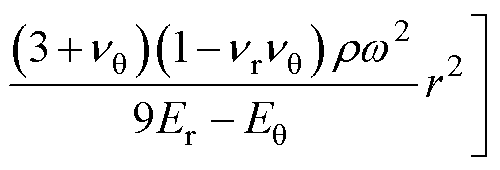 (10)
(10)
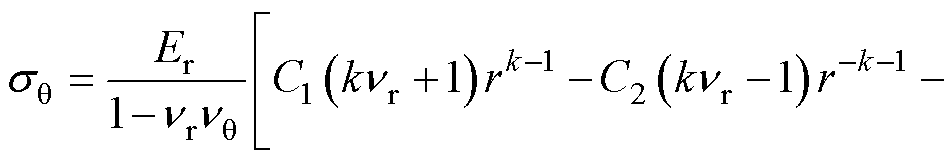
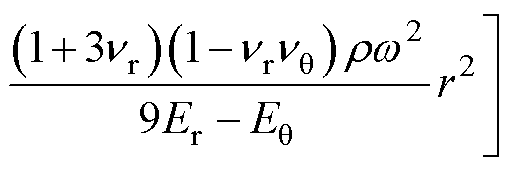 (11)
(11)
当材料各向同性时,式(10)和式(11)可表示为
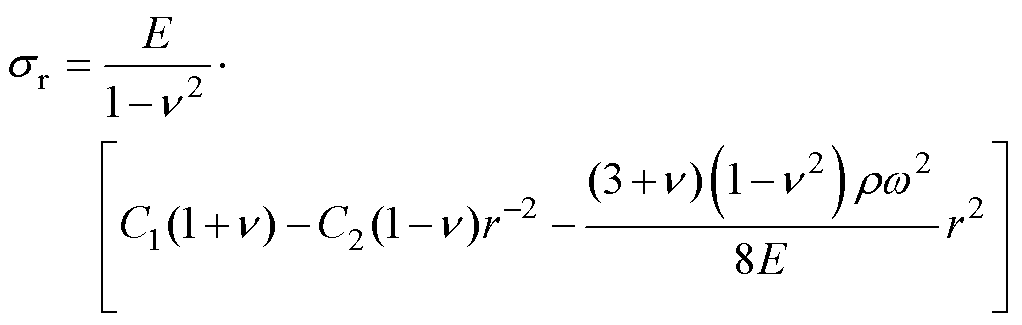 (12)
(12)
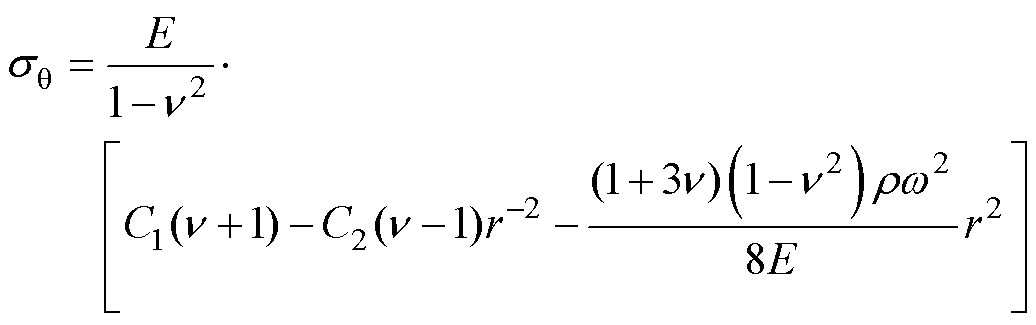 (13)
(13)
可知,求解应力分布的关键是确定表达式中的待定积分常数。两个待定常数需两个边界来确定,即圆筒内、外表面的受力情况。
圆筒受力示意图如图5所示,当圆筒表面受均匀力,内外表面受到的压强分别为Pin和Pout。图中标出了压强的参考正方向,与拉应力对应。当圆筒表面受正压力时,Pin和Pout为负值。根据给定条件,边界条件为
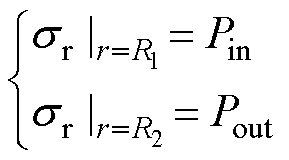 (14)
(14)
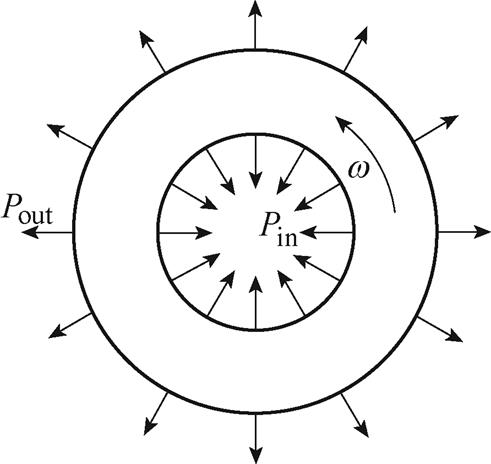
图5 圆筒受力示意图
Fig.5 Force on cylinder
由此边界条件可解出待定常数C1和C2。由式(12)和式(13)即得应力分布表达式,可表示为
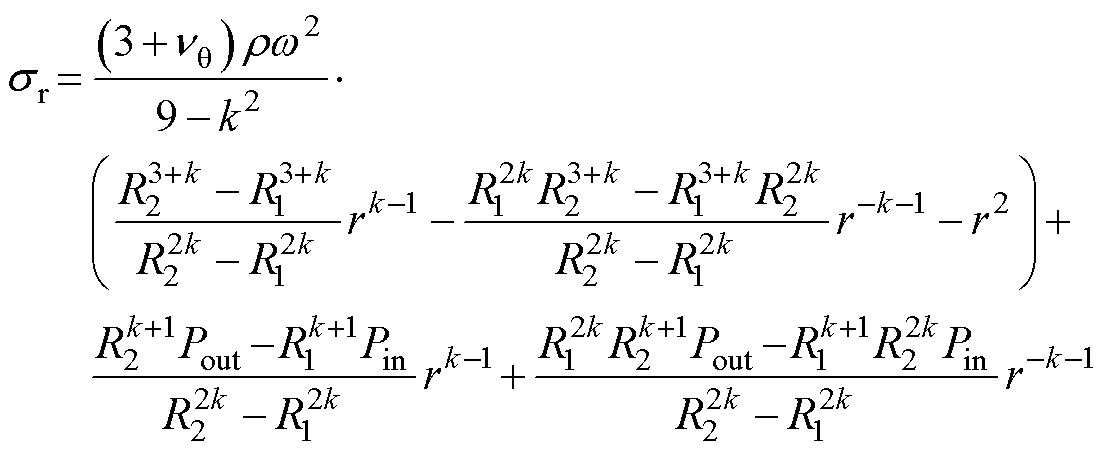 (15)
(15)
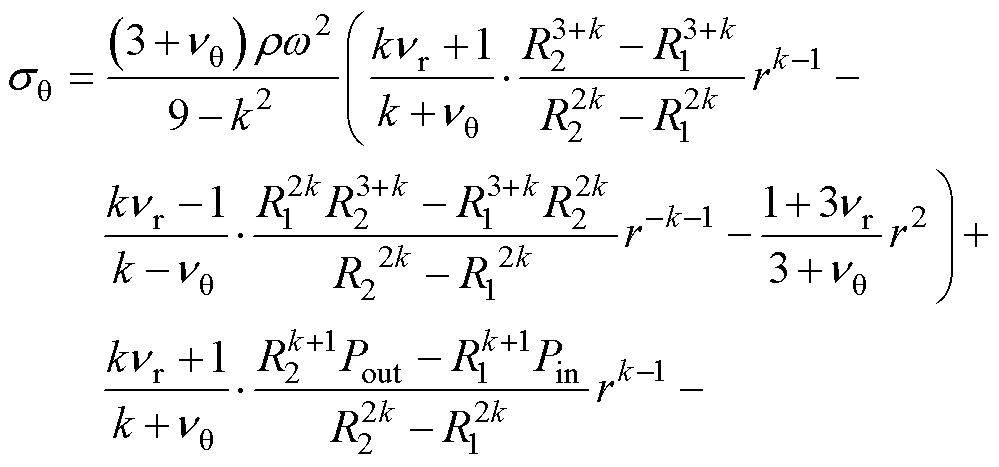
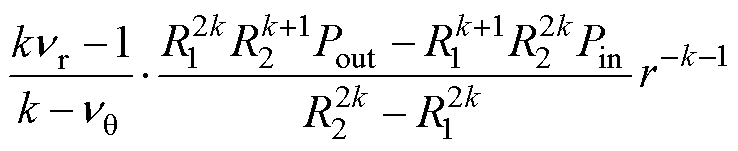 (16)
(16)
当材料各向同性时,式(15)和式(16)可简化为
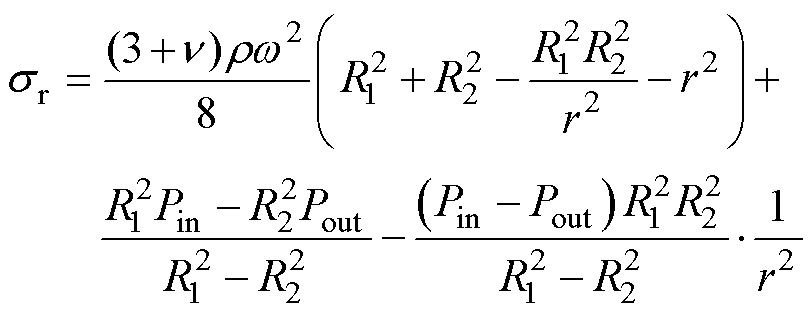 (17)
(17)
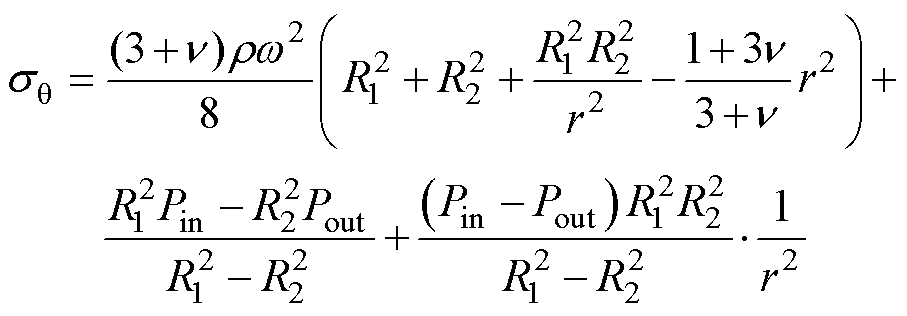 (18)
(18)
高速电机转子的转轴和永磁体通常采用各向同性材料,即满足式(4),而护套材料既有各向同性(如钛合金)也有各向异性(如碳纤维)。由于各向同性材料可看作是各向异性材料的特殊情况,本节以各向异性的护套和各向同性的转轴和永磁体为例进行转子应力分析。
表1 转子各部件材料属性
Tab.1 Material properties of each component of rotor
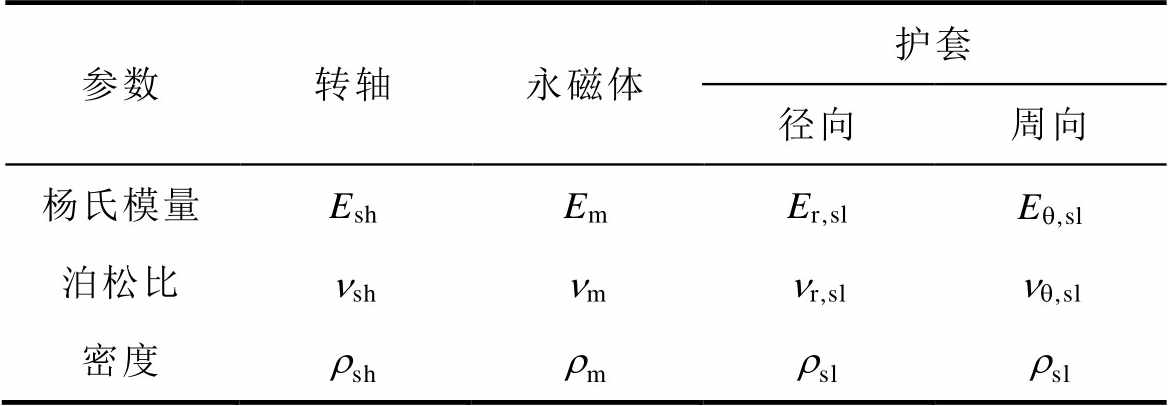
参数转轴永磁体护套 径向周向 杨氏模量EshEmEr,slEq,sl 泊松比nshnmnr,slnq,sl 密度rshrmrslrsl
以计算永磁体应力为例,把表1中材料属性代入式(17)和式(18),结合转子尺寸,可得到永磁体的应力分布为
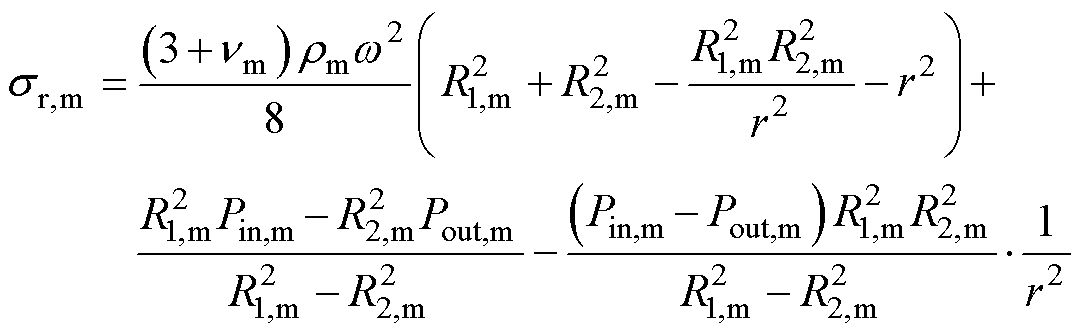 (19)
(19)
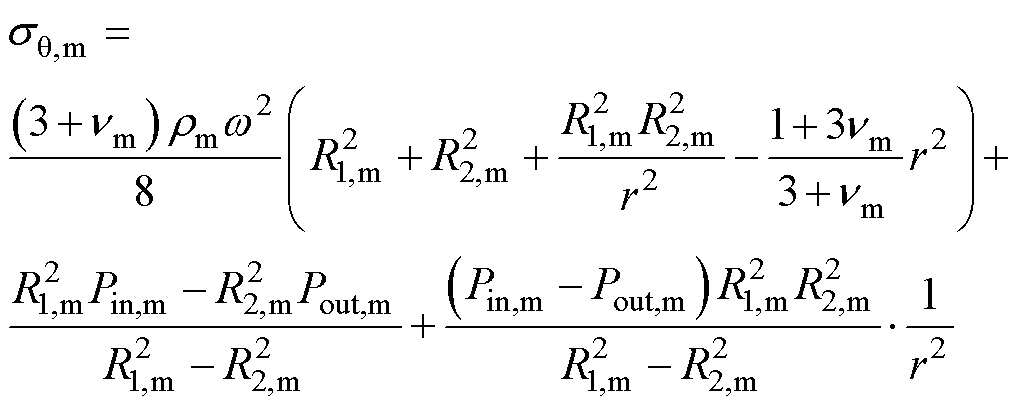 (20)
(20)
同理可求转轴和护套的应力分布,限于篇幅,相关方程不再一一列出。至此,可求出整个转子的应力分布。从上述表达式可知,总的应力由旋转分量和表面压力分量叠加而成。从理论上论证了给高速转子的永磁体加护套的原因——因高速旋转造成的拉应力可与来自护套的压力相抵消,抵消的程度由护套施加的压力决定。因此,若要精确计算转子应力,不仅要准确计算高速旋转导致的应力,还要正确获取护套施加的压力。高速旋转导致的应力计算较容易,而因护套压力抵消的应力由于涉及过盈技术,计算较复杂,因而有必要研究过盈方式对应力的影响。
过盈装配是获得预紧力的有效手段[26],具体有压入法和温差法两种。图6为温差法的过盈装配流程:初始状态下,轴径大于孔径;通过热胀冷缩原理,使孔径变大或轴径变小;当轴径不大于孔径时,将轴安入孔中,待两者恢复常温,完成装配。
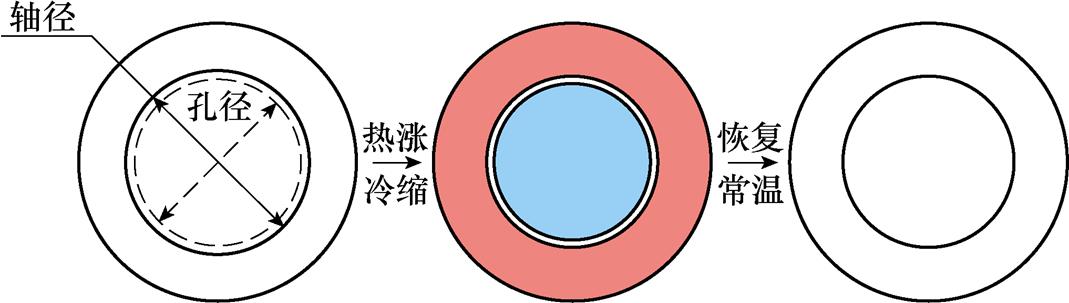
图6 温差过盈装配
Fig.6 Shrink fitting by temperature difference
考虑机械加工过程,圆筒(柱)的尺寸指的是常温下未装配前各零部件尺寸。过盈量一般由轴或孔的其中一方提供,视具体情况而定。也就是过盈量在轴上或者孔上,通常不会由两者同时提供。以下举例说明。现有半径为10 mm的轴和孔,若要实现过盈配合,则需把轴做大或把孔做小。若过盈量要求0.1 mm,则有两种方案:方案1:轴的半径为10.1 mm,孔的半径为10 mm;方案2:轴的半径为10 mm,孔的半径为9.9 mm。
这两种方案导致的应力分布不同,装配后交界面所在的半径位置也不同。对于方案1,交界面所在区间为10~10.1 mm;对于方案2,交界面所在区间为9.9~10 mm。过盈配合后,两个零件的交界面上的压强相等,用此压强衡量两种方案带来的应力差异是合适的。
没有过盈量时,设内圆柱半径同时也是圆筒内径为Ra,圆筒外径为Rb。加入过盈量后,设过盈量为DR。对于两种过盈方式,各零件的尺寸见表2。
表2 两种过盈方式的加工尺寸
Tab.2 Processing dimensions of two shrink fitting modes

参数方案1方案2 轴半径Ra+DRRa 圆筒内径RaRa-DR 圆筒外径RbRb
静止时,对于方案1过盈方式,根据式(9)计算轴外缘位移ui1为
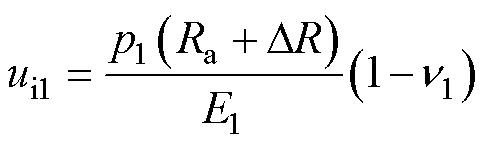 (21)
(21)
式中,E1为轴的杨氏模量;n1为轴的泊松比;p1为方案1过盈方式的接触面压强,参考方向与图5一致,下同。
圆筒内缘位移uo1为
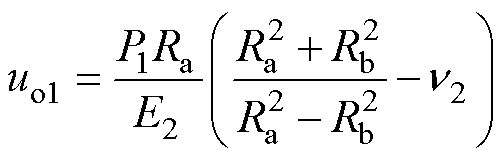 (22)
(22)
式中,E2为圆筒的杨氏模量;n2为圆筒的泊松比。
过盈量与以上两位移量满足
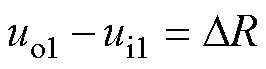 (23)
(23)
联立式(21)~式(23),得到方案1过盈方式的接触面压强为
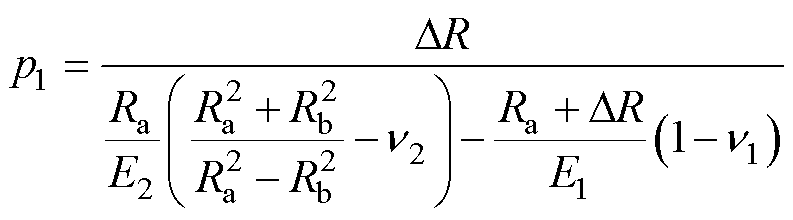 (24)
(24)
同理,方案2过盈方式的接触面压强为
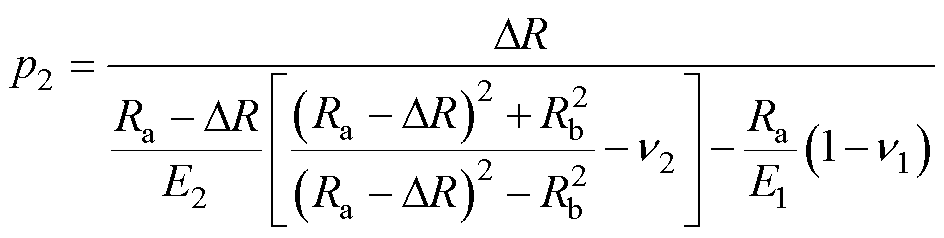 (25)
(25)
为便于讨论,假设轴和圆筒为同一种材料,则式(24)和式(25)可简化为
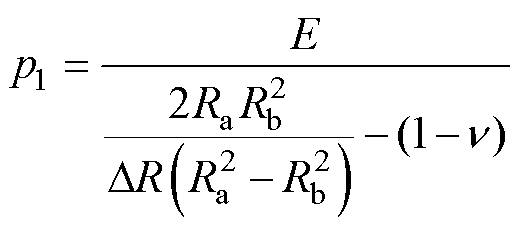 (26)
(26)
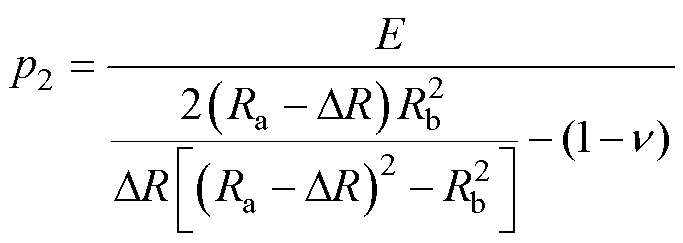 (27)
(27)
当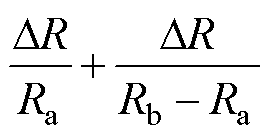 趋于零时,则可得到
趋于零时,则可得到
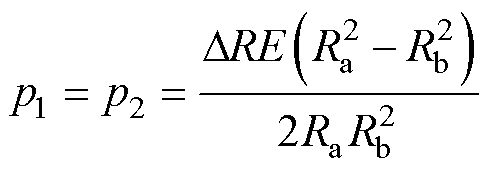 (28)
(28)
式(28)的意义是:当过盈量相较于零件尺寸很小时,两种过盈方案产生的应力效果一样,条件中Ra是圆柱的半径,Rb-Ra则表示了圆筒的径向厚度,但式(28)只在数学上有意义。
若抛开极限条件,定义虚拟的“方案3过盈方式”,这种方案产生的接触面压强为
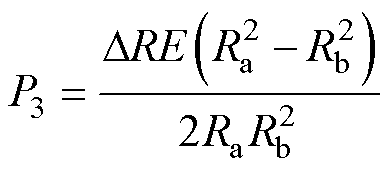 (29)
(29)
式中,p3为虚拟过盈方式的接触面压强。
式(29)没有给DR、Ra和Rb加以条件限制。下面将结合示意图对虚拟过盈量进行阐述。图7已将圆柱(筒)沿圆周方向展开,在未过盈装配前,如图7a所示,圆柱半径和圆筒内径相等,都为Ra,这与实际有差别。因为要实现过盈配合,轴和孔的尺寸必定不相等,但这里实现的是虚拟过盈,所以不必不相等。如图7b所示,有一虚拟介质在两零件间产生,其厚度为DR,此虚拟空间的特点是:其内部应力处处相等,均为p3,p3为负数,表示受压应力。
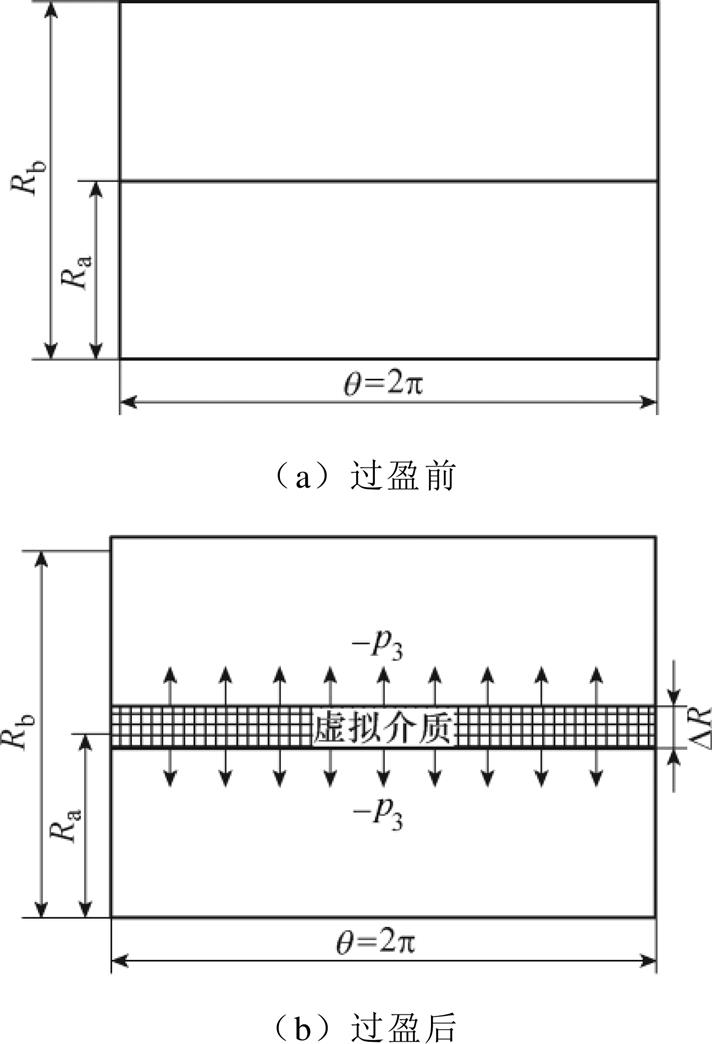
图7 虚拟过盈过程
Fig.7 Course of fictive shrink fitting
根据虚拟介质内部应力特点,其会在与两个零件的接触面上施加-p3的压强给两个零件。圆柱外缘位移ui3计算式为
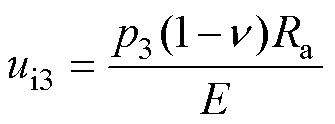 (30)
(30)
圆筒内缘位移uo3计算式为
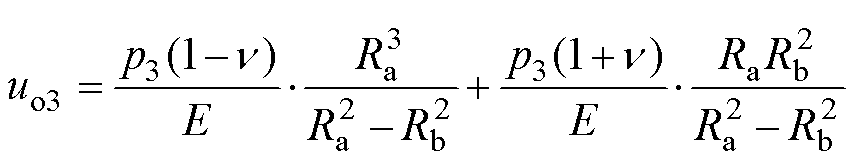 (31)
(31)
式(31)和式(30)两个位移之差即虚拟介质的厚度,表示为
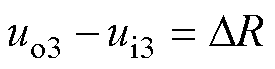 (32)
(32)
联立式(30)~式(32),解出接触面压强,即式(29)。式(29)无需考虑过盈量是由轴还是孔提供,只需知道未加过盈量前的零件尺寸和需要的过盈量,便可计算接触面压强。从式(28)可知,当过盈量相对于轴和护套的尺寸很小时,虚拟过盈的算法和两种实际过盈的算法相等。但在工程上,一般不追求零误差算法,可以接受在工程允许范围内的误差。
下面通过算例说明虚拟过盈算法和实际过盈算法之间的差别。取杨氏模量E=200 GPa,泊松比n= 0.28,过盈量为0.1 mm,0.5 mm<Ra<50 mm,0.5 mm<Rb-Ra<50 mm。用同一尺寸参数分别计算三种接触面压强,而后用离散系数来衡量三种算法的差别,离散系数CV的表达式为
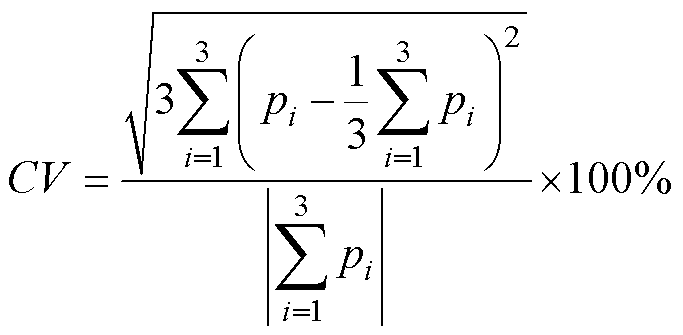 (33)
(33)
图8为不同尺寸(Ra和Rb)下三种算法算出的压强的离散系数。离散系数越大,数据的差异就越大。在靠近坐标值附近离散系数急剧上升。在原点附近,离散系数很大。而在其他不靠近坐标轴的区域,离散系数较小。当零件尺寸(圆柱半径和圆筒厚度)超过过盈量的20~30倍时,离散系数可达2 %以下。越远离坐标轴,离散系数越小。坐标分别代表了圆柱的半径和圆筒的厚度。以上结果表明,当过盈量相较于零件尺寸不能忽略时,两种实际的过盈方式或虚拟过盈方案计算的应力差别较大,在计算前一定要确定加工方案,选择对应的计算公式,否则会带来较大误差,从而影响转子的安全性。而当过盈量相较于零件尺寸可以忽略时,三种计算应力的方法算出来的结果几乎相同。计算的应力结果和实际方案差别很小,满足工程要求。
式(29)在过盈量相较于尺寸很小时与式(26)和式(27)接近的原因,可以从实际角度解释。应力是形变(应变)的结果,过盈量的存在迫使各零件在实际制造时尺寸带有公差,也就是轴径尺寸为正公差,或孔内径尺寸为负公差。如果过盈量较小,无论方案1还是方案2,因实际加工产生的尺寸改变DR可以忽略,轴径和孔内径视为同尺寸。对于方案1,认为Ra+DR=Ra;对于方案2,认为Ra-DR=Ra。以上便是实际意义,之后便可用虚拟过盈的思想解释式(30)~式(32),最终得到式(29)。
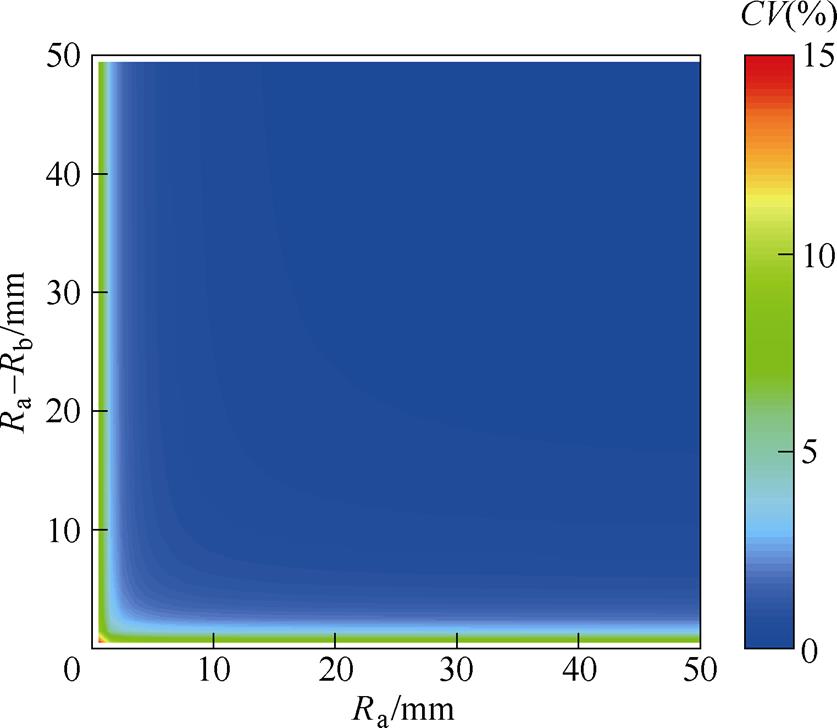
图8 不同尺寸的离散系数
Fig.8 Coefficient of variation over different dimensions
一般地,高速永磁电机转子的尺寸比例可参考图1,护套的厚度比护套包含的柱体尺寸小得多。因此,过盈量只需和护套的厚度作比较。若过盈量相对护套的厚度不可忽略(分界线是护套厚度,为过盈量的20~30倍,见图8),则需要对过盈方式加以重视,因为此时不同的过盈方式将对整体应力产生较大的影响。而若过盈量相对于护套厚度可以忽略不计,则无须对过盈方式加以关注,因为此时相同过盈量条件下不同的过盈方式对应力的影响很小,在工程允许的范围内。
以一台额定功率50 kW,额定转速40 000 r/min的高速永磁电机为例,用有限元方法计算不同过盈方式下转子的应力。
图9为电机的横截面示意图,表3列出了电机的主要结构与尺寸(注:表中尺寸未考虑过盈量)。转子铁心采用的材料是40Cr,永磁体材料为钐钴,护套材料为碳纤维。
不同过盈方式对应不同的加工尺寸:方案1:永磁体外径74.4 mm,护套内径74 mm;方案2:永磁体外径74 mm,护套内径73.6 mm。
以上两种过盈方式的过盈量DR均为0.2 mm,其余尺寸相同。有限元模型的条件与第1节中的假设条件一致。图10为额定转速下,使用不同过盈方式下永磁体和护套的应力分布。图10中除了给出采用两种实际加工过盈方式的应力分布,还给出了使用虚拟过盈算法的应力曲线。考虑到实际工况的复杂性,高速电机转子需经过超转120 %的校验,观察安全裕量。图11给出了转子在超转120 %的转速(48 000 r/min)下各部件的应力分布。
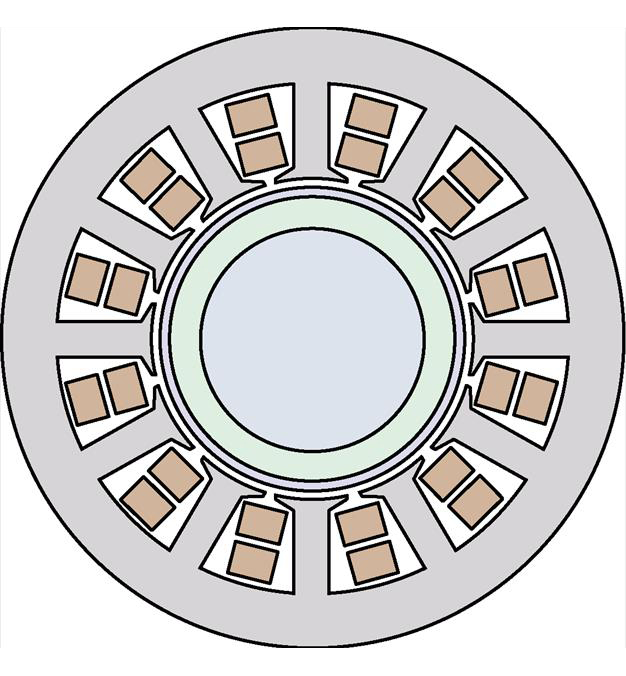
图9 电机截面
Fig.9 Cross section of machine
表3 电机的结构与尺寸
Tab.3 Dimensions and specifications of machine
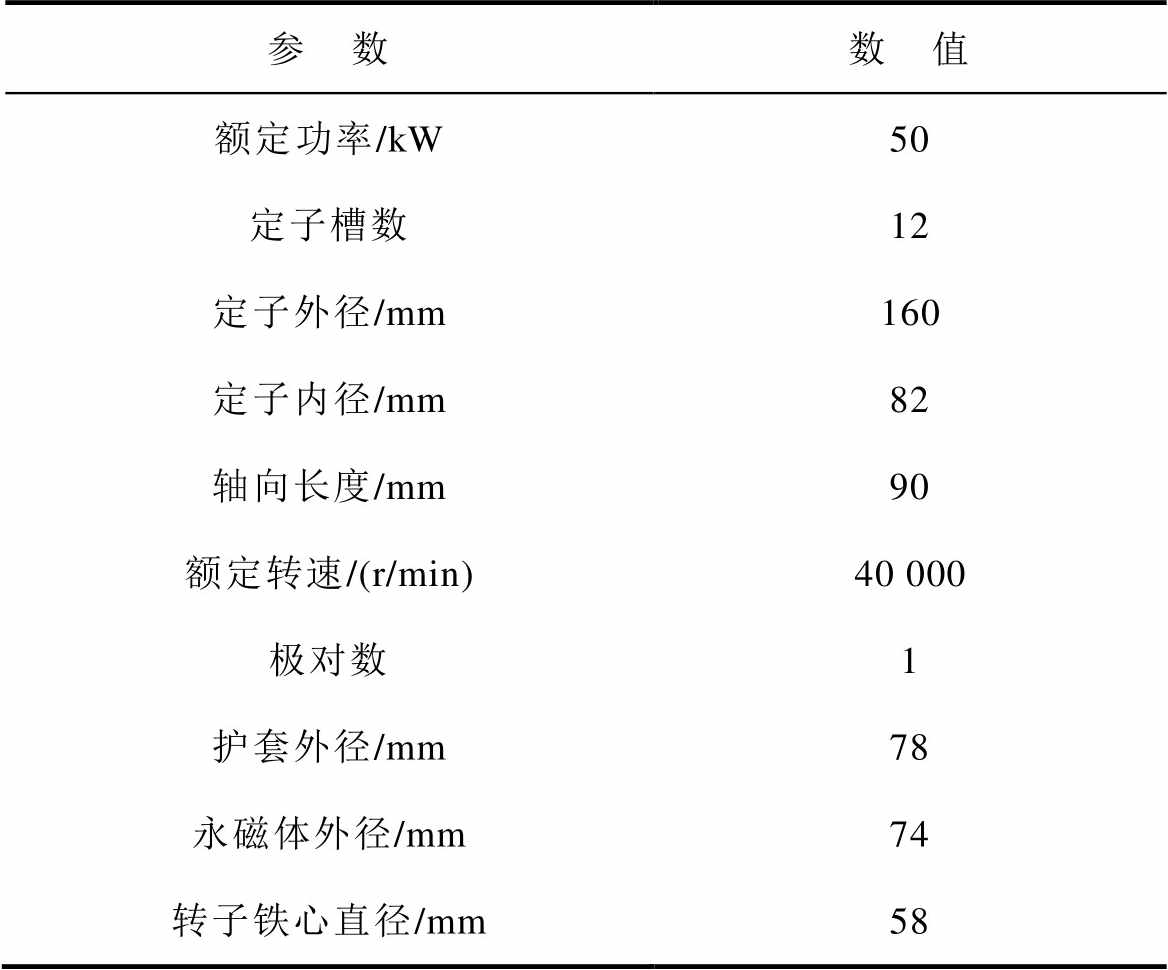
参 数数 值 额定功率/kW50 定子槽数12 定子外径/mm160 定子内径/mm82 轴向长度/mm90 额定转速/(r/min)40 000 极对数1 护套外径/mm78 永磁体外径/mm74 转子铁心直径/mm58
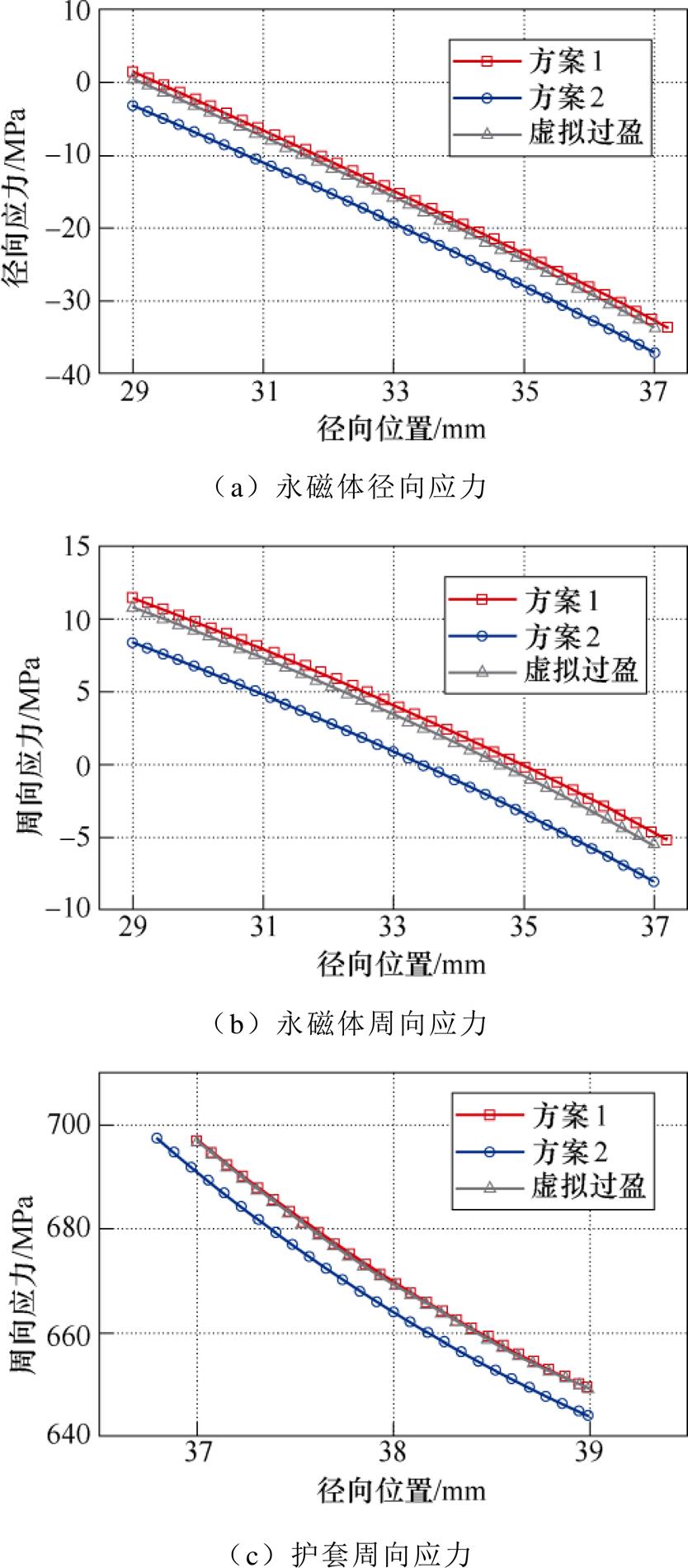
图10 额定转速下核心部件的应力
Fig.10 Stress of core components under rated speed
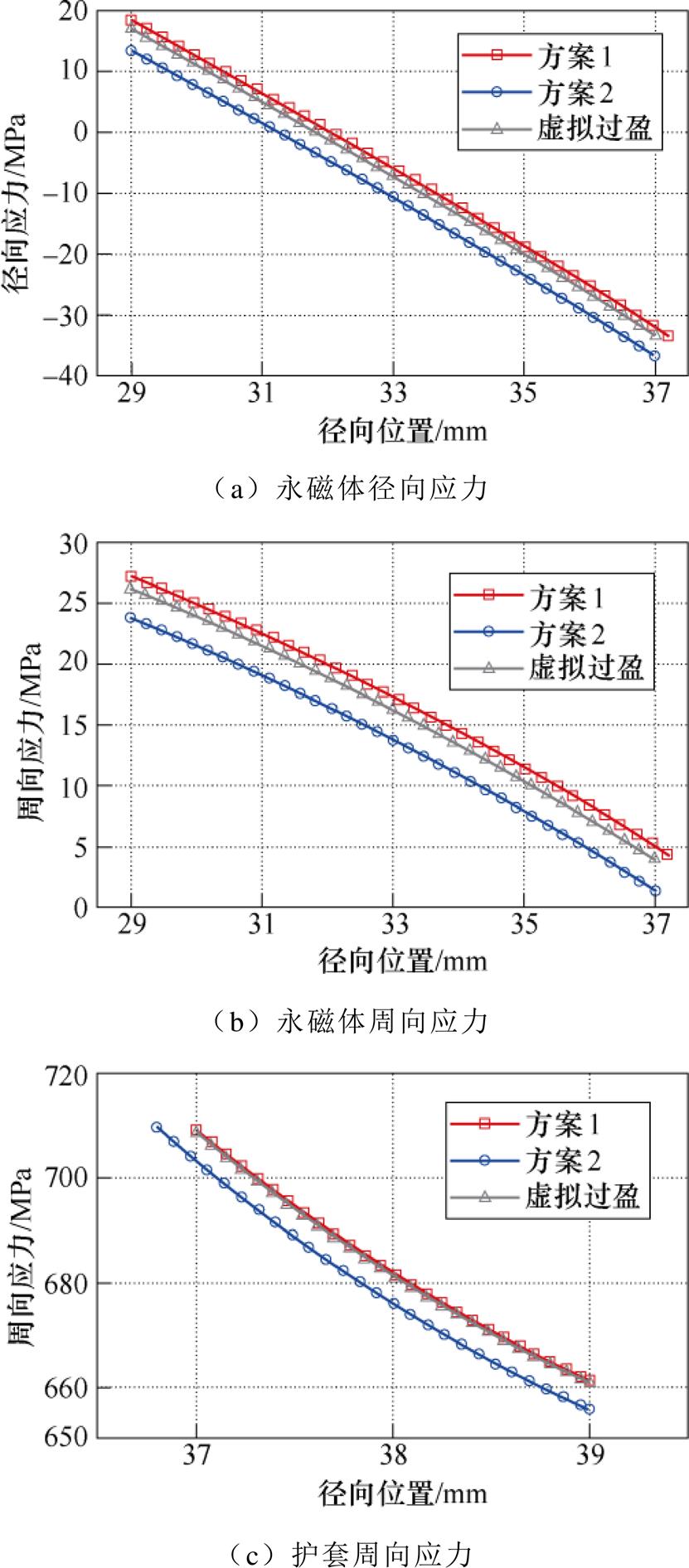
图11 48 000 r/min时核心部件的应力
Fig.11 Stress of core components at 48 000 r/min
由图10和图11可知,无论在额定转速还是超转下,采用过盈方案2时永磁体的整体应力低于采用过盈方案1的。此外,在转速相同的情况下,对于不同的过盈方式,护套的(周向)应力最大值几乎相等。说明护套厚度较小时,虽然过盈量相同,但不同的过盈方式将导致较为明显的应力差异,尤其是永磁体上的应力。
永磁体和护套的应力最大值都出现在其内表面。考虑到护套应力的最大值几乎相等,下面以永磁体的最大应力定义转子的安全度n,表达式为
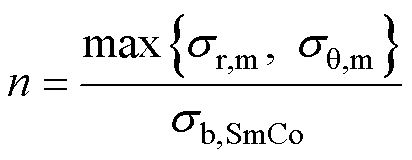 (34)
(34)
式中,sb,SmCo为钐钴材料的抗拉强度,sb,SmCo= 35 MPa。
表4为不同过盈方式和不同工况下转子核心部件的应力最大值及安全度。根据计算结果和应力对比,采用过盈方案2时转子有着更高的安全度,因此过盈方案2为更优的方式。
表4 应力对比
Tab.4 Stress comparison
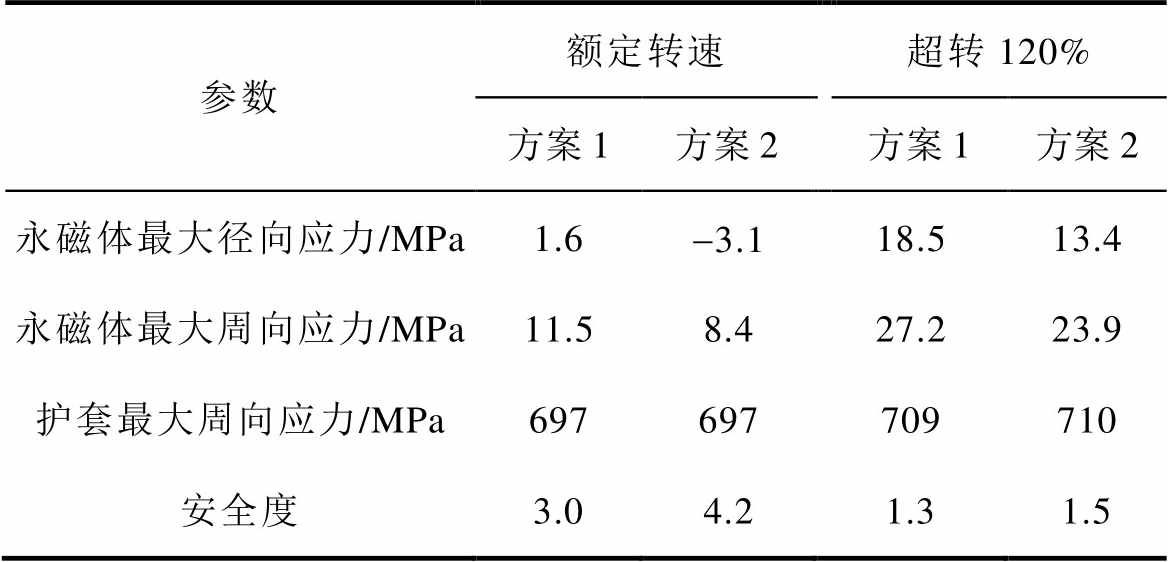
参数额定转速超转120% 方案1方案2方案1方案2 永磁体最大径向应力/MPa1.6-3.118.513.4 永磁体最大周向应力/MPa11.58.427.223.9 护套最大周向应力/MPa697697709710 安全度3.04.21.31.5
图12为采用过盈方案2,额定转速下转子各部件的应力分布。图12a为转轴的应力分布云图,考虑到40Cr为塑性材料,因此用冯·米塞斯应力来衡量。图12b为永磁体的径向应力和周向应力分布,图12c为护套的周向应力。
以上算例表明:当过盈量相对于护套厚度不可忽略时,不同的过盈方式将明显影响转子应力,尤其是核心部件永磁体。因此,有必要通过对比不同的过盈方式,选择更优的过盈方案,降低转子应力,提高电机的安全性与可靠性。
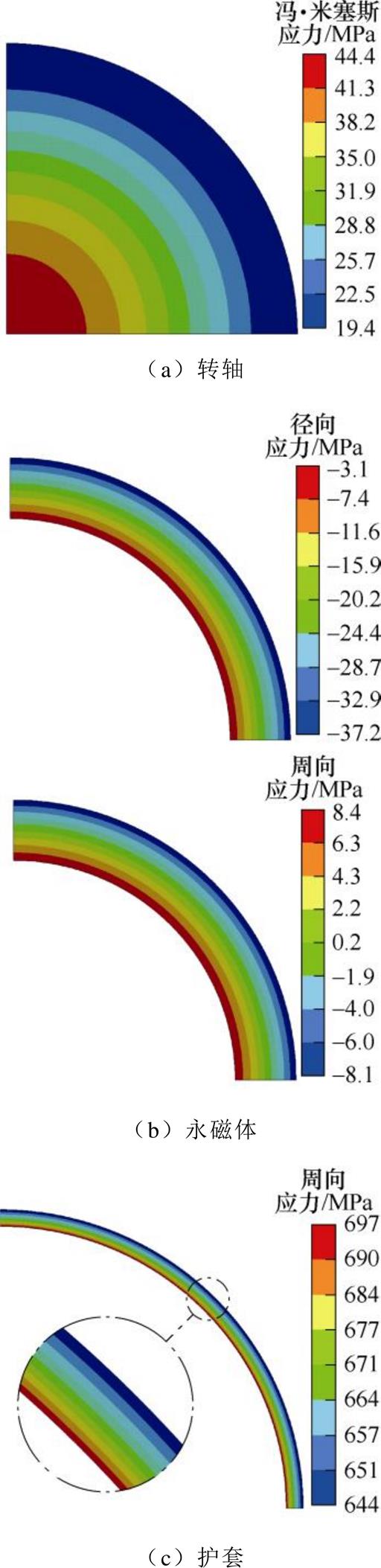
图12 额定转速下的转子应力
Fig.12 Rotor stress at rated speed
本文建立了常规表贴式高速永磁电机转子应力的解析模型,分析了不同过盈方式对转子应力的影响,提出了“虚拟过盈”的应力计算方法。过盈方式对应力的影响大小取决于过盈量和电机转子护套的尺寸。当护套厚度与过盈量的比值小于20~30时,不同的过盈方式对应力的影响较大。对一台50 kW、40 000 r/min的高速永磁电机在不同过盈方式下的转子应力进行了分析,相比于过盈方案1,过盈方案2能够有效降低永磁体的应力,提高转子的安全度。本文研究为高速永磁电机转子过盈方式的设计提供了理论指导。
参考文献
[1] 佟文明, 侯明君, 孙鲁, 等. 基于精确子域模型的带护套转子高速永磁电机转子涡流损耗解析方法[J]. 电工技术学报, 2022, 37(16): 4047-4059.
Tong Wenming, Hou Mingjun, Sun Lu, et al. Analytical method of rotor eddy current loss for high-speed surface-mounted permanent magnet motor with rotor retaining sleeve[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4047-4059.
[2] 王晓琳, 刘思豪, 顾聪. 基于自适应基准锁相环的高速永磁电机转子位置误差全补偿方法[J]. 电工技术学报, 2021, 36(20): 4308-4317.
Wang Xiaolin, Liu Sihao, Gu Cong. A rotor position error compensation algorithm for high-speed per- manent magnet motor based on phase-locked loop with adaptive reference[J]. Transactions of China Electrotechnical Society, 2021, 36(20): 4308-4317.
[3] 戴睿, 张岳, 王惠军, 等. 基于多物理场近似模型的高速永磁电机多目标优化设计[J]. 电工技术学报, 2022, 37(21): 5414-5423.
Dai Rui, Zhang Yue, Wang Huijun, et al. Multi- objective optimization design of high-speed per- manent magnet machine based on multi-physics approximate model[J]. Transactions of China Elec- trotechnical Society, 2022, 37(21): 5414-5423.
[4] 张丹, 姜建国. 高速磁悬浮永磁电机三电平无速度传感器控制[J]. 电工技术学报, 2022, 37(22): 5808- 5816.
Zhang Dan, Jiang Jianguo. Three-level sensorless control of high speed maglev permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5808-5816.
[5] 程文杰, 耿海鹏, 冯圣, 等. 高速永磁同步电机转子强度分析[J]. 中国电机工程学报, 2012, 32(27): 36-41.
Cheng Wenjie, Geng Haipeng, Feng Sheng, et al. Rotor strength analysis of high-speed permanent magnet synchronous motors[J]. Proceedings of the CSEE, 2012, 32(27): 36-41.
[6] Yu Wenfei, Liu Kai, Hua Wei, et al. A new high- speed dual-stator flux switching permanent magnet machine with distributed winding[J]. IEEE Transa- ctions on Magnetics, 2022, 58(2): 1-6.
[7] Liu Lin, Guo Youguang, Lei Gang, et al. Iron loss calculation for high-speed permanent magnet machines considering rotating magnetic field and thermal effects[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(8): 1-5.
[8] 赵士豪, 陈进华, 张驰, 等. 不均匀气隙表贴式永磁同步电机磁场解析计算[J]. 电工技术学报, 2022, 37(14): 3502-3513.
Zhao Shihao, Chen Jinhua, Zhang Chi, et al. Analytical calculation of magnetic field of permanent magnet synchronous motor with uneven air gap structure[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3502-3513.
[9] 董剑宁, 黄允凯, 金龙, 等. 高速永磁电机设计与分析技术综述[J]. 中国电机工程学报, 2014, 34(27): 4640-4653.
Dong Jianning, Huang Yunkai, Jin Long, et al. Review on high speed permanent magnet machines including design and analysis technologies[J]. Proceedings of the CSEE, 2014, 34(27): 4640-4653.
[10] 张凤阁, 杜光辉, 王天煜, 等. 高速永磁电机转子不同保护措施的强度分析[J]. 中国电机工程学报, 2013, 33(增刊1): 195-202.
Zhang Fengge, Du Guanghui, Wang Tianyu, et al. Rotor strength analysis of high-speed permanent magnet under different protection measures[J]. Proceedings of the CSEE, 2013, 33(S1): 195-202.
[11] 张凤阁, 杜光辉, 王天煜, 等. 高速电机发展与设计综述[J]. 电工技术学报, 2016, 31(7): 1-18.
Zhang Fengge, Du Guanghui, Wang Tianyu, et al. Review on development and design of high speed machines[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 1-18.
[12] 张超, 朱建国, 韩雪岩. 高速表贴式永磁电机转子强度分析[J]. 中国电机工程学报, 2016, 36(17): 4719-4727.
Zhang Chao, Zhu Jianguo, Han Xueyan. Strength analysis of high-speed surface-mounted permanent magnet motor rotor[J]. Proceedings of the CSEE, 2016, 36(17): 4719-4727.
[13] Uzhegov N, Kurvinen E, Nerg J, et al. Multi- disciplinary design process of a 6-slot 2-pole high- speed permanent-magnet synchronous machine[J]. IEEE Transactions on Industrial Electronics, 2016, 63(2): 784-795.
[14] Zhang Fengge, Du Guanghui, Wang Tianyu, et al. Rotor retaining sleeve design for a 1.12-MW high-speed PM machine[J]. IEEE Transactions on Industry Applications, 2015, 51(5): 3675-3685.
[15] 王继强, 王凤翔, 鲍文博, 等. 高速永磁电机转子设计与强度分析[J]. 中国电机工程学报, 2005, 25(15): 140-145.
Wang Jiqiang, Wang Fengxiang, Bao Wenbo, et al. Rotor design and strength analysis of high speed permanent magnet machine[J]. Proceedings of the CSEE, 2005, 25(15): 140-145.
[16] Du Guanghui, Xu Wei, Zhu Jianguo, et al. Rotor stress analysis for high-speed permanent magnet machines considering assembly gap and temperature gradient[J]. IEEE Transactions on Energy Conversion, 2019, 34(4): 2276-2285.
[17] 沈建新, 秦雪飞, 尧磊, 等. 高速永磁电机转子强度分析与护套设计[J]. 中国电机工程学报, 2022, 42(6): 2334-2345, 26.
Shen Jianxin, Qin Xuefei, Yao Lei, et al. Strength analysis and sheath design of high-speed permanent magnet motor rotor[J]. Proceedings of the CSEE, 2022, 42(6): 2334-2345, 26.
[18] Shen Jianxin, Hao He, Jin Mengjia, et al. Reduction of rotor eddy current loss in high speed PM brushless machines by grooving retaining sleeve[J]. IEEE Transactions on Magnetics, 2013, 49(7): 3973-3976.
[19] Fang Haiyang, Li Dawei, Qu Ronghai, et al. Rotor design and eddy-current loss suppression for high- speed machines with a solid-PM rotor[J]. IEEE Transactions on Industry Applications, 2019, 55(1): 448-457.
[20] 王天煜, 温福强, 张凤阁, 等. 兆瓦级高速永磁电机转子多场耦合强度分析[J]. 电工技术学报, 2018, 33(19): 4508-4516.
Wang Tianyu, Wen Fuqiang, Zhang Fengge, et al. Analysis of multi-field coupling strength for MW high-speed permanent magnet machine[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(19): 4508-4516.
[21] 刘威, 陈进华, 张驰, 等. 考虑轴间填充物的高速永磁电机转子强度分析[J]. 电工技术学报, 2018, 33(5): 1024-1031.
Liu Wei, Chen Jinhua, Zhang Chi, et al. Strength analysis of high speed permanent magnet machine rotor with inter-shaft filling[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1024-1031.
[22] 万援, 崔淑梅, 吴绍朋, 等. 扁平大功率高速永磁同步电机的护套设计及其强度优化[J]. 电工技术学报, 2018, 33(1): 55-63.
Wan Yuan, Cui Shumei, Wu Shaopeng, et al. Sheath design and strength optimization of flat high-power high-speed permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 55-63.
[23] 钱伟长. 电机设计强度计算的理论基础[M]. 合肥: 安徽科学技术出版社, 1992.
[24] 吴家龙. 弹性力学[M]. 北京: 高等教育出版社, 2001.
[25] 陈亮亮. 磁悬浮高速飞轮储能系统永磁电机转子强度分析及转子振动控制[D]. 杭州: 浙江大学, 2019.
[26] Bernard L, Daniel L. Effect of stress on magnetic hysteresis losses in a switched reluctance motor: application to stator and rotor shrink fitting[J]. IEEE Transactions on Magnetics, 2015, 51(9): 1-13.
Abstract In the design of a high-speed permanent magnet machine, the calculation and verification of rotor stress are very important, especially the stress of a permanent magnet. The existing research mainly focuses on the influence of shrink-fitting magnitude on rotor stress, but ignores the influence of shrink-fitting modes. The shrink fitting between the sleeve and the permanent magnet greatly impacts the rotor stress. Limited by the electromagnetic power, the stress margin left to the permanent magnet or sleeve is limited to improve the material utilization. If the difference of rotor stress under various shrink fitting modes is not considered in the design, the safety of rotor strength will be greatly reduced when the operating point of the machine is near the limit value of the material stress, which may even lead to the failure of the design of high-speed permanent magnet machine. Therefore, the influence of shrink-fitting modes on the rotor stress of high-speed permanent magnet machines should be addressed, and more attention must be paid to it when calculating the rotor stress. This paper studies the influence of shrink-fitting modes on the rotor stress of a high-speed permanent magnet machine.
Firstly, the stress field mathematical model of the unified geometric model of each rotor part is established in two-dimensional polar coordinates. The radial and circumferential stresses of the shaft, permanent magnet, and sleeve can be solved under different boundary conditions. It can be concluded that the rotor stress is the sum of the rotational component and the surface pressure component. The tensile stress caused by rotation can be offset by the pressure from the sleeve, and the degree of offset is determined by the pressure applied by the sleeve. Therefore, to calculate the rotor stress accurately, it is necessary to accurately calculate the stress caused by rotation and obtain the pressure applied by the sleeve. It is easy to calculate the stress caused by rotation, while the stress offset by the sleeve pressure is more complicated due to the shrink fitting, so it is necessary to study the influence of shrink-fitting modes on rotor stress. Then, based on the stress field mathematical model, the analytical calculation method of rotor stress under different shrink-fitting modes is further obtained, and the influence of different shrink-fitting modes on rotor stress is analyzed. Finally, taking a high-speed permanent magnet machine with rated power of 50 kW and rated speed of 40 000 r/min as an example, the rotor stress under different shrink-fitting modes is calculated by the finite element method. When the magnitude of shrink fitting relative to the sleeve thickness cannot be ignored, different shrink-fitting modes will significantly affect the rotor stress, especially the core component permanent magnet. Therefore, it is necessary to select a better mode by comparing shrink-fitting modes to reduce rotor stress and improve the safety and reliability of the machine. This paper provides theoretical guidance for the design of shrink-fitting modes of high-speed permanent magnet machine rotors.
keywords:High speed permanent magnet machine, stress, shrink fitting, mathematical model
DOI: 10.19595/j.cnki.1000-6753.tces.221036
中图分类号:TM351
国家自然科学基金(52007055)和湖南省自然科学基金(2021JJ40099)资助项目。
收稿日期 2022-06-06
改稿日期 2022-08-10
杨江涛 男,1991年生,博士,副教授,博士生导师,研究方向为特种电机及其控制。E-mail: yangjiangtao@hnu.edu.cn
冯垚径 女,1985年生,博士,副教授,博士生导师,研究方向为电机理论、设计与应用。E-mail: fengyaojing@hnu.edu.cn(通信作者)
(编辑 崔文静)