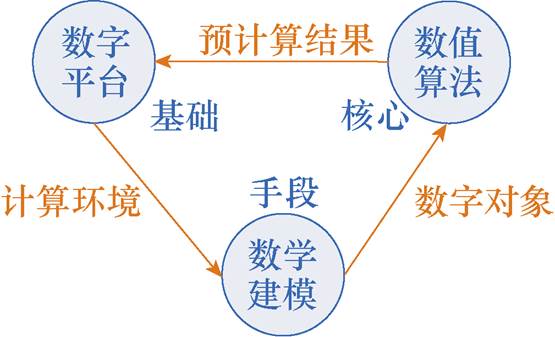
图1 数值仿真系统的计算流程关系
Fig.1 Computation flow diagram of numerical simulation
摘要 数值仿真是先进智能计算的基础与底层核心技术,而计算速度是数值仿真的核心性能指标。然而,随着高开关频率功率器件在电机驱动等系统中的应用,短时间约束给实时及在线数值仿真的计算速度带来了严峻挑战。当前数字平台的计算结构朝着并行化的趋势发展,并行计算被视为短时间约束下优化计算速度的有效途径,但现有的数值模型和数值算法大多基于顺序计算的串行模式,缺乏可并行执行的冗余并行度。因此,该文研究了数值算法的求解核心数值积分的并行优化方法,提出了计算前沿面的优化思路,为数值积分算法构造冗余并行度以实现并行计算,分析了其在数值精度与数值稳定性方面的影响,并讨论了在多步与高阶数值积分法上的可拓展性。同时,利用计算前沿面构造的冗余并行度,设计了数值模型的并行解耦分割,并应用于电驱系统实现了元件级的数值加速。最后,在硬件在环的实时数值环境中验证了优化方法的可行性、数值性能以及加速效果。
关键词:并行计算 电驱系统 计算前沿面 实时仿真 数值加速 数值积分
电机系统作为关键的基础部件,广泛应用于工业国防、航空航天等领域,是带动其发展的核心环节[1]。近年来,电动汽车的快速发展极大增加了电机系统的需求量[2]。同时受人工智能、大数据、云计算等智能计算促进,电机系统朝着数字化与智能化的趋势发展[3]。数值仿真作为智能计算的基础与底层核心技术[4],引起了学术界与工业界的重视[5]。
其中,数值计算速度是数值仿真性能的关键。然而,受电机驱动系统高频化应用趋势与数值仿真实时化、在线化使用需求的影响,一方面,高开关频率功率器件的应用[6],需要数值仿真系统具备超快的时间响应;另一方面,实时仿真[7]、数字孪生[8]等信息物理系统[9-10]的使用,对数值仿真系统有着极强的时间约束。因此,数值仿真的计算速度面临着严峻挑战。
数值仿真的执行过程如图1所示[11]。数字平台集成计算资源,为数值运算提供计算环境,数学建模将实际物理对象抽象成数学模型,由数值算法将连续域数学模型离散为数值模型,并对模型完成计算和更新。提升数值计算速度的思路按数值转化的流程可归纳为:数字平台上增加算力、数学模型与数值算法上降低计算量或等效并行。

图1 数值仿真系统的计算流程关系
Fig.1 Computation flow diagram of numerical simulation
通过增加算力来提升计算速度效果显著但通常会增加成本[12];降低计算量通过简化数学模型或采用先进的数值算法,前者如等值法[13]、查表法[14]等,后者如矩阵降维[13]、变步长[11]与离散事件机 制[5]等,在计算规模较大的场合效果明显,但其多数方法依赖物理对象的应用场景。在电力仿真领域,过去因为电力系统的发展,计算规模增加是限制计算速度的主要原因,因此降低计算量成为优化计算速度的主要技术路线。但随着SiC等功率器件在电动汽车中的应用,高频化的特征导致计算时限缩短至ns级,短时限逐渐成为限制计算速度的主导原因,降低计算量的优化空间有限。等效并行能在短时限下获得较高的加速比,且随着并行架构数字平台的发展,如多核中央处理器(Central Processing Unit, CPU)、图形处理器(Graphics Processing Unit, GPU)、可编程逻辑阵列(Field Programmable Gate Array, FPGA)[12]等,计算并行是短时限下优化计算速度的有效方式与新趋势。
现有并行加速的方法可分为等效网络划分和基于延迟解耦[15]两大类。等效网络划分根据节点关系将原网络等效降阶为多个同步的子网络,以实现并行,如状态空间节点法[16]与节点撕裂法[17]等,但其也仅适用节点多、规模大的仿真系统。基于延迟解耦包括插入延迟和自然延迟两种思路。前者通过注入时间延迟以解列时间顺序关系,因此注入延迟的变量可以视为独立等效的源,代表性方法包含延迟插入法[18]和VI耦合法[19]等。延迟插入的思路分割位置选择灵活,但引入的延迟会对数值精度和数值稳定性产生影响,因此常选取变化小的状态变量作为延迟插入点,或通过其他方式补偿延迟的影响,如插值方法[20]等,然而前者未从根本上避免延迟的影响,后者增加了计算复杂度。为克服此缺陷,自然延迟思路利用系统模型自身的延迟属性作并行分割,如传输线法[21]、直接映射法[22]与显示积分法[23]等,由于对数学模型本身有一定的要求,其应用的灵活性受限。综上所述,计算架构朝着并行化的趋势发展,但数值仿真的数学模型和数值算法仍多基于串行的方式建立,总体而言缺乏可并行执行的冗余并行度,导致并行分割时难以兼顾灵活性与数值性能。
针对上述问题,本文提出计算前沿面的思路为数值积分算法构造冗余并行度,实现数值积分的并行计算与数值模型间的并行分割,以完成并行加速。
1.1.1 算法结构与数值积分
算法结构是数值算法求解数学模型的基础,即以合理的架构将数学模型组织成适合离散数值求解的流程[11]。由于电力电子系统的数学模型类型通常以常微分方程(Ordinary Differential Equation, ODE)为主,因此其数值求解的数值积分方法是求解效率的核心。在数值算法上采用状态空间的算法结构将数学模型组织成式(1)的通式以便数值求解[14]。
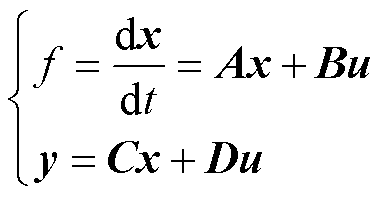 (1)
(1)
式中,x、u、y分别为状态变量、输入变量与输出变量;A、B、C、D为其系数矩阵。
状态空间的数值算法结构如图2所示。状态空间算法结构能够分离积分项,因此可灵活选取数值积分法。
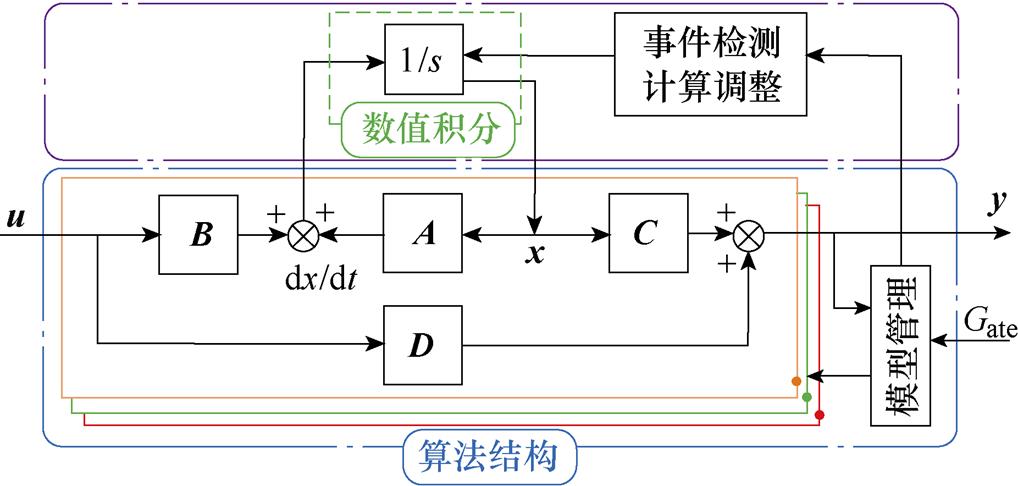
图2 状态空间的数值算法结构
Fig.2 Schematic diagram of state-space architecture
数值积分法多由式(2)的泰勒级数[24]衍生而来。
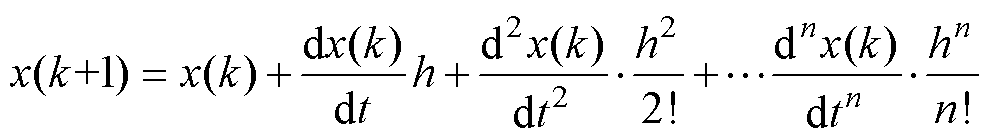 (2)
(2)
式中,h为计算步长;k为计算时刻。通过保留主要项舍弃高阶项完成数值求解,如前向欧拉(Forward Euler, FE)法、龙格-库塔(Runge-Kutta, RK)法等。
然而,舍弃的高阶项导致每个步长计算周期存在截断误差,因此误差累积会对数值求解的精度与稳定性产生影响。对此,常采用高阶或多步的数值积分以减小此影响,如RK法或阿达姆斯-巴什福斯法[24]等。然而,无论是数学模型或数值算法,在数值上均受输入输出关系的约束,因而在时间顺序上都是串行性质的,缺乏并行执行可能的冗余并行度,即使并行架构的数字平台也无法充分利用其并行的特征优势,导致效率低下。同时,高阶或多步的数值积分法一般存在多段的积分过程,增加了系统复杂度,特别给实时仿真的计算速度带来挑战。因此,本文引入计算前沿面的思想,其最初用以解决航天工业仿真领域中刚性ODE的分解问题[25],本文通过前沿面的设计改进数值积分,为其构造冗余并行度,在数值算法层面实现并行的计算,以此在数值模型层面完成数值解耦以实现并行加速。
1.1.2 计算前沿面的定义
由于数值积分法以时间步长迭代推进,因此可用时间轴上描述数值计算顺序关系的数值流表示状态量在每个计算步长下数值迭代的变化关系,进而将数值关系图形化。
预测校正(Predictor-Corrector, PC)法作为具有多段计算特征的数值积分法,“预测”采用显性方法避免迭代,“校正”采用隐性或高阶方法提升稳定性或精度,是最简单改进精度的方式。典型PC法为式(3)的改进欧拉(Heun)法[24],预测为FE法,校正为梯形法(Tustin),计算时序为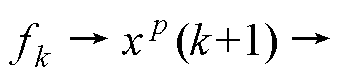
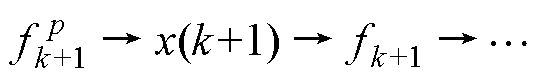 ,其中,p为阶数。改进欧拉法的数值流与计算前沿面如图3所示。
,其中,p为阶数。改进欧拉法的数值流与计算前沿面如图3所示。
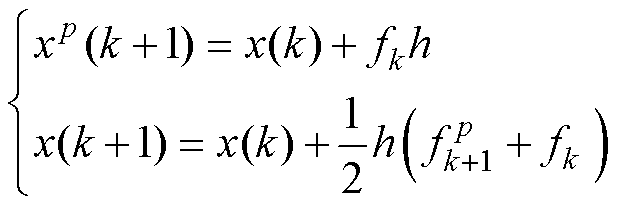 (3)
(3)
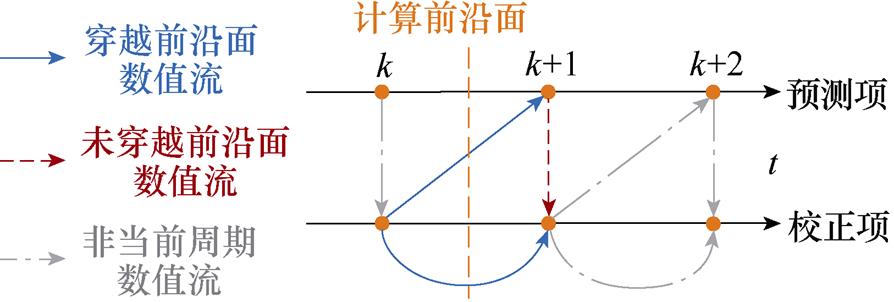
图3 改进欧拉法的数值流与计算前沿面
Fig.3 Numerical flow and computation front of Heun
图3中,上方时间轴表示Heun法预测过程在k+1时刻的计算任务,包括状态变量和导函数的计算,同理下方时间轴表示校正过程在k+1时刻的计算任务。
本文在其数值流上,引入计算前沿面,即在各段计算任务正在计算的时刻前,由数值积分过程中预计算的未来各值与已计算得到的所有值分割构成的虚线面,如图3所示。由于计算前沿面表征已计算与未计算的分割关系,因此,如果每个计算任务执行计算时所用到的数值都是穿越前沿面已计算时刻点上的数值,那么各段计算任务之间不存在数值依赖关系。即意味着如果所有数值流均穿越计算前沿面,那么各段计算任务之间可实现并行分割。基于这个思路,可知Heun法存在未穿越计算前沿面的数值流(红色标记),因此在数值上存在串行耦合。
1.2.1 优化原则
为了消除未穿越计算前沿面的数值流,实现数值积分算法的并行,可以通过两种方式解耦各段计算任务间的依赖关系:调整数值流或移动前沿面。
然而,解耦计算任务间的依赖关系存在一定的限制。由先前讨论,基于泰勒级数展开的数值积分法,根据迭代的方式、级数保留的阶数、历史项的步数,有显、隐性、低阶与高阶、单步与多步三种基本属性[24]。其中,阶数和步数主要影响数值积分的精度,而显、隐性主要对数值稳定域产生影响。由于数值稳定性影响数值仿真系统的正常运行,是数值算法的根本属性,因此其重要程度高于数值精度。同时,由于数值积分的阶数是由数值积分方法本身决定,几乎不受优化过程的影响,但数值积分的步数和显、隐性可能会被影响。因此,为了减小对数值积分算法原有属性的影响,在改进数值流计算依赖关系的过程中设定改进的优先级,即首要避免影响数值积分的显、隐性,其次避免数值积分步数的改变。
1.2.2 优化过程
直接调整数值流可实现各段任务的并行分割,但如图3所示,由于未穿越前沿面的数值流刚好位于预测与校正连接的流向上,该数值流关联的是校正过程梯形积分的隐性项。由于隐性项的计算在数值流图中的位置少且集中,因此调整隐性项的数值流会影响数值积分法的显、隐性,其具体表现为校正的隐性Tustin法退化为显性FE法。基于此,采取错开各段计算任务的当前计算时刻以调整前沿面的位置,进而实现各段计算任务的并行分割。改进欧拉法数值流的计算前沿面调整如图4所示。如图4a所示,针对预测过程,将当前计算时刻提前至k+2时刻,因此数值积分法计算前沿面的位置发生改变。随之未穿越前沿面的数值流发生改变,此前关联Tustin隐性项的数值流穿越前沿面,而改变后未穿越前沿面的数值流不关联隐性项。因此,在数值积分算法的步数范围内,可将该数值流调整为倍步计算,从而使其穿越计算前沿面,如图4b所示。
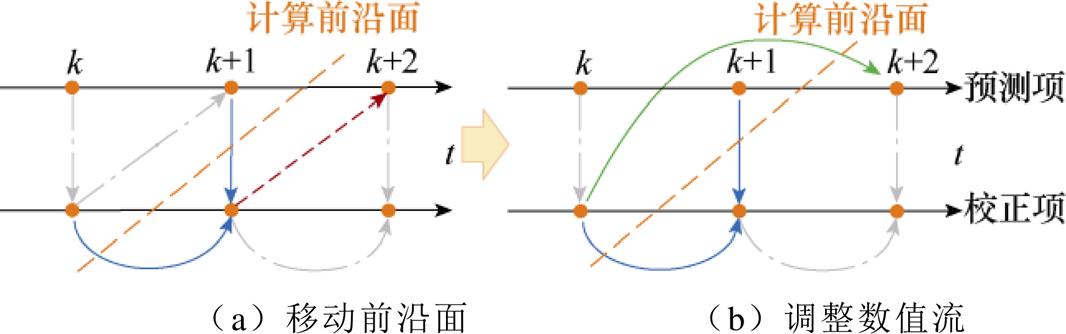
图4 改进欧拉法数值流的计算前沿面调整
Fig.4 Computation front optimization of numerical flow for Heun method
由此,改进Heun法的计算时序调整为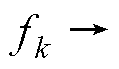
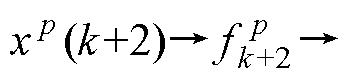 与
与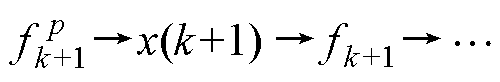 ,因此增加了冗余并行度,串行的计算被分为不存在计算依赖关系的两部分,可独立并行,则得改进Heun法为
,因此增加了冗余并行度,串行的计算被分为不存在计算依赖关系的两部分,可独立并行,则得改进Heun法为
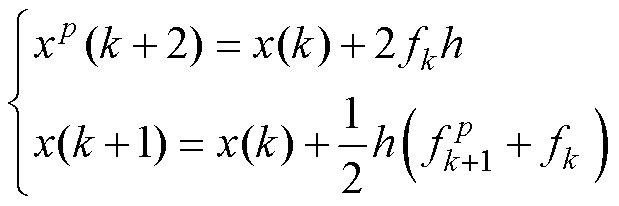 (4)
(4)
改进Heun法的计算时序被调整为两个独立并行的部分,一部分计算双倍步长的FE法;另一部分计算改进的Tustin法。没有计算依赖关系的部分可配置在并行的计算单元中,以此提高计算效率。
基于计算前沿面的优化方法,可以为数值积分方法构造冗余并行度,但由于数值流的调整,可能会在数值积分格式中引入局部的步长变化,因此会对数值积分算法的数值性能产生一定影响,主要包括数值精度与数值稳定性两方面。
1.3.1 数值精度分析
为了评估数值精度,假定式(3)的截断误差为R(k+1),那么可得到该时刻的精确值x*(k+1)为
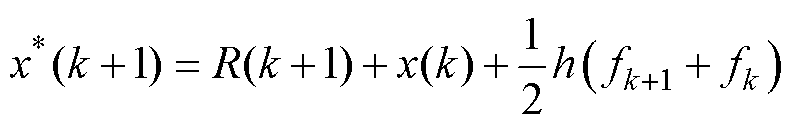 (5)
(5)
进一步可得改进后的算法(见式(4))相对精确值的误差,根据牛顿切线公式逼近可进一步化简为
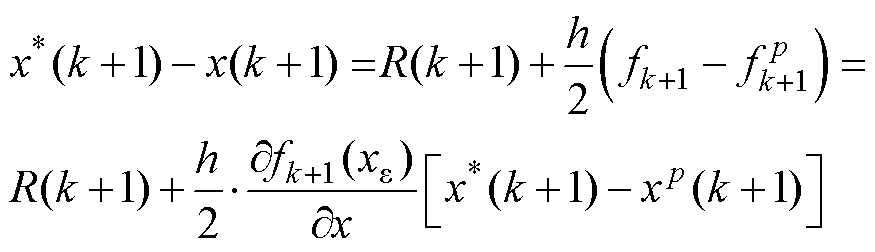 (6)
(6)
式中,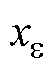 为x*(k+1)与
为x*(k+1)与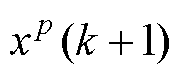 的中间值。根据Lipschitz连续性理论式(7):存在一个Lipschitz实数Lf,使得对于该函数上的每对点,连接它们直线斜率的绝对值不大于这个实数。则式(6)可推导为式(8)。
的中间值。根据Lipschitz连续性理论式(7):存在一个Lipschitz实数Lf,使得对于该函数上的每对点,连接它们直线斜率的绝对值不大于这个实数。则式(6)可推导为式(8)。
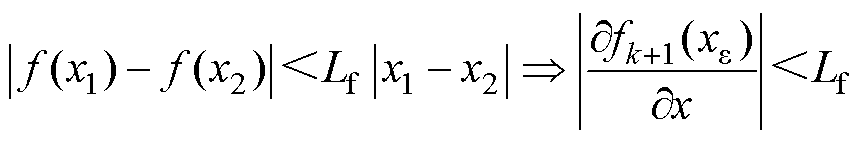 (7)
(7)
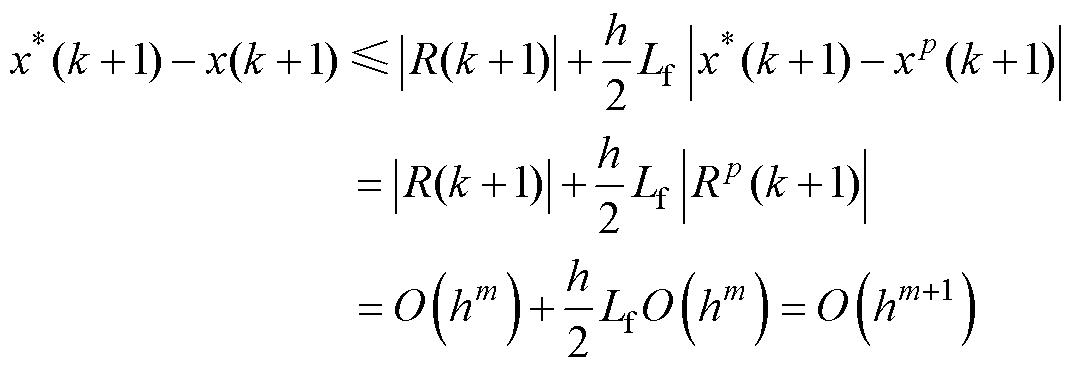 (8)
(8)
由此可知,若式(3)的预测计算采用m-1阶精度格式,则截断误差为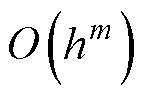 。在计算前沿面优化下,由式(8)可得,其截断误差为
。在计算前沿面优化下,由式(8)可得,其截断误差为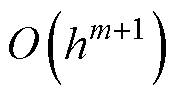 ,即具备m阶数值精度,较预测计算提高一阶。因此,相比于同等条件下采用一段计算的数值积分,改进方法本质上可通过并行增加的计算提高一阶精度,构造冗余并行度的同时以此避免并行分割后的系统通过牺牲数值精度来增加并行性能。
,即具备m阶数值精度,较预测计算提高一阶。因此,相比于同等条件下采用一段计算的数值积分,改进方法本质上可通过并行增加的计算提高一阶精度,构造冗余并行度的同时以此避免并行分割后的系统通过牺牲数值精度来增加并行性能。
因此,由式(4)可知,由于数值流调整的过程引入了倍步计算,在短时限步长较小的应用场景下,其对数值精度的影响可以忽略。然而,本文基于预测校正格式可以补偿倍步计算带来的精度损失。以FE法为例,选取包含FE法的Heun法作为优化对象,预测校正中FE法与Tustin结合的方式相比FE法提高了一阶数值精度。因此,改进Heun法的数值精度相比Heun法虽有所损失,但其数值精度比一段计算的FE法高一阶,因此可对倍步计算带来的数值精度损失进行一定的补偿,数值积分算法改进前后对比见表1。总之,相比于Heun法,改进Heun法缩短了计算时间,能实现计算加速;相比于FE法,改进Heun法通过增加校正过程提高了数值精度,增加的计算量并行处理,没有额外增加计算时间。此外,增加的计算可在后续环节中被用以设计数值模型的解耦分割。
表1 数值积分算法改进前后对比
Tab.1 Comparison of numerical integration methods

数值积分并行数量数值精度 前向欧拉法11 Heun法12 优化方法22
1.3.2 数值稳定性分析
数值稳定问题来自数值误差的累积,可由增长因子描述数值误差在迭代计算过程中的衰减特性。以FE法为例,结合式(1)与式(3)中的FE法,可得状态变量的迭代关系为式(9)。当式(10)满足时,数值误差可在迭代过程中衰减,保证数值稳定。当系数矩阵为一阶时,可以得到FE法的数值稳定域,如图5中(-1, 0)为圆心的单位圆包围的范围。
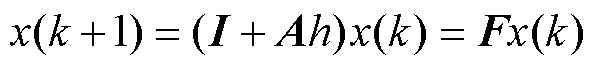 (9)
(9)
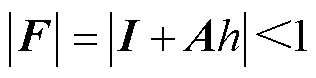 (10)
(10)
式中,I为单位矩阵,与系数矩阵A同阶;F为增长因子矩阵,其特征值决定了对应数值积分法的数值稳定性。
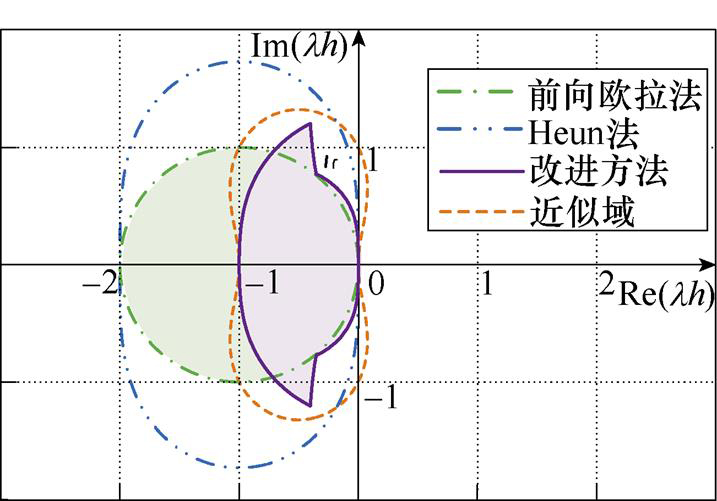
图5 改进方法的数值稳定域比较
Fig.5 Numerical stability domain comparison for optimization method
对于Heun法,由于校正过程采用了Tustin法,结合式(1)与式(3),其增长因子可推导为式(11),同理可获取其数值稳定域。由图5可知,相较于FE法,Heun法的数值稳定域被扩大,且呈椭圆状。
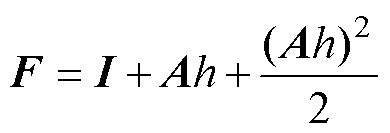 (11)
(11)
基于计算前沿面优化的改进Heun法,由于数值流的调整,其状态变量的迭代计算式由式(4)整理为式(12),可得其增长因子为式(13),由此可绘出改进Heun法的数值稳定域。由于式(13)的表达过于复杂,因此可考虑在式(12)中将x(k-1)项放松为x(k),则由式(14)推导得到改进Heun法的近似数值稳定域。
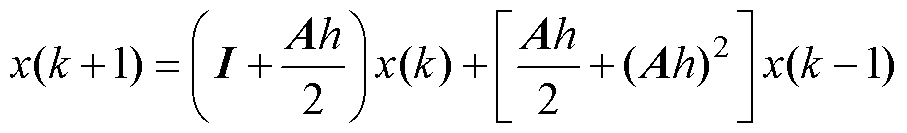 (12)
(12)
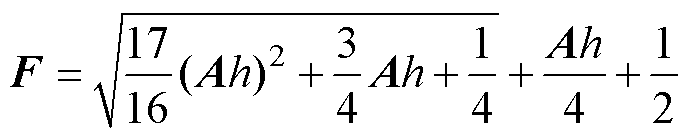 (13)
(13)
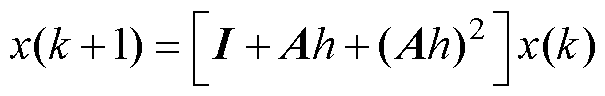 (14)
(14)
综上所述,基于计算前沿面改进的Heun法,由于优化过程中存在数值流的调整,使得改进后的数值稳定域范围约为改进前的一半,因此对数值稳定性有一定的影响。然而,在短时限步长较小的应用场景下,数值稳定性对改进方法的应用影响较小。并且,由于计算前沿面的应用具备一般性,因此可通过数值积分法的选取,避免数值稳定性的影响。
数值积分的阶数、步数与显、隐性是基本的数学属性。由于改进过程已涵盖显、隐性的影响,为说明一般性,将本文方法的应用推广至多步数值积分法与高阶数值积分法的冗余并行度构造。
1.4.1 多步数值积分法
计算前沿面的改进,一方面为串行数值积分构造冗余并行度实现并行计算;另一方面利用冗余的并行度,实现数值模型的解耦分割。由于后者只需两段计算的并行,因此具备两段计算特征的多步法即可满足数值模型分割的需求。
典型多步数值积分法的并行设计如图6所示。在式(15)的预测校正格式中,预测采用多步性质的显性Adams法、校正采用Tustin法。其数值流的计算前沿面如图6a所示。与Heun法的改进类似,为消除未穿越前沿面且关联隐性项的数值流,将校正过程的当前计算步延后至k时刻,如图6b所示。调整不关联隐性项的数值流,令其穿越前沿面,以保证算法在优化过程中的显、隐性不变,如图6c所示。根据改进的数值流,可得并行的算法格式见式(16)。多步法的一般形式见式(17)[24]。
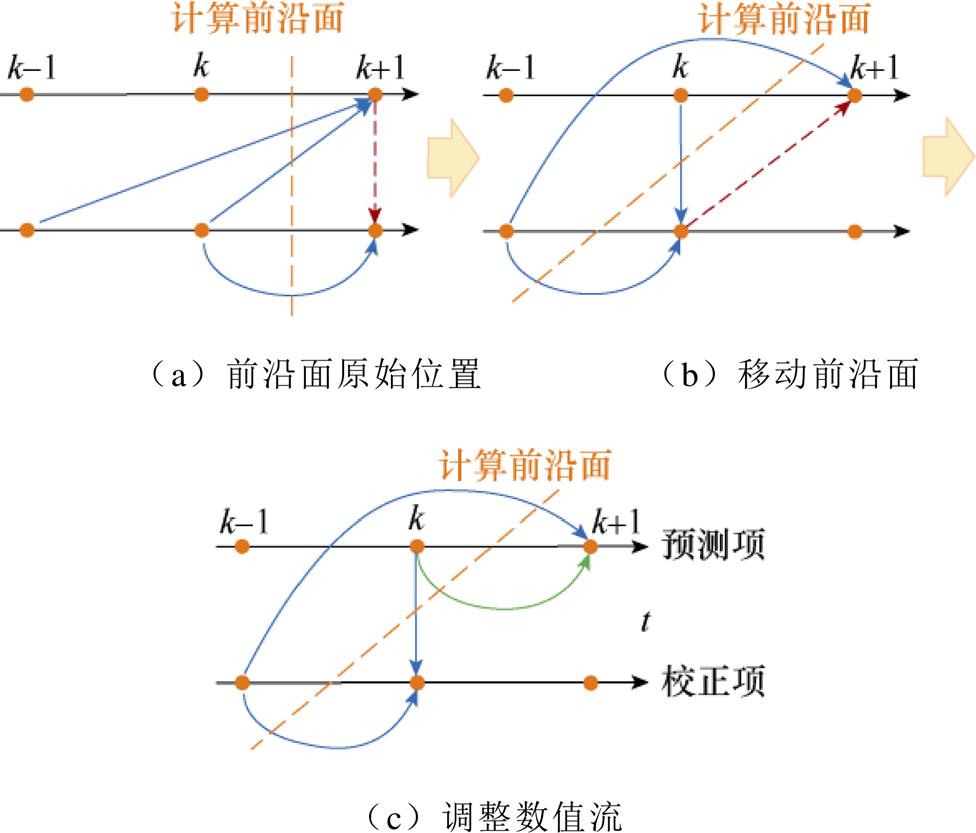
图6 多步格式的预测校正法数值流的计算前沿面调整
Fig.6 Computation front optimization of numerical flow for predictor-corrector method with multi-step behavior
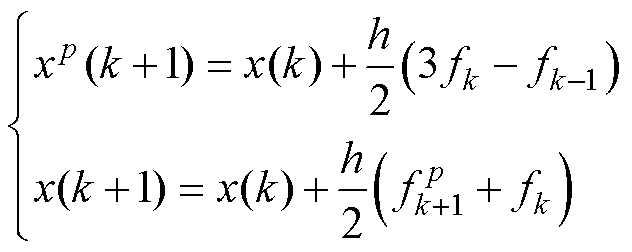 (15)
(15)
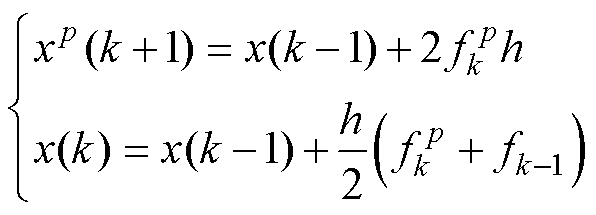 (16)
(16)
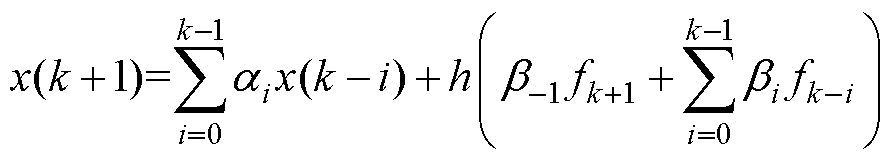 (17)
(17)
式中,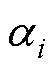 与
与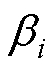 为积分系数。当
为积分系数。当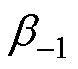 =0,多步法为显性;否则,为隐性。
=0,多步法为显性;否则,为隐性。
两段多步法采用预测校正的方式,一段采用显性格式避免隐性的数值迭代;一段采用隐性格式提高数值稳定域,因此显性用作预测计算,隐性用作校正计算。基于式(17),则通用的两段多步格式为
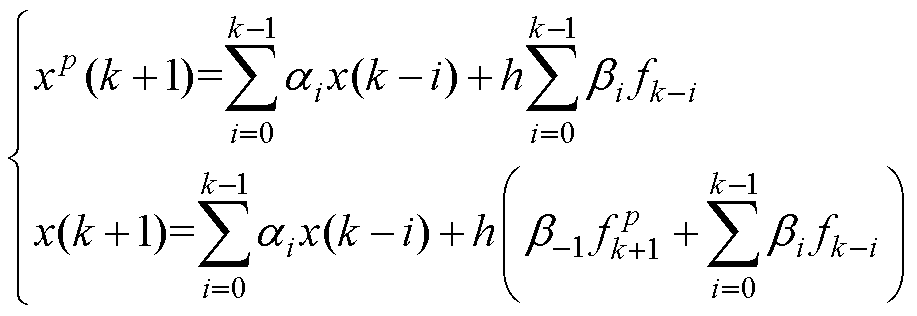 (18)
(18)
由此可得,两段通用多步法的计算前沿面调整如图7所示,并行的算法格式为
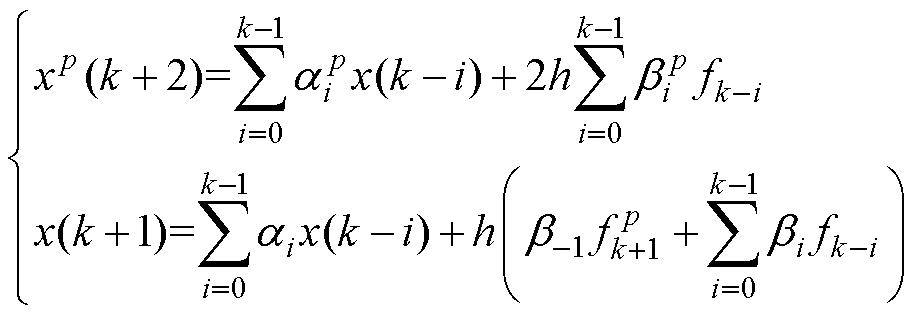 (19)
(19)
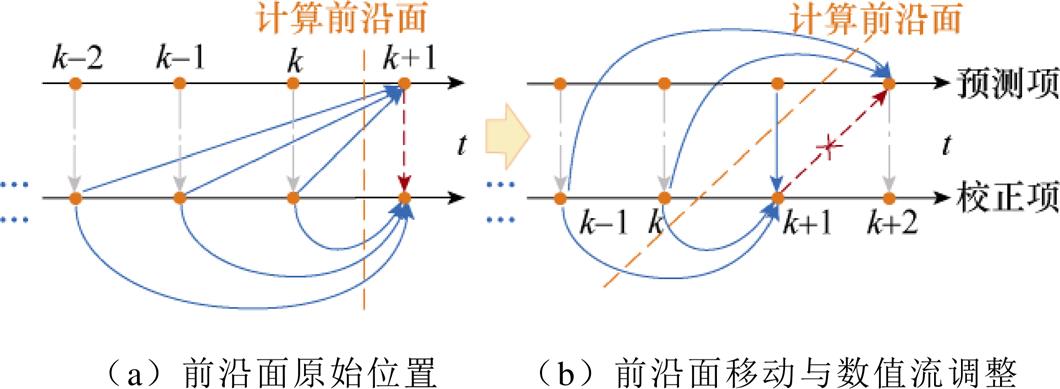
图7 两段通用多步法的计算前沿面调整
Fig.7 Computation front optimization of numerical flow for general form of two-stage multi-step method
因此,计算前沿面的优化方法可对一般形式的多步法进行优化改进,具备一般性。
1.4.2 高阶数值积分法
类似地,基于计算前沿面的思路可以应用到高阶数值积分法的并行优化中。高阶数值积分法的并行设计如图8所示。RK法由于精度高,是求解ODE最常用的高阶方法[24]。RK法可视为预测校正格式的扩展,各阶RK法通过一系列斜率K的线性组合作为预测值,以此提高数值精度,因此也导致计算过程存在多段的计算任务。式(20)给出了三阶精度四段计算的RK3法通用形式。其中,待定参数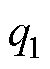 、
、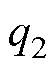 、
、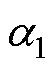 、
、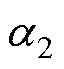 、
、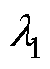 、
、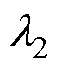 的取值满足条件式(21)的约束。
的取值满足条件式(21)的约束。
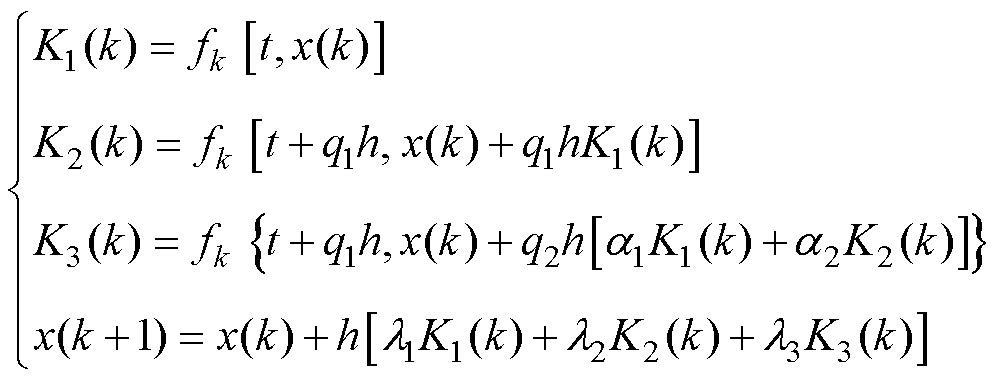 (20)
(20)
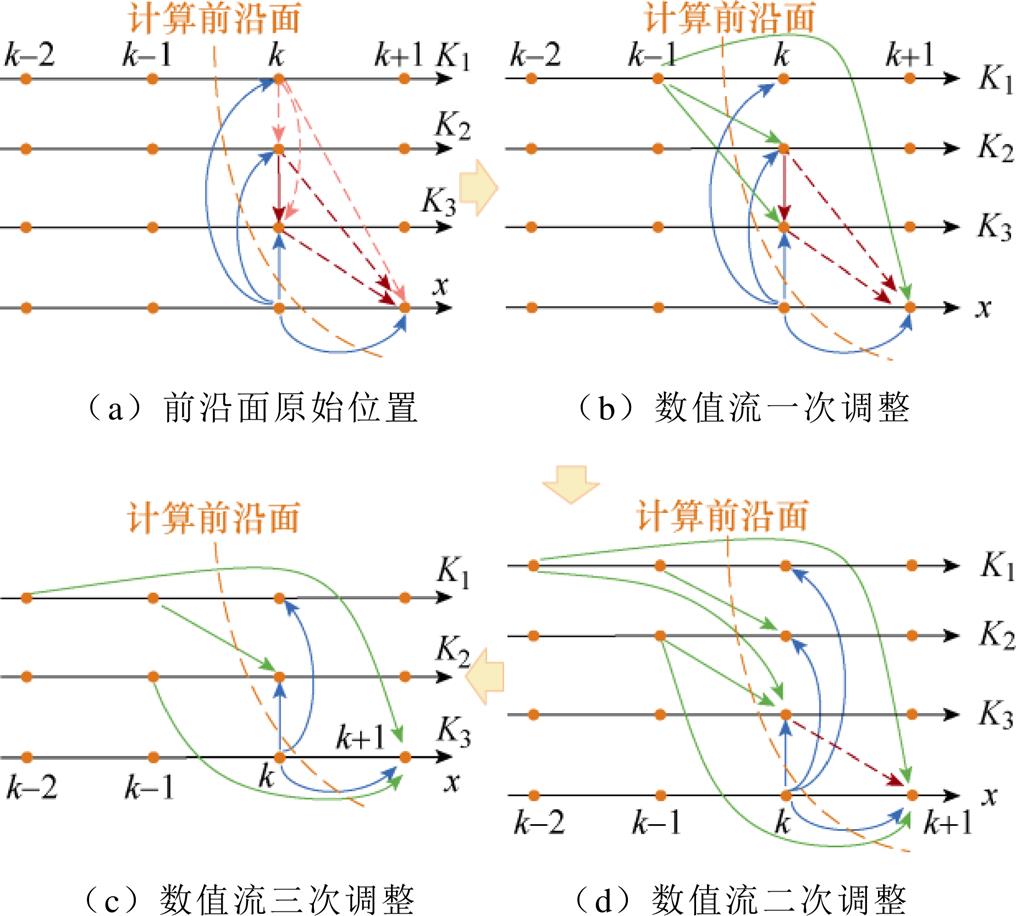
图8 三阶格式的龙格-库塔法数值流的计算前沿面调整
Fig.8 Computation front optimization of numerical flow for RK3 method
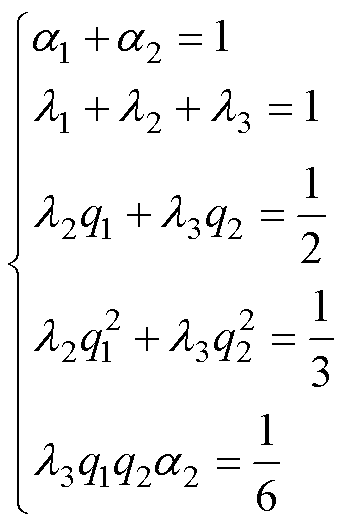 (21)
(21)
由此,RK3的计算前沿面可以推导,如图8a所示。通过图8b、图8c的二次优化调整,消除未穿越前沿面的数值流。根据图8c前沿面的关系可知,存在单个遗留的未穿越前沿面的数值流,因此可通过继续错步优化,或者直接合并斜率K3与状态值x的计算,如图8d所示,完成RK3法的并行化。据优化后的数值流,可得并行的RK3算法格式为
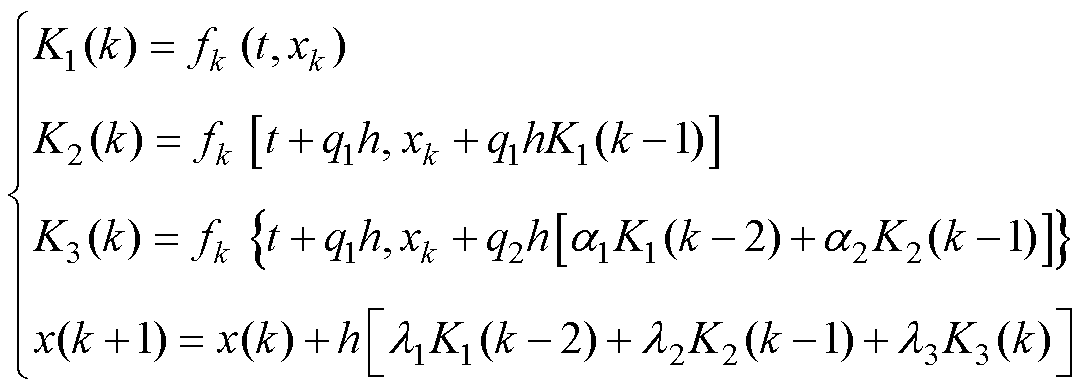 (22)
(22)
综上所述,结合数值积分公式在计算步数与精度阶数上的扩展讨论,本文所提计算前沿面的方法能适应不同数值积分方法,因此具备一般性。
根据上述分析可知,计算前沿面的优化方法为数值积分构造了冗余并行度,增加的计算量并行处理,没有额外增加计算时间。一方面,增加的计算可以补偿数值精度;另一方面,构造的冗余并行度可用以实现数值模型间的解耦分割[26]。
以电动汽车为例,纯电动汽车典型驱动系统拓扑结构如图9所示[11],包含整车控制器、电池单元、功率控制单元、电机、传动系及整车等。从控制的角度出发,实际系统可分为控制系统和被控对象两部分。控制系统包含软件层面的整车控制算法和电驱控制算法等;被控对象包含硬件层面的功率电路和机械单元等。被控对象功率电路部分的数值模型,由于其时间尺度小响应快,是约束计算速度的核心。
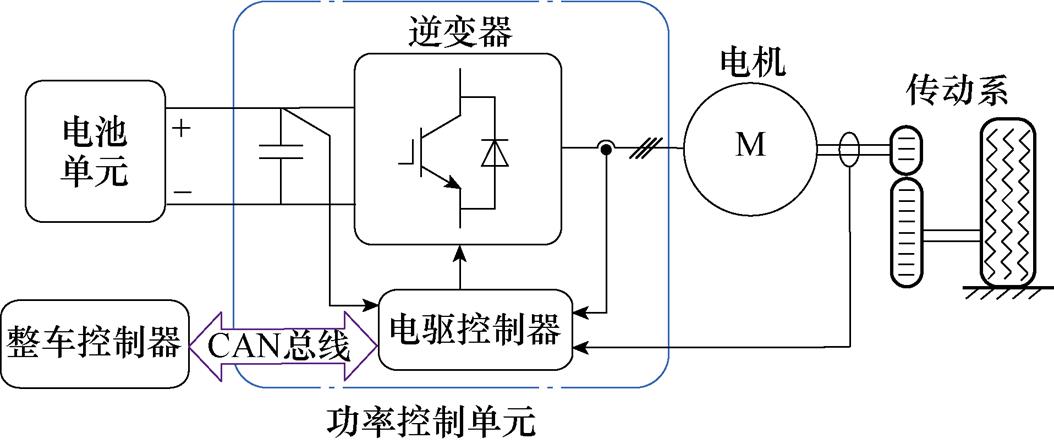
图9 纯电动汽车典型电驱动系统拓扑结构
Fig.9 Topology of electrical drive system for battery EV
其中电池单元简化为电容模型,电机为永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)的dq模型,其均含典型状态元件,适合采用状态空间的算法结构。对于逆变器,由于功率器件开关切换的特性是数值计算比较敏感的部分,因此本文采用L/C法[27]将逆变器中含功率器件和续流二极管的开关单元建模为历史电流源并联电感/电容的结构,电驱系统的数值模型如图10所示,由此形成的状态元件用以并行分割。
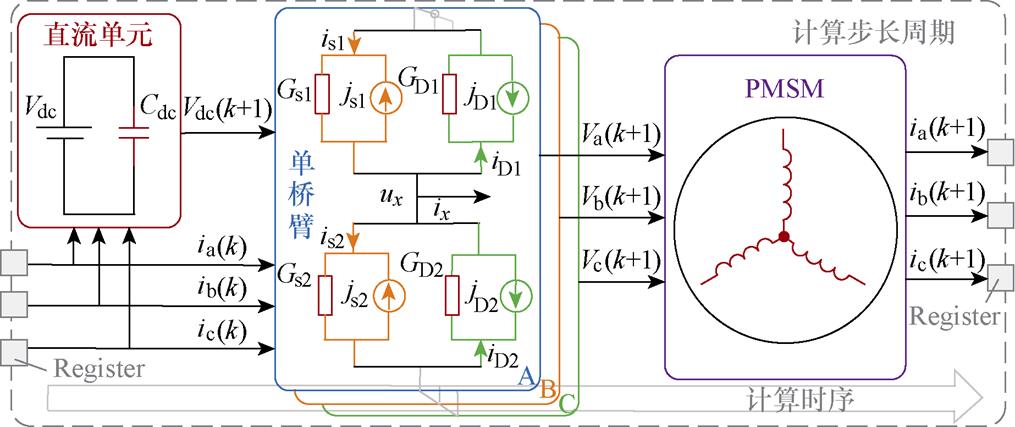
图10 电驱系统的数值模型
Fig.10 Numerical model of electrical drive system
受模型间输入输出关系的约束,传统数值模型的计算顺序是串行执行的,如图10所示。为了克服这一缺陷,不少研究者提出了在模型间采用插入延迟的方式进行模型分割[18],但引入的特征会对数值精度和稳定性产生影响。优化方法由于两段计算任务在时序上交错,导致预测采用倍步计算,因此可以利用其补偿数值模型因分割插入的延迟,基于并行数值积分的数值模型分割如图11所示。步长越小倍步计算的截断误差越小,同时由于预测与校正的计算是并行的,因此仅增加并行的计算资源而不增加计算时间,特别适合短时限下的数值加速,是高频化趋势下的有效方案。同时,由于采用状态空间的算法结构,数值积分求解ODE的对象一般选取状态元件的状态变量,以状态变量为模型间的输入输出接口,能使数值模型通过状态变量实现数值解耦。因此,基于计算前沿面改进优化的数值积分法对于分割数值模型天然有利。
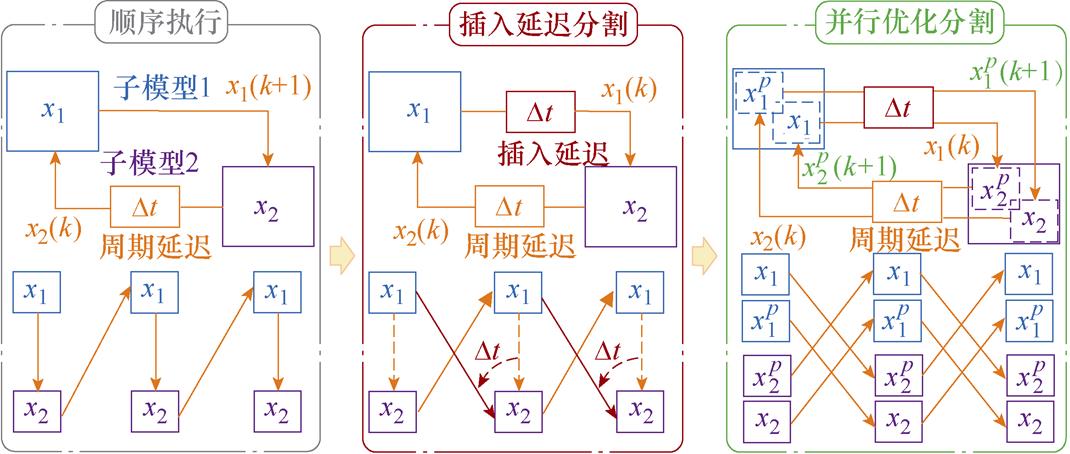
图11 基于并行数值积分的数值模型分割
Fig.11 Numerical model segmentation based on parallel numerical integration method
为简化讨论,本节应用最简单的预测校正格式离散状态变量,预测计算采用FE法,校正计算采用后向欧拉(Backward Euler, BE)法,其数值流与图3完全一致,以此讨论数值模型的分割过程。
2.3.1 逆变器模型的并行优化
逆变器采用L/C法建模,以含功率器件与续流二极管的开关元件作为建模单元,将其等效为受控电流源j并联恒值导纳Gs,开通时开关等效为小电感Ls,关断时开关等效为小电容Cs,则对应的电压vL和电流iC满足
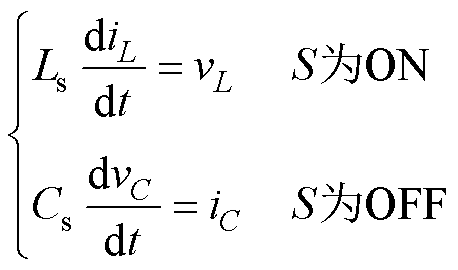 (23)
(23)
通过参数选取让开关时期电感电容等效的Gs相等,一方面可以避免开关期间导致的参数切换;另一方面可以方便优化后的数值积分算法进行并行分割。
采用BE法离散式(23),开关过程的小电感与小电容的数值模型分别为
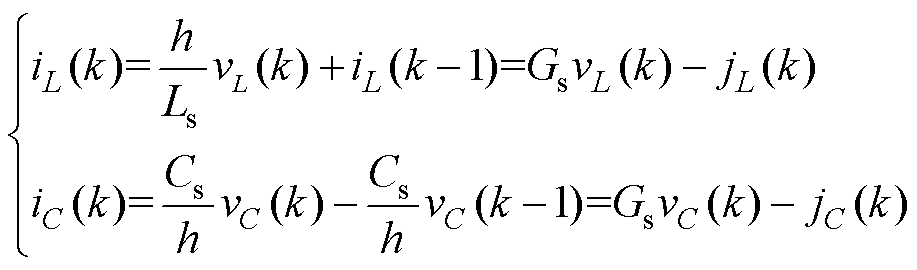 (24)
(24)
为提高L/C法数值求解的通用性,将其求解过程分为三部分:状态变量更新、历史电流源等效及节点矩阵求解。状态变量根据式(24)迭代,由此,电感电容的历史电流源等效为式(25),其中恒值导纳Gs表示为式(26)。节点矩阵求解,由式(27)的改进节点法描述历史电流源、恒值导纳与外围支路间的关系。
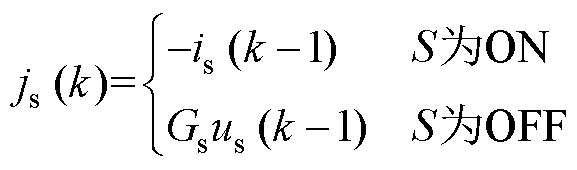 (25)
(25)
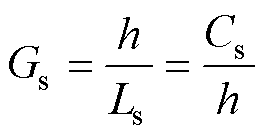 (26)
(26)
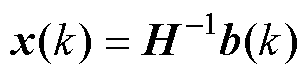 (27)
(27)
式中,H为导纳矩阵,描述了节点变量间的关系,因此状态变量x可以由输入变量b求解得出。
应用本文方法对L/C模型进行并行优化。式(24)改进为两段计算的预测校正法,预测倍步计算,校正不变。开关Ls与Cs的数值模型可写为式(28)与式(29)。
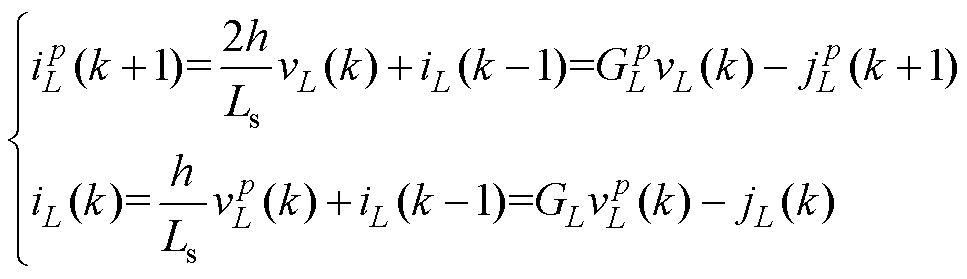 (28)
(28)
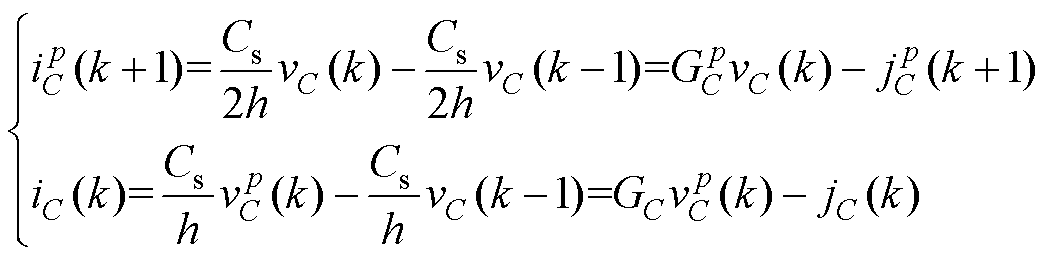 (29)
(29)
因此,预测的Gs调整为式(30),对比式(26)可知,式(30)无合适取值,这是由纯电感电容等效引起,实际上这也会导致L/C法在高频下的虚假数值振荡[27]。在此将关断处理为电容串联小电阻R,则式(30)更新为式(31)。开通和关断的历史电流源分别等效为式(32)和式(33),则状态变量更新可归一为式(34)。
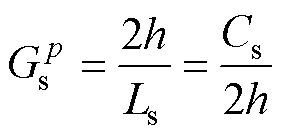 (30)
(30)
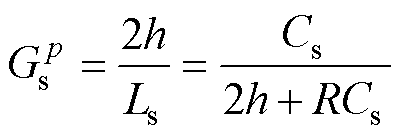 (31)
(31)
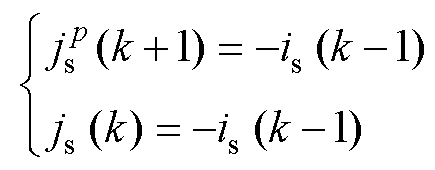 (32)
(32)
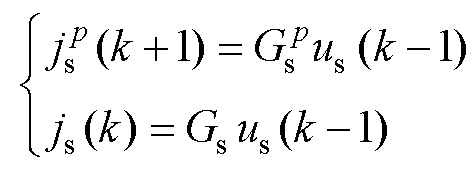 (33)
(33)
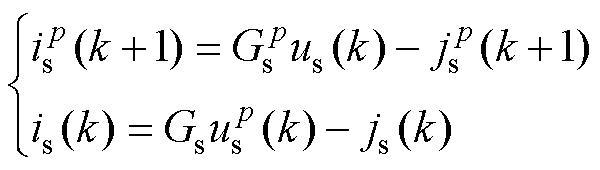 (34)
(34)
两段数值积分增加的计算量于并行计算单元中完成,增加计算资源但不增加计算时间。并行优化后的数值模型如图12所示。
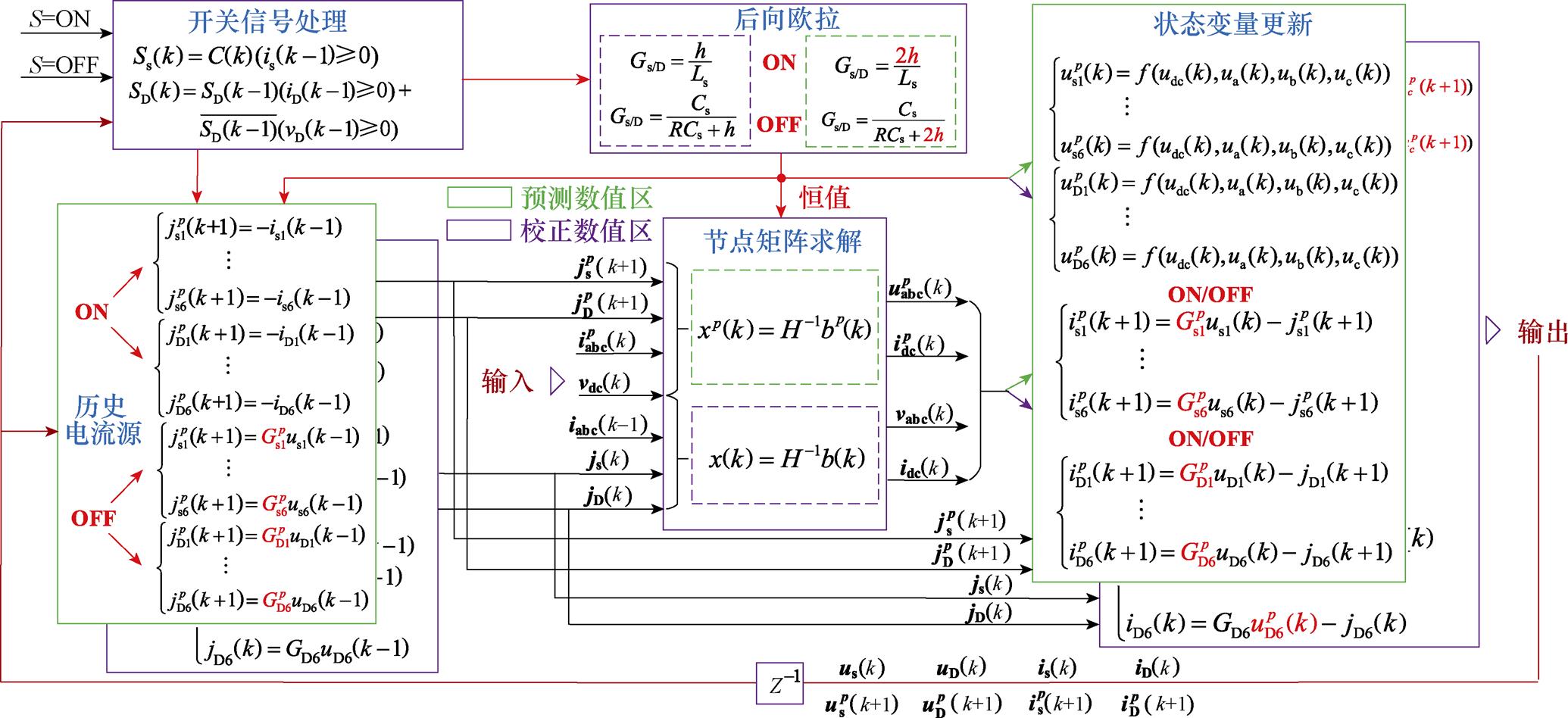
图12 含功率器件及其续流二极管的开关元件并行L/C数值模型
Fig.12 Optimized L/C model of switching elements including power device and freewheeling diode
2.3.2 永磁同步电机模型的并行优化
电动汽车的电机,常采用体积小、效率高的PMSM[28-29],其中的电磁部分相比于机械部分,其时间常数小、动态响应快,是电机数值模型中对计算速度较为敏感的部分,其电磁部分的dq模型(典型ODE)为
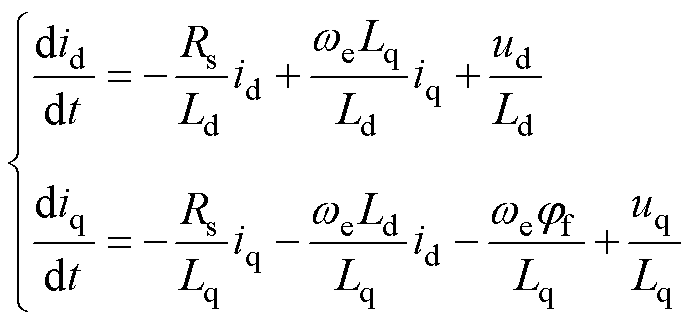 (35)
(35)
式中,id, iq、ud, uq、Ld, Lq分别为d、q轴的电流、电压与电感;Rs、jf、we分别为其定子电阻、永磁体磁链与转子角速度。忽略角速度对电磁部分数学模型的影响,采用FE法离散得
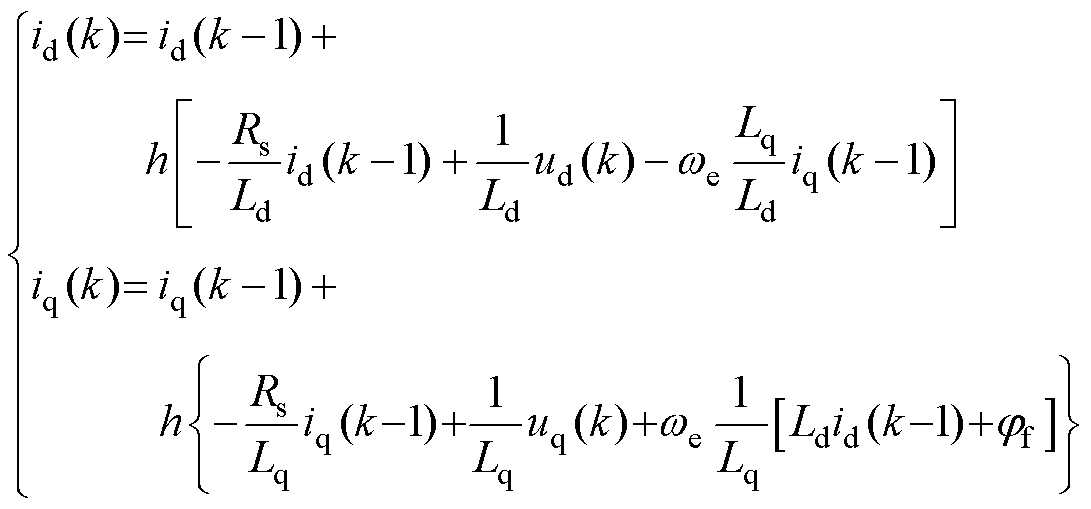 (36)
(36)
同理,应用改进并行的数值积分法,预测采用FE法,校正采用BE法。d、q电流的数值模型分别为
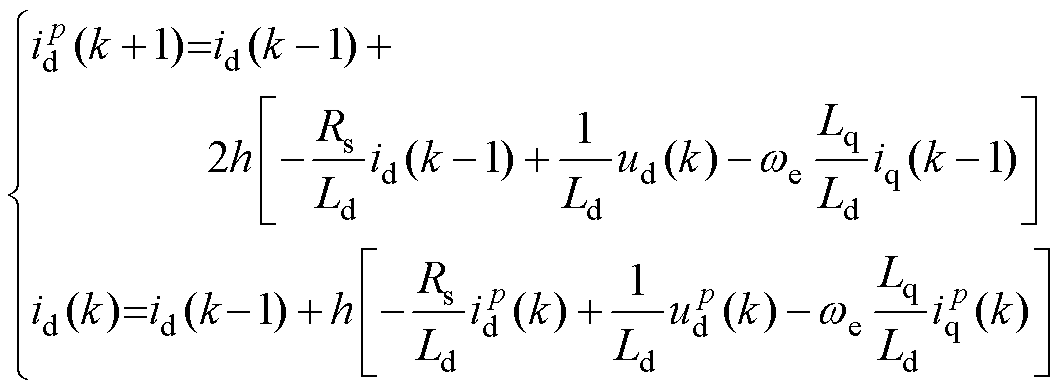 (37)
(37)
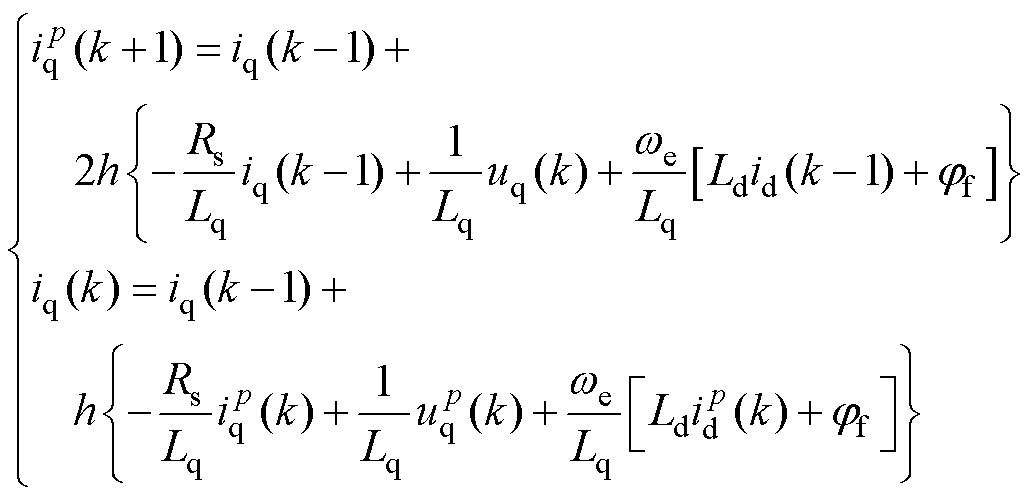 (38)
(38)
机械部分数值模型可类似推导,有
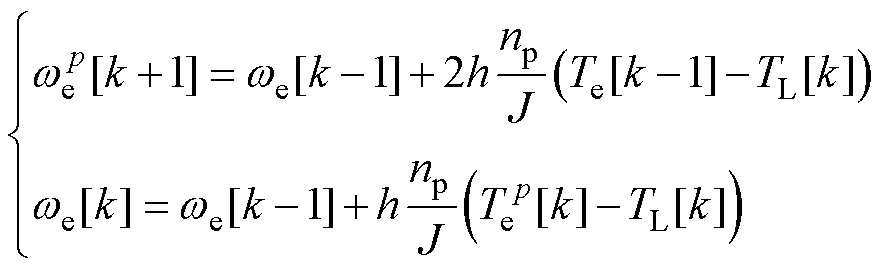 (39)
(39)
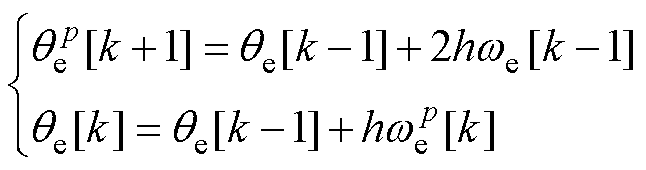 (40)
(40)
式中,np与J分别为电机的极对数、转动惯量;Te与TL分别为电磁转矩与负载转矩;qe为转子电角度。综上所述,优化的PMSM数值模型如图13所示。
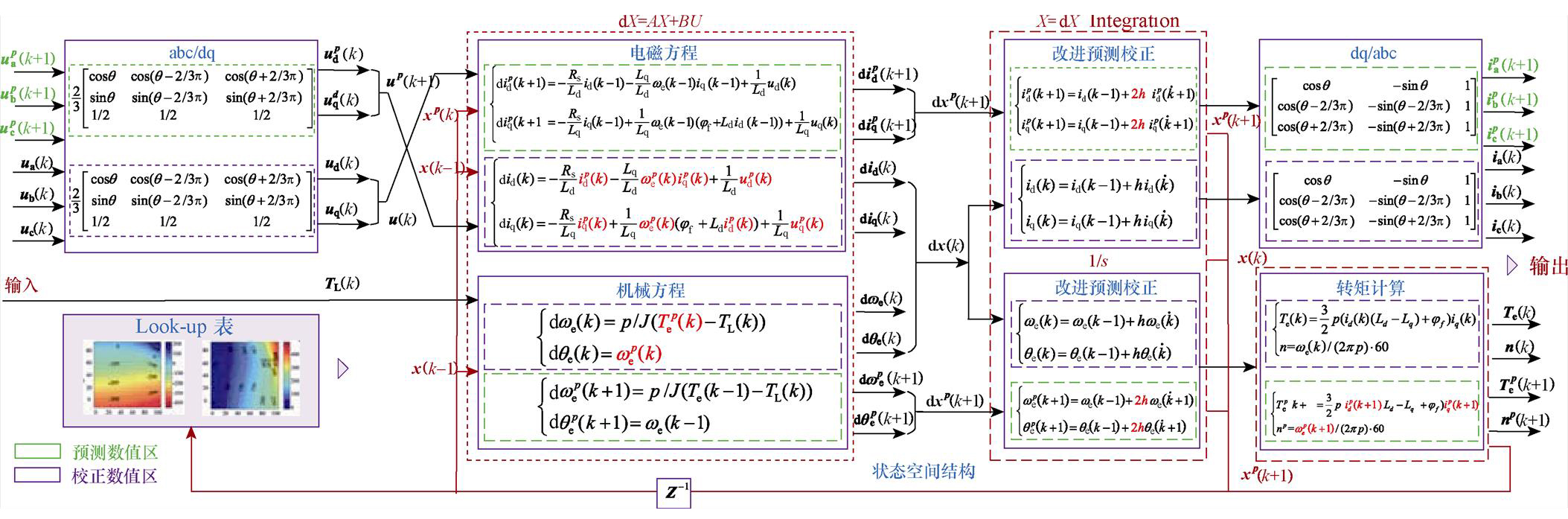
图13 并行优化的PMSM数值模型
Fig.13 Optimized PMSM numerical model
因此,采用两段计算的预测校正法替代逆变器及PMSM中原有一段计算的数值积分,利用基于前沿面优化增加的冗余并行度(见图11),电机驱动系统的数值模型分割如图14所示,实现元件级的解耦分割,以此完成并行加速。
为了验证方法的有效性,基于NI PXI的数字平台了搭建了如图15所示的硬件在环(Hardware in the Loop, HIL)实时仿真环境,并由上位机、实时仿真器、控制器、转接板及其附属电源构成。其中,上位机提供人机交互界面,完成仿真结果的波形显示、数据提取与结果分析,并通过TCP/IP协议与实时仿真器连接;实时仿真器的计算核心采用CPU/ FPGA结构,由CPU板卡(PXIe-8840)和FPGA板卡(PXIe-7857R)构成,二者通过PXIe总线进行通信。其中,CPU部分完成数据交互、通信管理等背景任务及实现慢速回路的机械负载模型仿真,步长为50 ms;FPGA部分实现快速回路的电力电子模型仿真,为使本文方法的验证效果更明显,将步长设为5 ms。同时,实际控制器采用矢量控制与SVPWM。实时仿真系统的整体实现架构如图16所示。本文讨论的功率电路数值模型使用LabVIEW开发在具有并行计算特征的FPGA中,其模型仿真的主要参数见表2,计算资源的占用情况见表3。
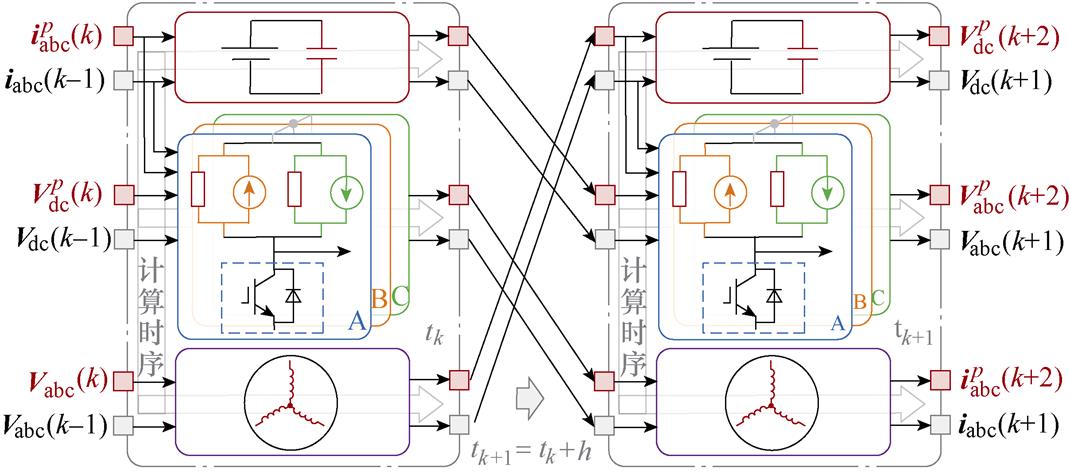
图14 电驱系统并行分割后的数值模型
Fig.14 Numerical model of electrical drive system based on parallel segmentation

图15 基于NI PXI硬件的实时仿真环境
Fig.15 Real-time simulation setup based on NI PXI
3.2.1 数值精度性能
为了验证实时仿真结果的准确性,在HIL中搭建了如图10所示的串行实时仿真模型,与此同时,在Simulink中搭建了与表2实时仿真参数一致的离线仿真模型。离线仿真的计算内核为CPU,同样为串行的计算时序。通过转矩负载的阶跃变化验证实时模型的有效性,转矩负载扰动下实时仿真与离线仿真测试如图17所示,针对电机的相电流响应与电磁转矩响应,提取扰动时刻附近的实时仿真结果,验证结果表明,串行计算的实时数值模型在稳态与动态的跟踪上与离线数值模型基本吻合,具备一定的准确度。动态过程存在微小的仿真偏差,这是由于硬件在环的实时仿真包含实际控制器,其控制算法部分非理想的运行环境造成的。
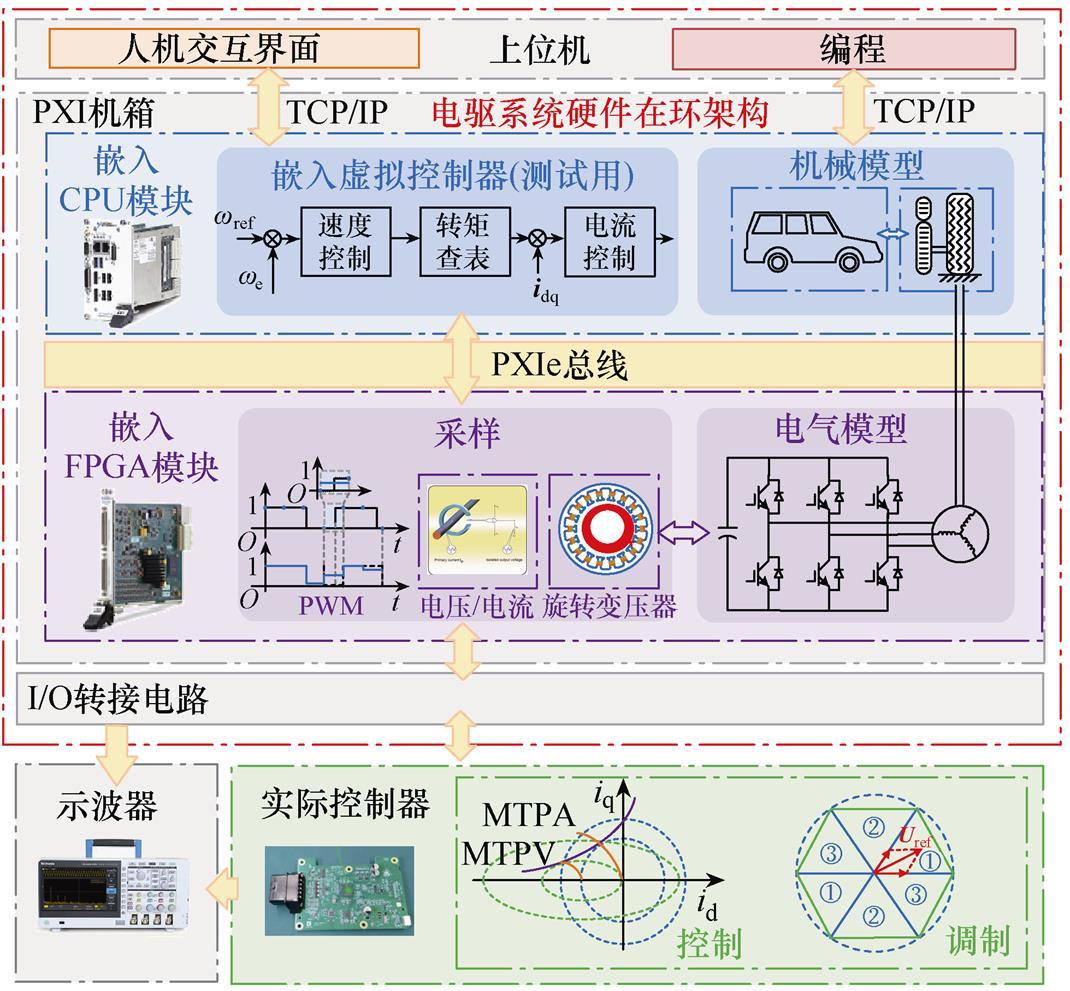
图16 实时仿真系统整体架构
Fig.16 Overall architecture of real-time simulation system
表2 实时仿真主要参数
Tab.2 Main parameters of real-time simulation
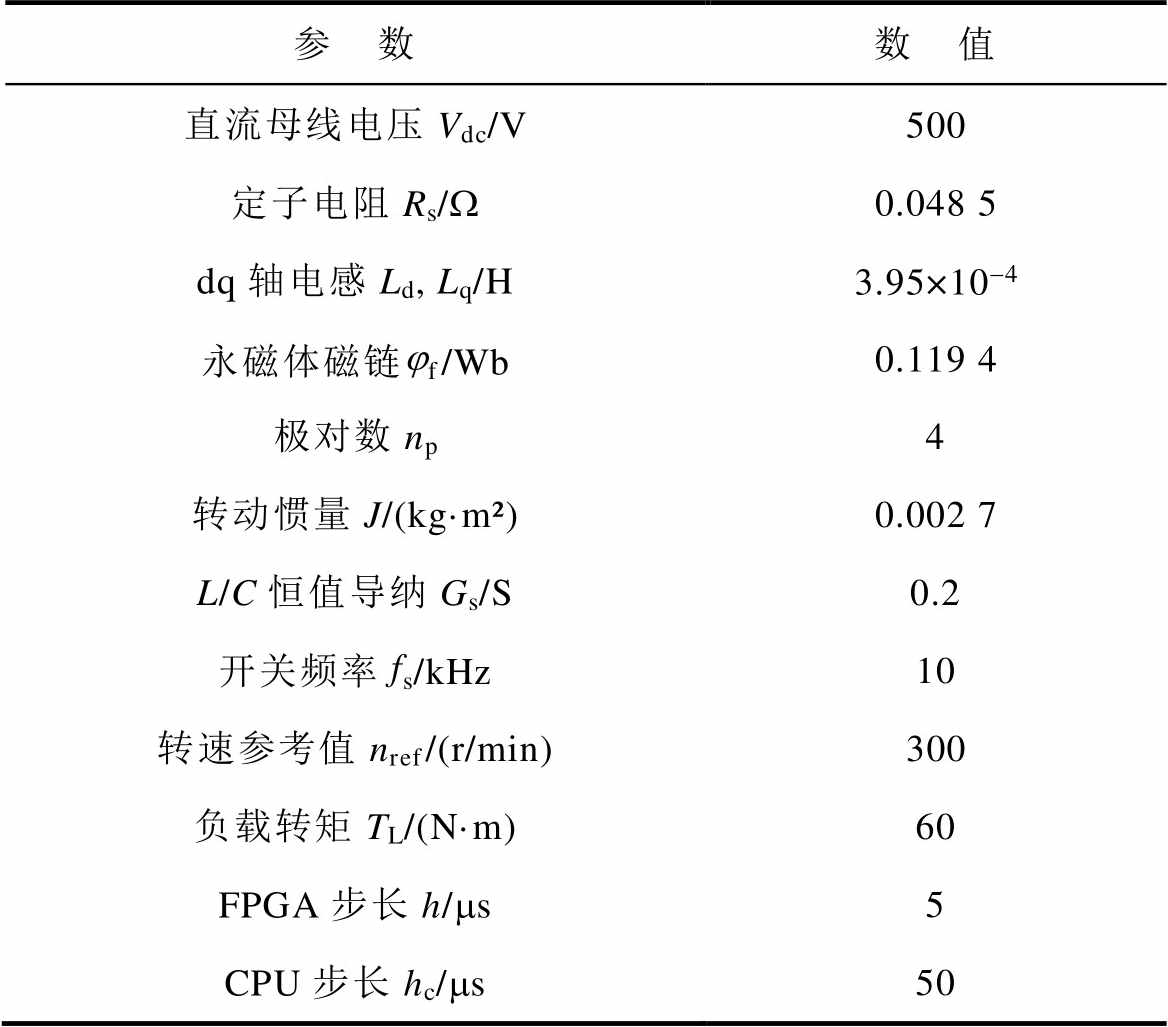
参 数数 值 直流母线电压Vdc/V500 定子电阻Rs/W0.048 5 dq轴电感Ld, Lq/H3.95×10-4 永磁体磁链jf/Wb0.119 4 极对数np4 转动惯量J/(kg·m²)0.002 7 L/C恒值导纳Gs/S0.2 开关频率fs/kHz10 转速参考值nref/(r/min)300 负载转矩TL/(N·m)60 FPGA步长h/ms5 CPU步长hc/ms50
表3 实时仿真硬件资源占用
Tab.3 Hardware resource utilization of real-time Simulation
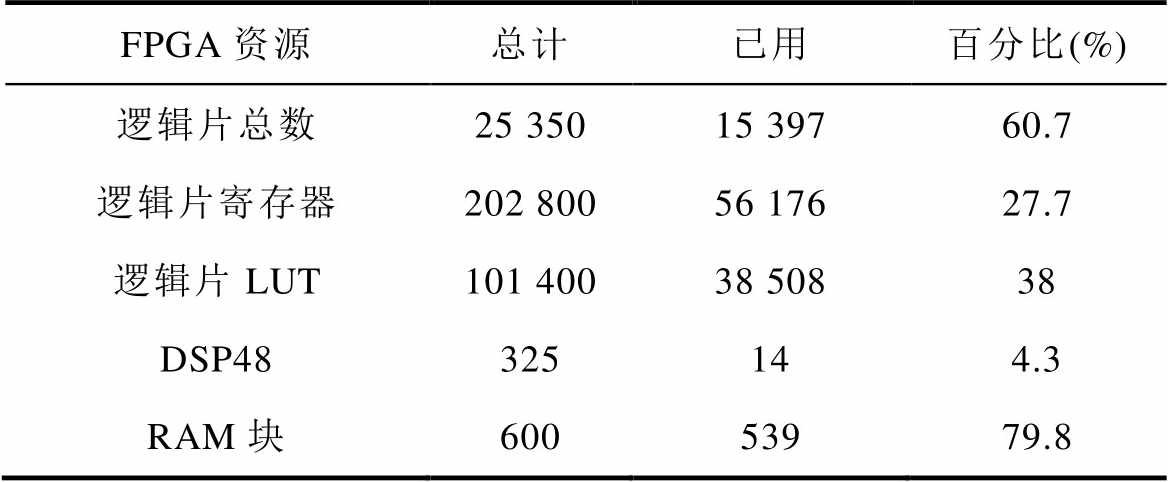
FPGA资源总计已用百分比(%) 逻辑片总数25 35015 39760.7 逻辑片寄存器202 80056 17627.7 逻辑片LUT101 40038 50838 DSP48325144.3 RAM块60053979.8
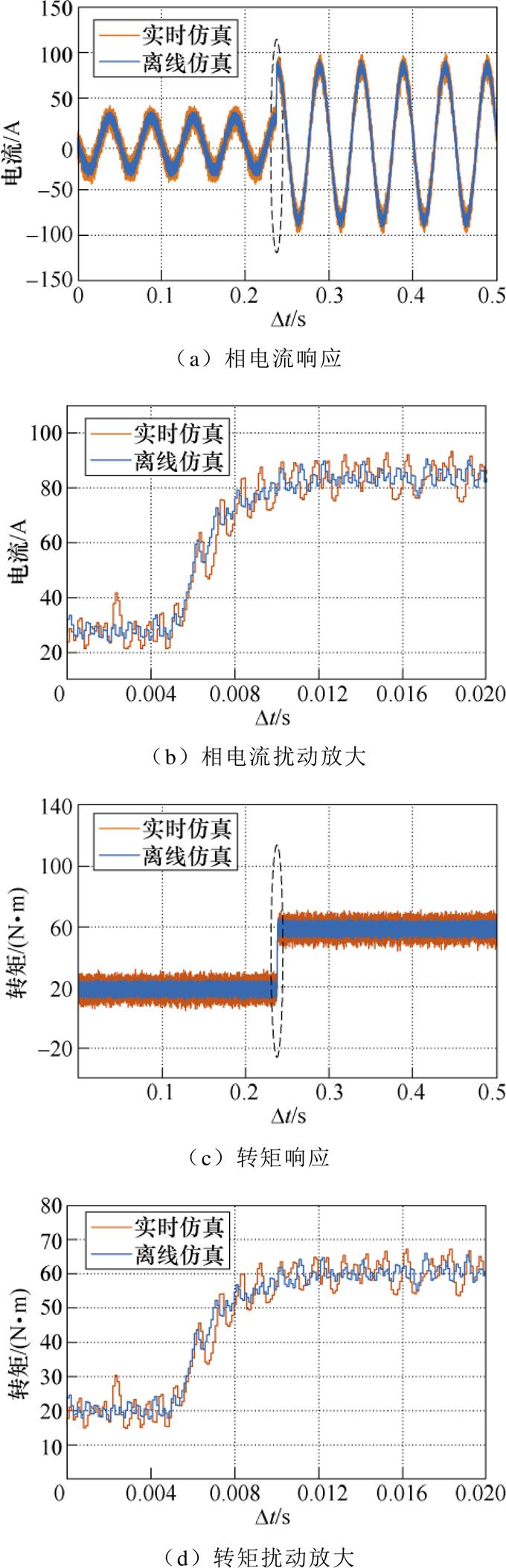
图17 转矩负载扰动下实时仿真与离线仿真测试
Fig.17 Real-time and offline simulation results at torque load disturbance
在串行计算的实时数值模型基础上,分别采用传统的延迟插入法与本文提出的优化方法解耦分割实时的数值模型(见图14),以此验证本文方法的优越性。延迟插入法采用图11中的方式分割数值模型;本文方法基于计算前沿面的优化,得到图12与图13的改进数值模型,利用冗余的并行度分割数值模型。根据得到的并行数值模型分别对三相电流、dq电流与转矩转速进行了测试比较。
延迟插入法与本文优化方法的时域响应及其误差测试结果如图18所示。图18a为PMSM三相电流的实时仿真比较,传统方法采用插入延迟的方式分割数值模型,引入的延迟导致仿真误差增加。对比其中单相电流对于串行实时仿真的相对误差,本文优化方法的相对误差降低至3 %以内。同样地,dq电流与电磁转矩仿真结果类似,如图18b、图18c所示。而对于图18d转速的实时仿真比较,本文方法与传统方法的相对误差类似,这是由于数值模型在转速计算过程中涉及多级积分运算,起到了数值滤波作用,这也是插入延迟类方法通常选取状态变量作为并行分割点的原因。综上所述,由对比结果可知,插入延迟的方式由于延迟的引入会影响数值仿真的精度,而本文方法能够实现同等并行加速的同时等效地减小延迟对数值精度的影响。并行方法相对串行仿真结果的误差比较见表4。由相对于串行仿真结果的误差测试表明,本文方法的各物理量在稳态下相对传统方法,其相对误差有所减小。
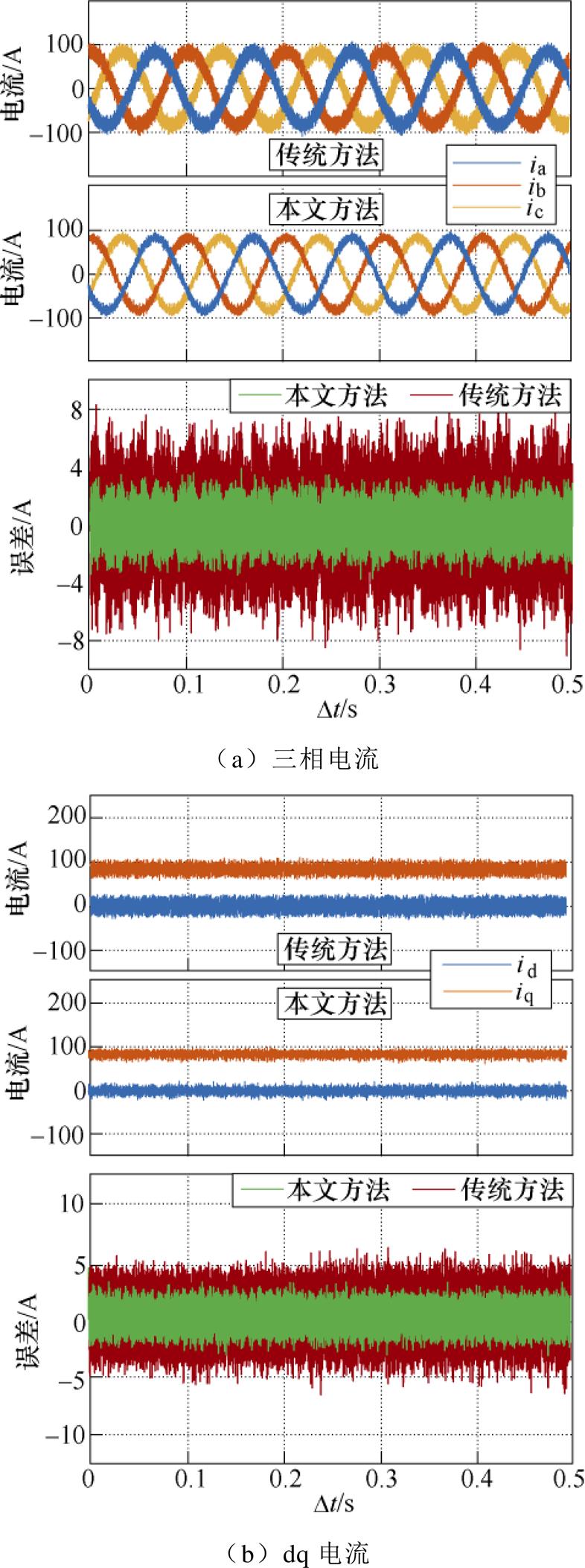
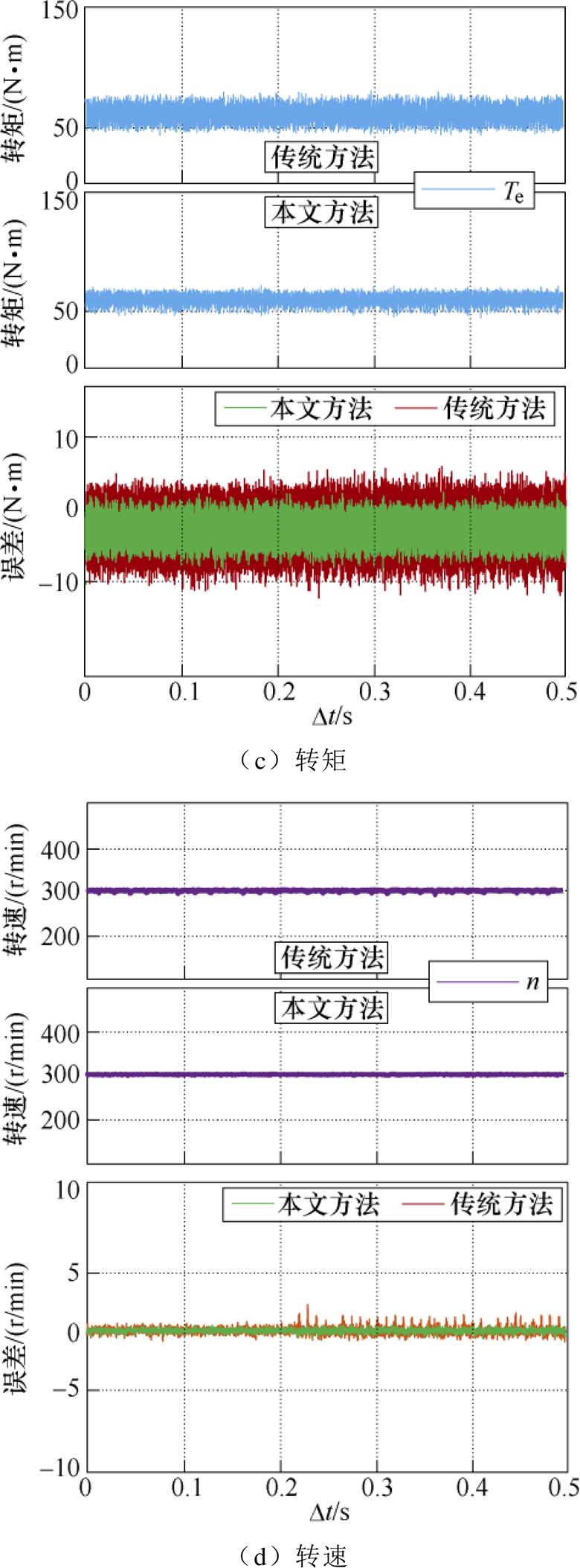
图18 延迟插入法与本文优化方法的时域响应及其误差测试
Fig.18 Time domain response of real-time simulation and error comparison with offline simulation for insertion-delay based method and proposed method
表4 并行方法相对串行仿真结果的误差比较
Tab.4 Error comparison of parallel methods relative to serial simulation results
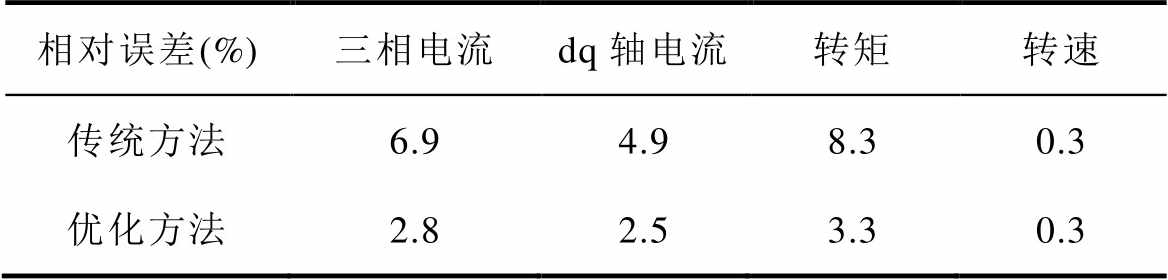
相对误差(%)三相电流dq轴电流转矩转速 传统方法6.94.98.30.3 优化方法2.82.53.30.3
此外,图19a为逆变器数值模型的输出电压,其中预测计算与校正计算的绝对误差在2.5 V以内,图19b为电机数值模型的相电流,预测计算与校正计算的绝对误差在1.5 A以内。因此,采用本文的优化方法,计算前沿面改进过程引入的倍步计算对数值求解结果的影响较小,基本可忽略,因此数值仿真的精度可以被保证。
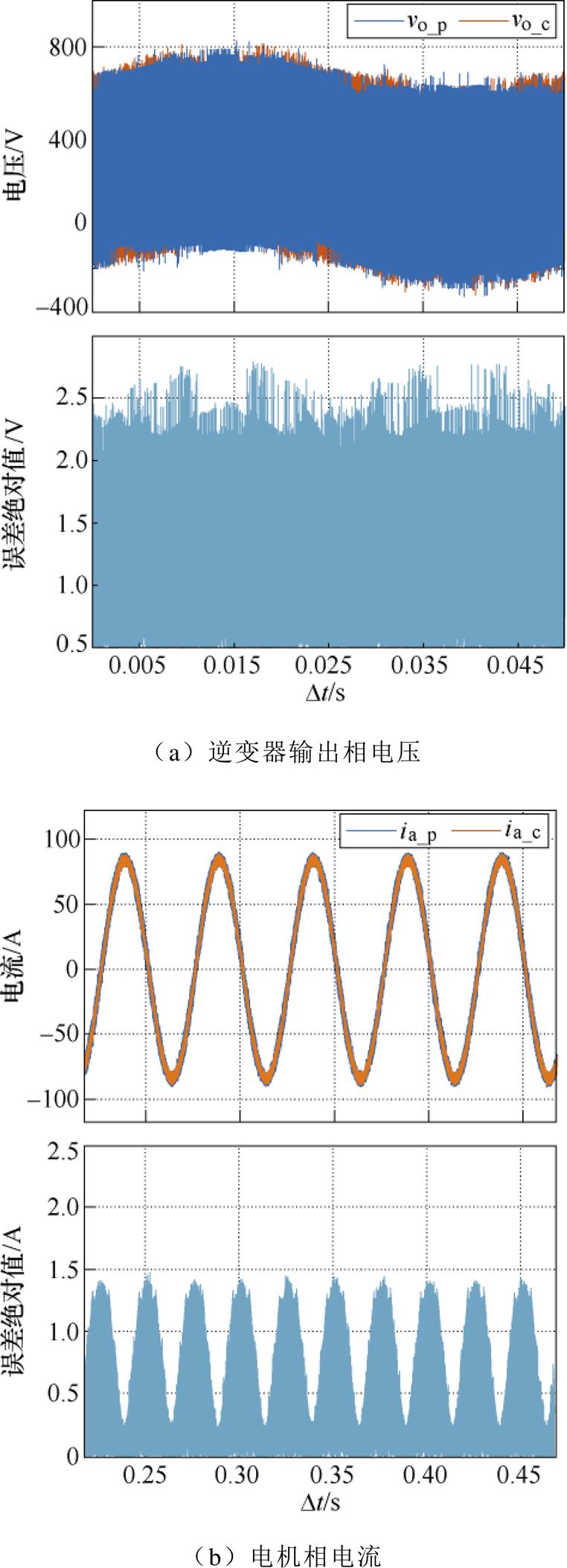
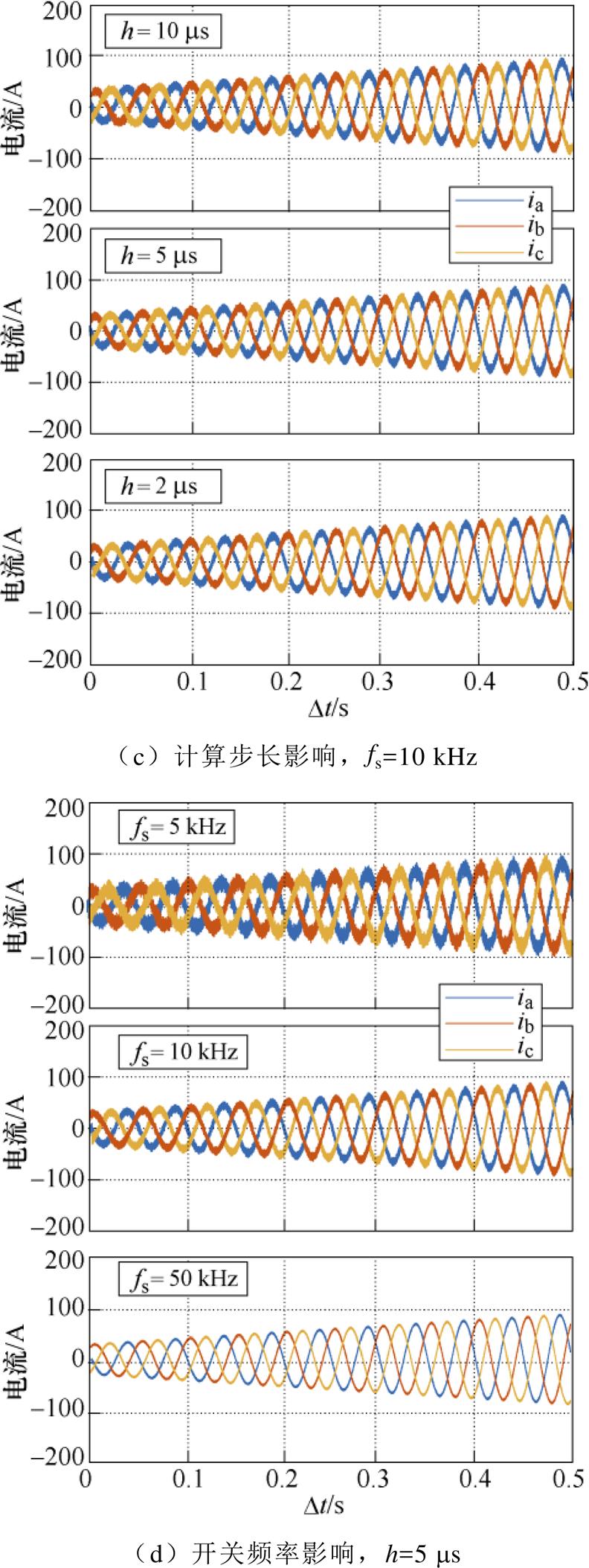
图19 本文方法的性能评估
Fig.19 Performance evaluation of optimized method
3.2.2 并行加速性能
为了评估优化方法的加速特性,表5给出了实时仿真中基于传统延迟插入方法、本文优化方法实现并行分割的数值模型,及其与串行的数值模型间的对比结果。FPGA中的数值模型被分割为直流单元、逆变器、电机模型三部分并行计算。优化方法的每部分采用双核计算单元处理预测与校正的两段并行计算,因此总并行单元数为6,计及加速比的并行单元数为3。相比于串行的数值模型,优化方法并行化后获得了1.72的加速比,并行效率达57.2 %。相比于传统基于延迟插入的并行分割方法,本文优化方法获得了同等的并行加速效果。但基于数值精度等方面的改进,本文方法具备综合的应用优势。目前,在数值算法上,并行计算的方法已有一定的研究,但应用于短时限约束下的电力电子实时数值仿真的并行加速方法较为有限。因此,本文方法具备一定的改进意义。与此同时,本文优化方法虽然实现了并行加速,但并行效率指标并非最优,这是由于分割后各并行单元的计算负载不平衡引起的。如在计算资源受限的情况下,为提升并行指标,可将直流单元与逆变器部分的计算合并,则数值仿真系统的并行效率可达到85.8 %。
表5 优化方法的并行性能
Tab.5 Parallel performance of optimization method
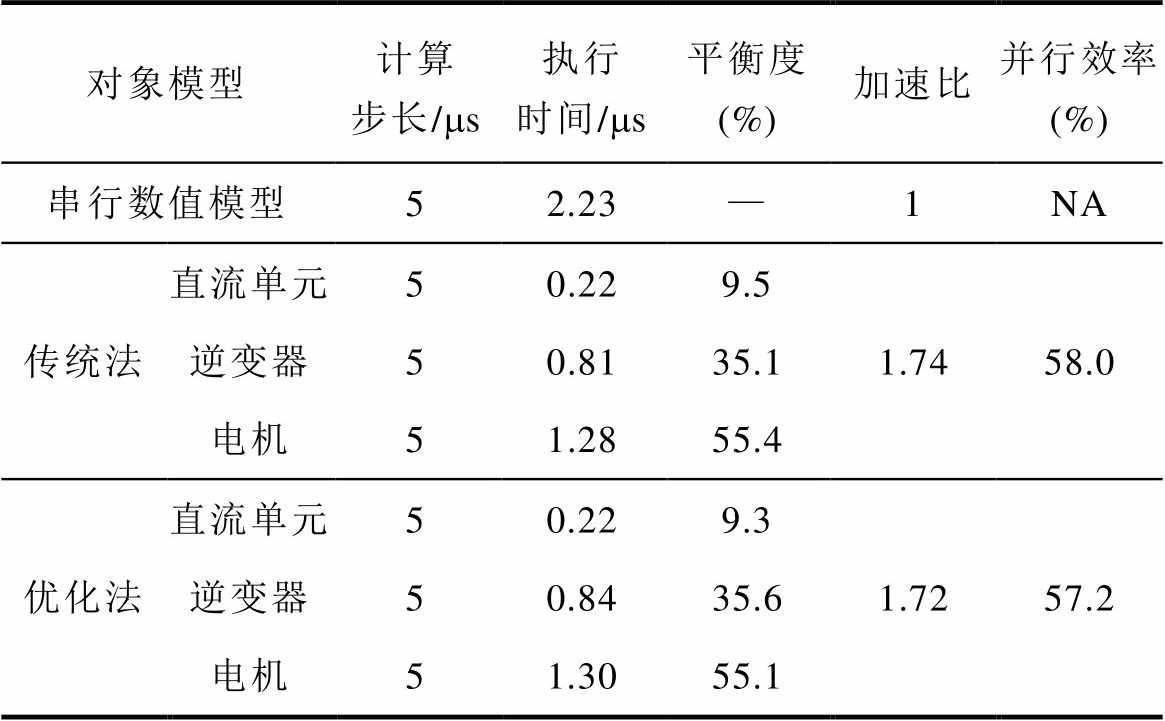
对象模型计算步长/ms执行时间/ms平衡度 (%)加速比并行效率 (%) 串行数值模型52.23—1NA 传统法直流单元50.229.51.7458.0 逆变器50.8135.1 电机51.2855.4 优化法直流单元50.229.31.7257.2 逆变器50.8435.6 电机51.3055.1
由于提升了加速比,相较于串行仿真而言,本文方法通过并行的方式释放了计算步长与开关频率在实时仿真中的约束范围,扩大了实时仿真的运行区域。实时仿真中计算步长与开关频率的约束关系如图20所示,以一个开关周期执行10次实时仿真计算为例,开关频率的增长,计算步长的短时限约束越明显。结合图19c、图19d的实时仿真结果,其分别为负载转矩逐渐增大的条件下,计算步长与开关频率的变化对本文方法的影响。计算步长增加对数值性能有一定影响,但本文方法在设定的步长范围内没有出现数值稳定问题,而且通过计算速度的提升扩大了实时仿真的步长选择范围。不同于串行实时仿真受到开关频率增加引发的计算时间缩短的限制,采用本文方法的并行实时仿真能够覆盖不同开关频率下的仿真需求,在短时限约束下的实时仿真具有一定的应用前景。
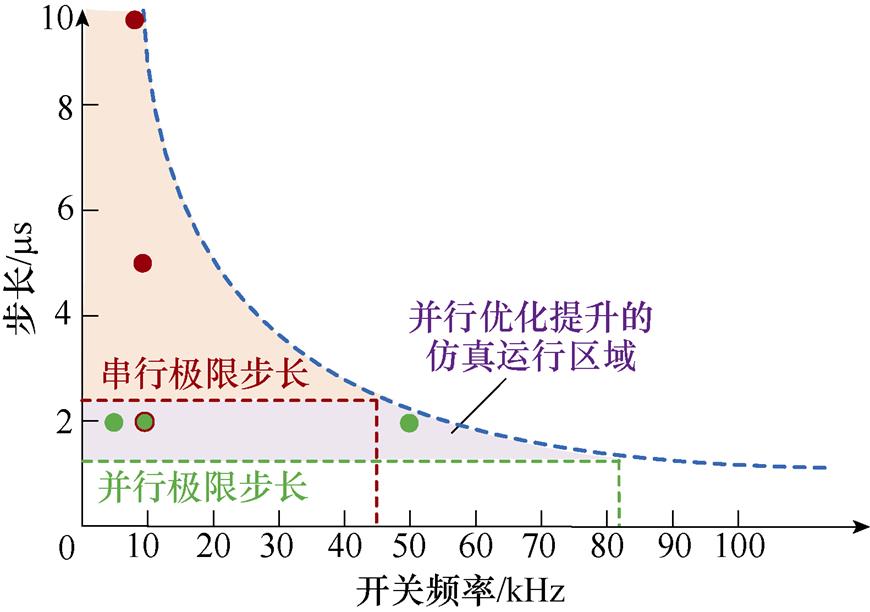
图20 实时仿真中计算步长与开关频率的约束关系
Fig.20 Constraints between step size and switching frequency in real-time simulation
基于硬件在环实时仿真在数值精度与并行加速两方面的验证结果表明,本文方法本质上是通过增加计算资源实现并行加速的同时保证计算精度。相比于传统方法,本文方法能降低并行分割带来的仿真误差,同时实现1.72倍的并行加速,扩大了实时仿真的运行范围,适合于短时限约束的应用场景。
与此同时,本文方法也存在一定的局限性。由于计算前沿面优化中存在数值流的调整,可能会在数值积分格式中引入局部的步长变化,优化方法虽然存在精度补偿机制,但对数值稳定域有一定影响,在大步长仿真的情况下存在数值不稳定的风险。本文方法在高阶或多步数值积分法的拓展上具备一般性,因此可通过数值积分方法的组合选取,避免大步长引发的数值不稳定。此外,由于本文方法适用于元件级的数值模型分割,因此可能存在计算负载不平衡的问题,导致并行加速比受到限制,尚有优化的空间。
计算速度是数值仿真的核心性能指标,而高开关频率功率器件的应用,给实时数值仿真在短时限约束下的计算速度带来严峻挑战。随着数字平台的计算结构朝着并行化的趋势发展,现有的数值模型和数值算法大多基于串行的计算模式,缺乏冗余并行度。本文研究了数值算法核心数值积分的并行优化方法,提出计算前沿面的思路为数值积分法构造冗余并行度,并利用其设计数值模型的并行分割,实现并行加速。将本文方法应用于电驱系统数值模型的硬件在环实时仿真,可以得到以下结论:
1)数值积分的计算关系通过数值流转化成图形关系,计算前沿面能够揭示数值积分算法的可并行性。在一定条件下通过计算前沿面的移动和数值流的调整,可为数值积分方法构造冗余并行度,实现并行计算。
2)计算前沿面的优化由于存在数值流的调整,可能会在数值积分格式中引入局部的步长变化,对于数值性能有一定影响,适合短时限约束下的并行加速。计算前沿面通过改进预测校正格式引入精度补偿机制,可以保证数值精度。由于计算前沿面的方法具备一般性,数值稳定域面积的减小可以通过数值积分的选取来克服其在大步长应用中的局限。
3)利用构造的冗余并行度,可以实现数值模型的并行分割。通过改进电驱系统逆变器与电机的数值模型,实现并行加速。硬件在环实时仿真的验证结果表明,优化方法降低了并行分割带来的计算误差,并实现1.72的加速比和57.2 %的并行效率,扩大了实时仿真的运行范围。受限于计算负载的不平衡,加速比和并行效率仍然有优化的空间,相关研究将在后续的工作中开展。
参考文献
[1] 马伟明, 王东, 程思为, 等. 高性能电机系统的共性基础科学问题与技术发展前沿[J]. 中国电机工程学报, 2016, 36(8): 2025-2035.
Ma Weiming, Wang Dong, Cheng Siwei, et al. Common basic scientific problems and development of leading-edge technology of high performance motor system[J]. Proceedings of the CSEE, 2016, 36(8): 2025-2035.
[2] International Energy Agency. Global EV outlook 2020[Z]. 2020.
[3] 袁立强, 陆子贤, 孙建宁, 等. 电能路由器设计自动化综述—设计流程架构和遗传算法[J]. 电工技术学报, 2020, 35(18): 3878-3893.
Yuan Liqiang, Lu Zixian, Sun Jianning, et al. Design automation for electrical energy router-design work- flow framework and genetic algorithm: a review[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3878-3893.
[4] 江悦, 沈小军, 吕洪, 等. 碱性电解槽运行特性数字孪生模型构建及仿真[J]. 电工技术学报, 2022, 37(11): 2897-2908.
Jiang Yue, Shen Xiaojun, Lü Hong, et al. Con- struction and simulation of operation digital twin model for alkaline water electrolyzer[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2897-2908.
[5] Zhao Zhengming, Tan D, Shi Bochen, et al. A breakthrough in design verification of megawatt power electronic systems[J]. IEEE Power Electronics Magazine, 2020, 7(3): 36-43.
[6] 张栋, 范涛, 温旭辉, 等. 电动汽车用高功率密度碳化硅电机控制器研究[J]. 中国电机工程学报, 2019, 39(19): 5624-5634, 5890.
Zhang Dong, Fan Tao, Wen Xuhui, et al. Research on high power density SiC motor drive controller[J]. Proceedings of the CSEE, 2019, 39(19): 5624-5634, 5890.
[7] Mojlish S, Erdogan N, Levine D, et al. Review of hardware platforms for real-time simulation of elec- tric machines[J]. IEEE Transactions on Transportation Electrification, 2017, 3(1): 130-146.
[8] Ruba M, Nemes R O, Ciornei S M, et al. Digital twin real-time FPGA implementation for light electric vehicle propulsion system using EMR organi- zation[C]//2019 IEEE Vehicle Power and Propulsion Conference (VPPC), Hanoi, Vietnam, 2020: 1-6.
[9] 薛禹胜, 谢东亮, 薛峰, 等. 支持信息-物理-社会系统研究的跨领域交互仿真平台[J]. 电力系统自动化, 2022, 46(10): 138-148.
Xue Yusheng, Xie Dongliang, Xue Feng, et al. A cross-field interactive simulation platform for suppor- ting research on cyber-physical-social systems[J]. Automation of Electric Power Systems, 2022, 46(10): 138-148.
[10] 吴巨爱, 薛禹胜, 谢东亮, 等. 电动汽车参与电量市场与备用市场的联合风险调度[J/OL]. 电工技术学报, DOI: 10.19595/j.cnki.1000-6753.tces.221386.
Wu Juai, Xue Yusheng, Xie Dongliang, et al. The joint risk dispatch of electric vehicle in day-ahead electricity energy market and reserve market[J/OL]. Transactions of China Electrotechnical Society,DOI: 10.19595/j.cnki.1000-6753.tces.221386.
[11] 何绍民, 杨欢, 王海兵, 等. 电动汽车功率控制单元软件数字化设计研究综述及展望[J]. 电工技术学报, 2021, 36(24): 5101-5114.
He Shaomin, Yang Huan, Wang Haibing, et al. Review and prospect of software digital design for electric vehicle power control unit[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5101- 5114.
[12] Shu Dewu, Wei Yingdong, Dinavahi V, et al. Cosimu- lation of shifted-frequency/dynamic phasor and elec- tromagnetic transient models of hybrid LCC-MMC DC grids on integrated CPU-GPUs[J]. IEEE Transa- ctions on Industrial Electronics, 2020, 67(8): 6517- 6530.
[13] 郭琦, 卢远宏. 新型电力系统的建模仿真关键技术及展望[J]. 电力系统自动化, 2022, 46(10): 18-32.
Guo Qi, Lu Yuanhong. Key technologies and pro- spects of modeling and simulation of new power system[J]. Automation of Electric Power Systems, 2022, 46(10): 18-32.
[14] Allmeling J H, Hammer W P. PLECS-piece-wise linear electrical circuit simulation for Simulink[C]// Proceedings of the IEEE 1999 International Con- ference on Power Electronics and Drive Systems. PEDS'99, Hong Kong, China, 2002: 355-360.
[15] Bai Hao, Liu Chen, Breaz E, et al. A review on the device-level real-time simulation of power electronic converters: motivations for improving performance[J]. IEEE Industrial Electronics Magazine, 2021, 15(1): 12-27.
[16] Dufour C, Mahseredjian J, Bélanger J. A combined state-space nodal method for the simulation of power system transients[J]. IEEE Transactions on Power Delivery, 2011, 26(2): 928-935.
[17] Ould-Bachir T, Blanchette H F, Al-Haddad K. A network tearing technique for FPGA-based real-time simulation of power converters[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3409-3418.
[18] Milton M, Benigni A. Latency insertion method based real-time simulation of power electronic systems[J]. IEEE Transactions on Power Electronics, 2018, 33(8): 7166-7177.
[19] Lin Ning, Dinavahi V. Detailed device-level electro- thermal modeling of the proactive hybrid HVDC breaker for real-time hardware-in-the-loop simulation of DC grids[J]. IEEE Transactions on Power Elec- tronics, 2018, 33(2): 1118-1134.
[20] 张宏俊, 郝正航, 陈卓, 等. 适用于模块化多电平换流器实时仿真的建模方法[J]. 电力系统自动化, 2017, 41(7): 120-126.
Zhang Hongjun, Hao Zhenghang, Chen Zhuo, et al. Modeling method for real time simulation of modular multilevel converter[J]. Automation of Electric Power Systems, 2017, 41(7): 120-126.
[21] Hui S Y R, Christopoulos C. Modeling non-linear power electronic circuits with the transmission-line modeling technique[J]. IEEE Transactions on Power Electronics, 1995, 10(1): 48-54.
[22] Chalangar H, Ould-Bachir T, Sheshyekani K, et al. Methods for the accurate real-time simulation of high-frequency power converters[J]. IEEE Transa- ctions on Industrial Electronics, 2022, 69(9): 9613- 9623.
[23] Grégoire L A, Blanchette H F, Bélanger J, et al. Real-time simulation-based multisolver decoupling technique for complex power-electronics circuits[J]. IEEE Transactions on Power Delivery, 2016, 31(5): 2313-2321.
[24] Cellier F E, Kofman E. Continuous system simu- lation[M]. New York, US: Springer, 2010.
[25] 陈丽容, 刘德贵. 求解刚性常微分方程的并行Rosenbrock方法[J]. 计算数学, 1998, 20(3): 251- 260.
Chen Lirong, Liu Degui. Parallel Rosenbrock methods for stiff ordinary differential equations[J]. Mathematica Numerica Sinica, 1998, 20(3): 251-260.
[26] Liu Chen, Bai Hao, Zhuo Shengrong, et al. Real-time simulation of power electronic systems based on predictive behavior[J]. IEEE Transactions on Indu- strial Electronics, 2020, 67(9): 8044-8053.
[27] 李子润, 徐晋, 汪可友, 等. 电力电子换流器离散小步合成实时仿真模型[J]. 电工技术学报, 2022, 37(20): 5267-5277.
Li Zirun, Xu Jin, Wang Keyou, et al. A discrete small-step synthesis real-time simulation model for power converters[J]. Transactions of China Electro- technical Society, 2022, 37(20): 5267-5277.
[28] He Shaomin, Xu Zhiwei, Chen Min, et al. General derivation law with torque-free achieving of integral on-board charger on compact powertrains[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 1791-1802.
[29] 章回炫, 范涛, 边元均, 等. 永磁同步电机高性能电流预测控制[J]. 电工技术学报, 2022, 37(17): 4335-4345.
Zhang Huixuan, Fan Tao, Bian Yuanjun, et al. Predictive current control strategy of permanent magnet synchronous motors with high performance[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4335-4345.
Abstract The computation speed is the key performance of numerical simulation, which is the foundation and underlying core technology of intelligent computing. However, with the application of high switching- frequency power devices in electric drive systems, the constraint of short computation time has led to great challenges for computation speed in real-time or online numerical simulation. At the same time, with the trend of parallel architecture in digital platforms, parallel computing is considered an effective way to optimize the computation speed with short time constraints. However, the state-of-the-art numerical models and algorithms are based on serial computation, lacking of redundant parallelism. Therefore, the computation front design methodology is proposed to construct the redundant parallelism for numerical integration, so the numerical model can be decoupled and parallel computed based on the redundant parallelism to accelerate the numerical simulation.
Firstly, the relationship between numerical integration and algorithm structure in power electronic simulation is discussed, which is the key to the numerical solution of ordinary differential equations (ODE). The computation front involved in numerical integration optimization is proposed, and the redundant parallelism construction process of the optimization method is described based on the predictor-corrector method. Secondly, the influence of the proposed method on the numerical performance is evaluated from numerical precision and numerical stability. The parallel computing resources are utilized in the proposed method to improve the numerical precision without increasing the computation time. Although the numerical stability domain changes during the optimization process, the influence on numerical simulation is limited, especially in applications with small step sizes. Thirdly, the possibility of general application is discussed from the multistep-step integration method and high-order integration method, proving that the computation front can be extended to different integration methods. Finally, the parallel numerical model is designed and applied to the electrical drive system based on the redundant parallelism constructed by the proposed method. As a result, the model-level numerical acceleration is achieved.
The real-time simulation environment of hardware in the loop (HIL) is demonstrated to verify the proposed method. The real-time simulation with a serial computing model is compared with offline simulation in Simulink, so the effectiveness of self-defined HIL based on NI PXI is verified. Then, the real-time simulation with a parallel computing model is compared between the latency insertion method and the proposed method. The results show that the relative error with the proposed method is reduced to less than 3 %, and the numerical precision of parallel simulation is improved. Moreover, the speedup ratio and parallel efficiency are 1.72 and 57.2 %, respectively, which expands the step size selection range of real-time simulation.
The following conclusions can be drawn from the real-time simulation analysis: (1) The redundant parallelism of numerical integration can be constructed based on the computation front to realize parallel computation. (2) The local step size of numerical integration is potentially changed during optimization, which may affect the numerical performance. Thus, the proposed method with accuracy compensation is designed based on the predictor-corrector method, which can reduce the simulation error. (3) The parallel acceleration can be achieved without accuracy reduction, but the parallel efficiency is limited due to an unbalanced computation load, which could be discussed in future research.
keywords:Parallel computation, electrical drive system, computation front, real-time simulation, numerical acceleration, numerical integration
何绍民 男,1994年生,博士研究生,研究方向为高效能电机系统数字化设计与验证、电力电子实时仿真技术。E-mail: shirmin001@zju.edu.cn
杨 欢 男,1981年生,教授,博士生导师,研究方向为分布式发电与微电网、智能配用电、高效能电机系统等。E-mail: yanghuan@zju.edu.cn(通信作者)
DOI: 10.19595/j.cnki.1000-6753.tces.220982
中图分类号:TM46; TP337
国家自然科学基金资助项目(52177062)。
收稿日期 2022-05-31
改稿日期 2022-09-20
(编辑 崔文静)