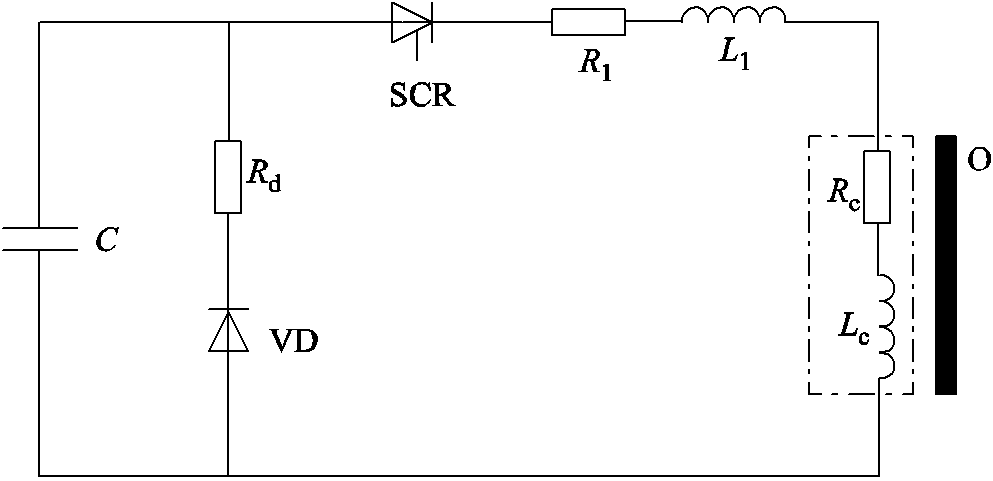
图1 脉冲线圈放电电路
Fig.1 Circuit of pulsed coil discharge
摘要 在飞机和风机叶片电脉冲除冰中,为了提高线圈的脉冲效果,降低除冰装置质量,实现系统的微功耗设计,需要优化线圈结构。脉冲线圈作为脉冲除冰、脉冲焊接等应用中能源转换的关键部件,其瞬态电磁场求解复杂,一般难以得到解析解。为了研究线圈结构参数对脉冲效果的影响,该文通过推导脉冲线圈的场-路数学方程,建立脉冲线圈和目标物的物理模型,并采用有限元软件对脉冲线圈的瞬态电磁场进行计算,得到脉冲线圈电磁参数时变特性。通过脉冲线圈的脉冲冲量试验对模型的准确性进行验证,在此基础上,分析线圈匝数、截面尺寸和线圈匝间距等结构参数对脉冲电流、脉冲力、脉冲效果的影响,为电脉冲除冰应用微功耗化设计提供优化思路和技术路线。
关键词:脉冲线圈 瞬态电磁场 脉冲效果 结构参数
相比常见的电热融冰法,电脉冲除冰是一种功耗小、速度快的除冰方式[1-2],其中能量转换部件为脉冲线圈。脉冲线圈在脉冲焊接[3-4]、无损探伤[5-7]、新型直流断路器[8]和无线传输[9]等领域也有应用,其作为电能转换为机械能或电能的关键部件不可或缺。在不同领域中,由于实现的目标不同,脉冲线圈的结构、电磁参数、布置和使用方式差别很大。在脉冲焊接和新型直流断路器的试验测试中,脉冲线圈将瞬时的电能通过磁场转化为目标物中的机械能,使目标物产生塑性形变或位移。
国内外针对脉冲线圈的不同应用领域研究各有侧重点。脉冲焊接主要关注目标物的塑性形变和不同异形金属件的焊接效果;新型直流断路器更关注目标物的受力过程;而在电脉冲除冰中,研究人员则将重点集中在目标物的电动力学、结构动力学和除冰效果等方面,但由于电磁场瞬态计算较为复杂,大部分的瞬态问题暂时无法得到精准的时域解析解[10]。目前,俄罗斯已升级至第四代电脉冲除冰系统,采用新材料和新结构,其质量比第三代系统更轻,并进一步提升了系统可靠性,使其除冰环境温度降低至-50℃。由于我国的飞机对除冰的需求比俄罗斯低,在国内还未广泛应用微功耗、轻量化的电脉冲除冰系统[11]。随着计算机的发展,数值计算在电磁场的应用越来越多[12],但对电脉冲除冰情景下的瞬态电磁场研究较少。特别是在不同电路参数下,脉冲线圈的电磁场变化及脉冲效果都缺乏相应的研究。
在20世纪,苏联、美国先后在飞机机翼电脉冲除冰方面开展研究,苏联已经成功地将其应用在伊尔系列飞机上,美国也已将其实现商业化[13]。目前我国主要在美国威奇塔州立大学(Wichita State University, WSU)飞机机翼电脉冲除冰方法的研究基础上开展相关探究。
美国R. A. Henderson博士利用M. H. S. Ei-Markabi和F. M. Freeman提出的电磁场建模技术,建立一种计算脉冲线圈的电磁场传输线模型,该模型初步计算线圈的放电电流、铝板所受的脉冲力,但它是一种通过频域近似计算的方法[14]。R. L. Schrag和W. D. Bernhart等提出了关于脉冲线圈的电磁场Bernhart-Schrag模型,通过将线圈和目标物同时划分为矩形单元,并建立单元间的电感矩阵,求得目标物的电磁力,但未对脉冲线圈结构参数进行分析[15]。南京航空航天大学李清英等认为,在电频率一定时,脉冲电流峰值最大则脉冲效果最好,并以此提出了线圈的设计方法[13]。E. Moehle等对铝板上的电脉冲力进行电磁场和结构动力学耦合分析,并进行除冰试验,验证仿真的有效性[16],但同样未对线圈进行优化分析。郭涛在此基础上建立了电脉冲除冰的有限元分析模型,为了降低计算难度,使用空心圆柱体来等效脉冲线圈[17],但在数值计算中,程序无法区别线圈截面和尺寸信息,对脉冲线圈的电气参数计算不准确,难以说明线圈的尺寸参数和匝数对计算结果的影响。重庆大学王洋洋等提出一种针对瞬态电磁场计算的有限元耦合方法,对导体域采用边光滑有限元法(Edge Smooth-Finite Element Method, ES-FEM),对非导体域采用边界元法(Boundary-Elements Method, BEM),能够提高求解速度和精度,但未将该方法应用于脉冲线圈的瞬态电磁场计算中[18]。同时重庆大学黄廷帆等在试验研究中发现[19],随着脉冲线圈匝数的增加,线圈电阻和电感同时增大,获得的总脉冲冲量呈上升趋势。相对于不变的电容和能量条件下,脉冲电路中的电流峰值会下降,出现峰值电流的时间滞后,进而使脉冲力峰值降低。在试验中需要控制的变量太多,且单个线圈在多次试验后,局部过高的温度会影响线圈电阻,进而影响试验结果。此外,在电脉冲除冰的研究中,普遍使用平面式螺旋线圈,线圈截面主要为矩形,仅部分研究使用了圆形截面的线圈。
综上所述,已有学者对脉冲线圈及目标物进行电磁场、电磁力计算和数值计算方法的研究,但均未对其结构参数的影响进行深入探索。本文从电路和电磁场的基本原理出发,建立矩形截面的脉冲线圈和目标物物理模型,确定电路参数、瞬态电磁场的控制方程及边界条件,通过数值方法计算不同线圈下的电气参数和瞬态电磁场,具体分析线圈尺寸、线圈匝数、线圈内外径结构参数对脉冲电流、脉冲力和脉冲冲量的影响,得到固定电路参数下,较优的脉冲线圈结构参数,对电脉冲除冰应用微功耗的优化设计具有一定的指导。
脉冲线圈放电过程是一种RLC的欠阻尼二阶电路,其电路如图1所示。其中,C为充、放电电容,作为放电电路的电源;VD为钳位二极管,用来保护电容;Rd为钳位二极管自带电阻;SCR为晶闸管,当电容充电完成准备除冰时,可通过控制电路控制其闭合;Rl和Ll分别为线路的电阻和电感,其值基本不变;Rc和Lc分别为线圈的电感和电阻;O为目标物,通常为铝板。

图1 脉冲线圈放电电路
Fig.1 Circuit of pulsed coil discharge
对于图1所示电路,可以得到其二阶电路中的电流方程为
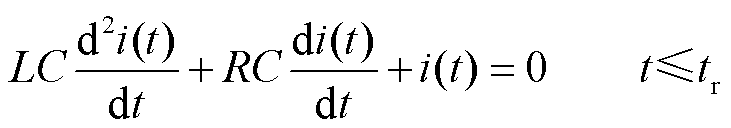 (1)
(1)
式中,i(t)为脉冲电路电流(A);L为电路电感(H),由线路电感和线圈电感组成;C为放电电容(F);R为电路电阻(Ω),由线路电阻和线圈电阻组成;tr为电容反向充电时刻(s)。由于钳位二极管的作用,线圈不会对电容反向充电。
在本文中,反向电流只会通过钳位二极管自行耗尽,且主要研究0~tr内的过程。线路参数和电容参数在瞬态计算中基本无明显变化,但在目标物涡流的影响下,线圈电阻、电感变化很大,这将给场-路耦合带来困难。
由式(1)可进一步得到脉冲电流为
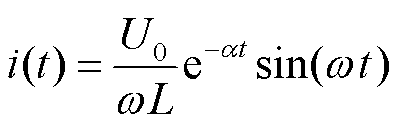 (2)
(2)
其中
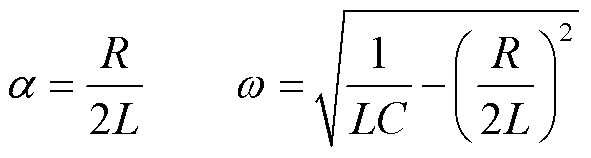
式中,U0为电容初始放电电压(V);α为振荡电路的衰减系数;ω为衰减角频率。
为了求解脉冲线圈的瞬态电磁场,本文从麦克斯韦方程出发,将目标域分解为感应域(目标物)、源域(线圈)和空气域三个部分,如图2所示。采用矢量磁位A和标量电位φ来表示场域的控制方程及其边界条件。式(3)和式(4)分别为位函数A、φ的定义,并采用库伦规范。
 (3)
(3)
 (4)
(4)
式中,B为求解域的磁感应强度(T);E为求解域的电场强度(V/m)。

图2 待求解的目标域
Fig.2 The target domain to be solved
对于源域和空气域,有
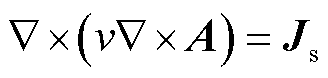 (5)
(5)
式中,v为空气域的磁阻率(H-1),在本文中无导磁材料,其磁阻率基本一致; 为源电流密度(A/m2)。
为源电流密度(A/m2)。
对于感应域(目标物),有
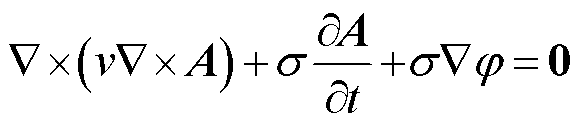 (6)
(6)
式中,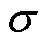 为感应域的电导率(S/m)。
为感应域的电导率(S/m)。
求解域的边界条件分别为
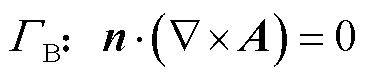 (7)
(7)
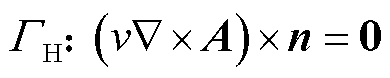 (8)
(8)
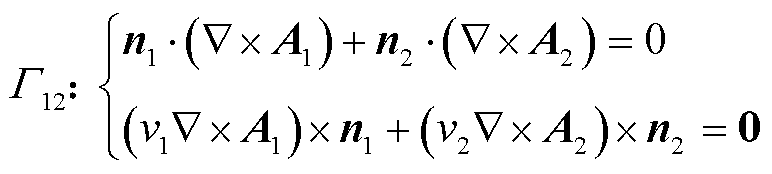 (9)
(9)
式中,n、n1、n2分别为空气域、源域和感应域边界相应表面的外法向分量;v1、v2分别为源域和感应域的磁阻率;A1、A2分别为源域和感应域的矢量磁位;ГB和ГH是空气域与外部相连的两种不同边界,并分别规定边界的磁感应强度的法向分量和磁场强度的切向分量为零;Г12为感应域和非感应域的边界。
在脉冲线圈的计算中,通过位函数A、φ作为中间变量进行耦合。由法拉第定律可以得到线圈电压方程为
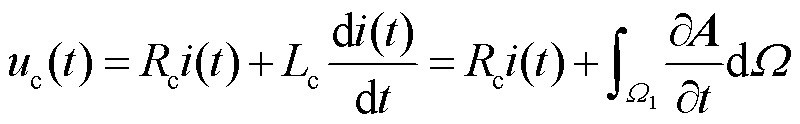 (10)
(10)
式中,uc(t)为线圈电压(V);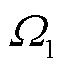 为源域空间的每匝线圈。而在电路方程中有
为源域空间的每匝线圈。而在电路方程中有
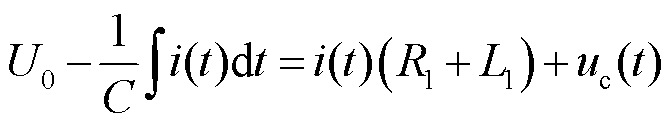 (11)
(11)
联立式(10)和式(11),即可实现场-路耦合。
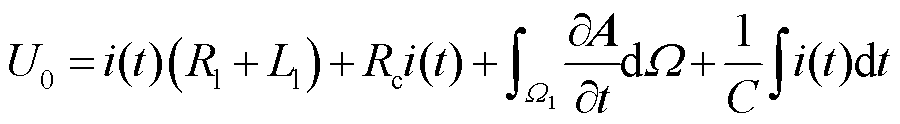 (12)
(12)
1.4.1 目标物的脉冲力密度分布
通过式(3)、式(4)、式(13)计算得到瞬态磁场磁感应强度B和目标物内的感应涡流Je,利用电磁力公式可以获得目标物的脉冲力密度分布,进而可以得到脉冲力F分布。
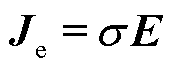 (13)
(13)
式中,Je为目标物内涡流密度(A/m2)。
本文所采用的数值计算模型如图3所示。由图3及电磁原理可得,目标物中的涡流主要垂直穿入/穿出在rOz平面。根据左手定理,目标物所受电磁脉冲力主要为z轴方向上,故在本文中主要研究脉冲力的z轴分量Fz,可得
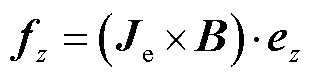 (14)
(14)
式中,fz为目标物在z轴方向所受脉冲力密度(N/m2); 为z方向上的单位向量。
为z方向上的单位向量。
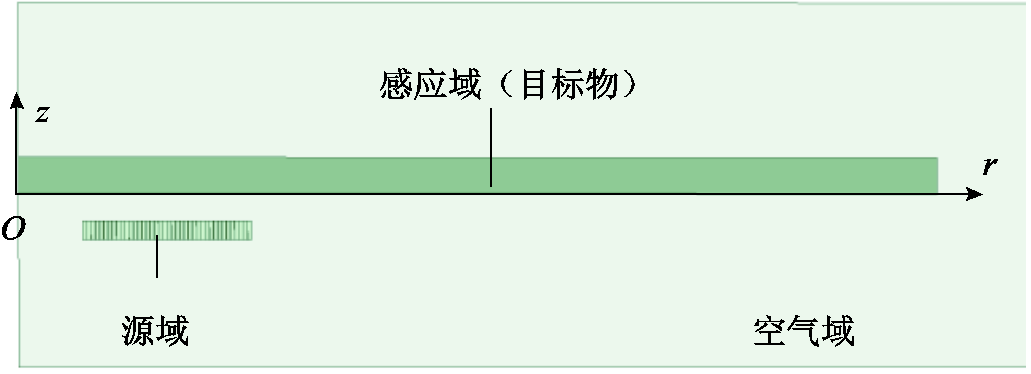
图3 数值计算模型
Fig.3 The numerical computation model
1.4.2 目标物的脉冲合力及冲量
将目标物上所有单元所受脉冲力进行体积分,可以得到目标物所受脉冲合力。根据分析可知,目标物所受r轴方向脉冲力较小,同时,目标物在除冰时主要依靠z轴方向的脉冲力,故本文重点分析在z轴方向的分量。
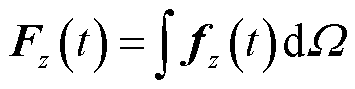 (15)
(15)
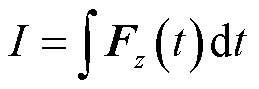 (16)
(16)
式中,Fz(t)为目标物在z轴方向所受脉冲力(N);I为目标物在z轴方向所获得的冲量(N·s)。
将目标物所受脉冲合力对时间求积分可以得到目标物在一次脉冲作用下获得的冲量,如式(16)所示,脉冲冲量可以进一步表征脉冲力的作用效果。根据除冰试验,可以发现除冰效果与脉冲冲量呈正相关。
有限元仿真需要对电脉冲线圈和目标物进行物理建模,若对实际脉冲线圈进行有限元计算会十分复杂,为了更好地研究其线圈形状参数与脉冲效果的关系,由于脉冲电路频率低于10 kHz,故需要作以下假设:①忽略位移电流对电磁场的影响;②忽略在电容器放电期间的目标物的外界受力及运动情况;③将模型简化为二维轴对称(rOz)模型,同时将螺旋线圈近似用同心圆线圈替代,计算模型如图3所示,以铝板下表面为z=0 mm。
模型中,源域材料为铜(电导率为5.8×107 S/m,相对磁导率为0.999 991),目标物材料为铝(电导率为3.48×107 S/m,相对磁导率为1.000 021),本文主要研究线圈结构参数,故并未对材料进行深入探究。除3.3节中所提到铝板与引用文献的测试情况一致外,本文所研究的目标物直径为100 mm、高为4 mm,线圈与目标物间隙为3 mm,空气域尺寸为300 mm×300 mm×100 mm。
由于脉冲电流将在目标物中感应出涡流,故需要对目标物网格进行趋肤深度距离内的细化。将频率f设定为1 kHz,通过目标物材料的磁导率μ和电导率σ,根据式(17)可得其趋肤深度d,由此将该范围内的网格进一步细化。
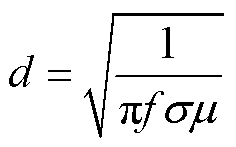 (17)
(17)
本文中40匝线圈模型的单元参数见表1,其中单元大小和单元数量均为各个工况下的最大结果。针对二维电磁场-路耦合计算,为减少计算总时长,加快电路电流衰减速度,将Rd值设置较大,故模型时间设置见表2,并保存每个时间步。
表1 40匝线圈模型的单元参数
Tab.1 The unit parameters of the 40-turning coil model

区域单元面积/mm2单元数量 最小最大标准差 源域0.000 60.045 60.0035 920 目标物0.171 61.862 60.341 3591 空气域0.000 236.883 13.338 77 409 共计———13 920
表2 模型瞬态时间参数
Tab.2 Model transient time parameters

求解总时长/ms求解步长/μs时间积分方法 1.55Backward Euler
2.3.1 脉冲线圈的电气参数
在研究脉冲线圈涡流场的过程中发现,有无目标物对脉冲线圈的电磁参数有很大影响。无目标物时,脉冲线圈电阻、电感基本不随频率的变化而变化;有目标物时,其电阻、电感都将随源域的频率改变而发生变化。
匝数为40、100的线圈在有目标物条件下的电阻、电感曲线如图4所示。可以看出,在有目标物时,线圈电阻随频率的增大而增大,线圈电感随频率的增大而减小。对于大匝数的线圈而言,在频率低于1 kHz以下时,电阻变化较缓,而在1~10 kHz时,电阻将快速增大;相反,电感的变化呈现先快后缓的趋势。脉冲除冰中,其瞬时频率不会较大,其峰值也在数百微秒,故取1 kHz为作为趋肤深度频率。
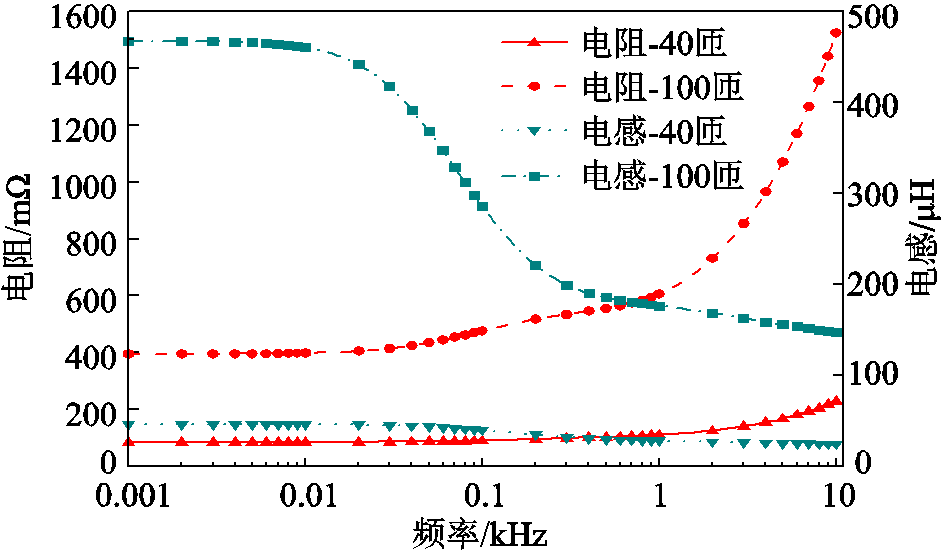
图4 线圈电阻、电感随频率的变化
Fig.4 Coil resistance and inductance change with frequency
相同内径、相同线圈截面、相同匝间距的不同匝数线圈电阻、电感的计算结果见表3。随着线圈匝数的增大,线圈的外径也将变大,在相同目标物的条件下,线圈的电阻、电感较无目标物时变化更大,这将影响线圈的脉冲效果。
表3 有、无目标物条件下的线圈电阻、电感
Tab.3 Resistance and inductance with and without target

线圈匝数无目标物有目标物 直流1 kHz1 kHz 电阻/mΩ电阻/mΩ电感/μH电阻/mΩ电感/μH 4085.4785.80246.266110.4128.229 50122.03122.5479.287163.6844.468 60164.67165.38124.63228.7164.025 70213.38214.34184.21228.7164.025 80268.18269.41259.94393.13114.16 90329.05330.59353.74494.74142.72 100395.99397.88467.52606.46176.52 110469.02471.29603.2729.19214
2.3.2 脉冲线圈的瞬态磁场
在目标物不变的情况下,脉冲线圈的瞬态磁场分布主要由脉冲线圈参数和脉冲电路共同作用,即脉冲电流的分布。
内径为14 mm的40匝线圈在目标物上产生的磁感应强度分布如图5所示。图6是不同位置点上,目标物沿轴向和径向的磁感应强度分布。由图5可知,当脉冲合力最大时,在目标物上出现最大的磁感应强度B=2.682 7 T。
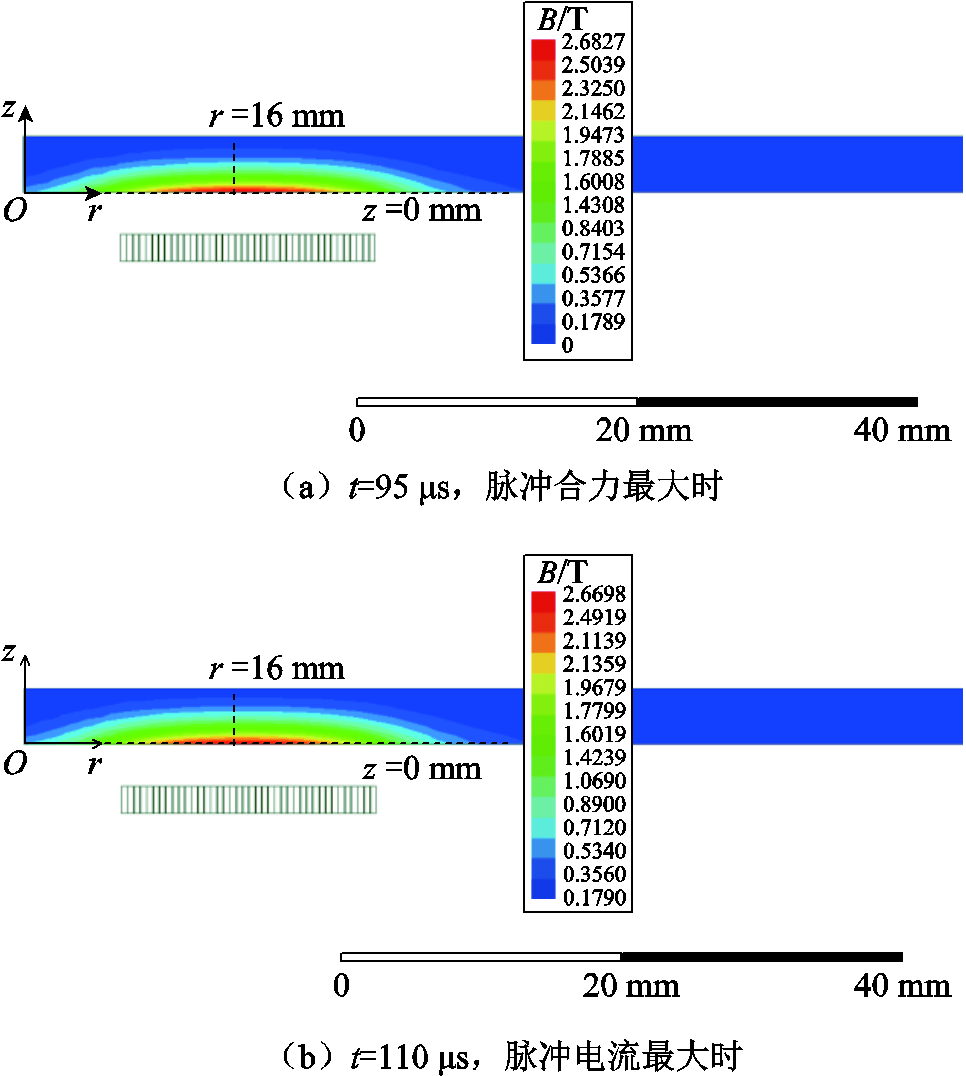
图5 目标物中磁感应强度分布
Fig.5 Magnetic induction field distribution in the target
由图5、图6可知,当t=95 μs时,对于z=0 mm这条线,磁感应强度的径向分量Br在r=0~16 mm之间单调递增,在r=16~100 mm之间单调递减,在r=16 mm、z=0 mm处出现极大值2.720 T;磁感应强度纵向分量Bz分别在r=8 mm、r=24 mm上出现极值,但该值较小,即铝板在r轴方向所受脉冲力较小,故后文并不对Bz和脉冲力的r向分量(Fr)进行研究。对于r=16 mm这条线,Bz在z=1~4 mm之间单调递减,即目标物距线圈越远的区域感应脉冲力越小。
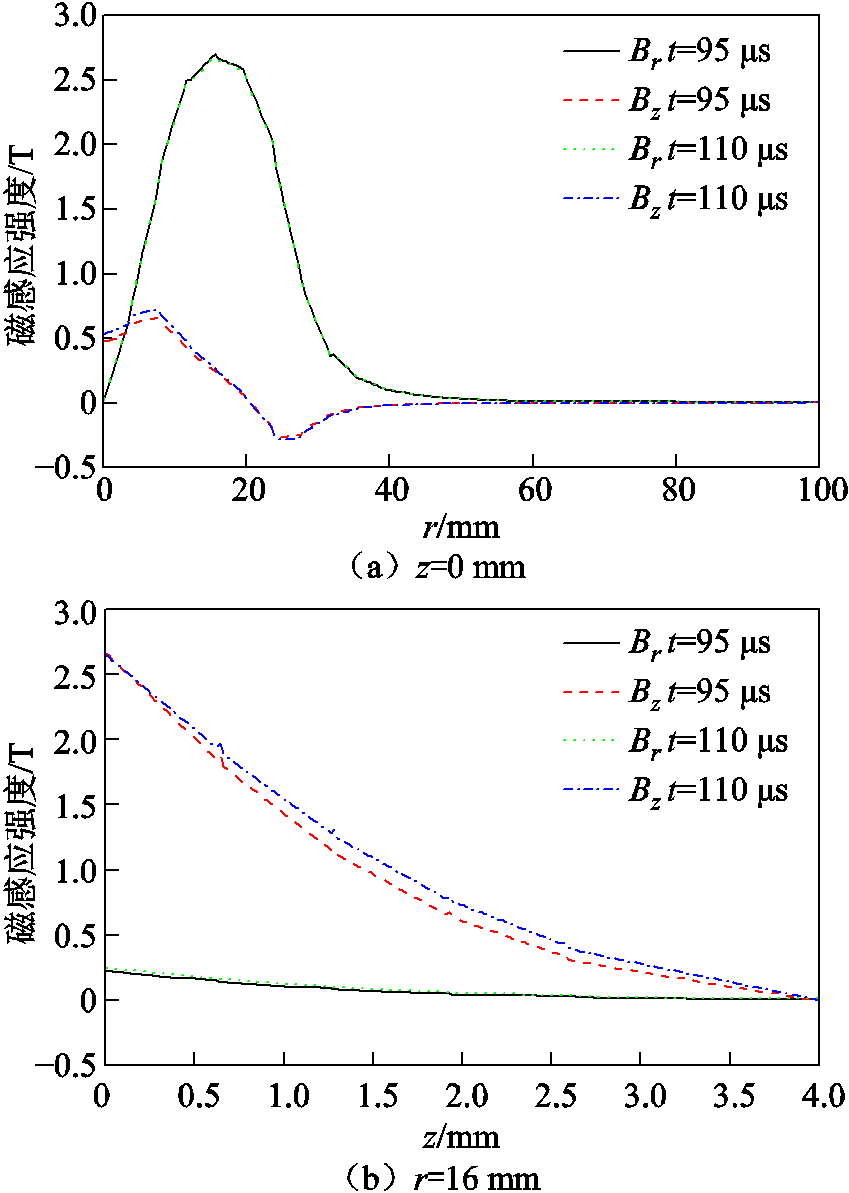
图6 目标物上磁感应强度分布
Fig.6 Magnetic induction intensity distribution on the target
2.3.3 目标物的感应涡流
进一步地,可以得到目标物内涡流密度的分布,如图7、图8所示。可以看出,在如图3所示的模型中,电流和涡流密度都只垂直穿入/穿出于图3中的线圈截面。
图7为不同时刻下目标物涡流密度场分布,可以看出涡流密度主要集中在靠近线圈的区域内,随着目标物的其他区域与源域距离增大,涡流密度呈指数式下降,最大值和最小值之间相差大约1 000倍。

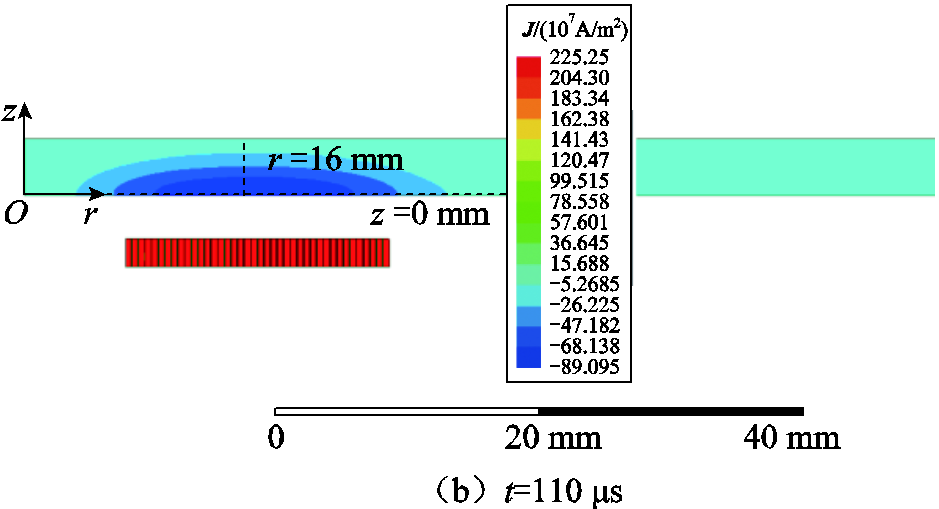
图7 目标物的涡流密度场分布
Fig.7 The current density field distribution target eddy
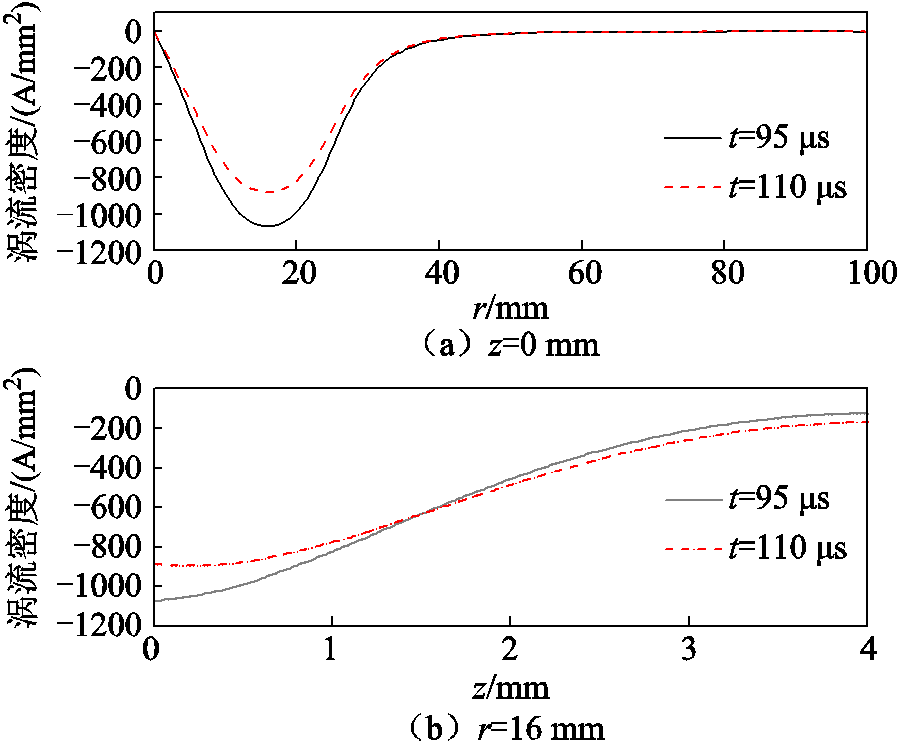
图8 目标物内涡流密度随位置变化
Fig.8 Eddy current density in the target varies with position
图8为目标物不同位置的涡流密度分布沿轴向和径向的变化,可以得到,在脉冲力最大时,涡流密度最大,而在脉冲电流最大时,涡流密度下降,表明涡流和脉冲合力峰值时间超前于脉冲电流峰值。由图8a可以看出,涡流主要集中在线圈内、外径对应的区域;由图8b可发现,随着高度的增加,目标物涡流密度逐渐降低。
2.3.4 目标物的脉冲力及冲量
根据目标物的涡流密度和磁感应强度,可以得到不同位置上的脉冲力分布。由于模型被划分为许多三角形单元,通过平均值来表征该区域内的脉冲力密度分布。不同时刻目标物的脉冲力密度分布如图9所示。图9a是目标物最底面的脉冲力分布,可见脉冲力在z=0 mm、r=4~32 mm以外的区域都近似为零,表明目标物能够产生脉冲力的区域面积同线圈面积近似;图9b是目标物沿r=16 mm处的脉冲力分布,当z>2.5 mm后,磁感应强度和涡流密度都比较小,脉冲力基本接近于零。
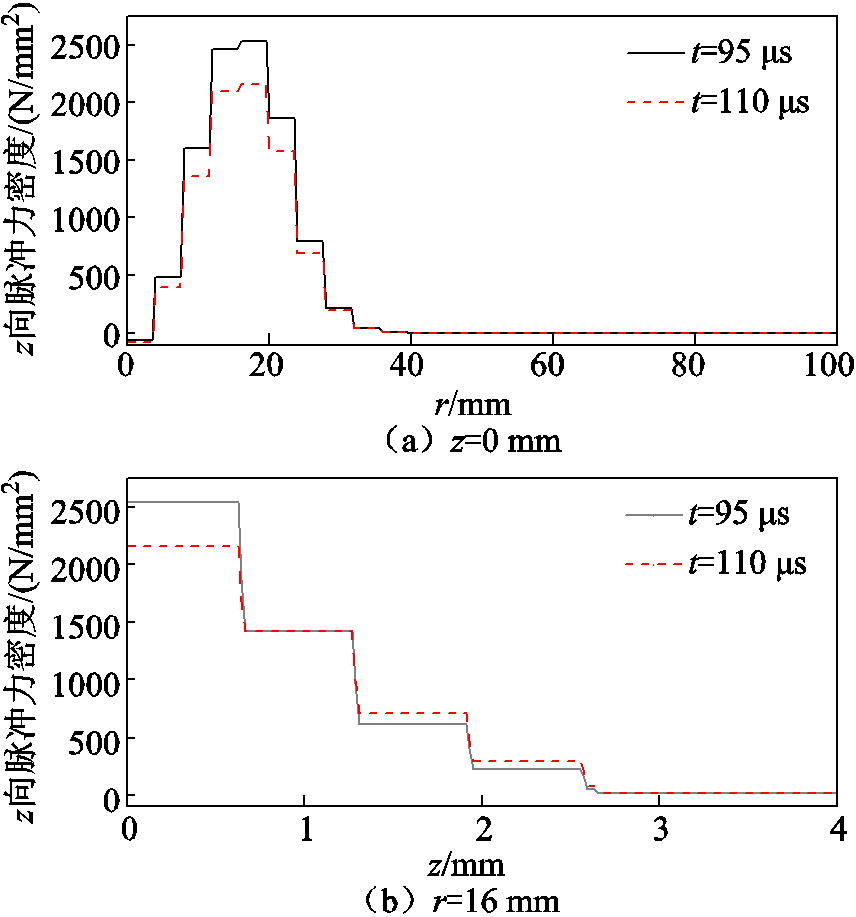
图9 目标物的脉冲力密度分布
Fig.9 Pulse force density distribution of the target
进一步地,通过对脉冲力依次进行空间、时间上的积分,最终得到40匝线圈下的目标物受到的冲量为0.742 8 N·s。
本文对40、50、60匝线圈进行加工,得到如图10所示的脉冲线圈,测量其不同条件下的电阻、电感,并同2.3.1节中的进行比较,其结果见表4。需要说明的是,为简化计算,未对线圈的进、出线进行建模,表3中的电阻总体较测量值小15~25 mΩ,该部分电阻在计算中并入R1。

图10 脉冲线圈实物
Fig.10 Pulsed coil
表4 线圈电感、电阻的测量值
Tab.4 Measurement of coil inductance and resistance

线圈匝数无目标物有目标物 直流电阻/mΩ1 kHz电感/μH1 kHz电阻/mΩ1 kHz电感/μH 4010146.3130.528.4 50144.578.2186.944.4 60188.75122.6253.463.9
同时,利用文献[20]中所采用的摆锤法,实时测量上述三种线圈的脉冲效果,并同计算得到的结果进行比较,结果见表5。
表5 脉冲冲量的计算值和测量值比较
Tab.5 Comparison of calculated and measured impulses

线圈匝数计算结果/(N·s)测量结果/(N·s)误差(%) 400.742 80.657 811.4 501.043 60.895 314.2 601.308 61.196 18.6
总体来说,仿真结果与测量结果相差较小,最大误差为14.2%。导致误差的主要原因有:①测量过程中存在各方面的误差,如摆锤自身运动过程中的消耗、测量精度的误差;②数值计算模型较为理想,目标物和线圈一直保持相同距离,而实际中,目标物将作为非固定物体进行运动,故实测值总体小于计算值。综上所述,数值计算与测量结果相近,具有较高的可信度。
脉冲线圈结构参数的变化,将导致脉冲线圈的电磁参数变化,在相同目标物和相同放电电路条件下,线圈电流分布的变化会导致求解空间磁场的变化,最终将改变脉冲线圈的脉冲效果。而脉冲电流峰值时刻,脉冲合力并未达到最大值,在本节中,主要对脉冲合力峰值时刻展开讨论。
如图10所示,实际线圈属于紧密绕制,故线圈的匝间距仅为加上两端漆层的扁线厚度。在本节中,电容参数保持不变,均为C=400 μF、U0=DC 1 200 V,通过测量得到线路阻抗和各个接触电阻为Rl=0.275 Ω、Ll=1 μH、Rd=10 Ω。
固定线圈内径、截面尺寸、匝间距,改变线圈匝数,得到不同线圈匝数的脉冲合力的峰值和峰值时间、脉冲冲量见表6。图11为不同匝数脉冲力峰值时刻,z=0 mm上脉冲力密度沿r轴的变化。
表6 不同线圈匝数的脉冲效果
Tab.6 Impulse effect of different coil turns

线圈匝数脉冲合力峰值/kN峰值时间/μs脉冲冲量/(N·s) 404.425 9950.742 8 505.027 51201.043 6 605.351 81451.328 8 705.480 51701.586 5 805.478 61951.814 3 905.392 82152.016 2 1005.255 92402.195 3 1105.087 72602.355 5
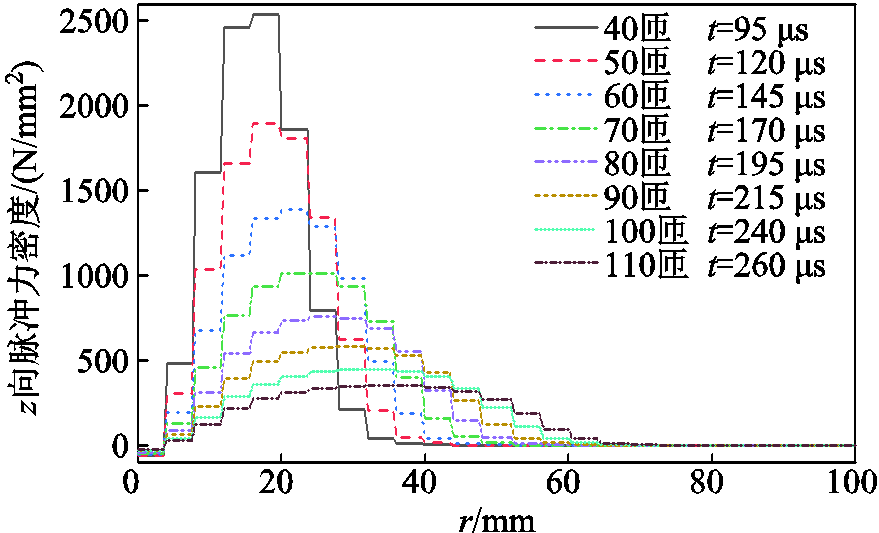
图11 不同匝数脉冲力密度随距离的变化
Fig.11 Variation of pulse force density with distance for different turns
随着匝数的增大,其电阻、电感将增大,而在其他计算参数不变的条件下,脉冲合力峰值先增大后减小,峰值时间随着电阻、电感的增大而增大。匝数的增大使得脉冲电流下降,降低z向脉冲力的峰值;同时也增大脉冲电流作用的面积,使得目标物上更大面积的磁感应强度发生变化,从而产生涡流,形成脉冲力,因此线圈脉冲冲量会随匝数的增大而持续增大。
但线圈外径逐渐增大时,导致线圈阻抗增大,脉冲频率下降,无法实现在高应变率下的除冰。尤其是当线圈外径超过目标物的外径后,其除冰效果将大幅下降。
固定线圈内径、匝间距、匝数,改变线圈截面尺寸。脉冲线圈触发时需瞬间通过数kA电流,为了装置可靠性和耐久度,其截面不能太小。同时,受制作工艺和线圈加工绕制的制约,本文选取线圈截面为0.2 mm×4 mm(宽×高,下同)、0.3 mm×2.67 mm、0.4 mm×2 mm三种保持相同截面积的尺寸(分别记为S1~S3),和0.4 mm×2 mm、0.4 mm×3 mm、0.4 mm×4 mm、0.4 mm×6 mm、0.4 mm×8 mm、0.4 mm×10 mm六种保持相同宽度的尺寸(分别记为S3、W1~W5)来探究其截面尺寸的影响,计算结果如图12所示和见表7。
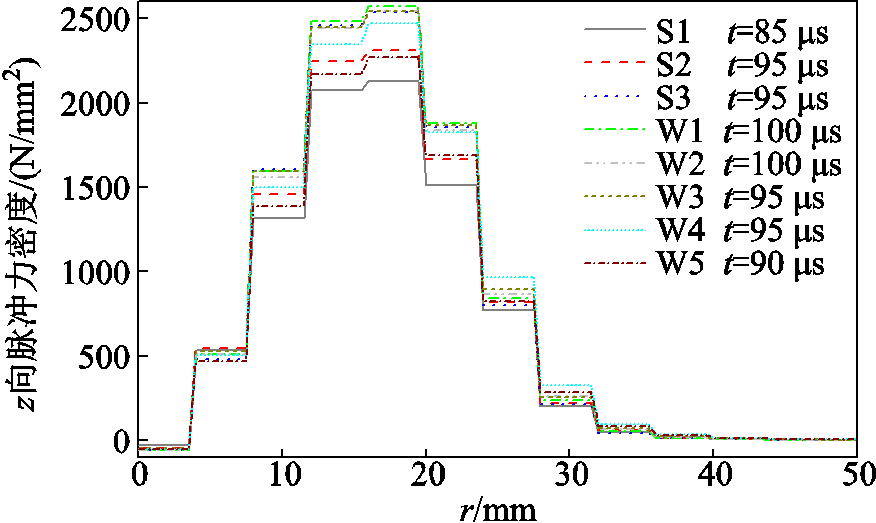
图12 不同截面尺寸脉冲力密度随距离的变化
Fig.12 Variation of pulse force density with distance for different section dimensions
表7 不同截面尺寸线圈的脉冲效果
Tab.7 Impulse effect of coils with different cross-sectional dimensions

组别截面尺寸/(mm×mm)脉冲合力峰值/kN峰值时间/μs脉冲冲量/ (N·s) 截面积一定S10.2×43.648 0950.606 2 S20.3×2.674.107 5950.687 7 S30.4×24.425 9950.742 8 截面宽度一定W10.4×34.692 81000.775 2 W20.4×44.738 61000.771 7 W30.4×64.593 7950.725 8 W40.4×84.606 5950.720 0 W50.4×104.121 1900.611 7
结合表7和图12发现,当截面宽度保持一定时,脉冲线圈的电阻随截面积增大而减小,脉冲电流峰值将增大,脉冲效果将有所提升。尽管脉冲电流总体呈增大趋势,但随着高度的进一步增加,越来越多脉冲电流分布在远离目标物的区域,导致目标物上的磁感应强度不高。0.4 mm×2 mm、0.4 mm× 6 mm和0.4 mm×10 mm的线圈在脉冲力峰值时的磁感应强度和涡流密度分布如图13所示,在目标物上仅表现磁感应强度,在线圈上表现涡流密度。脉冲量和脉冲力峰值及时间相关,一般情况下,线圈电阻减小,脉冲合力峰值和脉冲量增大。增大线圈截面高度提高电阻,其脉冲力峰值和脉冲量呈减小趋势。因此,在保证耐流的前提下,需要对截面高度进行限制。

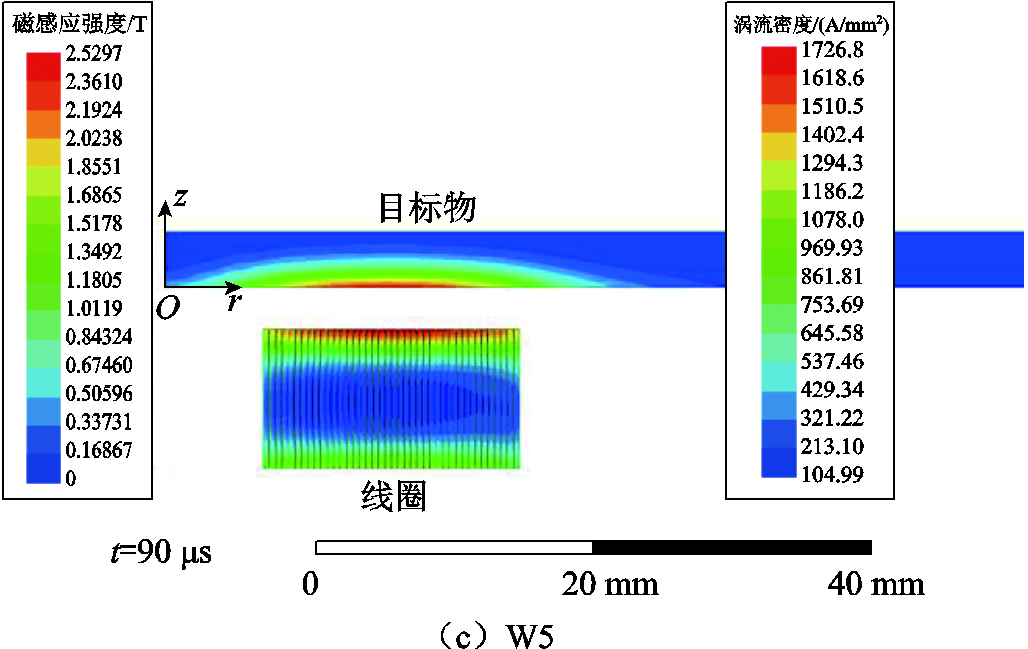
图13 不同截面的线圈涡流密度和目标物磁感应强度分布
Fig.13 Current density and target magnetic induction distribution at different cross-sections
本文讨论的0.4 mm×2 mm截面尺寸的线圈都属于紧密绕制,如图10所示。但由于漆层的存在,导致每匝之间存在间隙。在3.2节中所出现的0.2 mm×4 mm和0.3 mm×2.67 mm的脉冲线圈,若要在相同匝数下保证与0.4 mm×2 mm线圈具有相同的内、外径结构,则需要通过改变线槽基底、绕制方法和漆层厚度等方法实现。
同样对于0.4 mm×2 mm截面尺寸的线圈的匝间距,可以通过改变线槽基底来增大线圈的匝间距,从而改变线圈的内外径。不同外径和内径线圈的脉冲效果见表8和表9。
表8 不同外径线圈的脉冲效果
Tab.8 Impulse effect of coils with different outer diameters

编号线圈外径/mm匝间距/ mm脉冲合力峰值/kN峰值时间/μs脉冲冲量/ (N·s) O1500.464.425 9950.742 8 O29214.179 3900.772 6 O31311.53.648 7900.736 2 O417023.18900.701 0
表9 不同内径线圈的脉冲效果
Tab.9 Impulse effect of coils with different inner diameters

编号线圈内径/mm匝间距/ mm脉冲合力峰值/kN峰值时间/μs脉冲冲量/ (N·s) I11540.464.478 52351.928 8 I211214.024 71601.385 9 I3731.53.564 11201.042 8 I43423.170 4950.794 5
1)表8中,保持线圈内径为14 mm、匝数为40匝,通过改变匝间距来改变线圈外径。随着匝间距的增大,脉冲力合力峰值逐渐下降;而脉冲冲量在匝间距为1 mm时到达最大值,随后开始逐渐下降。
2)表9中,保持线圈外径为190 mm、匝数为40匝,通过改变匝间距,改变线圈内径。脉冲合力峰值、峰值时间、脉冲冲量均随着匝间距的增大而下降。
可见,当截面尺寸、匝数不变时,随着匝间距的增大,脉冲力峰值和脉冲冲量均呈下降趋势。故在线圈设计中,线圈的匝间距应该尽量减小。
此外,对比两表结果,不同外径下,电感、电阻随匝间距的增加而增加;不同内径下,电感、电阻的变化趋势相反。表9中不同内径线圈的电感、电阻较表8中的不同外径线圈变化更大,表明其脉冲效果变化更为明显,从而线圈外圈匝比内圈匝对电磁参数、脉冲效果的影响更大。
不同内、外径下脉冲力密度随r向距离的变化如图14所示,无论是在保持线圈外径还是内径的前提下,随着匝间距的增大,脉冲力密度分布都更加平缓。保持内径时,峰值时间较保持外径时更短,脉冲力峰值更大;但保持外径时,脉冲冲量更大,脉冲力作用时间更长。
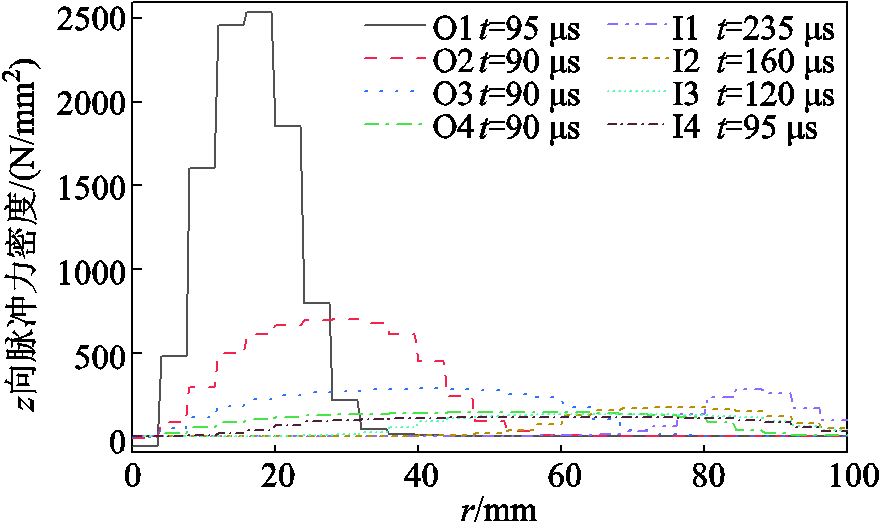
图14 不同内、外径下脉冲力密度随距离的变化
Fig.14 Variation of pulse force density with distance under different inner and outer diameters
综上所述,增加匝数、减小匝间距、增大每匝线圈的截面积和减小线圈高度将增大脉冲冲量。但过多的匝数会使脉冲力峰值下降,而当线圈超出目标物的范围时,脉冲冲量将不会增加。据此,采用0.8 mm×2 mm的线径绕制60匝,匝间距为1 mm,其内、外径分别为72 mm、190 mm时,在同样的电路参数条件下,脉冲合力峰值为6.992 9 kN,峰值时间为210 μs,脉冲冲量为2.591 6 N·s,能够得到较大的脉冲合力峰值和脉冲冲量,取得较好的脉冲效果。
为了进一步检验所设计线圈的电脉冲除冰效果,考虑铝板在叶片覆冰和防、除冰试验中的相似性,有学者采用铝板简化真实机翼进行了防冰除冰试验[21-22]。结合本文的仿真结果和实际条件,预先选择尺寸长×宽×高为500 mm×500 mm×2 mm的6061铝板作为除冰目标,在重庆大学人工气候室内进行了覆冰铝板的除冰试验。当线圈匝数为60匝,放电电压为DC 1 400 V,储能电容为400 μF时,单次除冰动作即可完成10 mm雨凇的除冰,其除冰结果如图15所示。

图15 铝板的脉冲除冰过程
Fig.15 Pulse de-icing process for aluminum plate
在优化脉冲线圈设计时,应以脉冲力峰值和脉冲冲量作为主要目标。同时考虑脉冲除冰不能改变目标物的外观,脉冲力只能使目标物产生弹性应变、避免塑性应变等因素。结合单个线圈尺寸和线圈截面积的限制条件,通过调整线圈截面尺寸、线圈个数、线圈位置来限制目标物部分区域的脉冲力,从而在目标物表面产生弹性应变,进而有效除冰。
1)在频域计算中,有无目标物对脉冲线圈的电阻、电感影响较大,实际测量40、50、60匝脉冲线圈的电路参数和脉冲效果,验证了模型的正确性。
2)匝数对线圈脉冲峰值力的影响存在极值;过度增加线圈高度反而会降低脉冲效果;线圈外圈匝比内圈匝对电磁参数、脉冲效果的影响更大。
3)需结合目标物材料、尺寸和覆冰等情况合理地限制线圈截面的高度,调整线圈的匝数、截面、匝间距及内、外径,获得较优的线圈结构参数,并且进行了相应的铝板除冰验证。
4)在本文的基础上将开展优化脉冲线圈的结构动力学和除冰准则方面的研究,为进一步优化脉冲线圈,实现脉冲除冰应用微功耗化设计提供优化思路和技术路线。
参考文献
[1] 蒋兴良, 张志劲, 胡琴, 等. 再次面临电网冰雪灾害的反思与思考[J]. 高电压技术, 2018, 44(2): 463-469. Jiang Xingliang, Zhang Zhijin, Hu Qin, et al. Thinkings on the restrike of ice and snow disaster to the power grid[J]. High Voltage Engineering, 2018, 44(2): 463-469.
[2] 欧阳虹, 蒋兴良, 涂振华, 等. 磁浮接触轨电脉冲除冰的试验研究[J]. 高电压技术, 2022, 48(4): 1553-1560. Ouyang Hong, Jiang Xingliang, Tu Zhenhua, et al. Experimental study on electro-impulse de-icing of maglev contact rail[J]. High Voltage Engineering, 2022, 48(4): 1553-1560.
[3] 李成祥, 石鑫, 周言, 等. 针对H型线圈的电磁脉冲焊接仿真及线圈截面结构影响分析[J]. 电工技术学报, 2021, 36(23): 4992-5001. Li Chengxiang, Shi Xin, Zhou Yan, et al. Electromagnetic pulse welding simulation for H-type coil and analysis of the influence of coil cross-sectional structure[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4992-5001.
[4] 周纹霆, 董守龙, 王晓雨, 等. 电磁脉冲焊接电缆接头的装置的研制及测试[J]. 电工技术学报, 2019, 34(11): 2424-2434. Zhou Wenting, Dong Shoulong, Wang Xiaoyu, et al. Development and test of electromagnetic pulse welding cable joint device[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2424-2434.
[5] Sophian A, Tian G Y, Taylor D, et al. Electromagnetic and eddy current NDT: a review[J]. Insight, 2001, 43(5): 302-306.
[6] 段志荣, 解社娟, 李丽娟, 等. 基于磁力传动式阵列涡流探头的管道缺陷检测[J]. 电工技术学报, 2020, 35(22): 4627-4635. Duan Zhirong, Xie Shejuan, Li Lijuan, et al. Detection of defects in pipeline structures based on magnetic transmission eddy current array probe[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4627-4635.
[7] Park D G, Angani C S, Rao B C, et al. Detection of the subsurface cracks in a stainless steel plate using pulsed eddy current[J]. Journal of Nondestructive Evaluation, 2013, 32(4): 350-353.
[8] 陈龙龙, 魏晓光, 焦重庆, 等. 混合式高压直流断路器分断过程电磁瞬态建模和测试[J]. 电工技术学报, 2021, 36(24): 5261-5271. Chen Longlong, Wei Xiaoguang, Jiao Chongqing, et al. Electromagnetic transient modeling and test of hybrid DC circuit breaker[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5261-5271.
[9] 程时杰, 陈小良, 王军华, 等. 无线输电关键技术及其应用[J]. 电工技术学报, 2015, 30(19): 68-84. Cheng Shijie, Chen Xiaoliang, Wang Junhua, et al. Key technologies and applications of wireless power transmission[J]. Transactions of China Electrotechnical Society, 2015, 30(19): 68-84.
[10] 金亮, 李育增, 杨庆新, 等. 大规模工程电磁场的亿自由度可扩展并行计算方法[J]. 电工技术学报, 2022, 37(3): 589-598. Jin Liang, Li Yuzeng, Yang Qingxin, et al. Extensible parallel computing method with hundreds of millions of freedoms for large-scale engineering electromagnetic field[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 589-598.
[11] 王洋洋. 微功耗飞机电脉冲除冰系统理论与实验研究[D]. 重庆: 重庆大学, 2020.
[12] Biro O, Preis K. On the use of the magnetic vector potential in the finite-element analysis of three-dimensional eddy currents[J]. IEEE Transactions on Magnetics, 1989, 25(4): 3145-3159.
[13] 李清英, 白天, 朱春玲. 电脉冲除冰系统的电磁场分析[J]. 南京航空航天大学学报, 2011, 43(1): 95-100. Li Qingying, Bai Tian, Zhu Chunling. Electromagnetic field analysis for electro-impulse de-icing system[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 43(1): 95-100.
[14] Henderson R A. Theoretical analysis of the electrical aspects of the basic electro-impulse problem in aircraft de-icing applications[D]. Wichita: Wichita State University, 1986.
[15] Zumwalt G W, Schrag R L, Bernhart W D, et al. Electro-impulse de-icing testing analysis and design[R]. NASA Contractor Report 4175, 1988.
[16] Moehle E, Haupt M, Horst P. Coupled magnetic and structural numerical simulation and experimental validation of the electro impulse de-icing[C]//54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, Massachusetts, USA, 2013: 1494.
[17] 郭涛. 机翼电脉冲除冰系统电磁力及其除冰过程仿真研究[D]. 南京: 南京航空航天大学, 2017.
[18] 王洋洋, 蒋兴良. 边光滑有限元-边界元耦合法计算二维瞬态涡流场[J]. 哈尔滨工业大学学报, 2021, 53(3): 137-141, 151. Wang Yangyang, Jiang Xingliang. Calculation of 2D transient eddy current field by ES-FEM-BEM coupling method[J]. Journal of Harbin Institute of Technology, 2021, 53(3): 137-141, 151.
[19] Huang Tingfan, Jiang Xingliang, Chen Yu, et al. Experimental study on electro-impulse de-icing of wind turbine blades[C]//2021 6th Asia Conference on Power and Electrical Engineering (ACPEE), Chongqing, China, 2021: 205-209.
[20] 黄廷帆. 金属表面覆冰的电磁脉冲除冰方法研究[D]. 重庆: 重庆大学, 2021.
[21] Wang Yangyang, Jiang Xingliang. Design research and experimental verification of the electro-impulse de-icing system for wind turbine blades in the Xuefeng mountain natural icing station[J]. IEEE Access, 2020, 8: 28915-28924.
[22] Chen Long, Yang Qingbao, Yang Xue, et al. Numerical investigation of heat transfer performance of graphene-doped anti-/deicing component[J]. Thermal Science and Engineering Progress, 2022, 28: 101098.
Abstract Electro-impulse de-icing of atmospheric structures is a low-power consumption and fast de-icing method. Pulsed coil is a key component in the conversion of energy for electro-impulse de-icing. Of which the structural parameters need to be optimized, so as to improve the de-icing effect of the electro-impulse de-icing system and promote the development of the system’s low-power consumption and lightweight.
Most researches on pulsed coil at home and abroad focus on the electrodynamics, structural dynamics and de-icing effect on the target. However, the influence of different structural parameters on the transient electromagnetic fields and impulse effects of pulsed coils has been little studied.
Aiming at the above problems, this paper started from the basic principle of circuit and electromagnetic field, simplified the electro-impulse de-icing system, deduced the field-circuit mathematical equation of pulsed coil, established the physical model of pulsed coil and rectangular cross section target, and determined the circuit parameters, the governing equation and boundary conditions of transient electromagnetic field. Based of which, the calculation methods of magnetic induction intensity, target eddy current, impulse force and impulse were obtained. The transient electromagnetic field of the pulsed coil is analyzed by finite element software, and the time-varying characteristics of the pulsed coil’s electromagnetic parameters were obtained.
In this paper, the electrical parameters and transient electromagnetic fields under different coils were calculated, which shows that the presence of the target had a great influence on the resistance and inductance of the pulsed coil. The circuit parameters and impulse effects of 40, 50 and 60 turns pulsed coils are measured by the impact pendulum test, which verifies the correctness of the model. Through comparative analysis, it is found that :(1) the number of turns has a great influence on the peak value of the pulse force. With the increase of the number of turns, the impulse effect gradually increases. However, the gradual increase in the outer diameter of the coil leads to an increase in coil impedance and a decrease in pulse frequency, making it impossible to achieve de-icing at high strain rates, in particular, the outer diameter of the coil exceeding the outer diameter of the target. (2) Excessive increase in coil height will reduce the impulse effect. With the increase of the coil height, the non-uniform distribution characteristics of the pulse current in the coil become more obvious, especially the pulse current density in the area far from the target increases, resulting in the reduction of the impulse effect. (3) With the increase of the coil turn-to-turn distance, the distribution of the pulsed coil is wider, which makes the pulse force on the target more uniform, but the peak of the pulse force density still appears in the middle region of the coil. (4) The outer turns of the coil have greater influence on electromagnetic parameters and impulse effect than the inner turns.
By reasonably limiting the height of the coil cross-section and adjusting the number of turns, cross-section, turn-to-turn distance and inner and outer diameter of the coil in combination with the target material, dimensions and icing, the optimal structural parameters of the pulsed coil under fixed circuit parameters were obtained (60 turns winding, 0.8 mm×2 mm wire diameter, 1 mm turn spacing, 72 mm inner diameter and 190 mm outer diameter).
Under the initial conditions of C=400 μF and U0=DC 1 200 V, the pulse force of 6.992 9 kN on the target, with a peak time of 210 μs and a pulse impulse of 2.591 6 N·s. The corresponding de-icing tests on aluminum plates were carried out using the above pulsed coil with good de-icing results.
keywords:Pulsed coil, transient electromagnetic field, impulse effect, structural parameters
陈 宇 男,1996年生,博士研究生,研究方向为输电线路覆冰与防冰。E-mail:cqueecy@cqu.edu.cn(通信作者)
蒋兴良 男,1961年生,博士,教授,博士生导师,研究方向为能源装备安全与灾害防御。E-mail:xljiang@cqu.edu.cn
DOI:10.19595/j.cnki.1000-6753.tces.220883
中图分类号:TM8; TM15
重庆市技术创新与应用发展专项重点项目(cstc2021jscx-dxwtBX0001)和南方电网有限责任公司防冰减灾重点实验室支撑项目(GZKJXM20190748)资助。
收稿日期 2022-05-23
改稿日期 2022-08-07
(编辑 李 冰)