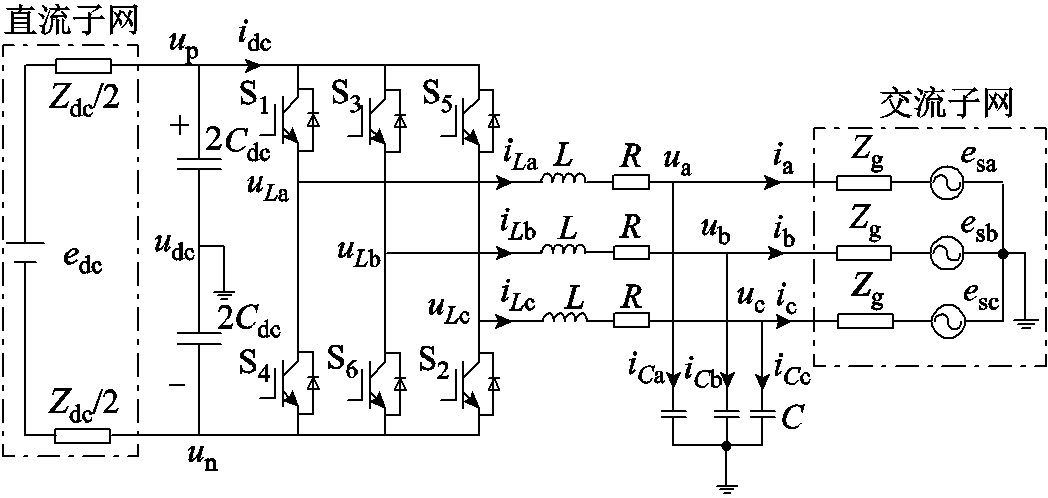
图1 交直流混合微电网主电路拓扑结构
Fig.1 Main circuit structure of AC-DC hybrid microgrid
摘要 交直流混合微电网因其高效的新能源消纳性能,成为未来电网的重要发展形式。然而交直流混合微电网的互联结构使其故障响应更为复杂,严重影响微电网安全运行能力。该文基于双向功率变换器连接交流子网和直流子网的交直流混合微电网结构,针对故障引起的交互影响问题展开研究。首先选取交流子网和直流子网的典型故障情况,分析故障分量在子网间传播引起的谐波频次变化和故障回路的暂态过程;然后,分别推导交直流子网电气量在考虑系统互联结构下的表达式,得出非故障子网对故障的响应结果,揭示混合微电网故障传播机理;最后基于Matlab/Simulink平台搭建交直流混合微电网模型,并针对不同故障类型进行仿真分析,以验证推导的正确性。
关键词:交直流混合微电网 双向功率变换器 故障传播 机理分析
“碳达峰、碳中和”目标的制定将加速可再生能源分布式发电的高度渗透。综合考虑分布式发电系统的间歇性和不确定性,其大规模并网运行将严重影响电力系统的安全稳定运行。此外,分布式发电系统装机容量的增加将会导致日益突出的新能源消纳问题[1-2]。为有效地解决上述问题,交直流混合微电网结构被广泛应用。然而,交直流互联结构使交直流微电网的故障响应变得复杂,使其在故障下的性能进一步恶化[3]。因此,研究交直流混合微电网故障传播机理,可为后续变换器的控制和继电保护的设计提供参考,对提升微电网安全运行能力具有重要意义。
目前已有的混合微电网故障机理研究多集中在交流侧故障机理分析及其对直流侧的影响上。交流侧故障及不平衡工况会导致负序分量的产生,进而经过AD-DC变换器造成直流电压的二倍频波动[4-5]。当直流子网采用双极供电方式时,直流侧电容中点接地可以减少正负极电压和电流的不平衡度[6],然而此结构为交流接地故障的零序分量在系统间的传播提供通路,使直流侧受工频谐波的影响[7-8]。在此基础上,文献[9]结合故障分量和开关函数,推导得出在不对称故障时交流侧受3次谐波为主要频次的奇次谐波扰动,这对负序分量仅引起系统二倍频扰动的认知进行了补充。相比于常规交流电网系统,交直流混合微电网含有更多的电力电子器件及各类分布式电源(Distribute Generation, DG),其低惯性使得系统抗干扰能力降低[10]。交流侧故障形成的谐波扰动令DG的输出功率产生波动[11],更不利于混合微电网的稳定运行。
交流系统故障引发的逆变侧换相失败是直流输电系统中最常见的故障之一[12],交直流系统间的交互影响使换相失败问题更为复杂,为此已有文献提出换流装置的控制策略及继电保护措施[13],但换相失败情形下的系统建模和机理分析有待深入研究。典型的直流故障特征表现为短路电流急剧增加,这不仅要考虑对直流线路的限流措施,还要解决直流故障对功率变换器和交流设备的影响[14]。文献[6]分析了直流电缆线路发生极间短路和单极接地故障的暂态过程,并提出定位接地故障的方法。文献[15-17]提出了直流配电网极间短路电流计算模型,但未考虑直流故障对交流线路和变换器的影响。文献[18]将变换器内的二极管用可关断电子管代替,虽然实现了利用换流器对直流故障的隔离,但投资成本高且控制复杂化。
由此可见,混合微电网交流侧故障传播机理的研究较多,直流故障机理分析虽在不同容量的系统中进行研究,但多针对极间短路故障及其限流措施,单极接地故障电流的计算模型鲜有涉及。此外,交直流混合微电网整体的故障交互影响缺少系统性的结论,本文在此互联系统中开展故障传播机理分析,为后续设计故障下的混合微电网协同控制策略提供理论基础。
综上所述,考虑到交直流混合微电网供电可靠性和电气安全性,本文依托直流子网双极供电的TT系统构建交直流混合微电网拓扑结构[19-20],由双向功率变换器(Bidirectional Power Converter, BPC)建立交流子网和直流子网的联系,如图1所示。针对交直流混合微电网故障下的交互影响问题,本文选取几种交流子网和直流子网的典型故障情况,分别推导交直流子网电气量在考虑系统互联下的表达式,较为完整地总结混合微电网非故障侧对故障的响应结果,揭示了混合微电网的故障传播机理。最后基于Matlab/Simulink平台搭建混合微电网模型并针对不同故障类型进行仿真分析,以验证推导的正确性。

图1 交直流混合微电网主电路拓扑结构
Fig.1 Main circuit structure of AC-DC hybrid microgrid
交直流混合微电网中交流子网的故障类型可分为对称故障和不对称故障,其中对称故障为三相短路故障,不对称故障包括单相接地故障、两相相间短路故障、两相接地短路故障,均会产生负序分量,且接地故障还将使系统中存在零序分量。
系统中主要参数及含义如下:edc为直流电压源,Zdc为直流子网内阻,udc为直流母线电压,Cdc为直流子网稳压电容,uLa、uLc、uLb为功率桥端电压,iLa、iLb、iLc为交流滤波电感电流,ua、ub、uc与ia、ib、ic为交流子网相电压、相电流,L、R、C分别为交流子网滤波器的电感、电阻、电容,Zg为交流子网等效阻抗,esa、esb、esc为交流子网电压源。
三相短路故障是对称故障,在直流侧正负极电压平衡时电容中点接地结构可等效简化为图2结构,基于此分析三相短路故障下的直流子网响应情况。

图2 等效拓扑结构
Fig.2 Equivalent topology
交直流混合微电网功率变换器开关器件的开关函数定义为
 (1)
(1)
结合开关函数,对双向功率变换器的交流出口侧列写三相KVL方程可得
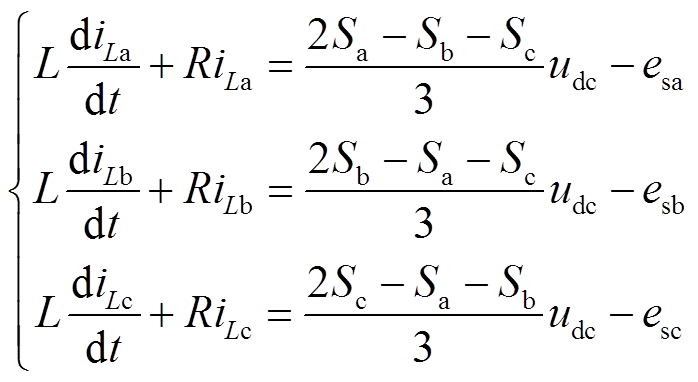 (2)
(2)
根据式(1)构建的BPC开关函数模型,忽略录波器的分压和分流,交、直流子网的电压和电流关系[21]为
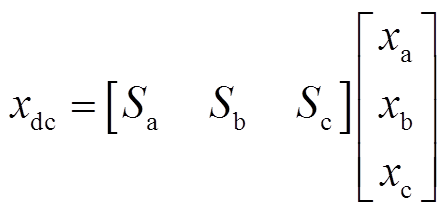 (3)
(3)
式中,x代表电压或电流。
结合基尔霍夫电流定律和式(3),在直流侧电容正极处有
 (4)
(4)
假设交流子网发生三相短路故障,交流电动势等效为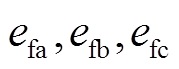 ,单相等效电阻为
,单相等效电阻为 ,其数值与三相短路故障点距BPC交流出口距离和交流输电线路参数相关。以开关状态
,其数值与三相短路故障点距BPC交流出口距离和交流输电线路参数相关。以开关状态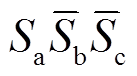 为例,代入上述KCL和KVL方程,整理得到此开关状态下直流母线电压故障响应的二阶非齐次线性微分方程为
为例,代入上述KCL和KVL方程,整理得到此开关状态下直流母线电压故障响应的二阶非齐次线性微分方程为
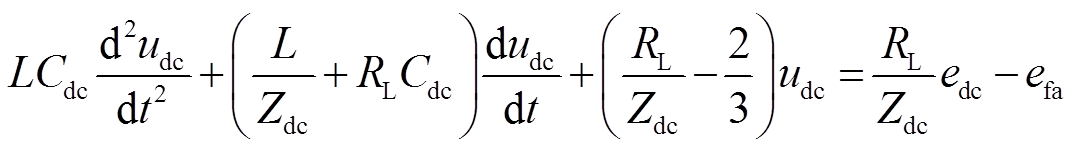 (5)
(5)
式(5)的全解由通解和特解组成,其中通解根据式(6)齐次微分方程得到。
 (6)
(6)
功率变换器开关器件的常规运行状态有六种: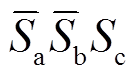 、
、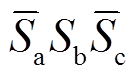 、
、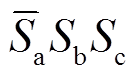 、
、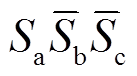 、
、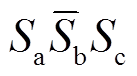 、
、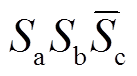 。上述状态代入式(2)~式(4),均可得到式(6)的齐次线性方程形式,因此式(6)对一般情况下的的开关状态具备普适性。
。上述状态代入式(2)~式(4),均可得到式(6)的齐次线性方程形式,因此式(6)对一般情况下的的开关状态具备普适性。
经计算,通解的特征根为

式中,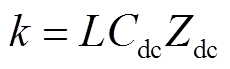 。
。
可见特征根无论形式如何,其实部均为负数,即式(6)的通解是衰减函数,因此在三相短路故障下该系统暂态响应是收敛的[22]。
式(5)的特解对应系统的稳态响应,若发生三相短路故障时a相等效电动势为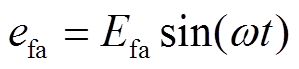 ,特解
,特解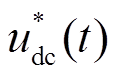 应设为
应设为
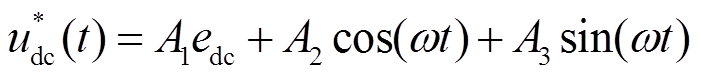 (8)
(8)
经计算求得
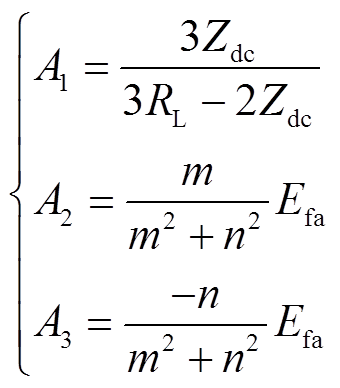 (9)
(9)
式中,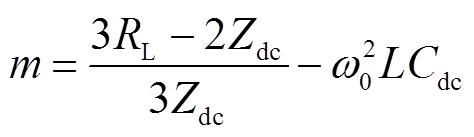 ,
,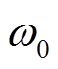 为交流子网角频率;
为交流子网角频率;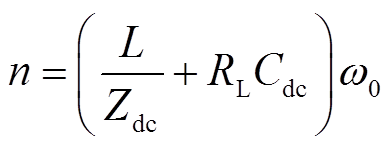 。
。
因此式(5)的特解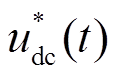 可进一化简为
可进一化简为
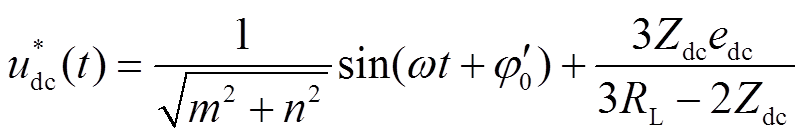 (10)
(10)
式中,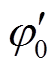 为式(8)三角函数项合并化简的相位。
为式(8)三角函数项合并化简的相位。
由于直流子网线路阻抗数值较小,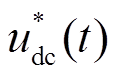 中的正弦分量可忽略,直流侧母线电压可表示为
中的正弦分量可忽略,直流侧母线电压可表示为
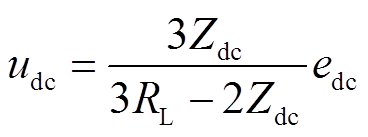 (11)
(11)
综上所述,交流子网发生三相短路故障时,交流故障点位置将直接影响直流子网母线电压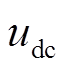 的稳态值。具体表现为
的稳态值。具体表现为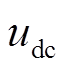 跌落幅度与故障点和BPC间的电气距离
跌落幅度与故障点和BPC间的电气距离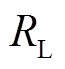 大小成反比,即故障离BPC远时
大小成反比,即故障离BPC远时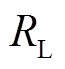 大,
大,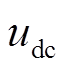 跌落幅度小,故障离BPC近时
跌落幅度小,故障离BPC近时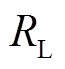 小,
小,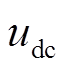 跌落幅度大。
跌落幅度大。
由于所有的不对称故障都将产生负序分量,此外图1所示的直流子网采用双极供电方式且电容中点直接接地,此结构可为接地故障下的零序分量提供通路。因此,本节同时考虑交流子网负序分量和零序分量对直流子网的影响情况。
1.2.1 负序分量对直流子网的影响
在单相接地故障引起的三相电网不平衡条件下,交流子网的视在复功率S为
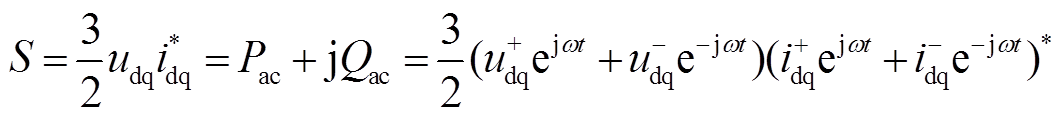 (12)
(12)
式中, 、
、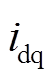 为同步旋转坐标系下的电压和电流;
为同步旋转坐标系下的电压和电流;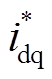 为dq轴电流分量
为dq轴电流分量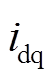 的共轭复矢量;
的共轭复矢量;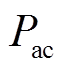 、
、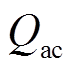 分别为BPC向交流子网传输的有功功率、无功功率。
分别为BPC向交流子网传输的有功功率、无功功率。
求解式(12)可得
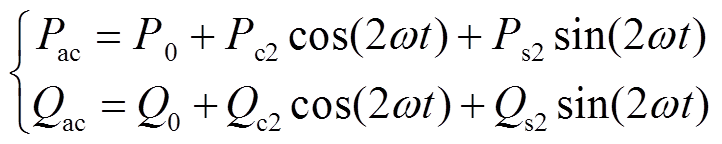 (13)
(13)
式中,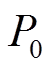 、
、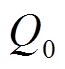 分别为有功功率、无功功率平均值;
分别为有功功率、无功功率平均值;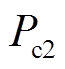 、
、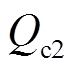 、
、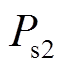 、
、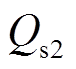 为各2次谐波项的峰值,其数值与同步旋转坐标系下正、负序电压和电流相关。
为各2次谐波项的峰值,其数值与同步旋转坐标系下正、负序电压和电流相关。
根据功率守恒原则,在Pac含有二次谐波的同时,直流子网功率也存在与交流子网二倍频波动相等的部分。因此,在负序分量作用下,系统中传输功率含有二次谐波。
将式(3)中的开关函数做傅里叶级数展开[23],可得
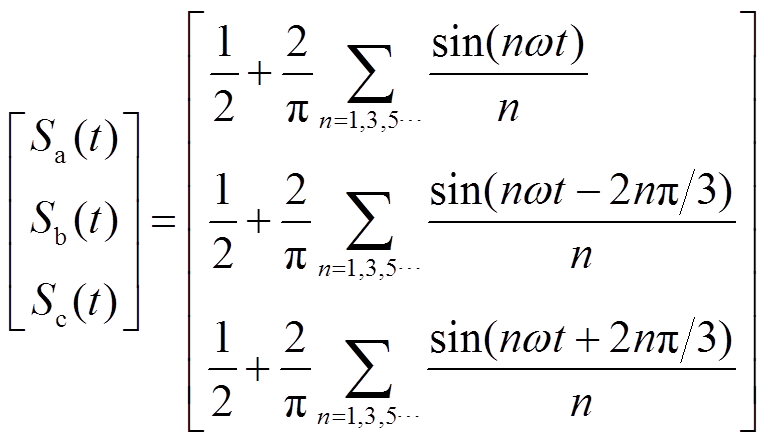 (14)
(14)
为简化分析过程,只计及其中的常数项和基频分量,开关函数的傅里叶级数展开式简化为
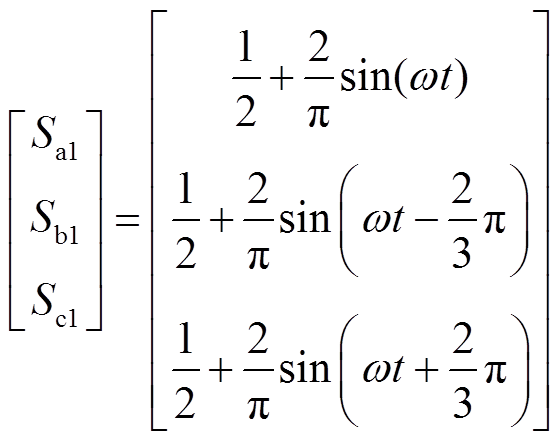 (15)
(15)
将交流子网的不平衡电流解耦为正序、负序分量,由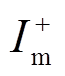 、
、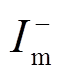 、
、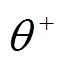 、
、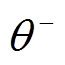 表示正、负序电流的幅值和相位。
表示正、负序电流的幅值和相位。
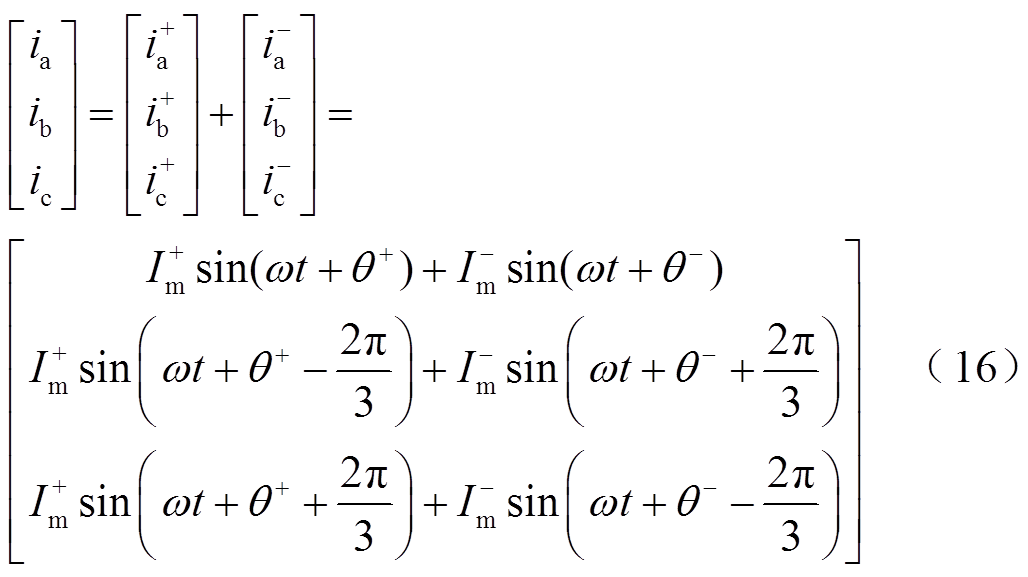
将式(15)、式(16)代入式(3),得直流侧电流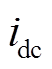 为
为
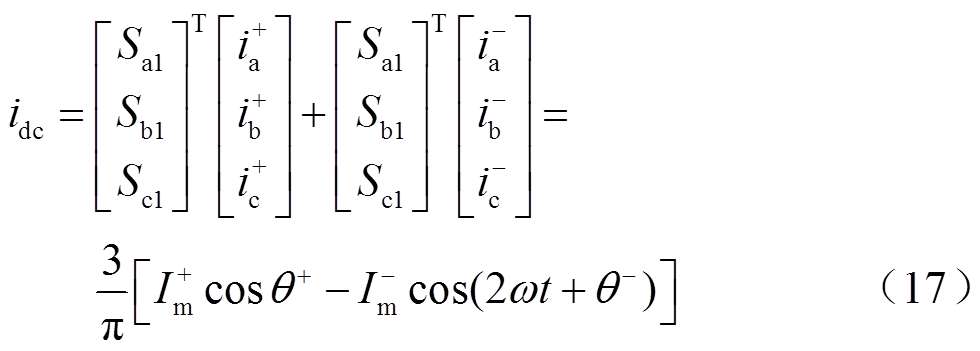
式(17)中开关函数和交流电流正序分量的作用结果对应着直流母线电流的常数项,而负序分量则通过BPC传播至直流子网形成二倍频谐波扰动。同时2次谐波电流也将引起直流电压波动,产生二倍频谐波电压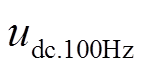 。
。
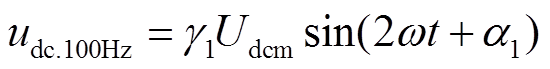 (18)
(18)
式中, 为直流电压幅值;
为直流电压幅值;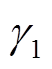 为2次谐波含有率;
为2次谐波含有率;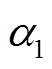 为2次谐波初始相位。联立直流电压二倍频波动量和式(15),可得直流子网的二倍频扰动对交流子网电压形成的反馈作用。
为2次谐波初始相位。联立直流电压二倍频波动量和式(15),可得直流子网的二倍频扰动对交流子网电压形成的反馈作用。
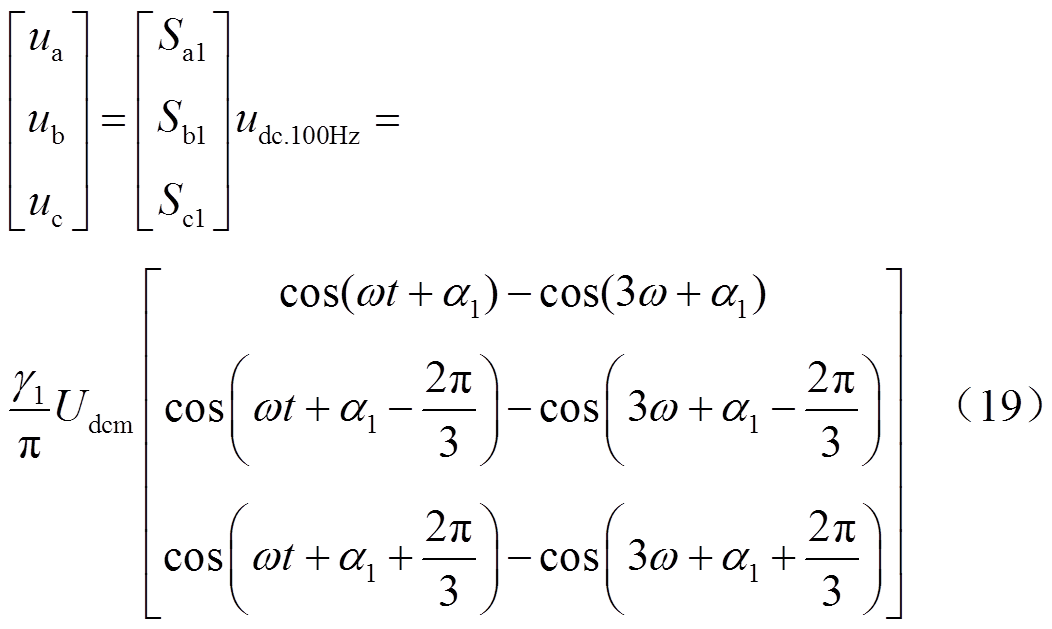
综上所述,交流子网单相接地故障产生的负序分量和开关函数基频分量将引发直流子网电压、电流的二倍频波动;并且2次谐波因系统互联而反作用到交流子网,导致交流电压产生3次谐波。由于3次谐波呈现零序分量特征,这将进一步扩大零序分量对交流子网的影响,恶化系统稳定运行能力。
1.2.2 零序分量对直流子网的影响
交直流混合微电网中接地故障零序分量通路如图3所示,交流子网零序电流为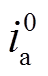 、
、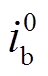 、
、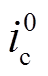 。
。
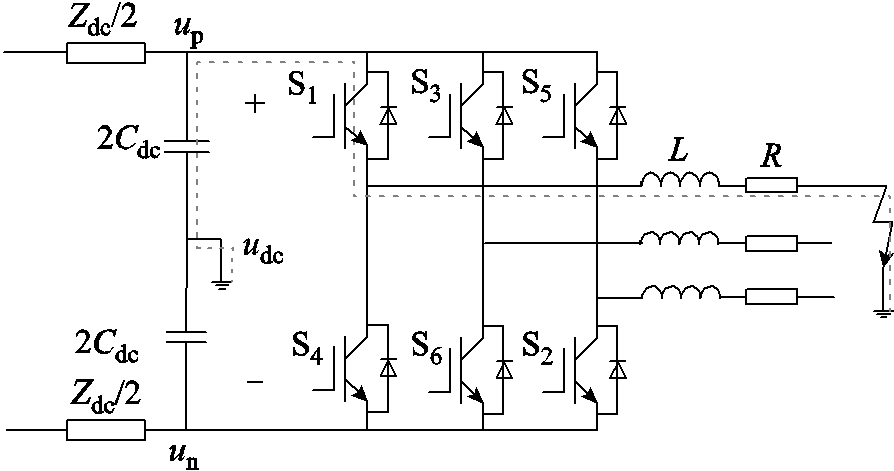
图3 接地故障零序分量通路
Fig.3 Ground fault zero-sequence component path
零序分量通过BPC传播至直流子网时,直流电流变化为
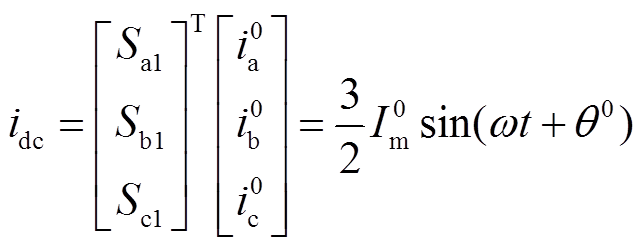 (20)
(20)
式中,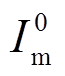 、
、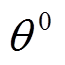 分别为交流零序分量幅值和初始相位。
分别为交流零序分量幅值和初始相位。
由式(20)可知,交流电流零序分量传播至直流子网会使直流电流出现工频波动,同时也产生工频谐波电压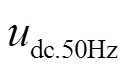 。
。
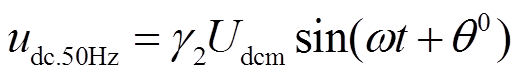 (21)
(21)
式中,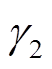 为工频谐波含有率。
为工频谐波含有率。
联立开关函数式(15)和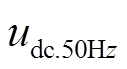 可得
可得
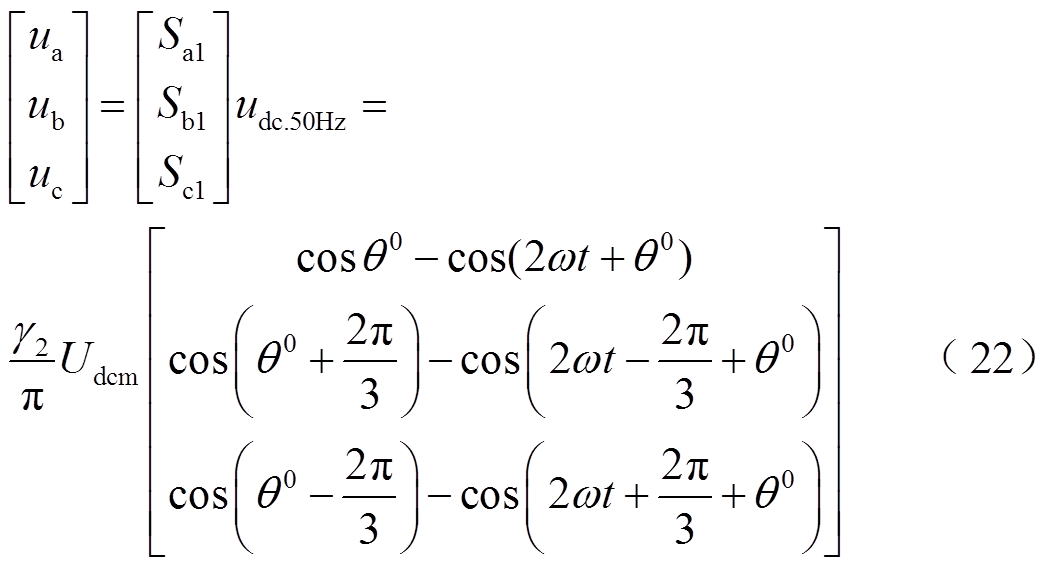
上述分析表明交流子网单相接地故障下的零序故障分量通过BPC传播到直流子网,引发直流电压、电流的工频波动,并且因系统互联再反作用到交流子网,导致交流电压产生2次谐波。
综合故障分量引起的谐波扰动及其在交直流子网间的传播过程,可见基波形式的负序分量和大小相等、相位相同的零序分量首次通过BPC在直流子网形成的2次谐波、工频谐波,再次通过BPC反作用到交流子网产生3次谐波、2次谐波。经计算验证,以上分析过程仅适用于零序分量和负序分量在交直流子网间传播引起的谐波扰动。对于更高频次的谐波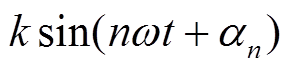 ,在流经BPC时谐波频次变化情况为
,在流经BPC时谐波频次变化情况为
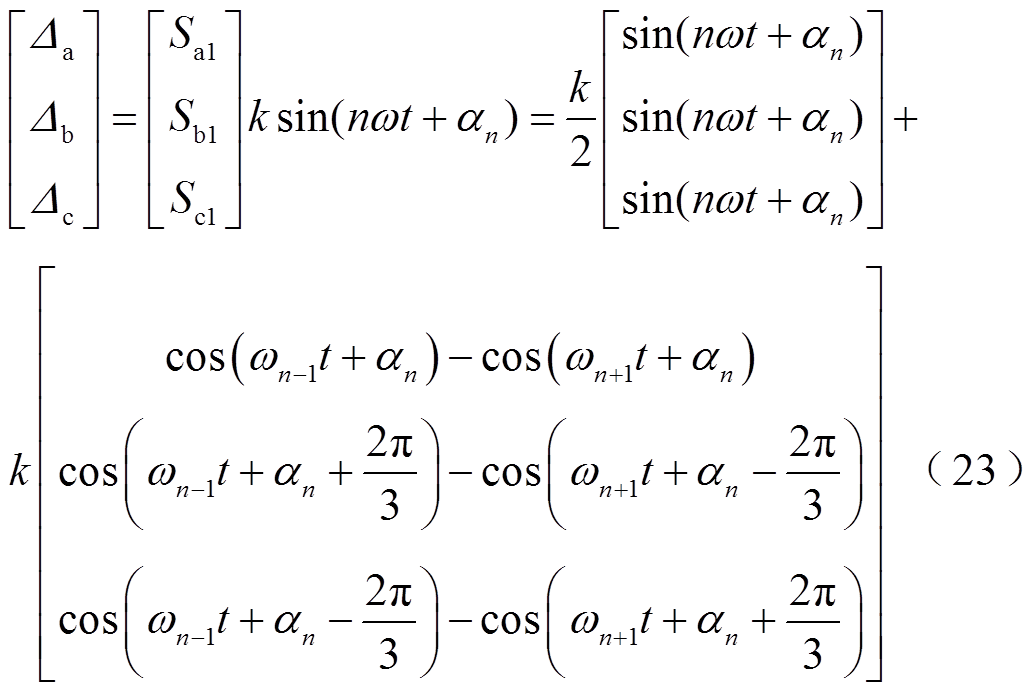
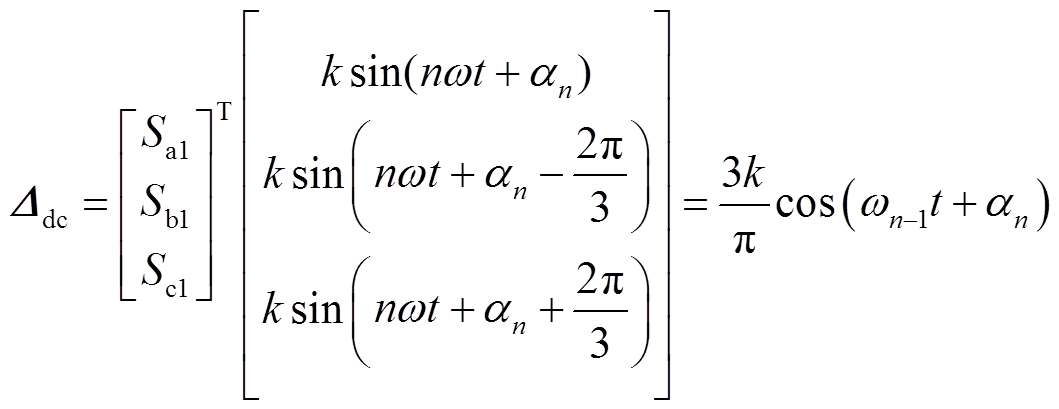 (24)
(24)
式中,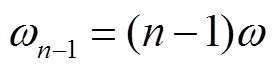 ;
;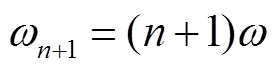 。
。
由式(23)可知直流子网n次谐波经BPC变换到交流子网时,产生频次为n-1、n+1的谐波扰动;式(24)中交流子网n次谐波经BPC变换到直流子网时,产生频次为n-1的谐波扰动。
直流子网的典型故障类型有极间短路故障和单极接地故障。由于直流子网内阻小使得故障电流大且上升速度快,为避免烧毁BPC的绝缘栅双极晶体管(Insulated Gate Bipolar Transistor, IGBT),故障瞬间IGBT因其自我保护功能可立即关断。然而,交流子网会通过续流二极管供给短路电流,这将无法隔离直流故障,进而影响整个系统的安全稳定运行[13]。
直流子网极间短路故障如图4所示。故障初始电容放电阶段,直流电容电压udc大于交流线电压,形成二阶RLC放电回路。
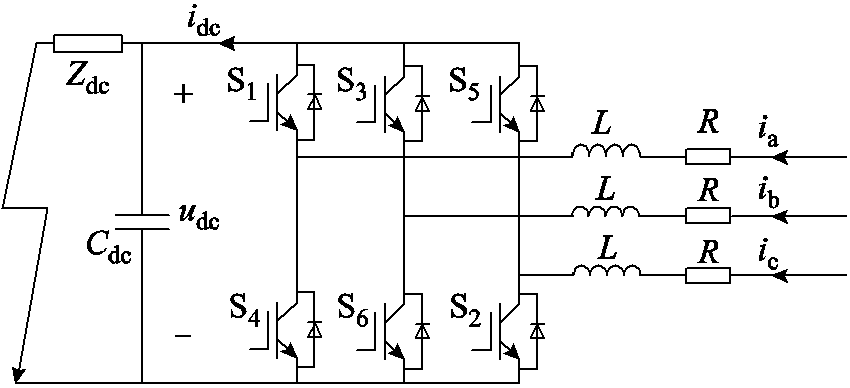
图4 直流子网极间短路故障
Fig.4 Interpole short circuit fault of DC sub-grid
由于直流子网阻尼满足 ,电容电压在欠阻尼状态下衰减振荡过零。当udc低于交流线电压时进入到交流馈流阶段,此时二极管遵循不控整流的自然换相原则导通,交流电源和直流电容同时向故障点放电,如图5所示。
,电容电压在欠阻尼状态下衰减振荡过零。当udc低于交流线电压时进入到交流馈流阶段,此时二极管遵循不控整流的自然换相原则导通,交流电源和直流电容同时向故障点放电,如图5所示。
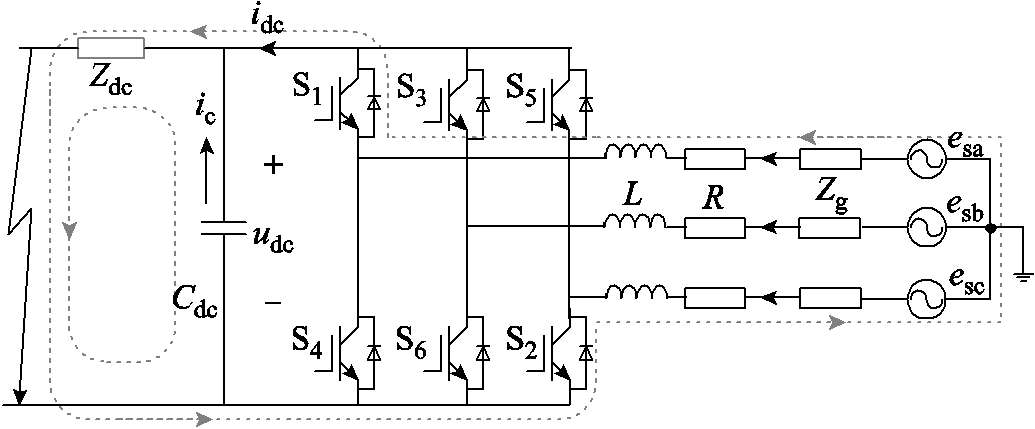
图5 交流馈流阶段短路电流路径
Fig.5 Short-circuit current path in AC feed stage
当直流电压udc衰减振荡过零时进入二极管同时导通阶段,直流子网短路电抗的反电动势使BPC的所有二极管同时导通,从而将直流电压udc钳位为零。直流子网形成一阶放电回路,同时因续流二极管全部导通,交流子网等效为发生三相短路[24],如图6所示。
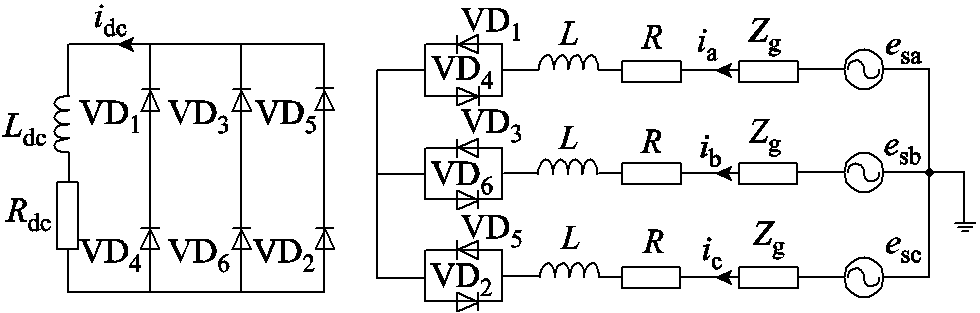
图6 二极管同时导通阶段等效图
Fig.6 Equivalent diagram of all diodes conducting
以极间短路故障时,交流子网a相短路电流的暂态响应为例:设t=0时刻电压源过零,a相电压为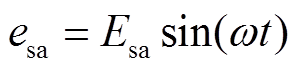 ,
,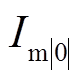 为a相瞬时电流值,
为a相瞬时电流值,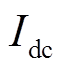 为直流短路电流瞬时值。
为直流短路电流瞬时值。
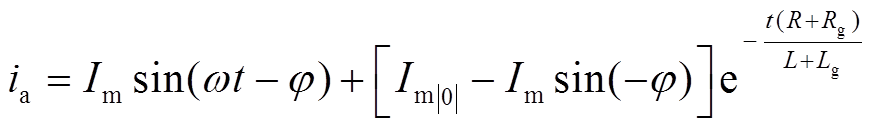 (25)
(25)
 (26)
(26)
式中,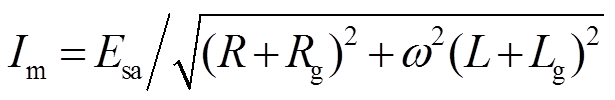 ;
;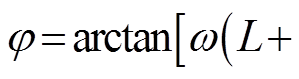
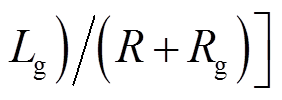 。
。
根据式(25),在二极管同时导通阶段内,交流短路电流由周期分量和非周期分量构成,直流短路电流随时间增加而衰减。达到稳态后,由于三相电路对称,各相交流短路电流呈现正弦变化且幅值相等、相位差120°,其幅值大小取决于交流电源幅值和交直流子网短路回路的总阻抗。
直流子网单极接地故障如图7所示。故障初始电容放电阶段,直流子网正极电压up大于交流相电压,形成了RLC放电回路。当up衰减到低于交流子网相电压时,进入交流馈流阶段,如图8所示。由于交流子网是正常运行状态,仍对直流子网母线供电,在正极电容电压up因接地保持为零时,负极un电位由-0.5 udc变为-udc,正负极电位差仍是udc。
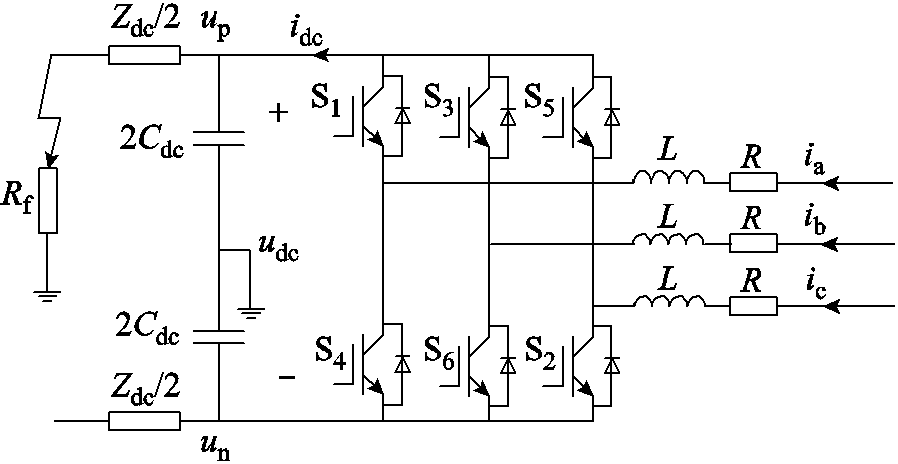
图7 直流子网单极接地故障
Fig.7 Positive cable ground fault of DC sub-grid
在交流馈流阶段中,下桥臂二极管阳极与直流子网负极线路相连,前述分析得负极线路电位为-udc,因此下桥臂二极管处于关断状态;上桥臂二极管阴极电位接近于0,阳极电位变化与交流源一致,故其导通情况和交流电压值的变化紧密相关。具体分为六个阶段,如图9所示。

图8 单极接地故障交流馈流阶段
Fig.8 Single-pole ground-fault AC feed-in stage

图9 分段示意图
Fig.9 Segmented schematic
阶段Ⅰ~Ⅵ所对应二极管导通情况见表1。
表1 各阶段二极管导通情况
Tab.1 Diode conduction at each stage

阶段导通二极管 ⅠVD1、VD5 ⅡVD1 ⅢVD1、VD3 ⅣVD3 ⅤVD3、VD5 ⅥVD5
对阶段Ⅰ的故障情况进行分析,其短路电流路径如图10所示。
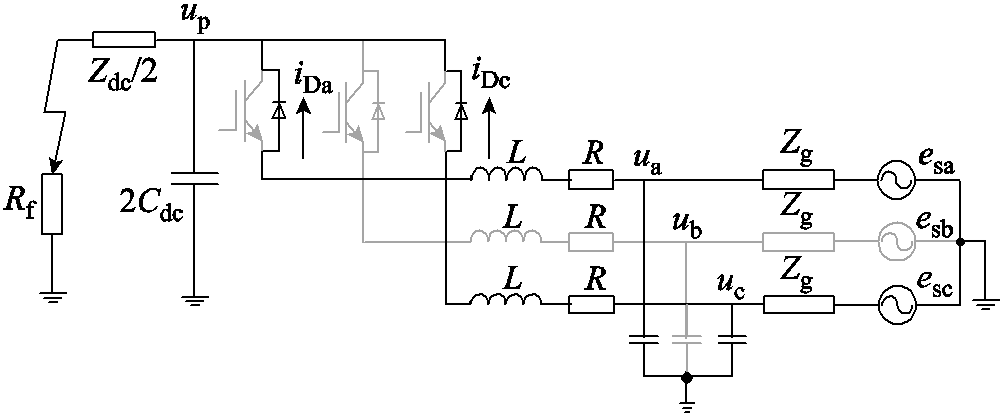
图10 阶段Ⅰ各桥臂二极管导通情况
Fig.10 Diode conduction of each bridge arm in stageⅠ
a相短路电流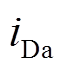 满足如下微分方程:
满足如下微分方程:
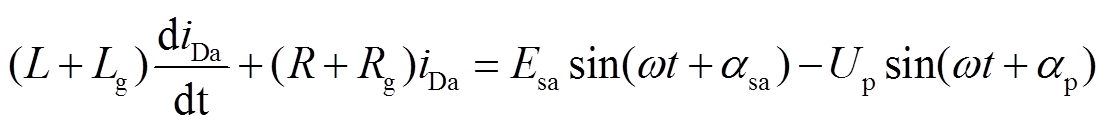 (27)
(27)
式中,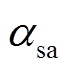 、
、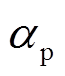 分别为a相电压源和直流侧正极电容电压的初始相位。通过计算一阶非线性方程(27)可得该阶段短路电流
分别为a相电压源和直流侧正极电容电压的初始相位。通过计算一阶非线性方程(27)可得该阶段短路电流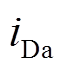 由周期分量
由周期分量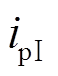 和非周期分量
和非周期分量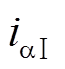 组成。
组成。
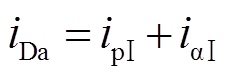 (28)
(28)
其中,周期分量为
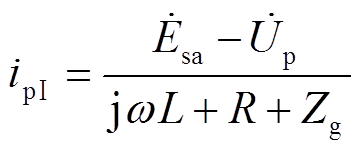 (29)
(29)
根据节点电压法计算短路电流周期分量为
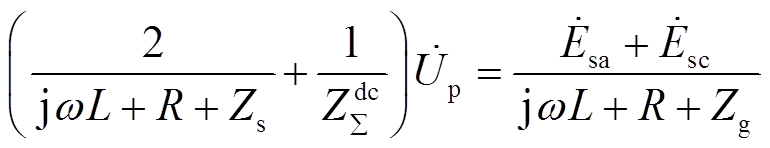 (30)
(30)
式中,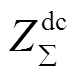 为直流子网内阻和稳压电容等值阻抗,有
为直流子网内阻和稳压电容等值阻抗,有
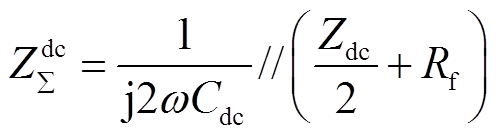 (31)
(31)
由于直流子网内阻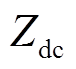 远小于交流子网等效阻抗与滤波器阻抗,可忽略
远小于交流子网等效阻抗与滤波器阻抗,可忽略 项,同时为简便计算令初相位
项,同时为简便计算令初相位 0°,因此稳态短路电流周期分量可近似为
0°,因此稳态短路电流周期分量可近似为
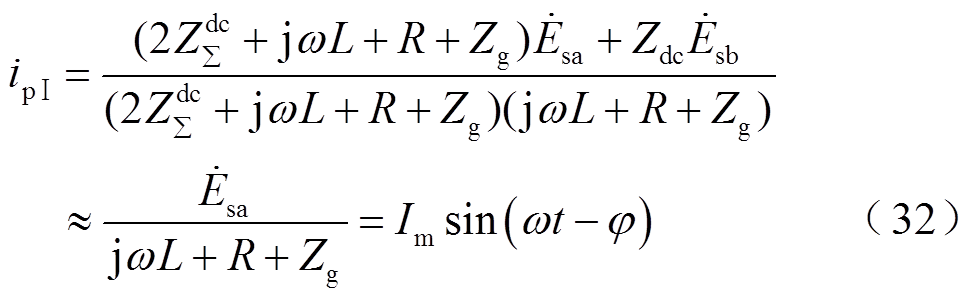
设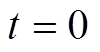 时刻a相电流为
时刻a相电流为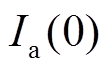 ,非周期分量表达式为
,非周期分量表达式为
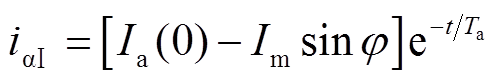 (33)
(33)
阶段Ⅰ的持续时间约为1/6个周期,即3.33 ms。因此非周期分量在短时间内变化不大,故将其近似为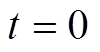 时刻的值,即
时刻的值,即
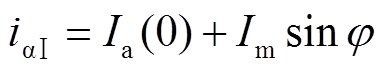 (34)
(34)
由式(32)、式(34)可得阶段Ⅰ内的全电流公式为
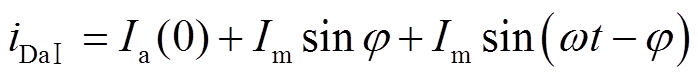 (35)
(35)
在阶段Ⅰ~阶段Ⅲ,a相电压均为正值,对应的稳态短路电流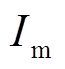 为正值;在阶段Ⅳ~阶段Ⅵ,a相电压过零点变为负值,稳态短路电流也为负值,用
为正值;在阶段Ⅳ~阶段Ⅵ,a相电压过零点变为负值,稳态短路电流也为负值,用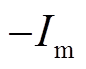 替换。按照上述推导过程,阶段Ⅱ~阶段Ⅵ的a相全电流表达式为
替换。按照上述推导过程,阶段Ⅱ~阶段Ⅵ的a相全电流表达式为
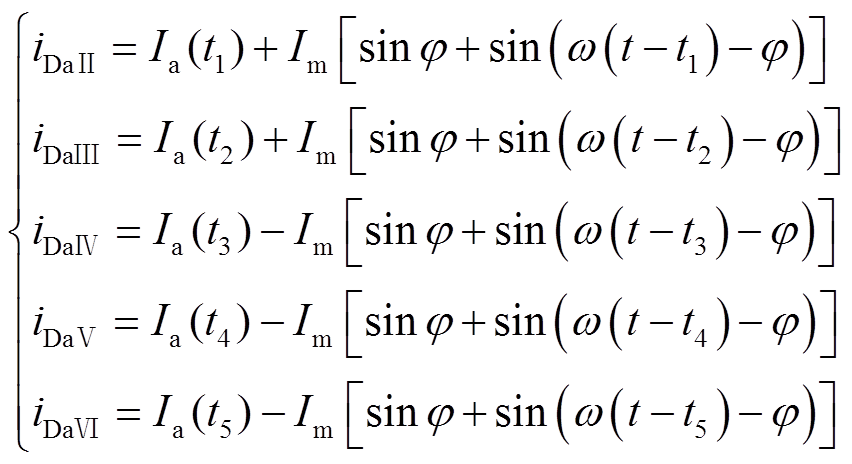 (36)
(36)
式中,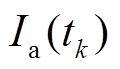 为
为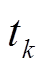 时刻的a相电流瞬时值,当k=1、2、3时,
时刻的a相电流瞬时值,当k=1、2、3时,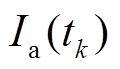 表示为
表示为
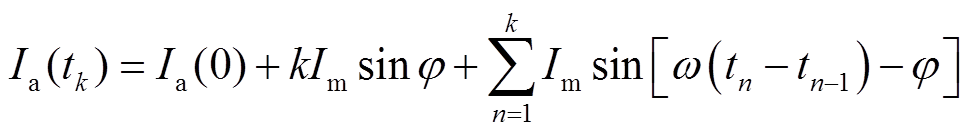 (37)
(37)
当k=4、5时,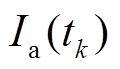 表示为
表示为
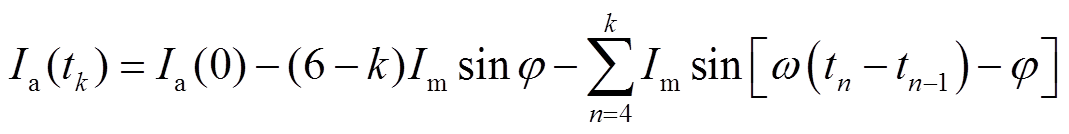 (38)
(38)
交流电压源为正弦波且各相相差120°,根据图7的阶段划分,每一阶段时长为占1个周期的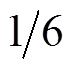 ,因此
,因此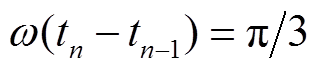 ,式(37)、式(38)简化为
,式(37)、式(38)简化为
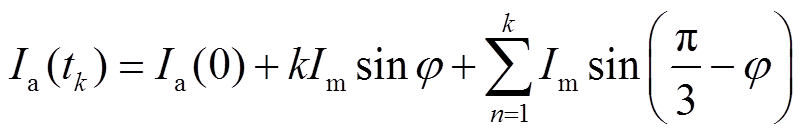 (39)
(39)
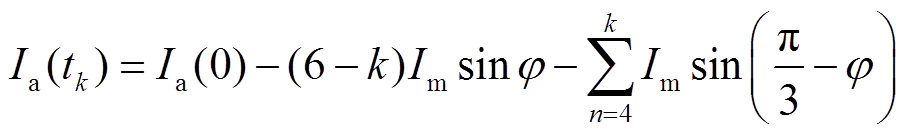 (40)
(40)
自 时刻开始新一周期的变化,a相电压仍然对应Ⅰ~Ⅵ阶段的变化过程,该时刻交流子网故障电流表达式为
时刻开始新一周期的变化,a相电压仍然对应Ⅰ~Ⅵ阶段的变化过程,该时刻交流子网故障电流表达式为
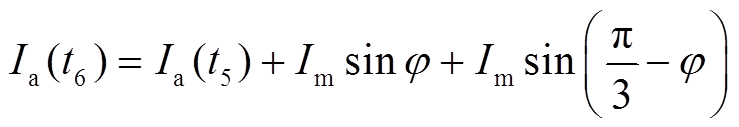 (41)
(41)
由式(40)可得
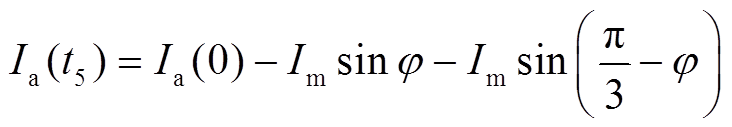 (42)
(42)
将式(42)代入式(41)得
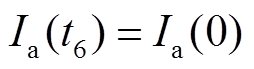 (43)
(43)
由式(43)可知,经过六阶段的变化,a相电流在周期末t6时刻的值恰好与周期初始(t=0)时的电流值相等,即每个周期的故障电流在都将循环进行阶段Ⅰ~阶段Ⅵ的变化过程。
因此在直流子网单极接地故障、交流子网正常运行的前提下,交流馈流暂态阶段中BPC借助交流电压变化实现换流,因此不同电压值对应的导通回路也不相同。经过推导各阶段故障电流表达式,可见第n+1个周期初始时刻电流值与第n个周期初始的电流值相等,说明交流电流呈现周期性变化特点,且因二极管的单相导通特性,各相交流电流均为正值。
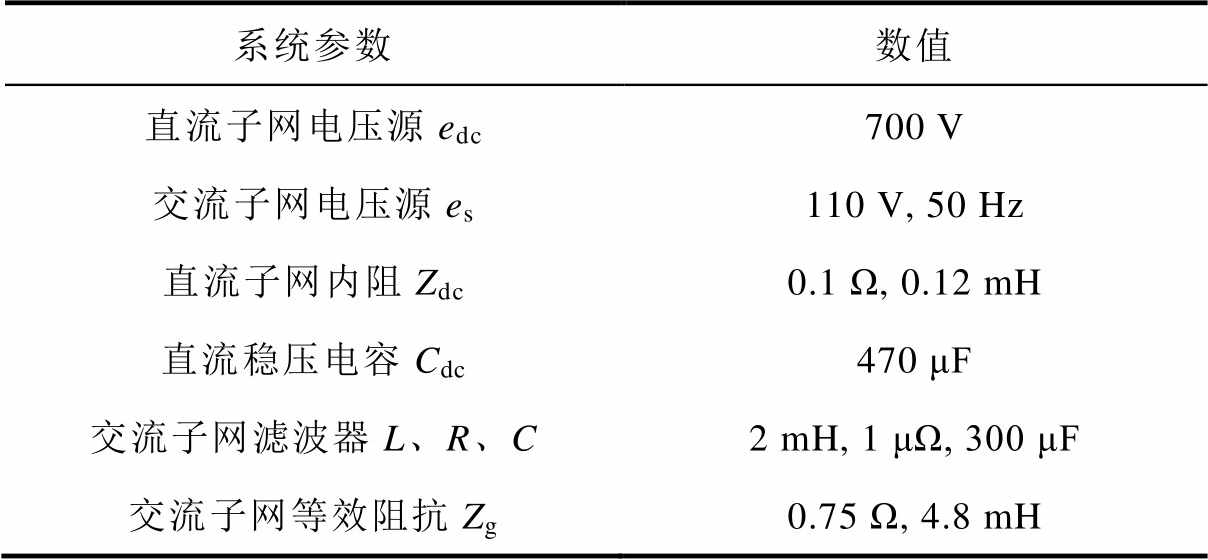
为验证上述交直流子网故障交互影响分析,借助Matlab/Simulink平台搭建图1所示的交直流混合微电网结构,仿真模型相关参数见表2。
表2 仿真模型相关参数
Tab.2 Simulation model related parameters
系统参数数值 直流子网电压源edc700 V 交流子网电压源es110 V, 50 Hz 直流子网内阻Zdc0.1 Ω, 0.12 mH 直流稳压电容Cdc470 μF 交流子网滤波器L、R、C2 mH, 1 μΩ, 300 μF 交流子网等效阻抗Zg0.75 Ω, 4.8 mH
交流子网故障时,直流子网正常运行,双向功率变换器工作在逆变状态,其交流出口处相电压有效值为220 V。
交流子网三相短路故障时直流母线电压幅值的变化情况如图11所示。0.4 s时发生三相短路故障,当故障距BPC交流出口1 km时,直流电压由688 V降至613 V;当故障距BPC交流出口3 km时,直流电压由688 V降至646 V。
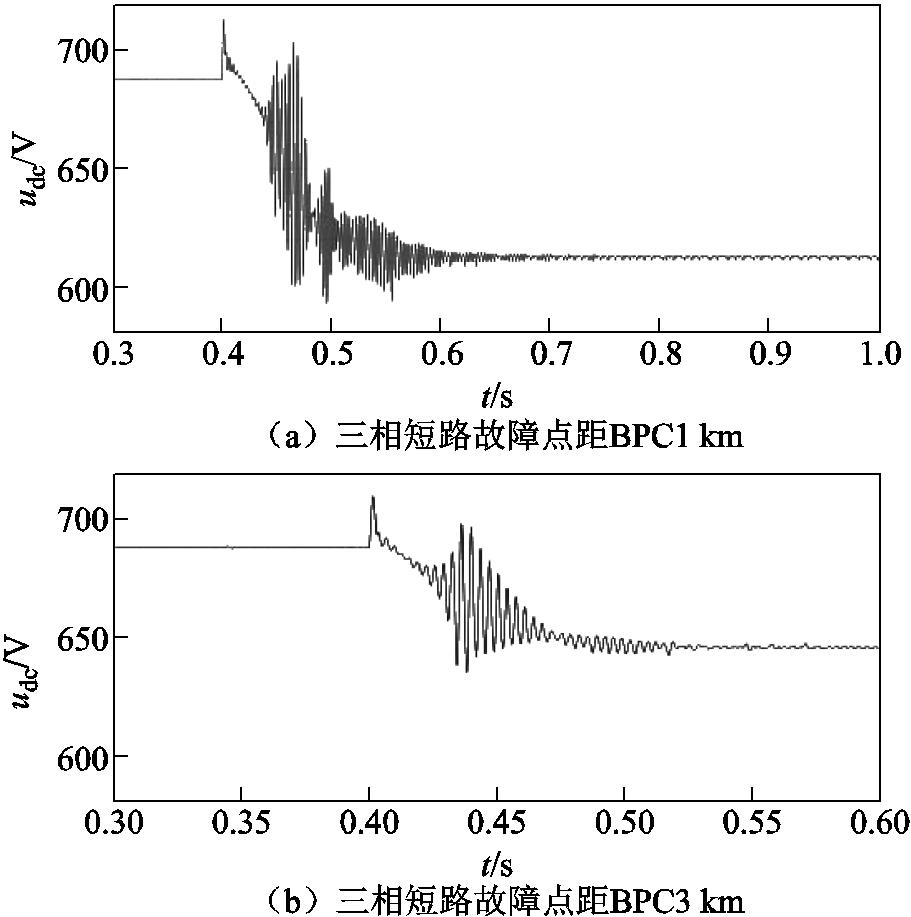
图11 三相短路故障时直流子网响应情况
Fig.11 DC sub-grid condition at three-phase short-circuit fault
可以明显比较出在交流子网三相短路故障情况下,故障点离变换器越近,电压跌落幅度越大,验证了式(8)直流母线电压跌落幅度与故障点距双向功率变换器交流出口距离成反比的结论。
图12为交流子在单相接地故障下的BPC交流出口处传输功率变化曲线。仿真系统设置在0.4 s时发生单相接地故障,观察图中P_output、Q_output波形,经测量得其波动周期为0.01 s,由此证实系统中传输功率因故障产生的负序分量引发二倍频波动。对于直流子网电容中性点直接接地的交直流混合微电网结构,正、负极电容电压up、un因接地故障的零序分量而受到工频共模扰动的影响,但对直流母线电压的影响较小,其电压偏移率仅为±0.465%,如图13所示。
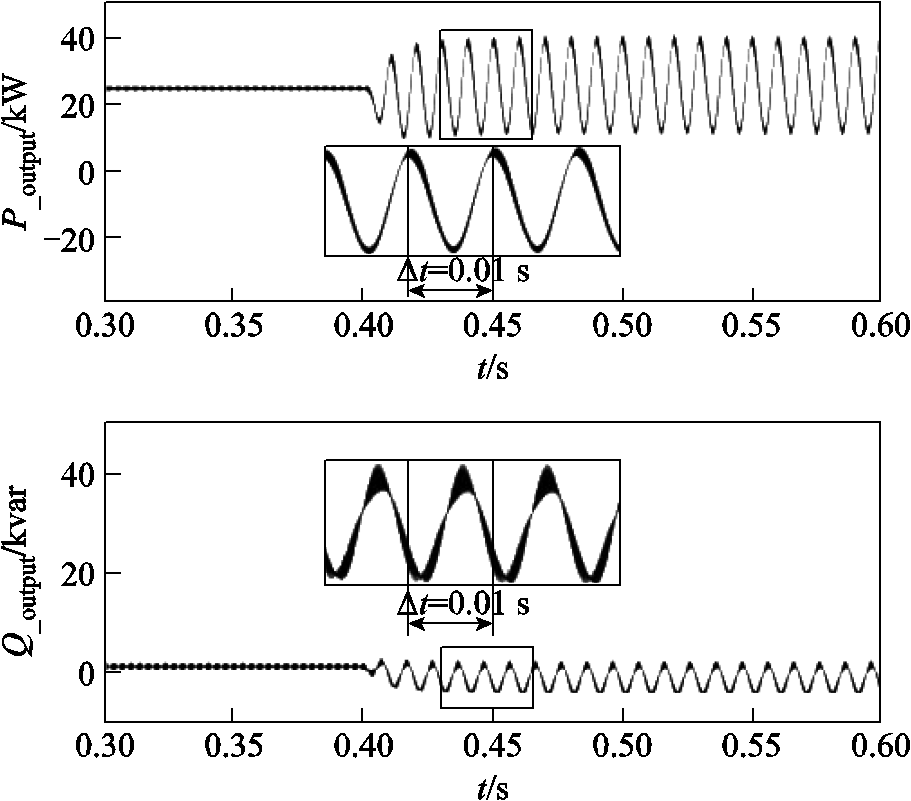
图12 不对称故障时的传输功率波形
Fig.12 Transmission power waveform during asymmetric fault
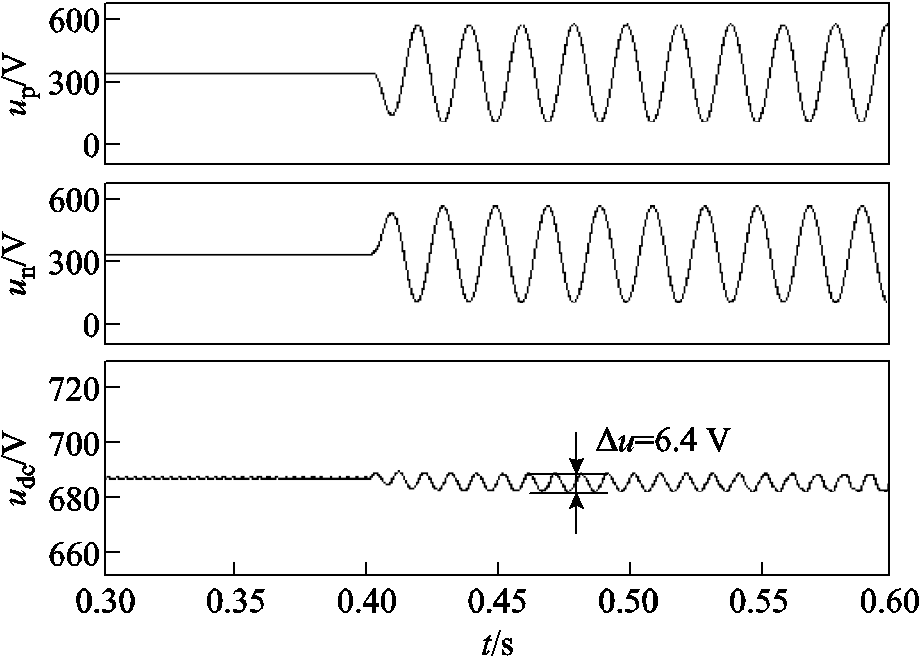
图13 接地故障时的直流子网电压波形变化情况
Fig.13 Changes of DC sub-grid voltage waveform during ground fault
为对比负序分量和零序分量引发的不同谐波影响,仿真模型设置两相接地短路故障和两相相间短路故障,采用Simulink平台中FFT模块对交直流子网进行谐波分析。图13为两类故障下的交流电压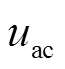 和直流电流
和直流电流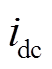 谐波含量示意图,其中两相接地短路故障会产生负序分量和零序分量,而两相相间短路故障仅有负序分量。根据图14所示,
谐波含量示意图,其中两相接地短路故障会产生负序分量和零序分量,而两相相间短路故障仅有负序分量。根据图14所示, 在两相接地故障下的工频谐波含量为41.3%,远高于两相短路故障时3.1%的工频谐波含量;而两相相间短路故障中,
在两相接地故障下的工频谐波含量为41.3%,远高于两相短路故障时3.1%的工频谐波含量;而两相相间短路故障中, 所含谐波分量以2次谐波为主。在两相接地短路故障下
所含谐波分量以2次谐波为主。在两相接地短路故障下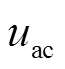 的2次谐波含有率最高;而两相相间短路时的
的2次谐波含有率最高;而两相相间短路时的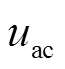 主要受到3次、5次谐波影响。由此,可见交流子网的负序分量传播到直流子网后产生2倍频为主的谐波扰动,再反作用到交流子网产生3倍频为主的谐波扰动;而零序分量使得直流子网受到工频谐波的影响较大,经BPC变换后使交流子网主要受到2次谐波的影响。
主要受到3次、5次谐波影响。由此,可见交流子网的负序分量传播到直流子网后产生2倍频为主的谐波扰动,再反作用到交流子网产生3倍频为主的谐波扰动;而零序分量使得直流子网受到工频谐波的影响较大,经BPC变换后使交流子网主要受到2次谐波的影响。

图14 不同故障类型下idc、uac谐波含量示意图
Fig.14 Schematic diagram of harmonic content of idc and uac under different fault types
直流子网故障时,交流子网正常运行,双向功率变换器工作在整流状态,直流母线电压为700 V。
图15为直流子网极间短路故障下的交流电流响应波形。由于在二极管同时导通阶段交流子网等效为发生三相短路故障,交流电流也迅速增大为三相短路电流,随着电流中非周期分量的衰减,三相电流稳态下呈现正弦对称波形。稳态时计算结果与仿真结果下的电流幅值分别为67.24 A、65.5 A,误差为2.66%,基本符合式(25)电流表达式。
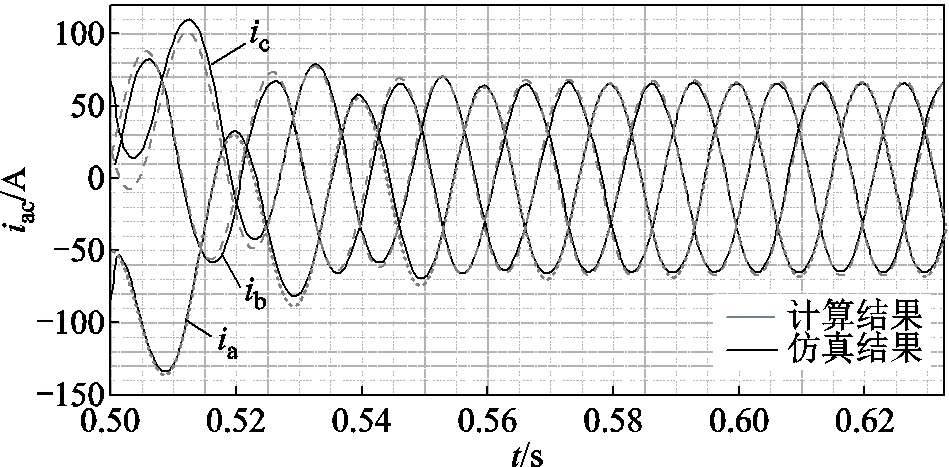
图15 极间短路故障时的交流电流波形
Fig.15 AC current waveforms of interpole short-circuit fault
图16为直流子网单极接地时a相故障电流波形。根据3.2节分析,在交流馈流阶段因二极管工作在不控整流的状态,交流短路电流单向变化,计算结果中的故障电流峰值为76.1 A,略大于仿真结果的73.06 A,误差为4.11%。
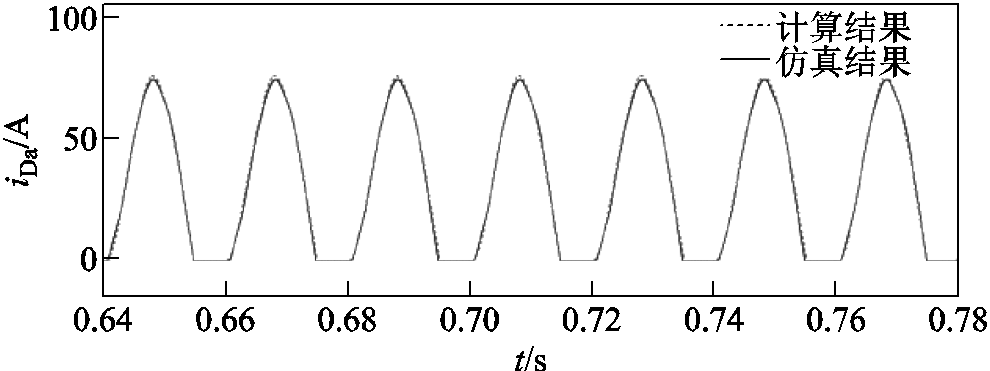
图16 单极接地故障时的交流电流波形
Fig.16 AC current waveform of single-pole ground fault
由于理论分析时,不计及直流子网内阻Zdc,若考虑其对短路电流的影响,短路电流的增长速度将慢于衰减速度。式(41)的电流表达式具体修正为
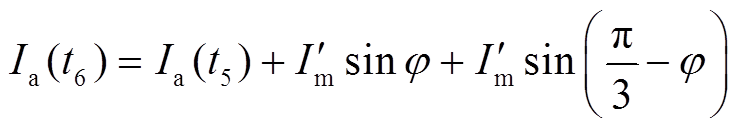 (44)
(44)
 (45)
(45)
其中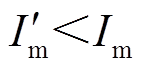 ,即实际上
,即实际上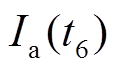 阶段Ⅵ内故障电流将衰减为0,且由于二极管的单向导通特性电流维持在0值,直至下个周期再次重复六个阶段的变化过程。图17为b相交流电压与故障电流在Ⅰ~Ⅵ阶段内的对应关系:0.664 s为周期开始时刻,各阶段占时3.33 ms。阶段Ⅰ内故障电流值为0,这是由于回路中的阻抗特性,测量可得故障电流响应滞后交流电压3.63 ms。
阶段Ⅵ内故障电流将衰减为0,且由于二极管的单向导通特性电流维持在0值,直至下个周期再次重复六个阶段的变化过程。图17为b相交流电压与故障电流在Ⅰ~Ⅵ阶段内的对应关系:0.664 s为周期开始时刻,各阶段占时3.33 ms。阶段Ⅰ内故障电流值为0,这是由于回路中的阻抗特性,测量可得故障电流响应滞后交流电压3.63 ms。
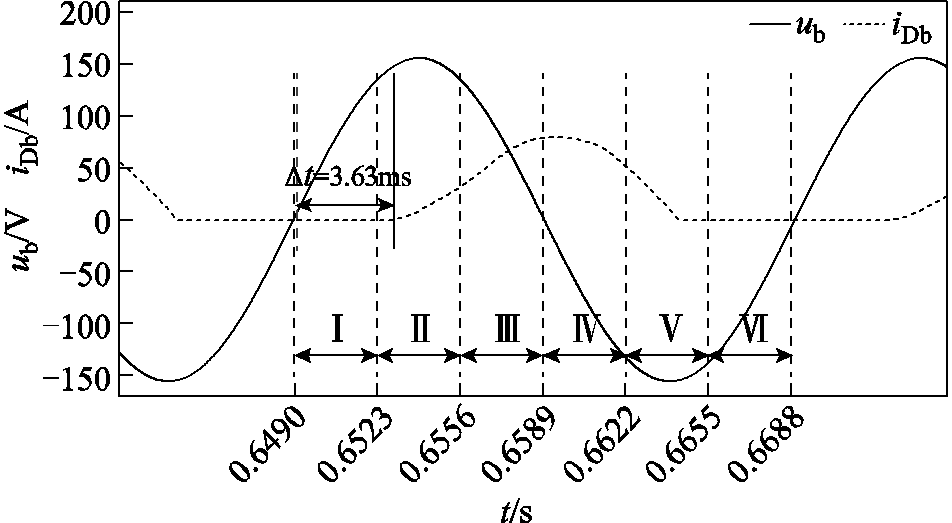
图17 b相Ⅰ~Ⅵ阶段交流电压与故障电流的对应关系
Fig.17 Corresponding relationship between AC voltage and fault current in phase I~VI stage of b-phase
将表1中的相关参数代入式(45),得到交流电流滞后交流电压角度为 °,而示波器测量所得的滞后时间转换成角度为65.3°,基本验证了仿真结果与理论计算的对应性。当交流电压在阶段Ⅳ~Ⅵ内过零为负时,故障电流也随之衰减,并且在阶段Ⅵ内将为0,与式(44)理论分析一致。
°,而示波器测量所得的滞后时间转换成角度为65.3°,基本验证了仿真结果与理论计算的对应性。当交流电压在阶段Ⅳ~Ⅵ内过零为负时,故障电流也随之衰减,并且在阶段Ⅵ内将为0,与式(44)理论分析一致。
图18将极间短路故障和单极接地故障的续流二极管电流波形进行对比。直流子网两类故障的暂态过程都经历了电容放电阶段和交流馈流阶段,但极间短路故障二极管电流相比于单极接地故障时出现急剧过电流的现象,约为正常运行时的3倍。其不同之处在于尽管处于电容放电阶段,两类故障下的电容电压都因系统欠阻尼状态而满足振荡过零的条件,但单极接地时有交流子网支撑的非故障极电压可维持udc不过零,从而不会进入类似二极管同时导通的第Ⅲ阶段,交流子网也不存在三相短路电流。
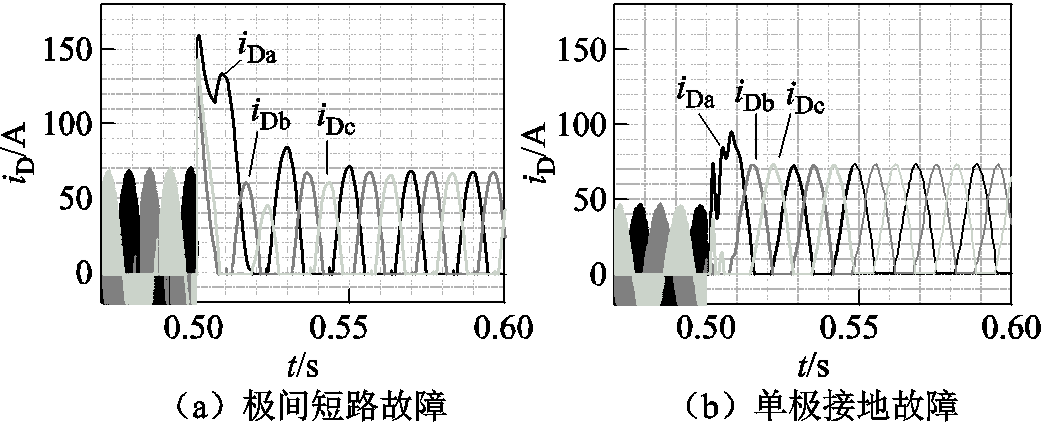
图18 续流二极管电流波形
Fig.18 Freewheeling diode current waveforms
本文基于双向功率变换器连接交流子网和直流子网的交直流混合微电网拓扑结构,进行故障传播机理研究,并在Matlab/Simulink平台对理论推导结果进行了仿真验证,其故障相应情况总结如下:
1)交流子网三相短路故障造成直流母线电压跌落,且故障点距BPC越近,跌落幅度越大。此外,交流n次谐波经BPC变换到直流子网产生n-1次谐波扰动;直流n次谐波经BPC变换到交流子网分别产生n-1、n+1次谐波扰动。
2)直流子网极间短路故障时,交流子网可等效为三相短路故障的状态;直流子网单极接地故障时,续流二极管工作在不控整流的状态,且因其单向导通作用使得交流短路电流波形不再呈现正弦变化。同时,理论推导的短路电流表达式计算结果与仿真结果的误差不超过5%。此外,经过对比两类故障下的续流二极管电流波形,极间短路故障相比于单极接地时的故障电流急剧增加,更易损坏开关器件。
参考文献
[1] 姜云鹏, 任洲洋, 李秋燕, 等. 考虑多灵活性资源协调调度的配电网新能源消纳策略[J]. 电工技术学报, 2022, 37(7): 1820-1835. Jiang Yunpeng, Ren Zhouyang, Li Qiuyan, et al. An accommodation strategy for renewable energy in distribution network considering coordinated dispatching of multi-flexible resources[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1820-1835.
[2] Nejabatkhah F, Li Yunwei. Overview of power management strategies of hybrid AC/DC microgrid[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 7072-7089.
[3] 葛平娟, 肖凡, 涂春鸣, 等. 考虑故障限流的下垂控制型逆变器暂态控制策略[J]. 电工技术学报, 2022, 37(14): 3676-3687. Ge Pingjuan, Xiao Fan, Tu Chunming, et al. Transient control strategy of droop-controlled inverter considering fault current limitation[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3676-3687.
[4] 郭文娇, 任春光, 王磊, 等. 电压不平衡时交直流双向功率变换器的控制策略[J]. 电网技术, 2016, 40(3): 925-930. Guo Wenjiao, Ren Chunguang, Wang Lei, et al. Control method of bidirectional AC/DC converter with unbalanced voltage in hybrid micro-grid[J]. Power System Technology, 2016, 40(3): 925-930.
[5] Ren Chunguang, Han Xiaoqing, Wang Lei, et al. High-performance three-phase PWM converter with a reduced DC-link capacitor under unbalanced AC voltage conditions[J]. IEEE Transactions on Industrial Electronics, 2018, 65(2): 1041-1050.
[6] Yang Jin, Fletcher J E, O'Reilly J. Short-circuit and ground fault analyses and location in VSC-based DC network cables[J]. IEEE Transactions on Industrial Electronics, 2012, 59(10): 3827-3837.
[7] 杨杰, 郑健超, 汤广福, 等. 电压源换相HVDC站内交流母线故障特性及保护配合[J]. 中国电机工程学报, 2010, 30(16): 6-11. Yang Jie, Zheng Jianchao, Tang Guangfu, et al. Internal AC bus fault characteristics of VSC-HVDC system and protection coordination[J]. Proceedings of the CSEE, 2010, 30(16): 6-11.
[8] 高一波, 徐习东, 金阳忻, 等. 交流侧接地故障对直流配电网电压平衡影响[J]. 电网技术, 2014, 38(10): 2665-2670. Gao Yibo, Xu Xidong, Jin Yangxin, et al. Impact on the voltage balancing of DC distribution network under AC side grounding fault[J]. Power System Technology, 2014, 38(10): 2665-2670.
[9] 朱永强, 刘康, 张泉, 等. 混合微电网交流侧故障传播机理及抑制方法[J]. 电机与控制学报, 2020, 24(4): 1-11. Zhu Yongqiang, Liu Kang, Zhang Quan, et al. Fault propagation mechanism and suppression method on AC side of hybrid microgrid[J]. Electric Machines and Control, 2020, 24(4): 1-11.
[10] 董新洲, 汤涌, 卜广全, 等. 大型交直流混联电网安全运行面临的问题与挑战[J]. 中国电机工程学报, 2019, 39(11): 3107-3119. Dong Xinzhou, Tang Yong, Bu Guangquan, et al. Confronting problem and challenge of large scale AC-DC hybrid power grid operation[J]. Proceedings of the CSEE, 2019, 39(11): 3107-3119.
[11] 许阔, 王婉君, 贾利虎, 等. 混合微电网交流不对称故障对直流系统的影响[J]. 中国电机工程学报, 2018, 38(15): 4429-4437, 4643. Xu Kuo, Wang Wanjun, Jia Lihu, et al. Influence of AC unbalanced faults on DC system of hybrid AC/DC microgrid[J]. Proceedings of the CSEE, 2018, 38(15): 4429-4437, 4643.
[12] 梁旭明, 张平, 常勇. 高压直流输电技术现状及发展前景[J]. 电网技术, 2012, 36(4): 1-9. Liang Xuming, Zhang Ping, Chang Yong. Recent advances in high-voltage direct-current power transmission and its developing potential[J]. Power System Technology, 2012, 36(4): 1-9.
[13] 宋金钊, 李永丽, 曾亮, 等. 高压直流输电系统换相失败研究综述[J]. 电力系统自动化, 2020, 44(22): 2-13. Song Jinzhao, Li Yongli, Zeng Liang, et al. Review on commutation failure of HVDC transmission system[J]. Automation of Electric Power Systems, 2020, 44(22): 2-13.
[14] 李斌, 何佳伟. 柔性直流配电系统故障分析及限流方法[J]. 中国电机工程学报, 2015, 35(12): 3026-3036. Li Bin, He Jiawei. DC fault analysis and current limiting technique for VSC-based DC distribution system[J]. Proceedings of the CSEE, 2015, 35(12): 3026-3036.
[15] 徐可寒, 张哲, 刘慧媛, 等. 光伏电源故障特性研究及影响因素分析[J]. 电工技术学报, 2020, 35(2): 359-371. Xu Kehan, Zhang Zhe, Liu Huiyuan, et al. Study on fault characteristics and its related impact factors of photovoltaic generator[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 359-371.
[16] Liu Jian, Tai Nengling, Fan Chunju, et al. A hybrid current-limiting circuit for DC line fault in multiterminal VSC-HVDC system[J]. IEEE Transactions on Industrial Electronics, 2017, 64(7): 5595-5607.
[17] Chen Dong, Xu Lie, Yu J. Adaptive DC stabilizer with reduced DC fault current for active distribution power system application[J]. IEEE Transactions on Power Systems, 2017, 32(2): 1430-1439.
[18] Baran M E, Mahajan N R. Overcurrent protection on voltage-source-converter-based multiterminal DC distribution systems[J]. IEEE Transactions on Power Delivery, 2007, 22(1): 406-412.
[19] 杨美辉, 周念成, 王强钢, 等. 基于分布式协同的双极直流微电网不平衡电压控制策略[J]. 电工技术学报, 2021, 36(3): 634-645. Yang Meihui, Zhou Niancheng, Wang Qianggang, et al. Unbalanced voltage control strategy of bipolar DC microgrid based on distributed cooperation[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 634-645.
[20] 李露露, 雍静, 曾礼强, 等. 低压直流双极供电系统的接地型式研究[J]. 中国电机工程学报, 2014, 34(13): 2210-2218. Li Lulu, Yong Jing, Zeng Liqiang, et al. Researches on grounding types of low-voltage DC bipolar distribution systems[J]. Proceedings of the CSEE, 2014, 34(13): 2210-2218.
[21] 张兴, 张崇巍. PWM整流器及其控制[M]. 北京: 机械工业出版社, 2012.
[22] 薛雪, 王子龙, 王全金, 等. 基于RLC二阶电路的直流配电网故障测距实验设计[J]. 实验技术与管理, 2021, 38(12): 160-164. Xue Xue, Wang Zilong, Wang Quanjin, et al. Experimental design of DC distribution network fault location based on RLC second-order circuit[J]. Experimental Technology and Management, 2021, 38(12): 160-164.
[23] 易桂平. 电网电压不平衡条件下微网恒功率控制策略研究[J]. 电工技术学报, 2015, 30(14): 377-387. Yi Guiping. Micro-grid constant power control strategy analysis under grid voltage imbalance[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 377-387.
[24] 李斌, 李晔, 何佳伟, 等. 基于模块化多电平的柔性直流系统故障稳态特性分析[J]. 电力系统保护与控制, 2016, 44(21): 1-8. Li Bin, Li Ye, He Jiawei, et al. Stable fault characteristic analysis of the DC system based on modular multilevel converter[J]. Power System Protection and Control, 2016, 44(21): 1-8.
Abstract The AC-DC hybrid microgrid will become an important development form of the future power grid due to the efficient renewable energy consumption performance. However, the interconnection structure of AC-DC hybrid microgrid complicates the fault response and decreases the system robustness. In this paper, the typical structure of hybrid microgrid includes AC sub-grid, DC sub-grid, and a bidirectional power converter (BPC), and the response characteristics of non-fault sub-grid to fault are analyzed. The systematic and complete fault response characteristic analysis results can provide a theoretical basis for the design of hybrid microgrid cooperative control or cooperative protection strategy under fault conditions.
The harmonic frequency change principle and the transient process of the fault loop caused by the propagation of fault components between sub-grids under typical fault conditions are analyzed in this paper. On this basis, the voltage and current expressions of the AC and DC sub-grids are deduced respectively with the consideration of the system interconnection structure. And then, the response results of the non-faulty sub-grid to the faulty sub-grid are obtained, which reveals the fault propagation mechanism of the hybrid microgrid. In the state of AC sub-grid fault, the harmonic transformation process caused by the propagation of negative sequence components and zero sequence components generated by symmetrical faults and asymmetric faults through BPC is deeply analyzed, and the general harmonic transformation expression is given. For the inter pole short-circuit fault and single pole grounding fault of DC sub-grid, this paper analyzes the transient process of short-circuit current loop in different stages, and deduces the expression of AC short-circuit current affected by DC sub-grid faults. The magnitude of the short-circuit current under a single-pole grounding fault is related to the BPC switch state. And the short-circuit current is characterized in the form of a piecewise function, by dividing the switch state of BPC, Furthermore, an AC-DC hybrid microgrid model is built and simulated for different fault types based on the Matlab/Simulink platform. And the following conclusions can be drawn:
1) DC bus voltage drop will be caused by three phase short-circuit fault. And the closer the faulted point is to BPC, the greater the drop amplitude is. In addition, (n+1)-th harmonics will be generated in DC sub-grid, when the n-th harmonic on the AC sub-grid is converted to DC sub-grid. And the (n+1)-th harmonics in DC sub-grid will react to the AC sub-grid and generate (n±1)-th harmonics.
2) AC sub-grid can be equivalent to the state of three-phase short-circuit fault, when a inter pole short-circuit occurs in DC sub-grid. In case of single pole grounding fault of DC sub-grid, the freewheeling diode works in the state of uncontrolled rectification, and the AC short-circuit current waveform no longer presents sinusoidal changes due to the unidirectional conduction. At the same time, the error between theoretical derivation and simulation results is less than 5%. Compared with the fault current of single-pole grounding, the fault current increases more rapidly in the inter pole short-circuit fault state by comparing the freewheeling diode current waveforms under two types of faults, which is more likely to damage the switching device.
keywords:AC-DC hybrid microgrid, bidirectional power converter, fault propagation, mechanism analysis
DOI:10.19595/j.cnki.1000-6753.tces.220834
中图分类号:TM713
国家自然科学基金联合基金重点项目(U1910216)和山西省基础研究计划青年科学研究项目(202203021212288)资助。
收稿日期 2022-05-16
改稿日期 2022-07-30
张 一 女,1997年生,硕士研究生,研究方向为交直流混合微电网、双向功率变换器控制。E-mail:m13115202590@163.com
张佰富 男,1992年生,讲师,研究方向为电力系统运行与控制,新能源发电与智能电网等。E-mail:zhangbaifu92@163.com(通信作者)
(编辑 赫蕾)