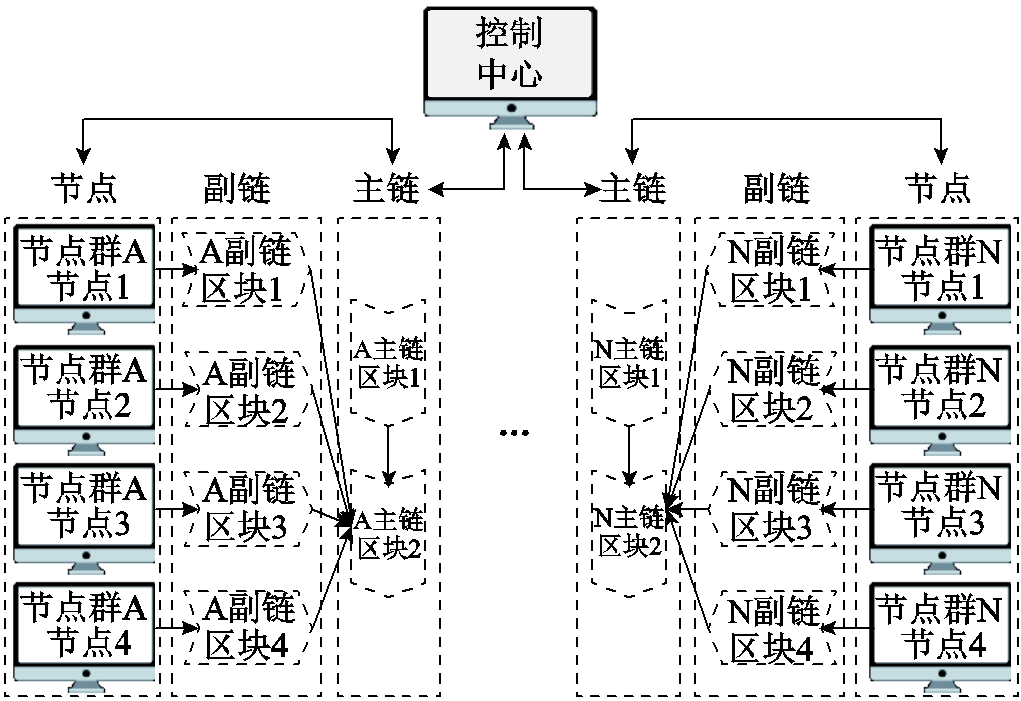
图1 BD-PSO算法结构
Fig.1 Structure diagram of BD-PSO
摘要 为提高虚拟电厂(VPP)的调度运行效率和信息安全水平,该文对区块链技术进行改进,并将其运用到VPP的优化调度过程中。首先以VPP分布式运行环境为背景,提出基于区块链的分布式粒子群优化算法和优化计算工作量证明共识算法;然后根据该算法,对传统区块链系统进行改进,形成了适用于VPP的优化计算型区块链系统;最后基于此系统建立了VPP结构模型,并提出相应的调度策略。仿真结果表明,优化计算型区块链系统能够较好地适应VPP运行环境,可以有效提高VPP调度效率,同时基于该系统建立的VPP模型和提出的调度策略,在降低系统运行成本、提高风/光消纳水平、减少二氧化碳排放量等方面相比传统VPP具有显著优势。
关键词:虚拟电厂 区块链 分布式 共识算法 粒子群优化算法
近年来,以风电、光伏、电动汽车、储能装置、可控负荷为代表的分布式能源数量增长迅速,由于此类分布式能源具有单机容量小、设备数量大、分布范围广等问题,其大规模接入将会对电网的可靠性和稳定性产生影响。虚拟电厂(Virtual Power Plant, VPP)技术[1-2]通过先进的计量、通信、控制技术,将多个不同利益群体整合成一个可控虚拟实体,参与电网调度和电力市场交易,并为系统提供容量和调峰、填谷服务[3],降低了分布式能源的运行风险和管理难度,促进了可再生能源消纳,提升了电网稳定性[4-7]。
但VPP具有的分布式特性也导致其存在一些问题[8-12]:
1)现有的集中式、集中-分散式和完全分散式VPP控制方式无法在灵活性、兼容性、扩展性上达成一致最优,影响VPP整体运行效果。
2)由于VPP内部之间依靠网络实现双向通信,各发电、负荷单元之间的出力、需求信息数据容易遭到外部恶意攻击篡改,造成VPP调度运行出错,导致成本增加或设备故障。
3)风、光等可再生能源出力具有不确定性和随机性,当其出现急剧变动时,如果VPP不能及时进行快速调整,将导致其惩罚成本上升,影响系统整体效益。
4)VPP的分布式特性导致其内部各单元之间整合难度大,调度协调困难。在现有的研究中通常使用智能优化算法进行计算,但此类算法没有针对分布式特性进行适配,在计算时间和准确性上仍存在诸多问题,导致交易成本的上升和效率的下降。
为解决上述问题,部分研究将区块链应用于VPP,建立了基于区块链技术的VPP架构和交易模式。文献[8]提出一种能源区块链网络模型并应用于VPP的调度运行过程,提高了VPP稳定性与数据安全性;文献[9]利用区块链共识机制结合等耗量微增率准则,使负荷在机组之间合理分配,实现了VPP的分布式调度。文献[10]提出适用于VPP的实用拜占庭容错算法共识机制,实现了区块链下VPP两阶段鲁棒优化调度,提高了系统的容错能力;文献[11]提出基于区块链技术的VPP分布式能源交易智能合约,帮助分布式能源供应商制定电价,提高交易效率;文献[12]进一步建立了基于区块链技术的VPP商业运营架构和电力交易模式。以上研究将区块链与VPP结合,提出基于区块链的VPP架构模型,但并未针对VPP运行特点对优化算法和区块链共识机制做出相应的改进,未将区块链技术与VPP的调度优化进一步结合,也未考虑可再生能源出力波动对区块链VPP调度速度、经济性的影响,仍有一定的改进空间。
本文针对上述问题,在分析区块链基本结构与应用于VPP可行性的基础上,提出适用于VPP运行环境的区块链-分布式粒子群优化算法(Blockchain-based Distributed Particle Swarm Optimization algorithm, BD-PSO),以及优化计算工作量证明(Proof of Optimization Calculation Workload,POCW)共识算法,并结合上述算法提出优化计算型区块链(Optimizing Computational Blockchains, OCB)系统提高系统运行效率,最终建立基于OCB的虚拟电厂(OCB-VPP)结构模型与调度策略。通过某区域实际数据,对比分析了OCB-VPP与传统VPP在应对可再生能源出力波动、提高系统经济效益与降低碳排放水平方面的差异,分析了BD-PSO算法在计算速度和计算精度上的优势,验证了所提模型的有效性和经济性。
区块链技术本质上是一种分布式共享数据库。其通过结合分布式数据存储、点对点传输、共识机制、加密算法等计算机技术,使存储在区块链中的数据具有去中心化、不可篡改、痕迹保留、操作追溯、公开透明、集体维护等特征,保证其内部信息和数据的诚信、透明与安全[13-15]。区块链技术为解决信息不对称问题,以及实现多个主体之间的协作信任与一致行动奠定了基础。区块链的上述特点与VPP的分布式特征,以及对信息安全、交易效率、灵活控制方面的需求相契合,因此区块链技术可应用于VPP,解决VPP内部各发电、负荷单元之间双向通信、快速交易、协调调度等问题。
区块是区块链系统的基本组成部分。区块头部包括版本号、前一区块哈希值、时间戳、Merkle根、挖矿难度、随机数六个部分。区块主体中封装了交易信息和数据。区块链系统分别由数据、网络、共识、激励、合约和应用六层结构组成[16-18]。数据层主要包括区块;网络层中包含系统组网、数据传输和验证等规则;共识层主要为共识算法;激励层中包含系统激励机制,通过该机制吸引节点加入和主动维护系统;合约层主要包含系统算法和智能合约;应用层则主要用于实现该区块链系统的实际应用场景。区块链系统各节点之间通过上述六层结构,可在保证信息安全的前提下逐步自动完成交易和数据传输的任务。
考虑到现有区块链技术主要应用于分布式记账系统,与VPP在效率和灵活性方面的要求不匹配,所以本文对区块链相关技术进行改进,提出并建立适用于VPP的区块链优化算法、共识机制、VPP模型与调度策略。
VPP的调度优化问题是一个多变量、多约束、高维度、非线性、连续和离散变量混合的数学优化问题,目前的主流VPP优化智能算法如粒子群、遗传、光线寻优算法等,以及Yalmip、Cplex等求解器,并未对VPP的分布式特性进行针对性改进,导致计算时间较长。
本文针对VPP的分布式特性,利用区块链技术分发和收集数据、信息、指令,提出BD-PSO优化算法。将VPP内每个用户视作一个计算节点,参与到求解运算中,最大限度地利用系统内算力,该算法结构如图1所示。

图1 BD-PSO算法结构
Fig.1 Structure diagram of BD-PSO
该算法原理为:
1)当系统有优化计算任务时,控制中心根据当时参与的节点数量与运算求解难度,将所有参与节点分为若干个节点群(群数量与求解速度成正比,与精度成反比;群内节点数量与求解精度成正比,与速度成反比),各节点群相应产生对应的区块链。随后控制中心将求解问题代入粒子群算法,随机产生大量的初始种群并均分后,与计算所需其余数据打包形成区块,链接到各节点群对应的区块链,作为群区块链的初始区块。
2)各节点群内的所有节点根据初始区块内容采用线性递减权重粒子群算法(Lin-WPSO)进行独立的优化计算。而由于粒子群这类智能算法具有结果不确定的特性,所以各节点群内部节点之间产生的结果不可能相同,同时各节点群之间因为所分配到的初始数据不同,也会导致节点群之间结果不同,这一特性会使系统内产生大量不同计算结果。
3)针对上述特性,BD-PSO算法设定当节点群内部所有节点完成单次计算后,各节点在群内广播计算结果,每个节点在收到的结果中选择最优的一个,并打包生成区块并行连接到群区块链的副链中。随后,在副链中此次计算产生的多个并行区块,逐个尝试链接到主链,群内各节点使用共识算法对该区块进行验证,通过验证的区块即为有效区块(该区块包含信息为最优解),一旦产生有效区块则停止验证,然后将该区块正式链接到主链中。
4)控制中心读取各群区块链,再取各节点群结果中的最优解为本次迭代计算结果,随后打包生成区块链接到所有群区块链中,群内各节点读取区块内容更新计算结果,进行下一次迭代。
通过上述过程可以发现,经分布式改进并结合区块链形成的BD-PSO算法,通过多节点并行计算,产生了比原算法更多的计算结果,且在使用区块链进行信息验证和传递以保证安全的基础上,进行了更大范围的最优结果比较,防止陷入局部最优,可以在提高算法精确度的同时,减少迭代次数和计算时间。其计算速度可表示为
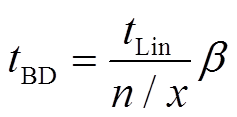 (1)
(1)
式中,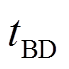 、
、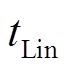 分别为BD-PSO算法和Lin-WPSO算法对于同一个计算任务所需时间;n为节点总数; x为一个节点群包含的节点数量;β为系统网络信息传输延迟系数。
分别为BD-PSO算法和Lin-WPSO算法对于同一个计算任务所需时间;n为节点总数; x为一个节点群包含的节点数量;β为系统网络信息传输延迟系数。
在区块链系统中,多个节点需要针对同一个操作、指令达成共识[19-20](判断该区块包含的信息是否真实,若真实则允许该区块链接到区块链,反之则禁止),以便系统正常运行。但节点中包含着故障和恶意节点,这类节点在运行时存在不能发送数据或发出恶意数据的情况,最终导致共识过程失败,阻碍系统运行,因此需要采用某种共识算法对该过程进行约束,保证系统的一致性和安全性。
2.2.1 工作量证明共识算法
目前的区块链系统中使用最广泛的共识算法为工作量证明共识算法(Proof of Work, PoW)。在使用PoW的区块链系统中,新区块的生成和验证流程如下。
1)当某节点参与到生成新区块的过程中时,该节点首先需要对系统内新产生的交互信息进行打包和哈希运算,从而生成新的Merkel根(Merkel根用于快速校验和索引区块数据),并封装到区块组成新的区块头部。
2)随后对区块头部进行多次SHA256运算(该运算过程为无规律的穷举运算,耗费时间长),如运算结果小于目标值则证明完成,向全网广播;如结果大于等于目标值则改变区块头部中的随机数,重新进行运算,如此循环直至符合要求。
3)当某节点率先向全网广播宣布自己完成时,全网节点对该结果进行验证,如果承认该区块有效的节点数超过50%,则该区块有效。
在此过程中如果想要对已经生成的区块信息进行修改,或者否决某一区块,恶意节点的算力必须远超越任何一个节点,才能保证自己总是能率先完成计算,同时至少控制全网超过50%以上节点,才能确保区块通过验证,成为有效区块。所以PoW算法的安全性(在某一系统中支持的最大恶意节点数量)为
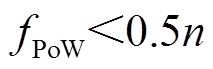 (2)
(2)
式中,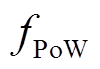 为PoW区块链系统可以容纳的恶意节点数量。
为PoW区块链系统可以容纳的恶意节点数量。
由此可知,PoW算法虽然具有较高的容错率,但其在生成新区块时需要进行大量的哈希运算,消耗系统内大量的算力资源,且该运算过程中产生的计算结果实际上并没有作用;同时VPP系统的各个节点受限于功耗和体积方面的限制,其算力不可能太高,因此完成一次运算并验证需要消耗大量的时间,难以应对可再生能源的突发出力波动和电网临时调度任务的速度要求,因此PoW算法不适用于本文的VPP模型,需要对其进行改进,提高适用性和运算速度。
2.2.2 工作量证明共识算法优化
本文对PoW共识机制进行改进,将PoW算法中需要重复进行的哈希运算,替换为使用BD-PSO算法的优化计算过程,提出优化计算工作量证明共识算法。该算法具体流程如下:
1)当某一节点需要生成新的区块时,与PoW相同首先对接收到的广播信息进行打包,生成Merkel根。
2)在验证环节首先取消耗费大量时间的SHA256运算。当各节点需要验证某一区块是否为有效区块时,若该区块为优化计算产生的结果,则令各节点分别对区块包含的计算结果进行验算(将计算结果代入BD-PSO算法重新计算,判断该结果是否符合系统约束和边界条件,以及运行成本是否最优)。若该区块为指令、操作或信息等单纯数据内容(如发电、负荷预测申报等信息),则将BD-PSO算法计算结果默认为1,以表示该区块为单纯数据区块,直接进行下一步。
3)对于包含优化计算结果的区块,如果有超过50%的节点验算该结果有效时,则该区块通过共识算法验证,为有效区块。
4)对于包含单纯数据内容的区块,则对该区块是否有效进行判断投票,如果具有超过50%的节点投票认同该数据时,则该区块通过共识算法验证,为有效区块。
综上所述,由于继承了PoW算法50%节点认同的特性,因此POCW算法安全性与PoW类似,即
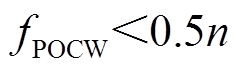 (3)
(3)
式中,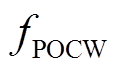 为POCW区块链系统可以容纳的恶意节点数量。
为POCW区块链系统可以容纳的恶意节点数量。
因此采用POCW共识算法后系统被入侵成功的概率可如图2所示。由于用户的智能家居设备一般通过路由器接入互联网,入侵路由器后即可通过路由器控制相应设备,所以采用POCW共识算法的VPP以路由器被入侵的概率数据进行比较。而普通VPP是控制中心的计算机或服务器独立进行计算和控制,因此以单台计算机或服务器被入侵的概率数据进行比较(但上述的两个概率没有准确的数据,因此只能根据路由器防护差易遭受入侵,而服务器防护较好不容易被攻破的情况,为其分别取一个较高的值0.8和较低的值0.1来进行比较,能够体现出两数据概率随节点数量变化的趋势即可)。
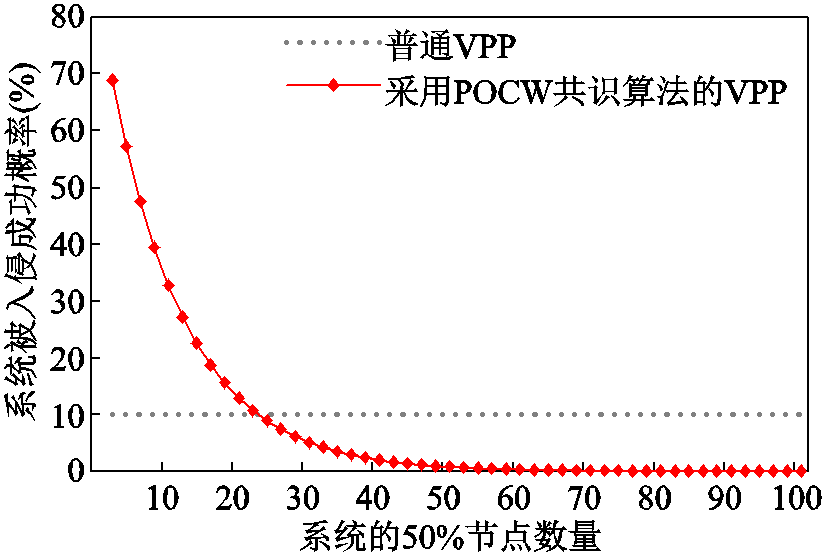
图2 算法安全性对比
Fig.2 Algorithm security comparison diagram
从图2中可以发现,随着系统内节点数量的增加,采用POCW共识算法的VPP被入侵成功的概率呈指数形式下降。在系统的50%节点数为30时被入侵成功的概率约为5.1%,在概率统计上基本为不可能事件,若节点再进一步增多,则可能性无限接近于零。这是因为POCW共识算法具有50%节点认同才能生成区块的特性,节点越多,入侵需要控制的节点越多,入侵难度就越大。而传统VPP由于只通过控制中心的一台计算机或服务器进行计算和控制,系统安全性与节点数量无关,因此一旦该服务器被攻破,整个系统也就被控制。
综上所述,经过改进的POCW算法,在继承了PoW算法安全性特点的同时,适应了区块链VPP的结构,可以与本文提出的BD-PSO算法配合,提高系统的计算速度和运行效率,为区块链VPP运行奠定基础。
2.3.1 优化计算型区块链系统
在基于PoW共识算法的区块链系统中,不包含优化算法,且共识验证时间较长,不能应用于区块链VPP。本文对基于PoW区块链系统进行改进,提出优化计算型区块链(Optimize Computing Blockchain, OCB),以适应区块链VPP在调度中优化计算的要求。
优化计算型区块链系统结构如图3所示。首先将BD-PSO优化算法与区块链结合,加入区块链数据层,并将PoW共识算法中采用的SHA256算法更改为本文改进的BD-PSO算法,形成POCW共识算法,在保证系统的安全性与交易效率的基础上,充分利用系统内节点算力,提高区块的生成验证速度。
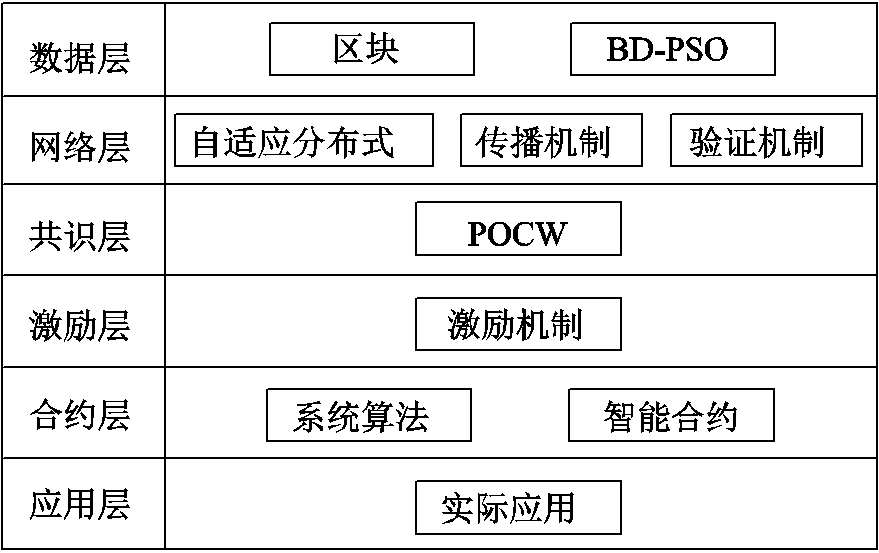
图3 优化计算型区块链系统结构
Fig.3 OCB system structure diagram
然后将网络组网机制由PoW区块链系统的完全分布式,更改为与VPP和BD-PSO算法相适应的自适应分布式。
自适应分布式组网机制是根据VPP实际运行特性结合本文改进的优化算法和共识算法特性改进形成的新型组网机制,结合了集中式和集中-分布式VPP控制方式的优点。即VPP系统内各节点可根据当前任务的不同,改变组网结构,以便在适应VPP调度运行特性和区块链、算法要求的基础上,提高VPP控制效率。例如,单纯数据交互时计算量小,不会对VPP控制中心产生较大影响,因此可使用集中式结构,控制中心直接通过OCB网络对各节点进行控制;优化计算时除主OCB网络外,还包括各群内的群OCB网络,群OCB网络可视为VPP下级控制中心,此时VPP控制中心通过各群OCB网络实现集中-分散式控制。
2.3.2 OCB-VPP系统结构
基于优化计算型区块链建立的OCB-VPP系统结构如图4所示。OCB-VPP内部包括多个已联网的发电、用电、储能用户,各用户之间、用户与控制中心之间利用网络进行通信和控制,各用户之间的发电、用电需求通过控制中心进行统一协调调度。OCB是系统内数据和信息传输载体,控制中心与所有节点之间的交互均通过OCB网络进行,保障通信和数据的安全。
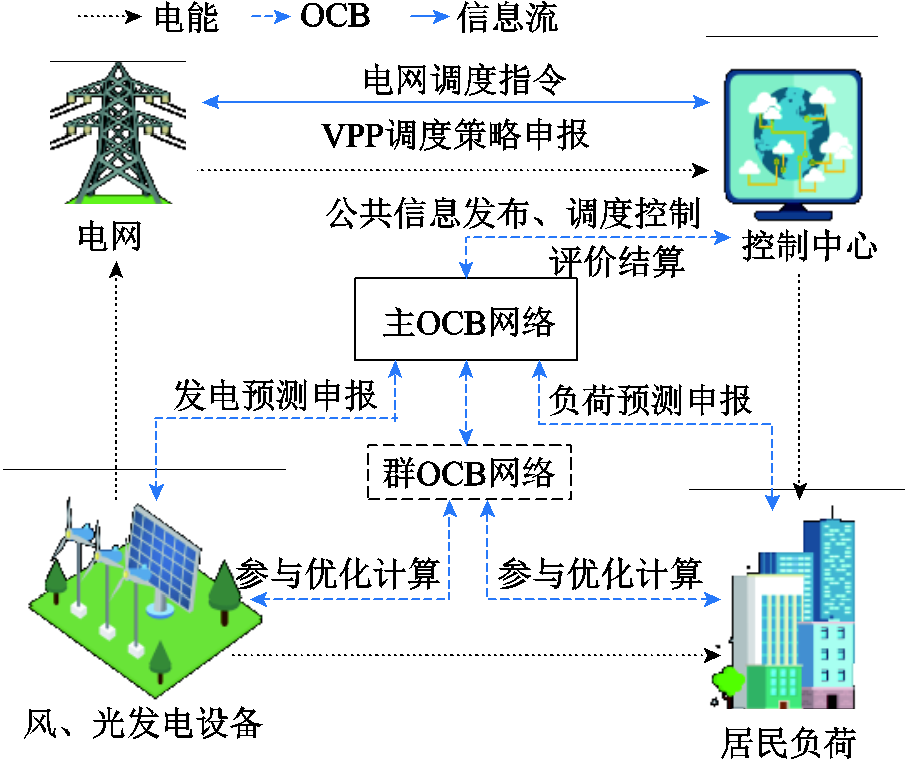
图4 OCB-VPP系统结构示意图
Fig.4 Schematic diagram of OCB-VPP structure
系统内节点之间的交互主要分为两类:首先是调度的优化计算过程,需要使用OCB配合BD-PSO优化算法并结合POCW共识算法完成;其次,系统内还包含大量的不需要进行优化计算的单向、双向信息数据传输,如控制中心向各节点发送气象预报数据、节点之间相互发送发电和负荷预测等申报信息、控制中心反馈各节点执行评价等过程。上述过程不需要进行复杂运算,只需要保障交互信息的快速、可靠和安全,因此应用于该过程的OCB需要将BD-PSO的计算过程默认为1,即各节点不需要使用BD-PSO进行计算即可生成区块。
OCB-VPP的调度运行过程主要分为三部分,系统调度流程如图5所示。
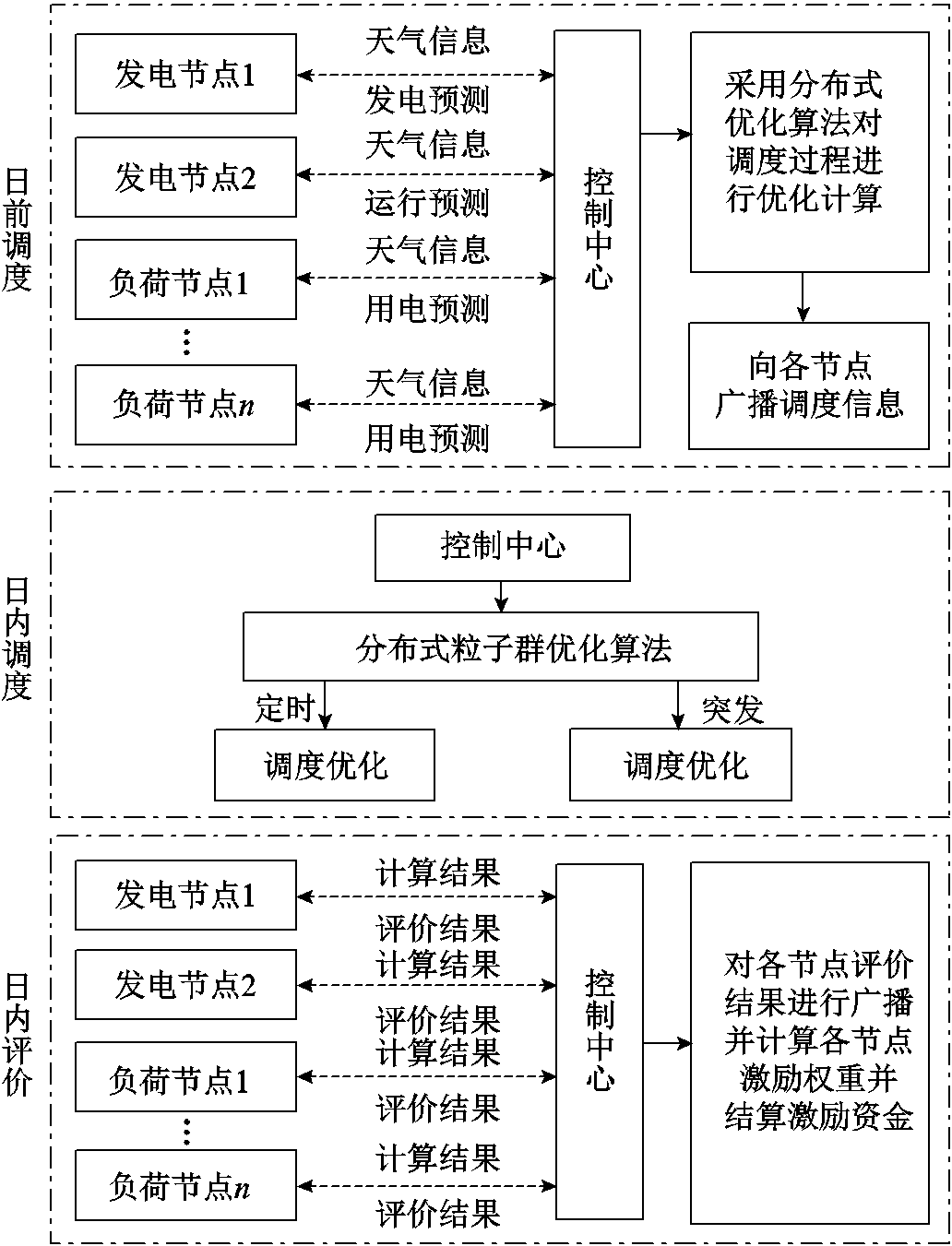
图5 系统调度流程
Fig.5 System scheduling process
1)日前调度阶段,各发电、负荷单元根据控制中心下发的气象预报数据对自身第二日的出力和负荷曲线进行预测,通过共识算法验证后生成区块链接到OCB。控制中心读取OCB数据并整理后,形成待优化计算问题,分配至各节点群进行计算(计算流程如2.1节所示)。计算结果通过共识算法验证后,控制中心生成新的区块链接到OCB作为日前调度方案。
2)日内调度阶段,主要包含实时优化调度和突发优化调度两个部分。对于实时优化调度,该过程得益于本文改进的BS-PSO优化算法,其消耗时间能够大幅减少,因此在优化过程中可以采取短间隔、多次数的优化计算,提高系统调度准确性,其间隔时间需要根据VPP、电网调度以及电力市场具体情况而定。其过程、目标函数、约束条件与日前阶段相同,不再赘述。对于突发情况的优化调度,如电网故障、可再生能源出力变化等问题导致的调度调整,利用BS-PSO优化算法的特性,可通过调整节点群和群内节点的数量,在保证计算精度的情况下,迅速完成调度计算,确保调度任务的顺利执行和减少惩罚费用。
3)日内评价阶段,主要是对各单元节点在调度过程中的完成表现进行评价,作为后续分配计算任务和激励结算的依据。对于计算任务的评价,每次计算完成后各单元节点会向系统广播自身计算结果,VPP控制中心根据各单元计算结果与最终写入到OCB中的实际值进行比较,比较结果作为单元节点的计算准确度进行广播。由于每次计算任务的分配,参与节点的选取需要根据计算准确度由高到低进行选择,同时,其计算准确度也会影响到优化计算中对节点的选取,有利于促进各用户升级和维护计算机。
在本文构建的OCB-VPP模型中,包含风力、光伏发电机组、储能电池、燃气轮机(发电、产热)、电加热设备(补充产热)和小区居民负荷,OCB-VPP以系统最小运行成本为目标,优化系统内各单元调度情况。系统收益为削峰填谷、余电上网收益,成本包括购电费用、设备投资和折现、碳排放成本,以及由于电力不足导致的失负荷惩罚费用,目标函数为
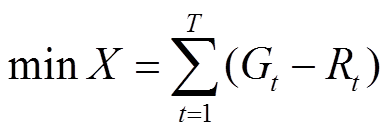 (4)
(4)
式中,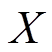 为系统单日运行成本;
为系统单日运行成本;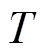 为系统调度周期,包含24个调度时段;
为系统调度周期,包含24个调度时段;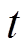 为某调度时段;
为某调度时段;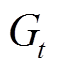 、
、 分别为
分别为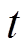 时段系统运行成本、收益,有
时段系统运行成本、收益,有
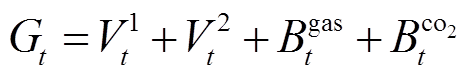 (5)
(5)
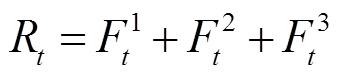 (6)
(6)
式中,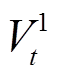 、
、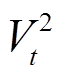 分别为系统购电、失负荷惩罚成本;
分别为系统购电、失负荷惩罚成本;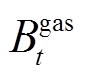 、
、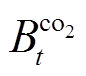 分别为燃气轮机燃料成本、系统碳排放成本;
分别为燃气轮机燃料成本、系统碳排放成本;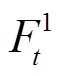 、
、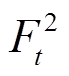 、
、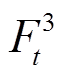 分别为风、光发电、燃气轮机余电上网收益及储能电池削峰填谷收益。
分别为风、光发电、燃气轮机余电上网收益及储能电池削峰填谷收益。
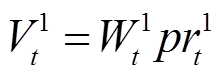 (7)
(7)
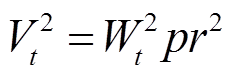 (8)
(8)
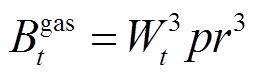 (9)
(9)
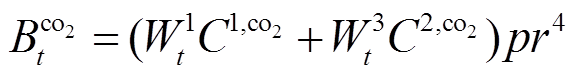 (10)
(10)
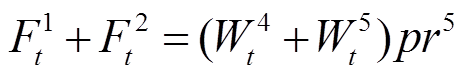 (11)
(11)
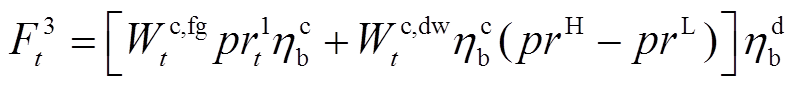 (12)
(12)
式中,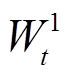 、
、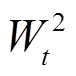 、
、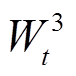 、
、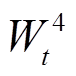 、
、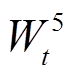 分别为
分别为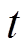 时段系统购电、失负荷、燃气轮机出力以及风、光和燃气轮机余电上网电能;
时段系统购电、失负荷、燃气轮机出力以及风、光和燃气轮机余电上网电能;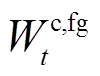 、
、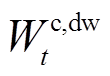 分别为风、光发电和电网对储能电池的充电能量;
分别为风、光发电和电网对储能电池的充电能量;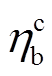 、
、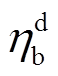 分别为储能电池充电、放电效率;
分别为储能电池充电、放电效率;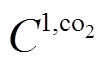 、
、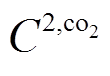 为电网购电、燃气轮机发电单位碳排放;
为电网购电、燃气轮机发电单位碳排放;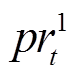 、
、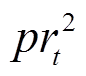 、
、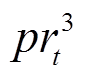 、
、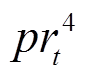 、
、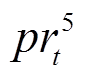 分别为
分别为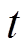 时段电网电价、失负荷惩罚、天然气价格、碳排放成本和余电上网单价;
时段电网电价、失负荷惩罚、天然气价格、碳排放成本和余电上网单价;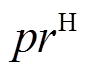 、
、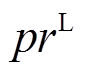 分别为电网峰时电价、低谷电价。
分别为电网峰时电价、低谷电价。
1)电能平衡约束
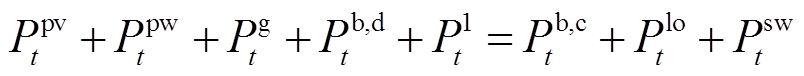 (13)
(13)
式中,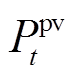 、
、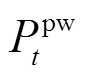 、
、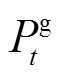 、
、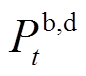 分别为
分别为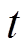 时段系统风、光发电机组、燃气轮机和储能电池出力功率;
时段系统风、光发电机组、燃气轮机和储能电池出力功率;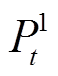 为
为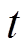 时段系统购电功率;
时段系统购电功率;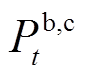 、
、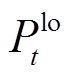 、
、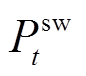 分别为
分别为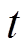 时段电池充电功率、居民电负荷功率和余电上网功率。
时段电池充电功率、居民电负荷功率和余电上网功率。
2)热能平衡约束
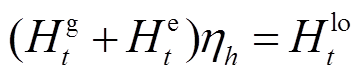 (14)
(14)
式中,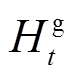 、
、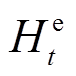 分别为
分别为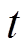 时段燃气轮机、电加热装置产热量;
时段燃气轮机、电加热装置产热量; 为供热管网运行效率;
为供热管网运行效率;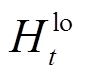 为
为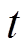 时段系统热负荷需求量。
时段系统热负荷需求量。
3)储能电池充放电约束
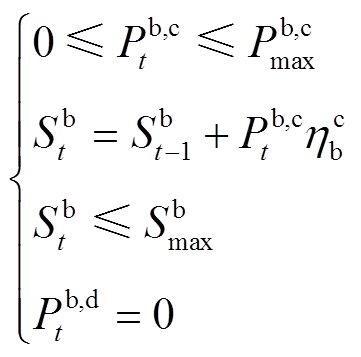 (15)
(15)
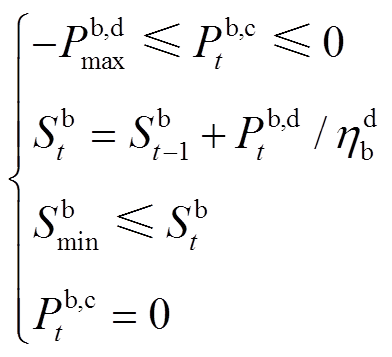 (16)
(16)
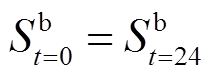 (17)
(17)
式中,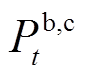 为
为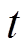 时段电池充电功率;
时段电池充电功率;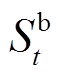 为
为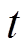 时段储能电池能量;
时段储能电池能量;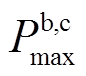 、
、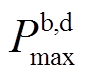 分别为储能电池充、放电最大功率;
分别为储能电池充、放电最大功率;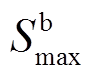 、
、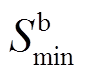 分别为储能电池充、放电最大深度。
分别为储能电池充、放电最大深度。
4)燃气轮机约束
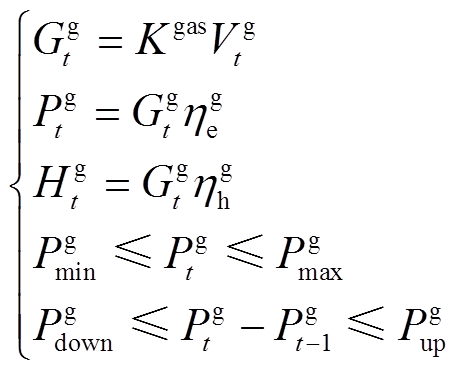 (18)
(18)
式中,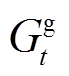 为
为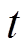 时段燃气轮机天然气燃烧后总功率;
时段燃气轮机天然气燃烧后总功率;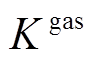 、
、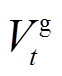 分别为天然气单位热值、
分别为天然气单位热值、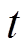 时段天然气进气量;
时段天然气进气量;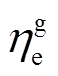 、
、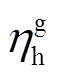 分别为燃气轮机发电、产热功率;
分别为燃气轮机发电、产热功率; 、
、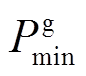 分别为燃气轮机电功率输出上、下限;
分别为燃气轮机电功率输出上、下限;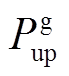 、
、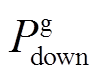 分别为燃气轮机输出电功率爬坡率上、下限。
分别为燃气轮机输出电功率爬坡率上、下限。
本文以某智慧社区数据为例,将本文构建的OCB-VPP与传统VPP在系统运行成本、新能源消纳量、碳排放量及调度速度等方面进行对比分析。VPP由该社区内风、光发电机组、居民电/热负荷、储能电池、燃气轮机、电加热装置等辅助设备构成,上述设备均通过自身的控制计算机加入OCB系统,成为多个独立节点,共同参与调度优化的计算任务,并接受OCB系统的控制。在四个季节的典型日内,该社区风、光发电机组出力和居民热、电负荷曲线如图6所示。
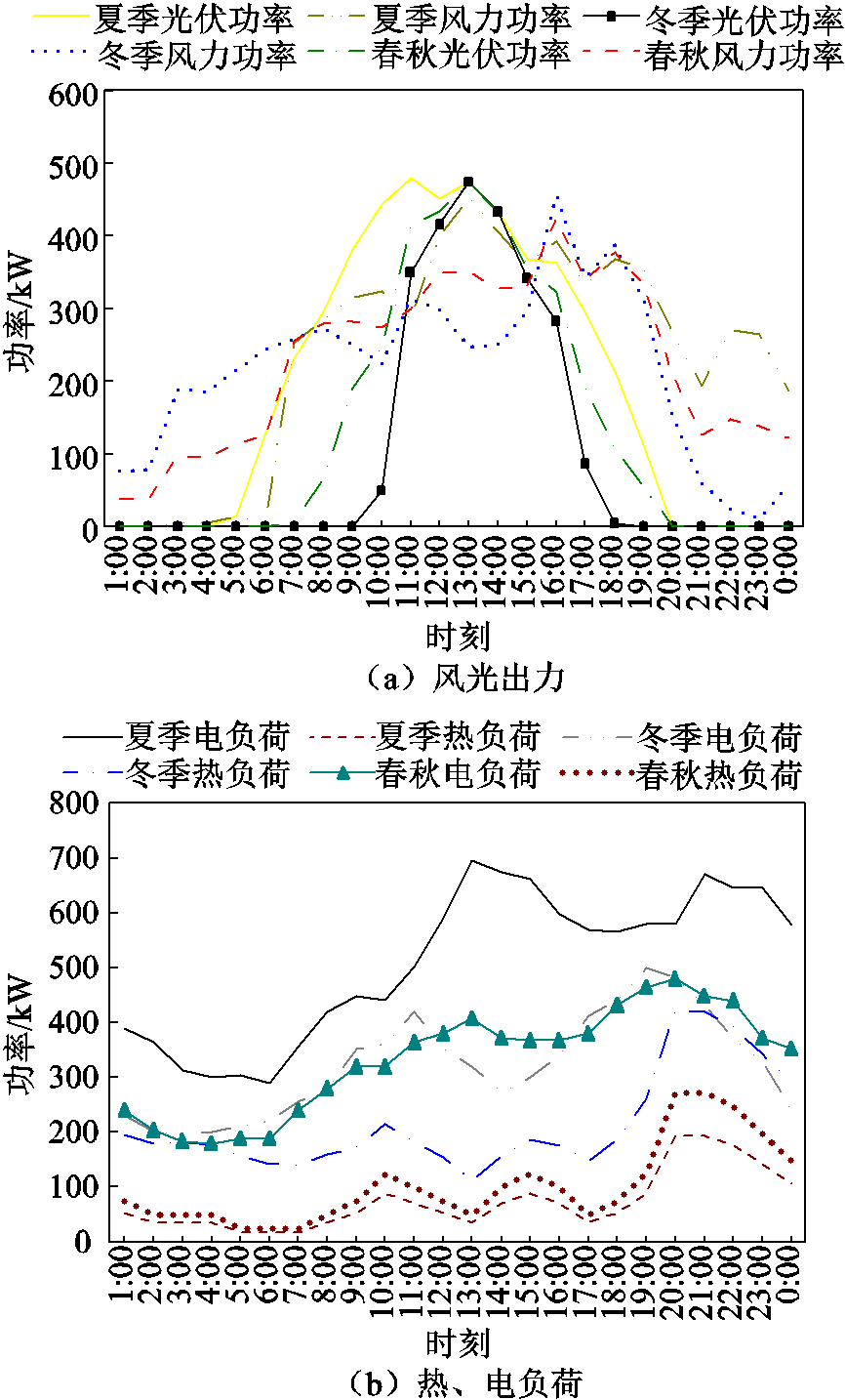
图6 负荷与风光出力曲线
Fig.6 Load, wind power and photovoltaic power output curve
社区内各设备参数见表1。设备参数参考自文献[21-23],并根据当前最新进展进行调整。
表1 设备参数
Tab.1 Equipment parameter
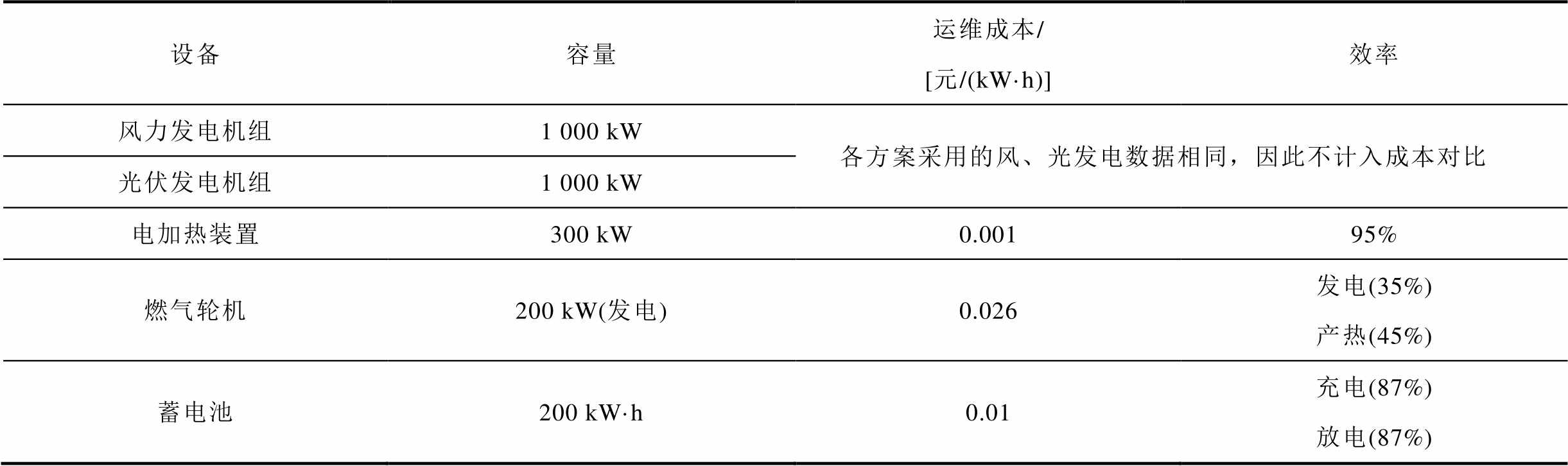
设备容量运维成本/[元/(kW·h)]效率 风力发电机组1 000 kW各方案采用的风、光发电数据相同,因此不计入成本对比 光伏发电机组1 000 kW 电加热装置300 kW0.00195% 燃气轮机200 kW(发电)0.026发电(35%)产热(45%) 蓄电池200 kW·h0.01充电(87%)放电(87%)
为验证上述所提模型的有效性,本文设定两种方案进行对比分析。
方案1:VPP采用常规集中控制方式,VPP控制中心对所有发电、负荷单元进行单向通信和控制;调度优化计算过程也由控制中心单独进行。
方案2:采用本文构建的OCB-VPP模型,各单元之间可通过区块链双向安全通信;调度优化计算过程也采用本文提出的基于区块链的分布式优化算法进行。
仿真环境为Matlab R2019a,各方案计算机配置相同,均为CPU i5 8400,RAM 16 GB,方案2利用Matlab并行计算工具箱编写并模拟区块链网络(模拟OCB网络内各个节点共同参与优化计算)。在计算中需要使用的其他重要参数见表2[24-25]。
表2 其他重要参数
Tab.2 Other important parameters

参数数值 失负荷惩罚10倍实时电价 电网电能单位碳排放量/[kg/(kW·h)]0.81 天然气单位碳排放/(kg/m3)2.165 天然气单价/(元/m3)2.7 碳排放单价/(元/t)30 余电上网单价/[元/(kW·h)]0.4 分时电价/[元/(kW·h)]0.417(0:00—7:00)\ (23:00—24:00),0.894(8:00—22:00)
为验证本文改进的BD-PSO优化算法具有良好性能,设定方案1分别使用Lin-WPSO算法、光线寻优算法(Light Ray Optimization Algorithm, LRO)、鲸鱼优化算法(Whale Optimization Algorithm, WOA),方案2使用BD-PSO算法进行计算,对比分析四种算法在计算精度和速度方面的差异。算法参数设定为:惯性权重最大值和最小值分别为0.9、0.4,方案1和方案2中算法粒子种群个数及迭代次数经多次实验后发现,分别取400和1 000、90和1 000(方案1采用的Lin-WPSO算法易陷入局部最优,故增加其粒子种群数)时效果最佳,学习因子c1=c2=2.05。WOA算法种群数为400,迭代次数1 000,初始游动因子为2,螺旋系数为3;LRO初始步长取值为变量初始范围最大值,步长更新系数为0.986,试探方向点为0.4个步长,迭代次数1 000。寻优变量为燃气轮机发电功率、向电网购电功率、电池充、放电功率、电加热功率。
以上述社区在夏季典型日下运行数据为背景,四种算法各求解10次,取平均值后结果见表3。
表3 算法性能
Tab.3 Algorithm performance

参数BD-PSO算法Lin-WPSO算法WOA算法LRO算法 最优值收敛次数/次927883875614 计算时间/s31.5467.1958.6236.93 单日运行成本/元-1 974.36-2 325.94-2 198.56-2 479.01
从表3中可以看出,在计算速度和计算精度上本文改进的BD-PSO优化算法较其余三种算法均具有明显优势。BD-PSO优化算法由于采用了分布式计算,计算时间大幅减少,相比Lin-WPSO、WOA、LRO算法分别下降了53.06%、46.20%、14.60%,单日运行成本分别减少了351.58元、224.20元、504.65元,计算精度分别提高了15.12%、10.19%、20.36%。可以发现,虽然Lin-WPSO、WOA、LRO算法的最优值迭代次数更少,但其最优值却远不如BD-PSO算法,究其原因是因为其过早陷入了局部最优。
两算法迭代结果对比如图7所示,Lin-WPSO、WOA、LRO算法在前期迭代速度较快。其中LRO算法在70次之前始终处于领先位置,但之后则基本停止了最优值的更新,这也说明了这三类算法全局搜索能力差,易陷入局部最优的特性,特别是LRO算法,虽然拥有较快的计算速度,但陷入局部最优的可能性是最大的。而BD-PSO算法虽然在前期的迭代速度较慢,但在中后段通过对众多节点产生的大量不同计算结果进行比较,仍保持了较强的寻优能力,最终超过了其余三种算法。
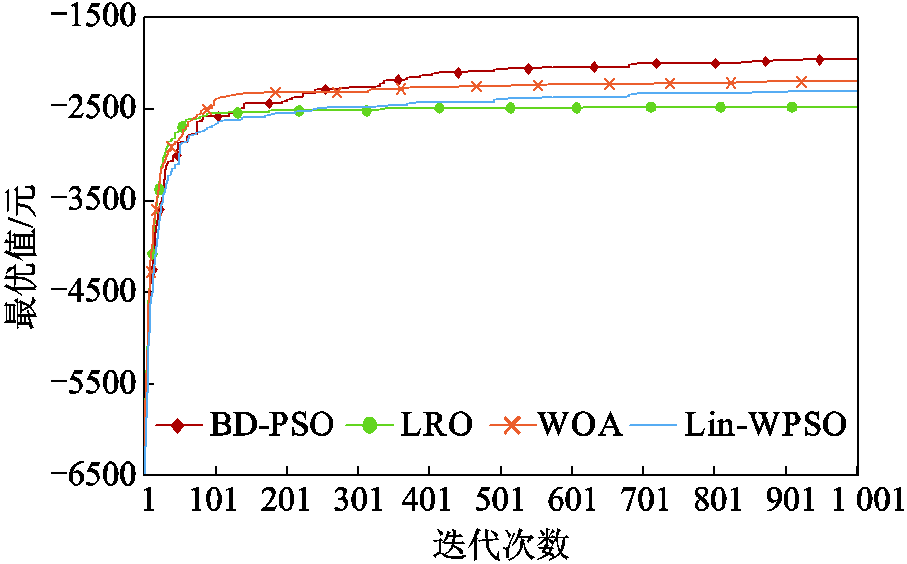
图7 两算法迭代结果对比
Fig.7 Comparison of the iterative results of the two algorithms
将本文设定的两种方案(方案1使用Lin-WPSO算法)在上述场景下进行单元出力调度优化计算,方案1系统各单元24 h内电、热能调度情况如图8所示。
从图8a中可以发现,蓄电池在该方案的三个场景中发挥的作用均不大(放电较少),在夏、冬和春秋各季节的典型日环境下,蓄电池放电总计分别为444.51 kW·h、422.01 kW·h、622.01 kW·h,仅占各自电负荷的3.69%、5.55%、7.93%。导致系统购电量增加,增加了系统运行费用,各季节电负荷购电量分别为3 927.63 kW·h、3 799.67 kW·h、2 525.69 kW·h,分别占各自电负荷的32.65%、49.93%、32.20%。其原因在于,一般VPP在总体控制方式下难以对多设备联合运行进行良好的优化,各自运行状态难以达到最优,使蓄电池没有起到最大程度的削峰填谷作用。
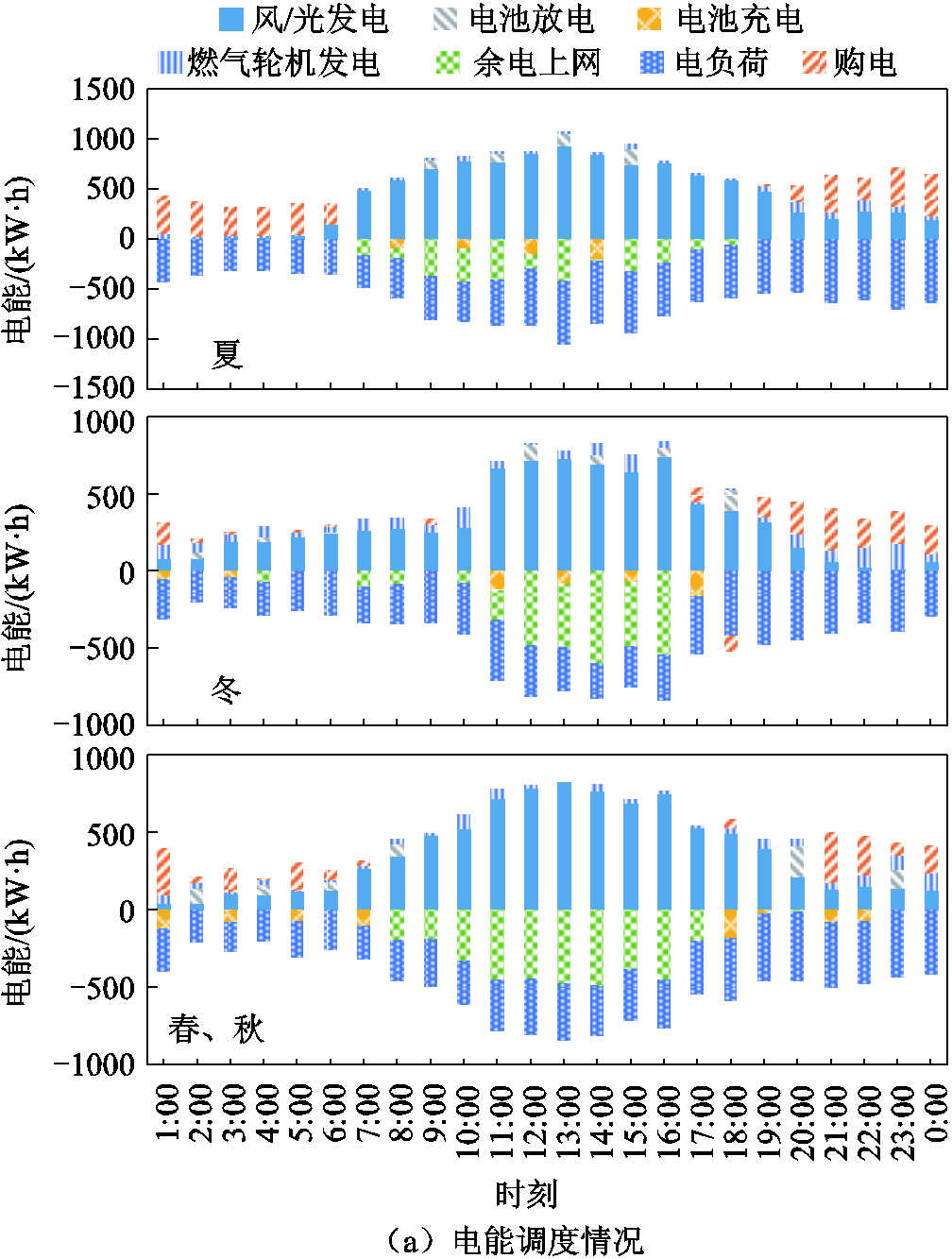
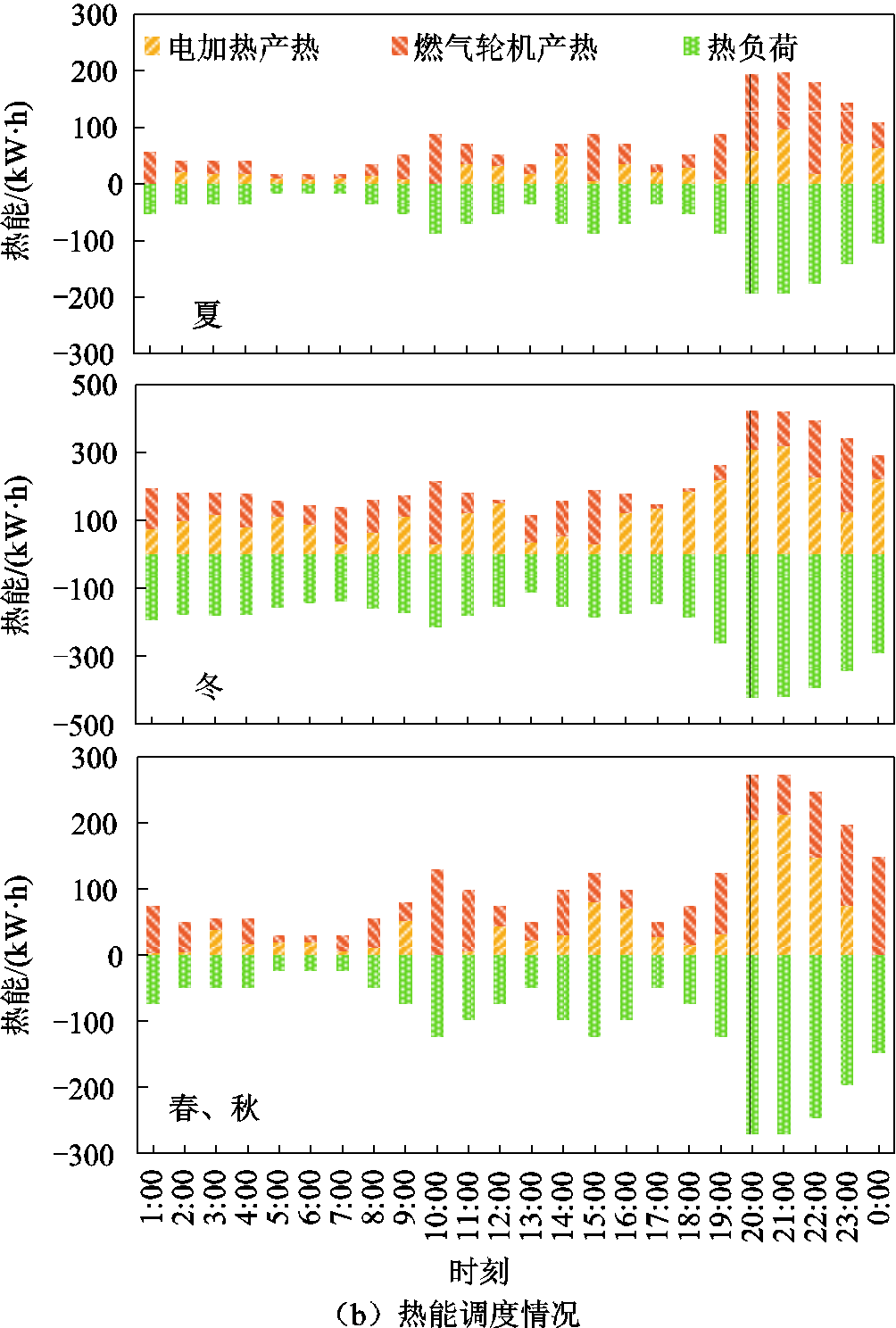
图8 方案1系统各单元调度情况
Fig.8 The scheduling situation of each unit of the system in scheme one
同时,从图8b可以发现蓄电池放电的减少也使燃气轮机的运行状态更加活跃,增加了天然气费用。燃气轮机在夏、冬、春秋各季节下的发电量分别占电负荷的6.98%、20.46%、12.98%;产热量分别占热负荷的65.21%、41.45%、56.47%,燃气轮机产热量超出负荷需求部分分别为33.26 kW·h、12.86 kW·h、44.09 kW·h,燃气轮机高强度运行在其经济效益极差的时段,造成了资源的浪费和运行成本升高。
图9为方案2系统各单元调度情况,得益于OCB-VPP的强大优化能力,各设备运行状态更为合理。从图9a中可以发现,蓄电池在该方案的三个场景中放电量明显增加,在夏、冬和春秋各季节的典型日环境下,蓄电池放电总计分别为607.47 kW·h、507.74 kW·h、729.17 kW·h,占各自电负荷比例相较方案1分别上升1.36%、1.12%、1.36%。使系统各季节电负荷购电量减少,较方案1分别下降了635.44 kW·h、659.04 kW·h、709.72 kW·h。
同时,燃气轮机在各季节下的发电量占电负荷比例较方案1分别下降了0.31%、2.05%、0.81%;产热量占热负荷比例较方案1分别下降了-19.5%、2.95%、3.52%,燃气轮机产热量超出负荷需求部分分别为4.35 kW·h、0 kW·h、12.36 kW·h,较方案1下降了86.92%、100%、71.97%,燃气轮机运行状态下降,同时运行集中在系统热、电负荷缺口较大时段,更有利于发挥其最大经济效益。
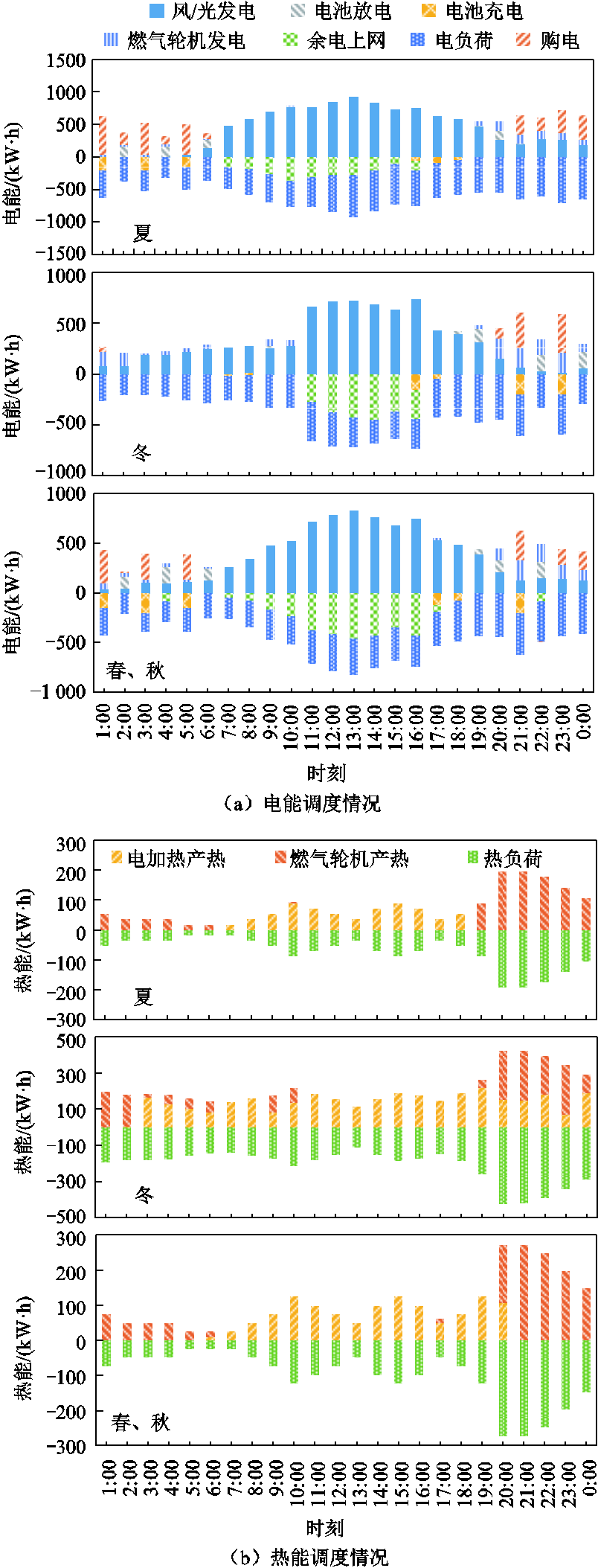
图9 方案2系统各单元调度情况
Fig.9 The scheduling situation of each unit of the system in scheme two
两种方案在各季节典型日内风、光电能消纳情况如图10所示。
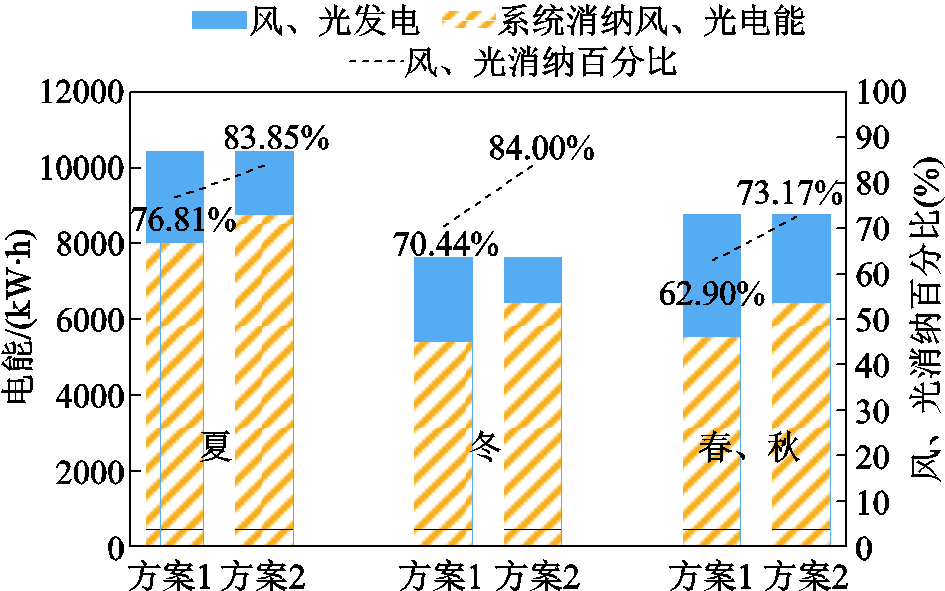
图10 两方案风、光出力剩余电能消纳情况
Fig.10 Energy consumption of wind and photovoltaic power generation in the two scenarios
由图10可知,方案2相比方案1,夏、冬和春秋季节系统消纳的风、光电能均有所上升。分析其原因在于,方案2的OCB-VPP得益于系统架构和优化算法的优越性,使其能充分利用各设备的调度能力,精确匹配供、给需求,在满足负荷与安全要求的基础上,增加高经济效益设备的使用率,减少低经济效益设备的运行,从4.2节中对燃气轮机和蓄电池运行情况的分析可以证明。
方案2对于蓄电池和燃气轮机的积极和精确使用,使系统购电量大幅减少,各个季节购电量较方案1总共减少19.55%,有利于提高风、光电能的利用水平。总体来看,方案1各季节消纳的风、光电能百分比分别为76.81%、70.44%、62.90%,方案2在方案1基础上分别提高了7.04%、13.56%、10.27%,充分说明了OCB-VPP在促进可再生能源消纳方面的优势。
两方案在夏、冬和春秋各季节典型日下系统运行费用见表4。由表4可知,方案2与方案1相比,系统在夏、冬、春秋各季节典型日内的运行成本分别下降了15.11%、9.20%、19.26%,充分体现了OCB-VPP在提高系统经济性上相比传统VPP具有显著优势。
从表4中可以发现,方案2在系统运行成本上具有优势的原因,主要是OCB-VPP凭借其较强的优化能力,可以精准匹配出力与负荷需求,从而使购电费用、失负荷惩罚费用大幅减少,相比方案1总计分别下降了19.55%、73.91%。同时精准匹配使方案2的风、光电能消纳水平提高,系统使用了更多的低成本电能,减少了额外购电带来的不必要浪费,使运行成本进一步下降。
表4 系统运行费用
Tab.4 System operation cost(单位:元)

参数方案1方案2 总运行成本夏-2 307.93-1 959.24 冬-3 649.51-3 313.90 春、秋-1 792.49-1 447.18 购电成本夏-2 112.94-1 658.16 冬-2 711.59-2 256.37 春、秋-1 671.87-1 191.36 余电上网收益夏967.71674.18 冬903.27488.80 春、秋1 301.73941.51 天然气成本夏-777.06-741.84 冬-1 440.23-1 295.94 春、秋-942.03-912.29 碳排放成本夏-148.28-126.74 冬-162.09-136.83 春、秋-93.44-93.44 设备运维成本夏-68.55-67.74 冬-123.89-113.56 春、秋-83.98-81.11 失负荷惩罚夏-168.80-38.94 冬-114.990 春、秋-289.02-110.49
同时,方案2天然气费用与碳排放成本也略有减少,在减少系统成本的同时,也对环境更加友好。
在本文构建的两个方案中,均包含了燃气轮机,燃气轮机运行时燃烧天然气,生成的副产物包括水和二氧化碳。同时,在不计算设备在生产阶段产生的二氧化碳排放前提下,两个方案中的碳排放还包括向电网购电产生的等效碳排放,各方案碳排放计算结果如图11所示。
由图11可知,方案2相比方案1在各个季节典型日的碳排放量均有所下降。方案1在夏、冬、春秋季节典型日内累计碳排放量分别为3 707.11 kg、4 052.14 kg、2 683.15 kg,方案2在方案1的基础上碳排放量分别降低了14.58%、15.58%、12.94%。
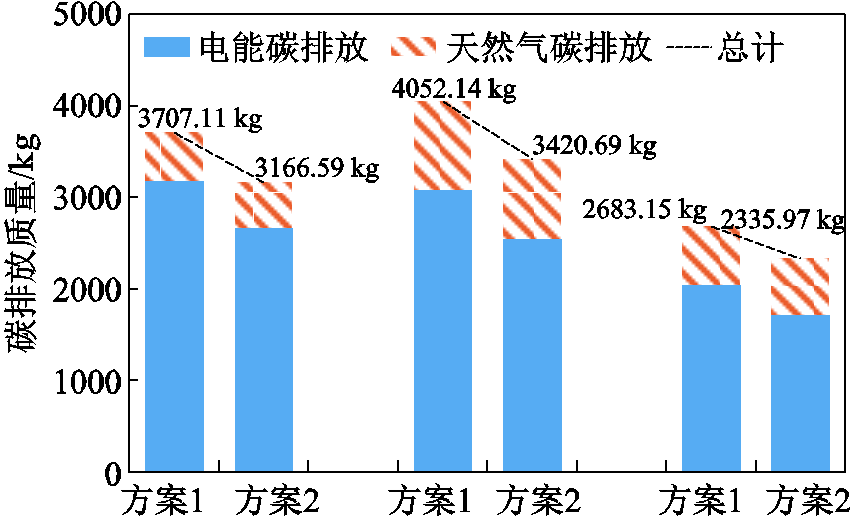
图11 两方案系统碳排放量
Fig.11 Carbon emissions of the two options
其中,夏、冬、春秋季节典型日内方案1的天然气碳排放和电能碳排放分别为525.73 kg、3 181.38 kg,974.41 kg、3 077.73 kg,637.34 kg、2 045.81 kg;方案2在三个季节内的天然气碳排放和电能碳排放分别下降了为4.53%、16.18%,10.02%、17.34%,3.16%、15.99%。可以看出碳排放量的降低大部分来自于电能碳排放的降低,天然气碳排放的降低幅度较电能更小,这与4.2节中对于购电量和蓄电池与燃气轮机的运行情况分析也是一致的。
总体来看,由于OCB-VPP架构和BD-PSO算法带来的效率提升,使其在优化计算的精确性上有所提高,能够更好地匹配各个发电设备和负荷需求,降低购电量和燃气轮机运行状态,因此使方案2在各个季节的总碳排放量均低于方案1。所以本文提出的OCB-VPP相比传统VPP在减少碳排量上具有一定优势。
本文将改进后的区块链技术应用于VPP,以期解决VPP信息安全和调度运行效率低下导致的系统经济效益下降问题。首先对粒子群优化算法进行改进,提出了BD-PSO优化算法和POCW共识算法,以适应VPP分布式的特点以及在调度效率方面的要求;其次结合上述算法特点,对传统区块链进行改进,形成了适用于VPP的OCB区块链系统;最后根据该算法与区块链系统提出了基于OCB的OCB-VPP系统模型,并提出相应的调度策略。通过对比分析得出以下结论:
1)本文改进的BD-PSO优化算法对比Lin-WPSO、WOA、LRO算法在计算速度和计算精度上均具有显著优势。BD-PSO算法在Lin-WPSO算法的基础上,产生了更多的计算结果,在更大的范围内进行了比较,优化了原算法易陷入局部最优的缺点,在计算速度和计算精度上分别提高了53.06%、15.12%。
2)OCB-VPP系统对比传统VPP系统,得益于系统架构和算法性能带来的提升,在调度的效率和精确性上具有优势,使系统的运行成本显著降低。各季节典型日成本总计减少13.29%,碳排放量总计降低14.55%,系统风/光消纳量总计提高9.95%,系统经济效益和能源利用率得到了明显提升。
本文仅考虑了OCB-VPP在电网调度背景下的运行情况,但其如何加入电力市场,提供现货、期货以及调峰、调频等辅助方面的服务,还需要对系统架构进一步改进,并提出相应的调度策略;同时在实际的应用场景下,如何建立对应的区块链平台,并与用户设备对接,有待今后进一步研究。
参考文献
[1] 李翔宇, 赵冬梅. 基于模糊-概率策略实时反馈的虚拟电厂多时间尺度优化调度[J]. 电工技术学报, 2021, 36(7): 1446-1455. Li Xiangyu, Zhao Dongmei. Research on multi-time scale optimal scheduling of virtual power plant based on real-time feedback of fuzzy-probability strategy[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1446-1455.
[2] 麻秀范, 余思雨, 朱思嘉, 等. 基于多因素改进Shapley的虚拟电厂利润分配[J]. 电工技术学报, 2020, 35(S2): 585-595. Ma Xiufan, Yu Siyu, Zhu Sijia, et al. Profit allocation to virtual power plant members based on improved multifactor dhapley value method[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 585-595.
[3] 赵昊天, 王彬, 潘昭光, 等. 支撑云-群-端协同调度的多能园区虚拟电厂:研发与应用[J]. 电力系统自动化, 2021, 45(5): 111-121. Zhao Haotian, Wang Bin, Pan Zhaoguang, et al. Research and application of park-level multi-energy virtual power plants supporting cloud-cluster-end multi-level synergetic dispatch[J]. Automation of Electric Power Systems, 2021, 45(5): 111-121.
[4] 周玮, 蓝嘉豪, 麦瑞坤, 等. 无线充电电动汽车V2G模式下光储直流微电网能量管理策略[J]. 电工技术学报, 2022, 37(1): 82-91. Zhou Wei, Lan Jiahao, Mai Ruikun, et al. Research on power management strategy of DC microgrid with photovoltaic, energy storage and EV-wireless power transfer in V2G mode[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 82-91.
[5] 郑重, 苗世洪, 李超, 等. 面向微型能源互联网接入的交直流配电网协同优化调度策略[J]. 电工技术学报, 2022, 37(1): 192-207. Zheng Zhong, Miao Shihong, Li Chao, et al. Coordinated optimal dispatching strategy of AC/DC distribution network for the integration of micro energy Internet[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 192-207.
[6] 陈张宇, 刘东, 刘浩文, 等. 基于精细化需求响应的虚拟电厂优化调度[J]. 电网技术, 2021, 45(7): 2542-2550. Chen Zhangyu, Liu Dong, Liu Haowen, et al. Optimal dispatching of virtual power plant based on refined demand response[J]. Power System Technology, 2021, 45(7): 2542-2550.
[7] 赵东元, 胡楠, 傅靖, 等. 提升新能源电力系统灵活性的中国实践及发展路径研究[J]. 电力系统保护与控制, 2020, 48(24): 1-8. Zhao Dongyuan, Hu Nan, Fu Jing, et al. Research on the practice and road map of enhancing the flexibility of a new generation power system in China[J]. Power System Protection and Control, 2020, 48(24): 1-8.
[8] 佘维, 胡跃, 杨晓宇, 等. 基于能源区块链网络的虚拟电厂运行与调度模型[J]. 中国电机工程学报, 2017, 37(13): 3729-3736. She Wei, Hu Yue, Yang Xiaoyu, et al. Virtual power plant operation and scheduling model based on energy blockchain network[J]. Proceedings of the CSEE, 2017, 37(13): 3729-3736.
[9] 周国亮, 李刚. 区块链背景下虚拟电厂分布式调度策略研究[J]. 计算机工程与应用, 2020, 56(15): 268-273. Zhou Guoliang, Li Gang. Research on distributed scheduling strategy of virtual power plant considering blockchain[J]. Computer Engineering and Applications, 2020, 56(15): 268-273.
[10] 任建文, 张青青. 基于能源区块链的虚拟电厂两阶段鲁棒优化调度[J]. 电力自动化设备, 2020, 40(8): 23-33. Ren Jianwen, Zhang Qingqing. Two-stage robust optimal scheduling of virtual power plant based on energy blockchain[J]. Electric Power Automation Equipment, 2020, 40(8): 23-33.
[11] Lu Jing, Wu Shihong, Cheng Hanlei, et al. Smart contract for distributed energy trading in virtual power plants based on blockchain[J]. Computational Intelligence, 2021, 37(3): 1445-1455.
[12] 周洪益, 余爽, 柏晶晶, 等. 基于区块链技术的虚拟电厂交易管理模式研究[J]. 电力需求侧管理, 2021, 23(1): 72-76. Zhou Hongyi, Yu Shuang, Bai Jingjing, et al. Research on trading pattern of virtual power plant based on blockchain technology[J]. Power Demand Side Management, 2021, 23(1): 72-76.
[13] Kavousi-Fard A, Almutairib A, Al-Sumaitic A, et al. An effective secured peer-to-peer energy market based on blockchain architecture for the interconnected microgrid and smart grid[J]. International Journal of Electrical Power & Energy Systems, 2021, 132: 107171.
[14] Regueiro C, Seco I, Diego S, et al. Privacy-enhancing distributed protocol for data aggregation based on blockchain and homomorphic encryption[J]. Information Processing & Management, 2021, 58(6): 102745.
[15] 黄伟, 左欣雅, 刘弋铭. 基于多区块链结构的综合能源系统调度构架[J]. 电力系统自动化, 2021, 45(23): 12-20. Huang Wei, Zuo Xinya, Liu Yiming. Multiple blockchains based dispatching architecture for integrated energy system[J]. Automation of Electric Power Systems, 2021, 45(23): 12-20.
[16] 邵奇峰, 金澈清, 张召, 等. 区块链技术: 架构及进展[J]. 计算机学报, 2018, 41(5): 969-988. Shao Qifeng, Jin Cheqing, Zhang Zhao, et al. Blockchain: architecture and research progress[J]. Chinese Journal of Computers, 2018, 41(5): 969-988.
[17] Dzobo O, Malila B, Sithole L. Proposed framework for blockchain technology in a decentralised energy network[J]. Protection and Control of Modern Power Systems, 2021, 6(1): 31.
[18] Wang Lei, Ma Yichao, Zhu Liuzhu, et al. Design of integrated energy market cloud service platform based on blockchain smart contract[J]. International Journal of Electrical Power & Energy Systems, 2022, 135: 107515.
[19] Li Wei, Wang Lixia, Wang Dawei. Power energy supply and demand scheduling method based on blockchain technology[J]. Journal of Physics: Conference Series, 2021, 1994(1): 012001.
[20] 杨锡运, 陶准, 黄欣欣, 等. 基于异构能源区块链的综合能源系统交易模型[J]. 电力自动化设备, 2021, 41(9): 224-231. Yang Xiyun, Tao Zhun, Huang Xinxin, et al. Transaction model of integrated energy system based on heterogeneous energy blockchain[J]. Electric Power Automation Equipment, 2021, 41(9): 224-231.
[21] 任洪波, 吴琼, 任建兴. 基于需求侧视角的天然气分布式热电联产系统节能效益研究[J]. 中国电机工程学报, 2015, 35(17): 4430-4438. Ren Hongbo, Wu Qiong, Ren Jianxing. Energy performance assessment of combined heat and power system based on demand-side viewpoint[J]. Proceedings of the CSEE, 2015, 35(17): 4430-4438.
[22] 熊宇峰, 司杨, 郑天文, 等. 考虑热电综合利用的光伏储氢独立供能系统容量优化配置[J]. 中国电力, 2020, 53(10): 66-73. Xiong Yufeng, Si Yang, Zheng Tianwen, et al. Optimal capacity configuration of solar-hydrogen independent power-supply system considering electricity-heat comprehensive utilization[J]. Electric Power, 2020, 53(10): 66-73.
[23] 方仍存, 杨洁, 周奎等. 计及全生命周期碳成本的园区综合能源系统优化规划方法[J]. 中国电力, 2022, 55(12): 135-146. Fang Rengcun, Yang Jie, Zhou Kui, et al. Optimal planning method of IES considering carbon cost from the perspective of the whole life cycle[J]. Electric Power, 2022, 55(12): 135-146.
[24] 孙益文. 低碳经济下我国天然气产业投资战略研究[D]. 东营: 中国石油大学(华东), 2016.
[25] 李嘉琪, 李柏姝. 面向生命周期的燃料电池低碳优化设计[J]. 时代汽车, 2020(21): 124-125. Li Jiaqi, Li Boshu. Low-carbon fuel cell optimization design for life cycle[J]. Auto Time, 2020(21): 124-125.
Abstract At present, there are four problems in the actual operation of the virtual power plant(VPP): (1) The centralized, centralized-decentralized and fully decentralized control modes of the VPP currently used cannot achieve common optimization in flexibility, compatibility and scalability, which will affect the overall operation effect of the VPP. (2) Because the VPP uses the network for two-way communication, the power generation and load data of each unit in the system are vulnerable to malicious attacks and tampering by hackers, which makes the operation process of the VPP wrong, resulting in increased system costs or equipment failures. (3) Wind, solar and other renewable energy power generation has uncertainty and randomness. If the VPP cannot quickly adjust the operation state when the power generation situation changes dramatically, it will lead to the increase of penalty costs and affect the overall benefits of the system. (4) The distributed characteristics of VPP make it difficult to integrate and coordinate the internal units. In the existing research, intelligent optimization algorithm is usually used to calculate the scheduling strategy of VPP, but such algorithm does not adapt to the distributed characteristics of VPP, and there are still deficiencies in calculation time and accuracy, which will lead to the rise of system operation cost and the decline of operation efficiency. To solve these problems, this paper proposes a VPP model and scheduling strategy based on optimized computing block-chain system to improve the information security level and operation efficiency of VPP.
Firstly, the basic structure of the block-chain system and the feasibility of the combination of block-chain technology and VPP are studied, and then on this basis, block-chain based distributed particle swarm optimization algorithm (BD-PSO) and proof of optimization calculation workload (POCW) consensus algorithm suitable for VPP operation environment are proposed, improve the computing speed of scheduling optimization problems. Thirdly, the improved BD-PSO algorithm and POCW algorithm are used to improve the traditional block-chain, and an optimized computational block-chains (OCB) system is proposed to improve the adaptability of the combination of block-chain and VPP and improve the operation efficiency of the system. Finally, the OCB virtual power plant (OCB-VPP) structure model and scheduling strategy are established based on OCB. Through the actual data of a certain region, the differences between OCB-VPP and traditional VPP in coping with the fluctuation of renewable energy output, economic benefits of the system and carbon emissions are compared and analyzed. The advantages of BD-PSO algorithm in calculation speed and accuracy are analyzed, and the effectiveness and economy of the proposed model are verified.
The simulation results of actual data in a certain area show that: (1) BD-PSO algorithm produces more calculation results based on Lin-WPSO algorithm, which are compared in a larger range, optimizes the disadvantage that the Lin-WPSO algorithm is easy to fall into local optimization, and improves the calculation speed and accuracy by 50.19% and 9.86% respectively. (2) Compared with the traditional VPP system, OCB-VPP system benefits from the improvement of system architecture and algorithm performance, and has advantages in scheduling efficiency and accuracy, which significantly reduces the operation cost of the system. The typical daily cost of each season is reduced by 13.29%, the carbon emission is reduced by 14.53%, the wind / light consumption of the system is increased by 9.95%, and the economic benefits and energy utilization of the system have been significantly improved.
Finally, the following conclusions are drawn through analysis: (1) compared with Lin-wPSO, WOA and LRO algorithms, the improved BD-PSO optimization algorithm in this paper has significant advantages in calculation speed and accuracy. Therefore, BD-PSO optimization algorithm is very suitable for the VPP environment with complex and changeable operating conditions. (2) OCB-VPP structure is more suitable for VPP, which can improve the information security level and operation efficiency of VPP. (3) Compared with traditional centralized VPP, OCB-VPP structure can reduce system operation costs, reduce carbon emissions and improve renewable energy utilization.
keywords:Virtual power plant, block-chain, distributed, consensus algorithm, particle swarm optimization algorithm
DOI:10.19595/j.cnki.1000-6753.tces.220881
中图分类号:TM732
国家自然科学基金(51767023)、新疆维吾尔自治区研究生科研创新计划(XJ2022G041)和天山英才培养计划(2022TSYCLJ0019)资助项目。
收稿日期 2022-05-23
改稿日期 2022-07-31
刘雨佳 男,1998年生,硕士研究生,研究方向电力系统控制与优化调度。E-mail:1104680459@qq.com
樊艳芳 女,1971年生,教授,博士生导师,研究方向为新能源并网技术及电力系统保护与控制。E-mail:fyf3985@xju.edu.cn(通信作者)
(编辑 赫蕾)