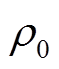 和相关系数矩阵
和相关系数矩阵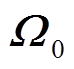 ,有
,有摘要 针对风电出力预测误差对区域间可用输电能力(ATC)评估的影响,提出一种计及风电出力相关性和条件风险价值(CVaR)的电力系统区域间ATC概率评估方法。首先,通过基于历史风电出力数据的相关系数矩阵和Copula函数,构建计及风电场出力空间相关性的风电出力预测误差概率模型;接着,基于获得的计及风电出力空间相关性的风电出力预测误差修正风电场出力预测值;然后,提出一种计及风电出力相关性和CVaR的ATC概率评估双层优化模型,下层模型以基态下发电成本和风险费用最小为目标,上层模型以极大化区域间ATC为目标,通过基态下和极限状态下机组的出力作为上下层模型间的交互信息;在此基础上,利用Karush-Kuhn-Tucker(KKT)最优条件,对下层模型进行转换,将双层优化模型转换为均衡约束的数学规划(MPEC)模型;进一步,将MPEC模型转换为混合整数二阶锥规划问题,进而实现概率ATC的求解;最后,通过PJM-5节点测试系统和吉林西部电网进行算例分析,结果验证了所提方法的可行性和有效性。
关键词:可用输电能力 风电出力相关性 条件风险价值 双层优化模型
大规模开发利用风、光等新能源,是加快我国实现能源结构低碳清洁转型,实现“碳达峰、碳中和”战略目标的重要手段。中国国家可再生能源中心在《中国可再生能源展望》中提到“预计到2050年,中国新能源发电占比将达70%以上”[1]。大规模新能源并网发电必将成为未来电力系统的发展趋势和重要特征[2-3],但新能源出力的波动性和随机性对区域间可用输电能力(Available Transfer Capability, ATC)评估带来了新的挑战[4]。
目前,电力系统区域间ATC评估主要分为确定性求解方法和概率性求解方法。确定性ATC求解方法计算速度快、容易实现,主要方法包括重复潮流法[5]、连续潮流法[6]、最优潮流法[7]和灵敏度法[8]等。然而,确定性计算方法通常是在系统各运行条件确定的条件下计算区域间ATC,未考虑风电出力不确定性对区域间ATC的影响。
相对于确定性ATC评估方法,概率ATC评估方法可对风电出力等不确定因素进行量化分析,并通过数理统计的方法得到区域间ATC的概率分布和统计特征[9-10],其主要求解方法有:随机规划法[10]、蒙特卡洛模拟[4]、区间优化算法[11]等。文献[9]提出基于稀疏多项式混沌展开的概率ATC计算方法,研究风电出力不确定性对区域间ATC的影响;文献[10]采用随机规划法和扩展潮流相结合的方法,快速计算输电可靠性裕度,研究了风电功率随机波动对输电能力的影响;文献[11]为改善蒙特卡洛方法计算效率低的问题,利用区间优化方法对风电不确定性进行处理,该方法只需考虑不确定性变量的上下边界,不需要计算大量风电出力的样本,通过大M法和强对偶理论求解ATC的乐观解和悲观解,进而准确获得区域间ATC可能的范围。然而,同一地区相邻风电场间出力空间相关性会影响风电出力的预测准确度[12-14],间接影响区域间ATC的计算精度。为此,文献[12]计及随机变量间的相关性影响,采用拉丁超立方采样与Cholesky分解相结合,获得计及随机变量相关性的风电出力场景,以较少的采样场景得到较高的计算精度,提升了ATC的计算效率;文献[13]计及风电出力相关性对区域间ATC的影响,采用双层优化模型对ATC进行评估,并证明了不同风电出力相关系数、风电并网位置及负荷水平对ATC评估均存在影响;文献[14]建立了计及风电出力相关性的二阶锥动态随机最优潮流模型,从风电场出力相关性角度出发,研究降低风电出力不确定性对ATC计算结果影响的方法,提升了ATC的计算精度;文献[15]分析了风电场间出力预测误差的时空相关性对区域间ATC评估结果的影响,证实了区域间ATC会随风电出力相关系数的变化而变化。
上述文献研究了风电出力不确定性对区域间ATC的影响,并计及风电出力相关性,构建了符合实际风电场出力相关性的风电出力预测模型,减小了风电出力的预测误差,提升了ATC的计算精度。然而,在实际运行中,风电出力的不确定性,将会影响电力系统调度人员制定的最优发电计划,导致系统出力有可能偏离最优发电计划,产生额外的运行风险费用[16]。因此,在高渗透率风电汇集地区概率ATC评估过程中,不仅要考虑风电出力不确定性和相关性对区域间ATC评估的影响,同时也要考虑机组出力调整产生的风险费用对ATC的影响。
针对上述问题,本文将风电出力历史数据和Copula函数相结合,构建风电出力的相关性模型,避免因风电场间出力相关性估计不准而产生较大的风电出力预测误差,影响ATC的评估精度,同时引入条件风险价值CVaR(conditional value-at-risk)量化风电出力不确定性产生的风险费用,以期更准确、全面地评估区域间ATC。为此,首先通过历史风电出力数据的相关系数矩阵和Copula函数构建计及空间相关性的风电出力预测误差概率模型,借助满足实际风电场出力相关性的风电出力预测误差数据修正风电场出力预测值,进而将修正后的风电出力预测作为计算区域间ATC的输入;然后,提出计及风电出力相关性和CVaR的区域间ATC双层优化模型,其中,上层模型极大化区域间ATC,下层模型为现有输电协议(Existing Transfer Capability, ETC)计算模型,以最小化基态下的发电成本和风险费用为目标;在此基础上,根据下层模型的Karush-Kuhn-Tucker(KKT)条件将计及风电出力相关性和CVaR的概率ATC评估双层优化模型转换为均衡约束的数学规划(Mathematical Program With Equilibrium Constraints, MPEC)问题;进一步,将该MPEC模型转换为易求解的混合整数二阶锥规划问题,并调用Mosek求解器进行求解,得到不同风险水平及风电预测误差相关性的区域间概率ATC期望;最后,通过PJM-5节点测试系统和吉林西部电网对所提计及风电出力相关性和CVaR的概率ATC评估方法进行分析、验证。
为提升风电出力预测精度,本节首先通过历史风电出力数据计算各风电场间出力的相关系数,得到风电场间的相关系数矩阵;然后,通过风电场出力预测的概率分布和Copula函数构建计及空间相关性的风电出力预测误差概率模型;根据满足实际风电场出力相关性的风电出力预测误差数据和风电场出力预测值修正风电场的出力预测,进而将修正后的风电出力预测作为计算区域间ATC的输入。
为此,首先根据历史风电出力数据计算得到风电场间相关系数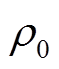 和相关系数矩阵
和相关系数矩阵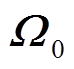 ,有
,有
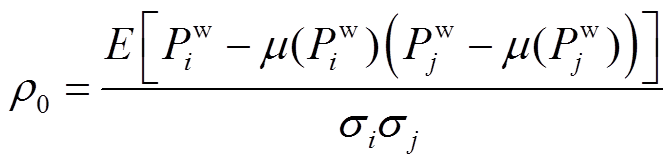 (1)
(1)
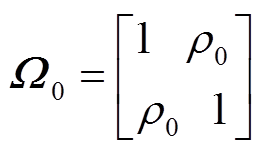 (2)
(2)
式中,E[·]为风电出力期望值;μ为风电出力平均值;Pw i和Pw j分别是第i个和第j个风电场出力的历史数据;σi和σj分别为第i个和第j个风电场出力的标准差。
风电出力预测误差可用不同概率分布方法进行描述。文献[9,13]分别采用Beta分布和Weibull分布处理风电出力预测误差,而文献[16-17]采用正态分布对预测误差进行描述。为获得符合实际风电场出力相关性的风电出力预测误差PTwi-Pwi,首先,假设风电出力预测误差服从均值为0、标准差为 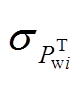 的正态分布,基于式(3)所示的风电场出力的概率分布函数,进行蒙特卡洛随机抽样,从而获得初始风电功率预测误差场景[16]。
的正态分布,基于式(3)所示的风电场出力的概率分布函数,进行蒙特卡洛随机抽样,从而获得初始风电功率预测误差场景[16]。
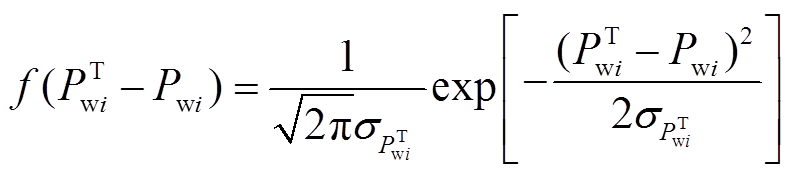 (3)
(3)
式中,Pwi为第i个风电场出力预测值;PTwi为第i个风电场出力实际值;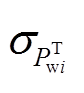 为标准差;f(PTwi-Pwi)为风电出力预测误差的概率分布。
为标准差;f(PTwi-Pwi)为风电出力预测误差的概率分布。
通过改变相邻两风电场出力概率分布函数中的标准差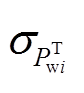 可获得不同初始风电出力预测的误差场景,然后根据式(1)和式(2)计算不同初始风电预测误差场景下风电场出力的相关系数矩阵Ω。对比Ω与
可获得不同初始风电出力预测的误差场景,然后根据式(1)和式(2)计算不同初始风电预测误差场景下风电场出力的相关系数矩阵Ω。对比Ω与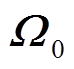 ,将Ω与
,将Ω与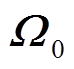 相近的风电场出力预测误差场景认为是符合实际风电场出力相关性的风电出力预测误差场景。
相近的风电场出力预测误差场景认为是符合实际风电场出力相关性的风电出力预测误差场景。
假设式(3)得到的风电出力预测误差场景的多元联合概率分布函数为H(·),则存在一个Copula函数C(f(ΔPw1), f(ΔPw2) , , f(ΔPwn))与风电出力预测误差的多元联合分布函数H(
, f(ΔPwn))与风电出力预测误差的多元联合分布函数H(![]() )对应。Copula函数的拟合优度指标即欧氏距离d,d值越小表明该Copula函数越贴近经验概率分布函数,可通过欧式距离d选取最优的Copula函数[18]。通过对比各类Copula函数的欧氏距离d,本文采用式(4)所示的t-Copula函数拟合满足实际风电场空间相关性的风电出力预测误差的多元概率分布。
)对应。Copula函数的拟合优度指标即欧氏距离d,d值越小表明该Copula函数越贴近经验概率分布函数,可通过欧式距离d选取最优的Copula函数[18]。通过对比各类Copula函数的欧氏距离d,本文采用式(4)所示的t-Copula函数拟合满足实际风电场空间相关性的风电出力预测误差的多元概率分布。
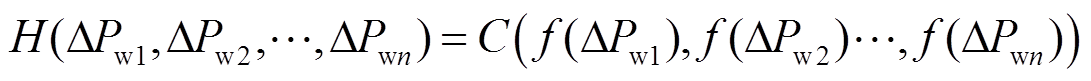 (4)
(4)
式中,H(![]() )为风电出力预测误差的联合分布函数;C(
)为风电出力预测误差的联合分布函数;C(![]() )为与H(
)为与H(![]() )对应的n元t-Copula函数;n为风电场的个数;ΔPwn为第n个风电场的风电出力预测误差,
)对应的n元t-Copula函数;n为风电场的个数;ΔPwn为第n个风电场的风电出力预测误差,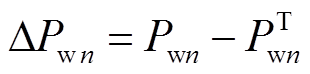 ;f(
;f(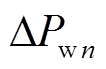 )为第n个风电场出力预测误差的概率分布。C(
)为第n个风电场出力预测误差的概率分布。C(![]() )具体形式如式(5)所示,式中相关参数可通过式(3)各风电场出力预测误差的概率分布f(ΔPw1), f(ΔPw2),
)具体形式如式(5)所示,式中相关参数可通过式(3)各风电场出力预测误差的概率分布f(ΔPw1), f(ΔPw2), , f(ΔPwn)计算得到。
, f(ΔPwn)计算得到。
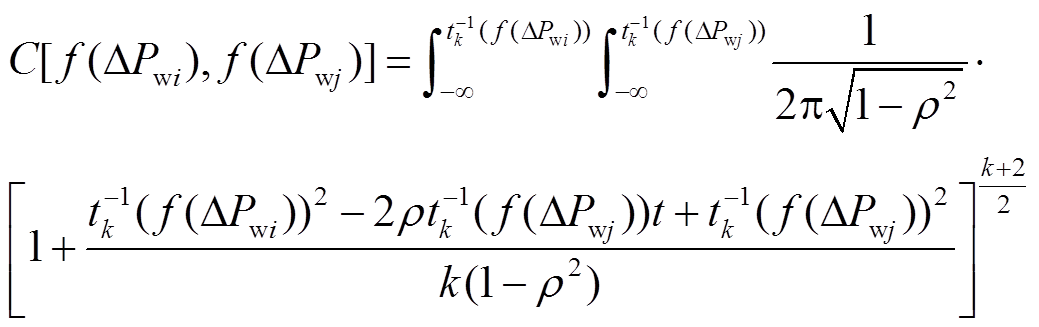 (5)
(5)
式中,f(ΔPwi)为第i个风电场出力预测误差的概率分布;ρ为两风电场的相关系数;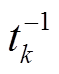 (∙)为自由度为k的一元t分布函数的反函数。
(∙)为自由度为k的一元t分布函数的反函数。
对式(5)的t-Copula函数进行随机抽样可得到风电出力预测误差场景及不同场景下风电出力预测误差的概率。进而,根据已知时间段内第s个场景下的风电出力预测值Pwi和出力预测误差ΔPswi得到修正后的风电场出力预测PT,swi,有
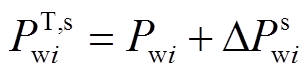 (6)
(6)
通过式(6)得到的修正后的风电场出力预测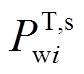 即为计及风电场间出力相关性的风电出力预测值。
即为计及风电场间出力相关性的风电出力预测值。
在评估区域间ATC时,计及同一地区临近风电场间出力的相关性,可提高风电场出力预测精度,降低风电出力不确定性对ATC评估精度的影响。但风电出力不确定性带来的系统运行风险同样对区域间ATC评估结果产生影响。为此,本文引入条件风险价值量化风电出力不确定性导致的风电出力误差,进而提出一种计及风电出力相关性和条件风险价值的概率ATC评估方法。
风电出力的不确定性[19]将导致运行人员需调整常规机组出力,使得系统偏离最优经济状态,产生额外的燃料费用和调整费用。为此,本文定义该部分费用为风电出力不确定性带来的系统运行风险费用,其表达式为
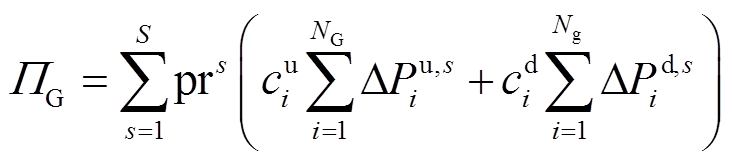 (7)
(7)
式中,ΠG为风险费用;ΔPu,s i为在第s个风电预测误差场景下第i台常规机组向上调整的出力;ΔPd,s i为在第s个风电预测误差场景下第i台常规机组向下调整的出力;cu i 为第i台常规机组爬坡成本;cd i为第i台常规机组滑坡成本;prs为第s个风电出力预测误差场景对应的概率;NG和Ng分别为每个场景下常规机组上调出力和下调出力的数量;S为场景总数。
为量化风险费用对区域间ATC的影响,本节进一步引入条件风险价值CVaR对风电功率预测误差产生的运行风险进行量化。对于不同的风电预测误差场景,发电成本整体呈现离散分布,在给定置信水平ε∈(0,1)下,发电成本超过风险价值(Value-at-Risk, VaR)的概率为(1-ε)×100%,CVaR可近似为具有较高发电成本的概率为(1-ε)×100%的场景集合对应的期望成本[20]。风电出力不确定性带来的系统运行风险费用VaR、CVaR为
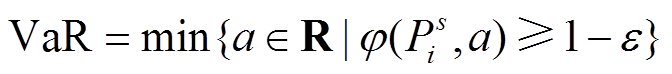 (8)
(8)
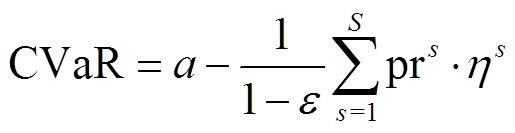 (9)
(9)
式中,Ps i为第s个风电出力预测误差场景下常规机组的有功出力;φ(Ps i, α)为风险费用ΠG不低于阈值α的概率;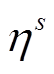 为场景s下调度总成本超出的值,其值为正数[16]。
为场景s下调度总成本超出的值,其值为正数[16]。
为量化风电出力不确定性对区域间ATC的影响,本文在概率ATC评估模型中计及风电出力不确定性带来的运行风险费用,引入CVaR对运行风险费用进行量化。为此,构建一种计及风电出力相关性和CVaR的概率ATC评估双层优化模型,上层模型以极大化区域间ATC为目标,下层模型以基态下发电成本和风险费用最小为目标。双层ATC评估模型中,通过基态下机组出力和极限状态下机组出力作为上下层模型间的交互信息。下层模型基于计及条件风险价值的ETC评估模型,确定基态下的发电机组出力Pi并传递给上层,进而对上层模型在极大化区域间ATC的过程中产生影响,同时将极限状态下的发电机出力P1 i传递给下层,对下层模型的爬坡约束产生影响。
2.2.1 上层模型
本文上层模型采用计及回路相角约束的二阶锥松弛交流潮流模型[21],该模型以极大化区域间概率ATC期望为目标,其目标函数为
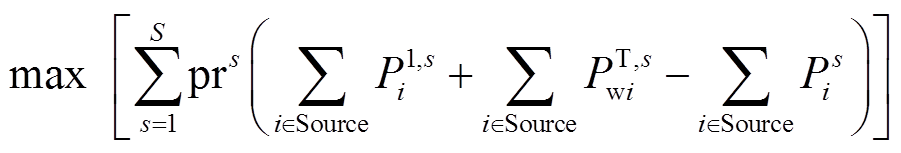 (10)
(10)
式中,Source为送电区域发电机节点的集合;P1,s i为场景s中位于节点i的常规机组极限状态下有功输出;Ps i为场景s下位于节点i的常规机组基态有功出力。
上层模型中除了目标函数外,还包括功率平衡约束、电压幅值约束、发电机有功和无功出力约束、线路热稳定约束等约束。
1)功率平衡约束
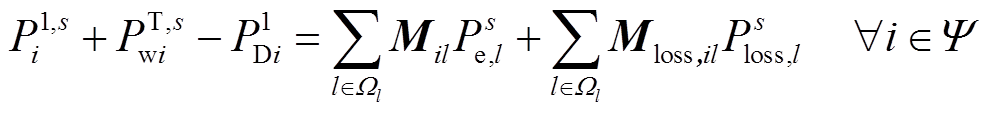 (11)
(11)
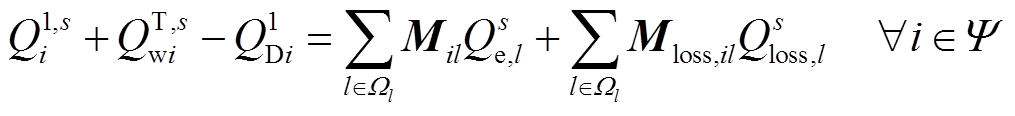 (12)
(12)
式中,Ψ为所有节点的集合;Ωl为线路集合;P1Di为极限状态下的负荷水平;QT,s wi为场景s下风电场的无功出力;Mil和Mloss,il分别为节点支路关联矩阵和节点支路网损关联矩阵,其中i、l分别表示矩阵的第i行和第l列;Psloss,l和Qs loss,l分别为场景s的线路有功、无功网损;Ps e,l、Qs e,l分别为场景s的各支路有功、无功潮流。
2)节点电压约束
电网节点电压约束包括电压降落方程、节点电压上下限约束和回路相角约束,具体表达式为
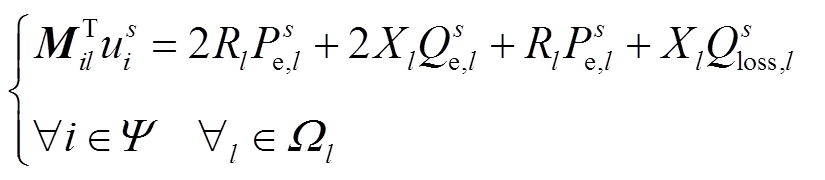 (13)
(13)
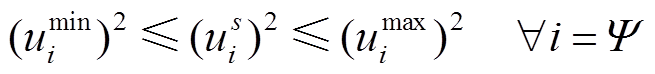 (14)
(14)
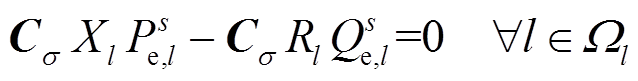 (15)
(15)
式中,Cσ为支路和回路组成的关联矩阵;Rl为支路l的电阻;Xl为支路l的电抗;us i为场景s的各节点电压;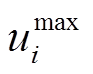 和
和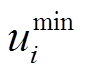 分别为节点电压的上限和下限。
分别为节点电压的上限和下限。
3)机组出力约束
在极大化区域间ATC时,各机组出力不得超过其出力限值,因此各机组出力需满足
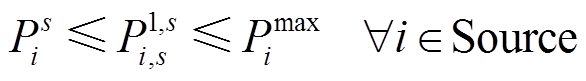 (16)
(16)
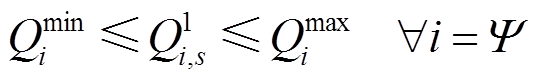 (17)
(17)
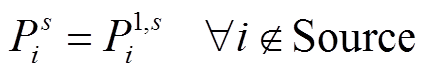 (18)
(18)
式中,Pmax i为常规机组有功出力上限;Qmax i和Qmin i分别为常规机组无功出力的上限和下限。
4)线路热稳定极限约束
系统正常运行时,线路潮流不得超过线路热稳定极限,为此线路潮流需满足
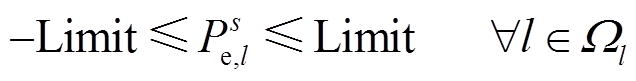 (19)
(19)
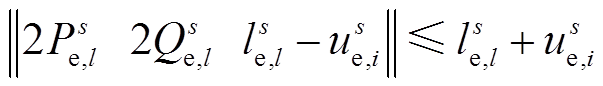 (20)
(20)
式中,us e,i为末端电压的二次方项;利用ls e,l代替有功网损和无功网损中的非线性项。
5)负荷约束
本文在求解ATC过程中,将维持送端负荷水平不变而极大化受端负荷水平,送、受端负荷需满足
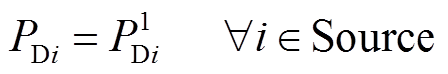 (21)
(21)
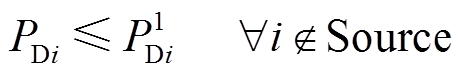 (22)
(22)
式中,PDi为节点i基态下的负荷。
2.2.2 下层模型
所提双层模型中的下层模型为计及风电出力相关性和CVaR的ETC评估模型,其目标函数由发电成本和CVaR两部分组成,详细表达式为
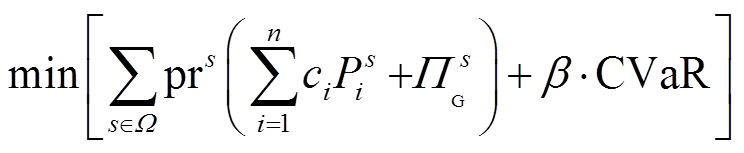 (23)
(23)
式中,ci为第i台常规机组的发电成本($/MW);Ps i 为第i台常规机组在第s个风电出力预测误差场景下的有功出力;β为风险系数;Πs G为由于风电出力存在不确定性,第s个场景系统为达到功率平衡所需承担的风险费用。CVaR表达式为
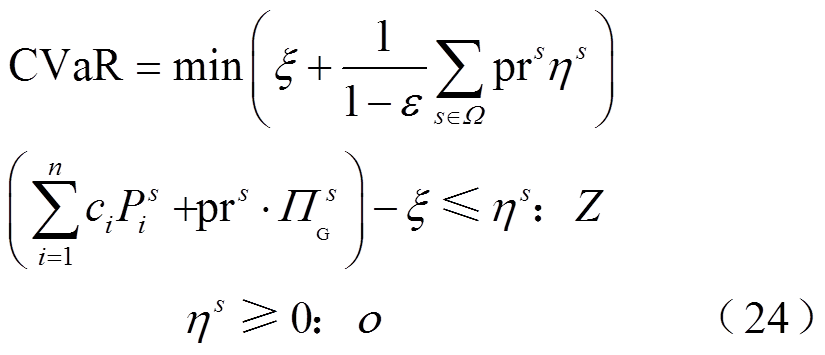
式中,ζ为引入的辅助变量;Z、o为对偶变量。
下层模型中,除式(24)的CVaR约束外,相比于上层模型的约束条件式(11)和式(22),下层模型的约束条件引入了常规机组上调、下调出力以满足风电出力不确定性带来的影响,同时还需对功率平衡约束、节点电压幅值约束、发电机有功出力约束、无功出力约束、线路热稳定约束等进行重构。
1)功率平衡约束
相比于上层模型功率平衡约束,下层模型由于计及了风电出力相关性的出力预测误差,需引入传统机组上调或下调出力以满足功率实时平衡需要,即
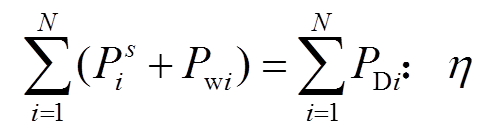 (25)
(25)
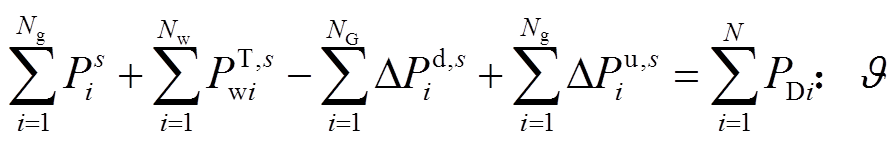 (26)
(26)
式中,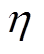 和
和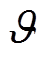 为功率平衡方程对应的对偶变量;Nw为风电场的数量。
为功率平衡方程对应的对偶变量;Nw为风电场的数量。
2)线路传输热稳定约束
由于下层模型采用直流潮流模型进行建模,下层模型的线路热稳定约束可直接利用发电转移因子(Generation Shift distributed Factors, GSF)矩阵进行建模。且调整常规机组出力,导致系统的潮流分布发生变化,为保证线路传输容量不越限,需对变化后的线路潮流重新进行约束,即
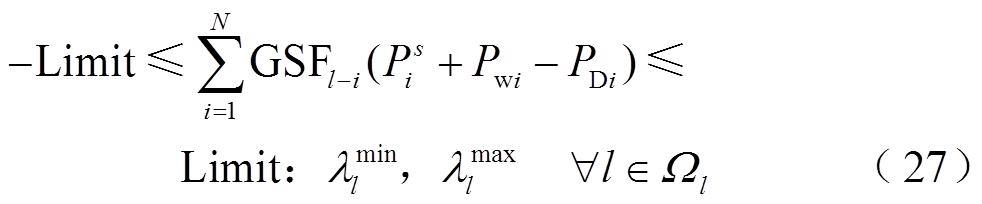
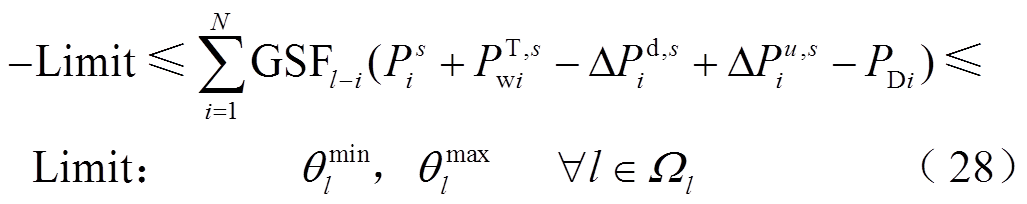
式中,GSFl-i为发电转移因子,表示节点i注入网络中的功率对支路l潮流的影响;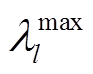 、
、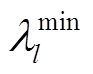 和
和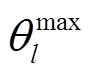 、
、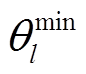 分别为式(27)和式(28)对应的对偶变量。
分别为式(27)和式(28)对应的对偶变量。
3)机组出力约束
相比于上层模型的机组出力约束,常规机组上调\下调出力后仍不能超过其出力限值,因此机组出力约束为
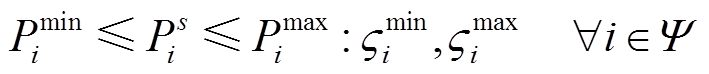 (29)
(29)
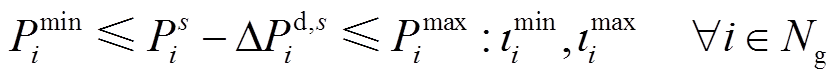 (30)
(30)
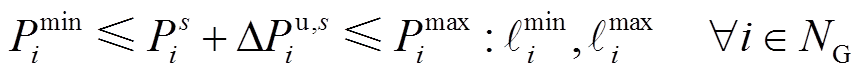 (31)
(31)
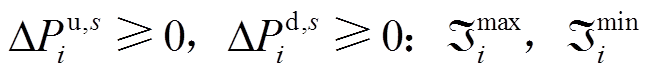 (32)
(32)
式中,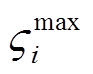 、
、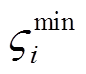 、
、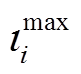 、
、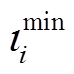 、
、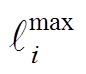 、
、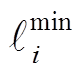 、
、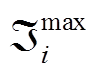 、
、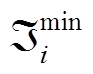 分别为式(29)~式(32)相关的对偶变量。
分别为式(29)~式(32)相关的对偶变量。
4)爬坡约束
基态下发电机出力与极限状态下发电机出力同样受到爬坡约束,即
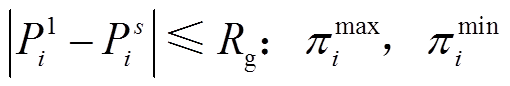 (33)
(33)
式中,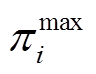 、
、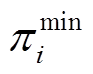 为式(31)相关的对偶变量;Rg为常规机组的爬坡速率。
为式(31)相关的对偶变量;Rg为常规机组的爬坡速率。
上述双层模型通过下层模型确定基态下的发电机组出力Pi并传递给上层,在上层模型中求解所得的极限状态下机组出力P1 i通过下层模型的爬坡约束式(33)交互信息,由于其具有耦合关系,难以对其直接求解。需对下层模型进行转换,通过构建下层模型拉格朗日函数,基于KKT条件[22],将所提计及风电出力相关性和CVaR的概率ATC评估双层模型转换为MPEC模型,转换后的MPEC模型为(式(37)为所有互补性约束的集合,完整的MPEC模型详见附录式(A1)~式(A13))
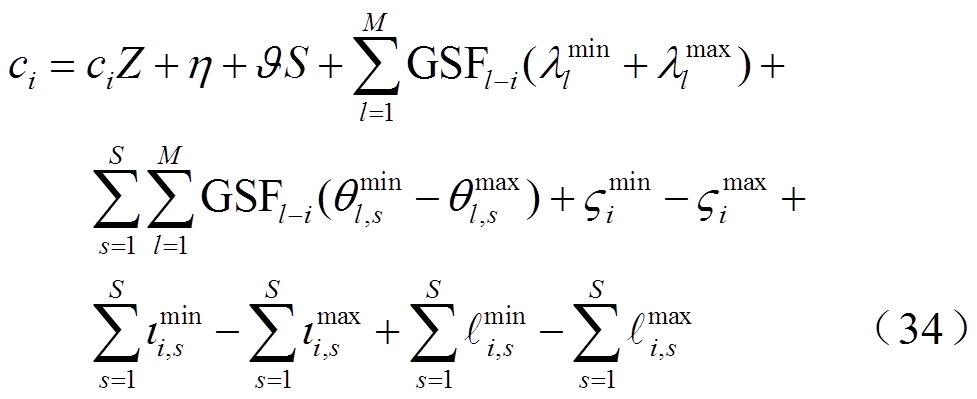
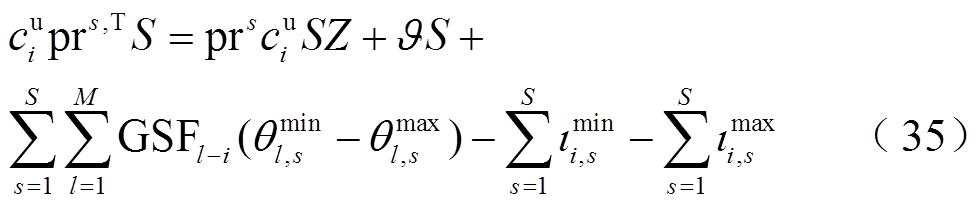
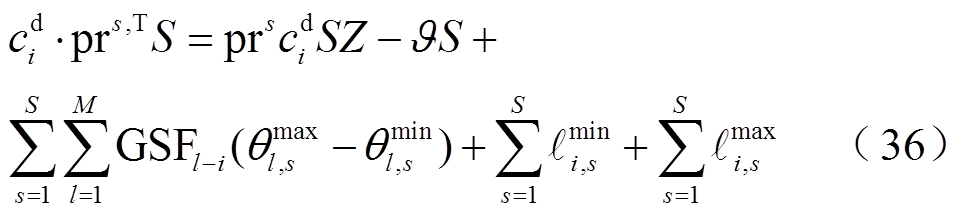
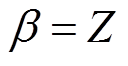 (37)
(37)
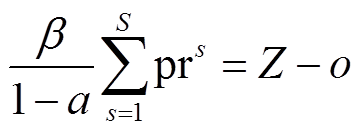 (38)
(38)
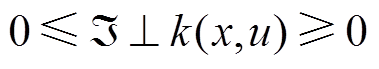 (39)
(39)
式中,符号⊥表示两个向量的乘积等于0;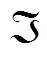 为原问题不等式约束条件k(x,u)对应所有对偶变量;prs,T为修正后的风电场出力场景对应的概率。
为原问题不等式约束条件k(x,u)对应所有对偶变量;prs,T为修正后的风电场出力场景对应的概率。
将MPEC模型中存在的非线性约束消除,利用大M法[23]通过引入0-1变量,将所提计及风电出力相关性和CVaR的概率ATC评估双层模型转换为易于求解的混合整数二阶锥问题(整体模型见附录式(A14)~式(A36)),有
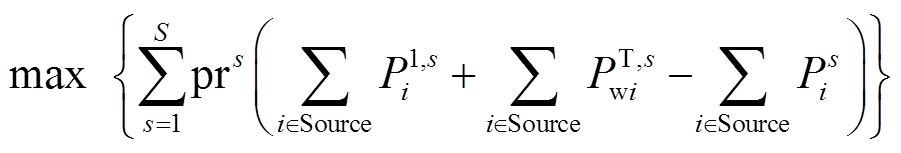 (40)
(40)
s.t. 式(11)~(22),式(23)~式(26),式(34)~式(38)
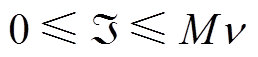 (41)
(41)
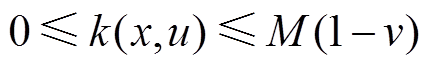 (42)
(42)
式中,M包括Mz,Mo,Mmin λ, Mmax λ, Mminθ, Mmax θ, Mmin ζ, Mmax ζ, Mmin ι, Mmax ι,MminƖ, MmaxƖ,为足够大的常数;v包括νz,νo,νmin λ,l, νmax λ,l, νmin θ,l, νmax θ,l, νmin ζ,I, νmax ζ,i, vmin ι,i, vmax ι,i, vminƖ,i, vmaxƖ,i,为辅助二进制变量。
转换后的混合整数二阶锥规划问题,可通过改变总发电成本置信水平、风险系数和风电出力相关性系数评估不同场景下的概率ATC期望。该模型可在CVX平台下建模,并通过Mosek进行求解。
为进一步量化分析概率ATC评估结果,利用统计分析的方法,求取下列ATC概率统计指标。
ATC最大值
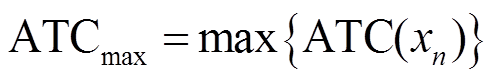 (43)
(43)
ATC最小值
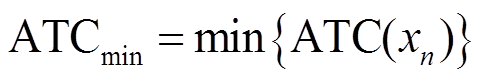 (44)
(44)
ATC期望值
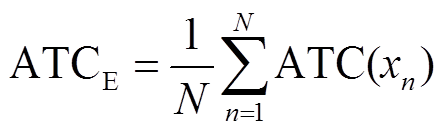 (45)
(45)
ATC方差
 (46)
(46)
ATC风险概率
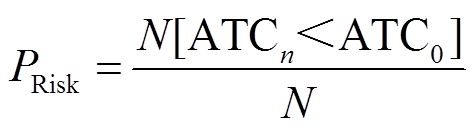 (47)
(47)
式中,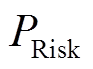 为ATC值小于某一设定ATC值时的概率值[4];N为场景总数。
为ATC值小于某一设定ATC值时的概率值[4];N为场景总数。
综上所述,本文所提计及风电出力相关性和CVaR的概率ATC评估流程如图1所示,具体步骤如下:
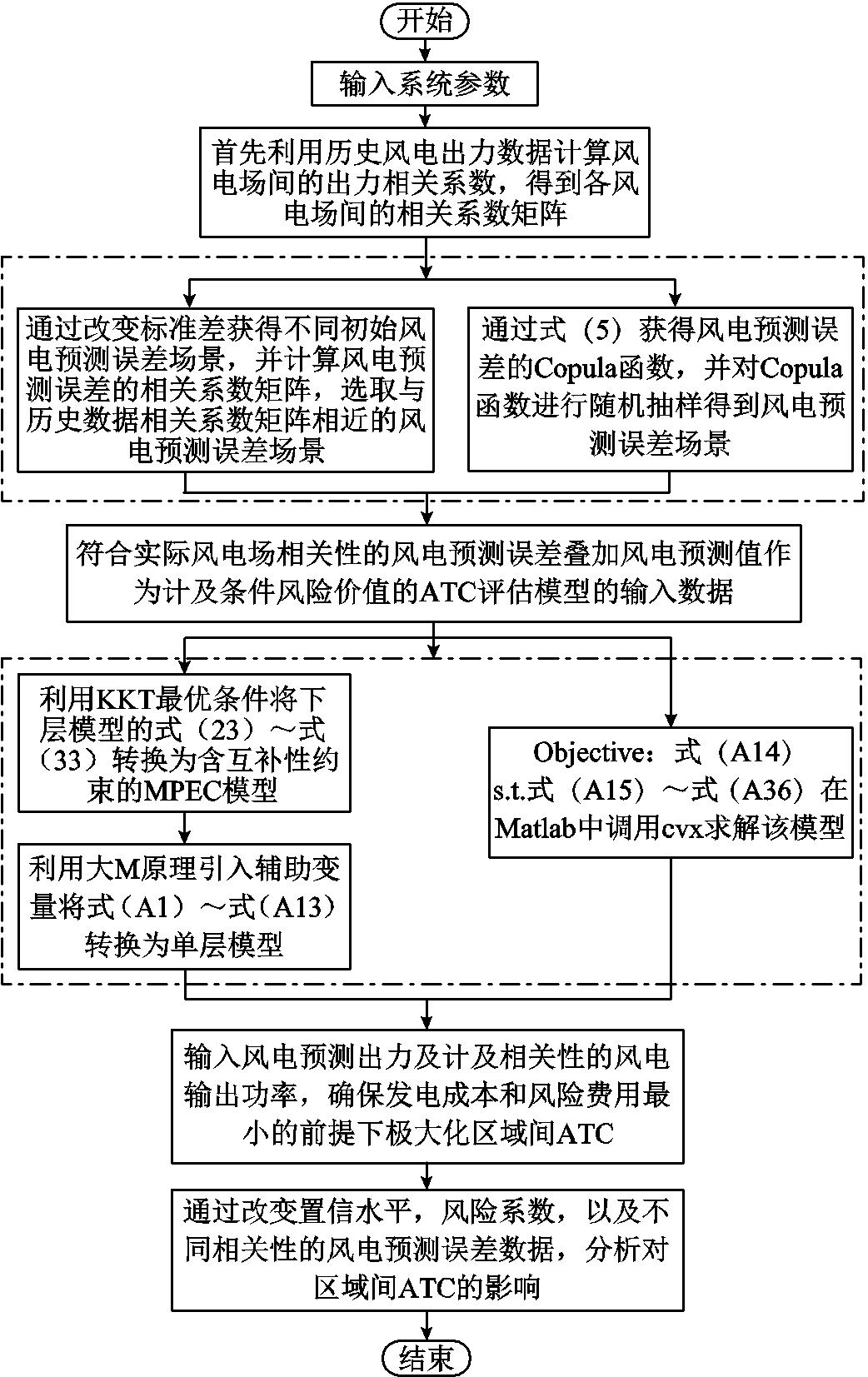
图1 计及风电出力相关性和条件风险价值的区域间ATC概率评估流程
Fig.1 Flow chart of the proposed ATC evaluation approach considering wind power correlation and conditional value at risk
1)首先利用历史风电出力数据计算风电场间的出力相关系数ρ0,得到各风电场间历史数据的相关系数矩阵Ω0。
2)改变式(3)中相邻两风电场出力概率分布函数中的标准差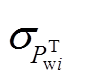 获得不同初始风电出力预测的误差场景,然后根据式(1)和式(2)计算不同初始风电预测误差场景下风电场出力的相关系数矩阵Ω。对比Ω与Ω0,将Ω与Ω0相近的风电场出力预测误差场景认为是符合实际风电场出力相关性的风电预测误差场景。
获得不同初始风电出力预测的误差场景,然后根据式(1)和式(2)计算不同初始风电预测误差场景下风电场出力的相关系数矩阵Ω。对比Ω与Ω0,将Ω与Ω0相近的风电场出力预测误差场景认为是符合实际风电场出力相关性的风电预测误差场景。
3)根据式(3)得到的风电出力预测误差场景和各风电场出力预测误差的概率分布f(ΔPw1), , f(ΔPwn),采用式(5)所示的t-Copula函数拟合满足实际风电场间的空间相关性的风电出力预测误差多元概率分布。然后对t-Copula函数进行随机抽样得到风电出力预测误差场景及不同场景下风电出力预测误差的概率,进而根据风电出力预测值Pwi和风电出力预测误差ΔPs wi计算经修正后的风电场出力预测值PT,s wi,即为计及风电场间出力相关性的风电场出力预测值。
, f(ΔPwn),采用式(5)所示的t-Copula函数拟合满足实际风电场间的空间相关性的风电出力预测误差多元概率分布。然后对t-Copula函数进行随机抽样得到风电出力预测误差场景及不同场景下风电出力预测误差的概率,进而根据风电出力预测值Pwi和风电出力预测误差ΔPs wi计算经修正后的风电场出力预测值PT,s wi,即为计及风电场间出力相关性的风电场出力预测值。
4)利用KKT最优条件,将下层模型的式(23)~式(33)转换为含互补约束的MPEC模型;并利用大M原理通过引入0-1变量将式(A1)~式(A13)转换为易求解的单层模型,具体模型见式(A14)~式(A36)。输入风电预测出力及计及相关性的风电预测误差等,求解概率ATC期望。
5)通过改变总发电成本的置信水平ε、风险系数β及不同相关系数的风电预测误差,分析风险水平及风电预测误差对区域间ATC的影响。
本节进一步通过PJM-5节点测试系统和吉林西部电网分析、验证所提区域间概率ATC评估方法的有效性和实用性。
修改后的PJM-5节点测试系统如图2所示。如图所示该系统划分为发电和受电两个区域。图中线路1-2、1-4、1-5、2-3、3-4和4-5的传输极限分别为400 MW、200 MW、200 MW、300 MW、200 MW和240 MW;PL2、PL3和PL4基态负荷均为270 MW;发电机G1、G3和G4有功容量分别为210 MW、520 MW和200 MW,发电报价分别为30 $/MW、40 $/MW和35 $/MW,发电机G1、G3和G4机组爬坡/滑坡成本均为75 $/MW和78 $/MW;风电场W1和W5预测功率分别为200 MW和150 MW。
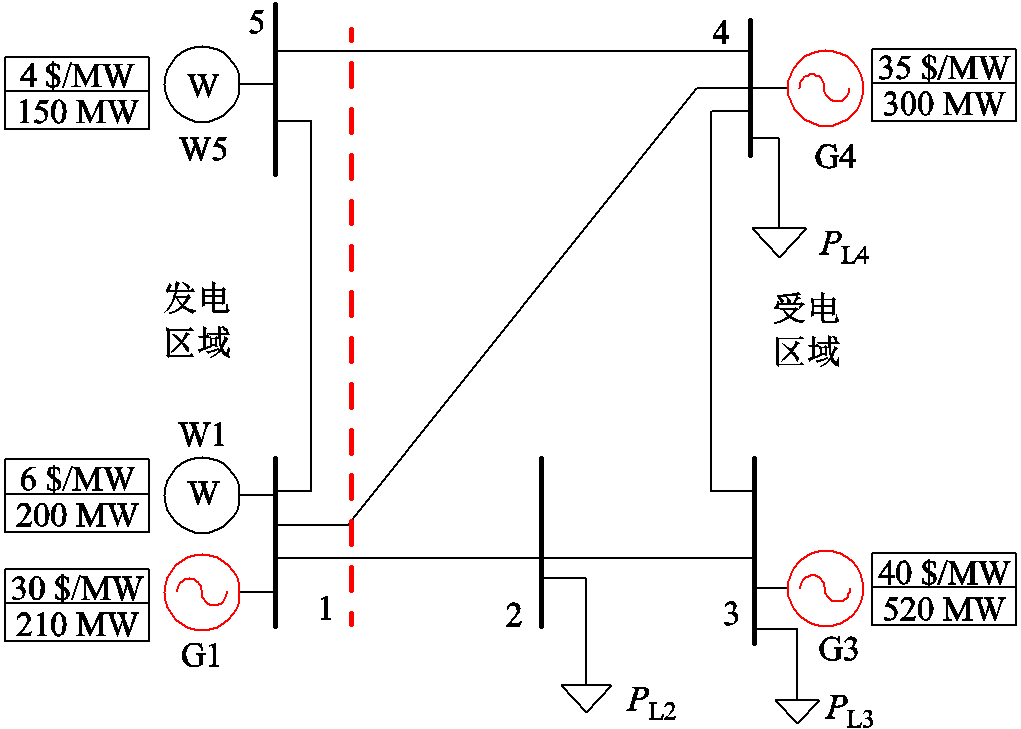
图2 改进的PJM-5节点系统
Fig.2 Modified PJM 5-bus test system
为验证所提方法的准确性和有效性,并对比风电预测误差相关性和风电出力不确定性产生的风险费用对区域间ATC的影响,本节设置了以下四种情况进行分析。
情况1:不计及风电出力空间相关性,随机生成风电出力预测误差场景。
情况2:计及风电出力空间相关性,生成风电出力预测误差场景。
情况3:随机生成不计及风电出力空间相关性的风电出力预测误差场景,考虑风电出力不确定性产生的风险费用。
情况4:生成计及风电出力相关性的预测误差场景,同时考虑风电出力不确定性产生的风险费用。
根据两风电场历史出力数据计算得到的两风电场出力的相关系数为0.88。为构建符合实际风电场出力相关性的风电出力预测误差数据,假设两风电场出力预测误差分别服从σ1=10%μ、σ2=10%μ,σ1=10%μ、σ2=15%μ和σ1=10%μ、σ2=20%μ的正态分布。Copula函数可以独立于两风电场出力的概率分布构建两风电场出力的相关性结构,通过Copula函数建立两风电场出力的多元联合概率分布,对风电场间空间相关性进行建模。不同Copula函数的欧氏距离对比见表1,不同Copula函数类型的概率ATC期望对比见表2。
由表1和表2可以看出,t-Copula函数的欧式距离d最小,因此,本文采用t-Copula函数描述风电预测误差贴近经验概率分布;而Clayton-Copula函数的欧式距离d最大,因此利用Clayton-Copula函数获得的概率ATC期望与t-Copula函数获得的概率ATC期望偏差较大。以上结果证明了采用t-Copula函数描述风电出力预测误差概率分布的合理性。
表1 不同Copula函数的欧氏距离对比
Tab.1 Euclidean distance comparison of different Copula functions
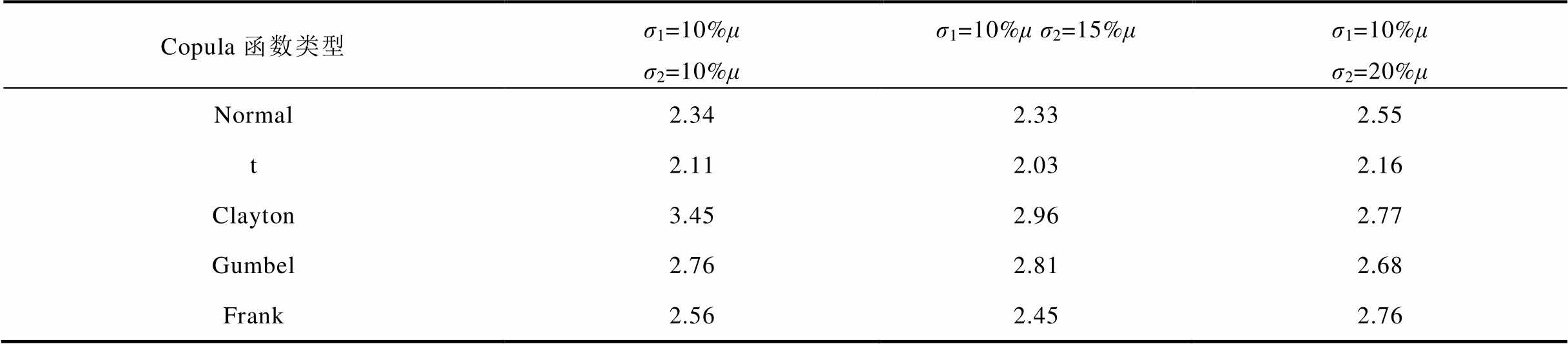
Copula函数类型σ1=10%μσ2=10%μσ1=10%μσ2=15%μσ1=10%μσ2=20%μ Normal2.342.332.55 t2.112.032.16 Clayton3.452.962.77 Gumbel2.762.812.68 Frank2.562.452.76
表2 不同Copula函数类型的概率ATC期望对比
Tab.2 Comparison of the probability ATC values of different Copula function types(单位:MW)

Copula函数类型情况1情况2情况3情况4 Normal195.6196.9187.3193.7 t195.9197.9186.8193.3 Clayton196.7199.5187.8192.1 Gumbel196.6195.5185.3194.1 Frank196.4196.2185.9193.9
当风电出力预测误差服从σ=10%μ的正态分布时,随机生成的风电出力预测误差和利用t-Copula函数获得的计及风电空间相关性的风电出力预测误差见表3。
表3 PJM-5节点测试系统各场景下风电出力预测误差及概率
Tab.3 Wind power forecast error and probability in each scenario in PJM 5-bus test system
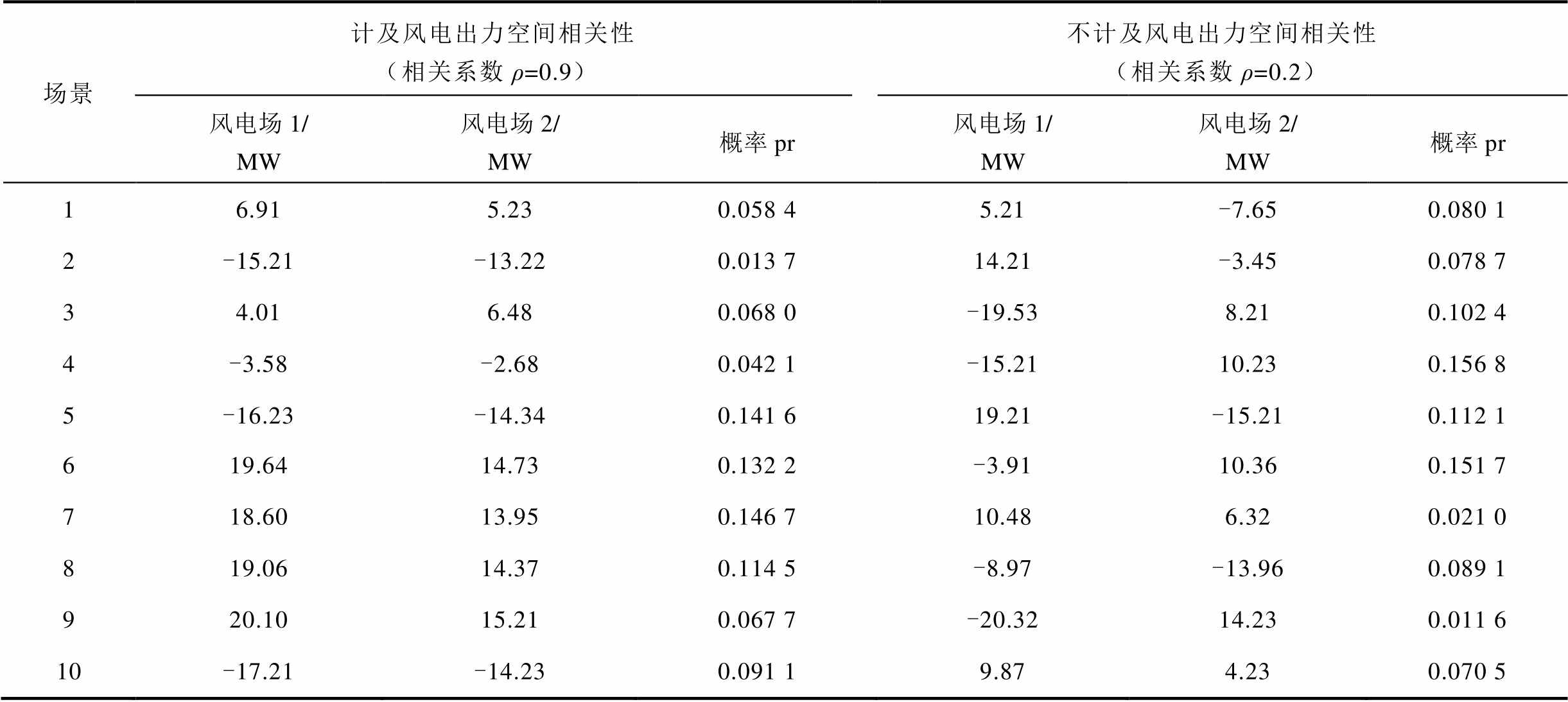
场景计及风电出力空间相关性(相关系数ρ=0.9)不计及风电出力空间相关性(相关系数ρ=0.2) 风电场1/ MW风电场2/ MW概率pr风电场1/ MW风电场2/ MW概率pr 16.915.230.058 45.21-7.650.080 1 2-15.21-13.220.013 714.21-3.450.078 7 34.016.480.068 0-19.538.210.102 4 4-3.58-2.680.042 1-15.2110.230.156 8 5-16.23-14.340.141 619.21-15.210.112 1 619.6414.730.132 2-3.9110.360.151 7 718.6013.950.146 710.486.320.021 0 819.0614.370.114 5-8.97-13.960.089 1 920.1015.210.067 7-20.3214.230.011 6 10-17.21-14.230.091 19.874.230.070 5
4.1.1 不同情况区域间概率ATC期望结果对比分析
针对所设置的四种情况,利用表3的风电出力预测误差数据对PJM-5节点系统区域间ATC进行概率评估。将总发电成本的置信水平设定为80%,风险系数设为2。对应的概率ATC期望评估结果如图3所示,概率ATC统计指标结果对比见表4,总发电成本结果如图4所示。
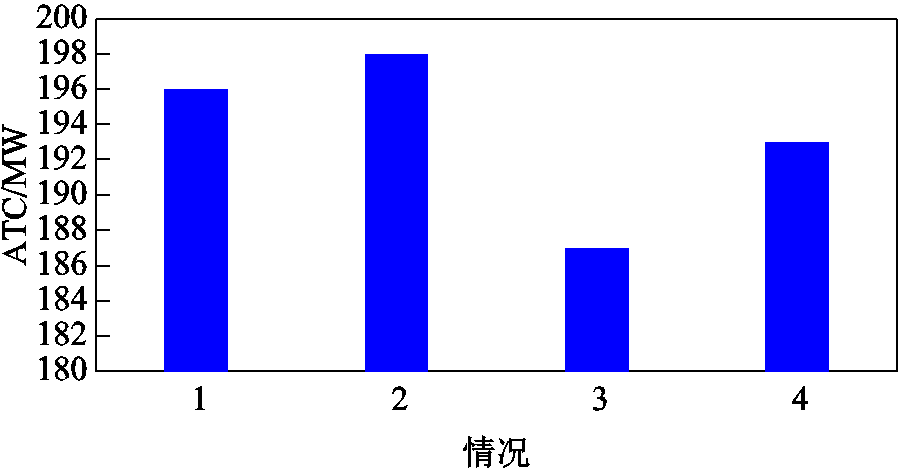
图3 不同情况下PJM-5节点测试系统概率ATC期望评估结果
Fig.3 Probabilistic ATC results of PJM 5-bus test system under different cases
表4 ATC统计指标结果对比
Tab.4 Comparison of ATC statistical indicators

情况ATCE/MWATCV/MWATCmin/MWATCmax/MWPRisk 1195.94.22193.1196.90.4 2197.96.28193.2201.20.2 3186.84.25184.1198.10.5 4193.36.22189.8196.20.6
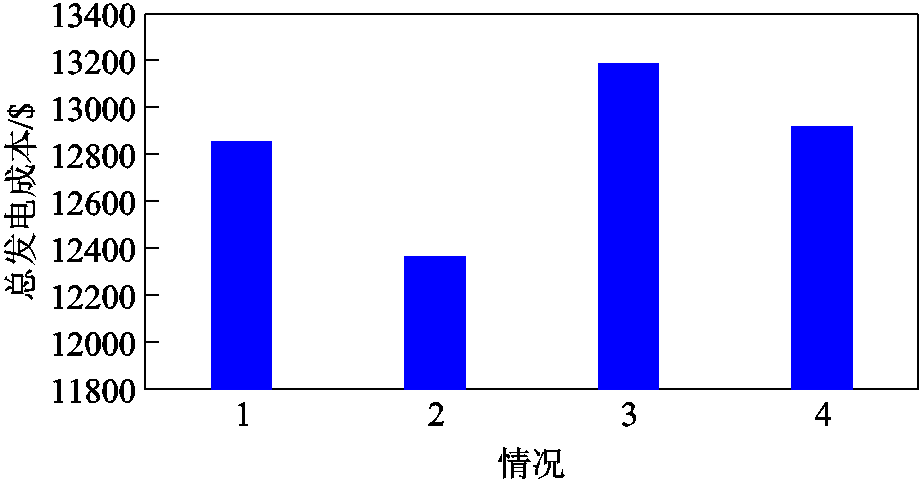
图4 不同情况下PJM-5节点测试系统总发电成本
Fig.4 Total generation costs of PJM 5-test system under different cases
对比图3中四种情况的概率ATC期望可看出:情况1的概率ATC期望为195.9 MW,此时支路4-5的传输功率分别为240 MW,支路4-5达到热稳定极限,且送电区域G1达到出力上限;情况2的概率ATC期望为197.9 MW,此时支路4-5和支路1-5均达到热稳定极限;情况3的概率ATC期望为186.8 MW,此时支路4-5和支路3-4达到热稳定极限,且G4达到出力上限;情况4的概率ATC期望为193.3 MW,此时支路4-5和支路1-4达到热稳定极限。由图3的ATC计算结果和表1的风电出力预测误差可以看出:计及风电场间出力相关性后,情况2和4的风电出力预测误差的相关系数为0.9与实际风电场间的出力相关系数0.88相近,即情况2和4的风电出力预测误差更能表征实际风电场的出力预测误差,有效地提升了区域间ATC的计算精度,提高了区域间ATC。因此,在计算高比例新能源电网的区域间ATC时,需计及风电场间出力相关性对风电出力预测误差的影响,实现对区域间ATC的准确评估。通过表4中概率ATC方差结果可以看出:对比于情况2和4,情况1和3下ATC方差较低,证明了考虑风电预测误差相关性后ATC的波动性增强;通过表4中风险概率和概率ATC期望结果可以看出:对比于情况1和2,情况3和4下风险概率较高,概率ATC期望较小,主要原因在于,情况3和情况4在评估区域间ATC时计及了风电出力不确定性产生的风险费用,系统为规避风电出力不确定性所带来的运行风险,结果更加保守,因此区域间ATC的期望值较小,而情况1和情况2未考虑风电出力不确定性产生的风险费用,计算结果较乐观。
对比图4中四个情况的总发电成本可看出:情况1和情况2的总发电成本分别为1.28×105 $和1.23×105 $,情况3和情况4的总发电成本分别为1.32×105$和1.29×105 $。由于情况3和情况4在情况1和情况2的基础上考虑了风电出力不确定性带来的风险费用,从而导致发电成本的增加,使得总发电成本高于情况1和情况2,若不考虑风险费用,计算得到的ATC结果过于乐观,不能有效量化出风电出力不确定性对系统运行带来的风险,有可能导致断面关键支路越限;进一步,对比图4中情况2与情况1、情况4与情况3的总发电成本可知:由于情况2和4在情况1和3基础上考虑了风电场间出力的空间相关性,得到的风电场出力预测值更能真实反映实际风电场的出力,减小了风电出力不确定性的影响,降低了系统运行的风险费用。
因此,在评估含高比例风电的电力系统概率ATC时,不仅要考虑风电出力不确定性及相关性,还要考虑机组出力调整产生的风险费用对区域间ATC计算结果的影响。
4.1.2 置信水平和风险系数对区域间ATC的影响
实际运行时,调度决策者可通过总发电成本的置信水平和风险系数来反映其规避风电出力不确定性带来的系统运行风险程度,因此本节进一步研究了置信水平和风险系数对ATC计算结果的影响。
首先,借助情况3和情况4分析总发电成本的置信水平对区域间概率ATC期望的影响,图5给出了总发电成本的置信水平在0.1~0.9时区域间概率ATC的期望。图6为不同置信水平对系统总发电成本的影响。
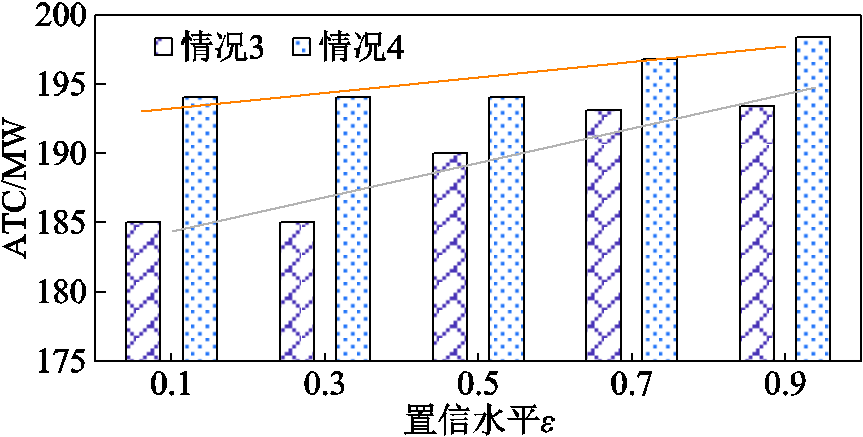
图5 不同置信水平下PJM-5节点测试系统概率ATC
Fig.5 Probabilistic ATC results of PJM-5 bus test system probability under different confidence levels
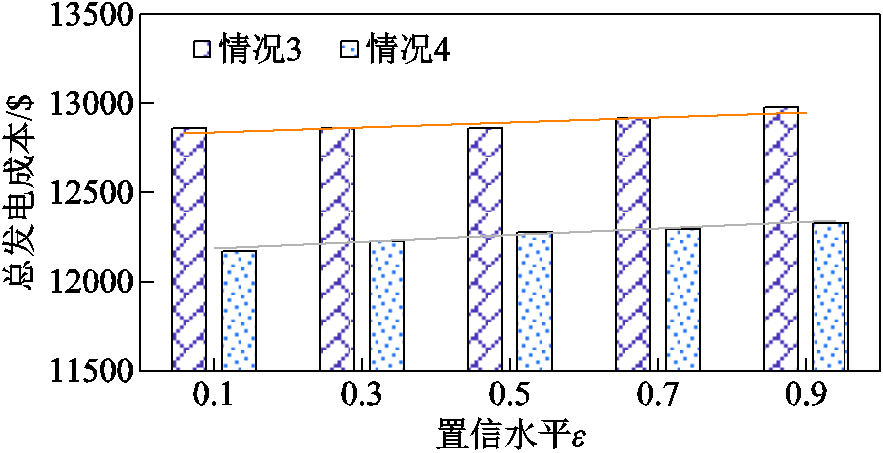
图6 不同置信水平下PJM-5节点测试系统总发电成本
Fig.6 Total generation costs of PJM 5-bus test system under different confidence levels
由图5和图6可看出:当总发电成本的置信水平ε从0.1增加到0.9时,区域间概率ATC期望增加了约10 MW,总发电成本也不断提高。随着区域间ATC不断增加,系统区域间联络线剩余传输容量将逐渐增大,以应对最严重的故障情况;同时,系统总发电成本不断提高,也反映了运行人员极力规避因风电出力不确定性所带来的系统运行风险,以增强系统的运行可靠性。
图7进一步根据情况4分析了风险系数对区域间概率ATC的影响。由式(23)可知:当风险系数β取值较小时,运行人员在追求发电成本较小的目标同时,将面临较大的成本波动风险。当风险系数逐渐增大时,运行人员开始极力规避成本波动的风险,即系统运行人员将面临较高的发电成本但成本波动风险较小。
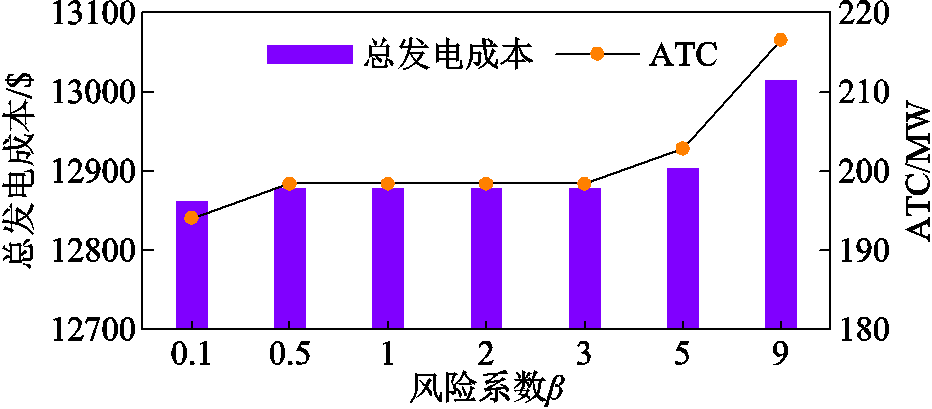
图7 不同风险系数下PJM-5节点测试系统概率ATC期望
Fig.7 Probabilistic ATC results of PJM 5 bus test system under different risk coefficients
由图7可以看出:风险系数较小时,即风险系数β在0.1~3.0之间时,随着风险系数的增加,区域间概率ATC期望从196 MW增加至199 MW,总发电成本从1.28×105 $增加至1.29×105 $,概率ATC期望和总发电成本均增加较小;风险系数较大时,较小的风险水平降低都会造成较大的总发电成本增加,同时概率ATC期望增加较快。由于风险系数较小时,风电出力不确定性导致的风险费用相比于传统机组的发电成本较小,因此对区域间ATC和总发电成本影响较小。
4.1.3 不同相关系数对区域间ATC的影响
本节进一步根据风电出力预测误差的不同空间相关性,分析风电场间出力相关性对概率ATC期望的影响。
假设风电出力预测误差分别服从s =10%m、s =15% m和s =20% m(s为标准差,m为期望)的正态分布。利用式(1)计算得出两风电场预测误差均满足σ=10%,其相关系数ρ为0.9;两风电场预测误差满足σ=10%和σ=15%时,其相关系数ρ为0.5;两风电场预测误差满足σ=10%和σ=20%时,其相关系数ρ为0.7。图8给出了不同相关系数对区域间概率ATC期望和发电成本的影响。
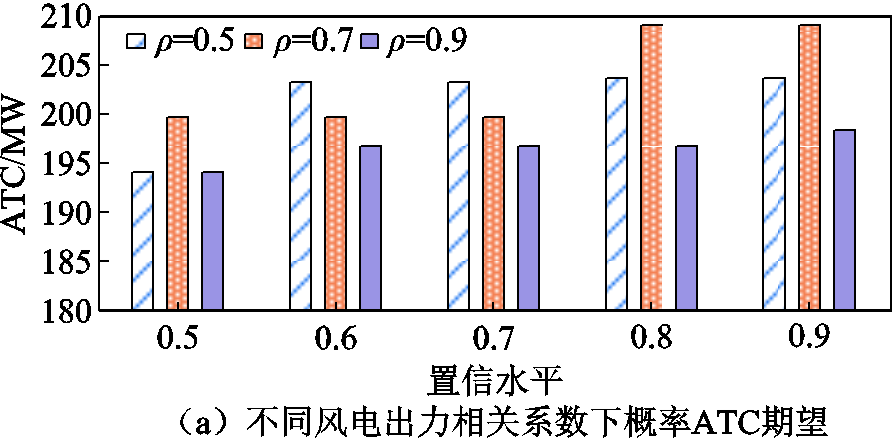
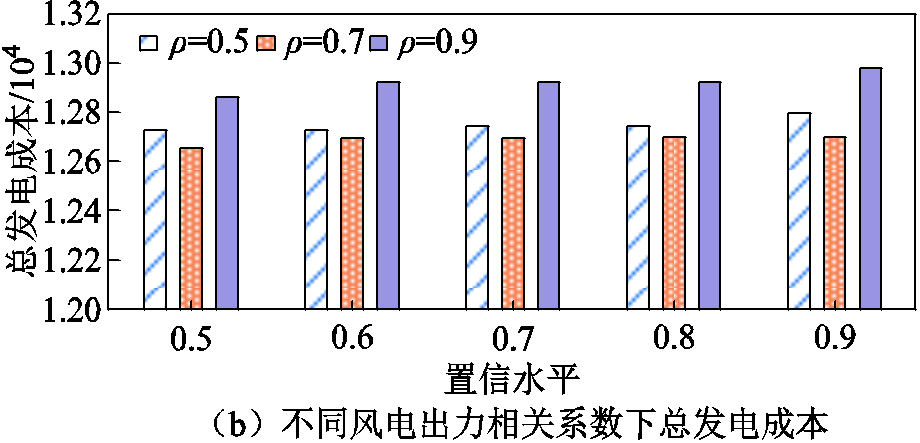
图8 不同风电出力相关系数下PJM-5节点测试系统概率ATC期望和总发电成本
Fig.8 Probabilistic ATC results and total generation costs of PJM 5-bus test system under different correlation coefficients of wind power forecast errors
由图8可以看出:相关系数在不同总发电成本的置信水平下对区域间概率ATC期望的影响不同。当置信水平取90%时,随着相关系数从0.5增加至0.9时,风电场出力相关性逐渐增大,区域间概率ATC期望先增大后减小;当置信水平取70%时,区域间概率ATC期望随相关系数的增加,逐渐减小,不同相关系数下的风电预测误差场景不同,导致基态下各发电机组出力不同,进而影响概率ATC期望。同样可以看出,随着相关系数的增加,总发电成本先减小后增加。由此可见:在含高比例风电的电力系统ATC评估过程中,需计及总发电成本的置信水平和风电场间相关性对ATC评估结果的影响。
为验证本文所提计及风电出力相关性和CVaR的区域间概率ATC评估方法的实用性,本节进一步以吉林西部电网为例对所提方法进行实用性验证,吉林西部电网拓扑结构如图9所示。将图中系统分为两个区域,变电站DA、XZ,风电场LF、XAL、LS和光伏电站ZWS位于送电区域;变电站ZL、TN、XH、QJ、ST、TS,火电厂BC,风电场HYP、风电场SL和风电场DB位于受电区域。输电断面由TS-DA线、TS-XZ线、ZL-XZ线构成,其线路热稳定极限分别为253 MW、611 MW、289 MW。送电区域风电场LF、XAL、LS和光伏电站ZWS容量分别为197.5 MW、49.5 MW、99 MW和200 MW;受电区域火电厂BC、风电场HYP、风电场SL和风电场DB容量分别为400 MW、198 MW、49.5 MW和49.5 MW。基于文献[24]中各电源的成本参数,风电场LF、XAL、LS及光伏电站ZWS的发电成本分别为289元/MW、258元/MW、276元/MW和291元/MW;火电厂BC、风电场HYP、风电场SL和风电场DB的发电成本分别为521元/MW、249元/MW、198元/MW、和191元/MW;火电厂BC的爬坡和滑坡成本分别为654元/MW和662元/MW。分析在不同置信水平及风电出力相关性对区域间概率ATC期望的影响。
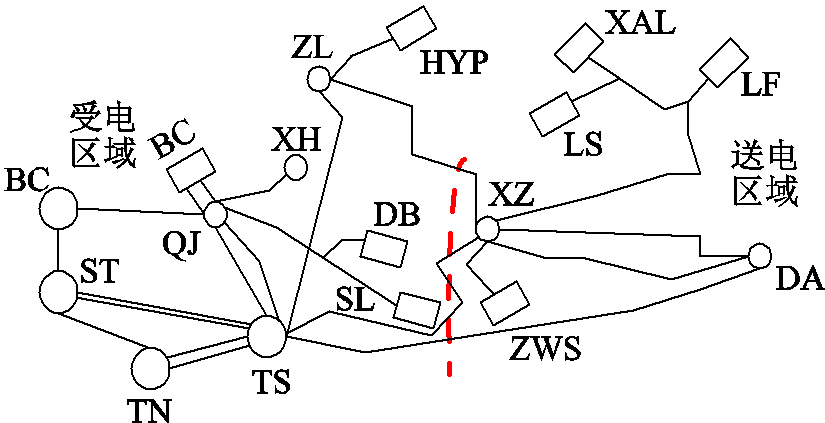
图9 吉林西部电网
Fig.9 Power gird in western Jilin
首先,根据风电场SL与DB的历史出力数据计算得到的SL与DB的风电出力相关系数为0.86。假设风电场SL和DB的出力预测误差服从σ=10%μ和σ=15%μ正态分布的两种场景,利用相关系数矩阵计算得出:两风电场预测误差均满足σ=10%μ时其相关系数为0.9;两风电场预测误差满足σ=10%μ和σ=15%μ时,其相关系数为0.7;两风电场预测误差满足σ=15%μ和σ=10%μ时,其相关系数为0.5。计及风电出力空间相关性的风电预测误差见表5,不同相关系数及置信水平对ATC期望的影响见表6。
表5 不同场景下风电场SL和DB出力预测误差
Tab.5 Wind power forecast errors of SL and DB in different scenarios(单位:MW)

场景两风电场预测误差满足σ=10%μ两风电场预测误差满足σ=15%μ 风电场SL风电场DB风电场SL风电场DB 11.791.422.213.65 2-3.61-3.221.212.35 31.012.26-3.53-4.11 4-1.58-1.971.243.23 5-2.23-2.14-4.21-5.14 6-3.64-3.21-3.98-2.36 72.601.933.484.62 84.062.17-3.27-3.96 9-1.10-2.61-2.32-4.23 10-2.21-2.274.274.34
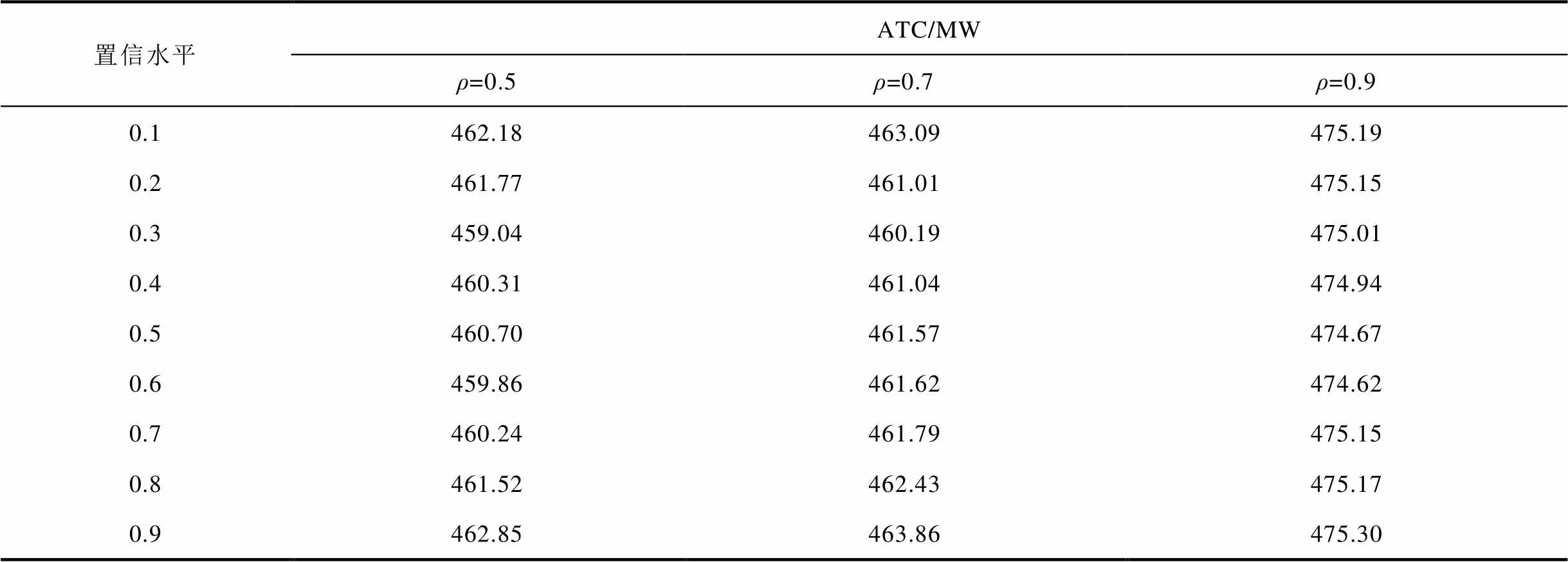
表6 置信水平和风电出力相关性对吉林西部电网概率ATC影响
Tab.6 Influence of confidence level and wind power correlation on probabilistic ATC results of power grid in western Jilin
置信水平ATC/MW ρ=0.5ρ=0.7ρ=0.9 0.1462.18463.09475.19 0.2461.77461.01475.15 0.3459.04460.19475.01 0.4460.31461.04474.94 0.5460.70461.57474.67 0.6459.86461.62474.62 0.7460.24461.79475.15 0.8461.52462.43475.17 0.9462.85463.86475.30
由表6结果可以看出:随着相关系数ρ从0.5增加到0.9,不同置信水平下对区域间概率ATC期望的影响不同。当置信水平取90%时,概率ATC期望随相关系数的增加从462.85 MW增加到475.30 MW;当置信水平取20%时,随相关系数的增加,概率ATC期望随相关系数的增加,先减小后增大,不同相关系数下的风电预测误差场景不同,且不同置信水平反映调度决策者对规避风电出力不确定性导致带来的系统运行风险不同,导致基态下各发电机组出力不同,进而影响概率ATC期望。
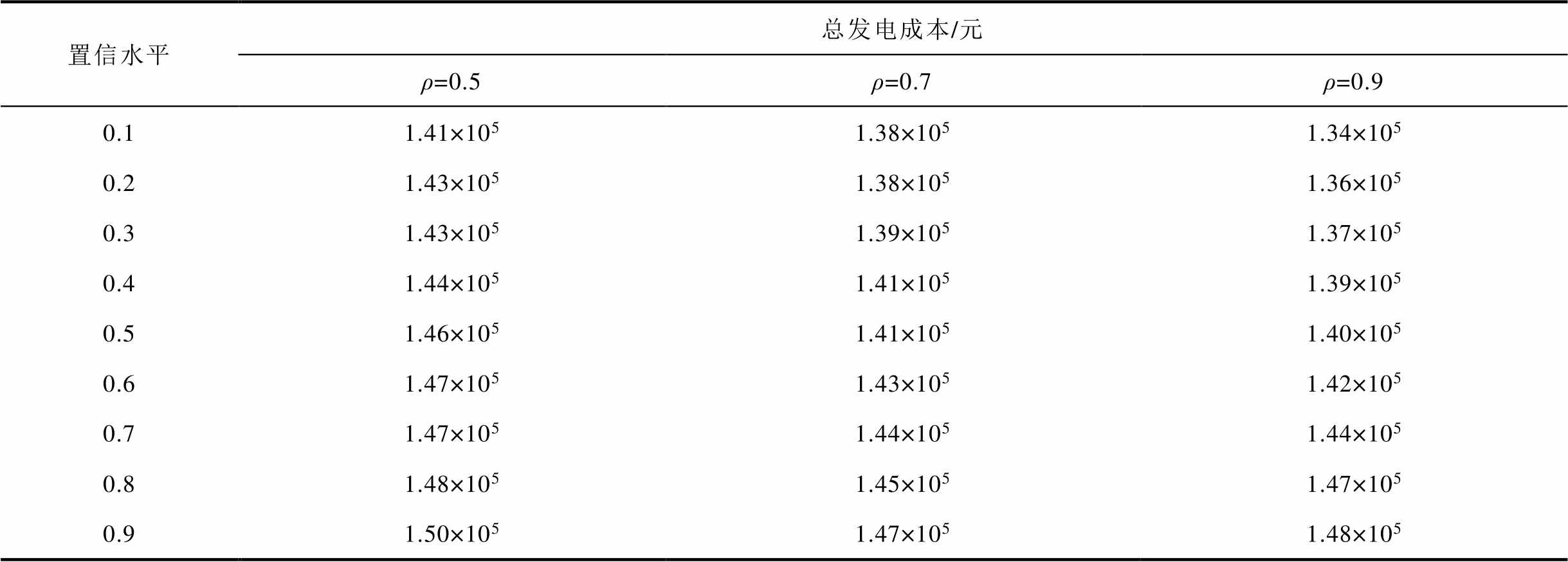
不同置信水平及风电出力相关性对总发电成本的影响见表7。两风电场出力相关系数为0.9时,随置信水平的增加,系统对安全性的要求增加,此时总发电成本从1.34×105元增加至1.48×105元;当置信水平为70%时,随相关系数的增加,总发电成本逐渐减小;当置信水平为90%时,随着相关系数的增加,总发电成本先减小后增加。
表7 置信水平和风电出力相关性对吉林西部电网总发电成本影响
Tab.7 Influence of confidence level and wind power output correlation on total generation costs of power grid in western Jilin
置信水平总发电成本/元 ρ=0.5ρ=0.7ρ=0.9 0.11.41×1051.38×1051.34×105 0.21.43×1051.38×1051.36×105 0.31.43×1051.39×1051.37×105 0.41.44×1051.41×1051.39×105 0.51.46×1051.41×1051.40×105 0.61.47×1051.43×1051.42×105 0.71.47×1051.44×1051.44×105 0.81.48×1051.45×1051.47×105 0.91.50×1051.47×1051.48×105
上述结果表明,在高渗透率风电汇集地区,总发电成本的置信水平以及风电预测误差的相关性均会对区域间ATC的评估结果产生影响。系统运行人员可根据对风险的规避程度设置置信水平,并计及风电场间出力相关性的预测风电场出力,以确保准确、全面地评估区域间ATC。
本文针对风电场间出力相关性和风电出力不确定性对区域间ATC的影响,提出了一种计及风电出力相关性和CVaR的区域间ATC概率评估方法,通过PJM-5节点测试系统和吉林西部电网对所提方法进行分析验证,相关结论如下:
1)所提风电预测误差相关性建模方法,通过获得符合实际风电场相关性的风电出力预测误差修正风电场出力预测值。在评估ATC的过程中,减小因风电出力不确定性带来的预测误差,降低系统运行的风险费用,并提升区域间ATC的计算精度。
2)所提计及CVaR的ATC评估模型,通过引入CVaR量化风电出力的不确定性产生的风险费用。当总发电成本的置信水平ε和风险系数β逐渐增加时,系统对安全性的要求增加,区域间概率ATC期望和总发电成本不断提高。系统运行人员可根据实际情况,综合考虑系统运行的经济性与安全性,合理设置总发电成本的置信水平。
3)所提计及风电出力相关性和CVaR的区域间ATC概率评估方法,验证了风电出力相关系数在不同总发电成本置信水平下对区域间概率ATC期望的影响不同。应合理设定置信水平,并计及风电预测误差相关性,以更准确、全面地评估区域间ATC。
本文主要考虑各风电场预测误差的空间相关性,后续将在本文研究的基础之上,考虑风电场间时空相关性对ATC的影响。
附 录
通过构建下层模型的拉格朗日函数,并根据所构建的拉格朗日函数和下层模型的KKT最优条件[23],可将双层模型转换为含互补性约束的单层模型,转换后的单层模型为(其中式(A2)~(A13)对应正文式(37))
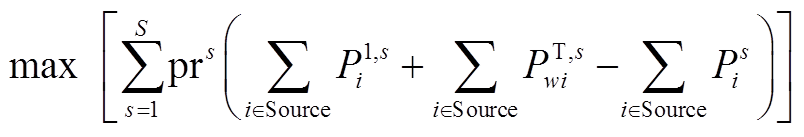 (A1)
(A1)
s.t. 式(9)~式(20),式(22)~式(24),式(32)~式(36)
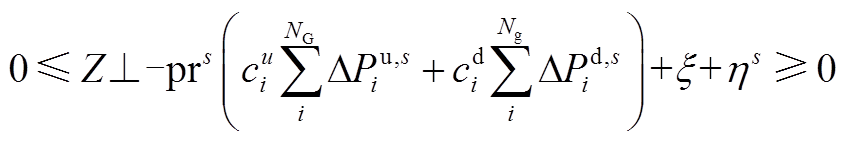 (A2)
(A2)
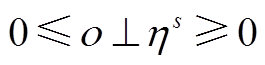 (A3)
(A3)
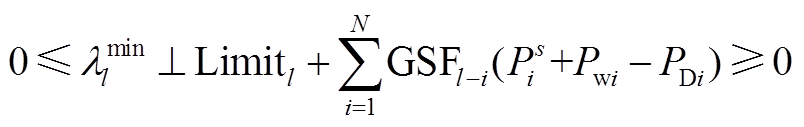 (A4)
(A4)
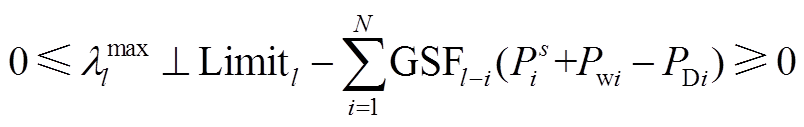 (A5)
(A5)
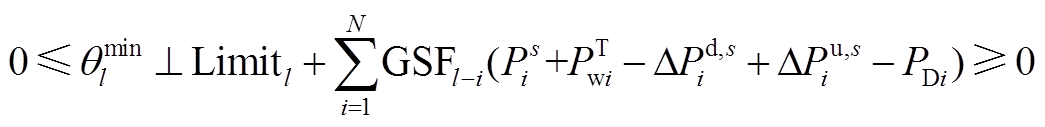 (A6)
(A6)
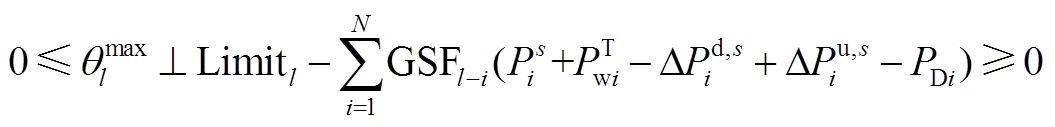 (A7)
(A7)
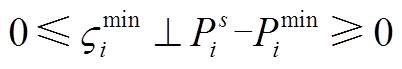 (A8)
(A8)
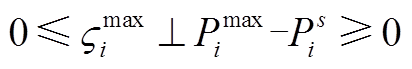 (A9)
(A9)
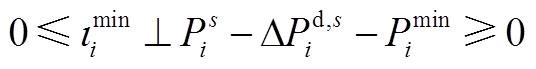 (A10)
(A10)
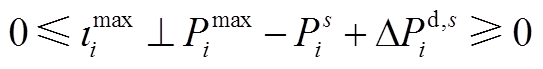 (A11)
(A11)
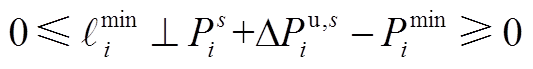 (A12)
(A12)
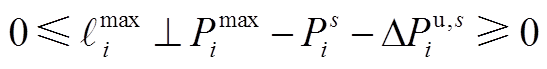 (A13)
(A13)
基于KKT条件中的互补性约束[25],通过引入0-1变量,最终将含非线性项的非线性单层模型转换为混合整数二阶锥规划问题,为
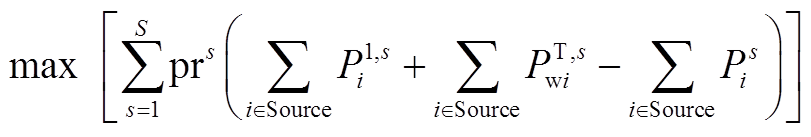 (A14)
(A14)
s.t.式(9)~式(20),式(22)~式(24),式(32)~式(36)
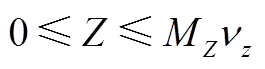 (A15)
(A15)
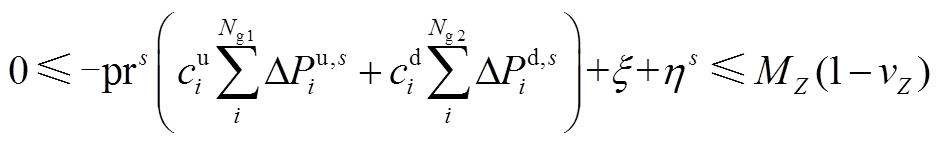 (A16)
(A16)
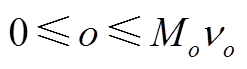 (A17)
(A17)
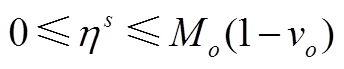 (A18)
(A18)
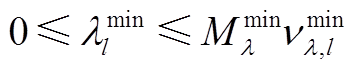 (A19)
(A19)
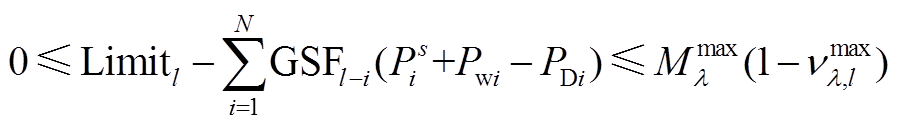 (A20)
(A20)
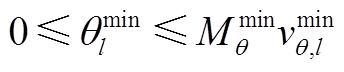 (A21)
(A21)
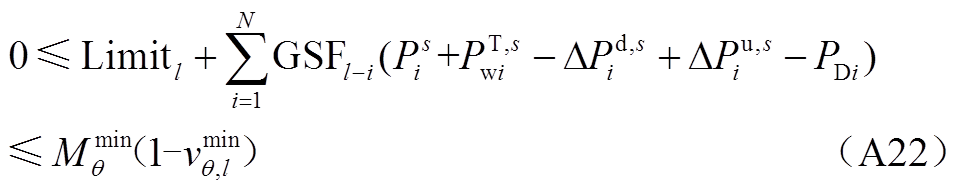
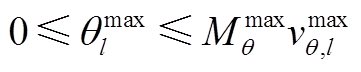 (A23)
(A23)
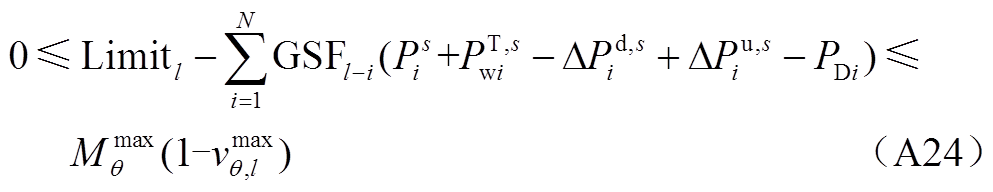
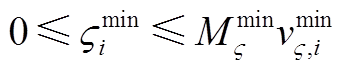 (A25)
(A25)
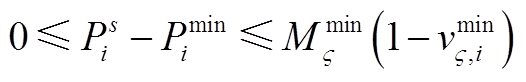 (A26)
(A26)
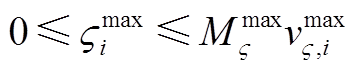 (A27)
(A27)
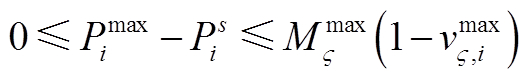 (A28)
(A28)
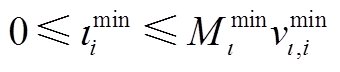 (A29)
(A29)
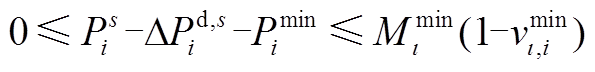 (A30)
(A30)
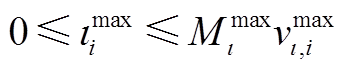 (A31)
(A31)
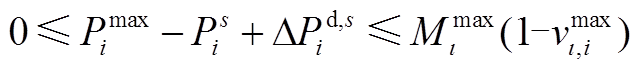 (A32)
(A32)
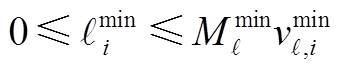 (A33)
(A33)
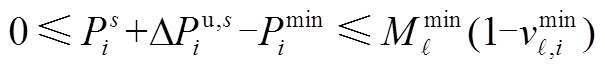 (A34)
(A34)
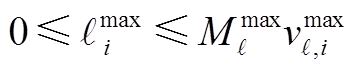 (A35)
(A35)
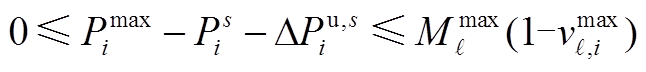 (A36)
(A36)
式(A14)~式(A36)为转换后的整体模型,对应正文式(38)~式(40),该模型为混合整数二阶锥规划模型,可借助Mosek求解器直接求解。
参考文献
[1] 姜海洋, 杜尔顺, 朱桂萍, 等. 面向高比例可再生能源电力系统的季节性储能综述与展望[J]. 电力系统自动化, 2020, 44(19): 194-207. Jiang Haiyang, Du Ershun, Zhu Guiping, et al. Review and prospect of seasonal energy storage for power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2020, 44(19): 194-207.
[2] 周博, 艾小猛, 方家琨, 等. 计及超分辨率风电出力不确定性的连续时间鲁棒机组组合[J]. 电工技术学报, 2021, 36(7): 1456-1467. Zhou Bo, Ai Xiaomeng, Fang Jiakun, et al. Continuous-time modeling based robust unit commitment considering beyond-the-resolution wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1456-1467.
[3] 麻秀范, 王戈, 朱思嘉, 等. 计及风电消纳与发电集团利益的日前协调优化调度[J]. 电工技术学报, 2021, 36(3): 579-587. Ma Xiufan, Wang Ge, Zhu Sijia, et al. Coordinated day-ahead optimal dispatch considering wind power consumption and the benefits of power generation group[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 579-587.
[4] 陈厚合, 李国庆, 张芳晶. 风电并网系统区域间概率可用输电能力计算[J]. 电力系统保护与控制, 2014, 42(21): 59-65.Chen Houhe, Li Guoqing, Zhang Fangjing. Calculation of probabilistic available transfer capability of wind farm incorporated system[J]. Power System Protection and Control, 2014, 42(21): 59-65.
[5] 白浩, 于力, 姜臻, 等. 考虑售电侧放开后的配电网供电能力计算方法[J]. 电力系统保护与控制, 2020, 48(10): 99-105. Bai Hao, Yu Li, Jiang Zhen, et al. Calculation method of power supply capacity of a distribution network considering the opening of power sale side[J]. Power System Protection and Control, 2020, 48(10): 99-105.
[6] 王艳玲, 韩学山, 周晓峰. 基于扩展潮流的输电断面最大传输能力[J]. 电力系统保护与控制, 2011, 39(13): 20-24, 31. Wang Yanling, Han Xueshan, Zhou Xiaofeng. The total transfer capability of cross-section of transmission line based on expanded power flow[J]. Power System Protection and Control, 2011, 39(13): 20-24, 31.
[7] 杨海涛, 江晶晶, 赵敏, 等. 基于模型预测控制的区域综合能源系统运行优化方法[J]. 电气技术, 2022, 23(4): 7-13. Yang Haitao, Jiang Jingjing, Zhao Min, et al. Operational optimization method of regional integrated energy system based on model predictive control[J]. Electrical Engineering, 2022, 23(4): 7-13.
[8] 王晨旭, 唐飞, 刘涤尘, 等. 基于双层代理模型的概率-区间潮流计算及灵敏度分析[J]. 电工技术学报, 2022, 37(5): 1181-1193. Wang Chenxu, Tang Fei, Liu Dichen, et al. Probabilistic-interval power flow and sensitivity analysis using double layer surrogate method[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1181-1193.
[9] 孙鑫, 王博, 陈金富, 等. 基于稀疏多项式混沌展开的可用输电能力不确定性量化分析[J]. 中国电机工程学报, 2019, 39(10): 2904-2914. Sun Xin, Wang Bo, Chen Jinfu, et al. Sparse polynomial chaos expansion based uncertainty quantification for available transfer capability[J]. Proceedings of the CSEE, 2019, 39(10): 2904-2914.
[10] 李锴, 党杰, 孙鑫, 等. 计及风电功率不确定性的电力系统输电可靠性裕度快速评估[J]. 电网技术, 2019, 43(9): 3337-3343. Li Kai, Dang Jie, Sun Xin, et al. Fast evaluation of transmission reliability margin of power systems considering wind power uncertainty[J]. Power System Technology, 2019, 43(9): 3337-3343.
[11] Kou Xiao, Li Fangxing. Interval optimization for available transfer capability evaluation considering wind power uncertainty[J]. IEEE Transactions on Sustainable Energy, 2020, 11(1): 250-259.
[12] 罗钢, 石东源, 蔡德福, 等. 计及相关性的含风电场电力系统概率可用输电能力快速计算[J]. 中国电机工程学报, 2014, 34(7): 1024-1032. Luo Gang, Shi Dongyuan, Cai Defu, et al. Fast calculation of probabilistic available transfer capability considering correlation in wind power integrated systems[J]. Proceedings of the CSEE, 2014, 34(7): 1024-1032.
[13] Chen Houhe, Fang Xin, Zhang Rufeng, et al. Available transfer capability evaluation in a deregulated electricity market considering correlated wind power[J]. IET Generation, Transmission & Distribution, 2018, 12(1): 53-61.
[14] 田园, 汪可友, 李国杰, 等. 计及风电相关性的二阶锥动态随机最优潮流[J]. 电力系统自动化, 2018, 42(5): 41-47. Tian Yuan, Wang Keyou, Li Guojie, et al. Dynamic stochastic optimal power flow based on second-order cone programming considering wind power correlation[J]. Automation of Electric Power Systems, 2018, 42(5): 41-47.
[15] 惠鑫欣. 计及风速时空相关性的风电并网系统可用输电能力计算[D]. 吉林: 东北电力大学, 2018.
[16] 郑义, 白晓清, 苏向阳. 考虑风电不确定性的Φ-散度下基于条件风险价值的鲁棒动态经济调度[J]. 电力自动化设备, 2021, 41(2): 63-70. Zheng Yi, Bai Xiaoqing, Su Xiangyang. Robust dynamic economic dispatch considering uncertainty of wind power based on conditional value-at-risk under Φ-divergence[J]. Electric Power Automation Equipment, 2021, 41(2): 63-70.
[17] 蒋海峰, 张曼. 基于混合半云模型的相关性风速及风电场并网可靠性分析[J]. 电力系统自动化, 2020, 44(22): 127-133. Jiang Haifeng, Zhang Man. Analysis on correlation-based wind speed based on mixed half-cloud model and grid-connection reliability of wind farm[J]. Automation of Electric Power Systems, 2020, 44(22): 127-133.
[18] 马然, 栗文义, 齐咏生. 风电机组健康状态预测中异常数据在线清洗[J]. 电工技术学报, 2021, 36(10): 2127-2139. Ma Ran, Li Wenyi, Qi Yongsheng. Online cleaning of abnormal data for the prediction of wind turbine health condition[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2127-2139.
[19] Tefera K, Tripathy P, Adda R. Electromagnetic and mechanical stress analysis of wind-driven synchronous reluctance generator[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(1): 107-114.
[20] Carrion M, Philpott A B, Conejo A J, et al. A stochastic programming approach to electric energy procurement for large consumers[J]. IEEE Transactions on Power Systems, 2007, 22(2): 744-754.
[21] Baradar M, Hesamzadeh M R, Ghandhari M. Second-order cone programming for optimal power flow in VSC-type AC-DC grids[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4282-4291.
[22] 张迪, 苗世洪, 周宁, 等. 分布式发电市场化环境下各交易主体响应行为模型[J]. 电工技术学报, 2020, 35(15): 3327-3340. Zhang Di, Miao Shihong, Zhou Ning, et al. Research on response behavior model of trading entities considering the marketization environment of distributed generation[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3327-3340.
[23] Li Fangxing, Bo Rui. DCOPF-based LMP simulation: algorithm, comparison with ACOPF, and sensitivity[J]. IEEE Transactions on Power Systems, 2007, 22(4): 1475-1485.
[24] 王思聪. 中国海陆风电成本研究[J]. 宏观经济研究, 2019(8): 170-175. Wang Sicong. A study on onshore and offshore wind power cost in China[J]. Macroeconomics, 2019(8): 170-175.
[25] 张儒峰, 姜涛, 李国庆, 等. 考虑电转气消纳风电的电-气综合能源系统双层优化调度[J]. 中国电机工程学报, 2018, 38(19): 5668-5678, 5924. Zhang Rufeng, Jiang Tao, Li Guoqing, et al. Bi-level optimization dispatch of integrated electricity-natural gas systems considering P2G for wind power accommodation[J]. Proceedings of the CSEE, 2018, 38(19): 5668-5678, 5924.
Abstract To consider the impact of wind power output forecasting errors on the assessment of available transfer capability (ATC), this paper proposes a probabilistic ATC assessment method of power system considering wind power correlation and conditional value-at-risk (CVaR).
First of all, the correlation coefficient between wind farms is calculated through the historical wind power output data, and the correlation coefficient matrix among wind farms is obtained. Then, the probability distribution and Copula function of wind farm output prediction are used to construct a probability model of wind power output prediction error considering spatial correlation. According to the wind power output forecast error data and wind farm output prediction value that meet the correlation of actual wind farm output, the output prediction of wind farm is corrected, and then the revised wind power output forecast is used as the input for calculating interregional ATC.
After that, this paper proposes a bi-level optimal model considering the correlation of wind power output and CVaR for probabilistic ATC assessment. The lower level model aims to minimize the generation cost and risk under the base state. The upper level model aims at maximizing inter-regional ATC by taking power output under base state and extreme state as the interaction information between the upper and lower level models. On this basis, the Karush-Kuhn-Tucker (KKT) optimal conditions are used and the bi-level model is converted into a mathematical program with equilibrium constraints (MPEC) model. The MPEC model is further transformed into a mixed integer second-order cone programming form, and then the probabilistic ATC can be solved.
Finally, the PJM-5 bus test system and Jilin Western Power Grid are used to analyze the example. In the PJM-5 bus test system, when the confidence level is taken by 90%, as the correlation coefficient increases from 0.5 to 0.9, the correlation of wind farm output gradually increases, and the inter-regional probability ATC expectation first increases and then decreases; when the confidence level is taken at 70%, the inter-regional probability ATC expectation gradually decreases with the increase of the correlation coefficient, and the wind power prediction error scenarios under different correlation coefficients are different, resulting in different output of each generator set in the ground state, which in turn affects the probability ATC expectation. In the actual system of Jilin Western Power Grid, it can also be seen that the correlation coefficient and confidence level of wind power forecast error have an impact on the probability ATC expectation. It can be seen that in the ATC evaluation process of power system with a high proportion of wind power, it is necessary to consider the confidence level of total power generation cost and the influence of wind farm correlation on the ATC evaluation results.
The proposed wind power prediction error correlation modeling method corrects the wind farm output prediction value by obtaining the wind power output prediction error that conforms to the actual wind farm correlation. In the process of evaluating ATC, the confidence level should be reasonably set, and the prediction error caused by the uncertainty of wind power output should be reduced by taking into account the correlation of wind power forecast error, the risk cost of system operation should be reduced, and the calculation accuracy of ATC between regions should be improved.
Keywords:Available transfer capability, wind power output correlation, conditional value-at-risk, bi-level optimal model
DOI:10.19595/j.cnki.1000-6753.tces.220725
中图分类号:TM73
吉林省自然科学基金资助项目(YDZJ202101ZYTS194)。
收稿日期 2022-05-04
改稿日期 2022-07-18
李 雪 女,1986年生,博士,教授,博士生导师,研究方向为电力系统安全性与稳定性、电力系统高性能计算、电力市场。E-mail: xli@neepu.edu.cn
张儒峰 男,1990年生,博士,教授,硕士生导师,研究方向为综合能源系统分析与优化运行。E-mail: zhangrufeng@neepu.edu.cn(通信作者)
(编辑 赫蕾)