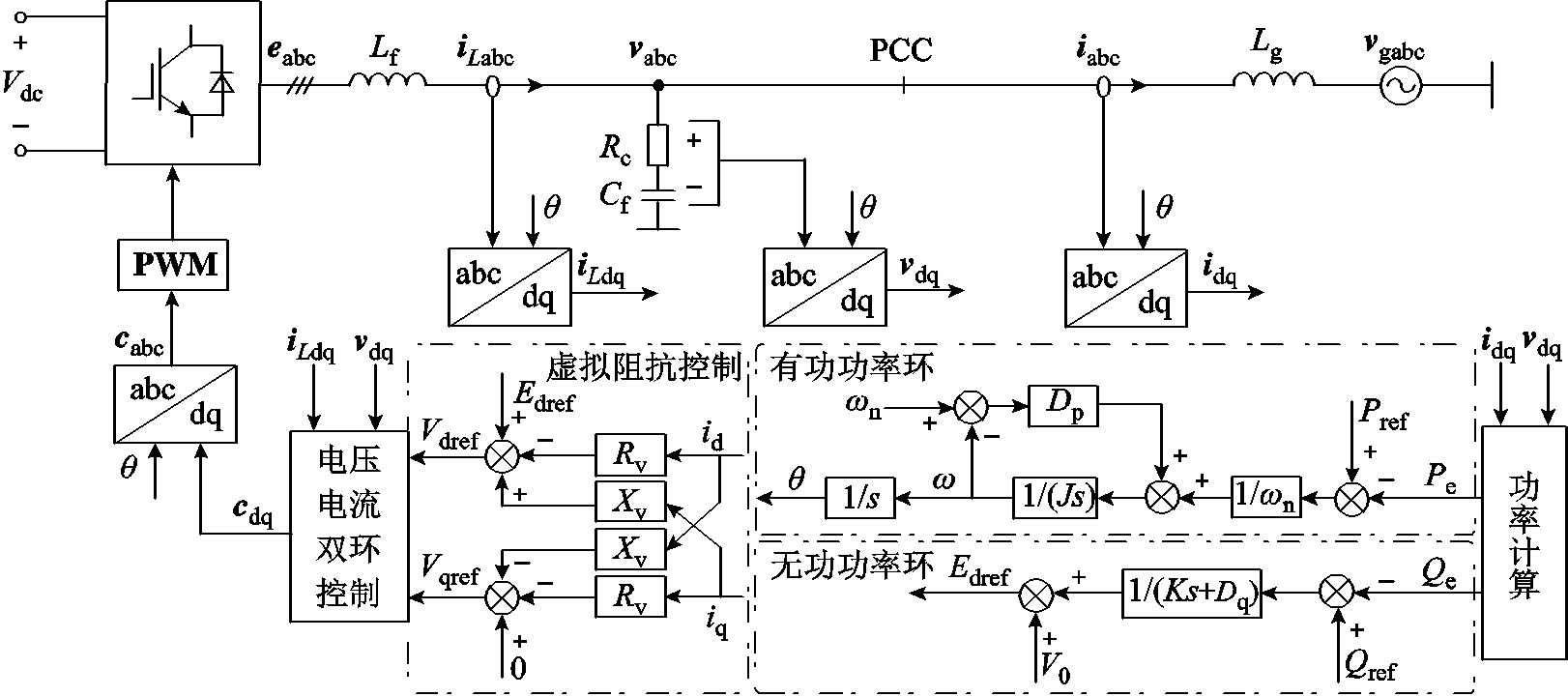
图1 VSG主电路拓扑及控制框图
Fig.1 Main circuit topology and control block diagram of VSG
摘要 在分布式发电高渗透率的微电网中,虚拟同步发电机(VSG)因可提供必要的频率和电压支撑而被广泛关注,其并网稳定性研究已成为热点问题。该文首先在获得VSG输出序阻抗矩阵的基础上,通过建立单输入单输出(SISO)等效模型,并结合Nyquist准则对VSG进行并网稳定性分析;然后,针对正负序之间存在的频率耦合现象,基于所建SISO等效序阻抗模型,对比分析了考虑频率耦合效应前后的VSG输出阻抗特性,揭示了频率耦合效应对VSG并网稳定性的影响机理,以及造成VSG并入强电网失稳的根本原因;最后,在上述机理分析的基础上,提出一种用于提升系统稳定性的虚拟阻抗简化设计方法,该方法从提升系统的幅值裕度的角度出发,直接利用SISO等效输出阻抗与电网阻抗二者的交互关系实现虚拟阻抗的定量计算,简化了虚拟阻抗的设计过程。仿真结果验证了稳定性分析的正确性以及虚拟阻抗设计方法的有效性。
关键词:虚拟同步发电机 SISO等效序阻抗模型 频率耦合效应 稳定性分析 虚拟阻抗设计
虚拟同步发电机[1-2](Virtual Synchronous Generator, VSG)通过引入有功-频率和无功-电压控制来模拟传统同步发电机的外部特性,可为分布式发电高渗透率的微电网提供必要的频率和电压支撑[3],是一种友好的新能源发电并网手段。近年来,VSG的并网稳定性引起了国内外学者的广泛兴趣,所涉及的VSG输出阻抗建模、稳定性分析、稳定性改善控制策略等诸多问题亟需开展系统且深入的研究。
目前,VSG并网稳定性的分析方法主要有状态空间法[4]和阻抗分析法[5]两种。状态空间法将电源和负载视为整体,统一建立状态方程,并通过特征值轨迹来判定系统稳定性[6]。由于该方法主要依靠数学模型,故在其基础上进行稳定性改善控制存在一定困难。阻抗分析法最初源于DC-DC变换器系统的控制器设计[7],后被广泛应用于并网稳定性问题的研究[8-12]。与状态空间法相比,阻抗分析法物理意义更加明确,控制器设计与实现也更为方便。阻抗分析法通常是将逆变器和电网视作两个系统,分别用戴维南或诺顿等效电路来描述其各自的外部特性[8],然后结合电网络和控制理论对该互联系统进行稳定性分析。2019年,文献[9]率先将阻抗分析法应用于电压型和电流型VSG的并网稳定性分析,但为了简化分析,忽略了内环控制和频率耦合效应。文献[10]建立了考虑电压电流内环的VSG序阻抗模型,但是由于没有考虑频率耦合效应,导致50Hz附近阻抗测量值和理论值存在一定偏差;文献[11]建立了考虑频率耦合的VSG序阻抗模型,对比频率耦合效应对VSG稳定性分析结果的影响,指出频率耦合效应在稳定性分析中不应被忽略。频率耦合效应表现为并网逆变器正负序阻抗之间的耦合作用,相应的输出阻抗将是一个二阶非对角矩阵[12]。针对该多输入多输出(Multi-Input and Multi-Output, MIMO)系统,其稳定性判断多采用基于回率矩阵[13]或回差矩阵[14]的广义Nyquist准则(Generalized Nyquist Criterion, GNC)。文献[6]依据回率矩阵特征值的两条Nyquist曲线对并网逆变器的稳定性进行了分析,但由于涉及矩阵的特征值计算,过程较为复杂。文献[15]提出一种基于回差矩阵行列式的Bode图来判断系统稳定性的方法,有助于简单直观地获取复杂互联系统的稳定性情况。但由于回率或回差矩阵判稳的方法均无法实现正负序解耦,因此在其基础上进行稳定性控制设计存在一定困难。为简化稳定性分析过程,文献[16]提出一种将MIMO系统dq阻抗模型转换为单输入单输出(Single Input and Single Output, SISO)系统等效序阻抗模型的方法,并证明了该SISO模型具有与MIMO模型相同的临界稳定条件。基于相同原理,文献[17]分析了跟网型逆变器与电网之间的交互稳定性,并对比了考虑频率耦合效应前后系统稳定性分析结果的差别。文献[18]应用该方法对构网型逆变器VSG的并网稳定性进行研究,并从阻抗交互的角度讨论了考虑和忽略频率耦合效应对系统相位裕度的影响。但以上研究尚未指明造成VSG并入强电网失稳的根本原因,关于频率耦合效应对VSG输出阻抗特性影响的机理分析仍有待深入,以便更有针对性地实现稳定控制器设计。
关于提升并网逆变器系统稳定性的方法,目前主要有虚拟阻抗[19]、有源阻尼[20-21]和电网电压前馈[22-23]等方法。其中虚拟阻抗具有重塑逆变器的输出阻抗[24]、减少功率耦合[25]、改善系统动态特性[26]和提高系统稳定性[27]的优点,因而被广泛应用于VSG控制。文献[25]通过引入虚拟电感以降低系统的功率耦合,并给出最佳解耦的物理解释,指出过大的虚拟电感值会恶化功率解耦性能,加剧电网无功功率不足,增加电压源变流器的容量需求。文献[28]提出了一种适合微电网在孤岛模式下稳定运行的VSG控制策略,在基本VSG控制器中加入虚拟阻抗环节,解决了非线性负载恶化微电网系统供电质量的问题,实现对微电网谐波的灵活抑制。文献[29]提出一种基于线路阻抗实时精确计算的VSG虚拟阻抗自适应算法,能自动平衡因线路阻抗不一致带来的功率不均衡和环流问题,使系统性能进一步提高。文献[11]通过加入虚拟阻抗,提升了VSG正序阻抗的幅值和相位,增强了系统的稳定性,但没有给出虚拟阻抗的设计方法。文献[30]从提升相位裕度角度出发,提出一种基于稳定性约束的虚拟阻抗最小值的计算方法,但该方法需要通过循环迭代求取耦合频段内VSG正序阻抗的最大值,过程较为复杂。总体而言,现有用于改善VSG并网稳定性的虚拟阻抗的设计方法并未充分利用VSG输出阻抗的特性及其与电网阻抗的交互特性,仍有进一步简化的空间。
根据上述问题,本文针对VSG并网稳定性及虚拟阻抗设计开展研究工作。首先,通过构建VSG的SISO等效序阻抗模型,采用传统的Nyquist准则对VSG并网稳定性进行分析。然后揭示了频率耦合效应对VSG并网稳定性的影响机理及造成VSG并入强电网失稳的根本原因。接着,基于上述机理分析结果,提出了一种用于提升VSG并网稳定性的虚拟电感定量设计方法。理论分析和仿真算例均表明,本文所提方法简单有效,并且对于不同电网阻抗和系统参数均具有很好的适用性。
鉴于SISO等效序阻抗模型物理意义明确,且具有正、负序可独立分析的优点,故本文以此为基础开展稳定性分析及稳定控制器设计。本节重点给出VSG输出序阻抗矩阵及其SISO等效模型的构建过程。
电压型VSG的电路拓扑及控制框图如图1所示[11]。图中Vdc为直流侧电压,由储能单元提供;ex、vx、vgx、iLx、ix分别为VSG内电动势、VSG输出电压、电网电压、滤波电感电流和并网电流,其中x=a、b、c,分别表示A,B,C三相;Lf、Cf、Rc分别为滤波电感、滤波电容和阻尼电阻;Lg为电网电感;Pe、Qe分别为VSG实际输出的有功功率和无功功率;Pref、Qref、V0、w、wn、q分别为有功功率指令值、无功功率指令值、VSG空载电动势、VSG输出角频率、额定角频率和VSG电角度;J、Dp、K、Dq分别为虚拟惯量、有功下垂系数、电压系数和无功下垂系数;Rv、Lv分别为虚拟电阻和虚拟电感。整个控制回路由功率外环、虚拟阻抗环和电压电流内环组成。

图1 VSG主电路拓扑及控制框图
Fig.1 Main circuit topology and control block diagram of VSG
逆变器的输出阻抗是阻抗分析法的前提,已有文献针对VSG的输出阻抗开展了相关研究[9]。考虑到文章的完整性,下面给出VSG输出阻抗矩阵公式的主要推导过程。公共耦合点(Point of Common Coupling, PCC)。
对于工频为f0的对称三相系统,当在PCC处注入频率为fp正序扰动电压时,VSG的输出电压和电流中将产生频率为fp的正序分量,同时还会产生与扰动频率相差二倍基频,即频率为fp-2f0的负序分量,这种现象被称作频率耦合效应[12]。为表述方便,在此统一对电压和电流的频域表达式进行定义。以A相为例,若采用符号X1、Xp和Xn分别表示VSG的输出电压va、输出电流ia和滤波电感电流iLa的基频分量、频率为fp的正序分量和频率为fp-2f0的负序分量,则它们频域表达式统一定义为
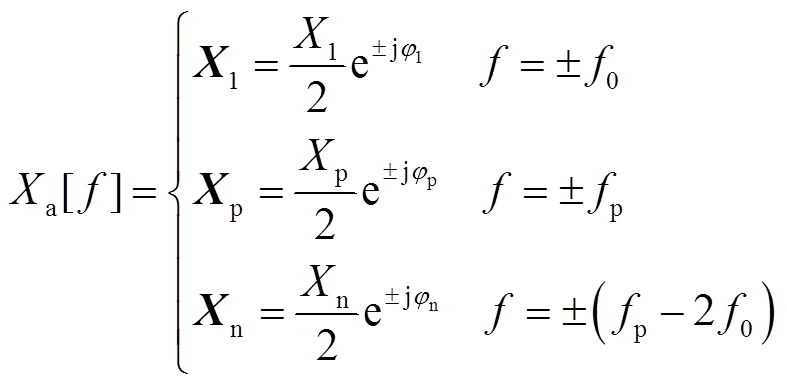 (1)
(1)
对VSG输出序阻抗的推导需综合考虑控制系统和物理系统的约束方程,下面将通过对各个控制环节及物理系统进行建模,推导出VSG的输出序阻抗解析公式。
1.2.1 功率环建模
功率外环控制框图如图1所示,其工作过程如下:首先基于瞬时功率理论对有功和无功进行计算,然后经低通滤波器Gf(s)消除高频分量后送入VSG控制环节,以得到VSG输出电压大小和相位的指令值[18]。当系统中同时含有正序和负序小扰动时,根据瞬时功率理论,可得到频域下有功和无功表达式为[9]
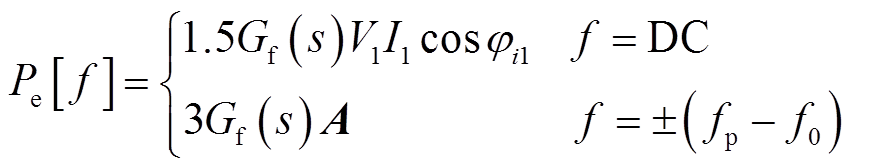 (2)
(2)
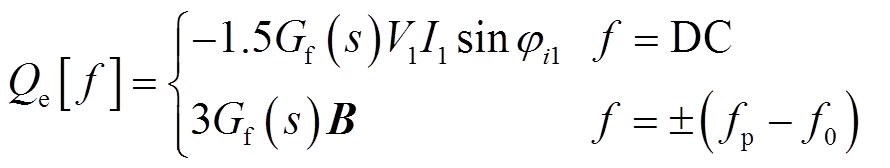 (3)
(3)
式中,Gf(s)为一阶低通滤波器的传递函数,Gf(s)= w1p/(s+w1p),w1p为截止频率;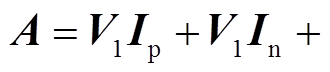
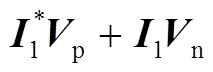 ;
;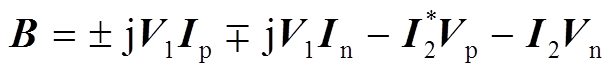 ;
;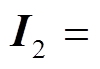
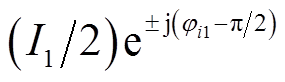 ;上标“*”表示共轭运算;V1、I1和ji1分别为基波电压、电流的幅值和基波电流的初相位。
;上标“*”表示共轭运算;V1、I1和ji1分别为基波电压、电流的幅值和基波电流的初相位。
结合式(2)、式(3)和图1中的有功功率-频率控制环及无功-电压控制环,可得VSG输出电压的相位q[f ]及其大小Edref [f]的频域表达式为
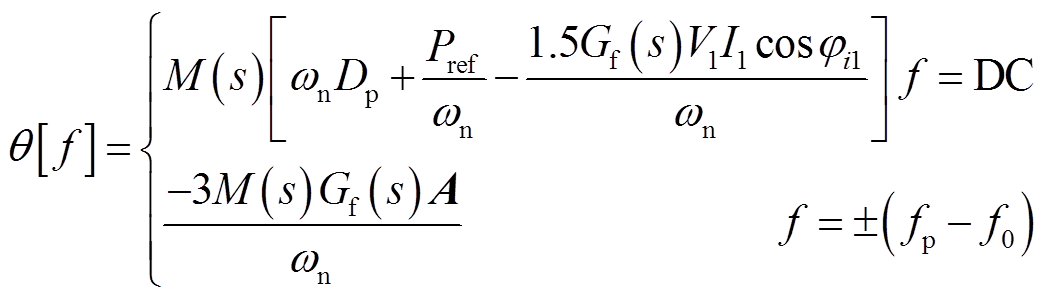 (4)
(4)
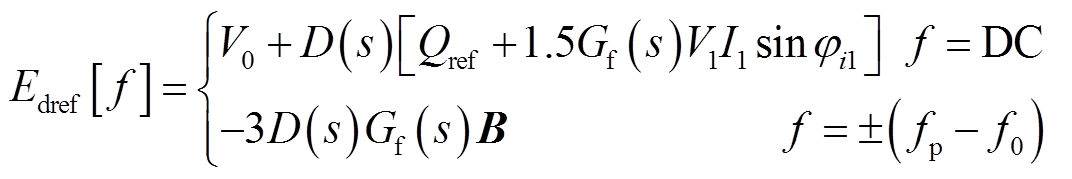 (5)
(5)
式中,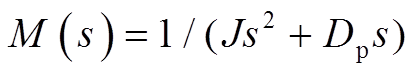 ;
;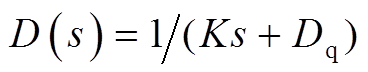 。
。
1.2.2 含虚拟阻抗的电压电流双环控制建模
通常在VSG控制中引入虚拟阻抗控制以实现有功和无功解耦,其控制框图示于图1之中,实现方式之一是通过输出电流在虚拟阻抗上的压降对电压参考值Edref加以矫正[18]。根据控制框图,加入虚拟阻抗后的电压参考值为
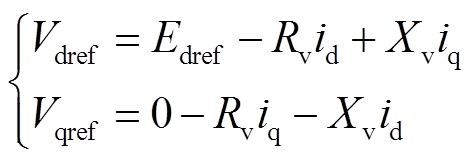 (6)
(6)
经对虚拟阻抗和电压、电流双环控制建模,可得dq坐标系下的调制波cdq的频域表达式,如式(7)和式(8)所示。
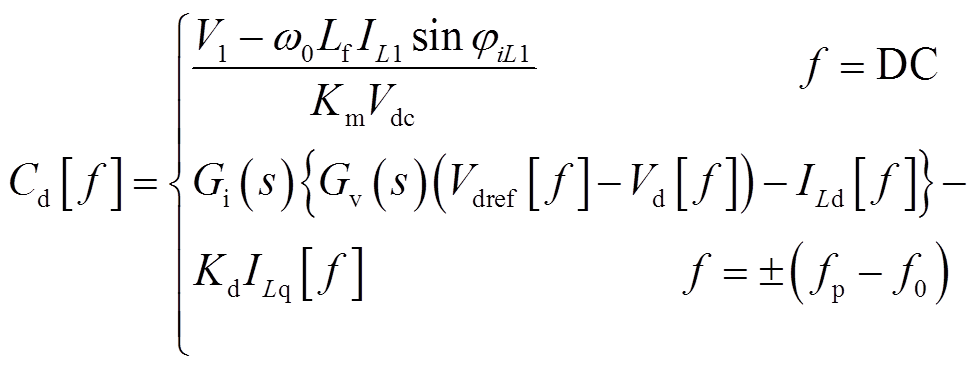 (7)
(7)
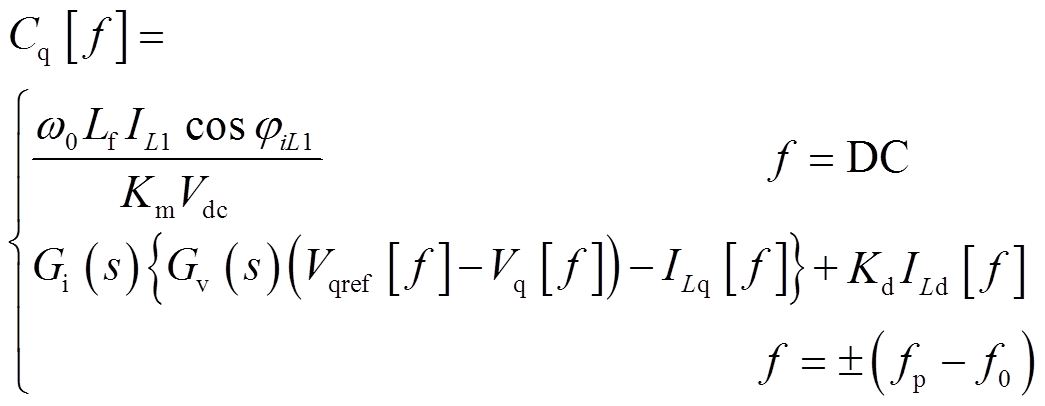 (8)
(8)
式中,Km为调制系数,Km=1/Vdc;Kd为电流环解耦系数,Kd=w0Lf;IL1和jiL1分别为基波滤波电感电流的幅值和初相位;Gv(s)和Gi(s)分别为电压外环和电流内环的PI调节器;Vd[f]、Vq[f]、Id[f]、Iq[f]和ILd[f]、ILq[f]分别为VSG输出电压、输出电流和滤波电感电流在dq坐标系下的频域表达式,具体示于附录式(A1)~式(A6)。
将式(6)代入式(7)、式(8),并经Park反变换,可得A相内电动势ea的频域表达式,见附录式(A7)。
1.2.3 VSG输出序阻抗矩阵建模
根据电路拓扑,可得主电路的谐波小信号模型为[18]
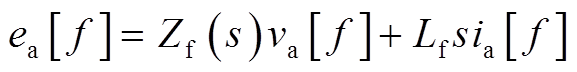 (9)
(9)
式中,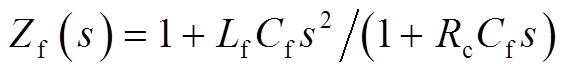 。
。
将附录式(A7)和式(1)代入式(9),经整理可得VSG输出序阻抗矩阵为
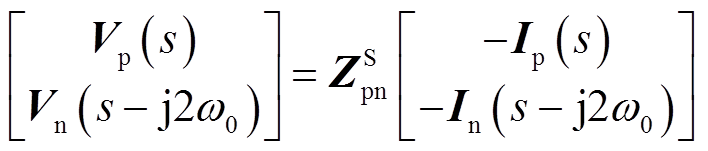 (10)
(10)
其中
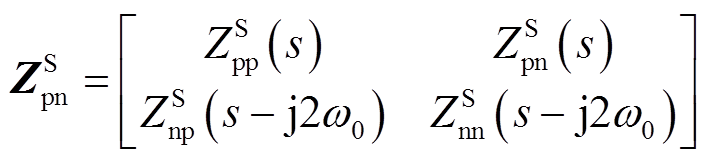
式中,矩阵中各元素表达式详见附录式(A8)~式(A12)。可见,VSG输出序阻抗矩阵的非对角元素不为0,说明正负序之间存在频率耦合,因此VSG属于非镜像解耦系统[31]。
1.2.4 SISO等效序阻抗模型
图1的VSG并网系统可视为图2所示的互联网络,其中含上标“S”的变量代表其位于VSG侧,含上标“L”的变量代表其位于电网侧;下标“p”和“n”分别代表正序和负序分量。uinj为注入的电压扰动,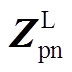 为电网输入阻抗。由于电网为镜像解耦系统[31],即正负序间不存在频率耦合,故其仅为一个二阶对角阵,且两对角元素相等,同为sLg。
为电网输入阻抗。由于电网为镜像解耦系统[31],即正负序间不存在频率耦合,故其仅为一个二阶对角阵,且两对角元素相等,同为sLg。
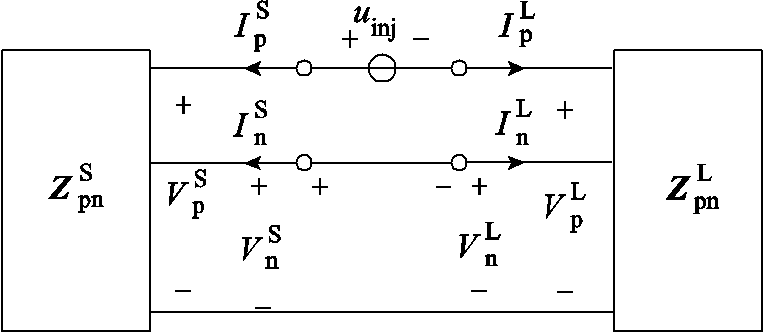
图2 VSG和电网等效双口网络
Fig.2 Equivalent dual-port network of VSG and grid
将VSG侧各序电压与电流的比值定义为正序输出阻抗Zppseries和负序输出阻抗Znnseries,可推得其表达式为
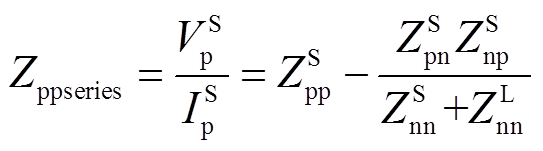 (11)
(11)
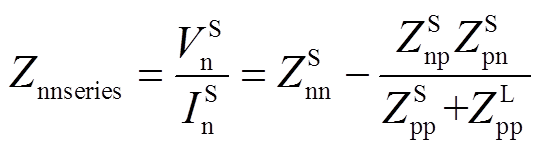 (12)
(12)
由式(11)和式(12)可以看出,通过将表征频率耦合效应的Zpn和Znp归算到VSG的输出序阻抗中,可将MIMO模型转换为SISO等效模型[16],因此仍可利用传统的Nyquist准则分析系统的稳定性。
为了验证SISO等效序阻抗模型的准确性,在Matlab/Simulink中搭建了仿真模型,其中系统参数见附表1。采用扫频法获得的VSG的SISO等效序阻抗频率特性曲线如图3所示,图中同时给出了式(11)和式(12)的理论计算结果。通过对比可以看出二者吻合得良好,验证了SISO等效序阻抗模型的正确性。
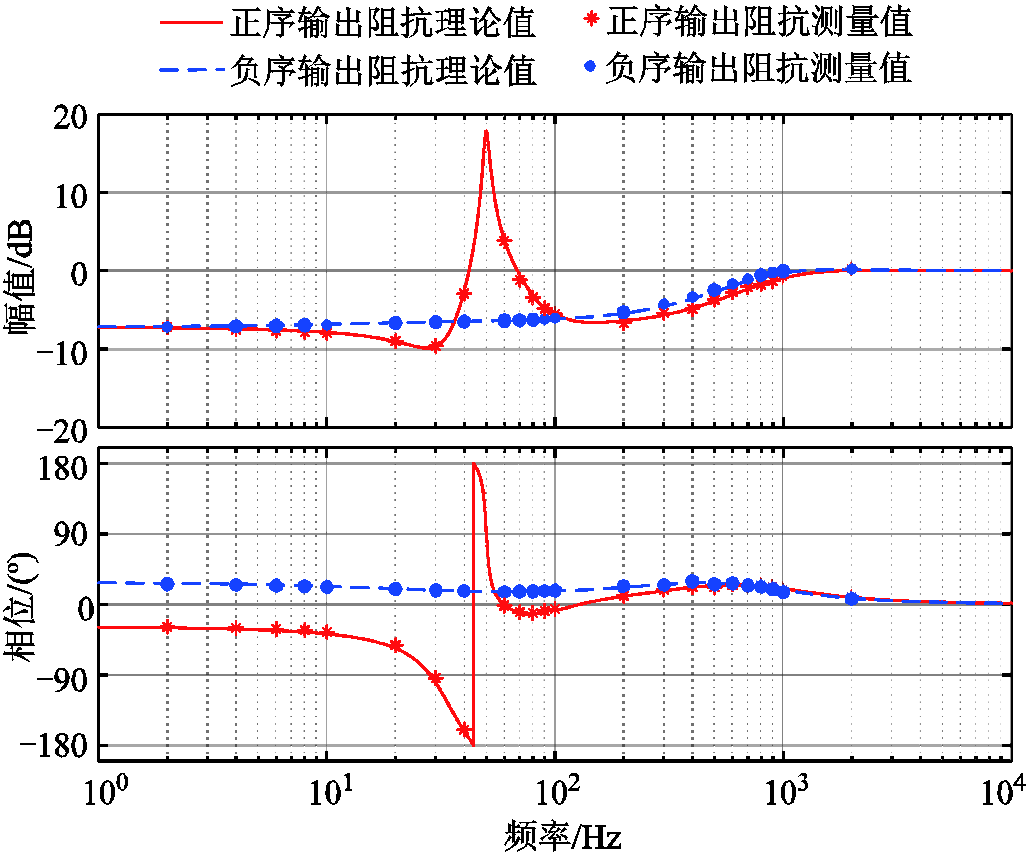
图3 SISO等效序阻抗的理论曲线和仿真结果
Fig.3 Theoretical curves and simulation results of SISO equivalent sequence impedance
相比于跟网型逆变器,电压控制型VSG在连接弱电网时体现出更好的并网稳定性,这源于其独特的输出阻抗特性,但频率耦合效应对输出阻抗的影响机理分析仍需要进一步完善。本节将通过对VSG并网系统稳定性的分析和频率耦合效应对正序输出阻抗的影响的讨论,揭示导致VSG并入强电网失稳的根本原因,并为后续稳定控制器提供设计依据。
由于电压控制型VSG对外视为电压源,故可将VSG的输出阻抗与电网阻抗之比视为开环传递函数进行稳定性分析[8]。相应地,基于SISO等效序阻抗模型的正序阻抗比IRvsgvp(s)和负序阻抗比IRvsgvn(s)计算公式分别为
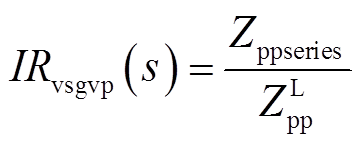 (13)
(13)
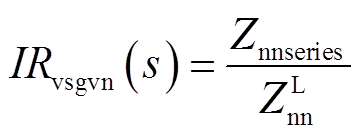 (14)
(14)
传统的Nyquist判稳准则可描述为
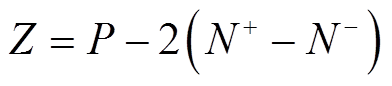 (15)
(15)
式中,P为上述阻抗比在右半平面的极点数;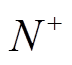 和
和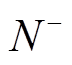 分别为阻抗比的正频率Nyquist曲线在(-1, j0)点左侧正穿越(逆时针)和负穿越(顺时针)的次数;Z为闭环传递函数在右半平面的极点数。当且仅当正、负序阻抗比都满足Nyquist判稳准则时,VSG与电网交互的系统才是稳定的。Nyquist曲线与单位圆相交的频率即系统的截止频率,与单位圆相交的位置决定了系统的相位裕度。对于具有两个或多个截止频率的条件稳定系统,相位裕度应由最高的截止频率决定[32]。
分别为阻抗比的正频率Nyquist曲线在(-1, j0)点左侧正穿越(逆时针)和负穿越(顺时针)的次数;Z为闭环传递函数在右半平面的极点数。当且仅当正、负序阻抗比都满足Nyquist判稳准则时,VSG与电网交互的系统才是稳定的。Nyquist曲线与单位圆相交的频率即系统的截止频率,与单位圆相交的位置决定了系统的相位裕度。对于具有两个或多个截止频率的条件稳定系统,相位裕度应由最高的截止频率决定[32]。
为了验证SISO等效序阻抗模型的正确性,本节针对VSG并入不同强度的电网进行稳定性分析。电网强度的划分可通过系统的短路比(Short Circuit Ratio, SCR)来描述[33]。一般来说,SCR超过20~25为强电网,SCR低于6~10为弱电网,SCR低于2为极弱电网。仿真算例中分别选取电网阻抗为0.7 mH(SCR=22)、1.916 6 mH(SCR=8.04)、3 mH(SCR=5.14)、8.5 mH(SCR=1.81)四种工况进行稳定性分析。
以附表1的额定工况为例,考虑和忽略频率耦合效应下的正负序阻抗比的Bode图如图4所示。可以看出,当频率趋近于+∞时,正、负序阻抗比的幅值均趋近于0,相位趋于-90°,这是因为二者的分母均比分子高一阶。需要说明的是,如果开环传递函数分子和分母的阶数不相等,在绘制Nyquist曲线时,还有必要补全ω→∞过程中与s平面闭合曲线Γs沿顺时针方向的1/4圆所对应的Nyquist轨迹段[34]。与该段轨迹对应的Bode图补线绘于图4中,可见当频率从+∞变化至∞的过程中,阻抗角将从-90°增加至0°,这说明所补充的Nyquist轨迹段不会穿越负实轴,对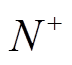 和
和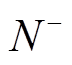 的数值没有影响,因此在后续稳定性分析时,此段Nyquist轨迹无需考虑。
的数值没有影响,因此在后续稳定性分析时,此段Nyquist轨迹无需考虑。
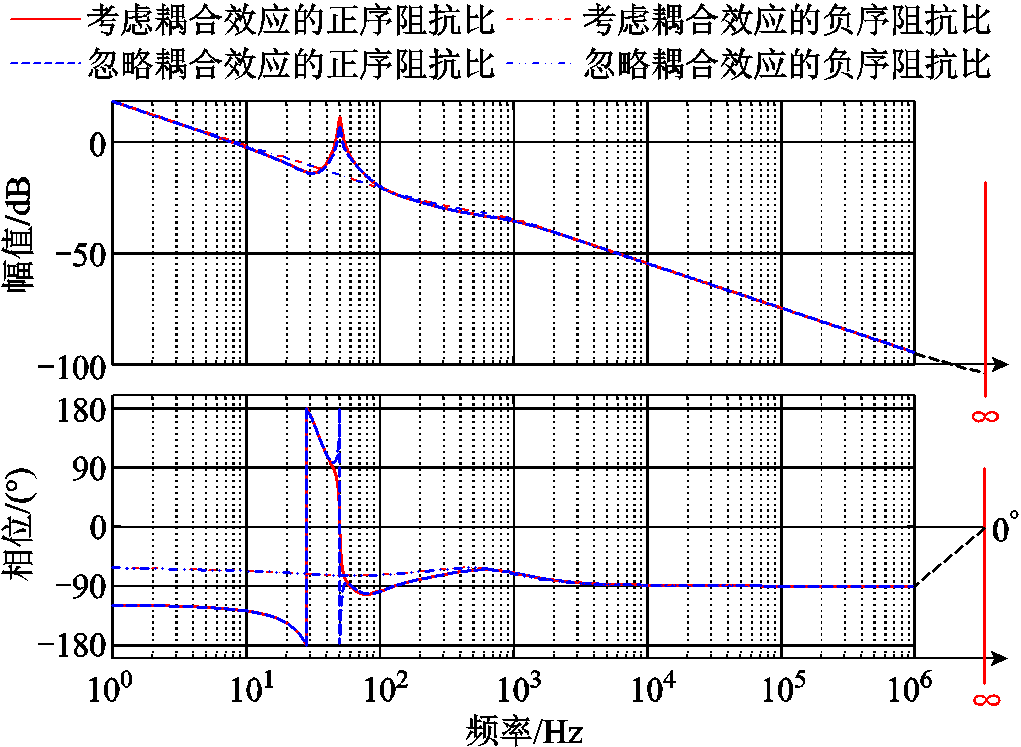
图4 正负序阻抗比的Bode图
Fig.4 Bode plots of IRvsgvp(s) and IRvsgvn(s)
上述四种工况下正负序阻抗比的正频率Nyquist曲线如图5所示,其中系统参数见附表1。由于无论是否计及频率耦合效应,正、负序输出阻抗均不存在右半平面极点,因此根据式(13)和式(14)可知,IRvsgvp(s)和IRvsgvn(s)也不含有右半平面极点,即P=0。将P=0代入式(15)可知,当且仅当IRvsgvp(s)和IRvsgvn(s)二者的正频率Nyquist曲线在(-1, j0)点左侧正、负穿越次数均相等时,系统才是稳定的。
考虑频率耦合效应时,VSG接入不同强度电网下的IRvsgvp(s)和IRvsgvn(s)的正频率Nyquist曲线如图5a所示。对于负序阻抗比IRvsgvn(s),其正频率Nyquist曲线始终不会穿越负实轴,说明负序系统始终处于稳定状态。其原因可结合图3予以解释,对于负序输出阻抗Znnseries,其阻抗角一直处于[-90°, 90°],为一无源阻抗,因此,其与电网阻抗相串联将始终保持稳定,这说明在VSG的稳定性分析时,仅需关注正序系统的稳定性问题。观察正序阻抗比IRvsgvp(s)的正频率Nyquist曲线可知,随着电网阻抗的减小,IRvsgvp(s)的正频率Nyquist曲线在穿越负实轴时从(-1, j0)点右侧逐渐向左移动,这意味着正序系统的稳定裕度逐渐减小。当电网阻抗减小至约1.916 6 mH时,IRvsgvp(s)的正频率Nyquist曲线将恰好负穿越(-1, j0)点两次,此即为正序系统的临界失稳状态。两次负穿越对应的频率分别为27.8 Hz和 72.2 Hz(二者之和为100 Hz,互为耦合频率),意味着系统中将会出现这两个频率的振荡。以上分析表明,随着电网强度增加(电网阻抗的减小),VSG的并网稳定性将随之变差,这与跟网型逆变器的稳定性特点正好相反。
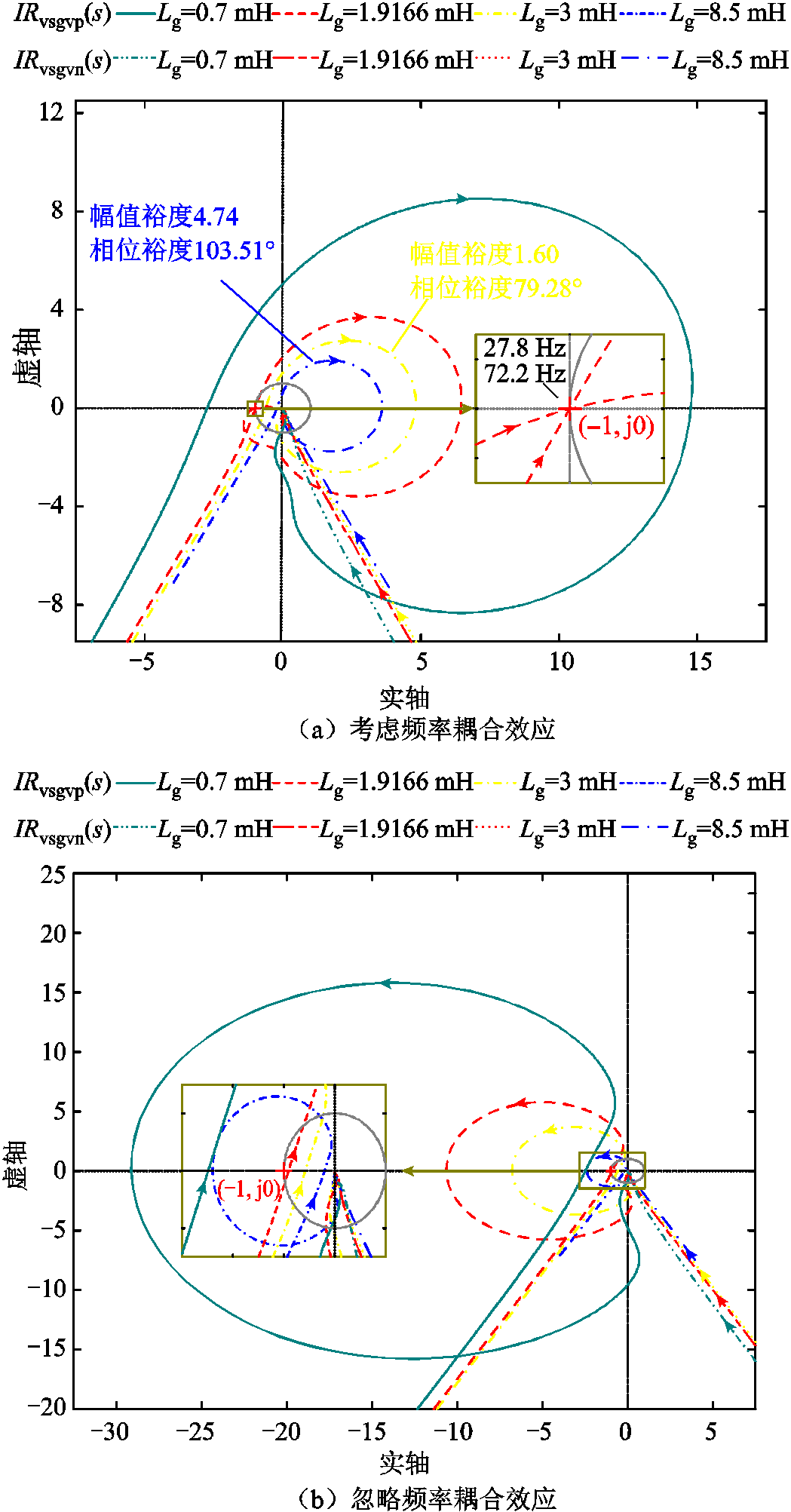
图5 不同工况下正负序阻抗比的正频率Nyquist曲线
Fig.5 Positive frequency Nyquist plots of IRvsgvp(s) and IRvsgvn(s) with different working conditions
图5b为忽略频率耦合效应时IRvsgvp(s)和IRvsgvn(s)的正频率Nyquist曲线,可以看出无论强电网还是弱电网,IRvsgvp(s)的正频率Nyquist曲线均存在两次穿越负实轴的情况,且正穿越点均位于(-1, j0)点左侧。随着电网阻抗减小,负穿越点会逐渐向(-1, j0)点左侧移动,当电网阻抗下降到0.7 mH时,Nyquist曲线在(-1, j0)左侧正负穿越各1次,系统才处于稳定状态。对于负序IRvsgvn(s),其正频率Nyquist曲线始终不穿越负实轴。
综合IRvsgvp(s)和IRvsgvn(s)二者分析结果可得,若忽略频率耦合效应,分析结果为电网强度越强系统越稳定,这一结论显然与考虑频率耦合效应的精SISO确判稳模型所得结果相悖。因此说明在VSG并网稳定性判断时必须计及正负序耦合,相关验证将在2.2节给出。
为了验证2.1节的分析结论,图6给出了电网电感Lg=1.916 6 mH(经2.1节分析后所得系统临界稳定下的电网电感值)时的并网电流波形,系统参数见附表1。以A相电流为例,取时间窗为0.5 s的时域波形进行频谱分析,所得结果如图7所示。可以看出,此种情况下系统失稳,且并网电流主要谐波频率为28 Hz和72 Hz,这与2.1节中得到的振荡频率非常接近,验证了基于SISO等效序阻抗模型的VSG并网稳定分析方法的正确性。
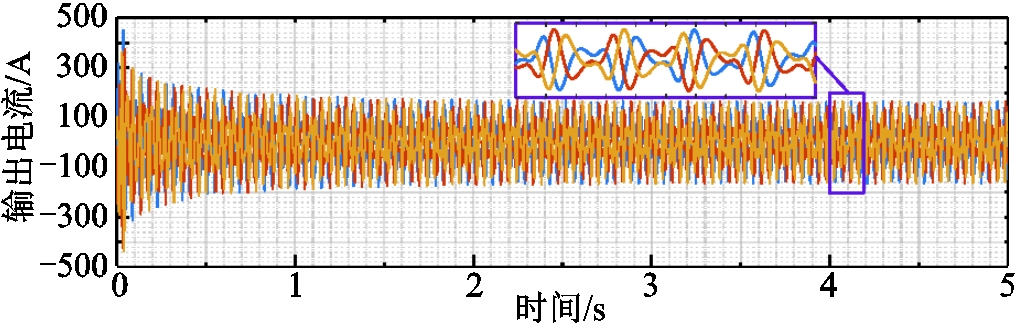
图6 VSG输出电流波形
Fig.6 Output current waveforms of VSG
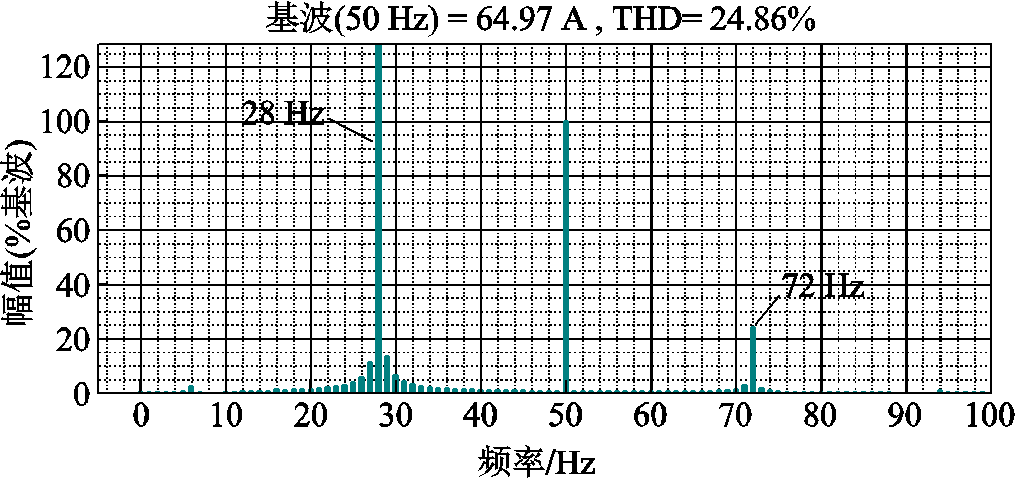
图7 A相输出电流FFT分析
Fig.7 FFT analysis of phase A output current
图8从有功功率角度展示了不同电网阻抗对系统稳定性的影响。从图8a可以看出,当电网阻抗为0.7 mH时,有功功率曲线振荡失稳;当电网阻抗增加到1.916 6 mH时,有功功率的时域波形如图8b所示,由于系统处于临界失稳状态,因此有功功率曲线呈现出等幅振荡特征;比较图8c和图8d可知,随着电网阻抗不断增大,有功功率动态响应逐渐从欠阻尼过渡到过阻尼状态,说明系统的稳定裕度逐渐增大,这也与图5a给出的幅值裕度和相位裕度变化规律相符。上述仿真结果均验证了2.1节理论分析的正确性。
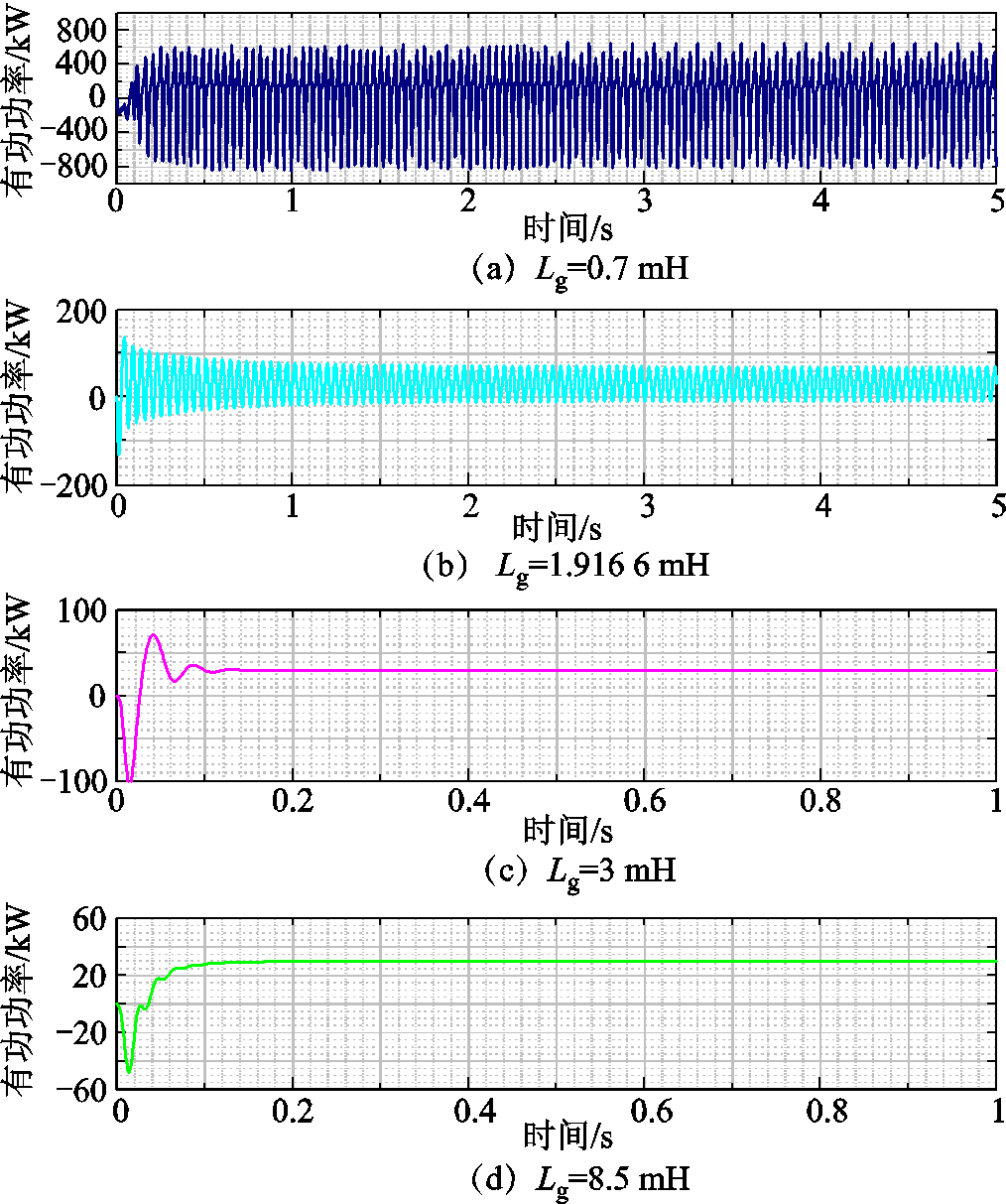
图8 不同电网阻抗下的有功功率曲线
Fig.8 Active power curves with different grid impedance
由2.1节的稳定性分析结果可知,正序系统的稳定性分析必须考虑频率耦合效应的影响。因此,为了进一步明确造成VSG并入强电网失稳的根本原因,本节通过对比分析考虑频率耦合前后的VSG正序输出阻抗特性,揭示频率耦合效应对VSG并网稳定性的影响机理,并为后续基于虚拟阻抗的稳定性控制器设计提供依据。
图9分别展示了在附表1的额定系统参数下,考虑频率耦合效应前后VSG正序阻抗Zpp和Zppseries,以及耦合项Zpn和Znp的频率特性。从图9b可以看出,Zpn在基频50 Hz附近存在尖峰幅值,而在其他频段处幅值非常小,因此频率耦合效应对正序阻抗的影响主要集中在基频附近。
定义频率耦合效应的影响频段为[f1, f2],从图9a中可以看出,忽略频率耦合效应时,正序阻抗Zpp在此频段内主要体现为容性特征,且在[f1, 50 Hz]频带表现为负阻容性,故容易在弱电网中引发振荡问题。而考虑频率耦合效应后,正序输出阻抗Zppseries在[f1, f2]频段内将由容性变为感性,具体见表1,其与电网的阻抗特性基本一致,因而在与感性弱电网互联时具有较好的稳定性。图5a和图5b的稳定性对比结果也验证了这一结论,故频率耦合效应在基频附近对正序阻抗的影响是导致VSG并入强电网失稳的根本原因,因此在稳定性分析中必须采用SISO精确模型。
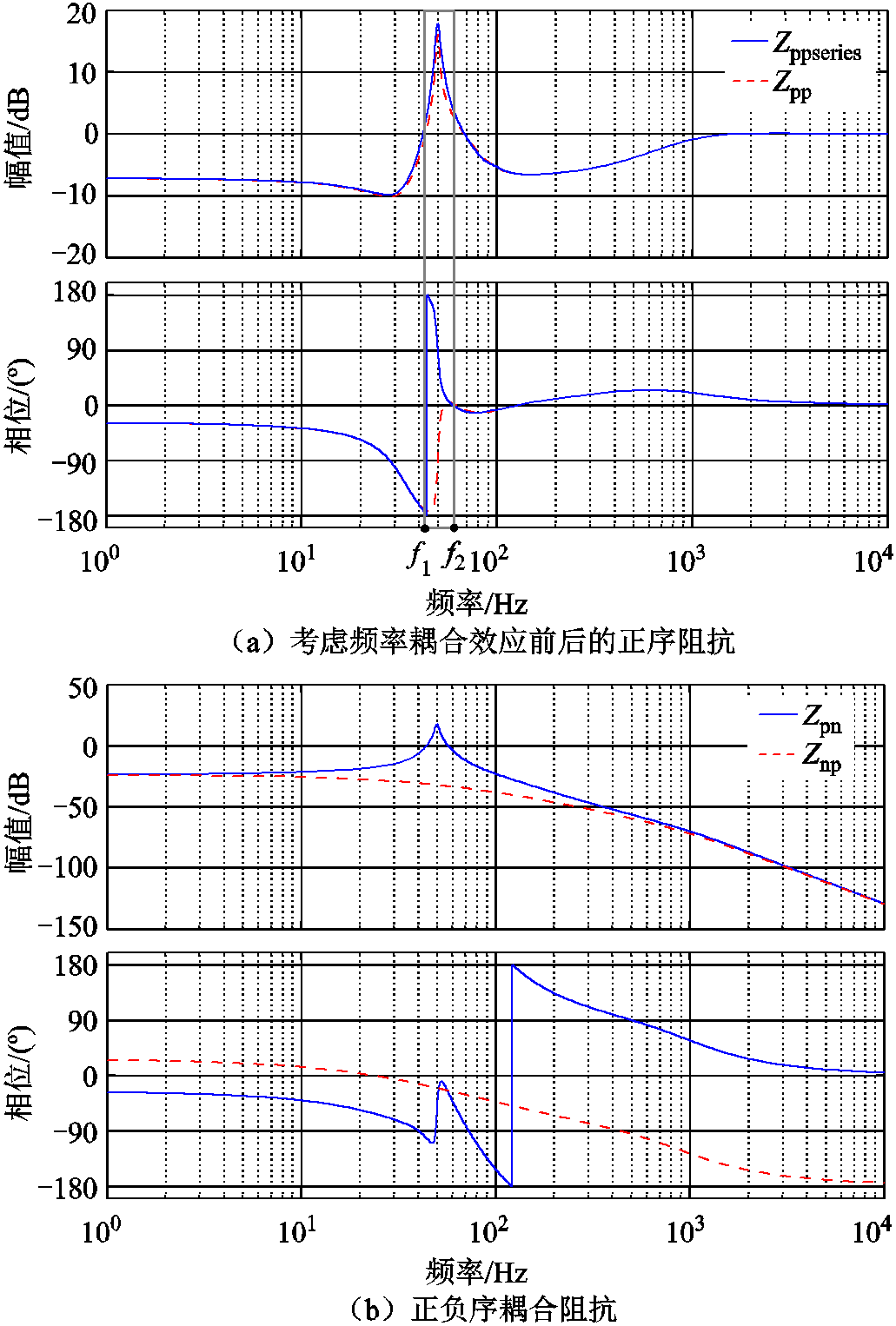
图9 VSG输出阻抗的Bode图
Fig.9 Bode plots of VSG output impedance
表1 频率耦合效应对正序阻抗特性的影响机理
Tab.1 The influence mechanism of frequency coupling effect on positive sequence impedance characteristics

频率耦合效应影响频段ZppZppseries [f1,50 Hz]负阻容性负阻感性 (50 Hz, f2]阻容性阻感性
下面进一步分析Zpp和Zppseries的阻抗特性对稳定性分析和虚拟阻抗设计的影响。由图9a可知,忽略频率耦合效应时,Zpp的相位两次穿越-90°,对应正序阻抗比IRvsgvp(s)的正频率Nyquist曲线正负穿越负实轴各一次。根据前文所述,由于IRvsgvp(s)没有右半平面极点,因此若要保证正序系统的稳定,则要求两次穿越需位于(-1, j0)点的同一侧。观察图9a可以发现,由于Zpp在正穿越负虚轴时具有很大的尖峰幅值,因此若要保证正序系统的稳定,应使电网阻抗的幅值在Zpp的相位两次穿越-90°时都位于Zpp以下,这意味电网阻抗越小,正序系统的稳定裕度越高。这一点与图5b给出的变化规律相符。而对于正序输出阻抗Zppseries,由于其相频曲线仅存在一个-90°穿越点,因此只要保证电网阻抗在穿越点处的幅值大于Zppseries,即可保证正序系统的稳定,即电网阻抗越大,系统的稳定裕度越高,图5a的分析结果也验证了这一点。考虑到虚拟阻抗的加入相当于等效增加了电网阻抗,因此若依据Zpp进行基于虚拟阻抗的稳定性改善设计,反而会恶化系统的稳定性改善效果,这显然与基于SISO的精确模型的分析结论相悖。
综合以上关于频率耦合效应的机理分析可知,无论是进行稳定性分析,还是用于提升系统稳定性的控制器设计,均必须采用计及频率耦合效应的SISO精确模型。根据上述分析可知,Zppseries在特定频段所呈现的负阻容性区是影响系统稳定的关键原因,因此可通过合理设计虚拟阻抗来改善系统稳定性。
需再次强调,由于负序系统始终处于稳定状态,故下文只针对正序系统进行虚拟阻抗设计。
现有改善系统稳定性的方法中,一种主要思路是以提升系统相位裕度[30]为目标进行虚拟阻抗设计。这种方法的具体实现过程为:首先根据VSG输出阻抗和电网阻抗幅频曲线确定交点频率f;然后将f代入相位约束条件反解出虚拟阻抗的取值范围。但是,由于VSG输出阻抗表达式较为繁琐,特别在考虑频率耦合和电压、电流双环控制的情况下,其表达式更加复杂,难以实现解析求解。
为简化设计过程,本文在上述稳定性机理分析基础上提出了一种基于SISO等效输出阻抗模型的虚拟电感Lv简化设计方法。该方法从提升系统的幅值裕度出发,目标是通过选择合理的虚拟电感以增加等效电网阻抗Zgv,使其在Zppseries的相位穿越-90°对应频点fx处(即IRvsgvp(s)的正频率Nyquist曲线穿越负实轴对应的频点)的幅值大于Zppseries的幅值,从而避免IRvsgvp(s)的正频率Nyquist曲线从(-1, j0)左侧穿越来保证系统稳定。
需要说明的是,用于改善系统稳定性的虚拟阻抗设计还需讨论以下两个关键前提:①根据式(11)可知,Zppseries与电网电感Lg相关,在虚拟阻抗量化设计时是否还需同时考虑Lg改变所带来的Zppseries的变化;②将虚拟阻抗归算至电网侧来实现虚拟阻抗量化设计是否可行。这两个关键问题将在3.1节和3.3节予以讨论,以使本文所提方法更加有据可依。
用于改善VSG并网稳定性的虚拟阻抗设计需综合考虑VSG正序输出阻抗与电网电感二者间的数值关系。由式(11)知,VSG正序输出阻抗与电网电感相关,理论上虚拟阻抗的设计需要一个迭代过程,但无疑增加了设计难度。为寻求简化的可能性,此处首先明确电网电感变化对正序输出阻抗的影响。本文采用正序输出阻抗关于电网电感的灵敏度来予以评价。定义Zppseries的幅值和阻抗角对Lg的相对灵敏度为
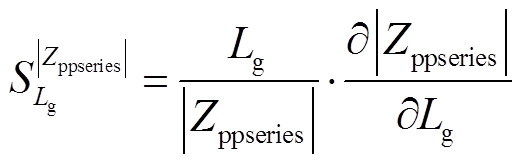 (16)
(16)
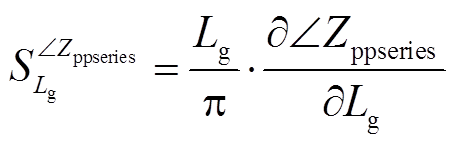 (17)
(17)
图10分别给出了不同电网强度下的Zppseries的幅值和相位关于Lg的灵敏度,其中系统参数见附表1。由图10可知,电网电感的变化仅会对50~100 Hz附近的正序输出阻抗影响较大,而在Zppseries表现为负阻容性的临界频点fx附近,可认为电网电感的变化对正序输出阻抗阻抗特性基本没有影响,即随着电网电感的变化,正序输出阻抗的相频曲线始终从同一频点穿越-90°。
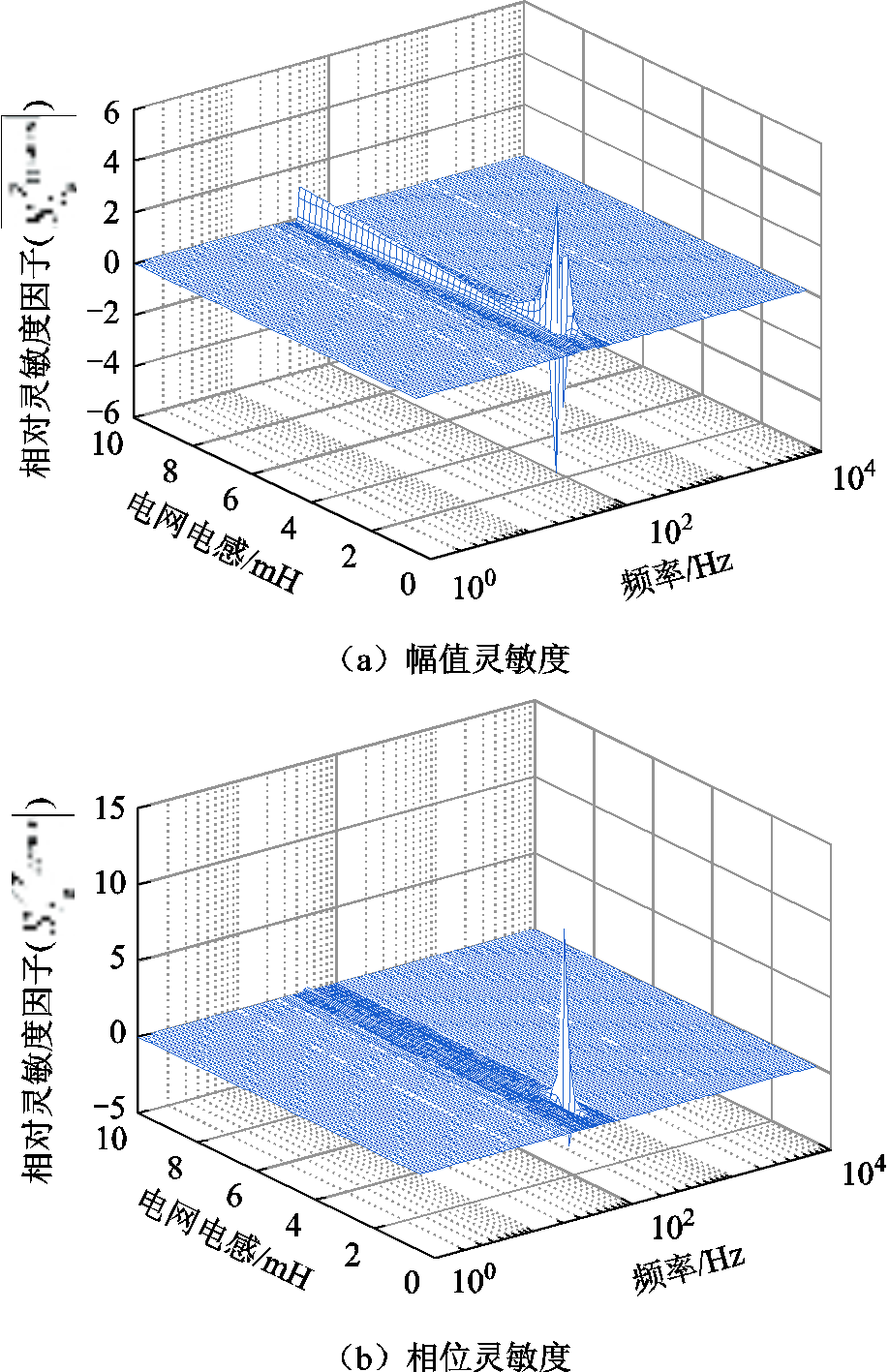
图10 正序输出阻抗对电网电感的灵敏度分析
Fig.10 Sensitivity analysis of positive sequence output impedance to grid inductance
该结论为本文提出的用于提升系统稳定性的虚拟阻抗的简化设计方法奠定了基础。因此,在后续虚拟阻抗的设计中,可依据某一电网阻抗下的Zppseries求解fx,只要将加入虚拟阻抗后的等效电网阻抗在频点fx处的幅值提升至Zppseries幅值之上,即可满足系统的稳定性要求。
虚拟阻抗的引入相当于增加了线路的等效串联阻抗,考虑到双环控制下电压外环能跟踪指令值,因此近似认为VSG的输出阻抗由Zvsg和Zv串联构成。为了简化虚拟阻抗的设计过程,可以将控制侧的虚拟阻抗等效归算到电网侧,即将虚拟阻抗视作与电网阻抗串联,此种处理方式的合理性将在3.3节予以解释。此时原公共耦合点将由PCC变为PCC′[35],加入虚拟阻抗之后的VSG并网系统如图11所示。
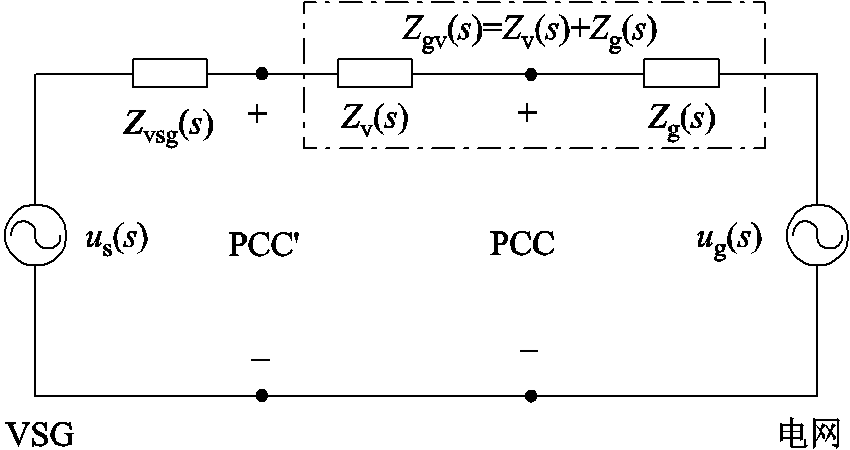
图11 加入虚拟阻抗之后的VSG并网系统
Fig.11 VSG system with virtual impedances
根据2.1节的分析,若使系统满足稳定性要求,应保证加入虚拟阻抗后,正序阻抗比的正频率Nyquist曲线在(-1, j0)点左侧正穿越次数(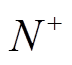 )等于负穿越次数(
)等于负穿越次数(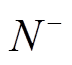 )。结合图5a和图10a可知,此时系统稳定性条件则转换为正序阻抗比的正频率Nyquist曲线应始终从(-1, j0)点右侧穿越。
)。结合图5a和图10a可知,此时系统稳定性条件则转换为正序阻抗比的正频率Nyquist曲线应始终从(-1, j0)点右侧穿越。
图12展示了VSG与电网阻抗的交互情况。如2.3节所述,正序输出阻抗Zppseries在低于50 Hz频段的负阻容性区是导致并网系统失稳的关键原因。为便于阐述,将Zppseries的相频曲线穿越-90°时对应的频率记为fx,即IRvsgvp(s)的正频率Nyquist曲线穿越负实轴时对应的频率。根据3.1节的灵敏度分析可知,在fx附近,电网电感Lg的变化对正序输出阻抗Zppseries的影响可以忽略,故此处以Lg=1 mH为例讨论虚拟阻抗的设计,系统参数见附表1。
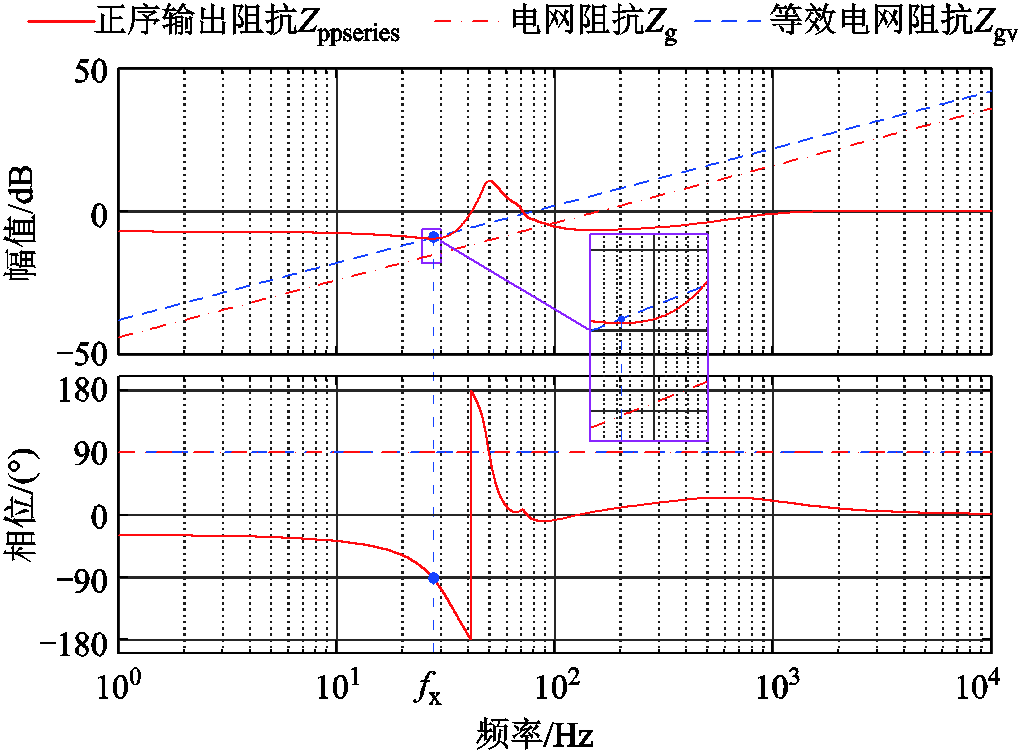
图12 VSG与电网阻抗交互图
Fig.12 Interaction diagram of VSG and grid impedance
根据图12可知,没有加入虚拟阻抗前,电网阻抗在fx处的幅值小于|Zppseries(j2πfx)|,此时IRvsgvp(s)的正频率Nyquist曲线将从(-1, j0)点左侧穿越,系统失稳。欲使正序系统保持稳定,需保证IRvsgvp(s)在fx处的模值低于0 dB,由此可知,将存在一电网阻抗阈值Zgmin,其在频点fx处的幅值与Zppseries大小相等,只要系统等效电网阻抗大于该值,IRvsgvp(s)的正频率Nyquist曲线将不会从(-1, j0)点左侧穿越,系统可维持稳定。
鉴于Zppseries在低频下的负阻容性区,因此将虚拟阻抗Zv设计为纯感性则有利于提高系统的稳定性[36],且选择纯感性虚拟阻抗也不会带来VSG频率稳定性劣化的问题[37]。观察图12可知,加入虚拟阻抗后,系统的等效电网阻抗Zgv增加至Zgv=Zv+Zg[35],其在fx处的幅值被提升到正序输出阻抗幅值曲线以上,使得IRvsgvp(s)的正频率Nyquist曲线仅从(-1, j0)点右侧穿越,从而提升了系统的幅值裕度。综上所述,稳定性约束条件可表达为
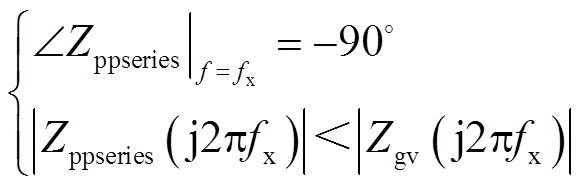 (18)
(18)
由分析可知,电网阻抗越小,系统的稳定裕度越低。文献[25]亦指出,当电网阻抗大于电网阻抗阈值时,虚拟阻抗就不再需要。由于虚拟阻抗的加入相当于增加了线路上的等效串联阻抗,因此对虚拟电感最小值Lvmin的要求,应保证在其加入之后,将等效电网阻抗调整到临界稳定状态所对应的电网阻抗阈值Zgmin之上。据此,虚拟电感的设计方法转换为求取临界稳定状态所对应的电网阻抗阈值Zgmin的问题。
在本文所给定的系统参数下,可求得图12所对应的fx为27.442 Hz,利用式(18),Zgmin在fx处的幅值应与Zppseries(j2πfx)的幅值相等,即
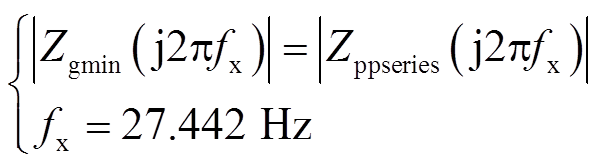 (19)
(19)
由此计算出临界稳定状态下所对应的电网电感阈值Lgmin约为1.92 mH,该数值与基于图5a分析得出的电网电感阈值大致相同,这说明只要在某一电网阻抗下通过计算或测量获得VSG的正序输出阻抗Zppseries,即可利用本文方法快速且准确地得到系统临界稳定状态的电网阻抗阈值Zgmin。在获得该阈值后,可根据等效电网阻抗与实际电网阻抗的关系确定出Lvmin,即
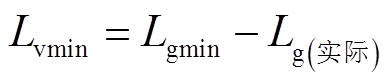 (20)
(20)
需要说明的是,根据式(20)可知,在获得电网电感阈值Lgmin之后,需根据电网电感参数以确定合适的虚拟电感参数。关于电网电感的测量,现有文献已开展了大量的工作[38-41],并已成功地应用于变流器系统用以实现控制参数的自适应调节[29]。考虑到电网电感的测量及虚拟阻抗的自适应调节可采用现有方法实现或事先保留一定裕度,故不再赘述。
上述设计方法的前提是将虚拟阻抗视为与电网阻抗相串联的等值阻抗。考虑到虚拟阻抗实际是通过控制系统实现的,在理论上并不完全等同于在物理系统中串入等值阻抗。因此上述虚拟电感定量设计方法的合理性必须予以解释,以使本文所提方法更加有据可依。
本节通过比较以下两种情况的幅值裕度和相位裕度来解释可将虚拟阻抗直接归入电网侧的原因。情况1:将虚拟阻抗归入电网侧,此时等效电网阻抗Zgv即为s(Lg+Lv),VSG的正序输出阻抗不计及虚拟阻抗的影响,其即为Zgv对应的Zppseries;情况2:将虚拟阻抗归算至控制侧,此时VSG的正序输出阻抗将包含虚拟阻抗控制环节,记作Z′ppseries,此时的电网阻抗Zg即为真实电网阻抗sLg,该情况即为理论上的准确模型。
图13给出了以上两种情况下的阻抗Bode图,其中电网阻抗和虚拟阻抗均取1 mH,系统参数见附表1。将Zppseries与Z′ppseries的相频曲线穿越-90°时对应的频点记作fx1,其即为正序阻抗比穿越负实轴所对应的频率。根据频点fx1处VSG正序输出阻抗和网侧阻抗幅频曲线的相对位置关系即可获得两种情况下系统的幅值裕度,分别记作h1和h2,显然有h2>h1>1,说明与情况1相比,情况2具有更好的稳定性。同时,频点f2和f3分别为两种情况下幅值曲线的最高频交互点,根据f2和f3可获得两种情况下系统的相位裕度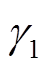 、
、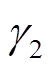 ,可知
,可知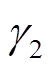 >90°>
>90°>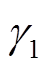 ,表明情况2具有更大的相位裕度。综合以上分析可以得出,将虚拟阻抗归算至控制侧的稳定裕度始终大于归算至电网侧,即将虚拟阻抗归算至电网侧若满足稳定性要求,则归算至控制侧的准确模型必定稳定。这说明本文方法所得的虚拟电感本身就包含一定的稳定裕量,同时可以带来简化设计的优点。
,表明情况2具有更大的相位裕度。综合以上分析可以得出,将虚拟阻抗归算至控制侧的稳定裕度始终大于归算至电网侧,即将虚拟阻抗归算至电网侧若满足稳定性要求,则归算至控制侧的准确模型必定稳定。这说明本文方法所得的虚拟电感本身就包含一定的稳定裕量,同时可以带来简化设计的优点。
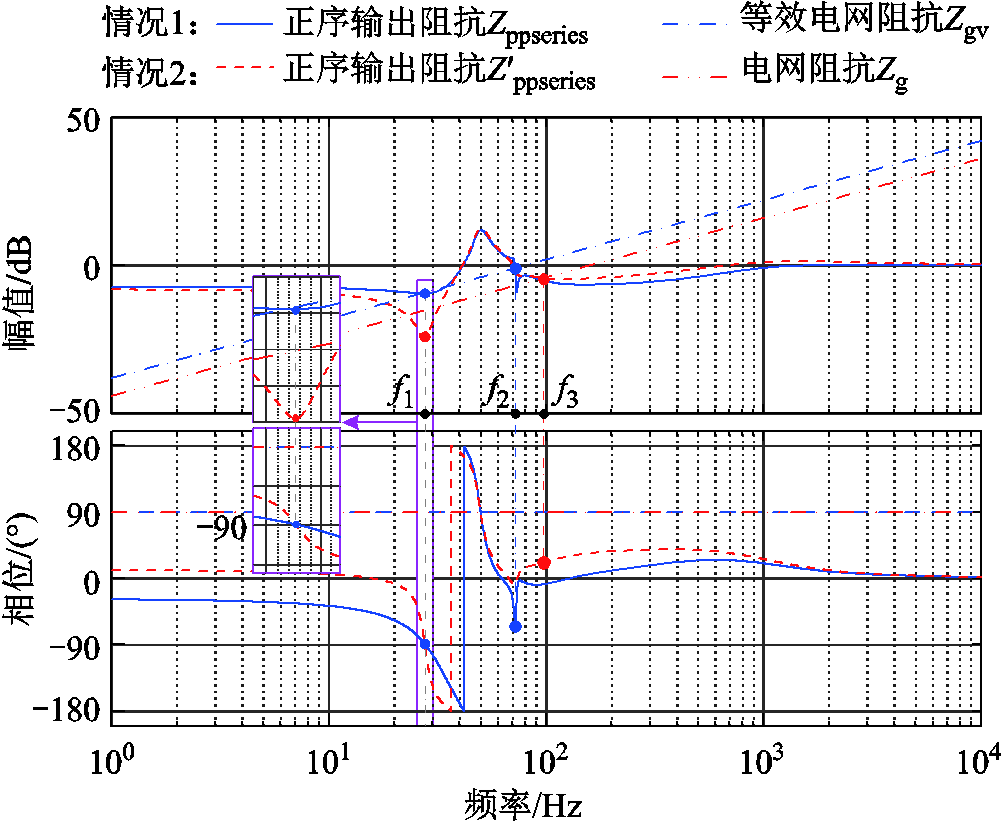
图13 虚拟阻抗归算至控制侧和网侧的阻抗交互对比
Fig.13 Impedance interaction comparison plot for two different cases
综上所述,采用本文方法所得到的虚拟电感最小值Lvmin是保证系统稳定的充分条件,虽然其数值上与理论值会略有偏差,但可有效地简化虚拟阻抗的量化计算过程。而且,系统的稳定控制本身需保有一定的稳定裕度,因此本文所提出的虚拟阻抗定量设计方法完全可胜任稳定控制器的设计。需要说明,虚拟电感并非越大越好,其最大值需根据功率输出能力的约束进行设计,但其并非本文研究重点,具体可参考相关文献[30]。
采用附表1的系统参数,本部分通过在Matlab/Simulink中搭建VSG并网系统来验证所提出的虚拟阻抗设计方法的正确性。
本仿真算例中电网电感Lg为1mH,根据式(19)和式(20),可确定满足系统稳定运行条件的虚拟电感最小值Lvmin= 0.92 mH。仿真中,0.5 s前不引入虚拟阻抗控制,0.5 s时加入0.92 mH的虚拟电感,相应的并网电流波形如图14所示。可以看出,加入虚拟电感之前,系统处于失稳状态;加入虚拟电感后,系统逐渐恢复稳定运行,并在0.9 s左右重新达到稳定状态。因此,验证了本文虚拟阻抗最小值边界设计方法的准确性。
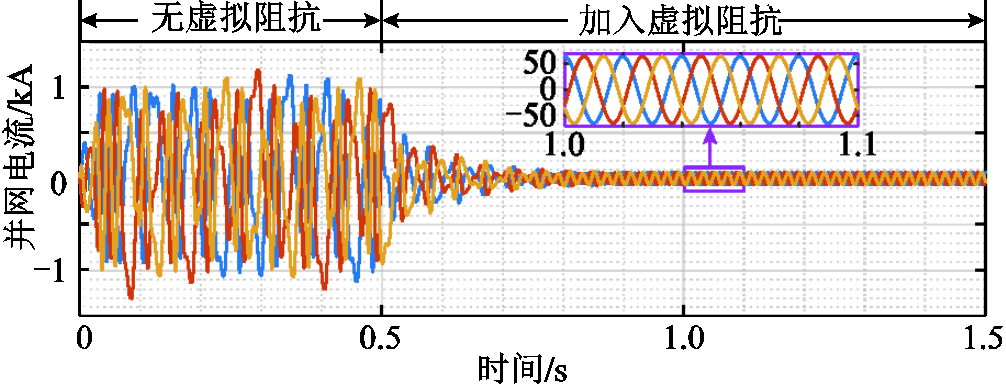
图14 加入虚拟阻抗前后的并网电流波形
Fig.14 Grid-connected current waveforms before and after adding virtual impedance
图15分别给出了三种不同虚拟阻抗和电网阻抗组合下的并网电流波形,其中情况1:Lg=1.5 mH,Lv=0.5 mH;情况2:Lg =1 mH,Lv =0.5 mH;情况3:Lg =1 mH,Lv =1 mH。
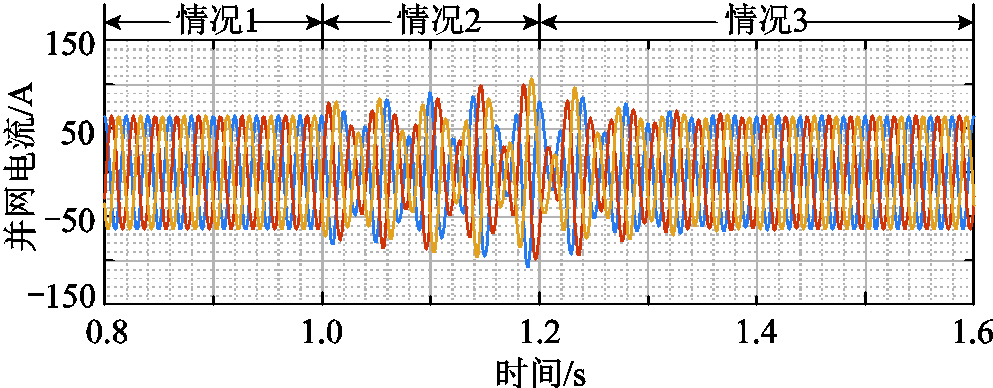
图15 不同电网阻抗和虚拟阻抗下的并网电流波形
Fig.15 Grid-connected current waveforms with different grid impedance and virtual impedance
由3.2节的分析可知,在附表1系统参数下,临界稳定状态所对应的电网电感阈值为1.92 mH,则对于电网电感取值为1 mH和1.5 mH,能使系统稳定的虚拟电感的最小值分别为0.92 mH和0.42 mH。从图15中可以看出,在0.8~1 s时段,由于Lg=1.5 mH,因此Lv=0.5 mH满足稳定性约束,系统可稳定运行;在1~1.2 s时段,将Lg减小至1 mH,则Lv=0.5 mH小于稳定条件的虚拟电感最小值,系统发生振荡失稳;1.2 s时保持Lg=1 mH不变,将虚拟电感调整为1 mH,系统重新满足稳定约束条件,此时系统逐渐恢复稳定运行,并在1.43 s左右再次达到稳定状态。
以上算例在说明本文所提虚拟阻抗设计方法有效性的同时,进一步验证了该方法对电网阻抗的适应性,即当电网阻抗变化后,电网电感阈值保持不变,因此只需根据式(20)重新计算满足系统稳定运行条件的虚拟电感最小值,即可保证VSG在不同电网阻抗条件下的稳定。
图16分别给出了不同虚拟惯量J和虚拟电感Lv组合下的并网电流波形,其中电网电感Lg始终保持1 mH不变。情况1:J=0.013 kg·m2、Lv=1 mH;情况2:J=0.013 kg·m2、Lv=0 mH;情况3:J=0.13 kg·m2、Lv=1 mH;情况4:J=0.13 kg·m2、Lv=1.3 mH。根据本文方法,对于J=0.013 kg·m2和J=0.13 kg·m2,利用式(19)可求得稳定条件下的电网电感阈值分别为1.92 mH和2.16 mH。则对于电网电感取值为1 mH,能使系统稳定的虚拟电感的最小值分别为0.92 mH和1.16 mH。
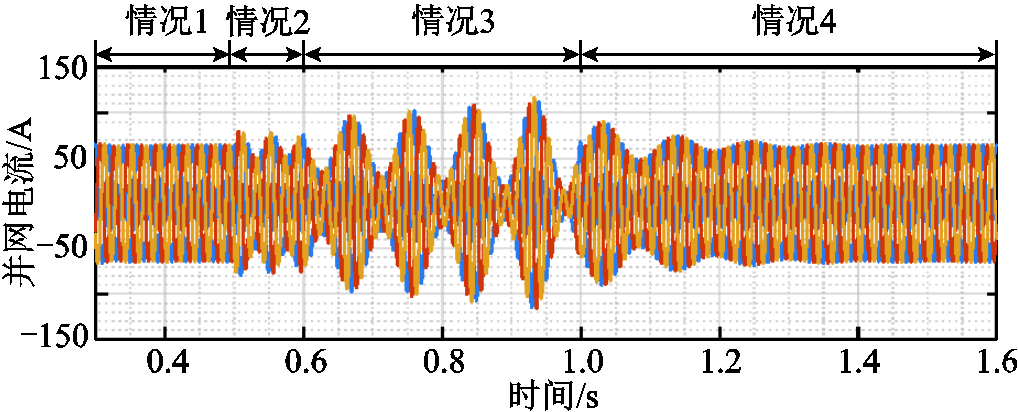
图16 不同虚拟惯量和虚拟阻抗下的并网电流波形
Fig.16 Grid-connected current waveforms with different virtual inertia and virtual impedance
情况1,虚拟惯量J=0.013 kg·m2,因此满足系统稳定运行条件的虚拟电感最小值Lvmin=0.92 mH,由于Lv=1 mH满足虚拟电感设计要求,系统可稳定运行;情况2,保持J和Lg不变,减小Lv至0,由于Lg<Lgmin,因此系统失稳;情况3,在t=0.6 s时将虚拟惯量J由0.013kg·m2变为0.13kg·m2,保持Lg和 Lv与情况1相同,由于Lv=1 mH小于满足系统稳定运行的虚拟电感最小值,因此系统继续失稳运行;情况4,在t=1 s时将Lv增加至1.3 mH,则Lv大于J=0.13 kg·m2对应的Lvmin,由于调整后的虚拟电感重新满足稳定性要求,系统再次恢复稳定运行,并在1.6 s左右重新进入稳定状态。
上述算例以虚拟惯量J为例,验证了本文所提出的虚拟阻抗设计方法对于不同控制参数的适应性。当控制参数变化后,由于Zppseries改变,因此应根据式(19)和式(20)所给出的设计方法重新求取满足系统稳定运行的虚拟电感,即可保证VSG并网系统的稳定运行。
本文针对VSG并网稳定性问题所涉及SISO等效序阻抗建模、并网稳定性机理分析及基于虚拟阻抗的稳定性改善控制器设计方法进行了全面系统的研究,所得结论如下:
1)本文在获得VSG输出序阻抗矩阵的基础上,依据SISO等效序阻抗模型对VSG并网稳定性进行了分析,并通过 Simulink仿真对其准确性进行了验证。该模型与基于矩阵的广义Nyquist准则判稳方法相比,不仅简化了计算过程,而且为后续虚拟阻抗的量化设计奠定了基础。
2)虽然频率耦合效应仅对基频50Hz附近的正序阻抗特性产生影响,但其却是VSG并网稳定性判断的关键所在。如采用忽略频率耦合效应的简化模型,无论在稳定性分析,还是在基于虚拟阻抗的稳定性控制器设计上,其结论均相悖于精确模型的分析结果。通过进一步分析,正序输出阻抗Zppseries在特定频段所表现的负阻容性是造成VSG并入强电网失稳的根本原因,可据此有针对性地对虚拟阻抗值量化设计来提升系统稳定裕度。上述机理分析为后续虚拟阻抗的量化设计提供了指导。
3)在上述结论基础上,本文基于SISO等效序阻抗模型,提出了一种用于改善VSG并网稳定性的虚拟电感Lv简化设计方法。该方法从提升系统的幅值裕度出发,通过将等效电网阻抗Zgv在正序输出阻抗Zppseries的相位穿越-90°对应的频点处的幅值提升到Zppseries以上,从而保证正序阻抗比的正频率Nyquist曲线仅从(-1,j0)点右侧穿越,实现系统稳定性改善。此外,本文还对所提方法得以简化的原因及其合理性进行了论证。分析结果表明,本文方法可直接通过计算或测量Zppseries进行虚拟电感的设计,避免了传统方法所需的反复迭代和复杂运算,并且对不同电网阻抗和控制参数具有很好的适用性。结合仿真算例,本文方法的有效性得到了验证。
附 录
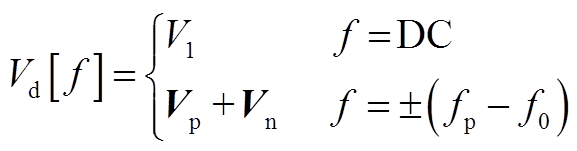 (A1)
(A1)
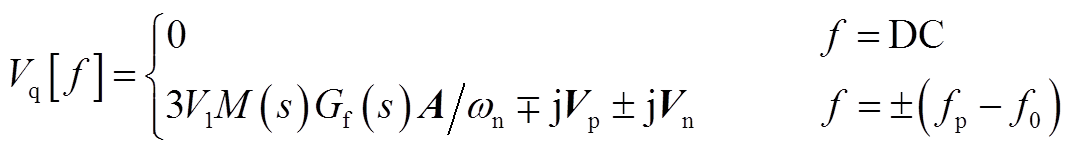 (A2)
(A2)
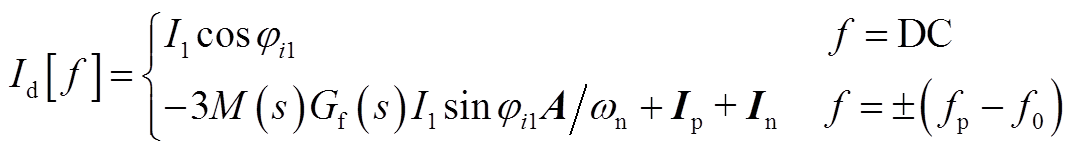 (A3)
(A3)
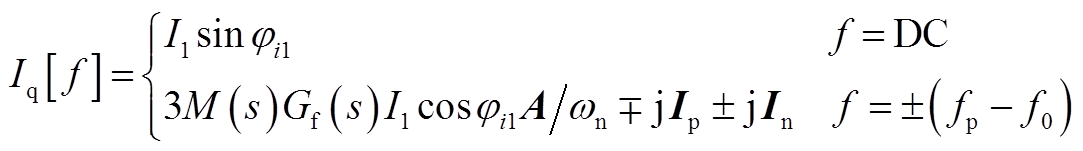 (A4)
(A4)
 (A5)
(A5)
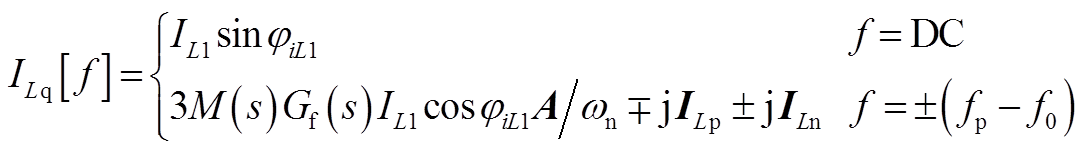 (A6)
(A6)
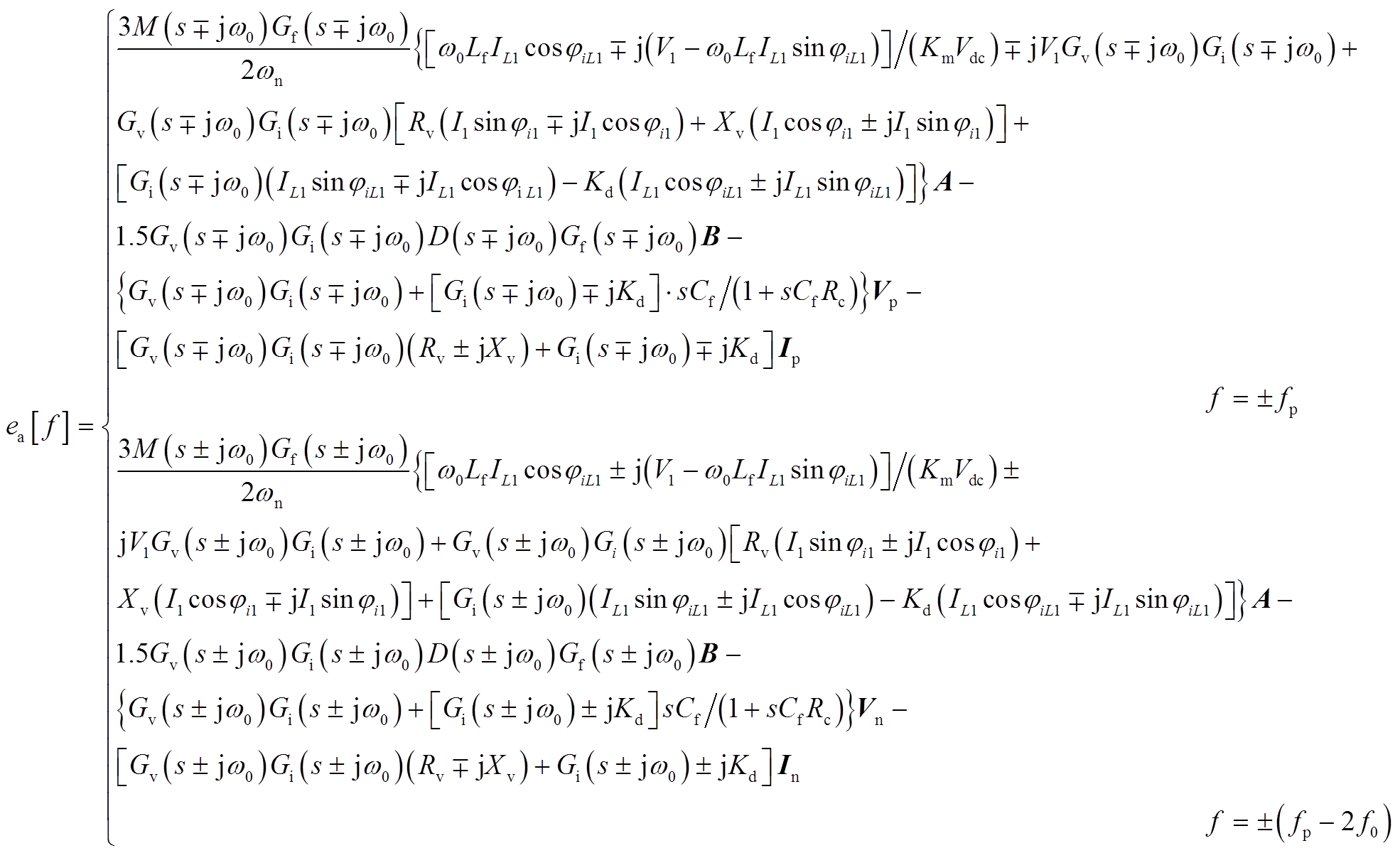 (A7)
(A7)
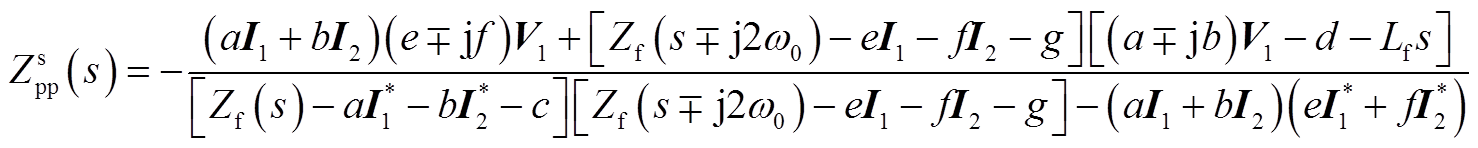 (A8)
(A8)
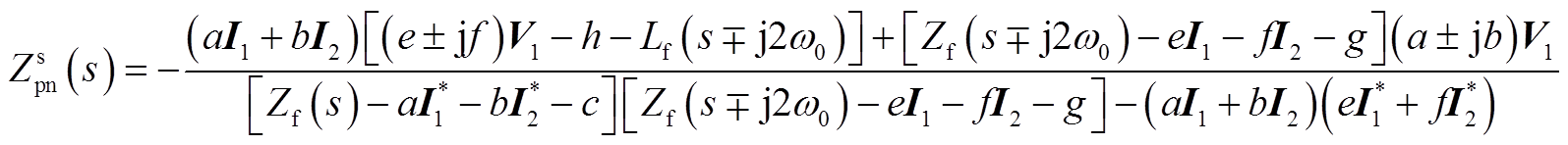 (A9)
(A9)
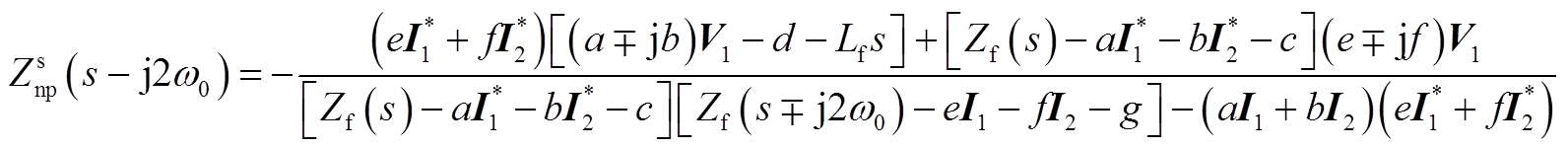 (A10)
(A10)
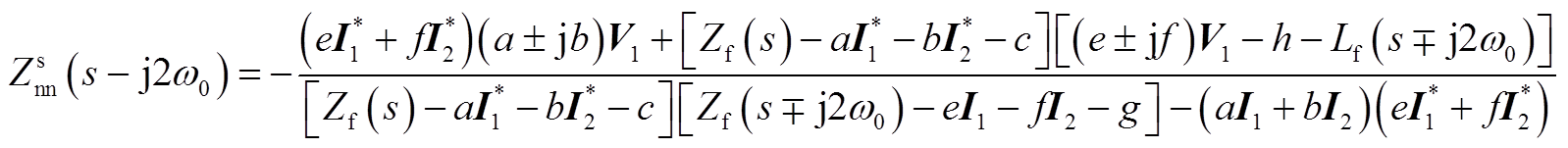 (A11)
(A11)
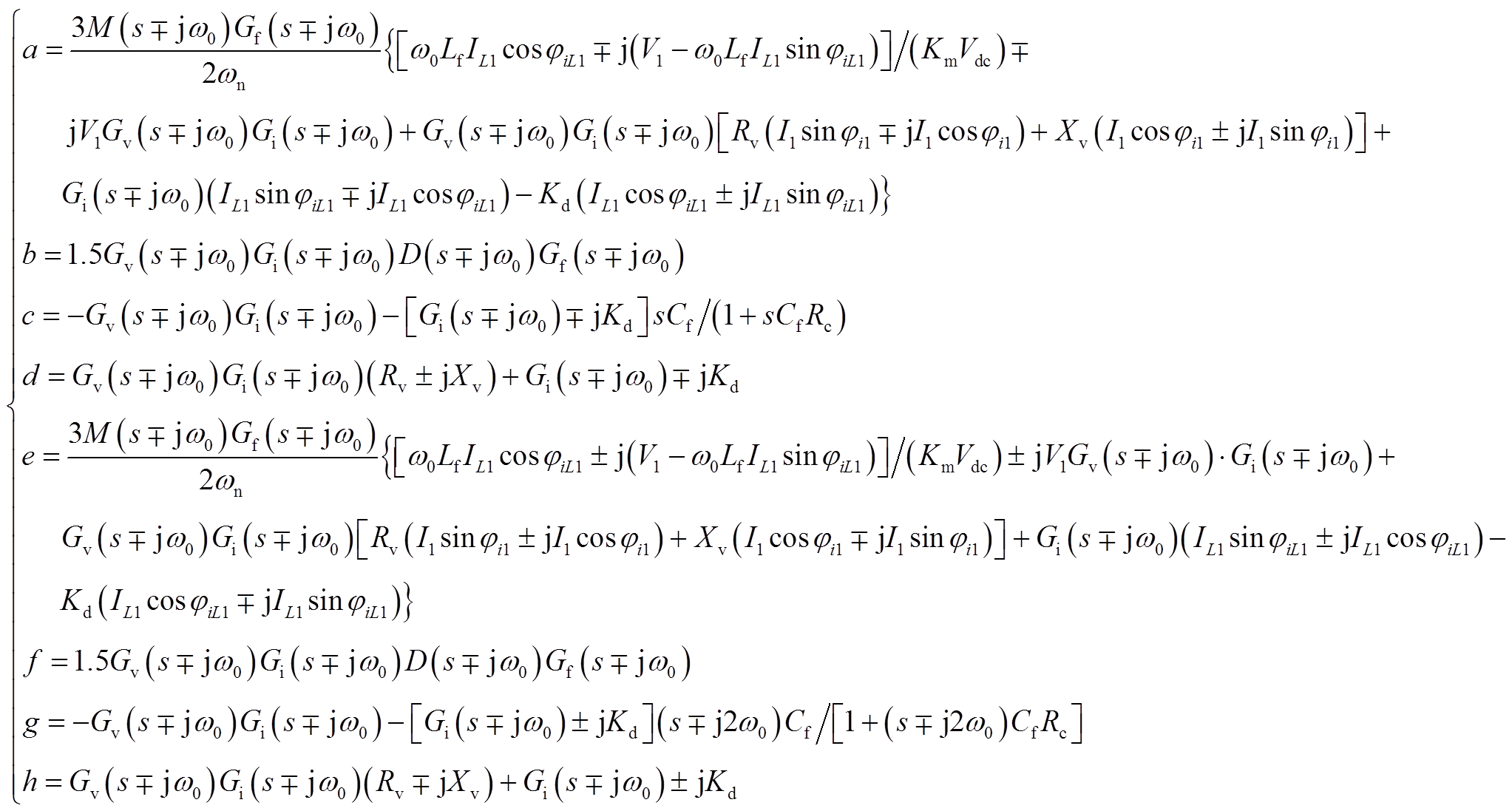 (A12)
(A12)
附表1 系统仿真参数
App.Tab.1 System simulation parameters

参数数值 有功指令值Pref/kW无功指令值Qref/var300 虚拟惯量J/(kg·m2)0.013 电压系数K6.5 P-f下垂系数DpQ-V下垂系数Dq5320 电压外环比例系数kpv电压外环积分系数kiv250 电流内环比例系数kpi电流内环积分系数kii650 直流电压Vdc/V800 调制系数Km1/800 额定线电压幅值V0/V311 开关频率fsw/kHz10 基波频率f0/Hz50
(续)

参数数值 滤波电感Lf/mH2 滤波电容Cf/mF阻尼电阻Rc/Ω2001 线路电感Lg/mH7
参考文献
[1] 任碧莹, 邱姣姣, 刘欢, 等. 基于虚拟同步发电机双机并联系统的参数自调节优化控制策略[J]. 电工技术学报, 2019, 34(1): 128-138. Ren Biying, Qiu Jiaojiao, Liu Huan, et al. Optimization control strategy of self-adjusting parameter based on dual-parallel virtual synchronous generators[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 128-138.
[2] 缪惠宇, 梅飞, 张宸宇, 等. 基于虚拟阻抗的虚拟同步整流器三相不平衡控制策略[J]. 电工技术学报, 2019, 34(17): 3622-3630. Miao Huiyu, Mei Fei, Zhang Chenyu, et al. Three phase unbalanced control strategy for virtual synchronous rectifier based on virtual impedance[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3622-3630.
[3] 于彦雪, 关万琳, 陈晓光, 等. 基于序阻抗的虚拟同步机同步频率谐振现象[J]. 电工技术学报, 2022, 37(10): 2584-2595. Yu Yanxue, Guan Wanlin, Chen Xiaoguang, et al. Synchronous frequency resonance in virtual synchronous generator based on sequence-impedance[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2584-2595.
[4] Kalcon G O, Adam G P, Anaya-Lara O, et al. Small-signal stability analysis of multi-terminal VSC-based DC transmission systems[J]. IEEE Transactions on Power Systems, 2012, 27(4): 1818-1830.
[5] 邹小明, 杜雄, 王国宁, 等. 三相并网逆变器频率耦合机理分析及稳定性判定[J]. 电力系统自动化, 2018, 42(18): 57-63. Zou Xiaoming, Du Xiong, Wang Guoning, et al. Frequency coupling mechanism analysis and stability judgement for three-phase grid-connected inverter[J]. Automation of Electric Power Systems, 2018, 42(18): 57-63.
[6] 年珩, 杨洪雨. 不平衡运行工况下并网逆变器的阻抗建模及稳定性分析[J]. 电力系统自动化, 2016, 40(10): 76-83. Nian Heng, Yang Hongyu. Impedance modeling and stability analysis of grid-connected inverters under unbalanced operation conditions[J]. Automation of Electric Power Systems, 2016, 40(10): 76-83.
[7] Middlebrook R D. Input filter considerations in design and application of switching regulators[C]//IEEE Power Electronics Specialists Conference, Cleveland, OH, USA, 1976: 366-382.
[8] Sun Jian. Impedance-based stability criterion for grid-connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078.
[9] Wu Wenhua, Chen Yandong, Zhou Leming, et al. Sequence impedance modeling and stability comparative analysis of voltage-controlled VSGs and current-controlled VSGs[J]. IEEE Transactions on Industrial Electronics, 2019, 66(8): 6460-6472.
[10] Peng Yang, Yin Taiyuan, Li Mingxuan, et al. A sequence impedance modeling of VSG with consideration of inner loops control[C]//2019 4th IEEE Workshop on the Electronic Grid (eGRID), Xiamen, China, 2020: 1-5.
[11] Shi Kai, Wang Yu, Sun Yuxin, et al. Frequency-coupled impedance modeling of virtual synchronous generators[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3692-3700.
[12] Kazem Bakhshizadeh M, Wang Xiongfei, Blaabjerg F, et al. Couplings in phase domain impedance modeling of grid-connected converters[J]. IEEE Transactions on Power Electronics, 2016, 31(10): 6792-6796.
[13] Wen Bo, Boroyevich D, Burgos R, et al. Inverse nyquist stability criterion for grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2017, 32(2): 1548-1556.
[14] 李信栋, 苟兴宇. 多输入多输出线性定常系统稳定裕度的分析与改进[J]. 控制理论与应用, 2014, 31(1): 105-111. Li Xindong, Gou Xingyu. Analysis and improvement of stability margin for multi-input multi-output linear time-invariant systems[J]. Control Theory & Applications, 2014, 31(1): 105-111.
[15] 李彪. 基于谐波线性化的三相并网逆变器系统建模和稳定性分析[D]. 重庆: 重庆大学, 2019.
[16] Zhang Chen, Cai Xu, Rygg A, et al. Sequence domain SISO equivalent models of a grid-tied voltage source converter system for small-signal stability analysis[J]. IEEE Transactions on Energy Conversion, 2018, 33(2): 741-749.
[17] 武相强, 王赟程, 陈新, 等. 考虑频率耦合效应的三相并网逆变器序阻抗模型及其交互稳定性研究[J]. 中国电机工程学报, 2020, 40(5): 1605-1616. Wu Xiangqiang, Wang Yuncheng, Chen Xin, et al. Sequence impedance model and interaction stability research of three-phase grid-connected inverters with considering coupling effects[J]. Proceedings of the CSEE, 2020, 40(5): 1605-1616.
[18] 杜燕, 赵韩广, 杨向真, 等. 考虑频率耦合效应的虚拟同步发电机序阻抗建模[J]. 电源学报, 2020, 18(6): 42-49. Du Yan, Zhao Hanguang, Yang Xiangzhen, et al. Sequence impedance modeling of virtual synchronous generator considering frequency coupling effect[J]. Journal of Power Supply, 2020, 18(6): 42-49.
[19] Yang Dongsheng, Ruan Xinbo, Wu Heng. Impedance shaping of the grid-connected inverter with LCL filter to improve its adaptability to the weak grid condition[J]. IEEE Transactions on Power Electronics, 2014, 29(11): 5795-5805.
[20] 郭强, 周琛力, 李山. 面向电流源型PWM整流器直流侧电压的多环路控制策略[J]. 电工技术学报, 2022, 37(8): 2051-2063. Guo Qiang, Zhou Chenli, Li Shan. A multiple loops control strategy based on DC link voltage of current source PWM rectifiers[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 2051-2063.
[21] 游逍遥, 刘和平, 苗轶如, 等. 带恒功率负载的双极性直流系统稳定性分析及其有源阻尼方法[J]. 电工技术学报, 2022, 37(4): 918-930. You Xiaoyao, Liu Heping, Miao Yiru, et al. Stability analysis and active damping method of the bipolar DC system with constant power loads[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 918-930.
[22] Zhang Xueguang, Xia Danni, Fu Zhichao, et al. An improved feedforward control method considering PLL dynamics to improve weak grid stability of grid-connected inverters[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 5143-5151.
[23] 徐健, 曹鑫, 郝振洋, 等. 基于电网谐波电压前馈的虚拟同步整流器电流谐波抑制方法[J]. 电工技术学报, 2022, 37(8): 2018-2029. Xu Jian, Cao Xin, Hao Zhenyang, et al. A harmonic-current suppression method for virtual synchronous rectifier based on feedforward of grid harmonic voltage[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 2018-2029.
[24] 袁敞, 丛诗学, 徐衍会. 应用于微电网的并网逆变器虚拟阻抗控制技术综述[J]. 电力系统保护与控制, 2017, 45(9): 144-154. Yuan Chang, Cong Shixue, Xu Yanhui. Overview on grid-connected inverter virtual impedance technology for microgrid[J]. Power System Protection and Control, 2017, 45(9): 144-154.
[25] Wen Tiliang, Zou Xudong, Zhu Donghai, et al. Comprehensive perspective on virtual inductor for improved power decoupling of virtual synchronous generator control[J]. IET Renewable Power Generation, 2020, 14(4): 485-494.
[26] 代维, 秦文萍, 任春光, 等. 含同步机微电网中基于解耦下垂的自适应虚拟阻抗控制[J]. 中国电机工程学报, 2020, 40(14): 4486-4495. Dai Wei, Qin Wenping, Ren Chunguang, et al. Adaptive virtual impedance control based on decoupling droop in microgrid with synchronous generators[J]. Proceedings of the CSEE, 2020, 40(14): 4486-4495.
[27] 周兵凯, 杨晓峰, 李继成, 等. 一种用于优化LC-DAB级联系统稳定性的虚拟阻抗控制技术[J]. 电工技术学报, 2021, 36(18): 3946-3956. Zhou Bingkai, Yang Xiaofeng, Li Jicheng, et al. Virtual impedance control technology for stability optimization of LC-DAB cascaded system[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3946-3956.
[28] 石荣亮, 张兴, 徐海珍, 等. 光储柴独立微电网中的虚拟同步发电机控制策略[J]. 电工技术学报, 2017, 32(23): 127-139. Shi Rongliang, Zhang Xing, Xu Haizhen, et al. A control strategy for islanded photovoltaic-battery-diesel microgrid based on virtual synchronous generator[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 127-139.
[29] 温春雪, 黄耀智, 胡长斌, 等. 虚拟同步发电机接口变换器并联运行虚拟阻抗自适应控制[J]. 电工技术学报, 2020, 35(增刊2): 494-502. Wen Chunxue, Huang Yaozhi, Hu Changbin, et al. Adaptive control of virtual impedance in parallel operation of virtual synchronous generator interface converter[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 494-502.
[30] 杜燕, 朱轲, 杨向真, 等. 考虑频率耦合的VSG虚拟阻抗优化设计[J]. 高电压技术, 2022, 48(12): 5057-5067. Du Yan, Zhu Ke, Yang Xiangzhen, et al. Optimal design of virtual synchronous generator virtual impedance considering frequency coupling[J]. High Voltage Engineering, 2022, 48(12): 5057-5067.
[31] Rygg A, Molinas M, Zhang Chen, et al. A modified sequence-domain impedance definition and its equivalence to the dq-domain impedance definition for the stability analysis of AC power electronic systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(4): 1383-1396.
[32] 胡寿松. 自动控制原理[M]. 7版. 北京: 科学出版社, 2019.
[33] Etxegarai A, Eguia P, Torres E, et al. Impact of wind power in isolated power systems[C]//2012 16th IEEE Mediterranean Electrotechnical Conference, Yasmine Hammamet, Tunisia, 2012: 63-66.
[34] Cao Wenchao, Ma Yiwei, Wang F. Sequence-impedance-based harmonic stability analysis and controller parameter design of three-phase inverter-based multibus AC power systems[J]. IEEE Transactions on Power Electronics, 2017, 32(10): 7674-7693.
[35] 屈子森, 蔡云旖, 杨欢, 等. 基于自适应虚拟阻抗的虚拟同步机功率解耦控制策略[J]. 电力系统自动化, 2018, 42(17): 58-66. Qu Zisen, Cai Yunyi, Yang Huan, et al. Strategy of power decoupling control for virtual synchronous generator based on adaptive virtual impedances[J]. Automation of Electric Power Systems, 2018, 42(17): 58-66.
[36] 陈杰, 闫震宇, 赵冰, 等. 下垂控制三相逆变器阻抗建模与并网特性分析[J]. 中国电机工程学报, 2019, 39(16): 4846-4856. Chen Jie, Yan Zhenyu, Zhao Bing, et al. On the impedance modelling and grid-connected characteristics of the three-phase droop controlled inverter[J]. Proceedings of the CSEE, 2019, 39(16): 4846-4856.
[37] Yang Yaqian, Xu Jiazhu, Li Chang, et al. A new virtual inductance control method for frequency stabilization of grid-forming virtual synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2023, 70(1): 441-451.
[38] Familiant Y A, Huang Jing, Corzine K A, et al. New techniques for measuring impedance characteristics of three-phase AC power systems[J]. IEEE Transactions on Power Electronics, 2009, 24(7): 1802-1810.
[39] 谢少军, 季林, 许津铭. 并网逆变器电网阻抗检测技术综述[J]. 电网技术, 2015, 39(2): 320-326. Xie Shaojun, Ji Lin, Xu Jinming. Review of grid impedance estimation for gird-connected inverter[J]. Power System Technology, 2015, 39(2): 320-326.
[40] 李杨, 帅智康, 方俊彬, 等. 基于阻抗测量的多逆变器系统稳定性校验方法[J]. 电力系统自动化, 2021, 45(11): 95-101. Li Yang, Shuai Zhikang, Fang Junbin, et al. Stability check method for multi-inverter system based on impedance measurement[J]. Automation of Electric Power Systems, 2021, 45(11): 95-101.
[41] Timbus A V, Rodriguez P, Teodorescu R, et al. Line impedance estimation using active and reactive power variations[C]//2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 2007: 1273-1279.
Abstract In microgrid with high penetration of distributed generation, the generalized Nyquist criterion based on return rate matrix or return difference matrix is often used to analyse the grid-connection stability of virtual synchronous generator (VSG), but the calculation process is complicated. Besides, existing studies have not identified the root cause of the instability of VSG's integration into the strong grid, and the mechanism analysis of the influence of frequency coupling effect on the output impedance characteristics of VSG remains to be deepened. In terms of stability improvement, existing virtual impedance design methods do not take full advantage of the characteristics of VSG output impedance and its interaction with the grid impedance, and there is still room for further simplification. Therefore, this paper conducts a comprehensive and systematic research on the mechanism analysis of microgrid VSG grid-connection stability and the design method of virtual impedance.
Firstly, on the basis of obtaining VSG output sequence impedance matrix, this paper analyses the grid-connection stability of VSG by establishing single input single output (SISO) equivalent model and combining with Nyquist criterion. Secondly, based on the established SISO equivalent sequence impedance model, the influence mechanism of frequency coupling effect on the output impedance characteristics of VSG and the root cause of the instability of VSG's integration into the strong grid are compared and analysed. Finally, based on the above mechanism analysis, this paper proposes a virtual impedance simplified design method to improve system stability, from the perspective of improving the amplitude margin of the system, this method directly uses the interaction relationship between SISO equivalent output impedance and grid impedance to realize the quantitative calculation of virtual impedance, which simplifies the design process of virtual impedance.
The results are as follows: first, the stability analysis method based on SISO equivalent sequence impedance model can easily obtain accurate stability analysis results, the results show that the instability of the system is caused by the sub-synchronous oscillation near the fundamental frequency of 50 Hz. Second, the influence of frequency coupling effect on VSG positive sequence output impedance is mainly concentrated around the fundamental frequency 50 Hz. Considering the frequency coupling effect before and after, VSG positive sequence impedance changes from capacitive to inductive in the frequency band affected by frequency coupling effect. Lastly, near the critical frequency point where VSG's positive sequence output impedance shows negative resistance capacitance, the influence of grid inductance changes on its impedance characteristics can be ignored. Therefore, the virtual impedance design method based on SISO equivalent sequence impedance proposed in this paper can quickly and accurately obtain the critical threshold of virtual inductance.
The following conclusions can be drawn from the above results: (1) The stability analysis method of VSG grid-connection system based on the SISO equivalent sequence impedance model can simplify the analysis process and lay a foundation for the subsequent quantitative design of virtual impedance. (2) Although the frequency coupling effect only affects the positive sequence impedance characteristics near the fundamental frequency 50 Hz, but this is the key to judging the stability of the VSG grid-connection. Through further analysis, the negative resistance capacitance of VSG positive sequence output impedance in a specific frequency band is the root cause of the instability of VSG's integration into the strong grid, the virtual impedance value can be quantitatively designed according to this point to improve the system stability margin. (3) On the basis of the above conclusions, this paper proposes a virtual impedance simplified design method based on the SISO equivalent sequence impedance model. From the perspective of improving the amplitude margin of the system, this method can be used to design virtual inductance directly by calculating or measuring VSG positive sequence output impedance. It avoids the repeated iteration and complex calculation required by traditional methods, and has good applicability to different grid impedance and control parameters.
keywords:Virtual synchronous generator (VSG), SISO equivalent sequence impedance model, frequency coupling effect, stability analysis, virtual impedance design
DOI:10.19595/j.cnki.1000-6753.tces.230077
中图分类号:TM712
国家自然科学基金资助项目(52207102)。
收稿日期 2023-01-18
改稿日期 2023-04-08
刘 欣 男,1980年生,博士,副教授,硕士生导师,研究方向为新能源发电系统建模与控制、电力电子系统电磁兼容和瞬态特性研究。E-mail:liuxinhust@163.com
郭志博 男,1998年生,硕士研究生,研究方向为新能源发电系统建模与控制。E-mail:gzb_ncepu@163.com(通信作者)
(编辑 赫蕾)