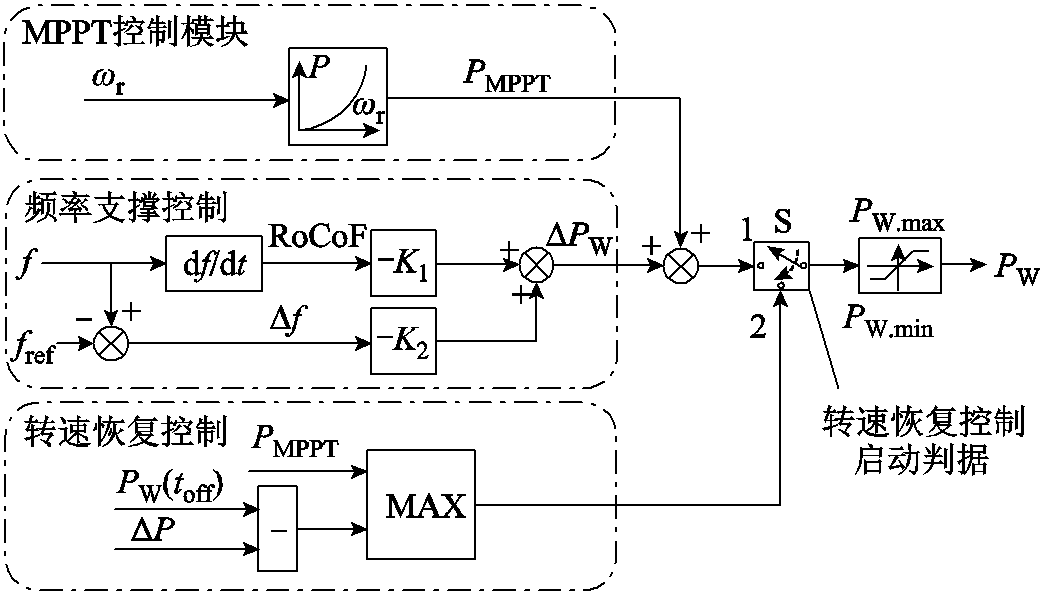
图1 综合虚拟惯性控制框图
Fig.1 Control diagram of combined virtual inertia control
摘要 针对现有的双馈风电机组转速恢复策略无法兼顾抑制频率二次跌落和转速恢复性能的问题，提出一种基于变系数PI控制的转速恢复策略。首先，揭示转速恢复策略启动时刻、有功减载量对频率二次跌落和转速恢复性能的影响机制；其次，提出基于定系数PI控制的双馈风电机组转速恢复策略，初步实现有功减载量以“先抑后扬”的输出方式进行转速恢复；然后，针对基于定系数PI控制的转速恢复策略的不足，根据不同运行工况，将PI控制系数与风机转速建立耦合关系，提出基于变系数PI控制的自适应转速恢复策略，实现了在兼顾抑制频率二次跌落的同时，保障转速恢复性能；最后，通过EMTP-RV软件搭建不同扰动、风电渗透率的电力系统模型，验证了所提策略的有效性。
关键词：双馈风电机组 自适应转速恢复 频率二次跌落 PI控制
随着我国能源结构的深化改革，可再生能源装机占比日益增加，高比例可再生能源接入和高比例电力电子化将成为电力系统的主要特征[1-2]。风能被普遍认为是最具有应用前景的可再生能源，由于风电机组不具备惯量响应和调频能力，导致电力系统抗扰能力下降[3]；在风电渗透率持续增长背景下，系统调频供需矛盾日益突出，当面临故障切机、负荷突变等扰动时，电力系统安全受到极大威胁[4]。
双馈风力发电机（Doubly-Fed Induction Generator, DFIG）含有丰富的转动惯量、宽泛的转速调节范围，通过在DFIG转子侧控制器中附加频率控制回路，模拟同步发电机的惯量响应和一次调频特性，释放自身转子动能，为受扰系统提供频率支撑[5-7]。国内外发布的一些电网导则明确提出联网风电场需要具备主动参与系统调频的能力[8-9]。
文献[10]为了便于风电机组参与一次调频，提出了一种基于频率变化率（Rate of Change of Frequency, RoCoF）分段的风电机组一次调频自适应控制方法；文献[11]采用遗传算法实现机组频率控制系数随机组转速变化而改变，提出同时考虑调频效益和调频成本的变系数虚拟惯量控制策略；文献[12]提出计及风机有效旋转动能的频率控制方法，使风机充分利用有限的转子动能参与系统调频，提高频率稳定性。
目前大多调频控制的能量来源于风机转子旋转动能，但调频控制结束后，风机转速低于最大功率跟踪控制（Maximum Power Point Tracking, MPPT）所对应的最优转速，不仅使风能利用率降低，而且过低的转速可能导致风机失速，因此，在风机参与调频后必须进行转速恢复控制，保障风电场的经济效益及系统稳定[13-14]。文献[15]提出了频率支撑阶段结束后直接切换至MPPT运行模式的转速恢复方法，虽然可以快速恢复转速，但是有功功率突变会引起严重的频率二次跌落，甚至低于扰动引起的频率最低点[16]；文献[17]对风电场内不同风电机组给定不同的转速恢复延时，避免所有机组都在同一时间进入转速恢复状态，从而减缓所有机组同时启动转速恢复引起的频率二次跌落；文献[18]通过扩张观测器动态估计风电机组捕获机械功率，进而设计恒加速功率转速恢复方法，但仍存在一定程度的有功突变，造成频率二次跌落；文献[19]初步探索了有功减载量对频率二次跌落的影响，然而未构建出具体的二次频率跌落模型，也未探索转速恢复时间对频率二次跌落的影响；文献[20]采用储能装置实现风储相互协调的动态频率调节，消除频率二次跌落，但储能装置成本较高，在大规模风电场配置并不经济；文献[21-22]考虑将下垂系数与电网频率变化率耦合，提出一种考虑最优状态动态恢复的风电持续调频策略，需整定的控制参数较多，给实际工程应用造成困难。此外，目前转速恢复策略只能单方面实现抑制频率二次跌落或保障转速恢复性能。
针对现有的DFIG转速恢复策略无法兼顾抑制频率二次跌落和转速恢复性能的问题，本文提出一种变系数PI控制的自适应DFIG转速恢复策略。首先在文献[19]基础上，揭示转速恢复控制中控制参数对转速恢复性能和频率二次跌落的影响机制，提出在频率恢复阶段启动转速恢复控制，有功减载量以“先抑后扬”的方式输出，既能减小转速恢复初期功率突变造成的频率二次跌落，又能使有功减载量逐步增加加快转速恢复；然后，提出基于定系数PI控制的双馈风电机组的转速恢复策略，初步实现有功减载量以“先抑后扬”的输出方式进行转速恢复，为克服基于定系数PI控制的转速恢复控制仍存在功率突变及不适应不同工况等不足，引入时变的PI控制增益，提出基于变系数PI控制的转速恢复策略，兼顾抑制频率二次跌落和转速恢复性能；最后，基于EMTP-RV软件搭建了含DFIG的电力系统模型，在不同风电渗透率及扰动场景下，验证提出自适应转速恢复策略的有效性。
DFIG利用转子中储存的动能参与系统调频，调频过程分为频率支撑控制（动能释放阶段，A-B-C）和转速恢复控制（动能吸收阶段，C*-D-A）。两者根据一定逻辑实现时序控制，其控制框图如图1所示；调频和转速恢复过程的轨迹如图2所示。
图1 综合虚拟惯性控制框图
Fig.1 Control diagram of combined virtual inertia control
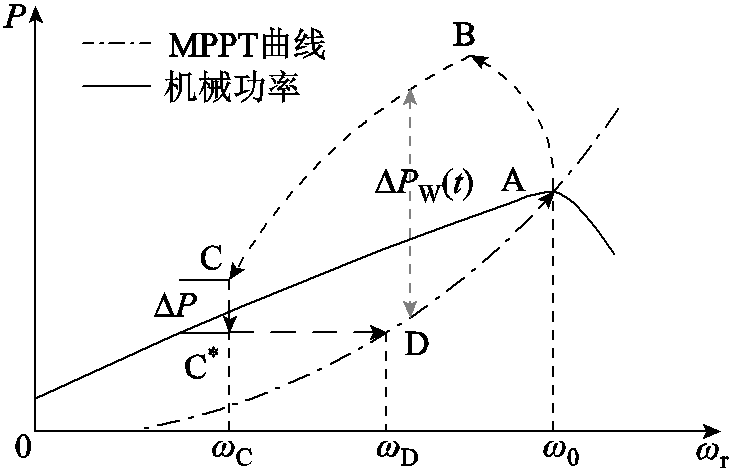
图2 DFIG有功功率-转速曲线
Fig.2 DFIG active power-speed curve
在图1和图2中，ωr为DFIG转速；PMPPT为MPPT模式下的输出功率；ΔPW为DFIG参与调频增发的电磁功率；f为系统频率；RoCoF为系统频率变化率；toff为DFIG退出调频的时刻；K1和K2分别为虚拟惯量控制和下垂控制的控制参数；fref为频率初始值；PW(toff)为toff时DFIG的输出功率；ΔP为DFIG转速恢复的有功减载量；PW.max和PW.min分别为DFIG输出的最大、最小限值；S为开关。
当系统中发生大小为ΔPL的扰动时，同步机组和DFIG共同参与调频，针对同步机组建立转子运动方程式[19]，有
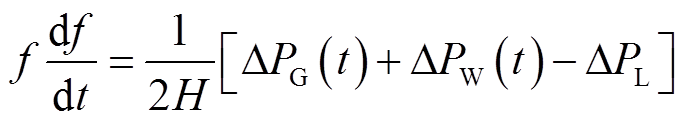（1）
式中，H为常规同步机组的惯性时间常数；ΔPG(t)为同步机组的增发功率。
DFIG参与调频期间，最大频率偏差Δfmax，如式（2）所示，具体推导过程见文献[19]。
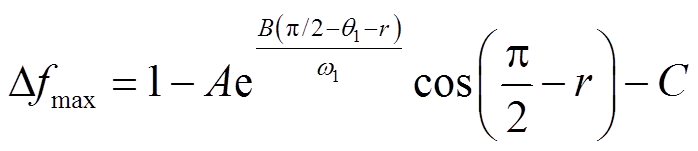（2）
式中，A、B、C、ω1、θ1、r均为中间变量，表达式为
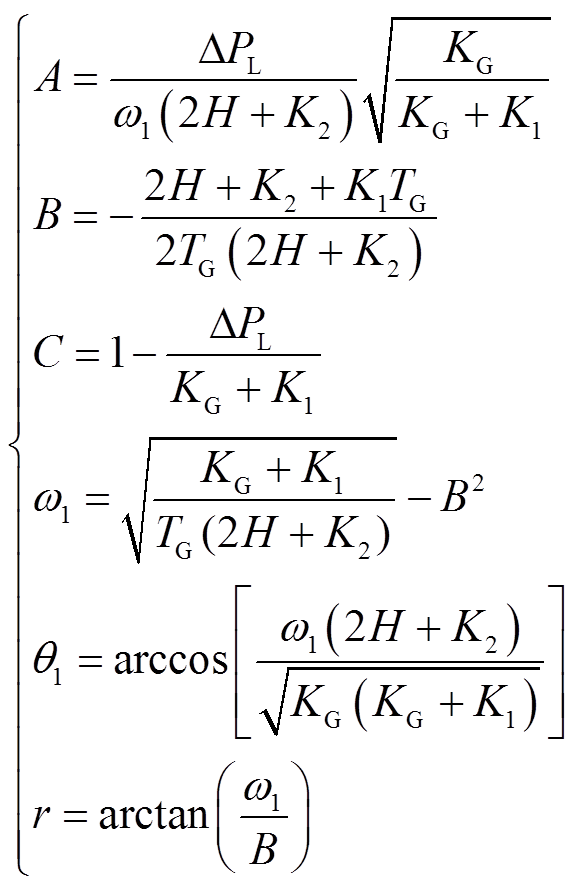（3）
式中，TG为同步机调速器动作的时间常数；KG为同步机的单位调节功率。
由式（3）可知，在系统的常规同步机组参数H、TG和KG已知条件下，Δfmax与K1、K2、ΔPL强相关。通过增大K1、K2可有效地减小Δfmax。
DFIG释放自身动能为系统提供频率支撑后，若转子动能得不到及时补充，不仅会导致风能利用率下降，甚至会造成DFIG失速，加剧系统的不平衡状态，进而造成严重的频率二次跌落[13]。
toff时转速恢复控制启动，DFIG通过减小电磁功率以满足转速恢复的充要条件（电磁转矩小于机械转矩），系统中不平衡功率ΔPE(toff)为
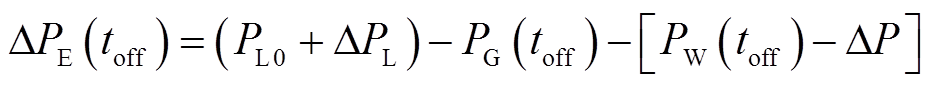（4）
式中，PL0为负荷初始值；PG(toff)为toff时刻同步发电机组的有功出力。
DFIG退出调频后，只有同步机组参与一次调频，转速恢复期间同步机组的转子运动方程可表示为
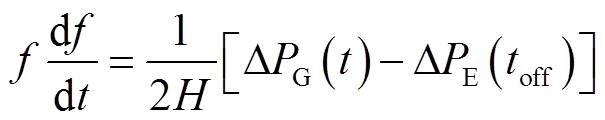（5）
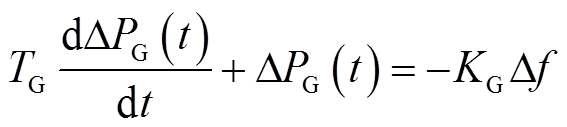（6）
将式（6）代入式（5）得到转速恢复阶段的频率变化式为
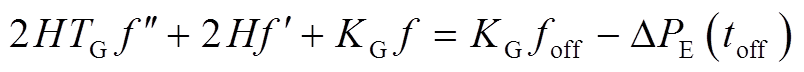（7）
式中，
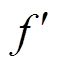和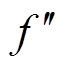
分别为系统频率的一阶导数和二阶导数；foff为toff时的系统频率。
式（7）初始条件为
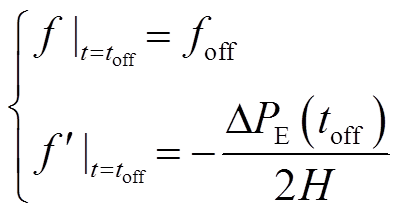（8）
将式（8）代入式（7），转速恢复期间系统频率的时域表达式为
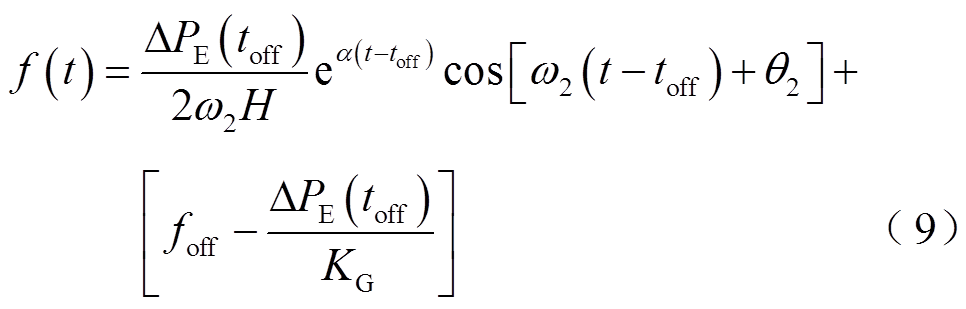
其中，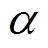
、ω2和θ2中间变量的表达式为
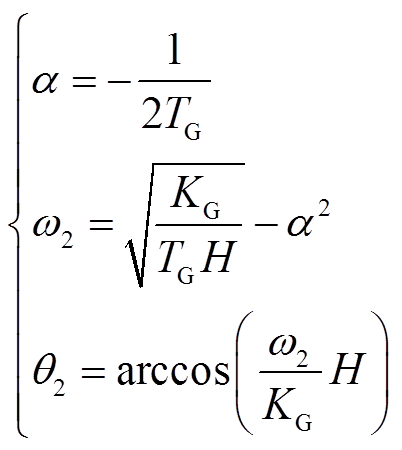（10）
进一步对式（9）求导，可求得频率二次跌落的最大偏差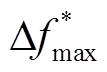
为
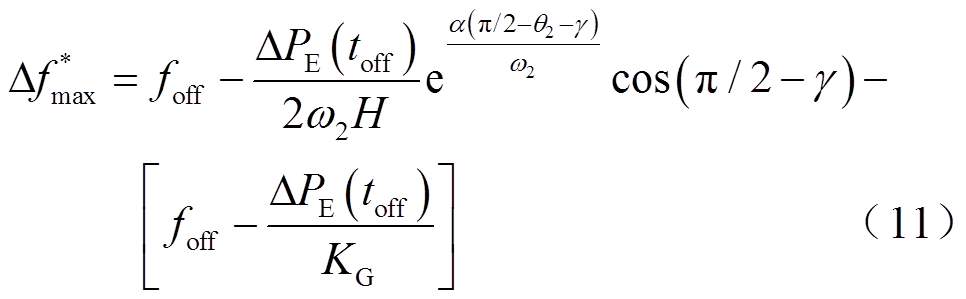
式中，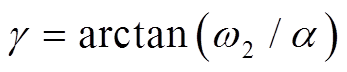
。
由式（11）可知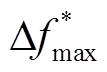，与ΔPE(toff)和foff存在密切关系。为进一步研究三者之间的关系，通过式（11）刻画出ΔPE(toff)与foff、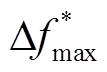的三维曲面图，如图3所示。结合图3和式（11）可知，随着ΔPE(toff)增大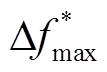，增大；随foff增大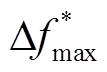，减小，foff增大会对频率二次跌落起到一定的抑制作用。在转速恢复初期，ΔPE(toff)主要由DFIG转速恢复期间ΔP产生，由式（4）可知，ΔPE(toff)与ΔP正相关；由于foff与toff强相关，选取不同的toff，可直接影响foff，故影响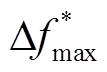的两个主要因素为toff和ΔP。
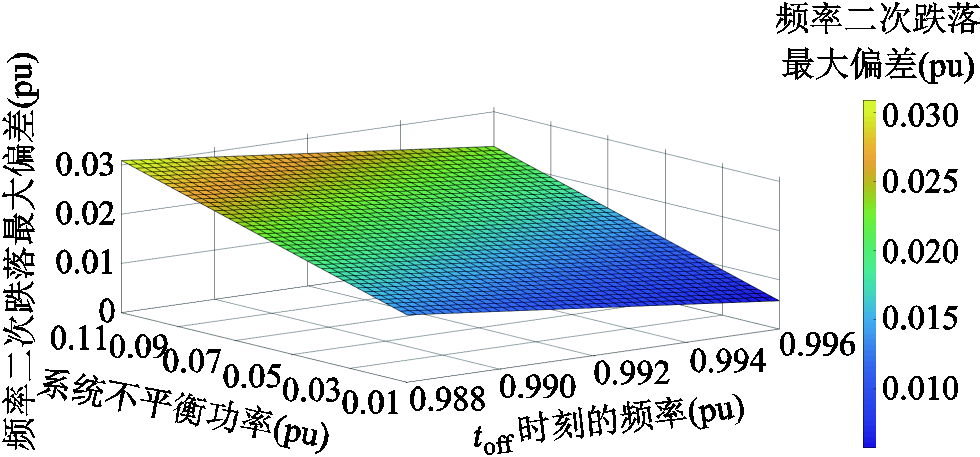
图3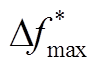 
与ΔPE(toff)和foff的变化曲线
Fig.3 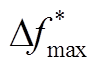with various of ΔPE(toff) and foff
目前，众多学者针对频率支撑策略进行了大量的研究，所提方法可有效地提高频率最低点，然而现有的转速恢复方法很难兼顾抑制频率二次跌落和转子转速恢复性能。为兼顾抑制频率二次跌落和转子转速恢复性能，本文首先揭示转速恢复策略启动时刻toff、有功减载量ΔP对转速恢复性能的影响机制，其次在图1的基础上，构建了基于PI控制的转速恢复策略。因此下面将重点介绍转速恢复策略，频率支撑策略详见文献[12,23]。
转速恢复策略的启动时刻可在以下代表阶段选取：频率最低点、频率恢复阶段、频率准稳态阶段；DFIG采用转速直接恢复方法，探索相同ΔP、不同toff对Δf*max的影响，仿真结果如图4所示。
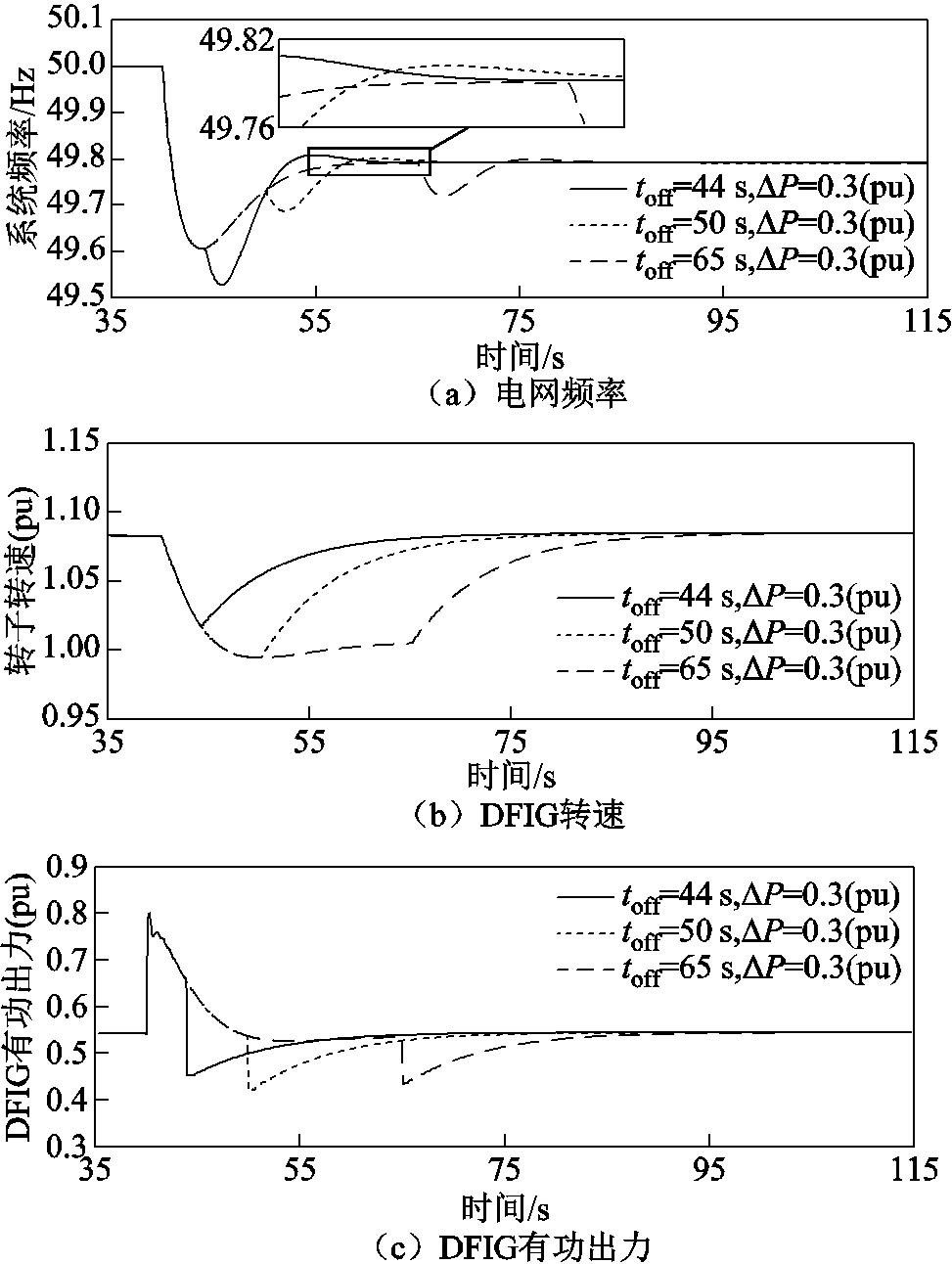
图4 仿真结果
Fig.4 Simulation results
在图4中，从频率二次跌落角度出发，在频率恢复阶段，电力系统有功功率存在差值，即有功增量大于负荷扰动值（ΔPG+ΔPW＞ΔPL），若启动转速恢复策略，DFIG有功出力降低，系统净负荷功率增加，ΔPE＜ΔP，频率下降0.053 Hz；若在频率最低点或准稳态阶段（ΔPG+ΔPW=ΔPL）启动转速恢复策略，ΔPE=ΔP，频率分别下降0.092 Hz、0.093 Hz，频率最低点时刻启动转速造成更严重的二次频率跌落深度（详见黑色实线）；从转速恢复角度出发，随转速恢复策略启动时间延后，转子转速恢复到稳态的时间增加。因此，综合考虑频率二次跌落与转速恢复速度，在频率恢复阶段启动转速恢复策略，可以抑制系统频率二次跌落且转速恢复速度较快。
在频率恢复阶段，随频率偏差减小，ΔPW(t)不断减小，DFIG的输出功率PW(t)逐渐靠近输入机械功率Pm，最终在转速最低点，实现DFIG的短暂稳态（PW(toff)=Pm）。综合考虑抑制频率二次跌落和转子转速恢复性能，为使转子转速尽快恢复，将频率恢复阶段中的典型时刻转子转速到达最低点作为转速恢复策略的启动判据。除转速最低点时刻外，频率恢复阶段的其他时间同样可以启动转速恢复策略，以后的研究将以转速恢复时间和二次频率跌落深度为目标函数，进一步探索不同转速恢复时间对转速恢复性能的影响。
转速恢复阶段DFIG输出功率PW(t)为
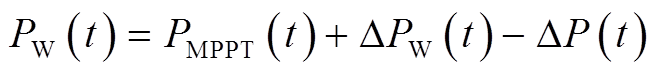（12）
转速恢复阶段电力系统和风电机组的转子运动方程式分别为
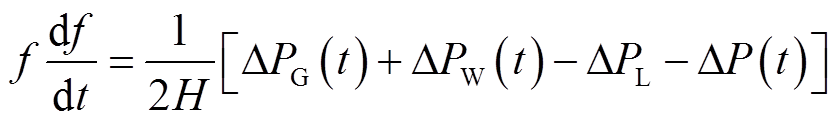（13）
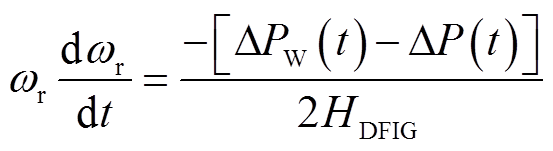（14）
式中，HDFIG为DFIG提供的虚拟惯量。
由式（13）和式（14）可知，通过改变ΔP(t)，可以调节转速恢复和频率二次跌落性能。在式（14）中，由于DFIG处于转速恢复期间，系统频率趋近于准稳态，致使ΔPW(t)变化很小，有功减载量ΔP(t)在转速恢复过程中占主导作用，使用较大的ΔP(t)可实现转子转速的快速恢复。但在转速恢复初期，DFIG有功突变导致ΔPE增加，造成严重的频率二次跌落，很难兼顾抑制频率二次跌落和转速恢复性能。为此，本文引入时变思想，实现ΔP(t)“先抑后扬”的输出方式，ΔP(t)逐渐增大，DFIG输出功率ΔPW(t)逐渐减小，抑制频率二次跌落，并随时间增长，ΔP(t)逐渐增加，DFIG输入与输出功率偏差增加，加快转速恢复。
为实现ΔP(t)以“先抑后扬”的输出方式进行转速恢复，本文提出了基于定系数PI控制的转速恢复策略，其控制框图如图5所示。ΔP(t)表达式为
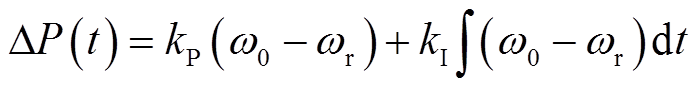（15）
式中，kP为比例控制系数；kI为积分控制系数；ω0为扰动前转子转速。
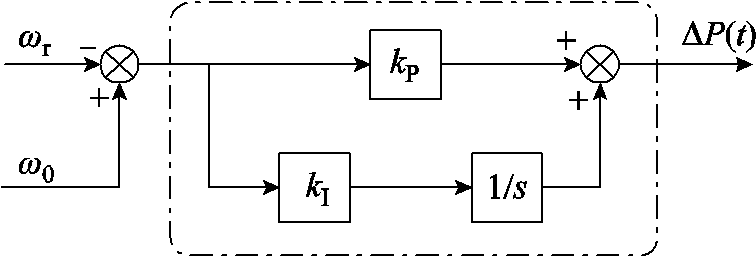
图5 基于PI控制的转速恢复策略框图
Fig.5 Block diagram of the recovery strategy with PI control
由式（15）和图5可知，DFIG转速偏差作为PI转速恢复控制的输入，ΔP(t)作为PI转速恢复控制的输出，通过P控制器调整有功减量ΔP(t)的大小，通过I控制器的积分作用消除转速的稳态误差，初步实现ΔP(t)“先抑后扬”的输出方式。
在不同工况下，基于PI控制的转速恢复策略输入的转速偏差随DFIG释放的旋转动能不同而存在差异，kP、kI采用固定系数会限制转子转速恢复速度，对频率二次跌落改善作用不大：kP过大，转速恢复速度快，但转速恢复初期功率突变大，造成的频率二次跌落严重；kP过小，转速恢复速度慢，并且由于kP不为0，功率突变仍存在，仍可能造成频率二次跌落；kI过小，造成误差积累过慢，转子转速恢复减慢；kI过大，会造成误差积累过快，转速恢复稳定后发生大波动。
针对上述定PI系数转速恢复策略的问题，引入时变思想，构建变系数PI控制的转速恢复策略，kP和kI分别为
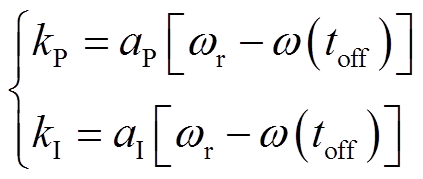（16）
式中，ω(toff)为toff时刻DFIG的转子转速；aP和aI分别为kP和kI的比例系数。
考虑到本文主要思想为实现ΔP以“先抑后扬”的输出方式进行转速恢复，采用正交实验法[24]初步确定aP和aI的值，未来将通过不同方法进一步探究PI系数整定方法及最优解。
通过式（16）将kP、kI与转子转速建立耦合关系，kP和kI随转速实时调整以适应在不同工况下恢复转速。在转速恢复初期，kP、kI随转速差值[ωr-ω(toff)]从0开始增加，实现ΔP(t)“先抑”的输出方式，在根源上抑制了功率突变带来的频率二次跌落问题；kP和kI随转速增加而增加，实现ΔP(t)“后扬”的输出方式，致使DFIG输入功率与输出功率偏差增加，加快转速恢复速度。为方便研究，本文对kP、kI采用同样形式的控制增益[ωr-ω(toff)]，未来将进一步挖掘不同PI控制增益对DFIG抑制频率二次跌落和转速恢复性能的影响，设计最优kP、kI。
基于变系数PI控制的自适应转速恢复策略如图6所示，其中，ωmax和ωmin分别为DFIG转子转速最大、最小限值。频率支撑阶段采用变系数控制策略[12]，根据DFIG转速状态调整控制系数，在高转速区域，采用较大的控制系数提高DFIG的调频能力；在低转速区域，采用近零系数避免DFIG过度减速现象，避免DFIG触及最低转速安全限制；通过检测最低转速，启动转速恢复策略。
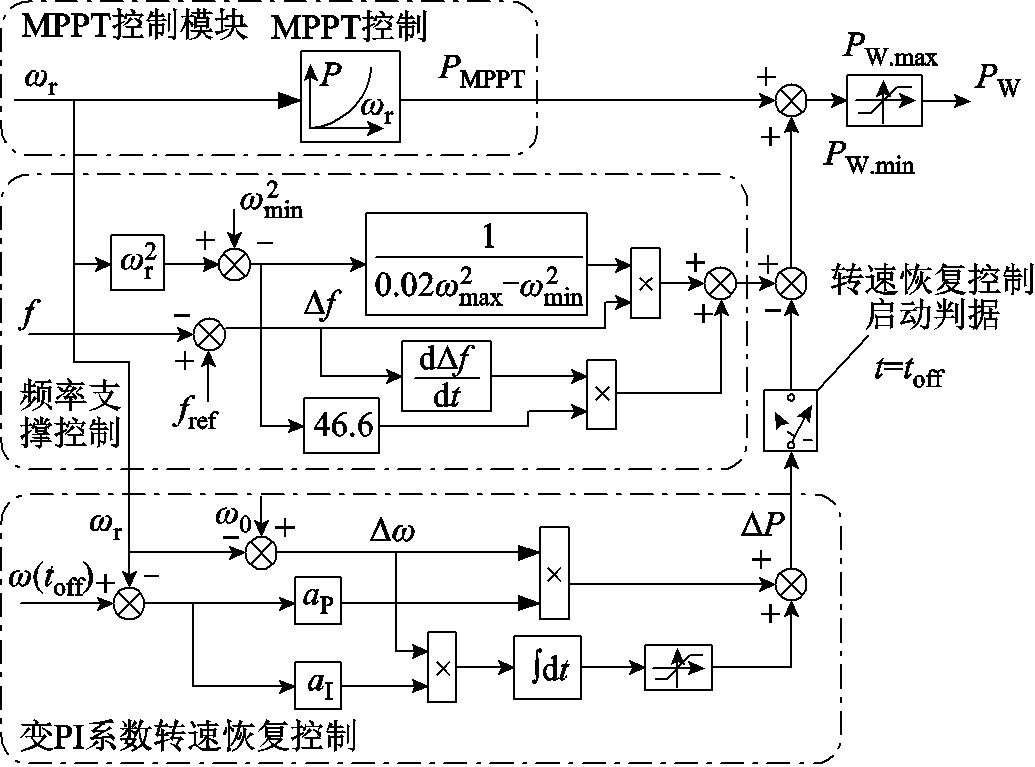
图6 基于变系数PI控制的DFIG转速恢复策略
Fig.6 DFIG speed recovery strategy with variable PI coefficient
为了验证本文提出转速恢复策略的有效性及良好的鲁棒性，在EMTP-RV仿真平台搭建了一个高风电渗透率的电力系统模型。该模型包括：6台同步发电机组成的火电厂、1个含DFIG的聚合风电场、1台异步电动机和350 MW的静负荷。其中DFIG聚合风电场由23台5 MW的DFIG组成。电力系统仿真模型结构如图7所示。
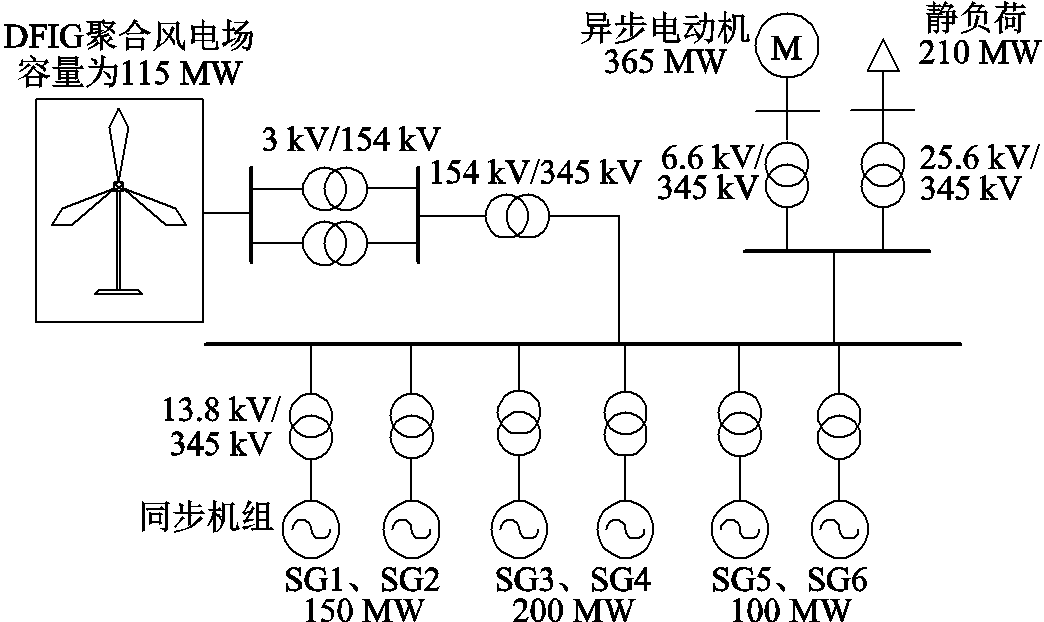
图7 电力系统仿真模型
Fig.7 Model of simulation system
本文采用控制变量法进行仿真对比实验，验证提出策略的有效性。在50 s切除同步发电机SG4作为功率扰动事件，频率支撑阶段采用图6所示的控制策略，在toff时刻启动转速恢复策略，对比传统转速恢复策略（DFIG退出调频）、定PI系数转速恢复策略（kP=1.5，kI=0.1）与变PI系数转速恢复策略（aP=5，aI=2），这三种转速恢复策略在不同扰动、不同风电渗透率下，转速恢复及频率二次跌落的情况。各算例设置见表1。
表1 算例设置
Tab.1 Case settings
算例扰动大小/MW风电渗透率(%)toff/s 1902050 21502053 31504056
3.1.1 算例1：风电渗透率为20%，扰动为90 MW
算例1的仿真结果如图8所示。由图8a～图8c可知，DFIG采用传统转速恢复策略时，直接移除频率支撑控制，造成0.116(pu)的功率突变，产生严重的频率二次跌落，频率跌落至49.69 Hz；转子吸收较多动能，转速快速恢复，在95 s转速恢复至初始值。
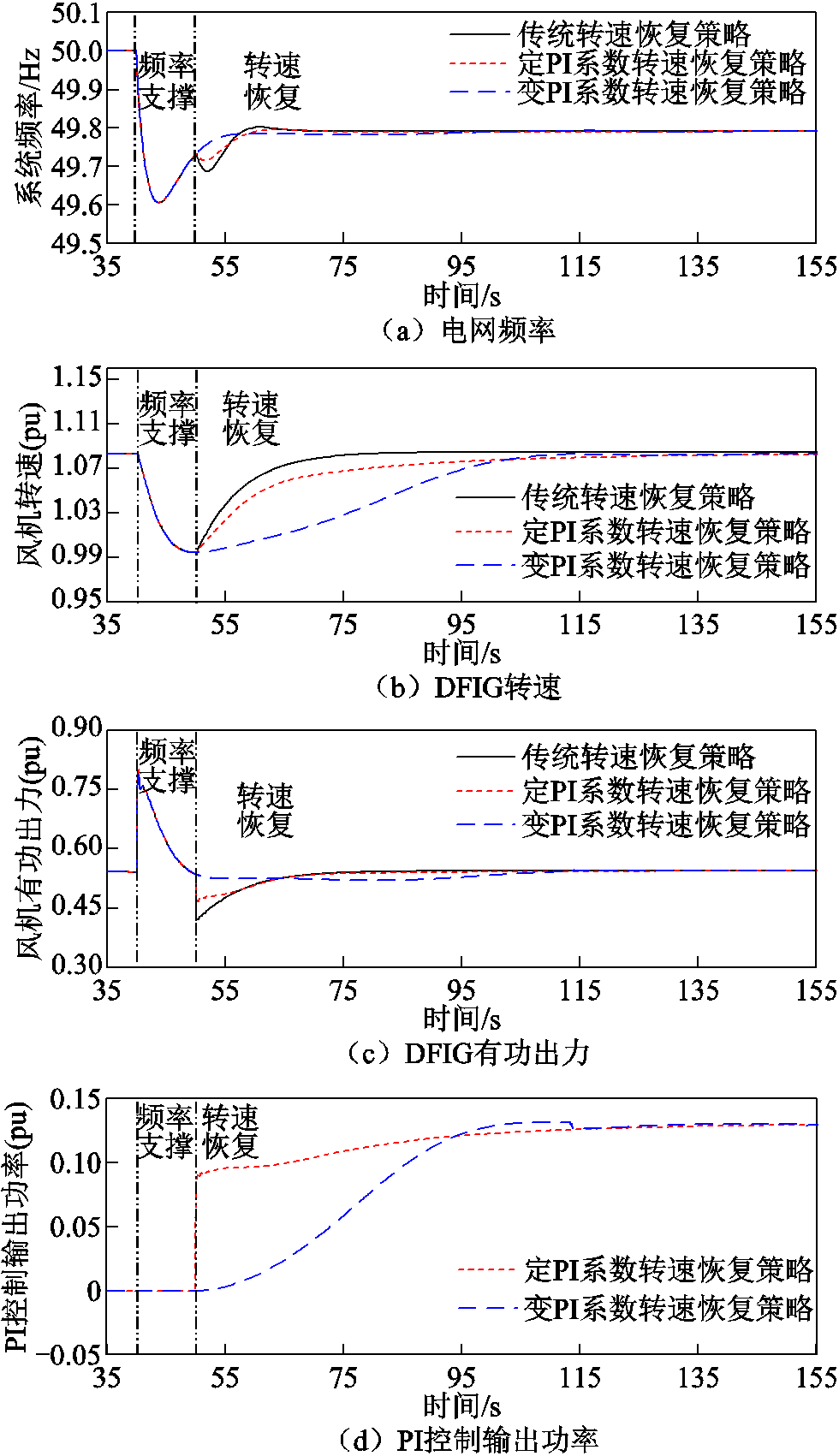
图8 算例1的仿真结果
Fig.8 Simulation results of Case 1
当DFIG采用定PI系数转速恢复策略时，转子转速恢复变慢，直到120 s时转子转速恢复稳定。但频率二次跌落得到改善，频率二次跌落最低点增加至49.72 Hz，这主要因为基于PI转速恢复控制策略初步实现有功减载量“先抑后扬”的输出方式，如图8d所示。然而在转速恢复初期，P控制器占据主导地位，转速恢复初期仍然存在功率突降，但相比传统转速恢复策略下降了0.082(pu)，从而抑制了频率二次跌落；随时间增长，I控制器占据主导地位，I控制器通过误差积累消除稳态误差，但由于较小且不变的控制增益，延长了转速恢复时间。
当DFIG采用变PI系数转速恢复策略时, 由于kP、kI与转速差值[ωr-ω(toff)]存在耦合关系，使ΔP能从0开始增加，实现ΔP(t)以“先抑后扬”的输出方式进行转速恢复。如图8d所示，在转速恢复初期，DFIG以ΔP为0的情况下启动转速恢复控制（“先抑”），在风机出力中ΔP(t)起主导作用，使DFIG总出力PW(t)逐步下降，且无功率突变，从根源上有效抑制了频率二次跌落；随时间增长，kP、kI随[ωr-ω(toff)]增大而增大，ΔP(t)与ΔPW(t)趋近相等，DFIG输出由MPPT出力占主导作用，105 s时，ΔP超过定PI系数转速恢复策略的ΔP（“后扬”），转速恢复加快（由于算例1为渗透率低，扰动小，转子释放动能少，转速恢复改善效果不明显）。
3.1.2 算例2：风电渗透率为20%，扰动为150 MW
不同扰动时，转子转速到达最低点的时间存在差异，foff不同，并且随扰动增大，转子释放动能增多。为了证明自适应转速恢复策略面对不同扰动的有效性，将切机容量增加到150 MW，算例2的仿真结果如图9所示。
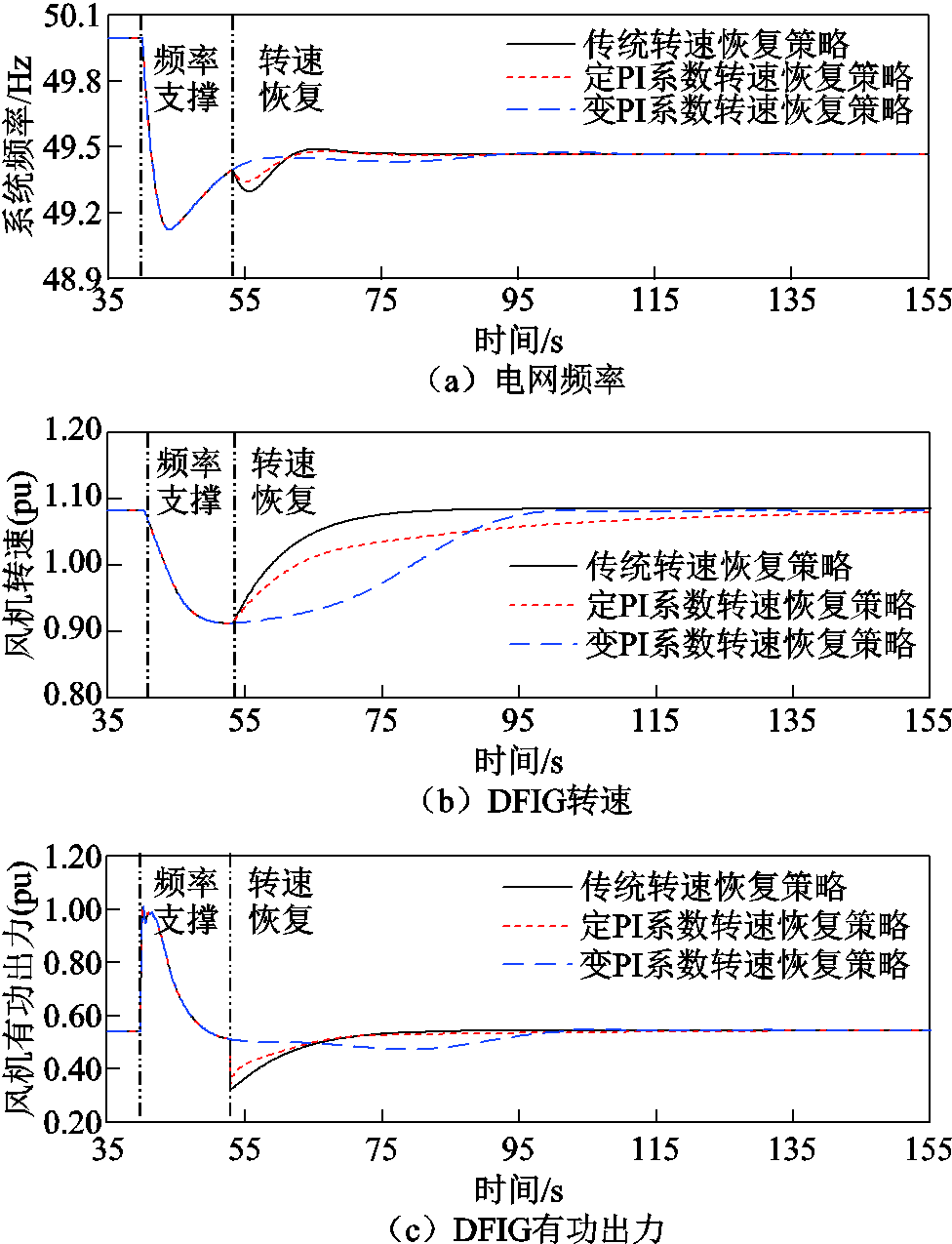
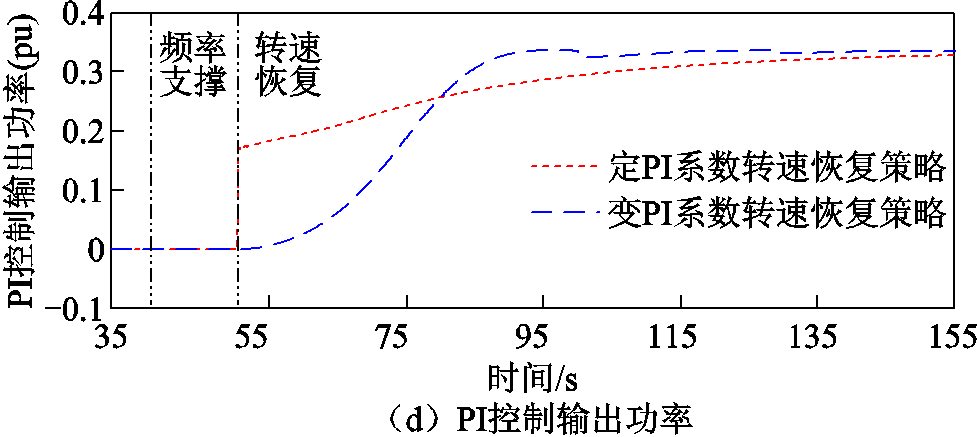
图9 算例2的仿真结果
Fig.9 Simulation results of Case 2
在采用传统转速恢复策略和定PI系数转速恢复策略时，DFIG频率二次跌落更加严重，频率二次跌落进最低点分别降低到49.30 Hz和49.34 Hz；转子转速恢复稳定的时间变长，分别为80 s和135 s。当采用变PI系数转速恢复策略时，无频率二次跌落，转速于98 s恢复稳定。从系统角度出发，有效抑制转速恢复初期的功率突变，消除频率二次跌落；从DFIG角度出发，ΔP以“先抑后扬”的方式输出，保障转速恢复性能。
算例3：风电渗透率为40%，扰动为150 MW。随着风电渗透率的增加，同步机调频比重减小，DFIG输出更多转子动能参与系统调频，转子转速大幅下降，转速恢复控制策略的toff与ΔPE(toff)均发生较大变化，导致转速恢复策略的性能受到影响。本文通过减少两台同步发电机，实现高比例风电渗透模型，算例3的仿真结果如图10所示。
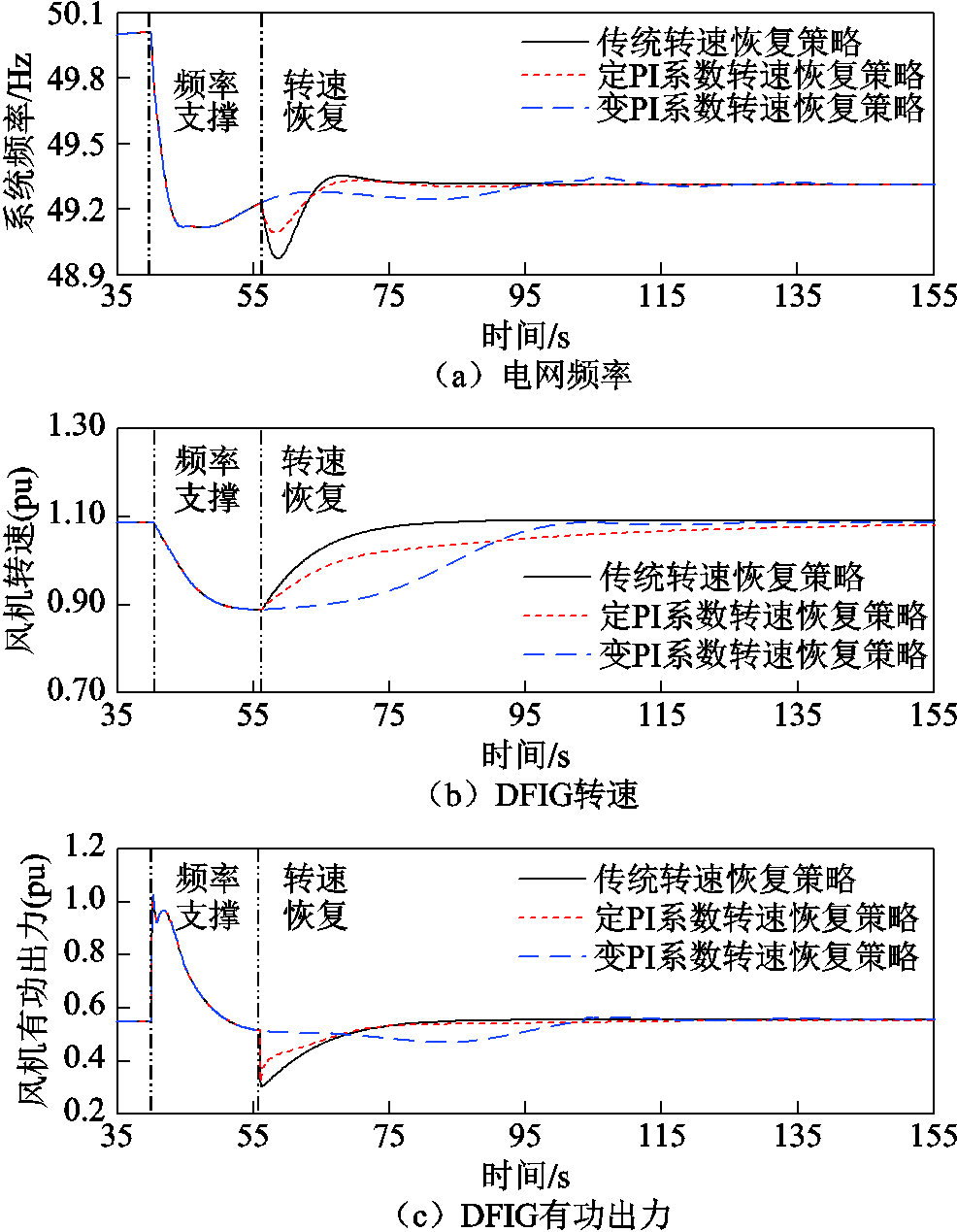
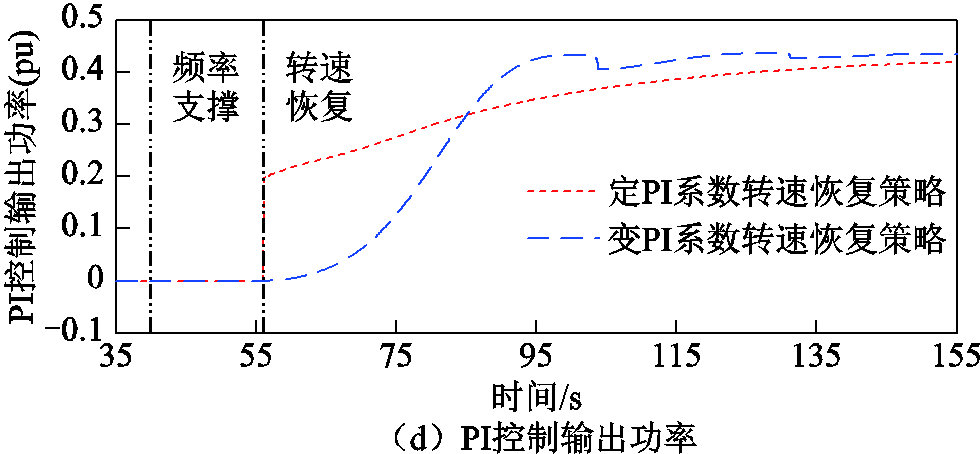
图10 算例3的仿真结果
Fig.10 Simulation results of Case 3
由图10可知，系统频率二次跌落比算例2更严重，采用传统转速恢复策略和定PI系数转速恢复策略时，频率二次跌落最低点分别为48.97 Hz、49.09 Hz，比频率一次跌落最低点小，对系统稳定造成巨大危害；转子转速分别在84 s、155 s恢复稳定。在采用变PI系数转速恢复策略时，无频率二次跌落，转速快速恢复。
为解决DFIG转速恢复策略不能兼顾抑制频率二次跌落和转子转速恢复性能的问题，本文首先揭示转速恢复控制启动时刻、有功减载量对抑制频率二次跌落的影响机制，其次提出一种基于变系数PI控制的自适应转速恢复策略，得出以下结论：
1）对转速恢复策略启动时间进行研究。从频率二次跌落的角度分析，在频率恢复阶段，启动转速恢复控制，系统不平衡功率更小，能有效地抑制转速恢复初期的功率突变；从转速恢复性能的角度分析，在频率恢复阶段启动转速恢复，转速恢复到稳态值的时间不至于太慢。
2）对转速恢复策略有功减载量进行研究。为减小转速恢复初期的功率突变，兼顾转子转速恢复性能，借助PI控制器实现有功减载量以“先抑后扬”的输出方式进行转速恢复。考虑到基于定系数PI控制的转速恢复策略无法适应不同工况、转速恢复初期仍存在功率突等问题，将比例、积分控制系数与转速建立耦合关系，设计了基于变系数PI控制的自适应转速恢复策略，实现了兼顾抑制频率二次跌落与转速恢复性能。
当前研究采用简化模型，与实际同步机组及风电机组调频模型存在一定差异，后期的工作将构建精细化风电机组和同步发电机组频率响应模型，量化分析风电机组控制参数二次频率跌落和转速恢复时间的影响，为风电机组整定频率控制参数提供参考。同时，进一步研究有效整定PI控制参数方法。
参考文献
[1] 康重庆, 姚良忠. 高比例可再生能源电力系统的关键科学问题与理论研究框架[J]. 电力系统自动化, 2017, 41(9): 2-11. Kang Chongqing, Yao Liangzhong. Key scientific issues and theoretical research framework for power systems with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2017, 41(9): 2-11.
[2] 李军徽, 侯涛, 穆钢, 等. 电力市场环境下考虑风电调度和调频极限的储能优化控制[J]. 电工技术学报, 2021, 36(9): 1791-1804. Li Junhui, Hou Tao, Mu Gang, et al. Optimal control strategy for energy storage considering wind farm scheduling plan and modulation frequency limitation under electricity market environment[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1791-1804.
[3] 朱博, 徐攀腾, 刘科, 等. 柔性直流与风电协同的受端系统频率调控方法[J]. 东北电力大学学报, 2021, 41(2): 86-93. Zhu Bo, Xu Panteng, Liu Ke, et al. Frequency control method for receiving end power system by DFIG and VSC-HVDC[J]. Journal of Northeast Electric Power University, 2021, 41(2): 86-93.
[4] 王洋, 杜文娟, 王海风. 风电并网系统次同步振荡频率漂移问题[J]. 电工技术学报, 2020, 35(1): 146-157. Wang Yang, Du Wenjuan, Wang Haifeng. Frequency drift of sub-synchronous oscillation in wind turbine generator integrated power system[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 146-157.
[5] 颜湘武, 崔森, 常文斐. 考虑储能自适应调节的双馈感应发电机一次调频控制策略[J]. 电工技术学报, 2021, 36(5): 1027-1039. Yan Xiangwu, Cui Sen, Chang Wenfei. Primary frequency regulation control strategy of doubly-fed induction generator considering supercapacitor SOC feedback adaptive adjustment[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1027-1039.
[6] 颜湘武, 孙雪薇, 崔森, 等. 基于转子动能与超级电容器储能的双馈风电机组惯量和一次调频改进控制策略[J]. 电工技术学报, 2021, 36(增刊1): 179-190. Yan Xiangwu, Sun Xuewei, Cui Sen, et al. Improved control strategy for inertia and primary frequency regulation of doubly fed induction generator based on rotor kinetic energy and supercapacitor energy storage[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 179-190.
[7] 颜湘武, 王德胜, 杨琳琳, 等. 直驱风机惯量支撑与一次调频协调控制策略[J]. 电工技术学报, 2021, 36(15): 3282-3292. Yan Xiangwu, Wang Desheng, Yang Linlin, et al. Coordinated control strategy of inertia support and primary frequency regulation of PMSG[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3282-3292.
[8] 国家市场监督管理总局, 国家标准化管理委员会. 风力发电机组电网适应性测试规程: GB/T 36994—2018[S]. 北京: 中国标准出版社, 2018.
[9] National Grid. Mandatory frequency response nation al grid [EB/OL]. 2016. https://www.nationalgrid.com/ sites/default/files/documents/Mandatory%20Frequency%20Response%20Guide%20v1.1.pdf.
[10] 单煜, 汪震, 周昌平, 等. 基于分段频率变化率的风电机组一次调频控制策略[J]. 电力系统自动化, 2022, 46(11): 19-26. Shan Yu, Wang Zhen, Zhou Changping, et al. Control strategy of primary frequency regulation for wind turbine based on segmented rate of change of frequency[J]. Automation of Electric Power Systems, 2022, 46(11): 19-26.
[11] 兰飞, 潘益丰, 时萌, 等. 双馈风电机组变系数虚拟惯量优化控制[J]. 电力系统自动化, 2019, 43(12): 51-59. Lan Fei, Pan Yifeng, Shi Meng, et al. Optimal variable-coefficient virtual inertia control for DFIG-based wind turbines[J]. Automation of Electric Power Systems, 2019, 43(12): 51-59.
[12] Lee J, Jang G, Muljadi E, et al. Stable short-term frequency support using adaptive gains for a DFIG-based wind power plant[J]. IEEE Transactions on Energy Conversion, 2016, 31(3): 1068-1079.
[13] 刘辉, 葛俊, 巩宇, 等. 风电场参与电网一次调频最优方案选择与风储协调控制策略研究[J]. 全球能源互联网, 2019, 2(1): 44-52. Liu Hui, Ge Jun, Gong Yu, et al. Optimization scheme selection of wind farm participation in grid primary frequency modulation and study of wind-storage coordination control strategy[J]. Journal of Global Energy Interconnection, 2019, 2(1): 44-52.
[14] 蔡国伟, 钟超, 吴刚, 等. 考虑风电机组超速减载与惯量控制的电力系统机组组合策略[J]. 电力系统自动化, 2021, 45(16): 134-142. Cai Guowei, Zhong Chao, Wu Gang, et al. Unit commitment strategy of power system considering overspeed load reduction and inertia control of wind turbine[J]. Automation of Electric Power Systems, 2021, 45(16): 134-142.
[15] Tarnowski G C, Kjar P C, Sorensen P E, et al. Variable speed wind turbines capability for temporary over-production[C]//2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 2009: 1-7.
[16] Kheshti M, Ding Lei, Nayeripour M, et al. Active power support of wind turbines for grid frequency events using a reliable power reference scheme[J]. Renewable Energy, 2019, 139: 1241-1254.
[17] Conroy J F, Watson R. Frequency response capability of full converter wind turbine generators in comparison to conventional generation[J]. IEEE Transactions on Power Systems, 2008, 23(2): 649-656.
[18] 刘璋玮, 刘锋, 梅生伟, 等. 扩张状态观测器在双馈风机虚拟惯量控制转速恢复中的应用[J]. 中国电机工程学报, 2016, 36(5): 1207-1217. Liu Zhangwei, Liu Feng, Mei Shengwei, et al. Application of extended state observer in wind turbines speed recovery after inertia response control[J]. Proceedings of the CSEE, 2016, 36(5): 1207-1217.
[19] 乔颖, 郭晓茜, 鲁宗相, 等. 考虑系统频率二次跌落的风电机组辅助调频参数确定方法[J]. 电网技术, 2020, 44(3): 807-815. Qiao Ying, Guo Xiaoqian, Lu Zongxiang, et al. Parameter setting of auxiliary frequency regulation of wind turbines considering secondary frequency drop[J]. Power System Technology, 2020, 44(3): 807-815.
[20] 赵晶晶, 李敏, 何欣芹, 等. 基于限转矩控制的风储联合调频控制策略[J]. 电工技术学报, 2019, 34(23): 4982-4990. Zhao Jingjing, Li Min, He Xinqin, et al. Coordinated control strategy of wind power and energy storage in frequency regulation based on torque limit control[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4982-4990.
[21] 劳焕景, 张黎, 宋鹏程, 等. 一种考虑最优状态动态恢复的风电持续调频策略[J]. 电网技术, 2020, 44(12): 4504-4512. Lao Huanjing, Zhang Li, Song Pengcheng, et al. Wind power sustained frequency regulation strategy with dynamic optimized state recovery behavior[J]. Power System Technology, 2020, 44(12): 4504-4512.
[22] 劳焕景, 张黎, 赵彤, 等. 考虑分组控制和有序恢复的风电调频策略[J]. 电力系统自动化, 2020, 44(16): 114-120. Lao Huanjing, Zhang Li, Zhao Tong, et al. Frequency regulation strategy for wind power considering grouping control and orderly recovery[J]. Automation of Electric Power Systems, 2020, 44(16): 114-120.
[23] Lao Huanjing, Zhang Li, Zhao Tong, et al. Innovated inertia control of DFIG with dynamic rotor speed recovery[J]. CSEE Journal of Power and Energy Systems, 2020, 8(5): 1417-1427.
[24] 高峰, 凌新梅, 王伟. 大型风电机组独立变桨控制器PI参数联合整定[J]. 太阳能学报, 2018, 39(2): 307-314. Gao Feng, Ling Xinmei, Wang Wei. PI parameters joint tuning for individual pitch controller of large wind turbine[J]. Acta Energiae Solaris Sinica, 2018, 39(2): 307-314.
Abstract Doubly-fed induction generator (DFIG) participates in frequency regulation to support the reduced system inertia. After frequency regulation, the rotor speed is lower than the optimal speed. It is necessary to regain the rotor speed, otherwise, the rate of wind energy utilization would be reduced, or stalling of DFIG even be caused. The existing rotor speed recovery methods only unilaterally improved the performance of speed recovery or reduced the size of frequency secondary drop. To address these issues, this paper suggests a variable-coefficient-PI-control speed recovery strategy.
Firstly, this paper revealed the influence mechanism of the amount of the active power reduction and the invitation of the recovery strategy on the frequency secondary drop and the speed recovery performance; secondly, a recovery strategy of the DFIG based on fixed-PI-coefficient control was proposed, the reduction output power with “rise after restrain” manner had been preliminarily constructed to speed recovery. Then, to solve the shortcomings of the recovery strategy with fixed-PI-coefficient, this paper established the coupling relationship between rotor speed of the doubly-fed induction generators and PI control coefficients according to different operating conditions, and then constructed an adaptive recovery strategy based on variable-PI-coefficient to ensure the speed recovery performance while suppressing the frequency secondary drop. Finally, power system model with various wind power penetrations and disturbances was modeled based on an EMTP-RV to investigate the effectiveness of the proposed rotor speed recovery strategy.
Simulation results on the different speed recovery strategies illustrate that, under the disturbance of 90 MW with the wind power penetration of 20%, since the DFIG directly removed the frequency support control strategy, it caused a sudden power change of 0.116(pu) so as to result in a frequency secondary drop of 49.69 Hz; the DFIG absorbed more kinetic energy during the short period, the rotor speed regained to the initial value at 95 s; when the DFIG used the fixed-coefficient-PI-control speed recovery strategy, the sudden power variation was reduced by 0.082(pu), the frequency secondary nadir was improved by 0.030 Hz, however, the time for the speed recovery was extended to 120 s; the use of variable-coefficient-PI-control speed recovery strategy started speed recovery without sudden power variation, as a result, no frequency secondary drop was caused, the amount of the active power reduction increase leaded to faster speed recovery during the latter period. When the disturbances increased to 150 MW, the variable-PI-coefficient speed recovery strategy could still maintain the better speed recovery performance and avoid secondary frequency drop. In the case of a large disturbance with a high wind penetration level, the frequency secondary drops for the direct rotor speed recovery and fixed-PI-coefficient speed recovery strategy were lower than the first frequency nadir caused by the disturbance, however, the variable-PI-coefficient speed recovery strategy could guarantee the speed recovery performance without causing a second frequency drop.
The following conclusions can be drawn from the simulation analysis: (1) In specific cases, the fixed-coefficient-PI-control speed recovery strategy can preliminarily constructed the “rise after restrain” manner of the active power reduction so as to mitigate the size of frequency secondary drop and ensure speed recovery performance by reasonably employing the parameters of PI controller. (2) The proposed variable-coefficient-PI-control speed recovery strategy can achieve the counterbalance between frequency secondary dip and rotor speed recovery performance compared to constant- coefficient-PI-control speed recovery strategy since the reduction output power with “rise after restrain” manner had been constructed to during the rotor speed recovery period.
Keywords: Doubly-fed induction generator (DFIG), adaptive rotor speed recovery, frequency secondary drop, PI control
DOI:10.19595/j.cnki.1000-6753.tces.220852
中图分类号：TM614
东北电力大学博士科研启动基金资助项目（BSJXM-2021209）。
收稿日期 2022-05-18
改稿日期 2022-08-17
王 鑫 男，1999年生，硕士研究生，研究方向为可再生能源联网控制技术。E-mail： 1954592617@qq.com
杨德健 男，1990年生，博士，讲师，研究方向为可再生能源联网控制技术。E-mail：yangdejian@neepu.edu.cn（通信作者）
（编辑 赫蕾）