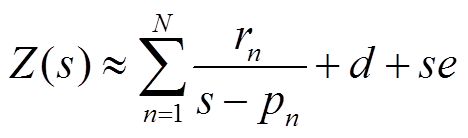 (1)
(1)
摘要 在舰船综合电力系统等复杂系统的电磁兼容设计验证中,迫切需要通过对强电磁设备的阻抗进行物理等效以便开展半实物电磁兼容试验。工程上常用矢量匹配法实现强电磁设备阻抗的等效电路网络建模,但由于存在“端口无源性”和非正值元件导致的“元件无源性”问题,不能确保等效电路网络的物理可实现性。为了解决这个问题,该文提出一种融合了矢量匹配法、留数摄动法和优化算法,并可物理实现的强电磁设备宽频段阻抗建模新方法。该方法首先通过矢量匹配法对强电磁设备的阻抗数据进行有理函数拟合;然后利用留数摄动法对矢量匹配法的结果进行“端口无源性”修正,并将其转化为等效电路网络;随后利用粒子群算法和天牛须算法对非正值元件进行修正,实现“元件无源性”修正;最后,通过典型实际案例验证了该方法的可靠性和正确性。
关键词:粒子群算法 无源网络 宽带网络 矢量匹配法 强电磁设备
随着电工新材料、电力电子新器件、控制新技术的快速进步,舰船综合电力系统等复杂系统的功率密度进一步提升,电压等级进一步提高,并逐渐朝中压直流输配电、高性能器件广泛应用的方向发展[1-2]。但是,由于在舰船综合电力系统等复杂系统中大规模采用功率变换模块[3-4],且由于开关频率快速提升导致的dv/dt和di/dt越来越高,给舰船综合电力系统等复杂系统带来了严重的电磁干扰隐患。因此,在舰船综合电力系统等复杂系统的电磁兼容设计阶段,迫切需要对系统中的强电磁设备进行电网络建模以便进行等效物理模拟,支撑开展半实物的电磁兼容测试,以更接近实际状态来评估系统的电磁兼容性能,并针对薄弱环节,提出针对性的抑制措施。
通常有两种不同的方法来进行强电磁设备阻抗建模:基于电路拓扑结构的简化电路建模方法和基于阻抗数据拟合的等效电路网络建模方法。基于电路拓扑结构的简化电路建模方法一般从实际强电磁设备的拓扑结构出发,经过简化得到电磁兼容模型,具有明确的物理意义,其参数由公式或Ansys等商业软件计算获得[5]。但是,由于在舰船综合电力系统等复杂系统的电磁兼容预测和设计中,难以确切地掌握各强电磁设备内部的详细拓扑结构等信息,比如各部分的接线方式和具体尺寸,因此难以获得设备的高频寄生参数,导致无法基于电路拓扑结构来建立其电磁兼容等效电路网络。基于阻抗数据拟合的等效电路网络建模方法是利用阻抗数据进行等效电路网络建模的一种有效方法,通常采用图像法或矢量匹配(Vector Fitting, VF)法将实测的阻抗数据转换为等效电路网络模型[6]。
图像法是一种利用阻抗数据直接建立其等效电路的建模方法,能够保证等效电路中的所有R、L、C参数均为正值,但是图像法的拟合精度相对较差,而且仅能用于只有一个峰值点的阻抗数据的建模。文献[7]指出,当阻抗数据波动较多时,如果想要精准拟合,则等效电路中存在非正值元件的概率较大,如果采用图像法进行等效电路的拟合,模型精度将会大大降低,因此对于舰船综合电力系统等复杂系统的强电磁设备阻抗建模,图像法较不适用。
矢量匹配法是一种将频域数据拟合为有理函数的方法,由于可以有效地避免在有理函数逼近过程中出现的病态矩阵问题,更加适用于舰船综合电力系统等阻抗数据波动较多的情况,成为目前应用最为广泛的端口等效电路网络建模方法[8]。迄今为止,矢量匹配法已经在架空输电线路、永磁同步电机、电力电子变换器等强电磁设备的阻抗建模中得到了广泛应用[9-11]。
为了降低舰船综合电力系统等复杂系统的电磁兼容设计风险,通常需要开展半实物电磁兼容试验,工程上常常需要在建立阻抗等效电路网络的基础上,搭建出由R、L、C等集中参数元件构成的物理电路,以实现对强电磁设备阻抗特性的物理等效。然而,利用矢量匹配法对强电磁设备阻抗进行建模时,不能有效地解决等效电路网络模型的“端口无源性”问题,很容易导致时域仿真时产生数值发散[12]。针对等效电路网络的“端口无源性”问题,文献[13]提出利用一阶摄动来调整Hermitian矩阵的虚特征值的方法,以实现“端口无源性”修正,但需要迭代多次才可以完成,耗时良久。文献[14]提出了将一阶特征值扰动引入二次规划算法的无源修正方法,以实现“端口无源性”修正,但是效率较低。文献[15]提出利用留数摄动法,通过二次规划优化参数,强制实现“端口无源性”修正,以牺牲拟合精度为代价,可以快速完成。
此外,将经由“端口无源性”修正的阻抗有理化函数转化为等效电路网络后,部分情况下等效电路网络中存在一些非正值的R、L、C元件,会导致“元件无源性”问题。文献[16]针对特高压电容分压器,利用模式搜索算法,对等效电路网络进行无源优化,但由于未经过“端口无源性”修正,使得等效电路网络含有较多的非正值元件,并且整个计算速度较慢、无源器件参数间相差可达三十个数量级,无法用R、L、C等集中参数元件构成物理电路进行半实物验证。文献[17]通过“分项-并项”将有理函数的有源极点与无源极点分开,再利用智能优化算法对有源极点进行修正,最终得到全部由无源元件组成的等效电路网络,但是其等效电路网络阶数较高,结构较为复杂,不易于物理实现。
为此,本文针对阻抗等效电路网络阶数较高、元件参数选取不合理且无法物理实现等问题,提出一种融合了矢量匹配法、留数摄动法和优化算法,并可物理实现的强电磁设备宽频段阻抗建模新方法。该方法建立的强电磁设备的等效电路网络阶数低、易于物理实现,且各元件参数选取较为合理,可由R、L、C等集中参数元件构成物理电路进行验证。该方法首先通过矢量匹配法对测试得到的阻抗数据进行有理函数拟合;然后利用留数摄动法对矢量匹配法的结果进行“端口无源性”修正,并将其转化为等效电路网络模型;随后利用粒子群(Particle Swarm Optimization, PSO)算法和天牛须(Beetle Antennae Search, BAS)算法对非正值元件进行修正,实现“元件无源性”修正;最后,通过实际案例验证本方法的可靠性和正确性。
根据矢量匹配法,可以将一个强电磁设备的阻抗模型用一个关于复频率s的有理函数表示为
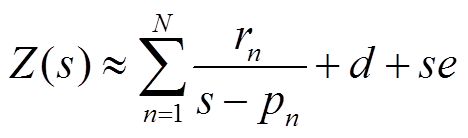 (1)
(1)
式中,rn和pn分别为留数和极点,它们均为实数或互为共轭复数对;d和e为实数;N为阶数。
基于测试数据Z(sk),sk为测试频点,k=1,2,…,K,K为测试频点个数,通过迭代可确定强电磁设备阻抗模型中的留数rn、极点pn、实数d和e。
首先,记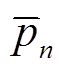 为初始极点,为了求解Z(s)的各系数,引入辅助函数σ(s)。将辅助函数σ(s)与强电磁设备内阻抗函数Z(s)相乘,并假设迭代过程中,σZ(s)与σ(s)有相同的极点
为初始极点,为了求解Z(s)的各系数,引入辅助函数σ(s)。将辅助函数σ(s)与强电磁设备内阻抗函数Z(s)相乘,并假设迭代过程中,σZ(s)与σ(s)有相同的极点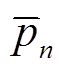 [18],并将其改写为相应的零极点形式,即
[18],并将其改写为相应的零极点形式,即
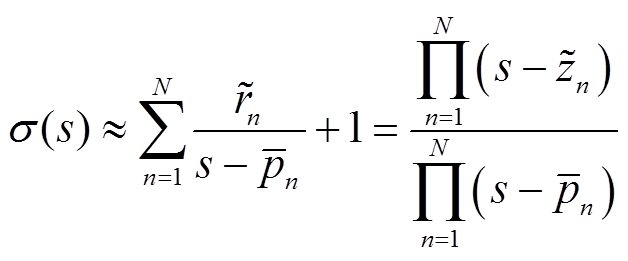 (2)
(2)
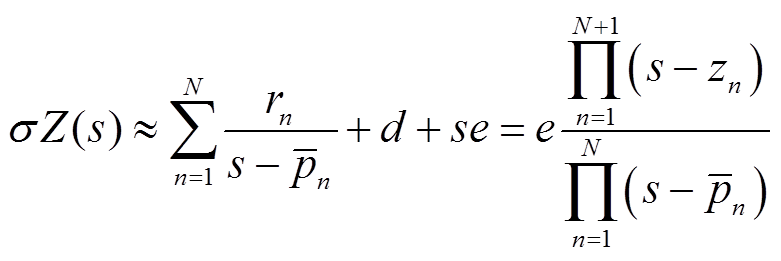 (3)
(3)
式中,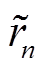 为辅助函数σ(s)的留数;
为辅助函数σ(s)的留数;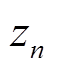 和
和 分别为σZ(s)和σ(s)的零点。
分别为σZ(s)和σ(s)的零点。
其次,利用式(2)和式(3),建立待求参数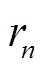 、
、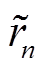 、d和e的线性方程,即
、d和e的线性方程,即
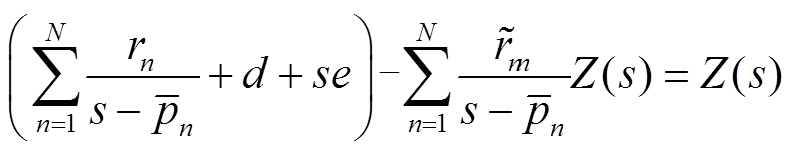 (4)
(4)
将测试数据Z(sk)及对应频点sk代入式(4),得到线性方程组的矩阵形式为
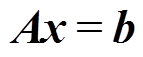 (5)
(5)
式中,A为K行2N+2列系数矩阵,其第k行表示为
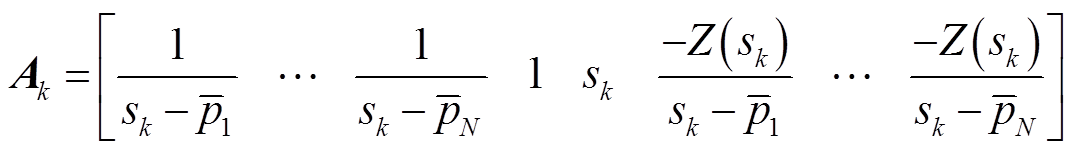 (6)
(6)
待求解向量x和已知向量b分别为
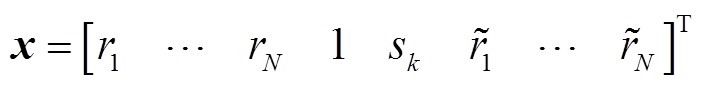 (7)
(7)
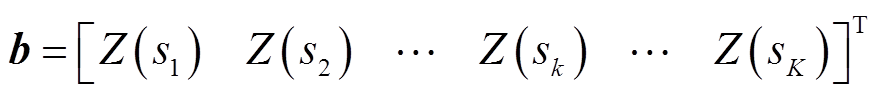 (8)
(8)
接着利用最小二乘法求解线性矩阵方程式(5)得到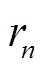 、
、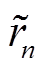 、d和e。需要注意的是,上述参数是在初始极点
、d和e。需要注意的是,上述参数是在初始极点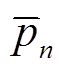 假设下得到的,故本次计算得到的
假设下得到的,故本次计算得到的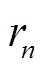 、
、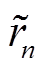 、d和e并不准确,因此有必要对初始极点
、d和e并不准确,因此有必要对初始极点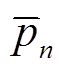 及参数
及参数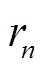 、
、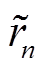 、d和e进行迭代修正。
、d和e进行迭代修正。
最后,根据式(2)和式(3),更新强电磁设备内阻抗模型输出函数Z(s),得到
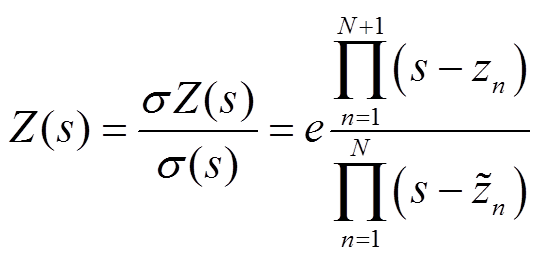 (9)
(9)
从式(9)可知,函数Z(s)的极点就是辅助函数σ(s)的零点,辅助函数σ(s)的零点就是下一次迭代Z(s)的初始极点。然后用σ(s)的零点代替初始假设的一系列初始极点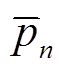 ,就可以获得新的
,就可以获得新的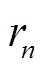 、
、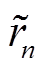 、d和e的解,循环迭代直到用式(1)参数化表达的Z(s)满足误差要求。
、d和e的解,循环迭代直到用式(1)参数化表达的Z(s)满足误差要求。
由于矢量匹配法是对强电磁设备的阻抗数据进行数学拟合,某些情况下会导致阻抗的有理函数达不到“端口无源性”的要求,极易造成时域仿真发散。本文为了解决这个问题,引入留数摄动法,具体方法如下。
根据电网络理论,一个无源网络必须满足两个条件:①无源网络阻抗可以表示为解析函数;②网络吸收的功率必须大于0。条件①由矢量匹配法自动满足,网络吸收的平均功率应按照式(10)计算。
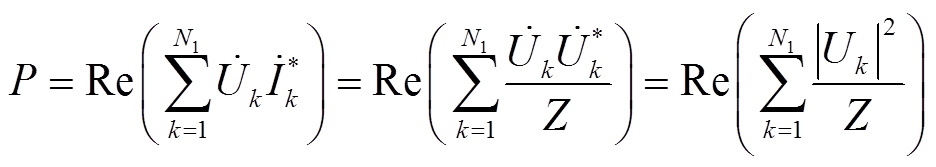 (10)
(10)
式中,Uk和Ik分别为网络中第k个端口的电压与电流;N1为网络的总支路数;“*”表示共轭运算。
因此,无源网络应满足的条件②即为Re(Z(s))>0,网络无源优化的目的即是令经过优化后的修正网络函数Gfit=Re(Z)的所有特征值均大于0。
故一个无源模型应该满足
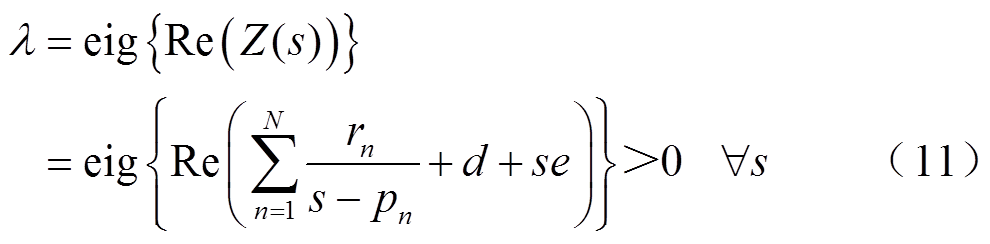
式中,λ为特征值;eig{·}为特征值求解。式(11)说明无源网络阻抗实部的所有特征值对于所有频率均为正。进一步,本文通过留数摄动法对式(1)进行修正。为了不改变原函数的性质,假设仅需要进行微小的修正,由此建立如式(12)~式(15)所示的约束方程。
 (12)
(12)
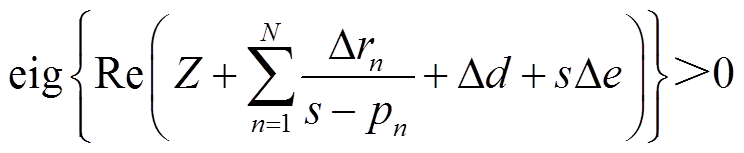 (13)
(13)
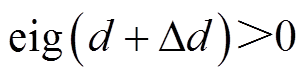 (14)
(14)
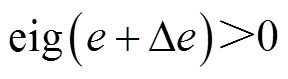 (15)
(15)
式中,ΔX为待求量,表示加在参数X上的修正偏差。约束式(12)是为了确保各参数的修正很微小;约束式(13)是为了确保经过修正后等效电路网络可以满足端口无源要求;约束式(14)和式(15)是为了确保参数d和e均为正值。
然后,根据式(12)~式(15)建立无源优化的二次规划方程[12],即
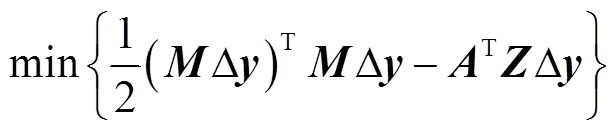 (16)
(16)
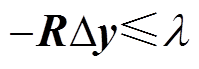 (17)
(17)
其中
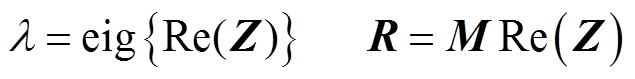
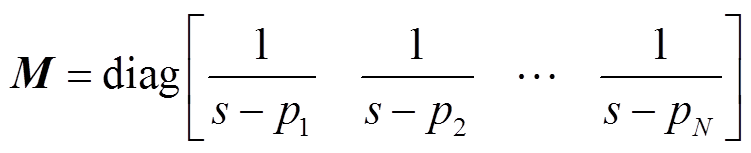
式中,Z为代入所有频点后形成的网络阻抗矩阵;y=[rn pn d e]T。
接着,对由各个端口的d和e组成的矩阵D和E分别进行正定化处理,即
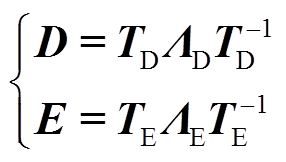 (18)
(18)
式中,TD和TE分别为D和E的标准化正交矩阵;ΛD和ΛE分别为D和E的特征值矩阵。将ΛD和ΛE中的负特征值用零代替,更新矩阵D和E,得到矩阵Dmod和Emod。
随后,利用二次规划算法计算满足约束条件式(16)和式(17)的最小二乘解,得到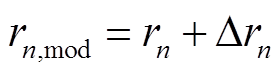 、
、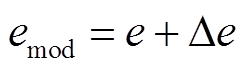 、
、 ,直至寻找到满足约束条件的修正参量,包括留数
,直至寻找到满足约束条件的修正参量,包括留数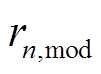 、一次项
、一次项 、常数项
、常数项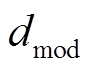 ;否则,将继续重复迭代。经过“端口无源性”修正后的内阻抗模型应为
;否则,将继续重复迭代。经过“端口无源性”修正后的内阻抗模型应为
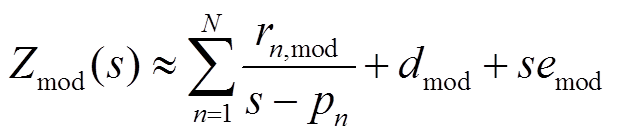 (19)
(19)
根据式(19)将经过修正后的留数、极点、一次项、常数项等参数信息,分为如图1所示的三种形式,每种形式用相应的子电路等效,最后将所有的子电路按串联方式连接,即可得到如图1所示的等效电路网络[19]。

图1 “端口无源性”修正后对应的等效电路网络
Fig.1 The equivalent circuit network corresponding to the "port passivity" correction
由于第1节得到的阻抗等效电路网络中常含有非正值元件,不能直接由R、L、C等集中参数元件构成物理电路,以实现阻抗的物理等效。因此有必要对其中的非正值元件进行修正,以实现“元件无源性”修正。相比于遗传算法等优化算法,粒子群(PSO)算法和天牛须(BAS)算法的原理更简单、参数更少、搜索速度更快、对计算机资源的占用更低[20-21],且经过大量实践证明,针对这一问题,在迭代次数相同时,与遗传算法等优化算法相比,PSO和BAS的优化效果更好。为了确保快速、高效地完成“元件无源性”修正,本文通过粒子群算法和天牛须算法,对非正值元件进行修正,以便于后期通过电容、电感及电阻物理实现等效电路网络,开展复杂电力系统的电磁兼容设计验证。
将目标函数设置为
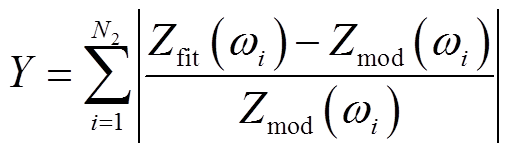 (20)
(20)
式中,ωi为第i个修正频点的角频率,i=1,2,…, N2;Zfit(·)为经过“元件无源性”修正后的电路阻抗函数。
基于优化算法的“元件无源性”修正流程如图2所示。在图2中的修正流程中,PSO和BAS均需要首先设置如式(20)所示的“元件无源性”修正的目标函数,在限值范围内随机设定各变量的初始值;然后更新步长等因子,进而更新各变量的选值,更新目标函数的最优值;如果满足结束要求,即可结束迭代,寻找到满足“元件无源性”修正的各元件参数。
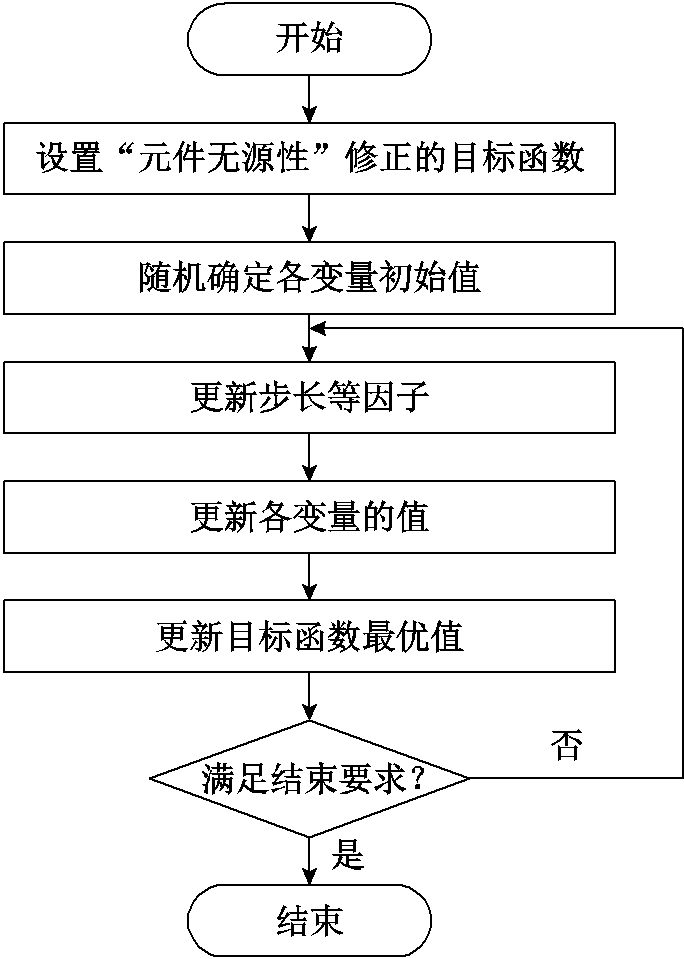
图2 基于优化算法的元件无源修正流程
Fig.2 Flowchart of passive correction of components based on optimization algorithm
可物理实现的强电磁设备阻抗的建模流程如图3所示。首先通过测试等方法获得强电磁设备的阻抗数据;然后通过矢量匹配法进行有理函数的拟合;随后,评估“端口无源性”状态,如果满足要求,则进行下一步,否则,需要先利用留数摄动法实现“端口无源性”修正,并将其转化为等效电路网络模型;接着对其“元件无源性”状态进行评估,如果满足要求,则可由R、L、C等集中参数元件构成物理电路进行验证,否则,需要先利用优化算法进行“元件无源性”修正;最后得到可物理实现的等效电路网络模型。
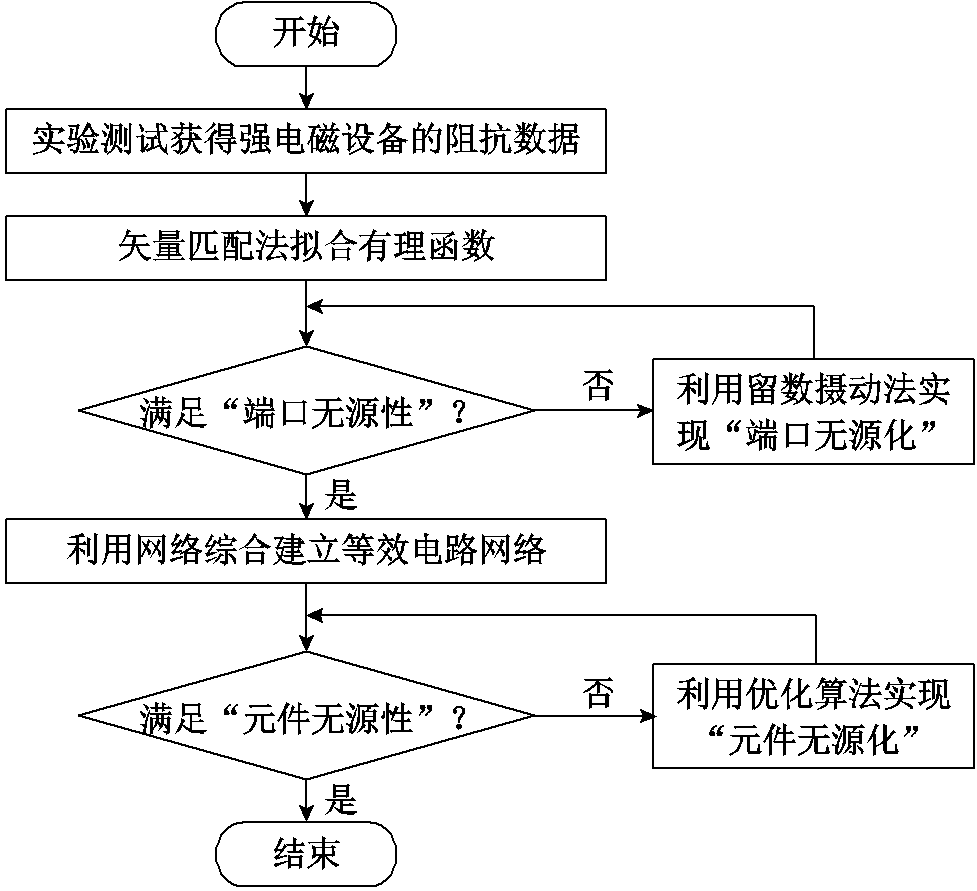
图3 可物理实现的强电磁设备阻抗的建模流程
Fig.3 Modeling process for physically realizable high- power electromagnetic device impedance
在进行舰船综合电力系统等复杂系统的传导干扰等效电路网络建模时,AC-AC变换器和永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)是两种典型的强电磁设备,因此为了验证本方法的正确性,本文以一台AC-AC变换器和PMSM进行实验验证。
首先,本文将上述方法应用到一台AC-AC变换器上进行建模验证与分析。该AC-AC变换器是将220 V、50 Hz的单相交流电转换为线电压为380 V、50Hz的三相交流电,其调制方式为空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM),开关频率为10 kHz,额定功率为1.5 kW。
结合WK 6500B阻抗分析仪的有效测量范围和国家军用标准GJB 151B—2013《军用设备和分系统电磁发射和敏感度要求与测量》中的CE102测试项目,在10 kHz~10 MHz频段内,对其进行阻抗测量。WK 6500B阻抗分析仪的偏置电压为1 V,阻抗测量方法如图4所示,将WK 6500B阻抗分析仪的输入端分别接在AC-AC变换器的两个输入端子上,测试频点个数为1 600个。

图4 AC-AC变换器的阻抗测量方法
Fig.4 Impedance measurement method of the AC-AC converter
然后,按照2.2节的流程搭建其可物理实现的等效电路网络,其中矢量匹配法的拟合阶数为8阶,AC-AC变换器经过“端口无源性”修正后的各元件参数见表1,其中下标n代表各子电路的个数。随后,本文分别利用PSO和BAS算法对这些非正值元件进行“元件无源性”修正,修正后的元件参数见表2,等效电路网络示意图如图5所示。
表1 AC-AC变换器“端口无源性”修正后的各元件参数
Tab.1 The parameters of each component after the correction of "port passivity" of the AC-AC converter

nR/ΩL/μHR0n/kΩC0n/pFR1n/kΩR2n/kΩC1n/pFLn/mH 125.93.05920.74388.5848.8114.774.3 2-6.62-9781.9212.7238.58.4 3-0.060.25759.90.023
表2 AC-AC变换器的“元件无源性”修正参数
Tab.2 "Component passivity" correction parameter of the AC-AC converter

算法C02/FR02/kΩR13/Ω PSO0.051 31.6941 BAS0.597 249.545.78
AC-AC变换器的幅频特性和相频特性对比结果分别如图6和图7所示,其中“VF初始结果”代表仅将实验测试数据进行矢量拟合的结果,还尚未进行“端口无源化”和“元件无源化”。可以发现,幅频特性和相频特性的拟合效果很好,并且PSO和BAS修正后的幅频特性拟合效果基本一致;BAS修正得到的相频特性更优,而且BAS计算时间更短;与相频特性相比,幅频特性拟合更优。而图7在1~10 MHz频率范围内,拟合精度不够高的主要原因在于:图1中每一个子电路对应的是式(20)的一个或两个极点,对表1的非正值元件修正,会导致对应的极点上的幅值和相位产生偏差;偏差较大是由于AC-AC变换器中含有非线性器件,对极值点的影响较大,且在这一频段范围内,其相频特性曲线有着较多的谐振点,当谐振点太多时,会导致误差不断叠加。
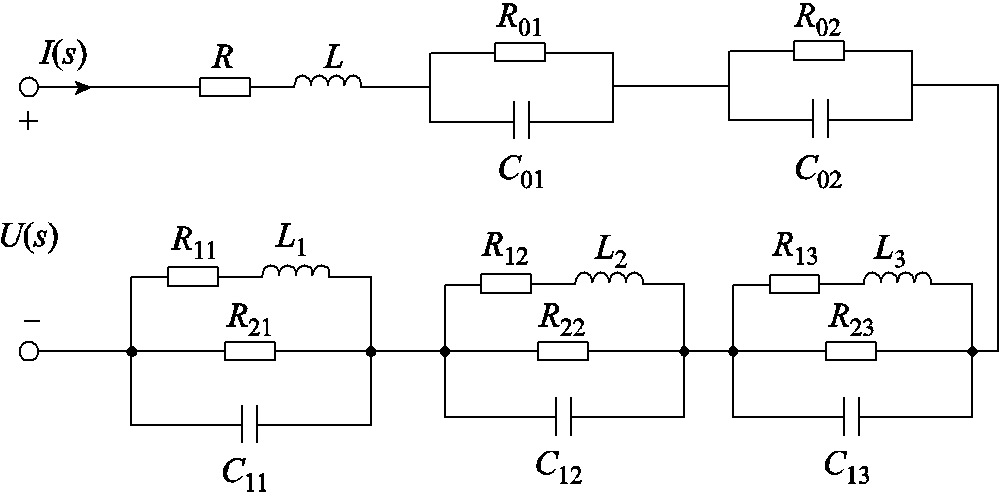
图5 AC-AC变换器的等效电路网络示意图
Fig.5 Equivalent circuit network diagram of the AC-AC converter
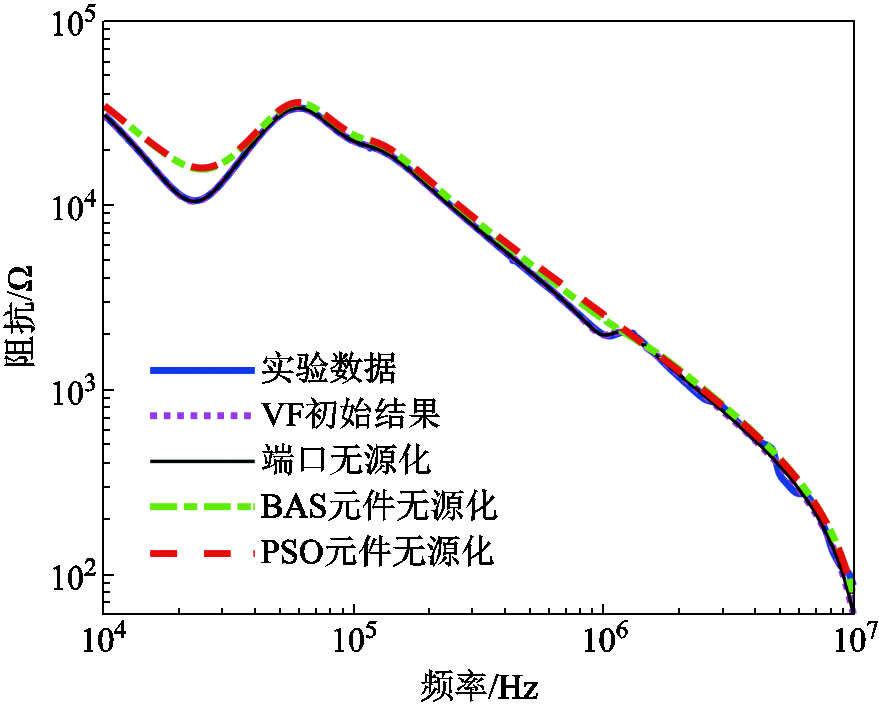
图6 AC-AC变换器幅频特性对比
Fig.6 Comparison of amplitude-frequency characteristics of the AC-AC converter
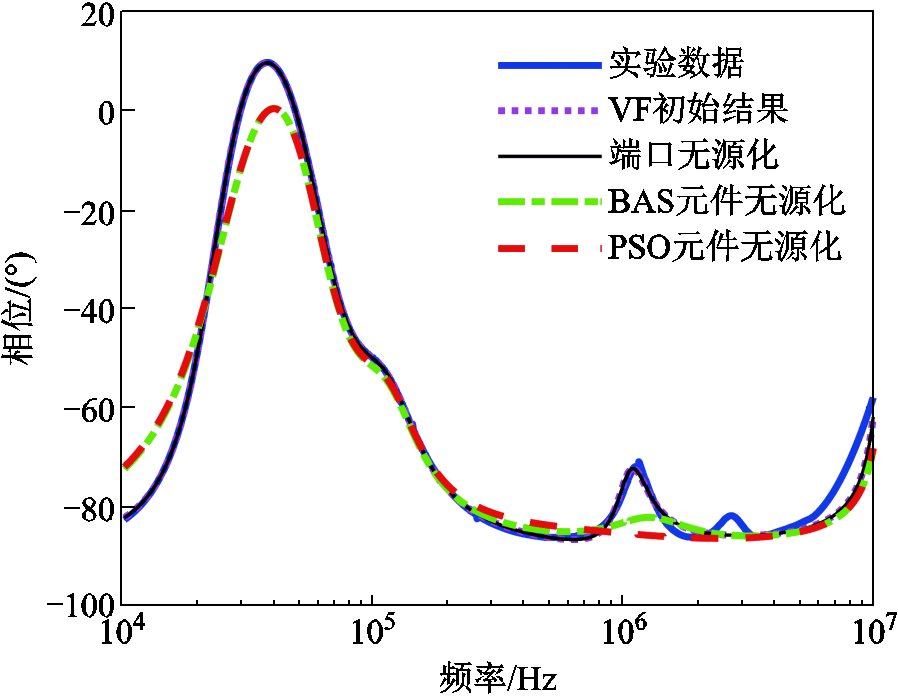
图7 AC-AC变换器相频特性对比
Fig.7 Comparison of phase-frequency characteristics of the AC-AC converter
此外,对于一些需要重点关注相频特性的场合,可以通过分段的方法,对效果较差的频段重新应用矢量匹配法,并建立相应的电磁兼容等效电路网络模型。本文以此AC-AC变换器为例,结合其幅频特性和相频特性曲线的特点与拟合较差的部分,重新对800 kHz~10 MHz范围内的阻抗数据进行矢量拟合,并进行相应的“端口无源性”和“元件无源性”修正,最终得到的AC-AC变换器幅频特性和相频特性对比结果分别如图8和图9所示。可以发现,在进行分段优化后,AC-AC变换器的幅频特性和相频特性拟合精度有了较大的提升,可以满足工程误差要求。
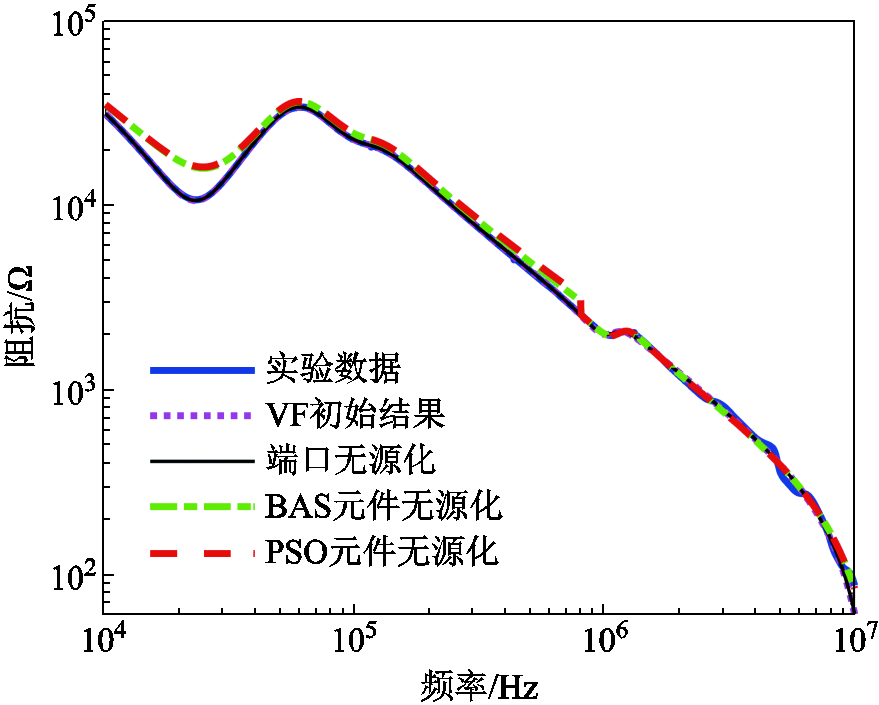
图8 分段优化后AC-AC变换器幅频特性对比
Fig.8 Comparison of amplitude-frequency characteristics of the AC-AC converter after segment optimization
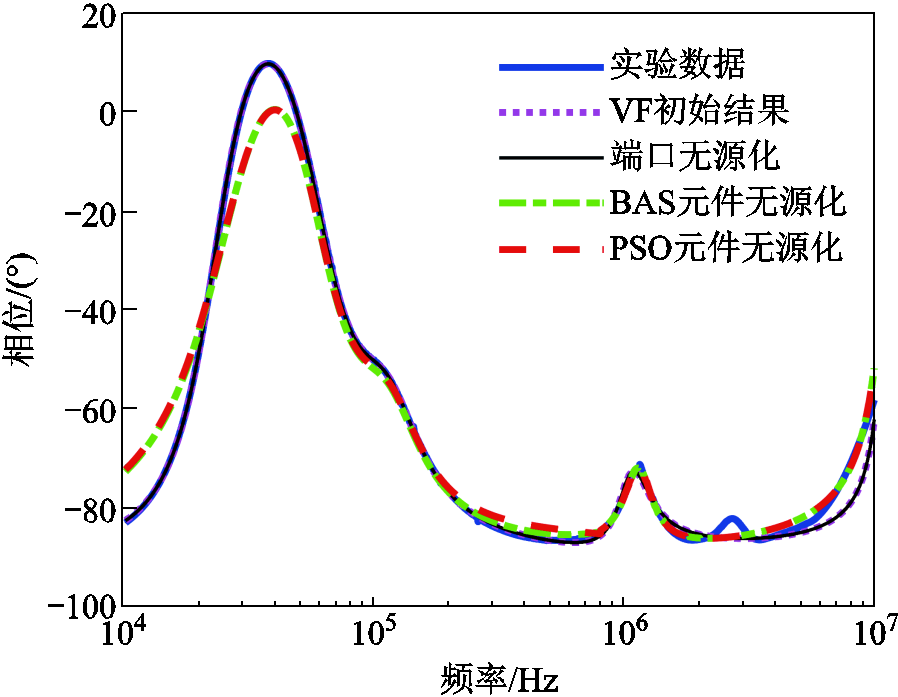
图9 分段优化后AC-AC变换器相频特性对比
Fig.9 Comparison of amplitude-frequency characteristics of the AC-AC converter after segment optimization
进一步地,对一台星形联结的永磁同步电机进行可物理实现的等效电路网络建模,该电机的型号为YYT-100L-5.5-302W,额定功率为5.5 kW,极对数为4,额定电压为380 V,额定频率为200 Hz。
与3.1节相同,结合WK 6500B阻抗分析仪的有效测量范围和国家军用标准GJB 151B—2013的CE102测试项目,在10 kHz~10 MHz的频率范围内,利用阻抗分析仪对其进行阻抗测量。WK 6500B阻抗分析仪的偏置电压为1 V,按照如图10所示的连接方式进行阻抗测量,将PMSM的三相电源输入端连接在一起,测试PMSM与机壳之间的共模阻抗,然后按照2.2节的流程搭建其可物理实现的等效电路网络,矢量匹配法的阶数为8阶,等效电路网络的各参数分别见表3和表4。
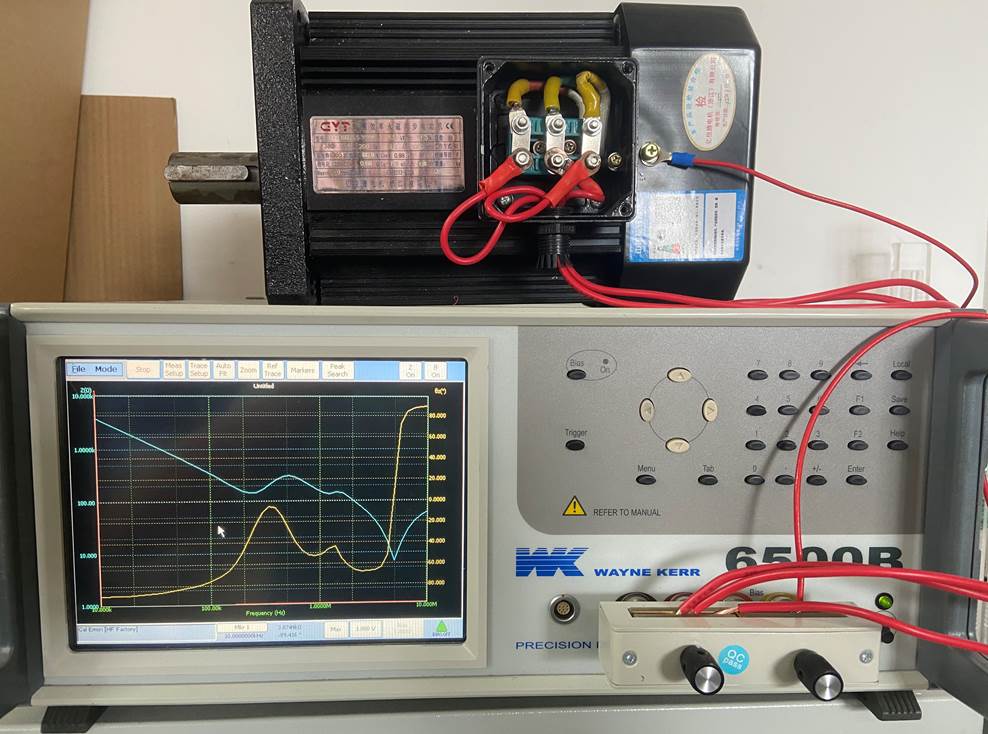
图10 永磁同步电机阻抗测量方法
Fig.10 Impedance measurement method of PMSM
表3 PMSM“端口无源性”修正后的各元件参数
Tab.3 The parameters of each component after the correction of "port passivity" of the PMSM

nR/ΩL/μHR0n/ΩC0n/nFR1n/ΩR2n/ΩC1n/nFLn/nH 18.342.121 9194.159.6416.11.835 709 2-56.9-13.712.8-1264.212 130 3-0.10.13-85.1-1.09
表4 PMSM的“元件无源性”修正参数
Tab.4 "Component passivity" correction parameter of the PMSM

算法R02/kΩR13/kΩR22/kΩC02/FC13/FL3/H PSO68.7528.531 00010.812 50.441 6 BAS35.1339.3097.640.430 80.616 20.202 6
PMSM的幅频特性和相频特性对比结果分别如图11和图12所示。根据图11和图12可以发现,PSO和BAS修正的幅频特性和相频特性基本一致,相比之下BAS的计算速度较快,且与图6和图7所示的AC-AC变换器的幅频特性曲线和相频特性曲线相比,拟合效果相对较好。
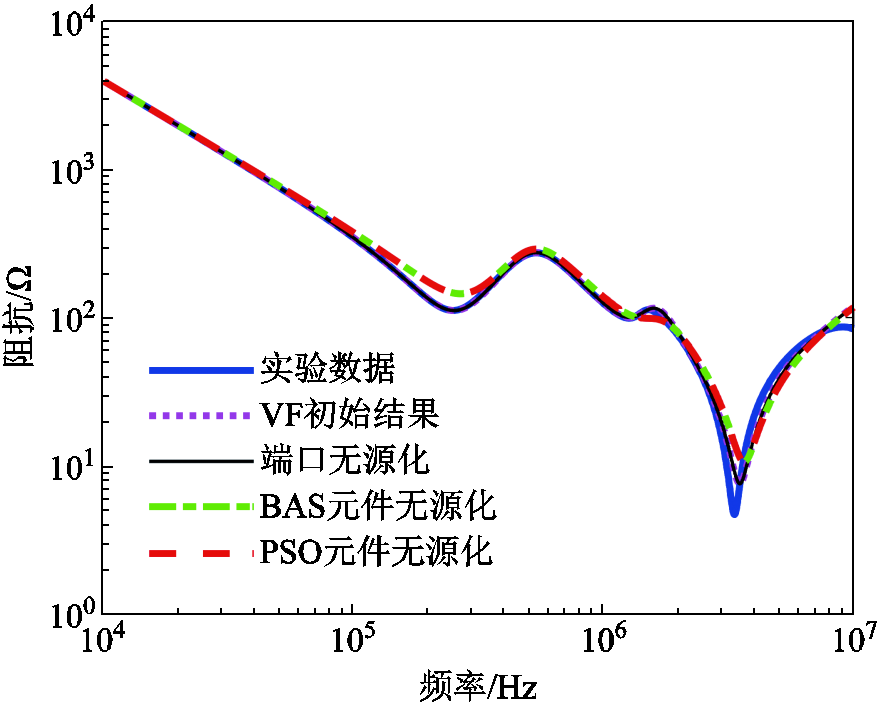
图11 PMSM幅频特性对比
Fig.11 Comparison of amplitude-frequency characteristics of the PMSM
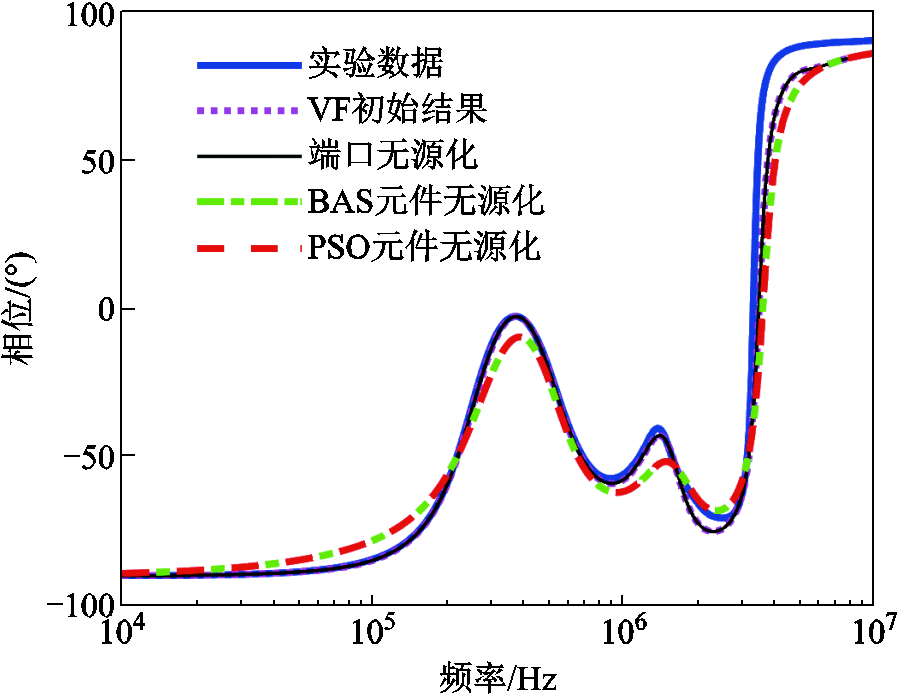
图12 PMSM相频特性对比
Fig.12 Comparison of phase-frequency characteristics of the PMSM
拟合效果相对较好的原因是PMSM中不包含非线性元件,对极值点的影响较小,且相对来说在高频情况下,PMSM的相频特性曲线的谐振点较少,由于优化算法带来的误差较小,“元件无源化”的拟合结果相对更好。
本文提出了一种融合了矢量匹配法、留数摄动法和优化算法,并可物理实现的强电磁设备宽频段阻抗建模新方法。该方法基于电机等强电磁设备的阻抗测量数据,首先利用矢量匹配法将强电磁设备实测的阻抗数据拟合为一个有理函数;然后利用留数摄动法对其进行修正,以实现“端口无源性”修正;最后利用PSO和BAS分别对等效电路网络中的一些非正值元件修正,以实现“元件无源性”修正。进一步,选取AC-AC变换器和永磁同步电机对该方法进行验证,证明了本文方法的正确性和可靠性,并发现相比于PSO算法,BAS算法更加适用于本文所提出的方法。
参考文献
[1] 刘计龙, 朱志超, 肖飞, 等. 一种面向舰船综合电力系统的模块化三端口直流变换器[J]. 电工技术学报, 2020, 35(19): 4085-4096. Liu Jilong, Zhu Zhichao, Xiao Fei, et al. A modular three-port DC-DC converter for vessel integrated power system[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4085-4096.
[2] 尚安利, 夏立, 王征. 舰船电力系统一体化系统模型和故障恢复研究[J]. 电工技术学报, 2016, 31(2): 163-170. Shang Anli, Xia Li, Wang Zheng. Research on integrated system model and service restoration method for warship power system[J]. Transactions of China Electrotechnical Society, 2016, 31(2): 163-170.
[3] 何杰, 刘钰山, 毕大强, 等. 开关变换器传导干扰抑制策略综述[J]. 电工技术学报, 2022, 37(6): 1455-1472. He Jie, Liu Yushan, Bi Daqiang, et al. Review of conducted electromagnetic interference suppression strategies for switching converters[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1455-1472.
[4] 陈垣, 张波, 谢帆, 等. 电力电子化电力系统多时间尺度建模与算法相关性研究进展[J]. 电力系统自动化, 2021, 45(15): 172-183. Chen Yuan, Zhang Bo, Xie Fan, et al. Research progress of interrelationship between multi-time-scale modeling and algorithm of power-electronized power system[J]. Automation of Electric Power Systems, 2021, 45(15): 172-183.
[5] Jia Xiaoyu, Hu Changsheng, Dong Bitao, et al. Influence of system layout on CM EMI noise of SiC electric vehicle powertrains[J]. CPSS Transactions on Power Electronics and Applications, 2021, 6(4): 298-309.
[6] Morales J, Medina E, Mahseredjian J, et al. Frequency-domain fitting techniques: a review[J]. IEEE Transactions on Power Delivery, 2020, 35(3): 1102-1110.
[7] Moghimi Haji M, Xu W, Geng Guangchao. Single-port and multi-port frequency-dependent network equivalents with numerically stable branches[J]. IET Generation, Transmission & Distribution, 2018, 12(3): 564-570.
[8] del Giudice D, Brambilla A, Linaro D, et al. Modular multilevel converter impedance computation based on periodic small-signal analysis and vector fitting[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2022, 69(4): 1832-1842.
[9] 宋鹏程, 张黎, 邹亮, 等. 一种改进的柔性直流系统IGBT行为模型[J]. 电工技术学报, 2021, 36(增刊1): 200-208. Song Pengcheng, Zhang Li, Zou Liang, et al. An improved IGBT behavioral model of voltage source converter based on HVDC[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 200-208.
[10] 解润生, 张国荣, 高凯, 等. 适用于频变输电线的动态相量谐波分析建模与仿真[J]. 电工技术学报, 2021, 36(15): 3200-3210. Xie Runsheng, Zhang Guorong, Gao Kai, et al. Modeling and simulation of dynamic phasor harmonic analysis for frequency-dependent transmission line[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3200-3210.
[11] 吴滨源, 李建文, 李永刚, 等. 用于谐波劣化分析的并网逆变器阻抗灰箱拟合方法[J]. 电工技术学报, 2022, 37(4): 942-953. Wu Binyuan, Li Jianwen, Li Yonggang, et al. A gray-box fitting method of grid-connected inverters impedance for the analysis of harmonic degradation[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 942-953.
[12] 司马文霞, 王惠, 杨鸣, 等. 考虑中间变压器饱和特性的电容式电压互感器宽频非线性模型[J]. 中国电机工程学报, 2021, 41(14): 5034-5043. Sima Wenxia, Wang Hui, Yang Ming, et al. Wideband and nonlinear model of capacitive voltage transformer considering the saturation of intermediate transformer[J]. Proceedings of the CSEE, 2021, 41(14): 5034-5043.
[13] Grivet-Talocia S. Passivity enforcement via perturbation of Hamiltonian matrices[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2004, 51(9): 1755-1769.
[14] Gustavsen B, Semlyen A. Enforcing passivity for admittance matrices approximated by rational functions[J]. IEEE Transactions on Power Systems, 2001, 16(1): 97-104.
[15] Gustavsen B. Fast passivity enforcement for pole-residue models by perturbation of residue matrix eigenvalues[J]. IEEE Transactions on Power Delivery, 2008, 23(4): 2278-2285.
[16] 王平, 张广勇, 李慧奇, 等. 特高压电容分压器宽频无源等效电路建模方法[J]. 高压电器, 2017, 53(6): 19-24, 29. Wang Ping, Zhang Guangyong, Li Huiqi, et al. Modeling the wideband passive equivalent circuit for UHV capacitor voltage transformer[J]. High Voltage Apparatus, 2017, 53(6): 19-24, 29.
[17] 梁贵书, 杜欣宇, 谢宇廷, 等. 电容式电压互感器的宽频无源电路模型[J]. 高电压技术, 2016, 42(1): 179-185. Liang Guishu, Du Xinyu, Xie Yuting, et al. Broadband passive circuit model of capacitor voltage transformer[J]. High Voltage Engineering, 2016, 42(1): 179-185.
[18] Gustavsen B, Semlyen A. Rational approximation of frequency domain responses by vector fitting[J]. IEEE Transactions on Power Delivery, 1999, 14(3): 1052-1061.
[19] 彭河蒙. 电动汽车电机驱动系统电磁干扰预测模型的研究[D]. 重庆: 重庆大学, 2015.
[20] 李家祥, 汪凤翔, 柯栋梁, 等. 基于粒子群算法的永磁同步电机模型预测控制权重系数设计[J]. 电工技术学报, 2021, 36(1): 50-59, 76. Li Jiaxiang, Wang Fengxiang, Ke Dongliang, et al. Weighting factors design of model predictive control for permanent magnet synchronous machine using particle swarm optimization[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 50-59, 76.
[21] Li Chunxu, Zhu Shuo, Sun Zhongbo, et al. BAS optimized ELM for KUKA iiwa robot learning[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2021, 68(6): 1987-1991.
Abstract Due to the large-scale use of power conversion modules in complex systems such as ship-integrated power systems and the increasing dv/dt and di/dt caused by the rapid increase of switching frequency, which brings serious electromagnetic interference risks to complex systems such as ship-integrated power systems. Therefore, in the electromagnetic compatibility design stage of complex systems such as ship-integrated power systems, it is urgent to model the electrical network of the strong electromagnetic equipment in the system to carry out equivalent physical simulation and support the hardware-in-the-loop electromagnetic compatibility test. The vector fitting method is commonly used in engineering literature to model the equivalent circuit network with the impedance of strong electromagnetic equipment. However, due to the problem of "port passivity" and "component passivity" caused by non-positive components, the physical realization of the equivalent circuit network cannot be ensured. To solve this problem, this paper proposes a new physically realizable wideband impedance modeling method for strong electromagnetic equipment, which integrates vector fitting method, residue perturbation method, and optimization algorithm.
Firstly, the impedance data of strong electromagnetic equipment are mathematically fitted by the vector fitting method, so that the discrete test data can be transformed into continuous rational functions. Secondly, considering the inherent "port passivity" problem caused by the vector matching method, the residual perturbation method is introduced to modify the results of the vector matching method to avoid the numerical divergence problem in the time domain simulation. Then, according to the knowledge of electrical networks, the rational function modified by "port passivity" is further transformed into equivalent circuit networks. Finally, to ensure the rapid and efficient completion of the "component passivity" correction, the particle swarm optimization algorithm (PSO) and the Beetle Antennae Search Algorithm (BAS) are utilized in this paper for their simpler principle,fewer parameters,faster search speed and less needof computer resources. The reason is that these two algorithms have many advantages such as simple principle, few parameters, fast search speed and low need of computer resources. Aiming at the non-positive components in the equivalent circuit network, these two algorithms are used to correct the "component passivity" of the whole equivalent circuit network, and an equivalent circuit network composed entirely of passive components is obtained.
To verify the correctness and reliability of this method, this paper selects AC-AC converter and permanent magnet synchronous motor as two typical pieces of equipment in the ship-integrated power systems. Combined with the effective measurement range of WK 6500B impedance analyzer and CE102 of national military testing standards GJB 151B—2013, these impedances are measured in the frequency band of 10 kHz~10 MHz, and its equivalent circuit network is established using the method proposed in this paper. By comparing the experimental data of the two devices with the simulation data of the equivalent circuit network, the proposed method can meet the error requirements of electromagnetic compatibility test, and the correctness and reliability of the proposed method can be verified. Through the verification and analysis of these two practical devices, it is found that the BAS is more suitable for the proposed method than the PSO.
Keywords:Particle swarm optimization, passive networks, wideband networks, vector fitting, high-power electromagnetic equipment
DOI:10.19595/j.cnki.1000-6753.tces.220833
中图分类号:TM341
重庆市自然科学基金项目(cstc2021ycjh-bgzxm0330, cstc2020jcyj- msxmX0825)和中央高校基本科研业务费项目(2020CDJ-LHZZ-078)资助。
收稿日期 2022-05-16
改稿日期 2022-08-06
徐寅翔 男,1998年生,硕士研究生,研究方向为电力电子设备间的电磁干扰预测。E-mail:xuyinxiang@cqu.edu.cn
刘其凤 男,1981年生,副研究员,硕士生导师,研究方向为电磁兼容预测与量化设计、电磁环境特性及防护等。E-mail:liuqifeng@cqu.edu.cn(通信作者)
(编辑 李冰)