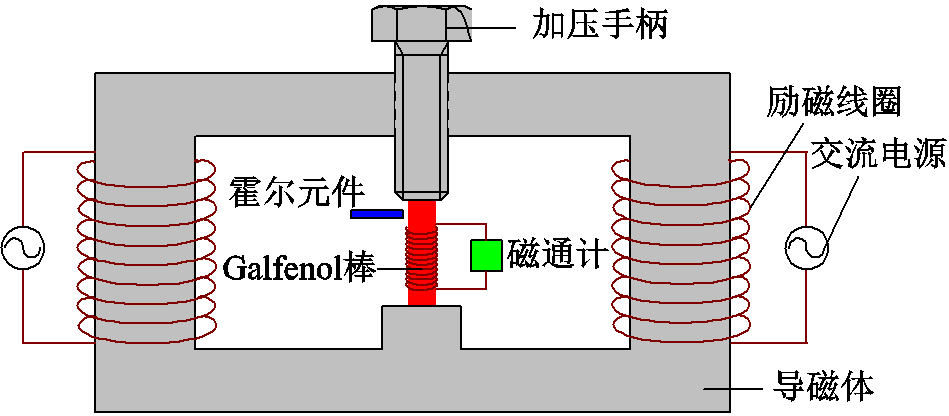
图1 双线圈磁特性测试系统原理
Fig.1 Schematic diagram of double coil magnetic characteristic test system
摘要 磁致伸缩材料具有应变大、响应速度快、稳定性好、频带宽的特点，是制作振动能量收集器的理想材料。当前磁致伸缩振动能量收集器建模主要利用线性压磁方程，此模型未能从材料自身耦合和磁路结构进行输出分析，导致输出预测误差较大。该文首先搭建了磁致伸缩材料磁特性测试装置，测试分析了磁致伸缩材料Galfenol合金在不同压应力尤其是大幅值应力下的磁特性；然后基于Gibbs自由能推导了Galfenol材料的全耦合非线性本构方程，进而构建了考虑漏磁、非线性、机磁耦合及饱和效应的振动能量收集器的等效电路模型，并对等效电路模型进行了非线性数学表征和参数识别；最后基于Galfenol材料设计了一个可以承受大幅值振动力的双棒型振动能量收集器样机，通过实验研究了收集器输出电压在不同力幅值、力频率、负载阻值等工况下的变化规律。实验结果与模型的计算结果对比分析表明，所建立的全耦合非线性等效电路模型可以准确预测振动能量收集器的输出电压特性。
关键词：振动能量收集器 Galfenol合金 全耦合非线性模型 等效电路 输出特性分析
目前，供配电技术已经较为成熟[1-2]，为人们生活和生产方式带来了极大的便利。但在一些偏远地区，例如野生动物保护区，生存着大量的野生动植物，为了及时记录动植物的生存状态，通常采用无线传感器和监控器等设备对保护区进行远程实时监控。无线传感器通常采用电池进行供电，然而电池存在供电时间短、污染环境、替换困难等缺点[3]，使得传感器的应用受到限制，因此利用环境中的能量为传感器提供不间断供电得到了国内外学者的广泛重视。环境能量通常以机械振动、热梯度、压力梯度和太阳辐射的形式存在。本文以其中的机械振动能量为背景，研究可应用于野生动物保护区的振动能量收集器，以收集动物运动时产生的能量，为检测动植物生态环境的电子设备提供可持续供电。
磁致伸缩材料、电致伸缩材料和压电材料是当前指导设计振动能量收集器的主流材料。相比之下，磁致伸缩材料具有机磁耦合系数大、灵敏度高、响应速度快等优点[4-5]，以磁致伸缩材料为核心制成的磁致伸缩振动能量收集器（Magnetostrictive Vibration Energy Harvester, MVEH），具有输出特性好、能量密度高、稳定性高的明显优势，尤其在应变能力和机电耦合方面更加突出。MVEH主要分为悬臂梁式和柱棒式，其中悬臂梁式多应用于高频低振幅（30～50 N）的振动力收集，具有输出效率高、输出电压大的优点[6]，但机械性能差，在受到较大的振动力冲击时容易损坏。柱棒式具有机械强度高、结构稳定等优点，目前多采用单棒式结构[7]，但其具有明显的导磁回路磁阻大、漏磁多、电磁转换效率低、输出电压小等缺点[8-9]。由于动物运动产生的振动力从几十牛顿到几千牛顿不等，其幅值较大、冲击力强。本文采用可承受大幅值振动力的柱棒式结构，设计一种新型双棒式磁致伸缩振动能量收集器。
早期学者们对磁致伸缩振动能量收集器的建模多为线性分析，文献[10]运用经典的机电耦合模型和线性压磁模型分析MVEH的输出电压，忽略了漏磁及材料的非线性，当施加的振动力幅值和频率分别为100 N和100 Hz时，此模型在输出电压预测中的相对误差为12.56%，没有达到良好的预测效果。而磁致伸缩材料具有明显的非线性，因此对MVEH的非线性建模尤为重要。文献[11]基于亥姆霍兹（Helmholtz）自由能并结合热动力学基本定理推导出MVEH的输出电动势预测模型，但将磁致伸缩材料棒等效为质量-弹簧-阻尼模型时忽略了施加振动力的变化引起的阻尼变化，导致在频率为10 Hz的正弦振动激励下，模型预测的输出电动势幅值的相对误差达到了11.7%。文献[12]基于吉布斯（Gibbs）自由能泰勒展开式和宏观连续介质力学原理，建立了超磁致伸缩材料的非线性磁-热-机多场耦合模型，该模型考虑预应力和温度的作用，可以预测不同预应力和温度共同作用下的磁致伸缩应变曲线，但其数学公式推导过程较为复杂，工作量较大。文献[13]提出了基于微观力学领域磁畴旋转的二维模型，将基于冯洛诺伊（Voronoi）图的离散化与混合有限元方法相结合，用来描述Galfenol的非线性行为，但运用的分析方法较为复杂，且未考虑预应力对输出特性的影响。文献[14]提出了一种新的简化方法，通过有限元分析预测磁致伸缩振动能量收集器的电功率输出，但是在收集器结构复杂的情况下，运用有限元方法分析计算的时间成本会大幅增加，且只有施加压力低于65 MPa时，模型计算相对误差才能低于10%。文献[15]提出了一种等效电路模型来分析水下阵列换能器的声学特性，通过比较其发射电压响应（Transmitting Voltage Response, TVR）谱和有限元分析结果，验证了等效电路的有效性,但是提出的等效电路模型没有考虑器件的漏磁及偏置磁场的影响，运用到收集器的输出特性预测分析中会导致误差较大。
本文基于Galfenol材料内部的Gibbs自由能并综合考虑了材料的机磁耦合和饱和效应建立了适用于MVEH的非线性本构方程模型，根据材料磁特性实验测试数据结合Matlab分析拟合对方程中的各个参数进行了识别。基于非线性本构方程模型构建适用于双棒式MVEH的电-磁-机全耦合三端口等效电路，该等效电路考虑了漏磁、偏置磁场、预应力等，并通过样机实验验证了全耦合三端口等效电路模型的准确性。
本文研究的MVEH核心材料选用Galfenol，是一种铁-镓合金（Fe81.6Ga18.4），具备优异的电磁性能、力学性能和磁致伸缩性能[16]。为了分析Galfenol的主要磁特性，进行了磁特性实验装置的搭建，其原理如图1所示。此实验平台是一个双输入和双输出系统，通过对材料施加磁场（磁场强度H）和机械（应力σ）两输入，测量其相应的机械（应变ε）和磁性（磁化强度M）输出变化响应。测试样品选择的是直径为5 mm、长度为10 mm的圆柱形Galfenol棒。将样品置于图1中Galfenol棒标识的位置，然后将50 Hz工频交流电流通入两个励磁线圈，使其产生相同方向的激励磁场，激励磁场通过导磁体汇入Galfenol棒。为了减小漏磁和磁路中的涡流损耗，导磁体由40片厚度为0.5 mm的高磁导率硅钢片沿着垂直于纸面方向堆叠而成。霍尔元件探头垂直置于棒的表面，用于测量磁场强度H。棒上绕有50匝感应线圈，线圈两端接入磁通计，用于测量磁感应强度B。加压手柄实现样品固定的同时可以根据需要给Galfenol棒施加不同的预压应力，预压应力的大小可以从压力传感器中读取。实验测试平台实物如图2所示。信号发生器和功率放大器用来给励磁线圈提供交流电，数据采集卡将霍尔元件采集到的磁场强度传输到计算机中进行输出显示。
图1 双线圈磁特性测试系统原理
Fig.1 Schematic diagram of double coil magnetic characteristic test system
图2 实验测试平台
Fig.2 Experimental test platform
实验测得的Galfenol棒在不同预压应力下的M-H曲线如图3所示。从图3中可以看出，铁-镓合金磁滞回线呈非线性，磁滞面积窄、矫顽场低、饱和磁化强度高。此外，还可以注意到三个截然不同的区域：区域一的曲线非常重叠且呈直线斜率；区域二的曲线斜率突然增大，此时的相对磁导率比区域一更高；区域三则为材料接近并达到磁饱和的区域。
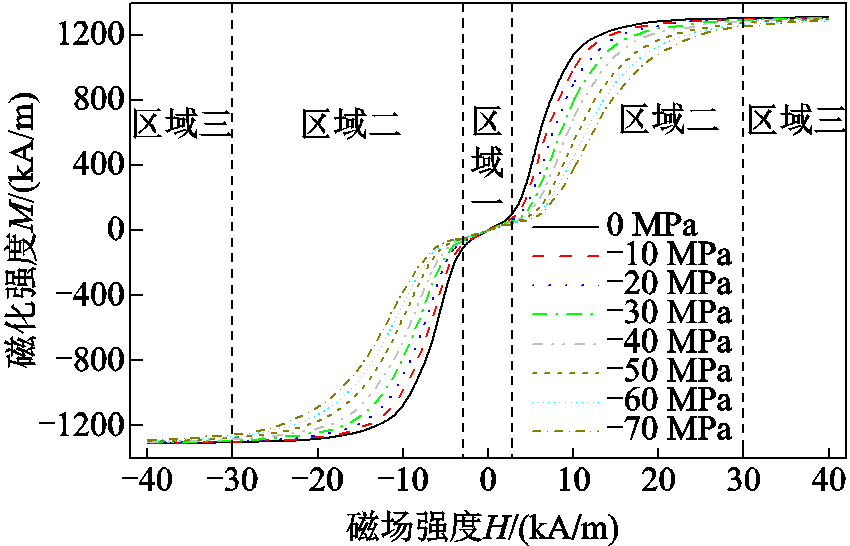
图3 Galfenol棒在各预应力下的M-H曲线
Fig.3 M-H curves of Galfenol rod under various prestresses
由图3的Galfenol磁特性分析可知，该材料磁滞回线窄、矫顽力较小。由文献[17]可知，Galfenol的磁损耗受温度影响较小，可以忽略温度对输出特性的影响。本文基于Galfenol材料的磁特性进行非线性机磁耦合模型构建，为了更方便地得到Galfenol棒内部的吉布斯自由能，假设工作过程中所施加的应力和磁场强度的方向始终与Galfenol棒轴向平行。满足以上假设条件时，对于任一磁场强度和压应力，Galfenol棒的吉布斯自由能[18]可以写为
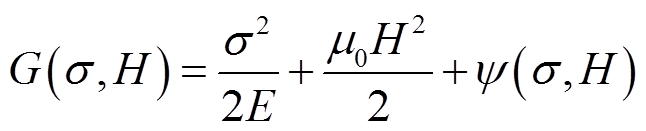（1）
式中，E为杨氏模量；μ0为真空磁导率。式（1）等号右侧的前两项分别构成机械能和磁能贡献的自由能，第三项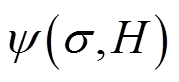
为磁致伸缩材料关于应力
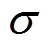与磁场强度H的能量解析函数，表征磁致伸缩材料的机磁耦合效应对吉布斯自由能的贡献。
吉布斯自由能是一个状态函数，应变ε和磁感应强度B可以由吉布斯自由能求微分得到。
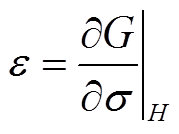（2）
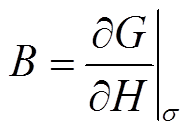（3）
式中，右下角标表示求导时将该参数视为常量。由式（2）和式（3）可知，确定函数ψ(σ, H)便可以得到非线性模型。假设函数ψ(σ, H)为
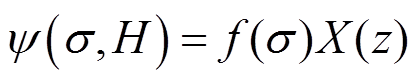（4）
式中，z=z(σ, H)，需要根据材料特性确定函数f(σ)、X(z)和z(σ,H)，以此来模拟材料的主要物理行为，如应力对饱和效应和磁化强度的影响。因此，结合式（2）和式（3）可得
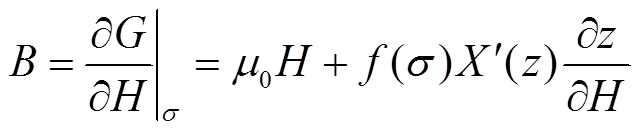（5）
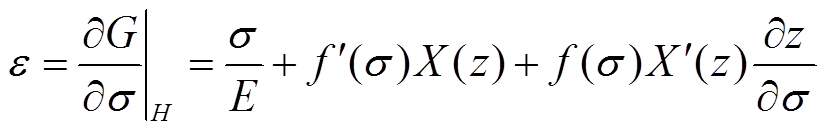（6）
式（5）和式（6）即为初步得到的磁致伸缩材料的非线性全耦合模型。根据经验公式，f(σ)和z(σ,H)通常假设[19]为
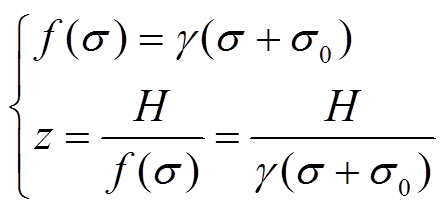（7）
式中，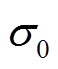
为材料在应力退火过程中所形成的内应力；γ为常数。将式（7）代入式（5）和式（6）可进一步将机磁耦合模型简化为
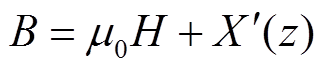（8）
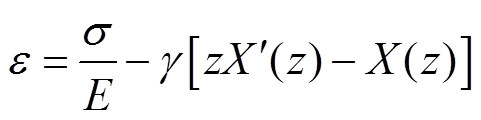（9）
材料中的磁感应强度B、磁场强度H与磁化强度M之间存在关系
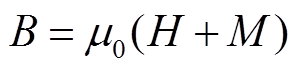（10）
结合式（8）可得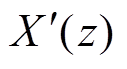
=μ0M。对于磁致伸缩材料，磁化强度M是关于H和σ的函数，对于具有饱和特性的磁化强度M，通常使用双曲正切函数来进行描述，即
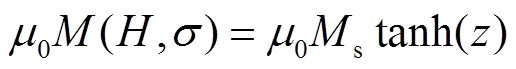（11）
式中，Ms为材料的饱和磁化强度。大量实验表明，式（11）在高磁场强度范围内对材料磁化强度的模拟较为准确，但在低磁场强度范围内误差较大，因此引入一项分母为高次项的函数对式（11）进行修正[20]，修正结果为
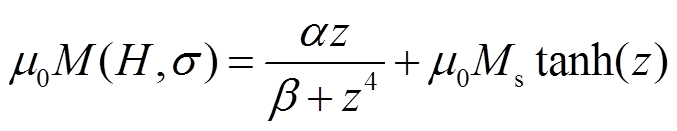（12）
式中，α、β为模型的修正因子。由式（12）可知，修正后的磁化强度模型由两项相加而成，在低磁场强度范围内，第一项起主要作用；当磁场强度较高时，由于第一项的分母含磁场强度的高次项，此时第二项起主要作用。联立式（5）～式（12）可以得到磁致伸缩材料棒最终的机磁耦合模型为
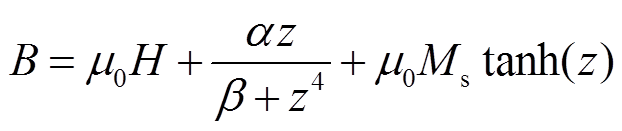（13）
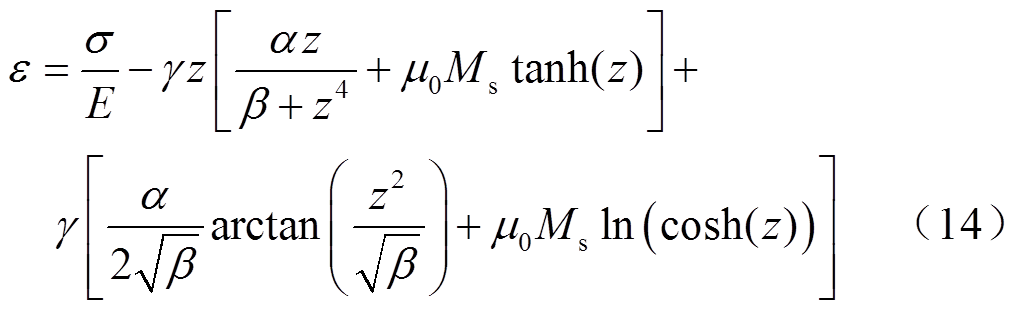
由式（13）和式（14）可知，机磁耦合模型中共有Ms、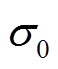、α、β、γ五个未知参数需要进行识别。其中饱和磁化强度Ms、材料内应力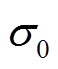是与材料自身属性相关的参数，可通过测量材料在不同预应力下的M-H曲线进行识别。
从图3中可以读出Galfenol棒的饱和磁化强度Ms=1 313 kA/m。根据式（12）可知，磁化强度M是关于H/(σ+σ0)的函数，且H/(σ+σ0)是M的唯一自变量，因此正确的σ0值应使所有预压应力下的 M-[H/(σ+σ0)]曲线重合。对于本文测试并使用的Galfenol样品，可发现当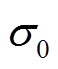= -50 MPa时，各预应力下的M-[H/(σ+σ0)]曲线高度重合，如图4所示。
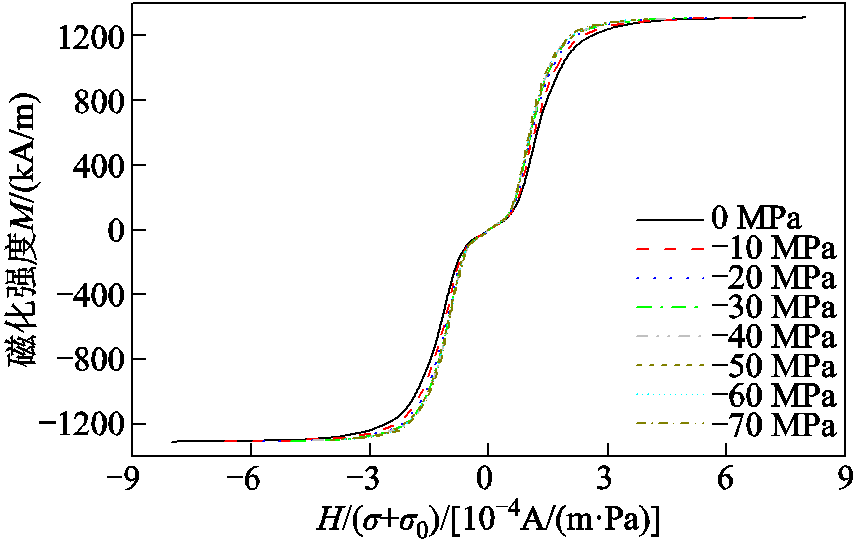
图4 Galfenol棒在各预应力下的M-[H/(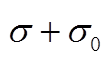
)]曲线
Fig.4 M-[H/(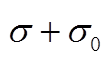)] curves of Galfenol rod under various prestress
与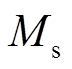
、
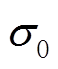的意义不同，α、β、γ这三个参数是为了使模型与实际相接近而引入的修正因子，没有实际物理意义，因此可以使用Matlab采用非线性最小二乘法[21]将模型与实验数据进行拟合求得。拟合结果为：α=-1.08、β=0.765 6、γ= -9.755×10-5。
为验证所提出模型的准确性，又测量了一组预应力为-5、-25、-45 MPa下的B-H曲线，如图5所示。对比相同预应力和磁场强度下的实验测量数据和模型计算数据发现，两组数据的最大误差为2.53%（磁场强度为20 kA/m、预应力为-45 MPa时），平均误差为0.68%，表明非线性本构方程模型预测Galfenol合金材料的磁特性具有良好准确性。
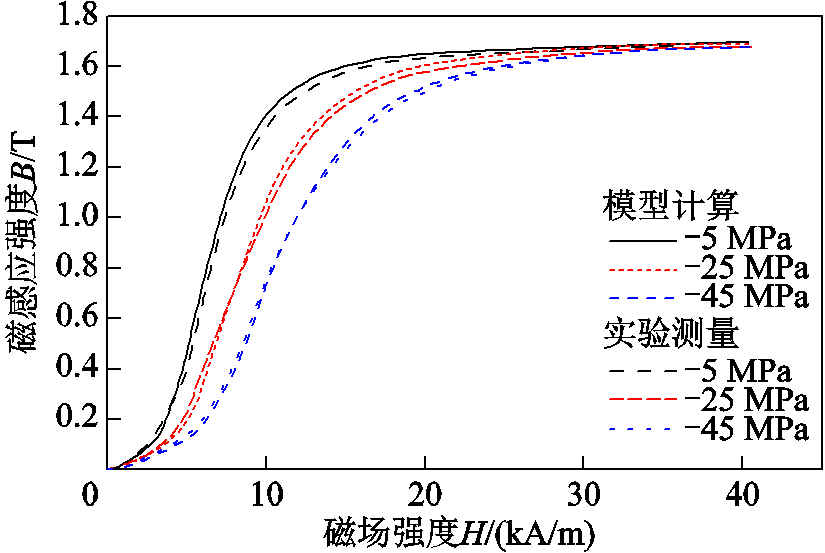
图5 模型计算与实验测量的B-H曲线
Fig.5 The B-H curves calculated by the model and measured by the experiment
为了简化分析MVEH等效输出模型，利用电路工具对整个系统进行建模可以更直观地分析MVEH的输出，本文通过特定的类比将MVEH全局系统的机械、磁和电与其等效电路相互联系起来。磁致伸缩材料应力表示为σ=F/S，应变表示为ε=x/l，磁通表示为ϕ=BS，其中F为所施加的振动压力，B为磁致伸缩棒中的磁感应强度，S为棒的横截面积，x为棒尖端的位移，l为棒的长度。将前面得出的本构方程式（13）乘以S，将式（14）乘以l，可以得到
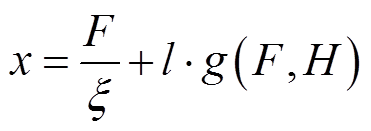（15）
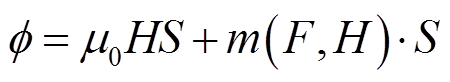（16）
其中
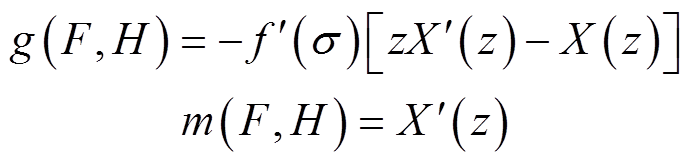
式中，ξ为样品的机械刚度，ξ=ES/l；µ0HS可以改写为lH/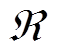
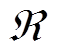，表示磁弹性棒的总磁阻的线性贡献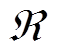，=l/(µ0S)。则式（15）和式（16）可改写为
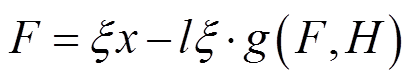（17）
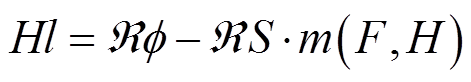（18）
式（17）为机械方程，采用机械量和电气量的类比，其中力F对应于电压V1，棒尖端的速度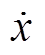
对应于电流i1；式（18）为磁性部分，应用磁路理论，Hl对应于磁压降Vg，磁通ϕ在磁阻棒内流动对应于电流ig，磁阻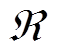由电阻Rg表示。从而得到
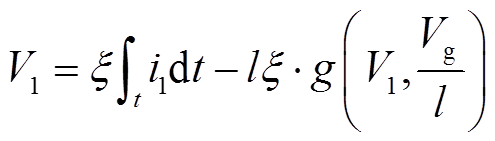（19）
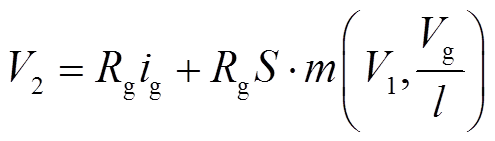（20）
式（19）和式（20）构成了一个双端口电路，其中式（19）表示机械端口，由串联电容（C=1/ξ=l/(ES)）电压和一个代表棒的非线性磁致伸缩响应相关电压源f1组成；式（20）构成了磁端口，由线性磁阻电压和磁致伸缩棒的非线性磁响应相关电压源f2组成。通过机电类比将非线性本构方程式（13）和式（14）中的机磁耦合关系用电路中的非线性相关控制电压源f1和f2表示，然后添加电端口感应输出电路，便可得到三端口等效电路模型，如图6所示。在等效电路中，线圈磁链采用Nig进行建模，N为感应线圈的匝数。当电流在线圈中流动时会影响磁致伸缩元件中的总磁通量，因此，在磁端口电路中串联一个与电端口感应线圈电路相对应的Ni2，非线性相关控制电压源Nig和Ni2被用来表征磁端口和电端口的耦合关系。图6中，Rcoil为感应线圈的电阻，i2为流过感应线圈的电流，Vout为输出电压；收集器的导磁回路由永磁体、硅钢片和Galfenol合金棒组成，因此需要增加相应的磁阻部分：硅钢片磁阻Rfe、气隙磁阻Rair、永磁体磁阻Rm，考虑到MVEH在工作时有一定的漏磁所以加入了漏磁阻Rleak，ileak为流过漏磁阻的电流；永磁体等效成数值为MmLm的电压源。
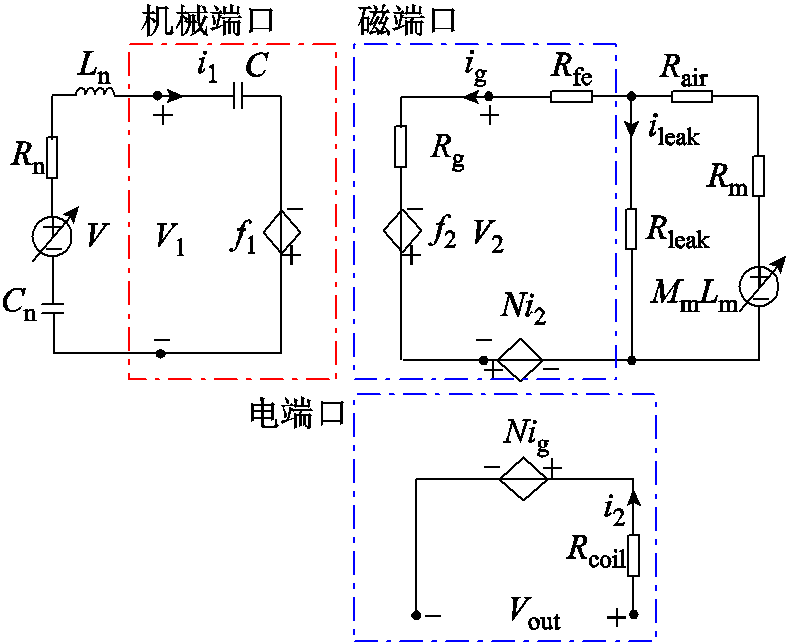
图6 单棒式MVEH电-磁-机全耦合三端口等效电路
Fig.6 Electro-magnetic-mechanical fully coupled three-port equivalent circuit of single rod MVEH
在机械端口，电压源V表示加力装置为整个系统提供的振动力，当考虑收集器的质量m、刚度k和阻尼c后，系统等效为由等效质量块、弹簧、阻尼器组成的动力学模型，可以通过机电类比法分别等效为机械电感Ln、机械电阻Rn、机械电容Cn[22]，其转换关系为
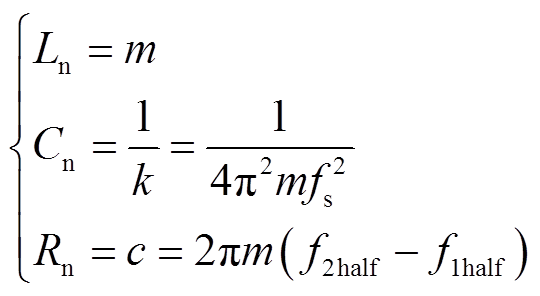（21）
式中，f1half和f2half为MVEH的半功率点频率；fs为谐振频率。利用阻抗分析仪对MVEH样机进行阻抗特性测试，确定MVEH的谐振频率点和机械结构参数。本实验所使用的阻抗分析仪型号为Agilent E4990A，扫频范围为20 Hz～10 MHz，量程为25 mΩ～40 MΩ，测量精度为±0.08%。由阻抗分析仪测试得到在设计范围内的MVEH谐振点为2.047 kHz。
辨识等效电路的所有参数后，MVEH的等效电路综合表达式为
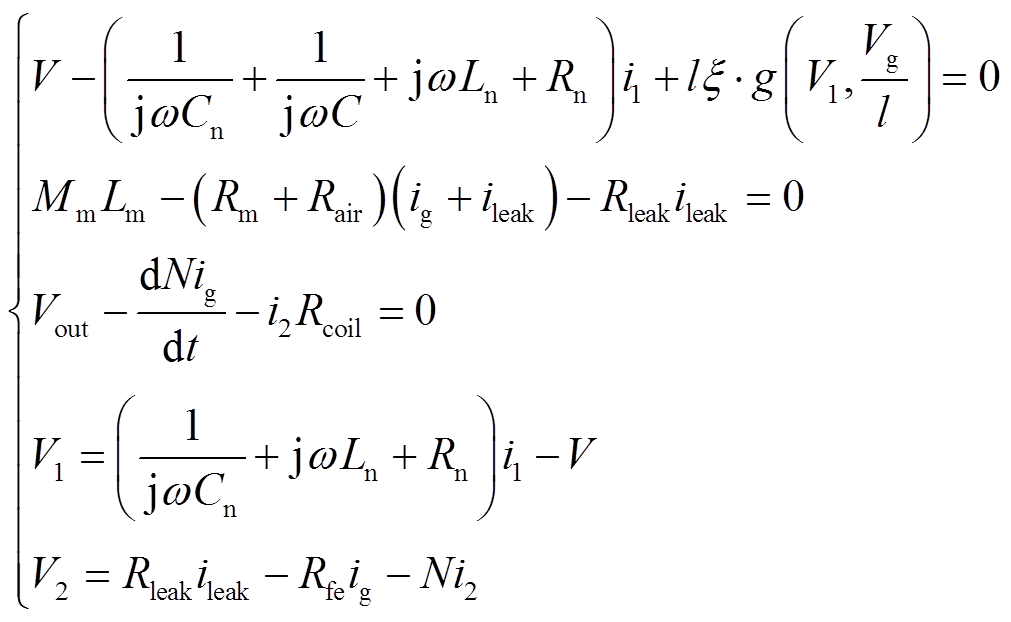（22）
通过以上类比分析并结合推导的磁致伸缩材料全耦合非线性本构方程式，构建了如图6所示的考虑了漏磁、偏置磁场、预应力等因素的电-磁-机全耦合三端口等效电路，公式组（22）为等效电路对应的综合数学表达式。结合材料特性实验测试数据及Matlab的非线性最小二乘法对等效电路中参数进行识别后，利用Multisim电路仿真计算软件对所建立的三端口等效电路模型进行仿真计算，并与后续样机实验测试的实际输出电压进行验证分析。
为了验证磁致伸缩材料非线性机磁耦合模型和类比得出的等效电路模型的准确性，本文设计了一台双棒式MVEH样机，其结构参数见表1，结构如图7所示。主体分为六部分，具有承受大幅振动力及固定作用的端座、构成闭合磁路的高导磁硅钢磁轭、核心部件Galfenol磁致伸缩棒、聚二甲基硅氧烷（Polydimethylsiloxane, PDMS）封装的软导磁材料粉末、感应线圈及提供偏置磁场的永磁体。
表1 样机结构相关参数
Tab.1 Prototype structure-related parameter
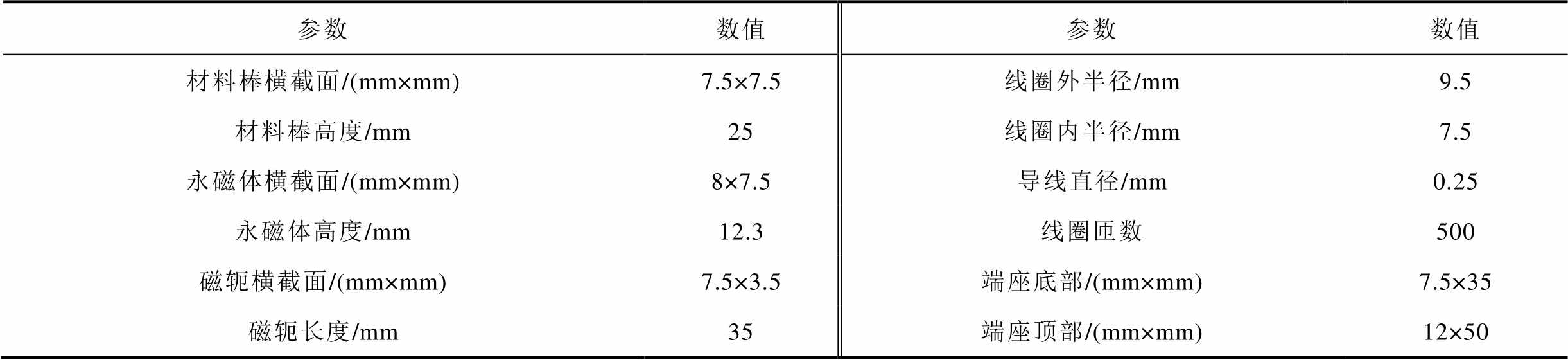
参数数值参数数值 材料棒横截面/(mm×mm)7.5×7.5线圈外半径/mm9.5 材料棒高度/mm25线圈内半径/mm7.5 永磁体横截面/(mm×mm)8×7.5导线直径/mm0.25 永磁体高度/mm12.3线圈匝数500 磁轭横截面/(mm×mm)7.5×3.5端座底部/(mm×mm)7.5×35 磁轭长度/mm35端座顶部/(mm×mm)12×50
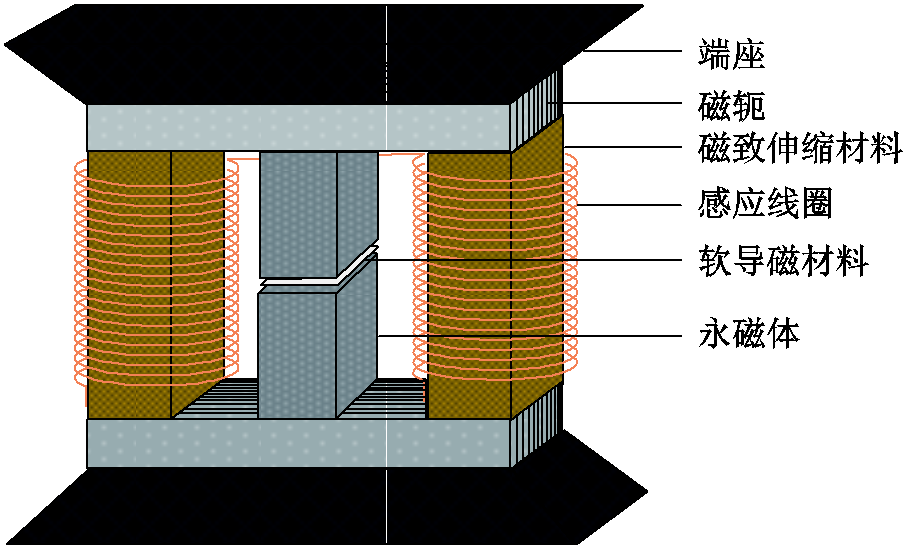
图7 MVEH结构部件示意图
Fig.7 Schematic diagram of structural components of MVEH
当幅值范围变化大的振动力施加在收集器上时，上端盖会将振动力经过磁轭传递到两侧的Galfenol合金棒，为提高转换效率和材料棒的内部磁场分布均匀度，将两块永磁体放置于器件中间位置并分为上下两部分，为材料棒提供偏置磁场。在外加磁场和应力共同作用下，Galfenol合金内部磁畴发生偏转进而引起磁化强度的变化，最后通过Galfenol合金棒四周的多匝感应线圈拾取并输出电压。
对应于所设计的收集大振动力的MVEH样机，可将图6所示的单棒式MVEH等效电路变换得到双棒式MVEH等效电路模型，如图8所示。其中左右两根Galfenol合金棒的等效三端口电路分别用不同线型突出区分，图中下标L和R分别表示左侧Galfenol合金棒和右侧Galfenol合金棒。当垂直振动力施加在上端盖，平面可以将振动力均匀分配给左右两侧的Galfenol合金棒，因此机械端口串联连接，其中电压源V表示加力装置为整个系统提供的振动力。在磁端口，永磁体等效为电压源MmLm，永磁体放置于收集器的中间位置，为两侧的Galfenol合金提供偏置磁场，因此两根Galfenol合金棒的磁端口电路部分并联连接。
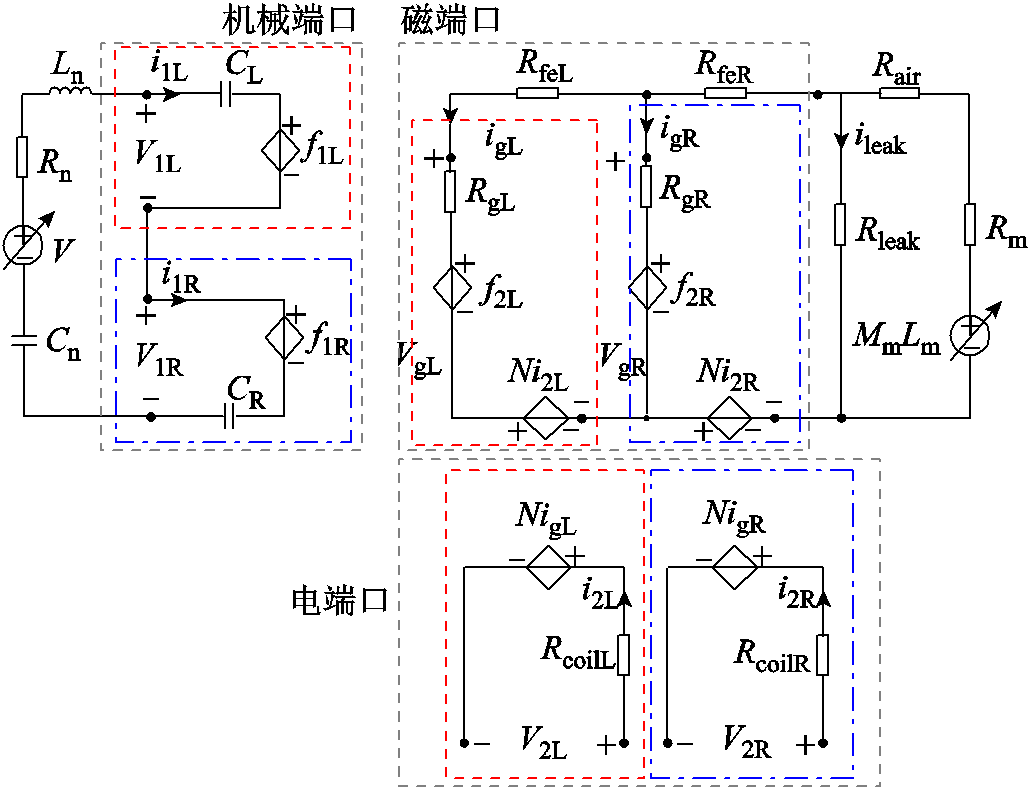
图8 双棒式MVEH电-磁-机全耦合三端口等效电路
Fig.8 Electro-magnetic-mechanical fully coupled three-port equivalent circuit of double-rods MVEH
为获取可调节频率和幅值大小的振动力，并分析施加振动力的幅值及频率大小对输出电压的影响情况，搭建变频变力的MVEH输出特性测试系统，其原理及实验装置分别如图9、图10所示。
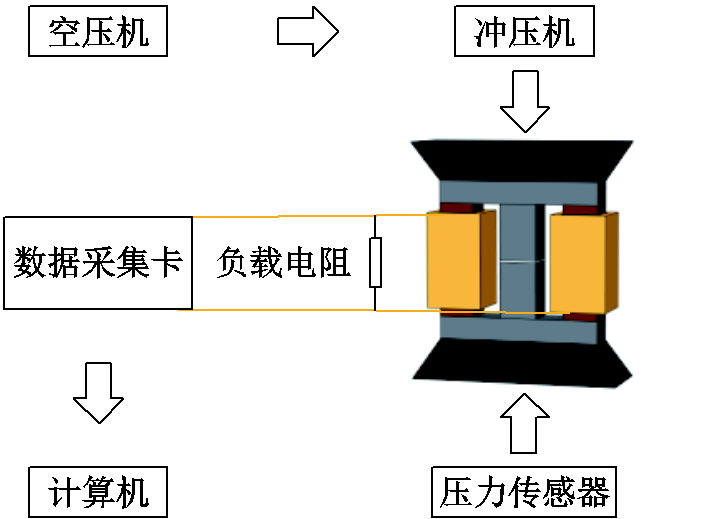
图9 实验测试系统搭建原理
Fig. 9 Schematic diagram of experimental test system
图10 MVEH 输出特性测试实验装置
Fig.10 MVEH output characteristic test device
MVEH输出特性测试系统的工作原理为：由空压机为气动冲压机提供压力，调节冲压机的压力阀和控制器可以改变垂直方向振动力的幅值及频率的大小，将设计的MVEH放置于冲压机施加压力的平面上，并将压力传感器放置在MVEH与气动式冲压机之间，用来实时监控振动力幅值大小，最后通过连接在感应线圈两端的数据采集卡采集输出的感应电动势，并由计算机保存数据。
4.3.1 振动力幅值及其频率对输出电压的影响
利用4.2节的MVEH输出特性测试系统中的冲压机对MVEH施加振动力，输出电压的大小由DH-8303型数据采集卡采集并传送至计算机显示。外接电阻负载阻值为10 kΩ时，输出电压单位时间（1 000 ms）内有效值随着垂直振动力的幅值及频率大小变化趋势如图11所示。
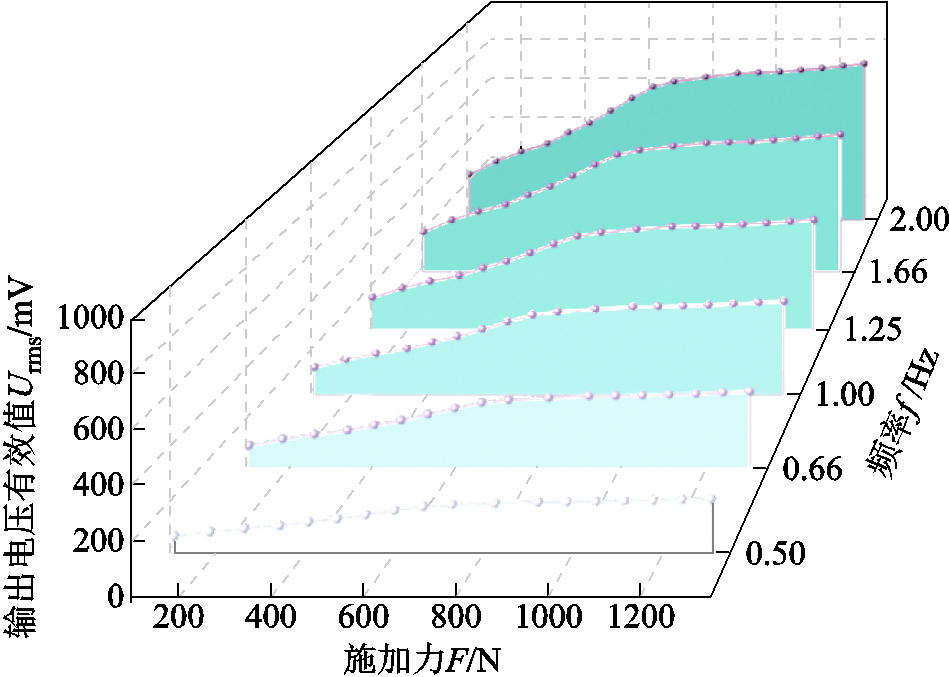
图11 输出电压有效值Urms与振动力幅值和频率的关系（负载阻值为10 kΩ时）
Fig.11 Relationship between output voltage RMS and amplitude and frequency of vibration (load resistance value is 10 kΩ)
引言中介绍到本文设计的MVEH可应用于野生动物保护区收集动物运动时的振动能量，因此所收集的振动力幅值及其变化范围较大。动物运动时产生的振动频率较低，因此设置本文施加的振动力幅值变化范围为115～1 310 N、以64 N为步长，频率变化范围为0.5～2 Hz。由图11可知，输出的电压有效值随着振动力幅值及频率的增大而增大，并在750 N出现线性度变化的拐点，这是因为根据Galfenol的磁化曲线特性，在受到压力的情况下，材料磁化曲线会从线性进入到非线性，临界点即膝点。
输出电压峰-峰值Upp与振动力幅值和频率的关系如图12所示，随着振动力幅值的增大，输出电压峰-峰值逐渐增加，最大值达到1 483 mV。而改变振动力的频率时，输出电压曲线几乎重叠，这是由于低频振动环境下，Galfenol材料棒远未达到其固有频率，改变频率对其电压峰-峰值输出影响并不大。
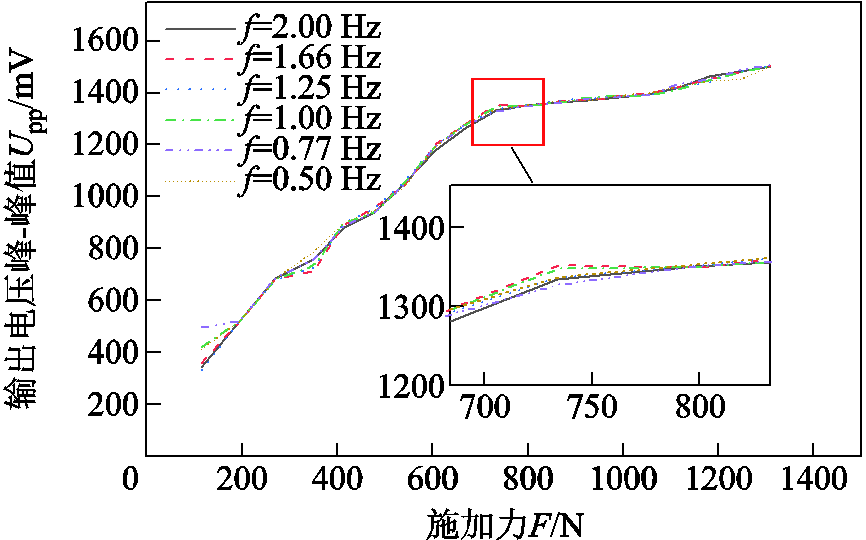
图12 输出电压峰-峰值Upp与振动力幅值和频率的关系
Fig.12 Relation between peak-to-peak value of output voltage and amplitude and frequency of vibration
为更清楚地说明振动力的幅值和频率对输出电压的影响规律，对单位时间内三种不同频率的单幅值振动力进行了实验研究。单位时间（1 000 ms）内，施加振动力频率分别1.0、1.5、2.0 Hz的垂直振动力波形如图13所示。
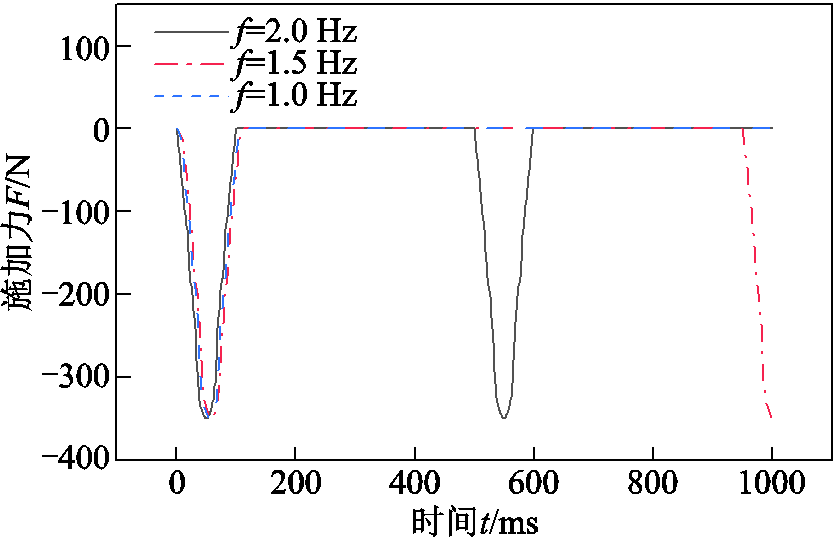
图13 单位时间内不同频率振动力波形
Fig.13 Vibration waveform of different frequencies in unit time
当上述三种不同频率的振动力施加在MVEH上时，其输出电压实时波形如图14所示。从图14中可以看出，不同频率的振动力下，各频率单次振动力下的输出电压波形几乎重叠，输出电压的峰-峰值大小也几乎没有差别。但是振动力频率越高，同一段时间内作用在MVEH上的振动次数就越多，导致输出电压周期数越多，从而同一段时间内的输出电压有效值随之增加。
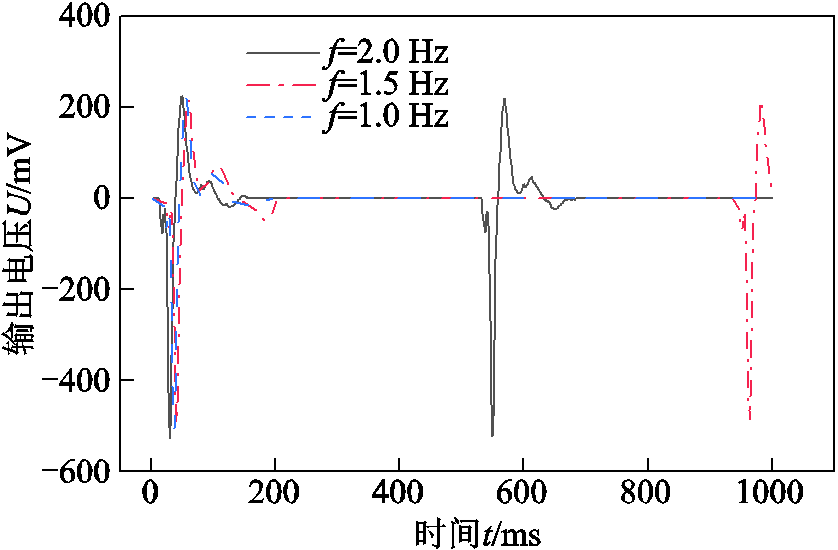
图14 单位时间内不同振动频率下输出电压波形
Fig.14 Output voltage waveform at different vibration frequencies in unit time
为了验证本文中构建的非线性等效电路模型的准确性，取F=350 N、频率f=1 Hz、负载R=10 kΩ时的单次振动力作为对比分析的输入条件，使用Multisim仿真计算软件进行仿真计算。图15展示了在单次垂直振动力下的模型计算和实验测试输出电压波形对比。
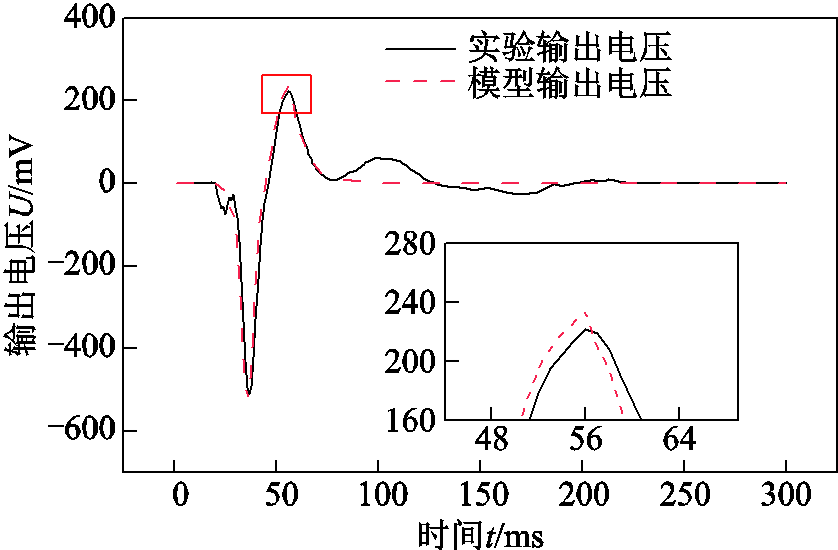
图15 模型计算与实验测试输出电压对比
Fig.15 Comparison of output voltage calculated by the model and measured by the experiment
图15中，等效电路模型计算得出的输出电压峰- 峰值和有效值分别为：Upp.sim=757.79 mV、Urms.sim= 223.98 mV；实验测试获取的输出电压峰-峰值和有效值分别为：Upp.ex=731.62 mV、Urms.ex=229.66 mV。实验结果和模型计算结果的相对误差为
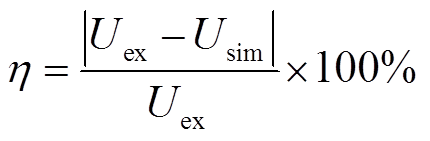（23）
由式（23）可计算得出电压峰-峰值和有效值的相对误差分别为ηpp=3.58%、ηrms=2.47%。
4.3.2 负载阻值大小变化对输出电压的影响
使用阻抗分析仪测得收集器内部阻抗值r为11.64 Ω。在感应线圈两段串联负载电阻，分析外界负载对收集器输出电压的影响。当负载阻值R为10 Ω、50 Ω、200 Ω、10 kΩ时，输出电压有效值随着振动力幅值和频率的变化趋势如图16所示。
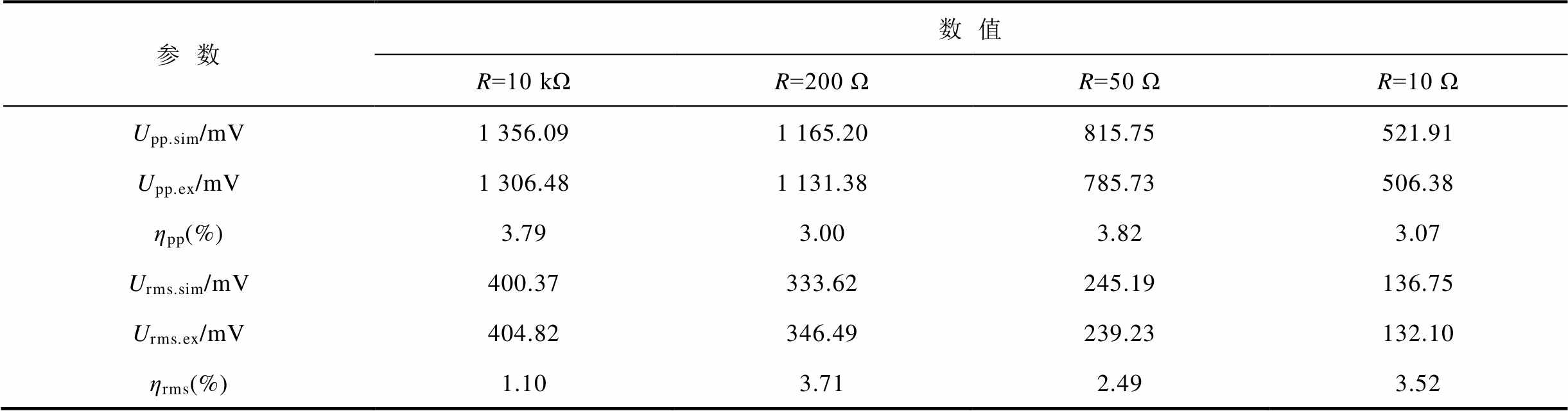
为了进一步验证模型准确性，进行了四组不同条件下的实验：选取振动力幅值F=755 N、频率f=1 Hz作为输入条件，外接负载分别为R=10 kΩ、R=200 Ω、R=50 Ω及R=10 Ω。图17依次显示了四组模型和实验输出电压波形。图17中四组不同外接负载条件下的模型预测与实验测试的输出电压峰-峰值、有效值及其相对误差见表2。
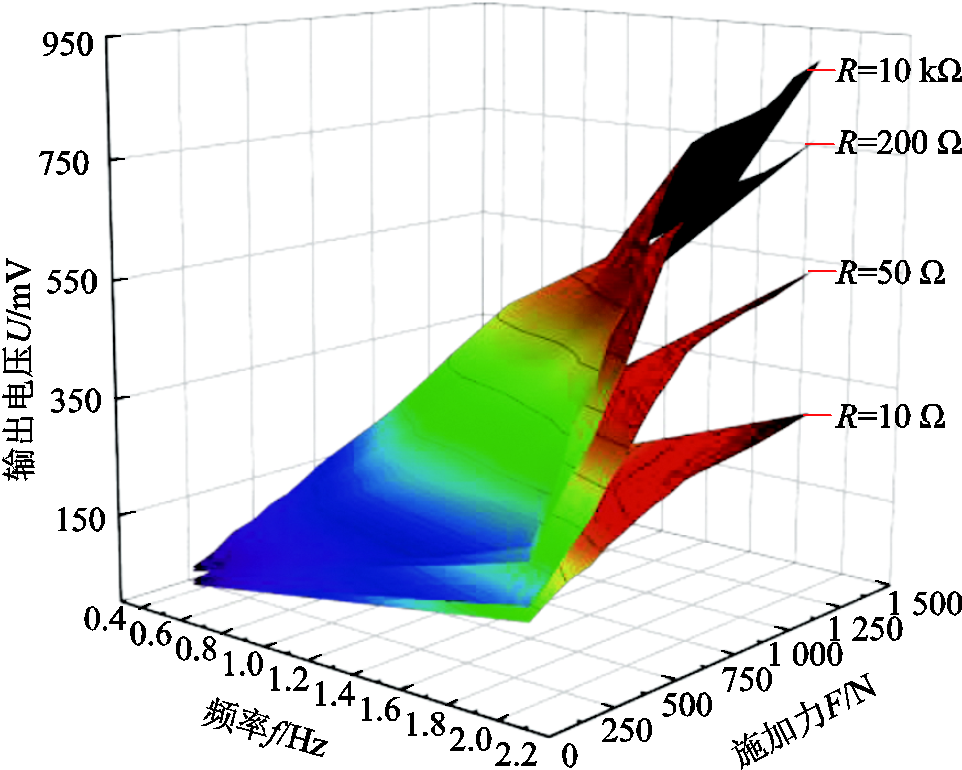
图16 输出电压有效值与振动力幅值和频率以及负载阻值的关系
Fig.16 Relation between output voltage RMS and amplitude and frequency of vibration and load
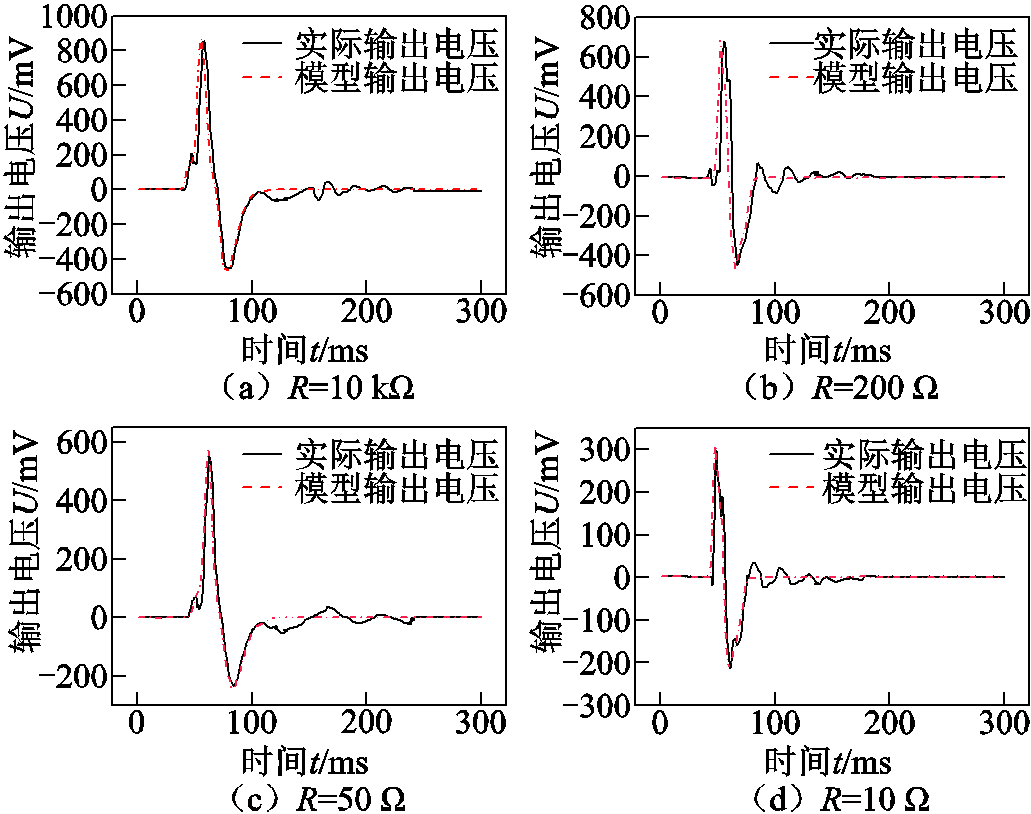
图17 四组模型计算与实验测得输出电压对比
Fig.17 Four sets of comparison of output voltage calculated by the model and output voltage measured by the experiment
表2 模型预测与实验测试输出电压的相对误差
Tab.2 Relative error of output voltages between model and experiment
参数数值 R=10 kΩR=200 ΩR=50 ΩR=10 Ω Upp.sim/mV 1 356.09 1 165.20815.75521.91 Upp.ex/mV1 306.481 131.38785.73506.38 ηpp(%)3.793.003.823.07 Urms.sim/mV400.37333.62245.19136.75 Urms.ex/mV404.82346.49239.23132.10 ηrms(%)1.103.712.493.52
表2数据显示，模型预测和实验测试的输出电压峰-峰值和有效值的相对误差均小于4%，证明了等效电路模型预测输出电压方法的有效性。几种不同模型预测结果的相对误差和模型复杂程度对比结果见表3。
表3 不同模型对比
Tab.3 Comparison of different models
模型相对误差(%)复杂程度 等效电路模型＜4较为简单 线性压磁方程模型12.56简单 输出电动势预测模型11.7简单 有限元分析模型＜10复杂
表3中数据显示，由于线性压磁方程模型[10]和基于亥姆霍兹自由能的输出电动势预测模型[11]在搭建过程中分别忽视了漏磁、等效阻尼的变化，导致两种模型在输出电压的预测中具有较大的误差，预测精度低于等效电路模型；有限元分析模型[14]对施加的压应力较为敏感，在不同的压应力范围段，预测精度也有差别，只有在施加压力低于65 MPa时，模型预测的相对误差才低于10%。其次，降低时间步长来提高模型精度会增加计算机计算时长，而且针对于结构复杂的能量收集器，计算时间会大幅增加。本文构建的全耦合非线性三端口等效电路模型在多次计算过程中都能良好地预测输出电压，且妥善地将材料间的漏磁、磁致伸缩材料的非线性等问题利用电路工具表达出来，使模型更加直观简洁。
1）本文基于磁致伸缩材料内部的吉布斯自由能并综合考虑了材料的机磁耦合和饱和效应建立了材料的非线性本构方程，通过材料特性测量装置和Matlab分析软件测试并识别了本构方程的参数，根据非线性本构方程和机电类比法构建适用于MVEH且考虑了漏磁、偏置磁场、预应力的电-磁-机全耦合三端口等效电路，用于准确地表征MVEH的电压输出特性。电路中的非线性相关控制电压源f1、f2表示磁端口和机械端口的耦合关系，电端口和磁端口耦合关系等效为非线性相关控制电压源Nig和Ni2。为验证模型的有效性，进行了不同输入和不同负载条件下的MVEH样机实验测试，模型计算和实验结果对比的相对误差均低于4%，表明该模型预测MVEH的电压输出特性具有良好的精准性。
2）设计并制作了一种应用于野生动植物保护区为无线传感设备持续供电的双棒式MVEH样机，为有效地收集动物运动所产生的幅值大的振动力，进行了一系列的实验来检验样机的输出性能。搭建了收集器输出特性测试系统并测试了不同负载条件下MVEH在变幅、变频振动力输入下的输出电压。根据实验测试结果，在施加的振动力幅值为115～1 310 N、频率为0.5～2 Hz的范围内，随着振动力幅值的增大，输出电压峰-峰值和有效值都随之增大，其中电压峰-峰值最大达到1 483 mV。实验测试验证了样机在承受幅值大的振动力的同时可以保证结构和输出的稳定性。
本研究可以为磁致伸缩振动能量收集器的非线性全耦合模型的构建、电压输出特性预测提供重要的理论指导。
参考文献
[1] 范兴明, 高琳琳, 莫小勇, 等. 无线电能传输技术的研究现状与应用综述(英文)[J]. 电工技术学报, 2019, 34(7): 1353-1380. Fan Xingming, Gao Linlin, Mo Xiaoyong, et al. Overview of research status and application of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1353-1380.
[2] 王照, 刘浩. 配电设备生命周期管理研究[J]. 电气技术, 2020, 21(12): 119-123. Wang Zhao, Liu Hao. Research on life-cycle management of distribution equipment[J]. Electrical Engineering, 2020, 21(12): 119-123.
[3] 薛明, 杨庆新, 章鹏程, 等. 无线电能传输技术应用研究现状与关键问题[J]. 电工技术学报, 2021, 36(8): 1547-1568. Xue Ming, Yang Qingxin, Zhang Pengcheng, et al. Application status and key issues of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.
[4] 朱逸凡. 碰撞式压电-电磁复合能量采集器研究[D]. 长春: 吉林大学, 2019.
[5] 黄文美, 夏志玉, 郭萍萍, 等. 变温条件下TbDyFe合金高频磁特性和损耗特性分析[J]. 电工技术学报, 2022, 37(1): 133-140. Huang Wenmei, Xia Zhiyu, Guo Pingping, et al. Analysis of high frequency magnetic properties and loss characteristics of TbDyFe alloy under variable temperature[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 133-140.
[6] 杨剑锋. 薄片式Galfenol能量收集器的设计与研究[D]. 杭州: 杭州电子科技大学, 2015.
[7] Deng Zhangxian, Dapino M J. Magnetic flux biasing of magnetostrictive sensors[J]. Smart Materials and Structures, 2017, 26(5): 055027.
[8] Viola A, Franzitta V, Cipriani G, et al. A magnetostrictive electric power generator for energy harvesting from traffic: design and experimental verification[J]. IEEE Transactions on Magnetics, 2015, 51(11): 1-4.
[9] Zucca M, Bottauscio O, Beatrice C, et al. A study on energy harvesting by amorphous strips[J]. IEEE Transactions on Magnetics, 2014, 50(11): 1-4.
[10] 孟爱华, 杨剑锋, 蒋孙权, 等. 柱棒式超磁致伸缩能量收集器的设计与实验[J]. 振动与冲击, 2017, 36(12): 175-180. Meng Aihua, Yang Jianfeng, Jiang Sunquan, et al. Design and experiments of a column giant magnetostrictive energy harvester[J]. Journal of Vibration and Shock, 2017, 36(12): 175-180.
[11] 何忠波, 柏果, 郑佳伟, 等. 柱棒式超磁致伸缩振动能量收集装置建模与实验[J]. 农业机械学报, 2019, 50(8): 400-409. He Zhongbo, Bai Guo, Zheng Jiawei, et al. Modeling and experiment of column-type giant magnetostrictive vibration energy harvesting device[J]. Transactions of the Chinese Society for Agricultural Machinery, 2019, 50(8): 400-409.
[12] Zhou Haomiao, Li Menghan, Li Xiaohong, et al. An analytical and explicit multi-field coupled nonlinear constitutive model for Terfenol-D giant magnetostrictive material[J]. Smart Materials and Structures, 2016, 25(8): 085036.
[13] Sathish Kumar R, Jayabal K. Micromechanically motivated constitutive model embedded in two-dimensional polygonal finite element framework for magnetostrictive actuators[J]. Journal of Applied Physics, 2019, 125(19): 194101.
[14] Ahmed U, Jeronen J, Zucca M, et al. Finite element analysis of magnetostrictive energy harvesting concept device utilizing thermodynamic magneto-mechanical model[J]. Journal of Magnetism and Magnetic Materials, 2019, 486: 165275.
[15] Pyo S, Roh Y. Structural design of an acoustic planar array transducer by using the equivalent circuit method[J]. Ultrasonics, 2020, 108: 106219.
[16] 李梦星, 张艳丽, 姜伟, 等. 机械应力下电工钢片磁滞与磁致伸缩回环滞后特性模拟[J]. 电工技术学报, 2022, 37(11): 2698-2706. Li Mengxing, Zhang Yanli, Jiang Wei, et al. Simulation of hysteresis and magnetostrictive loop hysteretic characteristics of electrical steel sheets under mechanical stress[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2698-2706.
[17] 翁玲, 常振, 孙英, 等. 不同磁致伸缩材料的高频磁能损耗分析与实验研究[J]. 电工技术学报, 2020, 35(10): 2079-2087. Weng Ling, Chang Zhen, Sun Ying, et al. Analysis and experimental study on high frequency magnetostrictive energy loss of different magnetostrictive materials[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2079-2087.
[18] Jin Ke, Kou Yong, Zheng Xiaojing. A nonlinear magneto-thermo-elastic coupled hysteretic constitutive model for magnetostrictive alloys[J]. Journal of Magnetism and Magnetic Materials, 2012, 324(12): 1954-1961.
[19] Clemente C S, Davino D. Modeling and characterization of a kinetic energy harvesting device based on galfenol[J]. Materials, 2019, 12(19): 3199.
[20] Meng Hao, Zhang Tianli, Jiang Chengbao. Cut-off frequency of magnetostrictive materials based on permeability spectra[J]. Journal of Magnetism and Magnetic Materials, 2012, 324(12): 1933-1937.
[21] 赵能桐, 高兵, 宁倩, 等. 考虑温度扰动的超磁致伸缩换能器电-磁-热-机耦合特性研究[J]. 中国电机工程学报, 2022, 42(16): 6116-6125, 6185. Zhao Nengtong, Gao Bing, Ning Qian, et al. Electrical-magnetic-thermal-mechanical coupling characteristics of giant magnetostrictive transducer considering temperature disturbance[J]. Proceedings of the CSEE, 2022, 42(16): 6116-6125, 6185.
[22] Cai Wanchong, Feng Pingfa, Zhang Jianfu, et al. Effect of temperature on the performance of a giant magnetostrictive ultrasonic transducer[J]. Journal of Vibroengineering, 2016, 18(2): 1307-1318.
Abstract Magnetostrictive vibration energy harvester (MVEH) uses the Villali effect of magnetostrictive rod or sheet to convert energy from mechanical vibrations to electrical energy. MVEH has obvious advantages in output stability, strain capacity and electromechanical coupling.In areas where power is not readily available, such as wildlife sanctuaries, MVEH can convert the abundant animal kinetic energy into electrical energy to power some sensing devices. However, multiple bidirectional coupling of mechanica-magnetic-electric and nonlinear characteristics occur in the process of energy conversion.In previous studies, the prediction models for the output characteristics of MVEH were mostly based on linear piezomagnetic equations, which do not allow for good prediction of the output voltage characteristics of the harvester due to the neglect of nonlinearities of materials.
In order to solve the problem of large errors in the prediction of the output voltage characteristics of the linear model. This paper constructs a mechanical-magnetic-electric three-port fully coupled nonlinear equivalent circuit model based on the Gibbs free energy. The model takes into account the effects of different compressive stresses, bias magnetic fields and leakage magnetism, et al. The core material chosen for the MVEH studied in this work is Fe81.6Ga18.4, which has excellent electromagnetic, mechanical and magnetostrictive properties. A magnetostrictive materials test platform has been built to analyse the main magnetic properties of Galfenol. Firstly, the M-H curves of the rod are tested in the compressive stress range of 0～70 MPa to obtain the trend of the magnetisation intensity of the Galfenol rod at different compressive stresses and bias magnetic fields. Secondly, based on the Gibbs free energy within the material and using a modified hyperbolic function to characterise the M-H curve clusters. A final machine-magnetic coupling model of the magnetostrictive Galfenol rod is constructed. To further simplify the analysis of the MVEH equivalent output model, the mechanical, magnetic and electrical aspects of the global system of MVEH are interlinked with their equivalent circuits using a specific electromechanical analogy to construct a three-port fully coupled nonlinear equivalent circuit model. In order to verify the accuracy of the predicted results of the equivalent circuit model, an experimental test system consisting of a pneumatic stamping press and an air compressor is built. It can provide MVEH with vibration forces varying in amplitude from 115 N to 1 310 N and in frequency from 0.5 Hz to 2 Hz to simulate the vibrations generated by animal movements in a practical application. In addition, a double-rods MVEH which can withstand large vibration force is designed. After several sets of experiments, the maximum actual output voltage of MVEH can reach 1 483 mV. Two groups of different vibration force input conditions and different external load resistance values are selected as comparison conditions. By comparing the peak-to-peak value of output voltage Upp and output voltageRMS Urms obtained from the actual test with the data predicted by the equivalent circuit model. The results show that when the vibration force amplitude F=350 N, frequency f=1 Hz, and external load R=10 kΩ, the relative errors are ηpp =3.58%, ηrms =2.47%. When the F=755 N, f=1 Hz and the external loads are R=10 kΩ, R=200 Ω, R=50 Ω and R=10 Ω respectively, ηpp are 3.79%, 3.00%, 3.82% and 3.07% respectively. ηrms are 1.10%, 3.71%, 2.49% and 3.52% respectively.
The relative errors η of Upp and Urms predicted by the model and experimentally tested are less than 4%, proving the effectiveness of the equivalent circuit model for predicting output voltage. In addition, the MVEH also ensures structural and output stability while withstanding large amplitude vibration forces. This study can provide some theoretical guidance for the construction of nonlinear fully coupled models of MVEH and the prediction of output voltage characteristics.
Keywords: Vibration energy harvesters, Galfenol,fully coupled nonlinear models, equivalent circuit, output characteristic analysis
DOI:DOI:10.19595/j.cnki.1000-6753.tces.220874
中图分类号：TM274
国家自然科学基金资助项目（51777053, 52077052, 52130710）。
收稿日期 2022-05-19
改稿日期 2022-09-28
黄文美 女，1969年生，博士，教授，研究方向为磁性材料与器件、电机电器及其控制。E-mail：huzwm@hebut.edu.cn（通信作者）
刘泽群 男，1998年生，硕士研究生，研究方向为磁性材料与器件、电机电器及其控制。E-mail：1195937663@qq.com
（编辑 李冰）