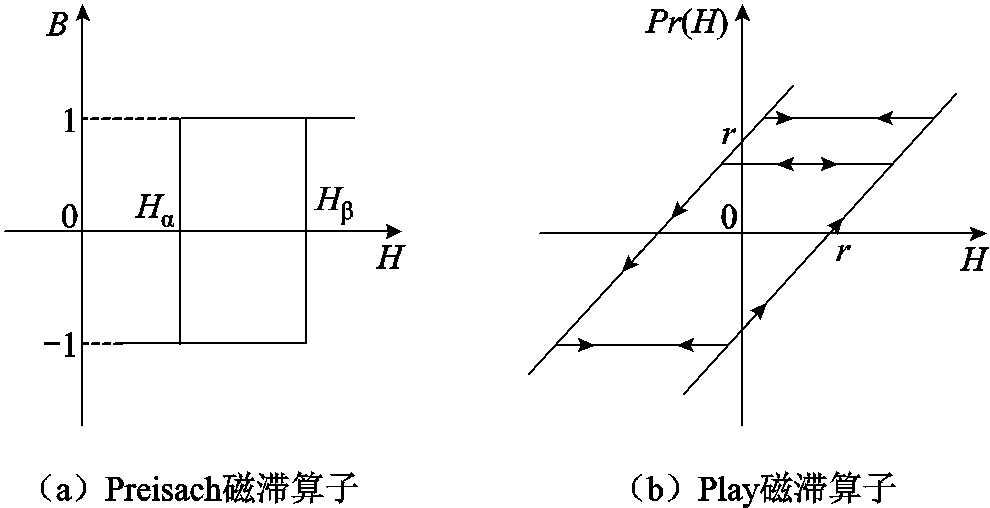
图1 两种标量磁滞算子
Fig.1 Two kinds of scalar hysteresis operators
摘要 铁磁材料磁滞建模是电气工程领域的基础性理论研究之一。该文基于深度置信网络(DBN)算法结合磁滞算子空间理论提出一种矢量磁滞模型。在模型结构中,引入郎之万函数作为映射函数对磁滞数据进行输入转换计算。利用多个磁滞算子构建算子空间生成高维算子数据,算子空间的数据输出作为DBN模型的输入,结合DBN算法表征算子数据与模型输出的非线性关系。利用样本的磁感应强度数据和生成的算子数据训练模型,获得模型参数。通过仿真表明构建的模型可以有效地描述铁磁材料在旋转磁化情况下的非线性特性和各项异性。同时,结合磁损分离理论改进磁损模型中相应的损耗系数,构建动态磁损计算模型,并将磁滞模型获得的数据应用于动态损耗计算。仿真表明,构建的磁滞模型可以有效地表征铁磁材料的实际磁化特性和损耗情况。
关键词:磁滞模型 深度置信网络算法 磁滞算子 磁滞损耗
电工装备如电机和变压器的优化设计中,铁心的电磁场分析至关重要[1-3]。构建描述铁磁性材料磁化特性的磁滞模型有助于提升电磁场分析的精度。传统的磁滞模型可以分为标量磁滞模型和矢量磁滞模型。标量模型的研究起步较早,其中,Preisach模型是一种经典的模型[4]。这一模型的建模思想是利用多个服从特定分布的磁滞算子共同描述材料的磁滞特性,该模型具备相当高的精度和有效性,然而相对过大的计算量和同余性是其不足之处。Jiles-Atherton(J-A)模型是另一种被广泛应用的基于物理意义的标量磁滞模型[5-6]。J-A模型的构建基于现有的畴壁移动和畴壁旋转的铁磁材料磁滞特性的数学理论,具有明确的物理特性而且计算量不大,但是其在描述小回环性质时不如Preisach模型,对材料的局部磁化特性的刻画不够强大。
在电工装备的实际运行中,磁场是一个矢量场,同时,在某些电工装备如变压器的T形结构处存在旋转磁场[7-8]。对此,标量磁滞模型很难精确地描述这一情况。相对而言,矢量磁滞模型可以有效地表征材料在矢量场情况下的磁滞特性。基于经典的Preisach模型,文献[9]提出了矢量Preisach模型,通过考虑不同磁化方向的标量模型的综合效应使之可以计算矢量的情况。相对而言,Stoner-Wohlfarth(S-W)模型是另一种基于材料微磁学机理提出的矢量磁滞模型,但是计算量也较大[10]。同时,由于它不能解释涡流损耗,不考虑各个粒子的相互作用以及磁化历史的影响,所以,该模型适用范围受限。结合上述两种模型的优点,2006年E. Della Torre课题组提出了一类混合矢量磁滞模型:一般矢量磁滞(Della Pinzaglia Cardelli, DPC)模型[11]。DPC模型本质上是对于传统的Preisach模型在矢量方向扩展。相对于传统的Preisach模型,DPC模型采用矢量磁滞算子参与计算。每个算子的输出为一个二维的或者三维的矢量,模型根据特定的分布综合算子的输出作为总的输出。相对而言,DPC模型的辨识仍然需要较长的时间,这一缺点在磁滞算子数目变多时更为明显。另一种考虑磁滞算子的模型是Play模型[12],不同于静止的DPC模型的磁滞算子,Play算子在材料的磁化过程中根据磁化轨迹的位置而变化。因此,Play模型需要的磁滞算子的数目较少,同时计算量和辨识时间都较少。然而Play模型的分布函数计算过程相对复杂。
铁磁材料的磁化机理涉及磁畴的运动过程,十分复杂。磁畴的运动机理涉及交换能、外场能、各项异性能等多种能量形式[13]。传统的磁滞模型,如Preisach模型、Play模型及DPC模型仅使用传统的数学工具,因此很难精确地表征材料的磁化过程。此外,J-A模型无法精确考虑精细的物理机理;S-W模型的模型磁化机理过于简化而且计算量过大,以上这些模型对于矢量磁滞建模物理机理不明确导致的非线性关系建模困难的问题。相对于传统模型,神经网络算法善于解决物理机理不明确的黑箱系统的建模问题。因此,很多学者采用神经网络技术构建磁滞模型。如文献[14]利用长短期记忆网络(Long Short-Term Memory Network, LSTM)构建机器人导管的磁滞模型,同时也证明了深度学习算法在磁滞模型构建中的有效性;文献[15]利用神经网络算法构建二维矢量磁滞模型,该模型具备较好的性能但是其多个神经网络的结构使得模型结构较为复杂,同时未能说明其数据保证不发散的原理;文献[16]采用前馈神经网络的结构以前一时刻的磁化数值递推求解后一时刻的数值,存在数据误差迁移的可能性,且不一定能表现小回环特征,以及不一定能够表现材料励磁特性;文献[17]结合循环神经网络(Recurrent Neutral Network, RNN)结构构建HRNN(Hysteretic-RNN)可以有效地描述材料的一阶回转曲线,在该模型中单个神经元类似于磁滞算子的结构,具备记忆特性,但是该模型为标量模型,不能推广到矢量情况。
考虑到传统磁滞模型与已有的神经网络类模型的不足之处,本文结合深度学习算法和传统模型中的磁滞算子的思想进行矢量磁滞建模。在模型构建中,通过引入宏观磁滞算子构成算子空间对输入的磁滞数据进行处理,将磁滞数据的磁滞特征转化为非线性特性。利用深度置信网络(Deep Belief Networks, DBN)对样本进行特征提取,表征这一非线性关系,构建矢量磁滞模型。由于DBN模型是数据驱动的,因此,材料本身不明确的物理机理的矢量磁滞建模问题被转换为深度学习网络训练问题。根据磁损分离理论改进相应的损耗系数使得矢量磁滞模型的数据进行损耗计算可以应用于动态情况。通过仿真数据可以证明本模型具有很好的精度和泛化能力。
铁磁材料的磁滞特性是一种复杂的非线性特性。磁滞模型中磁滞算子的作用是利用本身的记忆特性对输入的磁场强度函数{H1,H2,∙∙∙,Hn}和输出的磁通密度函数{B1,B2,∙∙∙,Bn}之间构建映射关系,其中n为磁滞模型的维数。通过磁滞算子的映射,每个确定的H生成多个算子值来定位B,也就是将磁性材料在B-H空间上的磁化状态唯一化。
传统磁滞算子有很多种,根据模型形式可以分为标量磁滞算子和矢量磁滞算子[18]。标量磁滞算子主要用于处理标量磁滞数据,如Preisach模型采用的继电特性的磁滞算子,以及基于齿轮滞后原理的Play算子等,两类算子特性如图1所示。

图1 两种标量磁滞算子
Fig.1 Two kinds of scalar hysteresis operators
相应地,矢量磁滞算子也有很多种。如考虑微磁学的相关理论的DPC算子、S-W算子和矢量单元算子,以及在标量Play算子基础上发展的矢量Play算子等。含有磁滞算子的磁滞模型一般可以表示为
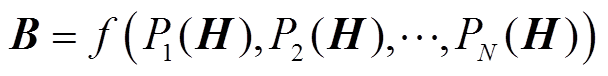 (1)
(1)
式中,Pi(H)为磁滞算子关于H的输出;N为磁滞算子的个数;f为非线性或者线性函数。特别地,对于标量Preisach模型f为线性函数。
通过对铁磁材料磁滞特性的分析,文献[19]提出了一种标量的宏观磁滞算子。这种磁滞算子可以有效地描述材料的磁滞特性中的记忆特性和擦除特性。算子的表达式为
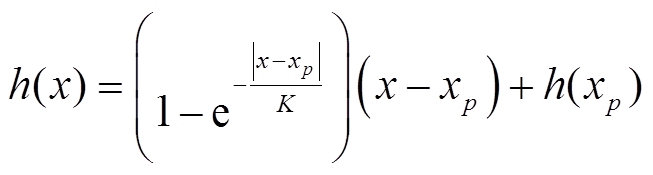 (2)
(2)
式中,h(x)为当前的输出;x为当前的输入;xp为距离当前输入最近的极值点;h(xp)为xp对应的输出值;K为压缩系数。显然,算子的当前输出是在历史极值点输出的基础上发生变化的。
采用如图2a中的输入为例说明该磁滞算子的特性。图2中,分别在算子的输入的上升支和下降支各有一个局部极值点,对应的算子输出产生一个小回环。小回环的产生证明了算子具备记忆特性。而小回环之后的数据与主回环有关,可以证明算子同时满足擦除特性。若不断在磁滞回线的最大值处生成多个磁滞回环,那么模型就产生一阶回转曲线。注意到,图中的磁滞回线不是关于横轴对称的,这是因为算子的输出与模型的初始值(对应于材料的剩磁状态)有关,在实际应用中,初始值根据之前磁化状态的轨迹确定。
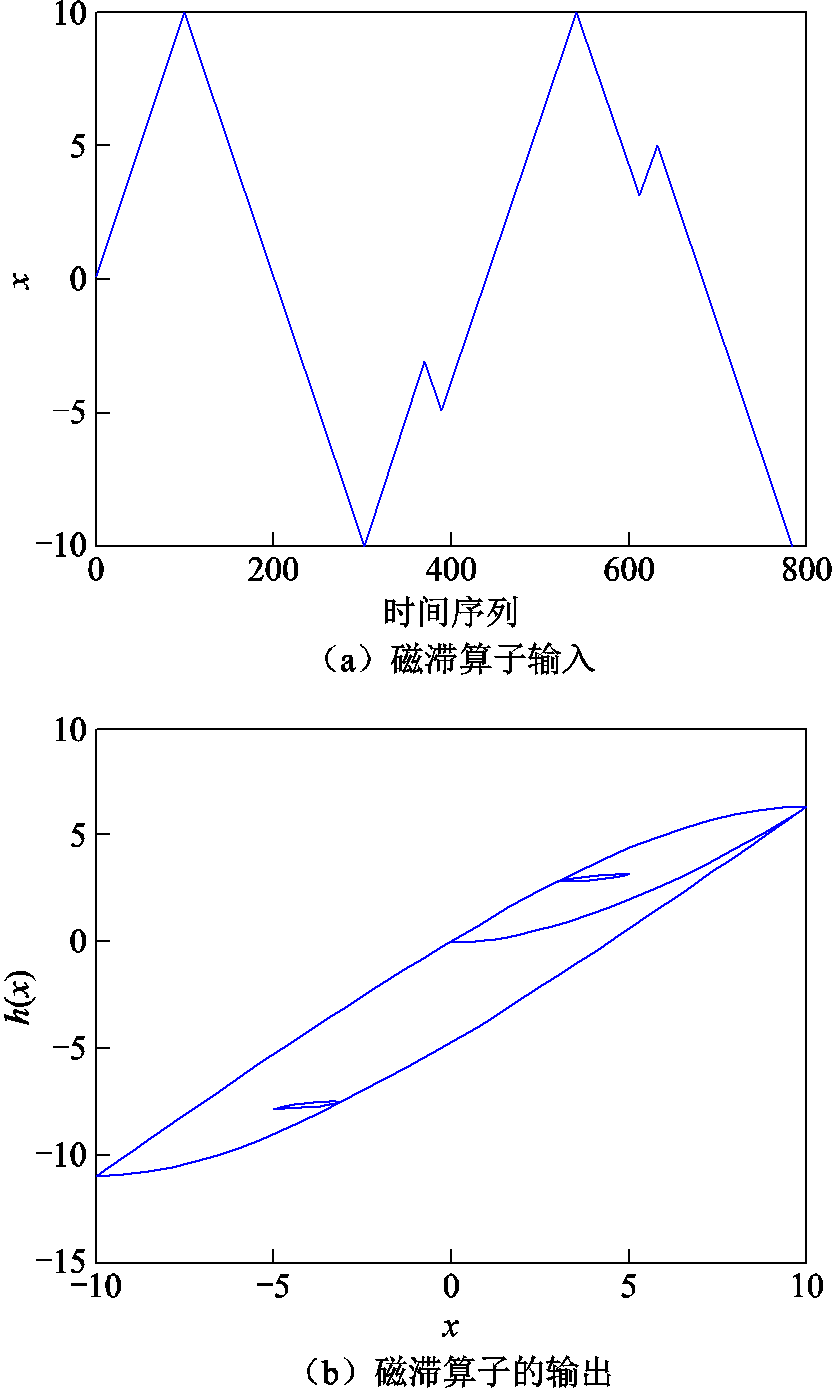
图2 宏观磁滞算子的特性
Fig.2 The properties of macroscopic hysteresis operators
为了精确表征算子的性能,在本算子中定义材料充磁过程:当铁磁材料当前的输入值(磁场强度H)的绝对值大于历史极值的绝对值时,材料处于充磁过程,此时,材料的磁化状态仅与当前的输入值相关。当材料处于充磁状态,算子的输出为
 (3)
(3)
式中,hE(x)为算子处于充磁状态当前的输出;x为当前的输入。在本文的仿真中,磁滞数据均为旋转磁化数据,材料未处于充磁状态。但是,式(3)的定义可以使得宏观磁滞算子在图2中的激励下的输出关于横轴对称,有利于完善宏观磁滞算子的特性。
将多个磁滞算子组合成一个集合,那么这样一个集合就构成了一个磁滞算子空间。如果算子空间中包含有m个磁滞算子,对于输入的H,经过算子空间运算可以产生m维的数据,即
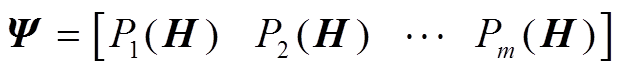 (4)
(4)
式中,Ψ为磁化状态矢量; 为第i个磁滞算子的输出。每个磁滞算子的输出表示它的磁化状态,相应的Ψ可以表述铁磁材料在当前输入的整体磁化状态。且这一状态与材料的磁通密度之间存在一种非线性的映射关系。磁滞算子空间理论是将深度学习算法应用于磁滞建模的理论基础。通过算子空间的处理,使得材料复杂的磁滞特性转换为高维数据与输出之间的映射特性。这样的数据关系可以通过深度学习算法进行处理。
为第i个磁滞算子的输出。每个磁滞算子的输出表示它的磁化状态,相应的Ψ可以表述铁磁材料在当前输入的整体磁化状态。且这一状态与材料的磁通密度之间存在一种非线性的映射关系。磁滞算子空间理论是将深度学习算法应用于磁滞建模的理论基础。通过算子空间的处理,使得材料复杂的磁滞特性转换为高维数据与输出之间的映射特性。这样的数据关系可以通过深度学习算法进行处理。
深度置信网络(DBN)算法是由G. E. Hinton 在2006年提出的一种生成模型。相对于传统的机器学习算法,DBN具有强大的特征提取能力与非线性表征能力。互补先验理论以及受限玻耳兹曼机(Restricted Boltzmann Machines, RBM)与有向连接神经网络的等效性原理作为DBN算法的理论基础保证了模型在实际应用中的有效性。近年来,DBN算法在图像识别、故障诊断、数据预测等领域得到大量的应用[20-22]。
DBN模型由多个RBM的堆叠实现深层的网络结构。RBM是一种基于能量的无监督模型,由可见层和隐藏层构成。RBM的结构如图3所示。图3中,W为权重,V-Layer为可见层,H-Layer为隐藏层。vi和hj分别为可见层与隐藏层的二值节点的取值(0或者1)。
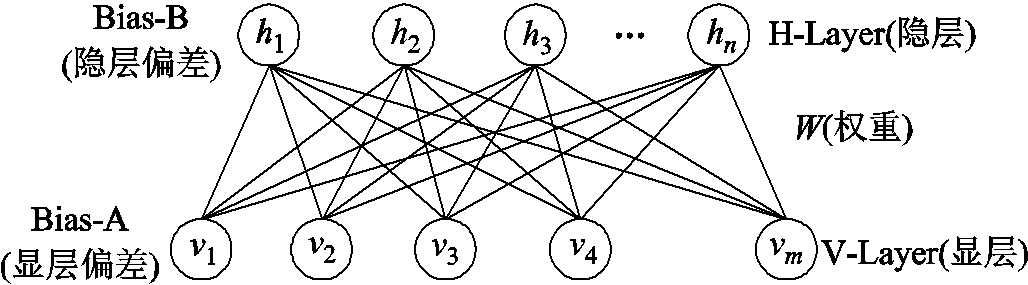
图3 RBM的结构
Fig.3 The structure of RBM
定义RBM的能量为
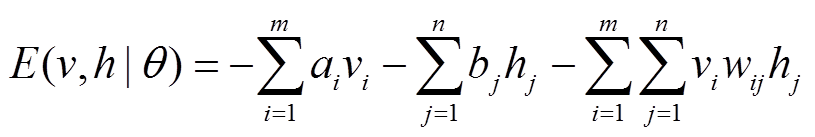 (5)
(5)
经过多个RBM堆叠,DBN的网络结构如图4所示。通常情况下,训练DBN需要两个步骤:①采用对比散度(Contrastive Divergence, CD)贪婪算法对单个RBM逐层无监督训练;②采用反向传播(Back Propagation, BP)算法或者醒眠算法对整个DBN网络进行全局参数微调。前者也被称作“预训练”,是一种无监督的训练方法,主要使网络参数可以尽量表征数据的特征分布;后者是一种有监督的训练,使模型可以有效拟合训练集的标签。
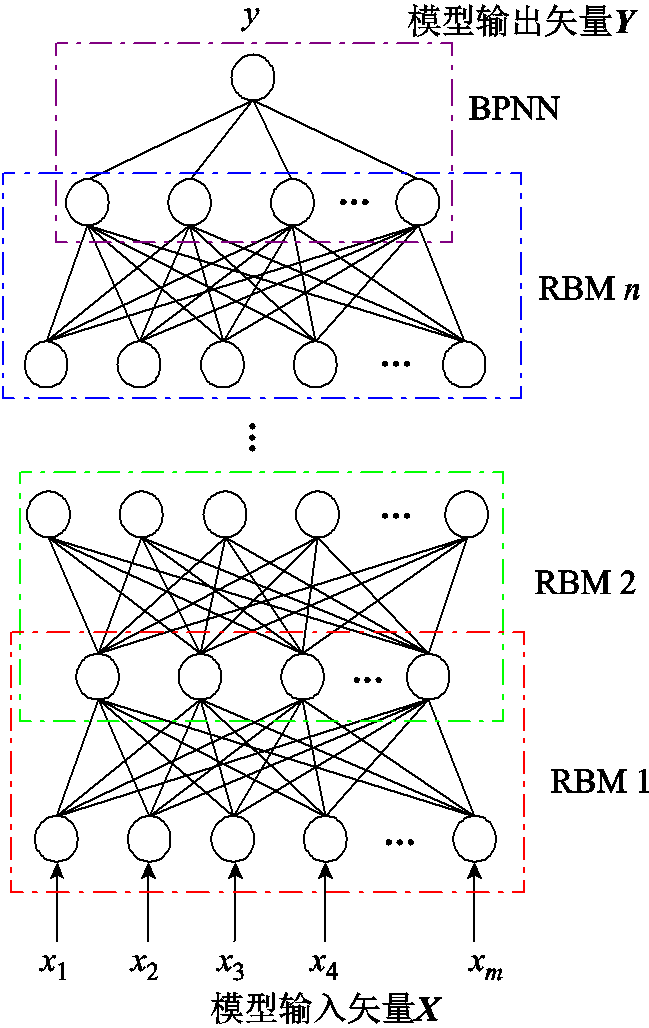
图4 DBN的结构
Fig.4 The structure of DBN
基于前文所述的宏观磁滞算子构成的算子空间和DBN算法,本文提出一种新结构的矢量磁滞模型,模型结构如图5所示。模型的大体结构分为输入映射函数、磁滞算子空间和DBN模型三个部分。
2.2.1 输入映射
在实际中的磁滞数据中,输入的H数据的变化范围从数A/m到数kA/m,而宏观磁滞算子的输入是无量纲且有限的,所以如果直接通过算子进行处理势必得不到合适的数据。为了适应宏观磁滞算子的特性且能体现磁滞现象的饱和特性,本文利用Langevin函数对磁滞数据进行输入映射。
在输入映射的过程中首先将磁滞数据H转换为极坐标的形式,获得数据的幅值和相位HA和θ。直接利用Langevin函数对幅值进行压缩映射,而相位保持不变。Langevin函数为
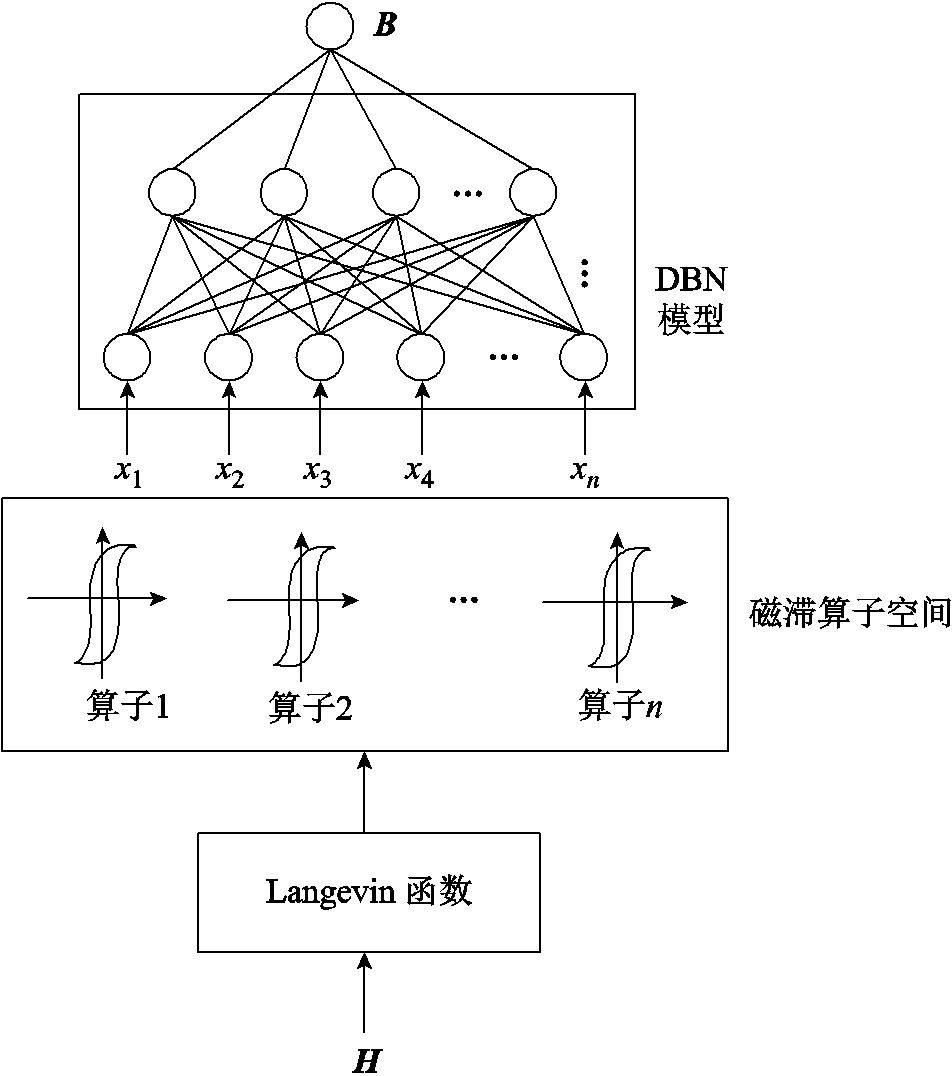
图5 矢量磁滞模型的结构
Fig.5 The structure of vector hysteresis model
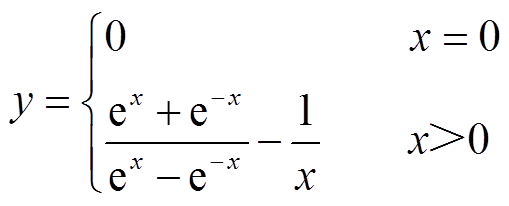 (6)
(6)
式中,x=HA/He。He主要用来调整Langevin函数的曲线形状,根据经验值可选取He=350 A/m,可以证明,当x→0时,y=0;x→∞时,y=1。
对于Langevin函数来说,输入的是磁场强度,输出的是无量纲的值。为了表明Langevin函数的特性,使函数输入的磁场强度的幅值由0增加到3000 A/m,Langevin函数的输出变化如图6所示。
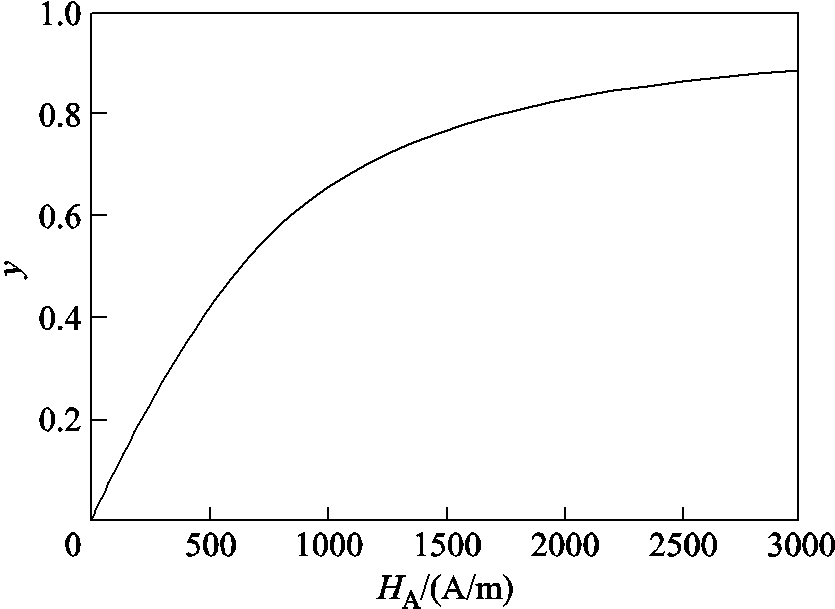
图6 Langevin函数
Fig.6 The Langevin function
由图6可以看出,随着磁场强度的增大,函数的输出存在饱和的现象,可以部分地体现材料的实际状况。
2.2.2 H空间中磁滞算子的分布——算子空间
H空间中磁滞算子的分布如图7所示。H空间中,在空间的右半平面确定n个方向(以原点出发构成n条射线),每个方向上放置一个磁滞算子。经Langevin函数映射后的磁化轨迹在H空间上的各个方向进行投影。显然,每个方向上H轨迹的投影区间是[-1,1](左半空间是负方向)。每个方向的投影在磁滞算子中计算获得相应算子的值,为了后续DBN的应用,经过调整初始值保证算子的输出在[0,1]之间,这些值作为后续DBN模块的输入。算子的数目就是输入DBN的数据的维数。
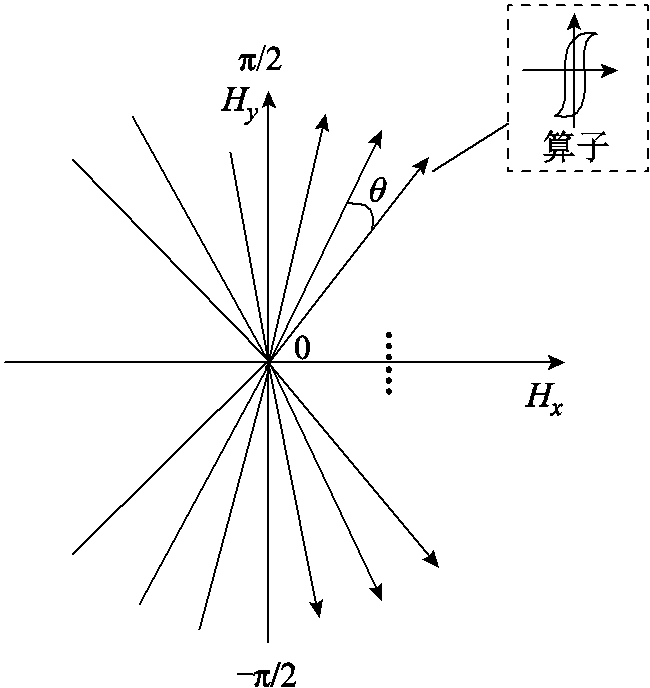
图7 H空间中磁滞算子的分布
Fig.7 The distribution of hysteresis operators in H space
算子空间中磁滞算子的数目和模型的精度存在一定的关系。如果算子的数目过多,那么模型的计算和训练的时间就会过长,造成算力的浪费。同时,如果算子的数目过少,那么模型很难完全地表征材料的磁化特性,因此,需要根据经验选取一个较为合适的值。图7所示H空间中设定64个算子,此时各个算子的位置的角度相差5.7°,可以保证模型的精确性。
2.2.3 DBN模型
在矢量磁滞模型的构建中,DBN模型主要用于表征算子输出的矢量数据与材料的磁感应数据的非线性关系。在DBN的参数获取过程中,根据磁滞数据生成的训练集进行训练,得到的DBN模型的参数。DBN的训练过程主要包含两部分:①采用CD算法对各层的RBM进行预训练,然后堆叠RBM获得模型初步的优化参数;②将训练获得的参数作为初始值,采用Nadam优化器进行参数的全局调优,获得模型最终的优化参数。
在训练中,RBM预训练的参数初始值采用生成的高斯分布的随机值(保证数值很小)。Nadam优化器的表达式为
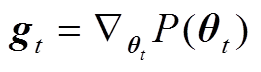 (7)
(7)
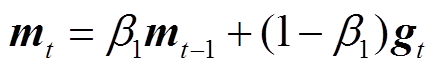 (8)
(8)
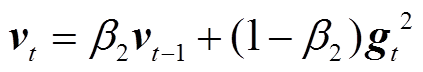 (9)
(9)
Nadam的参数更新规则为
 (10)
(10)
式中,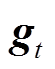 为梯度向量;
为梯度向量;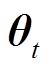 为模型参数向量;P为目标函数;
为模型参数向量;P为目标函数;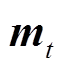 和
和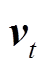 分别为梯度的一阶矩估计和二阶矩估计;η为学习率;t为迭代次数;β1和β2为优化器的修正参数;ε的作用是防止分母为0。
分别为梯度的一阶矩估计和二阶矩估计;η为学习率;t为迭代次数;β1和β2为优化器的修正参数;ε的作用是防止分母为0。
DBN模型的参数获得之后,整体的矢量磁滞模型可以用来计算磁滞数据和材料的磁滞损耗。整个矢量磁滞模型的构建流程如图8所示。
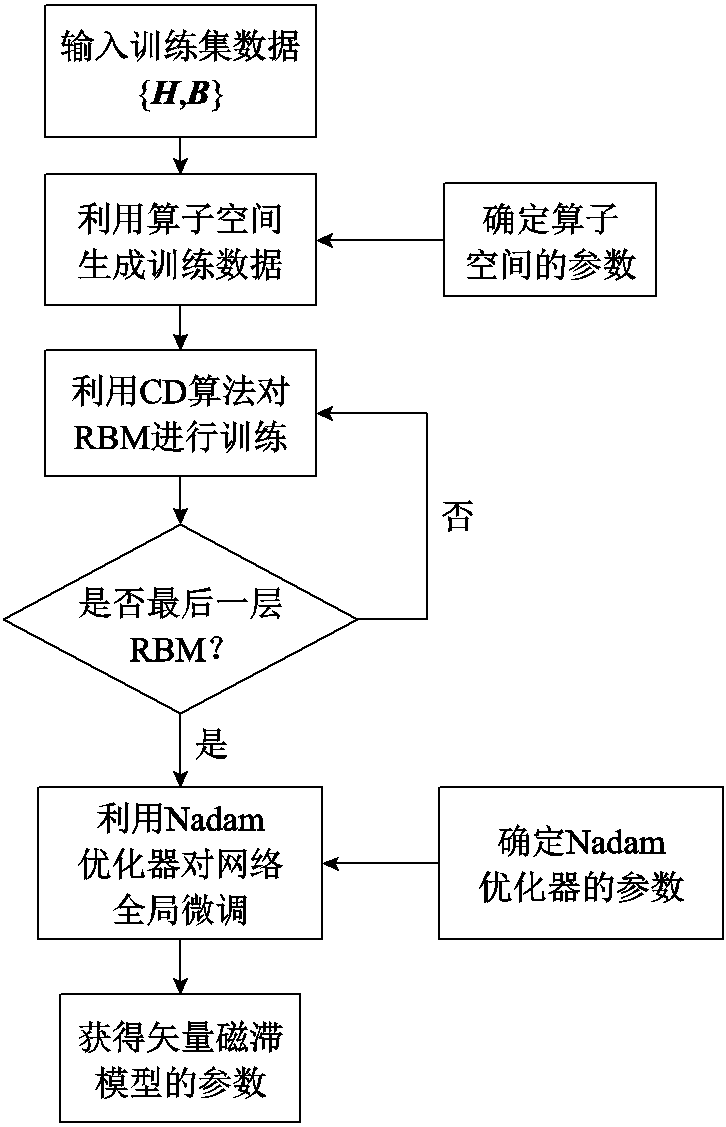
图8 矢量磁滞建模的流程
Fig.8 The flow chart of vector hysteresis modeling
本文利用二维矢量磁特性测试装置对无取向硅钢片B35A210的磁滞特性进行测量,获得材料的矢量磁滞数据。矢量磁特性磁测量装置的结构及铁心形状如图9所示。
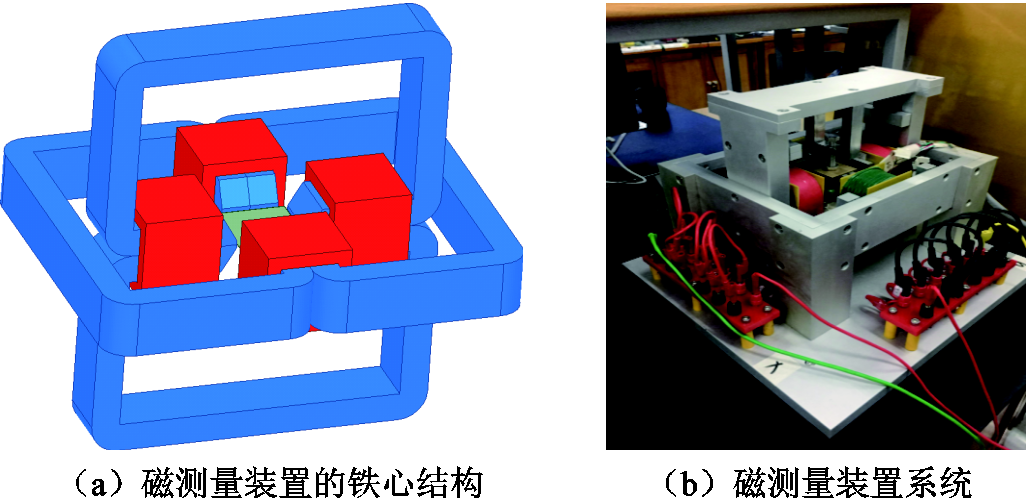
图9 二维矢量磁特性测试装置
Fig.9 The two-dimensional vector magnetic characteristics test device
在二维矢量磁特性测试装置中,两对“C型”铁心垂直安装,将含有待测样品的B-H传感装置放置在二维旋转磁特性测量装置的中心。由三层不同匝数的绕组组成多层励磁绕组,可以灵活地进行串并联,满足励磁的频率范围。装置采用组合式B-H传感结构,待测样品表面的B信号采用B探针法,避免了B线圈法对样品钻孔时造成的样品磁场分布的局部不均匀,同时采用H线圈法测量H信号。在实验测试中,控制样品处的磁通密度波形轨迹为圆形,测试H的轨迹。
在实际情况下,由于控制系统采样频率的存在,矢量磁测量装置不可能获得理想的静态数据,因此采用5 Hz的数据近似作为静态数据建模。在5 Hz条件下的矢量磁滞数据的特性见表1。表中,Bm是样本的磁通密度幅值;Hmax和Hmin分别是最大磁场强度和最小磁场强度;Tr或者Te表示数据集被当作训练集或者是测试集。为了将表1的数据可视化,部分样本的数据在图10中画出。其中,图10a为部分样本的磁滞数据的H轨迹,图10b为部分磁滞数据的B轨迹。
表1 磁滞数据的特性
Tab.1 The characteristics of hysteresis data

数据集的序号Bm/THmax/(A/m)Hmin/(A/m)Tr或Te Data 10.100 445.326.6Tr Data 20.298 381.743.1Tr Data 30.397 2100.150.4Tr Data 40.496 6117.563Te1 Data 50.598 6159.665.5Tr Data 60.696 2165.995.9Tr Data 70.795 1195.8118.8Tr Data 80.895 7231.0148.2Tr Data 90.996 6272.6182.3Te2 Data 101.094 7327.7224.1Tr Data 111.192 7390.1279.1Tr Data 121.292 4481.7346Tr Data 131.390 0609.0428.5Tr Data 141.489 8849.2544.9Te3 Data 151.587 01 643.0871.7Tr Data 161.690 34 292.52 175.4Tr Data 171.791 77 455.93 767.4Tr
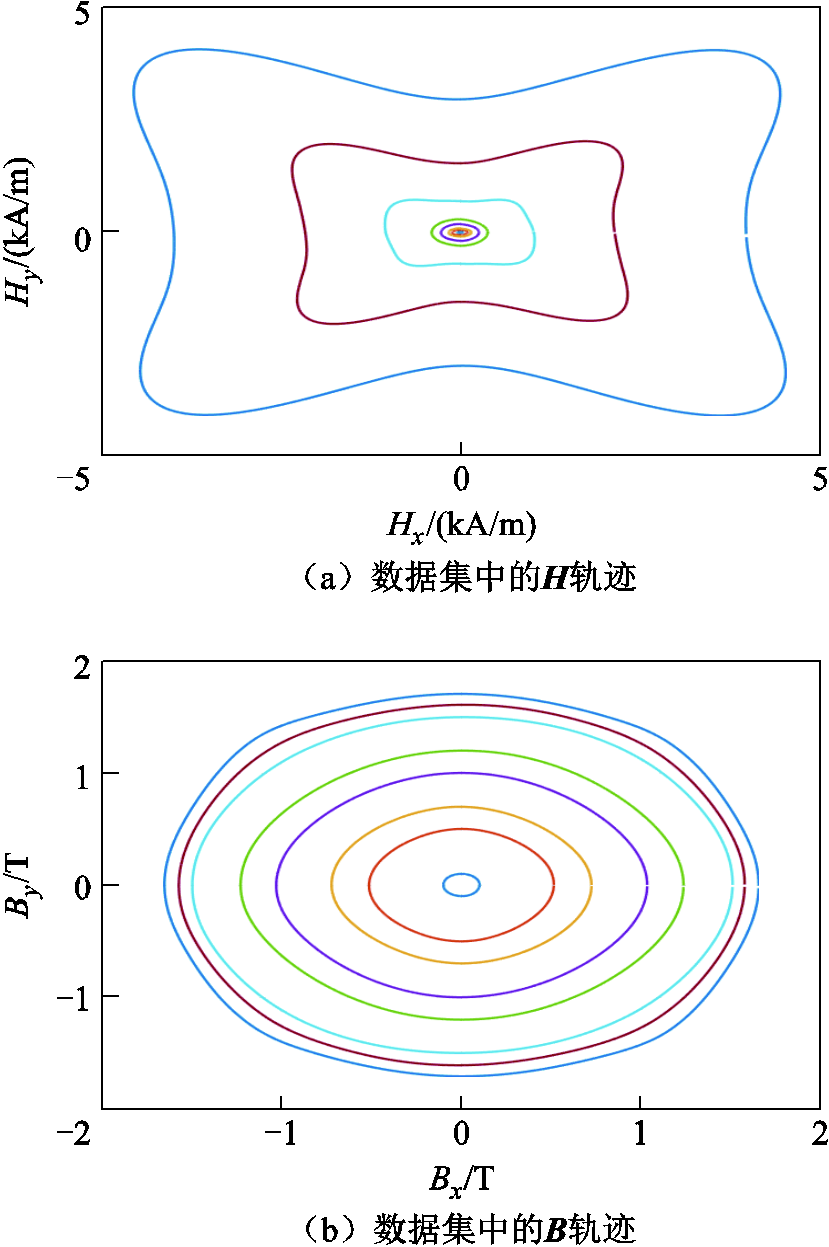
图10 数据集的可视化
Fig.10 The visualization of data sets
对于无取向硅钢而言,晶粒杂散分布近似为各向同性,但是材料的晶体结构方面存在晶格各向异性。材料在微观结构中存在的磁晶各向异性是导致其宏观磁化特性存在各向异性的原因。由表1和图10中可以看出,B轨迹是圆形的,而H轨迹随着材料磁通密度的变大由椭圆形变化为蝴蝶状,证明材料的各向异性也越来越大。另外,由表1中也可以看出,在高磁通密度的情况下,不同的磁化角度处的磁场强度的大小差异越来越大。由此可见,材料在高磁通密度情况下的各向异性更为明显。在选取材料测试集与训练集的情况下,测试集的样本兼顾高中低磁通密度的特性进行选取,已表征模型的泛化能力。在17组磁滞数据中选取14组作为训练样本,选取3组作为模型的测试样本,测试样本包含高中低磁通密度的情况(Bm= 0.5 T, 1 T, 1.5 T)。
在矢量磁测量系统中,通过控制B为不同幅值的圆形轨迹,产生17组磁滞数据集。在表1中,描述了这些数据集的特点。
在矢量磁滞模型中,通过算子空间可以获得64维的算子数据输入DBN,为了直观表现,图11展示了算子空间中-90°方向下算子对应于若干个数据集所产生的映射输出。

图11 算子的输出
Fig.11 The output of operator
通过对算子剩磁h(xp)的调整保证算子的对称性,事实上调整后的剩磁仍旧符合式(3)的表述。实际情况下,如果磁滞数据包含更复杂的磁化情况,在磁滞算子的计算中采用式(3)是必须的。
算子空间的数据输出作为DBN的输入,因此DBN的输入神经元为64个,DBN的输出为二维矢量磁通密度Bx、By。因此,DBN的输出节点为2。综合考虑,DBN模型结构确定为:64-100-40-20-2,采用3个RBM进行预训练。训练中,RBM的预训练采用CD算法,DBN的全局训练采用Nadam优化器,模型的主要优化参数见表2。
表2 DBN模型的优化参数
Tab.2 The optimized parameters of DBN model

算法参数数值 CD 算法迭代次数200 分支样本数100 学习率0.2 动量0.05 BP 算法(Nadam优化器)迭代次数1 200 分支样本数100 学习率0.001 0.9 0.9 10-8 激活函数sigmoid
矢量磁滞模型经过包含14组数据的训练集进行训练获得模型的参数,训练时间为109.02 s,所需的算力和建模的时间都在可接受范围。然后将训练好的模型分别在高、中、低磁通密度条件下(Bm=0.5 T, 1 T, 1.5 T)进行数据拟合,轨迹拟合的结果如图12所示。
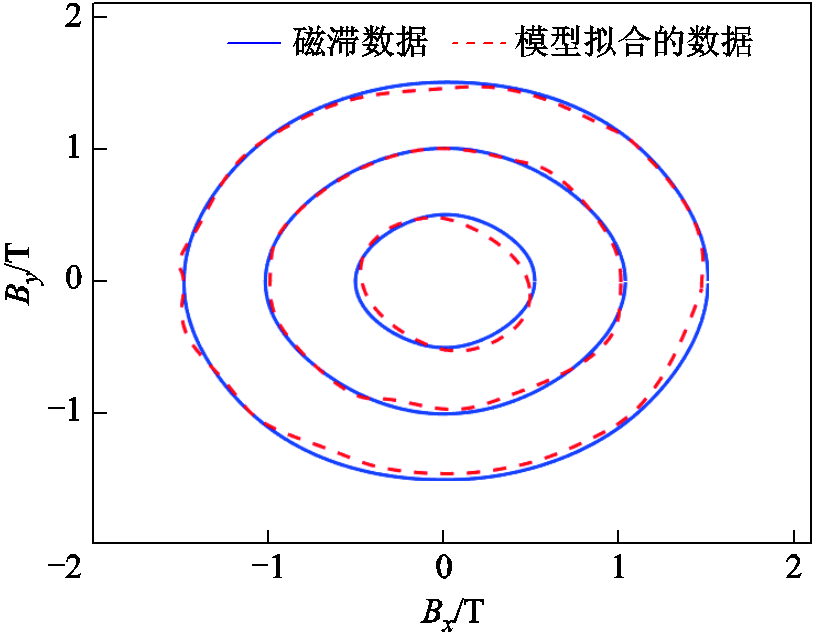
图12 磁滞模型的输出与磁滞数据的拟合
Fig.12 The fitting of output of the hysteresis model and hysteresis data
通过图12可以看出,模型计算得到的数据与原始的磁化数据轨迹拟合得比较好。可证明本模型具有较好的准确度与泛化能力。由于输入的H值存在各向异性,且随着B的增大,各向异性逐渐变大(由表1可得)。因此,可以证明本矢量模型可有效地表征铁磁材料的宏观各向异性。为了证明模型的表征能力,对矢量情况下测试集的磁滞数据在x轴和y轴进行分解,模型的拟合情况如图13所示。
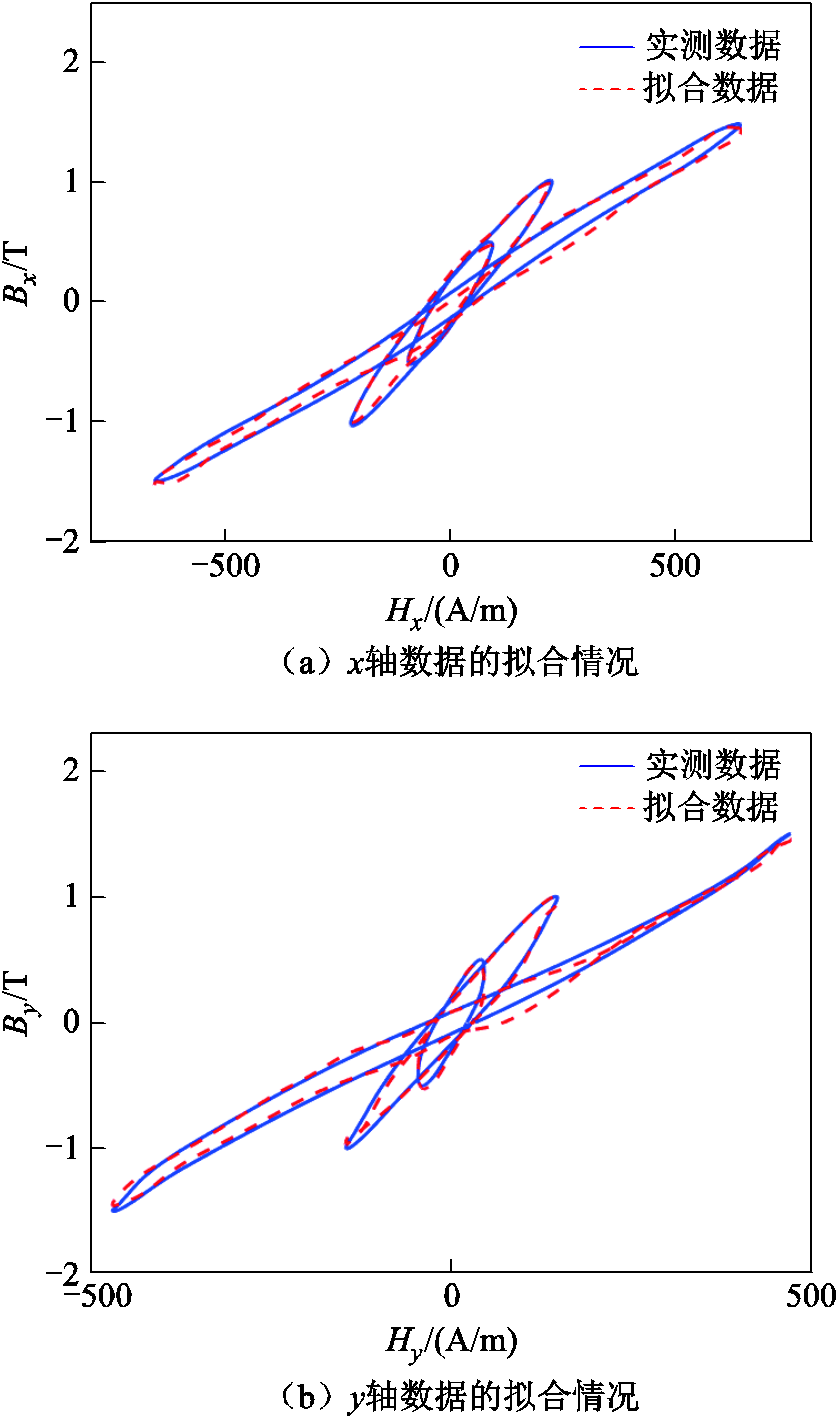
图13 测试集x轴和y轴数据的拟合情况
Fig.13 The fitting of x-axis and y-axis data of the test set
图13中,蓝色实线为测试数据,红色虚线为模型的拟合数据。可以明显地看出模型在x轴和y轴上数据中,在0.5 T、1.0 T、1.5 T情况下的拟合结果都比较好。这也证明提出的矢量模型对于磁滞数据在相位误差上也比较小,从而保证了磁损计算的可靠性。相对而言,模型在1.5 T的y轴数据的中、高磁通密度情况下的拟合结果存在一些误差,而其他情况的拟合结果相对更好。这是因为,一方面这一磁滞数据在高磁场强度下的磁滞特性相对较小,磁滞回线更为细长;另一方面,神经网络模型在处理多输出问题时误差相对较大,存在对特殊数据敏感性不强的可能。
为了定量地评估模型的性能,误差评估采用方均根公式,即
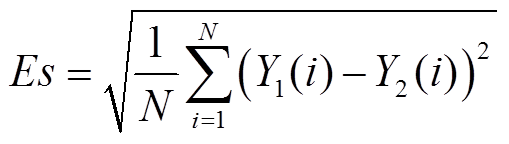 (11)
(11)
式中,N为数据集中的数据个数;Y1、Y2分别为模型的输出和原始数据值。误差的评估结果如图14所示。由图14可以看出模型的平均误差在0.05左右,精度在可接受范围内。同时每个测试集的误差相差不大,说明模型在不同的数据下稳定性较好。
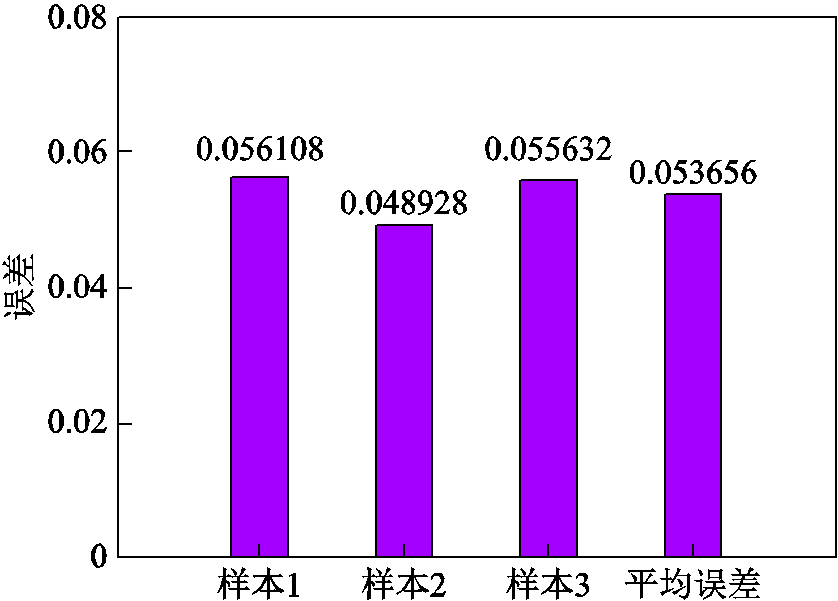
图14 模型的误差评估
Fig.14 The error evaluation of the model
对于本文所提的模型而言,由于深度学习算法本身是靠数据训练的,而根据二维矢量磁特性测试仪获得的磁滞数据本身体现了材料在宏观方向的各向异性,且磁通密度越大越明显。经过数据训练后,神经网络本身可以表征数据内在的联系,从而可以表现数据各向异性的特点,仿真的结果也证实了这一结论。
Berotti提出的磁损分离理论认为硅钢铁心损耗可以分解为磁滞损耗、经典的涡流损耗和异常损耗[23]。可表述为
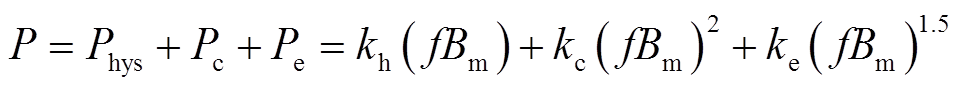 (12)
(12)
式中,P为总损耗;Phys、Pc和Pe分别为磁滞损耗、涡流损耗和异常损耗;kh、kc、ke分别为磁滞损耗系数、涡流损耗系数和异常损耗系数;f为频率;Bm为最大磁通密度值。
同时,基于模型的铁损计算公式为
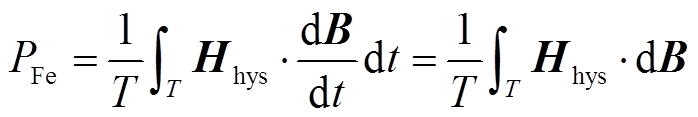 (13)
(13)
式中,Hhys和B分别为模型的输入磁场强度和输出磁通密度。通过式(13),利用本模型计算的准静态的磁滞数据计算可以得到磁损数据。
传统的磁损计算是将逆时针和顺时针的磁滞数据分别通过式(13)计算损耗,然后进行数据平均,认为通过这样的方式可以抵消材料的旋转各向异性以及材料在测量中存在的不确定性。本文将顺时针和逆时针的磁滞数据进行平均化然后采用式(13)进行铁磁损耗的计算。得到的结果与模型的磁损计算结果和材料的平均损耗进行对比,如图15所示。
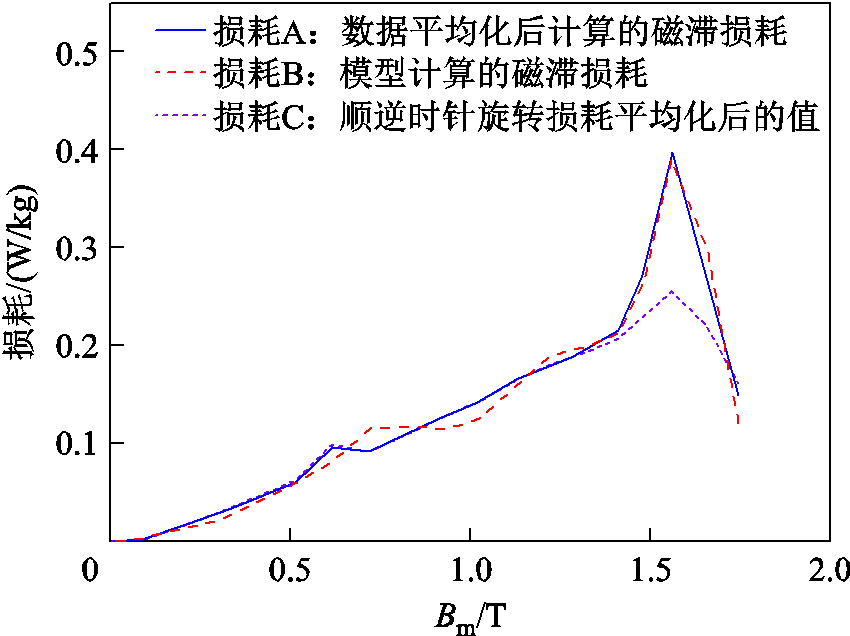
图15 各种计算方式的损耗对比
Fig.15 The comparison of loss of various calculation methods
为了方便表述,图15中,损耗A表示对原始的磁滞数据平均化后计算的损耗;损耗B表示对模型生成的磁滞数据计算的损耗;损耗C表示对原始的磁滞数据先分别计算顺时针旋转损耗和逆时针旋转损耗,然后再将损耗进行平均化得到的损耗。通过图15可以发现,在低磁通密度下三种计算方式之间的差别不大。但是,在高磁通密度下,损耗A和损耗B相差不大,这也变相地证明了本文构建的模型计算的数据在精度上和原始的磁滞数据很接近。相对而言,损耗A、B比损耗C要大一些。通过前述的数据分析可以看出,高磁通密度的磁滞数据的各向异性相对而言要大一些,这也是两种损耗计算方法差别较大的原因。单纯地将顺、逆时针的损耗进行平均化计算材料的损耗具有一定合理性。两者误差的差距主要在于材料的各向异性导致的两种不同的计算方式产生的数值误差。本文以损耗C作为标准,修正损耗计算模型。
本文的模型计算的数据是准静态的,所以包含一定的涡流和剩余分量。基于上述分析,本文改进传统的损耗模型为
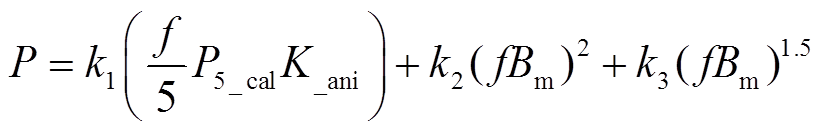 (14)
(14)
式中,P5_cal为磁滞模型计算的5 Hz条件下的铁磁损耗;K_ani为损耗考虑各向异性的折算系数,与最大磁通密度相关;k1、k2、k3分别为静损系数、涡流损耗系数和杂散损耗系数。在本文中,折算系数设定为与Bm相关的分段函数,设定为
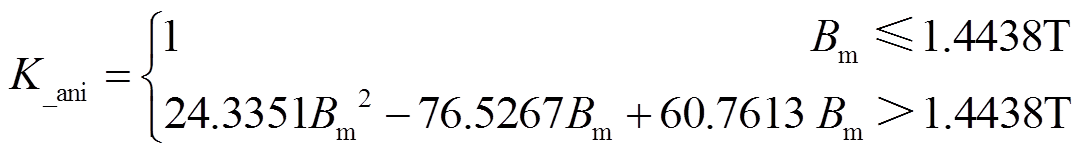 (15)
(15)
事实上,折算系数与顺、逆时针的数据误差相关,考虑到损耗模型中系数k1的限制,折算函数的选择有一定的经验性。本文根据样本点中各向异性比较大的后三个点的折算系数的值定为0.8、0.6、0.7,通过拟合的二次函数确定。
损耗模型的折算函数如图16所示。
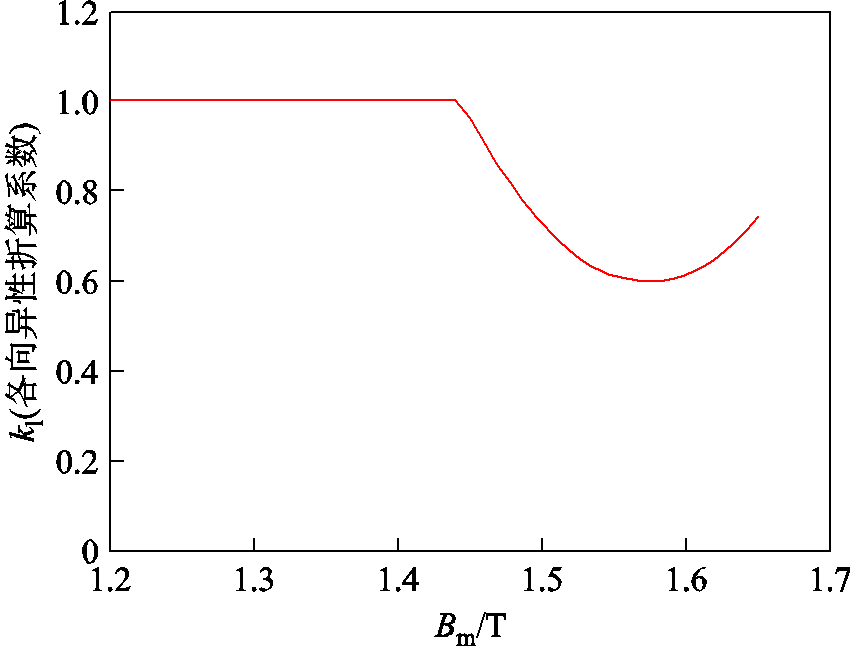
图16 损耗模型的折算函数
Fig.16 The discount function of loss model
材料磁损的计算对矢量数据是比较敏感的,实际数据中相位的偏差,以及顺、逆时针数据存在的误差等因素均可能造成磁损计算的偏差。实际应用中,应该通过多次实验确定不同旋转励磁的磁通密度幅值对应的铁磁损耗值,通过折算系数校核模型计算的磁损和实际磁损的偏差。通过这一方法可有效地保证磁损计算和模型磁特性表征的独立性,以及铁磁模型在损耗计算应用的可靠性。数据理想的情况下,折算系数可能为1。基于50 Hz和200 Hz的损耗数据采用混沌量子粒子群算法辨识模型相关系数[24],结果见表3。
表3 磁滞损耗模型的辨识系数
Tab.3 The identificated coefficients of hysteresis loss model

参数数值 k10.985 9 k21.176 4×10-5 k30.001 1
虽然后两个参数小几个量级,但是由于考虑频率的计算,后两部分损耗在总损耗中仍然占据一定的比例。依据辨识的模型计算的动态损耗和原始数据进行比较,动态损耗模型的拟合效果如图17所示。
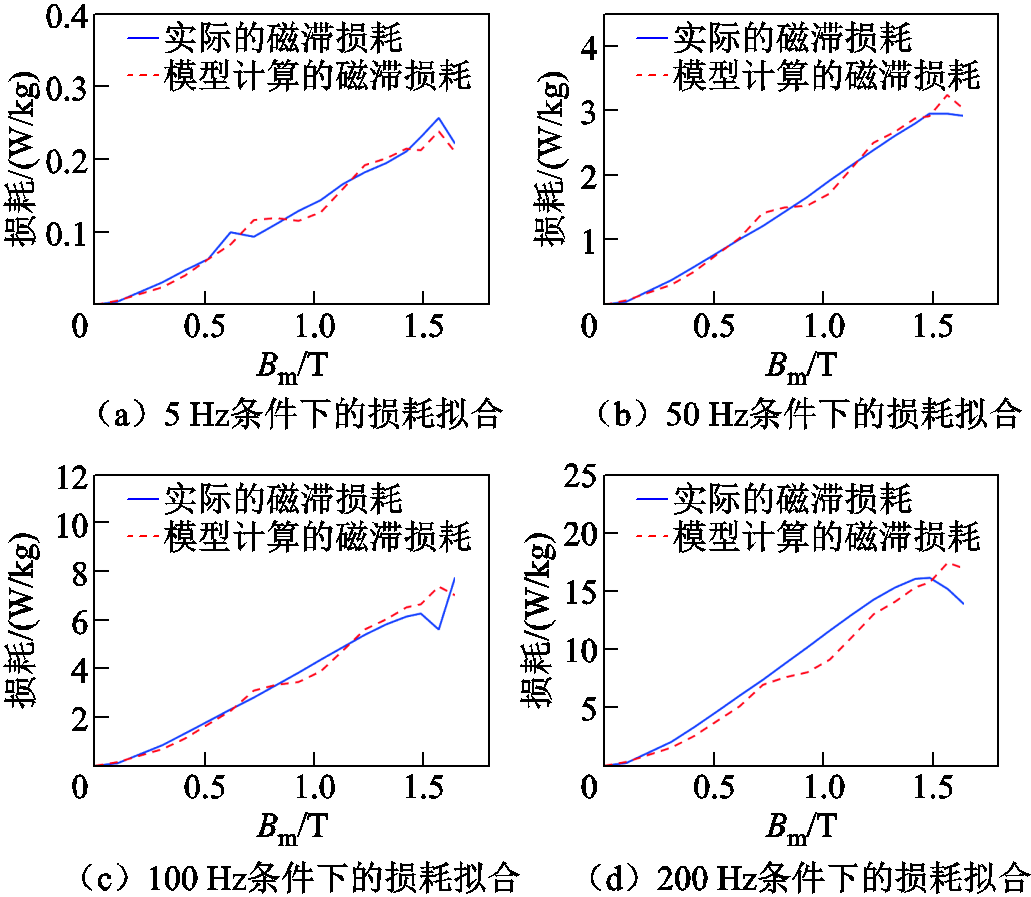
图17 动态损耗模型的拟合效果
Fig.17 The fitting of dynamic loss model
在图17中,各个频率的损耗拟合情况可以形象地表现出来。对于5 Hz损耗数据,采用折算系数计算后模型的输出与损耗数据的对比如图17a所示,可以看出模型的损耗计算与数据在高磁通密度条件下误差变小,同时,在高磁通密度阶段模型的损耗输出存在一个极大值,这一现象与实际情况是匹配的。因此,该图说明的是折算系数的作用。损耗模型的参数辨识由50 Hz和200 Hz的损耗数据进行,所以,在图17b和图17d中主要表现辨识算法的误差以及模型的复现效果。在图17c中利用辨识好的动态损耗模型对100 Hz的损耗数据进行泛化验证,可以看出模型具备较好的精度,证明了提出的损耗模型的泛化能力。为了对100 Hz损耗数据进行定量分析,引入相对误差,即
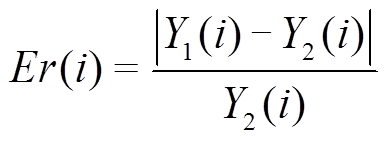 (16)
(16)
式中,Er(i)为第i个样本的相对误差。为了更加直观地表示,100 Hz损耗数据的17个样本的相对误差如图18所示。
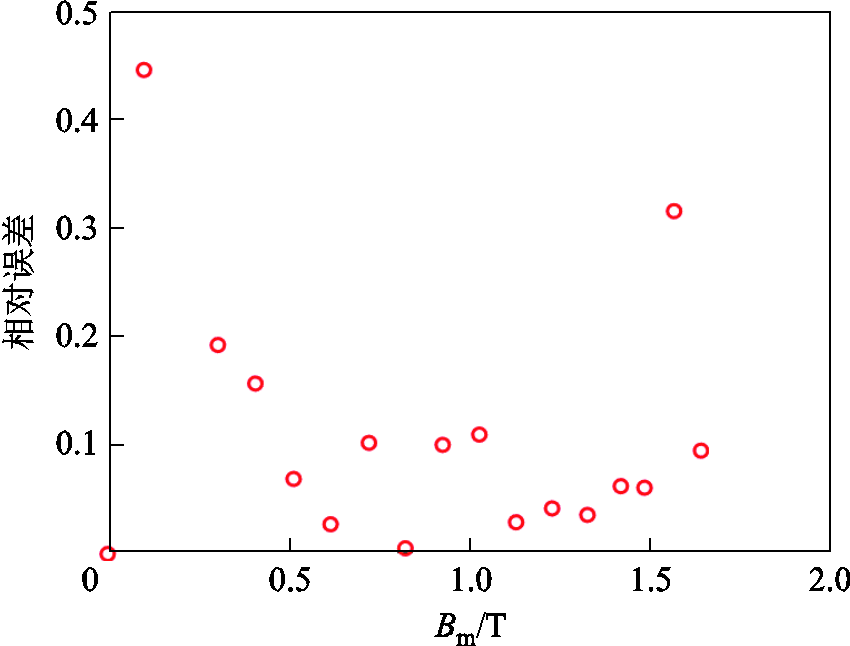
图18 100 Hz动态损耗的相对误差
Fig.18 The relative error of dynamic loss in 100 Hz
图18中,第一个样本为0样本,不具有统计意义。可以看出,大部分样本的相对误差在0.2以下,证明本模型具备较好的泛化能力。第二个样本的相对误差达到0.45,但是,第二个样本的原始数据为0.101 4,计算值为0.146 6,虽然相对误差较大,但其意义本身不大,这一计算结果在可接受范围内。第16个样本的相对误差达到0.315 9,其原始数据为5.574 7,计算值为7.335 7。但是注意到,在原始数据中,此点为一个极小值点,而模型计算的为一个极大值点。通过磁滞损耗理论以及其他三个频率下的特征描述可知,旋转损耗会在较高磁通密度时表现为一个极大值点。所以,该点应该是个极大值点,尽管计算的相对误差较大,但是模型是合理的。该误差的产生可能是装置测量导致的。总体来看,本磁滞损耗模型具备比较好的精度与泛化性能。
本文基于DBN算法结合磁滞算子空间理论提出一种矢量磁滞模型,并将该模型应用于B35A210无取向硅钢片的磁化轨迹验证和铁磁损耗计算中。通过仿真分析证明了针对矢量磁滞数据,该模型利用深度学习算法可以有效地表征材料在高、中、低等不同磁通密度条件下的各向异性和磁滞特性。同时通过改进动态损耗模型的相关系数,引入损耗折损系数表征材料的各向异性对损耗的影响,可以将本模型计算的磁滞数据应用于材料的动态损耗计算中。对实验数据的仿真证明了本模型具备较好的实用性和泛化能力。
参考文献
[1] Chen Weihua, Zhou Mingliang, Yan Xiaoheng, et al. Study on electromagnetic-fluid-temperature multiphysics field coupling model for drum of mine cable winding truck[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(2): 133-142.
[2] 李永建, 闫鑫笑, 张长庚, 等. 基于磁-热-流耦合模型的变压器损耗计算和热点预测[J]. 电工技术学报, 2020, 35(21): 4483-4491. Li Yongjian, Yan Xinxiao, Zhang Changgeng, et al. Numerical prediction of losses and local overheating in transformer windings based on magnetic-thermal-fluid model[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4483-4491.
[3] Paul S, Chang J. Fast model-based design of high performance permanent magnet machine for next generation electric propulsion for urban aerial vehicle application[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(2): 143-151.
[4] 赵小军, 刘小娜, 肖帆, 等. 基于Preisach模型的取向硅钢片直流偏磁磁滞及损耗特性模拟[J]. 电工技术学报, 2020, 35: (9): 1849-1857. Zhao Xiaojun, Liu Xiaona, Xiao Fan, et al. Hysteretic and loss modeling of silicon steel sheet under the DC biased magnetization based on the preisach model[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1849-1857.
[5] 李贞, 李庆民, 李长云, 等. J-A磁化建模理论的质疑与修正方法研究[J]. 中国电机工程学报, 2011, 31(3): 124-131. Li Zhen, Li Qingmin, Li Changyun, et al. Queries on the J-A modeling theory of the magnetization process in ferromagnets and proposed correction method[J]. Proceedings of the CSEE, 2011, 31(3): 124-131.
[6] 王旭, 张艳丽, 唐伟, 等. 旋转磁化下逆矢量Jiles-Atherton磁滞模型改进[J]. 电工技术学报, 2018, 33(增刊2): 257-262. Wang Xu, Zhang Yanli, Tang Wei, et al. Improvement of inverse vector Jiles-Atherton hysteresis model under rotating magnetization[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 257-262.
[7] 迟青光, 张艳丽, 任亚军, 等. 铁心旋转损耗模型改进与局部损耗测试[J]. 电工技术学报, 2018, 33(17): 3951-3957. Chi Qingguang, Zhang Yanli, Ren Yajun, et al. Improvement on rotational loss model and measurement of local loss in the iron core[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 3951-3957.
[8] 迟青光, 张艳丽, 曹政, 等. 电工钢片旋转损耗特性分析与损耗模型修正[J]. 中国电机工程学报, 2017, 37(8): 2418-2425. Chi Qingguang, Zhang Yanli, Cao Zheng, et al. Analysis of rotational loss property in an electrical steel sheet and correction of loss model[J]. Proceedings of the CSEE, 2017, 37(8): 2418-2425.
[9] 赵国生, 李朗如. 一种考虑磁滞可逆性的非线性矢量Preisach模型[J]. 中国电机工程学报, 2000, 20(1): 4-6, 10. Zhao Guosheng, Li Langru. A nonlinear vector Preisach model considering reversibility of the hysteresis[J]. Proceedings of the CSEE, 2000, 20(1): 4-6, 10.
[10] Stoner E C, Wohlfarth E P. A mechanism of magnetic hysteresis in heterogeneous alloys[J]. IEEE Transactions on Magnetics, 1991, 27(4): 3475-3518.
[11] Della Torre E, Pinzaglia E, Cardelli E. Vector modeling—part I: generalized hysteresis model[J]. Physica B: Condensed Matter, 2006, 372(1/2): 111-114.
[12] Zhu Lixun, Koh C S. A novel vector hysteresis model using anisotropic vector play model taking into account rotating magnetic fields[J]. IEEE Transactions on Magnetics, 2017, 53(6): 1-4.
[13] 迟青光, 张艳丽, 陈吉超, 等. 非晶合金铁心损耗与磁致伸缩特性测量与模拟[J]. 电工技术学报, 2021, 36(18): 3876-3883. Chi Qingguang, Zhang Yanli, Chen Jichao, et al. Measurement and modeling of lossand magnetostrictive properties for the amorphous alloy core[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3876-3883.
[14] Wu Di, Zhang Yao, Ourak M, et al. Hysteresis modeling of robotic catheters based on long short-term memory network for improved environment reconstruction[J]. IEEE Robotics and Automation Letters, 2021, 6(2): 2106-2113.
[15] Cardelli E, Faba A, Laudani A, et al. Two-dimensional magnetic modeling of ferromagnetic materials by using a neural networks based hybrid approach[J]. Physica B: Condensed Matter, 2016, 486: 106-110.
[16] Quondam Antonio S, Riganti Fulginei F, Laudani A, et al. An effective neural network approach to reproduce magnetic hysteresis in electrical steel under arbitrary excitation waveforms[J]. Journal of Magnetism and Magnetic Materials, 2021, 528: 167735.
[17] Veeramani A S, Crews J H, Buckner G D. Hysteretic recurrent neural networks: a tool for modeling hysteretic materials and systems[J]. Smart Materials and Structures, 2009, 18(7): 075004.
[18] 陈龙, 易琼洋, 贲彤, 等. 全局优化算法在Preisach磁滞模型参数辨识问题中的应用与性能对比[J]. 电工技术学报, 2021, 36(12): 2585-2593, 2606. Chen Long, Yi Qiongyang, Ben Tong, et al. Application and performance comparison of global optimization algorithms in the parameter identification problems of the Preisach hysteresis model[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2585-2593, 2606.
[19] Zhao Xinlong, Tan Yonghong. Modeling hysteresis and its inverse model using neural networks based on expanded input space method[J]. IEEE Transactions on Control Systems Technology, 2008, 16(3): 484-490.
[20] 李宝琴, 吴俊勇, 邵美阳, 等. 基于集成深度置信网络的精细化电力系统暂态稳定评估[J]. 电力系统自动化, 2020, 44(6): 17-26. Li Baoqin, Wu Junyong, Shao Meiyang, et al. Refined transient stability evaluation for power system based on ensemble deep belief network[J]. Automation of Electric Power Systems, 2020, 44(6): 17-26.
[21] Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507.
[22] 汪光远, 杨德先, 林湘宁, 等. 基于深度置信网络的柔性直流配电网高灵敏故障辨识策略[J]. 电力系统自动化, 2021, 45(17) :180-188. Wang Guangyuan, Yang Dexian, Lin Xiangning, et al. High-sensitivity fault identification strategy for flexible DC distribution network based on deep belief networks[J]. Automation of Electric Power Systems, 2021, 45(17): 180-188.
[23] 赵志刚, 徐曼, 胡鑫剑. 基于改进损耗分离模型的铁磁材料损耗特性研究[J]. 电工技术学报, 2021, 36(13): 2782-2790. Zhao Zhigang, Xu Man, Hu Xinjian. Research on magnetic losses characteristics of ferromagnetic materials based on improvement loss separation model[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2782-279.
[24] 王振树, 卞绍润, 刘晓宇, 等. 基于混沌与量子粒子群算法相结合的负荷模型参数辨识研究[J]. 电工技术学报, 2014, 29(12): 211-217. Wang Zhenshu, Bian Shaorun, Liu Xiaoyu, et al. Research on load model parameter identification based on the CQDPSO algorithm[J]. Transactions of China Electrotechnical Society, 2014, 29(12): 211-217.
Abstract The silicon steel sheet is the core material of electrical equipment, and its magnetization characteristics directly affect the operation mechanism of equipment. So, the hysteresis modeling of ferromagnetic materials is one of the basic theoretical studies in the field of electrical engineering. In this paper, a vector hysteresis model is proposed based on the deep belief network (DBN) algorithm and hysteresis operator space theory.
The structure of the model consists of three parts: input mapping function, operator space and DBN model. In this paper, the Langevin function is used as the input mapping function to calculate the input mapping of hysteresis data, so that the data can adapt to the characteristics of hysteresis operator in the subsequent structure and can reflect the saturation characteristics of hysteresis phenomenon. Hysteresis operators in multiple directions in H space construct a hysteresis operator space. And the magnetization trajectory of the material mapped by Langevin function is projected in all directions on H space. The high-dimensional hysteresis operator data is generated by calculating hysteresis operators in all directions. Then the output of the operator space is taken as the input of the DBN model. In the construction of vector hysteresis model, DBN model is mainly used to characterize the nonlinear relationship between the high-dimensional vector data output by the operator and the magnetic induction data of the material. The parameters of the vector hysteresis model are obtained by training the magnetic induction data of training samples and the operator data generated by the training samples. The model parameters are mainly obtained by training DBN parameters. And the training process of DBN mainly consists of two parts: (1) The CD algorithm is used to the pre-training of the RBM in each layer, then the RBMs are stacked to obtain the preliminary optimization parameters of the model. (2) The parameters obtained by pre-training are taken as initial values, and the Nadam optimizer is used for global parameter tuning to obtain the final optimization parameters of the model. The obtained model is fitted under the conditions of high, middle and low magnetic density (Bm=0.5 T, 1 T, 1.5 T) respectively, and it is proved that the trajectory error between the calculated data of the model and the original magnetization data is small. In addition, the x-axis and y-axis decomposition of the calculated vector hysteresis data also prove that the proposed vector model has a relatively small error in terms of phase for hysteresis data, thus ensuring the reliability of magnetic loss calculation. So, the simulation results of hysteresis data obtained by experiment show that the model can effectively describe the nonlinear characteristics and anisotropic of ferromagnetic materials under the rotation vector excitation.
Based on the magnetic loss separation theory, an improved loss calculation model is proposed in this paper. In the magnetic loss calculation model, the deviation between the magnetic loss calculated by the data calculated by the model and the actual magnetic loss is checked by the conversion function. Thus, the independence of the magnetic loss calculation and the characterization of the magnetic characteristics of the model are effectively guaranteed. And the data obtained by the hysteresis model is applied to the dynamic loss calculation. The simulation results show that the hysteresis model can fit the actual situation effectively.
keywords:Hysteresis model, deep belief network (DBN) algorithm, hysteresis operator, hysteresis loss
DOI: 10.19595/j.cnki.1000-6753.tces.211562
中图分类号:TM15
国家自然科学基金重点项目(52130710)、国家自然科学基金项目(51777055, 51977122)和河北省自然科学基金创新群体项目(E2020202142)资助。
收稿日期 2021-05-14
改稿日期 2021-06-14
马阳阳 男,1991年生,博士研究生,研究方向为电磁场理论、铁磁材料磁滞建模与深度学习。E-mail:1367767122@qq.com
李永建 男,1978年生,教授,博士生导师,研究方向为工程电磁场与磁技术、三维磁特性测量与建模。E-mail:liyongjian@hebut.edu.cn(通信作者)
(编辑 郭丽军)