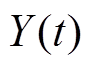 ,其数学表达式为
,其数学表达式为摘要 针对传统单性能退化量的油浸式电力变压器油纸绝缘剩余寿命预测方法难以全面反映油纸绝缘退化行为,且缺乏对多性能退化量间相关性的考虑,该文充分考虑退化过程的随机性和非线性,提出了一种基于二元非线性Wiener随机过程的变压器油纸绝缘剩余寿命预测方法。首先,基于非线性Wiener随机过程建立单性能退化量的油纸绝缘退化模型,刻画油纸绝缘退化过程的随机性和非线性;然后,基于Copula函数建立两性能相关的退化模型,更加全面地分析两性能退化量所反映的变压器油纸绝缘联合退化行为;最后,采用MCMC-Gibbs抽样算法估计模型未知参数,实现变压器油纸绝缘剩余寿命预测。该文以糠醛和甲醇含量作为性能退化量,依托加速热老化实验数据进行实例验证,对比单性能、两性能独立、两性能相关三种情况下的可靠度曲线及剩余寿命预测结果,结果表明,该文所提方法能够更加合理全面地描述退化过程,可靠度曲线更贴近真实结果。
关键词:电力变压器 油纸绝缘 剩余寿命 二元非线性Wiener Copula函数
作为电力系统的核心设备,油浸式电力变压器的运行寿命对电网的可靠供电具有重要意义[1-2]。对变压器进行性能可靠性分析和剩余寿命预测的目的在于预知其退化趋势与寿命终点,以便在变压器寿命终结前及时采取检修措施,避免停电事故发生。
变压器运行寿命主要取决于其绝缘性能,因此绝缘性能的可靠性分析和剩余寿命预测具有重要意义[3-4]。变压器投运初期,油纸绝缘系统有较好的物理和化学性能,但随着运行时间的延长,其性能逐渐发生不可逆的劣化。由于受环境、负荷等条件的影响,油纸绝缘退化过程复杂,呈现出随机性、非线性的特点。
传统的变压器油纸绝缘退化模型大多基于单性能退化量建立:例如早期以聚合度(Degree of Polymerization, DP)为性能退化量的零阶、一阶、二阶动力学油纸绝缘退化模型[5]和聚合度损失累积模型[6]。但零阶和一阶动力学模型缺乏对DP降解速率变化的考虑,在劣化后期误差较大;而二阶动力学模型和聚合度损失累积模型只适用于实验室温度条件,适用性低。为实现在线监测并提高适用性,有学者基于机器学习算法预测油纸绝缘剩余寿命:K. S. Madhavan等以糠醛含量为性能退化量,提出一种基于广义神经回归网络的变压器油纸绝缘剩余寿命预测模型[7];范贤浩等融合频域介电谱(Frequency Domain Spectroscopy, FDS)及支持向量机提出了一种考虑水分-老化协同效应的变压器油浸纸绝缘老化状态评估方法[8]。上述两种模型能够实现在线监测,但样本需求量较大,难以在工程实际中实现。考虑到油纸绝缘系统退化过程的随机性,有学者提出了基于随机过程的建模方法:张明泽等以糠醛含量作为性能退化量,提出了基于线性Wiener模型的变压器油纸绝缘剩余寿命预测方法[9],该模型虽然考虑到了变压器油纸绝缘劣化过程的随机性和剩余寿命预测的不确定性,但采用的线性模型不能很好地刻画油纸绝缘退化过程的非线性特性。
上述文献都是基于单性能退化量的建模方法,然而变压器油纸绝缘系统往往具有多个性能退化量,仅考虑单性能退化量的油纸绝缘退化模型难以全面地反映其退化过程,与实际情况偏差较大,因此,应考虑多个性能层面进行综合可靠性评估。为了更全面地描述变压器油纸绝缘系统的退化过程,部分学者综合考虑多个性能退化量建立油纸绝缘系统退化模型:R. Madavan基于数理统计建立了Weibull分布模型[10],此模型考虑到了介电强度、酸度等多个性能退化量,但为获得其平均寿命数据需进行多次不可逆的失效试验,实用性较低;M. M. Nezami等根据碳氧化合物和糠醛含量,提出了一种神经模糊逻辑模型,以估计油浸式变压器的寿命[11],该方法能够更全面地评估油纸绝缘系统的退化程度,但现场可采集的少量变压器退化数据难以满足这类方法对样本量的需求,且上述方法均未考虑多个性能退化量间的相关性。
总结现有变压器油纸绝缘剩余寿命预测研究存在的问题:①传统的基于Wiener随机过程的退化模型没有考虑退化过程非线性的情况;②上述部分方法均是基于单性能退化量建立退化模型,缺乏对退化过程多特征量特性的考虑;③Weibull分布模型和基于机器学习的变压器油纸绝缘剩余寿命预测方法缺乏对多性能退化量间相关性和退化过程随机性的考虑,且对样本数量均有较高的要求。
为解决以上问题,本文提出了一种基于二元非线性Wiener随机过程的变压器油纸绝缘剩余寿命预测方法。Copula函数是一种刻画变量间相关性的工具,建模简单、应用灵活、使用范围广[12-13],因此,本文采用Copula函数来描述两性能退化量间的相关性。本文所提方法具体步骤如下:首先,基于非线性Wiener随机过程建立单性能退化量的油纸绝缘退化模型;然后,基于Copula函数建立两性能相关的退化模型,由于似然函数过于复杂,未知参数较多,本文采用MCMC-Gibbs(Markov-Monte Carlo-Gibbs)抽样算法估计模型未知参数,并依据赤池信息量准则(Akaike Information Criterion, AIC)选择合适的Copula函数;最后,以糠醛含量和甲醇含量作为性能退化量,依托加速热老化实验数据进行实例验证,并比较单性能、两性能独立、两性能相关情形下的可靠度曲线及剩余寿命预测结果,以证明本文所提方法在可靠性评估及剩余寿命预测方面的优势及合理性。
Wiener过程是一种连续的随机过程,适用于非单调的随机过程建模[14-15],考虑到变压器油纸绝缘退化过程的非线性特点,本文采用非线性Wiener模型来进行建模。假设产品在t时刻的性能退化量为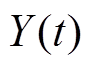 ,其数学表达式为
,其数学表达式为
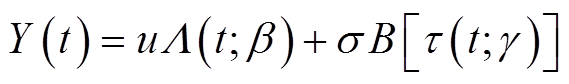 (1)
(1)
式中,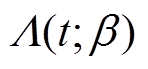 和
和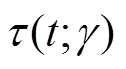 为关于时间的连续非减函数,
为关于时间的连续非减函数,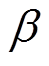 和
和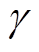 均为未知参数;
均为未知参数;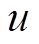 为漂移系数;
为漂移系数;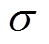 为扩散系数;
为扩散系数;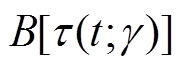 为非线性布朗运动,用来描述观测量
为非线性布朗运动,用来描述观测量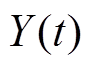 的随机性。
的随机性。
Copula函数是定义域为[0, 1]的二元分布函数,能够描述变量间的相关性,其实际意义是连接两个随机变量的边缘分布和联合分布,建立边缘分布和联合分布的映射关系,并将边缘分布和联合分布分开研究。Sklar定理是Copula函数的存在性定理,其基本内容是:若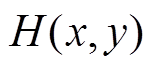 是一个具有连续边缘分布
是一个具有连续边缘分布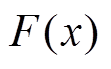 和
和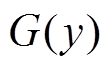 的二元联合分布函数,那么存在唯一的Copula函数C(·)使得
的二元联合分布函数,那么存在唯一的Copula函数C(·)使得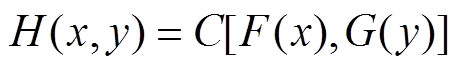 ;反之,如果C(·)是一个Copula函数,而F和G是两个任意的概率分布函数,那么由上式定义的H函数一定是一个联合分布函数,且对应的边缘分布刚好为F和G[16]。
;反之,如果C(·)是一个Copula函数,而F和G是两个任意的概率分布函数,那么由上式定义的H函数一定是一个联合分布函数,且对应的边缘分布刚好为F和G[16]。
根据上述内容,假设随机变量X和Y具有相关性,令二维随机变量(X, Y)的联合分布函数为H,边缘分布分别为F和G,由Sklar定理可知存在一个Copula函数C(·),使得
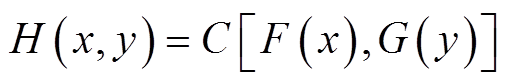 (2)
(2)
若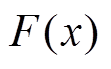 和
和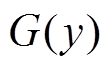 连续,则C(·)唯一确定。联合分布函数的概率密度函数为
连续,则C(·)唯一确定。联合分布函数的概率密度函数为
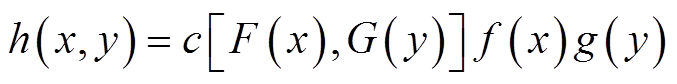 (3)
(3)
其中
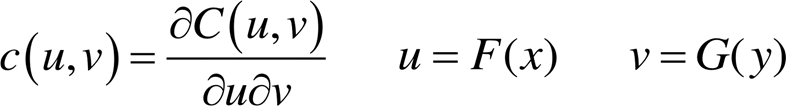
式中,c(·)为Copula函数C(·)的概率密度函数;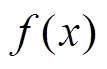 和
和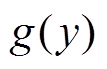 分别为边缘分布
分别为边缘分布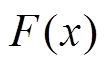 和
和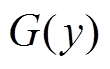 的概率密度函数。常见的二元Copula函数及其分布函数表达式见表1。
的概率密度函数。常见的二元Copula函数及其分布函数表达式见表1。
选择不同的Copula函数进行建模会出现不同的结果,因此根据实际情况,选择拟合效果好的Copula函数非常重要。赤池信息量准则(AIC)是衡量统计模型拟合优良性的一种标准,该准则从模型复杂度和模型拟合优度两方面考虑,选择出恰当的模型,其与似然函数和残差二次方和有一定的联系,AIC值越小说明所选择的模型越合适[17]。AIC准则突破了以往仅考虑模型拟合情况的评价标准,且具有适用性好的优点,因此本文依据AIC准则来选择合适的Copula函数。AIC准则的数学表达式为
表1 常见的几种二元Copula函数
Tab. 1 Several common binary Copula functions

Copula函数分布函数 Frank Gumbel Clayton
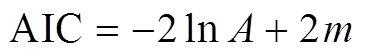 (4)
(4)
式中,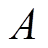 为模型对应的极大似然函数;
为模型对应的极大似然函数;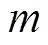 为模型中参数的个数。
为模型中参数的个数。
聚合度(DP)是表征油纸绝缘系统退化程度的最直接的性能退化指标,当DP下降到250时,认为绝缘性能失效[18],然而在工程实际中,DP无法实现在线检测。研究表明,糠醛含量与DP存在着一定的数学关系[19-20],且糠醛含量能够实现在线检测,因此被广泛用于绝缘纸的可靠性评估。但在油纸绝缘退化早期,糠醛含量低,难以检测,因此以糠醛为特征量的退化模型在评估早期退化时误差较大。A. Schaut等总结了甲醇含量在油纸绝缘退化评估方面的适用性[21],甲醇含量与DP之间同样存在着数学关系,且退化早期含量较高,因此可以更好地描述油纸绝缘早期退化。综上所述,本文选择甲醇与糠醛含量作为表征变压器油纸绝缘退化程度的性能退化量,将DP达到250时的糠醛和甲醇含量作为各自的失效阈值。
令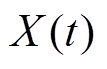 表示在t时刻变压器油纸绝缘退化模型的性能退化量,则性能退化量
表示在t时刻变压器油纸绝缘退化模型的性能退化量,则性能退化量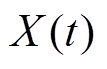 的退化轨迹可表示为
的退化轨迹可表示为
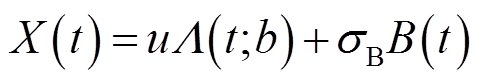 (5)
(5)
式中,u仍为漂移系数,是一个随机参数,且服从正态分布,即u~N(ua, σa2);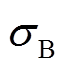 为扩散系数,是一个固定的未知参数;B(t)为标准布朗运动,也服从正态分布,即B(t)~N(0, t),用来表示油纸绝缘退化过程的随机动态特性。根据文献[22],两种常用的非线性Wiener模型分别为M1:Λ(t;b1)=exp(b1t)-1和M2:Λ(t;b2)=tb2。
为扩散系数,是一个固定的未知参数;B(t)为标准布朗运动,也服从正态分布,即B(t)~N(0, t),用来表示油纸绝缘退化过程的随机动态特性。根据文献[22],两种常用的非线性Wiener模型分别为M1:Λ(t;b1)=exp(b1t)-1和M2:Λ(t;b2)=tb2。
设性能退化量的失效阈值为ω,则性能退化量对应的设备失效时间(即寿命)T可定义为
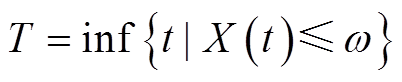 (6)
(6)
根据文献[16],寿命T的分布函数为
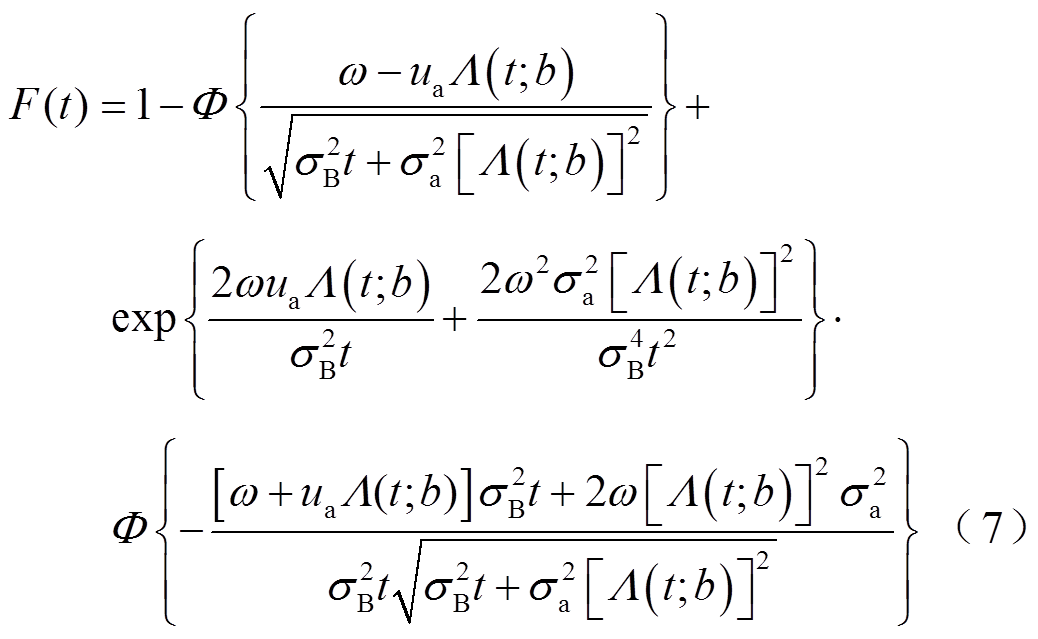
式中,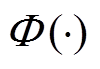 为标准正态分布的分布函数;
为标准正态分布的分布函数;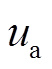 和
和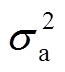 分别为漂移系数u服从的正态分布的均值和方差。则相应的可靠度函数为
分别为漂移系数u服从的正态分布的均值和方差。则相应的可靠度函数为
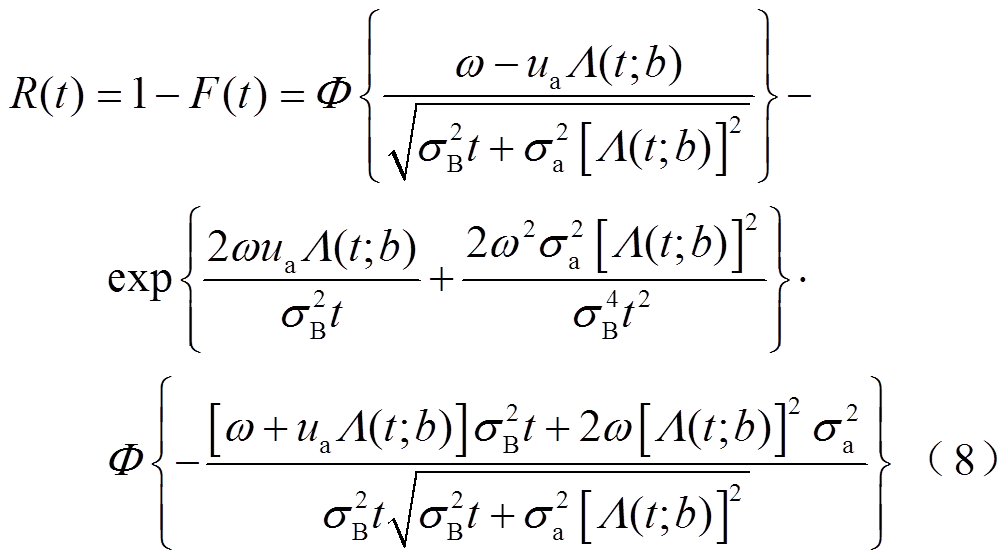
为建立两性能油纸绝缘系统退化模型,令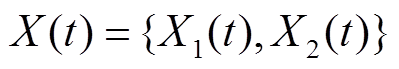 表示在t时刻变压器油纸绝缘系统的两个性能退化量,失效阈值记为
表示在t时刻变压器油纸绝缘系统的两个性能退化量,失效阈值记为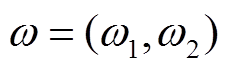 ,油纸绝缘寿命记为T,当任意一个性能退化量达到其失效阈值时油纸绝缘性能失效,因此寿命T可以表示为
,油纸绝缘寿命记为T,当任意一个性能退化量达到其失效阈值时油纸绝缘性能失效,因此寿命T可以表示为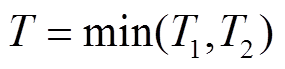 ,其可靠度为
,其可靠度为
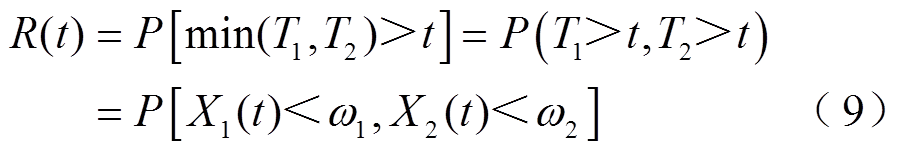
当两个性能退化量相互独立时,可靠度函数可以表示为
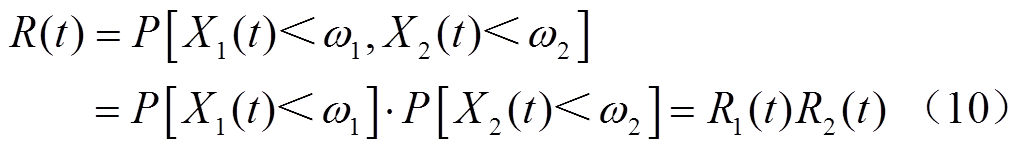
当两个性能退化量之间相互关联时,本文采用Copula函数来描述其相关关系。按照Sklar定理,存在唯一Copula函数使得式(11)成立。
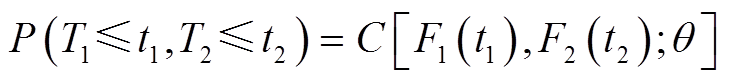 (11)
(11)
式中,θ为Copula函数的参数;两个边缘分布函数F1和F2的形式不要求相同。根据文献[16,23]可得式(9)的可靠度函数为
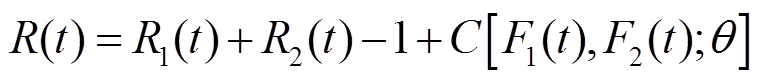 (12)
(12)
假设对油纸绝缘退化过程观测N次,用Xki(ti)表示第k个性能退化量在ti时刻的测量值,其中k为1或2,i=1, 2,…, N。由式(5)可得,每一步性能退化量的增量都可表示为
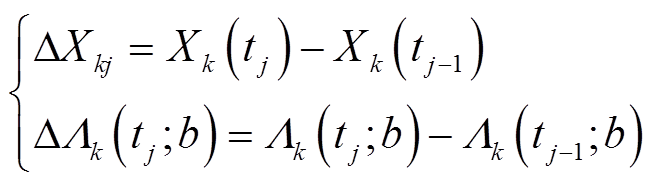 (13)
(13)
利用Wiener过程独立增量的性质可得,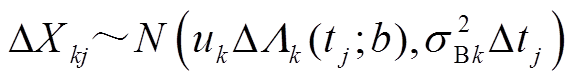 ,考虑到
,考虑到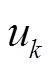 为随机变量,且
为随机变量,且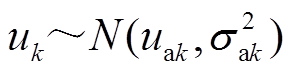 ,则性能退化量增量
,则性能退化量增量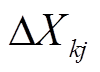 的概率密度函数为
的概率密度函数为
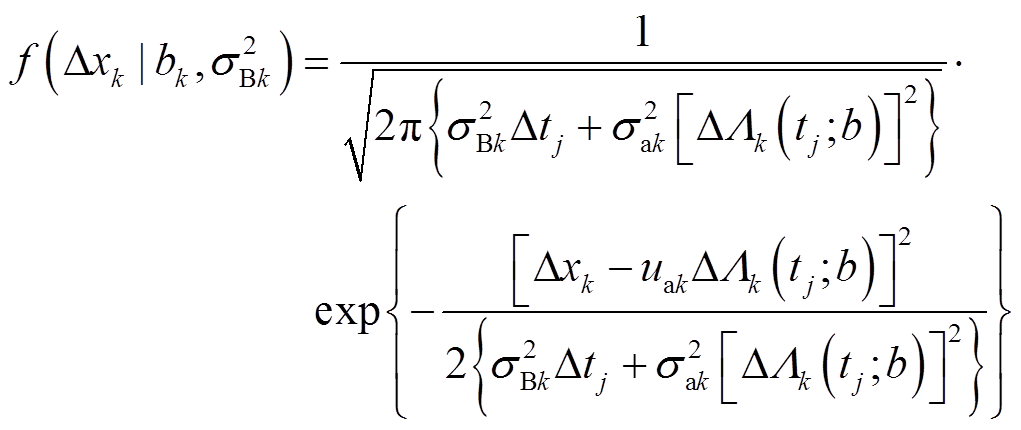 (14)
(14)
假设两个性能退化量在不同时间段内的相关性可以忽略,即当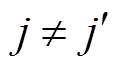 时,
时,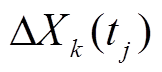 与
与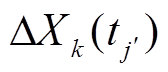 相互独立。考虑两个性能退化量增量
相互独立。考虑两个性能退化量增量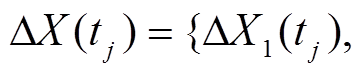
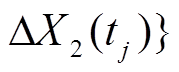 的联合分布函数H,根据Sklar定理,存在Copula函数C(·),使得
的联合分布函数H,根据Sklar定理,存在Copula函数C(·),使得
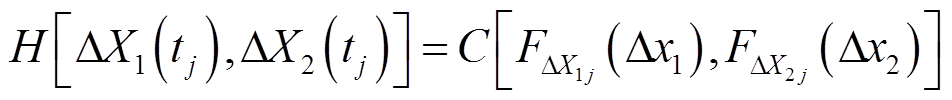 (15)
(15)
记模型未知参数为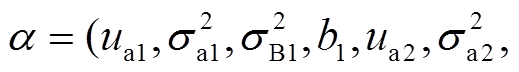
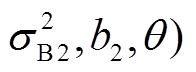 ,则可得到性能退化量的极大似然函数为
,则可得到性能退化量的极大似然函数为
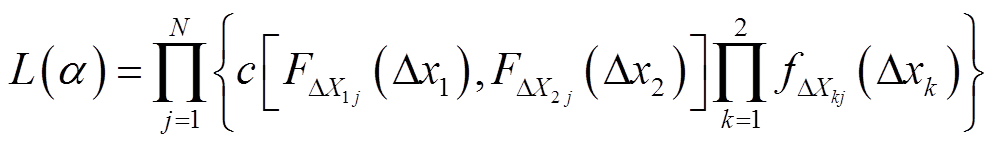 (16)
(16)
对似然函数两边取对数,可得
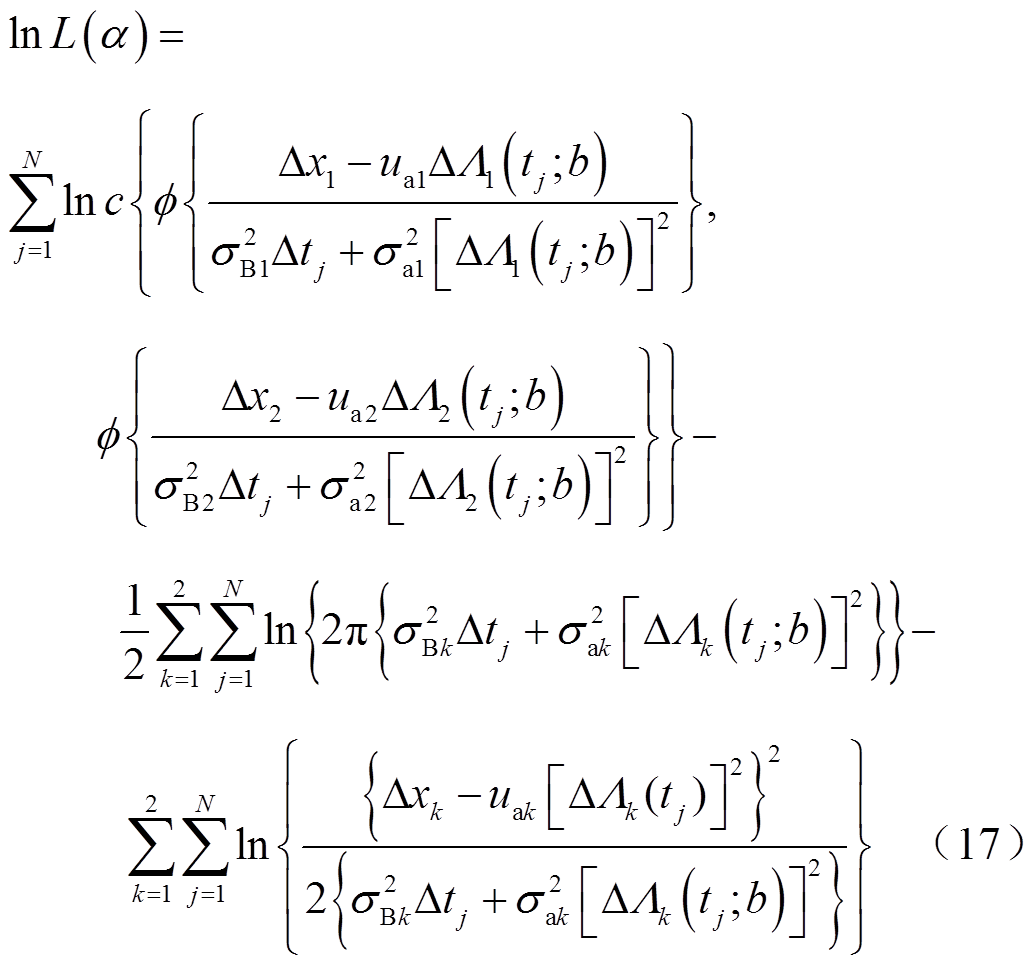
考虑到式(17)中有9个未知参数,且似然函数形式复杂,极大似然估计法将不再适用,因此本文采用MCMC-Gibbs抽样算法来估计模型未知参数。
MCMC(Markov-Monte Carlo)抽样算法基于马尔科夫链对未知变量进行抽样,得到未知参数的一条马尔科夫链,当其达到平稳分布时,即为未知参数的后验分布,通过后验分布的抽样点来作出统计推断。设α是一个n维随机变量,其概率密度函数为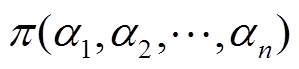 ,MCMC-Gibbs抽样的具体步骤如下:
,MCMC-Gibbs抽样的具体步骤如下:
1)给定任意一组马尔科夫链的初值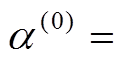
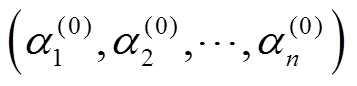 。
。
2)从条件分布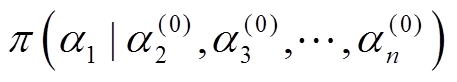 中抽取样本
中抽取样本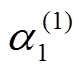 。
。
3)从条件分布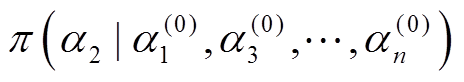 中抽取样本
中抽取样本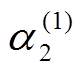 。依此类推,直至从条件分布
。依此类推,直至从条件分布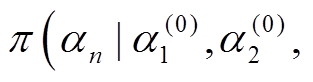
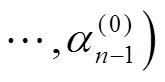 中抽取样本
中抽取样本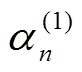 。
。
这样便完成了一次迭代,重复上述步骤,通过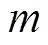 次迭代便可得到样本
次迭代便可得到样本
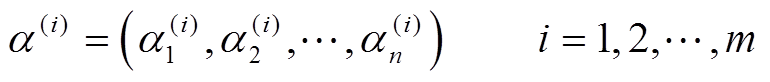 (18)
(18)
当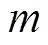 足够大时,
足够大时,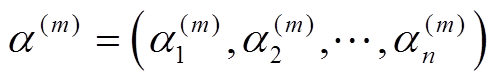 可看作
可看作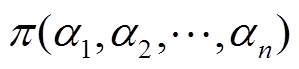 的近似值,由此可认为抽样所得到的随机样本来自目标分布
的近似值,由此可认为抽样所得到的随机样本来自目标分布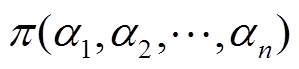 ,此时,可利用样本对未知参数进行估计。根据经验给定未知参数的先验分布
,此时,可利用样本对未知参数进行估计。根据经验给定未知参数的先验分布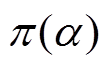 ,具体流程如图1所示。
,具体流程如图1所示。
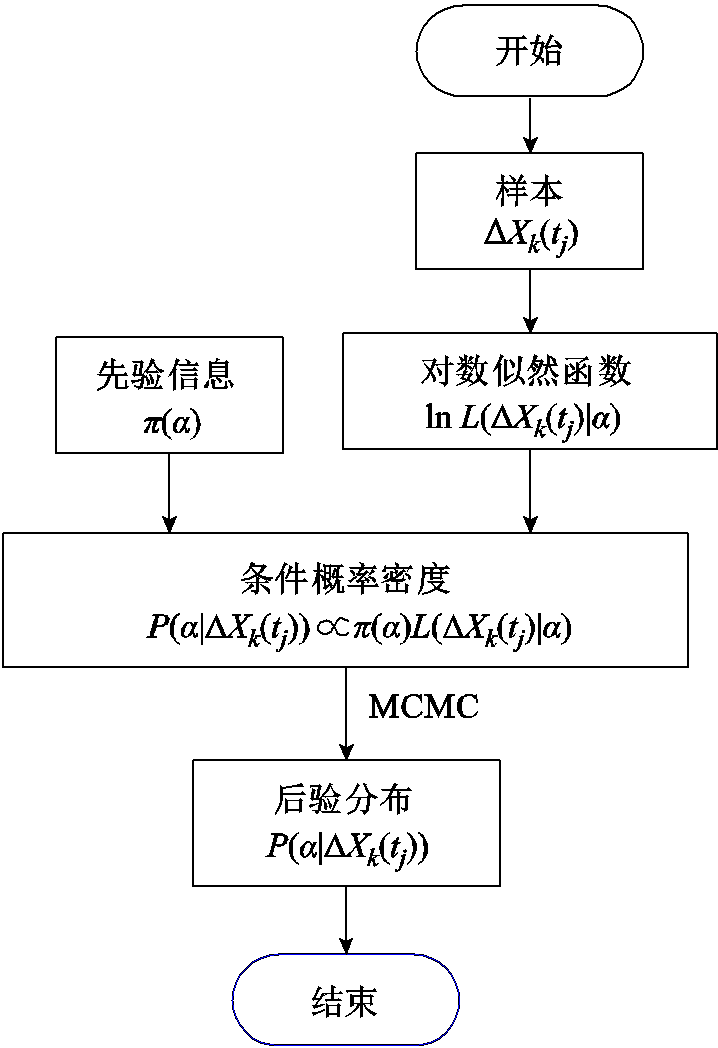
图1 MCMC方法估计未知参数流程
Fig.1 Flow chart of MCMC method to estimate unknown parameters
图2中给出一组110℃下绝缘纸加速老化试验中观测到的两个性能退化量的退化数据,数据来自于文献[24],其中绝缘油为克拉玛依25号变压器油,绝缘纸型号为JZGDL-075。糠醛含量的实际退化轨迹接近指数函数,因此令M1为Λ(t;b1)=exp(b1t)-1;甲醇含量的退化轨迹接近幂函数,因此令M2为Λ(t;b2)=tb2。
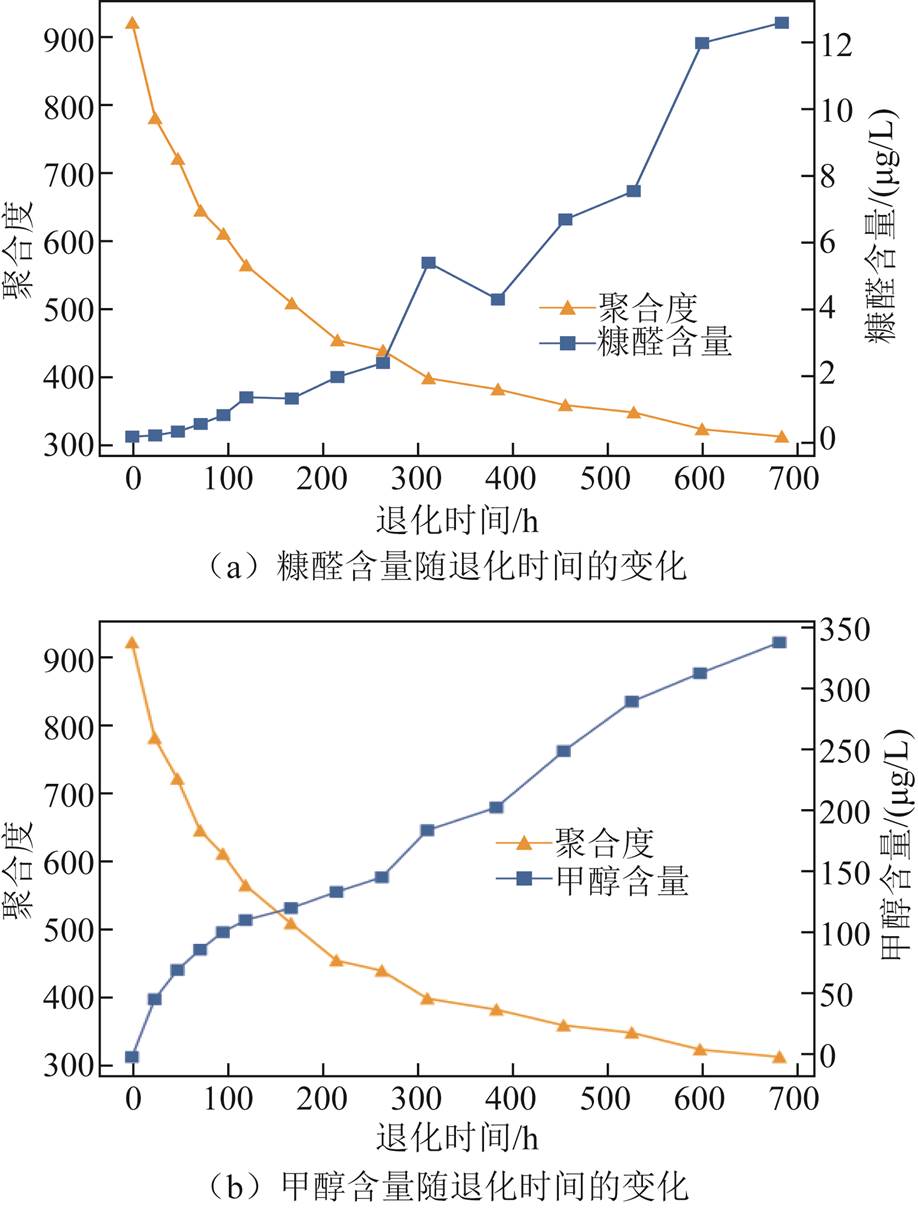
图2 油纸绝缘性能退化量随退化时间的变化
Fig.2 Variation of oil-paper insulation degradation with degradation time
采用MCMC算法估计不同Copula函数时退化模型的参数,并利用AIC准则选择合适的Copula函数,计算结果见表2。从表2中可以看出,针对该组数据,Frank Copula函数对应的AIC最小,因此选择Frank Copula函数来描述两个性能退化量之间的相关性。
表2 不同Copula函数的AIC计算结果
Tab.2 AIC values of the three Copula functions

参数FrankGumbelClayton -lnA-111.343 2-206.815 7-116.081 6 AIC240.686 3431.631 4250.163 3
根据所选择的Frank Copula函数建立退化模型,分别对两个性能退化量独立和相关时采用MCMC算法估计模型未知参数,抽取10 000个样本,表3中给出了第684个样本的两性能退化量相关的参数估计结果,表中MC误差即蒙特卡洛误差,是用来诊断算法收敛性的重要指标,需远小于估计量的标准差。部分参数的迭代过程如图3所示。
表3 MCMC方法模型参数估计结果
Tab.3 Parameter estimation results of MCMC method model
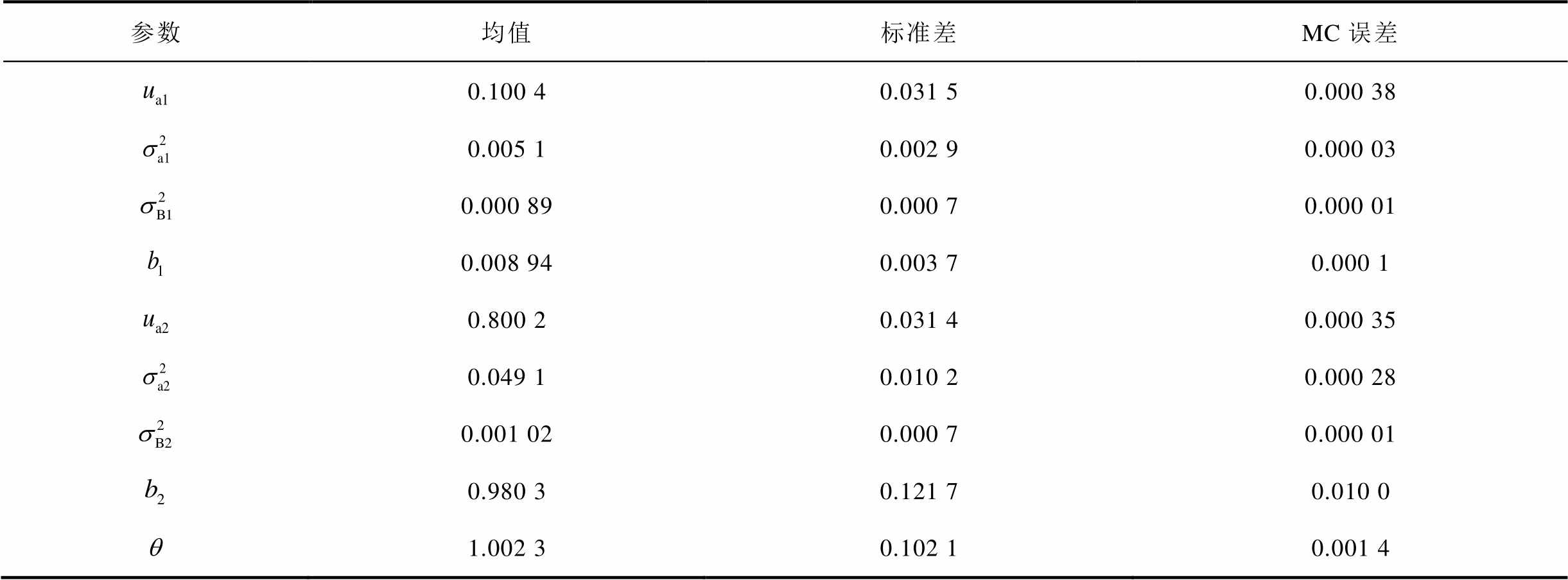
参数均值标准差MC误差 0.100 40.031 50.000 38 0.005 10.002 90.000 03 0.000 890.000 70.000 01 0.008 940.003 70.000 1 0.800 20.031 40.000 35 0.049 10.010 20.000 28 0.001 020.000 70.000 01 0.980 30.121 70.010 0 1.002 30.102 10.001 4
图3 部分参数的迭代过程
Fig.3 Iteration process of some parameters
将上述方法得到的模型参数代入2.2节的可靠度函数中,可获得油纸绝缘退化模型的单性能可靠度和综合可靠度曲线分别如图4和图5所示。
由图4可得,针对油纸绝缘退化早期,糠醛含量可靠度在400 h后仍为1,而甲醇含量可靠度约在300 h后开始下降,因此用甲醇含量来描述系统的早期退化更准确。这是由于退化早期,相对糠醛含量来说,甲醇含量更高,易于检测,测量误差较小。针对油纸绝缘退化后期,糠醛含量可靠度较甲醇含量可靠度更早接近0,退化后期糠醛含量变化明显,因此,能够更好地描述系统后期退化。针对整个寿命周期,两个性能退化量独立情形下的可靠度均高于相关时的可靠度,因此,忽略性能退化量之间的相关性可能会高估油纸绝缘系统的可靠性。
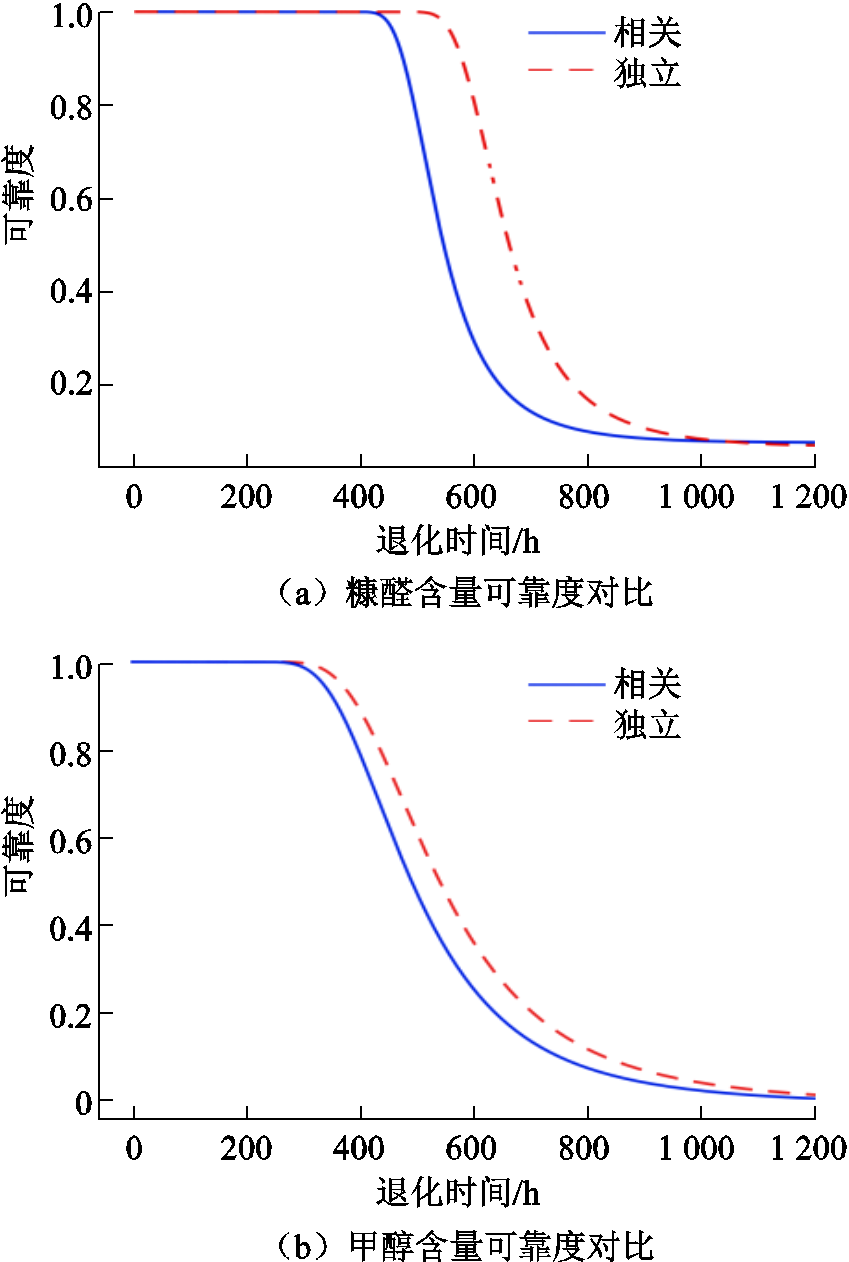
图4 油纸绝缘退化模型单性能退化量可靠度
Fig.4 Reliability curve of oil-paper insulation degradation model with single performance degradation
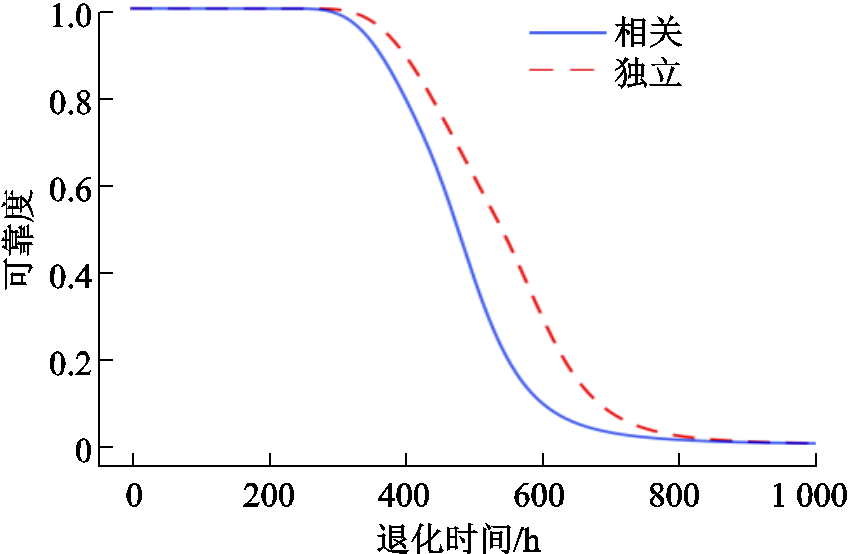
图5 油纸绝缘退化模型综合可靠度
Fig.5 Comprehensive reliability curve of oil-paper insulation degradation model
由图5可知,当退化时间达到600 h,独立情形下的综合可靠度为0.296 7,而相关情形下的综合可靠度为0.097 8,两种情形下的可靠度相差达到0.198 9,由此可以看出,独立和相关两种情形下,油纸绝缘系统的性能可靠度有较大差异,基于性能指标相关性的可靠性建模更符合实际情况。
对比图4与图5,单性能可靠度与两性能可靠度之间存在较大差异,油纸绝缘系统退化过程复杂,多个性能退化指标可以表征不同的退化特性,仅考虑单个性能退化量或忽略性能退化量之间的相关性的可靠性建模可能会高估系统可靠度,偏于危险。
假设油纸绝缘系统第k个性能退化量在ti时刻的剩余寿命为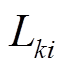 ,可定义为
,可定义为
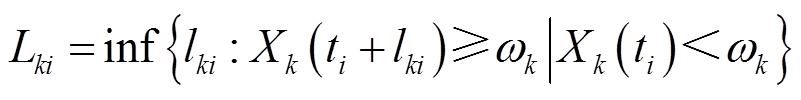 (19)
(19)
式中,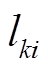 为第k个性能退化量在ti时刻的剩余寿命。
为第k个性能退化量在ti时刻的剩余寿命。
根据文献[25],两性能退化量在ti时刻的剩余寿命的概率密度函数可分别表示为
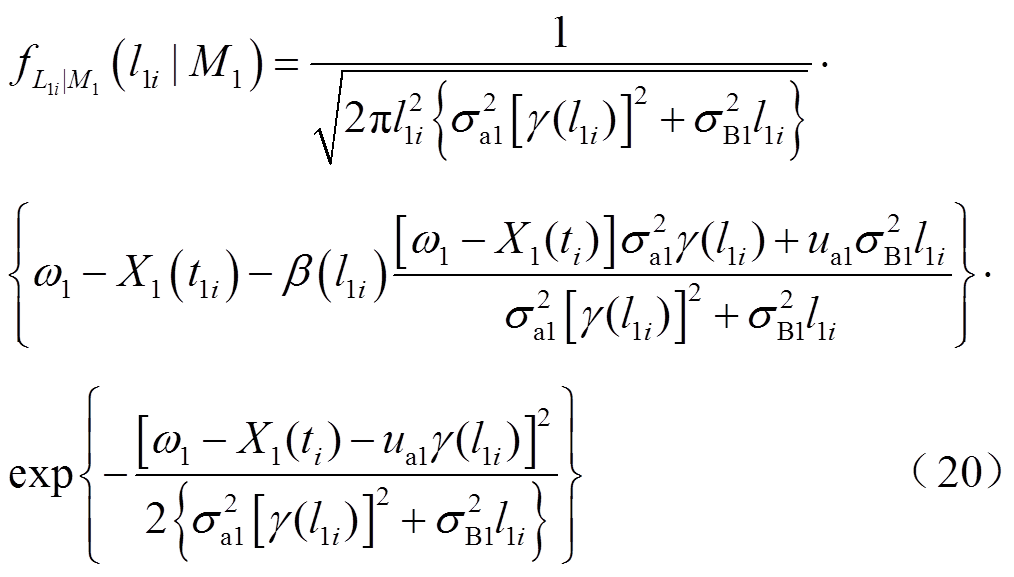
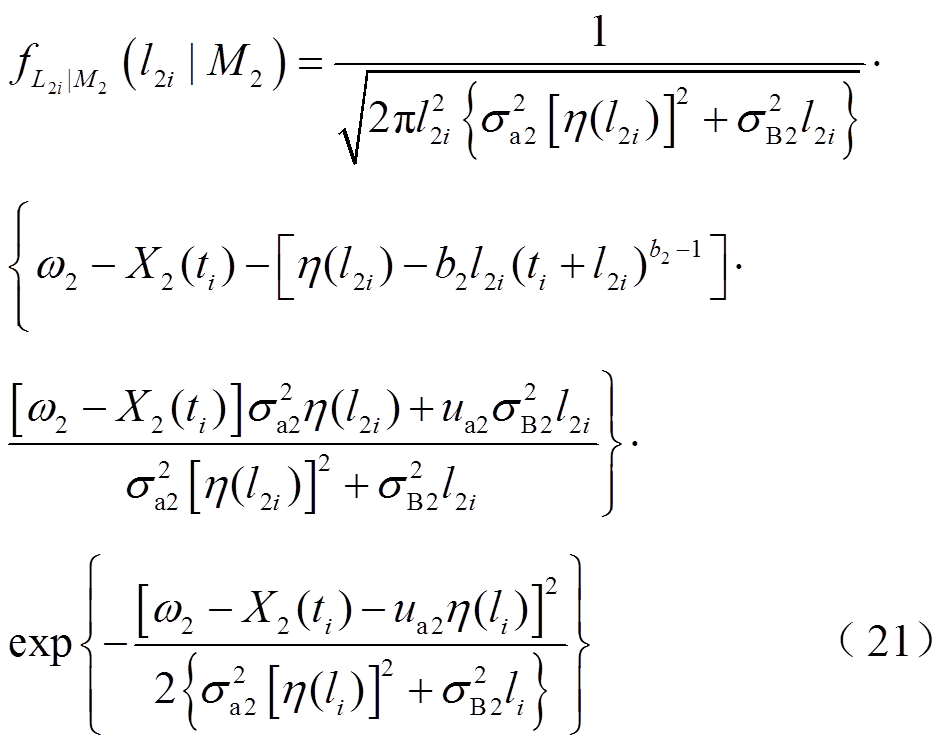
其中
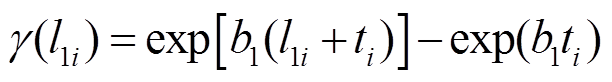
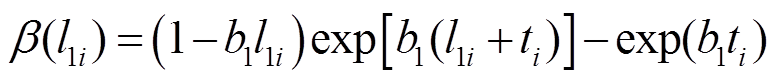
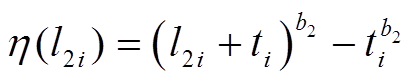
用上述方法估计不同时刻的未知参数,并代入剩余寿命的概率密度函数中,图6给出在385 h、456 h、528 h和600 h四个不同时刻,分别基于糠醛、甲醇和两性能相关的剩余寿命预测结果。
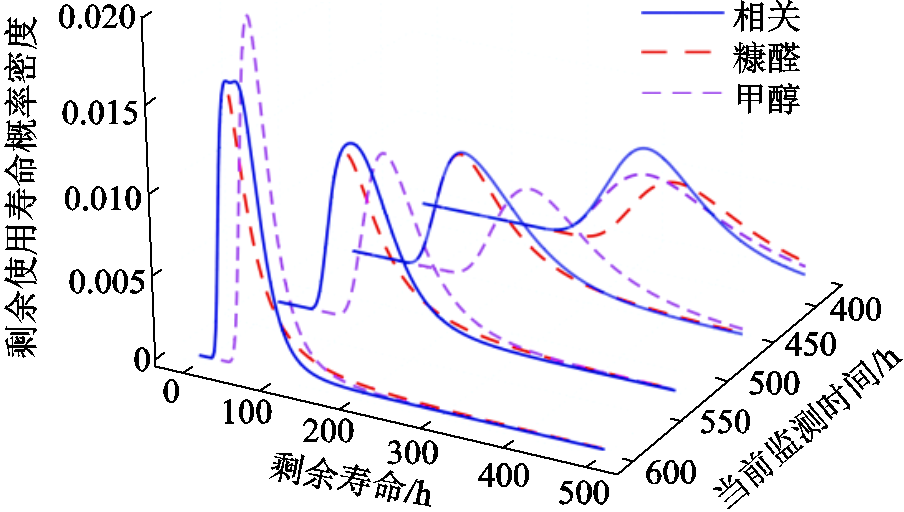
图6 剩余寿命概率密度曲线
Fig.6 Probability density curve of remaining life
由图6可以看出,随着退化时间的延长,油纸绝缘系统的剩余寿命预测不确定性降低,对比同一时刻的三条曲线,两性能相关性退化模型能够综合不同性能的剩余寿命预测结果的准确性和确定性,预测结果更加合理。因此,基于糠醛和甲醇两性能的退化模型能够为电力变压器健康状态评估提供更加可靠的参考依据。
针对变压器油纸绝缘剩余寿命预测中退化过程非线性、单个性能退化量难以全面反映其退化过程、多性能退化量间具有相关性的问题,本文基于Copula函数和非线性Wiener模型,提出了同时采用糠醛含量和甲醇含量两个性能退化量进行可靠性评估和剩余寿命预测的方法。采用加速老化实验数据进行实例验证,得到如下结论:
1)油纸绝缘系统糠醛含量与甲醇含量两个性能退化量在退化过程中存在相关关系,不同的Copula函数会出现不同的结果,本文基于AIC准则,证明Frank Copula函数在描述变压器油纸绝缘的糠醛含量与甲醇含量两性能退化量相关关系时具有更好的拟合优度。
2)本文分别比较了基于糠醛、甲醇、两性能独立、两性能相关等不同情形下的变压器油纸绝缘系统可靠度曲线,结果表明,单性能情形下的可靠度高于两性能情形下的可靠度,性能独立情形下的可靠度高于性能相关情形下的可靠度,考虑性能相关关系的二元变压器油纸绝缘可靠性评估方法较单性能可靠性评估方法更保守。对比实验数据可得,本文方法更符合实际测量结果,评估结果更加合理。
3)通过对比基于糠醛、甲醇及两性能相关情形下四个不同监测时刻的变压器油纸绝缘剩余寿命预测结果,可以看出,本文所提方法兼顾了预测结果的可靠性与准确性,能够为油浸式电力变压器的健康状态评估提供参考依据。
参考文献
[1] 杜江, 孙铭阳. 基于变权灰云模型的变压器状态层次评估方法[J]. 电工技术学报, 2020, 35(20): 4306-4316. Du Jiang, Sun Mingyang. Hierarchical assessment method of transformer condition based on weight-varying grey cloud model[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4306-4316.
[2] 李典阳, 张育杰, 冯健, 等. 变压器故障样本多维诊断及结果可信度分析[J]. 电工技术学报, 2022, 37(3): 667-675. Li Dianyang, Zhang Yujie, Feng Jian, et al. Multi-dimensional diagnosis of transformer fault sample and credibility analysis[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 667-675.
[3] Liao Ruijin, Xiang Bin, Yang Lijun, et al. Study on the thermal aging characteristics and bond breaking process of oil-paper insulation in power transformer[C]//Conference Record of the 2008 IEEE International Symposium on Electrical Insulation, Vancouver, BC, Canada, 2008: 291-296.
[4] Vasovic V, Lukic J, Mihajlovic D, et al. Aging of transformer insulation—experimental transformers and laboratory models with different moisture contents: part I—DP and furans aging profiles[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2019, 26(6): 1840-1846.
[5] Heywood R J, Stevens G C, Ferguson C, et al. Life assessment of cable paper using slow thermal ramp methods[J]. Thermochimica Acta, 1999, 332(2): 189-195.
[6] Ding H Z, Wang Z D. On the degradation evolution equations of cellulose[J]. Cellulose, 2008, 15(2): 205-224.
[7] Madhavan K S, Murthy T S R, Sethuraman R. Estimation of degree of polymerisation and residual age of transformers based on furfural levels in insulating oil through generalized regression neural networks[M]//Computational Intelligence, Theory and Applications. Berlin, Heidelberg: Springer, 2006: 751-756.
[8] 范贤浩, 刘捷丰, 张镱议, 等. 融合频域介电谱及支持向量机的变压器油浸纸绝缘老化状态评估[J]. 电工技术学报, 2021, 36(10): 2161-2168. Fan Xianhao, Liu Jiefeng, Zhang Yiyi, et al. Aging evaluation of transformer oil-immersed insulation combining frequency domain spectroscopy and support vector machine[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2161-2168.
[9] 张明泽, 刘骥, 陈昕, 等. 基于Wiener模型的变压器油纸绝缘老化剩余寿命评估方法[J]. 电工技术学报, 2018, 33(21): 5098-5108. Zhang Mingze, Liu Ji, Chen Xin, et al. Residual life assessment method of transformer oil-paper insulation aging based on Wiener modle[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 5098-5108.
[10] Madavan R, Balaraman S. Failure analysis of transformer liquid—solid insulation system under selective environmental conditions using Weibull statistics method[J]. Engineering Failure Analysis, 2016, 65: 26-38.
[11] Nezami M M, Wani S A, Khan S A, et al. Fuzzy approach for residual life assessment of paper insulation[C]//2017 3rd International Conference on Condition Assessment Techniques in Electrical Systems (CATCON), Rupnagar, India, 2018: 26-30.
[12] 周源, 吕卫民, 王少蕾, 等. 基于Copula函数耦合性建模的二元加速退化数据统计分析方法[J]. 兵器装备工程学报, 2018, 39(5): 160-165. Zhou Yuan, Lü Weimin, Wang Shaolei, et al. Statistical analysis method of bivariate degradation data based on dependency modeling via copula function[J]. Journal of Ordnance Equipment Engineering, 2018, 39(5): 160-165.
[13] 宋宇, 李涵. 基于核密度估计和Copula函数的风、光出力场景生成[J]. 电气技术, 2022, 23(1): 56-63. Song Yu, Li Han. Typical scene generation of wind and photovoltaic power output based on kernel density estimation and Copula function[J]. Electrical Engineering, 2022, 23(1): 56-63.
[14] 李天梅, 司小胜, 刘翔, 等. 大数据下数模联动的随机退化设备剩余寿命预测技术[J]. 自动化学报, 2022, 48(9): 2119-2141. Li Tianmei, Si Xiaosheng, Liu Xiang, et al. Data-model interactive remaining useful life prediction technologies for stochastic degrading devices with big data[J]. Acta Automatica Sinica, 2022, 48(9): 2119-2141.
[15] Ye Zhisheng, Xie Min. Stochastic modelling and analysis of degradation for highly reliable products[J]. Applied Stochastic Models in Business and Industry, 2015, 31(1): 16-32.
[16] 郝会兵. 基于贝叶斯更新与Copula理论的性能退化可靠性建模与评估方法研究[D]. 南京: 东南大学, 2016.
[17] 文冰梅, 赵联文, 黄磊. AIC准则与留一法交叉验证渐近等价的证明[J]. 统计与决策, 2022, 38(6): 40-43. Wen Bingmei, Zhao Lianwen, Huang Lei. Proof of the asymptotic equivalence between AIC criterion and LOOCV[J]. Statistics & Decision, 2022, 38(6): 40-43.
[18] 国家能源局. 电力设备预防性试验规程: DL/T 596—2021[S]. 北京: 中国电力出版社, 2021.
[19] 王健一, 刘雪丽, 孙建涛, 等. 油纸绝缘新型老化表征物研究进展与展望[J]. 中国电机工程学报, 2021, 41(21): 7517-7529. Wang Jianyi, Liu Xueli, Sun Jiantao, et al. Research progress and prospect of new aging characterization of oil-paper insulation[J]. Proceedings of the CSEE, 2021, 41(21): 7517-7529.
[20] 赵珩, 杨耀杰, 苗堃, 等. 油浸式电力变压器绝缘纸老化特征量的研究进展[J]. 变压器, 2020, 57(9): 38-43. Zhao Heng, Yang Yaojie, Miao Kun, et al. Research progress on aging indicator of insulating paper of OilImmersed power transformer[J]. Transformer, 2020, 57(9): 38-43.
[21] Schaut A, Autru S, Eeckhoudt S. Applicability of methanol as new marker for paper degradation in power transformers[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2011, 18(2): 533-540.
[22] Zhang Zhengxin, Si Xiaosheng, Hu Changhua, et al. Degradation data analysis and remaining useful life estimation: a review on Wiener-process-based methods[J]. European Journal of Operational Research, 2018, 271(3): 775-796.
[23] 周义蛟, 郭基联, 万巍, 等. 基于Wiener和Copula函数性能退化模型的减推力起飞可靠性收益评估研究[J]. 推进技术, 2019, 40(3): 667-674. Zhou Yijiao, Guo Jilian, Wan Wei, et al. A study on reliability benefit assessment of reduced thrust takeoff based on performance degradation model of Wiener and Copula functions[J]. Journal of Propulsion Technology, 2019, 40(3): 667-674.
[24] 彭磊, 付强, 李丽, 等. 基于变压器油中甲醇含量的绝缘纸聚合度检测方法[J]. 变压器, 2019, 56(3): 50-54. Peng Lei, Fu Qiang, Li Li, et al. Detection method for polymerization degree of insulation paper based on methanol content in transformer oil[J]. Transformer, 2019, 56(3): 50-54.
[25] Si Xiaosheng, Wang Wenbin, Hu Changhua, et al. Remaining useful life estimation based on a nonlinear diffusion degradation process[J]. IEEE Transactions on Reliability, 2012, 61(1): 50-67.
Abstract Oil-immersed transformer is one of the core equipment of power system, and its safe and stable operation is of great significance to the reliable power supply of power grid. The purpose of performance reliability analysis and remaining life prediction of transformer is to predict its degradation trend and life end, so that maintenance measures can be taken in time before the end of transformer life to avoid power failure. The operating life of transformer mainly depends on its insulation performance, so the reliability analysis of insulation performance and the remaining life prediction are of great significance.
Most of the traditional transformer oil paper insulation degradation models were based on single performance degradation. In view of the problem that the traditional prediction method of residual life of oil-paper insulation of oil-immersed power transformer with single performance degradation is difficult to fully reflect the degradation behavior of oil-paper insulation and the lack of consideration of the correlation between multi-performance degradation, considering the randomness and nonlinearity of the degradation process fully in this paper, a method for residual life prediction of transformer oil-paper insulation based on binary nonlinear Wiener random process was proposed. Firstly, based on nonlinear Wiener stochastic process, the oil-paper insulation degradation model with single property degradation quantity was established to describe the randomness and nonlinearity of oil-paper insulation degradation process. Then, based on Copula function, a degradation model with two performance correlation was established to analyze the joint degradation behavior of transformer oil-paper insulation reflected by two performance degradation quantities more comprehensively. However, different Copula functions would produce different results. Based on AIC criterion, this paper proved that Frank Copula function had better goodness of fit when describing the correlation between furfural and methanol degradation of transformer oil-paper insulation. Finally, because the likelihood function was too complex and there were many unknown parameters, this paper used MCMC-Gibbs sampling algorithm to estimate the unknown parameters of the model and predict the remaining life of transformer oil-paper insulation.
In order to verify the effectiveness and rationality of the proposed method, the contents of furfural and methanol were taken as performance degradation quantities, and the experimental data of accelerated thermal aging were used for example verification. The reliability curves and the prediction results of remaining life were compared under three conditions of single performance, two independent performance and two correlated performance. The results show that the reliability of the single performance case is higher than that of the two-performance case, and the reliability of the performance independent case is higher than that of the performance-dependent case. The reliability assessment method of oil paper insulation for transformer based on binary method considering performance correlation is more conservative than that based on single performance reliability assessment method. By comparing the experimental data, it can be seen that the proposed method is more consistent with the actual measurement results and the evaluation results are more reasonable. By comparing the prediction results of transformer oil paper insulation remaining life at four different monitoring times based on furfural, methanol and two performance correlation cases, it can be seen that the proposed method takes into account the reliability and accuracy of the prediction results, and can provide a reference for the health status assessment of oil-immersed power transformers.
keywords:Power transformer, oil paper insulation, residual life, bivariate nonlinear Wiener, Copula connect function
DOI:10.19595/j.cnki.1000-6753.tces.220865
中图分类号:TM85
收稿日期 2022-05-17
改稿日期 2022-06-17
赵洪山 男,1965年生,博士,教授,博士生导师,研究方向为电力系统动态分析与控制、主动配电网以及故障预测等。E-mail:zhaohshcn@126.com
曲岳晗 男,1995年生,博士研究生,研究方向为配电设备智能运维。E-mail:quyuehan0617@163.com(通信作者)
(编辑 李冰)