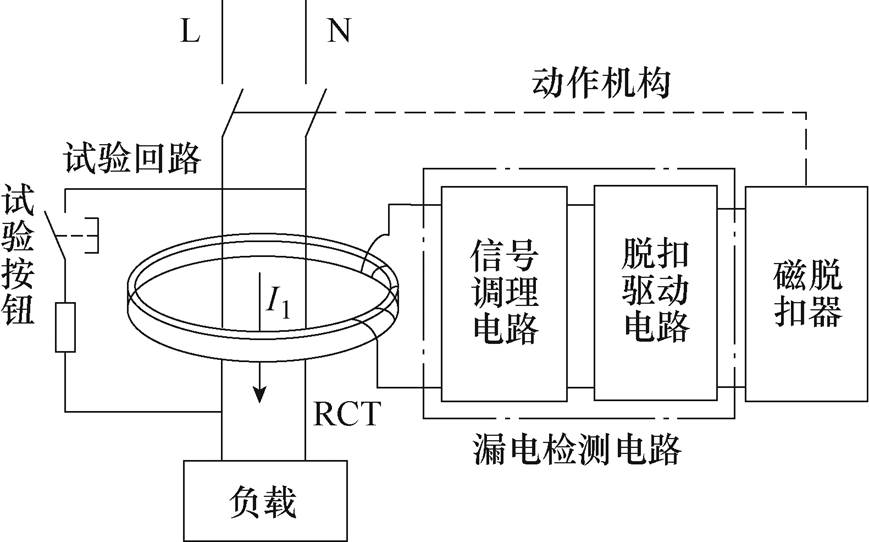
图1 电磁式漏电保护器原理
Fig.1 Schematic diagram of electromagnetic leakage circuit breaker
摘要 电磁式漏电保护是一种重要的漏电故障保护技术，其漏电保护特性受元器件参数影响大，导致批量生产工艺要求高、生产成本较高。该文针对电磁式漏电保护特性不稳定性问题开展研究。首先，分析漏电检测电路的工作原理，确定剩余电流互感器与补偿电容、补偿电阻之间的耦合关系；其次，分析剩余电流互感器铁心磁参数与漏电检测电路参数对漏电保护特性的影响，为剩余电流互感器及漏电检测电路的参数匹配设计提供依据；最后，分析补偿电容容差与剩余电流互感器铁心磁参数分散性对漏电保护特性稳健性的影响，确定铁心材料磁参数与漏电检测电路参数的匹配关系，进行剩余电流互感器及漏电检测电路参数的匹配设计，降低了元器件参数分散性对漏电保护特性的影响。
关键词：电磁式漏电保护 剩余电流互感器 漏电保护特性 稳健性 参数匹配设计
漏电保护技术是配电系统中一项重要的保护技术，可以用于防止人身触电伤亡和电气火灾事故的发生[1-3]。漏电保护器通过非接触式电流采集来检测线路中的剩余电流以实现漏电保护功能，根据其是否需要辅助电源，可以将其分为电子式与电磁式两种。电子式漏电保护器中剩余电流互感器二次回路的感应电压需经电子放大线路放大后激励脱扣器动作，因此具有灵敏度高、整定误差小等优点，但承受冲击能力和抗干扰能力较差、漏电特性易受到工作电压波动影响，导致其难以应用于重要场合。相比于电子式漏电保护器，电磁式漏电保护器无需辅助电压，剩余电流互感器（Residual Current Trans- former, RCT）二次回路的感应电压无需放大，便可直接激励磁脱扣器动作，同时其内部电磁元件具备抗冲击和抗干扰能力强的特点，零电压和断相后漏电保护特性不变，因此，电磁式漏电保护器在重要场合得到广泛应用[4-8]。但电磁式漏电保护器对生产工艺要求非常高，同时剩余电流互感器铁心材料在生产过程中的磁性能分散性较大，导致其保护特性不稳定，在批量生产过程中需要对互感器和磁脱扣器等元器件进行筛选，生产成本较高。因此，如何对剩余电流互感器参数进行优化，以减小其分散性，对漏电保护特性的影响具有重要的研究意义。
在互感器传输特性研究方面，有学者研究了互感器自身参数对传输特性的影响，发现铁心材料、铁心截面积、二次绕组匝数等均会对互感器传输特性产生影响[9-11]。还有学者针对线路中漏电电流存在直流分量时，剩余电流互感器传输能量减少的问题进行了分析，提出了相应的解决措施，提高了检测精度[12-16]。在对影响因素的分析方法上，目前大多采用控制变量的方法[17-19]。
在互感器与电路匹配关系研究方面，有学者用励磁电感代替互感器进行了简化分析，并在此基础上对取能电路进行设计，来提高互感器的输出能 量[20-23]。有学者建立了较为准确的互感器模型，可以精确仿真互感器在各种工况下的传输特性，为更加准确地分析二者之间的关系奠定了基础[24-27]。
本文针对电磁式漏电保护特性不稳定性问题开展研究，分析剩余电流互感器与补偿电阻、补偿电容之间的匹配关系，揭示电磁式漏电保护特性稳定性差的原因，并确定铁心材料参数设计范围以及最佳补偿电容和补偿电阻，提高电磁式漏电保护特性的稳健性，解决电磁式漏电保护器批量生产的制约因素。
电磁式漏电保护器一般由剩余电流互感器、漏电检测电路（信号调理电路和脱扣驱动电路）、磁脱扣器、试验按钮和断路器动作机构五部分构成，如图1所示。
图1 电磁式漏电保护器原理
Fig.1 Schematic diagram of electromagnetic leakage circuit breaker
当电力线路正常运行时，火线L与中性线N的电流相量和为零，剩余电流互感器二次侧无感应电信号输出，漏电保护器不动作；当电力线路中存在漏电故障时，L相电流与N相电流相量和不再为零，剩余电流互感器一次侧存在不平衡电流I1（漏电电流），二次侧有输出电压，其值随漏电电流的增加而增大。输出信号经过信号调理电路输出到脱扣驱动电路，当其值超过脱扣驱动电路动作阈值时，脱扣驱动电路会发出跳闸信号，驱动磁脱扣器脱扣，漏电保护器断开线路，实现漏电保护。
电磁式漏电检测电路原理如图2所示，信号调理电路包括补偿电路和储能电路。补偿电路由补偿电阻R1和补偿电容C1组成，储能电路由整流桥和储能电容C2组成，脱扣驱动电路中电压检测芯片的阈值电压为Uact。
图2 漏电检测电路原理
Fig.2 Schematic diagram of leakage detection circuit
为便于分析计算，根据补偿电容C1、储能电容C2两端电压大小，可以将漏电检测电路工作状态分为三种，如图3所示。图3中，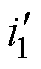
为一次电流折算到二次侧的等效电流；i2为二次电流；
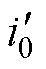为励磁电流折算到二次侧的等效电流；L0为励磁电感折算到二次侧的等效电感；Lr为磁脱扣器线圈电感。
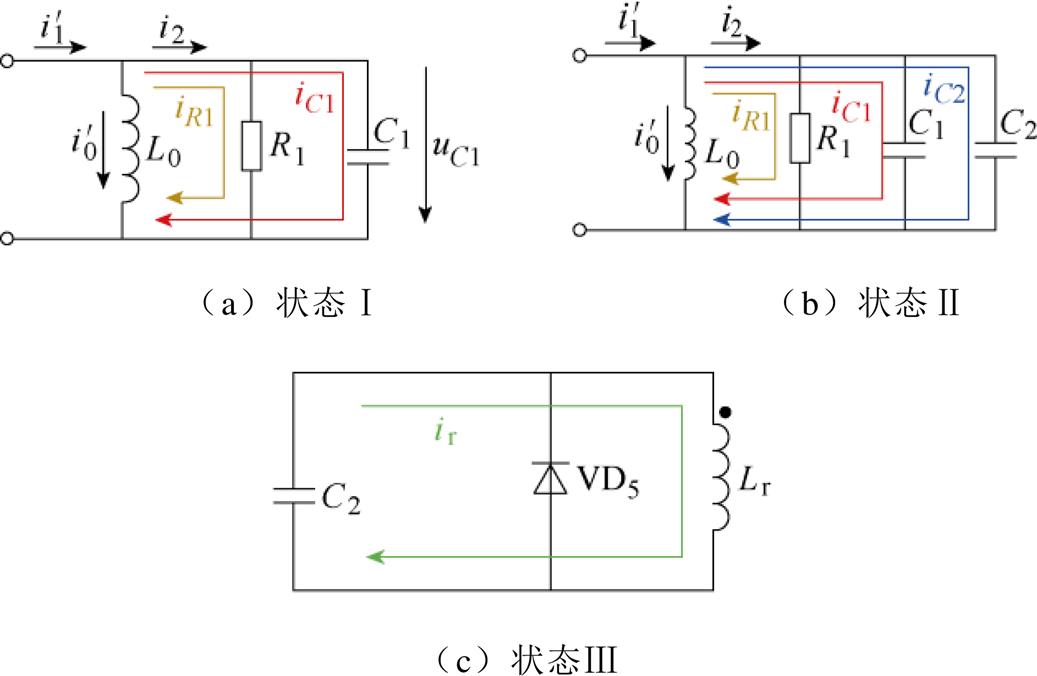
图3 漏电检测电路工作简化电路
Fig.3 Simplified circuit of leakage detection circuit
当补偿电容电压UC1小于储能电容电压UC2时，整流桥不导通，剩余电流互感器输出负载为R1和C1，电路工作于状态Ⅰ；当UC1=UC2时，整流桥导通，剩余电流互感器输出负载为R1、C1和C2，电路工作于状态Ⅱ；当UC2=Uact时，电压检测芯片输出电压使晶体管Q2导通，电路工作于状态Ⅲ。
若漏电电流I1小于漏电动作值IDd，稳态工作时整流桥不导通，储能电容充电最大电压UC2max为补偿电容C1上的电压最大值，且UC2max＜Uact，脱扣驱动电路不导通，磁脱扣器不动作。若漏电电流I1= IDd，则UC2max恰好能够达到Uact。因此，可以根据图3a进行漏电动作值IDd的影响因素分析。
若漏电电流I1＞IDd，UC2的理论稳态值会大于Uact，但实际中其值一旦达到Uact，电压检测芯片会发出信号驱动晶体管Q2导通，储能电容C2沿图3c中ir所示路径放电，磁脱扣器驱动漏电断路器断开线路，实现漏电保护。因此，可以根据图3b进行漏电动作时间的影响因素分析。
漏电检测电路虽然简单，但其特性影响因素复杂。由于漏电动作值IDd的制约，不能单纯地通过提高剩余电流互感器的性能来改善电磁式漏电保护特性的稳定性。因此，本文力图揭示电磁式漏电保护器合格率低的原因，通过检测电路参数的匹配设计，提高漏电保护特性稳定性，解决产品批量生产中的问题，提高合格率。
电磁式漏电保护器中磁脱扣器动作需要一定的驱动能量，因此漏电检测电路中储能电容C2和电压检测芯片的Uact必须大于一定值。基于此，本文假定储能电容C2和电压检测芯片Uact为确定值，进行漏电保护特性影响因素分析，需要解决以下问题：
（1）补偿电阻R1和补偿电容C1的匹配关系及其对漏电保护特性的影响。
（2）剩余电流互感器性能对漏电保护特性的影响。
（3）电磁式漏电保护特性一致性和稳健性设计。
漏电保护特性包括漏电动作值IDd与漏电动作时间td。动作值IDd应小于额定漏电动作电流IDn且大于额定漏电不动作电流IDno，一般情况下IDno= 0.5IDn，因此IDd的设计值一般为0.75IDn。
在进行漏电保护特性设计时，可以先确定漏电动作值IDd，再对IDn下的动作时间进行设计。漏电动作时间td包括三部分：储能电容C2电压达到判别电路阈值电压Uact的时间（即C2充电时间）tC、磁脱扣器动作时间tr、保护器机构动作时间tj。一般情况下tr与tj相对于tC来说较小，因此漏电保护器的动作时间主要由储能电容C2充电时间tC决定。
2.1.1 补偿电容与补偿电阻的匹配关系
剩余电流互感器确定情况下，要满足漏电动作值的要求，需要对补偿电阻R1和补偿电容C1进行匹配设计。为简化分析，先假设剩余电流互感器工作在线性区，即假设铁心磁导率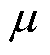
为常数，其励磁电感为
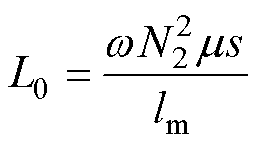（1）
式中，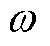
为漏电信号角频率，工频下为314 rad/s；N2为互感器二次侧匝数；s为剩余电流互感器铁心截面积；lm为剩余电流互感器铁心磁路长度。
由图3a可知，稳态情况下补偿电路电压UC1取决于剩余电流互感器励磁电感L0、补偿电阻R1和补偿电容C1，稳态电压UC1为
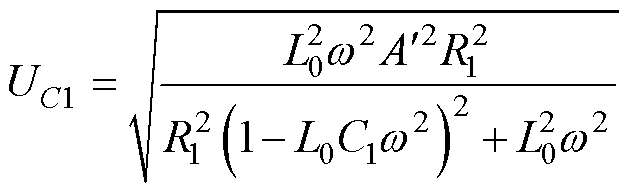（2）
式中，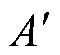
为一次电流折算到二次侧的等效电流幅值。当漏电电流为动作值IDd时，即在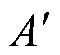=1.414IDd/N2情况下UC1=Uact，因此R1、C1与L0的关系为
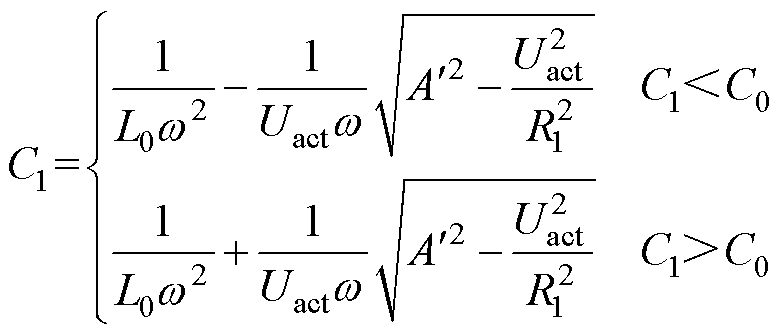（3）
式中，C0为谐振情况下的电容，即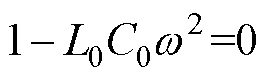
。由式（3）可以得到R1、C1的匹配关系曲线，如图4所示。
图4 R1、C1的匹配关系
Fig.4 Relationship between R1 and C1
由图4可知，剩余电流互感器确定情况下，补偿电阻R1存在最小值R1min，补偿电容C1存在下限值C1min与上限值C1max。
2.1.2 补偿电路参数对漏电动作时间的影响
补偿电容C1与补偿电阻R1在满足图4关系时，漏电动作值都符合要求，但在不同补偿电容和补偿电阻下其漏电动作时间不同。储能电容充电过程比较复杂，其过程包含图3a和图3b两种状态，储能电容电压变化的数学表达式较为复杂，但可以通过仿真分析其变化情况。某漏电检测电路实测参数为：剩余电流互感器匝数N=1 200匝、励磁电感L0= 300 H、阈值电压Uact=3 V、储能电容C2=363 nF、动作值IDd=22 mA。在此参数下进行仿真，得到R1、C1匹配关系及动作时间，如图5所示。由图5可知，在不同的R1、C1匹配参数下，虽然漏电动作值相同，但漏电动作时间相差很大，最短动作时间不到最长动作时间的一半；在谐振点附近补偿电阻最小，其动作时间也最长，且动作时间随补偿电容增大呈阶梯式变化。
对不同R1、C1参数下补偿电容与储能电容电压进行仿真，得到其动态变化过程，如图6所示。当UC1=UC2，整流桥导通，剩余电流互感器输出负载由R1、C1变为R1、C1和C2，等效电容容值变大，导致电压上升（下降）速度变缓，如图6a中电压波峰（波谷）呈现的现象。当UC1＜UC2时，整流桥不导通，储能电容不充电，因此储能电容电压呈现阶梯式上升，如图6b所示。
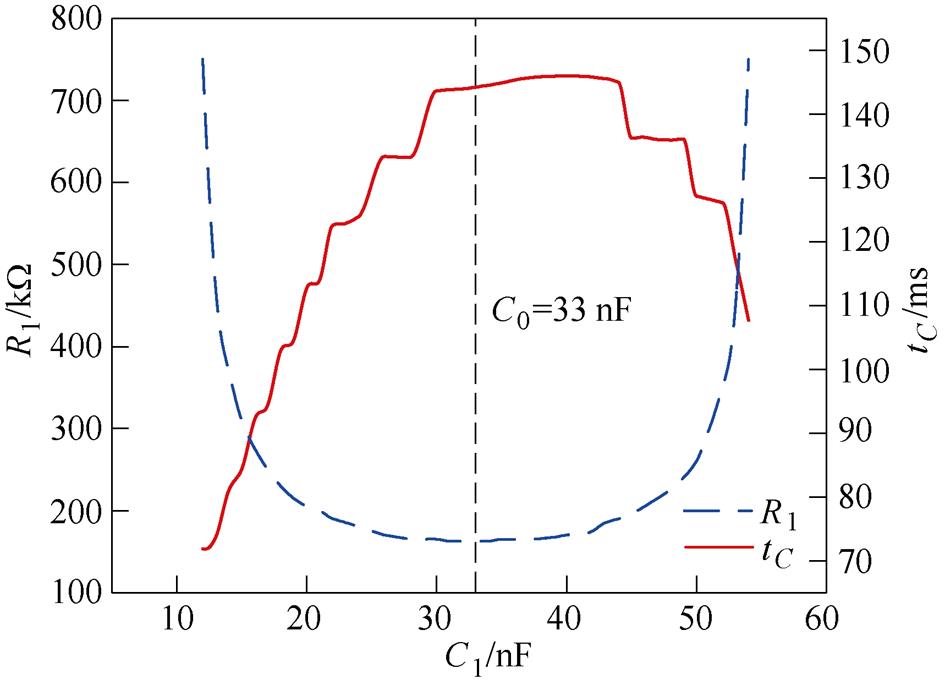
图5 铁心线性时R1、C1匹配关系及动作时间
Fig.5 Relationship between R1 and C1 and tC when the iron core is linear
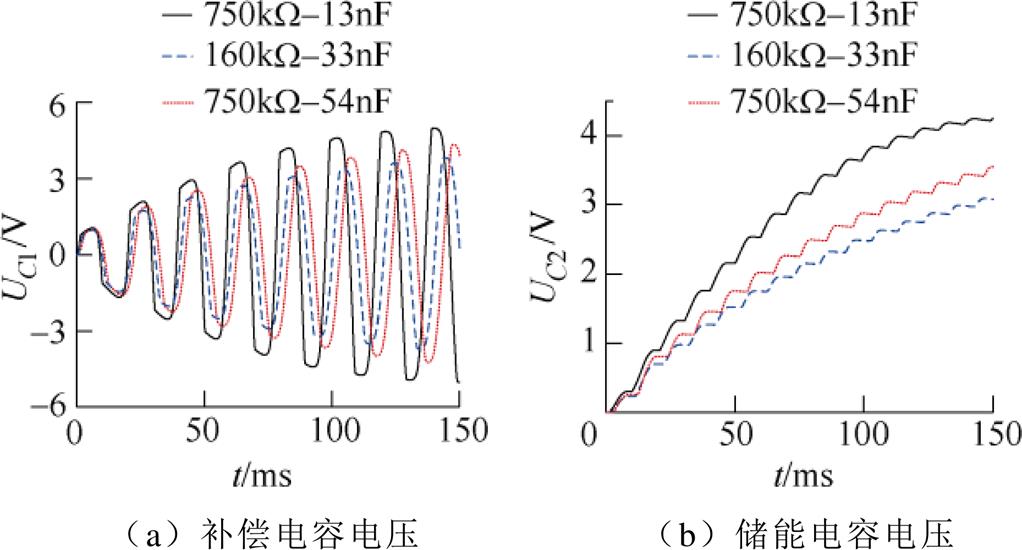
图6 储能电容电压和补偿电容电压
Fig.6 Voltage of energy storage capacitor and compensation capacitor
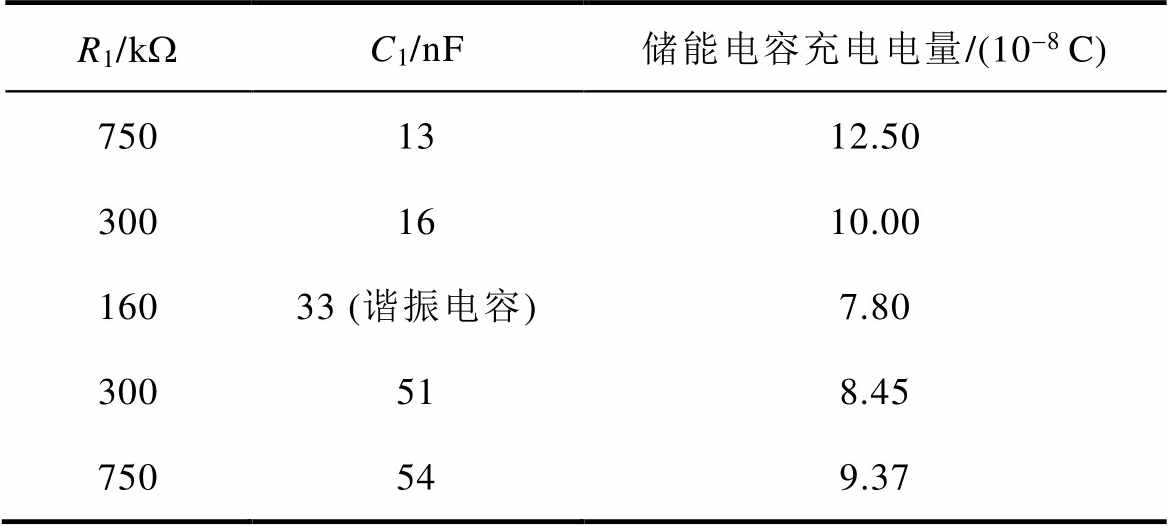
在不同R1、C1参数下进行储能电容充电电流仿真，其波形如图7所示，并计算一个周期内的It积分，获得该周期内电容的充电电量，见表1。
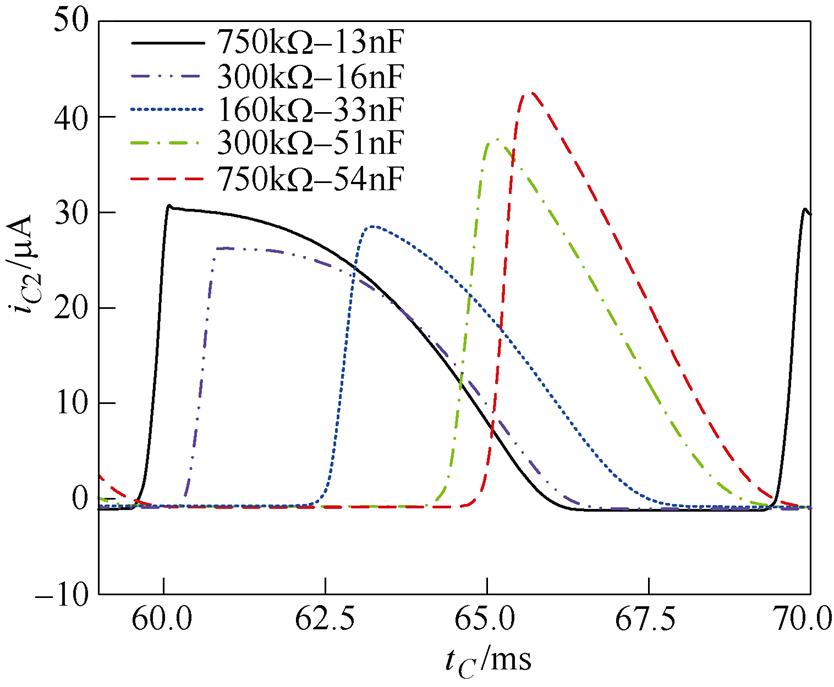
图7 储能电容充电电流
Fig.7 Charging current of energy storage capacitor
表1 储能电容充电电量
Tab.1 Electric quantity of energy storage capacitor
R1/kWC1/nF储能电容充电电量/(10-8 C) 7501312.50 3001610.00 16033 (谐振电容)7.80 300518.45 750549.37
从表1可以看出，当补偿电容为谐振电容时，一个充电周期内储能电容C2充电电量最小，因此在相同阈值电压下其动作时间最长。由图5可知，在相同补偿电阻下，有2个补偿电容C1与之匹配，一个大于谐振电容C0，一个小于C0。补偿电容越大其分流越大，一个周期内储能电容C2充电电量越小，因此其电压上升较慢，漏电动作较长。
2.2.1 线性情况下励磁电感对漏电保护特性的影响
剩余电流互感器性能主要取决于铁心尺寸、磁导率和线圈匝数。若剩余电流互感器工作在线性区，可以假设励磁电感为常数。因此，可以通过励磁电感分析剩余电流互感器性能对漏电保护特性的影响。
当励磁电感L0增大时，谐振电容值C0减小，反之亦然。由式（3）可知，不同励磁电感下，虽然补偿电容与补偿电阻的匹配关系发生变化，但补偿电容变化量只与励磁电感相关，即R1与C1的匹配关系曲线只是在坐标轴上平移。
当互感器线圈电流为22 mA时，测得1 200匝互感器的电感值在150～450 H之间。基于此，在进行仿真时采用等步长法，以50 H为步长进行了仿真分析，得到不同L0下对R1、C1的匹配关系及漏电动作时间的变化曲线如图8所示。由图8a可知，不同励磁电感L0下R1、C1的匹配关系曲线形状完全相同；由图8b可知，漏电动作时间变化规律也基本一致，最短动作时间tCmin出现在C1min处，最长动作时间tCmax出现在谐振电容C0附近，当20 nF＜C0＜40 nF时，动作时间最大值在140～150 ms之间；当C0＞40 nF时动作时间最大值在150～160 ms之间。
不同励磁电感L0下，最短、最长动作时间稍有差别，如图9所示。在一个储能电容充电周期内，若储能电容电压达不到阈值电压，则需要等待下一个充电周期。在全波整流充电情况下，其充电周期为10 ms，因此从图9中可以看到，在某电感值附近有近10 ms的变化。由图5可知，当C1=C1min时，动作时间最短，由式（3）可知，此时的补偿电阻应为无穷大。从图9可以看出，随着电感增大，最短动作时间趋于一个较小值，但当L0＞400 H时，最短动作时间略微上升，这是由于在电感较大时，由式（3）计算的C1min已经很小，甚至可能由0变负值，而实际中，电容不可能为负值。因此，在电感较大时的补偿电容最小为0，无法达到理论上的最小值，造成动作时间略微上升。从图8和图9可以看出，由于漏电保护动作值的制约，改变励磁电感，没有改变漏电动作时间的变化规律，即改变剩余电流互感器铁心磁性能，如提高磁导率等，不会改变漏电保护特性。
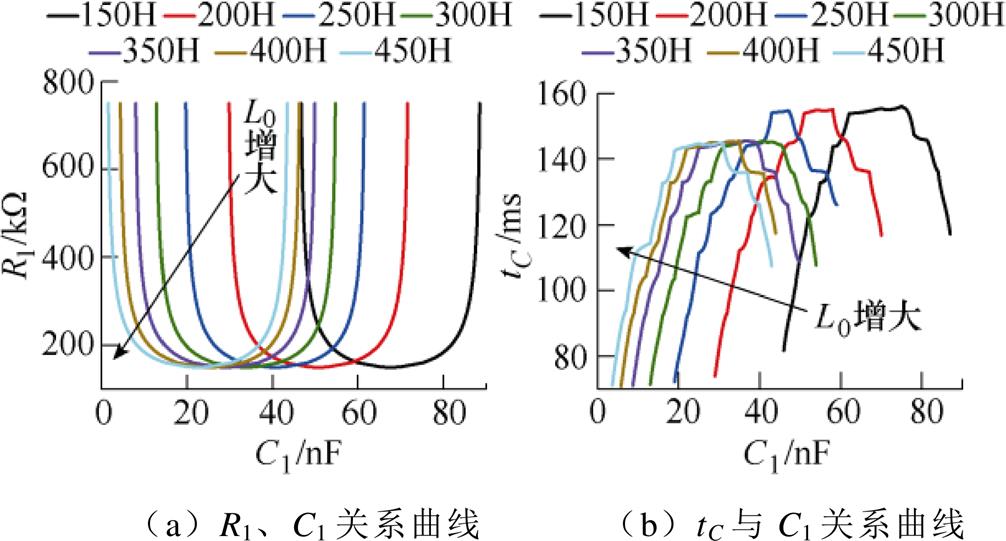
图8 不同L0下R1与C1的关系曲线及动作时间变化曲线
Fig.8 Relationship between R1 and C1 and tC under different L0
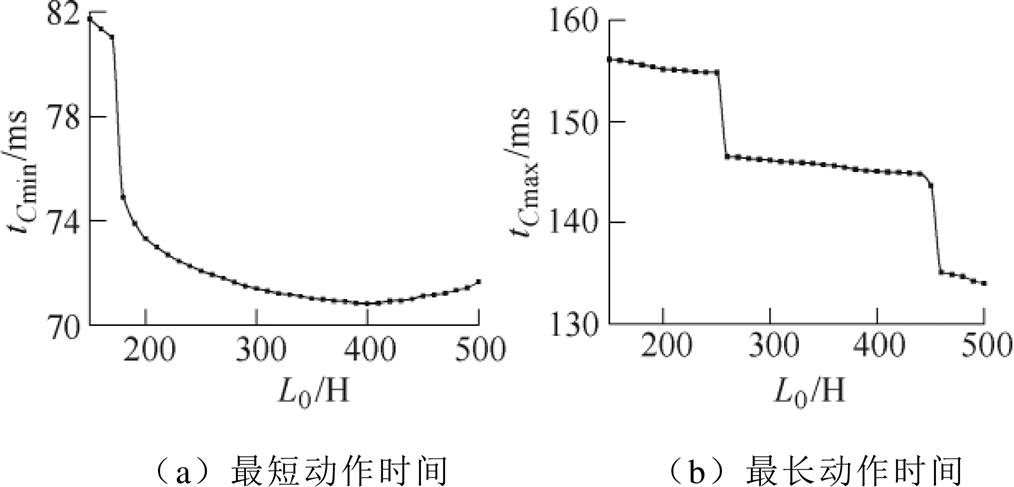
图9 不同L0下最短、最长动作时间
Fig.9 Shortest and longest tC under different L0
2.2.2 非线性情况下铁心磁性能对漏电保护特性的影响
在实际中，电磁式剩余电流互感器可能会工作在非线性区，其励磁电感不再是常数。虽然，在文献[27-28]中均提出了考虑磁饱和现象时铁心磁导率的表达式，但考虑电磁耦合关系时很难用解析方法进行理论分析。因此，根据饱和磁感应强度Bs、剩余磁感应强度Br和矫顽力Hc三个表征铁心磁性能的特征参量，建立了非线性剩余电流互感器模型，通过电路仿真来分析磁性能非线性的影响。剩余电流互感器与漏电检测电路原始参数见表2。在表2参数下进行仿真计算，可以得到R1、C1关系曲线及相应动作时间，如图10所示。
表2 剩余电流互感器与漏电检测电路原始参数
Tab.2 Original parameters of residual current transformer and leakage detection circuit
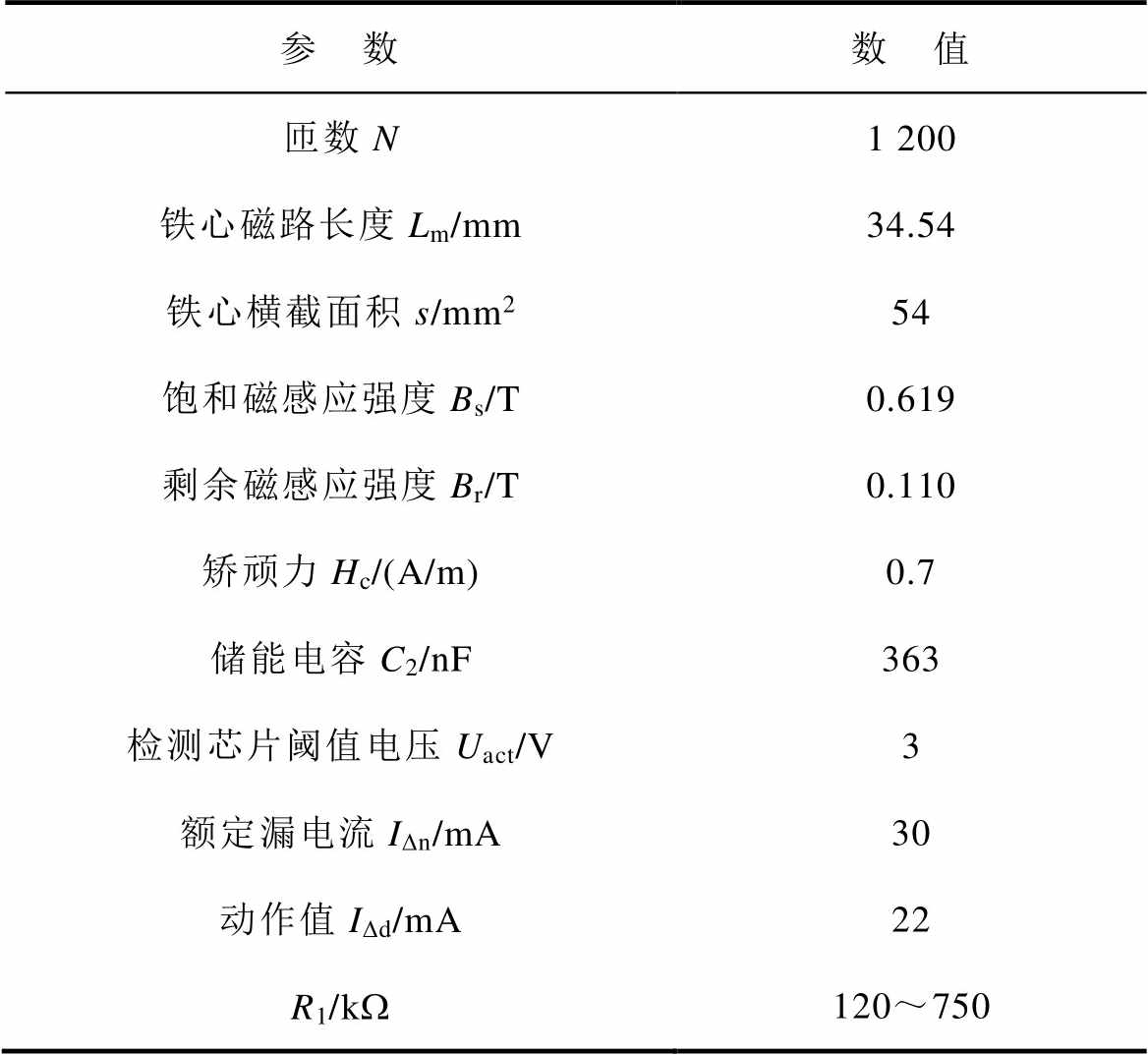
参 数数 值 匝数N1 200 铁心磁路长度Lm/mm34.54 铁心横截面积s/mm254 饱和磁感应强度Bs/T0.619 剩余磁感应强度Br/T0.110 矫顽力Hc/(A/m)0.7 储能电容C2/nF363 检测芯片阈值电压Uact/V3 额定漏电流IDn/mA30 动作值IDd/mA22 R1/kW120～750
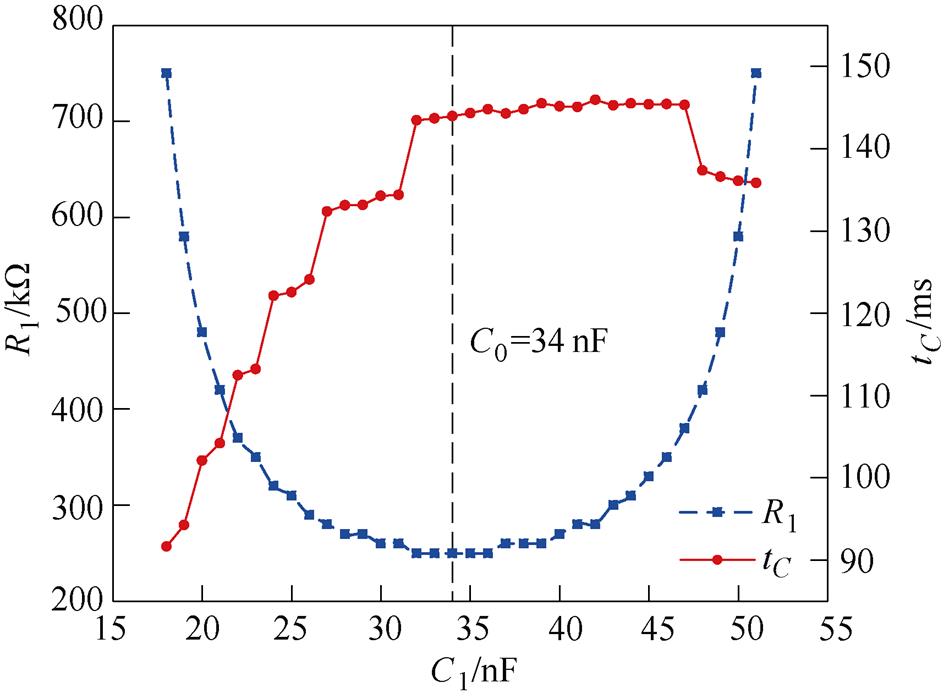
图10 铁心非线性时R1、C1匹配关系及动作时间
Fig.10 Relationship between R1 and C1 and tCwhen the iron core is non-linear
对比图10和图5，虽然剩余电流互感器工作在线性区与非线性区时R1、C1的匹配关系及动作时间有差异，但其变化规律相同，因此在励磁电感假设为常数情况下的分析，仍有指导意义。
在表2参数基础上，采用单因素轮换法分析补偿电路参数匹配关系和动作时间与铁心磁参数的关系，在磁参数Bs为0.4～1.3 T、Br为0.1～0.4 T、Hc为0.3～1.0 A/m情况下，进行仿真计算，其结果如图11所示。由图11可知，不同磁特性参数下补偿电阻、补偿电容之间的匹配关系曲线不完全相同，但都呈“U型”，动作时间变化趋势也与励磁电感为常数时基本相同。
图11 磁参数对R1、C1匹配及动作时间的影响
Fig.11 Relationship between R1 and C1 and tC under different magnetic parameters
实际测得某一剩余电流互感器参数见表3，通过实验得到了5组R1、C1参数组合使IDd=22 mA，测得了相应的动作时间，并通过仿真得到了相应参数下的动作值与动作时间，结果见表4。
表3 剩余电流互感器与漏电检测电路参数
Tab.3 Parameters of residual current transformer and leakage detection circuit
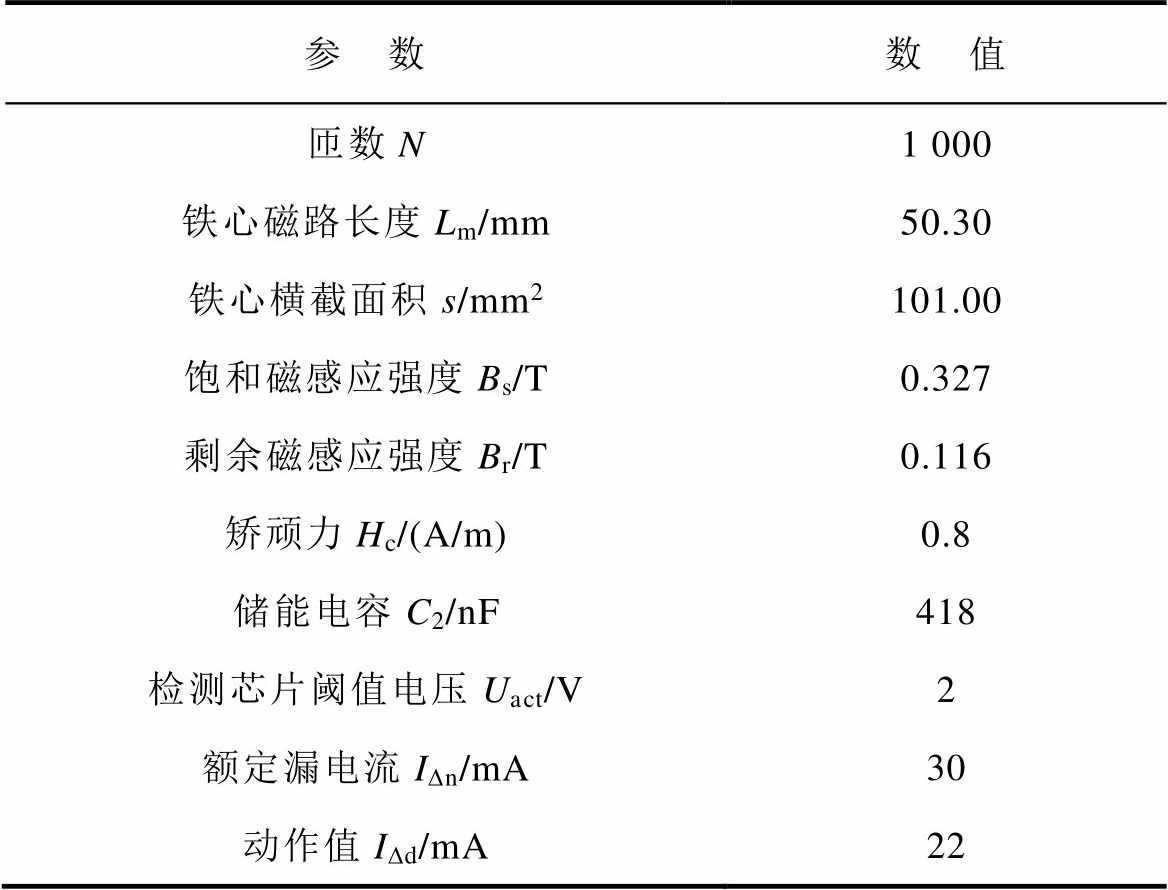
参 数数 值 匝数N1 000 铁心磁路长度Lm/mm50.30 铁心横截面积s/mm2101.00 饱和磁感应强度Bs/T0.327 剩余磁感应强度Br/T0.116 矫顽力Hc/(A/m)0.8 储能电容C2/nF418 检测芯片阈值电压Uact/V2 额定漏电流IDn/mA30 动作值IDd/mA22
表4 R1、C1参数及相应动作时间
Tab.4 Parameters of R1 and C1 and operating time
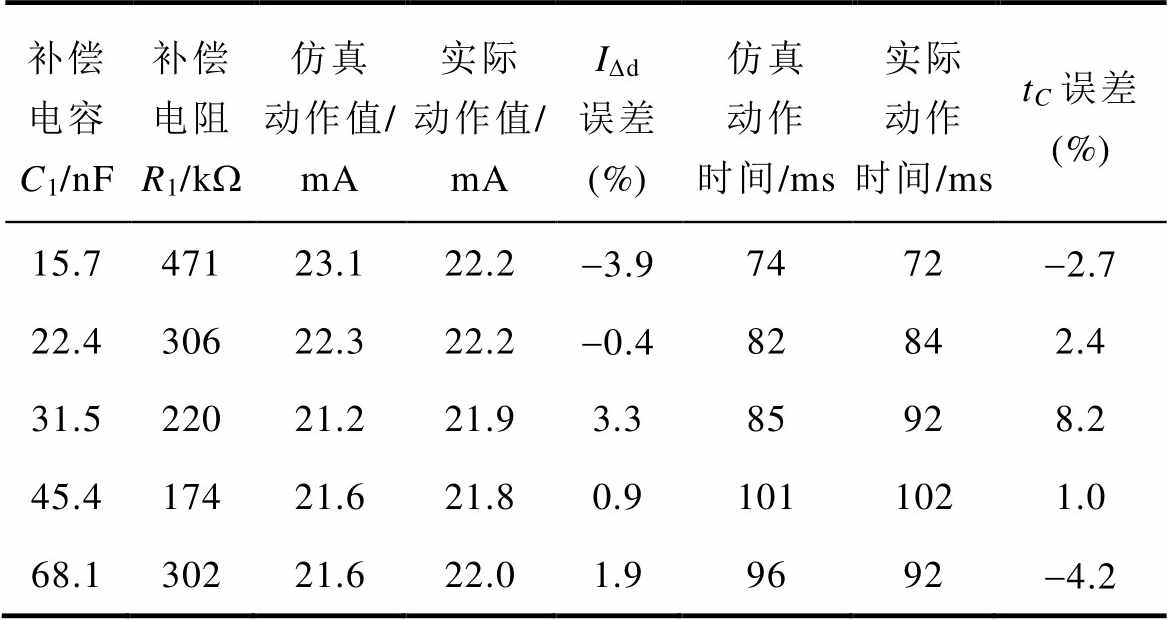
补偿电容C1/nF补偿电阻R1/kW仿真动作值/ mA实际动作值/ mAIDd误差 (%)仿真动作时间/ms实际动作时间/mstC误差 (%) 15.747123.122.2-3.97472-2.7 22.430622.322.2-0.482842.4 31.522021.221.93.385928.2 45.417421.621.80.91011021.0 68.130221.622.01.99692-4.2
由表4可知，不同补偿电容下，实验与仿真得到动作值误差均小于5 %，动作时间误差均小于10 %。由于在进行实验时无法控制电源合闸相位，造成补偿电容为31.5 nF时的动作时间和仿真结果相差较大，但误差在半个周期内，除此之外，其他几组数据的误差均小于5 %，验证了本文仿真方法的准确性。
3.1.1 补偿电容分散性对保护特性稳健性的影响
为分析补偿电容C1分散性对漏电动作值的影响，对式（2）进行变换可得
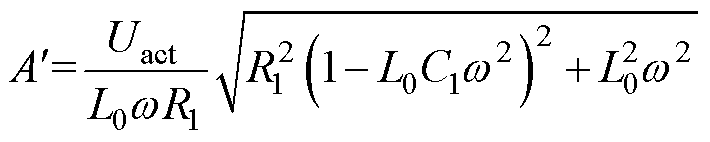（4）
则C1的绝对灵敏度为
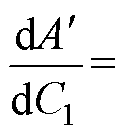
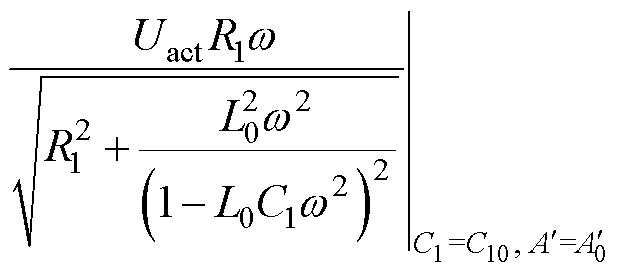（5）
C1的相对灵敏度为
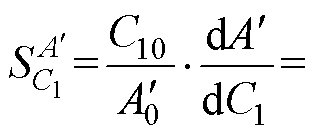
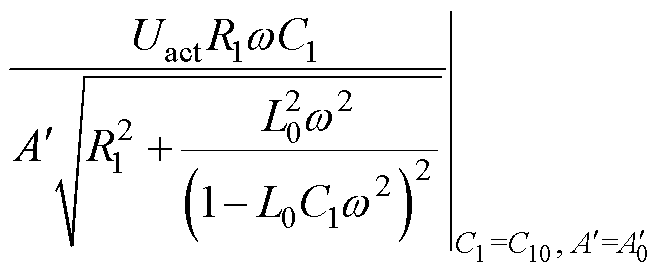（6）
由式（5）、式（6）可以得到不同电感值下灵敏度随C1变化曲线，如图12所示。
由图12可知，当补偿电容为谐振电容时灵敏度最低，即动作值最稳定，但此时动作时间最长。由图12a可知，绝对灵敏度以C1=C0为轴对称，励磁电感L0的变化不会影响绝对灵敏度的变化趋势；由图12b可知，C1＜C0时其相对灵敏度相较于C1＞C0时整体偏小。励磁电感越大，C1的相对灵敏度越小，当L0≥250 H时，C1＜C0时相对灵敏度S＜1.0，此时电容容差对动作值影响较小。因此，励磁电感应尽可能大，同时补偿电容小于谐振电容时，可以降低补偿电容的相对灵敏度，即可以减小补偿电容分散性对保护特性的影响。
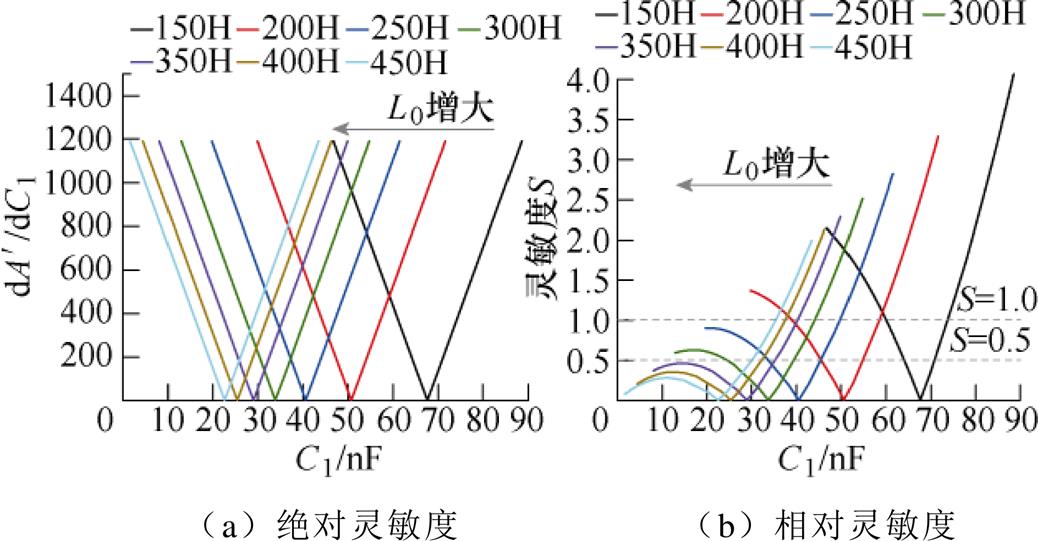
图12 不同电感下灵敏度随C1变化曲线
Fig.12 Relationship between sensitivity and C1 under different L0
由于动作时间随补偿电容增长呈阶梯状变化，在同一阶梯上，动作时间变化较小，由图10可知，将C1值设定在阶梯的中间时能够降低C1容差对动作时间的影响。
3.1.2 磁参数分散性对保护特性稳健性的影响
由图11可知，当Br＞0.2 T、Bs＞0.7 T时，R1、C1关系曲线及动作时间变化曲线较为密集，此时动作值、动作时间受Br分散性影响较小；Hc变化时R1、C1关系曲线间距较大，仅当补偿电容C1值接近谐振电容值C0时，Hc变化对动作值影响较小。在不同磁参数Br、Hc、Bs下，进行漏电动作值、动作时间的仿真计算，其结果如图13所示。
图13a、图13c、图13e中交点是在表2参数下的保护特性设计点，可知，Bs变化对动作值、动作时间影响最小，而Hc变化影响最大。由图13b、图13d、图13f可知，动作时间变化趋势与动作值基本一致，电容较小时动作时间相对较短。若动作值接近IDn时，则动作时间变化幅度较大，甚至超过300 ms的标准要求。因此，在参数设计时，应保证动作值受磁参数分散性影响较小，并与额定剩余电流动作值IDn之间存在一定裕度。
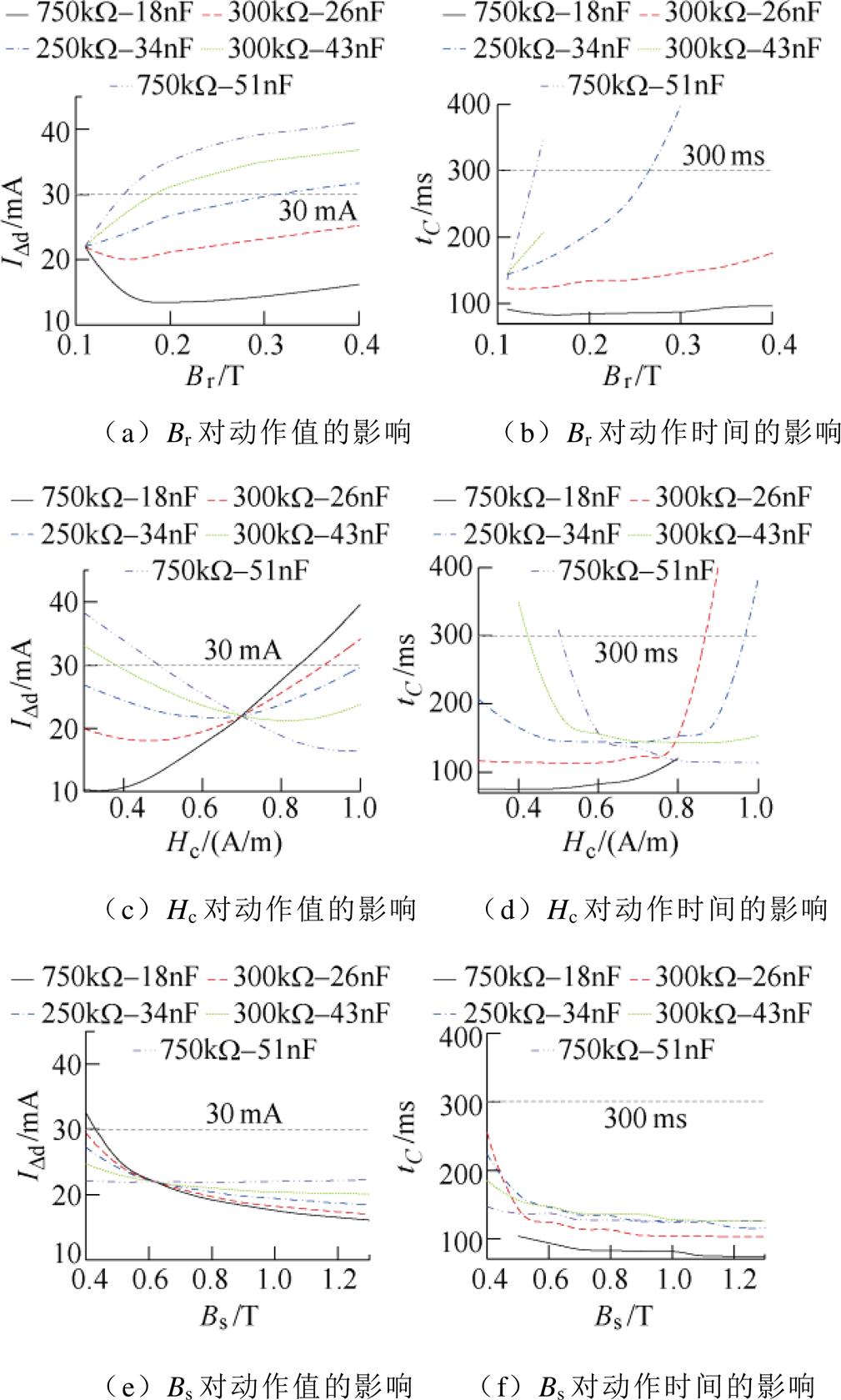
图13 剩余电流互感器磁参数对动作值、动作时间影响
Fig.13 Influence of magnetic parameters of residual current transformer on IDd and tC
为进一步明确Bs对动作值、动作时间的影响，仿真分析不同Bs下动作值、动作时间随Br、Hc的变化情况，如图14所示。
由图14可知，不同Bs下，动作值和动作时间随Br、Hc的变化曲线非常接近，证明了Bs变化对动作值、动作时间影响最小。因此，在进行磁性能参数设计时，可以先确定Bs，再分析Br与Hc分散性对动作值和动作时间的影响，本文将Bs确定为1.0 T。
对比图13c与图14c，增大Br后，Hc变化对动作值、动作时间的影响减小。在Bs=1.0 T、Br=0.2 T条件下，仿真分析Hc分别为0.6、0.7、0.8 A/m时的R1、C1匹配曲线与动作时间曲线，如图15所示。由图15可知，三组谐振电容值较为接近，补偿电容C1=18 nF时，其值接近谐振电容值，位于曲线的平缓区间。
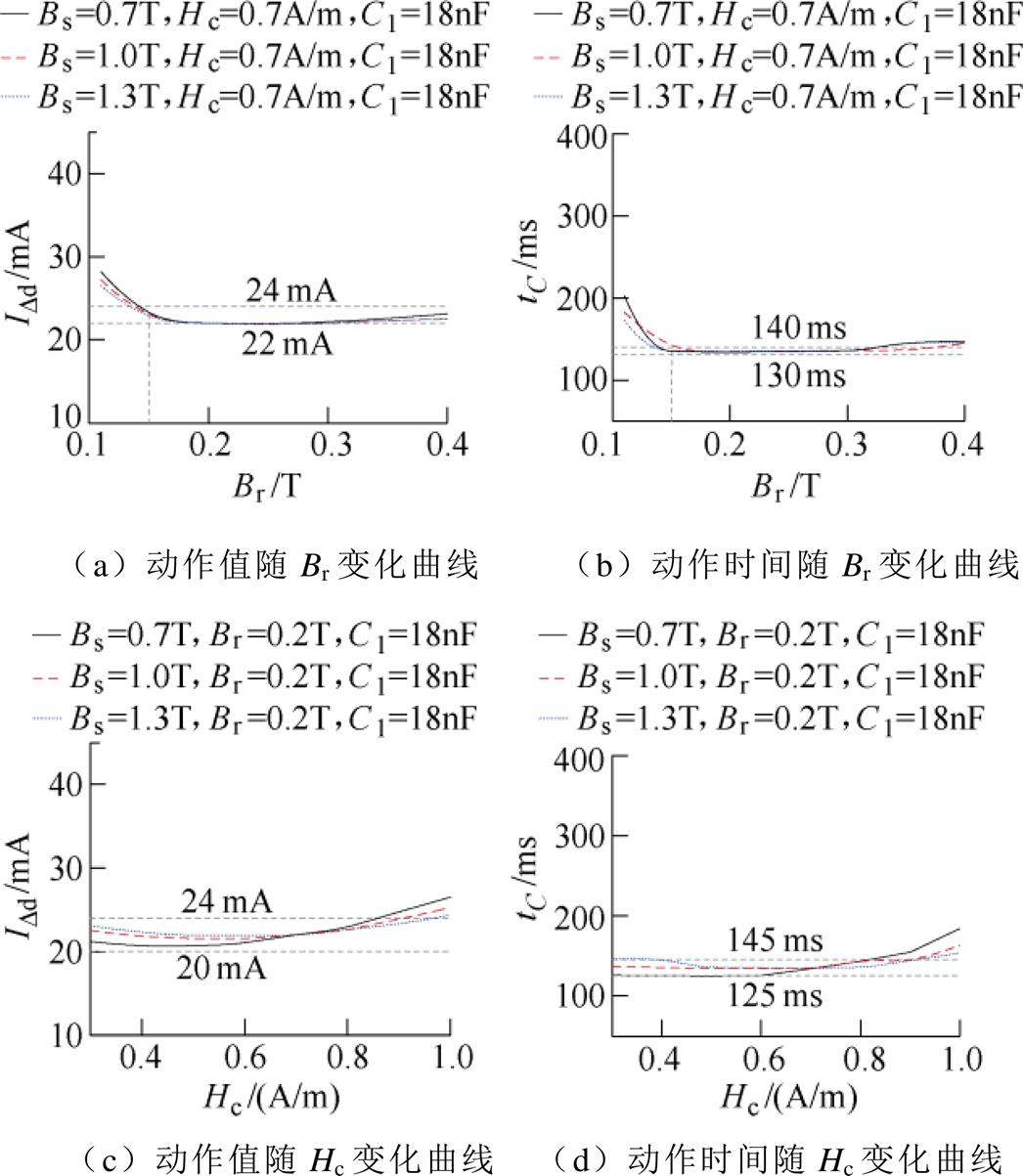
图14 不同Bs下磁参数对动作值、动作时间的影响
Fig.14 Influence of magnetic parameters on IDd and tC under different Bs
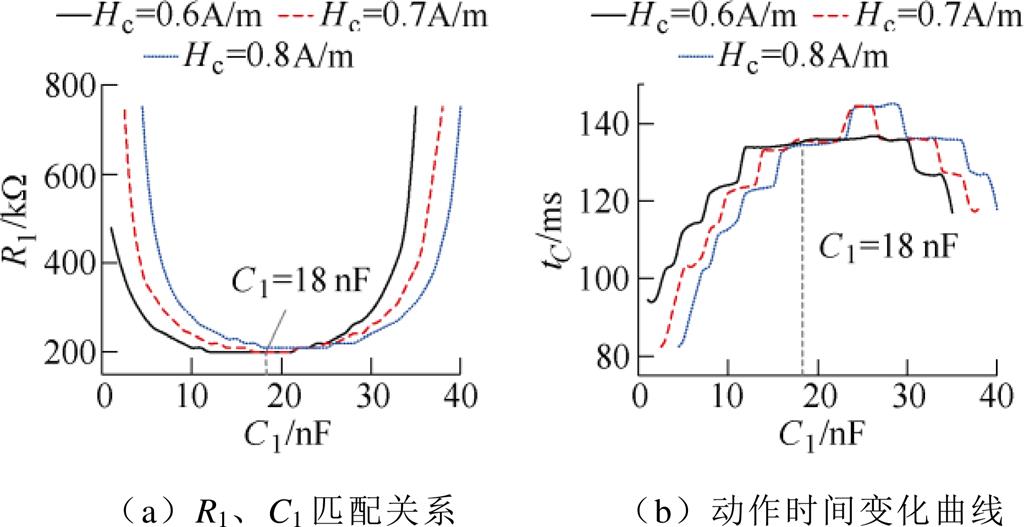
图15 不同Hc下R1、C1匹配关系及动作时间变化曲线
Fig.15 Relationship curves of R1 and C1 and tC under different Hc
综上可知，当补偿电容C1值确定后，通过Br与Hc的设计使补偿电容C1接近谐振电容，可以降低磁参数对动作值、动作时间的影响，从而提高漏电保护特性的稳健性。
3.2.1 漏电保护特性稳健性与磁参数关系分析
为进一步分析磁参数的影响，令k=Br/Hc，Bs=1.0 T，仿真分析动作值、动作时间随k的变化规律，从而明确Br、Hc设计范围。采用正交分析方法，对不同磁参数及匹配补偿电容和补偿电阻下的保护特性进行大量仿真，用于分析漏电保护特性稳健性。图16为几种典型仿真结果，其中实线为动作值变化曲线，虚线为动作时间变化曲线。动作值和动作时间变化曲线越平缓，平缓区间越大，说明漏电保护特性稳健性越好。
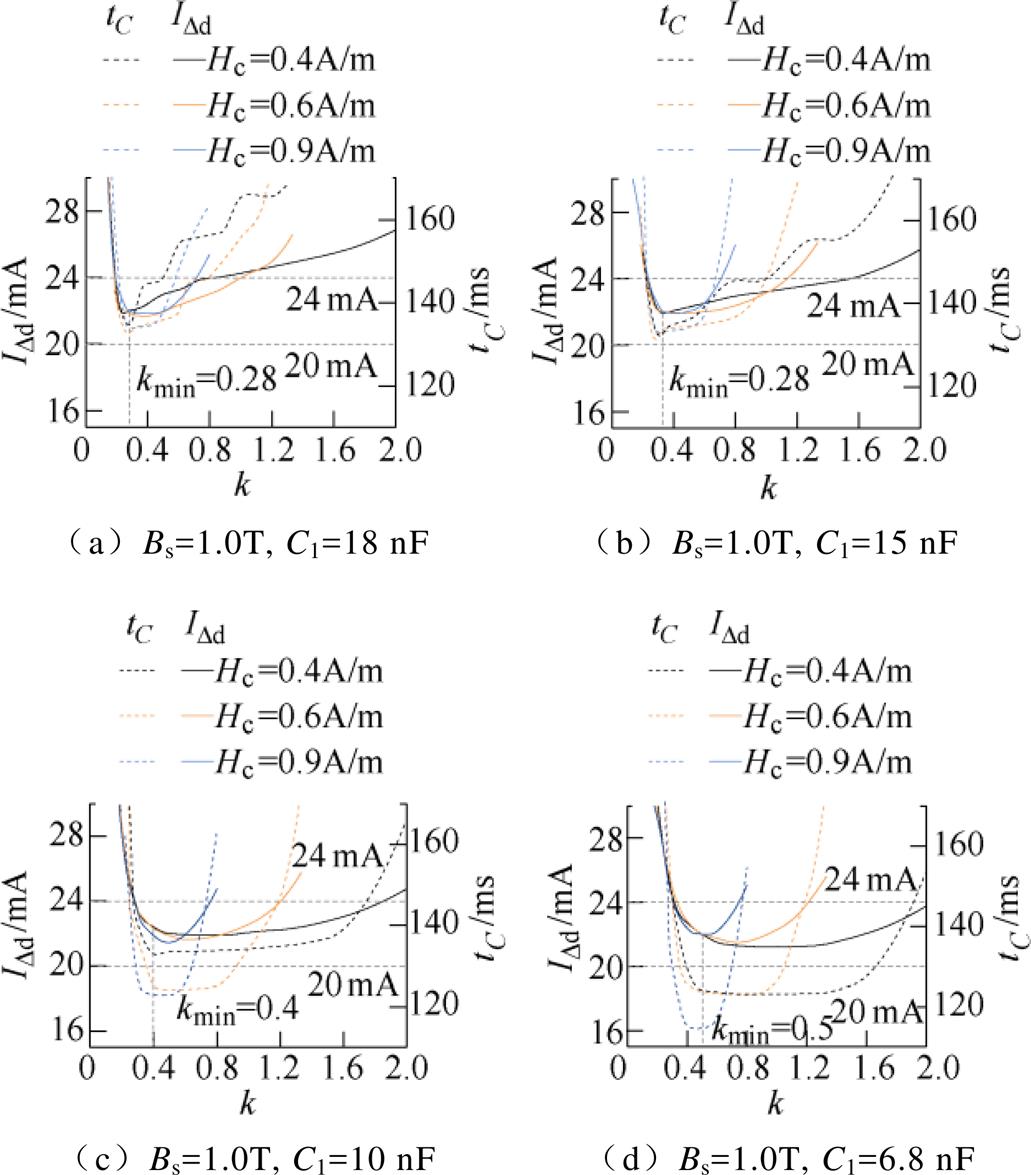
图16 不同Hc下k对动作值与动作时间的影响
Fig.16 Influence of k on IDd and tC under different Hc
从图16中可以发现，Hc=0.9 A/m时，其值较大，动作时间相对较短，但动作值和动作时间变化曲线的平缓区段较小，即保护特性稳定区间较小，其分散性对保护特性影响较大；在同一补偿电容值下，存在下限值kmin，Br/Hc＜kmin时，动作值与动作时间随k变化而变化得较快，保护特性受磁参数分散性影响较大，而Br/Hc＞kmin时，保护特性受磁参数分散性影响相对较小。另外，补偿电容C1越小，kmin越大，动作值与动作时间受剩余磁感应强度Br分散性的影响越小。当kmin＞0.4，且Br/Hc＞kmin时，动作值与动作时间变化曲线在不同矫顽力Hc下比较接近，此时Hc对动作特性影响较小。
实际中剩余磁感应强度Br与矫顽力Hc的分散性较大，一般可达±20 %左右。假设Br/Hc的基准值为k0，则因分散性引起的Br/Hc变化区间为(0.67～1.5)k0。因此，在磁参数设计时，可以使Br/Hc＞ 1.5kmin，就可以保证Br与Hc分散性在±20 %情况下Br/Hc仍大于kmin，从而保证了动作特性的稳定性。由图16可知，在C1=18 nF下，Br/Hc应大于0.42；在C1=15 nF下，Br/Hc应大于0.48；在C1=10 nF下，Br/Hc应大于0.6；在C1=6.8 nF下，Br/Hc应大于0.75。
3.2.2 设计方案对比分析
为提高电磁式漏电保护特性的稳健性，需要对剩余电流互感器与漏电检测电路参数进行综合设计，确定方法如下：
（1）确定Bs值。磁材料的饱和磁感应强度一般在1.0 T左右，因此本文选取Bs=1.0 T。
（2）补偿电容C1的取值范围。在实际中常用的电容值有6.8、10、15、18、22 nF等，由图16可知，补偿电容为6.8、10.0 nF时，动作值符合设计要求的范围宽，且保护特性变化平缓区段大，即保护特性稳健性高。因此，可以将6.8、10.0 nF作为补偿电容的设计值。
（3）铁心磁参数Br与Hc的设计。为减小保护特性受磁参数分散性的影响应尽量选取较小的矫顽力Hc，从图16可知，Hc为0.4 A/m时，无论动作值还是动作时间，其变化平缓段最大，Hc可以确定为0.4 A/m。由于要求Br/Hc＞1.5kmin，因此在补偿电容为6.8、10.0 nF下Br分别为0.30、0.24 T。
根据表2所示磁参数及以上方法确定的磁参数，并进行补偿电容C1与补偿电阻R1的匹配设计，确定三种方案，剩余电流互感器与补偿电路参数见表5。方案1和方案2为两种新设计的方案。
表5 剩余电流互感器与补偿电路参数
Tab.5 Parameters of RCT and compensation circuit
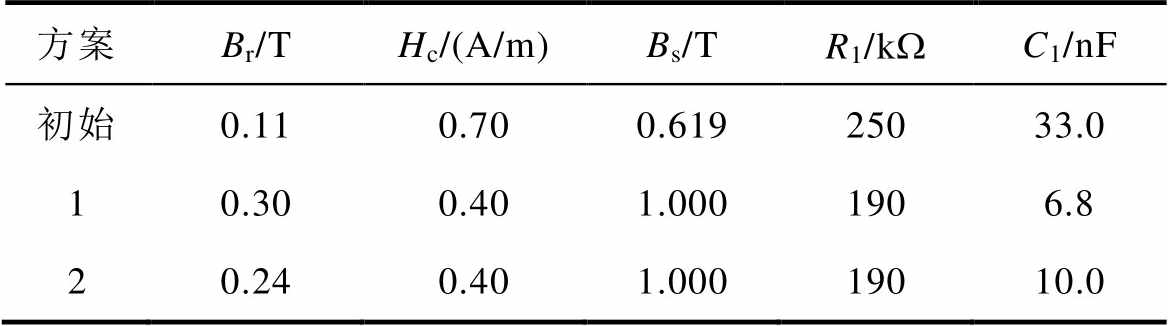
方案Br/THc/(A/m)Bs/TR1/kWC1/nF 初始0.110.700.61925033.0 10.300.401.0001906.8 20.240.401.00019010.0
为验证漏电保护特性的稳健性，对初始方案、方案1和方案2在剩余电流互感器磁参数极限偏差下的保护特性进行仿真，所得结果见表6。表中，“变化后①”是指C1减小10 %，且磁参数的变化使保护特性偏移增大；“变化后②”是指C1增大10 %，且磁参数的变化也使保护特性偏移增大。在这种情况下，补偿电容和磁参数的变化均使漏电保护特性变差，属于最严酷的情况。
表6 参数优化前后动作特性对比
Tab.6 Comparison of protection characteristics between original parameters and optimized parameters
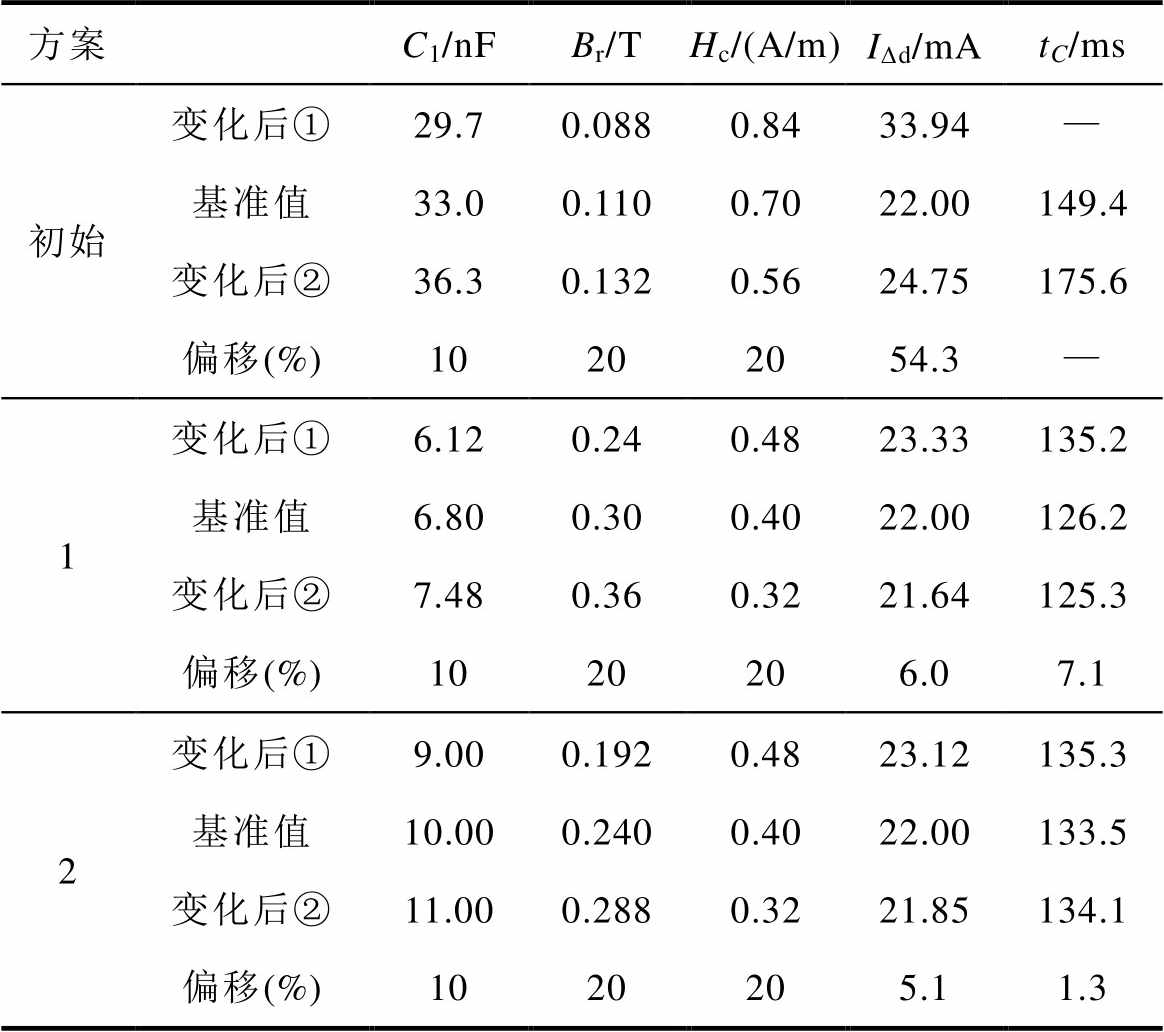
方案C1/nFBr/THc/(A/m)IDd/mAtC/ms 初始变化后①29.70.0880.8433.94— 基准值33.00.1100.7022.00149.4 变化后②36.30.1320.5624.75175.6 偏移(%)10202054.3— 1变化后①6.120.240.4823.33135.2 基准值6.800.300.4022.00126.2 变化后②7.480.360.3221.64125.3 偏移(%)1020206.07.1 2变化后①9.000.1920.4823.12135.3 基准值10.000.2400.4022.00133.5 变化后②11.000.2880.3221.85134.1 偏移(%)1020205.11.3
由表6可知，在初始方案的铁心磁参数下，通过补偿电阻、补偿电容的匹配，在理想情况下其漏电保护特性满足要求，但当元器件参数存在误差或因温度产生漂移时，其保护特性变化较大，甚至有可能无法满足标准要求。而通过稳健性分析得到的方案1和方案2，在相同参数变化情况下，无论是动作值还是动作时间变化都较小，即提高了电磁式漏电保护特性的稳健性。
本文分析了电磁式漏电保护特性影响因素，通过剩余电流互感器铁心材料磁参数与电路参数的设计，提高了漏电保护特性的稳健性，有助于电磁式漏电保护器的批量生产。主要结论如下：
1）分析了漏电检测电路与剩余电流互感器参数对漏电保护特性的影响。首先分析了剩余电流互感器与补偿电阻R1、补偿电容C1之间的匹配关系，发现当漏电动作值一定时，R1、C1匹配关系曲线呈“U型”；然后分析了R1、C1对动作时间的影响，发现动作时间随补偿电容C1增大先增大再减小，动作时间最大值出现在谐振电容附近，且随谐振电容的增大而增大。
2）分析了剩余电流互感器磁参数对保护特性的影响，发现当剩余电流互感器磁参数变化时，剩余电流互感器与补偿电阻、补偿电容之间的匹配关系不变，动作时间呈现的变化规律不变，仅补偿电容C1取值范围发生改变。
3）分析了补偿电容容差与剩余电流互感器铁心磁参数分散性对漏电保护特性的影响。发现当补偿电容值小于谐振电容时，其参数分散性对保护特性影响较小，同时Br/Hc存在一个最小值kmin，当Br/Hc＞1.5kmin时，漏电断路器保护特性受磁参数影响较小，基本上可以消除磁参数分散性对漏电保护特性的影响。
4）进行了剩余电流互感器磁参数的优化设计，并进行补偿电阻R1、补偿电容C1的匹配设计。经过优化设计，即使在参数漂移最严苛的情况下，动作值与动作时间的偏差均在10 %以下，减小了电路参数和磁材料参数分散性对漏电保护特性的影响，从而提高了漏电保护特性的稳健性。
虽然本文对实际的互感器及补偿电容、补偿电阻下的动作特性进行了测试，验证了论文仿真方法的准确性，但还需要采用不同特性的磁心材料进行稳健性设计结果的验证，将在技术转化应用过程中解决。
参考文献
[1] 刘帼巾, 李想, 王泽, 等. 基于Wiener过程电子式漏电断路器的剩余寿命预测[J]. 电工技术学报, 2022, 37(2): 528-536.
Liu Guojin, Li Xiang, Wang Ze, et al. Remaining life prediction of electronic residual current circuit breaker based on Wiener process[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 528-536.
[2] 胡博凯, 李奎, 牛峰, 等. 低压断路器机械特性状态监测方法研究[J]. 电工技术学报, 2022, 37(13): 3317-3330.
Hu Bokai, Li Kui, Niu Feng, et al. Research on condition monitoring method of mechanical charac- teristics of low-voltage circuit breaker[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(13): 3317-3330.
[3] 李奎, 张国盼, 郑淑梅, 等. 基于实时服役参数的交流接触器电寿命最大化控制策略[J]. 电工技术学报, 2021, 36(9): 1976-1985.
Li Kui, Zhang Guopan, Zheng Shumei, et al. A control strategy for maximizing the electrical life of AC contactors based on real-time operating para- meters[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1976-1985.
[4] 李奎, 李常宇, 牛峰, 等. 电磁式漏电断路器的空间磁场抗扰分析及屏蔽结构设计[J]. 电工技术学报, 2022, 37(9): 2161-2169.
Li Kui, Li Changyu, Niu Feng, et al. Anti-magnetic field interference analysis and shielding structure design of electromagnetic residual current circuit breaker[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2161-2169.
[5] 刘帼巾, 王泽, 李想, 等. 基于改进Bootstrap-Bayes的电子式剩余电流动作断路器可靠性评估[J]. 电工技术学报, 2022, 37(16): 4250-4258.
Liu Guojin, Wang Ze, Li Xiang, et al. Reliability evaluation of electronic residual current operated circuit breakers based on improved Bootstrap- Bayes[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4250-4258.
[6] Czapp S, Szultka S. Tripping limitations of residual current devices in photovoltaic installations[C]//2017 18th International Scientific Conference on Electric Power Engineering (EPE), Kouty nad Desnou, Czech Republic, 2017: 1-5.
[7] Luo Xiang, Du Yaping, Wang Xinghua, et al. Tripping characteristics of residual current devices under nonsinusoidal currents[J]. IEEE Transactions on Industry Applications, 2011, 47(3): 1515-1521.
[8] 李倩, 李奎, 王尧, 等. 脉动直流剩余电流下AC型漏电断路器动作特性分析[J]. 河南理工大学学报(自然科学版), 2020, 39(3): 100-107.
Li Qian, Li Kui, Wang Yao, et al. Analysis on tripping performances of AC-type leakage circuit breaker under pulsating DC residual current[J]. Journal of Henan Polytechnic University (Natural Science), 2020, 39(3): 100-107.
[9] 刘毅, 韩毅博, 刘思维, 等. 不同剩磁铁基纳米晶磁芯脉冲磁化特性[J]. 中国电机工程学报, 2016, 36(2): 577-584.
Liu Yi, Han Yibo, Liu Siwei, et al. Pulse mag- netization characteristics of Fe-based nanocrystalline cores with different remanences[J]. Proceedings of the CSEE, 2016, 36(2): 577-584.
[10] 郭琳云, 尹项根, 严新荣, 等. 配电网智能设备自取能电源的效率提升研究[J]. 中国电机工程学报, 2009, 29(增刊1): 217-221.
Guo Linyun, Yin Xianggen, Yan Xinrong, et al. Research of improving power efficiency for intelligent device self-power supply utilized in power distribution network[J]. Proceedings of the CSEE, 2009, 29(S1): 217-221.
[11] 刘亚东, 盛戈皞, 王葵, 等. 基于相角控制法的电流互感器取电电源设计[J]. 电力系统自动化, 2011, 35(19): 72-76.
Liu Yadong, Sheng Gehao, Wang Kui, et al. A new design of current transformer energy harvesting power supply based on phase angle control method[J]. Automation of Electric Power Systems, 2011, 35(19): 72-76.
[12] 郭一飞, 高厚磊. 直流偏磁对电流互感器暂态传变特性的影响[J]. 电力自动化设备, 2015, 35(12): 126-131, 144.
Guo Yifei, Gao Houlei. Effect of DC bias on transient transferring characteristics of current transformer[J]. Electric Power Automation Equipment, 2015, 35(12): 126-131, 144.
[13] 金能, 邢家维, 林湘宁, 等. 一种抗电流互感器饱和的工频变化量保护新方案[J]. 电工技术学报, 2018, 33(增刊1): 213-220.
Jin Neng, Xing Jiawei, Lin Xiangning, et al. A new scheme of frequency variation protection resisting current transformer saturation[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 213- 220.
[14] Xie Pengkang, Fang Zhen, Hu Jianping, et al. Tripping characteristics of residual current devices under different working conditions[C]//IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), Changsha, China, 2020: 2765-2769.
[15] Czapp S, Dobrzynski K, Klucznik J, et al. Low- frequency tripping characteristics of residual current devices[C]//2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 2017: 1-4.
[16] 李奎, 戴逸华, 牛峰, 等. 基于触发角识别的脉动直流剩余电流有效值检测方法[J]. 电力自动化设备, 2017, 37(5): 80-84.
Li Kui, Dai Yihua, Niu Feng, et al. Residual pulsating DC detection based on triggering angle identi- fication[J]. Electric Power Automation Equipment, 2017, 37(5): 80-84.
[17] 张保会, 李光辉, 王进, 等. 风电接入电力系统故障电流的影响因素分析及对继电保护的影响[J]. 电力自动化设备, 2012, 32(2): 1-8.
Zhang Baohui, Li Guanghui, Wang Jin, et al. Affecting factors of grid-connected wind power on fault current and impact on protection relay[J]. Electric Power Automation Equipment, 2012, 32(2): 1-8.
[18] 胡方, 杨文英, 赵瑞平, 等. 大功率直流接触器温度场仿真及影响因素分析[J]. 低压电器, 2011(23): 1-6.
Hu Fang, Yang Wenying, Zhao Ruiping, et al. Thermal simulation of high-power DC contactor and analysis of influencing factors[J]. Low Voltage Apparatus, 2011(23): 1-6.
[19] 汤蕾, 沈沉, 张雪敏. 大规模风电集中接入对电力系统暂态功角稳定性的影响(二): 影响因素分析[J]. 中国电机工程学报, 2015, 35(16): 4043-4051.
Tang Lei, Shen Chen, Zhang Xuemin. Impact of large-scale wind power centralized integration on transient angle stability of power systems—part Ⅱ: factors affecting transient angle stability[J]. Pro- ceedings of the CSEE, 2015, 35(16): 4043-4051.
[20] 刘铮, 樊绍胜, 胡劼睿. 基于阻抗匹配的输电线路在线取能方法研究[J]. 中国电机工程学报, 2019, 39(23): 6867-6876, 7100.
Liu Zheng, Fan Shaosheng, Hu Jierui. Research on on-line energy acquisition method for transmission lines based on impedance matching[J]. Proceedings of the CSEE, 2019, 39(23): 6867-6876, 7100.
[21] 程志远, 隋立程, 宋凯, 等. 谐振补偿式电流互感器取能方法的研究[J]. 电网技术, 2021, 45(12): 4896-4902.
Cheng Zhiyuan, Sui Licheng, Song Kai, et al. Resonance compensation current transformer energy extraction[J]. Power System Technology, 2021, 45(12): 4896-4902.
[22] 任晓东, 陈树勇, 姜涛. 电子式电流互感器高压侧取能装置的设计[J]. 电网技术, 2008, 32(18): 67-71, 76.
Ren Xiaodong, Chen Shuyong, Jiang Tao. Design of a high side energy extracting device for active elec- tronic current transformer[J]. Power System Tech- nology, 2008, 32(18): 67-71, 76.
[23] 娄杰, 陈常涛. 基于启动电流的电流互感器取能电源优化分析及实验验证[J]. 高电压技术, 2018, 44(6): 1774-1781.
Lou Jie, Chen Changtao. Optimization analysis and experiment verification of current transformer power supply based on starting current[J]. High Voltage Engineering, 2018, 44(6): 1774-1781.
[24] Liorzou F, Phelps B, Atherton D L. Macroscopic models of magnetization[J]. IEEE Transactions on Magnetics, 2000, 36(2): 418-428.
[25] Jiles D C, Atherton D L. Theory of ferromagnetic hysteresis[J]. Journal of Magnetism and Magnetic Materials, 1986, 61(1/2): 48-60.
[26] 雷阳, 段建东, 张小庆, 等. 电流互感器J-A模型参数辨识及大通流动模试验[J]. 中国电机工程学报, 2016, 36(增刊1): 240-245.
Lei Yang, Duan Jiandong, Zhang Xiaoqing, et al. Identification of current transformer J-A model parameters with large current dynamic simulation experiments[J]. Proceedings of the CSEE, 2016, 36(S1): 240-245.
[27] 李奎, 解晨雨, 牛峰, 等. 考虑非线性特性的剩余电流互感器建模及其输出调理电路参数设计[J]. 中国电机工程学报, 2022, 42(10): 3815-3826.
Li Kui, Xie Chenyu, Niu Feng, et al. Modeling of residual current transformer considering nonlinear characteristics and design of output conditioning circuit parameters[J]. Proceedings of the CSEE, 2022, 42(10): 3815-3826.
[28] Ramirez-Laboreo E, Sagues C, Llorente S. A new model of electromechanical relays for predicting the motion and electromagnetic dynamics[J]. IEEE Transa- ctions on Industry Applications, 2016, 52(3): 2545- 2553.
Abstract Electromagnetic leakage protection is an important leakage fault protection technology greatly influenced by component parameters and requires high requirements for the batch production process, resulting in high production costs. The problem of instability of electromagnetic leakage protection characteristics is studied to improve its robustness and to solve the constraints of batch production of electromagnetic leakage protectors.
Electromagnetic leakage protection characteristics, such as leakage operating current and operating time, depend on the parameters of the residual current transformer and its matching resistance and capacitance. If the leakage operating current is a specific value, the matching relationship curve of R1 and C1 is like the letter “U”. As C1 increases, the operating time tC increases and then decreases. The maximum value of operating time tC appears around the resonant capacitor, increasing with the increase of resonant capacitance. The inductance varies for different residual current transformer core magnetic parameters, resulting in different resistance and capacitance to be matched. However, the shape of the curve for the matching relationship between resistance and capacitance is the same, simply shifting on the axis, as shown in Fig.A1a, with a similar variation in the operating time tC, as shown in Fig.A1b.
Although different compensation capacitors C1 are available to meet the requirements of the leakage protection characteristics, the stability of the characteristics varies. The leakage protection characteristics are robust if C1 is smaller than the resonant capacitance, and the tolerance of C1 has less effect on it. At the same time, the leakage protection characteristics are also influenced by the magnetic parameters of the residual current transformer core, such as Bs, Br, and Hc. The stability of the leakage protection characteristics varies under different Bs, Br, and Hc, with Br and Hc having a large impact and Bs having a small impact. For the same value of compensation capacitance, there is a lower limit kmin for Br/Hc. If Br/Hc＜kmin, the leakage operating current and operating time will change rapidly with Br/Hc. While Br/Hc＞1.5kmin, the value of Br/Hc is guaranteed to be greater than kmin when the dispersion of Br and Hc reaches ±20 %. In this case, the leakage protection characteristics are less affected by the dispersion of magnetic parameters, and its robustness is good.
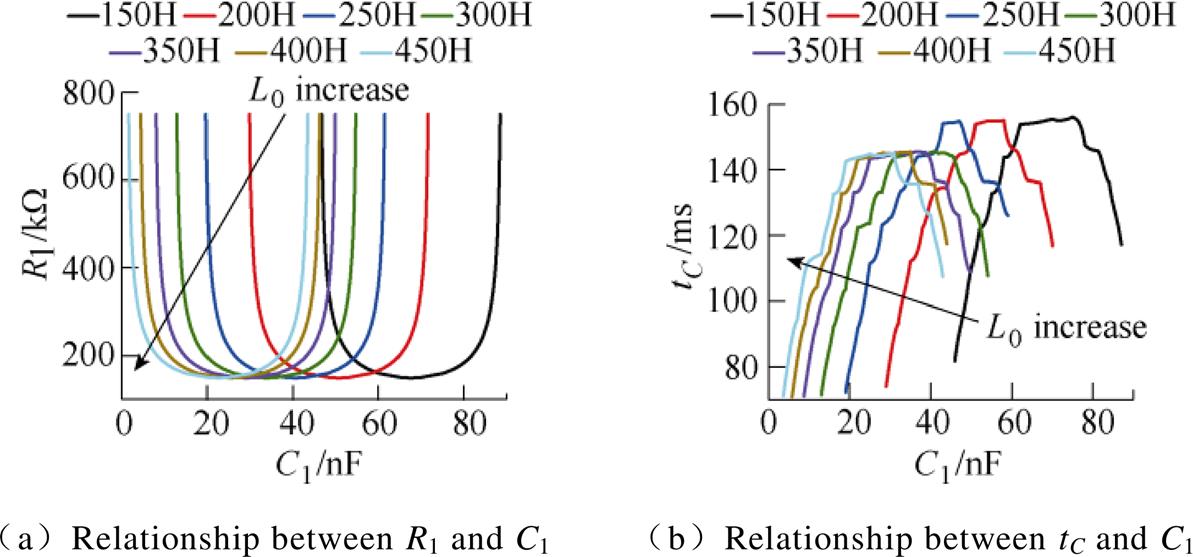
Fig.A1 Relationship between R1 and C1 and tC under different L0
According to the above analysis, the matching design of the residual current transformer and leakage detection circuit parameters are carried out, as shown in Tab. A1. Under the core magnetic parameters of the original scheme, the matching of R1 and C1 is carried out, and the leakage protection characteristics can meet the requirements. However, if the component parameters offset up to 10 % due to the dispersion of component parameters or the temperature of the environment, the value of leakage operating current ID exceeds the rated leakage operating current value IDn, and the leakage protector can not be operated with ID=IDn. With a 10% change in capacitance and the magnetic parameters shifted in the direction of the maximum shift in the protection characteristics, the offset of the leakage operating current value is less than 6 %, and the offset of operating time tC is less than 7.1 % with the optimized scheme 1 and 2. The robustness of the electromagnetic leakage protection characteristics is improved, which can be obtained from the fact that the protection characteristics vary less than the parameters of the components. The consistency and stability of the leakage protection characteristics can be ensured during manufacturing and operation with the optimized scheme, which is conducive to batch production.
Tab.A1 Influence of dispersion of parameters on the stability of protection characteristics under different design schemes
SchemeBr/THc/(A/m)Bs/TR1/kWC1/nFDIDd(%)DtC(%) Original Scheme0.110.700.61925033.054.3Unable to operate Optimized Scheme 10.300.401.0001906.86.07.1 Optimized Scheme 20.240.401.00019010.05.11.3
keywords：Electromagnetic leakage protection, residual current transformer, leakage protection characte- ristics, robustness, parameter matching design
国家自然科学基金（51977059）和河北省自然科学基金（E2020202042）资助项目。
收稿日期 2022-05-19
DOI: 10.19595/j.cnki.1000-6753.tces.220872
中图分类号：TM561
李 奎 男，1965年生，教授，博士生导师，研究方向为电器可靠性与试验技术、电器智能化理论与技术。E-mail: likui@hebut.edu.cn
武 一 女，1964年生，教授，硕士生导师，研究方向为智能控制系统研究与应用。E-mail: wuyi@hebut.edu.cn（通信作者）
改稿日期 2022-08-25
（编辑 崔文静）