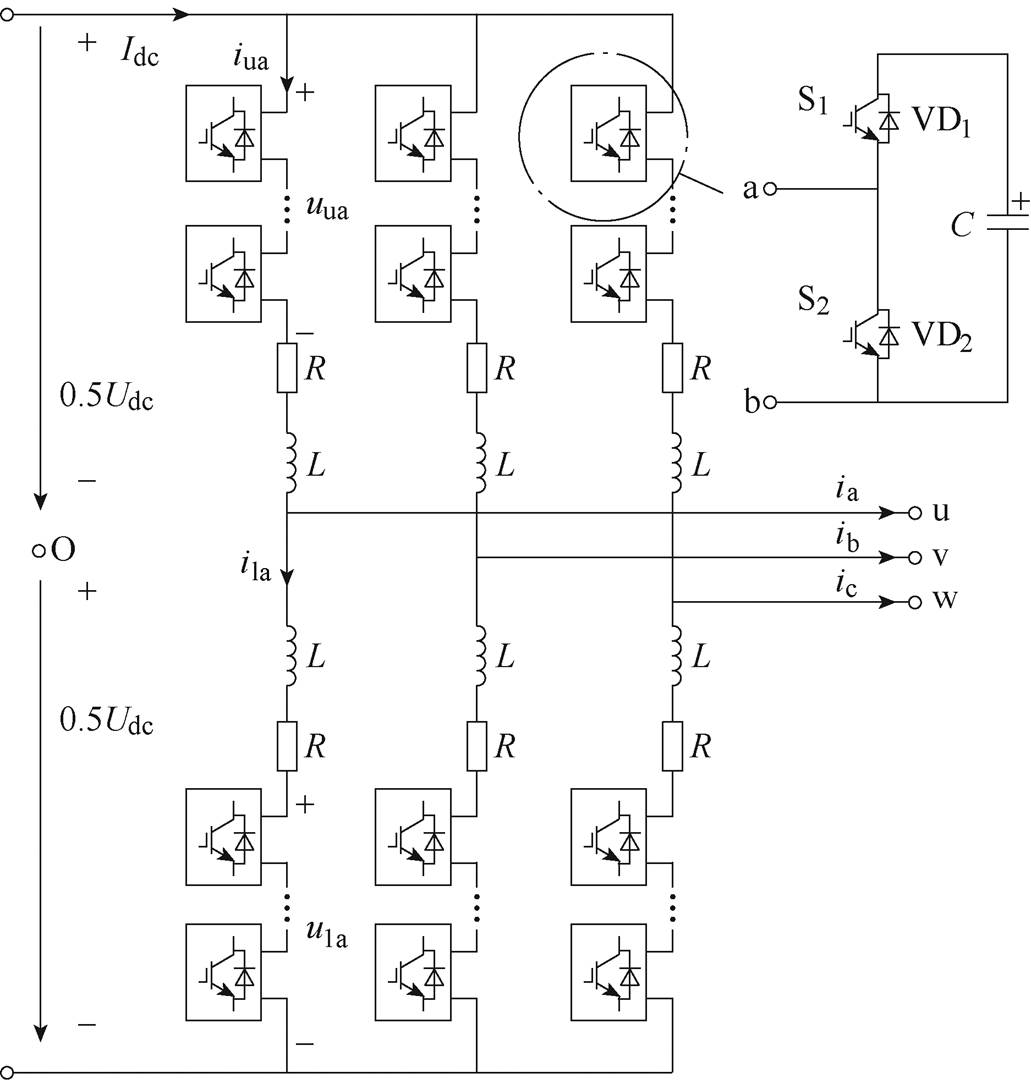
图1 三相MMC拓扑结构
Fig.1 Three phase MMC topology
摘要 模块化多电平换流器（MMC）广泛应用于高压大功率场合。MMC拓扑由大量的子模块（SM）组成，为了提高其运行可靠性，在其SM发生开路故障后，需要快速检测到故障并定位故障SM。现有研究基于经验的阈值设置在不同运行功率间难以推广。针对此，该文提出基于广义电容电压不平衡度的MMC子模块开路故障诊断策略。通过判断桥臂中电容电压最大SM的广义电容电压不平衡度是否超出设定阈值来检测故障，故障定位过程同样是基于该标志。通过理论分析，给出诊断阈值在不同运行功率下的设置方法。所提出的方法可以在不同功率点准确、快速地诊断出MMC子模块开路故障，并降低不同运行功率下阈值设置难度。最后通过硬件在环（HIL）平台验证了该方法的可行性。
关键词：模块化多电平换流器 广义电容电压不平衡度 故障诊断 运行功率
模块化多电平换流器（Modular Multilevel Con- verter, MMC）已在高压柔性直流（High Voltage Direct Current, HVDC）输电工程中得到了广泛应 用[1-4]。MMC开关损耗低，故障穿越能力强，更适用于柔性直流输电领域，因此在大规模风机并网、电力电子变压器等方面都有着广阔的应用前景[5-7]。
MMC拓扑由大量的子模块（Sub-Module, SM）组成，任何一个SM发生故障都会导致桥臂工作异常进而影响MMC的正常运行[8]。因此，快速检测到故障，并定位到故障SM是非常有必要的。功率半导体器件故障主要有短路故障和开路故障两种。其中，功率器件短路故障已有成熟的工业解决方案，而开路故障不易被发现，可能导致其他设备的二次损坏和系统的故障[9]。最近电平调制（Nearest Level Modulation, NLM）由于动态性能好、实现简便等优点，被广泛应用于高电平数的MMC中。因此本文重点研究了采用NLM策略时的MMC子模块开路故障诊断策略。
迄今为止，MMC的SM开路故障诊断方法主要可以分为三类：
第一类是基于硬件的故障诊断策略[10-11]。这些方法虽然简单可靠，但由于其需要引入额外的硬件电路，会导致系统成本显著增加。
第二类是基于人工智能（Artificial Intelligence, AI）的故障诊断策略。文献[12]中提出了基于SM电压相似性的故障诊断策略，通过计算同一桥臂中两两SM的电容电压相关系数来对故障SM进行定位。文献[13]提出了基于聚类算法的故障诊断策略，通过聚类算法对SM特征变量的二维轨迹模式进行识别，以此进行故障诊断。文献[14]提出了基于滑动时间窗（Sliding Time Window, STW）的故障诊断策略，根据相邻STW间的特征关系提出MMC的特征，并使用二维神经网络对MMC中的开路故障进行检测和定位。这些方法尽管无需额外硬件，但算法计算量较大，会导致控制器计算负担加重，进而影响故障诊断的快速性与准确性，这一点在故障SM数量较大时尤为显著。
第三类是基于模型的故障诊断策略。文献[15-16]应用滑模观测器检测并定位SM故障。文献[17]采用卡尔曼滤波器检测SM故障，并利用子模块电容电压值比较的方法定位SM。这些检测方法都是基于被测状态变量与估计值的比较，无需额外的传感器，但它们普遍存在计算复杂度高、诊断时间长等缺点。文献[18]中提出了基于单环定理的故障诊断策略，利用单环定理提供的平均谱半径来检测故障，利用箱线图的异常点识别来定位故障SM。文献[19]中通过判断子模块序列队首（First in the SM Number, FSN）来检测故障，并针对同一桥臂中多SM同时发生故障的情形提出了辅助定位策略。文献[20-21]中，首先计算桥臂电压的估计值和计算值的差异，然后通过与预设阈值比较以检测故障。文献[22]中是依据一组电压的估计值和计算值间的差异是否超出阈值判断是否存在故障。文献[23]则是依据输出电流或环流的估计值和计算值间的差异是否超出阈值判断是否存在故障，然后通过改进的保塔准则来对故障SM进行定位。文献[24]提出了一种基于改进泄放电阻电路（Rearranged Bleeding Resistor Circuit, RBRC）的故障检测方法，通过RBRC和SM开关函数的逻辑输出来识别故障。基于模型的故障诊断方法具备无需额外硬件、计算负担小、诊断时间快等优势，但其往往需要手动设置经验阈值，经验阈值设定直接决定了诊断方法的准确性，现有研究中的定位方法多是基于故障SM电容电压升高会超出阈值或故障SM与正常SM电容电压差会超出阈值，但这些定位依据会受运行功率影响，由于这些文献中并未给出这些定位依据与运行功率间具体关系，因而当MMC运行于不同功率时，现有策略阈值的设置及推广较为困难。
针对此，本文提出了基于广义电容电压不平衡度的MMC子模块开路故障诊断策略。该策略通过选取广义电容电压不平衡度作为诊断标志，能够快速准确地检测到子模块开路故障。与现有策略中手动设置经验阈值不同，本文通过理论分析，给出了不同运行功率下诊断阈值的准确设置方法。所提出的策略可以在不同功率点准确、快速地诊断出MMC子模块开路故障，并降低了不同运行功率下阈值设置难度。此外，所提策略可以应对桥臂中多个SM发生故障的情况，并通过利用均压控制的排序结果，大大减少了计算量，且可以在一个工频周期内完成诊断过程。
本文首先简要介绍了MMC的基本工作原理和电容电压平衡控制；然后，阐述了MMC子模块开路故障的两种类型，并详细分析了两种故障类型及不同功率流向条件下，故障子模块的电容电压变化；在此基础之上，提出了基于广义电容电压不平衡度的MMC子模块开路故障诊断策略，详细阐述了诊断过程，并给出了诊断阈值在不同运行功率下的准确设定依据；最后，通过硬件在环（Hardware-In- the-Loop, HIL）平台验证了该方法的可行性。
三相MMC拓扑结构如图1所示。MMC拓扑结构采用三相六桥臂结构，每相包含上、下两个桥臂，每个桥臂由N个子模块、桥臂电抗器L以及桥臂等效电阻R组成。
图1 三相MMC拓扑结构
Fig.1 Three phase MMC topology
对j（ j=a, b, c）相，根据KVL定律，上、下桥臂电压表示为
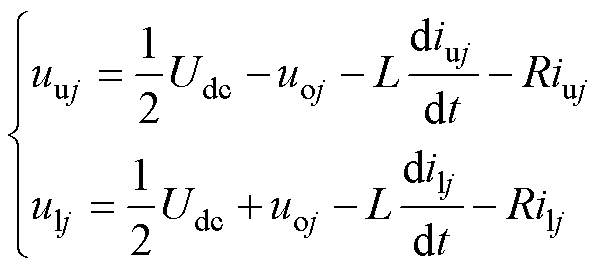（1）
式中，uuj和ulj分别为j相上、下桥臂中SM的总电压；Udc为直流母线电压；uoj为相对于中性点的输出电压；iuj和ilj分别为j相上、下桥臂电流。
对j相，根据KCL定律，上、下桥臂电流表示为
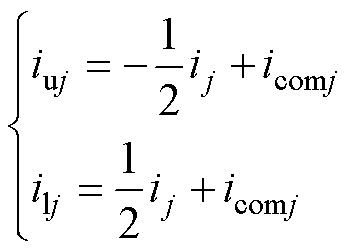（2）
式中，icomj为流过j相上、下桥臂的内部共模电流，由直流分量（Idc/3）和循环电流icirj构成。
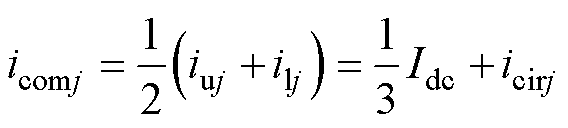（3）
半桥子模块结构如图1所示，由2个绝缘栅双极型晶体管（Insulated Gate Bipolar Transistor, IGBT）、2个反并联二极管和1个直流电容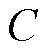
组成。正常运行时，SM的输出电压取决于IGBT的开关状态，可以表示为
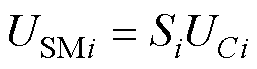（4）
式中，USMi为桥臂中序号为i对应SM的输出电压；UCi为该SM电容电压；Si为该SM对应开关函数。当S1导通、S2截止时，Si=1，SM被投入；当S1截止、S2导通时，Si=0，SM被切除。
以a相上桥臂为例说明MMC电容电压平衡控制具体实现过程：首先检测该桥臂中所有SM的电容电压，并计算出下一时刻需要投入的SM个数Non；接下来通过检测桥臂中电流方向，判断当前时刻SM电容充/放电状态；最后对桥臂中所有SM按照其电容电压值排序。当iua≥0时，桥臂电流对SM电容进行充电，此时投入桥臂SM电容电压最小的Non个SM，其余N-Non个SM切除；当桥臂电流iua＜0时，桥臂电流对SM电容进行放电，此时投入桥臂中SM电容电压最大的Non个SM，其余N-Non个子模块切除。
SM开路故障的两种类型如图2所示，SM开路故障类型可以分为S1故障、S2故障两种。SM在正常运行和开路故障等不同条件下的行为见表1。
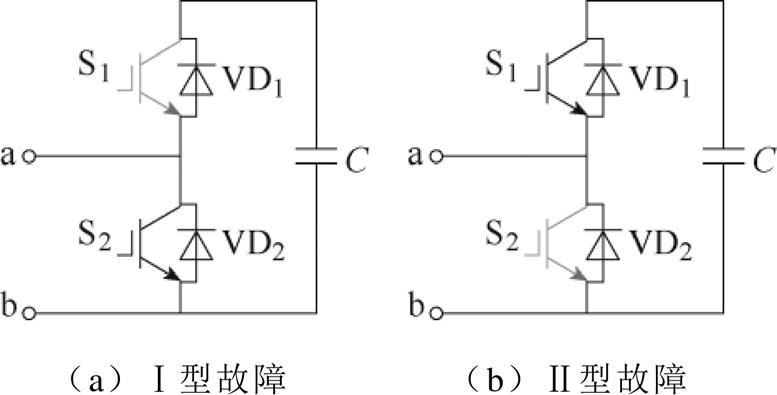
图2 SM开路故障的两种类型
Fig.2 Two types of SM open circuit faults
式（4）中，对于正常SM，其输出电压由开关函数和电容电压共同决定。而当SM发生开路故障时，存在一些异常行为，见表1。当S1故障时，本文称之Ⅰ型故障，故障SM在桥臂电流为正时正常工作，而在桥臂电流为负时故障SM电容始终被旁路；当S2故障时，本文称之Ⅱ型故障，故障SM在桥臂电流为负时正常工作，而在桥臂电流为正时故障SM电容始终被充电。
表1 不同状态下SM行为
Tab.1 SM behavior in different states
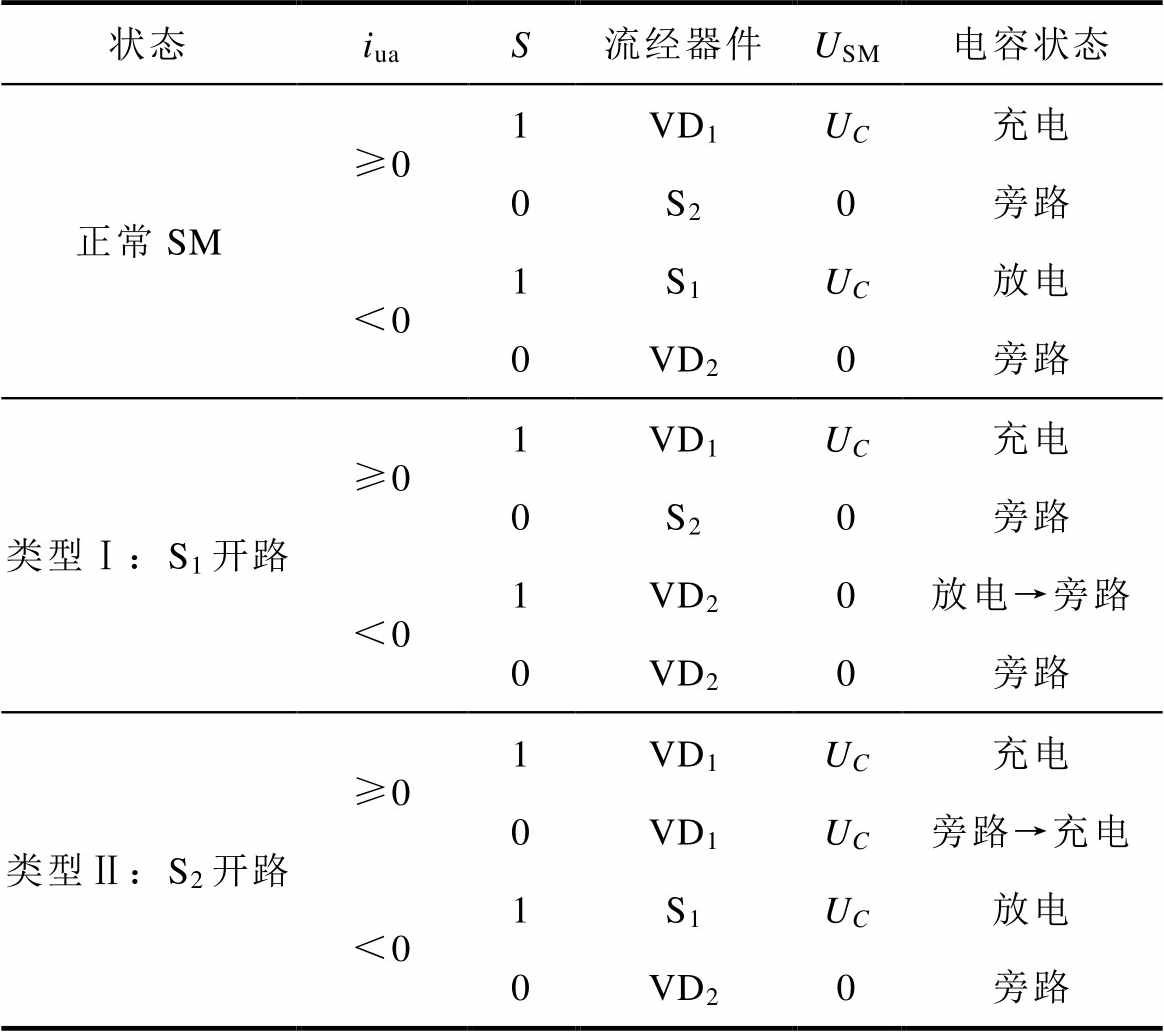
状态iuaS流经器件USM电容状态 正常SM≥01VD1UC充电 0S20旁路 ＜01S1UC放电 0VD20旁路 类型Ⅰ：S1开路≥01VD1UC充电 0S20旁路 ＜01VD20放电→旁路 0VD20旁路 类型Ⅱ：S2开路≥01VD1UC充电 0VD1UC旁路→充电 ＜01S1UC放电 0VD20旁路
在一个工频周期内，a相上桥臂单个SM的电容电压的变化可表示为
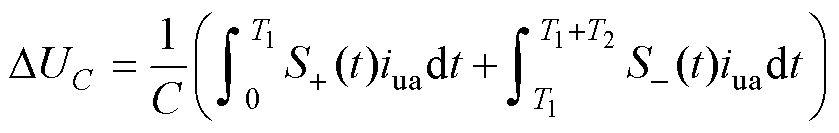（5）
式中，T1为一个工频周期中桥臂电流为正的时间；T2为一个工频周期中桥臂电流为负的时间；S+(t)为桥臂电流为正时开关函数；S-(t)为桥臂电流为负时开关函数。
根据式（2）、式（3），并忽略环流的影响，iua可以表示为
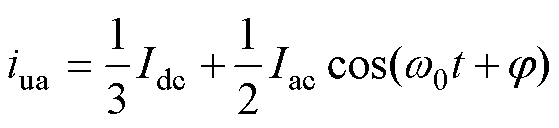（6）
式中，Iac为交流输出电流的幅值；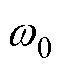
为基波频率；
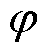为交流输出电流和电网电压之间的角度。
当发生Ⅰ型故障时，根据表1，T2时间段内故障SM电容始终被旁路，可等效为S-(t)恒为0，根据式（5），此时故障SM电容电压在一个工频周期内的变化取决于S+(t)，即为
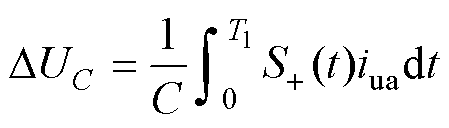（7）
根据均压控制，如果故障SM电容电压低于其他SM的电容电压，则它会像正常SM一样增加，根据式（7）可知，DUC＞0，而其余正常SM的DUC=0，这会导致故障SM电容电压成为桥臂SM中电容电压最大值，此后，由于均压控制，只要故障SM电容电压为最大值，则其在T1时间段内投入优先级最低，故障SM始终被切除，故障SM电容始终被旁路，即S+(t)恒为0，因此由式（7）可得DUC=0，此时故障SM电容电压变为零，能够实现电容电压平衡。但这种平衡状态会对桥臂电压和输出电压产生影响，故本文将该平衡状态称之为不当平衡。
当发生Ⅱ型故障时，根据表1，T1时间段内，故障SM电容始终充电，可等效为S+(t)恒为1，而T2时间段内，故障SM正常工作。此时式（5）变为
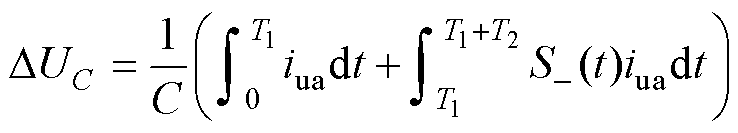（8）
1）当MMC工作于逆变模式时，式（6）中，Idc＞0。令故障SM在T1时间段内电容电压变化为DUC1，在T2时间段内电容电压变化为DUC2，当S-(t)=1，DUC2可取最小值DUC2_min，根据式（6）、式（8），DUC1及DUC2_min可分别表示为
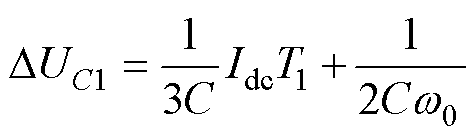
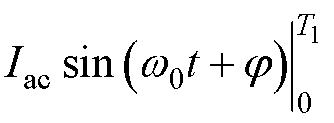（9）
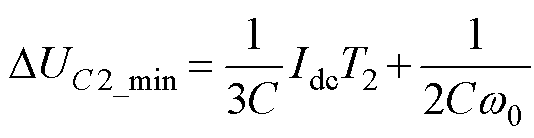
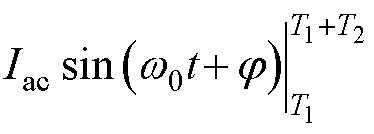（10）
将式（9）与式（10）相加可得DUC表达式为
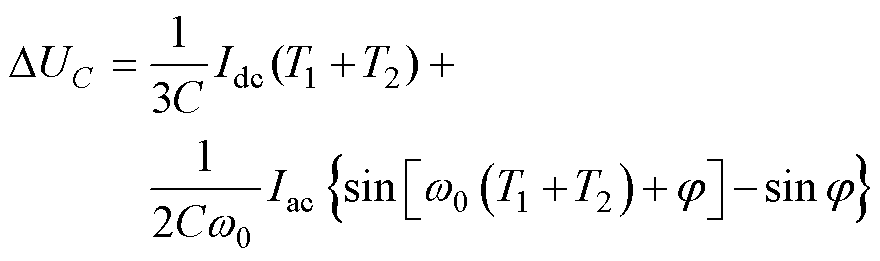（11）
由于T1、T2构成了一个工频周期，因此有
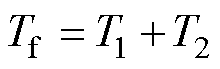（12）
式中，Tf为工频周期。
将式（12）代入式（11）可得
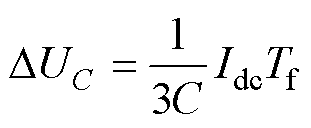（13）
可以看出故障SM即使在T2时间段内保持投入，其电容持续放电的情况下，依然有DUC＞0，因此故障SM电容电压无法保持平衡，且会不断增加。
2）当MMC工作于整流模式时，式（6）中，Idc＜0。由式（13）可知，若故障SM在T2时间段内保持投入，其电容持续放电，DUC＜0，因此当S-(t)取适当值时，故障SM电容电压能够保持平衡。
综上所述，采用NLM策略的MMC，在不同功率流向条件下，发生不同类型故障时，其故障SM的电容电压见表2。对于Ⅱ型故障而言，不同功率流向条件下，故障SM电容电压现象存在较大差异，因此需要提出有效的诊断方案。
表2 不同条件下子模块电容电压
Tab.2 SM capacitor voltage under different conditions
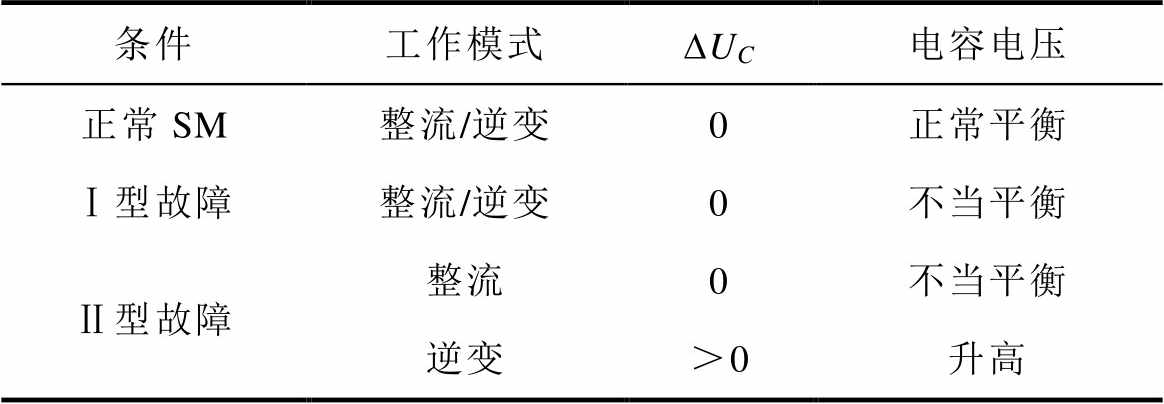
条件工作模式DUC电容电压 正常SM整流/逆变0正常平衡 Ⅰ型故障整流/逆变0不当平衡 Ⅱ型故障整流0不当平衡 逆变＞0升高
电容电压不平衡度s，定义为所有时刻各SM电容电压之间的最大偏差与SM电容电压额定值之比，所有时刻各SM电容电压之间的最大偏差及电容电压不平衡度分别为
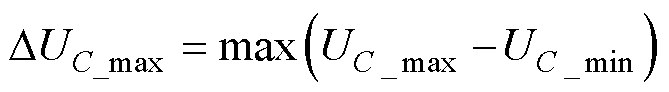（14）
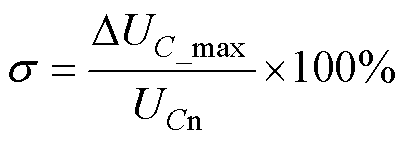（15）
式中，UC_max、UC_min为同一时刻所有SM电容电压中的最大值和最小值；DUC_max为所有时刻各SM电容电压之间的最大偏差；UCn为SM电容电压额定值。
由式（14）、式（15）可知，电容电压不平衡度只能针对于电容电压最大的SM，同时计算时需要一个工频周期，时间较长，因此本文参照电容电压不平衡度的定义，在其基础之上引入广义电容电压不平衡度的概念。任意子模块的广义电容电压不平衡度具体定义如下：当前时刻该SM与最小SM电容电压之间的偏差与SM电容电压额定值之比为
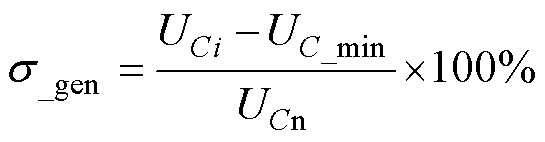（16）
对比式（15）、式（16）可以看出，对于正常SM而言，其广义电容电压不平衡度不大于系统电容电压不平衡度。
当发生Ⅰ型故障时，如2.1节分析，若故障发生时桥臂电流为正，则故障SM与正常SM状态相同，而当桥臂电流由正转负后，故障SM电容将始终被旁路，其电容电压保持不变，而其他正常SM则会根据均压控制依次被投入放电，电容电压将变小，因此电容电压不平衡度增大，故障SM为桥臂中电容电压最大子模块；若故障发生时桥臂电流为负，故障SM电容将始终被旁路，其电容电压保持不变，而其他正常SM则会根据均压控制依次投入放电，电容电压将变小，进而导致电容电压不平衡度增大，故障SM变为桥臂中电容电压最大子模块。
当发生Ⅱ型故障时，若故障发生时桥臂电流为正，则无论MMC工作于整流模式或逆变模式，故障SM电容始终被充电，电容电压不断升高，而其他正常SM则会根据均压控制依次被投入充电，电容电压增幅小于故障SM，因此电容电压不平衡度增大，故障SM为桥臂中电容电压最大子模块；若故障发生时桥臂电流为负，则故障SM与正常SM状态相同，而当桥臂电流由负转正后，故障SM电容始终被充电，电容电压不断升高，而其他正常SM则会根据均压控制依次被投入充电，电容电压增幅小于故障SM，因此电容电压不平衡度增大，故障SM为桥臂中电容电压最大子模块。
综上所述，无论在何种功率流向发生何种类型子模块开路故障，故障SM均为其产生故障特征时间段内对应的电容电压最大子模块，且电容电压不平衡度会增大，据此可提出故障诊断方法如下，诊断检测流程如图3所示。
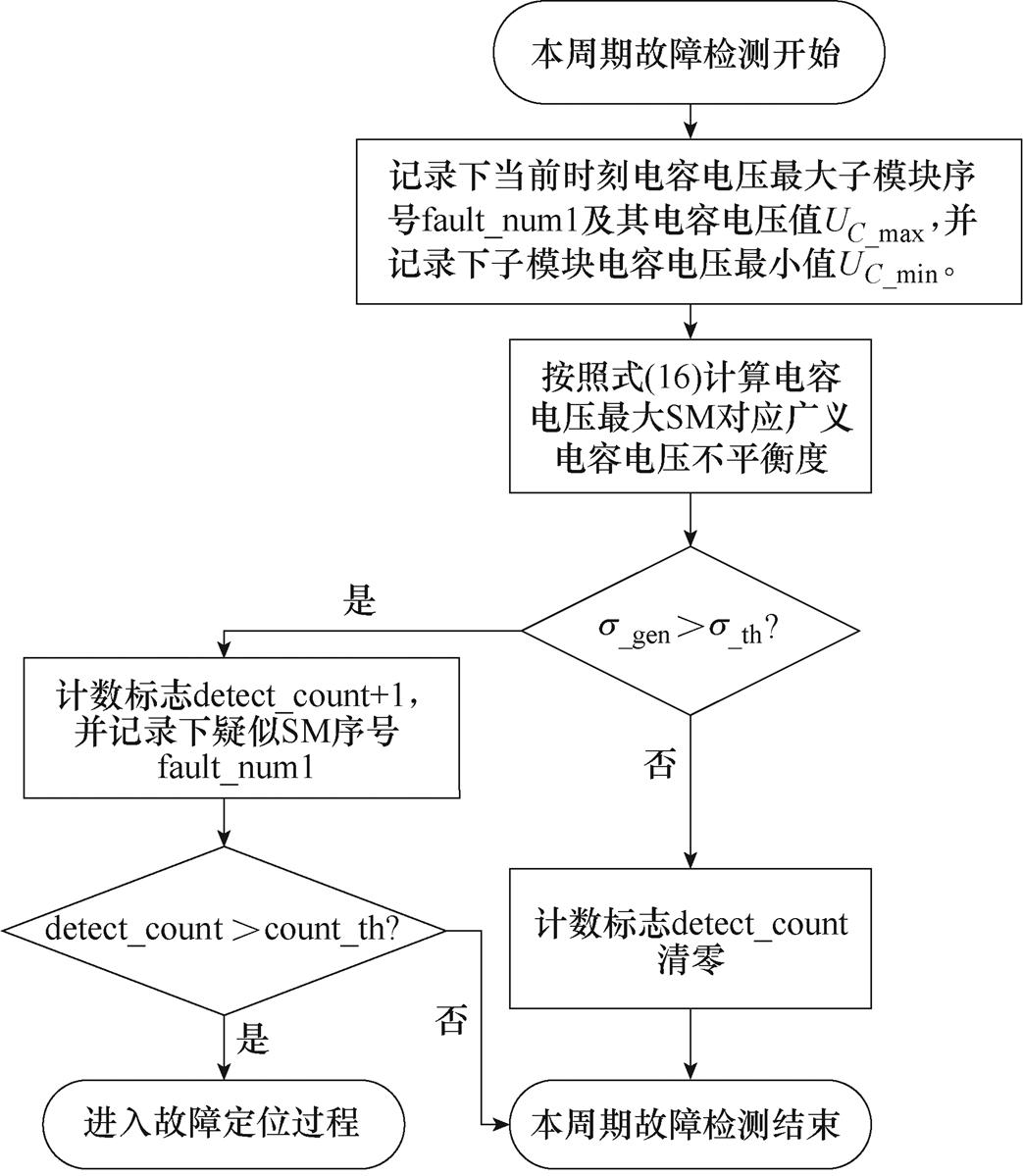
图3 检测流程
Fig.3 Detection flowchart
故障诊断具体实现步骤如下：
（1）根据均压控制排序结果，记录下当前时刻电容电压最大子模块序号fault_num1及其电容电压值UC_max，并记录下子模块电容电压最小值UC_min。
（2）由步骤（1）中记录的UC_max及UC_min，根据式（16）计算广义电容电压不平衡度s_gen。
（3）判断s_gen是否比设定阈值s_th大，若s_gen＜s_th，则说明此时不存在故障，将检测计数标志detect_count清零，本周期检测结束；若s_gen＞s_th，则将检测计数标志detect_count+1，同时记录下疑似SM序号fault_num1。
（4）判断detect_count是否比设定计数上限count_th大，若其小于count_th，说明未达计数上限，本周期故障检测过程结束；若其大于count_th，说明检测到故障，则进入故障定位过程。
计数阈值的存在是为了进一步消除误差与干扰的影响，同时避免短路故障SM造成的电容电压大幅下降造成的误诊断，防止故障误诊断情况的存在，可取count_th=3～5，本文取count_th=3。
根据故障SM数量及发生故障类型可将其分为以下两类，并分别进行说明：
（1）同一桥臂中单个SM发生故障或桥臂中两个SM同时发生Ⅰ型故障和Ⅱ型故障。在这种情况下，对于任意时刻其实际上只存在一个故障SM，因为Ⅰ型故障和Ⅱ型故障体现故障特性的时间段不同。根据3.1节中分析可知，当只存在一个故障SM时，该SM一定为桥臂中电容电压最大子模块，因此可以直接定位到故障SM。
（2）同一桥臂中两个或两个以上SM同时发生同种类型故障。以同一桥臂中两个SM同时发生故障为例说明，按照3.1节中分析，故障SM电容电压高于正常子模块电容电压，因此这两个故障SM为桥臂中SM电容电压最大及次之的子模块，据此可提出故障定位流程如图4所示。
故障定位具体过程如下：
（1）根据均压控制中排序结果，记录当前时刻电容电压大小排在第k位的SM序号number_k及其电容电压UC_number_k以及子模块电容电压最小值UC_min。
（2）按照式（16）计算SM序号number_k的广义电容电压不平衡度。
（3）判断广义电容电压不平衡度是否比设定阈值s_th大，若大于阈值，说明该SM为故障SM，将定位计数标志locate_count+1，之后再判断locate_ count是否比设定计数上限count_th大，若其小于count_th，说明未达计数上限，本周期故障定位过程结束，若其大于count_th，说明该SM为故障SM，将定位计数标志清零，k=k+1，继续判断下个位置的SM是否为故障SM；若广义电容电压不平衡度小于阈值s_th，说明该SM为正常SM，桥臂中只存在k-1个故障，输出故障SM数量及其对应序号，故障定位过程结束。
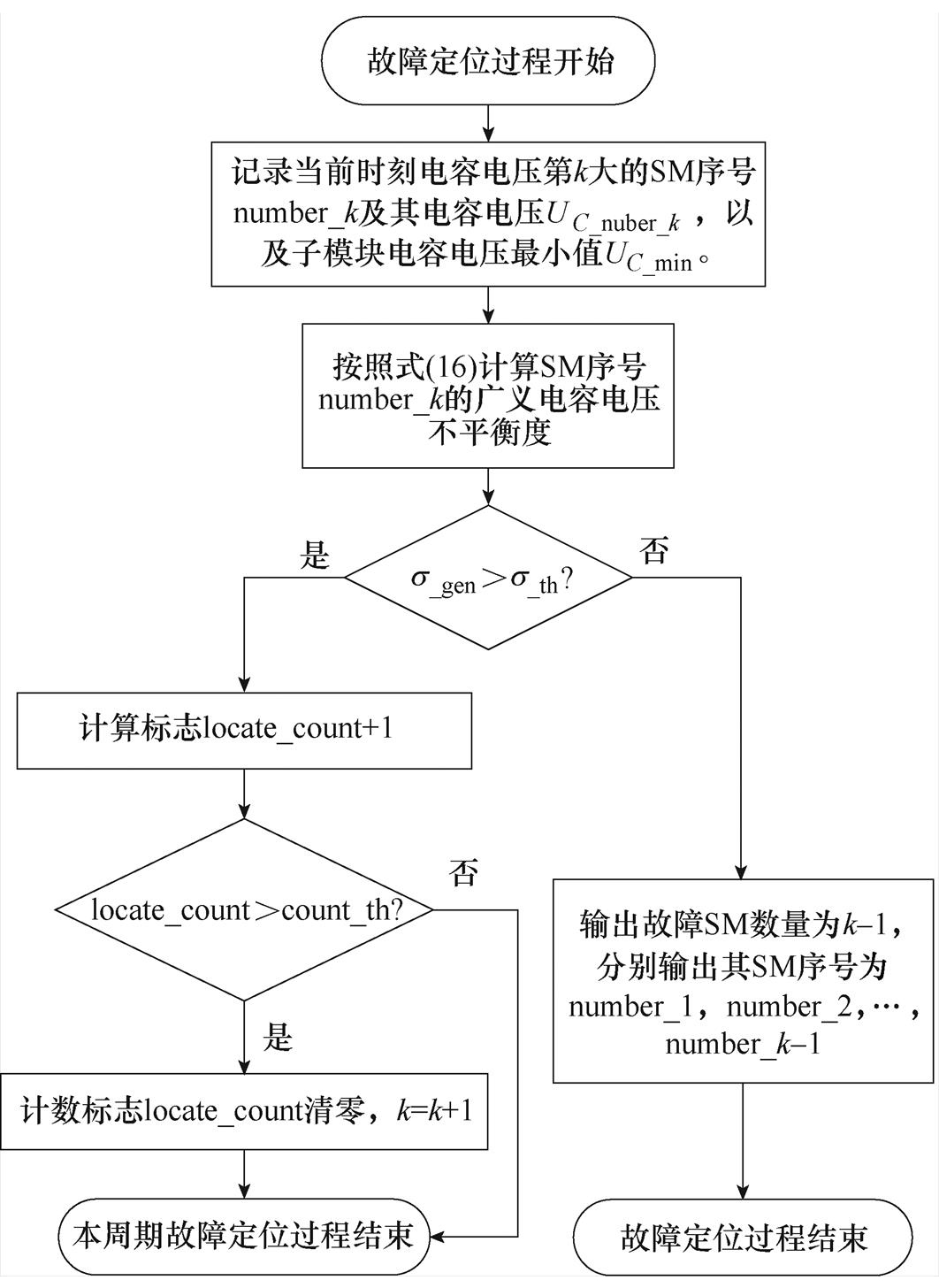
图4 定位流程
Fig.4 Location flowchart
由于均压控制，当MMC处于稳态运行时，电容电压不平衡度指标较低，而在发生几种类型故障时，电容电压不平衡度均会升高，因此阈值设定直接决定了上述诊断过程的准确性与快速性。
为保证正常运行时，故障诊断不发生误诊断现象，阈值设定时应大于正常运行时电容电压不平衡度snormal，而为保证开路故障发生时，故障诊断能够顺利动作，故障诊断设定阈值时应小于两种功率流向下发生两种类型开路故障时电容电压不平衡度中的最小值sfault，即阈值设定限制为
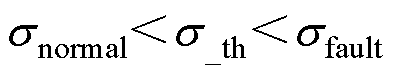（17）
由表2可知，发生Ⅰ型故障的SM在两种功率流向下电容电压最终均会保持不变；发生Ⅱ型故障的SM在MMC工作于逆变模式时，其电容电压会不断上升，而在MMC工作于整流模式时，其电容电压最大值相较于正常SM会上升，因此，整流模式下发生Ⅱ型故障时对应电容电压不平衡度在所有功率流向和故障类型中最小，即此种故障下电容电压不平衡度为sfault。
假设在桥臂电流由负转正时，故障SM电容电压为UC_faultlow，然后，在桥臂电流为正的时间段内，故障SM电容电压会不断升高，在桥臂电流由正转负时，故障SM电容电压达到最大值UC_faulthigh，则结合式（8），UC_faulthigh可表示为
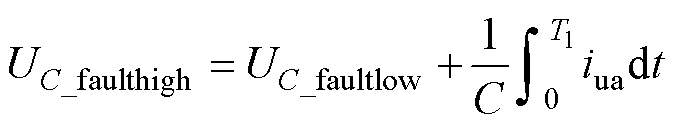（18）
由2.2节中分析可知，此时故障SM电容电压能够同正常SM一样平衡，只是其最大值相较于正常SM会上升，假设正常SM一个工频周期内最大值为UC_safehigh，最小值为UC_safelow，则sfault可以表示为
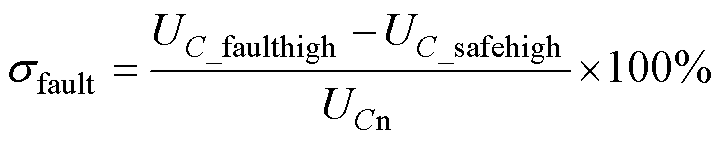（19）
根据文献[7]，UC_safelow、UC_safehigh分别表示为
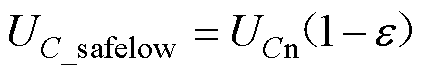（20）
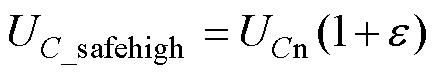（21）
式中，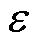
为电容电压波动率。而正常SM工频周期内最小值与故障SM工频周期内最小值基本相等，即UC_safehlow≈UC_faultlow，则由式（20）、式（21）得
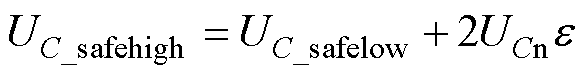（22）
将式（18）、式（22）代入式（19）可得
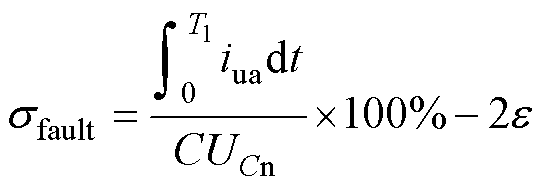（23）
将式（6）代入式（23），可得
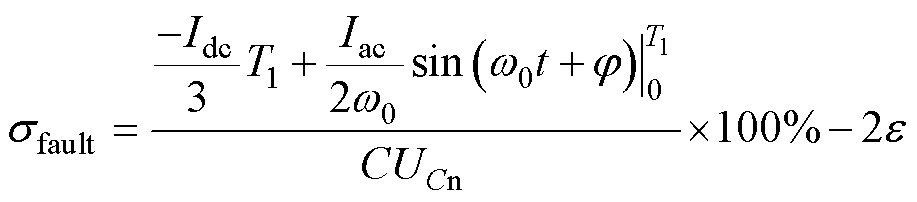（24）
双端MMC-HVDC系统如图5所示，图中，A端MMC采用定直流电压+定无功功率控制，工作于整流模式，B端MMC采用定有功功率+定无功功率控制，工作于逆变模式，以此为例说明不同功率下诊断阈值的设定方法。
图5 双端MMC-HVDC系统
Fig.5 Double-ended MMC-HVDC system
根据文献[7]，e 可表示为
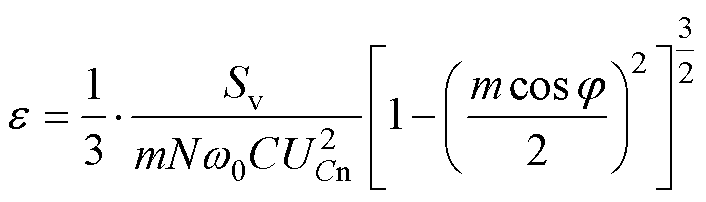（25）
式中，Sv和j 分别为Pv和Qv构成的视在功率及其功率因数角；m为调制比。
令A端MMC无功功率指令值为0，则有Sv=Pv,m≈1, cosj=1。则式（25）转化为
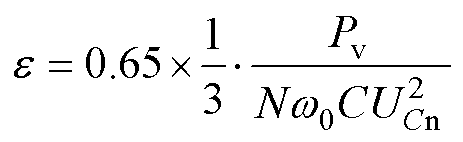（26）
将式（26）代入式（24），可得
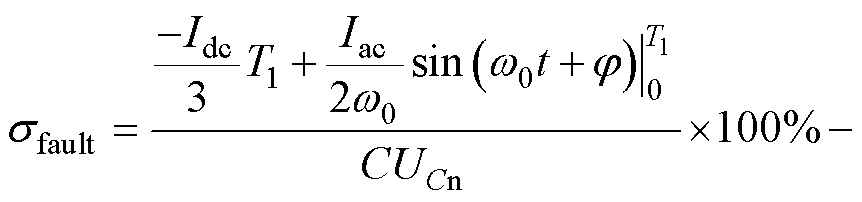
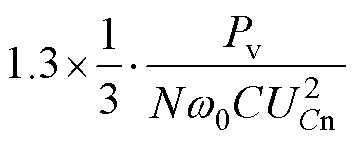（27）
而由于T1时刻式（6）=0，再结合j =0，则有
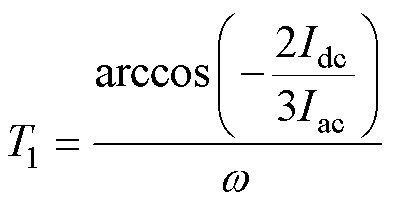（28）
而根据功率传输公式[9]有
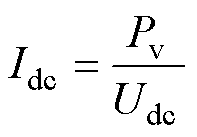（29）
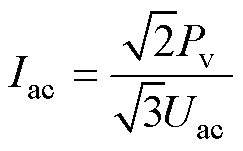（30）
式中，Uac为交流侧基频电压幅值。将式（29）、式（30）代入式（28），有
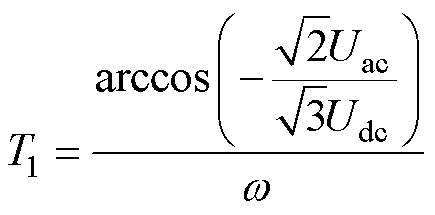（31）
从式（31）可以看出，T1为一定值，再将式（29）、式（30）代入式（27）可得
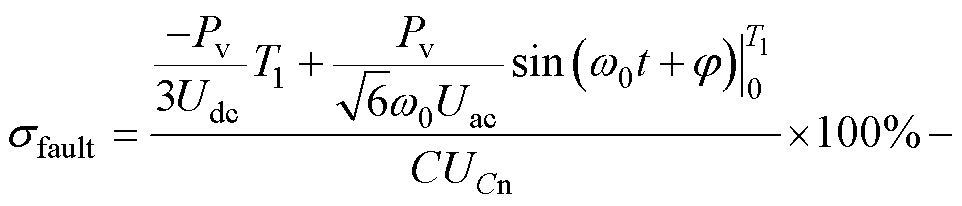
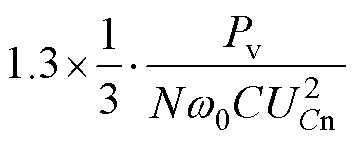（32）
由式（32）中可以得出，sfault与传输功率Pv的定量关系。而从式（17）中不难看出，s_th若接近于snormal，故障诊断速度将会上升，但对应抗干扰能力将会减弱，而s_th若接近于sfault，故障诊断速度将会下降，但对应抗干扰能力将会增强，实际设定时，可先由式（32）对应计算出此时运行功率下对应sfault，然后根据实际需求设置s_th。
与现有研究难以在不同运行功率间推广的依据相比，本文所提策略通过分析给出了诊断阈值与运行功率间的定量关系。基于此，当MMC运行功率发生改变时，可以相应地准确设置阈值，进而实现在不同运行功率下SM开路故障的准确诊断，同时降低了设定的难度，便于推广。
为了验证所提MMC子模块开路故障诊断策略的有效性，本文利用HIL平台进行实验验证，实验平台示意图如图6所示。HVDC系统的功率级模型经由上位机编译后，由目标机实时仿真，控制系统通过DSP TMS320F28335控制板实现。仿真模型结构如图5所示，调制方式采用NLM，控制周期设定为30 ms，仿真系统具体参数见表3。按照3.3节中故障阈值设定限制本文将所提策略中s_th设置为0.7sfault。
图6 硬件在环实验平台示意图
Fig.6 Diagram of hardware-in-loop experimental system
4.1.1 额定负载下发生Ⅰ型故障
由2.2节中分析可知，发生Ⅰ型故障时功率流向不会产生影响，因而整流模式下MMC与逆变模式下MMC故障现象及诊断过程一致，故只考虑A端MMC发生Ⅰ型故障，同时为验证所提策略可以适用于不同运行功率，分别考虑额定负载（Pv= 1.0(pu)）和空载（Pv=0.3(pu)）下发生故障的情形。令额定负载下A端MMC a相上桥臂序号为1、3的子模块发生Ⅰ型故障，实验波形如图7所示。在故障发生后，由于故障发生时桥臂电流为负，故障SM电容被旁路，其电容电压保持不变，与理论分析一致。从图7中s_th及s_gen波形可以看出，在故障发生前，MMC正常运行时，s_gen不会超出设定阈值s_th，正常运行时不会发生误诊断，诊断显示故障SM数量始终为零。而在故障发生后，s_gen超出设定阈值，系统可以快速检测到故障，随后进入故障定位过程，确定了当前桥臂中故障SM数量为2，序号分别为1和3，诊断用时为1.23 ms，验证了所提策略在这种情况下的适用性。
表3 仿真参数
Tab.3 Simulation parameters
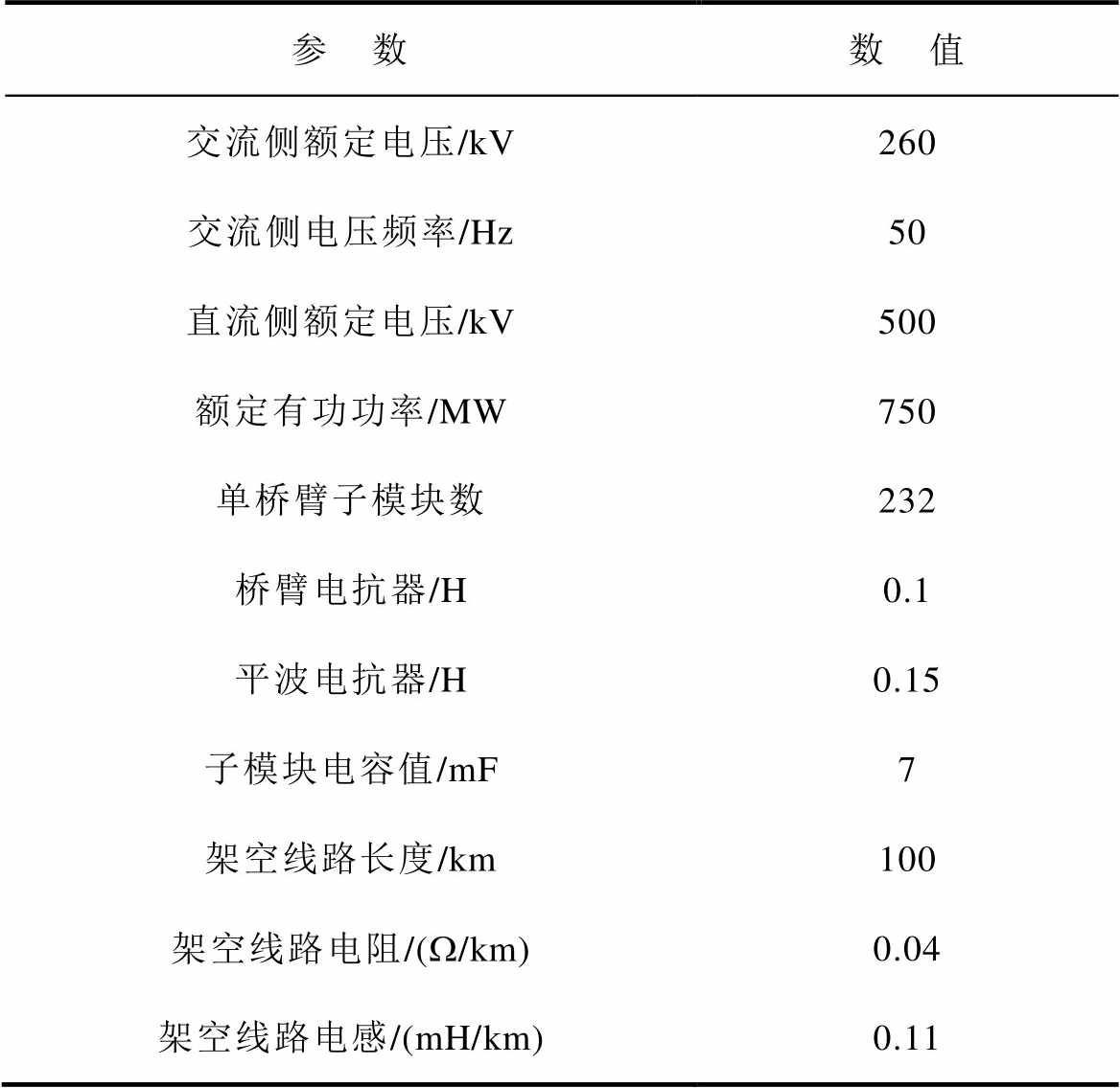
参 数数 值 交流侧额定电压/kV260 交流侧电压频率/Hz50 直流侧额定电压/kV500 额定有功功率/MW750 单桥臂子模块数232 桥臂电抗器/H0.1 平波电抗器/H0.15 子模块电容值/mF7 架空线路长度/km100 架空线路电阻/(W/km)0.04 架空线路电感/(mH/km)0.11
4.1.2 轻载条件下发生Ⅰ型故障
令轻载下A端MMC a相上桥臂序号为1、3的子模块发生Ⅰ型故障，实验波形如图8所示。从图8中s_th及s_gen波形可以看出，在故障发生后，s_gen超出设定阈值，系统可以快速检测到故障，随后进入故障定位过程，确定了当前桥臂中故障SM数量为2，序号分别为1和3，诊断用时为1.29 ms，验证了所提策略在这种情况下的适用性。同时综合图7、图8可以看出，所提策略可准确诊断到不同功率下的故障。
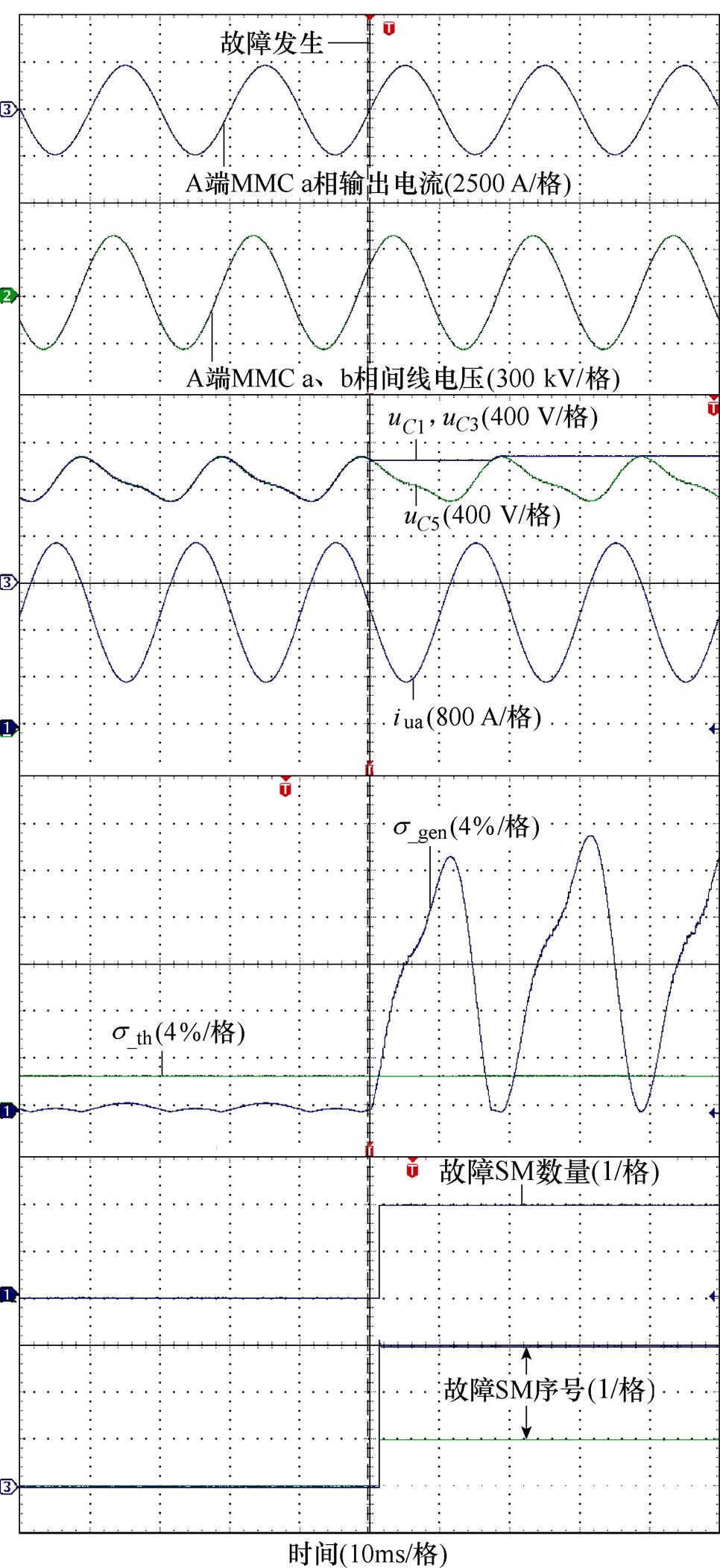
图7 整流模式MMC额定负载发生Ⅰ型故障实验波形
Fig.7 Experimental waveforms of type Ⅰ fault with rated load of MMC in rectifier mode
4.2.1 额定负载下发生Ⅱ型故障
由2.2节中分析可知，发生Ⅱ型故障时，功率流向会对故障现象及诊断过程产生较大影响，故分别考虑整流与逆变模式下MMC Ⅱ型故障情形，同时为验证所提策略可以适用于不同运行功率，分别考虑额定负载（Pv=1.0(pu)）和空载（Pv=0.3(pu)）下发生故障的情形。令额定负载下A端MMC a相上桥臂序号为1、3的子模块发生Ⅱ型故障，实验波形如图9所示。可以看出，故障时桥臂电流为负，故障SM能正常动作，而当桥臂电流变为正后，由于故障SM电容始终被充电，导致其电容电压迅速上升，最终会导致故障SM电容电压最大值增大，但仍能保持平衡，与理论分析一致。从图9中s_th及s_gen波形可以看出，在故障发生前，MMC正常运行时，s_gen不会超出设定阈值s_th，正常运行时不会发生误诊断，诊断显示故障SM数量始终为零。而在故障发生后，s_gen超出设定阈值，系统可以检测到故障，进入故障定位过程，确定了当前桥臂中故障SM数量为2，序号分别为1和3，诊断用时为17.43 ms，但由于故障时臂电流为负，因此实际诊断用时为6.28 ms，验证了所提策略在这种情况下的适用性。
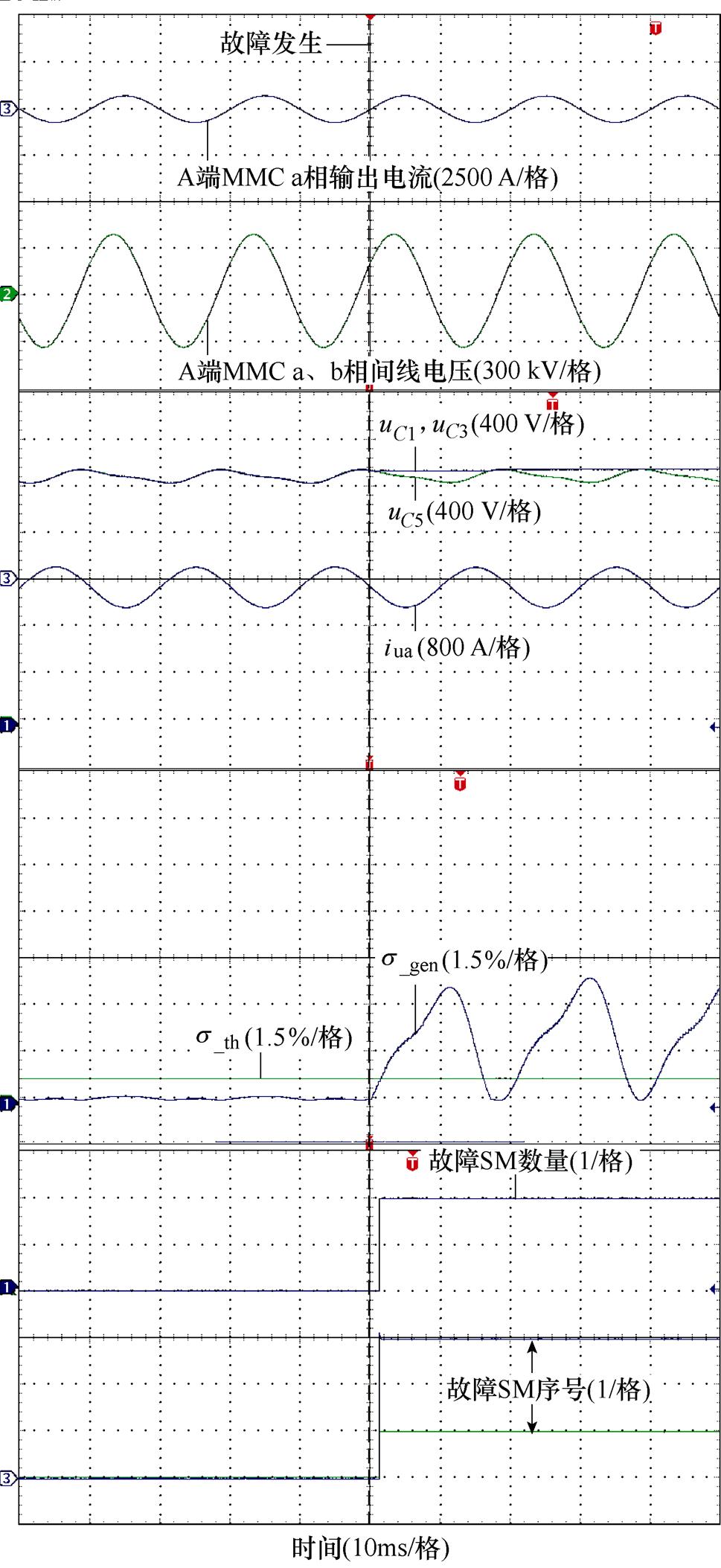
图8 整流模式MMC轻载发生Ⅰ型故障实验波形
Fig.8 Experimental waveforms of type Ⅰ fault with light load of MMC in rectifier mode
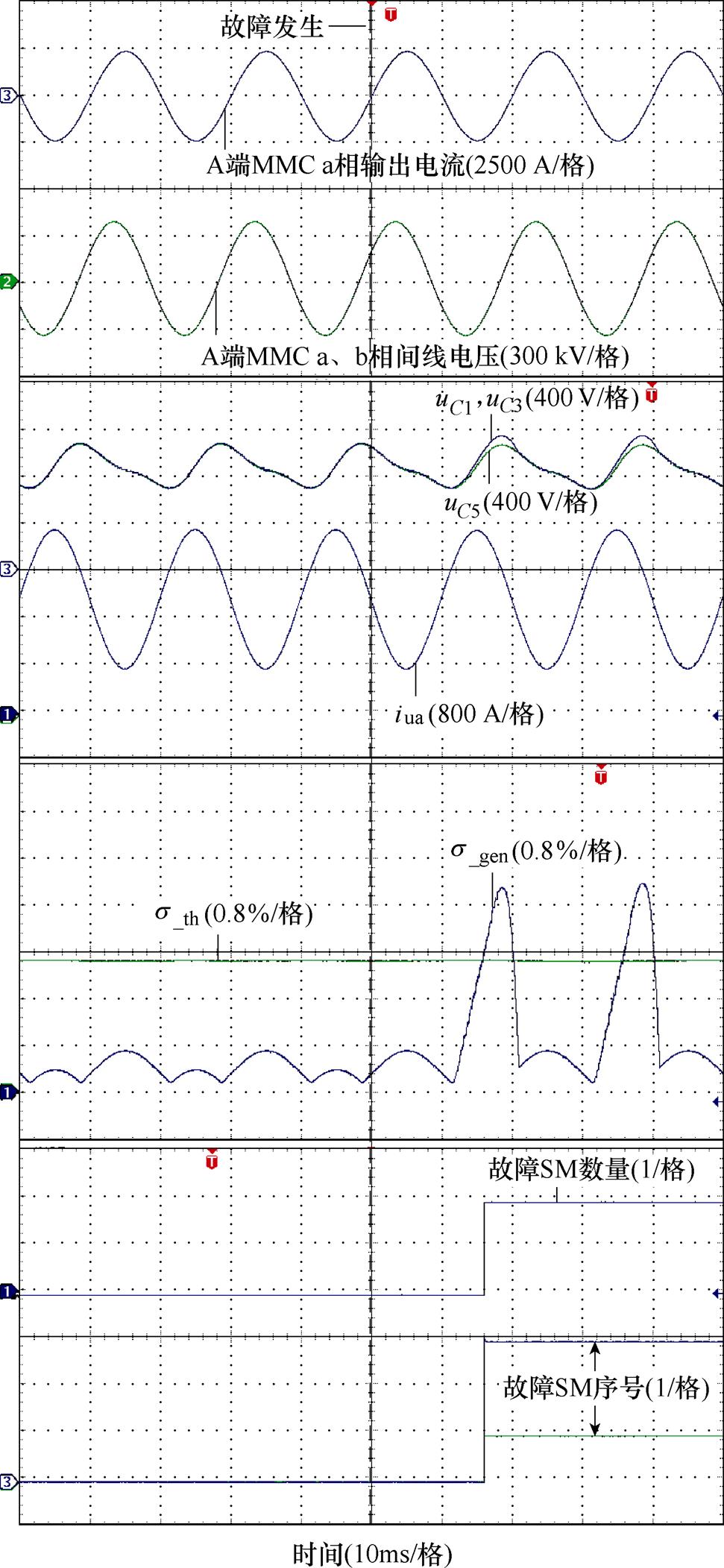
图9 整流模式MMC额定负载发生Ⅱ型故障实验波形
Fig.9 Experimental waveforms of type II fault with rated load of MMC in rectifier mode
4.2.2 轻载下发生Ⅱ型故障
令轻载下A端MMC a相上桥臂序号为1、3的子模块发生Ⅱ型故障，实验波形如图10所示。从图10中s_th及s_gen波形可以看出，在故障发生后，s_gen超出设定阈值，系统可以快速检测到故障，随后进入故障定位过程，确定了当前桥臂中故障SM数量为2，序号分别为1和3，诊断用时为17.8 ms，但由于故障时臂电流为负，因此实际诊断用时为6.7 ms，验证了所提策略在这种情况下的适用性。同时综合图9、图10可以看出，所提策略可准确诊断到不同功率下的故障。
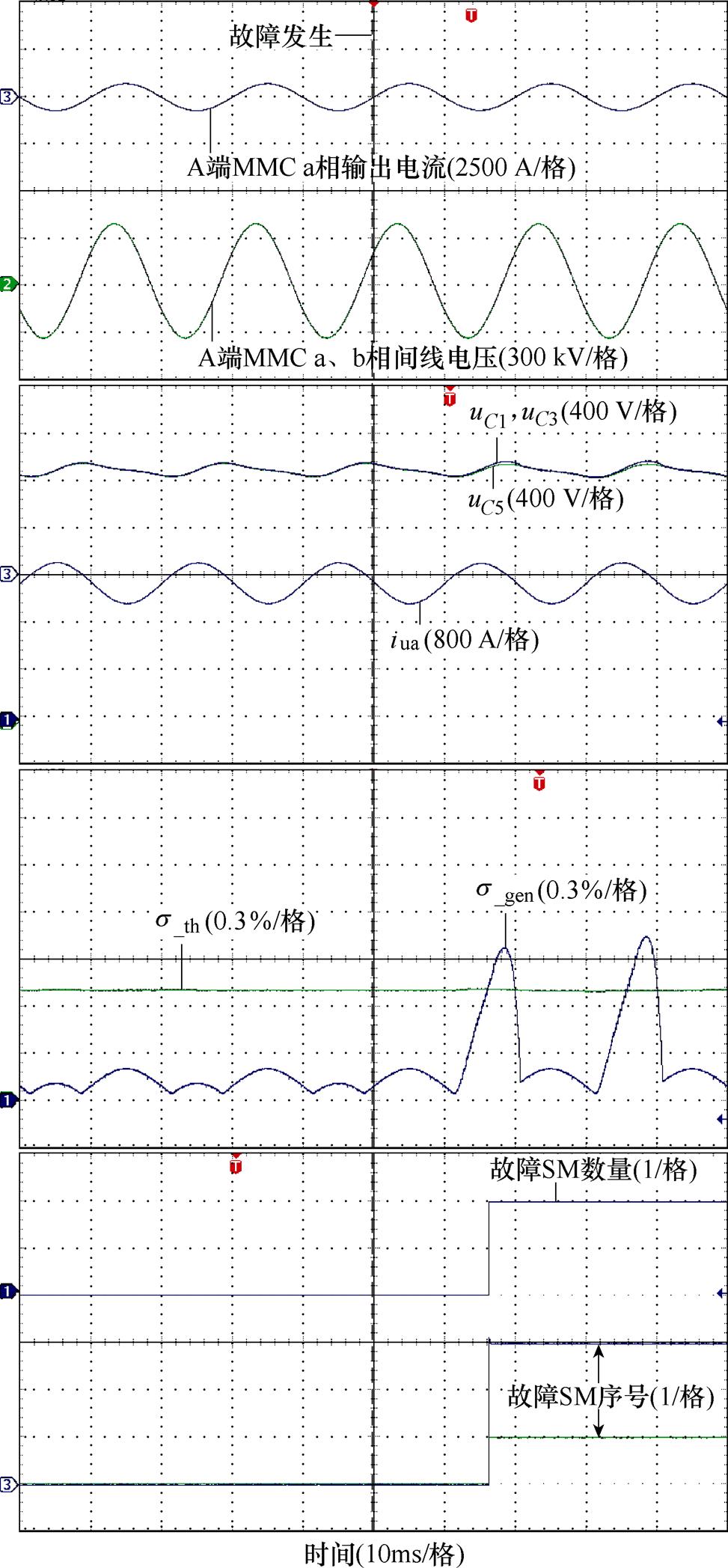
图10 整流模式MMC轻载发生Ⅱ型故障实验波形
Fig.10 Experimental waveforms of type II fault with light load of MMC in rectifier mode
4.3.1 额定负载下发生Ⅱ型故障
令额定负载下B端MMC a相上桥臂序号为1、3的子模块发生Ⅱ型故障，实验波形如图11所示。可以看出，故障发生时桥臂电流为正，故障SM电容始终被充电，电容电压迅速升高，最终导致故障SM电压不断升高，与理论分析一致。从图11中s_th及s_gen波形可以看出，在故障发生前，MMC正常运行时，s_gen不会超出设定阈值s_th，正常运行时不会发生误诊断，诊断显示故障SM数量始终为零。而在故障发生后，s_gen超出设定阈值，系统可以检测到故障，进入故障定位过程，确定了当前桥臂中故障SM数量为2，序号分别为1和3，诊断用时为1.02 ms，验证了所提策略在这种情况下的适用性。
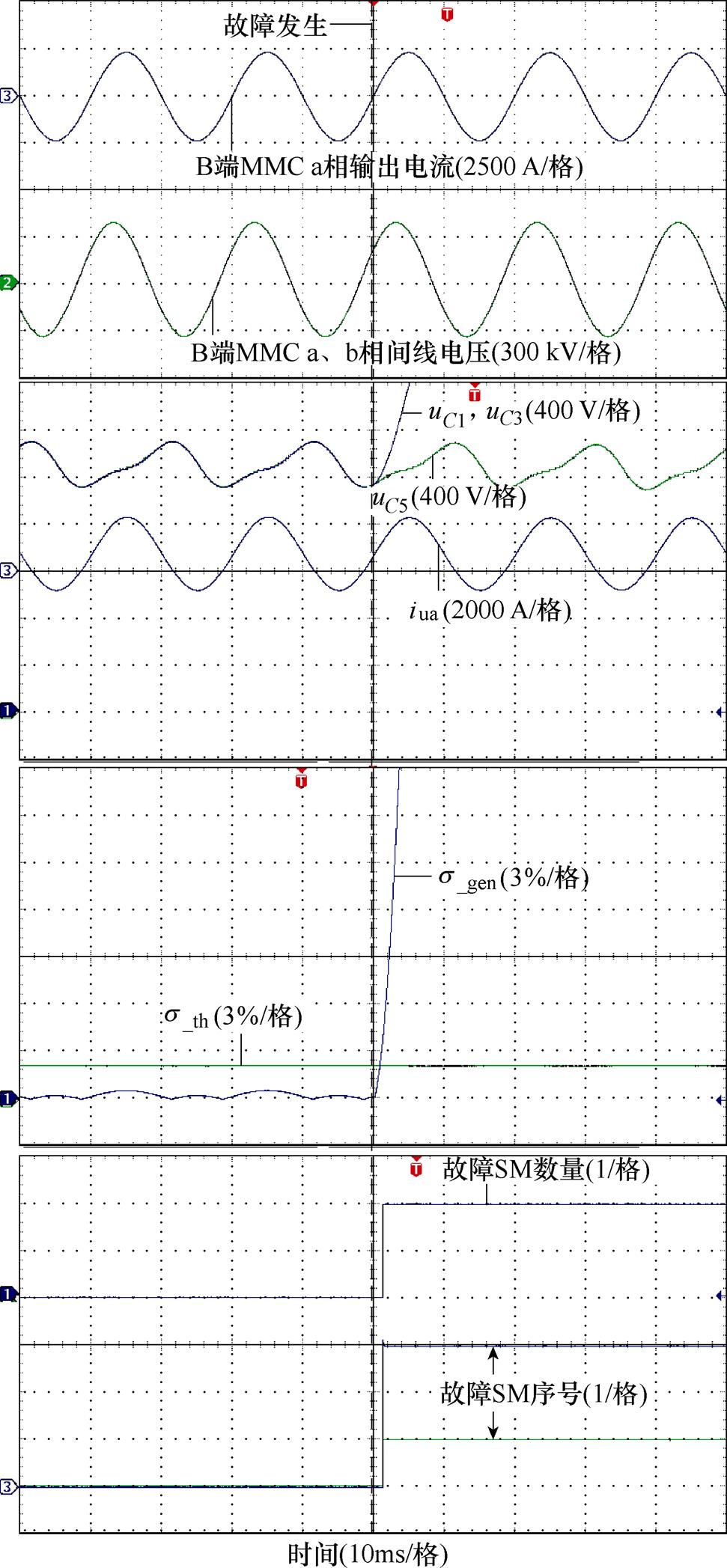
图11 逆变模式MMC额定负载发生Ⅱ型故障实验波形
Fig.11 Experimental waveforms of type II fault with rated load of MMC in inverter mode
4.3.2 轻载下发生Ⅱ型故障
令轻载下B端MMC a相上桥臂序号为1、3的子模块发生Ⅱ型故障，实验波形如图12所示。从图12中s_th及s_gen波形可以看出，在故障发生后，s_gen超出设定阈值，系统可以快速检测到故障，之后进入故障定位过程，确定了当前桥臂中故障SM数量为2，序号分别为1和3，诊断用时为1.15 ms，验证了所提策略在这种情况下的适用性。同时综合图11、图12可以看出，所提策略可准确诊断到不同功率下的故障。
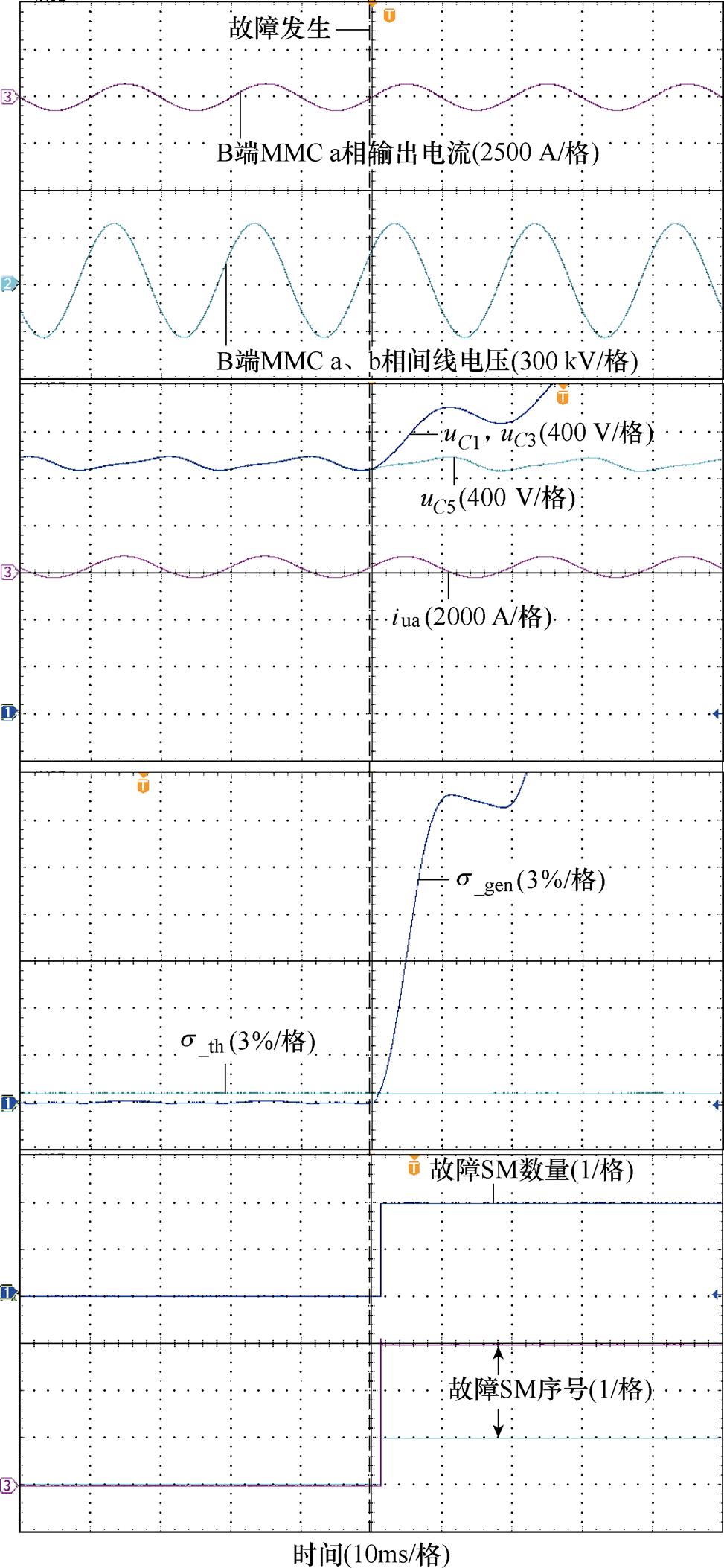
图12 逆变模式MMC轻载发生Ⅱ型故障实验波形
Fig.12 Experimental waveforms of type Ⅱ fault with light load of MMC in inverter mode
为进一步验证所提策略在不同运行功率下的可行性以及阈值设置的合理性，改变运行功率，在不同模式及不同类型故障下进行实验，记录其广义电容电压不平衡度，其中逆变模式下发生Ⅱ型故障对应广义电容电压不平衡度会随时间推移不断增加，因此记录了其在故障发生后0.05 s的值，并根据式（32）对整流模式下发生Ⅱ型故障对应广义电容电压不平衡度即sfault进行计算。不同模式及不同类型故障下的电容电压不平衡度实际值与计算值如图13所示。从图13a中可以看出，在运行功率相等时，整流模式下发生Ⅱ型故障的广义电容电压不平衡度相较于其他情形更小，证明了前述分析的正确性及阈值设置过程的合理性。在两种模式及故障类型中，选取的是整流模式下发生Ⅱ型故障对应广义电容电压不平衡度作为阈值设置的参考，而从图13b中可以看出，通过式（32）计算得到的sfault与其实际值基本一致，证明了验证前述分析与理论推导的准确性，进而验证了所提策略在不同运行功率下均可行。
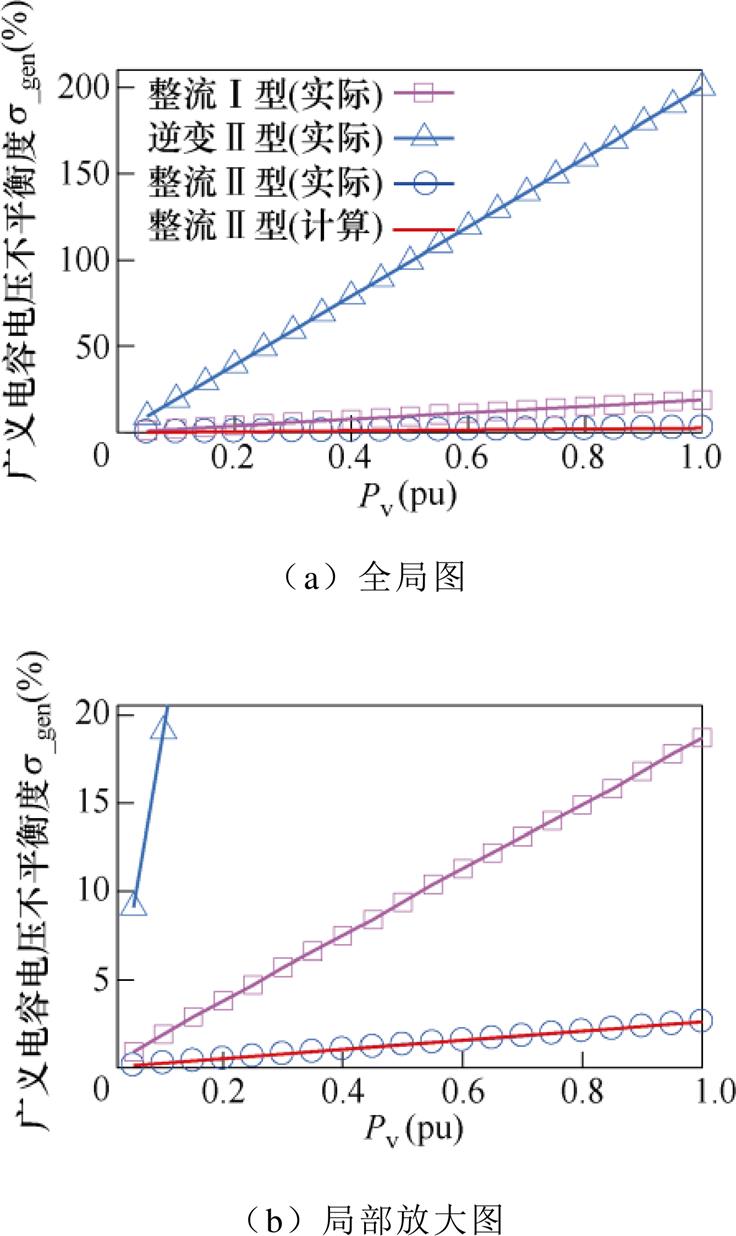
图13 不同模式及不同类型故障下的电容电压不平衡度实际值与计算值
Fig.13 Actual and calculated vaules of capaciotr voltage unbalance degree under different modes and different types of faults
综合上述实验波形，可以验证，所提策略能够准确快速地检测并定位到两种功率流向下的子模块开路故障，同时可以应对桥臂中多个SM发生故障的情况。更为重要的是，验证了本文分析给出的诊断阈值与运行功率间的定量关系准确性以及阈值设置的合理性，基于此，当MMC运行功率发生改变时，可以相应地准确设置阈值，进而实现在不同运行功率下SM开路故障的准确诊断，同时降低了设定的难度，便于推广。
为提升MMC的运行可靠性，需要在子模块发生开路故障时，快速检测到故障并定位到故障SM。本文针对采用NLM的MMC，提出了基于广义电容电压不平衡度的MMC子模块开路故障诊断方法，可解决现有研究中基于经验的诊断阈值在不同运行功率间难以推广的问题。具体得到以下结论：
1）发生开路故障的SM电容电压特性与故障类型及MMC工作模式有关。发生Ⅰ型故障的SM电容电压无论MMC工作于整流模式还是逆变模式最终均会保持不变，而发生Ⅱ型故障的SM，当MMC工作于逆变模式时，其电容电压将会不断增大，当MMC工作于整流模式时，其电容电压则会进入不当平衡状态。
2）引入了广义电容电压不平衡度的概念，提出了基于广义电容电压不平衡度的MMC子模块开路故障诊断策略。通过分析，选取了整流模式下SM发生Ⅱ型故障作为设置诊断阈值的情形，并通过计算推导给出了诊断阈值与运行功率间的定量关系，当MMC运行功率发生改变时，可以对应准确设置阈值，与现有研究相比降低了阈值设定的难度，便于推广。
3）HIL平台的实验结果验证了所提策略能够在不同运行功率下准确诊断出两种MMC子模块开路故障。此外，所提策略还可以应对桥臂中多个SM发生故障的情形，并可以在一个工频周期内完成诊断过程。
参考文献
[1] 尹太元, 王跃, 段国朝, 等. 基于零直流电压控制的混合型MMC-HVDC直流短路故障穿越策略[J]. 电工技术学报, 2019, 34(增刊1): 343-351.
Yin Taiyuan, Wang Yue, Duan Guozhao, et al. Zero DC voltage control based DC fault ride-through strategy for hybrid modular multilevel converter in HVDC[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 343-351.
[2] 杜东冶, 郭春义, 贾秀芳, 等. 基于附加带阻滤波器的模块化多电平换流器高频谐振抑制策略[J]. 电工技术学报, 2021, 36(7): 1516-1525.
Du Dongye, Guo Chunyi, Jia Xiufang, et al. Suppression strategy for high frequency resonance of modular multilevel converter based on additional band-stop filter[J]. Transactions of China Electro- technical Society, 2021, 36(7): 1516-1525.
[3] 罗永捷, 蒲羿, 宋勇辉, 等. 混合型模块化多电平换流器启动冲击电流特性分析及控制策略[J]. 电工技术学报, 2020, 35(增刊1): 49-59.
Luo Yongjie, Pu Yi, Song Yonghui, et al. The inrush current characteristics and control strategies of hybrid modular multilevel converter systems during start-up processes[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 49-59.
[4] 米彦, 万晖, 卞昌浩, 等. 基于模块化多电平换流器的模块化前后沿可调高压纳秒脉冲发生器的研制[J]. 电工技术学报, 2020, 35(6): 1279-1289.
Mi Yan, Wan Hui, Bian Changhao, et al. Design of modular high-voltage nanosecond pulse generator with adjustable rise/fall time based on modular multilevel converter topologies[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1279- 1289.
[5] 杨晓峰, 李泽杰, 薛尧, 等. 增强型柔性逆阻模块化多电平换流器的故障阻断特性分析[J]. 电工技术学报, 2019, 34(12): 2549-2557.
Yang Xiaofeng, Li Zejie, Xue Rao, et al. Fault blocking performance analysis of enhanced flexible reverse blocking multilevel modular converter[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2549-2557.
[6] 蔡洋, 郭文勇, 赵闯, 等. 模块化多电平换流器直流故障过电流精确计算与分析[J]. 电工技术学报, 2021, 36(7): 1526-1536.
Cai Yang, Guo Wenyong, Zhao Chuang, et al. The accurate calculation and analysis of overcurrent under modular multilevel converter DC fault[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(7): 1526-1536.
[7] 杨兴武, 杨帆, 薛花, 等. 基于占空比调制的模块化多电平换流器模型预测控制[J]. 电力系统自动化, 2021, 45(17): 134-142.
Yang Xingwu, Yang Fan, Xue Hua, et al. Duty-cycle modulation based model predictive control of modular multilevel converter[J]. Automation of Electric Power Systems, 2021, 45(17): 134-142.
[8] 于华龙, 黄伟煌, 梅红明, 等. 柔性直流输电系统同级双阀组直流电压平衡控制方法[J]. 电力系统自动化, 2021, 45(15): 134-142.
Yu Hualong, Huang Weihuang, Mei Hongming, et al. DC voltage balance control method for dual valve group in the same pole of flexible DC transmission system[J]. Automation of Electric Power Systems, 2021, 45(15): 134-142.
[9] 徐政. 柔性直流输电系统[M]. 2版. 北京: 机械工业出版社, 2017.
[10] Picas R, Zaragoza J, Pou J, et al. Reliable modular multilevel converter fault detection with reduntant voltage sensor[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 39-51.
[11] An Quntao, Sun Lizhi, Zhao Ke, et al. Switching function model-based fast-diagnostic method of open- switch faults in inverters without sensors[J]. IEEE Transactions on Power Electronics, 2013, 28(11): 4867-4872.
[12] Zhou Dehong, Qiu Huan, Yang Shunfeng, et al. Submodule voltage similarity based open-circuit fault diagnosis for modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2019, 34(8): 8008-8016.
[13] Yang Qichen, Qin Jiangchao, Saeedifard M. Analysis, detection, and location of open-switch submodule failures in a modular multilevel converter[J]. IEEE Transactions on Power Delivery, 2016, 31(1): 155- 164.
[14] Deng Fujin, Jin Ming, Liu Chengkai, et al. Switching open-circuit fault localization strategy for MMCs using sliding-Time window based features extraction algorithm[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(10): 10193-10206.
[15] Shao Shuai, Wheeler P W, Clare J C, et al. Fault detection for modular multilevel converters based on sliding mode observer[J]. IEEE Transactions on Power Electronics, 2013, 28(11): 4867-4872.
[16] Shao Shuai, Watson A J, Clare J C, et al. Robustness analysis and experimental validation of a fault detection and isolation method for the modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 155-164.
[17] Deng Fujin, Chen Zhe, Khan M R, et al. Fault detection and localization method for modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2014, 30(5): 2721-2732.
[18] Zhou Weihao, Sheng Jing, Luo Haoze, et al. Detection and localization of submodule open-circuit failures for modular multilevel converters with single ring theorem[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3729-3739.
[19] Geng Zhi, Han Minxiao, Khan Z W, et al. Detection and localization strategy for switch open-circuit fault in modular multilevel converters[J]. IEEE Transa- ctions on Power Delivery, 2020, 35(6): 2630-2640.
[20] Zhou Dehong, Yang Shunfeng, Tang Yi. A voltage- based open-circuit fault detection and isolation approach for modular multilevel converters with model-predictive control[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9866-9874.
[21] Chen Xingxing, Liu Jinjun, Deng Zhifeng, et al. A diagnosis strategy for multiple IGBT open-circuit faults of modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 191-203.
[22] Wang Zhen, Peng Li. Grouping capacitor voltage estimation and fault diagnosis with capacitance self-updating in modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 1532-1543.
[23] Yu Jin, Xiao Qian, Jia Hongjie, et al. A novel detection and localization approach of open-circuit switch fault for the grid-connected modular multilevel converter[J]. IEEE Transactions on Industrial Elec- tronics, doi:10.1109/TIE.2022.3153810.
[24] Liu Chengkai, Deng Fujin, Cai Xu, et al. Submodule open-circuit fault detection for modular multilevel converters under light load condition with rearranged bleeding resistor circuit[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 4600-4613.
Abstract Modular multilevel converters (MMC) have features of modular construction, redundancy configuration, and power scalability. The MMC topology is composed of a large number of series-connected submodules (SMs), and reliability is one of its important issues. The faults of the insulated gate bipolar transistor (IGBT) can generally be divided into short-circuit faults and open-circuit faults. The short-circuit fault is destructive, but now the gate driver is always integrated with short-circuit protection. In contrast, the open-circuit fault will not immediately damage the SM and may remain undetected for a long time. MMC’s SM open-circuit diagnosis strategy can be divided into hardware-based and software-based categories. The software-based strategies have the advantages of no additional hardware and fast diagnosis time. However, it often requires an empirical threshold, which is difficult to set when the MMC operates at different power.
Therefore, an open-circuit fault diagnosis strategy for MMC sub-modules based on generalized capacitor voltage unbalance degree (GCVUD) is proposed. The fault is detected by judging whether the GCVUD of the SM with the largest capacitor voltage in the arm exceeds the threshold. The remaining faulty SMs are located until the GCVUD of one SM is within the threshold according to the capacitor voltage sorting results. Moreover, to further eliminate the effects of errors and prevent fault misdiagnosis situations, a counting flag is used in the detection process and location process.
In this strategy, the threshold setting determines the accuracy and rapidity directly. The threshold shall be greater than the GCVUD to ensure no misdiagnosis during normal operation. On the other hand, the threshold shall be less than the minimum of the corresponding GCVUD in the case of two types of open-circuit faults. The type II fault of SM in rectifier mode is selected for setting the diagnostic threshold. The quantitative relationship between the diagnostic threshold and the operating power is given by calculation and deduction.
A detailed real-time digital simulation model of the MMC-HVDC system is built in a hardware-in-the-loop platform. The power-stage model is emulated by the target machine, and the control system is realized by the DSP TMS320F28335 control board. The experimental results verify that the voltage characteristics of the faulty SM are related to the type of fault and the MMC operating mode. The SM capacitor voltage under the type I fault will remain unchanged. The SM capacitor voltage will increase continuously in inverter mode but will keep an abnormal balance in rectifier mode. The GCVUD in the type II fault in rectifier mode is smaller than in other cases when the operating power is equal, and its calculated value is close to the actual value. The proposed strategy can accurately diagnose two types of MMC SM open-circuit faults at different operating powers. Before the fault occurs, the GCVUD will not exceed the threshold, so misdiagnosis will not occur during normal operation. If the fault occurs, the GCVUD exceeds the threshold, and the system can quickly detect the fault. Then, the number of faulty SMs and their serial numbers can be determined. In addition, the proposed strategy can cope with the cases of multiple SM failures in the arm and complete the diagnosis process within one fundamental frequency period.
keywords：Modular multilevel converter, generalized capacitor voltage unbalance degree, fault diagnosis, operating power
国家电网公司科技资助项目（5100-202156434A-0-0-00）。
收稿日期 2022-05-23
改稿日期 2022-09-20
DOI: 10.19595/j.cnki.1000-6753.tces.220898
中图分类号：TM46
武 鸿 男，1999年生，博士研究生，研究方向为模块化多电平换流器。E-mail: wuhong30@stu.xjtu.edu.cn
王 跃 男，1972年生，教授，博士生导师，研究方向为模块化多电平换流器、虚拟同步发电机、无线电能传输技术等。E-mail: davidwangyue@mail.xjtu.edu.cn（通信作者）
（编辑 陈 诚）