N。摘要 三相隔离型AC-DC-DC电源因其具有功率密度大、电气隔离等优点，在工业上应用广泛。但在一些负荷频繁投切的特殊应用场景下，如电泳、电镀等，基于传统PI控制的电源存在输出电压响应速度慢及纹波大的问题。为了提升电源的输出电压响应速度，该文在分析线性自抗扰控制中关键带宽参数与输出量之间关系的基础上，提出一种控制器带宽参数自适应调节的线性自抗扰控制（A-LADRC）方法以实现输出电压在负荷突变下的快速调节。而针对系统前级不控整流环节中电压六脉动分量对后级系统带来的输出电压纹波增大问题，设计一种根据系统输出电压反馈值，自适应调整变换器占空比补偿量的控制策略，以实现减小电压纹波的目的。最后通过一台400 V/50 A的实验样机对所提方法进行了验证，结果表明所提方法能够有效提升系统输出电压响应速度并减小电压纹波，具有较好的实际工程应用价值。
关键词：三相隔离型电源 移相全桥变换器 线性自抗扰控制 电压纹波 占空比补偿
三相隔离型AC-DC-DC电源具有功率密度大、易于扩展及电气隔离等优点，在工业上得到了广泛的应用[1-4]。在一些特殊应用场合（如电泳和电镀等），由于其负载通常频繁的投切，要求电源输出电压具有极快的响应速度，但因核心的隔离型DC-DC变换器是一种典型的非线性系统，在传统PI线性控制方法下其通常无法满足动态响应速度需求，更无法应对因负载突变带来的电压暂降或暂升问题，尤其是针对电压敏感型的直流负载。且由于前级AC- DC三相不控整流环节的影响，输出电压纹波通常较大，配置较大的滤波电容又会增加电源的成本。因此，亟须从控制层面来提升输出电压响应速度及减小纹波以解决大功率AC-DC-DC电源在特殊应用场景下遇到的问题。
在提升电源输出响应速度方面，近年来大量学者致力于研究隔离型DC-DC变换器新的控制方法，以获得良好的动态输出特性。文献[5]提出的一种滑模控制，具有优于传统PID控制的稳态和动态性能，但是其开关频率不稳定，易导致损耗和电磁干扰问题。文献[6]针对DC-DC变换器的非线性特性，提出用模糊逻辑控制器控制DC-DC变换器输出电压，尽管具有一定的优势，但其计算需求较高，不仅影响变换器在负载突然变化的反应速度，还增加了变换器的成本。文献[7]提出一种基于三重移相的模型预测控制策略，在解决端口功率耦合问题的同时对损耗进行了优化，但也存在计算量大的问题。文献[8]在移相全桥变换器的控制策略上，采用反向传播（Back Propagation, BP）神经网络和粒子群优化BP神经网络实现的各种双闭环PI控制效果，具有响应速度快和超调量小的优点。但是BP本身具有收敛速度慢、网络易陷入局部最小的缺点，不适合于工业应用。因而，针对大功率电源的核心DC-DC变换装置而言，具有良好动态响应且适合工业应用的控制方法具有较高的实际价值。
自抗扰控制（Active Disturbance Rejection Control, ADRC）技术是在传统PID控制基础上提出的改进策略，具有良好的抗干扰性能[9-10]。参数整定是ADRC设计的重要问题，由文献[11]提出的线性自抗扰控制（Linear Active Disturbance Rejection Control, LADRC），将传统ADRC线性化，减少可调参数数量的同时给出参数整定方法，并继承了原控制器的优点。文献[12]将LADRC应用于配电网逆变器控制中，验证了LADRC控制器稳定性良好，以及控制器具有动态跟踪响应速度和抗干扰能力。文献[13-14]将LADRC应用于伺服系统，设计了伺服系统中永磁同步电机的速度控制器和电流控制器，实现了控制器的高动态响应、强抗干扰和噪声抑制能力。以上文献中，线性自抗扰控制技术的优势都得到了充分验证。但应对较复杂的非线性系统时，受其固定的控制参数影响，面对动态变化的受控系统，控制效果不太理想，因此研究如何提高LADRC灵活调节能力具有实际意义。
同时，针对三相AC-DC-DC电源，受前级不控整流环节的影响，隔离型DC-DC变换器的直流输出电压具有周期性的六脉动分量。传统的PI控制器在脉动周期内反复调节，控制变换器的占空比来回振荡，脉动的抑制效果较差。文献[15-16]分别通过引入负载电流前馈、反馈，来抑制两级式单相逆变器的二次电流纹波。文献[17]提出了电流扰动前馈策略的陷波滤波器，对信号进行反馈调节，设计了一种带电压扰动前馈的反馈线性化策略来抑制变换器的输出电压纹波。文献[18-19]通过改进变换器以及滤波电路的电路结构，实现改善纹波的目的。文献[20]通过反馈线性化与输出扰动量前馈移相控制来抑制双有源桥DC-DC变换器的纹波电压。虽然外加电容电感能抑制脉动，但是考虑到工业应用的经济性，设计一种简单且易于实现的方法来减少隔离型DC-DC变换器输出电压的稳态纹波，以提高电能质量，具有可观的经济性和工程应用价值。
为了解决上述问题，提高系统的响应速度，本文提出了一种控制器带宽参数自适应调节的线性自抗扰控制（Adaptive Linear Active Disturbance Rejection Control, A-LADRC）方法。为了减小系统前级不控整流环节中电压六脉动分量引起的输出电压纹波增大问题，提出了一种占空比补偿控制策略。最后通过对一台20 kW的实验样机进行了验证。
本文所研究的系统拓扑结构如图1所示。为了节约成本，前级主要采用三相不控整流；后级隔离型DC-DC变换器通常采用移相全桥拓扑结构，后桶的拓扑结构决定了整个电源性能。三相交流电源经整流桥输出，通过LC滤波器滤波、稳压后，经由DC-DC大功率开关变换器及滤波装置向右端负载供电，将经L1、C1滤波输出的电压用ui表示。全桥电路中Llk为漏电感，通过控制全桥逆变电路的四个开关管S1～S4的开断，在T1前级得到交流方波电压，变压后再接入全桥整流电路VD5～VD8，经过滤波电感L2、稳压电容C2作用后输出电压uo，为负载供电。其中，变压器电压比为1N。
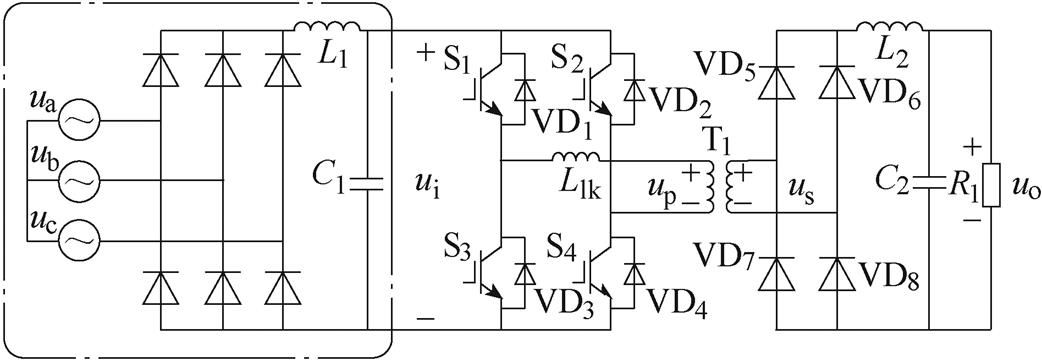
图1 AC-DC-DC模块拓扑结构
Fig.1 Topology structure of AC-DC-DC module
DC-DC大功率开关变换器采用移相PWM控制方式，同一桥臂的两个开关管互补导通，两个桥臂间对角开关管导通时错开的角度为移相角，该移相角决定了开关管的导通占空比。图2所示为忽略了死区时间的变换器工作原理波形，t0～t8为开关管工作的一个周期。
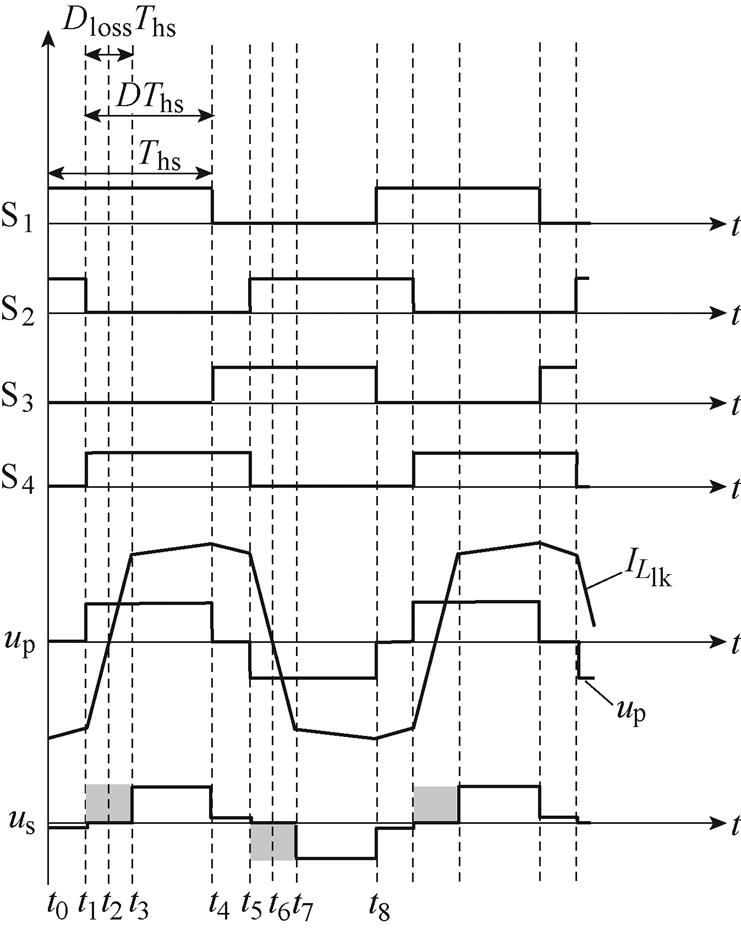
图2 大功率变换器工作原理波形
Fig.2 Waveforms of working principle of high power converter
图2中，up为变压器一次电压，其占空比为D；us为变压器二次电压；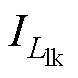
为流经漏电感电流。由于在t1～t3、t5～t7内谐振电感与开关管的结电容形成串联谐振，使变压器处于短接状态，由此导致二次电压占空比的丢失即图中阴影部分，设为Dloss；则变压器二次侧的有效占空比Deff为
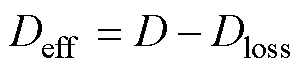（1）
由于全桥电路一般工作在深度连续状态，则Dloss简化后[21]可得
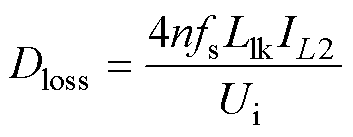（2）
式中，fs为变换器开关频率；IL2为滤波电感电流。
在系统前级三相桥式不控整流电路中，已知三相交流输入电压为
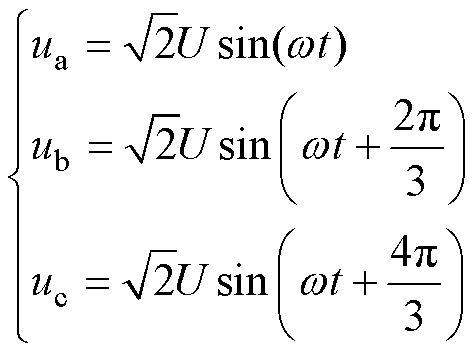（3）
式中，U为三相交流电压有效值，U=220 V；w 为角频率。
整流电路输出电压是周期性的非正弦函数，其中直流分量包括不同频率谐波。通过对整流输出电压进行傅里叶级数分解[22]可得到（m脉波为例）
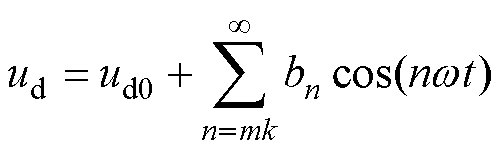（4）
式中，ud0为基波幅值；k =1, 2, 3,…；bn为n倍频谐波幅值。
三相桥式不控整流电路中m=6，滤波前整流输出电压取前三项得到
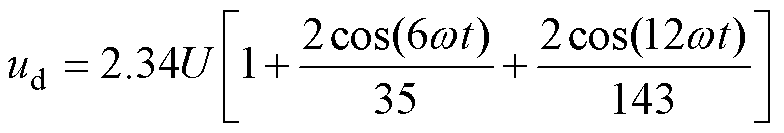（5）
输出电流可表示为
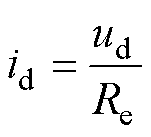（6）
式中，Re为后极电路等效阻抗。
不控整流输出电压电流经L1、C1滤波可得到输入到隔离型DC-DC变换器电压、电流ui、ii。通过微分方程计算可得
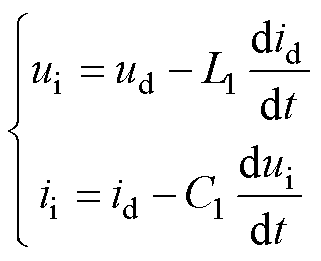（7）
给定隔离变压器前级逆变电路开关管实际导通状态函数D(t)，可得出隔离变压器一次电压、一次电流分别为
（8）
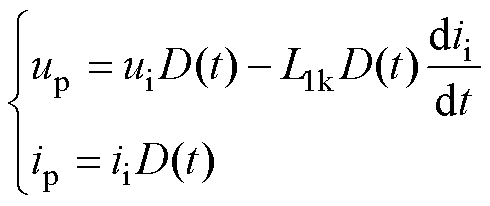（9）
式中，ip为变压器一次电流。已知隔离变压器电压比为1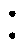N，可得变压器二次电压与二次电流分别为
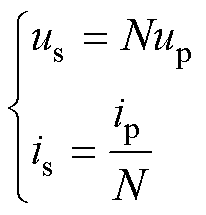（10）
图3所示为系统在一个周期内各阶段输出电压波形。从图3中可以看出，不控整流环节中输出电压六脉动分量含量较大。由二次电压us波形及局部放大图可以看出，受前级不控整流环节的影响，隔离型DC-DC变换器二次电压具有周期性的六脉动分量，甚至会直接影响输出电压uo的波形。因此，需要进一步研究如何提高系统电能质量，并改善隔离型DC-DC变换器输出电压的稳态纹波。
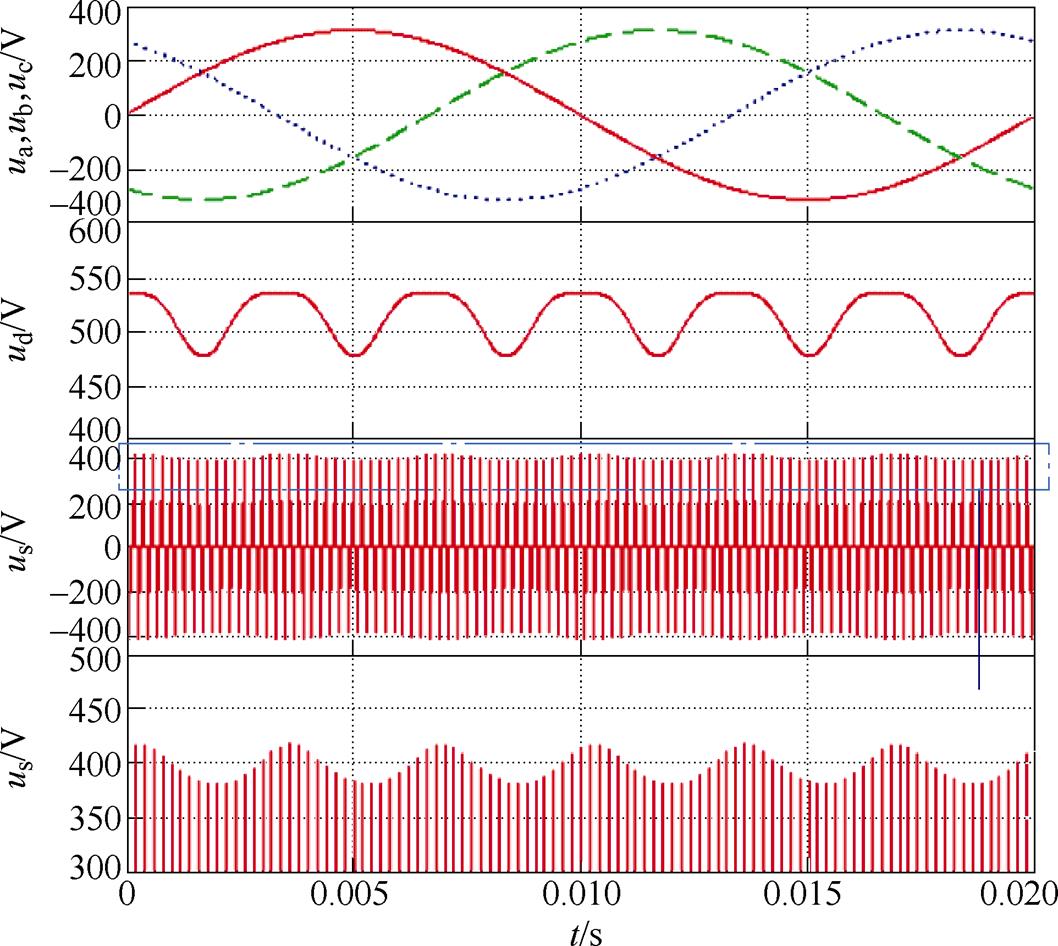
图3 各阶段输出电压波形
Fig.3 Output voltage waveforms at each stage
鉴于移相全桥DC-DC变换器的非线性和复杂性，基本的PI调节控制已无法满足工程应用中对调节速度等控制性能的需求。LADRC因其在非线性系统中良好的控制性能[12, 23]得到了广泛的应用，LADRC在保留ADRC优势的基础上减少了控制参数的选取，简化了非线性自抗扰控制器。控制器带宽较宽有利于提高抗扰度性能，但在本文研究的三相隔离型AC-DC-DC电源应用中，因传统LADRC是基于固定的控制器参数，因而无法应对突增负荷带来的电压暂降等响应问题，为此本文提出了一种可根据输出电流实时值灵活调整控制器带宽参数的A-LADRC方法，在解决实增负荷带来的电压暂降响应问题的同时提升了系统输出响应。本文针对系统前级不控整流环节中电压六脉动分量导致系统输出电压纹波增大的问题，提出了一种占空比补偿控制。
图4所示为本文所提A-LADRC及占空比补偿总控制框图。针对本文二阶研究系统，对A-LADRC参数进行整定。基于对线性状态误差反馈（Linear State Error Feedback, LSEF）控制与线性扩张状态观测器（Linear Extended State Observer, LESO）特征方程极点配置方法，在考虑实际工程应用的背景下对参数选取进行改进。
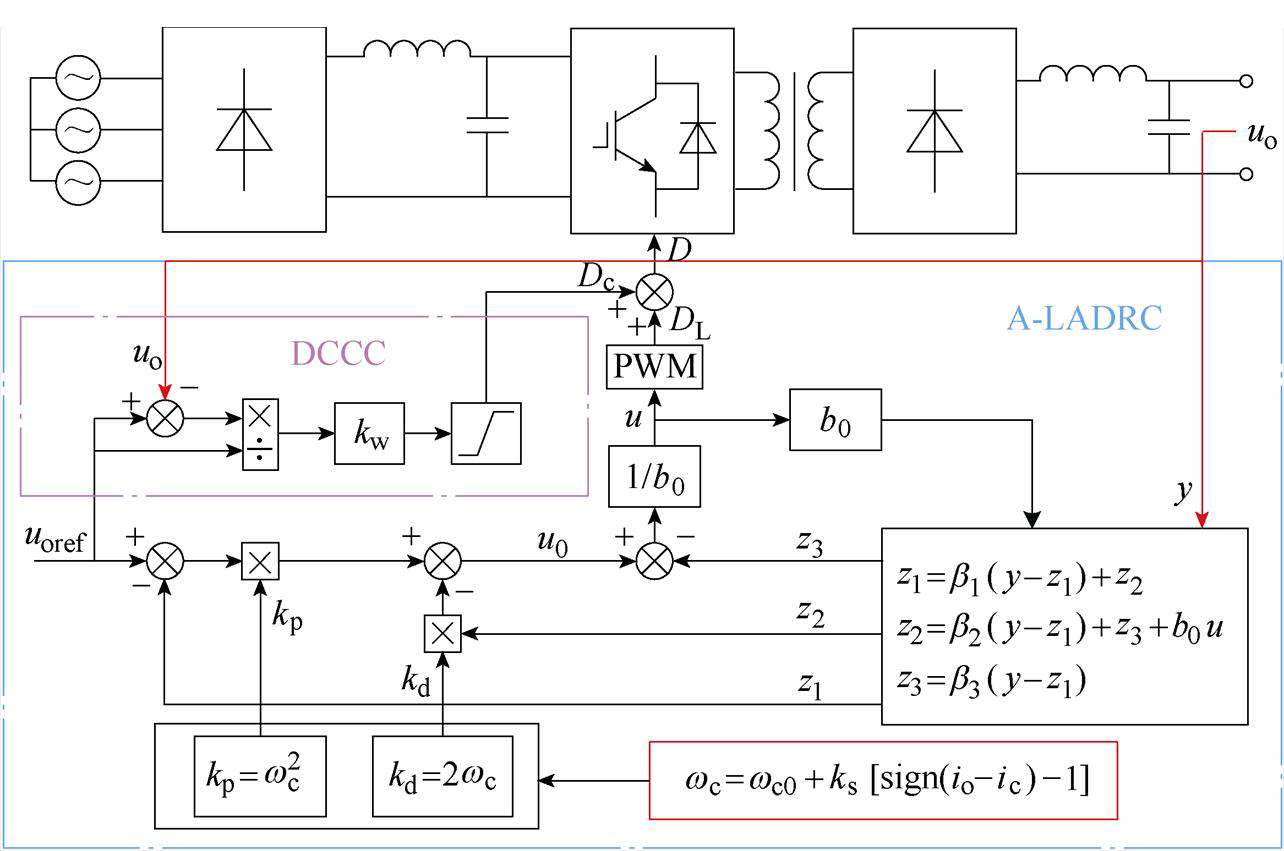
图4 所提基于A-LADRC及占空比补偿控制总结构框图
Fig.4 The proposed general structure block diagram based on A-LADRC and duty cycle compensation control
1）线性状态误差反馈控制
对于本文二阶研究系统，LSEF常用PD组合形式，控制表达式为
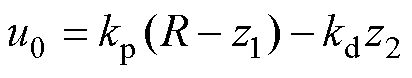（11）
式中，u0为LSEF输出控制量；R为系统给定的输入值；z1、z2为LESO观测出的状态变量；kp、kd为控制器的增益系数。控制率设计为
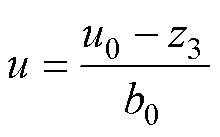（12）
式中，z3为LESO观测出的状态变量；b0为增益系数。
一般地，考虑二阶系统为
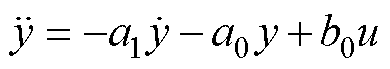（13）
式中，a1、a0为控制对象参数。
参考文献[12]中的极点配置法，令控制器带宽为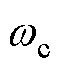
，将系统闭环极点配置于
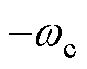处可得
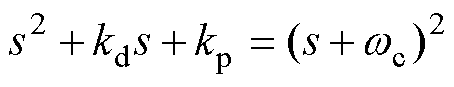（14）
通过式（14）能够得到控制器增益为
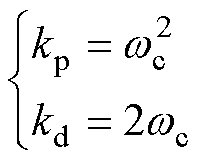（15）
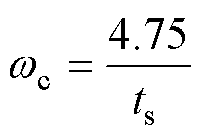（16）
式中，ts为系统调节时间。
基于传统LADRC，控制器带宽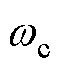与系统响应快速性密切相关如式（16）所示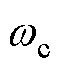，越大，控制器作用越强，系统响应越快速；但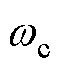过大也有可能使系统超调和振荡严重。
然而，传统LADRC依旧无法解决本文研究的移相全桥DC-DC变换器在实际应用过程中还存在突增负载带来的电压暂降或暂升现象的问题。通过实验验证，系统控制增益kp与kd的选取对大负载系统有较大的影响，而kp和kd的选取都与系统带宽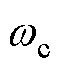有关，系统负载的大小可通过负载电流观测得出，因此针对本文负载突增问题，对LADRC参数的选取做了以下改进。
本文采用对系统带宽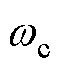自适应调节的方法，通过实时采集系统供给负荷端的电流值，同临界电流值比较，经过控制输出实际系统带宽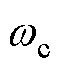。已知当系统工作于空载状态或轻载状态时，负载电流值较小，定义临界电流值为ic。
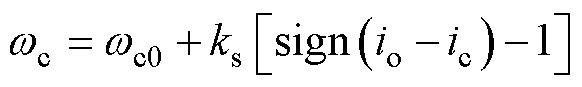（17）
其中
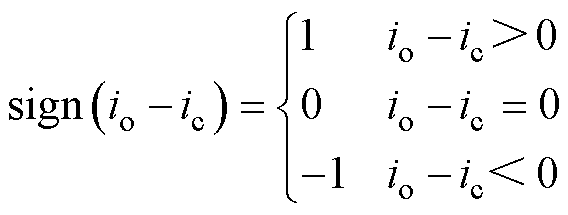（18）
式中，ks为自适应调节系数，考虑到系统空载或轻载状态下负载电流极小，因此可取ic=0.1 A，ks=50。
观察式（17）可知，当系统处于正常工作状态时，控制参数的系统带宽取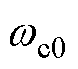
；当系统工作于空载或轻载状态下时，则通过调节系数可重新选取当前状态的最优值。
2）线性扩张状态观测器
LESO是控制算法的核心环节，可以根据系统的输入和输出信息，实时估计系统的状态变量，对非线性系统具有良好的抗扰效果。对于本文研究的二阶系统，LESO表达式可表示为
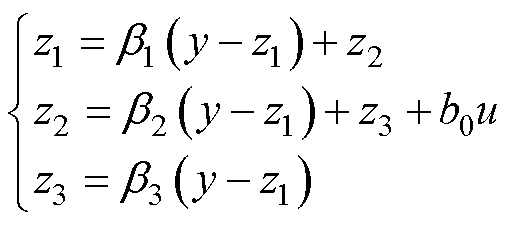（19）
式中，z1、z2、z3分别为状态变量；b1、b2、b3为观测器增益，通过选取合适的增益参数可实现观测器对状态变量的跟踪。
考虑到A-LADRC在实际工程应用中的可行性与控制参数整定的复杂性，同理可采用极点配置法，令观测器带宽为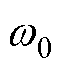
，可得
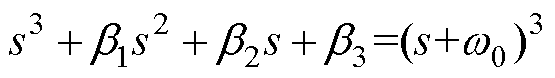（20）
依据式（20）可得观测器增益参数为
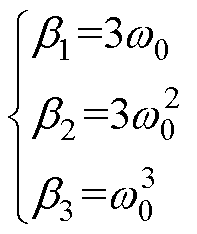（21）
由式（16）及式（21）可以看出，调整控制器带宽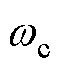及观测器带宽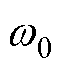能够实现控制器参数设计。其中观测器带宽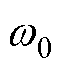一般取为4～10倍的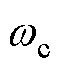[24]。结合文献[11]的参数整定方法，令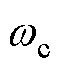=400(pu)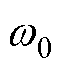，= 2 800(pu)时，控制效果最优。
3）A-LADRC传递函数
功率主电路的非线性并不十分强烈，使用同一套环路参数穿越多个工作点也是可行的。同时，本文所提出的A-LADRC具有一定的“鲁棒性”，使系统具有较强的带负载能力和抗干扰能力。因此，针对本文研究的非线性系统，研究其在某一稳态工作点附近的动态特性时，仍可以把它当作线性系统来近似，这样就可以通过小信号建模的方法来线性化系统的动态模型。为了进一步分析控制器各参数的选取对系统稳定性的影响，可对控制部分以及拓扑小信号进行建模。根据式（19）可求得其传递函数矩阵形式为
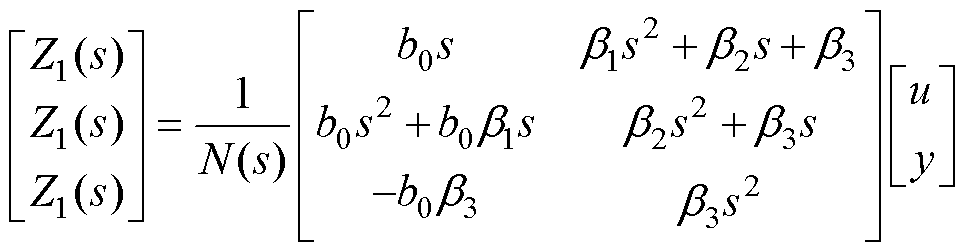（22）
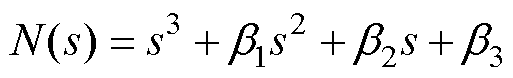（23）
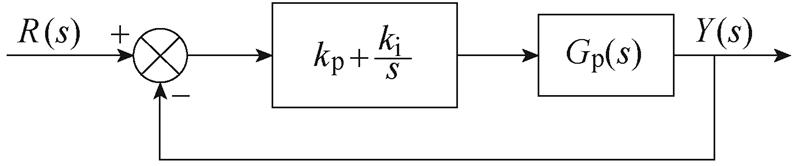
结合式（11）可得二阶A-LADRC控制器传递函数等效结构。图5所示为PI控制与A-LADRC传递函数等效框图。
（a）PI控制
（b）A-LADRC
图5 传递函数等效框图
Fig.5 Equivalent block diagram of transfer function
图5中，R(s)为输入信号，U(s)为控制信号，Y(s)为输出信号，Gp(s)为被控对象，Gc(s)为控制器，GF(s)为用于跟踪优化参考信号的滤波器。
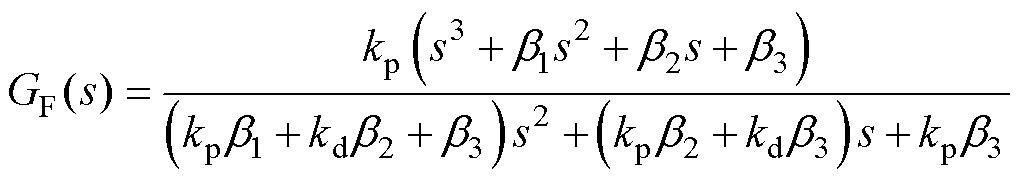（24）
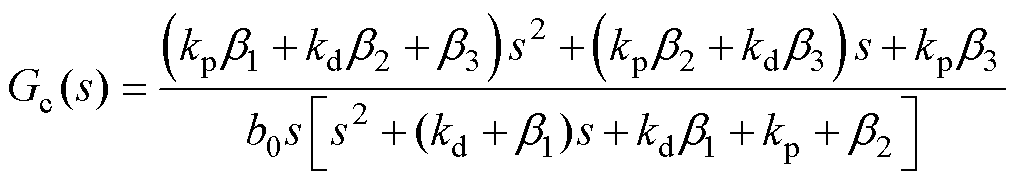（25）
参考文献[21]中所研究的移相全桥变换器零电压软开关（Zero Voltage Switching, ZVS）小信号模型，可推出被控对象传递函数Gp(s)为
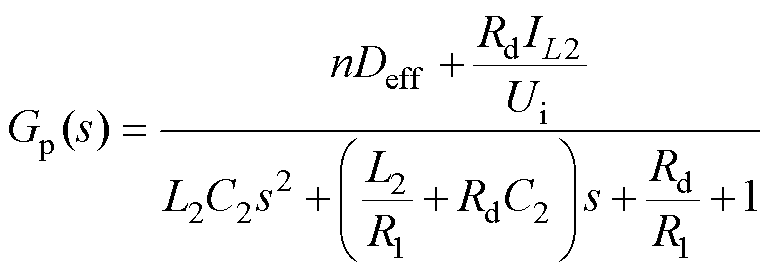（26）
式中，Rd为常数项。
因此，可得系统开环传递函数为
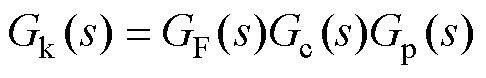（27）
系统闭环传递函数为
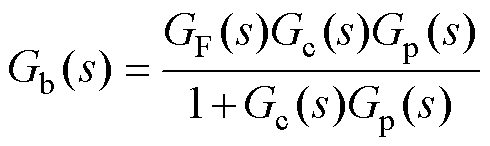（28）
为了验证A-LADRC的控制性能，画出A-LADRC以及PI控制下系统开环传递函数Bode图如图6所示。对比A-LADRC与PI控制的频域特性，由图6可以看出：低频段时，A-LADRC曲线幅值较大，指令跟踪效果强，低频扰动抑制能力较好；高频段时，A-LADRC曲线幅值较低，对高频噪声的抑制能力优于PI控制。
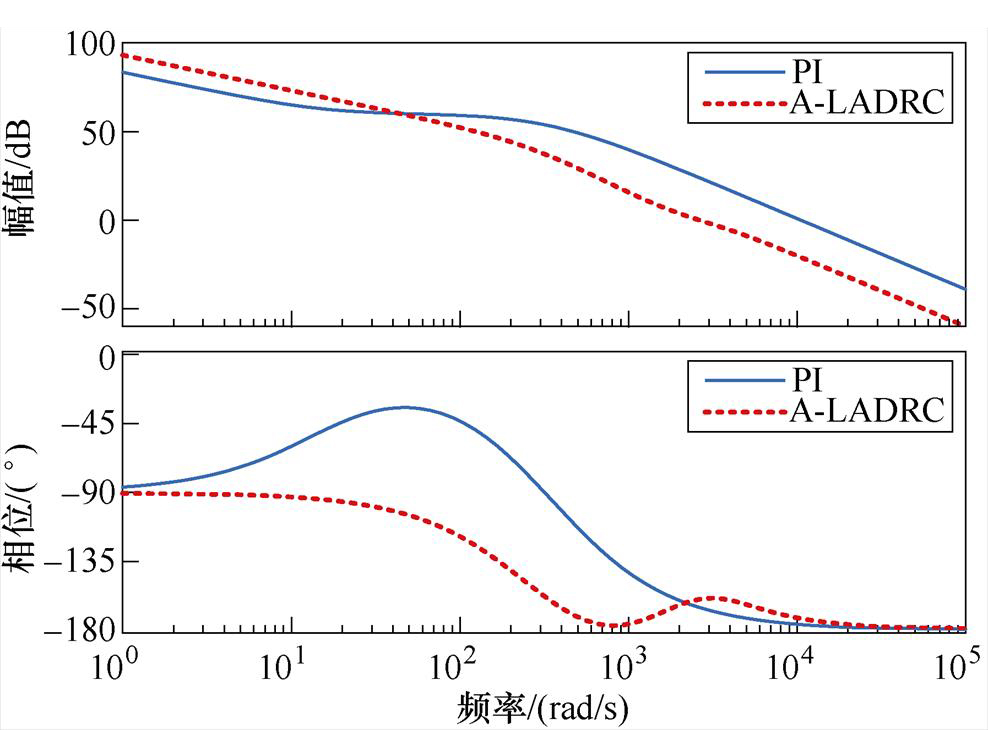
图6 系统开环传递函数伯德图
Fig.6 Bode plot of open loop transfer function of the system
当交流电网向直流负载供电时，不控整流电路输出的直流母线电压含有六脉动分量，最终体现在直流变换器输出电压同样含有六脉动的波动分量。通过外加电容电感也能减少输出电压的脉动[25-27]，但考虑到成本，本文从控制上寻求纹波改善的方法，提出一种占空比补偿控制（Duty Cycle Compen- sation Control, DCCC）策略。
在本文研究系统采用A-LADRC策略基础上，可以根据检测到的输出电压偏差量，给出变换器占空比的补偿量，辅助A-LADRC对系统输出电压进行微调。
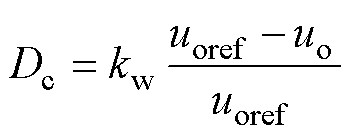（29）
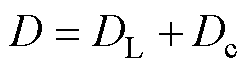（30）
式中，Dc为占空比补偿量；DL为A-LADRC的占空比；uoref为系统给定输出参考电压；uo为输出电压；kw为补偿系数。
图7所示为占空比补偿控制框图，当系统输出电压高于参考电压时，通过略微减小占空比D，抑制输出电压向上波动趋势；同理，当输出电压低于参考电压时，通过略微增大占空比，抑制输出电压减小的趋势。对于补偿系数kw的选取，通过实验分析，当kw取值较小时，对输出电压六脉动纹波抑制效果不明显，取值过大易造成纹波波动幅值增大，因此占空比补偿系数可取0.01。
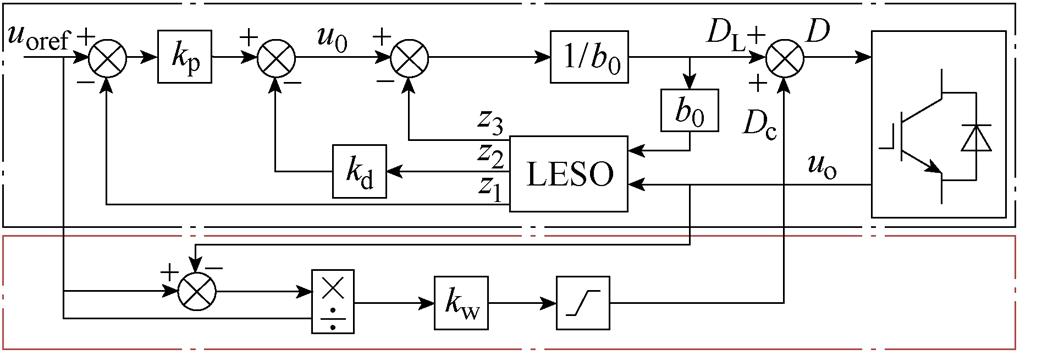
图7 占空比补偿控制框图
Fig.7 Duty cycle compensation control block diagram
图8所示为占空比补偿前后对比波形，由输出电压的波形可以看出，占空比补偿控制策略通过输出电压与参考值的偏差进行实时控制补偿，差值越大，补偿量越大，并且可以调节补偿系数控制补偿量的值。对系统实际运行中开关管占空比补偿前后进行对比，以一个波动周期内的系统输出电压波形为例，当电压位于峰值时，开关管导通时间缩短；位于波谷时，开关管导通时间延长，从而达到较好的补偿效果。通过选择合适的补偿系数，使得抑制系统输出波动达到最优，从而减小输出电压纹波幅值，同时，加快直流电压与电流的调节速度，减少电压暂降或暂升幅度，最终实现输出电压和电流的稳定。
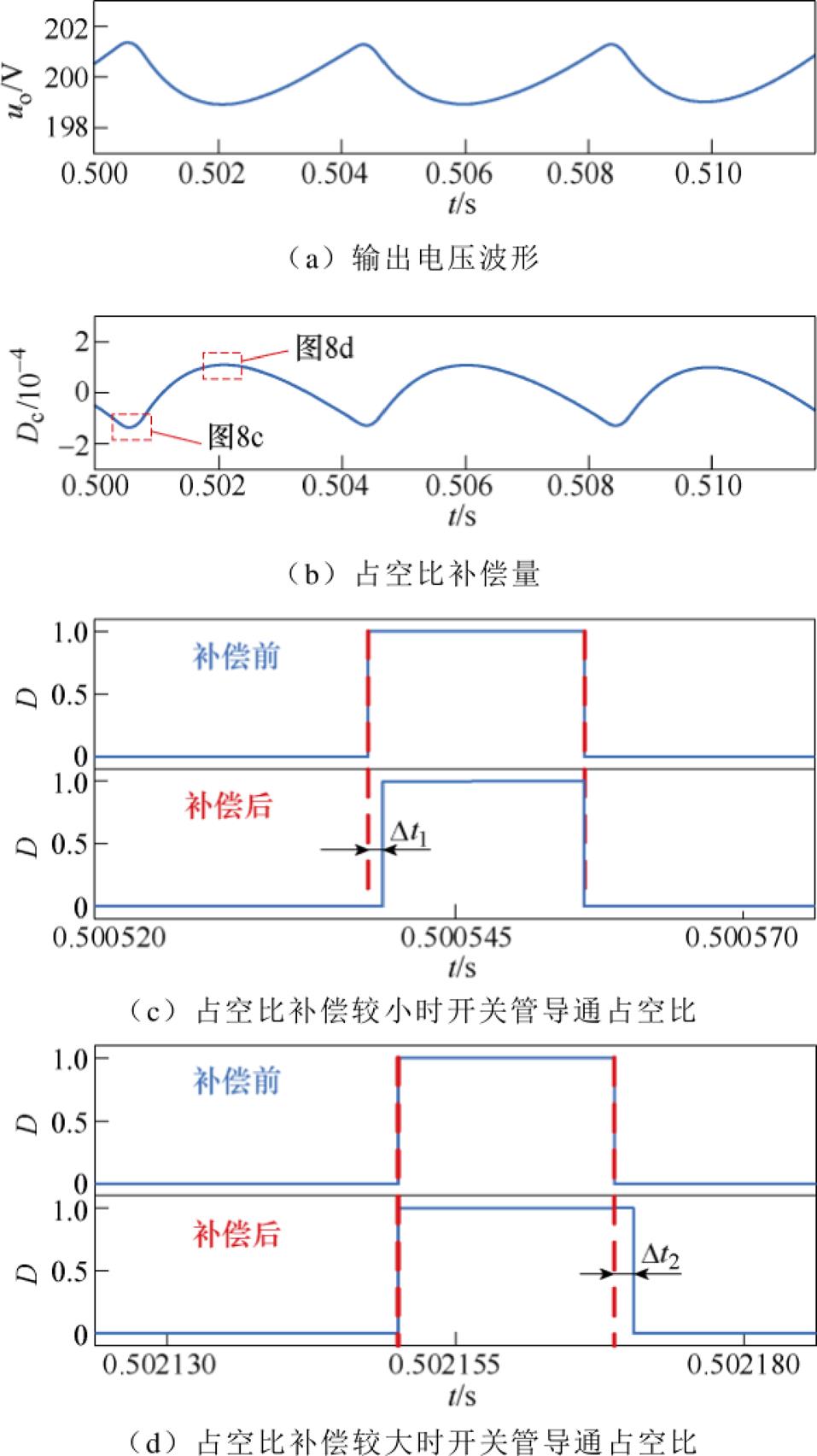
图8 占空比补偿前后对比
Fig.8 Duty cycle compensation before and after comparison
为了验证本文所提出的A-LADRC以及占空比补偿策略的有效性，本文通过由一台400 V/50 A实验样机、上位机与录波仪组成实验平台进行实验。通过实验平台对比验证PI控制与A-LADRC策略的优劣。系统及控制参数见表1。
表1 系统及控制参数
Tab.1 System and control parameters
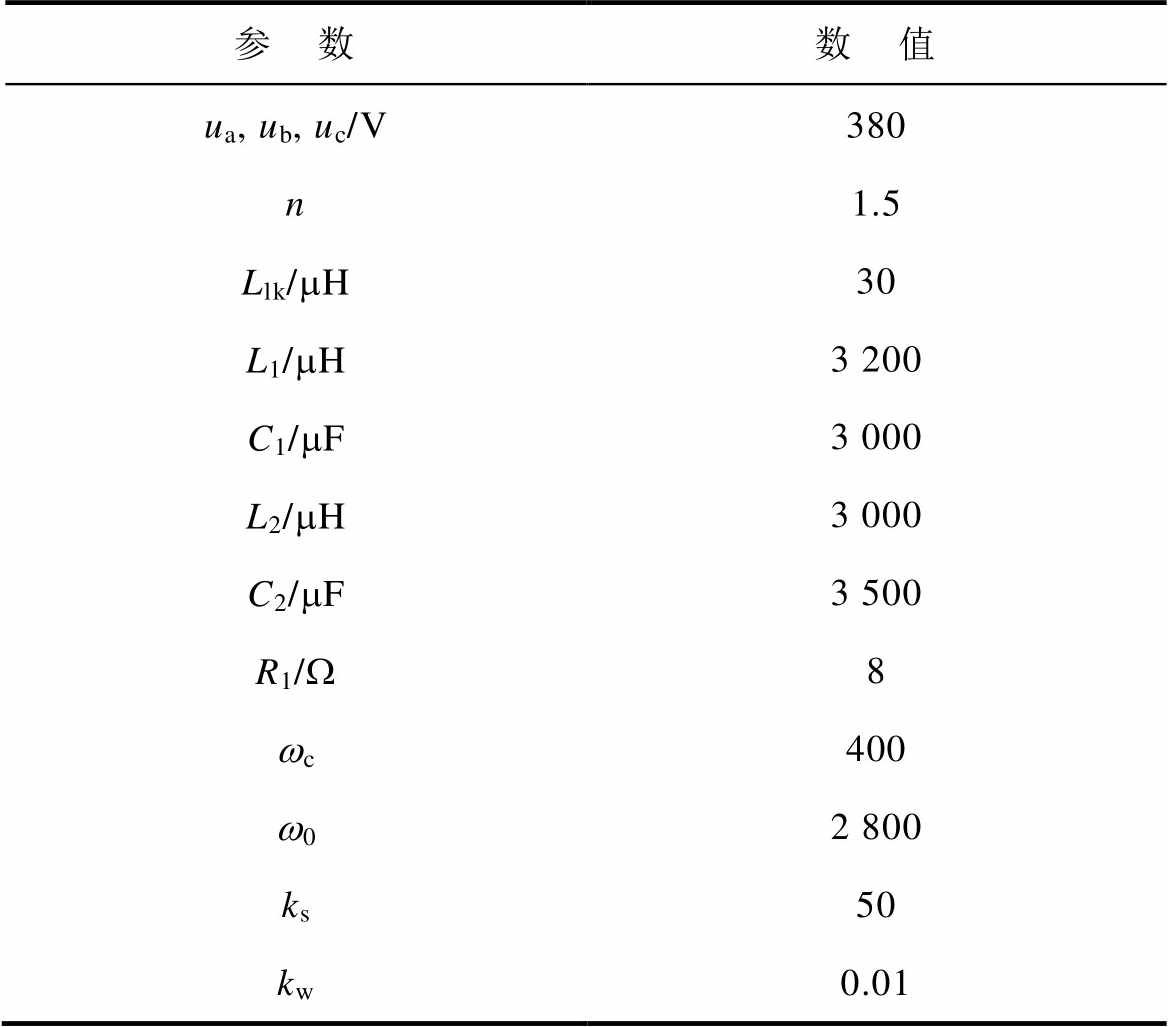
参 数数 值 ua, ub, uc/V380 n1.5 Llk/mH30 L1/mH3 200 C1/mF3 000 L2/mH3 000 C2/mF3 500 R1/W8 wc400 w02 800 ks50 kw0.01
在给定系统参数的前提下，分别采用PI控制、LADRC以及加入DCCC后的A-LADRC对输出电压进行控制，为了便于比较，通过录波仪录制功能，将不同控制输出波形显示于同一界面，得到系统起动时刻输出电压波形如图9所示。通过对比可以发现，系统达到稳态后，三种控制方法均可实现对给定输出电压200 V的跟踪控制。但基于A-LADRC及占空比补偿控制下的系统输出达到稳定所用时间最少，约为0.03 s，基于PI控制下系统达到稳定所用时间约为0.15 s，A-LADRC的响应速度优于传统PI控制。同时，观察加入占空比补偿后A-LADRC下系统启动时刻输出电压波形，在同一控制参数下系统输出超调显著减小，电压质量改善明显。
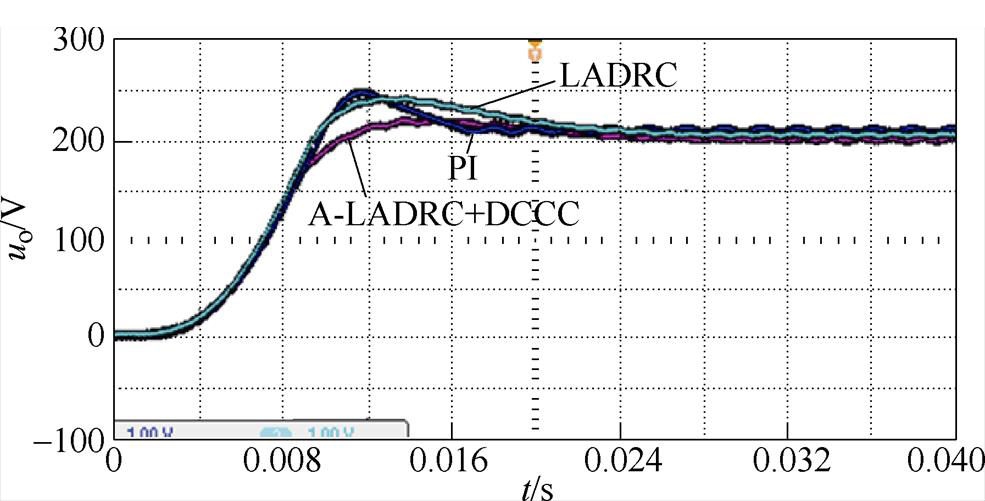
图9 不同控制下系统起动时刻输出电压响应波形
Fig.9 Output voltage response waveforms at system startup time under different controls
移相全桥DC-DC变换器在实际应用过程中还存在突增负载带来的电压暂降或暂升问题，为了模拟此类问题，设置初始负载为10 kΩ，此时系统处于空载状态，在0.6 s时刻使负载变为8 Ω，即系统由空载状态转变为负载状态。观察不同控制下系统输出电压电流波形。
图10、图11所示为不同控制方式下突增负载时系统输出电压和电流波形。从图中可以看出，突增负载后，A-LADRC及占空比补偿控制下输出响应较快，约0.07 s系统输出达到稳定200 V，而PI控制约经过0.45 s后稳定于200 V。PI控制下突增负载导致的电压暂降和电流暂升问题较为严重，电压衰减至30 V后缓慢上升，电压暂降幅度达85 %，电流突增至32 A后又降低至3.7 A缓慢上升。当采用本文提出的A-LADRC与占空比补偿控制应对突增负载系统时，从波形可以看出，电压仅降低至194 V，电流升高为24.2 A，电压暂降幅值相比于PI控制减小了约96 %，突增负载带来的电压暂降和电流暂降大幅减小。经过实验验证，当系统突减负荷时，基于A-LADRC及占空比补偿控制下输出电压电流突变幅值同样明显小于PI控制，限于篇幅不再赘述，进而验证了本文所提控制策略的有效性。
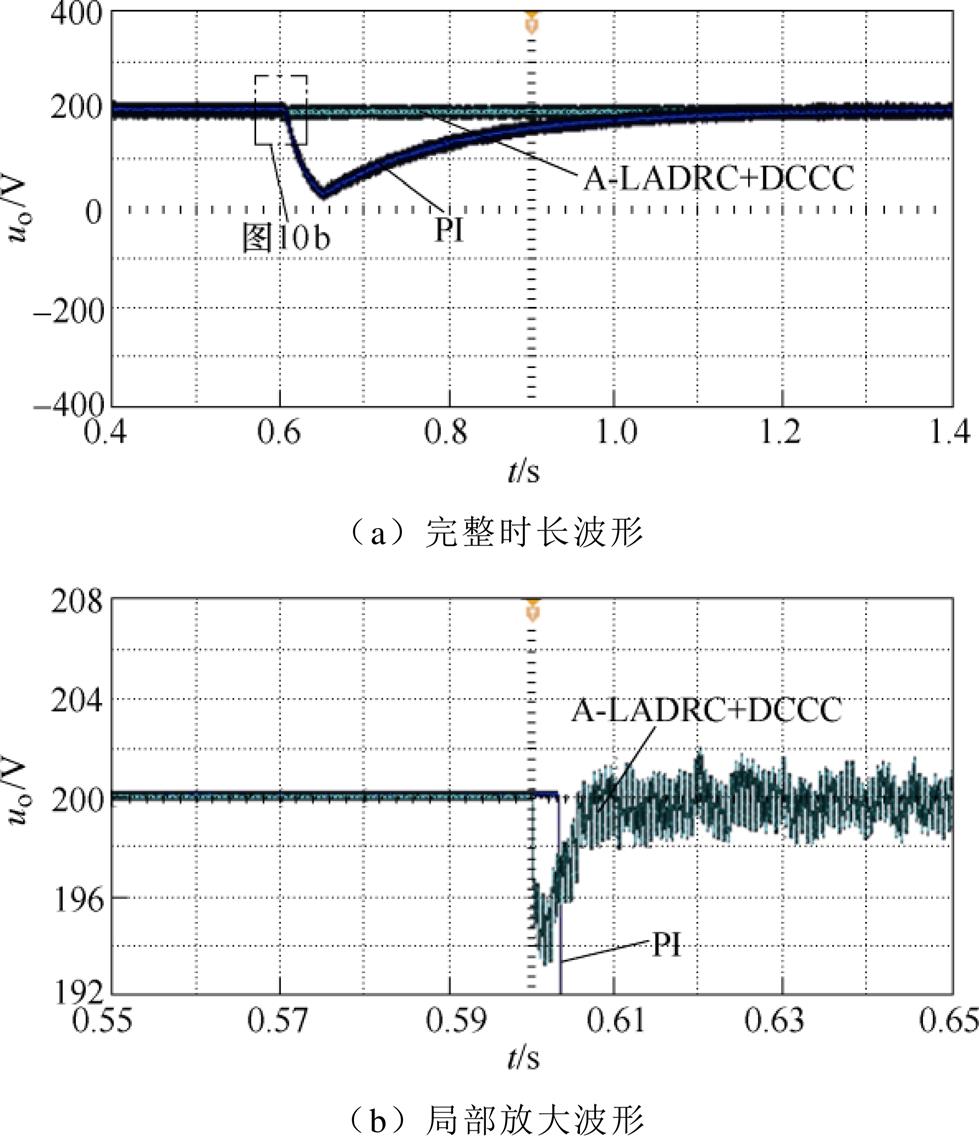
图10 突增负载时系统输出电压
Fig.10 System output voltage during sudden load
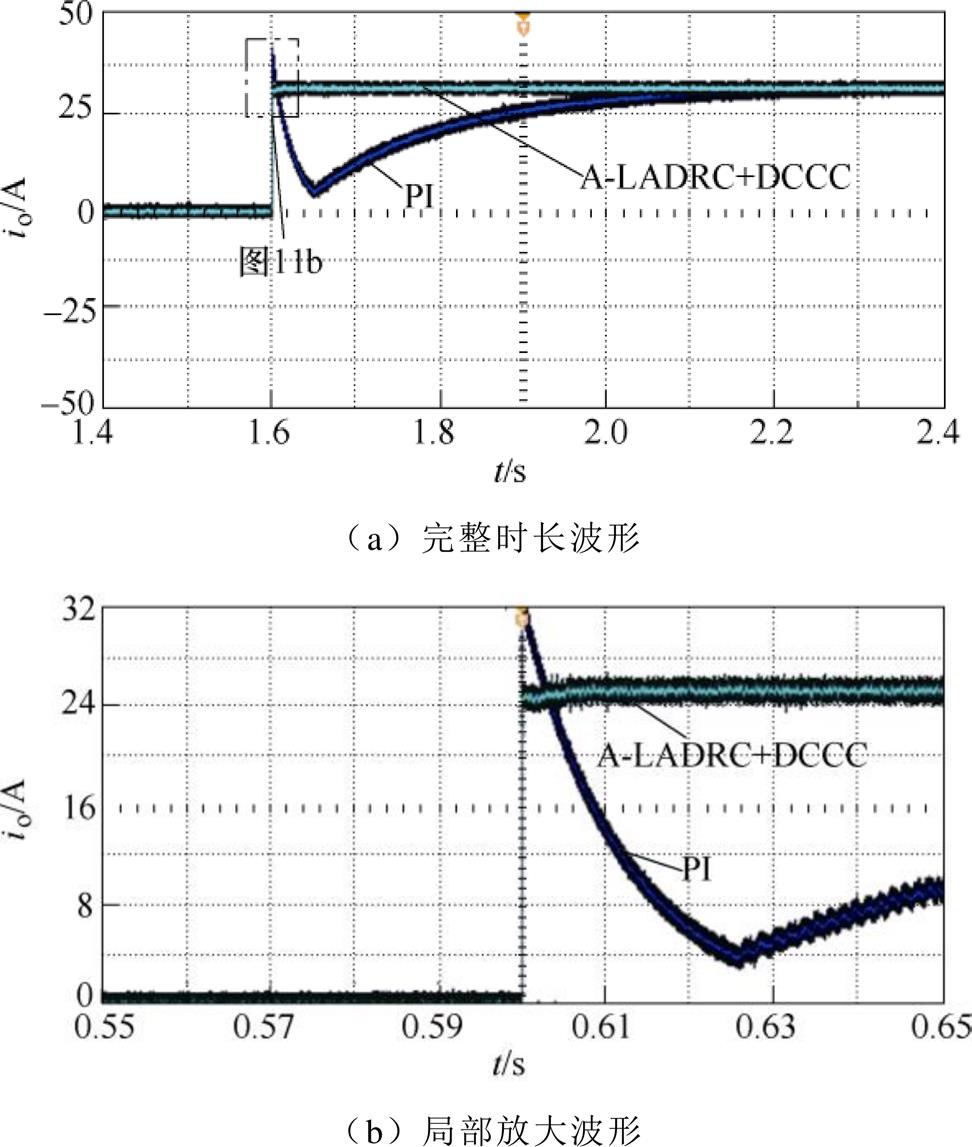
图11 突增负载时系统输出电流
Fig.11 System output current during sudden load
图12为不同控制下系统稳态时输出电压放大波形，为了更好地对比效果，通过调整示波器不同通道的位置将3个波形上下依次排列可得图12b。观察波形可知，当系统采用PI控制时，输出电压纹波波动幅值约为3.2 V。当系统控制采用LADRC策略时，输出电压不仅拥有较好的跟随特性，能够跟随由前级不控整流环节输出的六脉动分量，并且输出电压纹波波动幅值也有所降低，波动幅值约为1.5 V，纹波幅值相比PI控制降低了约50 %。最后观察在A-LADRC基础上，加入占空比补偿策略的稳态输出电压，由波形可以看出，输出六脉动分量显著降低，电压纹波波动幅值约为0.31 V，纹波幅值在LADRC的基础上再次降低80 %，验证了本文提出的电压纹波改善策略在大电流运行工况下的有效性。
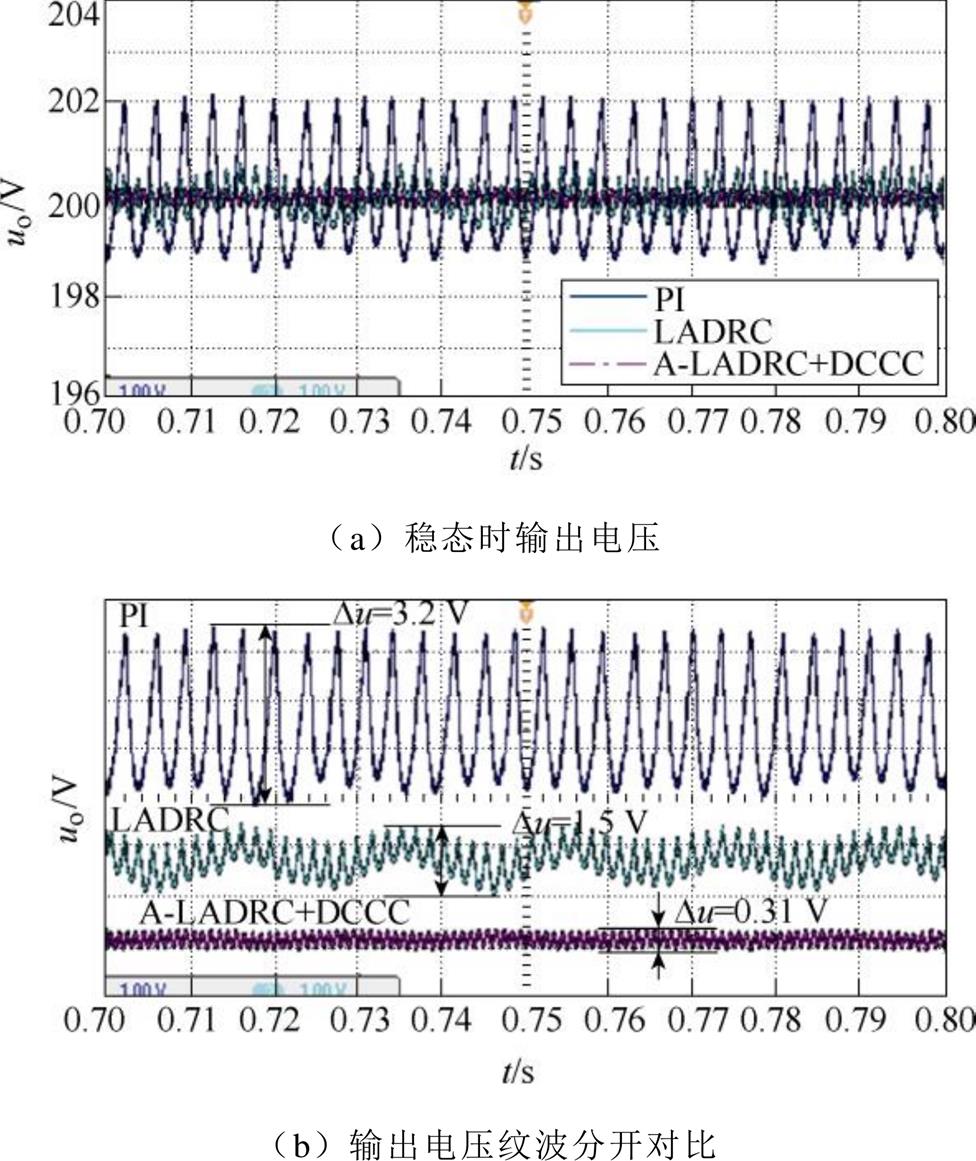
图12 不同控制下系统稳态时输出电压局部放大波形
Fig.12 Partially amplified waveforms of output voltage when the system is steady-state under different controls
三相隔离型AC-DC-DC电源应用广泛，为提高传统PI控制作用下系统输出响应速度和电压质量，本文提出了一种A-LADRC及占空比补偿控制策略，并通过实验验证了所提控制策略的有效性。得出结论如下：
1）通过建立控制器带宽参数与输出量之间关系，提出一种控制器带宽参数自适应调节的A- LADRC策略，从实验结果可以看出，所提方法能够有效缩短系统达到稳定的时间并且减小超调，显著提升了系统响应速度。
2）针对系统中存在的六脉动分量对输出电压产生的影响，设计了一种根据输出电压反馈值，自适应调整变换器占空比补偿量的控制策略。实验结果表明，输出电压纹波幅值较PI控制减小了约90 %。
3）通过实验样机，验证了本文所提控制策略对提高系统响应速度和改善输出电压纹波的有效性，具有较好的实际工程应用价值。
参考文献
[1] Lee S, Park J W. A new control for synchronous rectifier of phase-shifted full-bridge converter to improve efficiency in light-load condition[J]. IEEE Transactions on Industry Applications, 2021, 57(4): 3822-3831.
[2] 杨超, 许海平, 袁志宝, 等. 双PWM控制下三电平半桥隔离型双向DC-DC变换器的全局最小峰值电流研究[J]. 电工技术学报, 2020, 35(8): 1679-1689.
Yang Chao, Xu Haiping, Yuan Zhibao, et al. Global minimum peak current control of the three level isolated half-bridge bi-directional DC-DC converters with PWM-phase-shifting control[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1679- 1689.
[3] 张辉, 梁誉馨, 孙凯, 等. 直流微电网中多端口隔离型DC-DC变换器的改进虚拟电容控制策略[J]. 电工技术学报, 2021, 36(2): 292-304.
Zhang Hui, Liang Yuxin, Sun Kai, et al. Improved virtual capacitor control strategy of multi-port isolated DC-DC converter in DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 292 -304.
[4] 叶海涵, 陈武. 隔离型链式储能系统优化设计研究[J]. 电力工程技术, 2020, 39(4): 171-179.
Ye Haihan, Chen Wu. Optimization design of isolated cascaded energy storage system[J]. Electric Power Engineering Technology, 2020, 39(4): 171-179.
[5] 高明, 王大志, 李召. 移相全桥变换器的PWM全阶鲁棒滑模控制[J]. 电工技术学报, 2018, 33(10): 2293-2302.
Gao Ming, Wang Dazhi, Li Zhao. A PWM full order robustness sliding mode control for phase-shifted full-bridge converter[J]. Transactions of China Elec- trotechnical Society, 2018, 33(10): 2293-2302.
[6] Leso M, Zilkova J, Girovsky P. Development of a simple fuzzy logic controller for DC-DC con- verter[C]//2018 IEEE 18th International Power Elec- tronics and Motion Control Conference (PEMC), Budapest, Hungary, 2018: 86-93.
[7] 年珩, 叶余桦. 三端口隔离双向DC-DC变换器模型预测控制技术[J]. 电工技术学报, 2020, 35(16): 3478-3488.
Nian Heng, Ye Yuhua. Model predictive control of three-port isolated bidirectional DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3478-3488.
[8] Liu Hemiao, Zhao Yulian, Al Shurafa M, et al. A novel PID control strategy based on PSO-BP neural network for phase- shifted full-bridge current-doubler synchronous rectifying converter[C]//2021 IEEE 4th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 2021: 1241-1245.
[9] 高志强. 自抗扰控制思想探究[J]. 控制理论与应用, 2013, 30(12): 1498-1510.
Gao Zhiqiang. On the foundation of active dis- turbance rejection control[J]. Control Theory & Applications, 2013, 30(12): 1498-1510.
[10] 李志华, 曾江, 黄骏翅, 等. 基于线性自抗扰控制的微网逆变器时-频电压控制策略[J]. 电力系统自动化, 2020, 44(10): 145-154.
Li Zhihua, Zeng Jiang, Huang Junchi, et al. Time- frequency voltage control strategy of microgrid inverter based on linear active disturbance rejection control[J]. Automation of Electric Power Systems, 2020, 44(10): 145-154.
[11] Gao Zhiqiang. Scaling and bandwidth parameteri- zation based controller tuning[C]//Proceedings of the American Control Conference, Denver, CO, 2003: 4989-4996.
[12] Zhou Xuesong, Zhong Weibao, Ma Youjie, et al. Control strategy research of D-STATCOM using active disturbance rejection control based on total disturbance error compensation[J]. IEEE Access, 2021, 9: 50138-50150.
[13] 许文波, 魏泽宇, 孔伟, 等. PMSM伺服系统线性自抗扰控制器的参数整定[J]. 控制理论与应用, 2022, 39(1): 165-178.
Xu Wenbo, Wei Zeyu, Kong Wei, et al. Parameters tuning of linear active disturbance rejection controller for PMSM servo system[J]. Control Theory & Appli- cations, 2022, 39(1): 165-178.
[14] Lin Ping, Wu Zhen, Liu Kunzhi, et al. A class of linear-nonlinear switching active disturbance reje- ction speed and current controllers for PMSM[J]. IEEE Transactions on Power Electronics, 2021, 36(12): 14366-14382.
[15] 祝国平, 阮新波, 王学华, 等. 两级式单相逆变器二次纹波电流的抑制与动态特性的改善[J]. 中国电机工程学报, 2013, 33(12): 72-80, 188.
Zhu Guoping, Ruan Xinbo, Wang Xuehua, et al. Suppression of the second harmonic current and improvement of the dynamic performance for two- stage single-phase inverters[J]. Proceedings of the CSEE, 2013, 33(12): 72-80, 188.
[16] 刘斌, 贺建军, 粟梅, 等. 两级式单相逆变输入端纹波电流双反馈抑制[J]. 电工技术学报, 2013, 28(8): 187-193, 217.
Liu Bin, He Jianjun, Su Mei, et al. Input ripple current active mitigating for two-stage single-phase inverter based on double channel current feedback[J]. Transactions of China Electrotechnical Society, 2013, 28(8): 187-193, 217.
[17] Bandyopadhyay S, Qin Zian, Bauer P. Decoupling control of multiactive bridge converters using linear active disturbance rejection[J]. IEEE Transactions on Industrial Electronics, 2021, 68(11): 10688-10698.
[18] 丁杰, 高双, 赵世伟, 等. 基于耦合电感的对称式交错并联低输入电流纹波高增益DC-DC变换器[J]. 电工技术学报, 2021, 36(7): 1507-1515.
Ding Jie, Gao Shuang, Zhao Shiwei, et al. Symmetrical interleaved low input current ripple high step-up DC-DC converter based on coupled indu- ctor[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1507-1515.
[19] Zhou Yihan, Chen Guipeng, Wang Fei, et al. A ZVZCS hybrid dual full-bridge converter suitable for wide input voltage range[J]. IEEE Transactions on Industrial Electronics, 2021, 68(12): 12058-12068.
[20] 殷晓东, 罗登, 李祖勇, 等. 一种双向隔离DC-DC变换器二次纹波电压抑制方法[J]. 电工技术学报, 2018, 33(6): 1356-1363.
Yin Xiaodong, Luo Deng, Li Zuyong, et al. A second-order ripple voltage suppression algorithm of bidirectional isolation DC-DC converter[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(6): 1356-1363.
[21] 马树波. kW级全砖DC-DC模块电源的设计与实现[D]. 成都: 电子科技大学, 2020.
[22] 王兆安, 刘进军. 电力电子技术[M]. 5版. 北京: 机械工业出版社, 2009.
[23] 杨林, 曾江, 马文杰, 等. 基于改进二阶线性自抗扰技术的微网逆变器电压控制[J]. 电力系统自动化, 2019, 43(4): 146-153.
Yang Lin, Zeng Jiang, Ma Wenjie, et al. Voltage control of microgrid inverter based on improved second-order linear active disturbance rejection control[J]. Automation of Electric Power Systems, 2019, 43(4): 146-153.
[24] 梁青, 王传榜, 潘金文, 等. 线性自抗扰控制参数b0辨识及参数整定规律[J]. 控制与决策, 2015, 30(9): 1691-1695.
Liang Qing, Wang Chuanbang, Pan Jinwen, et al. Parameter identification of b0 and parameter tuning law in linear active disturbance rejection control[J]. Control and Decision, 2015, 30(9): 1691-1695.
[25] You Jiang, Cheng Lianbin, Fu Bin, et al. Analysis and control of input-parallel output-series based combined DC/DC converter with modified connection in output filter circuit[J]. IEEE Access, 2019, 7: 58264-58276.
[26] 黄先进, 赵鹃, 游小杰. 一种基于输入串联输出并联移相全桥变换器的改进交错控制方法[J]. 电工技术学报, 2020, 35(增刊1): 81-90.
Huang Xianjin, Zhao Juan, You Xiaojie. An improved interlace control method based on input series output parallel phase-shifted full-bridge converter[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(S1): 81-90.
[27] Zaoskoufis K, Tatakis E C. Isolated ZVS-ZCS DC-DC high step-up converter with low-ripple input current[J]. IEEE Journal of Emerging and Selected Topics in Industrial Electronics, 2021, 2(4): 464-480.
Abstract Three-phase isolated AC-DC-DC power supplies are widely used in industry due to their advantages of high power density and electrical isolation. However, in some particular application scenarios with frequent load switching, such as electrophoresis and electroplating, since the core isolated DC-DC converter is a typical nonlinear system, the power supply based on the traditional PI linear control method has slow output voltage response speed and large ripple, and cannot cope with the voltage sag or swell caused by the sudden change of load, especially for voltage-sensitive DC loads. Therefore, improving the output voltage response speed and reducing the ripple from the control level is urgent.
This paper analyzes the relationship between the key bandwidth parameters and output quantities in the linear active disturbance rejection control based on traditional linear active disturbance rejection control research. An Adaptive linear active disturbance rejection control (A-LADRC) method with adaptive adjustment of the controller bandwidth parameters is proposed. The proposed control method can collect the current value supplied to the load terminal by the system in real-time, and select it according to the designed controller bandwidth. According to the rules, the bandwidth parameters of the controller are adjusted online to realize the rapid adjustment of the output voltage under the sudden load change.
In view of the increase of the output voltage ripple caused by the voltage six-pulse component in the uncontrolled rectification of the front stage of the AC-DC-DC research system, the six-fold frequency pulsation of the power supply is analyzed by formula. Then a duty cycle compensation control (DCCC) strategy is designed to adaptively adjust the duty cycle compensation of the converter according to the feedback value of the system output voltage. This method can provide the compensation amount of the converter duty cycle according to the detectedoutput voltage deviation, assisting A-LADRC in fine-tuning the system output voltage to reduce voltage ripple.
Finally, the proposed method is verified by a 400 V/50 A experimental prototype. The experiments compare and verify the traditional PI control, linear active disturbance rejection control, and the A-LADRC with the duty cycle compensation control proposed in this paper. The experimental results show that among the output voltages at system startup under the same control parameters, the proposed A-LADRC control takes the least time to reach stability, and the time is 0.03 s, which is about 80 % less than that of the PI control, and overshoot is significantly reduced. In the sudden load simulation experiment, the output voltage dropped from 200 V to 30 V under PI control. Under the control method proposed in this paper, the output voltage only suddenly dropped to 194 V, and the sag amplitude was reduced by about 96 % compared with PI control. During PI control, the output voltage ripple fluctuation amplitude is 3.2 V. After using the control method proposed in this paper, the voltage ripple fluctuation amplitude is about 0.31 V, about 90 % lower than that of PI control. The results show that the proposed method can effectively improve the response speed of the system output voltage, reduce the voltage ripple, and solve the problems caused by the AC-DC-DC power supply in particular application scenarios from the control level.
keywords：Three-phase isolated power supply, phase-shifted full-bridge converter, linear active disturbance rejection control, voltage ripple, duty cycle compensation
国家自然科学基金资助项目（51807064）。
收稿日期 2022-05-23
改稿日期 2022-09-09
DOI: 10.19595/j.cnki.1000-6753.tces.220901
中图分类号：TM46
孟建辉 男，1987年生，博士，高级工程师，研究方向为新能源发电系统及其控制。E-mail: mengjianhui2008@163.com（通信作者）
吴小龙 男，1997年生，硕士研究生，研究方向为新能源发电系统及其控制。E-mail: 1621001066@qq.com
（编辑 陈 诚）