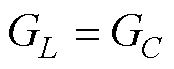（1）
摘要 电力电子系统较高的开关频率给传统以CPU为计算核心的电磁暂态（EMT）实时仿真带来了挑战。为了实现小步长实时仿真，该文提出并实现一款基于FPGA的EMT实时仿真解算器。该解算器的通用化框架分为离线和在线两部分，离线程序能够自动获取仿真模型的参数并生成计算数据，在线程序能够自动配置计算资源与控制逻辑。为了提高仿真速度，还提出一种低延迟的单周期浮点累加方法，用于构建解算器的基本计算单元。基于Xilinx Virtex7 xc7vx485t型FPGA芯片的评估与分析结果表明：相比某商业FPGA实时仿真解算器，该文解算器的仿真速度提高了一倍，仿真规模增加了29.69 %～79.17 %。最后，还通过两种电力电子变换器的实时仿真测试，验证了它的实际性能。所提解算器能够达到400 MHz的运行速度、100 ns级的仿真步长并保持较高的仿真精度，具有通用性强、自动化程度高、配置灵活等特点。
关键词：电力电子系统 FPGA实时仿真 通用解算器 浮点数乘累加
电磁暂态（Electro-Magnetic Transient, EMT）实时仿真在航空航天、轨道交通和电力系统等领域被广泛应用，贯穿于研发设计到验证测试等各个环节[1-3]。为了追求高功率密度、低总体谐波分布，电力电子系统的开关频率趋于高频化[4]。传统以CPU为计算核心的EMT实时仿真，它们以5～10 ms的最小仿真步长难以准确刻画开关的高频特性[5]。FPGA强大的并行计算能力、高带宽低延迟的I/O接口能够更准确地描述电力电子拓扑的开关事 件[1]。以FPGA为计算核心进行实时仿真已成为一种趋势[6-8]。
FPGA编程门槛高、开发周期长，增加了它用于实时仿真的难度。当前一种比较好的解决思路是基于通用解算器的仿真方法[9-13]。不同电路的数学模型可以统一为代数-微分方程组的形式[2]。如果方程求解程序实现了通用化，仿真时只需将其固化就可以处理不同的仿真对象，无需重复编程。Opal-RT公司在2011年公开了其FPGA实时仿真通用解算器的最早版本[9]，并提出新的浮点乘累加（Floating- Point Multiply-Accumulate, FPMAC）实现方法用于解算器的计算引擎[10]。为了提高仿真速度，MAC又被替换为并行度更大的向量点积（Dot Product, DP）[11]，但两者都未能很好地处理浮点累加运算，导致仿真速度受限。文献[12-13]提出了基于定点数的FPGA实时仿真解算器，可时钟频率仅有40 MHz。文献[14-16]针对有源配电网设计了基于矩阵分解运算的通用解算器，其用于机电暂态的仿真步长不太适合电力电子系统。
FPGA实时仿真的另一大难点是如何在完成高复杂度、大规模迭代计算的同时保证仿真的实时性。这不仅取决于计算核心的硬件能力，还与元器件的建模方法、电路方程的组织形式、解算器的框架以及程序设计等有关，尤其是开关器件模型，它几乎影响所有仿真环节。当前FPGA实时仿真中的开关模型主要有双值电阻模型与LC等效模型两类。双值电阻模型精度更高，但会造成电路方程的导纳矩阵时变。文献[14, 17]通过预存所有导纳矩阵逆矩阵的方法简化计算，不过仿真规模有限。LC等效模型具有恒定的开关导纳[18]，在当前FPGA实时仿真中广泛应用[19-20]。针对该模型引入人为振荡的问题，文献[21-23]已提出多种解决方案。
本文提出并实现了一款基于FPGA的电力电子系统EMT实时仿真通用解算器。相比文献[9-13]中报道的和现有的商业实时仿真解算器，它的特点在于：①依据仿真模型中状态量与测量量的情况，将基于固定导纳矩阵节点法（Fixed Admittance Matrix Nodal Method, FAMNM）生成的电路方程重写为状态空间的形式，提高仿真的实时性；②解算器通用框架分为离线与在线两部分，离线程序自动获取仿真模型的参数并生成计算数据，在线程序根据参数自动配置计算资源与控制逻辑，通用框架还可以配置资源的复用程度；③生成计算数据时考虑多个仿真工况的切换，并将多个数据拼接后再写入同一个初始化文件，以提高存储资源的利用率；④提出一种低延迟的单周期浮点累加实现方法，用于构建以FPMAC为基本计算单元的计算引擎，使得解算器最终取得极高的运行速度。
电路分析方法主要有节点分析法和状态空间法两种。节点分析法最早由Dommel博士提出，经过C. W. Ho等的改进，其相关理论已十分成熟[24-25]。在节点分析法的基础上，文献[9]结合LC等效开关模型提出的FAMNM是当前FPGA实时仿真的主流电路分析方法。LC等效开关模型将导通时的开关等效为电感，关断时的开关等效为电容[19]。经过数值积分方法离散后，如果开关等效电感和等效电容的导纳值GL、GC满足
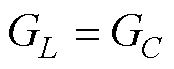（1）
那么开关导纳将不随开关状态变化，节点导纳矩阵也会保持固定不变。因此，FAMNM既保持了预存逆矩阵方法计算简单的优点，又不需要过多的存储资源。
对于一个有Nn个独立节点、Nvs个独立电压源的电路，根据FAMNM得到的节点方程为
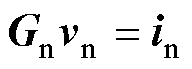（2）
式中，Gn为节点导纳矩阵；向量in包含Nn个节点注入电流和Nvs个独立电压源；向量vn为独立节点的电压和独立电压源的支路电流。
电力电子系统的节点方程是基于差分电路得出的，必须确定合适的数值积分方法。EMT仿真最常用的梯形法和后向欧拉法中，梯形法精度高，但用在含开关的电路时会有数值振荡[26]。通常选择后向欧拉法，因为它具有的阻尼作用可以较好地抑制开关动作引起的振荡，并且在实时仿真的步长下能够提供足够的精度和刚性[27]。
按照节点方程的解算流程，式（2）转换为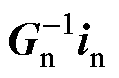
形式得到节点电压vn后，将依次更新支路电压、支路电流、历史电流源。这种串行求解方式以及节点电压、支路电流这些中间结果的求解过程，增加了解算程序的硬件复杂度与执行时间。
为此，本文依据仿真模型中状态量与测量量的情况，将节点方程重新组织为状态空间方程的形式，在减少计算量的同时增加计算的并行性。文献[9, 28-29]中已有类似做法，本文与它们的不同之处在于：直接更新仅与状态量和测量量相关的电压和电流，省略中间量（节点电压等）和无关项（电阻的电压电流、电感电压以及电容电流等）的计算。
假设电路中Nd个独立动态元件和Ns个开关在离散后分别形成了历史电流源向量ih_d、ih_s，它们共同组成状态向量x；Nu个独立输入源组成输入向量u。记
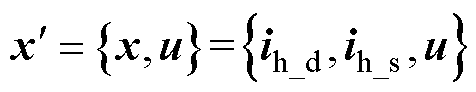（3）
式（2）中的向量in可以重新表示为
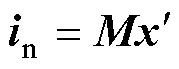（4）
矩阵M的(Nn+Nvs)×(Nd+Ns+Nu)个元素全部由-1, 0, 1组成。式（2）中的向量vn表示为
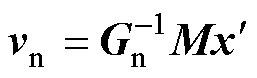（5）
相似地，将Nb个支路的支路电流向量ib表示为
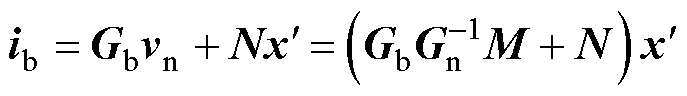（6）
式中，矩阵N的Nb×(Nd+Ns+Nu)个元素全部由-1, 0, 1组成的。支路导纳矩阵Gb含Nb×(Nn+Nvs)个元素，每行分别为相应支路的导纳。
记A=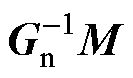
，B=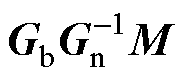
+N。根据算法1（见附录）的流程组织状态更新矩阵T。由于下一步长的ih_s需要从本步长的开关电压电流中选择，每个开关都在矩阵T中对应两行元素。
仿真模型中的各个测量量可以采用同样的方法组织输出矩阵P。既不是状态也未被测量的电气量将不会出现在矩阵[T;P]中，因此矩阵[T;P]的行数一般情况下是小于矩阵[A;B]的，这也是重写电路方程的意义。
最终状态空间形式的电路方程为
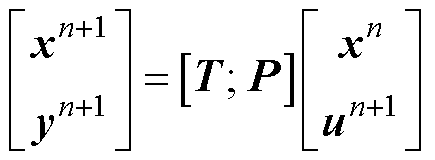（7）
式中，y为Nm个测量量对应的输出向量；上标n+1为当前仿真步长；n为上一仿真步长。矩阵[T;P]的行数Ntr为Nd+2Ns+Nm，列数Ntc为Nd+Ns+Nu。
得到式（7）后，仿真的迭代计算转为矩阵[T;P]与向量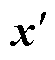
之间的矩阵向量乘（Matrix Vector Multipli- cation，MVM）运算。DP和MAC是两种最常见的实现MVM运算的单元，它们的结构示意图如图1所示。
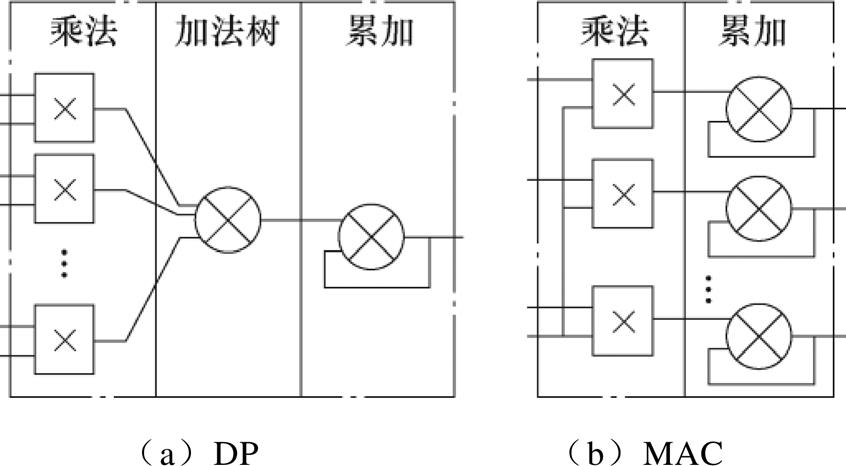
图1 DP与MAC的结构示意图
Fig.1 Structure diagrams of DP and MAC
理论上，DP拥有更大的并行度，不过有限的FPGA资源与变化的矩阵规模使得它很难达到理论上的并行度。此外，DP加法树复杂的二叉树结构不仅引入了延迟，可配置性还比较差。如Opal-RT的FPGA实时仿真解算器eHS，它的底层就是拥有8个乘法器的DP单元（DP8）[30]。这种情况下，即使电路规模只有11阶，也必须使用两个DP8单元。
相比之下，MAC自身相对独立的逻辑设计赋予了它极强的可拓展性。配合简单的控制逻辑，它很容易实现参数化配置。MAC的这些特点为根据仿真规模、资源数量、速度要求等因素灵活配置MAC单元的数量提供了可能，也是本文选择它完成MVM运算的原因。
本文设计的FPGA实时仿真解算器通用框架如图2所示。整个框架分为离线预处理、在线计算两个部分，离线部分为在线部分提供Nd、Ns和Nu等参数与计算数据{T;P}，在线部分负责更新状态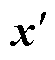与测量量y。
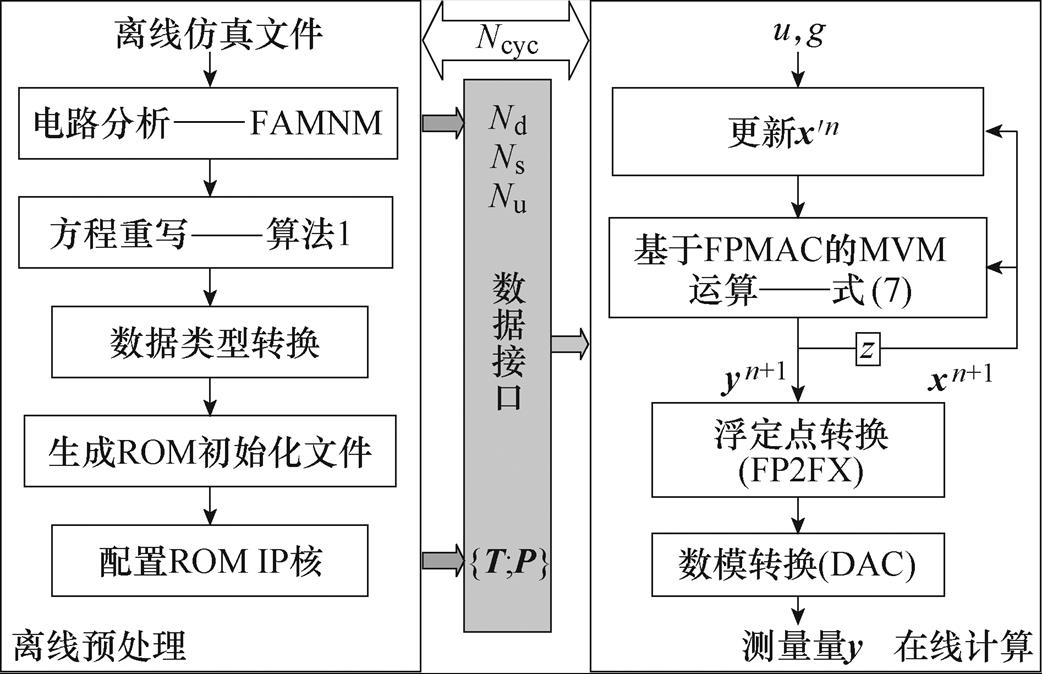
图2 解算器的通用框架
Fig.2 General framework of the proposed solver
2.1.1 离线部分
离线部分中，通过电路分析和方程重写得到更适合实时计算的电路方程；数据类型转换将Matlab默认的双精度浮点数转为IEEE-754标准下的单精度浮点数；ROM初始化文件为在线的MVM运算提供计算数据。本文在Matlab环境下，通过编写脚本完成上述所有离线预处理过程。
在具体实现时，首先，调用power_analyze命令生成Simulink模型的网表文件。该文件包含了电路的元器件参数与节点支路编号等信息。其次，利用这些信息按照FAMNM的规则组织电路的节点方程，并按照算法1的流程组织矩阵[T;P]。最后，根据参数Ncyc将数据类型转换后的矩阵[T;P]划为Ncyc个大小相同的分块，作为ROM的初始化数据{T;P}。其中，Ncyc为解算器中每个MAC单元的复用次数。
本文组织{T;P}的方法为：分块矩阵内部各行元素并行计算、不同分块矩阵之间串行计算。这样解算器中MAC单元的数量Nmac就等于各分块矩阵的行数Nbr。
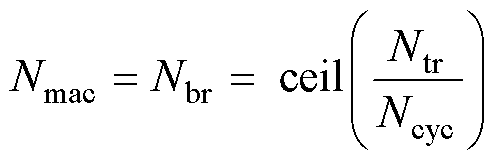（8）
式中，ceil(·)为向上取整函数。矩阵分块缺少的行填零补充，ROM初始化数据组织方式如图3所示。Ncyc=1时，矩阵[T;P]的所有行全部并行，此时解算器达到它的最大并行度。
考虑到多个仿真工况间的切换，以及提高存储资源的利用率，在生成计算数据时可以准备多组{T;P}，并将数据拼接后再写入同一个初始化文件中。
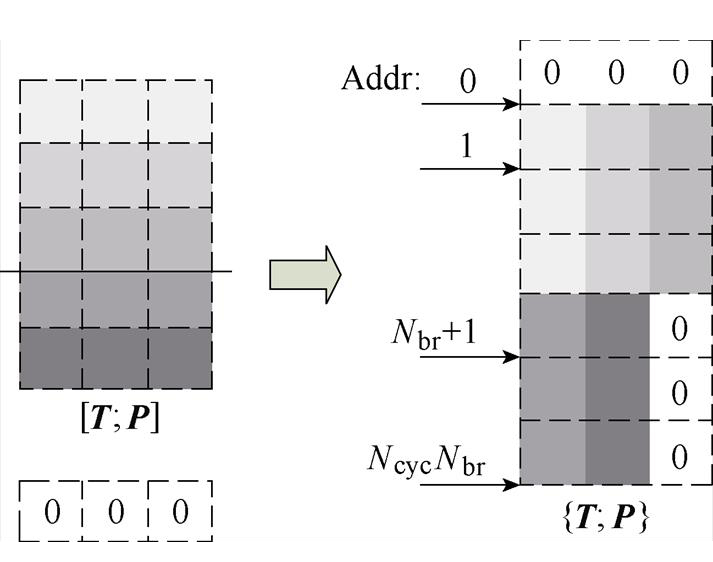
图3 ROM初始化数据组织方式
Fig.3 Organization of ROM initialization data
以图3为例，初始化数据{T;P}中首地址的全零行是解算器异步复位时的数据，从地址1到地址Nbr的每一个地址都写入第1个分块矩阵中的一列数据，从地址Nbr+1开始写入第2个分块的数据。{T;P}的总地址深度为NcycNbr+1。如果仿真模型有多个工况，如断路或者短路故障，将它们对应的{T;P}从地址NcycNbr+1接着写入，仿真时通过改变ROM读地址的偏移量切换工况。
由于Xilinx的BRAM资源一般以18 K、36 K为单位进行组合，最大位宽分别是36位、72位[31]。矩阵元素拼接如图4所示，9个32位的数据单独存储时需要9个18 K的BRAM，如果将9个数拼接成一个位宽为288的数据，此时存储将只需要8个18 K的BRAM，节省了12.5 %的BRAM资源。因此，通用解算器在离线预处理时将矩阵元素拼接成大位宽数据后再存储。
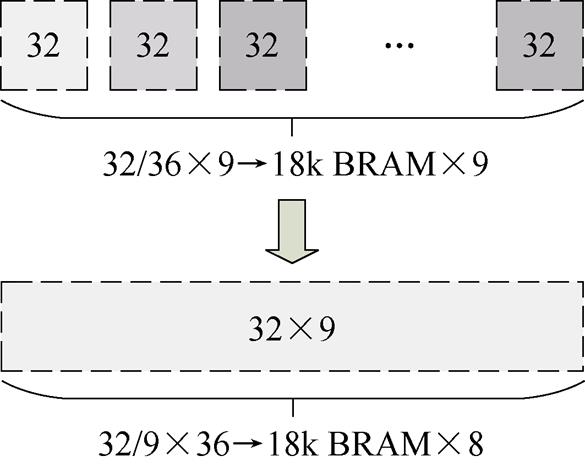
图4 矩阵元素拼接
Fig.4 Splicing of matrix elements
预处理程序默认只生成一个ROM初始化文件。如果分块矩阵的行数Nbr太大，这时就需要两个或者更多的ROM以及多个初始化文件。以Xilinx的Block Memory IP核为例，它支持的最大ROM位宽为4 608位，对应144个单精度浮点数[31]，即单个ROM初始化文件支持的最大Nbr为144。
2.1.2 在线部分
浮定点转换（FP2FX）、数模转换（DAC）的实现比较容易。基于MAC的MVM运算，它的数学原理虽然简单，但其FPGA程序设计却直接决定解算器的性能。向量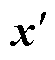中ih_d、u的更新直接按照式（7）进行，比较特殊的是ih_s的更新。由于xn+1中既有开关电压也有开关电流，ih_s需要根据开关的通断状态确定。记某个开关的电压、电流分别为vs、is，开关的通断状态为s（s=1，导通；s=0，关断），那么其历史电流源is_h可以表示为
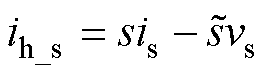（9）
因此，更新开关历史电流源首先要更新开关状态。
仿真中，全控型开关器件的状态由当前步长的开关信号g控制，但是不控型和半控型开关器件的状态还依赖开关上一步长的状态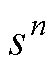
、电压
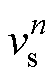和电流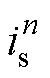
。如二极管的开关状态[9]表达式为
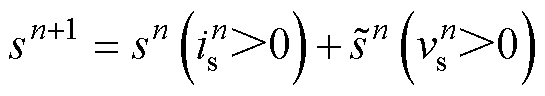（10）
同样地，如果将常用的IGBT反并联二极管模块当作一个整体，它的开关状态[9]为
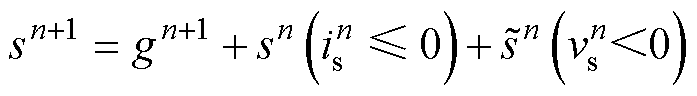（11）
在线部分的四个环节中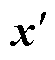，更新只是简单的选择判断逻辑、FP2FX利用厂家提供的IP核实现、DAC直接采用TI公司的软硬件解决方案，只有MVM运算比较复杂。为此，本文提出一种新的浮点累加方法，用于构建以FPMAC为基本计算单元的MVM运算架构，FPMAC单元与MVM运算整体架构如图5所示。
2.2.1 FPMAC单元
浮点运算的硬件复杂度比较高，尤其是FPMAC中的浮点累加计算，累加结果要经历取补、对阶、移位对齐等步骤才能再次累加，往往是整个硬件电路的性能瓶颈[32]。
为了提高浮点累加的速度，文献[33]通过插入寄存器的方法减短关键路径，但是反馈的累加结果在流水线结构中会引发“数据竞争”。还有文献[15, 34]将浮点数转为定点数降低累加的难度，不过定点数动态表示范围远不如浮点数广。由文献[32]提出、文献[35-36]优化的方法简化了浮点累加中移位对齐步骤的实现过程，并被用于Opal-RT的eHS解算器，但它对齐前的预处理过程仍有速度瓶颈。
本文通过双向移位对齐的方法实现低延迟的单周期浮点累加。在图5中，累加结果rfd反馈后直接进入累加器，只有符号数乘法的乘积rp根据对阶模块提供的结果进行移位对齐。若乘积的指数大，乘积rp左移；若累加结果的指数大，乘积rp右移。因为对齐仅由乘积rp双向移位完成，浮点累加的关键路径被进一步缩短，最终以极低的延迟实现单周期浮点累加。
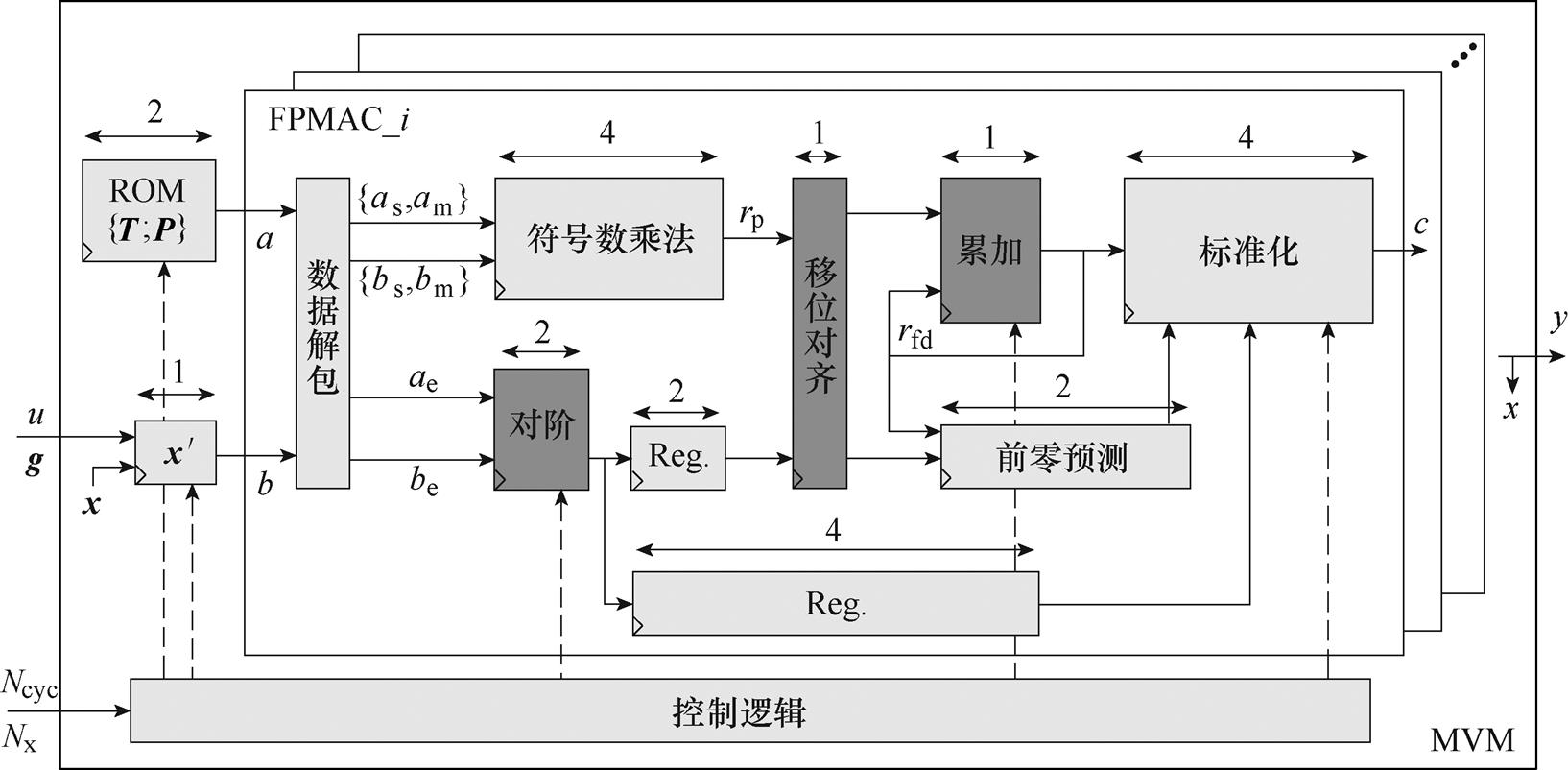
图5 FPMAC单元与MVM运算整体架构
Fig.5 Overall structure of FPMAC units and MVM operations
双向移位对齐的不足在于它使乘积rp的位宽增加了一半，后续累加、标准化等模块的位宽也随之增加。不过这些模块的逻辑比较简单，增加的位宽对解算器资源消耗的影响有限。
FPMAC除了浮点累加，还有符号数并行乘法和标准化两个步骤。符号数乘法通过乘法器IP核实现；标准化（包括前零预测）的原理与实现方法可见文献[37]。整个FPMAC单元采用深度流水线设计，输入输出延迟为10个节拍。图中标出了各模块的执行延迟，寄存器Reg.延迟多个节拍是为了数据同步。如果FPMAC单元的流水线启动延迟Nsp个节拍，那么单个仿真步长的总节拍数Ntp可以表示为
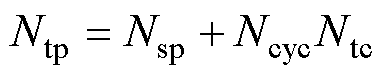（12）
MVM运算环节中FPMAC单元的数量根据离线环节提供的仿真参数自动适配。每个FPMAC单元的输入为a和b、输出为c，不同FPMAC单元间相互并行。整个MVM运算的输入除了初始化数据{T;P}，还包括Ncyc和Nx两个控制参数，其中Nx为向量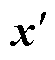的维数（Nx=Ntc）。图5中，下标“s”、“e”和“m”分别对应IEEE-754标准中浮点数的符号、指数和尾数[38]。
2.2.2 控制逻辑
解算器重要的控制逻辑有ROM读地址Addr、累加器清零信号Acc_clr、FPMAC输出使能信号Output_en。主计数器CNT从1～Ntp循环计数，整个解算器的控制逻辑根据它的计数值设计。
以图5中第i个FPMAC单元为例，ROM读操作的典型时序如图6所示。ROM的地址与数据之间的延迟为2个节拍，由于地址提前了一个节拍赋值，ROM实际读延迟只有一个节拍。结合FPMAC单元10个节拍的延迟，整个解算器流水线启动延迟共11个节拍（Nsp=11）。CNT计数值达到NcycNx后，ROM的地址被重置为0，a、b也同步为0；CNT计数值达到Ntp后，ROM地址开始为下一步长重新赋值。
图7为累加器清零信号Acc_clr的典型时序。由图5可知，新数据经历6个节拍到达累加器。当CNT的计数值在6～NcycNx+5之间时，子计数器cnt开始Ncyc次1～Nx的循环计数；否则，cnt保持为Nx。每当cnt=1时，Acc_clr置高。
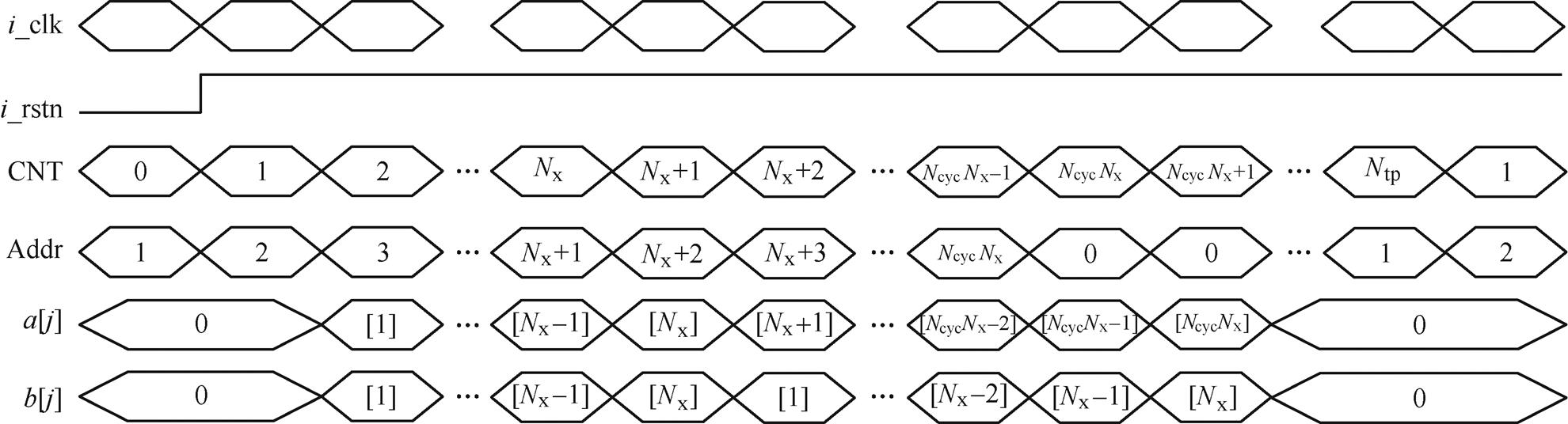
图6 ROM读操作典型时序
Fig.6 Typical timing of ROM read operations
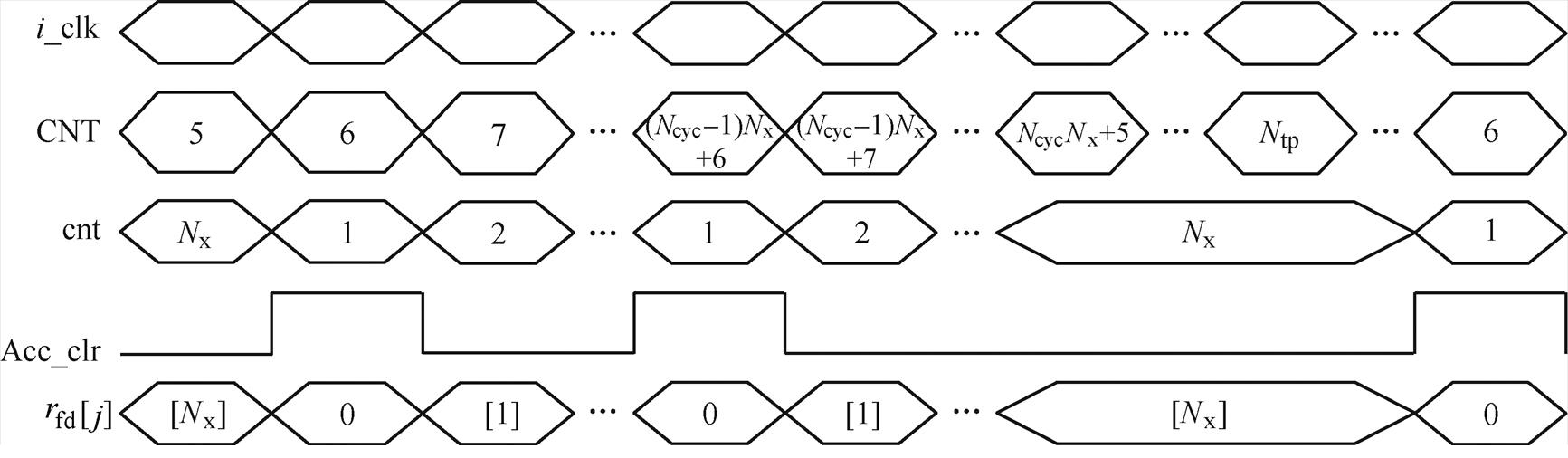
图7 累加器清零信号典型时序
Fig.7 Typical timing of the accumulator clearing signal
FPMAC输出使能信号Output_en的控制逻辑与图7相似。一组新数据经历Nsp个节拍才输出。当CNT的计数值在Nsp～NcycNx+Nsp之间时，cnt在1～Nx间循环计数；否则，cnt保持为Nx。每当cnt=1时，Output_en置高。
本文基于Xilinx ISE14.7环境完成解算器代码的开发与评估，目标器件为Virtex7 xc7vx485t，测试对象为如图8所示的三相两电平桥式变换器电路拓扑。仿真参数见表1，其中3个测量量分别为a相电压电流和a、b两相之间的线电压。
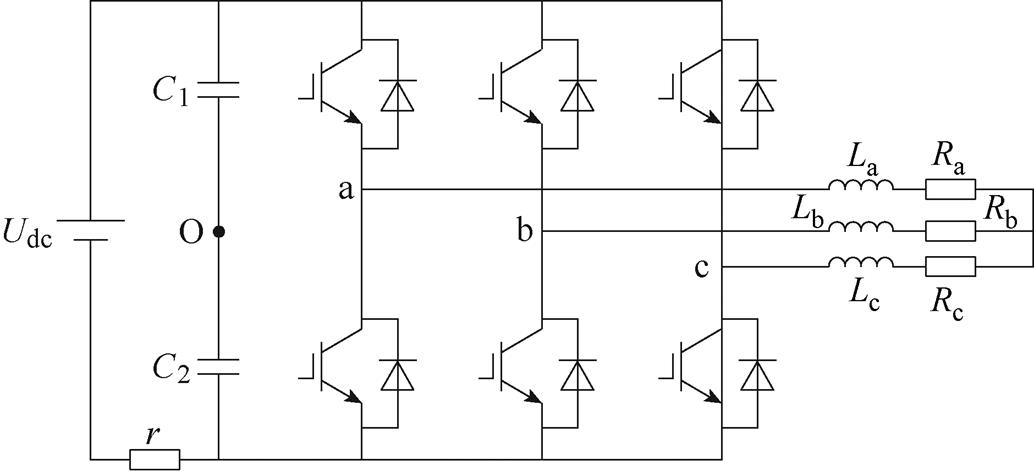
图8 三相两电平桥式变换器电路拓扑
Fig.8 Three-phase two-level bridge converter
解算器根据表1参数自动适配，表2列出了每个环节资源消耗的结果。MVM环节消耗了整个解算器程序86.25 %的寄存器资源、94.20 %的LUT资源和100 %的DSP资源。FP2FX环节将32位单精度浮点数转为Q(10, 6)格式的16位定点数，耗时6个节拍。DAC环节采用TI公司的解决方案，数据未列出。
表3是单个FPMAC单元和整个解算器的评估结果。FP2FX环节的代码规模取决于测量量个数，具有不确定性，评估时未将其包括在内。两个评估对象的关键路径都是乘法器IP核，因而它们拥有相同的关键路径延迟和最大时钟频率。在双向移位对齐的作用下，共3级流水线、消耗2个DSP的乘法器IP核，代替了浮点累加成为FPMAC的关键路径，这是FPMAC单元和解算器的最大时钟频率能够达到420.698 MHz的关键。
表1 变换器仿真参数
Tab.1 Simulation parameters of the converter
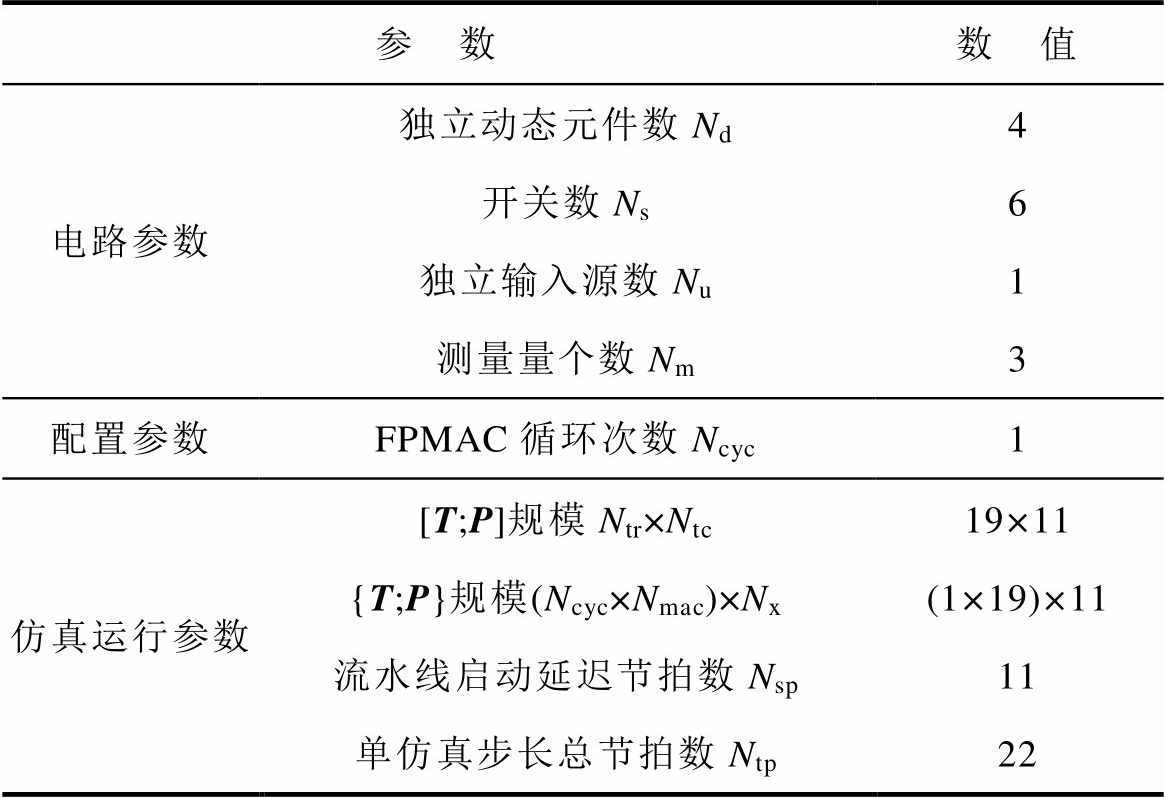
参 数数 值 电路参数独立动态元件数Nd4 开关数Ns6 独立输入源数Nu1 测量量个数Nm3 配置参数FPMAC循环次数Ncyc1 仿真运行参数[T;P]规模Ntr×Ntc19×11 {T;P}规模(Ncyc×Nmac)×Nx(1×19)×11 流水线启动延迟节拍数Nsp11 单仿真步长总节拍数Ntp22
表2 解算器各环节资源消耗
Tab.2 Resource consumption of each step in the solver
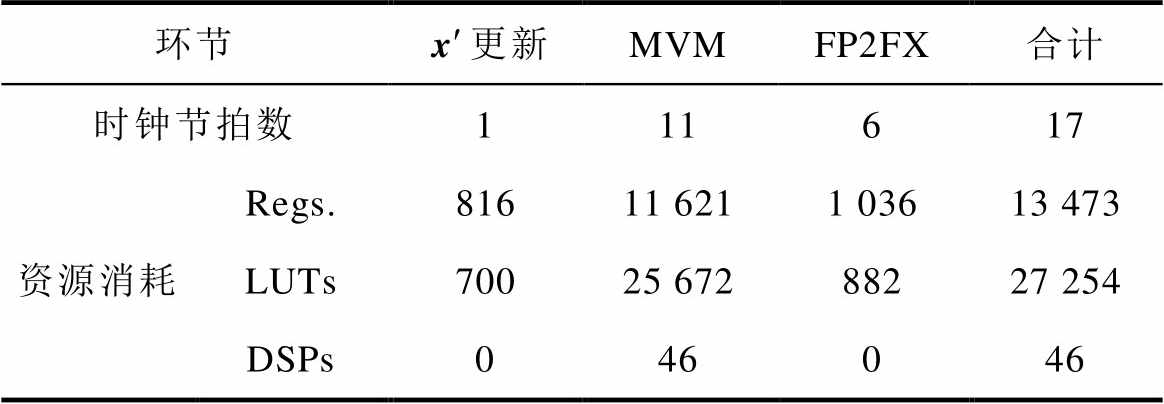
环节更新MVMFP2FX合计 时钟节拍数111617 资源消耗Regs.81611 6211 03613 473 LUTs70025 67288227 254 DSPs046046
表3 仿真模型评估结果（Ncyc=1）
Tab.3 Evaluation results of the simulation model (Ncyc=1)
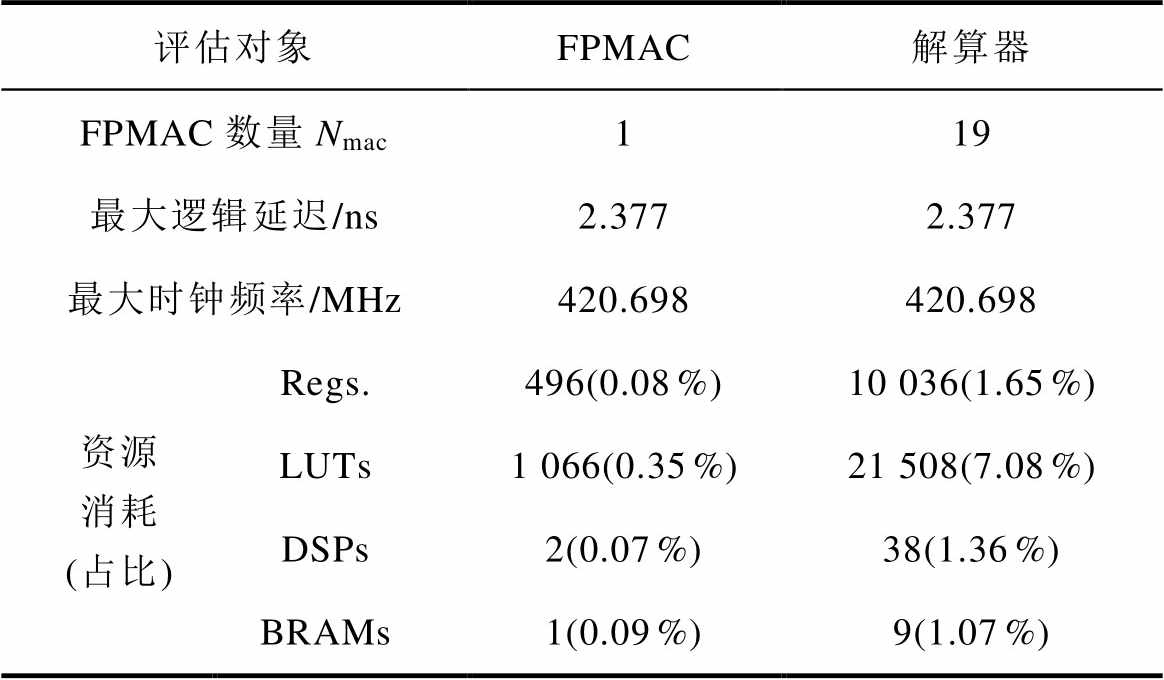
评估对象FPMAC解算器 FPMAC数量Nmac119 最大逻辑延迟/ns2.3772.377 最大时钟频率/MHz420.698420.698 资源消耗 (占比)Regs.496(0.08 %)10 036(1.65 %) LUTs1 066(0.35 %)21 508(7.08 %) DSPs2(0.07 %)38(1.36 %) BRAMs1(0.09 %)9(1.07 %)
解算器的初始化数据共消耗8个36 K、1个18 K的BRAM，如果矩阵元素不拼接则需要19个18 K的BRAM，多消耗2个18 K的BRAM。解算器资源消耗基本与它的FPMAC单元数量成正比，证实了MAC可拓展性极强。
3.2.1 仿真速度
本文解算器仿真步长Ts为
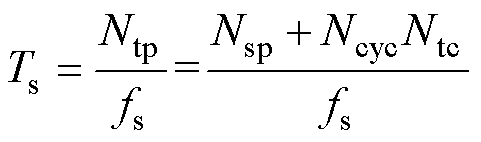（13）
式中，fs为FPGA仿真时的运行频率。表3所列解算器的最大时钟频率达到420.698 MHz，考虑到时间裕度，将fs设为400 MHz。Ncyc=1时，解算器达到最大并行度，Ts也达到最小值。
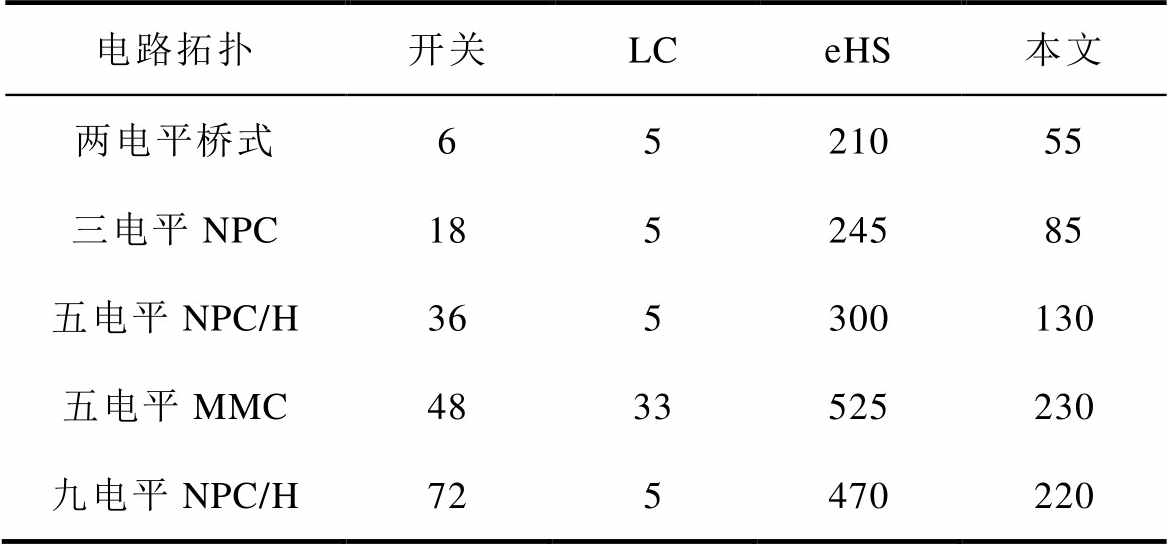
图8所示三相两电平桥式变换器模型的Ntp= 22，对应的最小Ts=55 ns。常见三相多电平拓扑接阻感负载时，它们相应的最小Ts见表4。结果显示，对于NPC/H九电平、五电平MMC这些较大规模的拓扑，最小Ts在55～200 ns之间；对于一般规模的拓扑，最小Ts通常约在100 ns级。
表4 常见多电平拓扑的最小Ts
Tab.4 Minimum values of Ts of several multi-level topologies （单位: ns）
电路拓扑开关LCeHS本文 两电平桥式6521055 三电平NPC18524585 五电平NPC/H365300130 五电平MMC4833525230 九电平NPC/H725470220
表4同时列出了Opal-RT eHS解算器对上述拓扑预估的最小Ts。可以发现，eHS的最小Ts是本文解算器的2.136～3.818倍，拓扑规模越小，差别越大。根据eHS解算器手册，其最大仿真频率为200 MHz，最小Ts=200 ns（同样是基于xc7vx485t型芯片）[39]。与本文解算器400 MHz的仿真速度相比，eHS解算器的最小Ts理应是本文解算的2倍。实际结果普遍大于2倍的原因如1.3节所述：eHS解算器底层计算单元是DP8。模型规模越小，DP8单元利用率越低，最小Ts差距也就越大。
3.2.2 仿真规模
由于MAC延迟相对固定、资源消耗基本呈线性，本节分别以仿真步长和FPGA硬件资源为约束条件预估解算器的仿真规模，即
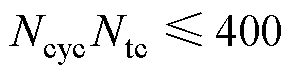（14）
一方面，fs=400 MHz时，解算器1ms仿真步长可以串行处理400个数据，对应矩阵[T;P]的列数或者向量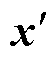
的维数为400；另一方面，考虑到解算器消耗最多的资源是LUT以及资源裕度，以70 %的LUT资源评估仿真规模。这些LUT资源可以支持175个FPMAC单元，即解算器最多支持矩阵的175行数据全并行计算。
式（15）为本文所提解算器仿真步长Ts与仿真规模之间的关系。基于所有指标能够同时到达最大值这一假设，本文预估了所提解算器的仿真规模，与文献[39]给出的Opal-RT eHS解算器仿真规模对比见表5。
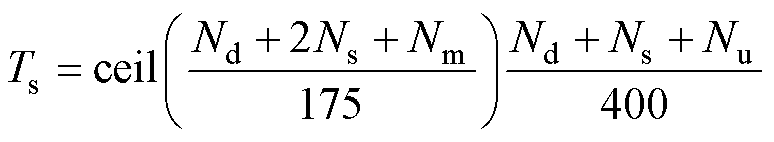（15）
表5 两种解算器仿真规模对比
Tab.5 Comparisons of simulation scale of two solvers
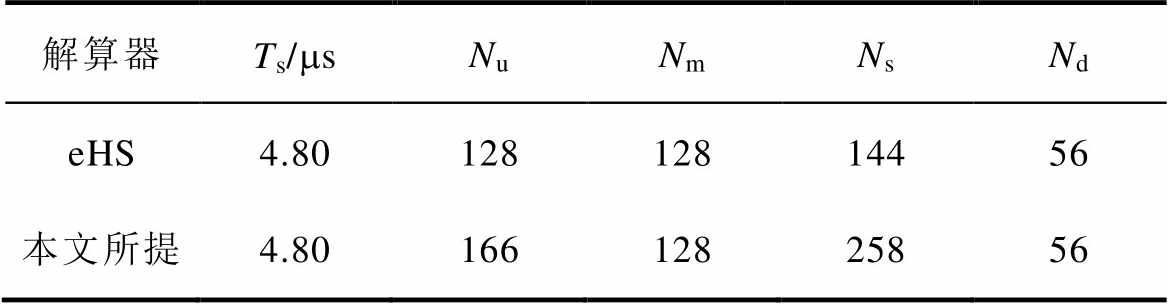
解算器Ts/msNuNmNsNd eHS4.8012812814456 本文所提4.8016612825856
相同条件下，本文解算器支持的输入源数量Nu增加了29.69 %，开关数量Ns增加了79.17 %。另外，eHS通过四种不同规模的计算引擎适配任意规模的电路拓扑[39]，资源利用率低、可配置性不好。本文解算器得益于MAC单元的灵活性，能够根据仿真规模与仿真需求，配置并生成定制化的计算引擎，资源利用率高、灵活性强。
图9为仿真测试的硬件平台，包括：Xilinx公司的VC707评估板、TI公司的DAC3484数模转换模块以及配套的FMC-DAC转接板。VC707评估板搭载了一块Virtex7 xc7vx485t型的FPGA芯片，DAC3484评估模块拥有4通道、16位分辨率和1.25GSPS的转换能力。同时，还有一台Opal-RT OP5700仿真机，用于比较eHS解算器与本文解算器的仿真结果。
图9 硬件平台
Fig.9 Hardware platform
4.2.1 算例一：三相两电平桥式变换器
为了验证解算器通用框架与FPGA程序的正确性，根据表6所列电气参数对两电平桥式变换器进行以下三种仿真：①变换器S函数模型在Matlab中的离线仿真，数据为双精度浮点格式；②变换器模型在本文所提解算器中的实时仿真；③变换器模型在eHS解算器中的实时仿真。两种实时仿真的数据都是单精度浮点格式。为了排除开关建模方法本身以及不同仿真步长对仿真结果的影响，三种仿真都基于LC等效开关模型，开关等效导纳设为1 S，仿真步长设为1 ms。
表6 两电平桥式变换器电气参数
Tab.6 Electrical parameters of two-level bridge converter
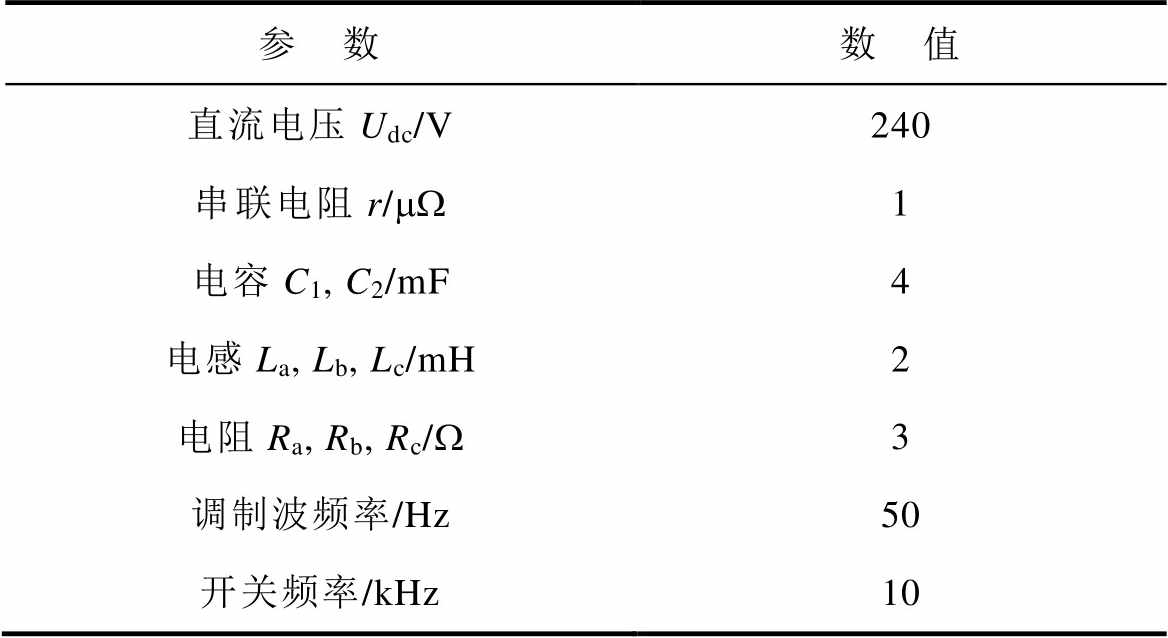
参 数数 值 直流电压Udc/V240 串联电阻r/mW1 电容C1, C2/mF4 电感La, Lb, Lc/mH2 电阻Ra, Rb, Rc/W3 调制波频率/Hz50 开关频率/kHz10
两电平桥式变换器a相电压测试结果如图10所示。无论是整体还是细节，三种仿真都反映出相电压波形存在“过脉冲”这一现象。该现象是由LC等效开关模型特性所引起，其机理与相关解决方法可以参考文献[22-24]。从过脉冲的包络线看，虽然eHS解算器的包络线形状明显比其他两种仿真平整，但却是不合理的。过脉冲反映的是开关模型等效LC元件的充放电过程，其幅值取决于开关的电压电流，其包络线形状应该与相电流波形一致。因此，本文解算器以及离线仿真的包络线形状更接近理论实际。本文解算器的包络线形状存在虚化，这是因为过脉冲幅值随着相电流的纹波在浮动。另外，从放大的细节看，本文解算器的过脉冲幅值普遍略小于离线仿真，这可能是波形在输出时受DAC电路的影响。
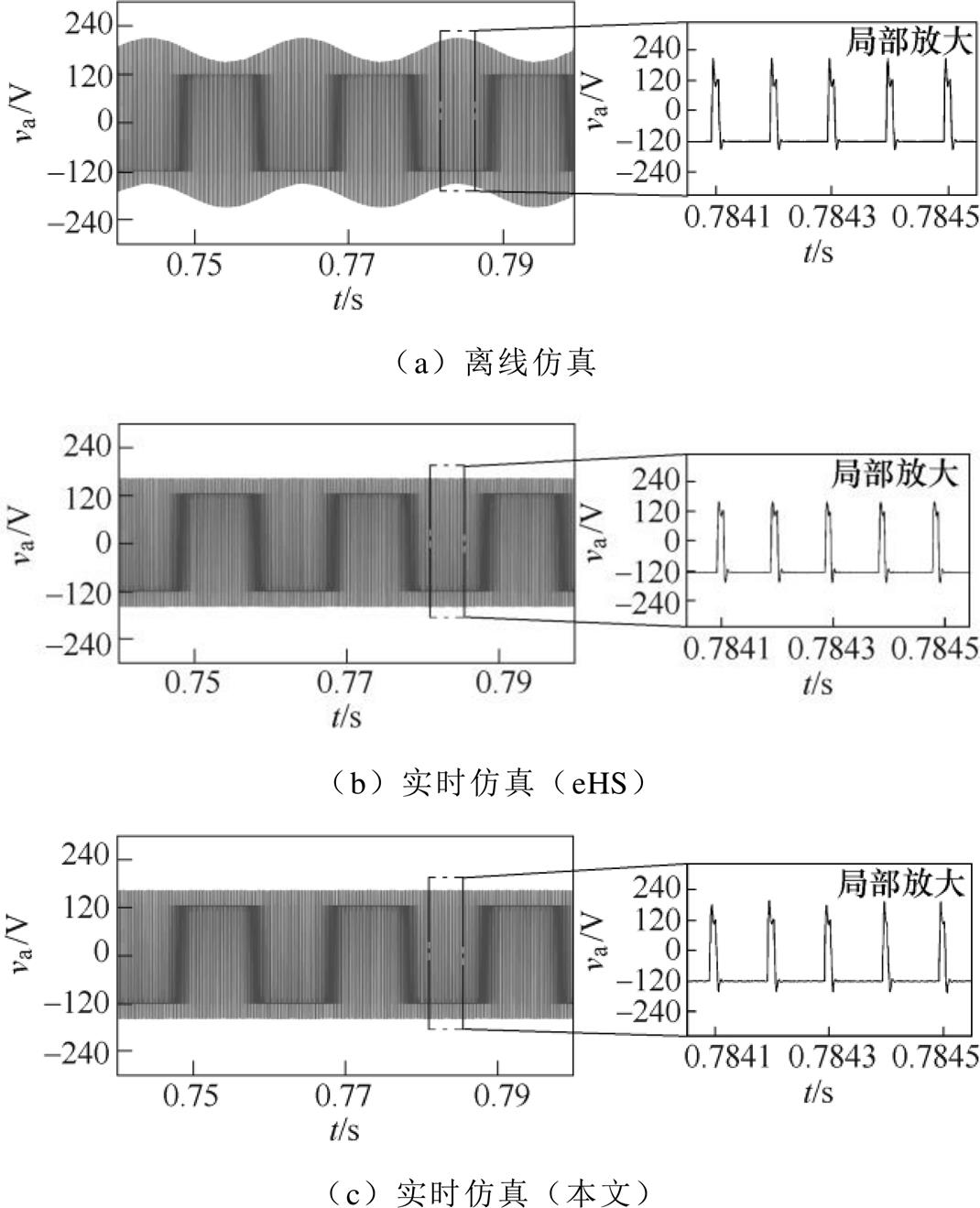
图10 两电平桥式变换器a相电压波形
Fig.10 Voltage waveforms of phase a from two-level bridge converter
图11是两电平桥式变换器a相电流波形。三种仿真波形总体上保持一致，但从放大的细节可以看出：与离线仿真相比，eHS解算器的电流纹波更小，最大误差率仅为1.87 %，而本文解算器的电流最大误差约为1.3 A的，最大误差率达到了3.47 %。原因可能有两个方面：①两种解算器的FPGA代码截断浮点计算结果的位宽不同；②两种解算器所在硬件平台的DAC电路设计不同。
为了验证本文解算器的多工况仿真能力，在Ra=Rb=Rc=3 W 的条件下，增加了电阻Ra=Rb=Rc=5 W 的工况。离线生成ROM初始化数据时，{T;P}里包含Ra, Rb, Rc为3 W 和10 W 两种工况的计算数据。仿真时，目前是通过定时器触发ROM读地址偏移量的变更，进而实现仿真工况的切换。
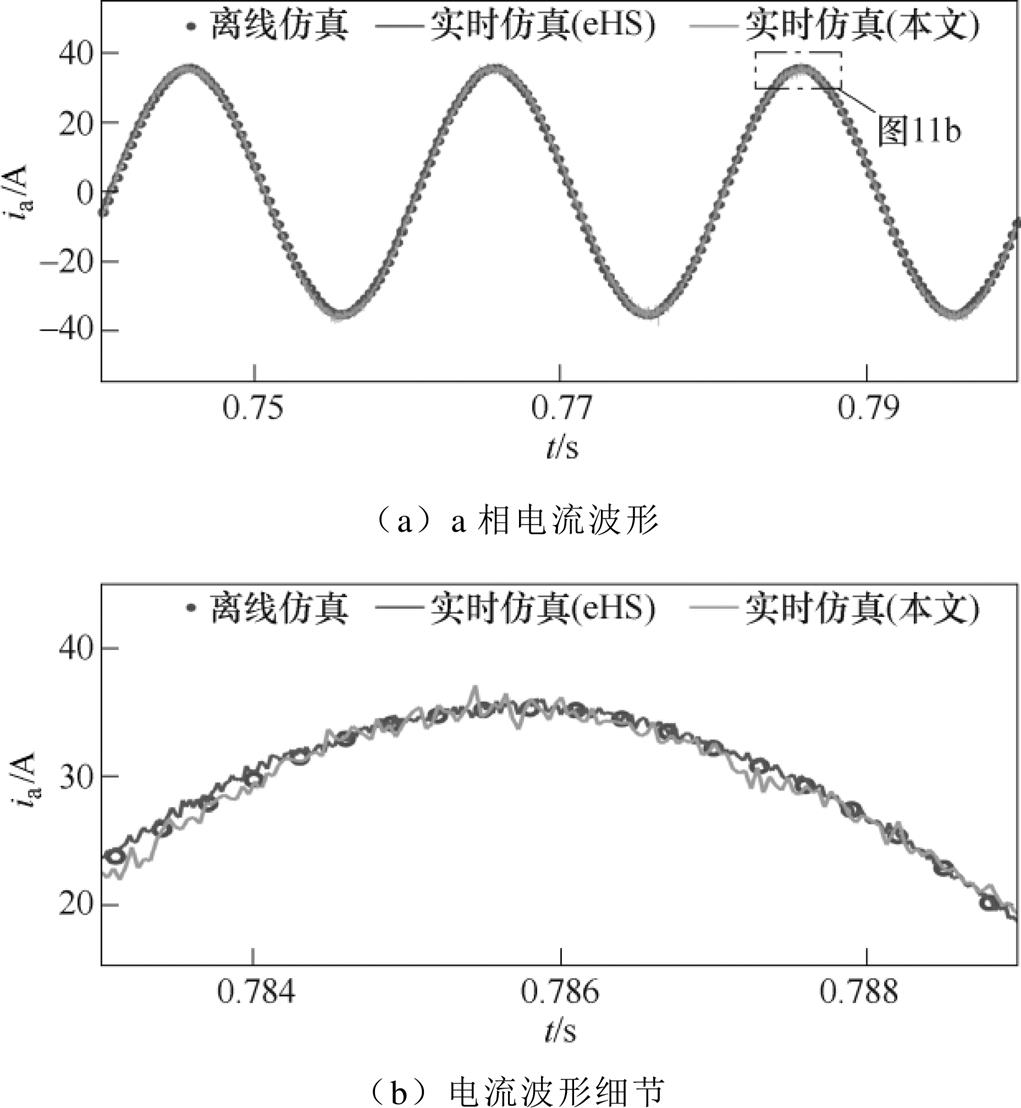
图11 两电平桥式变换器a相电流波形
Fig.11 Current waveforms of phase a from two-level bridge converter
工况切换时的a相电流波形如图12所示。可以发现，实时仿真的波形能够随着工况切换而正确变化。切换瞬间，电流发生突变，实时仿真的响应存在较小的波动。约1.2 ms后，实时仿真与离线仿真的波形再次贴合。测试结果证实了解算器具备在高开关频率下进行不同工况小步长实时仿真的能力。
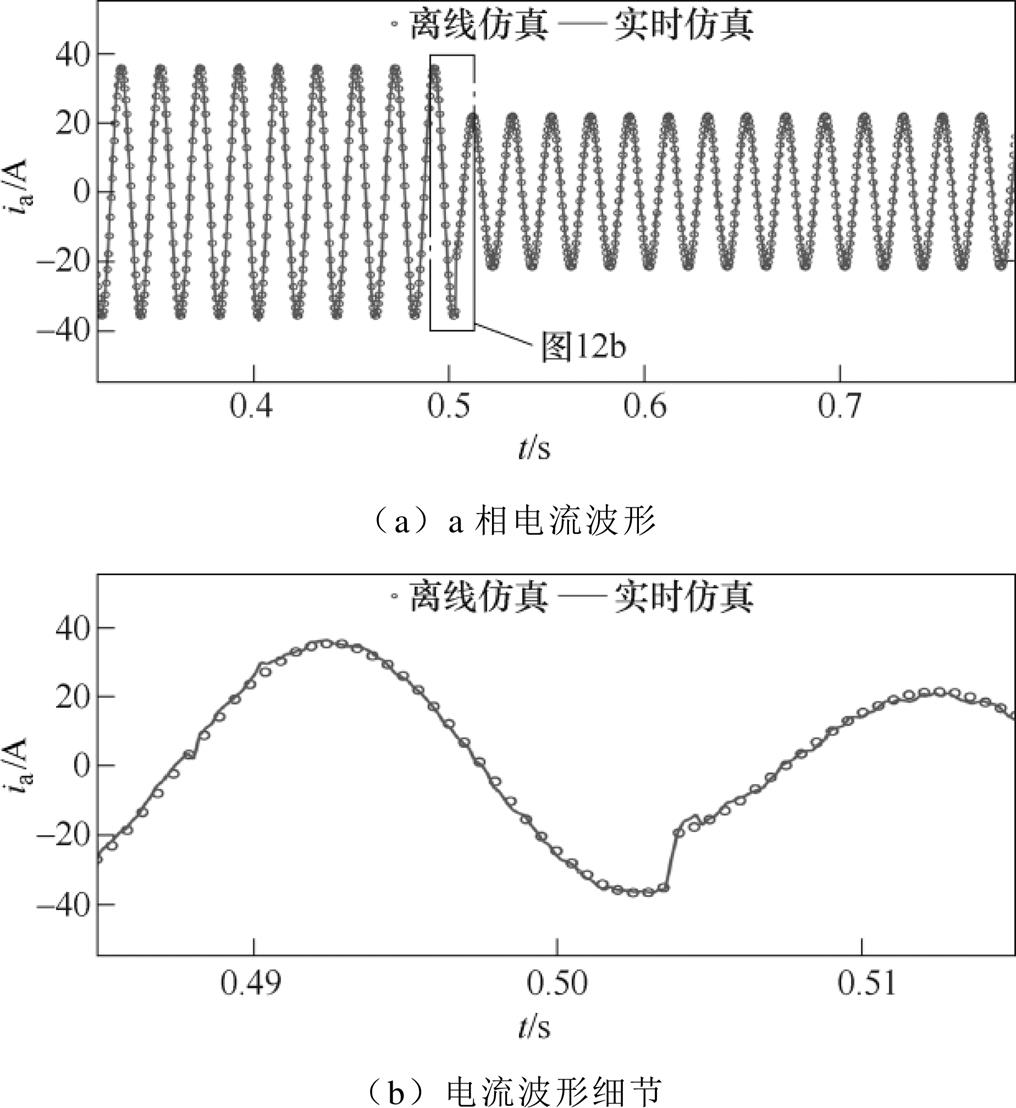
图12 工况切换时的a相电流波形
Fig.12 Current waveforms of phase a when working condition switching
4.2.2 算例二：三相三电平中点钳位变换器
为了验证解算器的通用性，将算例一的开关电路替换为中点钳位（Neutral Point Clamped, NPC）拓扑进行测试。变换器输出的相电压和相电流波形如图13、图14所示。相关结论与算例一的相同：相电压波形存在过脉冲，eHS解算器相电压的过脉冲包络线形状比较平整，却不如本文解算器以及离线仿真接近实际；与离线仿真相比，eHS解算器的电流纹波更小（1.12 %），本文解算器最大电流误差约为1.4 A（3.08 %）。离线仿真中，NPC拓扑的相电压最大幅值为181.2 V，大于两电平桥式拓扑的159.5 V。随着过脉冲幅值变大，受DAC电路的影响也更强，因此本文解算器的过脉冲幅值明显小于离线仿真。
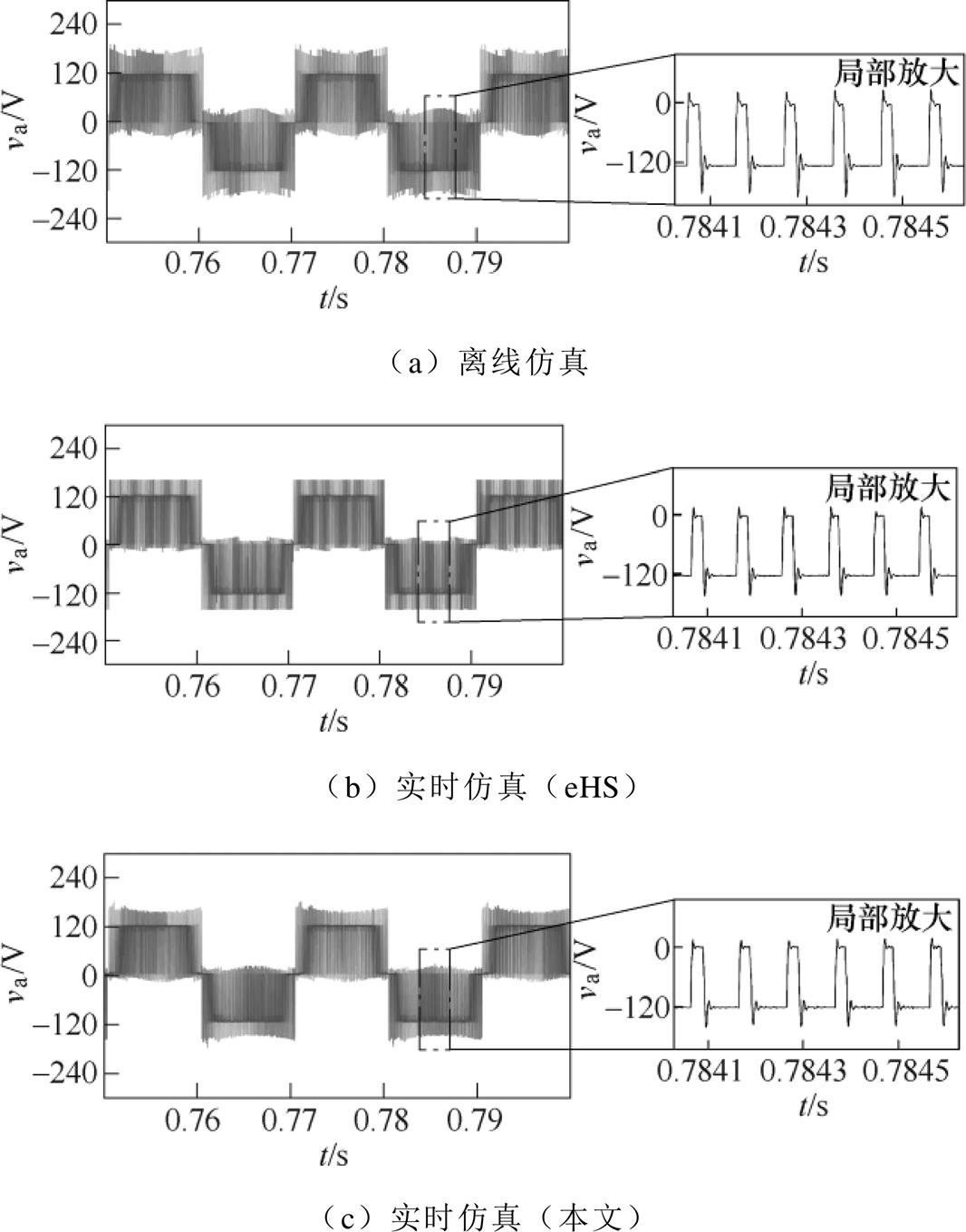
图13 NPC变换器a相电压波形
Fig.13 Voltage waveforms of phase a from NPC converter
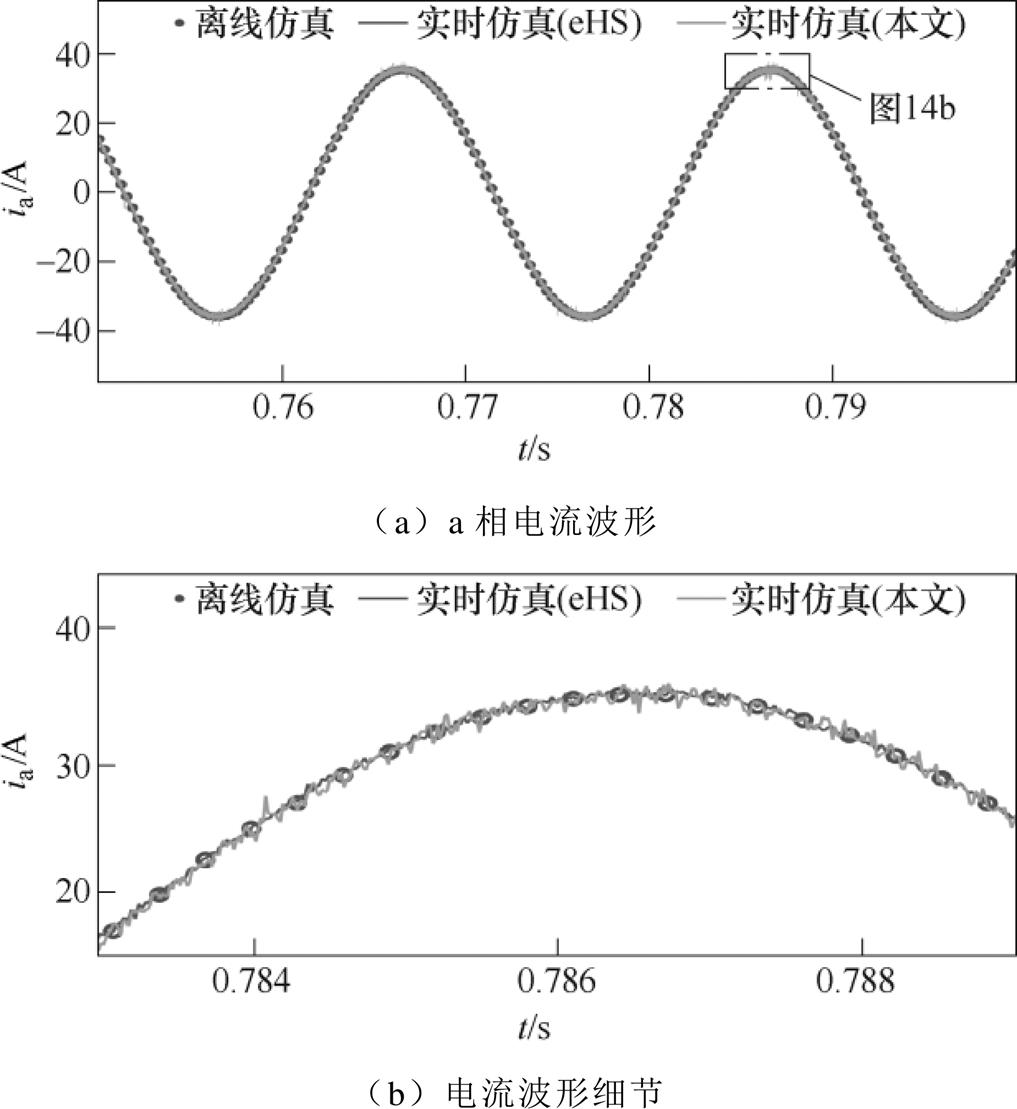
图14 NPC变换器a相电流波形
Fig.14 Current waveforms of phase a from NPC converter
本文提出并实现了一款基于FPGA的电力电子系统EMT实时仿真通用解算器。该解算器以高速FPMAC为基本计算单元，能够达到400 MHz的运行速度、100 ns级的仿真步长并保持较高的仿真精度，具有通用性强、自动化程度高、配置灵活等特点。在相同硬件条件下，它的仿真速度、仿真规模、资源利用率和使用灵活性都比Opal-RT公司的eHS解算器有优势。
后续除了通过更多算例测试解算器的性能外，还将从以下方面优化完善解算器的功能：消除LC等效开关模型的过脉冲、标幺化解算器数值、实现在线调参以及可将程序移植到国产FPGA芯片上等。
附 录
算法1：状态矩阵T组织流程 输入：x, A, B,节点对编号(j, k), 支路编号l输出：T for 1≤i≤Ndif x(i)对应电容元件T(i)←A(j)–A(k);else //x(i)对应电感元件T(i)←B(l);end ifend forfor Nd＜i≤Nd+NsT(2i-Nd-1)←A(j)–A(k); //对应开关电压T(2i-Nd)←B(l); //对应开关电流end for
参考文献
[1] 孙鹏琨, 葛琼璇, 王晓新, 等. 基于硬件在环实时仿真平台的高速磁悬浮列车牵引控制策略[J]. 电工技术学报, 2020, 35(16): 3426-3435.
Sun Pengkun, Ge Qiongxuan, Wang Xiaoxin, et al. Traction control strategy of high-speed maglev train based on hardware-in-the-loop real-time simulation platform[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3426-3435.
[2] 王成山, 李鹏, 王立伟. 电力系统电磁暂态仿真算法研究进展[J]. 电力系统自动化, 2009, 33(7): 97-103.
Wang Chengshan, Li Peng, Wang Liwei. Progresses on algorithm of electromagnetic transient simulation for electric power system[J]. Automation of Electric Power Systems, 2009, 33(7): 97-103.
[3] 王潇, 张炳达, 乔平. 一种面向微电网实时仿真的分块分层并行算法[J]. 电工技术学报, 2017, 32(7): 104-111.
Wang Xiao, Zhang Bingda, Qiao Ping. A block hierarchical parallel method for real-time simulation of microgrid[J]. Transactions of China Electro- technical Society, 2017, 32(7): 104-111.
[4] Chalangar H, Ould-Bachir T, Sheshyekani K, et al. Methods for the accurate real-time simulation of high-frequency power converters[J]. IEEE Transa- ctions on Industrial Electronics, 2022, 69(9): 9613- 9623.
[5] Mahseredjian J, Dinavahi V, Martinez J A. Simulation tools for electromagnetic transients in power systems: overview and challenges[J]. IEEE Transactions on Power Delivery, 2009, 24(3): 1657-1669.
[6] 郝琦, 葛兴来, 宋文胜, 等. 电力牵引传动系统微秒级硬件在环实时仿真[J]. 电工技术学报, 2016, 31(8): 189-198.
Hao Qi, Ge Xinglai, Song Wensheng, et al. Micro- second hardware-in-the-loop real-time simulation of electric traction drive system[J]. Transactions of China Electrotechnical Society, 2016, 31(8): 189-198.
[7] 朱建鑫, 胡海兵, 陆道荣, 等. 应用于级联STATCOM的高精度低成本全FPGA实时仿真模型研究[J]. 电工技术学报, 2019, 34(4): 777-785.
Zhu Jianxin, Hu Haibing, Lu Daorong, et al. The research on fully FPGA-based real-time simulation with high fidelity and low cost for the cascaded STATCOM[J]. Transactions of China Electrotech- nical Society, 2019, 34(4): 777-785.
[8] 李浩洋, 李泽, 郭源博, 等. 考虑开关管开路故障的三电平STATCOM建模与硬件在回路实时仿真[J]. 电工技术学报, 2019, 34(3): 552-561.
Li Haoyang, Li Ze, Guo Yuanbo, et al. Modeling and hardware-in-the-loop real-time simulation of three- level STATCOM considering switch open-circuit faults[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 552-561.
[9] Dufour C, Cense S, Ould-Bachir T, et al. General- purpose reconfigurable low-latency electric circuit and motor drive solver on FPGA[C]//Annual Con- ference on IEEE Industrial Electronics Society, Montreal, 2012: 3073-3081.
[10] Bachir T O, Dufour C, David J P, et al. Floating-point engines for the FPGA-based real-time simulation of power electronic circuits[C]//International Conference on Power Systems Transients (IPST), Delft, 2011: 1-7.
[11] Ould Bachir T, Dufour C, Bélanger J, et al. A fully auto- mated reconfigurable calculation engine dedi- cated to the real-time simulation of high switching frequency power electronic circuits[J]. Mathematics and Computers in Simulation, 2013, 91: 167-177.
[12] Razzaghi R, Paolone M, Rachidi F. A general purpose FPGA-based real-time simulator for power systems applications[C]//IEEE/PES Innovative Smart Grid Technologies Europe, Istanbul, 2014: 1-5.
[13] Razzaghi R, Mitjans M, Rachidi F, et al. An automated FPGA real-time simulator for power electronics and power systems electromagnetic transient applications[J]. Electric Power Systems Research, 2016, 141: 147-156.
[14] 王成山, 丁承第, 李鹏, 等. 基于FPGA的配电网暂态实时仿真研究(一): 功能模块实现[J]. 中国电机工程学报, 2014, 34(1): 161-167.
Wang Chengshan, Ding Chengdi, Li Peng, et al. Research on FPGA-based transient real-time simu- lation of distribution network, part Ⅰ: realization of functional modules[J]. Proceedings of the CSEE, 2014, 34(1): 161-167.
[15] 王成山, 丁承第, 李鹏, 等. 基于FPGA的配电网暂态实时仿真研究(二): 系统架构与算例验证[J]. 中国电机工程学报, 2014, 34(4): 628-634.
Wang Chengshan, Ding Chengdi, Li Peng, et al. Real- time transient simulation for distribution systems based on FPGA, part II: system architecture and algorithm verification[J]. Proceedings of the CSEE, 2014, 34(4): 628-634.
[16] Wang Zhiying, Zeng Fanpeng, Li Peng, et al. Kernel solver design of FPGA-based real-time simulator for active distribution networks[J]. IEEE Access, 2018, 6(1): 29146-29157.
[17] Majstorovic D, Celanovic I, Teslic N D, et al. Ultralow-latency hardware-in-the-loop platform for rapid validation of power electronics designs[J]. IEEE Transactions on Industrial Electronics, 2011, 58(10): 4708-4716.
[18] Pejovic P, Maksimovic D. A method for fast time- domain simulation of networks with switches[J]. IEEE Transactions on Power Electronics, 1994, 9(4): 449-456.
[19] Dagbagi M, Hemdani A, Idkhajine L, et al. ADC- based embedded real-time simulator of a power con- verter implemented in a low-cost FPGA: application to a fault-tolerant control of a grid-connected voltage- source rectifier[J]. IEEE Transactions on Industrial Electronics, 2016, 63(2): 1179-1190.
[20] Guo Xizheng, Tang Yiguo, Wu Mingkang, et al. FPGA-based hardware-in-the-loop real-time simu- lation implementation for high-speed train electrical traction system[J]. IET Electric Power Applications, 2020, 14(5): 850-858.
[21] 穆清, 周孝信, 王祥旭, 等. 面向实时仿真的小步长开关误差分析和参数设置[J]. 中国电机工程学报, 2013, 33(31): 120-129, 15.
Mu Qing, Zhou Xiaoxin, Wang Xiangxu, et al. Small- step switching error analysis and parameter setting for real-time simulation[J]. Proceedings of the CSEE, 2013, 33(31): 120-129, 15.
[22] Dufour C. Method and system for reducing power losses and state-overshoots in simulators for switched power electronic circuit: US, 9665672[P]. 2017-05-30.
[23] Li Zirun, Xu Jin, Wang Keyou, et al. A discrete small-step synthesis real-time simulation method for power converters[J]. IEEE Transactions on Industrial Electronics, 2022, 69(4): 3667-3676.
[24] Dommel H W. Digital computer solution of electro- magnetic transients in single and multiphase net- works[J]. IEEE Transactions on Power Apparatus and Systems, 1969, PAS-88(4): 388-399.
[25] Ho C W, Ruehli A, Brennan P. The modified nodal approach to network analysis[J]. IEEE Transactions on Circuits and Systems, 1975, 22(6): 504-509.
[26] Mahseredjian J. Computation of power system transients: overview and challenges[C]//IEEE Power Engineering Society General Meeting, Tampa, 2007: 1-7.
[27] Marti J R, Lin J. Suppression of numerical oscillations in the EMTP[J]. IEEE Power Engineering Review, 1989, 9(5): 71-72.
[28] 徐晋. 通用电力电子实时仿真方法研究及应用[D]. 上海: 上海交通大学, 2019.
[29] Ould-Bachir T, Dufour C, Bélanger J, et al. Effective floating-point calculation engines intended for the FPGA-based HIL simulation[C]//International Sym- posium on Industrial Electronics, Hangzhou, 2012: 1363-1368.
[30] Ould-Bachir T, Merdassi A, Cense S, et al. FPGA- based real-time simulation of a PSIM model: an indirect matrix converter case study[C]//Annual Con- ference of the IEEE Industrial Electronics Society, Yokohama, 2016: 3336-3340.
[31] Xilinx Inc. Block memory generator v8.4: LogiCORE IP product guide[EB/OL]. (2021-08-06)[2022-05-30]. https://docs.xilinx.com/content/dam/xilinx/support/documents/ip_documentation/blk_mem_gen/v8_4/pg058- blk-mem-gen.pdf.
[32] Vangal S R, Hoskote Y V, Borkar N Y, et al. A 6.2-GFlops floating-point multiply-accumulator with conditional normalization[J]. IEEE Journal of Solid State Circuits, 2006, 41(10): 2314-2323.
[33] Zhuo Ling, Morris G R, Prasanna V K. High- performance reduction circuits using deeply pipelined operators on FPGAs[J]. IEEE Transactions on Parallel and Distributed Systems, 2007, 18(10): 1377-1392.
[34] Chen Yuan, Dinavahi V. An iterative real-time non- linear electromagnetic transient solver on FPGA[J]. IEEE Transactions on Industrial Electronics, 2011, 58(6): 2547-2555.
[35] Ould-Bachir T, David J P. Performing floating-point accumulation on a modern FPGA in single and double precision[C]//IEEE Annual International Symposium on Field-Programmable Custom Computing Machines, Charlotte, 2010: 105-108.
[36] Ould-Bachir T, David J P. Self-alignment schemes for the implementation of addition-related floating-point operators[J]. ACM Transactions on Reconfigurable Technology and Systems, 2013, 6(1): 1-21.
[37] Oklobdzija V G. An algorithmic and novel design of a leading zero detector circuit: comparison with logic synthesis[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 1994, 2(1): 124-128.
[38] IEEE Standards 754-2008. IEEE standard for floating- point arithmetic[S]. New York: IEEE Computer Society Microprocess Standards Committee, 2008.
[39] OPAL-RT Inc. eFPGAsim v1.5: eHS user guide[EB/OL]. (2019-03-12)[2022-05-30]. https://www.opal-rt.com/ display/FPET/Main+features.
Abstract As the frequency of power electronic switches increases, the traditional electromagnetic transient (EMT) real-time simulation based on CPUs fails to describe the high-frequency characteristics of switches accurately. It has become a trend to take FPGAs as the hardware platforms for real-time simulation. However, the following challenges exist: (1) the high programming threshold and long development cycle make it difficult to conduct a real-time simulation based on FPGAs; (2) it is hard to ensure the real-time performance of simulation while completing high complexity and large-scale iterative calculation. Therefore, this paper proposes a real-time EMT simulation universal solver for power electronic systems based on FPGAs.
Firstly, a method that the node equation is reorganized into the form of a state space equation is proposed, and only the state quantity and measurement quantity in the simulation model are considered. As a result, the calculation quantity is reduced, and the calculation parallelism is increased. Secondly, the general framework of the FPGA real-time simulation solver is designed. The solver regards the fixed admittance matrix nodal method (FAMNM) as the switch modeling and circuit analysis method, and takes the multiply accumulator (MAC) for the basic computing unit. Its framework includes two parts, namely offline preprocessing and online calculation. The offline program of the solver can automatically obtain the parameters of the simulation models and generate the calculation data. A new organization method of FPGA ROM initialization data considering multiple simulation conditions is applied to improve the utilization of storage resources when generating calculation data, which splices and writes multiple data into the same initialization file. As the core of the online program, the matrix-vector multiplication (MVM) computing architecture can not only automatically configures computing resources and control logic according to parameters, but also automatically configure the reuse degree of resources by users. Finally, an implementation method of low-delay single-cycle floating-point accumulation is proposed. Rather than through a unidirectional shift, the alignment of the float-pointing accumulator is finished by a bidirectional shift, moving the shift alignment step out of the critical path of floating-point accumulation and realizing high-speed accumulation. The performance of the proposed solver is analyzed from two aspects of simulation speed and simulation scale: it can achieve a running speed of 400 MHz and a simulation step of 100 ns. Compared with the eHS solver from OPAL-RT under the same conditions, its simulation speed is doubled, and its simulation scale increases by 29.69 %～79.17 %. A two-level bridge converter and a three-level NPC converter are taken as test examples separately to verify the correctness and generality of the proposed solver. The real-time simulation at a high switching frequency is compared with the eHS solver based on an OP5700 simulator and the offline simulation based on Matlab. The results show that the maximum simulation errors of the proposed solver for the two examples are 3.47 % and 3.08 %, respectively.
The following conclusions can be drawn from the theoretical analysis and simulations. The proposed general solver based on FPGAs, with high-speed MAC as the basic computing unit, can achieve a running speed of 400 MHz, a simulation step of 100ns, and maintain a high simulation accuracy. It has the characteristics of strong versatility, high automation, and flexible configuration. Under the same hardware conditions, its simulation speed, simulation scale, resource utilization, and use flexibility are all superior to the eHS solver of OPAL-RT.
keywords：Power electronic systems, FPGA real-time simulation, general solver, floating-point multiply- accumulate
国防科技重点实验室资助项目（6142217200305）。
收稿日期 2022-05-26
改稿日期 2022-09-20
DOI: 10.19595/j.cnki.1000-6753.tces.220918
中图分类号：TM921
周 斌 男，1994年生，博士研究生，研究方向为电力电子系统的实时仿真建模与解算。E-mail: zhoubin5637@163.com
李卫超 男，1982年生，研究员，博士生导师，研究方向为大功率电能变换装置、电机控制。E-mail: liweichao3721@126.com（通信作者）
（编辑 陈 诚）