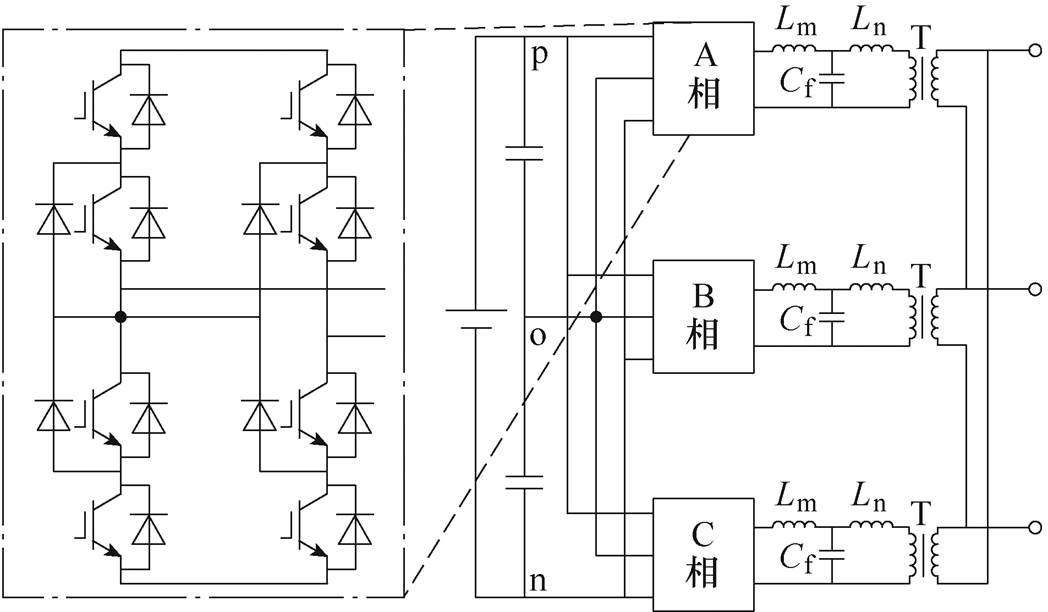
图1 组合式三相逆变电源拓扑
Fig.1 Topology diagram of combined three-phase inverter
摘要 中压大容量逆变电源可以实现中压直流至低压交流的电能变换，如何在低开关频率下实现较高的动态响应能力是其核心瓶颈问题之一。针对上述问题，该文尝试引入多次采样控制技术。首先，建立中点钳位（NPC）H桥组合式三相逆变电源主电路的状态空间平均模型，并基于Pade近似建立考虑多次采样的逆变电源系统级闭环模型。然后，基于上述模型分析不同采样次数下系统的动态特性，分析结果表明，多次采样能增大系统带宽、降低系统超调量和扩大系统控制参数的选取范围；进一步提出基于闭环带宽的采样次数选取方法。再次，分析闭环系统对控制参数的灵敏度，进而对控制参数进行全局优化。最后，通过等比例缩小实验平台验证了该文所提方法的有效性。
关键词：中压大容量逆变电源 多次采样 Pade近似 全局优化
随着交直流混合微电网的不断发展，中压大容量逆变电源将在船舶[1-3]、直流配电网[4-7]、可再生能源微电网制氢[8-10]等场合取得广泛应用。在典型中压直流配电系统中，逆变电源将中压直流变换至低压交流向负载供电[11]。图1为组合式三相逆变电源拓扑，其主电路包含三个单相二极管中点钳位三电平逆变单元、LC滤波器（Lm、Cf）及三相隔离变压器T。此拓扑具有以下优势：①输入与输出之间具有电气隔离；②变压器集成漏感Ln可作为输出侧的滤波电感，提高输出电压质量；③相较于三相三电平半桥逆变拓扑，其更适用于大功率应用场合[12]。
图1 组合式三相逆变电源拓扑
Fig.1 Topology diagram of combined three-phase inverter
对于中压大容量MW级逆变电源，通常选择较低的开关频率以降低系统的开关损耗。但较低的开关频率会引入显著的数字控制延迟，进而影响系统动静态性能，降低输出波形质量。对此，国内外许多学者通过改变采样策略减小控制延迟。文献[13]提出即时采样方法，将采样时刻相较于调制波装载时刻提前，介于两次调制波装载时刻之间，以减小数字控制器的计算延迟。文献[14]提出双采样模式的实时运算方法，通过占空比的大小实时选择采样模型，但这种采样模式仅适用单极性调制，难以应用于多电平逆变器。多次采样技术通过提高采样频率可以有效地降低计算延迟和PWM延迟[15]。文献[16]使用多次采样技术解决数字控制延迟导致逆变器输出电压失真的问题，仿真和实验结果表明，使用多次采样使逆变器的数字控制延迟明显降低，且输出电压质量明显提高。
在多次采样建模方面，现有文献对基于多次采样的调制环节建模主要使用小信号分析法。文献[17]使用小信号分析法建立了两次采样下调制环节模型，并验证了频域特性。文献[18]建立了不同载波下多次采样调制环节小信号模型，研究结果表明，保持开关频率不变，提高采样频率可以降低PWM延迟。基于多次采样的调制环节模型可以近似为纯延迟环节，文献[19]提出将非线性的纯延迟环节通过Pade近似等效。
在基于多次采样的控制策略及参数优化方面，许多学者将多次采样与不同的控制策略相结合使用，例如，文献[20]在DC-DC变换器中，将多次采样与滑模控制器相结合，通过多次采样提高带宽。文献[21]在模型预测控制中增加了多次采样技术，并将其运用在降压变换器中，结果表明，在开关周期内通过多次采样技术，定期更新模型的最优解，能更好地抑制干扰。而对于最常规的PID控制，文献[22]将基于多次采样的PI控制器与模型预测控制相比较，结果表明，二者的电流总谐波畸变率（Total Harmonic Distortion, THD）与动态特性相差不大。以上文献均分析了多次采样下的系统闭环控制性能，但未对控制参数设计开展深入研究。通常而言，控制参数通过经验法、零极点配置等方法获得，但这些方法计算出来的参数，难以保证系统性能均符合设计指标要求。文献[23]针对光伏发电系统提出了一种提高系统稳定性的控制参数全局优化方法，但未考虑多次采样的影响。
在上述研究基础上，本文针对中压大容量逆变电源，首先，建立组合式逆变电源的主电路状态空间平均模型，并基于Pade近似方法建立基于多次采样的系统闭环时域模型，求解闭环传递函数。其次，分析多次采样对系统特性的影响，并对系统闭环模型的控制器参数进行全局优化。最后，通过仿真与实验对比理论分析的正确性与优化方法的有效性。
单相逆变单元等效电路如图2所示。图中，Udc为直流母线电压，idci为正极输入电流（i=A, B, C），ii1为左桥臂电流，ii2为右桥臂电流，ui为逆变桥输出电压，iLi为滤波电感电流，it1i为变压器一次电流，uCfi为RC支路电压，uCi为滤波电容电压，uoi为变压器二次电压，C1、C2为直流侧支撑电容，S1～S8为IGBT，VD1～VD4为钳位二极管，Lm为滤波电感，Ln为变压器漏感，Cf为滤波电容，RC为阻尼电阻。
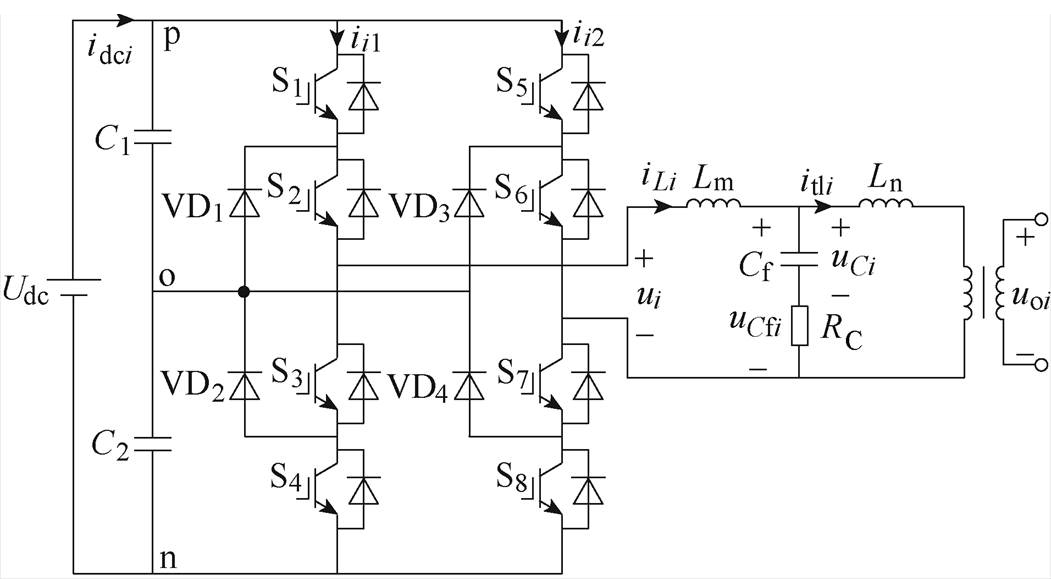
图2 单相逆变单元等效电路
Fig.2 Equivalent topology of single-phase inverter unit
使用状态空间平均法建立三相三电平全桥逆变电源状态空间模型，再使用小信号扰动法建立其小信号扰动模型。在建立逆变电源小信号模型前，做出以下假设：①系统已经工作在稳定状态；②电力电子开关元器件为理想元器件；③变压器为理想变压器；④直流母线电压恒定。
基于以上假设，逆变电源的状态方程表示为
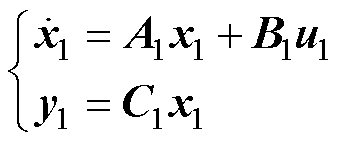（1）
选取状态变量x1=[iLA iLB iLC uCA uCB uCC it1A it1B it1C]T，输入变量u1=[dGA dGB dGC]T，输出变量y1=[uCfA uCfB uCfC]T，其中，dGA、dGB、dGC分别为A、B、C相的等效占空比，使用等幅值Park变换将abc坐标系下的小信号模型转换至dq旋转坐标系下得
（2）
式中，iLd、iLq分别为滤波电感电流iL的d、q轴分量；uCd、uCq分别为滤波电容电压uC的d、q轴分量；it1d、it1q分别为变压器一次电流的d、q轴分量；uCfd、uCfq分别为RC支路电压uCf的d、q轴分量；dGd、dGq分别为等效占空比dG的dq轴分量；A1为状态矩阵，表达式为
（3）
式中，w 为基波角频率；RLoad为等效至变压器一次侧的纯阻性负载。
逆变电源典型案例参数见表1。为了验证逆变电源小信号模型，针对表1算例，对d轴输入信号dGd(t)施加10 %、持续时间100 ms的小信号扰动，主电路小信号模型仿真结果如图3所示，表明上述小信号模型能够准确反映电路仿真的低频分量。
对于中压大功率逆变电源，使用无源阻尼RC会显著增加系统的损耗。为了降低系统损耗及抑制LCL滤波器的谐振尖峰，本文采用有源阻尼控制。考虑有源阻尼的电压电流双闭环控制框图如图4所示。图4中，有源阻尼电容电流IC(s)反馈系数H为
表1 逆变电源典型案例参数
Tab.1 Typical case parameters of inverter
参 数数 值 直流输入电压Udc/V4 500 开关频率fs/Hz1 000 额定输出电压Uo/V390 滤波电感Lm/mH980 变压器漏感Ln/mH640 滤波电容Cf /mF100 RC支路电压前馈系数a1 变压器一次电流前馈系数b1 电压环比例系数kup0.630 电压环积分系数tu0.045 5 电流环比例系数kip0.210 电流环积分系数ti0.002 2 电压基准值Ub/V2 550 电流基准值Ib/A620
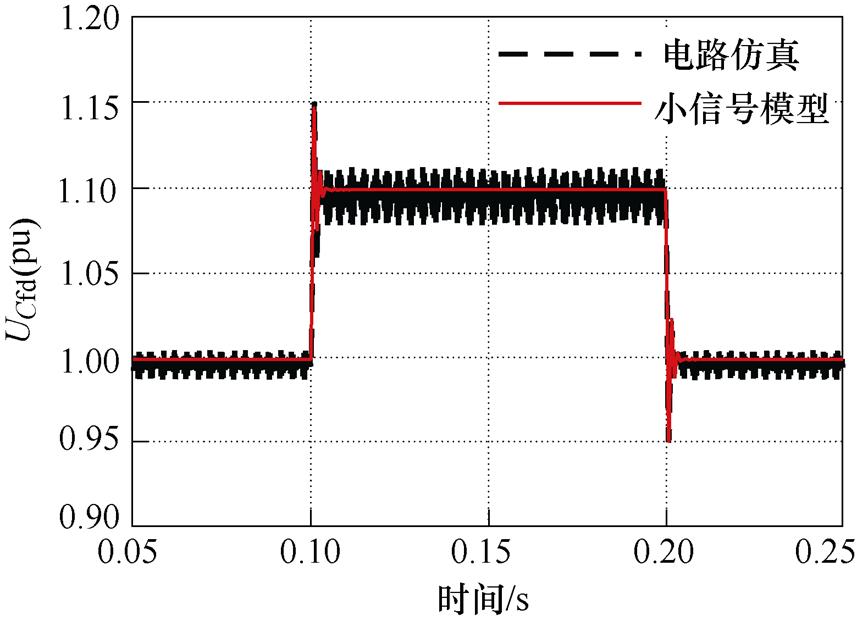
图3 主电路小信号模型仿真结果
Fig.3 Simulation results of the small-signal model of the maincircuit
图4 系统闭环控制框图
Fig.4 Structurediagramofclosed-loopcontrol
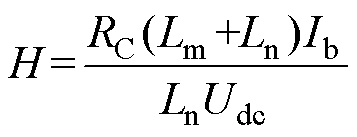（4）
式中，Ib为电流基准值。
对于表1中的典型参数，Ma(s)至UCf(s)的传递函数Bode图如图5所示。可知，无源阻尼、有源阻尼控制在低频段的增益和相位与无阻尼相同，在谐振频率附近，无源阻尼与有源阻尼能够较好地抑制LCL滤波的谐振峰值。
采用滤波电容电压外环与电流内环双环控制，并增加电压前馈以提高系统的快速响应能力。其中，GvPI(s)与GcPI(s)分别为电压外环与电流内环PI控制器，其表达式为
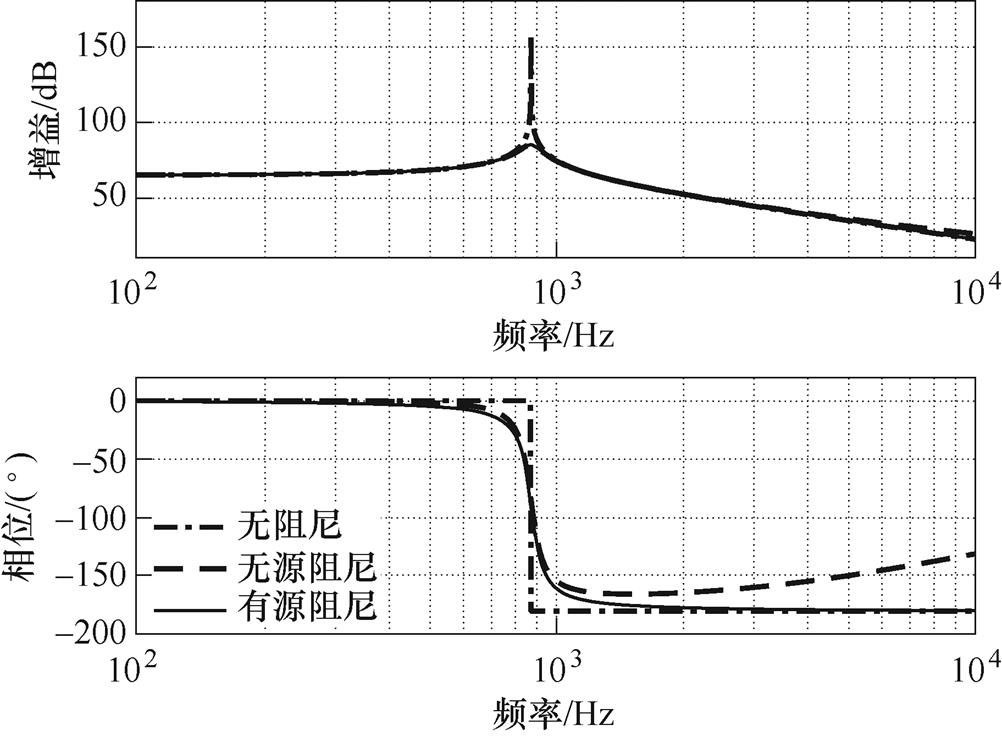
图5 不同阻尼方式下被控对象的Bode图
Fig.5 Bode diagram of the controlled object under different damping modes
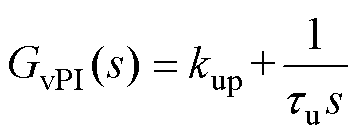（5）
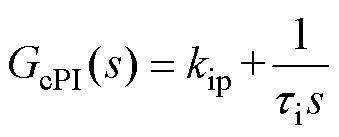（6）
式中，kup、tu分别为电压环PI调节器的比例系数与积分系数；kip、ti分别为电流环PI调节器的比例系数与积分系数。
多次采样是指在一个开关周期Ts内对系统的输出信号进行N（N≥2）次采样，并将每次采样后的信号送入控制器进行计算，将计算结果立即装载至调制器中，即采样频率与控制器计算频率fc为开关频率fs的N倍，多次采样控制原理如图6所示。图中，Tc为采样周期，Ts为开关周期，td1与td2分别为载波和调制波相交时刻与调制波更新时刻的时间差。
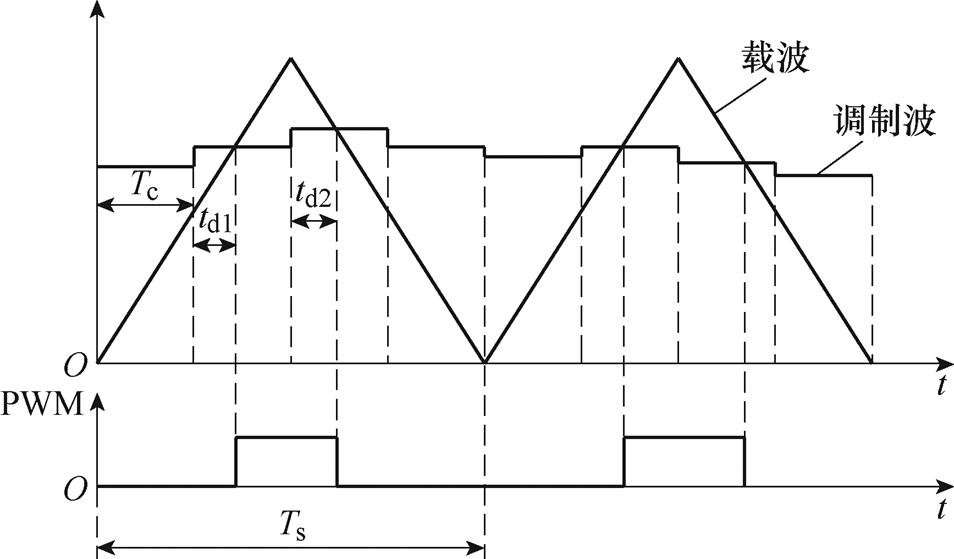
图6 多次采样控制原理
Fig.6 Principle of multisampling control
通过文献[17]可知，使用多次采样控制会对调制环节产生一定的影响，其中基于调制环节的多次采样模型可以表示为
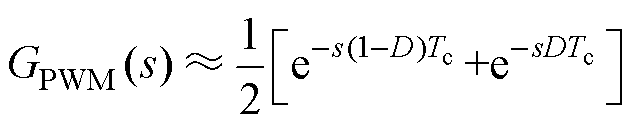（7）
式中，D为等效占空比。
文献[24]对式（7）中(1-D)Tc与DTc进行了简化，可得调制环节模型为
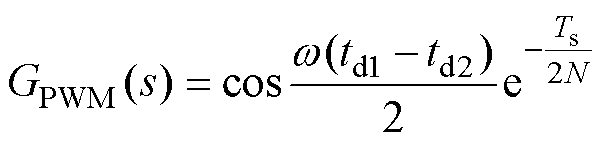（8）
td1与td2如图6所示。td1与td2非常接近，表明可以将多次采样条件下的PWM环节近似为纯延迟环节，即
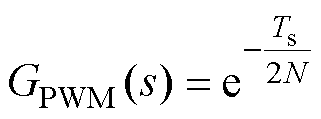（9）
当N→∞时，GPWM(s)=1，调制环节不再引入延迟，对应无延迟闭环模型。
根据信号流图与Mason公式可得在s域下系统的闭环传递函数G(s)为
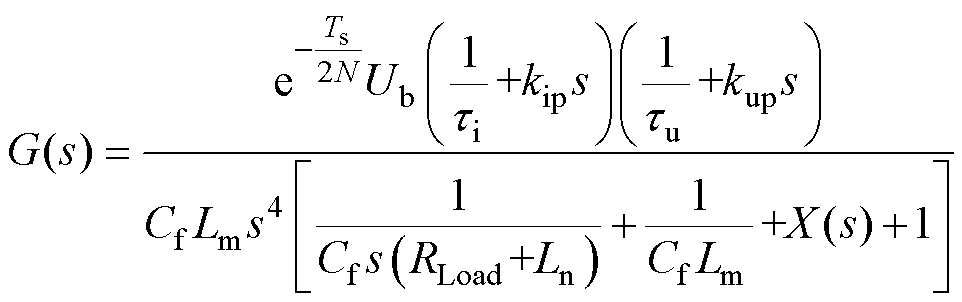（10）
其中
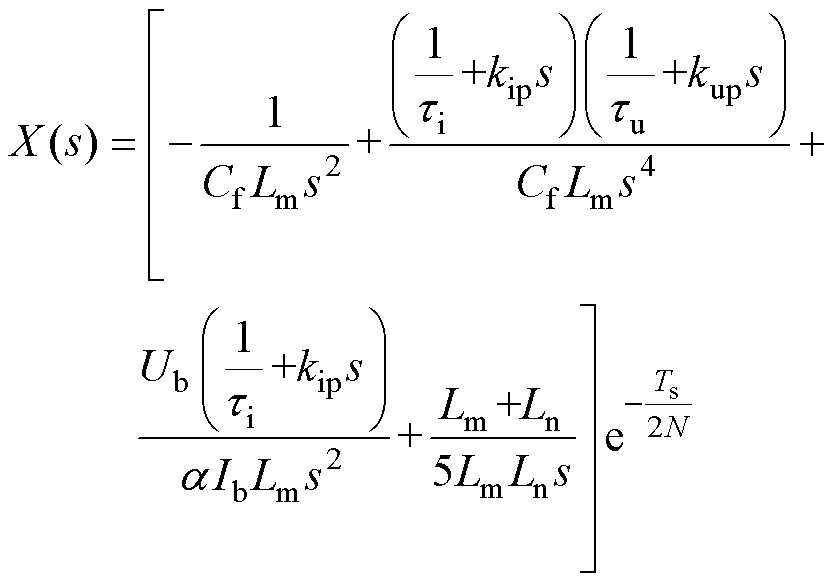（11）
通过Pade近似可以将延迟环节用有理函数表示为
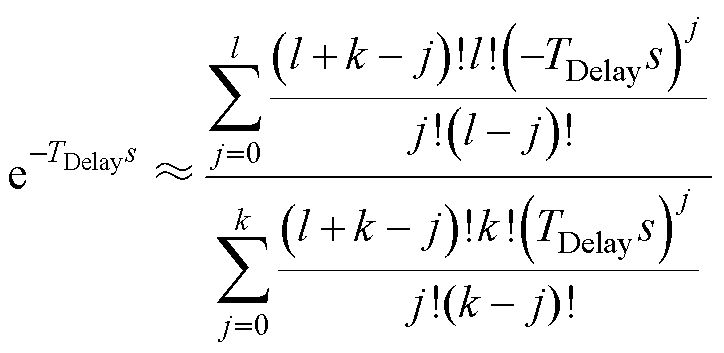（12）
以延迟TDelay=200 ms为例，一至四阶Pade近似的阶跃响应与相频特性曲线如图7所示。图7中，①为阶跃信号；②为纯延迟环节；③为一阶Pade近似；④为二阶Pade近似；⑤为三阶Pade近似；⑥为四阶Pade近似。
从图7可以看出，当Pade近似的阶数越高，近似越精确，但其计算量越大。通过分析比较，选择二阶Pade近似作为纯延迟环节的近似，可得其状态空间表达式为
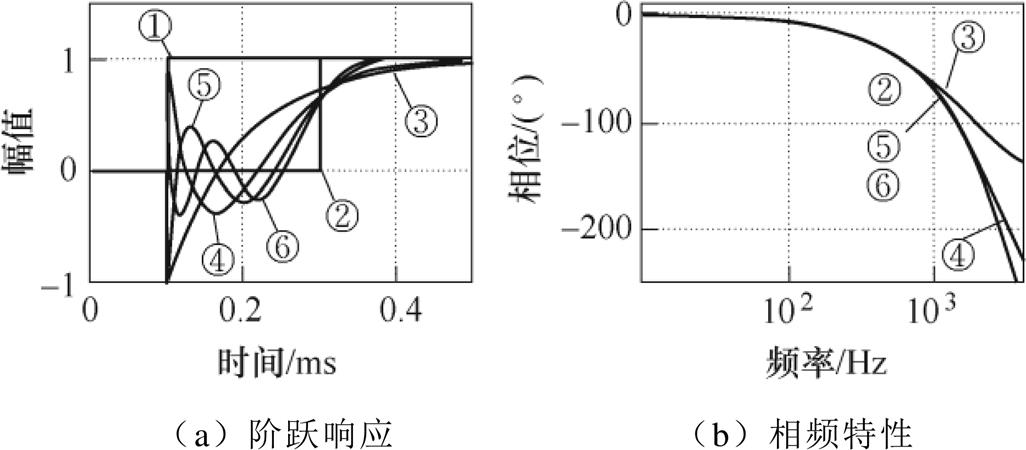
图7 Pade近似环节与纯延迟环节的阶跃响应和相频特性
Fig.7 Step response and phase frequency characteristics of the Pade approximation and time delay
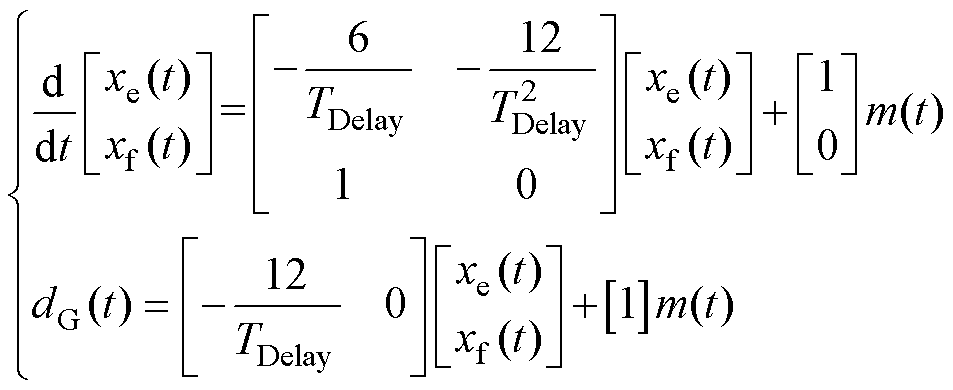（13）
式中，xe(t)、xf(t)为调制环节状态变量；m(t)为系统调制比。
使用Tustin变换将连续域的闭环传递函数G(s)离散化，并针对表1案例绘制了s域与z域的Bode图如图8所示。可知，当频率低于500 Hz时，连续模型与离散模型的幅频特性与相频特性能够很好地吻合，当频率高于500 Hz时，二者的增益差异随着频率的增大略有增大，其相位差异不明显。因此对于大容量逆变电源的低频特性，可以选择连续模型代替离散模型进行分析。
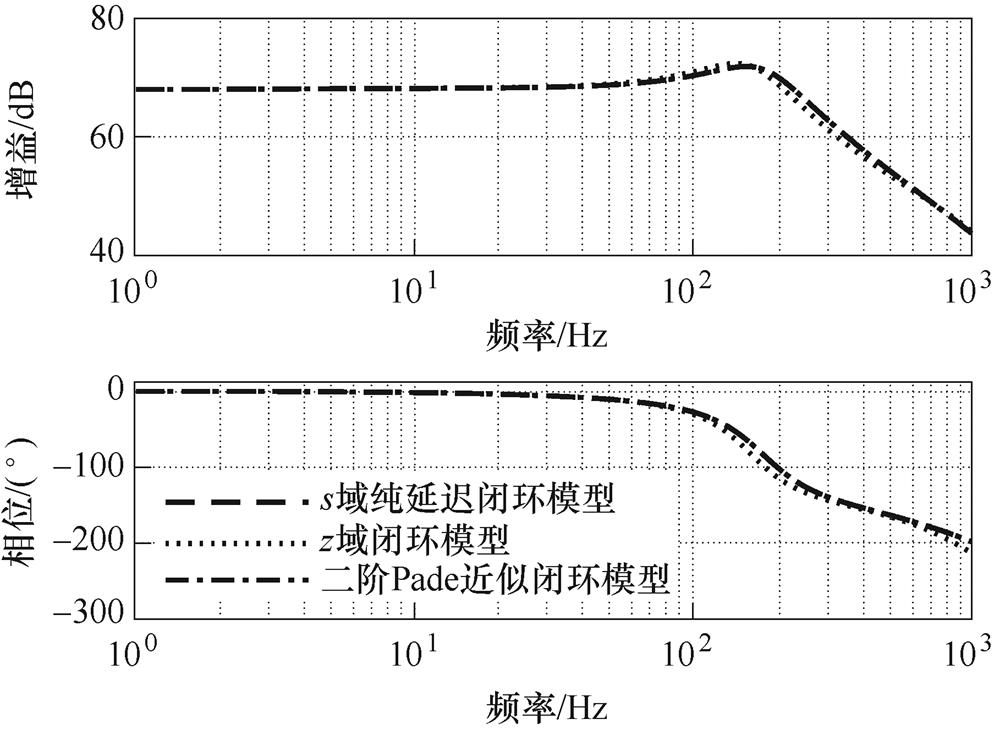
图8 闭环传递函数Bode图
Fig.8 Bode diagram of closed-loop transfer function
将控制环节、调制环节和主电路状态空间平均模型相结合，详细推导见附录，可得到在多次采样下逆变电源的闭环状态空间平均方程模型为
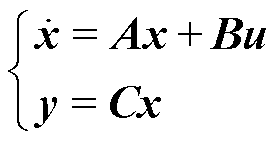（14）
为了验证二阶Pade近似与连续纯延迟闭环模型的差异，绘制了典型案例的Bode图，如图8中点画线与虚线所示。可知，二者较为接近，可以使用Pade近似模型替代离散模型。
为了验证闭环模型的准确性，在输入参考值施加幅值10 %、持续时间100ms的扰动，观察UCfd的动态响应变化，闭环模型时域验证如图9所示，可知本文闭环模型与电路仿真结果相吻合，验证了模型正确性。
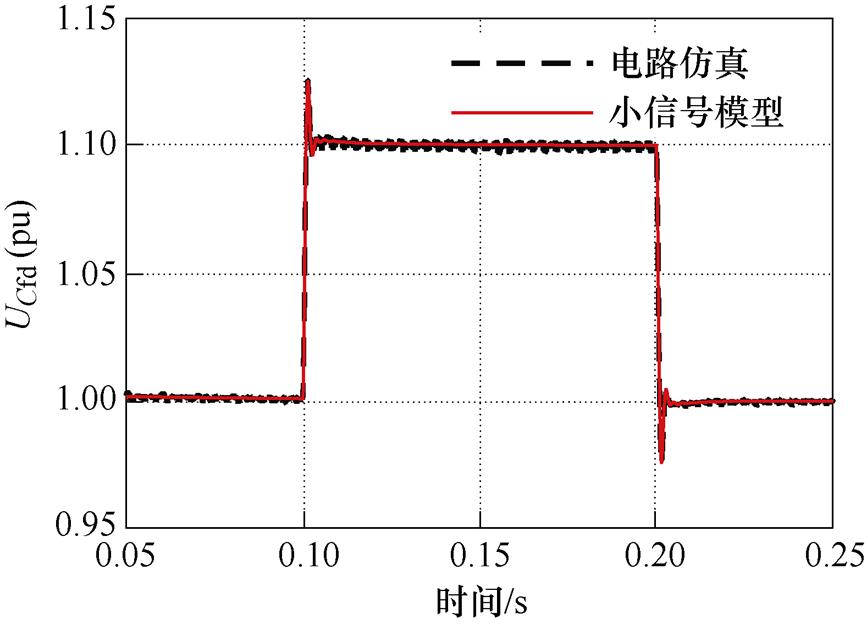
图9 闭环模型时域验证
Fig.9 Time domain validation of closed-loop model
为了比较不同采样次数N对系统动态性能的影响。使用表1算例，绘制N取不同值时系统的Bode图，如图10所示。从幅频特性可以看出，在低频段，采样次数对系统增益影响不大，在中高频段，当N越大时，系统幅频特性越接近无延迟闭环模型。从相频特性来看，在低频段，系统的相位差别不大；在中频段，随着N的增大，系统相位越接近无延迟闭环模型；但在高频段，由于数字控制引入延迟，其相频特性的变化趋势与无延迟闭环模型略有差异。
计算不同采样次数下闭环系统的带宽。图11为闭环带宽随采样次数变化的规律，图中，虚线为无延迟闭环模型带宽fIB，点线为80 %fIB。从图11可以看出，随着采样次数的增大，系统闭环带宽逐渐增大，且接近理想闭环模型带宽。但N增大到一定程度后，对系统的闭环带宽改善并不明显。对于表1所示的典型算例，无延迟闭环模型带宽为333 Hz，当N=5时，系统的闭环带宽为270 Hz，达到无延迟模型闭环带宽的80 %。
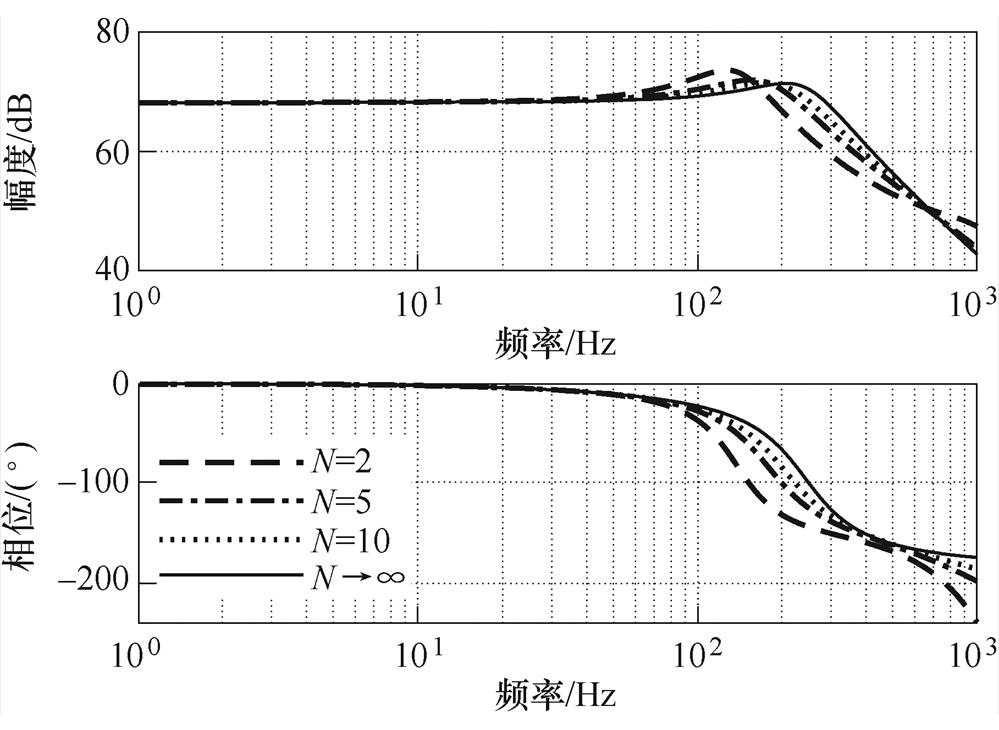
图10 不同采样次数下系统Bode图
Fig.10 Bode diagram of the system under different sampling times
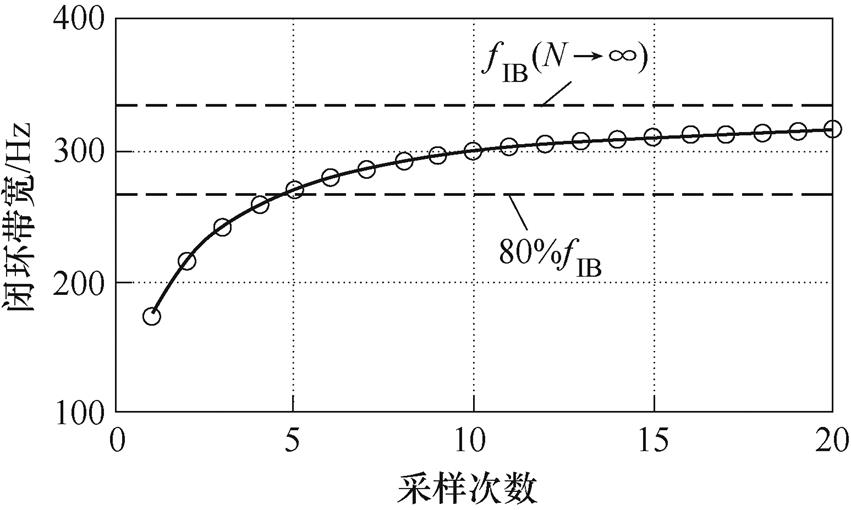
图11 闭环带宽与采样次数关系
Fig.11 The relationship of closed-loop bandwidth and sampling times
图12为系统的阶跃响应及性能对比，从图12a中可以看出，随着N的增加，系统的动态响应越接近连续模型，从图12b中可知，UCfd的阶跃响应超调量随着N的增加逐渐降低并趋于平缓。
双闭环PI控制的4个控制参数中，比例控制系数kup与kip对系统的动态特性影响较为明显，比例系数越大，系统的动态响应能力越强，但比例系统的增大会影响系统的稳定裕度。以kup为例，图13a与图13b分别绘制了单次采样和多次采样下，其余控制参数恒定，kup在[0.5, 20]内变化时系统的主导共轭极点变化规律。从图13中可以看出，在单次采样下，随着kup的增大，系统的主导极点逐渐从负半平面移到正半平面，系统从稳定变为不稳定；在N=10时，随着kup的增大，系统的稳定裕度逐渐降低，但系统主导极点仍在左半平面，系统保持稳定。多次采样可以提高系统比例参数的选取范围。
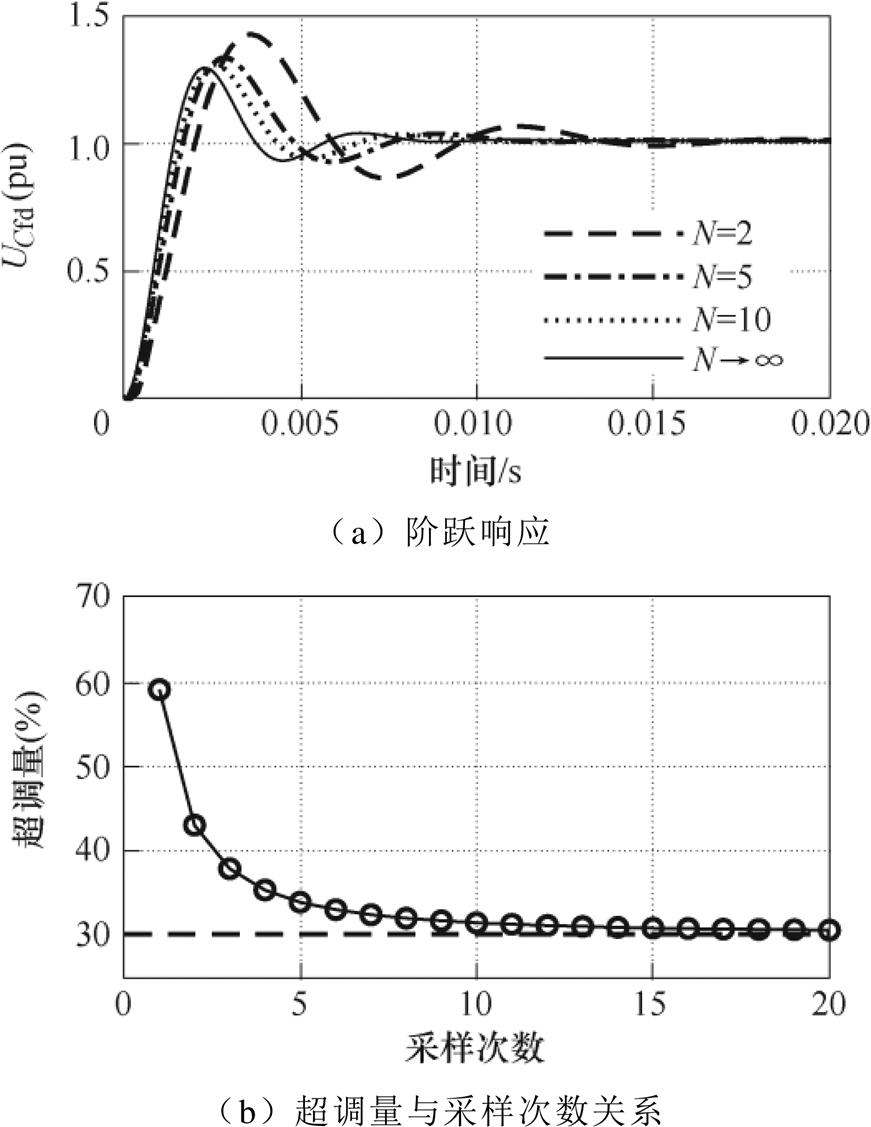
图12 系统阶跃响应及性能对比
Fig.12 System step response and performance comparison
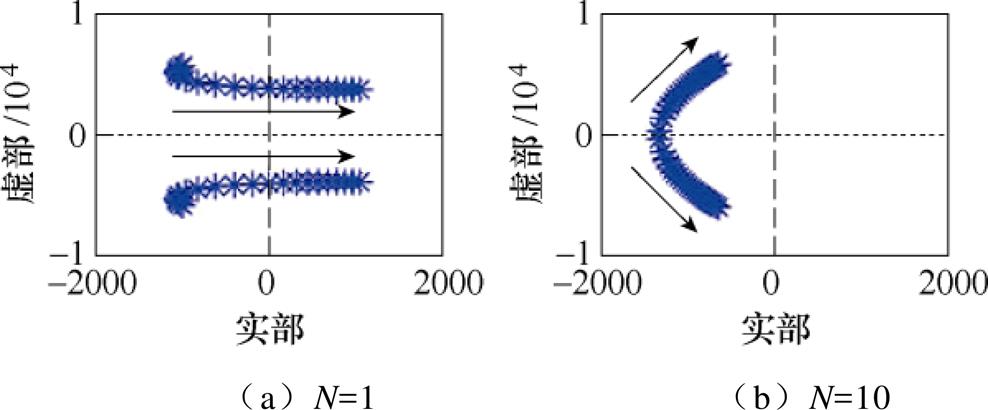
图13 kup变化系统主导极点分布
Fig.13 Dominant pole of the closed-loop control by varying kup
为了兼顾系统动态特性与数字控制器的计算负荷，选取采样次数的约束条件为：
（1）能够使得系统闭环带宽达到连续模型闭环带宽的80 %的采样次数最小值。
（2）数字控制器的计算负荷不超过70 %。
系统稳定工作时，参数的微小变化导致系统特征值发生相应变化，特征值灵敏度[25]提供了一种定量计算参数t 对特征值的影响程度的方法，常用于研究电力系统静态稳定性。
令vn、un分别为状态矩阵A的第n个左特征向量、右特征向量，ln为状态矩阵A的特征值。根据特征值的定义，分别有
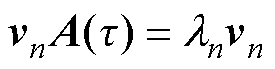（15）
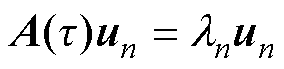（16）
由于ln、un为t 的隐函数，根据隐函数求导法则，对式（16）等号两边求t 的偏导数，可得
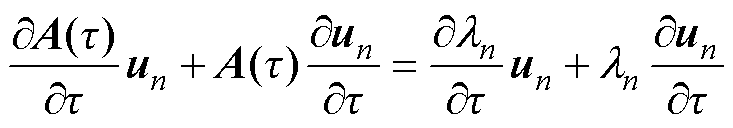（17）
式（17）两边同时左乘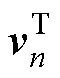
，结合式（15）、式（16）整理得第i个参数ti对第n个特征值ln的灵敏度为
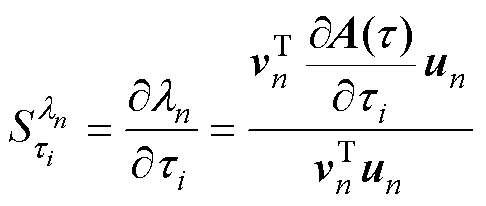（18）
则可以得到控制参数对逆变电源稳定性的影响。
系统特征值见表2，由表2可知，系统的7个特征值均分布在复平面的左侧，此逆变电源系统是小干扰稳定的，存在1个衰减模态和3个振荡模态。l1、l2和l3离虚轴最近，其余特征值均远离虚轴，可将l1、l2和l3视为主导特征值。
表2 系统特征值
Tab.2 System characteristic values
标号特征值振荡频率/Hz阻尼比 l1-35.5601 l2-230.7+784.2i124.80.282 l3-230.7-784.2i124.80.282 l4-1 813+6 340i1 0090.275 l5-1 813-6 340i1 0090.275 l6-1.577×104+1 261i200.70.997 l7-1.577×104-1 261i200.70.997
表3为表1中控制参数对主导特征值的灵敏度，灵敏度有正有负，灵敏度实部为正时，表示控制参数增大将使特征值的实部向正半轴移动，不利于系统的稳定。kup对l1实部的灵敏度为正，tu对l2和l3的灵敏度为正，kip对l1的灵敏度为正，ti对l1、l2和l3的灵敏度均为负。即kup与kip增大会使l1向正半轴移动，降低系统的稳定裕度。增大tu与kup会使l2和l3向正半轴移动，降低系统的稳定裕度。系统主导特征值l1、l2和l3随控制参数的变化轨迹如图14所示，其与理论计算变化规律一致。
表3 控制参数对主导特征值的灵敏度
Tab.3 The sensitivity of control parameters to main eigenvalues
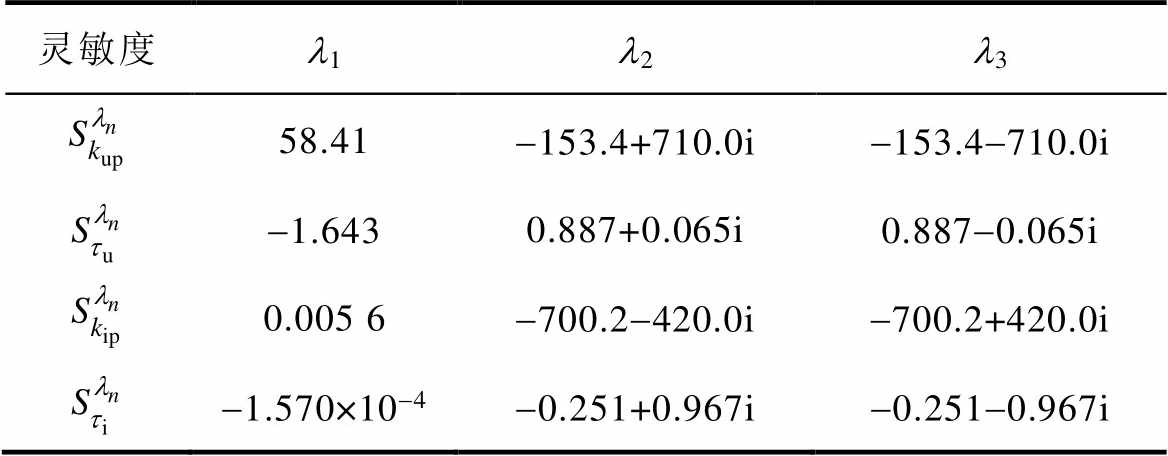
灵敏度l1l2l3 58.41-153.4+710.0i-153.4-710.0i -1.6430.887+0.065i0.887-0.065i 0.005 6-700.2-420.0i-700.2+420.0i -1.570×10-4-0.251+0.967i-0.251-0.967i
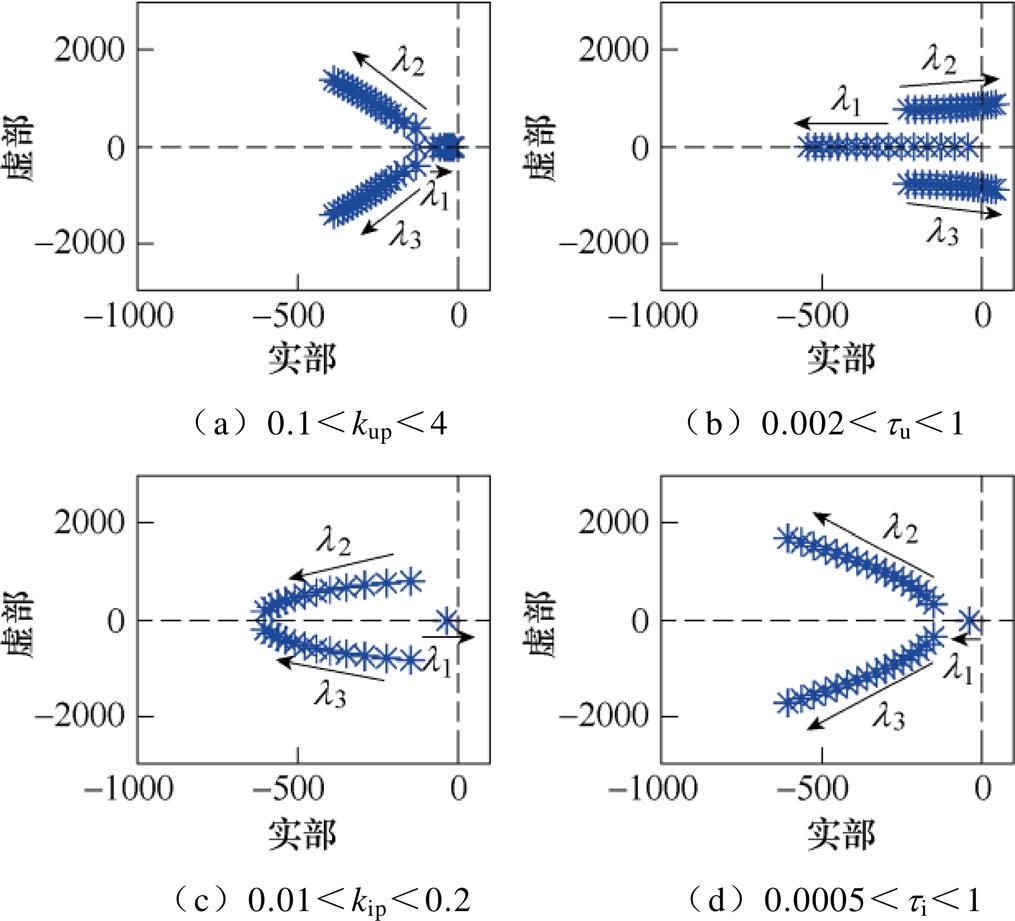
图14 系统特征值随控制参数变化轨迹
Fig.14 Trajectory of system characteristic values with varyingcontrol parameters
全局寻优算法是指在参数区间内按目标函数规则进行多次迭代，并对迭代结果进行比较，返回目标函数的最小值和对应的参数，即可搜索出参数区间内的全局最优值。该算法包含4个要素：目标函数、迭代初值、参数的取值范围和约束条件。
为了使系统能够尽快达到稳态值，要求系统主导特征值（主导极点）的实部要尽可能在左平面，且远离虚轴，故优化目标为
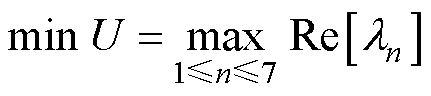（19）
约束条件主要考虑以下几点：
（1）系统的极点均位于复平面左半平面。
（2）通过设置合适的阻尼比，能够缩短系统的整定时间，减小系统超调量，一般设置阻尼比z 介于0.6～0.85之间。
（3）系统的动态响应速度与系统的闭环带宽fb存在一定的联系，带宽较高的系统动态响应更快。为了避免引入开关频率fs等高频谐波，fb一般小于0.5fs。
（4）对于系统电压的阶跃响应的最大值UCfmax限制为1.1倍的电压基准值Ub。
约束条件设置为
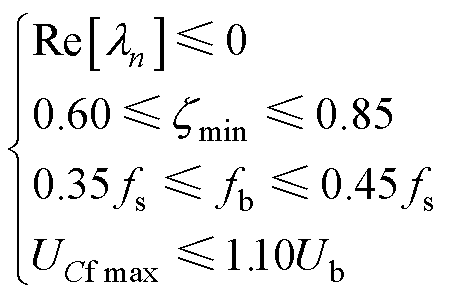（20）
在本算例中，根据灵敏度分析结果确定控制参数的取值范围分别为
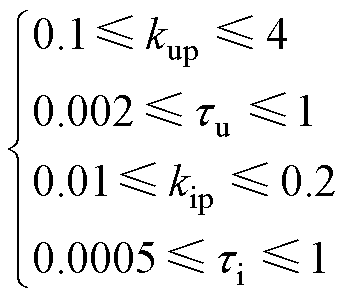（21）
以表1控制参数为初始值，运用上述优化方法得到kup=2.284、tu=0.101、kip=0.179、ti=0.052。
表4列出了寻优前后系统的主导极点，可以看出，寻优后系统的主导极点较寻优前主导极点远离虚轴，且阻尼比符合寻优所设定的边界条件。
表4 主导极点对比
Tab.4 Comparison of dominant poles
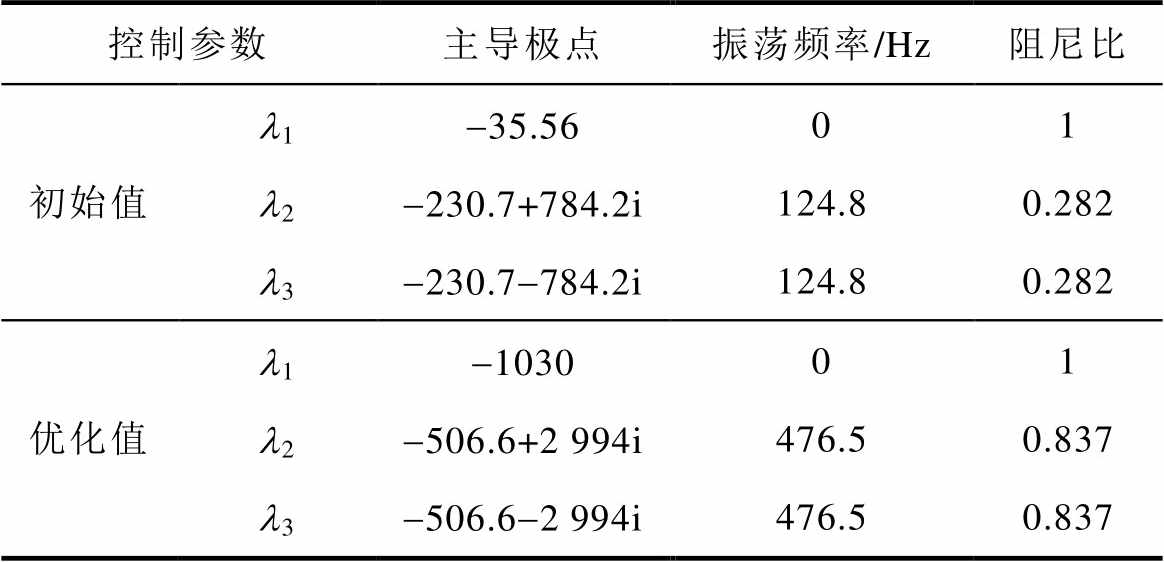
控制参数主导极点振荡频率/Hz阻尼比 初始值l1-35.5601 l2-230.7+784.2i124.80.282 l3-230.7-784.2i124.80.282 优化值l1-103001 l2-506.6+2 994i476.50.837 l3-506.6-2 994i476.50.837
图15为寻优前后系统的Bode图，从图中可以看出，相较于寻优前，系统的闭环带宽有所提升，通过计算闭环带宽由270 Hz提升至399 Hz，提升了47.78 %。
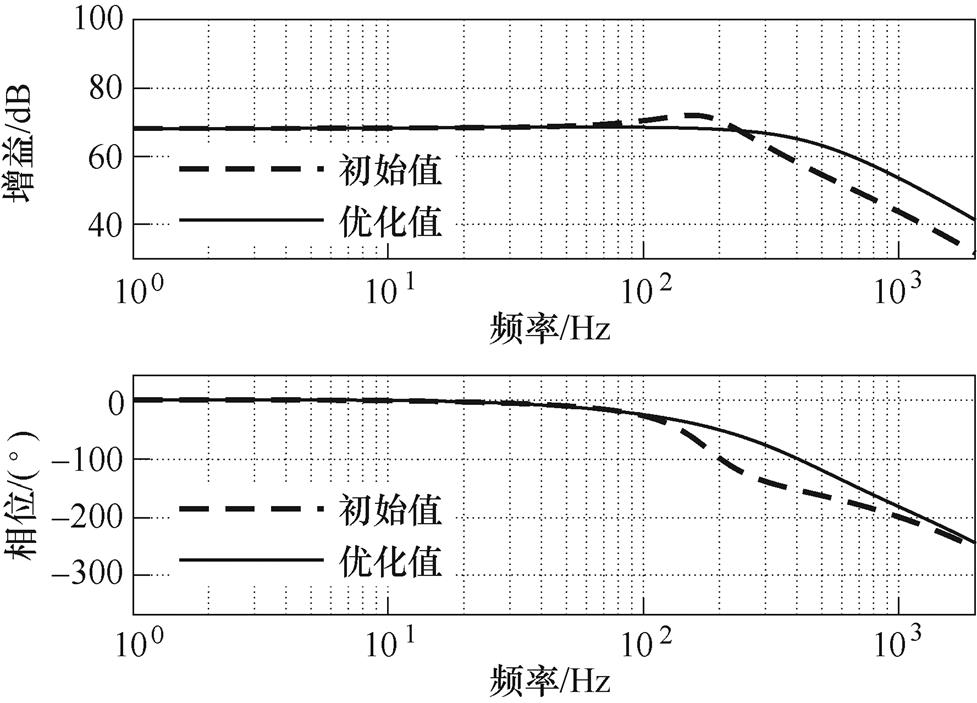
图15 系统Bode图对比
Fig.15 Comparison of system Bode diagram
图16为控制参数优化前后系统的阶跃响应对比，结果表明，寻优后系统阶跃响应的最大值为2 713 V，小于设定的最大值边界2 801 V，其最大值相较于寻优前减少了20.09 %。
搭建20 kW样机实物实验平台如图17所示，对全局优化算法的有效性和多次采样控制动态特性进行实验验证，20 kW样机实物实验平台参数见 表5。逆变电源控制系统以DSP+FPGA为核心。采用横河DL850对输出电压电流信号进行采集，采样率500 kS/s。
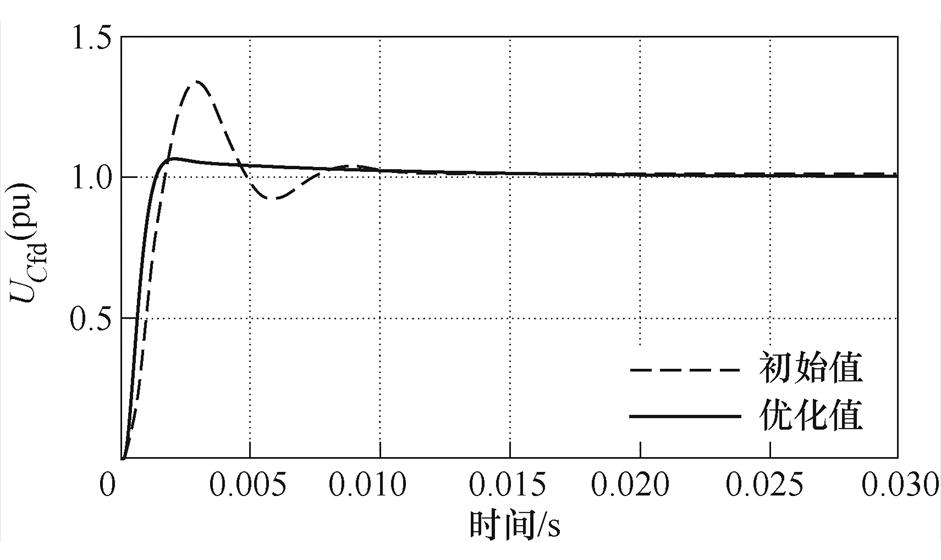
图16 系统阶跃响应比较
Fig.16 Comparison of systemstep respone
图17 20 kW逆变电源实验平台
Fig.17 Experimental platform of 20 kW inverter
表5 20 kW逆变电源样机参数
Tab.5 Parameters of 20 kW inverter
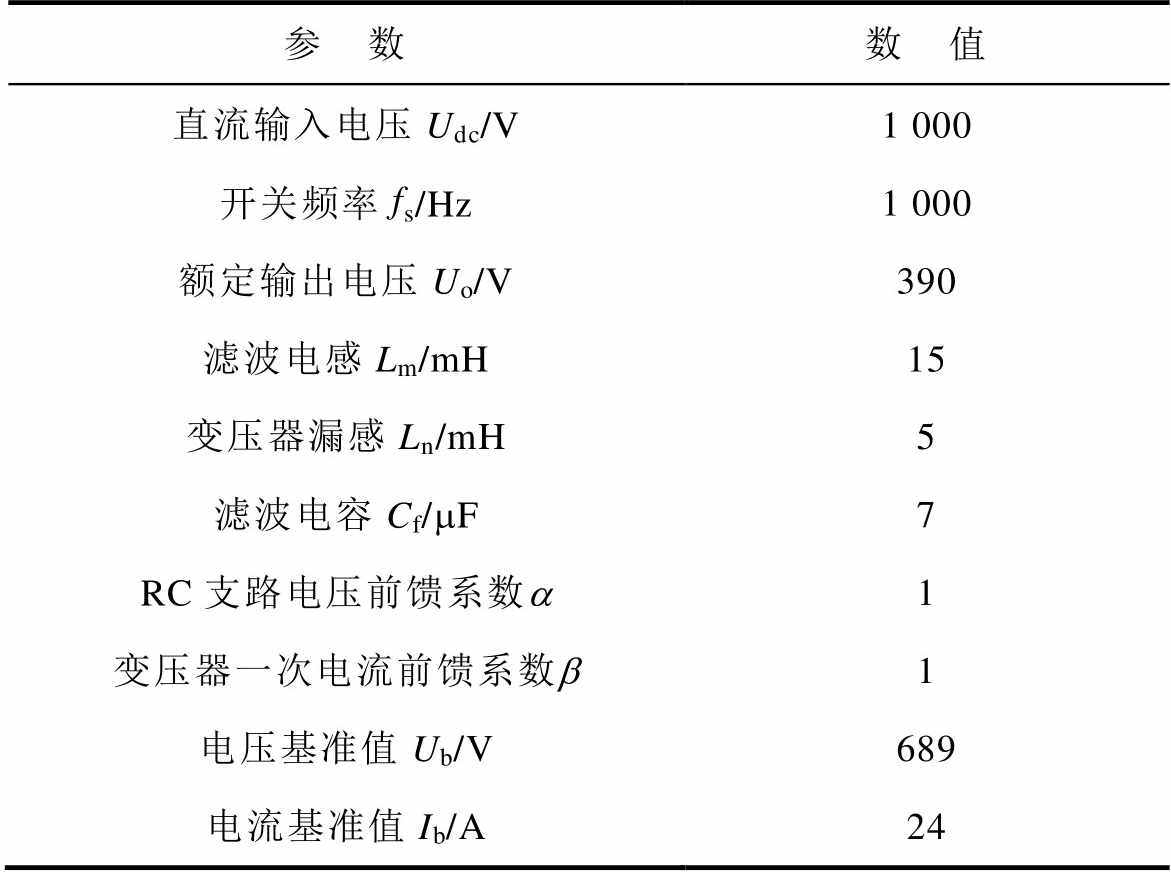
参 数数 值 直流输入电压Udc/V1 000 开关频率fs/Hz1 000 额定输出电压Uo/V390 滤波电感Lm/mH15 变压器漏感Ln/mH5 滤波电容Cf/mF7 RC支路电压前馈系数a1 变压器一次电流前馈系数b1 电压基准值Ub/V689 电流基准值Ib/A24
对比逆变电源在两组不同的控制参数下空载突加50 %的动态特性以验证全局优化算法的可行性。使用频域分析法计算出20 kW样机的控制参数初始值kup=0.75, tu=0.011, kip=0.138, ti=0.006，通过全局优化算法得到20 kW样机的控制参数优化值kup=1.8,tu=0.038, kip=0.44, ti=0.014。图18为两组参数下逆变电源20 kW样机空载突加半载（突加时刻为t =1 s）的实验波形。从图18b中可知，使用控制参数初始值时，系统电压跌落至88.2 V，电压经过33 ms恢复至稳态；使用控制参数优化值时，系统的电压跌落至220.6 V，经过9 ms左右恢复至稳态。从实验结果可知，使用优化后的控制参数，系统的动态特性优于使用初始控制参数的动态特性，验证了优化算法的有效性。
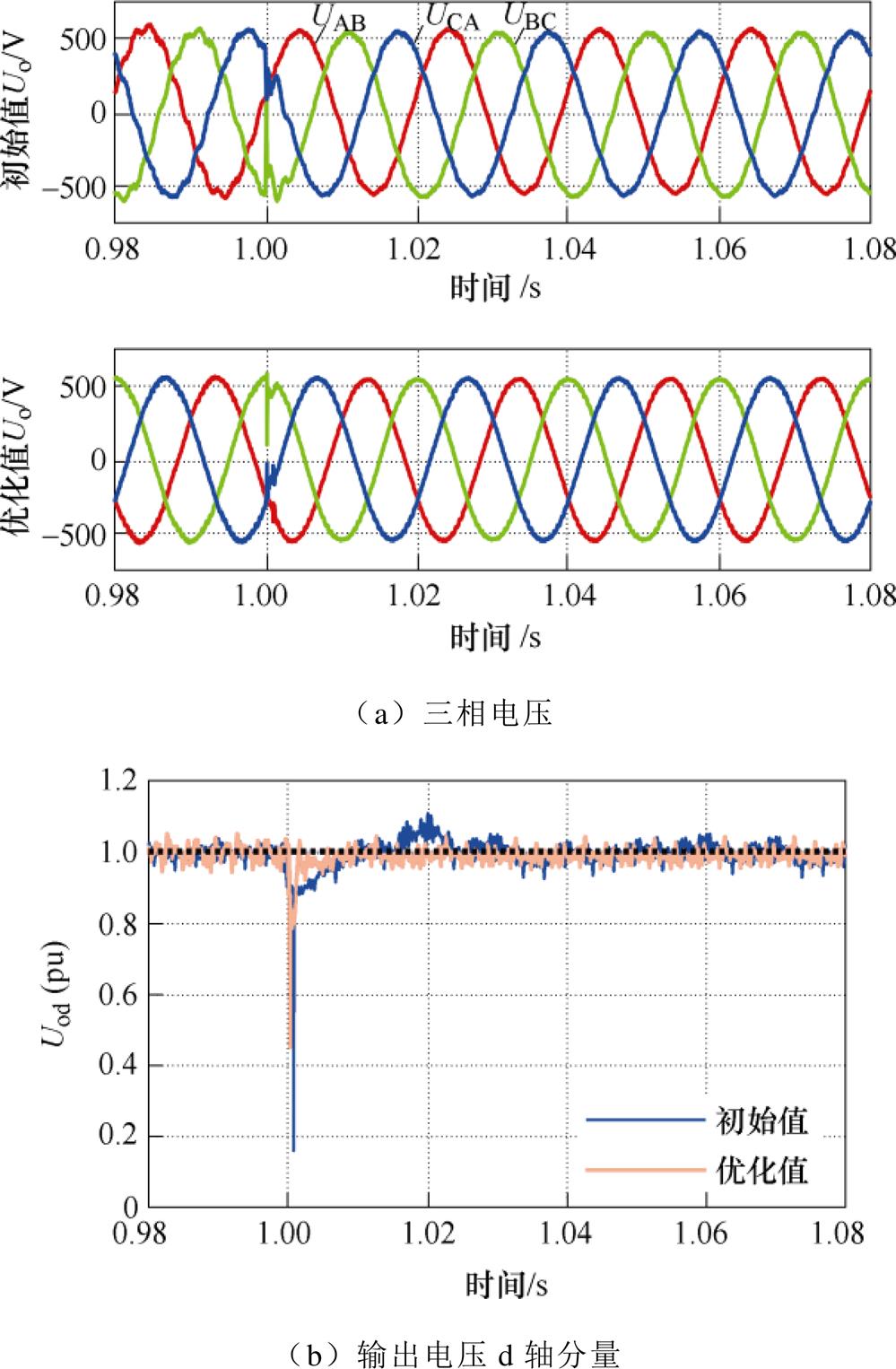
图18 全局优化实验波形
Fig.18 Validated waveforms of global optimization experiments
通过仅改变采样次数N进行空载突加50 %额定负载实验对多次采样控制动态特性进行验证。不同采样次数下输出电压d轴分量Uod、三相输出电压UAB、UBC、UCA和三相输出电流Ioa、Iob、Ioc波形如图19所示，其动态特性分析计算结果见表6。从结果中可看出，采样次数越高，在突加负载时电压跌落的越小，调节时间越短，但控制芯片计算负荷率增加。在N=2时，系统的电压跌落最多，恢复时间最长；N=10时，系统调节最快，但控制器的计算负荷率最大；N=5时，系统的调节时间与计算负荷率适中。
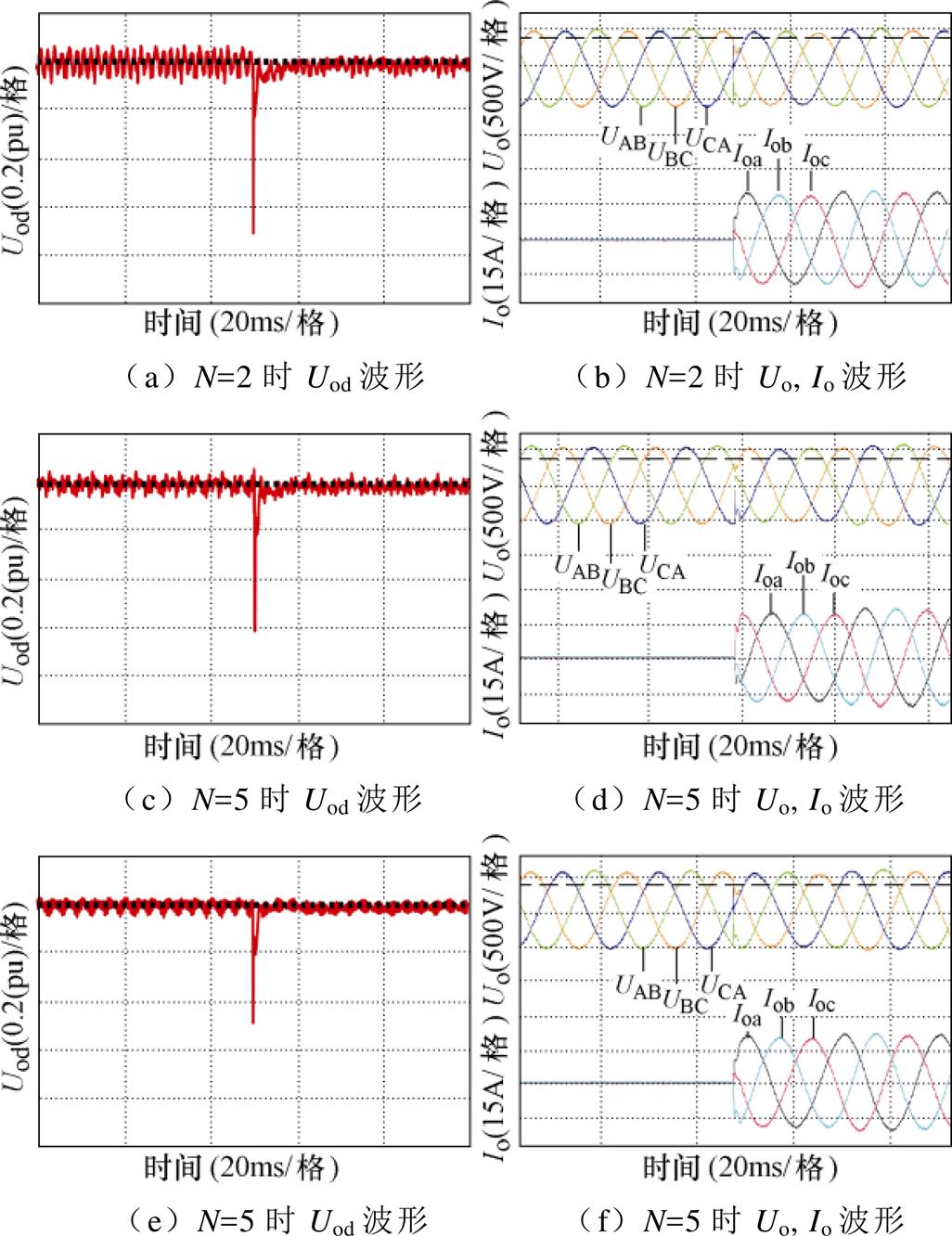
图19 多次采样特性验证实验波形
Fig.19 The experimental waveforms to verify multisampling characteristics
表6 系统动态特性与数字控制器负荷率
Tab.6 System dynamic characteristics and digitial contrdler load rate
采样次数N最低电压/V调节时间/ms数字控制器负荷率(%) 2165.522.317.01 5220.68.542.89 10292.34.885.68
针对中压大容量逆变电源在低开关频率下实现高动态响应能力的工程需求，本文建立了考虑多次采样的闭环模型，对模型动态特性进行分析，并搭建实验平台进行验证。本文结论如下：
1）使用二阶Pade近似将纯延迟环节化简为有理函数，并建立基于多次采样的逆变电源闭环模型，通过电路时域仿真验证了理论模型的正确性。
2）分析了采样次数对逆变电源动态特性的影响：采样次数越高，系统闭环带宽越接近无延迟闭环模型的带宽。在本文算例中，单次采样的闭环带宽为无延迟模型带宽的51.95 %，而采样次数N=5时，系统闭环带宽达到了无延迟闭环模型带宽的81.71 %。在此基础上，提出了一种兼顾闭环系统带宽和数字控制可实现性的采样次数选取方法。实验结果验证了所提方法的有效性。
3）在灵敏度分析的基础上，使用全局优化方法综合考虑电压外环、电流内环多个参数之间的耦合关系，设置约束条件寻找全局最优参数组合。本文算例中，寻优后系统的闭环带宽提高了47.78 %，系统阶跃响应的超调量降低了20.09 %。通过20 kW样机实验平台验证了优化算法的可行性。
附 录
逆变电源使用前馈解耦控制，可将式（2）中dq轴耦合的模型解耦，解耦后的主电路模型为
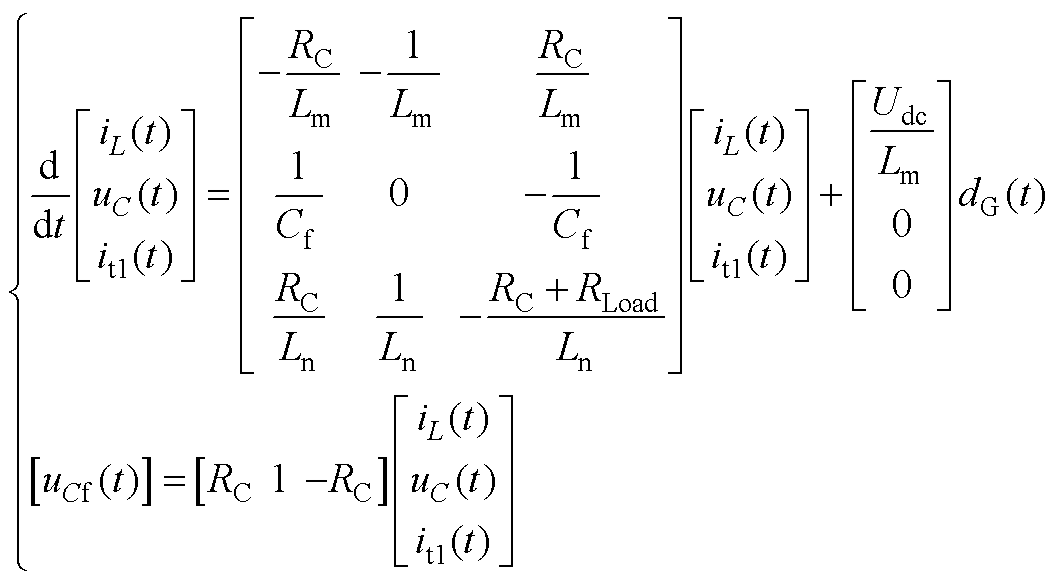（A1）
根据图4可列出逆变电源闭环控制状态空间方程。选择电压环与电流环PI控制积分的输出xu、xi作为状态变量，调制比m作为输出变量，可得控制环节的状态空间方程为
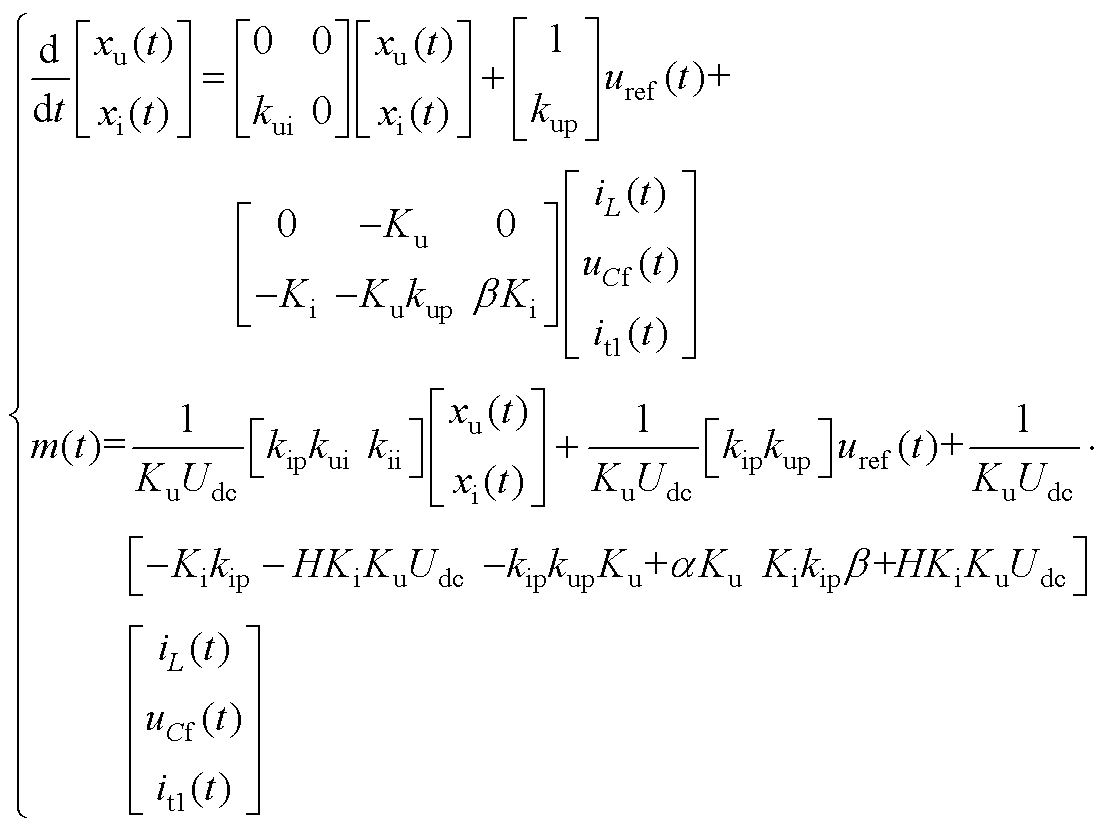（A2）
其中
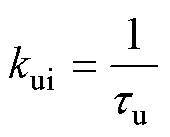
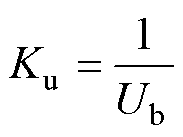
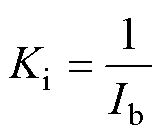
将式（13）、式（A1）、式（A2）相结合，可得到逆变电源闭环状态空间模型如式（14）所示。式中，状态变量x=[xu xi xe xf iLuCit1]T；输入变量u=[uref]；输出变量y=[uCf]。各矩阵的表达式为
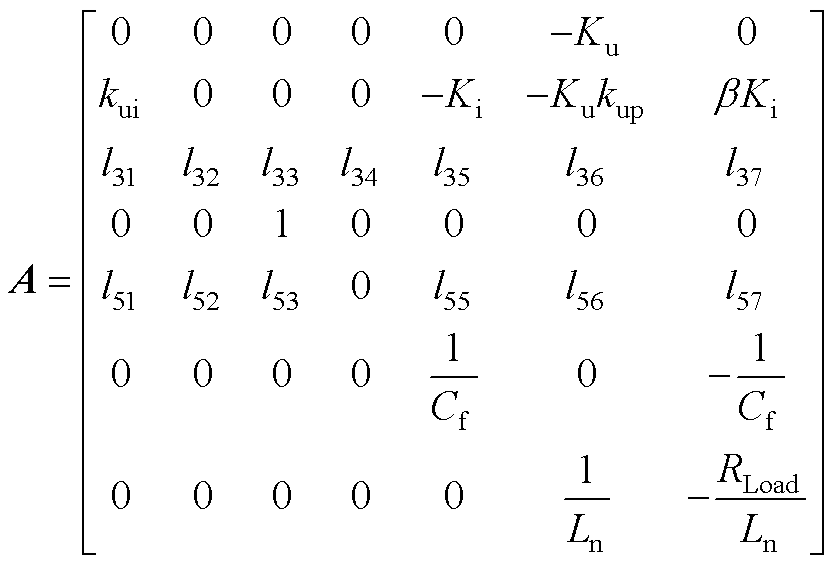
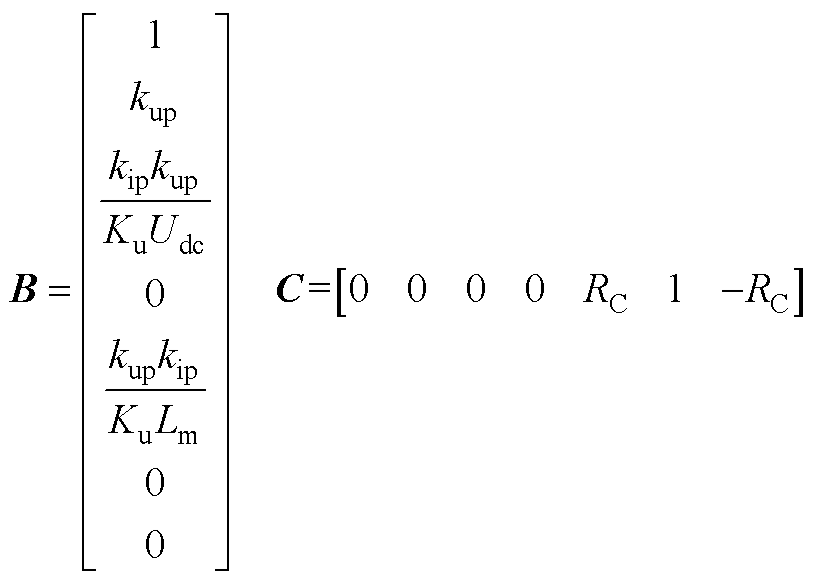
其中
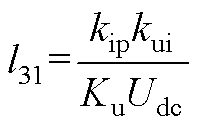
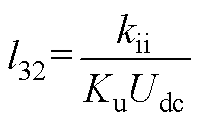
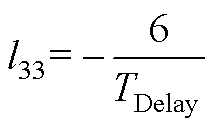
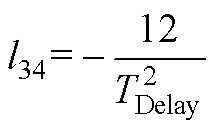
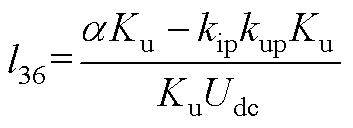
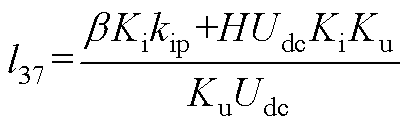
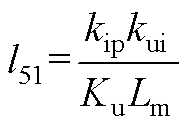
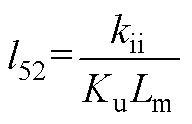
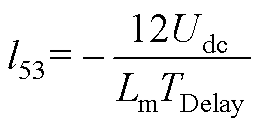
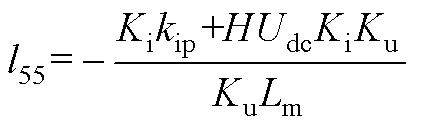
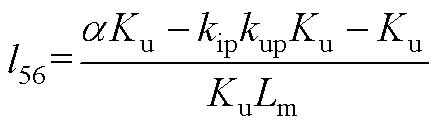
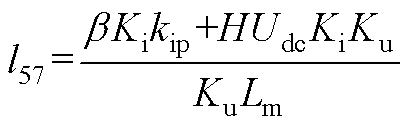
参考文献
[1] 马伟明. 电力电子在舰船电力系统中的典型应用[J].电工技术学报, 2011, 26(5): 1-7.
Ma Weiming. Typical applications of power electro- nics in naval ship power systems[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 1-7.
[2] 马伟明. 关于电工学科前沿技术发展的若干思考[J]. 电工技术学报, 2021, 36(22): 4627-4636.
Ma Weiming. Thoughts on the development of frontier technology in electrical engineering[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4627-4636.
[3] 李科峰, 高山, 刘计龙, 等. 有源中点钳位五电平逆变器悬浮电容预充电控制策略[J]. 电工技术学报, 2022, 37(8): 2064-2075.
Li Kefeng, Gao Shan, Liu Jilong, et al. Floating capacitor pre-charging control strategy for five-level active neutral-point-clamped inverter[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 2064- 2075.
[4] 李倩倩, 夏蓉花, 刘战, 等. 有源中点钳位型三电平并网逆变器多目标优化预测控制[J]. 电气技术, 2021, 22(7): 13-18.
Li Qianqian, Xia Ronghua, Liu Zhan, et al. Multi- objective optimal model predictive control for active neutral-point-clamped three-level inverter[J]. Electrical Engineering, 2021, 22(7): 13-18.
[5] 曹文远, 韩民晓, 谢文强, 等. 交直流配电网逆变器并联控制技术研究现状分析[J]. 电工技术学报, 2019, 34(20): 4226-4241.
Cao Wenyuan, Han Minxiao, Xie Wenqiang, et al. Analysis on research status of parallel inverters control technologies for AC/DC distribution net- work[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4226-4241.
[6] 于彦雪, 马慧敏, 陈晓光, 等. 弱电网下基于准静态模型的混合控制微电网逆变器同步稳定性研究[J]. 电工技术学报, 2022, 37(1): 152-164.
Yu Yanxue, Ma Huimin, Chen Xiaoguang, et al. Synchronous stability research of inverters in hybrid microgrid based on the quasi-static models under weak grid[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 152-164.
[7] 林霖, 裴忠晨, 蔡国伟, 等. 基于电力电子变压器的中压直流互联配电网协调控制方法[J]. 电力系统自动化, 2021, 45(8): 51-59.
Lin Lin, Pei Zhongchen, Cai Guowei, et al. Coordinated control method for medium-voltage DC interconnected distribution network based on power electronic transformer[J]. Automation of Electric Power Systems, 2021, 45(8): 51-59.
[8] 孙鹤旭, 李争, 陈爱兵, 等. 风电制氢技术现状及发展趋势[J]. 电工技术学报, 2019, 34(19): 4071- 4083.
Sun Hexu, Li Zheng, Chen Aibing, et al. Current status and development trend of hydrogen production technology by wind power[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4071-4083.
[9] 孙孝峰, 张绘欣, 张涵, 等. 一种用于电-氢多能互补型微电网的双有源桥集成Boost拓扑及其控制[J].电工技术学报, 2021, 36(10): 2092-2104.
Sun Xiaofeng, Zhang Huixin, Zhang Han, et al. Topology and control strategy of dual active bridge integrated boost circuit for electro-hydrogen multi- energy complementary microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2092- 2104.
[10] 郭小强, 魏玉鹏, 万燕鸣, 等. 新能源制氢电力电子变换器综述[J]. 电力系统自动化, 2021, 45(20): 185-199.
Guo Xiaoqiang, Wei Yupeng, Wan Yanming, et al. Review on power electronic converters for producing hydrogen from renewable energy sources[J]. Auto- mation of Electric Power Systems, 2021, 45(20): 185-199.
[11] 马伟明. 舰船动力发展的方向——综合电力系统[J].海军工程大学学报, 2002, 14(6): 1-5, 9.
Ma Weiming. Integrated power systems—trend of ship power development[J]. Journal of Naval Univer- sity of Engineering, 2002, 14(6): 1-5, 9.
[12] 张丹. 组合式多功能三相逆变器及其控制策略研究[D]. 马鞍山: 安徽工业大学, 2016.
[13] 潘冬华, 阮新波, 王学华, 等. 提高LCL型并网逆变器鲁棒性的电容电流即时反馈有源阻尼方法[J]. 中国电机工程学报, 2013, 33(18): 1-10, 21.
Pan Donghua, Ruan Xinbo, Wang Xuehua, et al. A real-time computation method with dual sampling modes to improve the current control performance of the LCL-type grid-connected inverter[J]. Proceedings of the CSEE, 2013, 33(18): 1-10, 21.
[14] Zhang Xing, Chen Peng, Yu Changzhou, et al. Study of a current control strategy based on multisampling for high-power grid-connected inverters with an LCL filter[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5023-5034.
[15] 周成, 江宏玲. 大功率并网逆变器多采样控制研究[J]. 大连交通大学学报, 2020, 41(3): 97-101.
Zhou Cheng, Jiang Hongling. Research on multi- sampling control of high powergrid-connected inver- ter[J]. Journal of Dalian Jiaotong University, 2020, 41(3): 97-101.
[16] Samanes J, Gubia E. Multisampled-capacitor-voltage active damping for parallel interleaved grid connected voltage source converters with LCL filter[C]//2017 19th European Conference on Power Electronics and Applications, Warsaw, Poland, 2017: 1-10.
[17] Van de Sype D M, De Gusseme K, Van den Bossche A P, et al. Small-signal Laplace-domain analysis of uniformly-sampled pulse-width modulators[C]//IEEE 35th Annual Power Electronics Specialists Confer- ence, Aachen, Germany, 2004: 4292-4298.
[18] Corradini L, Mattavelli P. Modeling of multisampled pulse width modulators for digitally controlled DC- DC converters[J]. IEEE Transactions on Power Elec- tronics, 2008, 23(4): 1839-1847.
[19] 刘春喜, 陈鹏荣, 高姬, 等. 中频逆变器数字控制延时的线性化近似[J]. 电源学报, 2015, 13(3): 55-61.
Liu Chunxi, Chen Pengrong, Gao Ji, et al. An approximation method of digital control delay in inverter[J]. Journal of Power Supply, 2015, 13(3): 55-61.
[20] Liu Guangyuan, Mattavelli P. Hysteresis droop con- troller with one sample delay for DC-DC converters in DC microgrids[C]//IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 2019: 2078-2084.
[21] Fischer C, Mariéthoz S, Morari M. Multisampled hybrid model predictive control for pulse-width modulated systems[C]//IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 2011: 3074-3079.
[22] Tomlinson M, Mouton T, Kennel R. Finite-control-set model predictive control with a fixed switching frequency vs. linear control for current control of a single-leg inverter[C]//IEEE International Symposium on Predictive Control of Electrical Drives and Power Electronics, Valparaiso, Chile, 2016: 109-114.
[23] 熊连松, 刘小康, 卓放, 等. 光伏发电系统的小信号建模及其控制器参数的全局优化设计方法[J]. 电网技术, 2014, 38(5): 1234-1241.
Xiong Liansong, Liu Xiaokang, Zhuo Fang, et al. Small-signal modeling of photovoltaic power gen- eration system and global optimal design for its controller parameters[J]. Power System Technology, 2014, 38(5): 1234-1241.
[24] 陈鹏. 基于多采样的大功率并网逆变器控制研究[D]. 合肥: 合肥工业大学, 2016.
[25] Nolan P J, Sinha N K, Alden R T H. Eigenvalue sensitivities of power systems including network and shaft dynamics[J]. IEEE Transactions on Power Apparatus and Systems, 1976, 95(6): 1318-1324.
Abstract The medium-voltage DC power system has broad application prospects in new energy, rail transportation, and integrated power system for ships. As the connection channel between a medium-voltage DC network and a low-voltage AC network, a medium-voltage high-capacity inverter power supply undertakes the task of supplying power for daily use and auxiliary equipment, which needs to meet the requirements of power quality, efficiency, power density, and reliability. The MW-level inverter power supply has a low switching frequency (500 Hz～2 kHz) due to the performance of existing mature medium-voltage high-capacity power electronics devices. The main challenge is to achieve high dynamic response capability at a low switching frequency. This paper focuses on the refinement model, characterization, control parameter optimization, and other related research work under the application of multisampling techniques for medium-voltage DC inverter power supplies.
Firstly, a state-space averaging model is established for the main circuit topology of the combined inverter and verified in the time domain. On this basis, a closed-loop control strategy containing double-closed-loop PI, feedforward decoupling, and active damping is adopted for the functional and index requirements of the inverter power supply in steady-state, dynamic, and grid-connected switching. A closed-loop state-space model under delay-free conditions is established to lay the foundation for the subsequent work.
Secondly, the basic principle and the PWM model based on multisampling are introduced. The pure delay link is a transcendental equation, which is reduced to a finite-dimensional polynomial using the Pade approximation instead of the delay link. The system-level closed-loop model of the inverter considering multisampling is developed based on the Pade approximation. The effect of multisampling on the dynamic characteristics of the system is investigated by a single-axis equivalent model. The analysis results show that increasing sampling times can reduce the digital control delay, increase the system’s closed-loop bandwidth, and reduce the step response overshoot. In this paper, the closed-loop bandwidth of a single sampling is 51.95 % of the delay-free model’s bandwidth, while the closed-loop bandwidth of the system reaches 81.71 % of the bandwidth of the delay-free closed-loop model when the sampling times N is 5. Accordingly, a sampling number selection method is proposed that considers the bandwidth of the closed-loop system and the achievability of digital control. A 20 kW prototype platform is built to verify the correctness of the model and analysis results.
Finally, according to the closed-loop model of the approximated inverter, the stability of the system is analyzed using the eigenvalue method, the sensitivity analysis of the PI control parameters to the eigenvalues is carried out, and the set of control parameters to be optimized is identified by sensitivity. Then, a mathematical model for control parameter optimization is established, and the final control parameters are obtained using a global optimization algorithm. In this paper, the closed-loop bandwidth of the optimized system is increased by 47.78 %, and the system's overshoot of the step response is reduced by 20.09 %. A 20 kW prototype platform verifies the effectiveness of the global optimization algorithm.
keywords：Medium-voltage high-power inverter, multisampling, Pade approximation, global optimization
国家自然科学基金项目（51907199）和中国博士后基金第64批面上项目（2018M643866）资助。
收稿日期 2022-07-18
改稿日期 2022-10-09
DOI: 10.19595/j.cnki.1000-6753.tces.221379
中图分类号：TM464
谢沁园 女，1998年生，硕士研究生，研究方向为电力电子与电力传动。E-mail: xqy329221315@qq.com
林克文 男，1989年生，助理研究员，研究方向为电力电子与电力传动。E-mail: kewenlin@163.com（通信作者）
（编辑 陈 诚）