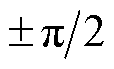 处有奇异点,因此难以保证PLL的全局收敛性。文献[16]通过增加一个额外的磁链观测器,利用观测误差构造出频率自适应算法,避免了奇异点问题。FLL无需PLL中的相位跟踪环节,直接利用正弦输入的误差反馈进行频率跟踪[22-25]。但是,上述方案均未考虑频率的变化率,因此当电机转速频繁变化时(如连续加减速),难以实时准确地跟踪频率。
处有奇异点,因此难以保证PLL的全局收敛性。文献[16]通过增加一个额外的磁链观测器,利用观测误差构造出频率自适应算法,避免了奇异点问题。FLL无需PLL中的相位跟踪环节,直接利用正弦输入的误差反馈进行频率跟踪[22-25]。但是,上述方案均未考虑频率的变化率,因此当电机转速频繁变化时(如连续加减速),难以实时准确地跟踪频率。摘要 磁链观测法是永磁同步电机在中高速区域一种有效的无传感器控制方案。但是由于逆变器非线性、初始位置误差、电流测量偏置等因素,磁链估计结果将不可避免地含有斜坡信号、直流偏置和各次谐波等多种干扰信号。这些干扰信号的存在将降低无传感器控制的稳态精度,增加转速波动,严重时甚至使系统失稳。针对这一问题,提出了基于扩张式主从自适应陷波滤波器(EMAF)的磁链观测方案。利用不同干扰信号的特性,EMAF可同时跟踪磁链观测中的多种干扰信号;通过对积分对象中的直流偏差进行反馈补偿,EMAF可消除积分环节产生的斜坡信号。进一步地,给出了EMAF的参数整定图解法,将多参数整定问题转换为单参数整定。另外,为了提高频率跟踪环节的动态性能,提出一种考虑电机运动方程的动态频率跟踪算法。相比锁相环或锁频环,该算法在频率变化时可减小频率跟踪误差,避免频率突变引起的暂态振荡。不同条件下的实验结果验证了所提方法的有效性。
关键词:永磁同步电机(PMSM) 无传感器控制 扩张式主从自适应陷波滤波器 参数整定 频率跟踪
近年来,永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)的无传感器控制系统因能够有效降低成本、提高空间利用率和可靠性,吸引了研究者的广泛关注[1-3]。PMSM的无传感器控制主要有高频信号注入[4-6]和模型估计法[7-11]两类,分别适用于低速和中高速区域。目前,主要通过二者的切换来实现宽调速范围。模型估计法可分为反电动势观测法和磁链观测法。由于转子磁链的幅值不随频率变化而变化——对于表贴式PMSM,其幅值为常数;对于内置式PMSM,有效磁链的幅值虽不是常数,但可利用电流直接计算。因此,相比反电动势观测法,磁链观测法在转速和电流时变的场合可获得更好的性能[12]。
但是,由于逆变器非线性、初始位置误差、电流测量偏置等因素,利用电压模型得到的磁链估计结果将含有直流偏置、各次谐波和斜坡信号等干扰信号[12-13]。这些干扰信号将严重影响PMSM无传感器控制的性能。因此,需消除上述干扰信号对磁链估计的影响,目前已有学者进行了相关研究。文献[14]提出了带有初始位置自适应辨识的磁链观测方案。但由于包含纯积分环节,这一方案难以实际应用。文献[15]在文献[14]的基础上,提出了鲁棒自适应磁链观测器,将初始位置辨识误差反馈至磁链观测器的输入,将纯积分环节转化为闭环观测器的形式,解决了积分饱和问题。但是,该方法未考虑电流测量值含有的直流偏差和谐波的影响,并且严格依赖磁链幅值这一参数。文献[13, 16]提出了一种带有频率自适应算法的磁链滑模观测器(Flux Sliding Mode Observer, FSMO)。该方法利用磁链的正交关系将纯积分环节转化为状态估计问题,再设计滑模观测器进行磁链估计,有效地消除了斜坡信号引起的积分饱和问题。但该方法同样未考虑直流偏置的影响,并且其谐波抑制能力需要与观测器响应速度取折中。文献[17]提出使用一种改进的二阶广义积分器进行磁链观测。该方法无需初位置检测,可以消除直流偏置并在一定程度上抑制谐波。但该方法无法完全消除谐波的影响,特别是在较低速时,谐波抑制能力较弱。另外,该方法需要先估计出反电动势,再利用估计结果进行磁链观测,这种观测器的级联结构将增加磁链观测误差。文献[18]采取另一种思路,将多个广义二阶积分器并联起来分别消除不同的干扰信号。但与文献[17]类似的是,该方法仍需先估计出反电动势。因此,目前已有方案难以做到在不影响观测器响应速度的同时消除磁链观测中的多种干扰信号。
另一方面,由于速度控制器和磁链观测均需要实时准确的频率信息,因此频率跟踪是一个重要环节。目前,应用较广泛的方法是锁相环(Phase-Locked Loop, PLL)[19]或者锁频环(Frequency-Locked Loop, FLL)[20]。文献[21]指出,PLL的应用将降低系统的动态性能,并提出了一种基于正切函数的PLL,解决了电机正反转切换时的不稳定问题。但正切函数在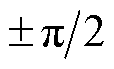 处有奇异点,因此难以保证PLL的全局收敛性。文献[16]通过增加一个额外的磁链观测器,利用观测误差构造出频率自适应算法,避免了奇异点问题。FLL无需PLL中的相位跟踪环节,直接利用正弦输入的误差反馈进行频率跟踪[22-25]。但是,上述方案均未考虑频率的变化率,因此当电机转速频繁变化时(如连续加减速),难以实时准确地跟踪频率。
处有奇异点,因此难以保证PLL的全局收敛性。文献[16]通过增加一个额外的磁链观测器,利用观测误差构造出频率自适应算法,避免了奇异点问题。FLL无需PLL中的相位跟踪环节,直接利用正弦输入的误差反馈进行频率跟踪[22-25]。但是,上述方案均未考虑频率的变化率,因此当电机转速频繁变化时(如连续加减速),难以实时准确地跟踪频率。
针对上述问题,本文的主要创新点总结如下:
(1)提出了扩张式主从自适应陷波滤波器(Extended Master-slave Adaptive notch Filter, EMAF),并将其应用于磁链观测。EMAF能够在不影响观测器响应速度的同时,消除磁链观测中的多种干扰信号,并且无需反电动势估计这一环节。
(2)针对EMAF中可调参数较多的问题,给出了一种简明有效的参数整定图解法。通过限定特征根的分布形式将多参数整定问题转化为单参数整定,并利用图解法避免了繁琐运算,具有较好的可移植性。
(3)提出了一种动态频率跟踪(Dynamic Fre- quency Tracking, DFT)算法。通过将电机运动方程纳入频率跟踪环节,DFT可提升频率跟踪的动态性能,特别是在转速时变的情况下。
表贴式永磁同步电机的电压-磁链方程可写为
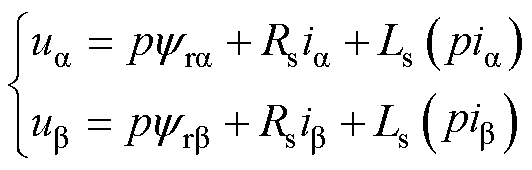 (1)
(1)
式中,ia,b、ua,b 和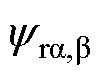 分别为电流、电压和转子磁链;Rs和Ls分别为定子电阻和电感;p为微分算子。
分别为电流、电压和转子磁链;Rs和Ls分别为定子电阻和电感;p为微分算子。
转子磁链可表示为
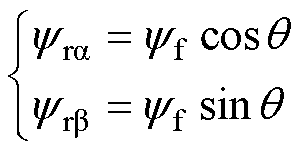 (2)
(2)
式中,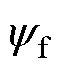 和q 分别为磁链幅值和转子位置。由式(2)可知,利用转子磁链可计算出转子位置。为此,需要估计出准确的转子磁链。由式(1)可知,转子磁链为
和q 分别为磁链幅值和转子位置。由式(2)可知,利用转子磁链可计算出转子位置。为此,需要估计出准确的转子磁链。由式(1)可知,转子磁链为
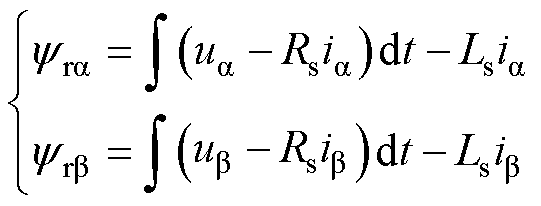 (3)
(3)
由于电流测量和A-D转换模块不可避免地含有直流偏差,经积分环节后将出现斜坡信号,造成积分饱和。除此之外,电流测量误差和初始位置检测误差将使磁链估计结果含有直流偏置;逆变器非线性还将引起5次、7次等谐波干扰。考虑这三类干扰信号,可将由式(3)计算出的转子磁链表示为
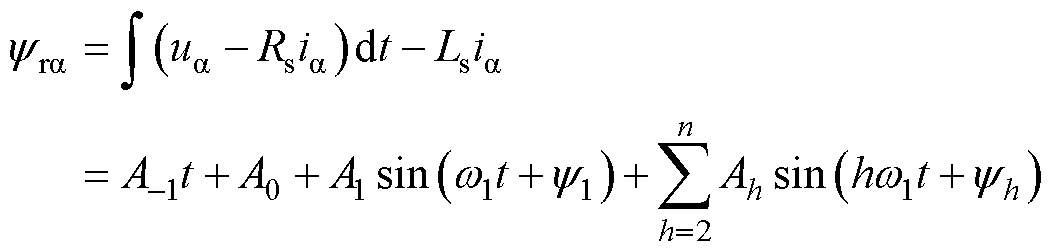 (4)
(4)
式中,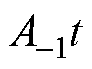 为斜坡信号,
为斜坡信号,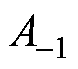 为该信号斜率,也是
为该信号斜率,也是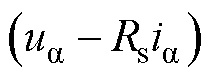 中的直流偏置;
中的直流偏置;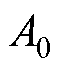 为直流偏置;
为直流偏置;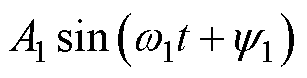 为基波信号;
为基波信号;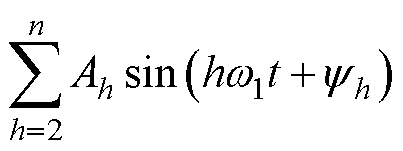 为各次谐波,h为谐波次数。这些干扰信号将增加位置估计误差,严重时可能导致系统不稳定。因此,消除这些干扰信号对于提高位置估计精度和稳定性具有重要意义。另外,磁链基波的准确估计以及转速的高性能控制均依赖快速准确的频率跟踪,因此提升频率跟踪的动态性能对于提升整体控制性能也很重要。
为各次谐波,h为谐波次数。这些干扰信号将增加位置估计误差,严重时可能导致系统不稳定。因此,消除这些干扰信号对于提高位置估计精度和稳定性具有重要意义。另外,磁链基波的准确估计以及转速的高性能控制均依赖快速准确的频率跟踪,因此提升频率跟踪的动态性能对于提升整体控制性能也很重要。
为消除干扰信号,本节提出EMAF。EMAF是由作者先前提出的主从自适应陷波滤波器(Mster- Slave Adaptive Notch Filter, MS-ANF)[22]发展而来。
首先,若仅考虑直流偏置与谐波,即假设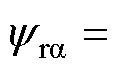
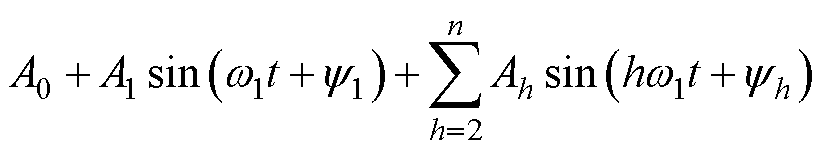 ,根据直流、基波和谐波信号的特性,可设计如下MS-ANF
,根据直流、基波和谐波信号的特性,可设计如下MS-ANF
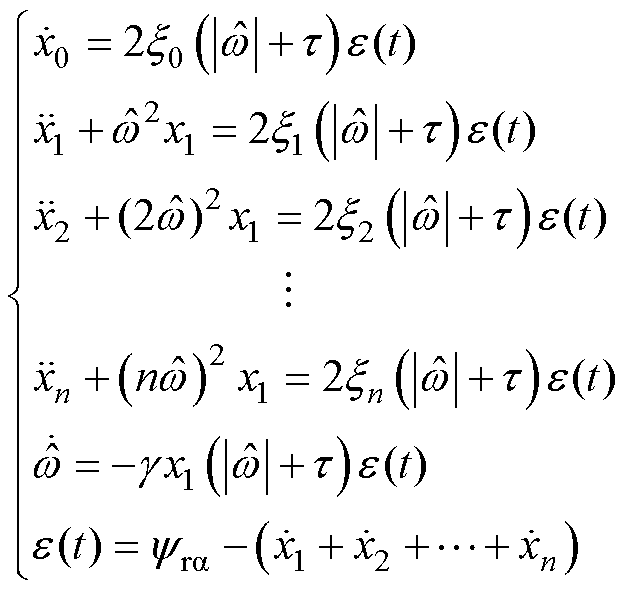 (5)
(5)
式中,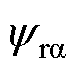 为输入信号;
为输入信号;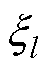 >0(l=0, 1, 2,
>0(l=0, 1, 2,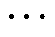 , n)为反馈增益;
, n)为反馈增益;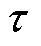 为足够小的正数,是为了确保反馈项不为零;
为足够小的正数,是为了确保反馈项不为零;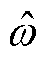 为频率估计;因子
为频率估计;因子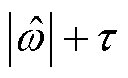 是为了归一化,有利于后文的参数整定。式(5)的解为
是为了归一化,有利于后文的参数整定。式(5)的解为
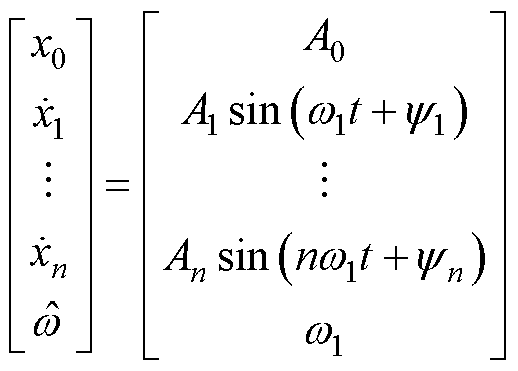 (6)
(6)
上述MS-ANF的稳定性分析见文献[22, 24]。由式(6)可知,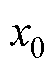 、
、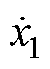 、
、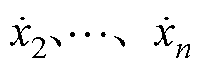 分别跟踪
分别跟踪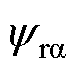 中的直流偏置、基波与各次谐波,从而达到消除直流偏置与谐波的目的。然而,式(5)无法消除斜坡信号。原因在于斜坡信号是无界的,无法通过上述直接跟踪的方式将其消除。
中的直流偏置、基波与各次谐波,从而达到消除直流偏置与谐波的目的。然而,式(5)无法消除斜坡信号。原因在于斜坡信号是无界的,无法通过上述直接跟踪的方式将其消除。
对于斜坡信号引起的积分饱和问题,目前较有代表性的方法是利用二阶广义积分器(Second Order Generalized Integrator, SOGI)[17]。但这类方法需要首先估计反电动势,再通过SOGI得到其积分,这将增加观测误差并导致动态性能下降。
考虑到斜坡信号的出现是由于积分对象存在直流偏差,本文引入一个新状态变量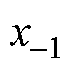 ,使其跟踪积分对象中的直流偏差,再将其补偿在积分对象中,从而达到消除斜坡信号的目的。
,使其跟踪积分对象中的直流偏差,再将其补偿在积分对象中,从而达到消除斜坡信号的目的。
以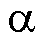 轴为例,将式(3)改写为
轴为例,将式(3)改写为
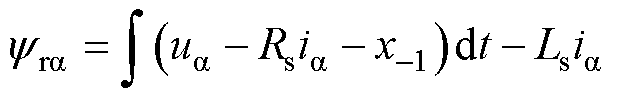 (7)
(7)
式中,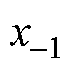 为引入的新状态变量。为了使
为引入的新状态变量。为了使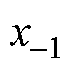 跟踪
跟踪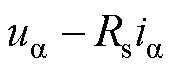 中的直流偏差,将式(5)扩张为
中的直流偏差,将式(5)扩张为
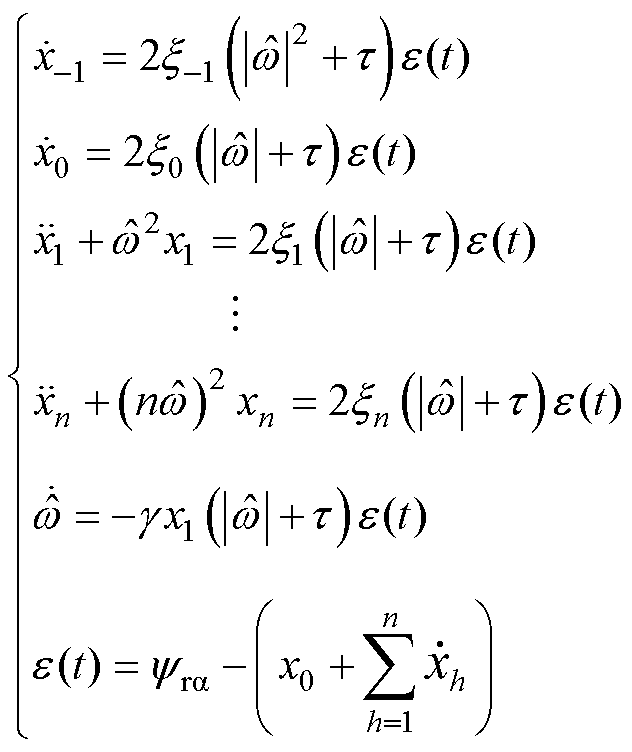 (8)
(8)
式(7)和式(8)联立起来构成了EMAF。下面分析EMAF的特性。
将式(7)重写为
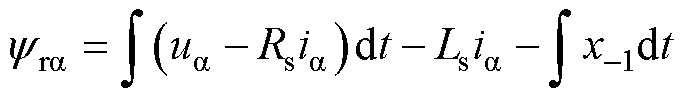 (9)
(9)
将式(9)代入式(8)中的最后一式,可得
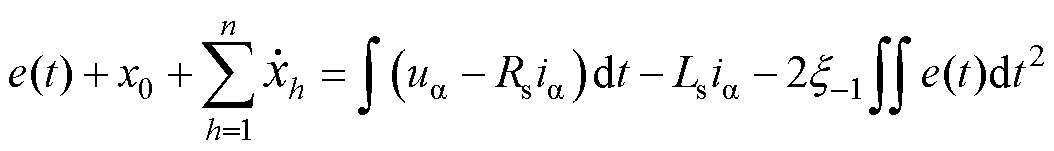 (10)
(10)
整理式(10),并考虑式(4),有
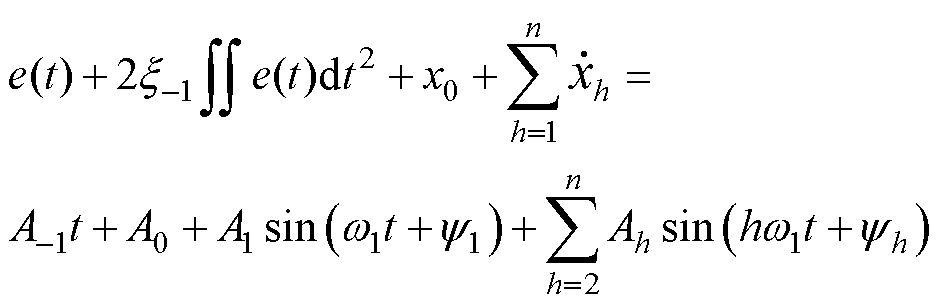 (11)
(11)
再结合式(8),易验证式(11)的解为
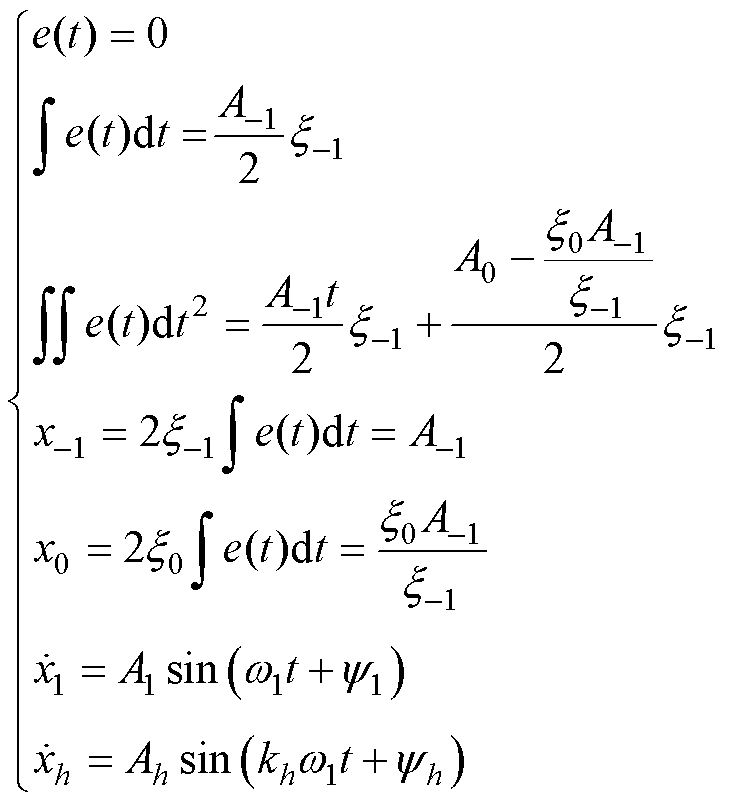 (12)
(12)
由式(12)可看出,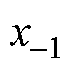 跟踪
跟踪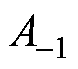 ,即积分对象
,即积分对象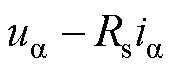 中的直流偏差。再将
中的直流偏差。再将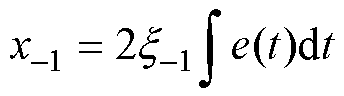 和
和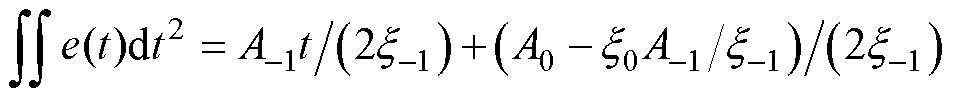 代入式(9),得
代入式(9),得
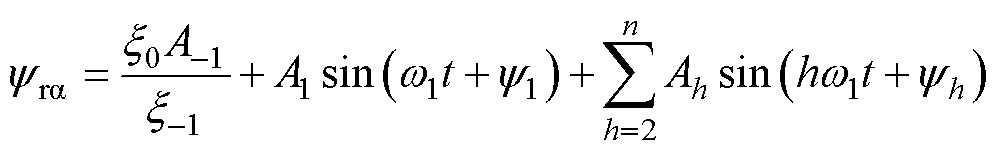 (13)
(13)
再由式(12)中的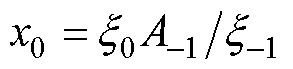 可知,x0跟踪
可知,x0跟踪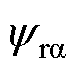 中的直流偏置;同时,
中的直流偏置;同时,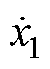 跟踪
跟踪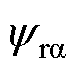 中的基波,
中的基波,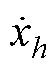 跟踪
跟踪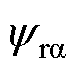 中的h次谐波。本文主要考虑5次和7次谐波。图1为
中的h次谐波。本文主要考虑5次和7次谐波。图1为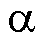 轴EMAF的结构框图,
轴EMAF的结构框图,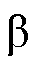 轴EMAF可设计为完全相同的结构。
轴EMAF可设计为完全相同的结构。
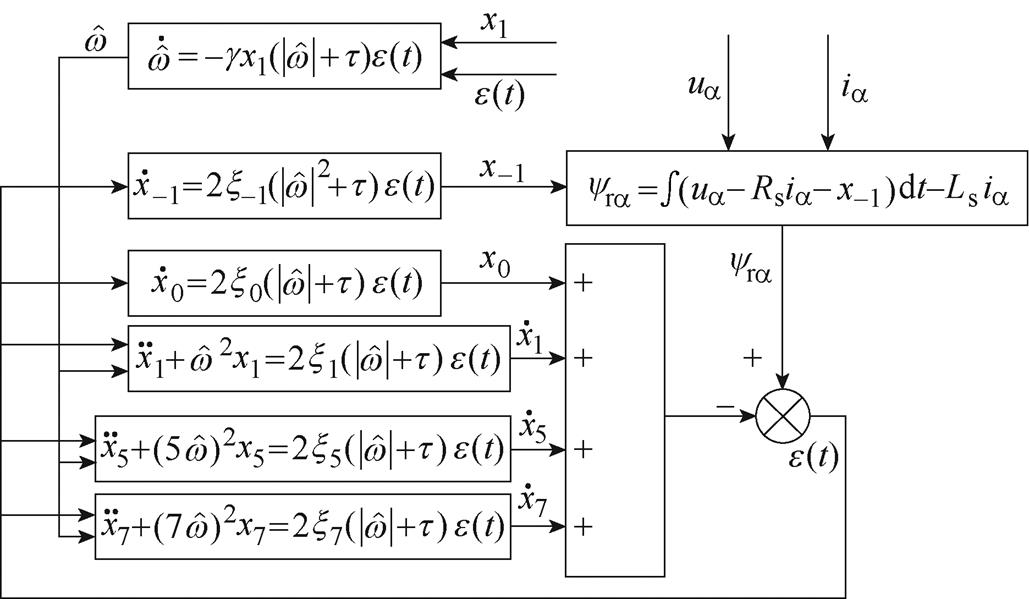
图1 EMAF的结构框图
Fig.1 Structure diagram of EMAF
为了便于分析,假设:输入信号为Y(t),其中包含直流偏置、基波与3次谐波,基波频率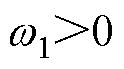 ,在稳态时
,在稳态时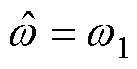 。根据2.2节,可设计EMAF来跟踪Y(t)的积分,考虑到
。根据2.2节,可设计EMAF来跟踪Y(t)的积分,考虑到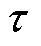 足够小,EMAF可表示为
足够小,EMAF可表示为
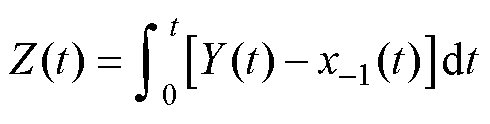 (14)
(14)
和
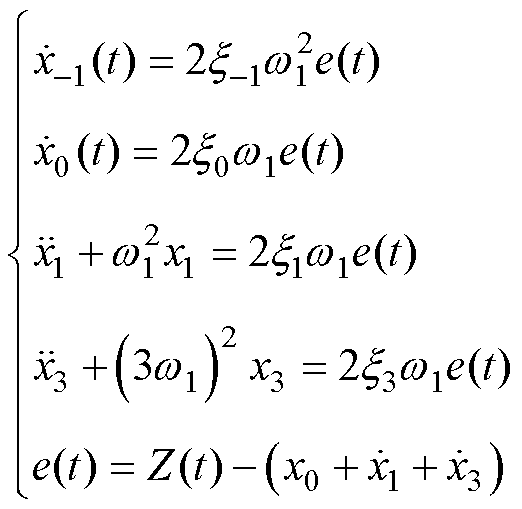 (15)
(15)
对式(15)中的后四式进行拉氏变换,可得
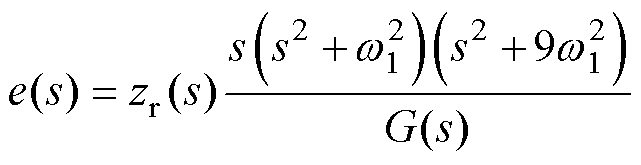 (16)
(16)
其中
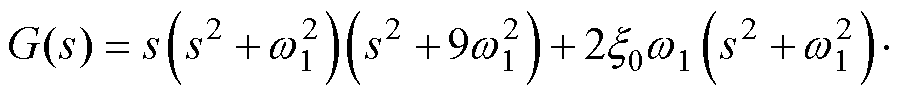
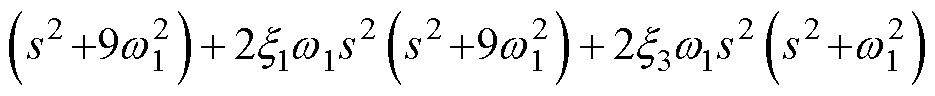
再将式(16)代入式(15)中的第三式,可得
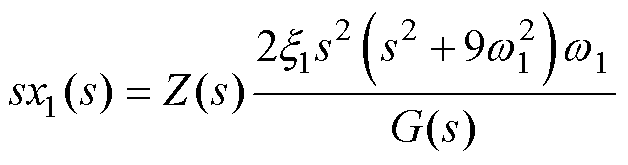 (17)
(17)
分别令s=j0,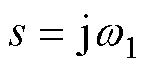 和
和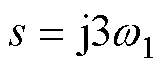 ,可得
,可得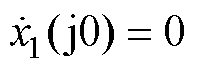 、
、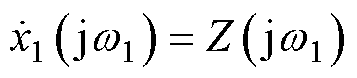 和
和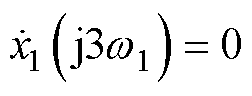 。因此,
。因此,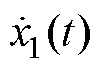 将准确跟踪Z(t)中的基波并且不受干扰信号的影响,表现出陷波滤波的特性。
将准确跟踪Z(t)中的基波并且不受干扰信号的影响,表现出陷波滤波的特性。
EMAF中的参数,即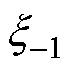 、
、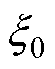 、
、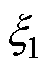 和
和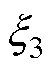 等影响EMAF的稳定性和收敛性能。由于可调参数较多,为便于实际应用,本文提出一种参数整定图解法。对式(14)和式(15)中第一式进行拉氏变换,得
等影响EMAF的稳定性和收敛性能。由于可调参数较多,为便于实际应用,本文提出一种参数整定图解法。对式(14)和式(15)中第一式进行拉氏变换,得
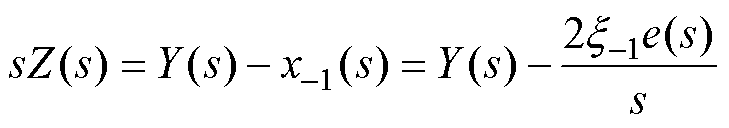 (18)
(18)
将式(16)代入式(18),得到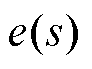 与
与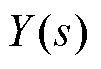 之间的传递函数为
之间的传递函数为
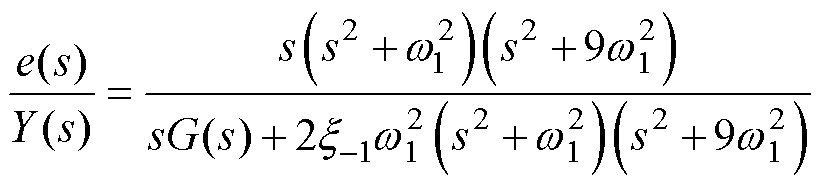 (19)
(19)
式中,右侧分母特征根决定了EMAF的稳定性与收敛性能。为了整定参数,需建立参数与特征根之间的关系。由于这些参数与特征根之间的关系比较复杂,本文通过限定特征根分布的方式来简化参数整定。令式(19)右侧分母多项式为
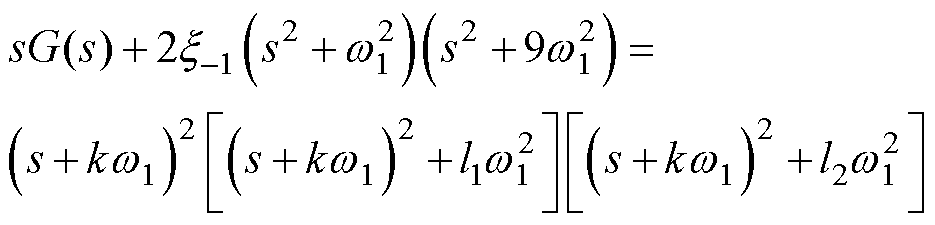 (20)
(20)
式中,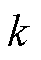 、
、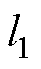 和
和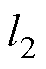 均为正常数。式(20)为一个六次多项式,并且最高次系数为1,而待确定的参数有7个(左侧含有4个待定参数:
均为正常数。式(20)为一个六次多项式,并且最高次系数为1,而待确定的参数有7个(左侧含有4个待定参数: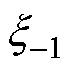 、
、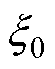 、
、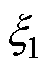 和
和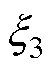 ,右侧引入了3个待定参数:
,右侧引入了3个待定参数: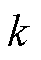 、
、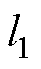 和
和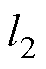 )因此,只需给定k值,其余参数便可唯一确定。这样,就将
)因此,只需给定k值,其余参数便可唯一确定。这样,就将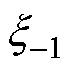 、
、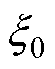 、
、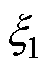 和
和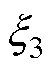 的整定问题转换成了k这一单参数的整定问题。
的整定问题转换成了k这一单参数的整定问题。
观察式(20)右侧可知,特征根被限定为: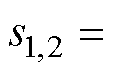
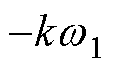 、
、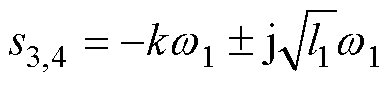 、
、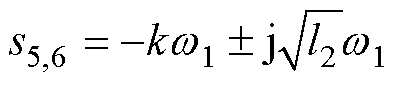 。k决定特征根实部,
。k决定特征根实部,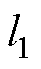 和
和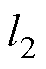 决定特征根虚部。又因为k确定后,
决定特征根虚部。又因为k确定后,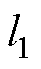 和
和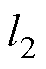 也随之确定,所以一旦确定了k,特征根的实部和虚部均确定。因此,为了获得满意的收敛性能,需考察k与
也随之确定,所以一旦确定了k,特征根的实部和虚部均确定。因此,为了获得满意的收敛性能,需考察k与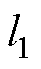 和
和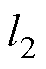 的关系。由于代数推导比较繁琐,本文采取图解法,步骤如下:
的关系。由于代数推导比较繁琐,本文采取图解法,步骤如下:
(1)给定一系列k值,对每一个k,在式(20)中取6个不同的s值,编程计算出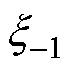 、
、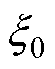 、
、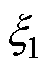 、
、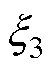 、
、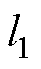 和
和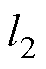 。
。
(2)得到一系列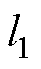 和
和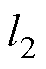 后,绘出它们与k的关系曲线。
后,绘出它们与k的关系曲线。
(3)观察k-l曲线选则合适的k值。确定k后,再计算相应的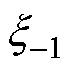 、
、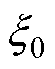 、
、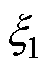 、
、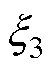 。
。
k-l曲线如图2所示。需要指出,由于在式(8)中,已经利用因子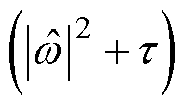 和
和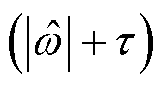 进行了归一化,因此不同频率下计算出的参数结果完全相同。
进行了归一化,因此不同频率下计算出的参数结果完全相同。
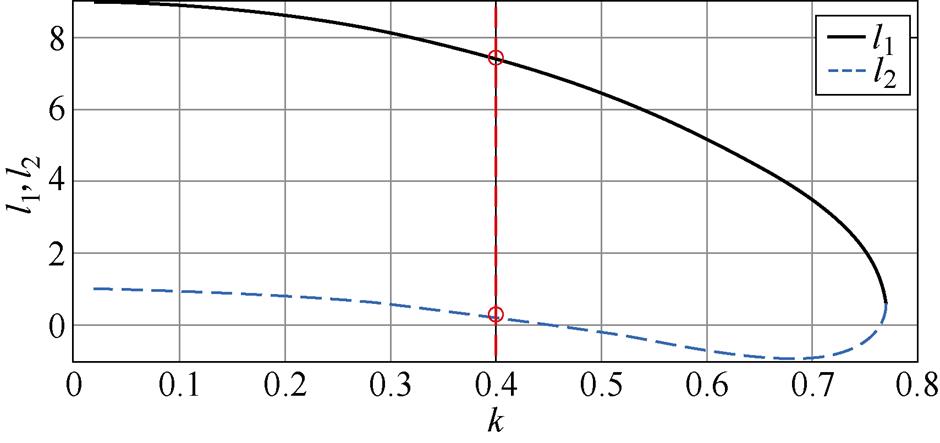
图2 l1、l2与k的关系曲线
Fig.2 Relationship curve of l1、l2 and k
观察图2可知,随着k增加,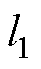 减小,
减小,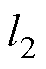 先减小后增大,并且当k>0.48时,
先减小后增大,并且当k>0.48时,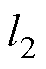 为负。为了获得较好的收敛性能,希望k较大,即特征根实部的绝对值较大,可增大收敛速度;同时希望
为负。为了获得较好的收敛性能,希望k较大,即特征根实部的绝对值较大,可增大收敛速度;同时希望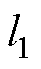 和
和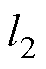 较小,即特征根虚部较小,可减小暂态振荡。另外,由式(20)可知,当
较小,即特征根虚部较小,可减小暂态振荡。另外,由式(20)可知,当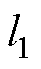 或
或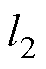 为负时,可能使特征根实部大于零,因此这里要求
为负时,可能使特征根实部大于零,因此这里要求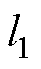 和
和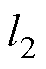 均为正。综合上述因素,并考虑一定裕度,可选取k=0.4。确定k之后可计算出
均为正。综合上述因素,并考虑一定裕度,可选取k=0.4。确定k之后可计算出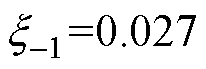 、
、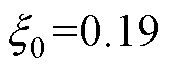 、
、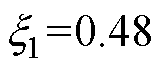 和
和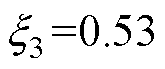 。
。
本节提出的参数整定方法具有较好的可移植性。对于不同的EMAF,只需改变式(20)的形式——EMAF中包含的二阶微分方程对应形如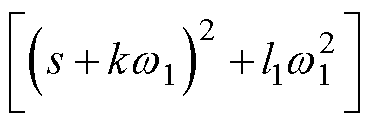 的因子,一阶微分方程对应形如
的因子,一阶微分方程对应形如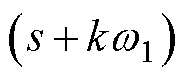 的因子。接下来按上述步骤作图,并观察k-l曲线选取合适的k,便可计算出待整定的参数。图解法的Matlab源程序见附录。
的因子。接下来按上述步骤作图,并观察k-l曲线选取合适的k,便可计算出待整定的参数。图解法的Matlab源程序见附录。
由第2节可知,对于EMAF,频率的准确跟踪至关重要。目前,具有代表性的频率跟踪方法主要有锁相环与锁频环。经简单推导可知,EMAF中的频率跟踪部分,即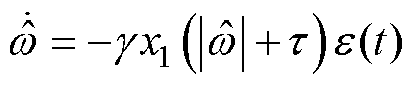 ,也可等效为锁频环[22]。利用锁相环(或锁频环)进行频率跟踪,当频率连续变化时,若带宽设置得较低,则难以实时跟踪时变的频率;若带宽设置得较高,则会增加噪声并影响稳定性。因此本节提出考虑电机运动方程的DFT。
,也可等效为锁频环[22]。利用锁相环(或锁频环)进行频率跟踪,当频率连续变化时,若带宽设置得较低,则难以实时跟踪时变的频率;若带宽设置得较高,则会增加噪声并影响稳定性。因此本节提出考虑电机运动方程的DFT。
得到磁链估计值,即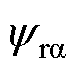 与
与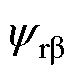 后,可计算出转子位置为
后,可计算出转子位置为
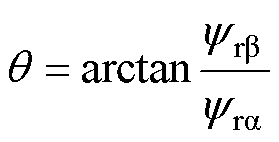 (21)
(21)
为了准确估计频率,考虑电机运动方程为
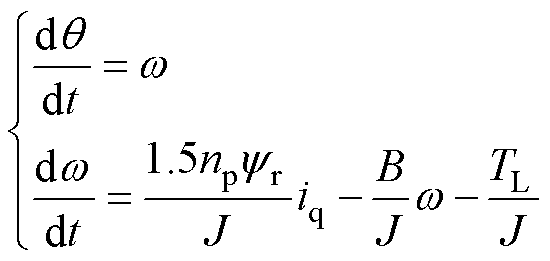 (22)
(22)
式中,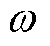 为转子的电角速度;np为转子极对数;B为摩擦系数;J为转动惯量。基于式(21)和式(22),设计如下扩张状态观测器(Extended State Observer, ESO)。
为转子的电角速度;np为转子极对数;B为摩擦系数;J为转动惯量。基于式(21)和式(22),设计如下扩张状态观测器(Extended State Observer, ESO)。
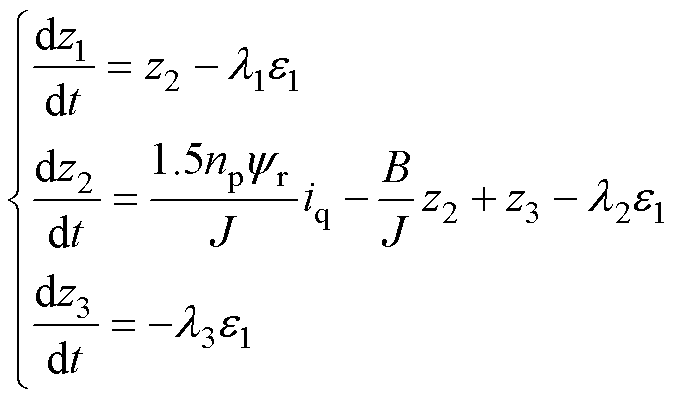 (23)
(23)
其中
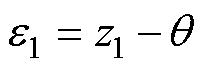
式中,l1、l2和l3为正常数。根据ESO理论[10],z1将跟踪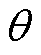 ,z2将跟踪
,z2将跟踪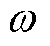 ,z3将跟踪
,z3将跟踪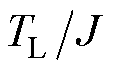 。但是,由于
。但是,由于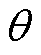 是在区间
是在区间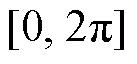 上的非连续变量(
上的非连续变量(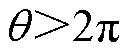 时会跳变至零),为了消除
时会跳变至零),为了消除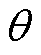 的跳变带来的影响,对式(23)中的
的跳变带来的影响,对式(23)中的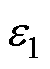 进行如下修正。
进行如下修正。
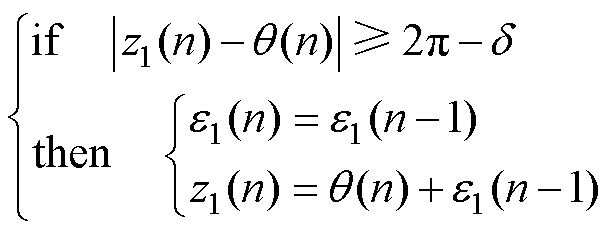 (24)
(24)
式中,n为n时刻;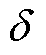 为一个足够小的正数。由式(24)可知,当
为一个足够小的正数。由式(24)可知,当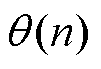 跳变时,
跳变时,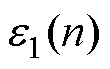 依然是连续的。式(23)与式(24)构成了本文提出的DFT。当电机转速连续变化时,由于式(23)考虑了频率的变化率,因此可获得更好的动态性能。后文实验将验证这一点。
依然是连续的。式(23)与式(24)构成了本文提出的DFT。当电机转速连续变化时,由于式(23)考虑了频率的变化率,因此可获得更好的动态性能。后文实验将验证这一点。
图3给出永磁同步电机无传感器控制的整体控制框图。基于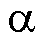 、
、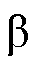 轴的电压方程设计EMAF,消除干扰信号并得到准确的
轴的电压方程设计EMAF,消除干扰信号并得到准确的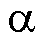 、
、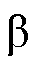 轴转子磁链;利用估计出的
轴转子磁链;利用估计出的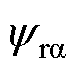 和
和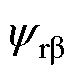 计算出转子位置,并利用动态频率跟踪算法得到频率;将估计出的频率反馈至EMAF,用于基波与各次谐波的跟踪,估计出的转子位置用于电流电压的坐标变换;同时,将估计频率反馈至速度控制器进行调速控制;电流环使用PI控制器,带宽设置为120;电流值通过电阻分压采样得到,算法中使用的电压值由控制器输出的电压给定代替;空间矢量调制采用固定频率的7段式SVPWM、对称规则采样;死区时间设置为2 ms。
计算出转子位置,并利用动态频率跟踪算法得到频率;将估计出的频率反馈至EMAF,用于基波与各次谐波的跟踪,估计出的转子位置用于电流电压的坐标变换;同时,将估计频率反馈至速度控制器进行调速控制;电流环使用PI控制器,带宽设置为120;电流值通过电阻分压采样得到,算法中使用的电压值由控制器输出的电压给定代替;空间矢量调制采用固定频率的7段式SVPWM、对称规则采样;死区时间设置为2 ms。
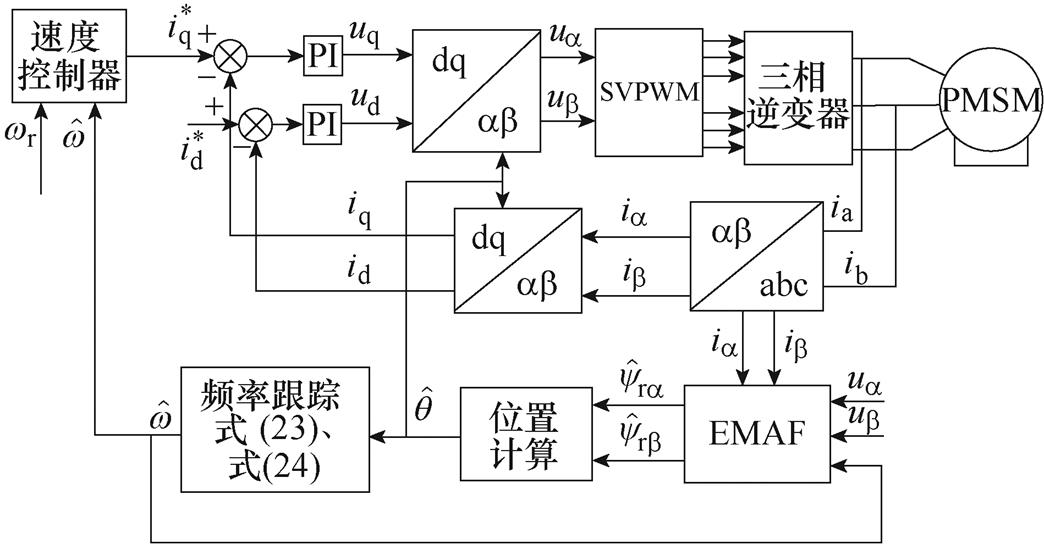
图3 永磁同步电机无传感器控制整体控制框图
Fig.3 The overall structure of sensorless control of PMSM
本文所提方法属于基于模型估计的无传感器控制方法,因此适用于中高速范围。由式(20)可知,提出的EMAF的特征根实部为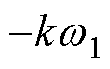 。为了保证整体系统的性能,观测环节的响应速度应当远大于控制环节。由于EMAF的特征根实部决定了其响应速度,因此本文要求其特征根实部的绝对值大于速度控制器带宽的5倍,即
。为了保证整体系统的性能,观测环节的响应速度应当远大于控制环节。由于EMAF的特征根实部决定了其响应速度,因此本文要求其特征根实部的绝对值大于速度控制器带宽的5倍,即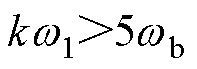 ,其中
,其中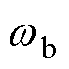 为控制器带宽,参数k按照第2节的整定方法选取为0.4。本文采用PI控制器,按照文献[26]中的方法进行参数整定,并以“对于阶跃速度指令,调速误差能够在1 s内衰减至初始误差的10%以下”为要求,利用表1中的电机参数可计算出速度控制器的闭环带宽最小可取为3.77。再由上述约束条件可知
为控制器带宽,参数k按照第2节的整定方法选取为0.4。本文采用PI控制器,按照文献[26]中的方法进行参数整定,并以“对于阶跃速度指令,调速误差能够在1 s内衰减至初始误差的10%以下”为要求,利用表1中的电机参数可计算出速度控制器的闭环带宽最小可取为3.77。再由上述约束条件可知 rad/s,即该方法适用的最低转速为112 r/min。
rad/s,即该方法适用的最低转速为112 r/min。
表1 永磁同步电机的参数
Tab.1 Parameters of PMSM

参 数数 值 额定功率/W200 额定电压/V24 定子电阻Rs/W0.79 定子电感Ls/mH0.5 转子磁链yr/Wb0.011 6 极对数np4 转动惯量J/(kg·m2)1.3×10-3
本节在恒定转速和连续时变转速的条件下,进行了实验以验证所提算法的有效性。图4为实验平台。直流电源提供电机直流侧电压,主控板芯片采用TMS320F28069,其频率为90 MHz。驱动芯片采用DRV8305,驱动板上集成了三相逆变器。逆变器开关频率和电流采样频率均为15 kHz。速度环周期与电流环周期分别为330 ms和66 ms。磁滞制动器提供负载转矩,采用可调电流源提供磁滞制动器所需的励磁电流。采用2 500线增量式编码器测量实际转子位置与速度。

图4 实验平台
Fig.4 The experimental platform
由于FSMO解决了积分饱和问题[13],并具有较好的稳定性和一定的谐波抑制能力,是一种近年来较常用的磁链观测方案。因此本节对比了使用FSMO与EMAF在不同转速下的磁链观测结果和位置-速度估计结果,并给出了EMAF的干扰信号跟踪结果,负载为额定负载2 N·m。FSMO的设计方法详见文献[13]。图5和图6分别给出了转速为150 r/min时,使用FSMO与EMAF的结果。对比图5与图6,可以看出,使用FSMO,位置估计的稳态最大误差约为0.075 rad,并且波动较大;使用EMAF,稳态最大误差减小到约为0.044 rad,且波动较小。另外,由图5与图6可知,使用EMAF也减小了速度估计值和实际值在稳态时的波动,提高了速度控制精度。图7给出了EMAF的其他输出,包括消除了斜坡信号但还未消除直流偏置与谐波的磁链估计、直流偏置、5次谐波和7次谐波。图8和图9给出了这两种方法在转速为2 000 r/min时的结果。同样可以看出,所提方法减小了位置误差以及转速波动,提升了稳态性能。
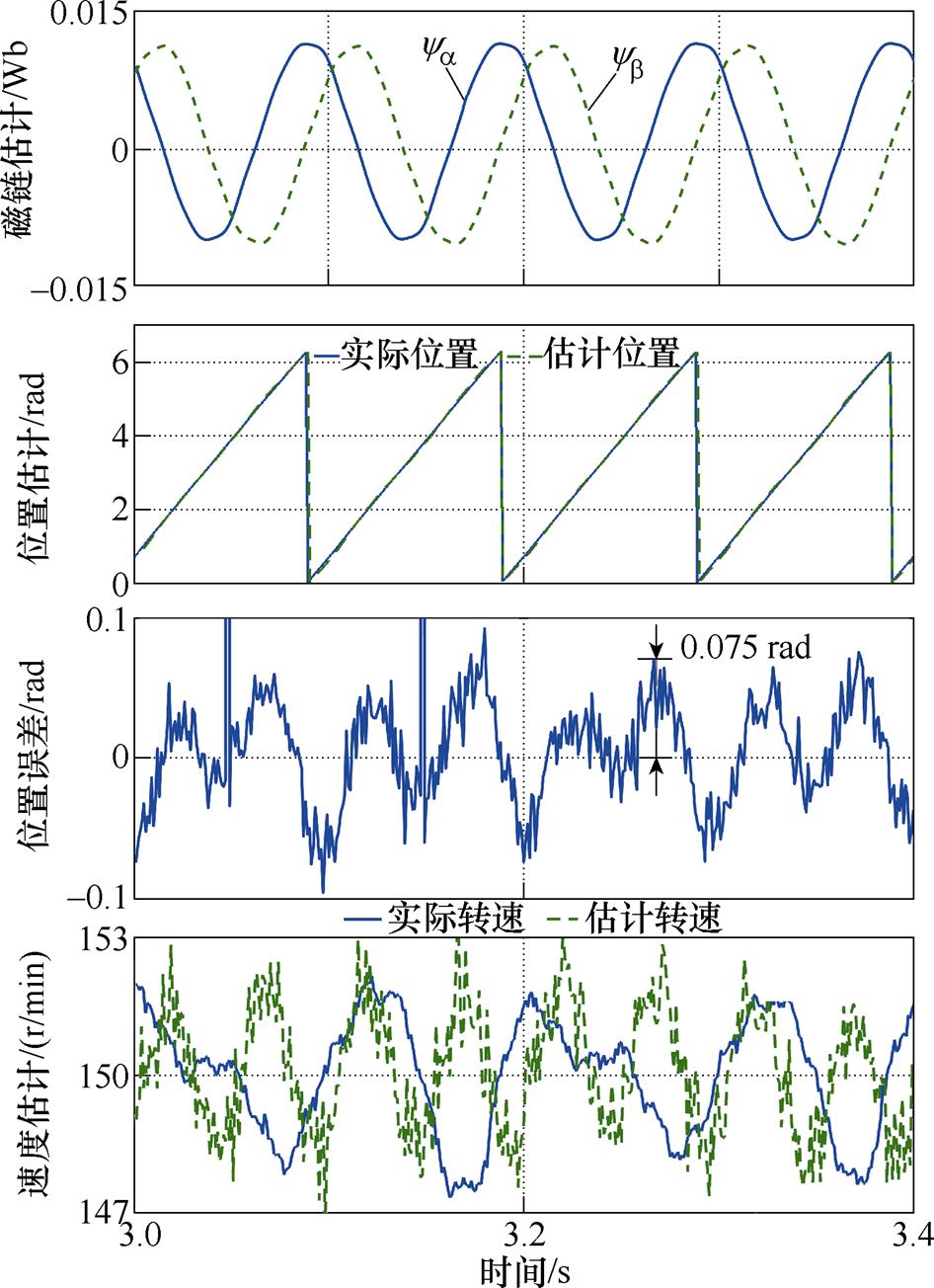
图5 使用FSMO的结果(150 r/min)
Fig.5 The results with FSMO at 150 r/min
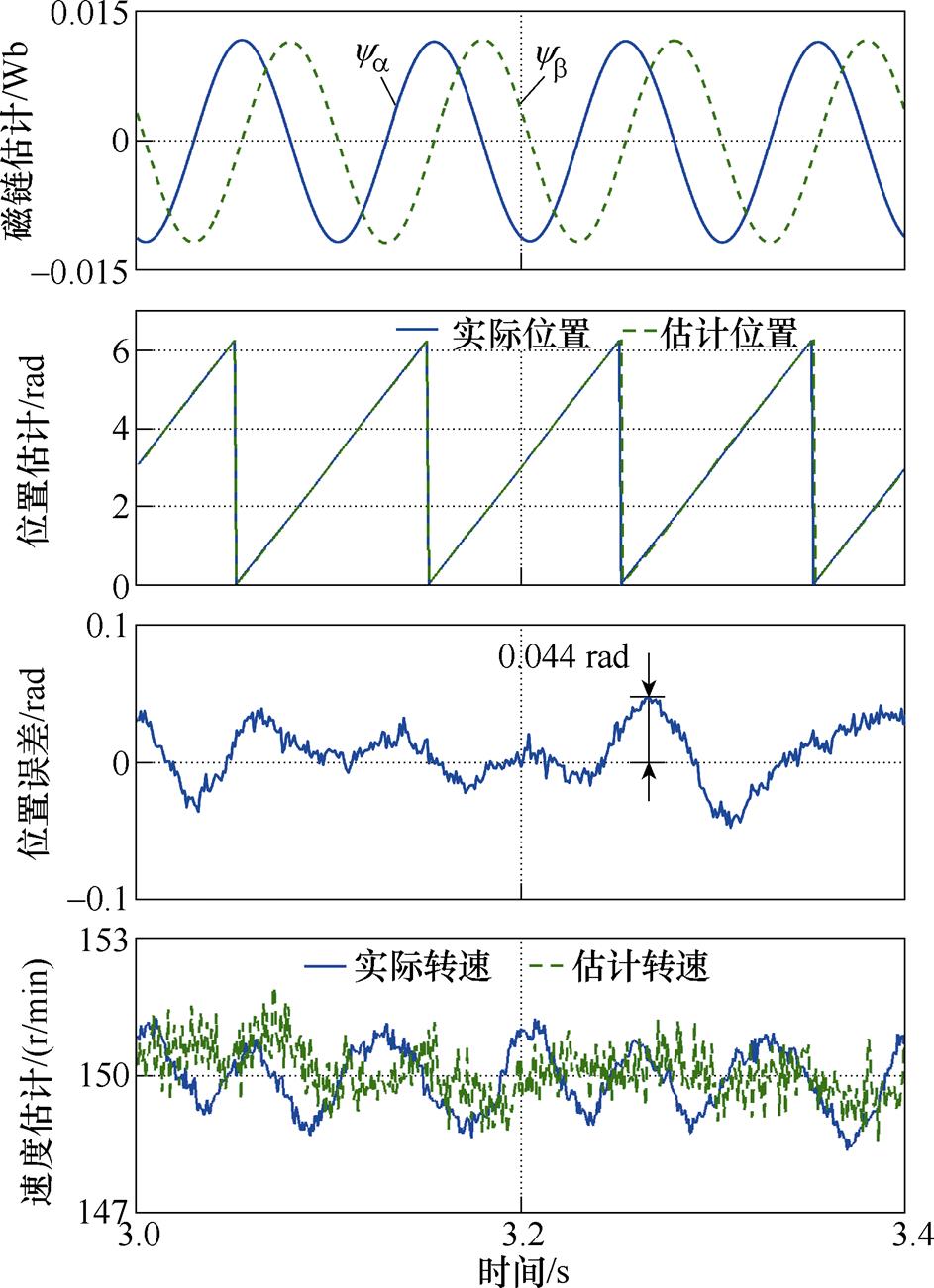
图6 使用EMAF的结果(150 r/min)
Fig.6 The results with EMAF at 150 r/min

图7 EMAF的输出(150 r/min)
Fig.7 The outputs of EMAF at 150 r/min
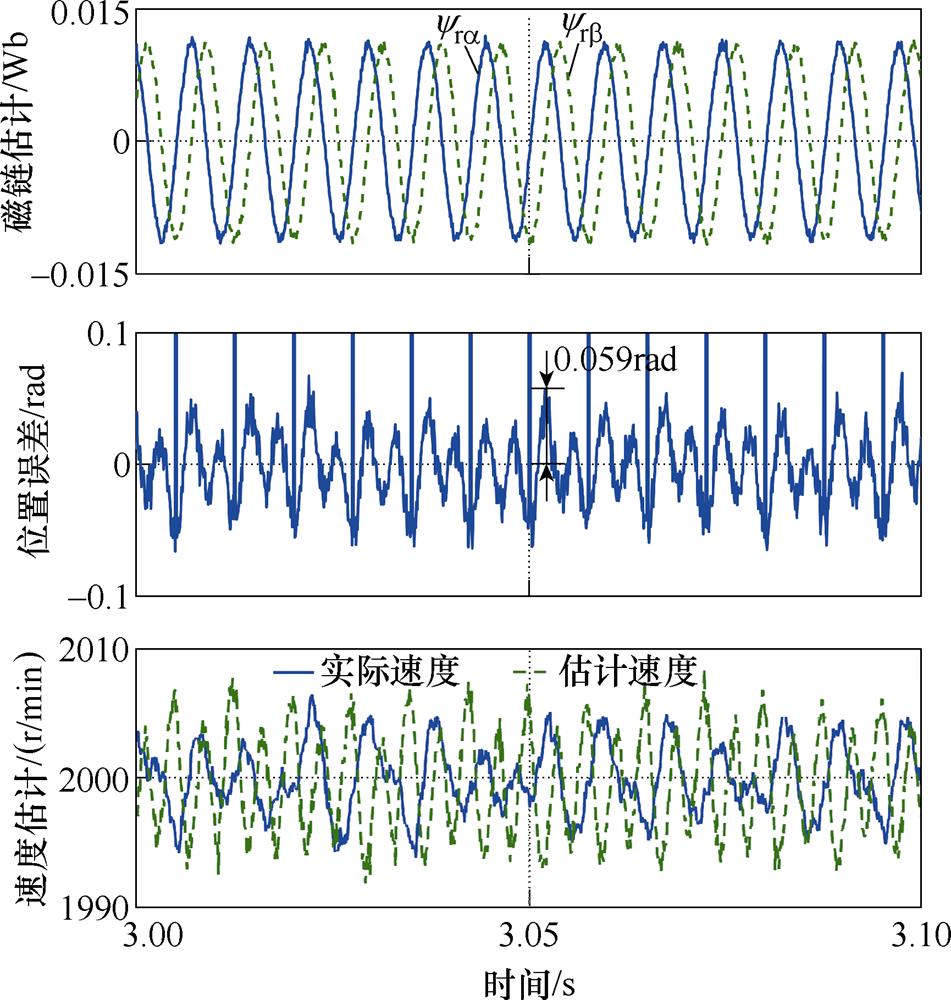
图8 使用FSMO的结果(2 000 r/min)
Fig.8 The results with FSMO at 2 000 r/min
本节在电机转速连续线性变化和正弦变化的条件下,对比了使用锁相环与DFT的性能。负载为1.5 N·m。为了使对比结果可靠,锁相环与DFT选取同样的带宽——200,磁链观测环节均采用EMAF,并且其他环节完全相同。
图10和图11给出了转速连续线性变化时,使用EMAF+PLL和EMAF+DFT的性能。可以看出,在连续加减速时,利用锁相环得到的频率估计出现了较大误差,约为27 r/min。此外,由图10a可看出,当转速由加速突变为减速时,转速估计出现了一定的振荡。而利用DFT得到的频率跟踪误差较小,约为5 r/min,并且在速度转折点处,未出现振荡。由图10b与图11b可看出,由于使用DFT提升了频率跟踪精度,位置误差也相应减小了,并且在速度转折点处,未出现较大的位置误差。图12和图13给出了转速正弦变化时两种方法的对比。转速给定值为
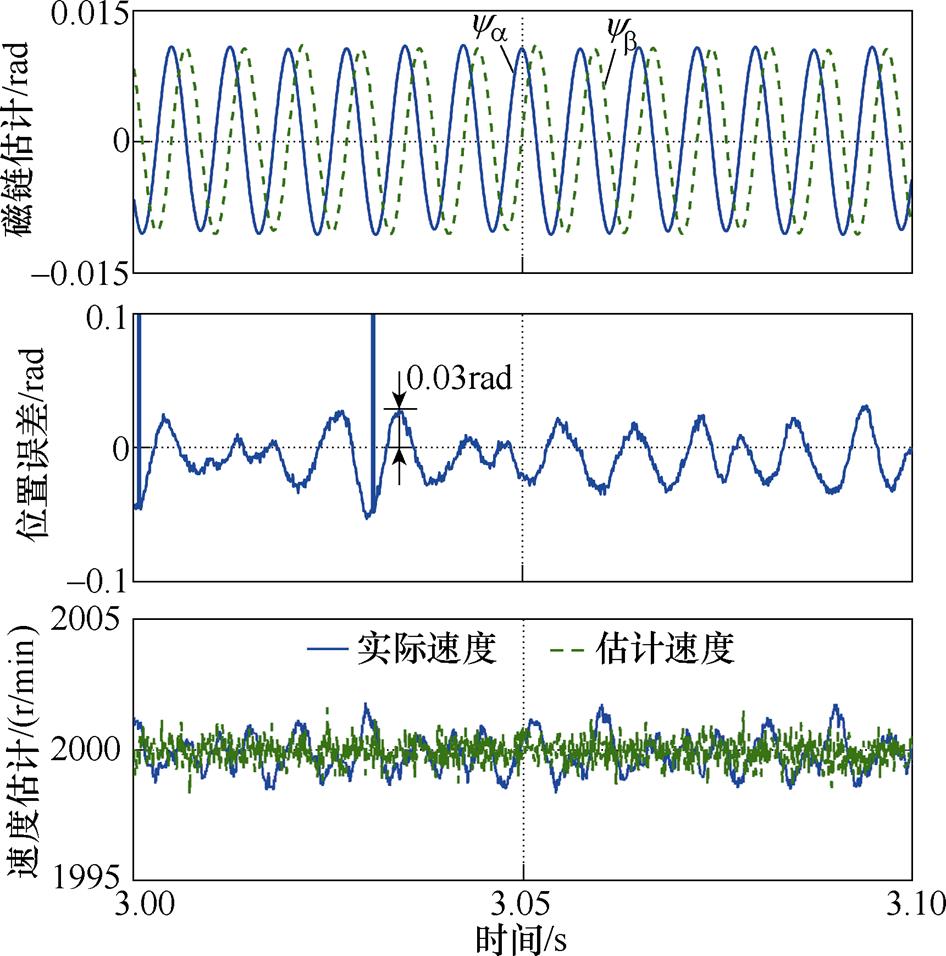
图9 使用EMAF的结果(2 000 r/min)
Fig.9 The results with EMAF at 2 000 r/min
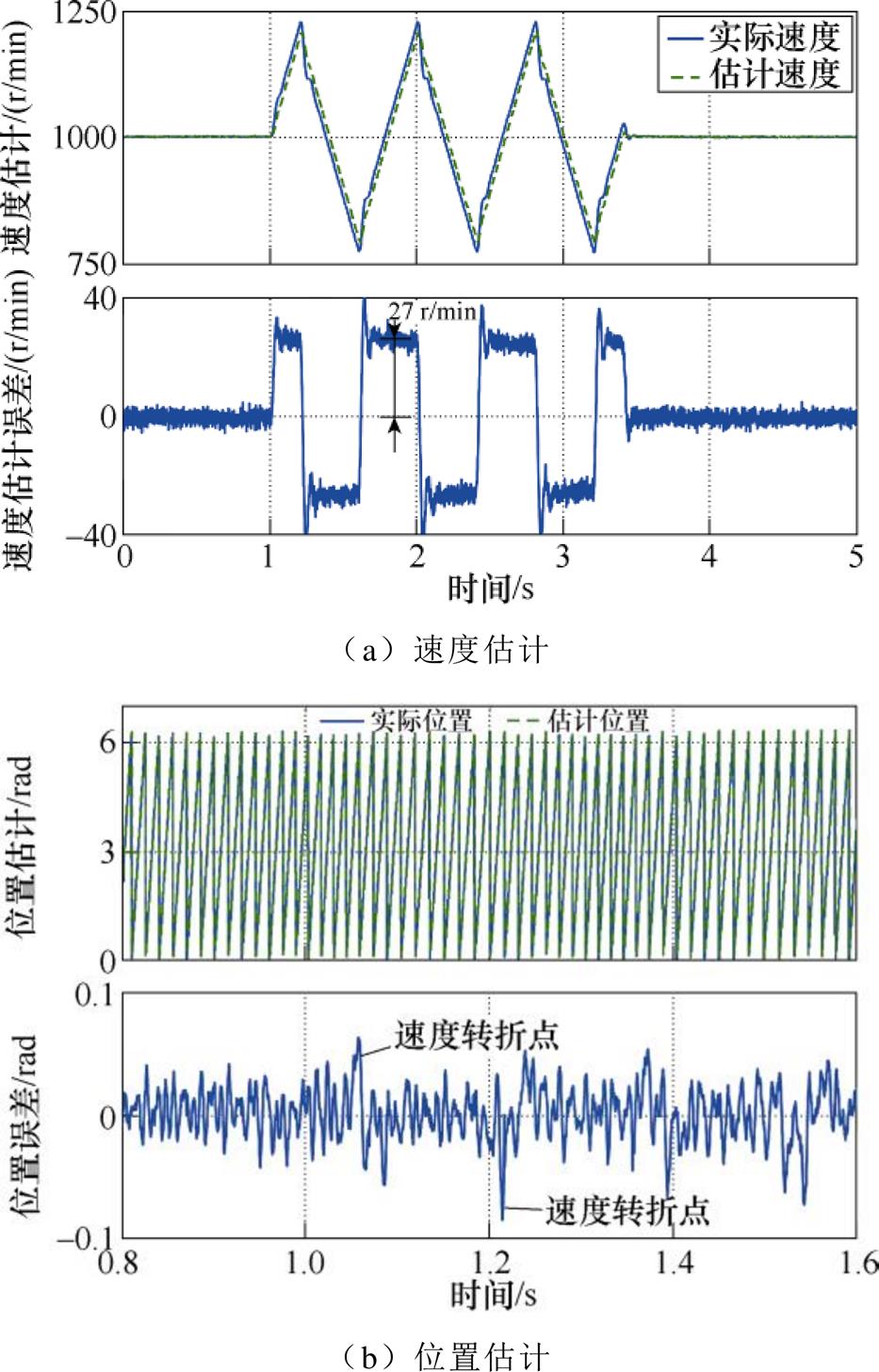
图10 使用EMAF+PLL在转速线性变化时的速度-位置估计
Fig.10 The results with EMAF+PLL under linear time-varying speed
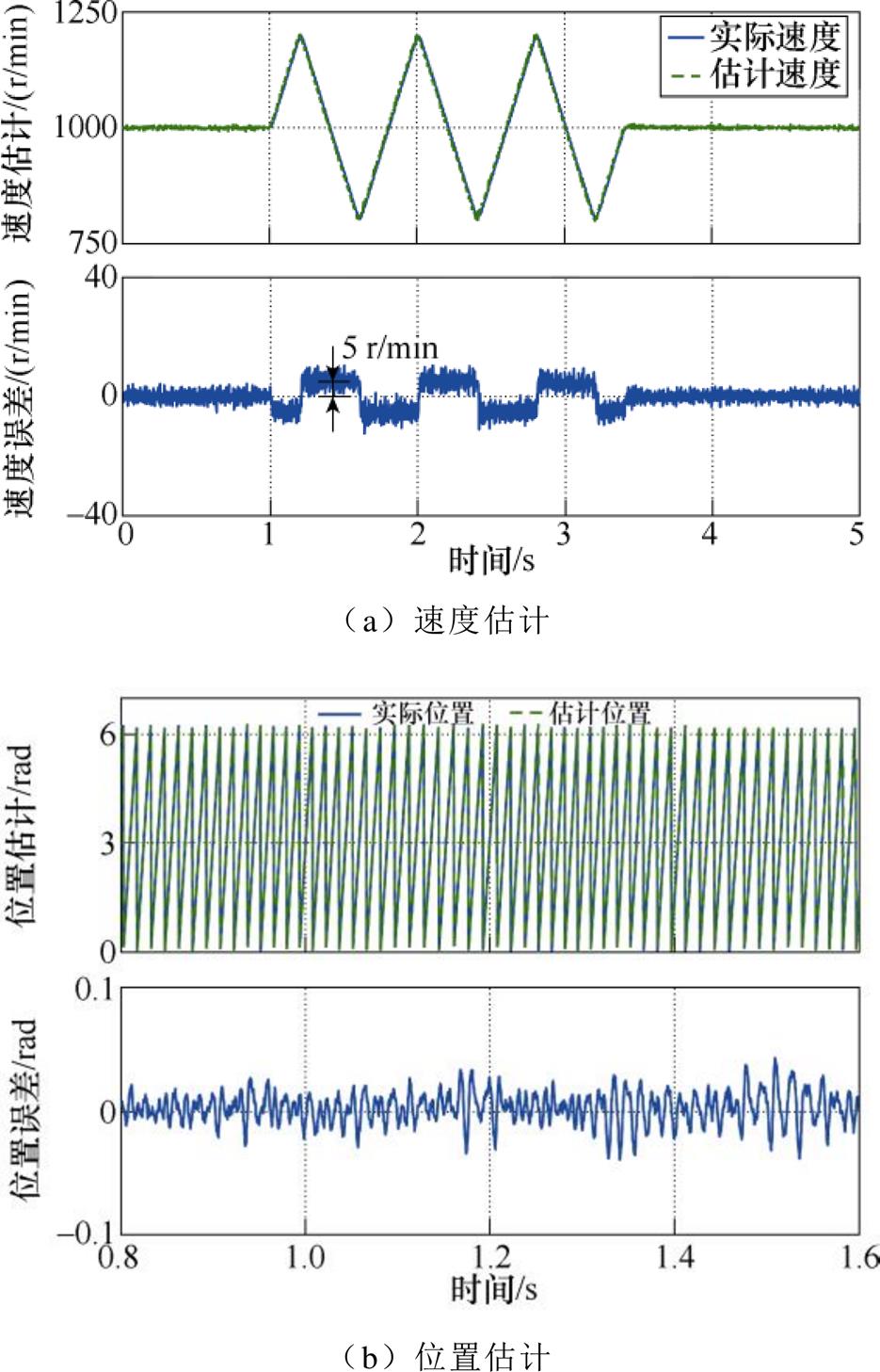
图11 使用EMAF+DFT在转速线性变化时的速度-位置估计
Fig.11 The results with EMAF+DFT under linear time-varying speed
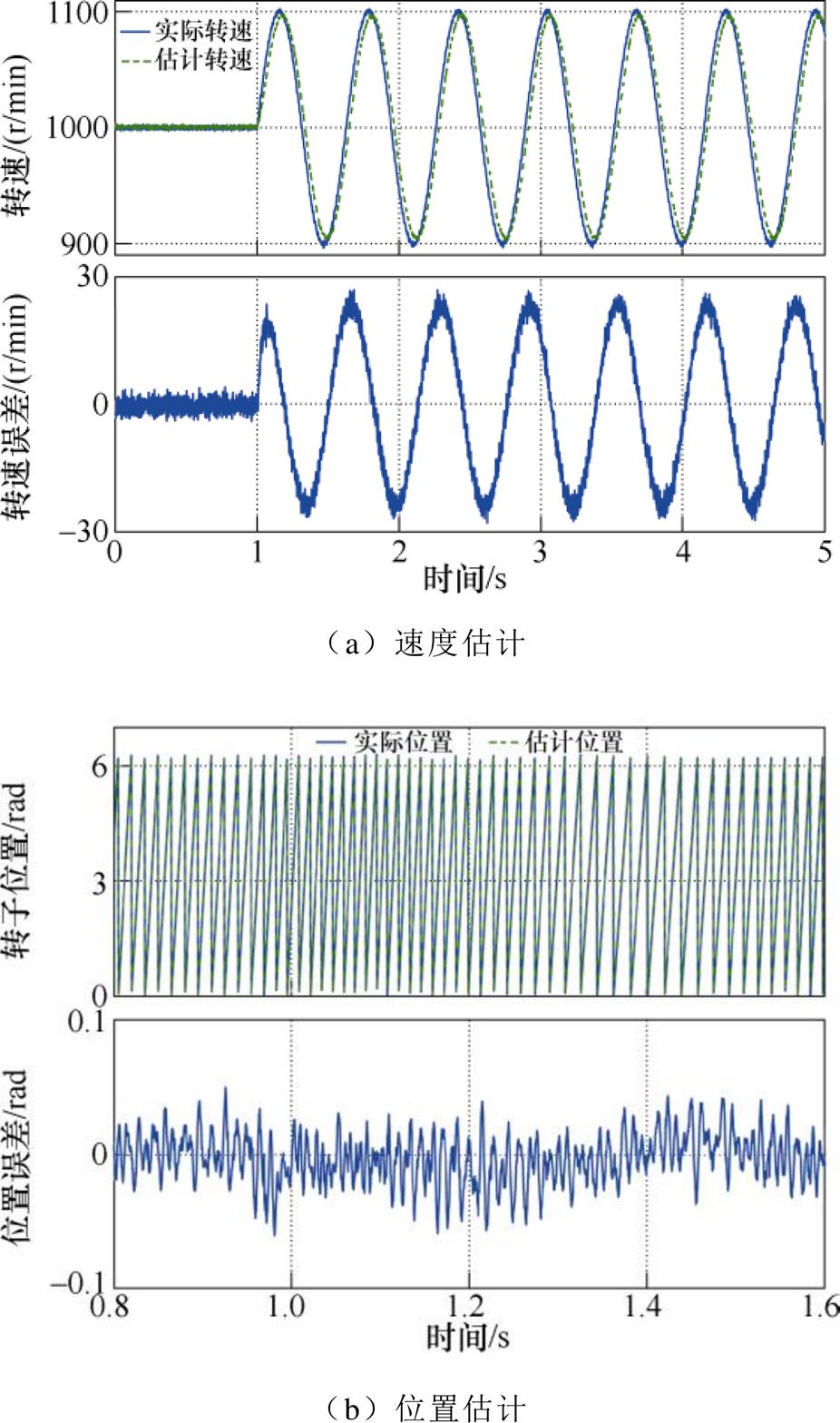
图12 使用EMAF+PLL在转速正弦变化时的速度-位置估计
Fig.12 The results with EMAF+PLL under sinusoidal speed
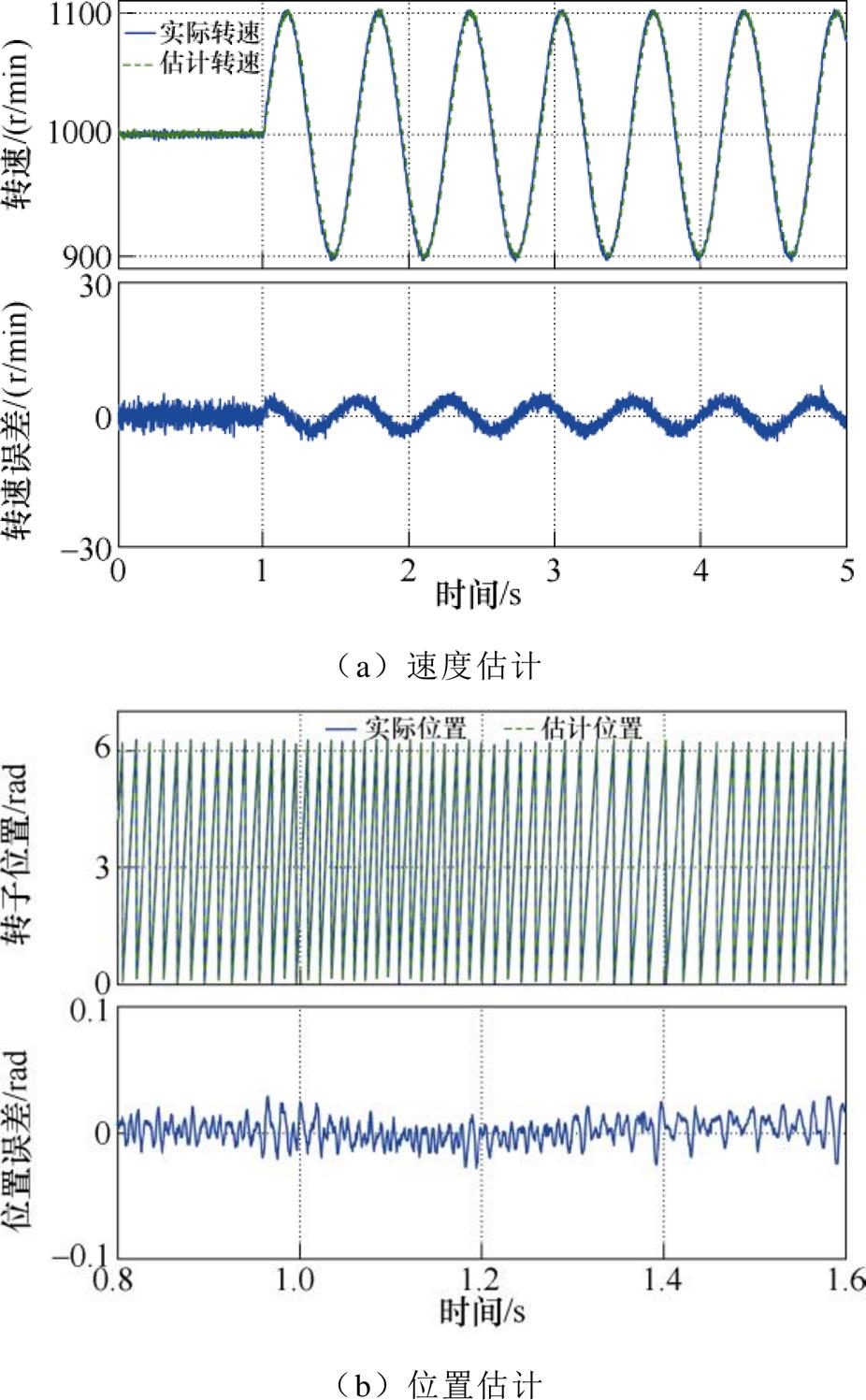
图13 使用EMAF+DFT在转速正弦变化时的速度-位置估计
Fig.13 The results with EMAF+DFT under sinusoidal speed
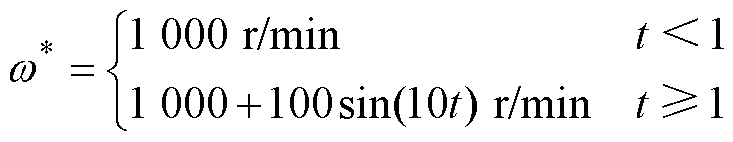
同样可以看出,使用DFT能够有效地减小转速时变情况下的频率跟踪误差,同时也减小了相应的位置估计误差。
本文针对永磁同步电机无传感器控制中磁链观测面临的干扰信号问题,提出了一种基于扩张式主从自适应陷波滤波器的磁链观测方案。该方案能够同时消除斜坡信号、直流偏置、各次谐波等干扰信号对磁链观测的影响。通过频域分析给出了EMAF的一种简明的参数整定图解法。除此之外,针对频率估计环节动态性能不佳的问题,提出了一种考虑电机运动方程的动态频率估计算法。基于EMAF与DFT,设计了永磁同步电机的无传感器控制方案。实验结果表明,提出的方法在不同转速下均能较好地消除干扰信号对位置-速度估计的影响;在转速连续变化时能够有效提升频率跟踪能力和动态性能。
附 录
y=zeros(1,5);x=zeros(5,5); w=500;
for j=1:1000
k=0.02+0.00075*j;
for i=1:6
s=i*k*w;
A=s^2+2*k*w*s+(k*w)^2;
y(1,i)=A^3-s^2*(s^2+w^2)*(s^2+9*w^2);
x(1,i)=2*(s^2+w^2)*(s^2+9*w^2);
x(2,i)=2*s*(s^2+w^2)*(s^2+9*w^2);
x(3,i)=2*w*s^3*(s^2+9*w^2);
x(4,i)=2*w*s^3*(s^2+w^2);
x(5,i)=-A^2*w^2;
x(6,i)=-A*w^4;
end
z=y*x^(-1);
a(j,1)=(sqrt(z(1,5)^2-4*z(1,6))+z(1,5))/2;
a(j,2)=(-sqrt(z(1,5)^2-4*z(1,6))+z(1,5))/2;
a(j,3)=k;
end
plot(a(:,3),a(:,1),a(:,3),a(:,2));
参考文献
[1] Huo Junya, Ding Dawei, Ren Zekun, et al. A novel flux-weakening control method with quadrature voltage constrain for electrolytic capacitorless PMSM drives[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(3): 279-287.
[2] Ge Yang, Yang Lihui, Ma Xikui. HGO and neural network based integral sliding mode control for PMSMs with uncertainty[J]. Journal of Power Elec- tronics, 2020, 20(5): 1206-1221.
[3] 阙鸿杰, 全力, 张丽, 等. 基于自适应滤波器在线解耦的磁场增强型永磁电机无位置传感器控制[J]. 电工技术学报, 2022, 37(2): 344-354.
Que Hongjie, Quan Li, Zhang Li, et al. Sensorless control of flux-intensifying permanent magnet synchronous motor based on adaptive Notch filter online decoupling[J]. Transactions of China Electro- technical Society, 2022, 37(2): 344-354.
[4] 刘旭, 牛大强, 曹阳, 等. 基于励磁绕组高频信号注入的混合励磁开关磁链永磁电机位置估计[J]. 电工技术学报, 2021, 36(20): 4297-4307.
Liu Xu, Niu Daqiang, Cao Yang, et al. Position estimation for hybrid excited switched flux PM machine by injecting high-frequency pulse into the field winding[J]. Transactions of China Electro- technical Society, 2021, 36(20): 4297-4307.
[5] Zhang Hang, Liu Weiguo, Chen Zhe, et al. Asymmetric space vector modulation for PMSM sensorless drives based on square-wave voltage- injection method[J]. IEEE Transactions on Industry Applications, 2018, 54(2): 1425-1436.
[6] 于安博, 刘利, 阚志忠, 等. 高频脉振信号注入永磁同步电机无滤波器初始位置辨识方法[J]. 电工技术学报, 2021, 36(4): 801-809.
Yu Anbo, Liu Li, Kan Zhizhong, et al. Initial position identification of PMSM with filterless high frequency pulse signal injection method[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 801-809.
[7] Ge Yang. A rotor flux observer with adaptive inter- fering signal elimination for SPMSM sensorless control[C]//2022 International Conference on Power Energy Systems and Applications (ICoPESA), Singapore, 2022: 609-616.
[8] Devanshu A, Singh M, Kumar N. An improved nonlinear flux observer based sensorless FOC IM drive with adaptive predictive current control[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 652-666.
[9] 张越雷, 黄科元, 蒋智, 等. 基于估算电流模型的永磁同步电机无速度传感器控制[J]. 电工技术学报, 2016, 31(11): 68-74.
Zhang Yuelei, Huang Keyuan, Jiang Zhi, et al. Speed sensorless control of PMSM based on estimated current model[J]. Transactions of China Electro- technical Society, 2016, 31(11): 68-74.
[10] Ge Yang, Yang Lihui, Ma Xikui. Sensorless control of PMSM using generalized extended state observer and adaptive resistance estimation[J]. IET Electric Power Applications, 2020, 14(11): 2062-2073.
[11] 章春娟, 王慧贞, 刘伟峰, 等. 基于宽频带同步基频提取滤波器的永磁同步电机转子位置与转速估计[J]. 电工技术学报, 2022, 37(4): 882-891.
Zhang Chunjuan, Wang Huizhen, Liu Weifeng, et al. Rotor position and speed estimation of permanent magnet synchronous motor based on wideband syn- chronous fundamental frequency extraction filter[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 882-891.
[12] 黄科元, 周佳新, 刘思美, 等. 考虑逆变器非线性永磁同步电机高频注入电感辨识方法[J]. 电工技术学报, 2021, 36(8): 1607-1616.
Huang Keyuan, Zhou Jiaxin, Liu Simei, et al. Inductance identification method of permanent magnet synchronous motor considering inverter nonlinearity based on high-frequency injection[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1607-1616.
[13] Ye Shuaichen. Design and performance analysis of an iterative flux sliding-mode observer for the sensorless control of PMSM drives[J]. ISA Transactions, 2019, 94: 255-264.
[14] Bobtsov A A, Pyrkin A A, Ortega R, et al. A robust globally convergent position observer for the per- manent magnet synchronous motor[J]. Automatica, 2015, 61: 47-54.
[15] Choi J, Nam K, Bobtsov A A, et al. Robust adaptive sensorless control for permanent-magnet synchronous motors[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3989-3997.
[16] Ye Shuaichen, Yao Xiaoxian. A modified flux sliding- mode observer for the sensorless control of PMSMs with online stator resistance and inductance esti- mation[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 8652-8662.
[17] Xu Wei, Jiang Yajie, Mu Chaoxu, et al. Improved nonlinear flux observer-based second-order SOIFO for PMSM sensorless control[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 565-579.
[18] Zhao Rende, Xin Zhen, Loh P C, et al. A novel flux estimator based on multiple second-order generalized integrators and frequency-locked loop for induction motor drives[J]. IEEE Transactions on Power Elec- tronics, 2017, 32(8): 6286-6296.
[19] Song Xinda, Fang Jiancheng, Han Bangcheng, et al. Adaptive compensation method for high-speed sur- face PMSM sensorless drives of EMF-based position estimation error[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1438-1449.
[20] 杨才伟, 王剑, 游小杰, 等. 二阶广义积分器锁频环数字实现准确性对比[J]. 电工技术学报, 2019, 34(12): 2584-2596.
Yang Caiwei, Wang Jian, You Xiaojie, et al. Accuracy comparison of digital implementation on the second-order generalized integrator frequency- locked loop[J]. Transactions of China Electro- technical Society, 2019, 34(12): 2584-2596.
[21] Lin Shuyi, Zhang Weidong. An adaptive sliding-mode observer with a tangent function-based PLL structure for position sensorless PMSM drives[J]. International Journal of Electrical Power & Energy Systems, 2017, 88: 63-74.
[22] Ge Yang, Yang Lihui, Ma Xikui. A harmonic com- pensation method for SPMSM sensorless control based on the orthogonal master-slave adaptive Notch filter[J]. IEEE Transactions on Power Electronics, 2021, 36(10): 11701-11711.
[23] 辛振, 赵仁德, 郭宝玲, 等. 基于二阶广义积分器-锁频环的异步电机同步角频率估计方法[J]. 电工技术学报, 2014, 29(1): 116-122.
Xin Zhen, Zhao Rende, Guo Baoling, et al. New induction motor synchronous angular frequency estimation method based on second order generalized integrator-frequency locked loop[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 116- 122.
[24] Mojiri M, Bakhshai A R. An adaptive Notch filter for frequency estimation of a periodic signal[J]. IEEE Transactions on Automatic Control, 2004, 49(2): 314- 318.
[25] 石荣亮, 张烈平, 王文成, 等. 基于改进型级联SOGI-FLL的虚拟惯量控制技术[J]. 太阳能学报, 2022, 43(1): 235-241.
Shi Rongliang, Zhang Lieping, Wang Wencheng, et al. Enhanced virtual inertia method for energy storage converters based on improved cascaded SOGI-FLL scheme[J]. Acta Energiae Solaris Sinica, 2022, 43(1): 235-241.
[26] 陈天, 厉茂海, 林睿. PMSM伺服系统的速度环控制器参数整定方法研究[J]. 制造业自动化, 2018, 40(12): 70-74.
Chen Tian, Li Maohai, Lin Rui. Research on parameter tuning method of speed loop controller in PMSM servo system[J]. Manufacturing Automation, 2018, 40(12): 70-74.
Abstract The model-based sensorless control of permanent magnet synchronous motor (PMSM) is effective at medium and high speed regions. Among several model-based methods, the flux observation method can achieve better performance because the rotor flux of PMSM is constant or calculable even when the speed or current is time-varying. However, due to the inverter nonlinearity, the initial position detection error, and the current measurement bias, the estimated flux will inevitably contain interfering signals such as ramp signal, DC bias, and harmonics. These interfering signals will reduce the steady-state accuracy of rotor position estimation, increase speed fluctuation, and even make the system unstable in severe cases.
Therefore, a flux observer based on an extended master-slave adaptive notch filter (EMAF) is proposed. The EMAF can track the signals containing multi-components by using their characteristics. Thus, considering the characteristic of interfering signals in estimated flux, we design the EMAF, which can accurately track these interfering signals. Besides, by introducing a new variable in EMAF, the dc deviation of integral terms is tracked and compensated, and the ramp signal caused by integrating is also eliminated. This method can directly estimate the rotor flux without estimating the back-EMF first. Since many parameters in EMAF need to tune, a parameter tuning graphical method of EMAF is given to simplify the tuning process, transforming the multi-parameter tuning into single-parameter tuning.
In addition, under varying speeds, the traditional phase-locked loop (PLL) can not accurately track the frequency, which degrades the dynamic performance. Therefore, a dynamic frequency tracking algorithm (DFT) is proposed. In this method, the motion equation is applied, and the extended state observer (ESO) is designed to estimate the frequency. Since the varying rate of the rotor speed is considered in ESO, compared with the phase-locked loop or frequency-locked loop, this method is more applicable under changing speed. Based on EMAF and DFT, the overall sensorless control system of PMSM is designed.
Compared the traditional flux sliding mode observer (FSMO) and the proposed EMAF under different speeds, the results show that the EMAF can effectively reduce the interfering signals, including the 5th and 7th harmonics, the dc bias, and the ramp signal, thus improving the accuracy of rotor position estimation and reducing the speed fluctuation. The bandwidths of the traditional PLL and the proposed DFT under linear changing and sine changing speeds are the same. The proposed DFT can greatly reduce the frequency tracking error when speed varies, thus improving the dynamic performance. Therefore, the proposed method is effective for enhancing the sensorless performance of PMSM.
keywords:Permanent magnet synchronous motor (PMSM), sensorless control, extended master-slave adaptive notch filter, parameters tuning, frequency tracking
国家自然科学基金(51877176)和陕西省教育厅服务地方专项项目(18JC024)资助。
收稿日期 2022-05-18
改稿日期 2022-07-04
DOI: 10.19595/j.cnki.1000-6753.tces.220858
中图分类号:TM921
葛 扬 男,1991年生,博士,讲师,研究方向为高性能电机控制。E-mail: gy@xaut.edu.cn(通信作者)
宋卫章 男,1980年生,教授,研究方向为节能环保型电源、特种电源系统及控制、永磁同步与同步磁阻电机高性能控制技术等。E-mail: SWZ@xaut.edu.cn
(编辑 崔文静)