图1 VTVPM结构和结构参数
Fig.1 Configuration and Geometric parameters of VTVPM
摘要 基于功率因数内在机理的研究,提出一种提升游标永磁电机(VPM)功率因数的设计方法,该方法采用分层优化,对影响电机功率因数的主要因素,即永磁磁链和同步电感,分别进行了理论推导和优化分析。该文首先对永磁磁链进行了优化设计,利用气隙谐波作为电机结构设计与电机电磁性能之间的中间桥梁,一方面,气隙谐波作为电机参数的设计目标,另一方面,也作为电机功率因数和其他相关电磁性能的设计变量。基于永磁磁链的分析,进一步优化相关参数对同步电感的影响,从而最终确定了VPM电机的优化设计方案。此外,为了验证该方法的有效性,对优化前后电机的电磁性能进行了分析评估。最后对优化后的电机进行了加工和实验测试,理论分析和实验结果表明所提出的VPM电机功率因数优化设计方法的有效性和合理性,提升了VPM电机在轮毂电机直接转矩驱动系统中的应用潜力。
关键词:游标永磁电机 功率因数 永磁磁链 同步电感 优化设计
近年来,游标永磁电机(Vernier Permanent Magnet Machine, VPM)因其在低速运行时的高转矩密度[1]这一显著特征而受到关注,并且已被广泛应用于电动汽车、航空航天和船舶驱动[2-5]等高端制造领域。然而,相比于传统永磁电机,随着VPM电机永磁体极对数和漏磁的增多,其功率因数通常相对较低[6]。这意味着在输出相同功率时,VPM电机所需的功率变换器的容量需要增加。一方面,这不仅导致电机应用成本的增加,另一方面也限制了其在轮毂驱动系统中的应用前景。实际上,在转子直接与轮毂相连,转矩直接传递给车轮的轮毂驱动系统中,其内部有限空间的高度集成化、精细化应用,是电动汽车等高端制造领域进一步发展的主要参考因素。因此,在轮毂电机直接转矩驱动系统中,提升轮毂电机的功率因数具有一定的研究意义和价值。
根据经典电机学理论,电机功率因数的定义为有功功率与视在功率的比值,也是电机输出电压与输入电流矢量相位差的余弦值,这反映了电机对于电能的利用率。而且,对于电机输出的有功功率,其主要部分为电磁功率,这在很大程度上取决于电机的转矩性能和运行转速。当电机转速一定时,电机的功率因数与转矩特性相关。此外,随着电机磁场调制理论的发展与完善,气隙磁通密度被认为是影响电机转矩等电磁性能的主要因素[7]。
如文献[8]所述,VPM功率因数低的关键原因是由永磁体产生的气隙磁通密度低,这意味着采用不同的永磁拓扑结构和改变永磁体位置以及用量,电机的功率因数能够得到改善。需要指出的是,这一理论发现,改变了由永磁磁动势和磁导相互作用产生的气隙磁通密度分布。事实上,为了解决上述问题,国内外电机领域的研究学者已经从电机设计角度,提出了多种提高VPM功率因数的方法。在以往研究中,轮辐式永磁体结构、Halbach永磁体结构、交替极永磁体结构的应用,改善了气隙磁通密度的分布,提高了电机功率因数[9-11]。然而,不同永磁体拓扑结构的应用,也导致一些问题的产生,如转矩脉动上升、电机损耗增加等问题。为了减小电机外圆漏磁的产生,文献[12]中的VPM采用了双定子的拓扑结构设计,提升了电机气隙磁通密度,提高了电机的功率因数。然而,由于电机的复杂结构(双层气隙和双定子结构),电机的实际加工和装配精度存在一定困难。与上述改变电机结构设计不同,文献[13]提出了在电枢绕组侧,采用辅助直流励磁的混合励磁结构,尽管VPM的功率因数得到了提升,同时不可避免地增加了电机铜损耗,也降低了一部分的电机转矩密度。此外,文献[14]提出以功率因数作为电机的设计目标之一,采用多目标遗传算法对VPM进行了优化,设计了一台轮辐式游标永磁电机(Spoke-Type Permanent Magnet Vernier Motor, STPMV)。为了提高电机的优化效率和精度,在优化过程中采用了多级灵敏度分析、近似模型等技术,使得STPMV电机具有较高的功率因数。
基于以上分析,目前关于磁场调制电机功率因数的相关研究主要集中于提出新型的电机结构[15-16]。这种方法本质上改变了磁场调制电机磁动势和磁导的分布,进而改善了电机气隙磁通密度,实现电机功率因数的提升。相反,磁场调制电机功率因数的内在机理却少有研究。因此,本文从电机功率因数基本原理出发,基于磁场调制原理,探索了磁场调制电机功率因数的内在机理,并提出了相应的提升磁场调制电机功率因数的设计方法。根据功率因数基本原理,在三相输入电流不变时,其主要与永磁磁链和同步电感相关。因此,本文采用分层优化,分别对永磁磁链层和同步电感层进行了理论推导和优化分析,并得出最终的优化设计。然后,对优化前后电机功率因数及其相关电磁性能进行了对比和分析。最后,对优化后的电机进行加工,并做了基础实验。仿真分析和实验结果验证了所提出优化方法的有效性和合理性,提升了VPM电机在轮毂电机直接转矩驱动系统中的应用潜力。
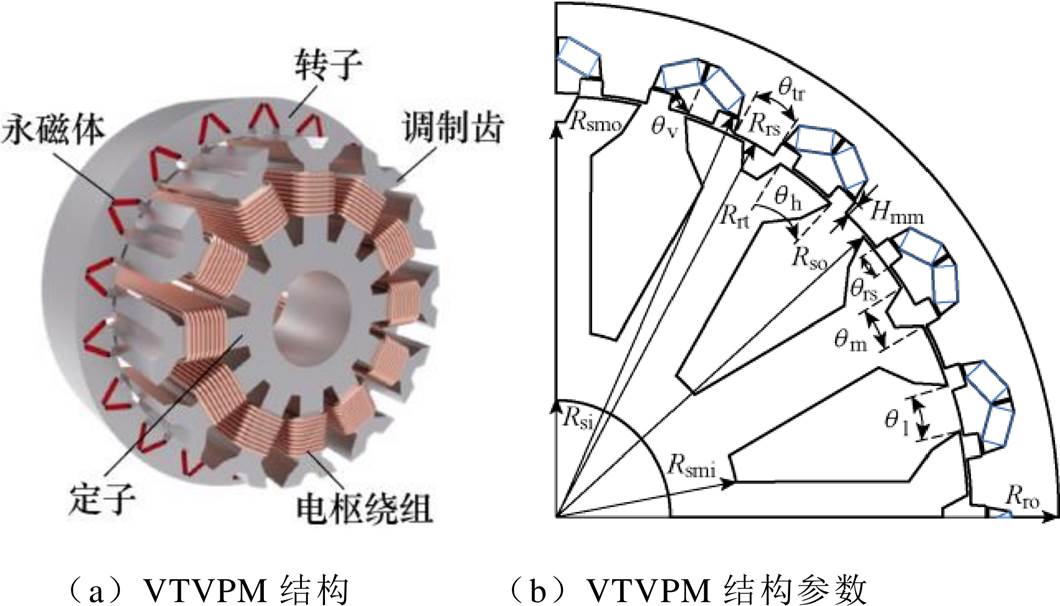
在本节中,选择V型游标永磁电机(V-Type Vernier Permanent Magnet Machine, VTVPM)作为优化设计的示例。本文VTVPM的拓扑结构如图1a所示,相关结构参数如图1b所示。图1b中,qv为永磁体倾斜角度;qtr和qrs分别为转子齿和转子槽所占角度;qh、qm、ql分别为定子齿、定子裂齿和定子槽所占角度;Rro、Rrs、Rrt分别为转子外径、转子槽半径和转子齿半径;Rso、Rsmo、Rsmi、Rsi分别为定子外径、定子裂槽半径、定子槽半径和定子内径;Hmm为转子槽深。

图1 VTVPM结构和结构参数
Fig.1 Configuration and Geometric parameters of VTVPM
该电机的极槽配比为19对极12槽24调制齿。电机定子采用调制齿结构设计,这不仅有利于最大化拓宽定子槽所占空间,在提升电机电枢绕组匝数的同时,在一定程度上缓解了电机散热的问题。此外,在电机转子内部,永磁体采用聚磁式V型拓扑结构设计,有助于增强电机永磁体的聚磁效应,减小永磁体漏磁和提升电机转矩特性。同时,为了进一步减小永磁体漏磁,在永磁体两端设计了端部磁障。同时,转子内圆侧虚拟槽的设计,进一步增强了电机磁场调制效应,且提升了VTVPM的转矩特性。VTVPM的基本参数见表1。
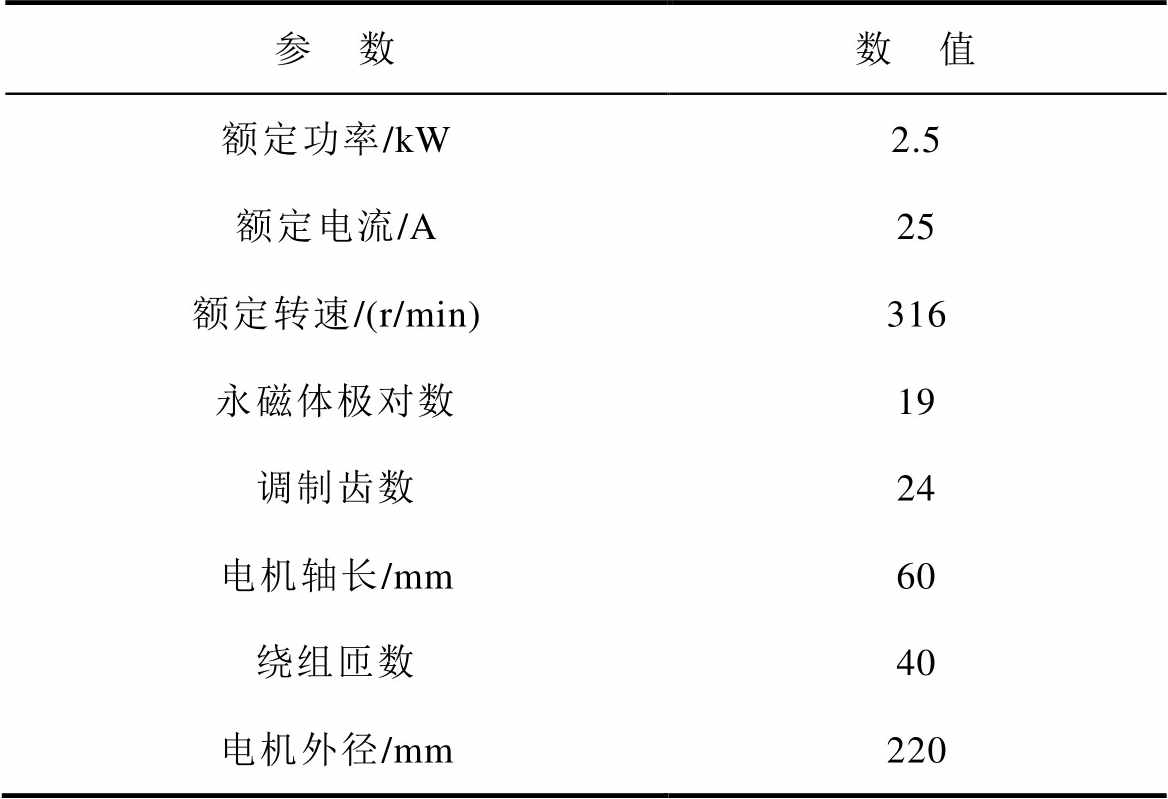
表1 VTVPM的基本参数
Tab.1 Basic parameters of VTVPM
参 数数 值 额定功率/kW2.5 额定电流/A25 额定转速/(r/min)316 永磁体极对数19 调制齿数24 电机轴长/mm60 绕组匝数40 电机外径/mm220
综上所述,定子齿的调制齿设计与转子的虚拟槽设计,大大增强了电机的磁场调制效应和电机转矩特性。同时,定子的调制齿结构设计,最大化地利用槽空间,增加绕组匝数的同时,缓解绕组散热问题。
本文基于功率因数内在机理的研究,提出了一种采用分层优化,提升游标永磁电机功率因数的优化设计方法,分别对永磁磁链层和同步电感层进行了理论推导和仿真优化。
由于VTVPM的凸极比约为1,通常采用直轴电流id=0的控制策略,且忽略绕组电阻,因此电机的功率因数[17]可表示为
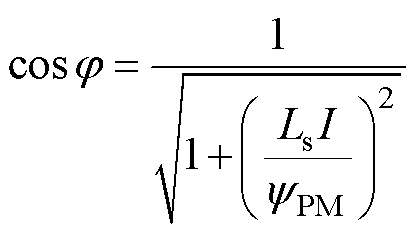 (1)
(1)
式中,Ls为同步电感;I为相电流的方均根值(Root Mean Square, RMS);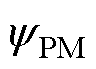 为永磁磁链的基波幅值。
为永磁磁链的基波幅值。
基于以上分析,在输入三相电流不变的情况下,电机功率因数主要与永磁磁链的基波幅值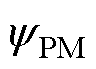 和同步电感Ls有关,这也验证了之前的研究,即永磁体产生的低气隙磁通密度是电机功率因数低的主要原因。因此,从气隙谐波磁场调制原理来看,提高永磁磁链基波幅值和降低电机同步电感的方案理论上可以提高游标永磁电机的功率因数。
和同步电感Ls有关,这也验证了之前的研究,即永磁体产生的低气隙磁通密度是电机功率因数低的主要原因。因此,从气隙谐波磁场调制原理来看,提高永磁磁链基波幅值和降低电机同步电感的方案理论上可以提高游标永磁电机的功率因数。
基于以上分析,本节对永磁磁链层和同步电感层进行了理论推导。首先,为了得出VTVPM磁路模型中参数的解析表达式,本节将首先根据电机的拓扑结构,获取永磁磁场的磁动势和磁导波形。根据磁场调制原理,得出仅由永磁体产生的气隙磁场的磁通密度及其谐波分布。其次,利用气隙磁通密度的谐波积分得出永磁磁链。根据理论推导,得出产生永磁磁链基波的气隙磁密主要工作谐波。然后,基于永磁磁链的研究,本节进一步对电机同步电感层进行了理论推导。最后,综合永磁磁链层和同步电感层的理论推导,得出最终的游标永磁电机功率因数提升的优化方法,为后面的仿真分析和结果验证提供了理论基础。
2.2.1 永磁磁链层的理论推导
为了探索气隙谐波和永磁磁通密度之间的关系,永磁磁动势(Magnetomotive Force, MMF)和磁导分布如图2所示。图2中,q1为永磁体占据的角度,同时也是转子齿所占角度;q2为转子槽占据的角度;q3为永磁体两对极之间的齿宽角;F为通过有效气隙永磁磁场MMF的幅值。
根据图2c中永磁磁场的MMF波形,傅里叶级数展开式[18]可表示为
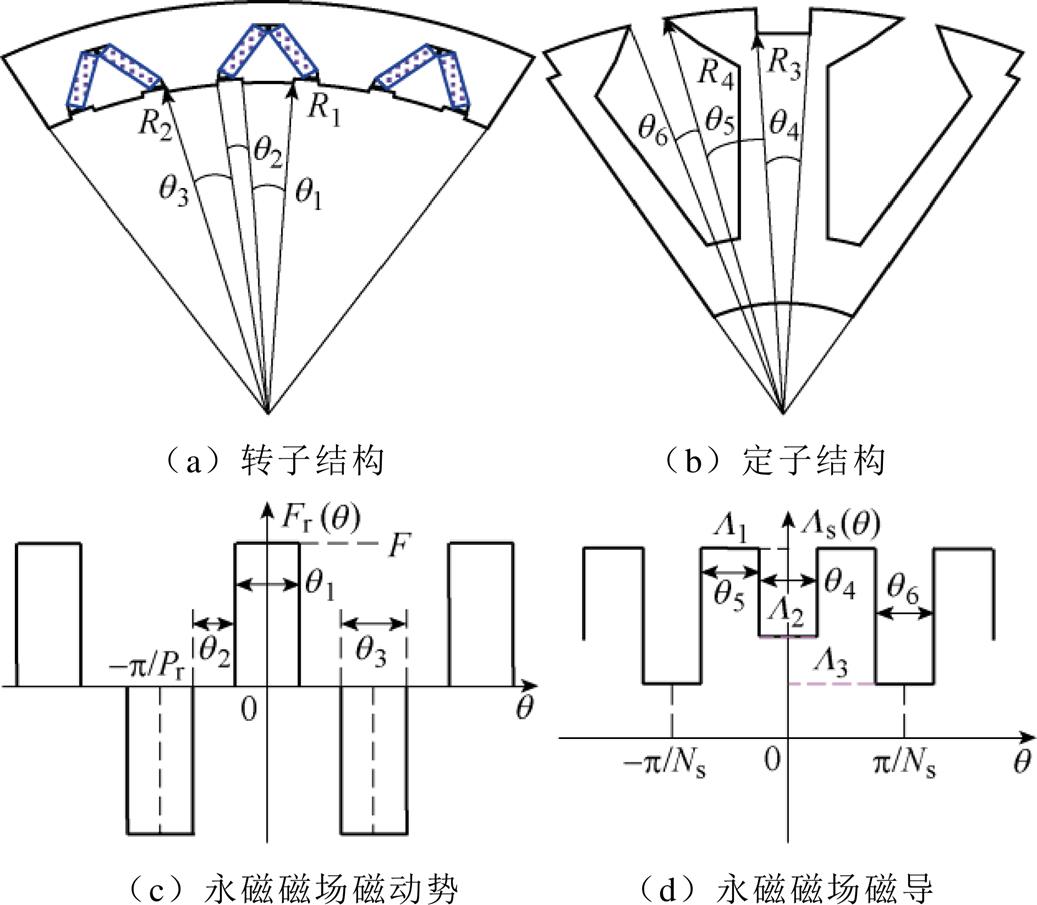
图2 VTVPM永磁磁场磁动势和磁导分布
Fig.2 Distribution of magnetomotive force and permeance in permanent magnet field of VTVPM
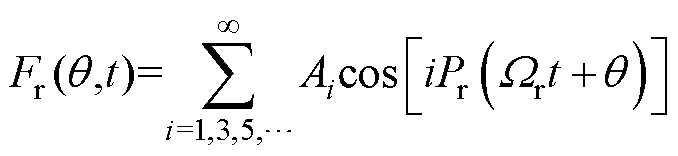 (2)
(2)
式中,Ai为第i次谐波的幅值;Pr为转子齿数,即永磁体的极对数;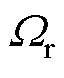 为转子旋转的机械角速度;q 为气隙周向位置。
为转子旋转的机械角速度;q 为气隙周向位置。
由于VTVPM的齿槽结构,磁导随转子的旋转而变化。此外,由于定子的调制齿结构,磁导呈现阶梯式变化,如图2d所示。图2d中,L1、L2、L3为由定子和气隙结构确定的磁导幅值;q4为两个调制齿间槽的角度;q5为单个调制齿所占角度;q6为相邻调制极(Flux Modulation Pole, FMP)间槽所占角度。因此,磁导的傅里叶级数展开式可以表示为
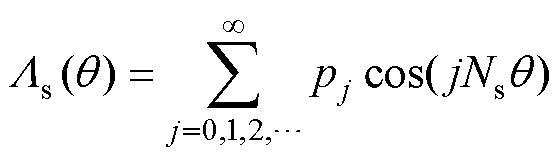 (3)
(3)
式中,pj为第j个磁导的谐波幅值;Ns为定子齿数。
随着转子旋转,永磁气隙磁场磁通密度随转子位置而变化。因此,根据电机理论,永磁体产生的气隙磁通密度可以表示为
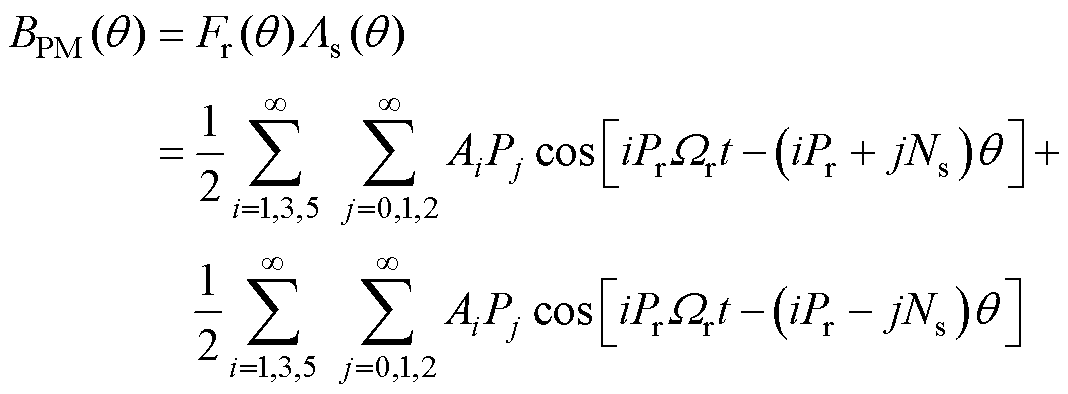 (4)
(4)
根据式(4),作为电机功率因数和电机结构参数的中间设计桥梁,永磁磁场气隙磁通密度是永磁MMF与定子磁导在垂直于磁场方向的单位面积上,彼此相互作用的结果。根据式(2),永磁体本身产生的谐波阶数为iPr(i=1, 3, 5,…)。从式(4)中可以看出,永磁体产生的气隙磁通密度通过定子-转子的调制效应产生一系列谐波,谐波的阶数k可总结为k=|iPr±jNs|(i=1, 3, 5,…; j=0, 1, 2,…)。
根据式(4)对永磁气隙磁通密度的分析,代入由永磁磁通密度的谐波分量积分产生的单个线圈的永磁磁链,可得
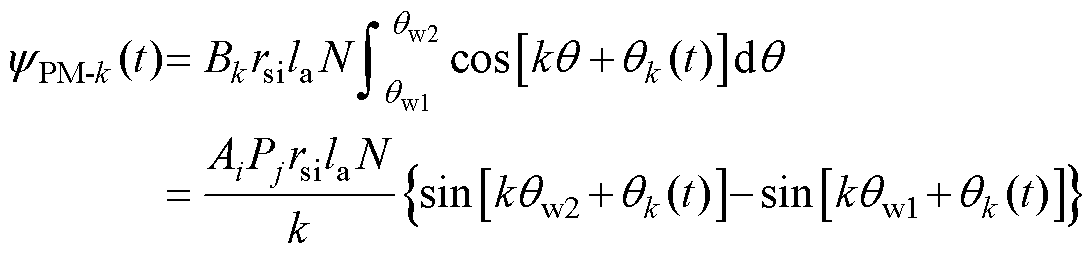 (5)
(5)
式中,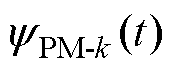 为每个线圈的永磁磁链;Bk、qk(t)分别为第k个永磁气隙磁通密度谐波的幅值和相位;rsi为电机定子的内径;N为线圈的绕组匝数;la为叠片长度;qw1和qw2为每个线圈的两个绕组侧的机械角度。根据式(5),每相的永磁磁链可通过线圈所产生的永磁磁链矢量叠加获得。
为每个线圈的永磁磁链;Bk、qk(t)分别为第k个永磁气隙磁通密度谐波的幅值和相位;rsi为电机定子的内径;N为线圈的绕组匝数;la为叠片长度;qw1和qw2为每个线圈的两个绕组侧的机械角度。根据式(5),每相的永磁磁链可通过线圈所产生的永磁磁链矢量叠加获得。
根据式(5)可知,当i=1时,由永磁磁通密度谐波积分产生的永磁磁链是总磁链的基波。因此,定义永磁磁链基波增强因子g,通过降低谐波增强因子g 值来提高永磁磁链的基波幅值,最终实现电机功率因数的提升。具体推导过程如下。
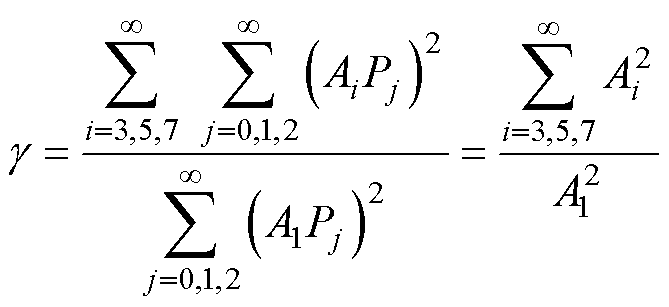 (6)
(6)
图3a显示了使用有限元分析法(Finite Element Analysis, FEA),计算VTVPM永磁磁通密度沿气隙圆周的波形。值得注意的是,360 °电气角度对应于电机的一个转子极距。图3b显示了VTVPM永磁磁通密度波形的谐波频谱。可以看出,由于定子-转子凸极的调制效应,VTVPM的气隙永磁磁通密度中存在许多空间谐波。选择幅值大于0.1 T的谐波分量,将其列为主要谐波。然后,根据不同谐波的i和j值,表2中列出了主要谐波的调制组合。
因此,从理论上讲,可以通过降低式(6)中的谐波增强因子g,增加永磁磁链的基波幅值以及增加的主要工作谐波,即5次、19次、43次谐波对总永磁磁链基波的贡献来提高电机的功率因数。
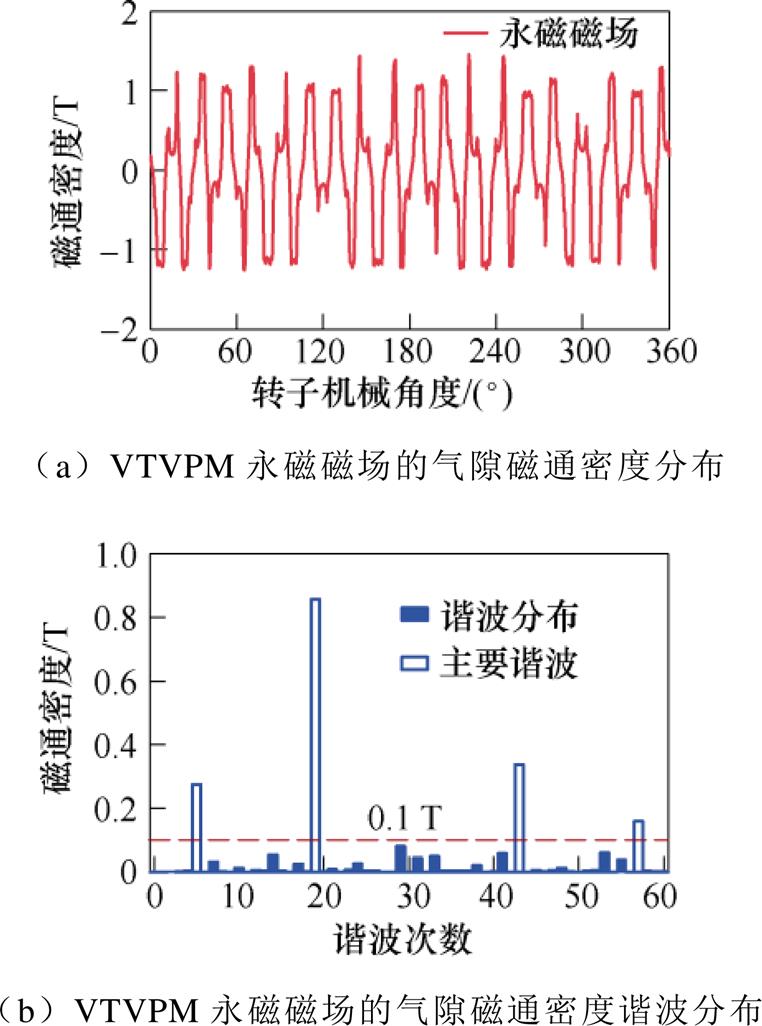
图3 VTVPM永磁磁场磁密和谐波分布
Fig.3 Permanent magnet magnetic flux density and harmonic distribution of VTVPM
表2 VTVPM主要谐波和调制组合
Tab.2 Major harmonics and modulated values of VTVPM

谐波调制组合 5次i=1, j=-1 19次i=1, j=0 43次i=1, j=1 57次i=3, j=0
2.2.2 同步电感层的理论推导
基于以上分析,进一步对同步电感层的优化设计进行理论推导。根据经典电机学理论,传统永磁电机同步电感Ls可表示为
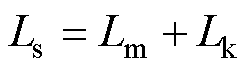 (7)
(7)
式中,Lm为主电感;Lk为漏电感。相比于主电感,漏电感可以忽略。因此,同步电感可近似等于主电感。根据经典绕组理论,可以计算定子任意两相的互感公式为
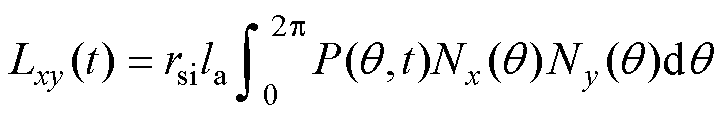 (8)
(8)
式中,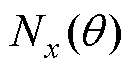 、
、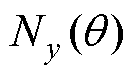 分别为x相、y相的绕组函数;
分别为x相、y相的绕组函数;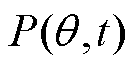 为气隙磁导函数。
为气隙磁导函数。
气隙磁导函数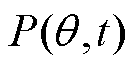 为
为
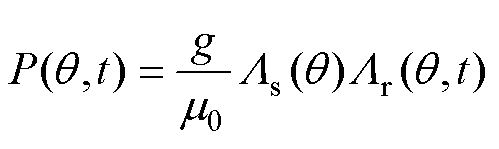 (9)
(9)
式中,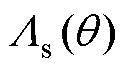 和
和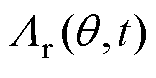 分别为定子侧和转子侧的磁导函数。当只考虑气隙磁导中的直流项和基波项时,定子和转子磁导函数为
分别为定子侧和转子侧的磁导函数。当只考虑气隙磁导中的直流项和基波项时,定子和转子磁导函数为
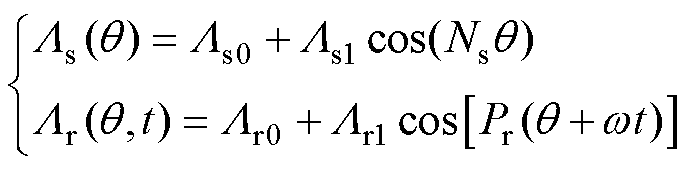 (10)
(10)
式中,g为气隙长度;m0为气隙磁导率;Ls0、Ls1分别为定子磁导的直流项和基波项;Lr0、Lr1分别为转子磁导的直流项和基波项。
将定转子磁导函数代入气隙磁导函数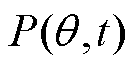 ,公式展开为
,公式展开为
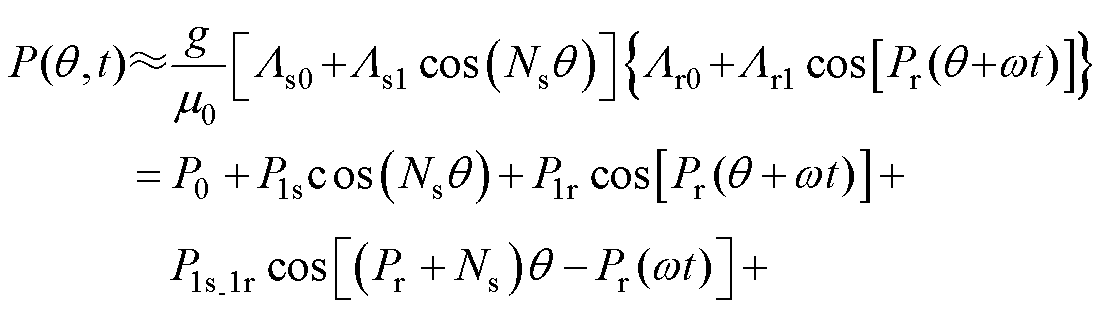
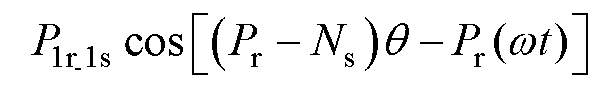 (11)
(11)
式中,P0为气隙磁导直流项;P1s为仅与定子相关的气隙磁导基波项;P1r为仅与转子相关的气隙磁导基波项;P1s_1r、P1r_1s为与定子和转子均相关的气隙磁导基波项。
根据式(8),以A相为例,A相自感与互感表达式为
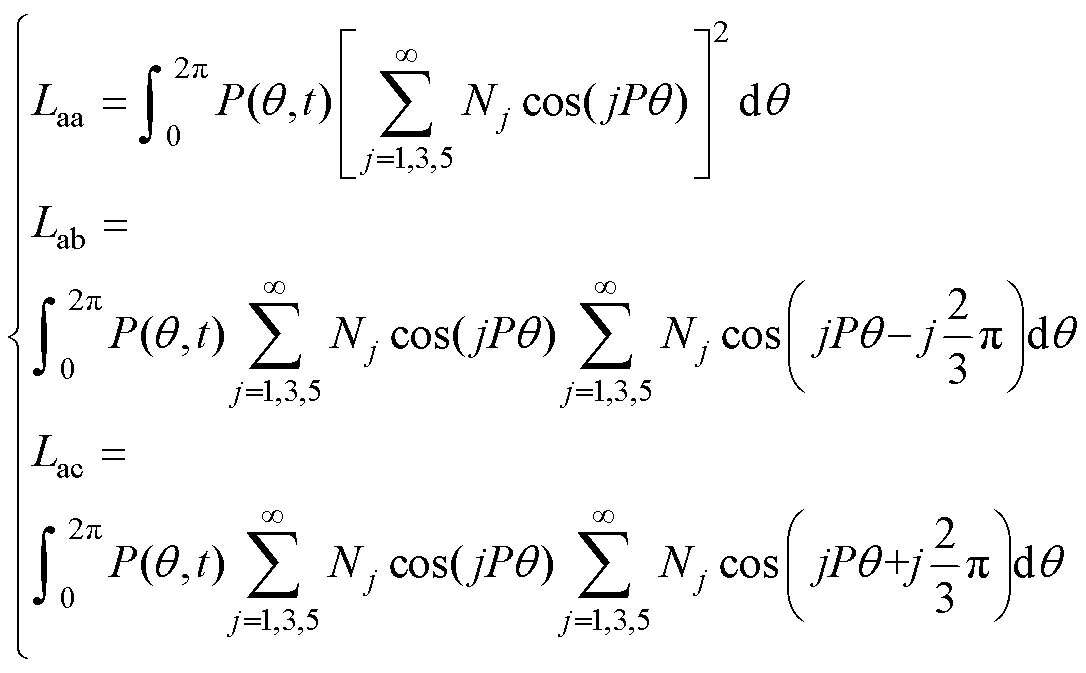 (12)
(12)
由于VTVPM的凸极比为1,其主电感Lm是自感和互感之间的差值。同时,同步电感Ls近似等于主电感,由此,根据式(11)、式(12),同步电感Ls表达式为
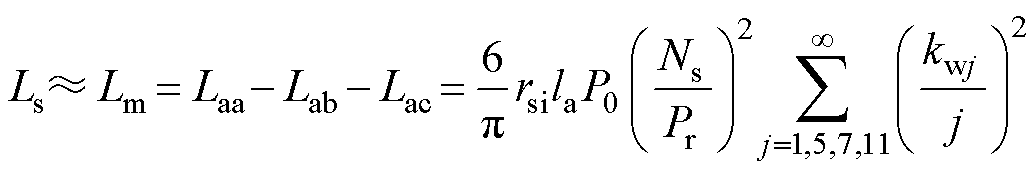 (13)
(13)
式中,P0为气隙磁导直流项;kwj为第j次谐波绕组因数。根据对定子和转子磁导波形的傅里叶分析,表达式P0可以表示为
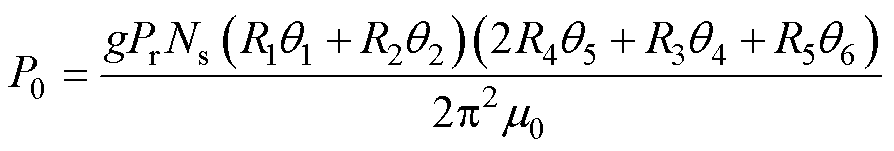 (14)
(14)
由此可以看出,同步电感与气隙磁导直流项P0线性相关。因此,选择P0作为关键设计参数,研究电机参数与同步电感之间的关系,进而反映电机功率因数的变化。
2.2.3 VTVPM功率因数内在机理及提升方法
基于以上分析,本节采用分层优化策略,分别从永磁磁链层和同步电感层,对VTVPM功率因数的内在机理进行了理论研究与公式推导。首先,根据电机经典功率因数公式,电机功率因数主要与永磁磁链和同步电感相关。因此,为了探究功率因数的内在机理,并提出相应的电机功率因数提升的优化设计方法,本节从优化永磁磁链和同步电感的角度出发,以谐波为桥梁,推导并建立了永磁磁链和同步电感与设计参数之间的内在联系,这为后面的优化设计和实验验证提供了理论基础。
基于上述分析,永磁磁链基波是影响电机功率因数的主要参数。在保持永磁体用量不变的前提下,选择转子齿宽角qtr和永磁倾斜角qv进行研究。同时,综合考虑参数变化对磁链基波幅值和负载转矩的影响。因此,设计参数的优化目标函数以及限制条件可定义为
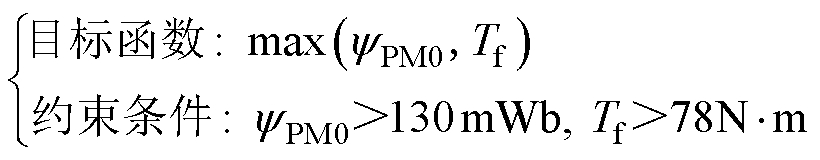 (15)
(15)
式中,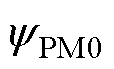 为永磁磁链的基本幅值;Tf为负载转矩。
为永磁磁链的基本幅值;Tf为负载转矩。
通过电机参数变化,探究对永磁磁链基波幅值和负载转矩之间的关系。相关结果如图4所示。
从图4可以看出,永磁磁链的基波幅值随着参数qtr和qv增大而先增大后减小,负载转矩随着qtr增大逐渐增大至基本保持不变,同时,随着qv增大,负载转矩在56 °取得极大值后不断减小。因此,可以认为,电机参数qtr和qv在1.5 °和56 °取得极值,即VTVPM的最优设计。根据表3,qv优化前后产生磁链基波的磁通密度幅值得到提升,同时,qtr优化前后磁通密度谐波略有降低,且产生磁链高次谐波的57th谐波幅值降低至接近于0。
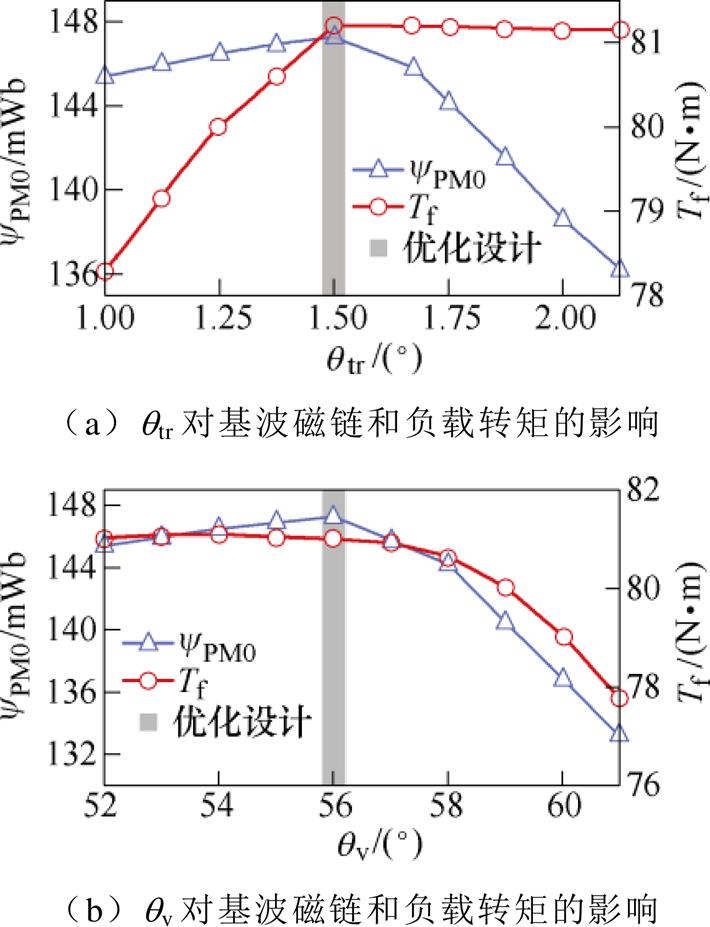
图4 参数对永磁磁链基波和负载转矩的影响
Fig.4 Influence of parameters on fundamental waves of permanent magnet flux linkage and load torque
表3 永磁磁通密度谐波优化前后对比
Tab.3 Comparison before and after optimization of permanent magnet density harmonic
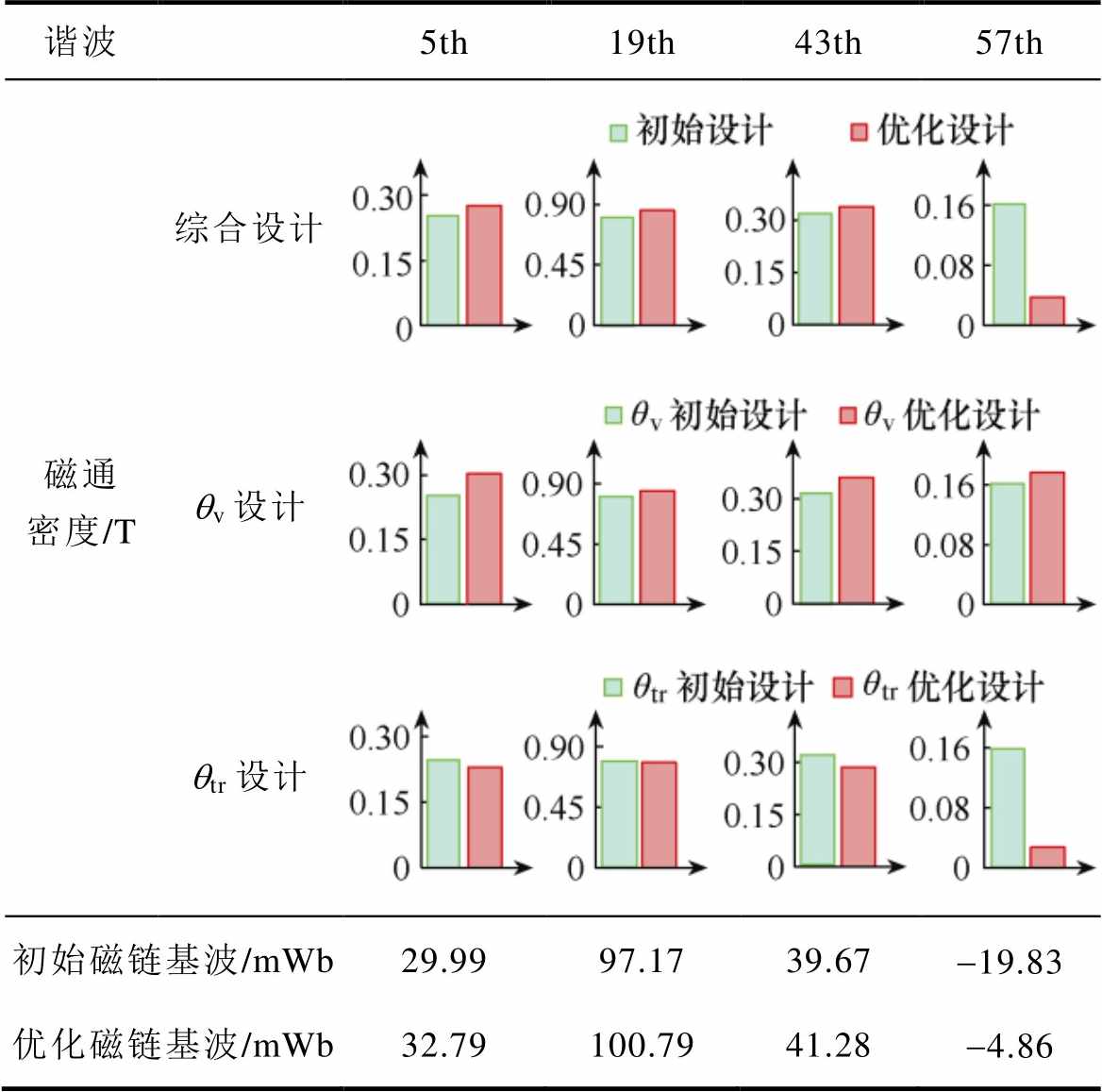
谐波5th19th43th57th 磁通密度/T综合设计 qv设计 qtr设计 初始磁链基波/mWb29.9997.1739.67-19.83 优化磁链基波/mWb32.79100.7941.28-4.86
表4 VTVPM优化前后参数和优化目标值
Tab.4 Parameters and optimization target values before and after VTVPM optimization
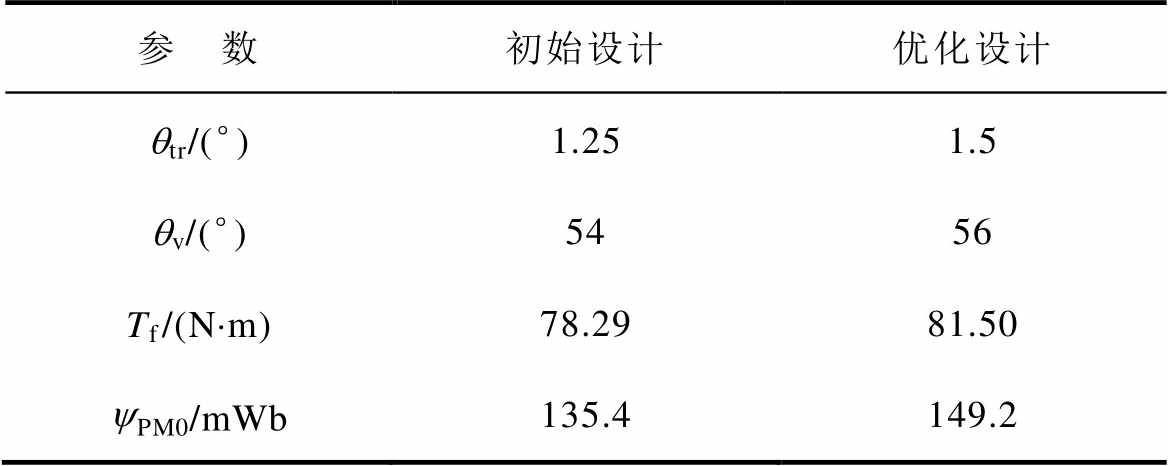
参 数初始设计优化设计 qtr/(°)1.251.5 qv/(°)5456 Tf/(N×m)78.2981.50 yPM0/mWb135.4149.2
基于以上对永磁磁链的研究和同步电感的理论推导,对参数P0对应参数进行优化设计。
根据图1b和式(14),气隙磁导直流项P0与定子和转子的结构参数相关,表5展示了VTVPM参数定义及表达式。
表5 VTVPM的优化参数定义
Tab.5 Optimization parameter definition of VTVPM
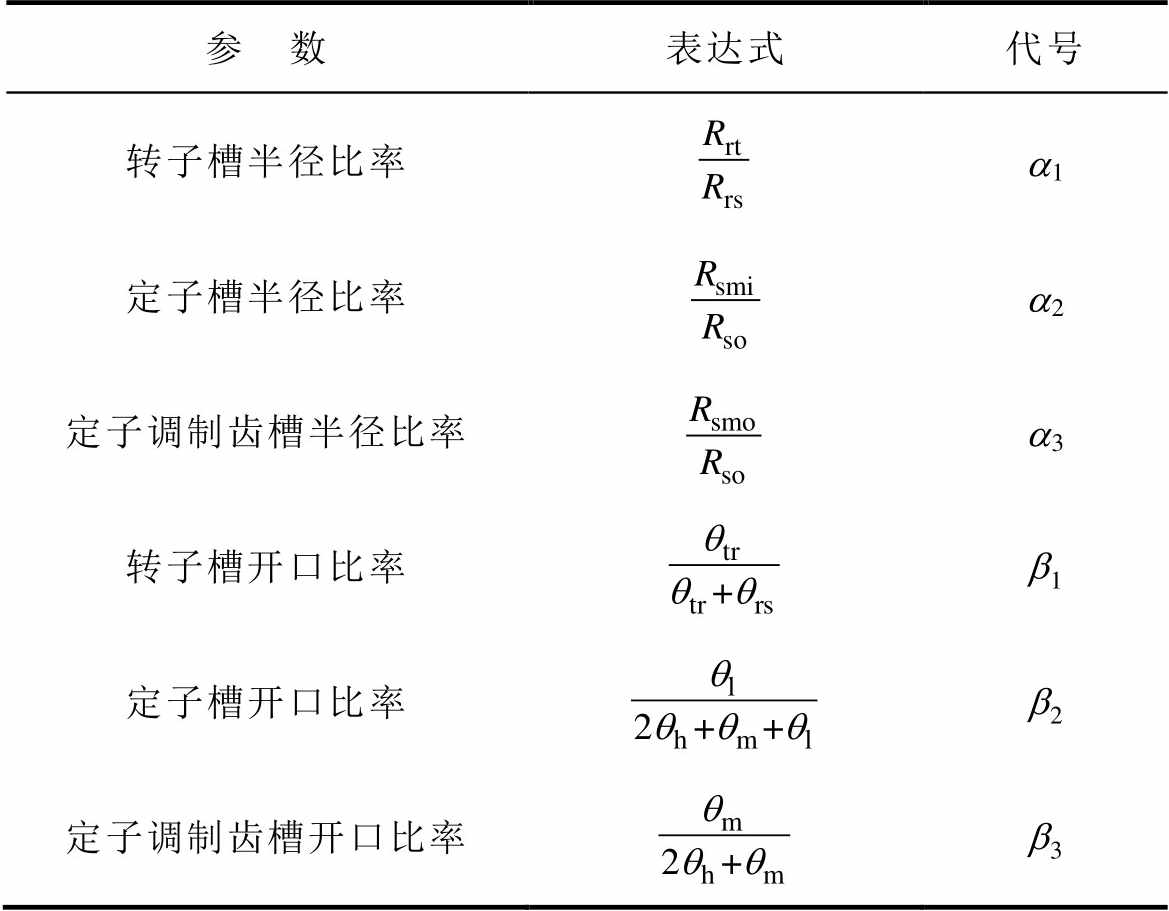
参 数表达式代号 转子槽半径比率a1 定子槽半径比率a2 定子调制齿槽半径比率a3 转子槽开口比率b1 定子槽开口比率b2 定子调制齿槽开口比率b3
基于以上分析,为了准确判别设计参数对同步电感的影响,并根据影响程度安排参数的优化顺序,本文采用了综合敏感度分析的方法,其中敏感度系数S(xi)可定义为
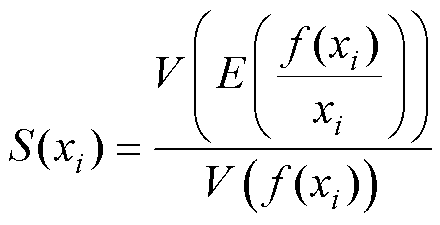 (16)
(16)
式中,xi为设计参数;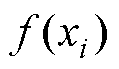 为优化目标;
为优化目标;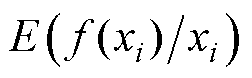 为xi取定值时f (xi)的平均值;
为xi取定值时f (xi)的平均值;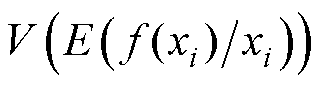 为
为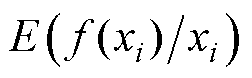 的方差,
的方差,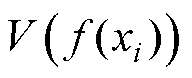 为
为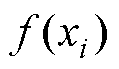 的方差。
的方差。
根据式(16),图5求取了电机参数关于同步电感的敏感度系数。根据电机参数的敏感度系数,依次选取b2与a2、b1与a1、以及b3与a3作为优化参数,具体优化过程如图6所示。
结合对电机永磁磁链的优化分析,表6展示了电机相关参数的优化结果。通过对相关参数的优化设计,同步电感由11.1 mH,降低至优化后的9.59 mH,同时,功率因数由0.54提升至0.67。
为了验证本文提出的分层优化方法的有效性,本节对与功率因数相关的电磁性能进行了分析和评估。
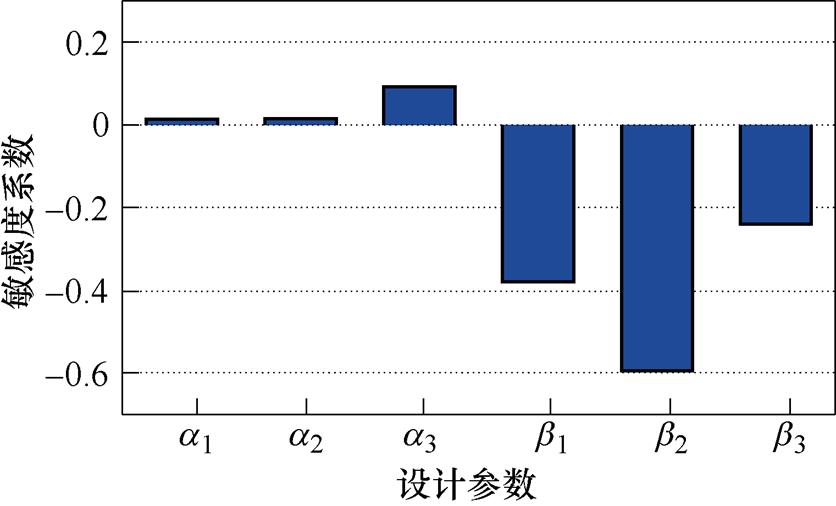
图5 VTVPM参数的敏感度分析
Fig.5 Sensitiveanalysis of VTVPM parameters
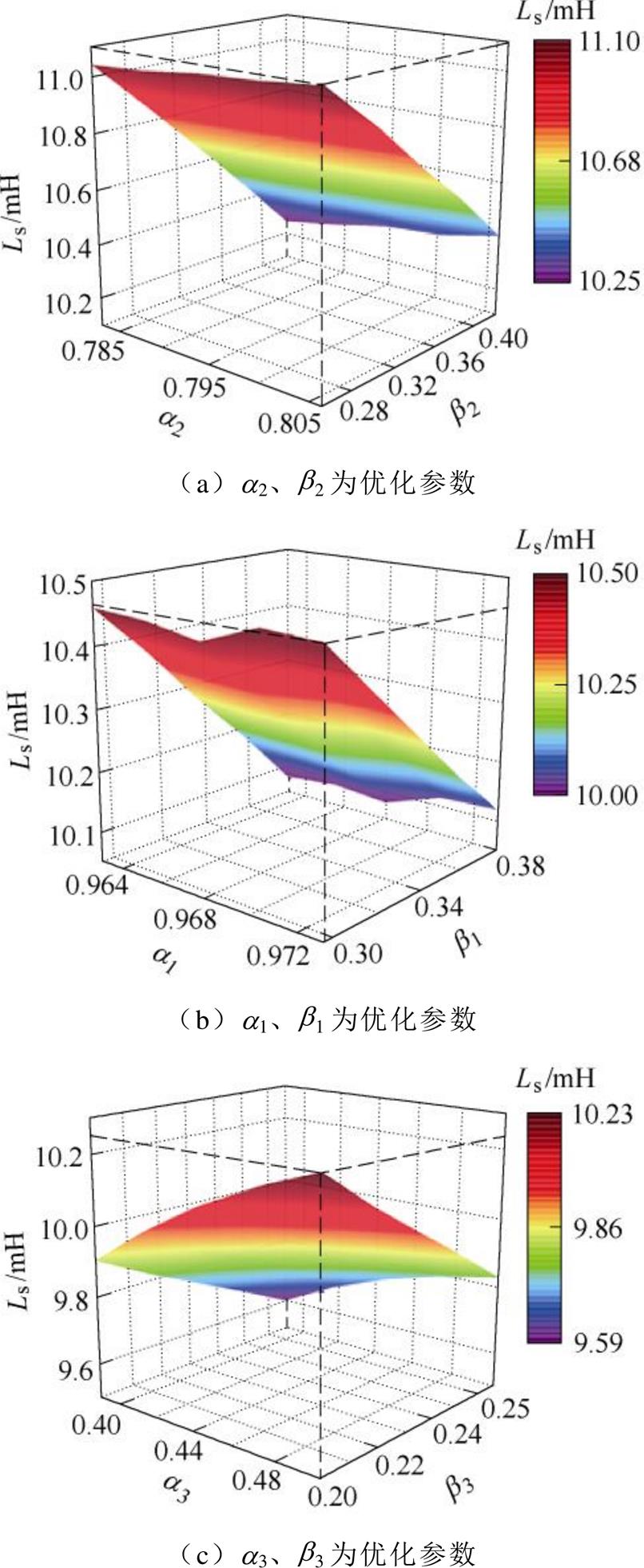
图6 VTVPM参数对同步电感的影响
Fig.6 Influence of VTVPM parameters on synchronous inductance
初始和优化设计电机的磁场分布和磁链分布如图7所示。从图7中可以直观地看出,与初始设计的磁路相比,优化电机的磁力线分布更密集,这表明优化电机的有效磁路大于初始电机,优化电机可以获得更高的磁通密度。优化后的电机磁通密度高于初始电机,这意味着优化后的VTVPM的功率因数得到了提升。
表6 VTVPM参数优化
Tab.6 Parameteroptimization of VTVPM
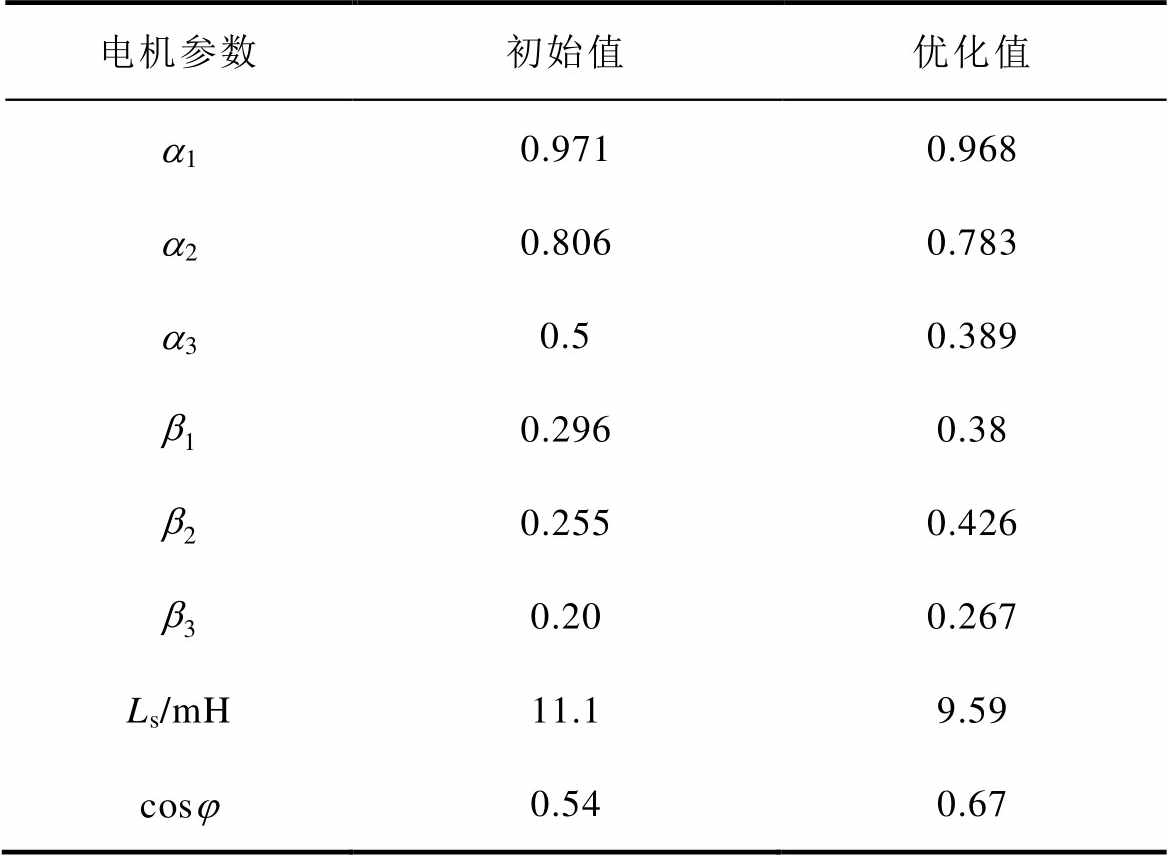
电机参数初始值优化值 a10.9710.968 a20.8060.783 a30.50.389 b10.2960.38 b20.2550.426 b30.200.267 Ls/mH11.19.59 cosj0.540.67
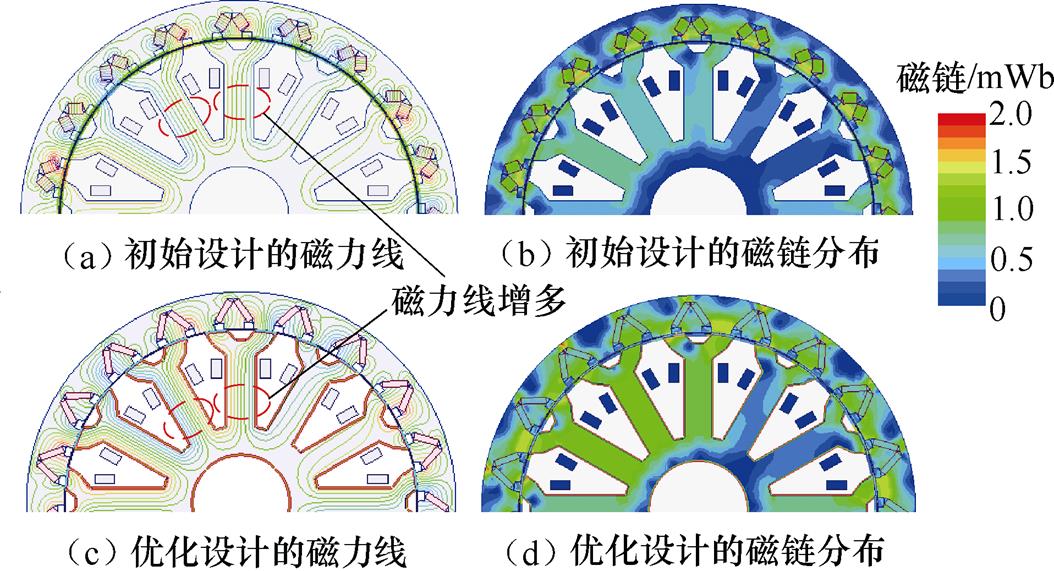
图7 VTVPM的磁场分布和磁力线分布
Fig.7 Magnetic field distributions and magnetic lines of flux distributions of the VTVPM
根据第2节提出的优化方法,分别对优化前后的永磁磁链和电感进行仿真验证。初始与优化VTVPM的永磁磁链和电感如图8所示。从图8a可以看出,优化前后永磁磁链的幅值提升了约4.16 %,这与之前理论分析,通过提升主要工作谐波幅值来提升永磁磁链基波幅值的理论推导相一致。如图8b所示,电感优化前后幅值明显降低,降低比例约为13.6 %,进一步验证了理论分析的正确性。
电机功率因数定义为负载电压基波和输入电流基波之间相位差的余弦值[19]。初始与优化VTVPM的功率因数如图9所示。从图9a中可以看出,优化电压的峰值比初始电压更接近电流的峰值,这意味着优化后的电机具有更高的功率因数。如图9b所示,电机功率因数从0.54增加到0.67。
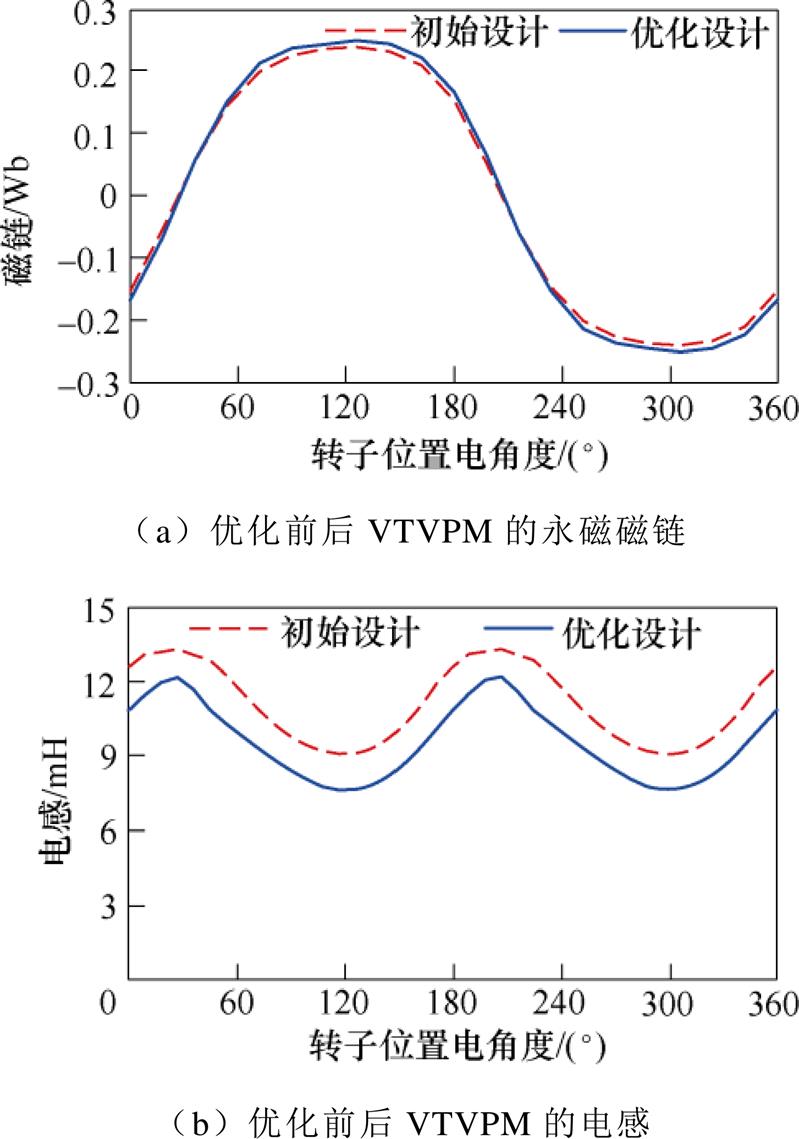
图8 初始与优化VTVPM的永磁磁链和电感
Fig.8 Initial and optimized permanent magnet flux linkage and inductance of VTVPM
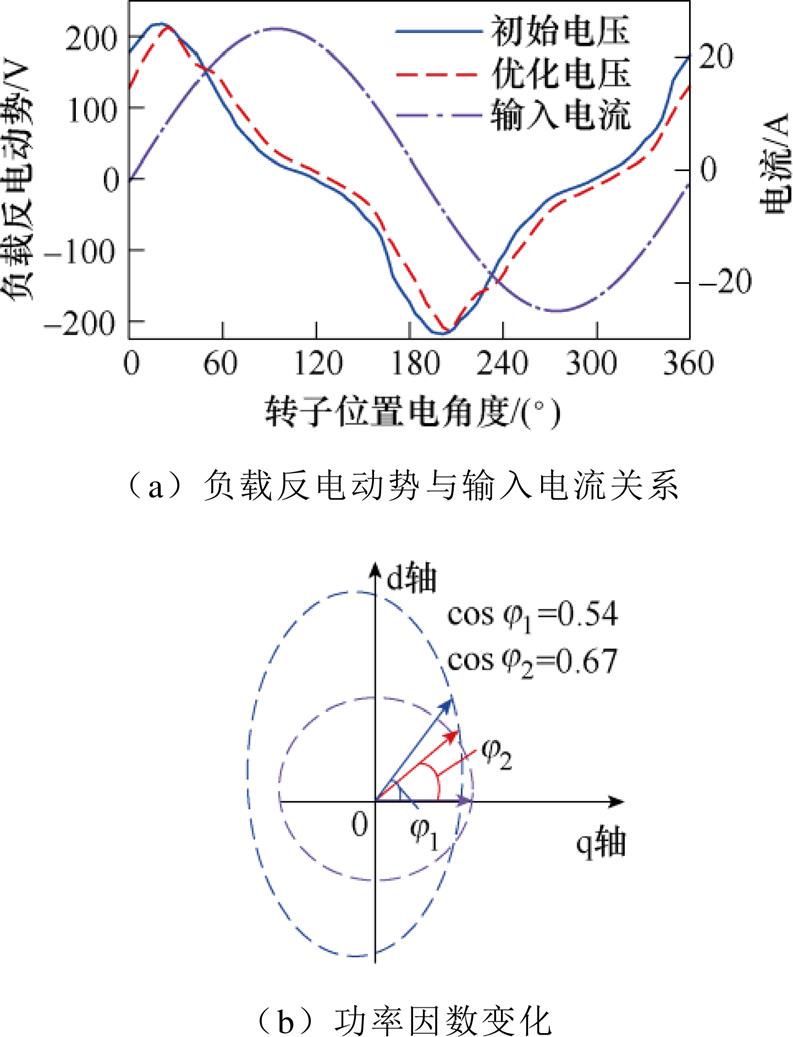
图9 初始与优化VTVPM的功率因数
Fig.9 Initial and optimized power factor of VTVPM
在轮毂电机应用中,空载反电动势会影响电机的输出转矩。为了验证功率因数对电磁性能的影响,图10显示了优化前后VTVPM的空载反电动势波形。在永磁体用量不变的前提下,反电动势的基波幅值从65 V增加到97 V,这意味着随着电机功率因数的增加,优化后的电机具有更高的转矩输出能力。
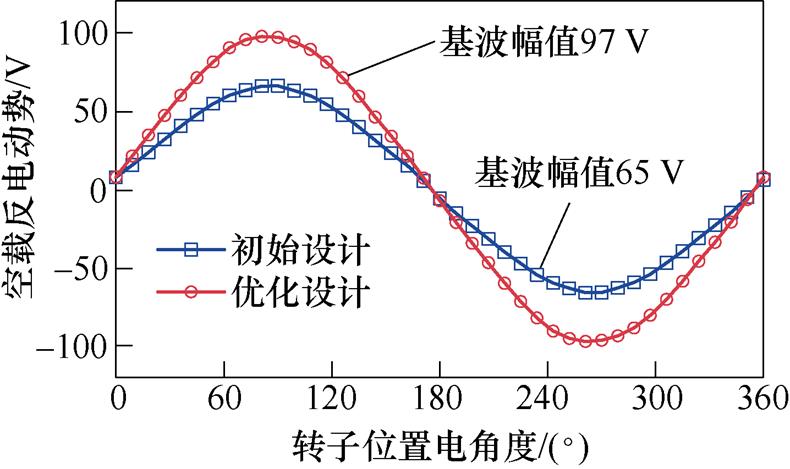
图10 初始与优化VTVPM的空载反电动势
Fig.10 Initial and optimized no-load back EMF of VTVPM
图11显示了优化前后电机转矩性能的比较结果。在图11a中,与初始电机相比,优化设计电机的齿槽转矩峰峰值降低了约14.04 %。VTVPM的输出转矩如图11b所示。从图中可以看出,相比于初始设计电机输出转矩的65.16 N×m,优化后的电机输出转矩平均值为76.94 N×m,输出转矩提高了18.07 %,同时,转矩脉动从2.60 %降低至1.73 %。通过以上对功率因数相关电磁性能的分析和比较,验证了该优化方法的合理性和有效性。
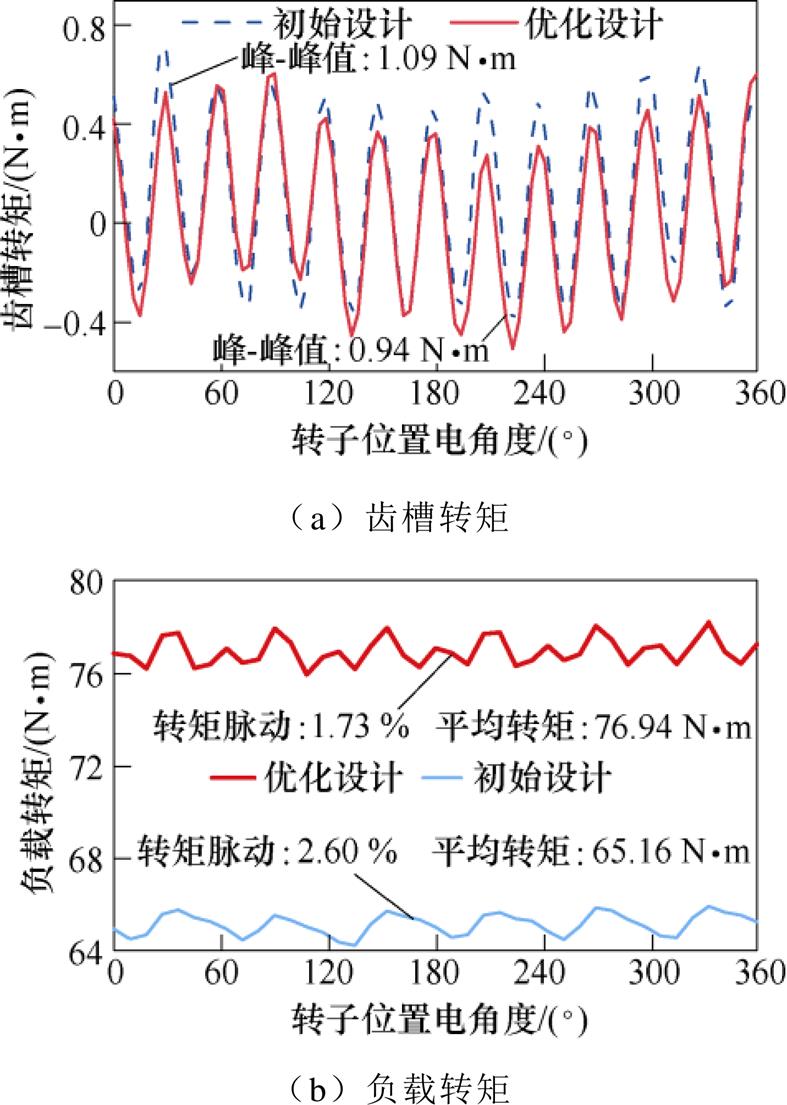
图11 初始与优化VTVPM的转矩特性
Fig.11 Initial and optimized torque characteristics of VTVPM
在上述分析和仿真的基础上,制作了样机,并搭建了实验平台。硅钢片、转子和定子如图12所示,相应的实验平台如图13所示。
VTVPM在300 r/min时的空载反电动势波形如图14所示。可以清楚地看到,电机的空载反电动势是正弦对称的,幅值为27 V,这有利于电机的控制。

图12 VTVPM的硅钢片、转子和定子
Fig.12 Silicon steel sheet, rotor and stator of VTVPM

图13 VTVPM的实验平台
Fig.13 Experimental platform of the VTVPM
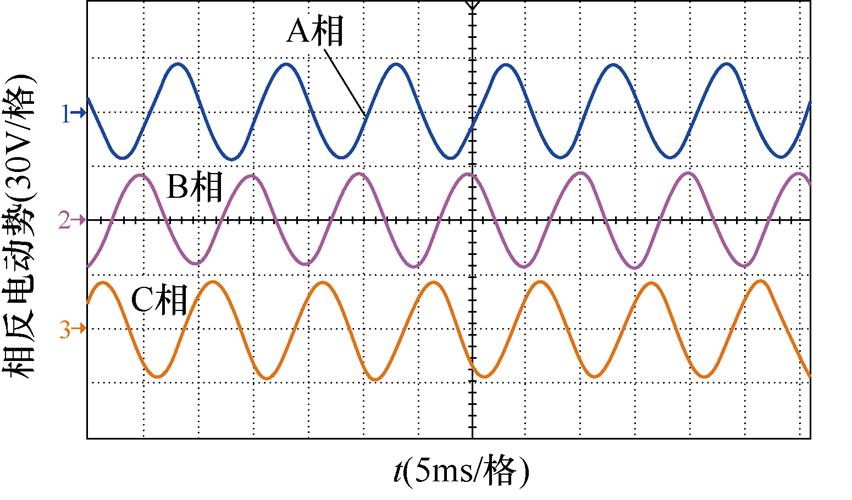
图14 VTVPM空载反电动势的实验波形
Fig.14 Experimental waveforms of no-load back EMF of VTVPM
图15a显示了样机在8 N×m负载转矩下的电流和电压的波形曲线。根据实验样机搭建的实验平台,通过电流探头测得相电流,隔离电压探头测得相电压,并导出电压和电流信号。通过对电压信号与电流信号进行快速傅里叶分解,得到电压与电流的基波波形。然后,根据波形之间的相位关系,测得的电机功率因数为0.70。图15b为仿真与实验测试的功率因数对比。可以看出,在该工作点下,电机功率因数的仿真值与实验值几乎一致,这进一步验证了本文提出的优化方法对提高游标电机功率因数的有效性。
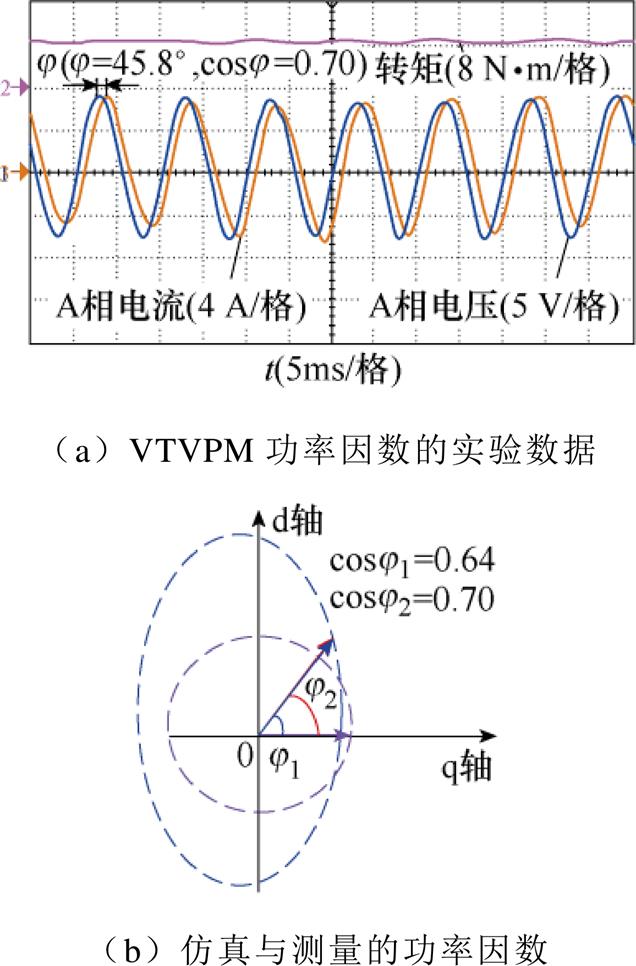
图15 VTVPM功率因数的实验数据
Fig.15 Experimental data of VTVPM power factor
本文基于对磁场调制电机功率因数的内在机理研究,提出了一种游标永磁电机功率因数的优化设计方法。在所提出的设计方法中,采用分层优化的思想,分别对永磁磁链层和同步电感层进行理论推导和优化分析。为了验证所提出优化方法的有效性,对比了优化前后电机功率因数及其相关电磁性能的变化,搭建了实验平台并进行了基础实验。结果表明,性能分析和实验结果验证了所提出的分层优化方法的有效性和合理性,提升了游标永磁电机在轮毂电机直接转矩驱动系统中的应用潜力。
参考文献
[1] Luo Jun, Kou Baoquan, Yang Xiaobao, et al. Develop- ment, design, and analysis of a dual-consequent-pole transverse flux linear machine for direct-drive appli- cations[J]. IEEE Transactions on Industrial Electro- nics, 2021, 68(7): 6097-6108.
[2] 赵士豪, 陈进华, 张驰, 等. 不均匀气隙表贴式永磁同步电机磁场解析计算[J]. 电工技术学报, 2022, 37(14): 3502-3513.
Zhao Shihao, Chen Jinhua, Zhang Chi, et al. Analytical calculation of magnetic field of permanent magnet synchronous motor with uneven air gap structure[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3502-3513.
[3] 黄海林, 李大伟, 曲荣海, 等. 磁齿轮复合永磁电机拓扑及应用综述[J]. 电工技术学报, 2022, 37(6): 1381-1397.
Huang Hailin, Li Dawei, Qu Ronghai, et al. A review of magnetic geared machines: topologies and appli- cations[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1381-1397.
[4] 高锋阳, 齐晓东, 李晓峰, 等. 不等宽不等厚Halbach部分分段永磁同步电机电磁性能解析计算与优化分析[J]. 电工技术学报, 2022, 37(6): 1398-1414.
Gao Fengyang, Qi Xiaodong, Li Xiaofeng, et al. Analytical calculation and optimization analysis of electromagnetic performance of Halbach partially- segmented permanent magnet synchronous motors with unequal width and thickness[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1398-1414.
[5] Wang Yubin, Feng Qi, Li Xianglin, et al. Design, analysis, and experimental test of a segmented-rotor high-temperature superconducting flux-switching generator with stationary seal[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11): 9047-9055.
[6] 石玉君, 程子活, 蹇林旎. 两种典型的场调制型永磁电机的对比分析[J]. 电工技术学报, 2021, 36(1): 120-130.
Shi Yujun, Cheng Zihuo, Jian Linni. Comparative analysis of two typical field modulated permanent- magnet machines[J]. Transactions of China Electro- technical Society, 2021, 36(1): 120-130.
[7] Zhu Xiaoyong, Jiang Min, Xiang Zixuan, et al. Design and optimization of a flux-modulated per- manent magnet motor based on an airgap-harmonic- orientated design methodology[J]. IEEE Transactions on Industrial Electronics, 2020, 67(7): 5337-5348.
[8] Lin Qifang, Niu Shuangxia, Fu W N. Design and optimization of a dual-permanent-magnet vernier machine with a novel optimization model[J]. IEEE Transactions on Magnetics, 2020, 56(3): 1-5.
[9] Chen Yiqiang, Zhu Xiaoyong, Quan Li, et al. A V-shaped PM vernier motor with enhanced flux- modulated effect and low torque ripple[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-4.
[10] Liu Yue, Li H Y, Zhu Z Q. A high-power factor vernier machine with coil pitch of two slot pitches[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.
[11] Du Yi, Xiao Feng, Hua Wei, et al. Comparison of flux-switching PM motors with different winding configurations using magnetic gearing principle[J]. IEEE Transactions on Magnetics, 2016, 52(5): 1-8.
[12] Fan Deyang, Quan Li, Zhu Xiaoyong, et al. Airgap- harmonic-based multilevel design and optimization of a double-stator flux-modulated permanent-magnet motor[J]. IEEE Transactions on Industrial Electronics, 2021, 68(11): 10534-10545.
[13] Yu Zixiang, Kong Wubin, Li Dawei, et al. Power factor analysis and maximum power factor control strategy for six-phase DC-biased vernier reluctance machines[J]. IEEE Transactions on Industry Appli- cations, 2019, 55(5): 4643-4652.
[14] Xu Liang, Zhao Wenxiang, Liu Guohai, et al. Design optimization of a spoke-type permanent-magnet vernier machine for torque density and power factor improvement[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3446-3456.
[15] 阙鸿杰, 全力, 张丽, 等. 基于自适应滤波器在线解耦的磁场增强型永磁电机无位置传感器控制[J]. 电工技术学报, 2022, 37(2): 344-354.
Que Hongjie, Quan Li, Zhang Li, et al. Sensorless control of flux-intensifying permanent magnet syn- chronous motor based on adaptive Notch filter online decoupling[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 344-354.
[16] Zhu Xiaoyong, Fan Deyang, Xiang Zixuan, et al. Systematic multi-level optimization design and dynamic control of less-rare-earth hybrid permanent magnet motor for all-climatic electric vehicles[J]. Applied Energy, 2019, 253: 113549.
[17] Wu Dingying, Xiang Zixuan, Zhu Xiaoyong, et al. Optimization design of power factor for an in-wheel vernier PM machine from the perspective of air-gap harmonic modulation[J]. IEEE Transactions on Indu- strial Electronics, 2021, 68(10): 9265-9276.
[18] Zhu Z Q, Liu Yue. Analysis of air-gap field modulation and magnetic gearing effect in fractional- slot concentrated-winding permanent-magnet synchronous machines[J]. IEEE Transactions on Industrial Elec- tronics, 2018, 65(5): 3688-3698.
[19] Silva C A, Bidaud F, Herbet P, et al. Power factor calculation by the finite element method[J]. IEEE Transactions on Magnetics, 2010, 46(8): 3002-3005.
Abstract In recent years, Vernier permanent magnet (VPM) machines have attracted increasing attention due to the advantages of high power density at low speed in the research field of electric vehicles (EVs), aerospace actuation, and ship propulsion. However, compared with traditional PM machines, VPM machines generally suffer from a low power factor due to increased PM pole number and flux leakage. Various methods have been proposed from the perspective of machine design to enhance the power factor of VPM machines. However, current research often focuses on the design and optimization of VPM, while the power factor improvement from the theory perspective needs to be addressed. Consequently, in this paper, the power factor mechanism of the magnetic field modulation machine is investigated based on the principle of magnetic field modulation, and a power factor improvement method is proposed for VPM.
Taking the V-type Vernier permanent magnet machine (VTVPM) as an example, the inherent mechanism of the power factor of the VTVPM is theoretically studied, and the formulas are derived from the permanent magnet flux linkage layer and synchronous inductance layer using the hierarchical optimization strategy. Firstly, according to the classical power factor formula of the machine, the power factor of the machine is mainly related to the permanent magnet flux linkage and synchronous inductance. Therefore, this paper, from the perspective of optimizing the permanent magnet flux linkage and synchronous inductance, taking harmonics as a bridge, derives and establishes the internal relationship between the permanent magnet flux linkage and synchronous inductance with the design parameters.
By the scanning analysis of the parameters qtr and qv of the permanent magnet flux layer motor, it can be concluded that qtr and qv obtain extreme values at 1.5 ° and 56 °, which is the optimal design of the VTVPM motor, and the amplitude of the fundamental wave of the permanent magnet flux linkage is increased from 135.4 mWb to 149.2 mWb. The synchronous inductance layer combines the sensitivity analysis and response surface methods to reduce the synchronous inductance from 11.1 mH to 9.59 mH. Finally, the power factor is increased from 0.54 to 0.67. In addition, the fundamental amplitude of the back EMF is increased from 65 V to 97 V, and the optimized machine load torque is close to 76.94 N·m, increased by 18.07 %. Moreover, the torque ripple is reduced from 2.60 % to 1.73 %. The simulation results verify the feasibility of the optimization design method.
Based on the study of power factor production mechanism of the field modulated machine, this paper presents an optimal design method for the power factor of the VPM machine. The proposed design method adopts hierarchical optimization to theoretically deduce and optimize the permanent magnet flux linkage and synchronous inductor layers, respectively. The power factor and other electromagnetic performance of the machine before and after optimization are compared. Finally, the prototype machine is built, and the basic experiments are carried out. Both the theoretical analysis and experimental results verify the effectiveness and rationality of the proposed optimization design method.
keywords:Vernier permanent magnet (VPM) machine, power factor, permanent magnet flux linkage, synchronous inductance, optimization design
国家自然科学基金资助项目(51937006, 51991385, 51877099, BK20220541)。
收稿日期 2022-05-31
改稿日期 2022-10-07
DOI: 10.19595/j.cnki.1000-6753.tces.220991
中图分类号:TM351
周健荣 男,1997年生,硕士,研究方向为磁场调制电机的设计与研究。E-mail: zhoujr987@163.com
樊德阳 男,1992年生,讲师,研究方向为新能源汽车高品质电机设计与控制。E-mail: Deyang.Fan@ujs.edu.cn(通信作者)
(编辑 郭丽军)