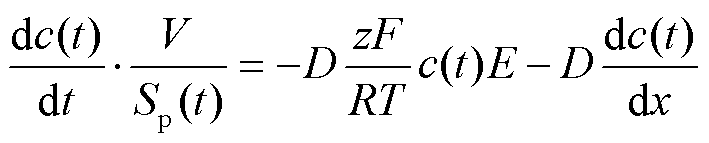（1）
摘要 目前在实验中通常采用间接的表征参量以衡量细胞电穿孔效应，为了能够在实验中找到一种直接的表征参量，该文提出了电穿孔面积这一新的表征参量及其测量方法。基于分子传输动力学，在脉冲电场下开展了荧光分子染色实验，然后通过对细胞荧光强度曲线进行数据处理，计算出脉冲期间形成的电穿孔面积，并研究了不同脉冲电场参数下的细胞膜电穿孔面积变化规律。结果表明，随着脉冲电场参数增强，细胞荧光强度增大，电穿孔效应增强，计算出的电穿孔面积数值与已有结论吻合，证实了该实验方法的可行性。此外，电穿孔面积随着电场强度、脉冲宽度和脉冲电冲击的增大而线性增大，为脉冲电场临床治疗提供了指导。
关键词：脉冲电场 电穿孔效应 电穿孔面积 分子传输 荧光染色实验
脉冲电场是一种有效治疗肿瘤的方法，其原理是细胞在电场的作用下，会在细胞膜内外侧感应出电位，当跨膜电压超过某一阈值时，细胞膜会发生击穿，即电穿孔[1-2]。细胞发生电穿孔后，膜通透性增大，一些分子（如荧光分子、化学药物和DNA等）可通过细胞膜进入细胞内。
目前在实验中有许多表征电穿孔效应的参量，如细胞活性、细胞凋亡坏死率、细胞膜通透性、电穿孔细胞百分比等。细胞活性通过检测细胞群体的健康情况以反映细胞的生理状态和代谢水平。细胞膜通透性利用细胞对荧光分子染料的摄取情况，观测细胞荧光强度的变化或计算电穿孔细胞百分比以反映电穿孔程度。
许多学者利用上述参量开展实验研究了脉冲电场参数对细胞膜电穿孔效应的影响[3]，如脉冲电场强度、脉冲宽度和脉冲个数等。米彦等[4]通过CCK-8（cell counting kit-8）法检测不同脉冲电场下的细胞活性发现，当固定脉冲宽度为300 ns、脉冲个数为100时，细胞活性随电场强度呈现S型衰减；当固定电场强度为6 kV/cm、脉冲个数为100时，细胞活性随脉冲宽度呈现S型衰减；当固定电场强度为6 kV/cm、脉冲宽度为300 ns时，细胞活性随脉冲个数呈现指数型衰减。T. Polajžer等[5]通过MTS（一种四唑盐类化合物）染色剂表征细胞的增殖和活性发现，随着电场强度的增大，细胞存活率下降，并且与脉冲相间延迟有关，当相间延迟较大时，脉冲电场在降低细胞存活率方面更有效。M. M. Sadik等[6]通过荧光显微镜观察电场下荧光分子碘化丙啶（Propidium Iodide, PI）在细胞内的空间分布和时间变化，实时反映了细胞对PI分子的摄取情况，发现随着观测时间的增大，进入细胞内的PI分子增多，细胞荧光强度增大。类似地，J. Dermol等[7]检测了脉冲电场下细胞膜通透性的变化并计算了电穿孔细胞的百分比，发现处于单个脉冲宽度为1 ms的电场下的电穿孔细胞百分比随着电场强度增大而增大。
此外，也有学者通过仿真研究了脉冲电场对电穿孔的影响[8-10]。K. A. DeBruin等[11]建立了单细胞电穿孔模型，发现电场冲击强度会增大微孔密度，但不会增加跨膜电压的最大值。刘红梅等[12-13]基于有限元仿真探究了脉冲参数的影响，并得出脉冲电场强度的增大会导致孔隙区域的扩张，细胞膜上的穿孔面积随着脉冲宽度的增加而增加，电穿孔程度随着电场强度的增大和脉冲宽度的延长而增加。类似地，吕彦鹏[14]在仿真中发现，电场强度越高，微孔密度越大，并用微孔面积比重反映电穿孔程度，微孔面积比重随着电场强度的增加而逐渐增加。
综上所述，在仿真中通常与电穿孔程度直接相关的表征参量为跨膜电压、电流密度、微孔密度、微孔半径和微孔面积等[15-16]，这些参量与微孔直接相关。而在实验中通常是从宏观上表征电场对细胞的杀伤效果或整体情况，与形成的微孔多少和大小等具体参量并不等效，也并不能直接地表征电穿孔效应，进而也不易建立仿真和实验的密切联系。因此，为找到一种能够直接衡量电穿孔效应的参量及实验测量方法，本文基于分子传输过程，通过开展PI分子荧光染色实验以测量出细胞膜电穿孔面积，并研究不同脉冲电场参数（电场强度和脉冲宽度）对电穿孔面积的影响。
当细胞膜完整时，PI分子不会进入细胞；而当发生细胞膜电穿孔时，PI分子会进入细胞内与核酸分子结合，发出荧光信号[17]。本文基于PI分子传输动力学和细胞膜的缺陷变化过程测量出细胞膜电穿孔面积。
当细胞膜穿孔后，PI分子进入细胞内部并与核酸结合。PI分子的传输一般用Nernst-Plank方程[18-19]来定量描述，即
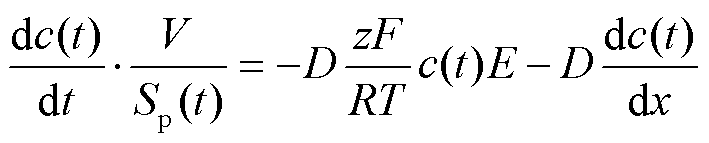（1）
式中，c(t)为穿过细胞表面的PI分子浓度；Sp(t)为渗透性结构缺陷表面积；V为细胞体积（当细胞半径为10 μm时，V=4.2×10-15 m3）；z为PI分子电荷；E为作用于分子的电场强度；F为法拉第常数；R为气体常数；D为PI分子的扩散系数，D=10-10 m2/s；dc(t)/dx为整个细胞膜的浓度梯度，如果已知细胞膜厚度d（如d=5 nm），则dc(t)/dx可近似表示为(cext-cint)/d，其中，cint为进入细胞内与核酸结合的PI分子浓度，cext为细胞外溶液的PI分子浓度。
式（1）中右侧第一项表示脉冲期间，由于电场引起的运输（电泳运输）；第二项表示脉冲作用后，PI分子的扩散迁移过程。在本文中，使用的脉冲电场宽度为800 μs，相较于荧光染色实验观测时间（100 s）非常短，因此电泳传输的贡献可忽略不计，主要考虑脉冲电场作用后的扩散传输，于是式（1）可写为
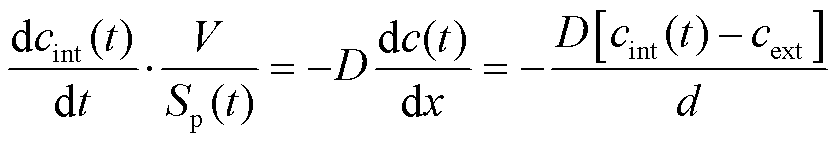（2）
其中，细胞外溶液的PI分子浓度cext=100 μmol/L，此浓度相对于细胞内的浓度很大，因此可视为恒定值，且等式右边的cint(t)近似为0。在一定条件下，细胞膜会重新密封，近似认为可渗透的结构性缺陷Sp(t)随时间呈现指数级下降[18]，即Sp(t)=Sp0e-t/τ，Sp0为脉冲后细胞膜上形成的初始孔隙面积，即脉冲结束时形成的微孔面积，τ为细胞膜上微孔重新密封的时间常数。将Sp(t)代入式（2）并进行时间积分，可得到进入到细胞内的PI分子浓度为
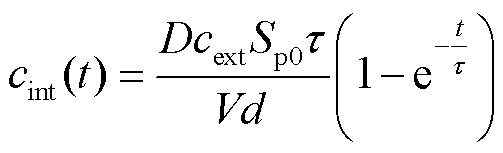（3）
目前大量的实验表明[20]，在一定范围内，结合的PI分子浓度随时间的变化过程可通过式（4）拟合。
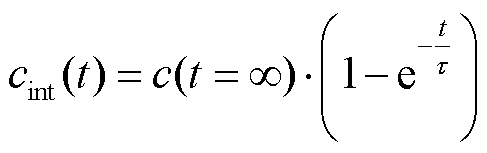（4）
式中，c(t=∞)为细胞内结合的PI分子饱和浓度值。在细胞结合的PI分子未达到饱和浓度前，细胞平均荧光强度Favg与结合PI分子的浓度成正比，即
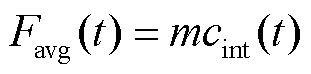（5）
式中，m为细胞平均荧光强度与结合的PI分子浓度的比例系数，为一常数。结合的饱和浓度值c(t=∞)与细胞荧光强度最大值Fmax成正比，与式（4）类似，细胞平均荧光强度随时间的变化可写为
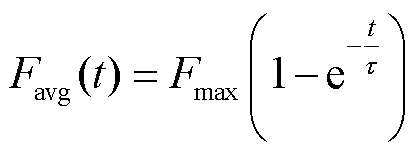（6）
联立式（3）～式（6）可得
（7）
于是可以得到电穿孔面积Sp0为
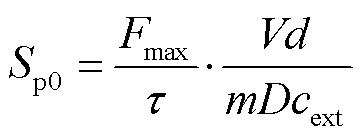（8）
其中，右侧第二个分式为常数，因此可通过细胞荧光染色实验测量出式（8）右侧第一个分式Fmax/τ，进而计算出电穿孔面积。
人黑色素瘤细胞A375由第三军医大学基础医学研究院捐赠，将细胞培养在含有10%胎牛血清（Gibco, USA）和1%青霉素-链霉素（Gibco, USA）的高葡萄糖改良杜氏伊格尔培养基（Dulbecco’s Modified Eagle Medium, DMEM）中，并放在37℃、CO2体积分数为5%、湿润的孵箱中培养，每隔1～2天传代一次。
实验装置示意图如图1所示，对A375细胞溶液施加脉冲电场，并在荧光显微镜下实时观察电场处理过程中细胞的荧光强度变化。
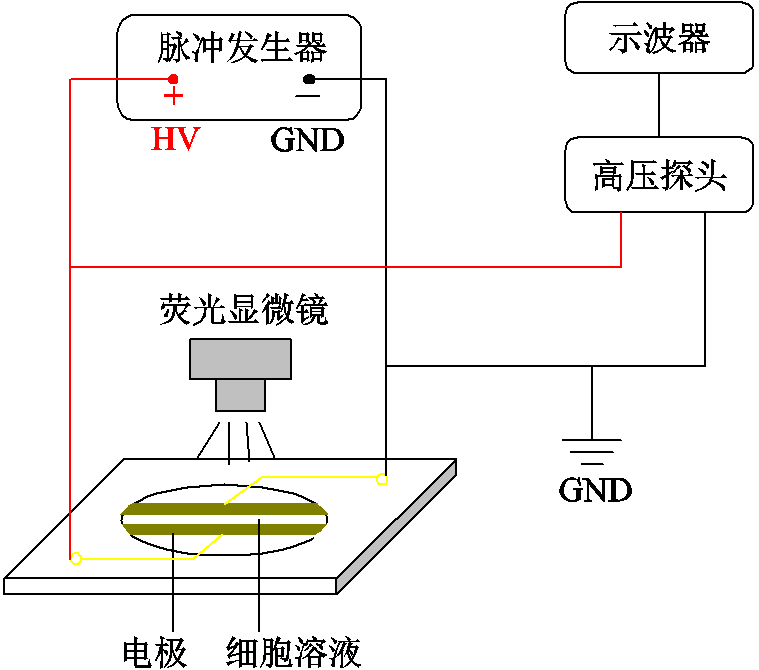
图1 实验装置示意图
Fig.1 Schematic of experimental setup
将1 mL A375细胞悬液（细胞数密度为4×105个/mL）加入到35 mm细胞培养皿（Eppendorf, Hamburg, Germany）中，然后放在37℃孵箱中1 h后取出，吸出培养基并用磷酸缓冲盐溶液（Phosphate Buffered Saline, PBS）清洗3遍后加入含有碘化丙啶浓度为100 μmol/L的PI溶液（Sigma，分子量为668 g/mol，激发波长为535 nm，发射波长为617 nm）的新鲜培养基，准备进行电场处理。采用自制的脉冲发生器[21]施加不同参数的脉冲电场至平板电极（电极间距为2 mm），细胞溶液两侧在不同电压幅值和不同脉冲宽度时的输出波形如图2所示，脉冲个数为1，每个参数均设置有6个水平值。当脉冲电场强度变化时，脉冲宽度固定为800 μs；当脉冲宽度变化时，脉冲电场强度固定为1 250 V/cm（电压为250 V）。
采用Leica DMi8 A倒置荧光显微镜系统（Leica Microsystems, Germany）实时拍摄电场处理过程中细胞的荧光强度变化，采用20×0.55干燥物镜进行放大。在脉冲电场施加前10 s开始实时荧光图像采集，曝光时间为30.18 ms，以1帧/s的速度采集图像100 s。
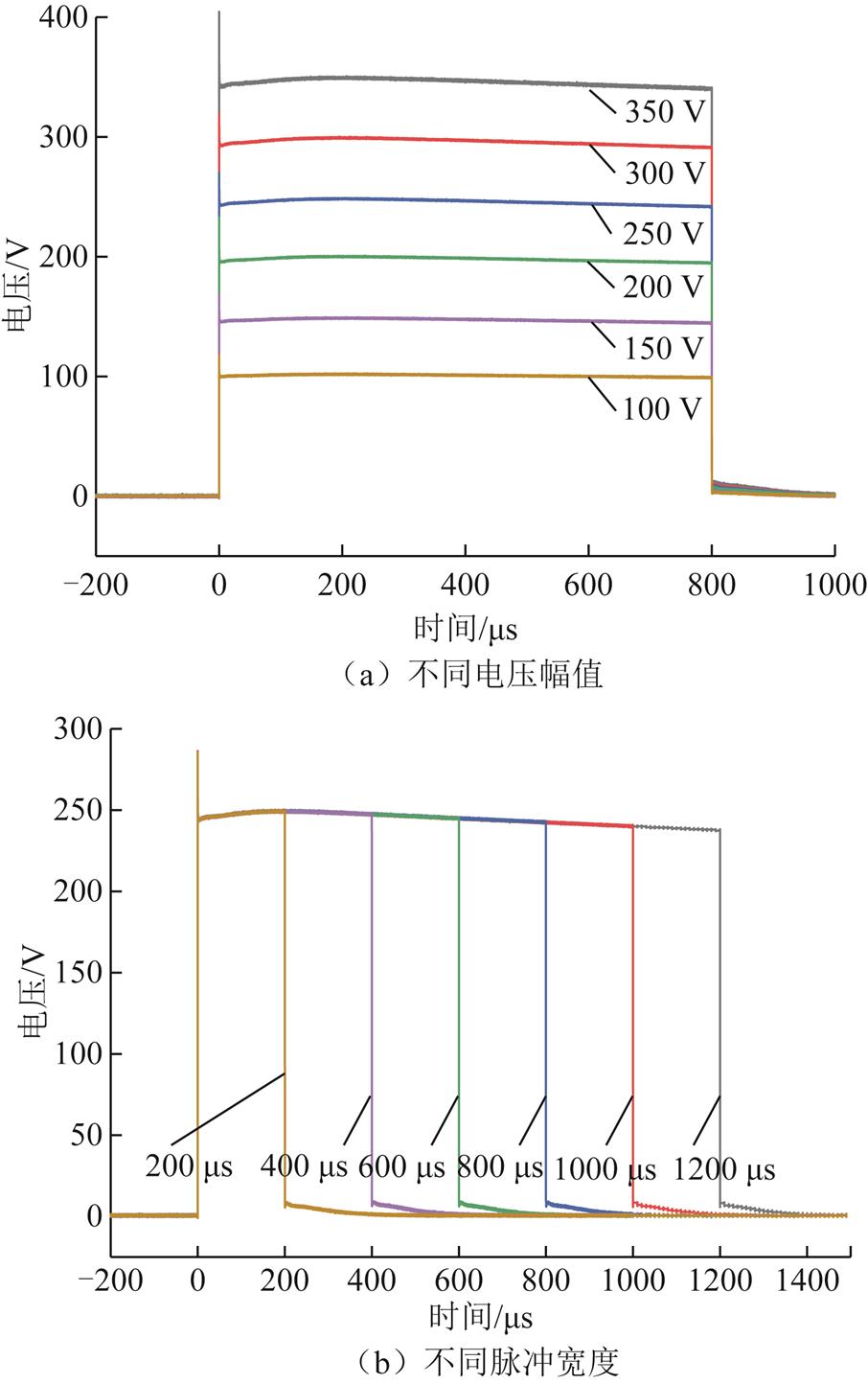
图2 不同幅值和宽度的脉冲电压波形
Fig.2 Pulse voltage waveforms of different amplitudes and widthes
使用Leica Application Suite X软件对拍摄的图像堆栈进行量化。在视野中选择40～50个细胞，取它们的荧光强度的平均值，然后减去脉冲施加前图像的荧光强度以去除背景信号，即可统计出脉冲电场作用期间和作用后细胞的平均荧光强度随拍摄时间的变化。
所有实验均独立重复3次，并使用OriginLab软件对实验数据进行统计分析。数据表示为平均值±标准偏差（mean±SD）。
由1.1节可知，在通过细胞荧光染色实验测量脉冲电场下形成的电穿孔面积时，式（8）右侧第二个分式中的m未知，因此需首先建立细胞荧光强度与细胞内结合的PI分子浓度间的关系（即求出二者的比值m）。本文对荧光显微镜系统进行校正，校正原理[22]为在细胞内结合的分子浓度饱和前，细胞内荧光强度与结合的PI分子浓度线性相关，细胞饱和结合时的荧光强度对应着能够饱和结合的PI分子的浓度。
为了获得细胞最大可达到的荧光强度，使用含有100 μmol/L PI染料的0.1%Triton X-100（一种快速裂解细胞组织的裂解液）对A375细胞进行化学裂解处理，然后在荧光显微镜下检测不同曝光时间（10.51、20.14、25.54、30.18、35.53、40.67 ms）下细胞的平均荧光强度，即细胞饱和荧光强度。
通过荧光强度校正将实验测得的PI染料荧光强度值转化为细胞内核酸结合的浓度，以获得二者的比例m，进而得到电穿孔面积。用0.1%Triton X-100通透细胞后，检测到的不同曝光时间下细胞的平均荧光强度校正曲线如图3所示。荧光强度与曝光时间呈线性关系，且实验曝光时间30.18 ms对应的饱和荧光强度约为50(au)。
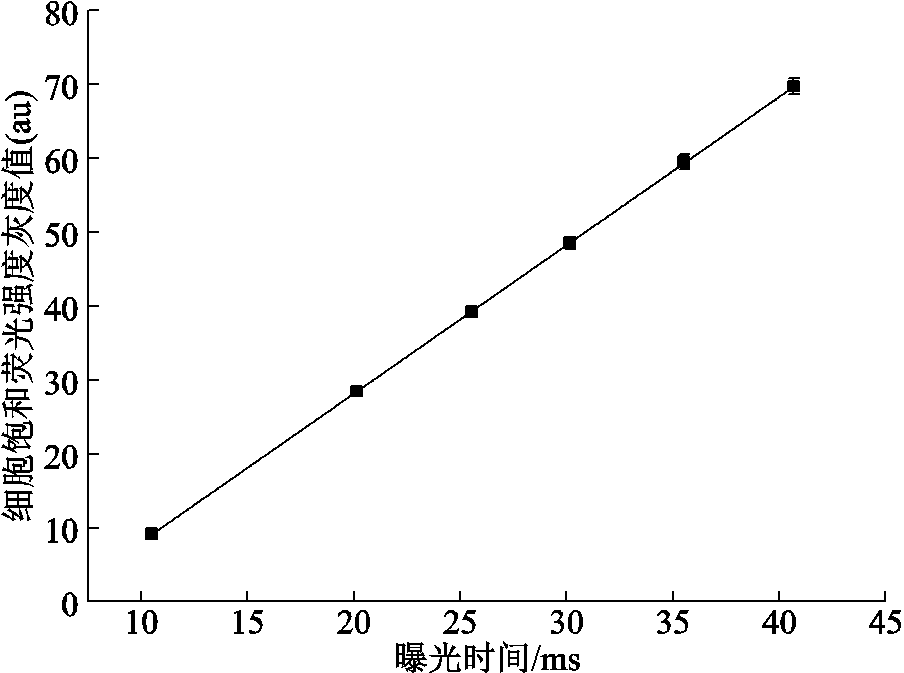
图3 荧光强度校正曲线
Fig.3 Fluorescence intensity calibration curve
假设人黑色素瘤细胞A375细胞（细胞半径近似为10 μm）内的结合位点为10 fmol[16,23]，即细胞内能够饱和结合的PI分子浓度为2.38 mmol/L。因此，在饱和荧光强度50(au)下对应的能够饱和结合的PI分子浓度为2.38 mmol/L，则测得的荧光强度与细胞内结合的PI分子浓度间的比例m为
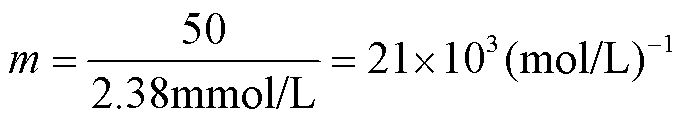（9）
在脉冲电场作用下，细胞荧光强度会发生变化，对不同脉冲电场强度和脉冲宽度下实时拍摄细胞图像的荧光强度进行量化，细胞平均荧光强度（含误差线）随时间的变化曲线如图4所示（“EP”表示脉冲电场开始作用）。从图4可知，脉冲电场参数（电场强度和脉冲宽度）越大，荧光强度曲线上移，进入到细胞内的PI分子越多，荧光强度越高，电穿孔效应越强。对于某一电场参数下的荧光强度变化曲线，荧光强度在脉冲作用时立即上升，随着观测时间的增加，荧光强度也随之增大，增大到某一值后，荧光强度不再上升，稳定在饱和值，这也说明了在设置的脉冲电场参数下，诱导的电穿孔是可逆的，即当脉冲电场撤去后，微孔能够慢慢恢复。
图4 不同脉冲电场参数下细胞平均荧光强度随时间变化曲线
Fig.4 Curves of the average fluorescence intensity of cells with time under different pulse field parameters
为得到不同脉冲电场参数下的电穿孔面积，对图4中各个脉冲电场参数下的细胞平均荧光强度曲线用函数Favg(t)=Fmax(1-e-t/τ)拟合，可得到荧光强度最大值Fmax（饱和值）和微孔恢复时间常数τ，如图5所示。
随着脉冲电场强度的增大，细胞荧光强度饱和值增大，意味着进入细胞内的PI分子增多；随着脉冲宽度增大，细胞荧光强度饱和值也增大，同样意味着进入细胞内的PI分子增多。
微孔恢复时间常数与细胞自身状态和细胞溶液有关，例如，随着细胞溶液电阻率的降低，微孔恢复时间常数降低；细胞骨架破坏，微孔恢复时间常数增大。脉冲电场一方面会破坏细胞膜结构，使微孔恢复时间常数增大；另一方面，在电穿孔过程中，细胞内物质泄漏，细胞溶液电导率增大，电阻率降低，使微孔恢复时间常数降低。在这两方面因素的共同作用下，微孔恢复时间常数在不同脉冲电场参数下有所不同。从图5a可以看出，改变脉冲电场强度时，随着电场强度增大，微孔恢复时间常数增大，可能是脉冲电场破坏细胞膜结构起主要作用；由图5b可知，当改变脉冲宽度时，微孔恢复时间常数与脉冲宽度无明显的依赖关系，可能是上述两种因素都发挥着重要作用并且互相影响。
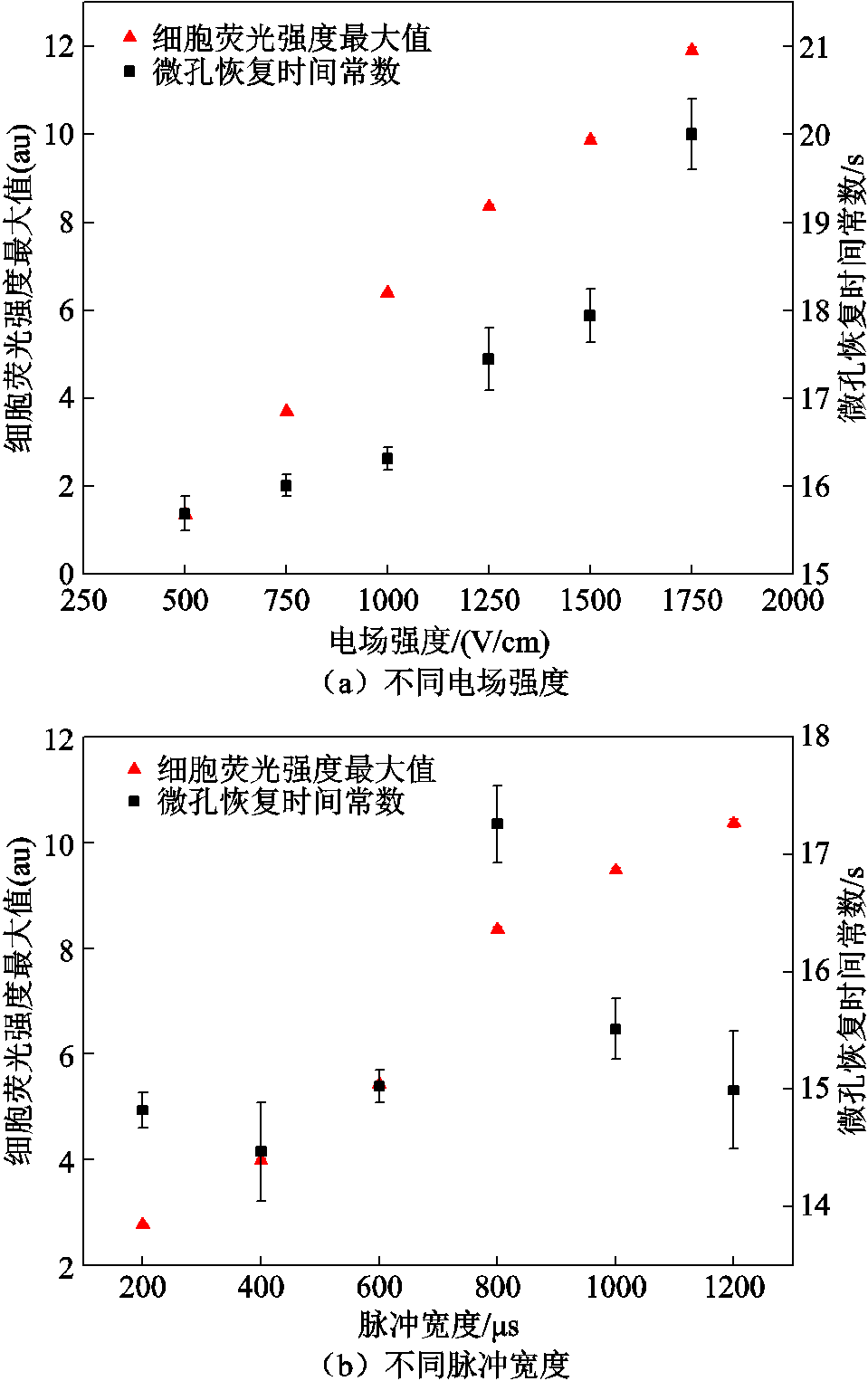
图5 不同脉冲电场参数下荧光强度最大值和微孔恢复时间常数
Fig.5 Maximum fluorescence intensity and pore recovery time constant under different pulsed electric field parameters
通过式（8）计算可得不同脉冲电场参数下的电穿孔面积，结果如图6所示。在改变脉冲电场强度和脉冲宽度时，计算得到的电穿孔面积数量级为10-15 m2，与细胞表面积之比近似为10-5，与文献[23]通过仿真估算的电穿孔面积比范围（10-3～10-5）相同。
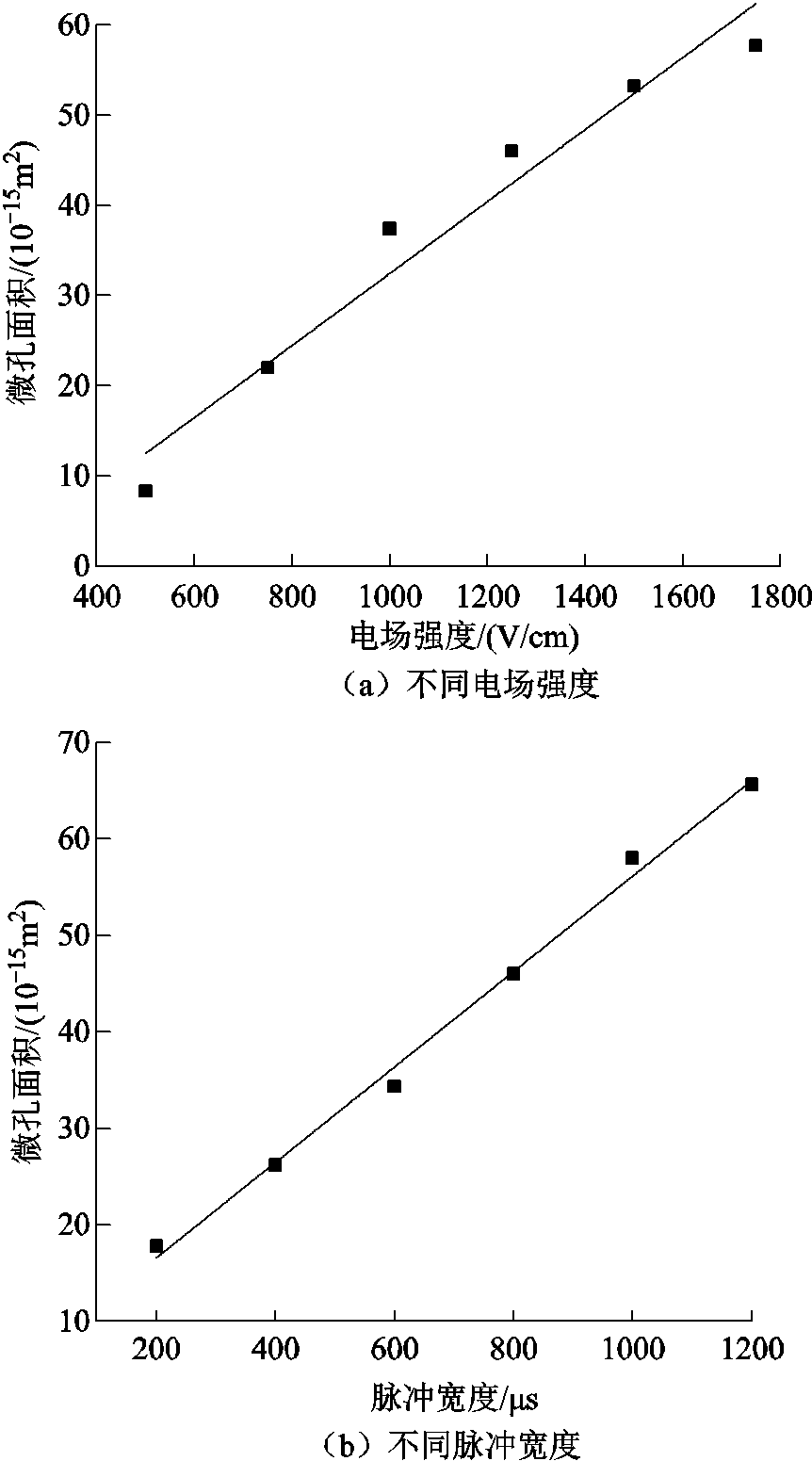
图6 不同脉冲电场参数下的电穿孔面积
Fig.6 Electroporation area under different pulsed electric field parameters
如图6a所示，当改变脉冲电场强度时，微孔面积随着电场强度的增大而增大，且二者近似呈线性关系，拟合函数关系式（R2=0.96）为
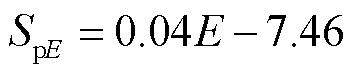（10）
式中，SpE为不同脉冲电场强度下的电穿孔面积，10-15 m2；E为脉冲电场强度，V/cm。
同样地，当改变脉冲电场宽度时，微孔面积随着脉冲宽度的增大而增大，如图6b所示，且二者近似呈线性关系，拟合函数关系式（R2=0.99）为
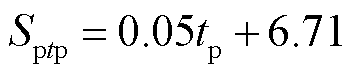（11）
式中，Sptp为不同脉冲宽度下的电穿孔面积，10-15 m2；tp为脉冲宽度，μs。
为了进一步分析电穿孔面积与脉冲电场强度和脉冲宽度两个参数间的综合关系，假设电穿孔面积与脉冲电场强度和脉冲宽度乘积有关，于是有
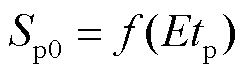（12）
式中，f (·)为描述脉冲电场强度和脉冲宽度乘积的函数，脉冲电场强度和脉冲宽度的乘积称为脉冲电冲击[24]。图7为电穿孔面积Sp0在不同脉冲电冲击Etp下的散点图，可以看出，电穿孔面积随着脉冲电冲击的增大而增大，且二者近似呈线性关系，拟合函数（R2=0.94）为
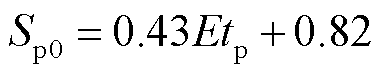（13）
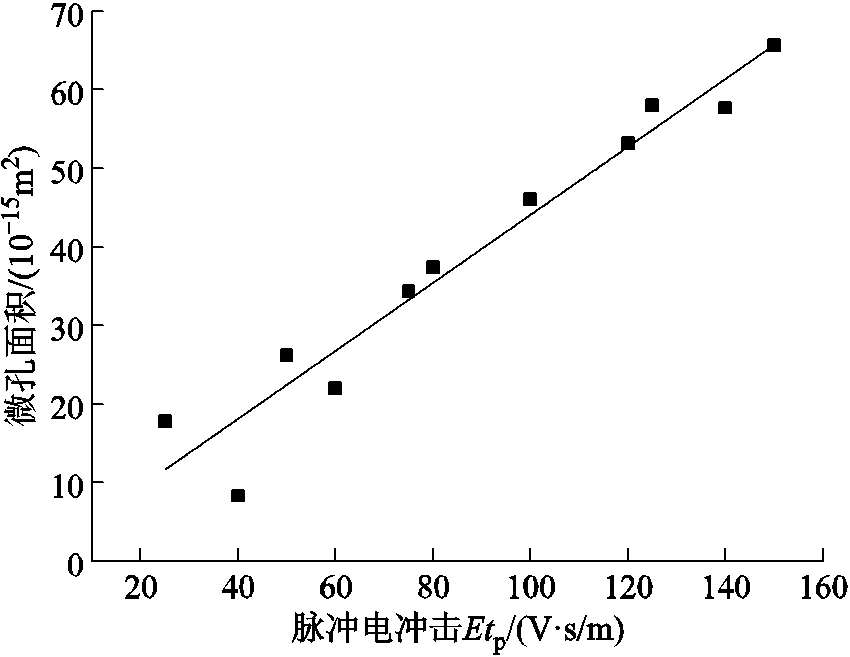
图7 电穿孔面积与脉冲电冲击Etp间的关系
Fig.7 Relationship between electroporation area and pulse electric impact Etp
从图7中可以看到，当脉冲电冲击较小时，微孔面积数值点距离拟合曲线较远，随着脉冲电冲击的增大，微孔面积的增加更趋近线性关系。
本文通过在脉冲电场下开展细胞荧光染色实验和数据处理，计算细胞膜上形成的电穿孔面积，并且计算出的电穿孔面积与文献中计算得到的数值在定量上接近。在利用荧光探针技术描述细胞电穿孔效应的过程中，大多数文献采用细胞荧光强度最大值[25]和电穿孔细胞百分比[7]等参量反映细胞膜的通透性。同样地，本文也可以用细胞荧光强度最大值反映细胞电穿孔效应，如图5所示，细胞荧光强度最大值随着脉冲电场参数（电场强度和脉冲宽度）的增大而增大。
虽然细胞荧光强度最大值可以反映电穿孔效应，但是仍难以建立其与电穿孔相关物理参数间的直接联系。于是，本文基于分子传输动力学，进一步通过细胞荧光强度最大值和微孔恢复时间常数计算得到电穿孔面积。其中，电穿孔面积与微孔数量和微孔半径有关，为细胞膜上各个区域形成的微孔面积的累积。微孔半径和数量是描述电穿孔效应的重要参量，对进出细胞膜的分子大小和多少有直接影响，如在电化学疗法、基因转染应用[26]中需要将化学药物和一些大分子传输到细胞内，因此，确定微孔半径和数量对应用电穿孔效应进行临床治疗具有重要意义。目前，通过高精度的检测设备（如高分辨率扫描电子显微镜和透射电镜等）可测量估计出细胞膜上形成的微孔大小，即微孔半径，假如利用本文的实验方法测量计算出细胞膜上形成的微孔面积，则可以估算出细胞膜上形成的微孔数量。因此，本文的实验方法也为进一步估计微孔数量提供了一种工具。
此外，有研究人员在仿真建模中也计算了细胞上形成的电穿孔面积，如刘红梅等[27]在脉冲电场强度为15 kV/cm、脉冲宽度为200 ns、脉冲数量为80个、频率为1 Hz时，利用COMSOL软件仿真出在A549细胞上形成的电穿孔面积约为2.257×10-10 m2，相对于细胞膜表面积的比例约为72%。吕彦鹏[14]在COMSOL中仿真出微孔面积比重随脉冲电场强度的变化，发现随着电场强度的增大，微孔面积比重增加，并用线性函数关系进行了拟合，与本文得到的微孔面积与脉冲电场强度的变化规律一致。但是，上述电穿孔面积的计算均是通过仿真方法，而本文通过实验和数据分析计算出细胞膜上形成的电穿孔面积，一方面可以与已有的仿真进行比较，从电穿孔面积角度为仿真的正确性提供新的验证思路；另一方面，后续可以联合仿真共同探究微孔面积与脉冲电场参数间的规律。
第2节的结果表明，细胞膜上形成的电穿孔面积与脉冲电场参数有关，且与脉冲电场强度、脉冲宽度和脉冲电冲击近似呈线性关系，下面从理论上对上述规律进行解释。
在脉冲期间，微孔形成速率[28-29]为
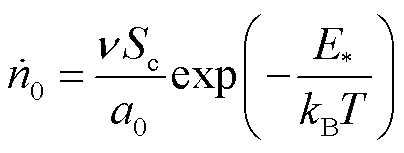（14）
式中，ν为脂质水平波动的频率；Sc为细胞膜面积；a0为每个脂质分子的面积；kB为玻耳兹曼常数；T为热力学温度；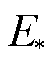
为从疏水孔转变为亲水孔所需的越过能垒。
根据微孔形成过程中的能量变化理论[30-31]可知，微孔越过能垒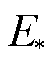由两个部分组成[32]：①没有电场情况时的能量屏障E0，取决于线张力和表面张力；②由电场诱导而引起的能量屏障的降低，与跨膜电压Vm有关。则微孔越过能垒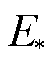可以表示为
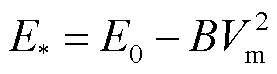（15）
式中，B为比例系数。假设细胞膜上单个微孔的面积为ap，将式（15）代入式（14）中，并进行时间积分，则在脉冲作用期间tp形成的微孔面积为
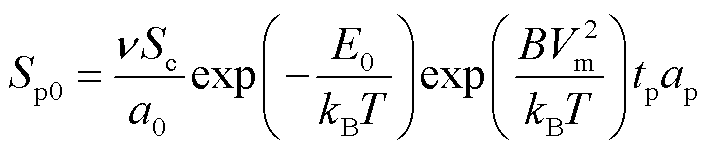（16）
从式（16）可以看出，微孔面积与跨膜电压Vm和脉冲宽度tp有关。
当脉冲宽度tp一定时，改变脉冲电场强度E时，从式（16）中可得
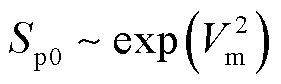（17）
式中，符号“～”表示线性关系。此外，细胞膜跨膜电压Vm与外加电场强度E的关系[33-34]为
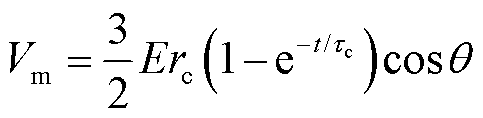（18）
式中，θ为细胞膜上任意一点法线方向与外加反向电场之间的夹角；
为细胞半径；τc为细胞膜充电时间常数，大约为75 ns[20,35]，而本文使用的脉冲宽度为百微秒级，远大于细胞膜充电时间常数，因此细胞膜已充电完成，式（18）可简化为
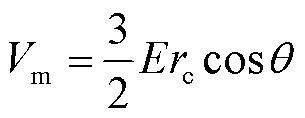（19）
于是，细胞膜跨膜电压的增加取决于脉冲电场强度。而当脉冲电场作用时，跨膜电压在脉冲施加后先立即增大而后稳定，不同电场强度下稳定后的跨膜电压相差很小[11,36]，因此，在较小的跨膜电压（电场强度）变化范围内，式（17）可近似为
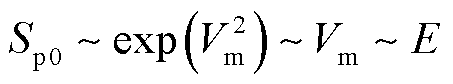（20）
即电穿孔面积与电场强度近似呈线性关系。
当脉冲电场强度E一定、改变脉冲宽度tp时，由式（19）可知，细胞膜上的跨膜电压不变，因此，微孔越过能垒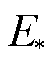不变，微孔形成速率不变，单位时间内形成的微孔数量不变。但是由式（16）可知，在脉冲期间累计形成的微孔数量会随着脉冲作用时间线性增加，于是微孔面积与脉冲作用时间tp（即脉冲宽度）呈线性关系，即
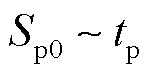（21）
综合来看，结合式（20）和式（21），当脉冲电场强度和脉冲宽度均改变时，电穿孔面积的变化规律为
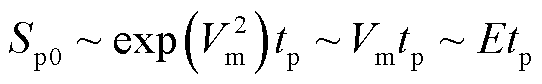（22）
因此，电穿孔面积与脉冲电场强度和脉冲宽度的乘积（脉冲电冲击）呈线性关系。
经过上述分析，电穿孔面积随着脉冲电场强度、脉冲宽度和脉冲电冲击的增大而增大，且均呈线性关系，定性上，通过这些理论分析得到的规律与实验得到的规律是一致的，也反映出本文电穿孔面积测量方法的合理性。通过电穿孔面积定量和定性上的比较，可以评估本文通过实验测量计算细胞电穿孔面积方法和结果的准确性。此外，在应用脉冲电场治疗肿瘤时，根据脉冲电场参数与形成的电穿孔面积的关系，可为提高治疗有效性提供指导。
对于本文使用的脉冲电场，从细胞荧光强度曲线可以发现，荧光强度在脉冲电场作用后先增加后达到饱和，发生的电穿孔为可逆的，而且若要用函数Favg(t)=Fmax(1-e-t/τ)进行拟合，也需满足细胞荧光强度有饱和值，因此本文的实验方法适用于可逆电穿孔领域，如电化学治疗和基因转染等应用。利用本文的实验方法，可测量计算出细胞在电场作用下形成的微孔面积。此外，根据本文得到的脉冲电场与电穿孔面积间的规律，可为脉冲电场治疗提供指导，如在电化学治疗中，线性增大脉冲电场参数（电场强度和脉冲宽度），电穿孔面积增大，进入到细胞内的药物更多，治疗更具有效性。
本文基于分子传输动力学，通过开展PI分子荧光染色实验，测量出在脉冲电场作用下形成的细胞膜电穿孔面积，并研究了脉冲电场参数（电场强度和脉冲宽度）对电穿孔面积的影响规律，得出以下结论：
1）随着脉冲电场参数（电场强度和脉冲宽度）增大，细胞荧光强度增大，电穿孔效应增强。
2）提出了一种直接表征电穿孔效应的参量及其实验测量方法，对细胞荧光强度曲线进行数据处理，可计算出脉冲期间形成的电穿孔面积，且实验测量的电穿孔面积数值与已有文献数值接近，证实了该方法的可行性。
3）电穿孔面积随着脉冲电场强度、脉冲宽度和脉冲电冲击的增大而线性增大，并从理论上进行了解释，得到的规律能够进一步为临床治疗提供指导。
参考文献
[1] Kinosita K, Tsong T Y. Formation and resealing of pores of controlled sizes in human erythrocyte membrane[J]. Nature, 1977, 268(5619): 438-441.
[2] Zimmermann U, Pilwat G, Riemann F. Dielectric breakdown of cell membranes[J]. Biophysical Journal, 1974, 14(11): 881-899.
[3] 姚陈果, 宁郡怡, 刘红梅, 等. 微/纳秒脉冲电场靶向不同尺寸肿瘤细胞内外膜电穿孔效应研究[J]. 电工技术学报, 2020, 35(1): 115-124. Yao Chenguo, Ning Junyi, Liu Hongmei, et al. Study of electroporation effect of different size tumor cells targeted by micro-nanosecond pulsed electric field[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 115-124.
[4] 米彦, 李盼, 刘权, 等. 纳秒脉冲电场联合多壁碳纳米管对皮肤癌细胞活性的剂量效应研究[J]. 电工技术学报, 2019, 34(22): 4849-4857. Mi Yan, Li Pan, Liu Quan, et al. Dose effect of the activity of skin cancer cells treated by nanosecond pulsed electric field combined with multi-walled carbon nanotubes[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4849-4857.
[5] Polajžer T, Dermol-Černe J, Reberšek M, et al. Cancellation effect is present in high-frequency reversible and irreversible electroporation[J]. Bioelectrochemistry, 2020, 132: 107442.
[6] Sadik M M, Li Jianbo, Shan J W, et al. Quantification of propidium iodide delivery using millisecond electric pulses: experiments[J]. Biochimica et Biophysica Acta (BBA)-Biomembranes, 2013, 1828(4): 1322-1328.
[7] Dermol J, Miklavčič D. Predicting electroporation of cells in an inhomogeneous electric field based on mathematical modeling and experimental CHO-cell permeabilization to propidium iodide determination[J]. Bioelectrochemistry, 2014, 100: 52-61.
[8] 米彦, 吴晓, 徐进, 等. 细胞膜力学性能对电穿孔影响的仿真研究[J]. 电工技术学报, 2022, 37(17): 4326-4334, 4400. Mi Yan, Wu Xiao, Xu Jin, et al. Simulation study on the effect of cell membrane mechanical properties on electroporation[J]. Transactions of China Electrote-chnical Society, 2022, 37(17): 4326-4334, 4400.
[9] 程显, 陈硕, 吕彦鹏, 等. 纳秒脉冲作用下核孔复合体影响细胞核膜电穿孔变化的仿真研究[J]. 电工技术学报, 2021, 36(18): 3821-3828. Cheng Xian, Chen Shuo, Lü Yanpeng, et al. Simulation study on the effect of nuclear pore complexes on cell electroporation under nanosecond pulse[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3821-3828.
[10] 胡亚楠, 包家立, 朱金俊, 等. 纳秒电脉冲对肝脏组织不可逆电穿孔消融区分布的时域有限差分法仿真[J]. 电工技术学报, 2021, 36(18): 3841-3850. Hu Yanan, Bao Jiali, Zhu Jinjun, et al. The finite difference time domain simulation of the distribution of irreversible electroporation ablation area in liver tissue by nanosecond electrical pulse[J]. Transactions ofChina Electrotechnical Society, 2021, 36(18): 3841-3850.
[11] DeBruin K A, Krassowska W. Modeling electroporation in a single cell. Ⅰ. Effects of field strength and rest potential[J]. Biophysical Journal, 1999, 77(3): 1213-1224.
[12] Liu Hongmei, Yao Chenguo, Mi Yan, et al. Multi-parameter analysis in single-cell electroporation based on the finite element model[C]//2016 IEEE International Power Modulator and High Voltage Conference (IPMHVC), San Francisco, CA, USA, 2016: 364-370.
[13] 刘红梅, 董守龙, 宁郡怡, 等. 纳秒脉冲高频透膜效应优先杀伤化疗抗性肿瘤细胞的仿真与实验研究[J]. 电工技术学报, 2019, 34(22): 4839-4848. Liu Hongmei, Dong Shoulong, Ning Junyi, et al. Simulation and experimental study on preferential killing of chemoresistance tumor cells induced by the high-frequency permeation effect of nanosecond pulse field[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4839-4848.
[14] 吕彦鹏. 协同脉冲电场增强不可逆电穿孔组织消融疗效的电学机理与实验研究[D]. 重庆: 重庆大学, 2019.
[15] 米彦, 徐进, 刘宏亮, 等. 基于网格传输网络模型的高频纳秒脉冲串作用下单细胞穿孔特性仿真[J]. 电工技术学报, 2018, 33(18): 4217-4230. Mi Yan, Xu Jin, Liu Hongliang, et al. Simulation on perforation features in a single-cell system exposed to high-frequency nanosecond pulse bursts based on mesh transport network model[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4217-4230.
[16] 李成祥, 李新皓, 柯强, 等. 纳/微秒复合脉冲提高细胞电融合效率的仿真与实验研究[J]. 电工技术学报, 2022, 37(6): 1522-1532. Li Chengxiang, Li Xinhao, Ke Qiang, et al. Simulation and experimental research on improving the efficiency of cell electrofusion by nano-microsecond pulsed electric fields[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1522-1532.
[17] Batista Napotnik T, Miklavčič D. In vitro electroporation detection methods-an overview[J]. Bioelectrochemistry, 2018, 120: 166-182.
[18] Pucihar G, Kotnik T, Miklavčič D, et al. Kinetics of transmembrane transport of small molecules into electropermeabilized cells[J]. Biophysical Journal, 2008, 95(6): 2837-2848.
[19] Neumann E, Toensing K, Kakorin S, et al. Mechanism of electroporative dye uptake by mouse B cells[J]. Biophysical Journal, 1998, 74(1): 98-108.
[20] Djuzenova C S, Zimmermann U, Frank H, et al. Effect of medium conductivity and composition on the uptake of propidium iodide into electropermeabilized myeloma cells[J]. Biochimica et Biophysica Acta (BBA) - Biomembranes, 1996, 1284(2): 143-152.
[21] Yao Chenguo, Dong Shoulong, Zhao Yajun, et al. High-frequency composite pulse generator based on full-bridge inverter and soft switching for biological applications[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(5): 2730-2737.
[22] Kennedy S M, Ji Z, Hedstrom J C, et al. Quantification of electroporative uptake kinetics and electric field heterogeneity effects in cells[J]. Biophysical Journal, 2008, 94(12): 5018-5027.
[23] Sukhorukov V L, Djuzenova C S, Frank H, et al. Electropermeabilization and fluorescent tracer exchange: the role of whole-cell capacitance[J]. Cytometry, 1995, 21(3): 230-240.
[24] Schoenbach K H, Joshi R P, Beebe S J, et al. A scaling law for membrane permeabilization with nanopulses[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2009, 16(5): 1224-1235.
[25] Dermol-Černe J, Miklavčič D, Reberšek M, et al. Plasma membrane depolarization and permeabilization due to electric pulses in cell lines of different excitability[J]. Bioelectrochemistry, 2018, 122: 103-114.
[26] Geboers B, Scheffer H J, Graybill P M, et al. High-voltage electrical pulses in oncology: irreversible electroporation, electrochemotherapy, gene electrotransfer,electrofusion, and electroimmunotherapy[J]. Radiology, 2020, 295(2): 254-272.
[27] Liu Hongmei, Yao Chenguo, Zhao Yajun, et al. In vitro experimental and numerical studies on the preferential ablation of chemo-resistant tumor cells induced by high-voltage nanosecond pulsed electric fields[J]. IEEE Transactions on Bio-Medical Engineering, 2021, 68(8): 2400-2411.
[28] Glaser R W, Leikin S L, Chernomordik L V, et al. Reversible electrical breakdown of lipid bilayers: formation and evolution of pores[J]. Biochimica et Biophysica Acta (BBA)-Biomembranes, 1988, 940(2): 275-287.
[29] Taupin C, Dvolaitzky M, Sauterey C. Osmotic pressure induced pores in phospholipid vesicles[J]. Biochemistry, 1975, 14(21): 4771-4775.
[30] Kotnik T, Rems L, Tarek M, et al. Membrane electroporation and electropermeabilization: mechanisms and models[J]. Annual Review of Biophysics, 2019, 48: 63-91.
[31] Chen C, Smye S W, Robinson M P, et al. Membrane electroporation theories: a review[J]. Medical and Biological Engineering and Computing, 2006, 44(1): 5-14.
[32] Muralidharan A, Rems L, Kreutzer M T, et al. Actin networks regulate the cell membrane permeability during electroporation[J]. Biochimica et Biophysica Acta Biomembranes, 2021, 1863(1): 183468.
[33] Kinosita K, Ashikawa I, Saita N, et al. Electroporation of cell membrane visualized under a pulsed-laser fluorescence microscope[J]. Biophysical Journal, 1988, 53(6): 1015-1019.
[34] Dimova R, Riske K A, Aranda S, et al. Giant vesicles in electric fields[J]. Soft Matter, 2007, 3(7): 817-827.
[35] Ahamed M K, Abu Sayem Karal M, Ahmed M, et al. Kinetics of irreversible pore formation under constant electrical tension in giant unilamellar vesicles[J]. European Biophysics Journal, 2020, 49(5): 371-381.
[36] 贡凌宇. 基于微流控芯片的单细胞电穿孔仿真与实验研究[D]. 重庆: 重庆大学, 2017.
Abstract In the field of electrobiology, simulation and experimental methods can be used to study the cell electroporation effect under pulsed electric field. In simulation, parameters such as transmembrane voltage, current density, pore density, pore radius and pore area are usually used to characterize the electroporation effect. In the experiment, the killing effect or the overall situation of the electric field on the cells is usually characterized macroscopically, which is not equivalent to the specific parameters such as the number and size of the pores formed, and it is not easy to establish a close relationship between simulation and experiment. Therefore, the electroporation area of cell membrane, a new characterization parameter to directly measure the electroporation effect, and its experimental measurement method are proposed in this paper.
Firstly, the measurement principle of cell electroporation area was analyzed based on the molecular transport dynamics, and it was found that the electroporation area could be measured and calculated by cell fluorescence experiment. Then, the fluorescent molecular staining experiment was carried out based on the above principle, the fluorescence intensity changes of cells under the electric field were captured in real time under the fluorescence microscope. Before carrying out cell electroporation experiments, the cell fluorescence intensity needs to be corrected to obtain the relationship between the cell fluorescence intensity and the intracellular concentration of propidium iodide ions. Next, the maximum cell fluorescence intensity and the pore recovery time constant were extracted from the fluorescence intensity curve under the action of the electric field, from which the electroporation area of cell membrane formed during the pulse could be calculated. Finally, experiments were carried out under different pulsed electric field parameters (field strength and pulse width) to study the relationship and law between cell electroporation area and pulsed electric field parameters, and the obtained laws were analyzed and explained theoretically.
Under the pulsed electric field parameters selected in this paper, the electroporation area calculated by the cell fluorescent staining experiment is in the order of 10-15 m2, which is quantitatively close to the value calculated in the literature. Under different pulse electric field parameters, with the increase of pulse electric field parameters (field strength and pulse width), the fluorescence intensity of cells increases, the fluorescence intensity curve moves up, and the electroporation effect is enhanced. Moreover, the calculated electroporation area increases with the increase of pulse field strength, pulse width and pulse electric shock, and all have a linear relationship. The obtained law is analyzed in combination with theory, and the laws obtained in this paper are qualitatively consistent with those in the existing literature. By comparing the electroporation area between this paper and the existing conclusions quantitatively and qualitatively, the accuracy of the method and results of calculating the cell electroporation area by experimental measurements can be evaluated. According to these laws, it can provide guidance for the pulsed electric field treatment. For example, in the electrochemotherapy, the pulsed electric field parameters (field strength and pulse width) are increased linearly, the electroporation area is increased, and more drugs enter the cells, and the treatment is more effective.
keywords：Pulsed electric field, electroporation effect, electroporation area, molecular transport, fluorescent staining experiment
国家自然科学基金项目（52077022, 51477022）和“111”引智项目（BP0820005）资助。
收稿日期 2022-05-10
改稿日期 2022-09-26
DOI: 10.19595/j.cnki.1000-6753.tces.220786
中图分类号：TM836；Q64
吴 晓 女，1996年生，硕士研究生，研究方向为高电压新技术。E-mail：20191102061t@cqu.edu.cn
米 彦 男，1978年生，教授，博士生导师，研究方向为高电压新技术。E-mail：miyan@cqu.edu.cn（通信作者）
（编辑 李 冰）