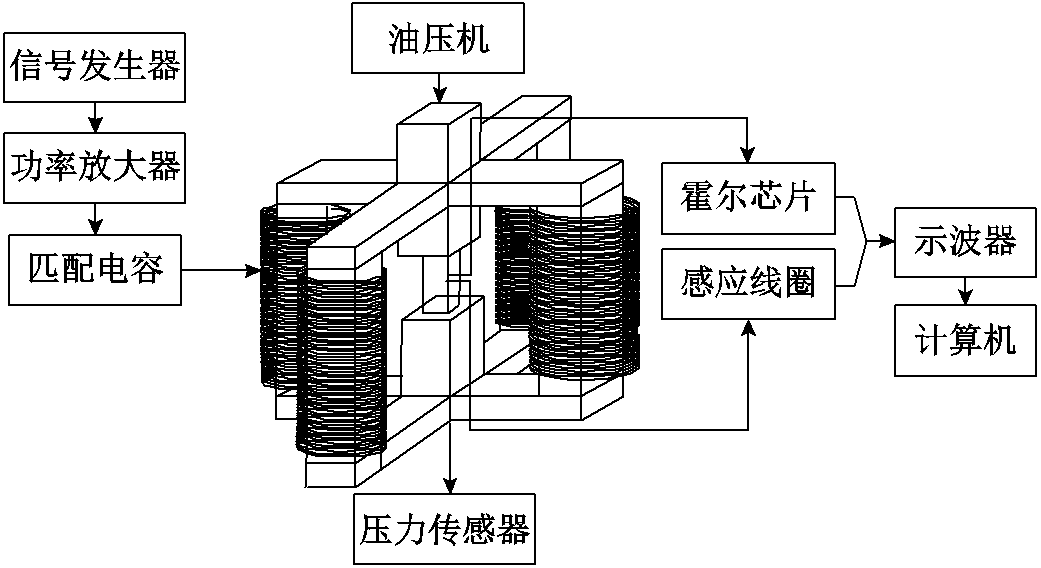
图1 测试系统原理
Fig.1 Test system schematic
摘要 高频大功率磁致伸缩换能器件的输出特性与其所受的压应力密切相关,施加一定的压应力可以提高其核心元件磁致伸缩棒材的磁致伸缩系数,增大器件输出功率,而不合适的压应力会使得器件性能恶化。该文搭建了磁致伸缩材料高频磁特性测试系统,测量了磁致伸缩材料铁镓合金棒材在不同激励条件下(变压应力σ、变励磁频率f和不同磁场强度H)的动态磁特性曲线。结果表明,当频率与磁场强度一定时,随着压应力的增加,高频磁特性中振幅磁导率减小、动态磁滞回线纵向变扁、磁能损耗减少。针对传统磁滞模型无法计及压应力影响的问题,在现有静态J-A磁滞模型的基础上,计及涡流损耗和剩余损耗,并采用分数阶导数修正高频涡流场表达式,建立了高频动态磁滞模型,再引入压应力相关项修正模型参数,得到与外施压应力相关的改进高频动态磁滞模型。将实验数据与模型计算结果进行对比分析,结果表明,在变压应力和高频激励条件下,模型计算结果与实测值吻合较好,最大误差为5.86%,平均误差为3.29%,验证了模型的准确性与可行性。
关键词:铁镓合金棒材 压应力 高频磁特性 改进的磁滞模型
磁致伸缩材料作为一种新型智能材料,能量密度高、耦合系数大,且兼具优良的应力灵敏性、磁致伸缩特性和力学性能,可广泛应用于换能器、传感器、精密机械控制等高新技术领域[1-2]。以磁致伸缩材料铁镓合金棒材为核心元件制成的高频大功率磁致伸缩器件,需要棒材工作在一定的压应力下以提高磁致伸缩应变、优化输出特性;而不合适的压应力会使得器件性能恶化。传统的磁滞模型难以准确地模拟出材料在变压应力条件下的磁特性[3],因此,有必要建立一种计及变压应力条件的铁镓合金棒材高频动态磁滞模型。但是,一方面由于高频条件下测试装置磁能损耗大,加之铁镓合金磁导率低,以往的实验平台[4]无法达到较高的磁通密度,难以获取建立模型需要的大量实验数据;另一方面,静态磁滞模型未考虑到铁磁材料的高频涡流损耗与剩余损耗,经修正后的动态模型[5]忽略了高频趋肤效应对材料内部磁场分布的影响,不适用于研究材料高频磁特性;此外,由于铁镓合金材料具有应力敏感性,在施加压应力时势必会引起棒材内磁场变化,一般的方法是在棒材内部有效场计算中引入应力相关项[6],但这会引起模型求解复杂化。
目前,对于磁性材料的磁滞特性模型研究主要分为两类:一是基于磁滞理论建立的Preisach模型、神经网络磁滞模型,这一类模型通过纯数学手段描述材料磁滞特性;二是基于磁畴理论建立的物理与数学相结合的J-A磁滞模型、自由能模型。其中,J-A磁滞模型是一种依据磁化机理建立的标量磁滞模型,具有稳定、准确、模型参数较少、物理含义明确,以及磁滞回线形状、大小与模型参数紧密相关等优点,因此在铁心磁滞建模领域得到了广泛应用。
文献[7]在变温条件下测试电工钢材料磁滞回线并提取J-A模型相关参数,研究电工钢材料的温度依赖性,通过将各参数表示为温度的函数,将热效应纳入现有模型,简化了模型识别过程。文献[8]基于磁弹性效应和J-A模型理论建立外施应力下的钢材磁特性模型,研究应力对钢材磁滞回线的影响,并采用Powell算法确定模型参数的应力依赖性,研究结果可较为准确地评估钢材所受应力。文献[9]基于考虑机械应力和晶体织构效应的多尺度模型,提出了J-A模型计及压应力条件下的优化形式,采用多尺度方法修正无磁滞磁化强度Man和损耗系数k,并利用实验结果进行参数识别,所得出的优化模型与实验结果吻合度较高。但上述研究建立的模型均为静态磁滞模型,仅适用于描述静态、准静态条件下材料的磁滞特性。
文献[10-11]基于能量守恒定律,考虑高频条件下电工钢材料的涡流损耗和剩余损耗,建立了计及直流偏置时变压器铁心材料磁化特性的高频动态J-A模型,模型计算结果具有通用性,但该研究没有研究变压应力条件下电工材料的磁滞特性。文献[12]通过引入频率、压应力相关项对J-A模型参数进行修正,较为准确地模拟出频率、压应力对变压器铁心硅钢片B-H曲线的影响。但由于该研究所基于的磁滞模型为静态模型,且实验测试频率小于1 kHz,无法用于准确地模拟更高频率(如超声应用)励磁条件下磁致伸缩材料的磁滞特性。
本文首先基于磁损耗理论搭建磁致伸缩棒材高频磁特性测试平台,测量磁致伸缩材料铁镓合金棒材在不同应力和励磁条件下的动态磁特性曲线并分析磁参数的变化趋势;然后在现有静态J-A磁滞模型的基础上,基于损耗分离理论建立计及涡流场和剩余损耗场的铁镓合金棒材动态J-A模型,采用分数阶导数修正高频涡流场表达式,使建立的动态磁滞模型适用于高频条件;最后基于实验测试数据并利用Matlab编写的J-A模型参数辨识程序求得不同压应力条件下的模型参数值,分析压应力对模型参数的影响,将各参数看作外施压应力σ的多项式函数,得到与外施压应力相关的改进高频动态磁滞模型。
为获取高频变压应力条件下铁镓合金棒材磁特性相关数据,本文设计了一种棒状铁镓合金高频磁特性测试装置。由于随着频率的升高,测试装置磁路损耗增加、绕组趋肤效应和邻近效应影响加剧,导致励磁线圈等效阻抗增大、励磁电流难以施加,加之铁镓合金棒磁导率低,使得被测棒材内部难以获得数值较高的磁通密度。为了解决上述问题,首先,基于磁损耗理论选取磁心损耗较低的高频导磁材料搭建磁路;然后,以提高电磁转化效率为目标,采用受高频趋肤效应和邻近效应影响小的利兹线绕制励磁线圈;最后,依据串联谐振原理进行阻抗匹配。测试装置整体采用四线圈结构,以提高励磁磁场大小,此外,为使压应力可传递到棒材上,上极头被设计为可上下自由活动。
本实验所搭建的测试系统原理如图1所示,测试平台可完成高频磁场施加、压应力加载、信号检测及数据处理功能。测试平台实物如图2所示。

图1 测试系统原理
Fig.1 Test system schematic

图2 测试系统实物
1—功率放大器 2—信号发生器 3—示波器 4—磁通计 5—油压机 6—高频磁特性测试装置(含磁路、励磁线圈、匹配电容、压力传感器) 7—霍尔芯片电源
Fig.2 Physical view of the test platform
高频磁场施加由信号发生器、功率放大器、匹配电容和所设计的高频磁特性测试装置完成。通过功率放大器放大并输出由信号发生器生成的高频电压,通过匹配电容加载到励磁线圈上以产生高频磁场,经高频导磁材料制成的磁路导入被测棒材中。应力的施加由油压机、压力传感器完成。通过油压机给棒材施加一定的压应力并在压力传感器上读取压应力数值。
平台采用感应线圈法和A1321LUA型霍尔芯片完成信号检测,当磁场改变时,缠绕在被测棒材上的感应线圈中的磁通量也会随之变化,由法拉第电磁感应定律得
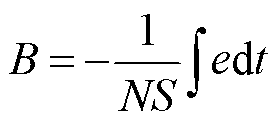 (1)
(1)
式中,B为磁通密度;N为感应线圈匝数;S为棒材横截面积;e为感应电压;t为时间。
霍尔芯片用来采集棒材上的磁场强度,由霍尔效应可知
![]() (2)
(2)
式中,H为磁场强度;I为芯片电流;UH为芯片感应电压;RH为霍尔系数;D为芯片厚度;μ0为真空磁导率。
感应线圈与霍尔芯片输出的信号由示波器与磁通计采集,并将数据导入计算机中,通过Matlab软件绘制H-t、B-t、B-H和M-H曲线(M为磁化强度)。
实验测试样品为叠堆结构铁镓合金棒材,叠片厚度为1 mm、高度为20 mm,棒材横截面尺寸为10 mm×10 mm。考虑到棒材磁特性与材料所受压应力σ、频率f、棒材上磁场强度H密切相关,本文采用控制变量法分别在不同压应力、频率、磁场强度下进行大量测试,结合铁镓合金棒材在水声频段的具体应用背景,实验测试压应力范围为0~60 MPa,频率范围为1~9 kHz,调节外加磁场,控制棒材上磁场强度H的范围为1 000~6 000 A/m,以此来绘制出变压应力条件下铁镓合金棒材在不同频率f和不同磁场强度H下的动态磁特性曲线。
频率f =5 kHz、磁场强度H=5 000 A/m时,不同压应力条件下铁镓合金的B-H曲线如图3所示。可知当磁场强度一定时,随着外施压应力提高,动态磁滞回线纵向变低,产生的磁通密度幅值降低,剩磁减小,磁能损耗降低。由此可见,外施压应力对材料磁畴壁移动和磁畴转动等行为有明显影响,这些影响可通过J-A模型参数变化体现出来。
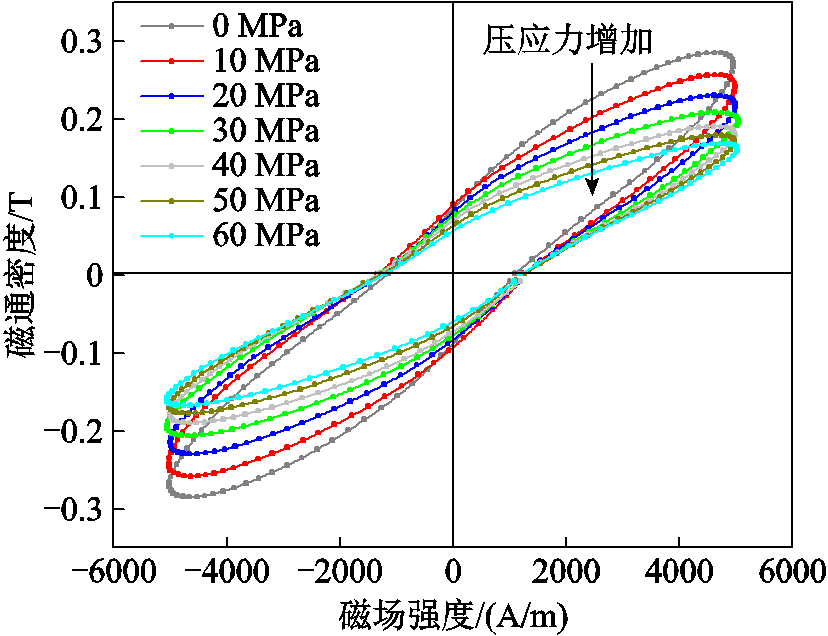
图3 不同压应力下的动态磁滞回线
Fig.3 Dynamic hysteresis lines under different compressive stresses
磁导率是表征材料动态磁特性的重要参数,图4所示为铁镓合金棒材在5 kHz频率下、磁场强度为5 000 A/m时,样品的振幅磁导率及实、虚部磁导率随压应力变化的曲线。从图4中可以发现,在外施压应力从0 MPa变化到60 MPa的过程中,样品的振幅磁导率及实、虚部磁导率随压应力的增大而减小,该样品振幅磁导率减小了40.89%(由0 MPa时的45.65 H/m下降到60 MPa的26.98 H/m)。在磁场强度一定时,随着振幅磁导率减小,铁镓合金棒材中产生的磁通密度幅值Bm相应减小,B-H回线纵向变低,棒材的剩磁和损耗减少。
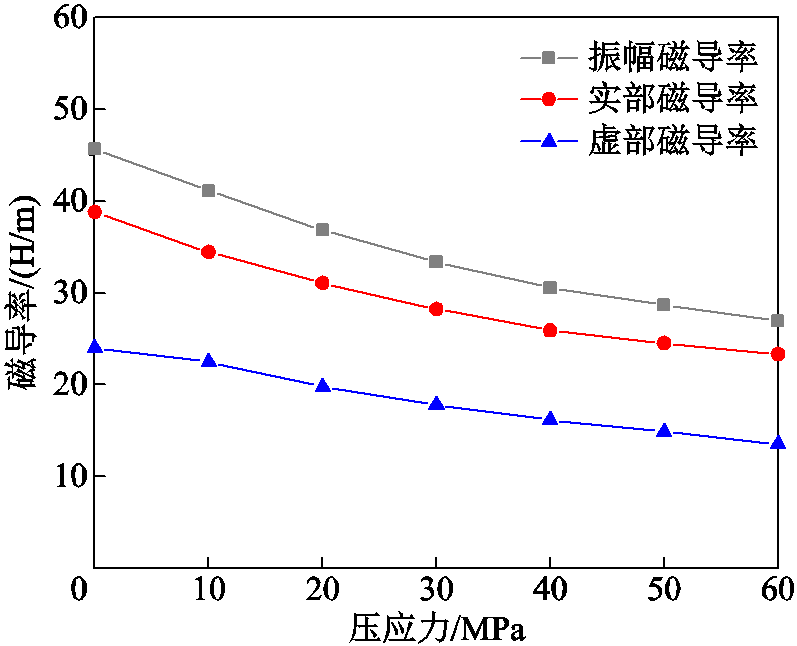
图4 振幅磁导率和实部、虚部磁导率与压应力关系
Fig.4 Relationship between amplitude permeability and real and imaginary part permeability and compressive stress
剩磁表示磁场减弱到零后,铁镓合金棒材中所剩的磁通密度大小,材料的磁能损耗则与磁滞回线的面积相关。图5所示为铁镓合金棒材在频率为5 kHz下、磁场强度为5 000 A/m时,剩磁Br及单位质量磁能损耗随外施压应力变化的曲线。从图5可以发现,随着外施压应力的增加,剩磁减少了38.04%(由0 MPa时的0.092 T减小到60 MPa时的0.057 T),磁能损耗减少了41.55%(由0 MPa时的862.21 W/kg降至60 MPa的503.96 W/kg),磁滞效应减弱。
由以上实验结果分析可知:随着压应力的增加,铁镓合金棒材磁导率减小,导磁性下降,材料的磁化过程越来越困难,但施加较大的压应力可以在磁场强度一定的情况下降低铁镓合金棒材磁损耗,同时剩磁降低,磁滞效应减弱。因此,为准确地描述铁镓合金棒材高频磁特性随外施压应力改变而变化的情况,需要建立一种计及压应力变化的高频动态磁滞模型。
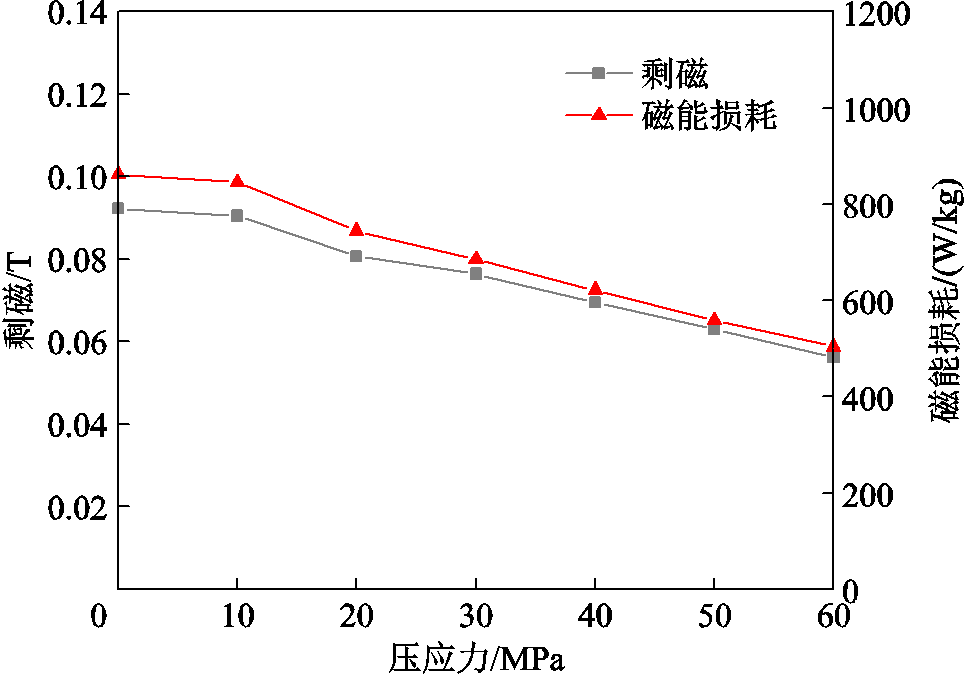
图5 剩磁、磁能损耗与压应力关系
Fig.5 Relationship between remanent magnetism and compressive stress
经典的J-A模型将磁畴磁化过程分解成不可逆分量Mirr和弹性分量Mrev,采用朗之万函数描述磁化强度M与磁场强度H之间的关系。在恒温条件下模型可表述为
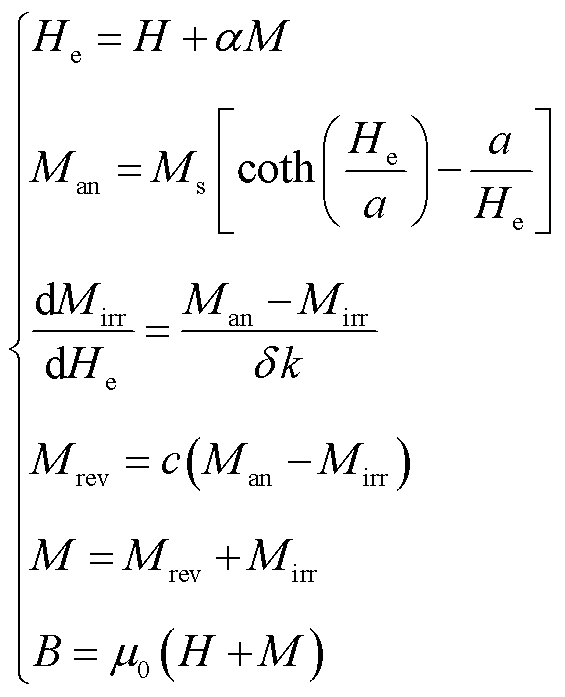 (3)
(3)
式中,Man为无磁滞磁化强度;Ms为饱和磁化强度;He为有效磁场强度;α为耦合系数;a为磁畴壁相互作用系数;k为损耗系数;c为不可逆损耗系数;δ=sign(dH/dt),sign为符号函数。
磁化强度M与磁场强度H的微分方程为
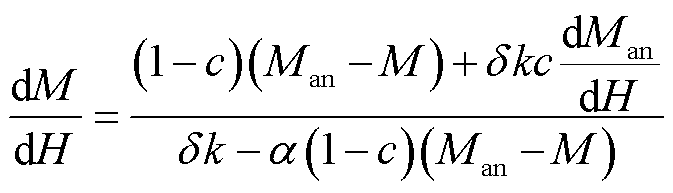 (4)
(4)
其中Ms、a、c、k、α为模型待定参数,数值确定后通过求解J-A模型便可绘制相应的M-H、B-H曲线。
当铁磁材料受到机械应力时,内部有效场He-σ可分解为不计压应力作用时的有效磁场He、应力退磁项DσM和附加机械应力场Hσ,材料中有效磁场表达式[13]可改写为
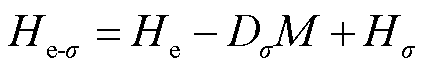 (5)
(5)
其中
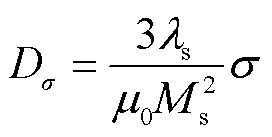 (6)
(6)
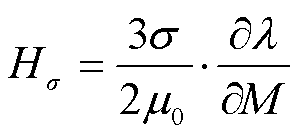 (7)
(7)
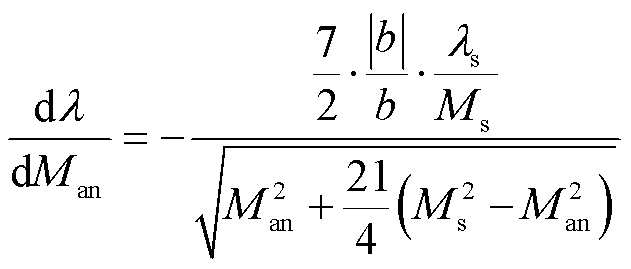 (8)
(8)
式中,He-σ为计及压应力影响的材料内部有效磁场强度;DσM为应力退磁项;λs为饱和磁致伸缩系数;λ为磁滞伸缩系数;b为磁弹性耦合常数。
在2.1节所述的静态J-A模型的基础上,考虑压应力影响下的模型修正为
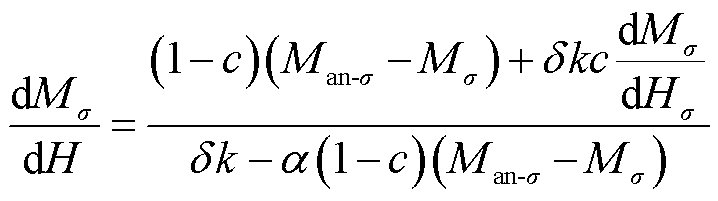 (9)
(9)
式中,Man-σ为含He-σ的无磁滞磁化强度;Mσ为含He-σ的动态磁化强度。
根据磁性材料的损耗分离理论,总损耗W由磁滞损耗Whys、涡流损耗Wed与剩余损耗Wex三部分组成,即
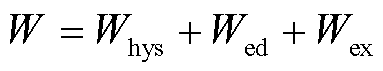 (10)
(10)
在静态、准静态条件下,材料内部磁场的趋肤效应可以忽略,可将叠片内部磁场视为均匀磁场;此外,经典的涡流损耗取决于材料厚度与电导率,所以假设它独立于机械应力,涡流损耗与涡流场的表达式分别为
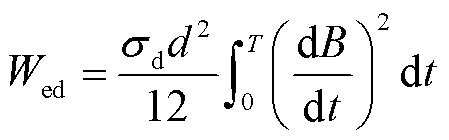 (11)
(11)
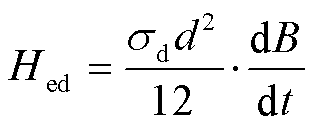 (12)
(12)
式中,σd为材料电导率;d为材料叠片厚度;T为磁化周期。
但随着频率的升高,趋肤效应影响加剧,材料内部磁场强度呈现出表面高、中心低的特点,使得未考虑磁场分布影响的传统方法计算值与实验值之间误差过大,因此引入R-L型分数导数,对高频涡流场进行修正。R-L型分数导数具体形式[14]为
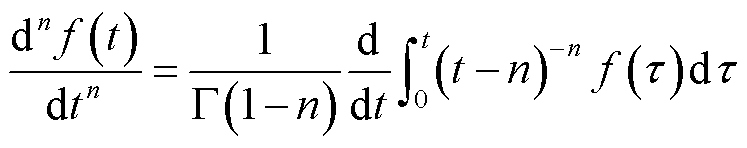 (13)
(13)
式中,非整数阶n的取值范围为(0, 1);Γ(·)为欧拉伽马函数。
R-L型分数阶导数为微分算子形式,自初始时刻0到当前时刻t的整个过程都可以考虑变量τ的影响,相较整数阶,分数阶更适用于幂律性、非局部等复杂情况[15]。由于非整数阶n可以为任意非负实数,因而采用分数微分算子描述的涡流损耗值表达式对频率具有依赖性,可保证高频涡流损耗的计算精度。
将传统涡流场表达式与R-L型分数阶导数相结合,推导出改进的涡流场表达式[16]为
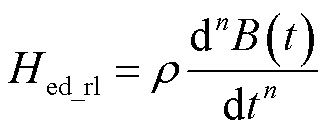 (14)
(14)
式中,ρ为阻尼系数。相应的涡流损耗表达式为
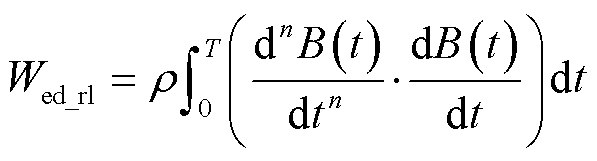 (15)
(15)
由于趋肤效应对剩余损耗几乎没有影响[17],在此只考虑修正涡流损耗项。剩余损耗与剩余损耗场可分别表示为
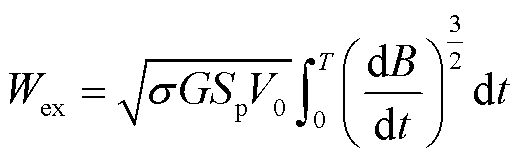 (16)
(16)
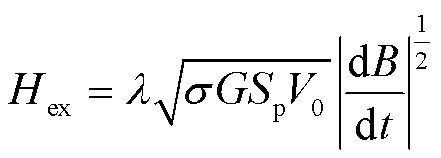 (17)
(17)
式中,Sp为叠片截面积;G=0.137 5;V0为统计参数,可利用总损耗和涡流损耗计算值的差值与频率的1/2次幂之间的线性关系取得[18]。
由此,总损耗可以进一步表示为
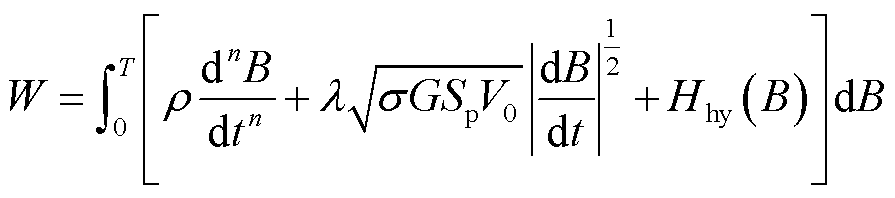 (18)
(18)
式中,Hhy(B)为可由静态J-A模型获取的磁滞损耗对应磁场强度分量。要确定参数ρ与n的值,首先,通过将参数n的值从1逐渐减小(步长设置为0.01)来进行调整;然后,固定参数n不变,调整参数ρ,直到采用式(18)计算的总损耗值接近实际测量的损耗值[19]。此处取n=0.98、ρ=0.142。
将改进涡流场Hed与剩余损耗场Hex的表达式代入关于有效场的表达式(3)中,得到含动态场的有效磁场强度为
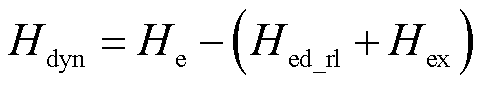 (19)
(19)
结合式(4)得到动态磁化微分表达式为
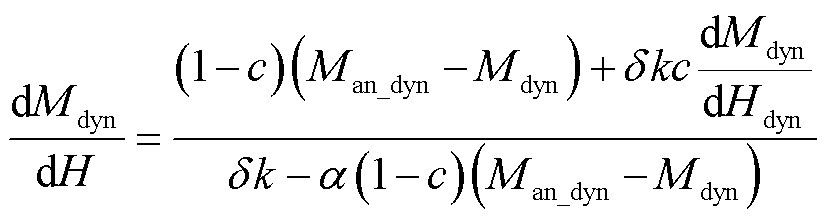 (20)
(20)
式中,Man_dyn为含Hdyn的无磁滞磁化强度;Mdyn为含Hdyn的动态磁化强度。
要建立高频条件下计及外施压应力的铁镓合金动态J-A磁滞模型,需要将2.2节中表达式较为复杂的He-σ与动态磁化微分表达式(20)相结合,但这会引起模型求解计算量增大;此外,还需准确地测量磁致伸缩系数λ,增加实验难度。因此,本文提出了基于式(20)的铁镓合金棒材高频变压应力模型的简便建模方法:将实测数据绘制成B-H曲线,然后采用混合粒子群算法,对J-A模型的五个参数(Ms、a、c、k、α)进行辨识,选取相应的拟合多项式,按照模型参数随压应力σ变化的规律,将J-A模型各个参数拟合为压应力σ的多项式函数,建立计及压应力影响的变系数高频磁滞模型。
要获取J-A模型参数值,需要对不同压应力下铁镓合金棒材磁滞回线实验样本数据进行参数辨识。公式法采用迭代运算,尽可能减小矫顽力Hc、剩磁Br、矫顽力点磁化率χc、无磁滞磁化曲线的初始磁化率χm等特殊点的计算误差,从而得到最优参数值,但此方法对初值及迭代次序敏感且精度不高;拟合法则以实测磁滞回线与计算磁滞回线吻合度最大为目标,通过优化算法实现参数的辨识,过程简单、执行效率高。本文采用将遗传算法中杂交的概念应用到粒子群算法中的混合粒子群算法,以计算的磁滞回线与实验获得的磁滞回线之间的磁场强度H的方均根误差作为目标函数,实现J-A模型的参数辨识,流程如图6所示。
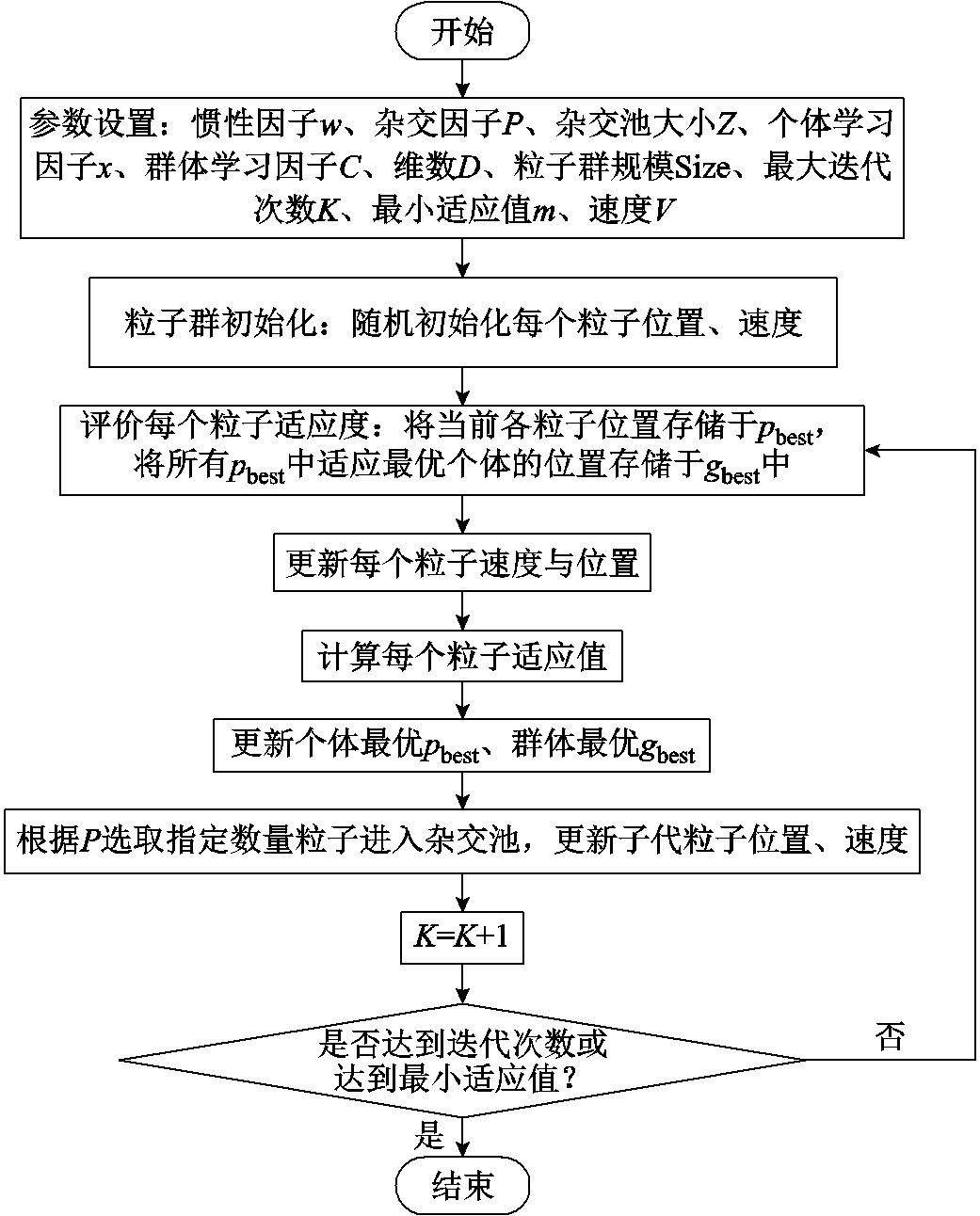
图6 J-A模型参数辨识流程
Fig.6 J-A model parameter identification flow chart
将不同外施压应力下(0~60 MPa)铁镓合金棒材B-H曲线数据导入上述辨识程序中,进行参数辨识,结果表明:由于铁镓合金棒材的应力敏感性,在受到外施压应力作用时,棒材磁滞特性势必受到影响,反映磁滞回线形状、面积的J-A模型参数(Ms、a、α、c、k)[20-21]也随之变化。相应的变化规律如图7所示。
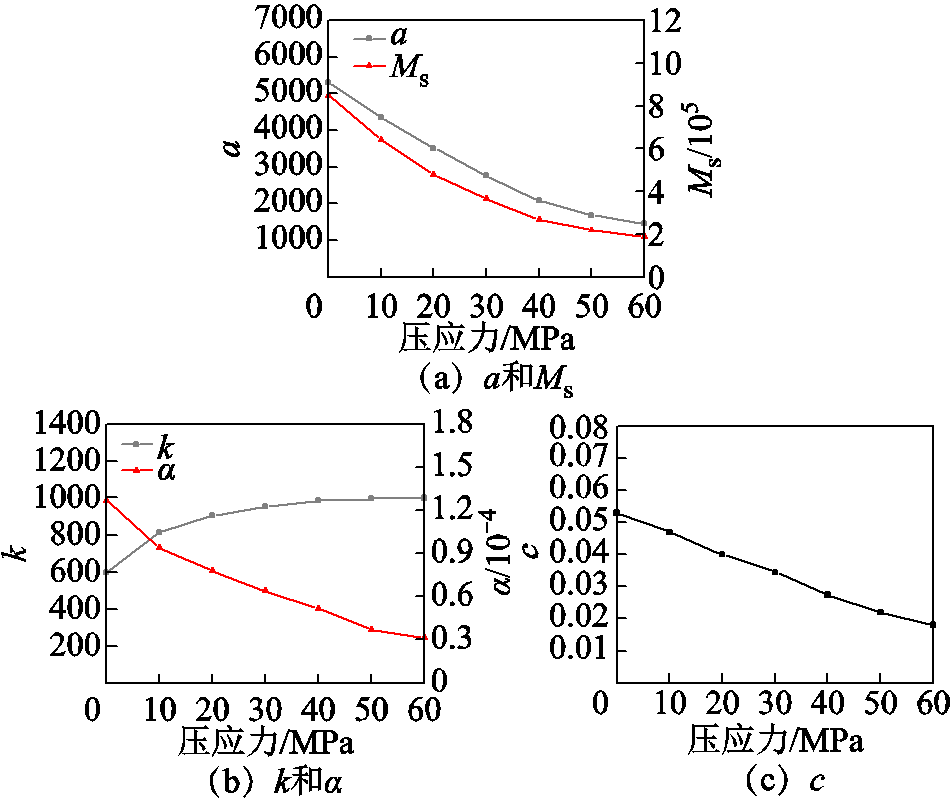
图7 模型参数的压应力相关性
Fig.7 Relationship between model parameters and externally applied stress
在此将模型各参数看作压应力σ的多项式函数,对于参数a、Ms、k、α宜用关于外施压应力σ的三次多项式进行拟合,其通式可表示为
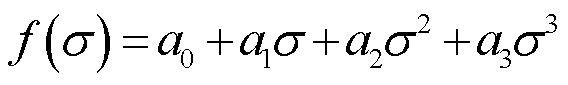 (21)
(21)
式中,a0~a3为多项式系数。而参数c的变化趋势可近似看作直线,采用一次多项式拟合,其通式可表示为
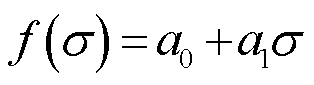 (22)
(22)
则模型参数表达式见表1。
表1 模型参数表达式
Tab.1 Model parameter expressions
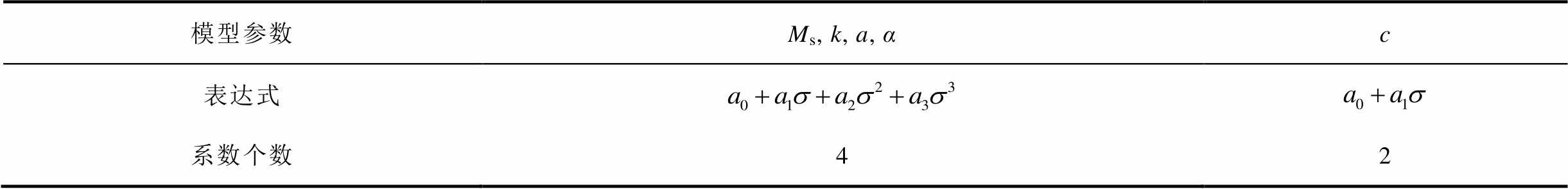
模型参数Ms, k, a, αc 表达式 系数个数42
其中,各参数的边界条件:a与k的取值范围为[0.2Hc, 5Hc];α取值范围为[0, Htip/Mtip],其中Htip和Mtip分别为顶点磁场强度和顶点磁化强度[22]; c的取值范围为[0, 1]。在边界条件给定的情况下,采用控制变量法,给定频率f与磁场强度H,改变外施压应力(本文的测试频率为1~9 kHz,磁场强度范围为1 000~6 000 A/m,压应力范围为0~60 MPa),将实验数据导入混合粒子群算法辨识程序,将各个参数拟合为压应力σ的多项式函数后,相应的多项式系数记录于表2。
表2 修正模型相关参数值
Tab.2 Correction of model-related parameter values

参数a0a1a2a3 Ms848 943.752-23 133.801256.737-0.922 k600.07522.911-0.5234.259×10-3 a5 306.11293.553-6.412×10-29.824×10-3 α1.269×10-74.532×10-91.411×10-101.751×10-12 c5.301×10-46.451×10-5
至此,通过混合粒子群算法对有限的实验数据进行参数辨识,将J-A模型各参数拟合为压应力σ的多项式函数,代入式(20)中,建立了计及压应力影响的变系数高频磁滞模型。根据各参数随压应力σ的变化规律,还可将模型推广至更宽的应用范围内。
为了验证所建立的计及压应力变化的高频动态J-A模型的准确性,在给定工作条件下(不同频率f、磁场强度H、外施压应力σ)测试铁镓合金棒材的磁滞特性。通过控制变量法分别绘制不同频率、磁场强度和外施压应力下的实测曲线,与模型计算结果进行对比,如图8~图10所示。
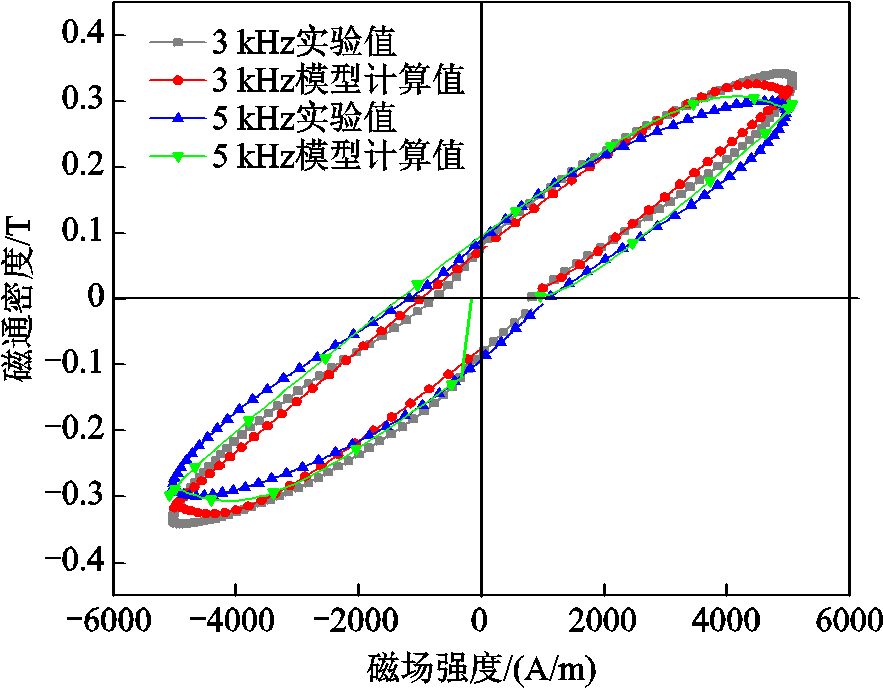
图8 不同频率下磁滞回线实验值与模型计算结果(H=5 000 A/m, σ=0 MPa)
Fig.8 Experimental values and model calculations of hysteresis lines at different frequencies (H=5 000 A/m, σ=0 MPa)
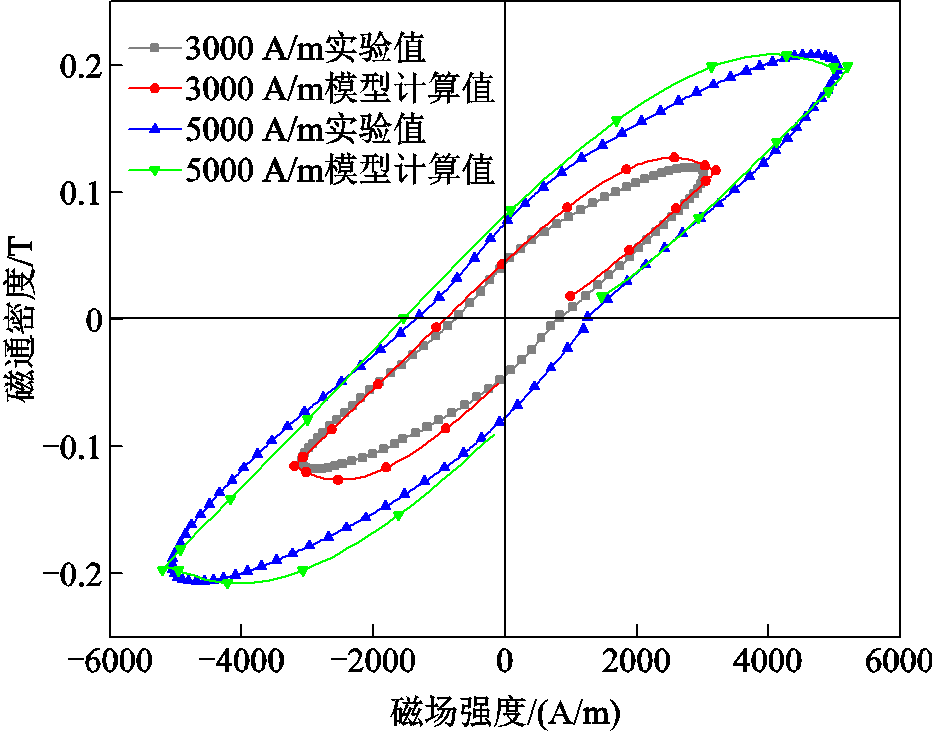
图9 不同磁场强度下磁滞回线实验值与模型计算结果(f =5 kHz, σ=30 MPa)
Fig.9 Experimental values and model calculations of hysteresis lines at different magnetic field strengths (f =5 kHz, σ=30 MPa)
为了表示模型的精确度,定义误差量E为
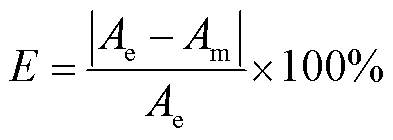 (23)
(23)
式中,Ae为实验测量的B-H曲线面积;Am为模型计算结果所得B-H曲线面积。
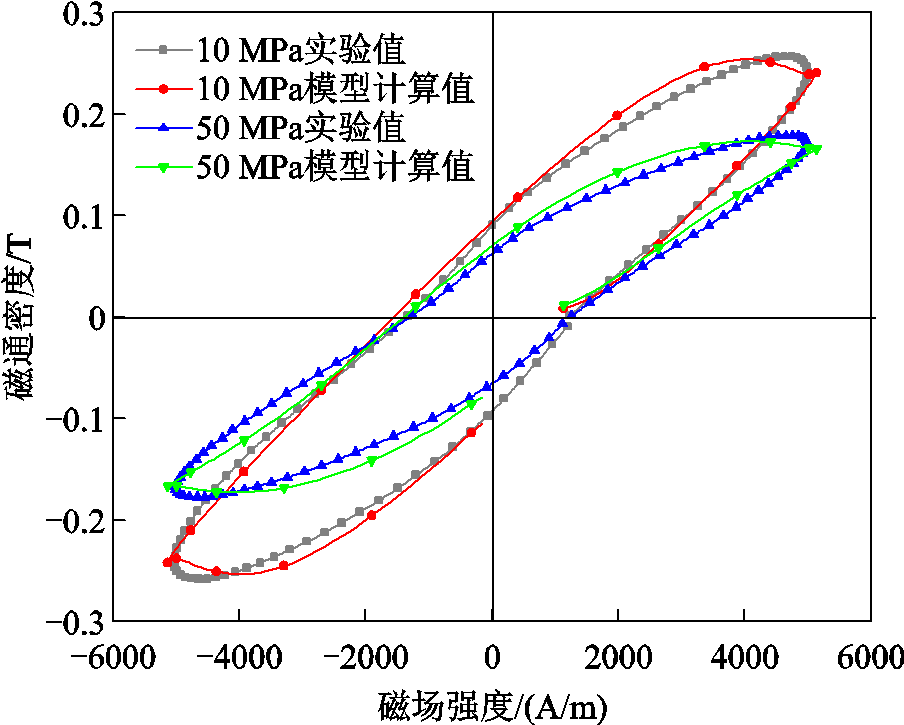
图10 不同压应力下磁滞回线实验值与模型计算结果(f =5 kHz, H=5 000 A/m)
Fig.10 Experimental values and model calculations of hysteresis lines under different compressive stresses (f =5 kHz, H=5 000 A/m)
图11所示分别为在磁场频率为1~9 kHz(H= 5 000 A/m、σ =0 MPa)、磁场强度为1 000~6 000 A/m(f =5 kHz、σ =30 MPa)和压应力为0~60 MPa(f = 5 kHz、H=5 000 A/m)的磁能损耗实验结果和模型计算结果的误差量。由于采用动态J-A磁滞模型并引入分数阶导数修正涡流损耗场,在高频激励下(f =1~9 kHz),模型计算结果频率适应性较好,最大误差量为6.88%,平均误差量为4.71%。此外,改进后的动态模型能反映出损耗量在磁场强度大小变化时的改变,在频率、外施压应力恒定(f =5 kHz、σ =0 MPa)时,不同磁场强度下(H=1 000~6000 A/m)所绘制的磁滞曲线较贴近实验值,最大误差量为6.99%,平均误差量为4.28%。在磁场频率、磁场强度恒定时(f =5 kHz、H=5 000 A/m),改变外施压应力条件下(σ =0~60 MPa),考虑到外施压应力对铁镓合金棒材磁特性的影响,将模型参数改写为外施加压应力σ的多项式函数,提高了计及压应力条件下的模型计算与实验结果的吻合性,最大误差量为5.86%,平均误差量为3.29%。
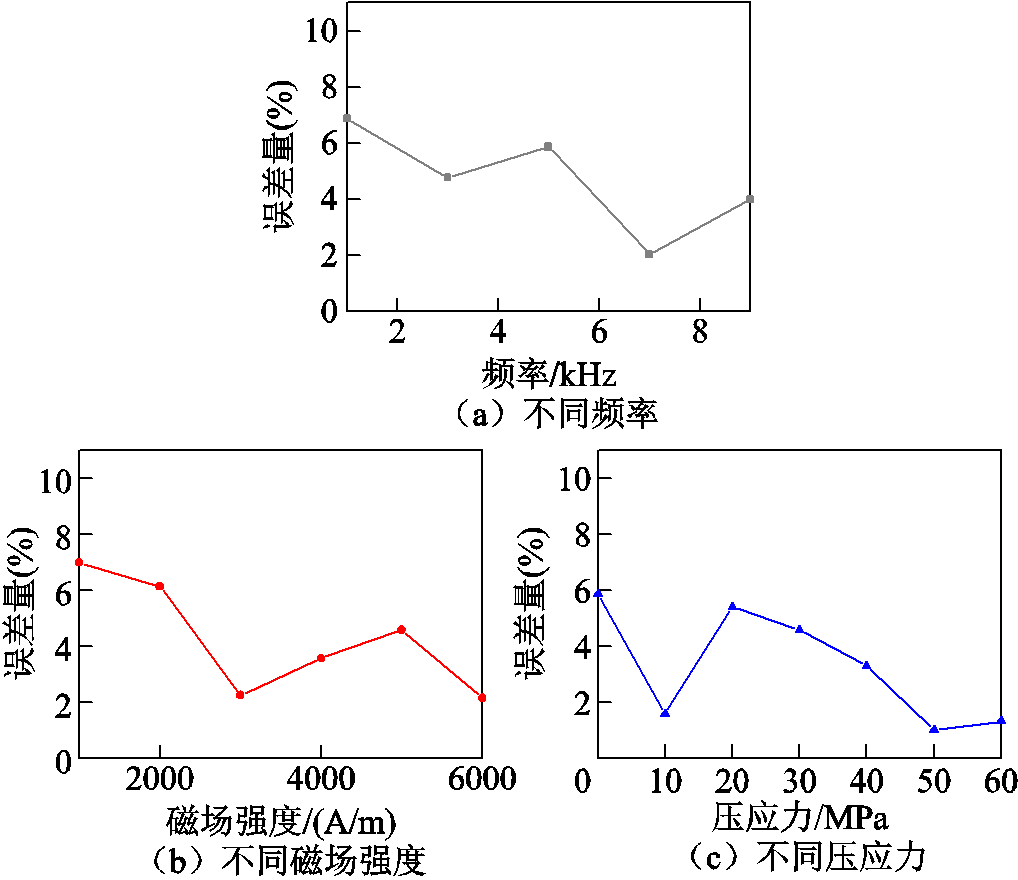
图11 不同频率、磁场强度和压应力下模型误差量
Fig.11 The amount of model error under different magnetic field frequency, magnetic field strength and compressive stress
本文搭建了外施压应力可控的磁致伸缩棒材高频磁特性测试平台,分析测试了不同压应力条件下铁镓合金棒材的高频磁特性,对现有的静态J-A模型进行改进,建立了计及压应力变化影响的高频动态磁滞模型。主要结论如下:
1)本文在磁场频率f =1~9 kHz、磁场强度H=1 000~6 000 A/m的条件下,测量了外施压应力从0 MPa增加到60 MPa时,铁镓合金棒材的动态磁滞回线,可知随着压应力增加,回线纵向变窄,振幅磁导率、剩磁和磁能损耗逐渐减小。
2)从经典的静态J-A模型出发,考虑高频涡流损耗场和剩余损耗场的影响,引入分数阶导数优化高频涡流场表达式,构建高频动态磁滞模型;采用拟合参数法计及压应力的影响,基于混合粒子群算法对不同压应力下的实验数据进行参数辨识,按照模型参数的变化的规律,将J-A模型各个参数拟合为压应力的多项式函数,建立了计及压应力影响的变系数高频磁滞模型。所建立的高频动态磁滞模型在高频磁场与应力场耦合的综合工况下,计算结果与实测值吻合性较好。在高频励磁下,由于引入分数阶导数对涡流场进行修正,使模型具有良好的频率适应性,最大误差量为6.88%,平均误差量为4.71%;在不同磁场强度下,最大误差量为6.99%,平均误差量为4.28%;通过拟合参数法,提高了模型的应力跟踪能力,在改变压应力σ时,最大误差量为5.86%,平均误差量为3.29%。
本文的研究工作可利用有限的实验数据,有效地预测铁镓合金棒材所受外界压应力变化时的高频磁特性变化,可为高频大功率磁致伸缩换能器件工程中的优化设计及性能调控提供理论和数据支持。
参考文献
[1] 翁玲, 梁淑智, 王博文, 等. 考虑预应力的双励磁线圈铁镓换能器输出特性[J]. 电工技术学报, 2019, 34(23): 4859-4869. Weng Ling, Liang Shuzhi, Wang Bowen, et al. Output characteristics of double-excited coil Fe-Ga transducer considering pre-stress[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4859-4869.
[2] Cao Shuying, Yue Xiufeng, Zheng Jiaju, et al. Dynamic coupled model of vibration system with galfenol damper considering eddy currents and hysteresis[J]. IEEE Transactions on Magnetics, 2020, 56(1): 1-4.
[3] 段娜娜, 徐伟杰, 李永建, 等. 一种考虑温度和压力影响的磁滞模型及其实验验证[J]. 电工技术学报, 2019, 34(13): 2686-2692. Duan Nana, Xu Weijie, Li Yongjian, et al. A temperature and stress dependent hysteresis model with experiment validation[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2686-2692.
[4] 杜杲娴, 杨鑫, 韦艳飞, 等. 稀土超磁致伸缩棒材特性测试平台优化与实验研究[J]. 电工技术学报, 2021, 36(18): 3867-3875. Du Gaoxian, Yang Xin, Wei Yanfei, et al. Optimization and experimental research on the test platform of rare-earth gaint magnetostrictive rod characteristics[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3867-3875.
[5] 赵志刚, 马习纹, 姬俊安. 基于AFSA与PSO混合算法的J-A动态磁滞模型参数辨识及验证[J]. 仪器仪表学报, 2020, 41(1): 26-34. Zhao Zhigang, Ma Xiwen, Ji Jun'an. Parameter identification and verification of J-A dynamic hysteresis model based on hybrid algorithms of AFSA and PSO[J]. Chinese Journal of Scientific Instrument, 2020, 41(1): 26-34.
[6] Hamada S, Louai F Z, Nait-Said N. Modeling and analysing the influence of both frequency and mechanical stress on ferromagnetic sheets NO Fe 3%Si using improved low frequency diffusion equation model[C]//2020 4th International Conference on Advanced Systems and Emergent Technologies (IC_ASET), Hammamet, Tunisia, 2020: 100-105.
[7] Messal O, Sixdenier F, Morel L, et al. Temperature dependent extension of the Jiles-Atherton model: study of the variation of microstructural hysteresis parameters[J]. IEEE Transactions on Magnetics, 2012, 48(10): 2567-2572.
[8] Jackiewicz D, Szewczyk R, Kachniarz M, et al. Modelling the influence of stresses on magnetic characteristics of the elements of the truss using extended Jiles-Atherton model[J]. Acta Physica Polonica A, 2017, 131(4): 1189-1191.
[9] Bernard L, Mailhé B J, Ávila S L, et al. Magnetic hysteresis under compressive stress: a multiscale-Jiles-Atherton approach[J]. IEEE Transactions on Magnetics, 2020, 56(2): 1-4.
[10] 李长云, 刘亚魁. 直流偏磁条件下变压器铁心磁化特性的Jiles-Atherton修正模型[J]. 电工技术学报, 2017, 32(19): 193-201. Li Changyun, Liu Yakui. Modified Jiles-Atherton model of transformer iron core magnetization characteristics with DC bias[J]. Transactions of China Electrotechnical Society, 2017, 32(19): 193-201.
[11] 陈彬, 秦小彬, 唐波, 等. 基于R-L分数阶导数的动态J-A磁滞模型及其特征参数辨识算法[J]. 中国电机工程学报, 2022, 42(12): 4590-4603. Chen Bin, Qin Xiaobin, Tang Bo, et al. Dynamic J-A hysteresis model based on R-L fractional derivative and its characteristic parameter identification algorithm[J]. Proceedings of the CSEE, 2022, 42(12): 4590-4603.
[12] Hussain S, Lowther D A. Prediction of iron losses using Jiles–Atherton model with interpolated parameters under the conditions of frequency and compressive stress[J]. IEEE Transactions on Magnetics, 2016, 52(3): 1-4.
[13] Malika Y, Sebti B, Adel B. A theoretical characterization of the coupling effects of frequency and mechanical stresses on the magnetic properties of the ferromagnetic material[C]//2018 International Conference on Communications and Electrical Engineering (ICCEE), El Oued, Algeria, 2019: 1-5.
[14] Zhang B, Gupta B, Ducharne B, et al. Dynamic magnetic scalar hysteresis lump model based on Jiles-Atherton quasi-static hysteresis model extended with dynamic fractional derivative contribution[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.
[15] 陈彬, 秦小彬, 万妮娜, 等. 基于R-L型分数阶导数与损耗统计理论的铁磁材料高频损耗计算方法[J]. 电工技术学报, 2022, 37(2): 299-310. Chen Bin, Qin Xiaobin, Wan Nina, et al. Calculation method of high-frequency loss of ferromagnetic materials based on R-L type fractional derivative and loss statistical theory[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 299-310.
[16] Ducharne B, Sebald G, Guyomar D, et al. Dynamics of magnetic field penetration into soft ferromagnets[J]. Journal of Applied Physics, 2015, 117(24): 243907.
[17] Zhao Hanyu, Ragusa C, Appino C, et al. Energy losses in soft magnetic materials under symmetric and asymmetric induction waveforms[J]. IEEE Transactions on Power Electronics, 2019, 34(3): 2655-2665.
[18] Zhao Hanyu, Ragusa C, de la Barrière O, et al. Magnetic loss versus frequency in non-oriented steel sheets and its prediction: minor loops, PWM, and the limits of the analytical approach[J]. IEEE Transactions on Magnetics, 2017, 53(11): 1-4.
[19] Liu Ren, Li Lin. Analytical prediction model of energy losses in soft magnetic materials over broadband frequency range[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 2009-2017.
[20] 李晓萍, 彭青顺, 李金保, 等. 变压器铁心磁滞模型参数辨识[J]. 电网技术, 2012, 36(2): 200-205. Li Xiaoping, Peng Qingshun, Li Jinbao, et al. Parameter identification of hysteresis loop model for transformer core[J]. Power System Technology, 2012, 36(2): 200-205.
[21] Rasilo P, Singh D, Aydin U, et al. Modeling of hysteresis losses in ferromagnetic laminations under mechanical stress[J]. IEEE Transactions on Magnetics, 2016, 52(3): 1-4.
[22] 王洋, 刘志珍. 基于蛙跳模糊算法的Jiles Atherton铁心磁滞模型参数确定[J]. 电工技术学报, 2017, 32(4): 154-161. Wang Yang, Liu Zhizhen. Determination of Jiles Atherton core hysteresis model parameters based on fuzzy-shuffled frog leaping algorithm[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 154-161.
Abstract The output characteristics of high-frequency and high-power magnetostrictive transducer devices are closely related to the compressive stress. Applying a certain compressive stress can increase the magnetostrictive coefficient of the core component magnetostrictive rod and increase the output power of the device. But an inappropriate compressive stress can deteriorate the performance of the device. To investigate the stress sensitivity of magnetostrictive rods under high frequency excitation conditions In this paper, we built a high-frequency magnetic property test system for magnetostrictive materials, and measured the dynamic magnetic property curves of iron gallium alloy rod under different excitation conditions (variable compressive stress, variable excitation frequency and magnetic field strength ). Based on the measured hysteresis lines, it shows that when the frequency and applied magnetic field strength are certain, with the increase of compressive stress, the magnetic permeability of iron gallium alloy rod decreases and the magnetization process of the material becomes more and more difficult. However, the applied larger compressive stress can reduce the magnetic loss of iron gallium alloy rod with a certain magnetic field strength, while the remanent magnetization decreases and the hysteresis effect is weakened, which improves the real-time of the rod.
To address the problem that conventional hysteresis models cannot account for the effects of compressive stress. Based on the existing static J-A hysteresis model, a high-frequency dynamic hysteresis model is established by taking into account the eddy current loss and residual loss and using fractional order derivatives to modify the high-frequency eddy current field expressions. Then improved high-frequency dynamic hysteresis model related to external applied compressive stress by introducing compressive stress-related terms to modify model parameters.
Analysis of the experimental data and the model calculation results show that the model calculation results have good frequency adaptation at high frequencies due to the consideration of the dynamic loss field and the introduction of fractional order derivatives. Comparing the model calculation results with the measured hysteresis loop area at high frequency excitation of f = 1~9 kHz, the maximum error amount is 6.88% and the average error amount is 4.71%. The model also reflects more accurately the change in the amount of loss when the magnitude of magnetic field strength is changed, with a maximum error of 6.99% and an average error of 4.28% under different magnetic field strengths (H=1 000~6 000 A/m). Due to the use of J-A model parameters with compressive stress correlation term, the model can effectively take into account the influence of compressive stress on the calculation results, and the calculation results have high accuracy under the conditions of variable external applied compressive stress (σ =0~60 MPa). The maximum error of hysteresis loop area is 5.86% and the average error is 3.29%. The model can use limited experimental data to effectively predict the variation of the high frequency magnetic properties of iron gallium alloy rod under variable compressive stress conditions. It provides theoretical and data support for the optimal design and performance regulation in the engineering of high-frequency high-power magnetostrictive transducer devices.
keywords:Rod gallium iron alloy, compressive stress, high frequency magnetic properties, improved hysteresis model
国家自然科学基金资助项目(51777053, 52077052, 52130710)。
收稿日期 2022-05-13
改稿日期 2022-06-24
DOI:10.19595/j.cnki.1000-6753.tces.220819
中图分类号:TM274
黄文美 女,1969年生,博士,教授,研究方向为磁性材料与器件、电机电器及其控制。E-mail:huzwm@hebut.edu.cn(通信作者)
陶 铮 男,1996年生,硕士研究生,研究方向为磁性材料与器件、电机电器及其控制。E-mail:961851321@qq.com
(编辑 李 冰)