 为输入电网的电流。不考虑变流器损耗时,输入并网点的功率即为P+jQ。
为输入电网的电流。不考虑变流器损耗时,输入并网点的功率即为P+jQ。摘要 随着风力发电的高比例接入电网,全功率风电机组的稳定运行能力面临着挑战。传统的网侧变流器采用锁相环(PLL)同步策略,构网型全功率风电机组的网侧变流器则基于功率同步策略,利用直流电压的动态特性实现直流电压同步的构网型控制。由于构网型控制存在功率耦合问题,无功通过耦合通道影响有功功率,进一步引起网侧直流电压的动态波动。该文针对网侧变流器构网型控制所存在的耦合问题,建立了直流电压-无功功率耦合模型,利用相对增益理论方法详细分析了系统参数对耦合效应的影响,并采用一种基于无功前馈的直流电压补偿方法,在实验中利用该方法可将由无功变化引起的直流电压动态超调降低81.8 %。通过实验验证了理论分析的正确性及所提方法的有效性。
关键词:全功率风电机组 网侧变流器 直流电压 耦合效应
随着可再生能源的发展,风力发电也得到快速发展[1]。全功率风力发电机组由于其高可靠性,得到了广泛的应用,在风力发电高比例接入电网的背景下,全功率风电变流器的稳定运行能力日渐面临挑战[2]。
全功率风电变流器由背靠背变流器组成,其中网侧变流器作为风力发电单元与电网的接口,其稳定运行能力对系统的稳定性起到关键作用[3-4]。传统的全功率网侧变流器采用锁相环(Phase-Locked Loop, PLL)同步控制方法,由于PLL和电流闭环相互耦合,PLL带宽过大会通过电流闭环使得系统稳定性降低[5]。针对PLL对并网系统的不利影响,国内外研究学者通过对同步发电机特性的模拟,提出基于功率同步的构网型控制,通过有功功率控制角度实现同步,代替了传统的PLL同步方案[6-8]。文献[9]对功率同步控制(Power Synchronization Control, PSC)的功率环和直流电压环建模与设计,表明PSC有很好的电压支撑能力。文献[10]对比了构网型控制和PLL控制的并网变流器,分析表明在高渗透率新能源发电背景下,基于PLL控制的并网变流器容易失稳,而采用构网型控制的并网系统依旧可以稳定运行且无锁相环的约束。文献[11]提出了利用直流电压进行同步的构网型控制原理,由直流电容的固有特性实现变流器的控制。文献[12]分析了不同类型的直流电压控制方法对构网型并网系统稳定性的影响。全功率风电网侧变流器的主要控制目标为直流电压控制[13],以保证功率的稳定传输。文献[14]提出全功率风电机组的网侧构网型控制方法,可在短路比为2的电网下稳定运行。文献[15]利用直流电容动态实现全功率风电机组网侧变流器的并网自同步,从而使全功率风电机组无需经过PLL并网运行。
目前,构网型控制的功率耦合问题是国内外学者的研究热点。文献[16]揭示了构网型控制功率耦合的机理,在输送有功功率时需要额外的无功功率,加大了对无功功率的需求。文献[17]对构网型控制的功率耦合进行了详细建模,表明功率耦合问题会受到控制参数及主电路参数的影响。文献[18]建立了宽频域功率动态耦合模型,分析表明功率耦合效应会加剧同步频率谐振。对功率耦合问题,文献[19]提出了一种基于自适应无功功率补偿的解耦策略。文献[20]通过虚拟阻抗的实时变动来补偿功角所带来的影响,消除有功功率对无功功率产生的影响。文献[21]采用相对增益分析的目标函数对角化解耦控制方法,将控制系统传递函数设置为对角矩阵实现功率解耦。文献[22]在基于虚拟功率控制方法的耦合路径中引入低通滤波器,实现有功无功的独立控制。文献[23-24]通过构建虚拟稳态同步输出阻抗,增加电流内环动态解耦补偿,在小功角条件不满足时完成有功无功解耦控制。
以上对于功率耦合问题的研究已较成熟,多关注于有功功率和无功功率的相互影响,所提解耦策略有效地解决了功率耦合问题。在全功率风电机组网侧变流器采用直流电压同步的构网型控制时,鲜有文献对功率耦合所引起的直流电压稳定性问题进行研究。当网侧变流器需要向电网输送无功功率,以提供电压主动支撑能力时,无功功率会通过耦合通道影响有功功率,从而影响直流电压的稳定性,降低系统的有效运行能力。本文首先介绍了全功率风电机组网侧变流器直流电压同步的构网型结构,建立了直流电压-无功功率耦合模型,通过相对增益理论,详细分析了控制参数对耦合效应的影响;然后,针对网侧耦合效应,提出一种基于无功前馈的直流电压补偿方法,降低了由于无功功率变化导致的直流电压波动问题;最后,在5 kW永磁同步全功率风电机组实验平台验证了理论分析的正确性及所提方法的有效性。
在全功率风电变流器中,机侧变流器控制功率输出,网侧变流器作为接入电网的接口,需要控制直流侧电容上的直流电压,以保证功率传输的稳定性。
全功率风电机组的网侧变流器并网主电路模型如图1所示,图中,Pref为机侧输入直流侧的功率,Vdc为直流电压,P和Q分别为网侧输出的有功功率和无功功率,采用LC滤波,Lf和Cf分别为滤波电感和滤波电容,Rg和Lg分别为电网线路电阻和电感,Cdc为直流侧电容,E∠0为远端电网的电压,保持恒定不变,U∠q 为并网点电压, 为输入电网的电流。不考虑变流器损耗时,输入并网点的功率即为P+jQ。
为输入电网的电流。不考虑变流器损耗时,输入并网点的功率即为P+jQ。
本文所分析的网侧变流器构网型控制,采用直流电压同步控制,其控制原理[15]为
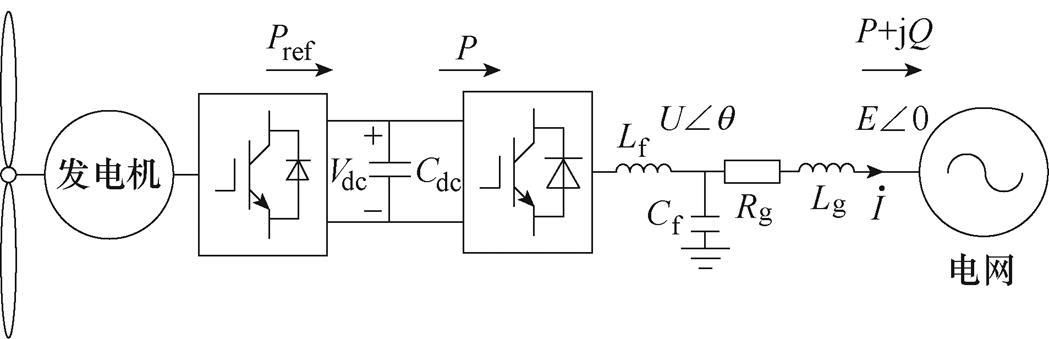
图1 网侧变流器并网主电路
Fig.1 Main circuit diagram of grid-side converter
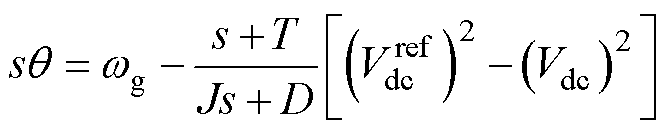 (1)
(1)
式中,q 为控制同步角度;wg为电网角频率;T为直流电压控制的时间参数;J为直流电压控制的惯量参数;D为直流电压控制的阻尼参数;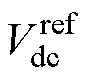 为直流电压控制给定值;s为拉普拉斯算子。直流电压同步控制框图如图2所示。
为直流电压控制给定值;s为拉普拉斯算子。直流电压同步控制框图如图2所示。
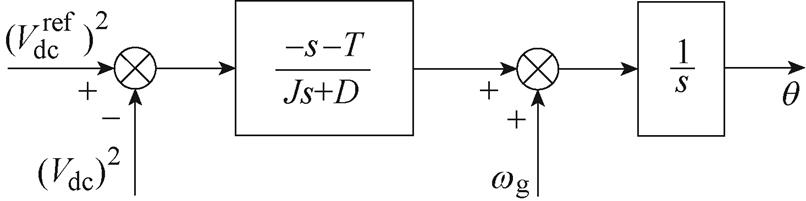
图2 直流电压控制框图
Fig.2 DC voltage control block diagram
在网侧变流器的直流电压控制模式中,机侧变流器输入直流侧的功率和直流电压动态关系为
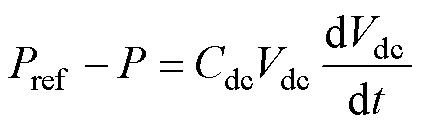 (2)
(2)
将式(1)代入式(2)中并整理[11]可得
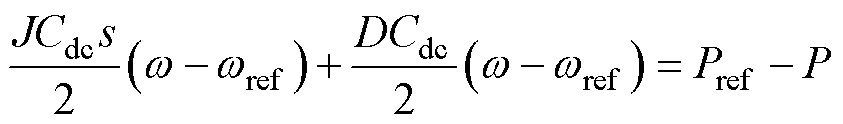 (3)
(3)
式中,w 为输出角频率;wref为额定角频率。式(3)通过模拟转子运动方程实现直流电压控制的构网型控制。
网侧变流器向电网输送无功功率,通过无功功率控制来提供电压支撑能力。本文采用如图3所示的无功功率控制方案。
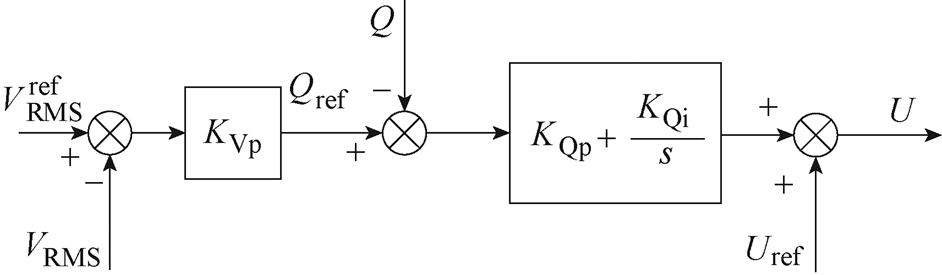
图3 无功功率控制框图
Fig.3 Reactive power control block diagram
图3中,Uref为并网点电压给定值,U为无功环输出电压,Qref为无功功率给定值,Q为无功功率反馈值,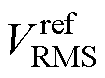 为并网点相电压有效值给定,VRMS为并网点相电压实际有效值,KVp为电压有效值外环比例系数,KQp和KQi分别为无功功率环比例和积分系数。在本文所采用无功控制结构中,KVp选择为0,则无功功率控制原理为
为并网点相电压有效值给定,VRMS为并网点相电压实际有效值,KVp为电压有效值外环比例系数,KQp和KQi分别为无功功率环比例和积分系数。在本文所采用无功控制结构中,KVp选择为0,则无功功率控制原理为
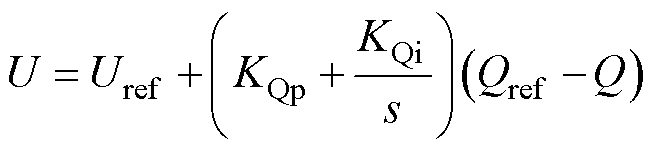 (4)
(4)
当并网点电压的幅值与理想值有偏差时,需要向电网输送无功以起到支撑电压作用,无功控制环路通过比例积分控制保证输出无功跟随给定,向电网提供电压的主动支撑。
图4为内环的控制框图,内环为交流电压环和电流环的级联结构,该结构广泛应用于构网型控制中[25]。在直流电压控制回路和无功功率控制回路分别获取同步角度q 和输出电压U后,同步角度q 作为uabc和iabc的坐标变换角度,由abc坐标系转化为dq坐标系,输出电压U作为交流电压环d轴给定信号,采用电网电压d轴定向,内环级联结构可实现并网点电压对外环指令的跟踪。其中,电压电流双闭环均采用PI控制,u为并网点电压,i为滤波电感电流,Ut为调制电压,下标abc表示三相静止坐标系下分量,下标d、q表示同步旋转坐标系下的d、q轴分量。电压环输出为电流环的给定值iref,调制电压经过空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)生产变流器的调制信号Sabc。由于在dq坐标系下存在d、q轴耦合,本文采用传统交叉解耦方式来消除d、q轴控制的耦合影响[26]。与外环控制相比,电压电流内环的带宽较大,其快速性更高,本文在建模过程中忽略其影响,认为内环反馈跟随给定。
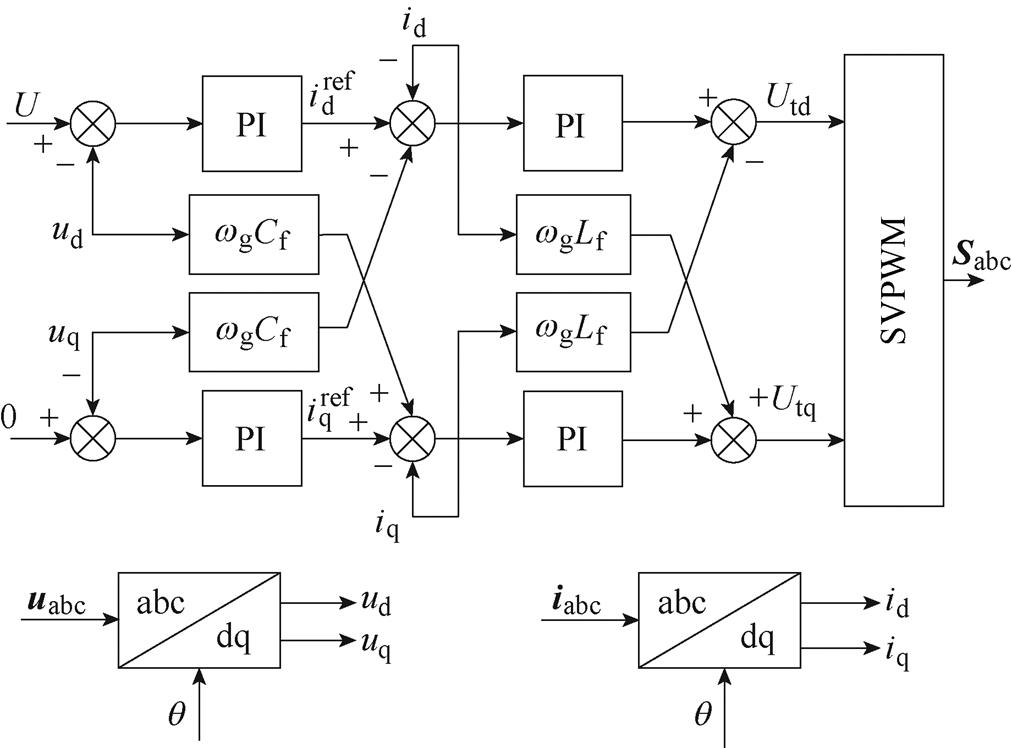
图4 内环控制框图
Fig.4 Inner loop control block diagram
VSG是基于线路潮流的有功功率和无功功率解耦条件下设计的。在图1中,并网变流器与交流母线之间流动的有功和无功功率可表示为
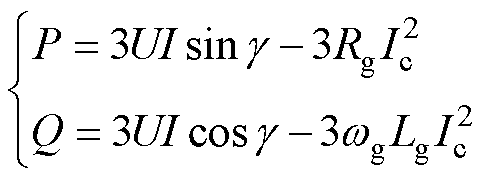 (5)
(5)
其中
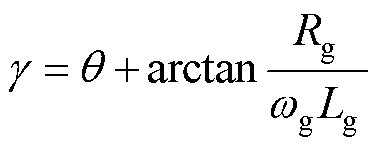
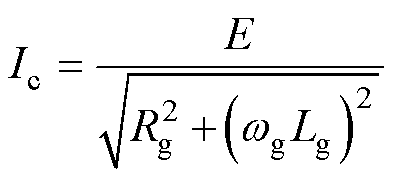
当认为同时满足内部和外部的功率解耦条件时,即较小的控制角度q 和线路呈纯感性,则可以作近似为: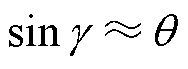 ,
,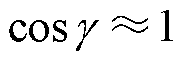 。代入式(5)可得
。代入式(5)可得
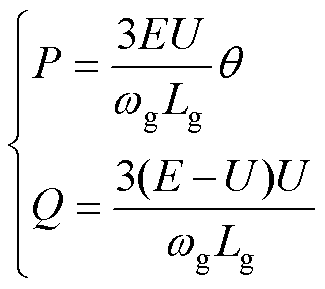 (6)
(6)
传统的功率解耦控制是基于式(6),利用角度q 实现有功功率P的控制,利用电压幅值U实现无功功率Q控制。当控制角度不够小,即不满足内部功率解耦条件时,或线路呈阻感性,即不满足外部功率解耦条件时,有功、无功控制通道之间产生了耦合,传统控制方法中,控制角度和电压的变化必将引起功率交叉量的变化,恶化系统的控制性能和稳定性。
由式(2)可知,当有功功率给定不变时,输入电网的有功功率变化会导致直流电压的变化。在风力发电高比例并网的背景下,网侧变流器要求能根据并网点电压的幅值情况,向电网输送相应的无功功率,以提供电压主动支撑。此时难以满足内部和外部的解耦条件,输入的无功功率将通过耦合通道引起有功功率的波动,再通过式(2)进一步影响直流电压控制的稳定性。
因此,有必要针对无功功率的变化对网侧变流器直流电压控制的耦合影响做进一步分析。
相对增益理论方法常用于分析多输入多输出系统中各通道之间的耦合问题[27]。在一个多输入多输出系统中,输入为X=[x1 x2… xn],输出为Y=[y1 y2 …yn]。假设xi是多输入多输出系统的第i个输入量,yj是第j个输出量,xi-yj通道的相对增益定义为第一放大因子pij和第二放大因子qij的比值,其中pij为其他通道打开时的xi-yj通道增益,qij为其他通道关闭且其他控制变量为常数的xi-yj通道增益。数学表达式可以写为
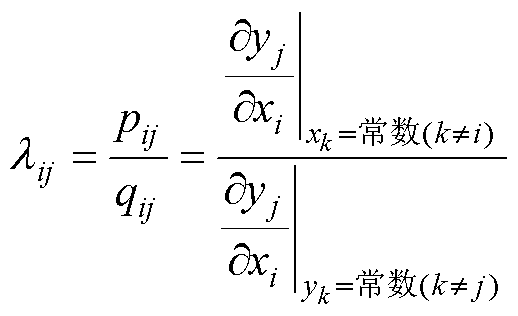 (7)
(7)
n个输入、n个输出的系统构成的相对增益矩阵为
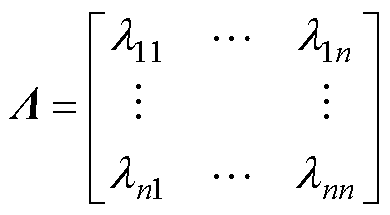 (8)
(8)
式中,元素lij的值所表明的意义为:①lij=0,表明输出yj不受输入xi的控制影响;②lij=1,表明输出yj只受输入xi的控制影响;③0<lij<1或lij>1,表明输出yj受除了输入xi外的输入量的影响,和其他通道存在耦合效应;④lij<0,表明该通道与其他通道间存在负耦合,用该通道的变量构成闭环控制时,会引起正反馈,使得系统不稳定。
相对增益矩阵反映了输入对输出控制作用的强弱,即各个控制通道的耦合程度,当相对增益矩阵为单位阵时,系统是解耦的。使用定义计算相对增益矩阵时较复杂,可以利用第一放大因子矩阵进行计算,有
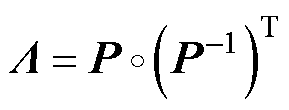 (9)
(9)
式中,“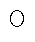 ”为矩阵的哈达玛积,即矩阵中各元素相乘;P为第一放大因子矩阵,对于n个输入、n个输出的系统,P为
”为矩阵的哈达玛积,即矩阵中各元素相乘;P为第一放大因子矩阵,对于n个输入、n个输出的系统,P为
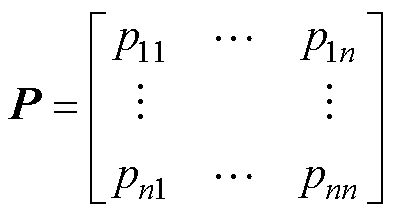 (10)
(10)
由以上理论可知,相对增益矩阵中的元素表明了各通道之间的耦合性,适用于复杂的多输入多输出系统。在网侧变流器的直流电压同步控制结构中,通过建模和计算得到相对增益矩阵,可利用对角线元素表征直流电压和无功功率之间的耦合关系。
当全功率风电机组网侧变流器采用直流电压同步控制结构,且考虑内部和外部解耦条件均不满足时,将式(5)在稳态工作点对q 和U进行小信号分析,可得
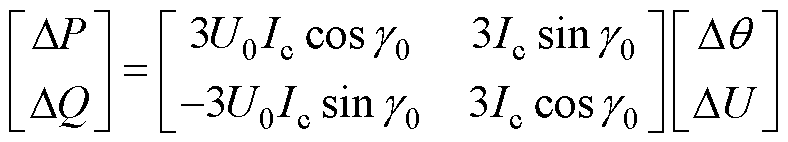 (11)
(11)
其中
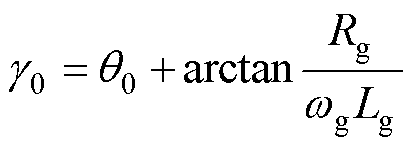
式中,下标“0”为稳态工作点处的值;“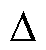 ”为小信号量。
”为小信号量。
由于直流电压的二次方的偏差表现出的趋势与直流电压相同,为方便分析,将直流电压的二次方作为分析量。在式(1)中,不考虑电网频率变换,以直流电压二次方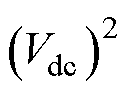 为控制变量,以控制角度q 为被控制变量,在稳态工作点处进行小信号分析,保留小信号量得到
为控制变量,以控制角度q 为被控制变量,在稳态工作点处进行小信号分析,保留小信号量得到
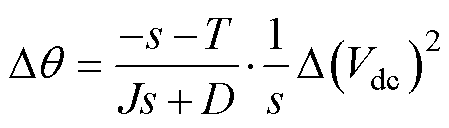 (12)
(12)
在认定无功功率给定为恒定值时,对式(4)的无功功率Q和输出电压U进行小信号分析可得
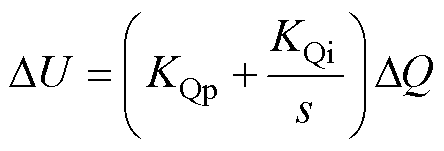 (13)
(13)
综合式(1)~式(6)、式(11)~式(13),得到考虑耦合效应时,由直流电压给定、无功功率给定到直流电压输出、无功功率输出的小信号闭环传递关系为
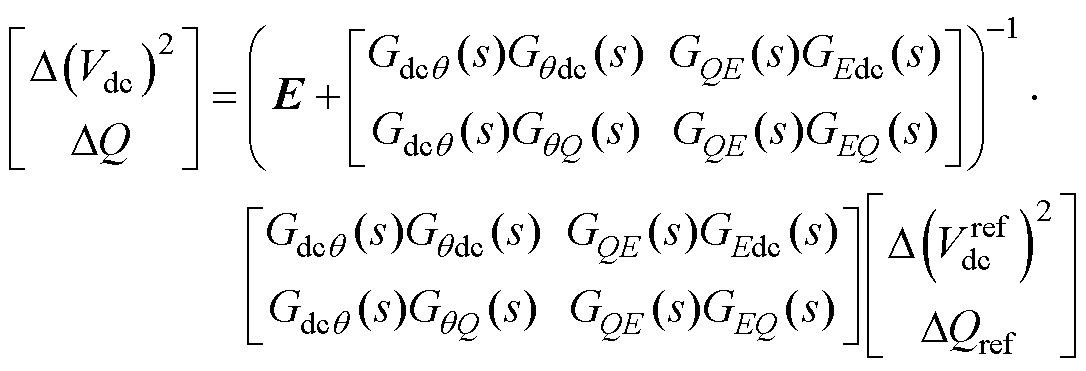 (14)
(14)
其中
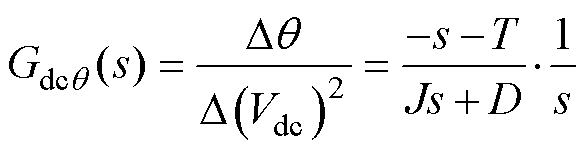 (15)
(15)
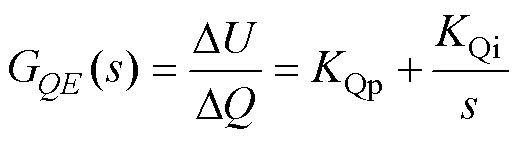 (16)
(16)
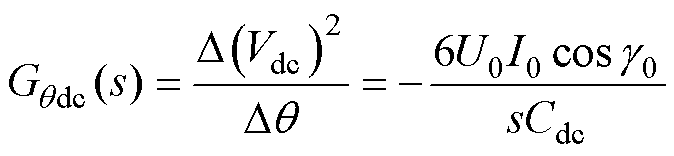 (17)
(17)
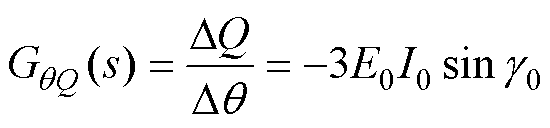 (18)
(18)
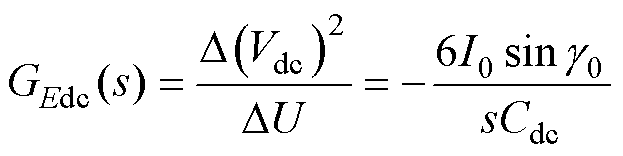 (19)
(19)
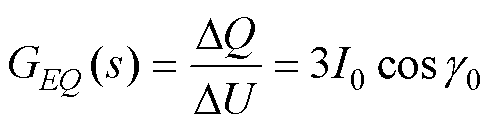 (20)
(20)
式中,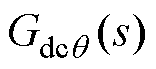 为由
为由 到
到 的传递函数;
的传递函数;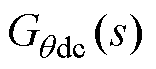 为由
为由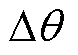 到
到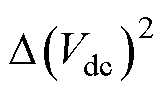 的传递函数;
的传递函数; 为由
为由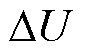 到
到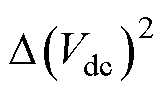 的传递函数;
的传递函数;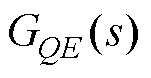 为由
为由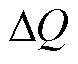 到
到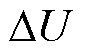 的传递函数;
的传递函数;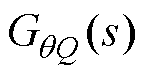 为由
为由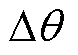 到
到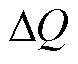 的传递函数;
的传递函数;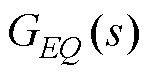 为由
为由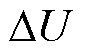 到
到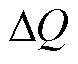 的传递函数。由式(14)得到考虑耦合效应的闭环模型框图,如图5所示。
的传递函数。由式(14)得到考虑耦合效应的闭环模型框图,如图5所示。
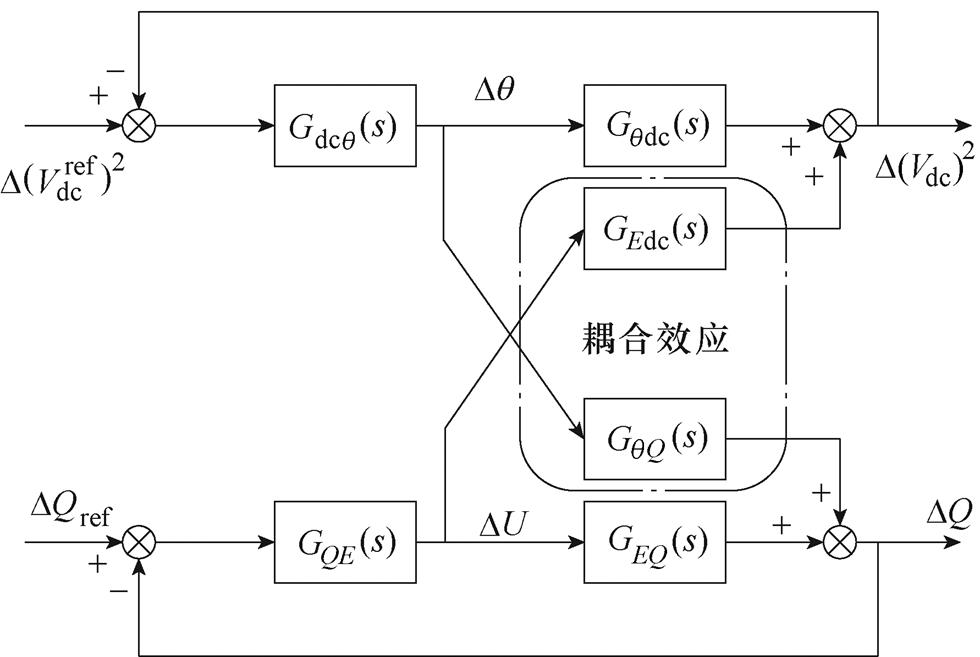
图5 网侧耦合效应闭环模型
Fig.5 Grid-side coupling effect closed-loop model
在图5中,直流电压控制环路和无功功率控制环路通过传递函数 和传递函数
和传递函数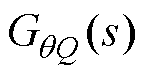 产生了耦合关系,无功功率控制环的输出电压
产生了耦合关系,无功功率控制环的输出电压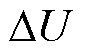 会通过
会通过 影响直流电压的控制,同时直流电压控制环的输出角度
影响直流电压的控制,同时直流电压控制环的输出角度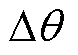 也会通过
也会通过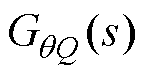 影响无功功率的控制。由图5可知,当需要补充额外无功功率以提供电压支撑时,网侧无功功率通过耦合效应影响直流电压的控制,同时,直流电压也通过耦合效应影响无功功率的控制。由于直流电压控制的稳定性影响整个系统的稳定,所以由网侧耦合效应引起的直流电压稳定性更需要引起重视。
影响无功功率的控制。由图5可知,当需要补充额外无功功率以提供电压支撑时,网侧无功功率通过耦合效应影响直流电压的控制,同时,直流电压也通过耦合效应影响无功功率的控制。由于直流电压控制的稳定性影响整个系统的稳定,所以由网侧耦合效应引起的直流电压稳定性更需要引起重视。
根据式(14)得到第一放大因子矩阵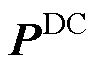 为
为
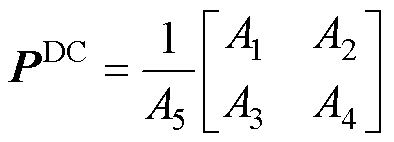 (21)
(21)
式中,A1~A5如附录式(A1)~式(A5)所示。
式(21)代入式(9)中可以计算得到直流电压控制的相对增益矩阵为
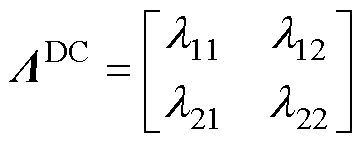 (22)
(22)
其中
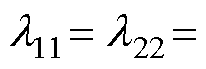
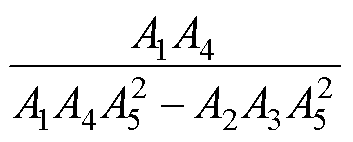
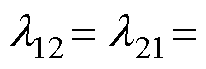
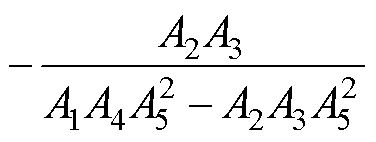
在第一放大因子矩阵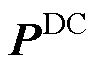 中,主对角线元素表示的是直流电压控制和无功功率控制环路的增益系数,副对角线元素则表示耦合效应引起的增益系数。而在相对增益矩阵
中,主对角线元素表示的是直流电压控制和无功功率控制环路的增益系数,副对角线元素则表示耦合效应引起的增益系数。而在相对增益矩阵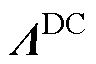 中,主对角线元素越接近于1、副对角线元素越接近于0,则表明耦合效应越小。
中,主对角线元素越接近于1、副对角线元素越接近于0,则表明耦合效应越小。
根据相对增益理论,分析控制参数对网侧耦合效应的影响,其默认参数见表1,绘制内部控制参数T、J、D、KQp、KQi变化时,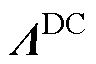 中表明网侧耦合效应的元素l12的伯德图,分别如图6~图10所示,在低、高频段l12幅值接近于0,在10 Hz频段处附近l12峰值幅值为0.33,表明网侧耦合效应主要存在于动态过程中,在稳态时系统不存在网侧耦合效应。
中表明网侧耦合效应的元素l12的伯德图,分别如图6~图10所示,在低、高频段l12幅值接近于0,在10 Hz频段处附近l12峰值幅值为0.33,表明网侧耦合效应主要存在于动态过程中,在稳态时系统不存在网侧耦合效应。
表1 控制环路参数
Tab.1 The parameters of control loop

参 数数 值 T(pu)30 J(pu)10 D(pu)50 000 KQp0.001 KQi0
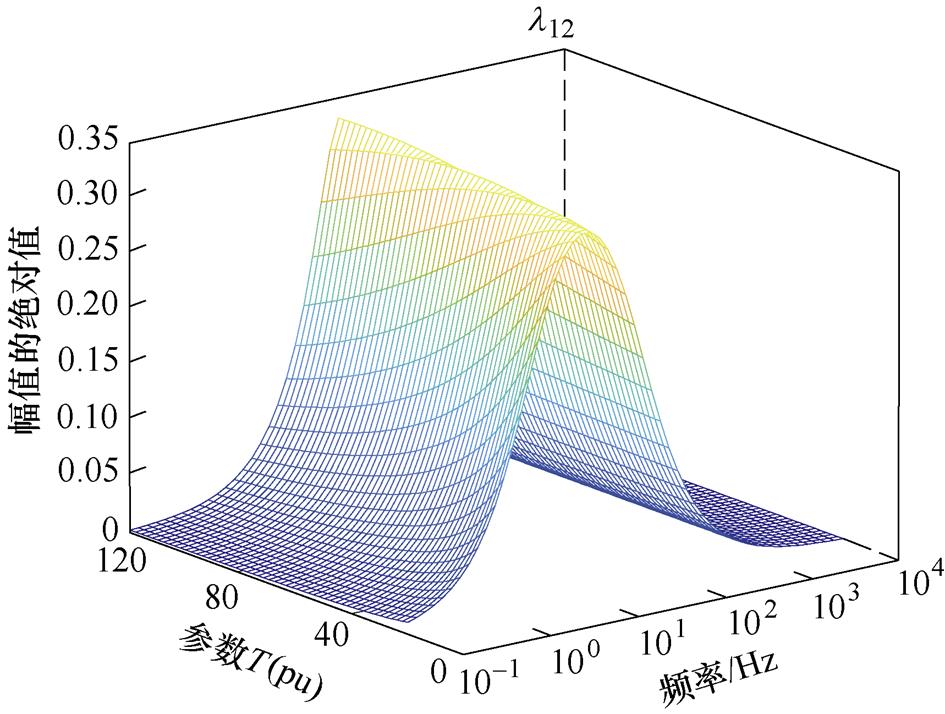
图6 参数T变化时l12幅值
Fig.6 Amplitude of l12 when parameter T changes
图6为参数T变化时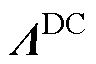 中表明网侧耦合效应的元素l12的伯德图,随着T增大,l12的峰值频率略有增加,峰值幅值几乎不变,由相对增益理论可知,T对网侧耦合程度影响不大,耦合频率会随着T增加而略有增大。图7为参数J变化时
中表明网侧耦合效应的元素l12的伯德图,随着T增大,l12的峰值频率略有增加,峰值幅值几乎不变,由相对增益理论可知,T对网侧耦合程度影响不大,耦合频率会随着T增加而略有增大。图7为参数J变化时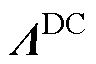 中表明网侧耦合效应的元素l12的伯德图,随着J增大,l12的峰值幅值从0.33增加到0.37,峰值频率不变,由相对增益理论可知,J增大会增加系统的耦合程度。图8为参数D变化时
中表明网侧耦合效应的元素l12的伯德图,随着J增大,l12的峰值幅值从0.33增加到0.37,峰值频率不变,由相对增益理论可知,J增大会增加系统的耦合程度。图8为参数D变化时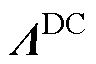 中表明网侧耦合效应的元素l12的伯德图,随着参数D增大,l12峰值幅值从0.33增加到0.57,而峰值频率不变,由相对增益理论可知,参数D增大会增加系统的耦合程度。由以上分析可知,在直流电压控制环路参数中,影响耦合程度的主要参数为J和D,为避免耦合程度加大,J和D的值不宜过大。
中表明网侧耦合效应的元素l12的伯德图,随着参数D增大,l12峰值幅值从0.33增加到0.57,而峰值频率不变,由相对增益理论可知,参数D增大会增加系统的耦合程度。由以上分析可知,在直流电压控制环路参数中,影响耦合程度的主要参数为J和D,为避免耦合程度加大,J和D的值不宜过大。
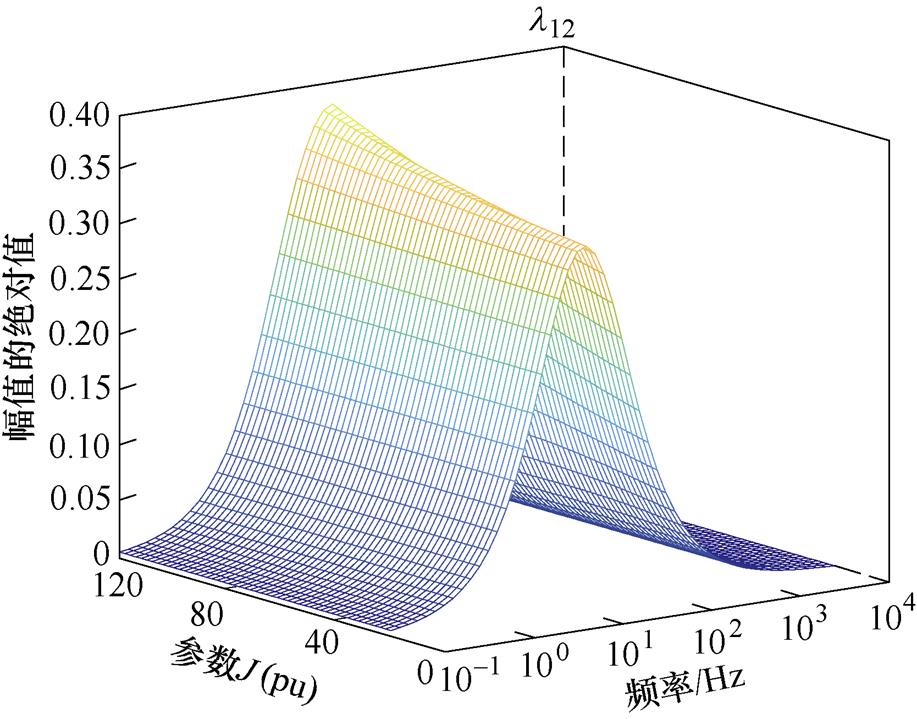
图7 参数J变化时l12幅值
Fig.7 Amplitude of l12 when parameter J changes
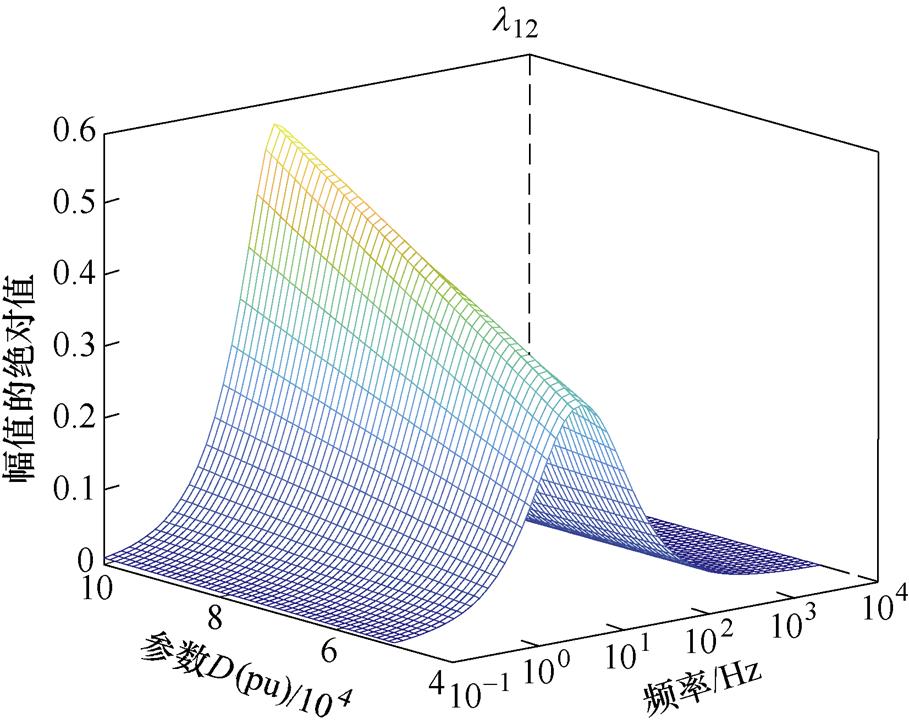
图8 参数D变化时l12幅值
Fig.8 Amplitude of l12 when parameter D changes
图9为参数KQp变化时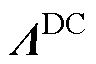 中表明网侧耦合效应的元素l12的伯德图,随着KQp增大,l12峰值幅值从0.33增加到0.65,峰值频率略有增加,由相对增益理论可知,KQp增大会增加系统的耦合程度,耦合频率略有增加。图10为参数KQi变化时
中表明网侧耦合效应的元素l12的伯德图,随着KQp增大,l12峰值幅值从0.33增加到0.65,峰值频率略有增加,由相对增益理论可知,KQp增大会增加系统的耦合程度,耦合频率略有增加。图10为参数KQi变化时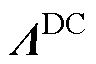 中表明网侧耦合效应的元素l12的伯德图,随着参数KQi增大,l12峰值幅值变化幅度较小,峰值频率增加到15 Hz附近,由相对增益理论分析可知,KQi增大会增加耦合频率,而对耦合程度影响较小。由以上分析可知,在无功功率控制环路参数中,影响耦合程度的主要为参数KQp,为避免耦合程度加大,KQp的值不宜过大。
中表明网侧耦合效应的元素l12的伯德图,随着参数KQi增大,l12峰值幅值变化幅度较小,峰值频率增加到15 Hz附近,由相对增益理论分析可知,KQi增大会增加耦合频率,而对耦合程度影响较小。由以上分析可知,在无功功率控制环路参数中,影响耦合程度的主要为参数KQp,为避免耦合程度加大,KQp的值不宜过大。
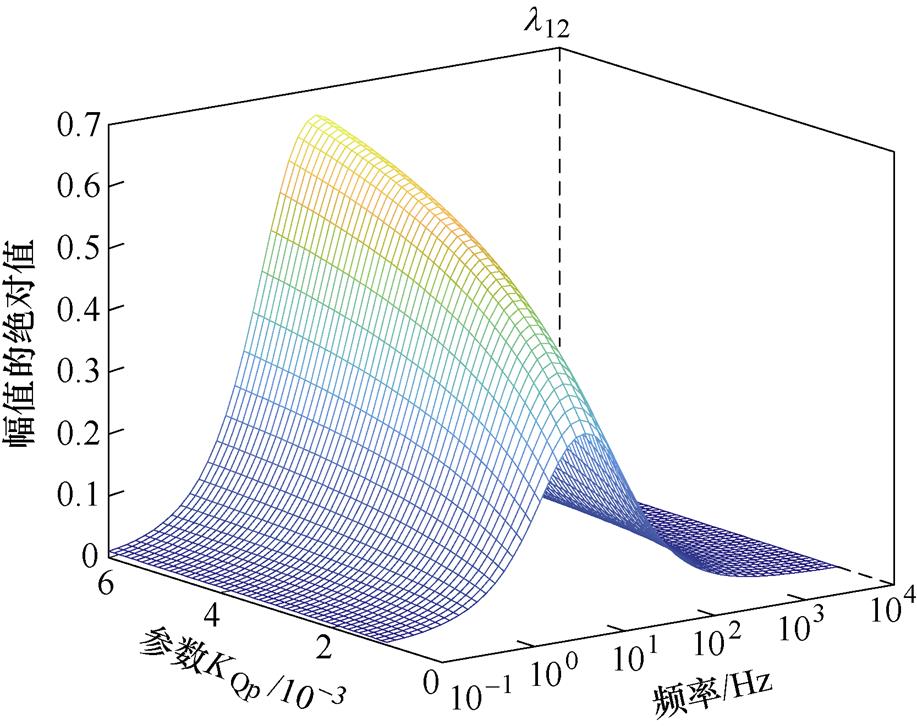
图9 参数KQp变化时l12幅值
Fig.9 Amplitude of l12 when parameter KQp changes
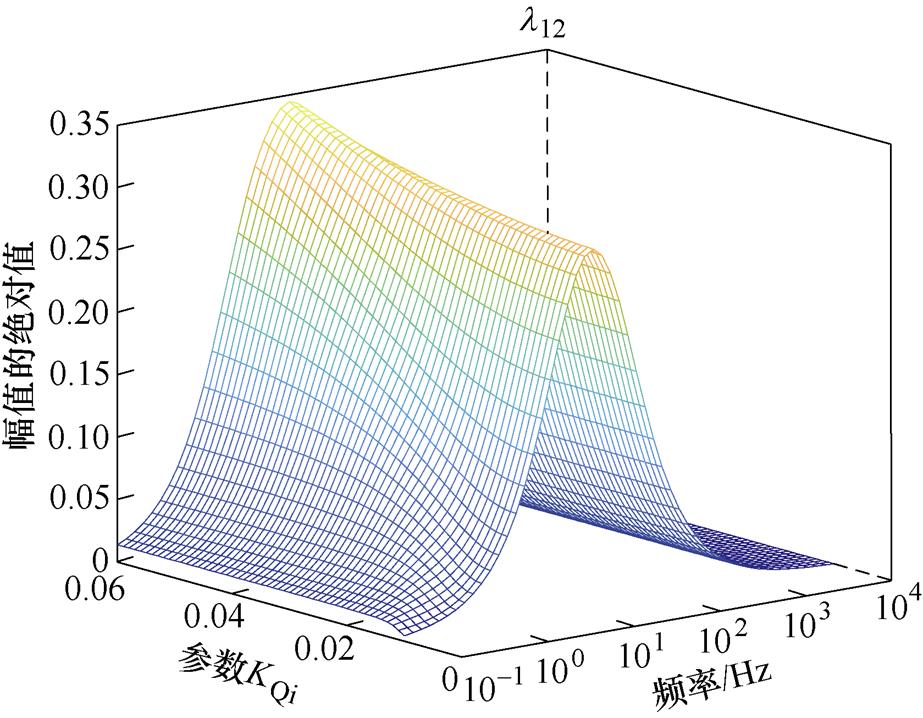
图10 参数KQi变化时l12幅值
Fig.10 Amplitude of l12 when parameter KQi changes
为减小耦合效应引起的直流电压波动,提出一种基于无功前馈的直流电压补偿策略,其控制框图如图11所示,通过无功功率偏差经过补偿系数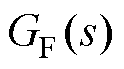 引入到直流电压控制环路中,
引入到直流电压控制环路中,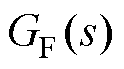 为高通滤波器,其控制作用只在动态过程起作用,不影响系统的稳态运行。
为高通滤波器,其控制作用只在动态过程起作用,不影响系统的稳态运行。
图11中,补偿系数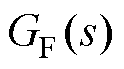 为
为
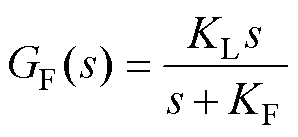 (23)
(23)
式中,KL为线路系数;KF为高通滤波器带宽。
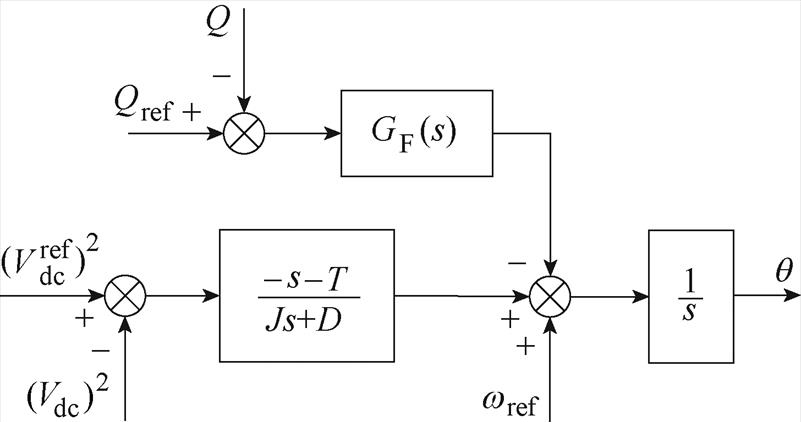
图11 基于无功前馈的直流电压补偿策略控制框图
Fig.11 Control diagram of DC voltage compensation method based on reactive power feedforward
按照第2节中建模方法,得到改进后考虑耦合效应的闭环模型框图如图12所示,改进后的考虑网侧耦合效应的直流电压闭环小信号模型如附录式(A6)所示,从而得到改进后第一放大因子矩阵 为
为
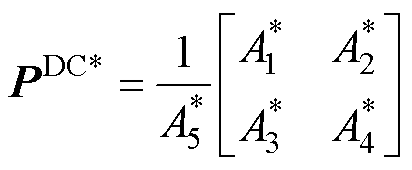 (24)
(24)
式中,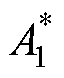 ~
~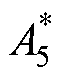 的值如附录式(A7)~式(A11)所示。
的值如附录式(A7)~式(A11)所示。
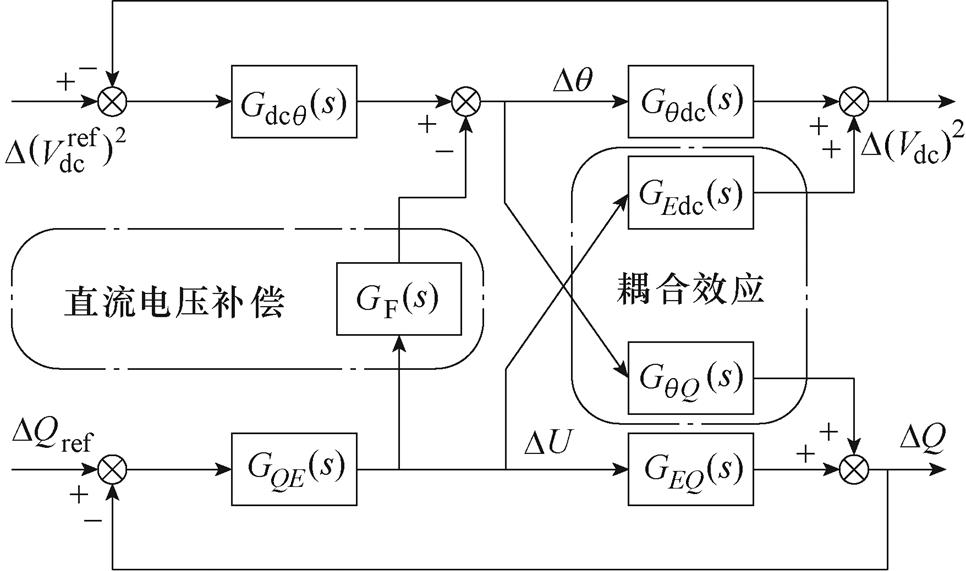
图12 改进后网侧耦合效应闭环模型
Fig.12 Improved grid-side coupling effect closed-loop model
将式(24)代入式(9)中可以计算得到直流电压控制的相对增益矩阵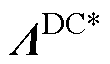 为
为
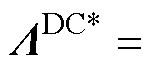
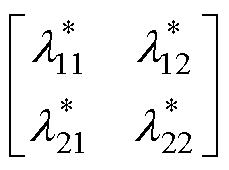 (25)
(25)
其中
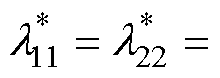
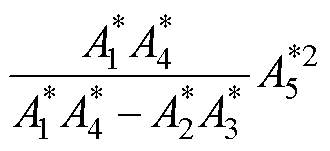
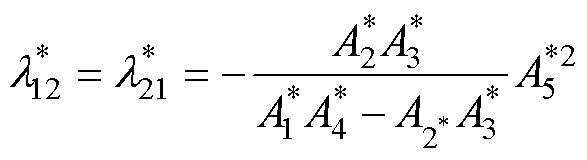
在式(23)中,线路系数KL是和线路电感Lg以及稳态工作点有关的量。当线路阻抗和有功功率给定发生变化时,参数KL需要随之调整,其设定应满足
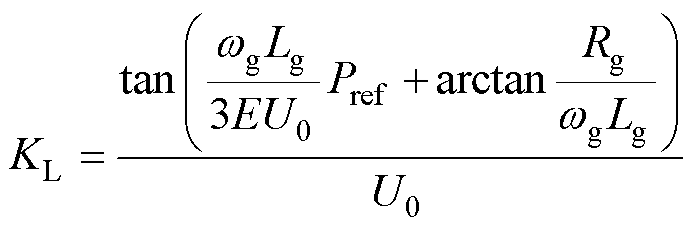 (26)
(26)
在确定参数KL后,高通滤波器带宽KF的设定,应使得式(24)中无功功率到直流电压的小信号传递函数满足
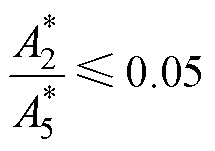 (27)
(27)
结合式(26)、式(27),得到KF取值应近似满足
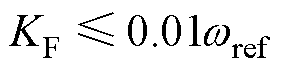 (28)
(28)
绘制参数KF变化时,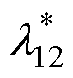 幅值变化情况如图13所示。
幅值变化情况如图13所示。
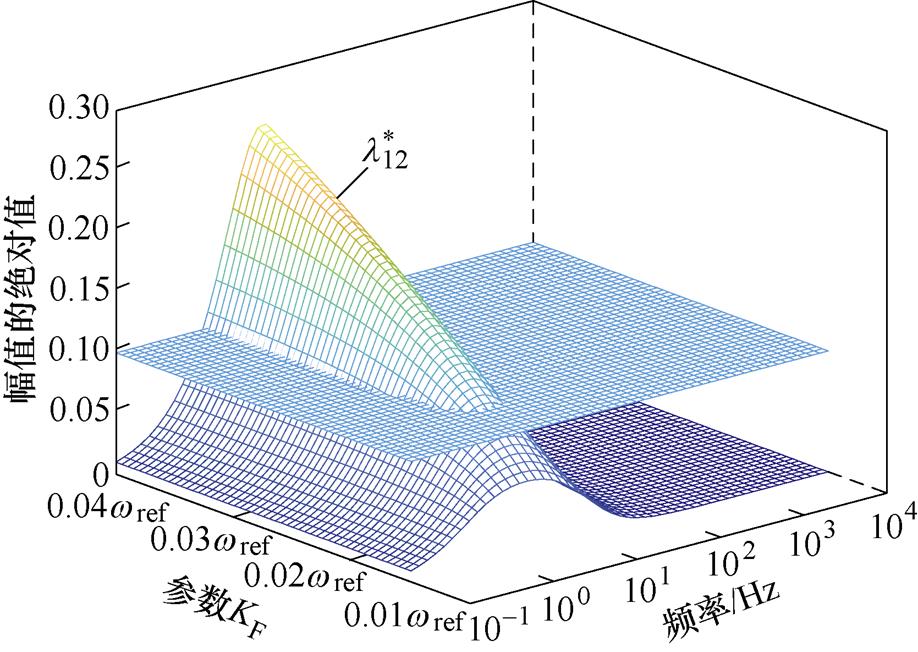
图13 参数KF变化时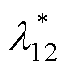 幅值
幅值
Fig.13 Amplitude of 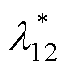 when parameter KF changes
when parameter KF changes
由图13可知,在使用基于无功前馈的直流电压补偿策略后,参数KF增大会影响其效果。选择KF≤ 0.02wref时,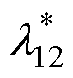 的峰值幅值减少到0.1以下,表明该方法有效地减小了网侧耦合效应。当KF选择满足式(28)时,
的峰值幅值减少到0.1以下,表明该方法有效地减小了网侧耦合效应。当KF选择满足式(28)时,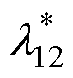 的峰值幅值降低至0.05以下,由相对增益理论分析可知,改进后网侧耦合效应的耦合程度降低。
的峰值幅值降低至0.05以下,由相对增益理论分析可知,改进后网侧耦合效应的耦合程度降低。
为验证理论分析的正确性及所提策略的可行性,在5 kW全功率风电实验平台上进行实验验证。实验平台如图14所示,原动机组由一台变频器和一台三相异步电动机组成,发电机组由一台5 kW永磁同步发电机、一组背靠背变流器以及LC滤波装置组成。原动机组中变频器对电动机进行V/f控制,三相异步电动机与永磁同步发电机同轴连接,模拟风力机为发电机提供机械转矩。发电机组中机侧变流器控制永磁同步发电机的定子电流,网侧变流器控制直流电压恒定,网侧采用理论分析中的构网型控制模式。实验平台相关参数见表2。

图14 5 kW全功率风电实验平台
Fig.14 5 kW full-power wind power experimental platform
表2 实验平台参数
Tab.2 The parameters of experimental platform
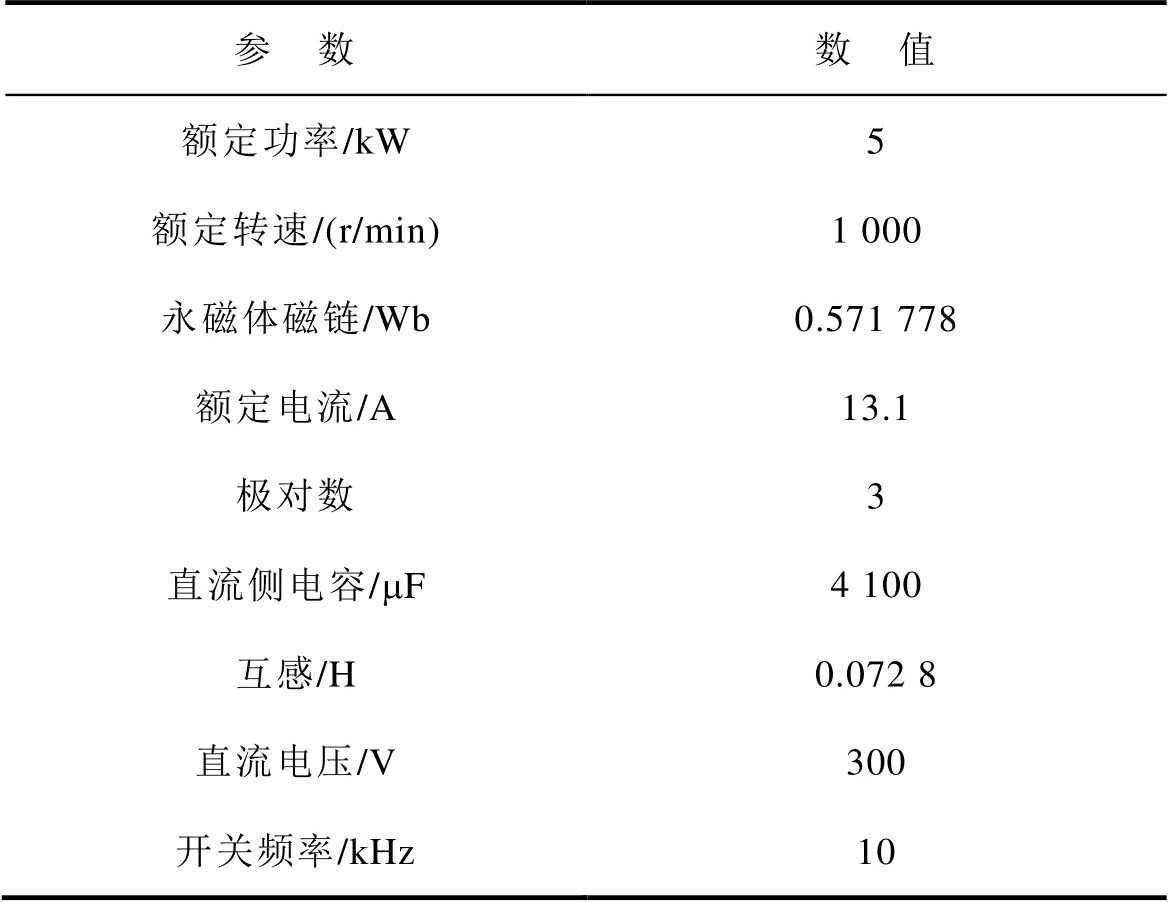
参 数数 值 额定功率/kW5 额定转速/(r/min)1 000 永磁体磁链/Wb0.571 778 额定电流/A13.1 极对数3 直流侧电容/mF4 100 互感/H0.072 8 直流电压/V300 开关频率/kHz10
为验证系统参数对网侧耦合效应影响,在机侧稳定运行,到达额定工作点后,网侧无功给定值由0(pu)(标幺值)阶跃到0.2(pu)(1 000 var),观测不同参数下直流电压和并网点有功功率的动态波形。
图15为直流电压环参数T变化时,无功阶跃的直流电压动态和并网点有功功率波形,在4.2 s发生无功功率阶跃。图15a为并网点有功功率波形,稳态时,有功功率在额定工作点处(1(pu)),在动态过程中,有功功率超调幅值为0.01(pu),随着参数T增大,其超调幅值不变,此时无功功率通过并网点有功功率影响到直流电压的动态过程。如图15b所示,随着参数T增大,直流电压的动态调节时间减小,峰值幅值变化不大,始终保持在-10 V,表明通过耦合程度变化较小。在相对增益理论分析中,耦合因子l12随T增大,峰值频率略有增加,峰值幅值几乎不变,即T对网侧耦合程度影响不大,耦合频率会随着T增加而略有增大,实验结果与理论分析相一致。
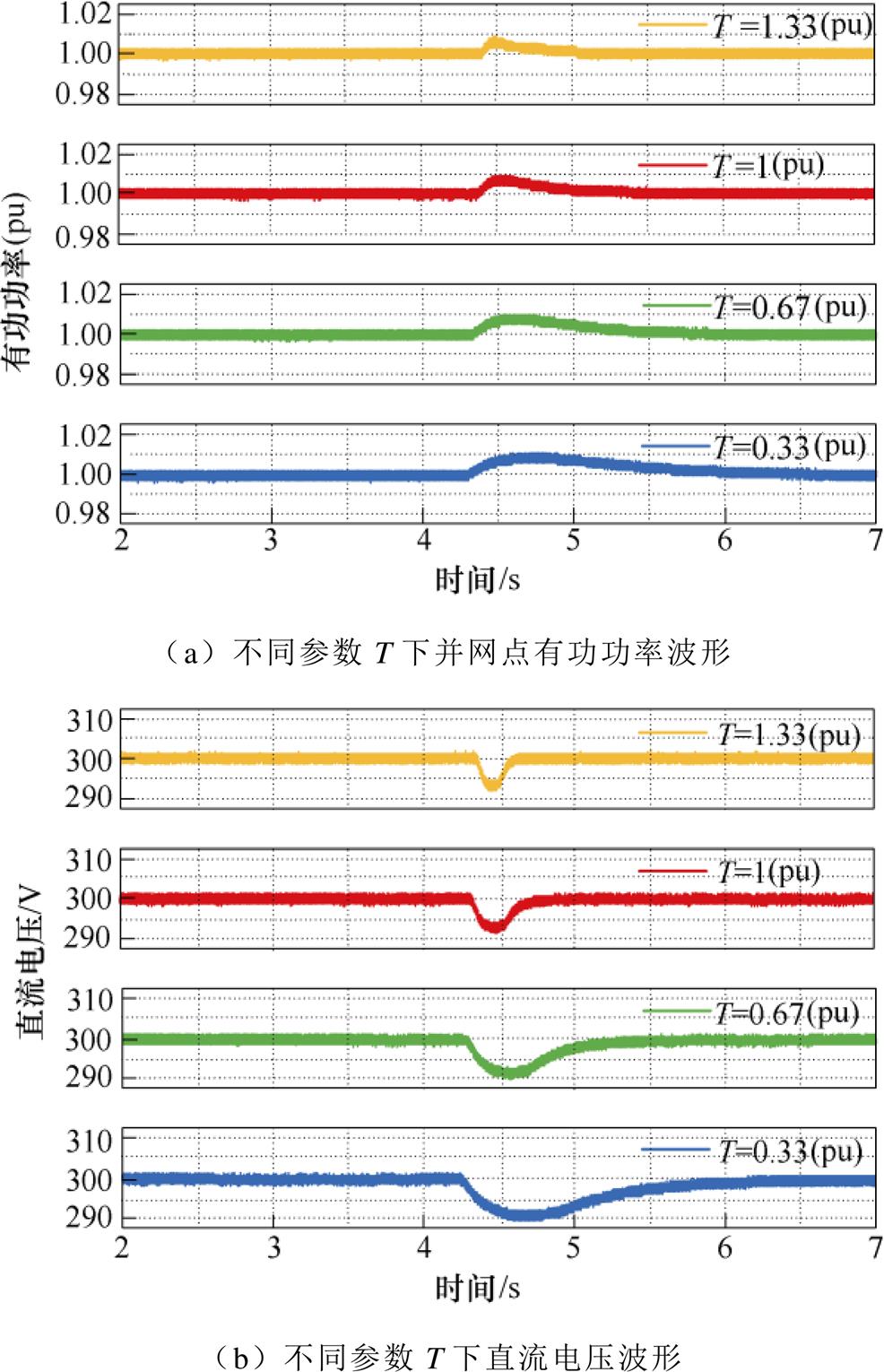
图15 直流电压环参数T对耦合效应影响
Fig.15 Influence of DC voltage loop parameter T on coupling effect
图16为直流电压环参数J变化时,无功阶跃的直流电压动态和并网点有功功率波形,在图16a中,4.2 s无功功率发生阶跃后,并网点有功功率超调量由J=10(1(pu))时的1.008(pu)增加到J=25(2.5(pu))时的1.015(pu)。在图16b中,随着参数J增大,直流电压动态过程峰值幅值略有增加,从10 V增加到18 V,表明耦合程度略有增大。在相对增益理论分析中,耦合因子l12随J增大,峰值频率不变,峰值幅值增大,即耦合程度会随着J增加而略有增大,实验结果与理论分析相一致。

图16 直流电压环参数J对耦合效应影响
Fig.16 Influence of DC voltage loop parameter J on coupling effect
图17为直流电压环参数D变化时,无功阶跃的直流电压动态和并网点有功功率波形,如图17a所示,4.2 s无功功率发生阶跃后,并网点有功功率超调量由D=50 000(1(pu))时的1.008(pu)增加到D=80 000(1.6(pu))时的1.022(pu)。在图17b的直流电压波形中,随着参数D增大,直流电压动态过程超调幅值从10 V增加到20 V,表明耦合程度增大。在相对增益理论分析中,耦合因子l12峰值幅值从0.33增加到0.57,而峰值频率不变,即参数D增大会增加系统的耦合程度,实验结果与理论分析一致。
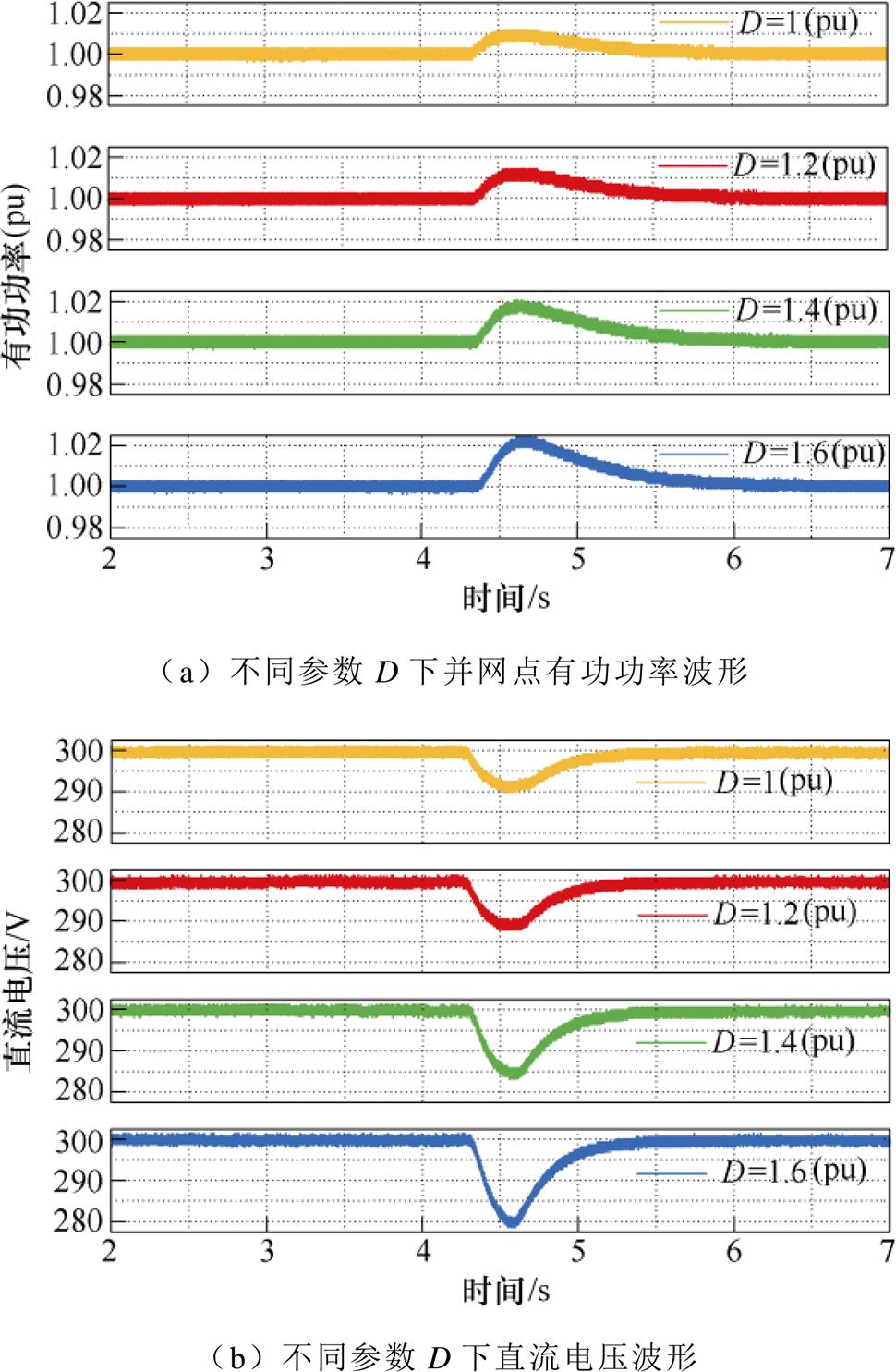
图17 直流电压环参数D对耦合效应影响
Fig.17 Influence of DC voltage loop parameter D on coupling effect
图18为无功功率环参数变化时,无功阶跃的直流电压和并网点有功功率的动态波形,在4.2 s时发生无功功率阶跃后,如图18a所示,随着参数KQP增大,并网点有功功率动态过程出现振荡,超调量由KQP=0.002时的1.008(pu)增加到KQP=0.003 5时的1.018(pu),且振荡频率增加。如图18b所示,随着参数KQP增大,直流电压的动态过程出现振荡,振荡幅值峰值由KQP=0.002时的-10 V增加到KQP= 0.003 5时的-22 V,且振荡频率增加,这表明耦合程度和耦合频率均增加。在相对增益理论分析中,耦合因子l12峰值幅值从0.33增加到0.65,峰值频率略有增加,即KQp增大会增加系统的耦合程度,耦合频率略有增加,实验结果与理论分析相一致。
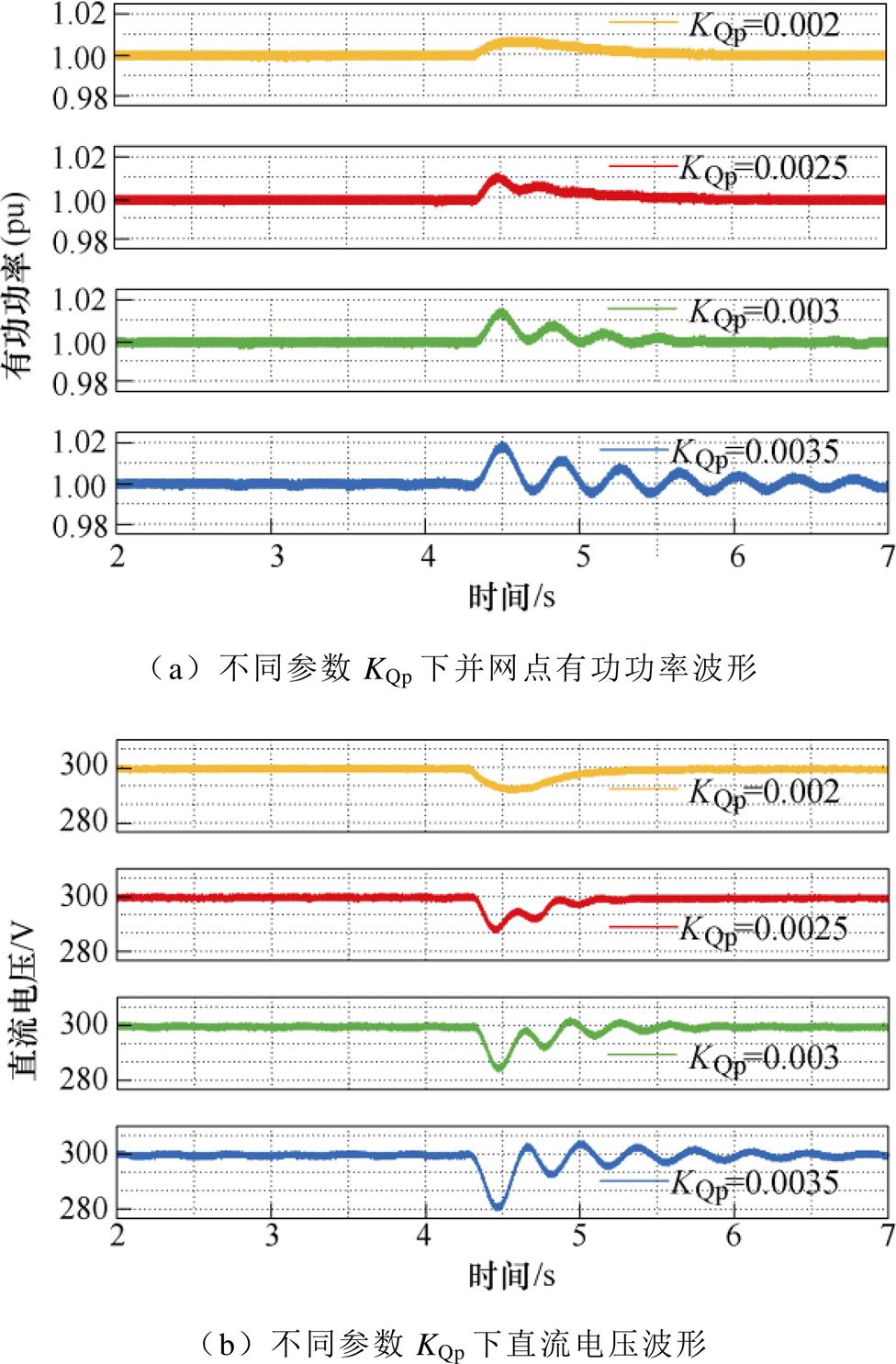
图18 无功环参数KQp对耦合效应影响
Fig.18 Influence of DC voltage loop parameter KQp on coupling effect
图19为无功功率环参数变化时,无功阶跃的直流电压和并网点有功功率的动态波形。如图19a所示,随着参数KQi增大,并网点有功功率动态过程出现振荡,振荡频率增加,超调量始终保持在1.008(pu)。如图19b所示,随着参数KQi增大,直流电压动态过程出现振荡,振荡幅值几乎不变,振荡频率增加,表明耦合程度变化不大,但耦合频率增加。在相对增益理论分析中,耦合因子峰值幅值变化幅度较小,峰值频率增加到15 Hz附近,即KQi增大会增加耦合频率,而对耦合程度影响较小,实验结果与理论分析相一致。

图19 无功环参数KQi对耦合效应影响
Fig.19 Influence of DC voltage loop parameter KQi on coupling effect
为验证所提补偿策略对抑制网侧耦合效应的可行性,在机侧稳定运行到达额定工作点(5 kW)后,网侧无功给定值由0(pu)阶跃到0.8(pu)(4 000var)。观测改进前后直流电压的动态波形。其中,参数KL由第2节中设计确定,与线路参数及工作点有关,KF参数选择为:KF=0.03wref、KF=0.01wref。

图20 改进前后耦合效应对比
Fig.20 Comparison of coupling effects before and after improvement
改进前后耦合效应对比如图20所示,在4.2 s时无功功率阶跃至0.8(pu),图20a为并网点有功功率波形,改进前动态过程超调量为1.05(pu),在改进后选择参数KF=0.03wref时,超调量降低为1.03(pu),选择参数KF= 0.01wref时,超调量降低为1.01(pu)。图20b为直流电压波形,改进前直流电压动态超调幅值为-22 V,采用本文提出的基于无功前馈的直流电压补偿策略时,选择参数KF=0.03wref,直流电压动态超调幅值降低至-13 V,选择参数KF=0.01wref,直流电压动态超调幅值降低至-4 V,降低了81.8 %。在相对增益理论分析中,选择KF≤ 0.02wref时,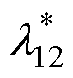 的峰值幅值减少到0.1以下,表明该方法有效减小了网侧耦合效应,即改进后网侧耦合效应的耦合程度降低,实验结果与理论分析相一致。
的峰值幅值减少到0.1以下,表明该方法有效减小了网侧耦合效应,即改进后网侧耦合效应的耦合程度降低,实验结果与理论分析相一致。
以上实验结果与第2节中理论分析基本一致,第2节中参数对耦合效应影响的分析得到了验证,证明所提基于无功前馈的直流电压补偿方法具有有效的直流电压波动抑制能力。
在全功率风电机组的网侧变流器的构网型控制中,由于功率模型存在有功功率和无功功率的耦合,导致在向电网输送无功功率时,会通过耦合通道影响直流电压的动态过程。本文利用相对增益理论的方法,分析了控制参数对耦合效应的影响,得出以下结论:
1)直流电压控制环路参数对耦合效应的影响。参数T增大时会提高降低直流电压的动态响应时间,对耦合程度无影响,参数J对直流电压的动态过程影响较小,参数D增大时,耦合程度随之增大,直流电压动态过程变差。
2)无功环控制参数对耦合效应的影响。参数KQp增大时,直流电压动态过程出现振荡,且振荡幅值增大,参数KQi增大时,直流电压动态过程振荡频率增加,但振荡幅值变化较小。
3)根据理论分析中参数KL和参数KF的设计,采用基于无功前馈的直流电压补偿策略后,由无功功率阶跃引起的直流电压动态过程振荡幅值减小、超调量降低,在选择合适参数KF时,可将由无功变化引起的直流电压动态超调降低81.8 %,改进后有效抑制了网侧的耦合效应。
本文的控制参数对耦合效应影响的分析可以为构网型全功率风电机组的参数设计提供进一步参考,所提无功补偿方法在工程实践中具有一定的应用前景。本文的研究未考虑故障电网条件,下一步可对电网不同场景下的耦合问题作更深入的研究。
附 录
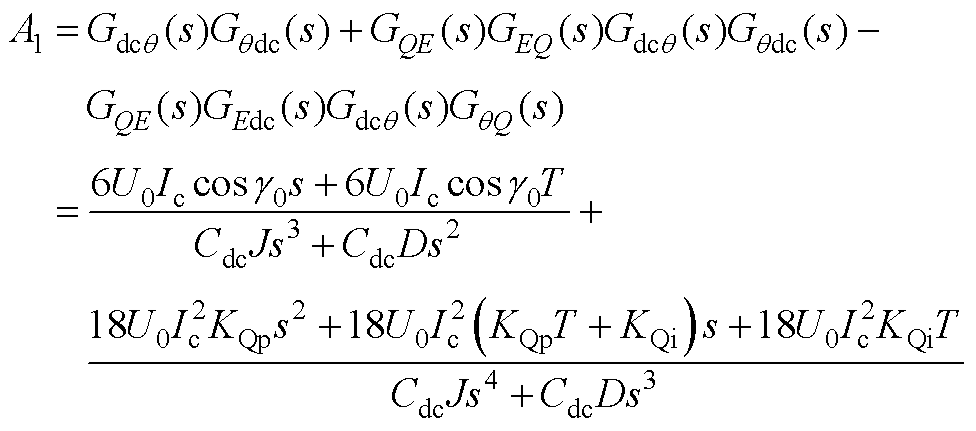 (A1)
(A1)
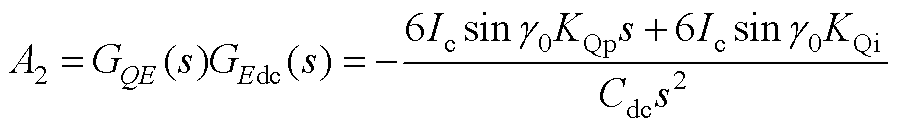 (A2)
(A2)
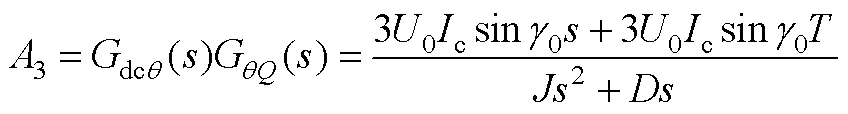 (A3)
(A3)
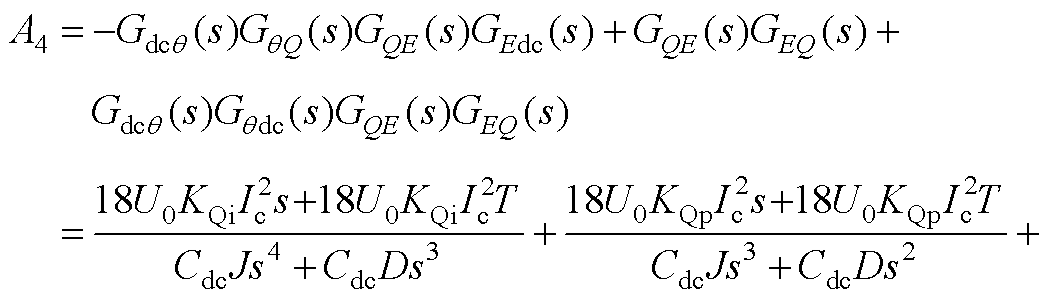
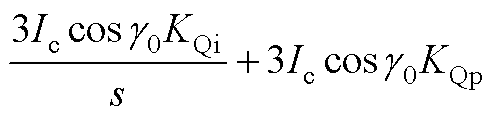 (A4)
(A4)
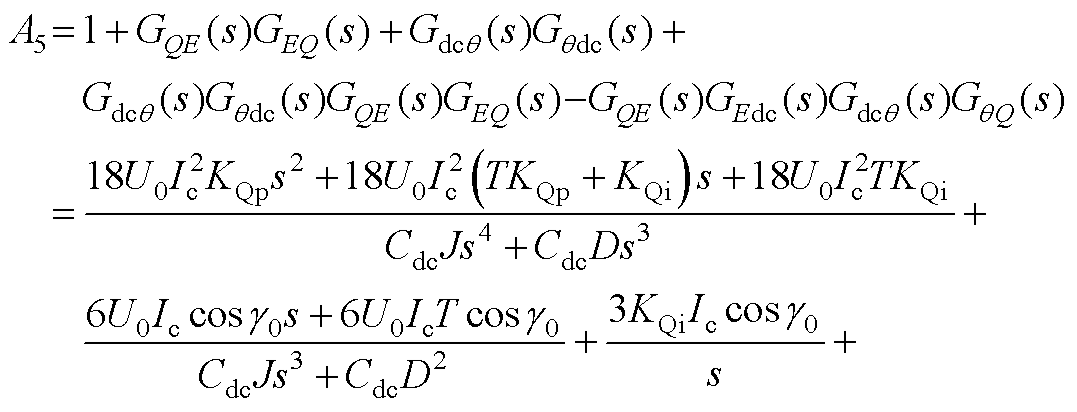
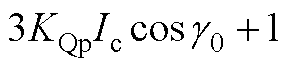 (A5)
(A5)
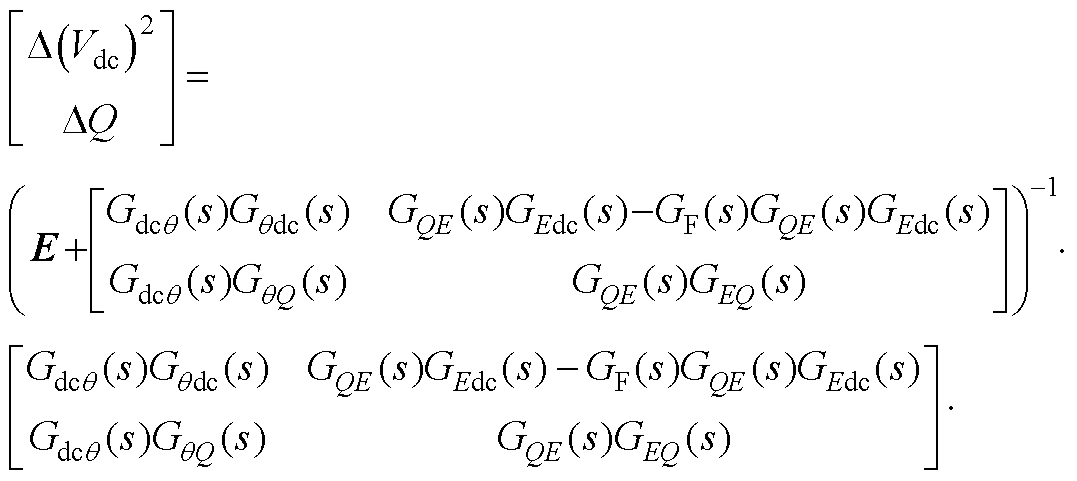
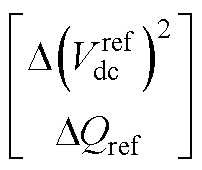 (A6)
(A6)
式中,E为单位矩阵。
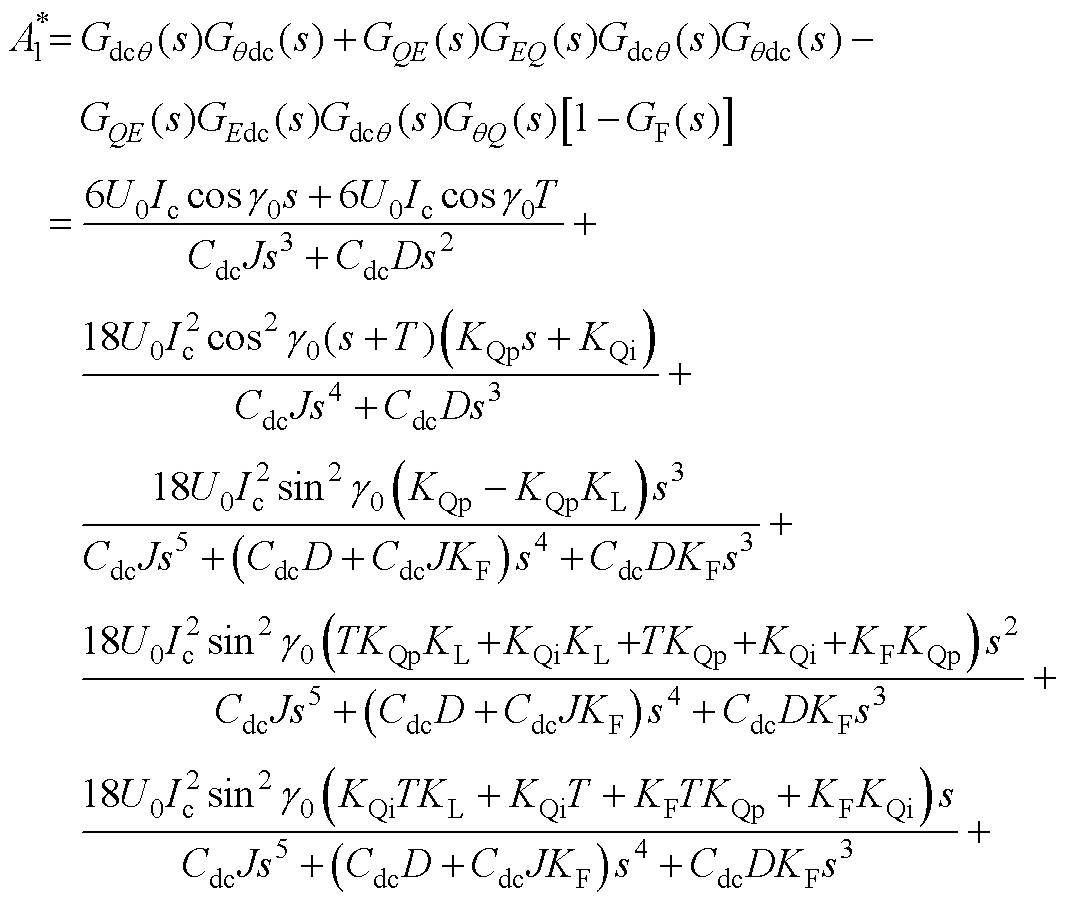
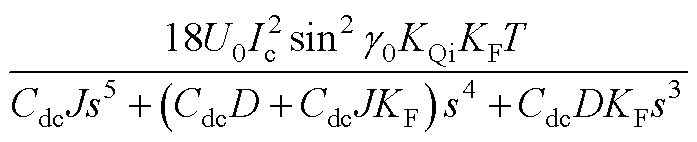 (A7)
(A7)
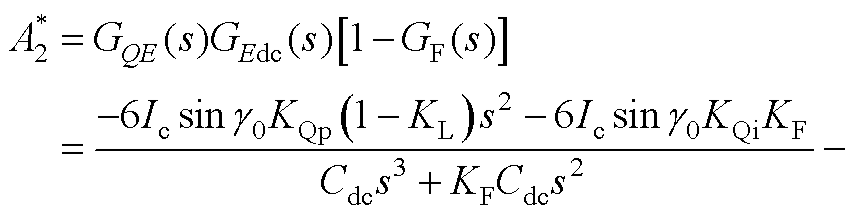
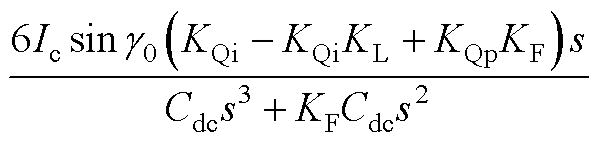 (A8)
(A8)
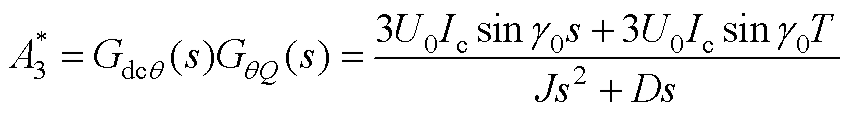 (A9)
(A9)
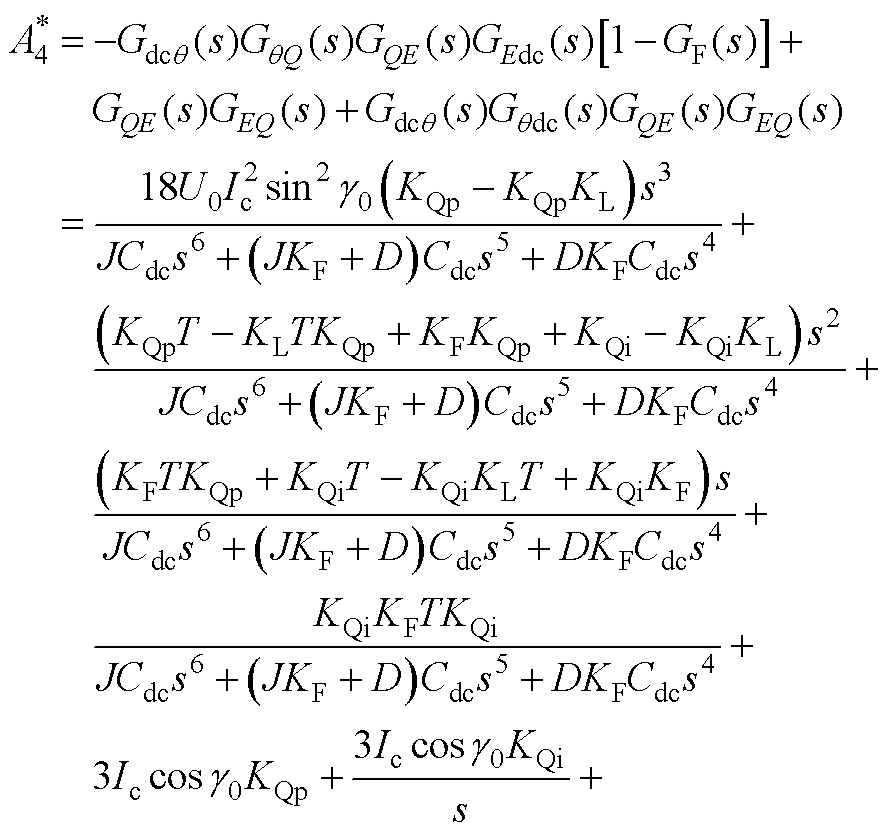
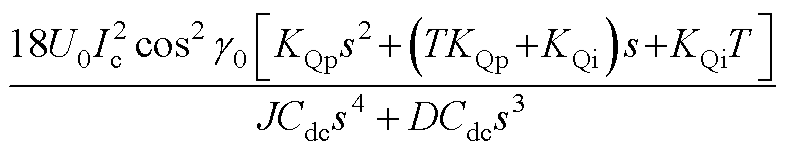 (A10)
(A10)

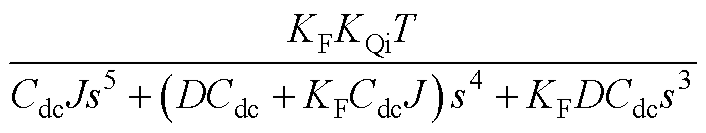 (A11)
(A11)
参考文献
[1] 王涛, 诸自强, 年珩. 非理想电网下双馈风力发电系统运行技术综述[J]. 电工技术学报, 2020, 35(3): 455-471.
Wang Tao, Zhu Ziqiang, Nian Heng. Review of operation technology of doubly-fed induction generator- based wind power system under nonideal grid conditions[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 455-471.
[2] 颜湘武, 王德胜, 杨琳琳, 等. 直驱风机惯量支撑与一次调频协调控制策略[J]. 电工技术学报, 2021, 36(15): 3282-3292.
Yan Xiangwu, Wang Desheng, Yang Linlin, et al. Coordinated control strategy of inertia support and primary frequency regulation of PMSG[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(15): 3282-3292.
[3] 吴广禄, 王姗姗, 周孝信, 等. VSC接入弱电网时外环有功控制稳定性解析[J]. 中国电机工程学报, 2019, 39(21): 6169-6183.
Wu Guanglu, Wang Shanshan, Zhou Xiaoxin, et al. Analytical analysis on the active power control stabi- lity of the weak grids-connected VSC[J]. Proceedings of the CSEE, 2019, 39(21): 6169-6183.
[4] 张学广, 付志超, 陈文佳, 等. 弱电网下考虑锁相环影响的并网逆变器改进控制方法[J]. 电力系统自动化, 2018, 42(7): 139-145.
Zhang Xueguang, Fu Zhichao, Chen Wenjia, et al. An improved control method for grid-connected inverters considering impact of phase-locked loop under weak grid condition[J]. Automation of Electric Power Systems, 2018, 42(7): 139-145.
[5] 杨苓, 陈燕东, 周乐明, 等. 弱电网下锁相环对三相LCL型并网逆变器小扰动建模影响及稳定性分析[J]. 中国电机工程学报, 2018, 38(13): 3792-3804, 4020.
Yang Ling, Chen Yandong, Zhou Leming, et al. Influence of PLL on small disturbance modeling and stability analysis of three-phase LCL grid-connected inverter in weak current network[J]. Proceedings of the CSEE, 2018, 38(13): 3792-3804, 4020.
[6] Zhong Qingchang, Weiss G. Synchronverters: inver- ters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.
[7] 陶亮, 孙建军, 查晓明, 等. 基于虚拟同步发电机技术的改进型背靠背起动方法[J]. 电工技术学报, 2020, 35(增刊2): 413-420.
Tao Liang, Sun Jianjun, Zha Xiaoming, et al. A modified back-to-back starting method based on virtual synchronous generator technology[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(S2): 413-420.
[8] 章艳, 高晗, 张萌. 不同虚拟同步机控制下双馈风机系统频率响应差异研究[J]. 电工技术学报, 2020, 35(13): 2889-2900.
Zhang Yan, Gao Han, Zhang Meng. Research on frequency response difference of doubly-fed indu- ction generator system controlled by different virtual synchronous generator controls[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2889- 2900.
[9] Harnefors L, Hinkkanen M, Riaz U, et al. Robust analytic design of power-synchronization control[J]. IEEE Transactions on Industrial Electronics, 2019, 66(8): 5810-5819.
[10] 伍文华, 周乐明, 陈燕东, 等. 序阻抗视角下虚拟同步发电机与传统并网逆变器的稳定性对比分析[J]. 中国电机工程学报, 2019, 39(5): 1411-1421.
Wu Wenhua, Zhou Leming, Chen Yandong, et al. Stability comparison and analysis between the virtual synchronous generator and the traditional grid- connected inverter in the view of sequence impe- dance[J]. Proceedings of the CSEE, 2019, 39(5): 1411-1421.
[11] Huang Linbin, Xin Huanhai, Wang Zhen, et al. A virtual synchronous control for voltage-source con- verters utilizing dynamics of DC-link capacitor to realize self-synchronization[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(4): 1565-1577.
[12] Guo Jian, Chen Yandong, Wang Lei, et al. Impedance analysis and stabilization of virtual synchronous generators with different DC-link voltage controllers under weak grid[J]. IEEE Transactions on Power Electronics, 2021, 36(10): 11397-11408.
[13] 董文凯, 杜文娟, 王海风. 弱连接条件下锁相环动态主导的并网直驱风电场小干扰稳定性研究[J]. 电工技术学报, 2021, 36(3): 609-622.
Dong Wenkai, Du Wenjuan, Wang Haifeng. Small- signal stability of a grid-connected PMSG wind farm dominated by dynamics of PLLs under weak grid connection[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 609-622.
[14] 桑顺, 张琛, 蔡旭, 等. 全功率变换风电机组的电压源控制(一): 控制架构与弱电网运行稳定性分析[J]. 中国电机工程学报, 2021, 41(16): 5604-5616.
Sang Shun, Zhang Chen, Cai Xu, et al. Voltage source control of wind turbines with full-scale converters (part Ⅰ): control architecture and stability analysis under weak grid conditions[J]. Proceedings of the CSEE, 2021, 41(16): 5604-5616.
[15] 贺家发, 宋美艳, 兰洲, 等. 适应于弱电网的永磁直驱风电机组虚拟惯量协调控制策略[J]. 电力系统自动化, 2018, 42(9): 83-90.
He Jiafa, Song Meiyan, Lan Zhou, et al. A virtual inertia coordinated control scheme of PMSG-based wind turbines in weak grids[J]. Automation of Electric Power Systems, 2018, 42(9): 83-90.
[16] Wen Tiliang, Zhu Donghai, Zou Xudong, et al. Power coupling mechanism analysis and improved decoupling control for virtual synchronous generator[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 3028-3041.
[17] Li Mingxuan, Wang Yue, Hu Weihao, et al. Unified modeling and analysis of dynamic power coupling for grid-forming converters[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 2321-2337.
[18] 李武华, 王金华, 杨贺雅, 等. 虚拟同步发电机的功率动态耦合机理及同步频率谐振抑制策略[J]. 中国电机工程学报, 2017, 37(2): 381-391.
Li Wuhua, Wang Jinhua, Yang Heya, et al. Power dynamic coupling mechanism and resonance suppression of synchronous frequency for virtual synchronous generators[J]. Proceedings of the CSEE, 2017, 37(2): 381-391.
[19] 姜静雅, 王玮, 吴学智, 等. 基于自适应无功功率补偿的虚拟同步机功率解耦策略[J]. 电工技术学报, 2020, 35(13): 2747-2756.
Jiang Jingya, Wang Wei, Wu Xuezhi, et al. Power decoupling strategy in virtual synchronous generator based on adaptive reactive power compensation[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2747-2756.
[20] 屈子森, 蔡云旖, 杨欢, 等. 基于自适应虚拟阻抗的虚拟同步机功率解耦控制策略[J]. 电力系统自动化, 2018, 42(17): 58-66.
Qu Zisen, Cai Yunyi, Yang Huan, et al. Strategy of power decoupling control for virtual synchronous generator based on adaptive virtual impedances[J]. Automation of Electric Power Systems, 2018, 42(17): 58-66.
[21] 李鹏, 杨世旺, 王阳, 等. 基于相对增益分析的目标函数对角化微网功率解耦控制方法[J]. 中国电机工程学报, 2014, 34(13): 2039-2046.
Li Peng, Yang Shiwang, Wang Yang, et al. Objective function diagonalization decoupling control of micro- grid power based on relative gain analysis[J]. Proceedings of the CSEE, 2014, 34(13): 2039- 2046.
[22] Wu Teng, Liu Zeng, Liu Jinjun, et al. A unified virtual power decoupling method for droop-controlled parallel inverters in microgrids[J]. IEEE Transactions on Power Electronics, 2016, 31(8): 5587-5603.
[23] 李明烜, 王跃, 徐宁一, 等. 松弛小功角约束条件的虚拟同步发电机功率解耦策略[J]. 电力系统自动化, 2018, 42(9): 59-68.
Li Mingxuan, Wang Yue, Xu Ningyi, et al. Power decoupling strategy for virtual synchronous generator relaxing condition of small power angle[J]. Auto- mation of Electric Power Systems, 2018, 42(9): 59-68.
[24] Zhao Fangzhou, Wang Xiongfei, Zhu Tianhua. Power dynamic decoupling control of grid-forming converter in stiff grid[J]. IEEE Transactions on Power Elec- tronics, 2022, 37(8): 9073-9088.
[25] Wang Jing, Chang N C P, Feng Xiaowei, et al. Design of a generalized control algorithm for parallel inverters for smooth microgrid transition operation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(8): 4900-4914.
[26] 张兴. PWM整流器及其控制策略的研究[D]. 合肥:合肥工业大学, 2003.
[27] 李鹏, 杨世旺, 殷梓恒. 基于相对增益矩阵的微网稳压解耦下垂控制方法[J]. 中国电机工程学报, 2015, 35(5): 1041-1050.
Li Peng, Yang Shiwang, Yin Ziheng. Voltage stabi- lization and decoupling droop control method for microgrid based on RGA[J]. Proceedings of the CSEE, 2015, 35(5): 1041-1050.
Abstract With the high proportion of wind power connected to the grid, the stable operation capability of full-power wind turbines is facing challenges. The traditional grid-side converter adopts a phase-locked loop (PLL) synchronization strategy. In a high-ratio power electronic system, the PLL is prone to phase-lock instability. The grid-side converter of the grid-forming full-power wind turbine adopts a power synchronization strategy based on the dynamic characteristics of the DC voltage to realize the grid-forming control of the DC voltage synchronization. In the grid-forming control of the full-power wind turbine grid-side converter using DC voltage synchronization, due to the power coupling problem in the grid-forming control, when the grid-side converter needs to transmit reactive power to the grid to provide active voltage support, the reactive power will affect the active power through the coupling channel, which will further affect the stability of the DC voltage and reduce the effective operation capacity of the system.
In order to analyze the coupling problem of reactive power and DC voltage in the grid-side converter, this paper first introduces the grid-forming control structure of the DC voltage synchronization of the grid-side converter of the full-power wind turbine and establishes the DC voltage-reactive power coupling model. Through the theory of relative gain, the influence of control parameters on the coupling effect is analyzed in detail. Then, aiming at the grid-side coupling effect, a DC voltage compensation method based on reactive power feedforward is proposed, which reduces the dynamic overshoot of DC voltage fluctuations due to reactive power variations; Finally, the theoretical analysis and the proposed method are verified on the experimental platform of the 5 kW permanent magnet synchronous full-power wind turbine.
The following conclusions can be drawn through the theoretical analysis results of the relative gain theory method and the verification of the experimental platform:
(1) The influence of DC voltage control loop parameters on the grid-side coupling effect: when parameter T increases, the dynamic response time of the DC voltage will be increased and reduced, but the grid-side coupling degree is not affected. Parameter J has little influence on the dynamic process of the DC voltage: when parameter D increases, the coupling degree of the grid side increases, and the dynamic process of DC voltage becomes worse.
(2) The influence of reactive loop control parameters on the grid-side coupling effect: when parameter KQp increases, the dynamic process of DC voltage oscillates, and the oscillation amplitude increases. When parameter KQi increases, the oscillation frequency of the dynamic process of DC voltage increases, but the oscillation amplitude changes little.
(3) According to the design of parameter KLand parameter KF in theoretical analysis, after adopting the DC voltage compensation strategy with reactive power feedforward, the oscillation amplitude and overshoot of the DC voltage dynamic process caused by reactive power steps are reduced. In the experiment, if the appropriate parameter KF is selected, the dynamic overshoot amplitude of the DC voltage can be reduced by 81.8%. This method effectively suppresses the coupling effect on the grid side.
keywords:Full-power wind turbine, grid-side converter, DC voltage, coupling effect
国家重点研发计划资助项目(2022YFB4202302)。
收稿日期 2022-07-28
DOI: 10.19595/j.cnki.1000-6753.tces.221462
中图分类号:TM464
谢 震 男,1976年生,教授,博士生导师,研究方向为大功率风力发电用并网变流器。E-mail: ppsd2003xie@sina.com(通信作者)
杨曙昕 男,1997年生,硕士研究生,研究方向为新能源发电系统并网技术。E-mail: 953835321@qq.com
改稿日期 2022-10-31
(编辑 崔文静)