
图1 传统LC滤波型电压源逆变器MPVC框图
Fig.1 Control block diagram of conventional MPVC for LC-filtered VSI
摘要 为解决传统模型预测控制在参数失配时预测误差增大的问题,该文提出一种适用于LC滤波型电压源逆变器的无模型预测电压控制策略。该策略建立了基于电压和电流双梯度的查询表,通过计算和存储上一时刻应用矢量作用下的电压和电流梯度,并结合当前时刻的采样值,实现未来时刻电压和电流的无模型预测;进一步重构状态空间预测方程,根据应用矢量作用下的电压和电流梯度实时更新未应用矢量的梯度值,保证了梯度的准确性;使用电压和电流双目标的价值函数进行跟踪评估,进而选取下一控制周期最优的矢量。该方法不依赖于任何系统参数、计算简单,且消除了传统无模型预测中梯度更新停滞现象,改善了输出电压性能。最后通过实验验证了所提方法的有效性和优越性。
关键词:电压源逆变器 LC型滤波 无模型预测电压控制 梯度更新
随着分布式发电、储能以及孤岛微电网系统的快速发展,三相LC滤波型电压源逆变器(Voltage Source Inverter, VSI)成为了可再生能源系统的关键设备[1]。为了实现期望的输出电压调节,研究人员在实际控制中通常采用多环路线性控制方法,该方法需要设置级联控制回路,导致其动态性能降低,参数调整困难。近年来,模型预测电压控制(Model Predictive Voltage Control, MPVC)因其具有响应速度快、约束处理简单、多目标控制能力强等优点,已广泛应用于VSI控制[2-5]。
文献[6]首次提出了LC滤波型VSI的MPVC策略,其通过离散的系统模型计算未来时刻的电压预测值,并利用价值函数选择最优的矢量。由于LC滤波器的电感电流和电容电压之间相互影响,以单一电压为控制目标很难得到满意的电压性能[6-7]。文献[8-9]在价值函数中加入电感电流追踪评估,实现了以电感电流和电容电压为双控制目标的价值函数评估,改善了电压质量。然而,基于MPVC的输出电压性能依赖精确的数学模型,建模的不确定性以及系统参数不可预见的变化会影响其稳态性能[10]。
为了消除模型参数对预测控制的影响,部分学者研究了无模型预测控制(Model-Free Predictive Control, MFPC)方法。该方法通过采用超局部模 型[11-12]、自回归输入模型[13]和查询表(Look-Up Table, LUT)[14-20]替代传统的预测模型,提高预测的鲁棒性。然而,基于超局部模型和自回归输入模型的MFPC方法的控制性能会受到电压和电流数据周期数的影响。当存储的电压和电流周期数增加时,MFPC的预测准确性随之提高,但这也占用了更多的存储空间,而且可能会降低系统的动态控制性能。当储存的电压电流周期数减小时,MFPC的预测准确性会降低。
基于LUT的MFPC方法原理简单、易于实现;其通过存储和更新一个控制周期中各个矢量作用下的电流梯度,实现鲁棒电流预测[14]。然而,该方法需要更新未应用矢量作用下的电流梯度,否则将导致梯度更新的停滞现象,增大预测误差。为此,文献[15-19]提出了多种电流梯度更新方法以减少停滞现象,改善其输出电流质量。文献[15]设置了电流梯度的更新频率,即某个电流梯度在50个控制周期内没有被更新,控制系统将在下一个控制周期强制使用其对应的矢量,从而实现电流梯度的更新;文献[16]利用过去3个控制周期采样的电流梯度对剩余的电流梯度进行更新;文献[17-18]建立了两个控制周期间的电流梯度关系,并利用该关系更新剩余的电流梯度;文献[19]通过应用矢量的幅值关系实现剩余梯度的更新;文献[20]在一个控制周期设置了3个采样点,通过多采样的方法提高了电流梯度的更新频率。目前,电流梯度的更新方法仍需被研究,且上述基于LUT的MFPC方法均针对L滤波型VSI系统提出,LC滤波型MFPC下LUT如何设计、梯度如何更新,尚未见报道。
本文针对LC滤波型VSI提出了一种基于电压电流双梯度全更新的无模型预测电压控制(Model- Free Predictive Voltage Control, MFPVC)方法。首先,该方法设计了电容电压梯度和逆变器侧电流梯度的查询表,基于梯度信息实现电压和电流的无参数预测;其次,该方法重构了状态空间预测方程,保证了每个控制周期中所有梯度的实时更新,消除了传统MFPC的停滞现象;此外,通过双目标的价值函数的使用,进一步提高了输出电压质量;最后,对所提方法的有效性进行了实验验证。
图1给出了LC型滤波VSI的传统MPVC方法控制框图,其拓扑在ab 静止坐标系中的数学模型可以表示为

图1 传统LC滤波型电压源逆变器MPVC框图
Fig.1 Control block diagram of conventional MPVC for LC-filtered VSI
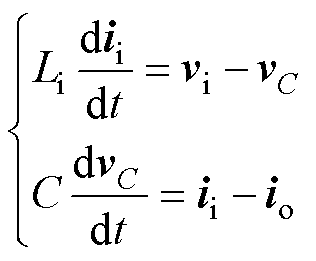 (1)
(1)
式中,Li为逆变器侧滤波电感;C为滤波电容;ii= iia+jiib 为ab 坐标系下的逆变器侧电感电流矢量;vx= vxa+jvxb ,x∈{0, 1,…, 7}为ab 坐标系下的逆变器侧输出电压矢量;vC=vCa+jvCb 为ab 坐标系下的电容电压矢量;io=ioa+jiob 为ab 坐标系下的负载侧输出电流矢量。
根据零阶保持方法,式(1)可以被离散为
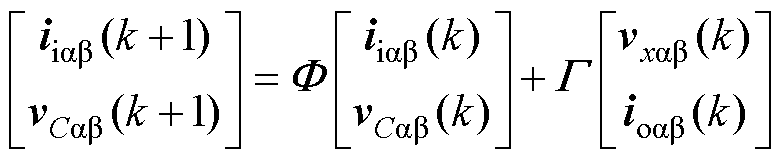 (2)
(2)
其中
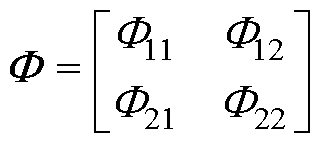
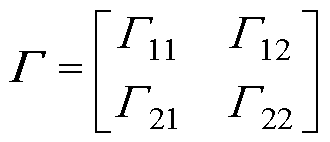
其中,系数矩阵 和
和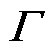 可以表示为
可以表示为
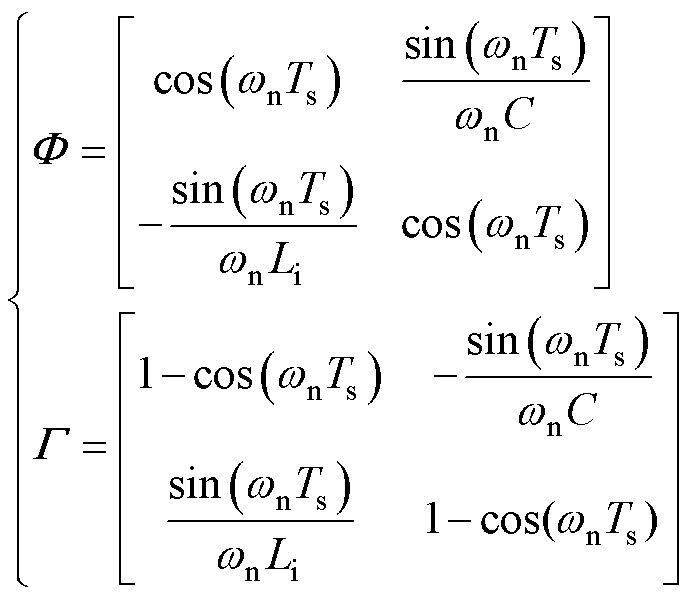 (3)
(3)
式中, 为LC滤波器的谐振频率;Ts为控制周期。
为LC滤波器的谐振频率;Ts为控制周期。
基于LC滤波的VSI通常以电容电压为主要控制目标。然而,根据式(1)可以得到,电感电流与电容电压相互影响。即LC滤波型VSI的电容电压不能通过逆变器侧输出电压直接调节,增加了电容电压控制的复杂性。因此,逆变器侧电感电流控制对于电容电压性能的提高至关重要,其与电容电压追踪将同时作为价值函数的评估目标。由于电容电压参考一般为正弦变量,其可以表示为
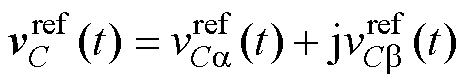 (4)
(4)
其中

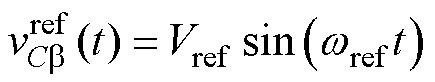
式中,上标“ref”代表参考值;Vref为电容电压参考幅值;wref为电容电压基频。
根据式(1),电感电流参考可以表示为
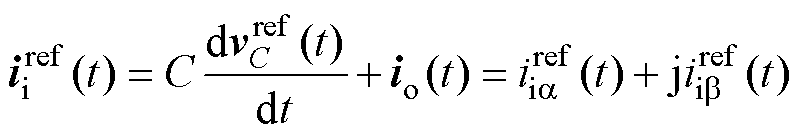 (5)
(5)
其中
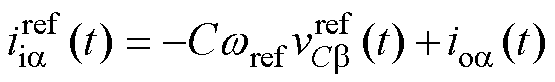
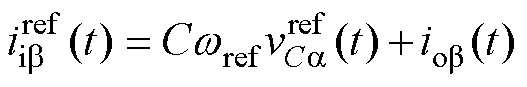
式(4)和式(5)的离散形式可以表示为
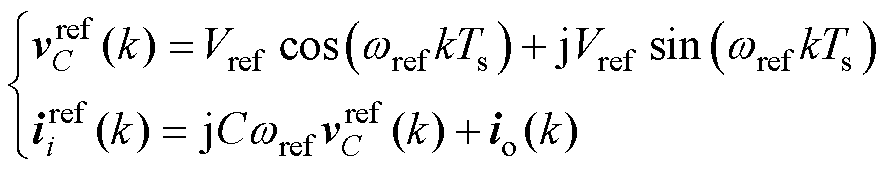 (6)
(6)
因此,基于电容电压和电感电流追踪的双目标价值函数gd可以表示为
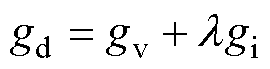 (7)
(7)
式中,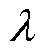 为权重因子;gv为电容电压追踪的价值函数;gi为电感电流追踪的价值函数,其可以表示为
为权重因子;gv为电容电压追踪的价值函数;gi为电感电流追踪的价值函数,其可以表示为
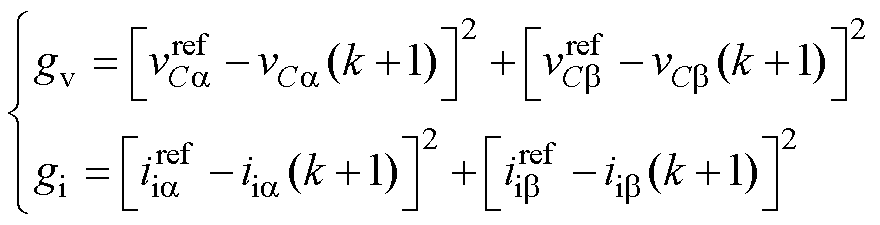 (8)
(8)
如图1所示,需要将8个矢量分别代入式(2),并将得到8个电压和电流预测值代入式(7)所示的双目标价值函数进行评估,最终选择使价值函数最小的矢量作为最优矢量,将其作用在下一个控制周期。然而,根据式(2)可知,电容电压预测和电感电流预测均会受到模型参数变化的影响,导致输出电压性能降低。
为了解决上述问题,本文提出了一种基于电压和电流双梯度实时更新的MFPVC方法,所提方法包括四个部分:MFPVC的基本原理、电压和电流梯度更新方法、停滞消除及所提方法的实现过程。
在每个控制周期中,采样得到的电容电压和电感电流可视为线性的。因此,在第k时刻采样的电容电压梯度和电感电流梯度可以表示为
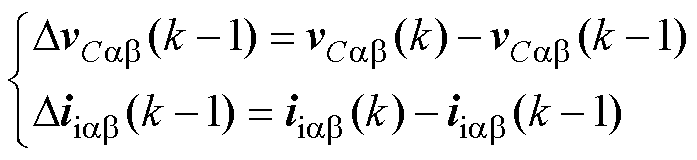 (9)
(9)
式中,DvCab(k-1)为电容电压梯度;Diiab(k-1)为电感电流梯度,其均由k-1时刻作用的矢量vxab(k-1)产生。同时,采样获得电压和电流梯度需要与应用的矢量相对应,并被存储在表1所示的LUT中用于电压和电流预测。
表1 所提方法查询表
Tab.1 LUT of the proposed method

电压矢量电流梯度电压梯度 v0Dii0DvC0 v1Dii1DvC1 v2Dii2DvC2 v3Dii3DvC3 v4Dii4DvC4 v5Dii5DvC5 v6Dii6DvC6 v7Dii7DvC7
因此,k+1时刻的预测电压和预测电流可以表示为
 (10)
(10)
由于k+2时刻的预测电压和电流由k-1时刻作用的矢量决定,式(10)中的电压和电流梯度可视为:DvCab(k)≈DvCab(k-1) 且Diiab(k)≈Diiab(k-1)。为了补偿一步控制延时,k+2时刻的预测电压和电流可以表示为
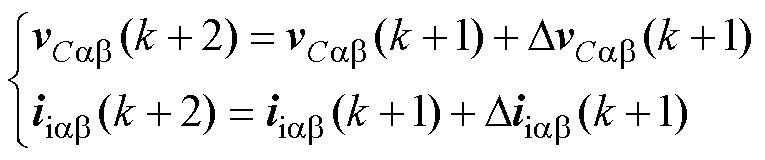 (11)
(11)
式中,DvCab(k+1) 和Diiab(k+1) 分别为8个候选矢量作用下的电压和电流梯度。为了得到最优的矢量并应用在下一控制周期,需要将8个候选矢量对应的电压和电流梯度代入式(11),并将得到8个电压和电流预测值代入式(7)所示的双目标价值函数进行评估,最终选择使价值函数最小的矢量作为最优矢量。
然而,仅通过电压和电流采样只能更新上一控制周期应用矢量作用下的梯度值,对于未应用的矢量,其对应的梯度值则无法更新,这种现象被称为停滞现象,将会增大预测误差,降低输出电压的性能。
为了消除停滞现象,并保证电压和电流梯度的准确性,提高预测精度,本节通过重构式(2)所示的状态空间预测模型,实现了每个控制周期中电压和电流梯度的实时更新。首先,式(2)可以重构为
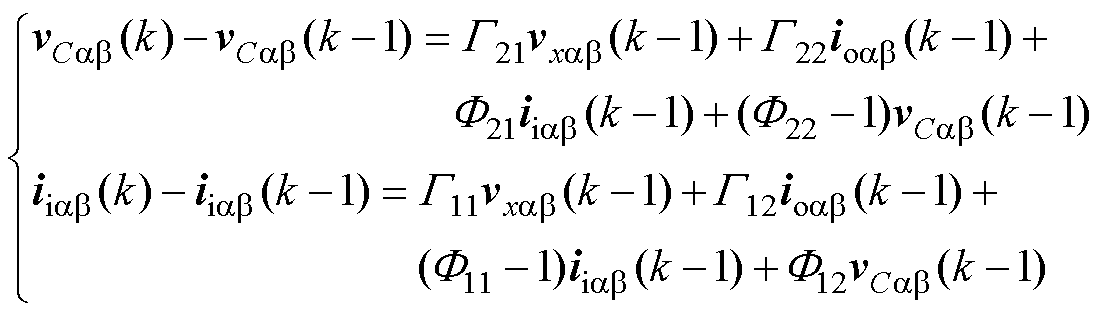 (12)
(12)
式中,vCab(k)-vCab(k-1)=DvCab(k-1),且iiab(k)-iiab(k-1)=Diiab(k-1)。因此,当式(12)中应用矢量vxab(k-1)变为剩余矢量vjab(k-1)时,其对应的电压和电流梯度可以表示为
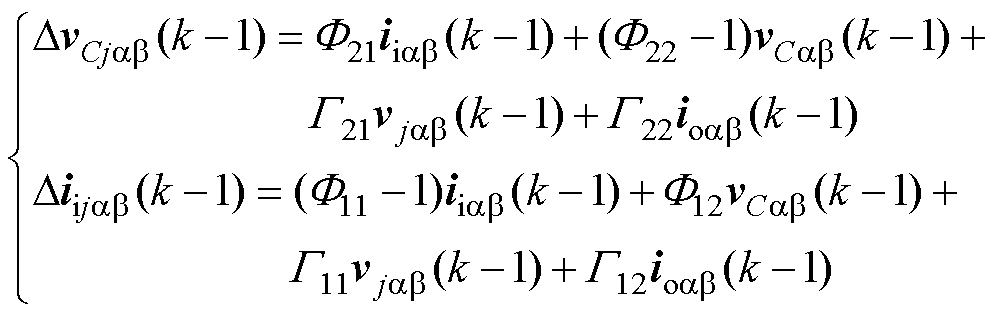 (13)
(13)
式中,j∈{0, 1,…, 7} 且j≠x。
将式(12)和式(13)相减可得
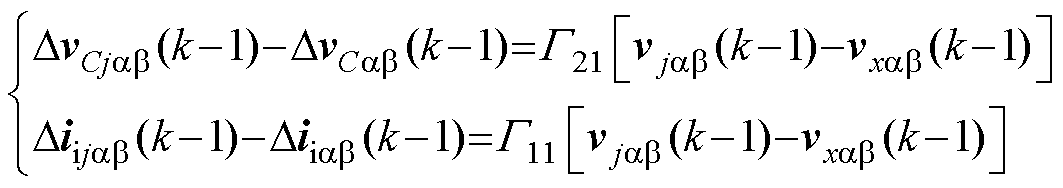 (14)
(14)
为了消除式(14)中的参数G21和G11,可以基于式(14)通过一步递推得到k-2时刻的电压电流梯度关系并分别表示为
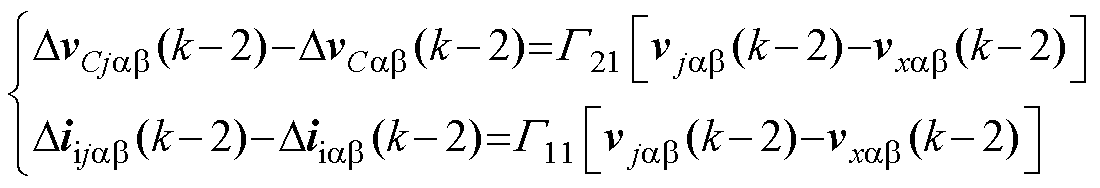 (15)
(15)
将式(14)和式(15)相除可以得到未应用矢量vjab(k-1) 作用下的电压和电流梯度值(DvCjab(k-1)和Diijab(k-1))并分别表示为
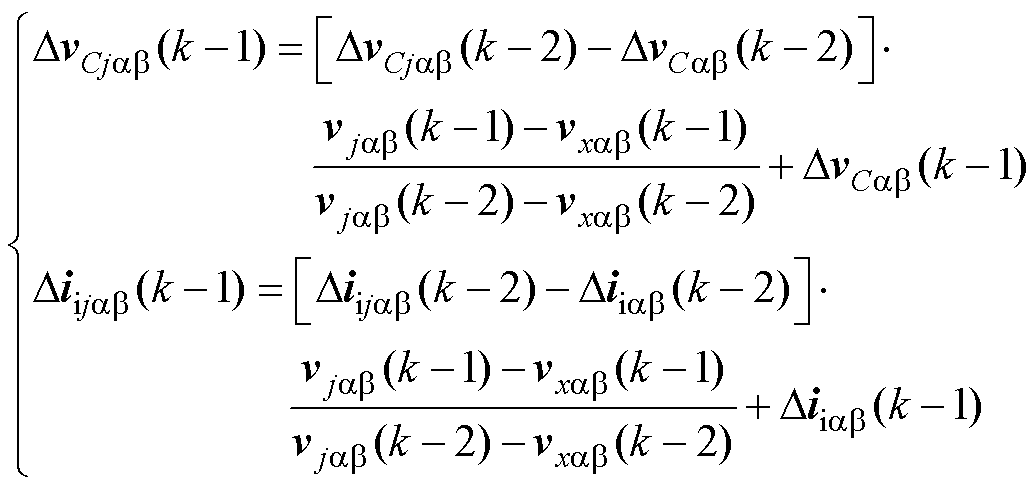 (16)
(16)
根据式(16)可知,电流梯度的计算会受公式分母数值的影响。本节将从以下两种情形分析剩余梯度的更新情况。
情形1:式(16)的分母值不为0时,其可以进一步化简为
 (17)
(17)
情形2:式(16)的分母趋近于0时,电流梯度的更新将不再生效。
不同矢量坐标分量如图2所示,以下八种情况可能导致其分母为0,分别为v0b=v1b,v2b=v3b,v4b=v7b,v5b=v6b,v0ab=v7ab,v1b=v4b,v3a=v5a 和v6a=v2a。
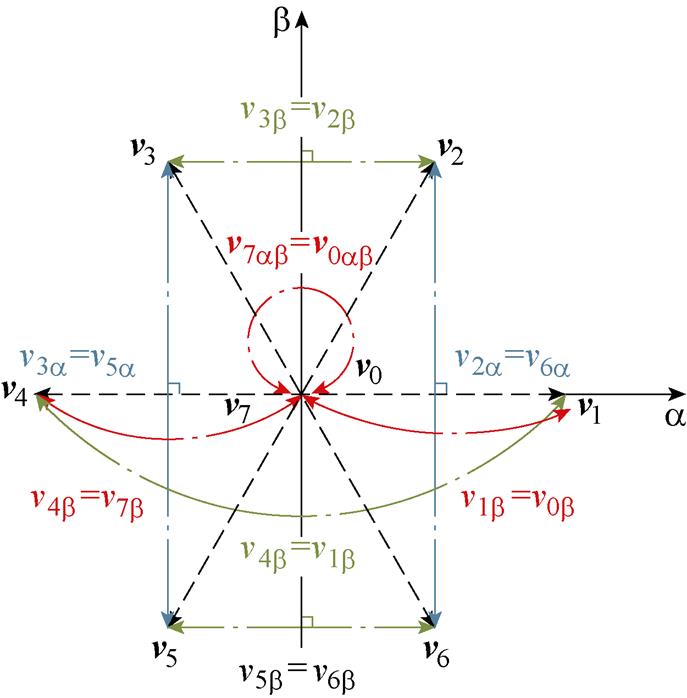
图2 不同矢量坐标分量
Fig.2 Coordinate component relationship between different vectors
根据式(14)可知,当矢量的坐标分量相等(即vjab(k-1)=vxab(k-1))时,其对应的电压和电流梯度也相等(即DvCjab(k-1)=DvCab(k-1),Diijab(k-1)= Diiab(k-1))。因此,更新式(16)可以重新表示为
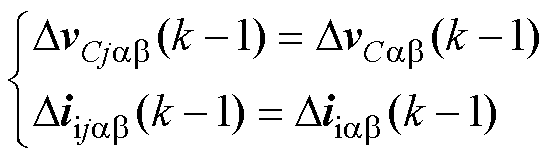 (18)
(18)
所提电流梯度更新方法如图3所示,所有电压和电流梯度均可以在一个控制周期内实时更新,消除了停滞现象。
图4为所提出MFPVC方法的控制框图,该方法主要由梯度更新、预测计算以及价值函数评估三部分组成。所提MFPVC实现过程如图5所示。由图5可知,该方法在实施预测控制时,首先,根据电压和电流采样,以及式(9)计算应用矢量作用下的电压和电流梯度;然后,根据式(16)、式(17)更新剩余矢量作用下的电压和电流梯度;其次,根据上一时刻应用的矢量,通过式(10)预测第k+1时刻的电压和电流,并根据式(11)分别预测8个矢量在k+2时刻的预测电压和电流;最后,根据式(7)所示的价值函数进行寻优评估,选择价值函数值最低的矢量作为最优矢量,并应用在下一控制周期。
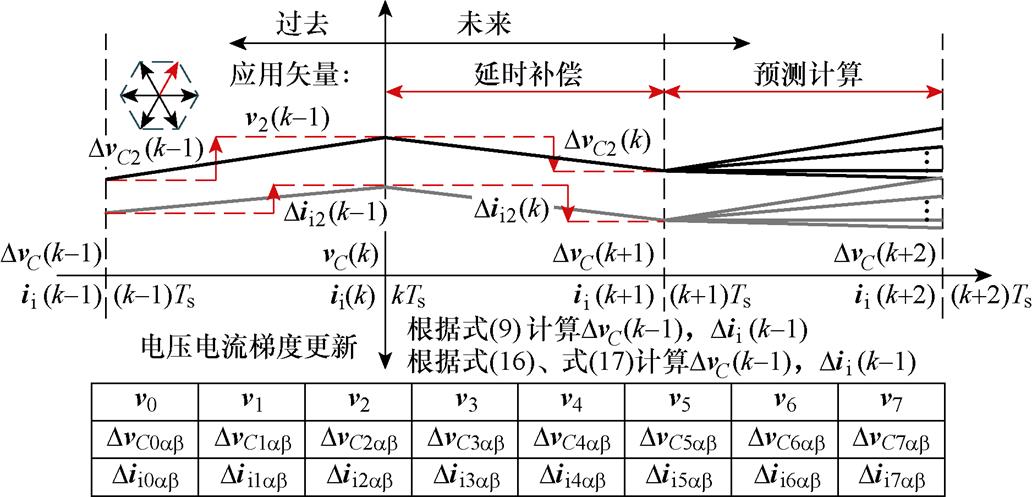
图3 所提电流梯度更新方法
Fig.3 The proposed current gradient updating method
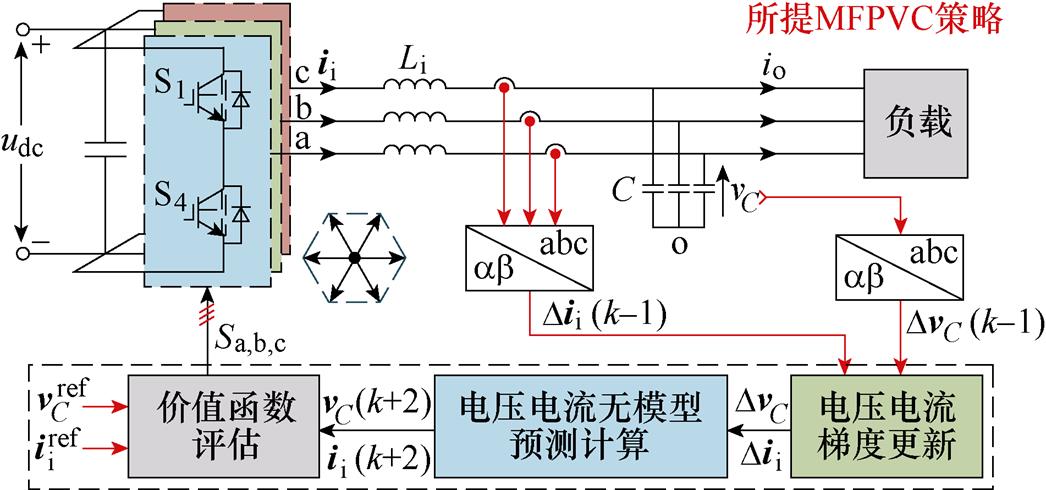
图4 所提MFPVC框图
Fig.4 Control block diagram of the proposed MFPVC
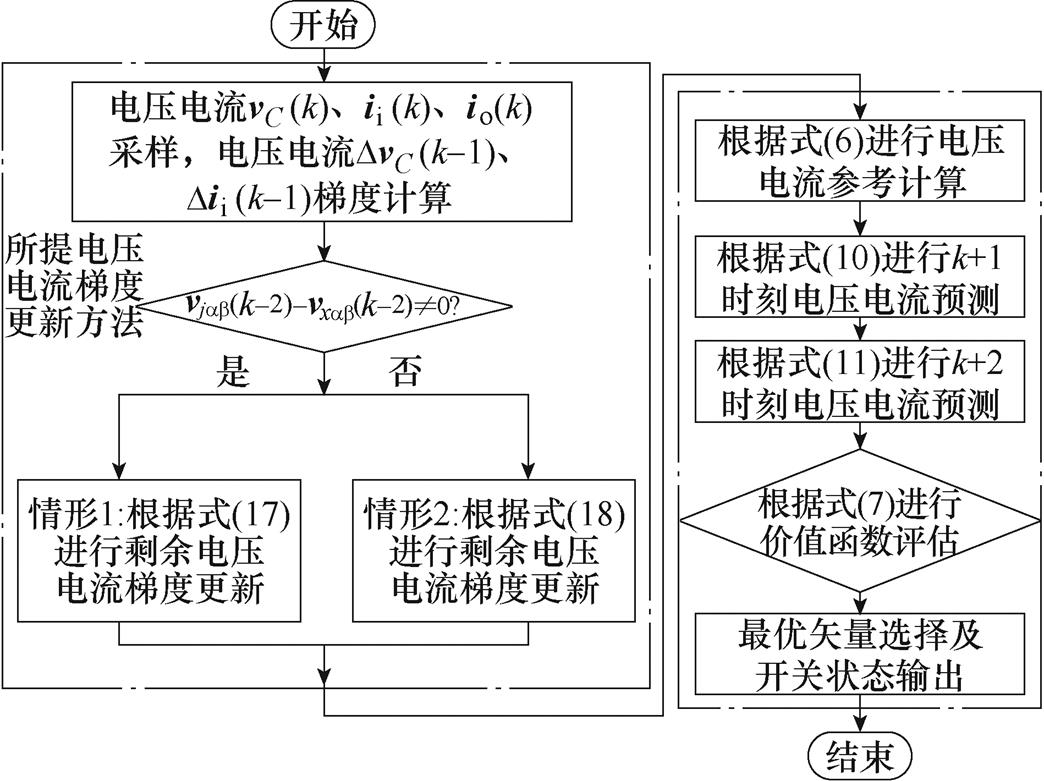
图5 所提MFPVC实现过程
Fig.5 Implementation process of proposed MFPVC
本节通过图6所示的实验平台验证了所提方法的有效性,其包括直流电压源、三相VSI、LC滤波器和交流负载。所有控制方案均在TMS320F28335中实现,系统和控制参数见表2。示波器型号为LeCroy-HDO4034,用于记录实验波形;电流探头型号为LeCroy-CP150,用于测量负载电流;电压探头型号为LeCroy-ADP300,用于测量电容电压。此外,文献[8]中的方法称为MPVC方法,式(9)所示更新方法称为传统更新方法,所提方法称为MFPVC方法。

图6 LC滤波型VSI实验平台
Fig.6 Experimental platform of LC-filtered VSI
表2 LC滤波型VSI系统和控制参数
Tab.2 System and control parameters of LC-filtered VSI
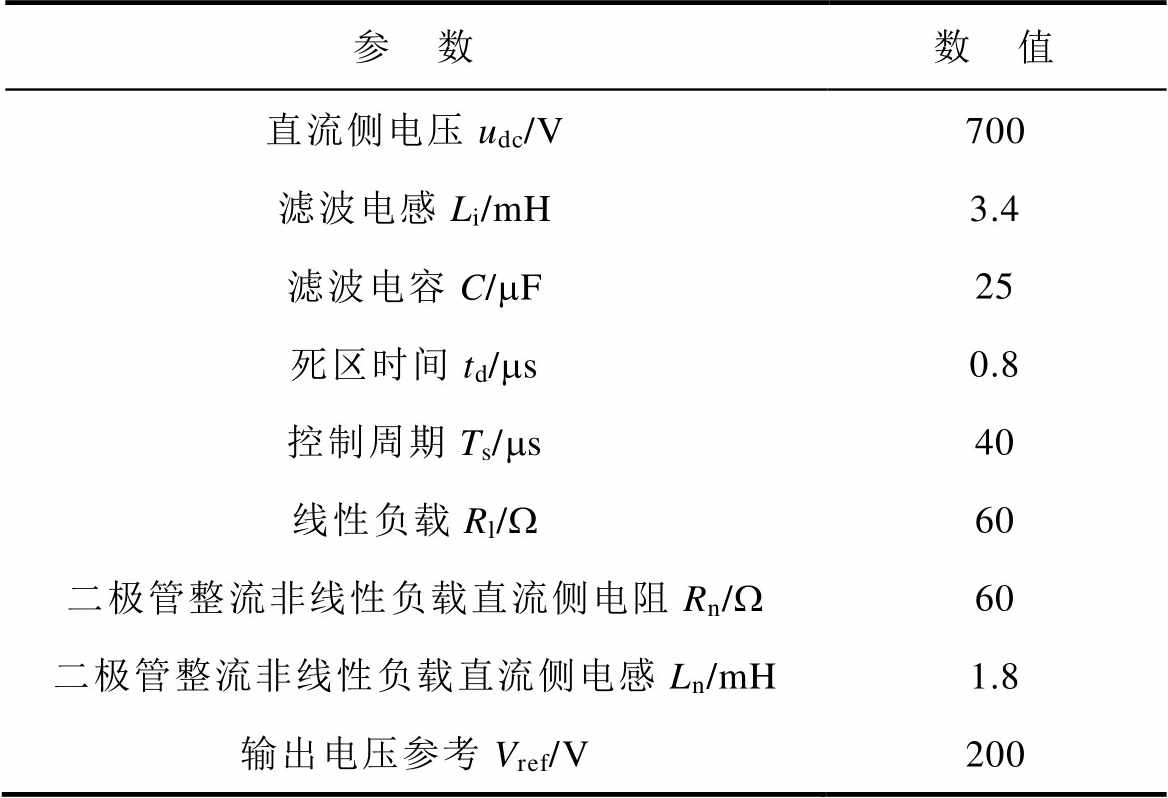
参 数数 值 直流侧电压udc/V700 滤波电感Li/mH3.4 滤波电容C/mF25 死区时间td/ms0.8 控制周期Ts/ms40 线性负载Rl/W60 二极管整流非线性负载直流侧电阻Rn/W60 二极管整流非线性负载直流侧电感Ln/mH1.8 输出电压参考Vref/V200
为了验证所提电压电流梯度更新方法的有效性,图7比较了传统更新方法以及所提MFPVC更新方法的电压性能。如图7a所示,由于传统更新方法仅更新应用矢量作用下的电压和电流梯度,剩余矢量的梯度值保持旧值,存在明显的停滞现象,导致电压纹波及其预测误差中出现尖峰。如图7b所示,当实施所提MFPVC更新方法时,由于停滞现象完全消除,因此其电压纹波和预测误差有效降低。为了进一步验证所提更新方法的电压追踪性能,计算a相电压方均根误差(Root Mean Squared Error, RMSE)为
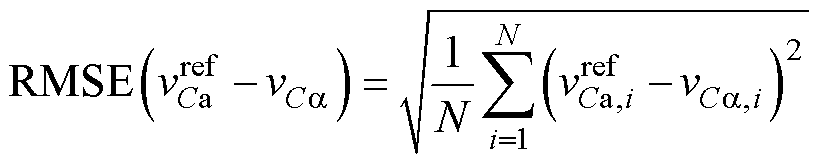 (19)
(19)
式中,N为采样点的数量。其中,传统更新方法的RMSE=6.91 V,所提MFPVC更新方法的RMSE= 3.66 V,较传统更新方法低3.25 V。
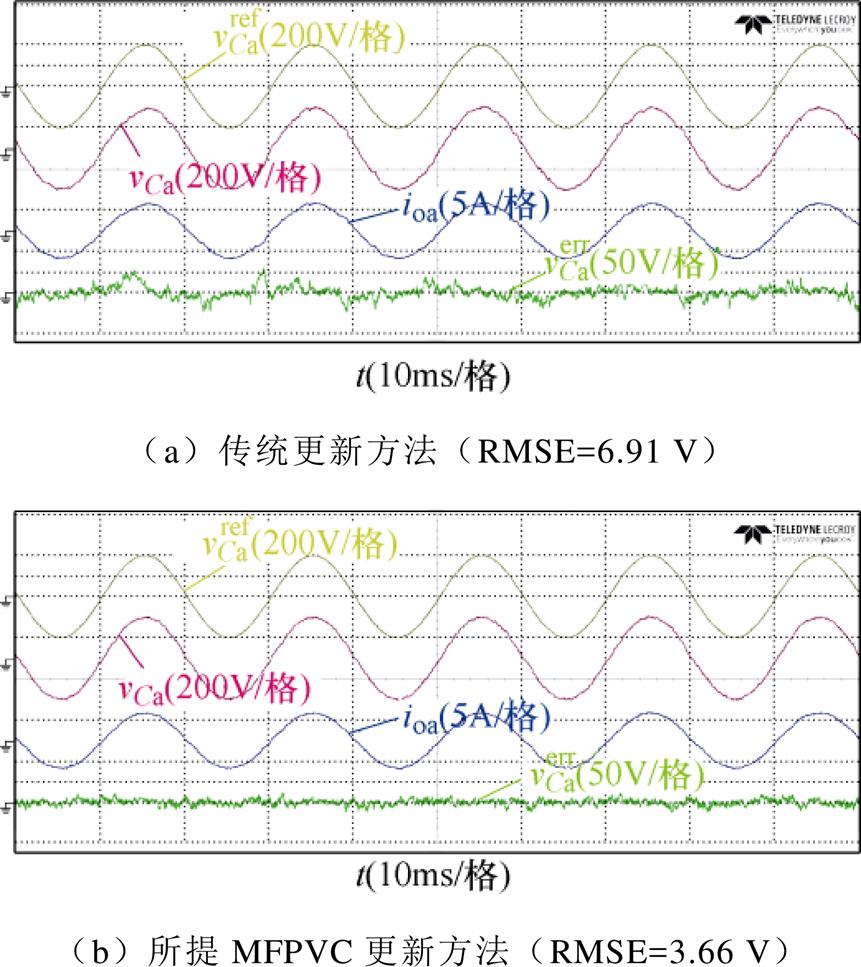
图7 不同更新方法下电压性能比较
Fig.7 Voltage performance comparison under different updating methods
图8比较了传统MPVC方法和所提MFPVC方法在线性负载下的稳态电压纹波、电压预测误差以及负载电流纹波,其中,参考电压为200 V。如图8a所示,当实施MPVC方法时,可以实现最优的电压跟踪,其具有最低的总谐波失真(Total Harmonic Distortion, THD)及稳态误差。如图8b所示,当实施MFPVC方法时,其输出电压THD由3.08 %增加到3.16 %,RMSE由3.47 V增加到3.66 V。这是因为所提方法的电压性能依赖电压及电流采样的准确性,而在实验过程中,由于采样噪声的存在,使得所提MFPVC方法的输出电压THD及电压预测误差略高于MPVC方法。

图8 线性负载时稳态性能比较
Fig.8 Steady-state performance comparison under nominal linear load
图9比较了传统MPVC方法和所提MFPVC方法在非线性负载下的电压追踪性能。上述两种方法均可准确追踪参考电压,没有明显的电压畸变。同样,由于所提方法受到采样噪声的影响,其THD和RMSE均略高于MPVC方法,输出电压THD由3.27 %增加到3.35 %,RMSE由3.53 V增加到3.71 V。
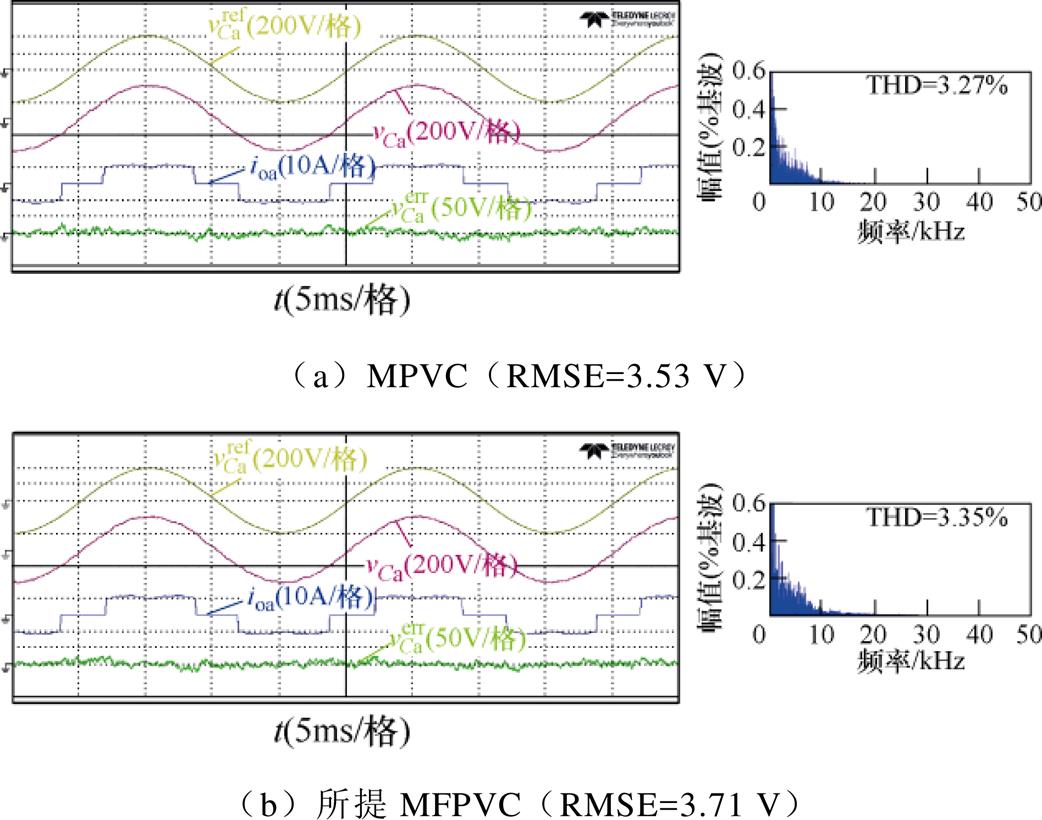
图9 非线性负载时稳态性能比较
Fig.9 Steady-state performance comparison under non-linear load
图10比较了参数失配时MPVC方法和所提MFPVC方法的电压纹波以及预测误差。由图10a和图10b可以看出,当电感的控制参数Lic由3.4 mH变为1.7 mH(即0.5Li)时,MPVC的RMSE由3.47 V增长到6.84 V,而所提MFPVC方法不受电感参数的影响,RMSE保持为3.66 V,与MPVC方法相比降低了3.18 V。由图10c和图10d可以看出,当电容的控制参数Cc由25 mF变为12.5 mF(即0.5C)时,MPVC方法RMSE由3.47 V增长到8.04 V;由于价值函数评估公式中存在电容参数,所提MFPVC方法的RMSE由3.66 V增加为4.45 V,其与MPVC相比降低了3.59 V。如图10e和图10f所示,当电感和电容的控制参数同时降低50 %(即0.5Li,0.5C)时,所提方法的RMSE比MPVC方法降低4.12 V。各参数失配条件下RMSE比较见表3。
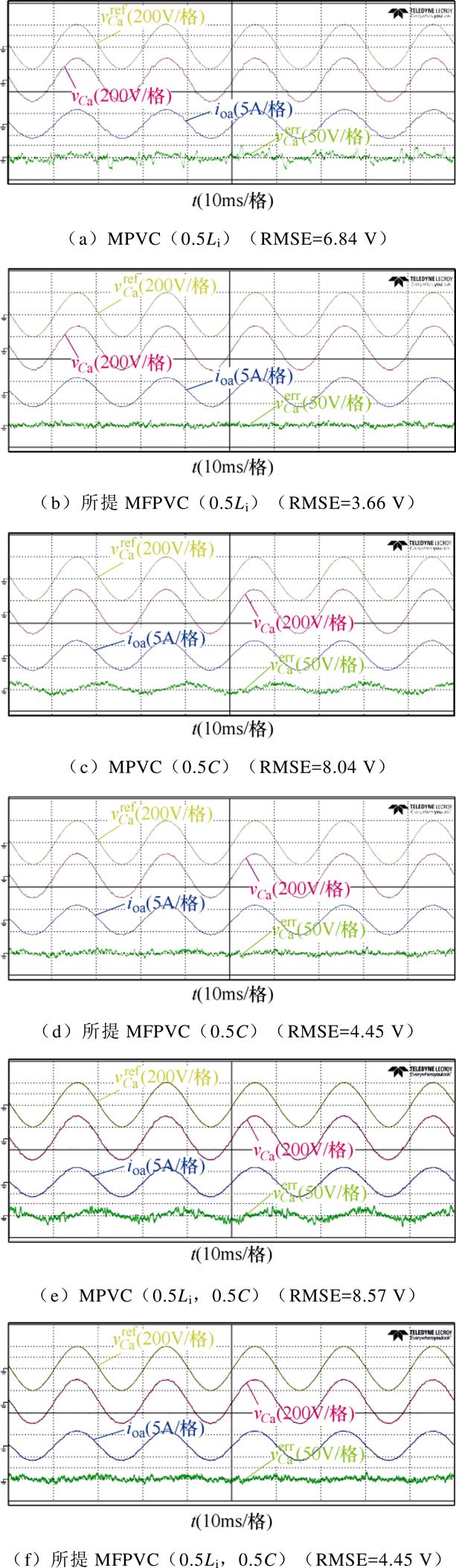
图10 参数失配时电压性能比较
Fig.10 Voltage performance comparison under mismatched parameter
为了进一步验证所提MFPVC方法在适应参数变化时的有效性,图11总结了传统MPVC方法和所提方法在电感控制参数由0.2Li变化为Li时,以及电容控制参数由0.2C变化为C时的实验结果。如图11所示,随着控制参数与实际参数误差增大,MPVC方法的RMSE由3.5 V增加到17.8 V,而所提方法的RMSE变化范围为3.6~5.4 V。尤其在0.2Li与0.2C的条件下,所提MFPVC方法的RMSE较传统MPVC方法降低了12.4 V,实验结果有效验证了所提方法在滤波器参数失配时优越的参数鲁 棒性。
表3 参数失配时RMSE比较
Tab.3 Comparision of RMSE under mismatched paramters (单位: V)

参数条件MPVCMFPVC Li, C3.473.66 0.5Li6.843.66 0.5C8.044.45 0.5Li, 0.5C8.574.45
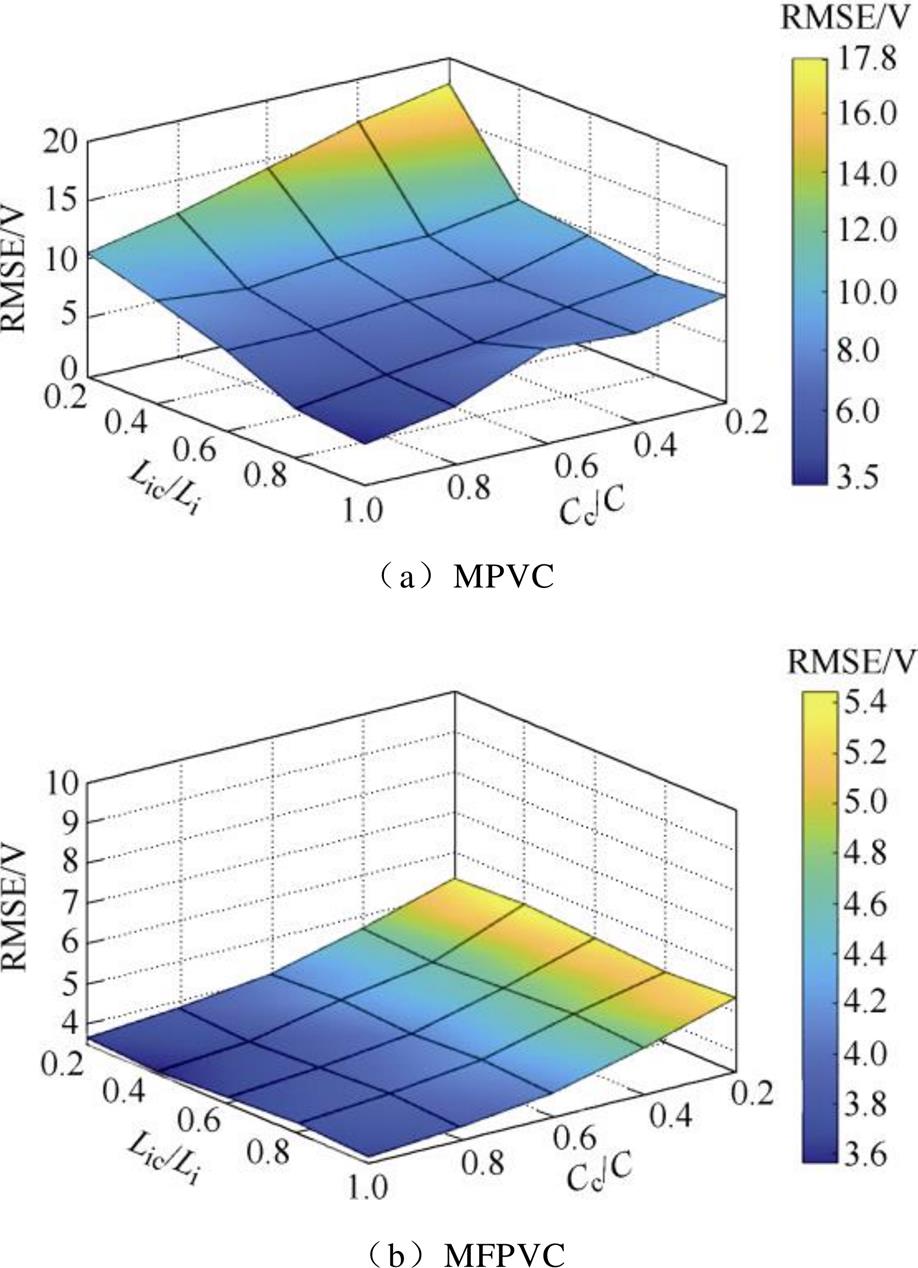
图11 参数失配时电压RMSE比较
Fig.11 Comparison of voltage RMSE under mismatched parameter
本文提出了一种基于电压和电流梯度实时更新的无模型预测电压控制方法,并在三相LC滤波型电压源逆变器平台进行实验测试。结果表明,所提方法具有以下优点:
1)所提方法具有良好的参数鲁棒性,在参数发生变化时显著降低了逆变器输出电压误差,改善了电压质量,并在参数准确的条件下实现了与MPVC相近的电压性能。
2)该方法提出了一种先进的电压电流梯度更新方法,实时更新所有矢量作用下的电压和电流梯度,消除了停滞现象及其引起的预测尖峰,进一步改善了输出电压质量。
后续研究可以将所提方法拓展到LCL滤波型VSI,或通过矢量组合进一步减小电压纹波。
参考文献
[1] Rocabert J, Luna A, Blaabjerg F, et al. Control of power converters in AC microgrids[J]. IEEE Transa- ctions on Power Electronics, 2012, 27(11): 4734- 4749.
[2] 郭磊磊, 金楠, 李琰琰, 等. 电压源逆变器虚拟矢量模型预测共模电压抑制方法[J]. 电工技术学报, 2020, 35(4): 839-849.
Guo Leilei, Jin Nan, Li Yanyan, et al. Virtual vector based model predictive common-mode voltage redu- ction method for voltage source inverters[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(4): 839-849.
[3] 柳志飞, 杜贵平, 杜发达. 有限集模型预测控制在电力电子系统中的研究现状和发展趋势[J]. 电工技术学报, 2017, 32(22): 58-69.
Liu Zhifei, Du Guiping, Du Fada. Research status and development trend of finite control set model predi- ctive control in power electronics[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 58-69.
[4] 郭磊磊, 金楠, 李琰琰, 等. 并网逆变器无电网电压传感器模型预测控制[J]. 电工技术学报, 2020, 35(12): 108-114.
Guo Leilei, Jin Nan, Li Yanyan, et al. Grid voltage sensorless model predictive control for grid- connected inverters[J]. Transactions of China Electro- technical Society, 2020, 35(12): 108-114.
[5] 李伟, 张勇军, 肖雄. 实时电感辨识的模型预测并网逆变器控制方法[J]. 电工技术学报, 2018, 33(15): 3450-3460.
Li Wei, Zhang Yongjun, Xiao Xiong. The model predictive grid-connected inverter control method based on real-time inductance identification[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3450-3460.
[6] Cortes P, Ortiz G, Yuz J I, et al. Model predictive control of an inverter with output $LC$ filter for UPS applications[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 1875-1883.
[7] Yaramasu V, Rivera M, Narimani M, et al. Model predictive approach for a simple and effective load voltage control of four-leg inverter with an output LC filter[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5259-5270.
[8] Dragičević T. Model predictive control of power converters for robust and fast operation of AC microgrids[J]. IEEE Transactions on Power Elec- tronics, 2018, 33(7): 6304-6317.
[9] Zheng Changming, Dragičević T, Majmunović B, et al. Constrained modulated model-predictive control of an LC-filtered voltage-source converter[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1967-1977.
[10] Zhang Yongchang, Jiang Tao, Jiao Jian. Model-free predictive current control of a DFIG using an ultra- local model for grid synchronization and power regu- lation[J]. IEEE Transactions on Energy Conversion, 2020, 35(4): 2269-2280.
[11] 芮涛, 尹政, 汪凤翔, 等. 基于双矢量的并网逆变器无模型预测电流控制策略[J]. 电工技术学报, 2023, DOI: 10.19595/j.cnki.1000-6753.tces.221461.
Rui Tao, Yin Zheng, Wang Fengxiang, et al. Model- free predictive current control strategy of grid- connected inverter based on double-vector[J]. Transa- ctions of China Electrotechnical Society, 2023,DOI: 10.19595/j.cnki.1000-6753.tces.221461.
[12] 张永昌, 屈祈延, 杨海涛. 基于空间矢量调制的Vienna整流器无模型预测电流控制[J]. 电工技术学报, 2022, 37(21): 5541-5547.
Zhang Yongchang, Qu Qiyan, Yang Haitao. Model free predictive current control of Vienna rectifier based on space vector modulation[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5541- 5547.
[13] Heydari R, Young H, Flores-Bahamonde F, et al. Model-free predictive control of grid-forming inver- ters with LCL filters[J]. IEEE Transactions on Power Electronics, 2022, 37(8): 9200-9211.
[14] Lin Chengkai, Liu Tianhua, Yu J T, et al. Model-free predictive current control for interior permanent- magnet synchronous motor drives based on current difference detection technique[J]. IEEE Transactions on Industrial Electronics, 2014, 61(2): 667-681.
[15] Lin Chengkai, Yu J T, Lai Y S, et al. Improved model-free predictive current control for synchronous reluctance motor drives[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3942-3953.
[16] Carlet P G, Tinazzi F, Bolognani S, et al. An effective model-free predictive current control for synchronous reluctance motor drives[J]. IEEE Transactions on Industry Applications, 2019, 55(4): 3781-3790.
[17] Hu Cungang, Yin Zheng, Rui Tao, et al. A novel double-voltage-vector model-free predictive current control method for two-level voltage source inver- ters[J]. IEEE Transactions on Industrial Electronics, 2023, 70(6): 5872-5884.
[18] Rui Tao, Yin Zheng, Hu Cungang, et al. Modulated model-free predictive current control for voltage source inverters with stagnation elimination and sampling disturbance suppression[J]. IEEE Transa- ctions on Power Electronics, 2023, 38(6): 6996-7008.
[19] Yu Feng, Zhou Chenhui, Liu Xing, et al. Model-free predictive current control for three-level inverter-fed IPMSM with an improved current difference updating technique[J]. IEEE Transactions on Energy Con- version, 2021, 36(4): 3334-3343.
[20] Agustin C A, Yu J T, Cheng Yushan, et al. Model-free predictive current control for SynRM drives based on optimized modulation of triple-voltage-vector[J]. IEEE Access, 2021, 9: 130472-130483.
Abstract This paper proposes a model-free predictive voltage control strategy for LC-filtered voltage source inverters to solve the problem that the prediction error increases when the parameters of conventional model predictive control are mismatched. The strategy establishes a look-up table based on the double gradients of voltage and current. By calculating and storing the voltage and current gradients under the action of the application vectors at the previous time, combined with the sampling values at the current time, the voltage and current at the future time can be predicted. The state space prediction equation is further reconstructed. The gradient value of the unapplied vector is updated according to the voltage and current gradients under the action of the applied vector. The voltage and current cost functions evaluate and select the optimal vector in the next control period. This method is independent of system parameters and simple, which can eliminate the stagnation of gradient updating in the conventional model-free prediction and improve the output voltage performance. Finally, simulation and experiment verify the effectiveness and superiority of the proposed method.
Firstly, the look-up table of the capacitor voltage gradient and the inverter-side current gradient is designed. Based on the gradient information, the voltage and current can be predicted without parameters. Secondly, the proposed method reconstructs the state-space prediction equation to ensure real-time updates of all gradients in each control period, eliminating the stagnation phenomenon of conventional model-free predictive control. In addition, the output voltage quality is further improved using the cost function with two control targets. Finally, the effectiveness of the proposed method is verified by experiments.
Simulation results on the voltage-current gradient updating show that the root mean square error (RMSE) of the conventional updating method is 6.91 V, and the RMSE of the proposed model-free predictive voltage control (MFPVC) updating method is 3.66 V, which is 3.25 V lower than that of the conventional updating method. Experimental results on the accurate model parameters show that the proposed method can achieve similar voltage performance with the conventional model predictive voltage control (MPVC). Experimental results on the inaccurate model parameters show that when the controller parameter mismatches the actual parameter, the proposed MFPVC produces smaller prediction errors than the conventional MPVC. Hence, the parameter robustness of the proposed MFPVC can be verified.
The following conclusions can be drawn from the simulation and experimental analysis: (1) The proposed method has good parameter robustness. When the parameters change, the output voltage error of the inverter is significantly reduced, the voltage quality is improved, and the voltage performance is similar to that of MPVC under the condition of accurate parameters. (2) This method proposes an advanced voltage and current gradient updating method, which can update the voltage and current gradient under all vectors in real time, eliminate the stagnation phenomenon and the predicted spikes, and further improve the output voltage quality.
In future studies, the proposed method can be extended to the LCL filter type VSI, or the voltage ripple can be further reduced by vector combination.
keywords:Voltage source inverter, LC filter, model-free predictive voltage control, gradient updating
国家自然科学基金项目(52207184)、安徽省科技重大专项(202103a05020019)和安徽省自然科学基金杰青项目(2108085J24)资助。
收稿日期 2022-09-27
DOI: 10.19595/j.cnki.1000-6753.tces.221815
中图分类号:TM464
尹 政 男,1996年生,硕士研究生,研究方向为变流器的调制与控制技术。E-mail: yz@stu.ahu.edu.cn
芮 涛 男,1990年生,讲师,研究方向为基于数据驱动的并网逆变器无参数预测控制技术。E-mail: 19057@ahu.edu.cn(通信作者)
改稿日期 2023-03-24
(编辑 崔文静)