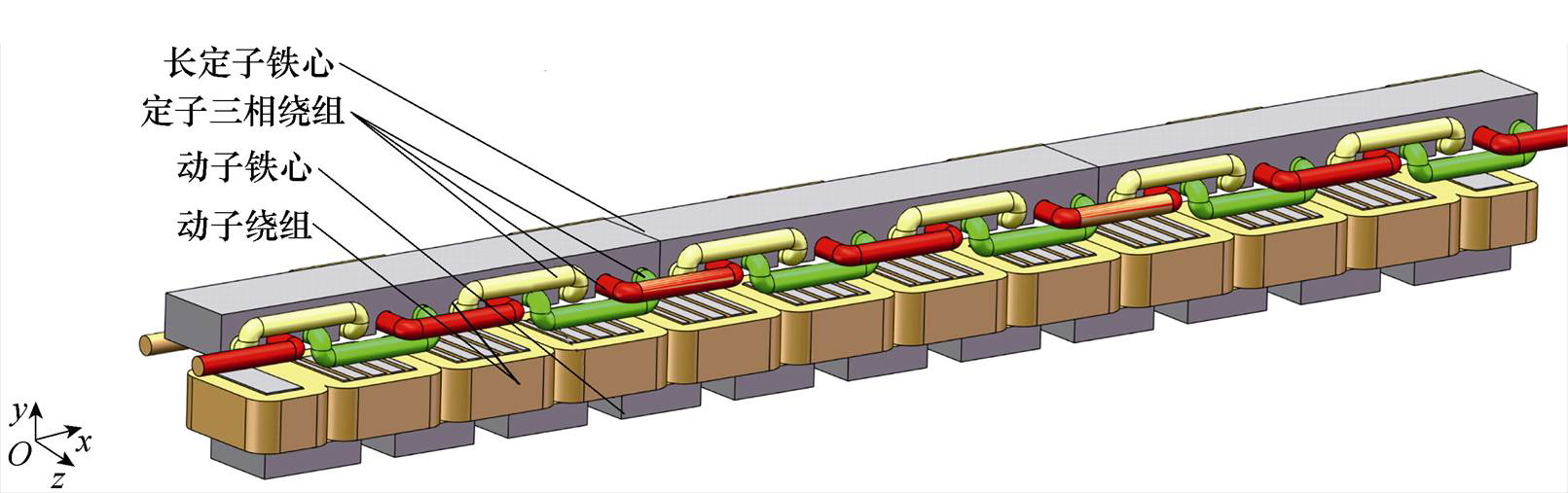
图1 高速磁浮直线电机三维模型图
Fig.1 Three dimensional model diagram of high-speed maglev linear motor
摘要 非晶合金作为一种低损耗铁心材料，在高速电机中具有较好应用前景。为探明非晶合金在高速磁浮直线电机中应用的可行性，该文针对常导型高速磁浮直线电机，采用改进的分布磁路法分别计算硅钢和非晶合金作为长定子铁心材料时的气隙磁通密度，并结合虚位移法对比计算两种材料下的静态悬浮力。首先，针对高速磁浮直线电机长定子与动子极距不等、动子极面直线发电机齿槽以及动子轭部不连续等特殊结构，对分布磁路法加以改进，分段表征磁导率并分段计算磁压降，进而计算得到硅钢、非晶长定子在不同励磁电流下精确的气隙磁通密度。在此基础上，采用虚位移法，对比计算基于两种长定子铁心材料下直线电机静态悬浮力，并进行有限元验证。最后，实测两种材料长定子直线电机的静态悬浮力，均能满足高速磁浮列车悬浮要求，进一步验证了解析计算结果的准确性，以及非晶合金长定子磁浮直线电机的合理性。
关键词：高速磁浮直线电机 非晶合金 分布磁路法 悬浮力
高速磁浮列车作为一种速度快、噪声小的陆上轨道交通工具，填补上了航空运输和高铁运输之间的速度空白，近年来成为备受关注的研究热点[1-4]。当列车以600 km/h高速运行时，为其提供动力的高速磁浮直线电机长定子铁耗也维持在较高水平。非晶合金作为一种良好的导磁材料，可以取代硅钢作为电机的铁磁材料来大幅降低高频旋转电机的铁心损耗，在高频旋转电机[5-9]中已有应用，在高速磁浮直线电机中，也有初步探讨[10]。然而非晶合金材料的饱和磁通密度相比于硅钢要小[11]，因此，非晶合金能否替代硅钢作为直线电机长定子的铁心材料需要进行深入研究，尤其电机静态悬浮力是首要考虑的性能。
近年来，国内外大量学者针对高速磁浮直线电机进行了诸多研究。高速磁浮直线电机按照悬浮原理分类，主要可以分为电磁悬浮型（吸力、常导型）和电动悬浮型（斥力、超导型）两种[12]。常导型高速磁浮直线电机利用悬浮电磁铁与轨道长定子之间的电磁吸力来使悬浮电磁铁实现悬浮，依靠长定子内部通入的可变频交变电流在气隙中形成的行波磁场与悬浮电磁铁产生的恒定电磁场相互作用牵引动子运动[13]。超导型高速磁浮直线电机利用动子侧的超导磁体与轨道上的无源线圈之间的相对运动来产生电磁斥力使动子侧实现悬浮，但是在动子静止和低速运行时不能悬浮[14]。目前两种高速磁浮直线电机均有应用[15]，常导型高速磁浮直线电机起步较早，技术相对成熟，国内已经在上海的高速磁浮运营线应用。现有的常导型高速磁浮直线电机长定子铁心均为硅钢材料[15-18]，对于低损耗的非晶合金能否替代硅钢作为高速磁浮直线电机长定子铁心材料鲜有研究。
为探明非晶合金在高速磁浮直线电机中应用的可行性，首要解决的问题是不同材料下高速磁浮直线电机静态悬浮力能否满足设计需求。为使高速磁浮直线电机静态悬浮力计算更加准确且能精准反映非晶合金长定子对悬浮力的影响，需要对直线电机气隙磁通密度进行精确计算。
常用的电机气隙磁通密度计算方法主要有分布磁路法、等效磁网络法等[19]。文献[20]针对双交替极横向磁通直线电机，采用等效磁网络法，建立了电机磁网络拓扑，对电机气隙磁通密度进行计算。文献[21]针对无槽双边长定子直线感应电动机，采用分布磁路法计算了直线感应电机的气隙磁通密度，经仿真验证发现计算结果吻合得较好。文献[22]针对六相圆筒式直线感应电机，考虑到不同于双边分段供电直线感应电机的以气隙中心线对称的特点，并计及边端铁心对磁通密度分布的影响，给出了一种优化改进后的直线感应电机分布磁路计算方法。可以看出，分布磁路法能较好地考虑长定子与动子极距不等、不对称齿槽结构及分布特性等因素的影响，加之其物理概念清晰，计算量不大，可以精确计算高速磁浮直线电机气隙磁通密度。
本文针对常导型高速磁浮直线电机，采用改进的分布磁路法，对比计算硅钢和非晶两种长定子铁心材料的静态悬浮力，以探明非晶合金替代硅钢作为长定子铁心材料的合理性。首先，充分考虑长定子与动子极距不等、动子极面直线发电机齿槽以及动子轭部不连续等特殊结构，将分布磁路法中各部分磁导率及磁压降进行分段表示，进而计算两种铁心材料下不同励磁电流对应的气隙磁通密度；其次，采用虚位移法，结合气隙磁通密度解析计算结果，对比计算基于两种长定子铁心材料下直线电机静态悬浮力，并利用有限元进行验证；最后，通过实测两种长定子铁心下高速磁浮直线电机悬浮力，进一步验证改进的分布磁路法计算结果的准确性，从而说明了非晶合金代替硅钢作为高速磁浮直线电机长定子铁心材料的可行性。
本文研究常导型高速磁浮直线电机，轨道作为直线电机长定子，位于悬浮电磁铁（动子）的上方，二者通过电磁吸力使列车达到稳定悬浮，其三维模型如图1所示。
图1 高速磁浮直线电机三维模型图
Fig.1 Three dimensional model diagram of high-speed maglev linear motor
悬浮电磁铁作为直线电机的动子位于长定子轨道的下方，共有10个整极和2个半极，相邻两个极构成一对极。当在悬浮电磁铁的励磁绕组中通入直流励磁电源时，长定子与动子之间形成闭合磁回路，二者之间的电磁吸力为列车提供悬浮力。长轨道作为高速磁浮直线电机长定子，其中均匀分布着三相对称绕组，在绕组通入三相对称电源时，会在气隙中感应出行波磁场[23]，其运行速度与电源频率有关。该行波磁场与动子侧的磁极相互作用，产生了使动子运行的推力。除此之外，动子侧整极的极面有预留的直线发电机齿槽，用于在列车运行时为列车供电。
在旋转电机以及部分长定子与动子极距相等的直线电机中，为方便计算，只针对1/4周期即半个极距下采用分布磁路法对电机磁路进行计算，再根据电机的高度对称性得到整个电机的磁路分布情 况[24]。直线电机横向截面图如图2所示。在高速磁浮直线电机中，有以下两点需要特别注意：①本文所研究的高速磁浮直线电机的长定子与动子的极距不同（见图2），其长定子与动子的齿槽的相对位置并不相对固定。因此，继续针对半个极下进行计算不能反映整个动子长度下电机的磁路分布情况且在一定程度上增加了计算复杂程度。②高速磁浮直线电机动子侧结构特殊，在修正气隙磁通密度初值时，需充分考虑励磁绕组齿槽和发电机绕组齿槽影响，以及不连续动子轭部的影响。
本文假设动子侧的中点（如图2中
点）与长定子齿部中点（见图2中O点）相对应。因此，可以将直线电机分为对称的两半，通过计算一半动子长度下直线电机的气隙磁通密度便可得到整个动子长度下的直线电机气隙磁通密度。以O点为坐标原点，沿纵向即动子运行的方向为x轴，沿垂向即垂直于长定子齿面向上为y轴，沿横向即垂直于直线电机横截面的方向为z轴建立空间直角坐标系。以动子极距为单元分别计算沿x轴方向5个整极以及1个半极下的气隙磁通密度（见图2）。
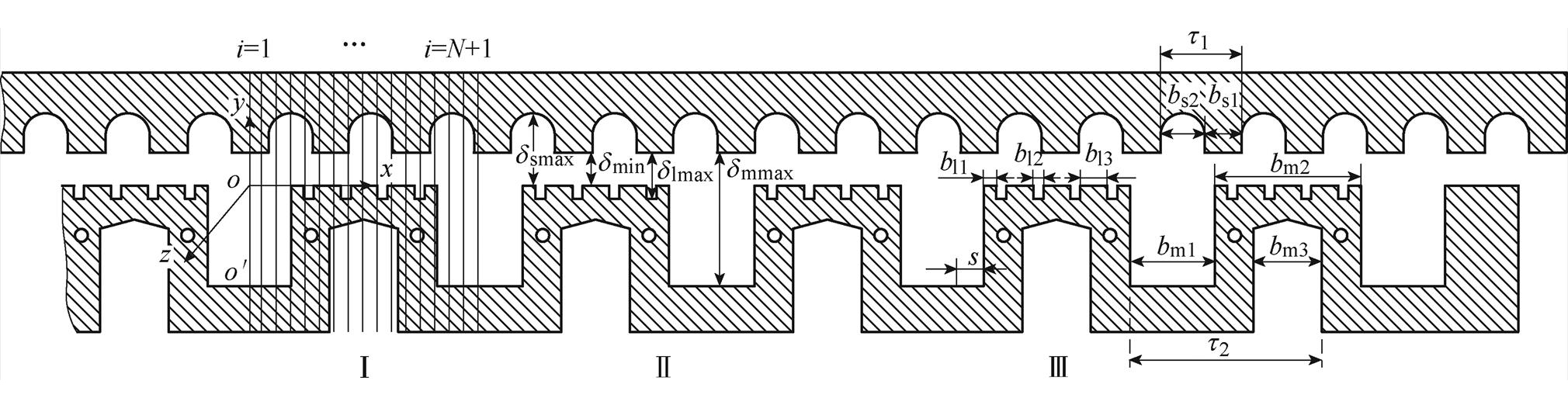
图2 直线电机横向截面图
Fig.2 Transverse section of linear motor
本小节以从坐标原点开始沿x轴正向的第一个动子整极为例来计算气隙磁通密度。将其均分为等距的N段，因此每个动子极距下有N+1个节点（见图2中Ⅰ区域所示）。
本文探究高速磁浮直线电机空载下的静态气隙磁通密度，并在此基础上计算直线电机空载下的静态悬浮力。因此，本文忽略电枢磁场，认为励磁磁场即为气隙磁场[25]。现有以下计算条件：①假设直线电机长定子为无限长；②忽略直线电机的边端效应；③假设定子电源为零；④动子与长定子相对位置固定，不会随时间变化；⑤为便于计算，将坐标原点置于如图2区域Ⅰ所示位置，且跟随动子运动。
1.3.1 磁动势计算
本文只针对高速磁浮直线电机悬浮电磁铁中的励磁电流产生的悬浮力。因此，长定子齿槽与动子齿槽之间的相对位置并不会影响动子侧励磁电流产生的磁动势随x的变化规律。设励磁绕组匝数为Na，直流电为I。结合如图2中Ⅲ区域所示的直线电机各部分参数，可以得到有电源产生的磁动势波形如图3所示[20]。
结合图3所示的磁动势波形，得到直线电机动子侧直流励磁电源产生的磁动势随x轴方向变化的表达式为
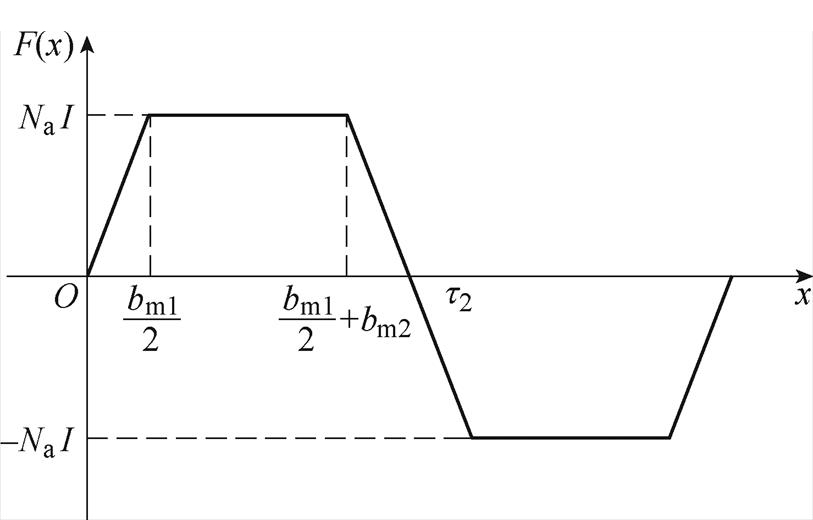
图3 励磁电流产生的磁动势波形
Fig.3 Waveform of magnetomotive force generated by excitation current
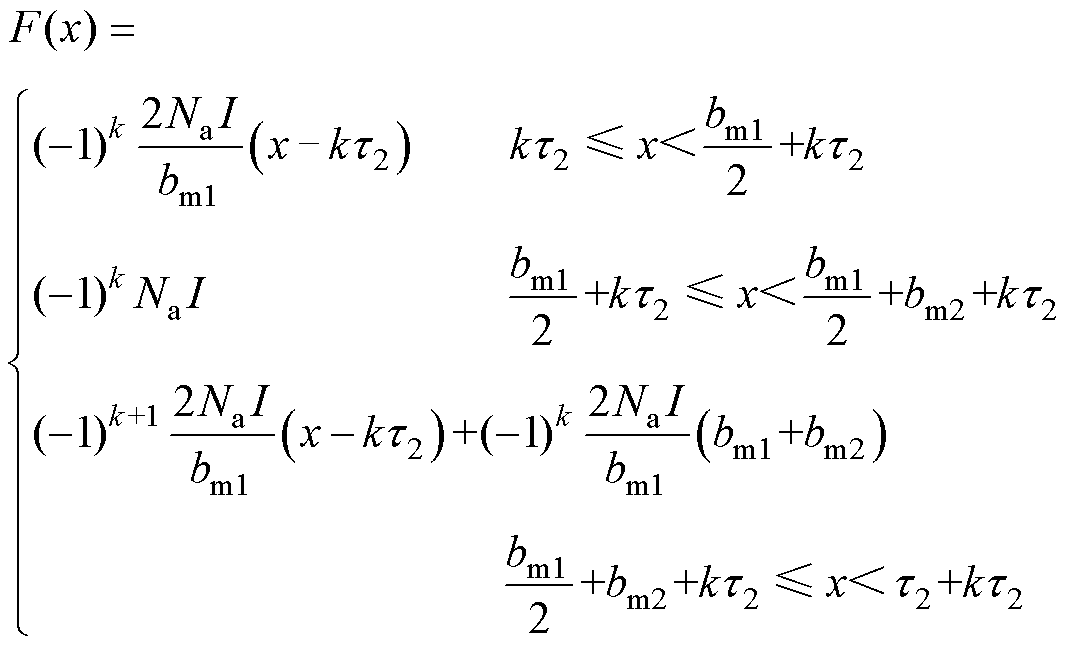（1）
式中，bm1为动子槽宽；bm2为动子齿宽；t2为动子齿距；k为从坐标原点到x之间动子侧整极的个数，k=0, 1, 2,…。具体见图2中的区域Ⅲ所示。
1.3.2 磁导率计算
图2区域Ⅱ中给出了高速磁浮直线电机长定子与动子之间不同部位对应的气隙长度。其中dmin表示忽略长定子与动子齿槽的存在时直线电机的气隙长度，dsmax表示长定子槽底到动子齿表面之间的气隙长度，dmmax表示动子槽底到长定子齿表面之间的气隙长度，dlmax表示直线发电机槽底到长定子齿表面之间的气隙长度。因此，直线电机各齿槽对应的磁导率为
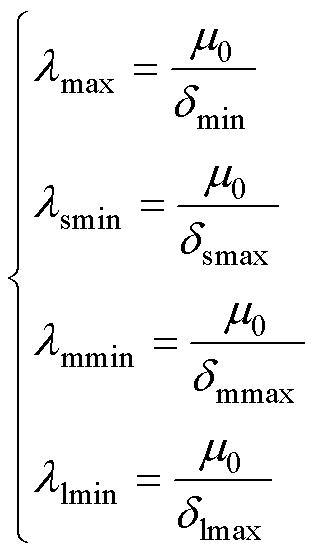（2）
式中，m0为空气磁导率，其值为4p×10-7；lmax、lsmin、lmmin和llmin分别为气隙长度dmin、dsmax、dmmax和dlmax对应的磁导率。
基于图2中建立的坐标系，结合式（2）中各部分气隙长度对应的气隙磁导率，得到只考虑长定子开槽时，气隙磁导率ls随x的变化规律为
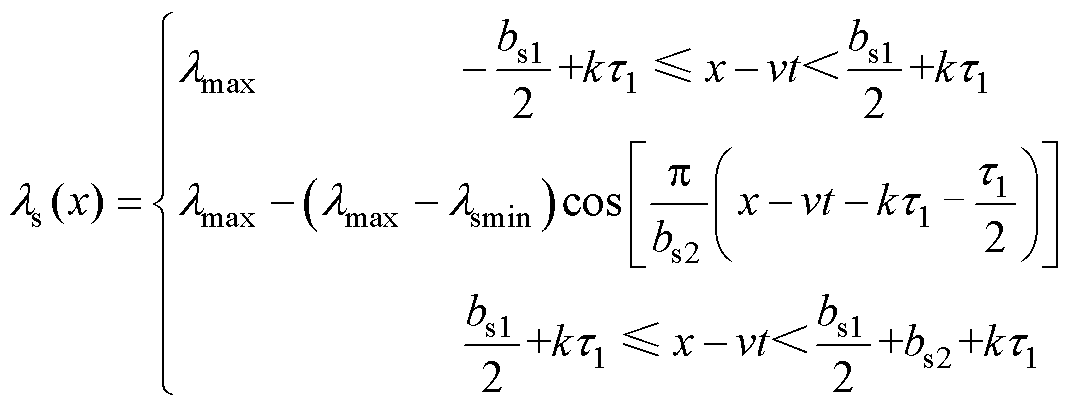（3）
式中，t1为长定子齿距；v为动子的运行速度，本小节旨在计算直线电机静态气隙磁通密度，所以v=0；t为动子侧运行时间；bs1为长定子齿宽；bs2为长定子槽宽；k为从坐标原点到x之间长定子齿距个数，k=0, 1, 2,…。具体见图2区域Ⅲ所示直线电机各部分尺寸。
只考虑动子侧开槽时，气隙磁导率lm随x的变化规律为
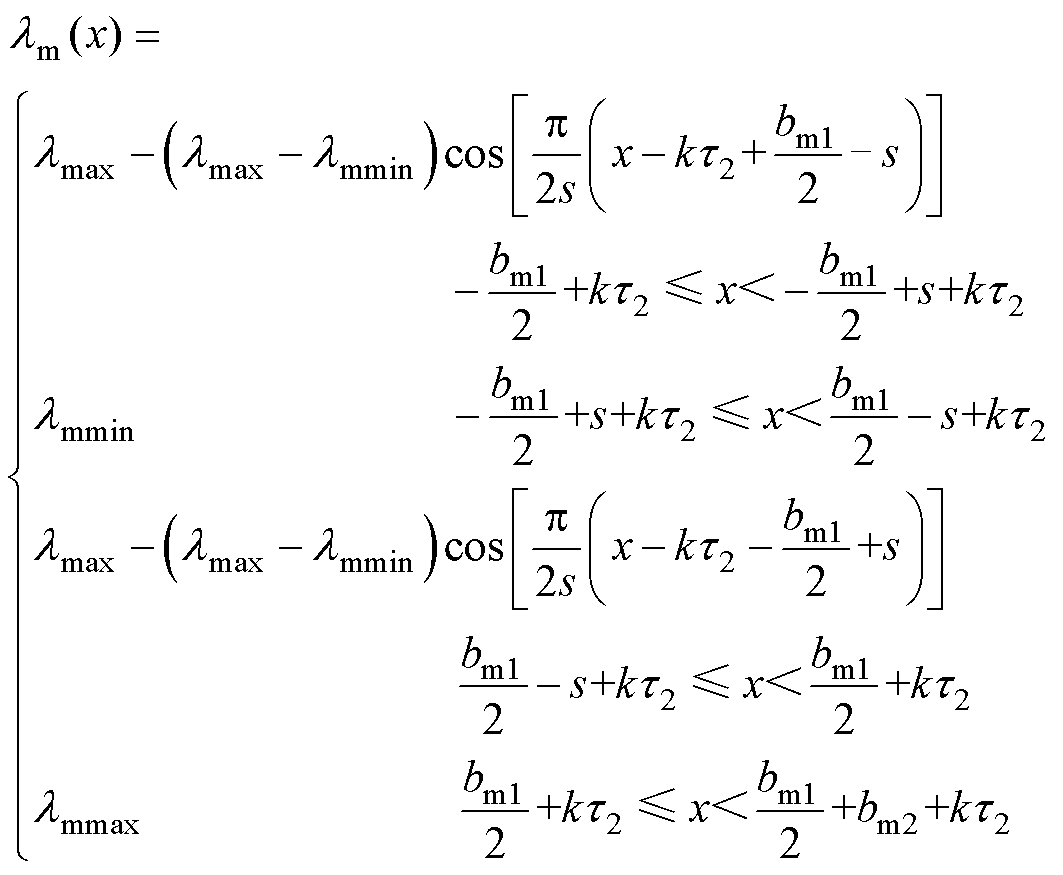（4）
式中，s为动子槽壁区余弦波的1/4周期长度。剩余参数与式（1）所示一致。
只考虑动子极面直线发电机齿槽时，气隙磁导率ll随x的变化规律为
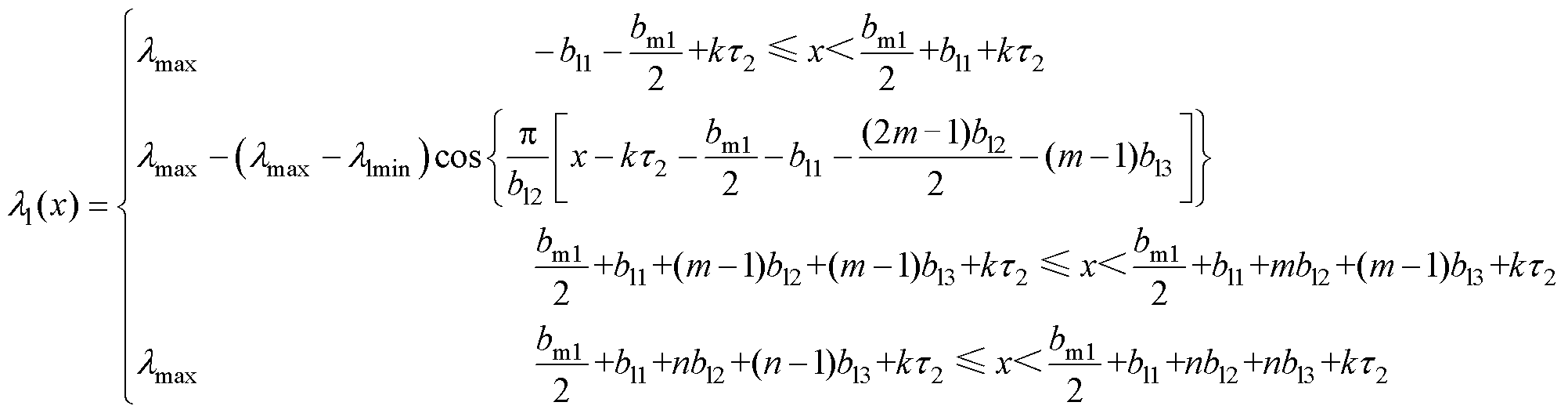（5）
式中，bl1为悬浮电磁铁表面直线发电机端部齿宽；bl2为直线发电机槽宽；bl3为直线发电机中部齿宽；m为悬浮电磁铁表面直线发电机槽的编号，m=1, 2, 3, 4；n为悬浮电磁铁表面直线发电机中间齿的编号，n=1, 2, 3。其他参数与式（1）所示一致。具体见图2区域Ⅲ所示的直线电机尺寸。
因此，在同时考虑高速磁浮直线电机长定子齿槽、悬浮电磁铁齿槽以及直线发电机齿槽后，得到高速磁浮直线电机气隙磁导率为
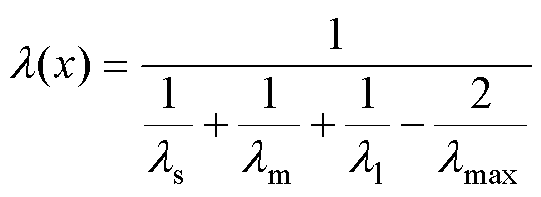（6）
结合式（1）和式（6）即可求得考虑长定子齿槽、动子齿槽以及直线发电机槽的影响条件下气隙磁通密度的初值为
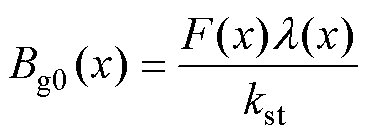（7）
式中，kst为预取的磁通密度饱和系数，一般取1～1.5之间。
在电机的磁路计算中，因为有饱和的存在，需要考虑电机齿部的实际磁通密度对气隙磁通密度的影响。分布磁路法根据电源产生的磁动势与电机内各部分磁压降相等的原理来对气隙磁通密度的初值进行修正。
本小节以从图2所示的坐标原点开始沿x轴正向的第一个整极为例，分别计算这一个极下的长定子与动子齿部压降和长定子与动子轭部磁压降。
1.4.1 直线电机齿部磁压降计算
根据磁通连续性原理并结合求解得到的气隙磁通密度初值，可以计算第i点处长定子齿部磁通密度Bst和动子齿部磁通密度Bmt分别为
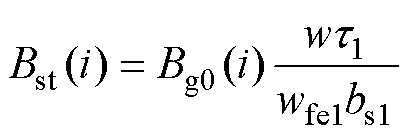（8）
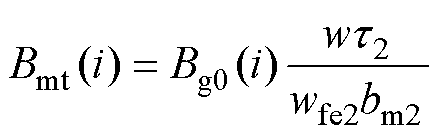（9）
式中，i为分段端点的标号，其值介于1～N+1之间；w为直线电机宽度；wfe1、wfe2分别为考虑叠压系数的长定子和动子宽度。
其中节点标号i与横坐标x的关系为
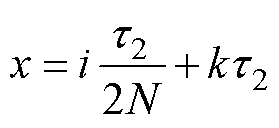（10）
因此，直线电机长定子齿部磁压降Fst以及动子齿部压降Fmt分别为
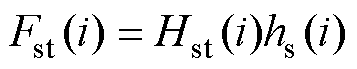（11）
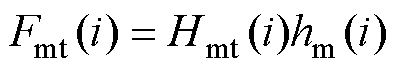（12）
式中，Hst、Hmt分别为各节点处长定子齿部以及动子齿部对应的磁场强度，是基于计算得到的齿部磁通密度并结合材料的B-H曲线求得；hs、hm分别为各节点对应的长定子齿部和动子齿部高度。
1.4.2 直线电机轭部磁压降
以第一个动子极为研究对象，根据磁通连续性原理，当i≤N/2+1时，第1节点与第i节点间气隙中心面上的垂向磁通等于第i节点处轭部截面上的纵向磁通；当i＞N/2+1时，第N+1节点与第i节点间气隙中心面上的垂向磁通等于第i节点处轭部截面上的纵向磁通。因此，得到长定子轭部磁通密度Bsc及动子轭部磁通密度Bmc分别为
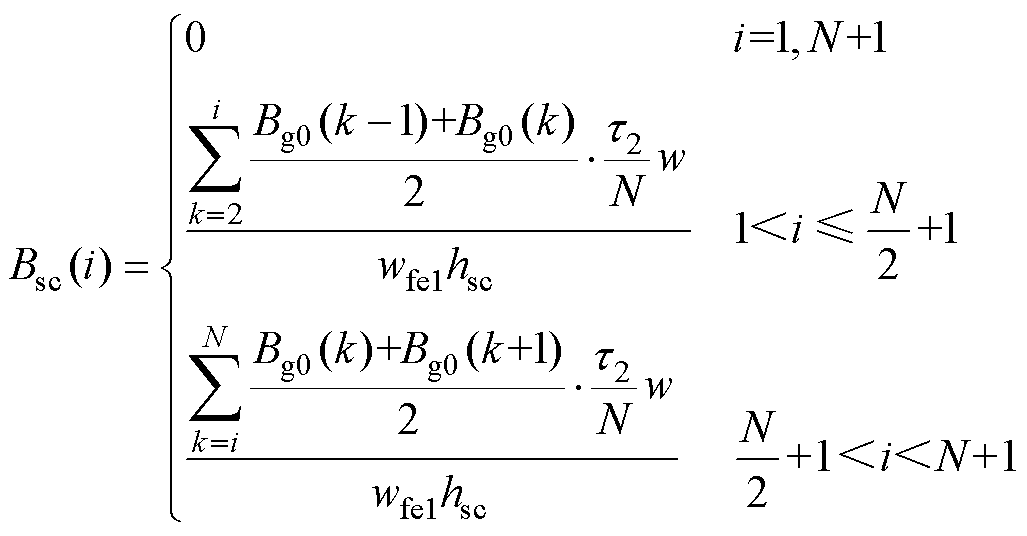（13）
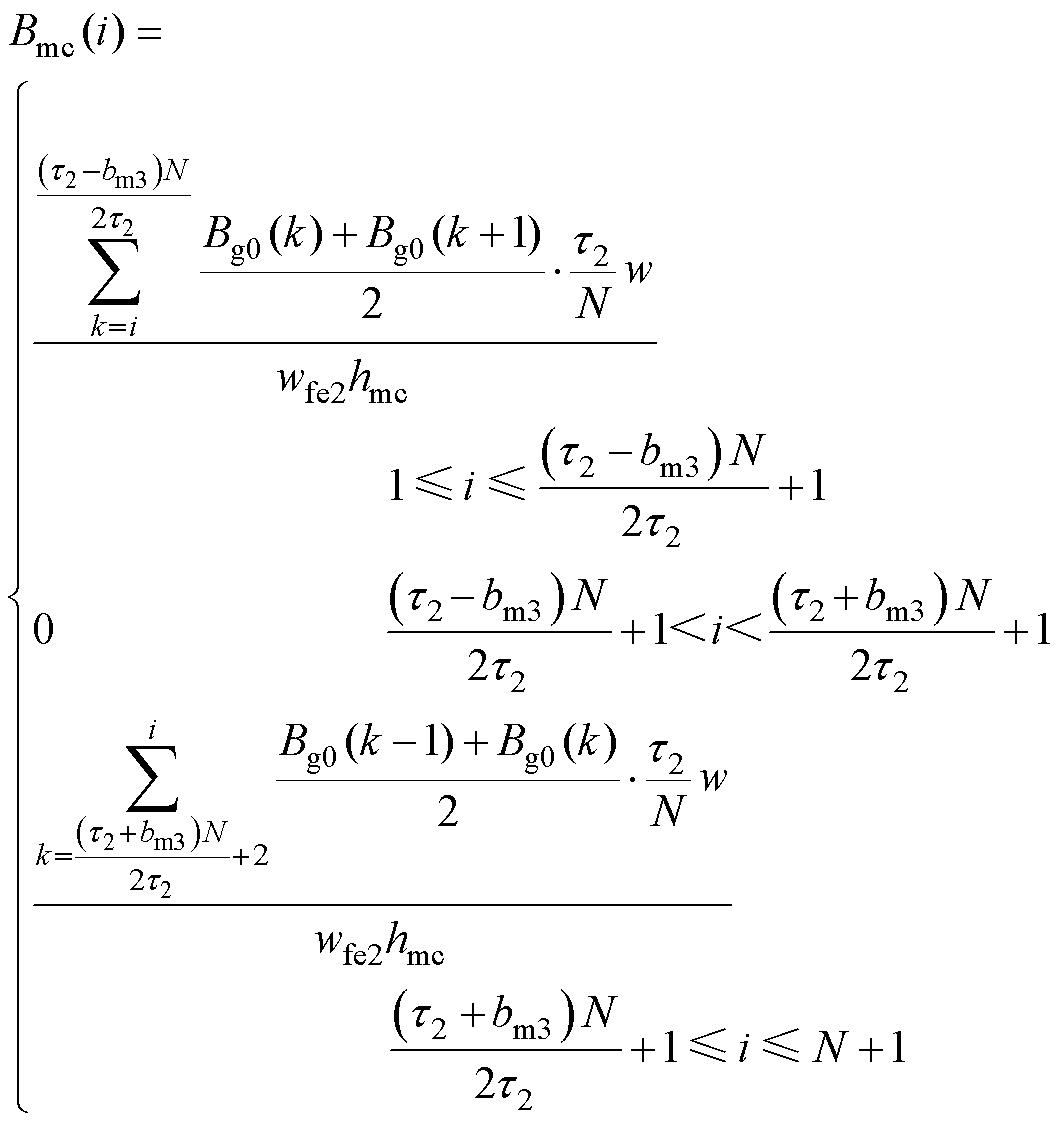（14）
式中，hsc、hmc分别为直线电机长定子轭部高度和动子轭部高度；bm3为直线电机动子轭部扣掉的空隙宽度。
因此，直线电机长定子轭部磁压降Fsc和动子轭部磁压降Fmc分别为
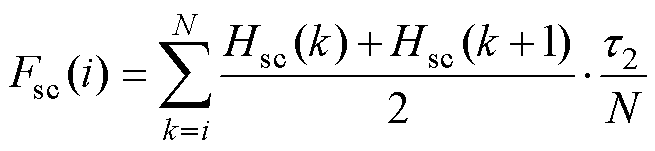（15）
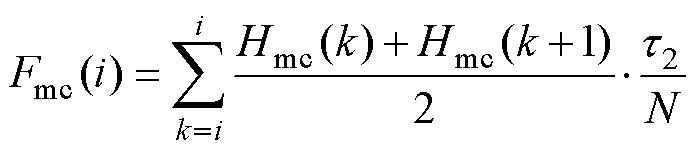（16）
式中，Hsc、Hmc分别为长定子轭部和动子轭部各节点处磁场强度，是根据求得的轭部磁通密度并结合各部分材料的B-H曲线求得。
基于1.4小节得到的直线电机一个极下各部分磁压降，可以求得高速磁浮直线电机的一个极下磁压降总和为
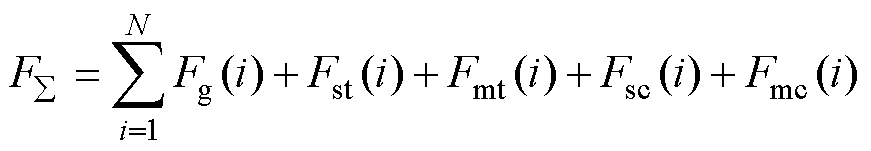（17）
式中，Fg为一个极下气隙中的磁压降，其值为
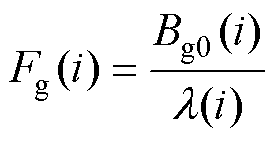（18）
因此，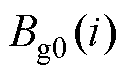
为第i节点处的气隙磁通密度初值。
因此，基于气隙磁通密度初值，根据由动子侧产生的直流励磁电源产生的磁动势与电机内部各部分的磁压降相等的原理，对气隙磁通密度进行修正，得到高速磁浮直线电机的实际的气隙磁通密度Bg[24]为
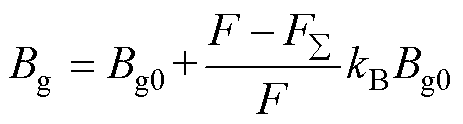（19）
式中，kB为经验系数，取值范围为0.05～0.5，饱和程度低时取大值，饱和程度高时取小值。
经过式（19）对气隙磁通密度初值进行修正，即可求得高速磁浮直线电机气隙磁通密度。因直线电机动子侧端部的气隙磁通密度受较多因素的影响，而解析计算并不能精确反映边端效应等因素对计算结果的影响。因此，为验证本文提出的改进分布磁路法计算直线电机气隙磁通密度的准确性，采用不同方法对比计算了直线电机中间八个极下的气隙磁通密度。图4给出了原分布磁路法、改进分布磁路法以及有限元仿真得到的高速磁浮直线电机气隙磁通密度曲线。
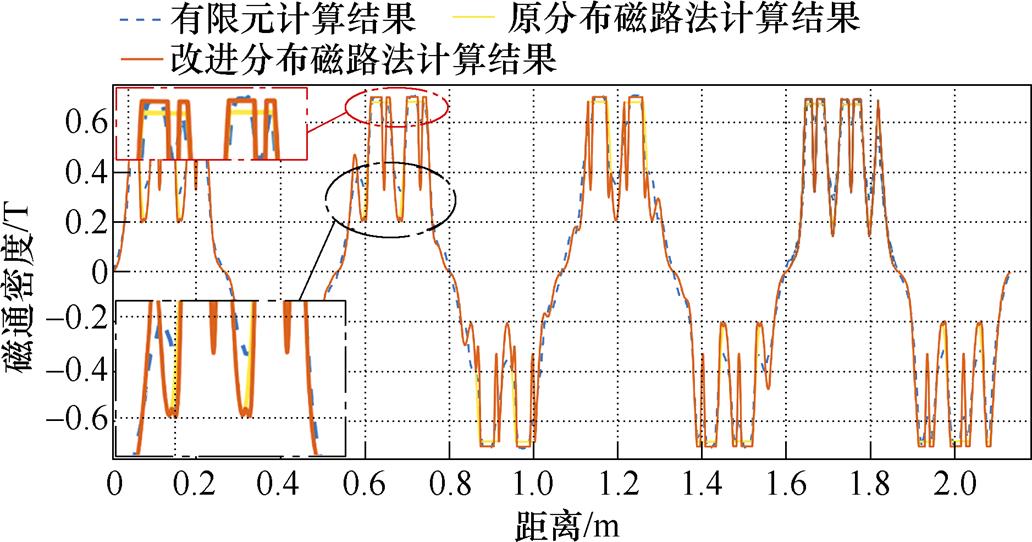
图4 高速磁浮直线电机气隙磁通密度
Fig.4 Air gap flux density of high-speed maglev linear motor
由图4可以看出，由于改进分布磁路法充分考虑了高速磁浮直线电机中发电机齿槽以及动子轭部不连续的特点，因此比未改进方法的计算精度更高。
为精确分析基于改进的分布磁路法与有限元法两种方法得到的计算结果之间的差异，分别对两种计算方法得到的气隙磁通密度曲线进行傅里叶分解，得到如图5所示的气隙磁通密度频谱图。
根据图5所示的气隙磁通密度频谱图可以看出，直线电机气隙磁通密度主要分解为基波和一些奇数次谐波分量。对比解析和有限元两种计算方法得到的气隙磁通密度基波分量可以看出，二者之间误差很小，仅有4.2 %，并且3次、5次、7次谐波分量误差很小。但是由于电机槽部漏磁等因素的影响，气隙磁通密度的9次、11次谐波分量误差较大。综上所述，在计算高速磁浮直线电机的气隙磁通密度时，基于分布磁路法的解析计算结果具有较高的准确度。
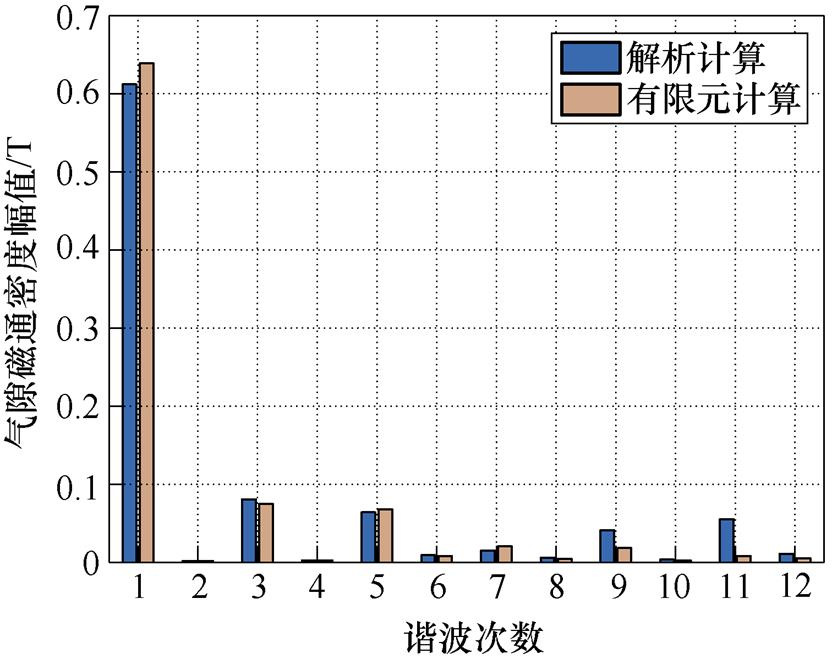
图5 气隙磁通密度频谱图
Fig.5 Spectrum of air gap magnetic density
虚位移法是通过假设物体在电磁力的作用下位移一段距离后各能量之间的关系来求解物体之间的电磁力。在高速磁浮直线电机中，悬浮电磁铁所受的悬浮电磁力主要由动子侧的直流励磁电源产生。因此，本文通过假设在动子侧直流励磁电源产生的电磁力的作用下沿垂向位移一段距离后各能量之间的关系来求解长定子与动子之间的电磁力，即为直线电机的悬浮力。
在工程应用中，为满足高速磁浮列车对悬浮力要求，需要在动子侧直流励磁电源单独作用时悬浮电磁铁所受的悬浮力满足一定的需求。因此，本文忽略直线电机长定子侧的励磁绕组，只针对动子侧直流励磁电源为5～45 A时所产生的悬浮力进行计算。此时，电机内部磁链保持不变，因此，悬浮力的计算公式为
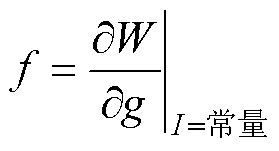（20）
式中，W为磁场中的能量；g为气隙长度。
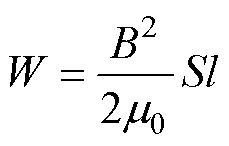（21）
式中，B为两块导磁材料之间的气隙磁通密度；S为气隙磁通密度B对应的铁心的横截面积；l为两铁心之间气隙长度。
将式（21）代入式（20）得到气隙磁通密度B所对应的横截面积为S时，两铁心之间的悬浮力为
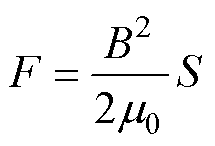（22）
基于式（22），结合高速磁浮直线电机磁通密度的分布情况，得到电磁力分段计算公式为
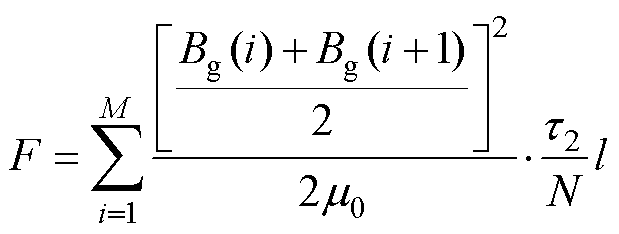（23）
式中，M为以t2/N为单元长度的直线电机总段数。
以硅钢作为直线电机长定子铁心材料时，其磁化特性曲线（B-H曲线）如图6中虚线所示，叠压系数为0.97；以非晶合金作为直线电机长定子铁心材料时，B-H曲线如图6中实线所示，考虑非晶合金带材很薄，仅有25 mm，因此在保证长定子厚度不变时，非晶合金的叠压系数设置为0.9。
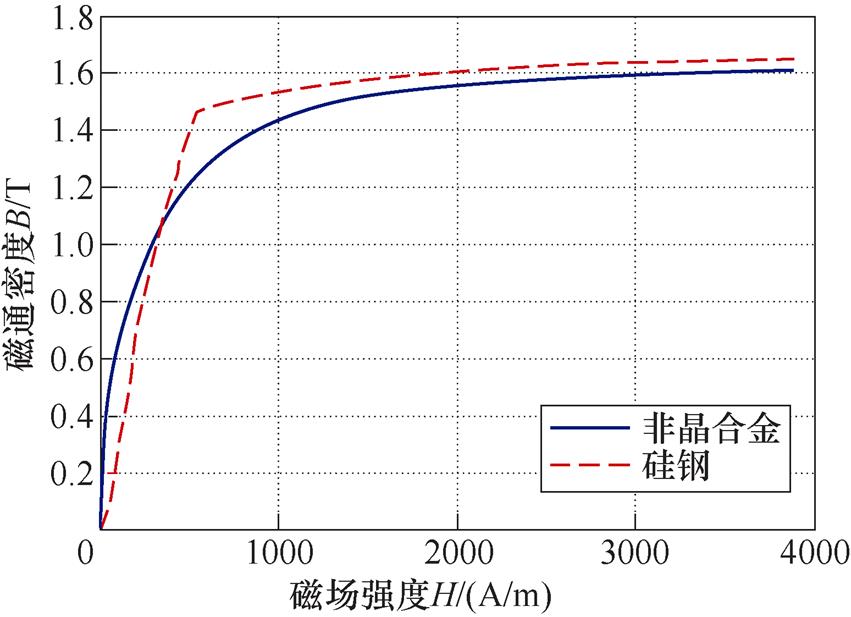
图6 两种材料的B-H曲线
Fig.6 B-H curves of two materials
为精确计算基于两种不同长定子下直线电机悬浮力的大小，本文基于分布磁路法，结合图6所示两种材料的磁化特性，对各励磁电流水平下的高速磁浮直线电机气隙磁通密度进行计算。图7给出了励磁电流为25 A、30 A、45 A时硅钢和非晶长定子直线电机气隙磁通密度的解析、有限元计算结果。对比基于改进后的分布磁路法求解得到的直线电机气隙磁通密度与有限元计算结果，可见，解析计算结果精确度较高；解析计算的误差主要来源于解析计算中未能充分考虑到电机槽中具有较大的漏磁。
在此基础上，结合式（23）即可求解不同励磁电流下基于两种长定子的直线电机的悬浮力。计算结果如图8所示。可以看出，同一励磁电流下，非晶长定子直线电机静态悬浮力略低于硅钢长定子直线电机的悬浮力；随着励磁电流的增大，两种材料长定子直线电机悬浮力均随励磁电流的增大而增大，且非晶材料相较硅钢而言饱和趋势变化略快，这与图6所示两种材料B-H曲线的变化规律吻合。
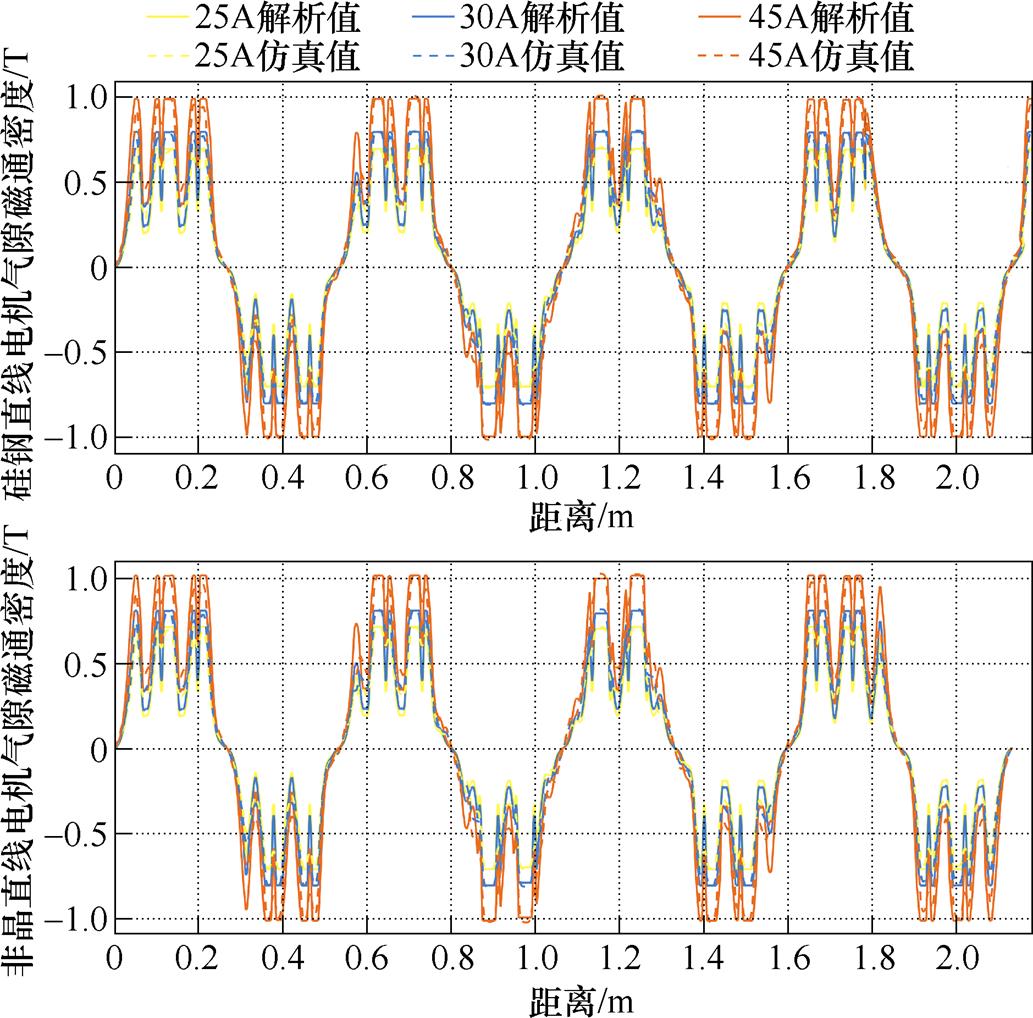
图7 励磁电流为25 A、30 A、45 A时两种材料长定子直线电机气隙磁通密度
Fig.7 Air gap magnetic density of linear motor with long stator made of two materials at excitation current of 25 A, 30 A and 45 A
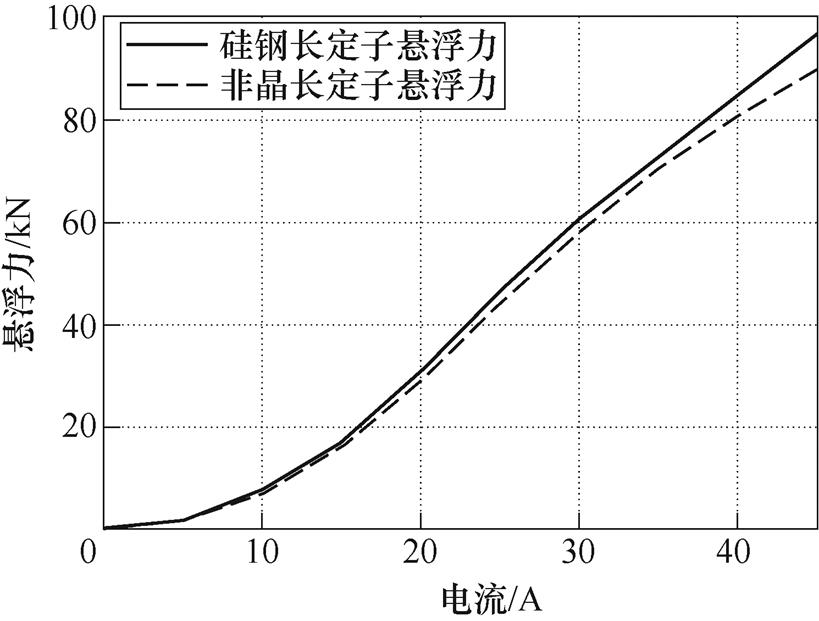
图8 基于两种材料长定子的直线电机悬浮力
Fig.8 Levitation force of linear motor based on two kinds of long stator
在额定励磁电流25 A时，两种材料长定子均可达到列车悬浮力40 kN要求；励磁电流超过30 A后，两种材料直线电机均进入饱和区；当励磁电流达到45 A时，为保障列车故障时的稳定悬浮，要求静态悬浮力不低于90 kN，两种材料长定子直线电机也都满足要求。
为验证高速磁浮直线电机悬浮力解析计算结果以及建立的有限元仿真模型的准确性，并进一步探究非晶合金作为长定子铁心材料时直线电机的悬浮力是否可以达到高速磁浮直线电机对悬浮力的要求，本小节分别实验测试以硅钢和非晶合金作为长定子铁心材料时直线电机悬浮力水平。高速磁浮直线电机的基本参数见表1。实验平台如图9所示。
表1 高速磁浮直线电机基本参数
Tab.1 Basic parameters of high-speed maglev linear motor
参 数数 值 长定子齿距t1/mm86 长定子槽宽bs2/mm46 长定子齿宽bs1/mm40 动子齿距t2/mm266.5 动子槽宽bm1/mm96.5 动子整极齿宽bm2/mm170 动子端极齿宽/mm85 励磁绕组匝数300 极数10个整极+2个端极
图9 实验平台
Fig.9 Experimental platform
以硅钢作为长定子铁心材料时直线电机悬浮力的解析计算值、有限元计算值以及实验值的对比如图10所示。
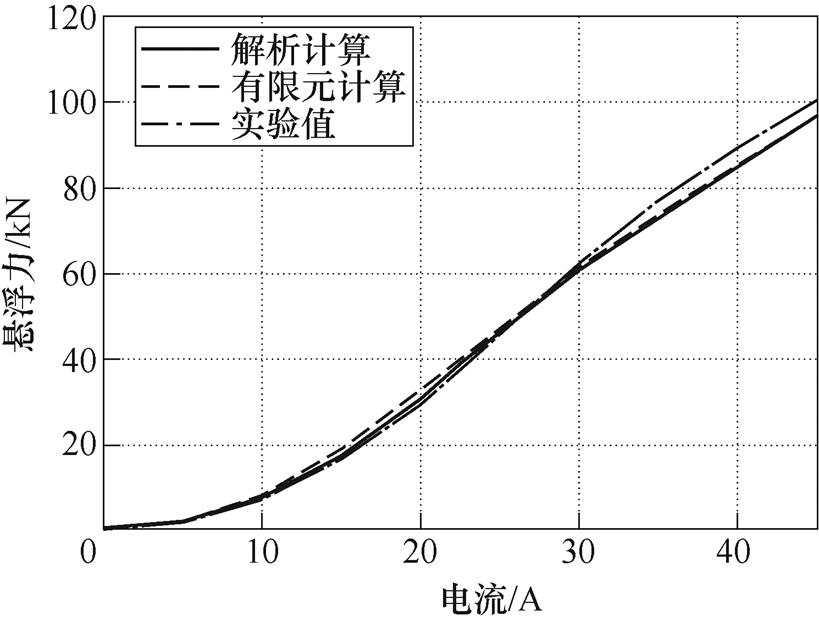
图10 基于硅钢长定子的悬浮力计算结果以及实验验证
Fig.10 Calculation results and experimental verification of suspension force based on silicon steel long stator
以非晶合金作为长定子铁心材料时直线电机的悬浮力解析计算值、有限元仿真值以及实验值的对比如图11所示。
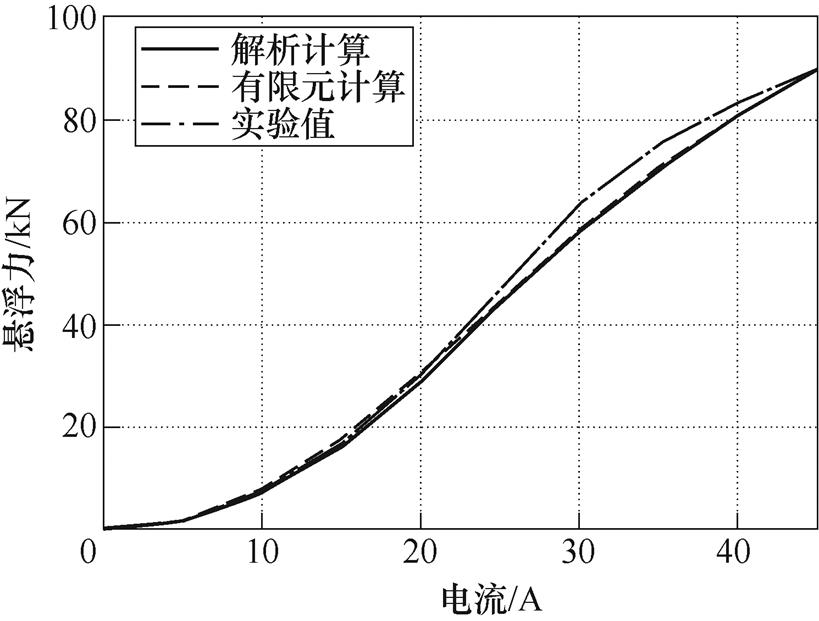
图11 基于非晶长定子的悬浮力计算结果以及实验验证
Fig.11 Calculation results and experimental verification of suspension force based on amorphous long stator
对比图10和图11中解析计算、有限元仿真计算以及实验测量得到的不同励磁电流下直线电机悬浮力，验证了基于改进后的分布磁路法计算直线电机静态悬浮力具有较高的准确度。计算值与实测值的误差主要来源于磁极端部漏磁以及磁化特性曲线与实测值的偏差。
为探究非晶合金取代硅钢作为高速磁浮直线电机长定子铁心材料的合理性，本文充分考虑直线电机长定子与动子极距不等，长定子、动子和直线发电机的齿槽结构及分布特征等因素的影响，采用改进的分布磁路法分别计算两种材料下不同励磁电流对应的直线电机气隙磁通密度，在此基础上采用虚位移法对比计算两种长定子铁心材料的静态悬浮力，并通过有限元以及实验验证。经过对结果的分析，得到如下结论：
1）本文采用改进的分布磁路法求得的高速磁浮直线电机气隙磁通密度波形与有限元仿真结果吻合较好。分别对二者进行傅里叶分解，结果表明，二者气隙磁通密度基波分量误差仅有4.2 %，且3次、5次、7次等奇次谐波含量基本一致。因此，在传统分布磁路法基础上分段表征磁导率并分段计算磁压降，可以充分考虑长定子与动子极距不等且不对称齿槽结构等因素，具有较高的计算精确度。
2）对比硅钢和非晶合金两种长定子铁心材料直线电机的静态悬浮力，可以看出，非晶合金长定子的悬浮力水平略低于硅钢长定子的悬浮力；但从应用需求看，非晶合金作为长定子铁心材料时的悬浮力依旧满足高速磁浮直线电机的要求。这也就证实了在直线电机静态悬浮力方面，非晶合金替代硅钢作为直线电机长定子铁心材料的可行性。
综上所述，非晶合金替代硅钢作为高速磁浮直线电机长定子铁心材料，不仅可以满足静态悬浮力等基本电磁性能需求，同时还可以大幅降低定子铁心损耗，具有较好的应用前景。
参考文献
[1] 熊嘉阳, 邓自刚. 高速磁悬浮轨道交通研究进展[J]. 交通运输工程学报, 2021, 21(1): 177-198.
Xiong Jiayang, Deng Zigang. Research progress of high-speed maglev rail transit[J]. Journal of Traffic and Transportation Engineering, 2021, 21(1): 177- 198.
[2] 朱进权, 葛琼璇, 王晓新, 等. 基于自抗扰和负载功率前馈的高速磁悬浮系统PWM整流器控制策略[J]. 电工技术学报, 2021, 36(2): 320-329.
Zhu Jinquan, Ge Qiongxuan, Wang Xiaoxin, et al. Control strategy for PWM rectifier of high-speed maglev based on active disturbance rejection control and load power feed-forward[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 320- 329.
[3] 赵牧天, 葛琼璇, 朱进权, 等. 中速磁悬浮列车分段式长定子永磁直线同步电机牵引控制策略[J]. 电工技术学报, 2022, 37(10): 2491-2502.
Zhao Mutian, Ge Qiongxuan, Zhu Jinquan, et al. Traction control strategy of segmented long stator permanent magnet linear synchronous motor for medium-speed maglev train[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2491-2502.
[4] 廖凯, 张润涛, 杨子安, 等. 交通能源融合大数据平台架构与应用[J]. 电力系统自动化, 2022, 46(12): 20-35.
Liao Kai, Zhang Runtao, Yang Zian, et al. Archite- cture and application of traffic-energy integrated big data platform[J]. Automation of Electric Power Systems, 2022, 46(12): 20-35.
[5] 迟青光, 张艳丽, 陈吉超, 等. 非晶合金铁心损耗与磁致伸缩特性测量与模拟[J]. 电工技术学报, 2021, 36(18): 3876-3883.
Chi Qingguang, Zhang Yanli, Chen Jichao, et al. Measurement and modeling of lossand magneto- strictive properties for the amorphous alloy core[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3876-3883.
[6] Tong Wenming, Li Shiqi, Sun Ruolan, et al. Modified core loss calculation for high-speed PMSMs with amorphous metal stator cores[J]. IEEE Transactions on Energy Conversion, 2021, 36(1): 560-569.
[7] 朱健, 曹君慈, 刘瑞芳, 等. 电动汽车用永磁同步电机铁心采用非晶合金与硅钢的性能比较[J]. 电工技术学报, 2018, 33(增刊2): 352-358.
Zhu Jian, Cao Junci, Liu Ruifang, et al. Comparative analysis of silicon steel and amorphous on the per- formance of permanent magnet synchronous motors on electric vehicles[J]. Transactions of China Elec- trotechnical Society, 2018, 33(S2): 352-358.
[8] Chai Feng, Li Zongyang, Chen Lei, et al. Effect of cutting and slot opening on amorphous alloy core for high-speed switched reluctance motor[J]. IEEE Transa- ctions on Magnetics, 2021, 7(2): 1-5.
[9] Tong Wenming, Sun Ruolan, Zhang Chao. Loss and thermal analysis of a high-speed surface-mounted PMSM with amorphous metal stator core and titanium alloy rotor sleeve[J]. IEEE Transactions on Magnetics, 2019, 55(6): 1-4.
[10] 孙玉玺, 高信迈, 包木建, 等. 基于非晶合金的高速磁浮直线电机长定子铁耗计算[J]. 大电机技术, 2022, 284(5): 21-27.
Sun Yuxi, Gao Xinmai, Bao Mujian, et al. Iron loss calculation of high-speed maglev linear motor based on amorphous alloy[J]. Large Electric Machine and Hydraulic Turbine, 2022, 284(5): 21-27.
[11] 宋守许, 杜毅, 胡孟成. 定子混合叠压再制造电机空载损耗计算与分析[J]. 中国电机工程学报, 2020, 40(3): 970-980.
Song Shouxu, Du Yi, Hu Mengcheng. Calculation and analysis of no-load iron loss of remanufactured motor with hybrid laminated stator core[J]. Proceedings of the CSEE, 2020, 40(3): 970-980.
[12] 胡道宇, 冯馨月, 张志华. 超导电动悬浮系统阻尼特性研究[J]. 中国电机工程学报, 2021, 41(13): 4679-4688.
Hu Daoyu, Feng Xinyue, Zhang Zhihua. Study on the damping characteristics of superconducting electro- dynamic suspension system[J]. Proceedings of the CSEE, 2021, 41(13): 4679-4688.
[13] 余浩伟, 寇峻瑜, 李艳. 600km/h高速磁浮在国内的适应性及工程化发展[J]. 铁道工程学报, 2020, 37(12): 16-20, 88.
Yu Haowei, Kou Junyu Li Yan. Adaptability and Engineering development of 600km/h high-speed maglev in China[J]. Journal of Railway Engineering Society, 2020, 37(12): 16-20, 88.
[14] 孙玉玲, 秦阿宁, 董璐. 全球磁浮交通发展态势、前景展望及对中国的建议[J]. 世界科技研究与发展, 2019, 41(2): 109-119.
Sun Yuling, Qin Aning, Dong Lu. Research on development and prospects of maglev transportation and suggestions to China[J]. World Sci-Tech R & D, 2019, 41(2): 109-119.
[15] 吕刚. 直线电机在轨道交通中的应用与关键技术综述[J]. 中国电机工程学报, 2020, 40(17): 5665-5675.
Lü Gang. Review of the application and key technology in the linear motor for the rail transit[J]. Proceedings of the CSEE, 2020, 40(17): 5665-5675.
[16] Cao Junci, Deng Xiaoqing, Jia Bo. Electromagnetic analysis and optimization of high-speed maglev linear synchronous motor based on field-circuit coupling[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(2): 118-123.
[17] 朱进权, 葛琼璇, 张波, 等. 考虑悬浮系统影响的高速磁悬浮列车牵引控制策略[J]. 电工技术学报, 2022, 37(12): 3087-3096.
Zhu Jinquan, Ge Qiongxuan, Zhang Bo, et al. Traction control strategy of high-speed maglev con- sidering the influence of suspension system[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3087-3096.
[18] Kang Jinsong, Mu Siyuan, Ni Fei. Improved EL model of long stator linear synchronous motor via analytical magnetic coenergy reconstruction method[J]. IEEE Transactions on Magnetics, 2020, 56(8): 1-13.
[19] 赵纪龙, 逯卓林, 韩青峰, 等. 轴向磁通永磁电机系统及关键技术前沿发展综述[J]. 中国电机工程学报, 2022, 42(7): 2744-2765.
Zhao Jilong, Lu Zhaolin, Han Qingfeng, et al. An overview on development of axial flux permanent magnet motor system and the key technology[J]. Proceedings of the CSEE, 2022, 42(7): 2744-2765.
[20] 罗俊, 寇宝泉, 杨小宝, 等. 双交替极横向磁通直线电机的基础研究[J]. 中国电机工程学报, 2019, 39(7): 1900-1908.
Luo Jun, Kou Baoquan, Yang Xiaobao, et al. Funda- mental study of dual consequent-pole transverse-flux linear motor[J]. Proceedings of the CSEE, 2019, 39(7): 1900-1908.
[21] 许金, 聂世雄, 马伟明, 等. 无槽双边长定子直线感应电动机磁路计算方法[J]. 中国电机工程学报, 2016, 36(10): 2793-2799.
Xu Jin, Nie Shixiong, Ma Weiming, et al. Magnetic circuit calculation of slot-less double-sided long primary linear induction motor[J]. Proceedings of the CSEE, 2016, 36(10): 2793-2799.
[22] 黄垂兵, 马伟明, 许金, 等. 六相圆筒式直线感应电机磁路计算及饱和特性分析[J]. 电工技术学报, 2018, 33(5): 1032-1039.
Huang Chuibing, Ma Weiming, Xu Jin, et al. Magnet circuit calculation and saturation characteristics analysis of six phase cylindrical linear induction motor[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1032-1039.
[23] 张千, 刘慧娟, 马杰芳, 等. 考虑后退行波的长初级双边直线感应电机电磁性能计算[J]. 电工技术学报, 2020, 35(7): 1398-1409.
Zhang Qian, Liu Huijuan, Ma Jiefang, et al. Calcu- lation of electromagnetic performance for long primary double sided linear induction motors con- sidering backward traveling wave[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1398- 1409.
[24] 刘治鑫, 王东, 余中军, 等. 基于磁性槽楔修正模型的感应电动机气隙磁场的分布磁路法[J]. 电工技术学报, 2019, 34(15): 3112-3123.
Liu Zhixin, Wang Dong, Yu Zhongjun, et al. Distributed magnetic circuit method for calculating air-gap magnetic field of induction motor based on modified model considering the effect of magnetic slot wedges[J]. Transactions of China Electro- technical Society, 2019, 34(15): 3112-3123.
[25] 章九鼎, 卢琴芬. 长定子直线同步电机齿槽效应的计算与影响[J]. 电工技术学报, 2021, 36(5): 964- 972, 1026.
Zhang Jiuding, Lu Qinfen. Calculation and influences of cogging effects in long-stator linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 964-972, 1026.
Abstract As a low-loss core magnetic conductive material, amorphous alloy can replace silicon steel as the ferromagnetic material of motor to greatly reduce the iron loss of high-speed maglev linear motor. In order to prove the feasibility of the application of amorphous alloy in high-speed magnetic levitation linear motor, the improved distributed magnetic circuit method was used to calculate the air gap magnetic density of silicon steel and amorphous alloy long stator linear motor, and the virtual displacement method was adopted to calculate the static levitation force of the two materials.
Firstly, the high-speed maglev linear motor has some unique structures, such as unequal pole distance between the long stator and mover, cogging on the polar surface of the mover, and discontinuity of the mover yoke. For this structure, the magnetic permeability was characterized in sections, the magnetic pressure drop was calculated in segments, and the distributed magnetic circuit method was improved. Then the accurate air gap magnetic density of silicon steel and amorphous long stator under different excitation currents was calculated. On this basis, the virtual displacement method was used to calculate the suspension force of a linear motor with a long stator made of two materials, and finite element verification was carried out. Finally, the static levitation force of this linear motor was measured, and both can meet the levitation requirements of high-speed maglev trains. The accuracy of the analytical results and the rationality of the amorphous alloy long-stator maglev linear motor were further verified.
The results of the air gap flux density of the linear motor show that the improved distributed magnetic circuit method is more accurate than the original method because the generator cogging and mover yoke’s discontinuity are considered. Accordingly, the analytical calculation results of the levitation force of the silicon steel and amorphous alloy long stator linear motor show that: (1) The static levitation force of the amorphous long-stator linear motor is slightly lower than that of the silicon steel long-stator linear motor under the same excitation current; (2) The levitation force of a linear motor with a long stator made of two materials increases with the increase of excitation current, and the saturation trend of amorphous materials changes slightly faster than that of silicon steel. When the excitation current is rated at 25 A, the long stator made of two materials can meet the requirement of 40 kN suspension force of the train. When the current exceeds 30 A, the linear motors of both materials enter the saturation zone. When it reaches 45 A, the static suspension force must be no less than 90 kN to ensure the stable suspension of the train under fault. In this case, the long stator linear motor made of two materials also meets the requirements. The simulation and experimental results of the levitation force show that the improved distributed magnetic circuit method has a high accuracy in calculating the static levitation force of the linear motor.
The following conclusions can be drawn from the analysis of calculation results: (1) The air gap flux density waveform of the high-speed maglev linear motor obtained by the improved distributed magnetic circuit method agrees with the finite element simulation results. (2) The levitation force level of an amorphous alloy long stator is slightly lower than that of a silicon steel long stator. However, from the perspective of application requirements, the suspension force of amorphous alloy as long stator core material still meets the requirements of the high-speed maglev linear motor. The feasibility of using amorphous alloy instead of silicon steel as the long stator core material of linear motor in terms of static levitation force of the linear motor is verified.
keywords：High-speed maglev linear motor, amorphous alloy, distributed magnetic circuit method, levitation force
青岛市科技计划重点研发专项资助项目（21-1-2-9-cl）。
收稿日期 2022-09-30
改稿日期 2022-11-23
DOI: 10.19595/j.cnki.1000-6753.tces.221852
中图分类号：TM359.4
包木建 男，1999年生，硕士研究生，研究方向为高速磁浮直线电机稳态性能分析。E-mail: baomujian@163.com
郑晓钦 女，1985年生，博士，副教授，硕士生导师，研究方向为多相电机及其系统的分析与控制。E-mail: zhengxiaoqin619@sina.com（通信作者）
（编辑 郭丽军）