
图1 偏心削极磁极结构示意图
Fig.1 Diagram of eccentric magnet shaping
摘要 该文以气隙磁通密度函数和永磁体磁化方向厚度函数为理论基础,结合卡特系数计算公式、磁路等效原理和分布磁路法,考虑定子开槽、极间漏磁、磁极边缘效应及磁路饱和等因素的影响,推导出表贴式永磁电机平行充磁条件下的正弦削极修正解析模型。而后建立有限元模型验证了解析模型的准确性,并与简化正弦削极电机、偏心削极电机进行仿真对比。结果表明修正正弦削极电机所得气隙磁通密度总谐波失真(THD)分别较简化正弦削极电机和偏心削极电机低41.3 %和23.4 %,径向电磁力密度THD分别较简化正弦削极电机和偏心削极电机低29.82 %和19.24 %,从而使电机转矩脉动降低。最后通过实验进一步验证了修正解析模型的准确性。该文提出的修正解析模型,不仅使电机的电磁性能得到了进一步优化,而且理论基础明晰,不用像偏心削极一样,需要进行遍历扫描寻优,提高了电机的设计效率,为高品质永磁电机的优化设计提供了参考。
关键词:永磁同步电机 正弦削极修正解析模型 平行充磁 分布磁路法
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)具有高转矩密度、高功率因数、高可靠性、高效率等优点,目前已经广泛应用于航天、交通运输、医疗、国防等领域[1-8]。通过减小PMSM气隙磁通密度谐波可以削弱电机气隙磁场径向电磁力谐波和转矩脉动,从而降低电机振动噪声和铁耗,提高电机的整体性能。因此,研究提高PMSM气隙磁场正弦度的电机设计方法,具有十分重要的意义。
PMSM气隙磁通密度的优化通常从本体设计和控制策略优化两个方面入手[9-12]。永磁电机削极技术是电机本体设计中最有效的途径之一。采用削极的方式改变转子永磁体或者转子铁心外表面极弧形状和长度并进行优化,可以达到增加电机径向气隙磁通密度正弦度、抑制转矩脉动和减振降噪的目 的[13-16]。针对表贴式永磁电机目前主要有偏心削极和正弦削极两种削极方式。偏心削极的磁极结构示意图如图1所示,该方法通过改变永磁体的极弧系数和外表面的偏心距,使电机气隙磁通密度的谐波含量达到最小,从而得到优化后的偏心磁极,使径向气隙磁通密度波形接近正弦[17-20]。偏心削极具有设计方法简单、加工工艺成熟等优点,因此在实际的工程应用中较为广泛,但是因为最优偏心距的变化受到漏磁、饱和、开槽、气隙长度、极弧系数、永磁体相对磁导率等多个因素的影响,在设计之初需要建立大量的仿真模型进行遍历扫描,时间成本高,而且这种削极方法对于气隙磁场的优化程度有限,很难满足高品质电机的需求。正弦削极是利用永磁体相对磁导率接近于空气的特性,将永磁体削减为正弦形状,以得到接近正弦的气隙磁通密度,正弦削极简化模型磁极结构示意图如图2所示,图中Dt是为了减小极间漏磁和边缘效应增加的边缘厚度。正弦削极相较于偏心削极,理论依据明晰,无需像偏心削极一样进行遍历扫描优化,可以大大减少前期电机设计的工作量[21]。
英国谢菲尔德大学诸自强教授等针对一台6槽4极电机进行削极研究,对比了正弦削极下永磁体边缘厚度不同时齿槽转矩和空载反电动势的波形,认为图2中Dt为0时,齿槽转矩较小,空载反电动势正弦度较高[21]。

图1 偏心削极磁极结构示意图
Fig.1 Diagram of eccentric magnet shaping
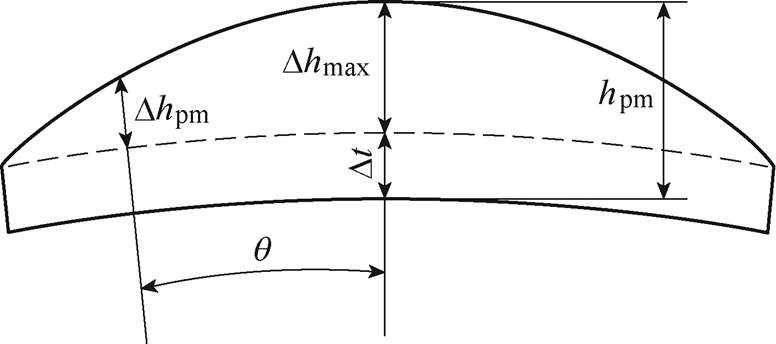
图2 正弦削极简化模型磁极结构示意图
Fig.2 Diagram of simplified sinusoidal magnet shaping
哈尔滨工业大学李勇教授等在正弦削极永磁磁极中注入3次谐波,以此达到在不提高电机转矩脉动的基础上提高电机平均输出转矩的目的[22]。王凯等以此为基础,利用Lagrange中值定理推导出径向充磁条件下转矩最大化的最优3次谐波注入因子。结果表明,磁极的优化使样机的平均转矩提高了9 %[23]。后续研究中,王凯等将3次谐波削极应用于五相电机,使注入的3次谐波与3次谐波电流作用,使得电机的输出转矩得到进一步提高[24]。
哈尔滨工业大学的柴凤教授等在永磁体正弦削极的基础上,依次注入3次、5次、7次和9次谐波,寻找到气隙磁通密度谐波含量最小的点,减小了电机的铁耗[25]。
沈阳工业大学张炳义等在传统正弦磁极结构的基础上,提出一种由导磁金属块和永磁体共同构成的表贴式磁极结构,通过改变导磁金属块的形状,提高电机气隙磁场的正弦度。此种磁极结构可以使永磁体按照简单的矩形结构加工,节省了永磁体用量,同时可以降低永磁体本身的涡流损耗,减小永磁体本身的退磁风险[26]。
上述对于正弦削极的研究,均是简单地将磁极的几何形状设计为正弦,忽略了极间漏磁、磁极边缘效应、定子开槽等因素的影响。因此,由这种简化模型所得的电机在基波气隙磁通密度幅值和气隙磁场正弦度两个方面均达不到理论预期效果。
海军工程大学胡鹏飞等对比了扇形和弓形磁极的转子磁通密度分布,并得出结论:在转子内圆直径和永磁体厚度相同的情况下,弓形磁极转子轭部材料的利用率更高,更利于提高电机转矩密度[27-28]。同时,弓形磁极的平底结构使其相比于扇形磁极具有更好的适装性,因此有必要对弓形磁极的正弦削极进行深入研究。
本文以气隙磁通密度函数和永磁体磁化方向厚度函数为理论基础,以气隙磁通密度的正弦化为目标,结合卡特系数计算公式、磁路等效原理和分布磁路法思想,考虑上述因素对气隙磁通密度的影响,建立了平行充磁条件下的正弦削极修正解析模型,并通过有限元仿真,与简化正弦削极永磁电机和偏心削极永磁电机进行了对比,证明了修正正弦削极技术的优越性,最后通过实验验证了修正模型的有效性和准确性。
对于表贴式永磁电机而言,未削极时气隙磁通密度[29]表达式为
 (1)
(1)
式中,Bg为电机气隙磁通密度;Br为永磁体剩磁; s 为漏磁系数,对于正弦削极曲线而言,只需从二维模型进行考虑即可,因此s 可视为极间漏磁系数;Kd 为卡特系数;Ks为磁路饱和系数;mr为永磁体相对磁导率;lg为气隙长度;hpm为永磁体厚度。
对于削极后的表贴式永磁电机,永磁磁极的外表面曲线 是关于空间角度
是关于空间角度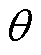 的变量,也可用如图3所示的R2表示。用
的变量,也可用如图3所示的R2表示。用 表示等效的极间漏磁系数,用
表示等效的极间漏磁系数,用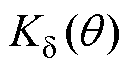 表示卡特系数,用
表示卡特系数,用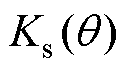 表示饱和系数。
表示饱和系数。
得到气隙磁通密度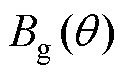 关于空间机械角度
关于空间机械角度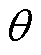 的表达式为
的表达式为
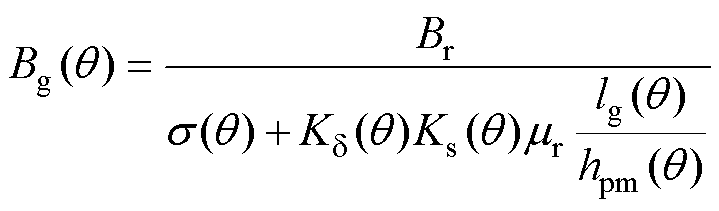 (2)
(2)
正弦削极修正模型磁极结构示意图如图3所示。对于修正正弦削极,气隙磁通密度波形的期望形状为正弦,表达式为
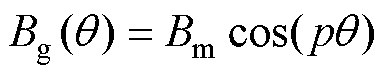 (3)
(3)
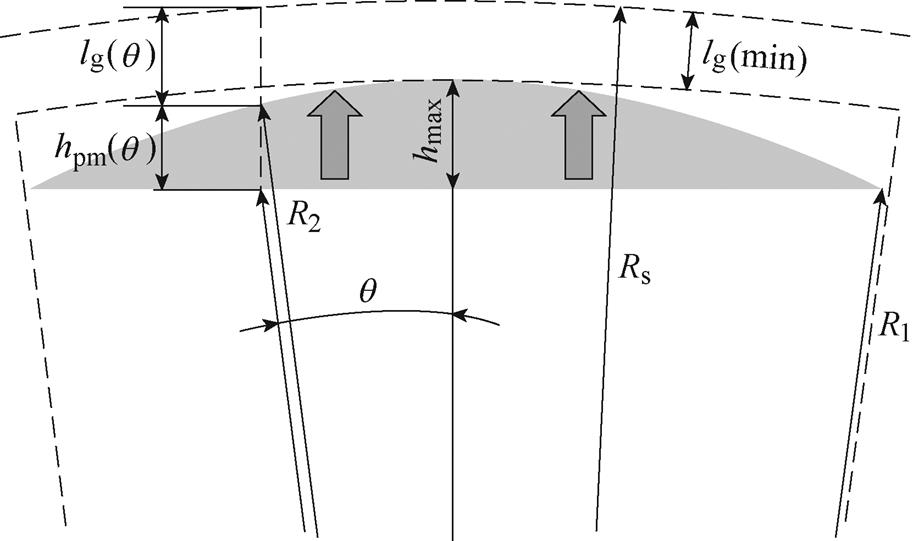
图3 正弦削极修正模型磁极结构示意图
Fig.3 Diagram of modified sinusoidal magnet shaping
式中,Bm为气隙磁通密度基波幅值;p为电机极对数。当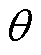 =0 °时,
=0 °时,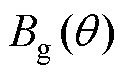 =Bm,
=Bm, =1,则Bm的表达式为
=1,则Bm的表达式为
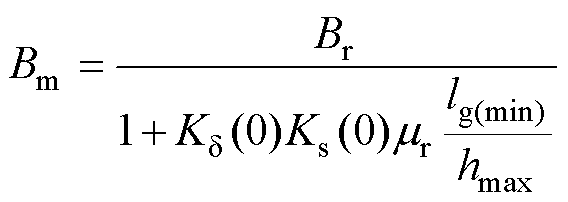 (4)
(4)
式中,lg(min)为最小气隙长度;hmax为永磁体最大厚度。
由式(2)~式(4)得
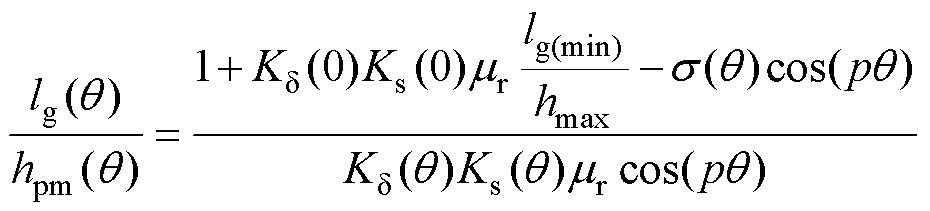 (5)
(5)
根据图3的几何关系,可得
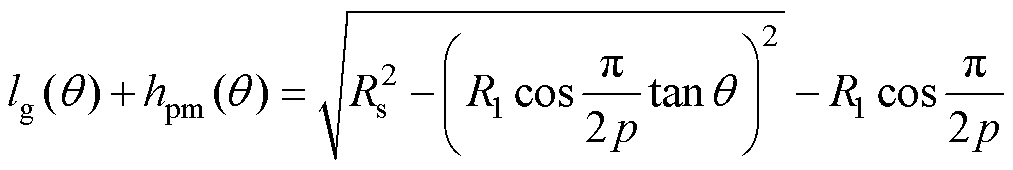 (6)
(6)
式中,Rs为定子内半径;R1为永磁体横截面底边端点到转子圆心的距离。
由式(5)、式(6)可以解得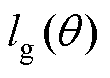 、
、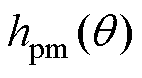 的表达式分别为
的表达式分别为
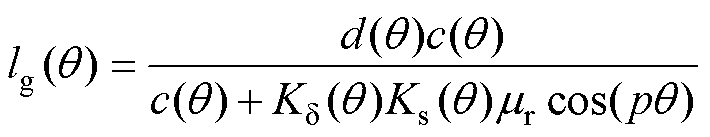 (7)
(7)
 (8)
(8)
其中
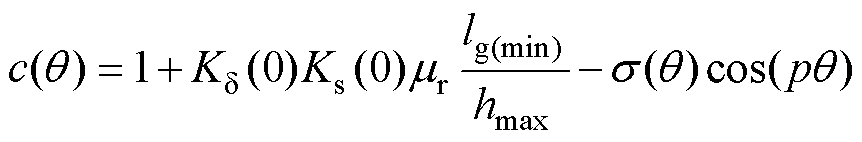 (9)
(9)
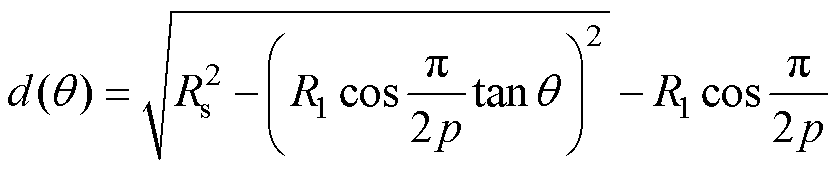 (10)
(10)
永磁体的外表面曲线 可以表示为
可以表示为
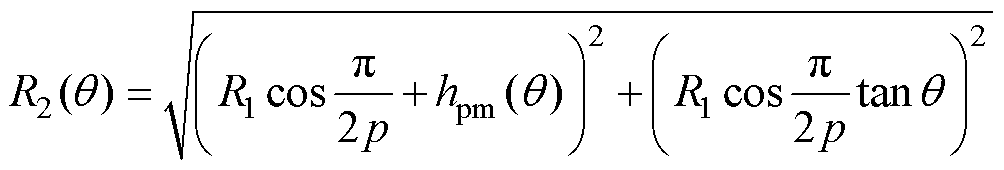 (11)
(11)
由上述推导可知,要得到精确的正弦削极公式,需要得到电机的卡特系数、饱和系数及极间漏磁系数,同时还要考虑电机磁极的边缘效应。
1.2.1 卡特系数
由定子开槽导致的气隙磁通密度畸变不受永磁体形状的影响,因此在推导削极公式时无需考虑定子开槽引起的相对比磁导的变化。此外,齿槽效应使得电机的等效气隙长度较实际的物理气隙长度有所增加,需要用卡特系数加以修正。
表贴式永磁电机的卡特系数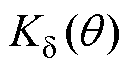 计算式为
计算式为
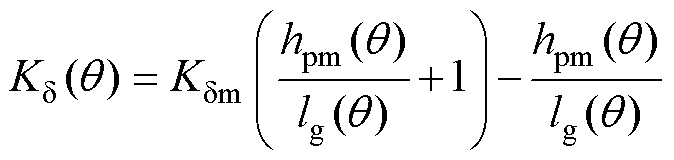 (12)
(12)
其中
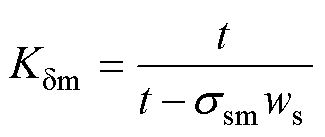 (13)
(13)
式中,ws为电枢槽口宽;t为电枢齿距;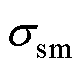 为槽宽缩减因子。
为槽宽缩减因子。
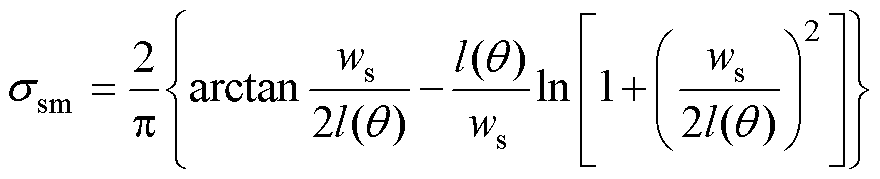 (14)
(14)
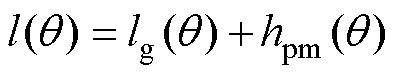 (15)
(15)
由式(6)可知, 不再是一个常数,而是随空间角度变化的量,因此,卡特系数也会随空间角度的变化而变化。
不再是一个常数,而是随空间角度变化的量,因此,卡特系数也会随空间角度的变化而变化。
1.2.2 漏磁及边缘效应的计算
磁极q轴附近的气隙磁通密度分布同时受到极间漏磁和边缘效应的影响。倘若对极间漏磁和边缘效应分别进行考虑则难以得到对应的削极公式。因此,需要研究将电机的极间漏磁和边缘效应的影响统一考虑的等效方法。
正弦削极表贴式永磁同步电机磁力线分布如图4所示。由图4发现,磁极的边缘效应和极间漏磁使得从d轴到q轴磁力线的方向逐渐偏移了永磁体的充磁方向。因此,空载时磁通的等效路径可分解为漏磁通路径和主磁通路径,对极间漏磁系数公式进行修正,得到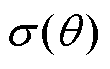 为
为
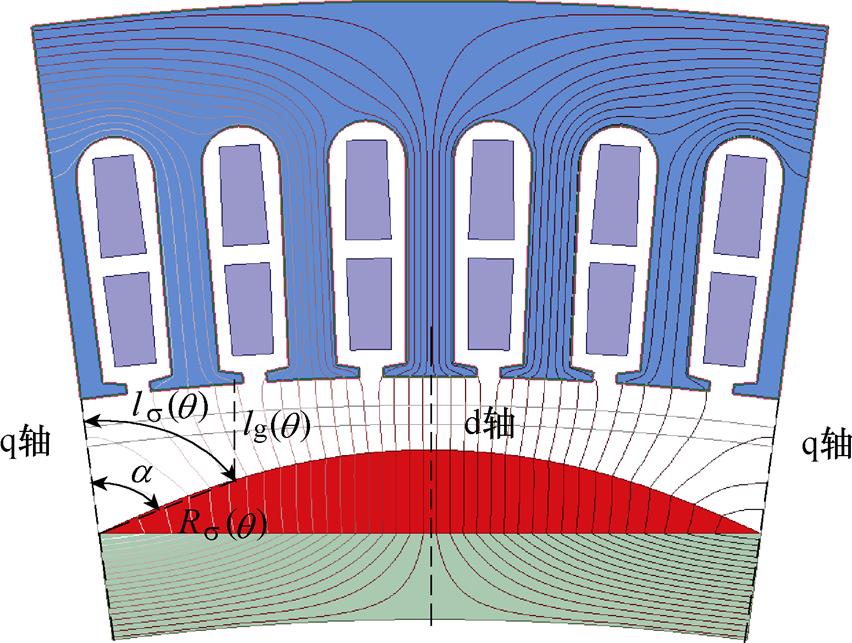
图4 正弦削极表贴式永磁同步电机磁力线分布
Fig.4 Flux line of surface-mounted permanent magnet synchronous motor with sinusoidal pole shape
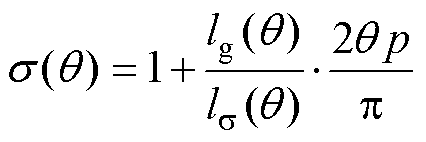 (16)
(16)
值得注意的是,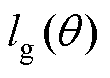 由式(7)所得。求解
由式(7)所得。求解 时,先令
时,先令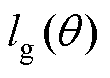 中的
中的 =1,
=1,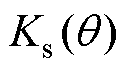 =1。
=1。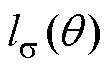 为等效漏磁路径长度,表达式为
为等效漏磁路径长度,表达式为
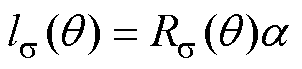 (17)
(17)
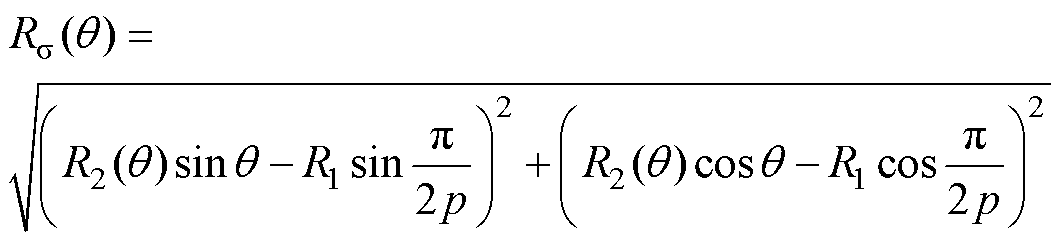 (18)
(18)
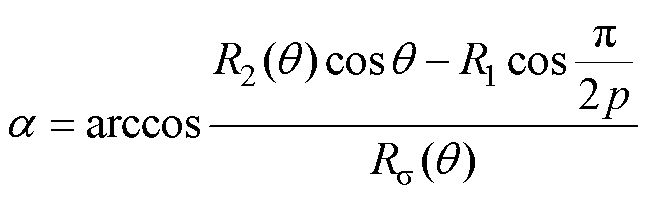 (19)
(19)
式中,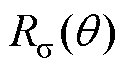 为漏磁路等效圆弧曲线的半径;
为漏磁路等效圆弧曲线的半径;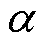 为漏磁路等效圆弧曲线对应的圆心角。
为漏磁路等效圆弧曲线对应的圆心角。
1.2.3 饱和系数的计算
对于饱和系数的计算,可以运用分布磁路法的思想,表贴式永磁电机磁路分布示意图如图5所示,可将电机沿径向和周向进行分区,在径向可将电机分为五个区:气隙区(Ⅰ)、定子齿部区(Ⅱ)、定子轭部区(Ⅲ)、永磁磁极区(Ⅳ)、转子轭部区(Ⅴ)。在磁路的周向上,采用图5所示的空间机械角度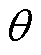 作为位置标识。
作为位置标识。
由图5可知,电机磁路满足
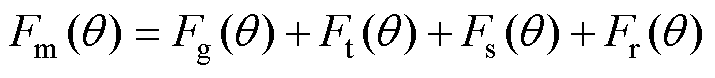 (20)
(20)
式中,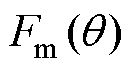 为区域Ⅳ产生的磁动势;
为区域Ⅳ产生的磁动势;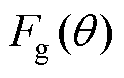 为区域Ⅰ的气隙磁压降;
为区域Ⅰ的气隙磁压降;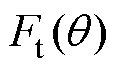 为区域Ⅱ的定子齿部磁压降;
为区域Ⅱ的定子齿部磁压降;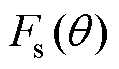 为区域Ⅲ的定子轭部磁压降;
为区域Ⅲ的定子轭部磁压降;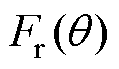 为区域Ⅴ的转子轭部磁压降。
为区域Ⅴ的转子轭部磁压降。
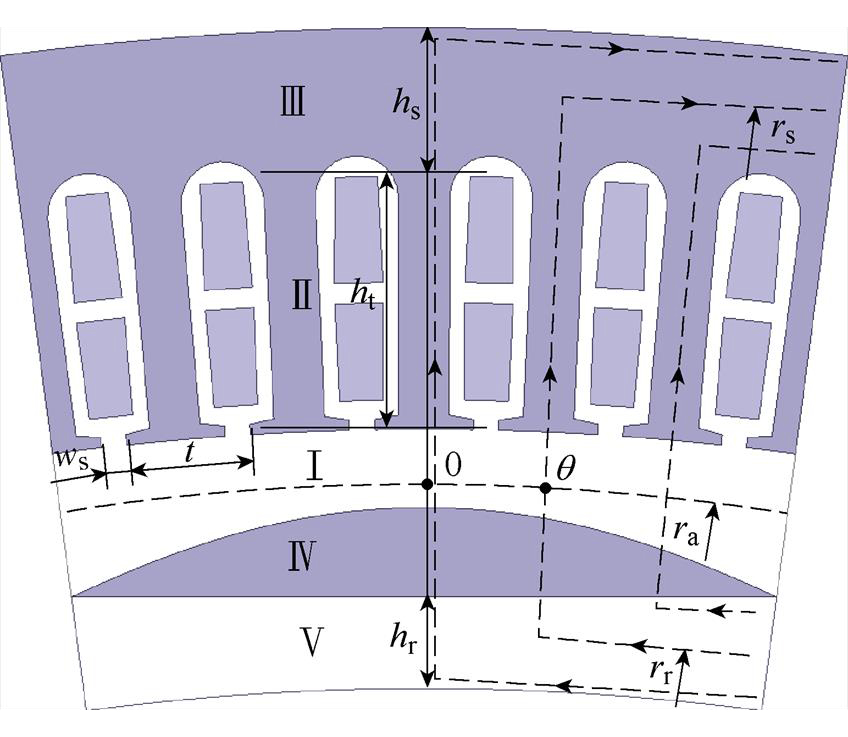
图5 表贴式永磁电机磁路分布示意图
Fig.5 Diagram of magnetic circuit distribution of surface-mounted permanent magnet motor
要求电机中各部分的磁压降,首先需要计算出各部分的磁通密度,根据磁通连续性定理,在空间角度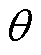 处,定子齿部的磁通密度计算公式为
处,定子齿部的磁通密度计算公式为
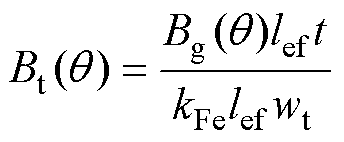 (21)
(21)
式中,kFe为定子铁心叠压系数;lef为定子铁心轴向长度;wt为定子齿宽;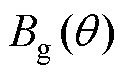 可由式(3)求得,求解
可由式(3)求得,求解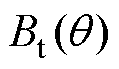 时,先令
时,先令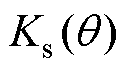 =1。
=1。
在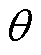 处的定子铁心轭部截面上的周向磁通,与气隙中线半径上的0到
处的定子铁心轭部截面上的周向磁通,与气隙中线半径上的0到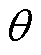 的总径向磁通相等,根据此原则可计算得到
的总径向磁通相等,根据此原则可计算得到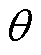 处定子轭部磁通密度
处定子轭部磁通密度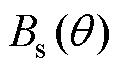 的表达式为
的表达式为
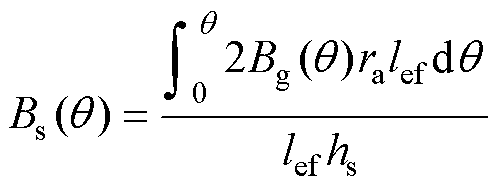 (22)
(22)
式中,ra为气隙中线半径;hs为定子磁轭厚度。转子轭部磁通密度的计算需要考虑极间漏磁的影响,可以表示为
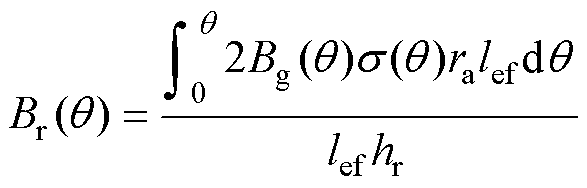 (23)
(23)
式中,hr为转子轭部厚度。
根据计算所得各部分的磁通密度,运用一维线性差值函数interp1得到各自的磁场强度为
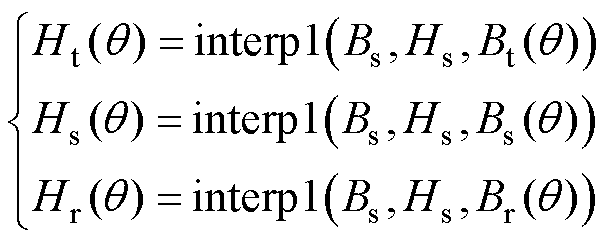 (24)
(24)
式中, 、
、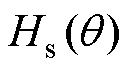 及
及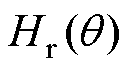 分别为定子齿部、定子轭部及转子轭部磁场强度;函数interp1(Bs, Hs,
分别为定子齿部、定子轭部及转子轭部磁场强度;函数interp1(Bs, Hs, 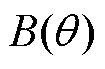 )使用查表法进行线性插值返回一维函数在特定查询点的插入值;Bs为磁通密度向量;Hs为对应磁通密度下的磁场强度;
)使用查表法进行线性插值返回一维函数在特定查询点的插入值;Bs为磁通密度向量;Hs为对应磁通密度下的磁场强度;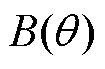 为待查询磁通密度,该函数返回在磁通密度为
为待查询磁通密度,该函数返回在磁通密度为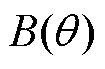 时的磁场强度
时的磁场强度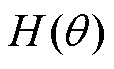 。
。
由此可以得到各部分的磁压降为
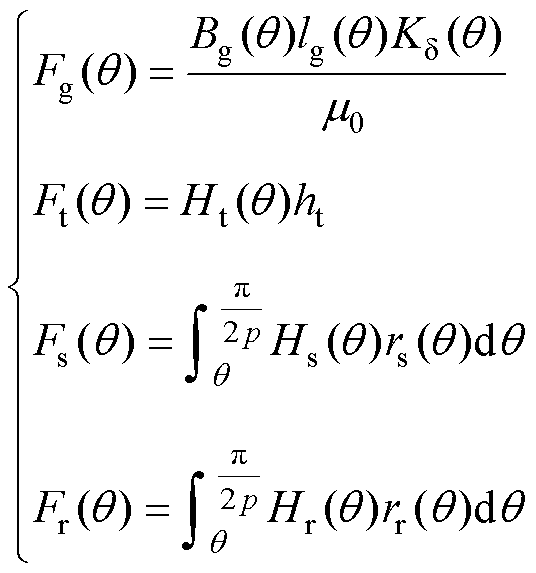 (25)
(25)
式中,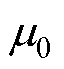 为真空磁导率;ht为齿高;
为真空磁导率;ht为齿高;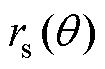 为磁路曲线在定子轭部时的半径;
为磁路曲线在定子轭部时的半径;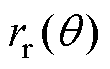 为磁路曲线在转子轭部时的曲线。
为磁路曲线在转子轭部时的曲线。
由此可以得到电机的饱和系数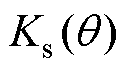 为
为
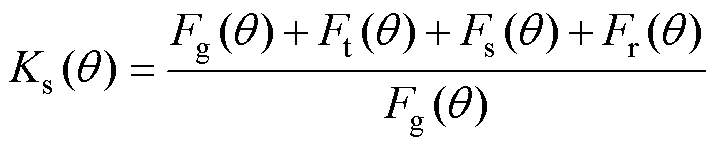 (26)
(26)
将计算的各系数代入式(8)中,可以计算出永磁体厚度随空间角度的变化;代入式(11)中则可以得到永磁磁极外表面曲线,以便于在有限元中建立磁极的几何模型。最终得到的修正正弦磁极如图6所示,可以看出,修正后的正弦磁极较简化模型得到的正弦磁极更加饱满,永磁体用量更高。

图6 正弦削极修正模型与简化模型对比
Fig.6 Comparison between modified sinusoidal pole and simplified sinusoidal pole
为验证正弦削极修正模型的准确性,建立了12对极144槽表贴式永磁电机有限元模型。与传统电机不同,目标电机为水下集成电机,定转子气隙中间需要有水流过,因此气隙较大,为7.7 mm,但这不影响对正弦削极修正模型准确性的验证。具体参数见表1。
表1 电机设计主要特征参数
Tab.1 Main machine design specification and parameters

参 数数 值 极数24 定子槽数144 额定转速/(r/min)630 额定电流峰值/A105 每相串联匝数96 轴向长度/mm94 定子外径/mm620 定子内径/mm561 齿宽/mm5 槽宽/mm2.5 最小气隙长度/mm7.7 永磁体剩磁/T1.09 相对磁导率1.05 永磁体最大厚度/mm8.8
正弦削极修正永磁电机模型有限元网格剖分如图7所示。由于所设计电机气隙较大,因此加密气隙部分网格以实现更高的仿真精度。
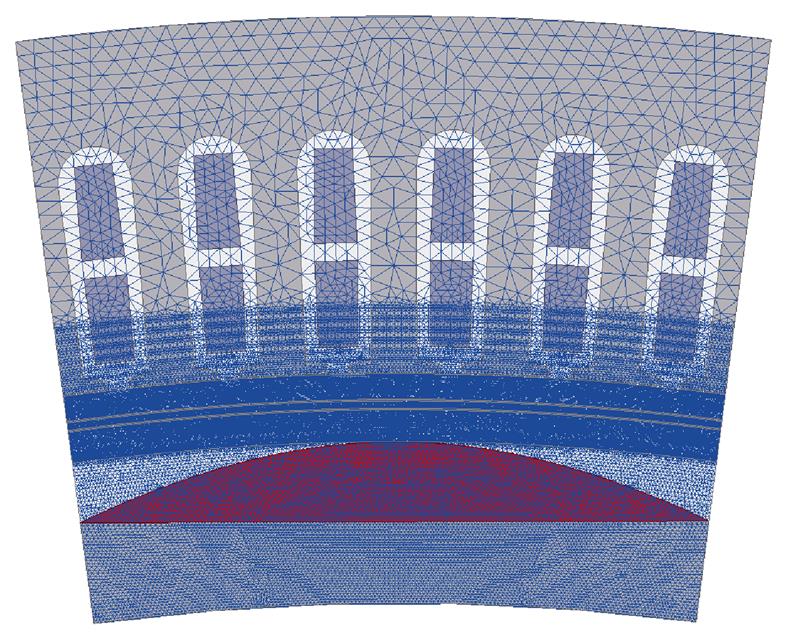
图7 正弦削极修正模型有限元剖分
Fig.7 Finite element mesh plot of modified sinusoidal pole
空载状态下,正弦削极修正模型的有限元磁通密度分布云图如图8所示。
电机空载相反电动势的解析表达式为
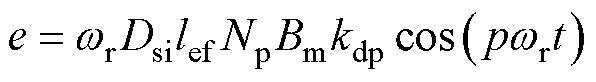 (27)
(27)
式中,Np为每相串联匝数;Dsi为定子内径;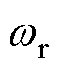 为转子角速度;kdp为绕组系数。由式(3)和式(27)可以分别得到气隙磁通密度和反电动势的解析解。与有限元结果对比分布如图9和图10所示。由图9和图10中解析解与有限元解的对比可以看出,无论是气隙磁通密度还是空载相反电动势,解析解的波形与有限元解一致性较高,两者在气隙磁通密度基波幅值和反电动势基波幅值上分别相差0.24 %和0.49 %,证明了解析模型的准确性。
为转子角速度;kdp为绕组系数。由式(3)和式(27)可以分别得到气隙磁通密度和反电动势的解析解。与有限元结果对比分布如图9和图10所示。由图9和图10中解析解与有限元解的对比可以看出,无论是气隙磁通密度还是空载相反电动势,解析解的波形与有限元解一致性较高,两者在气隙磁通密度基波幅值和反电动势基波幅值上分别相差0.24 %和0.49 %,证明了解析模型的准确性。
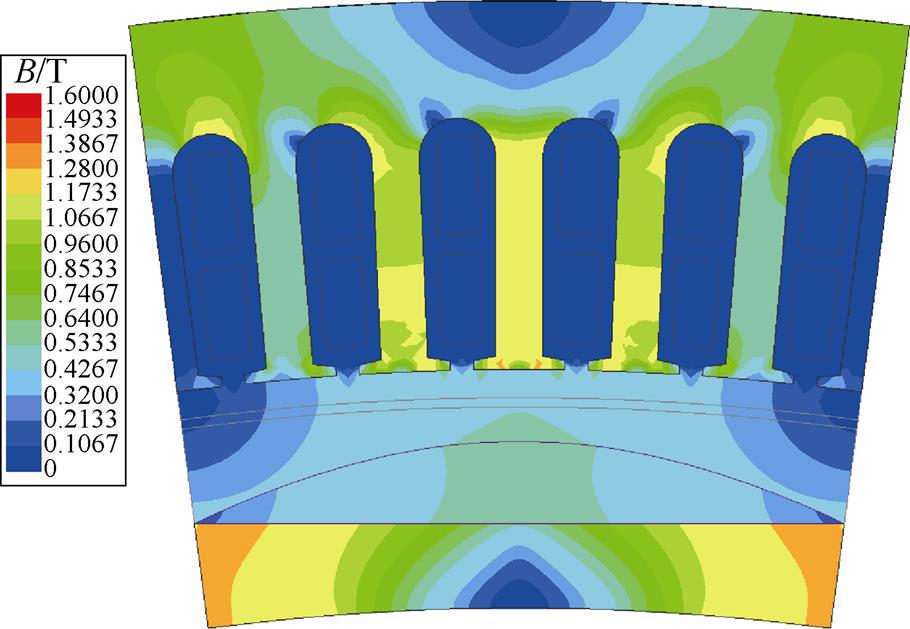
图8 正弦削极修正模型空载磁通密度分布云图
Fig.8 Magnetic density cloud map of modified sinusoidal pole under no-load condition
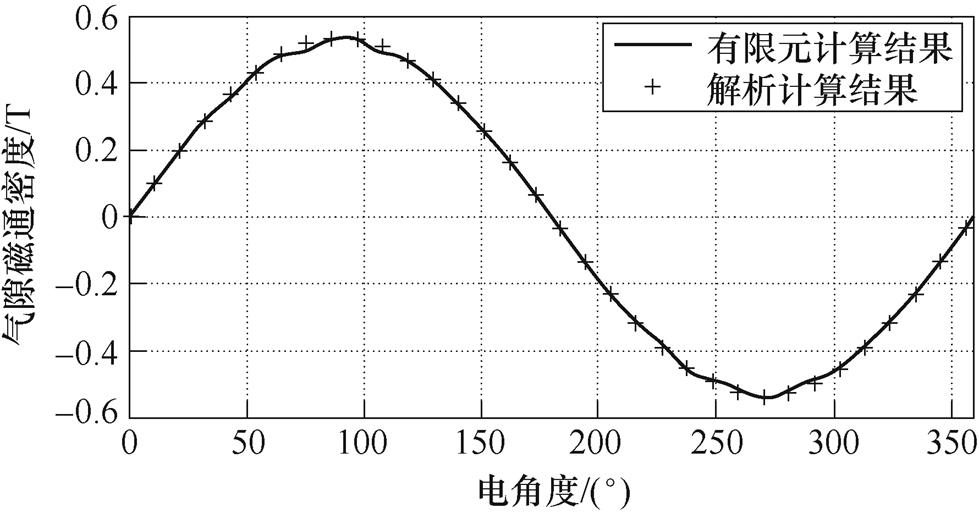
图9 气隙磁通密度波形的有限元与解析解对比
Fig.9 Comparison of air gap magnetic flux density waveform between finite element and analytical solutions
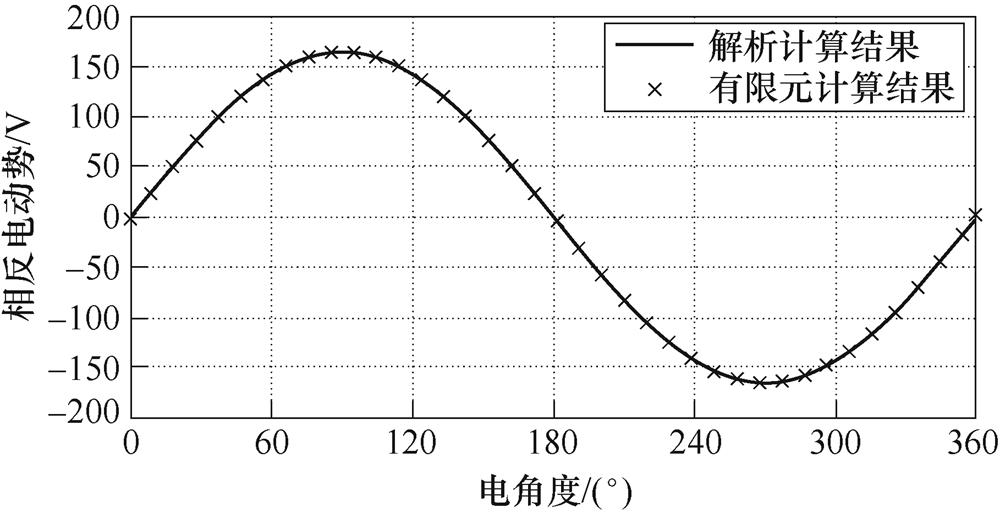
图10 相反电动势波形的有限元与解析解对比
Fig.10 Comparison between finite element and analytical solutions of phase induced electromotive force
为了验证正弦削极修正模型在减小气隙磁通密度谐波方面的优越性,按照表1中的参数建立了简化正弦削极、修正正弦削极和偏心削极三种不同磁极的电机仿真模型,并对比了相关电磁性能。其中偏心削极的最优参数是通过有限元遍历寻优得到,寻优方法如图11所示,在确定了最小气隙长度和定子结构后,通过改变永磁体极弧系数和偏心距来寻找使气隙磁通密度THD最小的点,最终得到当偏心距为200 mm、极弧系数为0.87时,气隙磁通密度的谐波含量最小。最终得到的三种磁极结构如图12所示。
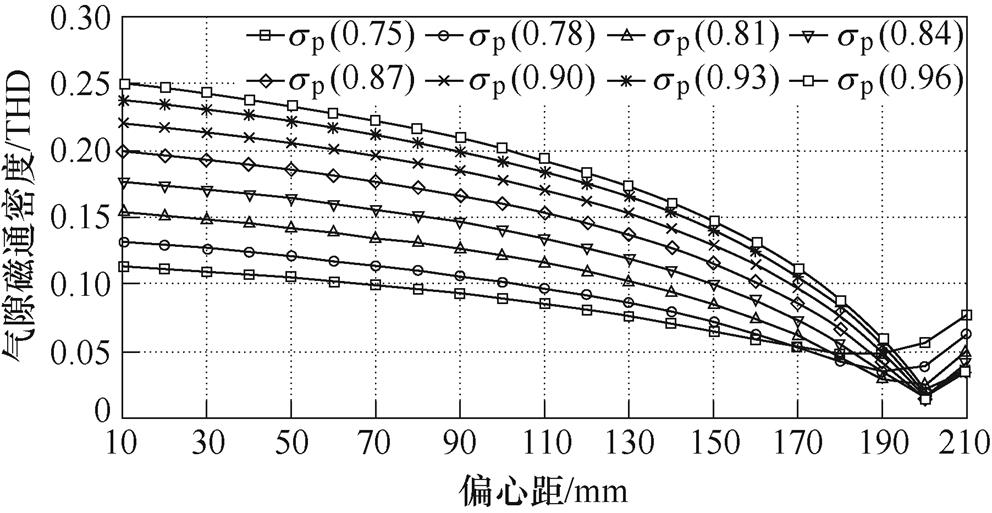
图11 径向气隙磁通密度THD随偏心距和极弧系数变化
Fig.11 Variation of radial air gap magnetic flux density THD with eccentricity and pole-arc coefficient
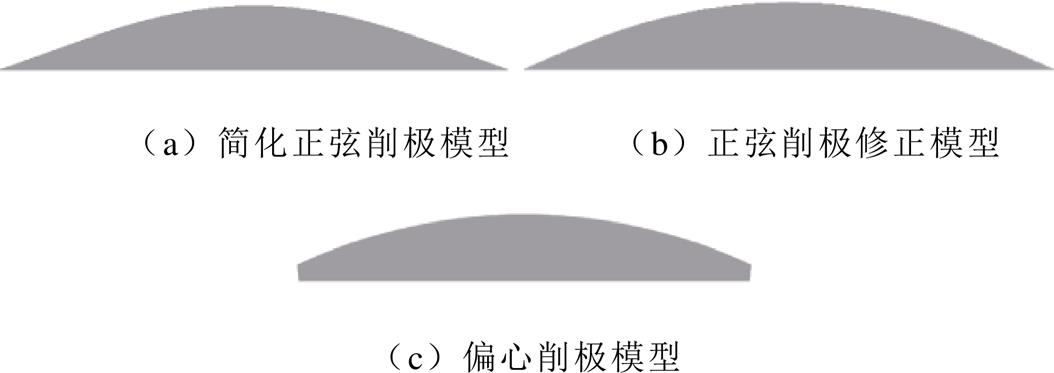
图12 不同磁极结构几何形状示意图
Fig.12 Diagram of geometric shape of different magnetic pole forms
图13a、图13b分别为三种磁极电机的空载气隙磁通密度波形和谐波分布对比,由图13a的波形对比可以看出,虽然气隙磁通密度最大值相差不大,修正正弦削极电机和偏心削极电机的气隙磁通密度波形较简化正弦削极电机更加饱满。由图13b可知,修正正弦削极电机的气隙磁通密度基波幅值较偏心削极低0.913 %,较简化正弦削极高2.82 %,但是修正正弦削极电机气隙磁通密度THD最小,分别较简化正弦削极电机和偏心削极电机低41.25 %和23.37 %,说明修正正弦削极电机的气隙磁通密度正弦度要优于另外两种削极电机。已知径向电磁力谐波是电机的重要噪声源,图14为不同磁极电机空载径向电磁力密度波形,图15为不同磁极电机的各阶次空载径向电磁力密度幅值的对比。总体上看,空载径向电磁力密度谐波均为偶数次,这是由于转子磁场为对称磁场,气隙磁通密度谐波均为奇数次(见图13b)。根据麦克斯韦应力张量法,径向电磁力由气隙磁通密度相互作用产生,因此在奇数次磁通密度谐波的相互作用下,产生的径向电磁力密度谐波均为偶数次。由图15可以看出,三种磁极电机的主力波(2次波)和开槽引起的10次、12次谐波幅值相近,而对于其他各阶次谐波而言,修正正弦削极电机均为最低或与最低值十分接近,其中在4次谐波处,修正正弦削极电机远低于另外两种电机,因此修正正弦削极电机的空间径向电磁力THD也是最低的,比简化正弦电机低29.82 %,比偏心削极电机低19.24 %。
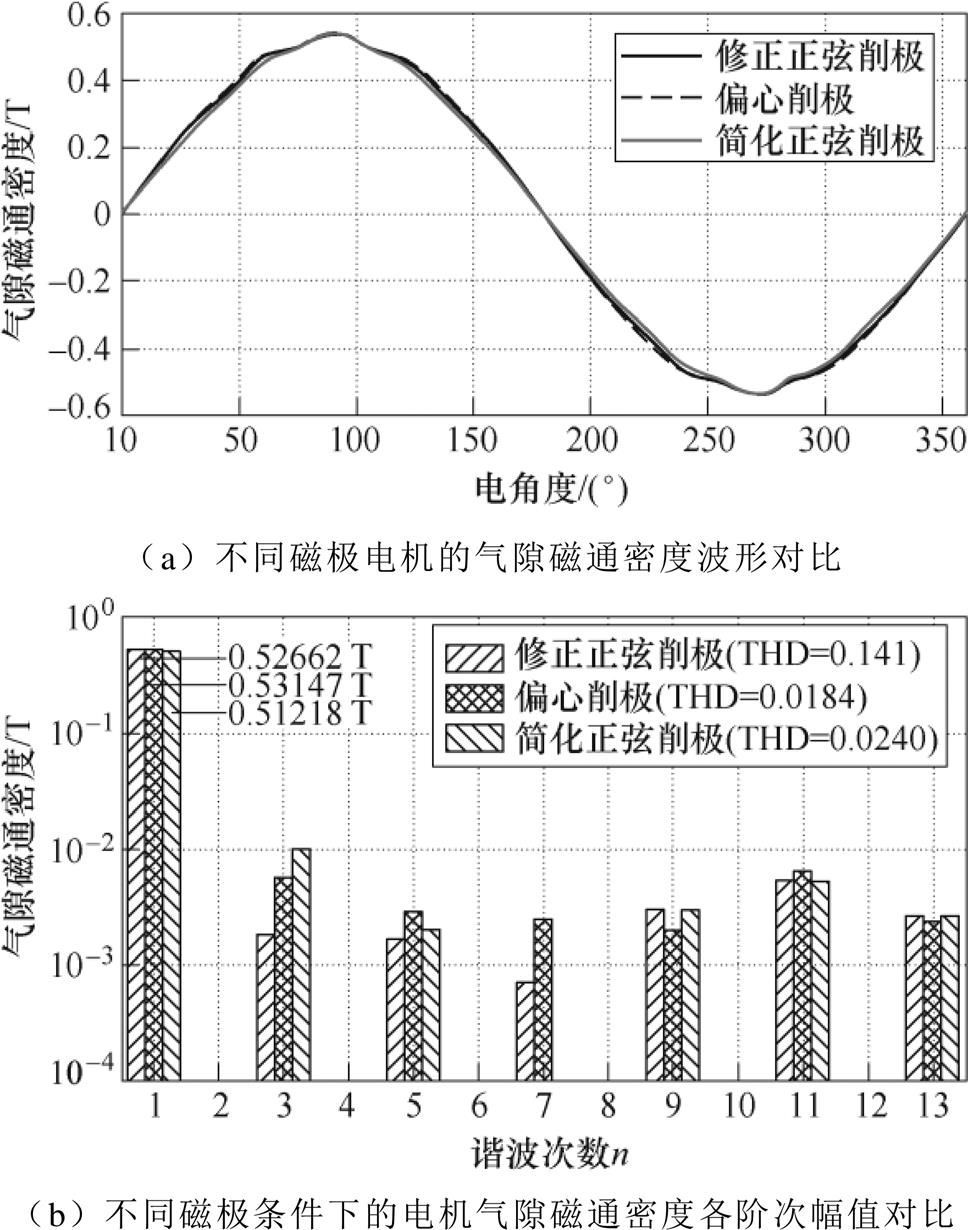
图13 不同磁极电机的气隙磁通密度波形及各阶次幅值对比
Fig.13 Air gap magnetic flux density waveforms and amplitude comparison of motors with different poles
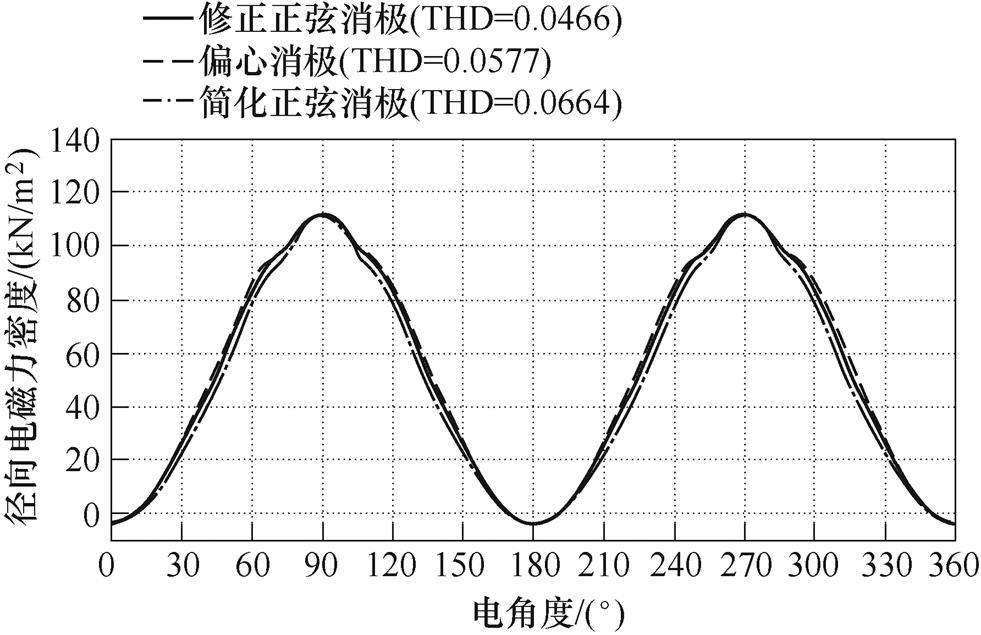
图14 不同磁极电机空载径向电磁力密度波形
Fig.14 Radial electromagnetic force density waves of motors with different poles under no-load condition
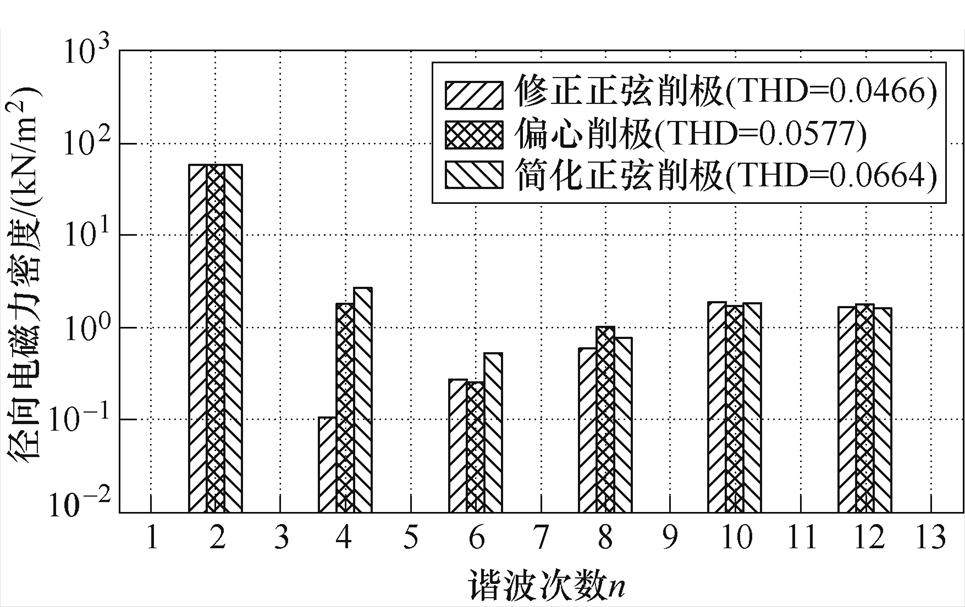
图15 不同磁极电机的空载径向电磁力密度各阶次幅值对比
Fig.15 Amplitude comparison of radial electromagnetic force density of motors with different poles under no-load condition
表2中依次展示了三种磁极电机的平均转矩、峰峰值转矩脉动、转矩波动幅值、齿槽转矩、平均气隙长度以及平均永磁体厚度的对比。从对比中可以看出,简化正弦削极电机的平均转矩最低,较修正正弦削极电机低2.72 %,但其转矩脉动较修正正弦削极电机高4.71 %;修正正弦削极电机的平均转矩较偏心削极电机低0.96 %,但转矩脉动较偏心削极电机低35.61 %;偏心削极电机的平均转矩最大,但是转矩脉动也较修正正弦削极电机和简化正弦削极电机更大。
表2 平均气隙长度、磁极厚度、转矩分量
Tab.2 Average air gap length, PM height, torque components
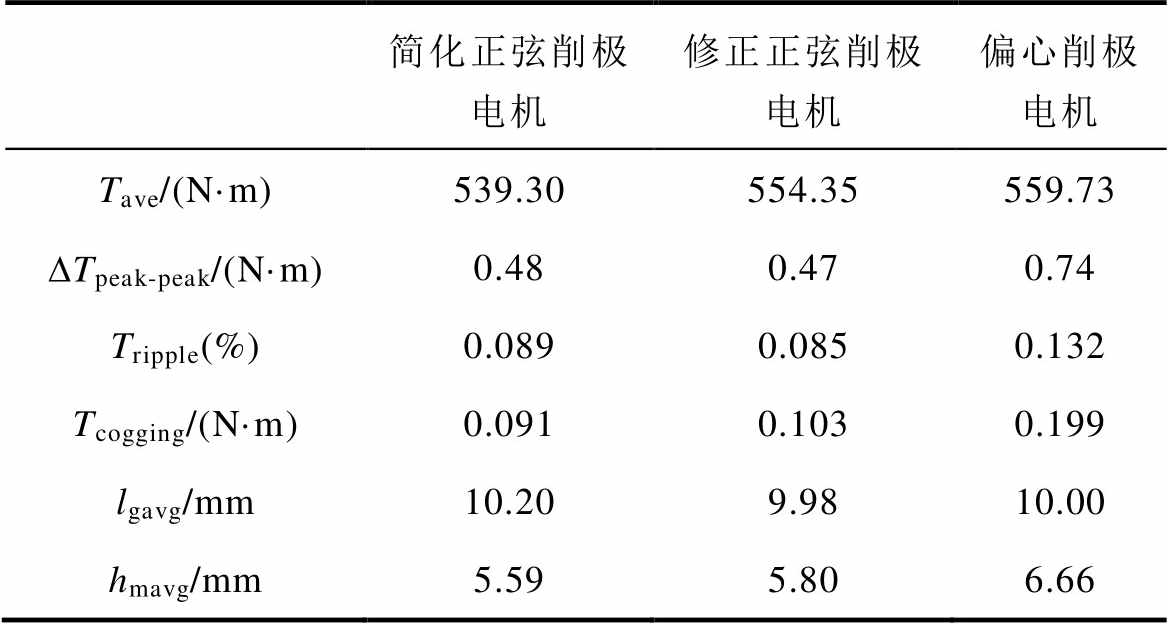
简化正弦削极电机修正正弦削极电机偏心削极电机 Tave/(N·m)539.30554.35559.73 DTpeak-peak/(N·m)0.480.470.74 Tripple(%)0.0890.0850.132 Tcogging/(N·m)0.0910.1030.199 lgavg/mm10.209.9810.00 hmavg/mm5.595.806.66
为验证正弦削极修正模型的准确性,按照设计参数,制造了一台修正正弦削极电机,如图16所示。对比中反电动势的解析解由式(27)计算得到,转矩的计算公式为
 (28)
(28)
式中,m为电机相数;Ipeak为电机相电流基波幅值。

图16 50 kW样机
Fig.16 50 kW prototype
图17所示为额定转速下样机空载相反电动势测试值与计算值波形的对比,可以看出,计算所得样机相反电动势的波形与测试值吻合度较高,基波幅值相差0.92 %,证明了解析模型的准确性;图18所示为额定工况下样机线电压测试值和有限元波形的对比,从图18中可以看到,有限元仿真的计算值于实验测试值吻合情况较好,对两者分别进行傅里叶分解并计算两者的THD可知,额定转速下有限元仿真得到的线电压,其THD为2.56 %,而同工况下样机实验测试所得线电压的THD为2.71 %,比有限元仿真结果略高。这是由于在实际的测试中,变频器提供的电流中存在非理想因素,含有一定的谐波分量,此外,在电机生产制造过程中会存在一定的加工误差,此误差在合理的范围内。图19所示为不同工况下解析计算与实验测试所得输出转矩的对比。图中d 表示为转矩误差,d <0表示解析计算值小于实验测试值,d>0表示解析计算值大于实验测试值。从图19中可看出,在各个工况下,实验测试得到的结果与解析计算值所得结果基本吻合。在额定工况下,解析计算值与测试值的偏差为1.13 %,说明了修正解析模型和相应有限元模型计算结果的准确性。
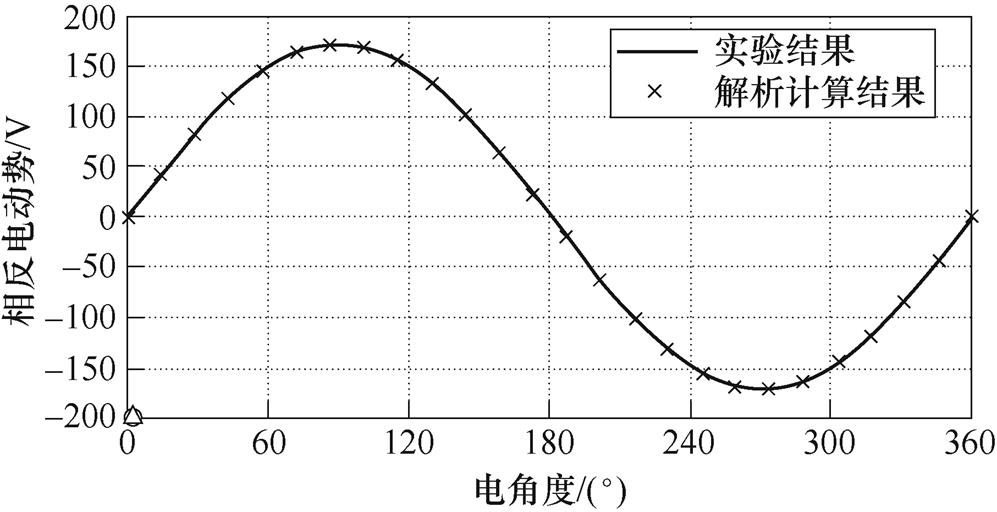
图17 额定转速下样机空载相反电动势测试值与计算值波形对比
Fig.17 Back electromotive force comparison of test value and calculated value of prototype at rated speed under no-load condition
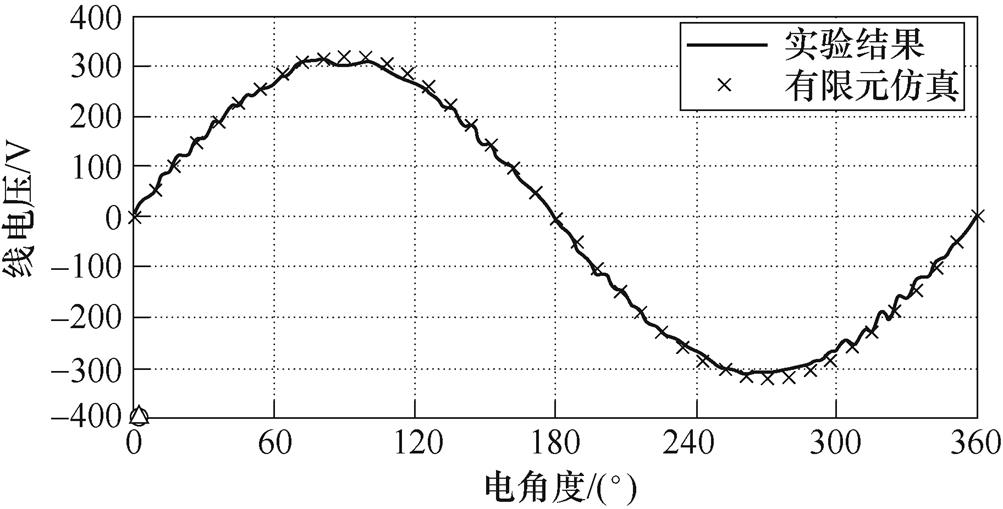
图18 额定工况下样机线电压测试值和有限元波形对比
Fig.18 Prototype line voltage comparison of test value and finite element value under rated working condition

图19 通入不同相电流时样机转矩解析值与测试值对比
Fig.19 Prototype torque comparison of analysis value and test value under different phase currents
为优化气隙磁场,使气隙磁通密度接近正弦,从而降低电机的径向电磁力谐波和峰峰值转矩脉动,本文以气隙磁通密度函数和永磁体磁化方向厚度函数为理论基础,运用卡特系数考虑定子开槽对气隙长度产生的影响,运用磁路等效原理考虑电机的极间漏磁和边缘效应,以分布磁路法思想计算电机的磁路饱和系数,推导出电机的气隙磁通密度计算公式和修正正弦削极公式,而后建立有限元模型验证了解析模型的准确性,并与简化正弦削极电机、偏心削极电机进行仿真对比,结果表明修正正弦削极电机所得气隙磁通密度的基波幅值和平均转矩明显高于简化正弦削极电机,与偏心削极电机十分接近,而气隙磁通密度THD、径向电磁力谐波以及转矩脉动则显著优于简化正弦削极电机和偏心削极电机,且本文提出的修正正弦削极设计方法相比于需要扫描寻优的偏心削极设计方法时间成本大幅减小,证明了修正正弦削极电机在电磁性能以及设计方法上的优越性,最后通过实验进一步验证了修正解析模型和有限元模型的准确性。
参考文献
[1] 马伟明. 关于电工学科前沿技术发展的若干思考[J]. 电工技术学报, 2021, 36(22): 4627-4636.
Ma Weiming. Thoughts on the development of frontier technology in electrical engineering[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4627-4636.
[2] 陈浈斐, 邢宁, 马宏忠, 等. 分数槽永磁电机永磁体谐波涡流损耗建模与分析[J]. 电工技术学报, 2022, 37(14): 3514-3527.
Chen Zhenfei, Xing Ning, Ma Hongzhong, et al. Analytical modeling and analysis of magnet harmonic loss in fractional slot permanent-magnet machines[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3514-3527.
[3] Xu Gaohong, Liu Guohai, Zhao Wenxiang, et al. Principle of torque-angle approaching in a hybrid rotor permanent-magnet motor[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 2580-2591.
[4] 邱子桢, 陈勇, 成海全, 等. 基于周期谐波扩频调制的永磁同步电机高频边带声振抑制[J]. 电工技术学报, 2022, 37(10): 2459-2468.
Qiu Zizhen, Chen Yong, Cheng Haiquan, et al. periodic harmonic spread spectrum modulation for high-frequency sideband vibro-acoustic suppression in permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(10): 2459-2468.
[5] 赵牧天, 葛琼璇, 朱进权, 等. 中速磁悬浮列车分段式长定子永磁直线同步电机牵引控制策略[J]. 电工技术学报, 2022, 37(10): 2491-2502.
Zhao Mutian, Ge Qiongxuan, Zhu Jinquan, et al. Traction control strategy of segmented long stator permanent magnet linear synchronous motor for medium-speed maglev train[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2491-2502.
[6] 朱洒, 曾峰, 陆剑波, 等. 考虑PWM谐波损耗的车用扁线内嵌式永磁同步电机效率图简化工程计算[J]. 电工技术学报, 2022, 37(22): 5687-5703.
Zhu Sa, Zeng Feng, Lu Jianbo, et al. simplified engineering calculation of efficiency map of interior permanent magnet synchronous machines with hairpin windings considering PWM-induced harmonic losses[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5687-5703.
[7] 刘计龙, 肖飞, 沈洋, 等. 永磁同步电机无位置传感器控制技术研究综述[J]. 电工技术学报, 2017, 32(16): 76-88.
Liu Jilong, Xiao Fei, Shen Yang, et al. Position- sensorless control technology of permanent-magnet synchronous motor-a review[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 76-88.
[8] 张丹, 姜建国. 高速磁悬浮永磁电机三电平无速度传感器控制[J]. 电工技术学报, 2022, 37(22): 5808- 5816.
Zhang Dan, Jiang Jianguo. Three-level sensorless control of high speed maglev permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5808-5816.
[9] Kim H, Han Yongsu, Lee K, et al. A sinusoidal current control strategy based on harmonic voltage injection for harmonic loss reduction of PMSMs with non-sinusoidal back-EMF[J]. IEEE Transactions on Industry Applications, 2020, 56(6): 7032-7043.
[10] Yang Y P, Peng M T. A surface-mounted permanent- magnet motor with sinusoidal pulsewidth-modulation- shaped magnets[J]. IEEE Transactions on Magnetics, 2019, 55(1): 1-8.
[11] 王凯, 孙海阳, 张露锋, 等. 永磁同步电机转子磁极优化技术综述[J]. 中国电机工程学报, 2017, 37(24): 7304-7317, 7445.
Wang Kai, Sun Haiyang, Zhang Lufeng, et al. An overview of rotor pole optimization techniques for permanent magnet synchronous machines[J]. Proceedings of the CSEE, 2017, 37(24): 7304-7317, 7445.
[12] Zhou Min, Zhang Xinxing, Zhao Wenxiang, et al. Influence of magnet shape on the cogging torque of a surface-mounted permanent magnet motor[J]. Chinese Journal of Electrical Engineering, 2019, 5(4): 40- 50.
[13] Liu Guohai, Zeng Yu, Zhao Wenxiang, et al. Permanent magnet shape using analytical feedback function for torque improvement[J]. IEEE Transa- ctions on Industrial Electronics, 2018, 65(6): 4619- 4630.
[14] Simón-Sempere V, Burgos-Payán M, Cerquides- Bueno J R. Cogging torque cancellation by magnet shaping in surface-mounted permanent-magnet motors[J]. IEEE Transactions on Magnetics, 2017, 53(7): 1-7.
[15] Simón-Sempere V, Simón-Gómez A, Burgos-Payán M, et al. Optimisation of magnet shape for cogging torque reduction in axial-flux permanent-magnet motors[J]. IEEE Transactions on Energy Conversion, 2021, 36(4): 2825-2838.
[16] Qi Ji, Zhu Z Q, Yan Luocheng, et al. Suppression of torque ripple for consequent pole PM machine by asymmetric pole shaping method[J]. IEEE Transa- ctions on Industry Applications, 2022, 58(3): 3545- 3557.
[17] Wu Lijian, Zhu Ziqiang. Analytical modeling of surface-mounted PM machines accounting for magnet shaping and varied magnet property distribution[J]. IEEE Transactions on Magnetics, 2014, 50(7): 1-11.
[18] Zhou Yu, Li Huaishu, Meng Guangwei, et al. Analy- tical calculation of magnetic field and cogging torque in surface-mounted permanent-magnet machines accounting for any eccentric rotor shape[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3438-3447.
[19] Zhou Yu, Li Huaishu, Ren Ningning, et al. Analytical calculation and optimization of magnetic field in spoke-type permanent-magnet machines accounting for eccentric pole-arc shape[J]. IEEE Transactions on Magnetics, 2017, 53(9): 1-7.
[20] 胡鹏飞, 王东, 靳栓宝, 等. 偏心磁极永磁电机气隙磁场正弦优化模型[J]. 电工技术学报, 2019, 34(18): 3759-3768.
Hu Pengfei, Wang Dong, Jin Shuanbao, et al. Sinusoidal optimization model for air gap magnetic field of eccentric magnetic pole permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3759-3768.
[21] Ruangsinchaiwanich S, Zhu Z Q, Howe D. Influence of magnet shape on cogging torque and back-EMF waveform in permanent magnet machines[C]//2005 International Conference on Electrical Machines and Systems, Nanjing, China, 2006: 284-289.
[22] Li Yong, Zou Jibin, Lu Yongping. Optimum design of magnet shape in permanent-magnet synchronous motors[J]. IEEE Transactions on Magnetics, 2003, 39(6): 3523-3526.
[23] Wang K, Zhu Z Q, Ombach G. Torque enhancement of surface-mounted permanent magnet machine using third-order harmonic[J]. IEEE Transactions on Mag- netics, 2014, 50(3): 104-113.
[24] Wang Kai, Zhu Z Q, Ombach G. Torque improvement of five-phase surface-mounted permanent magnet machine using third-order harmonic[C]//2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 2016: 1.
[25] Chai Feng, Liang Peixin, Pei Yulong, et al. Magnet shape optimization of surface-mounted permanent- magnet motors to reduce harmonic iron losses[J]. IEEE Transactions on Magnetics, 2016, 52(7): 1-4.
[26] 张炳义, 贾宇琪, 李凯, 等. 一种表贴式永磁电机磁极结构优化研究[J]. 电机与控制学报, 2014, 18(5): 43-48.
Zhang Bingyi, Jia Yuqi, Li Kai, et al. Study on magnetic pole structure of surface mounted PMSM[J]. Electric Machines and Control, 2014, 18(5): 43-48.
[27] 胡鹏飞, 王东, 靳栓宝, 等. 弓形磁极永磁电机谐波削极技术的优化研究[J]. 中国电机工程学报, 2020, 40(18): 5987-5997.
Hu Pengfei, Wang Dong, Jin Shuanbao, et al. Research on the optimization of harmonic pole shaping technologies for arcuate pole permanent magnet motors[J]. Proceedings of the CSEE, 2020, 40(18): 5987-5997.
[28] 杨奕. 永磁体形状对伺服电机性能的影响[J]. 电工技术, 2020(21): 162-164, 167.
Yang Yi. Influence of permanent magnet shape on servo motor performance[J]. Electric Engineering, 2020(21): 162-164, 167.
[29] 王秀和. 永磁电机[M]. 2版. 北京: 中国电力出版社, 2011.
Abstract Electric machines are gradually taking the place of traditional machines powered by fossil fuels in many industries for environmental issues, such as automobile industry and aviation industry. PMSM is usually the prime choice among all motor types because of its merits of high torque density, high power density, and high efficiency. Suppressing the noise and vibration of PMSM has become a key issue in recent years and the technology of pole shaping is one of the effective solutions. Eccentric magnet pole and sinusoidal magnet pole are most commonly used in pole shaping. When designing the eccentric magnet poles, much calculation and parameter sweeping are needed for optimization. The process is rather time-consuming, and the physical mechanism of eccentric pole shaping in making the air gap magnetic flux density sinusoidal needs to be clearer. Simplified sinusoidal pole shaping is to make the shape of magnet poles conform to sine function to make the air gap magnetic flux density sinusoidal. The mechanism is clear, and the designing process is time-saving. However, the influence of stator slot, pole-to-pole leakage, edge effect, and magnetic circuit saturation is not considered in simplified sinusoidal pole shaping. The air gap magnetic flux density needs to be more sinusoidal. Therefore, this paper proposes a modified sinusoidal pole shaping model, which optimizes the motor’s electromagnetic performance in a time-saving way and has a clear theoretical basis. The research object is an arcuate pole permanent magnet motor. Compared with a magnet pole with an arc bottom, an arcuate magnet pole can provide greater power density when the diameter of the rotor and the thickness of the magnet pole are the same. Besides, the model of the arcuate pole is more complex, and the derivation process is applicable to the model of the magnet pole with an arc bottom.
The functions of the air gap length and the thickness of the magnet are deduced. In the functions, the Carter coefficient formula is used to consider the influence of stator slots. Pole-to-pole leakage and edge effect are considered using the proposed leakage coefficient formula. Besides, the distributed magnetic circuit method is used to consider the saturation of the magnetic circuit. Compared with the model built by finite element analysis (FEA), the analytical model is accurate. Also, the fundamental component amplitude of the air gap magnetic flux density and the average torque of the modified sinusoidal pole shaping motor are higher than those of the simplified sinusoidal pole shaping motor and close to those of the eccentric pole shaping motor. Moreover, the total harmonic distortion (THD) of the air gap magnetic flux density of the modified sinusoidal pole shaping is 41.3 % and 23.4 % lower than that of the simplified sinusoidal pole shaping motor and the eccentric pole shaping motor, respectively. The THD of the radial electromagnetic force density of the modified sinusoidal pole shaping is 29.82 % and 19.24 % lower than that of the simplified sinusoidal motor and the eccentric motor, respectively. As a result, the torque ripple of the motor is reduced.
Therefore, the modified sinusoidal pole shaping model can save much time in the designing process and provide better performance in reducing vibration than the eccentric pole shaping model and simplified pole shaping model.
keywords:Permanent magnet motor, analytical model of modified sinusoidal pole shaping, parallel magnetization, distributed magnetic circuit method
国家自然科学基金资助项目(52207048, 51825703, 51977215, 51875573)。
收稿日期 2022-09-30
改稿日期 2022-12-27
DOI: 10.19595/j.cnki.1000-6753.tces.221853
中图分类号:TM341
赵浩然 男,1998年生,博士研究生,研究方向为集成化永磁推进电机设计与控制。E-mail: haoranzhaoh@163.com
胡鹏飞 男,1990年生,助理研究员,研究方向为集成化永磁推进电机设计。E-mail: 785141654@qq.com(通信作者)
(编辑 郭丽军)