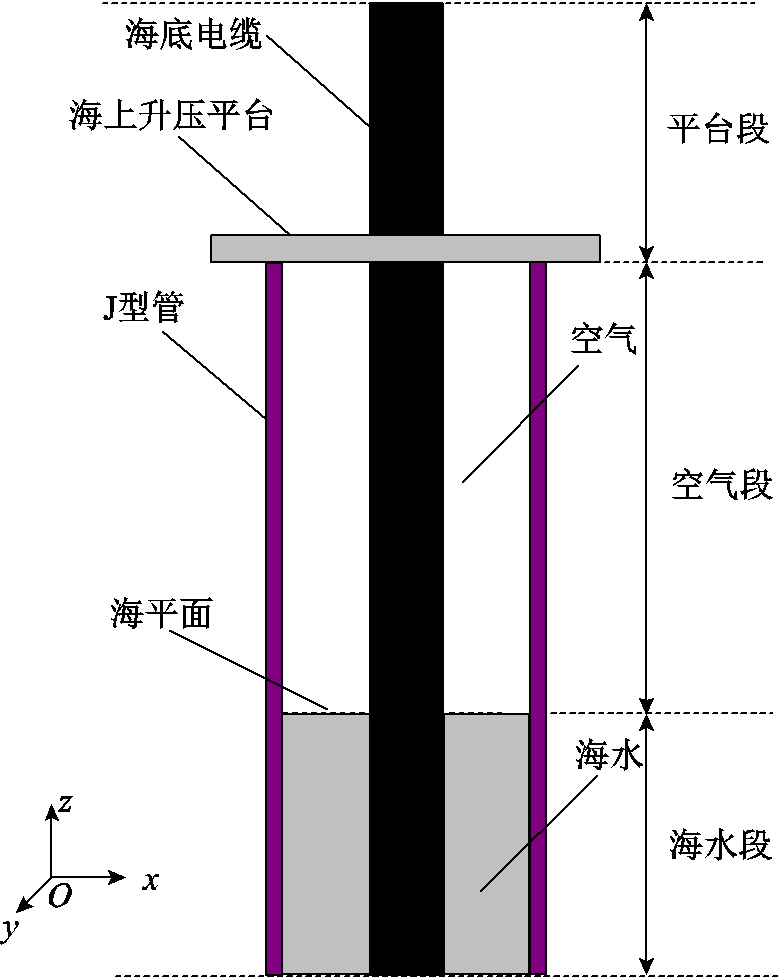
图1 J型管系统结构示意图
Fig.1 Structural diagram of J-tube system
摘要 海上风电场送出线路从升压站穿出首先需经过散热环境较差的J型管段,目前针对该区段海底电缆载流量的计算主要采用数值模拟法,而三维流体仿真计算非常耗时,因此难以推广使用。该文基于基本热分析方法提出了J型管段海底电缆径向-轴向传热解析模型,考虑温度沿轴向分布的差异,实现J型管段海底电缆载流量的快速计算。在计及导体电阻率随温度变化情况下,利用数值仿真软件建立海底电缆J型管系统三维热-流耦合数值模型,并与径向-轴向传热解析模型进行了对比计算。最后基于两种方法分析了J型管外径、太阳辐射强度和环境温度对J型管段海底电缆缆芯最高温度的影响规律。结果表明,J型管段海底电缆缆芯最高温度与太阳辐射强度和环境温度存在明显的线性关系,而J型管外径与海水温度对J型管段海底电缆缆芯最高温度影响较小,且解析法与数值仿真计算结果误差在5%以内。该文所提出针对J型管段海底电缆载流量计算的解析法高效准确,具有较好的工程应用价值。
关键词:海底电缆 J型管 解析法 数值模拟 载流量
近年来海上风电迅速发展,其中海底电缆作为海上风电场与陆地电网的重要连接枢纽,使得海底电缆输电技术有着迫切的研究需求[1-2],而海底电缆载流量的准确计算更是对减少海上风电场建设成本、保证整条线路的可靠高效运行、提升整个风电场的输送容量有着重要的意义[1,3]。
海底电缆的载流量是指在给定敷设方式和相应的环境条件下,能保证海底电缆在其所能承受的最高允许工作温度下稳态运行的载流能力。当缆芯流过电流大于载流量时,会使海底电缆绝缘层温度高于最高允许温度,从而导致海底电缆使用寿命大大缩短;当缆芯流过电流过小时,海底电缆的传输能力得不到充分利用,从而降低线路的经济性[4]。因此准确地评估不同敷设方式下海底电缆的载流量,明确海底电缆送出线路载流量的“瓶颈”,对于保障海上风电场安全稳定运行、最大程度地发挥海上风电经济效益、提高海上风电同其他发电技术的竞争力非常关键。
目前针对海底电缆载流量的评估标准或方法研究成果较少,已有研究大多集中于陆地电缆[5-8],因此海底电缆载流量的计算一般借鉴陆地电缆的建模和计算方法。现阶段电缆载流量的计算主要分为三类:解析法、数值解法和试验测试法。解析法基于IEC 60287标准所制定的等效热阻法,将温差、热流及热阻之间的关系与电路中的电压降、电流和电阻之间的关系相类比[9],将温度分布的“场”问题看作“路”问题进行分析。该方法计算方便快捷,但是在很多实际工程场合应用中还存在一定的局限性[10]。数值解法包括有限差分法、边界元法、有限元法和有限体积法[11-14],通过建立电缆及敷设环境模型,可以准确地模拟实际工况,具有精度高、适应性强等特点,近年来在电缆温度场和载流量分析中得到了越来越广泛的应用。试验测试法通过试验来确定实际的敷设情况,该方法通常成本较高、实施困难,且不具有通用性[15],实际工程中很少采用。
文献[16]分别利用经典热路法、有限元分析法和海底电缆热循环试验对110 kV单芯海底电缆进行载流量理论计算、温度场仿真和载流量试验研究,并比较了三种方法的利弊,初步证实其研究海底电缆载流量的可行性。文献[17]对直埋、隧道内、穿管段和空气中四种典型敷设环境下海底电缆的温度场分布进行了有限元分析和为期一年的长期可靠性试验,得到了四种典型环境下海底电缆系统沿线的温度分布,结果表明海底电缆线路穿管段和空气段缆芯的温度最高,是实际工程应用中的薄弱环节。文献[18]建立三芯铠装电缆的电磁-热耦合仿真模型,研究了缆芯电流在低频输电方式下的不均匀分布特性,并分析了应用IEC标准计算护套感应电压、损耗因子及载流量的误差。文献[19]利用有限元分析软件建立了海底电缆本体及其敷设环境的三维电-热-流耦合模型,研究了铺设和埋设两种敷设方式下海底电缆载流量、海水温度和海水流速对海底电缆径向温度及电场分布的影响,结果表明载流量是海底电缆径向温度和电场分布的主要影响因素,海水流动可以显著地降低海底电缆温度。文献[20]通过有限元模拟评估了海底土壤沉积物特性参数对高压直埋段海底电缆传热过程的影响,研究表明海底电缆的温度主要受到海底土壤的水渗透性、导热系数及海底电缆埋深的影响。文献[21]建立了无风条件下J型管段海底电缆二维热路模型,以及拓展的三维热路模型分析方法,并建立以表面传热系数来等效J型管内空气自然对流的三维有限元仿真模型,对热路模型进行了检验。目前针对海上风电送出平台J型管段海底电缆载流量计算分析较少,且已有研究基于简化模型,未考虑J型管内实际的自然对流换热过程。
针对以上问题,本文考虑海底电缆J型管空气段向海水段和平台段的轴向传热过程,提出J型管段海底电缆径向-轴向传热解析模型,并建立了三维热-流耦合数值模型。考虑导体电阻率随温度变化,研究J型管段海底电缆缆芯轴向传热特性,并采用所建立的解析模型分析J型管段海底电缆缆芯最高温度随J型管外径、太阳辐射强度、环境温度的变化规律,且与数值模拟方法进行了对比计算,验证了该解析模型计算J型管段海底电缆载流量的有效性。
典型海上风电送出线路J型管系统结构示意图如图1所示。

图1 J型管系统结构示意图
Fig.1 Structural diagram of J-tube system
根据海底电缆垂直方向上所处环境的不同可分成三段:
(1)平台段。海底电缆向上穿过海上升压平台后没有J型管保护,直接暴露于空气中,直至升压站。
(2)空气段,位于海平面与海上升压平台之间。工程上J型管顶端一般要求严格封闭,故在平台、海平面、J型管与海底电缆之间形成了一个充满空气的封闭空间。
(3)海水段,位于海平面与海床之间。工程中J型管底端不会严格封闭,故在海平面以下J型管与海底电缆之间充满海水。
当海底电缆缆芯通过电流时,忽略谐波情况,其损耗为导体的焦耳热损耗,对于交流海底电缆还存在绝缘介质损耗、金属护套和铠装的环流损耗,这些损耗以热量形式向外散热。J型管空气段海底电缆产生的热量首先以热传导形式传递给海底电缆外表面,然后以J型管内封闭空气的自然对流及海底电缆外表面与J型管内表面的热辐射形式传递给J型管,最后在J型管外表面以对流和辐射形式传递到外界空气中。传热学中三种传热方式控制方程[22]如下。
1)热传导
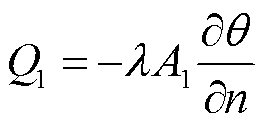 (1)
(1)
式中,Q1为热传导能量;λ为材料的导热系数;A1为垂直于导热方向的换热面积;θ为温度;n为等温线上的法向方向。
2)热对流
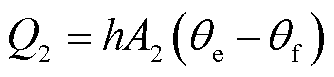 (2)
(2)
式中,Q2为热对流能量;h为表面传热系数;A2为对流换热表面积;θe为固体壁面温度;θf为周围流体温度。
3)热辐射
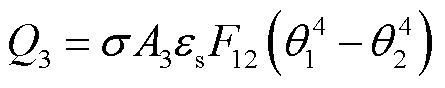 (3)
(3)
式中,Q3为热辐射能量;σ为斯忒藩-玻耳兹曼常量;A3为辐射表面积;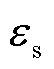 为系统发射率;F12为辐射换热的两个表面的角系数;θ1、θ2为两个表面的热力学温度。
为系统发射率;F12为辐射换热的两个表面的角系数;θ1、θ2为两个表面的热力学温度。
J型管内空气是一个自然对流换热过程,其传热流体场可通过三大守恒方程[23]来表述。
1)质量守恒方程
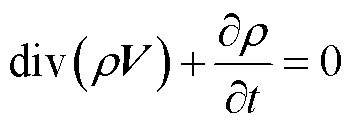 (4)
(4)
式中,V为流体流速;ρ为流体密度;t为时间。
2)动量守恒方程
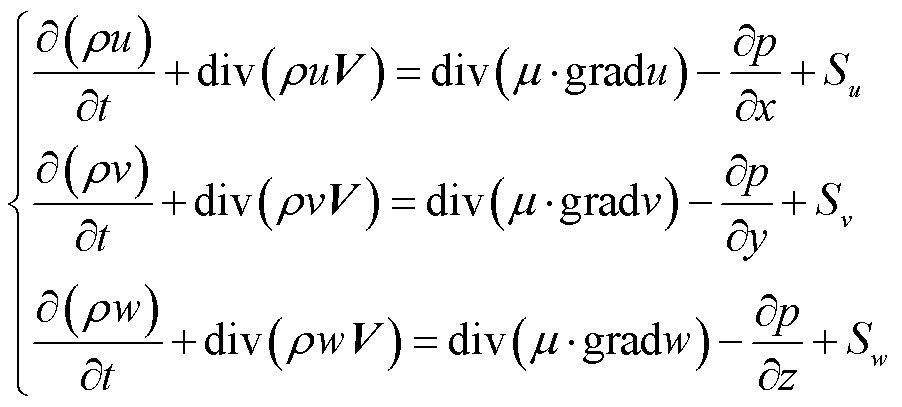 (5)
(5)
式中,u、v、w分别为流速V在x、y、z方向上的分量;μ为流体的动力粘度;p为流体压力;Su、Sv、Sw为动量守恒方程广义源项。
3)能量守恒方程
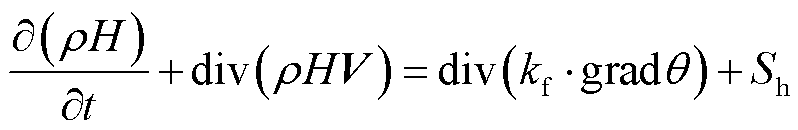 (6)
(6)
式中,H为比焓;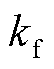 为流体导热系数;Sh为单位体积内焓生成率。
为流体导热系数;Sh为单位体积内焓生成率。
完整的计算模型需要包含边界条件,温度场计算常见的三类边界条件如下。
1)第一类恒温边界条件为
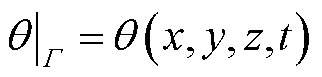 (7)
(7)
式中,Γ为物理边界。
2)第二类热流密度边界条件为
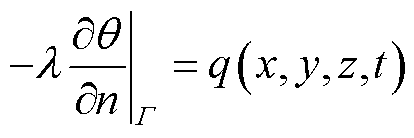 (8)
(8)
式中,q为热流密度。
3)第三类表面传热系数边界条件为
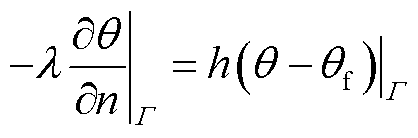 (9)
(9)
本文假设海底电缆与J型管垂直于海平面,且海底电缆位于J型管中心处;J型管外界空气流场自然对流换热过程一般以边界条件形式进行计算;海水导热性能较好,可忽略海水段自然对流过程,将海水等效为固体传热[19]。
文献[24]提出一种针对立管中电缆载流量的分析方法,其热路模型与J型管中海底电缆热路模型相似,类比电路概念,径向任意两个位置的温差为
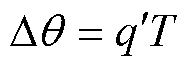 (10)
(10)
式中,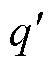 为单位长度海底电缆流过热阻的热量;T为单位长度海底电缆各圆环热阻层的等效热阻,其计算公式为
为单位长度海底电缆流过热阻的热量;T为单位长度海底电缆各圆环热阻层的等效热阻,其计算公式为
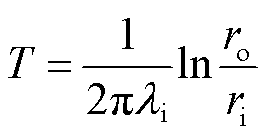 (11)
(11)
式中,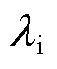 为海底电缆各层结构材料的导热系数;ro和ri分别为海底电缆各热阻层的外径与内径。
为海底电缆各层结构材料的导热系数;ro和ri分别为海底电缆各热阻层的外径与内径。
海底电缆表面与J型管内表面热通量可由热平衡公式计算,长度为L的海底电缆总热损等于来自海底电缆表面的对流换热和辐射换热之和,热平衡公式为
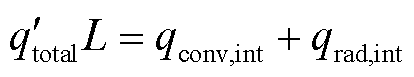 (12)
(12)
式中,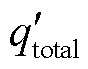 为海底电缆单位长度总热损。
为海底电缆单位长度总热损。
从海底电缆外表面到J型管内表面对流换热量为
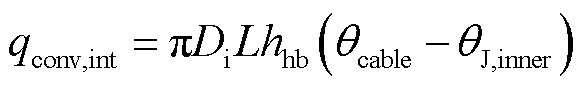 (13)
(13)
式中,Di为海底电缆外径;θcable为海底电缆表面温度;θJ,inner为J型管内表面温度;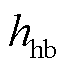 为海底电缆表面传热系数。
为海底电缆表面传热系数。
从海底电缆外表面到J型管内表面的辐射换热量为
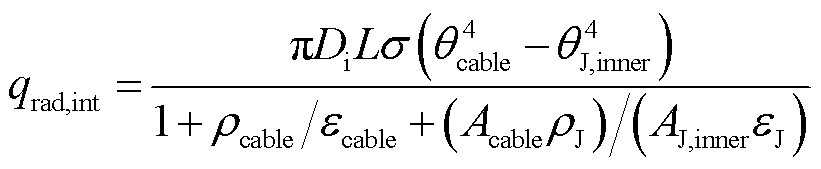 (14)
(14)
式中,εcable、εJ分别为海底电缆和J型管表面的发射率;ρcable、ρJ分别为相应的反射率;Acable、AJ,inner分别为海底电缆的外表面积和J型管的内表面积。
海底电缆表面传热系数可由经验公式(15)[24]确定。
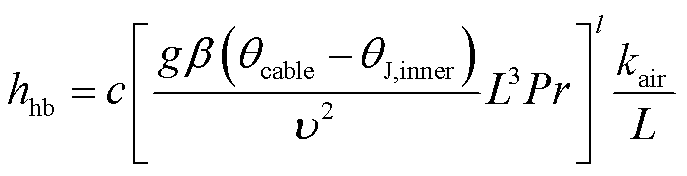 (15)
(15)
式中,g为重力加速度;β为空气热膨胀系数;Pr为空气普朗特数;υ为空气的运动粘度;kair为空气的导热系数;c与l为格拉晓夫数的函数,由实验研究确定[24]。
J型管内表面温度可由式(12)运用牛顿迭代法求出,基于热阻计算式(11)及式(10)可由J型管内表面温度计算出J型管外表面温度,之后可以求解J型管外表面与周围环境的热通量平衡关系式,即
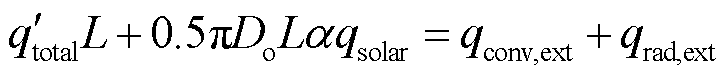 (16)
(16)
其中,J型管外表面与周围环境的对流换热量和辐射换热量分别为
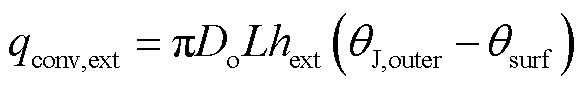 (17)
(17)
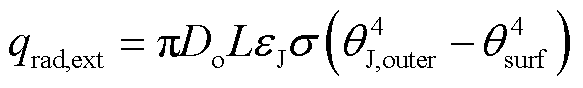 (18)
(18)
式中,hext为J型管外表面的表面传热系数;α为J型管表面的吸收率;qsolar为太阳辐射功率;Do为J型管的外表面直径;θJ,outer为J型管外表面温度;θsurf为周围环境温度。
根据以上径向传热分析模型可建立J型管段海底电缆载流量评估计算过程:首先设置缆芯温度范围[θa, θb],假设缆芯温度θc为温度范围的中间值;然后通过以上分析过程可计算出预测的周围环境温度θsurf,与实际环境温度θamb作对比;再根据误差采用二分法不断调整缩小缆芯温度取值范围;如此反复迭代计算,可得到满足精度要求Tol的缆芯温度值。
J型管空气段散热条件较差,而平台段和海水段散热条件相对较好,因此J型管空气段存在向海水段及平台段的轴向传热,当J型管空气段较短时,这种现象更为明显。本文参照传热学中等截面直肋导热模型[22]对J型管段海底电缆缆芯轴向传热进行近似,并考虑导体自身发热功率,建立J型管段海底电缆缆芯轴向传热的热平衡方程为
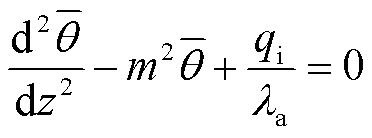 (19)
(19)
其中
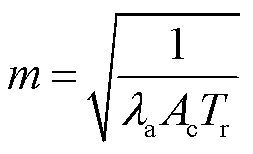
式中,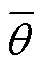 为缆芯温度θc和周围环境介质温度θ∞的温差,即
为缆芯温度θc和周围环境介质温度θ∞的温差,即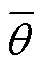 =θc-θ∞;z为缆芯轴向坐标;λa为海底电缆缆芯的导热系数;Ac为海底电缆缆芯横截面面积;Tr为海底电缆缆芯与周围环境介质径向等效总热阻;qi为海底电缆缆芯的热源密度。
=θc-θ∞;z为缆芯轴向坐标;λa为海底电缆缆芯的导热系数;Ac为海底电缆缆芯横截面面积;Tr为海底电缆缆芯与周围环境介质径向等效总热阻;qi为海底电缆缆芯的热源密度。
方程(19)可以求出解析解,其通解形式为
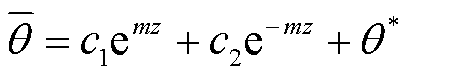 (20)
(20)
式中,c1、c2为待定常系数,可由边界条件求出;θ*为方程(19)的一个特解。
J型管空气段、海水段、平台段在交界面处满足连续性条件,即热流密度相等和温度相等,则有
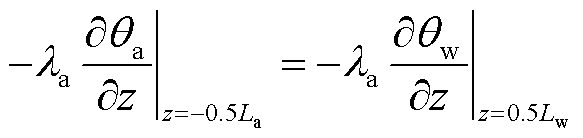 (21)
(21)
 (22)
(22)
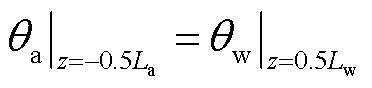 (23)
(23)
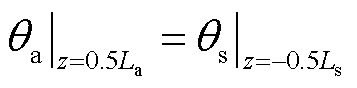 (24)
(24)
式中,θa、θw、θs分别为海底电缆J型管空气段、海水段与平台段的缆芯轴向温度分布;La、Lw、Ls分别为海底电缆J型管空气段、海水段与平台段长度;则各段中的轴向坐标z可分别表示为-0.5La≤z≤0.5La、-0.5Lw≤z≤0.5Lw、-0.5Ls≤z≤0.5Ls。
由式(20)~式(24)可得海底电缆J型管空气段导体轴向温度温度分布为
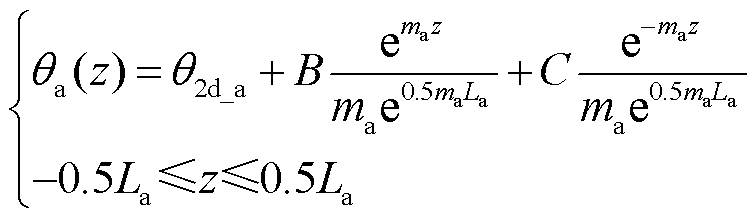 (25)
(25)
其中
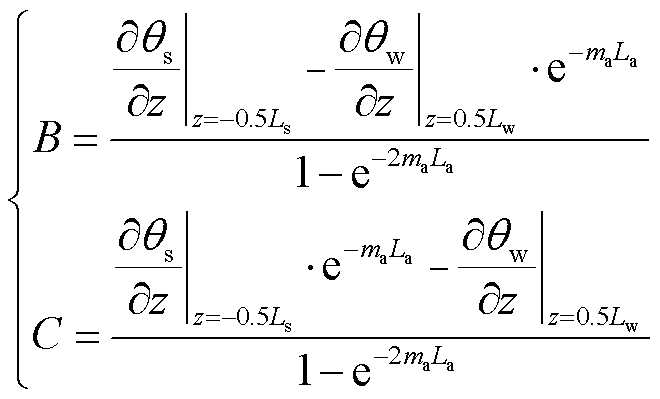 (26)
(26)
式中,θ2d_a为海底电缆J型管空气段海底电缆径向传热热路模型计算得到的缆芯温度;ma为空气段的m值。
同理,根据J型管段海底电缆平台段、海水段与空气段非接触端在无限远处轴向热流密度为零,结合式(21)和式(22)可得
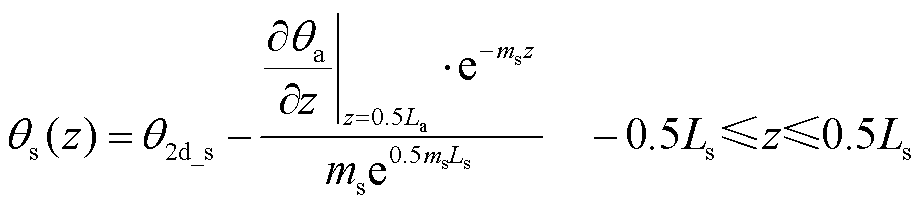 (27)
(27)
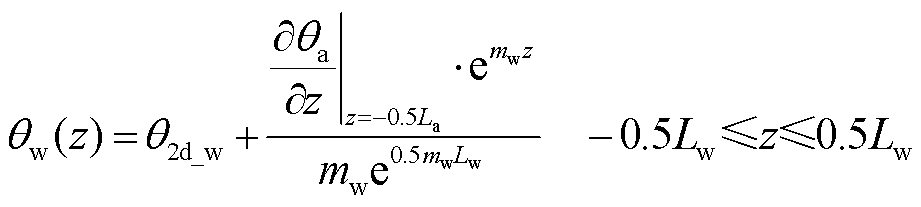 (28)
(28)
式中,θ2d_s、θ2d_w分别为J型管段海底电缆平台段与海水段径向传热热路模型计算得到的缆芯温度;ms和mw分别为平台段和海水段的m值。
由以上J型管段海底电缆径向和轴向热路分析模型可得到J型管段海底电缆载流量评估完整的迭代计算流程如图2所示。
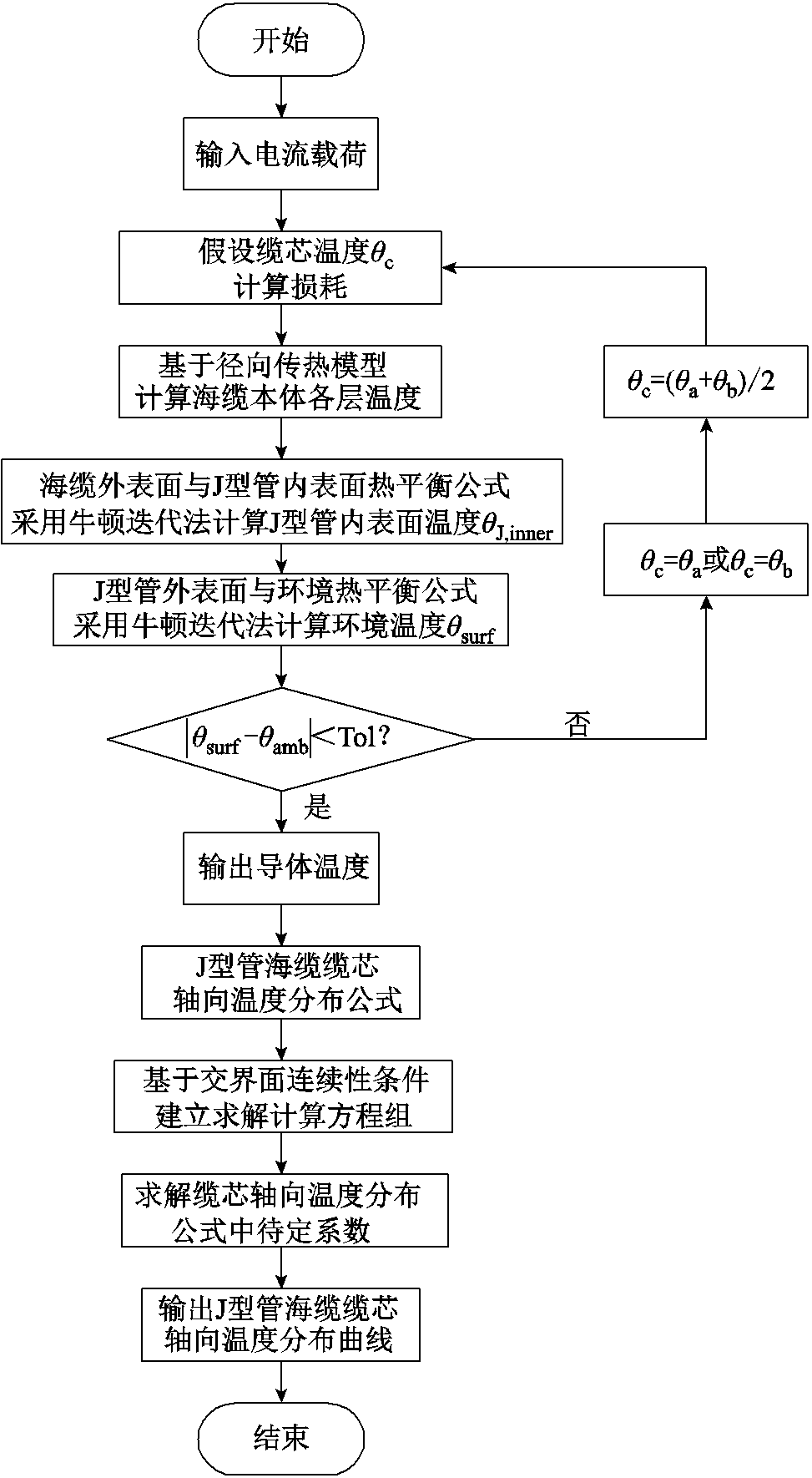
图2 J型管段海底电缆载流量评估迭代计算流程
Fig.2 Flow chart of iterative calculation for ampacity evaluation of submarine cable in J-tube section
本文建立包括空气段、海水段和平台段的J型管段海底电缆三维数值仿真模型,除了空气段为热-流耦合模型外,其他区域设置为固体传热。对于J型管与海底电缆之间空气的自然对流可以判定为湍流[25],由于k-ω剪切应力传输湍流模型兼具 k-ε和k-ω两种湍流模型特征,故本文选择该湍流模型。
对于空气段和平台段,周围空气通过施加表面传热系数来考虑与外界环境的之间的传热过程,表面传热系数[25-26]可表述为
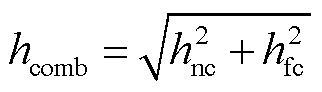 (29)
(29)
式中,hcomb为混合表面传热系数;hnc与hfc分别为自然表面传热系数和强迫表面传热系数。
对于空气段,hnc与hfc的计算如式(30)~式(35)所示,对于平台段方法类似。
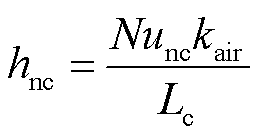 (30)
(30)
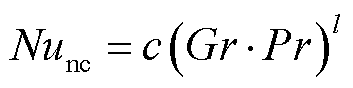 (31)
(31)
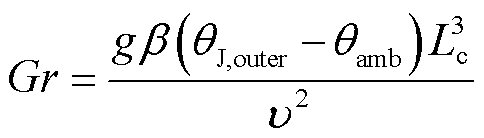 (32)
(32)
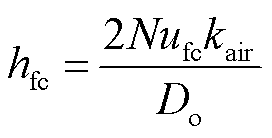 (33)
(33)
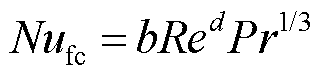 (34)
(34)
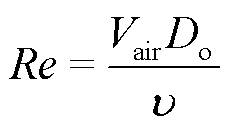 (35)
(35)
式中,Nunc、Nufc分别为自然对流和强迫对流的努塞尔数;Lc为特征尺寸;Gr为格拉晓夫数,反映自然对流过程中的流动方式;Pr为空气普朗特数,描述流体流动边界层与热边界层厚度之比;Re为雷诺数,表示惯性力和粘性力的相对大小;b、d取值由Re决定;Vair为环境风速。
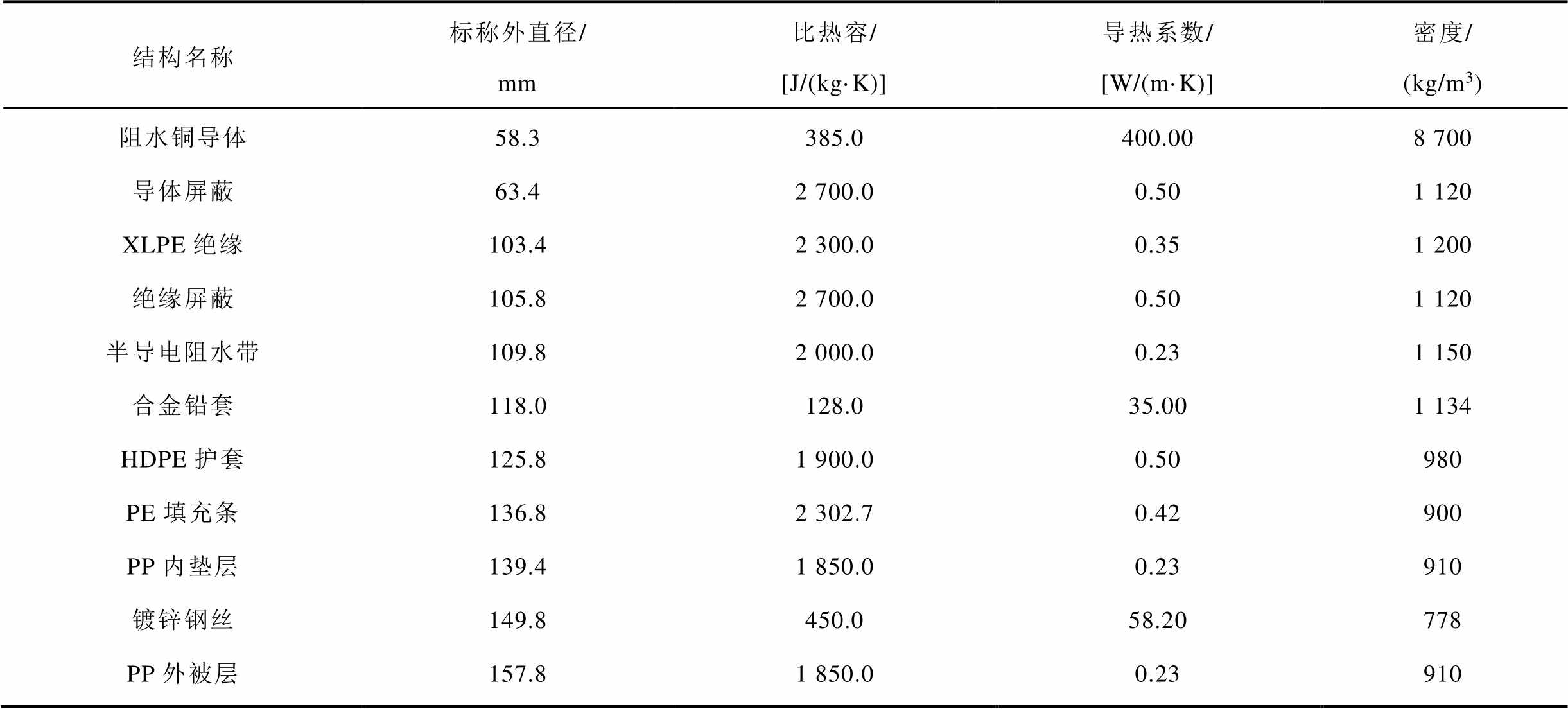
本文以直流±250 kV 交联聚乙烯(Cross Linked Polyethylene, XLPE)海底电缆为研究对象,其由11层不同结构组成,由内到外依次为阻水铜导体、导体屏蔽、XLPE绝缘、绝缘屏蔽、半导电阻水带、合金铅套、高密度聚乙烯(High Density Polyethylene, HDPE)护套、聚乙烯(Polyethylene, PE)填充条、聚丙烯(Polypropylene, PP)内垫层、铠装层、PP外被层。各层材料对应的参数见表1,J型管的尺寸与材料参数见表2。
表1 ±250kV XLPE海底电缆参数
Tab.1 Parameters of ±250 kV XLPE submarine cable
结构名称标称外直径/mm比热容/[J/(kg·K)]导热系数/[W/(m·K)]密度/(kg/m3) 阻水铜导体58.3385.0400.008 700 导体屏蔽63.42 700.00.501 120 XLPE绝缘103.42 300.00.351 200 绝缘屏蔽105.82 700.00.501 120 半导电阻水带109.82 000.00.231 150 合金铅套118.0128.035.001 134 HDPE护套125.81 900.00.50980 PE填充条136.82 302.70.42900 PP内垫层139.41 850.00.23910 镀锌钢丝149.8450.058.20778 PP外被层157.81 850.00.23910
表2 J型管材料参数
Tab.2 Material parameters of J-tube

结构名称标称直径/mm厚度/mm比热容/[J/(kg·K)]导热系数/[W/(m·K)]密度/(kg/m3) Q34550820480.048.007 850
基于上述模型,对海底电缆加载允许载流量2 000 A,海底电缆缆芯电阻率会随温度升高而明显增大。本文考虑电阻率随温度线性变化规律,即
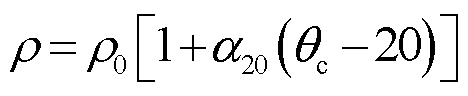 (36)
(36)
式中,ρ0为铜导体在20℃时的电阻率;α20为20℃时电阻率温度系数。
此外考虑夏季外界环境温度较高时情况,环境空气温度为40℃,海水温度为25℃;根据标准IEC 60287—2—1的规定,太阳辐射强度为1 000 W/m2,J型管外壁取太阳辐射吸收率为0.4,并注意到同一时刻J型管外壁只有一半面积可以有效地接收到太阳辐射;海底电缆与J型管表面的发射率分别为0.9和0.7。
本文采用流体仿真分析软件建立了J型管段海底电缆的热-流耦合模型,其数值模拟结果如图3、图4所示。由J型管空气段轴向中心高度处海底电缆截面温度分布云图可知,缆芯温度最高,海底电缆本体温度沿径向逐渐降低;根据海底电缆J型管段轴向温度分布可知,空气段海底电缆缆芯温度最高,且温度沿轴向分别向平台段与海水段逐渐降低。从J型管空气段内空气的流速分布云图可知,靠近海底电缆壁面空气流速较大,靠近J型管内壁面流速次之,中间流速最低,这是由于空气在J型管封闭腔体内沿着壁面上下循环流动造成的。
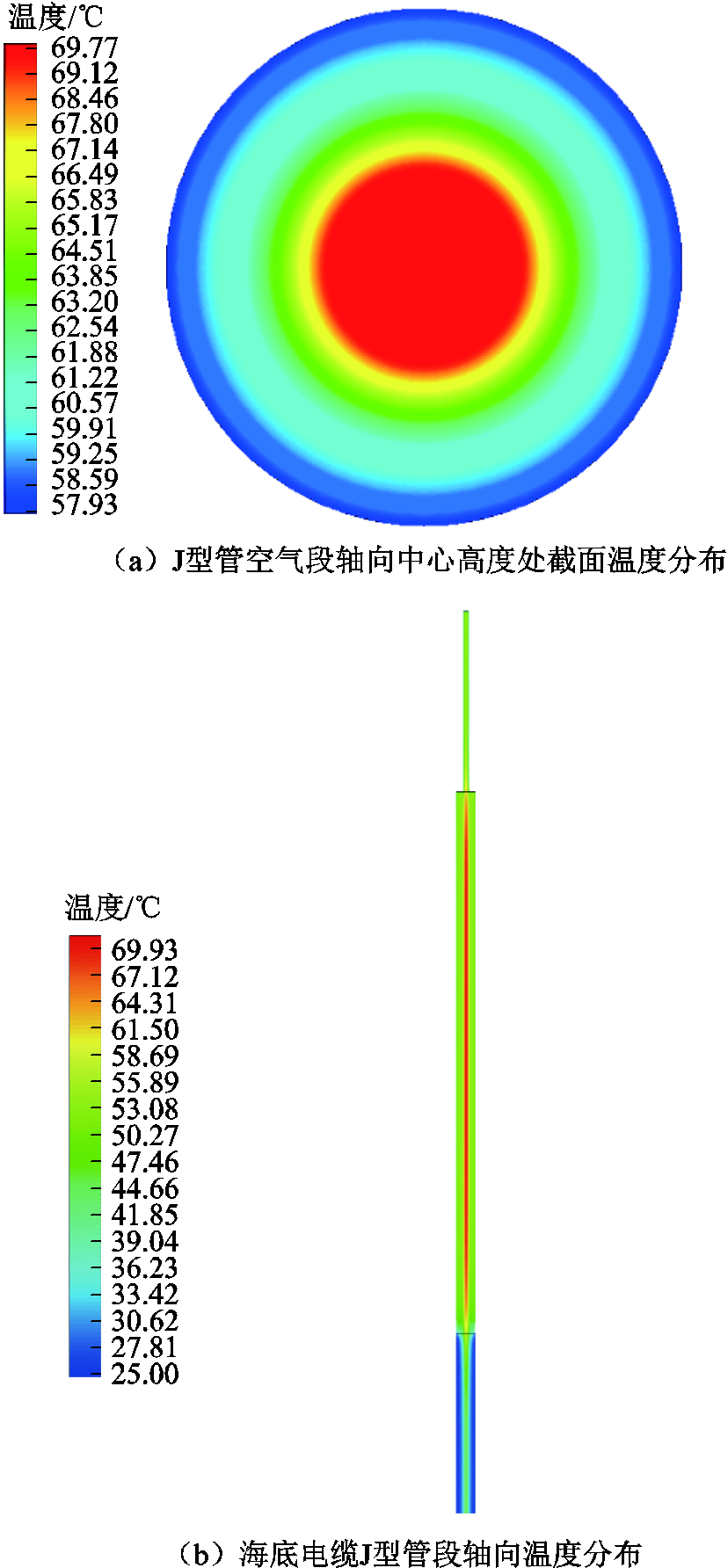
图3 仿真计算温度分布
Fig.3 Temperature distribution results of simulation calculation

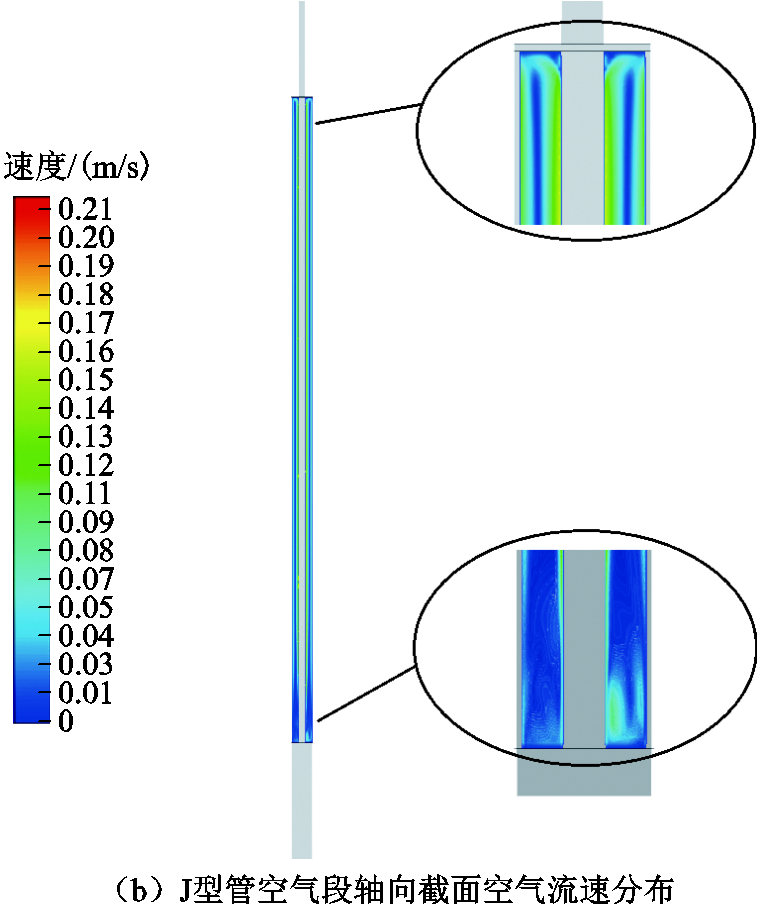
图4 仿真计算流速分布
Fig.4 Velocity distribution results of simulation calculation
J型管空气段海底电缆存在向海水段和平台段的轴向传热,因此应用基于径向传热的热路模型计算海底电缆载流量时,会因为轴向传热而造成一定误差。本文取海水段和平台段长度为5 m,而J型管空气段长度分别为5、10、15 m。基于数值模拟与轴向传热计算模型,本文计算了不同空气段长度下海底电缆缆芯的轴向温度分布,结果如图5所示。当J型管空气段长度为5 m时,轴向传热模型计算缆芯最高温度与数值法计算结果误差为3.0%;J型管空气段长度为10 m时,该误差为1.6%;J型管空气段长度为15 m时,该误差仅为1.1%。而实际海底电缆J型管空气段长度一般超过15 m,因此基于轴向传热模型的解析法已经可以满足工程应用要求。
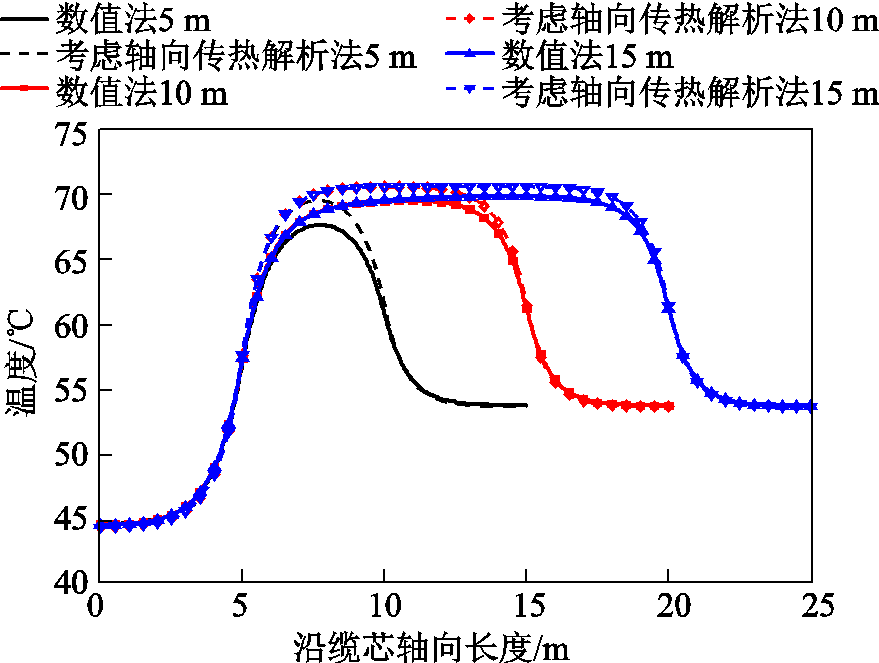
图5 不同空气段长度下缆芯轴向温度分布
Fig.5 Axial temperature distribution of the cable core conductor under different air section lengths
保持J型管壁厚为20 mm,改变其外径,其余条件参数不变,研究J型管尺寸参数对J型管段海底电缆缆芯温度的影响规律。
不同J型管外径下缆芯最高温度见表3。由表3可知,在J型管壁厚保持20 mm的条件下,J型管外径越大,J型管段海底电缆缆芯最高温度越低,但是增大J型管外径给缆芯带来的降温效果有限,数值模拟计算结果显示J型管外径每增加50 mm,温度变化小于0.4℃,而解析模型计算结果显示温度变化更小,因此可知J型管外径的增加对J型管段海底电缆载流量的提升效果有限。
表3 不同J型管外径下缆芯最高温度
Tab.3 Maximum temperature of cable core under different J-tube outer diameter

J型管外径/mm缆芯最高温度/℃ 数值模拟解析模型 45870.3070.04 50869.9370.00 55869.8369.98 60869.7069.97
太阳辐射有效吸收功率取值为0~500 W/m2,其余条件参数不变,对比研究不同太阳辐射强度对J型管段海底电缆缆芯温度的影响规律。
不同太阳辐射强度下J型管段海底电缆缆芯最高温度变化曲线如图6所示。由图6可知,缆芯最高温度随着太阳辐射强度的增加近似呈现线性上升的趋势,太阳辐射有效吸收功率每增加100 W/m2,海底电缆缆芯最高温度上升约4.8℃,且解析法与数值法计算结果趋势及规律基本一致。随着辐射强度的增加,解析法计算的结果相对数值模拟的误差略有增大,最大误差为2.8%。结果表明,太阳辐射强度对J型管段海底电缆载流量的影响较大,若能大幅减小J型管外壁对太阳辐射的吸收则可以显著地提升海底电缆的载流量。
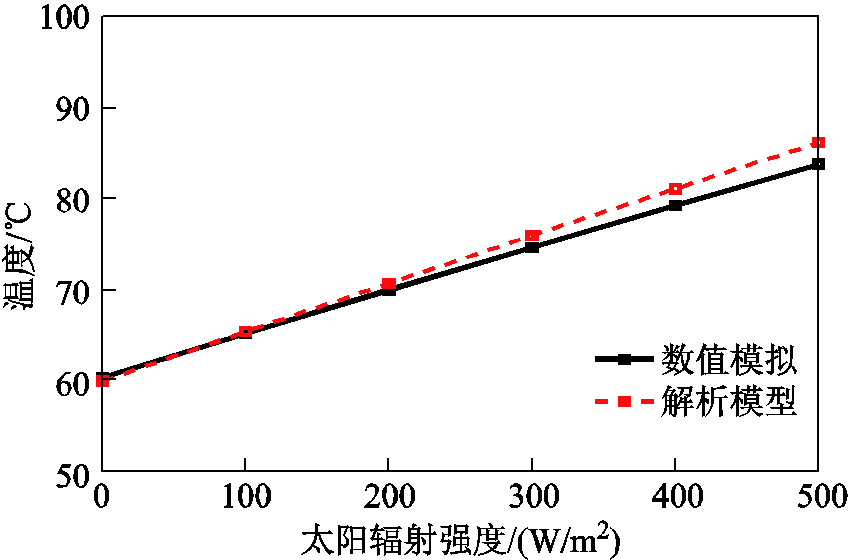
图6 不同太阳辐射下缆芯最高温度变化趋势
Fig.6 Variation trend of maximum temperature of the cable core conductor under different solar radiation
J型管段海底电缆环境温度包括空气温度和海水温度,空气温度直接影响J型管空气段海底电缆的散热,而海水温度通过影响海水段海底电缆散热间接影响空气段的海底电缆温度,因此有必要分别研究空气温度与海水温度对海底电缆缆芯最高温度的影响规律。其中海水段与平台段长度取值为5 m,空气段长度取值为15 m。
4.4.1 空气温度的影响
设外界空气温度分别为30、35、40、45℃,其余条件参数不变,对比研究了不同空气温度下J型管段海底电缆缆芯最高温度变化情况。
J型管段海底电缆缆芯最高温度随空气温度变化曲线如图7所示。由图7可知,海底电缆缆芯最高温度随空气温度升高近似线性增加,外界空气温度升高5℃,海底电缆缆芯最高温度也增加约5℃。此外,从图7中可以发现,解析法在不同空气温度下计算的缆芯最高温度与数值模拟法基本一致,误差在1%左右。

图7 不同空气温度下缆芯最高温度变化趋势
Fig.7 Variation trend of maximum temperature of the cable core conductor under different air temperatures
此外,为了研究不同太阳辐射强度和环境空气温度对J型管段海底电缆缆芯最高温度的综合影响因素,基于解析模型计算了在不同太阳辐射条件下,海底电缆缆芯最高温度随环境空气温度的变化规律,如图8所示。从图8可知,在不同太阳辐射条件下,J型管段海底电缆缆芯最高温度随着环境空气温度升高近似线性升高,但是随着太阳辐射强度的增大,海底电缆缆芯最高温度随着环境空气温度升高而升高的趋势略有降低。
4.4.2 海水温度的影响
海水温度分别为20、25、30℃,其余条件参数不变,研究了不同海水温度下J型管段海底电缆缆芯最高温度变化情况,结果见表4,可知海水温度对J型管空气段海底电缆缆芯最高温度几乎无影响。
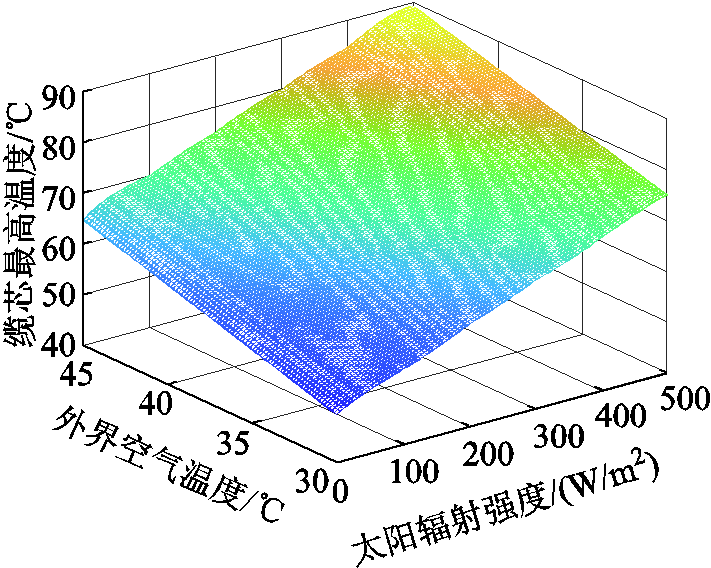
图8 不同太阳辐射下缆芯最高温度随空气温度的变化趋势
Fig.8 Variation trend of the maximum temperature of the cable core conductor with the air temperature under different solar radiations
表4 不同海水温度下缆芯最高温度
Tab.4 Maximum temperature of cable core under different seawater temperatures

海水温度/℃缆芯最高温度/℃ 数值模拟解析模型 2069.9170.00 2569.9370.00 3069.9570.00
本文提出了J型管段海底电缆径向-轴向传热模型,并在此基础上提出了适合J型管段海底电缆载流量计算的解析法,同时建立了三维J型管段海底电缆热-流耦合数值模型。基于解析法与数值模拟两种方法研究了J型管段海底电缆缆芯轴向传热特性,对比分析了J型管外径、太阳辐射强度和环境温度对海底电缆缆芯最高温度的影响规律,得出以下结论:
1)J型管空气段长度在大于10 m时,缆芯轴向温度分布的最高温度已形成明显平稳区段,此时基于径向-轴向热路模型的解析法与数值模拟法的误差在1.6%以内。
2)J型管外径增大时,J型管空气段海底电缆缆芯最高温度略有降低,但是J型管外径每增加50 mm,温度变化小于0.4℃;此外,虽然海水温度降低直接影响海水段海底电缆缆芯温度,但是对空气段海底电缆缆芯的最高温度也几乎无影响。
3)J型管段海底电缆缆芯最高温度随太阳辐射强度、空气温度的增加线性升高,太阳辐射有效吸收功率每增加100 W/m2,海底电缆缆芯最高温度上升约4.8℃;外界空气温度升高5℃,海底电缆缆芯最高温度上升约5℃。当太阳辐射强度增大时,海底电缆缆芯最高温度随空气温度升高而升高的趋势略有降低。
综上所述,本文针对J型管段海底电缆载流量计算所提出解析法与数值模拟对比结果最大误差在5%以内,初步验证了该解析法的有效性,可以满足一般工程应用的精度要求。
参考文献
[1] 李萌, 牛胜锁, 刘玉芹, 等. 基于多场耦合模型的海底电缆载流量和温度场计算研究[J]. 电测与仪表, 2018, 55(8): 12-16, 23. Li Meng, Niu Shengsuo, Liu Yuqin, et al. Calculation of temperature distribution and ampacity for submarine cables based on multi-physics field coupling model[J]. Electrical Measurement & Instrumentation, 2018, 55(8): 12-16, 23.
[2] 赵国亮, 陈维江, 邓占锋, 等. 柔性低频交流输电关键技术及应用[J]. 电力系统自动化, 2022, 46(15): 1-10. Zhao Guoliang, Chen Weijiang, Deng Zhanfeng, et al. Key technologies and application of flexible low-frequency AC transmission[J]. Automation of Electric Power Systems, 2022, 46(15): 1-10.
[3] 李翔宇, Gayan Abeynayake, 姚良忠, 等. 欧洲海上风电发展现状及前景[J]. 全球能源互联网, 2019, 2(2): 116-126. Li Xiangyu, Abeynayake G, Yao Liangzhong, et al. Recent development and prospect of offshore wind power in Europe[J]. Journal of Global Energy Interconnection, 2019, 2(2): 116-126.
[4] 刘云鹏, 许自强, 陈铮铮, 等. ±160 kV直流XLPE海底电缆载流特性仿真及试验[J]. 电力自动化设备, 2018, 38(2): 130-136. Liu Yunpeng, Xu Ziqiang, Chen Zhengzheng, et al. Simulation and experiment of ampacity characteristics for ±160 kV DC XLPE submarine cable[J]. Electric Power Automation Equipment, 2018, 38(2): 130-136.
[5] 梁永春, 李彦明, 柴进爱, 等. 地下电缆群稳态温度场和载流量计算新方法[J]. 电工技术学报, 2007, 22(8): 185-190. Liang Yongchun, Li Yanming, Chai Jinai, et al. A new method to calculate the steady-state temperature field and ampacity of underground cable system[J]. Transactions of China Electrotechnical Society, 2007, 22(8): 185-190.
[6] 魏艳慧, 郑元浩, 龙海泳, 等. 绝缘层厚度对高压直流电缆电场和温度场分布的影响[J]. 电工技术学报, 2022, 37(15): 3932-3940. Wei Yanhui, Zheng Yuanhao, Long Haiyong, et al. Influence of insulation layer thickness on electric field and temperature field of HVDC cable[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3932-3940.
[7] 张洪亮, 尹毅, 谢书鸿, 等. 不同金属屏蔽形式XLPE高压直流电缆载流量计算与试验验证[J]. 高电压技术, 2021, 47(6): 2117-2123. Zhang Hongliang, Yin Yi, Xie Shuhong, et al. Calculation and testing research on current rating capacity of XLPE insulated HVDC cable with different metallic screen type[J]. High Voltage Engineering, 2021, 47(6): 2117-2123.
[8] 吕安强, 李静, 张振鹏, 等. 夹具对高压绝缘电缆热学特性影响的有限元分析[J]. 电工技术学报, 2022, 37(1): 283-290. Lü Anqiang, Li Jing, Zhang Zhenpeng, et al. Finite element analysis for the influence of clamp on the thermal characteristics of high voltage insulated power cable[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 283-290.
[9] 吕安强, 寇欣, 尹成群, 等. 三芯海底电缆中复合光纤与导体温度关系建模[J]. 电工技术学报, 2016, 31(18): 59-65. Lü Anqiang, Kou Xin, Yin Chengqun, et al. Modeling of temperature relation between optical fiber and conductor in 3-core submarine power cable[J]. Transactions of China Electrotechnical Society, 2016, 31(18): 59-65.
[10] 赵建华, 袁宏永, 范维澄, 等. 基于表面温度场的电缆线芯温度在线诊断研究[J]. 中国电机工程学报, 1999, 19(11): 52-54, 68. Zhao Jianhua, Yuan Hongyong, Fan Weicheng, et al. Surface temperature field based online diagnoses study for electric cable’s conductor temperature[J]. Proceedings of the CSEE, 1999, 19(11): 52-54, 68.
[11] Weedy B M, El Zayyat H M. The current carrying capacity of power cables in tunnels[J]. IEEE Transactions on Power Apparatus and Systems, 1973, PAS-92(1): 298-307.
[12] Gela G, Dai J J. Calculation of thermal fields of underground cables using the boundary element method[J]. IEEE Transactions on Power Delivery, 1988, 3(4): 1341-1347.
[13] Hiranandani A. Calculation of conductor temperatures and ampacities of cable systems using a generalized finite difference model[J]. IEEE Transactions on Power Delivery, 1991, 6(1): 15-24.
[14] Al-Saud M S, El-Kady M A, Findlay R D. A new approach to underground cable performance assessment[J]. Electric Power Systems Research, 2008, 78(5): 907-918.
[15] 梁永春. 高压电力电缆载流量数值计算[M]. 北京: 国防工业出版社, 2012.
[16] 张磊, 宣耀伟, 乐彦杰, 等. 110kV单芯海缆的载流量计算、温度场仿真及其热循环试验研究[J]. 高压电器, 2016, 52(6): 135-140, 146. Zhang Lei, Xuan Yaowei, Le Yanjie, et al. Ampacity calculation, temperature simulation and thermal cycling experiment for 110 kV submarine cable[J]. High Voltage Apparatus, 2016, 52(6): 135-140, 146.
[17] 梁正波, 徐明忠, 陈锋, 等. 典型敷设环境下超高压海底电缆的热特性[J]. 高电压技术, 2019, 45(11): 3452-3458. Liang Zhengbo, Xu Mingzhong, Chen Feng, et al. Thermal characteristics of EHV submarine cable in typical layout environments[J]. High Voltage Engineering, 2019, 45(11): 3452-3458.
[18] 刘士利, 罗英楠, 刘宗烨, 等. 基于电磁-热耦合原理的三芯铠装电缆在低频输电方式下的损耗特性研究[J]. 电工技术学报, 2021, 36(22): 4829-4836. Liu Shili, Luo Yingnan, Liu Zongye, et al. Study on loss characteristics of three core armored cable under low-frequency transmission mode based on electromagnetic, thermal coupling principle[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4829-4836.
[19] 郝艳捧, 陈云, 阳林, 等. 高压直流海底电缆电–热–流多物理场耦合仿真[J]. 高电压技术, 2017, 43(11): 3534-3542. Hao Yanpeng, Chen Yun, Yang Lin, et al. Coupled simulation on electro-thermal-fluid multiple physical fields of HVDC submarine cable[J]. High Voltage Engineering, 2017, 43(11): 3534-3542.
[20] Hughes T J, Henstock T J, Pilgrim J A, et al. Effect of sediment properties on the thermal performance of submarine HV cables[J]. IEEE Transactions on Power Delivery, 2015, 30(6): 2443-2450.
[21] Chippendale R D, Pilgrim J A, Goddard K F, et al. Analytical thermal rating method for cables installed in J-tubes[J]. IEEE Transactions on Power Delivery, 2017, 32(4): 1721-1729.
[22] 杨世铭, 陶文铨. 传热学[M]. 4版. 北京: 高等教育出版社, 2006.
[23] Smolka J. CFD-based 3-D optimization of the mutual coil configuration for the effective cooling of an electrical transformer[J]. Applied Thermal Engineering, 2013, 50(1): 124-133.
[24] Hartlein R A, Black W Z. Ampacity of electric power cables in vertical protective risers[J]. IEEE Transactions on Power Apparatus and Systems, 1983, PAS-102(6): 1678-1686.
[25] 游磊. 海上风电场送出海缆载流量瓶颈区段与提升方法研究[D]. 广州: 华南理工大学, 2018.
[26] Anders G J. Rating of cables on riser poles, in trays, in tunnels and shafts-a review[J]. IEEE Transactions on Power Delivery, 1996, 11(1): 3-11.
Abstract The transmission line of offshore wind farm generally passes through the J-tube section with poor heat dissipation conditions,which is divided into three sections: platform section, tube air section and tube water section. The tube air section is often the weak point of ampacity of the submarine cable due to the closed air interlayer between the J-tube and the cable. There is no standard formula for calculating the ampacity of submarine cables in this laying section, which mainly depends on the numerical simulation. However, 3-D fluid simulation is time-consuming. This paper proposes an analytical model of radial-axial heat transfer of submarine cables in J-tube section, which takes into account the axial temperature distribution difference of submarine cable conductors and realizes the rapid calculation of ampacity of submarine cables in J-tube section.
Firstly, the radial thermal path model of the submarine cable in J-tube section is built according to the thermoelectric analogy method. The Nusselt number correlation formula is used to calculate the convection heat transfer coefficient between the submarine cable surface and the inner surface of J-tube. And the radiation heat transfer between the submarine cable surface and the inner surface of J-tube is considered. Secondly, the axial heat transfer of submarine cable conductor in J-tube section is approximated by the heat transfer model of medium cross-section straight rib, and the axial heat transfer model is built on the basis of its radial model. Finally, with the radial-axial thermal path model of the J-section submarine cable, the conductor temperature distribution of the J-tube submarine cable under the given current load can be quickly calculated by the dichotomy method.
Taking high voltage DC submarine cable as an example, a comparative calculation is carried out with the analytical model and the 3-D numerical model. The results show that when the length of tube air section is 5 m, the error between the maximum temperature of the conductor calculated by the axial heat transfer model and that calculated by the numerical method is 3.0%; the error is 1.6% when the length of tube air section is 10m; the error is only 1.1% when the length of tube air section is 15 m. The numerical simulation results show that the maximum temperature change is less than 0.4℃ when the outer diameter of J-tube increases by 50 mm, while the analytical model results show that the temperature change is smaller. The maximum temperature of the conductor increases linearly with the increase of solar radiation intensity. And the trend and law of the calculation results of the analytical method and the numerical method are basically consistent. With the increase of the radiation intensity, the error of the calculation results of the analytical method is slightly increased compared with the numerical method, and the maximum error is 2.8%. In addition, the maximum temperature of the conductor increases approximately linearly with the increase of ambient air temperature. The external ambient air temperature increases by 5℃, and the maximum temperature of the conductor also increases by about 5℃. The maximum conductor temperature calculated by the analytical method at different air temperatures is basically consistent with the numerical simulation method, with an error of about 1%.
The following conclusions can be drawn from the comparative calculation and analysis: (1) When the length of tube air section is greater than 10m, the maximum temperature of the axial temperature distribution of the cable conductor has formed an obvious stable section. (2) With the increase of the outer diameter of J-tube, the maximum temperature of the conductor decreases slightly; besides, the reduction of the seawater temperature directly affects the temperature of the conductor in tube water section, but has little effect on the maximum temperature of the conductor in tube air section. (3) The maximum temperature of the conductor in J-tube section increases linearly with the increase of solar radiation intensity and ambient air temperature. However, when the solar radiation intensity increases, the increasing trend of the maximum temperature of the conductor decreases slightly with the increase of air temperature.
keywords:Submarine cable, J-tube, analytical method, numerical simulation, ampacity
国家自然科学基金资助项目(51977152)。
收稿日期 2022-05-04
改稿日期 2022-10-17
DOI:10.19595/j.cnki.1000-6753.tces.220708
中图分类号:TM247
李 根 男,1990年生,博士研究生,研究方向为电磁装备多物理场数值计算。E-mail:912lg@163.com
杜志叶 男,1974年生,教授,博士生导师,研究方向为智能电气设备、特高压直流输电关键技术、电磁多物理场耦合计算技术。E-mail:Duzhiye@126.com(通信作者)
(编辑 李冰)