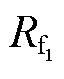；L2出线在故障点F2发生C相接地故障，接地点过渡电阻为
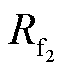；L3～Ln为母线上的健全出线；
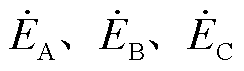为系统三相电源电动势；
为中性点电压，即为母线零序电压；
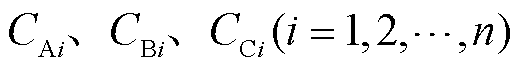分别为各条出线各相的对地零序电容。考虑到正序阻抗、负序阻抗远远小于零序阻抗，图1及以下分析中，均忽略正序阻抗、负序阻抗。由于母线接地概率很小，本文亦不考虑母线接地的情况。摘要 中性点不接地系统异名相两点接地且至少一个故障点过渡电阻较大时，故障电流较小出线保护不能直接切除，仍需依赖接地故障选线装置实现保护。根据故障边界条件建立不接地系统异名相两点接地故障复合序网，利用节点阻抗矩阵分别推导出两个接地点故障电流、系统零序电压等工频电气量随两个接地点过渡电阻的变化规律，并进一步分析了其对现有选线技术的影响。结果表明，异名相两点高阻接地时工频电气量总体特征与传统小电流接地故障特征相近，零序电压一般介于两个故障点单独接地时的零序电压之间，其中两个故障线路出口的零序电流既不符合故障线路特征也不符合健全线路特征，已有稳态选线原理并不完全适用。最后，利用数字仿真和现场数据验证了理论分析的正确性。
关键词：中性点不接地系统 异名相两点接地 工频电气量 稳态选线
我国中压配电网大都以小电流接地方式运行，其中以中性点不接地方式为主。据统计，单相接地故障占系统故障总数的80%以上[1-2]，而当系统发生单相接地故障时，非故障相对地电压的长期升高会威胁到系统已存在的绝缘薄弱环节，容易产生第二个接地点，从而形成异名相两点接地故障。据某省统计，在427起单相接地故障中，两点接地故障有12次，约占2.81%。当两个接地点过渡电阻均较小时，将产生较大的故障电流，由出线保护切除故障[1]；但当至少一个故障点过渡电阻较大时，其故障电流较小，出线保护将会拒动，仍需要依赖接地故障选线装置实现保护。
近年来，关于小电流接地故障保护技术的研究成果层出不穷[3-9]，现有选线技术按照原理可以分为外加信号法和故障信号法两类。外加信号法包括强注入法和弱注入法两大类，常见的外加信号法有中值电阻投切法[10-11]、调节消弧线圈补偿度法[12]及信号注入法[13]等。故障信号法包括稳态信号和暂态信号两大类，常见的故障信号法有零序导纳法[14]、小波法[15-17]和相电压极化量法[18]等。特别是，对于中性点不接地系统，通常认为单独利用故障工频信号也可实现选线，并且随着选线技术的成熟，有不少选线装置在利用故障暂态信号的基础上，仍融合了利用工频量的选线方法[19-20]。
当前单相故障检测技术与检测装置，无论是采取暂态量法还是稳态量法，一般都不能很好地处理两点接地故障，对第二次接地故障一般不做处理，导致故障长期存在，危害电网运行安全。由于重视程度不够，目前对于小电流接地系统异名相两点接地故障的研究相对不足。文献[21]归纳相继故障研究的要点与现状，包括演化机理、模式表示、场景筛选判据，并展望了相继接地故障研究重点与可能突破的方向。文献[22]建立两点接地故障仿真模型，通过仿真得到故障时相电压、零序电压和零序电流的特征，并基于此提出一种判断故障的方法，但只能判断两点接地故障类型，且缺乏理论推导。文献[23]结合两点接地故障发生时零序电流特征分量幅值及相位关系，提出一种配电网线路两点相继接地故障选线方法，但在实际相继接地故障中，第二故障点暂态特征存在特征不明显且衰减较快的情况，难以捕捉第二次故障的暂态信号。文献[24]针对单相接地引起的工频过电压及弧光过电压的影响因素和特点进行理论分析，进而得到引发相继故障的机理，但未涉及两点接地故障选线方法，也未涉及其对已有选线技术的影响。综上可知，在两点接地故障中，往往有些接地故障暂态特征不明显，有时容易错过故障暂态信息的采集，此时需要稳态量法进行故障检测。但目前针对不接地系统异名相两点接地故障工频特征的定量研究不足，亟须研究其工频故障特征。
本文建立中性点不接地系统异名相两点接地故障分析模型，利用节点阻抗矩阵推导出故障点零序电流（故障点电流的零序分量）等故障工频电气量的表达式；根据两个故障点过渡电阻的阻值大小变化，分析了不接地系统中故障工频电气量的特征，并与单点接地故障特征进行了对比；利用得出的故障特征，进一步分析了已有的工频量选线方法对于异名相两点接地故障的适应性，并提出了选线技术发展建议。最后，通过Matlab仿真和现场数据对理论分析进行了验证。
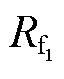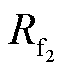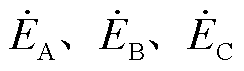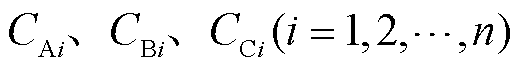中性点不接地系统异名相两点接地故障示意图如图1所示。系统共有n条出线，其中：L1和L2是母线上的两条故障出线，L1出线在故障点F1发生B相接地故障，接地点过渡电阻为；L2出线在故障点F2发生C相接地故障，接地点过渡电阻为；L3～Ln为母线上的健全出线；为系统三相电源电动势；为中性点电压，即为母线零序电压；分别为各条出线各相的对地零序电容。考虑到正序阻抗、负序阻抗远远小于零序阻抗，图1及以下分析中，均忽略正序阻抗、负序阻抗。由于母线接地概率很小，本文亦不考虑母线接地的情况。
根据已有对复故障类型的分类[25]，异名相两点接地故障属于串-串型双重复故障，且两个故障都是横向故障，其两个故障端口的阻抗参数等于故障点的节点阻抗参数；故障端口电流与故障点的故障分量相等；故障端口电压与故障点的电压相等。基于此类特点，可以利用节点阻抗矩阵进行推导计算，得到其矩阵形式的边界条件方程为
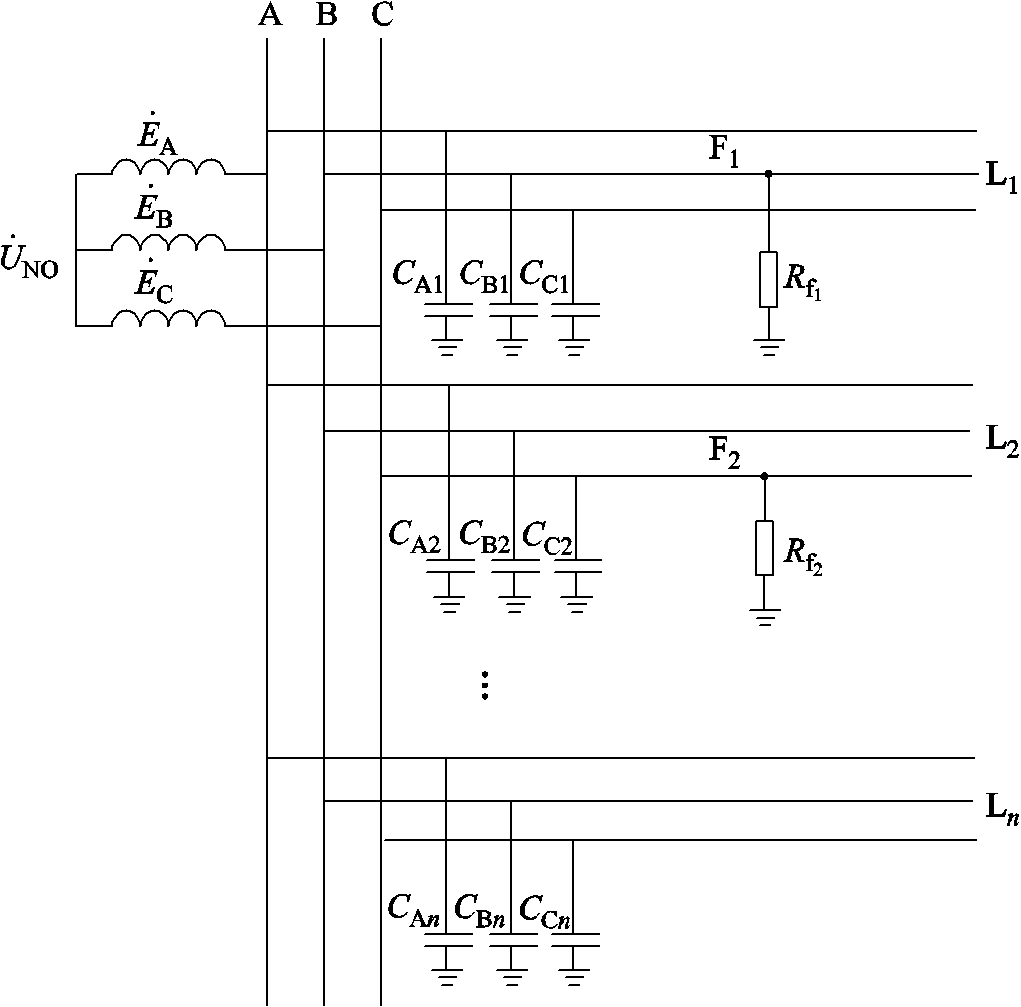
图1 不接地系统异名相两点接地故障示意图
Fig.1 The diagram of two-point grounding faults occurring on different phases in isolated neutral system
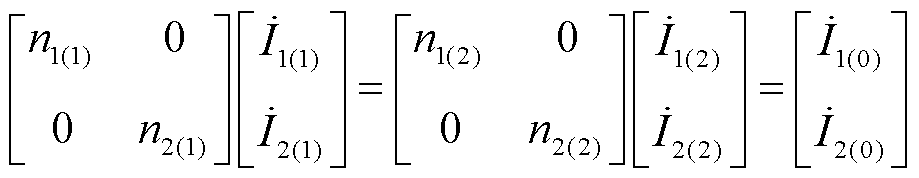（1）
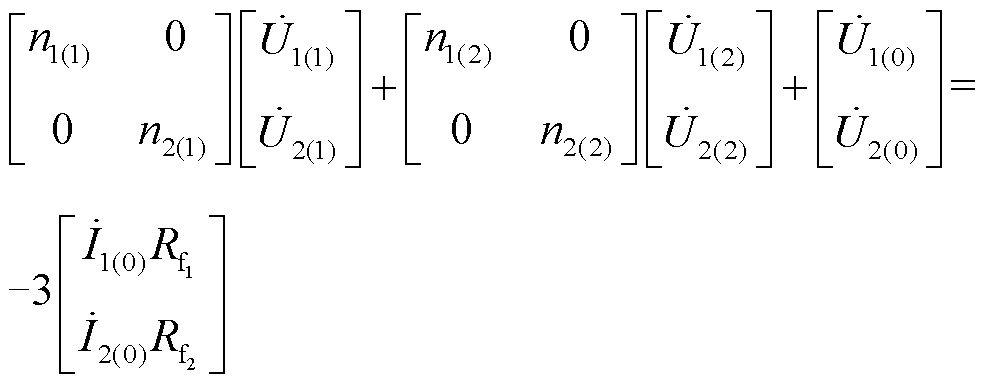（2）
式中，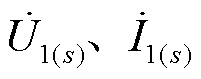
分别为第一故障口的三序电压、三序电流；
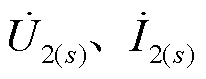分别为第二故障口的三序电压、三序电流；
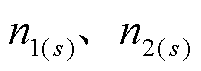分别为与两个故障特殊相有关的算子符号，用于归算基准相；s=0, 1, 2，分别表示零序、正序和负序。为便于计算，将A相设为基准相，相关算子符号取值见表1，其中
。
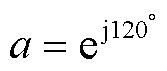表1 算子符号取值
Tab.1 Operator symbol value table
故障特殊相n0n1n2 A111 B1a2a C1aa2
统一基准相过程中，需要用到移相变压器。根据式（1）和式（2）所示边界条件方程，可得异名相两点接地故障复合序网如图2所示。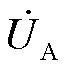
为基准相（A相）的相电压；CM为所有出线对地零序电容之和。
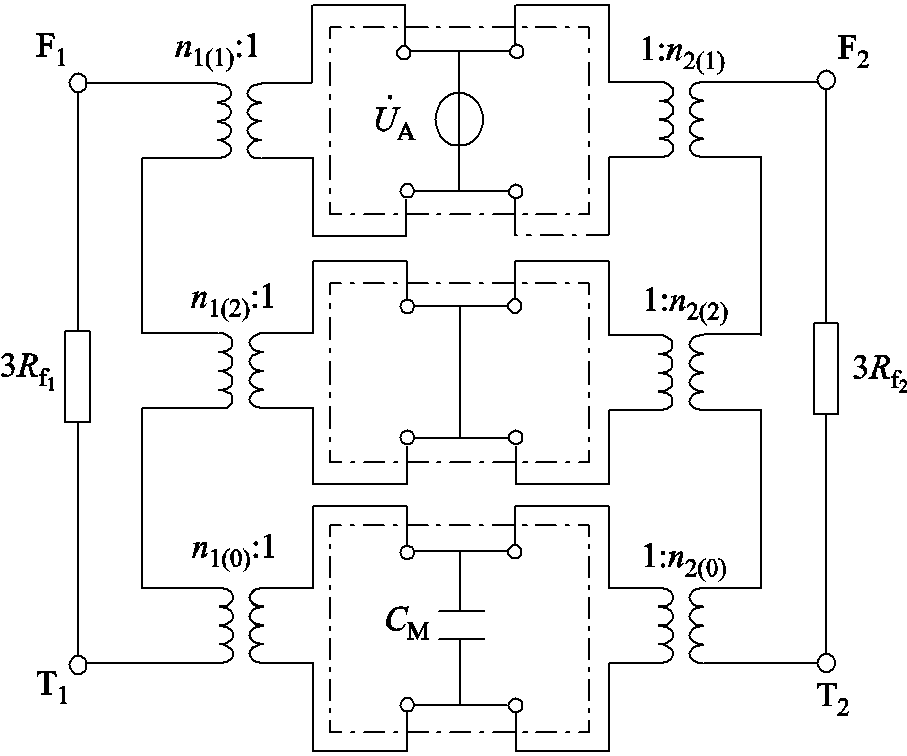
图2 不接地系统异名相两点接地故障复合序网
Fig.2 Compound sequence network of two-point grounding faults occurring on different phases
1.2.1 故障点工频电流分析
图2中，复合序网中的负序和零序网络均为无源双口网络，正序网络则为有源双口网络。各序网中两个故障端口的电流和电压间的关系，可用二端口网络阻抗型参数方程组表示为
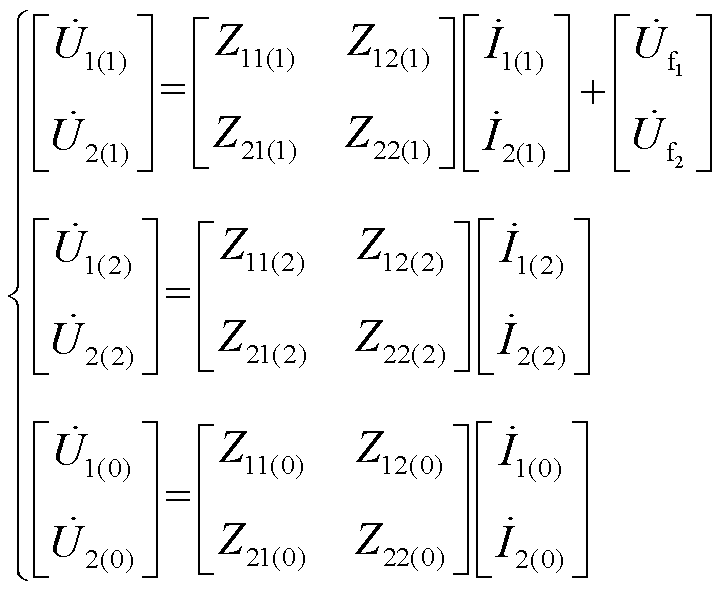（3）
式中，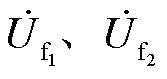
为两个故障口的开路电压，等于故障前故障相电压；
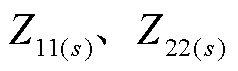为三个序网中两个故障端口之间的自阻抗；
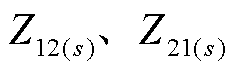为三个序网中两个故障端口之间的互阻抗。将式（1）～式（3）联立求解，可得到两个故障点的零序电流为
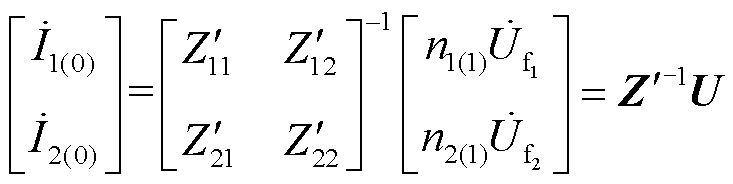（4）
式中，U为复合序网的故障口开路电压，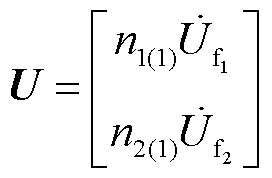
；
为复合序网口阻抗矩阵，是由两个故障点处的过渡电阻、三个序网中两故障端口之间的自阻抗和互阻抗组成，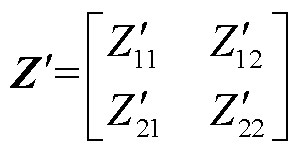
，其中
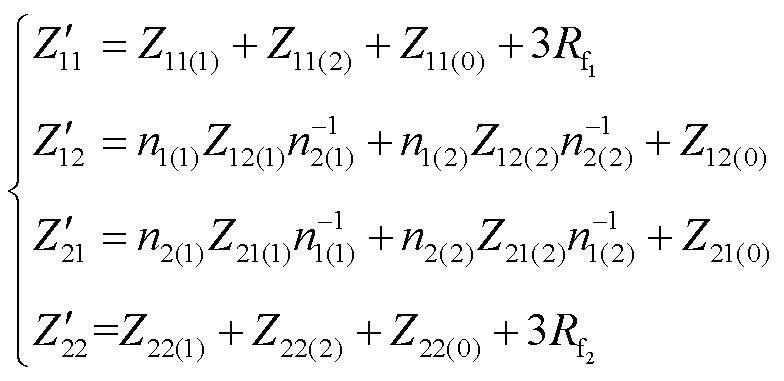（5）
在中性点不接地系统中，对于发生B相和C相两点接地的情况，其复合序网口阻抗矩阵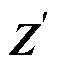
为
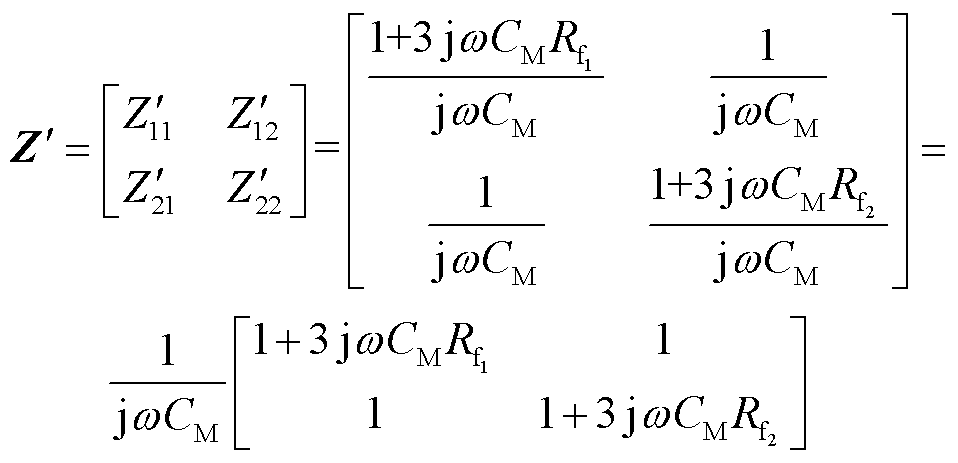（6）
式中，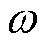
为工频角频率。
考虑到此时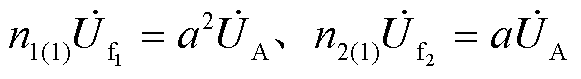
，可得到两个故障点处工频零序电流为
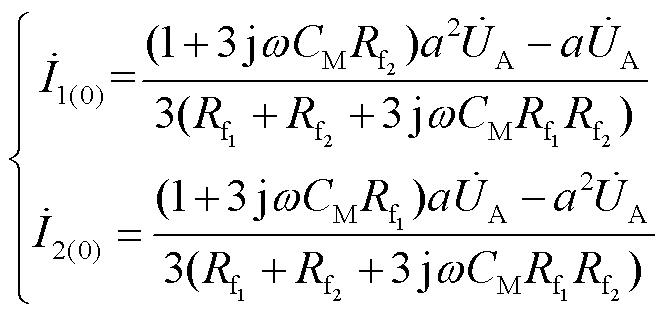（7）
根据文献[26]，GB 50613—2010标准规定：当中压配电网的电容电流小于10 A，宜采用不接地方式。为便于后续分析，本文以典型不接地系统总对地电容电流10 A为例，当两故障点过渡电阻分别在0～2 kΩ范围内变化时，由式（7）可以得到B相故障点工频零序电流随两个过渡电阻的变化趋势如图3所示，同时与B相单独接地时的故障点零序电流进行了比较。
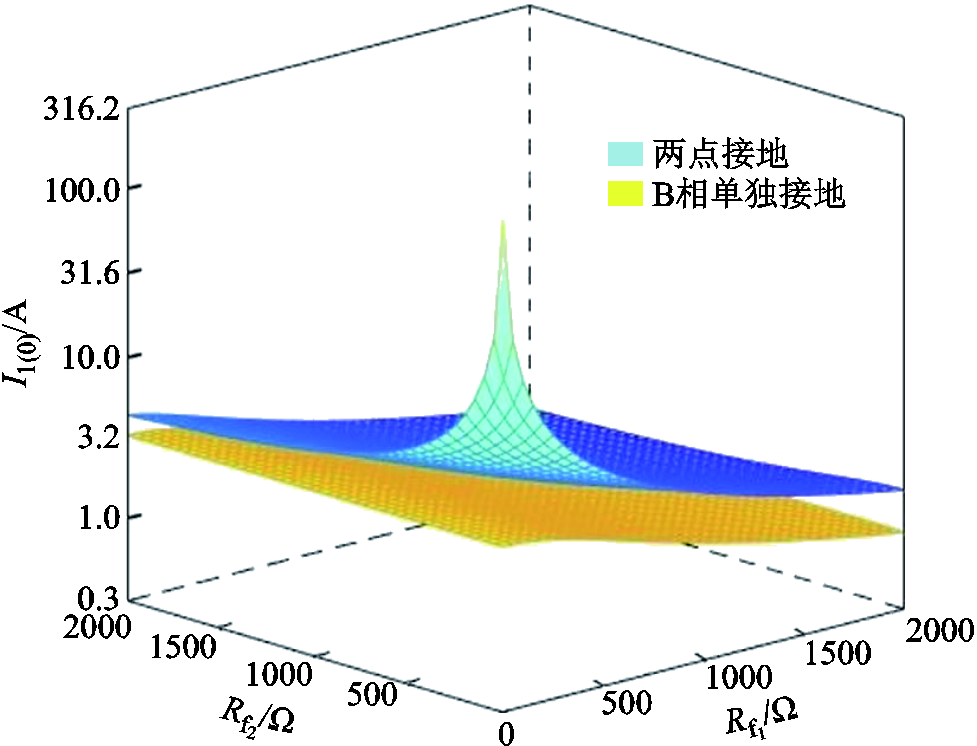
图3 B相故障点工频零序电流随过渡电阻的变化趋势
Fig.3 Tendency of power frequency current under phase B fault with the change of transition resistances
从图3中可知，两点接地时，故障超前相（B相）故障点的工频零序电流整体上随着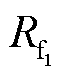
和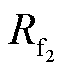的增大而减小；随着滞后相接地电阻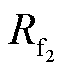的增大，零序电流无限趋近于超前相单独接地时的故障点零序电流；超前相故障点零序电流始终大于其单独接地时的故障点零序电流。
同理，根据式（7）亦可得到C相故障点零序电流随两个过渡电阻的变化趋势如图4所示。可见，随着故障滞后相（C相）接地点过渡电阻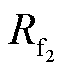的增大，两点接地时滞后相故障点零序电流单调减小；随着超前相故障点过渡电阻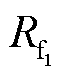的增大，零序电流呈现先减小后增大的趋势，最终无限趋近于滞后相单独接地时的故障点零序电流；当两个接地点过渡电阻满足式（8）时，两点接地时的滞后相故障点零序电流小于其单独接地时零序电流。
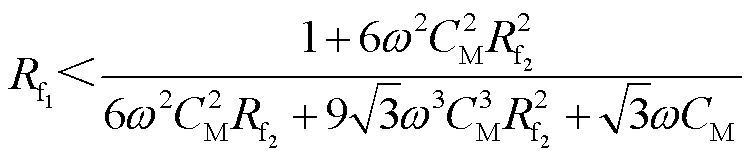（8）
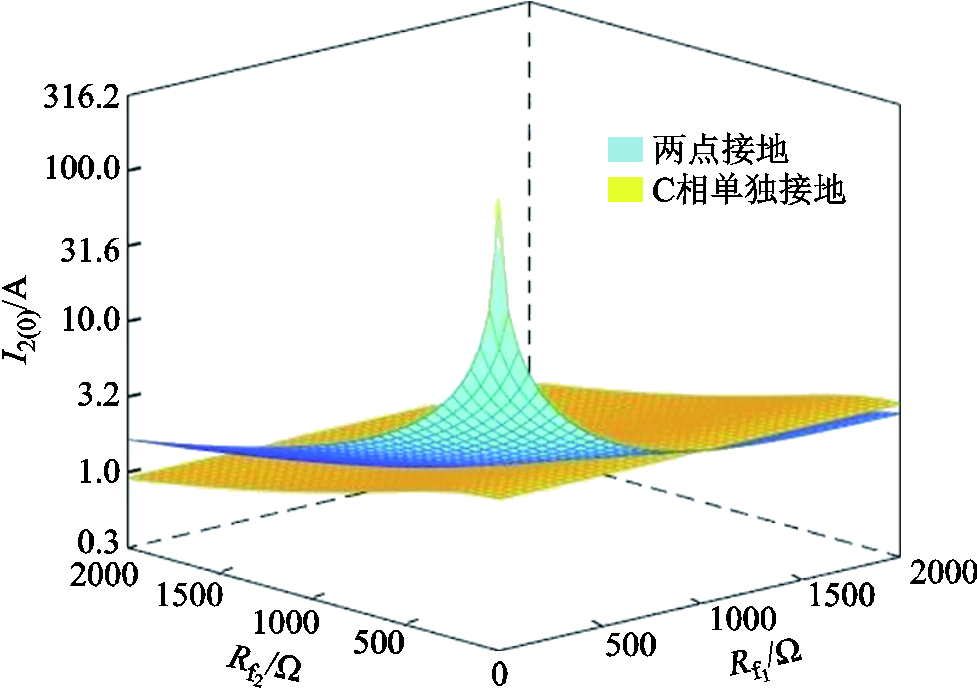
图4 C相故障点工频零序电流随过渡电阻的变化趋势
Fig.4 Tendency of power frequency current under phase C fault with the change of transition resistances
1.2.2 零序电压分析
将正负序网络的移相变压器移除，对复合序网进一步简化，根据基尔霍夫电压定理，可得故障点处零序电压表达式为
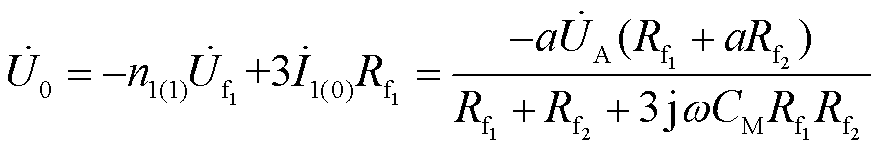（9）
由式（9）可得零序电压随两个过渡电阻的变化趋势，并将其与两个故障点单独接地时的零序电压作比较，如图5所示。
根据三种情况下的零序电压关系可知，当满足式（10）时，超前相单独接地时的零序电压大于两点接地时的零序电压。
图5 零序电压随两个过渡电阻大小的变化趋势
Fig.5 Tendency of zero-sequence voltage with the change of transition resistances
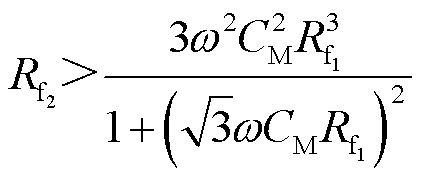（10）
同理，当满足式（11）时，滞后相单独接地时的零序电压大于两点接地时的零序电压。
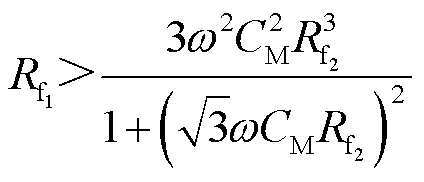（11）
同时满足式（10）和式（11），即两个故障点过渡电阻阻值相近时，两点接地时的零序电压要小于两条故障出线各自单独接地时的零序电压；在其他情况下，两点接地时的零序电压介于两条故障出线单独接地时的零序电压之间；而当两个接地点过渡电阻相差越大，两点接地的零序电压越接近于电阻较小故障点单独接地时的零序电压。
在零序网络中，由于线路阻抗与线路对地容抗相比小得多，可以忽略线路压降，即可认为系统中零序电压均满足上述规律。
据式（9），异名相两点接地时地电位轨迹如图6所示。
典型情况下地电位的变化规律为：
（1）当C相过渡电阻固定，B相过渡电阻为零时，异名相地电位位于点EB。随着B相过渡电阻不断增大，异名相两点接地故障地电位轨迹与C相单独接地时的地电位轨迹弧线ECN相交于点Gp（p=1,2,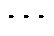
,7），体现为C相单点接地时的故障特征。
（2）随着C相过渡电阻增大，交点Gp不断向中性点N靠近，当两个故障点处过渡电阻都很大时，将不体现接地故障特征。
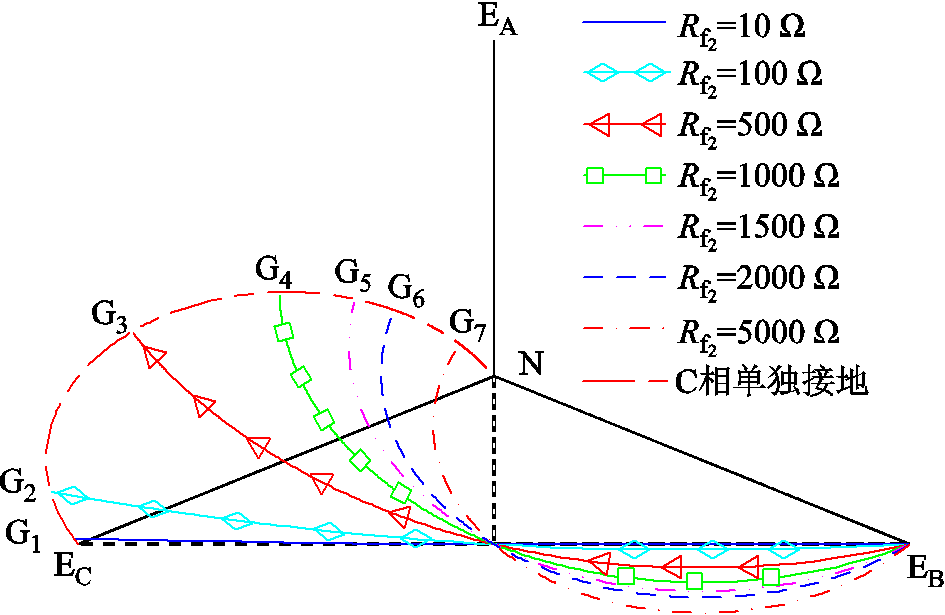
图6 异名相两点接地时的地电位分布
Fig.6 Distribution of ground potential when two-point grounding faults occurring on different phases
1.2.3 健全出线与故障出线工频零序电流分析
健全线路出口零序电流为零序电压激励下的对地零序电容电流，根据式（9）可得
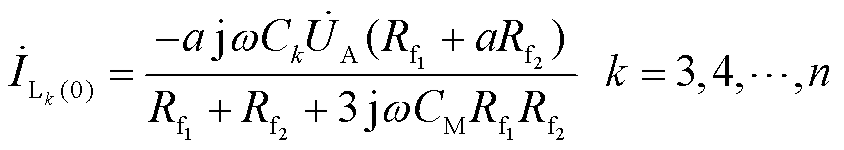（12）
即健全出线零序电流幅值与线路自身对地电容Ck成正比。结合式（9）和式（12）可知，伴随两个故障点过渡电阻的变化，健全出线零序电流幅值特征与零序电压的幅值特征相似；另外，健全出线零序电流的相位始终比零序电压相位超前π/2。
故障线路出口零序电流为故障点零序电流与线路自身对地电容电流的差值。
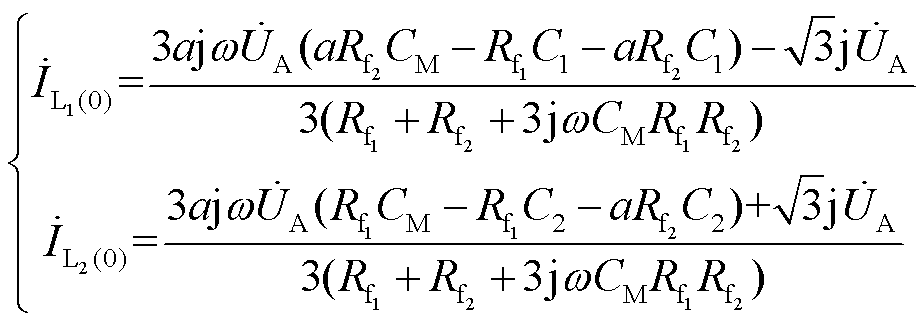（13）
式中，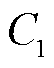
、
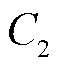分别为线路L1、L2自身对地电容。
进而，得到两条故障出线零序电流的比值为
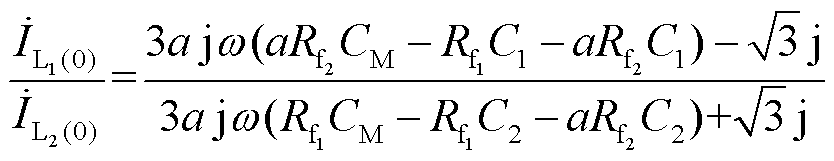（14）
将常用对地电容参数、工频角频率ω代入式（14）中，可知异名相两点接地时两条故障出线零序电流值的关系，主要与两个故障点过渡电阻及系统总对地电容相关。当满足式（15）时，有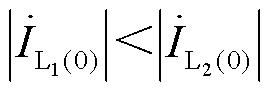
，即超前相故障出线零序电流的幅值小于滞后相故障出线零序电流。
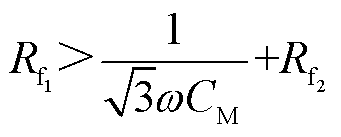（15）
两条故障出线零序电流与任意一条健全出线零序电流的比值为
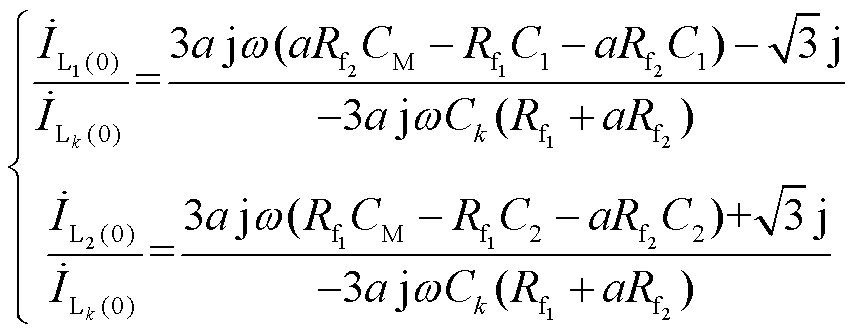（16）
由式（16）化简可得二者幅值之比为
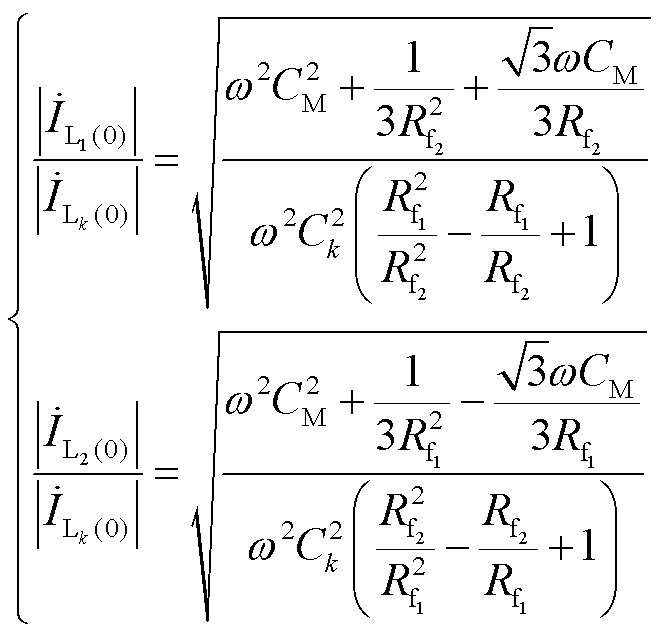（17）
当满足式（18）时，有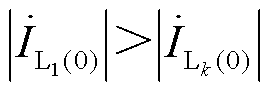
，即超前相故障出线零序电流的幅值大于健全出线零序电流。
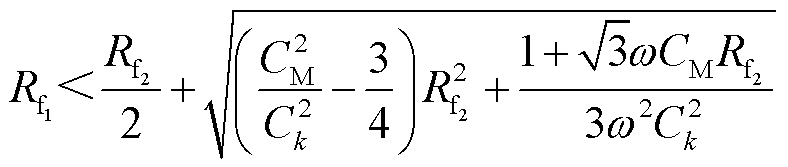（18）
当满足式（19）时，有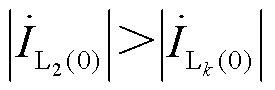
，即滞后相故障出线零序电流的幅值大于健全出线零序电流。
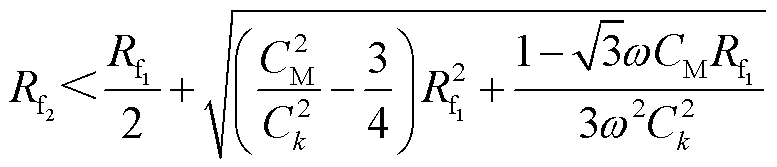（19）
通过分析可知，任何情况下式（18）和式（19）至少存在一个不等式成立，进而可以得到
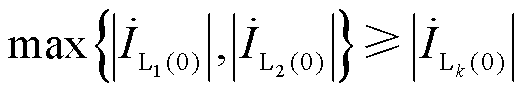（20）
根据式（16）可得两条故障出线零序电流与健全出线零序电流的相位差为
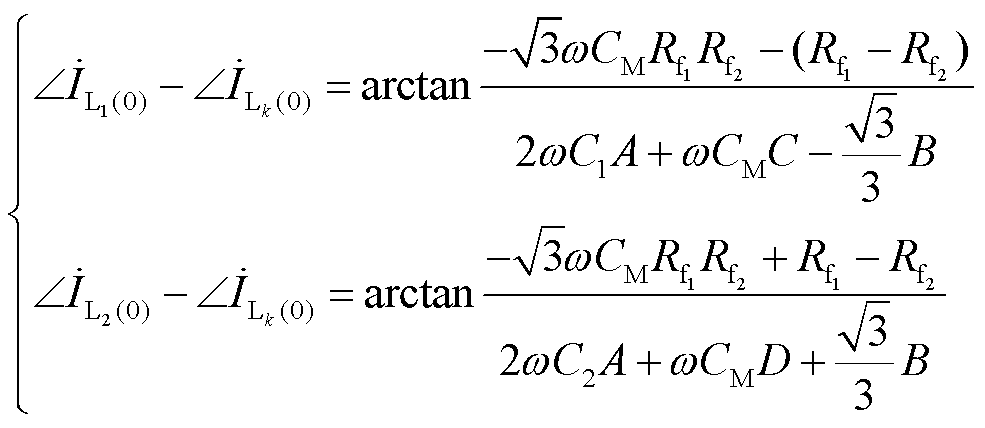（21）
其中
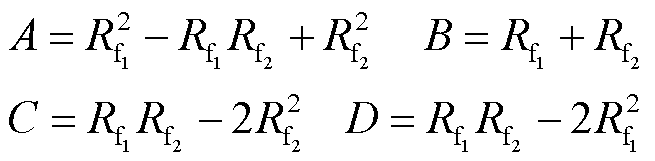
由式（21）可得，相位差与系统对地电容CM和故障线路对地电容C1、C2有关。当两个过渡电阻为定值时，超前相相位差与CM和C1分别成正比，滞后相相位差与CM成正比，与C2成反比。超前相故障出线零序电流与健全出线零序电流相位差为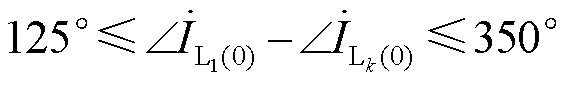
；滞后相故障出线零序电流与健全出线零序电流相位差为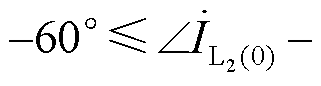
。
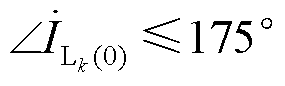综上可知，系统在异名相两点接地故障期间，至少存在一条故障出线零序电流的幅值大于各健全出线；两条故障出线零序电流与健全出线零序电流的相位差范围为
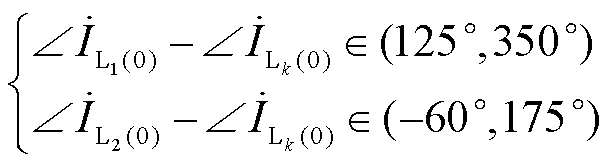（22）
对于不接地系统，可以利用故障工频信号实现选线，现有故障选线装置对单点接地故障选线的准确率较高，但绝大多数选线装置尚未具备两点接地故障的判断能力[22]。本节讨论异名相两点接地故障工频量信号对于现有选线原理的适用性，进而确定其对已有选线技术的影响并提出了选线技术发展建议。
根据1.2.2节分析，当两故障点过渡电阻相近时，两点接地时的零序电压幅值要小于两条故障出线各自单独接地时的零序电压；其余情况下，两点接地时的零序电压幅值介于两条故障出线单独接地时的零序电压之间。
现有选线方法常以零序电压幅值超越预设阈值作为故障启动条件，设该启动阈值为λUN，其中UN为系统额定相电压，λ为整定系数。可得到单点接地故障时，零序电压启动的最大过渡电阻Rx为
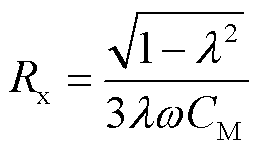（23）
当两点接地时，根据式（9），零序电压的启动条件为
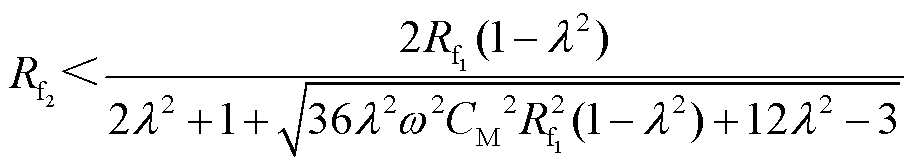（24）
以零序电压启动阈值为15%UN为例。根据式（23），单点接地时能够启动的最大过渡电阻Rx约为3 850 Ω。单点接地和两点接地期间，满足零序电压启动条件的过渡电阻变化区域如图7所示。
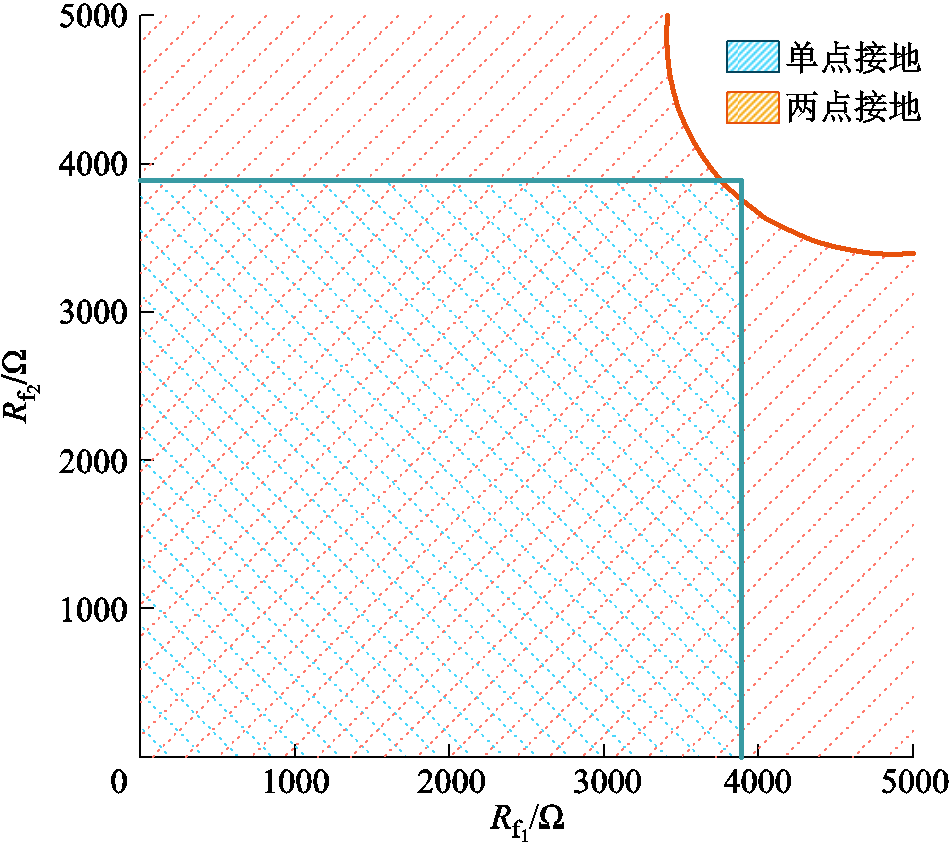
图7 满足零序电压启动阈值的区域
Fig.7 The area of meeting zero-sequence voltage start threshold
由图7可见，当发生单点接地故障，且首次故障的过渡电阻小于Rx时，系统零序电压始终大于零序电压启动阈值，满足选线装置启动要求；当相继发生第二次接地故障或同时发生两点接地故障时，只有在两个故障点过渡电阻均刚好接近耐过渡电阻能力最大值Rx的情况下，会导致系统零序电压略小于启动阈值，其余多数情况下仍可达到启动阈值水平。
若首次接地时的过渡电阻大于Rx，选线装置将无法启动，不能判断出首次接地故障的发生；当第二个故障点的过渡电阻较小，即满足式（24）时，会抬高系统零序电压，使选线装置满足零序电压启动判据，在两点接地期间启动。
常用的幅值比较法利用不接地系统故障出线工频零序电流幅值比健全出线大的特点，选择零序电流幅值最大的出线为故障出线，由于其不需设定阈值，使得比幅法具有一定的检测可靠性和灵敏度。根据式（20），发生异名相两点接地故障时，所有出线零序电流幅值最大的为其中一条故障出线。
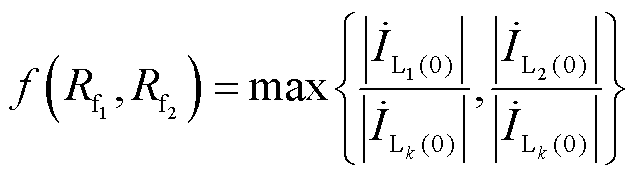（25）
式（25）表示在两条故障出线零序电流中，幅值较大者与健全出线零序电流幅值之比。以上文所述典型10 kV不接地系统为例，当两个故障点过渡电阻在0～5 kΩ范围内变化时，零序电流较大故障出线与健全出线的幅值比趋势如图8所示。
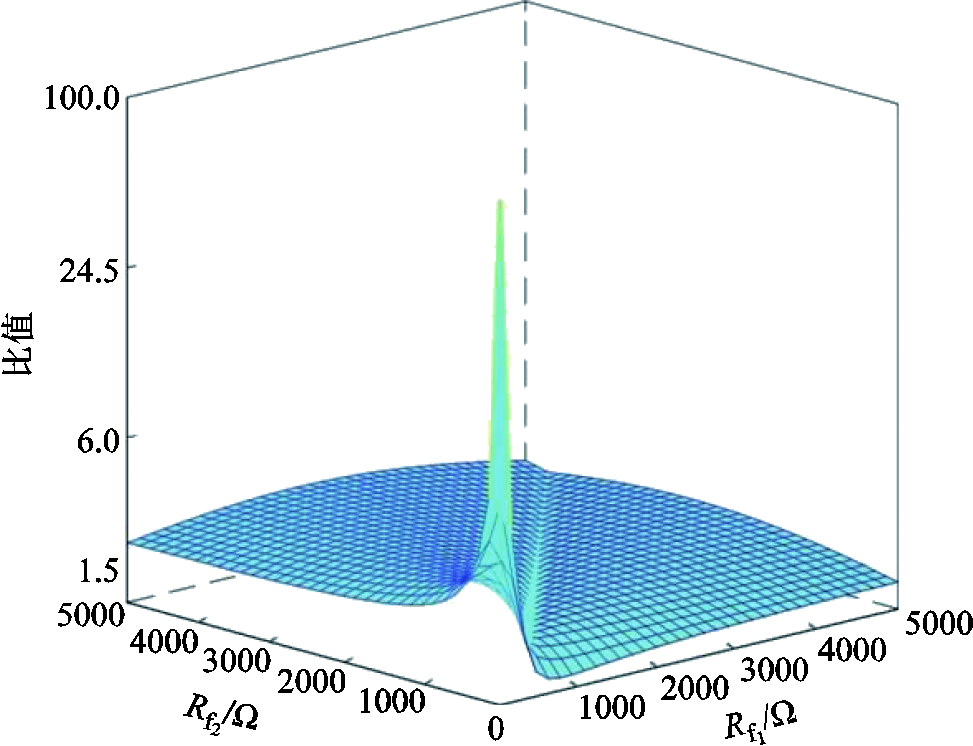
图8 零序电流较大故障出线与健全出线幅值比趋势
Fig.8 Trend of the amplitude ratio of zero-sequence current between faulty and healthy outlets
可以看出，当系统发生异名相两点接地故障时，至少存在一条故障出线零序电流幅值大于任意健全出线零序电流幅值。但目前安装在现场的常规选线装置只具有单点接地故障判断逻辑，无法检测到第二条故障出线的接地故障。
零序电流方向法是选择故障后与其他所有出线零序电流相位相反的出线为故障出线。由式（22）可知，当发生异名相两点接地故障时，两条故障出线与健全出线的工频零序电流相位关系并不是严格的反相关系，与两个故障相相序、两个故障点过渡电阻和系统总对地电容相关。
在现场实际应用中，当故障出线与健全出线零序电流的相位差α符合某一范围，即π-θ＜α＜π+θ时，则可认为故障出线与健全出线零序电流反相。假设整定值θ为π/6，根据式（21）可得
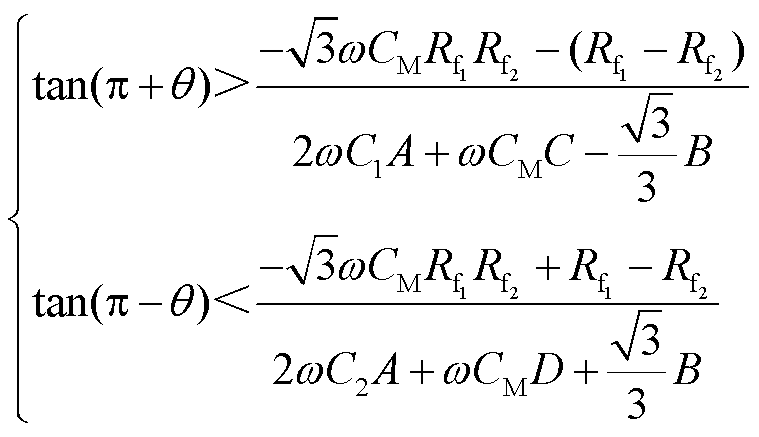（26）
结合式（22）故障出线与健全出线的相位差范围，可得到随着两个故障点过渡电阻的变化，在两点接地期间，利用零序电流相位信息选线的最大动作范围如图9所示。
可见，当两个故障点过渡电阻相差较大时，其中过渡电阻较小的故障出线相位能表现出明显的故障特征，与健全出线反相，而过渡电阻较大的故障出线则会被漏选。当两个过渡电阻相差不大且较小时，会漏选滞后相故障出线或拒动；当两个过渡电阻相差不大且较大时，均会拒动。
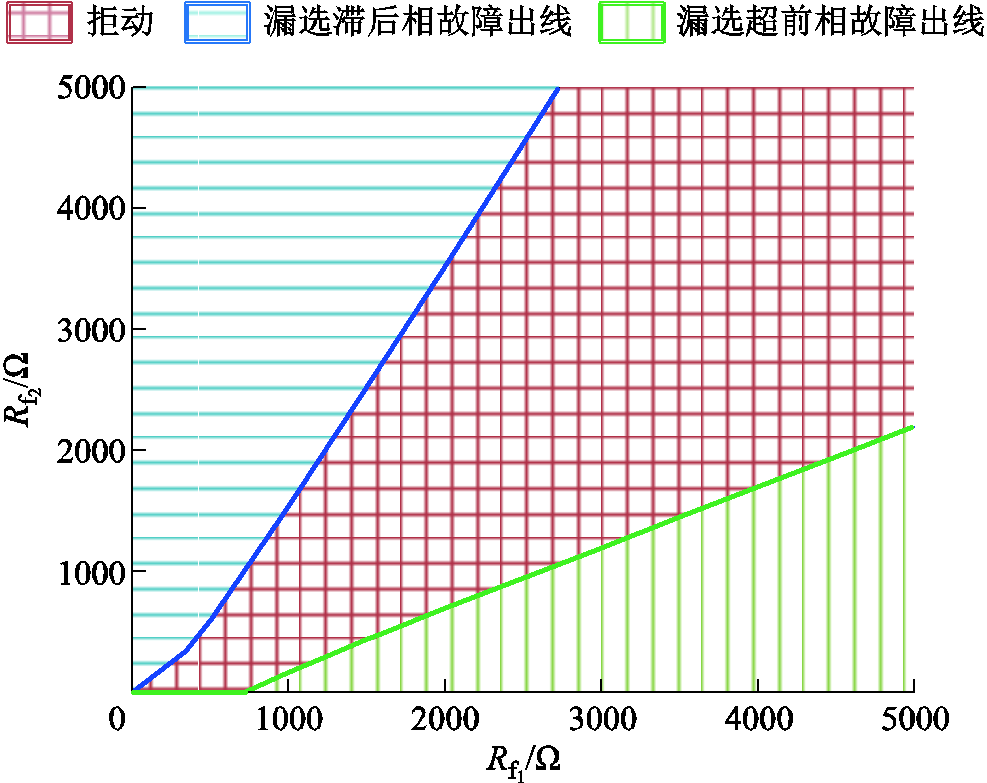
图9 选线动作情况
Fig.9 Analysis of line selection action
另外，群体比幅比相法综合利用了工频零序电流幅值与极性比较的优点，选出三条及以上工频零序电流幅值较大的出线作为候选线路，再通过相位比较选择出故障出线[27-28]。根据上述利用幅值信息进行选线的适应性分析，当系统发生异名相两点接地故障时，不能保证选出所有两条故障出线作为候选线路，可能会漏选；而由于两条故障出线的工频零序电流相位也不再具有明显的故障特征，该方法也极可能拒动。
对于传统单点接地故障，利用暂态信息进行选线拥有故障特征明显、准确率高的优势。但暂态选线技术依赖于故障发生瞬间的捕捉，故障暂态信息与故障时刻故障相的电压瞬时值关系密切。特别是对于不接地系统异名相两点接地故障，暂态法需要在故障持续期间进行连续检测，当后发故障初始相位太小、后发故障接地电阻较大且第二次接地故障发生在电压降低的非故障相时，暂态分量小且衰减速度快，容易错过暂态信息，此时只能用稳态信息进行选线。不接地系统异名相两点接地故障包括两点相继接地和两点同时刻接地两种情况，无论是相继接地故障还是同时刻接地故障，都存在两点同时接地的阶段，虽然部分稳态法只能正确选出一条故障线路，但是故障线路被切除后，只剩下一处接地故障，稳态量法就可以正确选出第二条故障线路并将其切除。稳态量法在两点接地故障选线中扮演了重要角色，提高了选线的准确率，降低了选线技术对于数字信号采集和处理能力的要求，节约了成本。
针对两点接地故障稳态选线技术的发展，可以在本文工频特征结论的基础上，进一步研究后发故障接地前后，故障线路与非故障线路工频特征的变化或研究先发故障线路切除前后，故障线路与非故障线路工频特征的变化。根据两个阶段故障线路与非故障线路工频特征变化差异，实现两点接地故障检测，并进一步缩短两点接地故障检测时间，提高检测效率。
针对两点接地故障暂态选线技术的发展，可以在本文工频特征结论的基础上，分析后发接地故障之后的间歇性弧光接地过程。当后发接地故障之后又发生了间歇性弧光接地故障，即后发接地故障之后又发生了熄弧再燃弧的情况，此时熄弧和燃弧的暂态分析与两点接地故障时稳态相关，针对以后两点接地故障暂态特征的研究可在本文稳态结论基础上进一步开展。
在Matlab/Simulink中搭建典型110 kV/10 kV中性点不接地系统异名相两点接地故障仿真模型，如图10所示。仿真模型中降压变压器高、低压侧额定电压分别为110 kV、10 kV，额定容量为20 MV·A；系统由电缆与架空线混合线路组成，母线处共设置五条出线（L1～L5），其中线路L1、L2分别发生B相、C相单点接地故障；线路参数采用文献[26]提供的标准参数，见表2；经计算可得，系统对地电容电流为10 A。
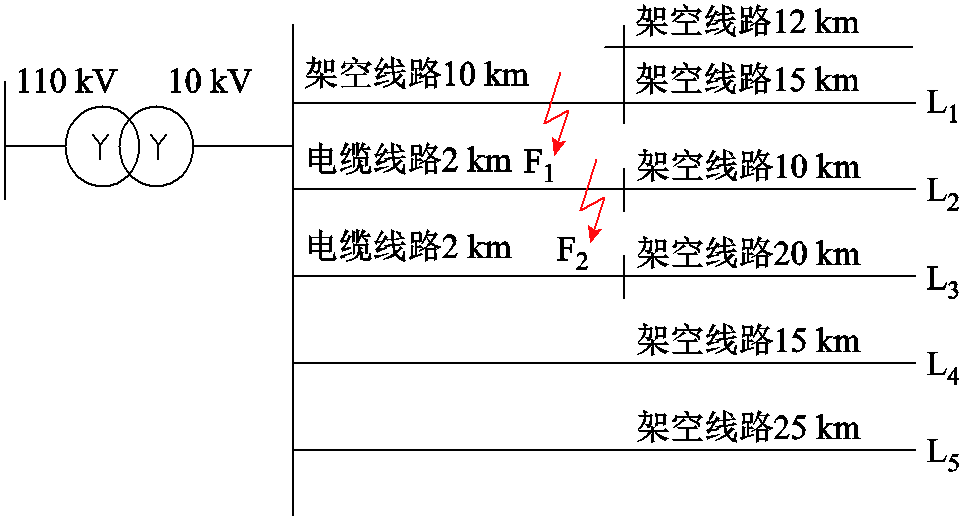
图10 仿真模型示意图
Fig.10 Schematic diagram of simulation model
表2 线路模型参数
Tab.2 Line model parameters
线路电阻/(Ω/km)电感/(mH/km)电容/(μF/km) 正序零序正序零序正序零序 架空线路0.170.321.023.560.120.006 电缆线路0.272.70.261.110.380.276
图11给出了当故障出线L1与L2的故障点过渡电阻分别为500 Ω和1 500 Ω时，系统仿真及根据式（7）和式（9）计算得出两个故障点工频电流和母线处零序电压的波形对比结果。
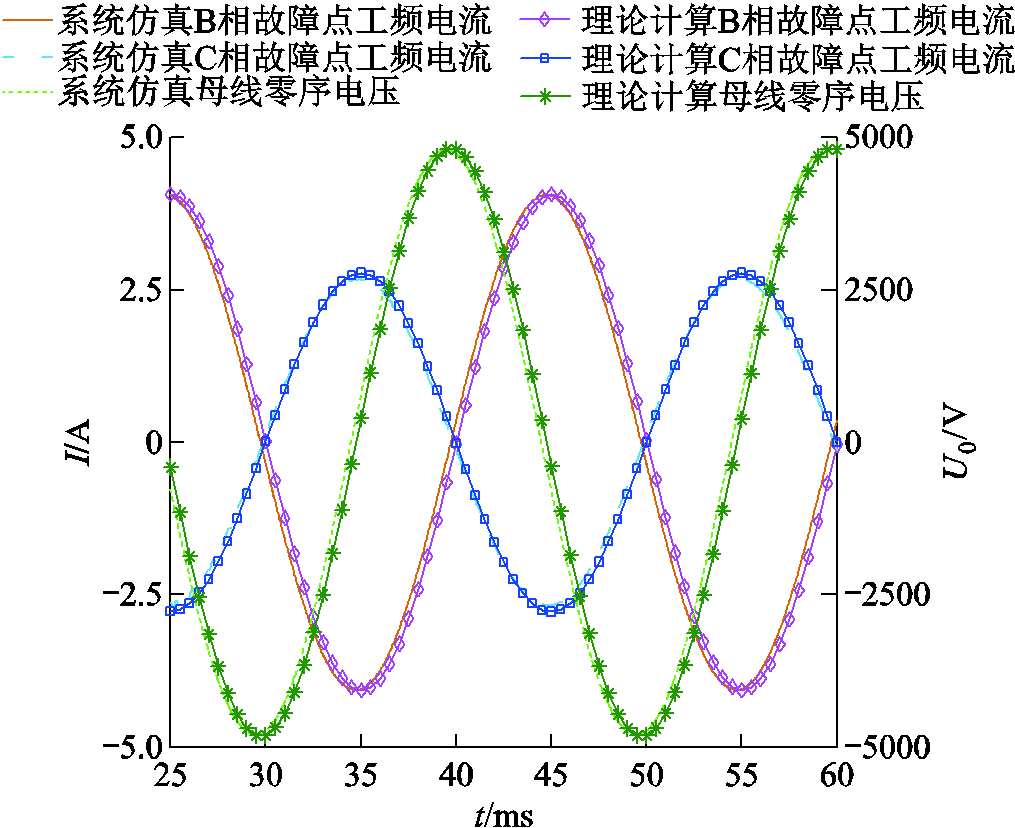
图11 理论计算值与仿真结果对比
Fig.11 Comparison of the calculated values and the simulation results
在不同过渡电阻下，两条故障出线L1、L2与健全出线L3的零序电流以及系统零序电压的仿真结果见表3。其中，故障出线与健全出线零序电流的相位差为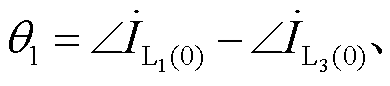
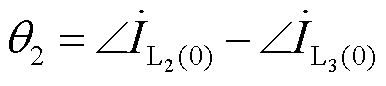。通过大量的仿真结果与理论计算的对比分析，二者结果一致，从而验证了本文理论计算部分的正确性。
从表3中仿真结果可知，系统发生异名相两点接地故障时，故障出线与健全出线零序电流幅值比和相位差的关系，与两故障点过渡电阻大小有关；一般情况下，两点接地时的零序电压幅值介于两条故障出线单独接地时的零序电压之间，只有当两个过渡电阻阻值相近时，两点接地时的零序电压幅值小于两条故障出线各自单独接地时的零序电压。
根据表3中选线结果可看出：当故障点过渡电阻较高时，系统零序电压未达到启动阈值水平，不能进入选线判别逻辑；异名相两点接地时，至少有一条故障出线零序电流幅值大于任意一条健全出线零序电流幅值，比较零序电流幅值可以且仅能选出其中一条故障出线；而两条故障出线零序电流与健全出线零序电流的相位差会受两个故障点过渡电阻影响，若使用零序电流方向法选线，将会漏选或拒动。以上结论，均与理论分析所得结果一致。
表3 不同过渡电阻下的数值仿真与已有选线方法结果
Tab.3 Results of simulation and existing line selection at different transition resistances
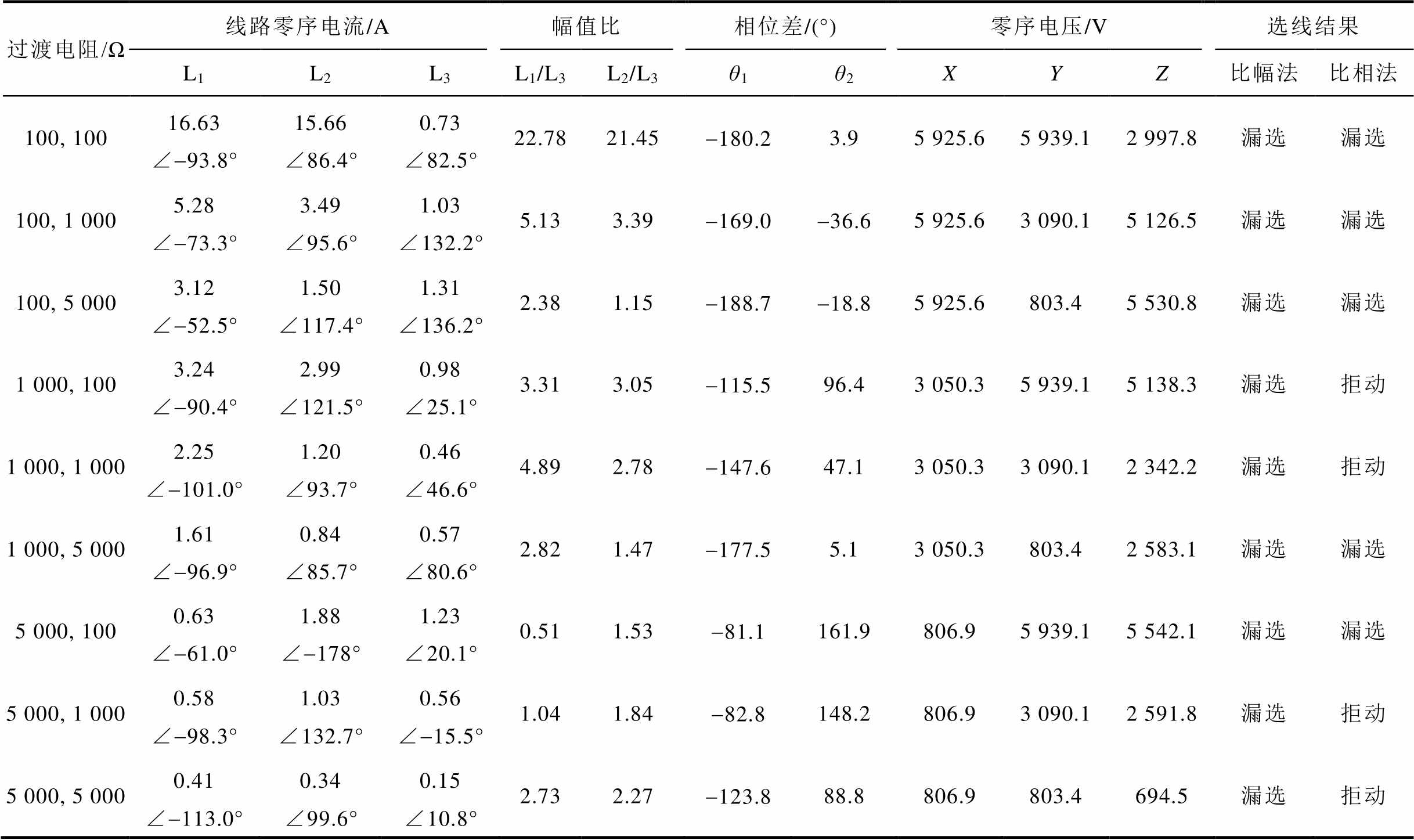
过渡电阻/Ω线路零序电流/A幅值比相位差/(°)零序电压/V选线结果 L1L2L3L1/L3L2/L3θ1θ2XYZ比幅法比相法 100, 10016.63∠-93.8°15.66∠86.4°0.73∠82.5°22.7821.45-180.23.95 925.65 939.12 997.8漏选漏选 100, 1 0005.28∠-73.3°3.49∠95.6°1.03∠132.2°5.133.39-169.0-36.65 925.63 090.15 126.5漏选漏选 100, 5 0003.12∠-52.5°1.50∠117.4°1.31∠136.2°2.381.15-188.7-18.85 925.6803.45 530.8漏选漏选 1 000, 1003.24∠-90.4°2.99∠121.5°0.98∠25.1°3.313.05-115.596.43 050.35 939.15 138.3漏选拒动 1 000, 1 0002.25∠-101.0°1.20∠93.7°0.46∠46.6°4.892.78-147.647.13 050.33 090.12 342.2漏选拒动 1 000, 5 0001.61∠-96.9°0.84∠85.7°0.57∠80.6°2.821.47-177.55.13 050.3803.42 583.1漏选漏选 5 000, 1000.63∠-61.0°1.88∠-178°1.23∠20.1°0.511.53-81.1161.9806.95 939.15 542.1漏选漏选 5 000, 1 0000.58∠-98.3°1.03∠132.7°0.56∠-15.5°1.041.84-82.8148.2806.93 090.12 591.8漏选拒动 5 000, 5 0000.41∠-113.0°0.34∠99.6°0.15∠10.8°2.732.27-123.888.8806.9803.4694.5漏选拒动
注：表中X、Y、Z分别表示L1单独接地、L2单独接地和两出线同时接地。
图12为山东某市DL变电站的现场故障波形，包含三条出线零序电流以及母线零序电压。系统为10 kV中性点不接地方式。经过查证，原为615线发生永久性接地故障，随后611线也发生了接地故障，形成两点接地。
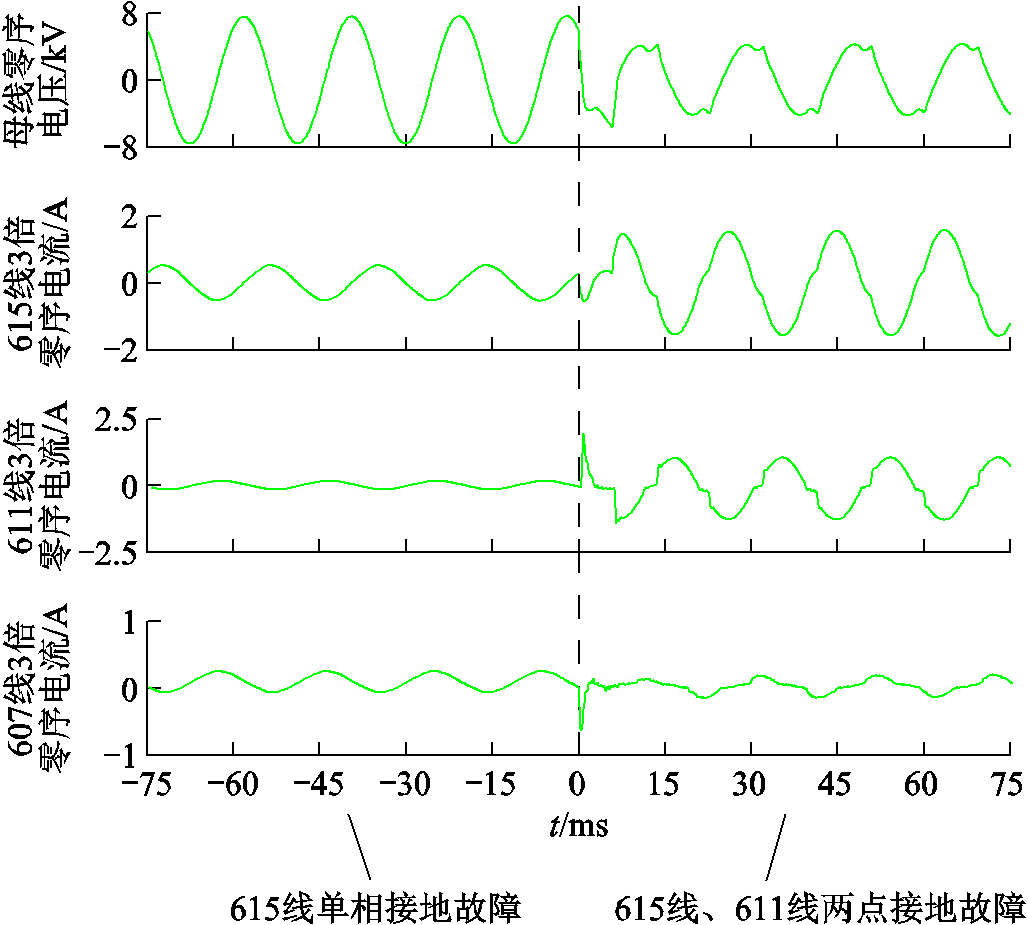
图12 现场故障电流以及母线零序电压波形
Fig.12 On-site waveforms of fault current and zero sequence voltage
通过现场录波可见，起初615线的零序电流相位与611线和607线零序电流近似相反，且615线幅值明显大于另两条出线，表现为典型的单点接地故障出线特征。当611线发生接地后，其工频零序电流幅值明显增大，相位与615线近似相反，而607线零序电流相位和611线近似相同、与615线近似相反，此时故障特征与单点接地时不再相同。与615线单独接地时零序电压相比，发生两点接地后母线零序电压幅值明显减小，可判断出先接地的故障点过渡电阻较小。
本文针对不接地系统异名相两点接地故障，根据故障边界条件建立其复合序网，推导出各故障工频电气量的解析表达式，并与两个故障点单独接地时的故障特征相比较。结果表明，当至少一个故障点过渡电阻较大时，异名相两点接地时工频零序电压与零序电流的幅值体现出单点接地的特征；至少存在一条故障出线的工频零序电流幅值大于健全出线；故障出线与健全出线工频零序电流的相位关系取决于两个故障相相序、两个故障点过渡电阻及系统对地总电容，一般不再有确定的相位关系；两点接地时的零序电压幅值在一般情况下介于两个故障点单独接地时的零序电压之间，当两个故障点过渡电阻相近时，两点接地时的零序电压最小。
对于不接地系统异名相两点接地故障，零序电压启动判据仍具有较高的耐过渡电阻能力，多数情况下可以达到启动阈值水平；两个故障线路出口零序电流一般既不符合故障线路特征也不符合健全线路特征，现有选线原理并不完全适用，利用幅值与相位信息进行选线，会发生漏选或拒动。
数字仿真和现场数据验证了本文理论分析部分的正确性，后续会进一步研究异名相两点接地时的暂态特征及其对暂态选线技术的影响。
参考文献
[1] 徐丙垠, 李天友, 薛永端. 配电网继电保护与自动化[M]. 北京: 中国电力出版社, 2017.
[2] 徐丙垠, 薛永端, 冯光, 等. 配电网接地故障保护若干问题的探讨[J]. 电力系统自动化, 2019, 43(20): 1-7. Xu Bingyin, Xue Yongduan, Feng Guang, et al. Discussion on several problems of earthing fault protection in distribution network[J]. Automation of Electric Power Systems, 2019, 43(20): 1-7.
[3] Topolanek D, Toman P, Ptacek M, et al. Evaluation of different solutions of faulted phase earthing technique for an earth fault current limitation[J]. CIRED - Open Access Proceedings Journal, 2017, 2017(1): 1107-1111.
[4] 王建元, 朱永涛, 秦思远. 基于方向行波能量的小电流接地系统故障选线方法[J]. 电工技术学报, 2021, 36(19): 4085-4096. Wang Jianyuan, Zhu Yongtao, Qin Siyuan. Fault line selection method for small current grounding system based on directional traveling wave energy[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4085-4096.
[5] 秦苏亚, 薛永端, 刘砾钲, 等. 有源配电网小电流接地故障暂态特征及其影响分析[J]. 电工技术学报, 2022, 37(3): 655-666. Qin Suya, Xue Yongduan, Liu Lizheng, et al. Transient characteristics and influence of small current grounding faults in active distribution network[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 655-666.
[6] Ding Xiaobing, Shi Zebing, Yu Jiang, et al. Protection method of small current grounding system based on phase current variation[C]//2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 2021: 243-247.
[7] 王晓卫, 刘伟博, 郭亮, 等. 基于不同时段内积投影的灵活接地系统高阻故障选线方法[J/OL]. 电工技术学报, 2023[2023-03-25].DOI:10.19595/j.cnki. 1000-6753.tces.221878. Wang Xiaowei, Liu Weibo, Guo Liang, et al. High impedance fault line selection method based on inner product projection of different time periods for flexible grounding systems[J/OL]. Transactions of China Electrotechnical Society, 2023[2023-03-25]. DOI:10.19595/j.cnki. 1000-6753.tces.221878.
[8] 喻锟, 胥鹏博, 曾祥君, 等. 基于模糊测度融合诊断的配电网接地故障选线[J]. 电工技术学报, 2022, 37(3): 623-633. Yu Kun, Xu Pengbo, Zeng Xiangjun, et al. Grounding fault line selection of distribution networks based on fuzzy measures integrated diagnosis[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 623-633.
[9] 张明一, 孙元章, 黎雄, 等. 改进时域反演算法在配电网故障定位中的应用[J]. 电力系统自动化, 2021, 45(15): 101-108. Zhang Mingyi, Sun Yuanzhang, Li Xiong, et al. Application of improved time reversal algorithm in fault location for distribution network[J]. Automation of Electric Power Systems, 2021, 45(15): 101-108.
[10] 明志强, 许虎. 经消弧线圈接地系统的中电阻快速选线方法[J]. 电网技术, 2009, 33(12): 112-114. Ming Zhiqiang, Xu Hu. Fast line selection method of medium resistance in grounding system via arc suppression coil[J]. Power System Technology, 2009, 33(12): 112-114.
[11] 李振兴, 万佳灵, 王新, 等. 基于中值电阻投切的故障选线与定位新方法[J]. 电力系统保护与控制, 2021, 49(7): 57-65. Li Zhenxing, Wan Jialing, Wang Xin, et al. A new method of fault line selection and location based on median resistance switching[J]. Power System Protection and Control, 2021, 49(7): 57-65.
[12] 邹浩斌, 胡少强, 刘利平, 等. 基于小扰动原理的单相接地选线装置[J]. 继电器, 2007, 35(2): 20-24. Zou Haobin, Hu Shaoqiang, Liu Liping, et al. Single-phase grounding line selection device based on small disturbance principle[J]. Power System Protection and Control, 2007, 35(2): 20-24.
[13] 王建元, 张峥. 基于注入信号与小波能量的小电流接地故障选线研究[J]. 电测与仪表, 2018, 55(5): 28-32. Wang Jianyuan, Zhang Zheng. Research on fault line selection of small current grounding based on injected signal and wavelet energy[J]. Electrical Measurement & Instrumentation, 2018, 55(5): 28-32.
[14] 栾晓明, 武守远, 贾春娟, 等. 基于改进零序导纳法的单相接地故障选线原理[J]. 电网技术, 2022, 46(1): 353-360. Luan Xiaoming, Wu Shouyuan, Jia Chunjuan, et al. Fault line selection principle of single-phase-to-ground fault based on improved zero-sequence admittance[J]. Power System Technology, 2022, 46(1): 353-360.
[15] Costa F B, Souza B A, Brito N S D, et al. Real-time detection of transients induced by high-impedance faults based on the boundary wavelet transform[J]. IEEE Transactions on Industry Applications, 2015, 51(6): 5312-5323.
[16] 叶宝柱, 薛超宇, 张惠娟, 等. 基于特征频带小波包分析的配电网故障选线的研究[J]. 电气工程学报, 2018, 13(2): 24-28. Ye Baozhu, Xue Chaoyu, Zhang Huijuan, et al. Research on fault line selection in distribution network based on feature band wavelet packet analysis[J]. Journal of Electrical Engineering, 2018, 13(2): 24-28.
[17] 贾清泉, 刘连光, 杨以涵, 等. 应用小波检测故障突变特性实现配电网小电流故障选线保护[J]. 中国电机工程学报, 2001, 21(10): 78-82. Jia Qingquan, Liu Lianguang, Yang Yihan, et al. Abrupt change detection with wavelet for small current fault relaying[J]. Proceedings of the CSEE, 2001, 21(10): 78-82.
[18] 管廷龙, 薛永端, 徐丙垠. 基于故障相电压极化量的谐振接地系统高阻故障方向检测方法[J]. 电力系统保护与控制, 2020, 48(23): 73-81. Guan Tinglong, Xue Yongduan, Xu Bingyin. Method for detecting high-impedance fault direction in a resonant grounding system based on voltage polarization of the fault phase[J]. Power System Protection and Control, 2020, 48(23): 73-81.
[19] 薛永端, 张秋凤, 颜廷纯, 等. 综合暂态与工频信息的谐振接地系统小电流接地故障选线[J]. 电力系统自动化, 2014, 38(24): 80-85. Xue Yongduan, Zhang Qiufeng, Yan Tingchun, et al. Faulty feeder identification based on combined transient and power-frequency components in resonant grounded systems[J]. Automation of Electric Power Systems, 2014, 38(24): 80-85.
[20] 金鑫, 薛永端, 彭振华, 等. 仅利用零序电流的谐振接地系统接地故障方向算法[J]. 电力系统自动化, 2020, 44(9): 164-170. Jin Xin, Xue Yongduan, Peng Zhenhua, et al. Grounding fault direction algorithm using zero-sequence current in resonant grounding system[J]. Automation of Electric Power Systems, 2020, 44(9): 164-170.
[21] 薛禹胜, 谢云云, 文福拴, 等. 关于电力系统相继故障研究的评述[J]. 电力系统自动化, 2013, 37(19): 1-9, 40. Xue Yusheng, Xie Yunyun, Wen Fushuan, et al. A review on cascading failures in power systems[J]. Automation of Electric Power Systems, 2013, 37(19): 1-9, 40.
[22] 吴凤翔, 顾兆雄. 小电流接地系统两点接地故障仿真分析[J]. 上海电力大学学报, 2020, 36(6): 524-528. Wu Fengxiang, Gu Zhaoxiong. Analysis of the cross-country grounded fault in the low current grounded system[J]. Journal of Shanghai University of Electric Power, 2020, 36(6): 524-528.
[23] 欧阳健娜, 俞小勇, 周杨珺, 等. 配网线路两点相继接地故障选线方法[J]. 南方电网技术, 2020, 14(6): 81-89. Ouyang Jianna, Yu Xiaoyong, Zhou Yangjun, et al. A fault line selection method for two-point successive grounding of power distribution lines[J]. Southern Power System Technology, 2020, 14(6): 81-89.
[24] 吴争荣, 蔡颖倩, 张俊潇, 等. 消弧线圈接地系统同母多回线相继故障分析[J]. 高电压技术, 2017, 43(7): 2402-2409. Wu Zhengrong, Cai Yingqian, Zhang Junxiao, et al. Fault analysis on successive fault of multi-feeders connected to the same bus in resonant grounding system[J]. High Voltage Engineering, 2017, 43(7): 2402-2409.
[25] 刘万顺, 黄少锋, 徐玉琴. 电力系统故障分析[M]. 3版. 北京: 中国电力出版社, 2010.
[26] 中华人民共和国住房和城乡建设部, 国家质量监督检验检疫总局. 城市配电网规划设计规范: GB 50613—2010[S]. 北京: 中国计划出版社, 2011.
[27] 徐丙垠, 薛永端, 李天友, 等. 小电流接地故障选线技术综述[J]. 电力设备, 2005(4): 1-7. Xu Bingyin, Xue Yongduan, Li Tianyou, et al. Review of line selection of grounding fault in non - effectively grounding network techniques[J]. Electrical Equipment, 2005(4): 1-7.
[28] 李鑫. 配电线路单相接地故障定位及选线研究[D]. 北京: 华北电力大学, 2018.
Abstract In isolated neutral system, when two-point grounding faults occurring on different phases take place and at least one of the transition resistances is large, the outgoing protection with the small fault current can not be directly removed, it still need to rely on the line selection device to achieve protection. At present, there are some problems in the research on the two-point grounding fault of the small current grounding system, such as lack of quantitative analysis, lack of line selection effect analysis, and difficult to be applied in practiceet al. To address these issues, based on the fault equivalent circuit, this paper analyzes the power frequency fault characteristics for two-point grounding faults occurring on different phases in isolated neutral system. Based on the fault characteristics, the adaptability of the existing power frequency line selection methods to the two-point grounding fault of the different phase is analyzed and the development suggestion of line selection technology is put forward.
Firstly, Setting up the compound sequence network of two-point grounding faults occurring on different phases, using the nodal impedance matrixes to respectively deduce the expressions of power frequency components, such as two grounding fault point currents, zero-sequence voltage, and so on. Secondly, analyze the characteristics of two-point grounding fault power frequency electrical quantity with the change of the transition resistances in ungrounded systems and compare them with the characteristics of single-point grounding faults. Finally, according to the fault characteristics, the limitation of the existing line selection methods are analyzed, and the development ideas of two-point grounding fault line selection technology are put forward.
The results show that, when the transition resistance of at least one fault point is large, the amplitudes of zero-sequence voltage and zero-sequence current of power frequency in two-point grounding of the different phase show the characteristics of single-point grounding. At least one fault feeder has a power frequency zero-sequence current amplitude greater than that of the healthy feeder. The phase relationship of zero-sequence current of power frequency between the fault feeder and health feeder depends on two fault phase sequences, transition resistance of two fault points and total capacitance to the ground of the system. Generally, there is no definite phase relationship. In general, the zero-sequence voltage amplitude when two fault points are grounded is between the zero-sequence voltage when two fault points are grounded separately. When the transition resistance of two fault points is similar, the zero-sequence voltage when two fault points are grounded is minimum. For two-point grounding faults occurring on different phases in isolated neutral system, the zero-sequence voltage starting criterion still has high resistance to transition resistance and can reach the threshold value in most cases.
The zero-sequence current at the outlet of two fault lines generally does not conform to the characteristics of both fault feeder and healthy feeder, and the existing line selection principle is not fully applicable. When the amplitude and phase information are used for line selection, missing selection or rejection will occur.
Development suggestions of line selection technology: (1) As for the development of steady-state line selection technology for two-point grounding fault, based on the conclusions of power frequency characteristics, the change of power frequency characteristics of faulty line and non-faulty line before and after subsequent fault, or the change of power frequency characteristics of faulty line and non-faulty line before and after first fault line removal can be further studied. According to the difference of power frequency characteristics between fault line and non-fault line in two stages, two-point grounding fault detection is realized and the detection time is further shortened to improve detection efficiency. (2) As for the development of transient line selection technology for two-point grounding fault, based on the conclusions of power frequency characteristics, the intermittent arc grounding process after subsequent fault can be analyzed.
Keywords：Isolated neutral system, two-point grounding faults occurring on different phases, power frequency components, the steady-state line selection
国家自然科学基金项目（52077221）和南方电网公司科技项目（046000KK52220008）资助。
收稿日期 2022-04-01
DOI:10.19595/j.cnki.1000-6753.tces.220473
中图分类号：TM713
亓志滨 男，1998年生，硕士研究生，研究方向为配电网接地故障检测与保护。E-mail：qizhibin90@126.com
田君杨 男，1981年生，博士，高级工程师，研究方向为电力系统继电保护与优化运行。E-mail：sumtjy@163.com（通信作者）
改稿日期 2023-03-27
（编辑 赫蕾）