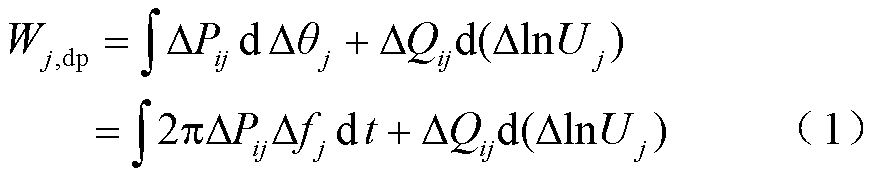
摘要 近年来，电力系统强迫振荡在电网中频繁发生，严重威胁到电网的安全稳定运行，快速、准确地定位强迫振荡源对抑制强迫振荡具有重要意义，但现有方法在分解具有高差异度多通道广域量测信息时难以准确提取强迫振荡模式分量，严重影响到强迫振荡源定位精度。为此，该文提出一种基于自适应投影多元经验模态分解（APIT-MEMD）的强迫振荡源定位方法。该方法首先采用APIT-MEMD通过构建自适应投影方向向量，实现对发电机多通道广域量测信息的同步分解，分离出表征不同振荡模式的固有模态函数（IMF）分量；然后，借助对数能量熵从众多IMF分量中提取出含强迫振荡模式的IMF分量；在此基础上，根据提取出的强迫振荡IMF分量，计算各发电机的耗散能量流，根据耗散能量流实现强迫振荡源定位；最后，通过WECC 179节点测试系统仿真数据和实际电网同步相量测量装置（PMU）实测数据对所提方法进行分析、验证，结果验证了所提方法的准确性和实用性。
关键词：电力系统 强迫振荡 振荡源定位 自适应投影多元经验模态分解 固有模态函数 耗散能量流
近年来，电力系统强迫振荡在电网中频繁发生，已成为威胁电网安全稳定运行的主要因素之一[1-3]。当强迫振荡的频率与系统固有振荡频率相同或接近时，将引发严重的共振现象，持续的共振将导致联络线传输功率降低，严重时有可能造成系统大规模解列[4-6]。针对强迫振荡具有明确扰动源，且失去扰动源后振荡将快速平息的特点，实际工程中较为常用的抑制措施是快速定位振荡源，进而切除强迫振荡源。因此，快速、准确地定位强迫振荡源是抑制强迫振荡的关键[7-9]。
为有效定位电力系统强迫振荡源，文献[10]根据强迫振荡期间相邻量测点间行波波速是否发生变化，实现振荡源定位；文献[11]利用广域量测信息构建割集能量，根据割集能量变化特点定位振荡源所在区域；文献[12]提出了耗散能量流（Dissipation Energy Flow, DEF）的相关理论，从能量的产生与消耗角度辨识振荡源，该方法仅需同步相量测量装置（Phasor Measurement Unit, PMU）的实测信息即可定位强迫振荡源；文献[13]在文献[12]的基础上改进了传统DEF的计算方法，所提方法无需估计各电气量稳态值，简化了计算过程。上述基于DEF的强迫振荡源定位方法因物理意义明确、定位效果良好，已在电网得到广泛应用。
然而在实际电网中，各PMU采集的量测信息中除强迫振荡模式信息外，还包含大量的冗余信息和噪声信息，无法直接用于耗散能量的计算。快速、准确地提取广域量测信息中的强迫振荡分量是提升强迫振荡源定位精度的关键[14]。为此，文献[15]引入带通滤波（Band-pass Filter, BF）提取广域量测信息中的强迫振荡模式分量定位强迫振荡源，有效地提升了强迫振荡源定位的精度和效率；文献[16]采用短时傅里叶同步压缩变换提取强迫振荡分量，进而借助DEF定位强迫振荡源；文献[17]提出采用连续小波变换（Continuous Wavelet Transform, CWT）分离出广域量测信息中表征强迫振荡的关键小波系数，有效避免了冗余信息和量测噪声对振荡源定位的干扰；文献[18]采用经验模态分解（Empirical Mode Decomposition, EMD），从广域量测信息中分解出含强迫振荡模式的固有本征模态分量（Intrinsic Mode Function, IMF），然后利用含强迫振荡模式的IMF分量计算系统强迫振荡期间各支路的势能变化量，根据支路势能变化趋势实现振荡源的自动识别。上述方法虽可有效地提取广域量测信息中的强迫振荡分量，但均为单通道方法，需对各通道量测信息逐一分解，计算效率较低且无法充分表征多通道量测信息间的相关性，导致各通道分离出的强迫振荡特征分量不同步，影响了振荡源定位的精度。为此，文献[19]采用多元经验模态分解（Multivariate EMD, MEMD）从多通道量测信息中同步提取出强迫振荡IMF分量，实现了强迫振荡源准确定位。
上述方法虽可提取广域量测信息中的强迫振荡分量进而实现强迫振荡源定位，但受算法复杂度、通道量测信息差异化、噪声等因素影响，现有方法对电力系统多通道量测信息中强迫振荡分量的提取效果仍有待完善，强迫振荡源定位精度和效率需进一步提升。为此，本文提出一种基于自适应投影多元经验模态分解（Adaptive-Projection Intrinsically Transformed Multivariate Empirical Mode Decomposition, APIT-MEMD）的强迫振荡源定位方法，首先，该方法通过构建自适应投影方向向量，将电力系统多通道广域量测信息自适应地分解为表征不同振荡模式的IMF分量；然后，借助IMF的对数能量熵筛选出含强迫振荡模式的IMF分量；在此基础上，根据所分解的含强迫振荡模式的IMF分量，计算各发电机耗散能量流，并依据强迫振荡源判据定位强迫振荡源；最后，以WECC 179节点测试系统仿真数据和实际电网强迫振荡PMU实测数据验证所提方法准确性和有效性。
当电力系统发生强迫振荡时，强迫振荡源将持续向网络注入能量，而非振荡源将持续从网络吸收能量。根据这一特点，文献[12]基于电力系统广域量测信息提出一种采用耗散能量流定位强迫振荡源的新方法，该方法定义节点i经支路Lij流入发电机j的耗散能量流为
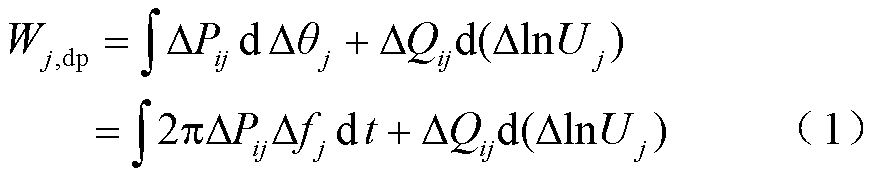
式中，Wj,dp为支路流入发电机j的耗散能量；ΔlnUj和Δθj分别为发电机j的电压幅值对数和电压相角相对稳态值的变化量；ΔPij和ΔQij分别为支路Lij的有功功率和无功功率相对稳态值的变化量；Δfj为发电机j的频率相对稳态值的变化量。
由式（1）求得发电机的耗散能量，根据基于耗散能量流的强迫振荡源定位判据可知[12]：若发电机j的Wj,dp为非负值，且变化趋势向上或保持不变，则发电机j持续吸收电网的振荡能量，为非振荡源；若发电机j的Wj,dp为负值，且变化趋势向下，则发电机j持续向电网中注入能量，为振荡源。
第1节简要介绍了基于广域量测信息的耗散能量流实用计算方法。然而实际应用时，为提高强迫振荡源定位的精度，需从广域量测信息中分解出含强迫振荡模式的时域分量，进而根据分解出的强迫振荡时域分量计算各发电机的耗散能量流。为此，本节引入APIT-MEMD对电力系统广域量测信息进行分解，以高精度提取电力系统的强迫振荡分量。
不同于MEMD，APIT-MEMD根据多通道量测信息在不同量测通道内的不均衡度，自适应调整投影方向，选取最优投影向量估计多通道量测信息的局部最优均值，实现多通道广域量测信息中强迫振荡分量的有效分离。
以发电机j处PMU采集的电压幅值、频率、有功功率和无功功率变化量构成的多通道量测信息矩阵Sj(t)为例，采用APIT-MEMD分解强迫振荡模式分量的基本原理如下：
首先，对多通道信号Sj(t)构建协方差矩阵C=E{SjT(t)Sj(t)}，其中E{·}是数学期望算子；对C进行特征分解得到对应的特征值及特征向量，即C=UΛUT，其中，Λ为特征值矩阵，U为对应特征向量矩阵；由于最大特征值λ1对应的左特征向量ν1表征了各量测通道内的最大不平衡度[21]，可自适应地确定量测信号的相关性；然后，通过在n维空间内构建与ν1方向完全相反的方向向量ν01=-ν1。根据ν1和ν01的方向重新定位投影生成的自适应方向向量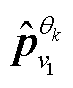
及
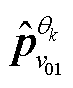；最后，将多通道信号Sj(t)沿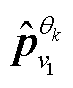及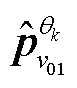
投影，并对投影信号极值点进行插值计算求取其多元包络线的局部均值，逐次生成IMF分量。
综上所述，采用APIT-MEMD分解多通道量测信号Sj(t)的详细流程如下[22]：
（1）对多通道信号Sj(t)的协方差矩阵C进行特征分解，得到特征值矩阵Λ及特征向量矩阵U，筛选出最大特征值λ1对应的左特征向量ν1。
（2）在n维空间内构造与ν1方向完全相反的向量ν01，即ν01=-ν1。
（3）在n-1维超球面建立Hammersley采样点集，生成一组方向向量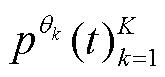
，进而计算各个方向向量到ν1的欧氏距离。
（4）针对与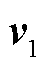
强相关的方向向量
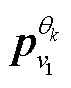，采用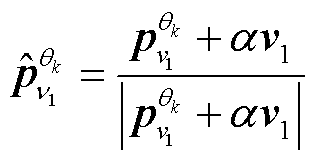
重新构建方向向量，其中α为各量测通道内信息的不平衡系数，其取值为[0, 1]。
（5）针对与ν01强相关的方向向量
，采用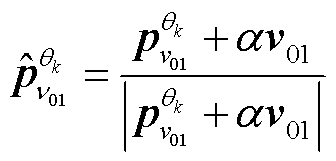
重新构建方向向量。
（6）采用自适应方向向量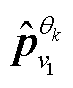及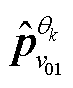进行高维空间局部均值m(t)估计。
需要指出的是：方向向量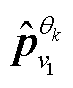与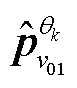的分布取决于α的取值。当α=0时，表明各量测通道间不存在信息不平衡，此时投影策略与MEMD一致；当α=1时，表明各量测通道间信息不平衡度极高。
通过逐次求取自适应局部均值，APIT-MEMD可将多通道量测信号分解为多组表征不同振荡模式的IMF矩阵与残差之和，经APIT-MEMD分解后的Sj(t)可表示为
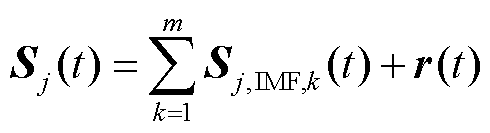（2）
式中，m为APIT-MEMD分解的IMF分量数量；r(t)为残差；Sj,IMF,k(t)为多通道量测信息矩阵Sj(t)的第k个IMF矩阵，表征了多通道量测信息的第k个振荡模式分量矩阵，即Sj,IMF,k(t)中各量测通道的IMF分量均含有相同的第k个振荡模式。
相对于EMD和MEMD，APIT-MEMD虽可更准确地估计电力系统多通道广域量测信息的局部最优均值，改善强迫振荡IMF分量的分解效果，但仍需从众多IMF分量中提取含系统强迫振荡模式的IMF分量。为此，本文引入对数能量熵来甄别含强迫振荡模式的IMF分量。
对于2.1节分解出的IMF分量Sj,IMF,k(t)，考虑到Sj,IMF,k(t)为发电机j电压幅值对数、频率、有功功率和无功功率变化量构成的多通道信号，因此需单独计算上述各电气量IMF的对数能量熵。以离散形式的电压幅值对数变化量的IMF分量ΔlnUj,IMF,k(τ)为例，其对数能量熵可定义为[2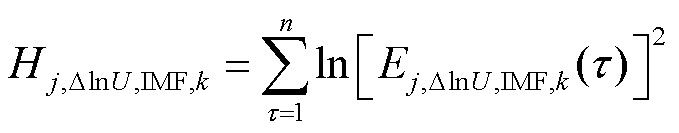3]
（3）
式中，τ为信号的离散采样点；n为IMF信号离散采样点的数量；Ej,ΔlnU,IMF,k(τ)为Sj,ΔlnU,IMF,k(τ)在采样点τ处的能量值，其中Ej,ΔlnU,IMF,k(τ)为[23]
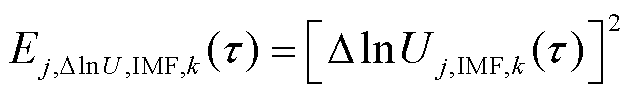（4）
类似地，根据式（3）可计算各通道量测信息IMF分量的对数能量熵。通常，对数能量熵越高的IMF分量包含的振荡信息量越大。为此，本文将各通道量测信息中对数能量熵最高的IMF分量认为是表征系统强迫振荡模式的IMF分量。
本节进一步利用APIT-MEMD分解出的强迫振荡模式IMF分量计算各发电机耗散能量，进而依据基于耗散能量流的振荡源判据，定位强迫振荡源。
针对获取的广域量测信息，首先以发电机为单元，构建含电压幅值对数、频率、有功功率和无功功率变化量的多通道量测信息矩阵S。以发电机j为例，含发电机j的电压幅值对数、频率、有功功率和无功功率变化量的多通道量测信息矩阵Sj为
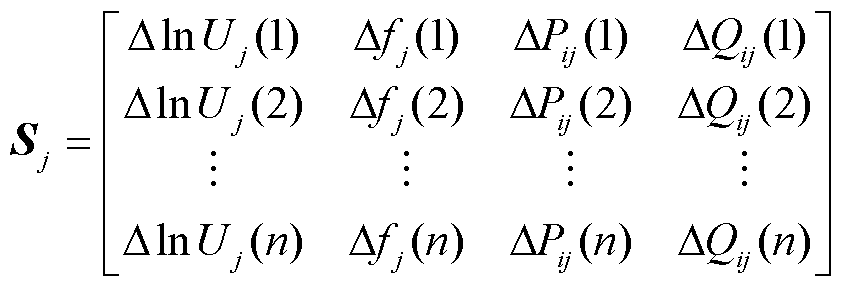（5）
式中，ΔlnUj(n)、Δfj(n)、ΔPij(n)、ΔQij(n)分别为发电机j的电压幅值对数、频率、有功功率和无功功率变化量在第n个采样点的值。对Sj进行APIT-MEMD分解，分解后的Sj可进一步表示为
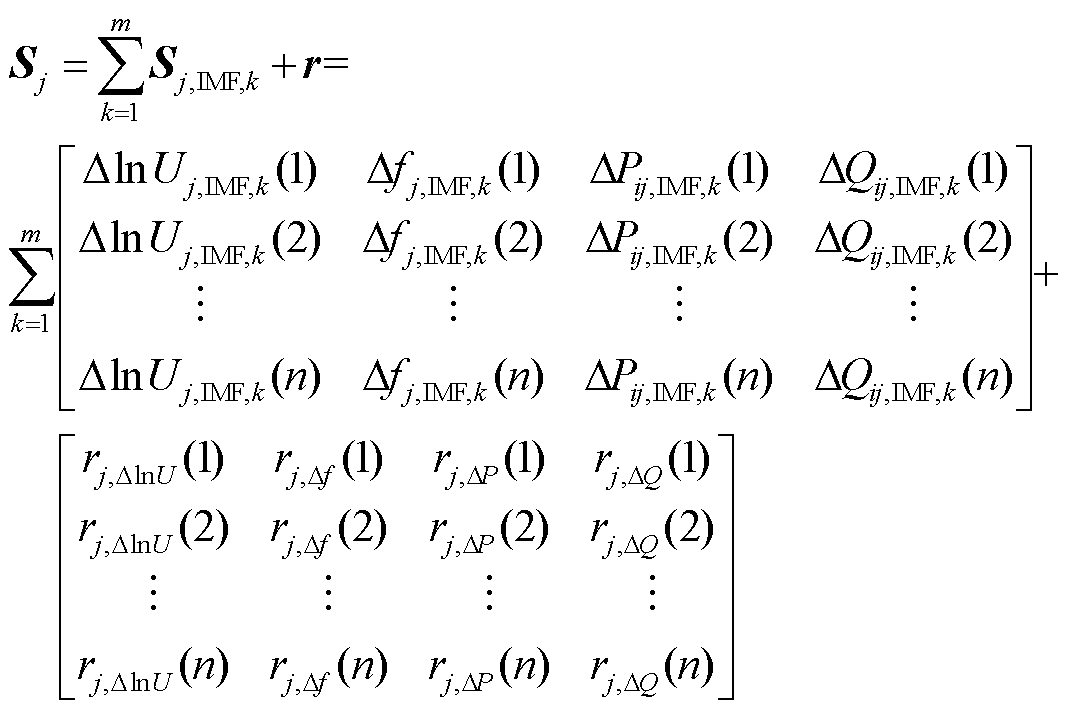（6）
式中，ΔlnUj,IMF,k(n)、Δfj,IMF,k(n)、ΔPij,IMF,k(n)、ΔQij,IMF,k(n)分别为发电机j的电压幅值对数、频率、有功功率和无功功率变化量的第k个IMF分量的第n个元素；rj,ΔlnU(n)、rj,Δf(n)、rj,ΔP(n)、rj,ΔQ(n)分别为发电机j的电压幅值对数、频率、有功功率和无功功率变化量残差向量的第n个元素。
进一步，根据式（3）和式（4）计算各IMF分量对数能量熵，则Sj的IMF分量对数能量熵矩阵Hj为
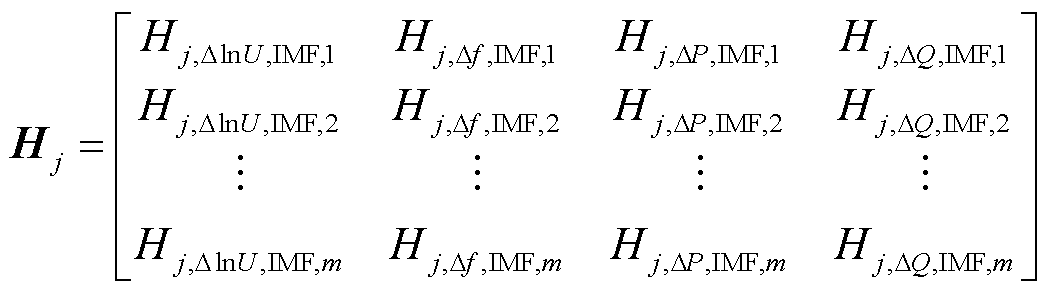（7）
式中，Hj,ΔlnU,IMF,m、Hj,Δf,IMF,m、Hj,ΔP,IMF,m、Hj,ΔQ,IMF,m分别为发电机j的电压幅值对数、频率、有功功率和无功功率变化量第m个IMF分量的对数能量熵。
由2.1节可知：式（5）的多通道量测信息矩阵Sj经APIT-MEMD分解出的第k个IMF矩阵Sj,IMF,k表征了多通道量测信息的第k个振荡模式分量矩阵。若第k个振荡模式为系统的强迫振荡模式，则Hj中第k行各对数能量熵将大于同一列的其余对数能量熵，则可认为式（6）中的第k个IMF矩阵Sj,IMF,k为系统强迫振荡模式的IMF矩阵，有
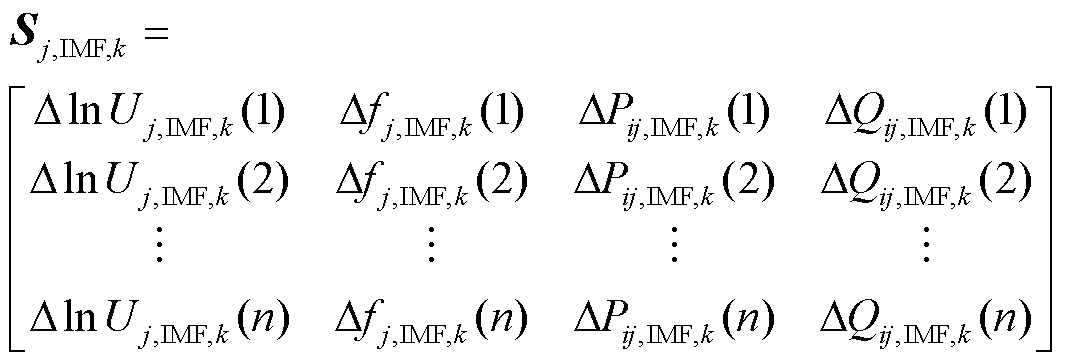（8）
将式（8）的强迫振荡模式IMF矩阵Sj,IMF,k中各量测通道IMF分量ΔlnUj,IMF,k、Δfj,IMF,k、ΔPij,IMF,k及ΔQij,IMF,k作为式（1）的耗散能量流计算输入，可得离散空间下，基于APIT-MEMD的耗散能量流Wj,dp,IMF为
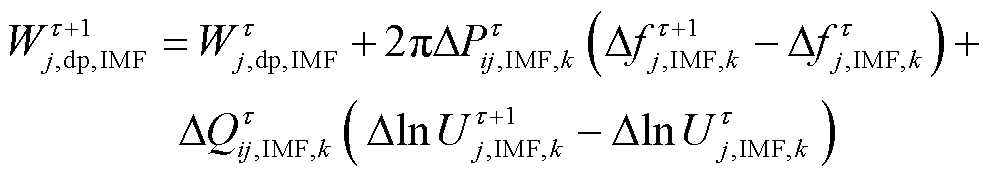（9）
式中，ΔPij,IMF,k和ΔQij,IMF,k分别为支路Lij的有功变化量ΔP和无功变化量ΔQ的强迫振荡IMF分量；Δfj,IMF,k为发电机j的Δf经APIT-MEMD分解的强迫振荡IMF分量；ΔlnUj,IMF,k为发电机j的ΔlnU经APIT-MEMD分解的强迫振荡IMF分量。
由于耗散能量流的变化趋势可用于定位强迫振荡源，为避免耗散能量曲线的变化趋势不明显影响振荡源定位效果，进一步对耗散能量流的相邻极小值点求差，以明晰耗散能量流的变化趋势，即
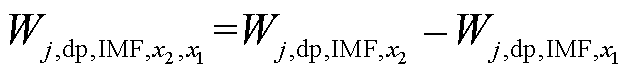（10）
式中，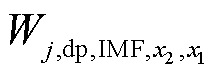
为发电机j耗散能量在x1和x2处能量差值；x1和x2分别为Wj,dp,IMF相邻的两个极小值点。根据耗散能量在相邻极小值点间变化量可判断发电机耗散能量变化趋势，进而定位强迫振荡源。
综上所述，采用APIT-MEMD分解的强迫振荡IMF分量计算各发电机耗散能量流定位强迫振荡源的判据为：若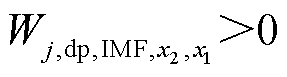
，且耗散能量曲线向上或不变，表明该发电机消耗振荡能量，为非振荡源；若
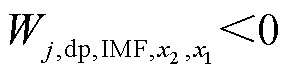，且耗散能量曲线向下，表明该发电机向电网注入振荡能量，为强迫振荡源。若网络中同时存在多个发电机耗散能量曲线向下，则相同时间内耗散能量下降最大的发电机为强迫振荡源。
综上所述，本文所提基于APIT-MEMD的强迫振荡源定位方法具体实施步骤如下：
（1）从PMU中获取各发电机电压幅值对数、频率、有功功率和无功功率量测信息，构建多通道量测信息相对稳态的变化量矩阵Sj。
（2）对多通道量测信息变化量矩阵Sj在高维空间建立自适应投影方向向量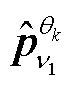
和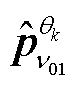
。
（3）对Sj沿自适应投影方向向量投影，逐次求取最优均值筛选出不同频率的IMF分量。
（4）根据式（7）计算发电机的对数能量熵矩阵Hj。
（5）筛选出能量熵值最高的IMF的分量作为强迫振荡分量予以保留，忽略其余分量。
（6）利用提取出的强迫振荡IMF分量，通过式（9）计算各发电机的耗散能量流，结合式（10）计算耗散能量的差值。
（7）依据强迫振荡源判据确定强迫振荡源。
本节分别以WECC 179节点测试系统和辽宁电网为例，分析、验证所提基于APIT-MEMD的强迫振荡源定位方法的准确性和可行性。
WECC 179节点测试系统拓扑结构如图1所示，该系统共有29台发电机，所有发电机阻尼系数均设置为4，各振荡模式阻尼良好。本节设置扰动如下：向发电机G79励磁系统持续注入0.46 Hz的正弦波激发出强迫振荡，采样频率为30 Hz，仿真时长为20 s。强迫振荡期间各发电机机端电压幅值对数、频率、有功功率和无功功率变化量仿真曲线如图2所示。
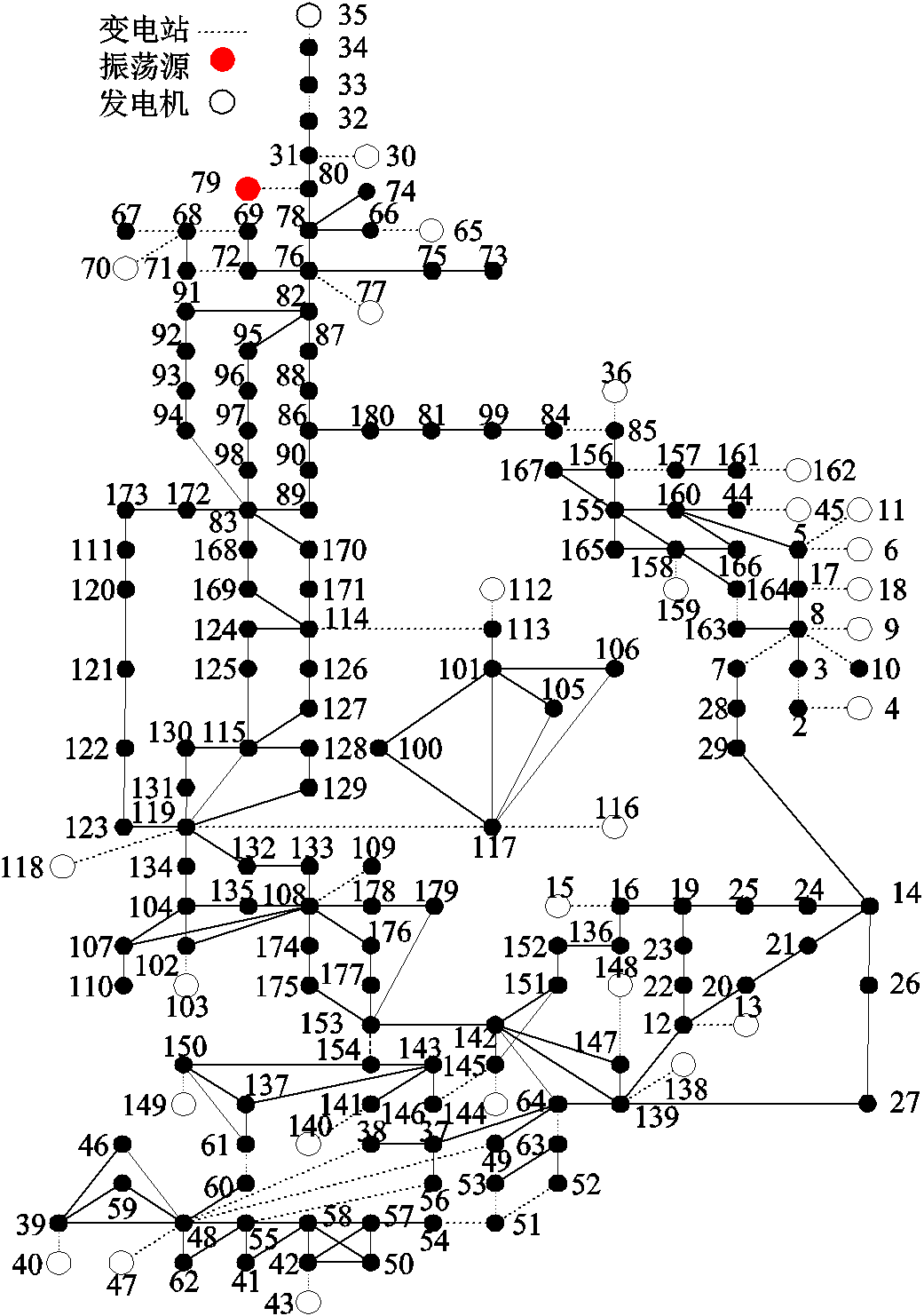
图1 WECC 179节点测试系统拓扑结构
Fig.1 WECC 179-bus test system
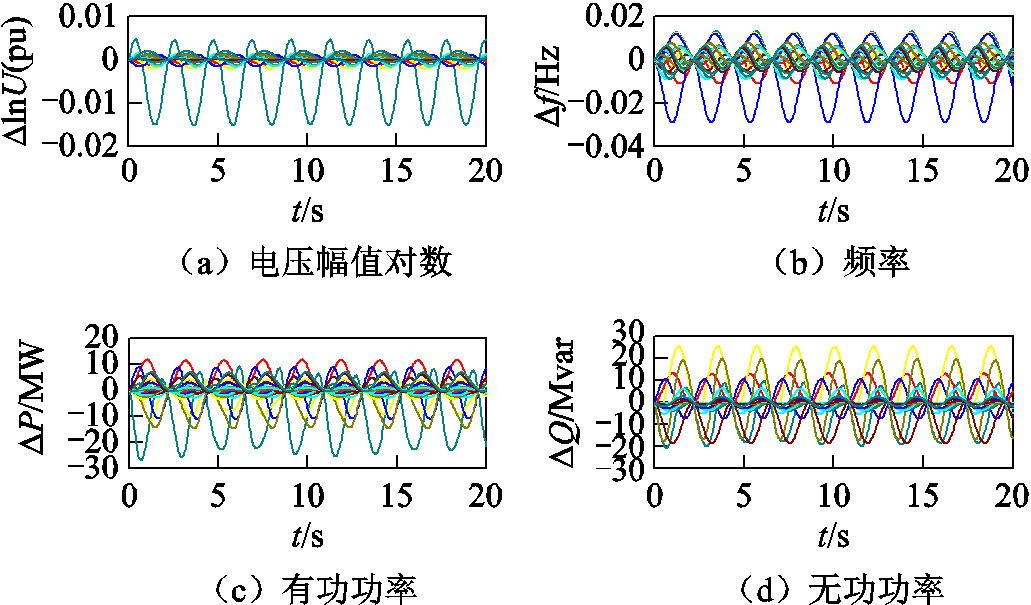
图2 WECC 179节点测试系统发电机参数仿真曲线
Fig.2 Simulated oscillation curves of generators in WECC 179-bus test system
4.1.1 APIT-MEMD准确性验证
根据所提方法，对图2中各发电机电压幅值对数、频率、有功功率和无功功率变化量构建式（5）形式的多通道量测信息矩阵Sj，然后对其协方差矩阵C进行特征分解，得到最大特征值λ1对应的左特征向量ν1，并构建其反方向向量ν01。根据信号的不平衡度重新确定自适应方向向量，设定信号不平衡系数α=0.3。进一步，对各发电机多通道量测信息矩阵Sj进行APIT-MEMD分解。最终Sj分解为4个IMF矩阵。发电机G79的Δf和ΔlnU经APIT-MEMD分解后的结果如图3所示。
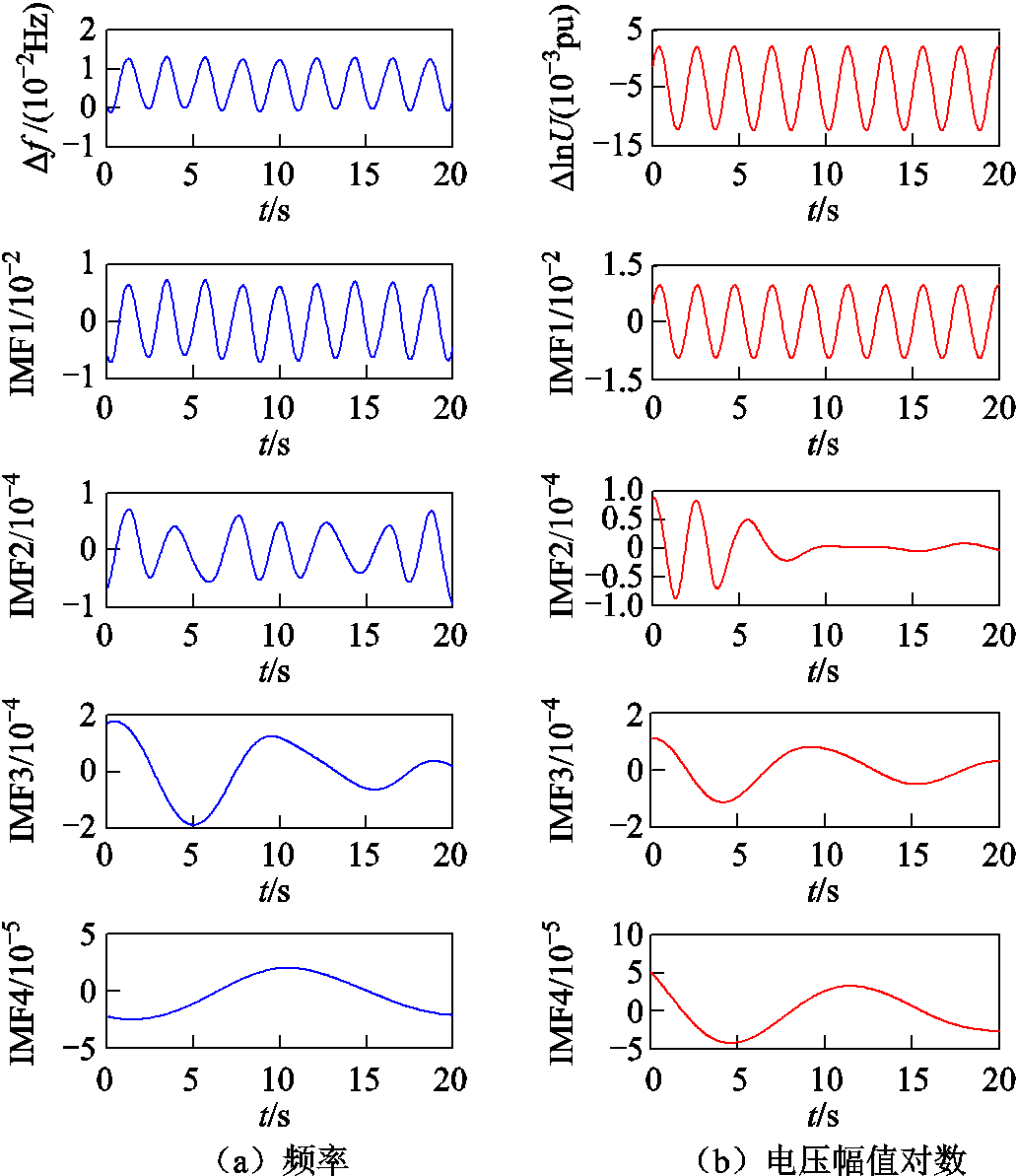
图3 基于APIT-MEMD的G79频率及电压幅值对数变化量IMF分量
Fig.3 IMFs of Δf and ΔlnU of G79 decomposed by APIT-MEMD
由图3可知，发电机G79的Δf和ΔlnU经APIT-MEMD共分解出4个IMF分量，随着逐次筛选，各IMF信号的振荡频率依次降低，包含的振荡信息量也依次减小。同时，在同次分解出的IMF分量中，各电气量波形基本一致，表明在逐次筛选过程中APIT-MEMD方法充分考虑了各量测通道间广域量测信息的相关性，使得同次分解出的IMF分量包含的振荡信息基本一致，方便后续耗散能量流的计算。进一步，计算各IMF的对数能量熵得到式（7）所示的Hj矩阵。受篇幅限制，部分发电机Δf和ΔlnU的IMF分量的对数能量熵值见表1。
表1 发电机频率及电压幅值对数变化量IMF分量的对数能量熵
Tab.1 Log energy entropy of each IMF decomposed from Δf and ΔlnU of generators in WECC 179-bus test system
编号ΔfΔlnU IMF1IMF2IMF3IMF4IMF1IMF2IMF3IMF4 G799.173.334.232.3213.635.737.704.07 G359.203.323.831.4510.273.125.673.79 G308.722.765.012.7611.062.954.050.93 G659.104.234.432.1511.183.454.862.32 G778.972.973.420.4511.143.296.193.24 G709.002.973.440.6511.313.486.363.35 G368.452.413.021.199.862.534.730.80 G1128.602.494.472.7410.373.355.754.13 G1628.452.562.730.048.150.913.660.89 G119.113.253.661.219.702.454.262.89 G69.043.183.591.1310.002.774.523.17 G458.492.632.790.208.440.933.100.42 G1598.362.532.740.138.621.413.380.93 G1188.162.193.862.1510.913.765.083.71 G1168.202.233.952.2410.873.745.033.71 G188.602.642.450.319.992.773.692.82 G138.742.732.700.769.842.063.710.38 G1388.782.772.990.819.952.003.771.43 G1038.202.271.150.1310.173.064.763.14 G98.632.682.700.299.772.483.852.19 G1488.732.712.890.659.471.683.281.07 G408.702.713.160.7210.122.614.051.60 G478.672.693.090.669.722.173.681.26 G1498.672.703.150.699.091.270.890.27 G1448.592.592.800.329.822.303.680.94 G48.682.712.990.228.871.712.551.71 G438.682.693.080.649.822.293.630.96 G1408.892.904.272.188.041.044.021.90 G158.882.853.141.099.772.194.142.26
显然，由表1可知：各发电机Δf和ΔlnU的IMF分量中IMF1对应的对数能量熵最高，远高于其余IMF分量，可知主导强迫振荡模式集中于IMF1中。为获取IMF1的振荡频率，对IMF1进行希尔伯特黄变换（Hilbert-Huang Transform, HHT），计算其瞬时频率，各发电机电压幅值对数、频率、有功功率和无功功率变化量信号IMF1对应的振荡频率均为0.46 Hz，与注入励磁系统的扰动频率一致，因此，可知IMF1可有效表征系统强迫振荡模式。进一步，分别计算其余电气变化量IMF分量的对数能量熵，其中IMF1对数能量熵值均为最高。因此，分别将提取的各发电机电压幅值对数、频率、有功功率和无功功率变化量的IMF1分量代入式（9），计算各发电机的耗散能量流并由式（10）计算能量差值，结果如图4所示。
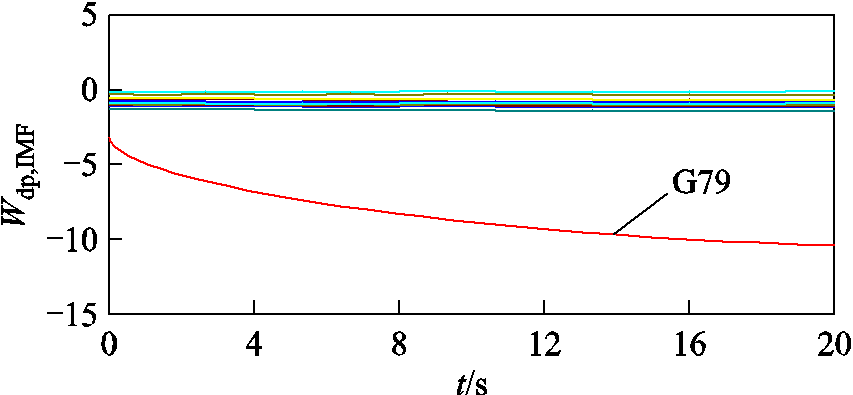
图4 基于APIT-MEMD的发电机耗散能量流
Fig.4 APIT-MEMD-based dissipation energy flows of generators
显然，图4中G79的耗散能量在0～20 s持续下降且为负值，结合强迫振荡源判据可知：发电机G79为强迫振荡源；其余发电机耗散能量在0～20 s均保持不变，为非振荡源。该辨识结果与仿真注入扰动的发电机一致，有效地验证了所提方法的准确性。
采用文献[15]所提传统耗散能量流方法计算的耗散能量流如图5所示。由图5可知：强迫振荡期间，发电机G79耗散能量为负且持续向下，为强迫振荡源，其余发电机无下降趋势，为非强迫振荡源，该定位结果与所提APIT-MEMD方法定位结果相同，有效地验证了所提方法的准确性。
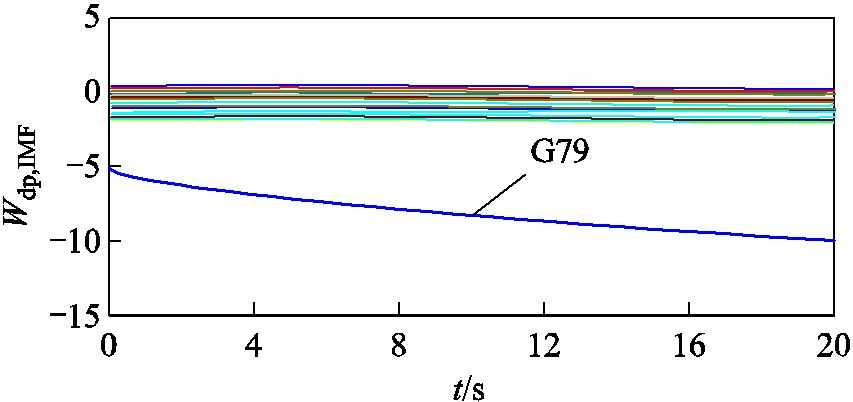
图5 基于传统耗散能量流的发电机耗散能量曲线
Fig.5 Traditional dissipation energy flows of generators
4.1.2 APIT-MEMD与EMD、MEMD结果对比
为分析所提方法的分离效果，本节进一步对比了APIT-MEMD、EMD[18]、MEMD[19]三种方法对发电机G79的仿真信号分解的差异性。
发电机G79的频率偏差量信号Δf和电压幅值对数变化量信号ΔlnU经EMD分解后的结果如图6所示。显然，由图6结果可知：发电机G79的Δf经EMD共分解出4个IMF分量，而ΔlnU经EMD共分解出3个IMF分量。上述结果表明：由于EMD对信号单通道分解时未能充分考虑各通道间量测信息的相关性，导致各通道分解的IMF数量不一致，分解效果较差。对比图3可知：本文所提APIT-MEMD方法对各电气量均提取出4个IMF分量，且各通道同次分解出的IMF振荡频率基本一致，与EMD相比，本文方法对多通道广域量测信息具有更好的振荡模式分离效果。
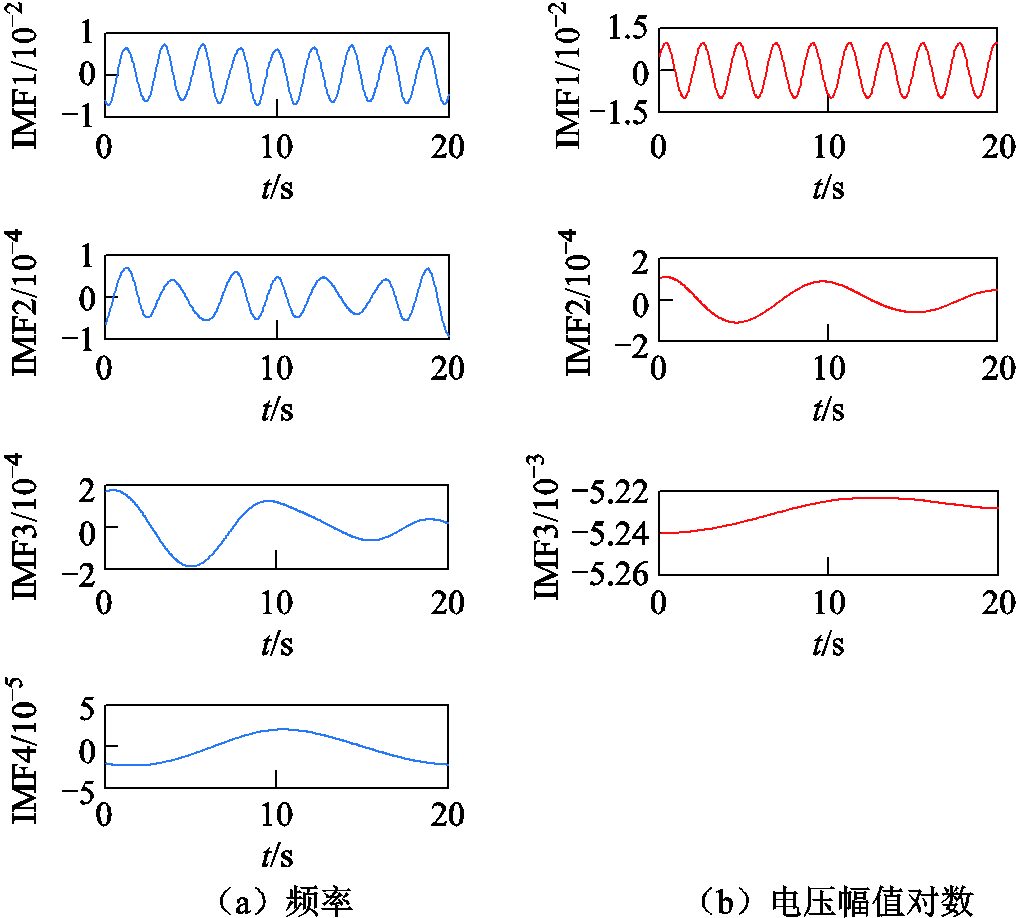
图6 基于EMD的发电机G79频率及电压幅值对数变化量IMF
Fig.6 IMFs of Δf and ΔlnU of G79 decomposed by EMD
APIT-MEMD与MEMD对发电机G79电压幅值对数变化量ΔlnU的分解效果对比如图7所示。由图7可知，强迫振荡分量均出现在IMF1中，对于同一多通道量测信号，APIT-MEMD相较于MEMD分解出更少的IMF，在有效提取强迫振荡模式分量基础上避免了信号的过度分解。图8进一步给出了两种方法分解得到的G79各电气变化量IMF1幅值占比。由图8可知，所提方法采用自适应投影，充分考虑了量测通道间的数据相关性，估计的局部均值更准确，分离出的IMF1效果更好。
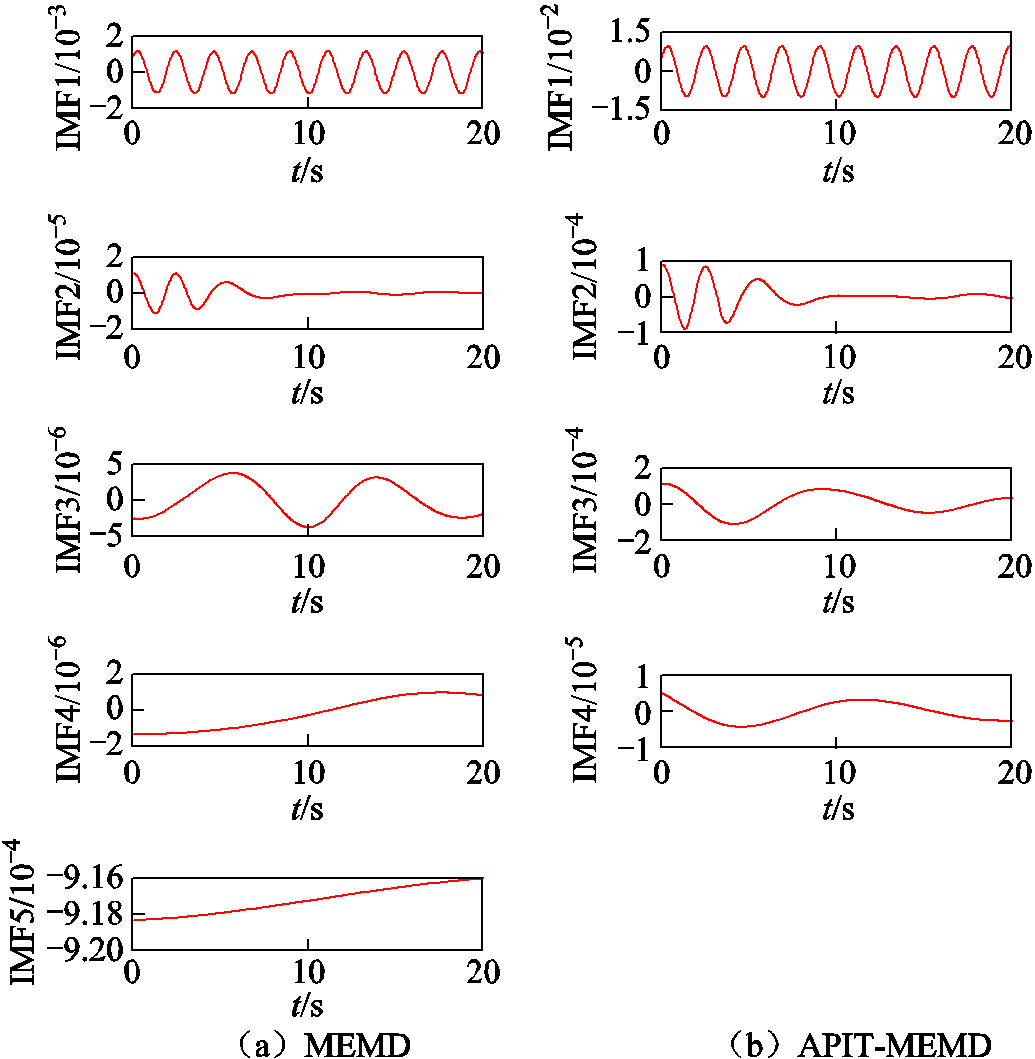
图7 APIT-MEMD与MEMD分解的IMF对比
Fig.7 Decomposed IMFs comparison between APIT-MEMD and MEMD
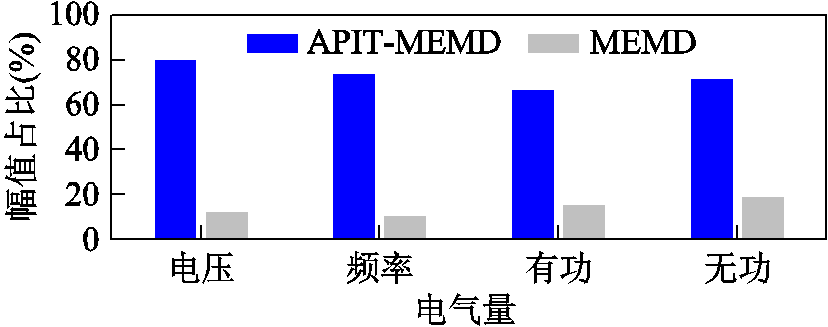
图8 APIT-MEMD与MEMD分解的IMF1幅值比对比
Fig.8 Amplitude ratio comparisons of IMFs between APIT-MEMD and MEMD
图9进一步给出了采用APIT-MEMD和MEMD分解的发电机G79多通道量测信息中频率变化量前三个IMF分量的频谱。由图9可知：MEMD分解出的各IMF分量带宽均明显大于APIT-MEMD，带宽约束性较差，存在较严重的模态混叠现象，而APIT-MEMD分解出的各IMF分量带宽跨度较小，其中IMF1仅存在0.46 Hz一个峰值，具有更好的强迫振荡分量分解效果。
图10给出了采用EMD和MEMD计算的耗散能量流结果，综合上述定位结果可知：与EMD和MEMD相比，采用本文所提方法求得的G79耗散能量流曲线具有更明显的下降趋势，更容易定位出振荡源，体现了所提方法的优越性。
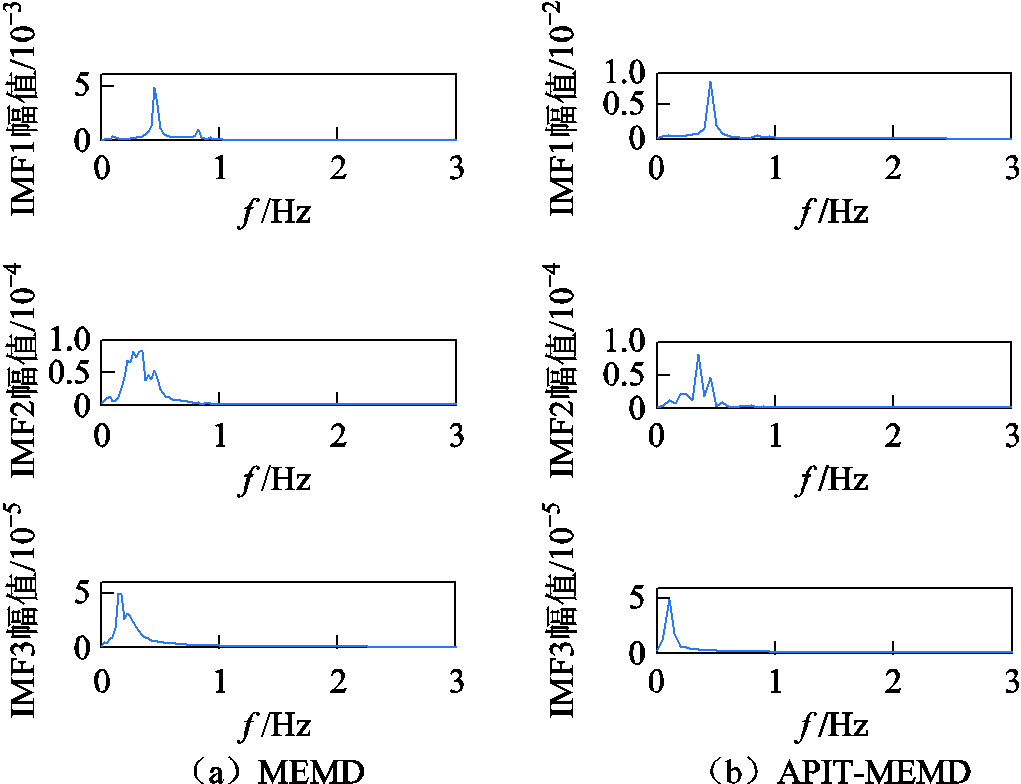
图9 基于APIT-MEMD和MEMD分解的IMF频谱
Fig.9 IMF spectrums decomposed by APIT-MEMD and MEMD
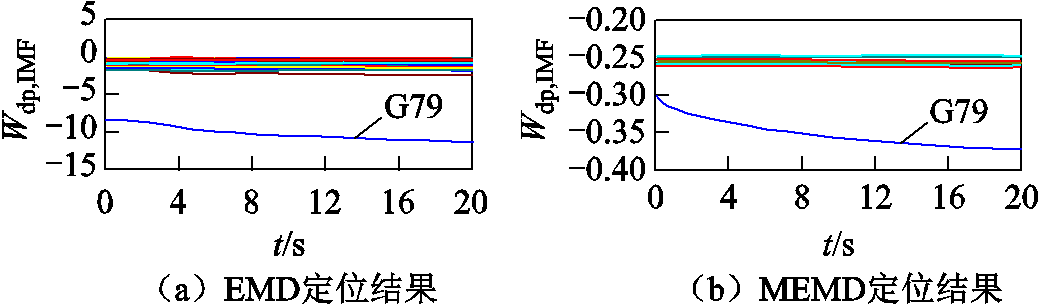
图10 基于EMD和MEMD的发电机耗散能量流
Fig.10 EMD and MEMD based dissipation energy flows of generators
APIT-MEMD、EMD和MEMD三种振荡源定位方法的计算耗时（计算平台硬件配置为：CPU Intel Core i5-11300H，主频3.1 GHz，内存16 GB）见表2。由表2结果可知：EMD计算时间为47.659 2 s、MEMD计算时间为19.817 9 s、APIT-MEMD计算时间为7.480 9 s，本文所提方法在计算效率上较EMD和MEMD分别提升了84.3%和62.2%。该结果表明：本文所提方法可有效提升振荡源定位的计算效率。
表2 不同方法计算效率对比
Tab.2 Computational efficiency comparisons among different methods
算法EMDMEMDAPIT-MEMD 计算时间/s47.659 219.817 97.480 9 计算效率提升(%)84.362.2—
4.1节通过WECC 179节点测试系统的仿真数据验证了所提方法定位强迫振荡源的准确性和有效性。本节以辽宁电网某次强迫振荡的PMU数据为例，进一步验证所提方法在实际系统中应用的可行性。本节选取了图11中强迫振荡源近区部分机组TPW、DD、DDT及ZH进行分析、验证。
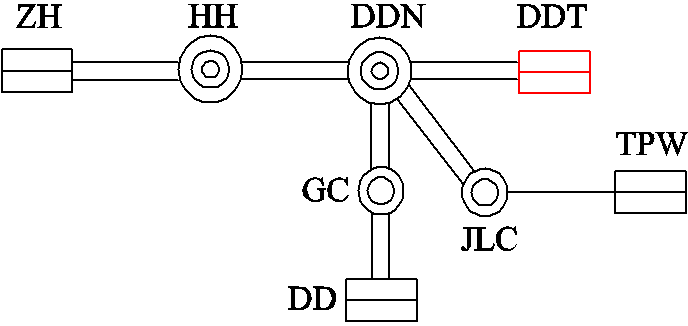
图11 DD地区电网拓扑结构
Fig.11 Grid topology in DD
图12给出了振荡期间30 s的PMU实测发电机TPW、DD、DDT和ZH的电压幅值、频率、有功功率和无功功率。
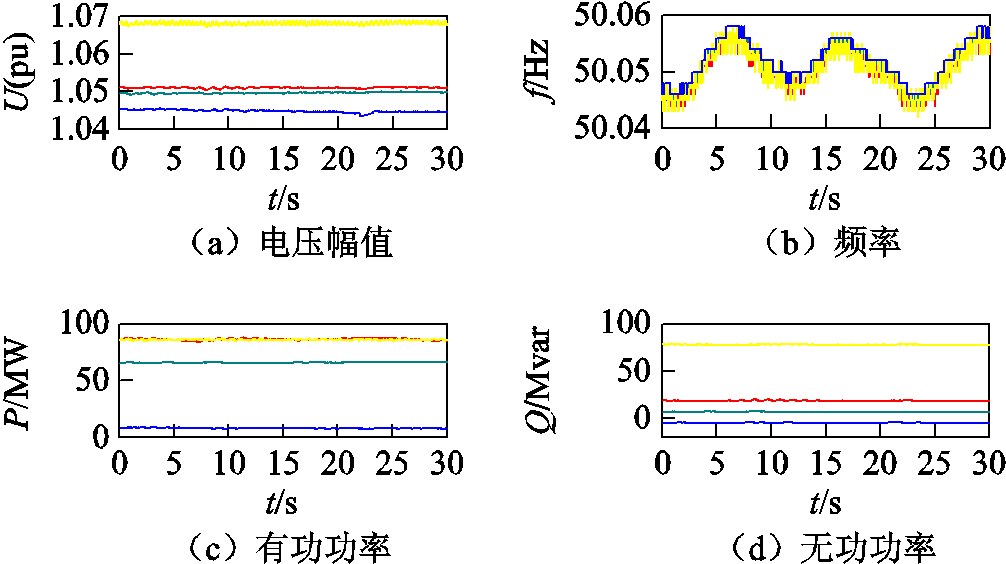
图12 辽宁电网PMU实测信息
Fig.12 Field-measurement PMU data in Liaoning Power Grid
首先，分别对TPW、DD、DDT及ZH发电机的电压幅值取对数，对各发电机电压幅值对数、频率、有功功率和无功功率量测数据构建式（5）形式的多通道量测信息矩阵Sj；然后对多通道矩阵Sj进行APIT-MEMD分解，各得到8个IMF分量。在此基础上，由式（7）计算各IMF对应的对数能量熵，结果见表3。
表3 DD地区各发电机实测信号IMF分量对数能量熵
Tab.3 log energy entropy of each IMF decomposed from field-measurements of generators in DD by using APIT-MEMD
参数编号DDTDDTPWZH DlnUIMF10.671 51.432 50.947 61.113 4 IMF22.7524.077 93.546 73.783 4 IMF36.238 17.340 35.972 46.740 7 IMF42.427 84.545 71.762 11.844 2 IMF50.486 50.922 00.880 81.028 6 IMF60.085 20.094 10.104 70.239 1 IMF70.016 80.043 00.020 80.027 9 IMF8———— DfIMF11.366 11.142 82.105 22.289 6 IMF23.477 14.317 32.562 84.770 5 IMF37.360 17.455 814.44 37.612 1 IMF42.447 64.564 73.105 43.933 8 IMF51.220 32.208 40.794 80.442 9 IMF60.191 80.341 40.494 30.270 7 IMF70.049 20.066 40.057 80.013 0 IMF8———— DPIMF11.558 41.142 54.838 11.372 6 IMF21.825 24.313 55.298 25.232 2 IMF37.821 77.453 78.045 511.260 7 IMF40.848 64.563 31.653 72.291 7 IMF51.464 42.204 74.272 11.238 4 IMF60.078 90.348 90.242 80.660 3 IMF70.046 10.067 40.023 40.021 9 IMF8———— DQIMF11.226 12.384 70.812 21.813 3 IMF23.346 73.980 82.644 82.730 1 IMF310.452 67.461 87.624 98.942 8 IMF43.830 92.230 32.675 55.016 9 IMF51.561 10.747 11.602 73.534 4 IMF60.215 80.224 10.593 80.984 6 IMF70.035 70.052 40.069 10.102 7 IMF8————
显然，由表3可知：发电机各电气变化量中，IMF3的对数能量熵在各发电机所有IMF分量中均为最高，可认为IMF3表征了系统的主导强迫振荡模式。进一步，对有功功率IMF3分量进行HHT求得的瞬时频率为1.57 Hz，与本次强迫振荡实际振荡频率一致，可知IMF3可有效表征强迫振荡模式。提取出的各电气变化量的IMF3分量如图13所示。
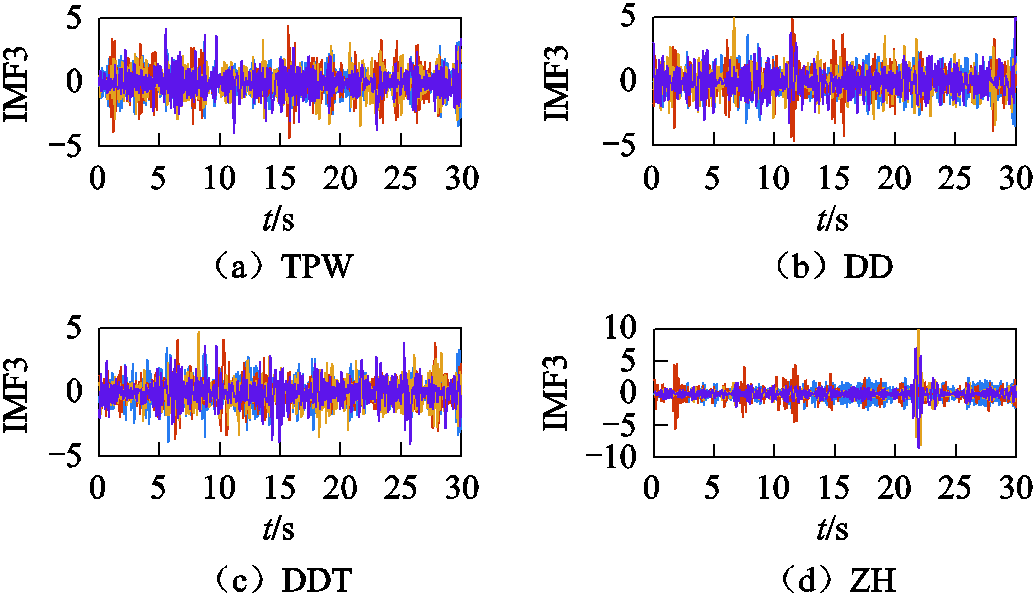
图13 发电机频率、电压幅值对数、有功功率和无功功率变化量的IMF3
Fig.13 IMF3 decomposed from the field-measurement Δf, ΔlnU, ΔP and ΔQ of the generators in DD
分别将图13中各发电机电压幅值对数、频率、有功功率和无功功率变化量的IMF3分量代入式（9）计算各发电机耗散能量流，并由式（10）计算能量差，结果如图14所示。
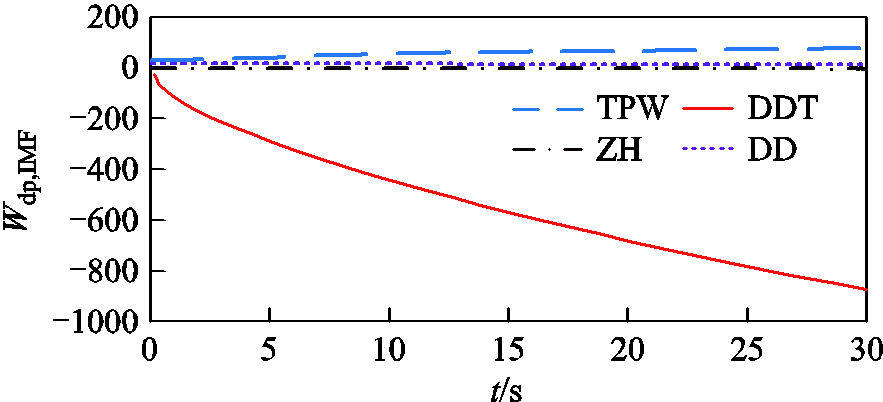
图14 基于实测PMU信息采用所提方法计算的发电机耗散能量流
Fig.14 APIT-MEMD-based field dissipation energy flow of generators using the field-measurement data
显然，由图14可知：DDT的耗散能量在整个量测时间段内均为负且持续向下，表明DDT在0～30 s期间持续向电网注入振荡能量，为振荡源；TPW、DD及ZH的耗散能量均无下降趋势，为非振荡源。
图15为传统DEF方法的定位结果，同样定位出DDT为强迫振荡源。对比图14和图15可知：所提APIT-MEMD方法由于可同步、准确地提取多通道广域量测信息中的强迫振荡分量，因此在整个时段内计算的DDT耗散能量持续向下，且下降趋势更为明显，可快速定位出强迫振荡源；而传统DEF方法受限于强迫振荡分量的提取精度，计算出的耗散能量在0～15 s内基本保持不变，无法准确定位强迫振荡源，不利于运行调度人员快速确定振荡源，为后续控制策略制定提供充裕的时间。上述结果表明，所提APIT-MEMD方法可利用PMU实测数据实现电力系统强迫振荡源的快速、准确定位，为后续强迫振荡源抑制措施制定提供充裕的时间。
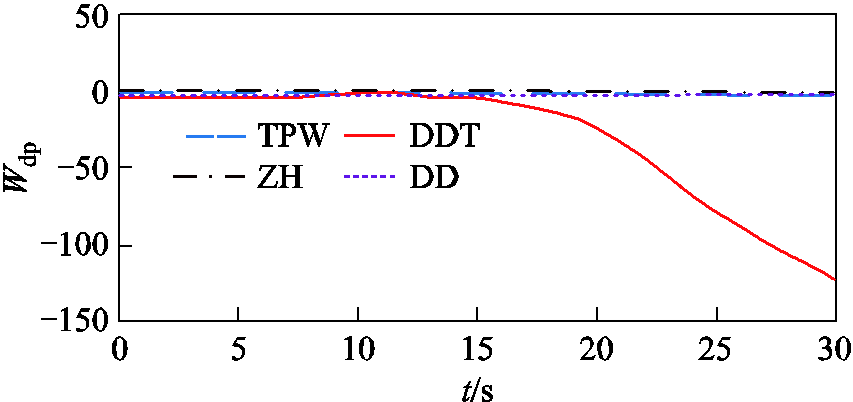
图15 基于实测PMU信息采用传统方法计算的发电机耗散能量流
Fig.15 Traditional field dissipation energy flow of generators using the field-measurement data
综上所述，本文所提基于APIT-MEMD的强迫振荡源定位方法可有效提取PMU实测数据中的强迫振荡IMF分量，准确定位出强迫振荡源，为运行人员制定相关控制措施提供参考。
本文提出了一种基于APIT-MEMD的电力系统强迫振荡源定位方法，通过WECC 179节点测试系统仿真数据和辽宁电网PMU实测数据对其进行分析、验证，相关结论如下：
1）所提APIT-MEMD方法可自适应构建投影方向向量估计局部最优均值，准确、完整地提取出含强迫振荡模式的IMF分量。与EMD相比，所提方法可实现多通道广域量测信息的强迫振荡分量同步提取；与MEMD相比，所提方法可在电力系统多通道广域量测信息差异较大时实现强迫振荡分量高精度提取。
2）相对基于EMD的强迫振荡源定位方法，所提方法通过同步提取发电机各电气量的强迫振荡IMF分量，大幅提升了耗散能量流的计算效率；与MEMD方法相比，所提方法通过精准估计局部最优均值，避免了对信号的过度分解，提升了计算精度。
3）所提基于APIT-MEMD的强迫振荡源定位方法完全不依赖系统详细模型及准确参数，仅根据发电机广域量测信息即可准确、有效地定位强迫振荡源。与传统DEF方法相比，所提方法有效地避免了广域量测信息中的冗余信息对振荡源定位的干扰，具有更高的强迫振荡源定位精度。
4）辽宁电网强迫振荡实测数据验证了所提方法可应用于实际电网的强迫振荡源定位，在基于广域量测信息的强迫振荡源定位中具有一定的工程参考价值。
参考文献
[1] 薛安成, 王嘉伟. 基于非光滑分岔的单机水电系统超低频频率振荡机理分析[J]. 电工技术学报, 2020, 35(7): 1489-1497. Xue Ancheng, Wang Jiawei. Mechanism analysis of ultra-low frequency oscillation of single hydropower system based on non-smooth bifurcation[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1489-1497.
[2] 陈剑, 杜文娟, 王海风. 采用深度迁移学习定位含直驱风机次同步振荡源机组的方法[J]. 电工技术学报, 2021, 36(1): 179-190. Chen Jian, Du Wenjuan, Wang Haifeng. A method of locating the power system subsynchronous oscillation source unit with grid-connected PMSG using deep transfer learning[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 179-190.
[3] 李雪, 于洋, 姜涛, 等. 基于稀疏增强动态解耦的电力系统振荡模式与模态辨识方法[J]. 电工技术学报, 2021, 36(13): 2832-2843. Li Xue, Yu Yang, Jiang Tao, et al. Sparsity promoting dynamic mode decomposition based dominant modes and mode shapes estimation in bulk power grid[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2832-2843.
[4] 冯双, 陈佳宁, 汤奕, 等. 基于SPWVD图像和深度迁移学习的强迫振荡源定位方法[J]. 电力系统自动化, 2020, 44(17): 78-91. Feng Shuang, Chen Jianing, Tang Yi, et al. Location method of forced oscillation source based on SPWVD image and deep transfer learning[J]. Automation of Electric Power Systems, 2020, 44(17): 78-91.
[5] 李阳海, 黄莹, 刘巨, 等. 基于阻尼转矩分析的电力系统低频振荡源定位[J]. 电力系统保护与控制, 2015, 43(14): 84-91. Li Yanghai, Huang Ying, Liu Ju, et al. Power system oscillation source location based on damping torque analysis[J]. Power System Protection and Control, 2015, 43(14): 84-91.
[6] Chen Lei, Min Yong, Chen Yiping, et al. Evaluation of generator damping using oscillation energy dissipation and the connection with modal analysis[J]. IEEE Transactions on Power Systems, 2014, 29(3): 1393-1402.
[7] Dosiek L, Zhou Ning, Pierre J W, et al. Mode shape estimation algorithms under ambient conditions: a comparative review[J]. IEEE Transactions on Power Systems, 2013, 28(2): 779-787.
[8] Myers R B, Trudnowski D J. Effects of forced oscillations on spectral-based mode-shape estimation[C]//2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 2013: 1-6.
[9] Sarmadi S A N, Venkatasubramanian V. Inter-area resonance in power systems from forced oscillations[J]. IEEE Transactions on Power Systems, 2016, 31(1): 378-386.
[10] 董清, 梁晶, 颜湘武, 等. 大规模电网中低频振荡扰动源的定位方法[J]. 中国电机工程学报, 2012, 32(1): 78-83, 15. Dong Qing, Liang Jing, Yan Xiangwu, et al. Locating method of disturbance source of low frequency oscillation in large scale power grid[J]. Proceedings of the CSEE, 2012, 32(1): 78-83, 15.
[11] 李文锋, 郭剑波, 李莹, 等. 基于WAMS的电力系统功率振荡分析与振荡源定位(1)割集能量法[J]. 中国电机工程学报, 2013, 33(25): 41-46, 9. Li Wenfeng, Guo Jianbo, Li Ying, et al. Power system oscillation analysis and oscillation source location based on WAMS part 1: method of cutset energy[J]. Proceedings of the CSEE, 2013, 33(25): 41-46, 9.
[12] 陈磊, 闵勇, 胡伟. 基于振荡能量的低频振荡分析与振荡源定位(一)理论基础与能量流计算[J]. 电力系统自动化, 2012, 36(3): 22-27, 86. Chen Lei, Min Yong, Hu Wei. Low frequency oscillation analysis and oscillation source location based on oscillation energy part one mathematical foundation and energy flow computation[J]. Automation of Electric Power Systems, 2012, 36(3): 22-27, 86.
[13] Maslennikov S. Dissipating energy flow method for locating the source of sustained oscillations[J]. International Journal of Electrical Power & Energy Systems, 2017, 88: 55-62.
[14] 姜涛, 张明宇, 李雪, 等. 基于正交子空间投影的电力系统同调机群辨识[J]. 电工技术学报, 2018, 33(9): 2077-2088. Jiang Tao, Zhang Mingyu, Li Xue, et al. Estimating coherent generators from measurement responses in power systems using orthogonal subspace projection[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 2077-2088.
[15] Chen Lei, Sun Ming, Min Yong, et al. Online monitoring of generator damping using dissipation energy flow computed from ambient data[J]. IET Generation, Transmission & Distribution, 2017, 11(18): 4430-4435.
[16] Estevez P G, Marchi P, Galarza C, et al. Non-stationary power system forced oscillation analysis using synchrosqueezing transform[J]. IEEE Transactions on Power Systems, 2021, 36(2): 1583-1593.
[17] 姜涛, 李孟豪, 李雪, 等. 电力系统强迫振荡源的时频域定位方法[J]. 电力系统自动化, 2021, 45(9): 98-106. Jiang Tao, Li Menghao, Li Xue, et al. Time-frequency domain location method for forced oscillation source in power system[J]. Automation of Electric Power Systems, 2021, 45(9): 98-106.
[18] 褚晓杰, 印永华, 高磊, 等. 基于经验模态理论的强迫振荡扰动源定位新方法[J]. 中国电机工程学报, 2014, 34(28): 4906-4912. Chu Xiaojie, Yin Yonghua, Gao Lei, et al. A new forced oscillation disturbance source location method based on empirical mode theory[J]. Proceedings of the CSEE, 2014, 34(28): 4906-4912.
[19] 姜涛, 刘博涵, 李雪, 等. 基于多元经验模态分解的电力系统强迫振荡源定位[J]. 中国电机工程学报, 2022, 42(22): 8063-8075. Jiang Tao, Liu Bohan, Li Xue, et al. Forced oscillation location in power systems using multiple empirical mode decomposition[J]. Proceedings of the CSEE, 2022, 42(22): 8063-8075.
[20] Min Yong, Chen Lei. A transient energy function for power systems including the induction motor model[J].Science in China Series E: Technological Sciences, 2007, 50(5): 575-584.
[21] 张艳军, 殷祥翔, 葛延峰, 等. 基于APIT-MEMD的电力系统低频振荡模式辨识新方法[J]. 电力系统保护与控制, 2020, 48(14): 165-174. Zhang Yanjun, Yin Xiangxiang, Ge Yanfeng, et al. Low frequency oscillation mode estimation in power systems using adaptive-projection intrinsically transformed multivariate empirical mode decom-position[J]. Power System Protection and Control, 2020, 48(14): 165-174.
[22] Hemakom A, Goverdovsky V, Looney D, et al. Adaptive-projection intrinsically transformed multivariate empirical mode decomposition in cooperative brain-computer interface applications[J]. Philosophical Transactions Series A, Mathematical, Physical, and Engineering Sciences, 2016, 374(2065): 20150199.
[23] Krishnan P, Yaacob S. Drowsiness detection using band power and log energy entropy features based on EEG signals[J]. International Journal of Innovative Technology and Exploring Engineering, 2019, 8(10): 830-836.
Abstract In recent years, forced oscillation occurs frequently in the power grid, which seriously threatens the stability of the power grid. Fast and accurate forced oscillation source location is very important to mitigate the forced oscillation. However, traditional methods are difficult to accurately extract the forced oscillation component from the multi-channel measurements, which significantly affects the accuracy of forced oscillation source location. To cope with this shortcoming, this paper proposes an adaptive-projection intrinsically transformed multivariate empirical mode decomposition (APIT-MEMD) based forced oscillation source location method. By accurately extracting the forced oscillation component implied in the multichannel measurements, the location accuracy and computational efficiency of the forced oscillation source are effectively improved.
Firstly, the intrinsic mode functions (IMFs) of the measurements, which represent different oscillation modes, are decomposed from the multichannel measurements via the proposed APIT-MEMD. Then, the IMF associated with the forced oscillation mode is separated from the decomposed IMFs by using the logarithmic energy entropy. Further, the APIT-MEMD-based dissipation energy flow (DEF) of each generator is calculated using the separated forced oscillation IMF, and the forced oscillation source is located by using the criterions of forced oscillation source. In this method, the proposed APIT-MEMD method can adaptively construct the projection direction vector to estimate the local optimal mean, and the IMF component associated with the forced oscillation mode is extracted accurately and completely.
Forced oscillation source location results of the WECC 179-bus test system and power grid field-measurements show that, the proposed APIT-MEMD method can accurately and completely extract the IMF component associated with the forced oscillation mode, which effectively improves the location accuracy and efficiency of forced oscillation source. Compared with EMD, the proposed method extracts 4 IMF components for each measurement, and the oscillation frequencies of IMFs decomposed by each channel are basically same. However, the extracted IMF components for each measurement of EMD method are different. Compared with the MEMD method, the proposed method decomposes fewer IMFs, which avoids excessive decomposition of signals on the basis of effectively extracting forced oscillation mode components. Furthermore, compared with the EMD and MEMD method, the dissipation energy flow calculated by the proposed method has a more obvious downward trend and is easier to locate the forced oscillation source, and the computational efficiency is improved by 84.3% and 62.2% respectively.
The following conclusions can be drawn from the simulation analysis: (1) Compared with EMD, the proposed method can extract forced oscillation components of multi-channel wide-area measurements synchronously. (2) Compared with the MEMD method, the proposed method can avoid the excessive decomposition of the multi-channel wide-area measurements and improves the calculation accuracy by accurately estimating the local optimal mean. (3) The forced oscillation source location method based on APIT-MEMD proposed in this paper is completely independent of the detailed model and accurate parameters of the system. The forced oscillation source can be accurately and effectively located only according to the wide-area measurements of the generator. (4) Compared with the traditional DEF method, the proposed method effectively avoids the interference of the redundant information in the wide-area measurement to the forced oscillation source location, and has higher forced oscillation source location accuracy.
keywords：Power systems, forced oscillation, oscillation source location, adaptive-projection intrinsically transformed multiple empirical mode decomposition, intrinsic mode function, dissipation energy flow
国家自然科学基金委员会-国家电网公司智能电网联合基金项目（U2066208）和国家自然科学基金项目（51877033）资助。
收稿日期 2022-04-06
改稿日期 2022-07-07
DOI:10.19595/j.cnki.1000-6753.tces.220503
中图分类号：TM712
姜 涛 男，1983年生，博士，教授，博士生导师，研究方向为电力系统安全性和稳定性、可再生能源集成、综合能源系统。E-mail: t.jiang@aliyun.com
李 雪 女，1986年生，博士，教授，博士生导师，研究方向为电力系统安全性与稳定性、电力系统高性能计算、电力市场。E-mail: xli@neepu.edu.cn（通信作者）
（编辑 赫蕾）