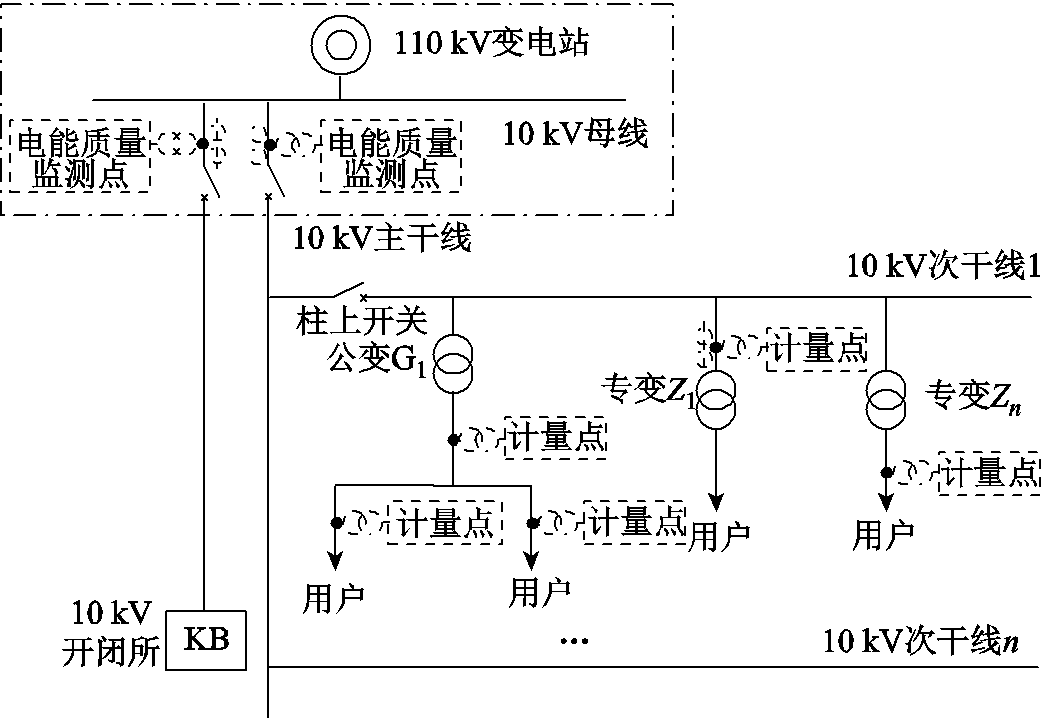
图1 电能质量监测点与用电计量点示意图
Fig.1 Schematic diagram of power quality monitoring point and electricity metering point
摘要 随着电力电子型用电设备的大量使用,电网公共连接点上干扰源用户的类型和数量越发增多,使得其电能质量扰动指标特征和时空特征更为复杂。针对目前电能质量监测装置难以对每条馈线上各终端用户均实现专门监测,且无法识别馈线上多个用户各自电能质量特征等问题,提出一种基于多源数据关联分析的工业用户电能质量特征识别方法。首先,以指标限值和累积分布图拐点为依据,提取监测点电能质量时间序列的超标和波动的数值及其时段,得到谐波关键指标、电压偏差、负序电压不平衡度等指标的扰动时序数据;其次,提出一种基于导数动态时间弯曲的时序距离计算方法,分析扰动时段下监测指标与工业用户用电数据的相关性,依据不同指标关联度识别用户的电能质量特征;最后,基于多类型干扰源仿真和实测算例,验证所提方法的可行性,可实现不同工业用户的电能质量特征识别。
关键词:电能质量特征识别 工业用户 时序数据 关联分析 导数动态时间弯曲
随着一条母线上工业用户负荷种类与数量的快速增加及电力电子型用电设备的广泛使用,多样化的电能质量特性加剧了公共连接点(Point of Common Coupling, PCC)电能质量问题的复杂性[1-3],增加了实施针对性治理工作的难度。识别工业用户电能质量多指标特征,对提高用户电能质量管理水平、引导用户参与主动治理具有重要意义。
在电能质量监测系统(Power Quality Monitoring System, PQMS)逐步部署至各个PCC处以后,电力企业能够获取海量且有价值的电能质量监测数据,有助于开展电能质量分析[4-5]。同一个干扰源用户在不同生产运行时段带来的多项扰动事件,以及同时刻下多个干扰源共同引起的扰动事件均体现在PQMS处多种电能质量稳态监测指标数据上,对传统的电能质量机理建模分析[6-7]提出了挑战。在现有多类型用户电能质量特征研究上,文献[8-9]基于电网关键节点的电能质量海量监测数据,进行监测点单时刻稳态指标特征聚类,具体分析了新能源、重大污染源、电气化牵引等工业用户特征,为用户总体特征分析提供了数据驱动思路。进一步,以下研究聚焦多时刻数据,并融入时空关联分析[10-16]。不同于秒级瞬时值电能质量复合扰动的相关性分析[10],文献[11-13]进行多节点分钟级时间序列关联分析,确定电能质量治理区域及主导扰动节点,对需治理用户的区域定位和影响分析有重要的意义。文献[14]构建一套干扰源电能质量治理需求画像标签体系,结合用户综合用电水平和电能质量发射水平来判断不同类型用户的治理需求级别。
上述数据驱动方法均基于PCC处PQMS稳态指标数据,无法区分各馈线上多种用户的稳态电能质量特征,而文献[15-16]关联分析了包括馈线各终端用户数据在内的多个数据源数据。文献[15]通过区间-仿射算法量化了不同分布式电源和谐波源用户功率波动对谐波、电压偏差和三相不平衡度三种电能质量指标的影响程度;文献[16]利用shape-DTW(shape-dynamic time warping)算法辅助计算谐波源用户责任,均通过量化用户功率波动与电能质量指标的波动相关性,体现不同用户的电能质量特征。
通过以上分析可知现有研究存在以下不足之处:①将馈线多分支上挂接的多个用户视为同一类用户群,并将监测系统采集到的数据视作用户群整体电能质量特征,无法细化识别馈线上各个多样化用户特征;②工业用户与电能质量扰动特征存在多对多的复杂关系,仅基于单一指标无法充分识别扰动事件特征及干扰源特征;③现有部分研究的基础数据为短时采样数据,需要采用专门设备进行额外测试,未能充分利用现有PQMS中的长时统计数据,同时无法契合长期性的电能质量现象和不确定的用户工况特点。
针对以上问题,本文在PCC处含有复杂多种扰动类型的情况下,利用长时间尺度数据关联方法,融合电能质量稳态监测数据和用户功率数据,综合考虑电能质量指标本身的时序特征以及与终端用户用电行为的关联特征,提出一种针对“多稳态指标类型-多工业用户”的多源时序数据关联分析方法,实现同一馈线下不同干扰源用户的扰动特征识别,以此避免机理分析在处理复杂多类型扰动之间交互影响时的困难。
为了实现延伸至终端用户的多类型稳态电能质量特征识别,本文通过关联分析现有多源系统的长时统计实测数据,得到各用户长时间的电能质量特征。
现有相关实测数据有两类:PCC(一般为变电站母线)处的电能质量监测点所得的电能质量指标统计数据以及各馈线用户计量点处智能电能表所得的用电数据,如图1[16]所示。前者反映了监测点所连接电力用户综合作用的电能质量水平;后者反映了不同工业用户的用电工况。

图1 电能质量监测点与用电计量点示意图
Fig.1 Schematic diagram of power quality monitoring point and electricity metering point
本文依据上述两类实测数据在时序上的关联关系,识别同一馈线下工业用户多电能质量指标特征,总体步骤如图2所示,主要研究包括时序特征筛选和用户电能质量指标特征识别两部分。
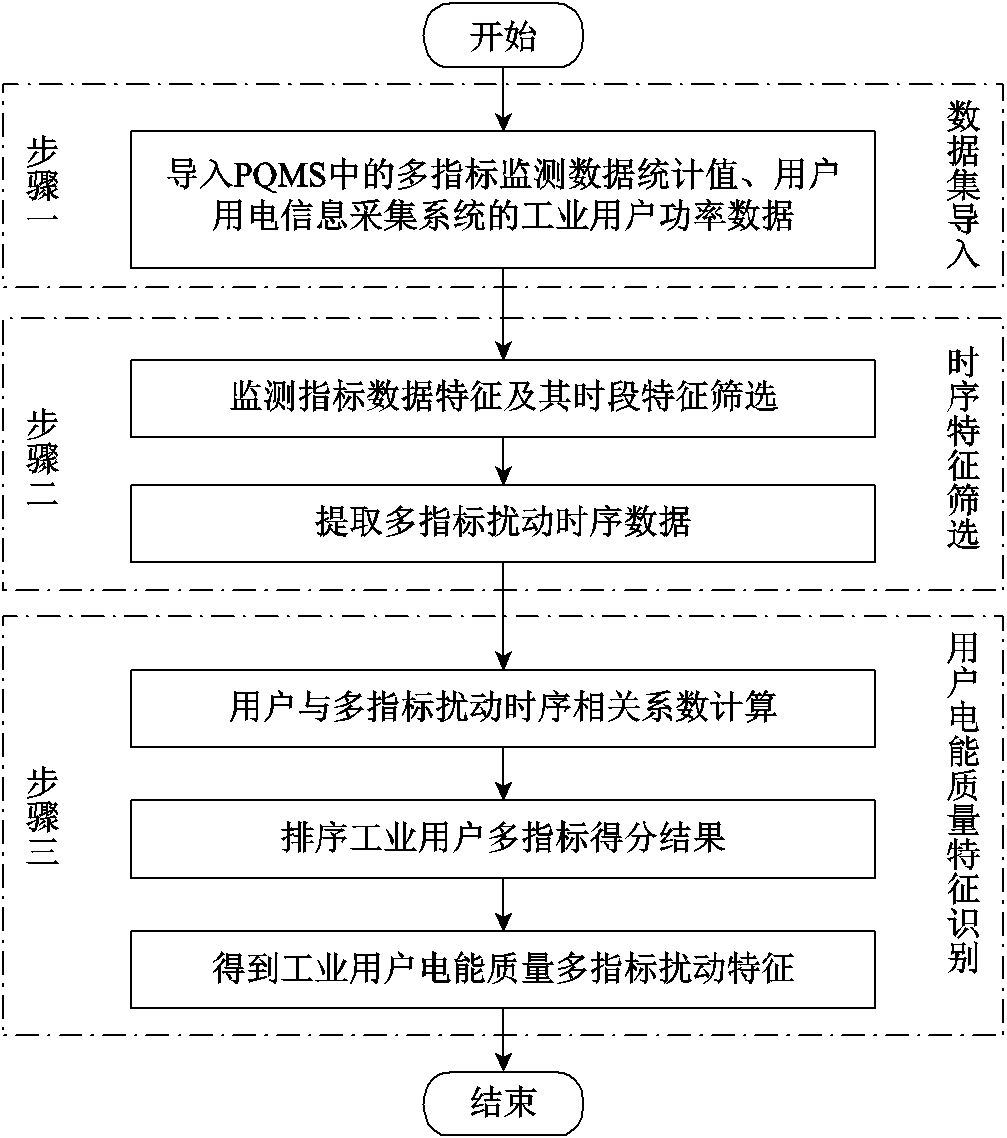
图2 工业用户电能质量特征识别算法流程
Fig.2 Flow chart of power quality characteristics identification of industrial users
1)时序特征筛选
首先将电能质量监测指标数据的越限和波动时段定义为扰动时段,依据指标限值和概率分布,提取电能质量时序超标、波动数值及其时段,并设立谐波关键指标筛选规则,得到谐波关键指标、电压偏差和负序电压不平衡度等指标的扰动时序数据。
2)用户多电能质量指标特征识别
提取扰动时段的用户功率数据,利用导数动态时间弯曲(Derivative Dynamic Time Warping, DDTW)算法,分析扰动时段下监测指标与工业用户用电数据的相关性,依据不同指标关联度识别用户的电能质量特征。
各类工业用户工况具有长时规律性以及短时不确定性的变化特点,PCC处电能质量稳态指标曲线随之呈现出周期性强且分钟级时段内波动较大的形态[17]。因此,本文从时序数值大小和趋势上,关注指标发生超标和大幅变化的时间段及其数值特征,归结为超标和波动两类具有显著特征的电能质量事件场景。
(1)超标场景,表现为指标波动幅值已超出国标限值的超标时段。在此时间区间内,测点电能质量水平受到严重影响。这类情况是电力公司电能质量管理工作中重点关注的问题,并制定标准明确规定了电能质量指标限值。因此,指标越限的超标场景应作为扰动特征分析的重点场景。
(2)波动场景,表现为指标虽无超标但变化趋势较大的时段。在实际曲线的某些时间区间内,虽然指标未超标,但数据变化量较大,区别于大部分情况下的正常指标数据,在此时段内,干扰源工况可能发生异常变化,对电能质量指标预测与预警具有现实意义[17-18]。因此,指标的波动也属于扰动特征分析场景。
同一日某10 kV监测点电能质量指标实际监测情况如图3所示,以电压总谐波畸变率UTHD和电压偏差Ud两个指标作为示例,说明波动场景分析的必要性。
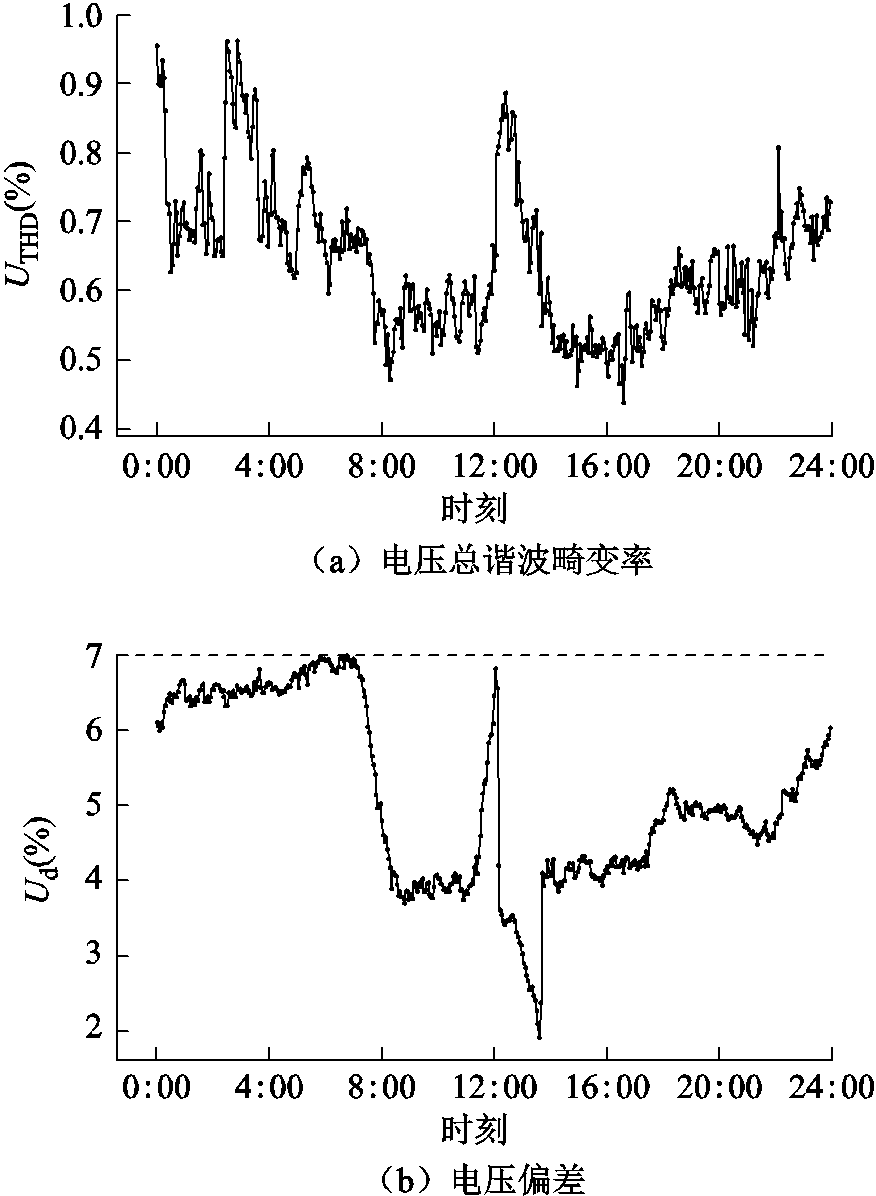
图3 同一日某10 kV监测点电能质量指标情况
Fig.3 Power quality indices of a 10 kV monitoring point on the same day
按限值的判定标准,在图3中这天内,UTHD全时段均未超出国标规定限值4.0%[19]。而电压偏差虽存在超标情况(限值线为7%[20]),但超标时刻较少。另外,从指标分布来看,前者在夜晚至凌晨及中午时段波动大,后者超标时刻点附近有较长一段时间内,指标均处于较高水平且波动极大。实际上,在凌晨与中午时段,该监测点的两种指标数值均发生显著变化。可见,仅依据国标限值设置固定界限可能遗漏重要时段及指标变化特征。
因此,综合考虑指标曲线的超标场景和波动场景,更有利于提取出电能质量指标的典型特征。
复合电能质量扰动中每时刻可能存在一个或多个事件[21-22],包括谐波、电压偏差、三相不平衡、电压闪变、间谐波等,参照国标的计算分析方法[19-20,23-25],可以分别得到谐波、电压偏差、负序电压不平衡度εU2、短时闪变[26]、间谐波电压含有率UIHR、电压波动Uf等指标数据。本文主要考虑问题较普遍严重且影响较大的谐波、电压偏差、负序电压不平衡度等指标类型,依次进行指标时序特征分析。
2.2.1 超标和波动序列筛选
由于不同类型指标的数据分布不一致,如图3a、图3b,两两数据整体长时关联程度低,仅部分时段具有波动相似性,故不便直接对多种监测指标时序进行关联分析。本文依据国标限值与时序数据累积分布[27],分别筛选指标超标时段及波动时段,并将各时刻合并成扰动时段,提取各个时段内电能质量多指标特征。
1)超标时刻筛选
根据电能质量领域标准文件[28]规定的限值,筛选超标时刻。当指标时序值大于国标限值时,则将对应的时间点划定为超标时刻。
2)波动时刻筛选
为有效筛选出波动时刻,本文基于指标数值的长时间概率分布情况,识别出异于大多数时刻分布的数值,并以此为依据提取对应的时序索引。
考虑电能质量指标本身具有长时低值、周期波动性,同时为保证时序索引提取的可靠性,本文采用最典型的3 min间隔的时序数据统计值展开研究,即分析样本为每天共480组、连续多天的时序数据,进而根据指标时序的累积分布图拐点确定波动时刻点。
累积分布图是累积分布函数(Cumulative Distribution Function, CDF)关于随机变量Y中任意取值y的曲线,记为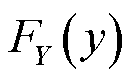 。
。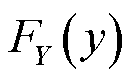 可以描述随机变量Y的概率分布,描述Y取值落在不大于y范围内的可能性,其定义式为
可以描述随机变量Y的概率分布,描述Y取值落在不大于y范围内的可能性,其定义式为
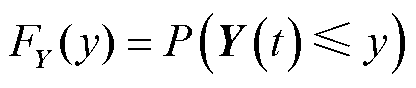 (1)
(1)
式中,Y(t)为时序变量;P(·)为概率函数。
计算累积分布函数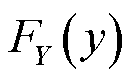 曲线拐点,记为y0,满足
曲线拐点,记为y0,满足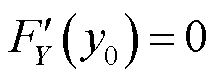 ,该点即为时序Y发生波动的数值点。将时序Y中取值为y0的时刻t0作为波动时刻,满足Y(t0)=y0。
,该点即为时序Y发生波动的数值点。将时序Y中取值为y0的时刻t0作为波动时刻,满足Y(t0)=y0。
假设在某时间段内获取某监测点的指标数据,以谐波、电压偏差、负序电压不平衡度三类指标扰动情况为例,由国标阈值和累积分布图拐点筛选处理后,得到的电能质量指标及其时序特征见表1。
表1 电能质量指标时序特征
Tab.1 Time sequence characteristics of PQ indices

时刻点指标特征 t1电压总谐波畸变率,电压偏差,负序电压不平衡 t2电压总谐波畸变率,5次谐波电流 t3电压偏差,负序电压不平衡,5、7次谐波电流 ……
3)超标及波动序列提取
经过上述超标及波动时刻的筛选过程,拆分了原有时段t1~tn内的连续等间隔时间点,得到一系列时刻点t'1~t'm,并且存在部分与其他时刻点间隔较大的离群点,将不便于后续长时间尺度下不同时序匹配分析。因此,需要进一步合并分布较为密集的时刻点,从而形成扰动时间区间,实现超标及波动时间序列提取。
划定最小扰动时段间隔Tlimit,扰动序列截取示意图如图4,将连续v个扰动时刻点合并为第一个时间区间,该区间对应时间段为DT1=[(t'v-t'v-1)+(t'v-1- t'v-2)+…+(t'2-t'1)],且其中两两相邻时刻点之间满足|t'j-t'i|min≤Tlimit,Tlimit取值可依据分析需要设置,如若划定允许最小扰动时间间隔为15 min,则将两两间隔在15 min之内的连续扰动时刻点视为同个扰动时段。接着,依次合并扰动时刻点,最终形成N个扰动时间区间(记为DT1,…,DTN)及其时间序列(记为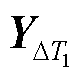 ,…,
,…,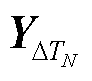 )。
)。
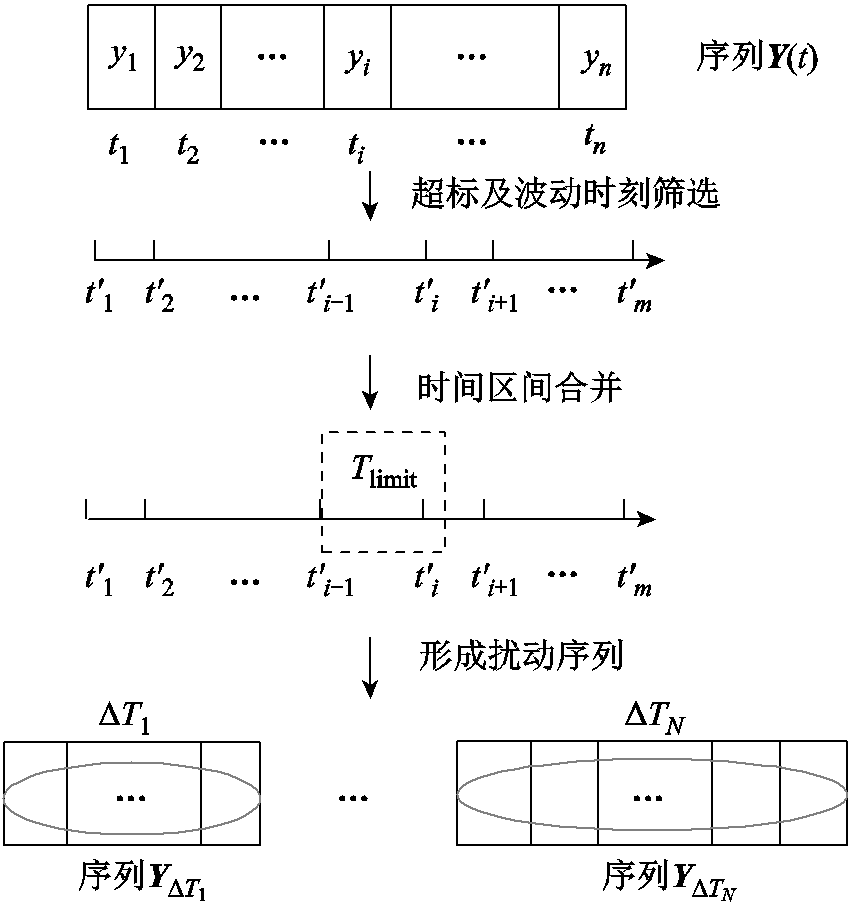
图4 扰动序列截取示意图
Fig. 4 Schematic diagram of disturbance sequence interception
2.2.2 多类型指标时序筛选
根据指标波动和超标特征,上述过程将原始指标时序数据拆分、合并后得到新的扰动序列。本节以谐波、电压偏差、负序电压不平衡度三种指标类型为例,说明多类型扰动指标时序筛选过程。其中谐波方面又可细分为电压总谐波畸变率、奇次谐波电流等谐波类指标。在后续关联量化计算时,特征识别必须更具针对性,因此需要取长时扰动的某个或某些谐波类指标作为谐波关键指标。
首先评估不同扰动序列的时间跨度,将跨度较大的谐波关键指标序列作为后续与用户功率时序匹配的对象。定义扰动时段占比τ如式(2)所示,计算新时间序列与原始时间序列数据的长度之比。
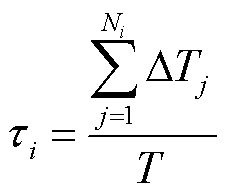 (2)
(2)
式中,τi为经截取后的指标i序列长度占原始时序全时段的比例;Ni为经截取后的指标i序列的时间区间数量;Tj为第j个时间区间的长度;T为原始时序全时段的长度。
接着,将各种谐波类型指标序列的时段跨度从高到低排序,根据如下规则选取某个指标的τ值作为阈值,将τ值不小于阈值τmin的谐波指标作为谐波关键指标。
规则一:若谐波指标时序的扰动时段占比{τ(谐波1),τ(谐波2),…,τ(谐波n)}中任意值均大于τ(电压偏差)或τ(负序电压不平衡度),则将后两者中的较小值作为阈值τmin,此时谐波代表性指标即为所有谐波指标。
规则二:若谐波指标时序的扰动时段占比{τ(谐波1),τ(谐波2),…,τ(谐波n)}中最大值τ(谐波)max均小于τ(电压偏差)与τ(负序电压不平衡度),则将谐波指标时序的扰动时段的τ(谐波)max作为阈值,此时谐波代表性指标包括阈值对应的谐波指标。
规则三:若τ(电压偏差)与τ(负序电压不平衡度)均大于谐波最小值τ(谐波)min,且谐波最大值τ(谐波)max大于τ(电压偏差)或τ(负序电压不平衡度)其一,即表现为{τ(谐波)max>τ(电压偏差)或τ(负序电压不平衡度)},{τ(电压偏差)与τ(负序电压不平衡度)>τ(谐波)min}的数值分布,则将τ(电压偏差)和τ(负序电压不平衡度)中的较小值作为阈值,此时谐波代表性指标为τ值大于阈值的部分谐波指标。
最后,提取谐波关键指标、电压偏差和负序电压不平衡度等其他指标的扰动时序数据。
传统的电能质量机理建模分析难以处理含有复杂多类型扰动之间的交互影响,而稳态电能质量监测统计数据的时序与干扰源负荷用电行为特征存在关联[14,16]。因此,在2.2节的基础上,利用长时间尺度数据关联方法,进一步计算扰动时段中时序数据与用户功率的相关系数,找出与指标具有强关联性的用户,实现电能质量特征与用户用电特征的匹配。
2.3.1 时间序列矩阵形式
在所筛选的扰动时段内,稳态指标x的扰动时间序列由N个扰动时序子集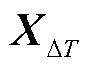 组合而成,记为
组合而成,记为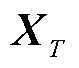 ,即
,即
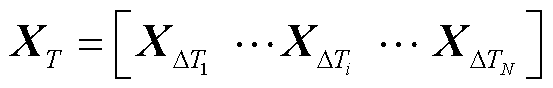 (3)
(3)
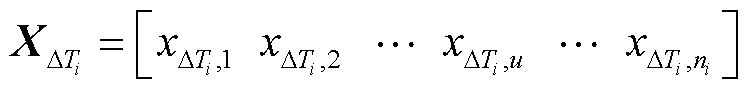 (4)
(4)
式中,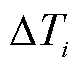 为某个子集i的扰动时段,1≤i≤N;ni为
为某个子集i的扰动时段,1≤i≤N;ni为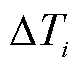 中的监测指标时序数据总数,
中的监测指标时序数据总数,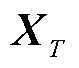 的数据总量可表示为
的数据总量可表示为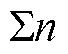 ;
;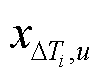 为在子集i内第u个扰动时刻的时序数据,1≤u≤ni。
为在子集i内第u个扰动时刻的时序数据,1≤u≤ni。
假设所分析的母线共连接了m个用户,提取相应扰动时段下的终端工业用户平均有功功率序列,分别记为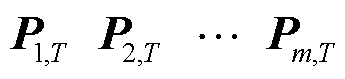 。如用户k的功率序列
。如用户k的功率序列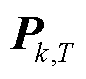 表示为
表示为
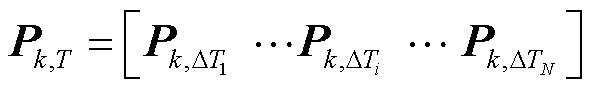 (5)
(5)
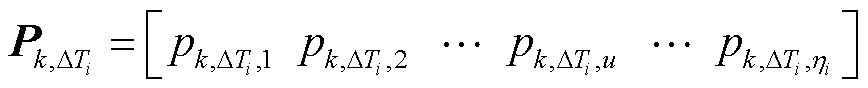 (6)
(6)
式中,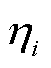 为
为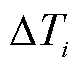 中的功率序列数据总数,1≤i≤N,
中的功率序列数据总数,1≤i≤N,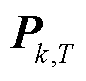 的数据总量可表示为
的数据总量可表示为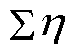 ;
;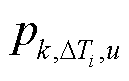 为第k个用户在
为第k个用户在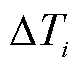 时段内第u个时刻的有功功率,1≤k≤m,1≤u≤ηi。
时段内第u个时刻的有功功率,1≤k≤m,1≤u≤ηi。
根据不同电能质量指标的扰动时段子集,形成时序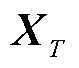 ,并且提取相应扰动时段下的终端工业用户用电数据时序,以用户k为例,即提取序列
,并且提取相应扰动时段下的终端工业用户用电数据时序,以用户k为例,即提取序列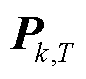 ,用于后续时序关联计算。
,用于后续时序关联计算。
2.3.2 用户多指标电能质量特征计算
电能质量监测数据与电力用户用电行为之间的关系体现为相应时间序列变化规律的相似性。由于上述两类量测数据来自不同的数据源,其存储时间间隔不一致。衡量时序相似性的传统方法,如皮尔逊相关系数,要求两者时序长度一致,不再适用于本文数据处理场景。
动态时间弯曲算法(Dynamic Time Warping, DTW)可以衡量两个非对齐时间序列的相似程度。通过序列之间的动态化匹配,可以得到电能质量监测数据和各个用户有功功率的特征矩阵之间的距离矩阵,从而定量分析各用户平均有功功率与电能质量指标的相关性[16]。
由于工业用户在特定用电时段内功率变化相对稳定,而DTW算法存在过度病态弯曲的缺陷,在匹配过程中使一个工业用户有功功率时间序列中连续多个同数值水平的值对应于电能质量时间序列的较长子序列,从而导致计算结果不精确。
因此,本文在DTW算法的基础上进行改进,利用综合考虑曲线形状特征和变化趋势的DDTW算法[29-30],来实现上述时序数据的匹配。与DTW类似,DDTW距离计算过程也采用迭代的方法,但对迭代初值做了导数预处理,其目的在于从时序数值上突显出指标变化特征,用以克服DTW算法的不足,进而计算时间序列两两元素间的欧式距离,形成DDTW距离矩阵。导数预处理的DDTW算法相较于DTW算法的具体改进效果详见算例3.3.1节部分。
对于实际中可能出现的噪声污染,直接对实际数据进行导数处理将增加噪声干扰的信噪比,影响指标时序数据与用户侧时序数据的关联匹配效果。因此,本文在获取原始实际数据时,首先对数据做平滑处理,具体方法为:使用一组滑动窗口,每li个时序数据取平均值,本文取li为10,即对相邻10个数依次求均值,得到平滑后的时序,以此减少噪声干扰对后续导数处理的影响。某监测点11次谐波电流指标处理前后的曲线如图5所示,该采样数据经平滑处理后,可消除局部尖峰干扰。
接着,对长度分别为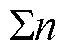 、
、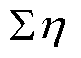 的监测数据XT与电力用户k平均有功功率
的监测数据XT与电力用户k平均有功功率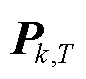 进行导数预处理,得到表征时序曲线特征和变化趋势的新序列,记为
进行导数预处理,得到表征时序曲线特征和变化趋势的新序列,记为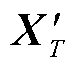 、
、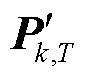 ,序列内任意一个元素分别记为
,序列内任意一个元素分别记为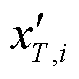 、
、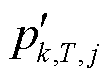 ,其计算公式分别为
,其计算公式分别为
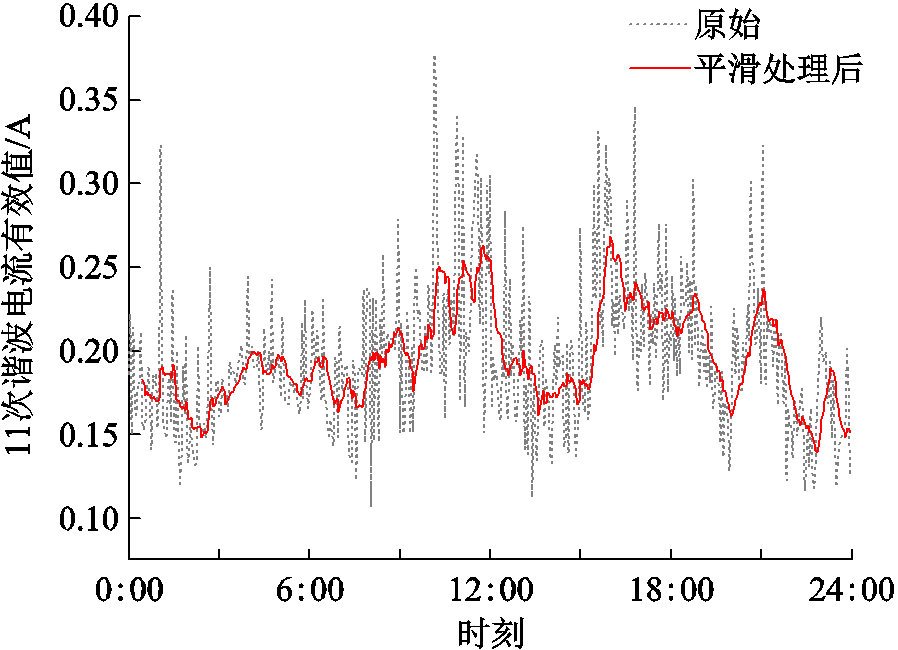
图5 某监测点11次谐波电流数据平滑处理前后曲线
Fig.5 Curve of the 11th harmonic current before and after smoothing of a monitoring point
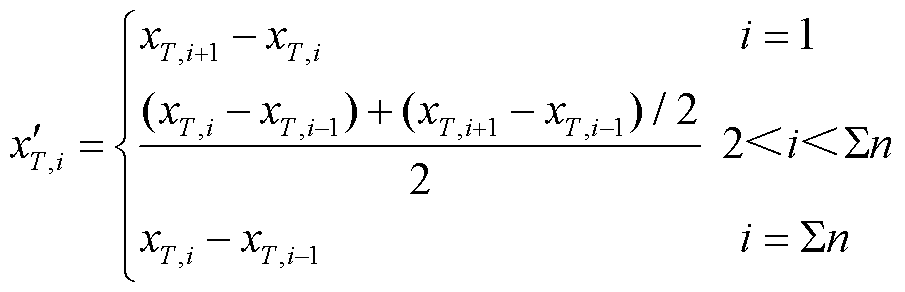 (7)
(7)
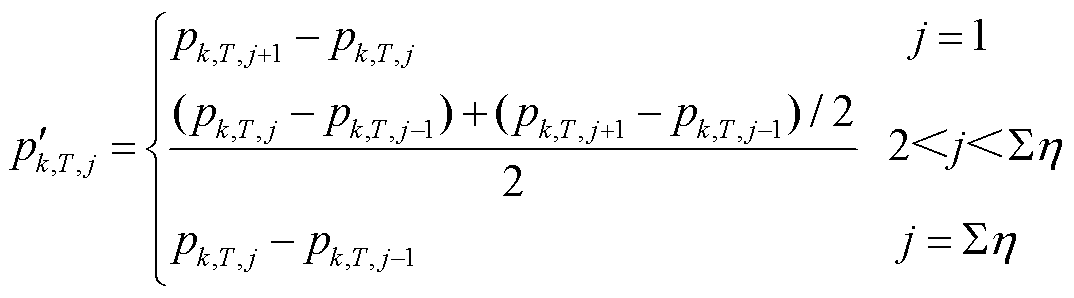 (8)
(8)
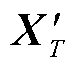 、
、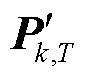 的量纲不一致,为了实现两者的可比性,计算两组序列的均值和方差,利用标准化方法,将上述若干组数据转换为无单位的分值,转换后的序列矩阵形式记为
的量纲不一致,为了实现两者的可比性,计算两组序列的均值和方差,利用标准化方法,将上述若干组数据转换为无单位的分值,转换后的序列矩阵形式记为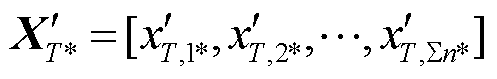 、
、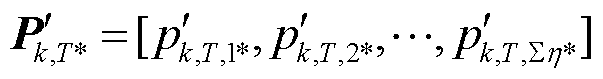 。
。
进一步地,进行DDTW距离计算,定义一个大小为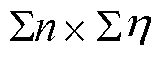 的距离矩阵D,有
的距离矩阵D,有
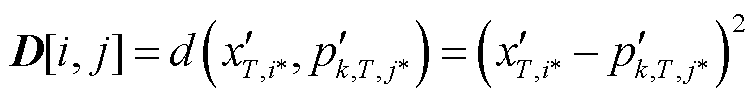 (9)
(9)
式中,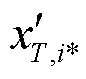 为特征矩阵
为特征矩阵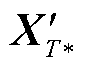 中第i个特征元素,
中第i个特征元素,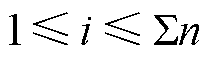 ;
;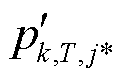 为
为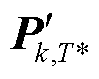 中第j个特征元素,
中第j个特征元素,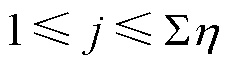 ;
;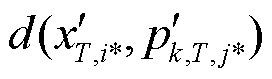 为两者欧氏距离二次方。
为两者欧氏距离二次方。
DDTW距离计算过程采用迭代的方法,记累积距离矩阵为S,初值为
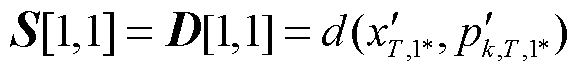 (10)
(10)
该矩阵中各元素计算方法如式(11)所示。
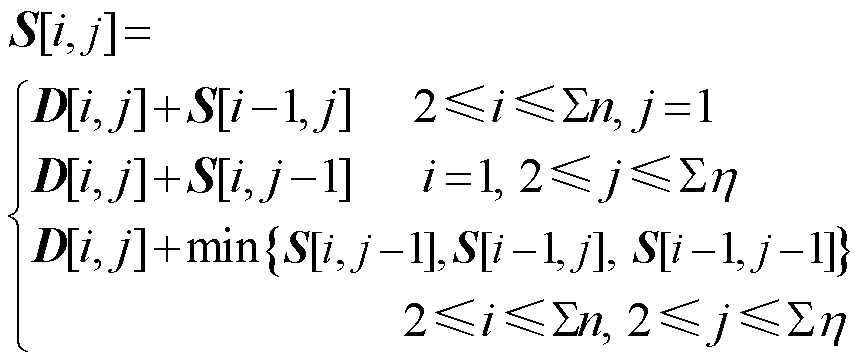 (11)
(11)
直至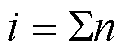 且
且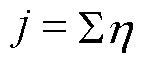 ,此时S[i, j]的数值即为两两时序的整体最小累积距离,也称两个序列的DDTW距离,记为
,此时S[i, j]的数值即为两两时序的整体最小累积距离,也称两个序列的DDTW距离,记为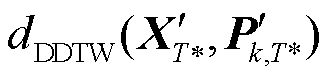 ,表征该用户k与指标数据在趋势特征和时间特征上的相似度,距离值越小,则两者在扰动时段上的相似度越高。
,表征该用户k与指标数据在趋势特征和时间特征上的相似度,距离值越小,则两者在扰动时段上的相似度越高。
时间序列DDTW计算示意图如图6所示,结合DDTW距离矩阵,计算两者时序数据的多时段关联结果计算,并根据式(12)进行归算,可以得到用户k在m个用户当中的相对关联系数结果w(k),从而准确刻画各用户的功率波动与该电能质量指标的关联系数大小。
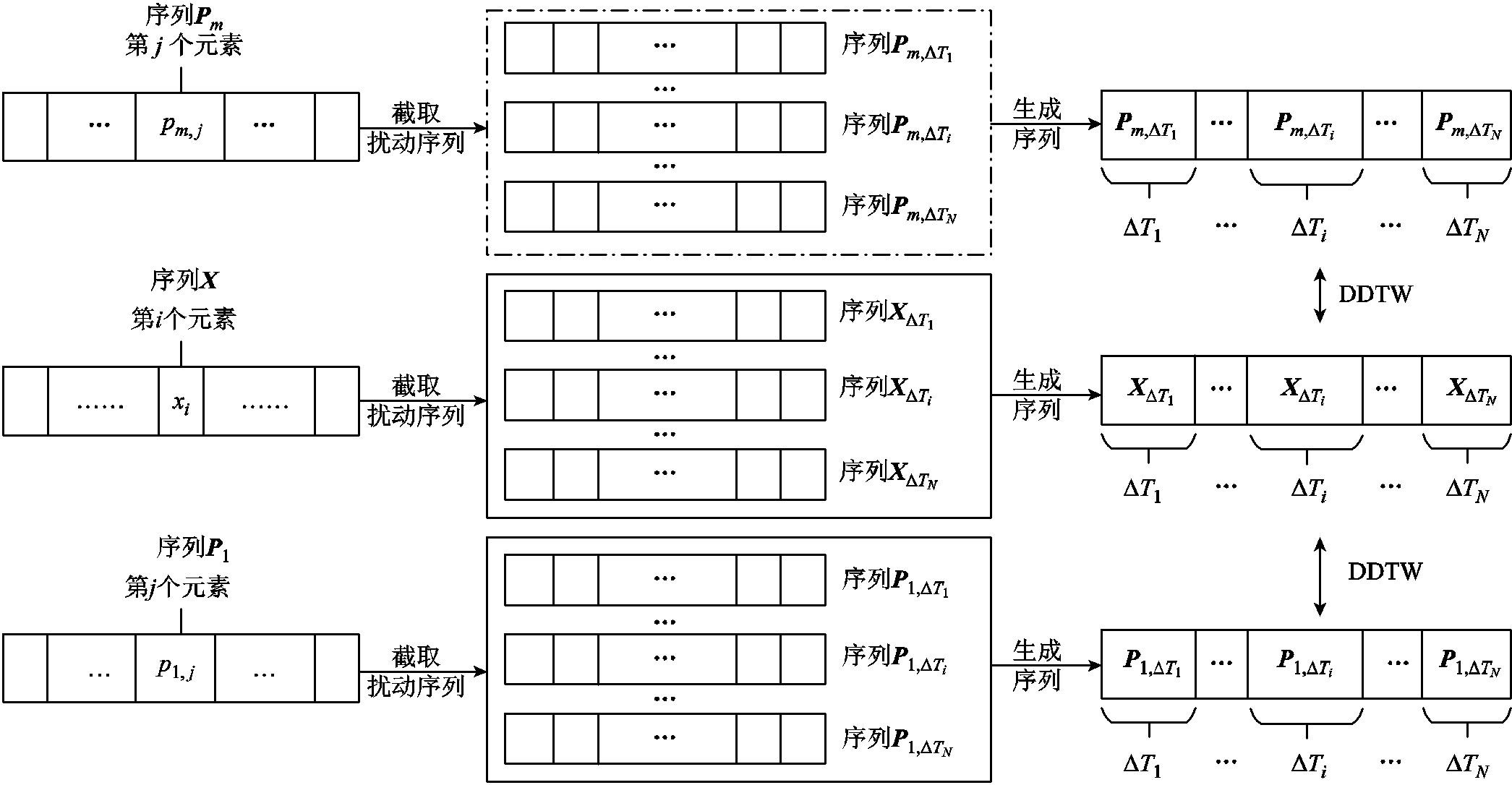
图6 时间序列DDTW计算示意图
Fig.6 Schematic diagram of time series DDTW calculation
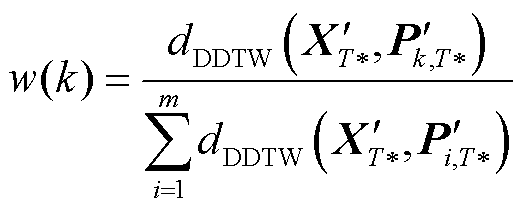 (12)
(12)
式中,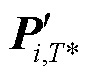 为扰动时段下经导数预处理、标准化后的任意用户i的功率时序。
为扰动时段下经导数预处理、标准化后的任意用户i的功率时序。
根据DDTW算法思想,当计算而得的距离结果dDDTW越小时,两者相似度越强,从而区分不同用户功率时序与不同指标时序的相似程度,实现用户电能质量特征识别。
采用Matlab/Simulink建立仿真算例,如图7所示,10 kV公共连接点(标识为a)下接有谐波干扰源负载、不平衡负载及三相线性负载。
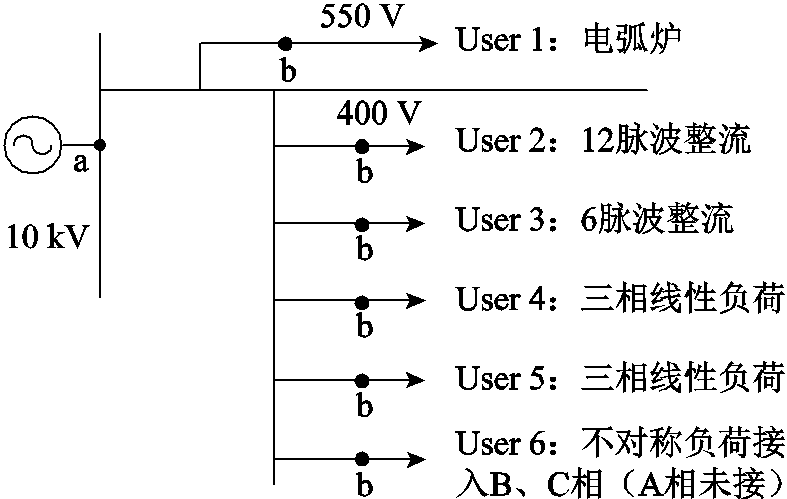
图7 仿真算例电气接线示意图
Fig.7 Schematic diagram of electrical wiring in simulation
随机设置不同用户的运行时段,其运行情况见表2,得到5个仿真日(24 h)的采样序列数据,选取三相总有功功率、电压偏差、三相电压不平衡度、电压总谐波畸变率、间谐波电压含有率、奇次谐波电流和电压波动指标进行分析。
表2 仿真算例工业用户容量与运行时段
Tab.2 Capacity and running time of industrial users in simulation
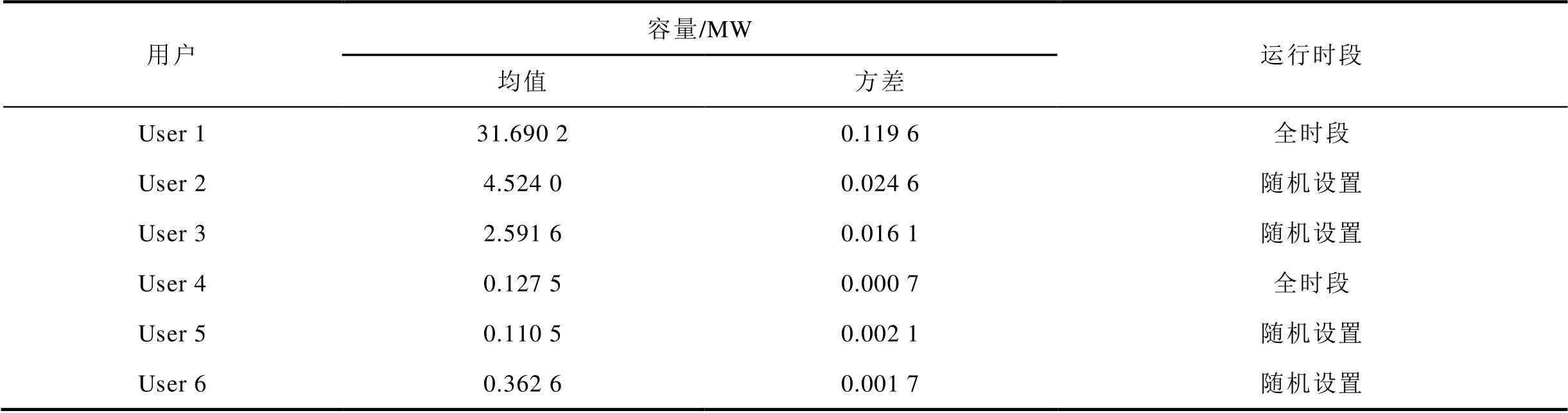
用户容量/MW运行时段 均值方差 User 131.690 20.119 6全时段 User 24.524 00.024 6随机设置 User 32.591 60.016 1随机设置 User 40.127 50.000 7全时段 User 50.110 50.002 1随机设置 User 60.362 60.001 7随机设置
由于仿真中主要建立了6、12脉波整流负荷模型,故5、7、11、13次奇次谐波电流较大,具有典型性,而其他次谐波电流数值较小,同时,实际现场的电能质量测试数据一般也体现出奇数次谐波较显著的情况。因此,本文采用5、7、11、13次典型谐波次数展开分析,其他次谐波指标如附图1所示。另外,由于存在电弧炉,该仿真场景下1.5次间谐波电压含有率UIHR1.5显著超标,故重点以该次指标展开分析,其他次UIHR指标如附图2所示。
根据国标中统计指标95%概率大值计算方法[25],得到PCC处电能质量监测数据统计值、用户侧(产权分界点标识为b)功率数据,除电压波动采样间隔为10 min[24]外,其他电能质量监测数据的采样间隔为3 min,用户侧功率数据Pi(1≤i≤6)间隔为15 min[31],采样数据的曲线如附图3、附图4所示。
依据10 kV电能质量指标限值,以及各指标时序累积概率分布曲线,得到不同扰动时刻下的指标特征。进一步,设置相邻两个扰动时刻点之间间隔限值为Tlimit,汇总所有扰动指标时刻点,形成多个扰动时间段。
当设置Tlimit为45 min时,可得到每个仿真日下的超标及波动扰动时段数以及时段分布情况,如图8和表3所示。
在该仿真场景下,整流器等非线性负荷带来的谐波扰动事件显著,特别是5、7、11、13谐波电流,以及1.5次间谐波电压含有率,存在长时间超标现象,且电压波动的扰动时段占比最小,因此,根据2.2.2节规则一,该场景下指标包括电压偏差、负序电压不平衡、电压波动、1.5次间谐波电压含有率以及所有谐波指标,谐波关键指标有电压总谐波畸变率、6k±1次谐波电流、12k±1次谐波电流,k=1。
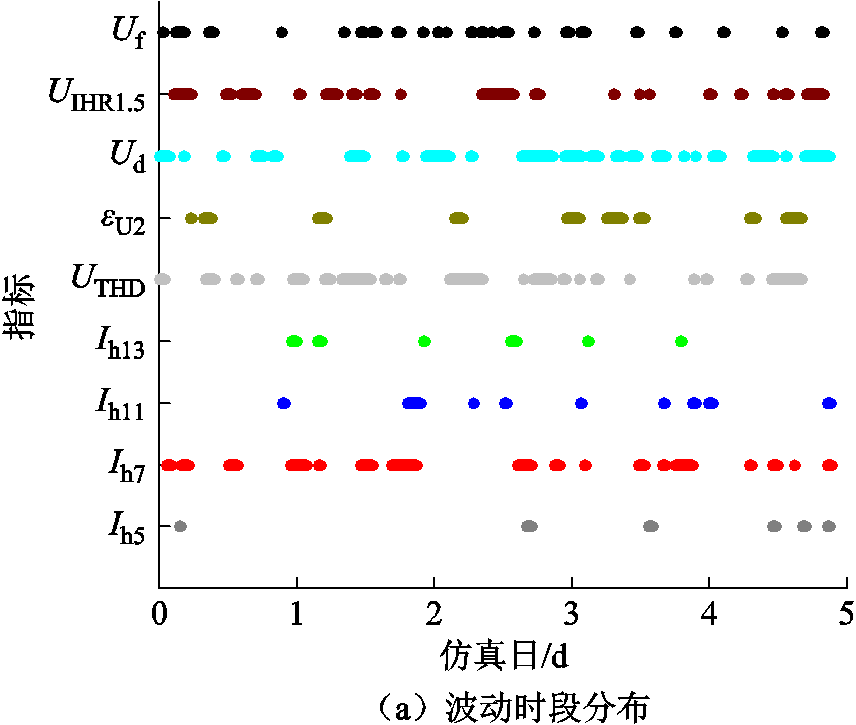
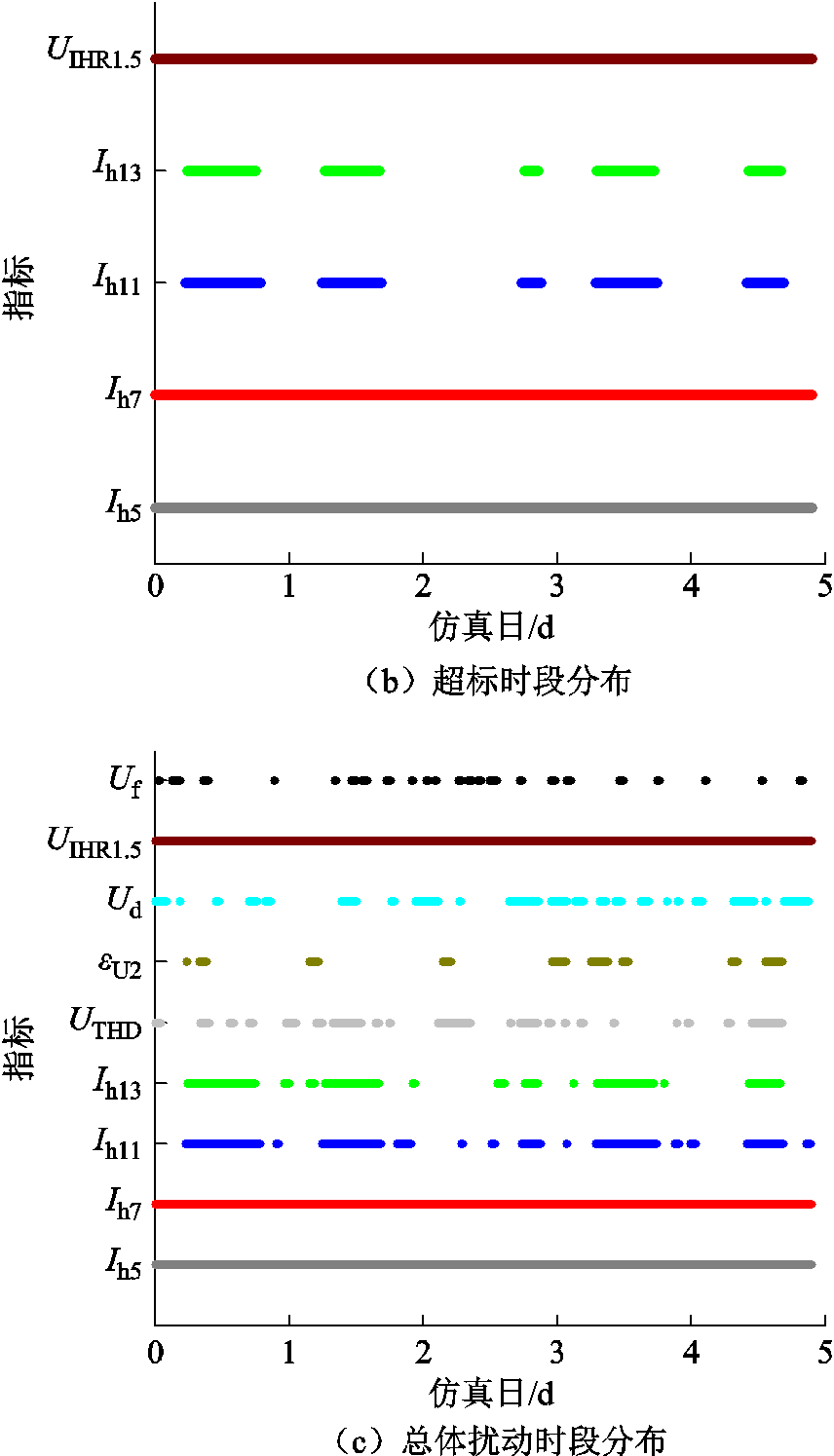
图8 不同电能质量指标扰动时段分布
Fig 8 Disturbed periods distribution of different power quality indices
表3 扰动时段数及占比(Tlimit=45 min)
Tab.3 Number and proportion of disturbed periods (Tlimit=45 min)
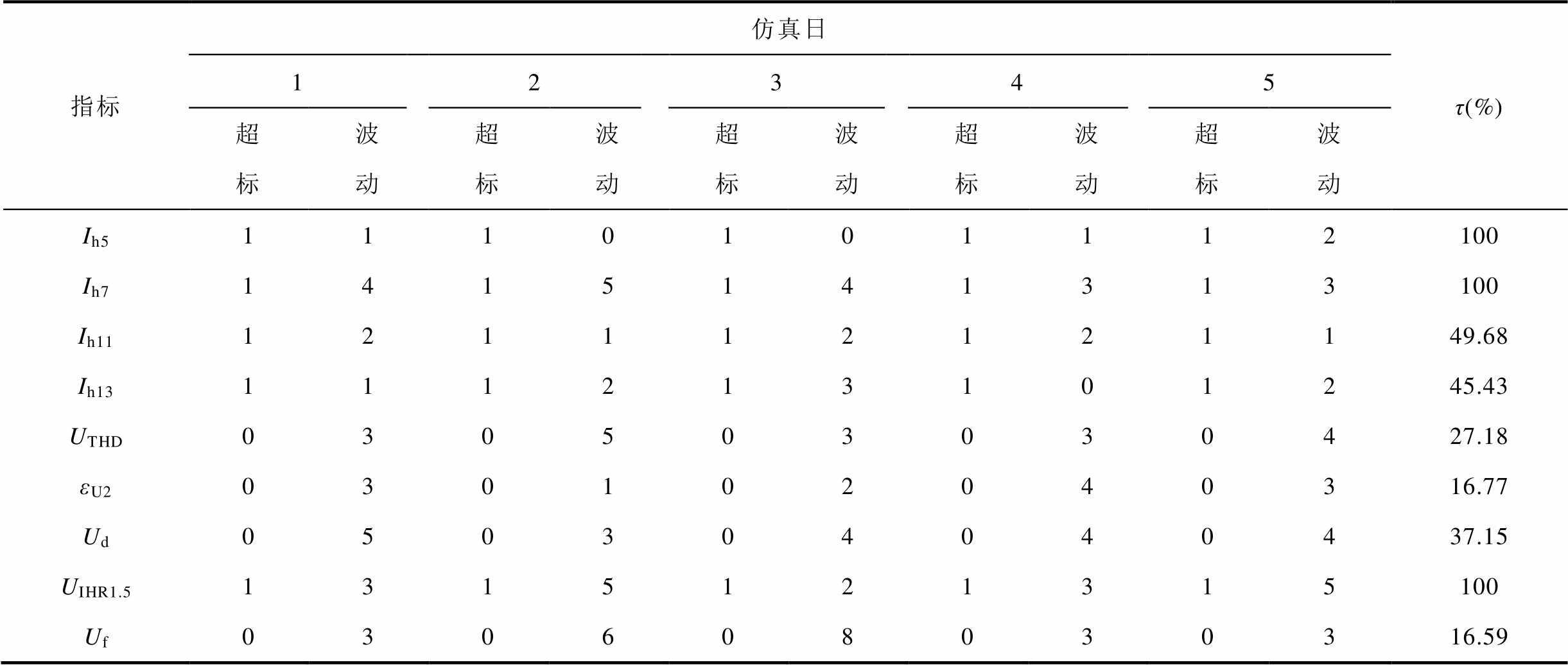
指标仿真日τ(%) 12345 超标波动超标波动超标波动超标波动超标波动 Ih51110101112100 Ih71415141313100 Ih11121112121149.68 Ih13111213101245.43 UTHD030503030427.18 εU2030102040316.77 Ud050304040437.15 UIHR1.51315121315100 Uf030608030316.59
3.3.1 DTW与DDTW关联系数结果对比
本文以表3中时间跨度最大的谐波关键指标(以7次谐波电流Ih7为例)与各个用户功率数据为基础,采用DDTW算法进行电能质量时序与用户用电时序的关联匹配计算,并与传统DTW算法[32]做算例对比,分析两者算法在本文的适用性。
由于本文所设置场景下,谐波关键指标扰动时段占比为100%,故将该指标的全时段时序数据代入DDTW算法中,根据式(12)归一化,计算得到各用户相对关联系数结果,如图9所示。
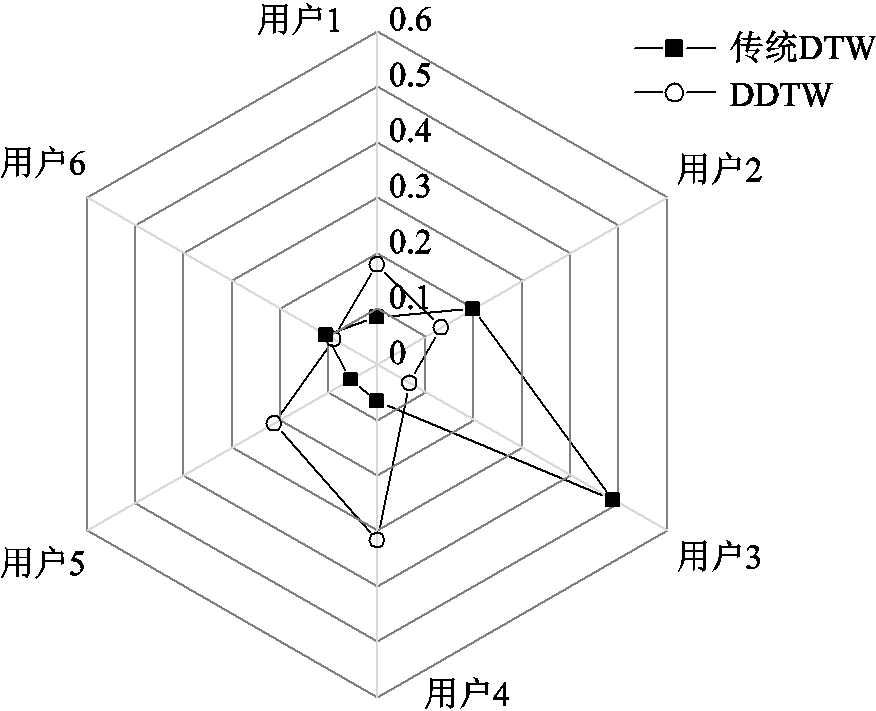
图9 Ih7指标相对关联系数
Fig.9 Relative correlation coefficient of the 7th harmonic current
由图9中可知,针对关键指标Ih7,观察用户3的DTW计算结果具有最大相对关联系数,意味着用户3的功率波动与(6k±1, k=1)次谐波电流变化的关联性最小,与仿真所设置的6脉波整流用户的特征不一致。因此,仅依据DTW算法进行时序匹配无法将主要电能质量问题准确划分到具有相应特征的用户上。
而图9中用户1、2、3、6的DDTW算法所得相对关联系数均处于较中心位置,相对关联系数较小,意味着其用电变化与指标波动具有强关联性,即将与7次谐波电流问题最为相关的非线性用户群均圈选出来,说明DDTW算法具有改进效果,克服了时序数据病态匹配的缺点,可有效筛选出时序上强相关的数据。
在上述4个用户组成的用户群中,用户3的dDDTW系数最小,认为该用户的用电行为与7次谐波电流问题最为相关,结合表3中5次谐波电流同样表现为全时段扰动,因此,在该场景下,对于用户3而言,需要重点治理(6k±1, k=1)次的特征次数谐波。
3.3.2 考虑扰动时段占比的关联计算
针对表3中扰动时序时段占比τ值最大的两个谐波指标Ih5、Ih7,3.3.1节已做相应分析,接下来围绕剩下的指标:Ih11(49.68%)、Ih13(45.43%)、UTHD(27.18%)、εU2(16.77%)、Ud(37.15%)、UIHR1.5(100%)、Uf(16.59%),将各指标的扰动序列依次按照式(8)进行计算,dDDTW结果见表4。
表4 各扰动时段DDTW计算结果
Tab.4 DDTW results of each disturbance period
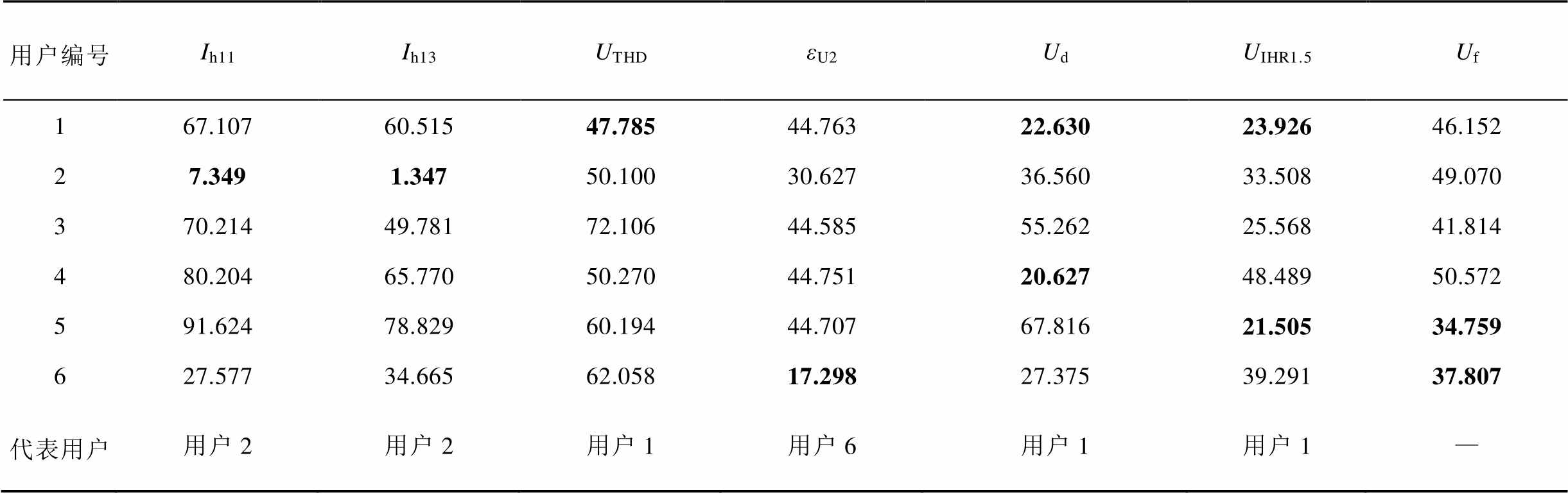
用户编号Ih11Ih13UTHDεU2UdUIHR1.5Uf 167.10760.51547.78544.76322.63023.92646.152 27.3491.34750.10030.62736.56033.50849.070 370.21449.78172.10644.58555.26225.56841.814 480.20465.77050.27044.75120.62748.48950.572 591.62478.82960.19444.70767.81621.50534.759 627.57734.66562.05817.29827.37539.29137.807 代表用户用户2用户2用户1用户6用户1用户1—
对比表4中,经扰动时段处理后的7个指标与用户的关联系数结果,可知:
1)(12k±1, k=1)次特征谐波Ih(12±1)方面,用户2的12k±1次谐波电流关联系数均最小,即其功率波动与指标数据集波动的相似性较其他用户而言大,其负荷性质为12脉波整流负荷,是造成PCC处(12 k±1, k=1)次特征谐波超标及波动的主要干扰源,与仿真设置一致。
2)对于电压总谐波畸变率UTHD,功率波动相似性最大的是用户1,其为容量较大的电弧炉,是造成该场景下总体谐波问题的主要工业用户类型,与仿真设置情况一致。
3)用户6的功率波动与负序电压不平衡指标εU2计算结果最小,即相似性最大,该用户为不平衡负荷,是造成监测点三相不平衡问题的主要干扰源,同样与仿真设置一致。
4)对于电压偏差指标Ud,功率波动相似性最大的分别是用户4和用户1,关联结果十分相近。但在仿真中用户4为线性负荷,且仿真中假设其每时每刻都在运行。具体分析可知,其他用户造成的电能质量污染综合作用在PCC上,线性用户4通过该点获取畸变电压,使得其用电功率变化趋势恰巧与PCC处电压变化情况相似,因此实际中不应将用户4作为引发电压偏差问题的关注用户。由于谐波与电压偏差具有关联性[33],因此在已明确用户1电能质量特征的情况下,可判断将用户1作为主要关注用户。
5)对于间谐波电压含有率UIHR1.5,计算结果表明,与之相似性较大的为用户5和用户1。结合该指标的扰动时段占比以及2个用户运行时段,可知较间断运行的用户5而言,长时间运行的用户1更有可能为造成UIHR1.5长时超标的主要用户。这与用户1、用户5分别为电弧炉、线性负荷的仿真情况相对应。
6)电压波动指标Uf与用户5、6的时序关联计算结果均较小,但从用户维度来看,这2个用户的强相似指标分别为UIHR1.5、εU2,在前文已判定出对应的代表用户,因此对所属电压波动指标特征的用户作保留处理。
可见,在PCC处复杂多种扰动类型的情况下,本文通过匹配不同类型稳态指标时序和用户侧用电时序之间的关联关系,能准确识别相应扰动下的用户特征。
3.3.3 与其他方法的识别结果对比
为分析本文所提方法相较于其他特征识别方法的优势,在该仿真场景中,与基于互信息方法的用户电能质量特征识别方法[14]进行对比,识别结果对比见表5。
表5 识别结果对比
Tab.5 Contrast of identification results

用户编号本文方法特征指标识别互信息方法[14]特征指标识别(判定阈值εÎ[-0.732 1, 0.422 6]) 1UTHD, Ud, UIHR1.5Ud, Ih(12±1), Ih(6±1) 2Ih(12±1)Ih(12±1), UTHD,Ud 3Ih(6±1)Ih7, UTHD 4—Ud, UTHD, Ih7, Ih11 5—Ud, UIHR1.5 6εU2εU2, Ud, UTHD
由表5可知,基于文中方法识别的用户电能质量特征均与仿真场景一一对应,而文献[14]基于最大互信息识别电能质量特征,获取的特征类型较多但不明确,且存在识别错误的现象。如用户6的特征识别结果有负序电压不平衡度、电压偏差与电压总谐波畸变率多个特征指标;对于线性用户4,误识别出Ud、UTHD、Ih7、Ih11共四类特征。这是因为文献[14]所提方法局限于分析时序数据的数值大小,而忽略了时间维度上的时序动态变化特点,导致识别结果缺乏典型性和准确性。
值得注意的是,文献[14]的基础数据均为PCC上同一时间尺度数据,而本文所分析的数据源于不同监测系统,数据的时间尺度不统一。因此,采用文献[14]方法进行算例对比时,需将本文间隔3 min的电能质量监测数据每5个为一组取均值,以此与15 min的功率数据进行时间尺度对齐,再利用最大互信息判定方法进行用户电能质量特征识别。而在实际工程中,常需面对多源数据融合分析的问题,本文所提方法考虑了不同时间尺度的时序数据特点,故较文献[14]更具实用价值。
为验证上述方法在工业用户生产运行场景中的有效性,利用某供电公司一个220 kV变电站10 kV母线(记为母线A)PCC处电能质量监测数据(如附图5所示),以及该母线所接馈线的数个工业用户的平均有功功率数据,进行分析计算。
采样数据情况具体如下:①PCC点电能质量监测数据包括各次谐波电流有效值、电压总谐波畸变率、负序电压不平衡度、电压偏差,取95%概率值,时间间隔为3 min;②用户侧数据包括各个工业用户的平均有功数据,时间间隔为15 min。
以国标规定限值为依据,在所选取的时段内,7个指标特征如图10所示。在所分析时段内扰动时段占比最高的为εU2(48.71%)、Ud(39.76%),谐波指标占比较小,根据2.2.2节的规则二,此处选取电压总谐波畸变率UTHD(18.24%)作为谐波类关键指标,不具体分析Ih5、Ih7、Ih11、Ih13等特征次数谐波指标(扰动时段占比分别为10.90%、9.36%、11.67%、13.98%)。
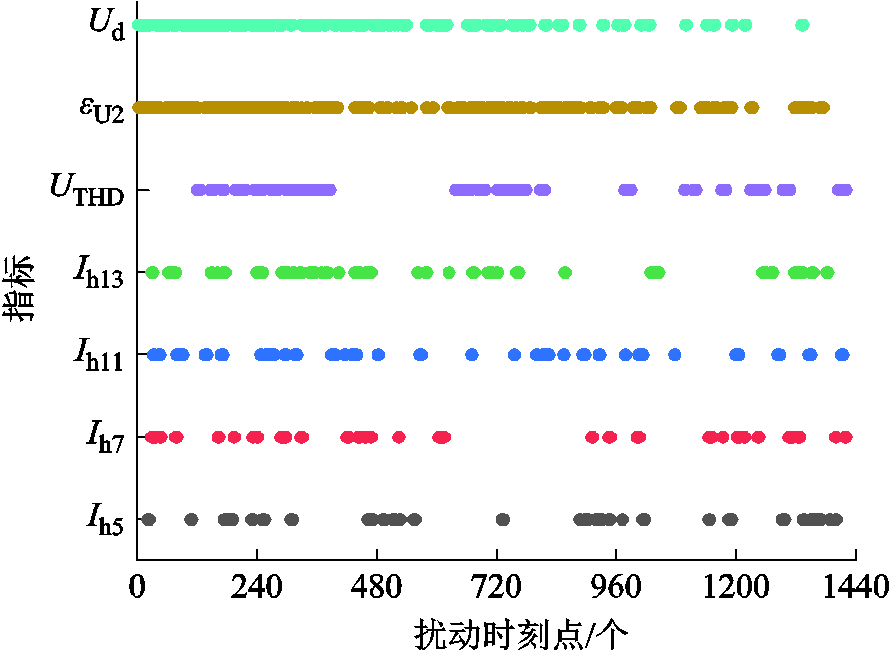
图10 不同电能质量指标时段分布
Fig.10 Time distribution of different power quality indices
计算得到监测数据与功率数据两两的DDTW结果,见表6。若用户与监测指标对应的系数越小,则关联性越强,需要重点关注并开展针对性治理。
表6 DDTW相对关联系数
Tab.6 DDTW relative correlation coefficient
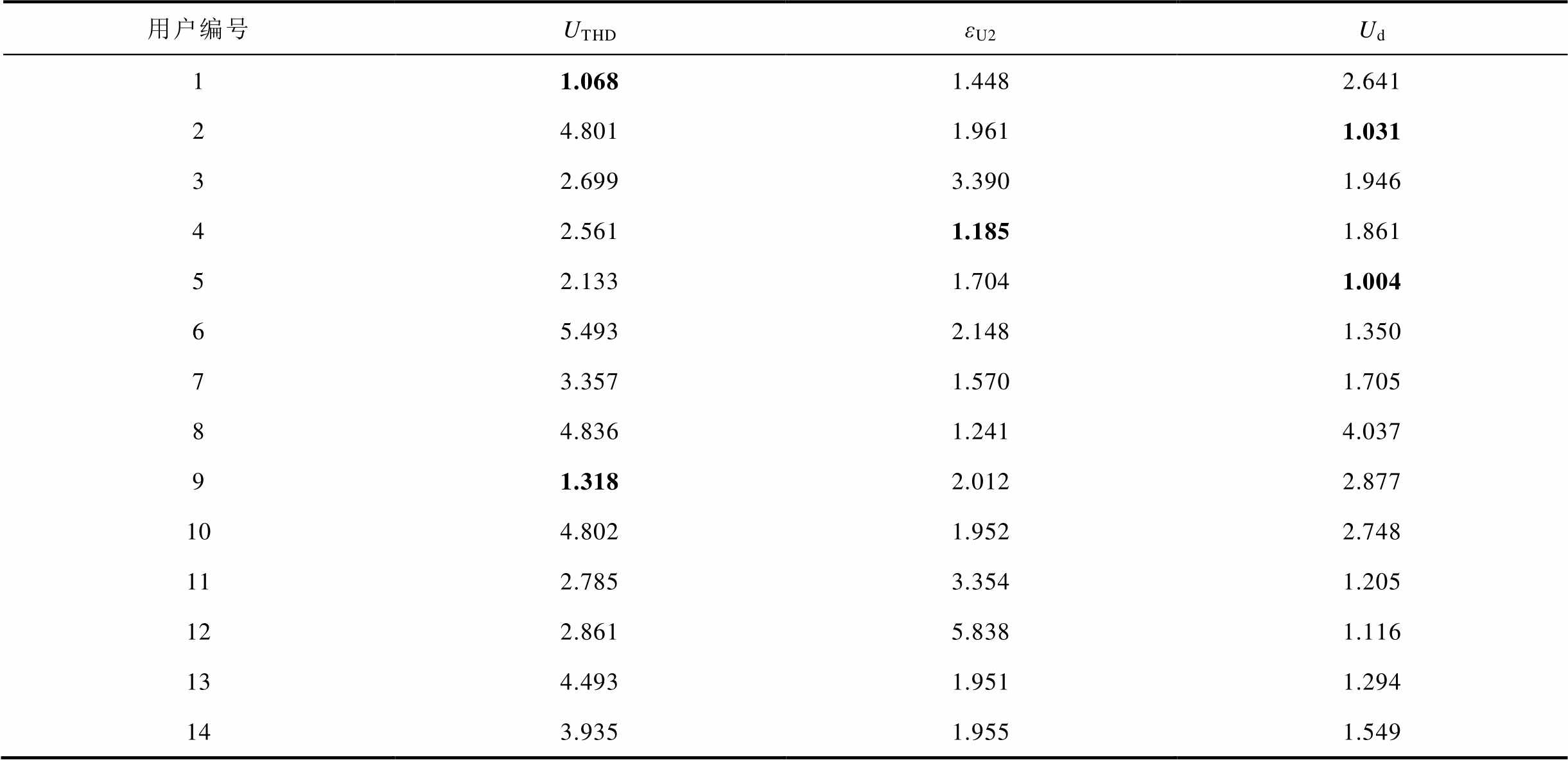
用户编号UTHDεU2Ud 11.0681.4482.641 24.8011.9611.031 32.6993.3901.946 42.5611.1851.861 52.1331.7041.004 65.4932.1481.350 73.3571.5701.705 84.8361.2414.037 91.3182.0122.877 104.8021.9522.748 112.7853.3541.205 122.8615.8381.116 134.4931.9511.294 143.9351.9551.549
对比表6中各指标计算结果可知:①相比其他用户结果,UTHD指标数据匹配母线A所接用户1、用户9时有较小值,因此,该区域内谐波问题与这两个用户最为相关;②εU2指标数据与用户4功率数据的计算系数最小,故该用户应对长时的负序电压不平衡问题进行治理;③用户2和用户5均与电压偏差Ud存在较大关联,治理时需要重点关注。经过调研可知,该母线A下接有冶金业、机械业等类型的工业用户,用电负荷主要为电加热负荷(含电弧炉、中频炉、电热炉、单/多晶硅生产设备)。
结合相对关联系数计算结果,可筛选出与各类电能质量问题强相关的代表性工业用户清单,主要用户信息见表7。
表7 主要用户信息
Tab.7 Main information of users

用户编号电能质量特征行业用电负荷 1UTHD铸造及其他金属制品制造电加热负荷(含电弧炉、中频炉、电热炉、单/多晶硅生产设备) 9UTHD铸造及其他金属制品制造 4εU2结构性金属制品制造 2Ud通用零部件制造 5Ud金属表面处理及热处理加工
各类电能质量问题与代表用户的对应关系分别是:①谐波:以用户1和用户9为代表的铸造及其他金属制品制造行业用户;②负序:以用户4为代表的结构性金属制品制造行业用户;③电压偏差:以用户2、用户5为代表的零部件制造和金属表面处理及热处理加工行业用户。经过现场调研和测试,算例分析结果与实际情况相符,可为确定具体电能质量问题管控对象提供参考。
本文综合考虑谐波、电压偏差及负序电压不平衡度指标,有效挖掘并利用电网公司现有多源数据的关联性,建立工业用户电能质量特征识别框架。该方法具有如下特点:
1)利用国标限值和概率分布方法,提取PCC处电能质量扰动时段,确定长时间尺度序列下的关键指标,能为未来电能质量指标精细化管理提供参考。
2)通过DDTW算法匹配监测点电能质量指标和用户侧功率时序数据,能够筛选出受功率波动影响大的代表性指标,实现不同用户的多类型电能质量稳态特征识别。
3)方法所需数据均可从电力公司现有相关系统获得,计算原理简单,实用性强,可便于集成在现有系统中,从而实现用户电能质量特征在线识别。
附 录
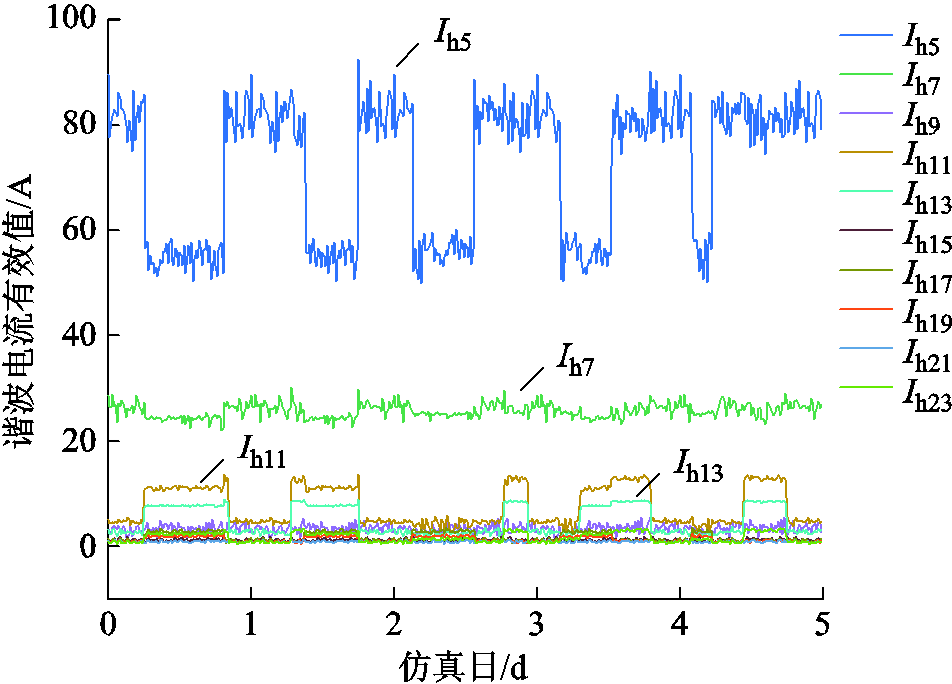
附图1 仿真场景谐波电流有效值曲线
App.Fig.1 Curves of harmonic current RMS in simulation
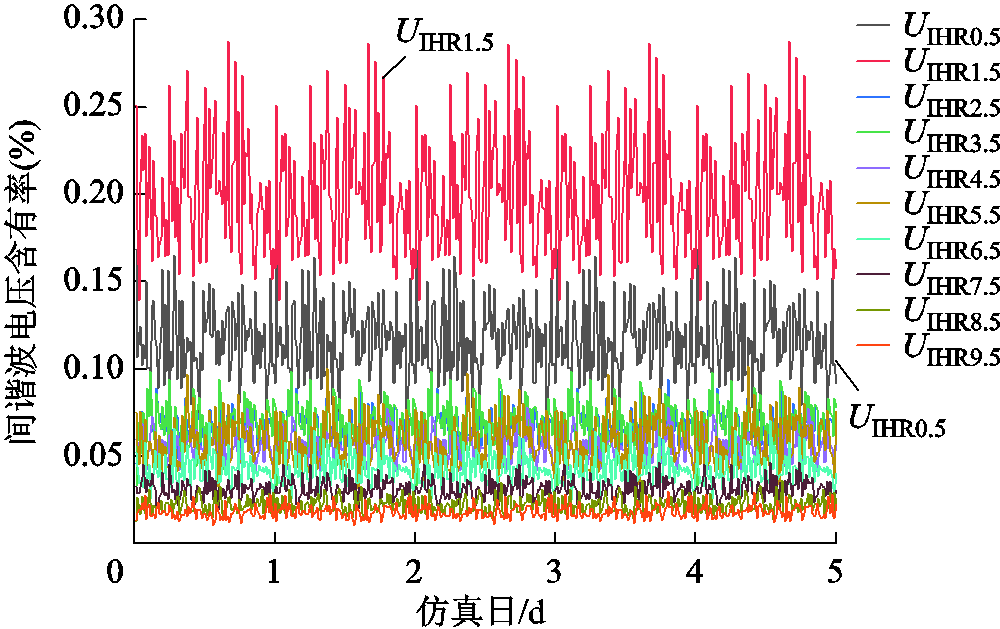
附图2 仿真场景间谐波电压含有率曲线
App.Fig.2 Curves of interharmonic ratio of voltage in simulation
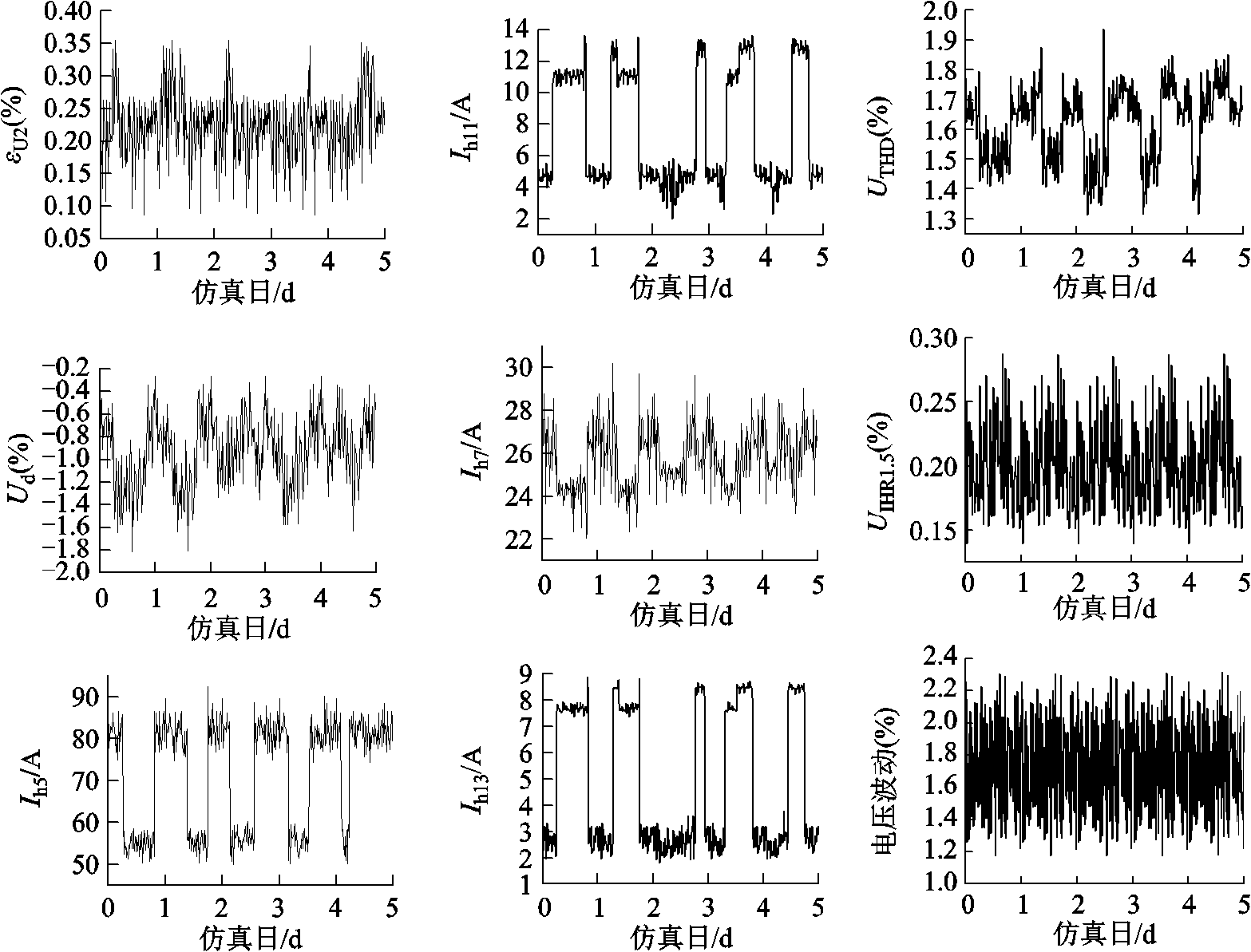
附图3 仿真场景PCC处电能质量监测数据曲线
App.Fig.3 Curves of power quality monitoring data at the PCC in simulation
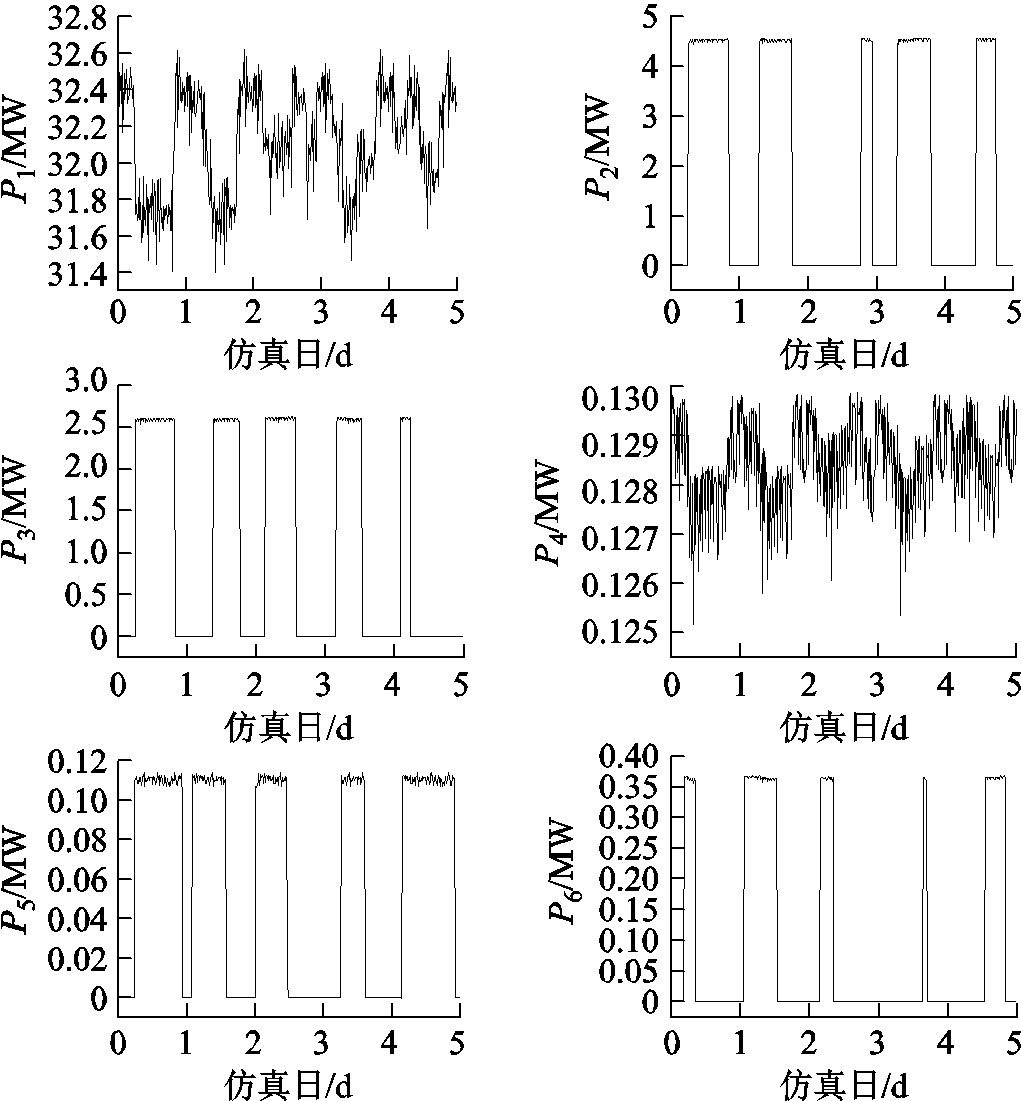
附图4 仿真场景用户侧有功功率数据曲线
App.Fig.4 Curves of active power data of users in simulation
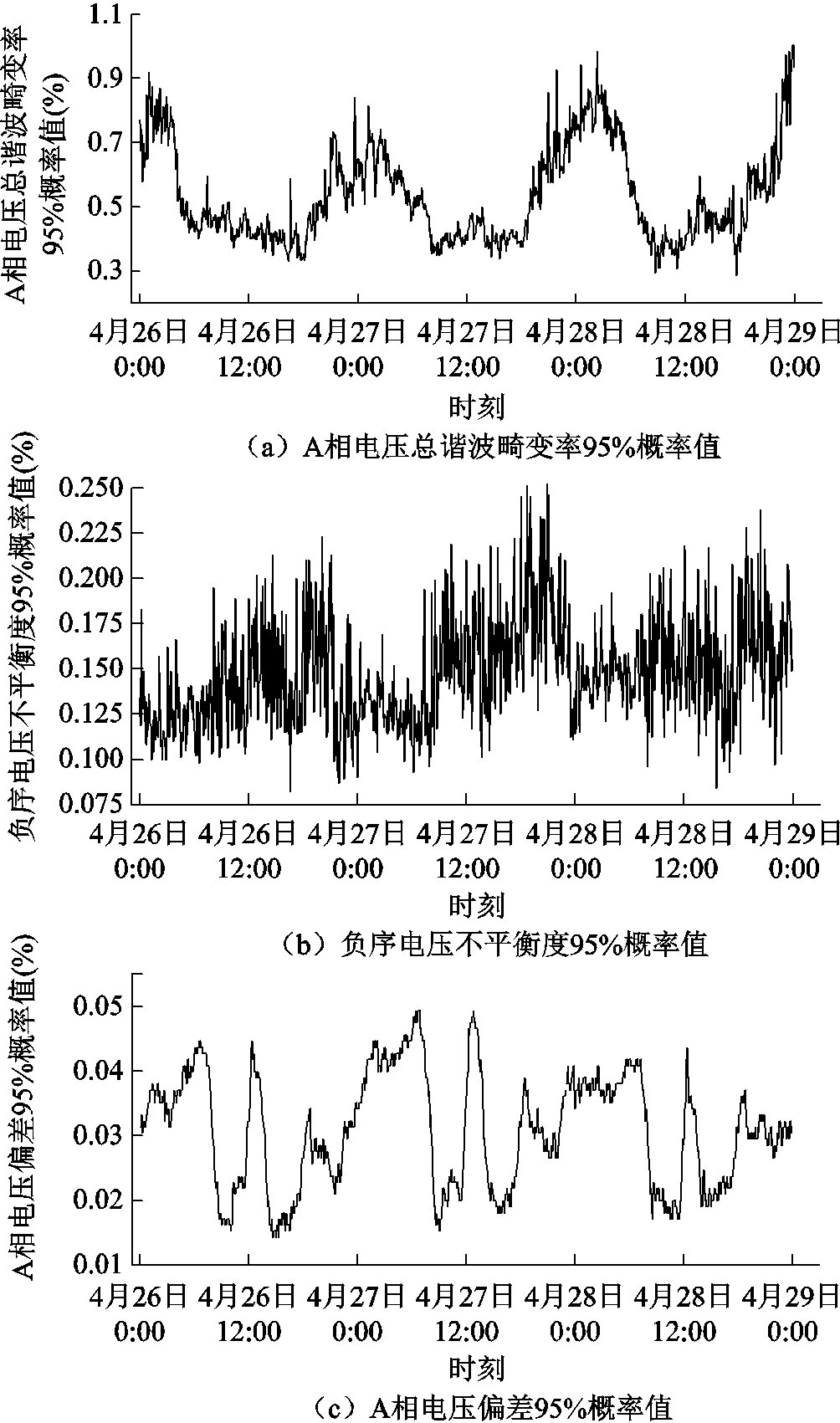
附图5 电能质量监测数据曲线
App.Fig.5 Curves of power quality monitoring data
参考文献
[1] 严静, 邵振国. 电能质量谐波监测与评估综述[J]. 电气技术, 2020, 21(7): 1-7. Yan Jing, Shao Zhenguo. Summary of harmonic monitoring and evaluation[J]. Electrical Engineering, 2020, 21(7): 1-7.
[2] 吴建章, 梅飞, 郑建勇, 等. 基于改进经验小波变换和XGBoost的电能质量复合扰动分类[J]. 电工技术学报, 2022, 37(1): 232-243, 253. Wu Jianzhang, Mei Fei, Zheng Jianyong, et al. Recognition of multiple power quality disturbances based on modified empirical wavelet transform and XGBoost[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 232-243, 253.
[3] 熊敏, 杨洪耕. 基于改进协方差特性的永磁直驱风电场谐波发射水平评估[J]. 电工技术学报, 2020, 35(3): 603-611 Xiong Min, Yang Honggeng. Assessment method of D-PMSG wind farm harmonic emission level based on the improved covariance characteristic[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 603-611
[4] 王鹤, 李石强, 于华楠, 等. 基于分布式压缩感知和边缘计算的配电网电能质量数据压缩存储方法[J]. 电工技术学报, 2020, 35(21): 4553-4564. Wang He, Li Shiqiang, Yu Huanan, et al. Compression acquisition method for power quality data of distribution network based on distributed compressed sensing and edge computing[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4553-4564.
[5] 杨挺, 李扬, 何周泽, 等. 基于矩阵填充的泛在电力物联网电能质量数据修复算法[J]. 电力系统自动化, 2020, 44(2): 13-21. Yang Ting, Li Yang, He Zhouze, et al. Matrix completion theory based recovery algorithm for power quality data in ubiquitous power Internet of Things[J]. Automation of Electric Power Systems, 2020, 44(2): 13-21.
[6] 张逸, 林才华, 邵振国, 等. 基于电子连续性方程的新型交流电弧炉通用模型[J]. 中国电机工程学报, 2021, 41(21): 7425-7433. Zhang Yi, Lin Caihua, Shao Zhenguo, et al. A novel general model of AC electric arc furnace based on electron continuity equation[J]. Proceedings of the CSEE, 2021, 41(21): 7425-7433.
[7] 肖湘宁, 廖坤玉, 唐松浩, 等. 配电网电力电子化的发展和超高次谐波新问题[J]. 电工技术学报, 2018, 33(4): 707-720. Xiao Xiangning, Liao Kunyu, Tang Songhao, et al. Development of power-electronized distribution grids and the new supraharmonics issues[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 707-720.
[8] 陈海涛. 电能质量监测海量数据分析研究[D]. 广州: 华南理工大学, 2013.
[9] 钟庆, 刘峰, 王钢, 等. 电能质量监测数据中间距离法聚类分析[J]. 电力系统及其自动化学报, 2016, 28(8): 69-73. Zhong Qing, Liu Feng, Wang Gang, et al. Middle distance clustering of power quality monitor data[J]. Proceedings of the CSU-EPSA, 2016, 28(8): 69-73.
[10] 李长松, 刘凯, 肖先勇, 等. 基于条件互信息特征选择法和Adaboost算法的电能质量复合扰动分类[J]. 高电压技术, 2019, 45(2): 579-585. Li Changsong, Liu Kai, Xiao Xianyong, et al. Classification of multiple power quality disturbances based on conditional mutual information feature selection method and Adaboost algorithm[J]. High Voltage Engineering, 2019, 45(2): 579-585.
[11] 于浩, 贾清泉, 李珍国, 等. 基于时间序列模式匹配的电能质量区域化治理[J]. 中国电机工程学报, 2019, 39(13): 3788-3798. Yu Hao, Jia Qingquan, Li Zhenguo, et al. Regionalization control for power quality based on time series pattern matching[J]. Proceedings of the CSEE, 2019, 39(13): 3788-3798.
[12] 孙海东. 电能质量时间序列关联分析及数据驱动治理策略研究[D]. 秦皇岛: 燕山大学, 2018.
[13] 石磊磊, 贾清泉, 孙海东, 等. 基于数据驱动的电能质量分区治理策略[J]. 中国电机工程学报, 2019, 39(4): 992-1001. Shi Leilei, Jia Qingquan, Sun Haidong, et al. Regional abatement strategy for power quality based on data driven[J]. Proceedings of the CSEE, 2019, 39(4): 992-1001.
[14] 汪颖, 喻梦洁, 卢宏, 等. 基于最大互信息的干扰源类型识别及电能质量需求画像技术[J]. 电力系统自动化, 2022, 46(9): 171-181. Wang Ying, Yu Mengjie, Lu Hong, et al. Interference source type identification and power quality demand portrait technology based on maximum mutual information[J]. Automation of Electric Power Systems, 2022, 46(9): 171-181.
[15] 秦梦雅. 基于区间-仿射算法的有源配电网电能质量综合评估[D]. 北京: 华北电力大学, 2020.
[16] 张逸, 王攸然, 刘航, 等. 基于监测数据相关性分析的用户谐波责任划分方法[J]. 电力系统自动化, 2020, 44(2): 189-197. Zhang Yi, Wang Youran, Liu Hang, et al. Determination method of user harmonic responsibility based on correlation analysis of monitoring data[J]. Automation of Electric Power Systems, 2020, 44(2): 189-197.
[17] 张逸, 姚文旭, 王康, 等. 考虑时序趋势分析的周期性谐波异常识别[J]. 电网技术, 2021, 45(3): 1117-1124. Zhang Yi, Yao Wenxu, Wang Kang, et al. Periodic harmonic anomaly recognition considering time series trend analysis[J]. Power System Technology, 2021, 45(3): 1117-1124.
[18] Cooke T A, Howe W R. Dynamic statistical process control limits for power quality trend data[C]//2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 2008: 1-5.
[19] 国家技术监督局. GB/T 14549—1993电能质量公用电网谐波[S]. 北京: 中国标准出版社, 1994.
[20] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 12325—2008电能质量供电电压偏差[S]. 北京: 中国标准出版社, 2009.
[21] 李云峰, 高云鹏, 蔡星月, 等. 自适应辛几何模态分解和短时能量差分因子在电能质量扰动检测中的应用[J]. 电工技术学报, 2022, 37(17): 4390-4400. Li Yunfeng, Gao Yunpeng, Cai Xingyue, et al. Application of adaptive symplectic geometry modal decomposition and short-time energy difference factor in power quality disturbance detection[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4390-4400.
[22] 肖贤贵, 李开成, 蔡得龙, 等. 一种电能质量扰动信号的联合去噪算法[J]. 电工技术学报, 2021, 36(21): 4418-4428. Xiao Xiangui, Li Kaicheng, Cai Delong, et al. A combined de-noising method for power quality disturbances events[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4418-4428.
[23] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 15543—2008电能质量三相电压不平衡[S]. 北京: 中国标准出版社, 2009.
[24] 国家质量监督检验检疫总局. GB 12326—2000电能质量电压波动和闪变[S]. 北京: 中国标准出版社, 2004.
[25] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 24337—2009电能质量公用电网间谐波[S]. 北京: 中国标准出版社, 2010.
[26] 邝昊云, 温和. 基于泰勒-傅里叶变换的电压闪变测量方法[J]. 电工技术学报, 2020, 35(22): 4798-4806. Kuang Haoyun, Wen He. Voltage flicker measurement based on Taylor-Fourier transform[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4798-4806.
[27] 冯丹丹, 王同勋. 一种电能质量扰动事件特征提取方法及系统: CN108053095A[P]. 2018-05-18.
[28] 张逸, 李渴, 邵振国, 等. 基于标准文件的电能质量领域本体构建方法[J]. 电力系统自动化, 2020, 44(17): 102-111. Zhang Yi, Li Ke, Shao Zhenguo, et al. Standard files based ontology construction method in power quality domain[J]. Automation of Electric Power Systems, 2020, 44(17): 102-111.
[29] 刘苏, 黄纯, 侯帅帅, 等. 基于DDTW距离与DBSCAN算法的户变关系识别方法[J]. 电力系统自动化, 2021, 45(18): 71-77. Liu Su, Huang Chun, Hou Shuaishuai, et al. Identification method for household-transformer relationship based on derivative dynamic time warping distance and density-based spatial clustering of application with noise algorithm[J]. Automation of Electric Power Systems, 2021, 45(18): 71-77.
[30] Górecki T, Łuczak M. Using derivatives in time series classification[J]. Data Mining and Knowledge Discovery, 2013, 26(2): 310-331.
[31] 国家电网公司. Q/GDW 1354—2013智能电能表功能规范[S]. 2013.
[32] 杨朝赟, 夏圣峰, 江南, 等. 基于相关性分析和长短时记忆网络的稳态电压质量指标预测[J]. 电力建设, 2021, 42(4): 9-16. Yang Chaoyun, Xia Shengfeng, Jiang Nan, et al. Prediction of steady-state indices of voltage quality based on correlation analysis and long short-term memory network[J]. Electric Power Construction, 2021, 42(4): 9-16.
[33] 朱明星, 张毅恒, 张华赢, 等. 考虑指标特性的区域电网电能质量评估方法[J]. 电力系统及其自动化学报, 2022, 34(8): 150-158. Zhu Mingxing, Zhang Yiheng, Zhang Huaying, et al. Regional power grid quality evaluation method considering index characteristics[J]. Proceedings of the CSU-EPSA, 2022, 34(8): 150-158.
Abstract The type and number of interference source users at the point of common coupling (PCC) are increasing. This makes the index and spatial-temporal characteristics of power quality (PQ) disturbance more complex. However, it is difficult for the PQ monitoring devices to monitor all terminal users of each feeder. Recently, some methods were presented to identify the PQ characteristics of multiple users, but most of them failed to accommodate long-term PQ phenomena and uncertain user operating conditions. To address these issues, this paper proposes a industrial users PQ characteristics identification method. Using derivative dynamic time warping (DDTW) to calculate the correlation of the existing multi-source data, it accurately identifies the PQ characteristics for industrial users.
Firstly, the over-limit and fluctuation periods of PQ monitoring index data are defined as disturbance periods. According to national standard limits and probability distribution, the over-limit and fluctuation values of PQ time series and their periods are extracted. Secondly, the screening rules of key harmonic indicators are set up to obtain the disturbance time series data of key harmonic indicators, voltage deviation and negative sequence voltage imbalance, so that the characteristics identification is more targeted. Thirdly, the user power data during the disturbance period are extracted, and the correlation between them and the monitoring indicators are calculated by using DDTW. Finally, the power quality characteristics of users are identified according to the correlation degree of different indicators.
The simulation results show that the proposed method can select the user groups most related to PQ problem, which is consistent with the simulation settings. In addition, compared with the traditional DTW algorithm, this shows that DDTW overcomes ill-conditioned matching of time series data, so as to effectively filter out the data with strong correlation in time series.To compare with the identification method based on mutual information, the power quality monitoring data with an interval of 3 minutes is averaged every 5 as a group, which is aligned with the power data of 15 minutes, and then the maximum mutual information decision method is used to identify the user power quality characteristics. The result shows that the maximum mutual information method obtains more types of characteristics and some errors.
The following conclusions can be drawn from the simulation and real measurement analysis: (1) Through the national standard limits and probability distribution method, it effectively determines key indicators for long time scale series. (2) The DDTW algorithm is used to match the power quality index of the monitoring point and the power time series data of the user side. In this way, it is more practical to select the representative indicators that are greatly affected by the power fluctuation. (3) The proposed method only needs long-term statistical data in the existing relevant systems. It is convenient to realize online identification of user power quality characteristics.
keywords:Power quality characteristics identification, industrial users, time series data, correlation analysis, derivative dynamic time warping
国家自然科学基金资助项目(51777035)。
收稿日期 2022-04-06
改稿日期 2022-06-05
DOI:10.19595/j.cnki.1000-6753.tces.220500
中图分类号:TM711
张 逸 男,1984年生,博士,硕士生导师,研究方向为电能质量、主动配电网及电力数据分析。E-mail:zhangyi@fzu.edu.cn(通信作者)
李 渴 女,1996年生,硕士研究生,研究方向为电能质量分析与控制技术。E-mail:llikefzu@163.com
(编辑 赫蕾)