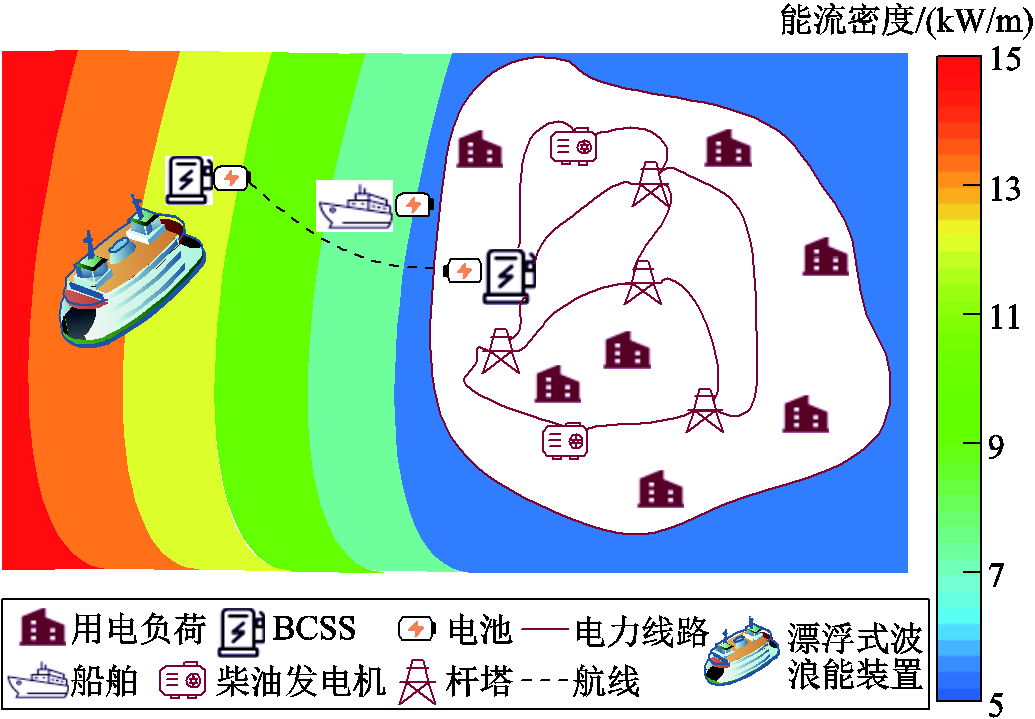
图1 基于换电船舶的孤岛微电网供能模式示意
Fig. 1 The isolated microgrid energy supply model based on power exchange vessels
摘要 当前,波浪能液压发电系统一般采用最大效率转化的控制策略,然而由于波浪能装置的间歇式出力特性,直接通过电池消纳会导致电池容量损耗进一步增大。在这种背景下,是否追求波浪能的最大效率转化值得商榷。为此,该文针对波浪能灵活接入的孤岛微电网系统,深入分析波浪能装置的工作原理,搭建波浪能液压系统的数学模型;在此基础上,以调度周期内的经济性最优为目标,综合考虑电池容量损耗和寿命损耗的影响,建立波浪能灵活接入下的孤岛微电网细粒化调度模型。仿真结果表明,相对于常规的孤岛微电网调度策略而言,在不同的波浪能出力场景下,该文所提的方案具有更优的经济性,为含波浪能的孤岛微电网经济运行策略提供了一个新的思路。
关键词:波浪能液压发电系统 储能快充容量损耗 细粒化调度 换电模式 最优功率跟踪策略
随着化石能源的不断减少,能源危机已经成为制约世界发展的关键性问题。与此同时,化石能源开发利用带来的环境污染、气候变化等问题也日益突出。在此背景下,大力发展可再生能源是实现“双碳目标”的重要途径。
目前,世界各国越来越重视海洋能的开发,据文献[1]统计,全世界建成的海洋能试验场已超过20个,投入的研发资金超过50亿元。究其原因,波浪能除了无污染、可再生、储量大等优势外,在长时间尺度上还具有出力恒稳、有效出力时间久等优点。因此,波浪能装置被广泛用于海水淡化[2]、制氢[3],并在海上石油平台、孤岛微电网、军事基地供能方面[4]崭露头角。对于波浪能装置的开发利用,许多专家学者做出了卓有成效的研究。早在20世纪70年代,就有国外科学家利用有限的船舶航行资料,分析计算了欧洲沿岸的海洋波浪能分布特征[5]。在此之后,文献[6]通过欧洲天气预报中心的海浪能再分析资料,研究分析了全球海域波浪能资源储量和分布情况,为波浪能的开发利用提供了理论可能。
此外,波浪能的资源分布除了受地球洋流的影响外,还与大陆架的距离有关。一般来讲,近海海域的波浪能资源较为匮乏,而远洋区域内的波浪能储存与转运等问题又给波浪能资源的消纳带来了新的挑战[7]。为此,以换电船舶为代表的移动式储能的发展为波浪能开发利用提供了新的视角[8-9]。在此背景下,电池通过船舶转移,将离岸式的波浪能装置生产的电能转移到电网的供电模式,成为了波浪能开发利用的新方向。
实际上,波浪能的出力特性不同于风、光等可再生能源,在短时间尺度上出力波动性较大,高效转化、利用较为困难[10]。为解决上述问题,专家学者对波浪能装置进行了一系列的开发与改良[11]。例如,文献[12-13]通过超级电容来平抑波能装置的功率波动,然而由于波能装置出力频繁,导致超级电容重复投切,影响系统的稳定性;文献[14]在能量转换环节加入了液压蓄能装置,解开了波况与电能输出之间的关联,实现了电能的稳定输出。基于波浪能液压发电装置,文献[15-16]分别针对其动力学以及能量转化系统进行了数学建模,探究了蓄能器压力、系统转速及其他电气转速的影响,为波能装置的自动控制理论发展奠定了基础。在此基础上,文献[17]注重波浪能的转化效率,提出了液压发电系统最大效率转化控制策略,实现了波能装置的高效能量转换。
但是这样的高效能量转换是有代价的。具体来说,液压发电系统在放电之前需要经历一定时间的蓄能,导致其出力曲线呈现出放电时间短、放电功率高的特点[18]。根据相关研究,蓄电池在面临这样的功率冲击时,容量损耗较正常运行方式会高出数倍[19]。因此,高效能量转换是以蓄电池损耗的大幅增加为代价的。在此背景下,选择最大效率转化策略是否一定达到经济性最优还亟待商榷,而如何找到一个效率和损耗的平衡点是值得探究的。
为此,本文首先对孤岛的供能模式进行了阐释;其次,深度分析了波浪能液压发电系统的组成和能量转化原理,搭建了波浪能液压系统细粒化模型;然后,总结现有控制策略存在的问题,提出适合孤岛微电网的波浪能最优功率跟踪(Optimal Efficiency Tracking, OET)策略;最后,以调度周期内的孤岛微电网成本最小为目标函数,量化分析储能的容量损耗成本,建立考虑波浪能装置接入的孤岛微电网调度模型,并设计了实际运行算例进行仿真验证,证明了本文所提调度策略相比较传统调度方案具有更好的经济性。本文的主要创新点如下:
1)深度分析波浪能装置的出力特性,搭建了波浪能液压发电系统的细粒化模型。
2)以孤岛微电网成本最小为目标,计及快充对蓄电池容量的损耗,建立考虑波浪能装置接入的孤岛微电网调度模型。
3)针对波浪能装置由船舶灵活接入电网的形态,基于船舶和电池的行为变量和位置变量,搭建船舶和电池交通流深度耦合的时空转移模型。
不同于陆地电网的开发,绝大多数的海岛由于远离大陆架,在工程实际中一般很难直接与陆地电网相连;此外,考虑到电缆造价成本较高、后期维护困难等问题,采用电缆供电模式未必是孤岛微电网能源开发的明智之举。因此,海岛微电网一般采用孤岛运行模式,依靠柴油机组等分布式能源机组支撑负荷运行。然而,随着可再生能源的大力发展,风、光等发电装置的接入给孤岛微电网供能提供了新的可能,在此背景下,本文提出了基于离岸式波浪能装置海岛微电网供能网络架构。
基于换电船舶的孤岛微电网供能模式如图1所示,该系统主要分为两部分:离岸式波浪能发电系统和孤岛微电网。其中,孤岛微电网主要由柴油发电机、用电负荷以及电池充电/换电站(Battery Charging and Switching Station, BCSS)构成。

图1 基于换电船舶的孤岛微电网供能模式示意
Fig. 1 The isolated microgrid energy supply model based on power exchange vessels
此外,根据图1所示的海域波浪能资源分布情况,将波浪能装置设置在离岸较远、波浪能资源较为丰富的海域。以上两者之间存在的地理隔阂,导致波浪能装置发电不能及时消纳,能量传输通道受阻。为解决上述问题,本文提出基于换电船舶的孤岛微电网供能模式。离岸式波浪能装置通过液压发电系统将波浪能转化为电能,并通过BCSS给电池进行充电;电池完成充电后通过船舶转运,在孤岛微电网处装卸,并与柴油发电机协同配合,共同对孤岛微电网提供功率支撑。
由于波浪能与海洋波浪功率存在强耦合关系,所以波浪能装置出力存在随机性较强的特点。此外,海浪总是周而复始地运行,这导致波浪能的能量变化也存在周期性,一个周期大概为2s至十几秒[20]。因此,波浪能直接并网将给电网带来较大的冲击。为解决上述问题,本文在波浪能能量转化环节加上液压蓄能装置,来实现波浪能装置的平滑出力。与此同时,为进一步减小波浪能装置对孤岛微电网的影响,本文将波浪能装置整流后与储能装置相连,不仅实现了波浪能的就地消纳,还减少了波浪能直接并网对电网的冲击。在此背景下,如何调度分布式能源以及储能设备的出力,实现孤岛微电网的经济安全运行是本文需要解决的问题。为此,本文提出了含波浪能装置的孤岛微电网细粒化调度策略,其调度模式如图2所示。
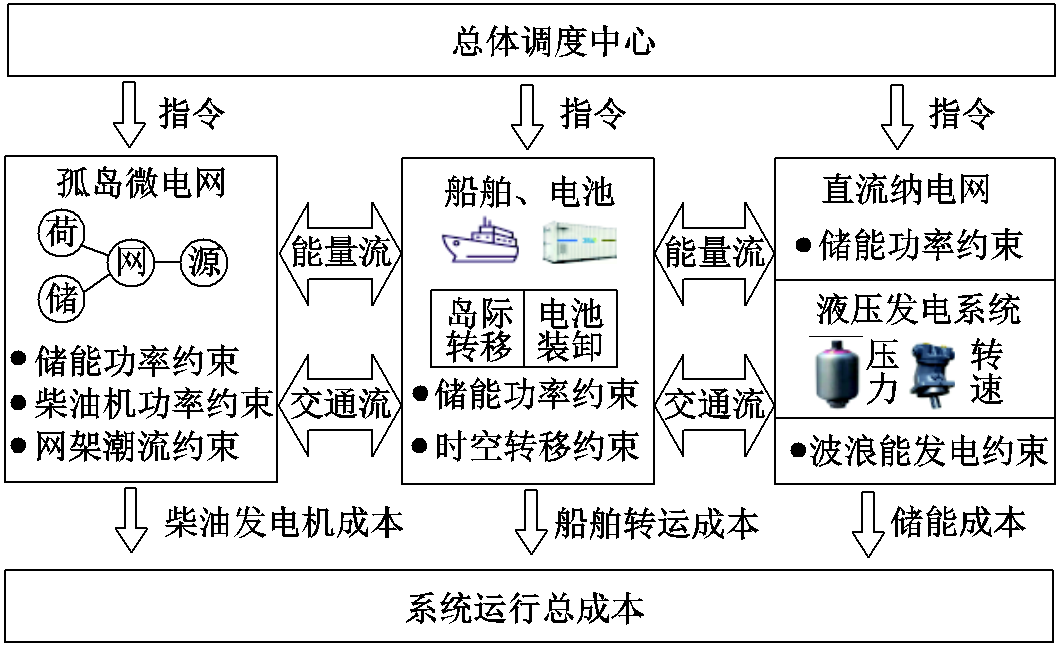
图2 含波浪能装置的孤岛微电网细粒化调度模式
Fig.2 Fine-grained scheduling model for isolated microgrids with wave energy devices
由图2可知,调度中心考虑到负荷需求变化,调整孤岛微电网源、储出力,实现孤岛微电网的功率平衡。此外,调度中心还根据船舶和电池的时空分布,对船舶的岛际转移和电池的装卸行为进行调度,引导电池在各站点间进行充、放电。与此同时,根据波浪能来波功率的不同,对波浪能液压发电系统的压力和转速进行细粒化调整,满足BCSS处电池的功率平衡约束。并在此基础上,考虑柴油机发电、船舶转运、储能损耗等成本,建立波浪能液压发电系统接入的孤岛微电网调度模型,实现孤岛微电网经济运行。
离岸式波浪能装置作为孤岛微电网调度模型中较为重要的一环,其建模的精确性也将直接影响调度方案的实际运行效果。为保证调度方案的可行性,本文对波浪能装置的内部结构进行深入研究,提出了波浪能细粒化模型以及适应孤岛微电网供能的控制运行策略。
含液压系统的波浪能装置结构如图3所示。由图3可知,液压发电系统主要包括液压控制系统、液压马达以及永磁同步电机。其工作原理如下:浮子随着波浪起伏,将油箱中的液压油压入蓄能器中;通过液压缸进一步做功,蓄能器压力逐渐升高,达到上限值时,液压控制系统动作,液压马达开始转动,与此同时,同步电动机开始发电,发电系统将液压能转化为电能输出;当海面波况较好时,蓄能器压力能够维持较高的压力水平,液压发电系统正常工作;当波况较差时,蓄能器压力低于下限值,液压控制系统关闭液压马达,等待下一个动作时刻。在理想的状况下,液压蓄能器实现前端能量捕获与后端发电环节的解耦,减少了波况的随机性和不确定性对电网的冲击,在工程实际中运用较为广泛。
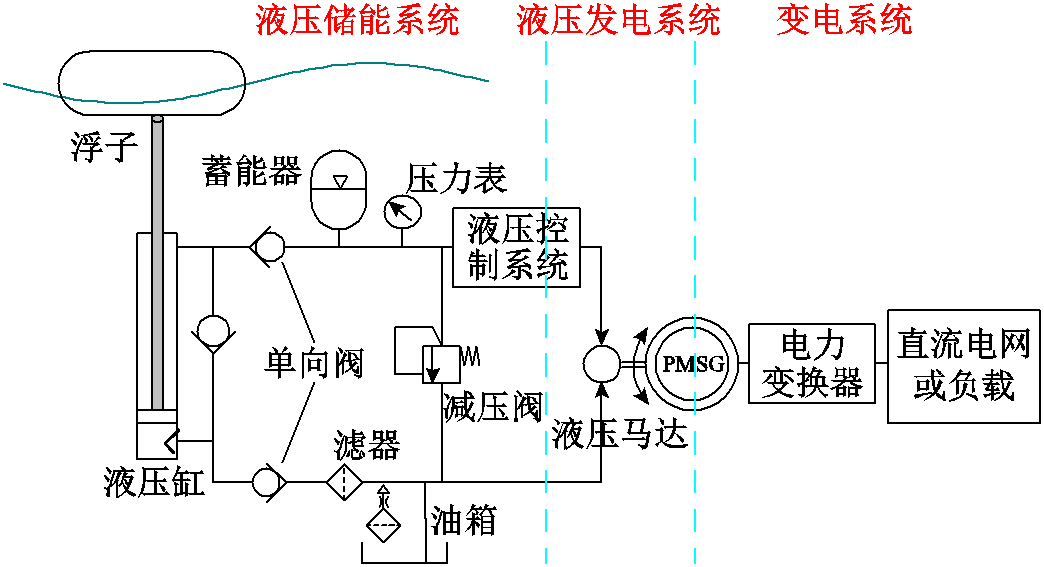
图3 含液压系统的波浪能装置结构
Fig.3 The structure of the wave energy device with hydraulic system
由于本文研究的重点为波浪能液压发电系统的细粒化建模,而液压管路的流阻损耗只会影响波浪能装置前端的波浪能捕捉和收集环节的转化效率,对液压发电系统模型不会造成影响。因此,本文建立的液压马达输出转矩模型为
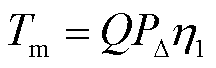 (1)
(1)
式中,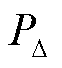 为液压马达进出口的压差;
为液压马达进出口的压差;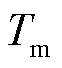 为液压马达的输出转矩;Q为液压马达排量;
为液压马达的输出转矩;Q为液压马达排量;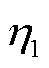 为液压马达的机械效率。
为液压马达的机械效率。
而液压马达输入功率主要取决于马达进出口压差与马达的排量。与此同时,考虑同步发电机经过电力变换器后直接与直流电网相连,并参考文献[21]中同步电动机和变流器的数学模型,推导出液压发电系统在电压负载下的数学模型为
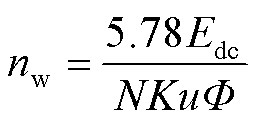 (2)
(2)
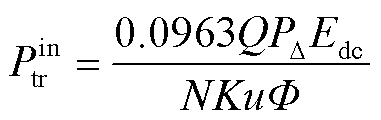 (3)
(3)
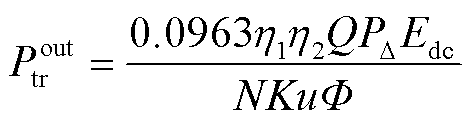 (4)
(4)
式中,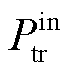 、
、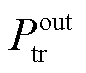 分别为波浪能液压发电系统的输入、输出瞬时功率值,N为发电机每相绕组的串联匝数,K为电动势绕组因数,
分别为波浪能液压发电系统的输入、输出瞬时功率值,N为发电机每相绕组的串联匝数,K为电动势绕组因数,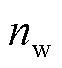 为液压发电系统的转速,u为电动机的极对数,Φ为永磁发电机磁通,上述参数为发电机参数,在系统稳态运行时,可以认为其保持不变;
为液压发电系统的转速,u为电动机的极对数,Φ为永磁发电机磁通,上述参数为发电机参数,在系统稳态运行时,可以认为其保持不变;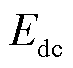 为直流电网的电压;
为直流电网的电压;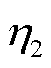 为液压马达的容积效率。由式(2)可知,在液压发电系统稳定运行时,液压马达的转速完全取决于直流电网的电压;此外,在较短的时间间隔内,可以认为蓄能器的压力保持不变。故由式(3)、式(4)可知,在直流电网电压确定的情况下,液压马达的输入、输出功率均与蓄能器压力成正比。
为液压马达的容积效率。由式(2)可知,在液压发电系统稳定运行时,液压马达的转速完全取决于直流电网的电压;此外,在较短的时间间隔内,可以认为蓄能器的压力保持不变。故由式(3)、式(4)可知,在直流电网电压确定的情况下,液压马达的输入、输出功率均与蓄能器压力成正比。
由式(2)~式(4)可知,波浪能液压发电系统的负载电压越高,液压发电系统的输出功率也越大。这样的特性与光伏等可再生能源的出力特性存在显著差异,因此,液压发电系统的控制策略不存在最大功率跟踪的问题。实际上,考虑到液压发电系统的流阻损耗以及蓄能器容量效应的影响[22],液压发电系统的机械效率和液压马达容积效率并不是一个常数,而是一个与系统转速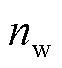 和压力
和压力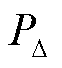 相关的变量,其关系式为
相关的变量,其关系式为
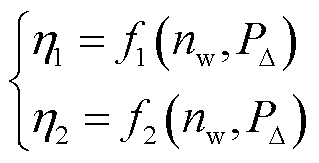 (5)
(5)
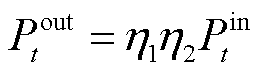 (6)
(6)
式中,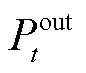 、
、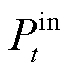 为液压发电系统在一个周期的平均输出和输入功率。由式(5)和式(6)可知,液压发电系统转化效率和液压发电系统的输出功率可以通过改变系统转速和压力进行调节。故实际工程中波浪能液压发电系统一般采用最大效率转化控制策略。
为液压发电系统在一个周期的平均输出和输入功率。由式(5)和式(6)可知,液压发电系统转化效率和液压发电系统的输出功率可以通过改变系统转速和压力进行调节。故实际工程中波浪能液压发电系统一般采用最大效率转化控制策略。
由上述分析可知,液压发电系统能够通过调节系统转速和蓄能器压力以求获得最大的转化效率。然而,波浪能最大效率的转化和孤岛微电网的最优调度并不完全匹配,其差异性主要体现在蓄电池快充损耗对整体调度经济性的影响。
波浪能发电与储能快充损耗关系如图4所示。由图4a可知,在一个发电周期内,液压发电系统发电机需要一段时间的蓄能过程,导致波浪能液压发电系统呈现出间歇性发电特性。与此同时,由于调度过程中直接通过储能电池对波浪能出力进行消纳,其间歇性发电特性对储能容量损耗的影响被进一步放大。
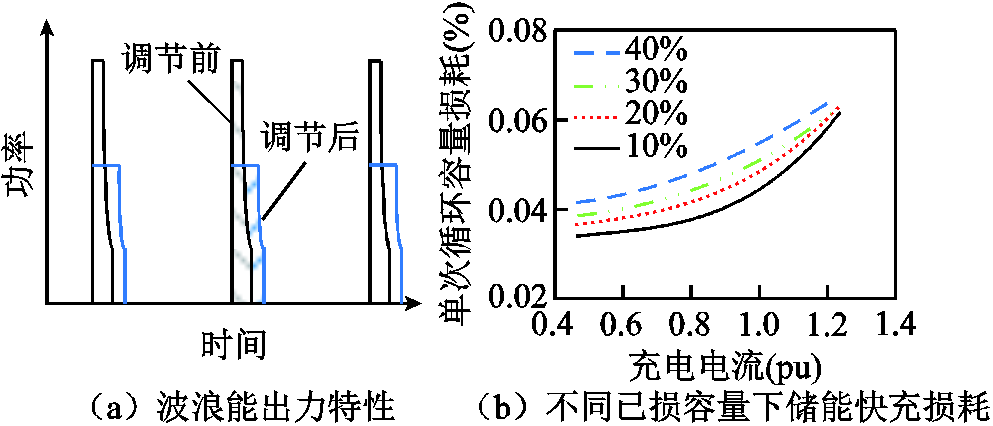
图4 波浪能发电与储能快充损耗关系
Fig.4 The relationship between wave energy generation and energy storage fast charging loss diagram
因此,本文针对储能电池快充容量损耗,搭建了适合波浪能发电系统的储能损耗模型。经过研究可知,储能的容量损耗不仅与充电电流相关,还与电池自身的已损容量相关。如图4b所示,充电电流变大、电池初始的已损容量升高,都会导致电池的单次循环容量损耗提高。该损耗模型为
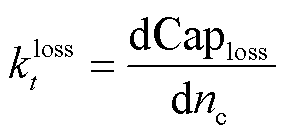 (7)
(7)
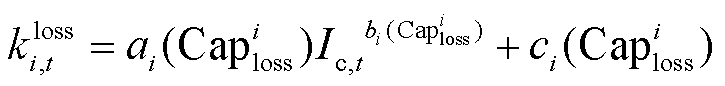 (8)
(8)
式中,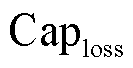 为电池的容量损耗;
为电池的容量损耗;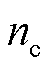 为电池的循环次数;当电池容量损耗为
为电池的循环次数;当电池容量损耗为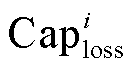 时,单次循环的电池容量损耗为
时,单次循环的电池容量损耗为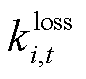 ;
;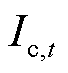 为充电电流;
为充电电流;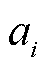 、
、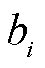 、
、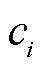 为与
为与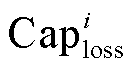 相关的储能容量损耗参数。式(7)为容量损耗的定义式;式(8)为储能快充损耗计算式,其相关参数见参考文献[23]中的实验数据。
相关的储能容量损耗参数。式(7)为容量损耗的定义式;式(8)为储能快充损耗计算式,其相关参数见参考文献[23]中的实验数据。
此外,由于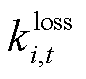 表示电池单次充放电循环过程中的容量损耗,需要将其转化到单个波浪能发电系统的调度周期内的储能损耗模型。该转化过程为
表示电池单次充放电循环过程中的容量损耗,需要将其转化到单个波浪能发电系统的调度周期内的储能损耗模型。该转化过程为
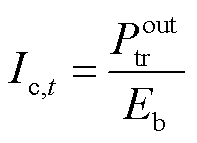 (9)
(9)
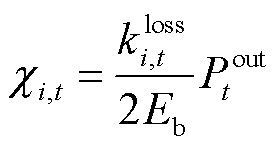 (10)
(10)
式中,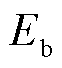 为电池容量;
为电池容量;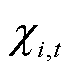 为t时刻电池的容量损耗。式(9)表示充电电流与充电功率之间的转化关系;式(10)表示电池调度尺度内的充放电容量损失关系式。
为t时刻电池的容量损耗。式(9)表示充电电流与充电功率之间的转化关系;式(10)表示电池调度尺度内的充放电容量损失关系式。
然而,在电池长期工作中,容量损耗是不断变化的,不同条件下充电过程对电池容量的损耗影响是不同的,即参数a、b、c随着容量损耗的提升而改变。以上特性使得电池的损耗模型异常复杂,难以进行直接求解。为此,本文将非额定条件下的放电过程等效到额定条件下,并且考虑电池在工作过程中的容量损耗是连续衰减的,对文献[23]给出的m个不同容量下的曲线进行平均。其等效过程为
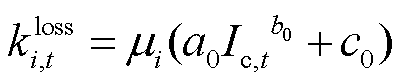 (11)
(11)
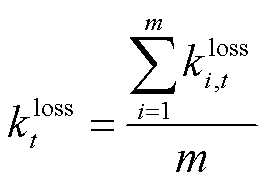 (12)
(12)
式中,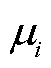 为等效系数;
为等效系数;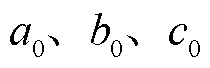 为额定条件下的储能容量损耗参数;
为额定条件下的储能容量损耗参数;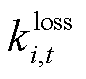 为拟合曲线的单次循环能量损耗。式(11)表示将容量损耗为
为拟合曲线的单次循环能量损耗。式(11)表示将容量损耗为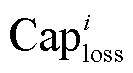 下的损耗曲线转化为额定条件下的关系式;式(12)表示计及电池全寿命周期的充电容量损耗模型。
下的损耗曲线转化为额定条件下的关系式;式(12)表示计及电池全寿命周期的充电容量损耗模型。
综上所述,关于蓄能器压力的调节将对调度模型产生较大的影响,具体解释如下:
(1)增大蓄能器压力可以提高液压发电系统的转化效率。在转速一定的情况下提高蓄能器压力,液压发电系统的转化效率增大。
(2)增大蓄能器压力导致电池的容量损耗提高。由式(9)可知,液压发电系统的输出功率与蓄能器压力成正比;与此同时,由式(10)~式(12)可知,输出功率提高导致就地消纳波浪能装置的储能电池容量损耗增加。
在这种背景下,如何兼顾两者的影响,求得经济性最优的方案是本文要解决的主要问题。为此,本文针对蓄电池的容量损失特性,在液压发电系统最大效率转化策略的基础上提出了最优效率跟踪策略,考虑到来波功率与电池充放电行为的影响,对蓄能器压力值进行了调整,以求得经济性更优的调度策略。
液压发电系统最优效率跟踪策略如图5所示。由图5可知,OET控制策略就是在最大效率转化策略的基础上,引入蓄电池充放电功率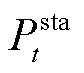 作为OET控制模块的输入信号,再根据液压发电系统的转速和最佳压力-转速曲线确定蓄能器的最佳压力
作为OET控制模块的输入信号,再根据液压发电系统的转速和最佳压力-转速曲线确定蓄能器的最佳压力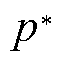 ,并将其作为蓄能器压力反馈控制的给定信号,控制液压发电系统的转化效率最优。
,并将其作为蓄能器压力反馈控制的给定信号,控制液压发电系统的转化效率最优。
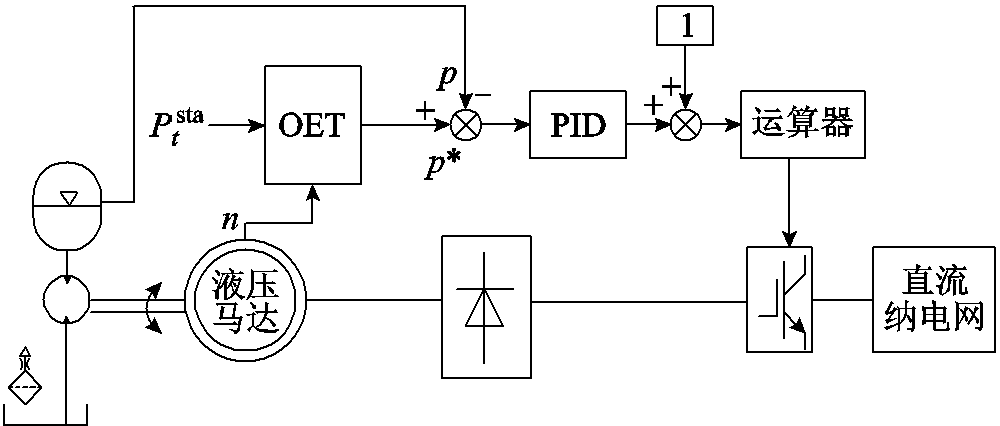
图5 液压发电系统最优效率跟踪策略
Fig.5 OET control strategy for hydraulic power generation systems
有必要提到,由于涉及流体力学知识,液压发电系统的损耗计算非常复杂,难以直接通过数学推导求得。因此,本文借鉴文献[17]中的方法,通过实验实测数据确定液压发电系统的最佳压力-转速曲线。液压发电系统不同系统转速和蓄能器压力情况下的转化效率如图6所示。
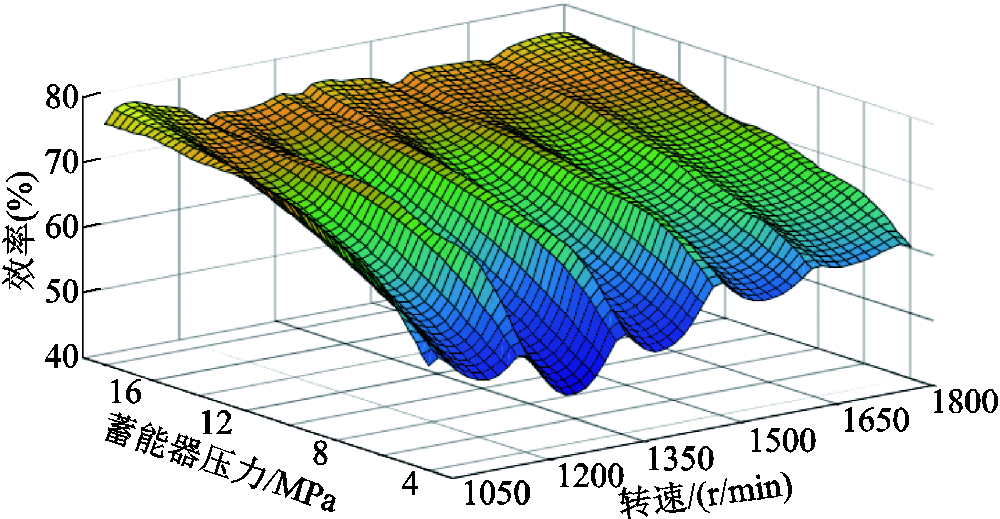
图6 液压发电系统转化效率
Fig.6 Hydraulic power generation system conversion efficiency
由图6可知,当系统转速较低,蓄能器压力较大时,液压发电系统的效率较高。尽管液压发电系统中的液压马达在转速越高时,其容积效率越大,但是,液压发电系统的总效率还与液压马达的机械效率和发电机组的效率等因素相关。在转速一定时,蓄能器压力越大,液压发电系统的转化效率越高,这是由于随着蓄能器压力的增大,液压管路的机械损失和流阻损失进一步减小,液压发电系统的整体转化效率提高。
基于电池换电的波浪能调度模型,以调度周期内的费用最少为目标函数,考虑孤岛微电网柴油发电机发电成本、船舶转移费用、电池循环寿命成本以及容量损耗成本。其目标函数为
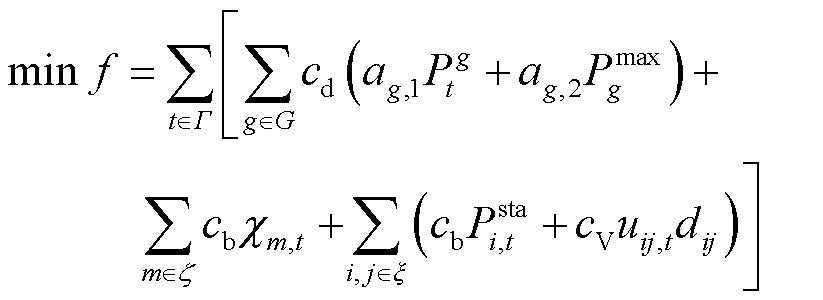 (13)
(13)
式中,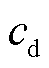 为柴油价格;
为柴油价格;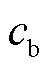 为电池价格;
为电池价格;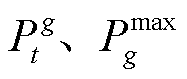 为柴油发电机输出功率和额定功率;
为柴油发电机输出功率和额定功率;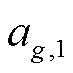 、
、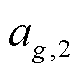 为柴油发电机的能耗参数;
为柴油发电机的能耗参数;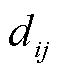 为节点i、j之间的距离;
为节点i、j之间的距离;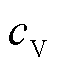 为船舶的转移费用;
为船舶的转移费用;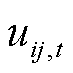 为t时刻船舶在线路ij上的位置变量,
为t时刻船舶在线路ij上的位置变量,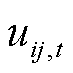 =1表示t时刻船舶位于线路ij上;
=1表示t时刻船舶位于线路ij上;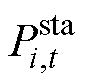 为所有在i站点的电池有功功率之和;
为所有在i站点的电池有功功率之和;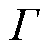 为调度时间集合;G为柴油发电机集合;
为调度时间集合;G为柴油发电机集合;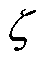 为电池集合;
为电池集合;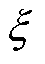 为BCSS站点集合。
为BCSS站点集合。
(1)波浪能约束条件
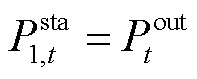 (14)
(14)
式中,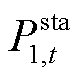 为波浪能装置节点的充放电功率。
为波浪能装置节点的充放电功率。
(2)电池调度约束
电池空间位置间的距离和转移时间由G(D, τ)来表示。其中距离D和转移时间τ表示为
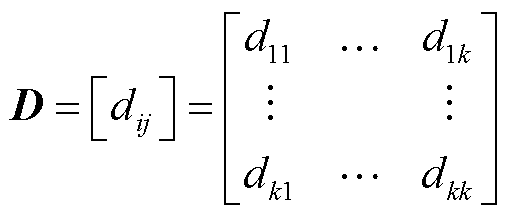 (15)
(15)
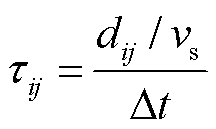 (16)
(16)
式中,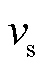 为船舶的运行速度;
为船舶的运行速度;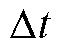 为调度时间尺度。
为调度时间尺度。
根据本文第1节的分析可知,在换电模式下,电池的时空转移与船舶的时空转移不完全相同,但又依赖于船舶的转移行为,这导致船舶和电池转移特性深度耦合。为解决此类问题,本文提出船舶与电池的转移模型如图7所示。

图7 船舶与电池的转移模型
Fig.7 Vessel and battery transfer model
在图7中,定义电池和船舶的状态变量集合为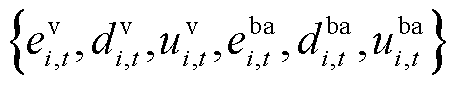 ,其中
,其中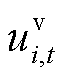 、
、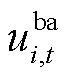 分别为船舶和电池t时刻在位置i的状态变量,属于空间变量,
分别为船舶和电池t时刻在位置i的状态变量,属于空间变量,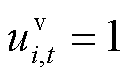 表示t时刻船舶位于i位置;
表示t时刻船舶位于i位置;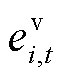 、
、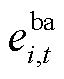 分别为船舶和电池t时刻到达位置i的状态变量,属于行为变量,
分别为船舶和电池t时刻到达位置i的状态变量,属于行为变量,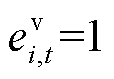 表示t时刻船舶到达i位置;
表示t时刻船舶到达i位置;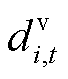 、
、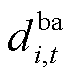 分别为船舶和电池t时刻离开位置i的状态变量,属于行为变量,
分别为船舶和电池t时刻离开位置i的状态变量,属于行为变量,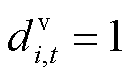 表示t时刻船舶离开i位置。则可得到上述状态变量的相关约束。
表示t时刻船舶离开i位置。则可得到上述状态变量的相关约束。
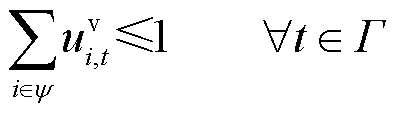 (17)
(17)
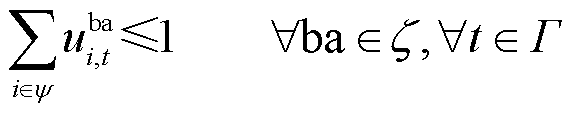 (18)
(18)
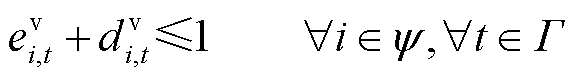 (19)
(19)
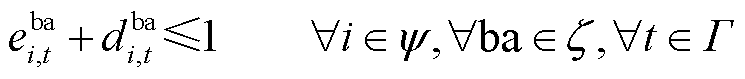 (20)
(20)
式中,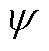 为电池和船舶所处的位置集合。
为电池和船舶所处的位置集合。
式(17)和式(18)分别表示船舶和电池空间位置的唯一性约束;式(19)和式(20)分别表示船舶和电池某时刻行为的单一性约束。
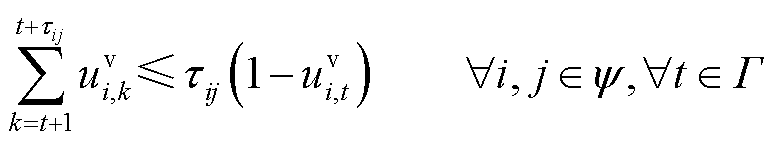 (21)
(21)
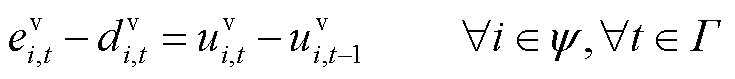 (22)
(22)
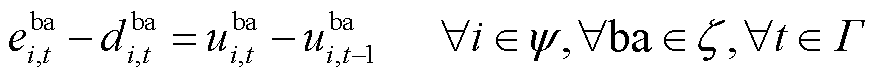 (23)
(23)
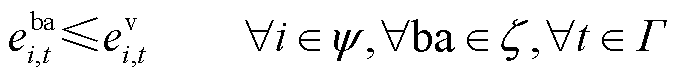 (24)
(24)
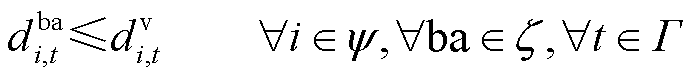 (25)
(25)
式(21)表示船舶转移过程的时间延时约束;式(22)和式(23)分别表示船舶和电池行为变量与位置变量的耦合关系;式(24)与式(25)表示电池的转移需要依赖船舶的转移行为。
(3)发电机约束
柴油发电机需要满足出力上下限约束和爬坡率约束,其中发电机爬坡率约束为
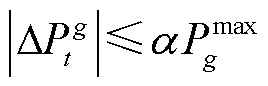 (26)
(26)
式中,α为柴油发电机的爬坡率限制值。
(4)储能约束
电池交通流与能量流耦合模型的约束条件为
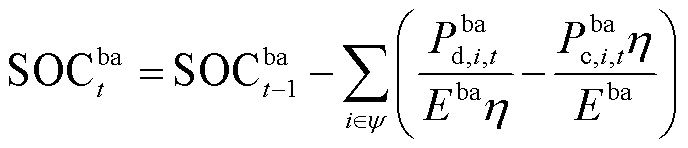 (27)
(27)
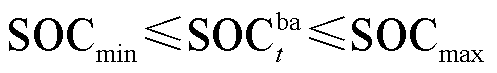 (28)
(28)
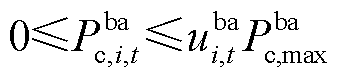 (29)
(29)
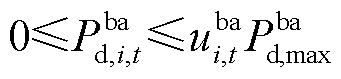 (30)
(30)
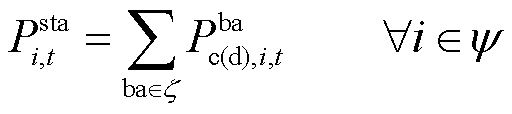 (31)
(31)
式中,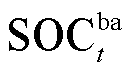 为t时刻电池的荷电状态(State of Charge, SOC);
为t时刻电池的荷电状态(State of Charge, SOC);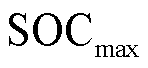 、
、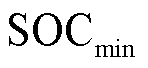 为电池SOC的最大与最小值;
为电池SOC的最大与最小值;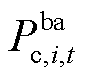 、
、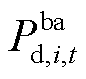 分别为t时刻电池ba的充、放电功率;
分别为t时刻电池ba的充、放电功率;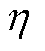 和
和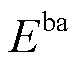 分别为电池的充放电效率和电池容量。式(27)表示电池荷电状态与充放电功率的约束条件;式(28)表示电池荷电状态的上下限约束;式(29)、式(30)表示电池的充放电功率与电池位置状态变量的耦合关系;式(31)表示BCSS站点充电功率与电池功率的耦合关系。
分别为电池的充放电效率和电池容量。式(27)表示电池荷电状态与充放电功率的约束条件;式(28)表示电池荷电状态的上下限约束;式(29)、式(30)表示电池的充放电功率与电池位置状态变量的耦合关系;式(31)表示BCSS站点充电功率与电池功率的耦合关系。
(5)微电网线路潮流约束
孤岛微电网存在实时功率平衡约束,各节点的潮流约束为
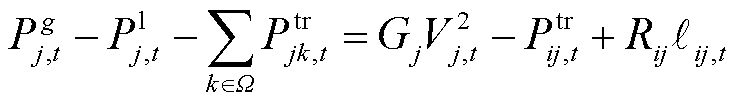 (32)
(32)
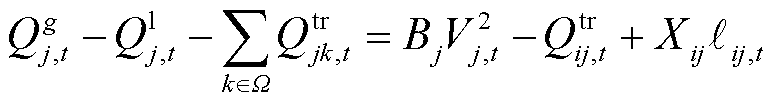 (33)
(33)
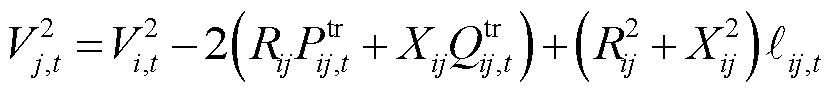 (34)
(34)
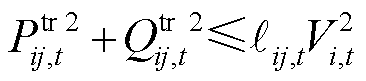 (35)
(35)
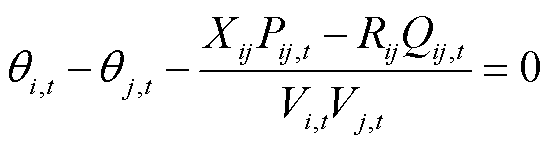 (36)
(36)
式中,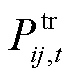 、
、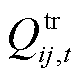 分别为t时刻节点i、j之间的线路传输的有功、无功功率;
分别为t时刻节点i、j之间的线路传输的有功、无功功率;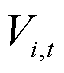 、
、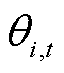 分别为t时刻节点i的电压值和相位;
分别为t时刻节点i的电压值和相位;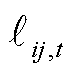 为t时刻线路ij的电流的二次方;
为t时刻线路ij的电流的二次方;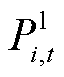 、
、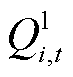 分别为t时刻节点i处的负荷有功、无功需求;
分别为t时刻节点i处的负荷有功、无功需求;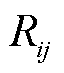 、
、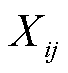 分别为线路ij的电阻、电抗;
分别为线路ij的电阻、电抗;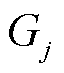 和
和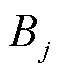 分别为节点j的电导和电纳。式(32)~式(34)表示线路ij上的潮流约束;式(35)表示传输功率的上限约束;式(36)表示电压的相位约束。
分别为节点j的电导和电纳。式(32)~式(34)表示线路ij上的潮流约束;式(35)表示传输功率的上限约束;式(36)表示电压的相位约束。
调度模型中包含非线性约束条件,难以直接进行求解。为此本文基于0-1线性化方案,将优化模型处理为混合整数线性规划问题(Multiple Integer Linear Problem, MILP),通过GUROBI对上述问题进行求解。线性化过程为
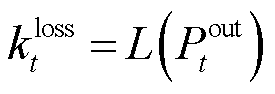 (37)
(37)
将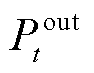 用
用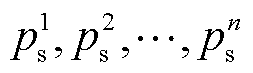 等分为n-1个区间,并引入n个权重变量
等分为n-1个区间,并引入n个权重变量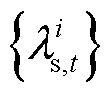 与n-1个布尔型变量
与n-1个布尔型变量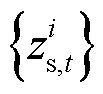 ,其中
,其中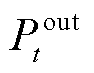 与间隔点
与间隔点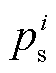 相关联,
相关联,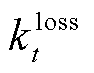 与
与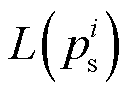 相关联。
相关联。
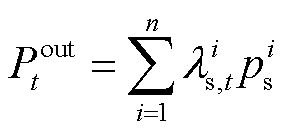 (38)
(38)
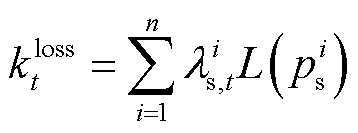 (39)
(39)
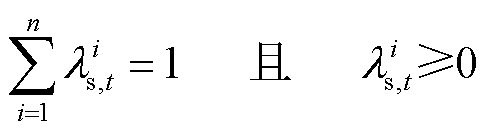 (40)
(40)
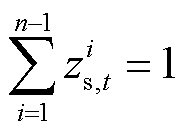 (41)
(41)
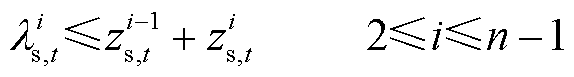 (42)
(42)
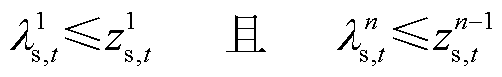 (43)
(43)
式(38)表示任意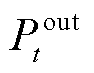 都可用间隔点以及权重系数的乘积之和表示;同理,式(39)表示
都可用间隔点以及权重系数的乘积之和表示;同理,式(39)表示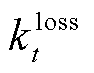 也可以通过权重系数及间隔点的函数值表示;式(40)表示权重变量满足的相关约束;式(41)表示在任意时刻只有一个布尔变量取值为1,即只有一个区间发挥作用;式(42)和式(43)保证了任意时刻只有两个相邻的权重系数不为0。
也可以通过权重系数及间隔点的函数值表示;式(40)表示权重变量满足的相关约束;式(41)表示在任意时刻只有一个布尔变量取值为1,即只有一个区间发挥作用;式(42)和式(43)保证了任意时刻只有两个相邻的权重系数不为0。
本文选取南海的某岛屿作为负荷中心岛,岛上的微电网采用改进的IEEE 6节点网络[24],其额定电压为10kV;岛上负荷选取南海某海岛常规负荷[25],并进行等比例调整。此外,考虑到供电可靠性问题,孤岛微电网配置两台额定功率为500kW的分布式柴油发电机。根据宜昌市发中船务有限公司提供的船舶相关数据,本文选取柴油发动机推动的船舶。此外,在距离人居岛20km外的海域上,存在漂浮式的波浪能生产基地,波浪能液压式发电装置的额定功率为400kW。为不失一般性,本文假设负荷中心岛和波浪能生产基地处都建有BCSS用于电池交换功率。本文采用的电力设备相关参数见表1。
表1 电力设备相关参数
Tab.1 Related parameters of electrical equipment

设备参数数值 储能电池电池容量/(kW·h)500 额定充放电功率/kW500 充放电效率(%)95 建造成本/[元/(kW·h)]4 500 充放电循环寿命/次6 000 船舶购置成本/万元40 航行平均速度/(km/h)20 使用寿命/a10 运输单位成本/[元/(t·km)]0.5 海底电缆投资成本/(万元/km)100 电阻/(Ω/km)0.32 电抗/(Ω/km)0.28 柴油发电机柴油费用/(元/L)6 损耗系数/(L/kW)0.23 损耗系数/(L/kW)0.057 5
另外,本算例考虑共有三个储能电池系统参与换电模型调度,其参数也表示在表1中。为了减小电池损耗,电池在使用过程中不宜过充过放,故设置电池SOC的最大值为0.9,最小值为0.1。为了保证调度周期的可重复性,设置在调度开始时两块电池位于负荷中心岛,一块电池位于漂浮式波浪能生产基地,并将每块电池初始的SOC设置为0.5。
考虑到波浪能出力的波动性,选取波浪能装置较高和较低两个场景,本算例中负荷和波浪能出力情况如图8所示,其中,场景1的波浪能出力较高。
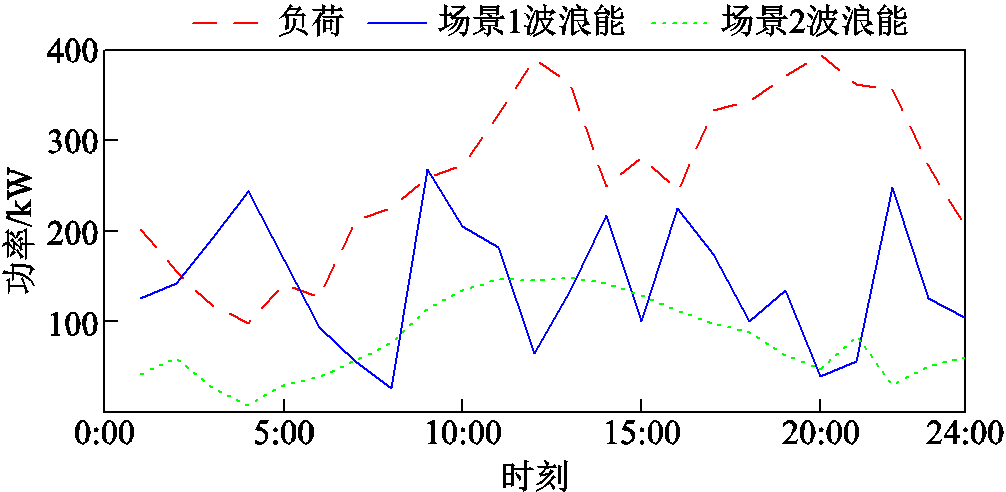
图8 孤岛微电网负荷与波浪能功率
Fig.8 Isolated microgrid loads with wave energy power
在Matlab R2017a的YALMIP平台调用GUROBI 9.0.3对第三节所建立的波浪能离散能源调度模型进行求解,并对以下调度方案展开分析:
1)波浪能调度
本文所提的波浪能调度不同于最大效率转化控制策略,在追求转化效率和储能快充损耗之间进行取舍,选择舍弃部分波浪能的转化效率,来获得经济性更优的含波浪能的孤岛微电网调度方案。波浪能细粒化调度结果如图9所示。
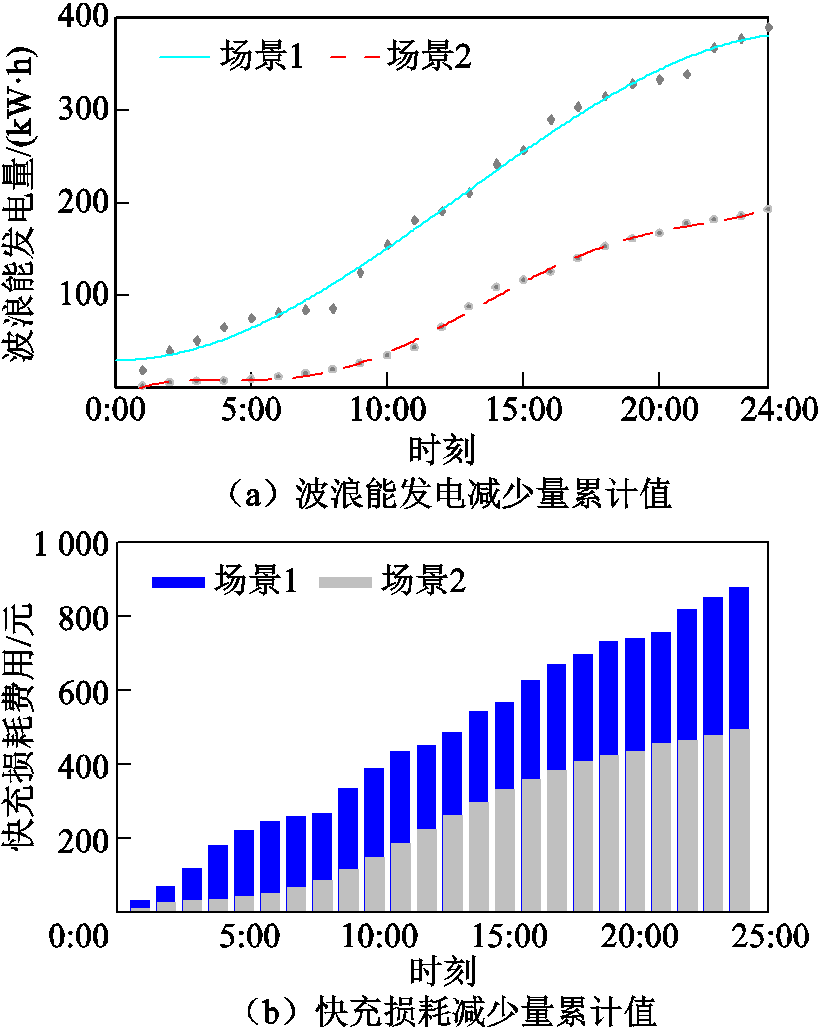
图9 波浪能细粒化调度结果
Fig.9 Wave energy fine-grained scheduling results
其中,图9a表示本文的调度策略相较于最大效率转化效率所舍弃的波浪能发电装置电能的累计值。在一个调度周期内,场景1损失的电能为382kW·h,场景2损失的电能为192kW·h。图9b表示本文所提的调度策略相较于最大效率转化策略下,储能少损失的容量所折合的费用。在一个调度周期内,场景1储能少损失的容量折换成损失费用为878.8元,场景2少损失费用为493.4元。由此可知,此处波浪能转化为电能的边际成本为2.5元/(kW·h)。
2)船舶与电池的调度方案
船舶在调度过程中作为电池的运输载具,往返于岛屿与漂浮式波能装置之间,完成电池的运输工作。船舶与电池的时空转移如图10所示,船舶1在场景1的运行路线为1→2→1→2→1→2→1→2→ 1→2,在一个调度周期内,船舶航行的时间为10h。为避免船舶在航行过程中因为柴油耗尽而停止工作,在调度周期开始前对船舶柴油进行补给,保证调度工作有序开展。
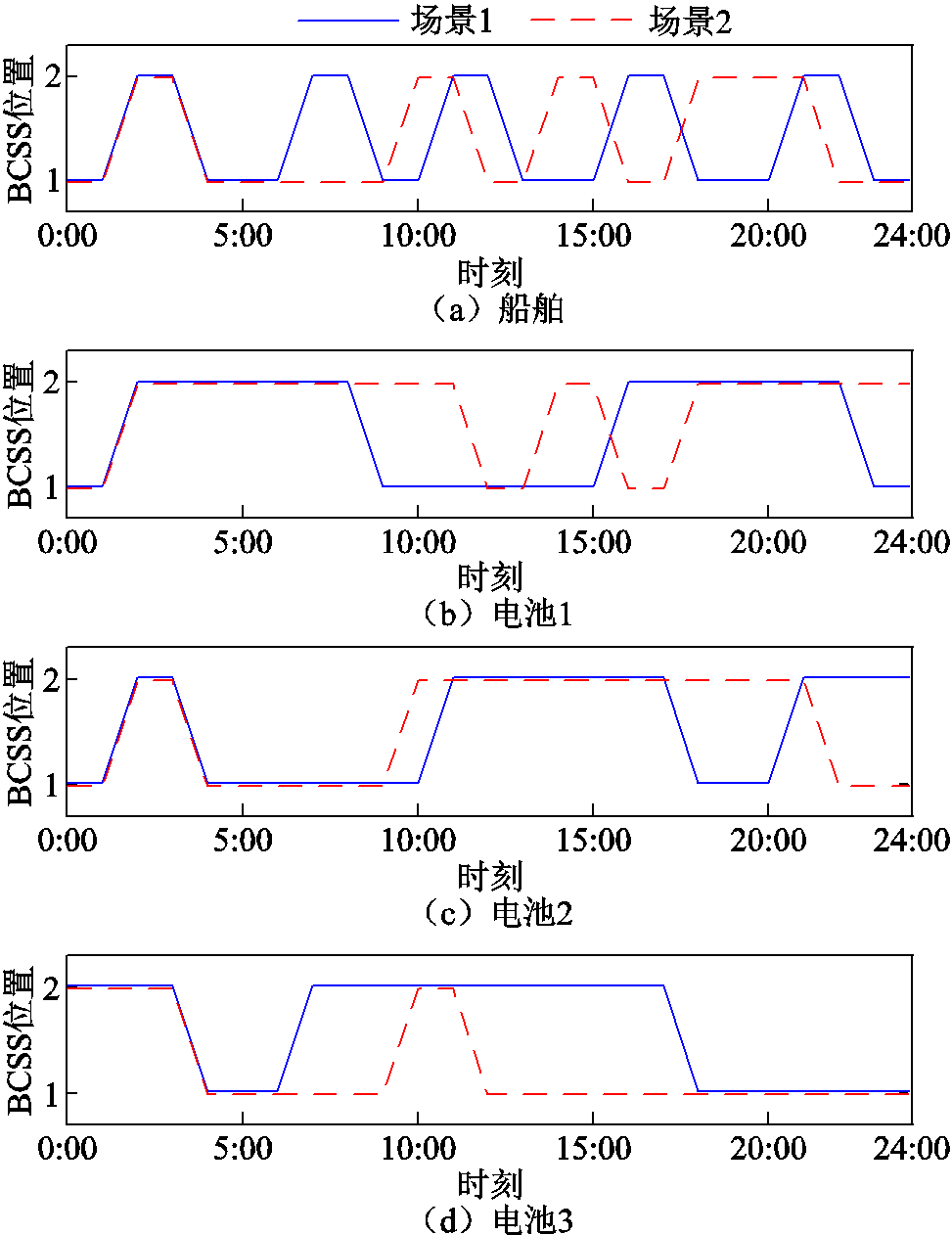
图10 船舶与电池的时空转移
Fig.10 Space-time transfer diagram of vessel and battery
电池换电模式下,由于电池的转移特性受限,在调度过程中需要依赖船舶的调度方案。由图10可知,任意电池在运输过程中的时空转移特性都与该时间船舶的转移特性保持一致。例如在场景1时,电池1在8:00~9:00时间段内,由充/换电站2向充/换电站1转移,而此时的船舶转移特性也恰好是由位置2指向位置1。综上所述,电池时空转移需依赖船舶的转移,与实际转移情况相符。
电池的充放电与SOC特性如图11所示,结合图10的时空转移特性可知,场景1调度开始时,电池1在BCSS1处放电,电池2位于BCSS1处,电池3在BCSS2处充电;1:00时船舶载着电池1、2前往BCSS2处进行充电,就地消纳波浪能装置发电;短暂时间后,船舶带着电池2、3前往BCSS1处,电池1在BCSS2继续充电。在这种工作模式下,船舶通过运载电池,将电能从波浪能发电装置处转移到负荷中心岛,完成了波浪能的消纳利用。
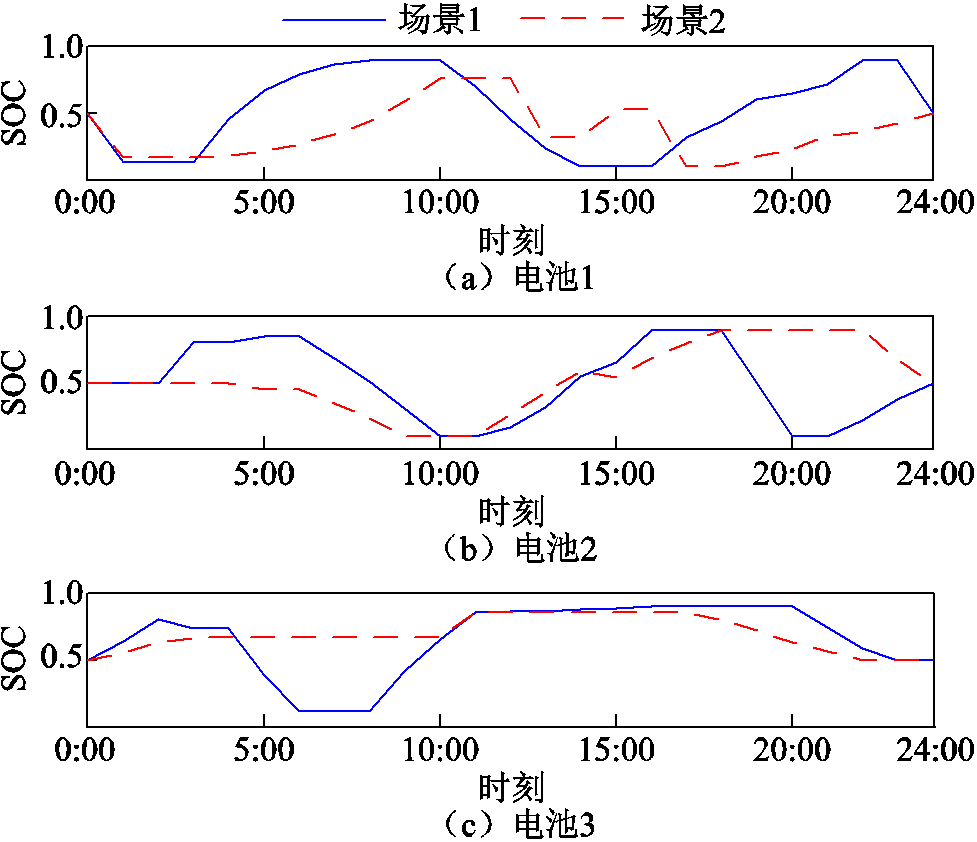
图11 储能电池的SOC变化
Fig.11 SOC variation graph of energy storage battery
3)微电网功率分布
孤岛微电网的功率分布情况如图12所示。在系统的调度周期内,柴油发电机与储能电池协调配合,共同满足微电网负荷用电需求。在低负荷时间段(1:00~6:00、14:00~17:00)电池全部在BCSS2处进行充电,微电网由柴油机组单独进行供电;在其他时间段,由于负荷用电需求较高,需要电池和柴油机协同调度来满足负荷需求;另外,在场景1下,由于波浪能出力较多,发电机相较于场景2出力较少。
此外,根据图10~图12还可以得出以下结论:
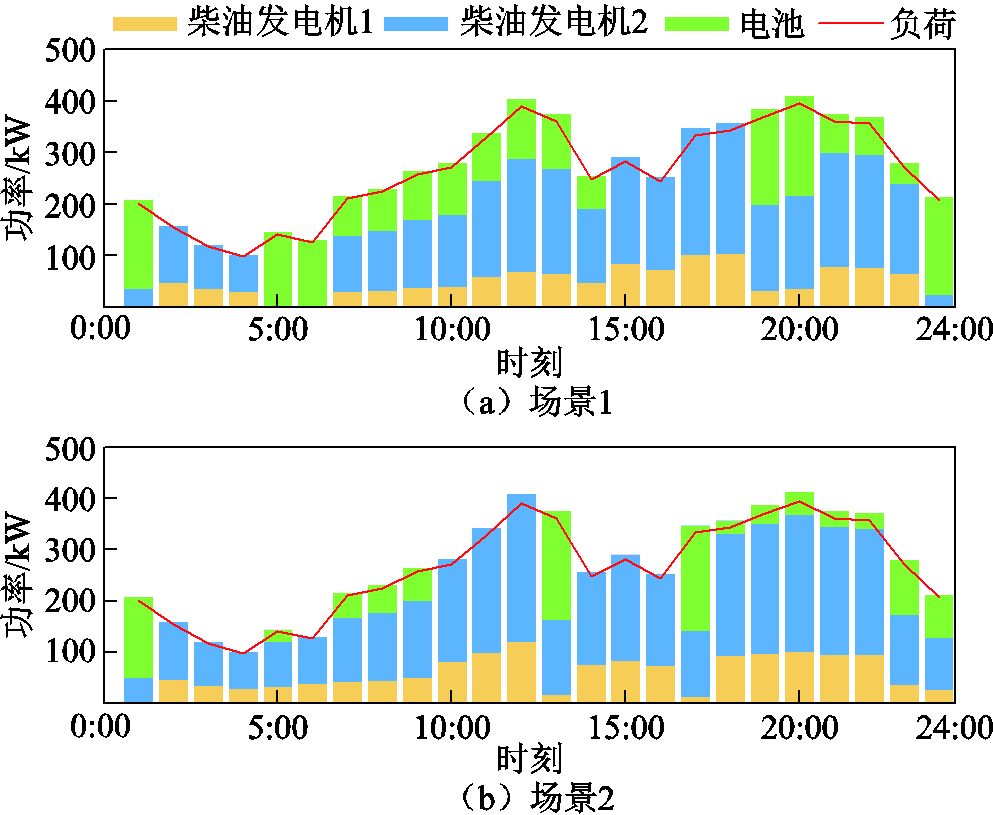
图12 孤岛微电网功率分布
Fig.12 Distribution graph of silo microgrid power
(1)受限于船舶转移速度与空间距离约束,电池物流运输具有明显的延时和离散特性,所以图10和图11所示的船舶转移特性曲线以及SOC变化曲线存在明显的时延特性;
(2)含波浪能装置的孤岛微电网系统兼具微电网实时功率平衡和岛际离散功率流的特点,如图12所示,柴油发电机、储能电池以及常规用电负荷都位于孤岛微电网中,功率流满足实时功率平衡的要求。
为突出本文所提调度策略的经济性,本文设计了三种对照方案:①本文所提的基于换电模式的孤岛微电网细粒化调度策略;②波浪能采取常规的最大效率转化控制策略,其他与方案①保持一致;③利用海底电缆来构建离岸式波浪能装置与孤岛微电网的传输通道,此外还在孤岛以及波浪能装置处各配置了500 kW的电池以平衡功率输出。
为了准确计算各方案的成本,本节的分析综合考虑了投资成本、运行成本和维护成本,并通过年限平均法[26]统一折算为年调度费用。不同方案的运行成本见表2。
表2 孤岛微电网不同调度方案的运行成本
Tab.2 Operating costs of different dispatching schemes for isolated microgrid

参数数值 方案①方案②方案③ 日电池容量损耗成本/元1 661.62 347723 日柴油机成本/元11 70911 4329 584 日储能电池寿命成本/元1 243.41 437539.5 日船舶航行成本/元1 8001 800- 年运行成本/万元599.1621.1395.8
由表2可知,本文所提的方案的年运行成本为599.1万元,相较于方案②而言,柴油机发电成本提高了10.11万元,而储能快充损耗和循环寿命减少32.08万元,总体经济性提高3.5%;与方案③相比,年运行费用增加了203.3万元。
进一步比较各方案的投资经济性,其中柴油发电机的造价为每台30万元,设备使用寿命为30年;海底电缆的初始投资成本为500万元/km(不考虑变电站的建设成本),使用寿命为30年;储能电池的建造成本为4.5元/(W·h),运行成本参照文献[26]折算到单次充放电成本进行计算;船体的造价参照舟山市造船厂的数据,以40万估算,使用寿命为10年。各方案的投资成本见表3。
表3 孤岛微电网不同调度方案的投资成本
Tab.3 Investment cost of different dispatching schemes for isolated microgrids

设备成本/万元 方案①方案②方案③ 柴油机1.81.81.8 电缆--300 船舶3.63.6- 总年均折旧额5.45.4301.8
综合表2和表3可知,本文所提方案的年综合成本为604.8万元,相较于方案②和方案③,经济性提高了3.4%和13.3%。方案③的运行成本虽然很低,但是海底电缆的投资成本过高,致使方案的年综合成本过高。综上所述,本文所提的孤岛微电网调度运行方案经济性最优。
本文搭建了波浪能细粒化模型,并通过理论分析和仿真验证,得出以下结论:
1)较之常规的供电策略,含漂浮式波浪能装置的孤岛微电网采用船舶换电模式供电具有更好的经济性。
2)孤岛微电网满足源荷储的实时功率平衡,船舶换电模式在能量传输上表现出离散、延时的特性,船舶换电模式实现了海岛能源的动态平衡。
3)液压发电系统细粒化调度策略通过对波浪能液压发电系统转速和蓄能器压力进行调控,相较于最大效率转化控制策略经济性提高了3.4%。
参考文献
[1] 张佳艺, 何礼鹏, 马立红, 等. 美国波浪能发电场建设对中国波浪能的启示[J]. 能源与节能, 2021(3): 5-7, 74. Zhang Jiayi, He Lipeng, Ma Lihong, et al. Enlightenment of American wave power generation yard construction on wave energy in China[J]. Energy and Energy Conservation, 2021(3): 5-7, 74.
[2] 徐超. 海流能驱动型制淡技术研究[D]. 杭州: 浙江大学, 2018.
[3] Wu You, Dai Haihong. Design and research of self-propelled wave energy collecting device based on hydrogen storage by seawater electrolysis[J]. IOP Conference Series: Earth and Environmental Science, 2020, 510(2): 022018.
[4] Azimov U, Birkett M. Feasibility study and design of an ocean wave power generation station integrated with a decommissioned offshore oil platform in UK waters[J]. International Journal of Energy and Environment, 2017, 8(2): 161-174.
[5] Hulls K. Wave power[J]. New Zealand Energy Journal, 1977, 50: 44-48.
[6] 郑崇伟, 贾本凯, 郭随平, 等. 全球海域波浪能资源储量分析[J]. 资源科学, 2013, 35(8): 1611-1616. Zheng Chongwei, Jia Benkai, Guo Suiping, et al. Wave energy resource storage assessment in global ocean[J]. Resources Science, 2013, 35(8): 1611-1616.
[7] 林湘宁, 陈冲, 周旋, 等. 远洋海岛群综合能量供给系统[J]. 中国电机工程学报, 2017, 37(1): 98-110. Lin Xiangning, Chen Chong, Zhou Xuan, et al. Integrated energy supply system of pelagic clustering Islands[J]. Proceedings of the CSEE, 2017, 37(1): 98-110.
[8] 汪致洵, 林湘宁, 刘畅, 等. 含换电船舶电能输运航路的远洋海岛群混合电能传输网络规划[J]. 中国电机工程学报, 2019, 39(12): 3420-3434. Wang Zhixun, Lin Xiangning, Liu Chang, et al. Hybrid power transmission network planning in pelagic islands based on power exchanging watercraft transport route[J]. Proceedings of the CSEE, 2019, 39(12): 3420-3434.
[9] 徐诗鸿, 张宏志, 林湘宁, 等. 基于换电船舶的远洋海岛离散能量优化调度策略研究[J]. 中国电机工程学报, 2020, 40(增刊1): 108-121. Xu Shihong, Zhang Hongzhi, Lin Xiangning, et al. Optimal discrete energy scheduling strategy for pelagic island based on electric vessel[J]. Proceedings of the CSEE, 2020, 40(S1): 108-121.
[10] 肖曦, 摆念宗, 康庆, 等. 波浪发电系统发展及直驱式波浪发电系统研究综述[J]. 电工技术学报, 2014, 29(3): 1-11. Xiao Xi, Bai Nianzong, Kang Qing, et al. A review of the development of wave power system and the research on direct-drive wave power system[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 1-11.
[11] 游亚戈, 李伟, 刘伟民, 等. 海洋能发电技术的发展现状与前景[J]. 电力系统自动化, 2010, 34(14): 1-12. You Yage, Li Wei, Liu Weimin, et al. Development status and perspective of marine energy conversion systems[J]. Automation of Electric Power Systems, 2010, 34(14): 1-12.
[12] 顾煜炯, 谢典, 和学豪, 等. 海岛直流微网复合储能系统控制策略设计与实现[J]. 电力自动化设备, 2018, 38(6): 1-6. Gu Yujiong, Xie Dian, He Xuehao, et al. Design and implementation of control strategy of hybrid energy storage system in island DC microgrid[J]. Electric Power Automation Equipment, 2018, 38(6): 1-6.
[13] 吴峰, 张小平, 鞠平. 电池储能在直接驱动式波浪能发电场并网运行中的应用(英文)[J]. 电力系统自动化, 2010, 34(14): 31-36. Wu Feng, Zhang Xiaoping, Ju Ping. Application of battery energy storage in the direct-drive wave energy conversion farm integrated into power grid[J]. Automation of Electric Power Systems, 2010, 34(14): 31-36.
[14] 王坤林, 盛松伟, 叶寅, 等. 波浪能装置中液压发电系统Boost变换机理及控制策略[J]. 电力系统自动化, 2017, 41(12): 173-178. Wang Kunlin, Sheng Songwei, Ye Yin, et al. Boost converter converting mechanism and control strategy for hydraulic power generation system in wave energy converter[J]. Automation of Electric Power Systems, 2017, 41(12): 173-178.
[15] 宋清超, 陈家伟, 蔡坤城, 等. 多电飞机用燃料电池-蓄电池-超级电容混合供电系统的高可靠动态功率分配技术[J]. 电工技术学报, 2022, 37(2): 445-458.Song Qingchao, Chen Jiawei, Cai Kuncheng, et al. A highly reliable power allocation technology for the fuel cell-battery-supercapacitor hybrid power supply system of a more electric aircraft[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 445-458.
[16] 刘颖昕, 秦健, 刘延俊. 液压蓄能式波浪能发电装置关键参数分析[J]. 山东大学学报(工学版), 2021, 51(6): 1-8. Liu Yingxin, Qin Jian, Liu Yanjun. The analysis of key parameters of hydraulic energy storage system of wave energy converter[J]. Journal of Shandong University (Engineering Science), 2021, 51(6): 1-8.
[17] 王坤林. 基于海岛直流纳电网波浪能发电场关键技术研究[D]. 广州: 华南理工大学, 2015.
[18] 方红伟, 宋如楠, 姜茹, 等. 振荡浮子式波浪能转换装置的全电气化模拟研究[J]. 电工技术学报, 2019, 34(14): 3059-3065. Fang Hongwei, Song Runan, Jiang Ru, et al. An oscillating buoy type wave energy converter with all-electrical analogue method[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 3059-3065.
[19] 何晨可, 朱继忠, 刘云, 等. 计及碳减排的电动汽车充换储一体站与主动配电网协调规划[J]. 电工技术学报, 2022, 37(1): 92-111. He Chenke, Zhu Jizhong, Liu Yun, et al. Coordinated planning of electric vehicle charging-swapping-storage integrated station and active distribution network considering carbon reduction[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 92-111.
[20] 高红, 肖杰. 基于模糊PI的波浪能液压转化系统平稳控制研究[J]. 机械工程学报, 2021, 57(10): 267-276. Gao Hong, Xiao Jie. Research on stabilization control of wave energy hydraulic conversion system based on fuzzy-PI[J]. Journal of Mechanical Engineering, 2021, 57(10): 267-276.
[21] 刘娜, 谭亦旻, 莫伟强, 等. 基于模拟退火算法的Halbach直线发电机优化设计[J]. 电工技术学报, 2021, 36(6): 1210-1218. Liu Na, Tan Yimin, Mo Weiqiang, et al. Optimization design of Halbach linear generator with simulated annealing algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1210-1218.
[22] 李言华, 王喜莲, 王小君. 液压蓄能式波浪能发电系统及其控制方案研究[J]. 太阳能学报, 2022, 43(1): 219-227. Li Yanhua, Wang Xilian, Wang Xiaojun. Research on hydraulic energy-storage wave energy generation system and its control scheme[J]. Acta Energiae Solaris Sinica, 2022, 43(1): 219-227.
[23] Gao Yang, Jiang Jiuchun, Zhang Caiping, et al. Lithium-ion battery aging mechanisms and life model under different charging stresses[J]. Journal of Power Sources, 2017, 356: 103-114.
[24] Wood A J, Wollenberg B F. Power Generation, Operation, and Control[M]. 2nd ed. New Jersey: John Wiley & Sons, Inc, 1996.
[25] Wu Chuantao, Sui Quan, Lin Xiangning, et al. Scheduling of energy management based on battery logistics in pelagic islanded microgrid clusters[J]. International Journal of Electrical Power & Energy Systems, 2021, 127: 106573.
[26] 刁涵彬, 李培强, 王继飞, 等. 考虑电/热储能互补协调的综合能源系统优化调度[J]. 电工技术学报, 2020, 35(21): 4532-4543. Diao Hanbin, Li Peiqiang, Wang Jifei, et al. Optimal dispatch of integrated energy system considering complementary coordination of electric/thermal energy storage[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4532-4543.
Abstract Currently, countries around the world are paying more attention to the development of ocean energy. However, wave energy has a large fluctuation in power output on short time scales, which makes it difficult to capture wave energy. Therefore, wave energy hydraulic power generation system generally adopts the control strategy of maximum power tracking, and the hydraulic power generation system needs to experience a certain time of energy storage before discharge, resulting in its power output curve showing the characteristics of short discharge time and high discharge power. According to the relevant research, the capacity loss of the battery will be several times higher than the normal operation mode when facing such a power shock. Therefore, the efficient energy conversion comes at the cost of a significant increase in battery losses. In this context, it is debatable whether choosing the maximum efficiency tracking strategy is necessarily economically optimal.
In this paper, for the islanded microgrid system with flexible wave energy access, firstly, the working principle of wave energy device is analyzed in depth and the mathematical model of wave energy hydraulic system is built; based on this, the economic optimality in the dispatching cycle is the goal, and a wave energy flexible access under The fine-grained dispatching model of the islanded microgrid with flexible wave energy access is established and solved by GUROBI. The simulation results show that the wave energy dispatching proposed in this paper is different from the maximum efficiency conversion control strategy, which makes a trade-off between the pursuit of conversion efficiency and the fast charging loss of energy storage, and chooses to discard part of the wave energy conversion efficiency to obtain a more economical dispatching scheme for islanded microgrids with wave energy. The power discarded in one dispatching cycle is 287 kW·h, and the cost of energy storage less loss in one dispatching cycle is 686 RMB. To highlight the economy of the dispatching strategy proposed in this paper, the following control schemes are designed: Scheme 1: the fine-grained dispatching strategy of the islanded microgrid based on the power exchange mode proposed in this paper; Scheme 2: the wave energy adopts the conventional maximum efficiency control strategy, and the other remains the same as Scheme 1; Scheme 3: the submarine cable is used to build the transmission channel between the offshore wave energy device and the islanded microgrid. The annual comprehensive cost of the proposed scheme in this paper is 6.048 million yuan, respectively, which is 3.4% and 13.3% more economical compared with scheme 2 and scheme 3.
Based on the above results, the following conclusions are drawn that: (1) the isolated island microgrid containing floating wave energy devices has better economy by using ship-for-power mode to supply power; (2) the isolated island microgrid satisfies the real-time power balance of source-load-storage, and the ship-for-power mode realizes the dynamic balance of island energy; (3) the fine-grained scheduling strategy of the hydraulic power generation system regulates the speed and accumulator pressure of the wave energy hydraulic power generation system, compared with the maximum conversion efficiency control strategy The economy is improved by 3.4%.
keywords:Wave energy hydraulic power generation system, energy storage fast charging loss, fine grain scheduling, power exchange mode, optimal efficiency trackin
广东电网公司电力规划专题研究项目资助(030400QQ00210001)。
收稿日期 2022-04-12
改稿日期 2022-06-27
DOI: 10.19595/j.cnki.1000-6753.tces.220582
中图分类号:TM71
李飞宇 男,1997年生,硕士研究生,研究方向为微电网规划及调度。E-mail:347199767@qq.com
林湘宁 男,1970年生,教授,博士生导师,研究方向为电力系统保护、分析与控制、新型发电技术和新型电网技术等。E-mail:xiangning.lin@hust.edu.cn(通信作者)
(编辑 李冰)