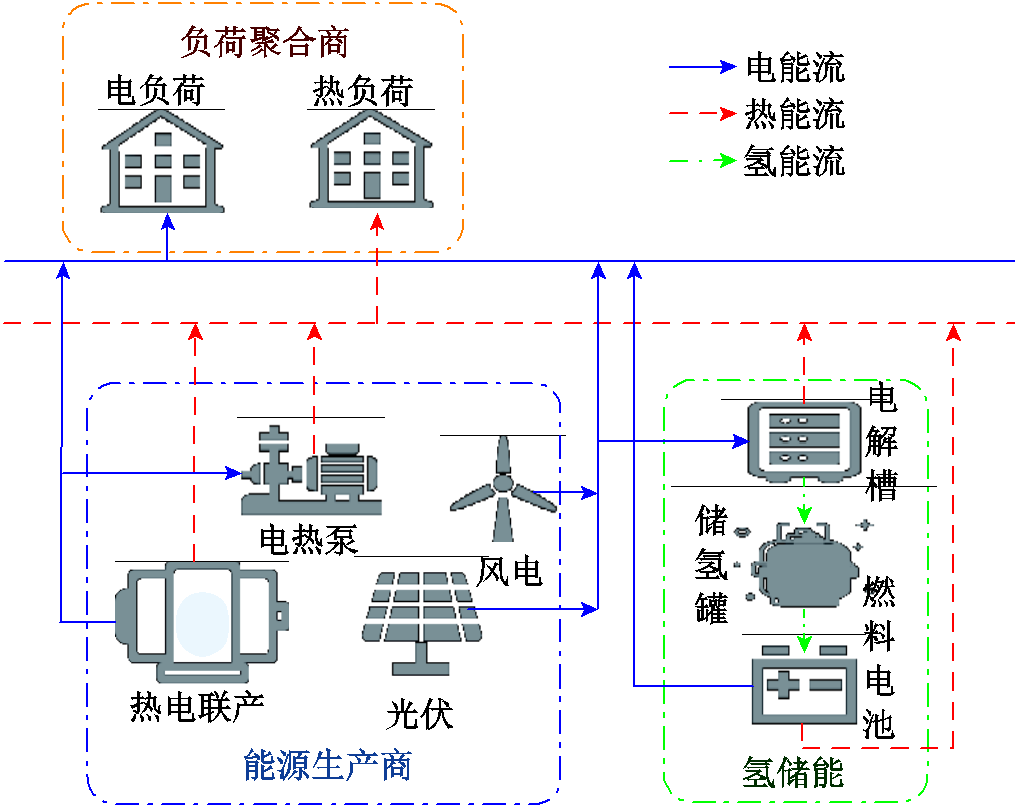
图1 EHH-IES结构
Fig.1 Structure of EHH-IES
摘要 为了提高可再生能源消纳，促进综合能源系统发展，该文提出一种计及风光不确定性的电-热-氢综合能源系统（EHH-IES）分布鲁棒优化方法。给出EHH-IES结构和氢储能（HES）耦合模型；基于分布鲁棒条件风险价值（DRCVaR）方法，以系统收益最大、全生命周期碳排放量最小和不确定性风险成本最小为目标，建立EHH-IES优化问题的博弈模型；应用拉格朗日对偶原理，将模型转换成半定规划问题并求解。算例结果表明，该优化方法可使EHH-IES总收益提高1.4%，全生命周期碳排放量减少2.9%，显著降低风光不确定性造成的经济风险。
关键词：综合能源系统 氢储能 分布鲁棒优化 不确定性 碳排放量
为顺应全球绿色低碳发展潮流，我国提出了“碳达峰、碳中和”的能源发展目标。为此，构建清洁低碳、安全高效的新型电力系统，推进电力源网荷储一体化和多能互补，成为当今能源系统发展的主要方向[1-3]。目前，我国电力系统运行灵活性不足，弃电现象严重，能源低碳转型仍然面临如何实现多能源系统协同发展的难题。储能系统通过充电和放电的削峰填谷作用，可以实现对电力系统的功率转移和存储，是解决灵活性问题的关键。
氢储能（Hydrogen Energy Storage, HES）具有质量能量密度高、可长时间存储、充放电过程无污染等优势，是极具潜力的新型大规模储能技术[4-6]，应用HES的多能源系统优化是近年来的研究热点。文献[7]针对氢-电混合储能系统提出一种源-储-网联合多时间尺度优化调度策略；文献[8]以电氢耦合系统为研究对象，提出考虑电氢耦合的混合储能微电网容量优化配置方法；文献[9]提出电热氢多种能源形式构成的多源协调储能优化模型，提高电网风电和光伏消纳能力并减轻电网调峰压力。上述文献对含氢储能的综合能源系统优化的研究是针对可再生能源与HES协同优化，主要关注HES作为储能的削峰填谷作用，对HES中的多种能源耦合的研究较少。文献[10]考虑HES的热平衡和热功率约束，提出提高风氢混合系统运行收益的优化调度方法，但是忽略了存储氢能的利用问题；文献[11]计及存储氢能的售氢收益，提出基于主从博弈的园区综合能源系统优化框架，并且分析了氢储能对各个博弈主体收益的影响，但是没有考虑HES热平衡和热约束。综上所述，HES中多种能源耦合的研究成果较少，且多以电能和热能、电能和氢能耦合为主，含电、热、氢多种能源的HES耦合模型值得深入研究。
双碳目标下，2030年风电和太阳能发电总装机容量要达到12亿kW以上，国内单位生产总值二氧化碳排放量要比2005年下降65%以上[12]。风光等可再生能源具有不确定性，高比例的可再生能源接入使得电力系统的经济运行面临着巨大挑战，严重制约了综合能源系统的发展[13]。
在电力市场中，用条件风险价值（Conditional Value at Risk, CVaR）方法处理可再生能源不确定性问题具有广泛的研究和应用。文献[14]针对园区级电-热综合能源系统，考虑综合需求响应与条件风险建立日前经济调度模型；文献[15]建立寡头竞争电力市场下含风电系统的电源投资扩展规划双层模型，采用CVaR方法度量投资规划博弈过程中竞争对手的不确定性给发电公司带来的投资风险。上述文献假设可再生能源机组出力或者出力预测误差服从某一特定分布，建立满足一定概率水平下的随机规划模型。在电力调度期的较短时段，机组出力或出力预测误差的概率分布是变化的，所以这种方法处理不确定性问题具有局限性。另一类常用的处理不确定性问题的方法是鲁棒优化方法，即假设不确定参数属于一个不确定集合，考虑最坏情况下的最优决策[16]。但这类方法一方面过于保守，另一方面没有利用数据间的概率统计信息导致计算复杂。结合随机规划和鲁棒优化的特点，近年来提出了基于期望、方差和协方差等矩信息不确定的分布鲁棒条件风险价值（Distributionally Robust Conditional Value at Risk, DRCVaR）方法解决可再生能源不确定性问题[17-19]。目前，应用DRCVaR方法处理电力系统可再生能源不确定性问题的研究成果不多，且并没有考虑大自然（可再生能源）和人工决策者的博弈关系，所以这部分值得进一步研究。
综上所述，本文提出一种计及风光不确定性的电-热-氢综合能源系统（Electricity-Heat-Hydrogen Integrated Energy System, EHH-IES）分布鲁棒优化方法。首先，分析EHH-IES的结构，给出含电、热、氢多种能源的HES耦合模型；然后，基于DRCVaR方法，以系统收益最大、全生命周期碳排放量最小和不确定性风险成本最小为目标，建立EHH-IES分布鲁棒优化问题的博弈模型；进而，通过拉格朗日对偶原理，将模型转换成半定规划问题进而求解；最后通过算例仿真验证了模型和方法的有效性。
本文提出的EHH-IES结构如图1所示，系统由HES、能源生产商（Energy Producer, EP）和负荷聚合商（Load Aggregator, LA）等主体组成，包括电能流、热能流、氢能流等三种能量流。
图1 EHH-IES结构
Fig.1 Structure of EHH-IES
HES是利用电-氢-电互变性发展起来的，主要包含电解槽（Electrolyser, EL）、储氢罐（Hydrogen Tank, HT）和燃料电池（Fuel Cells, FC）三个部分。在风光发电系统中，电力间歇产生的现象常有发生，利用富余的电力大规模制氢将电能转换为氢能储存起来，在电力输出不足时利用氢气转换为电能输送上网，这种模式能够有效地解决风光发电并网问题，同时也可以将此过程中产生的的氢气出售，提高经济性。
EP是系统能源的提供者，向LA提供所需的能量并以此获得收益。EP包括热电联产机组（Combined Heat and Power, CHP）、电热泵（Electric Heating Pump, ehp）、风电机组（Wind Turbine, wt）、光伏机组（Photovoltaic, PV）等设备。其中风光发电既可以直接用于满足LA负荷需求，也可以供给EL用于制氢。当EP提供的能量超过LA需求时，EL通过电氢转换消纳系统过剩能量，然后以氢能的形式存储；当EP提供的能量低于LA需求时，由FC补足系统缺少的能量。
HES模型如图2所示，其中EL消耗电能产生氢气，同时以水为工质将产生的热能参与到系统热循环中；FC可以燃烧氢气发电为系统提供电能，也可以通过水将产生的热能输送给LA的热负荷。
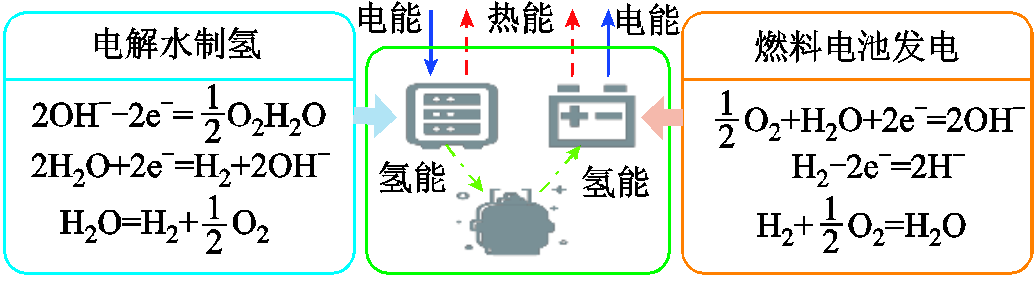
图2 HES模型
Fig.2 Model of HES
HES中电、热、氢三种能量耦合，内部多能联供联储特性[11]为
（1）
（2）
（3）
（4）
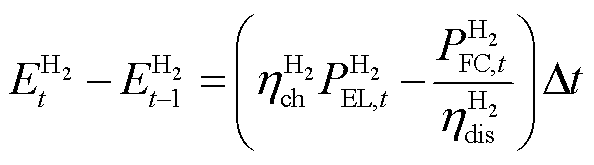（5）
式中，
、
、
分别为t时刻EL的耗电功率、产热功率、产氢功率；
和
分别为电制氢效率和余热利用效率；
、
、
分别为t时刻FC的发电功率、产热功率、耗氢功率；
和
分别为耗氢发电效率和余热利用效率；
为HT在t时刻存储的能量；
和
分别为氢气的充入和放出效率；Δt为单位步长，取1 h。
风光机组是EHH-IES中的能源提供者，其供电具有充足、安全、清洁的特点。大力发展风光等可再生能源是实现电力系统低碳转型的重要途径，但其具有不确定性，为电力系统规划带来巨大挑战。
本文采用随机规划和鲁棒优化相结合的分布鲁棒优化方法处理EHH-IES中风光不确定性问题，思路是假设风光机组可用出力的概率分布的矩信息属于一个不确定集，考虑集合中可用出力最坏情况下的系统最优的决策。在不确定性描述的研究中，椭球不确定集可以通过控制不确定度的大小，调整优化结果的保守程度，提高不确定集的准确性，在电力系统优化问题中具有广泛应用[20]，所以本文采用椭球不确定集
描述系统风光不确定性，即
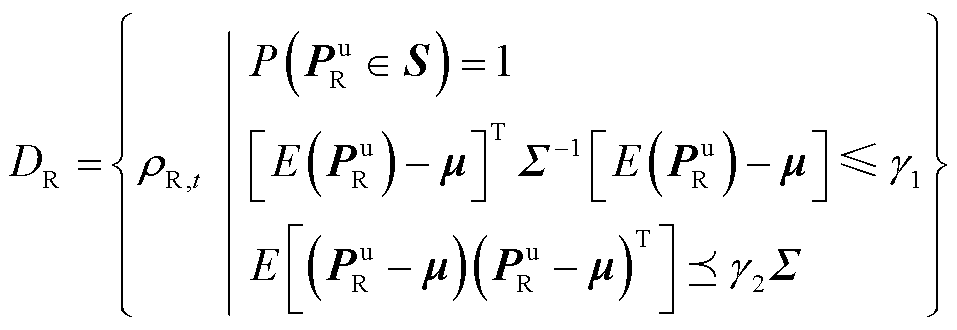（6）
式中，
为t时刻风光机组可用出力可能的概率分布；
为风光机组可用出力列向量；S为包含变量的任何闭凸集；
和
分别为风光机组可用出力均值列向量和方差矩阵；
和
为参数扰动水平，
、
；
表示半负定。
风光不确定性会引起系统波动，给其稳定运行造成一定的风险。当风光机组的可用出力大于决策出力时会产生弃电现象，当风光机组的可用出力小于决策出力时会产生供电不足现象，这两种现象都对EHH-IES运行产生重大影响。为量化风光不确定性对系统的影响，对其风险进行定量描述。
t时刻风光机组出力偏差成本为
（7）
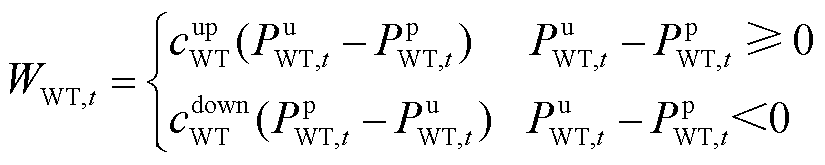（8）
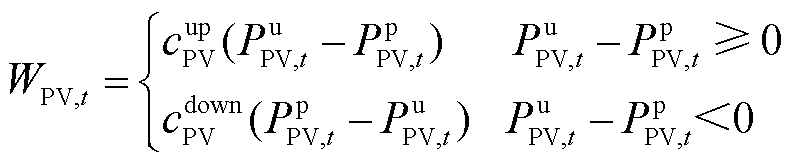（9）
式中，
、
、
分别为风光机组、WT、PV的出力偏差成本；
和
分别为t时刻WT和PV可用出力；
和
分别为t时刻WT和PV决策出力，
和
表示t时刻高估WT和PV出力，
和
表示t时刻低估WT和PV出力；
和
分别为高估WT和PV出力惩罚系数；
和
分别为低估WT和PV出力惩罚系数。
基于CVaR方法，置信水平为b时不确定性风险成本为
（10）
式中，VaR为置信水平b时风光机组出力的偏差成本；
为t时刻风光机组的可用出力。
由于式（10）的解析式难以直接求出，故引入关于a的函数将其转换为
（11）
其中
（12）
式中，
为概率分布下的期望值。
基于CVaR方法计算不确定性风险成本时采用确定的概率分布，没有考虑到电力调度期的较短时段内概率分布是变化的，会产生较大偏差，故本文用描述概率分布变化的椭球不确定来集刻画风光机组可用出力的概率分布。基于DRCVaR方法，最坏概率分布情况下的风光不确定性风险成本为
（13）
为满足构建清洁低碳、安全高效的新型电力系统要求，本文以收益最大、全生周期碳排放量最小、不确定性风险成本最小作为系统优化目标。
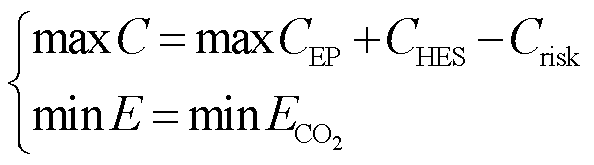（14）
式中，
和
分别为EP和HES收益；
为系统全生命周期的碳排放量。
由于EHH-IES收益、不确定性风险成本和全生命周期的碳排放量之间存在数量和维度差异，本文采用最小-最大归一化方法将多目标优化问题转换为单目标优化问题。
（15）
式中，
为归一化的总目标函数；
和
分别为基于运行经验的系统收益的最大值和最小值；
和
分别为基于运行经验的系统全生命周期碳排放量的最大值和最小值。
3.1.1 EP收益
EP向LA出售电能和热能获得收益，其中CHP、EHP组成的热电联产机组系统（CHPS）的运行需要燃料成本，而WT的PV可视为零边际成本。
（16）
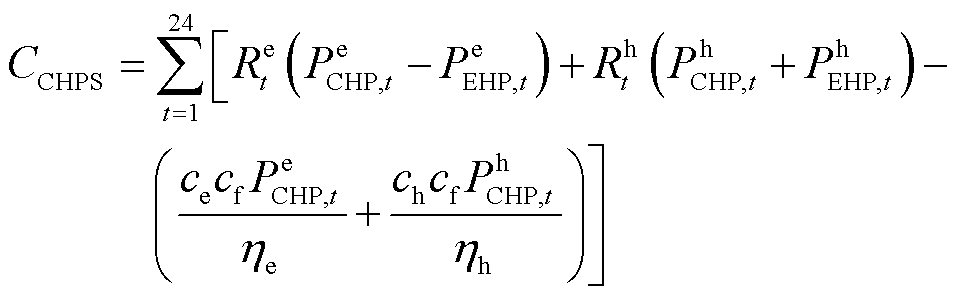（17）
（18）
（19）
式中，
、
、
分别为CHPS、WT、PV的收益；
、
、
、
分别为t时刻CHP电出力、CHP热出力、EHP电出力、EHP热出力；
和
分别为t时刻电价和热价；
和
分别为标准煤的电力当量和热力当量；
为标准煤的价格；
和
分别为CHP发电效率和产热效率。
3.1.2 HES收益
HES向LA出售电能和热能获得收益，还可以出售HT中存储的氢气获得收益。
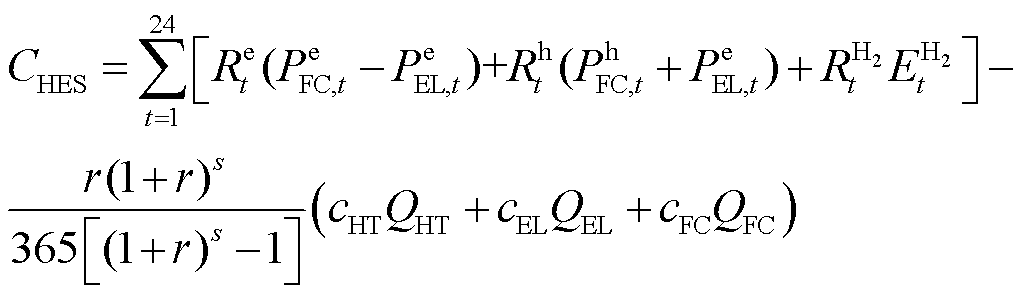（20）
式中，
为t时刻氢单位能量的价格；
、
、
分别为HT、EL、FC配置的容量，
、
、
分别为HT、EL、FC单位容量的价格；r和s分别为利率和系统寿命。
3.1.3 全生命周期碳排放量
基于生命周期评价方法对碳排放的度量包括直接碳排放量和间接碳排放量，需要经历确定机组的阶段和各阶段排放源、查询并确定碳排放因子和收集系统数据三个步骤[21-22]。本文WT、PV、CHP三个机组，筹建、建设、运行、报废四个阶段的系统全生命周期碳排放量为
（21）
式中，i表示WT、PV、CHP；j表示碳排放的四个阶段；
为t时刻机组i第j阶段的碳排放因子；
为t时刻机组i第j阶段的使用量。
为方便计算，式（21）可以改写为
（22）
式中，
为t时刻机组i的碳排放因子；
为t时刻机组i的使用量，本文中为
、
和。
3.2.1 功率平衡约束
在电力网络中，功率传输需要保证供给平衡，即
（23）
式中，
为t时刻LA的电负荷需求。
热力系统本身不需要时刻保证功率平衡，但研究的系统中热力系统与电力系统相连，因此热力系统也需要时刻满足功率平衡。
（24）
式中，
为t时刻LA的热负荷需求。
3.2.2 输出功率约束
CHP爬坡约束为
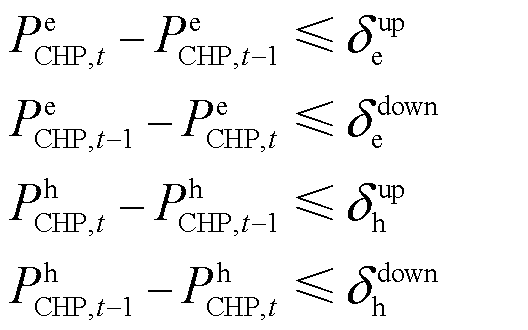（25）
式中，
、
、
、
分别为机组升电负荷、降电负荷、升热负荷、降热负荷时，单位时间内的最大变化量。
WT和PV的出力约束为
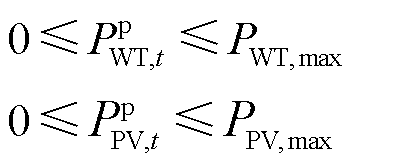（26）
式中，
和
分别为WT和PV的出力上限。
3.2.3 HES约束
FC和EL的功率约束及HT的容量约束分别为
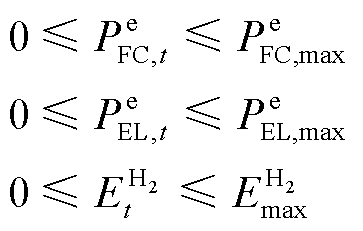（27）
式中，
和
分别为FC和EL电出力最大值；
为HT存储量的最大值。
计及风光不确定性的优化问题的决策主体有两个：一是人工决策者（决策变量），其所发出的调度指令能够平抑风光波动性对系统的影响，实现风光的高效消纳；二是大自然（随机变量），其不确定性倾向于使电力系统运行状况恶化，或使其运行成本升高。从工程博弈论观点看，大自然可以看作是“拟人化”的参与者，它与人工决策者一起构成广义的二人零和博弈关系。这类博弈问题的核心，即对不确定性作为决策成员之一的多主体决策问题中，设计各主体策略，以最大程度地抑制不确定性带来的不利影响，同时实现各主体的优化目标。
计及风光不确定性的分布鲁棒优化问题具有极大-极小结构的工程博弈格局，其中人工决策者希望极小化成本是容易理解的，而大自然是虚拟的对立方，企图使成本最大化，这是工程博弈论的一大特色。为了对工程博弈问题物理意义进行理解，文献[23]提出三项基本原则：①人工决策者的最佳选择是避免最坏情况。只要避免最坏情况的发生，即形成了一个合理的博弈格局，进而达到由两个参与者各自利益所强制形成的一种真正的均衡。②博弈双方最佳策略表示大自然先行决策，然后人工决策者介入。虽然从博弈观点看，这样决策顺序对人工决策者不公平，但是面对大自然这样的策略不明朗或有关信息不完备的博弈者，此时进行工程决策谈不上公平原则，最好的应对手段是先观察其最坏干扰（对大自然本身而言是其最佳策略），再构建应对之策。③人工决策者与大自然均满足理性要求。理性要求是指博弈参与者均期望通过博弈最大化己方收益。大自然作为博弈参与者是“理性”的，表现在大自然带来的不确定性总是会增加系统的支付，即降低系统的经济性或影响系统的运行安全。例如，突然出现的阵风绝不会使风电场输出更加平滑，因此大自然给系统带来的影响总是负面的，并企图极大化此负面影响，此即大自然的“理性”。
EHH-IES分布鲁棒优化问题的博弈模型结构如图3所示。从图3中可以看出，风光机组决策出力、CHPS出力和HES出力作为决策变量，风光机组可用出力作为随机变量，两者共同构成二人零和博弈的参与者。随机变量在椭球不确定集中寻找使系统总目标函数最小的决策，而决策变量在这种最坏情况下寻找使系统总目标函数最大的决策。
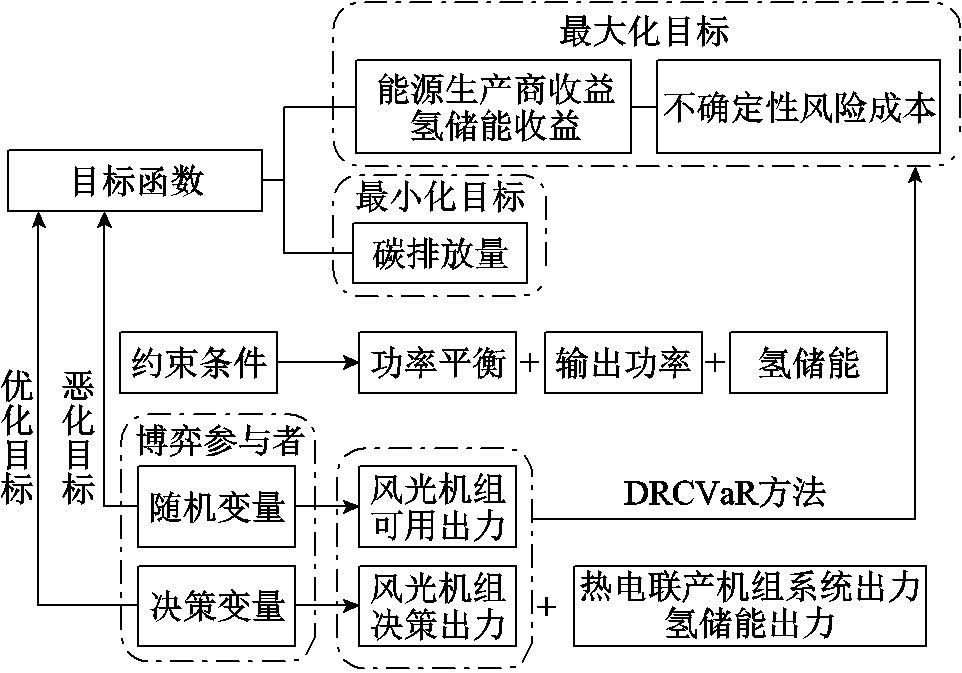
图3 博弈模型结构
Fig.3 Structure of game model
计及风光不确定性的EHH-IES分布鲁棒优化问题的博弈模型数学表达式为
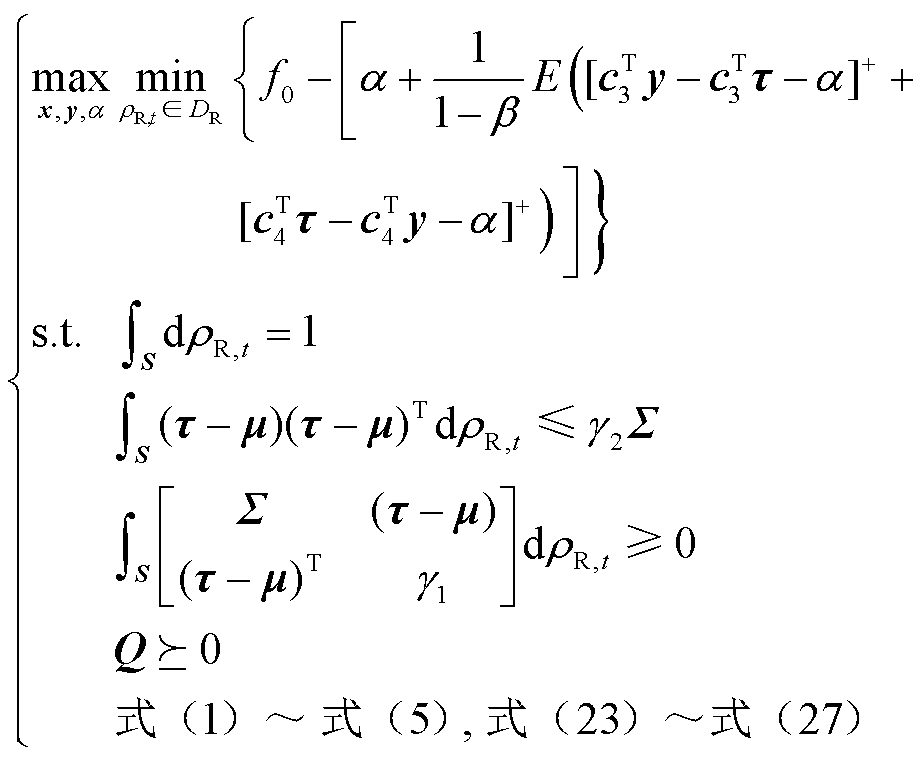（28）
（29）
式中，c1、c2、c3、c4为总目标函数的系数矩阵；c5为常数；x和y为决策变量的列向量，x包括
、
、
、
、
、
，y包括
和
；t 为随机变量的列向量，包括
和
。
EHH-IES分布鲁棒优化问题的最优解由博弈的纳什均衡确定，在均衡策略下没有一个博弈参与者能够通过单独更改策略达到更优的结果。对于本文的博弈模型，随机变量期望系统的总目标函数最小而决策变量期望系统的总目标函数最大，故纳什均衡
应满足
（30）
本文的博弈模型在数学上属于NP难题不能直接求解，需要把模型对偶处理再求解。为方便对偶转换，将目标函数改写成标准min-max形式为
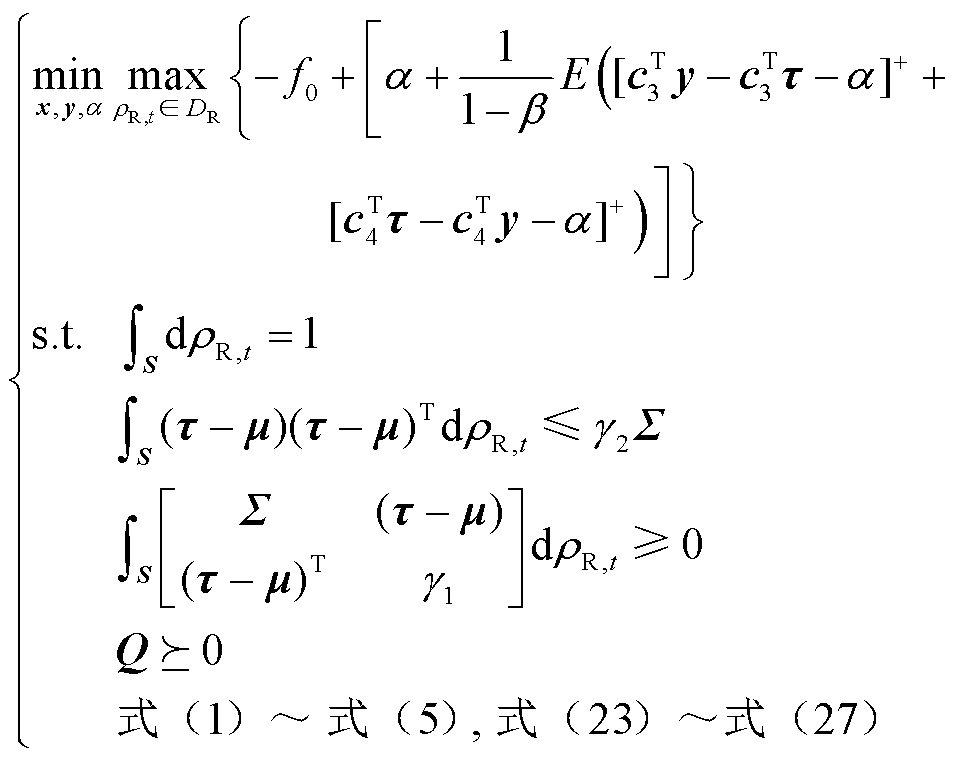（31）
采用拉格朗日对偶原理将模型转换为确定性的凸半定规划问题。
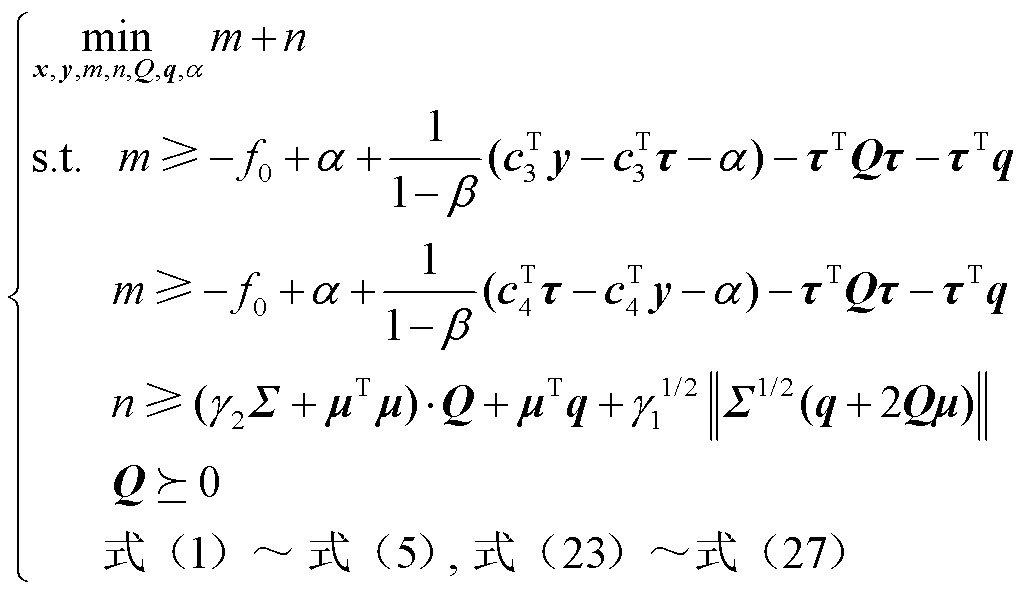（32）
式中，Q和q为对偶变量；m和n为松弛变量；“·”表示Frobenius积。
根据舒尔补理论，式（32）的第一个和第二个不等式约束可以转换为半定矩阵约束。
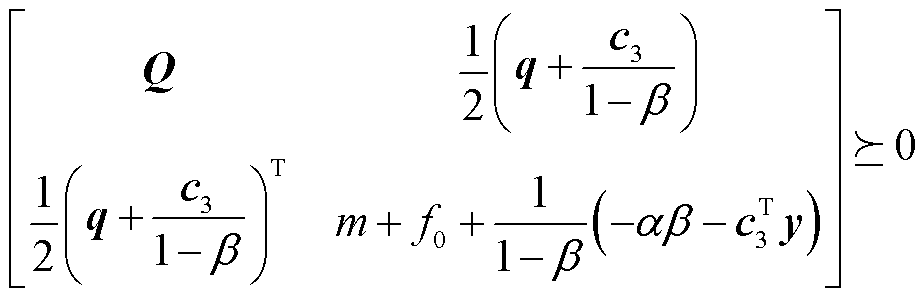（33）
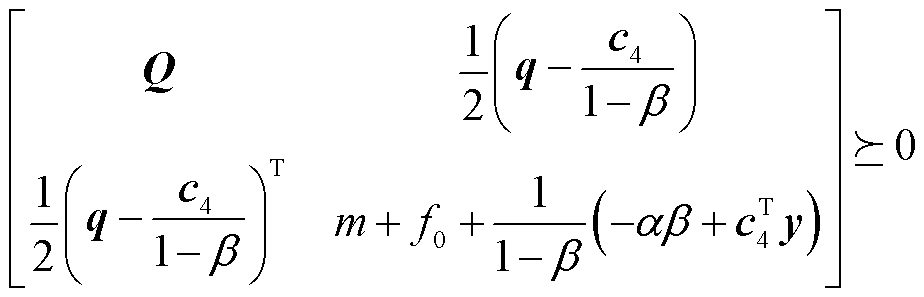（34）
以某工业园区的综合能源系统[24]为例，在Matlab环境下调用SDPT3求解器对本文提出的优化方法进行算例仿真。由于冬季LA热负荷具有典型性，所以本文在冬季典型日对系统进行仿真分析。LA电负荷、热负荷的功率预测曲线如图4所示。
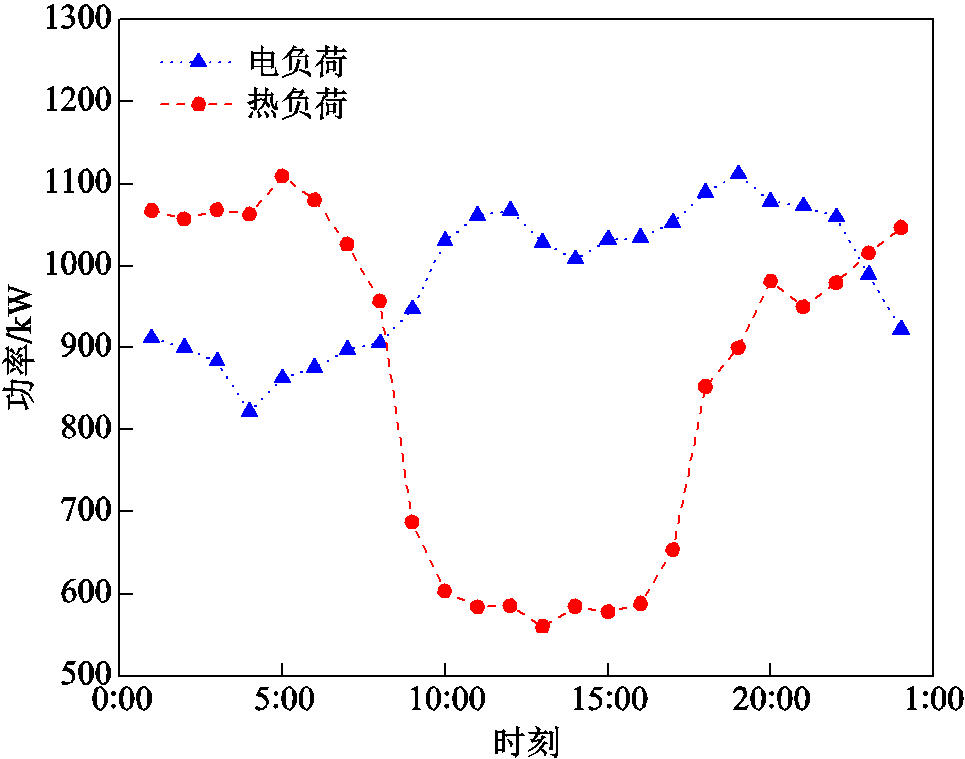
图4 冬季典型日LA功率预测曲线
Fig.4 User power forecast curve of the winter typical day
WT、PV各个时刻的历史数据的均值见表1，各个时刻的方差分别为0.680，0.564。采用分时电价，8:00—12:00、17:00—21:00峰时段，0:00—8:00、21:00—24:00谷时段，12:00—17:00平时段。峰、谷、平分时电价分别为1.25元/(kW∙h)、0.4元/(kW∙h)、0.8元/ (kW∙h)。CHPS和HES热价均为0.35元/(kW∙h)，HES的售氢价格为0.924元/(kW∙h)。
表1 WT、PV历史数据的均值
Tab.1 Mean of WT and PV historical data
时刻WT/kWPV/kW时刻WT/kWPV/kW 1:00672013:00636550 2:00636014:00672520 3:00528015:00612440 4:00672016:00588340
（续）
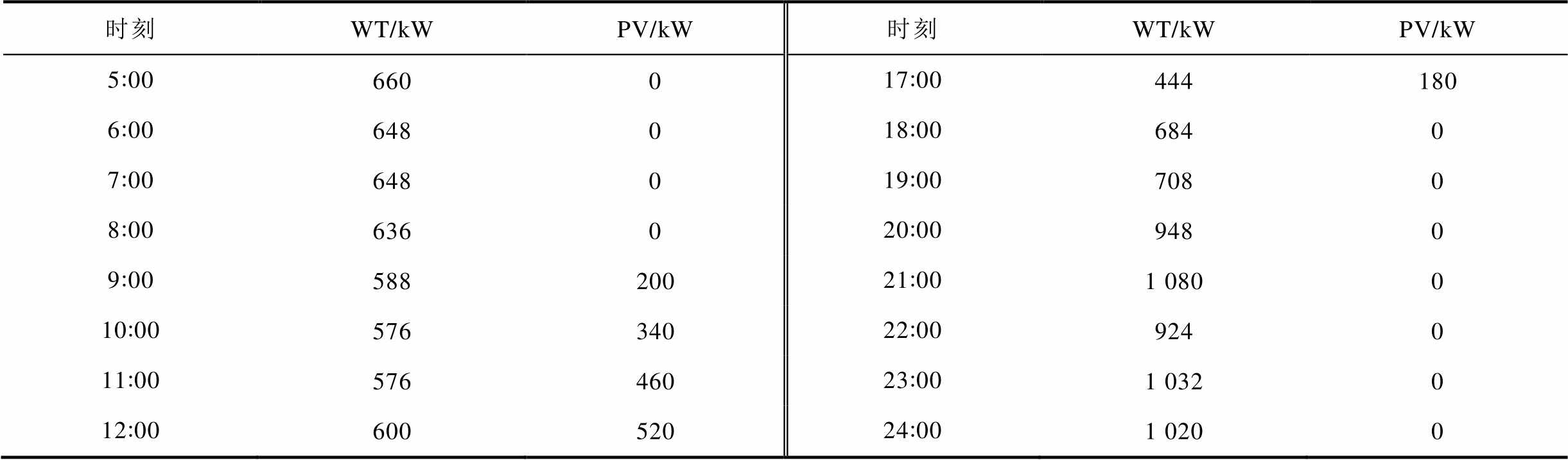
时刻WT/kWPV/kW时刻WT/kWPV/kW 5:00660017:00444180 6:00648018:006840 7:00648019:007080 8:00636020:009480 9:0058820021:0010800 10:0057634022:009240 11:0057646023:0010320 12:0060052024:0010200
CHPS、WT、PV、HES的容量、功率、转换效率等机组参数见表2，经济参数见表3。
表2 机组参数
Tab.2 Unit parameters
机组参数数值 WT容量/kW1 200 PV容量/kW1 000 CHP容量/kW600 纯凝工况下最小电出力/kW250 纯凝工况下最大电出力/kW600 最小燃料量最大抽汽量电出力/kW193 最小燃料量最大抽汽量热出力/kW300 最大热出力/kW650 产电效率(%)35.4 产热效率(%)89.2 EHP容量/kW200 电制热性能系数3 HES电解槽容量1 314 储氢罐容量(kW∙h)1 000 燃料电池容量226 氢能-电能转换效率(%)60 余热利用效率(%)88 氢气充放效率(%)98
表3 经济参数
Tab.3 Economic parameters
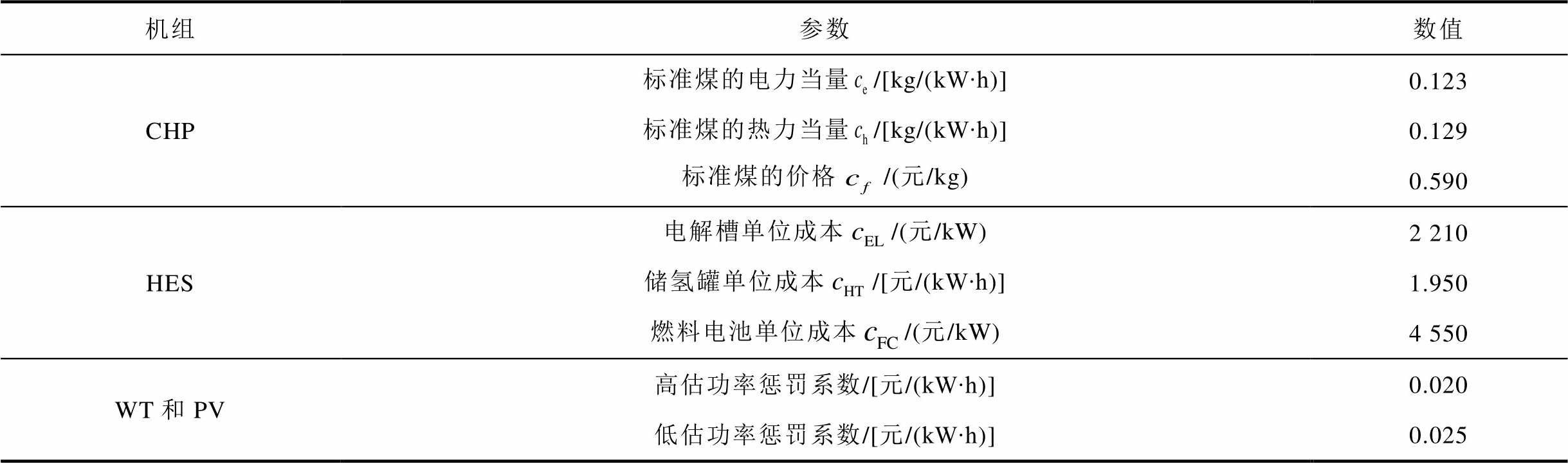
机组参数数值 CHP标准煤的电力当量/[kg/(kW∙h)]0.123 标准煤的热力当量/[kg/(kW∙h)]0.129 标准煤的价格/(元/kg)0.590 HES电解槽单位成本/(元/kW)2 210 储氢罐单位成本/[元/(kW∙h)]1.950 燃料电池单位成本/(元/kW)4 550 WT和PV高估功率惩罚系数/[元/(kW∙h)]0.020 低估功率惩罚系数/[元/(kW∙h)]0.025
4.2.1 纳什均衡策略
为验证本文提出的优化方法在经济性、低碳性和鲁棒性等方面的优越性，本文设置三个场景进行对比分析，场景分类见表4。
表4 场景分类
Tab.4 Scene classification
场景是否有HES是否用CVaR方法是否用DRCVaR方法 1××√ 2√√× 3√×√
场景1的纳什均衡策略即冬季典型日各机组的电、热出力情况如图5所示。LA电负荷需求由CHP和风光机组满足，LA热负荷需求由CHP和EHP满足。EHP消耗部分CHP的电能用于产热来满足LA的热能需求，同时实现热电解耦，提高机组的灵活性促进风光消纳。
场景2的纳什均衡策略即冬季典型日各机组的电、热出力情况如图6所示。场景2增加了HES，EL消耗电能产生氢气的同时将产生的热能参与到系统热循环中，FC消耗氢气发电为系统提供电能的同时，将产生的热能输送给热负荷。图6中可以看出，EL在8:00—14:00、20:00—24:00两个时间段消耗电能供给热能，但FC在一天24 h中的供电功率和产热功率均为零。说明在这种均衡策略下，HES中EL消耗风光机组过剩的电能制氢售氢，同时将过程中产生的热能供给热负荷，而FC未消耗氢能供给电能热能，而是直接出售氢能获得收益，这种策略未能充分发挥HES热电解耦的优势。
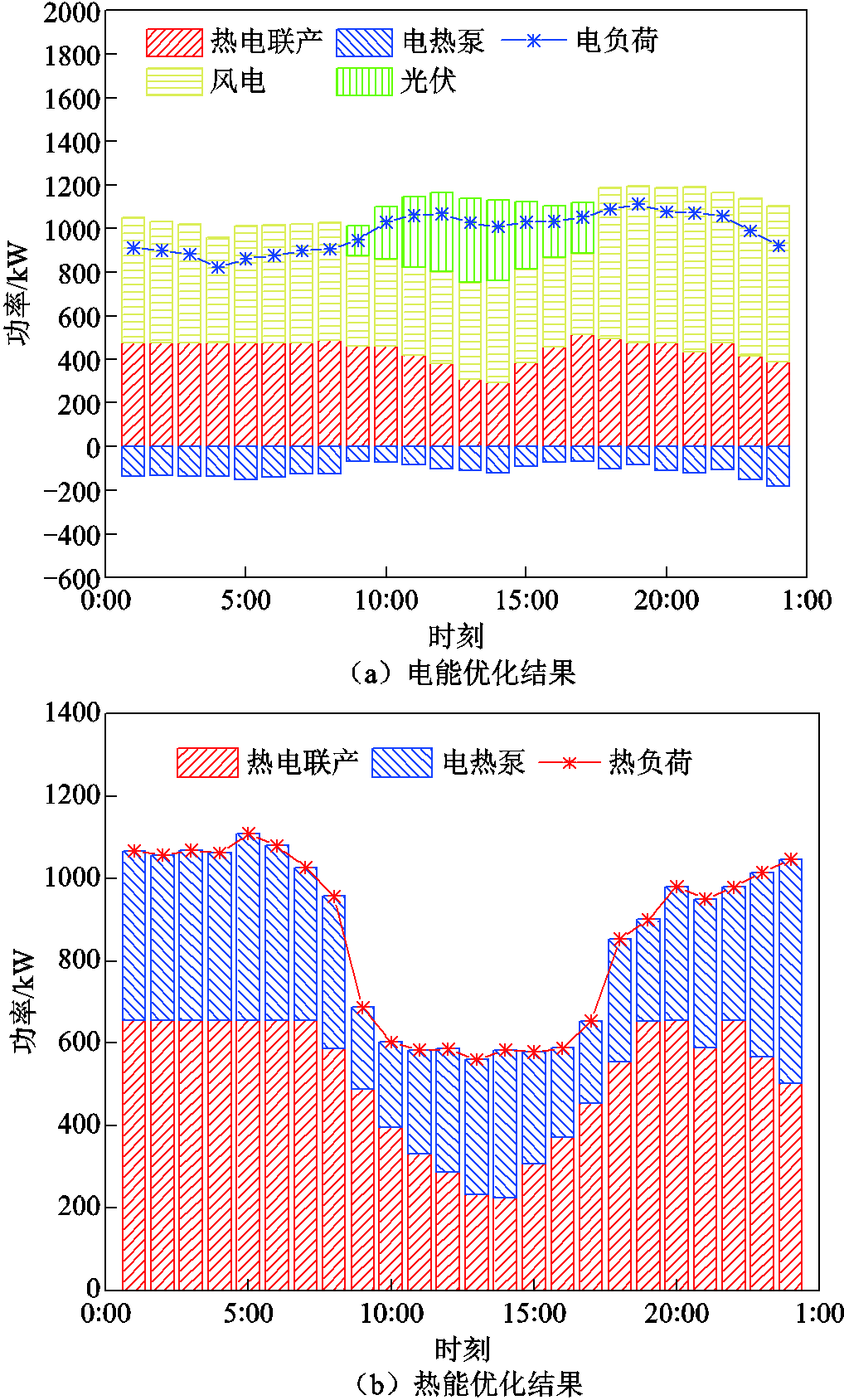
图5 场景1优化结果
Fig.5 Scenario 1 optimization results
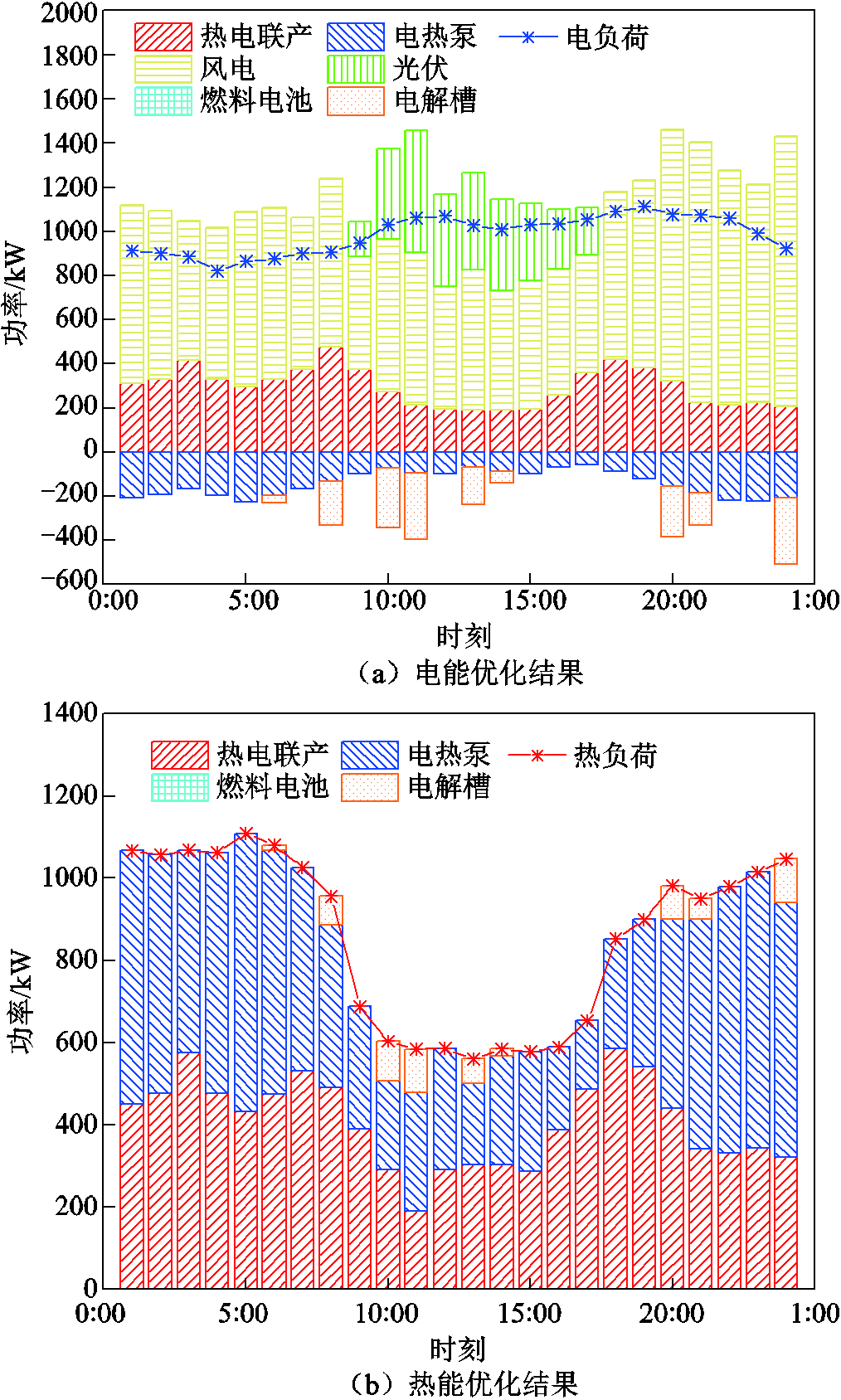
图6 场景2优化结果
Fig.6 Scenario 2 optimization results
场景3的纳什均衡策略即冬季典型日各机组的电、热出力情况如图7所示。场景3增加了HES并且使用DRcvar方法计算不确定性风险成本。图7中可以看出，EL在9:00—16:00、20:00—24:00两个时间段消耗电能并供给热能，FC在17:00—19:00两个时间段产生电能并供给热能，说明在这种均衡策略下HES充分发挥了对电力系统的功率转移和存储作用。
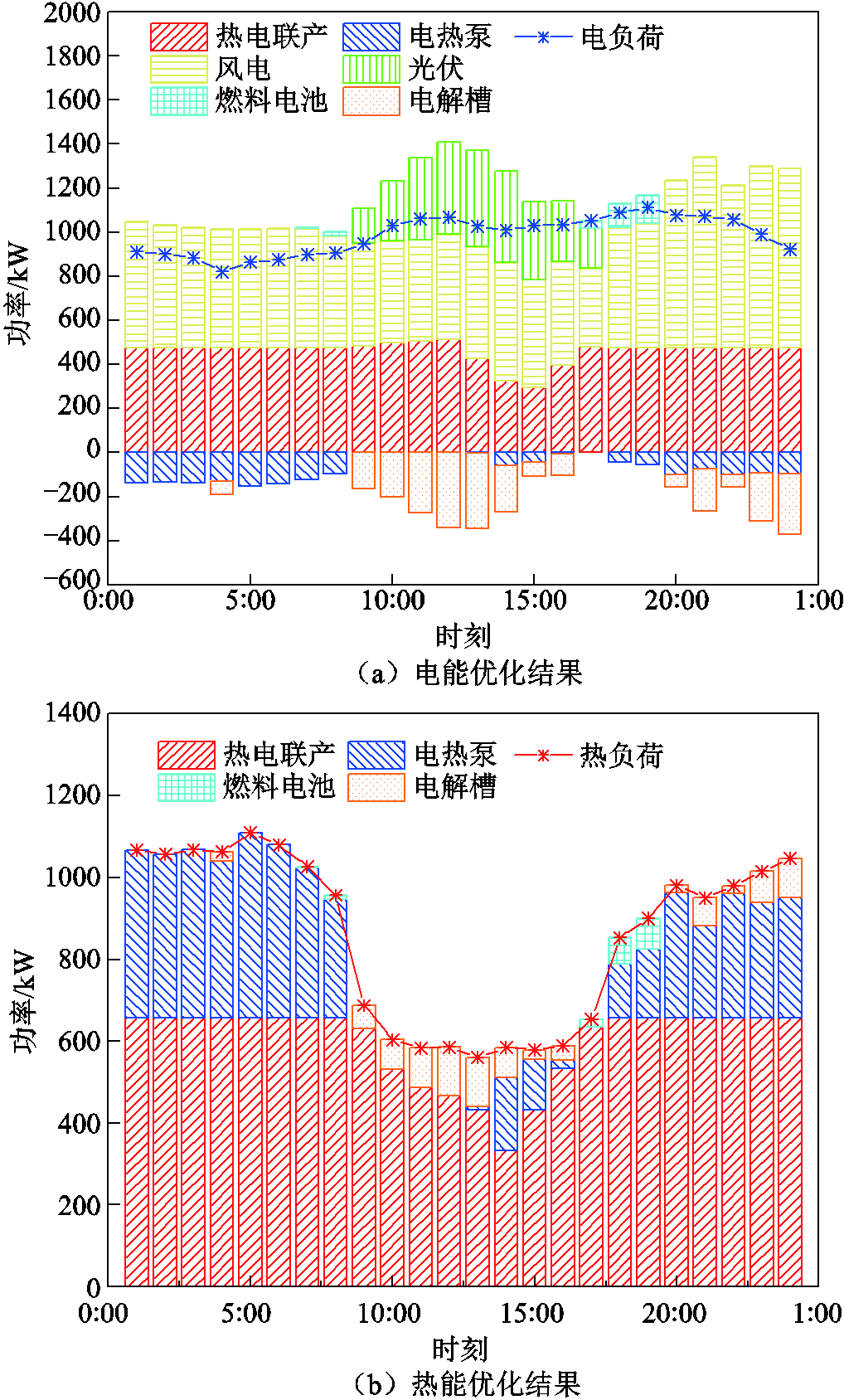
图7 场景3优化结果
Fig.7 Scenario 3 optimization results
图8和图9分别绘制了三种场景CHPS和风光机组出力，以便对三种场景下的均衡策略即机组出力进行对比分析。场景1和场景3的机组出力比较接近，但场景3的CHPS出力小一些，风光机组出力大一些，说明增加HES可以促进风电消纳。
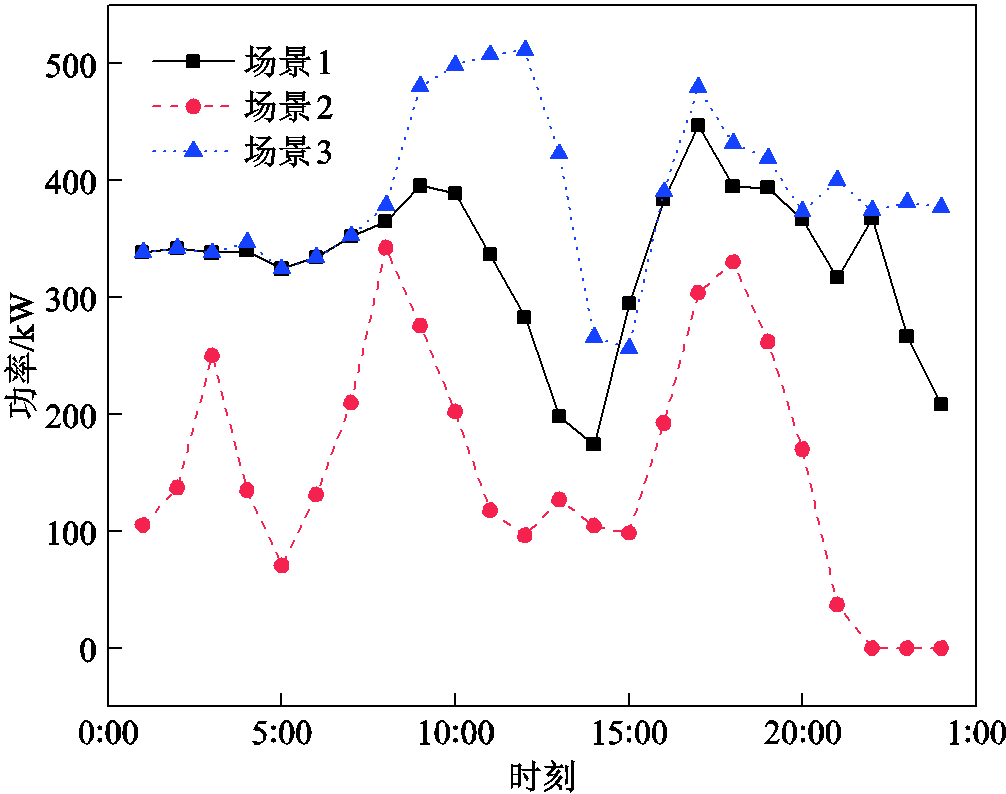
图8 三种场景CHPS出力
Fig.8 Output of CHPS in three scenarios
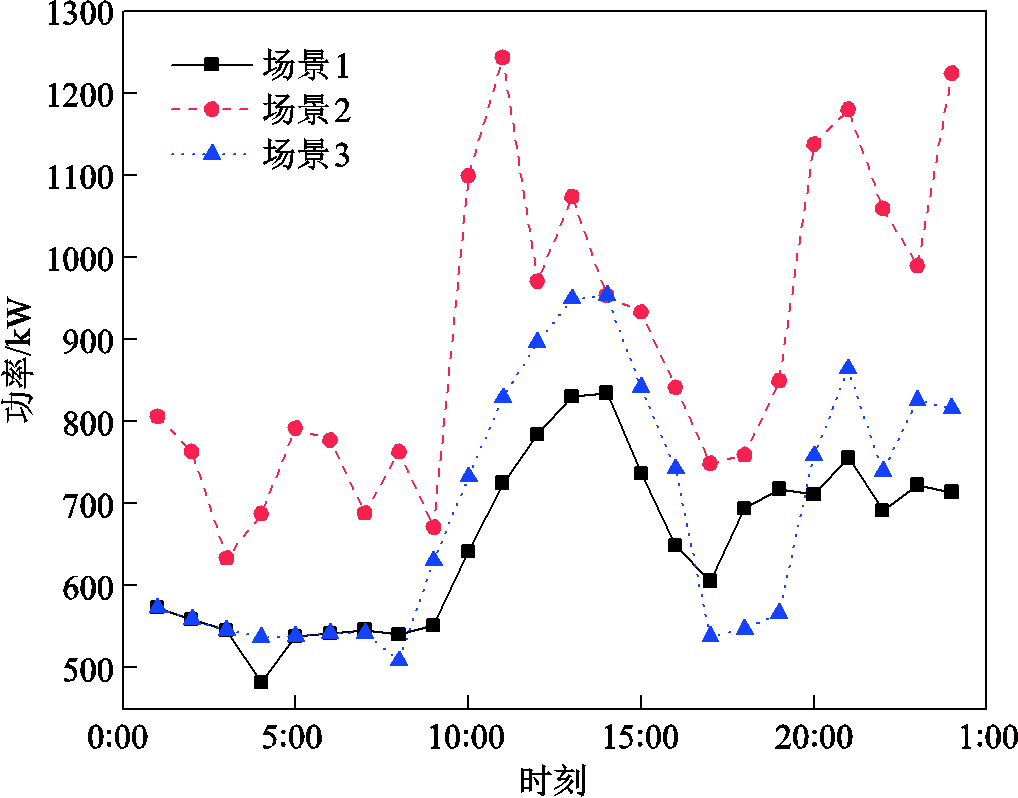
图9 三种场景风光机组出力
Fig.9 Output of WT and PV in three scenarios
从具体数据看，场景3系统总收益为2.0134万元，较场景1提高了1.4%，全生命周期碳排放量为10 053 t，较场景1减少了2.9%。场景3的HES收益为1665元，其中成本127元、售电收益333元、售热收益535元、售氢收益924元，售氢收益占HES收益的55.5%，说明由于HES的成本和转换效率较高，电能削峰填谷产生的收益较小。
场景2的CHPS出力小于场景1和场景3，风光机组出力大于场景1和场景3，原因是惩罚系数较高，场景2的风光机组决策出力的最优策略是最大程度接近风光机组可用出力，减少不确定性风险成本。由于风光机组可用出力在较短时段内是不确定的，这种方法会产生较大偏差，给电网安全稳定运行带来很大的风险。
4.2.2 HES优化结果分析
场景3的HES优化结果如图10和图11所示。从图10可以看出，FC主要在高电价的17:00—19:00时间段进行化学反应，释放电能和热能。EL在4:00、13:00—16:00、22:00—24:00和9:00—12:00这几个时段都利用电解水来制氢储氢。前几个时段是处于中低电价阶段，符合经济性原则，后面的时段制氢储氢是为了减少风光机组混合出力过剩造成的弃电现象的发生，同时也可以提高系统的经济性。HES中EL产氢功率、HT储氢量、FC耗氢功率如图11所示。由图可知，EL电解水制造的氢气大部分是储存在HT中，而不是通过FC耗氢产生电能和热能去满足用户的用能需求。说明目前HES的应用效果不是很理想，其大规模应用还需要进行相关研究，以实现在降低成本的同时提高能源转换效率。
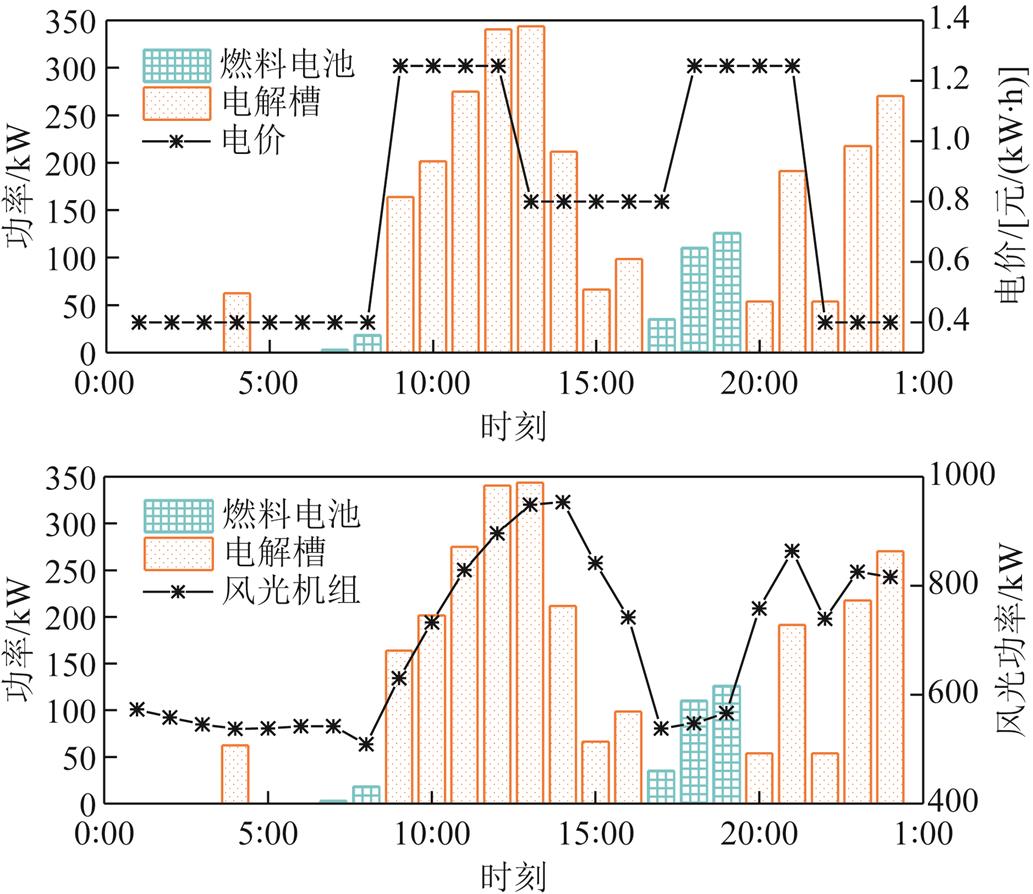
图10 HES优化结果
Fig.10 Optimization results of HES
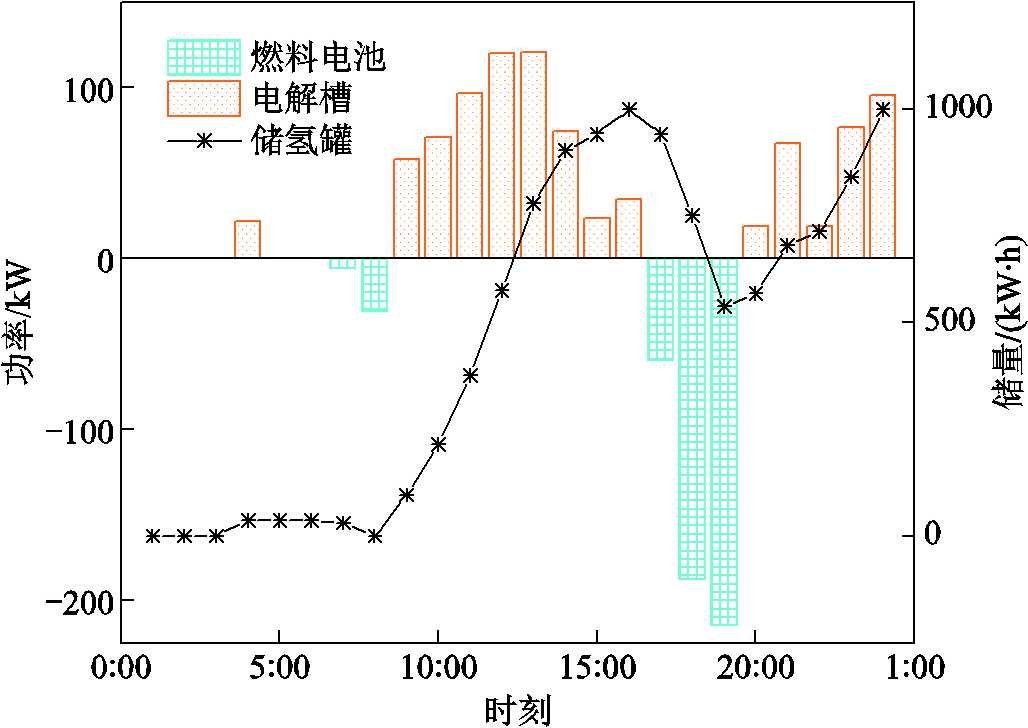
图11 HES储量变化曲线
Fig.11 Variation curve of HES
4.2.3 经济风险分析
为了对drcvar方法和cvar方法的性能进行比较，本文设计了随机模拟试验。其思路如下：①在不确定集中随机模拟10000次可能出现的风光机组可用出力情况；②在抽样得到的可用出力情景下，分别计算两种方法10000次随机模拟的不确定性风险成本和系统总收益；③计算两种方法下的经济风险，经济风险是指两种方法的优化结果总收益和随机模拟试验结果总收益之差[25]。本文以经济风险评价两种方法处理风光机组出力不确定性的能力，经济风险的数值越小，其处理不确定性的能力越强。
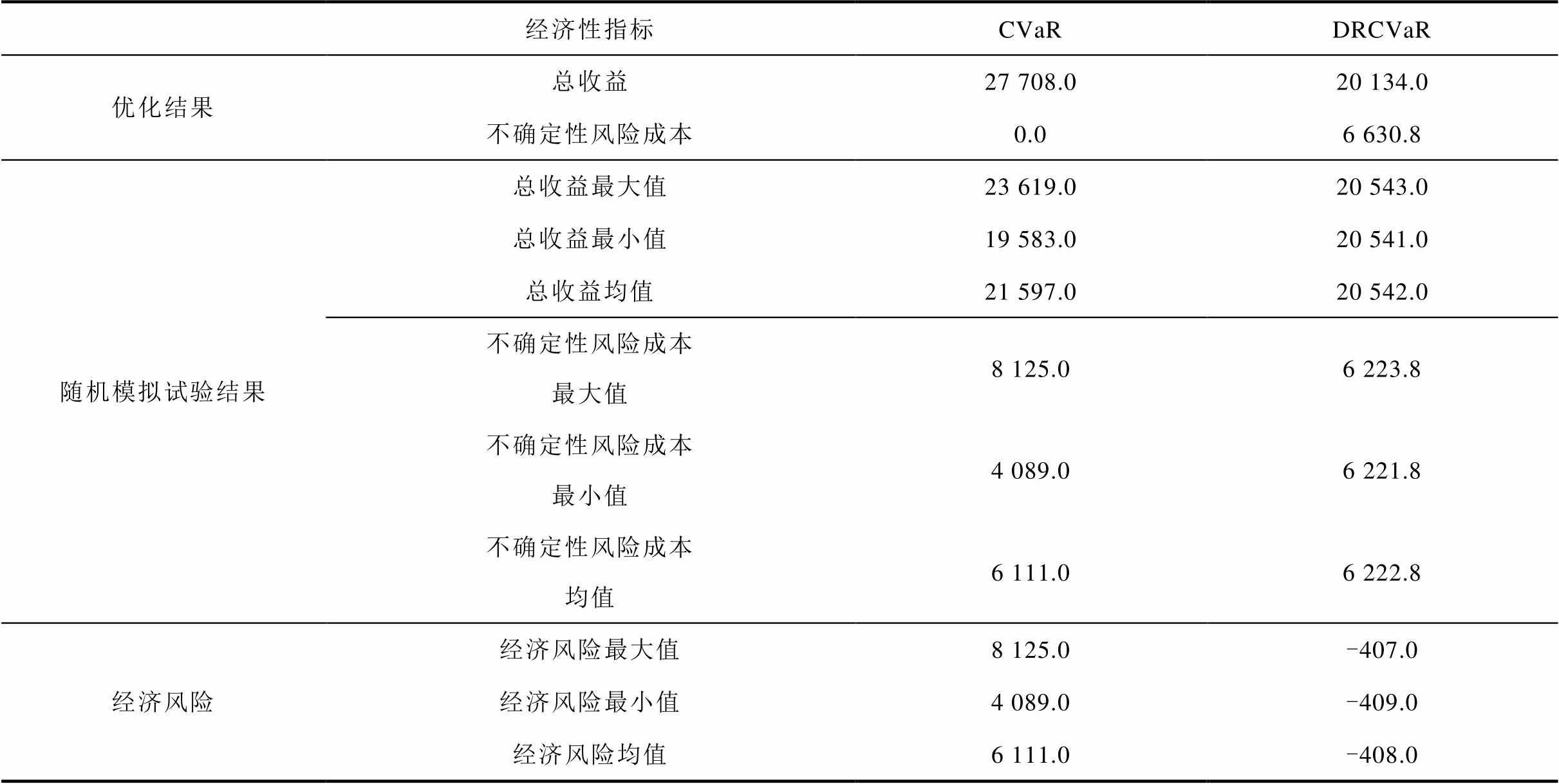
优化结果和随机模拟试验结果见表5，对cvar方法的优化结果和随机模拟试验结果进行对比。试验结果的不确定性风险成本远大于优化结果，说明风光机组可用出力在不确定的情况下很可能会低估不确定性风险，给系统的安全稳定运行带来巨大隐患；对drcvar方法的优化结果和随机模拟试验结果进行对比，试验结果的不确定性风险小于优化结果，说明风光机组可用出力在任一可能情况下，不确定性风险不会超过其优化结果，保证了系统的鲁棒性，也说明drcvar方法处理不确定性问题的性能优于cvar方法。对两种方法的结果进行对比，采用drcvar方法的经济风险的数值较小，说明其应对不确定性的能力较强。采用drcvar方法的不确定性风险成本为6 630.8元，占总收益的32.9%，高于cvar方法的风险成本，这是因为考虑了风光机组可用出力的一切可能，保证任一可能情况的风险不会大于这种情况的风险，即为提高系统的鲁棒性而牺牲掉一部分经济性。综上所述，本文提出的优化方法能有效抵御包括最恶劣干扰在内的一个干扰集，得到鲁棒性更优的优化策略。
表5 经济分析
Tab.5 Economic analysis （单位：元）
经济性指标CVaRDRCVaR 优化结果总收益27708.020134.0 不确定性风险成本0.06630.8 随机模拟试验结果总收益最大值23619.020543.0 总收益最小值19583.020541.0 总收益均值21597.020542.0 不确定性风险成本最大值8125.06223.8 不确定性风险成本最小值4 089.06221.8 不确定性风险成本均值6111.06222.8 经济风险经济风险最大值8125.0-407.0 经济风险最小值4 089.0-409.0 经济风险均值6111.0-408.0
4.2.4 置信水平影响分析
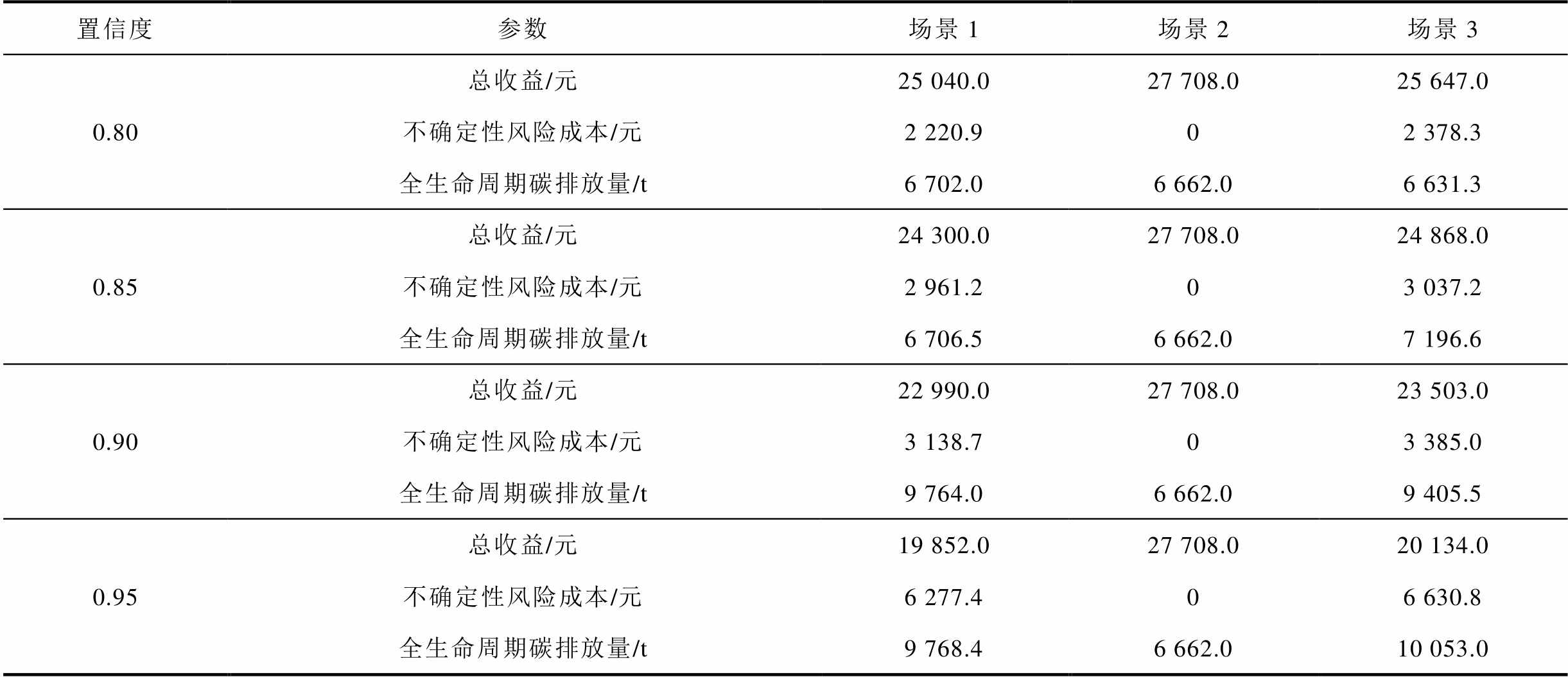
为分析不同置信水平对系统优化结果的影响，本文设置四种置信度，对不同置信度下的优化结果进行分析，具体见表6。
从表6中可以看出，随着置信度的提高系统总收益降低，不确定性风险成本增加，全生命周期的碳排放量增加。结果说明置信度越高，系统对不确定性的影响越敏感，系统鲁棒性的要求就越高。因此决策者要根据实际情况进行衡量，设置合理的置信水平以实现系统经济性和鲁棒性的协调统一。
表6 四种置信度优化结果
Tab.6 Optimization results in four confidence levels
置信度参数场景1场景2场景3 0.80总收益/元25040.027708.025647.0 不确定性风险成本/元2220.902378.3 全生命周期碳排放量/t6702.06 662.06631.3 0.85总收益/元24300.027708.024868.0 不确定性风险成本/元2961.203037.2 全生命周期碳排放量/t6706.56662.07196.6 0.90总收益/元22990.027708.023503.0 不确定性风险成本/元3138.703385.0 全生命周期碳排放量/t9764.06662.09405.5 0.95总收益/元19852.027708.020134.0 不确定性风险成本/元6277.406630.8 全生命周期碳排放量/t9768.46662.010053.0
针对双碳目标下构建清洁低碳安全高效的新型电力系统的要求，从HES和风光不确定性两个角度切入，构建计及风光不确定性的EHH-IES分布鲁棒优化问题的博弈模型，对模型进行拉格朗日对偶转换求解，结合算例仿真验证所提方法的性能。结果表明，应用含电、热、氢多种能源的HES耦合模型后，系统总收益提高了1.4%，全生命周期的碳排放量减少了2.9%，证明了发展和推广EHH-IES可以促进双碳目标的实现；基于DRCVaR方法的经济风险小于CVaR方法，说明本文提出的方法降低了风光不确定性给电力系统带来的风险；随着置信度的提高，系统总收益降低、不确定性风险成本增加、全生命周期碳排放量增加，因此，需要决策者根据实际情况进行衡量，设置合理的置信水平以实现电力系统的经济性、低碳性和鲁棒性的协调统一。
参考文献
[1] 吕佳炜, 张沈习, 程浩忠, 等. 考虑互联互动的区域综合能源系统规划研究综述[J]. 中国电机工程学报, 2021, 41(12): 4001-4021. Lü Jiawei, Zhang Shenxi, Cheng Haozhong, et al. Review on district-level integrated energy system planning considering interconnection and interaction[J]. Proceedings of the CSEE, 2021, 41(12): 4001-4021.
[2] Jiang Yibao, Wan Can, Botterud A, et al. Efficient robust scheduling of integrated electricity and heat systems: a direct constraint tightening approach[J]. IEEE Transactions on Smart Grid, 2021, 12(4): 3016-3029.
[3] 刁涵彬, 李培强, 王继飞, 等. 考虑电/热储能互补协调的综合能源系统优化调度[J]. 电工技术学报, 2020, 35(21): 4532-4543. Diao Hanbin, Li Peiqiang, Wang Jifei, et al. Optimal dispatch of integrated energy system considering complementary coordination of electric/thermal energy storage[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4532-4543.
[4] Hao Junhong, Chen Qun, He Kelun, et al. A heat current model for heat transfer/storage systems and its application in integrated analysis and optimization with power systems[J]. IEEE Transactions on Sustainable Energy, 2020, 11(1): 175-184.
[5] 荆涛, 陈庚, 王子豪, 等. 风光互补发电耦合氢储能系统研究综述[J]. 中国电力, 2022, 55(1): 75-83. Jing Tao, Chen Geng, Wang Zihao, et al. Research overview on the integrated system of wind-solar hybrid power generation coupled with hydrogen-based energy storage[J]. Electric Power, 2022, 55(1): 75-83.
[6] Tao Yuechuan, Qiu Jing, Lai Shuying, et al. Integrated electricity and hydrogen energy sharing in coupled energy systems[J]. IEEE Transactions on Smart Grid, 2021, 12(2): 1149-1162.
[7] 张昊天, 韦钢, 袁洪涛, 等. 考虑氢-电混合储能的直流配电网优化调度[J]. 电力系统自动化, 2021, 45(14): 72-81. Zhang Haotian, Wei Gang, Yuan Hongtao, et al. Optimal scheduling of DC distribution network considering hydrogen-power hybrid energy storage[J]. Automation of Electric Power Systems, 2021, 45(14): 72-81.
[8] 李奇, 赵淑丹, 蒲雨辰, 等. 考虑电氢耦合的混合储能微电网容量配置优化[J]. 电工技术学报, 2021, 36(3): 486-495.. Li Qi, Zhao Shudan, Pu Yuchen, Chen Weirong, et al. Capacity optimization of hybrid energy storage microgrid considering electricity-hydrogen coupling[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 486-495.
[9] 滕云, 王泽镝, 金红洋, 等. 用于电网调节能力提升的电热氢多源协调储能系统模型[J]. 中国电机工程学报, 2019, 39(24): 7209-7217, 7494. Teng Yun, Wang Zedi, Jin Hongyang, et al. A model and coordinated optimization for the multi-energy storage system of electricity heat hydrogen to regulation enhancement of power grid[J]. Proceedings of the CSEE, 2019, 39(24): 7209-7217, 7494.
[10] 司杨, 陈来军, 麻林瑞, 等. 考虑氢储能热平衡的风-氢混合系统优化调度方法[J]. 电器与能效管理技术, 2021(11): 15-21. Si Yang, Chen Laijun, Ma Linrui, et al. Optimal dispatching method of wind-hydrogen hybrid system considering heat balance of hydrogen energy storage[J]. Electrical & Energy Management Technology, 2021(11): 15-21.
[11] 熊宇峰, 司杨, 郑天文, 等. 基于主从博弈的工业园区综合能源系统氢储能优化配置[J]. 电工技术学报, 2021, 36(3): 507-516. Xiong Yufeng, Si Yang, Zheng Tianwen, et al. Optimal configuration of hydrogen storage in industrial park integrated energy system based on stackelberg game[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 507-516.
[12] 黄雨涵, 丁涛, 李雨婷, 等. 碳中和背景下能源低碳化技术综述及对新型电力系统发展的启示[J]. 中国电机工程学报, 2021, 41(增刊1): 28-51. Huang Yuhan, Ding Tao, Li Yuting, et al. Decarbonization technologies and inspirations for the development of novel power systems in the context of carbon neutrality[J]. Proceedings of the CSEE, 2021, 41(S1): 28-51.
[13] Lu Runzhao, Ding Tao, Qin Boyu, et al. Multi-stage stochastic programming to joint economic dispatch for energy and reserve with uncertain renewable energy[J]. IEEE Transactions on Sustainable Energy, 2020, 11(3): 1140-1151.
[14] 王昀, 谢海鹏, 孙啸天, 等. 计及激励型综合需求响应的电-热综合能源系统日前经济调度[J]. 电工技术学报, 2021, 36(9): 1926-1934. Wang Yun, Xie Haipeng, Sun Xiaotian, et al. Day-ahead economic dispatch for electricity-heating integrated energy system considering incentive integrated demand response[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1926-1934.
[15] 娄素华, 吕梦璇, 王永灿, 等. 考虑投资风险的含风电系统电源投资扩展规划研究[J]. 中国电机工程学报, 2019, 39(7): 1944-1956. Lou Suhua, Lü Mengxuan, Wang Yongcan, et al. Generation investment expansion planning for wind power accommodation considering investment risk[J]. Proceedings of the CSEE, 2019, 39(7): 1944-1956.
[16] Li Longfei, Xiao Jie, Zhao Yun, et al. Robust position anti-interference control for PMSM servo system with uncertain disturbance[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(2): 151-160.
[17] 许刚, 张丙旭, 张广超. 电动汽车集群并网的分布式鲁棒优化调度模型[J]. 电工技术学报, 2021, 36(3): 565-578. Xu Gang, Zhang Bingxu, Zhang Guangchao. Distributed and robust optimal scheduling model for large-scale electric vehicles connected to grid[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 565-578.
[18] Cao Yang, Wei Wei, Mei Shengwei, et al. Analyzing and quantifying the intrinsic distributional robustness of CVaR reformulation for chance-constrained stochastic programs[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4908-4911.
[19] Jabr R A. Distributionally robust CVaR constraints for power flow optimization[J]. IEEE Transactions on Power Systems, 2020, 35(5): 3764-3773.
[20] 李运龙, 李志刚, 郑杰辉. 考虑风电不确定性和相关性的多区域电网分布鲁棒经济调度[J]. 电力自动化设备, 2021, 41(8): 97-104. Li Yunlong, Li Zhigang, Zheng Jiehui. Distributionally robust economic dispatch of multi-regional power grid considering uncertainty and correlation of wind power[J]. Electric Power Automation Equipment, 2021, 41(8): 97-104.
[21] Huo Yuchong, Bouffard F, Joós G. Spatio-temporal flexibility management in low-carbon power systems[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2593-2605.
[22] 胡静哲, 王旭, 蒋传文, 等. 考虑区域碳排放均衡性的电力系统最优阶梯碳价[J]. 电力系统自动化, 2020, 44(6): 98-105. Hu Jingzhe, Wang Xu, Jiang Chuanwen, et al. Optimal tiered carbon price of power system considering equilibrium of regional carbon emission[J]. Automation of Electric Power Systems, 2020, 44(6): 98-105.
[23] 梅生伟, 魏韡, 刘锋. 电力系统控制与决策中的博弈问题——工程博弈论初探[J]. 控制理论与应用, 2018, 35(5): 578-587. Mei Shengwei, Wei Wei, Liu Feng. Game theoretical perspective of power system control and decision making: a brief review of engineering game theory[J]. Control Theory & Applications, 2018, 35(5): 578-587.
[24] 王海洋, 李珂, 张承慧, 等. 基于主从博弈的社区综合能源系统分布式协同优化运行策略[J]. 中国电机工程学报, 2020, 40(17): 5435-5445. Wang Haiyang, Li Ke, Zhang Chenghui, et al. Distributed coordinative optimal operation of community integrated energy system based on stackelberg game[J]. Proceedings of the CSEE, 2020, 40(17): 5435-5445.
[25] 梅生伟, 郭文涛, 王莹莹, 等. 一类电力系统鲁棒优化问题的博弈模型及应用实例[J]. 中国电机工程学报, 2013, 33(19): 47-56, 20. Mei Shengwei, Guo Wentao, Wang Yingying, et al. A game model for robust optimization of power systems and its application[J]. Proceedings of the CSEE, 2013, 33(19): 47-56, 20.
Abstract The operation flexibility of China's power system is insufficient, and the energy low-carbon transformation faces the problem of how to realize the coordinated development of multiple energy systems. Hydrogen energy storage (HES) can realize power transfer and storage of power system through peak shaving and valley filling of charging and discharging, which is the key to solve the flexibility problem. The existing research on the optimization of integrated energy system containing HES is aimed at the collaborative optimization of renewable energy and hydrogen energy storage, mainly focusing on the peak shaving and valley filling function of HES as energy storage. However, the research results of multiple energy coupling in HES are few, and most of them are electric energy and thermal energy, electric energy and hydrogen energy coupling. The HES coupling model containing electric, thermal and hydrogen energy is worth in-depth study. In view of the above situation, an electricity-heat-hydrogen integrated energy system (EHH-IES) model is established to study the coupling of electricity, heat and hydrogen.
In addition, renewable energy such as wind and solar in the integrated energy system is uncertain, and the high proportion of renewable energy access makes the safety and economic operation of the power system face great challenges, which seriously restricts the development of the integrated energy system. Therefore, combined with the characteristics of stochastic programming and robust optimization, a distributionally robust conditional value at risk (DRCVaR) method, based on moment information such as expectation, variance, and covariance, is proposed to quantify the risk of wind and solar uncertainties. Considering the game relationship between renewable energy and artificial decision makers, aiming at the maximum system revenue, the minimum carbon emissions in the whole life cycle and the minimum uncertainty risk cost, a zero-sum game model of EHH-IES distributed robust optimization problem is established. The model is transformed into a semi-definite programming problem by Lagrange duality principle and then solved. Finally, the effectiveness of the model and method is verified by numerical simulation.
In the case simulation, a comparative analysis is made on whether the HES coupling model is used and whether the DRCVaR method is used to quantify the risk of wind and solar uncertainties. The following conclusions can be drawn: (1) After applying the HES coupling model with multiple energy sources including electricity, heat and hydrogen, the total revenue of the system has increased by 1.4%, and the carbon emissions in the whole life cycle have decreased by 2.9%, which proves that the development and promotion of EHH-IES can give consideration to both economy and low carbon. (2) When adopting the optimization strategy of DRCVaR method to quantify the risk of wind and solar uncertainties, the economic risk of the system is less than the optimization strategy of conditional value at risk (CVaR) method, which shows that DRCVaR method effectively reduces the risk of wind and solar uncertainties to the system. (3) With the improvement of the confidence level, the total income of the system is reduced, the uncertainty risk cost is increased, and the carbon emissions of the whole life cycle are increased. This means that the decision-maker needs to measure according to the actual situation, and set a reasonable confidence level to achieve the coordination and unification of the system economy, low carbon and robustness.
keywords：Integrated energy system, hydrogen energy storage, distributionally robust optimization, uncertainties, carbon emission
国家自然科学基金（52176005）和国家重点研发计划（2018YFE-0106600）资助项目。
收稿日期 2022-05-07
改稿日期 2022-07-12
DOI:10.19595/j.cnki.1000-6753.tces.220759
中图分类号：TM73
吴孟雪 女，1997年生，硕士研究生，研究方向为综合能源系统优化。E-mail：wmx1583474781@163.com
房 方 男，1976年生，教授，博士生导师，研究方向为发电过程建模、控制与优化，综合能源系统优化配置和能量管控，智能发电理论与技术等。E-mail：ffang@ncepu.edu.cn（通信作者）
（编辑 赫蕾）