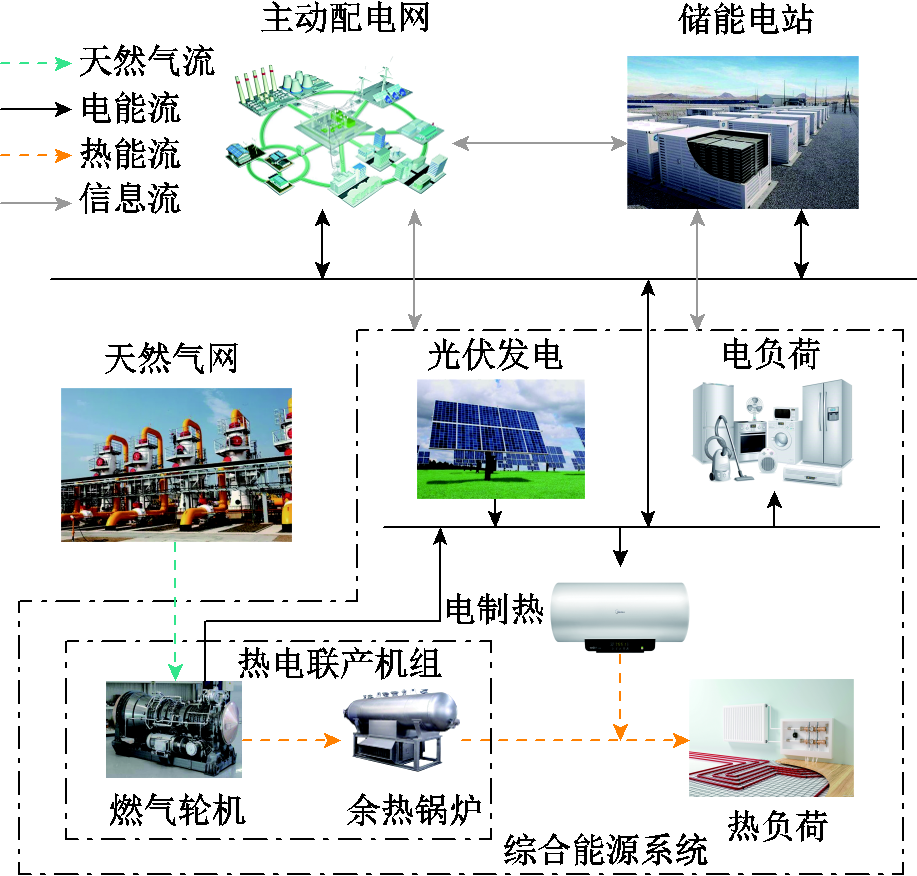
图1 含ESPS和IES的系统结构
Fig.1 Structure diagram of system with ESPS and IES
摘要 综合能源系统与储能电站在提高能源利用率方面具有显著优势,但如何建立综合能源系统与储能电站的协调优化策略是一个亟须解决的问题。为此,该文提出一种基于双向主从博弈的储能电站与综合能源系统经济运行策略。首先,在考虑储能电站作为用能主体和供能主体两重性的基础上分析了各主体间的博弈关系;其次,分别对综合能源系统、储能电站和主动配电网建立优化模型;然后,以主动配电网为领导者,储能电站为二级领导者,综合能源系统为跟随者,构建双向主从博弈模型,并从理论上证明该博弈存在唯一的均衡解;最后,通过算例仿真验证了所提策略能够有效地权衡综合能源系统、储能电站和主动配电网三者之间的利益关系,实现各主体间的利益均衡,提升系统整体的经济效益。
关键词:综合能源系统 储能电站 双向主从博弈 经济运行
随着“双碳”目标的提出,我国对能源利用率的要求在不断提高[1]。在这一背景下,综合能源系统(Integrated Energy System, IES)因其能实现多能互补,提高能源利用率而得到迅速发展[2-3]。IES在充分调用内部资源之外,还通过与主动配电网(Active Distribution Network, ADN)、储能电站(Energy Storage Power Station, ESPS)和天然气网等外部供能主体相连,有效地提高了IES供能可靠性[4]。然而,随着ESPS参与市场交易,如何实现IES与ESPS间的经济运行是一个亟须解决的问题。而充分利用各主体间的利益关系进行博弈是实现IES与ESPS经济运行的一条重要途径。
IES通常配置分布式储能,利用峰谷电价差来降低系统运行成本,同时储存新能源的余电[5]。但是,当前储能投资成本高,且IES规模不一使得储能的应用与发展受到严重限制,而将ESPS应用于IES是解决这一问题的有效方法。文献[6]将ESPS应用于IES,构建了考虑不同时间尺度的双层优化模型。该模型在显著降低用户成本的同时节约了储能资源。文献[7]建立了一种含ESPS的综合能源系统调峰调蓄协调运行模型,该模型能够促进新能源消纳,最大程度地实现系统的削峰填谷。但是,上述成果仅将ESPS作为IES的辅助供能设施,未能发挥ESPS在参与IES优化过程中作为独立主体的趋利性。为解决这一问题,文献[8]建立了一种ESPS参与调度决策的IES优化模型,该模型在实现IES经济最优的同时兼顾了ESPS的利益。文献[9]提出一种基于组合双向拍卖的ESPS服务机制,该机制解决了能量交易过程中单向拍卖存在的垄断竞争问题。然而,上述研究未考虑ESPS作为用能主体和供能主体的两重性,无法充分发挥ESPS作为独立主体参与经济运行的主动性,直接影响了系统中各主体的经济效益。鉴于此问题,文献[10]提出了一种考虑ESPS和IES的“源-储-荷”多时间尺度协调运行策略,该策略能够更好地利用ESPS和IES的快速调节能力,使系统运行成本达到最优。文献[11]提出了面向多类型储能系统、电转气设备和冷热电联产机组的多时间尺度协调运行模型,该模型能够提高系统用能效率,同时兼顾了系统的经济性。然而,上述研究未能利用ESPS与其他参与主体之间的博弈关系,未能充分发挥ESPS的参与潜能。
针对多主体参与IES经济运行的研究,采用博弈理论能够有效地发挥各主体参与市场竞价的主动性,兼顾各主体的经济效益[12]。文献[13]提出一种基于主从博弈的IES分布式协同优化策略,该策略兼顾了用户用能成本和满意度。文献[14-15]针对运营商定价策略与产消者能量需求间的博弈关系,提出一种基于主从博弈的分布式能量管理方法。该方法有利于参与主体收益提升、系统负荷特性改善。然而实际的IES在运行中通常涉及多个利益主体,上述模型并没有充分考虑各个利益主体之间的差异性。针对上述问题,文献[16]提出一种考虑阶梯型碳交易的IES多主体博弈协同优化方法,该方法有效地兼顾了系统的经济性和环保性。文献[17]以分布式能源站为领导者,用户为跟随者,构建基于多主多从博弈的能源交易模型,该模型实现了IES中各主体利益均衡。然而,以上研究均是以传统的主从博弈结构对参与主体进行博弈分析,未考虑参与主体既作为跟随者又作为领导者的双重性,以及该情况下两个主体间同时存在的主从关系与竞争关系,缺乏调动各主体参与优化的积极性。
针对上述问题,本文提出了一种基于双向主从博弈的ESPS与IES经济运行策略。该策略考虑ADN与ESPS之间存在的主从关系及竞争关系,构建了双向主从博弈经济运行模型,并从理论上证明了该博弈模型存在唯一的均衡解。该模型能够激发各主体参与协调运行的积极性,从而提升系统的整体经济效益。为求解上述模型,本文采用双层粒子群算法和CPLEX求解器求解。算例分析结果验证了本文所提经济运行策略的有效性和优越性。
含ESPS和IES的系统结构如图1所示,该系统内主要包含IES、ESPS和ADN等主体。各主体间相互连接,可进行能量交互,构成了一个可充分协调运行的多主体能源系统。各主体通过选择合理的竞价及能量交互策略,可有效提升系统的整体经济效益。
图1中,IES除自有机组供能外,还与ESPS、ADN相连,从而弥补功率缺额。其中,IES包含电能和热能,其内部优先消纳新能源来满足负荷需求。在IES出现功率余缺时,通过调节内部可控机组、调整负荷需求响应以及与外部供能主体进行能量交互来实现功率平衡。ADN是IES的主要供能主体,拥有对下级用能主体的自主定价权,以此实现自身效益的最大化。ESPS是IES的另一供能主体,同时也是ADN的用能主体,拥有向IES售电的自主定价权。ESPS通过协调控制充电功率及电价参与到供能主体的竞争中,从而实现自身盈利。

图1 含ESPS和IES的系统结构
Fig.1 Structure diagram of system with ESPS and IES
1.2.1 ADN经济运行模型
ADN是系统能量的主要来源,也是系统的领导者。ADN以动态售电价格为决策变量,以最大运行效益为优化目标,其目标函数为
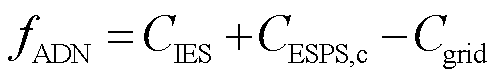 (1)
(1)
式中,![]() 为ADN与IES的功率交互收益;
为ADN与IES的功率交互收益;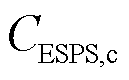 为ADN与ESPS的功率交互收益;
为ADN与ESPS的功率交互收益;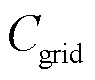 为ADN与外部电网的功率交互成本。
为ADN与外部电网的功率交互成本。
 (2)
(2)
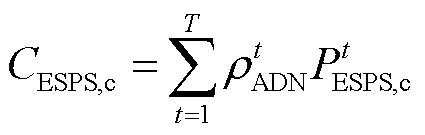 (3)
(3)
 (4)
(4)
式中,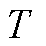 为调度周期时段数;
为调度周期时段数;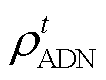 为ADN售电价格;
为ADN售电价格; 为IES与ADN间的交互功率;
为IES与ADN间的交互功率;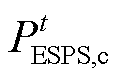 为ESPS的充电功率;
为ESPS的充电功率;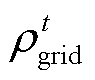 为外部电网的售电电价;
为外部电网的售电电价;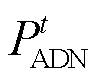 为ADN从外部电网的购电功率。
为ADN从外部电网的购电功率。
为避免ADN与ESPS间在电价过低时产生恶意竞争,两者间的功率交互满足如下保护机制。
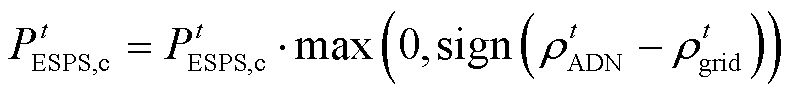 (5)
(5)
当 时,ADN的售电电价高于外部电网的售电电价,ADN从外部电网买电再向ESPS和IES售电存在利润空间,此时ESPS可以正常从ADN买电;当
时,ADN的售电电价高于外部电网的售电电价,ADN从外部电网买电再向ESPS和IES售电存在利润空间,此时ESPS可以正常从ADN买电;当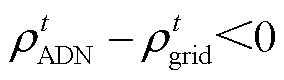 时,ADN的售电电价低于外部电网的售电电价时,ADN从外部电网买电再向ESPS和IES售电将处于亏损状态,为避免ESPS以低价从ADN购电后充电再以高价卖出,以恶意竞争的形式增加ADN的亏损,此时
时,ADN的售电电价低于外部电网的售电电价时,ADN从外部电网买电再向ESPS和IES售电将处于亏损状态,为避免ESPS以低价从ADN购电后充电再以高价卖出,以恶意竞争的形式增加ADN的亏损,此时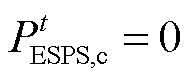 ,ESPS不能从外部电网买电。
,ESPS不能从外部电网买电。
ADN在制定动态电价和进行能量交互时需满足
 (6)
(6)
 (7)
(7)
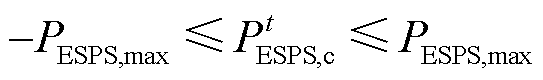 (8)
(8)
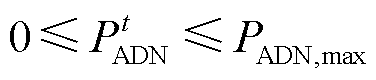 (9)
(9)
式中,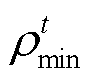 、
、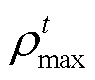 分别为最低、最高电价;
分别为最低、最高电价;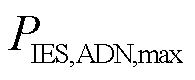 为ADN与IES间的最大传输功率;
为ADN与IES间的最大传输功率; 为ESPS的最大充、放电功率;
为ESPS的最大充、放电功率;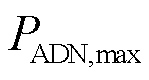 为ADN与外部电网间的最大传输功率。
为ADN与外部电网间的最大传输功率。
1.2.2 ESPS经济运行模型
ESPS根据ADN的动态电价,合理制定充电计划和电价策略,引导IES调整用能需求,实现电力系统的削峰填谷。ESPS以最大运行效益为目标,其目标函数为
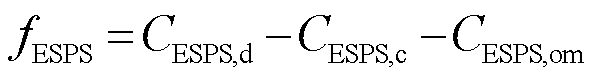 (10)
(10)
式中,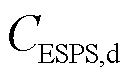 为ESPS与IES的功率交互收益;
为ESPS与IES的功率交互收益;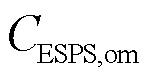 为ESPS的运行维护成本。
为ESPS的运行维护成本。
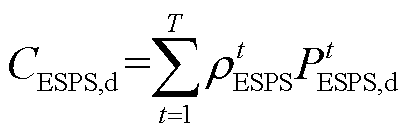 (11)
(11)
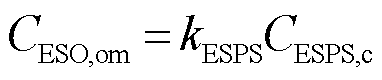 (12)
(12)
式中,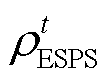 为ESPS的售电价格;
为ESPS的售电价格;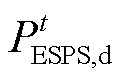 为ESPS向IES的放电功率;
为ESPS向IES的放电功率;![]() 为ESPS运行维护成本系数。
为ESPS运行维护成本系数。
ESPS的自主定价及功率交互满足
 (13)
(13)
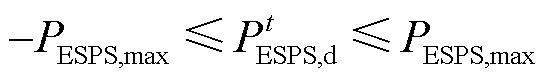 (14)
(14)
ESPS的储能状态满足
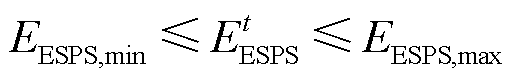 (15)
(15)
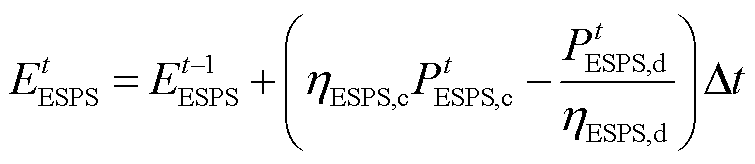 (16)
(16)
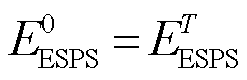 (17)
(17)
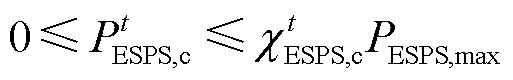 (18)
(18)
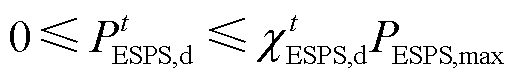 (19)
(19)
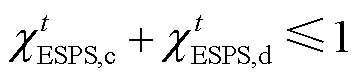 (20)
(20)
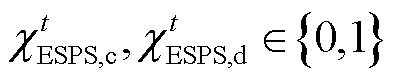 (21)
(21)
式中,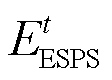 为ESPS的电量;
为ESPS的电量;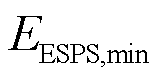 、
、 分别为ESPS容量的最小值、最大值;
分别为ESPS容量的最小值、最大值; 、
、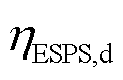 分别为ESPS的充、放电效率;
分别为ESPS的充、放电效率;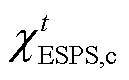 和
和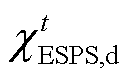 分别为ESPS的充、放电状态量。
分别为ESPS的充、放电状态量。
1.2.3 IES经济运行模型
具有良好的经济效益是推广IES广泛应用的前提。因此,本文以IES最大运行效益为目标,其目标函数为
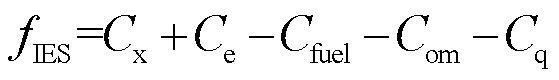 (22)
(22)
式中,![]() 为用电效用函数;
为用电效用函数;![]() 为IES的购售电成本;
为IES的购售电成本;![]() 为IES的燃料成本;
为IES的燃料成本;![]() 为IES的运行维护成本[17];
为IES的运行维护成本[17];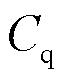 为削减热负荷和热能损耗造成舒适度下降的惩罚费用。
为削减热负荷和热能损耗造成舒适度下降的惩罚费用。
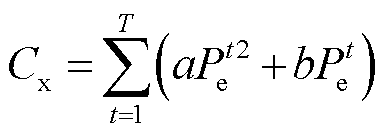 (23)
(23)
 (24)
(24)
 (25)
(25)
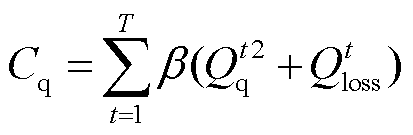 (26)
(26)
式中, 为调整后的电负荷功率;
为调整后的电负荷功率;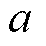 、
、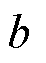 为用电效用函数的参数,其中a=-0.05,b=4[18];
为用电效用函数的参数,其中a=-0.05,b=4[18]; 、
、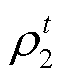 分别为ESPS、ADN的电价;
分别为ESPS、ADN的电价;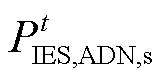 为IES向外部电网售电功率;
为IES向外部电网售电功率;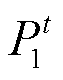 、
、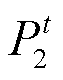 分别为IES与ESPS、ADN的交互功率;
分别为IES与ESPS、ADN的交互功率;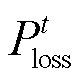 为电能损耗功率[19];
为电能损耗功率[19];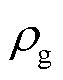 为天然气价格;
为天然气价格;![]() 为天然气热值;
为天然气热值;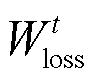 为天然气管道损耗值[20];
为天然气管道损耗值[20];![]() 为热电联产机组(Combined Heat and Power,CHP)的发电效率;
为热电联产机组(Combined Heat and Power,CHP)的发电效率;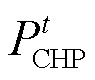 为CHP的输出电功率;
为CHP的输出电功率;![]() 为热负荷削减功率;
为热负荷削减功率;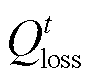 为热能损耗功率[21];
为热能损耗功率[21];![]() 为热负荷削减惩罚系数[22]。
为热负荷削减惩罚系数[22]。
根据电价信号的变化,IES内可平移电负荷可向电价谷时段平移以降低用电成本;IES内可削减部分热负荷以降低用热成本。可平移和可削减负荷需满足
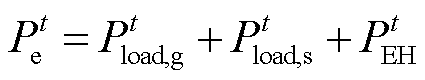 (27)
(27)
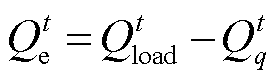 (28)
(28)
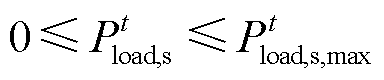 (29)
(29)
 (30)
(30)
式中,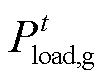 为固定电负荷;
为固定电负荷;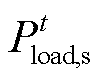 为可平移电负荷;
为可平移电负荷;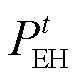 为电制热设备耗电功率;
为电制热设备耗电功率;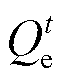 为调整后的热负荷功率;
为调整后的热负荷功率;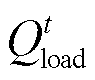 为调整前的热负荷功率;
为调整前的热负荷功率; 为可平移负荷最大值;
为可平移负荷最大值;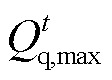 为可削减负荷最大值。
为可削减负荷最大值。
为确保安全稳定的运行,IES应满足
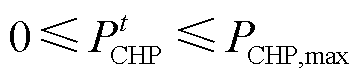 (31)
(31)
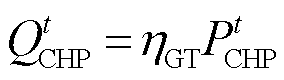 (32)
(32)
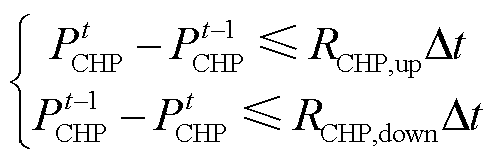 (33)
(33)
式中,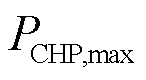 为CHP的最大输出电功率;
为CHP的最大输出电功率;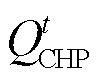 为CHP的制热功率;
为CHP的制热功率;![]() 为CHP的热电比;
为CHP的热电比;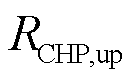 、
、 分别为CHP在相邻时段输出电功率的最大上升、下降速率。
分别为CHP在相邻时段输出电功率的最大上升、下降速率。
IES运行过程中,其功率平衡约束为
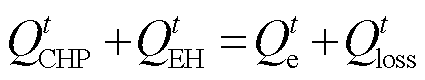 (34)
(34)
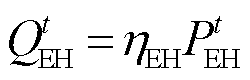 (35)
(35)
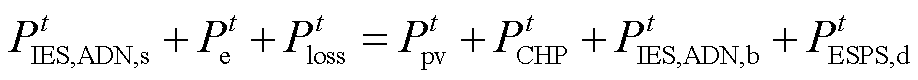 (36)
(36)
式中, 为电制热功率;
为电制热功率;![]() 为电制热设备转换效率;
为电制热设备转换效率;![]() 为光伏发电功率。
为光伏发电功率。
在含ESPS和IES的系统中,各主体间既有主从关系也有潜在的竞争关系,因此在主从博弈的基础上提出了双向主从博弈用以描述各主体间的博弈关系,从而实现系统的经济运行。本文提出的基于双向主从博弈的ESPS与IES经济运行模型框架如图2所示。IES、ESPS和ADN等主体之间通过能量交易确保系统整体平稳运行。各主体根据自身状态及效益目标制定能量交易策略以优化系统内部运行状态,从而满足各类负荷需求。

图2 双向主从博弈经济运行模型框架
Fig.2 Framework of bidirectional master-slave game economic operation model
ADN是系统可靠、稳定的供能主体,在经济运行中起领导者的作用。ADN通过制定动态售电价格,引导IES和ESPS响应其削峰填谷的电力需求调度,实现自身效益最大化。ESPS是系统的二级领导者,其利用自身充放电快速、灵活的特性,根据上级ADN的电价进行充电,并依据自主定价向下级系统进行售电。ESPS在系统中既起跟随者的作用又起领导者的作用,是双向主从博弈重要的中间环节。IES作为跟随者,根据外部电价合理调整内部机组出力及弹性负荷的调度,满足自身多种负荷需求,提升经济效益。
本文所提的双向主从博弈的具体步骤为:
(1)ADN作为领导者,制定初始售电价格策略。
(2)根据ADN制定的售电价格,ESPS响应ADN的电价策略,制定充电策略,并将充电策略上报给ADN;同时,ESPS向IES制定售电价格策略。
(3)IES根据ADN及ESPS的售电价格策略,优化调整内部能量转换设备出力,以及负荷需求响应情况,制定IES的购电策略,并将策略同时上报给ADN和ESPS。
(4)ADN根据ESPS和IES上报的购电策略更新售电价格,引导ESPS和IES进行动态调整,保证ADN自身经济效益最优。
(5)ESPS根据ADN更新的电价及IES的购电策略更新自身的充电策略和售电价格,使自身经济效益最优。
(6)重复步骤3)~步骤5),直至ADN的电价策略、ESPS充电和售电价格策略以及IES购电策略稳定不变,达到博弈均衡。
(7)系统以博弈均衡解为最终交易策略进行能量交易。
本文提出的双向主从博弈模型描述了ADN、ESPS和IES追求各自目标最优的决策过程。该过程考虑了ADN与ESPS、IES的主从关系、ESPS与IES的主从关系以及ADN与ESPS的竞争关系。双向主从博弈模型可表示为
 (37)
(37)
1)参与者:领导者ADN,二级领导者ESPS,跟随者IES。
2)策略集:领导者的售电价格策略为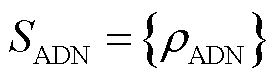 。二级领导者的充电策略以及售电价格策略为
。二级领导者的充电策略以及售电价格策略为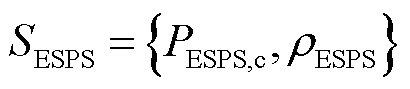 。跟随者的购电策略为
。跟随者的购电策略为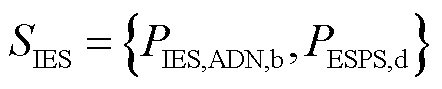 。
。
3)效用:各参与者的效用为前文所述各主体的目标函数,即式(1)、式(10)、式(22)。
在博弈模型中,对于一个策略方案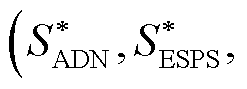
 ,其中
,其中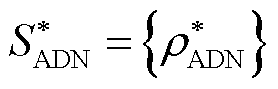 ,
, ,
, ,如果满足
,如果满足
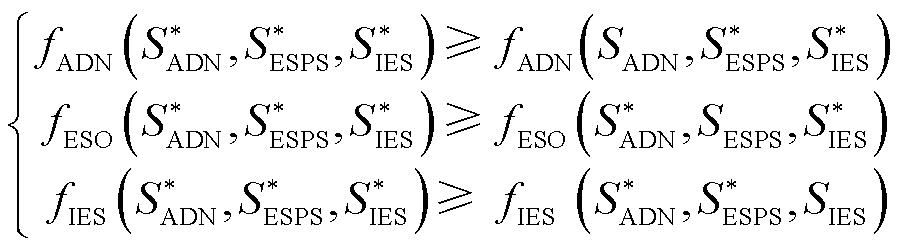 (38)
(38)
则策略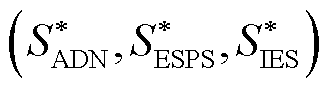 为该博弈的均衡解。
为该博弈的均衡解。
在多主体博弈中,其均衡解存在且唯一,当且仅当该模型满足以下三个条件[23]:①参与者的策略空间均为非空紧凸集;②给定领导者的策略,跟随者的最优解存在且唯一;③给定跟随者的策略,领导者的最优解存在且唯一。
证明如下:
1)由于ADN、ESPS和IES的策略集均为非空紧凸集,所以满足条件①。
2)当领导者ADN和ESPS给定电价策略时,求解跟随者IES的最优策略。对![]() 分别求关于
分别求关于![]() 的二阶偏导,可得
的二阶偏导,可得
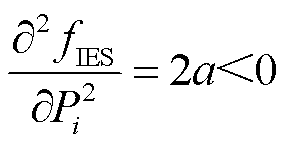 (39)
(39)
式(39)表明,![]() 的Hessian矩阵为负定矩阵,即IES的效用函数为凹函数,存在最优策略,满足条件②。
的Hessian矩阵为负定矩阵,即IES的效用函数为凹函数,存在最优策略,满足条件②。
将IES的最优策略代入ESPS的效用函数可得
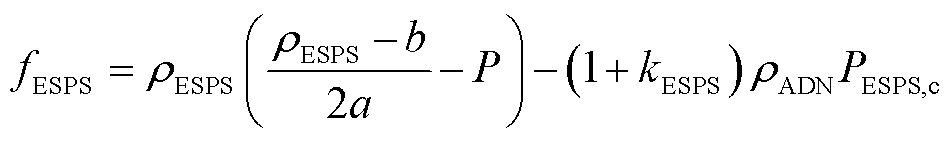 (40)
(40)
式中,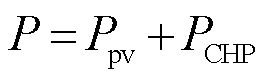 。
。
将ESPS的效用函数![]() 对
对![]() 求二阶偏导,可得
求二阶偏导,可得
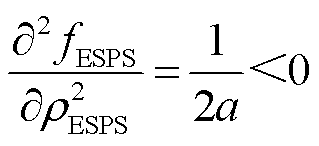 (41)
(41)
式(41)表明![]() 的Hessian矩阵为负定矩阵,即ESPS的效用函数为凹函数。所以,针对IES的最优策略,ESPS存在唯一的最优电价策略,满足条件③。
的Hessian矩阵为负定矩阵,即ESPS的效用函数为凹函数。所以,针对IES的最优策略,ESPS存在唯一的最优电价策略,满足条件③。
3)当ESPS作为跟随者时,ESPS的效用函数![]() 在充电策略
在充电策略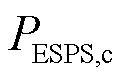 集合中呈线性变化,而线性函数是一类凹函数,所以
集合中呈线性变化,而线性函数是一类凹函数,所以![]() 是策略
是策略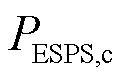 的连续拟凹函数。对于领导者ADN的最优策略,跟随者ESPS存在最优策略。
的连续拟凹函数。对于领导者ADN的最优策略,跟随者ESPS存在最优策略。
同理,ADN的效用函数![]() 在电价策略
在电价策略![]() 集合中呈线性变化,是关于策略
集合中呈线性变化,是关于策略![]() 的连续拟凹函数。所以,当跟随者ESPS和IES存在最优策略,领导者ADN有最优的电价策略。
的连续拟凹函数。所以,当跟随者ESPS和IES存在最优策略,领导者ADN有最优的电价策略。
上述研究表明,本文提出的双向主从博弈存在唯一的均衡解。
本文算例以IEEE 33节点电力系统[24]和比利时20节点天气系统为基础,构建了含ESPS和IES的系统模型,如图3所示。在IEEE 33节点电力系统的1节点接入了ESPS,6、11节点接入了CHP机组,5、8、10、16、20、24节点接入了光伏机组。同时,6、11节点的CHP机组分别与天然气系统的1、6节点相连。该系统的设备参数见表1,用户负荷需求和光伏发电预测数据如图4所示。仿真算例在Matlab平台上进行编程,采用双层粒子群算法[25]和CPLEX求解器进行求解。
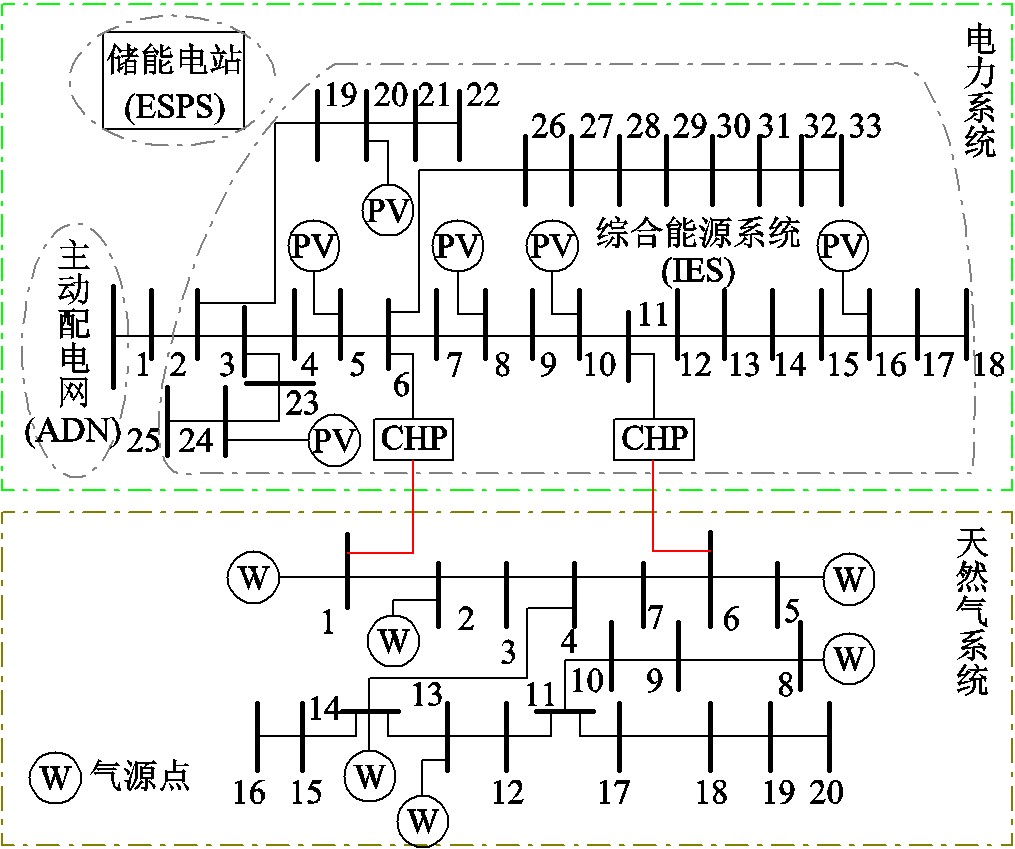
图3 含ESPS和IES的系统仿真算例拓扑结构
Fig.3 Topology diagram of system simulation example with ESPS and IES
表1 设备参数
Tab.1 Equipment parameters

参数数值 IES/(元/m³)3.24 /(kW·h/m³)9.78 0.4 /kW200 -0.05 4 0.1 0.8 /kW40, 40 0.9 ADN/kW300 /kW300 ESPS0.01 /kW300 /(kW·h)200, 1 300 0.95, 0.95
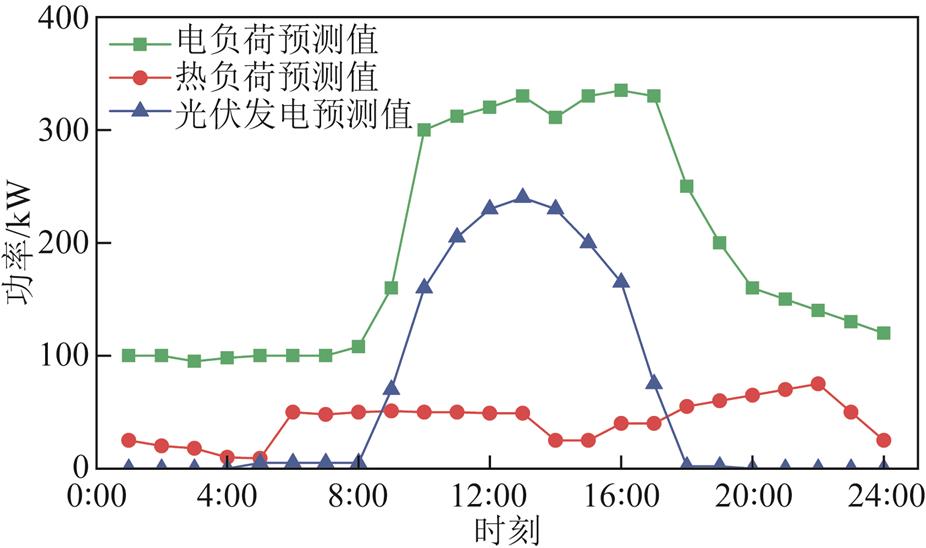
图4 电负荷、热负荷和光伏发电预测曲线
Fig.4 Electric load, heat load and photovoltaic power generation prediction curve
采用本文所提策略对含ESPS和IES的系统进行优化。ADN与ESPS电价策略如图5所示,IES电负荷平衡关系如图6所示,IES热负荷平衡关系如图7所示,ESPS储能容量状况如图8所示。
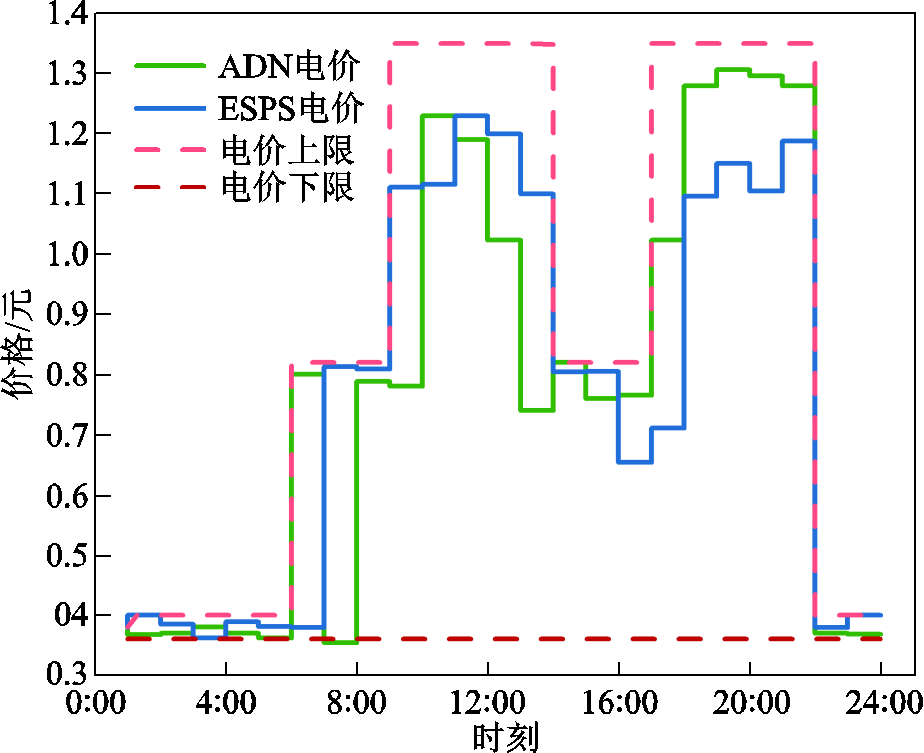
图5 ADN与ESPS电价策略
Fig.5 Electricity selling price of ADN and ESPS
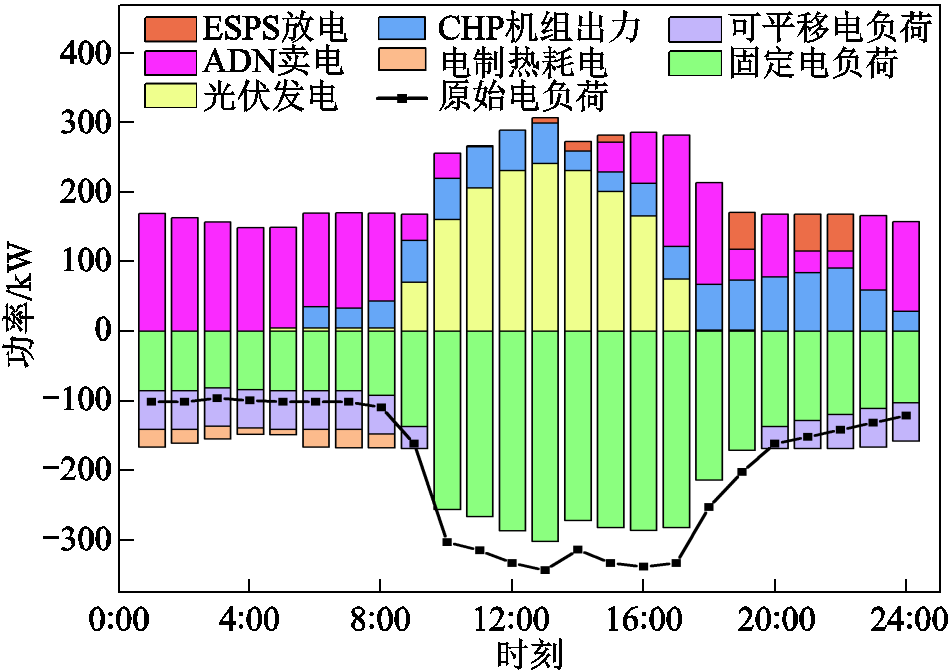
图6 电负荷平衡图
Fig.6 Electric load balance diagram
由图6可以看出,IES中可平移电负荷出现在1:00—9:00和20:00—24:00两个时段。这两个时段中ADN电价较低,IES可用低成本满足电负荷需求,提升用户效益。并且,可平移电负荷经调整后集中在两个连续时段内,有效地保证了可平移负荷用电的连续性。但在电价较高的20:00—22:00时段仍存在部分可平移电负荷,主要受到两方面影响:一方面是本方法的CHP机组采用以热定电的方式进行出力,可平移电负荷能灵活地平衡CHP机组产生的电能;另一方面是每个时段内可接受的可平移电负荷存在上限。
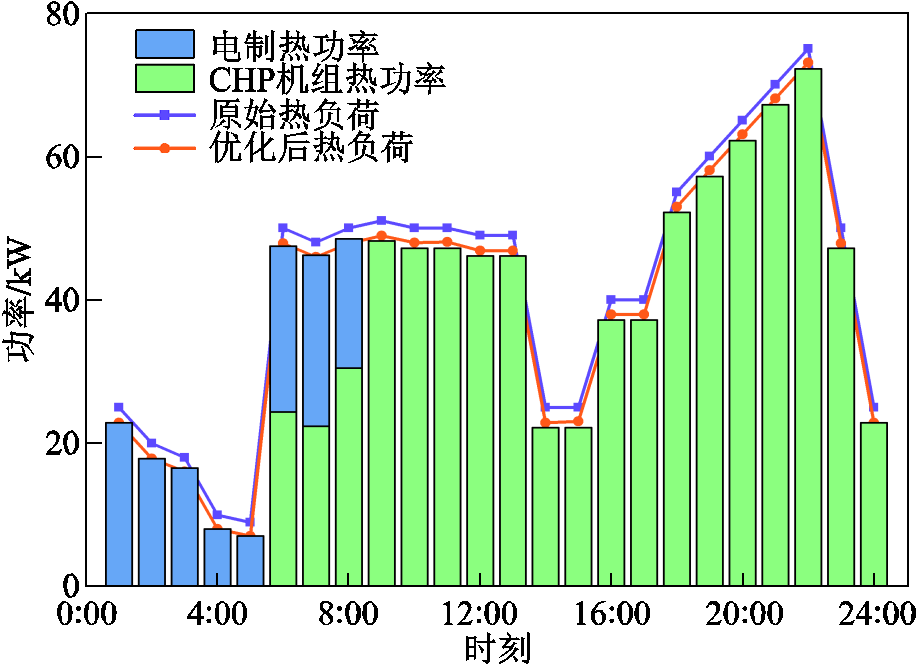
图7 热负荷平衡图
Fig.7 Heat load balance diagram
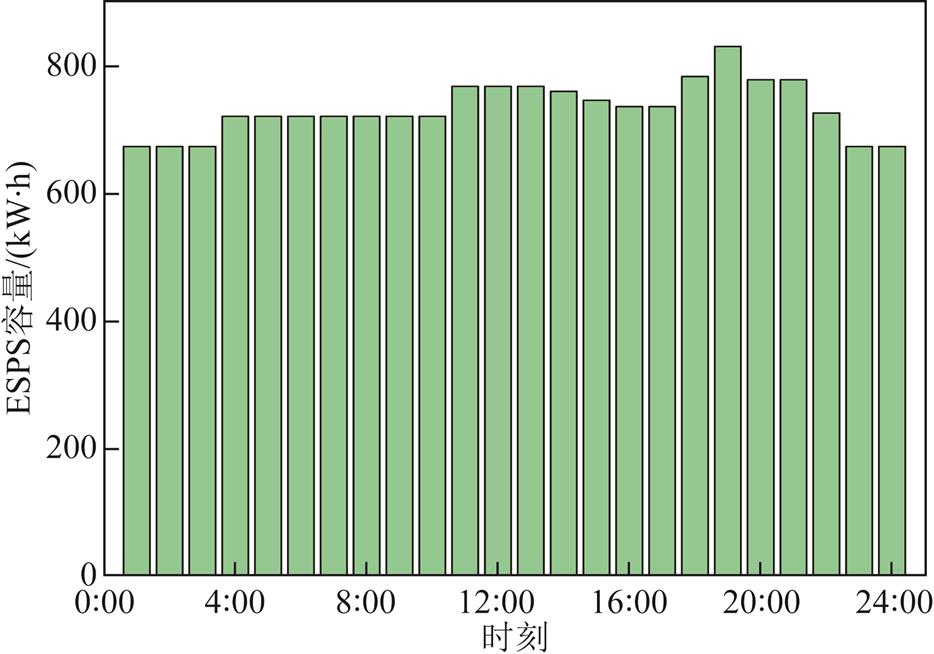
图8 ESPS储能容量变化
Fig.8 Change diagram of ESPS energy storage capacity
图7显示了IES中热负荷的供需平衡关系,可见热负荷在优化周期内均进行了削减。从热负荷的供能来源可以发现,在1:00—5:00时段内,热负荷由电制热设备供应,此时电价较低,采用电制热可有效降低供热成本。在6:00—8:00时段内热负荷激增,此时采用电制热和CHP机组供热结合的方式供热。随着电价的升高,热负荷的供应逐步转变为全由CHP机组供热,以此降低运行成本。结合图5与图8分析可知,采用本文所提方法,ESPS并未完全遵循“低充高放”的原则。ESPS集中在电价平时段以最大功率充电,并在电价峰时段向IES卖电。这一充放电模式有效降低了ESPS在电价谷时段充电给ADN造成的亏损,同时也降低了IES在电价峰时段的购电成本,有效地均衡了各参与主体的利益。
为验证本文所提双向主从博弈经济运行策略的有效性,设置三种经济运行方案进行对比分析。方案1:考虑ADN与ESPS的双重动态电价,即本文所提的双向主从博弈经济运行策略;方案2:考虑ADN动态电价,无ESPS参与经济运行;方案3:ADN和ESPS均为固定售电价,即各主体间无博弈关系。
按照上述三种方案进行仿真,得到的各主体效益优化结果见表2。
表2 各主体效益优化结果
Tab.2 Optimal benefit results of each subject

方案IES效益/元ESPS效益/元ADN效益/元整体效益/元 15 119.071.285.65 275.8 24 736.4—145.94 882.3 34 047.646.38.84 102.7
3.3.1 与不考虑ESPS的经济运行结果对比分析
为验证ESPS参与经济运行对系统效益的影响,本文首先对方案1和方案2的经济运行结果进行分析。三种方案优化后的电价对比如图9所示,采用方案1、方案2优化后的IES购电情况如图10所示。结合表2分析可知,相对于方案2,方案1中IES的效益增加了382.6元,提升了8.1%;ADN的效益减少了60.3元,降低了41.3%;ESPS获得了71.2元的效益;系统总效益增加了393.5元,提升了8.1%。这是因为方案1增加了具有主动性的ESPS,ESPS依赖ADN供能的同时又与ADN在售电过程形成竞争关系,各主体发生博弈导致方案1的电价相对降低。这也就造成了图10中IES从外部购电保持基本一致的情况下,IES的效益却得到了提升。虽然方案1中ADN的效益受到了不利影响,但这一方案有助于提升系统的整体效益,促进能源系统的良性运行。
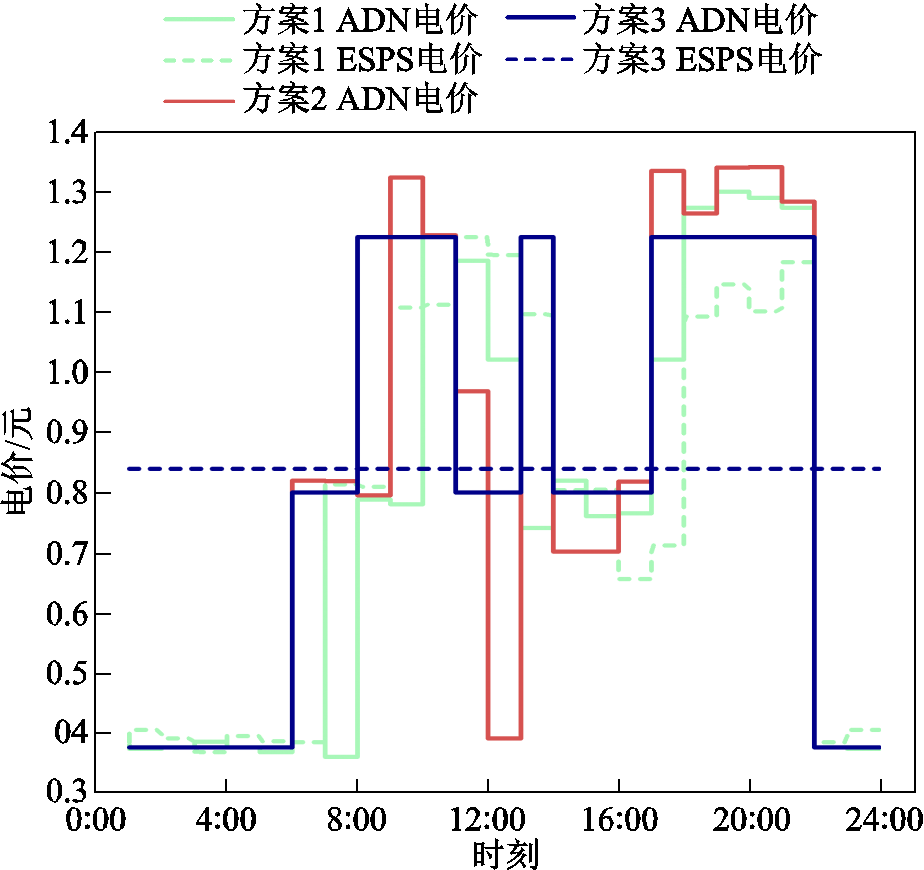
图9 电价对比
Fig.9 Electricity price comparison chart

图10 方案1和方案2下IES购电情况对比
Fig.10 Comparison diagram of IES power purchase under scheme 1 and scheme 2
3.3.2 与不考虑双重动态电价的经济运行结果对比分析
为验证动态电价对含ESPS和IES的系统经济运行的影响,对方案1和方案3进行对比分析。其中,采用方案1、方案3优化后的ESPS储能容量变化对比如图11所示、IES购电情况对比如图12所示。结合表2分析发现,相对于方案3,方案1中IES、ESPS和ADN主体的效益均得到提升。其中,IES的效益增加了1 071.4 元,提升了26.4%;ESPS的效益增加了24.9 元,提升了53.8%;ADN的效益增加了76.8元,提升了872.7%;系统总效益增加了1 173.1 元,提升了28.6%。在方案3中,ADN和ESPS均采用固定电价,各主体间无博弈,导致各主体不能充分发挥市场灵活性去获取更大的效益。结合图9与图11分析发现,相较于方案1,ESPS在利益驱使下主要在ADN电价谷时段时进行充电,在ADN电价峰时段时卖电。然而,由于ESPS售电价格固定,ESPS无法在负荷需求高峰时灵活提升电价来增加收益。同时,ESPS受到自身充放电功率限制,不能无限量地充放电,最终其效益相较于方案1大大降低。综合分析图11与图12可知,ADN虽然整体的售电价格较高,但受到ESPS“低充高放”的影响,在电价谷时段卖电量增多导致亏损,在电价峰时段卖电量减少导致收益降低,最终其效益受到极大的损失。对于IES,采用方案3优化运行,除18:00—22:00时段外,其购电价格均有所升高,并且在这一时段中受到ESPS放电功率的限制,无法大量购买廉价电能,最终导致购电成本增加,效益降低。综上分析,本文所提策略能够充分发挥各主体参与市场竞争的灵活性,提升系统经济效益,实现各主体的共赢。

图11 方案1和方案3下ESPS储能容量变化对比
Fig.11 Comparison diagram of changes in ESPS capacity under scheme 1 and scheme 3
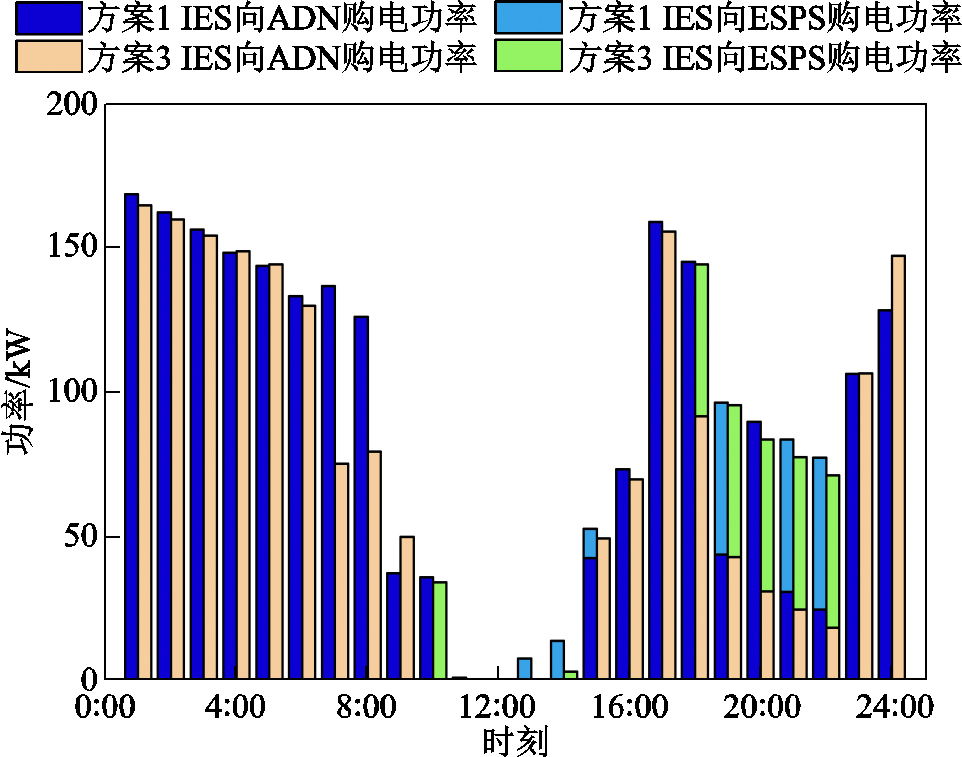
图12 方案1和方案3下IES购电情况对比
Fig.12 Comparison diagram of IES power purchase under scheme 1 and scheme 3
本文针对ESPS与IES的经济运行问题,充分考虑了IES、ESPS和ADN三者之间的博弈关系,提出一种基于双向主从博弈的ESPS与IES经济运行策略。该策略以ADN为领导者,ESPS为二级领导者,IES为跟随者,构建了双向主从博弈模型,并通过理论证明了该博弈模型存在唯一均衡解。最后,通过算例分析验证了本文所提经济运行策略的有效性和优越性。主要结论如下:
1)本文提出的经济运行策略考虑了ESPS作为用能主体和供能主体的两重性,充分发挥了ESPS参与经济运行的主动性,有效地促进了系统整体经济效益的提升。
2)现有研究仅考虑了供能主体的竞争关系或主从关系,并未同时考虑竞争关系与主从关系。本文所提策略综合考虑了ADN和ESPS间的主从和竞争关系,更贴合能源市场运行优化的实际状况。
3)经过三种方案对比分析,本文所提策略能够充分利用各主体间的博弈关系,提升系统的经济性,保证能源系统的互利共赢。
参考文献
[1] 张沈习, 王丹阳, 程浩忠, 等. 双碳目标下低碳综合能源系统规划关键技术及挑战[J]. 电力系统自动化, 2022, 46(8): 189-207. Zhang Shenxi, Wang Danyang, Cheng Haozhong, et al. Key technologies and challenges of low-carbon integrated energy system planning for carbon emission peak and carbon neutrality[J]. Automation of Electric Power Systems, 2022, 46(8): 189-207.
[2] 边晓燕, 史越奇, 裴传逊, 等. 计及经济性和可靠性因素的区域综合能源系统双层协同优化配置[J]. 电工技术学报, 2021, 36(21): 4529-4543. Bian Xiaoyan, Shi Yueqi, Pei Chuanxun, et al. Bi-level collaborative configuration optimization of integrated community energy system considering economy and reliability[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4529-4543.
[3] 陈岑, 武传涛, 林湘宁, 等. 计及上下游市场的园区综合能源商购售能策略[J]. 电工技术学报, 2022, 37(1): 220-231. Chen Cen, Wu Chuantao, Lin Xiangning, et al. Purchase and sale strategies of park integrated energy suppliers in wholesale and retail markets[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 220-231.
[4] 李勇, 姚天宇, 乔学博, 等. 基于联合时序场景和源网荷协同的分布式光伏与储能优化配置[J]. 电工技术学报, 2022, 37(13): 3289-3303. Li Yong, Yao Tianyu, Qiao Xuebo, et al. Optimal configuration of distributed photovoltaic and energy storage system based on joint sequential scenario and source-network-load coordination[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3289-3303.
[5] 张大海, 贠韫韵, 王小君, 等. 考虑广义储能及光热电站的电热气互联综合能源系统经济调度[J]. 电力系统自动化, 2021, 45(19): 33-42. Zhang Dahai, Yun Yunyun, Wang Xiaojun, et al. Economic dispatch of integrated electricity-heat-gas energy system considering generalized energy storage and concentrating solar power plant[J]. Automation of Electric Power Systems, 2021, 45(19): 33-42.
[6] 吴盛军, 李群, 刘建坤, 等. 基于储能电站服务的冷热电多微网系统双层优化配置[J]. 电网技术, 2021, 45(10): 3822-3832. Wu Shengjun, Li Qun, Liu Jiankun, et al. Bi-level optimal configuration for combined cooling heating and power multi-microgrids based on energy storage station service[J]. Power System Technology, 2021, 45(10): 3822-3832.
[7] 杨永标, 于建成, 李奕杰, 等. 含光伏和蓄能的冷热电联供系统调峰调蓄优化调度[J]. 电力系统自动化, 2017, 41(6): 6-12, 29. Yang Yongbiao, Yu Jiancheng, Li Yijie, et al. Optimal load leveling dispatch of CCHP incorporating photovoltaic and storage[J]. Automation of Electric Power Systems, 2017, 41(6): 6-12, 29.
[8] 李鹏, 周益斌, 李明哲, 等. 基于谈判博弈的含储能站利益主体的多能源站协同优化运行方法[J]. 高电压技术, 2021, 47(5): 1666-1677. Li Peng, Zhou Yibin, Li Mingzhe, et al. Cooperative optimal operation method of multiple energy stations with stakeholder of energy storage station based on negotiation game[J]. High Voltage Engineering, 2021, 47(5): 1666-1677.
[9] 孙偲, 郑天文, 陈来军, 等. 基于组合双向拍卖的共享储能机制研究[J]. 电网技术, 2020, 44(5): 1732-1739. Sun Cai, Zheng Tianwen, Chen Laijun, et al. Energy storage sharing mechanism based on combinatorial double auction[J]. Power System Technology, 2020, 44(5): 1732-1739.
[10] 金力, 房鑫炎, 蔡振华, 等. 考虑特性分布的储能电站接入的电网多时间尺度源储荷协调调度策略[J]. 电网技术, 2020, 44(10): 3641-3650. Jin Li, Fang Xinyan, Cai Zhenhua, et al. Multiple time-scales source-storage-load coordination scheduling strategy of grid connected to energy storage power station considering characteristic distribution[J]. Power System Technology, 2020, 44(10): 3641-3650.
[11] Cheng Shan, Wang Rui, Xu Jianyu, et al. Multi-time scale coordinated optimization of an energy hub in the integrated energy system with multi-type energy storage systems[J]. Sustainable Energy Technologies and Assessments, 2021, 47: 101327.
[12] 王雪纯, 陈红坤, 陈磊. 提升区域综合能源系统运行灵活性的多主体互动决策模型[J]. 电工技术学报, 2021, 36(11): 2207-2219. Wang Xuechun, Chen Hongkun, Chen Lei. Multi-player interactive decision-making model for operational flexibility improvement of regional integrated energy system[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2207-2219.
[13] 王海洋, 李珂, 张承慧, 等. 基于主从博弈的社区综合能源系统分布式协同优化运行策略[J]. 中国电机工程学报, 2020, 40(17): 5435-5445. Wang Haiyang, Li Ke, Zhang Chenghui, et al. Distributed coordinative optimal operation of community integrated energy system based on stackelberg game[J]. Proceedings of the CSEE, 2020, 40(17): 5435-5445.
[14] 马丽, 刘念, 张建华, 等. 基于主从博弈策略的社区能源互联网分布式能量管理[J]. 电网技术, 2016, 40(12): 3655-3662. Ma Li, Liu Nian, Zhang Jianhua, et al. Distributed energy management of community energy Internet based on leader-followers game[J]. Power System Technology, 2016, 40(12): 3655-3662.
[15] Ma Li, Liu Nian, Zhang Jianhua, et al. Energy management for joint operation of CHP and PV prosumers inside a grid-connected microgrid: a game theoretic approach[J]. IEEE Transactions on Industrial Informatics, 2016, 12(5): 1930-1942.
[16] 王瑞, 程杉, 汪业乔, 等. 基于多主体主从博弈的区域综合能源系统低碳经济优化调度[J]. 电力系统保护与控制, 2022, 50(5): 12-21. Wang Rui, Cheng Shan, Wang Yeqiao, et al. Low-carbon and economic optimization of a regional integrated energy system based on a master-slave game with multiple stakeholders[J]. Power System Protection and Control, 2022, 50(5): 12-21.
[17] 李咸善, 马凯琳, 程杉. 含多区域综合能源系统的主动配电网双层博弈优化调度策略[J]. 电力系统保护与控制, 2022, 50(1): 8-22. Li Xianshan, Ma Kailin, Cheng Shan. Dispatching strategy of an active distribution network with multiple regional integrated energy systems based on two-level game optimization[J]. Power System Protection and Control, 2022, 50(1): 8-22.
[18] 吴利兰, 荆朝霞, 吴青华, 等. 基于Stackelberg博弈模型的综合能源系统均衡交互策略[J]. 电力系统自动化, 2018, 42(4): 142-150, 207. Wu Lilan, Jing Zhaoxia, Wu Qinghua, et al. Equilibrium strategies for integrated energy systems based on Stackelberg game model[J]. Automation of Electric Power Systems, 2018, 42(4): 142-150, 207.
[19] 芮涛, 李国丽, 王群京, 等. 配电侧多微电网日前电能交易纳什议价方法[J]. 电网技术, 2019, 43(7): 2576-2585. Rui Tao, Li Guoli, Wang Qunjing, et al. Nash bargaining method for multi-microgrid energy trading in distribution network[J]. Power System Technology, 2019, 43(7): 2576-2585.
[20] 田晓翠, 董常龙, 杨正然, 等. 天然气管输损耗分析与控制综述[J]. 当代化工, 2014, 43(7): 1322-1325. Tian Xiaocui, Dong Changlong, Yang Zhengran, et al. Review of analysis and control for gas loss of pipeline[J]. Contemporary Chemical Industry, 2014, 43(7): 1322-1325.
[21] 孙鹏, 滕云, 回茜, 等. 考虑异质能流输运特性的多能源系统惯量极限优化[J]. 中国电机工程学报, 2022, 42(10): 3642-3656. Sun Peng, Teng Yun, Hui Qian, et al. Inertia limit optimization of multi-energy system considering the transport characteristics of heterogeneous energy flow[J]. Proceedings of the CSEE, 2022, 42(10): 3642-3656.
[22] Paudel A, Chaudhari K, Long Chao, et al. Peer-to-peer energy trading in a prosumer-based community microgrid: a game-theoretic model[J]. IEEE Transactions on Industrial Electronics, 2019, 66(8): 6087-6097.
[23] Yu Mengmeng, Hong S H. A real-time demand-response algorithm for smart grids: a stackelberg game approach[J]. IEEE Transactions on Smart Grid, 2016, 7(2): 879-888.
[24] 刁涵彬, 李培强, 吕小秀, 等. 考虑多元储能差异性的区域综合能源系统储能协同优化配置[J]. 电工技术学报, 2021, 36(1): 151-165. Diao Hanbin, Li Peiqiang, Lü Xiaoxiu, et al. Coordinated optimal allocation of energy storage in regional integrated energy system considering the diversity of multi-energy storage[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 151-165.
[25] 谢畅, 王蓓蓓,赵盛楠, 等. 基于双层粒子群算法求解电力市场均衡[J]. 电网技术, 2018, 42(4): 1170-1177. Xie Chang, Wang Beibei, Zhao Shengnan, et al. Equilibrium solution for electricity market based on bi-level particle swarm optimization algorithm[J]. Power System Technology, 2018, 42(4): 1170-1177.
Abstract When connected to energy supply entities such as active distribution networks (ADNs), energy storage stations (ESPSs) and natural gas networks, the energy supply reliability of the integrated energy system (IES) can be effectively improved. However, with the participation of ESPSs in market transactions, how to improve the initiative of ESPSs to realize the economic operation between the IES and the ESPS is an urgent problem to be addressed. Making full use of the interest relationship between various entities to game is an important way to achieve the economic operation of the IES and the ESPS. However, the game model adopted by the traditional economic operation method did not consider the duality of the participating subjects as both leaders and followers. This kind of game model cannot fully mobilize the initiative of the participating subjects.
To this end, a bidirectional master-slave game-based economic operation strategy is proposed for ESPS and IES in this paper. First,aiming at the economic benefits of the IES, ADN and ESPS, the corresponding economic operation models are established respectively. The models consider the constraints of each subject and the loss in energy transmission. Then,based on the duality of the ESPS as the energy supplier and the energy user, an energy interaction mechanism for the ADN, ESPS, and IES is constructed. The energy interaction mechanism considers the master-slave and competition relationship between the ADN and ESPS. Third,a bidirectional master-slave game model with the ADN as the leader, the ESPS as the secondary leader and the IES as the follower is proposed.The existence of the unique equilibrium solution of the proposed game strategy is proved theoretically in this paper. Finally, a simulation model is built based on the IEEE 33 node distribution network and Belgium’s 20 node natural gas network. The bi-level particle swarm optimization algorithm and CPLEX solver are used to perform the numerical simulation.Three kinds of economic operation schemes are set up for comparative analysis.Scheme 1 is the economic operation strategy proposed in this paper.In scheme 2, the dynamic electricity price of ADN is considered, and no ESPS participates in the economic operation.In scheme 3, both ADN and ESPS adopt fixed electricity prices, and there is no game relationship between each subject.Simulation results show that, compared with scheme 2 and scheme 3, the overall system benefit of scheme 1 is increased by 8.1% and 28.6%, respectively.This comparison results verify the superiority of the proposed strategy in improving economic benefits.
The following conclusions can be drawn from the simulation analysis: (1) The proposed strategy gives full play to the initiative of the ESPS participating in the economic operation. (2)The proposed strategy comprehensively considers the master-slave and competitive relationship between the ADN and ESPS, which is suitable for the actual scenario of the IES economic operation. (3)The proposed strategy can make full use of the game relationship between all subjects, improve the overall economic benefits of the system, and achieve mutual benefit and win-win results for all subjects.
Keywords:Integrated energy system, energy storage power station, bidirectional master-slave game, economical operation
国家自然科学基金资助项目(52107108)。
收稿日期 2022-06-20
改稿日期 2022-11-01
DOI:10.19595/j.cnki.1000-6753.tces.221164
中图分类号:TM732
王 灿 男,1987年生,副教授,博士生导师,研究方向为综合能源系统优化运行、微电网协调控制与优化运行等。E-mail:xfcancan@163.com(通信作者)
张 羽 女,1999年生,硕士研究生,研究方向为微电网协调控制与优化运行等。E-mail:yuzhang026@163.com
(编辑 赫蕾)