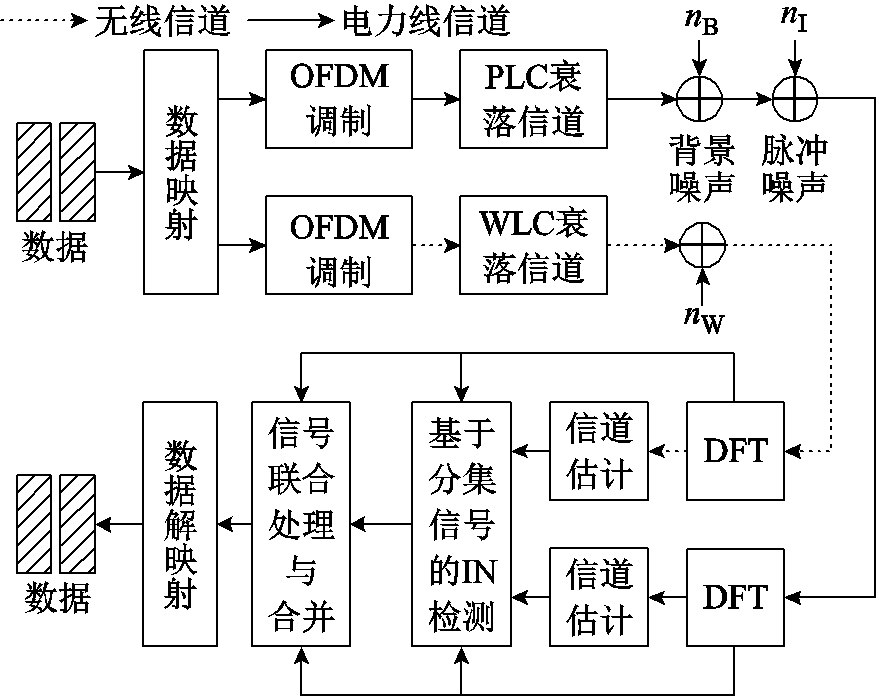
图1 双接口通信中的分集传输系统模型
Fig.1 Diversity transmission system model in dual interface communication
摘要 针对电力线与无线双接口通信中的电力线突发脉冲噪声（BIN）的干扰问题，提出一种基于分集信号抵消和自适应阈值估计（DSC-ATE）的BIN抑制算法。首先，利用电力线和无线并行信道传输相同的分集信号，接收端通过分集信号抵消获得脉冲噪声样本，降低峰平比对阈值估计的影响；然后利用噪声样本对非线性函数的最佳阈值进行估计；最后对脉冲噪声进行抑制处理。为了提高算法的鲁棒性和可扩展性，该文通过引入折扣因子和学习率来实现算法在复杂度和精度之间的有效折中。与已有的非线性处理算法相比，该方法不需要噪声的先验统计信息，并可根据信道环境的变化自适应地调整阈值。仿真结果表明，所提算法在可靠性和阈值精度方面均具有显著提升。
关键词：双接口通信 突发脉冲噪声 数据样本 最佳阈值
信息的全面感知与通信是构建智能电网的基础与保障。智能电网覆盖范围广、拓扑结构复杂、接入设备多样化，单一的通信技术已无法满足各种场景的需求，因此混合通信已成为智能电网的关键技术[1-3]。其中电力线通信（Power Line Communication, PLC）覆盖范围广，无需额外布线；无线通信（Wireless Communication, WLC）接入灵活，可扩展性强，因此，将PLC和WLC技术紧密结合，可提升混合通信的系统性能，在智能电网和物联网中具有广泛的应用前景，已成为研究热点之一[4-7]。
然而，由于家用电器和电力电子设备开关的通断所引起的电压突变，导致电力线信道极易受到脉冲噪声（Impulse Noise, IN）的影响[8]。特别是突发性脉冲噪声，因其在多个连续的采样点上产生，不仅影响信号的解调和译码，还会影响电力线传输的同步性能。如何抑制双接口通信中电力线信道的脉冲噪声，进一步提高通信系统的覆盖范围及其接入的可靠性是亟待解决的关键问题之一。
目前，在脉冲噪声影响下的双接口通信系统中，研究人员多以理论性能和信号合并等技术[5,9-10]为重点。文献[5]将无线衰落的Gamma分布近似为对数正态（Log Normal, LogN）分布，从而将电力线与无线并行通信系统中的混合衰落问题转换为LogN-LogN同分布衰落问题，然后对系统误码率等理论性能进行了分析。文献[9]采用Middleton Class A脉冲噪声模型，研究了电力线和无线并行通信系统采用最大比合并、选择合并等算法的性能。然而这些研究往往只考虑了脉冲噪声对系统性能的影响，而没有从脉冲噪声检测和消除的角度提升性能。文献[10]针对不同类型的脉冲噪声和窄带干扰，提出了基于多级正交匹配追踪恢复算法，用来联合恢复脉冲噪声和窄带干扰，但双接口信号并列处理的复杂度较高。
相对于压缩感知算法[11-13]，基于非线性函数[14]的脉冲噪声抑制算法因其计算速度快、无需空子载波等优点获得研究人员的关注。其中应用最广泛的非线性函数包括置零[15]、削波/深削波[16]及其组合[17]。但是在正交频分复用（Orthogonal Frequency Division Multiplexing, OFDM）系统中，由于峰值平均比（Peak-to-Average Power Ratio, PAPR）的存在，如果不能获得精确的噪声阈值，将会导致部分有用信号被当作噪声处理，这极大地限制了非线性函数的性能。
近年来，对于非线性函数最佳阈值的确定逐渐受到关注[15,18-20]。文献[15]通过交织技术将突发脉冲噪声离散化，然后利用矩估计获得噪声统计参数并计算噪声门限，但该文忽略了信道衰落对系统的影响，此外交织技术还会增大系统的传输时延。对于脉冲噪声中的确定性信号，局部最优检测（Locally Optimal Detection, LOD）算法在低信噪比下检测性能最好[18]，接近理论最优解。但LOD算法需要精确知道噪声的概率密度函数（Probability Density Function, PDF），实际场景需要付出较大的算法代价。文献[19]将削波和时/频信道均衡相结合，在OFDM信号解调之前先做组合限幅，然后进行时/ 频均衡化，但是该方法对通信质量的提高并不明显，且阈值一般通过经验获取。针对脉冲噪声中的信号检测问题，文献[20]提出基于指数函数的非线性变换函数的设计与优化方法，为各种分布的脉冲噪声提供了一个统一的解决方法。以上文献都是在PLC中单独对脉冲噪声进行处理，没有涉及到电力线与无线的双接口通信环境。利用双接口通信中的分集信号的传输特性，可以为非线性函数的自适应阈值估计提供新的研究思路。
鉴于对双接口通信和非线性函数的分析，本文根据电力线和无线信道的独立性与差异性、分集信号的一致性，提出了一种基于双接口的分集信号抵消和自适应阈值估计（Diversity Signal Cancellation and Adaptive Threshold Estimation, DSC-ATE）的脉冲噪声抑制方法。该方法首先利用无线信道辅助电力线信道进行噪声样本的提取；然后通过噪声样本自适应地估计出脉冲噪声阈值；最后将脉冲噪声从接收信号中分离。与现有的方法相比，本文的主要贡献如下：
（1）针对双接口通信架构，提出一种基于分集信号抵消的噪声样本提取方法。利用电力线与无线传输信号的一致性提取出噪声样本，突破了传统混合通信中只使用电力线单独进行脉冲噪声处理的局限性，可应用于最佳阈值预测中。
（2）基于分集传输，构建了脉冲噪声的样本空间，包含低信噪比时（非正常通信）的噪声样本；结合非线性函数，提出了基于噪声样本的最佳阈值估计算法，可实现通信系统误码率最小化，不需要脉冲噪声的先验信息。
（3）对于非平稳环境中最佳阈值实时变化问题，通过引入学习率和折扣因子等参数调节算法的收敛速度，使算法能更好地利用噪声样本，提高鲁棒性，实现算法在稳健性和收敛速度的有效折中。
本文采用的双接口OFDM通信系统模型如图1所示。发送的信号分别在电力线和无线通信模块中进行OFDM调制，在电力线和无线信道中分集传输。其中无线信道受到瑞利衰落和高斯白噪声nW的影响，电力线信道受到对数正态衰落、背景噪声nB和脉冲噪声nI的影响。接收端的电力线和无线信号同时包含相同的发送信息，只有电力线信号中具有较大幅值的脉冲噪声，因此可以将离散傅里叶变换（Discrete Fourier Transform, DFT）后的信号通过抵消运算获得电力线信号中的脉冲噪声数据，即可在无线信道传输的分集信号辅助下，获得脉冲噪声数据。之后将电力线与无线信号进行合并处理和译码输出。将提取的脉冲噪声数据保存下来，即可建立数据样本空间，为本文算法或其他算法提供数据支持。
图1 双接口通信中的分集传输系统模型
Fig.1 Diversity transmission system model in dual interface communication
无线信道衰落hW满足瑞利分布，则PDF为
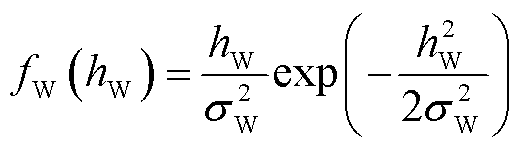（1）
式中，σW2为瑞利衰落参数。
电力线信道衰落hP满足LogN分布，其PDF为
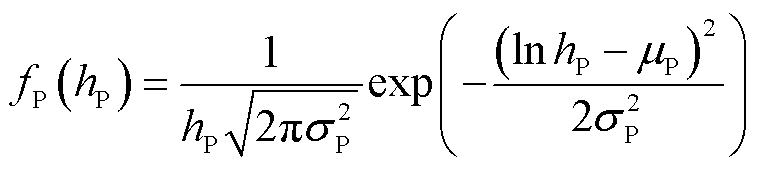（2）
式中，mP和σP2分别为lnhP的均值和方差。将信道衰落能量归一化[5]，可得σW2=0.5，mP=-σP2。
基于突发脉冲噪声在时间上的相关性[21]，本文建立了两状态马尔可夫-高斯（Two-State Markov-Gaussian, TSMG）模型[22]，如图2所示。
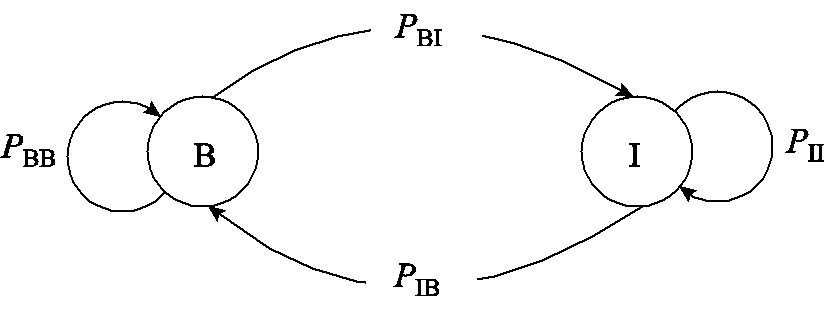
图2 TSMG噪声模型的马尔可夫链表示
Fig.2 Markov chain representation of TSMG noise model
在TSMG中，令电力线噪声的统计行为由噪声状态sk ∈{B,I}表示，其中B代表信道仅受背景噪声的干扰，I代表信道受到脉冲噪声的影响。噪声状态的产生过程可以用一个{s1, s2,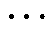
, sK}的序列表征。对于该模型，第K+1个噪声状态sK+1可用一阶马尔可夫过程表示为
（3）
因此噪声的状态变化过程可由状态转移概率Psksk+1=P(sk+1|sk)表示。根据状态转移概率，分别得到噪声处于状态I和状态B的概率PI和PB分别为
（4）
（5）
式中，PBI为状态B到状态I的转移概率；PIB为状态I到状态B的转移概率。可用参数ϛ= 1/(PBI+PIB)来描述噪声记忆的大小，ϛ =1表示噪声是无记忆的；ϛ ＞1表示噪声具有记忆，即存在时间相关性。
本节重点介绍基于分集信号抵消的脉冲噪声样本提取方法，给出算法的具体流程和结果分析，最后介绍此方法在非线性函数处理中的应用。
电力线与无线双接口通信系统在接收端进行信号处理的框架示意图如图3所示。首先在接收端去除电力线和无线时域信号循环前缀（Cyclic Prefix, CP），并利用导频信号进行理想信道估计；由于两个信道传输相同的信息，在理想信道估计下，可以通过抵消运算，去除掉电力线信号中与无线信号相同的数据部分，从而保留下电力线信号中的噪声样本；然后通过非线性函数提取出脉冲噪声并将其从电力线信号上消除；最后将分集信号进行合并处理以及译码输出。
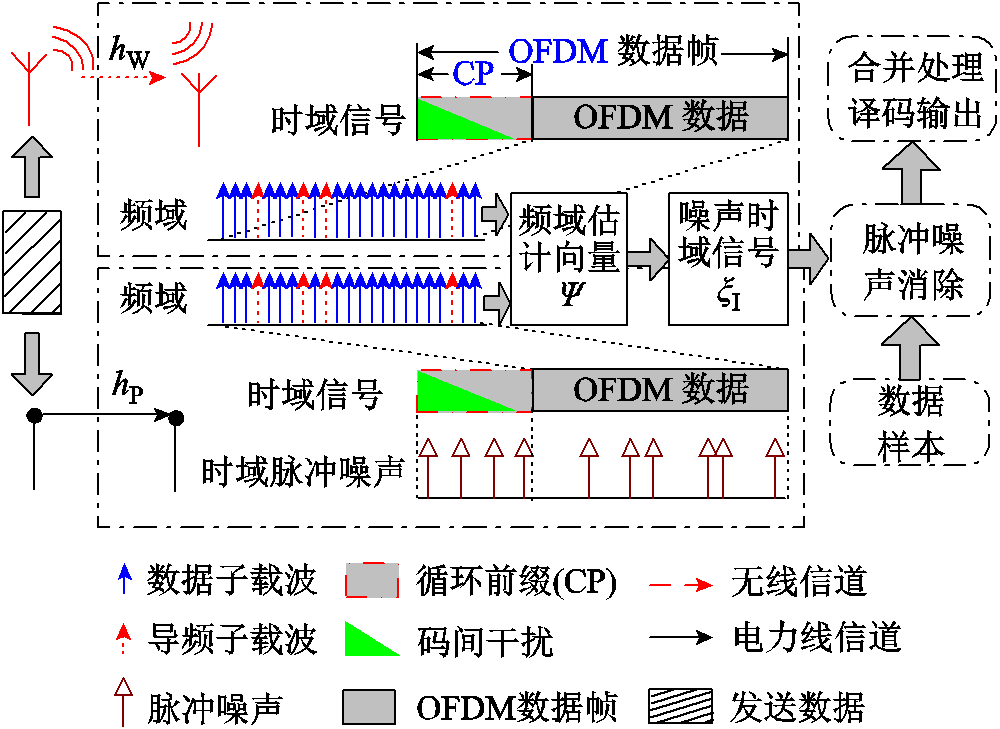
图3 双接口时频OFDM数据帧的脉冲噪声处理过程
Fig.3 The impulse noise processing of dual interface time-frequency OFDM data frame
第t个传输时刻的OFDM已调时域符号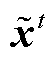
，经过信道衰落系数为hPt和hWt的电力线和无线并行信道传输相同的分集信号后，接收端接收到的电力线和无线的时域OFDM采样信号rPt 和rWt分别为
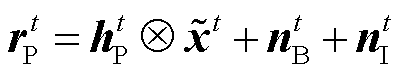（6）
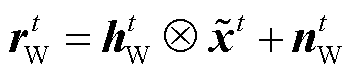（7）
式中，⨂代表卷积运算；nBt和nWt分别为电力线和无线信道上的时域高斯噪声向量，向量中的元素满足均值为零，方差分别为σB2和σ2BW；nIt为时域脉冲噪声向量，方差为σI2，且σI2/σB2≫1。将上述OFDM信号去除CP后进行DFT，获得的电力线和无线信道的等效的频域OFDM信号yPt和yWt可以分别表示为
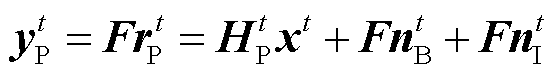（8）
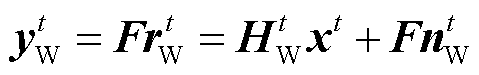（9）
式中，F为DFT算子；xt为第t时刻发送的OFDM频域符号向量，xt=[x1t x2t 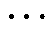xN t ]T，N为子载波的数量；HPt和HWt分别为电力线和无线的等效频域信道系数矩阵，由于利用CP来对抗多径信道造成的频率选择性衰落，本文忽略了码间串扰的影响，所以HPt和HWt均为对角矩阵，且HWt可逆。令yWt左乘矩阵Q可得
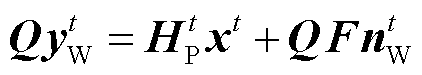（10）
式中，Q=HPt (HWt)-1，(HWt)-1表示HWt的逆矩阵。将式（8）与式（10）相减，可得到双接口信道中抵消数据信号后的噪声频域估计向量Ψt为
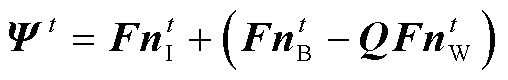（11）
式中，FnIt为时域脉冲噪声经DFT变换后的频域向量；FnBt −QFnWt表示双接口信道的背景噪声干扰项。
对Ψt进行逆离散傅里叶变换F*Ψt，获得噪声时域信号向量ξIt为
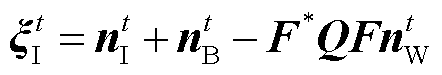（12）
在已知Q的条件下，可将ϖ=nBt−F*QFnWt近似为均值为0，方差为σG2的高斯分布。本文对噪声数据样本进行统计分析，ϖ的统计直方图如图4所示，且ϖ的分布与高斯分布CN～(0, σG2)高度重合。
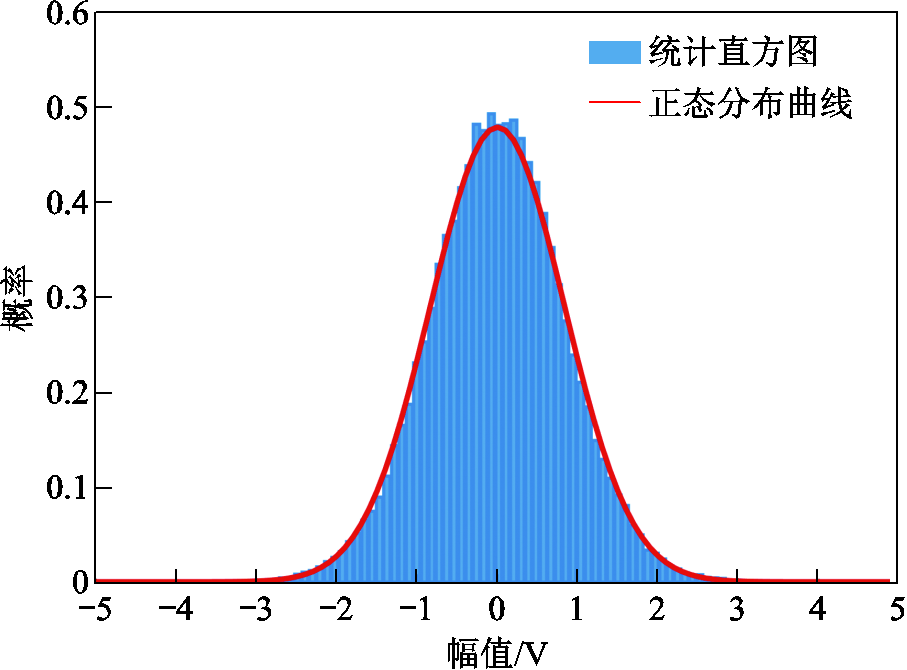
图4 概率密度统计
Fig.4 Chart of probability density statistical
噪声样本提取结果对比如图5所示，显示了基于双接口分集信号抵消的噪声数据提取效果，其中信噪比（Signal to Noise Ratio, SNR）SNR=10 dB。图5a、图5b分别为电力线和无线信道接收的时域信号，图5c给出了处理信号ξIt与实际脉冲噪声的对比结果。由图5a和图5b可知，OFDM系统中存在PAPR，导致在电力线信道中难以直接获取脉冲噪声的位置信息。进行分集信号抵消后，如图5c所示，由于ξIt只剩下背景干扰，PAPR的影响极小，因此可使用非线性变换获取脉冲噪声的位置信息。显然可以将图5c中的噪声数据保存下来，为最佳阈值估计算法提供大数据支持。
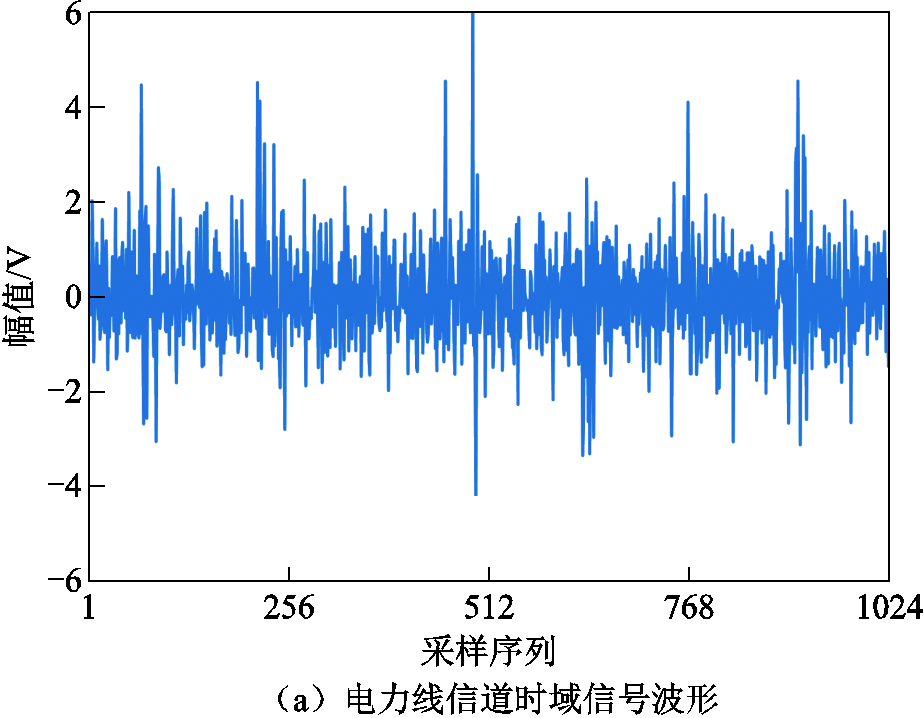
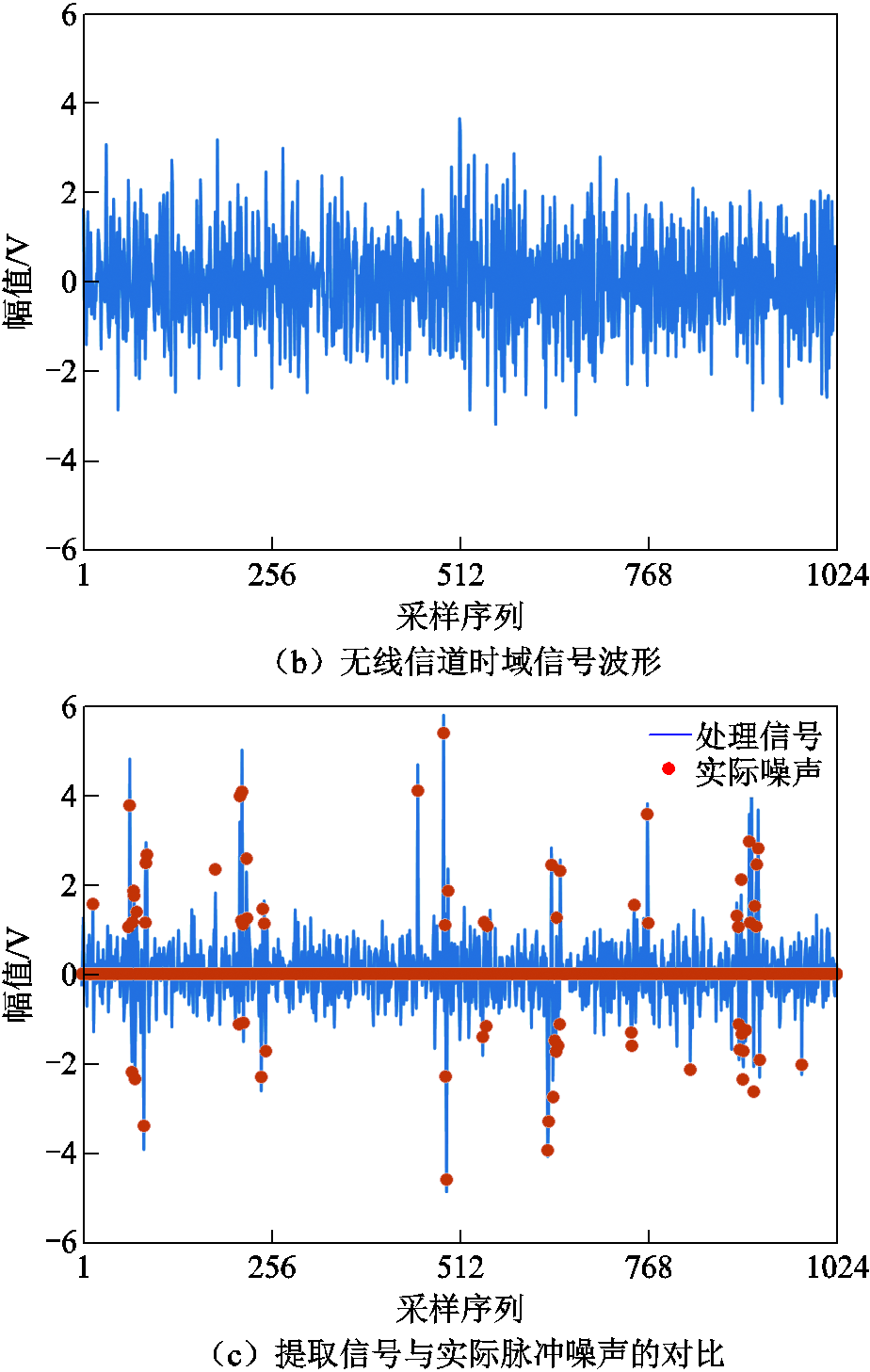
图5 噪声样本提取结果对比
Fig.5 Compare of noise sample extraction results
从图5c中可以看出，采用非线性函数中的置零算法[15]将幅值小于阈值Tt的噪声信号替换为零，保留幅值大于等于Tt的噪声信号最为简单有效。因此对ξIt中的第m个噪声元素采用置零变换为
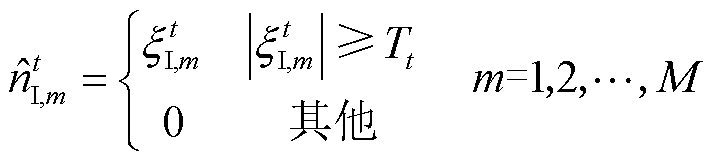（13）
式中，M为采样点总数；|⋅|表示取绝对值；向量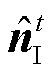
是ξIt的非线性变换输出。然后对yPt进行去除脉冲噪声的处理，即
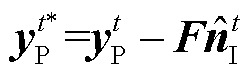（14）
随后将去除脉冲噪声后的电力线信号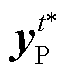
，与无线信号进行合并处理获得yt，最后对第k个子载波采用最大似然检测算法获得的估计符号
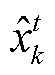为
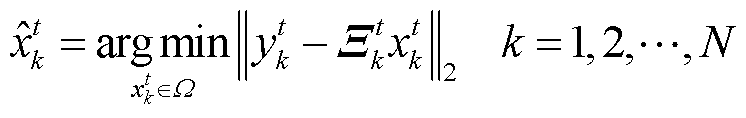（15）
式中，||⋅||2代表2-范数；Ω为调制信号星座点集合；Ξkt表示接收端在第t时刻第k个子载波上的等效信道系数；xkt为发射端的发送符号。
在本节中，首先简单介绍基于传统思路获得最佳阈值的方法，然后提出基于噪声样本的最佳阈值估计算法，并给出算法框图和具体流程。
准确估计出式（13）中的阈值T对算法性能至关重要。传统的加权组合准则（Weighted Combination Criterion, WCC）和Siegert准则（Siegert Criterion, SC）通过平衡脉冲噪声的检测概率和虚警概率，从而获得最佳阈值。由于WCC和SC所需的参数较少，因而获得广泛的研究[23]。
定义Pa为脉冲噪声的良好检测概率，Pb为虚警概率，其中综合目标函数为ηWCC =Pa-Pb，则WCC准则的最佳阈值TWCC为[22]
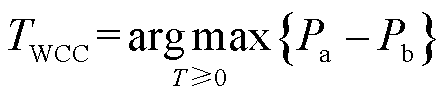（16）
如式（16）所示，WCC准则的关键步骤是以检测概率和虚警概率的综合函数为目标来确定最佳阈值TWCC。由式（16）可知，ηWCC越大，虚警概率和漏检概率就越小。与文献[22]中的求解步骤相同，在已知脉冲噪声的功率σI2和背景干扰的功率σG2的条件下，可以先分别给出Pa和Pb的公式，再将目标函数ηWCC对阈值T求偏导，可得最佳阈值TWCC为
（17）
同理，令目标函数ηSC=PIPa+PB(1-Pb)，参考文献[22]的步骤即可得到SC准则的最佳阈值TSC。
图6对比了在不同信噪比下，误码率（Bit Error Rate, BER）、ηWCC和ηSC随阈值T的变化情况。可以看出，以BER最小化为目标存在最佳阈值T*，但最佳阈值T*和两种准则获得的阈值TWCC、TSC存在一定的偏差。这是因为两种准则都是以检测概率和虚警概率为综合目标求解阈值，而不是直接使用BER作为优化目标。
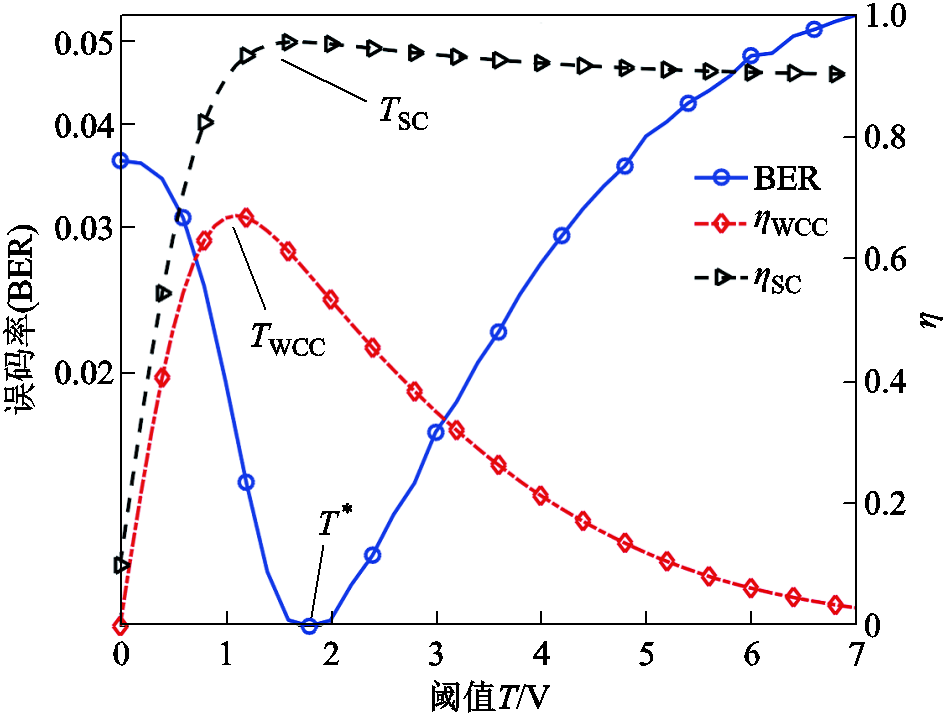
图6 WCC/SC与BER的最佳阈值对比分析
Fig.6 Comparative analysis of the best threshold between WCC/SC and BER
传统阈值估计算法需要精确的噪声参数。由于通信环境的非平稳性，导致参数的获取较为困难，且传统算法获取的阈值与真实的最优解之间存在一定的偏差。
受到基于数据驱动的机器学习[12,24-25]和迁移学习[26-28]的启发，通过噪声样本和梯度下降法来获取非线性函数的最佳阈值是处理脉冲噪声的一个新思路。对比传统算法，基于噪声样本的优化算法可以根据实际环境不断调节参数，以达到直接对目标函数进行优化，减小偏差的目的。由于没有公开的脉冲噪声数据库，可利用本文提出的分集抵消算法构建噪声样本数据库，并用于最佳阈值估计。为了保证算法的实时性，还需要利用最新的噪声样本进行阈值的迭代更新，以应对环境或参数的变化。
最佳阈值估计算法和目标函数的选择密切相关，需要针对不同的通信场景和性能指标建立具体的目标函数。本文主要给出以下两种形式：
1）最小化BER。在OFDM通信系统中，使用BER评价算法性能最为常见，这也是服务质量（Quality of Service, QoS）的重要指标之一。本文通过式（15）的译码判决获得的符号，与发送端发送的符号进行比较，从而获得误码率。Pr(yt(Tt))表示在第t时刻使用阈值Tt获得的OFDM误码率，有
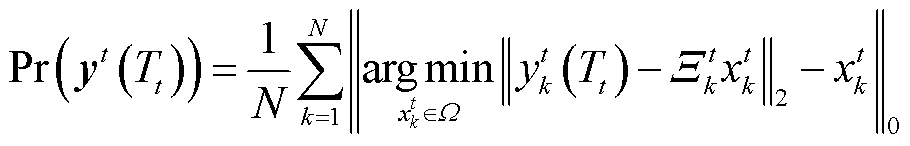（18）
式中，||⋅||0代表0-范数（即非零元素的数量）。目标函数为
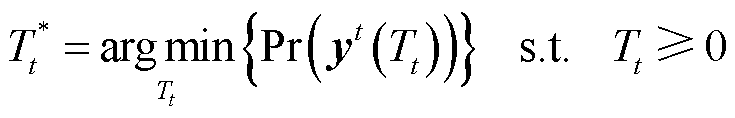（19）
2）最大化传输速率Rt：传输速率和信道质量直接相关。当归一化信道带宽后，可通过消除信道中的脉冲噪声，提高等效信噪比，也就间接性地提高了信道的传输能力。因此可基于短包理论[28]，以有限长编码的传输速率最大化为目标优化噪声阈值，其平均传输速率可以表示为
（20）
式中，γkt (Tt)为接收端第t时刻第k个子载波的等效信噪比；V为信道色散；L为编码长度；Q-1(⋅)为反函数；ε为误码率，则目标函数为
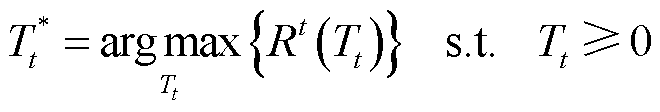（21）
不同目标函数的特性表现相似，可以采用相同的优化设计方法，本文重点对以最小化BER为目标函数的优化过程进行介绍。
在第t时刻，由于接收端只能获得信号yPt、yWt以及信道系数矩阵HPt和HWt，所以无法直接获得第t时刻的误码率，无法进行阈值优化。基于实时噪声样本的构建/更新，本文将最小化当前时刻误码率问题转换为最小化噪声样本误码率问题，从而获得当前时刻的最佳阈值Tt*，其表达式为
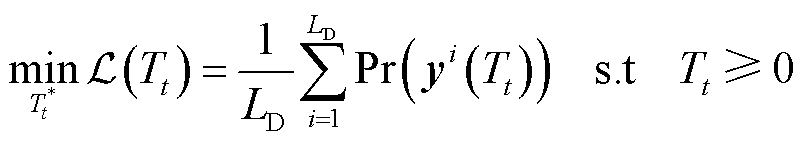（22）
式中，LD为噪声样本的大小。随机信道条件下，LD的选择需要考虑计算精度和复杂度的折中。
如图7所示，在第t时刻进行阈值更新时，首先要根据折扣因子Γ计算数据样本中各个时刻的权重λi，i=1,2,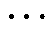, LD；然后根据前一时刻（即第t-1时刻）的阈值Tt-1，结合权重λi对数据样本DEN求误码率；随后通过梯度下降法获得阈值Tt-1对应的误码率的梯度值∇(Tt-1)；最后使用学习率
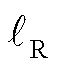更新当前时刻的阈值Tt*=Tt-1+ℓR∙∇(Tt-1)。附录中介绍了Tt的求解过程，结果为
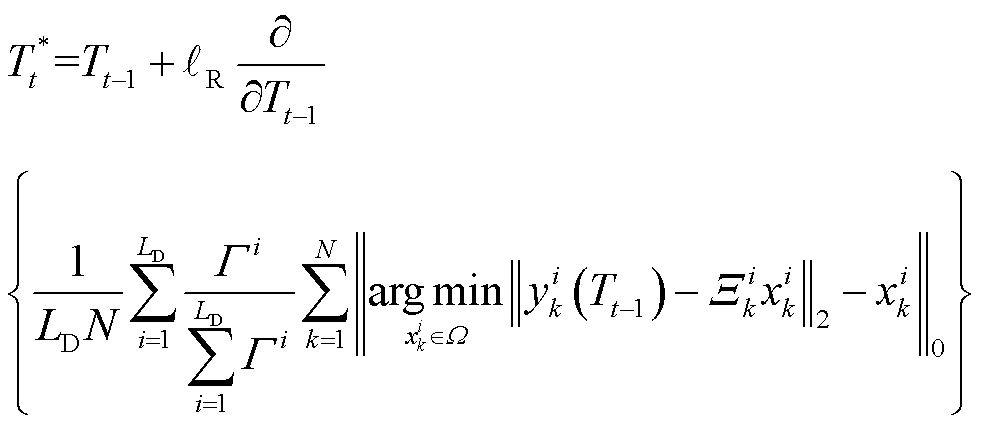（23）
除此之外，本文采用队列存储方式（先进先出准则）保存/更新噪声样本，从而保证噪声数据的有效性。此算法的具体步骤如下所示。
算法1 基于噪声样本的阈值更新算法 输入：学习率，折扣因子Γ，迭代次数jMAX,误差精度δ，阈值Tt-11：从存储区中获取LD个数据样本DEN2：令Tt,0= Tt-13：循环j=1: jMAX4： 执行式（23）更新阈值Tt,j=Tt,j-1+ ∙∇(Tt,j-1)5： 如果绝对误差| Tt,j- Tt,j-1|≤δ成立6： 则算法收敛，退出循环7： 否则8： 算法未收敛，返回步骤49： 直到算法收敛或超出循环最大次数10：输出估计的阈值Tt*
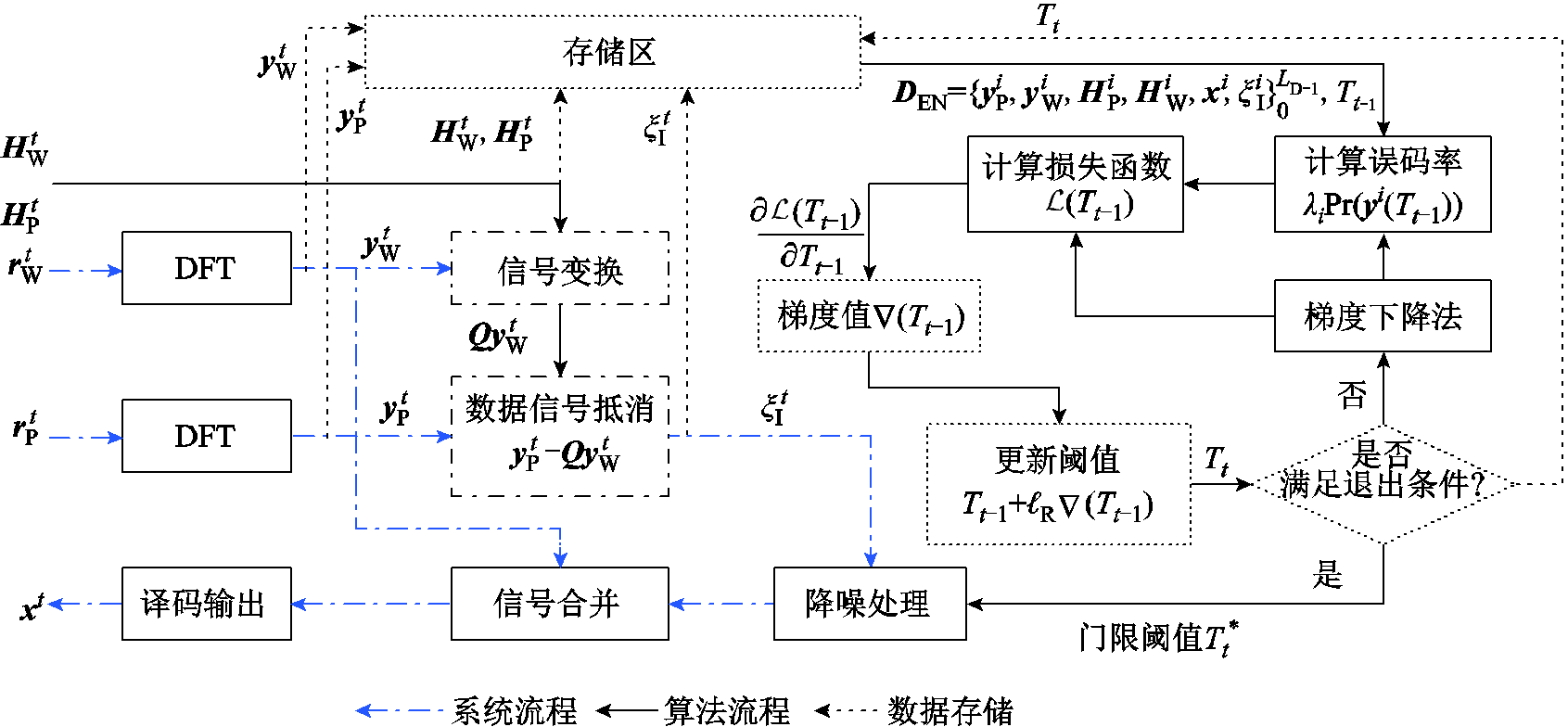
图7 基于数据样本的最佳阈值算法框图
Fig.7 Block diagram of optimal threshold algorithm based on data samples
通过上述步骤，可以获得更加精确的阈值。通过式（13）重构脉冲噪声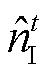
，并通过式（14）从解调之前的频域OFDM信号中减去重构的脉冲噪声，再将已经剔除脉冲噪声的接收信号进行合并处理、译码判决等操作即可获得数据符号。
下面从计算复杂度、阈值精度和更新速率等方面分析本文算法的特点。
1）复杂度分析。在以最小化BER为目标的过程中，本文算法的复杂度主要涉及判断、加减法和乘法三种运算。其中判断、加减法为运行效率最快的线性运算，主要包括式（13）非线性变换、式（14）脉冲噪声去除和式（18）译码判决三部分；乘法主要包括Ξktxkt、||⋅||2、DFT等计算。经过分析，在一次迭代计算中，线性运算量和乘法运算的复杂度均为O(kN)。
2）阈值精度。噪声样本直接来源于通信所处的物理环境，能准确地反映当前时刻的通信质量，在不需要噪声模型和参数的前提下获得更加精确的阈值。传统算法需要获得环境的统计数据和相关模型，会出现实际环境与模型不匹配的现象。
3）更新速率。当环境发生变化时，需要快速适应信道或者环境的动态变化。通过学习率和折扣因子，本文算法DSC-ATE可根据环境变化动态调整阈值，减小与实际阈值的偏差。而传统算法受到统计模型的约束，当模型参数不变时，无法快速调整阈值。
为了验证所提算法对脉冲噪声的抑制性能，本文进行了数值仿真。参考文献[10, 22]，不失一般性，仿真和计算过程中的参数设置见表1。已知电力线和无线信道的衰落分布，式（6）和式（7）中的信道增益是随机产生的，即算法处理过程中的每个样本对应的信道增益是不同的。在本次仿真中，本文选取置零[15]、指数拖尾[20]进行比较。除此之外，本文还对比了加权组合准则与Siegert准则的效果[22]。为更好地分析不同算法的性能，若无特别说明，所有算法都会在双接口并行通信系统中运行仿真。
表1 系统仿真参数
Tab.1 The parameters of system simulation
参数数值 采样点数量M1 024 子载波数量N512 电力线信道衰落系数σP2/dB2 无线信道衰落系数σW20.5 脉冲噪声概率0.1 记忆参数ϛ10 σI2/σB2 /dB20 调制方式正交相移键控 误差精度d/V0.01 数据样本长度LD /帧200 学习率15～35 折扣因子Γ0.7～1.0
由于参数的选择对于本文算法DSC-ATE的稳健性和运行效率至关重要，因此图8～图10分别给出了噪声样本长度LD、学习率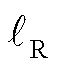以及折扣因子Γ对DSC-ATE算法性能的影响，并为后面的仿真给出合适的参数。
图8 标准差的变化趋势图
Fig.8 The variation trend of Standard Deviation
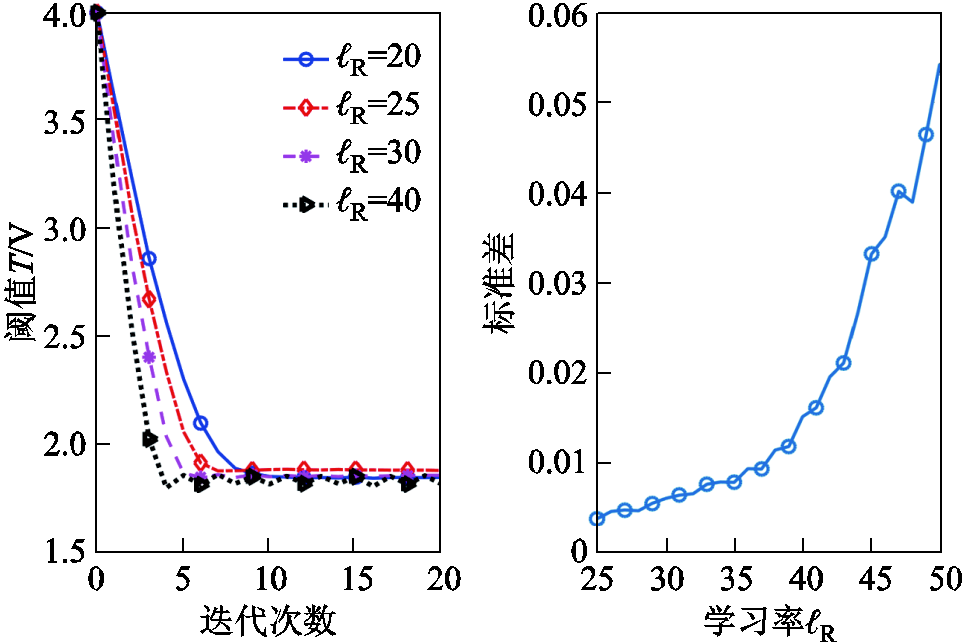
图9 DSC-ATE算法的收敛性能分析
Fig.9 Convergence performance analysis of DSC-ATE algorithm
算法收敛后的稳定性随学习率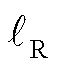和数据样本长度LD变化的三维趋势如图8所示，其中SNR=10 dB，Γ =1，标准差是指在平稳环境中，各个时刻的估计阈值与长期平均阈值的偏差程度。由图8可知，学习率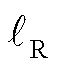固定时，LD越小，阈值波动性越大；LD越大，阈值越稳。但是LD过大会增加计算、存储负担和数据样本获取时间，使得阈值的更新速度变慢。因此可根据精度和复杂度等实际需要选择LD。
不同学习率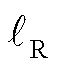的收敛趋势如图9所示，其中SNR=10 dB，Γ =1，LD=200。图9a为算法收敛速度与迭代次数的关系，图9b为各个时刻的估计阈值与平均阈值的标准差。从图9中可以看出，学习率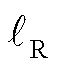较小时，算法需要的迭代次数较多；随着学习率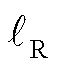的增加，算法收敛速度越来越快，但波动性也越来越大。例如，当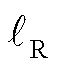=25时，算法需要迭代8次，标准差为0.004；当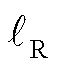=40时，收敛次数仅为5次，但是标准差增加到0.014，且当学习率继续增加时，标准差呈指数形式增加。为了实现收敛速度与阈值精度的折中，学习率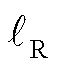应小于40，因此在后续的仿真中本文以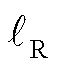=30作为基准。
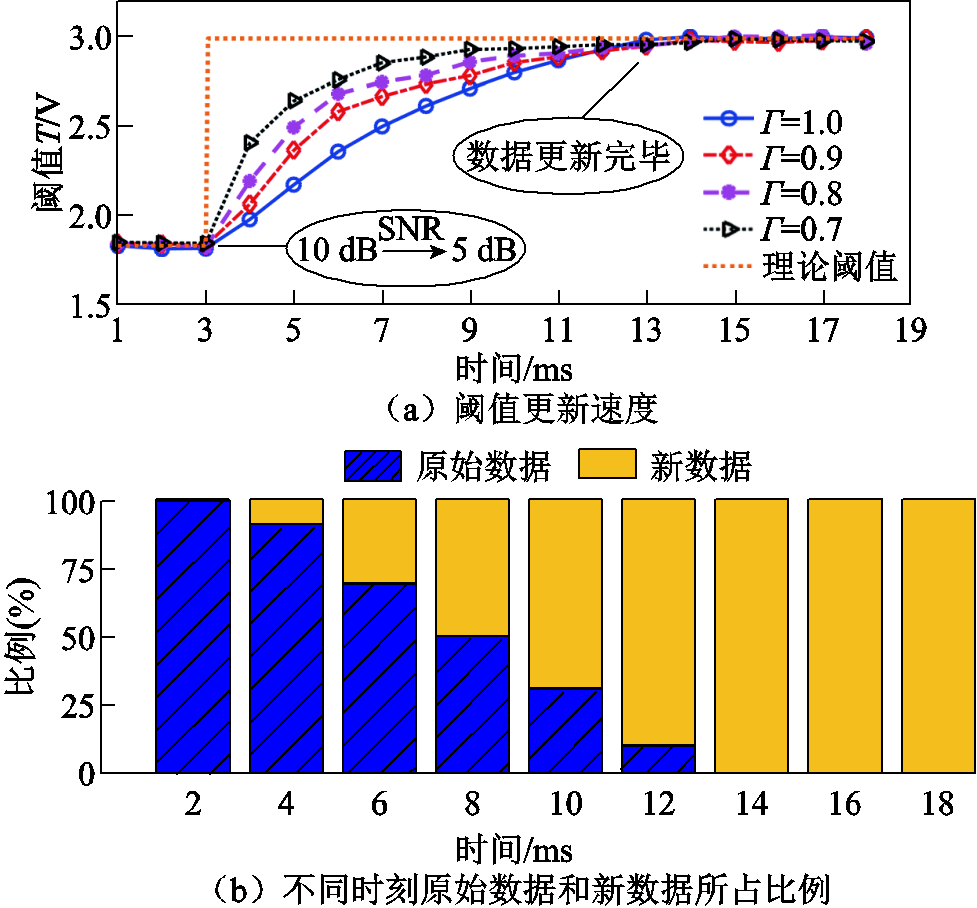
图10 折扣因子对算法反映时间的影响
Fig.10 Effect of the discount factor on reflection time of the algorithm
折扣因子对算法反映时间的影响如图10所示，展示了信道环境发生变化时本文算法的性能表现。假设每个OFDM符号周期为50 μs[10]（包括数据和CP部分），其中LD=200，所以大约需要10 ms才能更新完噪声样本数据库。从图10中可以看出，通过调节折扣因子Γ的大小，改变数据样本中的权重，在获得少量数据时就可以改变当前时刻的阈值。例如当折扣因子Γ =0.7时，新数据只占据总样本的40%，即只需收集4 ms的数据，阈值就可以从1.85更新到2.86，与最佳阈值2.99仅有0.13的误差。而对于Γ=1，则新数据要占总样本的80%（需要收集8ms的数据）才能达到相同的效果。这是因为在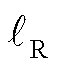
和LD固定时，Γ越小，算法越注重近期的新数据，计算中新数据在更新阈值时所占的权重越大，算法反映时间就越短。因此当数据样本存在一定的差异性时，本文算法可以快速调整阈值，从而保证精度不会明显降低。
不失一般性，后面仿真中，本文选择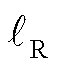=30、LD=200、Γ =0.7作为系统的参数使用。
不同算法估计的阈值与蒙特卡洛仿真（Monte Carlo Simulation, MCS）获得的最佳阈值的对比见表2。由表2可见，本文算法DSC-ATE在不同信噪比下获得的阈值精度明显高于其他算法，能接近最佳阈值，WCC和SC在不同信噪比下都有不同程度的误差。其中WCC估计的阈值明显低于最佳阈值，且误差较大，而SC的阈值误差明显小于WCC，这是因为SC同时考虑了脉冲噪声产生的平均概率，因此计算的结果也更加精确。而本文算法由于经过预处理，抵消了电力线信号中的数据部分，因此降低了PAPR的影响。另外，目标函数采用了最小化BER，从而减小了系统偏差。
表2 最佳阈值对比分析
Tab.2 Comparative analysis of optimal threshold
SNR/dB最佳阈值/V MCS仿真DSC-ATEWCCSC 14.3304.4652.8814.304 43.2803.2892.0983.153 82.2802.1781.3712.068 121.5301.4810.8881.349 161.1301.0540.5750.879
不同阈值下的BER性能分析如图11所示，对比了在不同信噪比下，采用不同算法在不同阈值Tt情况下的误码率。从图11中可以看出，当SNR＞5 dB时，本文所提算法性能优于其他算法，且随着SNR增大，性能越来越好。三种算法都存在最佳阈值Tt*使得BER最小。随着SNR的增加，阈值Tt对BER的影响越明显，因此需要更加精确的阈值估计方法来提升系统BER等性能。显然本文的算法具有较好的精度和灵活性。
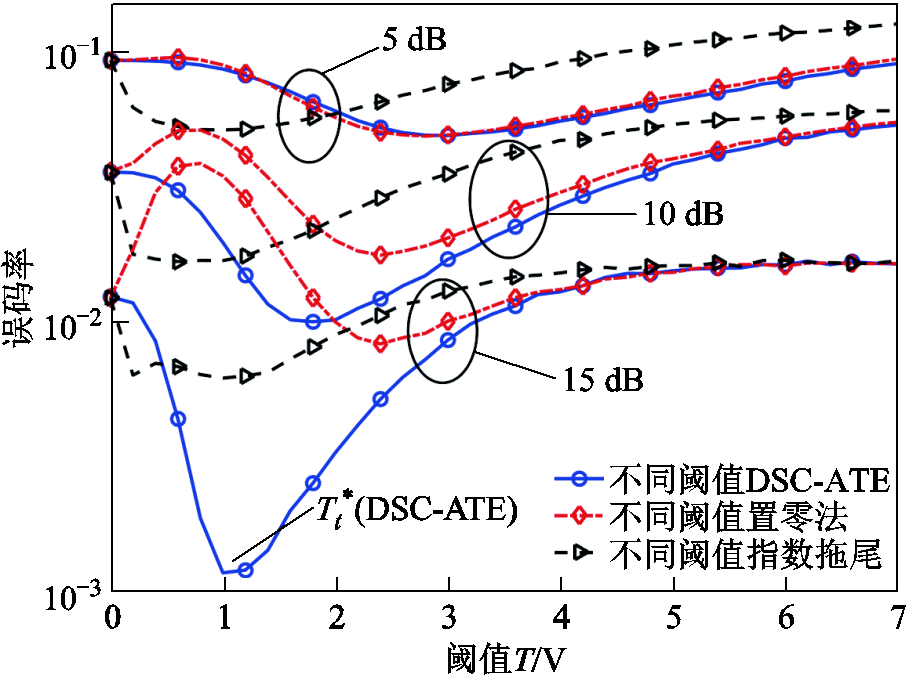
图11 不同阈值下的BER性能分析
Fig.11 Performance analysis of BER under different thresholds
BER性能分析如图12所示。为了更好地分析，本文绘制了在只使用单接口电力线信道进行信号传输（总发射功率相同）时的性能，并采用置零算法对脉冲噪声进行处理。在没有使用任何脉冲噪声抑制算法时，系统的误码率较大，此时对应图中的“无处理”曲线。本文算法DSC-ATE的BER性能始终优于WCC和SC，且随着SNR的增加，性能差异越来越大。值得注意的是，当SNR＞4 dB后，即使对双接口系统不进行脉冲噪声的处理，其BER也低于单接口PLC的，这是因为随着SNR的增加，分集传输所带来的增益逐渐发挥作用。
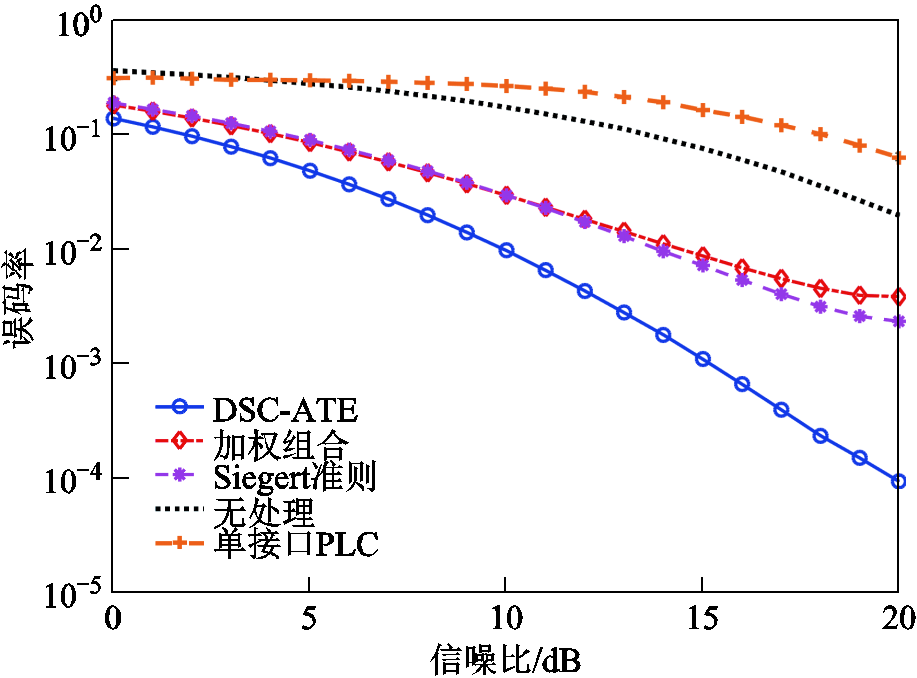
图12 BER性能分析
Fig.12 Performance analysis of BER
图13和图14为不同算法传输速率的性能对比图。仿真主要根据式（21）中以传输速率最大化为目标进行优化。不失一般性，取编码长度L=400，误码率ε=10-5。其中归一化的传输速率Rt可由式（20）计算得到，等于N个子载波速率的平均值，与脉冲噪声消除后的等效信噪比密切相关。
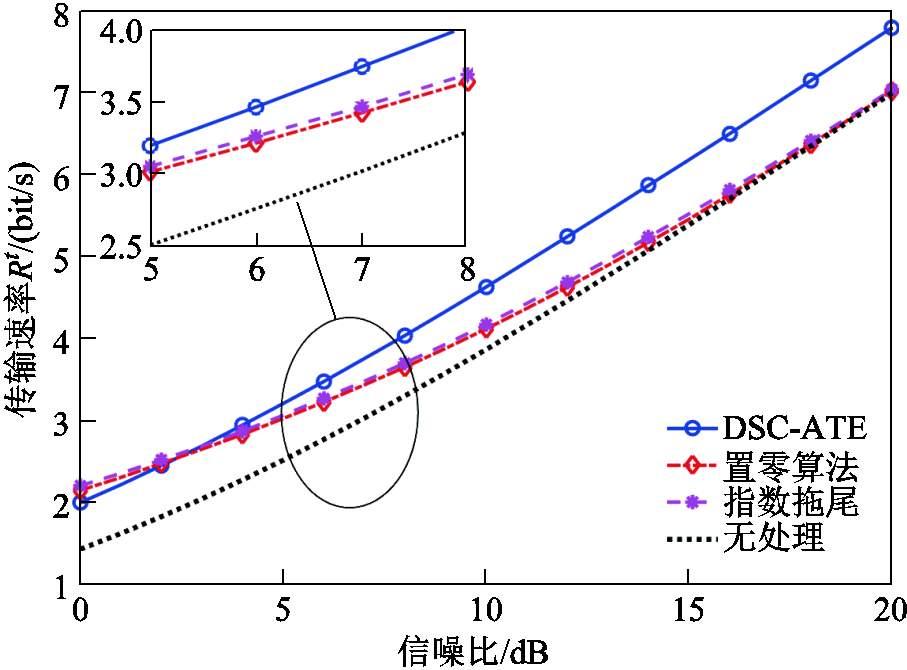
图13 不同算法的传输速率Rt性能分析
Fig.13 Performance analysis of transmission rate Rt of different algorithm
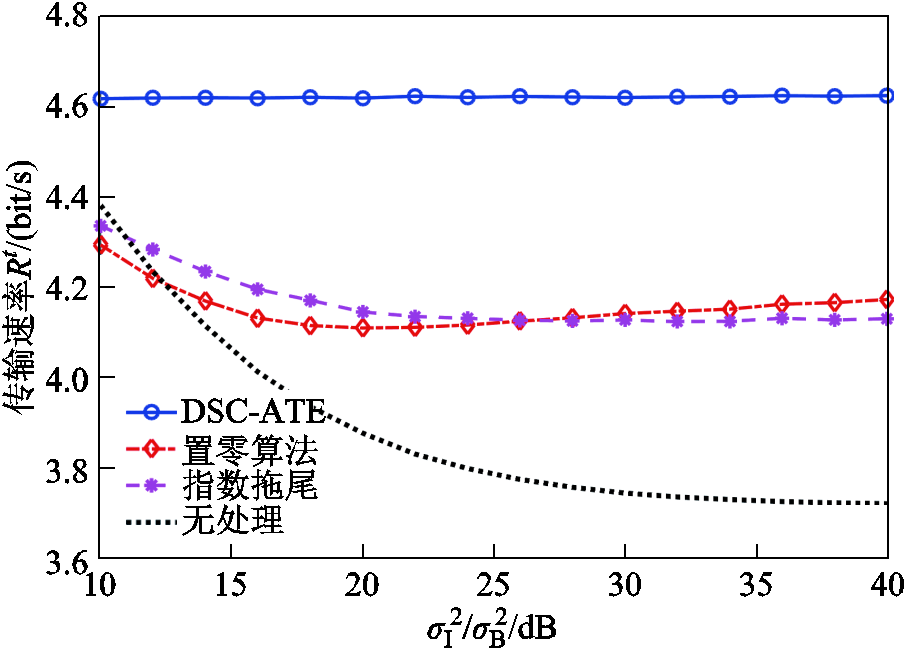
图14 传输速率Rt性能分析
Fig.14 Performance analysis of transmission rate Rt
不同算法的传输速率Rt性能分析如图13所示。从中可以看出，当SNR＞4 dB后，本文算法的Rt明显高于其他算法。随着SNR的增大，置零算法和指数拖尾算法的性能越来越差，这是因为随着SNR的增加，脉冲噪声的幅值越来越小，而信号幅值保持不变，导致脉冲噪声与信号的区分度不明显而造成虚警概率的增加，降低了算法的性能。本文算法由于预先消除了信号功率，只剩下背景干扰，没有PAPR的干扰，因此算法性能始终优于其他两种算法。
图14给出了不同算法的传输速率Rt随σI2/σB2的变化趋势图。其中SNR=10 dB。从中可以看出，对于置零算法，随着σI2/σB2的增加，Rt先降低后增加。而对于指数拖尾算法，Rt始终降低，且当σI2/σB2 ＜25 dB时，指数拖尾算法的性能优于置零算法。而本文算法的Rt几乎不受影响，且始终高于其他算法，说明了本文算法对σI2/σB2的不确定性具有一定的稳健性。这是因为当SNR确定后，由于本文算法在进行非线性变换之前进行了预处理，抵消了数据部分，因此影响本文算法性能的只有背景噪声，又因为σI2/σB2 ≫ 1，所以性能的变化较小。
本文设计了一种基于分集信号抵消和自适应阈值估计的算法用来抑制双接口通信中电力线信道中的突发脉冲噪声。首先考虑分集信号的一致性，利用无线信道辅助电力线信道进行预处理，提取出噪声样本。为了精确地估计出噪声阈值，利用数据样本与目标函数最小/大化算法迭代估计噪声阈值，从而确定脉冲噪声的位置信息。仿真结果表明，该方法能有效地提高突发脉冲噪声的抑制能力和通信系统的可靠性。今后可针对窄带噪声、混合噪声等其他噪声模型，将本文算法与稀疏理论、压缩感知等相结合进行研究，以研究本文算法对其他噪声的消除性能。
附 录
引理1：定义第t-1时刻和第t时刻的阈值分别为Tt-1和Tt*，令第t时刻的发送数据为xkt；第k个子载波上的等效信道系数为Ξkt，去除脉冲噪声后的电力线信号与无线信号进行最大比合并为ykt；调制信号星座点集合为Ω；学习率为
，数据子载波数量为N，折扣因子为Γ，数据样本DEN。则以最小误码率为目标，基于平均误码率和梯度下降算法的最佳阈值可表示为
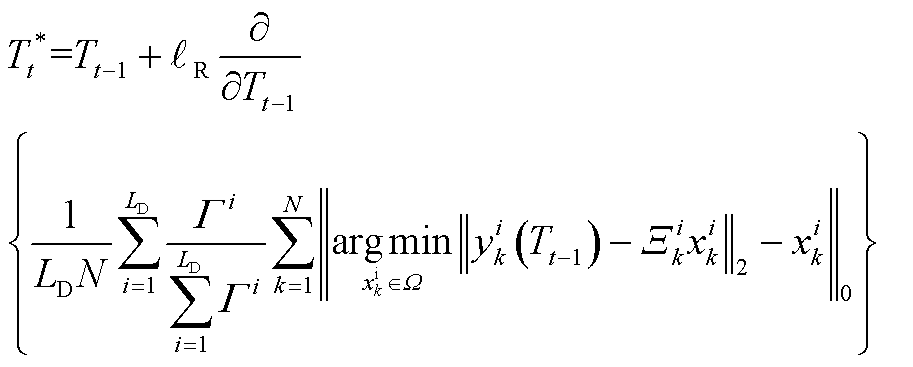（A1）
证明：已知第t-1时刻的阈值Tt-1，调制信号星座点集合为Ω，则在第t时刻，从数据样本中按照堆栈（后进先出准则）的方式获取LD帧的数据。根据最大似然法，可得到第i个数据帧第k个子载波的判决结果为
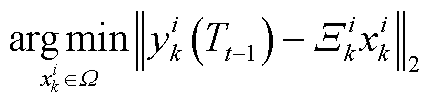（A2）
则第i个数据帧的误码率可以表示为
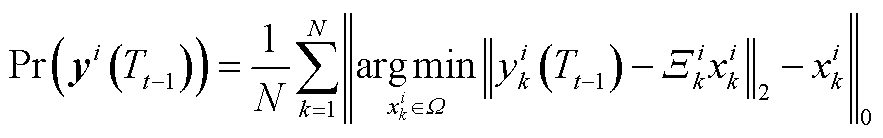（A3）
因此可得LD个数据帧的平均误码率为
（A4）
在非平稳环境中，距离当前时刻越远的旧数据，参考价值越低，而越新鲜的数据，其参考价值越高。因此需要对不同时刻的数据分配不同的权重，从而保证算法的稳定性和阈值的精度，则函数ℒ(Tt-1)可被改进为
（A5）
式中，λi为不同时刻的权重系数，是折扣因子Γ进行幂次运算后的归一化，即
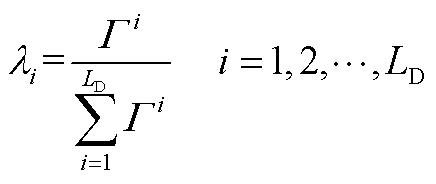（A6）
由于采用堆栈的读取方式，i越小，表示数据越新鲜。从中可以看出，Γ越小，系统越注重近期的数据；Γ越大，系统会兼顾长期的数据，这将驱动阈值更加快速有效地收敛。通过最小化目标函数ℒ (Tt-1)，可将当前阈值Tt-1更新为Tt*，首先，对ℒ (Tt-1)求梯度可得
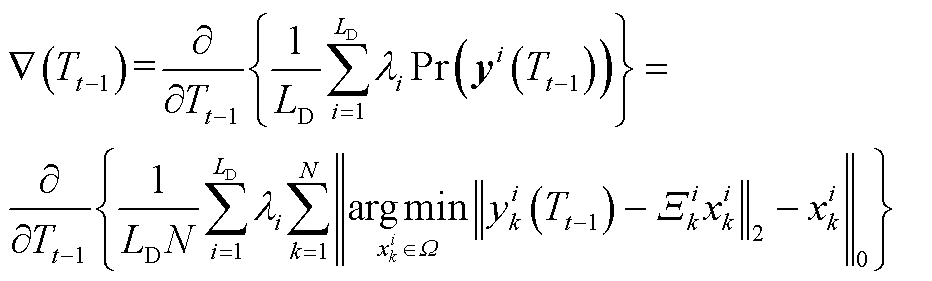（A7）
最终，第t时刻更新阈值Tt*为
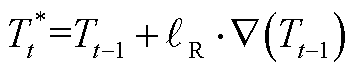（A8）
即
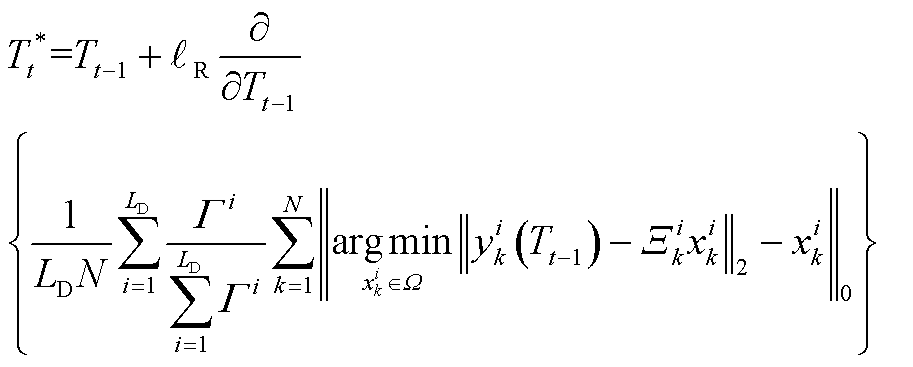（A9）
证明完毕。
参考文献
[1] de L Filomeno M, de Campos M L R, Poor H V, et al. Hybrid power line/wireless systems: an optimal power allocation perspective[J]. IEEE Transactions on Wireless Communications, 2020, 19(10): 6289-6300.
[2] Liu Huanlin, Zhu Pingxin, Chen Yong, et al. Power allocation for downlink hybrid power line and visible light communication system[J]. IEEE Access, 2020, 8: 24145-24152.
[3] 黄彦钦, 余浩, 尹钧毅, 等. 电力物联网数据传输方案：现状与基于5G技术的展望[J]. 电工技术学报, 2021, 36(17): 3581-3593. Huang Yanqin, Yu Hao, Yin Junyi, et al. Data transmission schemes of power Internet of Things: present and outlook based on 5G technology[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3581-3593.
[4] Qian Yuwen, Yan Jiahui, Guan Haibing, et al. Design of hybrid wireless and power line sensor networks with dual-interface relay in IoT[J]. IEEE Internet of Things Journal, 2019, 6(1): 239-249.
[5] Chen Zhixiong, Wang Lijiao, Han Dongsheng, et al. A unified performance analysis of relaying communication system for IoT application with hybrid fading[J]. IEEE Internet of Things Journal, 2020, 7(1): 570-583.
[6] 蒲红红, 刘晓胜, 韩铭, 等. 电力线通信信道下协作非正交多址接入系统的分布式机会中继选择[J]. 电工技术学报, 2020, 35(11): 2306-2318. Pu Honghong, Liu Xiaosheng, Han Ming, et al. Distributed opportunistic relay selection for cooperative non-orthogonal multiple access power line communication networks[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2306-2318.
[7] 史燕平, 王丽娇, 李秀彩, 等. 电力线和无线双媒质通信系统的自适应中继协议[J]. 电力自动化设备, 2021, 41(6): 171-179. Shi Yanping, Wang Lijiao, Li Xiucai, et al. Adaptive relay protocol for power line-wireless hybrid media communication system[J]. Electric Power Automation Equipment, 2021, 41(6): 171-179.
[8] Bai Tong, Zhang Hongming, Wang Jingjing, et al. Fifty years of noise modeling and mitigation in power-line communications[J]. IEEE Communications Surveys & Tutorials, 2021, 23(1): 41-69.
[9] Lai S W, Shabehpour N, Messier G G, et al. Performance of wireless/power line media diversity in the office environment[C]//2014 IEEE Global Communications Conference, Austin, TX, USA, 2015: 2972-2976.
[10] Elgenedy M, Awadin M M, Hamila R, et al. Sparsity-based joint NBI and impulse noise mitigation in hybrid PLC-wireless transmissions[J]. IEEE Access, 2018, 6: 30280-30295.
[11] 邓蓉, 谭周文, 肖郭璇, 等. 基于压缩感知的电力线脉冲噪声抑制[J]. 电工技术学报, 2018, 33(23): 5555-5563. Deng Rong, Tan Zhouwen, Xiao Guoxuan, et al. Impulse noise suppression in power line communication based on compressed sensing[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5555-5563.
[12] 吕新荣, 李有明, 国强. MIMO-OFDM系统的信道与脉冲噪声联合估计方法[J]. 通信学报, 2021, 42(12): 54-64. Lyu Xinrong, Li Youming, Guo Qiang. Joint channel and impulsive noise estimation method for MIMO-OFDM systems[J]. Journal on Communications, 2021, 42(12): 54-64.
[13] Gao Shuang, Zheng Jianping. Clipping noise recovery of OTFS signals using reliability-based compressed sensing[J]. IEEE Transactions on Vehicular Technology, 2021, 70(7): 7187-7192.
[14] 罗忠涛, 郭人铭, 詹燕梅. 脉冲噪声非线性变换设计的研究综述[J]. 系统工程与电子技术, 2021, 43(7): 1971-1980. Luo Zhongtao, Guo Renming, Zhan Yanmei. Review of nonlinear transformation design for impulsive noise[J]. Systems Engineering and Electronics, 2021, 43(7): 1971-1980.
[15] 谭周文, 刘宏立, 成运. 低压电力线通信自适应脉冲噪声抑制[J]. 电力系统及其自动化学报, 2022, 34(1): 129-136. Tan Zhouwen, Liu Hongli, Cheng Yun. Adaptive mitigation of impulsive noise in low-voltage power line communication[J]. Proceedings of the CSU-EPSA, 2022, 34(1): 129-136.
[16] Rožić N, Banelli P, Begušić D, et al. Multiple-threshold estimators for impulsive noise suppression in multicarrier communications[J]. IEEE Transactions on Signal Processing, 2018, 66(6): 1619-1633.
[17] Zhidkov S V. Analysis and comparison of several simple impulsive noise mitigation schemes for OFDM receivers[J]. IEEE Transactions on Communications, 2008, 56(1): 5-9.
[18] Vadali S R K, Ray P, Mula S, et al. Linear detection of a weak signal in additive cauchy noise[J]. IEEE Transactions on Communications, 2017, 65(3): 1061-1076.
[19] Kim Y C, Bae J N, Kim J Y. Novel noise reduction scheme for power line communication systems with smart grid applications[C]//2011 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 2011: 791-792.
[20] 罗忠涛, 詹燕梅, 郭人铭, 等. 脉冲噪声中基于指数函数的可变拖尾非线性变换设计[J]. 电子与信息学报, 2020, 42(4): 932-940. Luo Zhongtao, Zhan Yanmei, Guo Renming, et al. Variable tailing nonlinear transformation design based on exponential function in impulsive noise[J]. Journal of Electronics & Information Technology, 2020, 42(4): 932-940.
[21] 张慧, 卢文冰, 赵雄文, 等. 基于最小二乘支持向量机和小波神经网络的电力线通信信道噪声建模研究[J]. 电工技术学报, 2018, 33(16): 3879-3888. Zhang Hui, Lu Wenbing, Zhao Xiongwen, et al. Noise modeling for power line communication channel using the LS-SVM and wavelet neural networks[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3879-3888.
[22] Alam M S, Selim B, Kaddoum G, et al. Mitigation techniques for impulsive noise with memory modeled by a two state Markov-Gaussian process[J]. IEEE Systems Journal, 2020, 14(3): 4079-4088.
[23] Ndo G, Siohan P, Hamon M H. Adaptive noise mitigation in impulsive environment: application to power-line communications[J]. IEEE Transactions on Power Delivery, 2010, 25(2): 647-656.
[24] 臧海祥, 程礼临, 刘玲, 等. 基于数据驱动的太阳辐射估计和预测研究与展望[J]. 电力系统自动化, 2021, 45(11): 170-183. Zang Haixiang, Cheng Lilin, Liu Ling, et al. Research and prospect for data-driven estimation and prediction of solar radiation[J]. Automation of Electric Power Systems, 2021, 45(11): 170-183.
[25] Zheng Jialin, Zhao Zhengming, Shi Bochen, et al. A discrete state event driven simulation based losses analysis for multi-terminal megawatt power electronic transformer[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4): 275-284.
[26] 臧海祥, 郭镜玮, 黄蔓云, 等. 基于深度迁移学习的时变拓扑下电力系统状态估计[J]. 电力系统自动化, 2021, 45(24): 49-56. Zang Haixiang, Guo Jingwei, Huang Manyun, et al. State estimation for power systems with time-varying topology based on deep transfer learning[J]. Automation of Electric Power Systems, 2021, 45(24): 49-56.
[27] 陈剑, 杜文娟, 王海风. 采用深度迁移学习定位含直驱风机次同步振荡源机组的方法[J]. 电工技术学报, 2021, 36(1): 179-190. Chen Jian, Du Wenjuan, Wang Haifeng. A method of locating the power system subsynchronous oscillation source unit with grid-connected PMSG using deep transfer learning[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 179-190.
[28] She Changyang, Sun Chengjian, Gu Zhouyou, et al. A tutorial on ultrareliable and low-latency communi-cations in 6G: integrating domain knowledge into deep learning[J]. Proceedings of the IEEE, 2021, 109(3): 204-246.
Abstract Hybrid power line and wireless communication has wide application prospect in the Internet of Things. How to suppress the pulse noise of the power line channel in dual interface communication and improve the reliability of communication system is one of the key problems to be solved urgently. Aiming at the interference problem of power line burst pulse noise (BIN) in the power line and wireless dual interface communication, this paper put forward a BIN suppression algorithm based on diversity signal cancellation and adaptive threshold estimation (DSC-ATE), by using the independence and difference of power line and wireless channel and the consistency of diversity signal. In DSC-ATE, the wireless channel is used to assist the power line channel to extract the noise samples, and then the pulse noise threshold is estimated adaptively through the noise samples, finally the pulse noise is separated from the received signal.
The traditional OFDM system has the problem of peak-to-flat ratio PAPR, which is difficult to obtain the position information of pulse noise directly in the power line channel. Based on the dual-interface communication architecture, a noise sample extraction method based on diversity signal cancellation is proposed, which improves the accuracy of noise detection and can be applied to the optimal threshold prediction. The simulation results show that after diversity signal cancellation, the effect of PAPR is minimal because only background interference remains, and the precise position information of impulse noise can be obtained by using nonlinear transformation, which provides data support for the optimal threshold estimation algorithm.
Secondly, the sample space of impulse noise is constructed by means of signal cancellation processing in diversity transmission, in which the noise data of low SNR ensures the diversity of samples. Then, an optimal threshold estimation algorithm based on noise sample data and nonlinear functions is proposed, which can minimize the bit error rate of the communication system and does not require the prior information of impulse noise. The simulation result shows that the performance of threshold precision, transmission rate, and bit error rate under different SNRs of the algorithm is superior to the traditional algorithms such as the weighted combination criterion (WCC) and siegert criterion (SC). The proposed algorithm also has certain robustness and robustness under different channel fading and noise parameters.
Finally, aiming at the problem of pulse noise elimination in non-stationary environment, the noise threshold is iteratively estimated by using the data sample and the objective function minimization/maximization algorithm, so as to determine the location information of the pulse noise. The convergence rate of the algorithm is adjusted by importing parameters such as learning rate and discount factor, and the threshold can be dynamically adjusted according to the changes of the environment, so as to achieve the effective compromise between the robustness and convergence rate of the algorithm. The simulation result shows that when the learning rate of the algorithm is fixed, the larger the data sample length is, the smaller and more stable the threshold fluctuation is. However, the large data sample length will increase the computational burden, storage burden, and data sample acquisition time, which slow down the update speed of the threshold. In the future, the proposed algorithm DSC-ATE can be combined with sparse theory and compressed sensing for other noise models such as narrowband noise, to further improve the universality of the algorithm.
keywords：Dual interface communication, burst impulse noise, data samples, optimal threshold
国家自然科学基金（61601182）和中央高校科研业务费专项资金（2021MS070）资助项目。
收稿日期 2022-05-04
改稿日期 2022-07-20
DOI:10.19595/j.cnki.1000-6753.tces.220721
中图分类号：TM73; TN91.6
陈智雄 男，1983年生，副教授，硕士生导师，研究方向为物联网技术、电力系统通信。E-mail：zxchen@ncepu.edu.cn（通信作者）
张志坤 男，1995年生，硕士研究生，研究方向为电力系统通信。E-mail：zkzhang@ncepu.edu.cn
（编辑 赫蕾）