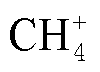数密度约增加2×1015 m-3；当针板距离小于10 μm时，电场畸变较大，满足场致发射条件，汤森放电和场致发射共同存在，平均电子能量上升两次；大于或等于10 μm时，电场强度畸变程度变弱，低于场致发射电场强度临界值，放电机制为汤森放电，平均电子能量只上升一次。摘要 研究爆炸性环境下微间隙放电过程及特性对本质安全电路的研究具有指导性意义，但目前爆炸性环境下的微间隙放电特性尚不明晰，且大多从宏观角度进行研究，缺少微观层面的理论分析，该文根据程控微间隙放电实验装置的电极结构，基于流体动力学理论模拟研究了甲烷/空气混合气体在低电压微间隙放电动态过程。通过改变极距、甲烷/空气混合气体体积分数的变化来分析对电子密度、各种正离子数密度、电场强度和平均电子能量的影响，从微观层面分析了微间隙放电机理，并通过试验验证了仿真结果的真实性和可靠性。经研究发现：阴极板附近的正离子鞘层区使得阴极板场强发射发生畸变，畸变为原来的3～5倍，电场强度大于场致发射所需临界电场强度，放电过程中存在场致发射；甲烷体积分数在3.5%～13.5%范围变化时，体积分数每增加5%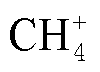，数密度约增加2×1015 m-3；当针板距离小于10 μm时，电场畸变较大，满足场致发射条件，汤森放电和场致发射共同存在，平均电子能量上升两次；大于或等于10 μm时，电场强度畸变程度变弱，低于场致发射电场强度临界值，放电机制为汤森放电，平均电子能量只上升一次。
关键词：爆炸性环境 针板电极 流体动力学理论 微间隙放电
随着5G通信及人工智能技术的发展，煤矿开采也越来越智能化，各种智能化设备的涌现对矿井下供用电技术也提出更加苛刻的要求。工作在爆炸性环境的供、用电设备必须满足防爆要求，同时满足功率不断增大的要求。本质安全型防爆措施是最佳防爆方法，要求设备内部的电路在规定的条件下，正常工作下或规定的故障状态下产生的电火花和热效应均不能点燃爆炸性混合物，即电路是本质安全的[1]。然而由于对电源发生短路故障时火花放电机理不清晰，电源在甲烷/空气混合气体环境下发生短路火花放电时电子及各种粒子演绎规律不清楚，导致目前采用过度防爆、抑爆措施使得本安电源输出功率较小。现阶段研究大多是基于IEC火花实验装置进行本安评价，根据特性曲线建立放电模型或对放电特性进行实验研究等。文献[2]基于火花试验装置进行大量实验测量并得到了放电的伏安特性表，即电压与电极间距和电流值的关系表。文献[3]建立了电容性电路放电电压指数模型来描述电容性电路和混合电路非振荡放电时功率及能量的传递过程。文献[4]以插值法对简单电容电路的最小点燃曲线进行拟合，对最小点燃曲线进行了数值化。文献[5]根据可模拟变换器输出短路放电特性进行等效电路，并通过实验验证输出放电特性本质安全判据的正确性。孟庆海等[6]提出了模拟电感和模拟电容电路的本安性能评价判据，对它们可能带来的危险进行评估。这些基本上是研究宏观特性，目前火花放电机理尚不清晰，放电时通道内各种粒子演化过程、电子浓度、温度、电子能量等都不清楚。成永红等[7]通过实验对400 μm以下的击穿特性进行研究，并对不同物理尺度介电系统的放电击穿特性进行了总结。柴钰等[8]仿真研究了N2-O2混合气体在纳米尖端场域的微间隙放电过程，但极板间隙为长间隙，对短间隙的研究不清楚。文献[9]采用粒子法（Particle-in-Cell/Monte Carlo Collision, PIC/MCC）进行仿真，分析了爆炸性气体环境下微间隙放电机制，但文中的电极仿真模型为板板结构。廖瑞金等[10]研究了棒板电极在6 kV电压下的负电晕放电过程，分析讨论了重离子的组成成分及其分布特性，但该研究为高电压下的放电过程。何彦良等[11]对不同电场、不均匀系数下的负直流电晕放电进行了仿真计算，研究了SF6/N2混合气体负直流电晕电流脉冲特性。由于目前相对于高电压长间隙击穿放电较多，对微间隙低电压火花放电研究较少，且对此方面的研究又可以增加本质安全电路的微观理论研究，因此对微间隙低电压放电进行研究很有意义。
火花放电是一种复杂的物理化学反应过程，放电时间为ns级，放电与电极材料、形状、周围环境温度、湿度、介质等参数有关，采用实验方法很难诊断和测量出放电通道中各种粒子演化过程。此外甲烷属于易燃易爆气体，进行实验时会存在安全隐患。近年来，随着电子技术和半导体科学技术发展，人们开始借助于计算机对放电进行模拟仿真研究，数值模拟方法在揭示放电机理及放电过程粒子演化具有明显优势[12-14]。如D. Herrebout等[15]建立了甲烷等离子体的流体模型对各个离子的密度进行预测仿真，并进行试验验证，但模型是一维的，不能对甲烷放电动态过程作出整体分析。V. Ivanov等[16]通过粒子法与流体动力学方法对比，分析了引起电子积累的机理和确定放电稳态的过程，但未对仿真结果进行实验验证。文献[17]采用流体-化学动力学混合方法对甲烷-氮气混合气体在微间隙的放电动态过程进行仿真，但研究针对长间隙下的特性，且气体介质只有甲烷和氮气混合，对其他因素的影响未做研究。文献[18]在针-板结构下对甲烷放电进行等离子体仿真，总结了反应生成物质以及主要粒子的生成路径。
为进一步明确爆炸性环境下微间隙放电[19-21]的特性和机理，指导本质安全电路的设计，本文基于程控微纳放电试验装置的电极结构，并在甲烷/空气混合气体环境下建立放电物理模型，通过流体动力学对放电进行二维建模仿真，仿真考虑了电场分布、粒子输运、动量传递等机理，最终得到放电过程中轴向电子密度、各种正离子数密度等放电参数的变化特性，从而阐明了等离子体微间隙的放电机理。
程控微间隙击穿放电试验装置如图1所示。甲烷/空气混合气体充满图1a主视图中的密闭气室，给电极两端施加电压，将平板电极固定，铜针电极在步进电机带动下逐渐向另外一个电极靠近。通过图1b俯视图中的玻璃罩可以观察击穿放电现象。
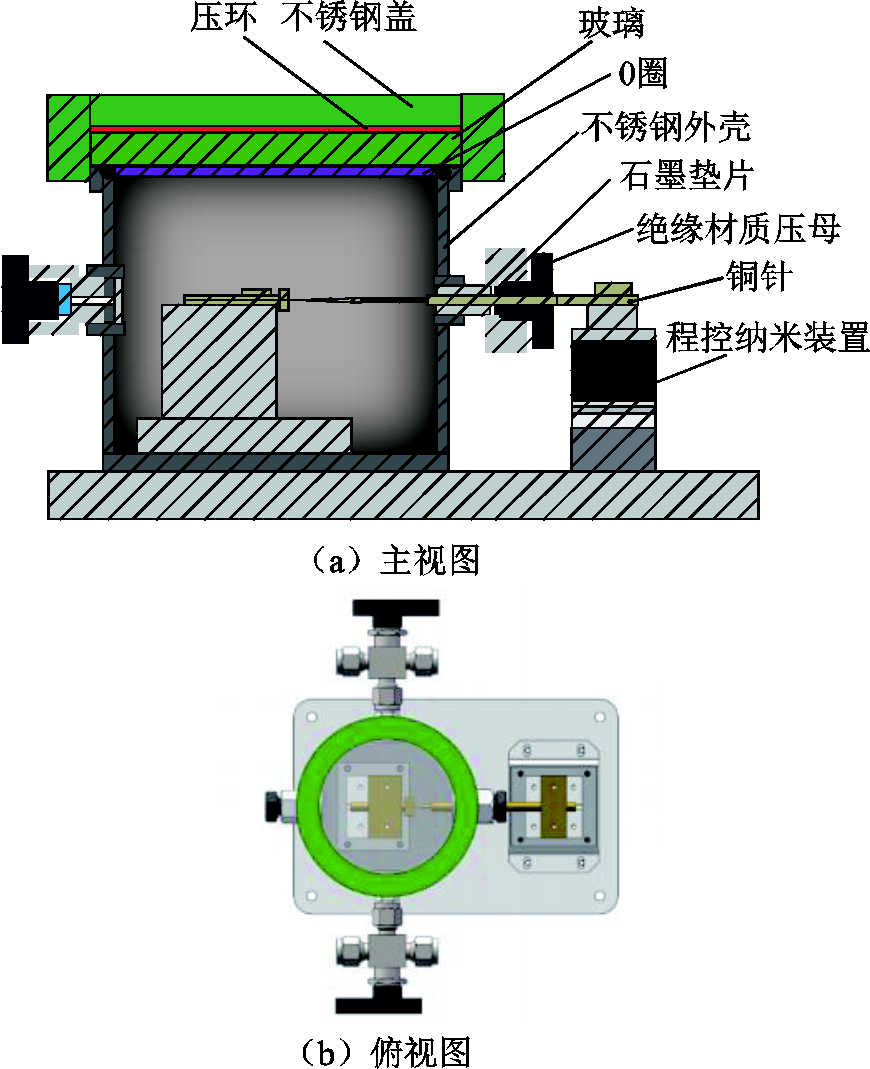
图1 程控微间隙击穿放电试验装置
Fig.1 Program controlled micro gap breakdown discharge test device
本文基于程控微间隙击穿放电试验装置的电极结构建立二维的针板电极仿真模型如图2所示。下极板的半径为10 μm，针电极尖端处的曲率半径为 0.5 μm，针、板两电极之间的气体间隙d为6 μm。针板都为铜，其中针电极接保护电路并接正电压150 V，板电极接地，R为1 kΩ，C为1 pF。
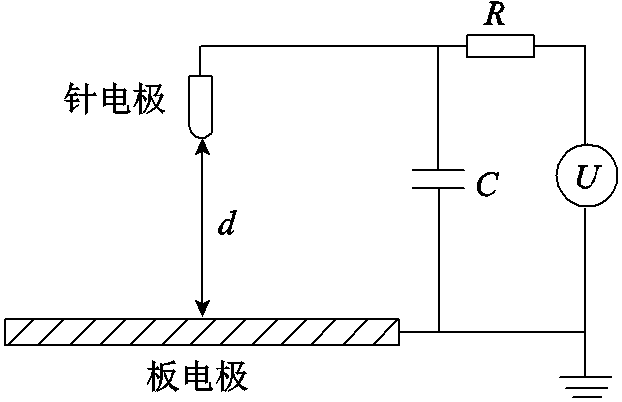
图2 仿真模型
Fig.2 Simulation model
对所建立的物理仿真模型采用等离子体流体动力学进行模拟，在气体放电中涉及许多碰撞反应，反应类型有弹性碰撞、电离碰撞、激发碰撞、物质反应、电子吸附和表面反应。因此仿真计算前需要通过麦克斯韦电子能量分布函数对各粒子连续性方程、电子能量约束方程和电场泊松方程进行求解[22]，图3为计算流程示意图。
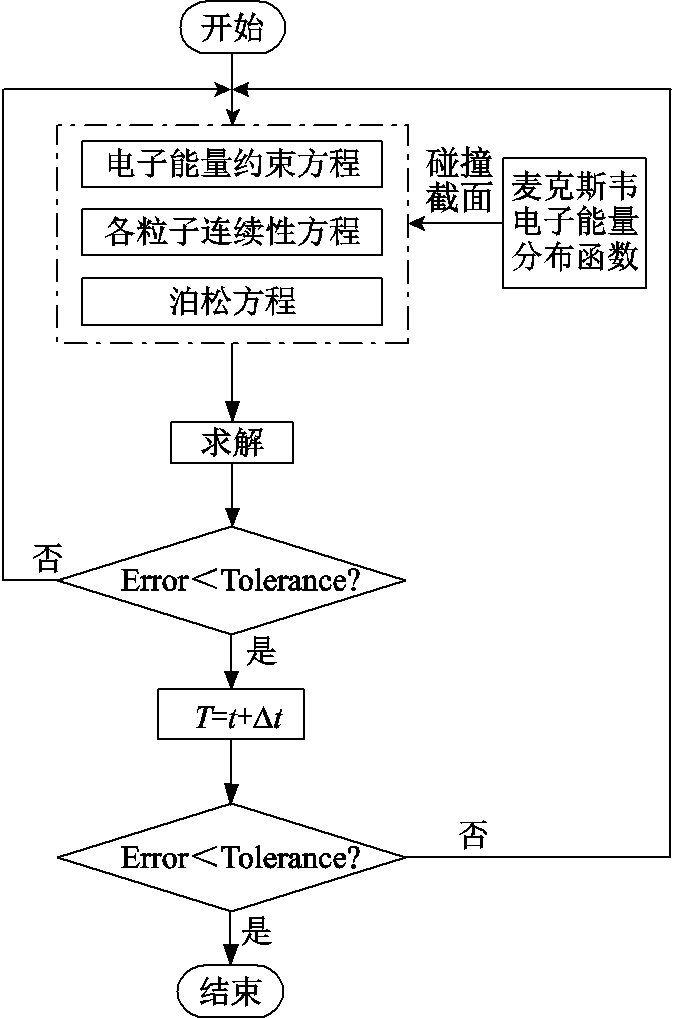
图3 计算流程示意图
Fig.3 Schematic diagram of calculation flow
各粒子（电子和正、负离子）的连续性方程[23]为
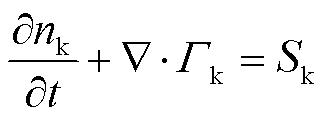（1）
式中，nk为电子和正、负离子的粒子数密度，m-3；Sk为包含了电子和正、负离子之间由于碰撞反应而引起的产生速率和消失速率，m-3·s-1；Γk为电子和正、负离子通量，即
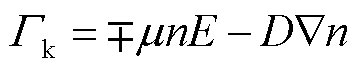（2）
式中，μ为粒子的迁移率；n为粒子数密度；E为电场强度；D为粒子的扩散系数。式（2）中右边第一项中的正号代表正离子，负号代表电子和负离子。
泊松方程为
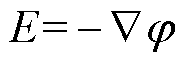（3）
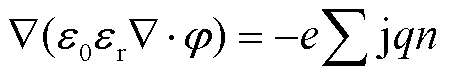（4）
式中，φ为电势；ε0为真空介电常数；εr为气体的相对介电常数；e为电子电荷；q为粒子电荷。
因为反应系数是电子温度的函数，所以通过求解电子的能量守恒方程可以得到电子温度，电子能量平衡方程[24]为
（5）
式中，KB为玻耳兹曼常数；Te为电子温度；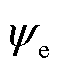
为电子能量通量；me为电子质量；M为气体的平均分子质量；vel为弹性碰撞频率；Tg为气体温度；ri和Δεi分别为第i次反应的速率和由非弹性碰撞引起的能量损失。
放电是在一个密闭容器中进行的，当离子碰撞器壁时，电子以指定的概率从壁表面发射出来，因此在壁处，电子通量Γe和电子能量通量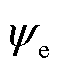满足边界条件[25-26]
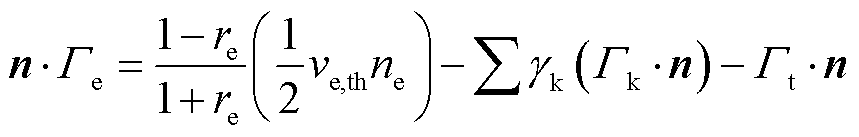（6）
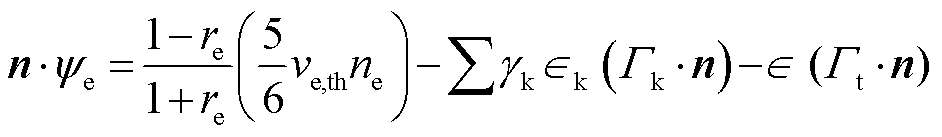（7）
式中，n为向外单位向量；re为反射系数；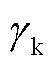
为二次电子发射系数；ve,th为电子热速率，m/s；
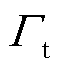为热发射通量，m-2·s-1；
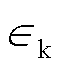为粒子的热离子能量；
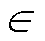为平均热离子能量。用电子流或离子流轰击物体表面，使之发射电子的过程叫二次电子发射，二次电子发射系数通常取值范围在 0.001～0.5[27]。二次电子的平均初始电子能量通常在1～5 eV[28]，为了仿真爆炸性气体在最易击穿的条件下的特性参数，根据汤森放电理论，仿真中设置二次发射系数取最大值0.5，平均初始电子能量为5 eV。
正、负离子通量在正极和负极的边界条件为
（8）
式中，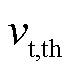
为正、负离子的热速率系数；
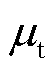为正、负离子的迁移率；
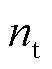为正、负离子数密度；
为电离系数。
中性粒子通量在正极和负极的边界条件为
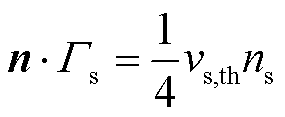（9）
式中，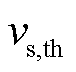
为中性粒子的热速率系数；
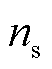为中性粒子数密度。
对于电场泊松方程，针电极与外电路连接，板电极接地。此外，对于求解域外边界，取开放边界条件，所有粒子满足
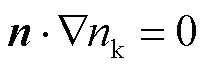（10）
电势满足
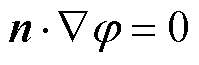（11）
程控微间隙击穿放电试验装置中充满甲烷/空气混合气体，其中空气中N2:O2的体积分数比约为78%: 21%，甲烷的体积分数在8.5%左右时最易引爆[29]。因此对于初始浓度要保证仿真收敛，一般最多的粒子作为质量约束，即设置N2来自质量约束，CH4初始摩尔分数为0.085，O2初始摩尔分数为0.183，其他均设为0.001。合适的初始离子数密度可以加快仿真的收敛速度，且不会改变仿真特性。设置针电极处离子数密度最大，远离针电极按高斯分布递减。
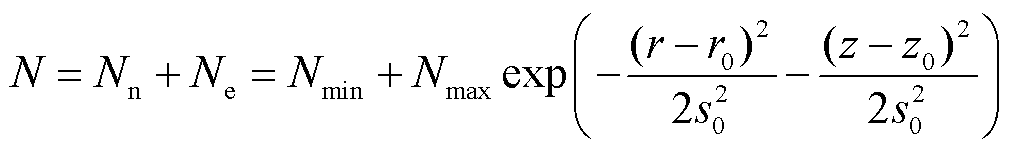（12）
式中，Nn为除电子外其他粒子浓度；Ne为电子浓度；Nmax为初始时刻最大粒子数密度，Nmax=1×1013m-3；Nmin为初始时刻最小粒子数密度，Nmin= 1×109 m-3；r0、z0分别为针尖的横、纵坐标；s0为高斯分布域，取s0=25 μm。
对于初始离子的数密度要遵循电中性原则，设置主要离子N+ 2来自电中性约束，其他离子具体参数：电子初始数密度为1×1013m-3，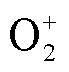
初始数密度 1×1012m-3，O-初始数密度1×1012m-3，CH+ 4初始数密度1×1012m-3，CH+ 3初始数密度1×1012m-3，
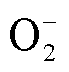初始数密度1×1012m-3，N+ 4初始数密度1×1012m-3，O+ 4初始数密度1×1012m-3，N2O+ 2初始数密度1×1012m-3。本文将气体放电时的环境温度设置为293.1 K，背景压强设置为1 atm（l atm=1.103×105 Pa）。
由于反应比较复杂，为了降低计算过程中的复杂度，主要考虑了15种粒子，主要的等离子体化学反应式见表1，表面反应式见表2。其中与电子有关的化学反应的反应速率系数通过电子能量分布函数获得，电子碰撞反应的反应速率由截面数据计算得出，截面数据从LXcat数据库中导出。
表1 等离子体化学反应
Tab.1 Plasma chemical reaction
序号反应方程反应类型反应速率 R1e+O2→O2+e弹性碰撞由碰撞截面计算 R2e+N2→N2+e 弹性碰撞由碰撞截面计算 R3e+CH4→CH4+e 弹性碰撞由碰撞截面计算 R4e+O2→O+ 2+2e 电离碰撞由碰撞截面计算 R5e+N2→N+ 2+2e 电离碰撞由碰撞截面计算 R6e+O2→O+O-电离碰撞由碰撞截面计算 R7e+CH4→CH+ 4+2e 电离碰撞由碰撞截面计算 R8e+CH4→CH+ 3+2e+H 电离碰撞由碰撞截面计算 R9e+CH4→CH3+e+H 激发碰撞由碰撞截面计算 R10e+CH4→CH2+e+2H 激发碰撞由碰撞截面计算 R11e+N2→e+ N* 2激发碰撞由碰撞截面计算 R12N+ 2+O2→O+ 2+ N2物质反应6.0×10−17 mol·s-1·m-3 R132N2+O+ 2→N2O+ 2+N2物质反应9.0×10−43 mol·s-1·m-6 R14N2O+ 2+N2→O+ 2+2N2物质反应4.3×10−10 mol·s-1·m-3 R15N2O+ 2+O2→O+ 4+N2物质反应1.0×10−15 mol·s-1·m-3
（续）
序号反应方程反应类型反应速率 R16O+ 2+2O2→O+ 4+O2物质反应2.4×10−42 mol·s-1·m-6 R17O+ 4+O- 2→3O2物质反应1.0×10−13 mol·s-1·m-3 R18e+O+ 4→2O2电子吸附1.4×10−42(300/Te)0.5 mol·s-1 R19e+O+ 2→2O电子吸附2.0×10−13(300/Te) mol·s-1 R20e+2O2→O2+O- 2电子吸附2.0×10−41(300/Te) mol·s-1·m-6 R212e+N+ 2→N2+e电子吸附5.651×10−27Te-0.8 mol·s-1 R22e+N+ 2+N2→2N2电子吸附3.6×10−10 mol·s-1·m-3
表2 表面反应
Tab.2 Surface reaction
序号反应方程反应类型εi/eV R1O+ 2→O2表面反应0.55 R2N+ 4→2N2表面反应0.55 R3N2O+ 2→O2+N2表面反应0.55 R4O+ 4→2O2表面反应0.55 R5CH+ 4→CH4表面反应0.55 R6CH+ 3→CH3表面反应0.55 R7O- 2→O2表面反应00 R8O-→O表面反应00
根据课题组前期实验的数据，锥形电极的击穿电压相对较小且最易击穿，但实际针电极不能完全制成锥形，因此对于针电极采用较小的曲率半径，并根据Mason公式[30]验证电极的曲率半径和极板间距是否满足
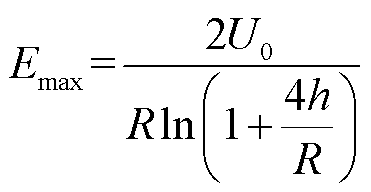（13）
式中，R为曲率半径；h为针板电极间距；U0为试验所加电压。
最后仿真设置针板间距为6 μm，电压为150 V，观察仿真区域内不同时刻电子密度分布图、中轴线处正负离子数密度变化曲线、沿轴向的各个粒子数密度变化曲线。
微间隙放电机理主要观察电子密度的动态变化过程，通过模拟气体放电过程得到不同时刻电子密度分布，如图4所示。放电过程、电子密度的变化可分为四个阶段，图4a和图4b之间的时间段内为电子密度缓慢上升阶段，此时电子密度峰值增长到2.24×1013m-3；图4b和图4c之间的时间段为电子密度快速上升阶段，峰值从2.24×1013m-3增长到6.23×1013m-3；第三阶段如图4c～图4e的时间段，电子密度继续上升到峰值2.84×1015m-3后，出现下降趋势，电子密度下降到7.97×1013m-3；第四阶段为放电稳定阶段，电子密度逐渐达到平稳状态如图4f所示。
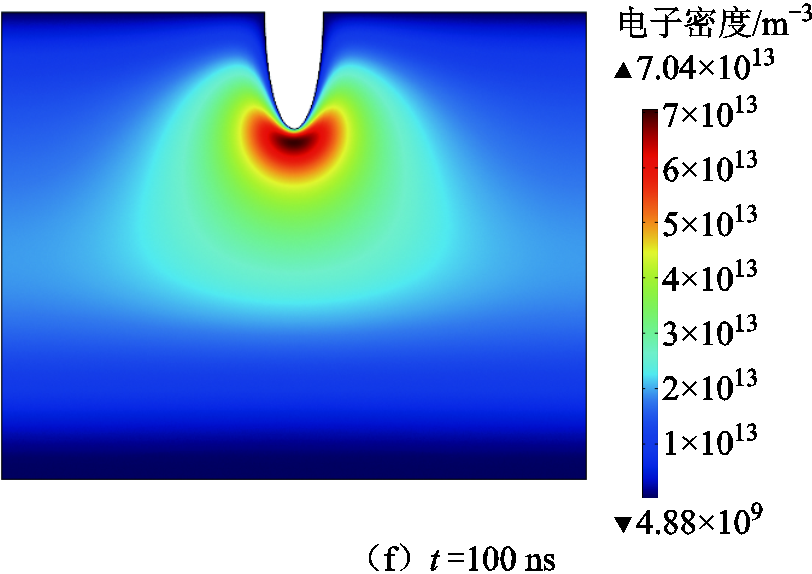
图4 不同时刻电子密度分布
Fig.4 Electron density distribution at different times
当放电初期，电场强度主要与静电场边界条件有关，针尖处电场强度为2×107 V/m，阴极板电场强度为1.2×107 V/m。游离在极间隙的电子与间隙中的其他气体分子发生电子碰撞电离反应程度较低，总体表现为在电场作用下向阳极移动，电子密度处于缓慢上升阶段。8～10 ns内，随着电子在电场中获取的能量增多，电子在向阳极移动的过程中所发生的碰撞电离也越来越剧烈，尤其在电场强度较大的针尖附近，碰撞后发生电离的概率更大，电子密度快速上升。当放电时间到达40 ns时，更多的电子运动到阳极，由于电子运动速度比正离子运动速度快，一些到达阳极的电子不仅碰撞电离的概率增加，电子与正离子复合的概率也有所增加，使得电子密度增长变缓。40 ns以后，到达阳极的电子一部分被吸收，另一部分在针尖附近不断累积形成了负离子鞘层，并使阳极附近的电场强度增加，除针尖区域处的电场强度高以外，中轴线上其他位置电场强度已经下降到1.1×107 V/m左右，造成电子在针尖处因复合而消失的速率不断增强，从而导致阳极处的电子密度相对减小，因此，电子密度出现下降趋势，继续发展，放电逐渐进入平稳阶段。
图5为中轴线附近正、负离子数密度分布，可以看出正离子数密度峰值随时间的发展向阴极移动后又远离阴极，且在距离阴极板2 μm附近形成正离子鞘层。同样，电子与其他负离子向阳极运动，电子密度峰值先向阳极运动后又在距离针尖0.5 μm附近也形成负离子鞘层。
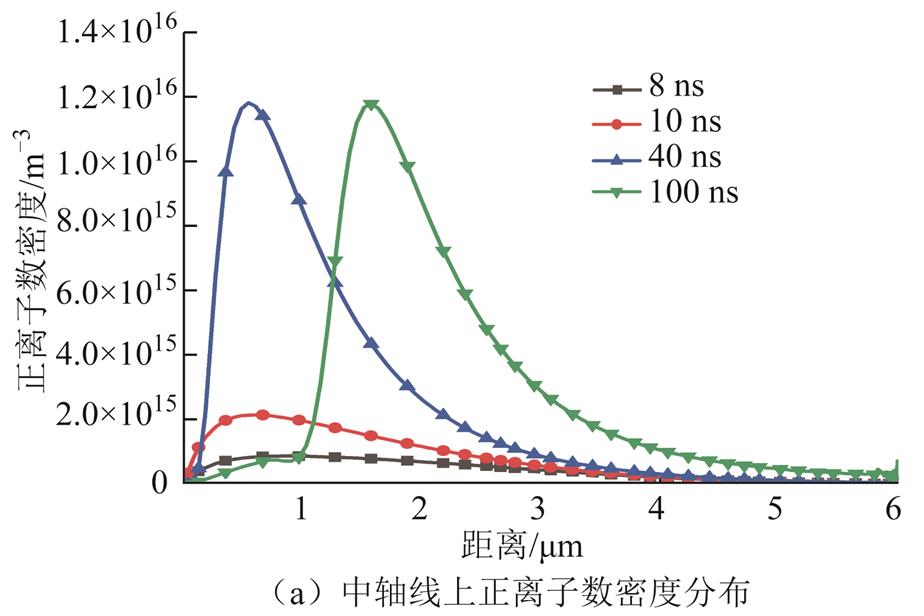
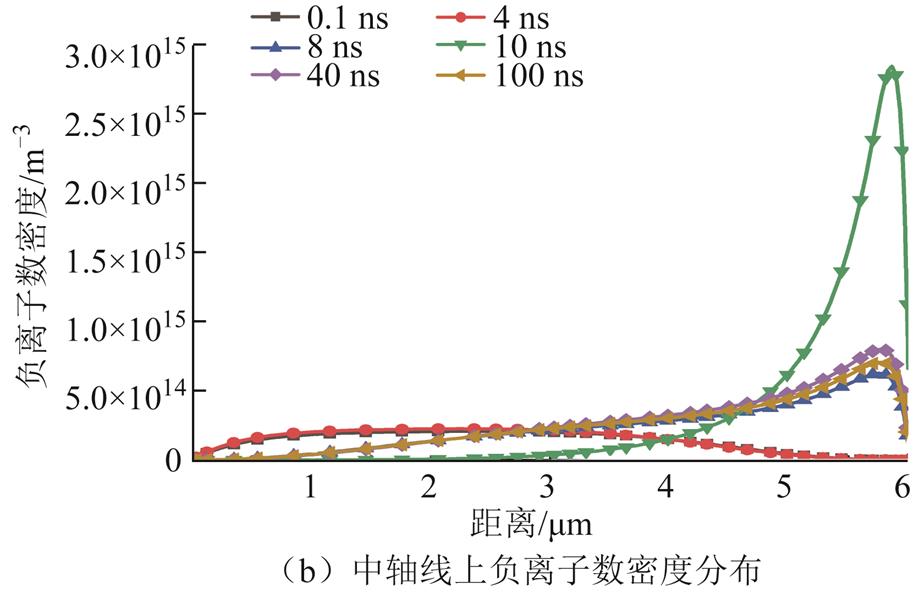
图5 中轴线上正负离子数密度分布
Fig.5 Positive and negative ion number density distribution on the central axis
电场的变化在一定程度上决定了微间隙放电机制，通过仿真软件得到了微间隙放电程中轴线电场变化情况，如图6所示。
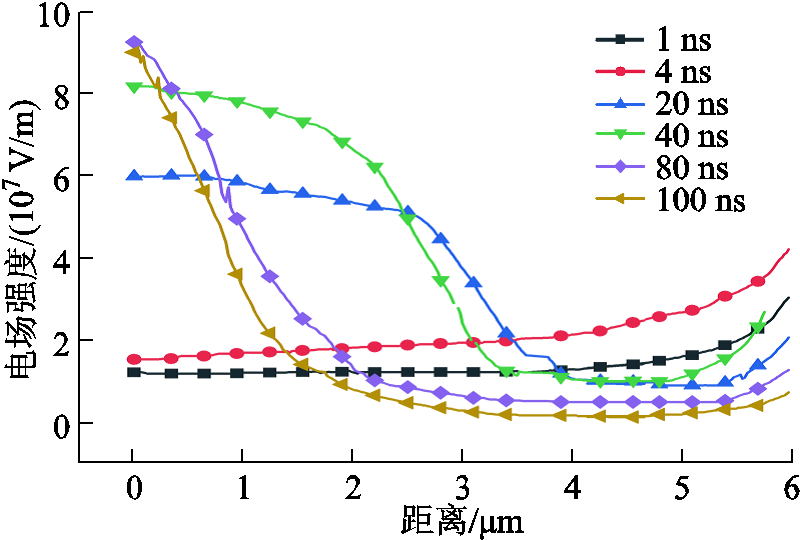
图6 中轴线不同时刻电场分布
Fig.6 Electric field distribution of central axis at different times
放电初期，电场强度随中轴线靠近阳极逐渐变大。当放电时间达到20 ns时，由于正、负鞘层区的形成，电场开始出现畸变现象，并随着时间推移，在80 ns时，电场强度畸变了4倍左右，此处电场强度达到了9.2×107 V/m。根据Fowler-Nodheim公式[31]可计算得到金属表面能够发射电子的临界电场强度为2×109 V/m左右，而光滑电极表面的场增强因子一般在15～30[32]，因此可以认为间隙电场在6.7×107 V/m时可形成阴极场致电子发射[33]，具体计算过程为
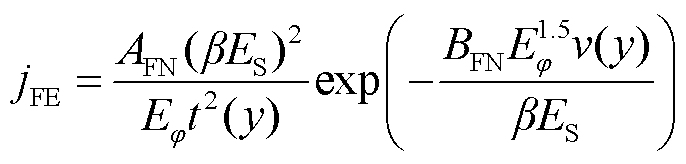（14）
式中，β为场增强因子；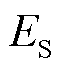
为间隙电场强度；Eφ为表面功函数，eV；常数AFN=1.541×10-6，BFN= 6.830 9×109；函数v(y)和t2(y)分别为
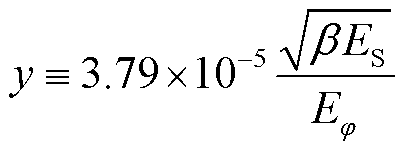
在中轴线0～2 μm处的电场畸变最严重，正、负离子在阴极和阳极附近形成鞘层，电场的畸变使得在阴极板附近的电场强度达到了阴极场致发射电子的电场强度临界值，因此在放电的过程中还存在着场致发射。
放电是一个复杂的物理化学过程，为了进一步对其中放电机理进行研究，主要考虑正离子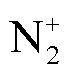
、
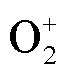和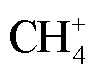
与电子在中轴线上随时间的密度变化，如图7所示。由图7可知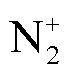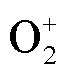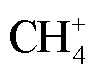，、、这三种正离子的数密度发展规律大致相同。施加电压后，针板电极间隙内部的游离电子会和N2、O2、CH4外层电子发生电子碰撞电离反应，从而产生新的电子和正离子，所产生的正离子随时间增加而增加，且逐渐向阴极移动。对比三种正离子数密度，发现它们的数密度相差不大，这是由于N2与O2、CH4相比，性质较为稳定，导致电子碰撞多以弹性碰撞为主。随着放电时间增加，各带电粒子数密度及数密度峰值位置均发生改变，这与电场分布有关。
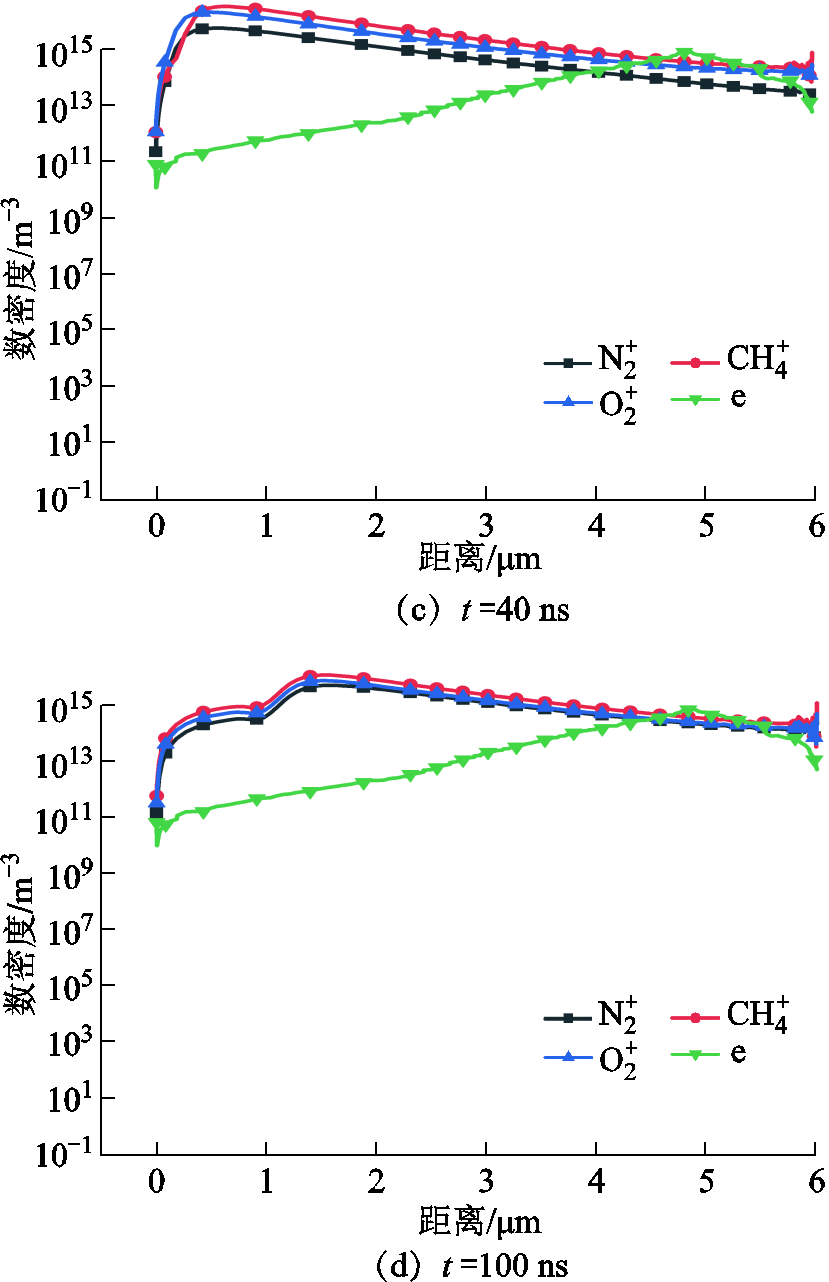
图7 中轴线上的各个离子密度分布曲线
Fig.7 Density distribution curve of each ion on the central axis
根据图6、图7c和图7d可知，在电极附近形成鞘层引起的电场畸变不仅使电场强度满足了场致发射的所需条件，而且加快了正离子到达阴极的速度，使得正离子到达阴极后发生二次电离，正离子数密度略微下降，电子数密度增加，峰值出现在正、负鞘层区。综上所述，在微间隙放电过程中不仅存在汤森放电，还存在阴极场致电子发射。
为了研究针板极间距对气体放电的影响，设置阳极电压为150 V，甲烷体积分数为8.5%，分别对针板间距6 μm、8 μm和10 μm进行仿真。改变针板间距发现，针板间距越小，电场强度越大，导致离子碰撞反应发生得更加剧烈，离子碰撞反应速率增加，同时还会增强场致发射；针板间距越大，电场强度越小，离子碰撞反应速率下降，场致发射减弱。图8为不同极间距平均电子能量随时间的变化曲线。由图8可知，极间距为6 μm时的平均电子能量达到12 eV，随着极间距的增大，平均电子能量减小，这是由于间距增加，电场强度下降，导致离子碰撞反应速率下降，放电过程不剧烈，造成平均电子能量下降。对比6 μm、8 μm和10 μm发现，当针板距离为6 μm、8 μm时，平均电子能量先上升后稳定短暂时间后再次出现上升趋势，最后达到稳定；而当针板间距为10 μm时，平均电子能量并未出现再次上升的趋势。通过对三种间距下的电场强度变化分析可知，当针板间距为6 μm、8 μm时，电场强度的畸变使得其依然满足场致发射所需条件，场致发射使得电子数密度增加，碰撞电离程度增大，因此平均电子能量出现再次上升趋势。当针板间距为10 μm时，电场强度畸变程度已无法满足场致发射条件，因此电子平均电子能量不会出现再次上升趋势。综上所述，针板极间距不仅影响粒子碰撞电离程度，还影响放电机制，当针板极间距大于等于10 μm时，放电过程不再存在场致发射。
图8 不同极间距平均电子能量随时间的变化曲线
Fig.8 Variation curve of average electron energy with time at different pole spacing
为了研究不同甲烷含量对微间隙气体放电的影响，设置甲烷体积分数为3.5%、8.5%和13.5%时对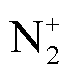
、
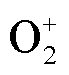和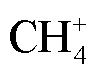
离子数密度仿真数据进行分析，得到不同甲烷浓度下正离子数密度随时间变化曲线如图9所示。
仿真结果显示，不同甲烷体积分数下N2+数密度随时间变化曲线基本不变，最终维持在4×1015m-3左右，这主要与空气中N2较为稳定有关。与N2相比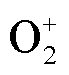，数密度随甲烷体积分数变化而比较明显地变化。当甲烷体积分数小于8.5%时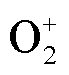，数密度随甲烷体积分数增加而增大；但当甲烷体积分数大于8.5%时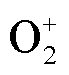，数密度将维持在6×1015m-3左右，不再随甲烷体积分数增加而增大。CH4+离子数密度随着甲烷体积分数的增加而增大。在甲烷体积分数为3.5%～13.5%范围内，甲烷体积分数每增加5%，CH4+数密度将增长约2×1015m-3。
为研究当甲烷体积分数大于8.5%时，O2+数密度将不再随甲烷体积分数增加而增大的原因，分别将混合气体中O2体积分数增加5%、10%，甲烷体积分数设置为13.5%进行仿真。仿真结果如图10所示。
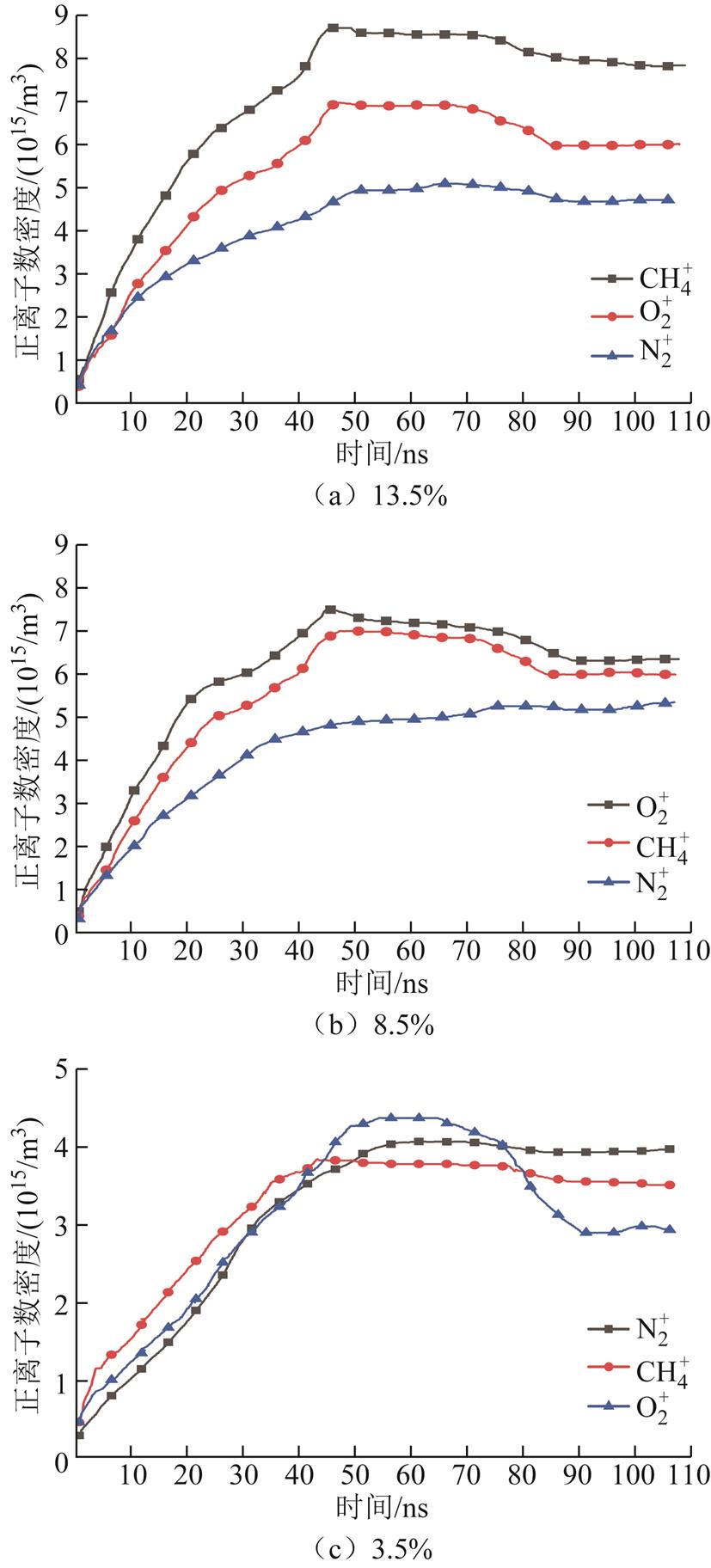
图9 不同甲烷含量下正离子数密度随时间变化曲线
Fig.9 Variation curve of positive ion number density with time under different methane concentrations
图10 混合气体中增加O2体积分数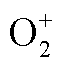
数密度变化曲线
Fig.10 Variation curve of 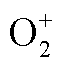number density with increasing O2 concentration in mixed gas
图10中显示，相比甲烷体积分数设置为13.5%，O2为空气原本比例时，随着O2体积分数增加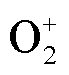，数密度由原来的基本不变变化为随着O2体积分数增加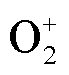，数密度增大。因此，当甲烷体积分数大于8.5%时，O2+数密度将不再随甲烷体积分数增加而增大的原因是混合物气体中O2比例一定，发生放电过程中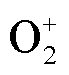的电离速度与复合速度达到了动态平衡，且电离和复合均达到了饱和程度，因此即使混合物中甲烷含量增加也不会使得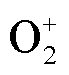数密度增加。综上所述，在放电过程中，O2与CH4对放电的贡献率要大于N2对放电的贡献率，放电以O2与CH4的碰撞电离为主。
甲烷/空气混合气体微间隙放电系统主要有两大部分组成：微间隙放电装置和放电波形采集装置。其中放电装置主要包括：程控步进电机（功率为42 W，步进最小增量为10 nm）、放电密闭气室、Itech IT8818可调直流电源、光学试验平台、真空泵、配气装置。波形采集装置主要包括：RIGOL DS4024示波器（采样率为2.5 GS/s）、KEITHLEY 2634B源表（电流测量范围0.1 fA～10 A）、电压、电流探头。试验平台如图11所示，其具体试验流程为：首先电源给电极两端施加0.1 V电压，将一个电极固定，通过计算机操作步进电机移动另外一个电极，每次步进0.1 μm，通过源表测量回路中电流，在电极移动过程中源表示数突然增大时则判断两电极间短路，并记录该位置为电极零点。
图11 实验平台
Fig.11 Experimental platform
设定甲烷体积分数分别为3.5%、8.5%和13.5%，极间距为6 μm，极间电压为150 V。运用图11实验装置进行放电试验，通过示波器测得相应参数下的典型放电波形如图12所示。
图12显示，放电电流会出现两次上升趋势，甲烷体积分数增加，放电时间减小，但当甲烷体积分数大于8.5%时，放电时间不再随甲烷体积分数增加而变小，这与仿真结果分析中正离子鞘层区引起电场畸变，存在场致发射相符合。同时从微观角度解释空气中甲烷体积分数为8.5%时最易发生爆炸的原因是空气中O2含量一定，放电过程中甲烷体积分数小于8.5%时，O2碰撞电离产生的正离子会随着甲烷体积分数增加而增加，对甲烷被点燃引爆起到重要作用[34]；大于或等于8.5%时，O2碰撞电离达到饱和状态，所产生的正离子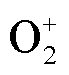数密度将不再随甲烷体积分数增加而增大，正离子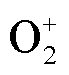对甲烷在燃烧爆炸过程中的“辅助”作用达到饱和，且在甲烷体积分数小于8.5%时，间隙击穿时间会随着甲烷体积分数的增加而减小；而甲烷体积分数大于8.5%时，间隙击穿电压会随着甲烷体积分数的增加而增加，因此空气中甲烷体积分数为8.5%时最易爆炸。
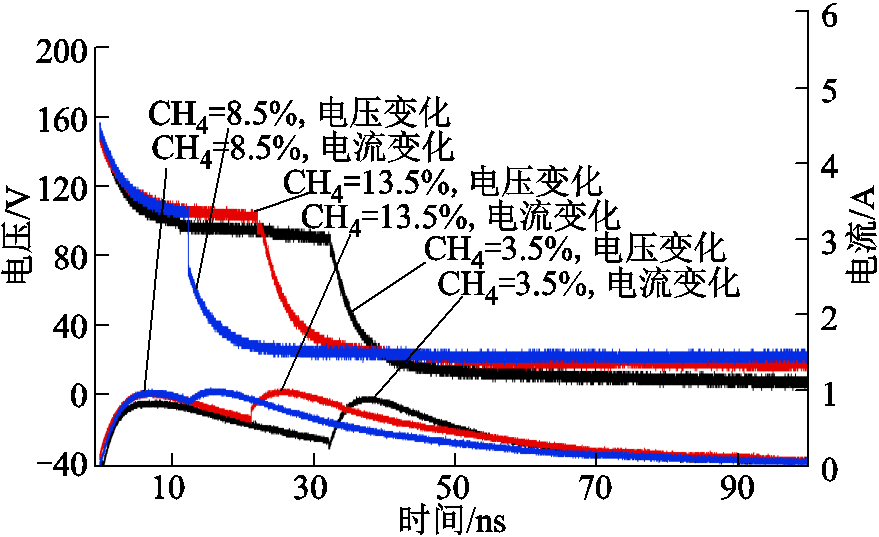
图12 不同甲烷体积分数下放电电压、电流波形
Fig.12 Discharge voltage and current waveforms under different methane concentrations
图13为针板距离分别为6 μm、8 μm和10 μm的微间隙放电实验结果。图13中显示，当针板间隙为10 μm时电流仅上升一次，说明放电过程中场致发射几乎不存在，距离变化对电场强度的影响大于畸变对电场强度的影响，实验结果与仿真结果相一致。因此，本文对微间隙放电的仿真为甲烷与空气混合气体下放电特性及机理研究提供了新的参考。
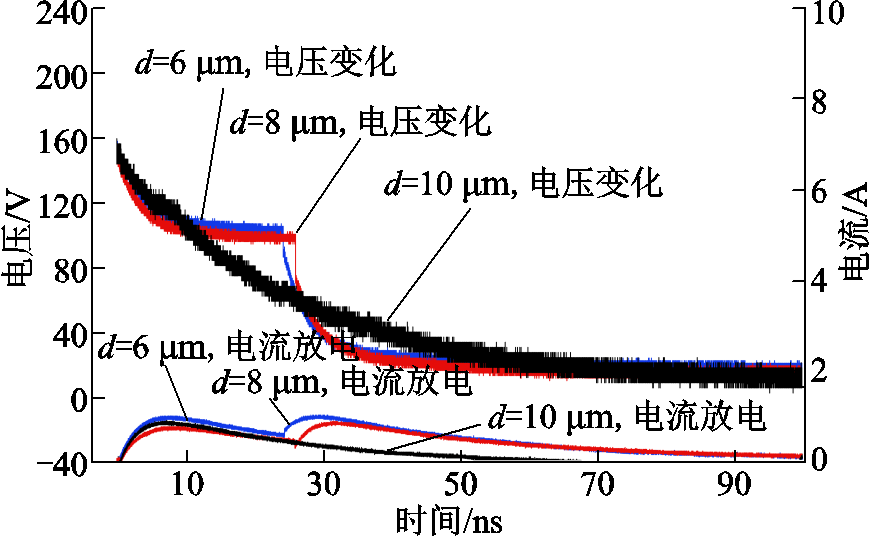
图13 不同间隙下放电电压、电流波形
Fig.13 Discharge voltage and current waveforms under different gaps
本文根据程控微间隙放电实验装置的电极结构，基于流体动力学理论建立了二维针-板仿真模型，在极板间距为6 μm、电压为150 V条件下对甲烷/空气混合气体的放电进行了模拟，分析了放电的微观动态过程，主要得出以下结论：
1）微间隙放电过程中，会在正极约2 μm处、负极约0.5 μm处形成鞘层区，其中阴极板附近的正离子鞘层区使得阴极板电场强度发生畸变，畸变为原来的3～5倍，电场强度大于场致发射所需临界场强，放电过程中还存在场致发射。
2）甲烷体积分数在3.5%～13.5%范围变化时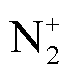，数密度相对稳定约为4×1015m-3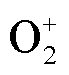，数密度在甲烷体积分数小于8.5%时随着甲烷体积分数增加而增加。甲烷体积分数大于等于8.5%时，混合气体中O2碰撞电离达到饱和，不随甲烷含量增加而增加。甲烷增加会影响碰撞电离产生的
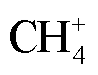数密度，体积分数每增加5%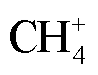，数密度增加约2×1015m-3。
3）改变极间间距，影响场内电场强度，进而影响放电机制，当针板距离小于10 μm时，电场畸变较大，满足场致发射条件，汤森放电和场致发射共同存在，平均电子能量上升两次；针板距离大于或等于10 μm时，电场畸变强度变弱，低于场致发射电场强度临界值，此时放电机制为汤森放电，平均电子能量只上升一次。
参考文献
[1] 南阳防爆电气研究所. 防爆电气标准汇编第二分册: GB 3846—2010[S]. 2011.
[2] Uber C, Hilbert M, Felgner A, et al. Electrical discharges caused by opening contacts in an ignitable atmosphere-part I: analysis of electrical parameters at ignition limits[J]. Journal of Loss Prevention in the Process Industries, 2019, 61: 114-121.
[3] 刘建华. 爆炸性气体环境下本质安全电路放电理论及非爆炸评价方法的研究[D]. 徐州: 中国矿业大学, 2008.
[4] 王玉婷, 刘树林, 马一博, 等. 简单电容电路最小点燃电压曲线的数值化研究[J]. 电工技术学报, 2014, 29(增刊1): 345-350. Wang Yuting, Liu Shulin, Ma Yibo, et al. Research on digitization of the minimum ignition voltage curve of simple capacitive circuit[J]. Transactions of China Electrotechnical Society, 2014, 29(S1): 345-350.
[5] 刘树林, 崔强, 李勇. Buck变换器的输出短路火花放电能量及输出本质安全判据[J]. 物理学报, 2013, 62(16): 168401. Liu Shulin, Cui Qiang, Li Yong. Output short-circuit spark discharging energy and output intrinsic safety criterion of Buck converters[J]. Acta Physica Sinica, 2013, 62(16): 168401.
[6] 孟庆海, 田媛. 本质安全电路模拟储能元件潜在危险性分析及其本质安全判据[J]. 电工技术学报, 2022, 37(3): 676-685. Meng Qinghai, Tian Yuan. Analysis of potential hazards of analog energy storage components in the intrinsic safety circuits and their intrinsic safety criteria[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 676-685.
[7] 成永红, 孟国栋, 董承业. 微纳尺度电气击穿特性和放电规律研究综述[J]. 电工技术学报, 2017, 32(2): 13-23. Cheng Yonghong, Meng Guodong, Dong Chengye. Review on the breakdown characteristics and discharge behaviors at the micro & nano scale[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 13-23.
[8] 柴钰, 张妮, 刘杰, 等. 微尺度下N2-O2电晕放电的动态特性二维仿真[J]. 物理学报, 2020, 69(16): 183-192. Chai Yu, Zhang Ni, Liu Jie, et al. Two-dimensional simulation of dynamic characteristics of N2-O2 corona discharge at micro scale[J]. Acta Physica Sinica, 2020, 69(16): 183-192.
[9] 王党树, 古东明, 栾哲哲, 等. 基于PIC/MCC法爆炸性气体环境下的微尺度放电特性[J]. 高电压技术, 2021, 47(3): 805-815. Wang Dangshu, Gu Dongming, Luan Zhezhe, et al. Micro-scale discharge characteristics in explosive gas environment based on PIC/MCC method[J]. High Voltage Engineering, 2021, 47(3): 805-815.
[10] 廖瑞金, 刘康淋, 伍飞飞, 等. 棒-板电极直流负电晕放电过程中重粒子特性的仿真研究[J]. 高电压技术, 2014, 40(4): 965-971. Liao Ruijin, Liu Kanglin, Wu Feifei, et al. Simulative study on characteristic of heavy particles in negative bar-plate DC corona discharge[J]. High Voltage Engineering, 2014, 40(4): 965-971.
[11] 何彦良, 丁未, 孙安邦, 等. 电场不均匀系数对SF6/N2混合气体负直流电晕电流脉冲特性的影响[J]. 电工技术学报, 2021, 36(15): 3124-3134. He Yanliang, Ding Wei, Sun Anbang, et al. Effect of electric field non-uniformity coefficient on current pulse characteristics of negative DC corona in SF6/N2 gas mixtures[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3124-3134.
[12] Levko D, Raja L L. Fluid versus global model approach for the modeling of active species production by streamer discharge[J]. Plasma Sources Science and Technology, 2017, 26(3): 035003.
[13] 王伟, 杨悦民, 雷肖, 等. 基于有限元分析的大容量叠装电抗器温度场研究[J]. 高压电器, 2022, 58(8): 267-274. Wang Wei, Yang Yuemin, Lei Xiao, et al. Research on temperature field of large capacity stacked reactor based on finite element analysis[J]. High Voltage Apparatus, 2022, 58(8): 267-274.
[14] 古海良, 周继贺, 蒋文明, 等. 低压预制母线温升特性的建模仿真研究[J]. 高压电器, 2022, 58(7): 214-222. Gu Hailiang, Zhou Jihe, Jiang Wenming, et al. Modeling and simulation study on temperature rise of low-voltage prefabricated busbar[J]. High Voltage Apparatus, 2022, 58(7): 214-222.
[15] Herrebout D, Bogaerts A, Yan M, et al. One-dimensional fluid model for an rf methane plasma of interest in deposition of diamond-like carbon layers[J]. Journal of Applied Physics, 2001, 90(2): 570-579.
[16] Ivanov V, Proshina O, Rakhimova T, et al. Comparison of a one-dimensional particle-in-cell-Monte Carlo model and a one-dimensional fluid model for a CH4/H2 capacitively coupled radio frequency discharge[J]. Journal of Applied Physics, 2002, 91(10): 6296-6302.
[17] 柴钰, 弓丽萍, 张晶园, 等. 微纳电离式矿井甲烷传感器安全放电及敏感机理仿真[J]. 电工技术学报, 2019, 34(23): 4870-4879. Chai Yu, Gong Liping, Zhang Jingyuan, et al. Simulation of safe discharge and sensitive mechanism of micro-nano ionized mine methane sensor[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4870-4879.
[18] 赵曰峰, 王超, 王伟宗, 等. 大气压甲烷针-板放电等离子体中粒子密度和反应路径的数值模拟[J]. 物理学报, 2018, 67(8): 085202. Zhao Yuefeng, Wang Chao, Wang Weizong, et al. Numerical simulation on particle density and reaction pathways in methane needle-plane discharge plasma at atmospheric pressure[J]. Acta Physica Sinica, 2018, 67(8): 085202.
[19] M Torres J, Dhariwal R S. Electric field breakdown at micrometre separations in air and vacuum[J]. Microsystem Technologies, 1999, 6(1): 6-10.
[20] 孟国栋, 折俊艺, 应琪, 等. 微米尺度气体击穿的数值模拟研究进展[J]. 电工技术学报, 2022, 37(15): 3857-3875. Meng Guodong, She Junyi, Ying Qi, et al. Research progress on numerical simulation of gas breakdown at microscale[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3857-3875.
[21] Go D B, Venkattraman A. Microscale gas breakdown: ion-enhanced field emission and the modified Paschen’s curve[J]. Journal of Physics D: Applied Physics, 2014, 47(50): 503001.
[22] Chen C H, Yeh J A, Wang P J. Electrical breakdown phenomena for devices with micron separations[J]. Journal of Micromechanics and Microengineering, 2006, 16(7): 1366-1373.
[23] Georghiou G E, Papadakis A P, Morrow R, et al. Numerical modelling of atmospheric pressure gas discharges leading to plasma production[J]. Journal of Physics D: Applied Physics, 2005, 38(20): R303-R328.
[24] 伍飞飞, 廖瑞金, 杨丽君, 等. 棒—板电极直流负电晕放电特里切尔脉冲的微观过程分析[J]. 物理学报, 2013, 62(11): 115201. Wu Feifei, Liao Ruijin, Yang Lijun, et al. Numerical simulation of Trichel pulse characteristics in bar-plate DC negative corona discharge[J]. Acta Physica Sinica, 2013, 62(11): 115201.
[25] Wang Qiao, Ning Wenjun, Dai Dong, et al. Characteristics and mechanisms of transition from filament to homogeneous glow in atmospheric helium dielectric barrier discharges under variation of the applied voltage amplitude[J]. Journal of Physics D: Applied Physics, 2019, 52(20): 205201.
[26] Lazarou C, Belmonte T, Chiper A S, et al. Numerical modelling of the effect of dry air traces in a helium parallel plate dielectric barrier discharge[J]. Plasma Sources Science and Technology, 2016, 25(5): 055023.
[27] 刘学悫. 阴极电子学[M]. 北京: 科学出版社, 1980.
[28] Ramses, Snoeckx, . Influence of N2 concentration in a CH4/N2 dielectric barrier discharge used for CH4 conversion into H2[J]. International Journal of Hydrogen Energy, 2013, 38(36): 16098-16120.
[29] (美)伯纳德·刘易斯(Bernard Lewis), (美)京特·冯·埃尔贝(Guenther von Elbe)著. 燃气燃烧与瓦斯爆炸[M]. 王方, 译. 北京: 中国建筑工业出版社, 2010.
[30] Sekimoto K, Takayama M. Negative ion formation and evolution in atmospheric pressure corona discharges between point-to-plane electrodes with arbitrary needle angle[J]. The European Physical Journal D, 2010, 60(3): 589-599.
[31] Forbes R G, Deane J H B. Reformulation of the standard theory of Fowler-Nordheim tunnelling and cold field electron emission[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2007, 463(2087): 2907-2927.
[32] Descoeudres A, Levinsen Y, Calatroni S, et al. Investigation of the DC vacuum breakdown mechanism[J]. Physical Review Special Topics - Accelerators and Beams, 2009, 12(9): 092001.
[33] 徐翱, 金大志, 王亚军, 等. 场致发射影响微间隙气体放电形成的模拟[J]. 高电压技术, 2020, 46(2): 715-722. Xu Ao, Jin Dazhi, Wang Yajun, et al. Simulation on influence of field emission to the gas discharge in micro-scale gaps[J]. High Voltage Engineering, 2020, 46(2): 715-722.
[34] Sekimoto K, Takayama M. Negative ion formation and evolution in atmospheric pressure corona discharges between point-to-plane electrodes with arbitrary needle angle[J]. The European Physical Journal D, 2010, 60(3): 589-599.
Abstract Electrical equipment working in explosive environment should meet the requirements of intrinsic safety. Domestic and foreign scholars evaluate the intrinsic safety based on the voltage and current characteristic curves of the discharge measured by IEC-SSTA spark test device. However, the discharge mechanism and particle change law in case of equipment failure are not clear. In the design of intrinsically safe electrical equipment, there will be transition explosion-proof, which limits the improvement of intrinsically safe output power, resulting in that the output power of intrinsically safe equipment can only reach about 20 W. Therefore, based on the electrode structure of the program-controlled micro-nano discharge test device, the discharge physical model is established in the methane-air mixture environment. The discharge parameters such as axial electron density, various positive ion density and so on are obtained by two-dimensional modeling and simulation of the discharge through hydrodynamics, thus clarifying the discharge mechanism of plasma micro-gap.
Firstly, a two-dimensional discharge model is established based on the electrode structure, and the boundary conditions are set. Secondly, add the chemical reaction equation and set the conditions such as the cross section data involved in the reaction. Then, set the initial gas concentration and particle density. Finally, the simulation is carried out to obtain the data by changing the electrode distance and the concentration of methane-air mixture. According to the simulation, the influence of the change on the electron density, the number density of positive ions, the electric field strength and the average electron energy is analyzed, and the micro-gap discharge mechanism is analyzed from the microscopic level.
At the initial stage of discharge, the degree of electron collision ionization reaction between the electrons in the electrode gap and other gas molecules is relatively low, and the electron density is in a slow rising stage. As the energy gained by the electrons in the electric field increases, the collision ionization becomes more and more intense, and the electron density increases rapidly. With the development of motion, the probability of recombination of electrons and positive ions also increases, which slows the growth of electron density. In general, the electron density first increased to the peak and then decreased, and the discharge continued to develop and gradually entered a stable stage. Then change the pole spacing to get the conclusion that the pin-plate spacing not only affects the particle impact ionization degree, but also affects the discharge mechanism. When the needle plate spacing is greater than or equal to 10 μm, there is no field emission in the discharge process. After changing the concentration of methane, it can be concluded that the contribution rate of O2 and CH4 to the discharge is greater than that of N2, and the discharge is mainly the collision ionization of O2 and CH4. Finally, experimental verification is carried out. The experimental results are consistent with the simulation results, which verify the correctness of the theoretical analysis.
The following conclusions can be drawn from the simulation analysis: (1) During micro-gap discharge, sheath area will be formed at about 2 μm of the positive electrode and about 0.5 μm of the negative electrode. The positive ion sheath area near the cathode plate distorts the field intensity emission of the cathode plate. (2) When the methane concentration changes from 3.5% to 13.5%, the number density of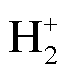 
is relatively stable about 4×1015 m-3, the number density of 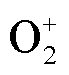increases with increasing methane concentration when methane concentration is less than 8.5%. When the methane concentration is greater than or equal to 8.5%, the O2 collision ionization in the mixed gas reaches saturation and does not increase with the increase of methane concentration. (3) The change of electrode distance affects the electric field intensity between electrodes and the discharge mechanism.
Keywords：Explosive environment, needle plate electrode, hydrodynamic method, micro gap discharge
国家自然科学基金面上项目（51776177）和国家自然基金科学青年项目（51604217）资助。
收稿日期 2022-04-08
改稿日期 2022-06-12
DOI: 10.19595/j.cnki.1000-6753.tces.220560
中图分类号：O461; TM863
王党树 男，1976年生，副教授，研究方向为电力电子技术。E-mail：wangdangshu@126.com（通信作者）
邓 翾 女，1997年生，硕士研究生，研究方向为电力电子技术。E-mail：1030390582@qq.com
（编辑 郭丽军）